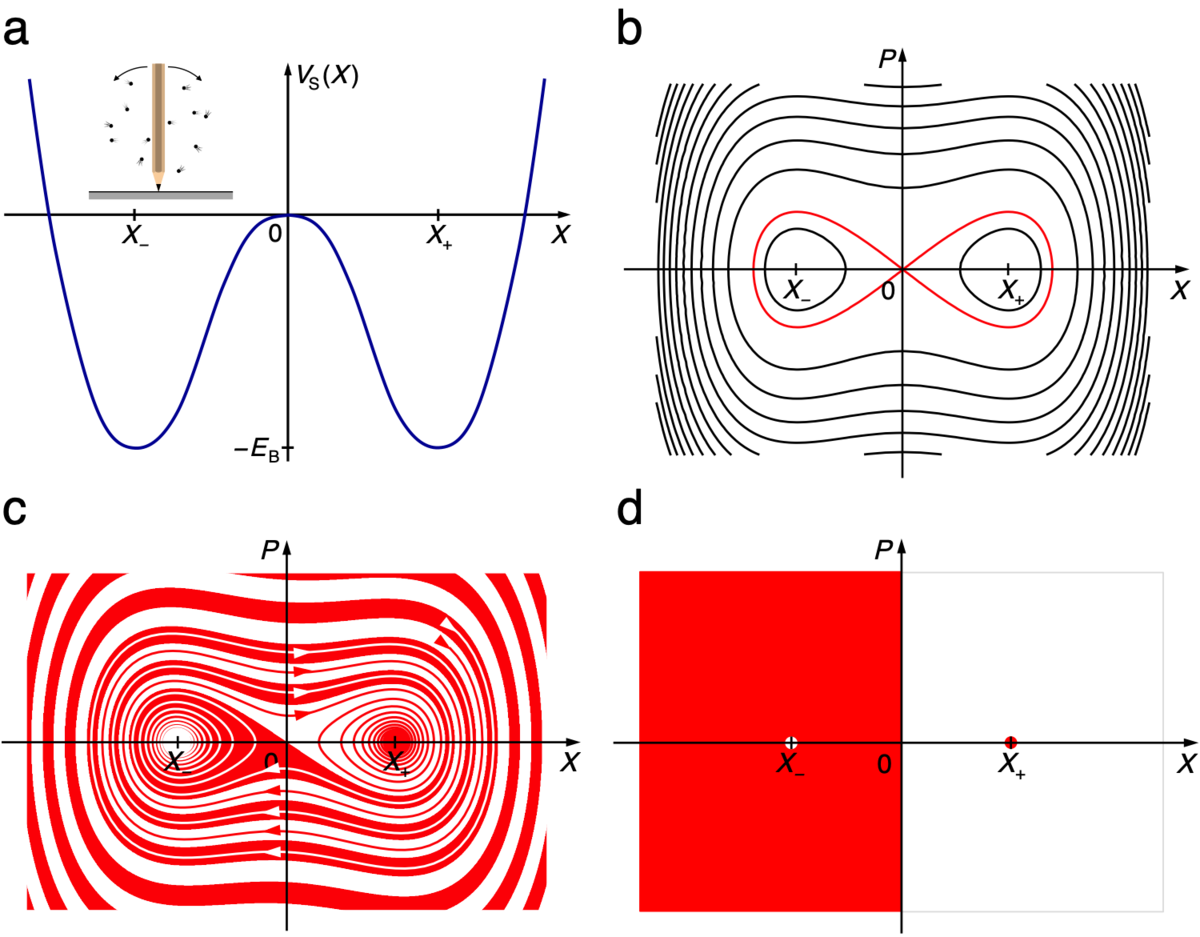
We construct a microscopic model to study discrete randomness in bistable systems coupled to an environment comprising many degrees of freedom. A quartic double well is bilinearly coupled to a finite number N of harmonic oscillators. Solving the time-reversal invariant Hamiltonian equations of motion numerically, we show that for N=1, the system exhibits a transition with increasing coupling strength from integrable to chaotic motion, following the KAM scenario. Raising N to values of the order of 10 and higher, the dynamics crosses over to a quasi-relaxation, approaching either one of the stable equilibria at the two minima of the potential. We corroborate the irreversibility of this relaxation on other characteristic timescales of the system by recording the time dependences of autocorrelation, partial entropy, and the frequency of jumps between the wells as functions of N and other parameters. Preparing the central system in the unstable equilibrium at the top of the barrier and the bath in a random initial state drawn from a Gaussian distribution, symmetric under spatial reflection, we demonstrate that the decision whether to relax into the left or the right well is determined reproducibly by residual asymmetries in the initial positions and momenta of the bath oscillators. This result reconciles the randomness and spontaneous symmetry breaking of the asymptotic state with the conservation of entropy under canonical transformations and the manifest symmetry of potential and initial condition of the bistable system.