Preprint

Article

Quantitative Mereology: An Essay to Derive Physics Laws from a Philosophical Concept

Altmetrics

Downloads

559

Views

2152

Comments

Georg J. Schmitz^*

This version is not peer-reviewed

Submitted:

26 July 2019

Posted:

28 July 2019

You are already at the latest version

Alerts

Abstract

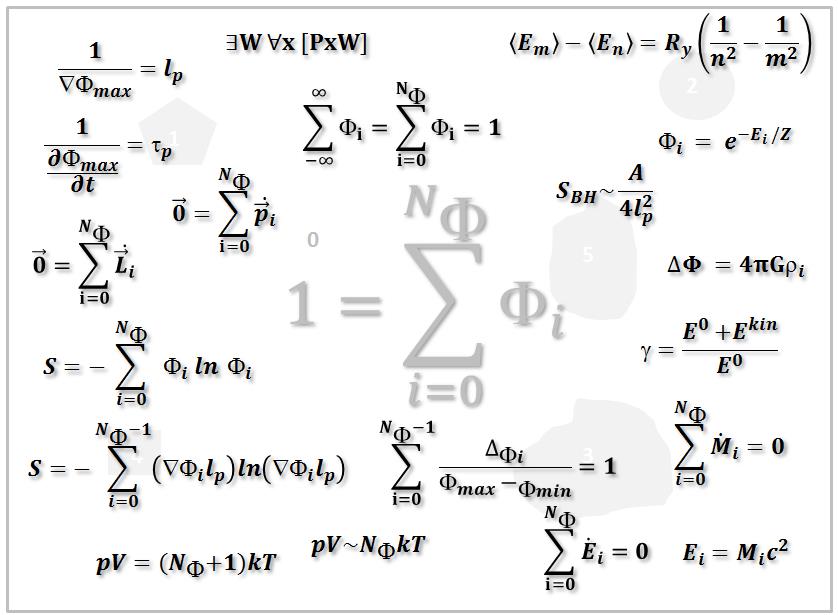
Mereology stands for the philosophical concept of parthood and is based on a sound set of fundamental axioms and relations. One of these axioms relates to the existence of a universe as a thing having part all other things. The present article formulates this logical expression first as an algebraic inequality and eventually as an algebraic equation reading in words: The universe equals the sum of all things. “All things” here are quantified by a “number of things”. Eventually this algebraic equation is normalized leading to an expression The whole equals the sum of all fractions. This introduces “1” or “100%” as a quantitative – numerical - value describing the “whole”. The resulting “basic equation” can then be subjected to a number of algebraic operations. Especially squaring this equation leads to correlation terms between the things implying that the whole is more than just the sum of its parts. Multiplying the basic equation (or its square) by a scalar allows for the derivation of physics equations like the entropy equation, the ideal gas equation, an equation for the Lorentz-Factor, conservation laws for mass and energy, the energy-mass equivalence, the Boltzmann statistics, and the energy levels in a Hydrogen atom. It further allows deriving a “contrast equation” which may form the basis for the definition of a length and a time scale. Multiplying the basic equation with vectors, pseudovectors, pseudoscalars and eventually hypercomplex numbers opens up the realm of possibilities to generate many further equations.

Keywords:

Subject: Physical Sciences - Mathematical Physics

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.