Quantum Mechanical and Optical Analogies in Surface Gravity Water Waves

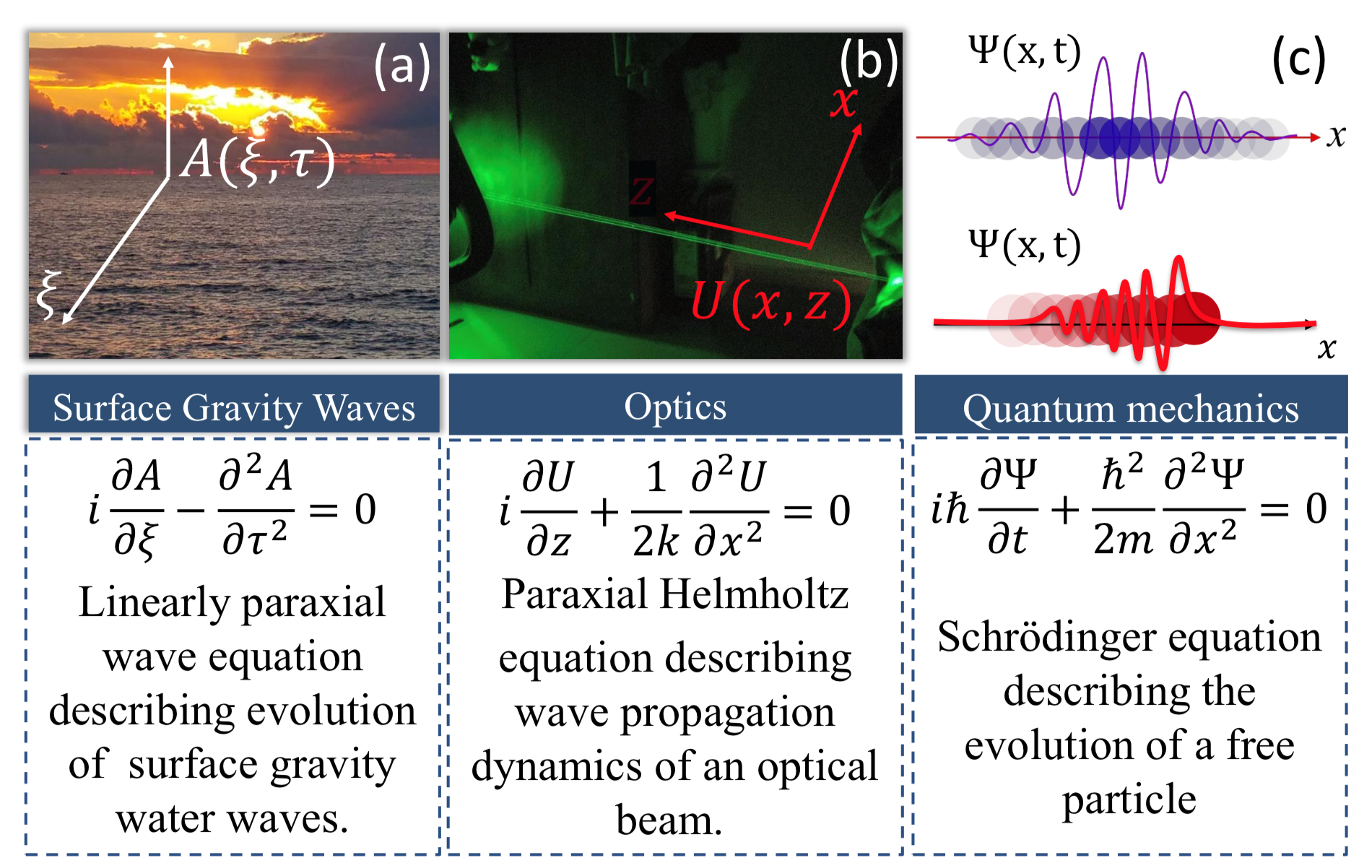
Recently a new class of experiments in the field of surface gravity waves has emerged. These experiments serve as demonstration of an analogy to a broad variety of phenomena in optics and quantum mechanics. In particular, experiments involving Airy water-wave packets were carried out. The Airy wave packets have attracted tremendous attention in optics and quantum mechanics owing to their unique properties, spanning from an ability to propagate along parabolic trajectories without spreading, and to accumulating a phase that scales with the cubic power of time. Non-dispersive Cosine-Gauss wave packets and self-similar Hermite-Gauss wave packets, also well known in the field of optics and quantum mechanics, were recently studied using surface gravity waves as well. These wave packets demonstrated self-healing properties in water wave pulses as well, preserving their width despite being dispersive. Finally, this new approach also allows to observe diffractive focusing from a temporal slit with finite width.