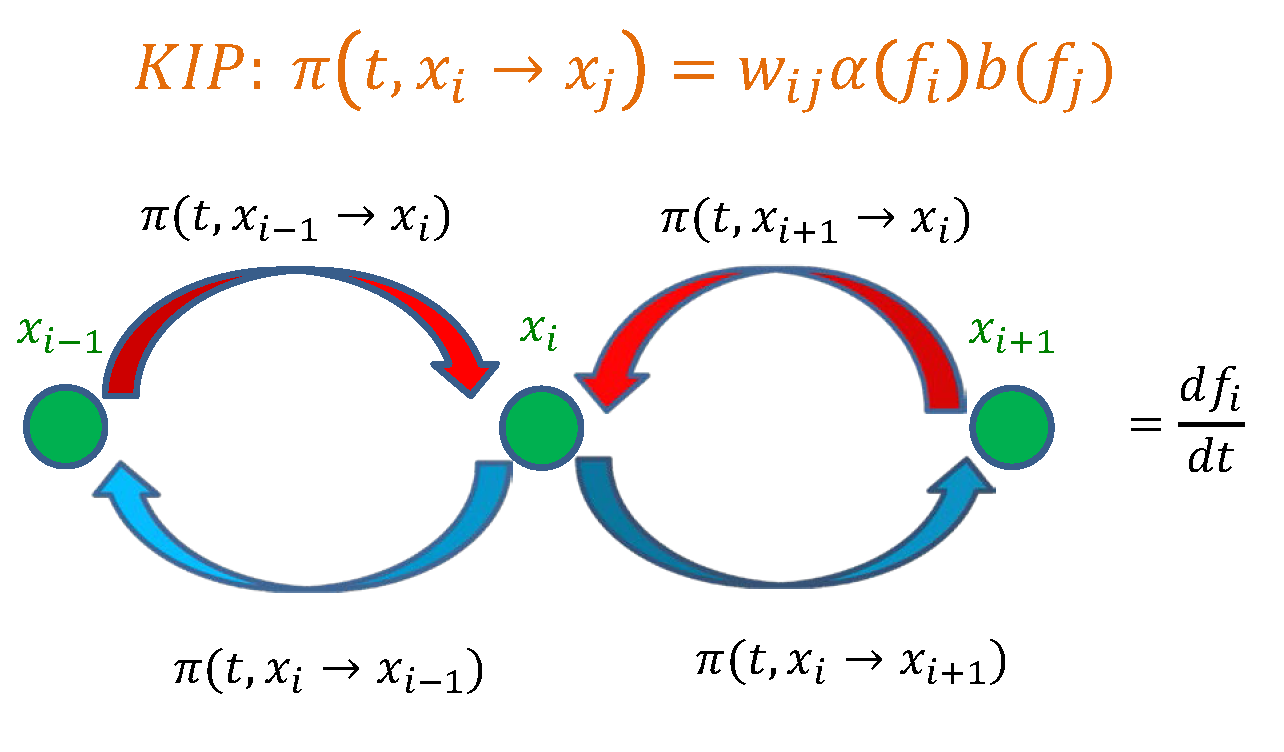
Master equations define the dynamics that govern the time evolution of various physical processes on lattices. In the continuum limit, master equations lead to Fokker-Planck partial differential equations that represent the dynamics of physical systems in continuous spaces. Over the last few decades, nonlinear Fokker-Planck equations have become very popular in condensed matter physics and in statistical physics. Numerical solutions of these equations require the use of discretization schemes. However, the discrete evolution equation obtained by the discretization of a Fokker-Planck partial differential equation depends on the specific discretization scheme. In general, the discretized form is different from the master equation that has generated the respective Fokker-Planck equation in the continuum limit. Therefore, the knowledge of the master equation associated with a given Fokker-Planck equation is extremely important for the correct numerical integration of the latter, since it provides a unique, physically motivated discretization scheme. This paper shows that the Kinetic Interaction Principle (KIP) that governs the particle kinetics of many body systems, introduced in [G. Kaniadakis, Physica A 296, 405 (2001)], univocally defines a very simple master equation that in the continuum limit yields the nonlinear Fokker-Planck equation in its most general form.