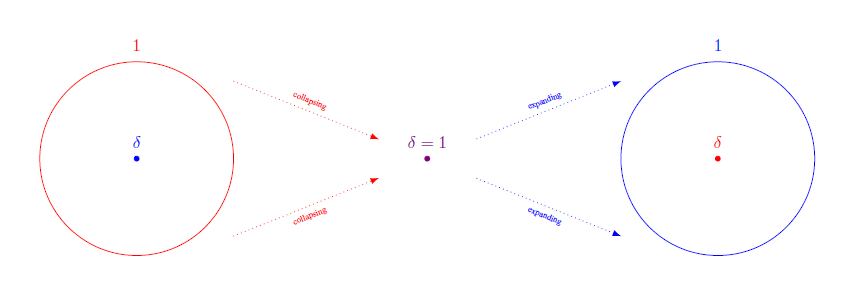
In previous studies we found that generalized functions can be smooth, discrete, periodic or discrete periodic and they can either be local or global and they are regular or generalized functions. We also saw that these properties were related to Poisson’s summation formula on one hand and to Heisenberg’s uncertainty principle on the other. In this paper, we interlink these studies and show that scalars (real or complex numbers) considered as trivial functions are discrete and periodic, local and global as well as regular and generalized, simultaneously. However, this is also a paradox because it means that Dirac’s δ and 1 (its Fourier transform) coincide. They both are unity. We show that δ and 1 coincide in the sense of scalars (real or complex numbers) but they differ in the sense of (generalized) functions. This result can moreover be related to Max Born’s principle of reciprocity. It also answers an open question in present-day quantum mechanics because it means that the Dirac delta squared is simply delta.