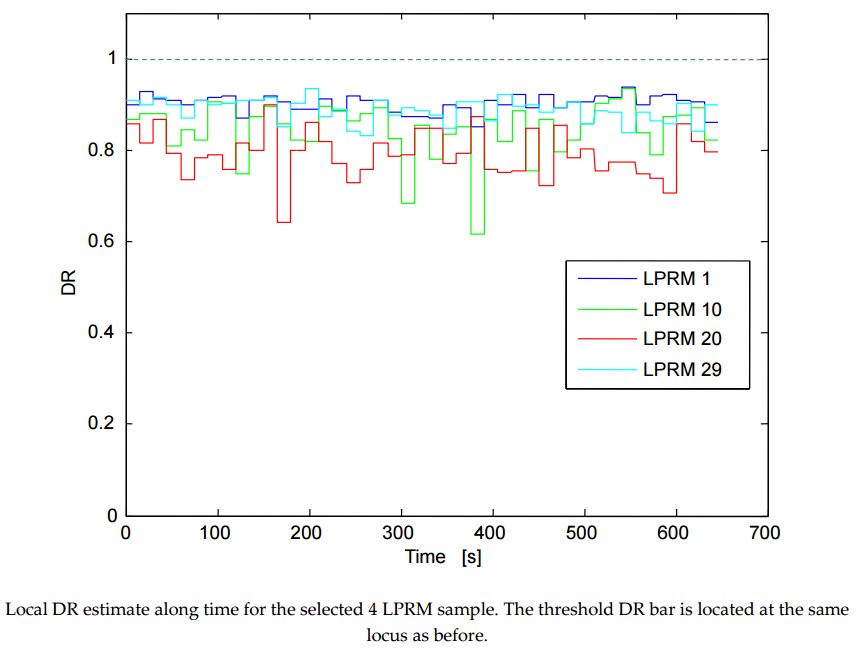
There are currently around 78 Nuclear Power Plants (NPP) in the world based on Boiling Water Reactors (BWR). The current parameter to assess BWR instability issues is the linear Decay Ratio (DR). However, it is well known that BWRs are complex non-linear dynamical systems that may even exhibit chaotic dynamics that normally preclude the use of the DR when the BWR is working at a specific operating point during instability. In this work a novel methodology based on an adaptive Shannon Entropy estimator and on Noise Assisted Empirical Mode Decomposition variants is presented. This methodology was developed for real-time implementation of a stability monitor. This methodology was applied to a set of signals stemming from several NPPs reactors (Ringhals-Sweden, Forsmark-Sweden and Laguna Verde-Mexico) under commercial operating conditions, that experienced instabilities events, each one of a different nature