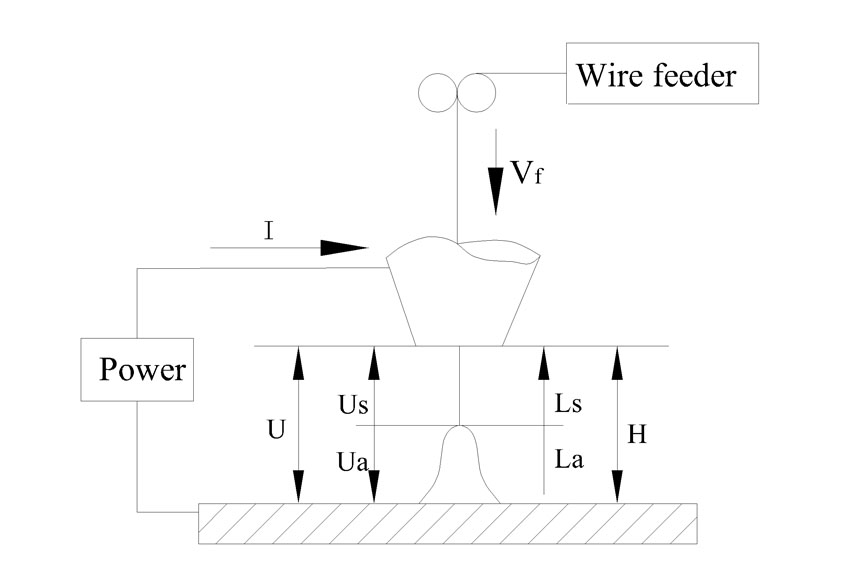
Arc sensors have been used in seam tracking and widely studied since the 80s; commercial arc sensing products for T and V shaped grooves have been developed. However, it is difficult to use these arc sensors in narrow gap welding because arc stability and sensing accuracy are not satisfactory. Pulse gas melting arc welding (P-GMAW) has been successfully applied in narrow gap welding and all position welding processes, so it is worthwhile to research P-GMAW arc sensing technology. In this paper, we derived a linear mathematical P-GMAW model for arc sensing, and the assumptions for the model are verified through experiments and finite element methods. Finally, the linear characteristics of the mathematical model were investigated. In torch height changing experiments, uphill experiments, and groove angle changing experiments the P-GMAW arc signals all satisfied the linear rules. In addition, the faster the welding speed, the higher the arc signal sensitivities; the smaller the groove angle, the greater the arc sensitivities. The arc signal variation rate needs to be modified according to the welding power, groove angles, and swing or rotate speed.