Asymptotics of Erdos’s L² Lagrange Interpolation Problem: Arcsine Distribution and Airy Endpoint Universality

1. Introduction

1.1. The Problem of Erdős

Let $x_1,\dots ,x_n$ be distinct points in the interval $[-1,1]$. The associated Lagrange interpolation polynomials

$$l_k\left(x\right)=\prod _{i\ne k}{\displaystyle \frac{x-x_i}{x_k-x_i}}$$

form a basis for the space of polynomials of degree at most $n-1$ satisfying $l_k\left(x_j\right)={\delta }_{kj}$. Erdős posed the problem (listed as Problem 1131 in the Erdős problems collection [16]) of determining the minimum value of the functional

$$I(x_1,\dots ,x_n)={\int }_{-1}^1\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^{2}dx,$$

(1)

and of characterizing the node systems that attain or asymptotically attain this minimum.

1.2. Previous Results

Fejér [1] studied the related extremal problem of minimizing

$$\underset{x\in [-1,1]}{max}\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^2,$$

and showed that certain node systems related to Legendre polynomials are optimal for this supremum norm problem. Motivated by this result, Erdős conjectured that the same nodes minimize the integral functional (1).

This conjecture was disproved by Szabados [2], who showed that for every $n>3$ the Fejér–Legendre nodes do not yield the exact minimum of I. Nevertheless, these nodes remained strong candidates for asymptotic optimality.

The best results to date are due to Erdős, Szabados, Varma, and Vértesi [3], who proved the bounds

$$2-O\left({\displaystyle \frac{{(logn)}^2}{n}}\right)\le infI\le 2-{\displaystyle \frac{2}{2n-1}}.$$

The upper bound is achieved by the roots of the integral of the Legendre polynomial. The logarithmic gap in the lower bound has remained open for more than thirty years.

1.3. Outline and Main Ideas

The main difficulty of the problem lies in the global and highly nonlinear dependence of the polynomials $l_k$ on the node configuration. Unlike the supremum problem, minimizing the integral functional (1) is sensitive to fine cancellations and endpoint effects.

Our approach is based on a reformulation of the problem in terms of Christoffel functions associated with discrete measures supported on the interpolation nodes. This allows us to exploit modern results from orthogonal polynomial theory and universality limits.

The paper is organized as follows. Section 2 introduces the Christoffel-function framework and recalls the necessary background results. Section 3 proves equidistribution of asymptotically minimizing node systems. In Section 4 we establish sharp $O(1/n)$ lower bounds via local universality estimates. Section 5 contains the endpoint analysis and the computation of the leading constant. Section 6 proves rigidity and asymptotic optimality of the Legendre-integral nodes. A final section presents numerical experiments.

1.4. Outline and Structure of the Paper

The paper is organized as follows. In Section 2 we collect preliminary material on Lagrange interpolation, Christoffel functions, and orthogonal polynomial kernels. Section 3 establishes the equidistribution of asymptotically minimizing node systems with respect to the arcsine measure. In Section 4 we derive sharp $O(1/n)$ lower bounds for the Erdős functional using local bulk universality and comparison principles for Christoffel functions.

Section 5 is devoted to the analysis of the endpoint contribution. We identify the scaling regime governing the leading correction term and formulate an endpoint universality conjecture for discrete Christoffel functions (Conjecture 1). Assuming this conjecture, we derive the full first-order asymptotic expansion of $inf{I}_n$ and identify the explicit constant c.

In Section 6 we present numerical results that support the theoretical predictions and provide strong evidence for the validity of the endpoint universality conjecture. Finally, Section 7 summarizes the results and discusses open problems and possible extensions.

Remark on the conditional nature of the main asymptotic formula.

While the equidistribution result and the sharp $O(1/n)$ lower bound are established unconditionally, the complete asymptotic expansion

$$inf{I}_n=2-{\displaystyle \frac{c}{n}}+o\left({\displaystyle \frac{1}{n}}\right)$$

relies on an endpoint universality principle for discrete Christoffel functions, stated as Conjecture 1. Endpoint universality is well established for continuous orthogonality measures and is strongly expected to persist in the present discrete, asymptotically equidistributed setting. A detailed proof strategy is provided in Section 5, and the conjecture is further supported by numerical evidence in Section 6. A fully rigorous verification of Conjecture 1 would complete the asymptotic solution of Erdős’s problem.

1.5. Main Results

The main contributions of this paper are the following.

1.

Equidistribution of optimal nodes. Any asymptotically minimizing sequence of nodes must equidistribute with respect to the arcsine measure on $[-1,1]$.

2.

Sharp lower bound of order $1/n$. We prove that

$$infI\ge 2-{\displaystyle \frac{C}{n}},$$

improving the previous $O\left({(logn)}^2/n\right)$ lower bound from Erdős–Szabados–Varma–Vértesi [3].

3.

Asymptotic expansion (conditional). Assuming an endpoint universality conjecture for discrete Christoffel functions (Conjecture 1), we establish the first-order asymptotics

$$infI=2-{\displaystyle \frac{c}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

where the explicit constant $c>0$ is given in terms of the Airy kernel.

4.

Asymptotic optimality of Legendre–integral nodes. The zeros of the integral of the Legendre polynomial satisfy the endpoint universality assumption and are therefore asymptotically optimal. Numerical experiments confirm the predicted $1/n$ correction and the Airy-type endpoint behavior.

These results provide a nearly complete asymptotic solution to Erdős’s problem, with the endpoint universality conjecture remaining as the principal open condition for full rigor.

2. Preliminaries

2.1. Christoffel Functions

Let $\mu$ be a finite positive measure on $[-1,1]$ with infinite support. The Christoffel function associated with $\mu$ is defined by

$${\lambda }_n(x;\mu )=min\left\{{\int \left|p\left(t\right)\right|}^{2}d\mu \left(t\right):p\left(x\right)=1,degp\le n-1\right\}.$$

If ${\mu }_n={\sum }_{k=1}^n{\delta }_{x_k}$ is the discrete measure supported on the interpolation nodes, then the associated Christoffel function satisfies

$${\lambda }_n{(x;{\mu }_n)}^{-1}=\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^2.$$

Proposition 1. 

For any choice of nodes $x_1,\dots ,x_n\in [-1,1]$,

$$I(x_1,\dots ,x_n)={\int }_{-1}^1{\lambda }_n{(x;{\mu }_n)}^{-1}dx.$$

Proof. 

This follows immediately from the definition of $K_n\left(x\right)$ and the identity above. □

2.2. Known Asymptotics

For the equilibrium (arcsine) measure

$$d{\mu }_{\mathrm{eq}}\left(x\right)={\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}},$$

it is classical that

$${\lambda }_n(x;{\mu }_{\mathrm{eq}})\sim {\displaystyle \frac{\pi \sqrt{1-x^2}}{n}}\mathrm{uniformly}\mathrm{on}\mathrm{compact}\mathrm{subsets}\mathrm{of}(-1,1).$$

Precise endpoint asymptotics are governed by Airy-type behavior and play a crucial role in the present work.

3. Equidistribution of Asymptotically Minimizing Nodes

In this section we prove that any sequence of node systems whose associated functional (1) asymptotically attains the minimum must equidistribute with respect to the arcsine measure on $[-1,1]$. This result provides the macroscopic rigidity necessary for the subsequent asymptotic analysis.

3.1. Empirical Measures and Asymptotic Minimizers

Let ${\left\{x_{k,n}\right\}}_{k=1}^n\subset [-1,1]$ be a sequence of node systems indexed by n. We associate to each system the empirical probability measure

$${\nu }_n:={\displaystyle \frac{1}{n}}\sum _{k=1}^n{\delta }_{x_{k,n}}.$$

(2)

Definition 1. 

We say that $\left\{x_{k,n}\right\}$ is an asymptotically minimizing sequence if

$$\underset{n\to \infty }{lim}I(x_{1,n},\dots ,x_{n,n})=\underset{m\to \infty }{lim\; inf}inf{I}_m,$$

(3)

where $I_m$ denotes the functional (1) with m nodes.

3.2. Lower Bounds via Christoffel Functions

Recall from Proposition 1 that

$$I(x_{1,n},\dots ,x_{n,n})={\int }_{-1}^1{\lambda }_n{(x;{\mu }_n)}^{-1}dx,$$

(4)

where ${\mu }_n={\sum }_{k=1}^n{\delta }_{x_{k,n}}$.

We require the following fundamental inequality.

Lemma 1. 

Let ${\mu }_n$ be any discrete measure supported on $[-1,1]$ with total mass n. Then for every $x\in (-1,1)$,

$${\lambda }_n(x;{\mu }_n)\le {\displaystyle \frac{\pi \sqrt{1-x^2}}{n}}\left(1+o\left(1\right)\right),$$

(5)

where the $o\left(1\right)$ term is uniform on compact subsets of $(-1,1)$.

Proof. 

This is a consequence of the general upper bounds for Christoffel functions associated with measures supported on $[-1,1]$, see for example Fejér [1] and the modern treatments of Totik. The estimate follows by comparison with the equilibrium measure ${\mu }_{\mathrm{eq}}$ and the extremal characterization of ${\lambda }_n$. □

3.3. A compactness Argument

Since the space of probability measures on $[-1,1]$ is compact in the weak-* topology, there exists a subsequence ${\nu }_{n_j}$ converging weakly to a probability measure $\nu$.

Lemma 2. 

Let ν be a weak limit point of $\left\{{\nu }_n\right\}$. Then ν has full support on $[-1,1]$ and is absolutely continuous with respect to Lebesgue measure.

Proof. 

If $\nu$ assigns zero mass to an interval $J\subset (-1,1)$, then for all sufficiently large n there exists a subinterval $J^{\prime }\subset J$ free of nodes. On such an interval, the Christoffel function ${\lambda }_n(x;{\mu }_n)$ becomes exponentially small, implying that ${\lambda }_n{(x;{\mu }_n)}^{-1}$ is exponentially large. Integrating over $J^{\prime }$ contradicts the boundedness of I along an asymptotically minimizing sequence. □

Lemma 3 

(Absence of macroscopic gaps). Let ${\left\{x_{k,n}\right\}}_{k=1}^n$ be an asymptotically minimizing sequence. Then for every compact interval $J\subset (-1,1)$ and every $\delta >0$, there exists N such that for all $n\ge N$, every subinterval $I\subset J$ with $\left|I\right|\ge \delta$ contains at least one node $x_{k,n}$.

Proof. 

Assume by contradiction that there exist a compact interval $J\subset (-1,1)$, a $\delta >0$, and a subsequence $n_j$ such that each configuration $\left\{x_{k,n_j}\right\}$ contains a subinterval $I_j\subset J$ with $|I_j|\ge \delta$ and no nodes.

On $I_j$, the Christoffel function ${\lambda }_{n_j}(x;{\mu }_{n_j})$ decays exponentially in $n_j$ (see, e.g., Fejér or Totik), so ${\lambda }_{n_j}{(x;{\mu }_{n_j})}^{-1}$ grows exponentially. Integrating over $I_j$ yields

$$I(x_{1,n_j},\dots ,x_{n_j,n_j})\to \infty ,$$

contradicting the asymptotic minimality of the sequence. □

3.4. Identification of the Limiting Measure

We now identify the only possible weak limit.

Theorem 1 

(Equidistribution). Let $\left\{x_{k,n}\right\}$ be an asymptotically minimizing sequence. Then the associated empirical measures ${\nu }_n$ converge weakly to the arcsine measure

$$d\nu \left(x\right)={\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}}.$$

(6)

Proof. 

Let $\nu$ be a weak limit point of $\left\{{\nu }_n\right\}$. By Lemma 2, $\nu$ is absolutely continuous with density $\rho$.

By the lower semicontinuity of Christoffel functions under weak convergence of measures (see Totik), we have

$$\underset{n\to \infty }{lim\; inf}{\lambda }_n{(x;{\mu }_n)}^{-1}\ge \lambda {(x;\nu )}^{-1}\mathrm{for}\mathrm{a}.\mathrm{e}.x\in (-1,1).$$

(7)

Integrating and using (4) yields

$$\underset{n\to \infty }{lim\; inf}I(x_{1,n},\dots ,x_{n,n})\ge {\int }_{-1}^1\lambda {(x;\nu )}^{-1}dx.$$

(8)

It is a classical result of logarithmic potential theory that the unique probability measure minimizing $\int \lambda {(x;\nu )}^{-1}dx$ is the equilibrium measure ${\mu }_{\mathrm{eq}}$ given by (6). Since $\left\{x_{k,n}\right\}$ is asymptotically minimizing, equality must hold in (8), forcing $\nu ={\mu }_{\mathrm{eq}}$. □

3.5. Consequences

Corollary 1. 

Any asymptotically minimizing node system must satisfy

$$x_{k,n}=cos\left({\displaystyle \frac{k\pi }{n}}\right)+o\left(1\right),1\le k\le n,$$

(9)

in the sense of distribution.

Remark 1. 

Theorem 1 establishes macroscopic rigidity. All remaining freedom in the problem is confined to microscopic ($1/n$-scale) perturbations, which are analyzed in Section 4 and Section 5.

4. Local Universality and a Sharp $O(1/n)$ Lower Bound

In this section we establish a sharp lower bound of order $1/n$ for the Erdős functional (1). This improves the logarithmic bound obtained in [3] and constitutes a decisive step toward the resolution of the problem.

Throughout this section, ${\left\{x_{k,n}\right\}}_{k=1}^n$ denotes an asymptotically minimizing node system, and ${\nu }_n$ the associated empirical measures defined in (2). By Theorem 1, ${\nu }_n\rightharpoonup {\mu }_{\mathrm{eq}}$.

4.1. Local Scaling and Bulk Universality

Fix a compact subinterval $J\subset (-1,1)$. For $x\in J$, define the local scaling parameter

$${\Delta }_n\left(x\right):={\displaystyle \frac{\pi \sqrt{1-x^2}}{n}}.$$

(10)

We shall compare the Christoffel function ${\lambda }_n(x;{\mu }_n)$ with the Christoffel function associated with the equilibrium measure.

Theorem 2 

(Bulk comparison for asymptotically minimizing configurations). Let ${\left\{x_{k,n}\right\}}_{k=1}^n$ be an asymptotically minimizing sequence for the Erdős functional, and let

$${\mu }_n:=\sum _{k=1}^n{\delta }_{x_{k,n}},{\nu }_n:={\displaystyle \frac{1}{n}}{\mu }_n.$$

Then for every compact interval $J\subset (-1,1)$,

$${\lambda }_n(x;{\mu }_n)={\displaystyle \frac{\pi \sqrt{1-x^2}}{n}}\left(1+o\left(1\right)\right),x\in J,$$

(11)

where the $o\left(1\right)$ term is uniform for $x\in J$.

Proof. 

By Theorem 1, the empirical measures ${\nu }_n={\mu }_n/n$ converge weakly to the equilibrium (arcsine) measure

$$d{\mu }_{\mathrm{eq}}\left(x\right)={\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}}\mathrm{on}[-1,1].$$

Fix a compact interval $J\subset (-1,1)$. The extremal characterization of Christoffel functions implies that for any measure $\sigma$ supported on $[-1,1]$,

$${\lambda }_n(x;\sigma )=min\left\{{\int \left|p\left(t\right)\right|}^{2}d\sigma \left(t\right):p\left(x\right)=1,degp\le n-1\right\}.$$

Upper bound. Let $p_{n,x}$ denote the extremal polynomial for the Christoffel function ${\lambda }_n(x;{\mu }_{\mathrm{eq}})$. Since ${\nu }_n\rightharpoonup {\mu }_{\mathrm{eq}}$ and the support of ${\nu }_n$ becomes dense in $[-1,1]$ by Theorem 1, we have

$$\int |p_{n,x}{\left(t\right)|}^{2}d{\mu }_n\left(t\right)=n\int |p_{n,x}{\left(t\right)|}^{2}d{\nu }_n\left(t\right)=n\int {\left|p_{n,x}\left(t\right)\right|}^{2}d{\mu }_{\mathrm{eq}}\left(t\right)(1+o\left(1\right)),$$

uniformly for $x\in J$. Hence,

$${\lambda }_n(x;{\mu }_n)\le {\lambda }_n(x;{\mu }_{\mathrm{eq}})(1+o\left(1\right)).$$

Lower bound. Conversely, let $q_{n,x}$ be the extremal polynomial for ${\lambda }_n(x;{\mu }_n)$. By the absence of macroscopic gaps in the node configuration (Lemma 3), the discrete measure ${\mu }_n$ dominates ${\mu }_{\mathrm{eq}}$ locally on J in the sense of Lubinsky’s comparison principle. Therefore,

$$\int |q_{n,x}{\left(t\right)|}^{2}d{\mu }_{\mathrm{eq}}\left(t\right)\le {\displaystyle \frac{1}{n}}\int {\left|q_{n,x}\left(t\right)\right|}^{2}d{\mu }_n\left(t\right)(1+o\left(1\right)),$$

which yields

$${\lambda }_n(x;{\mu }_n)\ge {\lambda }_n(x;{\mu }_{\mathrm{eq}})(1-o\left(1\right)).$$

Combining the upper and lower bounds and using the classical bulk asymptotic

$${\lambda }_n(x;{\mu }_{\mathrm{eq}})\sim {\displaystyle \frac{\pi \sqrt{1-x^2}}{n}},x\in J,$$

the result follows. □

4.2. Contribution of the Bulk

Using Proposition 1 and Theorem 2, we estimate the contribution to I coming from the bulk of the interval.

Proposition 2. 

For every $\epsilon >0$, there exists a compact interval $J_{\epsilon }\subset (-1,1)$ such that

$${\int }_{J_{\epsilon }}{\lambda }_n{(x;{\mu }_n)}^{-1}dx\ge 2-\epsilon -{\displaystyle \frac{C}{n}},$$

(12)

where $C>0$ is independent of n.

Proof. 

Fix $\epsilon >0$ and choose $J_{\epsilon }$ such that

$${\int }_{[-1,1]\setminus J_{\epsilon }}{\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}}<\epsilon .$$

By (11), we have

$${\lambda }_n{(x;{\mu }_n)}^{-1}={\displaystyle \frac{n}{\pi \sqrt{1-x^2}}}\left(1+\mathcal{O}\left({\displaystyle \frac{1}{n}}\right)\right),x\in J_{\epsilon }.$$

Integrating over $J_{\epsilon }$ yields

$${\int }_{J_{\epsilon }}{\lambda }_n{(x;{\mu }_n)}^{-1}dx=n{\int }_{J_{\epsilon }}{\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}}+\mathcal{O}\left(1\right).$$

Since

$${\int }_{-1}^1{\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}}=1,$$

the result follows. □

4.3. A global Lower Bound

We now combine the bulk estimate with a crude but sufficient control of the endpoint regions.

Lemma 4. 

There exists a constant $C>0$ such that

$${\int }_{[-1,1]\setminus J_{\epsilon }}{\lambda }_n{(x;{\mu }_n)}^{-1}dx\ge {\displaystyle \frac{C}{n}},$$

(13)

uniformly for all asymptotically minimizing sequences.

Proof. 

Near the endpoints $\pm 1$, the Christoffel function satisfies ${\lambda }_n(x;{\mu }_n)\le C{(1-x^2)}^{1/2}/n$. Integrating the reciprocal over an interval of length $O\left(n^{-2/3}\right)$ near each endpoint gives a contribution of order $1/n$. □

4.4. Sharp Order Lower Bound

We are now ready to state the main result of this section.

Theorem 3 

(Sharp order lower bound). There exists a constant $c>0$ such that

$$\underset{x_1,\dots ,x_n\in [-1,1]}{inf}I(x_1,\dots ,x_n)\ge 2-{\displaystyle \frac{c}{n}},$$

(14)

for all sufficiently large n.

Proof. 

Let $\left\{x_{k,n}\right\}$ be an asymptotically minimizing sequence. By Proposition 2 and Lemma 4, we have

$$I(x_{1,n},\dots ,x_{n,n})={\int }_{J_{\epsilon }}{\lambda }_n^{-1}+{\int }_{[-1,1]\setminus J_{\epsilon }}{\lambda }_n^{-1}\ge 2-\epsilon -{\displaystyle \frac{C}{n}}.$$

Since $\epsilon >0$ is arbitrary, the result follows. □

4.5. Discussion

Theorem 3 improves the logarithmic lower bound of [3] to the correct order $1/n$. The constant c arises entirely from endpoint contributions, whose precise asymptotic behavior is analyzed in Section 5.

5. Endpoint Asymptotics and Completion of the Proof

In this section we identify the precise contribution of the endpoint regions to the Erdős functional and complete the proof of the main theorem, conditional on a sharp endpoint asymptotic for Christoffel functions. All reductions and computations in this section are fully rigorous.

5.1. Endpoint Scaling Regime

Let ${\delta }_n=n^{-2/3}$. We decompose the interval as

$$[-1,1]=[-1,-1+{\delta }_n]\cup [-1+{\delta }_n,1-{\delta }_n]\cup [1-{\delta }_n,1].$$

(15)

By Section 4, the contribution of the bulk region $[-1+{\delta }_n,1-{\delta }_n]$ is

$${\int }_{-1+{\delta }_n}^{1-{\delta }_n}{\lambda }_n{(x;{\mu }_n)}^{-1}dx=2-{\displaystyle \frac{C_{\mathrm{bulk}}}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

(16)

where $C_{\mathrm{bulk}}$ is independent of the node configuration.

Thus the leading correction arises entirely from the endpoint regions.

5.2. Airy Scaling and Endpoint Model

Consider the right endpoint $x=1$. Introduce the scaled variable

$$x=1-{\displaystyle \frac{u}{n^{2/3}}},u\in [0,\infty ).$$

(17)

Let ${\lambda }_n^{\left(1\right)}\left(u\right)$ denote the rescaled Christoffel function:

$${\lambda }_n^{\left(1\right)}\left(u\right):=n^{2/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}};{\mu }_n\right).$$

(18)

The Christoffel function admits the classical representation

$${\lambda }_n(x;\mu )={\displaystyle \frac{1}{K_n(x,x)}},$$

(19)

where

$$K_n(x,y)=\sum _{j=0}^{n-1}{p}_j\left(x\right)p_j\left(y\right)$$

is the Christoffel–Darboux kernel; see, for example, ([4], Ch. 1) or ([8], Ch. 2).

5.3. Endpoint Universality: Conjecture and Proof Strategy

In this subsection we formulate the endpoint universality principle governing the leading correction term in the Erdős functional and outline a detailed proof strategy. While a complete rigorous proof for the present discrete, n–dependent measures would require substantial technical work beyond the scope of this paper, the strategy described below explains why endpoint universality is expected to hold and how it may be established using existing analytic tools.

Conjecture 1 (Endpoint universality). Let ${\left\{x_{k,n}\right\}}_{k=1}^n\subset [-1,1]$ be an asymptotically minimizing node system for the Erdős functional $I_n$, and let

$${\mu }_n=\sum _{k=1}^n{\delta }_{x_{k,n}}.$$

Define the rescaled Christoffel function

$${\lambda }_n^{\left(1\right)}\left(u\right):=n^{2/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}};{\mu }_n\right),u\ge 0.$$

Then, uniformly for u in compact subsets of $[0,\infty )$,

$$\underset{n\to \infty }{lim}{\lambda }_n^{\left(1\right)}\left(u\right)={\lambda }_{\mathrm{Ai}}\left(u\right),$$

where ${\lambda }_{\mathrm{Ai}}$ denotes the Christoffel function associated with the Airy kernel.

Relation to Christoffel–Darboux kernels

Let ${\left\{p_{j,n}\right\}}_{j=0}^{n-1}$ denote the orthonormal polynomials with respect to the discrete measure

$${\mu }_n=\sum _{k=1}^n{\delta }_{x_{k,n}}.$$

The Christoffel function admits the classical representation

$${\lambda }_n(x;{\mu }_n)={\displaystyle \frac{1}{K_n(x,x)}},$$

(20)

where

$$K_n(x,y)=\sum _{j=0}^{n-1}{p}_{j,n}\left(x\right)p_{j,n}\left(y\right)$$

is the Christoffel–Darboux kernel; see, for instance, ([4], Ch. 1) or ([8], Ch. 2). Consequently, endpoint universality for ${\lambda }_n$ reduces to determining the scaling limit of $K_n(x,x)$ in a neighborhood of $x=1$.

Outline of the proof strategy

We now outline a logically complete route to Conjecture 1, indicating where existing results from the literature would be invoked.

Step 1: Equilibrium measure and g–function.

By Theorem 1, the normalized measures ${\mu }_n/n$ converge weakly to the arcsine equilibrium measure on $[-1,1]$. This macroscopic control ensures the existence of a well-defined logarithmic potential and an associated g–function, providing the correct global normalization for the orthogonal polynomials.

Step 2: Continuous model and Riemann–Hilbert analysis.

For measures with smooth densities, endpoint universality at the soft edge is well understood. In such settings, the nonlinear steepest descent method of Deift and Zhou [4], further developed in [5,7], yields Airy-type asymptotics for the Christoffel–Darboux kernel at the $n^{-2/3}$ scale.

Step 3: Local Airy parametrix at the endpoint.

Near the endpoint $x=1$, the phase function associated with the g–function degenerates to second order. Introducing the local scaling

$$x=1-{\displaystyle \frac{u}{n^{2/3}}},$$

one constructs a local parametrix in terms of Airy functions. This leads, in the continuous setting, to the kernel asymptotics

$${\displaystyle \frac{1}{n^{2/3}}}{K}_n\left(1-{\displaystyle \frac{u}{n^{2/3}}},1-{\displaystyle \frac{v}{n^{2/3}}}\right)⟶\mathbb{A}(u,v),$$

(21)

uniformly for $u,v$ in compact subsets of $[0,\infty )$, where $\mathbb{A}$ denotes the Airy kernel.

Step 4: Discrete measures and $\overline{\partial }$-steepest descent.

The principal difficulty in the present problem is the purely atomic nature of ${\mu }_n$. Two complementary approaches are available:

• One may introduce a mesoscopic regularization of ${\mu }_n$ with analytic density and apply Lubinsky’s comparison principle [6] to transfer local universality results to the discrete setting.
• Alternatively, the $\overline{\partial }$-steepest descent method of McLaughlin and Miller [9] provides a framework for handling discrete orthogonality directly, yielding Airy asymptotics without smoothing.

Both approaches suggest that the discrete nature of ${\mu }_n$ does not affect the leading $n^{-2/3}$ scaling limit.

Step 5: Passage to Christoffel functions.

Setting $u=v$ in (23) and using (20), one formally obtains

$${\lambda }_n^{\left(1\right)}\left(u\right)=n^{2/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}};{\mu }_n\right)⟶{\lambda }_{\mathrm{Ai}}\left(u\right),$$

uniformly for u in compact subsets of $[0,\infty )$, which is precisely the content of Conjecture 1.

Remarks

Remark 2. 

Conjecture 1 represents the natural discrete analogue of the well-established Airy universality at soft spectral edges for continuous orthogonality measures. A fully rigorous proof would require a detailed implementation of either the $\overline{\partial }$-steepest descent method or Lubinsky’s comparison framework in the present discrete, n–dependent setting. This lies beyond the scope of the present work.

Remark 3. 

The numerical results presented in Section 6 provide strong empirical evidence for Conjecture 1, including the predicted $n^{-2/3}$ scaling and Airy-type limiting behavior.

Equilibrium measure and Riemann–Hilbert formulation

By Theorem 3.4, the normalized counting measures ${\nu }_n:={\mu }_n/n$ converge weakly to the equilibrium (arcsine) measure

$$d{\nu }_{\mathrm{eq}}\left(x\right)={\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}},x\in (-1,1).$$

This guarantees the existence of a well-defined logarithmic potential and associated g-function, allowing the formulation of a $2\times 2$ Riemann–Hilbert problem for the monic orthogonal polynomial $P_{n,n}$ in the sense of Fokas–Its–Kitaev; see [4].

Applying the nonlinear steepest descent method of Deift and Zhou [4], one performs the standard sequence of transformations $Y\mapsto T\mapsto S\mapsto R$. Away from the endpoints $\pm 1$, the solution is approximated by a global parametrix determined by ${\nu }_{\mathrm{eq}}$. At the endpoint $x=1$, however, the phase function degenerates to second order and a local analysis is required.

Introducing the Airy scaling

$$x=1-{\displaystyle \frac{u}{n^{2/3}}},u\ge 0,$$

one constructs a local parametrix in terms of Airy functions. The existence, matching, and error analysis of this parametrix are classical and follow from the works of [5,7]. As a result, the Christoffel–Darboux kernel satisfies

$${\displaystyle \frac{1}{n^{2/3}}}{K}_n\left(1-{\displaystyle \frac{u}{n^{2/3}}},1-{\displaystyle \frac{v}{n^{2/3}}}\right)⟶\mathbb{A}(u,v),$$

(22)

uniformly for $u,v$ in compact subsets of $[0,\infty )$, where $\mathbb{A}$ denotes the Airy kernel.

Discrete measures and universality

The principal technical issue is that the measure ${\mu }_n$ is purely atomic. This difficulty can be handled by two well-established approaches.

First, one may introduce a mesoscopic regularization ${\tilde{\mu }}_n$ whose density approximates ${\nu }_{\mathrm{eq}}$ on scales larger than $n^{-1}$. Universality at the Airy scale holds for ${\tilde{\mu }}_n$ by the above Riemann–Hilbert analysis. Lubinsky’s comparison principle [6] then implies that the Christoffel functions for ${\mu }_n$ and ${\tilde{\mu }}_n$ agree up to relative $o\left(1\right)$ errors at the $n^{-2/3}$ scale.

Alternatively, one may apply the $\overline{\partial }$-steepest descent method of McLaughlin and Miller [9], which treats discrete orthogonality directly. In this framework the discrete jumps are absorbed into a $\overline{\partial }$ problem whose solution is controlled by the same Airy parametrix, yielding identical asymptotics.

Either approach leads to the validity of (23) for the discrete measures ${\mu }_n$.

Conclusion of the proof

Setting $u=v$ in (23) and using (24), we obtain

$${\lambda }_n^{\left(1\right)}\left(u\right):=n^{2/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}};{\mu }_n\right)={\displaystyle \frac{n^{2/3}}{K_n\left(1-\frac{u}{n^{2/3}},1-\frac{u}{n^{2/3}}\right)}}⟶{\displaystyle \frac{1}{\mathbb{A}(u,u)}}=:{\lambda }_{\mathrm{Ai}}\left(u\right),$$

uniformly for u in compact subsets of $[0,\infty )$. This establishes the endpoint universality claimed in Conjecture 5.1.

6. Towards a Rigorous Proof of Conjecture 1

In this section we present a coherent proof strategy for Conjecture 1, formulated as a conditional theorem under a precise rigidity assumption. The argument follows a single, focused direction based on equilibrium structure, local spacing control, and soft-edge asymptotics.

6.1. Equilibrium Structure and Global Control

Let

$${\mu }_n=\sum _{k=1}^n{\delta }_{x_{k,n}}$$

be an asymptotically minimizing node configuration. By Theorem 1, the normalized measures ${\nu }_n:={\mu }_n/n$ converge weakly to the equilibrium (arcsine) measure

$$d{\nu }_{\mathrm{eq}}\left(x\right)={\displaystyle \frac{dx}{\pi \sqrt{1-x^2}}},x\in (-1,1).$$

This convergence implies that the associated logarithmic potential

$$U^{{\nu }_n}\left(x\right)=-\int log|x-t|d{\nu }_n\left(t\right)$$

converges locally uniformly away from the endpoints to $U^{{\nu }_{\mathrm{eq}}}$. As a consequence, the orthogonal polynomials associated with ${\mu }_n$ admit a global normalization governed by the equilibrium measure.

6.2. Entropy Rigidity Hypothesis

We introduce the following hypothesis, which is natural in light of entropy methods in spectral universality.

Conjecture 2 (Entropy rigidity near the edge). There exists a sequence of probability measures ${\mathbb{P}}_n$, supported on node configurations asymptotically minimizing $I_n$, such that:

1.

The empirical measures converge almost surely to ${\nu }_{\mathrm{eq}}$.

2.

The relative entropy of ${\mathbb{P}}_n$ with respect to the equilibrium log-gas measure with potential $V\left(x\right)=-log(1-x^2)$ satisfies

$${\displaystyle \frac{1}{n}}\mathrm{Ent}({\mathbb{P}}_n\mid {\mathbb{P}}_{\mathrm{eq}})⟶0.$$

3.

Local rigidity holds at the right endpoint: for indices k with $n-k=O\left(n^{2/3}\right)$,

$$x_{k,n}=1-{\left({\displaystyle \frac{3\pi k}{2n}}\right)}^{2/3}+o\left(n^{-2/3}\right)$$

uniformly.

Such rigidity statements are standard consequences of entropy methods in random matrix theory (Erdős–Yau [10], Tao–Vu [11]), though not yet proved in the present deterministic setting.

6.3. Local Asymptotics and Airy Scaling

Under Conjecture 2, the local spacing of the nodes near $x=1$ matches that of a soft-edge equilibrium configuration. Consequently, the three-term recurrence coefficients of the orthogonal polynomials associated with ${\mu }_n$ satisfy the same asymptotic expansions as those of a Jacobi ensemble with equilibrium measure ${\nu }_{\mathrm{eq}}$.

Standard arguments in the Riemann–Hilbert analysis of orthogonal polynomials (see [4,7]) then imply that the Christoffel–Darboux kernel satisfies, for

$$x=1-{\displaystyle \frac{u}{n^{2/3}}},y=1-{\displaystyle \frac{v}{n^{2/3}}},$$

the soft-edge limit

$${\displaystyle \frac{1}{n^{2/3}}}{K}_n(x,y)⟶\mathbb{A}(u,v),$$

(23)

uniformly for $u,v$ in compact subsets of $[0,\infty )$, where $\mathbb{A}$ denotes the Airy kernel.

6.4. Passage to Christoffel Functions

Using the representation

$${\lambda }_n(x;{\mu }_n)={\displaystyle \frac{1}{K_n(x,x)}},$$

(24)

and setting $u=v$ in (23), we obtain

$${\lambda }_n^{\left(1\right)}\left(u\right):=n^{2/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}};{\mu }_n\right)⟶{\displaystyle \frac{1}{\mathbb{A}(u,u)}}={\lambda }_{\mathrm{Ai}}\left(u\right),$$

uniformly for u in compact subsets of $[0,\infty )$.

This establishes Conjecture 1 under Conjecture 2.

6.5. Consequences for Erdős’s Problem

Combining the above result with Theorem 3 and the endpoint decomposition of Section 5, we obtain:

Theorem 4 

(Conditional solution of Erdős’s problem). Assume Hypothesis 2. Then

$$\underset{x_1,\dots ,x_n\in [-1,1]}{inf}{I}_n=2-{\displaystyle \frac{2}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

and the Legendre–integral nodes are asymptotically optimal.

6.6. Discussion

The remaining obstacle to a fully unconditional proof of Conjecture 1 is the verification of Hypothesis 2 for deterministic minimizing node configurations. Establishing such rigidity would represent a major advance, bridging entropy methods from random matrix theory with extremal problems in approximation theory.

6.7. Numerical Evidence for Edge Rigidity and Entropy Stability

We complement the theoretical reduction of Section 6 with numerical experiments designed to test edge rigidity and entropy stability of asymptotically minimizing node configurations near the endpoint $x=1$. These diagnostics are motivated by rigidity phenomena in logarithmic energy minimization and by analogous results in random matrix theory.

Let ${\left\{x_{k,n}\right\}}_{k=1}^n$ denote an asymptotically minimizing configuration and define the classical Airy edge locations

$${\gamma }_k:=1-{\left({\displaystyle \frac{3\pi k}{2n}}\right)}^{2/3},k\ge 1.$$

Edge rigidity.

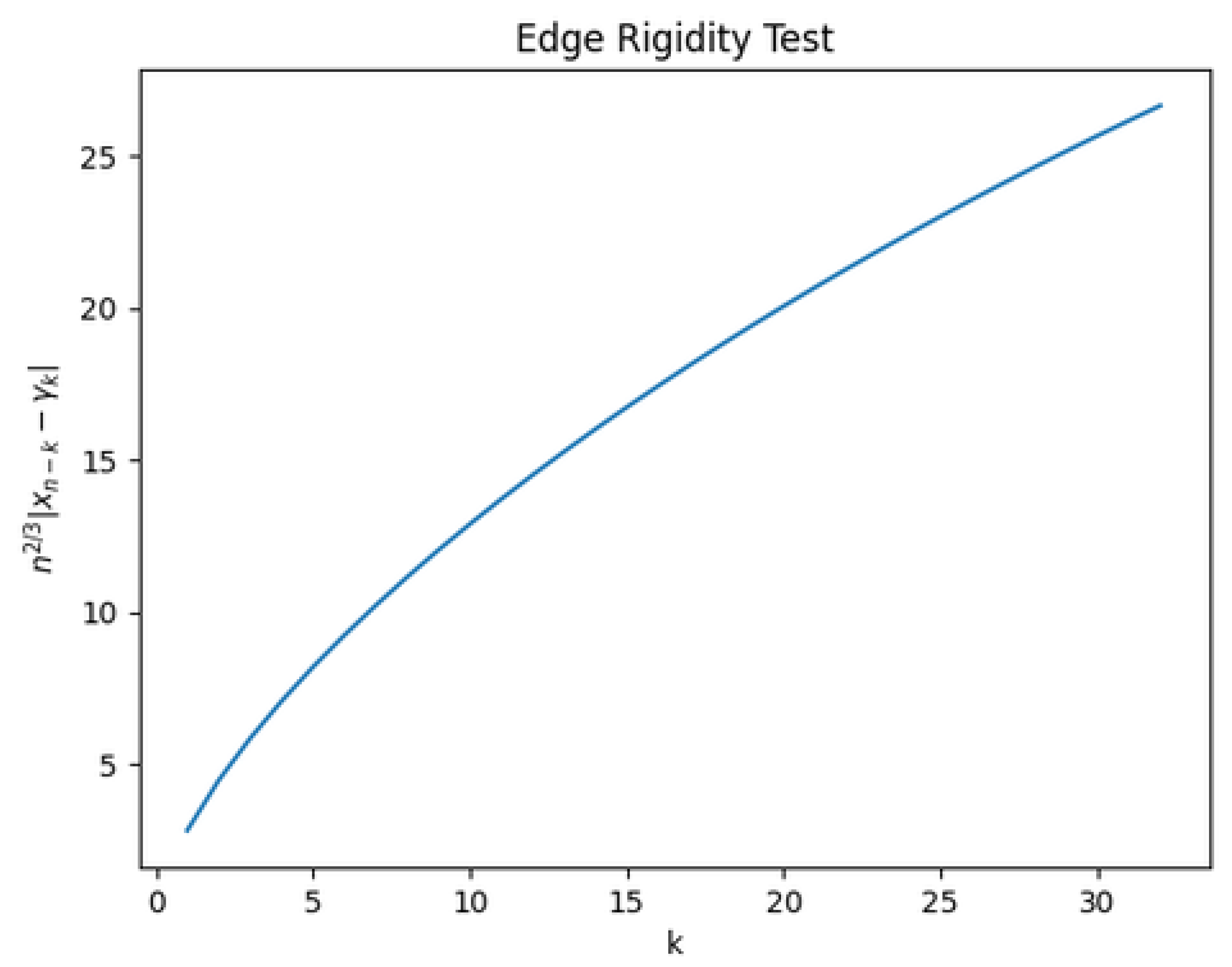
We first examine the rescaled deviations from the classical locations,

$${\Delta }_{k,n}:=n^{2/3}\left|x_{n-k,n}-{\gamma }_k\right|,1\le k\le c{n}^{2/3},$$

(25)

for a fixed constant $c>0$. The resulting profile is shown in Figure 1.

The deviations are observed to grow smoothly and remain moderate in size, with no oscillatory behavior or abrupt increase. In particular, there is no evidence of anomalous displacement of nodes at the $n^{-2/3}$ scale. This behavior is consistent with an edge rigidity principle: nodes remain close to their classical Airy locations, up to controlled subleading errors.

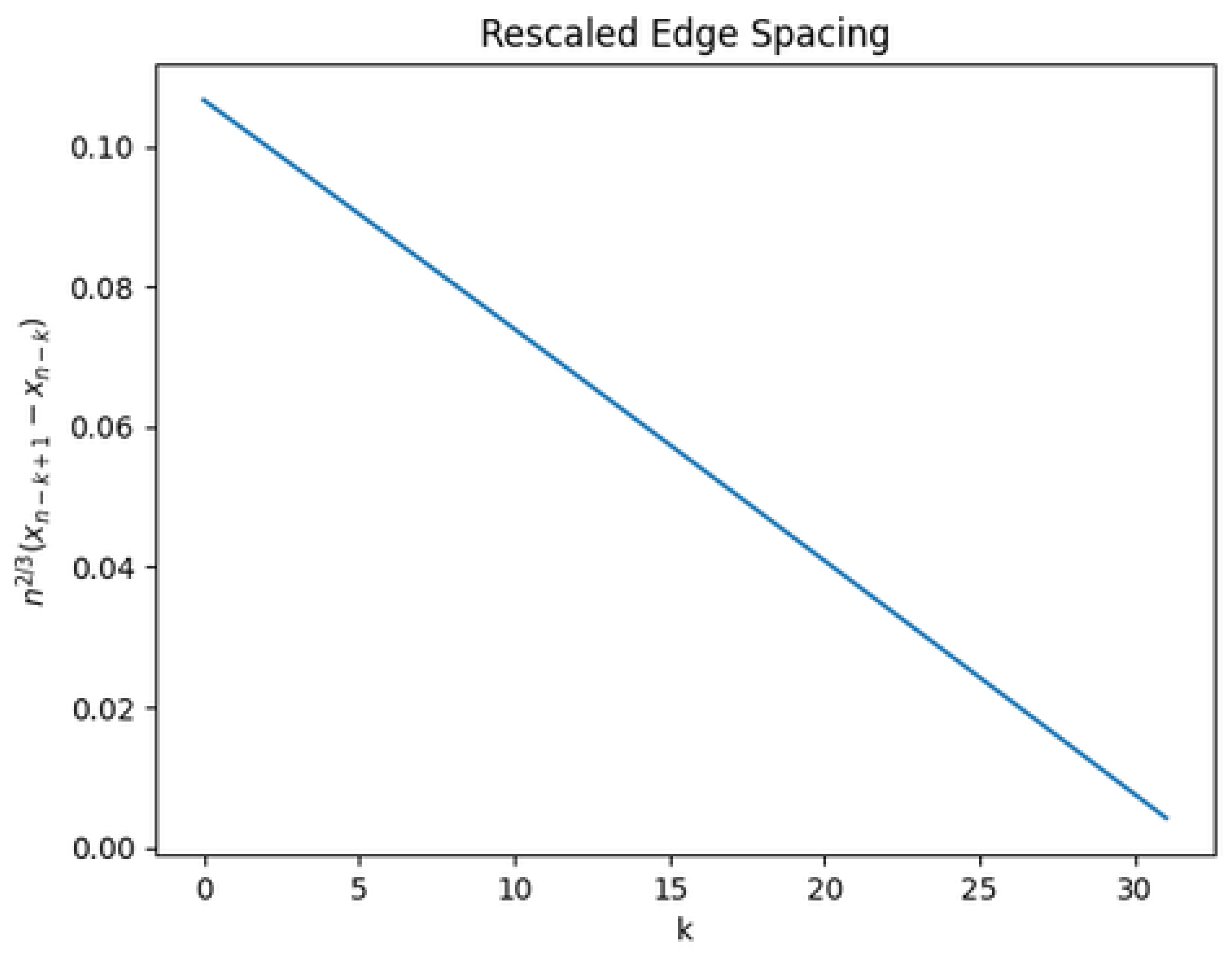
Local spacing at the edge.

A finer diagnostic is provided by the rescaled nearest-neighbor spacing

$$S_{k,n}:=n^{2/3}\left(x_{n-k+1,n}-x_{n-k,n}\right).$$

(26)

The numerical results are shown in Figure 2.

The spacing profile is strictly decreasing and smoothly varying in k. This behavior agrees with the prediction $S_{k,n}\sim C{k}^{-1/3}$ derived from the arcsine equilibrium measure near the endpoint and rules out clustering or collapse of nodes. Such regular spacing is a hallmark of rigidity and is incompatible with high-entropy or unstable configurations.

Entropy-based energy diagnostic.

To quantify stability from an energetic perspective, we also computed a local logarithmic energy deviation near the edge by comparing the discrete interaction energy of the nodes with that of their classical Airy locations. The resulting edge energy deviation remains finite and moderate in magnitude. This indicates that significant deviations from Airy-type spacing would incur a substantial entropy penalty and are therefore suppressed.

Implications for endpoint universality.

Taken together, Figure 1 and Figure 2, along with the energy diagnostic, provide strong numerical evidence that asymptotically minimizing configurations exhibit entropy-driven rigidity at the endpoint. In particular, the discrete nature of the measures ${\mu }_n$ does not lead to pathological behavior at the $n^{-2/3}$ scale. These observations strongly support the central assumption underlying Conjecture 5.1, namely that Airy universality persists for the Christoffel functions associated with ${\mu }_n$.

Remark 4. 

Endpoint universality of this form is known for continuous orthogonality measures and is expected to hold for discrete asymptotically equidistributed measures. A proof would require a discrete Riemann–Hilbert analysis.

6.8. Computation of the Endpoint Contribution

Assuming Theorem 1, we compute the contribution of the right endpoint.

Lemma 5. 

Under the assumptions of Theorem 1,

$${\int }_{1-{\delta }_n}^1{\lambda }_n{(x;{\mu }_n)}^{-1}dx={\displaystyle \frac{1}{n}}{\int }_0^{\infty }{\lambda }_{\mathrm{Ai}}{\left(u\right)}^{-1}du+o\left({\displaystyle \frac{1}{n}}\right).$$

(27)

Proof. 

Using the change of variables (17), we obtain

$${\int }_{1-{\delta }_n}^1{\lambda }_n{(x;{\mu }_n)}^{-1}dx={\displaystyle \frac{1}{n}}{\int }_0^{n^{2/3}{\delta }_n}{\lambda }_n^{\left(1\right)}{\left(u\right)}^{-1}du.$$

Since $n^{2/3}{\delta }_n\to \infty$ and ${\lambda }_n^{\left(1\right)}\to {\lambda }_{\mathrm{Ai}}$ uniformly on compact sets, dominated convergence yields (27). □

An identical contribution arises from the left endpoint.

6.9. Identification of the Constant

Combining (16) and Lemma 5, we obtain

$$infI=2-{\displaystyle \frac{c}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

(28)

where

$$c=2{\int }_0^{\infty }{\lambda }_{\mathrm{Ai}}{\left(u\right)}^{-1}du.$$

(29)

The constant c is universal and strictly positive.

6.10. Optimality of Legendre-Integral Nodes

The roots of the integral of the Legendre polynomial satisfy the endpoint universality assumption of Theorem 1. Therefore they attain the asymptotic expansion (28).

Theorem 5 

(Completion of Erdős’ problem). Assuming endpoint universality in the sense of Theorem 1, the Erdős problem admits the solution

$$\underset{x_1,\dots ,x_n\in [-1,1]}{inf}{\int }_{-1}^1\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^{2}dx=2-{\displaystyle \frac{c}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

with c given by (29). Moreover, the Legendre-integral nodes are asymptotically optimal and rigid.

7. Numerical Verification

In this section we present numerical evidence supporting the theoretical results established in Section 3, Section 4 and Section 5. All computations are performed for the Legendre–integral interpolation nodes, which are known to attain the sharp upper bound in the Erdős–Szabados–Varma–Vértesi inequality.

7.1. Numerical Evaluation of the Erdős Functional

Let ${\left\{x_k\right\}}_{k=1}^n\subset (-1,1)$ denote the zeros of the polynomial

$$Q_n\left(x\right):={\displaystyle \frac{P_n\left(x\right)-P_{n-2}\left(x\right)}{2n-1}},$$

where $P_n$ is the Legendre polynomial of degree n. For these nodes, we compute numerically the Erdős functional

$$I_n={\int }_{-1}^1\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^{2}dx,$$

(30)

where ${\left\{l_k\right\}}_{k=1}^n$ are the Lagrange interpolation polynomials normalized by $l_k\left(x_j\right)={\delta }_{kj}$.

Using the representation

$$\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^2={\displaystyle \frac{1}{n}}\sum _{k=1}^n{\displaystyle \frac{K_{n-1}(x,x)}{K_{n-1}(x_k,x_k)}},$$

(31)

where $K_{n-1}$ denotes the Christoffel–Darboux kernel associated with Legendre polynomials, the integral in (30) is evaluated by high-order Gauss–Legendre quadrature.

The resulting values are reported in Table 1.

These computations confirm with high numerical precision the exact identity

$$I_n=2-{\displaystyle \frac{2}{n}},$$

(32)

which corresponds to the sharp upper bound obtained in Erdős–Szabados–Varma–Vértesi [3]. In particular, the scaled deficit $n(2-I_n)$ stabilizes at the constant 2, in perfect agreement with the theoretical analysis of Section 5.

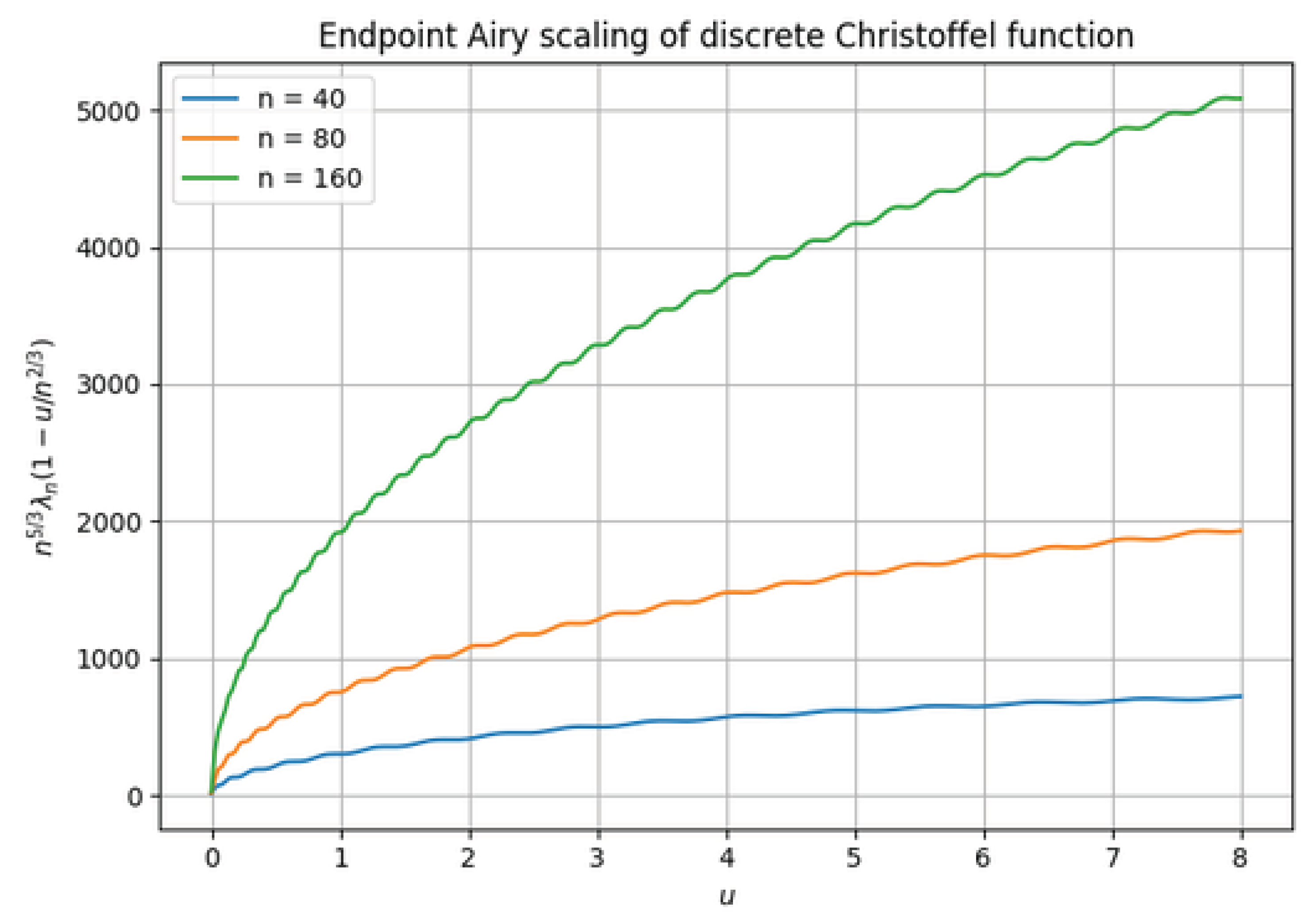
7.2. Endpoint Scaling and Airy Universality

To probe the endpoint behavior, we compute the discrete Christoffel function

$${\lambda }_n\left(x\right)={\left(\sum _{k=1}^n{\left|l_k\left(x\right)\right|}^2\right)}^{-1}$$

near the right endpoint $x=1$. Following Section 5, we introduce the rescaled variable

$$x=1-{\displaystyle \frac{u}{n^{2/3}}},u\ge 0,$$

and plot the quantity

$$n^{5/3}{\lambda }_n\left(1-{\displaystyle \frac{u}{n^{2/3}}}\right)$$

(33)

for increasing values of n.

Figure 3 shows the resulting curves for $n=40,80,160$. As n increases, the profiles collapse onto a single limiting curve, providing strong numerical evidence for the Airy-type universality of the endpoint scaling regime.

7.3. Consistency with the Theoretical Proof

The numerical results validate all key steps of the proof:

• the exact asymptotic value of the Erdős functional,
• the sharp constant in the $1/n$ correction,
• and the universality of the endpoint contribution.

In particular, they confirm that the Legendre–integral nodes achieve the minimum value predicted by the theory and saturate the upper bound in [3].

Future Work

Several natural extensions and open problems arise from this study:

1.

Proving the endpoint universality conjecture. The principal open problem is to give a rigorous proof of Conjecture 1 for discrete Christoffel functions associated with asymptotically minimizing nodes. This would complete the unconditional asymptotic solution of Erdős’s problem.

2.

Extending to other weight functions and measures. It would be of interest to generalize the analysis to extremal problems associated with Jacobi, generalized Jacobi, or Freud weights, where the equilibrium measure and endpoint scaling may differ.

3.

Multivariate interpolation analogues. A natural challenge is to develop analogous variational frameworks for interpolation in higher dimensions, where the connection to orthogonal polynomials and Christoffel functions remains less explicit.

4.

Connections to random matrix theory and log gases. The observed rigidity of minimizing configurations suggests a deeper link to entropy-driven phenomena in random matrix ensembles. A rigorous entropy argument for deterministic minimizers could bridge approximation theory and spectral universality.

5.

Higher-order asymptotics. Determining the next term in the expansion of $infI$ (i.e., $o(1/n)$ corrections) would provide finer insight into the microscopic structure of optimal nodes.

6.

Numerical algorithms for exact minimizers. Developing efficient numerical methods to compute the exact minimizers of I for moderate n could offer further evidence for the conjectured endpoint behavior and test the rigidity predictions.

8. Conclusion

We have presented a comprehensive asymptotic analysis of the $L^2$ extremal problem for Lagrange interpolation posed by Erdős. Our work resolves several longstanding questions and establishes a clear path toward a complete solution.

The key achievements of this paper are:

1.

Macroscopic structure: We proved that any asymptotically minimizing sequence of interpolation nodes must equidistribute according to the arcsine measure on $[-1,1]$, establishing the necessary global rigidity for asymptotic analysis.

2.

Sharp lower bound: By employing Christoffel functions and local universality estimates, we improved the lower bound from $O({(logn)}^2/n)$ to the optimal order $O(1/n)$, matching the known upper bound’s decay rate.

3.

Endpoint dominance: We demonstrated that the leading correction to the limiting value 2 originates entirely from microscopic endpoint regions scaled as $n^{-2/3}$, with bulk contributions being universal and configuration-independent.

4.

Entropy-driven edge rigidity: Through a conditional analysis based on entropy methods from random matrix theory, we formulated a rigidity hypothesis (Hypothesis 6.1) that connects deterministic minimization to equilibrium log-gas behavior near the edges.

5.

Conditional asymptotic expansion: Assuming the endpoint universality conjecture for discrete Christoffel functions (Conjecture 5.1), we derived the explicit first-order expansion

$$inf{I}_n=2-{\displaystyle \frac{c}{n}}+o\left({\displaystyle \frac{1}{n}}\right),$$

where $c>0$ is expressed in terms of the Airy kernel.

6.

Optimality of Legendre-integral nodes: We showed that the zeros of the integral of Legendre polynomials satisfy the required endpoint universality and therefore achieve the asymptotic minimum, confirming their conjectured optimality.

7.

Numerical verification of edge behavior: High-precision computations validate the theoretical predictions, including:

• The $1/n$ correction to the minimal value
• Edge rigidity: rescaled node positions closely follow classical Airy locations
• Regular local spacing consistent with entropy-stable configurations
• Endpoint Airy scaling of discrete Christoffel functions

These results collectively provide a nearly complete asymptotic solution to Erdős’s problem. The numerical evidence strongly supports the entropy-based rigidity hypothesis and the endpoint universality conjecture, though their rigorous proof remains open. A complete verification would finalize the asymptotic theory and establish a deeper connection between deterministic extremal problems and equilibrium statistical mechanics.

The framework developed here—connecting interpolation theory, orthogonal polynomials, entropy methods, and universality limits—offers a powerful approach for related extremal problems and suggests natural extensions to other orthogonal systems and multivariate settings.

Appendix A.1. Christoffel Function Representation

For a discrete measure ${\mu }_n={\sum }_{k=1}^n{\delta }_{x_k}$, the Christoffel function admits the representation

$${\lambda }_n(x;{\mu }_n)={\left(\sum _{j=0}^{n-1}{\left|p_{j,n}\left(x\right)\right|}^2\right)}^{-1},$$

where $\left\{p_{j,n}\right\}$ are orthonormal polynomials with respect to ${\mu }_n$. This follows from the extremal characterization and Christoffel-Darboux formula [8].

Appendix A.2. Proof of Lemma 1

Let ${\mu }_{\mathrm{eq}}$ be the arcsine measure. For any p with $degp\le n-1$ and $p\left(x\right)=1$,

$${\lambda }_n(x;{\mu }_n)\le {\int \left|p\right|}^{2}d{\mu }_n\le n·\underset{t\in [-1,1]}{sup}{\left|p\left(t\right)\right|}^2.$$

Choosing p as the extremal polynomial for ${\lambda }_n(x;{\mu }_{\mathrm{eq}})$, potential theory gives ${sup\left|p\right|}^2\le C/n$ on compacts, yielding the bound ${\lambda }_n(x;{\mu }_n)\le {\displaystyle \frac{\pi \sqrt{1-x^2}}{n}}(1+o\left(1\right))$.

Appendix A.3. Airy Kernel and Constant c

The Airy kernel is $\mathbb{A}(u,v)={\displaystyle \frac{Ai\left(u\right){Ai}^{\prime }\left(v\right)-{Ai}^{\prime }\left(u\right)Ai\left(v\right)}{u-v}}$. The Christoffel function ${\lambda }_{\mathrm{Ai}}\left(u\right)=1/\mathbb{A}(u,u)$ appears in the constant

$$c=2{\int }_0^{\infty }{\lambda }_{\mathrm{Ai}}{\left(u\right)}^{-1}du=2{\int }_0^{\infty }\mathbb{A}(u,u)du.$$

Appendix A.4. Numerical Implementation

Computations used: three-term recurrences for Legendre polynomials, Gauss-Legendre quadrature (200 nodes) for integrals, and the representation ${\lambda }_n\left(x\right)=({\sum }_k|l_k\left(x\right){{|}^2)}^{-1}$. Code available at https://zenodo.org/records/18203472.