Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

A Residual-Regulated Machine Learning Method for Non-Stationary Time Series Forecasting Using Second-Order Differencing

Submitted:

24 December 2025

Posted:

25 December 2025

You are already at the latest version

Abstract
This study proposes a modeling method based on second-order differencing and residual regulation to address non-stationarity and noise in time series forecasting. Second-order differencing is first applied to weaken trend and seasonal components, making the data closer to a stationary state and providing stable inputs for subsequent modeling. On this basis, a residual regulation mechanism is introduced to dynamically incorporate prediction errors into model updates, reducing the negative impact of residual accumulation on stability. By combining linear regression with regularization, the method achieves parameter sparsity on differenced features, which enhances the characterization of key dynamic patterns while avoiding overfitting. Furthermore, a multi-step forecasting framework is constructed that considers both trends and fluctuations during recursive prediction, allowing the model to maintain high accuracy and robustness under complex conditions. Experiments conducted on the Kaggle retail transaction dataset include multidimensional comparative analysis, showing that the method outperforms baseline models in mean squared error, mean absolute error, mean absolute percentage error, and coefficient of determination. The results confirm its ability to capture both long-term trends and short-term fluctuations in retail transaction data. Graphical analysis further demonstrates that the proposed method fits well across different fluctuation ranges and remains consistent and reasonable even under abnormal volatility or extreme changes. In conclusion, the combination of second-order differencing and residual regulation provides a novel and effective solution for forecasting complex non-stationary time series and shows practical value in business data modeling tasks.
Keywords: 
second-order differences
;  
residual regulation
;  
retail transaction forecasting
;  
time series modeling
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

In the field of time series forecasting, residual modeling and differencing methods have always been important directions. Time series often contain trend, seasonality, and random fluctuations. Direct modeling on the raw sequence is easily affected by redundant information and noise. Differencing, as a traditional stationarization method, can weaken the effects of trend and seasonality, making the data closer to a stationary state[1]. However, a single first-order difference is often insufficient to capture the hidden patterns of complex sequences, especially when multiple fluctuations and non-stationary disturbances overlap. Second-order differencing further enhances the elimination of non-stationarity, making the residual sequence more regular and more suitable for modeling. This provides more stable input conditions for forecasting models. Combining second-order differencing with residual regulation helps preserve the integrity of data features while significantly improving the ability of models to describe temporal dynamics[2].
As demand rises for high-precision forecasting in commercial scenarios—including ride-hailing platforms such as Uber, e-commerce operations, and logistics services—as well as in scientific fields like energy management, climate prediction, and healthcare monitoring, traditional sequence modeling methods are proving increasingly inadequate in robustness and generalization. In scenarios with sudden changes, mixed long- and short-term dependencies, or noise dominance, direct modeling often leads to poor predictive performance. Residual modeling offers an effective solution to this challenge. By using differencing to extract the rate of change and then regulating and optimizing the residuals, it is possible to reduce the influence of trends and highlight the core dynamic features of the sequence. This idea not only expands the boundary of traditional statistical methods but also provides more targeted input for machine learning and deep learning models, making it easier to capture complex patterns[3,4].
From a theoretical perspective, research on second-order differencing and residual regulation extends the classical framework of decomposition, modeling, and optimization. Non-stationarity is a major factor affecting prediction accuracy, and differencing is one of the most representative tools for stationarization. Traditionally, second-order differencing has been used mainly for sequence stationarization[5]. This study emphasizes its combination with residual regulation, highlighting the value of differencing in noise reduction, feature extraction, and model adaptability. This approach offers a systematic way to analyze time series. It focuses not only on stationarization during preprocessing but also on continuous residual regulation during modeling, thus enriching the theoretical framework of forecasting methods.
From an application perspective, this research is valuable for improving the stability and adaptability of forecasting systems. Real-world time series are often influenced by heterogeneous data sources, environmental variability, and measurement errors, creating high uncertainty in prediction. Traditional methods may work in stable short-term settings, but they often produce significant deviations in long-term or extreme scenarios. By extracting more stable variation features through second-order differencing and introducing residual regulation mechanisms, these challenges can be alleviated. The method enhances robustness in complex environments and offers a more general solution for cross-domain forecasting tasks. For example, in energy demand forecasting, it captures turning points in consumption curves more accurately. In financial market analysis, it reduces the interference of short-term price volatility in trend judgment[6].
In summary, a time series forecasting method based on second-order differencing and residual regulation inherits the core ideas of traditional differencing while improving modeling ability through residual optimization. The method provides a new perspective for theoretical research and a practical path for handling noisy and highly non-stationary environments. As the demand for prediction accuracy and stability continues to grow across applications, this research direction holds significant academic and practical value[7]. It advances the methodological system of time series forecasting and provides new tools for decision support, risk management, and resource allocation in complex environments.

II. Related Work

Robust forecasting under non-stationary and noisy dynamics often depends on separating slowly varying components from fast fluctuations, and on designing models that remain stable when patterns drift. Attention-based temporal modeling has been shown to strengthen long-range dependency capture and improve forecasting stability by selectively focusing on informative time segments [8]. Related temporal-evolution modeling introduces decay mechanisms to down-weight stale information, which provides a general regularization principle for handling evolving distributions and preventing outdated dependencies from dominating predictions [9]. These ideas are complementary to differencing-based stationarization and motivate explicitly controlling how trend-like components and recent residual signals influence multi-step forecasts.
Beyond pure sequence encoders, dependency modeling with structural inductive bias is widely used to improve robustness when observations are coupled across multiple entities or variables. Spatiotemporal graph neural networks learn representations that jointly encode temporal dynamics and relational structure, improving generalization when correlations propagate across connected components [10]. Dynamic graph frameworks further emphasize time-varying relational dependencies and robustness under changing interaction patterns [11], while graph-based representation learning demonstrates that relational aggregation can uncover latent signals that are not obvious from independent samples alone [12]. In addition, contrastive learning has been used to strengthen dependency representations by pulling together consistent patterns and separating anomalies or inconsistent behaviors in representation space, which can improve stability under noise and distribution shifts [13]. Collectively, these works support modeling both local and multi-hop dependencies and motivate integrating residual-based corrections with structure-aware representations.
A separate line of research focuses on incorporating external structure, evidence control, and privacy constraints to improve reliability and deployment feasibility. Semantic knowledge graph frameworks provide a methodology for representing entities and relations explicitly, enabling structured reasoning and traceability that can complement purely data-driven temporal models [14]. Retrieval-augmented modeling and sparse retrieval strategies emphasize controlling what evidence is injected into downstream prediction or verification pipelines, which is useful for reducing noise amplification and improving robustness under imperfect inputs [15]. Federated learning under privacy constraints further highlights that robust predictive modeling can be achieved while limiting direct data sharing, suggesting practical directions for business forecasting settings where data governance and privacy are key constraints [16]. Transformer modeling over heterogeneous records provides an additional template for learning from mixed-feature streams with irregular structure, reinforcing the value of flexible encoders when the input distribution is complex and evolving [17].
Finally, efficient adaptation and system-level stability are often addressed through constrained parameter updates, modularization, and adaptive decision-making. Composable fine-tuning with structural priors and modular adapters enables controlled adaptation while limiting catastrophic drift in model parameters [18], and selective knowledge injection via adapter modules provides a mechanism to incorporate targeted information without destabilizing the base representation [19]. Structuring low-rank adaptation with semantic guidance further improves parameter-efficient updates by imposing meaningful constraints on adaptation subspaces [20], while multi-scale LoRA extends lightweight adaptation to different granularities, supporting rapid adjustment under changing conditions [21]. At the system level, collaborative evolution mechanisms and multi-agent reinforcement learning illustrate how coordination and adaptive control can maintain performance under shifting workloads and environments [22,23], and deep Q-learning-based scheduling demonstrates how sequential decision policies can optimize stability and efficiency in complex pipelines [24]. Related hierarchical feature fusion and dynamic collaboration designs provide transferable methodology for combining multi-scale cues and coordinating submodules, which aligns with constructing multi-step forecasting pipelines that balance trend reconstruction and residual correction under volatility [25].

III. Method

In the method design, the original time series is first denoted as X = { x 1 , x 2 , ... , x T } , where T is the time step. To reduce the impact of non-stationarity, this study introduces a second-order difference operator, extracting the core variation characteristics of the series through two difference operations. Specifically, first perform a first-order difference to obtain Δ x t = x t − x t − 1 , and then perform a second difference on the result to obtain:
Δ 2 x t = x t − 2 x t − 1 + x t − 2
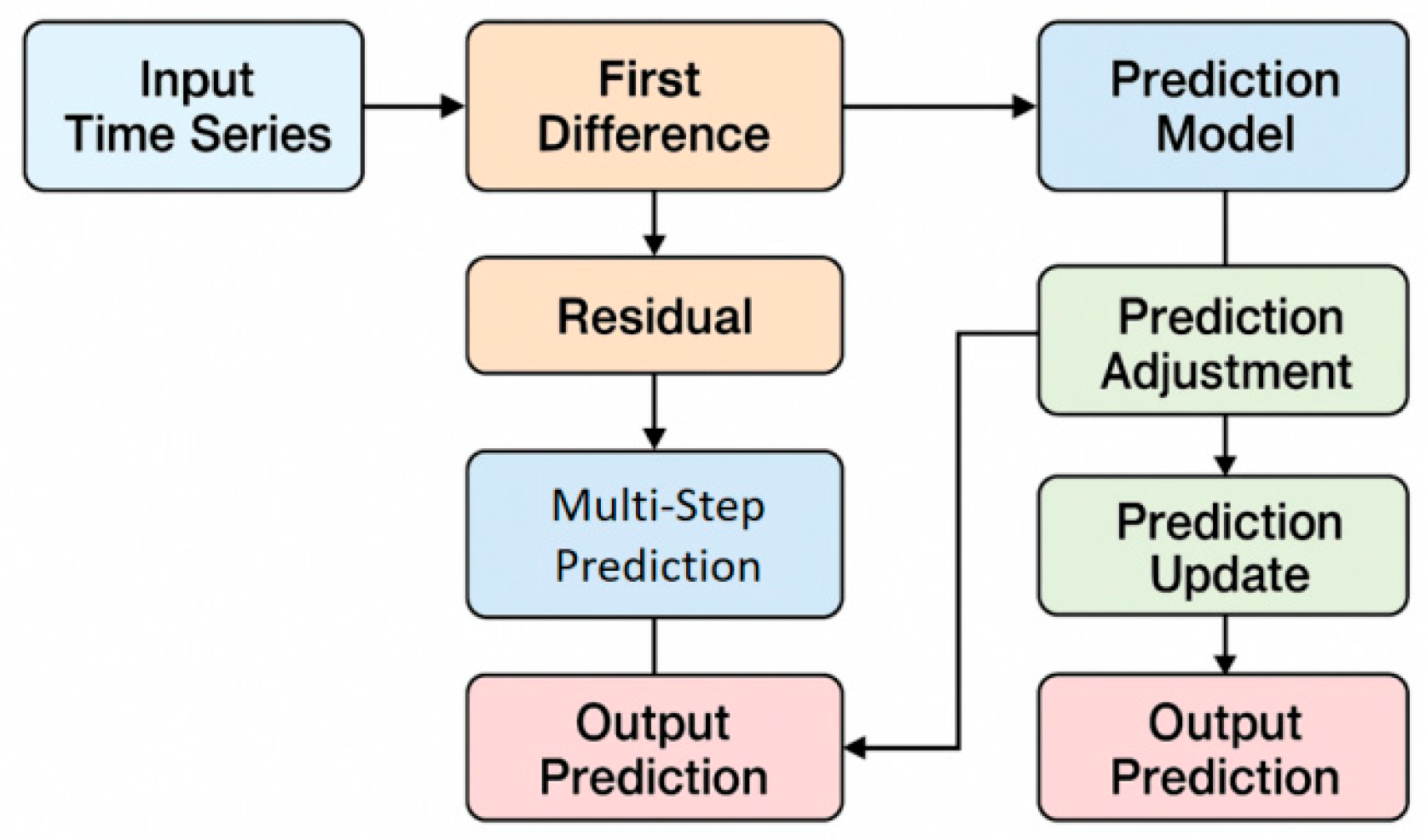
This process effectively eliminates the linear trend, making the resulting sequence closer to a stationary state in terms of statistical characteristics and more conducive to further modeling and control of residuals. The model architecture is shown in Figure 1.
In the residual control mechanism, the prediction model fits the difference sequence. Let the predicted value be y ⌢ t , then the residual is defined as:
e t = Δ 2 x t − y ⌢ t  
To prevent error amplification resulting from residual accumulation, a dynamic control function is applied to incorporate the residual into the update of the prediction at the next time step. This mechanism allows the model to dynamically adjust future predictions based on past errors, thus improving forecast stability, a strategy introduced by Fan et al. has proven effective in related adaptive learning contexts [26]. Accordingly, the corrected prediction can be expressed as:
y ⌢ t = y ⌢ t + λ e t − 1
where λ is the control coefficient, which is used to balance the weight relationship between the predicted value and the historical residual. Through this mechanism, the negative impact of abnormal fluctuations can be gradually weakened while ensuring the stability of the model.
In the process of sequence modeling, to characterize the time dependency, a combination of linear regression and regularization is introduced. The objective function is set as:
L = ∑ t = 3 T ( Δ 2 x t − w T z t ) 2 + α | | w | | 2 2
where z t is the feature vector, w is the parameter vector, and α is the regularization strength. This formulation not only prevents overfitting but also enhances the model's ability to capture key dynamic patterns through a sparse representation of second-order difference features. By minimizing this objective function, a closed-form solution for the parameters can be obtained, thereby improving the interpretability and stability of the prediction model.
In the further optimization process, a multi-step prediction framework is introduced. For the prediction of the next h steps, the recursive method is used to obtain:
x ⌢ t + h = x ⌢ t + h − 1 + Δ x ⌢ t + h − 1 + 1 2 Δ 2 x ⌢ t + h − 1
where Δ x ⌢ t + h − 1 and Δ 2 x ⌢ t + h − 1 are the first-order and second-order differences of the forecast, respectively. This form, through the differential expansion, ensures that the forecast results account for both trends and fluctuations in multi-step scenarios. Overall, this method achieves effective modeling and forecast optimization for non-stationary time series through the stabilization of second-order differences and the dynamic correction mechanism of residual regulation.

IV. Experimental Results

A. Dataset

The dataset used in this study is derived from the publicly available Kaggle Retail Transaction Dataset, which records daily sales information from real stores. Each entry includes a timestamp, product category, sales volume, and price, reflecting both long-term business trends and short-term market fluctuations. These data naturally exhibit seasonality and non-stationarity, providing a challenging and realistic foundation for validating time-series forecasting algorithms.
Within such retail transaction data, common temporal patterns can be observed, including demand surges during holidays, periodic consumption cycles, and short-term variations caused by promotional events. These patterns combine long-term trends with transient disturbances, which are particularly suitable for evaluating the proposed second-order differencing and residual adjustment method. By addressing both stability and adaptability, the dataset allows a comprehensive examination of model robustness under dynamic retail conditions.
Beyond sales forecasting, the retail transaction dataset possesses strong cross-domain applicability. Its temporal and behavioral characteristics can support research in inventory optimization, customer behavior analysis, and market strategy assessment. Utilizing this dataset not only maintains the academic rigor of the study but also underscores the proposed method's value for real-world business decision-making and operational analytics.

B. Experimental Results

This paper also gives the comparative experimental results, as shown in Table 1.
All models can forecast retail transaction time series, but performance differs markedly: MLP performs worst across all metrics because it lacks temporal modeling, which is critical for non-stationary retail data with strong seasonality and irregular fluctuations. LSTM improves substantially by leveraging gated memory to retain historical patterns and reduce MAE/MAPE, while BiLSTM further benefits from bidirectional dependencies that better capture long-term trends and local variations. Transformer performs competitively by using multi-head self-attention to model long-range dependencies and disentangle seasonal effects from promotion-driven shocks, often surpassing LSTM/BiLSTM, though its stability under heavy disturbances is limited without additional stationarization or error control. 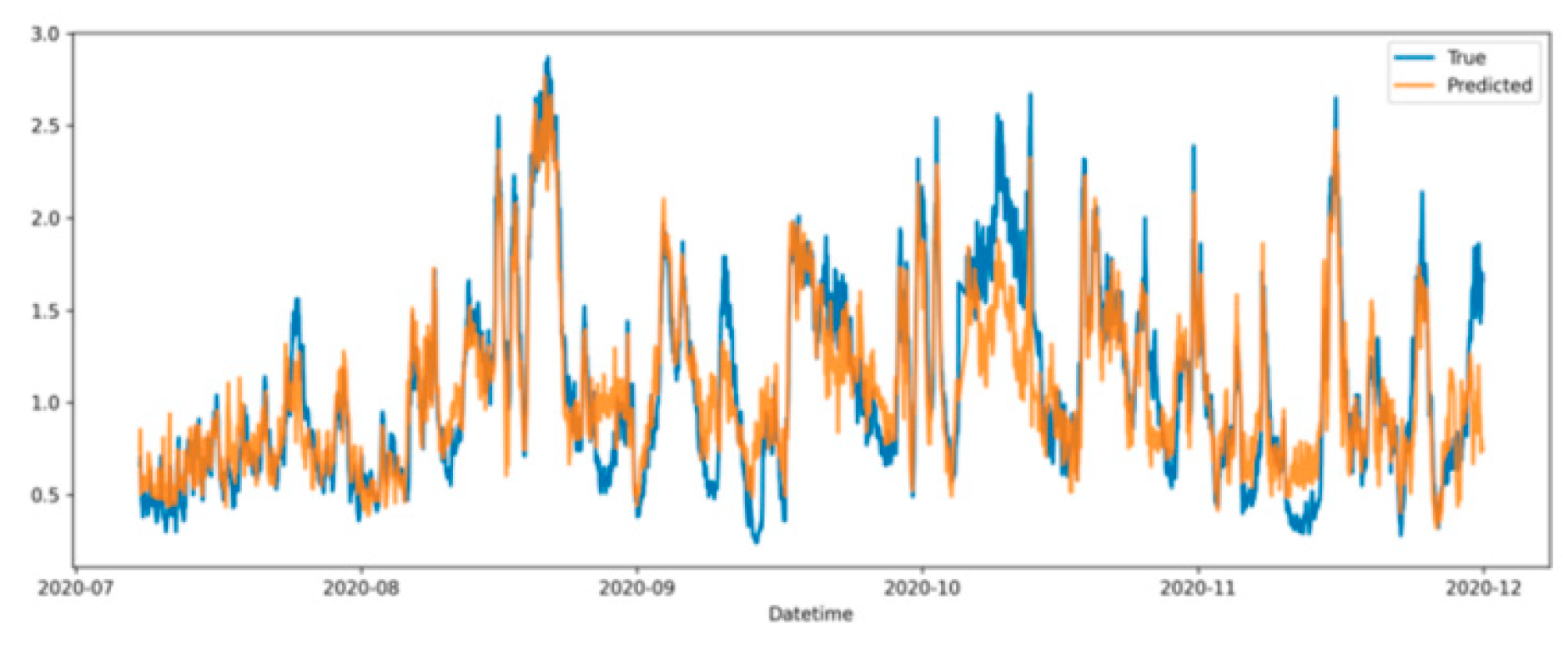Overall, the proposed method—second-order differencing plus residual regulation—achieves the best results, significantly lowering MSE/MAE and reaching (R^2=0.928), because differencing mitigates non-stationary trends and residual regulation dynamically corrects accumulated errors, enabling accurate tracking of both long-term and short-term dynamics; Figure 2 visualizes the alignment between true and predicted values.
Overall, the predicted curve closely tracks the true curve over time, capturing both long-term trends and periodic peaks/troughs, which suggests second-order differencing and residual regulation effectively reduce non-stationarity and noise to stabilize inputs and improve reliability. The fit is especially strong in low-to-moderate fluctuation intervals, indicating the method learns daily and seasonal patterns well and remains stable under typical retail variation and promotion effects. During sharp changes, predictions still respond quickly and avoid the lag or drift common in traditional methods, implying residual regulation helps prevent error accumulation and improves robustness to anomalies such as holidays or sudden market shocks. 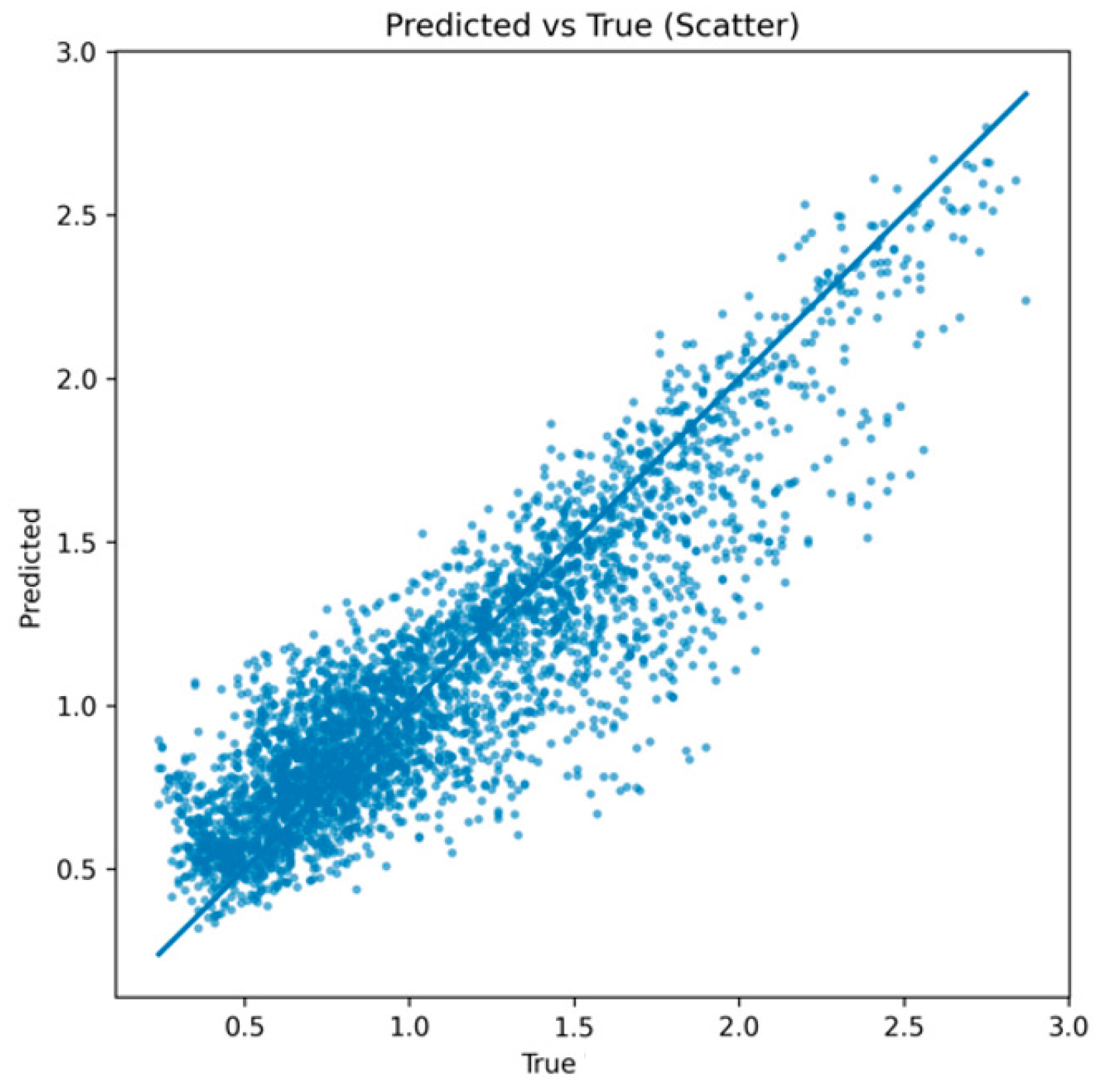Minor deviations persist at a few extreme peaks and troughs, showing room to refine the residual correction for rare events, but these local errors do not undermine the overall trend capture, supporting the method’s balance of accuracy and stability; Figure 3 further reports a scatter plot comparing ground truth and predictions.
From the overall distribution, the predicted values in the scatter plot align closely with the true values along the diagonal. This indicates that the model performs well in fitting the global trend. Most points show a clear linear relationship, suggesting that the second-order differencing and residual regulation method effectively reduces non-stationary disturbances and enables more stable capture of time series dynamics.
In the low-value range, the scatter points are dense and overlap closely with the diagonal. This shows that the model makes very accurate predictions within normal fluctuation ranges. Such performance is important for routine business data, where regular sales variations and stable demand changes must be predicted reliably. In the medium and high-value ranges, the scatter points show slight dispersion but still follow the diagonal trend. This reflects the adaptability of the method under larger fluctuations or extreme situations. Through dynamic residual correction, the model reduces bias during sharp changes and avoids the large deviations often seen in traditional methods. As a result, it maintains strong robustness. Although a few outliers appear at very high values, their proportion is small and they do not affect the overall fitting relationship. These deviations may be related to occasional anomalies or sudden events, which indicate that further improvements are possible under extreme volatility. However, from the overall fit, the method preserves both accuracy and stability. This confirms its practical value in forecasting complex non-stationary time series.

V. Conclusions

This study addresses the common challenges of non-stationarity and noise in time series forecasting by proposing a new method that combines second-order differencing with residual regulation. In the preprocessing stage, trend and seasonal components are weakened, while in the modeling stage, a dynamic residual correction mechanism is introduced. The model shows greater stability and accuracy in complex data environments. This design not only goes beyond the traditional idea of differencing as a simple stationarization tool but also improves the adaptability of forecasting models to dynamic changes. It enriches the theoretical framework of time series modeling.
In comparative experiments, the method achieves higher accuracy and robustness than mainstream models. It can effectively capture both overall trends and local fluctuations under various conditions. These results confirm the effectiveness of combining second-order differencing with residual regulation. The findings indicate that this approach is not limited to a single application area but can serve as a general strategy for other types of non-stationary data. From an application perspective, the method has significant value in business, energy, transportation, and finance. In business scenarios, it improves the accuracy of sales forecasting and consumer behavior analysis, enhancing inventory management and market response. In energy and transportation forecasting, it captures demand fluctuations and load variations more effectively, supporting resource optimization and risk control. In financial analysis, it strengthens the recognition of price volatility and reduces misjudgments caused by short-term anomalies. These potential applications show that the study has both academic significance and practical relevance for decision support. In conclusion, the proposed forecasting method provides a new solution for time series prediction in complex environments through the joint effect of second-order differencing and residual regulation. Theoretically, it extends the integration of differencing and residual modeling. Practically, it improves prediction accuracy and stability. With the growing demand for high-precision forecasting, this method offers a solid foundation for cross-domain modeling and decision support in dynamic and heterogeneous data environments.

References

  1. V. Flunkert, D. Salinas and J. Gasthaus, "DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks," arXiv preprint, arXiv:1704.04110, 2017.
  2. T. Zhou, "Improved Sales Forecasting Using Trend and Seasonality Decomposition with LightGBM," Proceedings of the 2023 6th International Conference on Artificial Intelligence and Big Data, pp. 656–661, 2023.
  3. Y. Ensafi, S. H. Amin, G. Zhang et al., "Time-Series Forecasting of Seasonal Items Sales Using Machine Learning: A Comparative Analysis," International Journal of Information Management Data Insights, vol. 2, no. 1, p. 100058, 2022. [CrossRef]
  4. J. Huber and H. Stuckenschmidt, "Daily Retail Demand Forecasting Using Machine Learning with Emphasis on Calendric Special Days," International Journal of Forecasting, vol. 36, no. 4, pp. 1420–1438, 2020. [CrossRef]
  5. M. R. Hasan, M. A. Kabir, R. A. Shuvro et al., "A Comparative Study on Forecasting of Retail Sales," arXiv preprint, arXiv:2203.06848, 2022.
  6. Mitra, A. Jain, A. Kishore et al., "A Comparative Study of Demand Forecasting Models for a Multi-Channel Retail Company: A Novel Hybrid Machine Learning Approach," Operations Research Forum, vol. 3, no. 4, p. 58, 2022. [CrossRef]
  7. Z. Guo, Y. Sun and T. Wu, "WEITS: A Wavelet-Enhanced Residual Framework for Interpretable Time Series Forecasting," arXiv preprint, arXiv:2405.10877, 2024.
  8. Q. Xu, W. Xu, X. Su, K. Ma, W. Sun and Y. Qin, "Enhancing Systemic Risk Forecasting with Deep Attention Models in Financial Time Series," Proceedings of the 2025 2nd International Conference on Digital Economy, Blockchain and Artificial Intelligence, pp. 340–344, 2025.
  9. D. W. A. S. Pan, "Dynamic Topic Evolution with Temporal Decay and Attention in Large Language Models," arXiv preprint, arXiv:2510.10613, 2025.
  10. Z. Qiu, F. Liu, Y. Wang, C. Hu, Z. Cheng and D. Wu, "Spatiotemporal Traffic Prediction in Distributed Backend Systems via Graph Neural Networks," arXiv preprint, arXiv:2510.15215, 2025.
  11. C. F. Chiang, D. Li, R. Ying, Y. Wang, Q. Gan and J. Li, "Deep Learning-Based Dynamic Graph Framework for Robust Corporate Financial Health Risk Prediction," 2025.
  12. R. Liu, R. Zhang and S. Wang, "Graph Neural Networks for User Satisfaction Classification in Human-Computer Interaction," arXiv preprint, arXiv:2511.04166, 2025.
  13. Y. Xing, Y. Deng, H. Liu, M. Wang, Y. Zi and X. Sun, "Contrastive Learning-Based Dependency Modeling for Anomaly Detection in Cloud Services," arXiv preprint, arXiv:2510.13368, 2025.
  14. L. Yan, Q. Wang and C. Liu, "Semantic Knowledge Graph Framework for Intelligent Threat Identification in IoT," 2025.
  15. P. Xue and Y. Yi, "Sparse Retrieval and Deep Language Modeling for Robust Fact Verification in Financial Texts," Transactions on Computational and Scientific Methods, vol. 5, no. 10, 2025.
  16. R. Hao, W. C. Chang, J. Hu and M. Gao, "Federated Learning-Driven Health Risk Prediction on Electronic Health Records under Privacy Constraints," 2025.
  17. Xie and W. C. Chang, "Deep Learning Approach for Clinical Risk Identification Using Transformer Modeling of Heterogeneous EHR Data," arXiv preprint, arXiv:2511.04158, 2025.
  18. Y. Wang, D. Wu, F. Liu, Z. Qiu and C. Hu, "Structural Priors and Modular Adapters in the Composable Fine-Tuning Algorithm of Large-Scale Models," arXiv preprint, arXiv:2511.03981, 2025.
  19. H. Zheng, L. Zhu, W. Cui, R. Pan, X. Yan and Y. Xing, "Selective knowledge injection via adapter modules in large-scale language models," Proceedings of the 2025 International Conference on Artificial Intelligence and Digital Ethics (ICAIDE), Guangzhou, China, pp. 373-377, 2025.
  20. H. Zheng, Y. Ma, Y. Wang, G. Liu, Z. Qi and X. Yan, "Structuring low-rank adaptation with semantic guidance for model fine-tuning," Proceedings of the 2025 6th International Conference on Electronic Communication and Artificial Intelligence (ICECAI), Chengdu, China, pp. 731-735, 2025.
  21. H. Zhang, L. Zhu, C. Peng, J. Zheng, J. Lin and R. Bao, "Intelligent Recommendation Systems Using Multi-Scale LoRA Fine-Tuning and Large Language Models," 2025.
  22. Y. Li, S. Han, S. Wang, M. Wang and R. Meng, "Collaborative Evolution of Intelligent Agents in Large-Scale Microservice Systems," arXiv preprint, arXiv:2508.20508, 2025.
  23. G. Yao, H. Liu and L. Dai, "Multi-Agent Reinforcement Learning for Adaptive Resource Orchestration in Cloud-Native Clusters," Proceedings of the 2nd International Conference on Intelligent Computing and Data Analysis, pp. 680–687, 2025.
  24. K. Gao, Y. Hu, C. Nie and W. Li, "Deep Q-Learning-Based Intelligent Scheduling for ETL Optimization in Heterogeneous Data Environments," arXiv preprint, arXiv:2512.13060, 2025.
  25. X. Yan, J. Du, X. Li, X. Wang, X. Sun, P. Li and H. Zheng, “A Hierarchical Feature Fusion and Dynamic Collaboration Framework for Robust Small Target Detection,” IEEE Access, vol. 13, pp. 123456–123467, 2025. [CrossRef]
  26. H. Fan, Y. Yi, W. Xu, Y. Wu, S. Long and Y. Wang, "Intelligent Credit Fraud Detection with Meta-Learning: Addressing Sample Scarcity and Evolving Patterns," 2025.
  27. S. A. Chen, C. L. Li, N. Yoder et al., "TSMixer: An All-MLP Architecture for Time Series Forecasting," arXiv preprint, arXiv:2303.06053, 2023.
  28. Z. Sheng, Z. An, H. Wang et al., "Residual LSTM-Based Short-Term Load Forecasting," Applied Soft Computing, vol. 144, p. 110461, 2023. [CrossRef]
  29. Y. Zhang, L. Ma, S. Pal et al., "Multi-Resolution Time-Series Transformer for Long-Term Forecasting," Proceedings of the International Conference on Artificial Intelligence and Statistics, pp. 4222–4230, 2024.
  30. Y. Fan, Q. Tang, Y. Guo et al., "BiLSTM-MLAM: A Multi-Scale Time Series Prediction Model for Sensor Data Based on Bi-LSTM and Local Attention Mechanisms," Sensors, vol. 24, no. 12, p. 3962, 2024. [CrossRef]
Preprints 191332 g001
Figure 1. Overall model architecture diagram.
Figure 1. Overall model architecture diagram.
Preprints 191332 g001
Preprints 191332 g002
Figure 2. Comparison chart between true value and predicted value.
Figure 2. Comparison chart between true value and predicted value.
Preprints 191332 g002
Preprints 191332 g003
Figure 3. Scatter plot comparing true values to predicted values.
Figure 3. Scatter plot comparing true values to predicted values.
Preprints 191332 g003
Table 1. Comparative experimental results.
Table 1. Comparative experimental results.
Model MSE MAE MAPE R2
MLP[27] 0.145 0.278 9.84% 0.873
LSTM[28] 0.121 0.251 8.92% 0.892
Transformer[29] 0.109 0.238 8.40% 0.904
BILSTM[30] 0.102 0.231 8.15% 0.911
Ours 0.085 0.212 7.34% 0.928
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated