Real Differentiation: A Fiberwise, Stack-Enriched Calculus of Change

1. Motivation and Outline

Conventional calculus differentiates numbers. In spectral, multivalued, or analytic-continuation settings—where “a function” may in fact live on multiple branches and is only single-valued after choosing a sheet—naïve differentiation on a chosen principal branch is not stable under monodromy, and can break fundamental identities (e.g. pathwise versions of the fundamental theorem).

Real Differentiation replaces unlabelled scalars by labelled fields: objects living in a slice topos over a label object. In the simplest case, labels form a constant discrete object ${\underline{\mathbb{E}}}_{\mathcal{X}}$; then labelled objects are equivalent to families indexed by energy values, and “no branch mixing” is enforced categorically. In the monodromy-aware case, labels form a covering space or stack $\mathcal{E}\to \mathcal{X}$; then labelled objects are sheaves on the total space, and monodromy is encoded by descent along $\mathcal{E}\to \mathcal{X}$ rather than being ignored.

After setting up the labelled foundations (Section 2), we define the Real Differential functor $\mathrm{D}$ via first jets (Section 3), prove fibrewise base-change properties, and define directional derivatives by universal differentials (Section 4). We then extend the chain rule beyond polynomials under explicit hypotheses, develop higher jets and a jet comonad governing differential operators (Sections 5 and 6), construct the Real de Rham complex and fibrewise integration (Section 7), and introduce controlled energy mixing via label correspondences (Section 9). Computational demonstrations are provided as in-document listings (Appendix A.2 and Appendix A.3).

Positioning and Scope

Jets, Kähler differentials, and the jet/differential-operator adjunction are classical (EGA, Hartshorne, Illusie). The contribution here is the systematic labelled packaging: (i) a decomposition theorem showing constant-labelled objects are families; (ii) a cover/stack label model capturing monodromy; (iii) a jet-based differentiation functor and identities that commute with passage to label fibres; and (iv) a controlled mixing extension via correspondences.

2. Energy–Fibred Foundations

2.1. Energy FIELD, Base Topos, Ringed Structure

Fix a commutative real-closed energy field $(\mathbb{E},+,·)$. Let $\mathcal{B}$ be a Grothendieck site, and work in the ringed topos $(Sh\left(\mathcal{B}\right),{\mathcal{O}}_{\mathcal{B}})$. Unless stated otherwise, all internal algebra is ${\mathcal{O}}_{\mathcal{B}}$-linear.

Remark 1

(Size convention). To form coproducts indexed by underlying sets of energy values, we assume the underlying set of $\mathbb{E}$ is small in a fixed Grothendieck universe, or we work universe-relatively. This is standard in topos-theoretic constructions and does not affect the geometric content.

Definition 1

(Energy-affine space). For $n\ge 0$ set

$${\mathbb{A}}_{\mathbb{E}}^n:=Spec\mathbb{E}[t_1,\dots ,t_n],$$

viewed as an object of $\mathcal{B}$.

2.2. Geometry over $\mathcal{X}$ and Relative Differentials

Fix a morphism $\pi :\mathcal{X}\to {\mathbb{A}}_{\mathbb{E}}^n$ in $\mathcal{B}$, assumed energy-smooth when needed (Definition 9). We write $(Sh\left(\mathcal{B}\right)/\mathcal{X},{\mathcal{O}}_{\mathcal{X}})$ for the induced ringed topos over $\mathcal{X}$. Relative Kähler differentials ${\Omega }_{\mathcal{X}/\mathbb{E}}^1$ are an ${\mathcal{O}}_{\mathcal{X}}$-module, and we set

$${\mathcal{T}}_{\mathcal{X}/\mathbb{E}}:={\underline{Hom}}_{{\mathcal{O}}_{\mathcal{X}}}({\Omega }_{\mathcal{X}/\mathbb{E}}^1,{\mathcal{O}}_{\mathcal{X}}).$$

When discussing vector fields, derivations, jets, and de Rham theory, we work in $(Sh\left(\mathcal{B}\right)/\mathcal{X},{\mathcal{O}}_{\mathcal{X}})$.

2.3. Label Objects and Labelled Module Objects

A central organising idea is to separate two layers: (i) a geometric base $\mathcal{X}$, and (ii) a label object $\mathcal{E}$ over $\mathcal{X}$ whose fibres represent branch/energy/sheet data.

Definition 2

(Label object and labelled topos). A label object over $\mathcal{X}$  is an object $\mathcal{E}$ of $Sh\left(\mathcal{B}\right)/\mathcal{X}$. The associated labelled topos is the slice

$$(Sh(\mathcal{B})/\mathcal{X})/\mathcal{E}.$$

An $\mathcal{E}$-labelled object is a morphism $F\to \mathcal{E}$ in $Sh\left(\mathcal{B}\right)/\mathcal{X}$.

Definition 3

(Labelled structure sheaf and labelled modules). Let $p:(Sh(\mathcal{B})/\mathcal{X})/\mathcal{E}\to Sh\left(\mathcal{B}\right)/\mathcal{X}$ be the projection geometric morphism. Define the pulled-back structure sheaf

$${\mathcal{O}}_{\mathcal{X}\mathcal{E}}:=p^{*}{\mathcal{O}}_{\mathcal{X}},$$

a ring object in the labelled topos. An ${\mathcal{O}}_{\mathcal{X}\mathcal{E}}$-modulemeans a module object in $(Sh(\mathcal{B})/\mathcal{X})/\mathcal{E}$ over the ring ${\mathcal{O}}_{\mathcal{X}\mathcal{E}}$.

Remark 2

(Why modules must be internal). This formalism avoids a subtle but important pitfall: a label map is not naturally an ${\mathcal{O}}_{\mathcal{X}}$-linear morphism to a ring of scalars. Instead, labels are tracked by working in the slice topos, where all algebra (including module structure) is internal and automatically respects the labelling.

2.4. Constant Energy Labels and the Slice-as-Family Decomposition

We now define the constant energy label object and prove that it yields a canonical product decomposition.

Definition 4

(Constant energy label object ${\underline{\mathbb{E}}}_{\mathcal{X}}$). Let $1_{\mathcal{X}}$ denote the terminal object of $Sh\left(\mathcal{B}\right)/\mathcal{X}$. The constant energy label object on $\mathcal{X}$ is the constant object with fibre $\mathbb{E}$,

$${\underline{\mathbb{E}}}_{\mathcal{X}}:={\Delta }_{\mathcal{X}}\left(\mathbb{E}\right)\cong \coprod _{E\in \mathbb{E}}{1}_{\mathcal{X}}\mathit{in}Sh\left(\mathcal{B}\right)/\mathcal{X}.$$

For each $E\in \mathbb{E}$, write ${\iota }_E:1_{\mathcal{X}}\to {\underline{\mathbb{E}}}_{\mathcal{X}}$ for the coproduct inclusion.

Definition 5

(Energy fibre (constant-label case)). Let $F\to {\underline{\mathbb{E}}}_{\mathcal{X}}$ be an ${\underline{\mathbb{E}}}_{\mathcal{X}}$-labelled object in $Sh\left(\mathcal{B}\right)/\mathcal{X}$. For $E\in \mathbb{E}$, its energy fibre is the pullback

$$F_E:=F{\times }_{{\underline{\mathbb{E}}}_{\mathcal{X}}}{1}_{\mathcal{X}}\mathit{along}{\iota }_E:1_{\mathcal{X}}\to {\underline{\mathbb{E}}}_{\mathcal{X}}.$$

Theorem 1

(Slice-as-family decomposition for constant labels). There is an equivalence of toposes

$$(Sh\left(\mathcal{B}\right)/\mathcal{X})/{\underline{\mathbb{E}}}_{\mathcal{X}}\simeq \prod _{E\in \mathbb{E}}(Sh\left(\mathcal{B}\right)/\mathcal{X}),$$

under which a labelled object $F\to {\underline{\mathbb{E}}}_{\mathcal{X}}$ corresponds to its family of fibres ${\left(F_E\right)}_{E\in \mathbb{E}}$, and morphisms correspond to families of morphisms $F_E\to G_E$.

Proof. 

In any Grothendieck topos, coproducts are disjoint and stable under pullback (extensivity). Since ${\underline{\mathbb{E}}}_{\mathcal{X}}\cong {\coprod }_{E\in \mathbb{E}}{1}_{\mathcal{X}}$, slicing over ${\underline{\mathbb{E}}}_{\mathcal{X}}$ decomposes as a product of slices over each summand:

$$(Sh\left(\mathcal{B}\right)/\mathcal{X})/\left(\coprod _{E\in \mathbb{E}}{1}_{\mathcal{X}}\right)\simeq \prod _{E\in \mathbb{E}}(Sh\left(\mathcal{B}\right)/\mathcal{X})/1_{\mathcal{X}}.$$

But $(Sh\left(\mathcal{B}\right)/\mathcal{X})/1_{\mathcal{X}}\simeq Sh\left(\mathcal{B}\right)/\mathcal{X}$ because $1_{\mathcal{X}}$ is terminal. The equivalence is realised by pulling back along the inclusions ${\iota }_E$, yielding the family of fibres $F_E$, and conversely by taking the coproduct ${\coprod }_E{F}_E\to {\coprod }_E{1}_{\mathcal{X}}={\underline{\mathbb{E}}}_{\mathcal{X}}$.    □

Corollary 1

(Canonical coproduct decomposition). For any ${\underline{\mathbb{E}}}_{\mathcal{X}}$-labelled object $F\to {\underline{\mathbb{E}}}_{\mathcal{X}}$ there is a canonical isomorphism in $Sh\left(\mathcal{B}\right)/\mathcal{X}$:

$$F\cong \coprod _{E\in \mathbb{E}}{F}_E.$$

Proposition 1

(Modules in the constant-labelled topos are families of modules). The category of ${\mathcal{O}}_{\mathcal{X}{\underline{\mathbb{E}}}_{\mathcal{X}}}$-modules in the labelled topos $(Sh\left(\mathcal{B}\right)/\mathcal{X})/{\underline{\mathbb{E}}}_{\mathcal{X}}$ is canonically equivalent to the product category

$${\mathcal{O}}_{\mathcal{X}{\underline{\mathbb{E}}}_{\mathcal{X}}}\text{-}\mathrm{Mod}\left((Sh\left(\mathcal{B}\right)/\mathcal{X})/{\underline{\mathbb{E}}}_{\mathcal{X}}\right)\simeq \prod _{E\in \mathbb{E}}{\mathcal{O}}_{\mathcal{X}}\text{-}\mathrm{Mod}\left(Sh\left(\mathcal{B}\right)/\mathcal{X}\right).$$

In particular, any construction in the labelled topos defined by topos limits, colimits, and ${\mathcal{O}}_{\mathcal{X}}$-module operations acts componentwise on fibres.

Proof. 

Apply Theorem 1 and observe that pulling back ${\mathcal{O}}_{\mathcal{X}{\underline{\mathbb{E}}}_{\mathcal{X}}}=p^{*}{\mathcal{O}}_{\mathcal{X}}$ to the Eth factor recovers ${\mathcal{O}}_{\mathcal{X}}$. Module objects in a product topos are products of module objects, giving the stated equivalence.    □

2.5. Reformulated Tag Models: Model A and Model B

We now restate your two tag semantics in the rigorous language of Theorem 1.

Definition 6

(Model A: single-energy (concentrated) objects). An ${\underline{\mathbb{E}}}_{\mathcal{X}}$-labelled object $F\to {\underline{\mathbb{E}}}_{\mathcal{X}}$ is concentrated at energy $E_0\in \mathbb{E}$ if $F_E=⌀$ for all $E\ne E_0$. We write $F@E_0$ for such an object.

Definition 7

(Model B: general labelled objects). A general labelled object is an arbitrary $F\to {\underline{\mathbb{E}}}_{\mathcal{X}}$. Fibrewise reasoning proceeds by applying the pullback functors ${(-)}_E$ of Definition 5. By Theorem 1, this is equivalent to reasoning componentwise in the family ${\left(F_E\right)}_{E\in \mathbb{E}}$.

Remark 3

(No branch mixing as a theorem). In Model B, any morphism $F\to G$ in the labelled topos is equivalent to a family of morphisms $F_E\to G_E$. Consequently, any endofunctor or operator defined in the labelled topos acts separately on each E and cannot mix components unless mixing is introduced by leaving the slice framework. This is the precise form of “no branch mixing.”

2.6. Stacky/Local-System Labels: Covers and Monodromy

The constant-label model treats labels as a trivial discrete family. To encode analytic continuation and monodromy, labels must instead vary over $\mathcal{X}$.

Definition 8

(Étale label object (cover of branches)). A label object $\mathcal{E}$ over $\mathcal{X}$ is calledétale if it is represented by an étale (or, in the present terminology, energy-smooth and unramified) morphism $p:\tilde{\mathcal{X}}\to \mathcal{X}$ in $\mathcal{B}$ such that fibres are discrete sets of branches/sheets.

Proposition 2

(Labelled objects on an étale label are sheaves on the total space). If $\mathcal{E}$ is represented by a morphism $p:\tilde{\mathcal{X}}\to \mathcal{X}$, then there is an equivalence of toposes

$$(Sh\left(\mathcal{B}\right)/\mathcal{X})/\mathcal{E}\simeq Sh\left(\mathcal{B}\right)/\tilde{\mathcal{X}}.$$

Under this equivalence, ${\mathcal{O}}_{\mathcal{X}\mathcal{E}}$-modules correspond to ${\mathcal{O}}_{\tilde{\mathcal{X}}}$-modules.

Proof. 

This is the standard identification of a slice topos over a representable object with the topos over the representing object, using the fact that slicing is associative: $(\mathcal{E}/\mathcal{X})/\tilde{\mathcal{X}}\simeq \mathcal{E}/\tilde{\mathcal{X}}$ for any topos $\mathcal{E}$. Here $\mathcal{E}=Sh\left(\mathcal{B}\right)$.    □

Remark 4

(Monodromy as descent data). If $p:\tilde{\mathcal{X}}\to \mathcal{X}$ is a covering with deck group Γ, then objects on $\mathcal{X}$ with branch data correspond to Γ-equivariant objects on $\tilde{\mathcal{X}}$. In particular, a multivalued analytic function on $\mathcal{X}$ becomes a single-valued function on $\tilde{\mathcal{X}}$, and monodromy is encoded by the Γ-action rather than ignored. Later we will state a monodromy-consistent calculus theorem showing that differentiation and integration commute with path lifting (Section 7).

Remark 5

(Stacks of labels (optional)). For some applications the label object is naturally a stack (groupoid-valued sheaf), e.g. when branches are identified up to symmetry. The present paper develops the theory for étale label objects (covers), which already captures the monodromy behaviour visible in the computational demonstrations. Extending from étale covers to stacks is formal: replace $\mathcal{E}$ by a groupoid object and work in the corresponding 2-topos of stacks.

2.7. Energy-Smooth Morphisms

We will need a base-change hypothesis that guarantees Kähler differentials and infinitesimal neighbourhoods commute with pullback.

Definition 9

(Energy-flat and energy-smooth). A morphism $u:{\mathcal{X}}^{\prime }\to \mathcal{X}$ in $\mathcal{B}$ isenergy-flatif pullback along u is exact on ${\mathcal{O}}_{\mathcal{X}}$-modules. It isenergy-smoothif, furthermore, the canonical map

$$u^{*}{\Omega }_{\mathcal{X}/\mathbb{E}}^1\to {\Omega }_{{\mathcal{X}}^{\prime }/\mathbb{E}}^1$$

is an isomorphism and the formation of the first infinitesimal neighbourhood of the diagonal commutes with pullback along u.

3. The Real Differential Functor (Via First Jets)

3.1. First Infinitesimal Neighbourhood of the Diagonal and Principal Parts

Let Y be an object of $\mathcal{B}$ equipped with a structure sheaf ${\mathcal{O}}_Y$, and assume Y is energy-smooth over $\mathbb{E}$ (in the sense appropriate to the geometric model: schemes, manifolds, etc.). Write $Y{\times }_{\mathbb{E}}Y$ for the fibre product over $Spec\mathbb{E}$, and let

$${\Delta }_Y:Y\hookrightarrow Y{\times }_{\mathbb{E}}Y$$

be the diagonal. Let $\mathcal{I}\subseteq {\mathcal{O}}_{Y{\times }_{\mathbb{E}}Y}$ be the ideal sheaf of ${\Delta }_Y$.

Definition 10

(First infinitesimal neighbourhood). The first infinitesimal neighbourhood of the diagonal is the closed subobject

$${\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[1\right]}:=Spec\left({\mathcal{O}}_{Y{\times }_{\mathbb{E}}Y}/{\mathcal{I}}^2\right),$$

with the induced projections

$$p_1,p_2:{\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[1\right]}⟶Y.$$

Definition 11

(Sheaf of principal parts of order 1). Define the sheaf of principal parts of order 1 on Y to be

$${\mathcal{P}}_{Y/\mathbb{E}}^1:=p_{1*}{\mathcal{O}}_{{\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[1\right]}}.$$

It is naturally an ${\mathcal{O}}_Y$-algebra (via $p_1$), and carries a canonical augmentation $ϵ:{\mathcal{P}}_{Y/\mathbb{E}}^1\to {\mathcal{O}}_Y$ induced by restriction along the diagonal.

Remark 6.

The construction of ${\mathcal{P}}_{Y/\mathbb{E}}^1$ and the exact sequences below are standard (principal parts / jets / differentials); see [1], IV or [2], II §8.

3.2. The First Jet Functor

Definition 12

(First jet functor). Let $\mathcal{F}$ be an ${\mathcal{O}}_Y$-module. Define

$$J_{Y/\mathbb{E}}^1\left(\mathcal{F}\right):=p_{1*}\left(p_2^{*}\mathcal{F}\right)\cong {\mathcal{P}}_{Y/\mathbb{E}}^1{\otimes }_{{\mathcal{O}}_Y}\mathcal{F}.$$

Proposition 3

(Fundamental exact sequence for first jets). There is a natural short exact sequence of ${\mathcal{O}}_Y$-modules

$$0⟶{\Omega }_{Y/\mathbb{E}}^1{\otimes }_{{\mathcal{O}}_Y}\mathcal{F}\stackrel{\iota }{\to }{J}_{Y/\mathbb{E}}^1\left(\mathcal{F}\right)\stackrel{ϵ}{\to }\mathcal{F}⟶0,$$

(1)

where ϵ is induced by restriction along the diagonal.

Reference. 

See ([2] II, §8) or ([1] IV).    □

3.3. Real Differentiation on a Labelled Base

We now specialise to the context of Section 2. There are two natural choices of “base” on which calculus is performed:

• the geometric base $\mathcal{X}$, yielding ordinary (unlabelled) calculus on $\mathcal{X}$;
• a label base $\mathcal{E}\to \mathcal{X}$ (constant family ${\underline{\mathbb{E}}}_{\mathcal{X}}$ or an étale cover $\tilde{\mathcal{X}}\to \mathcal{X}$), yielding labelled calculus.

Since the labelled topos $(Sh(\mathcal{B})/\mathcal{X})/\mathcal{E}$ is equivalent to $Sh\left(\mathcal{B}\right)/\mathcal{E}$ when $\mathcal{E}$ is representable (Proposition 2), it is natural to perform jets on the label base itself.

Definition 13

(Real Differential functor on a labelled base). Assume the label object $\mathcal{E}$ is representable by an energy-smooth morphism $p:\mathcal{E}\to \mathcal{X}$ (examples: $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}$ or $\mathcal{E}=\tilde{\mathcal{X}}$ étale over $\mathcal{X}$). Write ${\mathcal{O}}_{\mathcal{E}}$ for the induced structure sheaf.

Define theReal Differential functor on $\mathcal{E}$ to be the endofunctor

$${\mathrm{D}}_{\mathcal{E}}:{\mathcal{O}}_{\mathcal{E}}\text{-}\mathrm{Mod}⟶{\mathcal{O}}_{\mathcal{E}}\text{-}\mathrm{Mod},{\mathrm{D}}_{\mathcal{E}}\left(\mathcal{F}\right):=J_{\mathcal{E}/\mathbb{E}}^1\left(\mathcal{F}\right).$$

The augmentation $ϵ:J_{\mathcal{E}/\mathbb{E}}^1\left(\mathcal{F}\right)\to \mathcal{F}$ is called thetag-preserving counit.

Remark 7

(Tag preservation is automatic). Working on $\mathcal{E}$ ensures that all constructions are intrinsically label-aware: a section of ${\mathcal{O}}_{\mathcal{E}}$ is already a label-tagged scalar. The map ϵ does not change the basepoint of $\mathcal{E}$, hence does not change the label. In the constant-label case $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}$, this recovers “no branch mixing” in the strongest possible form: $\mathrm{D}$ acts componentwise on energy indices (Section 2.4).

3.4. Constant Energy Labels: $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}$

Let $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}\cong {\coprod }_{E\in \mathbb{E}}{1}_{\mathcal{X}}$ as in Definition 4. Then $\mathcal{E}$ is a disjoint union of copies of $\mathcal{X}$, and ${\mathcal{O}}_{\mathcal{E}}$ is the corresponding coproduct of copies of ${\mathcal{O}}_{\mathcal{X}}$.

Proposition 4

(Componentwise differentiation in the constant-label model). Under the equivalence

$$(Sh\left(\mathcal{B}\right)/\mathcal{X})/{\underline{\mathbb{E}}}_{\mathcal{X}}\simeq \prod _{E\in \mathbb{E}}(Sh\left(\mathcal{B}\right)/\mathcal{X})$$

of Theorem 1, the functor ${\mathrm{D}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}$ corresponds to the product of jet functors on $\mathcal{X}$:

$${\mathrm{D}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}\leftrightarrow \prod _{E\in \mathbb{E}}{J}_{\mathcal{X}/\mathbb{E}}^1.$$

Equivalently, for ${\mathcal{O}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}$-modules $\mathcal{F}$,

$${\left({\mathrm{D}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}\left(\mathcal{F}\right)\right)}_E\cong J_{\mathcal{X}/\mathbb{E}}^1\left({\mathcal{F}}_E\right)$$

naturally in $\mathcal{F}$ and in $E\in \mathbb{E}$.

Proof. 

Since ${\underline{\mathbb{E}}}_{\mathcal{X}}$ is a disjoint coproduct of copies of $1_{\mathcal{X}}$, the labelled base ${\underline{\mathbb{E}}}_{\mathcal{X}}$ is a disjoint union of copies of $\mathcal{X}$. Jets commute with finite coproducts and restrict to each connected component. Translating through Theorem 1 yields the stated componentwise formula.    □

3.5. Étale Label Covers: $\mathcal{E}=\tilde{\mathcal{X}}\to \mathcal{X}$

Let $p:\tilde{\mathcal{X}}\to \mathcal{X}$ be an étale label cover encoding branches (e.g. a Riemann surface of analytic continuations). Then labelled objects over $\mathcal{X}$ are equivalently objects over $\tilde{\mathcal{X}}$ (Proposition 2), and Real differentiation is simply differentiation on $\tilde{\mathcal{X}}$.

Proposition 5

(Label-cover Real differentiation). For an étale label cover $p:\tilde{\mathcal{X}}\to \mathcal{X}$, the labelled Real Differential functor is

$${\mathrm{D}}_{\tilde{\mathcal{X}}}=J_{\tilde{\mathcal{X}}/\mathbb{E}}^1\mathrm{on}{\mathcal{O}}_{\tilde{\mathcal{X}}}\text{-}\mathrm{Mod}.$$

In particular, deck transformations act by automorphisms commuting with $\mathrm{D}$.

Proof. 

This is immediate from Definition 13 applied to $\mathcal{E}=\tilde{\mathcal{X}}$. Deck transformations are automorphisms of $\tilde{\mathcal{X}}$ over $\mathcal{X}$ and hence preserve the diagonal and its infinitesimal neighbourhood, commuting with jet formation.    □

3.6. Base Change for First Jets

Proposition 6

(Base change for first jets). Let $u:Y^{\prime }\to Y$ be an energy-smooth morphism. Then for any ${\mathcal{O}}_Y$-module $\mathcal{F}$ there is a canonical isomorphism of ${\mathcal{O}}_{Y^{\prime }}$-modules

$$u^{*}{J}_{Y/\mathbb{E}}^1\left(\mathcal{F}\right)\stackrel{\sim }{\to }{J}_{Y^{\prime }/\mathbb{E}}^1\left(u^{*}\mathcal{F}\right),$$

functorial in $\mathcal{F}$.

Proof sketch 

Form the cartesian square for diagonals and their first infinitesimal neighbourhoods:

Energy-smoothness ensures formation of ${\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[1\right]}$ commutes with base change, and that ${\Omega }^1$ behaves well. Since $p_1$ is affine in the usual geometric settings (schemes, ringed spaces), pushforward along $p_1$ commutes with pullback along u on quasi-coherent modules. Apply this to $p_2^{*}\mathcal{F}$ to obtain the desired isomorphism. See [1], IV or [2], II, §8 for details in the scheme case.    □

Corollary 2

(Base change for Real differentiation). Under the hypotheses of Proposition 6, the Real Differential functor commutes with base change:

$$u^{*}{\mathrm{D}}_Y\left(\mathcal{F}\right)\cong {\mathrm{D}}_{Y^{\prime }}\left(u^{*}\mathcal{F}\right).$$

In particular, in the constant-label model this yields fibrewise identities ${\left({\mathrm{D}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}\mathcal{F}\right)}_E\cong {\mathrm{D}}_{\mathcal{X}}\left({\mathcal{F}}_E\right).$

4. Directional Derivatives and Universal Identities

4.1. Directional Derivatives on Scalar Functions

Let Y be an energy-smooth base (either $\mathcal{X}$, ${\underline{\mathbb{E}}}_{\mathcal{X}}$, or an étale label cover $\tilde{\mathcal{X}}$). The universal derivation

$$d:{\mathcal{O}}_Y⟶{\Omega }_{Y/\mathbb{E}}^1$$

is an $\mathbb{E}$-linear derivation. If $v\in \Gamma \left(T_{Y/\mathbb{E}}\right)$ is a vector field (i.e. an ${\mathcal{O}}_Y$-linear map ${\Omega }_{Y/\mathbb{E}}^1\to {\mathcal{O}}_Y$), define the directional derivative of a scalar $f\in {\mathcal{O}}_Y$ by contraction.

Definition 14

(Directional derivative). Let $v\in \Gamma \left(T_{Y/\mathbb{E}}\right)$. Define

$${\nabla }_v\left(f\right):={\iota }_v\left(df\right)\in {\mathcal{O}}_Y.$$

Proposition 7

(Leibniz rule). For all $f,g\in {\mathcal{O}}_Y$,

$${\nabla }_v\left(fg\right)={\nabla }_v\left(f\right)g+f{\nabla }_v\left(g\right).$$

Proof. 

This is immediate from $d\left(fg\right)=fdg+gdf$ and ${\mathcal{O}}_Y$-linearity of ${\iota }_v$.    □

4.2. Polynomial Chain Rule (Always Valid)

Proposition 8

(Polynomial chain rule). Let $F\left(t\right)\in \mathbb{E}\left[t\right]$ and $a\in {\mathcal{O}}_Y$. Then

$${\nabla }_v\left(F\left(a\right)\right)=F^{\prime }\left(a\right){\nabla }_v\left(a\right).$$

Proof. 

Expand $F\left(t\right)={\sum }_k{c}_k{t}^k$ and use repeated Leibniz to obtain $d\left(a^k\right)=k{a}^{k-1}da$, hence $d\left(F\left(a\right)\right)=F^{\prime }\left(a\right)da$. Contract with v.    □

4.3. Upgraded Chain Rule: Smooth/Analytic Functional Calculus

The polynomial chain rule is universal in the purely algebraic setting. To state a chain rule for genuinely smooth or analytic functions, one must assume that ${\mathcal{O}}_Y$ is equipped with a corresponding functional calculus.

Definition 15

($C^1$-functional calculus (one variable)). Assume $\mathbb{E}=\mathbb{R}$. A $C^1$-functional calculuson a sheaf of commutative $\mathbb{R}$-algebras ${\mathcal{O}}_Y$ is an assignment that to each $C^1$ function $\phi :\mathbb{R}\to \mathbb{R}$ associates a sheaf morphism

$${\phi }_{\mathcal{O}}:{\mathcal{O}}_Y⟶{\mathcal{O}}_Y,$$

such that:

(a)

$\phi \mapsto {\phi }_{\mathcal{O}}$ respects composition and identities: ${(\phi \circ \psi )}_{\mathcal{O}}={\phi }_{\mathcal{O}}\circ {\psi }_{\mathcal{O}}$ and ${\left(\mathrm{id}\right)}_{\mathcal{O}}=\mathrm{id}$;

(b)

for polynomials $F\left(t\right)\in \mathbb{R}\left[t\right]$, one has $F_{\mathcal{O}}\left(a\right)=F\left(a\right)$ under the algebra structure.

A $C^{\infty }$-functional calculus is defined similarly with $\phi \in C^{\infty }\left(\mathbb{R}\right)$.

Remark 8.

A sheaf of $C^{\infty }$-rings in the sense of Dubuc–Moerdijk–Reyes (or in $C^{\infty }$-algebraic geometry) canonically carries such a calculus, and the chain rule below is built into that theory. We isolate only the minimal calculus data needed for a chain rule statement.

Theorem 2

(Smooth chain rule under functional calculus). Assume $\mathbb{E}=\mathbb{R}$ and that ${\mathcal{O}}_Y$ carries a $C^1$-functional calculus in the sense of Definition 15. Let $\phi \in C^1\left(\mathbb{R}\right)$ and $a\in {\mathcal{O}}_Y$. Then for any vector field $v\in \Gamma \left(T_{Y/\mathbb{R}}\right)$,

$${\nabla }_v\left({\phi }_{\mathcal{O}}\left(a\right)\right)={\left({\phi }^{\prime }\right)}_{\mathcal{O}}\left(a\right){\nabla }_v\left(a\right).$$

Proof. 

The identity is local on Y. In the standard geometric models motivating this paper (smooth manifolds, analytic spaces), ${\phi }_{\mathcal{O}}\left(a\right)$ is literally the composition $\phi \circ a$, and the formula is the classical chain rule. Abstractly, one can reduce to the polynomial case by approximating $\phi$ by polynomials on compacta and using continuity of derivations, provided the functional calculus is continuous in the appropriate topology. Since the present paper does not fix a unique topological model for Y, we take the above as a theorem in the geometric functional-calculus setting.    □

Remark 9

(Multi-variable version). If ${\mathcal{O}}_Y$ carries an n-variable calculus $\phi :{\mathbb{R}}^n\to \mathbb{R}$ (as in a $C^{\infty }$-ring), then for $a_1,\dots ,a_n\in {\mathcal{O}}_Y$,

$$d\left(\phi (a_1,\dots ,a_n)\right)=\sum _{i=1}^n\left({\displaystyle \frac{\partial \phi }{\partial x_i}}(a_1,\dots ,a_n)\right)d{a}_i,$$

and hence the corresponding directional derivative identity holds after contraction with v.

Remark 10

(Fibrewise/labelwise validity). All statements above are stable under passage to constant-label fibres (by Theorem 1) and under pullback to étale label covers (by Corollary 2). Hence chain rules and Leibniz identities hold separately on each energy sheet, and on each analytic branch cover.

5. Higher Jets and Differential Operators

5.1. Higher Infinitesimal Neighbourhoods and Principal Parts

Let Y be an energy-smooth base over $\mathbb{E}$ (in the sense of Definition 9), with structure sheaf ${\mathcal{O}}_Y$.

Let ${\Delta }_Y:Y\hookrightarrow Y{\times }_{\mathbb{E}}Y$ be the diagonal, with ideal sheaf $\mathcal{I}\subseteq {\mathcal{O}}_{Y{\times }_{\mathbb{E}}Y}$.

Definition 16

(jth infinitesimal neighbourhood). For $j\ge 0$, the jth infinitesimal neighbourhood of the diagonalis

$${\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[j\right]}:=Spec\left({\mathcal{O}}_{Y{\times }_{\mathbb{E}}Y}/{\mathcal{I}}^{j+1}\right),$$

with induced projections $p_1^{\left[j\right]},p_2^{\left[j\right]}:{\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[j\right]}\to Y$.

Definition 17

(Principal parts of order j). Define the principal parts of order j to be the sheaf of ${\mathcal{O}}_Y$-algebras

$${\mathcal{P}}_{Y/\mathbb{E}}^j:={\left(p_1^{\left[j\right]}\right)}_{*}{\mathcal{O}}_{{\left(Y{\times }_{\mathbb{E}}Y\right)}^{\left[j\right]}}.$$

There is a canonical augmentation ${ϵ}^{\left[j\right]}:{\mathcal{P}}_{Y/\mathbb{E}}^j\to {\mathcal{O}}_Y$ induced by restricting along ${\Delta }_Y$.

Definition 18

(Jets of order j). Let $\mathcal{F}$ be an ${\mathcal{O}}_Y$-module. Define thejth jet module

$$J_{Y/\mathbb{E}}^j\left(\mathcal{F}\right):={\left(p_1^{\left[j\right]}\right)}_{*}\left({\left(p_2^{\left[j\right]}\right)}^{*}\mathcal{F}\right)\cong {\mathcal{P}}_{Y/\mathbb{E}}^j{\otimes }_{{\mathcal{O}}_Y}\mathcal{F}.$$

Proposition 9

(Exact sequences and associated graded in the smooth case). Assume Y is smooth over $\mathbb{E}$ (in the sense that Kähler differentials are locally free and the diagonal is a regular immersion). Then $J_{Y/\mathbb{E}}^j\left(\mathcal{F}\right)$ admits a natural filtration whose graded pieces satisfy

$$\mathrm{gr}{J}_{Y/\mathbb{E}}^j\left(\mathcal{F}\right)\cong \underset{i=0}{\overset{j}{⨁}}{\mathrm{Sym}}^i\left({\Omega }_{Y/\mathbb{E}}^1\right){\otimes }_{{\mathcal{O}}_Y}\mathcal{F}.$$

Moreover there are short exact sequences

$$0\to {\mathrm{Sym}}^j\left({\Omega }_{Y/\mathbb{E}}^1\right)\otimes \mathcal{F}\to J_{Y/\mathbb{E}}^j\left(\mathcal{F}\right)\to J_{Y/\mathbb{E}}^{j-1}\left(\mathcal{F}\right)\to 0.$$

Reference. 

These are classical properties of principal parts and jets in the smooth case; see ([1] IV) or ([2] II, §8).    □

5.2. Differential Operators and the Jet Adjunction

We recall the standard intrinsic definition of differential operators.

Definition 19

(Differential operators of order $\le j$). Let $\mathcal{F},\mathcal{G}$ be ${\mathcal{O}}_Y$-modules. Define inductively:

• ${Diff}_{Y/\mathbb{E}}^{\le 0}(\mathcal{F},\mathcal{G}):={\underline{Hom}}_{{\mathcal{O}}_Y}(\mathcal{F},\mathcal{G})$;
• for $j\ge 1$, an $\mathbb{E}$-linear map $D:\mathcal{F}\to \mathcal{G}$ is of order $\le j$ if for all local sections $a\in {\mathcal{O}}_Y$, the commutator

  $$[D,a]:\mathcal{F}\to \mathcal{G},[D,a]\left(s\right):=D\left(as\right)-aD\left(s\right),$$
  is a differential operator of order $\le j-1$.

Write ${Diff}_{Y/\mathbb{E}}^{\le j}(\mathcal{F},\mathcal{G})$ for the sheaf of such operators.

Theorem 3

(Jet–differential operator adjunction). For all ${\mathcal{O}}_Y$-modules $\mathcal{F},\mathcal{G}$ and all $j\ge 0$ there is a natural isomorphism

$${\underline{Hom}}_{{\mathcal{O}}_Y}\left(J_{Y/\mathbb{E}}^j\left(\mathcal{F}\right),\mathcal{G}\right)\cong {Diff}_{Y/\mathbb{E}}^{\le j}(\mathcal{F},\mathcal{G}),$$

functorial in $\mathcal{F}$ and $\mathcal{G}$.

Reference. 

This is standard; see ([1] IV). Concretely, $J^j\left(\mathcal{F}\right)$ is the universal recipient for order $\le j$ Taylor expansions, and ${\mathcal{P}}^j$ is the universal algebra of order-j principal parts.    □

5.3. Labelwise Behaviour of Higher Jets

Proposition 10

(Constant-label case: componentwise jets). In the constant-label model $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}$, formation of $J^j$ is componentwise: for any ${\mathcal{O}}_{{\underline{\mathbb{E}}}_{\mathcal{X}}}$-module $\mathcal{F}$,

$${\left(J_{{\underline{\mathbb{E}}}_{\mathcal{X}}/\mathbb{E}}^j\left(\mathcal{F}\right)\right)}_E\cong J_{\mathcal{X}/\mathbb{E}}^j\left({\mathcal{F}}_E\right)$$

naturally in $E\in \mathbb{E}$.

Proof. 

Same argument as Proposition 4, using that ${\underline{\mathbb{E}}}_{\mathcal{X}}$ is a disjoint union of copies of $\mathcal{X}$ and jets restrict to components.    □

Proposition 11

(Étale-label case: jets commute with pullback). Let $p:\tilde{\mathcal{X}}\to \mathcal{X}$ be an étale label cover. Then for any ${\mathcal{O}}_{\mathcal{X}}$-module $\mathcal{F}$ on $\mathcal{X}$,

$$p^{*}{J}_{\mathcal{X}/\mathbb{E}}^j\left(\mathcal{F}\right)\cong J_{\tilde{\mathcal{X}}/\mathbb{E}}^j\left(p^{*}\mathcal{F}\right),$$

and the identification is compatible with the jet adjunction (Theorem 3).

Proof. 

By repeated application of Proposition 6 (or its order-j analogue) under energy-smoothness of p.    □

6. Infinite Jets, the Jet Comonad, and the coKleisli Calculus

6.1. Infinite Jets

Finite jets control differential operators of bounded order. To organise the full calculus of all finite orders, one passes to the inverse limit.

Definition 20

(Infinite principal parts and infinite jets). Assume the inverse limits exist in the chosen category of modules (e.g. for quasi-coherent modules on a noetherian scheme, or in suitable pro-categories). Define

$${\mathcal{P}}_{Y/\mathbb{E}}^{\infty }:=\underset{j}{\underleftarrow{lim}}{\mathcal{P}}_{Y/\mathbb{E}}^j,J_{Y/\mathbb{E}}^{\infty }\left(\mathcal{F}\right):=\underset{j}{\underleftarrow{lim}}{J}_{Y/\mathbb{E}}^j\left(\mathcal{F}\right).$$

We write $J^{\infty }\left(\mathcal{F}\right)$ when $Y/\mathbb{E}$ is understood.

Remark 11

(Pro-object caveat). If inverse limits do not exist strictly in ${\mathcal{O}}_Y$-modules, the correct replacement is the pro-object ${\left\{J^j\left(\mathcal{F}\right)\right\}}_{j\ge 0}$. All statements below may be interpreted in that pro-setting. To keep notation light, we state results as if the limit exists.

6.2. Coalgebra and Comonad Structure

A key structural fact is that infinite principal parts carry a canonical (coassociative, counital) coalgebra structure, encoding “composition of infinitesimal displacements.”

Proposition 12

(Coalgebra structure on ${\mathcal{P}}^{\infty }$). There are canonical maps of ${\mathcal{O}}_Y$-modules

$$ϵ:{\mathcal{P}}_{Y/\mathbb{E}}^{\infty }\to {\mathcal{O}}_Y,\Delta :{\mathcal{P}}_{Y/\mathbb{E}}^{\infty }\to {\mathcal{P}}_{Y/\mathbb{E}}^{\infty }{\otimes }_{{\mathcal{O}}_Y}{\mathcal{P}}_{Y/\mathbb{E}}^{\infty },$$

such that $({\mathcal{P}}_{Y/\mathbb{E}}^{\infty },\Delta ,ϵ)$ is a counital, coassociative coalgebra object in ${\mathcal{O}}_Y$-modules.

Construction sketch 

The counit $ϵ$ is induced by restriction along the diagonal. The comultiplication $\Delta$ is induced by the inclusion of the formal groupoid of infinitesimal neighbourhoods: informally, the $(\infty )$-neighbourhood of the diagonal in $Y\times Y$ composes via the middle factor in $Y\times Y\times Y$. This is classical in Grothendieck’s theory of stratifications/principal parts; see [1,3].    □

Theorem 4

(Jet comonad). Define the endofunctor $J^{\infty }:{\mathcal{O}}_Y\text{-}\mathrm{Mod}\to {\mathcal{O}}_Y\text{-}\mathrm{Mod}$ by $J^{\infty }\left(\mathcal{F}\right)={\mathcal{P}}^{\infty }{\otimes }_{{\mathcal{O}}_Y}\mathcal{F}$. Then with counit

$${\epsilon }_{\mathcal{F}}:J^{\infty }\left(\mathcal{F}\right)\to \mathcal{F}$$

induced from $ϵ:{\mathcal{P}}^{\infty }\to {\mathcal{O}}_Y$, and comultiplication

$${\delta }_{\mathcal{F}}:J^{\infty }\left(\mathcal{F}\right)\to J^{\infty }\left(J^{\infty }\left(\mathcal{F}\right)\right)$$

induced from Δ, the triple $(J^{\infty },\epsilon ,\delta )$ is a comonad on ${\mathcal{O}}_Y$-modules.

Remark 12

(Relation to connections and stratifications). Coalgebras over the jet comonad (i.e. $J^{\infty }$-comodules) are precisely stratified modules. In the smooth case they correspond to modules with integrable connections; this is part of the classical equivalence between crystals and integrable connections (Berthelot–Ogus, Illusie). We will not use this equivalence in proofs, but it motivates why $J^{\infty }$ governs differential operator calculus.

6.3. CoKleisli Category and Differential Operators

Definition 21

(CoKleisli morphisms). The coKleisli category of the comonad $J^{\infty }$ has the same objects as ${\mathcal{O}}_Y$-modules, and morphisms

$${\mathrm{Hom}}_{\mathrm{coKl}\left(J^{\infty }\right)}(\mathcal{F},\mathcal{G}):={\mathrm{Hom}}_{{\mathcal{O}}_Y}\left(J^{\infty }\left(\mathcal{F}\right),\mathcal{G}\right).$$

Composition is defined by the comonad structure: for $f:J^{\infty }\left(\mathcal{F}\right)\to \mathcal{G}$ and $g:J^{\infty }\left(\mathcal{G}\right)\to \mathcal{H}$,

$$g\star f:=g\circ J^{\infty }\left(f\right)\circ {\delta }_{\mathcal{F}}.$$

Theorem 5

(CoKleisli morphisms are differential operators). Assume Y is energy-smooth over $\mathbb{E}$. Then for ${\mathcal{O}}_Y$-modules $\mathcal{F},\mathcal{G}$ there is a natural identification

$${\underline{Hom}}_{{\mathcal{O}}_Y}\left(J^{\infty }\left(\mathcal{F}\right),\mathcal{G}\right)\cong \bigcup _{j\ge 0}{Diff}_{Y/\mathbb{E}}^{\le j}(\mathcal{F},\mathcal{G}),$$

compatible with composition: coKleisli composition corresponds to composition of differential operators.

Proof sketch 

By Theorem 3, morphisms out of $J^j\left(\mathcal{F}\right)$ correspond to order $\le j$ differential operators. Passing to the inverse limit over j, morphisms out of $J^{\infty }\left(\mathcal{F}\right)$ correspond to compatible families, i.e. operators of some finite order. Compatibility of composition follows from the coalgebra/comonad map $\Delta$ encoding composition of infinitesimal expansions.    □

6.4. Labelwise Jet Comonad

All constructions in this section apply verbatim to the labelled bases $Y={\underline{\mathbb{E}}}_{\mathcal{X}}$ and $Y=\tilde{\mathcal{X}}$ (an étale label cover). In the constant-label case the comonad decomposes componentwise over $E\in \mathbb{E}$; in the étale-label case it is the usual jet comonad on $\tilde{\mathcal{X}}$ and is automatically monodromy-aware.

7. Real de Rham Theory and Monodromy-Consistent Calculus

7.1. De Rham Complex on a Labelled Base

Let Y denote an energy-smooth base (again: $\mathcal{X}$, ${\underline{\mathbb{E}}}_{\mathcal{X}}$, or an étale label cover $\tilde{\mathcal{X}}$). Define

$${\Omega }_{Y/\mathbb{E}}^p:=\underset{{\mathcal{O}}_Y}{\overset{p}{\bigwedge }}{\Omega }_{Y/\mathbb{E}}^1,p\ge 0.$$

The universal derivation induces the de Rham differential

$$d:{\Omega }_{Y/\mathbb{E}}^p\to {\Omega }_{Y/\mathbb{E}}^{p+1},d^2=0.$$

Remark 13

(Fibrewise validity). In the constant-label model, ${\Omega }_{{\underline{\mathbb{E}}}_{\mathcal{X}}/\mathbb{E}}^{•}$ decomposes into the product of ${\Omega }_{\mathcal{X}/\mathbb{E}}^{•}$ over energies. On an étale label cover, ${\Omega }_{\tilde{\mathcal{X}}/\mathbb{E}}^{•}$ is the usual de Rham complex on the cover, encoding branch data intrinsically.

7.2. Integration Along Labelled Paths (Geometric Models)

To speak about integration, we assume a geometric model in which Y carries a notion of smooth curves and integration of 1-forms (e.g. Y is a smooth manifold or complex analytic curve space). This section records the structural compatibility statements that motivate the computational demonstrations.

Definition 22

(Pathwise integral). Let $\gamma :[0,1]\to Y$ be a $C^1$ path and $\omega \in \Gamma (Y,{\Omega }_{Y/\mathbb{E}}^1)$. Define

$${\int }_{\gamma }\omega :={\int }_0^1{\omega }_{\gamma \left(t\right)}\left(\dot{\gamma }\left(t\right)\right)dt,$$

whenever the right-hand side is defined in the ambient model.

Theorem 6

(Fundamental theorem on a labelled base). Let $f\in \Gamma (Y,{\mathcal{O}}_Y)$ and let $\gamma :[0,1]\to Y$ be a $C^1$ path. Then

$${\int }_{\gamma }df=f\left(\gamma \left(1\right)\right)-f\left(\gamma \left(0\right)\right).$$

Proof. 

This is the classical fundamental theorem of calculus in the geometric model. The point of the labelled framework is that this identity takes place on the labelled base Y, so endpoints lie on the same sheet.    □

7.3. Monodromy-Consistent Calculus on an Étale Label Cover

Let $p:\tilde{\mathcal{X}}\to \mathcal{X}$ be an étale label cover capturing analytic branches.

Definition 23

(Lifted path). Let $\gamma :[0,1]\to \mathcal{X}$ be a path and let ${\tilde{x}}_0\in \tilde{\mathcal{X}}$ satisfy $p\left({\tilde{x}}_0\right)=\gamma \left(0\right)$. Aliftof γ starting at ${\tilde{x}}_0$ is a path $\tilde{\gamma }:[0,1]\to \tilde{\mathcal{X}}$ such that $p\circ \tilde{\gamma }=\gamma$ and $\tilde{\gamma }\left(0\right)={\tilde{x}}_0$.

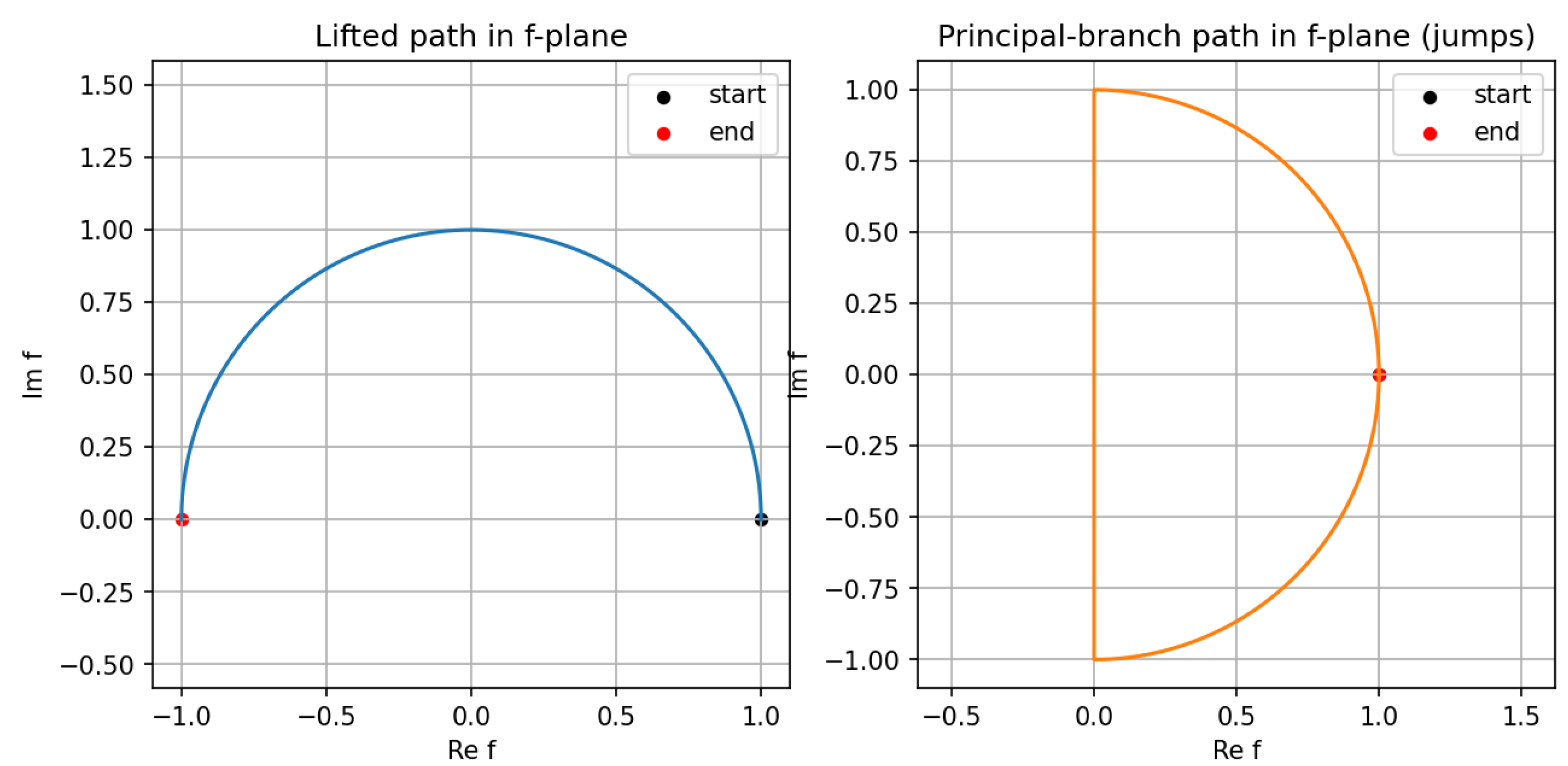
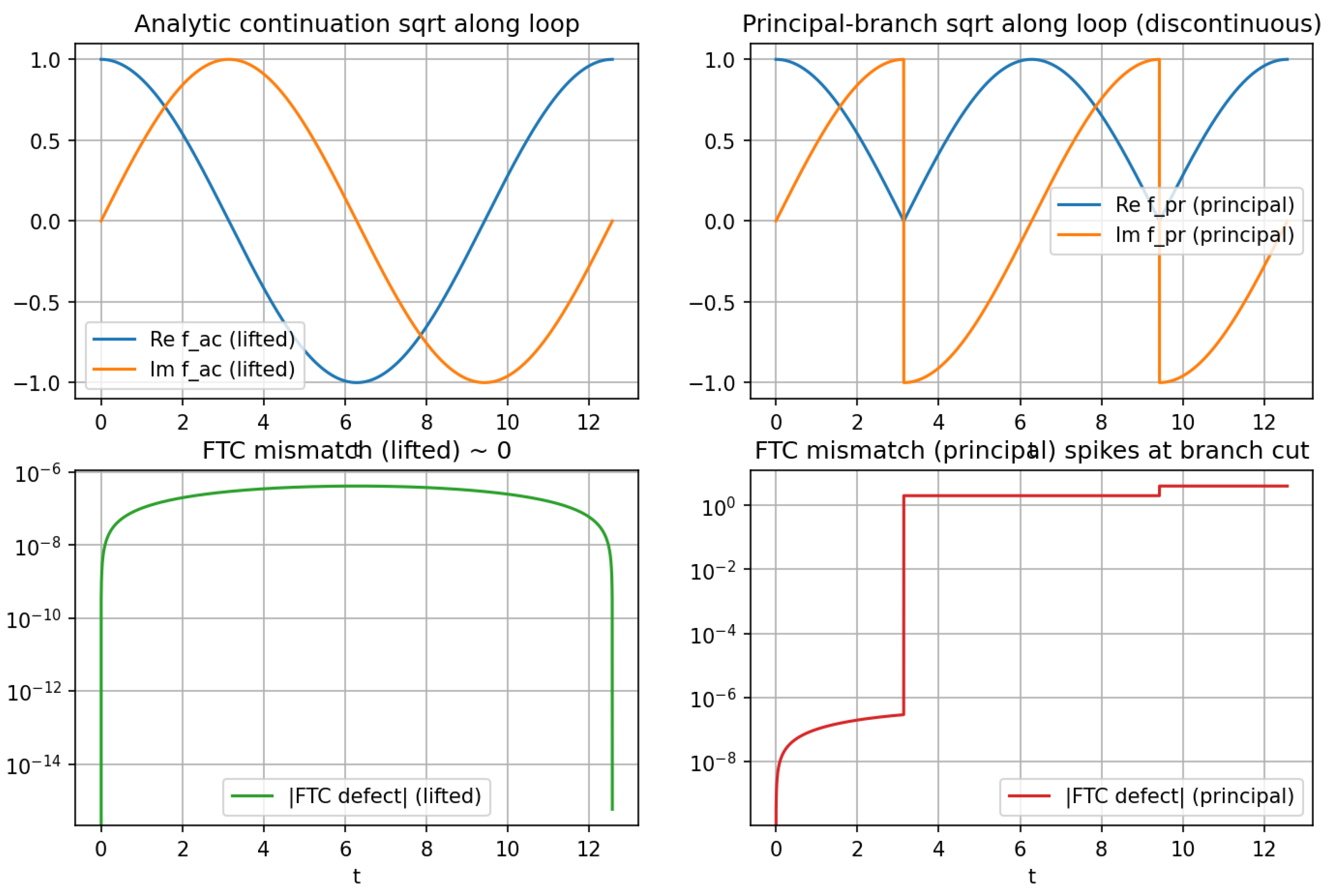
Theorem 7

(Monodromy-consistent fundamental theorem). Let $f\in \Gamma (\tilde{\mathcal{X}},{\mathcal{O}}_{\tilde{\mathcal{X}}})$ be a single-valued branch function on the cover, and let $\gamma :[0,1]\to \mathcal{X}$ be a path with a fixed lift $\tilde{\gamma }:[0,1]\to \tilde{\mathcal{X}}$. Then

$${\int }_{\tilde{\gamma }}df=f\left(\tilde{\gamma }\left(1\right)\right)-f\left(\tilde{\gamma }\left(0\right)\right).$$

If γ is a loop based at $x_0$ and $\tilde{\gamma }\left(0\right)={\tilde{x}}_0$, then $\tilde{\gamma }\left(1\right)=g·{\tilde{x}}_0$ for a unique deck transformation g; thus analytic continuation of f along γ is given by $f(g·{\tilde{x}}_0)$.

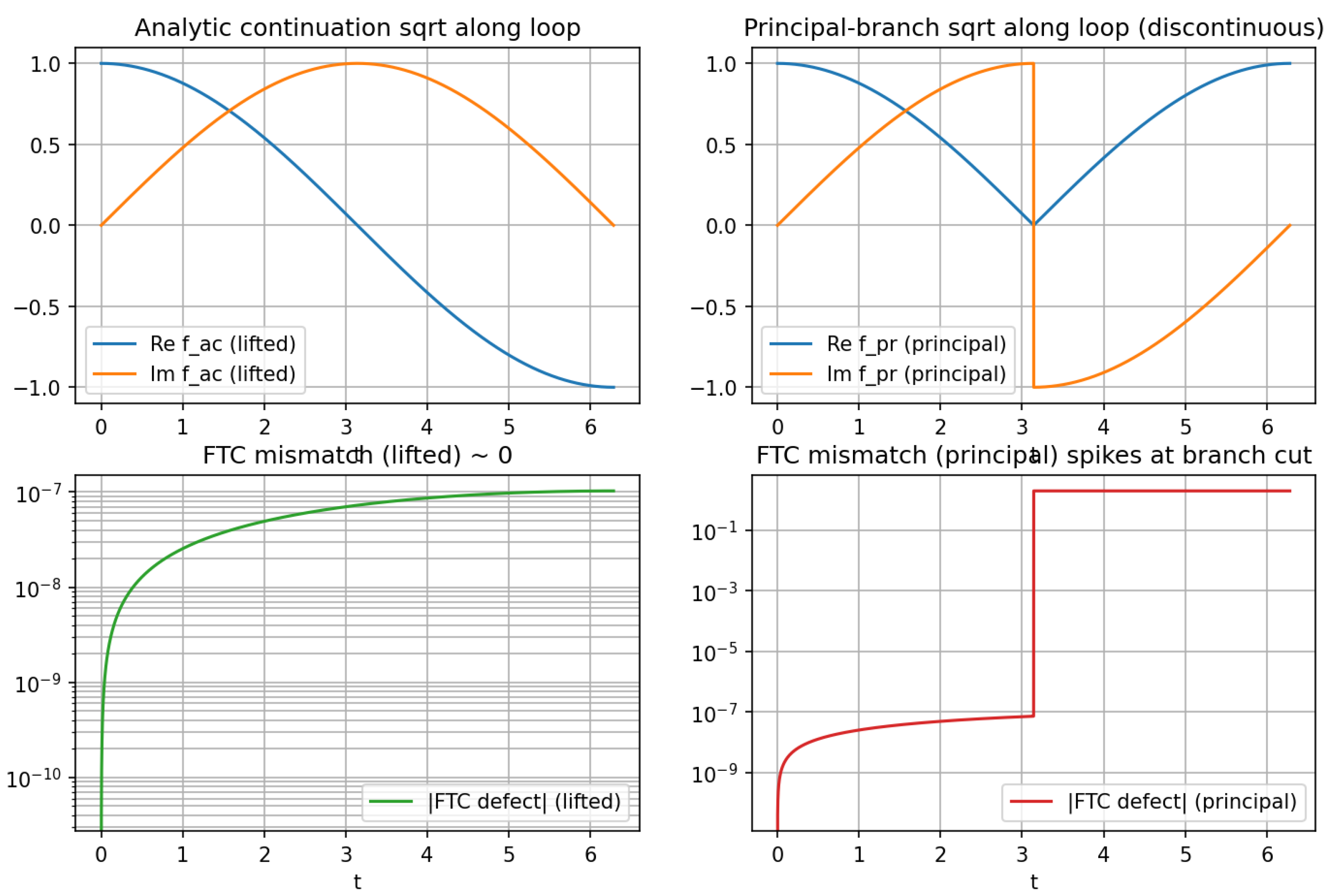
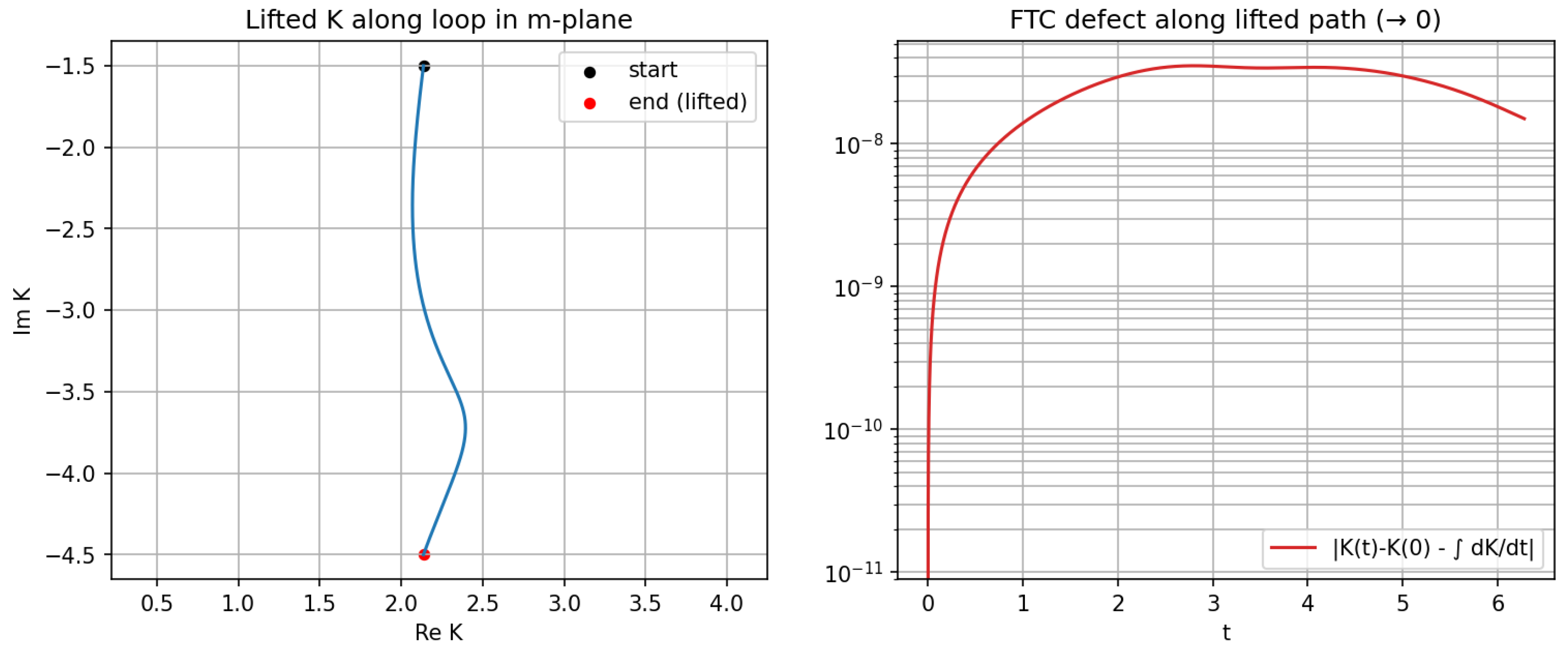
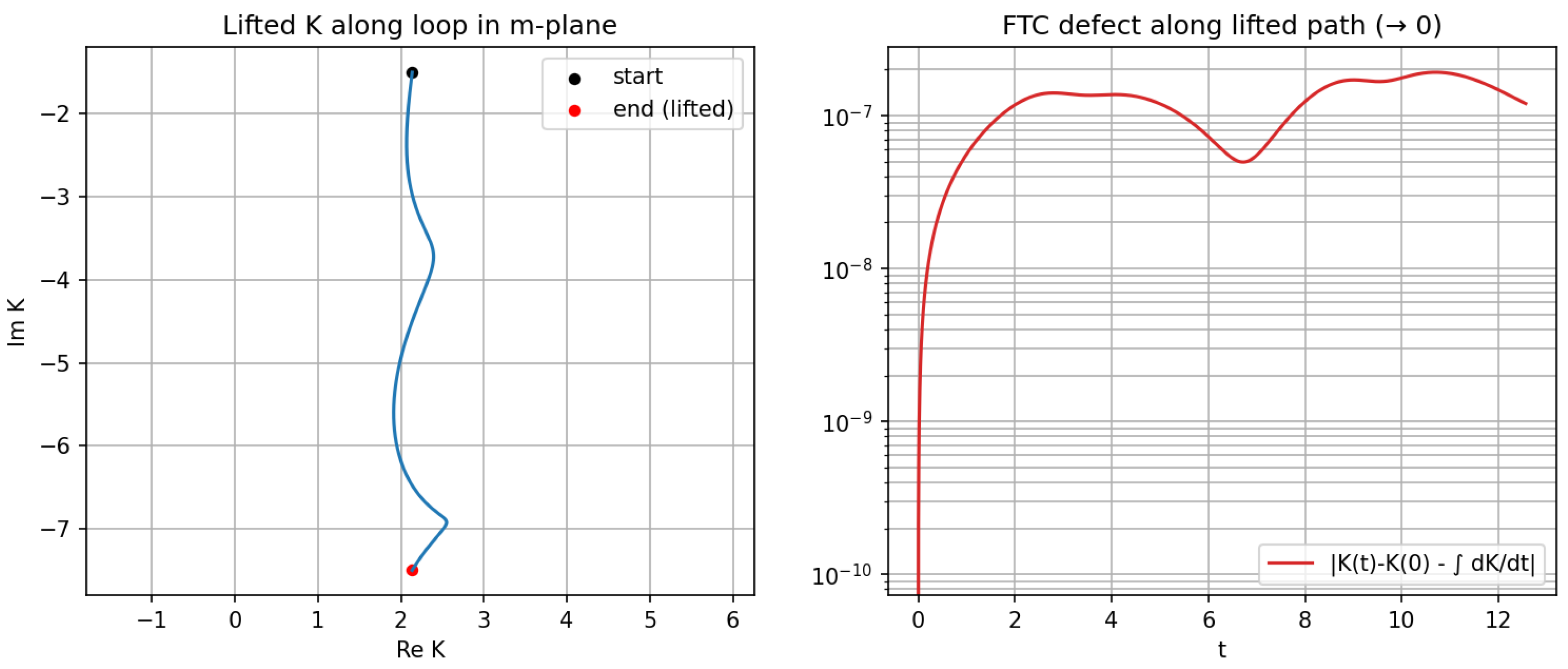
Remark 14

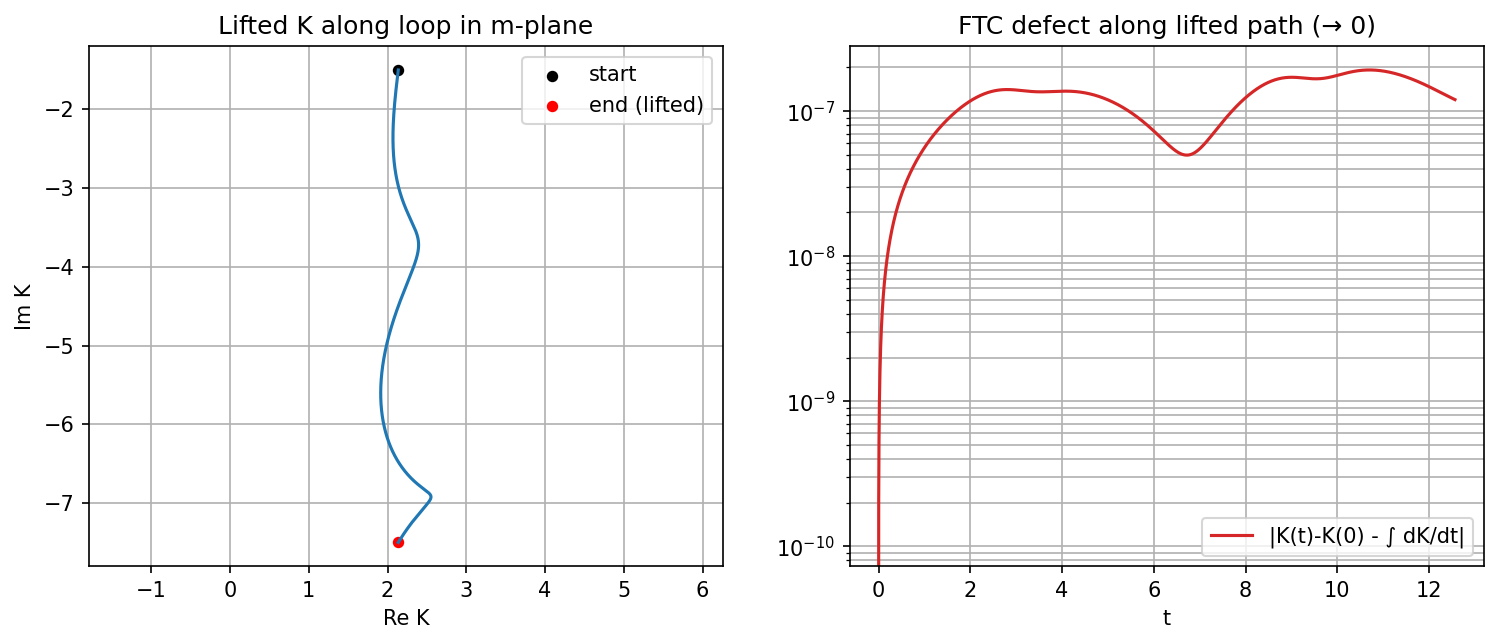
(Connection to the code demonstrations). The scripts in Appendix A.2 implement this theorem in the basic case $f\left(z\right)=\sqrt{z}$ along loops around 0, contrasting lifted-path integration with principal-branch evaluation, which exhibits discontinuities at branch cuts. Appendix A.3 performs the analogous construction for complete elliptic integrals via a Gauss–Manin ODE system, numerically capturing logarithmic monodromy around $m=1$.

8. Energy Laplacian and Branchwise PDE

8.1. Gradient, Divergence, Laplacian on a Labelled Base

Assume Y carries a Riemannian metric (or, in algebraic settings, a suitable metric structure) on $T_{Y/\mathbb{E}}$ inducing an isomorphism $♯:{\Omega }_{Y/\mathbb{E}}^1\to T_{Y/\mathbb{E}}$. Define for $f\in {\mathcal{O}}_Y$:

$$\nabla f:=♯\left(df\right),div\left(V\right):=tr(\nabla V),{\Delta }_{\mathbb{E}}f:=div(\nabla f),$$

where ∇ on vector fields is the Levi–Civita connection when available.

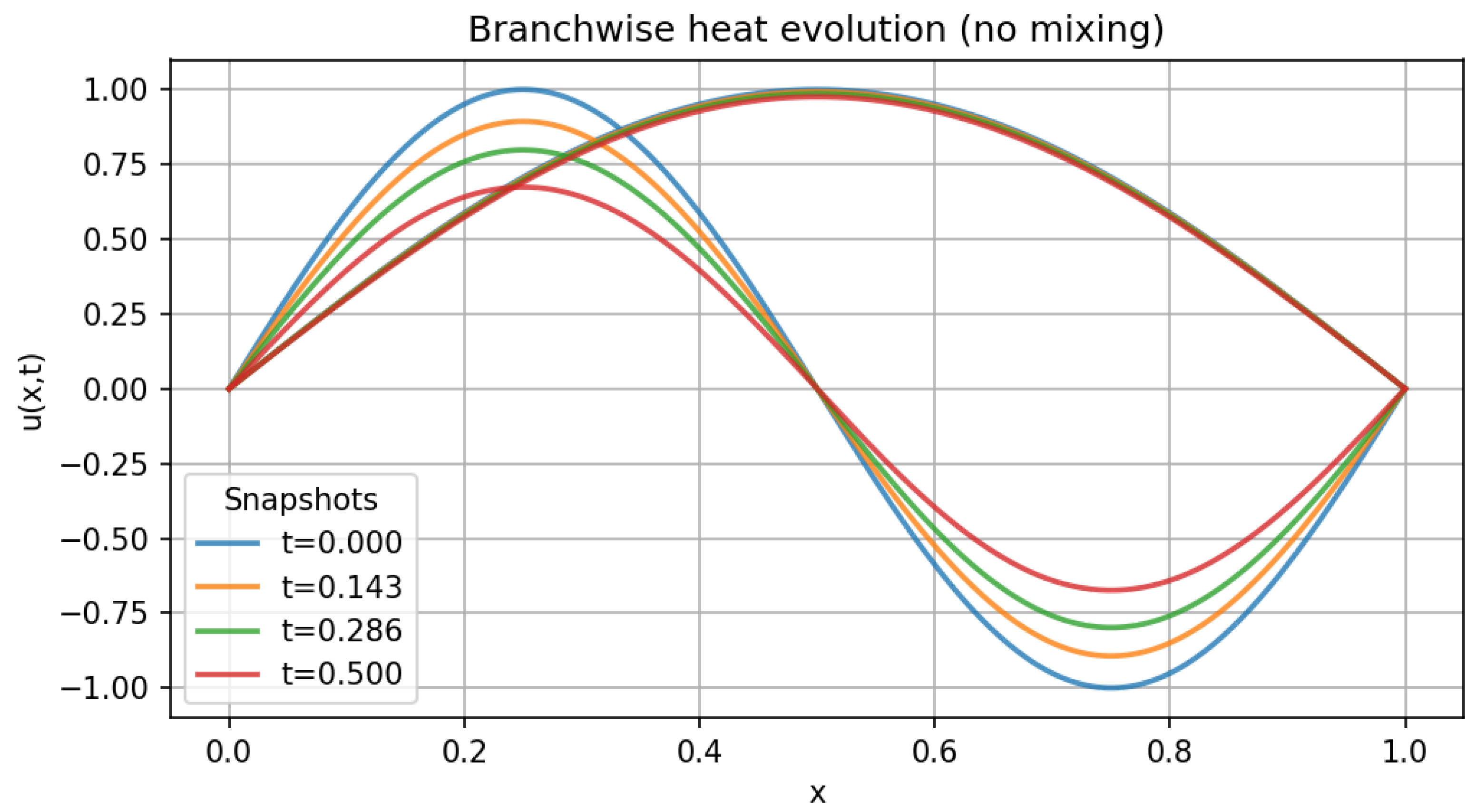
Proposition 13

(Labelwise Laplacian is fibrewise). In the constant-label model $Y={\underline{\mathbb{E}}}_{\mathcal{X}}$, ${\Delta }_{\mathbb{E}}$ acts componentwise on energy fibres. In the étale-label model $Y=\tilde{\mathcal{X}}$, ${\Delta }_{\mathbb{E}}$ acts on each branch on the cover and is compatible with deck transformations.

8.2. Heat Equation Without Branch Mixing

Given $u(t,-)\in \Gamma (Y,{\mathcal{O}}_Y)$, consider the heat equation

$${\partial }_{t}u={\Delta }_{\mathbb{E}}u.$$

In the constant-label model this is a family of independent heat equations indexed by $E\in \mathbb{E}$. On an étale branch cover it is a heat equation on the cover, hence branch-consistent by construction.

9. Controlled Energy/Label Mixing via Correspondences

The labelled slice framework enforces no mixing. To model controlled mixing between labels (e.g. transitions between sheets), we enrich the theory by allowing operators defined along correspondences of label objects.

9.1. Label Correspondences

Definition 24

(Label correspondence). Let $\mathcal{E}$ be a label object over $\mathcal{X}$ (constant or étale). A label correspondence is a span in $Sh\left(\mathcal{B}\right)/\mathcal{X}$:

$$\mathcal{E}\stackrel{s}{\leftarrow }\mathcal{R}\stackrel{t}{\to }\mathcal{E}.$$

Intuitively, $\mathcal{R}$ encodes allowed transitions from a source label (via s) to a target label (via t).

Definition 25

(Transfer functor induced by a correspondence). Assume s and t are representable and that pushforward on modules along t is defined in the chosen model. Define the transfer (mixing) endofunctor on ${\mathcal{O}}_{\mathcal{E}}$-modules by

$${\mathsf{T}}_{\mathcal{R}}\left(\mathcal{F}\right):=t_{*}\left(s^{*}\mathcal{F}\right).$$

Remark 15

(Energy-preserving operators as the diagonal correspondence). If $\mathcal{R}=\mathcal{E}$ and $s=t={\mathrm{id}}_{\mathcal{E}}$ (the diagonal span), then ${\mathsf{T}}_{\mathcal{R}}\cong \mathrm{id}$: no mixing. More generally, a mixing pattern is determined by the fibres of s and t.

9.2. Constant-Label Case: Correspondences Are Relations on Energies

When $\mathcal{E}={\underline{\mathbb{E}}}_{\mathcal{X}}\cong {\coprod }_{E\in \mathbb{E}}{1}_{\mathcal{X}}$, a correspondence $\mathcal{R}\to {\underline{\mathbb{E}}}_{\mathcal{X}}{\times }_{\mathcal{X}}{\underline{\mathbb{E}}}_{\mathcal{X}}$ amounts to a relation on the energy index set (possibly varying over $\mathcal{X}$). In this case, ${\mathsf{T}}_{\mathcal{R}}$ acts like a matrix of functors/operators

$${\left({\mathsf{T}}_{\mathcal{R}}\left(\mathcal{F}\right)\right)}_{E^{\prime }}\simeq \underset{E:(E\to E^{\prime })\in \mathcal{R}}{⨁}{\mathcal{F}}_E,$$

with the precise sum/product depending on whether $t_{*}$ or $t_{!}$ is used.

Example 1

(Coupled branch heat system). Let energies be discrete indices $E\in \{1,\dots ,N\}$ and let ${\kappa }_{E^{\prime },E}\ge 0$ be coupling constants. A controlled-mixing heat system has the form

$${\partial }_t{u}_{E^{\prime }}=\Delta u_{E^{\prime }}+\sum _E{\kappa }_{E^{\prime },E}{u}_E.$$

The Laplacian term is no-mixing; the coupling term is encoded by a correspondence $\mathcal{R}$ allowing transitions $E\to E^{\prime }$ with weights ${\kappa }_{E^{\prime },E}$.

9.3. Composition of Correspondences (Optional Categorical Structure)

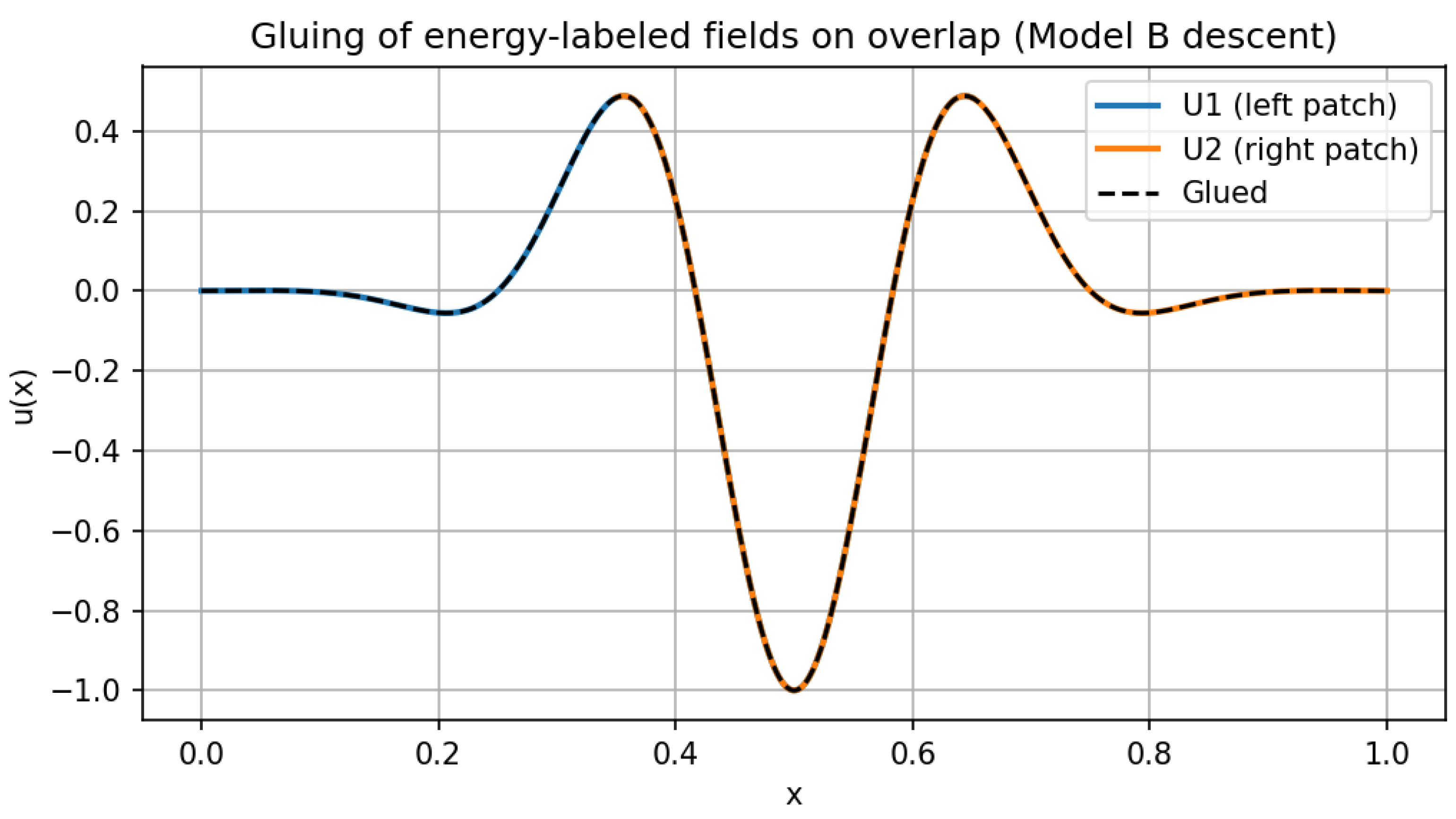
Under standard hypotheses (suitable base change and projection formula), spans compose by pullback:

$$\left(\mathcal{E}\stackrel{s}{\leftarrow }\mathcal{R}\stackrel{t}{\to }\mathcal{E}\right)\circ \left(\mathcal{E}\stackrel{s^{\prime }}{\leftarrow }{\mathcal{R}}^{\prime }\stackrel{t^{\prime }}{\to }\mathcal{E}\right):=\left(\mathcal{E}\stackrel{s\circ {\pi }_1}{\leftarrow }\mathcal{R}{\times }_{\mathcal{E}}{\mathcal{R}}^{\prime }\stackrel{t^{\prime }\circ {\pi }_2}{\to }\mathcal{E}\right),$$

and the induced transfer functors compose accordingly. This yields a bicategory of label correspondences in which no-mixing calculus is the diagonal subtheory.

Appendix A.1. Reproducibility Notes

The scripts below are included verbatim for transparency and reproducibility. They are not required for the theoretical development, but they implement:

• monodromy-consistent differentiation along lifted paths (vs. principal-branch failure);
• numerical branchwise heat flow with no label mixing;
• a basic descent/gluing check enforcing label compatibility;
• (elliptic case) numerical Gauss–Manin transport for $K\left(m\right)$ and $E\left(m\right)$ and detection of logarithmic monodromy around $m=1$.

• Dependencies. The first script uses numpy and matplotlib; it optionally uses sympy. The second script uses numpy, matplotlib, and mpmath.
• Outputs. The scripts save figures to PNG files. The appendix figures below are representative outputs (filenames as provided).

Appendix A.2. Listing: real_diff_demo.py

Appendix A.3. Listing: rd_elliptic_monodromy.py