Submitted:
09 December 2025
Posted:
10 December 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
3. Data and Methods
3.1. Impulse Response Between the Exchange Rate and the Oil Price

3.2. VAR-DCC- GARCH Estimator
3.2.1. The Estimation of the VAR-DCC-GARCH Model
3.2.2. Econometric Estimation Methodology
3.2.3. VAR Model
3.2.4. VAR-DCC-Model
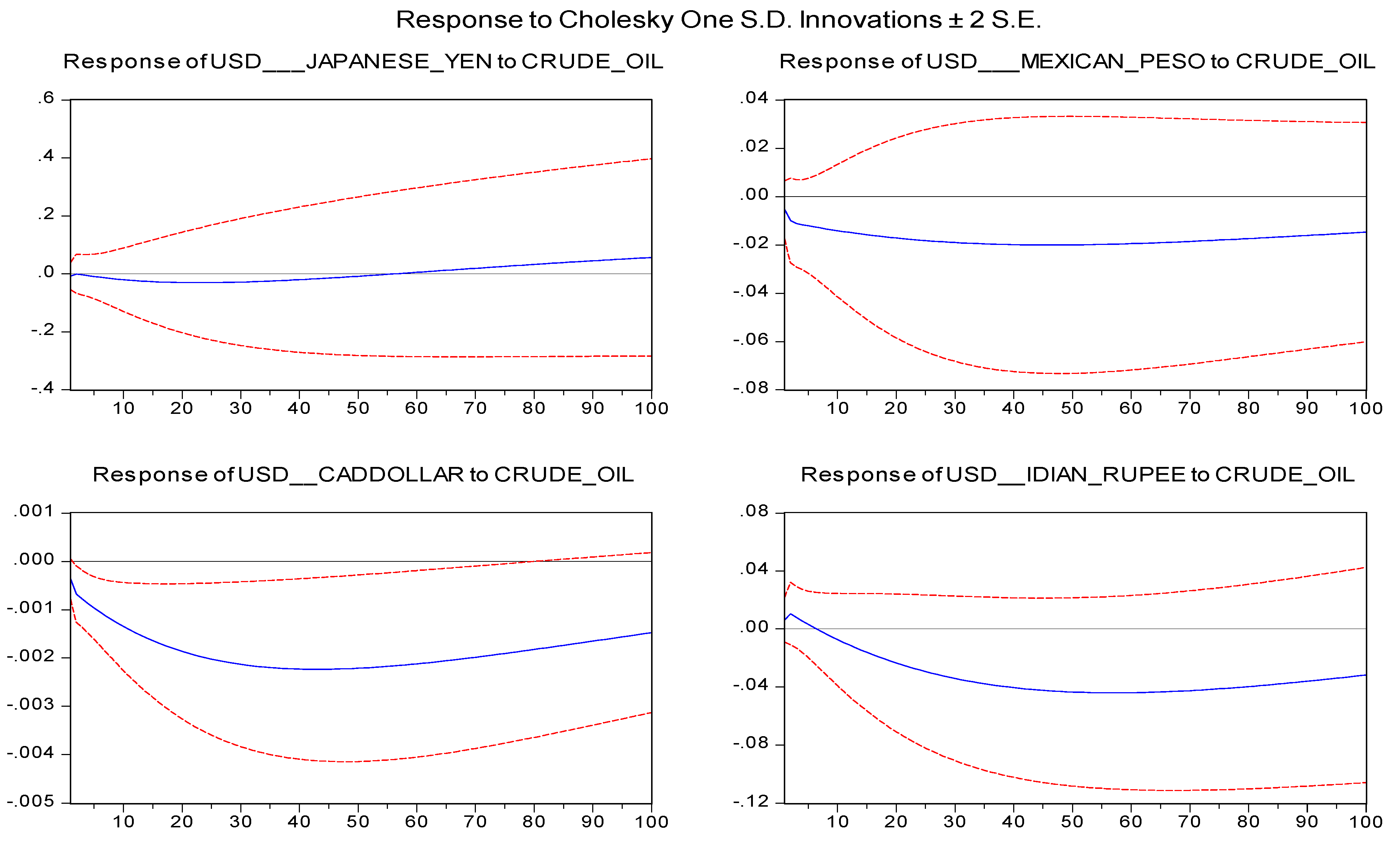
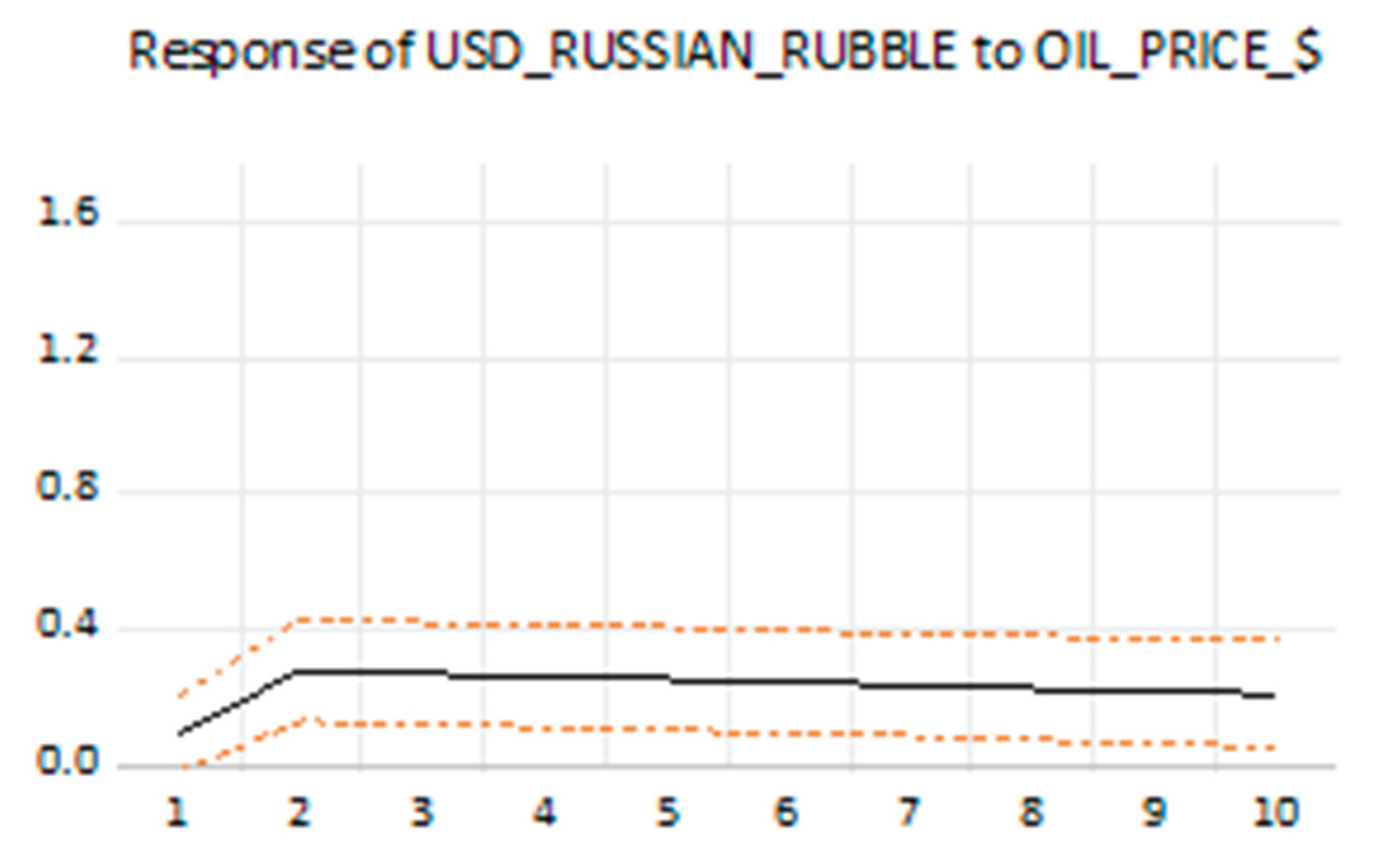
4. Results
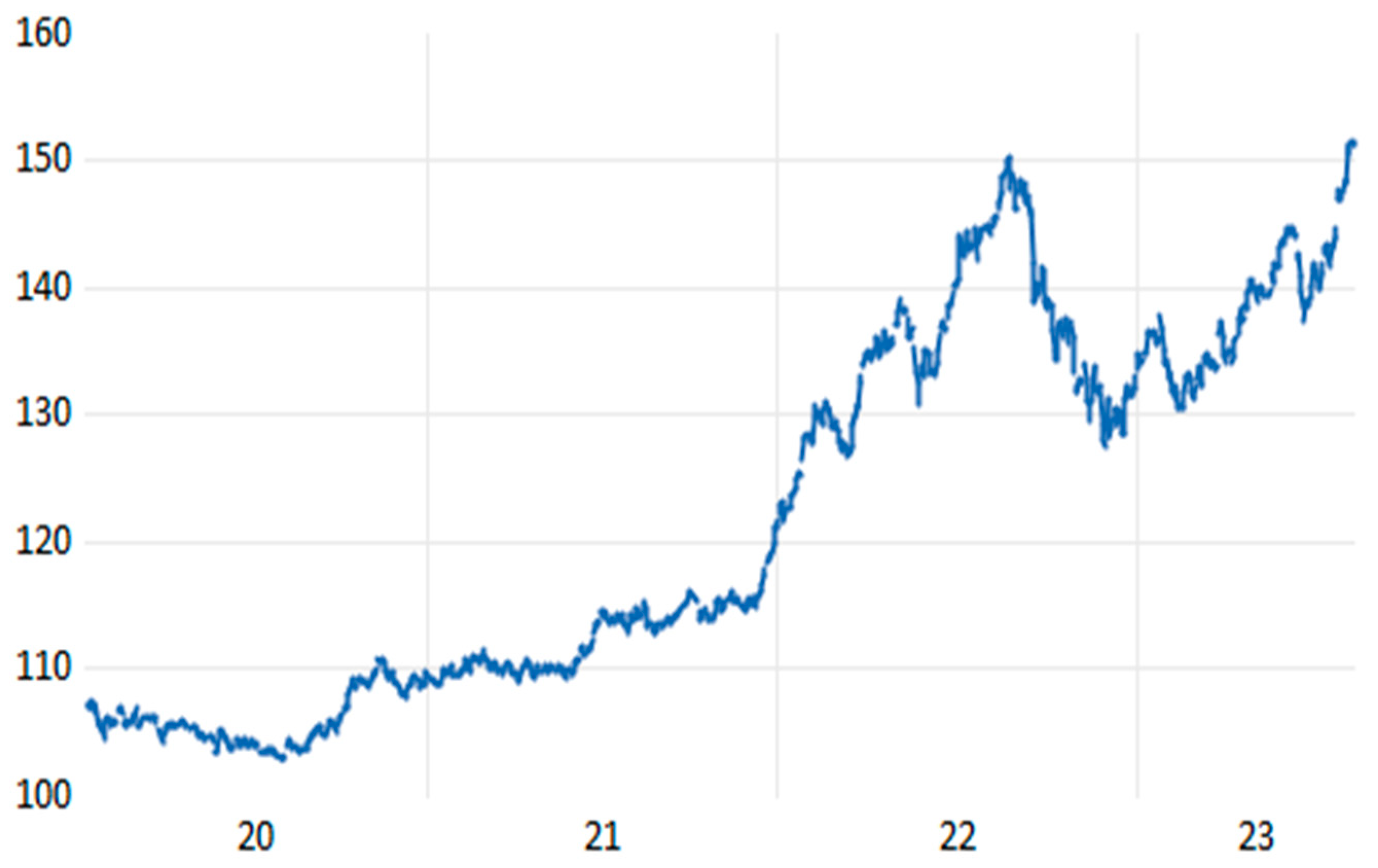
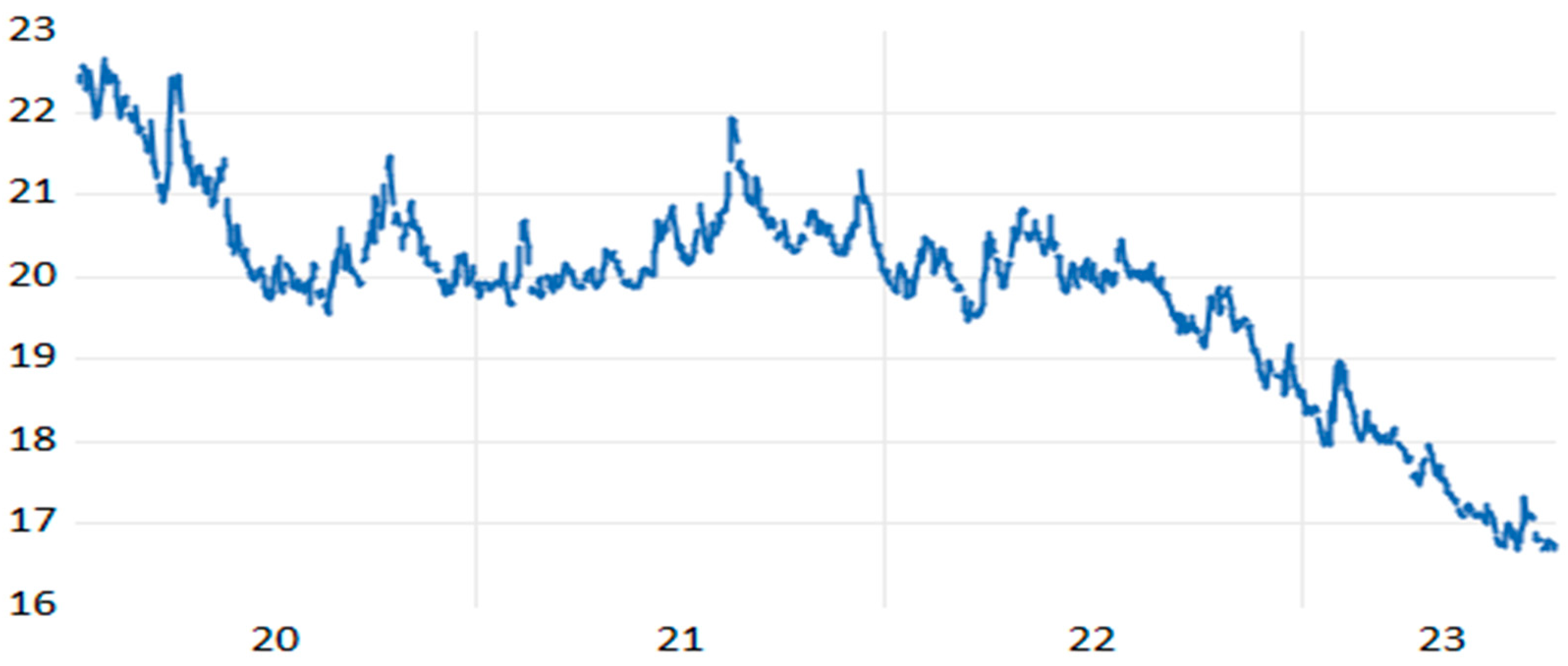
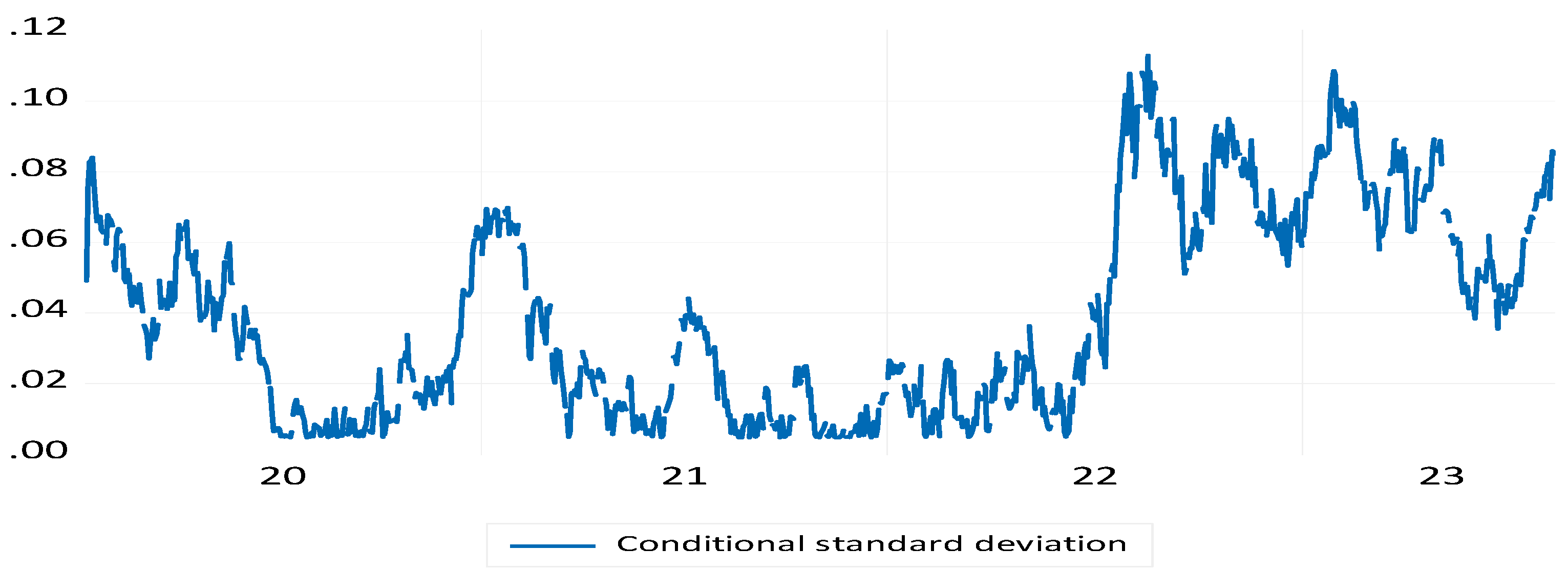
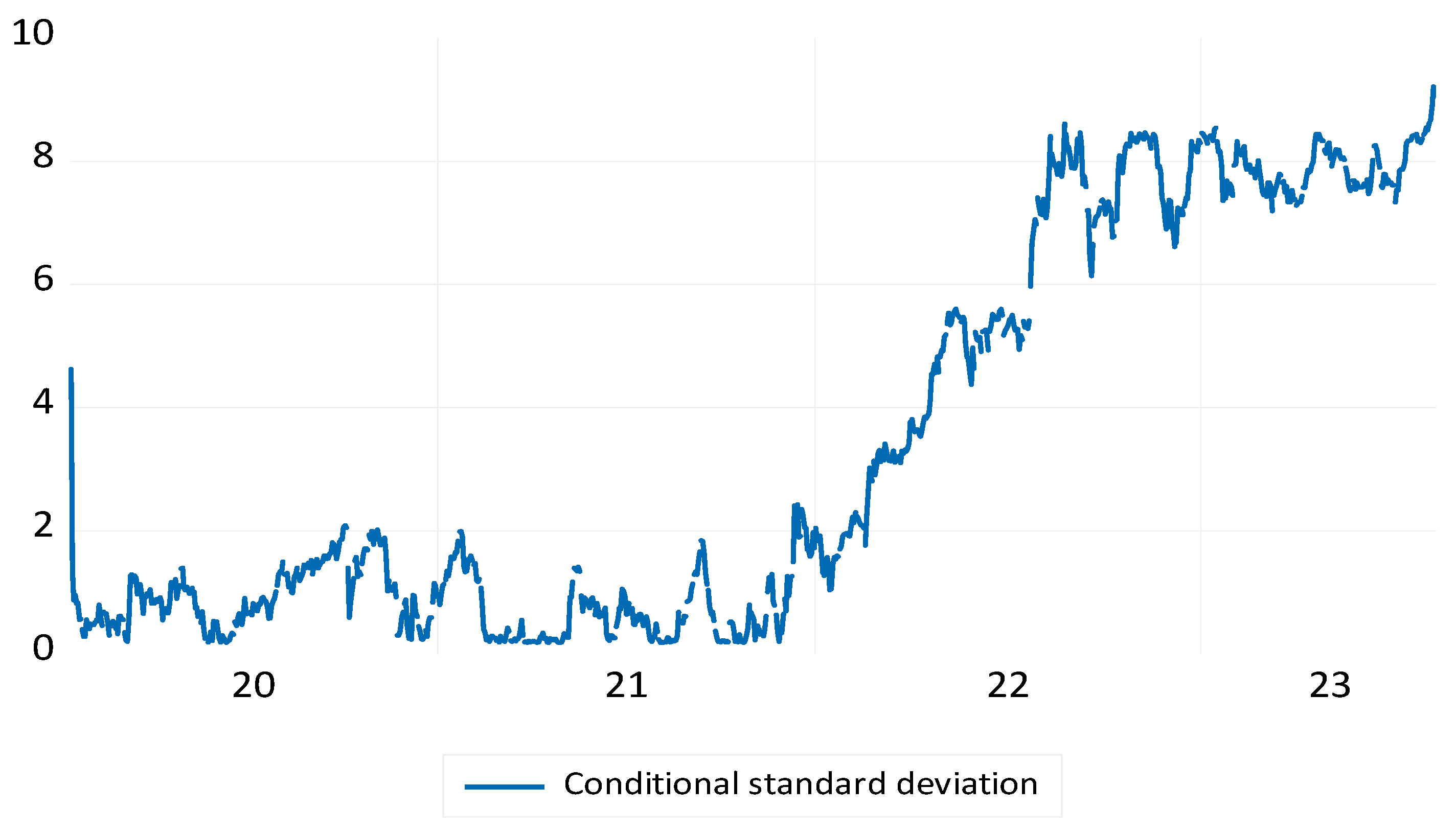
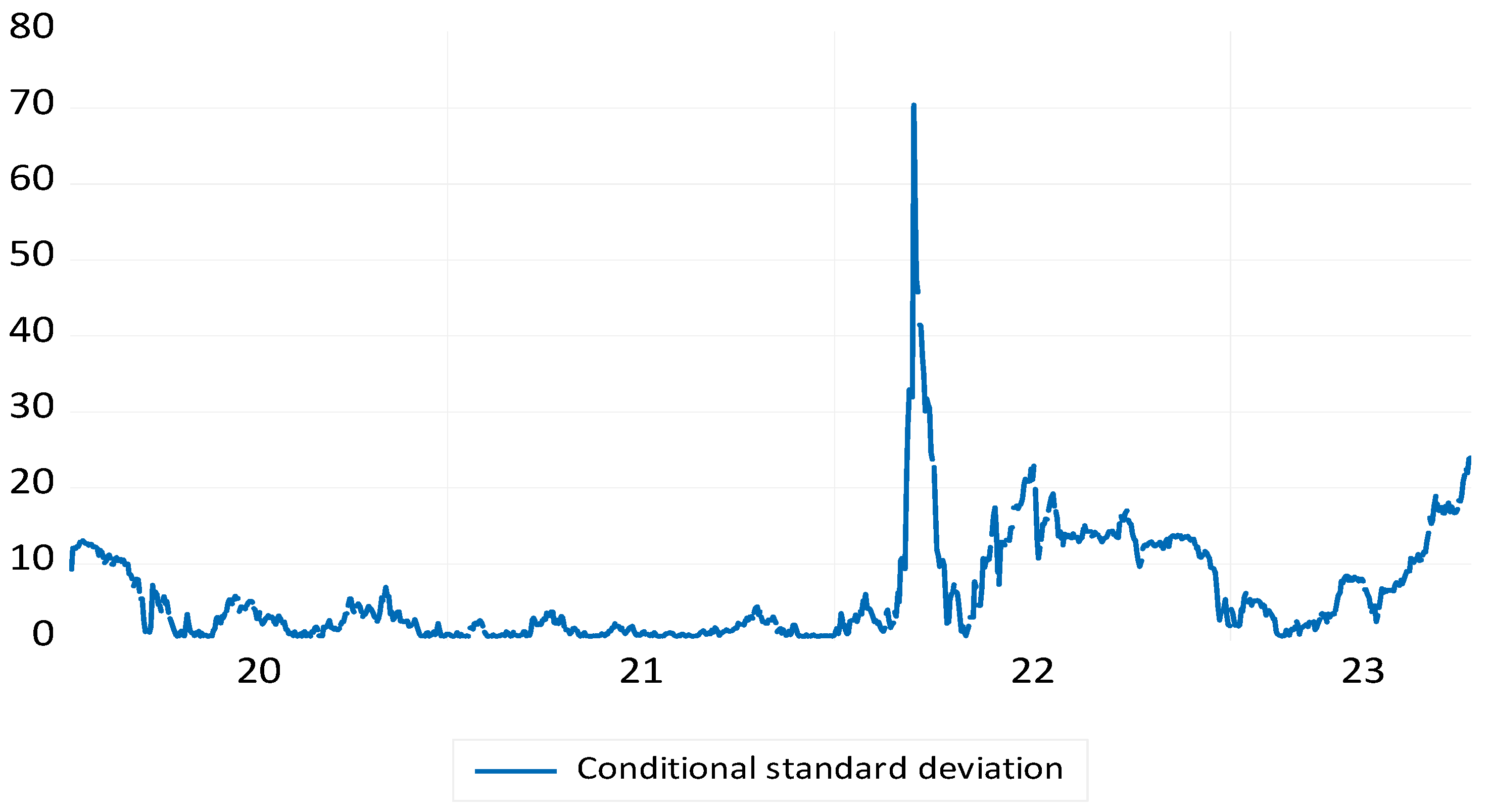
5. Conclusion and Policy Implications
References
- Atems, B.; Kapper, D.; Lam, E. Do exchange rates respond asymmetrically to shocks in the crude oil market? Energy Econ. 2015, 49, 227–238. [Google Scholar] [CrossRef]
- Asadi, M.; Roubaud, D.; Tiwari, A.K. Volatility spillovers amid crude oil, natural gas, coal, stock, and currency markets in the US and China based on time and frequency domain connectedness. Energy Econ. 2022, 109. [Google Scholar] [CrossRef]
- Bloomberg, S.B.; Harris, E.S. The commodity-consumer price connection: fact or fable? Federal Reserve Board of New York. Economic Policy Review 1995, 21–38. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econ. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Cappiello, L.; Engle, R.F.; Sheppard, K. Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. J. Financial Econ. 2006, 4, 537–572. [Google Scholar] [CrossRef]
- Chkir, I.; Guesmi, K.; Ben Brayek, A.; Naoui, K. Modelling the nonlinear relationship between oil prices, stock markets, and exchange rates in oil-exporting and oil-importing countries. Res. Int. Bus. Finance 2020, 54, 101274. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Huang, S.; An, H.; Gao, X.; Wen, S.; Hao, X. Themultiscaleimpactofexchangerates ontheoil-stocknexus:evidencefromChinaandRussia. Appl. Energy 2017, 194, 667–678. [Google Scholar] [CrossRef]
- Ji, Q.; Liu, B.-Y.; Fan, Y. RiskDependenceofCoVaRandStructuralChangeBetweenOil PricesandExchangeRates:ATime-varyingCopulaModel. Energyeconomics 2018. [Google Scholar]
- Jiang, Y.; Feng, Q.; Mo, B.; Nie, H. Visiting the effects of oil price shocks on exchange rates: Quantile-on-quantile and causality-in-quantiles approaches. North Am. J. Econ. Finance 2020, 52. [Google Scholar] [CrossRef]
- Krugman, P. OilandtheDollar. In Economic InterdependenceandFlexibleExchangeRates; INBahandari, JS, Putnam, BH, Eds.; MITPress: Cambridge,MA, 1983. [Google Scholar]
- Kyriazis, N.; Corbet, S. The role of international currency spillovers in shaping exchange rate dynamics in Latin America. Q. Rev. Econ. Finance 2024, 94, 1–10. [Google Scholar] [CrossRef]
- Umar, Z.; Aziz, M.I.A.; Zaremba, A.; Tran, D.K. Modelling dynamic connectedness between oil price shocks and exchange rates in ASEAN+3 economies. Appl. Econ. 2023, 55, 2676–2693. [Google Scholar] [CrossRef]
- Xu, Y.; Han, L.; Wan, L.; Yin, L. Dynamic link between oil prices and exchange rates: A non-linear approach. Energy Econ. 2019, 84. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Ren, X. Asymmetric effects of crude oil prices and USD exchange rate on precious metals returns:Evidence from pre and during COVID-19 outbreak. Heliyon 2023, 9, e21996. [Google Scholar] [CrossRef] [PubMed]
| Data | Description |
| Energy | Crude oil price in US Dollar per Barrel |
| Mexican | Peso Mexican to US $ |
| Japanese yen | Japanse Yen to US $ |
| Russian | Ruble Russian to US $ |
| Chinese | Yuan Chinese to US$ |
| Australian | Australian dollar to US $ |
| Crude oil | USD/Japanese Yen | USD/Mexican Pesos | USD/Canadian Dollar | USD/Indian Rupee | USD/Russian Rubble | |
| Mean | 72.35074 | 118.6943 | 20.28068 | 1.305822 | 76.49582 | 73.04935 |
| Median | 74.49000 | 111.4400 | 20.10270 | 1.301000 | 75.13100 | 73.66030 |
| Maximum | 133.1800 | 150.3200 | 25.11300 | 1.462200 | 83.03700 | 143.0000 |
| Minimum | 9.120000 | 102.8300 | 17.08000 | 1.203900 | 70.80800 | 51.45000 |
| Std. Dev. | 24.96555 | 13.60424 | 1.454220 | 0.049583 | 3.529688 | 9.239425 |
| Skewness | -0.056550 | 0.651157 | 0.658737 | 0.264079 | 0.620975 | 1.446933 |
| Kurtosis | 2.580234 | 1.889411 | 4.135947 | 2.409354 | 1.983891 | 10.34939 |
| Jarque-Bera | 7.173937 | 111.1962 | 114.8662 | 23.83080 | 97.73954 | 2511.115 |
| Probability | 0.027682 | 0.000000 | 0.000000 | 0.000007 | 0.000000 | 0.000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





