Substituent Effects in the Thermal Decomposition of 1,2,4-Triazol-3(2H)-Ones and Their Thione Analogues: A DFT Study with Functional Performance

Rosalinda Ipanaque-Chávez; Marcos Loroño; Tania Cordova-Sintjago; Miguel Ponce-Vargas; José L. Paz

doi:10.20944/preprints202512.0474.v1

Submitted:

03 December 2025

Posted:

04 December 2025

You are already at the latest version

Abstract

This computational study investigates the thermal decomposition of 1,2,4-triazol-3(2H)-ones and their thione analogues using Density Functional Theory (DFT). The reaction proceeds via a concerted, six-membered cyclic transition state, primarily driven by the breaking of the N–N bond. A key finding is that the accuracy of the calculated activation energies (Ea) strongly depends on the choice of the DFT functional. For sulfur-containing systems (thiones), the hybrid functional APFD (with 25% Hartree-Fock exchange) provides the most reliable results, effectively describing their higher polarizability. In contrast, for oxygen-containing systems (triazolones), the dispersion-corrected functional B97D-GD3BJ (with 0% Hartree-Fock exchange) delivers superior accuracy by better modeling electrostatic and dispersion interactions. The -CH₂CH₂CN group at the N-2 position acts not only as a protecting group, but also stabilizes the transition state through non-covalent interactions. Electron-withdrawing substituents slightly increase the Ea, while electron-donating groups decrease it. Sulfur analogues consistently show significantly lower activation energies (by ~40 kJ/mol) than their oxygen counterparts, explaining their experimentally observed faster decomposition. This work establishes a dual-methodology computational framework for accurately predicting the kinetics of these reactions, providing valuable insights for the regioselective synthesis of biologically relevant triazole derivatives via controlled pyrolysis.

Keywords:

DFT

;

triazole

;

regioselective

;

kinetics

;

reaction mechanisms

;

NBO

;

IGM

Subject:

Chemistry and Materials Science - Theoretical Chemistry

Introduction

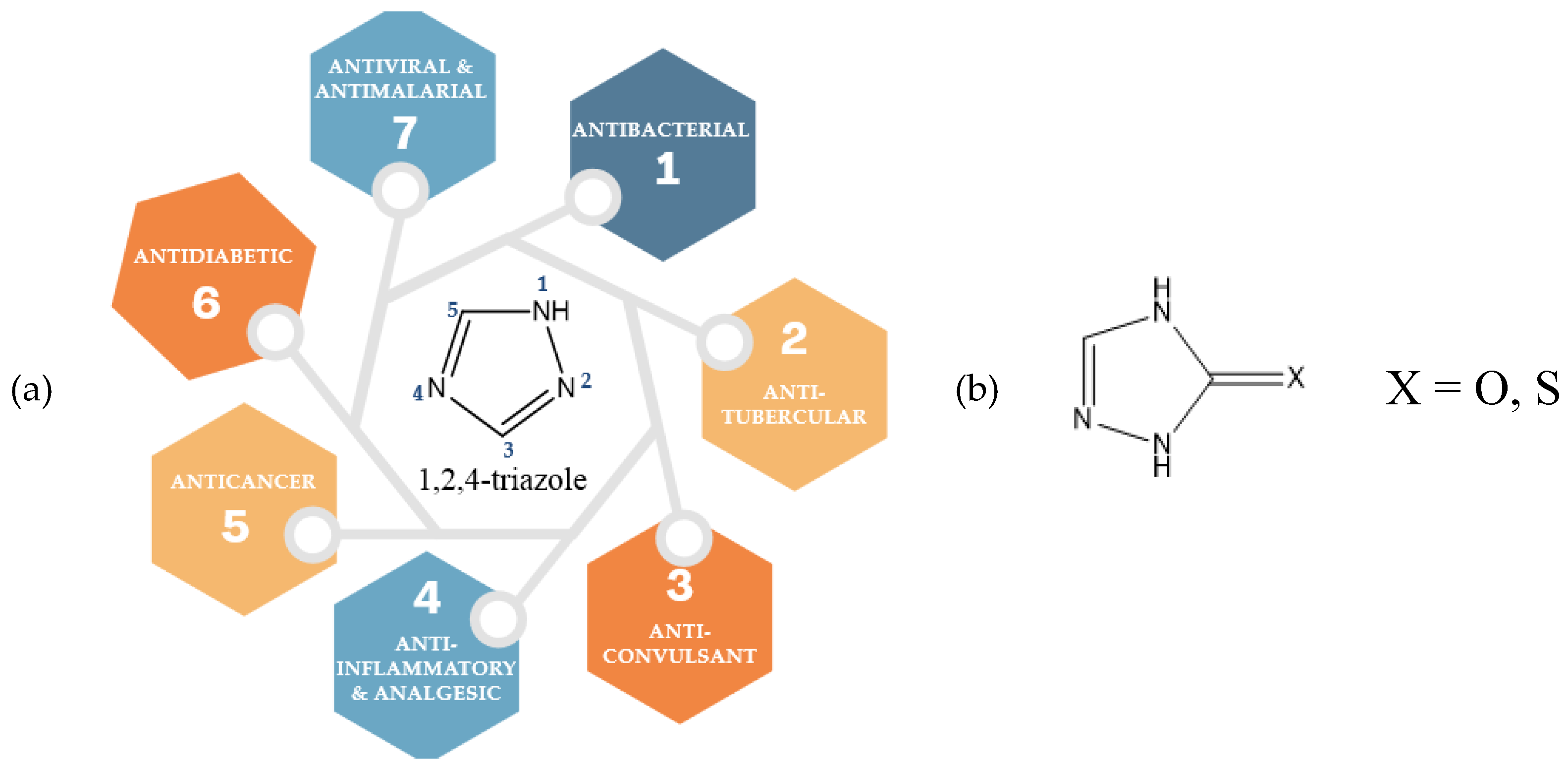
Nitrogen-containing five-membered heterocycles, particularly triazoles, play a pivotal role in medicinal and materials chemistry due to their pharmacological versatility and thermal stability [1,2]. Among these, 1,2,4-triazole derivatives stand out for their broad biological activities, including antifungal, antiviral, and anticancer properties [3,4,5,6,7]. 1H-1,2,4-triazole-5(4H)-one is depicted in Scheme 1b. Substituting oxygen for sulfur to form triazole-thione derivatives enhances its antiproliferative and anticonvulsant effects, as documented in previous studies [8,9] (Scheme 1).

An experimental work by Al-Awadi et al. studied the thermal decomposition of 4-arylideneimino-2-cyanoethyl-1,2,4-triazole-3(2H)-ones/thiones in the gas phase and proposed a unimolecular concerted mechanism via a six-membered cyclic transition state (TS), as shown in Scheme 2. Triazole-thione derivatives exhibited reactivity 10³ times faster than their oxygenated analogues at 500 K [10]. While this difference in reactivity was initially attributed to the greater thermodynamic stability of π bonds (C=S vs. C=O) and enhanced protophilicity [10,11], the underlying electronic and steric details remained unresolved.

This study focuses on 2-ethyl or 2-(2-cyanoethyl)-1,2,4-triazol-3(4H)-ones/thiones (R = CH₂CH₂CN) with N-2 substitution, aiming to facilitate regioselective functionalization at other ring nitrogen sites. Controlled pyrolysis of 2-cyanoethyl derivatives allows sequential deprotection at N-4 and N-2, offering a strategic pathway for synthesizing 2- and 4-substituted 1,2,4-triazoles with potential biological applications. For the studied system, Al-Awadi et al. highlighted the critical influence of the -CH₂CH₂CN group at the triazole N-2 position on activation energy (Eₐ) through steric and electronic interactions with the TS [12].

Advances in computational chemistry enable precise exploration of these mechanisms. A previous theoretical investigation of the gas-phase thermal decomposition of 4-arylideneimino-1,2,4-triazol-3(2H)-ones/thiones, studied the reaction mechanism through a one-step, six-membered cyclic TS [13]. This work suggested that N–N bond elongation was the driving force, with Wiberg bond indices indicating slightly advanced bond-breaking processes relative to X-Y bond formation.

In this theoretical work, we are re-evaluating the oxygen/sulfur influence in the reaction mechanism and assessing the sulfur atom effect on the Eₐ and exploring the intrinsic electronic dynamics, including the role of hybrid functionals in Hartree-Fock exchange (%HF) contributions and their impact on Eₐ predictions. We employ the APFD (Austin-Frisch-Petersson with dispersion) method [14], paired with the def2-TZVP basis set, as a reference, alongside other functionals with varying percentages of HF contributions. Non-covalent interactions in the TS, involving compounds other than -CH₂CH₂CN, such as: -H; -CH₂CH₃; -CH₂CH₂-CS-CH₃; -CH₂CH₂-CO-CH₃; and -CH₂CH₂-S-CH₃, were also studied to understand their possible influence on the reaction mechanism. The different TSs were analysed via the Independent Gradient Model (IGM) [15,16,17,18], through the descriptors

δ

g or

δ

q, to elucidate reactivity differences between S/O analogues.

Computational Methods

1.: Thermodynamic Properties and Wiberg Bond Index

Density functional theory (DFT) calculations were performed using the Gaussian16 program suite [19]. We employed a combination of pure and hybrid exchange functionals, with the Def2-TZVP basis set, to determine the geometric parameters for all reactants, transition states (TSs), and products involved in the studied reactions. Each stationary structure was characterized as a minimum or a first-order saddle point through analytical frequency calculations. An empirical dispersion correction (gd3bj) was applied where necessary [20].

Thermal corrections to Enthalpy, Gibbs, and Entropy were evaluated at the experimental temperature of 500 K [21]. Intrinsic reaction coordinate (IRC) calculations [22] were conducted for all cases to confirm that the localized TS structures correctly connected the corresponding minimum of reactants and products. Single-point energy calculations were performed with multiple functionals using the Def2-TZVP basis set [23] to derive energy profiles and kinetic parameters. Bonding characteristics of reactants, TSs, and products were analyzed using the natural bond orbital (NBO) method of Reed and Weinhold [24,25]. The NBO formalism, which provided Wiberg bond indices [26], was used to track reaction progress. These analyses were performed using the NBO program [27], integrated into Gaussian16.

For kinetic parameter calculations, classical transition state theory (TST) [28,29] was applied. The rate constant k(T) for each elementary step—assuming a transmission coefficient of unity—was expressed as:

k (T) = \frac{K_{b} T}{h} \exp (\frac{- ∆ G^{‡} (T)}{R T}),

[1]

where

k_{B}

, h, and R are the Boltzmann constant, Planck constant, and universal gas constant, respectively.

{∆ G}^{‡} (T)

represents the standard-state free energy of activation at temperature T. Activation energies (

E_{a}

) and Arrhenius pre-exponential factors (A) were derived from TST from:

E_{a} = ∆ H (T) + R T,

[2]

A = \frac{e k_{B} T}{h} \exp (\frac{∆ S^{‡} (T)}{R}) .

[3]

Wiberg bond indices were computed for bonds undergoing formation or cleavage in reactants, TSs, and products. The relative bond index variation at the TS (

δ B_{i}

) for each bond i was defined as [30]:

δ B_{i} = \frac{(B_{i}^{T S} - B_{i}^{R})}{(B_{i}^{P} - B_{i}^{R})},

[4]

where superscripts R, TS, and P denote reactants, TSs, and products, respectively. The reaction progress (%EV) was quantified as:

% E V = 100 δ B_{i}

[5]

The average bond index advancement (

δ B_{a v}

) and reaction synchronicity (

S_{S}

) were calculated as [30]:

δ B_{a v} = \frac{1}{n} \sum δ B_{i},

[6]

S_{S} = 1 - S_{A}, w h e r e S_{A} = \frac{1}{(2 N - 2)} \sum \frac{|δ B_{i} - δ B_{a v}|}{δ B_{a v}}

[7]

where,

S_{A}

represents absolute asynchronicity, and

S_{S}

ranges from 0 (complete asynchronicity) to 1 (perfect synchronicity).

2.: IGM Bond Index IBSI

The IBSI (Independent Gradient Model-based Bond Index [31]) and its descriptor

{δ g}^{p a i r}

was derived from the Independent Gradient Model (IGM). The IGM-

δ

scheme. This approach is designed to identify and quantify molecular interactions by analyzing electron density (ED) topology, specifically its gradient ∇ρ. By plotting

{δ g}^{p a i r}

against the ED, oriented with the sign of the second Hessian eigenvalue (λ₂). The method captures a wide range of interactions, including covalent bonds, transition-metal bonding, hydrogen bonds, and van der Waals forces, regardless of the presence of bond critical points (BCPs).

For an atom pair, the IBSI (

∆ g^{p a i r})

measures the electron sharing per squared unit distance and is calculated as:

∆ g^{p a i r} = \int_{V} \frac{δ g^{p a i r}}{d^{2}} d V .

[8]

where d is the internuclear distance. To standardize comparisons, the

∆ g^{p a i r}

is normalized to 1 for the H₂ molecule.

In accordance with the method, for a system with interacting fragments A and B,

δ g^{p a i r}

is defined as:

δ g^{p a i r} = \nabla ρ^{I G M} - \nabla ρ = |\frac{𝜕 ρ_{A}}{𝜕 x}| + |\frac{𝜕 ρ_{B}}{𝜕 x}| - |\frac{𝜕 ρ_{A}}{𝜕 x} + \frac{𝜕 ρ_{B}}{𝜕 x},|

[9]

where the equation applies to all three spatial directions (x, y, z). Non-zero

{δ g}^{p a i r}

values exclusively indicate interactions: stronger interactions correspond to larger

δ g

magnitudes.

The IBSI index is versatile, applicable to diverse bonding scenarios beyond closely related molecules. It is particularly useful for tracking bond formation/cleavage during reactions and predicting intrinsic bond strengths in transition states. Changes in IBSI values across reaction pathways provide insights into distinct phases of chemical bonding evolution.

To enhance the visualization of

{δ g}^{p a i r}

signatures in 2D plots, the descriptor

δ

q can be further introduced:

δ q = \frac{\nabla ρ^{I G M}}{\nabla ρ} .

[10]

Unlike

δ

g, the

δ

q is more sensitive to weak interactions (e.g., hydrogen bonds) as the gradient electronic density (∇ρ) tends to zero.

3.: Selection of the Calculation Level

The selection of an appropriate basis set is fundamental for the reliability of quantum chemical calculations. While smaller basis sets, such as 6-311G(d,p), are often adequate for optimising molecular geometries or calculating vibrational frequencies [32], they may lack the flexibility required to accurately describe electron density-dependent properties—such as interaction energies or non-covalent interactions. For this reason, we employed the Def2-TZVP basis set. This is a triple-zeta split-valence basis set augmented with polarization functions, which offers a superior description of the electron distribution compared to double-zeta or minimal basis sets. Furthermore, Def2-TZVP provides an excellent balance between computational cost and accuracy for properties sensitive to electron correlation, such as those central to this study.

Regarding the exchange-correlation functional, we employed the APFD hybrid functional as an initial reference functional. It is a well-developed and parameterised functional that combines accurate and balanced performance across a wide range of chemical applications [33]. APFD integrates a portion of exact Hartree-Fock exchange with density functional exchange and correlation, along with an empirical dispersion correction (D3). This combination makes it particularly robust for describing challenging electronic environments, including compounds containing sulfur and oxygen, as well as non-covalent interactions (e.g., van der Waals forces and hydrogen bonding).

For hybrid functionals, the percentage of Hartree-Fock (HF) exchange is a key adjustable parameter that can be optimized for specific properties. Unlike standard hybrid functionals, the B97D-GD3BJ functional is a pure generalized gradient approximation (GGA) functional [34], containing 0% HF exchange. Its accuracy for non-covalent interactions stems from its built-in, empirically parameterized dispersion (GD3BJ). This makes it a powerful tool that often outperforms hybrids like B3LYP for systems where dispersion forces are dominant. Comparisons with other hybrids such as B3LYP-GD3BJ (20% HF) [35,36], M06-2X-D3(0) (54% HF) [37], and O3LYP-GD3BJ (11.61% HF) [38], highlight B97D’s advantages for oxygen-rich and dispersion-sensitive systems, as we have noticed here in our study with several triazole derivatives containing oxygen.

The Gaussian16 package allows you to configure custom hybrid functionals via the parameters a,b, and c in the exchange-correlation equation [19]:

{X C}^{F u n t i o n a l} = {a E}_{x}^{l o c a l} + (1 - a) E_{x}^{H F} + {b E}_{x}^{n o n - l o c a l} + {c E}_{c}^{n o n - l o c a l} + {(1 - c) E}_{c}^{l o c a l}

[11]

These are adjusted using IOP commands (e.g., IOp(3/76=mmmmmnnnnn)), where the characters m and n values encode P1–P6 to weight Slater local exchange, non-local terms, and exact HF contributions. This flexibility enables precise functional design for specific electronic structure challenges.

Hybrid functionals integrate exact exchange to reduce self-interaction errors, with range-separated hybrids modulating this contribution based on inter-electron distances. For chemical kinetics (e.g., barrier calculations), higher exact exchange percentages are often essential. The B97 functional family, for instance, shows dual optima for reaction barriers: ~16% HF (local) and ~45% HF (global). Such insights guide functional selection to balance accuracy and cost for mechanistic studies. However, B97D functional has no HF contribution and is very popular for non-covalent interactions. In this work, various functionals with different HF exchange contributions were selected, aiming to obtain a new one (equation 11) if significant differences from existing functionals were observed.

Based on our theoretical results, we concluded that the APFD functional, complemented by B97D-GD3BJ benchmarks and customizable hybrids, ensures robust modeling of triazole thermolysis. This approach captured electronic effects (e.g., sulfur’s role in lowering Ea), non-covalent interactions, and reaction dynamics while maintaining computational tractability. The methodology aligns with our goal of unraveling substituent and mechanistic influences on thermal decomposition pathways.

Results and Discussion

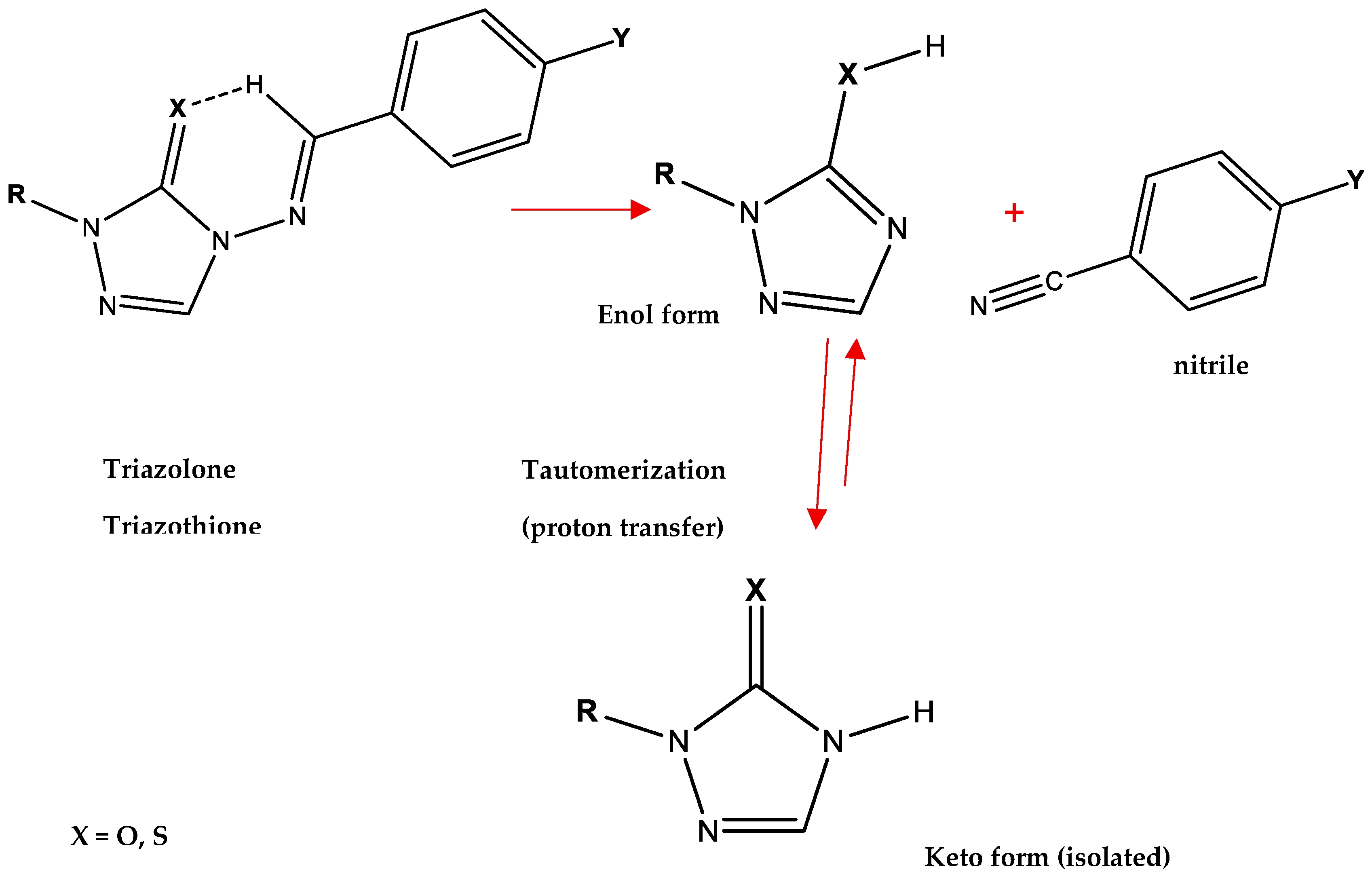
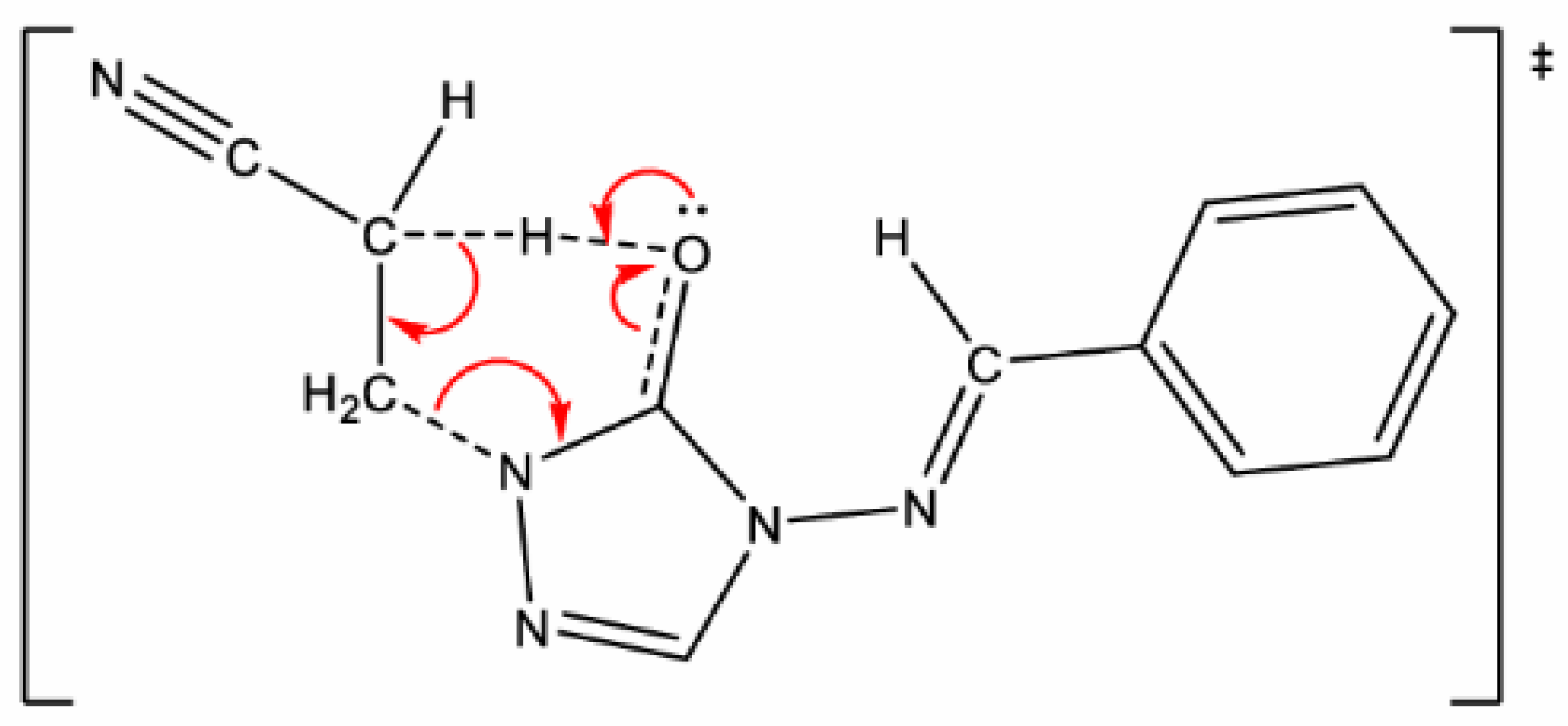
The mechanism depicted in Figure 2 was used for theoretical calculations, using a variety of functionals. The cyclic six-membered transition state in these eliminations involves a proton transfer to oxygen or sulfur, resulting in the formation of the enol form of the triazolone or triazothione, along with an aromatic nitrile, as illustrated in Scheme 3. The enol form tautomerizes with the corresponding keto form of the product, which is the product isolated in experimental work.

To determine the most appropriate model, we compared the calculated thermodynamic parameters with the experimental values. Table 1 shows the thermodynamic parameters and activation energies (Ea) calculated at APFD/def2-TZVP (25% HF) theoretical level, for 4-arylideneimino-1,2,4-triazol-3(2H)-ones (I–V) and their thione analogues (VI–X), shown in Figure 1, with R = H. For sulfur derivatives (VI–X), discrepancies emerge between calculated and experimental Ea values, particularly significant for Y=H (29.0% error) and Y=Cl (27.1% error). Oxygen analogs (I–V) show consistently high deviation (average ~20%), peaking at 39.0% for Y= -OMe. Calculations reveal a systematic ~40 kJ/mol gap between sulfur (X=S) and oxygen (X=O) derivatives, favoring decomposition in sulfur systems (e.g., 160.40 kJ/mol for X=S/Y=H vs. 199.77 kJ/mol for X=O/Y=H). However, critical inconsistencies persist: the X=O/Y=-OMe case shows the highest discrepancy (39.0%, Ea =197.47 kJ/mol vs. exp. 142.1 kJ/mol), while for sulfur, substituents Y=H and Cl yield unusually high errors (29.0% and 27.1%), despite the exceptional accuracy for X=S/Y= -OMe (1.4% error). These divergences underscore the APFD functional’s sensitivity to combining electronegativity, steric, and polarity effects of substituents.

The pronounced 29.0% error in activation energy (Ea) for sulfur (X=S/Y=H) with APFD (25% HF), contrasted with 14.4% for oxygen (X=O/Y=H), stems from how Hartree-Fock (HF) exchange modulates self-interaction error (SIE) in transition states (TS). Sulfur’s high polarizability exacerbates SIE in hybrid functionals: while pure/near-zero HF functionals like B97D-GD3BJ (0% HF) yield exceptional accuracy for X=S/Y=H (Ea= 121.59 kJ/mol, -2.2% error), hybrids with >20% HF (e.g., wB97XD at 100% HF) overestimate Ea by 40.7–55.2% due to exaggerated charge localization. APFD’s 25% HF strikes a poor balance for sulfur, over-stabilizing reactants by inadequately correcting delocalization in the TS.

To gain a better understanding of the errors in the determinations of activation energies, several functionals were selected with varying percentages of Hartree-Fock (HF), ranging from 0% to 100%. The results are presented in Table 2 and Table 3 for 4-benzylideneimino-1,2,4-triazole-3(2H)-one (2H) and 4-benzylideneimino-1,2,4-triazole-3(2H)- one (R = H, Y = H), as displayed in bold characters in Table 1. Oxygen-containing TSs, tolerate moderate HF exchange: B3LYP-GD3BJ (20% HF) reduces the error to 5.8% for X=O/Y=H, while pure functionals (e.g., BLYP, 0% HF) underestimate Ea by 13.8% due to insufficient exchange repulsion. APFD’s intermediate 25% HF performs better for oxygen (14.4% error) than sulfur, where low polarizability reduces SIE sensitivity. Sulfur’s diffuse electrons demand minimal HF exchange (0–15%) to model charge dispersion during N–N bond rupture, whereas oxygen’s lesser polarizability benefits from 20–25% HF to avoid spurious stabilization.

This dichotomy explains APFD’s failure for X=S/Y=H and highlights the need for system-specific HF tuning: sulfur requires dispersion-corrected, low-HF functionals (e.g., B97D), while oxygen achieves optimal accuracy with moderate-HF hybrids (e.g., B3LYP, or B97D).

The systematic errors in activation energy calculations observed across hybrid functionals (Table 2 and Table 3)—particularly HF-exchange-induced inaccuracies—also prompted us to an exploration of Gaussian16’s IOP keyword customization to modify, for example, BLYP’s exchange parameters, which, being a pure functional, would allow us to modify its contribution in percentage HF.

Blyp iop(3/76=1000002000) iop(3/77=0720008000) iop(3/78=0810010000), 20% HF

Blyp iop(3/76=1000001500) iop(3/77=0720008500) iop(3/78=0810010000), 15% HF

The goal is to mimic B3LYP’s behavior. This parameterization adjusted the pure BLYP functional to emulate B3LYP’s Hartree-Fock exchange fraction through non-standard weighting of Slater/local and non-local exchange-correlation terms (P1-P6) in Gaussian’s modified XC-functional equation. Despite this targeted tuning, results showed no significant improvement over established hybrids like M062X (54% HF) [39], PBE0 (25% HF) [40], or BHANDHLYP (50% HF) [41], indicating that merely adjusting HF percentage within the BLYP framework fails to resolve intrinsic limitations for transition state modeling. The persistent discrepancies suggest that fundamental functional design—not just HF exchange magnitude is needed to improve the accuracy of calculated thermodynamic parameters for triazole decomposition.

As shown, the systematic benchmarking in Table 2 and Table 3 reveals that APFD (25% HF) provides the most reliable activation energies for sulfur-containing triazoles, maintaining consistent errors (e.g., 10–13% for X=S/R=H/Y=substituents) while accurately capturing substituent trends, despite a slight overestimation versus pure functionals. Conversely, for oxygen analogues, B97D-GD3BJ (0% HF) delivers superior accuracy, reducing errors to ≤7.5% (Table 3: X=O/Y=H Eₐ = 160.62 kJ/mol vs. exp. 174.6 kJ/mol, −6.7% error) by mitigating self-interaction error and better describing electrostatic/dispersion forces in the transition state. This dichotomy, where sulfur’s polarizability favours APFD’s hybrid character, and oxygen’s lesser polarizability benefits from B97D’s dispersion-corrected pure DFT, establishes the dual-methodology approach for studying cyano group effects (Figure 2.

DFT calculations have been used to explain the differences [43] in reactivities of oxygen and sulfur-containing species, in terms of the hardness and softness of acids and bases, HSAB. Calculations show the frontier orbitals of sulfur compounds have a smaller energy gap compared to their oxygen analogs, explaining the increased orbital interaction (covalency) in sulfur-based bonding. DFT-based population analyses, like Mulliken or Bader charges, reveal the electrostatic character of bonds. Hard-hard interactions (like those with oxygen) are dominated by charge-charge attraction, while soft-soft interactions (like those with sulfur) are driven by orbital overlap.

Having identified a suitable model for the study, we proceeded to vary the R group from H to -CH2-CH2-CN and the Y group to H, NO2, Me, OMe, and Cl, in 4-arylideneimino-1,2,4-triazol-3(2H)-one and thione analogs. Activation energies were calculated at the APFD-Def2-TZVP level of theory to verify the model already established.

Table 4 shows the calculated thermodynamic parameters for the structures shown in Figure 2, using B97D-GD3BJ for 4-arylideneimino-1,2,4-triazol-3(2H)-one derivatives and APFD for the corresponding thiones; all calculations were carried out with def2-TZVP basis set. The transition state has a six-member ring geometry, as shown in Figure 1.

Table 5 shows the results obtained for the case of the functional B97D-GD3BJ. The table also indicates other R groups, including: CH₂CH₂-CO-CH₃, CH₂CH₂-CS-CH₃, CH₂CH₂-O-CH₃, and CH₂CH₃. These groups were aggregated to affect the six-ring transition state mechanism. In general, the activation energy remains constant at about 160 kJ/mol.

Table 5 also shows that the O-compounds (e.g., R=CH₂CH₂CN, Y=H) at the B97D-GD3BJ theoretical level, the calculated activation energy was 162.21 kJ/mol, aligning closely with experimental values (error: –6.7%), whereas APFD overestimates (Ea = 199.50 kJ/mol, +23.4% error). Conversely, for S-systems (e.g., R=CH₂CH₂CN, Y=Cl), APFD predicts Ea = 163.36 kJ/mol with minimal error (0.2–13.1%), while B97D-GD3BJ underestimates (Ea = 124.68 kJ/mol). This divergence stems from B97D-GD3BJ’s superior handling of dispersion-driven non-covalent interactions in O-TS (0% HF exchange), in contrast to APFD’s 25% HF exchange better captures S-TS steric/electronic effects during N–N bond cleavage.

We found that substituent effects on energies of activation are small for O-systems, and S-systems: Eelectron-withdrawing groups (e.g., NO₂) raise Ea for both systems (O: 162.21 → 166.14 kJ/mol; S: 162.34 → 166.67 kJ/mol), while electron-donating groups (OCH₃/CH₃) slightly reduce Ea (S-OCH₃: 162.03 kJ/mol). Large R-groups (e.g., glucosyl) increase Ea for O (157.01 kJ/mol vs. cyanoethyl’s 162.21 kJ/mol), highlighting steric constraints. S-compounds consistently exhibit lower Ea than O-analogues (ΔEa ≈ 37 kJ/mol), confirming in agreement with experimental values; 10³× faster thiocarbonyl decomposition. Hybrid functionals with high HF exchange (e.g., M062X, 54% HF) overestimate Ea by 43–55% for S-systems, underscoring APFD’s balanced parametrization. For regioselective synthesis, B97D-GD3BJ/Def2-TZVP is recommended for O-triazoles, while APFD/Def2-TZVP optimizes predictions for S-triazolothiones, enabling precise kinetic control [44].

The experimental work by Al-Awadi et al. also demonstrated that the -CH₂CH₂CN group on R undergoes pyrolytic decomposition at 800 K, as shown in Scheme 4. Our DFT calculations at the APFD/Def2-TZVP level explored this side reaction by replacing the -CN group with -H, -CS-CH₃, -S-CH₃, and -CO-CH₃. The results indicate that these alternative decompositions occur at higher activation energies, consistently above 200 kJ/mol, making them less favorable than the primary six-membered ring mechanism. For the specific case of the -CH₂CH₂-CS-CH₃ group, reported in Table 6, the calculated activation energies are notably comparable to those of the main pathway. For instance, with sulfur (X=S), APFD predicts an Eₐ of 149.75 kJ/mol, while B97D-GD3BJ gives a lower value of 107.80 kJ/mol. This suggests that this side reaction could compete with the main reaction pathway for sulfur-containing systems where the energy barrier is significantly lower.

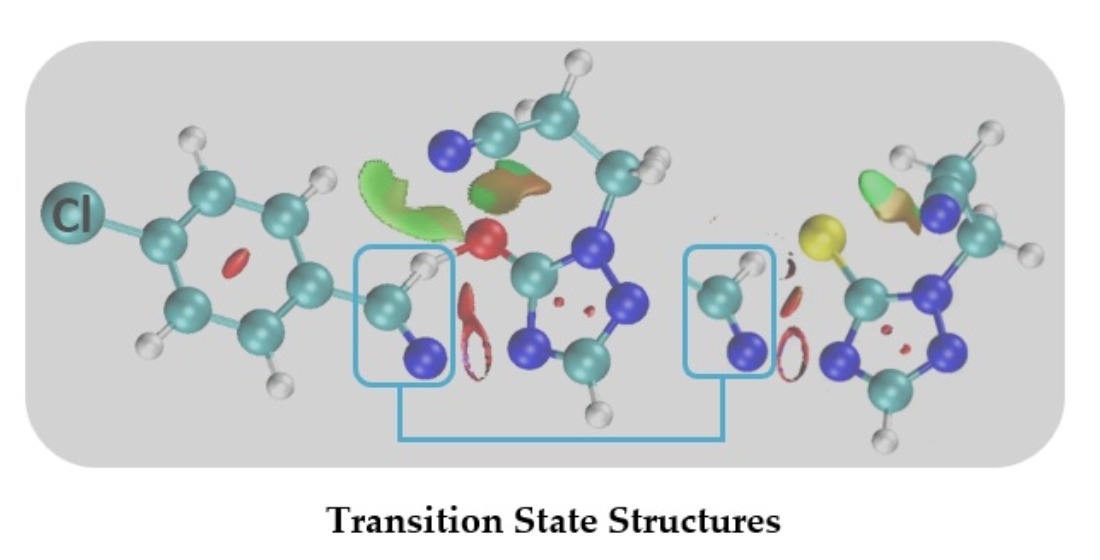
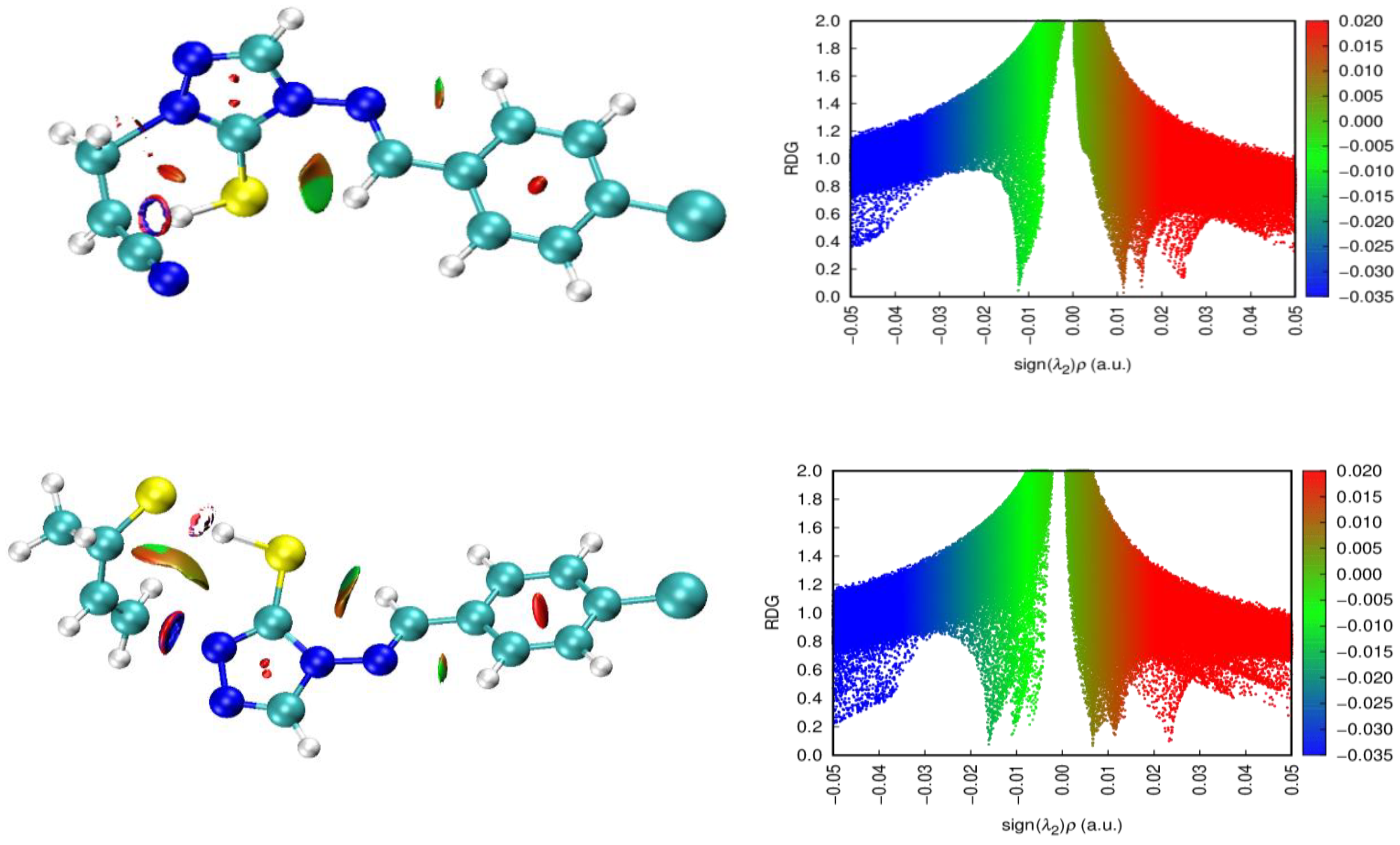
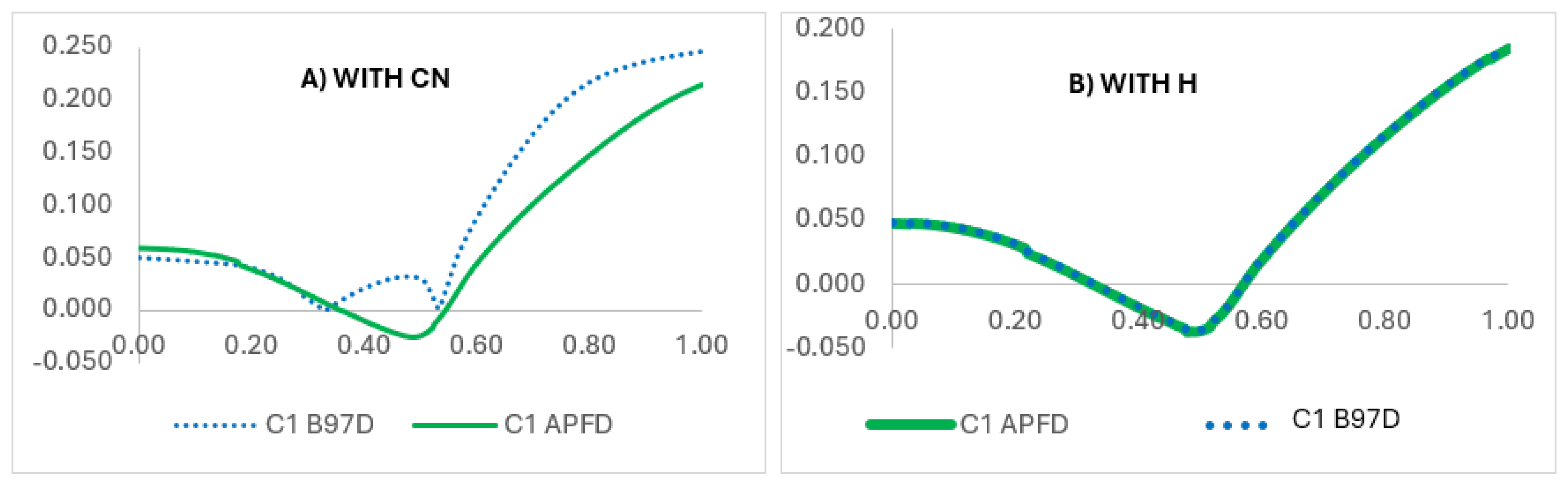
Figure 3 depicts the non-covalent interactions (NCI), comparing -CH₂CH₂CN, and -CH₂CH₂CSCH₃, green color indicates non-covalent interactions, blue is associated with strong attractive interactions (π bond), and red to strong repulsion interactions. These NCI calculations indicate that hydrogen atoms from these R groups could compete with the primary hydrogen (H12) involved in the six-membered ring transition state, potentially “trapping” the sulfur or oxygen atom in a different reaction coordinate. By applying the optimal functional model, we established APFD for sulfur and B97D for oxygen, where we observe that these large side chains, especially thioester-like groups, provide competitive pathways that influence the regioselectivity of the decomposition, underscoring the complex interplay between the main and side reactions in these systems.

After a systematic analysis of the calculated activation energies (Eₐ) across various functionals (Table 1, Table 2 and Table 3), it was determined that for sulfur-containing systems (X=S), the hybrid functional APFD (25% Hartree-Fock exchange) proved most suitable, providing consistent errors (~10–13%) and correctly capturing stereo electronic and polarizability effects during N–N bond cleavage. In contrast, for oxygen-containing systems (X=O), the B97D-GD3BJ functional (0% HF, dispersion-corrected) offered superior accuracy, reducing errors to ≤7.5% by effectively mitigating self-interaction errors and better describing electrostatic and dispersion interactions in the transition state. Based on these findings, the dual model APFD/Def2-TZVP for sulfur and B97D-GD3BJ/Def2-TZVP for oxygen was adopted. This model was subsequently applied to study systems with R = –CH₂CH₂CN and two Y substituents (Cl and H), enabling a reliable comparison of IRC energy profiles and NBO charge analyses.

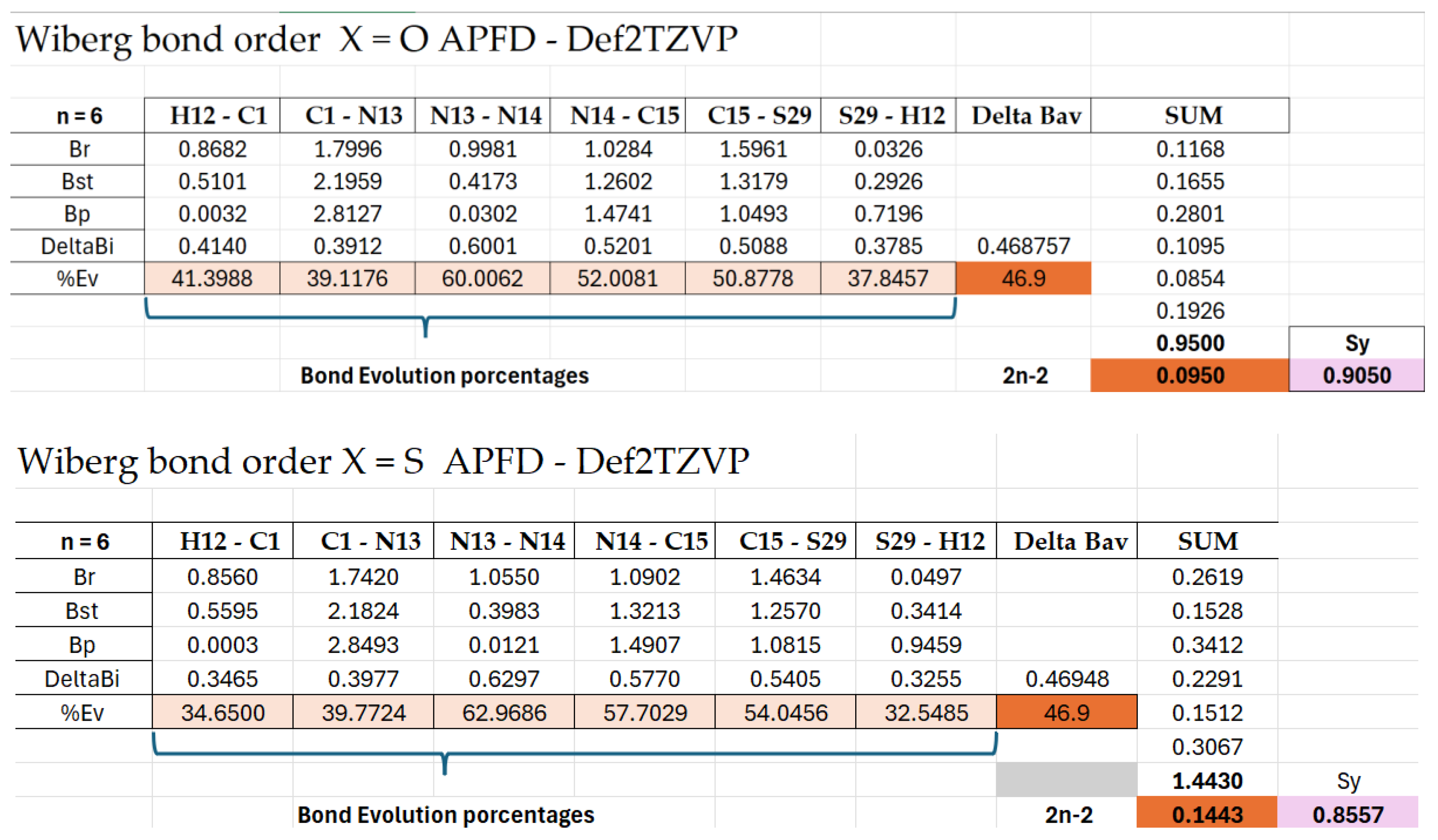
Wiberg NBO analysis was used to measure the progress of the reaction, studying the bonds involved in the process from the reactants to the products [23]. Bi is defined as the sum of the squares of the off-diagonal density matrix elements between atoms. The bond index between two atoms is a measure of the bond order and, hence, of the bond strength between two atoms. Thus, if the evolution of the bond indices corresponding to the bonds being made or broken in a chemical reaction is analyzed along the reaction path, a very precise image of the timing and extent of the bond-breaking and the bond-making processes at every point can be achieved [27]. The Wiberg bond indices corresponding to the bonds being made or broken in the reactions, for the reactants, TSs, and products, were studied and collected in Table 7 and Table 8.

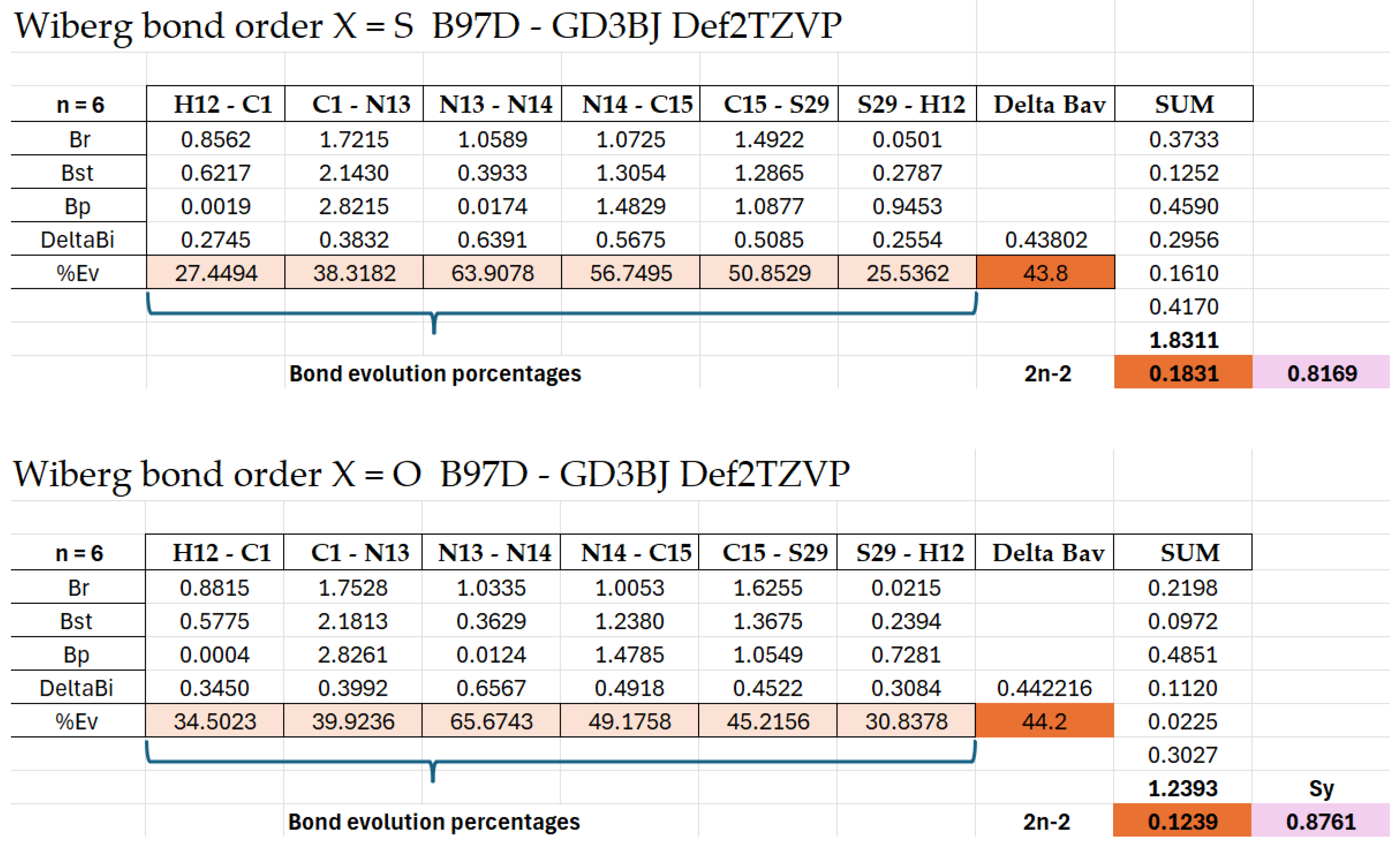
Results from said Tables show that the breaking of the N13-N14 bond is the most advanced process (more than 60% in all the reactions). Also advanced are the N14-C15 double bond formation and the C15-X29 double-bond breaking. The less advanced ones were the C-N triple-bond formation (between 38-40%) and, most of all, the H migration from C to X, where the C—H bond is broken in 40-41% of cases in the oxotriazoles (I–IV)R=b, and only in 31-32% of cases in the thiotriazoles (V–VIII)R=b. While the X-H bond is formed in 35-37% of cases in the oxotriazoles I-IV, only in 30-31% of cases were observed in the thiotriazoles (V–VIII)R=b). The elongation of the N-N bond seems to be the driving force for the reactions studied, instead of the migration of the H6 atom from C1 to X. The calculated ΔBav values for the studied reactions range from 0.43 to 0.47, showing that the TS is early in the reaction coordinate. Here, the TS structure is closer to the reactants than to the products.

The synchronicity (Sy) parameter of the bond-breaking and the bond processes indicates that the bond-breaking processes are slightly more advanced (an average of 63%) than the bond-forming ones (an average of 52%).

The Sy also revealed a key differential behaviour between sulfur and oxygen systems depending on the computational method used. For sulfur, the APFD functional (25% HF exchange) yields low synchronicity (~0.83), indicating a less synchronous and more gradual mechanism, consistent with sulfur’s higher polarizability and the need for a hybrid treatment that properly captures charge dispersion during N–N bond cleavage. For oxygen systems, the B97D-GD3BJ functional (0% HF) gives similarly low synchronicity (~0.83), reflecting its ability to model electrostatic and dispersion interactions in a more rigid transition state. However, when the functionals are reversed, using APFD for oxygen and B97D for sulfur, the synchronicity is artificially elevated (~1), suggesting an artificially concerted mechanism. This occurs because APFD over-stabilizes the oxygenated TS covalently, while B97D underestimates the stereo electronic effects of sulfur, leading to an apparent perfect synchronicity that does not correspond to the physicochemical reality. This discrepancy underscores the criticality of selecting the appropriate functional for each system, as the specific electronic nature of each heteroatom demands a distinct balance between exact exchange and dispersion correction.

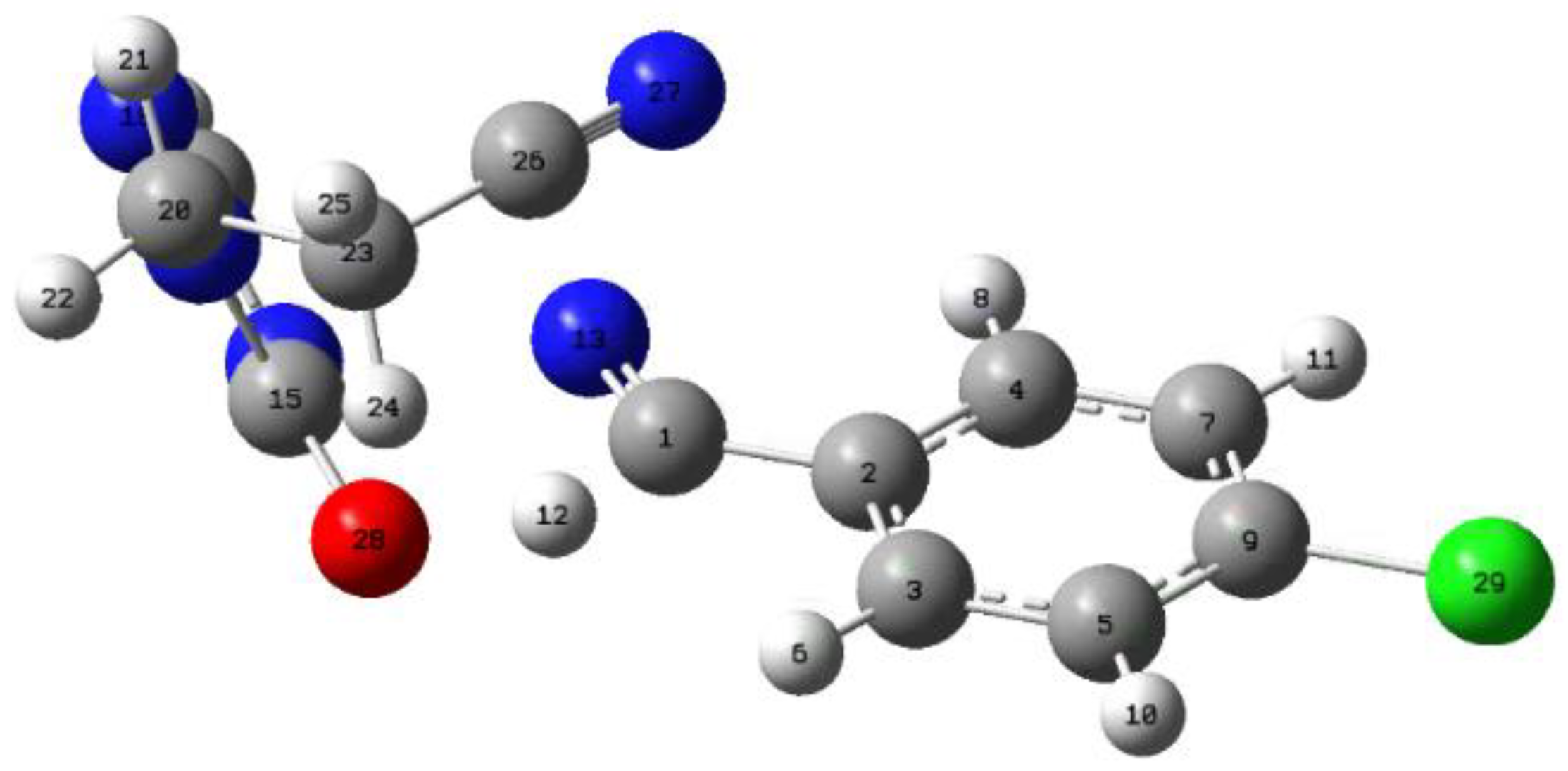
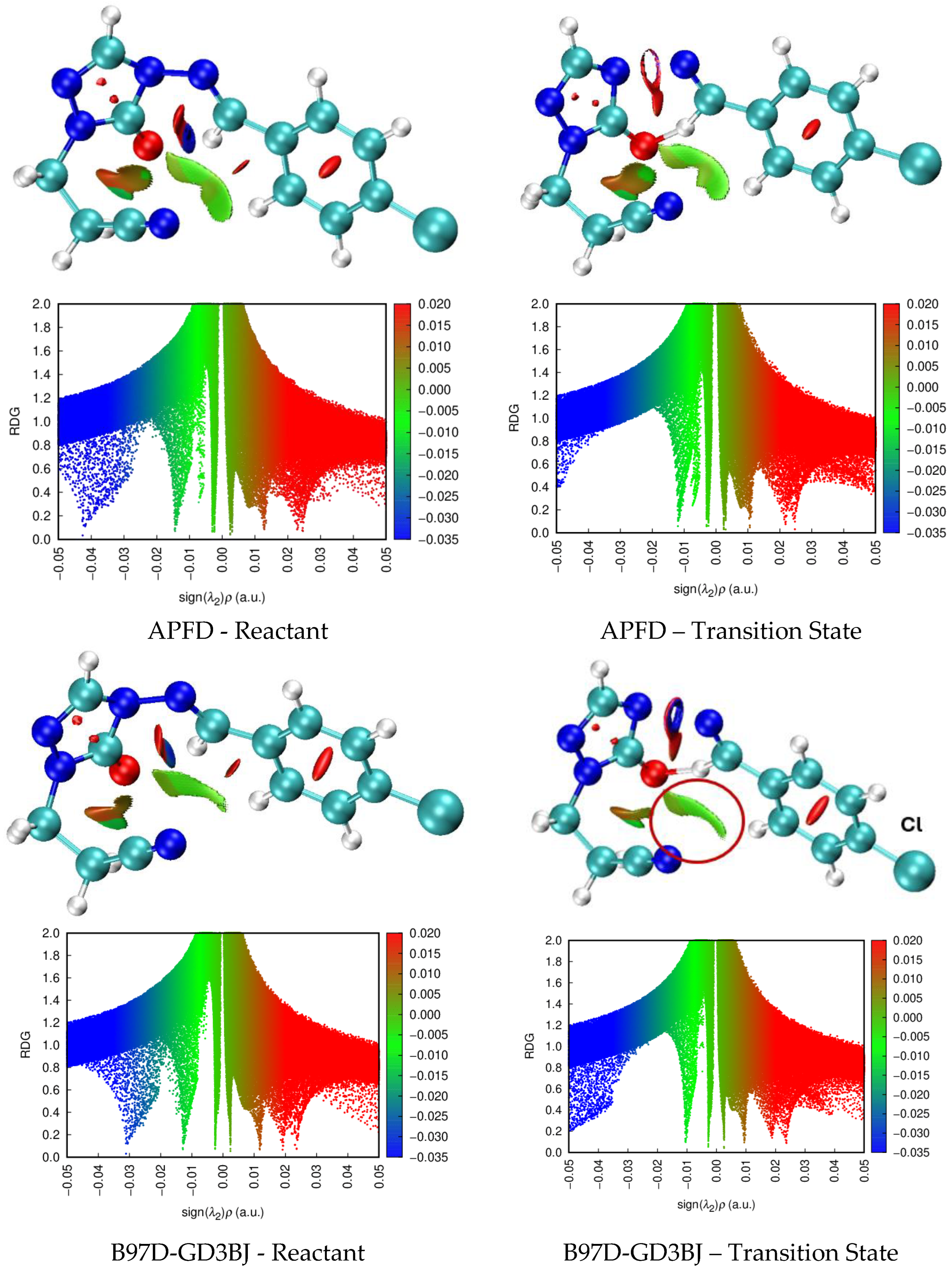
An intrinsic coordinate reaction (IRC) study was performed at the B97D-GD3-BJ/def2-TZVP level. This method is widely used in quantum chemical analysis and the prediction of reaction mechanisms. The IRC gives a unique connection from a given transition structure to local minima of the reactant and product. In this work, the experimental activation energies are between 150 and 180 kJ/mol in general, depending on the type of substituent. For the decomposition mechanism study, IRC profiles were computed with 241 points between reactants and products using the options (IRC=stepsize=3 and maxcycles=200), ensuring proper convergence for all species. The NBO charge analysis focused on the molecule depicted in Figure 4, which features the -CH₂CH₂CN group positioned above the transition state in oxygen-containing systems. This study compared this system to its analogue where the -CH₂CH₂CN group was replaced by a hydrogen atom (-H), to evaluate the substituent’s electronic and steric effects.

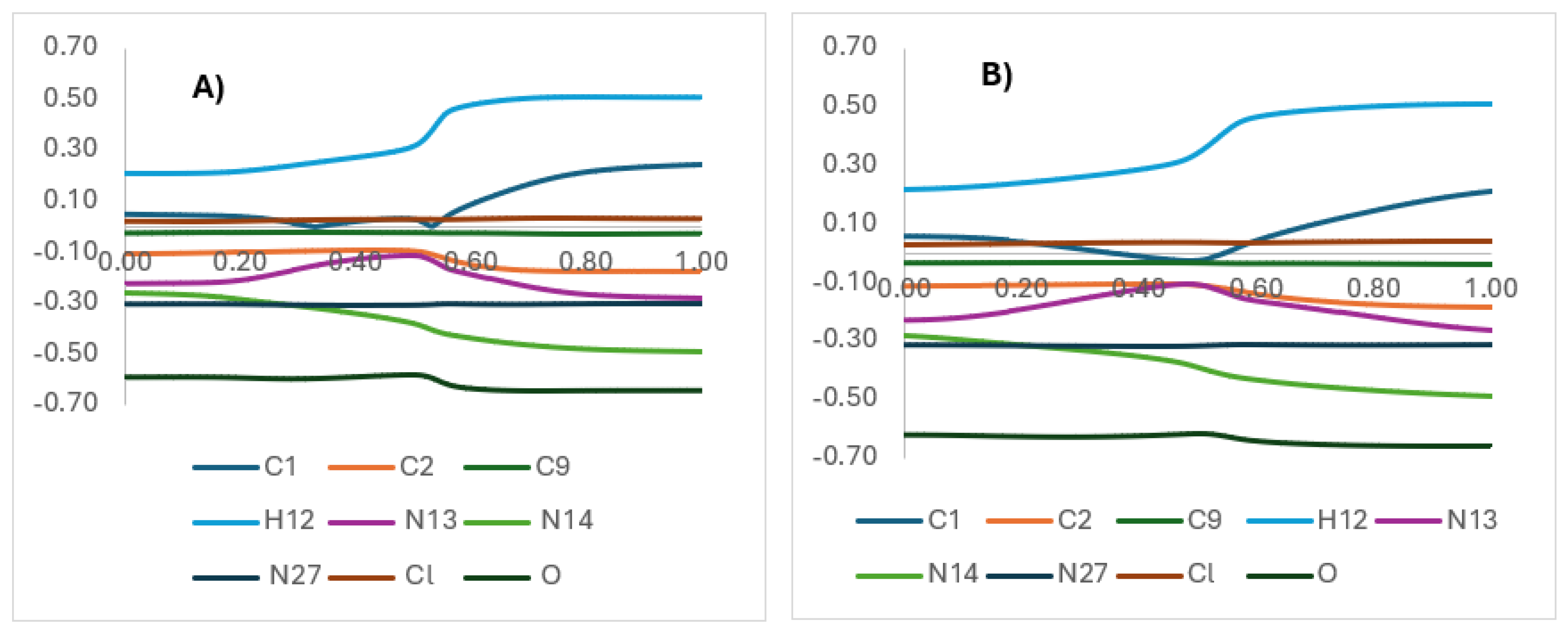
The detailed IRC analysis revealed how the presence of the -CH₂CH₂CN group significantly modifies the electronic environment of the six-membered transition state (TS). NBO charge analyses (Figure 5, Figure 6A, and Figure 7) show that at carbon C1 (from which the hydrogen migrates to oxygen), a peculiar electron redistribution occurs when using the B97D-GD3BJ functional (0% HF, dispersion-corrected), which provides a better description for oxygenated systems.

The presence of the -CH₂CH₂CN group induces additional electron density contours (Figure 6A, in yellow) that are not present when the group is replaced by a hydrogen (Figure 6B), suggesting a non-covalent stabilization of the TS through dispersion or electrostatic interactions.

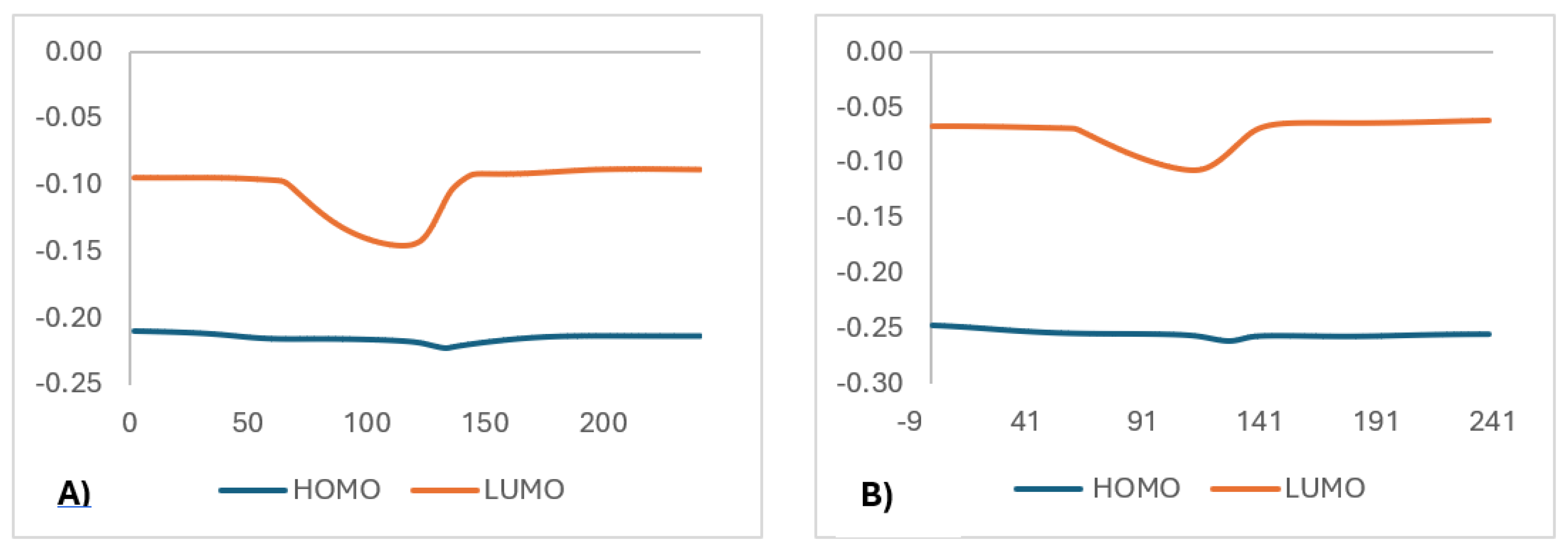
This stabilization is supported by HOMO-LUMO calculations (Figure 7), where the B97D-GD3BJ functional shows a closer proximity between the frontier orbitals, indicating a better description of reactivity and a lower activation energy, consistent with experimental values. In contrast, the APFD functional (25% HF) overestimates the activation energy due to a poorer ability to capture non-covalent interactions. Finally, the NBO charge analysis of the chlorine atom (Figure 8) consistently shows a loss of electron density, regardless of the functional use, suggesting an electron-withdrawing effect that likely favors charge transfer toward the -CN group. This group ultimately adopts a stabilized configuration in an aromatic system. This electron-withdrawing effect of chlorine could facilitate hydrogen migration by making carbon C1 more electrophilic, consistent with the lower activation energy observed in systems with electron-accepting substituents.

The Independent Gradient Model (IGM)

The IGM model is used here to obtain insights into both strong and weak interactions in molecular systems. The method was used to represent the isosurfaces of interaction between structures. Figure 9 shows how structures change in transition states when placing substituents or switching between sulfur or oxygen. Using the output of the IRC calculations, each structure was extracted from the reactants to the products, in total 241 points were extracted per level of theory, depending on whether it is sulfur or oxygen, in total there were 241*4 = 961 structures analyzed under the IGM-IBSI scheme, the densities were evaluated and then the 2D contours were studied, for each IRC point involved. In this case, the bonds involved in the TS were used, but adding the effect of the chlorine atom and the -CH₂CH₂CN group to identify any non-covalent interactions. The entire process was carried out automatically with a unix script. The param. igm file is required to run the IGMPLOT software. In the case of 2D graphics, the GNUPLOT software was used. At the 121 IRC point, corresponding to the transition state, TS, specifically for the B97D-GD3BJ—Def2-TZVP-Oxygen system with substituents -CH₂CH₂CN and Chlorine, we calculated several important parameters, including the IBSI (intrinsic bond strength). The Pair Density Asymmetry (PDA) provides users with a simple tool to assess inductive effects on specific bonds in molecules. The PDA index gives a measure of the electron density (ED) asymmetry between two atoms and the direction of the asymmetry.

The parameter

\nabla

g represents the magnitude of the electron density gradient embedded in the interaction region between a pair of atoms. This value quantifies the spatial variation of the electron density (ρ) in the bond zone or non-covalent interaction. Critical Point Analysis, which gives us the Laplacian (Lap), and the eigenvalues of the Hessians are given in Table 9, for several pairs of atoms as shown in Figure 10.

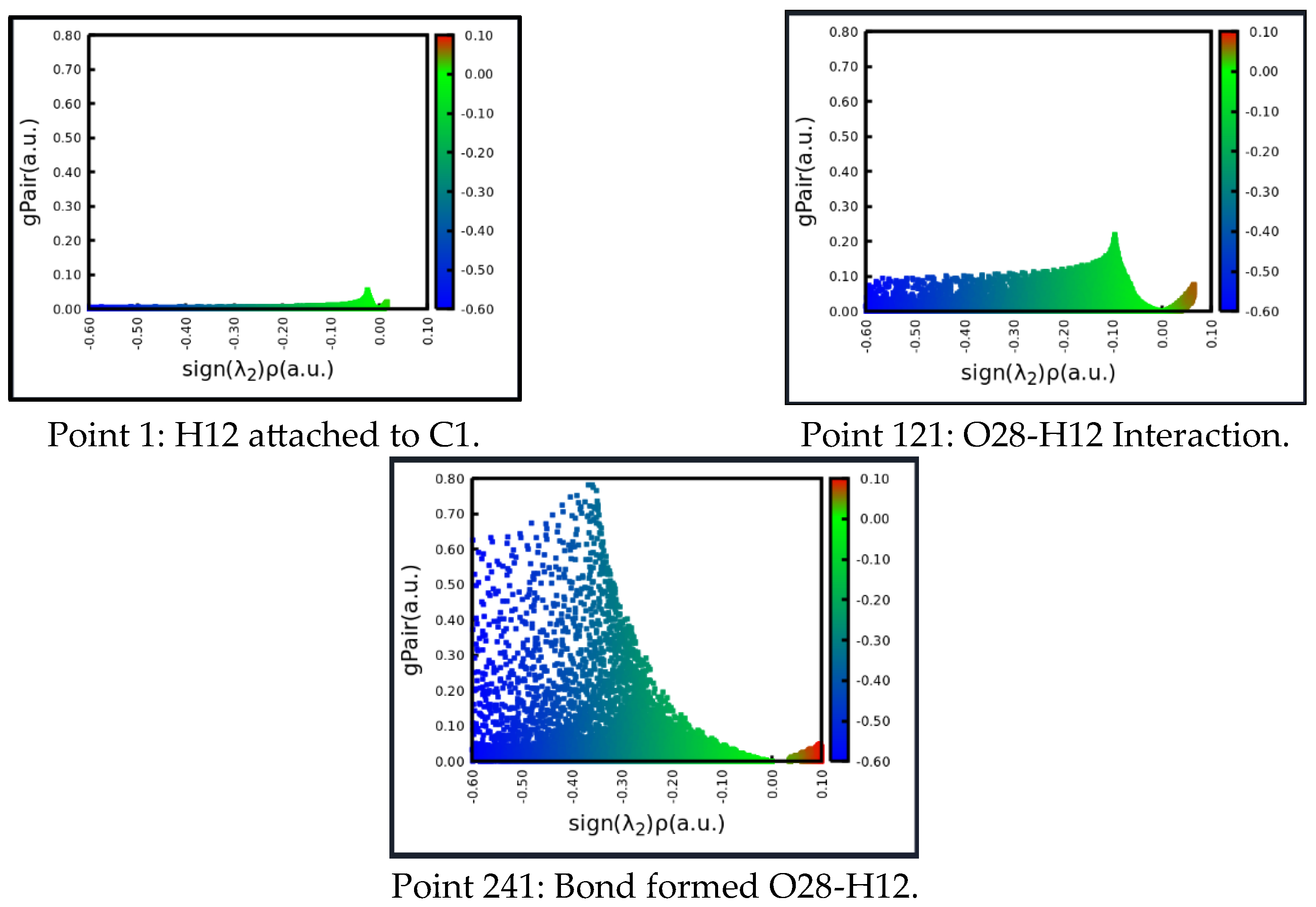
The values of the analysis of critical points were performed for each point in the path of the IRC study. In this case, if we worked with oxygen at the B97D-GD3BJ level, each pair of atoms was studied. Figure 11 represents the area found from each interaction. At point 1, there is no strong interaction between O28 and hydrogen 12. At point 121, it corresponds exactly to the transition state, and the area of interaction increases. Finally, when the complete transfer of hydrogen to oxygen has occurred, and a definite O28-H12 bond is formed, its area or profile is quite high.

Table 10 shows the same calculation as in Table 9, but now with the APFD/Def2-TZVP level of theory. Point 121 (Transition State) from an IRC calculation.

A Comparison of IGM calculations between APFD and B97D-GD3BJ functionals reveal significant differences in key interactions. For the O28-H12 bond, the APFD calculation shows a shorter distance (1.334 Å) vs. B97D (1.434 Å), with a higher IBSI (0.438 vs. 0.336), indicating greater strength in APFD. However, the density asymmetry (PDA) is reversed: in APFD, the density flows from H12 to O28 (H12→O28, PDA=267.9), while in B97D, it flows from O28 to H12 (O28←H12, PDA=249.8), suggesting differences in the polarization of the bond. For C9-Cl29, both functionals coincide in direction (C9→Cl29) and magnitude (IBSI ~0.75, PDA ~323), confirming a stable polar covalent bond. In N13-N14, APFD presents higher IBSI (0.220) and asymmetry (N14→N13, PDA=1.0), while B97D shows lower strength (IBSI=0.160) and perfect symmetry (PDA=0.0), evidencing a more marked non-covalent trait with B97D. 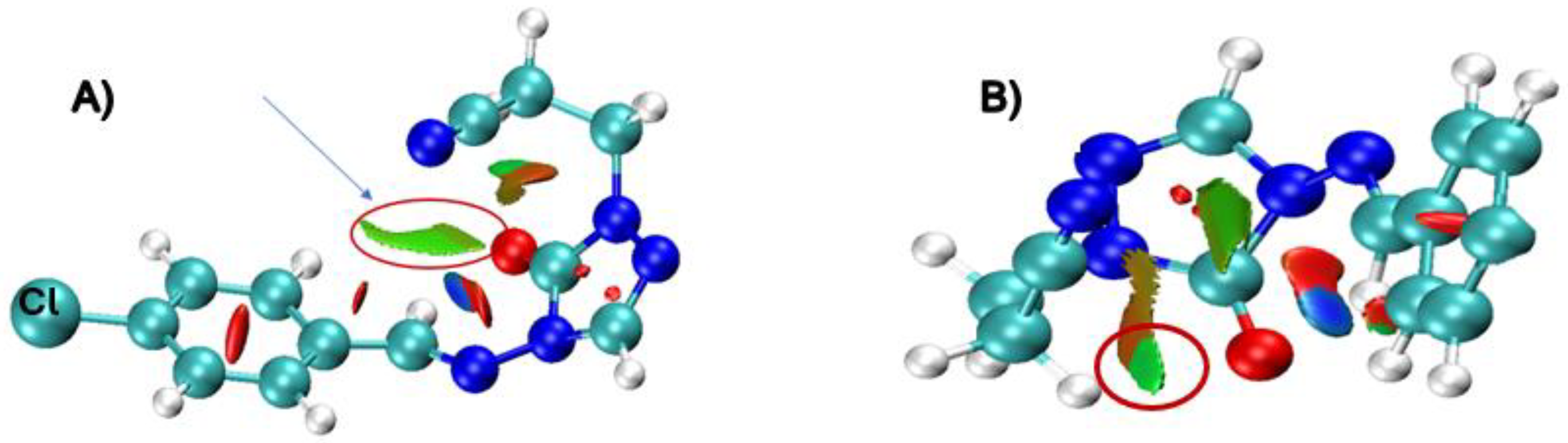A deeper analysis of the distribution of the atoms according to the IBSI analysis in Table 9 and Table 10 can be seen in the presence of a non-covalent interaction between the -CH₂CH₂-CN group and the atoms that will eventually be involved in the six-membered ring in the transition state. Figure 12 A). Similarly, there is an interaction between one of the hydrogens of the -CH₂-CH(H)-CN group and oxygen, Figure 12 B).

Figure 13 shows more clearly the non-covalent interactions and the 2D NCI profiles to highlight the interactions by the number of green peaks in the middle of the graph.

The two calculation models, APFD and B97D-GD3BJ, exhibit remarkable differences; the blue dots indicate a strong interaction of the N-N bond breaking, which is key to understanding the determining stage, as shown by the NBO analysis and the Wiberg indices. In the case of the model with B97D-GD3BJ, a marked influence of the N-N bond is still shown. The influence of the -CH₂CH₂CN group is not observed in the case of replacing oxygen with sulfur, but the interaction of hydrogen, -CH₂-CH(H)-CN, is observed, Figure 14.

Below, we present an analysis of the critical points and their different properties when exchanging oxygen for sulphur. The results are presented in Table 11 and Table 12.

Table 11. Critical Point Analysis for the B97D-GD3BJ-Def2-TZVP, X = S, Y = Cl. R =-CH₂CH₂CN (TS). Point 51 from the IRC calculation.

Bond	d(Angs)	δg	IBSI	PDA (×10⁻¹)	Asymmetry Direction	rho	Lap	bcp_x	bcp_y	bcp_z	L1	L2	L3
H24-S29	2.9	0.118	0.019	252.5	H24→S29	0.009	0.026	-2.277	-1.151	-1.354	-0.007	-0.005	0.038
S29-H12	1.925	0.431	0.162	384.7	S29←H12	0.057	0.051	-0.689	0.62	-1.32	-0.077	-0.076	0.205
H12-C1	1.159	0.736	0.762	212.1	H12→C1	0.235	-0.699	-0.013	0.834	-0.612	-0.623	-0.622	0.545
C1-N13	1.238	2.006	1.822	30.9	C1→N13	0.428	-0.861	0.128	1.296	0.323	-1.037	-0.946	1.122
N13-N14	2.012	0.7	0.241	1.3	N13←N14	0.077	0.154	-1.224	1.796	0.509	-0.107	-0.104	0.364
N14-C15	1.363	1.769	1.325	38.1	N14←C15	0.337	-1.058	-2.39	1.239	-0.342	-0.779	-0.666	0.387
C15-S29	1.693	1.728	0.839	292.5	C15→S29	0.217	-0.399	-2.052	0.593	-1.497	-0.262	-0.237	0.099
C9-C128	1.739	1.6	0.737	322.5	C9→C128	0.202	-0.306	5.092	-0.485	0.035	-0.331	-0.311	0.335

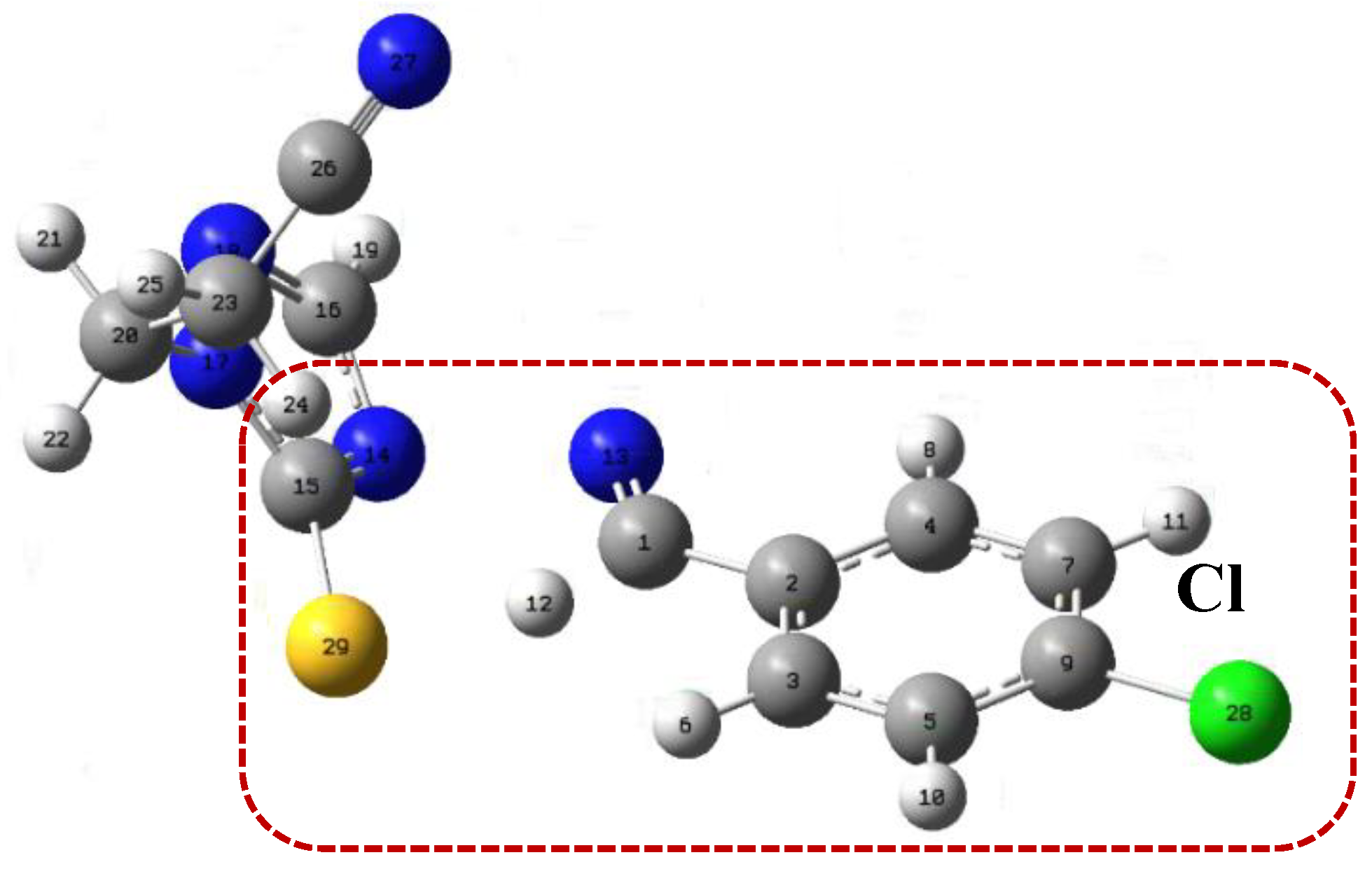
Table 12. Critical Point Analysis for the APFD-Def2-TZVP, X = S, Y = Cl. R =-CH₂CH₂CN (TS). Point 121 from the IRC calculation.

Bond	d(Angs)	δg	IBSI	PDA (×10⁻¹)	Asymmetry Direction	rho	Lap	bcp_x	bcp_y	bcp_z	L1	L2	L3
H24-S29	2.911	0.107	0.018	250.4	H24→S29	0.009	0.026	-2.192	1.126	1.304	-0.006	-0.005	0.037
S29-C15	1.699	1.688	0.814	291.2	S29←C15	0.216	-0.398	-1.951	-0.612	1.47	-0.262	-0.233	0.097
C15-N14	1.34	1.795	1.392	38.5	C15→N14	0.354	-1.191	-2.341	-1.258	0.35	-0.836	-0.706	0.351
N14-N13	2.037	0.641	0.215	0.8	N14→N13	0.072	0.155	-1.169	-1.803	-0.512	-0.096	-0.094	0.345
N13-C1	1.214	2.013	1.903	29.8	N13←C1	0.446	-0.639	0.189	-1.288	-0.35	-1.1	-1.029	1.491
C1-H12	1.226	0.678	0.628	203.8	C1←H12	0.195	-0.485	-0.012	-0.833	0.614	-0.486	-0.481	0.483
H12-S29	1.773	0.539	0.239	416.7	H12→S29	0.081	-0.002	-0.637	-0.627	1.295	-0.124	-0.12	0.241
C9-C128	1.724	1.626	0.762	324.2	C9→C128	0.21	-0.347	5.102	0.488	-0.045	-0.346	-0.326	0.325

In Table 11 and Table 12, the properties of critical points for the sulfur-containing system (X=S) are compared at two theoretical levels: B97D-GD3BJ (Table 11, IRC point 51) and APFD (Table 12, IRC point 121). Both methods show significant differences in key interactions. For example, in the H12-S29 bond, the IBSI (bond strength index) is higher in APFD (0.239) than in B97D-GD3BJ (0.162), suggesting a stronger interaction in the former. Additionally, the PDA (Pair Density Asymmetry) for this bond is more pronounced in B97D-GD3BJ (384.7) than in APFD (416.7), indicating greater polarization in the former case. For the N13-N14 bond, both methods show similar IBSI values (~0.22–0.24), but the PDA is slightly higher in B97D-GD3BJ (1.3 vs. 0.8 in APFD), reflecting a minor difference in electron density distribution. The C15-S29 bond also has a higher IBSI in APFD (0.814 vs. 0.839 in B97D-GD3BJ), though the direction of asymmetry (C15→S29) remains consistent in both cases.

It is worth noting that, in the case of the sulfur-containing system at the B97D-GD3BJ level, we struggled with convergence near the transition state (TS), probably due to its lack of Hartree-Fock exchange, requiring coarser steps to stabilize the computation. In contrast, APFD (25% HF + dispersion) handled the IRC smoothly at stepsize=3, highlighting its robustness for TS descriptions. While the larger stepsize in B97D-GD3BJ preserved the overall reaction pathway, it likely sacrificed fine details of weak interactions (e.g., non-covalent bonds) critical for accurate IBSI/PDA analysis. This trade-off underscores the importance of functional selection when mapping reaction mechanisms, with hybrid functionals like APFD offering a better balance for IRC precision in polarizable systems like sulfur-containing triazoles.

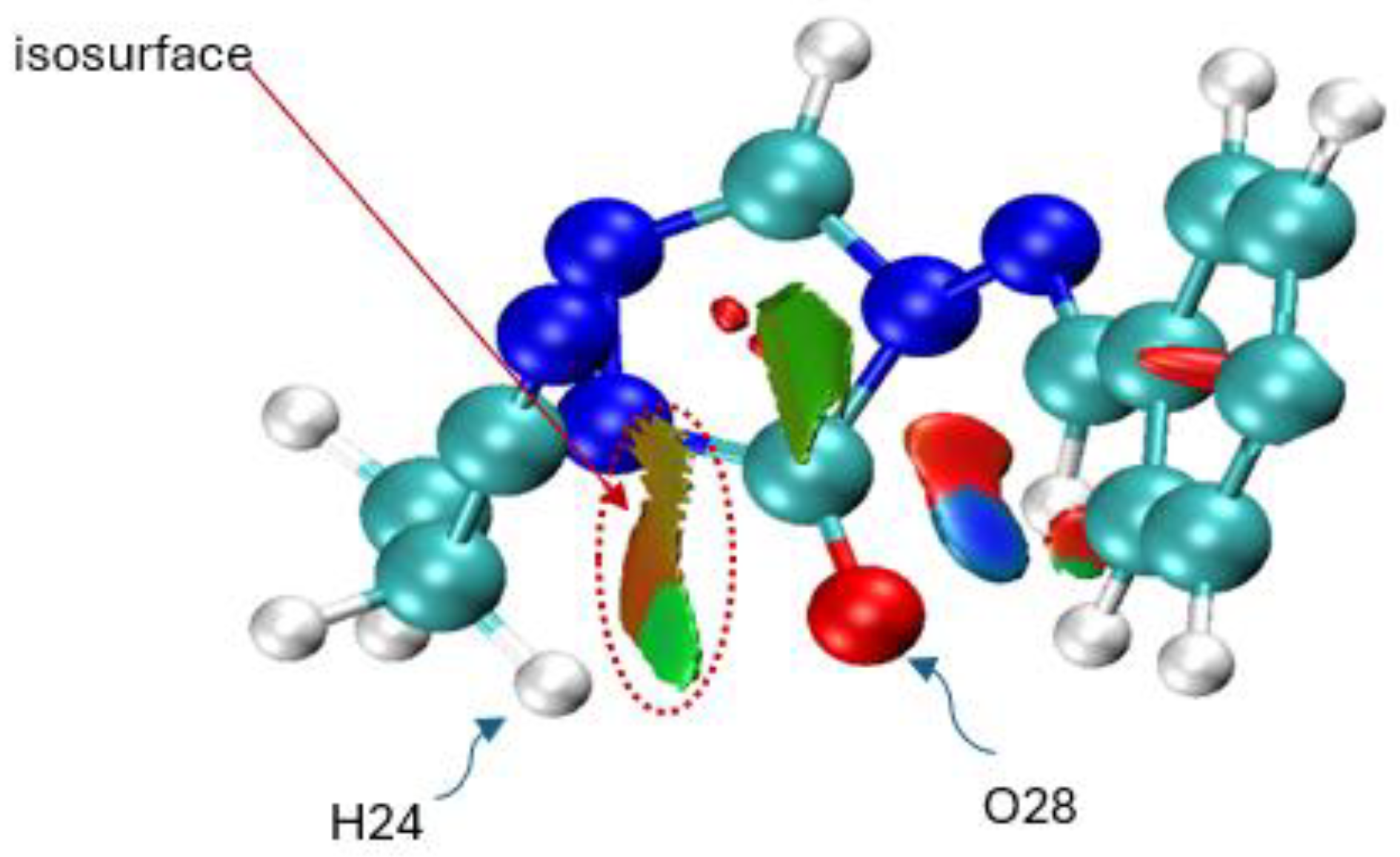
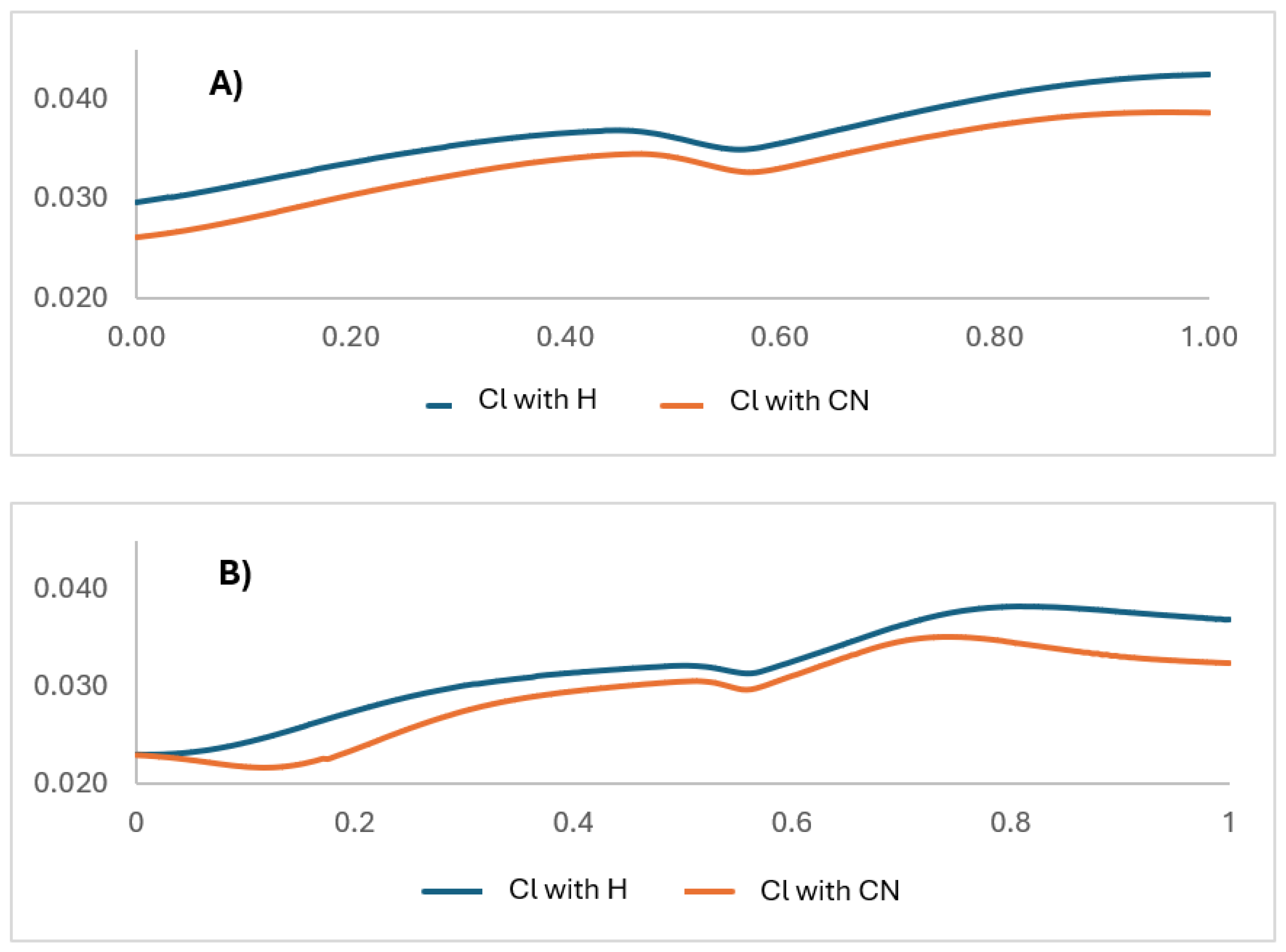
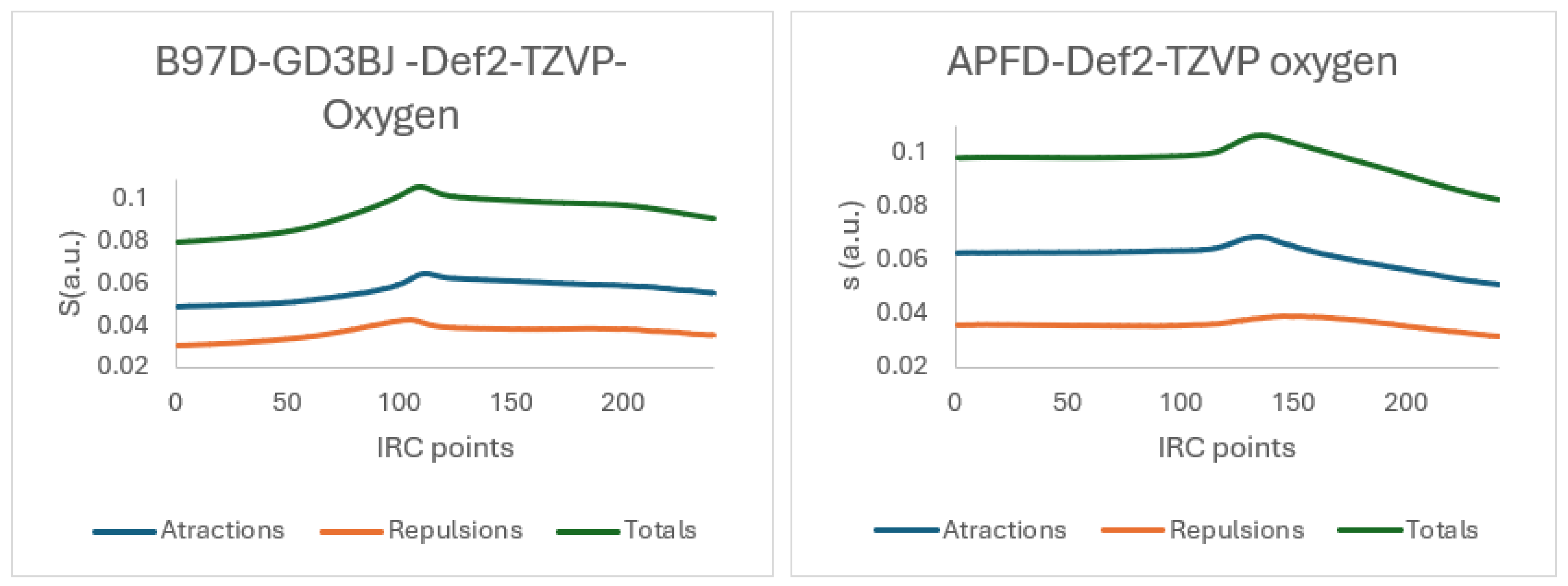
Another interesting effect observed is the interaction of hydrogen H24 from the -CH₂CH₂CN group with the oxygen atom (O28), an effect previously analyzed in our study when this group was substituted to probe potential competitive side reactions. Figure 15 quantifies this weak, attractive non-covalent interaction (NCI) that stabilizes the six-membered ring transition state. The data reveals a key difference between the APFD and B97D-GD3BJ functionals: APFD calculates this H24-O28 interaction to be stronger and occurring earlier along the reaction path (higher IBSI, shorter distance). At the same time, B97D models it as weaker and more delayed. This discrepancy highlights how the choice of functional influences the description of such stabilizing interactions. Crucially, this specific interaction was not observed in the sulfur analogues, which is consistent with sulfur’s larger atomic radius and lower electronegative compared to oxygen, preventing close contact with the H24 hydrogen. Thus, this interaction is a unique stabilizing feature for the oxygenated system, fine-tuning the reaction landscape without overriding the primary decomposition mechanism.

As detailed in the NBO charge analysis section, it consistently shows that the chlorine atom loses electron density throughout the IRC, confirming it acts as an electron donor rather than a classical withdrawing group in this specific system. The IBSI calculation shows that the C9-Cl bond strength remains remarkably stable and strong (~0.75) throughout the entire reaction coordinate, regardless of the functional used. This indicates the C-Cl bond is not breaking; instead, it is acting as a stable conduit for electron donation. The constant bond strength, coupled with the chlorine’s increasing positive charge, suggests it is feeding electron density into the aromatic system to stabilize the developing negative charge on the triazole ring during the N-N bond cleavage. This donation is ultimately driven by the powerful electron-withdrawing effect of the newly formed nitrile (-CN) group in the final product, which creates a strong thermodynamic pull, making chlorine a net donor to compensate. Thus, the chlorine substituent electronically stabilizes the six-membered cyclic transition state not by withdrawing density, but by providing it, fine-tuning the energy landscape and lowering the activation barrier.

Finally, to quantify the participation of the -CH₂CH₂CN group on the transition state of six members, the interaction was quantified by analyzing the fragments as indicated in Figure 16. The study was only performed for the case of oxygen in the two energy levels B97D-GD3BJ and APFD.

The shift observed between the B97D-GD3BJ (left) and APFD (right) plots in Figure 17 reflects differences in how these functionals model non-covalent interactions (NCIs) between the -CH₂CH₂CN group and the transition state fragments during the IRC analysis. The B97D-GD3BJ functional, which lacks Hartree-Fock (HF) exchange but includes dispersion corrections, emphasizes dispersion-driven interactions, resulting in a more pronounced and slightly delayed (shifted) attraction profile (blue peaks) as the reaction progresses. In contrast, the APFD functional, with 25% HF exchange and dispersion, balances electrostatic and dispersion effects, leading to an earlier and sharper peak in the attraction profile, indicating stronger stabilization of the TS at an earlier stage. This shift suggests that APFD’s hybrid character accelerates the stabilization of NCIs due to better handling of charge polarization, while B97D’s dispersion-centric approach delays this stabilization, reflecting its sensitivity to weaker, long-range interactions. The consistent blue dominance in both plots confirms that attractive interactions prevail, but the timing and intensity differences highlight the critical role of functional choice in describing how substituents like -CH₂CH₂CN modulate TS stability and reaction kinetics.

Conclusions

This DFT study elucidates the thermal decomposition mechanism of 1,2,4-triazol-3(2H)-ones/thiones, confirming a concerted six-membered cyclic transition state primarily driven by N–N bond elongation (60–63% advanced). A critical finding is that functional selection impacts accuracy: B97D-GD3BJ at 0% HF excels for oxygen systems by mitigating self-interaction error and better describing electrostatic/dispersion interactions in the TS; while APFD at 25% HF is optimal for sulfur analogues, balancing polarizability and charging dispersion during N–N cleavage. The -CH₂CH₂CN group acts not only as a thermally labile protecting group for regioselective synthesis but also stabilizes the TS via non-covalent interactions, with electron-withdrawing/donating substituents raising/lowering Ea, respectively. Sulfur’s polarizability consistently lowers Ea by ~40 kJ/mol compared to oxygen, explaining the experimental reactivity gap. This work provides a robust predictive framework for designing triazole-based therapeutics through controlled pyrolysis, underscoring the necessity of system-tailored computational methods for mechanistic fidelity in heterocyclic chemistry.

Author Contributions

Conceptualization, R. I. C. and M. L.; formal analysis, R. I. C., M. L., M. P. V. and T. C. S.; investigation, R. I. C. and M. L.; methodology, R. I. C., M. L. and M. P. V.; supervision, J. L. P.; validation, T. C. S.; visualization, R. I. C. and M. L.; writing– original draft, R. I. C. and M. L.; writing– review & editing, T. C. S. and J. L. P.

Data Availability Statement

All computational details and data are available upon request.

Acknowledgments

The authors thank the Facultad de Química e Ingeniería Química de la Universidad Nacional Mayor de San Marcos, particularly the DEINPRO research group, for the use of the high-performance computing system utilized for most of the theoretical calculations presented in this work. Rosalinda Ipanaque-Chávez extends his sincere gratitude to the Postgraduate Program of the Faculty of Chemical and Chemical Engineering. This research was funded by the Universidad Nacional Mayor de San Marcos under Rectoral Resolution No. 00671-2024-R-UNMSM, with project code C25071291.:

Conflicts of Interest

There are no conflicts to declare.

References

Kumar, A.; Singh, A. K.; Singh, H.; Vijayan, V.; Kumar, D.; Naik, J.; Thareja, S.; Yadav, J. P.; Pathak, P.; Grishina, M.; et al. Nitrogen-Containing Heterocycles as Anticancer Agents: A Medicinal Chemistry Perspective. Pharmaceuticals 2023, 16, 299. [Google Scholar] [CrossRef]
Wibowo, A.; Mohammed, M. F.; Shaameri, Z.; Rashid, F. N. A. A.; Pungot, N. H.; Hamzah, A. S. Five-Membered Nitrogen Heterocycles as New Lead Compounds in Drug Discovery. Heterocycles 2022, 105, 244–286. [Google Scholar] [CrossRef]
Aly, A. A.; Hassan, A. A.; Makhlouf, M. M.; Bräse, S. Chemistry and Biological Activities of 1,2,4-Triazolethiones—Antiviral and Anti-Infective Drugs. Molecules 2020, 25, 3036. [Google Scholar] [CrossRef]
Šermukšnytė, A.; Kantminienė, K.; Jonuškienė, I.; Tumosienė, I.; Petrikaitė, V. The Effect of 1,2,4-Triazole-3-thiol Derivatives Bearing Hydrazone Moisty on Cancer Cell Migration and Growth of Melanoma, Breast, and Pancreatic Cancer Spheroids. Pharmaceuticals 2022, 15, 1026. [Google Scholar] [CrossRef]
Jasim, A. M.; Omar, T. N.-A.; Abdulhadi, S. L. Sulfur Derivatives of 1,2,4-Triazole: Recently Developed Compounds, Structure Activity Relationship, and Biological Activity: Review Article. Iraqi Journal of Pharmaceutical Sciences 2024, 33, 1–21. [Google Scholar] [CrossRef]
De La Rosa, M.; Kim, H. W.; Gunic, E.; Jenket, C.; Boyle, U.; Koh, Y.; Korboukh, I.; Allan, M.; Zhang, W.; Chen, H.; Xu, W.; Nilar, S.; Yao, N.; Hamatake, R.; Lang, S. A.; Hong, Z.; Zhang, Z.; Girardet, J.-L. Tri-Substituted Triazoles as Potent Non-Nucleoside Inhibitors of the HIV-1 Reverse Transcriptase. Bioorg. Med. Chem. Lett. 2006, 16, 4444–4449. [Google Scholar] [CrossRef] [PubMed]
Dong, W.-L.; Liu, Z.-X.; Liu, X.-H.; Li, Z.-M.; Zhao, W.-G. Synthesis and Antiviral Activity of New Acrylamide Derivatives Containing 1,2,3-Thiadiazole as Inhibitors of Hepatitis B Virus Replication. Eur. J. Med. Chem. 2010, 45, 1919–1926. [Google Scholar] [CrossRef] [PubMed]
Karakıtçük-Iyidoğan, A.; Başaran, E.; Tatar-Yılmaz, G.; Oruç-Emre, E. E. Development of New Chiral 1,2,4-Triazole-3-thiones and 1,3,4-Thiadiazoles with Promising in Vivo Anticonvulsant Activity Targeting GABAergic System and Voltage-Gated Sodium Channels (VGSCs). Bioorg. Chem. 2024, 151, 107662. [Google Scholar] [CrossRef]
Sirakanyan, S. N.; Spinelli, D.; Geronikaki, A.; Hakobyan, E. K.; Petrou, A.; Kartsev, V. G.; Yegoryan, H. A.; Paronikyan, E. G.; Zuppiroli, L.; Jughetsyan, H. V.; et al. New Triazole-Based Hybrids as Neurotropic Agents. RSC Adv. 2024, 14, 32922–32943. [Google Scholar] [CrossRef] [PubMed]
Al-Awadi, N. A.; Ibrahim, Y. A.; Dib, H.; Kaul, K. Gas-Phase Elimination Reactions of 4-Arylideneimino-2-cyanoethyl-1,2,4-triazol-3(2H)-ones, Their Thione Analogues and 2-Glucosyl-1,2,4-triazole-3(2H)-thiones: A Kinetic and Mechanistic Study. J. Phys. Org. Chem. 2002, 15, 324–329. [Google Scholar] [CrossRef]
Hadad, C. M.; Rablen, P. R.; Wiberg, K. B. C-O and C-S Bonds: Stability, Bond Dissociation Energies, and Resonance Stabilization. J. Org. Chem. 1998, 63, 8668–8681. [Google Scholar] [CrossRef]
Al-Awadi, N. A.; Ibrahim, Y. A.; Kaul, K.; Dib, H. Regioselective Synthesis of 1,2,4-Triazol-3(2H)-ones and their 3(2H)-Thiones: Kinetic Studies and Selective Pyrolytic Deprotection. Heteroat. Chem. 2003, 14, 50–55. [Google Scholar] [CrossRef]
León, L. A.; Notario, R.; Quijano, J.; Vélez, E.; Sánchez, C.; Quijano, J. C.; Al-Awadi, N. A Density Functional Theory Study of the Gas-Phase Elimination Reactions of 4-Arylideneimino-1,2,4-triazol-3(2H)-ones and Their 3(2H)-thione Analogues. Theor. Chem. Acc. 2003, 110, 387–394. [Google Scholar] [CrossRef]
Austin, A.; Petersson, G. A.; Frisch, M. J.; Dobek, F. J.; Scalmani, G.; Throssell, K. A Density Functional with Spherical Atom Dispersion Terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef]
Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately Extracting the Signature of Intermolecular Interactions Present in the NCI Plot of the Reduced Density Gradient versus Electron Density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef]
Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef]
Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. Analysis of the Interaction Energy in Biomolecular Systems via the Independent Gradient Model (IGM). J. Chem. Theory Comput. 2020, 16, 2680–2691. [Google Scholar]
Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar] [CrossRef]
Grimme, S.; Hansen, A.; Brandenburg, J. G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed]
McQuarrie, D. A.; Simon, J. D. Molecular Thermodynamics; University Science Books: Sausalito, CA, 1999. [Google Scholar] [CrossRef]
Fukui, K. A Formulation of the Reaction Coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
Reed, A. E.; Weinhold, F. Natural Bond Orbital Analysis of Near-Hartree–Fock Water Dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
Reed, A. E.; Curtiss, L. A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
Wiberg, K. B.; Haven, N. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1967, 23, 1083–1096. [Google Scholar] [CrossRef]
Glendening, E. D.; Landis, C. R.; Weinhold, F. NBO 6.0: Natural Bond Orbital Analysis Program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
Muller, O. H. The Polarographic Method of Analysis. J. Chem. Educ. 1942, 19, 249. [Google Scholar] [CrossRef]
Benson, S. W. The Foundations of Chemical Kinetics; McGraw-Hill: New York, 1960. [Google Scholar]
Moyano, A.; Pericàs, M. A.; Valenti, E. A Theoretical Study on the Mechanism of the Thermal and the Acid-Catalyzed Decarboxylation of 2-Oxetanones (β-Lactones). J. Org. Chem. 1989, 54, 573–582. [Google Scholar] [CrossRef]
Klein, J.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. A New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef] [PubMed]
Frisch, M. J.; Pople, J. A.; Binkley, J. S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
Lin, Y. S.; Li, G. D.; Mao, S. P.; Chai, J. D. Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections. J. Chem. Theory Comput. 2013, 9, 263–272. [Google Scholar] [CrossRef]
Najibi, A.; Goerigk, L. The Non-Local Kernel in van-der-Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ωB97M-V Approaches. J. Chem. Theory Comput. 2018, 14, 5725–5738. [Google Scholar] [CrossRef] [PubMed]
Zaier, R.; Martel, A.; Antosiewicz, T. J. Effect of Benzothiadiazole-Based π-Spacers on Fine-Tuning of Optoelectronic Properties of Oligothiophene-Core Donor Materials for Efficient Organic Solar Cells: A DFT Study. J. Phys. Chem. A 2023, 127, 10555–10569. [Google Scholar] [CrossRef] [PubMed]
Elias, R. S.; Saeed, B. A.; Kamounah, F. S.; Duus, F.; Hansen, P. E. Strong Intramolecular Hydrogen Bonds and Steric Effects Involving C=S Groups: An NMR and Computational Study. Magn. Reson. Chem. 2020, 58, 154–162. [Google Scholar] [CrossRef] [PubMed]
Wang, Y.; Verma, P.; Jin, X.; Truhlar, D. G.; He, X. Revised M06 Density Functional for Main-Group and Transition-Metal Chemistry. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 10257–10262. [Google Scholar] [CrossRef] [PubMed]
Edet, H. O.; Louis, H.; Gber, T. E.; Idante, P. S.; Egemonye, T. C.; Ashishie, P. B.; Oyo-Ita, E. E.; Benjamin, I.; Adeyinka, A. S. Heteroatoms (B, N, S) Doped Quantum Dots as Potential Drug Delivery System for Isoniazid: Insight from DFT, NCI, and QTAIM. Heliyon 2024, 10, e40199. [Google Scholar] [CrossRef] [PubMed]
Savenko, E. S.; Kostjukov, V. V. Theoretical Study of the Excitation of Proflavine H-Dimers in an Aqueous Solution: The Effect of Functionals and Dispersion Corrections. Phys. Chem. Chem. Phys. 2023, 25, 12259–12276. [Google Scholar] [CrossRef]
Jacquemin, D.; Wathelet, V.; Perpète, E. A.; Adamo, C. Extensive TD-DFT Benchmark: Singlet-Excited States of Organic Molecules. J. Chem. Theory Comput. 2009, 5, 2420–2435. [Google Scholar] [CrossRef]
Bednarska, J.; Zalesny, R.; Bartkowiak, W.; Ośmiałowski, B.; Medved, M.; Jacquemin, D. Quantifying the Performances of DFT for Predicting Vibrationally Resolved Optical Spectra: Asymmetric Fluoroborate Dyes as Working Examples. J. Chem. Theory Comput. 2017, 13, 4347–4359. [Google Scholar] [CrossRef]
Lefebvre, C.; Klein, J.; Khartabil, H.; Boisson, J.-C.; Hénon, E. IGMPlot: A Program to Identify, Characterize, and Quantify Molecular Interactions. J. Comput. Chem. 2023, 44, 1750–1766. [Google Scholar] [CrossRef]
Menconi, G.; Tozer, D. J. Diatomic Bond Lengths and Vibrational Frequencies: Assessment of Recently Developed Exchange-Correlation Functionals. Chem. Phys. Lett. 2002, 360, 38–46. [Google Scholar] [CrossRef]
Stuyver, T.; Shaik, S. Unifying Conceptual Density Functional and Valence Bond Theory: The Hardness—Softness Conundrum Associated with Protonation Reactions and Uncovering Complementary Reactivity Modes. J. Am. Chem. Soc. 2020, 142, 20002–20013. [Google Scholar] [CrossRef]
Wieczorkiewicz, P.; Krygowski, T.; Szatyłowicz, H. Substituent Effects and Electron Delocalization in Five-Membered N-Heterocycles. Phys. Chem. Chem. Phys. 2024. [CrossRef] [PubMed]

Scheme 1. Biological activities of triazole and triazole-thione derivatives.

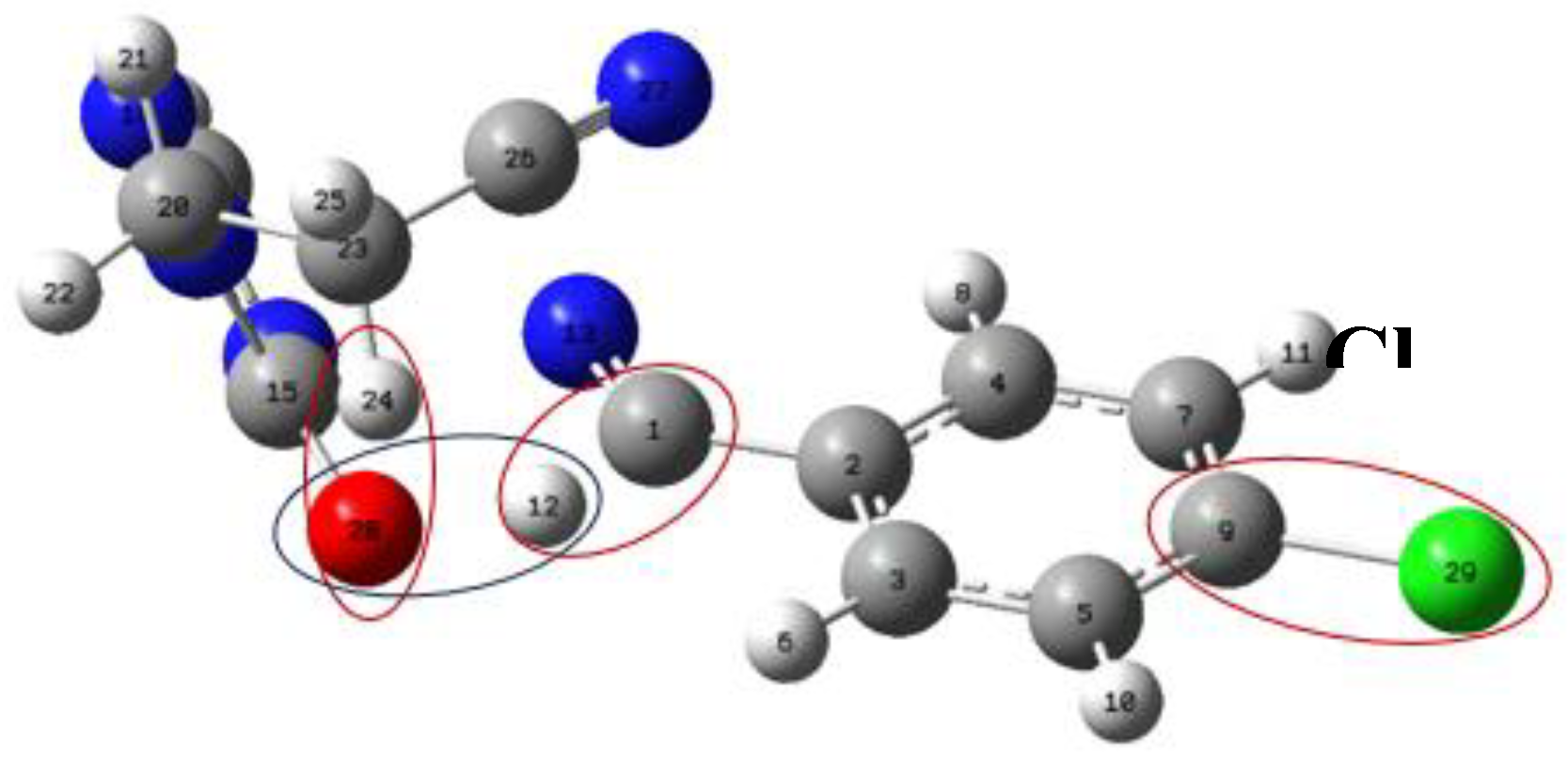
Scheme 2. Proposed mechanism and compounds studied for gas-phase unimolecular decomposition of 4-arylideneimino-R-1,2,4-triazol-3(2H)-ones/thiones. (A) Reactant structure with R-group variations: -H (a), or -CH₂CH₂CN (b); B) Six-membered cyclic transition state (TS) structure showing concerted bond cleavage (N-N) and hydrogen migration (H→X). The Table shows the series (I_R-VIII_R) with substituents X (O/S) and Y (H, Cl, Me, OMe) studied computationally.

Scheme 3. Elimination mechanism proceeds via a cyclic six-membered transition state, showing the proton transfer to oxygen or sulfur to form the enol form of the triazolone or triazothione, along with the aromatic nitrile. Subsequent tautomerization of the enol form to the keto form yields the product isolated experimentally.

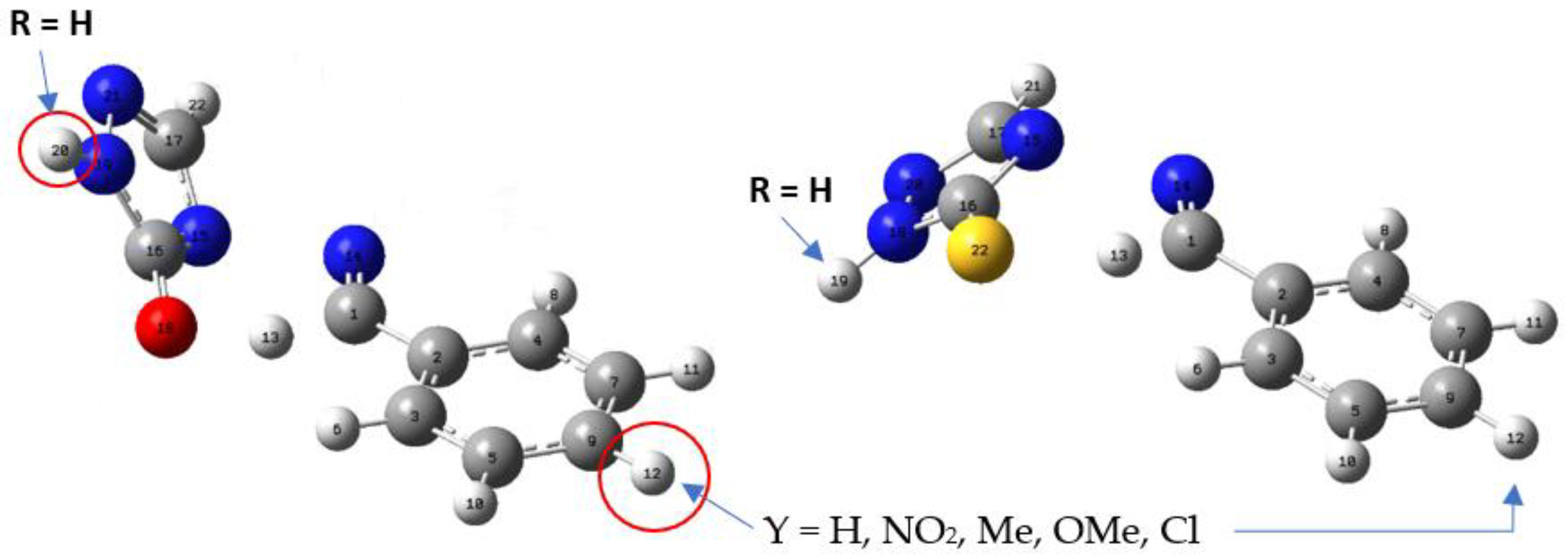
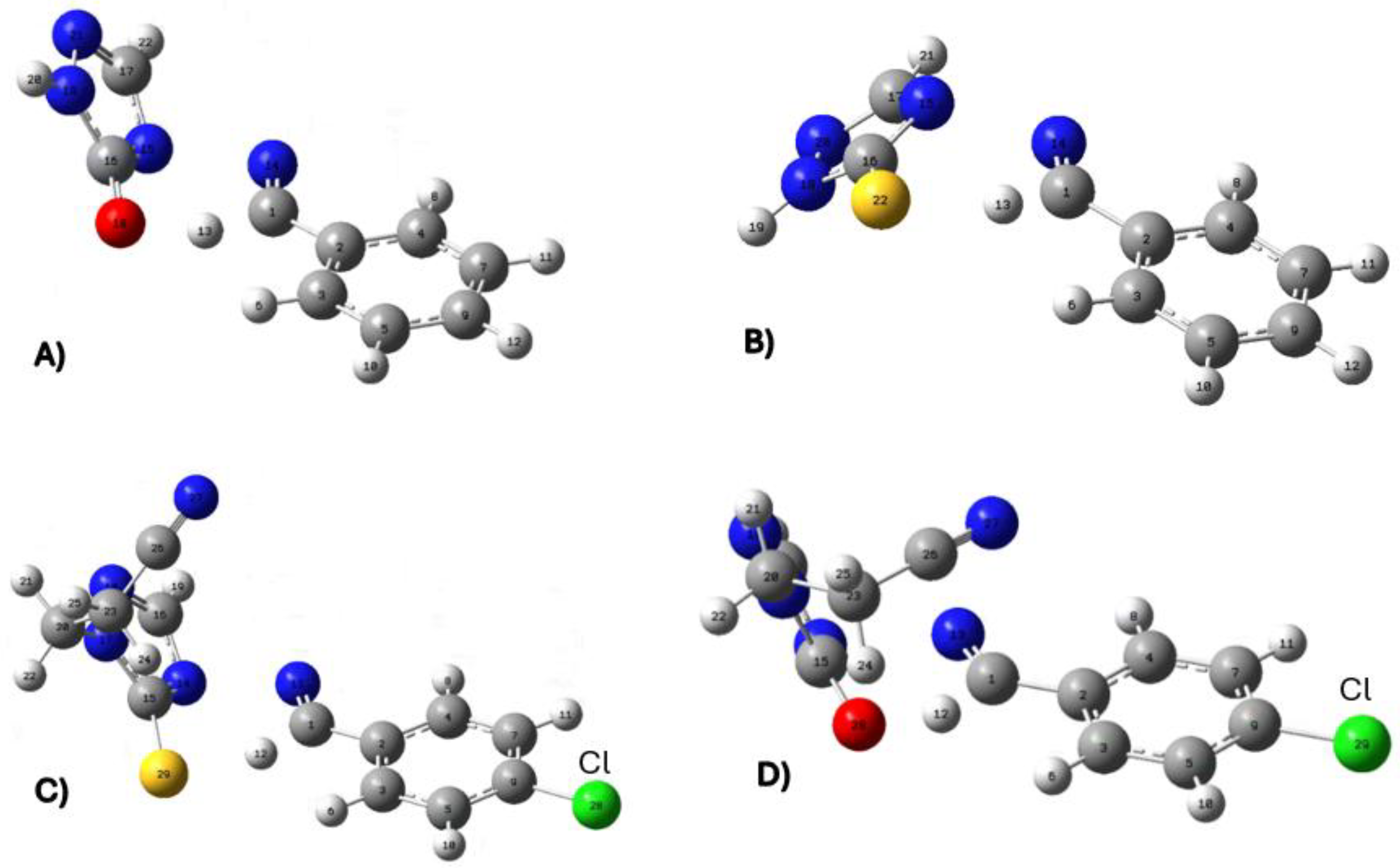
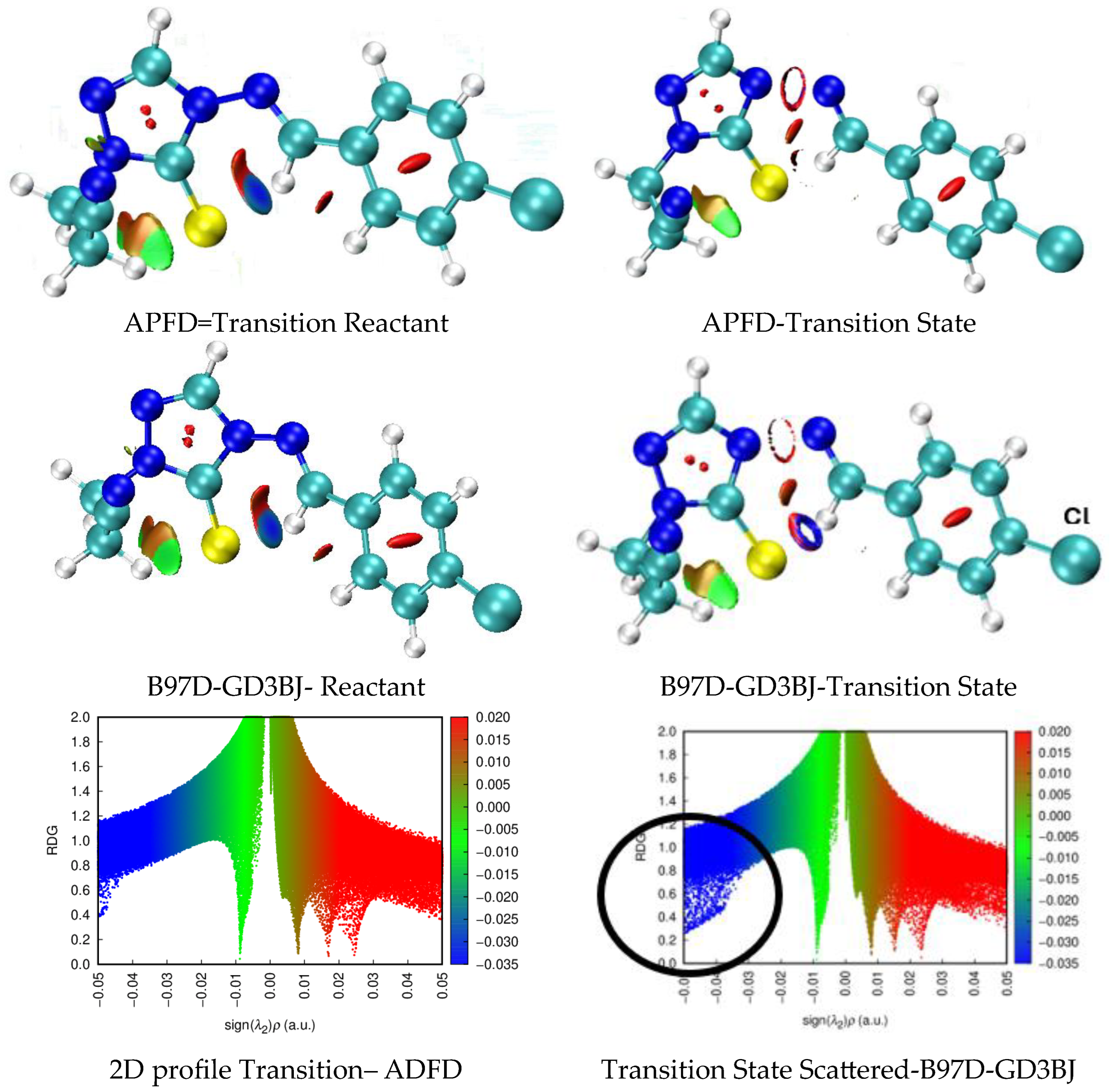
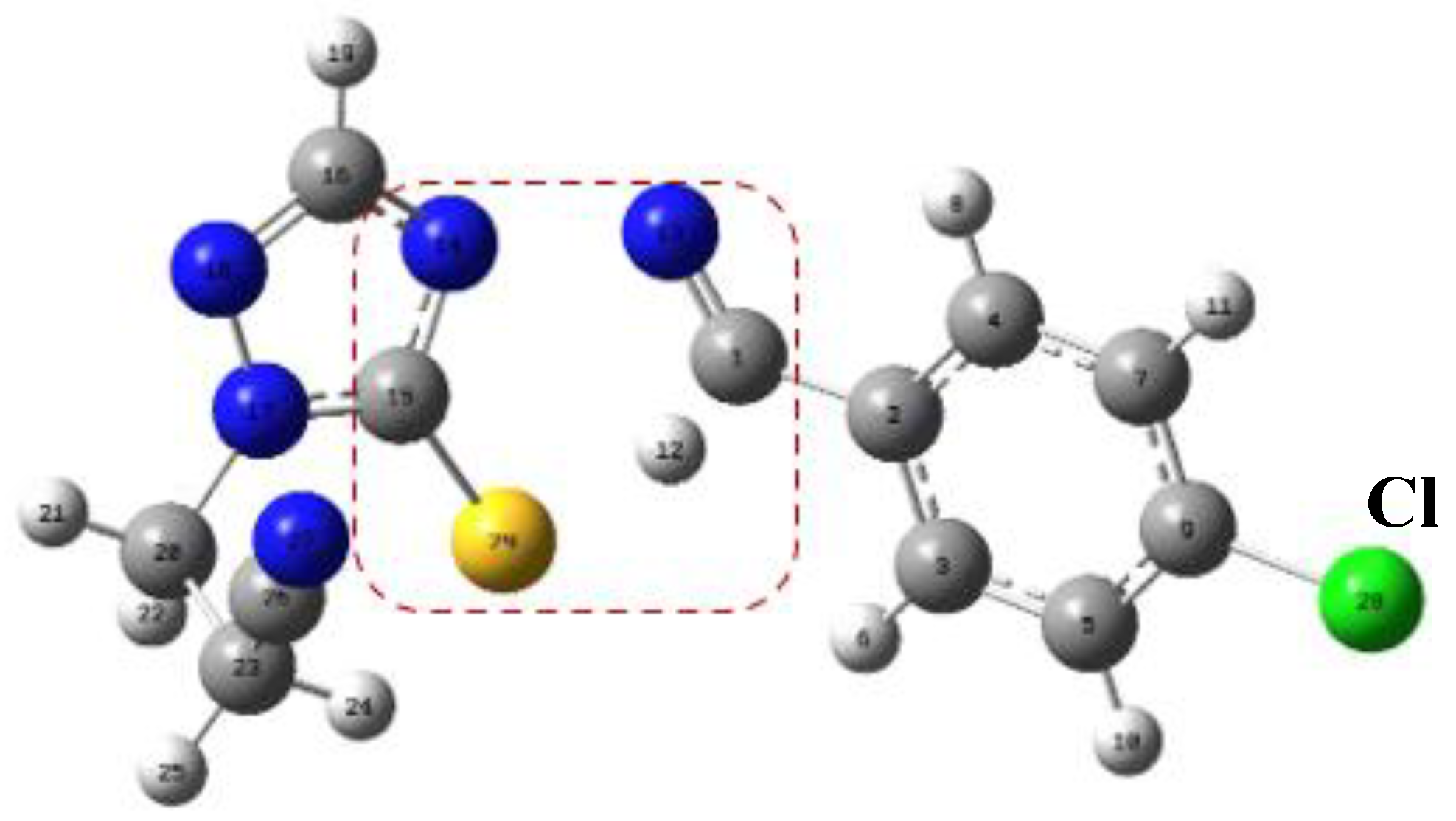
Figure 1. TS structures calculated at the level of APFD-Def2-TZVP theory. The TS of the 4-arylideneimino-1,2,4-triazol-3(2H)-one, on the left, shows a hydrogen attracted to the oxygen atom. The TS of the thione analogue on the right side shows the hydrogen atom closer to the carbon atom than the sulfur atom. The arrows indicate the position of the substituents.

Figure 2. Structure of the TS for 4-arylideneimino-1,2,4-triazol-3(2H)-one and thione analog derivatives, by comparing with Figure 1, we are incorporating the -CH₂CH₂CN group and its variants.

Scheme 4. Mechanism of decomposition for the -CH₂CH₂CN group.

Figure 3. Non-covalent interactions, NCI, involving the group -CH2CH2CN (A) and -CH2CH2-CS-CH3 (B). In the above picture, green color is related to non-covalent interactions, blue to strong interactions (π bond), and red to strong repulsion interactions. Here we use Y = Cl, X = S, at the APFD–def2–TZVP level of theory.

Figure 4. IRC and NBO studied molecule, where the -CH₂CH₂CN is over the TS structure.

Figure 5. A) NBO B97D-GD3BJ and B) APFD charges using the -CH₂CH₂CN group.

Figure 6. A detailed description of the C1 charge with the two methods, with and without -CH₂CH₂CN (CN). A) In blue, the two extra figures with CN, and B) we replace the whole group -CH₂CH₂CN with H.

Figure 7. HOMO and LUMO calculation for the carbon C1 using the group -CH₂CH₂CN. The case A) Using B97D—GD3BJ, and for the case B) APFD.

Figure 8. NBO charges the Chlorine atom. A) APFD, B) B97D-GD3BJ in both cases with and without -CN group.

Figure 9. Molecular structures (TS) under study, at the level of APFD-Def2-TZVP theory. The small differences correspond to changes in the substituents. A) X=O, R=-CH₂CH₂CN, and Y=Cl.

Figure 10. The area used to calculate the IBSI index represents the measure of the interaction strength present. These surfaces were integrated and presented as IBSI in these schemes. Each variable has its meaning in the interaction. Mainly, the parameters are calculated at the critical point of bonding between the two selected atoms—B97D-GD3BJ / Def2-TZVP theory level.

Figure 11. Graphical representation of the H12—O28 interaction. At the beginning, the interaction is very low, then in the transition state, a link is established, to finally generate a strong interaction. The integration of these areas represents the IBSI index and opens an index for each point in the IRC profile. Rendering B97D-GD3BJ / Def2-TZVP.

Figure 12. Determined structures of the model in Figure 10, at theory level B97D-GD3BJ and the base set def2-TZVP. The figure shows two views. In view (A) shows the non-covalent interaction between the -CH₂CH₂CN group on a green isosurface. In view (B), the interaction of one of the hydrogens of the -CH₂-CH(H)-CN group and oxygen (green color) is observed.

Figure 13. Non-covalent interactions with your 2D profiles with different functionalities with an oxygen atom.

Figure 14. Non-covalent interactions with your 2D profiles with different functionalities with a sulfur atom.

Figure 15. Critical Data Graphs Interaction: H24----O28 B97D-GD3BJ (Blue) APFD (Orange) for the Def2-TZVP basis set. Data from an IRC calculation (241 points).

Figure 16. Fragment definitions: (Frag1:CN) with (Frag2: some atoms of the transition state and the benzene ring, as shown in the figure above in circles). At the theory levels B97D-GD3BJ and APFD with the same basis set Def2-TZVP.

Figure 17. Quantification of fragment interaction: (Frag1:CN) with (Frag2: some atoms of the transition state and the benzene ring, as shown in Figure 16). At the theory level, APFD-Def2-TZVP.

Table 1. Thermodynamic parameters evaluated at the APFD/Def2-TZVP, HF =25% level of theory, enthalpies, Gibbs, entropies, and Activation energies in kJ/mol for all the reactants and transition states involved in the reactions studied (J/mol K).

X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)	% Error Ea (kJ/mol)	Ea (kJ/mol) Experimental
Sulfur	H	H	156.25	158.18	-3.87	160.40	29.0	124.3 ± 0.8
Sulfur	H	NO₂	160.85	161.98	-2.27	165.01
Sulfur	H	Me	159.56	146.49	26.15	163.72	5.8	154.8 ± 0.1
Sulfur	H	OMe	154.67	158.23	-7.11	158.83	1.4	156.7 ± 0.2
Sulfur	H	Cl	157.86	159.97	-4.18	162.02	27.1	127.5 ± 0.4
Oxygen	H	H	195.62	194.91	1.40	199.77	14.4	174.6 ± 2.5
Oxygen	H	NO₂	201.10	197.22	7.67	205.21
Oxygen	H	Me	198.62	182.86	31.54	202.78	18.4	171.0 ± 0.9
Oxygen	H	OMe	193.31	194.07	-1.52	197.47	39.0	142.1 ± 2.4
Oxygen	H	Cl	197.19	196.26	1.88	201.35	16.8	172.4 ± 2.1

Table 2. Calculated thermodynamic parameters using different functionals/Def2-TZVP, HF= 20–100% level of theory, for all the reactants and transition states. The parameters were evaluated for: 4-benzylideneimino-1,2,4-triazol-3(2H)-one and 4-benzylideneimino-1,2,4-triazol-3(2H)-thione.

Functional	X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)	% Error Ea (kJ/mol)
B3LYP GD3BJ P2 = 20%	Sulfur	H	H	143.07	144.80	-3.47	147.22	18.4
M062X P2=54%	Sulfur	H	H	173.60	174.28	-1.36	177.76	43.0
BHandHLYP P2=50%	Sulfur	H	H	188.71	189.19	-0.96	192.87	55.2
wB97XD P2=100%	Sulfur	H	H	170.66	172.56	-3.77	174.83	40.7
BLYP P2 = 20%	Oxygen	H	H	148.57	148.76	-0.37	152.73	-13.8
PBE0 P2=25%	Oxygen	H	H	210.68	209.22	2.86	214.83	21.3
M062X P2=54%	Oxygen	H	H	208.68	205.86	5.64	212.84	20.2
B3LYP P2 = 20%	Oxygen	H	H	184.04	183.05	-39.89	188.20	6.3
B3LYP GD3BJ P2=20%	Oxygen	H	H	183.29	182.98	0.62	187.45	5.8

Table 3. Calculated thermodynamic parameters using different functionals/Def2-TZVP, HF = 0% level of theory. for all the reactants and transition states, the parameters were evaluated for 4-benzylideneimino-1,2,4-triazol-3(2H)-one and 4-benzylideneimino-1,2,4-triazol-3(2H)-thione.

^Functional	X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)	% Error Ea (kJ/mol)
^MO6L	Sulfur	H	H	134.97	137.91	-5.89	139.12	11.9
MO6L (GD3)	Sulfur	H	H	135.03	138.04	-6.02	139.19	12.0
B97D (GD3BJ)	Sulfur	H	H	117.43	120.04	-5.21	121.59	-2.2
HCTH407^$	Sulfur	H	H	133.61	135.20	-3.17	137.77	10.8
HCTH407	Oxygen	H	H	175.49	175.60	-0.21	179.65	1.4
B97D (GD3BJ)	Oxygen	H	H	156.46	137.41	12.60	160.62	-6.7
BLYP	Oxygen	H	H	148.57	148.76	-0.37	152.72	-13.8
MO6L	Oxygen	H	H	175.75	175.07	1.36	179.91	1.6

^$ [42].

Table 4. Thermodynamic parameters were calculated at APFD/Def2-TZVP HF = 25% level of theory, for all the reactants and transition states involved in the reactions studied.

Functional	X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)	% Error Ea (kJ/mol)
APFD	Sulfur	CH₂CH₂CN	Cl	159.21	158.09	2.23	163.36
APFD	Sulfur	CH₂CH₂CN	H	158.18	156.04	0.10	162.34	2.7
APFD	Sulfur	CH₂CH₂CN	Me	159.02	159.71	-1.39	163.17	0.2
APFD	Sulfur	CH₂CH₂CN	OMe	157.87	157.02	1.70	162.03	4.7
APFD	Sulfur	CH₂CH₂CN	NO₂	162.51	162.63	-4.43	166.67	13.1
APFD	Oxygen	CH₂CH₂CN	H	195.34	184.68	0.69	199.50	23.4
APFD	Oxygen	CH₂CH₂CN	NO₂	201.07	197.81	6.51	205.22	32.7
MO6L	Oxygen	CH₂CH₂CN	NO₂	180.74	186.62	-11.77	184.89	19.6
APFD	Oxygen	CH₂CH₂CN	Me	194.46	214.06	-6.70	198.61	9.4
APFD	Oxygen	CH₂CH₂CN	OMe	194.34	195.53	-2.38	198.50	7.1
APFD	Oxygen	CH₂CH₂CN	Cl	201.72	198.20	7.04	205.88

Table 5. Energies evaluated at the B97D-GD3BJ/Def2-TZVP HF = 0% level of theory, enthalpies, Gibbs, entropies*, and activation energies in kJ/mol for all the reactants and transition states involved in the reactions studied. *(J/mol K).

X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)
Sulfur	CH₂CH₂CN	Cl	120.52	121.78	-2.52	124.68
Sulfur	CH₂CH₂CN	OCH₃	118.75	121.39	-5.22	122.91
Sulfur	CH₂CH₂CN	CH₃	114.73	118.35	-7.24	118.89
Sulfur	CH₂CH₂CN	NO₂	123.59	121.82	3.55	127.75
Sulfur	CH₂CH₂CN	H	118.94	120.26	-2.63	123.10
Oxygen	CH₂CH₂CN	OCH₃	157.23	155.49	3.50	161.39
Oxygen	CH₂CH₂CN	CH₃	157.41	156.77	1.28	161.56
Oxygen	CH₂CH₂CN	Cl	159.29	161.22	-3.85	163.45
Oxygen	CH₂CH₂CN	NO₂	161.98	165.37	-6.78	166.14
Oxygen	CH₂CH₂CN	H	158.05	158.29	-0.47	162.21
Oxygen	CH₂CH₂-CO-CH₃	Cl	154.87	161.65	-13.55	159.03
Oxygen	CH₂CH₂-CS-CH₃	Cl	150.84	157.05	-12.44	155.00
Oxygen	CH₂CH₂-O-CH₃	Cl	156.69	159.09	-4.81	160.85
Oxygen	CH₂CH₃	Cl	158.42	158.04	0.76	162.58

Table 6. Thermodynamic parameters were evaluated at the APFD and B97D-GD3BJ/Def2-TZVP levels of theory for all reactants and transition states involved in the studied reactions.

Functional	X	R	Y	ΔH (kJ/mol)	ΔG (kJ/mol)	ΔS (J/Kmol)	Ea (kJ/mol)
APFD P2 = 25%	Sulfur	CH₂CH₂-CS-CH₃	Cl	145.59	146.94	-2.69	149.75
APFD P2 = 25%	Oxygen	CH₂CH₂-CS-CH₃	Cl	170.21	184.30	-28.19	174.37
B97D GD3Bj P2 = 0%	Oxygen	CH₂CH₂-CS-CH₃	Cl	148.74	156.83	-16.18	152.90
B97D GD3Bj P2 = 0%	Sulfur	CH₂CH₂-CS-CH₃	Cl	103.64	102.18	2.93	107.80

Table 7. Wiberg bond indices, Bi, of reactants, transition states, and products under the scheme of the TS shown after the Table, percentage of evolution (%E_V) through the chemical process of the bond indices at the transition states. The degree of advancement of the transition states, ΔBav, and absolute synchronicities (Sy). Values calculated at the APFD/Def2-TZVP level of theory.

Table 8. Wiberg bond indices, Bi, of reactants, transition states, and products, calculated at the B97D-GD3BJ/Def2-TZVP level of theory. Atom numbers are depicted in Figure 5. The percent evolution (%EV) through the chemical process of the bond indices at the transition states, degree of advancement of the transition states, ΔBav, and absolute synchronicities (S) are shown.

Table 9. Critical Point Analysis for the B97D-GD3BJ / Def2-TZVP, X = O, Y = Cl. R =-CH₂CH₂CN, point 121 (Transition State) from an IRC calculation.

Bond Pair	d(Angs)	δg	IBSI	PDA (×10⁻¹)	Asymmetry Direction	rho	Lap	bcp_x	bcp_y	bcp_z	L1	L2	L3
H24-O28	2.512	0.093	0.02	135.1	H24 → O28	0.011	0.042	-2.114	1.344	1.163	-0.01	-0.007	0.058
O28-H12	1.434	0.497	0.336	249.8	O28 ← H12	0.1	0.1	-1.075	-0.363	1.293	-0.215	-0.213	0.528
H12-C1	1.212	0.693	0.656	205.9	H12 → C1	0.204	-0.542	-0.474	-0.716	0.864	-0.523	-0.519	0.5
C1-N13	1.225	2.025	1.878	30.3	C1 → N13	0.439	-0.781	-0.263	-1.432	0.091	-1.064	-0.991	1.274
N13-N14	2.165	0.538	0.16	0	N13–N14	0.054	0.125	-1.705	-1.892	0.079	-0.067	-0.063	0.254
N14-C15	1.369	1.751	1.301	38.6	N14 ← C15	0.339	-1.052	-2.711	-1.034	0.686	-0.802	-0.681	0.431
C15-O28	1.269	1.987	1.717	84.2	C15 → O28	0.372	-0.609	-2.421	-0.326	1.136	-0.95	-0.826	1.167
C9-C129	1.739	1.598	0.735	322.5	C9 → C129	0.202	-0.306	4.731	0.253	-0.028	-0.33	-0.311	0.335

Table 10. Critical Point Analysis for the APFD/ Def2-TZVP, X = O, Y = Cl. R =-CH₂CH₂CN (TS). Point 121 del perfil IRC.

Bond	d(Angs)	δg	IBSI	PDA (×10⁻¹)	Asymmetry Dir.	rho	Lap	bcp_x	bcp_y	bcp_z	L1	L2	L3
H24-028	2.476	0.082	0.019	137.5	H24→028	0.012	0.049	-2.297	1.376	1.105	-0.011	-0.007	0.066
028-C15	1.269	1.955	1.689	84.8	O28←C15	0.373	-0.601	-2.386	-0.295	1.05	-0.967	-0.849	1.215
C15-N14	1.349	1.764	1.348	38.9	C15→N14	0.352	-1.189	-2.619	-1.012	0.645	-0.85	-0.71	0.371
N14-N13	2.035	0.653	0.22	1	N14→N13	0.072	0.151	-1.581	-1.892	0.118	-0.096	-0.092	0.339
N13-C1	1.214	2.002	1.889	29.5	N13←C1	0.445	-0.589	-0.211	-1.392	0.14	-1.087	-1.043	1.542
C1-H12	1.259	0.656	0.576	200.2	C1←H12	0.18	-0.425	-0.498	-0.593	0.854	-0.45	-0.444	0.469
H12-028	1.334	0.559	0.438	267.9	H12→028	0.127	0.045	-1.062	-0.252	1.221	-0.314	-0.31	0.668
C9-C129	1.725	1.622	0.759	323.9	C9→C129	0.209	-0.347	4.739	0.278	-0.059	-0.344	-0.324	0.321

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.