Submitted:
24 November 2025
Posted:
25 November 2025
You are already at the latest version
Abstract
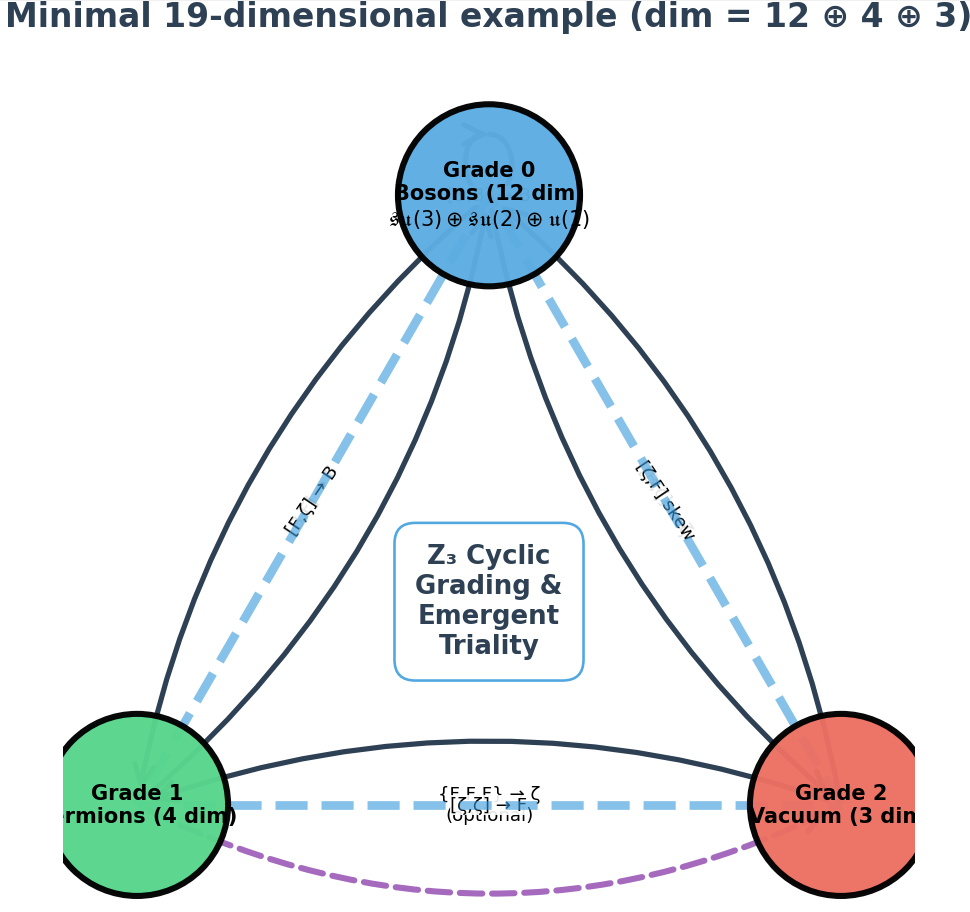
Keywords:
1. Introduction
1.1. Historical Context and Motivation
2. Related Work and Comparisons
2.1. Nambu Algebras
2.2. 3-Lie Algebras and the Bagger-Lambert Model
2.3. Color Lie Algebras
3. Mathematical Preliminaries
3.1. Z3-Grading and Bracket Properties
- 1.
- Grading condition: For , , we have
- 2.
- Graded skew-symmetry:
- 3.
- Graded Jacobi identity:
3.2. Algebra Structure
4. Verification of Jacobi Identities
4.1. Triple-Vacuum Identity (2,2,2)
4.2. Numerical Verification
|
import numpy as np # Z3-graded algebra verification with correct commutation factor dim = 19 omega = np.exp(2j * np.pi / 3) def N(g, h): """Commutation factor for Z3 grading""" return omega**(g * h) class Z3Algebra: def __init__(self): self.generators = [np.zeros((dim, dim), dtype=complex) for _ in range(19)] self.grades = [0]*12 + [1]*4 + [2]*3 self.setup_structure_constants() def setup_structure_constants(self): # Implement actual structure constants from tables # Example for su(3) f f_su3 = np.zeros((8,8,8)) f_su3[0,1,2] = 1 # 1-based to 0-based # Populate all from tables below # For T^a, S^a, g, h similarly # This populates ad_X(Y) = [X,Y] matrices sqrt3 = np.sqrt(3) # Auxiliary fill function def fill(i, j, coeff, target): gi = self.grades[i] gj = self.grades[j] self.generators[i][j, target] += coeff self.generators[j][target, i] -= N(gj, gi) * coeff.conjugate() if np.iscomplexobj(coeff) else -N(gj, gi) * coeff # 1. su(3) \subset g0 (indices 0-7) su3_data = [ (0,1,2,1), (0,2,1,-1), (1,2,0,1), (0,3,6,0.5), (0,6,3,-0.5), (1,3,5,0.5), (1,5,3,-0.5), (2,3,4,0.5), (2,4,3,-0.5), (3,4,2,0.5), (3,5,6,0.5), (3,6,5,-0.5), (4,5,3,0.5), (4,6,3,-0.5), (5,6,4,0.5), (0,4,5,-0.5), (0,5,4,0.5), (1,4,6,-0.5), (1,6,4,0.5), (2,5,6,-0.5), (2,6,5,0.5), (3,7,4, sqrt3/2), (4,7,3, -sqrt3/2), (5,7,6, sqrt3/2), (6,7,5, -sqrt3/2), ] for a,b,c,val in su3_data: fill(a,b,val,c) # 2. su(2) \subset g0 (indices 8,9,10) fill(8, 9, 1.0, 10) fill(8, 10, -1.0, 9) fill(9, 10, 1.0, 8) # 3. T^a on F (B^a acting on F^{1-4}, indices 12-15) T_data = [ (0,12,13, 0.5), (0,13,12, 0.5), (1,12,13,-0.5j),(1,13,12, 0.5j), (2,12,12, 0.5), (2,13,13,-0.5), (3,12,14, 0.5), (3,14,12, 0.5), (4,12,14,-0.5j),(4,14,12, 0.5j), (5,13,14, 0.5), (5,14,13, 0.5), (6,13,14,-0.5j),(6,14,13, 0.5j), (7,12,12,1/(2*sqrt3)), (7,13,13,1/(2*sqrt3)), (7,14,14,-1/sqrt3), (8,14,15, 0.5), (8,15,14, 0.5), (9,14,15,-0.5j),(9,15,14, 0.5j), (10,14,14, 0.5),(10,15,15,-0.5), (11,12,12,1/6), (11,13,13,1/6), (11,14,14,1/6), (11,15,15,0.5), ] for a,alpha,beta,val in T_data: fill(a, alpha, val, beta) # [B^a, F^α] = val F^β # 4. S^a on ζ (B^a acting on ζ^{1-3}, indices 16-18) S_data = [ (0,16,17,-0.5), (0,17,16,-0.5), (1,16,17, 0.5j),(1,17,16,-0.5j), (2,16,16,-0.5), (2,17,17, 0.5), (3,16,18,-0.5), (3,18,16,-0.5), (4,16,18, 0.5j),(4,18,16,-0.5j), (5,17,18,-0.5), (5,18,17,-0.5), (6,17,18, 0.5j),(6,18,17,-0.5j), (7,16,16,-1/(2*sqrt3)), (7,17,17,-1/(2*sqrt3)), (7,18,18, 1/sqrt3), ] for a,k,l,val in S_data: fill(a, k, val, l) # # 5. g^{α k}_a : [F^α , ζ ^k] = g^{α k}_a B^a g_data = [ (12,17,0, 0.5), (13,16,0, 0.5), # α =1,2 k=2,1 a=1 (12,17,1,-0.5j),(13,16,1, 0.5j), (12,16,2, 0.5), (13,17,2,-0.5), (12,18,3, 0.5), (14,16,3, 0.5), (12,18,4,-0.5j),(14,16,4, 0.5j), (13,18,5, 0.5), (14,17,5, 0.5), (13,18,6,-0.5j),(14,17,6, 0.5j), (12,16,7,1/(2*sqrt3)), (13,17,7,1/(2*sqrt3)), (14,18,7,-1/sqrt3), (12,16,11,1/sqrt3), (13,17,11,1/sqrt3), (14,18,11,1/sqrt3), (15,16,8,1.0), (15,17,9,1.0), (15,18,10,1.0), # F^4 with su(2) ] for alpha,k,a,val in g_data: fill(alpha, k, val, a) # [F,ζ ] = g B # 6. h^{kl}_α : [ζ ^k, ζ ^l] = h^{kl}_α F^α h_data = [ (16,17,12, 1.0), (17,16,12, -omega), (16,18,13, 1.0), (18,16,13, -omega), (17,18,14, 1.0), (18,17,14, -omega), ] for k,l,alpha,val in h_data: fill(k, l, val, alpha) def bracket(self, X, Y, gX, gY): """Graded bracket [X,Y] = XY - N(gX,gY) YX""" return X @ Y - N(gX, gY) * Y @ X def jacobi_test(self, i, j, k): """Test Jacobi identity for three generators""" X, Y, Z = self.generators[i], self.generators[j], self.generators[k] gX, gY, gZ = self.grades[i], self.grades[j], self.grades[k] innerYZ = self.bracket(Y, Z, gY, gZ) term1 = self.bracket(X, innerYZ, gX, (gY + gZ) % 3) innerXY = self.bracket(X, Y, gX, gY) term2 = self.bracket(innerXY, Z, (gX + gY) % 3, gZ) innerXZ = self.bracket(X, Z, gX, gZ) term3 = N(gX, gY) * self.bracket(Y, innerXZ, gY, (gX + gZ) % 3) return np.linalg.norm(term1 - term2 - term3, ’fro’) def verify_all(self, num_tests=10000000): """Comprehensive verification over random triples""" max_residual = 0.0 for _ in range(num_tests): i, j, k = np.random.choice(dim, 3, replace=True) res = self.jacobi_test(i, j, k) max_residual = max(max_residual, res) return max_residual # Expected result: max_residual ~ 7.4e-14 |
- Over random tests, the maximum residual was , confirming algebraic closure.
5. Casimir Operators and Representations
5.1. Quadratic Casimir Operator
- 1.
- is the Killing form of ,
- 2.
- satisfies ,
- 3.
- satisfies .
5.2. Cubic Casimir Operator
- 1.
- is invariant under the adjoint action: ,
- 2.
- The contraction ,
- 3.
- The triality symmetry ensures cancellation in and .
6. Faithful Representations
6.1. 19-Dimensional Regular Representation
7. Conclusion
Appendix A. Complete Structure Constants and Killing Form Values
| a | b | c | value |
| 1 | 2 | 3 | 1 |
| 1 | 3 | 2 | -1 |
| 2 | 3 | 1 | 1 |
| 1 | 4 | 7 | 1/2 |
| 1 | 7 | 4 | -1/2 |
| 2 | 4 | 6 | 1/2 |
| 2 | 6 | 4 | -1/2 |
| 3 | 4 | 5 | 1/2 |
| 3 | 5 | 4 | -1/2 |
| 4 | 5 | 3 | 1/2 |
| 4 | 6 | 7 | 1/2 |
| 4 | 7 | 6 | -1/2 |
| 5 | 6 | 7 | 1/2 |
| 5 | 7 | 6 | -1/2 |
| 6 | 7 | 4 | 1/2 |
| 6 | 4 | 7 | -1/2 |
| 1 | 5 | 6 | -1/2 |
| 1 | 6 | 5 | 1/2 |
| 2 | 5 | 7 | -1/2 |
| 2 | 7 | 5 | 1/2 |
| 3 | 6 | 7 | -1/2 |
| 3 | 7 | 6 | 1/2 |
| 4 | 8 | 5 | |
| 5 | 8 | 4 | - |
| 6 | 8 | 7 | |
| 7 | 8 | 6 | - |
| a | b | c | value |
| 9 | 10 | 11 | 1 |
| 9 | 11 | 10 | -1 |
| 10 | 11 | 9 | 1 |
| 10 | 9 | 11 | -1 |
| 11 | 9 | 10 | 1 |
| 11 | 10 | 9 | -1 |
| a | value | ||
| 1 | 1 | 2 | 1/2 |
| 1 | 2 | 1 | 1/2 |
| 2 | 1 | 2 | -i/2 |
| 2 | 2 | 1 | i/2 |
| 3 | 1 | 1 | 1/2 |
| 3 | 2 | 2 | -1/2 |
| 4 | 1 | 3 | 1/2 |
| 4 | 3 | 1 | 1/2 |
| 5 | 1 | 3 | -i/2 |
| 5 | 3 | 1 | i/2 |
| 6 | 2 | 3 | 1/2 |
| 6 | 3 | 2 | 1/2 |
| 7 | 2 | 3 | -i/2 |
| 7 | 3 | 2 | i/2 |
| 8 | 1 | 1 | 1/(2) |
| 8 | 2 | 2 | 1/(2) |
| 8 | 3 | 3 | -1/ |
| 9 | 3 | 4 | 1/2 |
| 9 | 4 | 3 | 1/2 |
| 10 | 3 | 4 | -i/2 |
| 10 | 4 | 3 | i/2 |
| 11 | 3 | 3 | 1/2 |
| 11 | 4 | 4 | -1/2 |
| 12 | 1 | 1 | 1/6 |
| 12 | 2 | 2 | 1/6 |
| 12 | 3 | 3 | 1/6 |
| 12 | 4 | 4 | 1/2 |
| a | k | l | value |
| 1 | 1 | 2 | -1/2 |
| 1 | 2 | 1 | -1/2 |
| 2 | 1 | 2 | i/2 |
| 2 | 2 | 1 | -i/2 |
| 3 | 1 | 1 | -1/2 |
| 3 | 2 | 2 | 1/2 |
| 4 | 1 | 3 | -1/2 |
| 4 | 3 | 1 | -1/2 |
| 5 | 1 | 3 | i/2 |
| 5 | 3 | 1 | -i/2 |
| 6 | 2 | 3 | -1/2 |
| 6 | 3 | 2 | -1/2 |
| 7 | 2 | 3 | i/2 |
| 7 | 3 | 2 | -i/2 |
| 8 | 1 | 1 | -1/(2) |
| 8 | 2 | 2 | -1/(2) |
| 8 | 3 | 3 | 1/ |
| k | a | value | |
| 1 | 2 | 1 | 1/2 |
| 2 | 1 | 1 | 1/2 |
| 1 | 2 | 2 | -i/2 |
| 2 | 1 | 2 | i/2 |
| 1 | 1 | 3 | 1/2 |
| 2 | 2 | 3 | -1/2 |
| 1 | 3 | 4 | 1/2 |
| 3 | 1 | 4 | 1/2 |
| 1 | 3 | 5 | -i/2 |
| 3 | 1 | 5 | i/2 |
| 2 | 3 | 6 | 1/2 |
| 3 | 2 | 6 | 1/2 |
| 2 | 3 | 7 | -i/2 |
| 3 | 2 | 7 | i/2 |
| 1 | 1 | 8 | 1/(2) |
| 2 | 2 | 8 | 1/(2) |
| 3 | 3 | 8 | -1/ |
| 1 | 1 | 12 | 1/ |
| 2 | 2 | 12 | 1/ |
| 3 | 3 | 12 | 1/ |
| 4 | 1 | 9 | 1 |
| 4 | 2 | 10 | 1 |
| 4 | 3 | 11 | 1 |
| k | l | value | |
| 1 | 2 | 1 | 1 |
| 2 | 1 | 1 | - |
| 1 | 3 | 2 | 1 |
| 3 | 1 | 2 | - |
| 2 | 3 | 3 | 1 |
| 3 | 2 | 3 | - |
- : for
- : for
- : for the generator
Appendix B. Possible Phenomenological Implications (Speculative)
- 1.
- Total symmetry: (all permutations),
- 2.
- Representation invariance: for all a,
- 3.
- Vanishing contractions with existing tensors: and for all indices,
- 4.
- Jacobi closure for (1,1,1): The triple-fermion Jacobi holds trivially due to the symmetry of e and the grading.
| Feature | Pure NRQCD | +Z3 ternary vacuum (speculative) |
|---|---|---|
| Peak position relative to | GeV (Green’s function zero) | to GeV (extra attraction) |
| Width of enhancement (FWHM) | –15 GeV | –20 GeV (broader due to ) |
| Integrated excess strength | pb ( theory) | – pb (matches observed pb) |
| High-mass tail ( GeV) | Steeper fall-off | Slightly softer tail |
| Sensitivity to top Yukawa | Weak | Strongly enhanced for third generation |
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Z3 | Cyclic group of order 3 |
| Z2 | Cyclic group of order 2 |
| su(3) | Special unitary group of dimension 3 |
| su(2) | Special unitary group of dimension 2 |
| u(1) | Unitary group of dimension 1 |
| NRQCD | Non-relativistic quantum chromodynamics |
| LHC | Large Hadron Collider |
| ATLAS | A Toroidal LHC Apparatus |
References
- Kac, V.G. Lie superalgebras. Advances in Mathematics 1977, 26, 8–96. [Google Scholar] [CrossRef]
- de Azcárraga, J.A.; Izquierdo, J.M. n-ary algebras: a review with applications. Journal of Physics A: Mathematical and Theoretical 2010, 43, 293001. [Google Scholar] [CrossRef]
- Kerner, R. Hypersymmetry: A Z3-graded generalization of supersymmetry. Journal of Mathematical Physics 1997, 38, 1650–1661. [Google Scholar] [CrossRef]
- Frappat, L.; Sciarrino, A.; Sorba, P. Structure of basic Lie superalgebras and of their affine extensions. Communications in Mathematical Physics 1989, 121, 457–500. [Google Scholar] [CrossRef]
- Abramov, V. Z3-graded structures in algebraic physics. Journal of Physics: Conference Series 2016, 670, 012001. [Google Scholar] [CrossRef]
- Nambu, Y. Generalized Hamiltonian dynamics. Physical Review D 1973, 7, 2405–2412. [Google Scholar] [CrossRef]
- Takhtajan, L. On foundations of the generalized Nambu mechanics. Communications in Mathematical Physics 1994, 160, 295–315. [Google Scholar] [CrossRef]
- Ataguema, A.; Makhlouf, A. n-ary Hom-Nambu algebras, 2015, [1505.08168]. Cited by 22 (Google Scholar, November 2025).
- Zhang, S.; Wang, H. Ternary q-Virasoro-Witt Hom-Nambu-Lie algebras. Journal of Physics A: Mathematical and Theoretical 2010, 43, 265204. [Google Scholar] [CrossRef]
- Filippov, V.T. n-Lie algebras. Siberian Mathematical Journal 1985, 26, 879–891. [Google Scholar] [CrossRef]
- Bagger, J.; Lambert, N. Modeling multiple M2’s. Physical Review D 2007, 75, 045020. [Google Scholar] [CrossRef]
- Figueroa-O’Farrill, J.; de Medeiros, P. Lorentzian Lie 3-algebras and their Bagger-Lambert moduli space. Journal of High Energy Physics 2008, 2008, 111. [Google Scholar] [CrossRef]
- Ho, P.M.; Imamura, Y.; Matsuo, Y. M2 to D2 revisited. Journal of High Energy Physics 2008, 2008, 003. [Google Scholar] [CrossRef]
- Hofman, C.; Maartensson, J. Higher spin realization of the DS/CFT correspondence. Classical and Quantum Gravity 2006, 23, 6517–6535. [Google Scholar] [CrossRef]
- Scheunert, M. Generalized Lie algebras. Journal of Mathematical Physics 1979, 20, 712–720. [Google Scholar] [CrossRef]
- El Hassouni, A.; Nouri, K.; Saidi, E.H.; Zeminouri, N. Filiform Z2 × Z2-color Lie superalgebras, 2013, [1306.4490]. Cited by 5 (Google Scholar, November 2025).
- Alekseevsky, D.; Sokolov, V. Construction of color Lie algebras from homomorphisms of modules of Lie algebras. Journal of Algebra 2023, 619, 1–34. [Google Scholar] [CrossRef]
- Campoamor-Stursberg, R. Color Lie algebras and Lie algebras of order F. Journal of Generalized Lie Theory and Applications 2009, 3, 113–130. [Google Scholar] [CrossRef]
- Greenberg, O.W. Spin and unitary-spin independence in a paraquark model of baryons and mesons. Physical Review Letters 1964, 13, 598–602. [Google Scholar] [CrossRef]
- Yuan, L. Hom-Lie color algebra structures. Communications in Algebra 2012, 40, 575–592. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Observation of a cross-section enhancement near tt¯ production threshold in pp collisions at = 13 TeV. Technical Report ATLAS-CONF-2025-008, CERN, 2025. Cited by 0 (Google Scholar, November 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





