Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Identifying Seismic Anomalies Through Latitude‐ Longitude Mesh Analysis

Submitted:

19 December 2025

Posted:

22 December 2025

You are already at the latest version

Abstract
Analysing seismic data with modern statistical methods has opened up the possibility of predicting major earthquakes and those of specific magnitudes. However, comprehensive analysis for each location is particularly labour-intensive, while such data necessitates continuous observation. It is therefore desirable to detect anomalies with ease. We demonstrate that this objective can be achieved not by examining complex regional ge-ometries, but simply by dividing the study area into a mesh. Moreover, unexpected properties emerged from the data collected in this manner, which we also present.
Keywords: 
earthquake prediction
;  
calculation method
;  
programming
;  
latitude–longitude grid running head: mesh analysis
Subject: 
Environmental and Earth Sciences  -   Geophysics and Geology

Introduction

Modern statistical methods enable the detection of anomalies that precede major earthquakes. Such anomalies can be identified even from simple records, including time and magnitude (Konishi, 2025d). For earthquakes of magnitude 6–7, some degree of prediction appears feasible, provided that such records are available (Konishi, 2025a). Precursor swarms are frequently observed prior to large events, and their identification—alongside anomalous magnitude distributions—may offer valuable insights into seismic hazard.
Historically, seismological research has not fully incorporated these modern statistical approaches. As a result, certain empirical laws—such as the Gutenberg–Richter law for magnitude distribution (Gutenberg and Richter, 1944) and the Omori formula for aftershock decay (Omori, 1895; Utsu, 1957; Utsu et al., 1995) —remained widely accepted for decades, despite mounting evidence of their limitations (Konishi, 2025d, c). While these models have played a foundational role in the development of seismology, their continued use without critical re-evaluation may hinder progress. Accordingly, research grounded in such assumptions should be interpreted with caution, particularly when drawing conclusions about earthquake mechanisms.
The principal difficulty is that the recorded data are often extremely voluminous, making regional examination laborious (JMA, 2025c, d; Konishi, 2025a). In addition, the administrative areas defined by local authorities are typically irregular in shape (JMA, 2025e). As earthquakes can occur at any time, continuous monitoring is essential, yet maintaining such monitoring across an entire country, such as Japan, is particularly demanding.

Materials and Methods

Data

Comprehensive seismic source data were employed. These consist of CSV-formatted records of earthquake date and time, epicentre location, and magnitude, organised annually (JMA, 2025c, f). As compilation requires several years, the most recent dataset available as of November 2025 is from 2022 (JMA, 2025c). More recent data are available (JMA, 2025f), but these are organised daily, making download cumbersome; therefore, sampling at intervals of several days was applied. Monthly reports are also published, but these are provided as PDF files, rendering extraction laborious (JMA, 2025g, d). The comprehensive catalogue includes lower magnitudes than the monthly reports.

Grid Construction

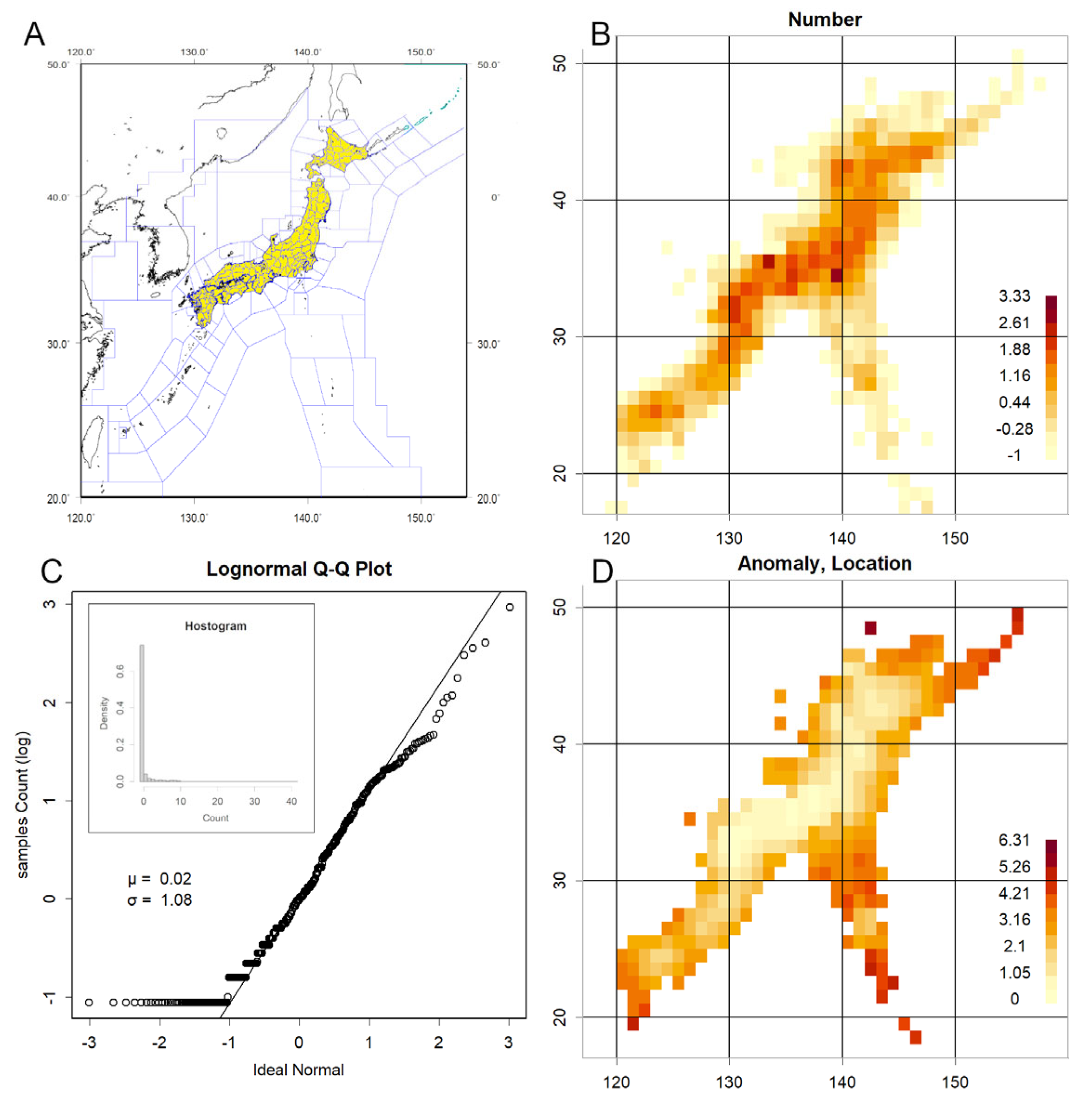
Date, location, and magnitude were extracted from the seismic dataset. To facilitate spatial analysis, the entire Japanese archipelago was partitioned into a grid composed of 1° latitude by 1° longitude cells. Each cell was treated as a discrete unit, and the corresponding magnitude records were aggregated accordingly. The grid was visualised as a mosaic of rectangular tiles; although the longitudinal span of each tile decreases with increasing latitude, this division was adopted primarily for practical reasons.
The choice of a 1° resolution was guided by several considerations. First, it aligns naturally with the coordinate format of epicentre records, which are typically reported in degrees. Second, it proved compatible with standard plotting functions in R, enabling efficient visualisation. Most importantly, this resolution provided a suitable balance between spatial granularity and data completeness. As illustrated in Figure S5, this would be the finest resolusion; attempts to increase the resolution to 0.5° resulted in numerous empty cells, particularly in regions with lower seismic activity. Conversely, coarser grids—such as 4°—led to excessive spatial aggregation, with single tiles encompassing vast areas (e.g., one tile covering nearly the entirety of Hokkaido), thereby obscuring localised patterns.
The 1° grid thus emerged as an empirically optimal resolution for Japan, offering sufficient detail without compromising data coverage. For regions with lower seismic frequency, coarser grids may be more appropriate. Additionally, in high-latitude areas where longitudinal convergence becomes significant, adjustments such as doubling or tripling the longitudinal span may be warranted.
Should finer resolution be desired, a sliding window approach could be employed by shifting the grid in 0.1° increments and averaging the resulting 100 outputs. The R code has been designed to accommodate such operations; however, this would entail a substantial increase in computational time—potentially requiring several days to generate a single averaged image. For this reason, such an approach was not pursued in the present study.

Statistical Analysis

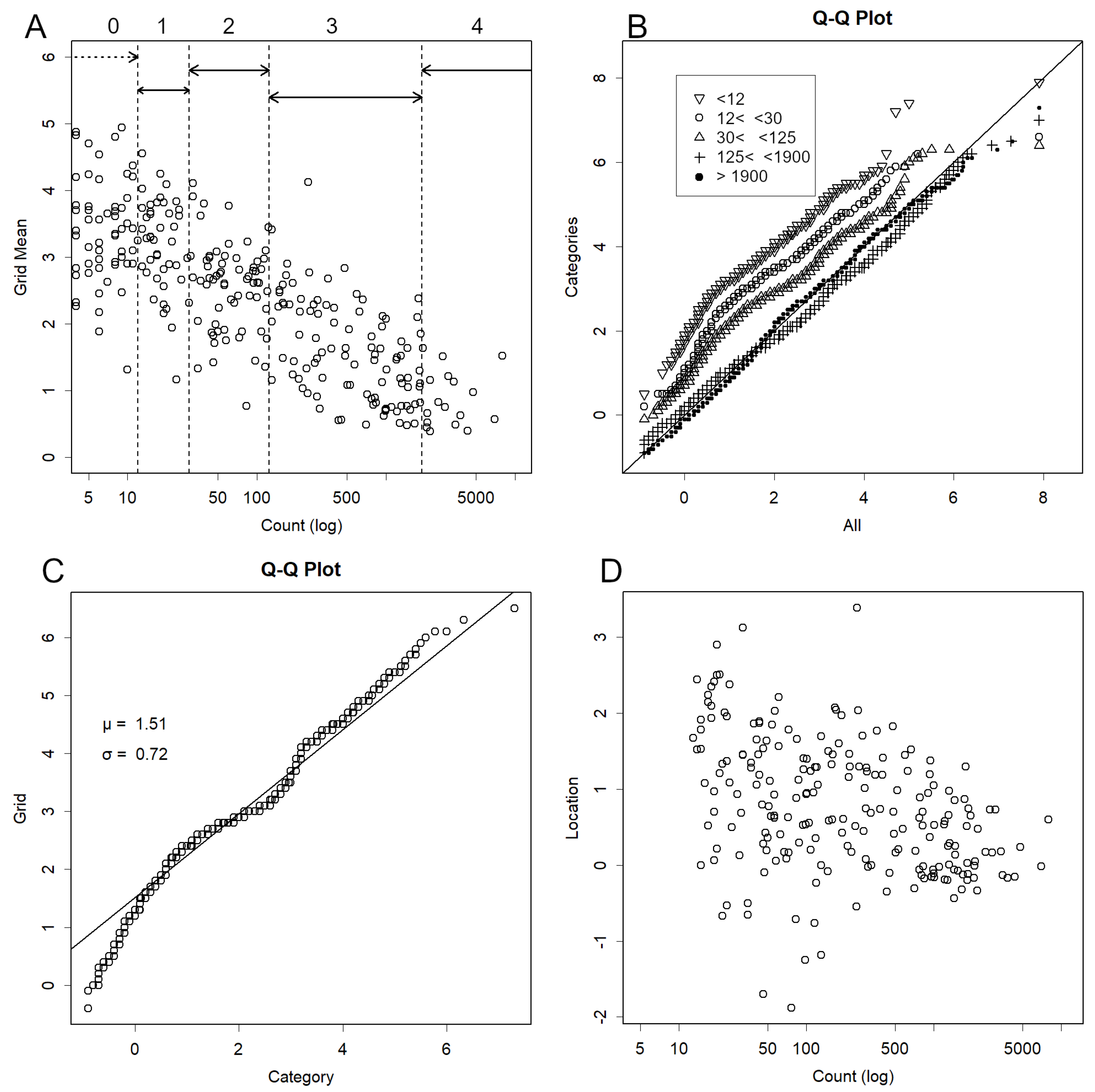
The number of epicentres in each grid was recorded. For each grid, a quantile–quantile (QQ) plot was generated, comparing magnitudes within the grid against magnitudes across multiple grids as background (Konishi, 2025a, d; Tukey, 1977). This yielded a linear relationship, from which the intercept (location) and slope (scale) were recorded.
Magnitudes in monthly reports follow a normal distribution (Konishi, 2025d), whereas the comprehensive catalogue differs slightly (Konishi, 2025a). The lower frequency of very small magnitudes introduces curvature in the relationship, leading to deviations in mean or standard deviation estimates. To standardise the data, QQ plots were employed to determine parameters, thereby assessing whether the distribution in a given grid deviated significantly from the majority.

Error Estimation

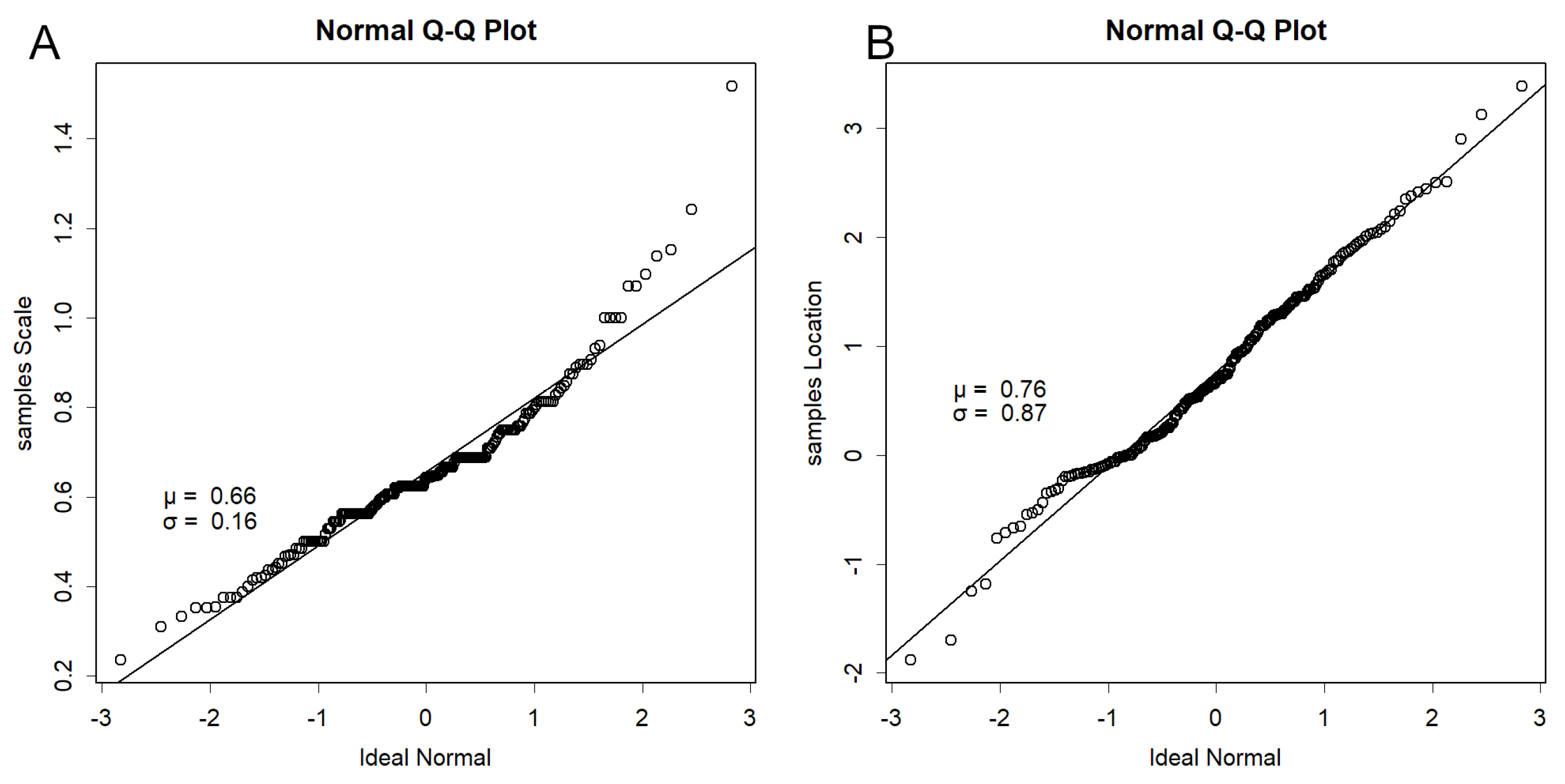
Parameter estimation with small sample sizes introduces substantial error. For example, when estimating location from sample data, the error is known to be σ / n   (Stuart and Ord, 1994). To investigate error in QQ plots, simulations were conducted. Random samples were drawn, QQ plots generated, and values calculated. Sample size was increased from 2 to 400 to examine estimation behaviour.

Normalisation

In the actual data, smaller counts tended to correspond to larger mean magnitudes. To account for this, grids were divided into five categories based on count, and measurements were performed accordingly. The QQ plot used to determine parameters employed the full dataset for the category to which the grid belonged as background. QQ plots were also conducted for counts, location, and scale against well-known distribution forms to investigate distribution patterns.

Case Studies

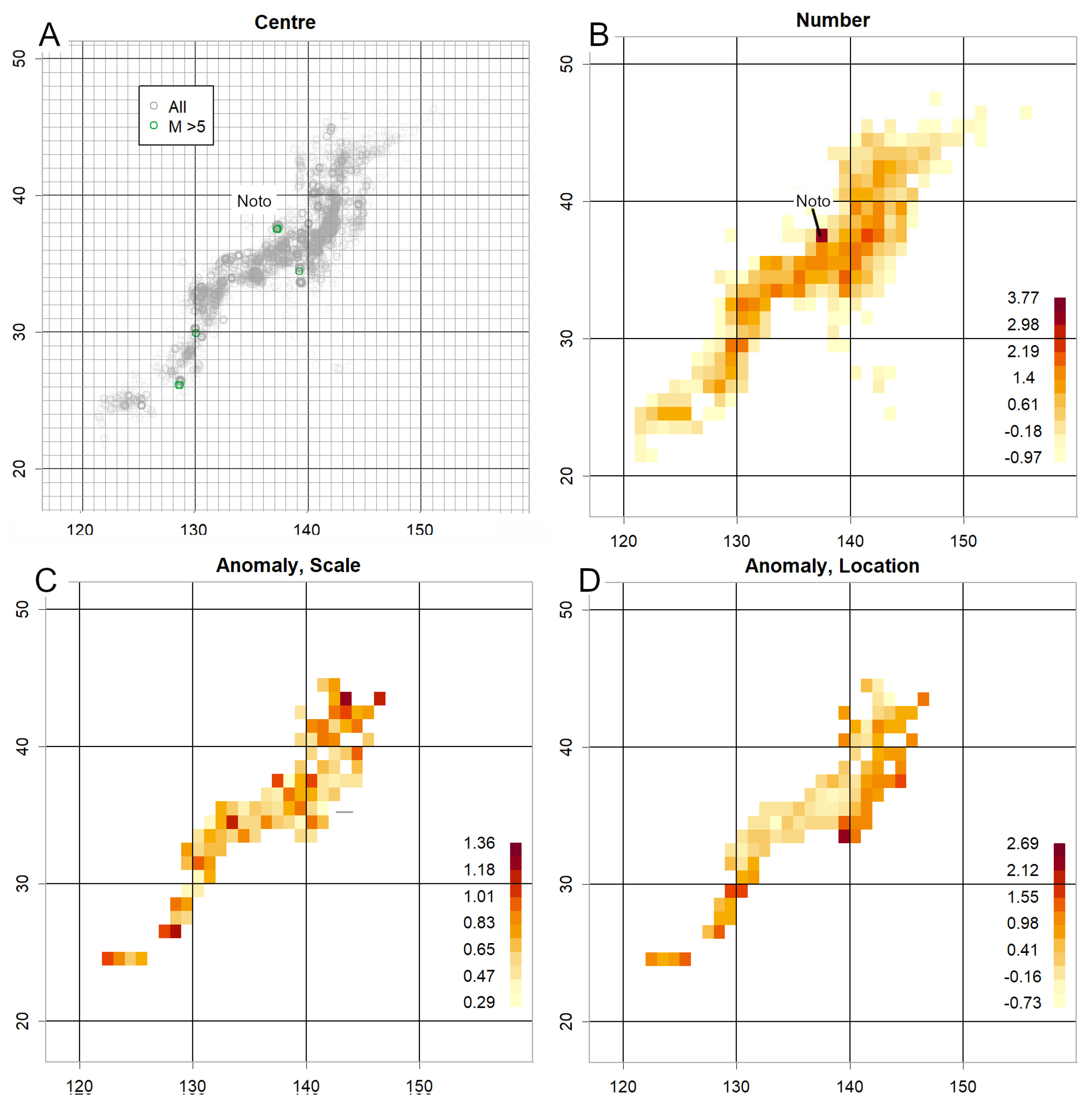
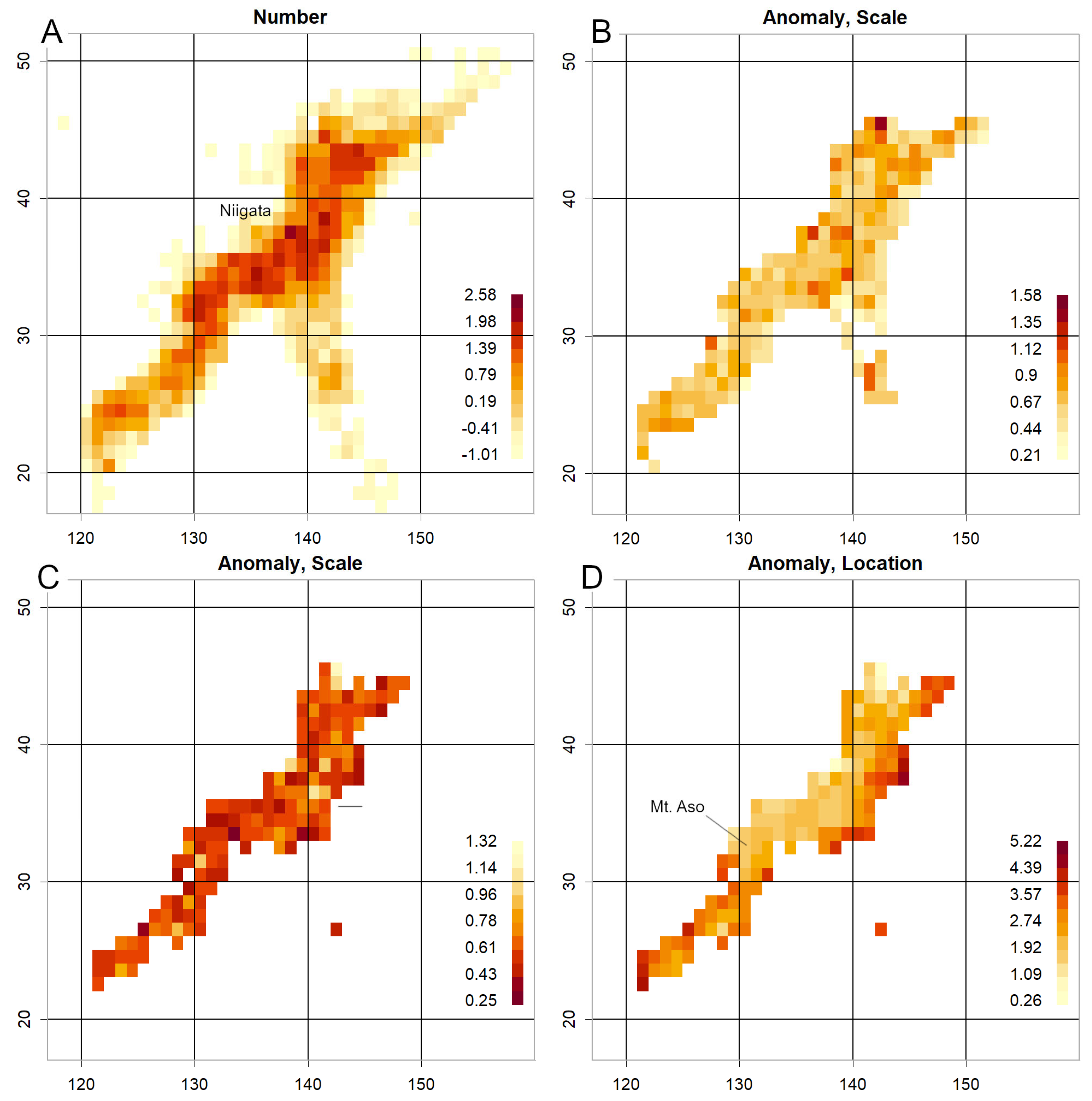
To evaluate whether the method could detect earthquakes in advance, anomalies in the investigated parameters were examined for the Mid Niigata Prefecture Earthquake (October 2004, M6.8) (JMA, 2024c), the 2011 Tohoku Earthquake (M9) (JMA, 2011), the Kumamoto Earthquake (April 2016, M7.3) (JMA, 2016), and the Noto Peninsula Earthquake (January 2024, M7.6) (JMA, 2024b).

Implementation

All calculations were performed using R (R Core Team, 2025). The code is provided in the Supplement. As two types of data with different formats were used, two versions of the code are supplied. Some figures utilise data provided by the Japan Meteorological Agency (JMA) (JMA, 2025f), realised using the open-source technology Leaflet (Agafonkin, 2025).

Visualisation and Legend

Gri data are visualised by arranging square tiles corresponding to 1° latitude by 1° longitude segments. This was implemented using the image function in R, which maps numerical values to colours across a defined spatial grid. To aid interpretation, a legend is displayed to the right of each figure.
The legend represents an arithmetic sequence spanning the minimum and maximum values present in the figure. Each tile is assigned a single colour according to its corresponding value, using the same scale as the legend. The colour palette can be easily modified within the R code. For the present study, a palette optimised for colour-blind accessibility was selected to ensure broader readability.

Some Notes

In this study, verification frameworks such as ETAS (Zhang et al., 2024) and CSEP (Research Center for Earthquake Forecast 2025) were not employed. These models are grounded in assumptions and formulae that have recently been called into question (Konishi, 2025d, c). Accordingly, the present approach offers a more straightforward perspective on seismic phenomena, distinct from established paradigms.
To detect anomalies, comparisons were made using nationwide data from the same time period. This decision was not arbitrary. Initially, we considered constructing a control dataset by averaging data from several previous years. However, this approach proved ineffective due to a marked increase in the number of observed epicentres in recent years. This rise is likely attributable to the deployment of more sensitive seismic instrumentation following the 2011 Tohoku earthquake (JMA, 2011; Konishi, 2025a; The Headquarters for Earthquake Research Promotion, 2009). As a result, comparisons with historical data are fundamentally problematic. Should this trend of improved detection continue, the most appropriate baseline for comparison will ultimately be contemporary data from across Japan.
While excluding the target location from the national average might enhance anomaly sensitivity, implementing such a procedure would significantly complicate the programming. This, in turn, would hinder secondary use and increase both computational cost and processing time. For these reasons, this refinement was not pursued in the present analysis.
No uniform nationwide threshold has been defined in this study. Such an approach would likely be inappropriate, given that seismic risk varies considerably by region. This spatial heterogeneity becomes increasingly evident upon closer examination of the data. For instance, analysis of data from 1994 reveals that in the Hanshin region, only a single grid cell exhibited a notable anomaly, with a scale of approximately 1.5 (Konishi, 2025c). This cell was situated directly above the Seto Inland Sea interface, where the Philippine Sea Plate converges with the Eurasian Plate—a tectonically active zone known for its seismic potential. Notably, the Great Hanshin–Awaji Earthquake struck this very region the following year (JMA, 2025b). Had such an anomaly occurred in a less seismically sensitive area, a more cautious, observational approach might have been justified. However, determining the significance of such anomalies requires not only geological context but also several years of operational experience. As such, the establishment of region-specific thresholds remains a subject for future investigation.

Results

Data Caracteristics

Figure 1A illustrates the geographical relationship between Japan and neighbouring countries (JMA, 2025e). The area enclosed by the red line represents the regional boundaries defined by the Japan Meteorological Agency (JMA). Figure 1B onwards are presented at essentially the same scale. Subsequent figures display data from a grid dividing Japan into one-degree latitude and longitude squares, arranged in a mosaic pattern. The grid size is smaller than that used for oceans but slightly larger than the JMA’s land divisions. Panel B shows the number of recorded epicentres within these grids. Observations extend over a considerable oceanic area, with the entire Japanese archipelago fully covered. As the count numbers follow a log-normal distribution (Figure 1C) (Konishi, 2025a), z-scores were derived from the logarithms of the counts. Since magnitudes follow a normal distribution (Konishi, 2025d), their parameters—scale and location—were estimated using the mean and standard deviation here, respectively. Panel D represents the location estimated from the mean, appearing higher in areas with low counts in Panel B and lower in inland areas with high counts.
To confirm this trend, Figure 2A shows the relationship between count numbers and grid mean, revealing a clear correlation. To investigate anomalies, it was necessary to examine whether distributions differed from the majority. As low-count data predominate, indicating higher location values, normalisation with respect to count was required. Magnitudes were therefore divided into five categories. Figure 2B presents a QQ plot comparing magnitude data for each category against the overall background. Category 4, with the highest counts, broadly aligned with the overall quantile, whereas Category 0, with the lowest counts, exhibited a significantly higher location. Scale, however, remained approximately constant.
For each category, magnitudes and QQ plots (Konishi, 2025a; Tukey, 1977) were generated for each grid, using all magnitudes belonging to that category as background. An example is shown in Figure 2C, with another in Figure S1. Approximately 1,500 such plots were produced per time point. Overall, a linear relationship was obtained, and slope and intercept were estimated using a robust method. Categorisation substantially mitigated the influence of count on location, although some residual effect persisted (Figure 2D). With fewer counts, greater noise was introduced (Figure S2AB), resulting in smaller scale values (S2A) and higher location values (S2B). This tendency was particularly pronounced when counts were ≤12. Consequently, grids with counts below this threshold were excluded. As precursory swarms typically involve very large counts, such errors are unlikely to affect prediction.
Figure 3A shows a normal QQ plot compiling the slope (scale) from QQ plots introduced in Figure 2C and Figure S1. While broadly following a normal distribution, the highest points tended to be elevated, reflecting strong earthquakes associated with higher σ values. Figure 3B shows the normal QQ plot for intercepts (location), which also roughly followed a normal distribution. If grid data were randomly selected, QQ plots would yield μ = 1 for scale and μ = 0 for location (Figure S2AB). In practice, μ was smaller for scale and much higher for location, illustrating that grid data are not randomly selected. At low counts, scale tended to be estimated as large and location as small (Figure S2B), elevating μ in Figure 3B. Both σ values were relatively large; if selection were random, σ would be at least an order of magnitude smaller. This indicates considerable variation in data characteristics between grids.
If grid data were randomly selected, QQ plots would yield μ = 1 for scale and μ = 0 for location (Figure S2AB). In practice, μ was smaller for scale and much higher for location, confirming that grid data are not randomly selected. At low counts, scale tended to be estimated as large and location as small (Figure S2B), elevating μ in Figure 3B. Both σ values were relatively large; if selection were random, σ would be at least an order of magnitude smaller. This indicates considerable variation in data characteristics between grids.
Categorisation ensured that scale no longer depended on count, though it remained consistently below the expected value of 1 (S2C). Normalization allowed data to be treated independently of count (S2D). Slightly elevated average seismicity was observed in oceanic regions extending from Etorofu Island along the Pacific subduction zone, through the Sanriku coast and Izu Islands, to the Ryukyu Islands and Taiwan (Bird, 2003; Maruyama, 1994; Matsukawa, 2009; Nishimura, 2021). This phenomenon is commonly observed, though not invariably present.

Case Studies

2021. Tohoku Earthquake

Figure 4 shows data from 1 January to 10 March 2011, preceding the 11 March 2011 Tohoku earthquake. Epicentre locations (Figure 4A) reveal numerous large precursory swarms off Sanriku. Event counts (Figure 4B) were high along the Sanriku coast. Location values (Figure 4C) were elevated, and scale values (Figure 4D) exceptionally high. Regions with high counts coupled with high scale and location values are prone to large earthquakes (Konishi, 2025d). Supporting QQ plots are shown in Figure S1: Sanriku data (S1A) exhibited markedly elevated μ and σ values, while Akita offshore data (S1B) showed more moderate During the same period, earthquake activity increased in northern Nagano Prefecture (Figure 4B), with a corresponding rise in scale. This may have been a precursor to the 12 March 2011 earthquake (M6.7), although no strong precursory swarm was observed (Figure 4A) (Konishi, 2025d).
During the same period, earthquake activity increased in northern Nagano Prefecture (Figure 4B), with a corresponding rise in scale. This may have been a precursor to the 12 March 2011 earthquake (M6.7), although no strong precursory swarm was observed (Figure 4A) (Konishi, 2025d).

2024. Noto Earthquake

Figure 5A shows results sampled over two weeks in May 2023, revealing a concentration of large earthquakes around Noto. Counts increased (Figure 5B), and scale rose accordingly (Figure 5C), though location anomalies were not evident (Figure 5D).

2004. Niigata Earthquake and 2016 Kumamoto Earthquake

Figure 6A and B show results prior to the 2004 Niigata Chuetsu earthquake (M6.8). Counts were elevated near the mainshock epicentre (Figure 6A), and surrounding scale was heightened (Figure 6B). Data from 2015 (Figure 6C and D) show reduced scale and location in the Kumamoto region. Such anomalies were also confirmed during the Tokara eruption (Konishi, 2025b). The reduction in σ at volcanic sites likely indicates increased volcanic activity (Konishi, 2025a), particularly where counts are high.
The Pacific side frequently exhibited higher location values (Figure 4C, Figure 5D, Figure 6D, Figures S2D, S3A, S4B). The Sea of Japan side was generally lower, though one consistently high location offshore in the central Sea of Japan (S3A) suggests susceptibility to strong earthquakes.
Particularly low σ values indicate magnitude concentration, often associated with frequent small earthquakes linked to volcanic activity, as observed in Tokara in 2025 (Konishi, 2025b) and around Mount Aso in 2015 (Figure 6D). Similar reductions were noted prior to the 2000 Miyakejima eruption (Figure S3C) and during the 2017 volcanic activity from Myojin Reef to Iwo Jima (Figure S3D).

Recent Examples

Short observation periods complicate calculations, as at least 12 data points per grid cell are required. Figure 5 covers approximately two weeks, while Figure S4 shows the most recent three-week period. Measurement ranges were narrow, and areas where measurement was impossible increased, particularly in marine regions. Restricting analysis to grids with >100 counts further reduced coverage (Figure S5). Nevertheless, anomalies were confirmed. In May 2023, a swarm in Noto increased σ (Figure 5C, Figure S5C). In recent three-week data, elevated location values were observed along the Sanriku coast (Figures S4A, S4B). The Tokara Islands swarm continues (JMA, 2025a), with increasing activity near Suwanose Island, likely elevating location values (Konishi 2025b). Given the low σ, volcanic activity may still be ongoing. No volcanoes under alert were identified in Honshu where σ was low (Figure S5D). Elevated counts and locations were observed from the Sakishima Islands to Taiwan, though σ remained unchanged. When restricted to counts >100, this location increase disappeared, suggesting it may be an artefact of low counts (Figure S5D).

2025. Iwate-Oki Earthquake

During manuscript preparation, a magnitude 6.7 earthquake occurred along the Sanriku coast on 9 November, where location values had been rising (Figure S4A). A 10-day extension was therefore added (Figure 7). Subsequent activity shifted from offshore Fukushima to offshore Iwate (Figure 7A). Epicentres from 3–8 November revealed concentrated location values (Figure 7B). Elevated location values were confirmed (Figure 7C and Figure S6A), though scale did not increase significantly. Daily magnitudes (Figure 7D) showed sharply rising counts in November, with consistently high location values above average. This state persisted prior to the major earthquake. A t-test of magnitudes from 1–8 November, before the main quake, yielded a p-value < 2.2 × 10⁻¹⁶, too small for R to compute, confirming statistical significance.

Discussion

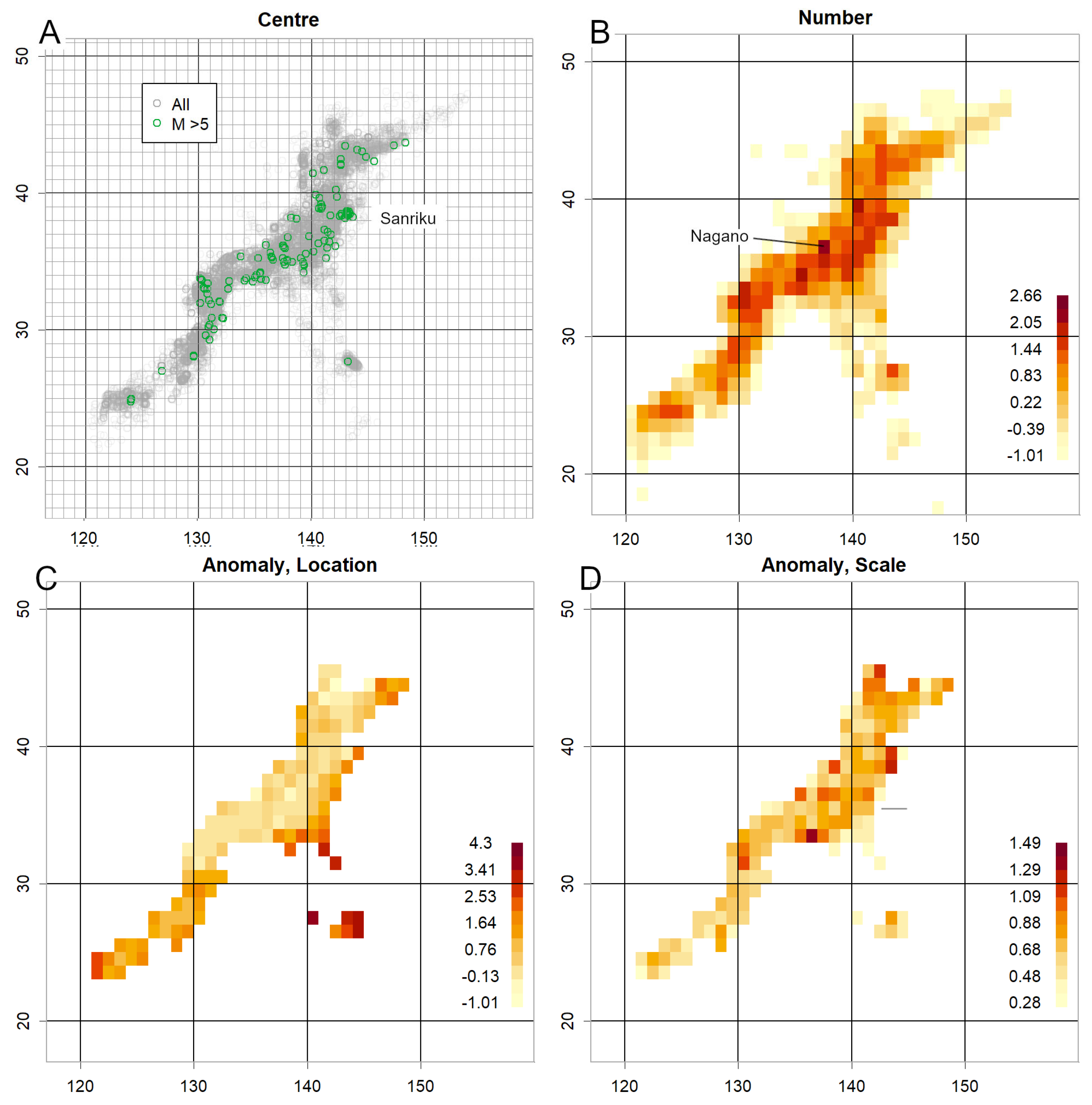
Regarding grid magnitudes exhibiting considerably low σ (Figure 3A): theoretically, σ should equal 1 if selection were random (Figure S2A), yet in practice it is approximately 0.6. This is unlikely to be an artefact of estimation. Although such results are common when estimating with very few data points (Figure S2A), here at least 12 data points were available. Each grid can be considered as the interior of squares with sides of approximately 100 km, corresponding to a radius of 1°. The properties of nearby epicentres are likely similar, whether related to fault presence or plate slip. Most data are collected over a year and are not necessarily continuous, yet earthquakes occurring within a grid likely share similar mechanisms. Consequently, σ becomes smaller, indicating that significant differences in magnitude are unlikely.
Underestimation of scale suggests clustering of magnitude values within a grid. This may occur if volcanic activity increases the number of earthquakes caused by magma movement (Konishi, 2025b). Such phenomena have been observed during several volcanic episodes (Figure 6C, S3CD). Near the First Kashima Seamount, σ is low but consistently exceeds the measurement range (Figure 4D, Figure 5C, Figure 6C, Figures S3C, S4D), and has only been measured once (Figure S3D). Volcanic activity may therefore be occurring in this vicinity, which is also a fault-rich area at the northern end of the Japan Trench (Nakajima, 2025). Intensified observation may be warranted. Similarly, the offshore area in the central Japan Sea, where location readings are consistently high (Figure S3AB), also shows low σ values, suggesting possible volcanic activity (Figure S3CD) (Japan Coast Guard, 2013).
Other explanations for low σ are also plausible. For example, Sanriku and Chiba Prefecture exhibited low σ values similar to those observed for Myojin Reef and Iwo Jima (Figure S3D), despite lacking notable volcanoes. Low σ values therefore indicate potential hazards but require careful scrutiny. For volcanic activity estimation, this method should be combined with others, as eruptions can occur without accompanying low σ values, as observed at Sakurajima. Such eruptions likely involve minimal magma movement. Further investigation using independent geophysical datasets may help clarify the origin of low-σ anomalies, particularly in volcanic regions.tyot
Regarding grid magnitudes indicating significantly high locations (Figure 3B): most grids contain limited data, with locations having fewer than 12 data points constituting approximately 80% of the total—a characteristic of the log-normal distribution (Figure 1C). These locations are predominantly marine (Figure 1B, Figure 6A), where measurement is difficult. Observations in such areas are feasible only for events exceeding a certain magnitude threshold. Consequently, the overall mean value tends to be elevated, even after categorisation.
To normalise, QQ plots were presented by category. Alternatively, one could average the data and apply a correction, such as a spline function aligning the M4 position with that in Figure 2B. This would avoid biased estimation errors arising from low counts (Figure 2AB). However, such an approach was not employed, as it would inevitably yield the desired data shape, undermining analytical falsifiability (Thornton, 2023). Rigorous methodology entails certain inconveniences, and exclusion of low-count data is likely more appropriate, as such data are probably unnecessary.
Regarding the cause of count numbers following a log-normal distribution (Figure 1C): earthquake intervals fundamentally follow an exponential distribution (Konishi, 2025d), and it was initially considered whether the inverse of count numbers might correspond to this. In practice, however, this was not the case (Konishi, 2025a), likely because each grid possesses a different λ. Log-normal distributions typically emerge from the synergy of multiple random factors (Stuart and Ord, 1994). Magnitude represents the energy released by an earthquake in logarithmic terms, so its normal distribution (Figure 3B) indicates that energy itself follows a log-normal distribution (Konishi, 2025d). Similarly, earthquake frequency may be determined by the synergistic effect of such factors. The recent high frequency and elevated location of earthquakes off the Sanriku coast suggest that several of these factors have been consistently active. The addition of new factors would likely increase both event frequency and magnitude synergistically. This is probably what triggered the most recent earthquake (M6.7) and caused their rapid increase within a short period.
Whilst a consolidated earthquake catalogue simplifies calculations, even the most recent data are available only on a daily basis (JMA, 2025f). Calculations are feasible with two weeks’ (Figure 5) or three weeks’ worth of data (Figure S4). However, the requirement for at least 12 counts narrows the observation range, leaving marine areas underrepresented (Figure 5B, Figures S4A, S5). Nevertheless, meaningful insights can still be obtained, warranting continued investigation. Particular caution is required when anomalies appear in locations with high counts, as location and scale values typically converge with those of other grids (Figure 2B) (Konishi, 2025a). Significant deviations in such cases likely indicate meaningful phenomena.
Elevated location and scale values at high-count sites are particularly hazardous, as they increase the expected probability of a large earthquake (Konishi, 2025d). This phenomenon was observed prior to the 2011 Tohoku earthquake (Figure 4) and the 2024 Noto earthquake (Figure 5). When anomalies are detected, verification using the classification system employed by the Japan Meteorological Agency is advisable. The simplest method is to compare magnitude data from these locations with others using QQ plots ) (Konishi, 2025a) (Figure 2C, Figure S1AB, 7C). Such verification is crucial, as anomalies may provide the basis for earthquake prediction. Many JMA classifications cover smaller areas than the grid used here, so anomalies are expected to appear more sharply defined; surrounding areas should also be examined, as responsibility for issuing instructions to residents lies with local authorities.
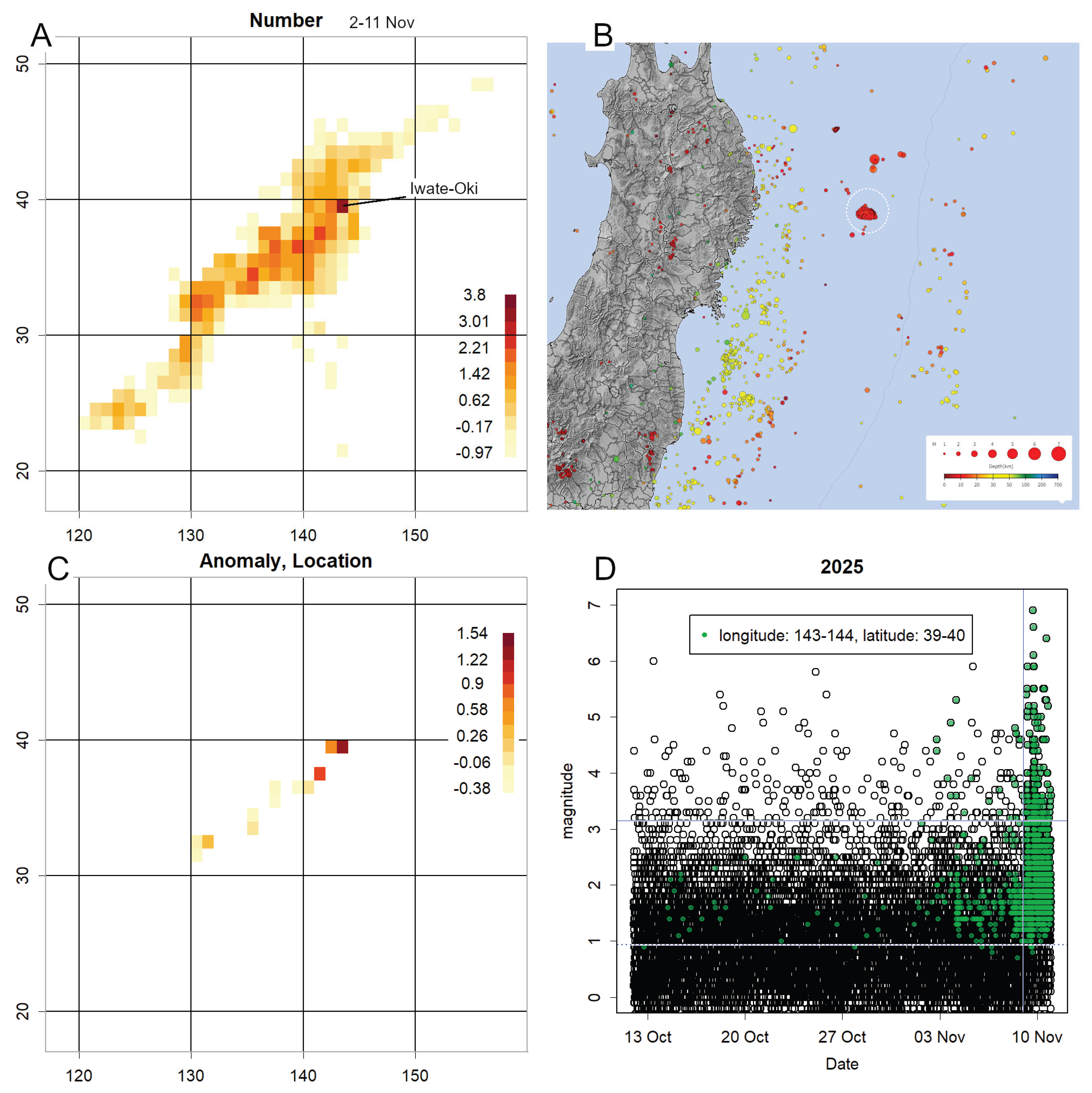
Immediately prior to the M9 Tohoku earthquake, a precursor swarm with an extremely high location was observed (JMA, 2011; Konishi, 2025d). The recent earthquake off Iwate Prefecture may correspond to this (Figure 7D). Between 1 and 8 November, counts in this grid increased sharply, with large magnitudes and extremely low P-values. Thus, when a sudden increase in counts is accompanied by elevated location or scale values, the situation should be judged hazardous. For example, the geometric mean of daily counts from 3–8 November was 35, with a z-score exceeding 3 (compared with ~0.5 prior to 1 November). The sudden emergence of such values in a grid of this size warrants vigilance.
At present, the Iwate earthquake appears to be decaying, accompanied by numerous aftershocks (Figure 7D and Figure S6B) (Utsu et al., 1995). Whether convergence will occur remains unclear until further data are available. Due to these aftershocks, both magnitude and counts remain high, and the anomaly persists. Should scale increase, the hazard would be considerable.
To date, only large earthquakes accompanied by swarm activity have been investigated, resulting in high counts (Konishi, 2025d). Focusing on such events may be advisable. The R code includes a presentation option limiting plots to grids with counts >100 (Figures S5, 7C). Scale can pose problems both when high and when low, and different colour charts are used to enhance readability (Figures S4CD).
This method can be implemented automatically. Provided conditions are set appropriately for the region, R performs calculations efficiently, requiring little computation time. For Japan, this approach is sufficient. However, results are not always conclusive. For example, the 2018 Eastern Iburi earthquake (M6.7) was not predicted. An anomaly (Konishi, 2025d) that might have been detected by combining several regions into a single QQ plot was obscured. Using a 4° interval instead of 1° revealed the anomaly, but the grid became too coarse, covering most of Hokkaido and hindering site identification. Similarly, the 2021 Fukushima earthquake could not have been predicted without monthly rather than annual data. Anomalies are likely easier to detect during swarm activity (Konishi, 2025d). Attempts to shorten the period in Iburi resulted in insufficient data, highlighting a trade-off between simplicity and sensitivity.
Apart from the recent Iwate event, no evidence has been found of the high-magnitude precursor swarms observed immediately before the Thoku mainshock (JMA, 2011; Konishi, 2025d). In most cases, the period preceding the mainshock was quiet (Konishi, 2025d). Consequently, even if anomalies are detected, the timing of the mainshock cannot generally be determined. Several methods have been proposed to predict the timing of major earthquakes (Nagao et al., 2014; Tanaka et al., 2004; Varotsos et al., 2024a; Varotsos et al., 2024b). However, given Japan’s high frequency of large earthquakes, it is difficult to distinguish whether such findings are coincidental or represent underlying phenomena. Their validity does not yet appear established (JMA, 2024a). Nevertheless, should reliable timing determination become possible, it would greatly enhance practical utility.

Conclusions

This study demonstrates that setting a grid across an area approximately the size of Japan enables straightforward visualisation and analysis of seismic data. Anomalies detected through such automated methods should be investigated in greater detail. As earthquakes occur unpredictably, continuous monitoring remains essential. Evidence suggests that anomalies may precede major earthquakes by several months to a year; however, sudden spikes in counts may indicate imminent activity, though exceptions exist. Consequently, even when alerts are issued, sustained vigilance over extended periods is required. In this context, raising public awareness alongside the dissemination of warnings is of critical importance.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: Examples of QQ plots per grid; Figure S2: Simulation of the effect of count size on parameter estimation; Figure S3. Examples of location and scale; Figure S4. Example created using data from the most recent three weeks; Figure S5. Example with display restricted by count numbers; Figure S6. QQ plots before and after the mainshock in Iwate Oki earthquake; Scripts for the catalog.txt and Scripts for each day.txt: the R-codes. Those are available in zenodo, https://doi.org/10.5281/zenodo.17983156.

Funding

This research received no external funding.

Data Availability Statement

All the data used can be downloaded from JMA homepage (JMA, 2025c, f). R source code is available in the Supplementary Materials.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Agafonkin, V. Leaflet, an open-source JavaSCript library for mobile-fienendly interactive maps. 2025. Available online: https://leafletjs.com/.
  2. Bird, P. An updated digital model of plate boundaries: Geochemistry. Geophysics, Geosystems 2003, 4(no. 3). [Google Scholar] [CrossRef]
  3. Geospatial Information Authority of Japan (GSI). Standard map. 2025. Available online: https://maps.gsi.go.jp/.
  4. Gutenberg. B., and C. F. Richter, 1944, Frequency of Earthquakes in California. Bulletin of the Seismological Society of America 34(no. 4), 185–188. [CrossRef]
  5. Japan Coast Guard. The submarine volcano in TOKARA Islands Volcanic Eruption Prediction Liaison Committee Bulletin (JMA). 2013, 115, 235–236. Available online: https://www.jma.go.jp/jma/kishou/shingikai/ccpve/Report/115/kaiho_115_37.pdf.
  6. JMA, 2011, Great East Japan Earthquake. Available online: https://www.jma.go.jp/jma/menu/jishin-portal.html (accessed on 11/3 2025).
  7. JMA, 2016, 2016 Kumamoto Earthquake Investigation Report. Available online: https://www.jma.go.jp/jma/kishou/books/gizyutu/135/gizyutu_135.html (accessed on 11/4 2025).
  8. JMA. About earthquake prediction. 2024a. Available online: https://www.jma.go.jp/jma/kishou/know/faq/faq24.html.
  9. JMA. Related information on the 2024 Noto Peninsula Earthquake. 2024b. Available online: https://www.jma.go.jp/jma/menu/20240101_noto_jishin.html.
  10. JMA. Hanshin-Awaji (Hyogoken-Nanbu) Earthquake Special Site. 2025a. Available online: https://www.data.jma.go.jp/eqev/data/1995_01_17_hyogonanbu/index.html.
  11. JMA. Assessment of seismic activity off the coast of the Tokara Islands. 2025b. Available online: https://www.static.jishin.go.jp/resource/monthly/2025/20250703_tokara_2.pdf.
  12. JMA. Earthquake Monthly Report (Catalog Edition). 2025c. Available online: https://www.data.jma.go.jp/eqev/data/bulletin/hypo.html (accessed on 11/2 2025).
  13. JMA. Summary of seismic activity for each month. 2025d. Available online: https://www.data.jma.go.jp/eqev/data/gaikyo/.
  14. JMA. Epicenter location names used in earthquake information (Japan map). 2025e. Available online: https://www.data.jma.go.jp/eqev/data/joho/region/.
  15. JMA. List of epicenter location. 2025f. Available online: https://www.data.jma.go.jp/eqev/data/daily_map/index.html.
  16. JMA. Earthquake information. 2025g. Available online: https://www.data.jma.go.jp/multi/quake/index.html?lang=en.
  17. Konishi, T. Exploratory Statistical Analysis of Precursors to Moderate Earthquakes in Japan. GeoHazards 2025a, 6((4)), 82. [Google Scholar] [CrossRef]
  18. Konishi, T. Earthquake Swarm Activity in the Tokara Islands (2025): Statistical Analysis Indicates Low Probability of Major Seismic Event: GeoHazards. 2025b, 6(no. 3), 52. Available online: https://www.mdpi.com/2624-795X/6/3/52. [CrossRef]
  19. Konishi, T. Visualising Earthquakes: Plate Interfaces and Seismic Decay: Preprints. 2025c, 189197. [Google Scholar] [CrossRef]
  20. Konishi, T. Seismic pattern changes before the 2011 Tohoku earthquake revealed by exploratory data analysis: Interpretation. 2025d, T725–T735. [Google Scholar] [CrossRef]
  21. Maruyama, S. Plume tectonics: Journal - Geological Survey of Japan 1994, 100(no. 1), 24–49. [CrossRef]
  22. Matsukawa, H. Macro system friction: Hyomen Kagaku. 2009, 30(no. 10), 548–553. [Google Scholar] [CrossRef]
  23. Nagao, T.; Orihara, Y.; Kamogawa, M. Precursory Phenomena Possibly Related to the 2011M9.0 Off the Pacific Coast of. Journal of Disaster Research 2014, 9(no. 3), 303–310. [Google Scholar] [CrossRef]
  24. Nakajima, J. The Tokyo Bay earthquake nest, Japan: Implications for a subducted seamount. Tectonophysics 2025, 906, 230728. [Google Scholar] [CrossRef]
  25. Nishimura, T. Volcanic eruptions are triggered in static dilatational strain fields generated by large earthquakes. Scientific Reports 2021, 11(no. 1), 17235. [Google Scholar] [CrossRef] [PubMed]
  26. Omori, F. On the After-shocks of Earthquakes. 1895. Available online: https://repository.dl.itc.u-tokyo.ac.jp/records/37571 (accessed on 2 7).
  27. Research Center for Earthquake Forecast; University of Tokyo. Collaboratory for the Study of Earthquake Predictability (CSEP). 2025. Available online: https://wwweprc.eri.u-tokyo.ac.jp/study/project/csep.html.
  28. R Core Team, 2025, R: A language and environment for statistical computing: R Foundation for Statistical Computing.
  29. Stuart, A.; Ord, J. K. Distribution theory; Kendall's advanced theory of statistics: Hodder Arnold, 1994. [Google Scholar]
  30. Tanaka, H.; Varotsos, P. A.; Sarlis, N. V.; Skordas, E. S. A plausible universal behaviour of earthquakes. Proceedings of the Japan Academy, Series B 2004, 80(no. 6), 283–289. [Google Scholar] [CrossRef]
  31. The Headquarters for Earthquake Research Promotion, 2009, Promoting new earthquake research. Available online: https://www.jishin.go.jp/main/suihon/honbu09b/suishin090421.pdf (accessed on 11/2 2025).
  32. Thornton, S., ed. 2023, Karl Popper. Edited by E. N. Zalta, and U. Nodelman, The {Stanford} Encyclopedia of Philosophy: Metaphysics Research Lab, Stanford University.
  33. Tukey, J. W. Exploratory data analysis; Addison-Wesley Pub. Co: Behavioral Sciences: Quantitative Methods: Reading, Mass., 1977. [Google Scholar]
  34. Utsu, T. Magnitude of earthquakes and occurance of their aftershocks: Journal of the Seismological Society of Japan, 2nd ser. ed; 1957; Volume 10, no. 1, pp. 35–45. [Google Scholar] [CrossRef]
  35. Utsu, T.; Ogata, Y.; Matsu'ura, R. S. The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. Journal of Physics of the Earth 1995, 43(no. 1), 1–33. [Google Scholar] [CrossRef]
  36. Varotsos, P. A.; Sarlis, N. V.; Nagao, T. Complexity measure in natural time analysis identifying the accumulation of stresses before major earthquakes. Scientific Reports 2024a, 14(no. 1), 30828. [Google Scholar] [CrossRef] [PubMed]
  37. Varotsos, P. A.; Skordas, E. S.; Sarlis, N. V.; Christopoulos, S.-R. G. Review of the Natural Time Analysis Method and Its Applications: Mathematics. 2024b, 12(no. 22), 3582. Available online: https://www.mdpi.com/2227-7390/12/22/3582. [CrossRef]
  38. Zhang, H.; Ke, S.; Liu, W.; Zhang, Y. A combining earthquake forecasting model between deep learning and epidemic-type aftershock sequence (ETAS) model. Geophysical Journal International 2024, 239(no. 3), 1545–1556. [Google Scholar] [CrossRef]
Preprints 190512 g001
Figure 1. Description of figures. A. Japan and its neighbouring countries. The red lines indicate the divisions defined by the Japan Meteorological Agency ((GSI), 2025; JMA, 2025e). As the original map was likely based on a Mercator projection, distances were adjusted at 10-degree intervals of longitude to ensure a consistent scale. B. Grid-based count data (hereafter referred to as the 2004 data; z-scores calculated on a logarithmic scale) shown at the same scale as in A, and consistently thereafter. C. Normal QQ plot of count data and log-transformed z-scores. Superimposed is a histogram without logarithmic transformation, illustrating that very small counts occur most frequently. D. Average magnitude per grid. Areas with fewer counts tend to exhibit higher average magnitudes.
Figure 1. Description of figures. A. Japan and its neighbouring countries. The red lines indicate the divisions defined by the Japan Meteorological Agency ((GSI), 2025; JMA, 2025e). As the original map was likely based on a Mercator projection, distances were adjusted at 10-degree intervals of longitude to ensure a consistent scale. B. Grid-based count data (hereafter referred to as the 2004 data; z-scores calculated on a logarithmic scale) shown at the same scale as in A, and consistently thereafter. C. Normal QQ plot of count data and log-transformed z-scores. Superimposed is a histogram without logarithmic transformation, illustrating that very small counts occur most frequently. D. Average magnitude per grid. Areas with fewer counts tend to exhibit higher average magnitudes.
Preprints 190512 g001
Preprints 190512 g002
Figure 2. Effect of count size. A. Relationship between grid count (z-score) and grid mean value. Smaller counts are associated with higher means. Accordingly, the data were divided into five categories (0–4, shown at the top of the graph). Counts below 12 (zero counts) were excluded (Category 0), and the remaining data were partitioned at counts of 30, 125, and 1900. The data used here, and up to Figure 3, are from 2004. B. QQ plots were generated for each category, using the entire dataset as the background. The intercept decreases from Category 1 to Category 4, while the slope remains approximately constant. C. Example of a QQ plot created for each grid count, using the data for that category as the background. Approximately 1500 such plots were produced for each dataset. As linear relationships were obtained, robust methods were applied to estimate the intercept (“location”) and slope (“scale”) for each category, which were then recorded. D. Relationship between recorded location and count. Categorisation reduces the slope tendency observed in Panel A, though a residual trend remains, particularly for very small counts.
Figure 2. Effect of count size. A. Relationship between grid count (z-score) and grid mean value. Smaller counts are associated with higher means. Accordingly, the data were divided into five categories (0–4, shown at the top of the graph). Counts below 12 (zero counts) were excluded (Category 0), and the remaining data were partitioned at counts of 30, 125, and 1900. The data used here, and up to Figure 3, are from 2004. B. QQ plots were generated for each category, using the entire dataset as the background. The intercept decreases from Category 1 to Category 4, while the slope remains approximately constant. C. Example of a QQ plot created for each grid count, using the data for that category as the background. Approximately 1500 such plots were produced for each dataset. As linear relationships were obtained, robust methods were applied to estimate the intercept (“location”) and slope (“scale”) for each category, which were then recorded. D. Relationship between recorded location and count. Categorisation reduces the slope tendency observed in Panel A, though a residual trend remains, particularly for very small counts.
Preprints 190512 g002
Preprints 190512 g003
Figure 3. QQ plots for parameters. A. Example of a Normal QQ plot for recorded scale. B. Example of a Normal QQ plot for recorded location. Both are compared with an ideal normal distribution and appear normally distributed.
Figure 3. QQ plots for parameters. A. Example of a Normal QQ plot for recorded scale. B. Example of a Normal QQ plot for recorded location. Both are compared with an ideal normal distribution and appear normally distributed.
Preprints 190512 g003
Preprints 190512 g004
Figure 4. Data from January to 10 March 2011, prior to the 2011 Tohoku earthquake (M9). A. Epicentre. Numerous earthquakes of M > 5 occurred in the Sanriku region. B. Count. Highest along the Sanriku coast, with elevated values also in Nagano. C. Location. High in Sanriku, with counts exceeding 12. D. Scale. Extremely high in Sanriku. The combination of high frequency with large location and scale values indicates a strong likelihood of a major earthquake. Elevated regions are also observed around Nagano.
Figure 4. Data from January to 10 March 2011, prior to the 2011 Tohoku earthquake (M9). A. Epicentre. Numerous earthquakes of M > 5 occurred in the Sanriku region. B. Count. Highest along the Sanriku coast, with elevated values also in Nagano. C. Location. High in Sanriku, with counts exceeding 12. D. Scale. Extremely high in Sanriku. The combination of high frequency with large location and scale values indicates a strong likelihood of a major earthquake. Elevated regions are also observed around Nagano.
Preprints 190512 g004
Preprints 190512 g005
Figure 5. Data sampled over a two-week period in May 2023, prior to the 2024 Noto earthquake (M7.6). A. Large earthquakes occurred frequently around Noto. B. Counts were particularly high in Noto. C. Counts exceeded 100. Although the dataset is limited, the scale is clearly much larger in Noto. D. Location was not particularly large.
Figure 5. Data sampled over a two-week period in May 2023, prior to the 2024 Noto earthquake (M7.6). A. Large earthquakes occurred frequently around Noto. B. Counts were particularly high in Noto. C. Counts exceeded 100. Although the dataset is limited, the scale is clearly much larger in Noto. D. Location was not particularly large.
Preprints 190512 g005
Preprints 190512 g006
Figure 6. Data from the ten months immediately preceding the 2004 Mid Niigata Prefecture Earthquake (M6.8). A. Counts are elevated near the epicentre. B. Scale. Elevated in this vicinity. C–D. Data from 2015, prior to the 2016 Kumamoto Earthquake (M7). In the region surrounding Mount Aso, both scale and location are low, suggesting increased volcanic activity.
Figure 6. Data from the ten months immediately preceding the 2004 Mid Niigata Prefecture Earthquake (M6.8). A. Counts are elevated near the epicentre. B. Scale. Elevated in this vicinity. C–D. Data from 2015, prior to the 2016 Kumamoto Earthquake (M7). In the region surrounding Mount Aso, both scale and location are low, suggesting increased volcanic activity.
Preprints 190512 g006
Preprints 190512 g007
Figure 7. Data for the ten days following Figure S4. A. The centre of counts shifted offshore Iwate Prefecture. B. Epicentre locations for 3–8 November, concentrated within the white dotted circles. Individual magnitudes are high (depicted by larger circles; legend at bottom right). C. Location. Owing to the short period, only data with more than 100 counts are displayed. The superimposed figure does not obscure the original data. D. Time record of magnitude throughout the period. Only this grid’s data are displayed in green. The horizontal blue dotted line represents the mean, while the solid line indicates a position 3σ above the mean. The vertical line marks 0:00 on 9 November, just before the mainshock occurred (the mainshock itself was at 17:03). This illustrates that magnitudes in this grid were elevated even before the mainshock, though the overall distribution changed from the morning of 9 November.
Figure 7. Data for the ten days following Figure S4. A. The centre of counts shifted offshore Iwate Prefecture. B. Epicentre locations for 3–8 November, concentrated within the white dotted circles. Individual magnitudes are high (depicted by larger circles; legend at bottom right). C. Location. Owing to the short period, only data with more than 100 counts are displayed. The superimposed figure does not obscure the original data. D. Time record of magnitude throughout the period. Only this grid’s data are displayed in green. The horizontal blue dotted line represents the mean, while the solid line indicates a position 3σ above the mean. The vertical line marks 0:00 on 9 November, just before the mainshock occurred (the mainshock itself was at 17:03). This illustrates that magnitudes in this grid were elevated even before the mainshock, though the overall distribution changed from the morning of 9 November.
Preprints 190512 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated