Submitted:
13 November 2025
Posted:
14 November 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
2.1. Low-light Image Enhancement
2.2. Mamba-based Methods
3. Preliminaries
3.1. State Space Model
3.2. Hausdorff Dimension
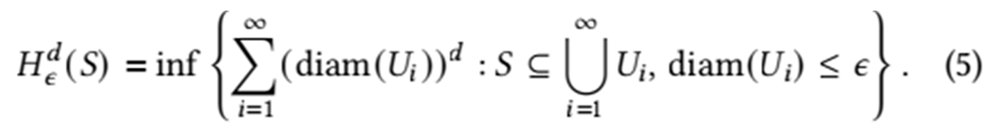
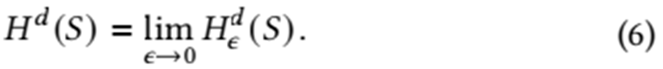
4. Methodology
4.1. Hausdorff Dimension’s Implications for
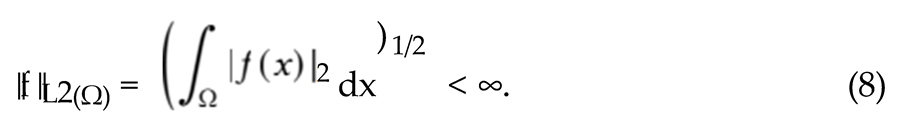
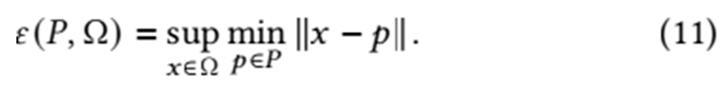
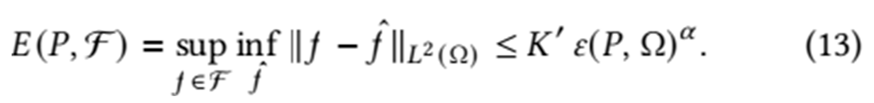
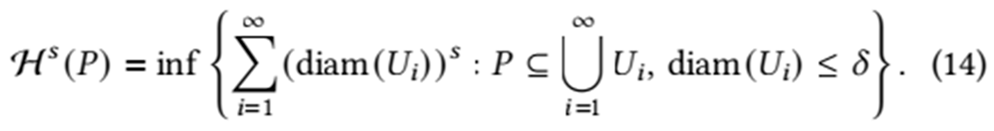

4.2. Hilbert Scan & Peano Scan

 |

5. Experiment
5.1. Experiment Settings

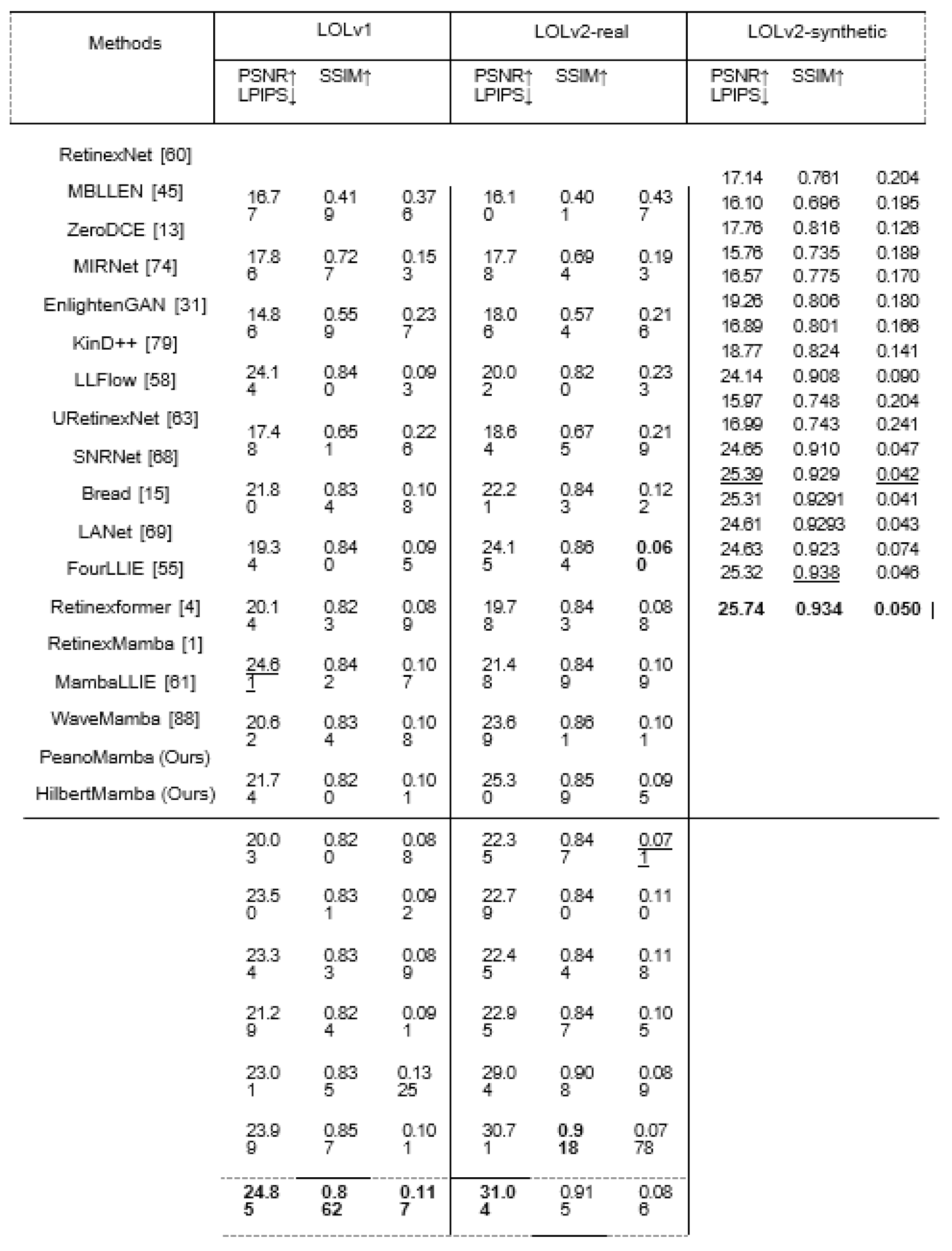
5.2. Comparison with State-of-the-Art Methods
5.3. Comparison with Different Scanning Paths
6. Conclusion
 |



References
- Jiesong Bai, Yuhao Yin, Qiyuan He, Yuanxian Li, and Xiaofeng Zhang. 2024. Retinexmamba: Retinex-based Mamba for Low-light Image Enhancement. arXiv:2405.03349 [cs.CV] https://arxiv.org/abs/2405.03349.
- Steven Bart, Zepeng Wu, YE Rachmad, Yuze Hao, Lan Duo, and X. Zhang. 2025. Frontier AI Safety Confidence Evaluate. Cambridge Open Engage (2025). [CrossRef]
- Jiang Bian, Helai Huang, Qianyuan Yu, and Rui Zhou. 2025. Search-to-Crash: Gen- erating safety-critical scenarios from in-depth crash data for testing autonomous vehicles. Energy (2025), 137174.
- Yuanhao Cai, Hao Bian, Jing Lin, Haoqian Wang, Radu Timofte, and Yulun Zhang. 2023. Retinexformer: One-stage retinex-based transformer for low-light image enhancement. In ICCV. 12504–12513.
- Jie Chen, Ziyi Li, Lu Li, Jialing Wang, Wenyan Qi, Chong-Yu Xu, and Jong-Suk Kim. 2020. Evaluation of multi-satellite precipitation datasets and their error propagation in hydrological modeling in a monsoon-prone region. Remote Sensing 12, 21 (2020), 3550.
- Heng-Da Cheng and XJ Shi. 2004. A simple and effective histogram equalization approach to image enhancement. Digit. Signal Process. 14, 2 (2004), 158–170.
- Ronald, A. DeVore and George G. Lorentz. 1993. Constructive Approximation. Springer.
- Gerald, A. Edgar. 2007. Measure, Topology, and Fractal Geometry. Springer.
- Kenneth, J. Falconer. 2003. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons.
- Albert Gu and Tri Dao. 2023. Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752 (2023).
- Albert Gu, Karan Goel, and Christopher Ré . 2021. Efficiently modeling long sequences with structured state spaces. arXiv preprint arXiv:2111.00396 (2021).
- Zhihao Gu, Fang Li, Faming Fang, and Guixu Zhang. 2019. A novel retinex-based fractional-order variational model for images with severely low light. IEEE TIP 29 (2019), 3239–3253.
- Chunle Guo, Chongyi Li, Jichang Guo, Chen Change Loy, Junhui Hou, Sam Kwong, and Runmin Cong. 2020. Zero-reference deep curve estimation for low-light image enhancement. In CVPR. 1780–1789.
- Hang Guo, Jinmin Li, Tao Dai, Zhihao Ouyang, Xudong Ren, and Shu-Tao Xia. 2024. MambaIR: A Simple Baseline for Image Restoration with State-Space Model. arXiv preprint arXiv:2402.15648 (2024).
- Xiaojie Guo and Qiming, Hu. 2023. Low-light image enhancement via breaking down the darkness. IJCV 131, 1 (2023), 48–66.
- Yuze Hao. 2024. Comment on’Predictions of groundwater PFAS occurrence at drinking water supply depths in the United States’ by Andrea K. Tokranov et al., Science 386, 748-755 (2024). Science 386 (2024), 748–755.
- Yuze Hao. 2025. Accelerated Photocatalytic C–C Coupling via Interpretable Deep Learning: Single-Crystal Perovskite Catalyst Design using First-Principles Calculations. In AI for Accelerated Materials Design-ICLR 2025.
- Yuze Hao, Lan Duo, and Jinlu He. 2025. Autonomous Materials Synthesis Labora- tories: Integrating Artificial Intelligence with Advanced Robotics for Accelerated Discovery. ChemRxiv (2025). [CrossRef]
- Yuze Hao and Yueqi Wang. 2023. Quasi liquid layer-pressure asymmetrical model for the motion of of a curling rock on ice surface. arXiv preprint arXiv:2302.11348 (2023).
- Yuze Hao and Yueqi Wang. 2025. Unveiling Anomalous Curling Stone Trajec- tories: A Multi-Modal Deep Learning Approach to Friction Dynamics and the Quasi-Liquid Layer.
- Yuze Hao, X Yan, Lan Duo, H Hu, and J He. 2025. Diffusion Models for 3D Molecular and Crystal Structure Generation: Advancing Materials Discovery through Equivariance, Multi-Property Design, and Synthesizability. (2025).
- David Hilbert. 1891. Ueber die stetige Abbildung einer Linie aufein Flächenstück. Math. Ann. 38 (1891), 459–460.
- Shih-Chia Huang, Fan-Chieh Cheng, and Yi-Sheng Chiu. 2012. Efficient contrast enhancement using adaptive gamma correction with weighting distribution. IEEE TIP 22, 3 (2012), 1032–1041.
- Tao Huang, Xiaohuan Pei, Shan You, Fei Wang, Chen Qian, and Chang Xu. 2024. Localmamba: Visual state space model with windowed selective scan. arXiv preprint arXiv:2403.09338 (2024).
- Xinyue Huang, Ziqi Lin, Fang Sun, Wenchao Zhang, Kejian Tong, and Yunbo Liu. 2025. Enhancing Document-Level Question Answering via Multi-Hop Retrieval- Augmented Generation with LLaMA 3. arXiv:2506.16037 [cs.CL] https://arxiv. org/abs/2506.16037.
- Xinyue Huang, Chen Zhao, Xiang Li, Chengwei Feng, and Wuyang Zhang. 2025. GAM-CoT Transformer: Hierarchical Attention Networks for Anomaly Detection in Blockchain Transactions. INNO-PRESS: Journal of Emerging Applied AI 1, 3 (2025).
- XinyuJia, Weinan Hou, Shi-Ze Cao, Wang-Ji Yan, and Costas Papadimitriou. 2025. Analytical hierarchical Bayesian modeling framework for model updating and uncertainty propagation utilizing frequency response function data. Computer Methods in Applied Mechanics and Engineering 447 (2025), 118341.
- XinyuJia and Costas Papadimitriou. 2025. Data features-based Bayesian learning for time-domain model updating and robust predictions in structural dynamics. Mechanical Systems and Signal Processing 224 (2025), 112197.
- Xinyu Jia, Omid Sedehi, Costas Papadimitriou, Lambros S Katafygiotis, and Babak Moaveni. 2022. Nonlinear model updating through a hierarchical Bayesian modeling framework. Computer Methods in Applied Mechanics and Engineering 392 (2022), 114646.
- Hai Jiang, Ao Luo, Haoqiang Fan, Songchen Han, and Shuaicheng Liu. 2023. Low-light image enhancement with wavelet-based diffusion models. ACM Trans. Graph. 42, 6 (2023), 1–14.
- Yifan Jiang, Xinyu Gong, Ding Liu, Yu Cheng, Chen Fang, Xiaohui Shen, Jian- chao Yang, Pan Zhou, and Zhangyang Wang. 2021. EnlightenGAN: Deep light enhancement without paired supervision. IEEE TIP 30 (2021), 2340–2349.
- Daniel J Jobson, Zia-ur Rahman, and Glenn A Woodell. 1997. A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE TIP 6, 7 (1997), 965–976.
- Chongyi Li, Chunle Guo, Linghao Han, Jun Jiang, Ming-Ming Cheng, Jinwei Gu, and Chen Change Loy. 2021. Low-light image and video enhancement using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 44, 12 (2021), 9396–9416.
- Chongyi Li, Jichang Guo, Fatih Porikli, and Yanwei Pang. 2018. LightenNet: A convolutional neural network for weakly illuminated image enhancement. Pattern Recognit. Lett. 104 (2018), 15–22.
- Ziyi Li, Kaiyu Guan, Wang Zhou, Bin Peng, Zhenong Jin, Jinyun Tang, Robert F Grant, Emerson D Nafziger, Andrew J Margenot, Lowell E Gentry, et al. 2022. Assessing the impacts of pre-growing-season weather conditions on soil nitrogen dynamics and corn productivity in the US Midwest. Field Crops Research 284 (2022), 108563.
- Ziyi Li, Kaiyu Guan, Wang Zhou, Bin Peng, Emerson D Nafziger, Robert F Grant, Zhenong Jin, Jinyun Tang, Andrew J Margenot, DoKyoung Lee, et al. 2025. Com- paring continuous-corn and soybean-corn rotation cropping systems in the US central Midwest: Trade-offs among crop yield, nutrient losses, and change in soil organic carbon. Agriculture, Ecosystems & Environment 393 (2025), 109739.
- Dong Liang, Ling Li, Mingqiang Wei, Shuo Yang, Liyan Zhang, Wenhan Yang, Yun Du, and Huiyu Zhou. 2022. Semantically contrastive learning for low-light image enhancement. In AAAI, Vol. 36. 1555–1563.
- Seokjae Lim and Wonjun Kim. 2020. DSLR: Deep stacked Laplacian restorer for low-light image enhancement. IEEE TMM 23 (2020), 4272–4284.
- Jiarun Liu, Hao Yang, Hong-Yu Zhou, Yan Xi, Lequan Yu, Yizhou Yu, Yong Liang, Guangming Shi, Shaoting Zhang, Hairong Zheng, et al. 2024. Swin- UMamba: Mamba-based unet with imagenet-based pretraining. arXiv preprint arXiv:2402.03302 (2024).
- Risheng Liu, Long Ma, Jiaao Zhang, Xin Fan, and Zhongxuan Luo. 2021. Retinex- inspired unrolling with cooperative prior architecture search for low-light image enhancement. In CVPR. 10561–10570.
- Xichang Liu, Helai Huang, Jiang Bian, Rui Zhou, Zhiyuan Wei, and Hanchu Zhou. 2025. Generating intersection pre-crash trajectories for autonomous driving safety testing using Transformer Time-Series Generative Adversarial Networks. Engineering Applications of Artificial Intelligence 160 (2025), 111995.
- Yue Liu, Yunjie Tian, Yuzhong Zhao, Hongtian Yu, Lingxi Xie, Yaowei Wang, Qixiang Ye, and Yunfan Liu. 2024. VMamba: Visual state space model. arXiv preprint arXiv:2401.10166 (2024).
- Kin Gwn Lore, Adedotun Akintayo, and Soumik Sarkar. 2017. LLNet: A deep autoencoder approach to natural low-light image enhancement. PR 61 (2017), 650–662.
- Ilya Loshchilov and Frank Hutter. 2017. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101 (2017).
- Feifan Lv, Feng Lu, Jianhua Wu, and Chongsoon Lim. 2018. MBLLEN: Low- light image/video enhancement using CNNs.. In BMVC, Vol. 220. Northumbria University, 4.
- Jun Ma, Feifei Li, and Bo Wang. 2024. U-Mamba: Enhancing long-range de- pendency for biomedical image segmentation. arXiv preprint arXiv:2401.04722 (2024).
- Long Ma, Tengyu Ma, Risheng Liu, Xin Fan, and Zhongxuan Luo. 2022. Toward fast, flexible, and robust low-light image enhancement. In CVPR. 5637–5646.
- Benoit B. Mandelbrot. 1982. The Fractal Geometry of Nature. W.H. Freeman and Company.
- Jiří Matoušek. 1999. Geometric Discrepancy: An Illustrated Guide. Springer.
- Giuseppe Peano. 1890. Sur une courbe, qui remplit toute une aire. Math. Ann. 36, 1 (1890), 157–160.
- Jiaming Pei, Jinhai Li, Zhenyu Song, Maryam Mohamed Al Dabel, Mohammed JF Alenazi, Sun Zhang, and Ali Kashif Bashir. 2025. Neuro-VAE-Symbolic Dynamic Traffic Management. IEEE Transactions on Intelligent Transportation Systems (2025).
- Jiaming Pei, Wenxuan Liu, Jinhai Li, Lukun Wang, and Chao Liu. 2024. A review of federated learning methods in heterogeneous scenarios. IEEE Transactions on Consumer Electronics 70, 3 (2024), 5983–5999.
- Jiaming Pei, Marwan Omar, Maryam Mohamed Al Dabel, Shahid Mumtaz, and Wei Liu. 2025. Federated Few-Shot Learning With Intelligent Transportation Cross-Regional Adaptation. IEEE Transactions on Intelligent Transportation Sys- tems (2025).
- Xiaohuan Pei, Tao Huang, and Chang Xu. 2024. Efficientvmamba: Atrous selective scan for light weight visual mamba. arXiv preprint arXiv:2403.09977 (2024).
- Chenxi Wang, Hongjun Wu, and Zhi Jin. 2023. FourLLIE: Boosting low-light im- age enhancement by fourier frequency information. In ACMInt. Conf. Multimedia. 7459–7469.
- Lukun Wang, Xiaoqing Xu, and Jiaming Pei. 2025. Communication-Efficient Federated Learning via Dynamic Sparsity: An Adaptive Pruning Ratio Based on Weight Importance. IEEE Transactions on Cognitive Communications and Networking (2025).
- Wenjing Wang, Chen Wei, Wenhan Yang, and Jiaying Liu. 2018. GLADNet: Low- light enhancement network with global awareness. In IEEE Conf. Autom. Face Gesture Recognit. (FG). IEEE, 751–755.
- Yufei Wang, Renjie Wan, Wenhan Yang, Haoliang Li, Lap-Pui Chau, and Alex Kot. 2022. Low-light image enhancement with normalizing flow. In AAAI, Vol. 36. 2604–2612.
- Zhou Wang, Alan C Bovik, Hamid R Sheikh, and Eero P Simoncelli. 2004. Image quality assessment: from error visibility to structural similarity. IEEE TIP 13, 4 (2004), 600–612.
- Chen Wei, Wenjing Wang, Wenhan Yang, and Jiaying Liu. 2018. Deep retinex decomposition for low-light enhancement. arXiv preprint arXiv:1808.04560 (2018).
- Jiangwei Weng, Zhiqiang Yan, Ying Tai, Jianjun Qian, Jian Yang, and Jun Li. 2024. MambaLLIE: Implicit Retinex-Aware Low Light Enhancement with Global-then- Local State Space. NeurIPS 2024 (2024).
- Jan C Willems. 1986. From time series to linear system—Part I. Finite dimensional linear time invariant systems. Automatica 22 (1986), 561–580.
- Wenhui Wu, Jian Weng, Pingping Zhang, Xu Wang, Wenhan Yang, and Jianmin Jiang. 2022. URetinex-Net: Retinex-based deep unfolding network for low-light image enhancement. In CVPR. 5901–5910.
- Yicheng Xiao, Lin Song, Shaoli Huang, Jiangshan Wang, Siyu Song, Yixiao Ge, Xiu Li, and Ying Shan. 2024. GrootVL: Tree Topology is All You Need in State Space Model. arXiv preprint arXiv:2406.02395 (2024).
- Zhaohu Xing, Tian Ye, Yijun Yang, Guang Liu, and Lei Zhu. 2024. SegMamba: Long-range Sequential Modeling Mamba For 3D Medical Image Segmentation. arXiv preprint arXiv:2401.13560 (2024).
- Jingzhao Xu, Mengke Yuan, Dong-Ming Yan, and Tieru Wu. 2022. Illumination guided attentive wavelet network for low-light image enhancement. IEEE TMM 25 (2022), 6258–6271.
- Shuo Xu, Yuchen ***, Zhongyan Wang, and Yexin Tian. 2025. Fraud Detec- tion in Online Transactions: Toward Hybrid Supervised–Unsupervised Learning Pipelines. In Proceedings of the 2025 6th International Conference on Electronic Communication and Artificial Intelligence (ICECAI 2025), Chengdu, China. 20–22.
- Xiaogang Xu, Ruixing Wang, Chi-Wing Fu, and Jiaya Jia. 2022. SNR-aware low-light image enhancement. In CVPR. 17714–17724.
- Kai-Fu Yang, Cheng Cheng, Shi-Xuan Zhao, Hong-Mei Yan, Xian-Shi Zhang, and Yong-Jie Li. 2023. Learning to adapt to light. IJCV 131, 4 (2023), 1022–1041.
- Wenhan Yang, Shiqi Wang, Yuming Fang, Yue Wang, and Jiaying Liu. 2020. From fidelity to perceptual quality: A semi-supervised approach for low-light image enhancement. In CVPR. 3063–3072.
- Wenhan Yang, Wenjing Wang, Haofeng Huang, Shiqi Wang, and Jiaying Liu. 2021. Sparse gradient regularized deep retinex network for robust low-light image enhancement. IEEE TIP 30 (2021), 2072–2086.
- Xunpeng Yi, Han Xu, Hao Zhang, Linfeng Tang, and Jiayi Ma. 2023. Diff-Retinex: Rethinking Low-light Image Enhancement with A Generative Diffusion Model. In ICCV. IEEE, 12268–12277.
- Syed Waqas Zamir, Aditya Arora, Salman Khan, Munawar Hayat, Fahad Shahbaz Khan, and Ming-Hsuan Yang. 2022. Restormer: Efficient transformer for high- resolution image restoration. In CVPR. 5728–5739.
- Syed Waqas Zamir, Aditya Arora, Salman Khan, Munawar Hayat, Fahad Shahbaz Khan, Ming-Hsuan Yang, and Ling Shao. 2020. Learning enriched features for real image restoration and enhancement. In ECCV. Springer, 492–511.
- Syed Waqas Zamir, Aditya Arora, Salman Khan, Munawar Hayat, Fahad Shahbaz Khan, Ming-Hsuan Yang, and Ling Shao. 2022. Learning enriched features for fast image restoration and enhancement. IEEE Trans. Pattern Anal. Mach. Intell. 45, 2 (2022), 1934–1948.
- Hongwei Zhang, Meixia Tao, Yuanming Shi, and Xiaoyan Bi. 2022. Federated multi-task learning with non-stationary heterogeneous data. In ICC 2022-IEEE International Conference on Communications. IEEE, 4950–4955.
- Kaibing Zhang, Cheng Yuan, Jie Li, Xinbo Gao, and Minqi Li. 2023. Multi-branch and progressive network for low-light image enhancement. IEEE TIP 32 (2023), 2295–2308.
- Richard Zhang, Phillip Isola, Alexei A Efros, Eli Shechtman, and Oliver Wang. 2018. The unreasonable effectiveness of deep features as a perceptual metric. In CVPR. 586–595.
- Yonghua Zhang, Xiaojie Guo, Jiayi Ma, Wei Liu, and Jiawan Zhang. 2021. Beyond brightening low-light images. IJCV 129 (2021), 1013–1037.
- Yonghua Zhang, Jiawan Zhang, and Xiaojie Guo. 2019. Kindling the darkness: A practical low-light image enhancer. In ACM Int. Conf. Multimedia. 1632–1640.
- Kaiyang Zhong, Yifan Wang, Jiaming Pei, Shimeng Tang, and Zonglin Han. 2021. Super efficiency SBM-DEA and neural network for performance evaluation. Information Processing & Management 58, 6 (2021), 102728.
- Rui Zhou, Weihua Gui, Helai Huang, Xichang Liu, Zhiyuan Wei, and Jiang Bian. 2025. DiffCrash: Leveraging Denoising Diffusion Probabilistic Models to Expand High-Risk Testing Scenarios Using In-Depth Crash Data. Expert Systems with Applications (2025), 128140.
- Rui Zhou, Helai Huang, Guoqing Zhang, Hanchu Zhou, and Jiang Bian. 2025. Crash-based safety testing of autonomous vehicles: Insights from generating safety-critical scenarios based on in-depth crash data. IEEE Transactions on Intelligent Transportation Systems (2025).
- Rui Zhou, Guoqing Zhang, Helai Huang, Zhiyuan Wei, Hanchu Zhou, Jieling Jin, Fangrong Chang, and Jiguang Chen. 2024. How would autonomous vehicles behave in real-world crash scenarios? Accident Analysis & Prevention 202 (2024), 107572.
- Weilian Zhou, Sei-Ichiro Kamata, Haipeng Wang, Man-Sing Wong, Huiying, and Hou. 2024. Mamba-in-Mamba: Centralized Mamba-Cross-Scan in Tokenized Mamba Model for Hyperspectral Image Classification. arXiv:2405.12003 [cs.CV] https://arxiv.org/abs/2405.12003.
- Lianghui Zhu, Bencheng Liao, Qian Zhang, Xinlong Wang, Wenyu Liu, and Xinggang Wang. 2024. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv preprint arXiv:2401.09417 (2024).
- J Zhuang, G Li, H Xu, J Xu, and R Tian. 2024. TEXT-TO-CITY Controllable 3D Urban Block Generation with Latent Diffusion Model. In Proceedings of the 29th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Singapore. 20–26.
- Wenbin Zou, Hongxia Gao, Weipeng Yang, and Tongtong Liu. 2024. Wave- Mamba: Wavelet State Space Model for Ultra-High-Definition Low-Light Image Enhancement. In ACM Multimedia 2024. https://openreview.net/forum?
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




