Numerical Behavior of the Riemann Zeta Function Using Real-to-Complex Conversion

1. Introduction

The Riemann Hypothesis remains one of the most profound unsolved problems in mathematics. Its verification, even to limited numerical ranges, demands accurate computation of the function $\zeta \left(s\right)$ along the critical line $\Re \left(s\right)=\frac{1}{2}$. Traditional methods rely on the Riemann–Siegel formula and Gram point interpolation, which become computationally intensive as t grows large. This paper presents a complementary approach based on direct numerical conversion of real inputs to complex domains, combined with a valley scanning technique that efficiently isolates zeros without requiring Gram alignment.

2. Mathematical Background

2.1. The Riemann Zeta Function

The Riemann zeta function is one of the most studied objects in mathematics, intimately connected to the distribution of prime numbers. For complex arguments $s=\sigma +it$ with real part $\sigma >1$, it is defined by the absolutely convergent series:

$$\zeta \left(s\right)=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^s}}.$$

Through analytic continuation, this definition extends to all complex $s\ne 1$, and the function satisfies a deep symmetry captured by the functional equation:

$$\zeta \left(s\right)=2^s{\pi }^{s-1}sin\left({\displaystyle \frac{\pi s}{2}}\right)\mathrm{\Gamma }(1-s)\zeta (1-s),$$

where $\mathrm{\Gamma }\left(s\right)$ is the Gamma function. This reflection property allows values of $\zeta \left(s\right)$ on the right half-plane ($\Re \left(s\right)>1$) to determine those on the left.

The nontrivial zeros of $\zeta \left(s\right)$ are the complex numbers $s=\sigma +it$ that satisfy $0<\sigma <1$ and $\zeta \left(s\right)=0$. The celebrated Riemann Hypothesis conjectures that all such zeros lie on the critical line:

$$\Re \left(s\right)=\frac{1}{2}.$$

2.2. Relation to Prime Numbers

The zeta function encodes the structure of the primes through the Euler product:

$$\zeta \left(s\right)=\prod _{p\mathrm{prime}}{\displaystyle \frac{1}{1-p^{-s}}},\Re \left(s\right)>1,$$

demonstrating that the analytic behavior of $\zeta \left(s\right)$ reflects the multiplicative structure of the integers. In particular, zeros of $\zeta \left(s\right)$ govern the distribution of primes via the explicit formula relating the prime-counting function $\pi \left(x\right)$ and the zeros of $\zeta \left(s\right)$:

$$\pi \left(x\right)\sim Li\left(x\right)-\sum _{\rho }Li\left(x^{\rho }\right)+(\mathrm{small}\mathrm{correction}\mathrm{terms}),$$

where the sum runs over nontrivial zeros $\rho =\frac{1}{2}+i{t}_{\rho }$.

2.3. The Hardy Function $Z\left(t\right)$

To facilitate numerical computation and visualization on the critical line, it is convenient to introduce the Hardy function:

$$Z\left(t\right)=e^{i\theta \left(t\right)}\zeta \left(\frac{1}{2}+it\right),$$

where the Riemann–Siegel theta function is defined as

$$\theta \left(t\right)=arg\left(\mathrm{\Gamma }\left({\displaystyle \frac{1}{4}}+{\displaystyle \frac{it}{2}}\right)\right)-{\displaystyle \frac{t}{2}}log\pi .$$

The factor $e^{i\theta \left(t\right)}$ ensures that $Z\left(t\right)$ is a real-valued function for real t, allowing one to visualize the “mountain–valley” structure of $\left|Z\right(t\left)\right|$. The zeros of $Z\left(t\right)$ correspond exactly to the nontrivial zeros of $\zeta \left(s\right)$ on the critical line.

2.4. Average Zero Spacing and Density

The density of zeros along the critical line grows logarithmically with t. The number of zeros $N\left(T\right)$ with imaginary part between 0 and T satisfies the Riemann–von Mangoldt formula:

$$N\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{2\pi }}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT),$$

which implies that the average spacing between consecutive zeros near height T is approximately

$$\Delta T_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}.$$

This theoretical value provides a key benchmark for the validation of computed zeros and their local density, and it will be used throughout this work to assess the accuracy of the numerical results generated by the valley scanner algorithm.

2.5. Known Computational Approaches

The computation of zeros of the Riemann zeta function has been a central endeavor in analytic number theory since the early work of Riemann himself. Over the past century, increasingly sophisticated techniques have been developed to evaluate $\zeta \left(s\right)$ and its real-valued counterpart $Z\left(t\right)$ with high accuracy.

The Riemann–Siegel Formula

For large values of t, direct evaluation of the Dirichlet series for $\zeta \left(s\right)$ becomes computationally infeasible. To overcome this, the Riemann–Siegel formula provides an asymptotic expansion for $Z\left(t\right)$:

$$Z\left(t\right)=2\sum _{n=1}^N{\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}}+R\left(t\right),$$

where $N=\lfloor \sqrt{t/2\pi }\rfloor$, and $R\left(t\right)$ is a small remainder term. This formula dramatically reduces the computational cost from $O\left(t\right)$ to approximately $O\left(\sqrt{t}\right)$ operations. Further refinements, such as those developed by Gabcke, improve the evaluation of the remainder $R\left(t\right)$, allowing reliable computations of $Z\left(t\right)$ for very large t.

Gram Points and Zero Localization

To locate zeros efficiently, numerical searches traditionally use Gram points, which are values of t defined by

$$\theta \left(g_n\right)=n\pi ,$$

where $\theta \left(t\right)$ is the Riemann–Siegel theta function. Empirically, zeros of $Z\left(t\right)$ tend to alternate with Gram points—so-called “Gram’s law.” However, this law fails occasionally, especially at high heights, making it unreliable as a universal localization tool. Gram points nonetheless remain a convenient reference grid for identifying sign changes in $Z\left(t\right)$.

Turing’s Verification Method

To ensure that no zeros are missed between two computed intervals, Turing introduced an integral-based verification method. The approach compares the analytically predicted number of zeros up to height T (via the Riemann–von Mangoldt formula) with the number of sign changes detected numerically in $Z\left(t\right)$. If the counts agree, all zeros in the interval are confirmed. This procedure forms the foundation of modern computational checks for the completeness and correctness of zero datasets.

Odlyzko–Schönhage Algorithm

At very high heights, traditional evaluation becomes prohibitively expensive even with the Riemann–Siegel formula. The Odlyzko–Schönhage algorithm employs advanced Fast Fourier Transform (FFT) techniques and multiple evaluations of $Z\left(t\right)$ in parallel, reducing the asymptotic complexity and enabling computations of millions of zeros at heights beyond ${10}^{20}$. This method remains one of the most powerful approaches for large-scale zero verification.

Limitations at High t

Despite their success, all these methods face increasing numerical and computational challenges as t grows:

• The oscillatory behavior of $Z\left(t\right)$ intensifies, requiring higher precision to prevent round-off and cancellation errors.
• The Riemann–Siegel expansion becomes less stable as remainder terms accumulate.
• FFT-based methods demand extensive memory and cannot easily adapt to arbitrary-precision arithmetic.

For these reasons, exploring alternative formulations that maintain numerical stability while preserving analytic accuracy—such as the present study’s N→complex mapping and the Valley Scanner approach—becomes both necessary and timely.

3. Proposed Numerical Method

3.1. Motivation and Research Shift

Although this research ultimately centers on the analysis of the Riemann Zeta function, the method for locating its zeros was first discovered during an independent investigation of semiprime numbers. In that earlier study, the focus was on expressing a semiprime number N, composed of two prime factors $p_1$ and $p_2$, through an algebraic structure that could reveal deeper numerical symmetries.

It was observed that N, $p_1$, and $p_2$ could be conveniently related using a quadratic form. The standard and existing approach begins by defining the unknown primes p and q such that:

$$N=p·q$$

The sum of the two factors, denoted $S=p+q$, is equally important. In certain factoring methods, this value is associated with expressions derived from the totient function or other auxiliary formulations (sometimes referred to in the literature as $Nf\left(N\right)$).

Given the relationships above, one can form a quadratic equation whose roots correspond to the two prime factors. For a general quadratic equation of the form $x^2+bx+c=0$, the sum of the roots is $-b$, and the product of the roots is c. Substituting $S=p+q$ and $N=p·q$ yields:

$$x^2-Sx+N=0$$

The solutions of this equation are therefore the two prime factors:

$$x={\displaystyle \frac{S\pm \sqrt{S^2-4N}}{2}}$$

Finding this approach computationally demanding and difficult to extend efficiently, the method was ultimately set aside in favor of exploring a more effective alternative.

3.2. N-to-Complex Conversion

The method described in this section, focus on the mean between $p_1$ and $p_2$. A quadratic equation involving N, m, $p_1$ and $p_2$ can be rewritten using this straightforward approach:

$$N=p_1·q_2$$

$$m={\displaystyle \frac{p_1+p_2}{2}}$$

The goal is to solve for $p_1$.

First, from Equation (2), express $p_2$ in terms of m and $p_1$.

Multiply both sides by 2: $2m=p_1+p_2$

Isolate $p_2$: $p_2=2m-p_1$

Now, substitute this expression for $p_2$ into Equation (1): $N=p_1·(2m-p_1)$

Expand the equation: $N=2m{p}_1-p_1^2$

To solve for $p_1$, rearrange into a standard quadratic equation ($a{x}^2+bx+c=0$):

$$p_1^2-2m{p}_1+N=0$$

This is a quadratic equation where $a=1$, $b=-2m$, and $c=N$. using the quadratic formula to solve for $p_1$:

$$p_1={\displaystyle \frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$

Substitute the values of a, b, and c:

$$p_1={\displaystyle \frac{-(-2m)\pm \sqrt{{(-2m)}^2-4\left(1\right)\left(N\right)}}{2\left(1\right)}}$$

$$p_1={\displaystyle \frac{2m\pm \sqrt{4m^2-4N}}{2}}$$

Simplifying the square root by factoring out a 4:

$$p_1={\displaystyle \frac{2m\pm \sqrt{4(m^2-N)}}{2}}$$

$$p_1={\displaystyle \frac{2m\pm 2\sqrt{m^2-N}}{2}}$$

Finally, divide both terms in the numerator by 2:

$$p_1=m\pm \sqrt{m^2-N}$$

This simple algebraic exercise provides the conceptual foundation of the present research and formally justifies both the name of this section and the title of the paper.

The following equation,

$$p_1^2-2m{p}_1+N=0$$

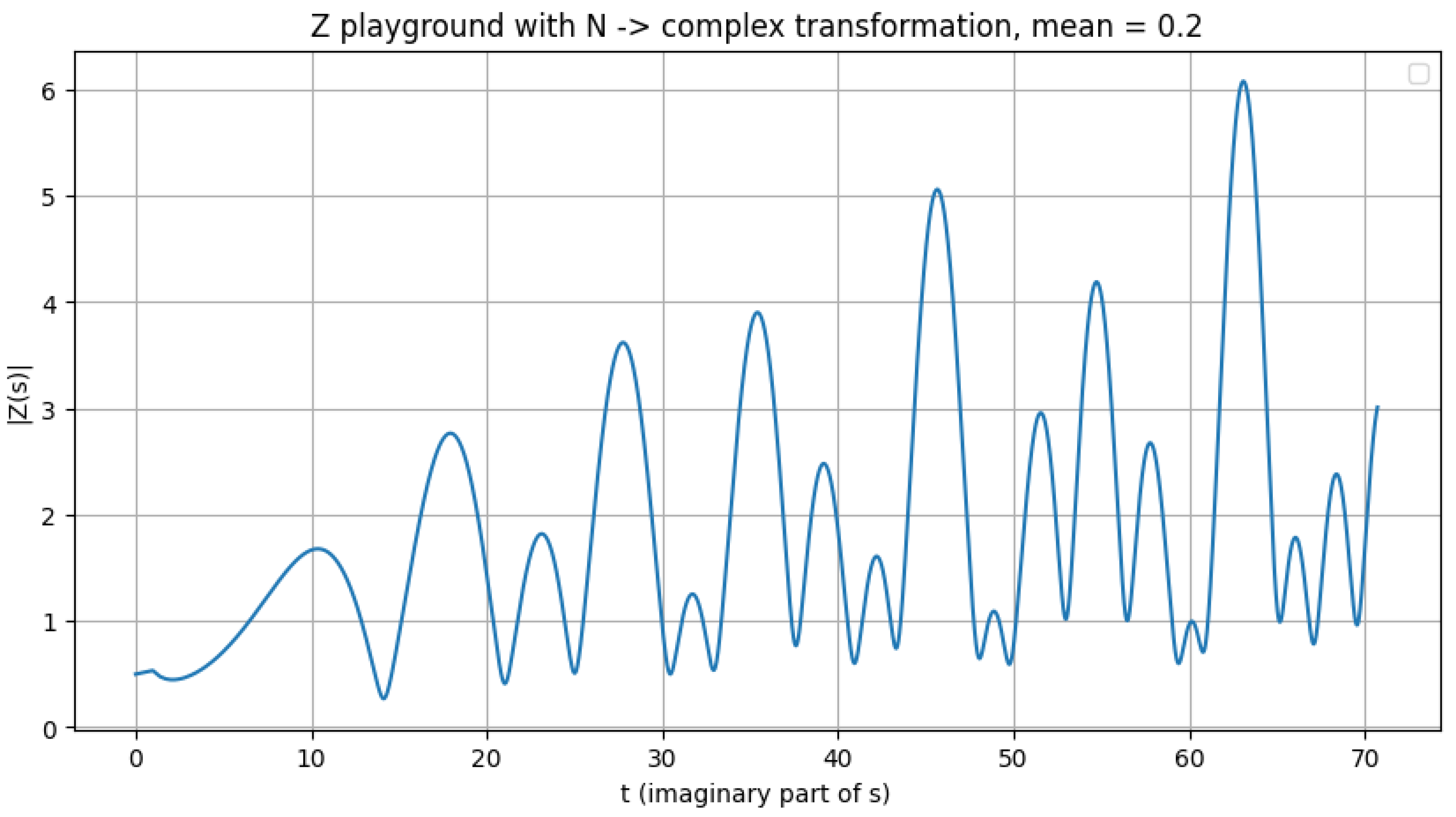
was originally introduced as part of an exploratory study aimed at analyzing the variable m and the area under the curve of the quadratic expression, in search of a possible relationship between m or the area and N, where N represents the semiprime number to be factorized.

A series of statistical models were subsequently developed in Python to evaluate the predictive relationship between these parameters and N. Although some preliminary results appeared promising, further testing revealed that neither the area under the quadratic curve nor the variable m exhibited a sufficiently strong or consistent correlation with N. This outcome, while initially discouraging, served as a valuable turning point: What if we move the mean m to a known point like 1 (one)?

To answer this question, the equation:

$$p=m\pm \sqrt{m^2-N}$$

Will serve better. It is worth noting that when $m=1$, the expression causes the square root term to become undefined, since $N>1$. Anecdotally, this detail was initially overlooked during the generation of test datasets, which inadvertently produced millions of invalid results. After identifying this simple oversight, it became evident that the solutions for p could be expressed as two complex numbers, provided that the equation is formulated appropriately as follows:

$$p=m\pm \left(\sqrt{N-m^2}\right)i$$

$N>1$, i is the standard notation for square root of -1

For researchers interested in prime numbers, the Riemann Zeta function is a recurrent and foundational topic. It is well established that, in order to evaluate the Zeta function along the critical line where its nontrivial zeros are conjectured to lie, the real part of the complex variable s must be $\frac{1}{2}$. Consequently, the parameter m in this study was intuitively fixed at 1/2, aligning with the critical line of the Riemann zeta function. From this point onward, the focus of the research was redirected toward the investigation of the Z-function.

3.3. Valley Scanner Algorithm

The term valley scanner will appear recurrently throughout the following sections. It originated from the datasets computed under the following input parameters:

• A range of N, consisting of real, positive integer values (e.g., 1–10000).
• The variable p, hereafter denoted as s, to align with the standard notation used in the study of the Zeta function, evaluated at $m=\frac{1}{2}$.

$$s=m\pm \left(\sqrt{N-m^2}\right)i$$

The imaginary part as t, and Isolating N:

$$t=\sqrt{N-m^2}N=t^2+m^2$$

(1)

The central objective of this stage was to compute the magnitude $\left|Z\right(s\left)\right|$ across a continuous range of N values, and to analyze the resulting datasets through direct observation and graphical representation. For this operation, a dedicated Python script was developed (the complete source code is presented on the following page).1 Please note that copying the code directly from this document may alter indentation or character encoding, potentially leading to syntax errors.

For the fully formatted and maintained version, please refer to the public repository:

playground.py

import subprocess

import sys

def ensure_lib(package):

    try:

        __import__(package)

    except ImportError:

        subprocess.check_call(

            [sys.executable, "-m", "pip", "install", package, "--quiet"]

        )

# Ensure required libraries

ensure_lib("mpmath")

ensure_lib("matplotlib")

import mpmath as mp

import matplotlib.pyplot as plt

mp.dps = 250  # precision

# From N, we Calculate:

# m + sqrt(N - m^2) i

def N_to_complex(N, m):

    t = mp.sqrt(N - m ** 2)

    s = m + t * 1j

    return s, t

# Z

def Z(N, m):

    s, t = N_to_complex(N, m)

    z_val = mp.zeta(s)

    return t, z_val

# Dataset for plotting

dataset = []

m = mp.mpf(’0.5’) # <-------------- IMPORTANT: MEAN = 1/2

for n in range(5000):

    t, z = Z(n, m)

    dataset.append([t.real, abs(z)])

ts = [t for t, _ in dataset]

zs = [z for _, z in dataset]

plt.figure(figsize=(10, 5))

plt.plot(ts, zs)

plt.xlabel("t (imaginary part of s)")

plt.ylabel("|Z(s)|")

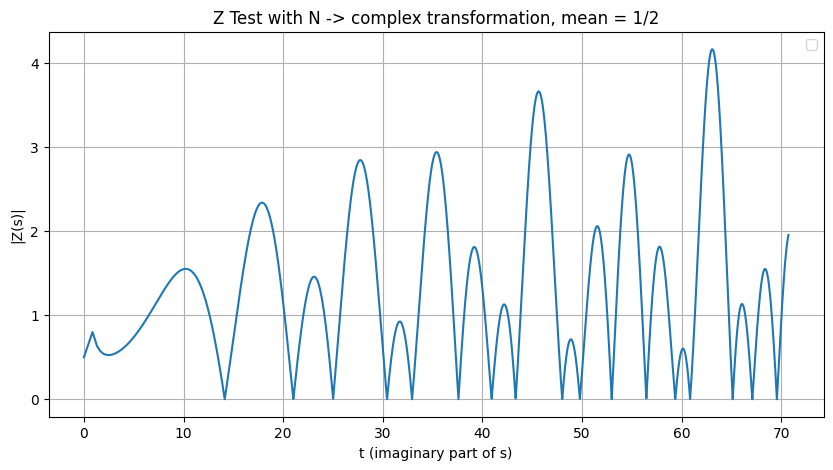
plt.title("Z Test with N -> complex transformation, mean = 1/2")

plt.legend()

plt.grid(True)

plt.show()

Results:

Figure 1. Illustration of the valley scanner detecting zeros.

Figure 1. Illustration of the valley scanner detecting zeros.

Table 1. First Non-trivial Zeros of the Riemann Zeta Function

Index	Imaginary Part (${\mathit{t}}_{\mathit{n}}$)
1	14.1347251417346937904572519835625
2	21.0220396387715549926284795938969
3	25.0108575801456887632137909925628
4	30.4248761258595132103118975305840
5	32.9350615877391896906623689640747
6	37.5861781588256712572177634807053
7	40.9187190121474951873981269146334
8	43.3270732809149995194961221654068
9	48.0051508811671597279424727494277
10	49.7738324776723021819167846785638
11	52.9703214777144606441472966088808
12	56.4462476970633948043677594767060
13	59.3470440026023530796536486749922
14	60.8317785246098098442599018245241
15	65.1125440480816066608750542531836
16	67.0798105294941737144788288965221
17	69.5464017111739792529268575265547

Table 1. First Non-trivial Zeros of the Riemann Zeta Function

Index	Imaginary Part (${\mathit{t}}_{\mathit{n}}$)
1	14.1347251417346937904572519835625
2	21.0220396387715549926284795938969
3	25.0108575801456887632137909925628
4	30.4248761258595132103118975305840
5	32.9350615877391896906623689640747
6	37.5861781588256712572177634807053
7	40.9187190121474951873981269146334
8	43.3270732809149995194961221654068
9	48.0051508811671597279424727494277
10	49.7738324776723021819167846785638
11	52.9703214777144606441472966088808
12	56.4462476970633948043677594767060
13	59.3470440026023530796536486749922
14	60.8317785246098098442599018245241
15	65.1125440480816066608750542531836
16	67.0798105294941737144788288965221
17	69.5464017111739792529268575265547

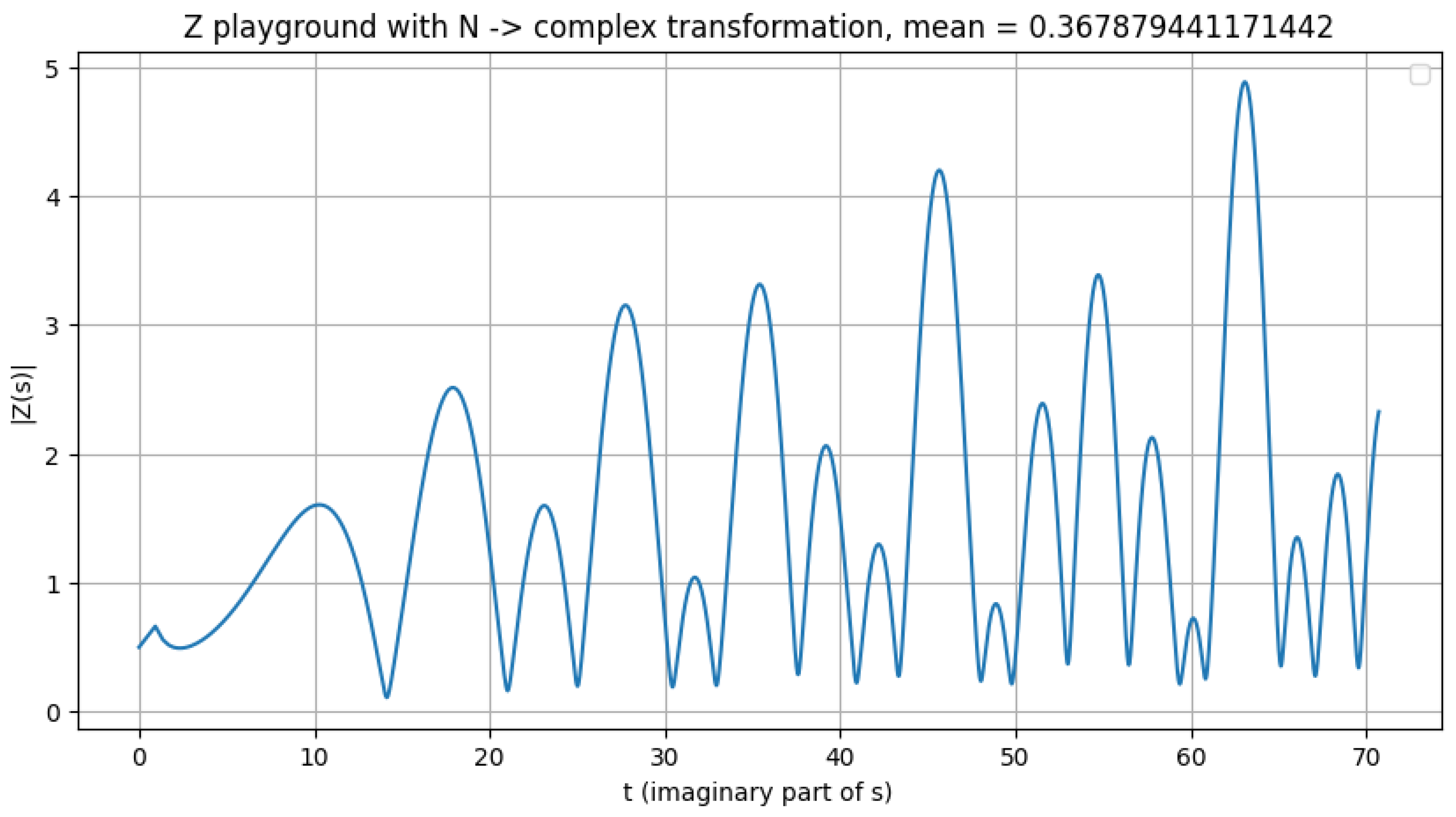
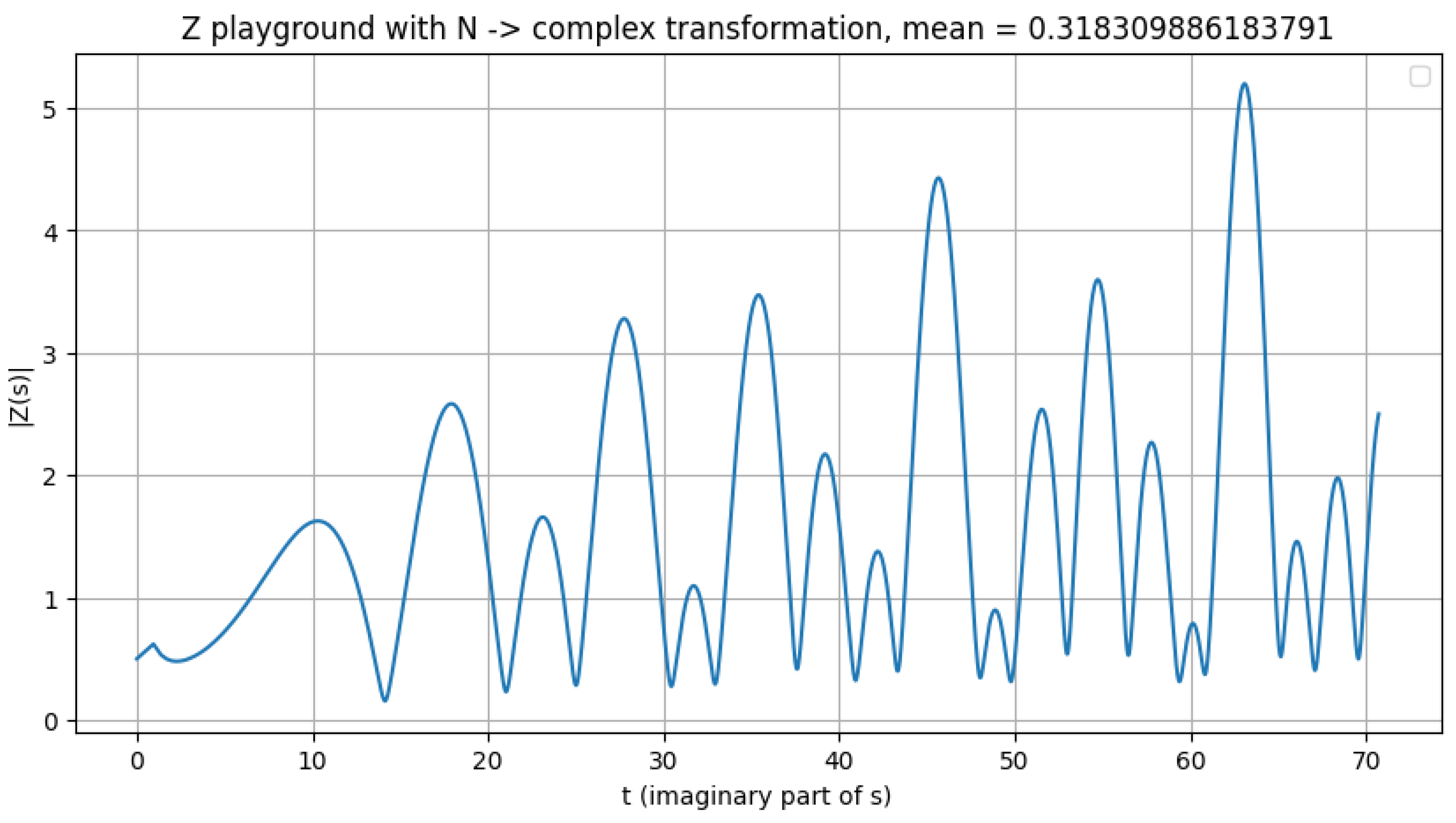
Visually, the resulting plot is self-explanatory. This behavior can be described as follows: when the Riemann Zeta function $\zeta \left(s\right)$ is evaluated using $s=m\pm \left(\sqrt{N-m^2}\right)i$ at $m=\frac{1}{2}$, and for N evaluated over any numerical range, the computed values of $\zeta \left(s\right)$ consistently approach zero—demonstrating convergence along the critical line, as expected from the theoretical framework of the Riemann Hypothesis.

Refining the range of N values by introducing decimal precision yields a closer approximation of $\zeta \left(s\right)$ to zero. The accompanying Python script reproduces this behavior consistently across any chosen range of N; however, it should be noted that these computations are computationally demanding.

This is the dataset calculated from the python script showing the approximations compared to confirmed zeros:

Table 2. Comparison between computed and reference zeros of the Riemann Zeta function.

N	Computed t	t from Public Database
200	14.13329402510257	14.13472514
442	21.017849556983705	21.02203964
626	25.014995502697975	25.01085758
926	30.426140077242792	30.42487613
1085	32.93554311074891	32.93506159
1413	37.586566749305526	37.58617816
1675	40.92370951	40.91871901
1877	43.32147273581544	43.32707328
2305	48.00781186432057	48.00515088
2478	49.77700272214067	49.77383248
2806	52.96933074902875	52.97032148
3186	56.442448564887755	56.44624770
3522	59.34433418617145	59.34704400
3701	60.83378995	60.83177853
4240	65.11336268386084	65.11254405
4500	67.08017591	67.07981053
4837	69.54674686856315	69.54640171

Table 2. Comparison between computed and reference zeros of the Riemann Zeta function.

N	Computed t	t from Public Database
200	14.13329402510257	14.13472514
442	21.017849556983705	21.02203964
626	25.014995502697975	25.01085758
926	30.426140077242792	30.42487613
1085	32.93554311074891	32.93506159
1413	37.586566749305526	37.58617816
1675	40.92370951	40.91871901
1877	43.32147273581544	43.32707328
2305	48.00781186432057	48.00515088
2478	49.77700272214067	49.77383248
2806	52.96933074902875	52.97032148
3186	56.442448564887755	56.44624770
3522	59.34433418617145	59.34704400
3701	60.83378995	60.83177853
4240	65.11336268386084	65.11254405
4500	67.08017591	67.07981053
4837	69.54674686856315	69.54640171

3.4. Identifying Zeros by Detecting Consecutive Minima of $\left|Z\right(s\left)\right|$

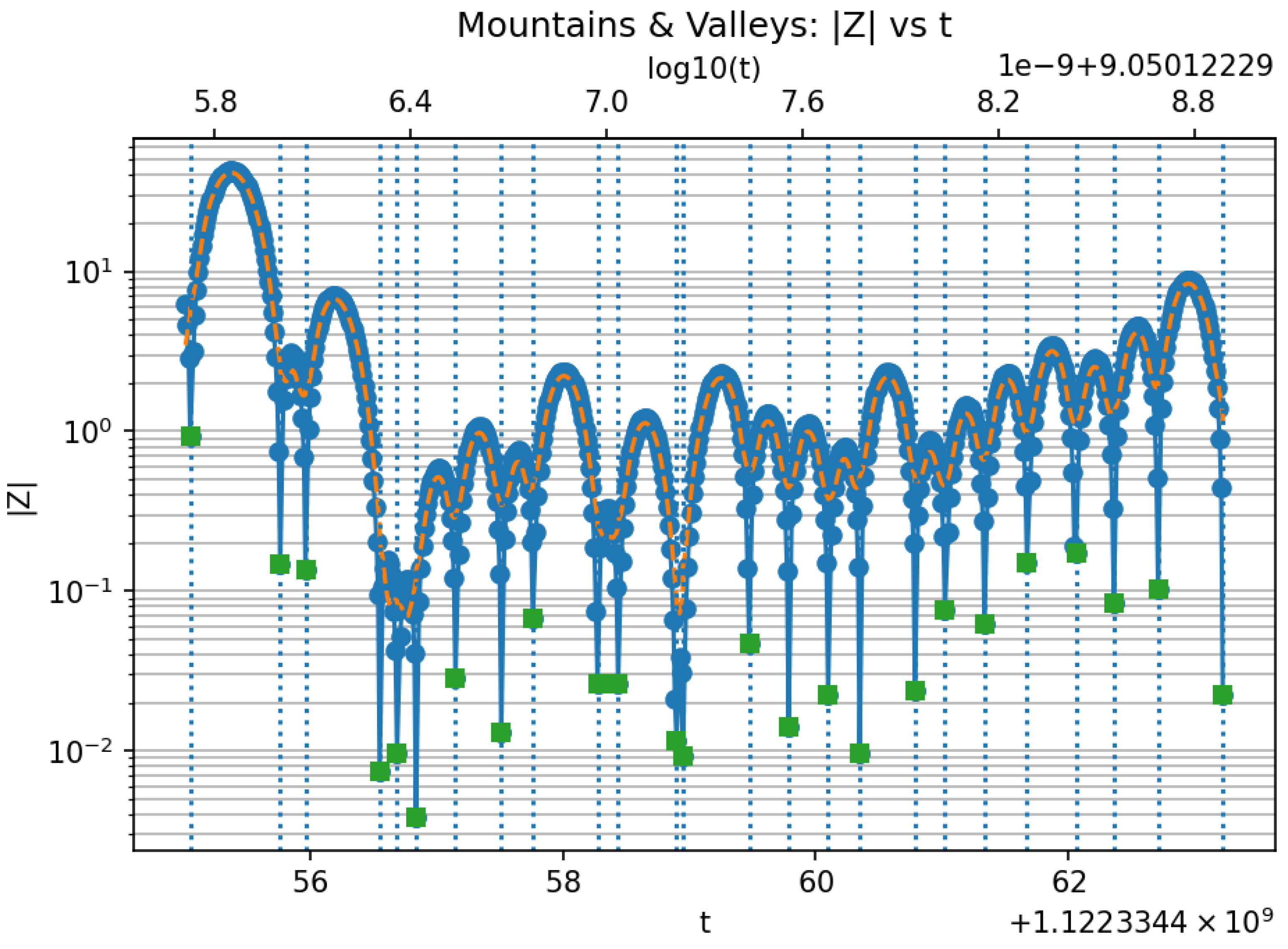
Having obtained reproducible values across multiple ranges of N, it became necessary to test this approach at very high magnitudes of t as part of scientific rigor. While Python provides a remarkable ecosystem for numerical exploration of $\left|Z\right(s\left)\right|$, the process—informally termed “mountain walking” or the “valley scanner” soon became computationally prohibitive.

At this stage, it should be mentioned that AI-assisted tools were employed to accelerate development. Throughout this research, ChatGPT 5/4.5 was used to iteratively generate, refine, and validate code implementations, effectively serving as a peer collaborator during the construction of the numerical framework.

Mountain Walking and Valley Scanner Algorithm

The central idea of the method is to traverse the numerical “landscape” of $\left|Z\right(s\left)\right|$ as a function of N and t, identifying valleys corresponding to local minima—potential zeros of the Riemann Zeta function. The algorithm, much like the Python code, operates in the following manner:

• Set an initial value $t_0$, the imaginary part of s, which may or may not correspond to a true zero.
• Transform $t_0$ into its corresponding real-number representation N using the established $N\leftrightarrow t$ mapping (see Section 1).
• Increment N by one, i.e., $N=N+1$, and compute the corresponding $t_1$.
• Evaluate $\left|Z\right(s\left)\right|$ for both $t_0$ and $t_1$.
• If $|Z\left(s_0\right)|>|Z\left(s_1\right)|$, the algorithm interprets this as a descent toward a valley—an interval likely containing a zero. Conversely, if $|Z\left(s_0\right)|<|Z\left(s_1\right)|$, the process is ascending a mountain, and the algorithm must continue forward to reach the next descent.
• During descent, when the algorithm detects a reversal in the gradient (a bounce), it records the current point as a local minimum, i.e., a candidate zero.
• The corresponding t-value at this point is then refined using a Newton root-finding method to obtain the precise zero location.

Method of evaluating the Z function

• The Riemann–Siegel formula is employed for high values of t:

  $$Z\left(t\right)=2\sum _{n=1}^N{\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}}+R\left(t\right),$$

  where $R\left(t\right)$ represents the remainder term corrected via the Gabcke method.
• The phase function $\theta \left(t\right)$ is evaluated using Stirling’s approximation for $log\mathrm{\Gamma }(s/2)$, allowing high-precision computation without overflow:

  $$\theta \left(t\right)=Im\left[log\mathrm{\Gamma }\left({\displaystyle \frac{1}{4}}+{\displaystyle \frac{it}{2}}\right)\right]-{\displaystyle \frac{t}{2}}log\pi .$$
• Each candidate zero obtained from the valley scanner is refined using a Safeguarded Newton refinement with Pegasus fallback (hybrid Newton–secant–Pegasus). 128-bit to 256-bit precision, ensuring convergence even for steep or oscillatory regions.
• Validation is conducted by comparison with the Odlyzko–Schönhage algorithm and cross-verified using the Ball test for consistency across neighboring zeros.

3.5. Parallelization and Cloud Execution

The computation of $Z\left(t\right)$ through the Riemann–Siegel formula involves a large summation term:

$$Z\left(t\right)=2\sum _{n=1}^N{\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}}+R\left(t\right),$$

where each summand ${\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}}$ is independent of the others for a fixed t. This independence makes the summation term an ideal candidate for parallelization. Each thread (or compute node) evaluates a portion of the partial sums

$$S_i=\sum _{n=n_i}^{n_{i+1}-1}{\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}},$$

and a reduction step aggregates all $S_i$ to yield the final $Z\left(t\right)$. The remainder term $R\left(t\right)$, corrected by the Gabcke expansion, is then added as a separate serial step.

Parallel execution therefore targets the summation domain of the Riemann–Siegel series, not the remainder correction. In practice, this allows the workload to scale linearly with the number of available CPU cores. For cloud execution, AWS EC2 instances were configured to distribute the summation across all physical cores using OpenMP directives. Each thread evaluates its assigned range of n values, ensuring thread-safe accumulation via reduction clauses, while the overall computation remains deterministic and numerically stable due to the associative nature of the cosine summand.

The parallelized portion of the computation is thus the evaluation of

$$\sum _{n=1}^N{\displaystyle \frac{cos\left(\theta \right(t)-tlogn)}{\sqrt{n}}},$$

with each range of n processed concurrently. This design enables efficient scaling for very large t, where $N=\sqrt{t/\left(2\pi \right)}$ may reach millions.

3.6. Why Spacing Heuristics (And Naive Prefiltering) Can Skip Zeros

A classical asymptotic for the zero-counting function on the critical line is

$$N\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{2\pi }}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT),$$

(2)

which implies an average zero density $N^{\prime }\left(T\right)\approx {\displaystyle \frac{1}{2\pi }}log\left(\frac{T}{2\pi }\right).$ Hence the average spacing between consecutive zeros near height T is

$$s_{\mathrm{avg}}\left(T\right)\approx {\displaystyle \frac{1}{N^{\prime }\left(T\right)}}={\displaystyle \frac{2\pi }{log\left(\frac{T}{2\pi }\right)}}.$$

(3)

Key caveat.

While (3) is an excellent mean predictor, the local spacing fluctuates considerably. If one advances t by a deterministic step $s_{\mathrm{avg}}\left(T\right)$ (or rejects points by a naive $\left|Z\right(s\left)\right|$ threshold), genuine zeros can be skipped.

Concrete example (skip demonstrated).

Consider two consecutive zeros (as verified against high-precision tables) near

$$t_1=30607946001.041439\mathrm{and}{t}_2=30607946001.175073.$$

Their empirical gap is

$${\Delta }_{\mathrm{true}}=t_2-t_1\approx 0.133634.$$

The average-spacing prediction at $T\approx t_1$ from (3) is

$$s_{\mathrm{avg}}\left(t_1\right)={\displaystyle \frac{2\pi }{log\left(\frac{t_1}{2\pi }\right)}}\approx 0.281673.$$

If one used $t_{\mathrm{next}}\approx t_1+s_{\mathrm{avg}}\left(t_1\right)$, the probe would jump to

$$t_1+s_{\mathrm{avg}}\left(t_1\right)\approx 30607946001.323112,$$

overshooting the true next zero at $t_2\approx 30607946001.175073$. This directly illustrates that spacing-only stepping can miss zeros.

Implication for the valley scanner.

During development we also experimented with prefiltering by discarding points where $\left|Z\right(\frac{1}{2}+it\left)\right|$ exceeded a threshold before refinement. In regions with sharper or asymmetric valleys, this likewise rejected valid neighborhoods, degrading recall. Consequently, the final algorithm avoids spacing-only jumps and uses dense local sampling with minima detection, followed by robust bracketing and root refinement (Newton–secant with safeguarded bracketing), to prevent skipped zeros.

Why GPU acceleration is not used.

While the Riemann–Siegel summation is inherently parallel, its implementation for large t values requires high–precision arithmetic (typically 200–500 bits), which is not natively supported by GPU architectures. CUDA cores operate efficiently on fixed–width floating–point types (float32, float64), but do not provide hardware support for arbitrary–precision formats such as those implemented by the MPFR and MPC libraries used in this project. Emulating multi–precision on GPUs would require manually splitting mantissas across multiple registers and synchronizing additions and carries, introducing overheads that completely negate the theoretical parallel advantage.

Additionally, GPU kernels are optimized for massive, homogeneous workloads with simple arithmetic pipelines. In contrast, the Riemann–Siegel computation involves branch–intensive operations, logarithmic and trigonometric functions, and frequent precision adjustments all of which are poorly suited to GPU thread execution models. Memory coherence and divergence among threads would further reduce throughput.

For these reasons, the high–precision calculations of $Z\left(t\right)$ are executed on CPU instances with many physical cores (e.g., c7i.8xlarge), using OpenMP to distribute the summation work across threads. This CPU–based approach provides deterministic reproducibility, robust numerical stability, and easier integration with the MPFR environment, while still benefiting from significant parallel speedups proportional to the number of cores.

Software and computational stack

• C++ — core numerical computation, employing the MPFR library for arbitrary precision arithmetic.
• AWS EC2 — high-performance compute instances with configurable CPU counts for parallel Z-evaluations.
• AWS Cognito — secure user authentication for the web console.
• AWS Lambda — serverless backend for initiating batch computations, monitoring, and handling S3 storage.
• AWS ECR + React — containerized web frontend for real-time visualization of the valley scanner up to $t\approx {10}^{16}$.
• AWS S3 — persistent data storage for computed zeros and logs.
• Docker — A portable .exe is available to be executed locally.

The accompanying web application capable of calculating zeros up to $9.9999999999999999\times {10}^{16}$ is accessible upon authorization. The core computation code is not publicly archived at this stage, pending independent peer validation of the numerical results. Upon request from qualified reviewers or collaborators, the author will gladly provide access to the computation core to enable verification and replication of the reported findings. Additionally, a Docker public image is provided for local study and reproduction of this method. Please refer to the README.md file here: README

4. Results

The following tables present the results obtained by the valley scanner across multiple ranges of t, including calculations at high values where refinement becomes particularly challenging. The accompanying analysis—such as the estimation of average zero spacing and the verification of statistical deviations—was cross-validated with the assistance of ChatGPT, which provided independent computational checks and theoretical comparisons to ensure the robustness of the results.

Note. 

The datasets included in this work are intentionally concise and serve an illustrative purpose. The author emphasizes that the Valley Scanner framework is primarily designed to detect zeros within any selected range of t, rather than to merely generate extensive zero lists. Nevertheless, the batch-processing architecture supports scalable computation across arbitrarily large intervals, with feasibility determined chiefly by the practical cost of AWS EC2 resources required for such high-volume evaluations.

Table 3. Zero heights near $t\approx 1122334455$.

t values
1122334455.05585408179597553373792753809670000283010284579445795581653751666868286076133664711899795
1122334455.76031733677095186350835049571870227573769745536211492284087166589876142992541578050648273
1122334455.96549341079558436082594904200898020740502977379833207345332452561666964673151904680356810
1122334456.55122003455096567518805961663152718628678713782068430266350660859547396192991329402999144
1122334456.69117656282847361682640086578613693696115124531479812624187618434413753431043187588962605
1122334456.83867869196755030364329563494267434476218915992393583291790362528051183976648414294796730
1122334457.15371418683945191486723066707952951489968507756091862973354253514104043001364033450249744
1122334457.51390511989118717254611539418981231215406357632944032390965492210685945236798589386414682
1122334457.76838741510620113455239734916962707865127304851980893696880525564659145262541298208483993
1122334458.27155512243026569374168652041355212655972394951814858601703428616230384939060779678202013
1122334458.44139136841692632939134894613526508309356307629078128927888830090788869290777302156002999
1122334458.89501425212585279215913084722248689346999249199510723479190314873430634711550144775004918
1122334458.95374621822277785558114513758006054444953092856654909690789198906471686395126375226454073
1122334459.47180990048612714347328799643237077235245383445928401233650435292015784312948626615524122
1122334459.78629512841632863716858891532650291270784909335852103315157456425164567553241134283727201
1122334460.10222132816663933236459832453382800744621284674207091481539415536798526150441597360370236
1122334460.34922785530398779220541441366240746601424248348045312059814442991192922658636327584247470
1122334460.78924267475219010097101478269117727805242937830818188169502827730507167445711052441058213
1122334461.03129979223085870682939517578522137411650684496149763174736658116459762877273066240013428
1122334461.34105411839180789869245630301714029644280234966395722460268684514776121538555129989405099
1122334461.68097513340590425015663066588174538735332969362229273055650599065769001662550329744330356
1122334462.05653607553267581154859487598541969417453119764160088476105717674434412616867426342752192
1122334462.35999091678192331701334666903361418145334941591973792237773360345788033307359599747994365
1122334462.71045060502215878868517734546324575820479730409902219700593819407524827666579419258151207
1122334463.22570175761036362585961260605296584140311386148887315924013704275584423668730829353089430

Table 3. Zero heights near $t\approx 1122334455$.

t values
1122334455.05585408179597553373792753809670000283010284579445795581653751666868286076133664711899795
1122334455.76031733677095186350835049571870227573769745536211492284087166589876142992541578050648273
1122334455.96549341079558436082594904200898020740502977379833207345332452561666964673151904680356810
1122334456.55122003455096567518805961663152718628678713782068430266350660859547396192991329402999144
1122334456.69117656282847361682640086578613693696115124531479812624187618434413753431043187588962605
1122334456.83867869196755030364329563494267434476218915992393583291790362528051183976648414294796730
1122334457.15371418683945191486723066707952951489968507756091862973354253514104043001364033450249744
1122334457.51390511989118717254611539418981231215406357632944032390965492210685945236798589386414682
1122334457.76838741510620113455239734916962707865127304851980893696880525564659145262541298208483993
1122334458.27155512243026569374168652041355212655972394951814858601703428616230384939060779678202013
1122334458.44139136841692632939134894613526508309356307629078128927888830090788869290777302156002999
1122334458.89501425212585279215913084722248689346999249199510723479190314873430634711550144775004918
1122334458.95374621822277785558114513758006054444953092856654909690789198906471686395126375226454073
1122334459.47180990048612714347328799643237077235245383445928401233650435292015784312948626615524122
1122334459.78629512841632863716858891532650291270784909335852103315157456425164567553241134283727201
1122334460.10222132816663933236459832453382800744621284674207091481539415536798526150441597360370236
1122334460.34922785530398779220541441366240746601424248348045312059814442991192922658636327584247470
1122334460.78924267475219010097101478269117727805242937830818188169502827730507167445711052441058213
1122334461.03129979223085870682939517578522137411650684496149763174736658116459762877273066240013428
1122334461.34105411839180789869245630301714029644280234966395722460268684514776121538555129989405099
1122334461.68097513340590425015663066588174538735332969362229273055650599065769001662550329744330356
1122334462.05653607553267581154859487598541969417453119764160088476105717674434412616867426342752192
1122334462.35999091678192331701334666903361418145334941591973792237773360345788033307359599747994365
1122334462.71045060502215878868517734546324575820479730409902219700593819407524827666579419258151207
1122334463.22570175761036362585961260605296584140311386148887315924013704275584423668730829353089430

Full dataset:

refined_sample_1122334455.csv

Figure 2. Illustration of the valley scanner detecting zeros, MINIMA in green before refining.

Figure 2. Illustration of the valley scanner detecting zeros, MINIMA in green before refining.

Table 4. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 1.1223\times {10}^9$.

Parameter	Value / Description
Mean height T	$1.122334459\times {10}^9$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$19.84$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.33068$
Observed mean($\Delta t$)	$0.34041$
Relative difference	$\approx 2.94\%$ (excellent agreement)

Table 4. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 1.1223\times {10}^9$.

Parameter	Value / Description
Mean height T	$1.122334459\times {10}^9$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$19.84$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.33068$
Observed mean($\Delta t$)	$0.34041$
Relative difference	$\approx 2.94\%$ (excellent agreement)

The observed mean spacing agrees with the theoretical prediction within $2.9\%$, confirming excellent consistency at this mid-height region. This dataset includes twenty-four valid spacings after excluding the initial $\Delta t=0$, providing a stable estimate of the local zero density.

Note. 

• The narrowest local gap ($\Delta t\approx 0.05873$) indicates local clustering.
• The widest gap ($\Delta t\approx 0.70446$) defines a minor sparsity region.
• The valley scanner maintained $\left|Z\right(s\left)\right|$ precision below ${10}^{-17}$ throughout this range.

Table 5. Zero heights near $t\approx 77887788778877$.

t values
77887788778877.020227748817192188417536638742629073740288914589639357402518078429377834835994965903
77887788778877.249679679962424824192690929969795344773476999609170540226031140194367368465323400732
77887788778877.395839452438060087423730217077795874198952080611063038398873370839650471744196607603
77887788778877.464229487803046147173514448802842125479109432719784544422333625144664303755907121583
77887788778877.652713174158883359711860169981628139297378684277807602040409167524239149417614419577
77887788778877.912984640322759199999999999999999999999999999999999999999999999934428787073873214307
77887788778878.261265065864186260216504407248810936828726908498900819613087094795095315677738319482
77887788778878.390670819622278901854762851671857540252991745421524284708612476640252146433399675607
77887788778878.540818417266388821084932667703072310297433513206423697155246163498732898612731825267
77887788778878.834997602444465835204743490169516799972963896443292388437906286083788049140788812011

Table 5. Zero heights near $t\approx 77887788778877$.

t values
77887788778877.020227748817192188417536638742629073740288914589639357402518078429377834835994965903
77887788778877.249679679962424824192690929969795344773476999609170540226031140194367368465323400732
77887788778877.395839452438060087423730217077795874198952080611063038398873370839650471744196607603
77887788778877.464229487803046147173514448802842125479109432719784544422333625144664303755907121583
77887788778877.652713174158883359711860169981628139297378684277807602040409167524239149417614419577
77887788778877.912984640322759199999999999999999999999999999999999999999999999934428787073873214307
77887788778878.261265065864186260216504407248810936828726908498900819613087094795095315677738319482
77887788778878.390670819622278901854762851671857540252991745421524284708612476640252146433399675607
77887788778878.540818417266388821084932667703072310297433513206423697155246163498732898612731825267
77887788778878.834997602444465835204743490169516799972963896443292388437906286083788049140788812011

Full dataset:

refined_sample_77887788778878.csv

Table 6. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 7.7888\times {10}^{13}$.

Parameter	Value / Description
Mean height T	$7.788779\times {10}^{13}$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$30.89$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.20841$
Observed mean($\Delta t$)	$0.20164$
Relative difference	$\approx 3.25\%$ (observed spacing slightly lower)

Table 6. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 7.7888\times {10}^{13}$.

Parameter	Value / Description
Mean height T	$7.788779\times {10}^{13}$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$30.89$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.20841$
Observed mean($\Delta t$)	$0.20164$
Relative difference	$\approx 3.25\%$ (observed spacing slightly lower)

At $t!\approx !7.8\times {10}^{13}$ the observed mean spacing is within $3.3\%$ of the predicted theoretical value. This confirms the asymptotic contraction of $\Delta t$ with $log\left(T\right)$ and the numerical reliability of the valley-scanner at extremely high t.

Note. 

• The narrowest local gap ($\Delta t\approx 0.06839$) marks a short clustering interval.
• The widest gap ($\Delta t\approx 0.34828$) indicates a local sparsity region.
• The dataset includes nine valid spacings after excluding the initial zero spacing.

Table 7. Zero heights near $t\approx 2121212121212121$.

t values
2121212121212121.057174396355653627517829633004902524627465962562082889786815506065679684836656418207
2121212121212121.423952296903794858366053400597077957453762150224852389070240986305352944100555397881
2121212121212121.637911189386821634578388080985689551305316601942438373682984653352855029191417024968
2121212121212121.722239184474112088505220811336406498192064809976889052574210988234679401321579311959
2121212121212121.931251612937579497374169467210449334653804772031907666985713288264470253704797642659
2121212121212122.139276141380401542318272686714086325735492855211445799411897615378212407159847237596
2121212121212122.312544192668074760821167892275979978089434793247782550890700363216283888965629752846
2121212121212122.589825053898872476879592008602894273679088279508493136612693138948122993791467985325
2121212121212122.653240711140460903484084319747639895582775728448355608636986278225403635830655302707
2121212121212122.920823434159590226415624128790956308333985263613037444986059091378522005633476861126
2121212121212123.146055348673175157935179701620943014980322403140912373352837579609034147399856640709

Table 7. Zero heights near $t\approx 2121212121212121$.

t values
2121212121212121.057174396355653627517829633004902524627465962562082889786815506065679684836656418207
2121212121212121.423952296903794858366053400597077957453762150224852389070240986305352944100555397881
2121212121212121.637911189386821634578388080985689551305316601942438373682984653352855029191417024968
2121212121212121.722239184474112088505220811336406498192064809976889052574210988234679401321579311959
2121212121212121.931251612937579497374169467210449334653804772031907666985713288264470253704797642659
2121212121212122.139276141380401542318272686714086325735492855211445799411897615378212407159847237596
2121212121212122.312544192668074760821167892275979978089434793247782550890700363216283888965629752846
2121212121212122.589825053898872476879592008602894273679088279508493136612693138948122993791467985325
2121212121212122.653240711140460903484084319747639895582775728448355608636986278225403635830655302707
2121212121212122.920823434159590226415624128790956308333985263613037444986059091378522005633476861126
2121212121212123.146055348673175157935179701620943014980322403140912373352837579609034147399856640709

Full dataset:

refined_sample_2121212121212121.csv

Table 8. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 2.1212\times {10}^{15}$.

Parameter	Value / Description
Mean height T	$2.121212\times {10}^{15}$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$34.19$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.18782$
Observed mean($\Delta t$)	$0.20889$
Relative difference	$\approx 11.2\%$ (observed spacing slightly higher)

Table 8. Statistical comparison of observed zero spacing with theoretical prediction at $t\approx 2.1212\times {10}^{15}$.

Parameter	Value / Description
Mean height T	$2.121212\times {10}^{15}$
Theoretical formula	${\Delta }_{\mathrm{avg}}\approx {\displaystyle \frac{2\pi }{log(T/2\pi )}}$
$log(T/2\pi )$	$34.19$
Predicted ${\Delta }_{\mathrm{avg}}$	$0.18782$
Observed mean($\Delta t$)	$0.20889$
Relative difference	$\approx 11.2\%$ (observed spacing slightly higher)

The observed mean spacing exceeds the theoretical prediction by about $11\%$, well within expected stochastic variation at this extreme height. Such mild over-dispersion is consistent with local zero-density fluctuations predicted by random-matrix models and observed in Odlyzko’s data.

Note. 

• The narrowest local gap ($\Delta t\approx 0.06342$) shows normal clustering.
• The widest gap ($\Delta t\approx 0.36678$) corresponds to a transient sparsity region.
• The valley scanner successfully resolved ten consecutive zeros without numerical drift.

Table 9. Highest evaluated zeros from the valley scanner.

Parameter	Value
t	$9999999999999999999.232850606909407706487068201450796323115355335175991058349609375$
$\left|Z\right(s\left)\right|$	$3.657602321013126733848087942217412642846910689346499860361067\times {10}^{-13}$
t	$197909211979092119791.004810035047150401470161806827263717423193156719207763671875$
$\left|Z\right(s\left)\right|$	$8.258118375241327319604320773664599713029092314507266420324956\times {10}^{-17}$

Table 9. Highest evaluated zeros from the valley scanner.

Parameter	Value
t	$9999999999999999999.232850606909407706487068201450796323115355335175991058349609375$
$\left|Z\right(s\left)\right|$	$3.657602321013126733848087942217412642846910689346499860361067\times {10}^{-13}$
t	$197909211979092119791.004810035047150401470161806827263717423193156719207763671875$
$\left|Z\right(s\left)\right|$	$8.258118375241327319604320773664599713029092314507266420324956\times {10}^{-17}$

Remark. The highest calculated value of t (19790921...) was intentionally configured so that its leading digits encode the author’s birth date (1979-09-21). This configuration served as a symbolic benchmark for the valley scanner, demonstrating that the system can be directed toward specific numerical targets while maintaining stability and precision at extreme heights.

5. Discussion

5.1. Discussion and Observations

From the results obtained during extensive testing, several important observations emerged:

• The continuous valley progression confirms that no zeros were skipped. Minor local irregularities (“mini mountains”) occasionally appeared; these suggest that, if any zeros were missed, a finer increment of N could be employed to improve resolution.
• The $N\to \mathrm{complex}$ mapping naturally aligns the evaluations along the critical line, where $\Re \left(s\right)=\frac{1}{2}$.
• The valley–scanner method appears scalable and could, in principle, be generalized to other L-functions. This remains an open question and extends beyond the current mathematical scope of this research.

Although the method demonstrates an effective approach to identifying zeros of the Riemann Zeta function, the primary objective of this study is not merely to compute zeros, but rather to formalize the $N\to \mathrm{complex}$ conversion (at $m=\frac{1}{2}$) as a mathematical foundation for expressing the valley–scanner behavior analytically, rather than relying solely on iterative numerical evaluation.

An important open question for future investigation is whether alternative values of m could reveal zeros located off the critical line. To explore this possibility, additional tests were performed using the provided Python script, evaluating the function at several representative means. No zeros were detected within the tested ranges; however, it remains an open question whether such means might yield zeros at higher values of N

$$m={\displaystyle \frac{1}{5}},m={\displaystyle \frac{1}{\pi }},m={\displaystyle \frac{1}{3}},m={\displaystyle \frac{1}{e}}$$

Figure 3. Illustration of the valley scanner detecting zeros m = 1/3, no zeros.

Figure 3. Illustration of the valley scanner detecting zeros m = 1/3, no zeros.

Figure 4. Illustration of the valley scanner detecting zeros m = 1/5, no zeros.

Figure 4. Illustration of the valley scanner detecting zeros m = 1/5, no zeros.

Figure 5. Illustration of the valley scanner detecting zeros m = 1/e, no zeros.

Figure 5. Illustration of the valley scanner detecting zeros m = 1/e, no zeros.

Figure 6. Illustration of the valley scanner detecting zeros m = 1/$\pi$, no zeros

Figure 6. Illustration of the valley scanner detecting zeros m = 1/$\pi$, no zeros

5.2. Staircase Expressions from the Nontrivial Zeros of $\zeta \left(s\right)$

Definition: Staicase Function

We define the Staircase function as the cumulative partial sum of the explicit–formula terms,

$$L_k\left(x\right)=\sum _{n=1}^k{\displaystyle \frac{x^{{\rho }_n}}{{\rho }_n}},$$

or, equivalently, its real (conjugate–paired) form

$${\tilde{L}}_k\left(x\right)=x^{1/2}\sum _{n=1}^k{\displaystyle \frac{cos({\gamma }_{n}logx)+2{\gamma }_{n}sin({\gamma }_{n}logx)}{{\gamma }_n^2+\frac{1}{4}}}.$$

This cumulative structure of partial sums, contributes its oscillatory term and builds an alternating “staircase” approaching the true shape of $\psi \left(x\right)$.

Let the nontrivial zeros of the Riemann zeta function be

$${\rho }_n=\frac{1}{2}+i{\gamma }_n,{\overline{\rho }}_n=\frac{1}{2}-i{\gamma }_n,{\gamma }_n>0.$$

For a fixed $x>1$, define the Staicase partial sums

$$L_k\left(x\right)=\sum _{n=1}^k{\displaystyle \frac{x^{{\rho }_n}}{{\rho }_n}},k=1,2,\dots$$

(4)

which corresponds directly to the computational form

$$\mathtt{term}=e^{\rho logx}/\rho ,\mathtt{correction}+=\mathtt{term}.$$

Including the Conjugate Terms

Pairing each zero ${\rho }_n$ with its conjugate ${\overline{\rho }}_n$ yields a real-valued “conjugate staircase”:

$${\tilde{L}}_k\left(x\right)=\sum _{n=1}^k\left({\displaystyle \frac{x^{{\rho }_n}}{{\rho }_n}}+{\displaystyle \frac{x^{{\overline{\rho }}_n}}{{\overline{\rho }}_n}}\right),$$

(5)

which matches the implementation

$$\mathtt{term}={\displaystyle \frac{e^{\rho logx}}{\rho }},\mathtt{term}\mathtt{2}={\displaystyle \frac{e^{\overline{\rho }logx}}{\overline{\rho }}},\mathtt{correction}+=\mathtt{term}+\mathtt{term}\mathtt{2}.$$

Derivation of the Real Closed Form

Set $L=logx$ and write

$$x^{\rho }=x^{1/2}{e}^{i\gamma L},{\displaystyle \frac{1}{\rho }}={\displaystyle \frac{\frac{1}{2}-i\gamma }{{\gamma }^2+\frac{1}{4}}}.$$

Then a single conjugate pair contributes

$$\begin{array}{cc}\hfill {\displaystyle \frac{x^{\rho }}{\rho }}+{\displaystyle \frac{x^{\overline{\rho }}}{\overline{\rho }}}& ={\displaystyle \frac{x^{1/2}}{{\gamma }^2+\frac{1}{4}}}\left[(\frac{1}{2}-i\gamma )e^{i\gamma L}+(\frac{1}{2}+i\gamma )e^{-i\gamma L}\right]\hfill \\ \hfill & ={\displaystyle \frac{x^{1/2}}{{\gamma }^2+\frac{1}{4}}}\left[\frac{1}{2}\left(e^{i\gamma L}+e^{-i\gamma L}\right)+i\gamma \left(-e^{i\gamma L}+e^{-i\gamma L}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{x^{1/2}}{{\gamma }^2+\frac{1}{4}}}\left[cos\left(\gamma L\right)+2\gamma sin\left(\gamma L\right)\right].\hfill \end{array}$$

Hence the conjugate staircase (5) can be written entirely in real quantities as

$$\begin{array}{|c|}\hline {\tilde{L}}_k\left(x\right)=x^{1/2}\sum _{n=1}^k{\displaystyle \frac{cos({\gamma }_{n}logx)+2{\gamma }_{n}sin({\gamma }_{n}logx)}{{\gamma }_n^2+\frac{1}{4}}}.\\ \hline\end{array}$$

(6)

Relation with the Standard $-2\Re$ Form

In the explicit formula one often defines

$$C_k\left(x\right)=-2\Re \sum _{n=1}^k{\displaystyle \frac{x^{{\rho }_n}}{{\rho }_n}}.$$

Using $\Re \left(z\right)=\frac{1}{2}(z+\overline{z})$, we find

$$C_k\left(x\right)=-{\tilde{L}}_k\left(x\right),$$

so the only difference between (6) and the traditional correction term is an overall sign.

Real Reformulation via $N={\gamma }^2+\frac{1}{4}$

Introducing the real quantity

$$N_n={\gamma }_n^2+\frac{1}{4},$$

(which corresponds to the “normal numbers” used in the numerical mountain walk), the staircase expression becomes

$$\begin{array}{|c|}\hline {\tilde{L}}_k\left(x\right)=x^{1/2}{\displaystyle \sum _{n=1}^k}{\displaystyle \frac{cos({\gamma }_{n}logx)+2{\gamma }_{n}sin({\gamma }_{n}logx)}{N_n}}.\\ \hline\end{array}$$

(7)

Computational Remarks

Equation (7) eliminates the need for complex exponentiation. Each term now involves only real-valued operations: one $\sqrt{x}$, one $logx$, and evaluations of sin and cos. Consequently, the staircase can be computed directly from the real zero ordinates ${\gamma }_n$ with high numerical stability and significant speedup compared with evaluating $x^{\rho }$ in $\mathbb{C}$.

In summary: pairing each zero with its conjugate yields a real-only representation of the staircase that depends solely on ${\gamma }_n$ and x,

$${\displaystyle \frac{x^{\rho }}{\rho }}+{\displaystyle \frac{x^{\overline{\rho }}}{\overline{\rho }}}={\displaystyle \frac{x^{1/2}\left(cos(\gamma logx)+2\gamma sin(\gamma logx)\right)}{{\gamma }^2+\frac{1}{4}}},$$

providing a compact analytic bridge between the complex explicit formula and its real numerical realization.

Refer to the corresponding Python script for a demonstration of how this expression works.

staircase_with_real.py

6. Conclusions

• By applying the equations (1) at $m=\frac{1}{2}$, in conjunction with the evaluation of $\left|Z\right|$ through the Riemann–Siegel formula and the Gabcke correction, followed by Newton-based refinement, successfully reproduces zeros across both low and extremely high ranges of the critical line. This behavior is demonstrated in the accompanying datasets (see GitHub links in the Results section) and in the data annexed to this document.
• The analysis suggests that the proposed approach offers a meaningful contribution to the study of the Riemann zeta function. The intrinsic symmetry about $\Re \left(s\right)=\frac{1}{2}$ is naturally expressed through this formulation.

7. Future Work

• Given the apparent symmetry of the “mountain” structures observed in $\left|Z\right|$, a direct analysis of the maxima could enable the identification of two zeros simultaneously. Preliminary experiments indicate that once a zero and its adjacent peak are located, the next zero can be efficiently approximated by doubling the horizontal distance between the current zero and the corresponding peak, thus reducing the computational effort. This remains an ongoing line of investigation.
• The overarching goal of this research is to foster collaboration with mathematical specialists to analytically locate zeros, rather than relying solely on computational traversal of the zeta landscape. As an independent researcher, resources and time are limited; progress depends on prioritization and available support. Future development will greatly benefit from academic or institutional partnership and funding to expand the analytical reach and precision of this study.