Prime Representing Constant in the Critical Strip

1. Introduction

Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. In 1737, the connection between the zeta function and prime numbers was discovered by Euler, who proved the identity.

$$\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^s}}=\prod _{pprime}{\displaystyle \frac{1}{1-p^{-s}}}$$

This study is about the Prime Representing Constant. It shows that the probability of $P_k$ is the smallest prime that does not divide n. Shows the relation of the critical strip and the Prime Representing Constant. Shows the composition of the Prime Representing Constant and how it infinitely generates all prime numbers in order. Demonstrate the relation of Riemann Zeta function and the Prime Representing Constant.

2. Method

The sequence 2, 3, 2, 3, 2, 5, 2,.., is a sequence of smallest primes that do not divide n. The probability of $P_k$ is the smallest prime that does not divide n, for some natural number can be written as:

$$P(P_k\mathrm{does}\mathrm{not}\mathrm{divide}\mathrm{n}\mathrm{and}{P}_1,P_1,...,P_{k-1}\mathrm{divide}\mathrm{n})=\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}\left({\displaystyle \frac{1}{P_i}}\right)$$

The average of the sequence is therefore given by

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}=\sum _{k=1}^{\infty }{P}_k\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}$$

which is the definition of Prime Representing Constant [1].

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}=2.9200509773161347120925629171120194...$$

$$f_{(n+1)}=\lfloor f_n\rfloor (f_{\left(n\right)}-\lfloor f_n\rfloor +1)$$

The floor of $f_n$ are all prime numbers

2.1. Riemann Zeta Function

The Euler product formula can be used to calculate the asymptotic probability that s randomly selected integers are set-wise coprime. The asymptotic probability that s numbers are coprime is given by a product over all primes,

$$\prod _{pprime}\left(1-{\displaystyle \frac{1}{p^s}}\right)={\displaystyle \frac{1}{\zeta \left(s\right)}}$$

Bernhard Riemann’s 1859 article "On the Number of Primes Less Than a Given Magnitude" [2] extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers.

If we substitute s = 1 then,

$$\prod _{pprime}\left(1-{\displaystyle \frac{1}{p^1}}\right)={\displaystyle \frac{1}{\zeta \left(1\right)}}$$

$$\prod _{pprime}\left(1-{\displaystyle \frac{1}{p^1}}\right)=\left(1-{\displaystyle \frac{1}{2}}\right)\left(1-{\displaystyle \frac{1}{3}}\right)\left(1-{\displaystyle \frac{1}{5}}\right)\left(1-{\displaystyle \frac{1}{7}}\right)...$$

2.2. Euler–Mascheroni Constant

$$\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}=\zeta \left(1\right)$$

In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:

$$\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}=1+{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{5}}+{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{7}}+...$$

The first n terms of the series sum to approximately ln n + $\gamma$ where ln is the natural logarithm and $\gamma$ is the Euler–Mascheroni constant.

$$\gamma =\underset{s\to 1^{+}}{lim}\sum _{n=1}^{\infty }\left({\displaystyle \frac{1}{n^s}}-{\displaystyle \frac{1}{s^n}}\right)$$

$$\gamma =\underset{s\to 1}{lim}{\displaystyle \frac{\zeta (1+s)+\zeta (1-s)}{2}}$$

$$\gamma =\underset{s\to 1}{lim}\left(\zeta \left(s\right)-{\displaystyle \frac{1}{(s-1)}}\right)$$

2.3. Analytical Continuation

The equation relates values of the Riemann zeta function at the points s and $1-s$ in particular relating even positive integers with odd negative integers, except for a simple pole at s = 1. The continuation to $0>\Re \left(s\right)\le 1$ can be obtained from the formula

$$\zeta \left(s\right)={\displaystyle \frac{1}{(s-1)}}+\sum _{n=1}^{\infty }{\int }_n^{n+1}\left({\displaystyle \frac{1}{n^s}}-{\displaystyle \frac{1}{x^s}}\right)dx$$

Using algebra, if we substitute ${\sum }_{n=1}^{\infty }{\int }_n^{n+1}\left({\displaystyle \frac{1}{n^s}}-{\displaystyle \frac{1}{x^s}}\right)dx$ with x then.

$$\zeta \left(s\right)={\displaystyle \frac{1}{(s-1)}}+x$$

Substituting s with ${\displaystyle \frac{1}{2}}$,

$$\zeta \left(1/2\right)={\displaystyle \frac{1}{(\frac{1}{2}-1)}}+x$$

$$\zeta \left(1/2\right)={\displaystyle \frac{1}{(-\frac{1}{2})}}+x$$

$$\zeta \left(1/2\right)=-2+x$$

all trivial zeros have interval of -2.

$$\zeta \left(1/2\right)=-2+x$$

$\zeta (1/2)\approx -1.46...$

$$-1.46...=-2+x$$

$$-1.46...=-2+0.539...$$

The number 2 is the smallest prime number. The smallest prime number that does not divide succeeding prime number is 2. Starting from 3, all prime numbers are odd numbers. The smallest prime that does not divide odd number is 2.

Table 1. Sequence of smallest prime that does not divide n.

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Prime	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	7

Table 1. Sequence of smallest prime that does not divide n.

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Prime	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	5	2	3	2	3	2	7

Table 2. In the Total row, 87/30 is equal to 2.9. It is approximately the Prime Representing Constant.

k	${\mathit{P}}_{\mathit{k}}$	Count	Product	Count/Product
1	2	15	30	15/30
2	3	10	30	10/30
3	5	4	20	4/30
4	7	1	7	1/30
Total		30	87	30/30

Table 2. In the Total row, 87/30 is equal to 2.9. It is approximately the Prime Representing Constant.

k	${\mathit{P}}_{\mathit{k}}$	Count	Product	Count/Product
1	2	15	30	15/30
2	3	10	30	10/30
3	5	4	20	4/30
4	7	1	7	1/30
Total		30	87	30/30

In the 1st row, 15/30 is equal to 1/2 and in the total row 30/30 is equal to 1.

$$\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}$$

if k = 1, then $P_1=2$

$$\left(1-{\displaystyle \frac{1}{P_1}}\right)\prod _{i=1}^{1-1}{\displaystyle \frac{1}{P_i}}$$

$$\left(1-{\displaystyle \frac{1}{2}}\right)\prod _{i=1}^0{\displaystyle \frac{1}{P_i}}$$

$$\left(1-{\displaystyle \frac{1}{2}}\right)$$

$${\displaystyle \frac{1}{2}}$$

2.4. Critical Strip and Prime Representing Constant

$$\sum _{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}=\sum _{k=1}^{\infty }\left(\prod _{i=1}^k{\displaystyle \frac{1}{P_i}}-\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}\right)$$

This is a telescoping sum:

$$=\left(1-{\displaystyle \frac{1}{P_1}}\right)+\left({\displaystyle \frac{1}{P_1}}-{\displaystyle \frac{1}{P_{1}P2}}\right)+...$$

$$=1+\prod _{i=1}^{\infty }{\displaystyle \frac{1}{P_i}}$$

${\prod }_{i=1}^{\infty }{\displaystyle \frac{1}{P_i}}$, tends to 0

$$=1+0$$

$$=1$$

The

$$\prod _{k=1}^{\infty }\left[\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}\right]$$

is equal to

$$\prod _{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)multipliedby\prod _{k=1}^{\infty }\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}$$

${\prod }_{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)$ tends to 0(product over primes converges to zero)

${\prod }_{k=1}^{\infty }{\prod }_{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}$ which tends very quickly to zero.

So

$$\prod _{k=1}^{\infty }\left[\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}\right],$$

the whole product tends to 0

The

$$\prod _{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)=\prod _{pprime}\left(1-{\displaystyle \frac{1}{p^s}}\right)={\displaystyle \frac{1}{\zeta \left(1\right)}}$$

$$\prod _{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)={\displaystyle \frac{1}{\zeta \left(1\right)}}=0$$

$$\zeta \left(1\right)={\displaystyle \frac{1}{{\prod }_{k=1}^{\infty }\left(1-\frac{1}{P_k}\right)}}$$

$$\zeta \left(1\right)=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}=\infty$$

Riemann Zeta function has the Prime Representing Constant in the critical line.

$$0.4999161085496864640353762556517134...\approx 0.5$$

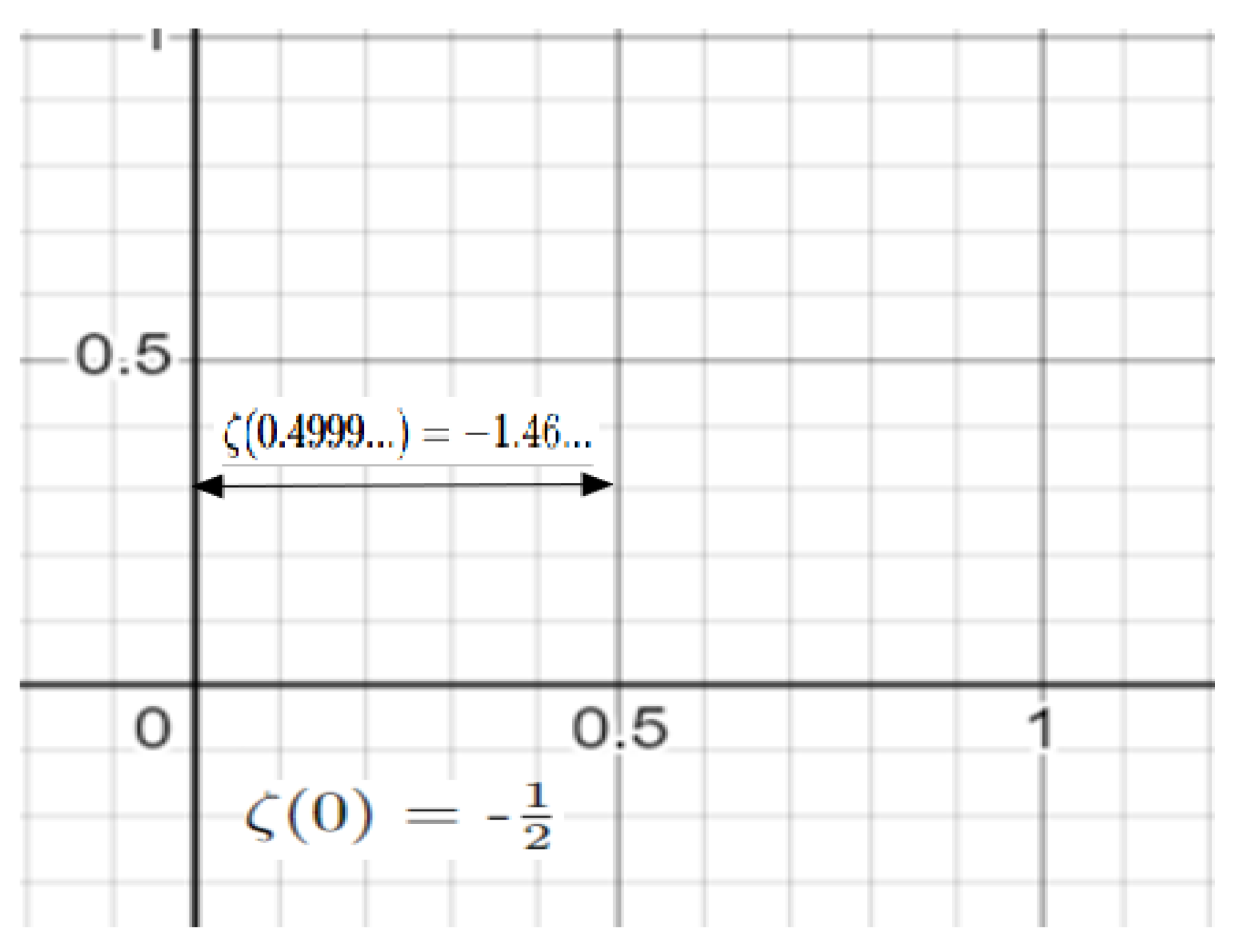
The $\zeta (0.4999161085496864640353762556517134...)$ is - 1.4600254886580673560462814585560097340...The result divided by $\zeta \left(0\right)$ is equal to the Prime Representing Constant.

Figure 1. Nontrivial zeros are aligning in the critical line.

Figure 1. Nontrivial zeros are aligning in the critical line.

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}={\displaystyle \frac{-1.460025488658067356046281458556009734...}{-1/2}}$$

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}={\displaystyle \frac{1.460025488658067356046281458556009734...}{1/2}}$$

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}=\left(2\right)(1.460025488658067356046281458556009734...)$$

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}=2.920050977316134712092562917112019468...$$

3. Result

$$\zeta \left(0\right)=-1/2$$

multiply by Prime Representing Constant is equal to

$$-1/2\left(\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}\right)=-1.460025488658067356046281458556009734...$$

$$-1/2\left(\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}\right)=\zeta (0.4999...)$$

$$\zeta \left(0\right)\left(\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}\right)=\zeta (0.4999...)$$

4. Discussion

The probability of $P_k$ is the smallest prime that does not divide n, for some natural number can be written as:

$$P(P_k\mathrm{does}\mathrm{not}\mathrm{divide}\mathrm{n}\mathrm{and}{P}_1,P_1,...,P_{k-1}\mathrm{divide}\mathrm{n})=\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}\left({\displaystyle \frac{1}{P_i}}\right)$$

The average of the sequence is therefore given by

$$\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}=\sum _{k=1}^{\infty }{P}_k\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}$$

Prime Representing Constant, the prime generator/operator, infinitely generates prime numbers in order.

$$\sum _{k=1}^{\infty }\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}=\sum _{k=1}^{\infty }\left(\prod _{i=1}^k{\displaystyle \frac{1}{P_i}}-\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}\right)$$

This is a telescoping sum equal to 1.

The product of

$$\prod _{k=1}^{\infty }\left[\left(1-{\displaystyle \frac{1}{P_k}}\right)\prod _{i=1}^{k-1}{\displaystyle \frac{1}{P_i}}\right],$$

tends to 0

The average of 0 and 1 is 1/2. The number 2 is the smallest prime number. This study shows that the smallest prime that does not divide $P_2$ up to $P_{\infty }$ is 2. The probability of 2 is the smallest prime that does not divide n to be 1/2.

$$\zeta \left(0\right)\left(\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}\right)=\zeta (0.4999...)$$

$$0.4999\approx 0.5$$

$$-1/2\left(\sum _{k=1}^{\infty }{\displaystyle \frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}\right)=-1.460025488658067356046281458556009734...$$

$$-1/2={\displaystyle \frac{-1.460025488658067356046281458556009734...}{{\sum }_{k=1}^{\infty }\frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}}$$

$$1/2={\displaystyle \frac{1.460025488658067356046281458556009734...}{{\sum }_{k=1}^{\infty }\frac{P_k-1}{{\prod }_{i=1}^{k-1}{P}_i}}}$$

These show the relation of prime numbers in the critical line 1/2 of the Riemann Zeta function.