Classifying Transportable vs. Non-Transportable Compounds Through Fundamental Energy Constraints

1. Introduction

Transport across biological membranes significantly influences the pharmacokinetic and toxicokinetic properties of drugs. Understanding active transport—especially efflux mechanisms—is essential, as these processes greatly impact a compound’s bioavailability, toxicity, and therapeutic efficacy. Active transport of molecules through cell membranes functions in parallel with passive diffusion; however, instead of being driven by concentration gradients, active transport is energy-dependent and can occur against such gradients. As passive membrane permeability increases for more hydrophobic chemicals, more energy is needed for their active transport to counteract their rate of passive diffusion. Given that cells have a limited energy budget, this work sets out to prove the existence of a membrane permeability threshold beyond which active transport of molecules is no longer energetically viable.

Efflux proteins located in the apical membrane such as P-glycoprotein/multi-drug resistant protein 1 (P-gp, MDR1), breast cancer resistance protein (BCRP) and multi-drug resistance associated protein 2 (MRP2) are responsible for actively pumping out foreign substances from cells, often reducing the efficacy of drug uptake (Juvale et al., 2022; Sharom, 2008). The resistance of cancerous tissue to multiple drugs is largely attributed to the over-expression of such efflux proteins, due to their role in decreasing the intracellular concentration of chemotherapeutic agents (Fletcher et al., 2010). Given the role of P-gp overexpression in multidrug-resistance (MDR), which reduces the efficacy of chemotherapeutics, antibiotics, and antivirals, there is a strong demand for cost-effective, rapid methods to identify P-gp substrates. Such methods could not only help predict a compound’s toxicity, bioavailability, and drug-drug interaction potential (Demel et al., 2009), but also enable the early elimination of problematic candidates, mitigating MDR-related challenges during drug discovery (Xue et al., 2004). Therefore, it is of great importance in the pharmaceutical industry to ascertain whether drugs are affected by such efflux transporters. Traditionally, the passive membrane permeability (P_m) of a compound, as well as the involvement of efflux transporters—quantified using a metric known as the efflux ratio (ER)— is determined through bidirectional transport assays using epithelial cell lines such as MDCK or Caco-2. Such assays have also been used to accumulate data on the chemical nature of efflux transporter substrates (Gombar et al., 2003; Li et al., 2014; Penzotti et al., 2002; Wang et al., 2011; Xue et al., 2004), in the hopes of enabling the development of predictive in silico models linking physicochemical properties to carrier-mediated efflux (i.e QSAR models (Chen et al., 2012)). However, the utility of such models is hindered by their limited interpretability, narrow chemical coverage due to limitation in the training datasets, as well as their reliance on inconsistent datasets.

Efforts have also been made to develop simple and fast interpretations of the molecular features that contribute to being an efflux substrate (Didziapetris et al., 2003; Gombar et al., 2003; Seelig, 1998). These studies aim to establish simple and widely-applicable "rules-of-thumb" for hit-to-lead optimisation. It has been suggested that such simple rules may have a greater impact than complex, predictive models (Demel et al., 2009). In this work, we propose another simple and easily applicable rule-of-thumb: compounds above a certain passive membrane permeability threshold are less likely to exhibit significant transporter-facilitated efflux. The objective of this study was to investigate this hypothesis and to see whether it could be translated into a rule for quick, membrane permeability-based separation of compounds that may exhibit significant transporter-facilitated efflux from those that cannot. The permeability-based separation proposed here does not differentiate between efflux substrates and non-substrates. Instead, it distinguishes compounds whose ADME properties can be significantly influenced by efflux transporters from those that cannot, regardless of whether they are actual substrates. A rule-of-thumb for permeability-based separation could be very useful if applied in drug classification, or could be used for the rational direction of lead optimisation towards desired efflux effects. Since it was shown recently by Dahley et al. (2024) that the biological Caco-2/MDCK membrane permeability of drugs is well predicted by the solubility diffusion model (SDM), permeability-based separation can in most cases be done without the need for experimental assays. Furthermore, since this rule is based on a fundamental physical principle (the energy limit of the cell) it is not restricted to P-gp only, but should be applicable to any ATP-consuming efflux transporter.

The aims of this study were (i) to evaluate existing MDCKII ER data for MDR1, BCRP and MRP2 and to identify a crude membrane permeability cut-off line above which compounds no longer seem to be affected by active efflux. Compounds that appear to violate the established threshold can then be identified as outliers and systematically investigated using a variety of measures. Secondly, it was aimed (ii) to identify compounds that lie at or near the threshold so they can be investigated with concentration-dependent monolayer efflux assays. These data can then be used to identify the maximal flux rate (i.e the maximal amount of compound that can be actively effluxed per time) and the corresponding energy plateau for such compounds. Finally, we aimed (iii) to link this energy limit with a certain P_m value and to perform a sensitivity analysis, highlighting all the caveats and limitations that come with such a rule-of-thumb P_m threshold.

2. Theory

2.1. Transport Model

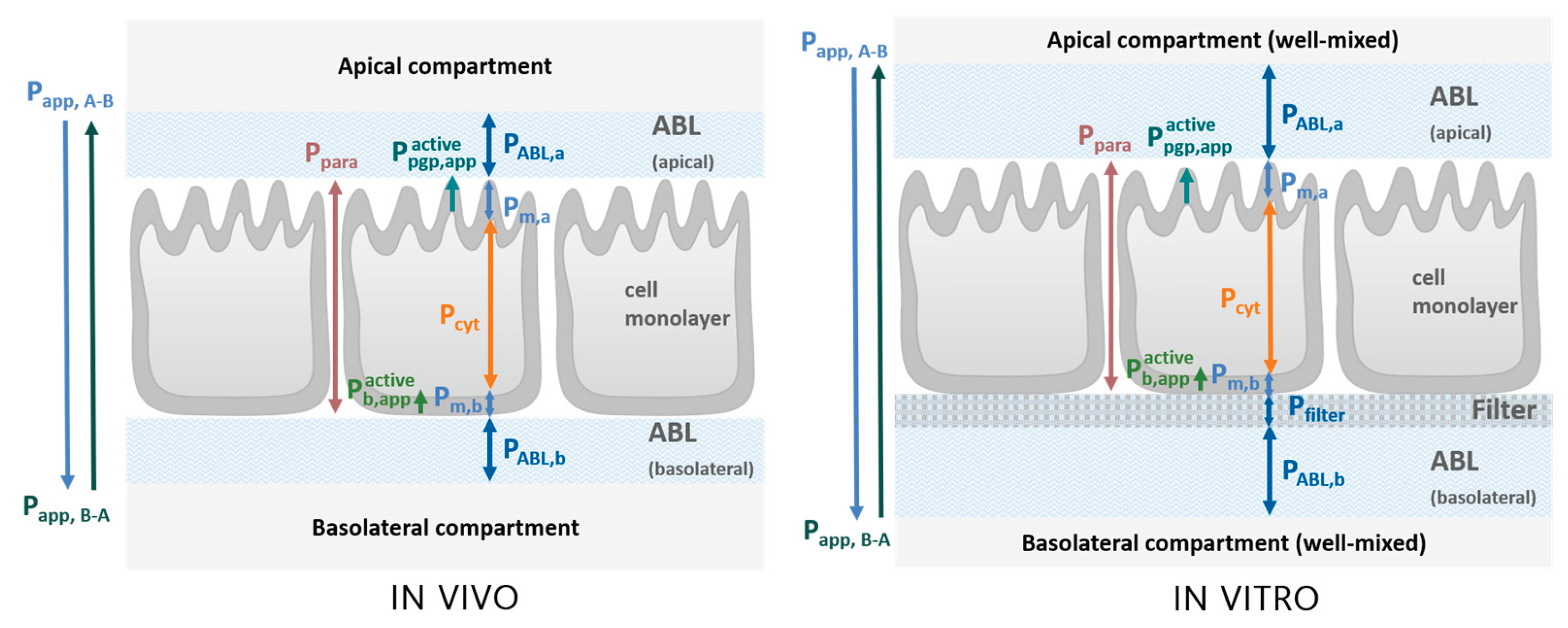
There are various resistances found in series and parallel that a compound encounters as it permeates from one compartment to another across a cell layer. This includes aqueous boundary layers (ABL), as well as the cell layer itself, consisting of the basolateral and apical membranes, as well as the cytosol. The permeability (P) through each barrier is inversely proportional to its resistance. As is evident in Figure 1, the unidirectional active transport facilitated by P-gp (denoted as $P_{pgp,app}^{active}$) and a basolateral uptake transporter (denoted as $P_{b,app}^{active}$ ) is found in parallel to the passive diffusion through the apical membrane (P_m,a). The in vitro situation during MDCK/Caco-2 assays is comparable to the in vivo scenario, save for the presence of a permeable filter on which cells are grown, as well as thicker unstirred water layers. A detailed description of the conceptual model used, as well as the various resistances and how they can be quantified can be found in Kotze et al. (2024b).

The total permeability through all these barriers which is measured by the transport assays is known as the apparent permeability, P_app, which is a function of all individual permeabilities found in series and parallel. P_app can be sub-divided into the contributions of these constituent parts, which allows for the individual evaluation and quantification of permeability through each layer, see Equations S1-1 to S1-8 in the Supplementary Materials S1 for modelled permeabilities and local compound concentrations as described in detail in Kotze et al. (2024b).

2.2. Maximal Active Transport Flux and Borderline Compounds

It is crucial to distinguish between the two different threshold values discussed in this work: the maximal flux and the associated maximal passive membrane permeability. The maximal flux, or J_pgp,active, refers to the maximum moles of compound that can be actively transported by any transporter per unit area and time (μmol/cm²/s) assuming the cell has limits to the energy it can invest in its transporters. The energy limit thus corresponds to the maximal J_pgp,active possible given limited energy production of the cell. Both the value for active efflux $P_{pgp,app}^{active}$ (cm/s) facilitated by P-gp from the apical membrane as well as the actively transported flux J_pgp,active at a given apical freely-dissolved concentration can be extracted from model fits of experimental MDCK data. A theoretical calculation of the maximal possible J_pgp,active given the cells ATP turnover can also be performed to compare with the empirical value as a plausibility check, see Supplementary Materials S1-2. However, J_pgp,active is an impractical metric, since it is complex to determine and not meaningful for the average scientist. Thus, we aimed to ultimately link it with passive membrane permeability, P_m, which is usually readily available, or easily determinable if not. The P_m threshold is thus the specific passive membrane permeability value where the rate of passive influx of a chemical would require an active efflux rate that exceeds the cell’s maximal J_pgp,active.

Chemicals which have a P_m value that exceeds the threshold P_m value would thus be unlikely to exhibit significant efflux, as their high permeability would impose an unsustainable energy demand on the cell. The connection between those two metrics, J_pgp,active and P_m, is provided by the assumption that almost all the compound passively diffusing into the cells is actively effluxed, which is a valid approximation for high efflux ratios. If membrane permeability poses the main passive resistance, passive influx corresponds to P_m*C_ext. For significant ER values, the energy limit can thus be approximated by the applied concentration-corrected membrane permeability, P_m*C_ext. Although concentrations in MDCK/Caco-2 efflux assays typically vary only within a narrow range (1–100 µM), therapeutic plasma concentrations span more than six orders of magnitude (Schulz and Schmoldt, 2003). It is therefore essential to take C_ext into account when defining the threshold.

Since J_pgp,active depends on several factors, the resultant P_m*C_ext threshold would not be a hard, definite cut-off line. Rather, it could be expected that there would be some intermediary window of transitionary permeability values that separate compounds that can be effectively effluxed from those that cannot. For compounds that have a P_m*C_ext value within this window (which we designate as “borderline compounds”) concentration plays a particularly pivotal role. For such borderline compounds, we observed concentration-dependent saturation of active transport. The rationale is that at low concentrations, compounds can be efficiently effluxed without substantially straining the cell’s energy budget. However, as concentration increases, the greater the amount of compound entering the cell, and the nearer the increased efflux would get to approaching the energy limit. Finally, at some higher concentration and above, the amount of compound passively permeating into the cell far exceeds what can be effluxed, since the energy budget has been depleted.

3. Material and Methods

3.1. Determination of Passive Membrane Permeability P_m

To determine the energy limit, a reliable P_m is needed. P_m can be determined experimentally, or predicted with in silico methods. According to the pH-partition hypothesis, only the neutral fraction (f_n) of a chemical can pass through membranes by passive diffusion due to its exceedingly hydrophobic nature (Shore et al., 1957), because the permeability of the ionic fraction is negligible in comparison (Ebert et al., 2018). The P_m of ionisable chemicals is therefore dependent on pH, or the neutral fraction f_n:

$$P_m=P_0\bullet f_n$$

(1)

The interconversion between the intrinsic permeability P₀ and P_m is straightforward when the neutral fraction is known. For all compounds in this study, pKa values were used to determine f_n at pH 7.4 according to Escher et al. (2020). Experimental pKa values were preferred, however, where no experimental pKa could be sourced, pKa values were instead determined using the software ACD/pKa GALAS from ACD/Percepta (version 2020.1.2, Advanced Chemistry Development, Inc. (ACD/Labs), Toronto, ON, Canada, www.acdlabs.com). For zwitterions, only the non-charged neutral species was assumed to permeate the membrane, and the respective fraction was calculated according to Ebert and Dahley (2024). See Tables S2-1 to S2-3 for details.

For epithelial cells such as the MDCK line used in this study, it is crucial to note that the apical membrane is folded to form microvilli. As a result, it is generally assumed to have a greater surface area than the basolateral membrane. If there is indeed a difference in surface area between the apical and basolateral membrane, it is suspected to have a significant effect on the resulting energy limit of this work. In our previous study we speculated that the factor of 24 (Palay, 1959) we routinely implemented to account for this increase in apical membrane surface area was likely too high (Kotze et al., 2024b). As such, in the main text of this study we used a more moderate apical membrane surface area factor (SA) of 7.5 (determined specifically for MDCKII cells as the mean value of these cells grown on different filters (Butor and Davoust, 1992)), and compared this to the two other proposed factors of 24 and 1 on the extreme ends of the probable range in the Supplementary Materials S1 (9–16). The factor of 1 naturally indicates that there is no difference in surface area between apical and basolateral membranes.

3.1.1. In Silico Prediction of P_m Using UFZ-LSERD/COSMO-RS

Experimental P_m values are the most reliable, so for this work such values were preferred when available for a given compound. When no reliably extracted experimental P₀ value was available for the calculation of P_m, P₀ was predicted according to the solubility-diffusion model (SDM) using hexadecane as a model for the hydrocarbon core of the membrane (Bittermann and Goss, 2017; Dahley et al., 2024; Walter and Gutknecht, 1986):

$${\mathrm{P}}_{0,\mathrm{S}\mathrm{D}\mathrm{M}}={\displaystyle \frac{{\mathrm{D}}_{\mathrm{h}\mathrm{e}\mathrm{x}}\bullet {\mathrm{K}}_{\frac{\mathrm{h}\mathrm{e}\mathrm{x}}{\mathrm{w}}}}{{\mathrm{x}}_{\mathrm{m}}}}$$

(2)

Where ${\mathrm{D}}_{\mathrm{h}\mathrm{e}\mathrm{x}}$ is the diffusion coefficient of the compound in hexadecane, ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$ is the hexadecane-water partition coefficient of the compound, and ${\mathrm{x}}_{\mathrm{m}}$ is thickness of the hexadecane-like hydrocarbon core of the cell membrane. The ${\mathrm{D}}_{\mathrm{h}\mathrm{e}\mathrm{x}}$ is assumed to be one tenth of the ${\mathrm{D}}_{\mathrm{w}}$ (Bittermann and Goss, 2017), and was thus calculated as a function of molecular weight of the compound, corrected to account for the temperature of 37 °C (Avdeef, 2010; Avdeef et al., 2005). The ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$ was determined using the LSER database (UFZ-LSER, 2025). ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$ values determined from experimental descriptors were preferred and duly sub-categorised. For compounds where experimental descriptors were not available, ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$ values determined from calculated descriptors were used instead. For the sake of comparison, ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$ values were also generated for all compounds using the quantum chemically-based software COSMOtherm (version C30, release 18, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, www.cosmologic.de)(Eckert and Klamt, 2002). COSMOtherm values were only used for zwitterions, and compounds with a molecular weight > 1000 g/mol. The P₀ of the MDCK cell membrane P_0,MDCK was then calculated from P_0,SDM using the empirical correlation determined by Dahley et al. (2024):

$${\mathrm{P}}_{0,\mathrm{M}\mathrm{D}\mathrm{C}\mathrm{K}}=0.84\mathrm{l}\mathrm{o}\mathrm{g}{\mathrm{P}}_{0,\mathrm{S}\mathrm{D}\mathrm{M}}-1.85$$

(3)

3.1.2. Experimental Determination of P_m with Bidirectional MDCK Assays

Membrane permeability P_m and the resultant P₀ values can also be determined with in vitro bidirectional assays. In this study, P₀ values for all compounds were preferentially sourced from our own experiments and from Ebert et al. (2024) who extracted P₀ values from experimental Caco-2/MDCK P_app data from several sources taking into account the many pitfalls of P₀ determination. As such they are considered the most reliable P₀ values available.

3.1.3. Experimental Determination of P_m with PAMPA and SDM

Using hexadecane as the membrane in HDM-PAMPA (Parallel Artificial Membrane Permeability Assay) has been shown an effective way to determine reliable experimental K_hex/w (Dahley et al., 2025). These ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values could then be used via Equations (2) and (3) to determine a P_m for MDCK cells that is much more reliable than those generated from predicted ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values (Dahley et al., 2024). For this work, HDM-PAMPA assays were performed for some compounds at suitable pH values. Detailed descriptions of the methodology used can be found in an accompanying study by Dahley et al. (2025). Further details about the experiments first reported in Dahley et al. (2025) that are relevant to this study (including the chemicals and reagents used, the experimental conditions, the experimentally obtained P_app, P₀ and K_hex/w values, as well as the resultant P_m values calculated from it, etc.) can be found in the Supplementary Materials S1 (3–4) and S2 (Tables S2-5 and S2-6).

3.2. Analysis of ER Data

3.2.1. Evaluation of ER Data from Literature

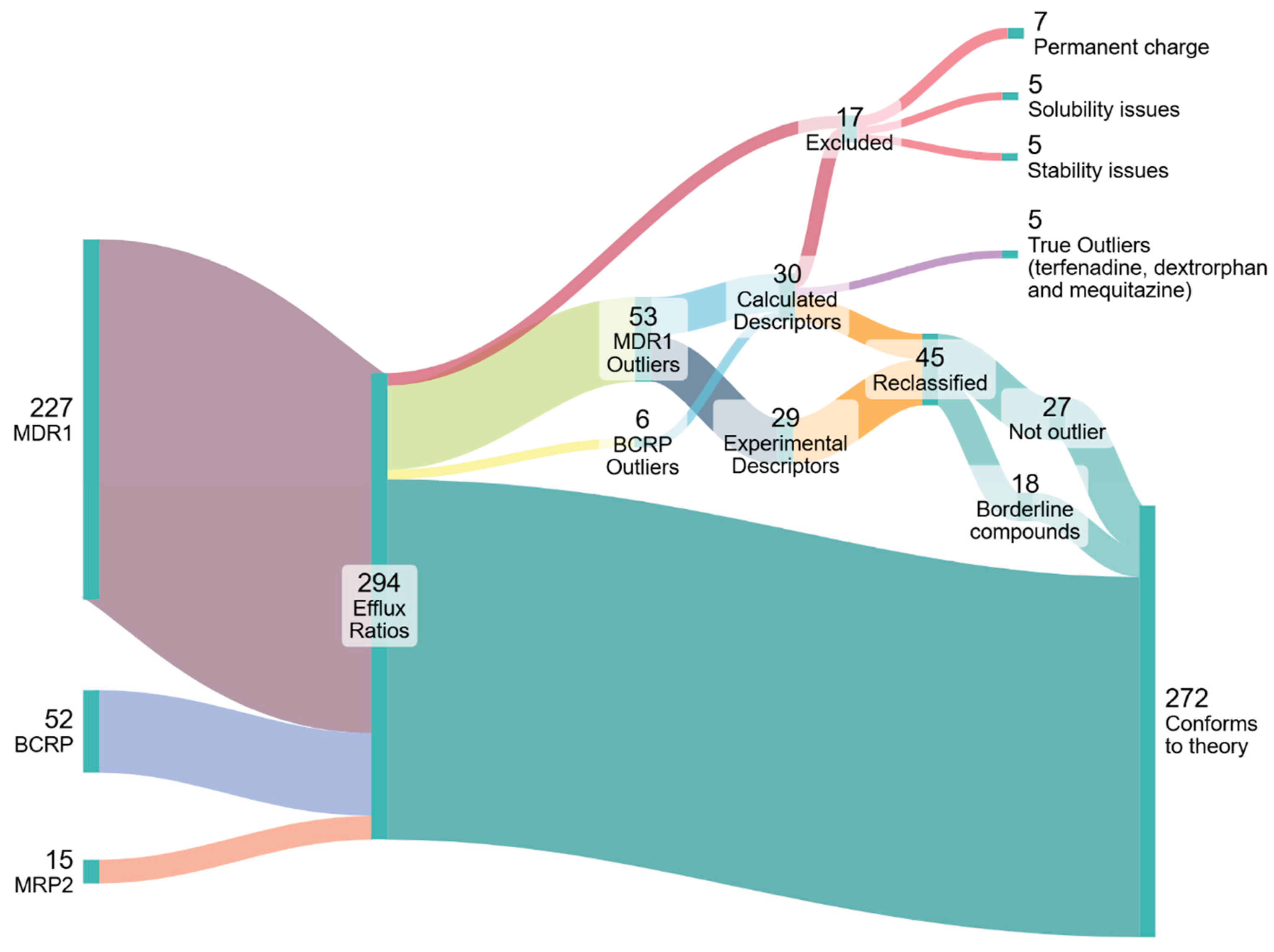
Three separate datasets of ER values were curated for P-gp, BCRP and MRP2 substrates as the three most clinically relevant apically-located efflux transporters. A literature search was performed to obtain compounds for which the ER was ≥ 2.5 (Wager et al., 2010), as determined with bidirectional MDCK transport assays. For compounds where ER values from more than one source were available, values from all sources were included in the analyses, even if some sources had a conflicting ER below the cut-off value. A total of 294 datapoints were gathered, representing 136 unique compounds, with those from MDCKII-MDR1 assays making up the bulk of the data, since MDCK-BCRP and MRP2 monolayer efflux assays are far less common. MDCKII-MDR1 assay data from 24 different sources were used (Callegari et al., 2011; Carrara et al., 2007; Chang et al., 2006; Chen et al., 2003; Chen et al., 2005; De Souza et al., 2009; Eriksson et al., 2006; Feng et al., 2008; Gertz et al., 2010; Hellinger et al., 2012; Huang et al., 2006; Liu et al., 2012; Luo et al., 2010; Mahar Doan et al., 2002; Obradovic et al., 2007; Park et al., 2011; Polli et al., 2001; Simoff et al., 2016; Tang et al., 2004; Taub et al., 2005; Troutman and Thakker, 2003; Wager et al., 2010; Wang et al., 2005a; Wegler et al., 2021). The dataset was comprised of 227 data points (i.e ER values) from 107 unique compounds. MDCK-BCRP assay data from 12 different sources were used (Chen et al., 2009; Feng et al., 2019; Mahringer et al., 2009; Marchetti et al., 2008; Muenster et al., 2008; Mukkavilli et al., 2018; Poirier et al., 2014; Polli et al., 2008; Wegler et al., 2021; Xiao et al., 2006; Ye et al., 2013; Zhang et al., 2015). The dataset was comprised of 52 data points from 33 different compounds. MDCK-MRP2 assay data from 8 different sources were used (Hong et al., 2014; Huisman et al., 2005; Jain et al., 2008; Lau et al., 2006; Nielsen et al., 2019; Tang et al., 2002; Williams et al., 2002; Zimmermann et al., 2008). The dataset was comprised of 15 data points from 11 different compounds. A fourth, separate dataset was also curated for compounds with insignificant ER values below the cut-off line. For this, data was obtained from 4 sources (Feng et al., 2008; Hellinger et al., 2012; Mahar Doan et al., 2002; Polli et al., 2001). This dataset was comprised of 125 datapoints representing 123 compounds. For all datasets, compounds with a permanent charge were excluded from further analyses since they have no neutral fraction that can passively permeate through the hydrophobic core of the membrane.

The P_m of each compound was then determined according to Equation (1) and the corresponding applied concentrations used by the respective studies were noted and used to calculate the concentration-corrected P_m values (P_m*C_ext). The MDCK ER values from the studies of all three transporters and the P_m*C_ext values determined for each respective compound are depicted in Figure 2. Tabulated values of Pgp/MDR1, BCRP and MRP2 substrates along with their chemical properties can be found in the Supplementary Materials (Tables S2-1, S2-2 and S2-3, respectively), along with the concentration-corrected P_m values (Table S2-4).

3.2.2. Re-Determining the ER of Outlier Compounds with Bidirectional MDCK Assays

Chemicals and Reagents

All chemicals and reagents can be found in the Supplementary Materials (S1-3).

Cells and Cell Culture

MDCKII-MDR1 cells were obtained from The Netherlands Cancer Institute (Amsterdam, The Netherlands). The cell medium was Dulbecco's modified Eagle medium (DMEM) (1X) + GlutaMAX™-I supplemented with 10 % foetal bovine serum (FBS), 100 U/mL penicillin and 100 µg/mL streptomycin. Cells were maintained at 37 °C in an atmosphere of 5 % CO₂ and passaged twice a week.

Bidirectional MDCK Assays

MDCK bidirectional transport assays were performed as described in Kotze et al. (2024a; 2024b). MDCKII-MDR1 cells (passages 20–40) were seeded at a density of 1.5 x 10⁵ cells/insert onto 12-well transwell inserts from CellQART (Northeim, Germany; pore size: 0.4 µm; filter thickness: 11.5 µm, porosity: 100 x 10⁶ pores/cm²). After seeding, cells were maintained as described in Section 3.2.2.2 and grown for 4 days. On the day before the experiment, the cell medium was refreshed. The transport buffer was HBSS and HEPES with a pH of 7.4. Stock solutions were prepared in the transport buffer. Prior to the experiment, the pH of the buffer and stock solutions was controlled with a rapid pH automated pH meter (Hudson Robotics, Inc., Springfield, NJ, USA), as was the pH of all samples after the completion of the experiment. Inserts were used in 12-well plates from TPP Techno Plastic Products AG (Trasadingen, Switzerland). Sampling occurred at 3–4 time intervals, the length of which was determined uniquely for each compound and direction of measurement in order to ensure sink conditions. Plates were placed in a Titramax and Inkubator 1000 orbital shaking incubator from Heidolph Instruments GmbH & Co. (Schwabach, Germany) at 450 rpm and 37 °C in between sampling steps. At the final sampling step, the donor compartment was sampled for mass balance calculations. The trans-epithelial electrical resistance (TEER) across the cell monolayer was measured for each insert at 37 °C using an EVOM epithelial tissue volt/ohmmeter (World Precision Instruments Inc., Sarasota, FL, USA) before and after the experiment to ensure that cell monolayer remained intact throughout the experiment. Lucifer yellow (LY) was also used as a paracellular marker to further verify the integrity of the cell monolayer. For this, the LY permeability of each insert was evaluated after the experiment by measuring the fluorescence intensity (excitation: 485 nm, emission: 538 nm) of basolateral compartment samples using a SpectraMAX Gemini EM spectrophotometer (Molecular Devices LLC., San Jose, CA, USA). Inserts exhibiting a LY permeability exceeding the pre-defined threshold of 1.5 x 10⁶ cm/s were excluded (Irvine et al., 1999), unless their P_app results were qualitatively consistent with those of replicate inserts that fell within the LY threshold..

Samples were analysed with an Infinity II 1260 LC system coupled with a 6420 triple quadrupole 145 with ESI source (Agilent Technologies Inc., Santa Clara, CA, USA). Either a Kinetex® F5 (2.6 µm; 100 Å; 50 * 3.0 mm) or C18 (2.6 µm; 100 Å; 50 * 3.0 mm) LC column was used (Phenomenex Inc., Torrance, CA, USA). P_app was calculated from acceptor compartment concentrations as described in Kotze et al. (2024b). P_app values at each timestep were corrected with the calculated recovery as done by Neuhoff (2003). Data are presented as the mean of the recovery-corrected P_app ± standard deviation of at least two timestep samples of both replicates. In order to account for lag time (Heikkinen et al., 2009), the first timestep in the A ⟶ B direction was excluded. The ER was calculated as the ratio of the mean P_app values in the B ⟶ A direction and A ⟶ B direction according to:

$$\begin{array}{c}ER\equiv {\displaystyle \frac{J_{\mathrm{B}⟶\mathrm{A}}}{J_{\mathrm{A}⟶\mathrm{B}}}}\equiv {\displaystyle \frac{P_{app,\mathrm{B}⟶\mathrm{A}}}{P_{app,\mathrm{A}⟶\mathrm{B}}}}\end{array}$$

(4)

3.2.3. Concentration-Dependent MDCK Assays for Borderline Compounds

Bidirectional MDCK-MDR1 assays were performed as described in Section 3.2.2.3 and Kotze et al. (2024b) to determine P_app values as well as the ER using stock solutions with varying concentrations. Concentrations were chosen to span the range of viable concentrations within the limits of the experimental procedure and LC-MS quantification. Where DMSO was required for solubility, the total concentration was kept constant at a limit of 0.1 %, and the transport buffer was supplemented with the same concentration to prevent a DMSO gradient between compartments. MDCK assays for this section were performed in triplicate, and sampling occurred at 4 consistent time intervals. Data from these assays are presented as the mean of the recovery-corrected P_app ± standard deviation of at least three timestep samples for all replicates.

3.2.4. Determination of $P_{pgp,app}^{active}$ and Maximal Flux J_pgp,active

The recovery-corrected A ⟶ B and B ⟶ A permeabilities determined for each concentration of the assays in Section 3.2.3 were used in the evaluation of the saturation experiments. The thickness of the apical and basolateral ABL, the thickness of the filter and its effective surface area, as well as the P₀, D_w, D_cyt and pKa of each respective compound were used to calculate the permeability through the individual resistances (ABLs, membranes, cytosol and filter). Paracellular permeability was calculated according to Bitterman et al. (2017) and a factor of 0.1 applied so that its final value matches the paracellular permeabilities typically observed for our MDCKII-MDR1 cell set-up (Kotze et al., 2024b). The external neutral fraction was once again calculated according to Escher et al. (2020) based on the compound's pKa values and the external pH. The neutral fraction in the cytosol was similarly calculated after determining the cytosolic pH as a function of the external pH according to Dahley et al. (2024).

The experimental P_app and known P₀ values were then used to fit the apparent permeabilities facilitated by P-gp and the basolateral uptake transporter $P_{pgp,app}^{active}$ and $P_{b,app}^{active}$. P_{app A⟶B} (see Eq. S1-3) was fitted at each concentration with the Excel SOLVER function which minimised the difference between the calculated and experimental apparent permeability by varying $P_{pgp,app}^{active}$. Using the extracted $P_{pgp,app}^{active}$as well as the starting concentrations (μmol L^-1), the calculation of compound concentrations adjacent to the apical membrane in the cytosol was possible (c_cyt,a) (see Eq. S1-6). The flux of actively transported compound, J_pgp,active, could then be calculated from $P_{pgp,app}^{active}$ * c_cyt,a in μmol cm^-2 s^-1. Ideally, a consecutive calculation would have been performed: First, for the basolateral transporter $P_{b,app}^{active}$, by fitting the B ⟶ A permeability (see Eq. S1-4) under the assumption that the apical membrane is not a significant resistance in this direction of transport. Then $P_{pgp,app}^{active}$ would be determined by fitting A ⟶ B permeability. However, due to unforeseen experimental effects, only A ⟶ B permeability could be fitted to determine ${PS}_{pgp,app}^{active}$, under the assumption of insignificant basolateral active transport. This is elaborated upon and justified in the Supplementary Materials (S1-7).

3.2.5. Linking the Maximal Flux Value with a Membrane Permeability Threshold

For the compounds that exhibited saturation effects in the concentration-dependent MDCK assays and thus evidently reached the maximal flux plateau, classic non-linear Michaelis-Menten fits for extracted J_pgp,active depending on C_cyt,a were performed using IGOR Pro 7 (WaveMetrics Inc., Lake Oswego, USA) to determine the maximal J_pgp,active. The maximal J_pgp,active was then used to calculate the corresponding threshold P_m value depending on ER (i.e the maximum passive membrane permeability a compound can have in order to potentially be affected by active efflux), again using the Excel solver function to optimize P_m for various $P_{pgp,app}^{active}$_, minimizing J_{pgp,active,max}- $P_{pgp,app}^{active}$*C_cyt,a. ER and C_cyt,a were calculated using Eq. S1-5 and S1-6, respectively. In contrast to our earlier assumption that nearly all compounds passively diffusing into the membrane are subsequently effluxed, this approach also allows determination of P_m for low ER values, where that assumption is not valid. In essence, P_m was back-calculated from P-gp activity, and it was determined what P_m value is possible for P-gp activity to equal the maximal flux value. Compound concentrations, paracellular transport and the apical membrane surface area were varied for the sensitivity analysis of the P_m threshold.

4. Results and Discussion

4.1. First Estimation of P_m*C_ext Limit

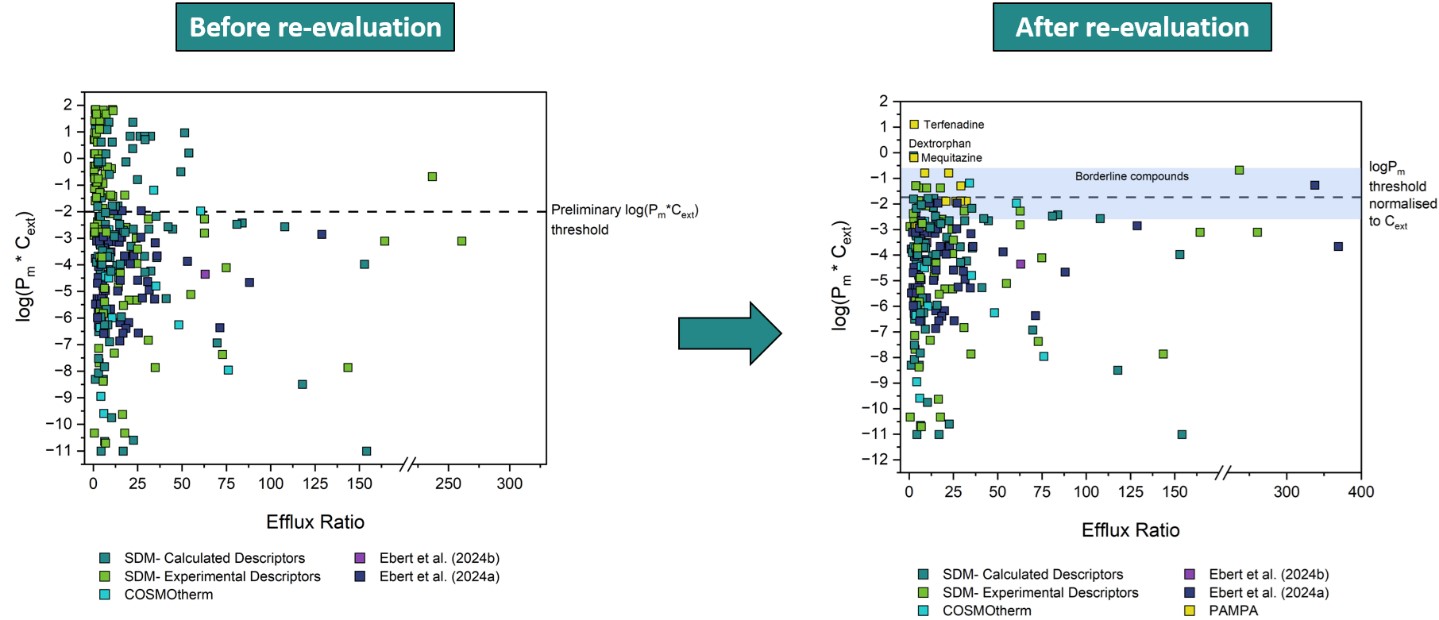
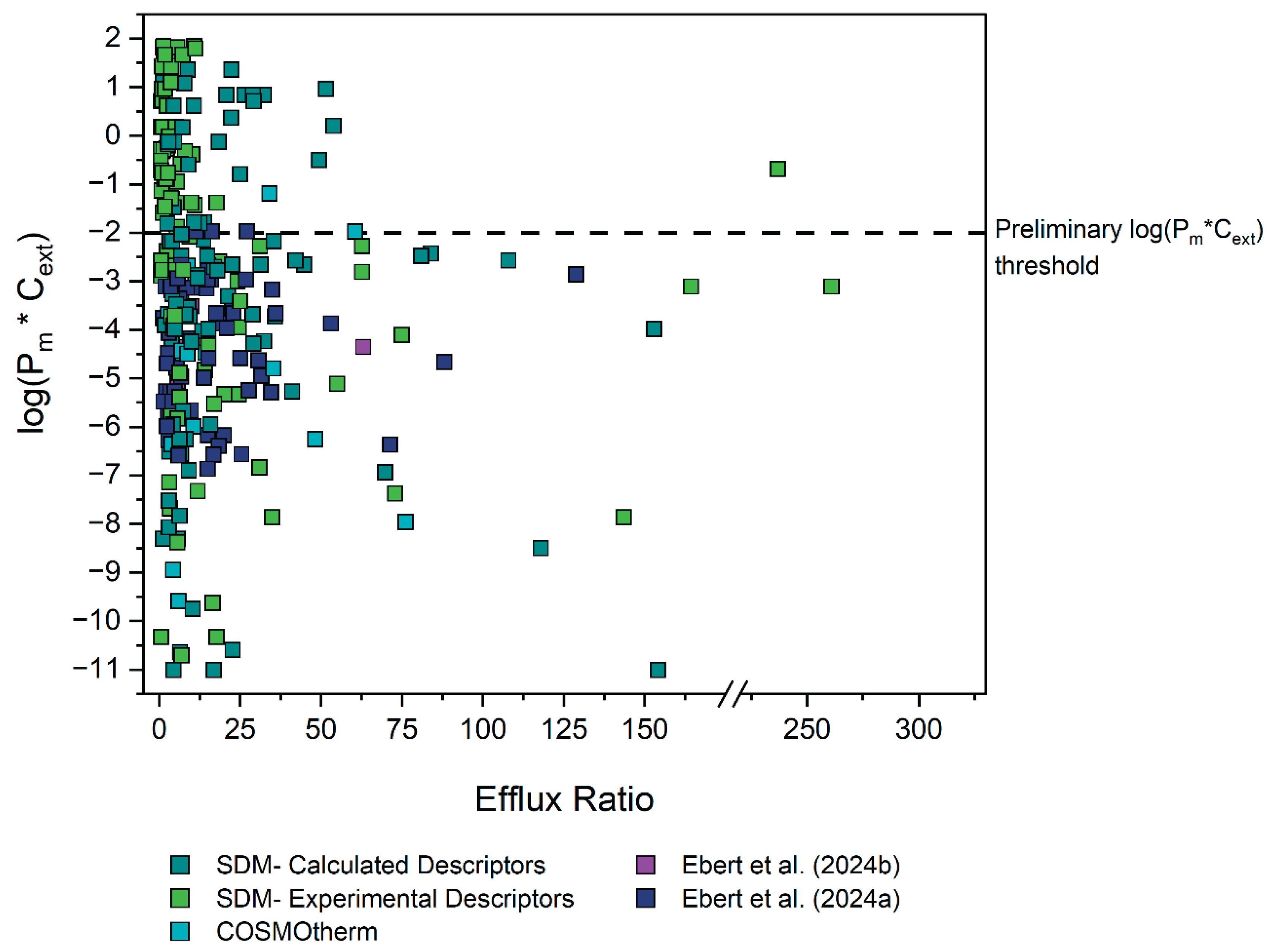
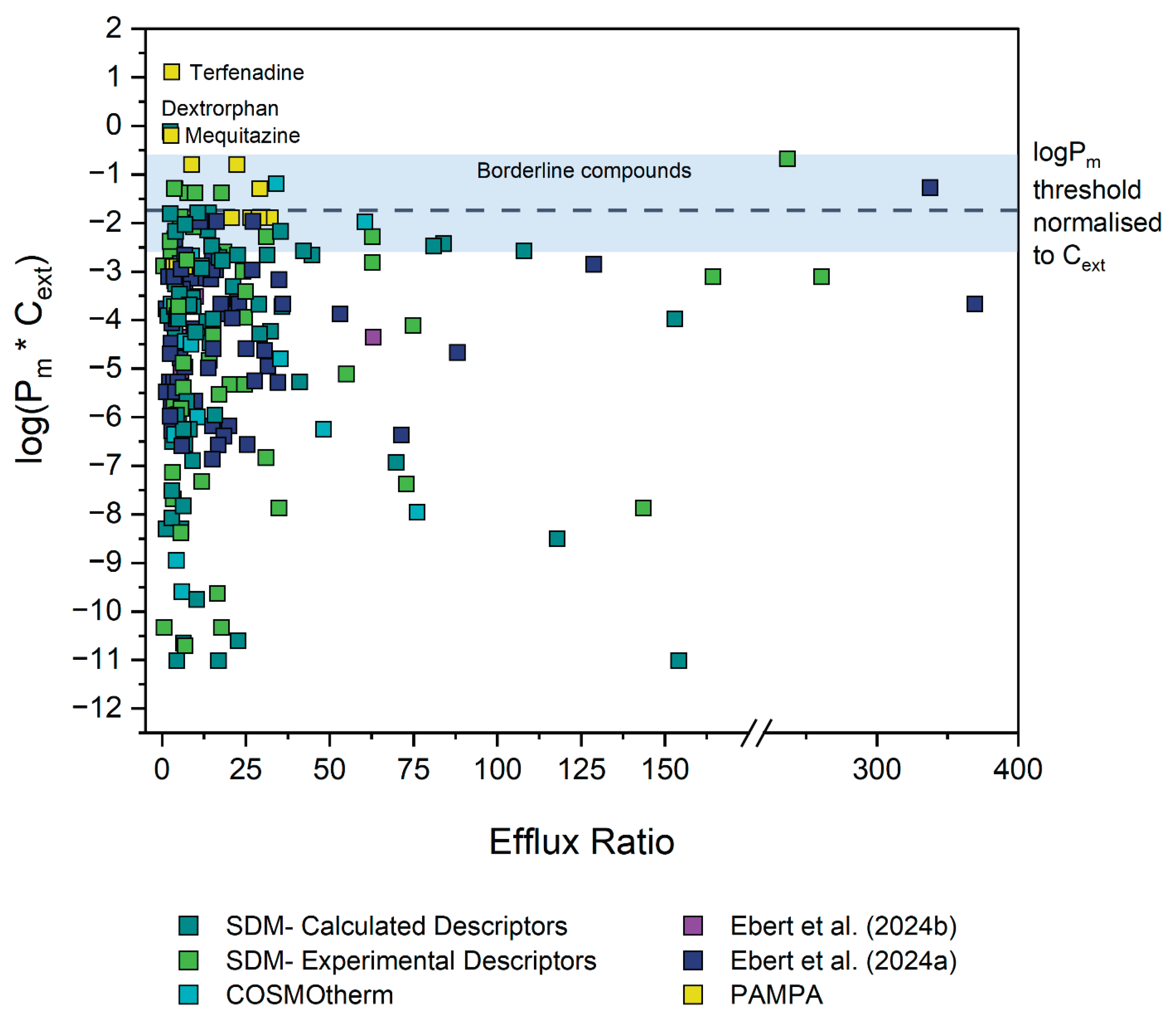
To validate our assumption of a P_m*C_ext limit for active transport, the efflux ratios for P-gp, BCRP and MRP2 substrates were extracted from literature as described in section 3.2.1. Figure 2 shows the P_m*C_ext plotted against the reported efflux ratios for a total of 286 datapoints, representing 132 unique compounds (after exclusions, see details in Section 3.3). Different colors indicate the source of each P_m value, which in turn reflects the reliability of the experimental or predicted data.

A rough approximation of the cut-off value for compound permeability was delineated to enable rational direction of the initial investigations. This cut-off P_m*C_ext value was determined by assessing the distribution of all the data (Figure 2). Particular weight was given to datapoints which had P_m*C_ext values based on the reliable P₀ values extracted by Ebert et al. (2024) and Ebert and Dahley (2024). Consequently, as a first approximation as to where the energy threshold (and thus concomitant membrane permeability threshold) could lie, a preliminary threshold of log(P_m*C_ext) = -2 was established, as it can be observed that none of the reliable experimental P_m*C_ext values by Ebert et al. were found above this.

4.2. Identification and Investigation of Outliers

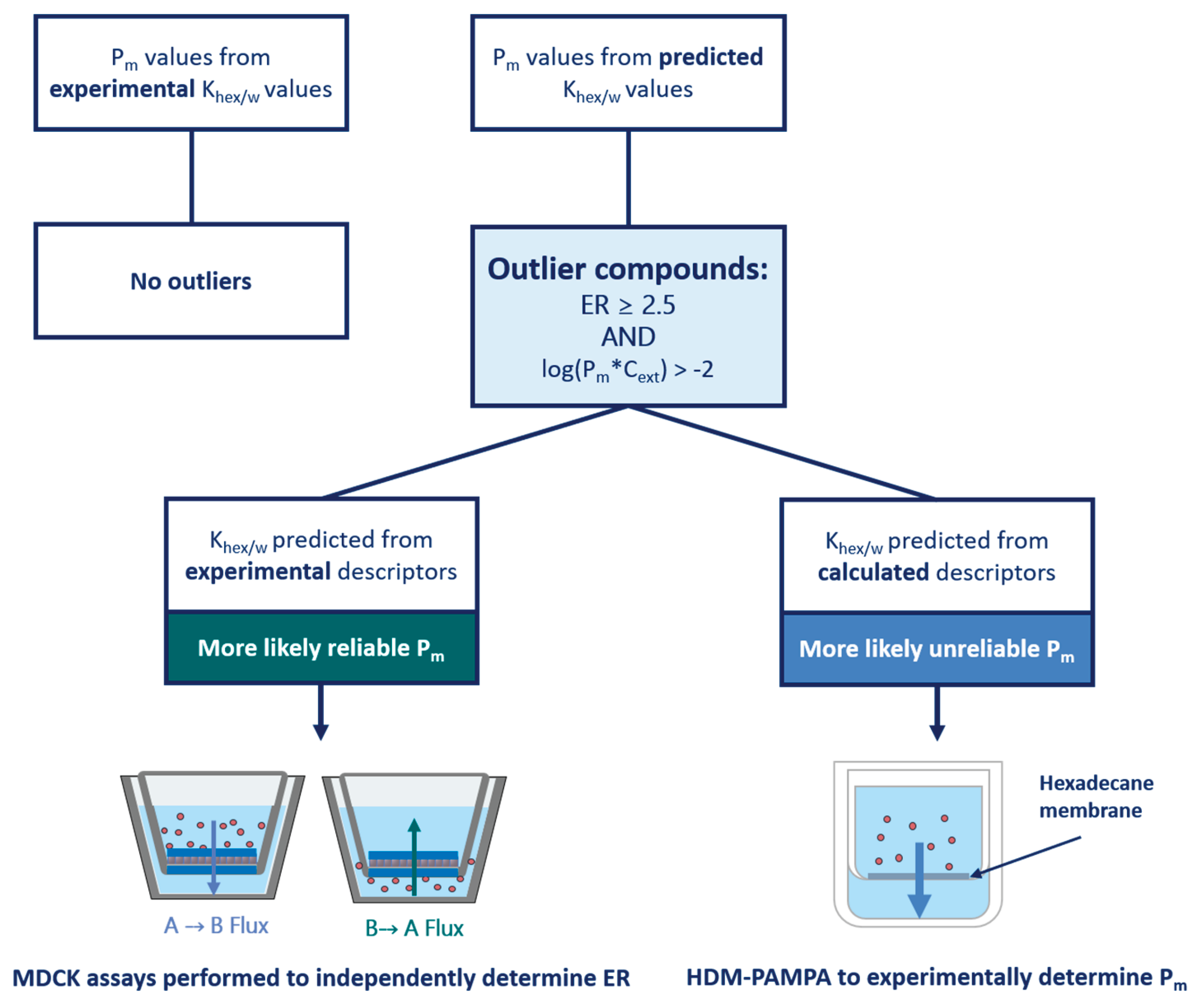
All 59 datapoints (41 compounds) with an ER ≥ 2.5 and with a log(P_m*C_ext) > -2 were thus identified as tentative outliers to our hypothesis, see Table S2-6. Owing to the specific threshold selection, this classification inherently resulted in all outliers having P_m values predicted from ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values, determined either with experimental or calculated descriptors. ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values determined from experimental descriptors are generally regarded as quite reliable, so for outliers in this category it was more likely that the reported ER values were erroneous. Thus, for outliers in this category, MDCK assays were preferentially performed to determine the ER independently in an attempt to reproduce the results of the original source study. Since only the MDR1 dataset had outliers in this category, only MDCKII-MDR1 assays were performed. ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values from calculated descriptors are deemed less reliable, so for outliers in this category it was generally assumed that the calculated P_m was false. For outliers in this category, HDM-PAMPA experiments were preferentially performed to obtain more reliable ${\mathrm{K}}_{\mathrm{h}\mathrm{e}\mathrm{x}/\mathrm{w}}$values as already described in Section 3.1.3. Figure 3 depicts a schematic summarising the aforementioned process of deciding how to probe each outlier compound. The aforesaid assumptions were merely used as a general guideline to determine which experimental method would be preferentially implemented to investigate a given outlier. However, for some compounds both MDCK as well as HDM-PAMPA were eventually performed.

4.3. Outlier Reclassification

Figure 4 represents the collection, analysis and reclassification of the data. Five outlier compounds (gefitinib, lopinavir, ritonavir, zotepine and dasatinib) were excluded for exhibiting stability and solubility issues that precluded reliable PAMPA/MDCK assays. It is worth noting that two thirds of the outlier compounds for the MDR1 dataset were contributed by only three of the 22 sources. Data sourced from Wager et al. (2010) represented more than 30% of the outliers. Moreover, except for one compound, all Wager et al. (2010) outliers fell in the "Experimental Descriptors" category, meaning that the ER value (not the P_m) is more likely dubious for these outliers. Significant ER values reported by Wager et al. and two other sources overrepresented in the outlier data— Obradovic et al. (2007) and Wang et al. (2005b)— were also often contradicted by one or more other sources, which would report no significant ER. As such, values from these sources were treated with caution. Accordingly, the 22 outliers from these sources were reclassified based on contradictory non-significant ER values produced by our own MDCK assays and/or by other sources. Two outliers were reclassified as non-outliers based on newly determined P_m values from PAMPA experiments. Ten outliers were reclassified as borderline compounds based on P_m values— often newly-determined with PAMPA— that placed their log(P_m*C) values between -2 and -1. The outliers, their reclassification and the basis for it can be found in Table S2-6 of the Supplementary Materials. The results of the MDCK and PAMPA assays can be found in the Supplementary Materials S1 (4 and 5) as well as S2 (Table S2-5).

After evaluation, there are three remaining outliers: dextrorphan, mequitazine and terfenadine. For dextrorphan, the reported ER of 2.6 barely surpasses the significance threshold and is thus not a very convincing outlier. This was also the case for mequitazine with an ER of 2.8. For terfenadine, our own MDCK assays did find a significant, albeit also very low ER value of 2.8. Furthermore, a newly-determined PAMPA K_hex/w value for terfenadine confirmed a log(P_m*C_ext) value of 0.08, therefore above the threshold. However, this compound exhibits very poor recovery in the MDCK assays— which would have likely been the case in the assays from the other sources as well. These poor recoveries may very well result in a false ER.

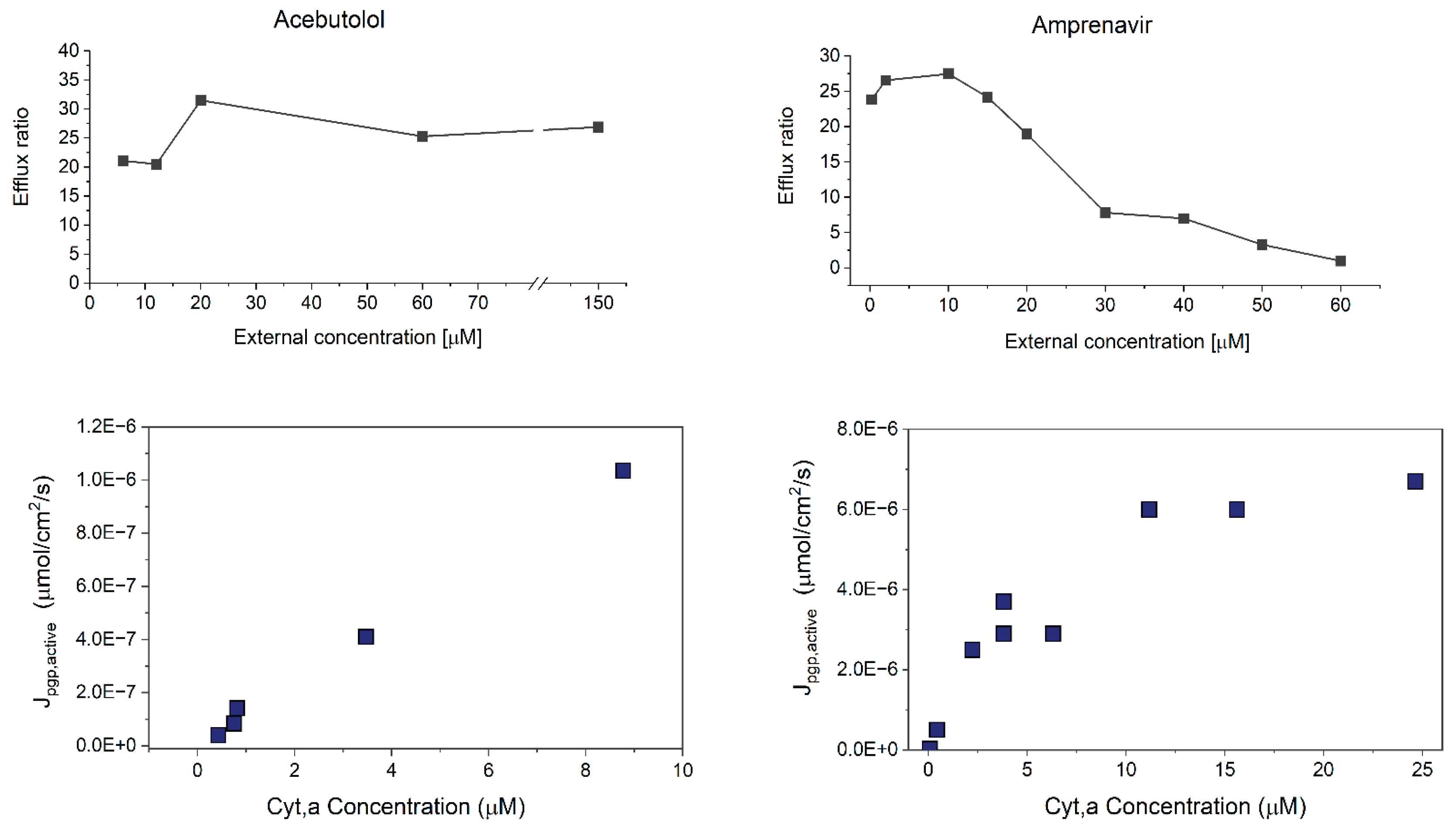
4.4. Concentration-Dependent Investigation of Borderline Compounds

Figure 5 shows the results of the concentration-dependence assays for a borderline compound (amprenavir) compared to a low P_m compound (acebutolol). The top panels show ER values as a function of applied assay concentration. The bottom panels show the J_pgp,active values (μmol/cm²/s) calculated as described in Section 3.2.4 from the P_app,A⟶B values at each concentration. Similar graphs for all compounds for which concentration-dependent experiments were performed can be found in the Supplementary Materials S1 (6, 9–11) along with tabulated P_app, recovery and ER values at each concentration. From Figure 5 it is evident that for the low P_m compound acebutolol, P-gp has not reached saturation, and there is no change in ER values even at very high concentrations. In contrast, for the borderline compound amprenavir the decline in ER values is attributed to classic saturation effects of the P-gp transporter. This supports our theory that there is concentration-dependent saturation of active transport for compounds near the maximal flux limit. The decline in ER can be attributed to classic saturation effects of the P-gp transporter. At low compound concentrations the P-gp transporter is not yet saturated and this results in high transport rates, resulting in high ER values. At higher concentrations, the transporter has likely reached saturation, and active transport no longer increases with concentration. Thus, passive permeation becomes more dominant as it increases proportionally with concentration.

The observed saturation effects coinciding with the energy plateau is likely no coincidence. Indeed, these two phenomena lead to the same result: no further increase in the activity of the transporter with increasing concentration past some maximal flux value. As such, the energy limit which is dictated by physical principles is enforced by the cell through the mechanism of saturation. While the concept of transporter saturation and its impact on transporter-facilitated efflux is not new (Heikkinen et al., 2010; Li et al., 2008; Tubic et al., 2006), this study is to our knowledge the first to link it to an energy threshold. It is important to note that this does not imply that every observed saturation effect is caused by an energetic limitation; rather, a saturation effect is always observed before the energetic limit is reached, which is plausible from an evolutionary perspective, as it avoids the energy depletion of the cell. It is unclear how exactly the saturation effect would be linked to the energy limit. One hypothesis is that ATP binding kinetics may become rate-limiting at high active transport rates; however, this potential relationship is beyond the scope of the present study.

Tachibana et al. (2010) had already applied a sophisticated model to extract J_{pgp,active,max} ​ (referred to as V_max in their work) from concentration-dependent measurements reported by Shirasaka et al. (2006) for verapamil, vinblastine, and quinidine. Their model accounted for passive permeation into and out of the cell on both the apical and basolateral sides of the membrane, as well as unidirectional P-gp transport. While our model for obtaining the K_m ​value differs from theirs, both approaches use the intracellular K_m parameter relevant for transporter saturation rather than the extracellular one. The main difference between their approach and ours is that we also included paracellular transport and ABL resistance. It should be emphasized that ABL resistance cannot simply be lumped together with passive permeability; only passive permeability runs in parallel with active transport, whereas the ABL does not. Moreover, paracellular transport can strongly influence P_app​, since P_app will not fall below P_para, even when P_trans ​is negligibly low because of active efflux.

Unfortunately, re-analyzing their published data with our model did not yield reliable results, as the evaluable concentration window was rather narrow. At higher concentrations, all compounds appeared to be limited by ABL effects (their data suggested a total ABL thickness of ~4 mm, compared to 426 µm in our experiments). As we were unfamiliar with their experimental setup, estimating paracellular transport was difficult. However, based on the predictions of Avdeef (2012), paracellular transport could have affected P_app ​at low concentrations for both vinblastine and quinidine. Furthermore, while we could extract a total membrane thickness, the distribution of the ABL between the apical and basolateral sides is critical for the evaluation, and this information was unavailable. In addition, recovery data were missing. Collectively, these factors prevented us from reliably applying our model to their dataset. A fourth compound, digoxin, was included in the study by Shirasaka et al. (2006). It showed no signs of saturation across the tested concentration range (up to 26 µM). With a P_0​ of 4.14 (Ebert et al., 2024), corresponding to a log P_m⋅C_ext of –2.72, this completely neutral compound lies well below our permeability threshold—fully consistent with our model. Finally, the V_max of 5.7 × 10⁻⁶ µmol/cm²/s for quinidine, obtained by Heikkinen et al. (2010) using a five-compartment model that accounted for ABL effects, is in good agreement with our own J_{pgp,active,max} of 9.7 × 10⁻⁶ µmol/cm²/s (for SA = 1) derived from our quinidine experiments.

As such, it is worth emphasising once again that experimental conditions are critical for obtaining meaningful results in MDCK efflux assays. We previously showed that pH can play a role in the false classification of compounds, as ER values can change based on the pH (Kotze et al., 2024b). Here once again it can be observed that using concentrations that are too high can easily lead to the erroneous conclusion that compounds are not P-gp substrates.

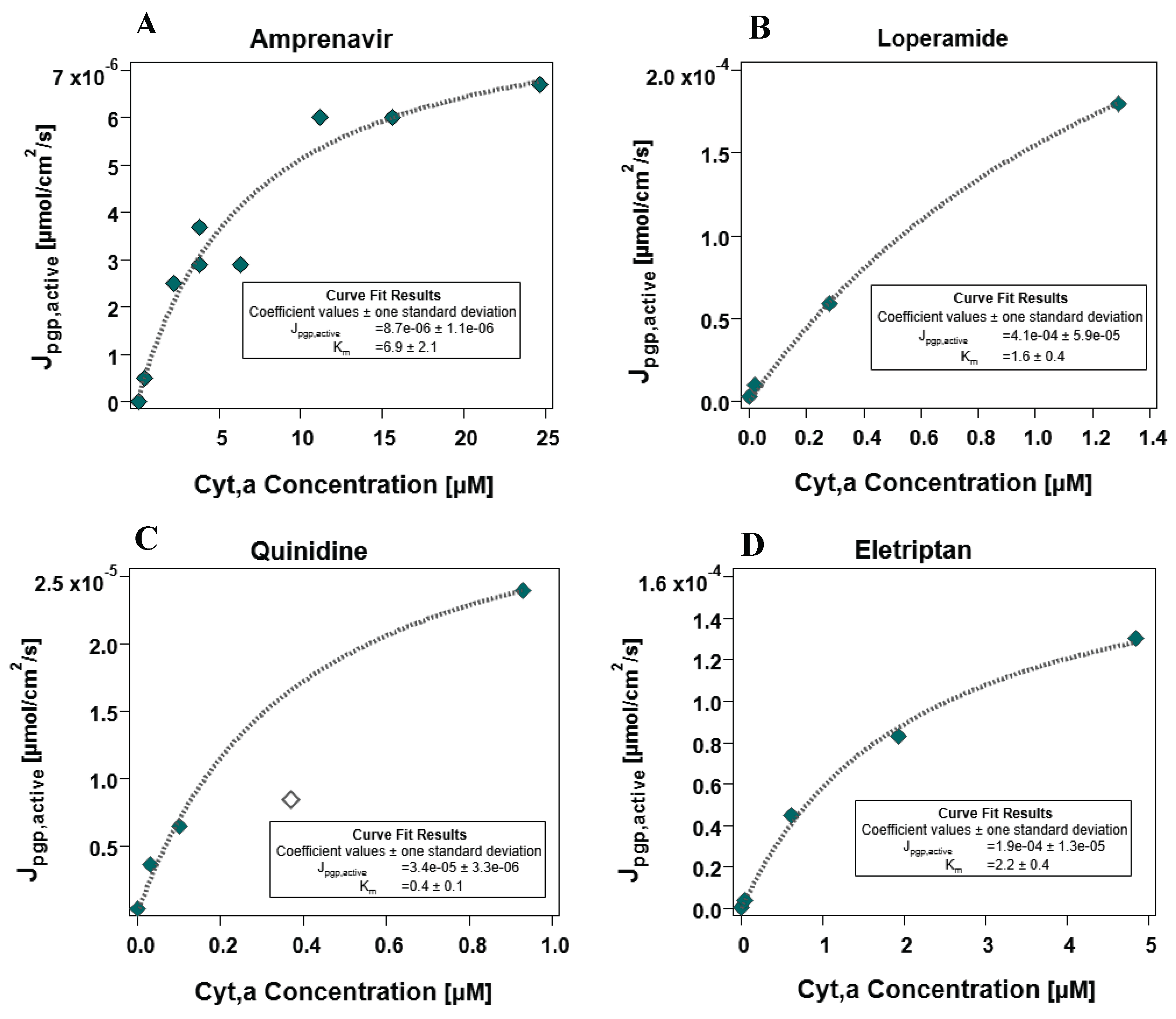
4.5. Empirical Determination of the Energy Limit

Four out of the six compounds suspected to be borderline compounds (for which concentration-dependent assays were performed) exhibited the expected plateau when the transport of these compounds started reaching the maximal J_pgp,active . Because these compounds exhibited saturation effects and evidently reached the maximal flux plateau, Michaelis-Menten fits were performed as described in Section 3.2.5, the results of which are depicted in Figure 6. The final J_{pgp,active,max} value was determined from the average of the individual maximum flux values determined for the four compounds depicted in Figure 6. Analogous fits for the same compounds using the other apical membrane surface area factors of 1 and 24 as well as the resultant mean J_pgp,active values in these cases can be found in the Supplementary Materials S1 (12–14). The mean (N=4) J_pgp,active determined for the case considered as most plausible (apical membrane surface area factor of 7.5) was determined to be 1.6 x 10^-4 μmol/cm²/s.

Since the maximal flux value is based on cellular energy constraints, we expect that all borderline compounds should plateau at the same maximal J_pgp,active. As is evident from Figure 6, this is not quite the case. This is easily explained when one considers the influence of P₀ values in determining J_pgp,active. P₀ values always come with some threshold of error, and the source of the P₀ is the biggest determining factor of the level of error. Quinidine has a very reliable experimental P₀ value determined from MDCK assays, whereas amprenavir and eletriptan both also have experimental (PAMPA-SDM) P₀ values. The results for loperamide, in contrast, are considered less precise because of uncertainty in predicted P₀ values. The P₀ for loperamide could not be determined via MDCK or PAMPA assays, and is thus based only on an SDM prediction. While SDM predictions derived from experimental descriptors can be quite accurate, experimental P₀ are more reliable. The uncertainty in the P₀ prediction for loperamide consequently results in greater uncertainty in its fitted J_{pgp,active,max} values. Though experimental P₀ values are generally reliable, they are still subject to error. The experimental P₀ for quinidine, amprenavir and eletriptan may still lead to an estimation that is off by one order of magnitude. Thus, the maximal J_pgp,active determined from these fits are fairly consistent within the inextricable error that comes with P₀ values.

This maximal J_pgp,active of 1.6 x 10^-4 μmol/cm²/s generated by the Michaelis-Menten fits for four borderline compounds is the energy threshold for efflux transport determined for the MDCKII-MDR1 cells used in this study. Essentially: it is unlikely that highly membrane-permeable compounds that have a higher flux demand for its effective efflux would be affected by any efflux transporter. As stated before, compounds that lie in the borderline window of membrane permeability could exhibit efflux, depending on their concentration.

4.6. Linking a Passive Membrane Permeability Threshold to the Energy Limit

While the J_pgp,active value is interesting, it must be linked with a more accessible metric such as membrane permeability to be useful in practice. As described earlier, for high ER J_pgp,active≈ J_passive,in, meaning almost all compound passively diffusing into the cell is actively transported out again. If the membrane poses the main resistance, J_passive,in corresponds to P_m*C_ext. However, this assumption is not valid for low ER values, or if other transport resistances are dominant. We thus used our model to calculate the maximum P_m that would lead to a specific ER assuming a maximal J_pgp,active of 1.6 x 10^-4 μmol/cm²/s as described in Section 3.2.5.

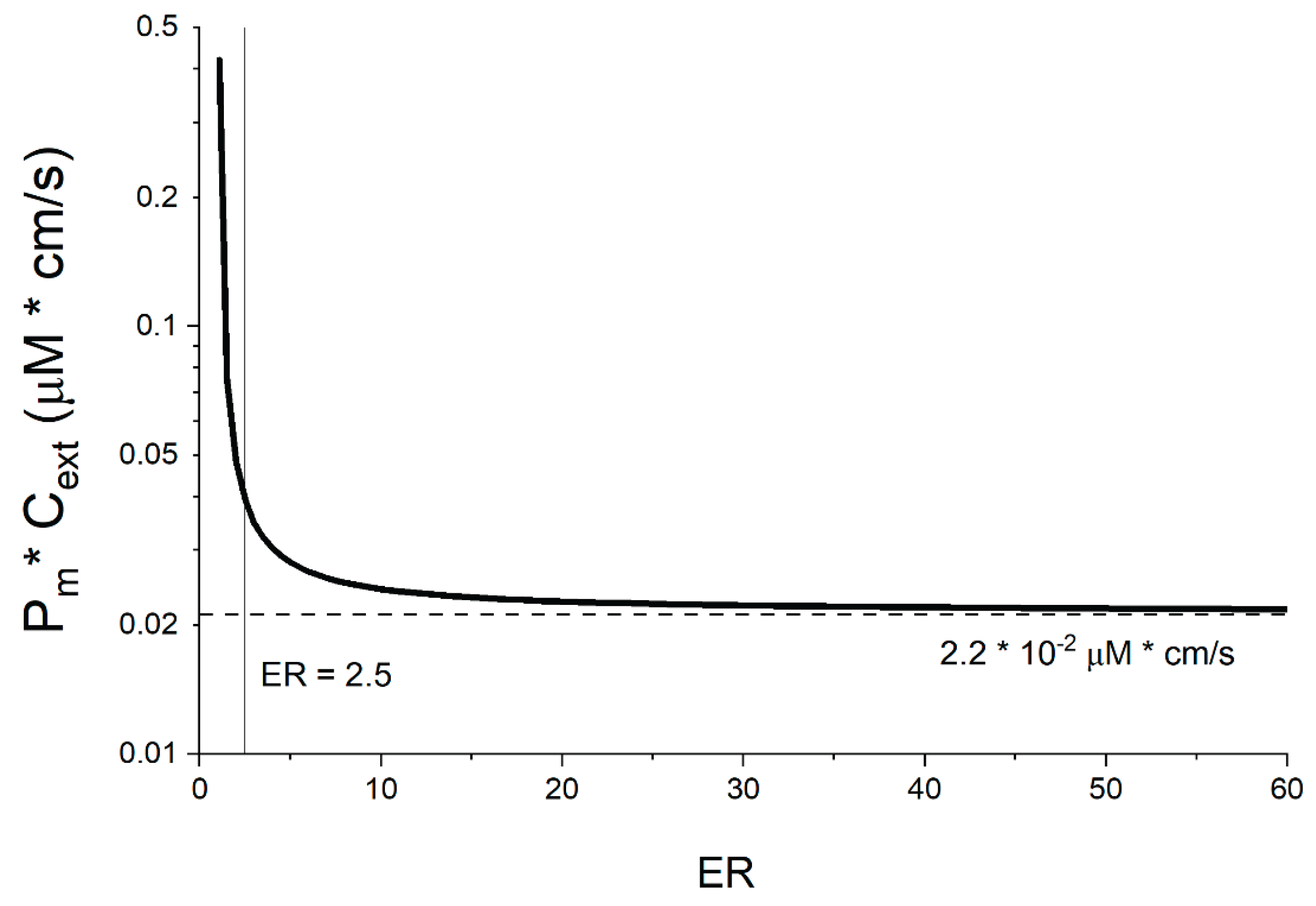
As is evident from Figure 7, the P_m*C_ext threshold stays constant across all ER values except in the lower ranges. To understand why this is, one needs to consider that at low ER values when P-gp is less active, passive back-flow of the compound from the cytosol is highly relevant, which is not the case for compounds with high ER values where P-gp is more active. In the low ER value range, in order to double the ER, active efflux has to increase substantially to compete with the passive backflow. However, even with a substantial increase in P-gp activity, there is only a modest drop in cytosol concentration. Thus, in the low ER ranges, P₀ has to decrease in order for the system to continue adhering to the maximal energy consumption value when the ER increases. In contrast, at higher ER values, active efflux dominates, making the passive backflow negligible. Doubling ER in this range involves proportionally smaller increases in P_pgp since it already vastly exceeds P₀, and active transport largely dictates the efflux. As a result, the cytosolic concentration decreases proportionally with the increase in P_pgp activity. Energy consumption remains the same despite the higher ER and reaches a plateau- leading to a concurrent P_m plateau. This is of course a simplified scenario, since the activity of the basolateral transporter and other factors also play a role— but it allows for a fundamental understanding of the phenomenon that can be observed in the lower ER ranges. However, this affects only a small percentage of the significant efflux ratios in our database (those that barely surpass the significance threshold), therefore, the plateau remains the most interesting value. However, this sharp increase in the P_m*C_ext limit for low ER values might explain the few remaining outliers that did indeed show low ER values (2.6–2.8). Especially when one considers that low recovery may also have resulted in an overestimation of ER.

4.7. Sensitivity Analysis of P_m Threshold

Though the energy threshold should be static across compounds and concentrations, translating J_pgp,active into a P_m value is dependent on various factors. Firstly, the apical membrane surface area factor SA is expected to be quite consequential, as this directly affects the maximal J_pgp,active value (see S1-11-S1-13). Fortunately, SA does not affect the extracted P_m threshold if we consider the maximal J_pgp,active that corresponds with the respective SA. For example, if the SA is increased by 3.2 (as is the case with 7.5 vs. 24), the extracted J_pgp,active is also increased by a factor of 3.2, but the extracted P_m*C_ext threshold is not affected (see S1-14). The determination of the P_m*C_ext threshold specific to our cells is thus not affected by the uncertainty of the SA factor. However, if a fixed maximal J_pgp,active is used to extract P_m, the resulting values will scale directly with SA (see Figure S1-10). This becomes critical when the energy limit is determined independently (e.g from ATP-turnover rates, see Supplementary Materials S1-2) because SA variability would then introduce a major source of uncertainty.

Secondly, as stated in the preceding section, the maximal J_pgp,active presented in this work was determined specifically for MDCK-MDR1 cells. The maximal flux value can be different for different cell types. MDCK cells likely have a higher energy limit than the average cell, since their energy needs are higher than that of other, less active cells (see Supplementary Materials S1-2). As such, it is critical to bear in mind that there will be differences between different cell types. Cells with higher energy demands/production are likely to have a higher maximal flux value. For example, in cancer cells an upregulation of mitochondrial respiration has been reported (Giddings et al., 2021), which would also suggest an increased J_{pgp,active,max}​. The observation that inhibition of the electron transport chain restored the cells’ drug sensitivity (Giddings et al., 2021) is fully consistent with our assumption of an energy limitation.

It was found that the energy limit of the cells and thus their maximal J_pgp,active is directly proportional to the corresponding P_m threshold. An increase in maximal flux shifts the logP_m threshold higher by the same factor. Thus, it has to be emphasised once again that the P_m threshold presented here is not a universal value, since it was determined for the MDCK-MDR1 cells at our disposal. Therefore, the exact same P_m cut-off cannot be used across all cell types. For example, cells of the blood-brain barrier (BBB) are more active than Caco-2 cells, since they express very high amounts of various efflux transporters to maintain stringent control of brain access. As such, if BBB cells have a higher maximal flux value, it is reasonable to conclude that this would allow for the efficient efflux of compounds with a higher passive membrane permeability. The higher density of mitochondria in the blood–brain barrier (Salmina et al., 2021) may result in a higher energetic limit (and thus higher P_m*C_ext​ threshold). This— together with the expected lower compound concentrations in the blood compared to the intestine— may explain why certain compounds have a high bioavailability, but low brain uptake if they are not actively effluxed in the gut, but are in the brain.

Finally, the importance of concentration for the P_m threshold was very apparent. As expected it was found that the P_m threshold is indirectly proportional to the concentration, since their product determines the passive diffusive flux rate through the membrane that counteracts active transport. The lower the compound concentration, the higher the threshold (and vice versa for an increasing concentrations). This is why the metric proposed for the threshold is not simply P_m, but rather the P_m-concentration product, P_m*C_ext (µM cm/s). Instead of the threshold shifting whenever a new concentration is considered, we found that when the P_m is normalised to concentration it always results in the same threshold, regardless of assay concentration applied.

The effect of paracellular transport, compound charge, as well as basolateral uptake on the P_m*C_ext threshold was also evaluated, but was found to be inconsequential (Supplementary Materials S1-16). Thus, the final log(P_m*C_ext) threshold for our MDCK-MDR1 cell system— determined empirically with borderline compounds—was found to lie at -1.7. This is slightly higher than the threshold considered initially for the identification of outliers, and as such did not result in the re-identification of more outliers not previously considered.

4.8. Re-Evaluation of Literature Data

Nearly 300 significant ER values from MDCK assays were collected from 46 different literature sources. Considering the spread of the initial experimental data, it was initially hypothesised that for MDCK cells, compounds with a P_m*C_ext value greater than 1 x 10^-2 cm/s would be too membrane permeable for the cell to maintain efficient efflux against their high rates of passive diffusion. From the outset, two thirds of the data did not contradict this hypothesis. That is, they were confirmed efflux substrates with a P_m*C_ext lower than 1 x 10^-2 cm/s. Figure 8 shows the distribution of the data of all three transporters after re-evaluation of the outliers, along with the final P_m*C_ext threshold line of 2.2 x 10^-2 cm/s (and borderline area) that was determined empirically in this study.

The depicted P_m*C_ext threshold is based on the J_{pgp,active,max} of 1.6 x 10^-4 μmol/cm²/s determined for our MDCK-MDR1 cells. Due to normalisation of the threshold P_m to external concentration, it is independent of assay concentration used.

It is remarkable that of all compounds reported in the literature as being substrates of one of the three major efflux transporter implicated in MDR, all have P_m*C_ext values either below the threshold, or they fall in the borderline window and exhibit only concentration-dependent efflux. This supports the theory that there is indeed a P_m limit for active efflux — and due to it being based on the fundamental principle of cellular energy constraints, that it is universal for three different transporters. Ultimately, there are only three unconvincing, low ER compounds which have a P_m*C_ext value above the threshold and its accompanying borderline window. This is notable as there is no shortage of pharmaceutical compounds with log(P_m*C_ext) values above the threshold. 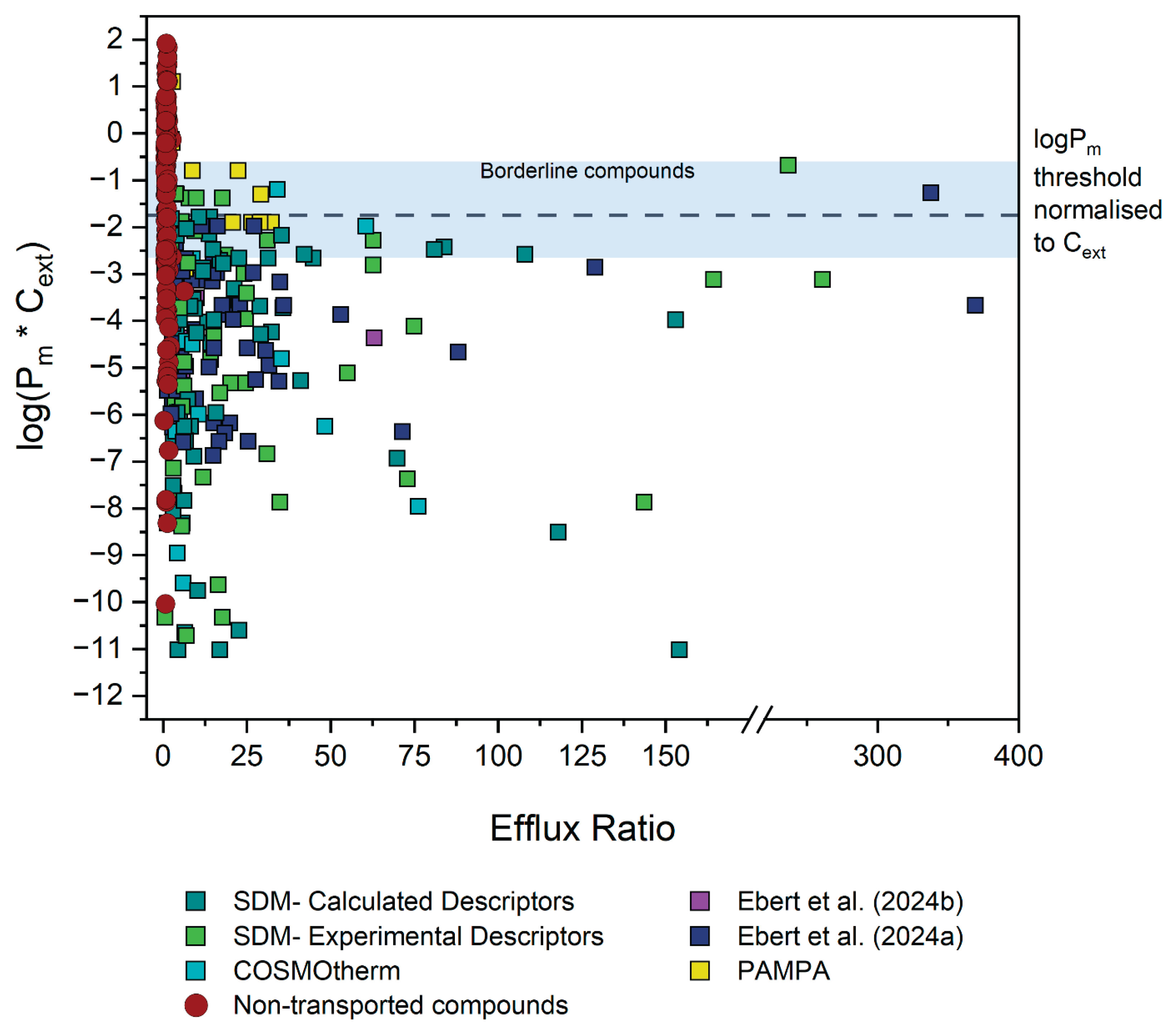As described in Section 3.2.1, 123 compounds with non-significant ER values were also evaluated. Figure 9 depicts the P_m*C_ext values for these compounds with ER values less than 2.5 in red, and as is evident about 60 % of them fall above the threshold. Compounds below the threshold may potentially be affected by efflux transport, and in vitro transwell assays for these compounds are warranted. However, compounds above the threshold are not expected to be affected by efflux transporters, and assays to check for an ER value would be unnecessary.

Our results align with the Biopharmaceutics Drug Disposition Classification System (BDDCS), which categorizes drugs into four classes according to solubility and intestinal permeability. According to Benet et al. (2011), efflux transport should be considered for Class II compounds (low solubility, high passive permeability), whereas membrane transporters—both uptake and efflux—play a critical role for Class III (high solubility, low permeability) and Class IV (low solubility, low permeability) drugs. In contrast, for Class I drugs (high solubility, high permeability), active transport is generally not relevant. This is fully consistent with our defined P_m*C_ext threshold, since we would not anticipate active transport under conditions of high permeability combined with high concentrations.

5. Conclusions

In this study, we propose an energy limit for active efflux which can be translated into a membrane permeability threshold value that can be used to simplify identification of compounds that can exhibit significant efflux. Nearly 300 ER values from MDCK assays of three transporters (P-gp, BCRP and MRP2) were sourced from literature to investigate this hypothesis. A systematic analysis of outlier compounds of a preliminary threshold (compounds with ER values greater than 2.5 and log(P_m*C_ext) values greater than -2) resulted in the reclassification of most outliers as conformers. Concentration-dependent transwell assays for borderline compounds enabled the more precise identification of the maximal flux value (J_{pgp,active,max}) of 1.6 x 10^-4 μmol/cm²/s for our MDCK-MDR1 cell systems. It was found that the energy limit seems to be enforced by the cell through the mechanism of saturation. The maximal J_pgp,active was then translated into a more accessible threshold P_m value. The threshold P_m was normalised to external concentration for a concentration independent P_m*C_ext threshold. This P_m*C_ext threshold falls within the mid-range of typical hydrophobicity/lipophilicity values for most chemicals of interest, making it relevant across a broad spectrum of compounds.

Our results confirm that passive membrane permeability (P_m*C_ext) can be used as a filtering metric to determine whether the pharmacokinetics of pharmaceutical compounds can be affected by efflux. If the energy limit of certain cells expressing an efflux transporter of interest is known or determined, then it can also be determined what the maximal membrane permeability of a compound can be that would still allow the maintenance of efficient efflux. Consequently, for compounds that have a P_m value above the threshold it can with some certainty be concluded that their disposition will likely not be affected by any efflux transporters relevant for those cells. However, accurate P_m values are absolutely critical for determining whether efflux can occur. This approach would reduce the need for time- and resource-intensive transport assays for compounds above the threshold. Furthermore, it can aid rational lead optimisation by enabling drugs of interest to be engineered for desired transporter interactions through adjustments in membrane permeability. Future research could extend the present framework to account for influx transport. In addition, the role of saturation as a cellular mechanism for maintaining efflux within the cell’s energy limit warrants further investigation. Finally, future studies could determine the energy limit and corresponding P_m*C_ext threshold for other cell lines.