Optical Flow-Based Algorithms for Real-Time Awareness of Hazardous Events

1. Introduction

The main objective of this review is to present a common algorithmic approach to a variety of real-time video observation challenges. These challenges arise from clinical and general practice scenarios where video observation can be critical for the safety and security of the monitored population. We will further address each of the scenarios and events separately and here we first introduce the generic idea of optical flow (OF) image and video processing.

OF is a powerful technique [1,2,3] that gives the reconstruction of object displacements from analyzing related pairs of images where the objects are recorded. Although the most common use is in inferring the velocities of moving objects from video sequences, it has also been successfully applied in stereo vision [4,5] for reconstructing depth information from the disparity between the images provided by two (or more) spatially separated cameras. There are numerous algorithms available but most of them use only the intensity information in the images and ignore the spectral content, the color. We have designed our own proprietary algorithm in [6] where all spectral components of the image sequences participate in parallel in the reconstruction process. In addition, our method, named SOFIA from Spectral Optical Flow Iterative Algorithm, provides iterative multi-scale reconstruction of the displacement field. The spatial scale or aperture parameter has been studied comprehensively earlier [3,4,5,7]. Our approach however, goes one step further and uses iteratively a sequence of scales, running from coarse-grained to fine, in order to stabilize the solution of the inverse problem without losing spatial resolution. Such multi-scale method provides hierarchical control over the level of detail that is needed for each individual application, ranging from large-scale global displacements to finer, pixel-level ones.

For global displacements, where individual pixels are not relevant, the reconstruction of the OF and subsequent aggregation of the velocity field is obviously a highly redundant procedure. For such applications we have developed a second proprietary algorithm [8], named GLORIA, where global displacements, such as translations, rotations, dilatations, shear or any other group transformations can be reconstructed directly without solving the OF problem at the pixel level. Such an approach assumes certain knowledge, or model behind the OF content, but it has significant computational advantages that allow usage in real-time applications. It gives as an output the group parameter variations that explain the differences in the sequences of images.

Figure 1 illustrates the overall spectrum of the OF applications reviewed here. For the majority of tasks, we refer to GLORIA global reconstruction. The latter is best suitable in scenarios where the overall behavior is relevant for detection or alerting and the exact localization of the process is not required. These are the cases for monitoring convulsive epileptic seizures, falls, respiratory disruptions, object tracking and image stabilization. For the application of detection and localization of explosions, we use the SOFIA algorithm. Here we briefly introduce the individual implementation modules and challenges.

The principal motivation for developing our OF remote detection techniques was the need for remote alerting of major convulsive seizures in patients with epileptic condition. Epilepsy is a debilitating disease of the central nervous system [9] that can negatively affect the lives of those suffering from it. There are various forms and suspected causes [10] for the condition, but in general, epilepsy manifests with intermittent abnormal states, fits or seizures that interrupt normal behavior. Perhaps the most disrupting types of epileptic seizures are the convulsive ones where the patient falls into uncontrollable oscillatory body movements [11,12]. During these states the individual is particularly vulnerable and at higher risk of injuries or even death. Especially hazardous are terminal cases of Sudden Unexpected Death in Epilepsy, or SUDEP [13,14]. The timely detection of epileptic seizures can therefore be essential for protecting the life of the patients in certain situations [15]. Because of the sudden, unpredictable occurrence of the epileptic seizures, a continuous monitoring of the patients is essential for their safety. Automated detection of seizures has long been studied [16,17,18,19] and effective techniques based on electroencephalography (EEG) signals are now in use in specialized diagnostic facilities. Those systems are however not directly applicable for home or residential facilities use as they require trained technicians to attach and control the EEG electrodes. The latter can also cause discomfort to the patient. Wearable devices that use 3D accelerometers are available and validated for use in patients [20,21,22,23,24]. Although effective and reliable, these devices need constant care, charging and proper attachment. They may, therefore, not be the optimal solution for some groups of patients. Their visible presence may also pose ethical issues related to stigmatization. Alternatively, bed mounted pressure or movement detectors are also used [25,26] but their effectiveness can be hampered by the position of the patient and the direction of the convulsive movements. Notably, both classes of the above-mentioned detectors rely on limited measures of movements from one single spatial point. These shortcomings can be resolved by using video observation that can provide a “holistic” view of the whole of substantial part of the patient’s body. Continuous monitoring by operators however, is a time and attention consuming process demanding great amounts of operator work[20–24load. In addition, privacy concerns may restrict or even prevent the use of manned video monitoring. To address these issues, automated video detection techniques have been investigated [27,28,29,30,31,32,33,34,35,36]. In these works, recorded video data has been used to analyze the movements of the patient and validate the detection algorithms. Such systems can be useful as tools for offline video screening and will increase the efficiency of the clinical diagnostic workflow. It is not always clear however, which of the proposed algorithms are suitable for real-time alerting of convulsive seizures.

In our work [37] we reported results from operational system for real time continuous monitoring and alerting. It employs the GLORIA OF reconstruction algorithm and is in use in a residential care facility. In addition, the system allows for continuous, on-the-fly, personalization and adaptation of the algorithm parameters [38] by using an unsupervised leaning paradigm. With this functionality, the alerting device finds optimal balance between specificity and sensitivity and can adjust its operational modalities in cases of changes of the environment or patient’s status.

In addition to detecting of convulsive epileptic seizures, we investigated the possibility of predicting post-ictal generalized electrographic suppression events (PGES) that may be a factor in the SUDEP cases [39]. In [40] we found, using spectral and image analysis of the OF, that in cases of tonic-clonic convulsive motor events, the frequency of the convulsions or the body movements per second, exponentially decreases towards the end of the seizure. We also developed and validated an algorithm for automated estimation of the rate of the decrease from the video data. Based on a hypothesis derived from a computational model [41], we related the amount of decrease of the convulsive frequency to the occurrence and the duration of a PGES events. This finding was further validated on cases with clinical PGES [42] and may provide a method for diagnosing and even alerting in real-time of possible post-ictal arrests of brain activity.

Another area of application of real-time optical flow video analysis is the detection and alerting for falls. Falls are perhaps the most common causes of injuries, especially among the elderly population [43,44,45,46]. Also, in the vulnerable population of epileptic patients, falls resulting from epileptic arrests can be a major complication factor [47,48,49]. Accordingly, a lot of research and development has been dedicated to the detection and prevention of these events [50,51,52,53,54,55,56]. The challenge of robust detection of falls has led to accumulating of empirical data in natural and simulated environments [57,58] and the development of new algorithms [59,60,61,62,63,64,65]. One of the major challenges is the reliable distinction of fall events from other situations in real-world data [66] and the comparison of the results to simulated scenarios [67]. As with the alerting for epileptic seizures, wearable devices provide solution [61,68] but also have their functional and support limitations. Non-wearable fall detection systems [69] have been also developed and implemented, including approaches based on sound signals [70,71,72] produced by a falling person.

Possibly the most reliable and studied fall detection systems are based on automated video monitoring [73,74,75,76,77,78,79,80,81,82]. Algorithms based on depth imaging [83], some using Microsoft Kinect stereo vision device, are also proposed [84]. Notably there are few works addressing the issue by comb[59–65ining multiple modalities [85]. The simultaneous use of video and audio signals has been found to improve the performance of the detector [86,87]. Recently, machine learning paradigms have been added to the detection techniques offering personalization of the methods [88,89,90,91,92,93]. Optical Flow is one of the widely spread methods for detecting falls in video sequences [89,94,95]. We applied our proprietary global motion reconstruction algorithm GLORIA in [93] where the six principal movement components are fed into a pre-trained convolutional neural network for classification. Such an approach allows including a fall alerting module to our integral awareness concept.

One of the potential causes of death during or immediately after epileptic seizures is respiratory arrest, or apnea [96]. Together with cardiac arrests [14] this may be a major confounding factor in the cases of SUDEP. While in cases of epileptic condition seizure detection can be the lead safety modality [97], the detection and management of apnea events for the general population is relevant as well [98,99]. The cessation of breathing is the most common symptom for the Sudden Infant Death Syndrome (SIDS) that usually occurs during sleep and the cause often relates to breathing problems.

Devices dedicated to apnea detection during sleep have been proposed and tested in various conditions. Especially relevant are methods based on non-obstructive contactless sensor modalities [100,101,102,103] including sensors inbuilt in smart phones [104]. A depth registration method using Microsoft Kinect sensor has also been investigated [105]. Perhaps the most challenging approaches for apnea detection and alerting are those using life video observations. Cameras are now available in all price ranges and they are suitable for day and night continuous monitoring of subjects. To automate the task of recognizing apnea events from video images in real time, researchers have developed effective algorithms. Numerous approaches have been proposed [106,107,108,109,110,111,112,113] in the literature. A common feature in these works is the tracking of the respiratory chest movements of the subject [114]. In our work [115], we applied global motion reconstruction of the video optical flow and subsequent time-frequency analysis followed by classification algorithms to identify possible events of respiratory movement arrests. In a recent patent application [US20230270337A1], tracking of respiratory frequency provides effective method for alerting of SIDS.

Optical flow reconstruction at pixel scale [6] was also used in the context of detection and quantification of explosions in public spaces [116]. Fast cameras registering images in time-loops provided view from multiple locations. Dedicated algorithm for 3D scene reconstruction was constructed to localize point events registered simultaneously from the individual cameras. This part of the technique goes outside the scope of the present work. The optical flow analysis, together with the reconstructed depth information, provided an estimate of the charge of the explosion. Explosion events were detected and quantified from the local dilatation component calculated as the divergence of the velocity vector field at suitable spatial scale. Further in the methods we give some more details of this concept, here we note that optical flow-based velocimetry has also been explored for near-field explosion tracking [117].

The last two topics of this survey concerns indirect application of the optical flow global motion reconstruction. The first application is dedicated to automated tracking of moving objects or subjects [118,119,120,121]. This is achieved by either defining a dynamic region of interest (ROI) containing the object or by applying physical camera movements such as pent, tilt and zoom (PTZ). This is valuable addition to the monitoring paradigms described above, as manual object tracking is an extremely labor intensive and attention demanding process. Automated tracking in video sequences has been extensively investigated especially for applications related to traffic management and self-driving vehicles [122,123,124,125,126] or surveillance systems [127,128]. Methods dedicated to human movements in behavioral tasks has also been reported [129] in applications where the objectives are mainly related to the challenge of computer-human interfaces [130,131,132]. In our approach published in [133] and in a filed patent application, we used the global movement parameters reconstruction GLORIA to infer the transformation of a ROI containing the tracked object. Leaving the technical description for the next paragraph, we note that OF based methods have been introduced in other works [134,135], however no use of the direct transformation parameter reconstruction has been made. To compare, our approach reduces the computational load and makes possible the implementation of the algorithm in real-time. In addition to the single camera-tracking problem, simultaneous monitoring from several cameras has been in the focus of interest of researchers [136,137,138,139,140,141,142]. We have addressed the multi-camera tracking challenge by adding adaptive algorithms [143] that reinforce the interaction between the individual sensors in the course of the observation process. Deep learning paradigm has been also employed [144] in multi-camera application for traffic monitoring. In our approach, the coupling between the individual camera tracking routines is constantly adjusted according to the correlations between the OF measurements. We have studied both linear correlation couplings and non-linear association measures. In this way, we have established a dynamic paradigm for video OF based sensor fusion reinforcement. The fusion between multiple sensor observations is a general concept that can be employed in a broader array of applications [145,146,147].

Finally, we introduce the application of GLORIA method to stabilizing of video sequences [US 2022/0207657] when artefacts from camera motion are present. Although optical flow techniques have been used earlier for stabilizing camera imaging [148,149,150], our approach brings two essential novel features. First, it uses the global motion parameters, namely translation, rotation, dilatation and shear directly reconstructed from the image sequence and therefore avoid the computationally demanding pixel-level reconstruction of the optical flow. Next, we use the group properties of the global transformations and integrate the frame-by-frame changes into an aggregated image transformation. For this purpose, the group laws of vector diffeomorphisms are applied as we explain later in the methods.

The rest of the paper is organized as follows. In the Materials and Methods section, we give the basic formulations of the methods used for the different tasks graphically presented as blocks in Figure 1. We start with the definition of our proprietary SOFIA and GLORIA optical flow algorithms. Next, the application of the GLORIA output for detecting convulsive seizures, falls and apnea adverse events is explained. The extension of the seizure detection algorithm to post-ictal suppression forecast is also presented. Explosion detection, localization and charge estimation from optical flow features is briefly explained. At the end of the methodological section, we focus on the use of global motion optical flow reconstruction for tracking objects and for stabilizing video sequences affected by camera movements.

In the Results section, we report our major findings from our work on the variety of applications. Some limitations and possible extensions of the methodology presented in the Discussion section. An overall assessment of the use of the proposed approaches is offered in the Conclusions.

2. Materials and Methods

In the next two subsections, we present in short, the methods introduced in our works [6,8].

2.1. Spectral Optical Flow Iterative Algorithm (SOFIA)

Here we recall the well-known concept of optical flow. A deformation of an object or a media can be described by the change of its positions according to some deformation parameter $t$ (time in the case of temporal processes):

$$x\left(t+\delta t\right)=x\left(t\right)+v(x,t)\delta t$$

(1)

In (1) $v(x,t)$ is the vector field generating the deformation with an infinitesimal parameter change $\delta t$which in the case of motion sequences is the time incremental step. We denote a multi-channel image registering a scene as $L^c\left(x,t\right);c=1,\dots ,N_c,x\in R^2$ (to simplify the notations we consider the channels to be a discrete set of spectral components or colors). If no other changes present in the scene, the image will change according to the “back-transformation” rule, i.e., the new image values at given point are those transported from the old one due to the spatial deformation.

$$L^c\left(x,t+\delta t\right)=L^c\left(x-v(x,t)\delta t,t\right)$$

(2)

Optical flow reconstruction is then an algorithm that attempts to determine the deformation field $v\left(x,t\right)$given the image evolution. Assuming small changes and continuous differentiable functions we can rewrite Equation (2) as a differential equation:

$$\begin{gathered} {\displaystyle \frac{d{L}^c}{dt}}=-\mathit{\nabla }{L}^c·v\equiv {\mathit{\nabla }}_v{L}^c; \\ {\mathit{\nabla }}_v\equiv v·\mathit{\nabla }\equiv \sum _k{v_k\mathit{\nabla }}_k; {\mathit{\nabla }}_k{L}^c\equiv {\displaystyle \frac{\partial L^c}{\partial x_k}} \end{gathered}$$

(3)

We use here notations from differential geometry where the vector field is a differential operator ${\mathit{\nabla }}_v$. From Equation (3) it is clear that in the monochromatic case $N_c=1$the deformation field is defined only along the image gradient and the reconstruction problem is underdetermined. On the contrary, if $N_c>2$ the problem may be over-determined as the number of equations will exceed the number of unknown fields (here and throughout this work we assume two spatial dimensions only although generalization to higher image dimensions is straightforward). However, if the spectrum is degenerate, for example when all spectral components are linearly dependent, the problem is still under-determined. To account for both under and over-determined situations we first postulate the following minimization problem defined by the quadratic local cost-function in each point $\left(x,t\right)$ of the image sequence as:

$$\begin{gathered} C\left\{L^c\left(x,t\right),v\left(x,t\right)\right\}\equiv \sum _c{\left|{\displaystyle \frac{d{L}^c\left(x,t\right)}{dt}}+\mathit{\nabla }{L}^c\left(x,t\right)·v(x,t)\right|}^2 \\ v\left(x,t\right)={argmin}_v\left[C\left\{v\left(x,t\right)\right\}\right] \end{gathered}$$

(4)

Clearly because the cost-function in Equation (4) is positive and the solution for $v\left(x,t\right)$always exists. However, this solution may not be unique because of possible zero modes, i.e., local directions of the deformation field along which the cost-functional is invariant.

Applying the stationarity condition for the minimization problem (1) and introducing the quantities:

$$H_k=-\sum _c{\displaystyle \frac{d{L}^c}{dt}}{\mathit{\nabla }}_k{L}^c; S_{kj}=\sum _c{\mathit{\nabla }}_k{L}^c{\mathit{\nabla }}_j{L}^c;j,k=\mathrm{1,2}$$

(5)

The equation for the velocity vector field minimizing the function is:

$$\sum _j{S}_{kj}\left(x,t\right)v_j\left(x,t\right)=H_k\left(x,t\right);$$

(6)

In definition (2) $S_{kj}$ will be referred as the structural tensor and $H_k$ as the driving vector field.

In some applications, it might be advantageous to look for smooth solutions for the optical flow equation. To formulate the problem, we modify the cost function so that in each Gaussian neighborhood of the point x on the image, the optical flow velocity field is assumed to be the spatially constant vector that can “explain” best the averaged changes in the image evolution in this neighborhood. Therefore, we can modify (literally blur or smoothen) the quadratic cost function (3) in each point $x$ of the image and its neighborhood as:

$$C^{\sigma }\left\{v\left(x\right)\right\}\equiv \sum _{y}G\left(x,y,\sigma \right)\sum _c{\left|{\displaystyle \frac{d{L}^c(y,t)}{dt}}+\mathit{\nabla }{L}^c(y,t)·v(x,t)\right|}^2$$

(7)

Where the Gaussian kernel is defined as:

$$G\left(x,y,\sigma \right)={\displaystyle \frac{1}{N_{\sigma }}}{e}^{-{\displaystyle \frac{{(x-y)}^2}{{\sigma }^2}}}$$

(8)

In Equation (8) the normalization factor ${\mathrm{N}}_{\mathsf{\sigma }}$ is conveniently chosen to provide unit area under the aperture function. Applying the stationarity condition to the so postulated smoothened cost function leads to the modified equation:

$$S_{kj}^{\sigma }\left(x,t\right)v_j\left(x,t\right)=H_k^{\sigma }\left(x,t\right)$$

(9)

The smoothened structural tensor and driving vector are obtained as:

$$\begin{gathered} H_k^{\sigma }\left(x,t\right)\equiv \sum _{y}G\left(x,y,\sigma \right)H_k\left(y,t\right); \\ S_{kj}^{\sigma }\left(x,t\right)\equiv \sum _{y}G\left(x,y,\sigma \right)S_{kj}\left(y,t\right) \end{gathered}$$

(10)

We can now invert the Equation (9) to obtain explicit unique solution (we skip here the introduction of a regularization parameter, leaving this to the original work) for the optical flow vector field, for a given scale:

$$v_j\left(x,t\right)={{\left(S_{kj}^{\sigma }\left(x,t\right)\right)}^{-1}H}_k^{\sigma }\left(x,t\right)$$

(11)

Let denote the solution as a functional of the image and its deformation, the scale parameter as:

$$v_j(x,t)=v_j\left\{L^c\left(x,t+\delta t\right),L^c\left(x,t\right),\sigma \right\}$$

(12)

We can approach now the task of finding a detailed optical flow solution by iteratively solving the optical flow equation for a series of ${\mathsf{\sigma }}^{\mathrm{n}}<{\mathsf{\sigma }}^{\mathrm{n}-1}<\dots {\mathsf{\sigma }}^1$decreasing scales using the solution of each coarser scale to deform the image and use it as input for obtaining the optical flow at the next finer scale. The iterative procedure can be expressed by the following iteration algorithm:

$$\begin{gathered} v^{\left(1\right)}\left(x,t\right)=v\left\{L^c\left(x,t+\delta t\right),L^c\left(x,t\right),{\sigma }^1,\rho \right\} \\ {v}^{\left(k+1\right)}\left(x,t\right)=v^{\left(k\right)}\left(x-w^{\left(k\right)}\left(x,t\right)\delta t,t\right)+w^{\left(k\right)}\left(x,t\right); \\ k=1\dots (n-1) \\ w^{\left(k\right)}\left(x,t\right)\equiv v\left\{L^c\left(x,t+\delta t\right),{ L}^c(x-v^{\left(k\right)}(x,t)\delta t,t),{\sigma }^{k+1},\rho \right\} \end{gathered}$$

(13)

The last iteration produces an optical flow vector field ${\mathrm{v}}^{\left(\mathrm{n}\right)}(\mathrm{x},\mathrm{t})$ representing the result of zooming-down through all scales.

2.2. Global Lie-Algebra Optical Flow Reconstruction Algorithm (GLORIA)

In some applications, it might be advantageous to look first or only for solutions for the optical flow equation that represent known group transformations.

$$v\left(x,t\right)\equiv \sum _a{A^u\left(t\right)v}^u\left(x\right), u=1\dots N_G$$

(14)

In Equation (5) $v^u\left(x\right)$ are the vector fields corresponding to each group generator and $A^u\left(t\right)$ are the corresponding transformation parameters, or group velocities in the case of velocity reconstruction context. We can then reformulate the minimization problem by substituting (5) into the cost-function (4) and consider it as a minimization problem for determining the group-coefficients $A^u\left(t\right)$.

$$\begin{gathered} C\left\{A\right\}\equiv \sum _{c,x}{\left|{\displaystyle \frac{d{L}^c(x,t)}{dt}}+\sum _u{A}^u\left(t\right)v^u\left(x\right)·\mathit{\nabla }{L}^c(x,t)\right|}^2 \\ A\left(t\right)={argmin}_A\left[C\left\{A\left(t\right)\right\}\right] \end{gathered}$$

(15)

Using notations from differential geometry, we can introduce the generators of infinitesimal transformations algebra as a set of differential operators.

$$G^u\left(x\right)\equiv \sum _k{v}_k^u{\left(x\right)\mathit{\nabla }}_k$$

(16)

The operators defined in (16) form the Lie algebra of the transformation group.

Applying the stationarity condition for the minimization problem (4) and introducing the quantities:

$$\begin{gathered} H^u=-\sum _{x,k,c}{v}_k^u\left(x\right){\displaystyle \frac{d{L}^c}{dt}}{\mathit{\nabla }}_k{L}^u; \\ S^{uq}=\sum _{x,k,j,c}{v}_k^u\left(x\right){\mathit{\nabla }}_k{L}^c{\mathit{\nabla }}_j{L}^c{v}_j^q\left(x\right);u,q=1\dots N_A \end{gathered}$$

(17)

The equation for the coefficients minimizing the function is:

$$\sum _q{S}^{uq}{A}^q=H^u$$

(18)

We can now invert Equation (18) to obtain the unique solution (we skip again the regularization step in case of singular matrix $S^{uq}$) for the optical flow vector field coefficients defined in (14):

$$A^q=\sum _u{\left(S^{uq}\right)}^{-1}{H}^u$$

(19)

We apply the above reconstruction method in sequences of two-dimensional images, restricting the transformations to the six parameters non-homogeneous linear group:

$$\begin{gathered} G^{{translations}_1}\left(x\right)={\mathit{\nabla }}_1; G^{{translations}_2}\left(x\right)={\mathit{\nabla }}_2; \\ {G}^{rotation}\left(x\right)=x_2{\mathit{\nabla }}_1-x_1{\mathit{\nabla }}_2; \\ {G}^{dilatation}\left(x\right)=x_1{\mathit{\nabla }}_1+x_2{\mathit{\nabla }}_2; \\ G^{{shear}_1}\left(x\right)=x_1{\mathit{\nabla }}_2;{ G}^{{shear}_2}\left(x\right)=x_2{\mathit{\nabla }}_1 \end{gathered}$$

(20)

Those are the two translations, rotation, dilatation and two shear transformations.

2.3. Detection of Convulsive Epileptic Seizures

Applying the algorithm GLORIA on the image sequence with the generators (20) produces six time series representing the rates of changes (group velocities) of the six two-dimensional linear inhomogeneous transformations.

$${L^c\left(x,y,t\right);c=\{R,G,B\}=>V}_g\left(t\right);g=\{TrX, TrY, Rot, Dil, ShX,ShY\}$$

(21)

We use next a set of Gabor wavelets (normalized to unit 1-norm and zero mean) with exponentially increasing wavelengths ${\mathit{f}}_{\mathit{k}}, k=1..200$

$$\begin{gathered} W_g\left(t,f_k\right)=\left|{\int }_{t^{\mathrm{\text{'}}}}d{t}^{\mathrm{\text{'}}}g\left(t-t^{\mathrm{\text{'}}},f_k\right)V_g\left(t^{\mathrm{\text{'}}}\right)\right| \\ g\left(t-t\text{'},f\right)=(e^{-{\pi }^2{\alpha }^2{f}^2{(t-t\text{'})}^2-i2\pi f(t-t\text{'})}-O_f)/N_f \\ W\left(t,f_k\right)\equiv {〈W_g\left(t,f_k\right)〉}_g; \\ W^q\left(f_k\right)\equiv {〈W\left(t,f_k\right)〉}_{t\in q} \\ f_k=f_{min}{e}^{(k-1)\mu } \end{gathered}$$

(22)

For the exact definitions and normalizations, we refer to earlier publications [26,35] and here we note that the wavelet spectrum in (22) is a time-average along each images sequence window denoted with q.

Next, we define the “epileptic content” as the fraction of the wavelet energy contained in the frequency range defined here as $\left[f_a,f_b\right]$.

$$E\left(q,f_a,f_b\right)\equiv {\displaystyle \frac{\sum _{f\in [f_a,f_b]}{W}^q\left(f\right)}{{\sum }_f{W}^q\left(f\right)}}$$

(23)

In the “rigid” application, as well as an initial setting for the adaptive scheme, we use the default range of $f\in \left[f_a,f_b\right]\equiv \left[2\dots 7\right] Hz$ that represents the most common observed frequencies in convulsive motor seizures. To compensate for different frequency ranges that may be used, we calculated also the same quantity in (3) but for a signal with “flat” spectrum representing random noisy input. Then we rescale the epileptic marker as

$$\check{E}\left(q,f_a,f_b\right)={\displaystyle \frac{E\left(q,f_a,f_b\right)-E_0(f_a,f_b)}{1-E_0(f_a,f_b)}}$$

(24)

Here $E_0$ is the relative wavelet spectral power of a white noise. Note that in (23) and (24) the quantity q is a discrete index representing the frame sequence number and corresponds, as stated earlier, to a time window conveniently chosen of approximately 1.5 seconds.

We use three parameters $[\mathrm{N},\mathrm{n},\mathrm{T}]$to detect an event (seizure alert) in real time. At each time instance, we take the seizure marker (3a) in the N preceding windows. If from those N, at least n have values $\check{E}$>T an event is generated and eventually (if within the time selected for alerts) sent as an alert to the observation post. The default values are [7 6 0.4]. This corresponds to a criterion that detects if from the past 10.5 seconds at least 9 seconds contain epileptic “charge” (24) higher than 0.4. These values are used in the rigid mode as well as an initial setting in the adaptive mode described in [37,38].

The design and operation of the adaptive algorithm, representing a reinforcement learning approach, goes beyond the scope of this work. We notice only that the proposed scheme adjusts both the frequency range and the detection parameters $[\mathrm{N},\mathrm{n},\mathrm{T}]$while performing the detection task. A clustering algorithm applied on the optical flow global movement traces (21) provides the labeling used for a “ground truth”. We refer to [38] for a detailed description of the unsupervised reinforcement learning technique.

2.4. Forecasting Postictal Generalized Electrographis Suppression (PGES)

The change in clonic frequency during a convulsive seizure can be modelled by fitting a linear equation to the logarithm of the inter-clonic interval [41] . If the times of successive clonic discharges for a given seizure are $t_k$ (marked for example by visual inspection of the EEG traces or in video recordings), then exponential slowing down can be formulated as:

$${ICI}_k\equiv t_{k+1}-t_k={C_{0}e}^{\alpha {\tau }_k};{\tau }_k\equiv {\displaystyle \raisebox{1ex}{${ (t}_{k+1}+t_k)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(25)

In Equation (25), $\mathsf{\alpha }$ is a constant defining the exponential slowing. Our hypothesis, validated in [41] is that the overall effect of slowing-down is a factor correlated to the PGES occurrence and duration. The total effect of ictal slowing for each seizure is quantified as

$${ICI}_{term}\equiv C_0{e}^{\alpha T_{seizure}}$$

(26)

In the above definition ${ICI}_{term}$ is the terminal inter-clonic interva, the $C_0$ and $\mathsf{\alpha }$ parameters are derived for each case from the linear fit procedure in Equation (25), and $T_{seizure}$ is the total duration of the seizure.

The optical flow technique was used to estimate the parameters of the ictal frequency decrease [40]. Starting point is the Gabor spectrum $W\left(t,f_k\right)$ as definedin Equation (22). Because of the exponential increase of the wavelet central frequencies, an exponential decrease of the clonic frequency will appear in a straight line in the time-spectral image. We use this fact to estimate the position and slope of such a line by applying two-dimensional integral Radon transformation, performing integration along all lines in the time-frequency space:

$$\begin{gathered} RW\left(r,\theta \right)\equiv \underset{-inf}{\overset{+inf}{\int }}W\left(t\left(u\right),f\left(u\right)\right)du \\ \left[t\left(u\right),f\left(u\right)\right]\equiv \left[\left(u\mathit{sin}\theta +r\mathit{cos}\theta \right),\left(r\mathit{sin}\theta -u\mathit{cos}\theta \right)\right] \end{gathered}$$

(27)

We applied further a simple global maximum detection for the $\mathrm{R}\mathrm{W}\left(\mathrm{r},\mathsf{\theta }\right)$ function and determine the angle and distance parameters of the dominant ridge line as

$$\left\{r_M,{\theta }_M\right\}=armax\left\{RW\left(r,\theta \right)\right\}$$

(28)

Finally, one can estimate from (22) and (25) the exponential constant $\mathsf{\alpha }$ as:

$$\alpha =\mu {\mathit{tan}}^{-1}\left({\theta }_M\right)$$

(29)

The above estimate was done for multiple video recordings of convulsive seizures and used to establish associations with the PGES occurrence and duration. For more technical and analytic insight, we refer to [40].

2.5. Detection of Falls

Here we present briefly only the essential parts of the fall detection algorithm originally introduced in [88]. In this original work, standard optical flow pixel-level algorithm was used but the general methodology, apart from some spatial correction factors, is applicable to the new GLORIA technique.

Assuming a position of the camera that laterally registers the space of observation, the motion component from the set (20), (21) relevant for detection of falls is the vertical velocity corresponding to the translational component $V_y\left(t\right)$ as function of time. Taking a discrete derivative of this time series, we can calculate the vertical acceleration $A_y\left(t\right)=V_y\left(t\right)-V_y\left(t-1\right)$. We can assume also that positive values of $V_y$ correspond to downward motion (otherwise we can invert the sign of the parameter).

From the functions$A_y\left(t\right)$and$V_y\left(t\right)$ we define a triplet of time-series features $\left\{A\left(t_A\right),V\left(t_V\right),D\left(t_D\right)\right\}$ corresponding to the local positive maxima of the functions $\left\{A_y\left(t\right),V_y\left(t\right),-A_y\left(t\right)\right\}$. These features are the maximal downward acceleration, velocity and deceleration. An event eligible for fall detection is characterized by these three features whenever the positions of the consecutive maxima are ordered as $t_A<t_V<t_D$.

In addition to the three optical flow derived features $\left\{A,V,D\right\}$ we use a forth one associated with the sound that a falling person may cause. For each window (we use windows of 3 seconds with two seconds overlap, step of one second) we calculate the Gaussian smoothened Hilbert envelope of the audio signal (aperture of 0.1 second) and take the ratio of the maximal to the minimal values. The ratio $S$ is then associated to all events in the corresponding window where the detection takes place. This way we obtain four features $\left\{A,V,D,S\right\}$ to classify an event as a fall.

The rest of the algorithm involves training technique, support vector machine (SVM) with a radial basis function kernel, to establish the domain in the four-dimensional feature space corresponding to fall events.

In reference [93] we propose a variant of this algorithm that employs all six reconstructed global movements and is enhanced with alternative machine learning techniques such as convolutional neural networks (CNN), skipping however the audio signal component. This approach is less sensitive to the position of the camera and avoids synchronization and reverberation problems associated with the audio registration in real world settings.

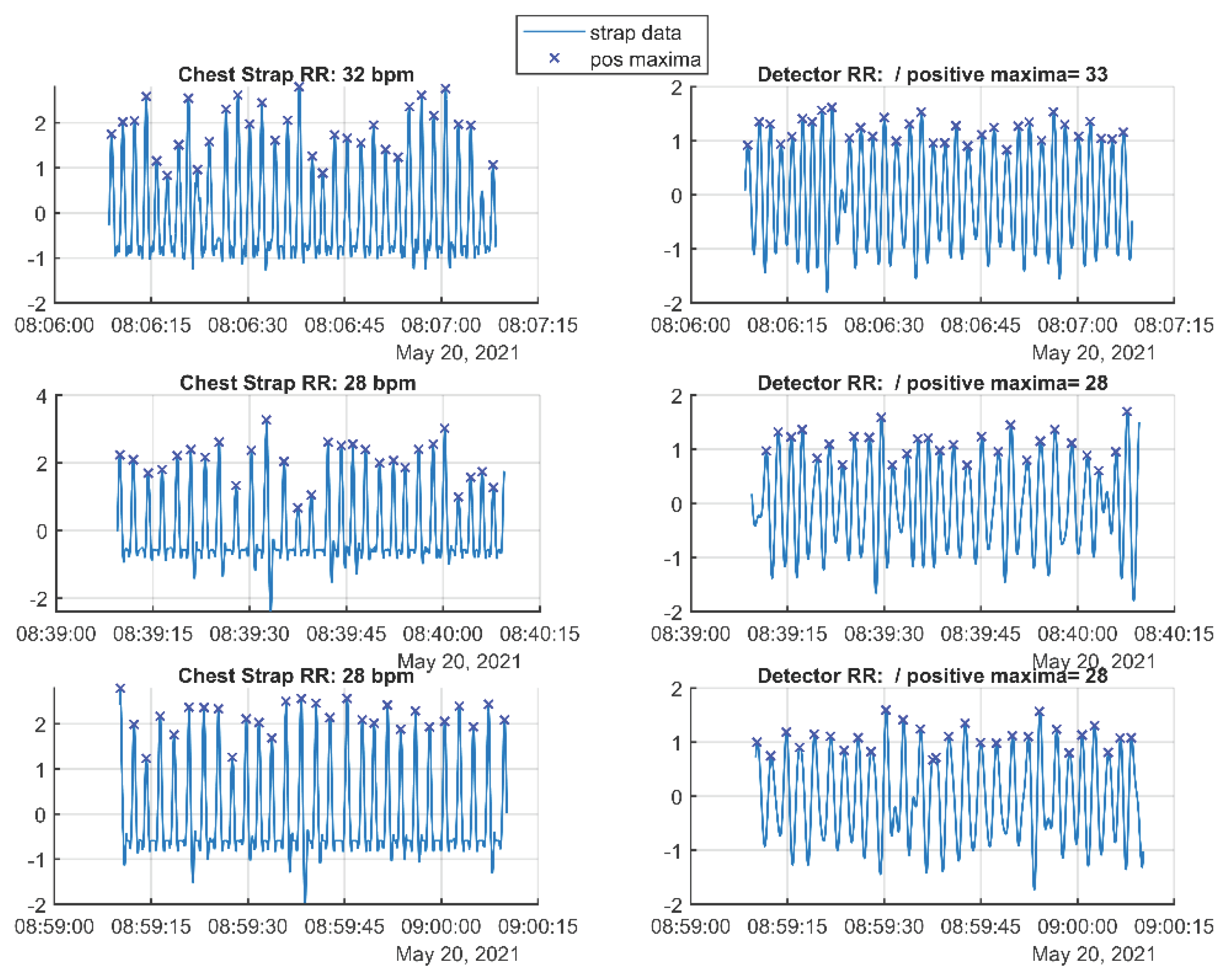
2.6. Detection of Respiratory Arrests, Apnea

Following the methodology of [115], the same optical flow reconstruction and Gabor wavelet spectral decomposition is used as with the convulsive seizure detection, repeating steps (21), (22). The relative spectrum essential for respiratory tracking is defined similarly to (23) but without the window-averaging of the spectra:

$$RE\left(t,f_a,f_b\right)\equiv {\displaystyle \frac{\sum _{f\in [f_a,f_b]}W\left(t,f\right)}{{\sum }_{f}W\left(t,f\right)}}$$

(30)

Where now $\left[f_a,f_b\right]=\left[\mathrm{0.1,1}\right]Hz$. The denominator in Equation (30) is the total spectrum for all wavelet central frequencies (0.08 to 5 Hz in this implementation):

$$TS\left(t\right)={\sum }_{f}W\left(t,f\right)$$

(31)

We note that up to this point the algorithm can be modularly linked to the seizure detection processing using the same computational resources.

The specific respiratory arrest events are detected by further post-processing of relative and total spectra defined in (30) and (31).

First, we define a range of 200 scales ${\mathrm{s}}_{\mathrm{k}}$($\mathrm{k}=\mathrm{1,2},\dots 200$), with exponentially spaced values in the range 25-500 pixels. For each scale, an aperture sigmoid template is defined for window $\mathsf{\tau }$:

$$S\left(\tau ,k\right)={N_k^S}^{-1}{\displaystyle \frac{e^{\tau /s_k}-e^{-\tau /s_k}}{e^{\tau /s_k}+e^{-\tau /s_k}}}{e}^{{-\left|\tau \right|}^2/{s_k}^2} ; \tau =[-3s_k:3s_k]$$

(32)

together with the Gaussian aperture template:

$$G\left(\tau ,k\right)={N_k^G}^{-1}{e}^{{-\left|\tau \right|}^2/{s_k}^2}$$

(33)

In Equations (32) and (33) L2 normalization was applied through the coefficients ${{\mathrm{N}}_{\mathrm{k}}^{\mathrm{S},\mathrm{G}}}^{-1}$, with ${\mathrm{N}}_{\mathrm{k}}$ defined as the squared sum of the kth aperture template. The time window in (32) and (33) is chosen to be of three scale lengths, as values outside this range are suppressed by the Gaussian aperture factor. Sigmoid time-scale modulation $\mathrm{m}$ can then be obtained using the convolutions between the filters and the $\mathrm{R}\mathrm{E}$ signal:

$$m\left(t,k\right)={\displaystyle \frac{\underset{\tau }{\overset{\infty }{\int }}S(t-\tau )RE\left(\tau \right)d\tau }{\underset{\tau }{\overset{\infty }{\int }}G(t-\tau )RE\left(\tau \right)d\tau }}$$

(34)

To quantify the presence of significant respiratory range power drops, we calculated the mean sigmoid modulation $\mathrm{M}$ over the scales that correspond to observed drop times:

$$M\left(t\right)={〈m(t,k)〉}_{k\in s_{drop}}$$

(35)

Drop times were observed to be between 4.0 and 8.2 seconds in test recordings, and correspond to filters ${s_{drop}\in [s}_{70},s_{129}]$.

Potential respiratory events are defined at the times of local positive maximums of $M\left(t\right)$,$t_M=\left\{t:M\left(t\right)>\mathit{max}\left(M\left(t-1\right),M\left(t+1\right)\right);M\left(t\right)>0\right\}$. The first feature to be used for apnea detection, the sigmoid modulation maximum is then:

$$SMM\left(t_M\right)=M\left(t_M\right)$$

(36)

A second classification feature quantifying the change of total power at the time of events may distinguish events due to apneas from events due to gross body movements. For each event we therefore calculated the total power modulation ($\mathrm{T}\mathrm{P}\mathrm{M}$), comparing the 2 s before, to the 2 s after the $\mathrm{M}$ maximum:

$$\begin{gathered} TPM\left(t_M\right)={\displaystyle \frac{{〈TS〉}_a-{〈TS〉}_b}{{〈TS〉}_a+{〈TS〉}_b}} \\ a=\left[t_M,t_M+2s\right]; b=\left[t_M-2s,t_M\right]; \end{gathered}$$

(37)

Presumably, the $\mathrm{T}\mathrm{P}\mathrm{M}$ feature has a small and often negative value for apnea events, and a high value (positive of negative) for gross body movement events.

The two quantifiers (36) and (37) are then used to train a support vector machine (SVM) as in the previous application. We refer to [115] for further details.

Monitoring of the respiratory rate in infants between 2 and 6 months of age is another application of respiratory rate detection. It is critical in infants because unprovoked respiratory arrest (for some reason, most often during deep sleep, the baby “forgets” to breathe) is the leading cause of SIDS, especially in infants between 2 and 6 months of age. As in the previous task of detecting respiratory arrests, particularly central apnea, we developed a reliable, automated, non-contact algorithm for real-time respiratory rate monitoring using a video camera. The settings for the present task are well defined, since the baby lies swaddled in a crib, and the camera is mounted above the crib. This allows for easy preliminary selection of a rectangular ROI that lies close to the frontal camera plane, covering the chest and abdomen, i.e., the places where the dominant respiratory movements (expansion and contraction) occur.

In the patent application [US20230270337A1] six methods are proposed for detecting the respiratory rate $S\left(t\right)$ that may be used in different situations.

The total movement in the video is quantified as in the previous applications by the spectral optical flow algorithm GLORIA giving directly the rates of the six motions (20) in the plane $V\left(t\right)=\left\{V_c\left(t\right) | c=1,..,6\right\}$.

In some cases, the number of motion degrees can be reduced. For example, when the ROI is in a plane close to the frontal plane, the vectors (elements of the vector field corresponding to the motions caused by respiration) are decomposed mainly along the dilation and shear transformation axes, with only a small part of the respiration being projected onto the translation and possibly rotation axes. In such a case, both translations and rotations may be omitted due to the lack of quantification of the respiratory signal. In other cases, due to the presence of different objects in the video or different camera positions, only rotation may be omitted or a different set of quantifier motions may be chosen.

The features of the vector $V\left(t\right)$ are analysed in a specific frequency interval (Breathing Frequency of Interest (BFOI), or the interval of frequencies to be used to look for respiratory activity [0.5, 1] Hz). After filtering, we created a new signal $Vh\left(t\right)$ containing only periodicities between 0.5 and 1 Hz. The featured signal $V\left(t\right)$ may be filtered in any manner. For example, using a band-pass filter (e.g., using the Fourier transform, Gabor wavelets, or a Hilbert-Huang transform (HH)). Then a respiratory rate detector S(t) is built. The $S\left(t\right)$ outputs a time-dependent signal $S_n\left(t\right)$ that represents the breathing of the subject where the distinct local maxima(s) above a certain threshold represent the times of inhaling and the local minima(s) under a certain threshold represent the times of exhaling.

The abbreviations for the six methods are: VFD, GSD, ICD, GMD, HFD, and SCD. Here we give a brief description of each of them.

VFD is a data-driven method, where the filtered signal is used directly. Therefore, the method directly uses the selected components of the movements’ vector field between every two consecutive frames. The filtered signal represents a series of time vectors, and therefore, a complex time series is assumed. The selected complex time series is summarised (vector sum). Then, the obtained complex time series is divided into two time series, one for its real part and one for its imaginary part. The upper spline envelope over the maxima of the real-part time series represents the $X$ coordinates of the proposed respiratory rate detector, corresponding to time. The upper spline envelope over the maxima of the imaginary-part time series represents the $Y$ coordinates of the proposed respiratory rate detector corresponding to the magnitude. This results in a determination of $VFD\left(t\right)$, which means the time (i.e., the $X$-coordinates) and magnitude (i.e., the $Y$-coordinates) of the proposed respiratory rate detector S(t).

The GSD is a model-driven method, based on dimensionality decrease, where the breath detector can be built from the situational model. One may use GSD when there is only one type of movement in the frame, specifically the motions caused by the subject’s breathing. In such a case, the rest is noise due to the camera itself and the recording conditions. The GSD may also be used when there are several other movements in the frame, partially correlated with breathing, caused by different physical sources, and where a linear correlation exists between the various physical sources and respiration. Then, the GSD eliminates the linear correlations between different data dimensions. GSD uses principal component analysis (PCA) to eliminate linear correlations between different data dimensions, thereby reducing noise and enhancing the signal generated by breathing, and reducing the dimensions to a single one. By doing so, the resultant signal (data in principle mode) corresponds to the subject’s inhalations and exhalations, corresponding to the local maxima/minima of the signal.

The ICD is a model-driven approach based on dimensionality reduction. The ICD method is used when there are several other movements in the frame, partially correlated with breathing, caused by different physical sources, and a nonlinear correlation or no correlation between the various physical sources and respiration (as opposed to the linear correlation discussed above regarding the GSD method). In the ICD, independent component analysis (ICA) is employed to eliminate the nonlinear correlations, yielding a set of statistically independent signals. This result is based on the idea that different physical sources generate the resulting signals. In some cases, it may not be clear which of the obtained set of signals represents respiration, and it is also possible that the breathing signal is not separated as an independent physical source. Still, rather, different parts of it are involved in the separated signals. In such cases, the ICD may still be used for building the respiratory rate detector $S\left(t\right)$ when additional information is available that can answer these questions. Otherwise, one may use the methods discussed below.

The GMD is a model-driven method, based on dimensionality reduction. The GMD method may be used when additional information is available that can address the questions discussed above regarding the ICD method. For the GMD method, the data is in the principal mode (after, for example, the use of the GSD method, discussed above). In the GMD method, the received signals are embedded in time to obtain the unknown variable and possible time dependencies. Then, the observed time series are converted to state vectors. A phase-space reconstruction procedure can then be used to verify the system order and reconstruct all dynamic system variables while preserving the system’s properties. For each time series, the phase-space dimension and time lag are estimated, and the highest time lag, along with its corresponding phase-space dimension, is chosen. For all the time series obtained so far, the phase space of the uniformly sampled time-domain signal is reconstructed with the chosen couple: a time delay and embedding dimension. PCA may then be used for every newly obtained state vector to build a new system (e.g., resulting signals matrix after PCA) with removed time delay correlations (using PCA to put the resulting signals’ matrix into a principal mode again, removing the linear correlations between the nonlinearities caused by time embedding). In some examples, the resulting signal matrix after PCA may still contain linear or nonlinear trends. In such cases, the typical trend may be removed by summing the time series cumulatively and detrending the results. This may result in a system noise that persists in the result. If so, the detrended signal may be decomposed into components using the HH, and the first HH component may be used as a resulting signal (thereby removing the HH residual).

The HFD is a model-driven, spectral contrast-based detector. In the HFD, the empirical decomposition-based detector’s signal can be represented by the ratio between the sum of the second spectrum of the HH transform components of the signals Vh(t) and the sum of the second spectrum of the HH transform component of the signals $V\left(t\right)$.

SCD builds a model-driven, spectral contrast-based detector. In the method, to use the frequency (spectral) information, the time-dependent spectral content is calculated in each of the chosen group velocities using convolutions with Gabor filters, as described in the Detection of respiratory arrests section.

The respiratory rate detector S(t) may be constructed using two or more of the methods mentioned above. For example, the respiratory rate detector $S\left(t\right)$ may be built (first) by using the first, second, third, and fourth methods (i.e., the VFD method, the GSD method, the ICD method, and the GMD method discussed above), and then (second) by using the fifth and sixth methods (i.e., the HFD method, and the SD and SCD methods discussed above). Preferably, the respiratory rate detector $S\left(t\right)$ may be constructed (first) by using the fourth method (i.e., the GMD method), and then (second) by using the sixth method (i.e., the SD and SCD methods). Sometimes, more than one of the first, second, third, and fourth methods (discussed above) may be selected for use in constructing the respiratory rate detector $S\left(t\right)$. Additionally, in some cases, both the fifth and sixth methods can be chosen. The use of additional methods confirms the initial results and leverages some specific aspects of the current case. One or more artificial intelligence or machine learning methods can be employed to detect and recognise anomalies, thereby adjusting the system’s response. The final step is to join some consecutive local maxima that are too close to each other in time.

For the examples shown in the Results section, we derived time series, representing the spatial transformations or group velocities: translational velocities along the two image axes. Here, we initially chose to omit rotation due to the lack of quantification of the respiratory signal. Furthermore, we construct the respiratory detector as follows:

We obtained the time-dependent spectral composition by averaging the time series over the five group velocities. We then filtered the resulting signal using an empirical decomposition with a stopping criterion for the last level that has at least $2*T$ maxima (where $T$ is the recording time in seconds). We then used the HFD to obtain $S1\left(t\right)$ as the respiratory detector. The initial assumption is that the individual local maxima of $S1\left(t\right)$ represent the respiratory times. Where by “separate local maxima” we assume a threshold $\tau$ that connects some maxima to one if in time they are too close (${∆t}_{i,i+1}<\tau$) to each other. Therefore, we joined several detections of the same event.

2.7. Detection and Charge Estimation of Explosions

In the original publication [116] we have shown that three-dimensional scene can be reconstructed from images taken from multiple cameras situated in general positions and intersecting their fields of view. This reconstruction can be used to localize explosions and estimate its charge. Here we reproduce only the part of the methodology related to the use of optical flow.

To localize specific events in each of the camera’s images, global motion reconstruction provided by the GLORIA algorithm is not sufficient. For the purpose we need the complete vector displacement, or velocity in this application, field. One possible approach is to apply the SOFIA algorithm, where equation (11) gives the reconstructed local and instantaneous velocity field $\overrightarrow{v}\left(x,y,t\right)\equiv \left\{v_x\left(x,y,t\right),v_y\left(x,y,t\right)\right\}$. We omit the scale parameter or sequence of scales for simplicity.

Explosions are detected as expansion events that can be characterized by the high positive divergence of the vector field. Because of the high velocities associated with such events, high speed cameras with 6000 frames per second were used. To avoid local fluctuations, we define a smoothened Gaussian spatial derivative of the vector field:

$$\begin{gathered} {\mathit{\nabla }}_a^{\sigma }\overrightarrow{v}\left(\overrightarrow{r},t\right)\equiv \iint {\displaystyle \frac{\partial }{\partial r_a}}G\left(\overrightarrow{r}-\overrightarrow{\rho },\sigma \right){\overrightarrow{v}\left(\overrightarrow{\rho },t\right)d}^2\overrightarrow{\rho } \\ \overrightarrow{r}\equiv \left\{x,y\right\}\equiv \left\{r_1,r_2\right\} \\ G\left(\overrightarrow{r},\sigma \right)\equiv {\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{\left|\overrightarrow{r}\right|}^2}{{\sigma }^2}}} \end{gathered}$$

(38)

The divergence of the vector field at the selected scale (our choice was $\sigma$ of 30 pixels but the results were not sensitive to this parameter) is:

$$Q^{\sigma }\left(\overrightarrow{r},t\right)\equiv {\mathit{\nabla }}_x^{\sigma }{v}_x\left(\overrightarrow{r},t\right)+{\mathit{\nabla }}_y^{\sigma }{v}_y\left(\overrightarrow{r},t\right)$$

(39)

From the quantity (39) we can localize the coordinates in the image plane and video sequence time (frame) of potential explosion events

$$\left\{{\overrightarrow{r}}_E,t_E\right\}={argmax}_{\overrightarrow{r},t}\left(Q^{\sigma }\left(\overrightarrow{r},t\right)\right)$$

(40)

The localization procedure is done simultaneously in all camera registrations and the position of the explosion in the three-dimensional scene is reconstructed from the generic formalism developed in [116].

Finally, as an overall estimation of the released energy by the explosion, the following expression was proposed:

$$W=\sum _{t=t_E}^{t_E+T}\iint {\left|\overrightarrow{v}\left(\overrightarrow{r},t\right)\right|}^2{d}^2\overrightarrow{r}$$

(41)

This quantity is calculated for all camera registrations and added with the corresponding distance corrections. We selected T=100 frames corresponding to 1/60 of а second, the time for a sound wave to cover slightly over five meters.

2.8. Object Tracking

Tracking of moving objects by using the global motion optical flow reconstruction method is introduced in detail in [133]. Although it can be applied to any group of transformations, our choice here is on the two translation rates and the dilatation (a global scale factor quantity) that are provided by the first three generators from Equation (20). We mark for clear interpretation the triplet $\left\{A^1,A^2,A^3\right\}$ of reconstructed parameters in (19) as $T_x^i$ and $T_y^i$ for the translations and $D^i$ for the dilatation, where $i$ indicates which two consecutive frames $\left\{i-1,i\right\}$ were used for the calculation. We restrict the current method to only these three transformations because we do not intend to rotate the region of interest (ROI) with the tracked object nor change the ratio between the ROI dimensions - $L_x,L_y$. In this way, our method is directly applicable to a situation where pan, tilt, and zoom (PTZ) hardware actuators are affecting the camera field of view that corresponds to the two translations (pen and tilt) and the dilatation (the zoom). Accordingly, we define the dynamic ROI with a triplet of values $\left\{X_c^i,Y_c^i,L^i\right\}$ representing the coordinates of the ROI center and the length of the ROI diagonal $L=\sqrt{L_x^2+L_y^2}$. Because of the fixed, constant ratio between the ROI dimensions, these three parameters uniquely define the ROI at each frame $i$.

In this notation, the ROI transformation driven by the translations and dilatation reconstructed parameters is:

$$\begin{gathered} X_C^i= X_C^{i-1} + T_x^i; { Y}_C^i= Y_C^{i-1} + T_y^i \\ L^i= L^{i-1}*\left(1 + D^i\right); \end{gathered}$$

(42)

Equations (42) define the ROI transition between from frame $i-1$ to frame $i$. Note that in the size transformation of ROI, we have assumed that for infinitesimal dilatations $e^D\cong 1+D$.

We have developed an extension of the single camera tracking algorithm to simultaneous multi-camera ROI tracking in [143]. In its simplest form, a linear model can describe the relationship between the tracking processes from $N$ cameras:

$$RO{I}_a\left(k\right)=\sum _{b\ne a}^N{W}_{ab}*RO{I}_b\left(k\right)+R_a$$

(43)

In (43) $a,b=\left\{1,\dots ,N\right\}$ are the labels of the individual cameras. $W_{ab}$ are $3x3$ transitional matrices and $R_a$ are $3x1$ offset vectors; $ROI\equiv \left\{{\mathrm{X}}_{\mathrm{c}}^{\mathrm{i}},{\mathrm{Y}}_{\mathrm{c}}^{\mathrm{i}},{\mathrm{L}}^{\mathrm{i}}\right\}$ is considered a vector as defined above. In the original work [143] a dynamic reinforcement algorithm based on quadratic cost-function minimization is proposed that can determine the $W_{ab},R_a$ interaction parameters from the tracking process. This way, the individual cameras start the tracking independently but, in the process, they begin to synchronize their ROIs. The linear model (43) has limited applications and we introduced non-linear interactions between the tracking algorithms. The details go beyond the scope of this review.

2.9. Image Stabilizing

The challenge of stabilizing image sequences affected by camera motion artefacts can be formulated as follows. Let the image sequence $\left\{L^c\left(x,t+k\delta t\right)\right\};k=\mathrm{0,1},\dots n$ contain an initial image for $k=0$ and the subsequent registrations that are affected or shifted by the motion artefacts. The objective of the methodology patented in [US 2022/0207657] is to build a filter that restores the sequence at any discrete index $k>0$ to the initial image that is conveniently chosen. To this end we recall Equation (2) and introduce am extra notation

$$L^c\left(x,t+k\delta t\right)=L^c\left(x-v^{\left(k\right)}\left(x\right),t+(k+1)\delta t\right)\equiv D_{v^{\left(k\right)}}\left\{L^c\right\}$$

(44)

Here ${\mathrm{D}}_{\mathrm{v}}\left\{{\mathrm{L}}^{\mathrm{c}}\right\}$ is a short abbreviation for the vector diffeomorphism acting on the image. Note that here we have used the image optical flow transformation “in reverse”. We use the optical flow reconstruction algorithm, introduced in the first two subsections of the methods, to find the vector diffeomorphism $v^k\left(x\right)$ that returns the current image to the previous one. Stabilizing the image sequence and removing motion artefacts due to camera motion involves reconstructing the corresponding vector field that connects the shifted images at all times to the initial one. To achieve this, we first stress that the application of two successive morphisms $v\left(x\right)$ and $g\left(x\right)$ is not equivalent to one with the sum of the two vector fields. More precisely, we need to “morph” the first vector field (shift its spatial arguments) by the second one:

$$D_g\left\{D_v\left\{L^c\right\}\right\}=D_{g+D_g\left\{v\right\}}\left\{L^c\right\}$$

(45)

Therefore, the resulting vector field generating the diffeomorphism from two successive vector diffeomorphisms is:

$$V\left(g,v\right)=g+{\mathrm{D}}_{\mathrm{g}}\left\{\mathrm{v}\right\}$$

(46)

The above equation gives the group convolution law for vector diffeomorphisms. We apply (46) iteratively to reconstruct the global transformation between the initial image and any subsequent image of the sequence:

$$V_{k+1}=V_k+D_{V_k}\left\{v_k\right\}$$

(47)

Here, $v_k$ is the infinitesimal vector-field transformation connecting the images $L^c\left(x,t+k\delta t\right)$ and $L^c\left(x,t+(k+1)\delta t\right)$. The resulting aggregated vector field $V_k\left(x\right)$ connects the k-th image to the original member $L^c\left(x,t\right)$ of the video sequence. Note again that also in (47) the diffeomorphisms transform the sequence members in the reverse direction, from the current image to the initial.

We define therefore the stabilized $k$-th image as

$${S{L}^c\left(x,t+k\delta t\right)\equiv D}_{V_k}{L}^c\left(x,t+k\delta t\right)$$

(48)

The above Equation (48) is the required filter that “recovers” the shifted images and transforms them closest to the initial one. The latter can be chosen arbitrarily. Depending on the application, it can be updated at any fixed number $\mathbf{n}$ of images, or updated when some appropriate condition is met, for example when the aggregated vector field ${\mathbf{V}}_{\mathbf{k}}\left(\mathbf{x}\right)$ exceeds certain norm and the stabilization procedure becomes unfeasible.

3. Results

In the above technique, we can use either the local OF reconstruction approach SOFIA (11) or the global motion OF reconstruction GLORIA (14). In the first case, we attempt to filter all changes due to movements in the image sequence. Perhaps more flexible as well as computationally faster is the second option. GLORIA algorithm allows selecting a subset of transformations to filter out, leaving the rest of the movements intact. In the case of oscillatory movements of a camera, we can choose to filter only one or both of the translational movements. Rotational, dilatational and other displacements will be still present in the video sequence as they may be part of the intended observation content.

In the next subsections, we show summaries of the main results reported in our works ordered by the applications presented in the previous section.

3.1. Spectral Optical Flow Iterative Algorithm (SOFIA)

The accuracy of optical reconstruction has been evaluated for multiple images, transformation fields and reconstruction parameters [6]. Our method, applied iteratively with sequence of scales [1, 2, 4, 8, 16] significantly outperforms the standard Matlab^® Horn-Schunk ‘opticalFlowHS’ routine with default parameters of smoothness: 1, Maximal Iterations: 10 and minimal velocity 0. The average reconstruction error, tested for 8 images and 20 random vector deformation fields of average magnitude 0.5 pixels and spatially smoothened to 32 pixels was 2.5%. Our results show also that the reconstruction precision depends on the number of iterations going from large to fine scales. Table 1 gives the average reconstruction error as function of the iteration scale.

We found also that the spectral content of the image can influence the accuracy of the OF reconstruction. Our method is intrinsically multi-spectral; images with low spectral dispersion (like monochromatic ones) give higher error than images with balanced spectral content. In addition, images with higher spatial wavelengths give better OF reconstruction accuracy than images containing more short distance details (textures). For a quantified version of the above statements we refer to the original work [6].

3.2. Global Lie-Algebra Optical Flow Reconstruction Algorithm (GLORIA)

Following the results from the validation tests described in [8], GLORIA reconstruction applied with the transformations (20) gives accuracy depending on the magnitude of the transformations. In Table 2 we show the average errors for the corresponding group parameters.

3.3. Detection of Convulsive Epileptic Seizures

Here we present some validation results that are from offline application of our seizure detection algorithm. We first note that there are several different instances of the detector and the specific details are reported in the corresponding original works. The basic component is however, the use of optical flow motion parameters reconstruction and a subsequent spectral filtering.

In the seminal work [36] we have analyzed the performance of the detector in 93 convulsive seizures recorded from 50 patients in our long-term monitoring unit. We show that for a suitable selection of the detection threshold, a sensitivity of 95% and a false positive (FP) rate of less than one FP per 24 hours is achievable.

Automated video-based detection of nocturnal convulsive seizures was later investigated in our residential care facility [35]. From 50 convulsive seizures, all were detected (100%) sensitivity and the FP rate was 0.78 per night. The detection delay in 78% of the cases was less than 10 seconds; maximal delay was of 40 seconds in one case. There were also other types of epileptic seizures registered in the study; the detector was less sensitive to motor events of non-convulsive patterns.

Detection and alerting for convulsive seizures in children were conducted in [34]. The dataset included 1661 full recorded nights of 22 children (13 male) with a median age of 9 years (range of 3-17 years). The video detection algorithm was able to detect 118 of 125 convulsive seizures, overall sensitivity 94%. The total FP detections were 81, rate 0.048 per night.

The adaptive paradigm proposed in [37,38] was tested on one patient exhibiting frequent tonic-clonic convulsive seizures. The total observation time was 230 days with 228 events detected by the system. This case study showed that with the default parameter settings the specificity, the percentage of true alarms was 70% corresponding to an average of 1 FP per 2.6 days. After applying parameter reinforcement optimization, the specificity was elevated to 93% corresponding to an average of 1 FP per 18 days. Unfortunately, no “ground truth” tracking of all possible seizures was available, the patient was in residential setting and no continuous video monitoring was installed. Therefore, we cannot report on the sensitivity for this cases study.

3.4. Forecasting (PGES)

In [41] we found that in accordance with results from a computational model, clinical clonic seizures exhibit an exponential decrease of the convulsion frequency or, equivalently, exponential increase of the inter-clonic intervals (ICI). We found also that there is a correlation between the terminal ICI and the duration of a post ictal suppression, PGES phase. The relation between the two was estimated from analyzing 48 convulsive seizures 37 of which resulted in PGES phase. The association measure is the amount of explained variation between two time series and is defined as:

$$h^2\left(T_{PGES},{ICI}_{terminal}\right)\equiv 1-{\displaystyle \frac{var\left({T_{PGES}|ICI}_{terminal}\right)}{var\left(T_{PGES}\right)}}$$

(49)

It is clear from Equation (49) that if the conditional variation between the two quantities is zero, meaning that one is an exact function of the other, the index is one. If the two quantities are independent, the conditional variation is equal to the total one and the index is zero. Note that the index (49) is asymmetric to its arguments. The value of this index for our sample series was 0.41. It is not a large value but it is statistically significant. The statistical significance of the index (49) can be estimated by taking a number (100 or more) of random permutations of the time stamps in one of the signals and calculating (49) in each of them to establish the probability $p$of obtaining the specific association value or higher by chance. In all our reported results we have at least $p<0.05$.

To automate the process of estimating the increase rate of the ICE from the OF analysis, we applied the technique in subsection 2.4 to 33 video sequences [40]. We found that the association indexes (49) between the manual and automated rate estimates are $h^2\left(automated,manual\right)=0.87$ and $h^2\left(manual,automated\right)=0.74$.

The efficient automated procedure allowed for further investigation of the relations between the PGES duration and the exit ICI in convulsive seizures. In [42] 48 cases of convulsive seizures with PGES and 27 without PGES were analyzed. An SVM classifier using the exit ICI and the seizure duration was constructed and after 50-fold training-performance repetitions, we reached a mean accuracy of 99.7%, mean sensitivity of 99.0% and mean specificity of 100%.

3.5. Detection of Falls

In the original work [87] we used two datasets for the development and testing of the fall detection algorithm; the publicly available Le2i fall detection database [60] and the SEIN fall database, a video database of recordings of genuine falls from people with epilepsy, collected at our center. The Le2i database contains 221 videos simulated by actors, with falls in all directions, various normal activities and challenges such as variable illumination and occlusions. Some of the videos were without audio track and were excluded, leaving 190 video fragments used for training and evaluation. The overall results from classifiers using only the video information (features $\left\{A,V,D\right\}$, see Section 2.5) and the full video and audio features $\left\{A,V,D, S\right\}$ are summarized in the Table 3 below.

Recently we applied for the full Le2i dataset a more advanced machine learning paradigm in [93] using only video data, but considering all six global movement parameters instead of only the vertical translational component, and we achieved a ROC AUC of 0.98.

3.6. Detection of Respiratory Arrests, Apnea

The results reported in [115] suggest that the position of the camera largely influences the detector performance. Sensitivity varies from 80% (worst position) to 100% (best position) and the average from all positions was 83%. The corresponding false positive rates (events per hour) were between 3.28 and 1.09, the average for all the positions: 2.17.

In addition, we tested also an early integration between the camera signals. In the averaged spectrum of the OF from Equation (22), third line, traces reconstructed simultaneously from all cameras were included. The sensitivity was 92.9% and the false positive rate 1.64 events per hour. These numbers are in-between the best and worst camera positions but better than the averaged single-camera performance. Such result is especially interesting in cases when the best camera position is unknown or the position of the patient may change during the observation.

To show the results of monitoring of the respiratory rate in infants between 2 and 6 months of age, we compared the proposed method with a ground truth, namely “Chest Strap” - a recognized (contact) method for detecting the rhythm of breathing. Figure 2 shows Chest Strap RR(respiratory rate) and Detector RR readings on the same one-minute segments of three infants.

The mean respiratory rhythms for all of the examined infants are shown in Table 4

The duration of the measurements (movies included in Table 4) is between 2 and 6 hours, in which the sleep phases alternate with the awake phases of the babies.

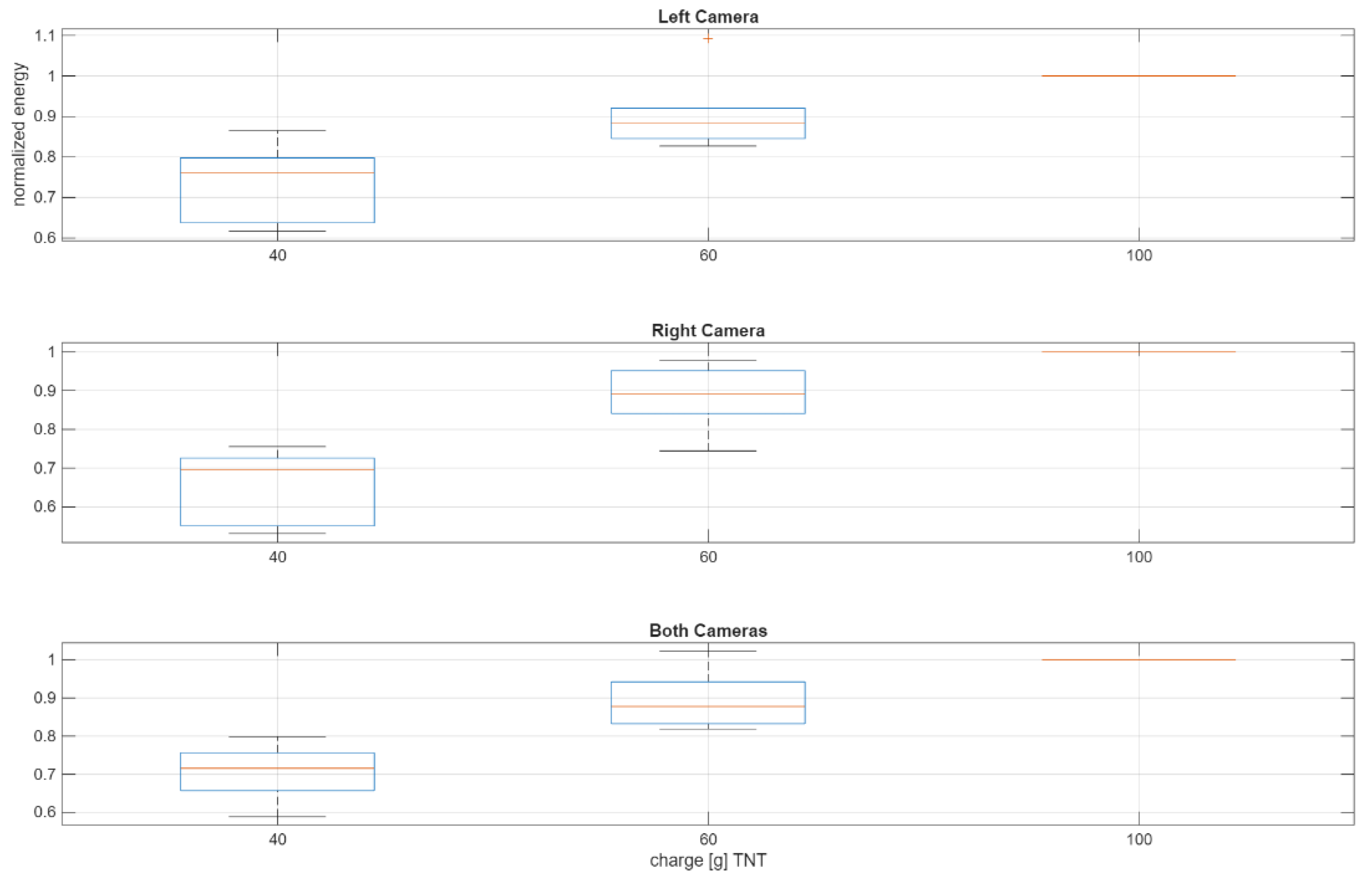
3.7. Detection and Charge Estimation of Explosions

In the article [116] explosions of three different charges 40,60 and 100 gram of TNT were performed at six locations. The spatial reconstruction and subsequent charge estimations were done by registrations with two cameras installed on separate locations at approximately 10 meters from the explosions. The reconstructed 3D coordinates from the OF localization in each camera were within 200mm of the actual explosion locations. The maximal relative error was therefore 0.2/10=0.02, or 2%.

Charge estimation was done for each camera separately and also by combining the energy estimates (41) of both cameras. In the original work we presented the raw estimates, here we also normalized all energy estimates to the corresponding ones from the largest charge (here with 100-gram TNT) for each explosion location in order to cancel the dependence on the distance to the camera.

Figure 3. The distributions over the six explosion locations of the normalized (to the charge of 100 g TNT) energy estimates registered from the left (upper plot), right (middle plot) and both (lower plot) cameras according to the test charge (horizontal axes in gram TNT). The boxplots show the average (red lines) normalized energy, the 25 and 75 percentiles (box tops and bottoms) and the 10 and 90 percentiles (the whiskers). Red stars are the outliers.

Figure 3. The distributions over the six explosion locations of the normalized (to the charge of 100 g TNT) energy estimates registered from the left (upper plot), right (middle plot) and both (lower plot) cameras according to the test charge (horizontal axes in gram TNT). The boxplots show the average (red lines) normalized energy, the 25 and 75 percentiles (box tops and bottoms) and the 10 and 90 percentiles (the whiskers). Red stars are the outliers.

From the figure, we see that the left camera gives better separation between the registered charges than the right one, while the combined estimate from both cameras interpolates the results.

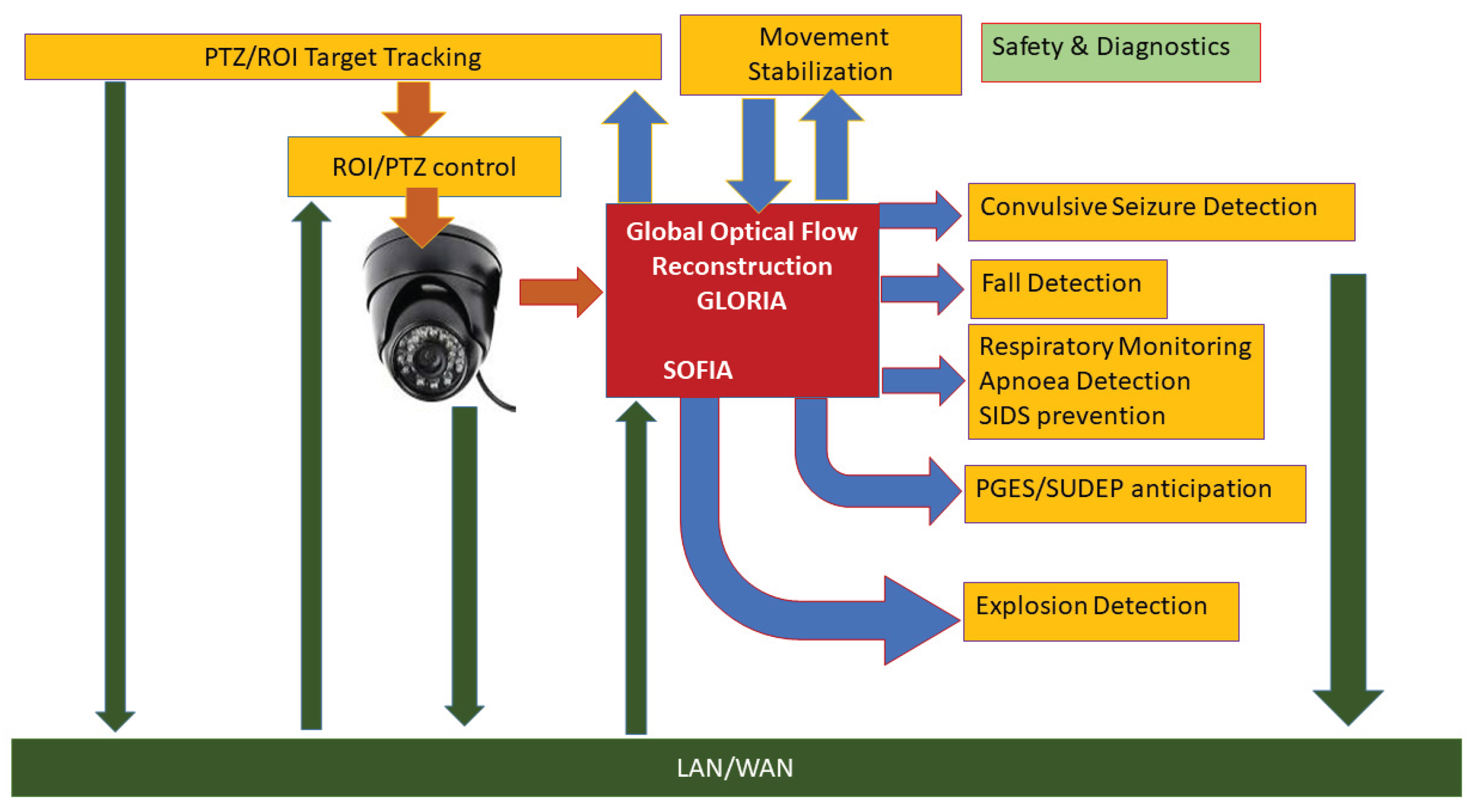
3.8. Object Tracking

The tracking algorithm based on Equation (42) was validated in [133] on both synthetic motion sequences and real-world registrations. In the first case, we have a ground truth for the actual displacement parameters and for the second, operator tracking gave the “gold standard”. In all cases the overall quality of automated tracking at every time sample (or frame number) $t$ is evaluated by the total deviation of the ROI coordinates ${∆}_{total}\left(t\right)\equiv \sqrt{{∆X_c\left(t\right)}^2+{∆Y_c\left(t\right)}^2+{∆L_x\left(t\right)}^2+{∆L_y\left(t\right)}^2}$.

In the tests with synthetic images (Gaussian blob moving with 2 pixels per framer change in the x-direction and 1 pixel per frame change in the y-direction) the deviation was 0.05 pixels for both directions resulting in a relative error of 2.5% and 5% for the (x, y) directions correspondingly. Dilatations were tracked with 10% relative deviation.

In the follow-up work [143] the effect of reinforcement between the tracking algorithms of two cameras was studied. Fifty-one videos were generated. The total deviation in both cameras was calculated and averaged over all frames. The linear fusion model showed marginal improvement, the deviation was reduced by less than 4%. Non-linear interaction between the tracking sequences resulted on average in 30% reduction of the deviation between the tracked and target ROI. We also investigated the influence of object speed on the effectiveness of the non-linear reinforcement. The effectiveness decreased with the increase of object velocity, the approach increased however significantly the accuracy of tracking of objects moving slower than 0.3 pixels/frame.

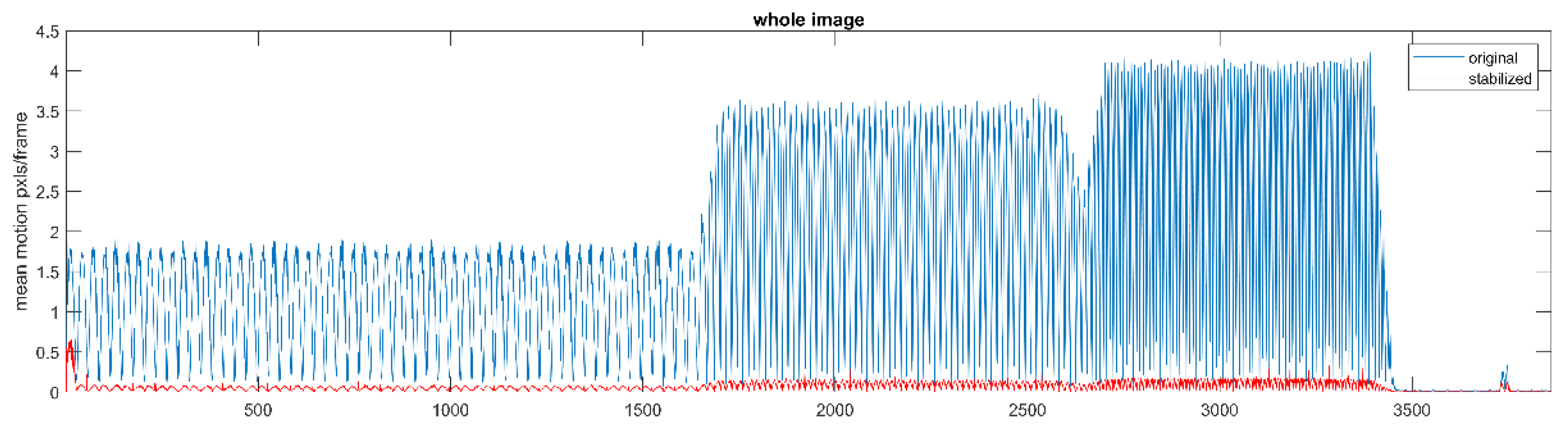
3.9. Image Stabilizing

The methodology published in the patent “US 2022/0207657 GLOBAL MOVEMENT IMAGE STABILIZATION SYSTEMS AND METHODS” was tested on multiple scenarios of moving cameras, moving objects or both. The extended analysis and validation of the method will be reported in a separate work. Here we present the result from a simple test where the camera was subject to oscillatory movements and the stabilizing algorithm was based on the global movement OF reconstruction GLORIA involving translations, rotation, dilatation and shear transformations. In Figure 4 we show the motion content of a video sequence, measured by the pixel-level OF reconstruction method SOFIA, before and after the stabilizing process.

The test demonstrates that the stabilizing algorithm compensates more than 95% of the motion related OF amplitude.

4. Discussion

Here we discuss the general concepts as well as some specific issues related to the methods and applications reviewed in this work. We also outline some limitations of our approaches and accordingly, speculate about possible extensions and future research.

Most of the challenges where we applied the optical flow concept relate to detection and awareness of events such as motor epileptic seizures, falls, apnea. In the case of post-ictal electrographic suppression prediction, the method can be used for both real-time alerting and off-line diagnosis of cases with higher risk of PGES. We note however that in general the task of detection events in real-time is related but not equivalent to classification of signals. The essential difference is in the requirement to recognize the event as soon as possible without possessing the data from the whole duration of the event. Classification of off-line data can be important for diagnostic purposes, but for real-time detection of convulsive seizures for example, reaction times within 5-10 seconds achievable with our technique [35], can be critical for avoiding injuries or complications. The two objectives, classification and alerting, can be part of one system in the context of adaptive approaches involving machine-learning paradigms. In [37] we have used off-line cluster-based classification of already detected or suspected events [38] as part of unsupervised reinforcement learning procedure for fine-tuning the on-line detector. The assumption is that the OF signal during the total duration of the convulsive seizure can provide reliable discrimination between the real seizure detections from the false ones. Therefore, detector parameters dynamically adapt to the classification of the previous detections used as training sets. This approach was applied and tested only for the seizure detection but in the future, it may be used in other adaptive detectors. In this context we realize also that for some alerting applications, machine-learning approaches can be difficult to develop and their advantages can be disputable. Falls for example, happen due to a broad variety of factors and unsupervised learning approaches may not be effective. Providing training sets for all of them on the other hand, can be a challenge as well. Validating and labeling cases is also a time-consuming process and in addition depends on the skills of the qualified observers. In such applications, universal model-based algorithm may provide a feasible alternative. Our guiding principle is the “hybrid” approach, using as much as possible model based “backbone” algorithms such as the computational model induced post-ictal suppression prediction in [41]. The refinement of the detectors or predictors can be further achieved by machine learning paradigms.

In the context of the previous comments, state classification may provide predictive information about forthcoming adverse events. We have explored such possibilities in the cases of PGES by relating the convulsive movements dynamics to post-seizure suppression of the brain activity. Another example is the observation that respiratory irregularities may be prodromal for the catastrophic events of SIDS. We have analyzed also possibilities for short-term anticipation of epileptic seizures, the results are promising but more statistical evidence has to be collected.

Both SOFIA and GLORIA algorithms provide early multi-channel data fusion. As seen from the Equations (2), (3), (4) and (15), the velocity, or displacement field to be reconstructed is common for all the spectral channels, or colors in case of traditional RGB camera. Additional sensor modalities such as thermal (contrast) imaging, depth detectors, radars or simply broader array of spectral sensors can be included. The intrinsic multichannel nature of our algorithms decreases the level of degeneracy of the inverse problem. OF reconstruction is in general, and especially in case of using single channel intensity images, an under determined problem as the local velocities in the directions of constant intensity can be arbitrary. This is less likely to occur in multichannel images and therefore early data fusion is advantageous for obtaining robust solution.

The image sequence-based reconstruction of global movements further allows for early integration, or fusion, of multi-camera registrations. Because the spatial information is largely truncated, time series from the cameras can be analyzed simultaneously as was shown in [115] in the example of respiratory arrest detection. Signal fusion can be also done in later processing stages, as is the case with explosion charge estimates [116]. The synergy between OF algorithms running on a set of cameras can be achieved as a dynamic reinforcement process, as shown in the application of tracking objects [143]. Sensor fusion paradigms can be also advantageous for the rest of the applications considered here and these may be subjects for further developments.

As described in the methods section, SOFIA is an iterative multi-scale algorithm. This means that we can control the levels of detail that we want to obtain in the solution. However, how do we choose these levels? In the current stage of applying the method, we have rigidly selected the sequences of scales according to the expected or assumed levels of detail that will be relevant for the specific analysis. In a more flexible and assumption free implementation, levels of detail may be possible to infer from the dynamic content of the video sequences. A simple approach will be to start at a coarse scale and then test whether the reconstructed displacement vector field “explains” sufficiently the changes in the frames. If not, a finer scale reconstruction will follow. We will address this extension in a future work.

Except for the part dedicated to image stabilization, all the applications here are assuming a static (or PTZ controlled in the case of object tracking module) camera observing scenes or objects. Optical flow derived algorithms can be extended to mobile cameras. The separation between the camera movement and the displacement of the registered objects will be subject to future investigations. One particular setup that can be of a direct benefit for the detection and alerting of convulsive epileptic seizures and of falls is the use of “egocentric” camera. The last can be the inbuilt camera of a smartphone, avoiding this way possible inconveniences associated with dedicated wearables. We believe that especially for detection of motor seizures, the direct application of the same algorithms used with static camera are applicable. The global movement reconstruction GLORIA may even be more effective in this setup as the whole scene will follow the convulsive movements of the patient. A test trial with wireless camera will be attempted in nearest future.

Our last remark concerns the issue of scalability of any system dedicated to real-world operation. Our approach, as stated in the Introduction and illustrated on Figure 1, allows for a common universal OF module linked to modular additions of various detectors. This feature distinguishes our paradigm from the variety of task-specific detectors that would require a separate processing implementation for each individual class of events. The last may be feasible only for small-scale applications like home use. In a typical care center, however, the number of residents that may need safety monitoring can be of order of 100 or more. It may be possible, but sometimes economically not realistic, that for each person a complete system will be installed. In addition, a video network supporting that many cameras (in some cases more than one camera per resident may be optimal) will be extremely loaded. Given that the OF reconstruction is the most computationally demanding part of the processing and that it is common for all detectors, a distributed system of smart cameras each with an uploaded GLORIA algorithm can provide the data for all the detectors running on centralized platform connected to observation stations. Indeed, OF signals are just six time-series per camera of relatively low sample rates (25-30 samples per second) and can easily be distributed to central processing servers over low-bandwidth network where the computationally light algorithms can run in parallel. We are considering these options within a pending institutional implementation phase.

5. Conclusions

The paradigm of optical flow reconstruction on a variety of levels, from fine scale pixel-level details to global movements, can be a common processing module providing data for a variety of video-based remote detectors. The detectors can be implemented separately, concurrently or working synchronously in parallel to selectively identify and alert for hazardous situations. Off-line implementations can be used for dedicated diagnostic or forensic algorithms. Global movement reconstruction can serve at the same time as input for automated tracking and image stabilizing algorithms. The major computational complexity, the OF inverse problem solution, is therefore centrally addressed providing thus significant reduction of subsequent processing resources.

6. Patents

• Karpuzov S, Kalitzin S., Petkov A, Ilieva S, Petkov G, METHOD AND SYSTEM FOR OBJECTS TRACKING IN VIDEO SEQUENCES https://patentscope.wipo.int/search/en/WO2025085981
• Petkov, G., Fornell, P., Ristic, B. and Trujillo, I., HB Innovations Inc, 2023. System and method for video detection of breathing rates. U.S. Patent Application 17/682,645. https://patents.google.com/patent/US20230270337A1/en
• Petkov G, Kalitzin S, Fornell P. Global movement image stabilisation systems and methods [US PATENT US20220207657A1/US11494881B2 citations (17)/(5)]. Available from: https://patents.google.com/patent/US11494881B2