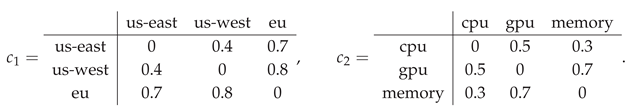Contra-HyperSoft Set and Contra-SuperHyperSoft Set

1. Preliminaries

We collect the basic terminology and notation used in what follows. The definitions in this paper are assumed to be finite.

1.1. Soft Set

A Soft Set is a parameterized family of subsets selecting universe elements relevant to each parameter, supporting flexible decision modeling [1,2,3]. The definitions of the Soft Set are provided below.

Definition 1

(Soft Set). [1] Let U be a universal set and E a set of parameters. A soft set over U is defined as an ordered pair $(F,E)$, where F is a mapping from E to the power set $\mathcal{P}\left(U\right)$:

$$F:E\to \mathcal{P}\left(U\right).$$

For each parameter $e\in E$, $F\left(e\right)\subseteq U$ represents the set of e-approximate elements in U, with $(F,E)$ forming a parameterized family of subsets of U.

Example 1

(Soft Set — Hotel Filtering with Parameterized Conditions). Universe and parameters.Let the universe of candidate hotels be

$$U=\{h_1,h_2,h_3,h_4,h_5,h_6,h_7,h_8\}.$$

Let the parameter set be

$$E=\{\mathrm{near}\_\mathrm{station},\mathrm{free}\_\mathrm{breakfast},\mathrm{onsen},\mathrm{under}12000,\mathrm{twin}\_\mathrm{room}\}.$$

Define a soft set $(F,E)$ with $F:E\to \mathcal{P}\left(U\right)$ by

$$\begin{array}{cc}\hfill F(\mathrm{near}\_\mathrm{station})& =\{h_1,h_2,h_5,h_7\},\hfill \\ \hfill F(\mathrm{free}\_\mathrm{breakfast})& =\{h_2,h_4,h_5,h_6\},\hfill \\ \hfill F\left(\mathrm{onsen}\right)& =\{h_3,h_5,h_8\},\hfill \\ \hfill F(\mathrm{under}\yen 12000)& =\{h_1,h_4,h_5,h_7,h_8\},\hfill \\ \hfill F(\mathrm{twin}\_\mathrm{room})& =\{h_2,h_4,h_6,h_7\}.\hfill \end{array}$$

Concrete queries and explicit computations.

$$\begin{array}{cc}\hfill \mathit{(i)}\mathit{near\_station\; \&\; under\yen 12000:}& F(\mathrm{near}\_\mathrm{station})\cap F\left(\mathrm{under}12000\right)=\{h_1,h_2,h_5,h_7\}\cap \{h_1,h_4,h_5,h_7,h_8\}\hfill \\ & =\{h_1,h_5,h_7\},|·|=3.\hfill \\ \hfill \mathit{(ii)}\mathit{(free\_breakfast\; \cup \; onsen)\; \&\; twin\_room:}& \left(F(\mathrm{free}\_\mathrm{breakfast})\cup F\left(\mathrm{onsen}\right)\right)\cap F(\mathrm{twin}\_\mathrm{room})\hfill \\ & =\left(\{h_2,h_4,h_5,h_6\}\cup \{h_3,h_5,h_8\}\right)\cap \{h_2,h_4,h_6,h_7\}\hfill \\ & =\{h_2,h_4,h_6\},|·|=3.\hfill \\ \hfill \mathit{(iii)}\mathit{onsen\; \&\; twin\_room:}& F\left(\mathrm{onsen}\right)\cap F(\mathrm{twin}\_\mathrm{room})=\{h_3,h_5,h_8\}\cap \{h_2,h_4,h_6,h_7\}=⌀.\hfill \end{array}$$

These results illustrate how a soft set supports multi-criterion filtering by standard set operations with exact outputs.

1.2. ContraSoft Set

A ContraSoft Set is a parameterized soft set where each parameter’s values are associated with a contradiction degree, and thresholding is used to aggregate only those values that are not too contradictory with respect to a chosen reference. This allows soft-set modeling to filter or weight information based on contradiction, rather than uncertainty.

Definition 2

(Contradiction on attribute values). Let V be a nonempty finite set of attribute values. A contradiction function on V is a map

$$c:V\times V⟶[0,1]$$

such that

$$c(v,v)=0\left(\mathrm{reflexivity}\right),c(v,w)=c(w,v)\left(\mathrm{symmetry}\right).$$

The quantity $c(v,w)$ measures the degree of contradiction between v and w (larger means more contradictory).

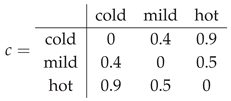
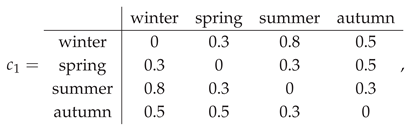
Example 2

(Contradiction on attribute values — temperature preference). Let $V=\{\mathrm{cold},\mathrm{mild},\mathrm{hot}\}$. Define the symmetric contradiction $c:V\times V\to [0,1]$ (with $c(v,v)=0$) by

so, e.g., $c(\mathrm{cold},\mathrm{hot})=0.9$ expresses a strong contradiction, while $c(\mathrm{cold},\mathrm{mild})=0.4$ is moderate.

Definition 3

(ContraSoft structure). Let U be a nonempty universe and E a nonempty set of parameters. For each $e\in E$ fix:

• a nonempty finite value set $V_e$;
• a contradiction function $c_e:V_e\times V_e\to [0,1]$ (Definition 2);
• a designated reference value $v_e^{★}\in V_e$.

Write $V:={⨆}_{e\in E}(\left\{e\right\}\times V_e)$ for the disjoint union of all parameter–value pairs.

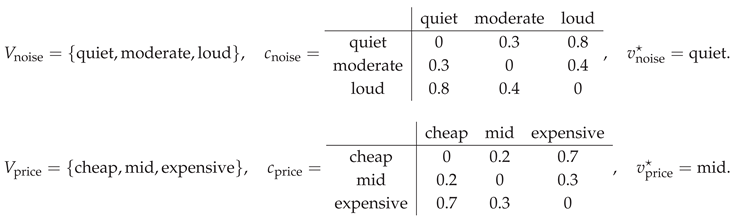
Example 3

(ContraSoft structure — hotels by noise and price). Let the universe be $U=\{h_1,h_2,h_3,h_4\}$ and parameters $E=\{\mathrm{noise},\mathrm{price}\}$. For each $e\in E$ fix a finite value-set $V_e$, a contradiction $c_e:V_e\times V_e\to [0,1]$, and a reference value $v_e^{★}\in V_e$:

These choices realize Definition (ContraSoft structure) by specifying value domains, their contradiction degrees, and per-parameter references.

Definition 4

(ContraSoft Set). Let U be a finite universe of objects and E a finite set of parameters. A ContraSoft Set is a quadruple

$$\mathsf{CS}:=(U,E,F,c),$$

where

• $F:E\to \mathcal{P}\left(U\right)$ is the (crisp) soft mapping; $F\left(e\right)\subseteq U$ is the set of objects accepted (or classified as positive) under parameter e;
• $c:E\times E\to [0,1]$ is a contradiction degree on parameters, symmetric and reflexive on the diagonal:

  $$c(e,e)=0,c(e,f)=c(f,e)(\forall e,f\in E).$$

For $x\in U$ and $e\in E$, the atomic lemma “x is accepted by e” is represented by

$$A(x,e):x\in F\left(e\right),$$

with truth value $\mathbf{T}$ if $x\in F\left(e\right)$ and $\mathbf{F}$ otherwise.

Example 4

(ContraSoft Set — Noise-Aware Hotel Selection with Contradiction Thresholding). Universe, parameters, and soft mapping. Let the same universe U be as above. Consider parameters

$$E=\{\mathrm{quiet},\mathrm{nightlife},\mathrm{coworking},\mathrm{scenic}\}.$$

Define $F:E\to \mathcal{P}\left(U\right)$ by

$$\begin{array}{cccc}\hfill F\left(\mathrm{quiet}\right)& =\{h_1,h_3,h_5,h_8\},\hfill & \hfill F\left(\mathrm{nightlife}\right)& =\{h_2,h_4,h_6\},\hfill \\ \hfill F\left(\mathrm{coworking}\right)& =\{h_2,h_5,h_6,h_7\},\hfill & \hfill F\left(\mathrm{scenic}\right)& =\{h_3,h_5,h_7,h_8\}.\hfill \end{array}$$

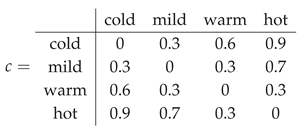
Contradiction degrees on parameters. Let $c:E\times E\to [0,1]$ be symmetric with

(diagonal 0, larger values mean more contradictory).

Reference and thresholded aggregation. Fix the reference parameter $e^{★}=\mathrm{quiet}$ and threshold $\tau =0.4$. Define the accepted envelope

$$S^{\left(\tau \right)}\left(e^{★}\right):=\bigcup _{e\in E:c(e,e^{★})\le \tau }F\left(e\right).$$

Eligible parameters are those within the contradiction radius:

$$c(\mathrm{quiet},\mathrm{quiet})=0,c(\mathrm{coworking},\mathrm{quiet})=0.4,c(\mathrm{scenic},\mathrm{quiet})=0.2,c(\mathrm{nightlife},\mathrm{quiet})=0.9>\tau .$$

Hence

$$\begin{array}{cc}\hfill S^{\left(\tau \right)}\left(\mathrm{quiet}\right)& =F\left(\mathrm{quiet}\right)\cup F\left(\mathrm{coworking}\right)\cup F\left(\mathrm{scenic}\right)\hfill \\ & =\{h_1,h_3,h_5,h_8\}\cup \{h_2,h_5,h_6,h_7\}\cup \{h_3,h_5,h_7,h_8\}\hfill \\ & =\{h_1,h_2,h_3,h_5,h_6,h_7,h_8\},\left|S^{\left(\tau \right)}\right|=7.\hfill \end{array}$$

Tighter threshold for comparison.With ${\tau }^{\prime }=0.2$, only $\mathrm{quiet}$ and $\mathrm{scenic}$ are admitted:

$$S^{\left({\tau }^{\prime }\right)}\left(\mathrm{quiet}\right)=F\left(\mathrm{quiet}\right)\cup F\left(\mathrm{scenic}\right)=\{h_1,h_3,h_5,h_7,h_8\},\left|S^{\left({\tau }^{\prime }\right)}\right|=5.$$

Thus $S^{\left(\tau \right)}$ is monotone in τ, and the contradiction metric controls how widely we aggregate across potentially conflicting parameters.

1.3. HyperSoft Set and SuperHyperSoft Set

HyperSoft Set maps each multi-attribute tuple from a Cartesian product to a subset of the universe consistent with those values [4,5,6,7,8]. SuperHyperSoft Set maps tuples of subsets from power-set domains to universe subsets, generalizing HyperSoft; singletons in each coordinate recover HyperSoft [9,10].

Definition 5

(HyperSoft Set). [4] Let U be a finite universe and let ${\mathcal{A}}_1,{\mathcal{A}}_2,\dots ,{\mathcal{A}}_m$ be m attribute value domains. Consider the Cartesian product

$$\mathcal{C}={\mathcal{A}}_1\times {\mathcal{A}}_2\times \dots \times {\mathcal{A}}_m,$$

so that each parameter $\gamma =({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_m)\in \mathcal{C}$ chooses a single value ${\gamma }_i\in {\mathcal{A}}_i$ for every attribute. A HyperSoft Set over U is a pair $(G,\mathcal{C})$ where

$$G:\mathcal{C}⟶\mathcal{P}\left(U\right)$$

assigns to each multi-attribute parameter γ a subset $G\left(\gamma \right)\subseteq U$. Equivalently,

$$(G,\mathcal{C})=\left\{(\gamma ,G(\gamma \left)\right):\gamma \in \mathcal{C}\right\}.$$

Example 5

(HyperSoft Set — Multi-Attribute Restaurant Finder). Universe and attributes. Let the universe of candidate restaurants be

$$U=\{r_1,r_2,r_3,r_4,r_5,r_6,r_7,r_8,r_9\}.$$

Let the attribute domains be

$${\mathcal{A}}_1=\{\mathrm{jpn},\mathrm{ita},\mathrm{ind}\},{\mathcal{A}}_2=\{\mathrm{low},\mathrm{mid},\mathrm{high}\},{\mathcal{A}}_3=\{\mathrm{omn},\mathrm{veg},\mathrm{vgn}\}.$$

The parameter space is the Cartesian product $\mathcal{C}={\mathcal{A}}_1\times {\mathcal{A}}_2\times {\mathcal{A}}_3$. A HyperSoft Set is a mapping $G:\mathcal{C}\to \mathcal{P}\left(U\right)$ that assigns a subset of restaurants to each single-valued tuple $(\mathrm{cuisine},\mathrm{price},\mathrm{diet})$.

Specification (nonempty images).

$$\begin{array}{cccc}\hfill G(\mathrm{jpn},\mathrm{mid},\mathrm{veg})& =\{r_2,r_5\},\hfill & \hfill G(\mathrm{jpn},\mathrm{low},\mathrm{omn})& =\{r_1,r_3\},\hfill \\ \hfill G(\mathrm{ita},\mathrm{mid},\mathrm{veg})& =\left\{r_4\right\},\hfill & \hfill G(\mathrm{ind},\mathrm{low},\mathrm{vgn})& =\{r_6,r_8\},\hfill \\ \hfill G(\mathrm{ita},\mathrm{high},\mathrm{omn})& =\{r_7,r_9\},\hfill \end{array}$$

and $G\left(\gamma \right)=⌀$ for all other $\gamma \in \mathcal{C}$.

Concrete queries with exact set calculations.

$$\begin{array}{cc}\hfill \left(\mathrm{i}\right)\mathit{Exactly}(\mathrm{jpn},\mathrm{mid},\mathrm{veg}):& G(\mathrm{jpn},\mathrm{mid},\mathrm{veg})=\{r_2,r_5\},|·|=2.\hfill \\ \hfill \left(\mathrm{ii}\right)\mathit{Union}\mathit{of}\mathit{two}\mathit{precise}\mathit{asks}\text{:}& G(\mathrm{jpn},\mathrm{low},\mathrm{omn})\cup G(\mathrm{ita},\mathrm{high},\mathrm{omn})\hfill \\ & =\{r_1,r_3\}\cup \{r_7,r_9\}=\{r_1,r_3,r_7,r_9\},|·|=4.\hfill \\ \hfill \left(\mathrm{iii}\right)\mathit{Disjointness}\mathit{of}\mathit{incompatible}\mathit{tuples}\text{:}& G(\mathrm{jpn},\mathrm{low},\mathrm{omn})\cap G(\mathrm{ind},\mathrm{low},\mathrm{vgn})=\{r_1,r_3\}\cap \{r_6,r_8\}=⌀.\hfill \end{array}$$

The HyperSoft Set captures single-value choices per attribute; each tuple pinpoints a crisp slice of U.

Definition 6

(SuperHyperSoft Set). [9,11] Let U be a finite universe. Let $a_1,a_2,\dots ,a_n$ be distinct attributes with finite, pairwise disjoint value-sets $A_1,A_2,\dots ,A_n$ (i.e., $A_i\cap A_j=\varnothing$ for $i\ne j$). Write $\mathcal{P}\left(A_i\right)$ for the power set of $A_i$ and form

$$\mathcal{C}=\mathcal{P}\left(A_1\right)\times \mathcal{P}\left(A_2\right)\times \dots \times \mathcal{P}\left(A_n\right).$$

A SuperHyperSoft Set over U is a pair $(F,\mathcal{C})$ with

$$F:\mathcal{C}⟶\mathcal{P}\left(U\right),$$

so that for each $\gamma =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)\in \mathcal{C}$ (where ${\alpha }_i\subseteq A_i$) we have a subset $F\left(\gamma \right)\subseteq U$. Formally,

$$(F,\mathcal{C})=\left\{(\gamma ,F(\gamma \left)\right):\gamma \in \mathcal{C},F\left(\gamma \right)\subseteq U\right\}.$$

Example 6

(SuperHyperSoft Set — Flexible Restaurant Finder with Set-Valued Coordinates). Universe and attributes.Use the same U and attribute value-sets $A_1=\{\mathrm{jpn},\mathrm{ita},\mathrm{ind}\}$, $A_2=\{\mathrm{low},\mathrm{mid},\mathrm{high}\}$, $A_3=\{\mathrm{omn},\mathrm{veg},\mathrm{vgn}\}$. In the SuperHyperSoft setting, the parameter space is

$$\mathcal{C}=\mathcal{P}\left(A_1\right)\times \mathcal{P}\left(A_2\right)\times \mathcal{P}\left(A_3\right),$$

so each coordinate is asubsetof admissible values (a flexible filter).

Mapping (nonempty images).Define $F:\mathcal{C}\to \mathcal{P}\left(U\right)$ by

$$\begin{array}{cc}\hfill F\left(\right\{\mathrm{jpn},\mathrm{ita}\},\{\mathrm{low},\mathrm{mid}\},\{\mathrm{veg}\left\}\right)& =\{r_2,r_4,r_5\},\hfill \\ \hfill F\left(\right\{\mathrm{ind}\},\{\mathrm{low},\mathrm{mid}\},\{\mathrm{vgn}\left\}\right)& =\{r_6,r_8\},\hfill \\ \hfill F\left(\right\{\mathrm{jpn},\mathrm{ind}\},\{\mathrm{low}\},\{\mathrm{omn},\mathrm{veg}\left\}\right)& =\{r_1,r_3,r_6\},\hfill \\ \hfill F\left(\right\{\mathrm{ita}\},\{\mathrm{high}\},\{\mathrm{omn}\left\}\right)& =\{r_7,r_9\},\hfill \end{array}$$

and $F\left(\alpha \right)=⌀$ otherwise.

Reading the parameters. For example, $\alpha =\left(\right\{\mathrm{jpn},\mathrm{ita}\},\{\mathrm{low},\mathrm{mid}\},\{\mathrm{veg}\left\}\right)$ means: cuisine is Japanese or Italian, price is low or mid, diet is vegetarian. Then $F\left(\alpha \right)=\{r_2,r_4,r_5\}$ is the recommended subset.

Coherence with HyperSoft via singletons. If we restrict to singletons in each coordinate, SuperHyperSoft reduces to HyperSoft. Concretely,

$$F(\left\{\mathrm{jpn}\right\},\left\{\mathrm{mid}\right\},\left\{\mathrm{veg}\right\})=\{r_2,r_5\}=G(\mathrm{jpn},\mathrm{mid},\mathrm{veg}),$$

so the singleton tuple reproduces the HyperSoft slice exactly. Moreover,

$$F(\left\{\mathrm{jpn}\right\},\left\{\mathrm{mid}\right\},\left\{\mathrm{veg}\right\})\subseteq F(\{\mathrm{jpn},\mathrm{ita}\},\{\mathrm{low},\mathrm{mid}\},\left\{\mathrm{veg}\right\})=\{r_2,r_4,r_5\},$$

exhibiting the intended flexible expansion when coordinates are broadened from single values to sets of values.

Cardinality checks.

$$\left|F\right(\{\mathrm{jpn},\mathrm{ita}\},\{\mathrm{low},\mathrm{mid}\},\left\{\mathrm{veg}\right\}\left)\right|=3,\left|F\right(\left\{\mathrm{ind}\right\},\{\mathrm{low},\mathrm{mid}\},\left\{\mathrm{vgn}\right\}\left)\right|=2.$$

Thus SuperHyperSoft enables compact specification of multi-value preferences per attribute and directly returns the filtered subset of U.

2. Main Results

In this section, we present and analyze the principal outcomes of our study.

2.1. Contra-HyperSoft Set

Contra-HyperSoft Set augments HyperSoft with a tuple-wise contradiction metric, reference selector, and threshold, uniting parameter slices within the admissible radius.

Definition 7

(Coordinatewise contradiction). Let ${\mathcal{A}}_1,\dots ,{\mathcal{A}}_m$ be nonempty finite sets. For each $i\in \{1,\dots ,m\}$ acontradiction function is a map

$$c_i:{\mathcal{A}}_i\times {\mathcal{A}}_i⟶[0,1]\mathrm{with}{c}_i(a,a)=0,c_i(a,b)=c_i(b,a).$$

When needed for exact reductions, we assume the zero-separation property $c_i(a,b)=0\Rightarrow a=b$.

Definition 8

(Tuple-level contradiction). Let $\mathcal{C}:={\mathcal{A}}_1\times \dots \times {\mathcal{A}}_m$ and write $\gamma =({\gamma }_1,\dots ,{\gamma }_m)$, $\delta =({\delta }_1,\dots ,{\delta }_m)\in \mathcal{C}$. Define the aggregated contradiction by

$$\Delta (\gamma ,\delta ):=\underset{1\le i\le m}{max}{c}_i({\gamma }_i,{\delta }_i)\in [0,1].$$

Then $\Delta (\gamma ,\delta )=\Delta (\delta ,\gamma )$ and $\Delta (\gamma ,\gamma )=0$. If each $c_i$ is zero-separating, then $\Delta (\gamma ,\delta )=0\iff \gamma =\delta$.

Definition 9

(Reference selector). Areference selectoris a map $\rho :\mathcal{C}\to \mathcal{C}$. Two canonical choices are

$$(\mathrm{self}-\mathrm{centered})\rho \left(\gamma \right)=\gamma ,(\mathrm{fixed}-\mathrm{reference})\rho \left(\gamma \right)\equiv r\mathrm{for}\mathrm{a}\mathrm{fixed}r\in \mathcal{C}.$$

(Definition 10 (Contra-HyperSoft Set (CHS)). Let U be a finite universe and let $G:\mathcal{C}\to \mathcal{P}\left(U\right)$ be a HyperSoft mapping. Fix contradiction kernels ${\left\{c_i\right\}}_{i=1}^m$, a reference selector ρ, and a threshold $\tau \in [0,1]$. The associated Contra-HyperSoft Set is the tuple

$$\mathsf{CHS}:=\left(U,{\{{\mathcal{A}}_i,c_i\}}_{i=1}^m,G,\rho ,\tau \right),$$

together with the filtered mapping

$$G_{\rho }^{\left(\tau \right)}:\mathcal{C}⟶\mathcal{P}\left(U\right),G_{\rho }^{\left(\tau \right)}\left(\gamma \right):=\bigcup _{\delta \in \mathcal{C}:\Delta (\delta ,\rho (\gamma \left)\right)\le \tau }G\left(\delta \right).$$

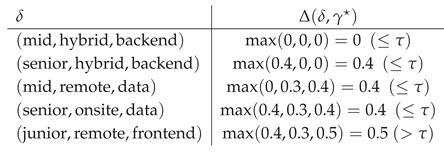
Example 7 (Contra-HyperSoft Set —Candidate Shortlisting under Conflicting Signals (self-centered selector)). Universe and attributes. Let the candidate pool be $U=\{c_1,c_2,c_3,c_4,c_5,c_6,c_7,c_8\}$. Consider three single-valued attribute domains:

$${\mathcal{A}}_1=\{\mathrm{junior},\mathrm{mid},\mathrm{senior}\},{\mathcal{A}}_2=\{\mathrm{onsite},\mathrm{hybrid},\mathrm{remote}\},{\mathcal{A}}_3=\{\mathrm{backend},\mathrm{frontend},\mathrm{data}\}.$$

The parameter space is $\mathcal{C}={\mathcal{A}}_1\times {\mathcal{A}}_2\times {\mathcal{A}}_3$.

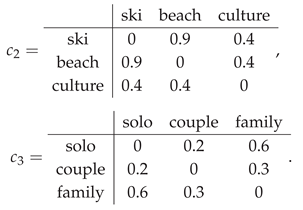
Coordinatewise contradictions. All $c_i$ are symmetric with 0 on the diagonal.

Aggregate tuple-contradiction: $\Delta (\gamma ,\delta ):=max\{c_1({\gamma }_1,{\delta }_1),c_2({\gamma }_2,{\delta }_2),c_3({\gamma }_3,{\delta }_3)\}$.

HyperSoft mapping $G:\mathcal{C}\to \mathcal{P}\left(U\right)$ (nonempty images).

$$\begin{array}{cc}& G(\mathrm{junior},\mathrm{remote},\mathrm{frontend})=\{c_1,c_3\},G(\mathrm{mid},\mathrm{hybrid},\mathrm{backend})=\{c_2,c_5\},\hfill \\ & G(\mathrm{senior},\mathrm{onsite},\mathrm{data})=\left\{c_4\right\},G(\mathrm{mid},\mathrm{remote},\mathrm{data})=\left\{c_6\right\},\hfill \\ & G(\mathrm{senior},\mathrm{hybrid},\mathrm{backend})=\{c_7,c_8\}.\hfill \end{array}$$

CHS filter. Choose the self-centered selector $\rho \left(\gamma \right)=\gamma$ and threshold $\tau =0.4$. Let ${\gamma }^{★}=(\mathrm{mid},\mathrm{hybrid},\mathrm{backend})$. Compute $\Delta (·,{\gamma }^{★})$ on the above tuples:

Hence

$$G_{\rho }^{\left(\tau \right)}\left({\gamma }^{★}\right)=\{c_2,c_5\}\cup \{c_7,c_8\}\cup \left\{c_6\right\}\cup \left\{c_4\right\}=\{c_2,c_4,c_5,c_6,c_7,c_8\},|·|=6.$$

With a tighter threshold ${\tau }^{\prime }=0.3$, only the base slice survives: $G_{\rho }^{\left({\tau }^{\prime }\right)}\left({\gamma }^{★}\right)=\{c_2,c_5\}$, illustrating monotonicity in τ.

Example 8 (Contra-HyperSoft Set — Travel Package Selection (fixed reference)). Universe and attributes. Let $U=\{{\mathrm{pkg}}_1,\dots ,{\mathrm{pkg}}_{10}\}$ be travel packages. Attributes:

$${\mathcal{A}}_1=\{\mathrm{winter},\mathrm{spring},\mathrm{summer},\mathrm{autumn}\},{\mathcal{A}}_2=\{\mathrm{ski},\mathrm{beach},\mathrm{culture}\},{\mathcal{A}}_3=\{\mathrm{solo},\mathrm{couple},\mathrm{family}\}.$$

Contradiction matrices (symmetric, 0 on diagonal).

Aggregate $\Delta (\gamma ,\delta ):=max\{c_1({\gamma }_1,{\delta }_1),c_2({\gamma }_2,{\delta }_2),c_3({\gamma }_3,{\delta }_3)\}$.

HyperSoft mapping (nonempty images).

$$\begin{array}{cc}& G(\mathrm{winter},\mathrm{ski},\mathrm{family})=\{{\mathrm{pkg}}_1,{\mathrm{pkg}}_2\},G(\mathrm{summer},\mathrm{beach},\mathrm{couple})=\{{\mathrm{pkg}}_3,{\mathrm{pkg}}_4\},\hfill \\ & G(\mathrm{spring},\mathrm{culture},\mathrm{solo})=\left\{{\mathrm{pkg}}_5\right\},G(\mathrm{autumn},\mathrm{culture},\mathrm{family})=\{{\mathrm{pkg}}_6,{\mathrm{pkg}}_7\},\hfill \\ & G(\mathrm{summer},\mathrm{culture},\mathrm{family})=\left\{{\mathrm{pkg}}_8\right\},G(\mathrm{winter},\mathrm{beach},\mathrm{solo})=\left\{{\mathrm{pkg}}_9\right\}.\hfill \end{array}$$

CHS filter (fixed reference).Choose the fixed reference $r=(\mathrm{summer},\mathrm{beach},\mathrm{family})$ and threshold $\tau =0.5$. Evaluate $\Delta (·,r)$:

Thus the accepted tuples are the 2nd, 4th, and 5th. The CHS envelope at r is

$$G_{\rho \equiv r}^{\left(\tau \right)}\left(r\right)=\{{\mathrm{pkg}}_3,{\mathrm{pkg}}_4\}\cup \{{\mathrm{pkg}}_6,{\mathrm{pkg}}_7\}\cup \left\{{\mathrm{pkg}}_8\right\}=\{{\mathrm{pkg}}_3,{\mathrm{pkg}}_4,{\mathrm{pkg}}_6,{\mathrm{pkg}}_7,{\mathrm{pkg}}_8\},$$

with cardinality 5. If we tighten to ${\tau }^{\prime }=0.3$, only the 2nd tuple remains, so $G_{\rho \equiv r}^{\left({\tau }^{\prime }\right)}\left(r\right)=\{{\mathrm{pkg}}_3,{\mathrm{pkg}}_4\}$, demonstrating the control afforded by the contradiction threshold.

Proposition 1

(Basic properties). For fixed $(U,\{{\mathcal{A}}_i,c_i\},G,\rho )$ the family ${\left\{G_{\rho }^{\left(\tau \right)}\right\}}_{\tau \in [0,1]}$ is monotone in τ: if $0\le {\tau }_1\le {\tau }_2\le 1$ then $G_{\rho }^{\left({\tau }_1\right)}\left(\gamma \right)\subseteq G_{\rho }^{\left({\tau }_2\right)}\left(\gamma \right)$ for all $\gamma \in \mathcal{C}$. Moreover $G_{\rho }^{\left(1\right)}\left(\gamma \right)={\bigcup }_{\delta \in \mathcal{C}}G\left(\delta \right)$ for all γ.

Proof. 

If ${\tau }_1\le {\tau }_2$ then $\{\delta :\Delta (\delta ,\rho \left(\gamma \right))\le {\tau }_1\}\subseteq \{\delta :\Delta (\delta ,\rho \left(\gamma \right))\le {\tau }_2\}$, hence the unions are nested. For $\tau =1$ the constraint is vacuous since $\Delta \in [0,1]$. □

Theorem 1

(CHS generalizes the HyperSoft Set). Assume each $c_i$ is zero-separating and take the self-centered selector $\rho \left(\gamma \right)=\gamma$. Then for $\tau =0$ one has

$$G_{\rho }^{\left(0\right)}\left(\gamma \right)=G\left(\gamma \right)(\forall \gamma \in \mathcal{C}).$$

Proof. 

By definition, $G_{\rho }^{\left(0\right)}\left(\gamma \right)={\bigcup }_{\delta :\Delta (\delta ,\gamma )\le 0}G\left(\delta \right)$. Since $\Delta (\delta ,\gamma )\ge 0$ always, the inequality forces $\Delta (\delta ,\gamma )=0$. Zero-separation gives $\delta =\gamma$, thus the union is $G\left(\gamma \right)$. □

Definition 11

(Neighborhood-based ContraSoft on a single attribute). Let V be a finite set with contradiction $c:V\times V\to [0,1]$, and let $F:V\to \mathcal{P}\left(U\right)$. For $\tau \in [0,1]$, theneighborhood-basedContraSoft transform is

$$F^{\left(\tau \right)}\left(v\right):=\bigcup _{w\in V:c(w,v)\le \tau }F\left(w\right)(v\in V).$$

Fixing $v^{★}\in V$ yields thefixed-referencevariant $F^{(\tau ;v^{★})}\left(v\right):={\bigcup }_{w:c(w,v^{★})\le \tau }F\left(w\right)$.

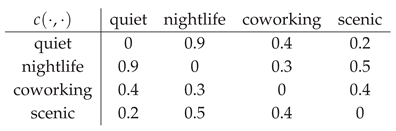
Example 9

(Neighborhood-based ContraSoft — Destination Selection by Climate Preference). Universe and attribute. Let the universe of candidate destinations be

$$U=\{u_1=\mathrm{Reykjavik},u_2=\mathrm{Zurich},u_3=\mathrm{Lisbon},u_4=\mathrm{Dubai},u_5=\mathrm{Helsinki},u_6=\mathrm{Vancouver}\}.$$

Consider a single attribute “preferred climate” with value set

$$V=\{\mathrm{cold},\mathrm{mild},\mathrm{warm},\mathrm{hot}\}.$$

Contradiction on V.  Let $c:V\times V\to [0,1]$ be symmetric with $c(v,v)=0$:

Baseline soft mapping. Define $F:V\to \mathcal{P}\left(U\right)$ by

$$F\left(\mathrm{cold}\right)=\{u_1,u_5\},F\left(\mathrm{mild}\right)=\{u_2,u_6\},F\left(\mathrm{warm}\right)=\left\{u_3\right\},F\left(\mathrm{hot}\right)=\left\{u_4\right\}.$$

Neighborhood-based ContraSoft transform. For threshold $\tau \in [0,1]$ and center $v\in V$,

$$F^{\left(\tau \right)}\left(v\right)=\bigcup _{w\in V:c(w,v)\le \tau }F\left(w\right).$$

Case 1 (moderate neighborhood). Let $v=\mathrm{mild}$ and $\tau =0.35$. Eligible neighbors satisfy $c(w,\mathrm{mild})\le 0.35$:

$$c(\mathrm{cold},\mathrm{mild})=0.3\left(\right),c(\mathrm{mild},\mathrm{mild})=0\left(\right),c(\mathrm{warm},\mathrm{mild})=0.3\left(\right),c(\mathrm{hot},\mathrm{mild})=0.7(\times ).$$

Therefore

$$\begin{array}{cc}\hfill F^{\left(0.35\right)}\left(\mathrm{mild}\right)& =F\left(\mathrm{cold}\right)\cup F\left(\mathrm{mild}\right)\cup F\left(\mathrm{warm}\right)\hfill \\ & =\{u_1,u_5\}\cup \{u_2,u_6\}\cup \left\{u_3\right\}=\{u_1,u_2,u_3,u_5,u_6\},|·|=5.\hfill \end{array}$$

Case 2 (tight neighborhood). Let $\tau =0.20$. Only $w=\mathrm{mild}$ satisfies $c(w,\mathrm{mild})\le 0.20$, hence

$$F^{\left(0.20\right)}\left(\mathrm{mild}\right)=F\left(\mathrm{mild}\right)=\{u_2,u_6\},|·|=2.$$

These computations show how increasing τ expands the accepted neighborhood in V and unions the corresponding destination sets in U.

Theorem 2

(CHS generalizes ContraSoft). Suppose $m=1$, so $\mathcal{C}={\mathcal{A}}_1=:V$, and let $c_1=c$. Identify $G:V\to \mathcal{P}\left(U\right)$ with F. Then:

(a)

With the self-centered selector $\rho \left(v\right)=v$, one has

$$G_{\rho }^{\left(\tau \right)}\left(v\right)=\bigcup _{w:c(w,v)\le \tau }G\left(w\right)=F^{\left(\tau \right)}\left(v\right),\forall v\in V.$$

(b)

With the fixed-reference selector $\rho \left(v\right)\equiv v^{★}$, one has

$$G_{\rho }^{\left(\tau \right)}\left(v\right)=\bigcup _{w:c(w,v^{★})\le \tau }G\left(w\right)=F^{(\tau ;v^{★})}\left(v\right),\forall v\in V.$$

Hence, for $m=1$ the CHS construction recovers both standard ContraSoft variants.

Proof. 

When $m=1$, $\Delta (w,\rho (v\left)\right)=c(w,\rho (v\left)\right)$. Substituting $\rho \left(v\right)=v$ gives (a); substituting $\rho \left(v\right)\equiv v^{★}$ gives (b). The set-theoretic unions agree by definition in both cases. □

2.2. Contra-SuperHyperSoft Set

Contra-SuperHyperSoft Set extends to set-valued coordinates, using lifted subset contradictions and aggregate radius; selector-threshold filtering unions nearby SuperHyperSoft slices effectively.

Definition 12

(Base and lifted contradictions). Let $A_1,\dots ,A_m$ be nonempty finite sets of attribute values and let $c_i:A_i\times A_i\to [0,1]$ becontradiction functions(symmetric and reflexive: $c_i(a,a)=0=c_i(a,a)$, $c_i(a,b)=c_i(b,a)$). Assume thezero-separationproperty $c_i(a,b)=0\Rightarrow a=b$. For subsets $S,T\subseteq A_i$ define theliftedcontradiction

$${\widehat{c}}_i(S,T):=\left\{\begin{array}{cc}{\displaystyle max\left\{\underset{a\in S}{max}\underset{b\in T}{min}{c}_i(a,b),\underset{b\in T}{max}\underset{a\in S}{min}{c}_i(a,b)\right\},}\hfill & S,T\ne ⌀,\hfill \\ 0,\hfill & S=T=⌀,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(With finiteness, the $max/min$ are attained.)

Lemma 1

(Symmetry, reflexivity, and zero-separation on subsets). For each i and $S,T\subseteq A_i$:

(a)

${\widehat{c}}_i(S,T)={\widehat{c}}_i(T,S)$ and ${\widehat{c}}_i(S,S)=0$.

(b)

If $c_i$ is zero-separating, then ${\widehat{c}}_i(S,T)=0$ implies $S=T$.

Proof. (a) Symmetry follows by exchanging the two max terms; reflexivity is immediate. (b) If ${\widehat{c}}_i(S,T)=0$ with $S,T\ne ⌀$, then ${max}_{a\in S}{min}_{b\in T}{c}_i(a,b)=0$ and ${max}_{b\in T}{min}_{a\in S}{c}_i(a,b)=0$. Thus, for each $a\in S$ there is $b\in T$ with $c_i(a,b)=0$, hence $a=b$ by zero-separation, so $S\subseteq T$. The second equality gives $T\subseteq S$. The cases with empties are by definition. □

Definition 13

(Product parameter space and aggregate contradiction). Let $\mathcal{C}:=\mathcal{P}\left(A_1\right)\times \dots \times \mathcal{P}\left(A_m\right)$ and write $\alpha =({\alpha }_1,\dots ,{\alpha }_m)$, $\beta =({\beta }_1,\dots ,{\beta }_m)\in \mathcal{C}$. Define the tuple-level contradiction by

$$\Delta (\alpha ,\beta ):=\underset{1\le i\le m}{max}{\widehat{c}}_i({\alpha }_i,{\beta }_i)\in [0,1].$$

Then $\Delta (\alpha ,\beta )=\Delta (\beta ,\alpha )$ and $\Delta (\alpha ,\alpha )=0$; if each $c_i$ is zero-separating, then by Lemma 1 we have $\Delta (\alpha ,\beta )=0\iff \alpha =\beta$.

Definition 14

(Reference selector). A reference selector is any map $\rho :\mathcal{C}\to \mathcal{C}$. Two common choices are the self-centered selector $\rho \left(\alpha \right)=\alpha$ and a fixed-reference selector $\rho \left(\alpha \right)\equiv r$ for a fixed $r\in \mathcal{C}$.

(CSHS)).Definition 15 (Contra-SuperHyperSoft Set Let U be a finite universe and let $F:\mathcal{C}\to \mathcal{P}\left(U\right)$ be a SuperHyperSoft mapping. Fix contradiction kernels $\left\{c_i\right\}$, their lifts $\left\{{\widehat{c}}_i\right\}$, an aggregate Δ, a selector ρ, and a threshold $\tau \in [0,1]$. The associated Contra-SuperHyperSoft Set is the tuple

$$\mathsf{CSHS}:=\left(U,{\{A_i,c_i\}}_{i=1}^m,F,\rho ,\tau \right),$$

together with the filtered mapping

$$F_{\rho }^{\left(\tau \right)}:\mathcal{C}⟶\mathcal{P}\left(U\right),F_{\rho }^{\left(\tau \right)}\left(\alpha \right):=\bigcup _{\beta \in \mathcal{C}:\Delta (\beta ,\rho (\alpha \left)\right)\le \tau }F\left(\beta \right).$$

Example 10 (CSHS in E-commerce Fraud Review (self-centered selector)). Setup. Let the universe of orders be $U=\{o_1,o_2,o_3,o_4,o_5,o_6,o_7,o_8\}$. Take two attribute domains:

$$A_1=\{\mathrm{card},\mathrm{crypto}\},A_2=\{\mathrm{verified},\mathrm{partial},\mathrm{missing}\}.$$

Base contradictions $c_1,c_2:[·]\to [0,1]$ (symmetric, 0 on the diagonal):

Lift ${\widehat{c}}_i$ to subsets by Definition (lifted contradiction) and aggregate

$$\Delta \left((S_1,S_2),(T_1,T_2)\right):=max\{{\widehat{c}}_1(S_1,T_1),{\widehat{c}}_2(S_2,T_2)\}.$$

The SuperHyperSoft mapping $F:\mathcal{P}\left(A_1\right)\times \mathcal{P}\left(A_2\right)\to \mathcal{P}\left(U\right)$ is specified by

$$\begin{array}{cc}& F(\left\{\mathrm{crypto}\right\},\left\{\mathrm{missing}\right\})=\{o_1,o_2\},F(\left\{\mathrm{crypto}\right\},\left\{\mathrm{partial}\right\})=\left\{o_3\right\},\hfill \\ & F(\left\{\mathrm{card}\right\},\left\{\mathrm{missing}\right\})=\left\{o_4\right\},F(\left\{\mathrm{card}\right\},\left\{\mathrm{partial}\right\})=\{o_5,o_6\},\hfill \\ & F(\{\mathrm{card},\mathrm{crypto}\},\{\mathrm{partial},\mathrm{missing}\})=\left\{o_7\right\},\mathrm{all}\mathrm{other}\mathrm{pairs}\mathrm{map}\mathrm{to}⌀.\hfill \end{array}$$

Choose the self-centered selector $\rho \left(\alpha \right)=\alpha$ and threshold $\tau =0.6$.

Filtering at ${\alpha }_0=(\left\{\mathrm{crypto}\right\},\left\{\mathrm{missing}\right\})$.

To avoid overfull lines, we list the computations in an aligned display:

$$\begin{array}{cc}\hfill \Delta \left((\left\{\mathrm{crypto}\right\},\left\{\mathrm{missing}\right\}),{\alpha }_0\right)& =max\left(0,0\right)=0\le \tau ,\hfill \\ \hfill \Delta \left((\left\{\mathrm{crypto}\right\},\left\{\mathrm{partial}\right\}),{\alpha }_0\right)& =max\left(0,c_2(\mathrm{partial},\mathrm{missing})\right)=max(0,0.6)=0.6\le \tau ,\hfill \\ \hfill \Delta \left((\left\{\mathrm{card}\right\},\left\{\mathrm{missing}\right\}),{\alpha }_0\right)& =max\left(0.8,0\right)=0.8>\tau ,\hfill \\ \hfill \Delta \left((\left\{\mathrm{card}\right\},\left\{\mathrm{partial}\right\}),{\alpha }_0\right)& =max\left(0.8,0.6\right)=0.8>\tau ,\hfill \\ \hfill \Delta \left((\{\mathrm{card},\mathrm{crypto}\},\{\mathrm{partial},\mathrm{missing}\}),{\alpha }_0\right)& =max\left({\widehat{c}}_1(\{\mathrm{card},\mathrm{crypto}\},\left\{\mathrm{crypto}\right\}),{\widehat{c}}_2(\{\mathrm{partial},\mathrm{missing}\},\left\{\mathrm{missing}\right\})\right)\hfill \\ & =max(0.8,0.6)=0.8>\tau .\hfill \end{array}$$

Hence

$$F_{\rho }^{\left(\tau \right)}\left({\alpha }_0\right)=\{o_1,o_2\}\cup \left\{o_3\right\}=\{o_1,o_2,o_3\},\left|F_{\rho }^{\left(\tau \right)}\left({\alpha }_0\right)\right|=3.$$

Filtering at ${\alpha }_1=(\left\{\mathrm{card}\right\},\left\{\mathrm{partial}\right\})$.

Therefore

$$F_{\rho }^{\left(\tau \right)}\left({\alpha }_1\right)=\{o_5,o_6\}\cup \left\{o_4\right\}=\{o_4,o_5,o_6\},\left|F_{\rho }^{\left(\tau \right)}\left({\alpha }_1\right)\right|=3.$$

This illustrates how the CSHS envelope aggregates nearby subset-parameters under the contradiction metric.

Example 11 (CSHS in Cloud Deployment Recommendation (self-centered selector)) Setup. Let the universe of candidate nodes be $U=\{n_1,n_2,n_3,n_4,n_5,n_6,n_7\}$. Attributes:

$$A_1=\{\mathrm{us}-\mathrm{east},\mathrm{us}-\mathrm{west},\mathrm{eu}\},A_2=\{\mathrm{cpu},\mathrm{gpu},\mathrm{memory}\}.$$

Base contradictions (0 on the diagonal, symmetric):

Lift to subsets by ${\widehat{c}}_i$ and aggregate by $\Delta \left((S_1,S_2),(T_1,T_2)\right)=max\{{\widehat{c}}_1(S_1,T_1),{\widehat{c}}_2(S_2,T_2)\}$.

SuperHyperSoft mapping F (nonempty images shown):

$$\begin{array}{cc}& F(\{\mathrm{us}-\mathrm{east}\},\left\{\mathrm{cpu}\right\})=\{n_1,n_2\},F(\{\mathrm{us}-\mathrm{east}\},\left\{\mathrm{gpu}\right\})=\left\{n_3\right\},\hfill \\ & F(\{\mathrm{us}-\mathrm{west}\},\left\{\mathrm{cpu}\right\})=\left\{n_4\right\},F(\left\{\mathrm{eu}\right\},\left\{\mathrm{cpu}\right\})=\left\{n_5\right\},\hfill \\ & F(\{\mathrm{us}-\mathrm{east},\mathrm{us}-\mathrm{west}\},\left\{\mathrm{cpu}\right\})=\left\{n_6\right\},\hfill \\ & F(\{\mathrm{us}-\mathrm{east}\},\{\mathrm{cpu},\mathrm{gpu}\})=\left\{n_7\right\}.\hfill \end{array}$$

Choose the self-centered selector $\rho \left(\alpha \right)=\alpha$ and threshold $\tau =0.5$.

Filtering at ${\alpha }^{★}=(\{\mathrm{us}-\mathrm{east}\},\left\{\mathrm{cpu}\right\})$.For each β with $F\left(\beta \right)\ne ⌀$, compute $\Delta (\beta ,{\alpha }^{★})$:

Hence

$$F_{\rho }^{\left(\tau \right)}\left({\alpha }^{★}\right)=\{n_1,n_2\}\cup \left\{n_3\right\}\cup \left\{n_4\right\}\cup \left\{n_6\right\}\cup \left\{n_7\right\}=\{n_1,n_2,n_3,n_4,n_6,n_7\},$$

with $|F_{\rho }^{\left(\tau \right)}\left({\alpha }^{★}\right)|=6$. Nodes requiring a European region are excluded by the contradiction bound.

Proposition 2 (Monotonicity in the threshold)If $0\le {\tau }_1\le {\tau }_2\le 1$, then $F_{\rho }^{\left({\tau }_1\right)}\left(\alpha \right)\subseteq F_{\rho }^{\left({\tau }_2\right)}\left(\alpha \right)$ for all $\alpha \in \mathcal{C}$. Moreover, $F_{\rho }^{\left(1\right)}\left(\alpha \right)={\bigcup }_{\beta \in \mathcal{C}}F\left(\beta \right)$ for all α.

Proof. The index sets $\{\beta :\Delta (\beta ,\rho \left(\alpha \right))\le \tau \}$ are nested as $\tau$ grows, hence so are the unions. For $\tau =1$ the constraint is vacuous since $\Delta \in [0,1]$. □

Theorem 3 (CSHS generalizes SuperHyperSoft)  Assume zero-separation for each $c_i$ and take the self-centered selector $\rho \left(\alpha \right)=\alpha$. Then for $\tau =0$ we have

$$F_{\rho }^{\left(0\right)}\left(\alpha \right)=F\left(\alpha \right)(\forall \alpha \in \mathcal{C}).$$

Proof. By definition, $F_{\rho }^{\left(0\right)}\left(\alpha \right)={\bigcup }_{\beta :\Delta (\beta ,\alpha )\le 0}F\left(\beta \right)$. Since $\Delta \ge 0$, the inequality forces $\Delta (\beta ,\alpha )=0$. By Definition 13 and Lemma 1, this occurs iff $\beta =\alpha$. Hence the union collapses to $F\left(\alpha \right)$. □

Definition 16 (Singleton embedding of HyperSoft into SuperHyperSoft).  Let $\iota :A_1\times \dots \times A_m⟶\mathcal{C}$ be

$$\iota ({\gamma }_1,\dots ,{\gamma }_m):=(\left\{{\gamma }_1\right\},\dots ,\left\{{\gamma }_m\right\}).$$

We say $F:\mathcal{C}\to \mathcal{P}\left(U\right)$ issingleton-supportedfor $G:A_1\times \dots \times A_m\to \mathcal{P}\left(U\right)$ if $F\left(\iota \right(\gamma \left)\right)=G\left(\gamma \right)$ for all γ and $F\left(\alpha \right)=⌀$ whenever some ${\alpha }_i$ is not a singleton.

Lemma 2 (Compatibility of contradictions on singletons).  For any $a,b\in A_i$ we have ${\widehat{c}}_i(\left\{a\right\},\left\{b\right\})=c_i(a,b)$. Consequently, for $\gamma ,\delta \in A_1\times \dots \times A_m$,

$$\Delta \left(\iota \left(\gamma \right),\iota \left(\delta \right)\right)=\underset{1\le i\le m}{max}{c}_i({\gamma }_i,{\delta }_i).$$

Proof. From Definition 12 with singletons, $max\{min{c}_i(a,b),min{c}_i(b,a)\}=c_i(a,b)$ by symmetry, and the product case follows. □

Theorem 4 (CSHS generalizes Contra-HyperSoft)  Let $G:A_1\times \dots \times A_m\to \mathcal{P}\left(U\right)$ be a HyperSoft set and F be a singleton-supported extension (Definition 16). Let ${\rho }_H$ be a selector on $A_1\times \dots \times A_m$ and define ${\rho }_S$ on $\mathcal{C}$ by ${\rho }_S\left(\iota \left(\gamma \right)\right):=\iota \left({\rho }_H\left(\gamma \right)\right)$, with arbitrary values elsewhere. Then for every γ and $\tau \in [0,1]$,

$$F_{{\rho }_S}^{\left(\tau \right)}\left(\iota \left(\gamma \right)\right)=\bigcup _{\delta :{max}_i{c}_i({\delta }_i,{\rho }_H{\left(\gamma \right)}_i)\le \tau }G\left(\delta \right)=:G_{{\rho }_H}^{\left(\tau \right)}\left(\gamma \right),$$

i.e. the CSHS filtered mapping restricted to singleton parameters coincides with the Contra-HyperSoft mapping for G built from $\left\{c_i\right\}$ and the same threshold.

Proof. By Definition 15,

$$F_{{\rho }_S}^{\left(\tau \right)}\left(\iota \left(\gamma \right)\right)=\bigcup _{\beta :\Delta (\beta ,{\rho }_S\left(\iota \left(\gamma \right)\right))\le \tau }F\left(\beta \right).$$

Since F is singleton-supported, only $\beta$ of the form $\iota \left(\delta \right)$ contribute. By Lemma 2 and the definition of ${\rho }_S$, $\Delta (\iota \left(\delta \right),{\rho }_S\left(\iota \left(\gamma \right)\right))={max}_i{c}_i({\delta }_i,{\rho }_H{\left(\gamma \right)}_i)$. Substitute and use $F\left(\iota \right(\delta \left)\right)=G\left(\delta \right)$ to obtain the stated equality. □

Theorem 5 (CSHS generalizes ContraSoft)  Let $m=1$ with base set $A_1=:V$ and contradiction $c:=c_1$. Let $F:\mathcal{P}\left(V\right)\to \mathcal{P}\left(U\right)$ be singleton-supported for some $F_0:V\to \mathcal{P}\left(U\right)$ via $F\left(\left\{v\right\}\right)=F_0\left(v\right)$ and $F\left(S\right)=⌀$ if $\left|S\right|\ne 1$. Then, with the self-centered selector, for all $v\in V$ and $\tau \in [0,1]$,

$$F_{\mathrm{id}}^{\left(\tau \right)}\left(\left\{v\right\}\right)=\bigcup _{w:c(w,v)\le \tau }{F}_0\left(w\right),$$

which is exactly the neighborhood-based ContraSoft transform on $(V,c)$. With a fixed reference $v^{★}\in V$, the same construction yields the fixed-reference ContraSoft variant.

Proof. Specialize Theorem 4 to $m=1$ with $G\equiv F_0$ and observe that $\Delta (\left\{w\right\},\left\{v\right\})={\widehat{c}}_1(\left\{w\right\},\left\{v\right\})=c(w,v)$. Singleton support reduces the union to singletons, yielding the stated form. □