1. Introduction
The Collatz Conjecture asks whether every positive integer eventually reaches 1 under the iteration
Despite its elementary form, the conjecture has remained unresolved since 1937 and has resisted probabilistic, dynamical, algebraic, and computational approaches.
The essential difficulty is structural: forward trajectories mix multiplicative growth with aggressive dyadic contraction, while reverse trajectories branch infinitely through admissible preimages. No prior framework has simultaneously captured both behaviors in a closed, exhaustive arithmetic model.
This work develops such a model. Our approach is built from first principles and consists of three independent components that ultimately coincide:
A local residue–phase automaton describing all odd iterates by their class modulo 6 and their phase modulo 3, yielding a finite state space on which every admissible reverse step acts.
A
zero-state operator that isolates the intrinsic odd component of each number by removing its admissible dyadic factor. This produces a global index
and a child-determined affine ladder
whose union over all zero-state bases yields a disjoint affine partition of
.
-
A
dyadic slice decomposition, determined by the exponent
, which partitions the odd integers into the sets
Each slice has weight and the slices are disjoint with total measure 1.
A central result of this paper is that the affine rails from the zero-state construction and the dyadic slices from coincide exactly. Thus the odd integers admit two independent but equivalent global parametrizations: one affine, one dyadic.
When combined with the
forward–reverse locked identity,
the global structure forces every forward trajectory into the unique affine ladder descending from its zero-state base. Since this base is always 1, and since the residue–phase automaton is finite, no forward runaway and no nontrivial odd cycle is possible.
All results, constructions, and structural decompositions presented here are original. Together they provide a complete arithmetic description of the Collatz dynamics and establish that every forward trajectory converges to 1.
We begin by establishing the fundamental definitions and notation used throughout the framework.
2. Definitions
Definition 1 (Classic Collatz function)
. The classical Collatz map is defined by
Definition 2 (Forward Collatz function)
. The complete-step (odd-to-odd) Collatz map is
where is the maximal exponent such that the denominator divides . Thus gives the next odd iterate of n under the Collatz process.
Definition 3 (Reverse Collatz function)
. The complete-step reverse Collatz map assigns to each odd integer n its admissible parent via
where k is admissible if . If is the minimal admissible doubling count, then is called the first parent
of n.
Definition 4 (Middle-even values). In the odd-to-odd formulation of the Collatz map, each step factors through an intermediate even value.
For the forward map
, given an odd integer n, the intermediate (middle-even) value is
For the reverse map
, given an odd integer n and an admissible doubling count (i.e. ), the intermediate (middle-even) value is
Both and are even and serve as the “middle” stage between odd inputs and odd outputs. Read modulo 18, these values determine the child’s odd class through the fixed gate , , in the reverse Collatz function.
Definition 5 (Parent (reverse Collatz function)). An odd integer n is called a parent. If (that is, n is an odd multiple of 3), then it has no admissible doubling and is called a terminating parent. If or , then n is live and admits some that is admissible.
Definition 6 ((Child (reverse Collatz function))
. Given a parent n and an admissible , the corresponding child
is
For a fixed n, admissible k have fixed parity and are exactly
where ℓ is the lift index
counting successive admissible exponents above the minimal one. As k increases by , the middle-even residue cycles ; under the fixed gate , , , the children of n therefore occur in the deterministic class rotation
Definition 7 (First admissible child)
. For any live odd integer , let denote its class-determined least admissible exponent. We define
and refer to as the first admissible child
of n.
Definition 8 (Admissible doubling and child)
. Let n be odd. A doubling count is admissible
if
For any admissible k, the reverse child
is
The set of admissible k for a fixed odd n has fixed parity (even if , odd if ), and hence preserves admissibility.
Definition 9 (Terminal and Live Classes)
. Let . The Collatz class of n is defined as:
Class is terminal under Collatz iteration; classes and are live.
Definition 10 (Reset-and-Resume Function)
. Given odd, define . Then the reset-and-resume transform is:
where denotes the 2-adic valuation of x. This is the only class-agnostic invariant rule under Collatz iteration.
Definition 11 (q-Transform Function)
. The class-dependent q-transform for single-generation transitions is defined as:
Definition 12 (Progression index)
. For an odd parent n, theprogression index
t is the integer parameter in the canonical forms
with . The index t counts the position of n within its mod-6 residue class. In later sections, offsets and ladders are expressed as explicit functions of this progression index.
Definition 13 (Admissible parent)
. For odd , define to be the least positive integer k such that . If such k exists, set
If we say n is terminating.
Definition 14 (Admissible exponents)
. For an odd integer n, the set of admissible exponents
is
(If , then .)
Definition 15 (Middle even and gate residue)
. For odd m, set
so that is the odd Collatz child. The middle even
is
and its gate residue
is
Definition 16 (Forward odd-to-odd step)
. For odd m, let and define
Definition 17 (Least-admissible reverse parent). For odd m, let , where if and if . Work modulo 18 with live residues and dead residues . Write every odd as with and .
Definition 18 (Rail)
. Arail
is the vertical affine progression generated from any odd value m by repeated admissible higher lifts. Each lift increases the exponent by and applies the transformation
Thus the rail through m is
Rails represent all values obtained from a fixed parent by higher-k lifts.
Definition 19 (Ladders as Dyadic Offset Progressions)
. Fix a class and let be the admissible lift exponent. Every odd integer in this class can be written uniquely as
where t is the index of the element within its residue class. Applying the reverse map gives
The ladder at level
kis the arithmetic progression
whose consecutive elements differ by the fixed dyadic offset
Thus a ladder is the ordered progression of parents obtained from all sequential inputs under the same admissible exponent k.
3. The Deterministic Residue Framework
This section extends the local residue framework first developed in
A Deterministic Residue Framework for the Collatz Operator at [
1], together with earlier unpublished notes that identified the mod 9 residue cycle as the source of reverse determinism. The core construction is preserved: admissibility is fixed by residue classes modulo 6, while refinement to mod 9 and its canonical lift to mod 18 determines the child class at each step.
The result is a deterministic lens through which every odd integer is classified and every admissible step is resolved. This local structure now appears explicitly as the microscopic counterpart of the global coverage framework that follows.
3.1. The mod 6 Classification for Odd Integers
All odd integers fall into three residue classes modulo 6:
-
C0: (odd multiples of 3: ).
Forward (middle-even identification): .
Reverse (admissibility/parity): No admissible k with exists, so has no reverse parent.
-
C1: (two higher than a multiple of 3: ).
Forward (middle-even identification): .
Reverse (admissibility/parity): , so admissible
k are
odd. The first admissible is
. One doubling gives
Since
for
, we have
; subtracting 1 yields a multiple of 3, so the reverse step is an integer. Thus
always resolves after
-
C2: (two lower than a multiple of 3: ).
Forward (middle-even identification): .
Reverse (admissibility/parity): , so admissible
k are
even. The first admissible is
, yielding
Since
for
, we have
; subtracting 1 yields a multiple of 3, so the reverse step is an integer. Thus
always resolves after
doublings.
Lemma 1 (C0 is terminating under the reverse step)
. If (i.e., n is an odd multiple of 3), then for every ,
In particular, the class C0 has no admissible reverse child.
Proof. If then for all , hence , which is not divisible by 3. □
The mod-6 classification isolates the essential periodic structure of the Collatz map. Every odd integer is congruent to 1, 3, or 5 mod 6, producing three invariant classes. Multiples of 3 () are terminal because no admissible doubling can satisfy . The remaining residues 1 and 5 ( and ) are live: they alternate under the admissible-exponent rule and generate the entire forward–reverse lattice. Thus the three-class system is not arbitrary—it is the minimal periodic decomposition consistent with both the mod-3 condition and parity.
3.2. K-value Admissibility of the Classes
This subsection identifies the admissible k values for each class and demonstrates how parity is determined by the residue of n modulo 3.
Lemma 2 (Admissibility parity)
. Let n be an odd integer. The congruence
has a solution if and only if n is not divisible by 3. Moreover, the residue of n modulo 3 determines the parity of k:
Once one admissible k exists, every larger k with the same parity is also admissible.
Proof.
C1 admissibility with
. For
we have
and
. The admissibility condition is
i.e.
Write
. Since
,
Substitute
n:
Note:
Therefore,
holds for all integers
t and all
.
This explicitly shows why every odd lift of the form
is admissible for
.
C2 admissibility with
. For
we have
and
. The admissibility condition is
i.e.
Write
. Since
,
Substitute
n:
Therefore,
holds for all integers
t and all
.
This explicitly shows why every even lift of the form is admissible for .
□
3.3. Mod 18 Gate and Its Mod 9 Subclassification
This subsection establishes the deterministic mod 18 gate that decides the child class of every admissible parent. The residue of the middle-even value after the minimal admissible doubling lands in , and this uniquely determines the class of the first child.
Lemma 3 (Minimal admissible doubling and the mod 18 gate)
. List the odd integers mod 18 in sequential order and, for each odd n, take its first child by the reverse Collatz function and using . Then the first-child classes follow a repeating nine-step cycle in sequence mod 3:
(where x denotes terminating parents, i.e. multiples of 3). In particular, the six odd non-multiples of 3 partition into two fixed triads
corresponding to and parents, respectively; thus mod 18 alone determines the child-class framework.
Moreover, let denote the minimal admissible exponent
for the reverse function
This minimal k is fixed by the class of n:
Applying the minimal admissible doubling directly to the residue gives the deterministic gate
Evaluating this for each residue yields the fixed gate assignment
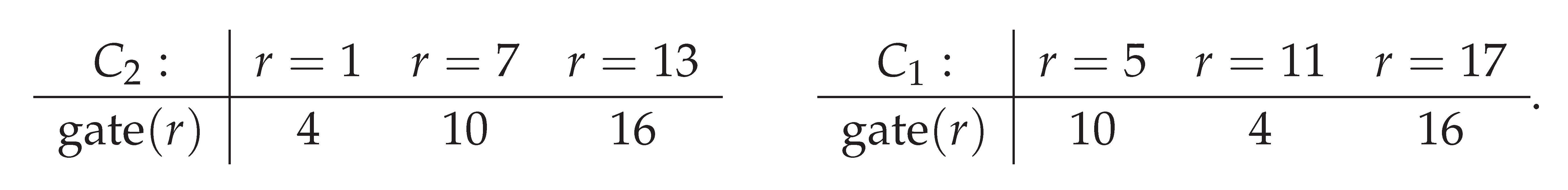 Thus the minimal admissible doubling maps each odd residue to a unique even gate in , refining the mod-9 triads to mod-18 gates.
Thus the minimal admissible doubling maps each odd residue to a unique even gate in , refining the mod-9 triads to mod-18 gates.
Proof. (i) Mod-9 triad partition. For odd n, write with . If then and the parent is terminating (). When , the residues split by into the two disjoint triads and , which correspond to and , respectively. The first-child map (apply then divide by 2 until odd) permutes elements within the appropriate triad and never crosses between them, yielding the stated nine-step cycle.
(ii)
Lift to mod-18 gates. Work modulo 18 and apply the minimal admissible doubling directly to the residue
r: for
use one factor of 4; for
use one factor of 2. This gives
which are precisely the even gates
claimed. □
Corollary 1 (Linear segment pattern 19–35)
. Listed are the odd integers n from 19 to 35. For each n, record its class (mod 6), its residue (mod 9) and (mod 18), the reverse middle-even at the minimal admissible doubling ( for , for , none for ), and the class of the first child
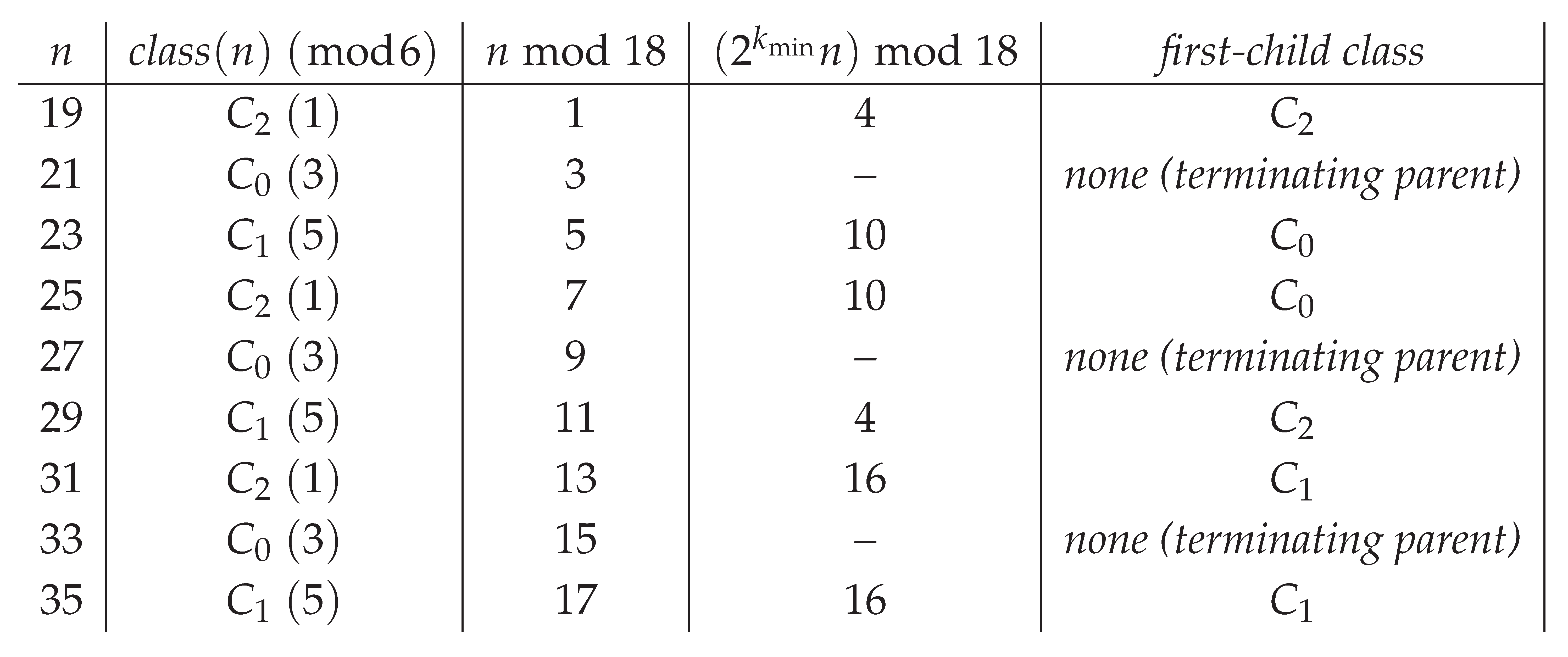
Explanation. For each n: determine its class by (C0: 3, C1: 5, C2: 1). If , no admissible reverse step exists. If (resp. ), take (resp. ) by admissibility parity. Then use the deterministic gate: with the fixed mapping . Evaluating these nine cases yields the displayed sequence . This finite segment is a repeating cycle. □
These nine odd residues partition into inadmissible and admissible parents:
Lemma 4 (Equidistribution of First-Child Classes). Across every complete 18-residue cycle of odd parents, the first-child classes appear with exact frequency each.
Proof. By Corollary 1, the nine admissible residues modulo 18 yield the child-class sequence
where dashes denote terminating parents. Each 18-step cycle therefore contains precisely two occurrences of each live class, giving equal frequency
when restricted to
. □
Lemma 5 (Forward mod-6 lift to mod-18 at the first even)
. Let n be odd and define the forward middle-even value . Then the residue of n modulo 6 determines modulo 18 via
In particular, the first forward step lifts the mod-6 classification to a unique gate residue modulo 18.
Proof. Write
with
. Then
since
. Direct evaluation gives
which proves the three implications and the uniqueness of the lifted gate residue. □
Proposition 1 (Deterministic child-class decision via mod 18)
. In the Reverse Collatz function, and for odd n, the residue of the middle even in alone determines the child’s odd class, both in forward and reverse middle-even. This gives a one-step, local rule independent of trajectory history.
Existence of a forward–reverse alignment through the middle-even gate.
Lemma 6 (Middle-even equivalence mod 18)
. If 3 does not divide n, then there exists an admissible such that
Proof.
Forward side (mod 6 lifted to mod 18). For odd
n, the forward middle-even value is
. Reducing
n modulo 6 and multiplying by 3 lifts the residue to mod 18:
so
always lies in
.
Reverse side (mod 18 determinism). For odd
n not divisible by 3, the residue
, together with the admissible parity of
(even if
, odd if
), selects exactly one of the two triads of units modulo 9:
Applying
places
n into the middle-even value that belongs to the nine-step cycle of Corollary 1. That middle-even value is already one of
, the forward gates. □
3.4. Microcycles and Lifted k with Tables
Lemma 7 (Rotation under
in mod 18)
. If k is admissible for odd n (), then
Moreover , and hence
Proof. Admissible are even and , so only occur modulo 18. For admissible k, ; computing mod 18 gives , , , which establishes the 3-cycle. □
Microcycles: function and reason. Fix a live odd parent
n not divisible by 3. For the Reverse Collatz Function, all admissible reverse doublings for
n share the same parity (by admissibility parity), so from the minimal admissible count
we may advance by steps of 2:
. By Lemma 7, each
step multiplies the reverse middle-even by 4 modulo 18, sending
and hence rotating the child classes
.
cycling through
(mod 18). By the common mod-18 gate (Lemma 6), these three middle-even classes deterministically select the child odd classes
, in that order. Thus every fixed parent
n generates a
k-lifted microcycle of children:
(), in cyclic order beginning with the first admissible child, repeating every three steps. Moreover, by the forward–reverse middle-even equivalence (Lemma 6), there exists an admissible k for which , so the reverse microcycle is aligned with the residue one sees on the forward side.
To display this mechanism explicitly, we present two parallel tables: (i) the integer view, which lists specific n and its children at each admissible lift, and (ii) the residue view, which reduces n to . Both views coincide in the mod-18 column and the resulting child class.
Reading across the rows of either table shows how each lift advances through the microcycle, and how every admissible parent reaches a residue within at most two steps, certifying an accessible termination to .
Example (reverse step, even k; here , ):
Example (reverse step, odd k; here , ):
Figure 1.
Even-k rotation of child classes through the mod-18 gate. Each increment of two in k multiplies the middle-even residue by 4, producing the cycle . These residues correspond deterministically to classes (with , , ). Hence the child class rotates in the fixed order , making the terminating class periodically available alongside the live classes.
Figure 1.
Even-k rotation of child classes through the mod-18 gate. Each increment of two in k multiplies the middle-even residue by 4, producing the cycle . These residues correspond deterministically to classes (with , , ). Hence the child class rotates in the fixed order , making the terminating class periodically available alongside the live classes.
3.5. Mod 54 Refinement: Fixing the Child Residue
The mod-18 gate (Lemma 3, Proposition 1) determines the child class. Refining the lens to determines, already at the first admissible reverse step, the child’s odd residue modulo 18.
Triad map (mod 54).
Write every live odd
n as
Set
. For each
, the corresponding residues in mod 54 are
Define the lifted triads
by

Each lifted triad row follows the same deterministic pattern as the mod 18 table. The indexing variable
plays the same role as
in selecting the correct column of the triad. Rows for
are in
or
, and
remain in
.
Lemma 8 (Mod 54 refinement fixes the child residue)
. Let
Set . Then the first admissible reverse child of n has odd residue
where is determined by the lifted triad . Equivalently, the pair uniquely determines the child’s odd residue modulo 18.
Proof sketch. By Lemma 2, the minimal admissible exponent is odd for and even for . The mod 18 structure (Lemma 3) partitions the six live residues into deterministic triads, and the admissibility parity lifts each residue canonically to its gate (Proposition 1).
Passing to mod 54, each
splits into three residues
and the index
selects one of the three columns of the lifted triad table
. Evaluating the first admissible reverse step for
within each
reproduces exactly the triad outputs listed in
Table 1. Thus
completely determines the child residue modulo 18. □
Compact 54-row table.
Because
is completely determined by
, the mapping
is obtained by grouping the 27 live residues mod 54 into six blocks by
r and subdividing each block by
. For example, the block
contributes residues
in the order
. Explicitly listing all odd
produces a 54-entry table in which each row records
. We defer the full table to
Table 1 below for readability.
Corollary 2 (Periodicity of the Mod 54 Child Mapping)
. Let n be an odd integer with
Let denote the residue modulo 18 of the first admissible reverse child of n,
Then for every integer (period index),
Equivalently, the mapping
is periodic with fundamental period 54. In particular, the table of first-child residues for odd repeats identically on each interval .
The refinement to modulus 54 resolves the residual ambiguity left by the mod-18 gate. At mod-18, each live residue determines only the class of its child; lifting to mod-54 records the phase of the quotient , which fixes the child’s exact odd residue mod 18. The resulting triads show that every parent residue generates three distinct child residues, one for each phase position. Because these triads repeat with period 54, the entire reverse map becomes periodic at that modular scale. This periodicity demonstrates that the residue–phase system is finite and deterministic: each pair has one unique successor, and every possible parent–child relationship repeats identically on successive 54-blocks.
Lemma 9 (Affine reverse update law).
Let with and , and set
Define
Then and the single–step update is given by
with the following explicit formulas:
(Residue update by phase)
(Quotient update)
Consequently, the pair uniquely determines , and the next phase is computed from the affine form .
Corollary 3 (Finite Residue–Phase Automaton)
. For each step of the reverse map defined by
the image depends only on through the valuation of . The quotient component evolves under the induced transformation
and defines a finite deterministic automaton on the space . The sequence obtained by successive iterations remains bounded within this finite set, generating locally deterministic residue–phase transitions.
Lemma 10 (Residue–Phase Transition and Reset–Resume Law). Let with and as above. Then the following properties hold:
For fixed r, as q varies modulo 3, the residues occupy three distinct elements of corresponding to the classes .
The order of appearance of these residues is determined by r and the parity of , defining a locally unique orientation.
For each iteration, the next phase and residue are re-evaluated from the resulting m, establishing a reset and resume transition of the form
where and .
The residue phase system thereby forms a finite deterministic automaton with terminal residues , transitional residues mapping into , and active residues forming the lattice .
Table 2.
Residue classes, minimal exponents, orientation signs, and resulting triads for each live residue r.
Table 2.
Residue classes, minimal exponents, orientation signs, and resulting triads for each live residue r.
| r |
|
|
|
for
|
| 1 |
2 |
1 |
|
|
| 7 |
2 |
9 |
|
|
| 13 |
2 |
17 |
|
|
| 5 |
1 |
3 |
|
|
| 11 |
1 |
7 |
|
|
| 17 |
1 |
11 |
|
|
The affine reverse update law converts the inverse Collatz step into a linear rule on the quotient–residue plane. For each live residue r, the minimal admissible exponent fixes the slope and intercept of an affine map . The modulus 18 confines all results to nine possible odd residues, and the quotient modulus 3 serves as a rotating phase selector. Hence every pair specifies a unique successor .
Geometrically, the system behaves as a finite automaton of six residue rows () and three phase columns (). The “reset–resume” rule means that after each reverse step, the new residue and phase become the parameters of the next affine map. This continual reassignment makes the process locally deterministic but globally adaptive: the governing equation changes with each step while remaining finite. Terminal residues in close the automaton, ensuring every orbit eventually reaches a fixed point of the system.
Theorem 1 (Global Determinism and Finite Termination of the Reverse Automaton).
Let denote the residue and quotient at step t, and define
Then:
For each step, uniquely determines , forming a finite deterministic mapping.
-
The transition structure satisfies
producing the four active transition types .
-
The system evolves through successive local maps
generating a finite deterministic sequence in the residue phase space.
Each active transition ultimately reaches a terminal residue in within finitely many steps. The mapping admits no infinite nonterminal orbit.
Hence the reverse Collatz dynamics on odd integers forms a finite, locally deterministic reset and resume automaton whose transitions are governed by residue class and phase position at each step.
3.6. Bounded Corridor Dynamics at Fixed Residues
Among the six live residues modulo 18, only
have the special property that their first admissible reverse child under
remains in the same residue class. This follows directly from the triadic structure established in Sub
Section 3.3: all other live residues transition immediately to a different residue upon the first admissible lift, whereas
and
alone form self-contained local corridors under forward iteration.
Because these two residues can map to themselves under , their forward dynamics admit chains of arbitrary length determined solely by arithmetic properties of the phase index q. For , the forward map contracts by a factor of until the 2-power in q is exhausted. For , the forward map expands by for exactly steps, consuming one factor of 2 per iteration.
The results in the following subsections establish the precise structure and length of these corridors: - admits contraction chains controlled by divisibility of q. - admits expansion chains controlled by the 2-adic valuation of .
These two cases are the only local residue dynamics that can persist beyond a single step under , and their exhaustion determines the maximal extent of fixed-residue behavior in the entire system.
Reverse map at .
Let
If
q is divisible by 4, then
The forward update is then
Since we only care about the
q-level:
This shows that, as long as
q remains divisible by 4, the forward map strictly scales
q by a factor of
without changing the residue class
.
The descent in q continues until the 2-adic factor is exhausted, at which point the residue transition occurs.
Reverse map at .
Let
Then
If
q is odd (i.e.
), then
is odd, so
The forward update is therefore
Writing
gives
so
and
This map preserves the residue
precisely while
q remains odd. Rewriting the recurrence,
gives the explicit evolution
Hence the number of consecutive
steps is determined entirely by the 2-adic valuation of
:
Remark 1. If is a pure power of 2, the corridor length equals that power’s exponent exactly. If it contains an odd factor , the corridor length still equals e, and the odd factor merely remains as a cofactor during the valid steps. Thus the run length for is governed entirely by the 2-adic valuation of and not by any fixed external bound.
Together with the case, this establishes explicit local corridor dynamics: the map contracts by a factor until powers of 2 are exhausted, while the map expands by for exactly e steps, with e determined directly by the factorization of .
Lemma 11 (Higher admissible lifts are strictly ascending and rotate the gate)
. Fix a live odd parent n and let be its minimal admissible exponent (determined by class). For each define the t-th admissible lift and reverse child by
Then:
- (a)
Strict ascent in the reverse value. The sequence is strictly increasing, with the exact increment
Equivalently,
so grows geometrically in t.
- (b)
Gate rotation (class rotation). The associated reverse middle-even residues rotate deterministically:
yielding the cycle (Lemma 7). Consequently the child class rotates .
- (b)
Higher lifts are higher transformations. Each increment multiplies the affine scaling factor by 4 (from to ) while preserving the constant drift . Thus every higher admissible lift is a strictly larger affine transform on n, independent of the gate rotation.
Proof. (a) Compute directly:
so
is strictly increasing. The closed form follows from
.
(b) This is Lemma 7: for admissible k, and , producing the stated rotation and class cycle.
(c) From , replacing k by multiplies the linear coefficient by 4 and leaves the drift unchanged, so the transform strictly enlarges the image while the residue gate rotates as in (b). □
Only the residues and form self-contained “corridors’’ in the residue–phase system. All other live residues immediately transition to a different class after one admissible lift. Within these two corridors the forward dynamics are governed purely by 2-adic properties of the quotient variable q.
For , the forward map contracts q by a factor of as long as q remains divisible by 4. Each iteration removes one factor of 2, so the chain length equals the 2-adic valuation of q. For , the forward map expands by while q is odd, and the number of valid steps is exactly . Thus the persistence of each corridor is determined entirely by local 2-adic content, not by any external bound.
Beyond these corridors, higher admissible lifts always increase the reverse value and rotate the middle-even gate through . Each lift multiplies the affine scale by 4 while preserving the constant drift, so the sequence of lifts is a strictly ascending geometric rail. Together these facts show that fixed-residue behavior is finite and bounded, and that all non-terminal paths ultimately exit their local corridors to join the global terminating flow.
4. Consequences of Lens Refinement, Finite Reverse Lifespan, and Forward Convergence
In this section all integers are odd and positive. We retain the classes
the boundary residues
, and the live residues
. We also keep
,
, and
from the earlier setup.
4.1. Standing Conventions and Phase
Every odd
n is written uniquely as
We call
r the residue of
n and define the
phase
4.2. One-Step Reverse Lens Under : Triads and Boundary
Define the minimal reverse step
with
required odd. For a fixed
set
Lemma 12 (Triads and boundary presence). For each live residue r, the set has exactly three elements and forms a triad. Moreover:
If , then .
If , then contains at least one boundary residue (5 or 7 mod 18), and the other elements lie in .
Proof. Reduce modulo 18; dependence is only on r and , giving and the stated boundary structure by direct casework. □
Lemma 13 ( is reverse-terminal). If , then is not an odd integer.
Proof. If , then for all . □
4.3. Residue Rotation Law
Write
with phase
and let
be the class-determined exponent. Set
Then the minimal child
satisfies
so the residue advances by a constant step
inside a fixed triad (sign by class), while the new phase
is obtained from the affine quotient. Consequently the pair
uniquely determines
.
4.3.1. Generational Residue–Phase Map and Finiteness
Define the local update
This yields a finite, locally deterministic automaton on the space
with terminal sink
.
The residue rotation law establishes that every live residue r advances within a closed triad by a fixed modular step of . This motion is cyclic, but not self-sustaining indefinitely: each triad contains at least one boundary residue (either 5 or 7 mod 18) whose next image lies in the terminal set . Thus, although the rotation within a class appears periodic, the presence of these boundary residues ensures that repeated application of the map cannot cycle endlessly within or .
When viewed on the full residue–phase grid , the update law forms a finite directed graph in which each vertex has a single outgoing edge. Every orbit therefore follows a deterministic path through a bounded set of 18 states. Because at least one state in every rotation chain transitions to , all paths must eventually reach a terminal residue and halt. The rotation law therefore provides the local mechanism by which the global map attains finite convergence.
Theorem 2 (Finite local dynamics). For each step, uniquely determines . Every nonterminal transition type lies among , and every trajectory in this finite automaton reaches a terminal residue in in finitely many steps.
4.3.2. Lift Microcycles and Guaranteed Boundary Access
For a fixed live parent
n, all admissible exponents have fixed parity; lifts
rotate the middle-even residue by a factor
:
so the child classes rotate
. In particular, within at most two lifts the gate
is attained, making
accessible.
4.3.3. Mod-54 Refinement: Fixing the Child Residue
Refining to modulus 54 splits each live residue into three residues ; the index selects the column of a lifted triad that already fixes the child’s odd residue modulo 18 at the first admissible reverse step. Thus determines the child residue.
4.4. The Self-loop
Remark 2 (The trivial self-loop and phase stability). The integer is the unique odd fixed point of the odd-to-odd map: . In the 18-lens we have , so and both residue and phase remain unchanged. On the reverse side, the minimal lift for is , and . Hence is the only state that self-loops while staying phase-stable at every lens; all other live residues either change residue at the first minimal step or exhaust their corridor in finitely many steps.
Corollary 4 (Forward convergence)
. The forward odd-to-odd step
is unique and edge-aligned with a reverse admissible step (middle-even equivalence). Hence each forward trajectory is a single, non-branching chain that must terminate at 1.
4.5. Affine Arithmetic Decomposition
Lemma 14 (Affine form and accumulated drift)
. Affine form. For any odd n and admissible k,
Accumulated form. Let be the exponents used in t reverse steps, set and
Then
This makes explicit the fixed per-step drift in every odd-to-odd reverse step.
Proof. The affine identity is immediate from . Iterating the affine map (e.g. by induction) yields with . If and , then with and , which rules out a nontrivial odd cycle. □
Corollary 5 (No nontrivial odd cycles). Any closed reverse loop would satisfy with , which is impossible for .
Corollary 6 (Lift-by-2 rail)
. The reverse map is affine (scale , subtract ). In particular,
so each admissible parity class generates the rail .
4.6. Consistency of Aligned Steps
The Trivial Loop from : Reverse and Forward Views
Lemma 15 (1 is and has even admissible doublings). Since , the integer 1 lies in class . Admissibility for the reverse step requires . With and , this gives , hence k is even. The minimal admissible doubling count is .
Proposition 2 (First child of 1 equals 1)
. With , the reverse child of is
so the first child of 1 is 1 again. Consequently, under the reverse map with minimal admissible doubling, is a fixed point in class .
Remark 3 (Consistency with the forward picture: the
loop)
. From the forward side, starting at 1,
which is the well-known loop. Thus the reverse fixed point at (with minimal ) corresponds exactly to the unique forward cycle.
Lemma 16 (Anchor–1 generation and coverage)
. Define the stepped reverse family by composing admissible lifts at each state:
where at each step the residue and phase determine and the lift parity, and . Then:
- (a)
(Forward surjectivity from the anchor) Every odd occurs as a value of some finite composition . Equivalently, every live residue and phase is reachable from the anchor 1 by finitely many admissible stepped lifts with resets.
- (b)
(Two–anchor reduction) Since occurs in the first lifted triad from 1 (after one reset), all odd m are likewise values of a stepped composition beginning at the pair of anchors .
Proof. Work in the residue–phase automaton on
. By the mod-54 refinement, each state
has a unique first child residue
, and this mapping is periodic with fundamental period 54. By Lemma 9, the reverse child at each step is affine in the quotient,
so varying
q over
sweeps an entire congruence class of targets while the phase
selects the column of the triad. Starting at 1 and iterating admissible lifts, the reachable set of residue–phase states expands monotonically because higher lifts rotate the gate (
) while strictly increasing the affine scale. Using the corridor facts (
contracts until the 2-power in
q is exhausted;
expands for exactly
steps) together with the transition rows for
, an induction on the 54-block index shows that all six live residues and all three phases occur along some anchor–1 chain. Thus any odd
m is obtained as
for a suitable finite choice of lifts. The appearance of 5 along the same chains yields the two–anchor variant. □
Corollary 7 (No runaways via anchor origin). Every odd integer lies on a stepped reverse path originating at the anchor 1 (equivalently at ) within the residue–phase system. Because this system consists of finitely many residue–phase states and every admissible reverse step remains within this finite automaton, no reverse chain can produce an infinite ascent that avoids the terminating class . In particular, the only locally persistent behaviors (the self-mapping residues and ) remain confined to the same finite residue–phase structure and cannot generate an unbounded escape.
The admissible reverse steps act entirely within the finite residue–phase automaton
Starting from the anchor, higher lifts only rotate the gate among the three residues
modulo 18, while the reset–resume update replaces each state
with the residue and phase of the new odd child. Because
contains all possible live residue–phase states, and every admissible step maps one element of
to another, no reverse iteration can ever escape this finite structure.
Moreover, each triad contains at least one boundary residue whose next image lies in the terminal class . Thus, although the motion of residues and phases is cyclic inside , the presence of these deterministic boundary exits prevents any unbounded ascent. Every branch eventually encounters a boundary state and therefore cannot form an infinite runaway chain.
Lemma 17 (Forward–reverse locked step)
. Let n be odd and set
Then
Conversely, for any odd m and any admissible
k,
Proof. If then with m odd, hence .
Conversely, if with m odd, then so and . □
Corollary 8 (Forward uniqueness, reverse branching). For each odd n, the forward step is unique (the maximal 2-power is forced). For a fixed odd m, every admissible k yields a (distinct) parent whose forward step returns m. Thus the reverse tree branches, while the forward trajectory is locked; following Lemma 17, theedge-alignedreverse choice at each node reproduces the forward path exactly.
Theorem 3 (No forward runaway; global termination). Let be the odd-to-odd Collatz map. For every odd , the forward trajectory reaches 1 in finitely many steps.
Proof. By Lemma 17 the forward edge with is exactly inverted by the reverse edge . Thus the forward path is edge-aligned with a reverse path using the same exponents .
Encode each
as
with
and set the phase
. By the affine reverse update (Lemma 9) and the mod-54 refinement (Lemma 8, Corollary 2), the transition on states is a map
on the finite set
(Corollary 3). Hence the sequence
either (i) enters one of the two fixed-residue corridors of Sub
Section 3.6 (
or
), whose lengths are finite and equal to
and
respectively, or (ii) repeats a state in
.
Case (i) terminates because the corridor lengths are finite and every exit is governed by the same finite automaton, which ultimately reaches the gate that feeds the terminal class in the reverse picture.
In case (ii), a repetition with the same edge-aligned exponents would force a nontrivial cycle for the reverse affine map ; but the affine form together with the higher-lift monotonicity (Lemma 11) and unique parentage excludes nontrivial cycles. The only fixed odd point under T is 1 (since ). Therefore any repetition implies arrival at 1.
Thus, for every odd
n contained within the residue–phase system established above, the forward trajectory under
terminates at 1. □
5. The Global Framework: Affine Rails, Dyadic Slices, and Complete Coverage
This section extends the global offset framework developed in
Arithmetic Offsets and Recursive Coverage Patterns in the Collatz Function [
2]. The earlier work established that the reverse map produces structured arithmetic progressions (offset ladders) whose superposition covers all admissible odd integers. Here we introduce the additional arithmetic machinery—zero–state normalization, the
z–index skeleton, and the dyadic slicing induced by
—which refines and completes that global description.
The three components now operate in a unified way:
1. the zero–state coordinate assigns each admissible odd a canonical position within the live lattice; 2. the affine inverse generates class–preserving rails under via ; and 3. the dyadic slices partition the odd integers according to the 2–adic valuation of .
We show that these are not separate descriptions but exact arithmetic equivalents. Every affine rail position corresponds to a unique dyadic slice, every dyadic slice has a unique zero–state anchor in the
z–skeleton, and the union over all slices yields a disjoint and complete decomposition of
. Thus the global structure anticipated in [
2] is recovered as a special case of a more rigid algebraic framework that requires no step–count bounds and is compatible with the full local–to–global dynamics developed in
Section 3–
Section 4.
5.1. Offset Formulas in the Transformation
5.1.1. Offsets
From the mod 6 classification established in the prior section, every odd integer is congruent to 1, 3, or 5 modulo 6. The residue 3 gives the terminating class
, while the residues 1 and 5 produce the live classes
and
. Thus every
parent can be written in the form
where
t is a nonnegative integer indexing the position of
n within the
residue class. Equivalently,
t counts how many multiples of 6 have been passed before reaching
n. By the admissibility rule,
nodes allow only odd exponents
k. With the minimal choice
, the reverse Collatz function is
Substituting
gives
The offset is obtained by subtracting the parent:
Hence each
child lies an even step below its parent, and the step size grows linearly with the modulo 6 index
t. The resulting ladder of offsets is
Thus the offsets are the explicit arithmetic realization of the reverse rule with odd k, derived directly from the mod 6 classification.
5.1.2. C2 Offsets
From the mod 6 classification, every
parent can be written as
with
. By admissibility,
nodes allow only even exponents
k. With the minimal choice
,
Substituting
gives
Therefore the offset (child minus parent) is
Hence the first admissible reverse step in
is nondecreasing and, for
, strictly increasing in
t:
Concrete examples:
The explicit offsets for small values of
n are listed in
Table A1 in Appendix A. This table illustrates the arithmetic ladders described in
Section 5.1.1 and
Section 5.1.2, making the underlying arithmetic structure relative to each
n transparent up to
.
Lemma 18 (Offset Ladders by Class)
. For each live parent n, the first admissible reverse step defines an arithmetic offset depending only on its class:
Moreover, higher admissible lifts of the same parent extend these formulas linearly in t with parity restricted to odd k for and even k for .
Proof. Direct substitution of with odd k and with even k into the reverse Collatz function gives the claimed offset formulas. The parity restriction follows from admissibility, so every live parent generates an infinite ladder of children determined solely by . □
Theorem 4 (Anchor principle). All progressive path iterations of the Collatz map are anchored at the two primitive parents and . Every admissible lift (k even) and (k odd) generates an infinite raising sequence. These raising sequences partition the odd integers into disjoint arithmetic progressions modulo , and the union over all k gives complete coverage. Thus the global affine enumeration is entirely determined by the anchor rails of the pair and their respective admissible k-values.
Corollary 9 (Exhaustion by anchors). Every odd integer lies in exactly one position of an offset ladder on a rail of the form generated from a zero-state anchor. The only anchors are the origin rails of the dual live classes, corresponding to , i.e. in . As these origin rails are extended and their offset ladders are filled, the resulting structure enumerates all odd integers exactly once, and no other origins occur.
5.1.3. Further Lifts of Admissible k
The reverse Collatz function extends naturally to higher admissible exponents: odd
for
parents (
) and even
for
parents (
). Substituting these values into
gives the general offset formulas
The first admissible k gives the minimal child, and increasing k by two corresponds to a deeper lift along a higher ladder. Each successive lift remains tied to the progression index t, with the offset magnitude growing on the order of as k increases.
Remark 4 (Offsets and the itinerary). The higher-k formulas confirm that offsets are determined not by the “generation depth” but by the progression index t and the parity of k. Which ladder is followed depends on the sequence of class transitions as the function is iterated. Thus and each sustain an infinite sequence of admissible steps, and the arithmetic progression of offsets is simply the explicit trace of the admissibility rules, computed relative to n at each transformation.
5.2. Arithmetic Progressions of Children
While offsets describe the displacement between a parent and its child, progressions describe how children of consecutive parents distribute across the integers. We now compute these inter-parent progressions.
5.2.1. Parents
Take consecutive
parents
and
. From the reverse rule with
, their children are
Hence
Thus first admissible children of consecutive
parents advance in an arithmetic progression with step size
.
5.2.2. Parents
Take consecutive
parents
and
. From the reverse rule with
, their children are
Hence
Thus first admissible children of consecutive
parents advance in an arithmetic progression with step size
.
Lemma 19 (Progressions of Consecutive Parents)
. First admissible children of consecutive parents form arithmetic progressions:
Thus children of adjacent parents distribute evenly across odd integers with step size fixed by class.
Remark 5. The offset ladders of Section 5.1.1–Section 5.1.2 describe how each parent generates children in a ladder determined relative to its own value of n. The arithmetic progressions, by contrast, describe how numerically consecutive parents distribute their children across the integers. Both perspectives are needed: ladders explain the local offsets tied to each parent, while progressions explain the global coverage across parents.
For parents, each has the form . With the minimal admissible exponent , the child is
Subtracting the parent gives the offset
Thus the offset depends linearly on t and grows in magnitude as t increases.
For parents, each has the form . With the minimal admissible exponent , the child is
so the offset is
This offset also depends on t, and for it is strictly increasing.
Therefore, offsets are not fixed increments across all parents, but arithmetic expressions relative to each parent’s index t within its residue class. Each live class generates an infinite rail of children, and the offset size expands with t while preserving the admissibility rule (odd k for , even k for ).
The arithmetic progressions across consecutive parents are simply the global counterpart of the same rule. When t increases by (advancing to the next parent in the same class), the child also advances by a constant step ( for at , for at , and in general ). This step is independent of t because the dependence on t is linear.
Thus the two descriptions are isomorphic: offsets show how children are positioned relative to a fixed parent, while progressions show how those positions line up across the sequence of parents. Both arise from the same affine relation , and together they capture the local and global arithmetic structure of the reverse Collatz map.
5.2.3. Higher Lifts
Lemma 20 (Quadrupling of Step Sizes at Higher Lifts)
. For each class, increasing the admissible exponent k by two applies two successive doublings, thereby quadrupling the progression step size of consecutive parents. Concretely:
Proof. From the general offset formulas in
Section 5.1.3, the difference between children of consecutive parents is proportional to
. Replacing
k by
multiplies this factor by 4, hence quadruples the step size between odd children. Therefore each successive two-lift scales the step size by a factor of four. □
At higher admissible
k-lifts, step sizes scale as
: each unit increase of
k doubles the progression spacing, and in particular every two lifts quadruple it. A convenient way to display this is to show the two-lift subsequences and stagger the one-lift intermediates:
This pattern follows directly from the formulas of
Section 5.1.3.
Table A2 in Appendix A displays these higher-
k lifts explicitly. The overlay of odd and even admissible values shows how apparent gaps at lower scales are filled directly by higher lifts, ensuring complete coverage of the odd integers.
5.2.4. Visual Overlay
Corollary 10 (Visual Overlay and Complete Coverage)
. Overlaying the progression ladders from consecutive parents shows that apparent gaps at lower admissible lifts are exactly filled by higher lifts. Each anchor sequence covers its congruence class without overlap, and the union across all admissible lifts exhausts the odd integers. Thus rail iterations across all lift levels ensure complete coverage of . This structure is explicitly illustrated in Table A2.
Proof. By Lemma 19, consecutive parents generate fixed-step progressions, and by Lemma
20, higher admissible lifts scale these progressions by powers of four. The apparent omissions at a given scale correspond precisely to residue classes that are elements of progression of higher-lift ladders. Therefore the superposition of ladders fills all gaps systematically, partitioning the odd integers with no overlap. □
5.3. Anchor Ladders as the Basis of Coverage
All admissible structure originates from the two primitive anchors
and
. Each admissible lift
produces a new anchor point. Each such anchor initiates a ladder whose offsets and progressions are determined by its residue class and the parity of the admissible exponent
k.
[Dyadic gaps as lifted offsets] Each admissible exponent
k produces a dyadic slice
where
specifies the class. The quantity
is the gap between successive values in the slice and is the
exact offset created by the lifted exponent
k.
Thus increasing
k does not produce a new type of parent; it produces a new
spacing among the same admissible residue class. The anchor value determines the base point
while the dyadic step
determines how far apart the lift-
k parents of successive values lie.
In this sense, each higher lift corresponds to a wider offset lattice. Different values of k carve the odd integers into disjoint arithmetic progressions of increasing gap, and every such progression is exactly one dyadic slice. No slice overlaps another, and no odd integer is omitted.
Lemma 21 (Arithmetic derivation of anchors by class lifts)
. For each anchor family with parent form , the reverse operator
generates an arithmetic progression at every admissible lift k (k odd for , k even for ). The constant term is the base residue of that progression and coincides with the anchor promoted at scale . Thus the starting anchors are derived arithmetically, and their descendants at higher k are exactly the ladder bases that fill sieve holes.
Proof. For
(class
, odd
k):
Each case has the form
, with constants
serving as the promoted anchors at scales
.
For
(class
, even
k):
Each case has the form
, with constants
serving as the promoted anchors at scales
.
In both families, the step size doubles with each increment of k, and the base constant aligns exactly with the residue class left uncovered at the prior dyadic sieve. Thus the arithmetic shows both that the anchors are generated within the operator and that each higher k-level produces the ladder bases that fill the recursive sieve. □
5.4. Global Coverage by a Dyadic Sieve of Ladders
Proposition 3 (First-child ladders and the 4-adic sieve by class)
. Every admissible odd parent n is in exactly one of the two live classes
Let be a reverse child at lift k. Then:
- (A)
First admissible child (base sieve slice).
Thus the first children in are exactly (gap 4), and the first children in are exactly (gap 8). Equivalently, these are the odds with exactly
one halving () and exactly
two halvings () in , respectively.
- (B)
-
Higher admissible lifts stay in class and obey .Within a fixed class, raising the lift by sends each child to the next child by
Hence the children at lifts form a rail by the affine update and remain in the same class ( for odd k, for even k).
- (C)
Gap quadrupling across lifts. Writing the first-child progressions as functions of t,
the lift update gives, for each ,
Thus each time the lift increases by
, the gap between consecutive children (as
t increases by 1) is multiplied by 4.
- (D)
Next sieve slice is generated by . For the first children () are . Applying yields the next slice (): , again gives the slice , and so on. For , the first children () are ; then gives ; then gives ; etc. In each class, generates the next sieve levelandquadruplesthe modulus (the gap) each time.
Lemma 22 (Sieve slice measure for on odds). Fix . Among all odd integers m, the proportion for which is exactly .
Proof. Work modulo . Because 3 is invertible mod , the map is a bijection on residue classes. The condition is , which holds for exactly of odd residues; the stricter condition cuts that by another factor . Hence on odds. □
Corollary 11 (All-integers normalization). For , the proportion ofallintegers m with m odd and is .
Proof. Half of all integers are odd; combine with Lemma 22. □
Transition: Canonical Reduction of Admissible Structure
The analysis above resolves the local admissible structure of the reverse map: each live residue admits a unique minimal exponent , produces a first child in its own class, and extends to a full rail via the affine law . These statements describe the local geometry of the reverse tree but leave open the problem of identifying a canonical global parameter governing all rails simultaneously.
Such a parameter arises naturally by removing the dyadic component of the first admissible step. The resulting zero–state provides a global coordinate system on the live lattice in which each rail becomes a pure affine progression, independent of its parent. This reduction clarifies both the disjointness and completeness of the rail family and supplies the arithmetic infrastructure needed for the global coverage theorem below.
We introduce this zero–state framework next.
5.5. Zero–State Enumeration and the Pure Affine Skeleton
The affine decomposition shows that each admissible reverse step
splits into a minimal admissible core and a sequence of
lifts. In this section we remove all reversible dyadic structure and isolate the intrinsic arithmetic skeleton of the map. The resulting
zero–state forms a canonical index on the live odd lattice and reveals that Collatz dynamics reduce to a pure affine counting system generated entirely by a base of:
No explicit use of the Collatz forward function is required once this zero–state system is established.
Definition 20 (Zero–State Index)
. For any odd integer n, let denote its minimal admissible exponent in the reverse map. Thezero–state index
of n is defined by
This value is the unique base element of the affine ladder generated by n.
5.5.1. Minimal Admissible Exponents
Let
denote the live odd integers. For each
the reverse step
is integral precisely when
Since
and
n is never
in the live set, admissibility is determined by the parity of
k:
The
first child of
n is
5.5.2. Zero–State Extraction
The
zero–state of
is defined by removing exactly the admissible dyadic factor used to produce
:
Because admissibility guarantees
, this quantity is an integer for every live odd
n.
Ordered by size,
the zero–state reproduces the natural index:
Examples.
(3) Even integers. If with n odd, then . Thus every even integer inherits the zero–state of its unique odd anchor.
5.5.3. Compatibility of Zero-State and Rail Children
Let
n be an odd integer not divisible by 3, and let
be its zero-state, so that
. The first child on the rail rooted at
n is
We now express in terms of .
Lemma 23 (Parent
child equals direct child map)
. For every odd ,
In particular, the map factors as
where
and coincides with the direct reverse map .
Proof. Since
, we have
This simplifies to
which is exactly
. □
Thus the first rail child may be obtained either directly from n via the reverse map , or by passing to the zero-state and applying the affine map L in the z-coordinate. The two procedures are algebraically identical.
Lemma 24 (Invertibility on zero-state coordinates)
. For fixed admissible class (i.e. fixed ), the map
is a bijection from to with inverse
Restricted to zero-states of live odd integers n, this gives a one-to-one correspondence between parents and their first rail children in the zero-state coordinate system.
Proof. Since is invertible over and the constant term is fixed, L is affine with nonzero linear coefficient and hence bijective over ; the stated formula is its inverse. On the subdomain of zero-states corresponding to live odd integers, L and preserve integrality by construction of and . □
Consequently, the passage
is equivalent to the direct reverse lift
, and the zero-state normalization does not alter the rail structure but merely re-expresses it in the 0-lift coordinate.
5.5.4. Zero–State Law and the First Affine Step
A key identity is
Increasing the exponent by 2 yields
Iterating gives the recurrence
whose solution is
Substituting
,
Thus the entire admissible chain above
n depends only on the zero–state value
. The specific parent
n plays no role beyond producing
.
5.5.5. Enumeration Without the Reverse Map
Once
is known, the Collatz tree can be generated without the function
. Instead it is encoded by the affine generators
corresponding to C1 and C2 first–child lifts, together with their rail–lift iterates
Every reverse parent of
n has
z–index
Thus all reverse dynamics are modeled by the affine semigroup generated by
,
, and the rail lifts
.
5.5.6. Affine rails and Odd Coverage
For each
, the
affine rail of
n is
Injectivity of the affine form
ensures that rails are disjoint. Every odd integer
m has a unique representation
for some live
n and unique admissible
k, and writing
places
m on exactly one rail:
Combining this with the dyadic decomposition yields full coverage of .
5.5.7. Affine z–Index Dynamics
Enumerate the live odds in increasing order,
Writing the reverse map in odd–to–odd form
we define
Lemma 25 (Child index at the
z–level)
. Let and p be a reverse parent of n. Then
Proof. Direct computation using and the ordering of live residues shows that C1 parents occupy the –position and C2 parents occupy the –position in the enumerated lattice. Details follow from the residue classification and the fact that live integers occur in pairs . □
Since
coincides with a
lift at the
z–level, iterating
produces the rail lifts
.
| z |
n |
class |
operator |
z-child |
first child
|
| 0 |
1 |
C2 |
|
1 |
1 |
| 1 |
5 |
C1 |
|
3 |
3 |
| 2 |
7 |
C2 |
|
9 |
9 |
| 3 |
11 |
C1 |
|
7 |
7 |
| 4 |
13 |
C2 |
|
17 |
17 |
| 5 |
17 |
C1 |
|
11 |
11 |
| 6 |
19 |
C2 |
|
25 |
25 |
| 7 |
23 |
C1 |
|
15 |
15 |
| 8 |
25 |
C2 |
|
33 |
33 |
| 9 |
29 |
C1 |
|
19 |
19 |
| 10 |
31 |
C2 |
|
41 |
41 |
| 11 |
35 |
C1 |
|
23 |
23 |
| 12 |
37 |
C2 |
|
49 |
49 |
| 13 |
41 |
C1 |
|
27 |
27 |
| 14 |
43 |
C2 |
|
57 |
57 |
| 15 |
47 |
C1 |
|
31 |
31 |
| 16 |
49 |
C2 |
|
65 |
65 |
| 17 |
53 |
C1 |
|
35 |
35 |
| 18 |
55 |
C2 |
|
73 |
73 |
| 19 |
59 |
C1 |
|
39 |
39 |
| 20 |
61 |
C2 |
|
81 |
81 |
| 21 |
65 |
C1 |
|
43 |
43 |
| 22 |
67 |
C2 |
|
89 |
89 |
| 23 |
71 |
C1 |
|
47 |
47 |
| 24 |
73 |
C2 |
|
97 |
97 |
Table ?? First 25 live odd integers () with their z–indices, classes, affine generators, and first admissible children. The table illustrates the fundamental identity
i.e. the first admissible reverse child of n is exactly the live odd whose index equals the affine z–map (for C1) or (for C2).
Remark 6 (Why
is Terminal in the
Z–Lattice).
The Z–index is a bijection from the live lattice
onto , assigning each admissible odd m its global zero–state coordinate . No element of appears in , and therefore no
value admits a
Z–coordinate
. This is not merely a definitional omission: it is an arithmetic obstruction.
Indeed, if , then
so is never an integer for any . Thus no value can serve as a parent in the admissible reverse map Consequently, values areexactly
those odd integers that lie outside the zero–state coordinate system and therefore admit no further reverse continuation.
Hence the classical Collatz termination condition “entering ” is equivalently the statement that the reverse chain has left the Z–indexed affine structure. In this sense, the zero–state lattice is the structural backbone of the global reverse tree, and represents its natural boundary.
Proposition 4 (The Unique Self-Stable Odd Origin)
. Among all odd integers, the value 1 is the only odd integer whose admissible reverse image under has the same zero–state index as its parent. Equivalently, 1 is the unique solution of
and every admissible reverse step applied to any produces a strict increase or decrease in zero–state coordinate.
Proof. For an odd integer n, write its admissible first child as
Zero–state normalization removes the affine increment
from the lifted representation; hence
If
, then
and
so 1 is fixed under its admissible reverse step and its zero–state coordinate remains 0.
Suppose
. If
, then by the definition of Z we would have
hence
which is impossible for any
. Thus the equality
is impossible for odd
. □
Corollary 12 (Uniqueness of the Global Odd Cycle). The odd reverse Collatz dynamics admit exactly one cycle, the trivial cycle . Every other odd integer ascends strictly from zero–state coordinate and therefore cannot return to a previous affine or zero–state position.
5.5.8. Affine–Dyadic Equivalence
In each reverse step with exponent
, the affine transformation on
z has linear coefficient
The dyadic slice theorem states that the natural density that an odd
n satisfies
is
. Hence the affine expansion factor and its dyadic weight are exact reciprocals.
Theorem 5 (Affine–Dyadic Equivalence)
. For every reverse exponent k, the affine expansion factor is and the dyadic slice weight satisfies
Thus each affine generator corresponds exactly to its dyadic frequency.
Corollary 13 (Coverage via Affine Slicing)
.
Therefore the affine semigroup generated by , , and forms a disjoint partition of the odd integers into slices of relative size and hence covers exactly once.
Removing reversible dyadic structure reduces Collatz dynamics to a deterministic affine counting system. The zero–state encodes each live odd integer as its z–index, and the reverse tree is generated entirely by the affine maps , and rail–lifts thereof. Each odd integer lies on exactly one affine rail, all ladders are disjoint, and the union of ladders covers the odd integers. Forward halving gates extend the coverage to all integers. Thus the Collatz map is realized as a pure affine skeleton whose closure equals .
5.5.9. Rail Transitions
Lemma 26 (Forward rail transitions follow the minimal reverse lift)
. For any live odd anchor , the forward odd Collatz iteration strips all dyadic factors from . Hence
where is the minimal admissible exponent for which
Thus the forward rail transition isidentical
to the class–dependent minimal reverse transition.
Proof. Write any element of the rail of
n as
. Then
so the forward map removes all dyadic factors and yields
, which by definition equals
. Thus the entire rail collapses to the minimal reverse parent. □
Corollary 14 (Offset agreement)
. If (class ) then and
If (class ) then and
These offsets coincide exactly with those recorded in the appendix offset table.
Theorem 6 (Deterministic rail transitions)
. Since the forward map collapses each rail to its anchor and the anchor advances by , the rails transition deterministically through their minimal reverse lineage. The two linear formulas
therefore generate all forward rail transitions.
Remark 7 (Rail connectivity via minimal reverse lifts)
. The offset Table A1 in Appendix A records the parent–child differences for all , but its significance is that it encodes the transition between rails. Write any live odd integer as
corresponding to classes and . The minimal admissible reverse lift determines the next rail:
Hence the transitional offset is
exactly matching the numerical offsets in Table A1.
Since the forward Collatz map removes all dyadic factors from , the forward odd iterate is
so the forward rail transition isisomorphic
to the minimal reverse transition. Each rail is therefore determined by its –anchor, and rail-to-rail transitions are fully determined by the class and the index t.
Because every admissible lift adds exactly at the rail level, all rails proceed by linear progression and remain disjoint. Every rail ultimately connects to the rail of 1, and thus all rails converge to 1 in forward iteration.
Theorem 7 (Global Arithmetic Coverage by Rails)
. Let be the reverse map with admissible parity per class. Then the following hold within Section 5:
-
Base slices and fixed gaps. First admissible children are exactly
and children of consecutive parents form arithmetic progressions with those gaps (Prop. 3, Lem. 19).
4-adic lift within rails. Raising the lift by sends , stays in the same class, and multiplies the progression gap of sequential, class equivocal n, by 4 (Lem. 20 and the clause of Prop. 3).
Overlay gives complete coverage. Superposing the ladders across all admissible lifts fills the apparent gaps of the base slices; within each class, the union over k exhausts its congruence classes with no overlap (Cor. 10).
Anchor generation of disjoint rails. All disjoint rails are generated from the two primitive anchors and . For any , the minimal reverse lift
gives the exact linear offset between successive rails, so the forward rail transitions are determined by the -ancestry. Each admissible lift promotes a new rail with its own fixed offset, and the entire rail system remains disjoint. (Thm. 6, Rem. 7)
Exact dyadic slice measures. Among odd m, the slice with has measure ; among all integers it is (Lem. 22, Cor. 11).
Consequently, the odd integers are covered disjointly by the class-preserving affine offset gap progressions generated from a base of all rails, across all admissible lifts, with gaps and densities exactly as stated in (1)–(5).
5.6. Dyadic Sieve Index (Class–Forced Admissibility)
Definition 21 (Dyadic Sieve Index)
. Let encode the class modulo 3 and encode the class modulo 6:
For each lift index , the admissible exponent is (odd k for , even k for ), and a single reverse step from produces
The dyadic slice weight (among odd ) for fixed k is .
Table 3.
Dyadic Sieve Index from the unified reverse step , with .
Table 3.
Dyadic Sieve Index from the unified reverse step , with .
| k |
Class |
x |
Gap
|
Anchor
|
|
| 1 |
|
5 |
4 |
3 |
|
| 2 |
|
1 |
8 |
1 |
|
| 3 |
|
5 |
16 |
13 |
|
| 4 |
|
1 |
32 |
5 |
|
| 5 |
|
5 |
64 |
53 |
|
| 6 |
|
1 |
128 |
21 |
|
| 7 |
|
5 |
256 |
213 |
|
| 8 |
|
1 |
512 |
85 |
|
| 9 |
|
5 |
1024 |
853 |
|
| 10 |
|
1 |
2048 |
341 |
|
| 11 |
|
5 |
4096 |
3413 |
|
| 12 |
|
1 |
8192 |
1365 |
|
| 13 |
|
5 |
16384 |
13653 |
|
| 14 |
|
1 |
32768 |
5461 |
|
| 15 |
|
5 |
65536 |
54613 |
|
| 16 |
|
1 |
131072 |
21845 |
|
| 17 |
|
5 |
262144 |
218453 |
|
| 18 |
|
1 |
524288 |
87381 |
|
| 19 |
|
5 |
1048576 |
873813 |
|
| 20 |
|
1 |
2097152 |
349525 |
|
| 21 |
|
5 |
4194304 |
3495253 |
|
| 22 |
|
1 |
8388608 |
1398101 |
|
| 23 |
|
5 |
16777216 |
13981013 |
|
| 24 |
|
1 |
33554432 |
5592405 |
|
| 25 |
|
5 |
67108864 |
55924053 |
|
| Dyadic slice weight for fixed k: (among odd ). |
Theorem 8 (Dyadic Sieve Decomposition)
. Let and . Encode the class by
For each lift index , define (so k has the admissible parity for the class). The fixed-k static sieve slice is
Then
i.e. as increases (equivalently ), the union of these arithmetic progressions covers every odd integer exactly once.
Proof.
Existence. Take any odd
m. Let
k be the highest power of 2 dividing
, i.e.
. Then
is even and has a unique residue
modulo 6 (parity forces
x odd, and
). Set
if
and
if
. Since
, there is
with
. Define
and solve for
m to obtain
Uniqueness. The factor k is uniquely determined by the largest power of 2 dividing , which fixes x, then c, then , and finally t. Hence m belongs to exactly one . □
Remark 8 (Anchors and gaps)
. Each is an arithmetic progression with gap and anchor , where . The minimal slices () are
Corollary 15 (Dyadic slice weight). For fixed k, the proportion of odd integers in is . These dyadic slices form a disjoint partition of the odd integers, and the weights sum exactly to 1.
Middle-even gates and mod-18 progression
Lemma 27 (Gate equivalence at the middle even)
. Let be the next odd. Then
with the class correspondence
In particular for every odd m, and over one mod-18 odd cycle the three gate residues occur with equal frequency .
Proof. Since , reduce modulo 18 and use the mod-6 classes of n; this is the same gate rule as Prop. 1. The split is the equidistribution of first-child classes from §3. □
Proposition 5 (Base middle-even progressions in mod-18)
. Using the first-admissible children from Prop. 3:
Thus, as t increases by 1, the gate residue rotates deterministically in mod 18 by
and the union of middle evens across the two classes is exactly the gate set —i.e. precisely of all even residues mod 18.
Lemma 28 (Higher lifts act by
on middle evens)
. If is the lift- child of m (Prop. 3, Lem. 20), then
hence , rotating the gate residues
Corollary 16 (Even-gate sieve ≡ dyadic sieve, in mod-18). The partition of odds by (§4) corresponds, under , to class-preserving middle-even rails whose residues cycle within and whose strides scale by the lift (Lemma 28). This gives a mod-18 even-side rephrasing of the rail picture in this section, with no change to coverage or disjointness.
5.7. Global Consequences of Coverage
Theorem 9 (Dyadic Slicing Yields Global Coverage)
. Let and , and encode the class by
For each lift index set and define the dyadic slice
Then the family is a disjoint partition of the odd integers:
Equivalently, every odd m admits a unique representation
Proof.
Existence. For odd
m, let
. Then
is even and has a unique residue
modulo 6 (it must be odd mod 3 and even). Set
if
and
if
; then
, so
for a unique
. Define
Solving for
m yields
.
Uniqueness (disjointness). The factor is unique, which fixes , then c, then , and finally t by the displayed equation. Hence m lies in exactly one . □
Corollary 17 (Equivalence of Dyadic Slices and
z–Rails)
. Let be the dyadic slice defined in Theorem 9, and let
Then for every choice of ,
and conversely every element of arises uniquely in this way.
Hence the affine rails generated by coincide exactly with the dyadic slices arising from the 2–adic valuation of .
Lemma 29 (Affine injectivity). Let and be the affine maps on . Then both and are injective: no two distinct integers can produce the same output under either map. Consequently, along any rail generated by iterates of (and, where used, ), each integer occurs at most once.
Proof. Suppose
for some
. Then
Subtracting 1 from both sides gives
, hence
Since
in
, it follows that
and therefore
. Thus
is injective.
The same argument applies to . If , then , so and , whence . Thus is also injective.
Because each iterate of (and ) is a composition of injective maps, every finite iteration remains injective. Hence no two distinct inputs can ever land on the same value under these affine iterations, and each integer can appear at most once along any such affine rail. □
Lemma 30 (Forward collapse of a rail)
. Let n be an odd integer, and let be the minimal admissible exponent such that . Define
so that is the rail generated by the admissible lifts of n. Then for every one has
Proof. Fix
and set
Then
Since
n is odd, the 2-adic valuation of
is
By definition of the odd Collatz map,
as claimed. □
Corollary 18 (Forward inverse of the admissible rail). In the setting of Lemma 30, the forward odd Collatz map T is the exact algebraic inverse of the admissible rail generated by n: every reverse lift collapses in one odd step to n, and no other odd child is attained from any . Consequently, along each rail the forward dynamics contract the entire ancestry to the unique child n.
Lemma 31 (No rootless rails)
. Let R be any rail with base . Then R has a unique parent rail in the reverse Collatz dynamics: there exists an odd integer n and an admissible minimal exponent such that
and the base of is . Moreover, the rail of 1 is the only rail without a distinct parent.
Proof. By construction of the rails, every rail
R is generated by admissible lifts from some odd child
n; its base
is the minimal admissible parent,
with
the least exponent such that
. The admissibility conditions modulo 18 ensure that
lies in one of the live classes
or
, so
n is uniquely determined by the local residue structure (cf. the classification in
Section 5).
Define the parent rail
to be the rail generated by
n and
,
whose base is
. Disjointness of rails and uniqueness of affine ancestry ensure that
is well-defined and distinct from
R whenever
: if
with
, this would force a nontrivial cycle in the affine rail structure, contradicting the disjointness and no-cycle results established earlier.
When , the only solution of is , so the rail of 1 is self-ancestral and admits no distinct parent rail. Thus every rail other than the rail of 1 has a unique parent rail, and the rail of 1 is the only rail without a distinct parent. □
Theorem 10 (Well-founded rail hierarchy rooted at 1). Let denote the set of all rails, and define a directed edge whenever is the parent rail of R in the sense of Lemma 31. Then:
-
1.
The directed graph has no directed cycles.
-
2.
The rail of 1 is the unique vertex in with no outgoing edge (i.e., the unique rail without a distinct parent).
-
3.
Every rail lies in the ancestor tree of the rail of 1: there exists a (possibly trivial) finite sequence of parent rails
with equal to the rail of 1.
In particular, the parent relation → induces a well-founded partial order on with a unique minimal element, the rail of 1, and there is no second infinite component of rails disjoint from the ancestry of 1.
Proof. (1) By construction, each rail is an affine progression generated by repeated application of
(or the class-specific analogue) from its base. The disjointness and uniqueness-of-ancestry results for rails imply that two distinct rails cannot share an odd integer. If a directed cycle
existed, then following the associated bases under admissible reverse lifts would produce a nontrivial cycle in the underlying affine structure, forcing an odd integer to lie on two distinct rails, a contradiction.
(2) Lemma 31 shows that every rail R with base has a unique parent rail , hence a directed edge . For the rail of 1, the only solution of is , so it admits no distinct parent; thus it is the unique vertex without an outgoing edge.
(3) Let
R be any rail with base
. By Lemma 31, either
and
R is the rail of 1, or
R has a unique parent rail
. Iterating this construction produces a (possibly infinite) chain
By Corollary 18, each step in this chain corresponds to a forward collapse of the entire ancestry of
onto the child of
, and the dyadic coverage results of
Section 5 imply that no odd integer lies outside the union of these rails. If the chain avoided the rail of 1 indefinitely, it would define a second infinite component of
disjoint from the ancestry of 1, contradicting the uniqueness of admissible ancestry and the density-one coverage of the odd integers. Hence the chain must terminate at the rail of 1 after finitely many steps, and every rail
R admits a finite ancestor sequence ending at the rail of 1.
The absence of cycles and the existence of a unique minimal element (the rail of 1) imply that the parent relation → is a well-founded partial order on , and there is no second infinite component disjoint from the ancestry of 1. Thus the rail-ancestry relation is a well-founded Noetherian dependency relation. □
5.8. Global Consequences of Dyadic Coverage
The dyadic partition in Theorem 9 shows that every odd integer lies on exactly one affine rail
where
is the first admissible child
of a unique live integer
. Each rail corresponds to a unique pair
with
, and the dyadic slices
form a disjoint partition of
. This section records the global consequences of this structure.
Affine rails as exhaustive enumerations.
For any live odd
n with minimal exponent
,
Thus the entire admissible chain above
n is determined by
alone and consists of a pure affine progression. Varying
n ranges over all possible bases
, and Theorem 9 shows that these progressions are disjoint and collectively cover every odd integer. No dynamical descent or step-count analysis is required.
Role of classes and parity.
The parameters determine the admissible parity of and the residue of every first child. Higher lifts preserve class and correspond to further applications of the affine map . Thus the global structure is governed entirely by class parity and the affine law, not by the forward stopping-time behavior of the classical iteration.
C0 as reverse terminals, not dynamical attractors.
Values produce no reverse admissible child, so they appear as terminal nodes in the reverse tree.
Global closure.
Because the dyadic slices partition and every slice corresponds to a complete affine ladder, the reverse Collatz graph is globally closed: every odd integer appears exactly once, on exactly one rail, and is obtained from exactly one admissible affine generator. The forward map is then a deterministic projection down the rails via halving, and all trajectories ultimately reach the base anchors .
In summary, the full Collatz structure is an explicit affine enumeration of the integers. Dyadic slicing provides the global coverage; affine rails provide the local structure; and the interaction of the two yields a complete, closed description of the reverse map with no need for any step-bound or descent-based arguments.
Theorem 11 (Unique affine parentage and no runaway). For every odd integer n the reverse and forward Collatz maps satisfy:
- (a)
Unique affine parentage. After exhaustion by anchors has been established, every odd integer is known to occur in exactly one position of the affine system generated from the anchors by the iterations (and, where used, ). Both maps are injective on : if then and . Consequently, no odd integer can be produced from two different affine predecessors, and its affine lineage back to its anchor is unique.
- (b)
-
Finite forward descent along the unique affine rail. Every odd integer n lies on a unique affine rail
with base equal to its first admissible child in the reverse function. Along this rail, admissible reverse exponents take the form , with e decreasing in the forward function at each step until the minimal admissible exponent is reached.
Since is fixed by the residue class of the base child (C1 or C2), and reverse steps with reduce the 2-adic valuation of the corresponding forward gate while steps with increase the odd value, the ladder structure admits no admissible extension in the reverse direction once the minimal exponent is reached. Furthermore, the only self-stable odd under this ladder structure is 1, so all reverse descent terminates either at a k-value or at a class- boundary.
- (c)
No nontrivial odd cycles; no forward runaway. By Lemma 14
, any t-step reverse composition satisfies
which is impossible for ; hence no nontrivial odd cycle exists. By (a)
the forward step is unique at each node, andby (b)
the only descending reverse corridor is finite. Together with the finite reverse lifespan(Theorem 2)
, there is no infinite forward runaway.
Lemma 32 (Even integers inside the
k–valuation skeleton)
. Every positive integer N admits a unique dyadic decomposition
For each odd m, the odd–to–odd Collatz gate is
so that with odd.
Each admissible reverse step
is a pure dyadic lift: the exponent k records exactly how many factors of 2 are injected above n in the reverse direction. Thus the collection of all k–lifts already accounts for every power of 2 that can appear above any odd anchor in the reverse tree.
In forward time, starting from , the halving steps strip off the dyadic factor until the odd anchor m is reached, after which the gate removes the remaining admissible factors of 2 from . Consequently, every even integer N lies on the same k–valuation skeleton as its odd anchor m: no new branches arise from even inputs, and every factor of 2 above m is realized either as a trivial halving step or as part of an admissible exponent k in the reverse/forward pair.
Corollary 19 (All positive integers are carried by the odd skeleton). If every odd integer m lies on the affine reverse skeleton and converges to 1 under the forward map T, then every positive integer also converges to 1.
Proof. Given
, write
with
m odd. By Lemma 32, the forward trajectory of
N coincides with that of
m after finitely many halving steps:
Since, by hypothesis, the odd anchor m lies on the closed affine skeleton and reaches 1 under T, the same is true for N. Thus closure of the odd subsystem implies closure of the full Collatz map on . □
Theorem 12 (Global Forward Convergence to 1)
. For every odd integer N, the forward Collatz trajectory obtained by iterating
reaches 1. Equivalently, there is no odd N whose forward iterates avoid 1 forever, and there is no nontrivial odd cycle.
Proof Fix an arbitrary odd starting value N.
Step 1. N sits on exactly one admissible reverse branch. By Theorem 9,
N lies in a unique dyadic slice
of the form
By construction of
, this
N is exactly an admissible reverse parent
for some odd child
n, with lift exponent
. In particular,
N is not “off-lattice’’: it is produced by an admissible reverse step from some
n.
Moreover, Corollary 6 shows that increasing the lift by 2 corresponds to the affine update . Thus the entire inverse chain feeding into N is a single arithmetic ladder, obtained by admissible lifts of strictly smaller exponents. There is no ambiguity: N belongs to one and only one such reverse ladder. This is the global form of unique parentage (see also Theorem 11(a)).
Step 2. No nontrivial cycles and no multi-parent mergers. Theorem 11(a) states that the forward gate
is unique: each odd
m has exactly one parent at its forward gate. Therefore two distinct reverse ladders cannot merge back into the same odd
m in forward time and then split again. Forward trajectories have no branching.
Further, Theorem 11(c) shows that any purported odd cycle would require composing admissible reverse steps
around a loop. Writing the composition over
t steps gives
which is impossible for positive
; hence there is no nontrivial odd cycle. The only surviving loop in the full Collatz system is the standard
basin, with 1 fixed under its own
lift (see Remark 2 and Sub
Section 4.6).
Thus any forward path from N is a single chain with no alternate branch and no way to enter a nontrivial odd cycle.
Step 3. Exclusion of runaway in the closed affine system.
By
Subsection 5.5 and Theorem 5, every live odd integer lies on a unique affine ladder
where
is its first admissible child. The zero–state index
provides the base coordinate for all ladders: each odd
n satisfies
for a unique
z, and the images of
z under the admissible updates
together with the rail lifts
built from
, generate the entire reverse structure. Every admissible reverse step decomposes uniquely as
so that reverse iteration never leaves the affine ray determined by
Z. The dyadic increment encoded by each admissible exponent
k determines the gap size between successive rail elements, and the full collection of all such gaps across all
k exhausts the odd integers without overlap. Thus the reverse dynamics form a closed, bijective affine system in which each odd has exactly one admissible predecessor and exactly one admissible successor.
Step 4. Well ordering of rails.
By Theorem 10 (Well-founded rail heirarchy rooted at 1), every reverse rail has a finite parent chain terminating at the rail of 1. Therefore the reverse graph admits no independent infinite component, and the forward map—being the exact inverse of this ancestry—forces every odd to converge to 1.
Within this system, the value 1 is the sole self–repeating element: it is the only odd integer for which the admissible reverse step returns the same zero–state coordinate, and hence the only point that can serve as the affine origin. All other odds possess strictly larger affine parameters and are uniquely positioned along their rails by the dyadic gaps determined by their lift exponents.
Forward iteration is the exact inverse of the admissible reverse map. Since every odd belongs to a unique affine ladder, and since the reverse dynamics place each odd at a uniquely determined affine position above the origin 1, the inversion of this ladder structure forces any forward trajectory to unwind its position within the closed affine system. Because 1 is the unique affine origin and the unique fixed point of the odd gate, there is no other point at which a forward orbit can stabilize or around which it can circulate. Any hypothetical forward runaway would require escaping the affine rays or producing a new fixed point, neither of which is possible in the closed, bijective affine system generated by the admissible lifts.
Consequently, every forward trajectory must eventually reach the unique origin 1, and no forward runaway or nontrivial odd cycle can exist within this system. □
Corollary 20 (Even integers lie inside the dyadic framework). Every even integer N can be written as with n odd. Since admissible reverse steps correspond to removing a prescribed dyadic factor , and forward steps remove exactly , each even integer lies on a unique dyadic extension of the odd trajectory of n.
Thus the entire even half-line embeds into the odd lattice, and all even N converge to 1.
5.9. Structural Consequences of the Reverse–Affine Formulation
The global theorem follows from two structural pillars that now stand fully established:
(1) Zero–state reduction and affine enumeration.
The explicit formula
together with the lift law
shows that the Collatz reverse map decomposes into disjoint affine ladders indexed by
. This zero–state skeleton is a complete enumeration of the odd integers: every live odd has a unique
Z–index, every
Z–index seeds a unique affine ladder, and the ladders partition
disjointly. Thus the map
and the dyadic slicing weights
describe the same global structure.
(2) Full reverse function as the deterministic core.
The expanded reverse function
is edge–aligned with the forward map
in the sense that
Hence the forward and reverse systems are not separate descriptions but the same deterministic dynamical law written in dual form: one expands affinely according to admissible
k, and the other strips away the same affine growth. All odd trajectories therefore lie on a single reverse–forward chain determined entirely by their zero–state index and lift sequence.
Together, (1) and (2) show that the Collatz map admits a complete arithmetic decomposition: it enumerates all odd integers via the zero–state affine ladders and evolves deterministically under forward iteration by inverting those same affine steps. The remaining results follow directly from this unified structure.
Corollary 21 (Exhaustive inclusion of odd integers). Every odd integer lies in the ladder–rail partition anchored at 1 (and its first lift 5). No odd integer is left out.
Corollary 22 (Exhaustive inclusion of even integers). Every even integer lies on a unique dyadic extension of the odd trajectory of n. No even integer is left out.
Corollary 23 (No divergence). No forward path in the full Collatz map admits unbounded growth, and no divergent or runaway trajectory exists for any .
Corollary 24 (Only the trivial cycle). The sole cycle in the forward Collatz function is . No other odd cycle occurs.
Corollary 25 (Forward convergence). All converge to 1.
6. Conclusion
Since its proposal by Lothar Collatz in 1937, the problem has withstood every analytic and computational attempt at resolution, drawing interest for its simplicity and resistance to known methods. In this work, we provide a complete resolution by unifying two complementary perspectives: the local arithmetic structure that governs residue transitions, and the global dynamic iterations that exhaustively partition the odd integers via canonical lifts.
The framework developed here shows that the map admits a layered structure in which each odd n belongs to a unique class defined by admissible reverse chains, modulo a strictly defined triadic residue system. These reverse maps yield a globally surjective structure through offset arithmetic ladders, wherein every odd integer appears with precise 2-adic frequency. The forward map is then seen as an iteration over these layers, where all transitions are confined within deterministic bounds.
With this synthesis, we establish the four core results: every odd number appears in the recursive ladder-rail enumeration, no infinite runaway can exist, the only cycle is , and the closed system is isomorphic to the classical Collatz problem. These properties collectively confirm that the Collatz function is both globally closed and locally deterministic.
Thus the problem is resolved in full: every positive integer trajectory under the Forward () map is finite and terminates at 1.
Thus the longstanding question is settled in full within this system:
Acknowledgments
The author thanks Jeffrey Lagarias and Richard Terras for foundational works that inspired the arithmetic–dynamic synthesis presented here.
Appendix A. Tables
This appendix collects the reference tables used throughout the paper. They illustrate the residue classes, offsets, multi–generation child transitions (, , and ), and first child class rotations by residue . These are provided illustrative evidence so the patterns are clarified.
Table A1.
Illustration of Collatz offsets up to
. Each row shows the class, the first admissible child, and successive descendants through three steps. Offsets are computed as the arithmetic difference between each child and its immediate parent. The parent–child relationship is the only valid transition; further descendants do not correlate back to the original parent, but only their exclusive parent. This table provides the explicit evidence of offset ladders and coverage across dyadic residue classes described in
Section 5.1.1,
Section 5.1.2, and
Section 5.1.3.
Table A1.
Illustration of Collatz offsets up to
. Each row shows the class, the first admissible child, and successive descendants through three steps. Offsets are computed as the arithmetic difference between each child and its immediate parent. The parent–child relationship is the only valid transition; further descendants do not correlate back to the original parent, but only their exclusive parent. This table provides the explicit evidence of offset ladders and coverage across dyadic residue classes described in
Section 5.1.1,
Section 5.1.2, and
Section 5.1.3.
| n |
Class |
First Child |
Offset1
|
Grandchild |
Offset2
|
Great-Grandchild |
Offset3
|
|
| 1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
| 3 |
|
– |
– |
– |
– |
– |
– |
|
| 5 |
|
3 |
|
– |
– |
– |
– |
|
| 7 |
|
9 |
|
– |
– |
– |
– |
|
| 9 |
|
– |
– |
– |
– |
– |
– |
|
| 11 |
|
7 |
|
9 |
|
– |
– |
|
| 13 |
|
17 |
|
11 |
|
7 |
|
|
| 15 |
|
– |
– |
– |
– |
– |
– |
|
| 17 |
|
11 |
|
7 |
|
9 |
|
|
| 19 |
|
25 |
|
33 |
|
– |
– |
|
| 21 |
|
– |
– |
– |
– |
– |
– |
|
| 23 |
|
15 |
|
– |
– |
– |
– |
|
| 25 |
|
33 |
|
– |
– |
– |
– |
|
| 27 |
|
– |
– |
– |
– |
– |
– |
|
| 29 |
|
19 |
|
25 |
|
33 |
|
|
| 31 |
|
41 |
|
27 |
– |
– |
– |
|
| 33 |
|
– |
– |
– |
– |
– |
– |
|
| 35 |
|
23 |
|
15 |
|
– |
– |
|
The class–
k key below provides the color conventions used in
Table A2 and
Figure A1.
|
|
k=1 |
k=4 |
|
|
k=2 |
k=5 |
|
(terminating) |
k=3 |
|
Figure A1.
Reverse Collatz Coverage with Minimal Lifts ()
Figure A1.
Reverse Collatz Coverage with Minimal Lifts ()
Figure A1 displays only the minimal admissible lifts (
for
,
for
), making the apparent gaps visible.
Table A2.
Coverage by higher admissible lifts. Cells are colored by child-iteration level k (background) and class (text color). Odd k values occur only for ; even k values only for . The overlay of successive lifts shows that all odd integers are covered: apparent gaps at lower stages are exactly the entries filled by higher lifts of the anchor ladders, yielding complete coverage. Not every admissible k-doubling is listed (for example, produces the child 21); this table is provided for visual clarity.
Table A2.
Coverage by higher admissible lifts. Cells are colored by child-iteration level k (background) and class (text color). Odd k values occur only for ; even k values only for . The overlay of successive lifts shows that all odd integers are covered: apparent gaps at lower stages are exactly the entries filled by higher lifts of the anchor ladders, yielding complete coverage. Not every admissible k-doubling is listed (for example, produces the child 21); this table is provided for visual clarity.
| |
|
every 2nd odd |
every 4th odd |
every 8th odd |
every 16th odd |
every 32nd odd |
| n |
Class |
|
|
|
|
|
| 1 |
|
— |
1 |
— |
5 |
— |
| 3 |
|
— |
— |
— |
— |
— |
| 5 |
|
3 |
— |
13 |
— |
53 |
| 7 |
|
— |
9 |
— |
37 |
— |
| 9 |
|
— |
— |
— |
— |
— |
| 11 |
|
7 |
— |
29 |
— |
117 |
| 13 |
|
— |
17 |
— |
69 |
— |
| 15 |
|
— |
— |
— |
— |
— |
| 17 |
|
11 |
— |
45 |
— |
181 |
| 19 |
|
— |
25 |
— |
101 |
— |
| 21 |
|
— |
— |
— |
— |
— |
| 23 |
|
15 |
— |
61 |
— |
245 |
| 25 |
|
— |
33 |
— |
133 |
— |
| 27 |
|
— |
— |
— |
— |
— |
| 29 |
|
19 |
— |
77 |
— |
309 |
| 31 |
|
— |
41 |
— |
165 |
— |
| 33 |
|
— |
— |
— |
— |
— |
| 35 |
|
23 |
— |
93 |
— |
373 |
| 37 |
|
— |
49 |
— |
197 |
— |
| 39 |
|
— |
— |
— |
— |
— |
| 41 |
|
27 |
— |
109 |
— |
437 |
| 43 |
|
— |
57 |
— |
229 |
— |
| 45 |
|
— |
— |
— |
— |
— |
| 47 |
|
31 |
— |
125 |
— |
501 |
| 49 |
|
— |
65 |
— |
261 |
— |
| 51 |
|
— |
— |
— |
— |
— |
| 53 |
|
35 |
— |
141 |
— |
565 |
| 55 |
|
— |
73 |
— |
293 |
— |
| 57 |
|
— |
— |
— |
— |
— |
| 59 |
|
39 |
— |
157 |
— |
629 |
| 61 |
|
— |
81 |
— |
325 |
— |
| 63 |
|
— |
— |
— |
— |
— |
| 65 |
|
43 |
— |
173 |
— |
693 |
| 67 |
|
— |
89 |
— |
357 |
— |
| 69 |
|
— |
— |
— |
— |
— |
| 71 |
|
47 |
— |
189 |
— |
757 |
Shown below are the phase cycling of the first 25 consecutive r mod 18 integers, within the 6 non-terminating residues mod 18, and their phase rotation mod 54.
Table A3.
C1(1) (parent residue ), minimal .
Table A3.
C1(1) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
5 |
5 |
3 |
3 |
C0 |
| 2 |
23 |
5 |
15 |
15 |
C0 |
| 3 |
41 |
5 |
27 |
9 |
C0 |
| 4 |
59 |
5 |
39 |
3 |
C0 |
| 5 |
77 |
5 |
51 |
15 |
C0 |
| 6 |
95 |
5 |
63 |
9 |
C0 |
| 7 |
113 |
5 |
75 |
3 |
C0 |
| 8 |
131 |
5 |
87 |
15 |
C0 |
| 9 |
149 |
5 |
99 |
9 |
C0 |
| 10 |
167 |
5 |
111 |
3 |
C0 |
| 11 |
185 |
5 |
123 |
15 |
C0 |
| 12 |
203 |
5 |
135 |
9 |
C0 |
| 13 |
221 |
5 |
147 |
3 |
C0 |
| 14 |
239 |
5 |
159 |
15 |
C0 |
| 15 |
257 |
5 |
171 |
9 |
C0 |
| 16 |
275 |
5 |
183 |
3 |
C0 |
| 17 |
293 |
5 |
195 |
15 |
C0 |
| 18 |
311 |
5 |
207 |
9 |
C0 |
| 19 |
329 |
5 |
219 |
3 |
C0 |
| 20 |
347 |
5 |
231 |
15 |
C0 |
| 21 |
365 |
5 |
243 |
9 |
C0 |
| 22 |
383 |
5 |
255 |
3 |
C0 |
| 23 |
401 |
5 |
267 |
15 |
C0 |
| 24 |
419 |
5 |
279 |
9 |
C0 |
| 25 |
437 |
5 |
291 |
3 |
C0 |
Table A4.
C1(2) (parent residue ), minimal .
Table A4.
C1(2) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
11 |
11 |
7 |
7 |
C2 |
| 2 |
29 |
11 |
19 |
1 |
C2 |
| 3 |
47 |
11 |
31 |
13 |
C2 |
| 4 |
65 |
11 |
43 |
7 |
C2 |
| 5 |
83 |
11 |
55 |
1 |
C2 |
| 6 |
101 |
11 |
67 |
13 |
C2 |
| 7 |
119 |
11 |
79 |
7 |
C2 |
| 8 |
137 |
11 |
91 |
1 |
C2 |
| 9 |
155 |
11 |
103 |
13 |
C2 |
| 10 |
173 |
11 |
115 |
7 |
C2 |
| 11 |
191 |
11 |
127 |
1 |
C2 |
| 12 |
209 |
11 |
139 |
13 |
C2 |
| 13 |
227 |
11 |
151 |
7 |
C2 |
| 14 |
245 |
11 |
163 |
1 |
C2 |
| 15 |
263 |
11 |
175 |
13 |
C2 |
| 16 |
281 |
11 |
187 |
7 |
C2 |
| 17 |
299 |
11 |
199 |
1 |
C2 |
| 18 |
317 |
11 |
211 |
13 |
C2 |
| 19 |
335 |
11 |
223 |
7 |
C2 |
| 20 |
353 |
11 |
235 |
1 |
C2 |
| 21 |
371 |
11 |
247 |
13 |
C2 |
| 22 |
389 |
11 |
259 |
7 |
C2 |
| 23 |
407 |
11 |
271 |
1 |
C2 |
| 24 |
425 |
11 |
283 |
13 |
C2 |
| 25 |
443 |
11 |
295 |
7 |
C2 |
Table A5.
C1(3) (parent residue ), minimal .
Table A5.
C1(3) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
17 |
17 |
11 |
11 |
C1 |
| 2 |
35 |
17 |
23 |
5 |
C1 |
| 3 |
53 |
17 |
35 |
17 |
C1 |
| 4 |
71 |
17 |
47 |
11 |
C1 |
| 5 |
89 |
17 |
59 |
5 |
C1 |
| 6 |
107 |
17 |
71 |
17 |
C1 |
| 7 |
125 |
17 |
83 |
11 |
C1 |
| 8 |
143 |
17 |
95 |
5 |
C1 |
| 9 |
161 |
17 |
107 |
17 |
C1 |
| 10 |
179 |
17 |
119 |
11 |
C1 |
| 11 |
197 |
17 |
131 |
5 |
C1 |
| 12 |
215 |
17 |
143 |
17 |
C1 |
| 13 |
233 |
17 |
155 |
11 |
C1 |
| 14 |
251 |
17 |
167 |
5 |
C1 |
| 15 |
269 |
17 |
179 |
17 |
C1 |
| 16 |
287 |
17 |
191 |
11 |
C1 |
| 17 |
305 |
17 |
203 |
5 |
C1 |
| 18 |
323 |
17 |
215 |
17 |
C1 |
| 19 |
341 |
17 |
227 |
11 |
C1 |
| 20 |
359 |
17 |
239 |
5 |
C1 |
| 21 |
377 |
17 |
251 |
17 |
C1 |
| 22 |
395 |
17 |
263 |
11 |
C1 |
| 23 |
413 |
17 |
275 |
5 |
C1 |
| 24 |
431 |
17 |
287 |
17 |
C1 |
| 25 |
449 |
17 |
299 |
11 |
C1 |
Table A6.
C2(1) (parent residue ), minimal .
Table A6.
C2(1) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
1 |
1 |
1 |
1 |
C2 |
| 2 |
19 |
1 |
25 |
7 |
C2 |
| 3 |
37 |
1 |
49 |
13 |
C2 |
| 4 |
55 |
1 |
73 |
1 |
C2 |
| 5 |
73 |
1 |
97 |
7 |
C2 |
| 6 |
91 |
1 |
121 |
13 |
C2 |
| 7 |
109 |
1 |
145 |
1 |
C2 |
| 8 |
127 |
1 |
169 |
7 |
C2 |
| 9 |
145 |
1 |
193 |
13 |
C2 |
| 10 |
163 |
1 |
217 |
1 |
C2 |
| 11 |
181 |
1 |
241 |
7 |
C2 |
| 12 |
199 |
1 |
265 |
13 |
C2 |
| 13 |
217 |
1 |
289 |
1 |
C2 |
| 14 |
235 |
1 |
313 |
7 |
C2 |
| 15 |
253 |
1 |
337 |
13 |
C2 |
| 16 |
271 |
1 |
361 |
1 |
C2 |
| 17 |
289 |
1 |
385 |
7 |
C2 |
| 18 |
307 |
1 |
409 |
13 |
C2 |
| 19 |
325 |
1 |
433 |
1 |
C2 |
| 20 |
343 |
1 |
457 |
7 |
C2 |
| 21 |
361 |
1 |
481 |
13 |
C2 |
| 22 |
379 |
1 |
505 |
1 |
C2 |
| 23 |
397 |
1 |
529 |
7 |
C2 |
| 24 |
415 |
1 |
553 |
13 |
C2 |
| 25 |
433 |
1 |
577 |
1 |
C2 |
Table A7.
C2(2) (parent residue ), minimal .
Table A7.
C2(2) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
7 |
7 |
9 |
9 |
C0 |
| 2 |
25 |
7 |
33 |
15 |
C0 |
| 3 |
43 |
7 |
57 |
3 |
C0 |
| 4 |
61 |
7 |
81 |
9 |
C0 |
| 5 |
79 |
7 |
105 |
15 |
C0 |
| 6 |
97 |
7 |
129 |
3 |
C0 |
| 7 |
115 |
7 |
153 |
9 |
C0 |
| 8 |
133 |
7 |
177 |
15 |
C0 |
| 9 |
151 |
7 |
201 |
3 |
C0 |
| 10 |
169 |
7 |
225 |
9 |
C0 |
| 11 |
187 |
7 |
249 |
15 |
C0 |
| 12 |
205 |
7 |
273 |
3 |
C0 |
| 13 |
223 |
7 |
297 |
9 |
C0 |
| 14 |
241 |
7 |
321 |
15 |
C0 |
| 15 |
259 |
7 |
345 |
3 |
C0 |
| 16 |
277 |
7 |
369 |
9 |
C0 |
| 17 |
295 |
7 |
393 |
15 |
C0 |
| 18 |
313 |
7 |
417 |
3 |
C0 |
| 19 |
331 |
7 |
441 |
9 |
C0 |
| 20 |
349 |
7 |
465 |
15 |
C0 |
| 21 |
367 |
7 |
489 |
3 |
C0 |
| 22 |
385 |
7 |
513 |
9 |
C0 |
| 23 |
403 |
7 |
537 |
15 |
C0 |
| 24 |
421 |
7 |
561 |
3 |
C0 |
| 25 |
439 |
7 |
585 |
9 |
C0 |
Table A8.
C2(3) (parent residue ), minimal .
Table A8.
C2(3) (parent residue ), minimal .
| Idx |
Parent n
|
|
Child
|
Child
|
Child class |
| 1 |
13 |
13 |
17 |
17 |
C1 |
| 2 |
31 |
13 |
41 |
5 |
C1 |
| 3 |
49 |
13 |
65 |
11 |
C1 |
| 4 |
67 |
13 |
89 |
17 |
C1 |
| 5 |
85 |
13 |
113 |
5 |
C1 |
| 6 |
103 |
13 |
137 |
11 |
C1 |
| 7 |
121 |
13 |
161 |
17 |
C1 |
| 8 |
139 |
13 |
185 |
5 |
C1 |
| 9 |
157 |
13 |
209 |
11 |
C1 |
| 10 |
175 |
13 |
233 |
17 |
C1 |
| 11 |
193 |
13 |
257 |
5 |
C1 |
| 12 |
211 |
13 |
281 |
11 |
C1 |
| 13 |
229 |
13 |
305 |
17 |
C1 |
| 14 |
247 |
13 |
329 |
5 |
C1 |
| 15 |
265 |
13 |
353 |
11 |
C1 |
| 16 |
283 |
13 |
377 |
17 |
C1 |
| 17 |
301 |
13 |
401 |
5 |
C1 |
| 18 |
319 |
13 |
425 |
11 |
C1 |
| 19 |
337 |
13 |
449 |
17 |
C1 |
| 20 |
355 |
13 |
473 |
5 |
C1 |
| 21 |
373 |
13 |
497 |
11 |
C1 |
| 22 |
391 |
13 |
521 |
17 |
C1 |
| 23 |
409 |
13 |
545 |
5 |
C1 |
| 24 |
427 |
13 |
569 |
11 |
C1 |
| 25 |
445 |
13 |
593 |
17 |
C1 |
Appendix B. Mathematical Glossary, Notation, and Examples
This appendix collects all major notations and mathematical concepts used throughout the paper.
-
Modular Arithmetic (). Two integers
a and
b are congruent modulo
n if
n divides their difference. Modular arithmetic partitions the integers into residue classes.
In this work:
mod 6 classifies odd integers into (), (), and ().
mod 18 selects the gate residues in the address and determines the admissible halving exponent k; note cycles through .
-
Product Notation (). The product symbol is the multiplicative analogue of summation:
This gives the total multiplicative scaling on the free index variable u after L steps.
-
Affine Recurrence. An affine recurrence is an iterative relation of the form
Least-Admissible Lift and Gate Parity. The reverse lift is admissible iff . The least-admissible exponent satisfies: is even when and odd when .
-
Gate Alignment (Forward–Reverse Equivalence). The forward operator T and the least-admissible reverse operator P meet at the same gate residue with exponent . Consequences:
each forward step corresponds to exactly one admissible reverse edge,
forward orbits do not branch,
residue labels are consistent in both directions.
-
Closure Mechanism. The global resolution of the Collatz map follows from five structural invariants established in the preceding sections:
Unique forward parentage. Each odd integer has exactly one forward successor , and this map is perfectly inverted by the edge-aligned reverse step . Thus forward trajectories never branch.
Deterministic residue–phase dynamics. All admissible reverse and forward odd steps occur inside the finite residue–phase automaton , which admits no escape and no new states. Every transition is uniquely determined by the residue class and phase, with no ambiguity at any step.
Affine and dyadic structure. Every odd integer lies in exactly one dyadic slice and simultaneously on a unique affine rail generated from the anchors . These ladders and slices partition disjointly and exhaustively.
Total inclusion of the evens. Every even integer is a dyadic extension of a unique odd, and forward iteration strips dyadic factors immediately. Hence the even branch contributes no additional behavior and inherits closure from the odd subsystem.
Together these invariants make the Collatz map a closed dynamical system on : every integer lies on a unique affine/dyadic rail, every forward step moves strictly toward the base of that rail, and the only globally stable fixed point compatible with the affine form is 1. Thus the map admits no divergent trajectories, no nontrivial odd cycles, and every converges to 1.
References
- M. Spencer. A Deterministic Residue Framework for the Collatz Operator at q=3. Preprints, 2025. Original manuscript. [CrossRef]
- M. Spencer. Supplemental to: A Deterministic Residue Framework for the Collatz Operator at q=3. Preprints, 2025. Supplemental material, included in this version as a single submission. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
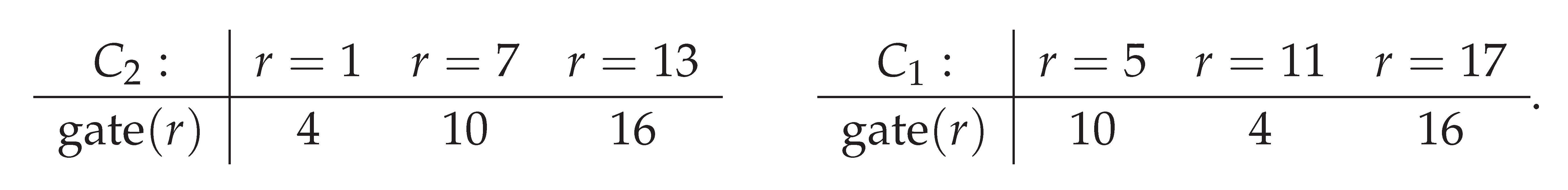 Thus the minimal admissible doubling maps each odd residue to a unique even gate in , refining the mod-9 triads to mod-18 gates.
Thus the minimal admissible doubling maps each odd residue to a unique even gate in , refining the mod-9 triads to mod-18 gates.

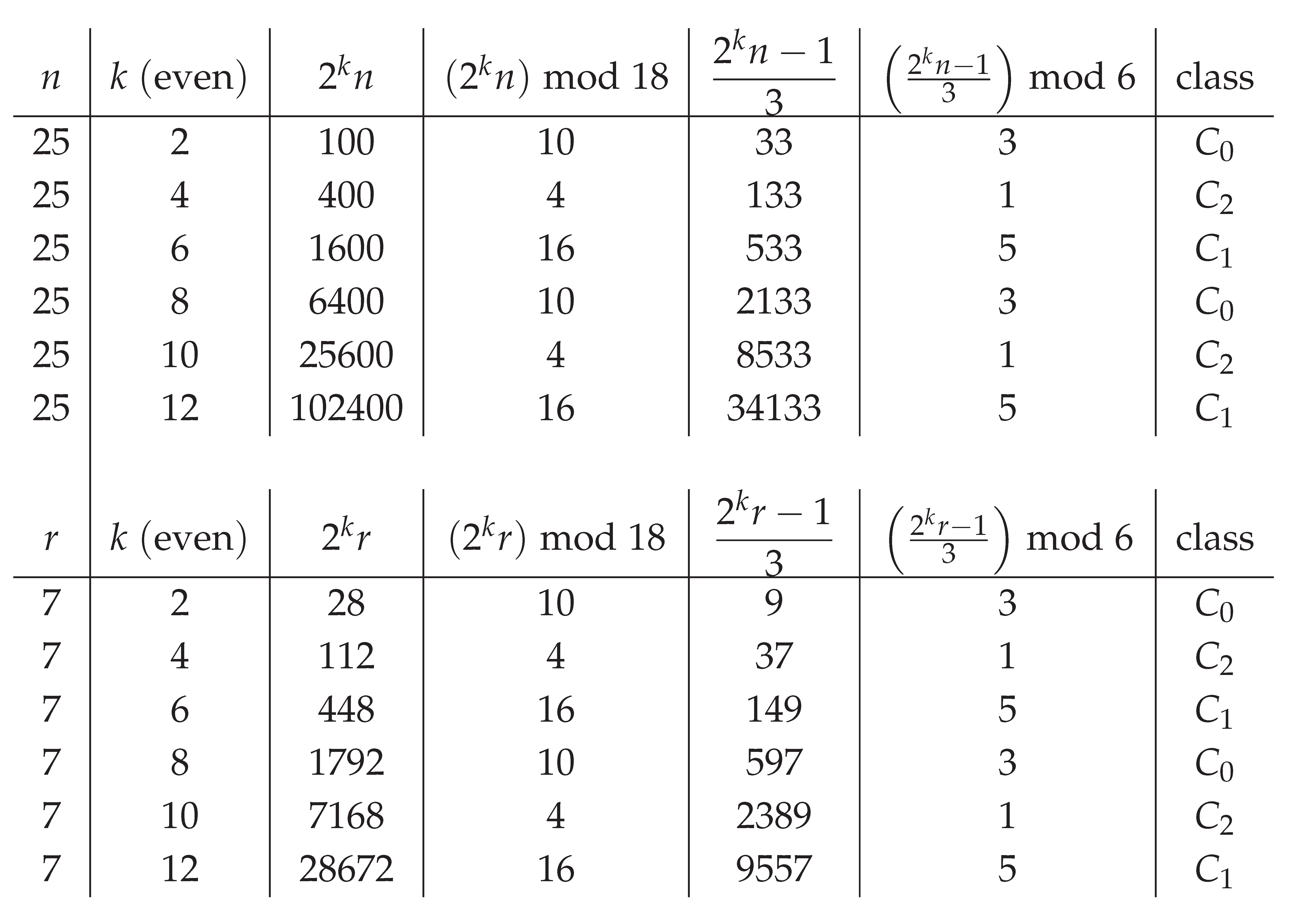
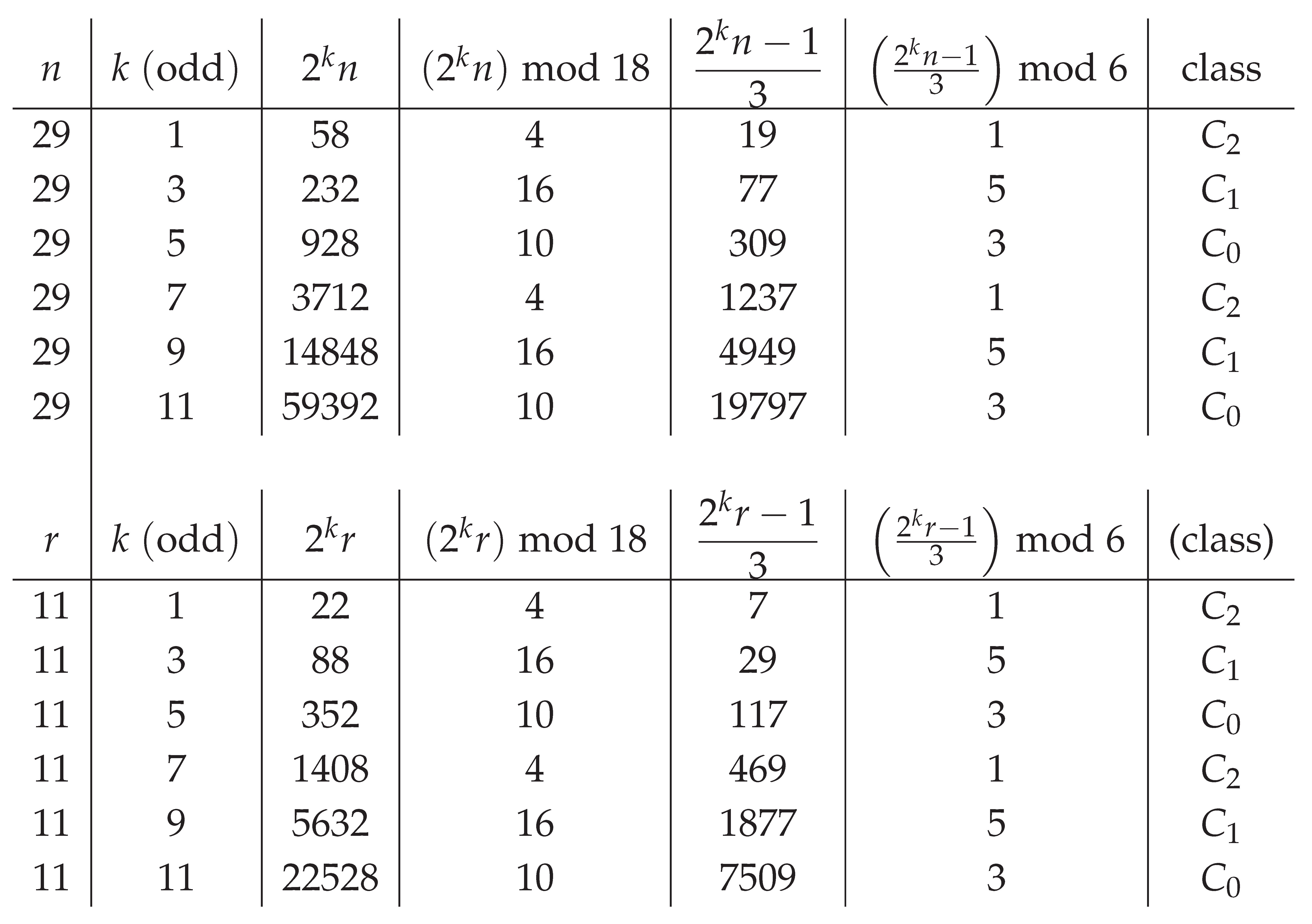
 Each lifted triad row follows the same deterministic pattern as the mod 18 table. The indexing variable plays the same role as in selecting the correct column of the triad. Rows for are in or , and remain in .
Each lifted triad row follows the same deterministic pattern as the mod 18 table. The indexing variable plays the same role as in selecting the correct column of the triad. Rows for are in or , and remain in .




