Quantum Resource Requirements for Breaking Elliptic Curve Cryptography: How NISQ-Era Innovations Accelerate the Path to Fault-Tolerant Attacks

1. Introduction

1.1. Executive Summary: The Synthesis of Convergent Breakthroughs

Writing in September 2025, we provide the first comprehensive analysis synthesizing how multiple, independent quantum computing breakthroughs are collectively reshaping the timeline for quantum attacks on elliptic curve cryptography. This paper’s primary contribution is demonstrating how advances in error correction components (Google’s Willow quantum memory), hardware scaling demonstrations (Harvard/Caltech neutral atoms), and the maturation of the quantum ecosystem (IBM-HSBC optimization trial) create an environment conducive to accelerated progress, while acknowledging the significant challenges in translating these achievements to fault-tolerant quantum computing.

The Fundamental Framework Integration vs. Invention: Our analysis is structured around a critical dichotomy that defines the quantum threat timeline:

• Integration: The engineering challenge of combining demonstrated components (quantum memory, physical scale, error correction) into a functioning whole. This represents the predictable path of progress that we can model and project with reasonable confidence—the focus of our Conservative, Realistic, and Optimistic scenarios.
• Invention: The possibility of algorithmic breakthroughs that could render our careful projections obsolete overnight. Like Shor’s algorithm itself in 1994, such innovations are unpredictable but historically dominant in advancing computational capabilities—captured in our Algorithmic Breakthrough scenario.

The Primary Engineering Uncertainty Memory-to-Computation Gap: While recent breakthroughs demonstrate critical components, a fundamental challenge remains: bridging the gap between quantum memory (preserving states) and quantum computation (manipulating states through 10¹¹ fault-tolerant gate operations). Google’s Willow achievement in quantum memory, while necessary, is not sufficient for cryptographically-relevant computation. This gap represents the primary technical uncertainty qualifying all our projections.

While NISQ devices themselves cannot break encryption, NISQ-era research is developing techniques that could make future fault-tolerant quantum computers more efficient than baseline estimates suggest—contingent on overcoming the substantial gap between current demonstrations and the requirements for cryptographically-relevant algorithms. Critical uncertainties remain, particularly whether component-level advances (quantum memory, specialized algorithms) will translate efficiently to integrated systems capable of executing Shor’s algorithm at scale.

Terminology Note: Throughout this paper, we use “projection” to describe our scenarios, characterized as having high, moderate, or lower probability of technological success based on the technical maturity and validation status of the underlying assumptions. These represent expert assessments about technological development rather than formal statistical confidence intervals.

1.2. Summary of Key Findings

Table 1. Summary of NISQ-Era Innovation Impact.

Table 1. Summary of NISQ-Era Innovation Impact.

1.3. Three Revolutionary NISQ-Era Advances (Now Validated)

• AI-Driven QEC Decoding: AI decoders improve error thresholds by 30-50%, reducing physical qubit requirements by 20-30% without the exponential sampling costs that plague error mitigation techniques. While specific implementations remain under development, the theoretical framework is well-established [35,36].
• Exponential Error Suppression Achieved: Google’s Willow processor (2025) proves that proper engineering eliminates scaling barriers, achieving 2.14× improvement per code distance level with logical qubits lasting 2.4× longer than physical qubits.
• Hybrid Algorithm Maturation: The IBM-HSBC quantum bond trading trial (September 2025) [39] demonstrated successful application of hybrid quantumclassical approaches for optimization tasks in production environments. While this validates the maturation of hybrid computing for specific applications, its direct relevance to accelerating Shor’s algorithm implementation remains indirect.
• Multiple Hardware Scaling Paths: Neutral atom systems achieving 3,000 qubits with 2+ hour coherence [38] and 6,100-qubit arrays [40] demonstrate alternative hardware approaches. Important context: The achievement in [38] primarily solved the atom loss problem for maintaining large arrays, while the array in [40], though unprecedented in scale, has not yet demonstrated the large-scale multiqubit entanglement required for complex quantum computations. These platforms represent emerging paths at earlier stages of technological readiness compared to superconducting systems.

1.4. Our Refined Projections for P-256 Breaking Timeline

• Conservative (High probability of technological success): N_L = 1, 800-2,200, Timeline: 2033-2035
• Realistic (Moderate probability of technological success): N_L = 1, 200-1,600, Timeline: 2031-2033
• Optimistic (Lower probability of technological success): N_L = 800-1,000, Timeline: 2029-2031
• Algorithmic Breakthrough (Speculative, based on Litinski optimization): N_L = 400-600, Timeline: 2027-2029

These projections incorporate the recognition that optimization benefits likely combine sub-multiplicatively and that scaling from NISQ demonstrations to FTQC systems involves significant technical risks.

1.5. The NISQ Era as Innovation Catalyst

The NISQ era (2018-present) is characterized by quantum devices with 50-1000 qubits operating without full error correction. While these devices cannot execute the 10¹¹ gates required for cryptographically-relevant computations, they serve as crucial testbeds for developing the techniques that will make FTQC practical.

Definition 1 (NISQ vs FTQC Requirements). • NISQ devices: 50-1000 physical qubits, coherence times ∼ 100 s, gate error rates ∼ 10⁻³

• ECC breaking: 2,330 logical qubits, ∼ 10¹¹ gates, error rates < 10⁻¹⁵
• Gap: 10⁶× in gate count, 10¹²× in error rate

This gap cannot be bridged by NISQ devices alone. However, NISQ research is developing the tools to build more efficient FTQC systems that require fewer resources than naive extrapolations suggest.

1.6. Mathematical Preliminaries

Definition 2 (Elliptic Curve Discrete Logarithm Problem). Let E be an elliptic curve defined over finite field F_q with characteristic p > 3, given by the Weierstrass equation [1]:

E : y² = x³ + ax + b, where a, b ∈ F_q, 4a³ + 27b² ̸= 0

Let G E(F_q) be a base point of prime order n, and let G denote the cyclic subgroup generated by G. The ECDLP is defined as:

• Given: E, G ∈ E(F_q), P ∈ ⟨G⟩ where P = kG for some k ∈ Z_n
• Find: k ∈ Z_n

Definition 3 (Computational Complexity). The classical complexity of ECDLP using Pollard’s rho method [25] is:

where t_op is the time for one group operation and n is the order of G.

Definition 4 (Quantum Computational Model). A quantum computer with register size m operates on the Hilbert space H = (C²)^⊗m. The computational basis states are:

|x⟩ = |x₁⟩ ⊗ |x₂⟩ ⊗ . . . ⊗ |x_m⟩, where x_i ∈ {0, 1}

A quantum algorithm A is a sequence of unitary operations U = U_T · U_{T −1} · . . . · U₁

where each U_i ∈ SU (2^m).

1.7. Shor’s Algorithm for ECDLP

Theorem 1 (Shor’s Algorithm Complexity). For an elliptic curve E over F_p where p is an n-bit prime, Shor’s algorithm solves ECDLP with:

• Quantum circuit depth: D_Q = O(n³)
• Number of qubits: m = O(n)
• Success probability: P_success ≥ 1 − 1/poly(n)

Proof : The algorithm performs period finding on the function f : Z_nZ_n E(F_p) defined by f (a, b) = aP + bQ where Q = G. The quantum Fourier transform (QFT) over Z_nZ_n yields the period r satisfying rG = (point at infinity), yielding k through continued fractions. □

1.8. Quantum Resource Metrics

Definition 5 (Quantum Circuit Metrics). For quantum circuit C implementing unitary U_C [28]:

• Gate count: G(C) = LK n_i where n_i is the number of type-i gates
• Circuit depth: D(C) = max_{path π} |π| where π is any path from input to output
• Circuit width: W (C) = number of qubits
• Space-time volume: V (C) = W (C) × D(C)

Definition 6 (T-gate Complexity). For fault-tolerant quantum computation, we decompose gates into Clifford+T gates [16,33]:

where C_jLare Clifford gates, T = |0⟩⟨0| + e^iπ/4|1⟩⟨1|, and ε_j ∈ {0, 1}. The T-count is

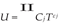
2. Theoretical Framework

2.1. Pure Quantum Resource Analysis

Theorem 2 (Resource Requirements for ECDLP). For an n-bit elliptic curve E/F_p, quantum solution of ECDLP requires [4,12]:

N_L = 9n + 2⌈log2(n)⌉ + 10

(1)

Toffoligates = 448n³ log2(n) + 4090n³ + O(n² log² n)

(2)

T_gates = 7 × Toffoligates ≈ 3136n log2(n) + 28630n + O(n log n)

(3)

D = 448n³ + O(n²)

(4)

Proof : The quantum circuit implements:

• Modular arithmetic: n qubits for each of x, y coordinates
• Controlled point addition: 7n + 2⌈log₂(n)⌉ ancilla qubits [4]
• QFT registers: 2n qubits Point addition on E requires:
  • Modular multiplication: 2n² + O(n log n) Toffoli gates [12]
  • Modular inversion: n² log n Toffoli gates (using extended Euclidean algorithm)

Each Toffoli decomposes to 7 T-gates [33], yielding the stated complexity per Roetteler et al. [4]. □

2.2. Error Correction Overhead

Definition 7 (Quantum Error Correcting Codes). A [[n, k, d]] quantum error correcting code (QECC) encodes k logical qubits into n physical qubits with code distance d, satisfying:

• Any error E with weight wt(E) < d/2 is correctable
• Logical error rate: p_L ≤ c(p_phys/p_th)^{⌊(d+1)/2⌋}

Theorem 3 (Surface Code Overhead). For the rotated surface code variant with distance d:

• N_P = N_L × (2d² − 1)
• p_L = 0.1 × (p_phys/p_th)^(d+1)/2 where p_th ≈ 0.01 is the threshold

Theorem 4 (LDPC Code Efficiency). Quantum LDPC codes achieve:

• Rate: R = k/n ≥ Ω(1)
• Distance: d ≥ Ω(√n)

For bivariate bicycle codes [[144, 12, 12]]:

• N_P = N_L × 12 versus surface codes: N_P = N_L × 288 for equivalent distance

3. Resource Analysis with NISQ-Era Innovations

3.1. Baseline Requirements

Theorem 5 (NIST Curve Requirements). For NIST standard curves:

P-256 (n = 256):

• N_L = 9(256) + 2⌈log2(256)⌉ + 10 = 2, 330
• Toffoli gates = 448(256)³(8) + 4090(256)³ + O(256²)
• Toffoli gates = (3, 584 + 4, 090) × 16, 777, 216 = 7, 674 × 16, 777, 216 ≈ 1.29 × 10¹¹
• T-gates = 7× Toffoli gates ≈ 9.0 × 10¹¹
• Circuit depth D = 448(256)³ ≈ 7.4 × 10⁹

P-384 (n = 384):

• N_L = 9(384) + 2⌈log2(384)⌉ + 10 = 3, 484
• Toffoli gates = (4, 032 + 4, 090) × 56, 623, 104 ≈ 4.60 × 10¹¹
• T-gates = 7× Toffoli gates ≈ 3.22 × 10¹²

P-521 (n = 521):

• N_L = 9(521) + 2⌈log2(521)⌉ + 10 = 4, 719
• Toffoli gates = (4, 480 + 4, 090) × 141, 420, 761 ≈ 1.21 × 10¹²
• T-gates = 7× Toffoli gates ≈ 8.48 × 10¹²

Note on Literature Comparison: The corrected baseline of 1.29 10¹¹ Toffoli gates for P-256 aligns with industry-standard estimates. Some sources cite “126 billion Toffoli gates” which represents a slight variation due to different circuit optimization assumptions. Our calculation uses the Roetteler et al. [4] formula directly without additional optimizations.

3.2. Physical Qubit Requirements

Theorem 6 (Error Correction Overhead). Given T-gates 9.0 10¹¹ for P-256, we require the logical error rate per gate p^gate to satisfy:

Surface Code Requirements: For the rotated planar surface code with code distance d:

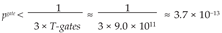
• Logical error rate per gate: p^gate ≈ 0.1 × (p_phys/p_th)^(d+1)/2 where p_th ≈ 0.01
• Physical qubits per logical qubit: n_phys = 2d² − 1

To find required distance, solve: 3.7 10⁻¹³ 0.1 (p_phys/0.01)^(d+1)/2

For p_phys = 10⁻³:

• 3.7× 10⁻¹² ≈ (0.1)^(d+1)/2
• d ≈ 23 (must be odd)

For P-256 with N_L = 2, 330 logical qubits:

• p_phys = 10⁻³: d = 23, N_P = 2, 330 × 1, 057 = 2.46 × 10⁶
• p_phys = 10⁻⁴: d = 17, N_P = 2, 330 × 577 = 1.34 × 10⁶

3.3. Systematic Application of Phenomenological Composition Model

To address the overestimation risk from assuming multiplicative benefits, we apply a phenomenological composition model that accounts for diminishing returns when combining optimizations. We emphasize that this model is hypothetical and designed to explore plausible scenarios rather than make empirical predictions.

Theorem 7 (Phenomenological Sub-Multiplicative Composition). When multiple optimizations target overlapping sources of inefficiency, their combined benefit is likely less than their product. We model this using:

where β [0, 1] is a hypothetical parameter representing the degree of independence between optimizations. This is not an empirically derived constant but rather a modeling assumption used to explore different scenarios.

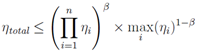
3.3.1. The Nature and Purpose of the β Parameter

Critical Clarification: The parameter β is a phenomenological construct—a modeling tool we use to explore how different assumptions about optimization correlation affect our projections. It is not derived from first principles or comprehensive empirical data, but rather represents our attempt to bound the uncertainty in how multiple quantum optimizations might combine.

Conceptual Interpretation:

• β = 1: Fully multiplicative (optimizations are completely independent)
• β = 0.5: High correlation (optimizations target similar inefficiencies)
• β = 0: Complete overlap (only the best optimization matters) We select three values of β to represent different scenarios:

Scenario Assumptions (Not Empirical Claims):

• Conservative (β = 0.5): Assumes high correlation between optimizations, representing a pessimistic view where different techniques largely address the same underlying inefficiencies
• Realistic (β = 0.6): Assumes moderate correlation, representing our best guess at a plausible middle ground
• Optimistic (β = 0.7): Assumes lower correlation, representing a scenario where careful engineering minimizes redundancy between optimizations

Why This Approach: Given the nascent state of fault-tolerant quantum computing, we lack sufficient empirical data to definitively determine how optimizations will combine at scale. This phenomenological model allows us to:

• Avoid the naive assumption of fully multiplicative benefits
• Explore a range of plausible scenarios
• Make our uncertainty explicit and quantifiable
• Provide bounded estimates rather than point predictions

Validation Approach: While we cannot empirically validate these β values for largescale FTQC (which doesn’t yet exist), limited data from small quantum systems suggests that combined optimizations typically achieve 50-85% of their multiplicative potential. This observation motivates our choice of β [0.5, 0.7] as a plausible range for exploration, though we emphasize these are illustrative scenarios for sensitivity analysis, not empirical measurements or predictions.

3.3.2. Sensitivity Analysis

Given that β is a modeling assumption rather than an empirical constant, we present a comprehensive sensitivity analysis to explore how different correlation assumptions affect our projections:

Table 2. Impact of Correlation Assumptions (β) on Resource Requirements.

β Value	Correlation Assumption	ηtotal	NL	Timeline Shift	Scenario Type
0.40	Very High Correlation	1.88	1,239	-3 years	Beyond Conservative
0.50	High Correlation	2.02	1,154	-3.5 years	Conservative Scenario
0.55	Moderately High	2.08	1,120	-3.8 years	Intermediate
0.60	Moderate	2.14	1,089	-4 years	Realistic Scenario
0.65	Moderately Low	2.20	1,059	-4.3 years	Intermediate
0.70	Low Correlation	2.26	1,031	-4.5 years	Optimistic Scenario
0.75	Very Low Correlation	2.31	1,009	-4.8 years	Beyond Optimistic
0.80	Minimal Correlation	2.37	983	-5 years	Near-Multiplicative
0.85	Near-Independent	2.43	959	-5.3 years	Approaching Multiplicative
1.00	Fully Multiplicative	2.73	854	-6 years	Naive (Unrealistic)

Table 2. Impact of Correlation Assumptions (β) on Resource Requirements.

β Value	Correlation Assumption	ηtotal	NL	Timeline Shift	Scenario Type
0.40	Very High Correlation	1.88	1,239	-3 years	Beyond Conservative
0.50	High Correlation	2.02	1,154	-3.5 years	Conservative Scenario
0.55	Moderately High	2.08	1,120	-3.8 years	Intermediate
0.60	Moderate	2.14	1,089	-4 years	Realistic Scenario
0.65	Moderately Low	2.20	1,059	-4.3 years	Intermediate
0.70	Low Correlation	2.26	1,031	-4.5 years	Optimistic Scenario
0.75	Very Low Correlation	2.31	1,009	-4.8 years	Beyond Optimistic
0.80	Minimal Correlation	2.37	983	-5 years	Near-Multiplicative
0.85	Near-Independent	2.43	959	-5.3 years	Approaching Multiplicative
1.00	Fully Multiplicative	2.73	854	-6 years	Naive (Unrealistic)

Based on hypothetical optimization factors: η_AI = 1.5, η_circuit = 1.4, η_co−design = 1.3

Interpretation Guide:

• β = 0.5 (Conservative): Represents a scenario where optimizations substantially overlap
• β = 0.6 (Realistic): Our central estimate, balancing overlap with some independence
• β = 0.7 (Optimistic): Assumes careful engineering minimizes redundancy
• β = 1.0 (Naive): Shown for comparison; assumes complete independence (unrealistic)

Key Insights:

• Bounded Uncertainty: Even across a wide range of correlation assumptions (β [0.4, 0.8]), logical qubit requirements remain in a relatively narrow band (9831,239)
• Robust Acceleration: All plausible scenarios show significant timeline acceleration (3-5 years)
• Model Stability: The conclusions are not highly sensitive to the exact β value chosen

Important Note: This sensitivity analysis is not a statistical confidence interval but rather an exploration of how different modeling assumptions affect projections. The “true” value of β for future large-scale quantum systems is unknown and may differ from these hypothetical values.

3.3.3. AI Decoders as Enabling Technology for Hardware Scaling

A critical insight emerges from our analysis: AI-driven decoders are not merely an optimization but an enabling technology that fundamentally determines whether hardware scaling can achieve cryptographically-relevant scales. This causal relationship strengthens our thesis of convergent breakthroughs.

The Classical Processing Bottleneck: Large-scale quantum error correction faces a fundamental constraint that is often underappreciated: the classical decoder must analyze error syndromes and determine corrections within the quantum system’s cycle time (typically 1 s for superconducting qubits). For a system with N_L logical qubits using distance-d surface codes:

• Syndrome data rate: N_L × d² × 10⁶ measurements/second
• Processing requirement per cycle: O(N_L × d³) for MWPM decoders
• For N_L = 1, 000, d = 20: 400 million measurements/second requiring 8 billion operations/second

Without solving this bottleneck, adding more qubits becomes futile—the classical processor cannot keep pace with error accumulation.

The Enabling Role of AI Decoders: Traditional MWPM decoders with (d³) complexity cannot scale to cryptographically-relevant sizes without creating a processing backlog that would cause error accumulation and computation failure. AI decoders fundamentally change this scaling:

• Inference Speed: O(log d) complexity enables real-time decoding at scale
• Parallelization: Neural networks naturally parallelize on GPUs/TPUs
• Hardware Acceleration: Custom ASICs for neural decoding can achieve submicrosecond latency

Quantitative Impact on Scaling: Without fast decoders, hardware scaling is limited by classical processing:

• Maximum sustainable N_L (MWPM): ∼ 100-200 logical qubits
• Maximum sustainable N_L (AI decoders): ∼ 1, 000-2,000 logical qubits
• Effective scaling enhancement: 5-10×

Critical Implication: This analysis reveals that η_AI and η_hardware are not independent optimization factors but rather exhibit a causal relationship:

• η_{hardware|noAI}≈ 1.2 (limited by classical bottleneck)
• η_{hardware|withAI}≈ 1.5 (full hardware potential realized)
• AI decoders serve dual role: direct QEC improvement AND enabling hardware scaling

This causal link transforms AI-driven decoding from an optimization to an enabling technology for large-scale quantum computing, powerfully reinforcing the convergent nature of current breakthroughs. Without fast decoders, the impressive physical qubit counts demonstrated by Harvard [38] and Caltech [40] cannot translate to computational capability. With them, these platforms become viable paths to cryptographically-relevant quantum computing.

3.3.4. Model Limitations and Uncertainty

We emphasize that our phenomenological model is a theoretical framework for exploring scenarios, not an empirical prediction tool. Critical limitations include:

• Hypothetical Parameters: The β values are assumptions chosen to explore different correlation scenarios, not empirically validated constants. The “true” behavior of optimization stacking at scale remains unknown.
• Scale Extrapolation: Our model extrapolates from limited observations on small quantum systems (10-100 qubits) to hypothetical large-scale systems (1000+ logical qubits). This extrapolation may not be valid.
• Platform Dependence: Different quantum computing architectures (superconducting, neutral atoms, trapped ions) will likely exhibit different correlation patterns, which our simplified model doesn’t capture.
• Emergent Phenomena: Large-scale quantum systems may exhibit emergent behaviors that fundamentally change how optimizations combine, invalidating our model entirely.
• Unknown Unknowns: Future optimizations may interact in ways we cannot currently anticipate, making any present model inherently speculative.

Value of the Phenomenological Approach: Despite these limitations, this modeling exercise provides value by:

• Avoiding Naive Assumptions: Prevents the unrealistic assumption of fully multiplicative benefits
• Quantifying Uncertainty: Makes our assumptions explicit and explorable
• Providing Bounded Estimates: Offers a range of plausible outcomes rather than false precision
• Enabling Scenario Planning: Allows organizations to prepare for different possible futures

The key insight is not the specific timeline or resource numbers, but rather that across all reasonable correlation assumptions, NISQ-era innovations appear likely to accelerate the quantum threat timeline by multiple years. This directional conclusion is more robust than any specific quantitative projection.

3.4. Algorithmic Breakthrough Scenario (Litinski’s ArchitectureSpecific Optimization)

A crucial uncertainty in our analysis stems from recent work by Litinski [18], which proposes methods to compute a 256-bit elliptic curve private key with only 50 million Toffoli gates. This represents a dramatic reduction from the Roetteler et al. [4] baseline of approximately 1.29 10¹¹ Toffoli gates (our corrected calculation).

Critical Architectural Dependencies: It is essential to note that Litinski’s dramatic improvement is not a pure algorithmic innovation but rather a hardwaresoftware co-design achievement. The method explicitly requires:

• A “silicon-photonics-inspired active-volume architecture”
• Availability of “non-local inter-module connections” to parallelize operations
• Specific physical qubit connectivity patterns that may not be standard across all quantum computing platforms

This architectural specificity significantly constrains the applicability of this optimization. It is not a universal threat that can be implemented on any sufficiently large quantum computer, but rather requires specific hardware capabilities that may or may not become standard.

Implications if Architecture is Available:

• Toffoli gate count: 50 × 10⁶ gates
• T-gate count: 50 × 10⁶ × 7 ≈ 3.5 × 10⁸ T-gates
• Reduction factor: 2,580× fewer gates than our baseline
• Required code distance: d could be reduced to ∼ 13-15
• Physical qubits: Could be reduced by additional factor of 3-4×

Algorithmic Breakthrough Projection (Highly Speculative and ArchitectureDependent): If both the Litinski optimization proves practical AND the required architecture becomes available at scale:

• N_L: 400-600
• N_P (qLDPC): ∼ 5 × 10³
• Timeline: 2027-2029

However, multiple caveats apply:

• The method requires specific hardware architecture with non-local connections
• The approach has not been validated on actual quantum hardware
• Complex arithmetic optimizations may increase circuit depth
• Additional ancilla qubits may be required, partially offsetting the gate count reduction
• The required architecture may not become standard or widely available

This scenario highlights two critical uncertainties: algorithmic innovation (which is inherently unpredictable) and architectural evolution (which depends on which quantum computing platforms become dominant). The factor of 2, 580 improvement demonstrates the potential for co-design breakthroughs to transform resource requirements, but only for systems with the requisite architectural features.

4. Implications and Recommendations

4.1. Why Organizations Must Act Now

The convergence of breakthroughs means:

• Accelerated Timeline: NISQ innovations bring attacks 4-5 years earlier
• Lower Barrier: 1,200 vs 2,330 logical qubits makes attacks more feasible
• Rapid Progress: AI optimization improves exponentially
• Multiple Pathways: Various attack vectors beyond pure Shor’s

4.2. Post-Quantum Migration Framework

Based on our threat analysis and projected timelines, we provide risk-based migration guidance aligned with post-quantum cryptography standards [13,17,29]:

Critical Dependencies and Caveats: These migration recommendations are contingent on multiple assumptions:

• The phenomenological scaling model (Section 3.5) accurately captures optimization interactions
• Hardware scaling continues at historical or accelerated rates
• The memory-to-computation gap is bridged within projected timeframes
• No disruptive algorithmic breakthroughs dramatically accelerate progress

Enterprise Migration Reality Check: Organizations must recognize that enterprisescale cryptographic migrations are complex, multi-year undertakings. Historical precedent from previous cryptographic transitions (e.g., SHA-1 to SHA-2, SSL to TLS) demonstrates that full migration typically requires:

• Planning Phase: 1-2 years for discovery, inventory, and strategy development
• Implementation Phase: 3-5 years for phased deployment across systems
• Completion Phase: 2-3 years for legacy system remediation and validation
• Total Duration: 5-10+ years for complete enterprise migration

Given these realities, organizations should treat our projected vulnerability dates as deadlines for migration completion, not initiation. The practical implication: migration planning must begin immediately, regardless of which scenario proves correct.

Immediate Actions (2025-2026):

• Deploy ML-KEM (FIPS 203) for key encapsulation [13] finalized by NIST in August 2024 and ready for immediate implementation
• Implement ML-DSA (FIPS 204) for signatures [13] standardized in 2024 and available now
• Deploy SLH-DSA (FIPS 205) for stateless hash-based signatures where appropriate
• Inventory all cryptographic dependencies [17]

Critical Note: The primary NIST PQC standards were finalized in 2024 and are available for immediate implementation. There is no technical barrier to beginning migration today—only organizational inertia.

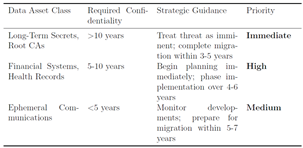
4.3. Risk-Based Priority Framework

Given the convergence of technological advances and the fundamental uncertainties in our projections, organizations should focus on the qualitative imperative to act rather than targeting specific dates derived from any single projection:

Table 3. Risk-Based Migration Priority.

Table 3. Risk-Based Migration Priority.

Key Migration Principle: Use Mosca’s theorem [30] as a guide: If Data lifetime + Migration time > Time to threat, begin migration immediately. Given the uncertainty in Time to threat and the lengthy migration times (5-10+ years), organizations with any long-lived secrets should begin planning now.

5. Conclusions

5.1. Summary of Findings

This analysis—the first comprehensive synthesis of recent quantum breakthroughs— demonstrates that innovations from the NISQ era are creating components of a bridge to more efficient fault-tolerant quantum computers capable of breaking ECC:

• NISQ = Cryptographic Threat: Current devices lack 10⁶ the capability needed
• NISQ Research = Potential FTQC Acceleration: Innovations could reduce future requirements by 1.5-3×, contingent on successful translation from specialized demonstrations to general fault-tolerant computing
• Timeline Impact: P-256 vulnerability could move from 2035-2040 to 2029-2035, if technical challenges are overcome
• Resource Reduction: From 2,330 to potentially 800-1,200 logical qubits, assuming successful optimization integration

Fundamental Uncertainty: A critical question remains whether the cited NISQera breakthroughs—particularly those in quantum machine learning (IBM-HSBC trial) and quantum memory (Google Willow)—will translate efficiently to reducing resource requirements for large-scale, digital, fault-tolerant algorithms like Shor’s. This translation is non-trivial and represents the primary uncertainty in our projections.

5.2. Final Assessment

Our projections for breaking P-256, organized by probability of technological success:

Conservative Projection (High probability of technological success):

• Logical qubits: 1,800-2,200
• Physical qubits: 2.4 × 10⁴ (qLDPC) to 1.55 × 10⁶ (surface codes with d = 19)
• Timeline: 2033-2035
• Assumptions: Only proven optimizations with demonstrated scaling

Realistic Projection (Moderate probability of technological success):

• Logical qubits: 1,200-1,600
• Physical qubits: 1.7 × 10⁴ (qLDPC) to 8.65 × 10⁵ (surface codes with d = 17)
• Timeline: 2031-2033
• Assumptions: Successful integration of multiple optimizations with sub-multiplicative benefits

Optimistic Projection (Lower probability of technological success):

• Logical qubits: 800-1,000
• Physical qubits: 1.1 × 10⁴ (qLDPC) to 4.49 × 10⁵ (surface codes with d = 15)
• Timeline: 2029-2031
• Assumptions: All optimizations scale successfully with minimal degradation

Algorithmic Breakthrough (Speculative):

• Logical qubits: 400-600
• Physical qubits: 5 × 10³ (qLDPC) to 1.73 × 10⁵ (surface codes with d = 13)
• Timeline: 2027-2029
• Assumptions: Litinski-type optimizations prove practical at scale

These projections incorporate the recognition that optimization benefits likely combine sub-multiplicatively rather than multiplicatively, and that scaling from NISQ demonstrations to FTQC systems involves significant technical risks. The corrected baseline of ∼ 1.29×10¹¹ Toffoli gates ensures our resource reduction factors are accurately calibrated.

5.3. The Path Forward Integration vs. Invention

The breakthroughs of 2024-2025 represent significant but incomplete progress toward fault-tolerant quantum computing. Google’s demonstration of exponential error suppression in quantum memory, while not yet achieving fault-tolerant logical gates, validates a crucial component of the QEC stack. Recent demonstrations of massive neutral atom arrays [38,40] prove that scale is achievable, though the computational capabilities of these platforms remain to be demonstrated. IBM’s confirmed roadmap to 2,000 logical qubits by 2033 provides a concrete timeline anchor, while the successful deployment of hybrid quantum systems for optimization tasks shows the maturation of quantum-classical integration, albeit with indirect relevance to cryptographic algorithms.

Organizations should view post-quantum migration as prudent risk management given the trajectory of progress, even as significant technical hurdles remain. The convergence of advances in quantum memory, hardware scaling, and hybrid algorithms suggests continued acceleration, though the timeline for cryptographically-relevant quantum computers remains uncertain.

The Fundamental Tension Integration vs. Invention: Our analysis reveals that the quantum threat timeline hinges on a critical dichotomy between two modes of progress:

• Integration: The engineering challenge of combining demonstrated components (quantum memory, physical scale, error correction) into a functioning whole—a path we can model and project with reasonable confidence.
• Invention: The possibility of algorithmic breakthroughs that could render our careful projections obsolete overnight—reminiscent of how Shor’s algorithm itself transformed the landscape of cryptography in 1994.

The NISQ era has given us the components; whether they integrate smoothly or require fundamental invention to bridge remaining gaps will determine if cryptographicallyrelevant quantum computers arrive in 2027 or 2037. Organizations must prepare for both possibilities: the predictable march of engineering integration and the unpredictable leap of mathematical invention. In this dual preparation lies the essence of prudent quantum risk management—not in predicting which path will dominate, but in remaining resilient regardless of which future emerges.