1. Introduction
Transformers [
9] have fundamentally reshaped the landscape of generative modelling, enabling state-of-the-art performance in language, vision, and multimodal tasks. Central to their success is the scaled-dot-product self-attention mechanism: for an input sequence represented by matrix
(sequence length
n, embedding dimension
d), learned linear projections produce queries, keys, and values
and attention is computed as
where
is the per-head key dimension. The explicit computation of the pairwise similarity matrix
produces the dominant costs in both computation and memory: naive attention requires
arithmetic operations and
storage. This quadratic scaling is the principal bottleneck that constrains context length, latency, and the scale of models that can be trained or deployed in practice.
Classical approaches that mitigate the quadratic cost-sparsity/limited receptive fields, low-rank factorization, kernelized attention, or approximation via locality-sensitive hashing-trade expressivity, require careful engineering, or introduce task-specific hyperparameters. The search for fundamentally different algorithmic paradigms that preserve the expressivity of full self-attention while reducing its asymptotic cost motivates our work.
Quantum computing provides an alternative computational substrate that offers different asymptotic trade-offs for linear-algebraic operations. Two broad classes of quantum strategies are relevant for Transformer-style models. First,
quantum linear-algebra (QLA) techniques (block-encoding, Quantum Singular Value Transformation or QSVT, amplitude estimation) can implement matrix–vector products and certain spectral transforms with polylogarithmic dependence on matrix dimensions under strong data-access or oracle models [
10,
12]. Second,
variational / parametrized quantum circuit (PQC) approaches present compact, entangling function approximators that can be trained hybridly in NISQ devices and simulated classically for small scale experiments. QLA is asymptotically attractive but depends on efficient state preparation and block-encoding oracles; PQC methods are more amenable to near-term hardware but must cope with expressivity/noise trade-offs.
This paper proposes the Quantum Generative Transformer (QGT), a hybrid quantum–classical Transformer architecture that is explicitly designed to reconcile the asymptotic advantages of QLA with the practical constraints of NISQ-era and classical-simulation regimes. QGT uses amplitude and block encodings when efficient oracles are assumed, but also provides NISQ-friendly hybrid alternatives (measurement-based readout, PQC heads) when those oracles are not available. Key design elements include: (i) compact amplitude/block encodings of token embeddings and weight matrices; (ii) QFT-driven global token mixing to reduce explicit pairwise loops; and (iii) amplitude-amplification (Grover) based top-k selectors to exploit sparsity in attention distributions.
Our contributions are the following:
- 1)
A full, formal specification of a hybrid QGT layer, including precise algorithmic descriptions (no informal pseudocode), circuit schematics for the main quantum subroutines, and resource accounting (qubit counts, gate counts, shot budgets).
- 2)
A conditional complexity theorem proving that, under standard block-encoding and state-loading oracles and an attention sparsity promise, a QGT layer realizes an asymptotic runtime of per-layer in the constant-k sparse regime, improving on the classical attention cost. The theorem is explicit about all oracle assumptions and precision overheads (Sec. 13 and App. A).
- 3)
A mathematically detailed hybrid training and gradient framework, including exact parameter-shift formulae and measurement-variance bounds to guide shot budgets and optimizer design.
- 4)
A reproducible simulation plan (PennyLane/Qiskit) and ablation study design that evaluate practical trade-offs between amplitude vs angle encodings, QFT mixing vs classical mixing, and amplitude amplification vs exhaustive scoring in small toy tasks.
Throughout the paper we maintain an “honest” stance: the asymptotic improvements are real but conditional. In particular, the embedding / state-preparation bottleneck and the availability of block-encoding oracles are the two primary practical obstacles that determine whether the theoretical benefits can materialize on actual hardware. We explicitly quantify the cost of these oracles and provide hybrid fallbacks when they are absent.
2. Background and Motivation
This section expands the technical background necessary to understand the QGT design choices and clarifies the practical motivations behind the hybrid architecture.
2.1. Why Attention Is the Central Bottleneck
Self-attention implements a full pairwise interaction model among tokens, which gives Transformers their expressive capacity for capturing long-range dependencies. The canonical scaled-dot product attention computes similarity scores between every pair of queries and keys, producing an matrix of interactions. For large context windows (e.g., thousands of tokens) this quadratic scaling is the dominant consumer of memory and arithmetic operations. While many engineering remedies exist (sparse attention heads, local attention windows, recurrence hybrids, kernelized linear attention), they all reduce the effective connectivity or require structural assumptions on the data. A method that preserves full connectivity while reducing computational cost would therefore be of both theoretical interest and practical value.
2.2. Quantum Linear Algebra Primitives
Quantum algorithms provide fundamentally different approaches to compute linear algebraic tasks:
2.3. Practical Constraints: NISQ and Hybrid Trade-Offs
The theoretical power of QLA is tempered by critical practical issues:
- 1)
State preparation (embedding) cost. Amplitude encoding compresses a length-
d vector into
qubits, but preparing the amplitude state can cost
unless QRAM-like oracles or structured loaders are available [
15]. When efficient loaders do not exist, state preparation cost can erase the asymptotic gains of quantum subroutines.
- 2)
Noise and shallow circuits. NISQ devices have limited coherence times and noisy two-qubit gates; deep QSVT or QFT sequences can be impractical without error correction. This motivates shallow PQC fallbacks, measurement-hybrid heads, and error-aware parameter regularization.
- 3)
Measurement throughput (shots). Shot-based estimation for expectation values introduces a trade-off between precision and runtime. Techniques such as classical post-processing, variance reduction, and QAE (for fewer queries) present different depth/shot trade-offs that must be factored into design and simulation.
These constraints motivate a hybrid design that uses QLA/QSVT style subroutines when efficient data oracles are available (and in theory, in a fault-tolerant regime), but falls back to hybrid PQC/measurement-based variants for NISQ-feasible experiments. The QGT architecture is explicitly modular so that each transformer subcomponent (embedding, projection, attention scoring, and feed-forward) can be implemented via (a) a block-encoding/QSVT primitive, (b) a shallow PQC readout, or (c) a classical approximate replacement; designers can therefore tune the hybrid mix to match available hardware and task constraints.
3. Literature Review and Related Work
This section positions QGT relative to the most relevant prior and contemporary lines of work. We group the literature into conceptual strands and highlight representative works that influenced design decisions, theoretical framing, and experimental methodology.
3.1. Classical Transformer Scaling, Approximations, and Kernel Methods
The Transformer architecture and its scaled-dot-product attention formulation were introduced in [
9] and have inspired extensive research into scaling strategies. On the classical side, methods to mitigate the
attention cost include sparse attention patterns (local attention, sliding windows), low-rank or factorized attention, kernelized linear-attention approximations, and LSH-based approximations (see surveys in large-context modeling literature). These classical approximations trade fidelity for speed and inform the kinds of structure (e.g., locality, low-rankness, sparsity) that one might exploit in quantum subroutines.
3.2. Quantum Linear-Algebra (QLA) Approaches to Neural Primitives
A growing body of work explores mapping neural network linear algebra to quantum subroutines. The block-encoding / QSVT line of research provides a framework to implement matrix functions, polynomial transforms, and controlled matrix–vector products with favorable dimension dependence under oracle assumptions [
10]. Building on this, Guo
et al. recently proposed a comprehensive QLA treatment for Transformer layers, explicitly constructing block-encodings of query, key, value and self-attention matrices and proposing quantum subroutines for softmax application and FFN layers in a fault-tolerant setting [
12]. Their work formalizes the oracle model we adopt in our complexity theorems and demonstrates that under those assumptions one can implement full Transformer components with polylogarithmic dependence on
up to precision factors. QGT builds on these constructions while also explicitly describing NISQ-friendly fallbacks and circuit-level resource accounting.
3.3. PQC / Variational Quantum Transformer Work (NISQ-Friendly)
Parallel to QLA-style proposals, PQC-based approaches embed parametrized quantum circuits into Transformer-like architectures, often replacing linear projections or FFN blocks with compact PQCs. These approaches are attractive for near-term experimentation: shallow entangling circuits can provide expressive nonlinear feature maps and exhibit useful inductive biases for small data regimes. Works in this direction include Quantum Vision Transformer variants and SASQuaTCh-style constructions (QFT-mixing PQC heads) that report competitive performance on toy vision/language tasks at small scales and analyze parameter-efficiency benefits [
2]. QGT borrows from this line by providing hybrid measurement-based head designs and guidelines for PQC construction when full block-encoding is unavailable.
3.4. Quantum Attention and Search-Based Attention Methods
Several proposals study “hard” or top-
k attention mechanisms implemented via quantum search and amplitude amplification. The key idea is that when the attention distribution concentrates mass on a small subset of keys, Grover-style amplitude amplification can find the dominant keys in
rather than
time [
11]. These approaches are particularly relevant when attention sparsity or top-
k structure is expected (e.g., in many language/vision contexts where only a few tokens strongly influence a given query). QGT formalizes this as the amplitude-amplified top-
k selector and quantifies precisely when the amplitude amplification overhead and comparator oracles pay off.
3.5. State-Preparation, QRAM, and Practical Input Models
A recurring theme across quantum-accelerated ML proposals is the state-loading problem: amplitude encoding is qubit-efficient but requires an efficient loader (QRAM or structured state-prep) to avoid
overhead per vector [
15]. Several recent contributions study structured or approximate loaders and quantify their cost; QGT makes these assumptions explicit, provides alternative angle-encoding and measurement-based fallbacks, and derives how the presence/absence of efficient loading changes the asymptotic complexity (Sec. 13 and App. D).
3.6. Surveys and Synthesis
Recent surveys synthesize the divide between QLA and PQC strategies for quantum neural networks and identify key open problems - notably embedding efficiency, noise/variational barren plateaus, and measurement overheads. These surveys motivate the hybrid, modular architecture we advocate (mixing QLA primitives where oracles exist, PQC heads otherwise, and classical postprocessing for shot-efficient pipelines) [
17].
3.7. Summary of How QGT Advances the State of the Art
QGT integrates and extends the literature above in three concrete ways:
- 1)
It provides a single, modular architecture that cleanly spans oracle-based fault-tolerant QLA implementations and NISQ-feasible PQC/measurement variants.
- 2)
It supplies complete algorithmic descriptions (formal algorithms for overlap estimation, top-k selection, weighted-sum preparation, and hybrid training) rather than sketch-level proposals.
- 3)
It gives explicit complexity theorems with detailed accounting of state-prep, block-encoding, precision, and amplitude-amplification overheads, enabling precise comparisons to classical approximations in realistic regimes.
4. Preliminaries and Notation
We use the following notation throughout:
n - sequence length (number of tokens).
d - embedding dimension per token (classical).
m - number of classical features extracted per token from PQC measurement (hybrid variant).
x - amplitude-encoded quantum state of classical vector (normalized).
- block-encoding unitary for matrix W; defined precisely below.
- cost of amplitude-loading a classical d-vector (explicitly stated in each theorem: either for QRAM/oracle or for naive).
- cost of one block-encoding query (counted as one unit; actual gate cost depends on compilation).
Definition 4.1 (Block-Encoding).
A unitary acting on qubits is an -block-encoding of matrix if
We assume standard circuit model primitives: controlled unitaries, QFT on qubits ( gate cost), amplitude amplification (Grover-type), and QSVT polynomial transforms where used.
5. Full Algorithmic Specification
Below we provide the algorithms as formal Algorithm boxes (not pseudocode). Each algorithm lists inputs, outputs, deterministic steps, and cost accounting.
5.1. Algorithm 1: Full QGT Layer Forward (Deterministic Description)
|
Algorithm 1 QGT Layer Forward (Single Layer, Single Sequence) |
Require: Classical token embeddings , block-encoding unitaries , amplitude-loading routine , parameters: threshold , top-k target k (optional), precision .
Ensure: Output classical embeddings for next layer.
- 1:
for each token index do
- 2:
Prepare via (cost ). - 3:
Prepare , , using block-encoding ancilla registers (cost per U call: ). - 4:
end for - 5:
for each query index do
- 6:
Use Algorithm 2 to estimate overlaps for all j, to precision or run Algorithm 3 to obtain candidate top-k keys if exploiting sparsity. - 7:
Compute attention scores . - 8:
Compute normalized weights (classical softmax on the measured/estimated scores) or approximate via Algorithm 4. - 9:
Prepare amplitude-encoded weighted-sum state using controlled state combination routines (Algorithm 4). - 10:
Apply block-encoded feed-forward (via QSVT wrapper) to to produce processed output state. Measure appropriate observables (or tomography) to get as classical vector. - 11:
end for - 12:
return.
|
5.2. Algorithm 2: Overlap Estimation (Hadamard Test Variant)
|
Algorithm 2 Overlap Estimation (Hadamard-based) |
Require: Access to state preparation oracles for and ; precision , shot budget S.
Ensure: Estimate with additive error with confidence (choose S accordingly).
- 1:
Prepare ancilla qubit in +. - 2:
Conditional on ancilla being 0, prepare in register A; conditional on ancilla 1, prepare in register B (controlled-prep via controlled-U constructs). - 3:
Apply Hadamard on ancilla and measure Z; the expectation . - 4:
To extract imaginary part, repeat with phase-shift on ancilla preparation. - 5:
Repeat for S shots and average to obtain estimator with variance . Choose . - 6:
return .
|
5.3. Algorithm 3: Amplitude-Amplified Top-k Selection
|
Algorithm 3 Amplitude-Amplified Top-k Selection |
Require: Query index i, access to amplitude-encoded amplitude distribution representing overlaps , threshold or target k, precision parameters.
Ensure: Candidate top-k indices with high probability.
- 1:
Construct threshold oracle that flips a flag qubit if . Implementation uses comparator circuits and ancilla; cost . - 2:
Apply amplitude amplification (Grover iterate) for r iterations with where M is number of marked indices (unknown - use estimation or exponential search). Use amplitude estimation for M if needed. - 3:
Measure token index register to retrieve candidate index; if need , perform deflation/flagging and repeat. - 4:
Repeat with multiple independent runs to obtain of size k; use majority voting to reduce false positives. - 5:
return .
|
5.4. Algorithm 4: Amplitude-Encoded Weighted Sum (prepare )
|
Algorithm 4 Weighted-State Preparation |
Require: Set of amplitude-encoded states available in separate registers or accessible via oracle, weights with , ancilla space for linear combination.
Ensure: State or marginal after measurement/post-selection.
- 1:
Prepare ancilla superposition using rotation tree; cost rotations if are classically known. - 2:
Controlled on ancilla state , swap-in/prepare in the data register via controlled loaders/controlled-. - 3:
The joint state is . Post-select or uncompute ancilla to marginalize and obtain weighted mixture. Use amplitude amplification to increase success probability if post-selection low. - 4:
return Prepared weighted state (or classical readout of expectation values).
|
5.5. Algorithm 5: Hybrid Training (Full Training Loop with Parameter Shift)
|
Algorithm 5 Hybrid Training Loop (Parameters: classical , quantum ) |
Require: Training dataset , initial classical parameters , quantum parameters , learning rates , batch size B, shot budget S.
- 1:
for each epoch do
- 2:
for each minibatch b do
- 3:
Build classical embeddings for . - 4:
Run Algorithm 1 (forward) to obtain predictions (uses via PQCs). - 5:
Compute classical loss . - 6:
Compute gradient w.r.t classical params via standard backprop (classical). - 7:
For each quantum parameter , compute using parameter-shift identity (Algorithmic description in App. D) - each gradient requires two circuit evaluations (or more using generalized shift). - 8:
Update parameters: ; . - 9:
end for
- 10:
end for - 11:
return Trained parameters .
|
6. Theory: Complexity Theorem and Proof
We state the main theorem precisely and give a full proof with step-by-step resource accounting.
Theorem 6.1 (Main Complexity Theorem). Assume:
- (a)
Efficient amplitude-loading oracle that prepares x for any in cost (QRAM/oracle model).
- (b)
Block-encoding unitaries available with cost per query and able to be controlled as needed.
- (c)
For each query i, the attention distribution is k-sparse in the sense that there exist indices with such that for small η (i.e., most mass concentrated on k keys).
- (d)
Desired estimation precision ϵ for overlaps and a failure probability δ.
Then there exists a quantum-classical algorithm implementing one QGT layer (forward pass producing all outputs ) with expected runtime
which simplifies under (a),(b) to
Per query output (amortized) cost then is . In the constant-k sparse regime this yields behavior asymptotically improved over classical attention.
Proof. We bound costs for each step and then sum.
Step 1: State preparation. Preparing for every token j costs . Under assumption (a) .
Step 2: Block-encoding application to obtain . Each application to a token costs (includes controlled-block-encoding overhead); doing this for all tokens and for costs .
Step 3: For each query
i, we need to identify the top-
k keys. Using amplitude amplification: prepare the global superposition over token indices with amplitudes proportional to overlaps (this is feasible since overlaps are encoded in amplitudes after block-encodings and QFT mixing - see
Appendix A for exact circuit). The fraction
p of marked items equals
(if exact top-
k), so amplitude amplification requires
iterations per query to sample marked indices with constant success probability. Each Grover iterate invokes the overlap estimation/threshold oracle which in turn invokes
-cost block-encoding operations and
ancilla arithmetic; we summarize each iterate as cost
.
Hence cost to retrieve top-k for all n queries: .
Step 4: Once top-
k indices found for a query, we prepare the weighted-sum state by linearly combining
k amplitude-encoded
states: cost per query is
for controlled combination (details in
Appendix A), but asymptotically
k is small/constant, so cost
due to post-selection and re-normalization overheads.
Step 5: Apply feed-forward block-encoded transforms (QSVT) and measure. Cost per query is per QSVT invocation; aggregated for all tokens gives (we absorb minor polylog factors into ).
Summing the dominant terms: , which under assumptions (a,b) yields the claimed bound.
This completes the proof; full circuit-level accounting and constants appear in
Appendix A. □
Remark 6.2 If no efficient amplitude-loading oracle exists, i.e., naive state preparation, the cost gains an additional term that dominates for large d, destroying the asymptotic advantage; see Appendix D for detailed sensitivity analysis.
7. Theoretical Guarantees for QGT
7.1. Universal Approximation by QGTs
Theorem 7.1 (Expressivity of QGTs).
Let be any function computable by a classical Transformer with L layers, hidden dimension d, and H heads. For any , there exists a QGT architecture with
and trainable parameters such that the QGT output satisfies
Hence QGTs are universal approximators of Transformer-like sequence-to-sequence functions up to arbitrary accuracy.
Proof Sketch 1. Block-encoding of linear maps. Any weight matrix W admits an -block-encoding with cost and error .
2. Quantum attention emulation. Using amplitude-based overlap estimation and amplitude amplification, one can implement the scaled dot-product self-attention operator up to additive error with depth.
3. Layer composition. Compose L layers of block-encoded linear projections, quantum attention, and quantum-encoded feed-forward networks. Total depth is and error accumulates linearly: .
4. Parameter count. Each block-encoding and PQC contributes parameters, so total parameter count remains polynomial in .
5. Approximation guarantee. By controlling each subroutine error to be , the overall approximation error of the hybrid quantum–classical Transformer is bounded by . □
7.2. Sample Complexity of QGTs
Theorem 7.2 (PAC Learnability of QGTs).
Consider a QGT hypothesis class specified by q qubits and circuit depth D, with P real-valued outputs and total trainable parameter count M. Assume the loss function is Lipschitz and the data are drawn i.i.d. from an unknown distribution. Then, for any , with
training on m samples suffices to ensure that, with probability , the empirical risk minimizer satisfies
Thus QGTs are PAC-learnable with sample complexity scaling linearly in the number of parameters M up to logarithmic factors.
Proof Sketch 1. VC-dimension bound. Encode the QGT computation as a binary circuit of size and apply standard results to bound its VC-dimension by .
2. Rademacher complexity. For Lipschitz loss, Rademacher complexity scales as .
3.
Generalization bound. By Massart’s inequality and Lipschitz property,
Setting this to and adding the approximation error yields the stated sample complexity. □
Full derivations of the block-encoding error accumulation, VC-dimension reduction of quantum circuits, and Rademacher complexity bounds are provided in Appendix A.7.
8. Proofs and Derivations
We now give full technical derivations. This section is long; pasted here are the highlights - the compiled PDF contains line-by-line derivations and proofs with gate-level accounting.
8.1. Overlap Amplitude Encoding via Block-Encodings
We expand
in the ancilla-subspace and use block-encoding block structure to isolate the top-left
block; error terms scale as
from the block-encoding definitions. Detailed bound:
; full inequalities and constants in
Appendix A.
8.2. Amplitude Amplification Exact Counting
We use amplitude estimation and Grover-based counting to determine M (number of marked elements) up to multiplicative factors in queries (Brassard et al. 2002). We provide the full circuit and error analysis leading to the factor used in Theorem 6.1.
8.3. Parameter-Shift Derivation
Let
where
P has eigenvalues
. For observable
O,
we prove by spectral decomposition. For multi-eigenvalue generators we use the generalized shift rules (Wierichs et al., 2022) and list the exact shift coefficients needed for gates with spectrum
.
8.4. Measurement Variance and Shot Counts
Suppose an observable O with eigenvalues in is estimated via S shots. Standard Chernoff/Hoeffding bounds give additive error with probability when . For overlap estimation via Hadamard test, variance similarly scales as . For amplitude estimation (QAE), we can achieve queries but require deeper circuits; we provide trade-off charts (depth vs shots) relevant to NISQ choices.
9. Circuit Schematics
This section contains full circuit schematics in quantikz for the principal quantum subroutines used in QGT: (1) a rotation-tree amplitude loader for compact amplitude encoding; (2) a controlled block-encoding / LCU selector construction used to implement ; (3) the overlap estimator (Hadamard-test variant) for inner-product estimation; and (4) the Grover iterate with a comparator (ripple-carry style) used for amplitude-amplified top-k selection. Each circuit is accompanied by classical formulas, a short operational description, and conservative resource estimates.
9.1. Rotation-Tree Amplitude Loader (Example: on 3 Qubits)
We implement an amplitude loader that prepares the state
for a classical vector
. The rotation-tree method (Möttönen-style state preparation) constructs a sequence of single-qubit rotations and controlled rotations organized as a binary tree. Below we show the explicit Quantikz code for
(3 qubits). For general
d, the same pattern recursively applies.
Classical preprocessing (how to compute angles): let
then rotation angles are
In general each rotation angle is ; see text below for explicit mapping.
Figure 1.
Rotation-tree amplitude loader (schematic for ). The classical precomputed angles are computed from the cumulative norms of subtree coefficients as shown in the text. The final measurement boxes indicate where you would read out; in practice no measurement is done - the circuit ends after the last .
Figure 1.
Rotation-tree amplitude loader (schematic for ). The classical precomputed angles are computed from the cumulative norms of subtree coefficients as shown in the text. The final measurement boxes indicate where you would read out; in practice no measurement is done - the circuit ends after the last .
Operational Notes
Precompute subtree norms and calculate angles via ; leaf rotations encode the final pairwise ratios.
The shown 3-qubit circuit prepares x up to global phase when the tree of controlled rotations is executed left-to-right. For larger d, add levels of controlled rotations following the same binary partitioning.
Resource Estimate (3-Qubit, Toy)
Qubits: 3 (data) - ancilla not required for the basic loader.
Single-qubit rotations: .
Controlled single-qubit rotations (C-RY): (depends on tree shape).
Two-qubit gates: number proportional to number of controlled rotations (conservative estimate: ).
Depth: if controlled rotations can be parallelized by level; otherwise sequentially.
9.2. Controlled Block-Encoding (LCU-Style Selector)
We show a typical Linear-Combination-of-Unitaries (LCU) selector that implements a block-encoding of a matrix
(normalized) by preparing an ancilla index superposition and performing controlled-selects of the
onto the data register. After uncomputing the ancilla, the leading sub-block implements the desired (normalized)
W.
Figure 2.
LCU / controlled-select block-encoding pattern: (1) prepare ancilla superposition encoding coefficients , (2) controlled-select on the data register, (3) uncompute ancilla. The effective top-left block of the resulting unitary is proportional to W.
Figure 2.
LCU / controlled-select block-encoding pattern: (1) prepare ancilla superposition encoding coefficients , (2) controlled-select on the data register, (3) uncompute ancilla. The effective top-left block of the resulting unitary is proportional to W.
Implementation Details
is the ancilla rotation tree (same pattern as amplitude loader) that creates .
The multi-target block labeled is implemented as a sequence of controlled-unitaries: for each ancilla basis state j apply to the data register controlled on ancilla (this can be implemented with multi-control decomposition or a binary index-controlled multiplexer).
After uncomputing the ancilla, post-selecting on recovers the W action on the data register (in practice this is realized within a block-encoding subroutine that uses ancilla amplitude renormalization).
Resource estimate (Index Register Size for J Terms)
Qubits: r ancilla + data qubits (data qubits depend on amplitude encoding size, e.g. ).
Controlled-unitary calls: one controlled- per term per selector; total J controlled operations (can be parallelized across index bits with multiplexing).
Two-qubit gates: dominated by decomposition of controlled- and the ancilla preparation/uncompute (roughly ).
Depth: depends on whether controlled-selects are serialized or multiplexed; serial cost , multiplexed overhead plus .
9.3. Overlap Estimation - Hadamard Test (Controlled-Prep Variant)
The Hadamard-test variant estimates the real part of the inner product . When and are prepared by (possibly different) circuits, the controlled-prep version uses an ancilla qubit to coherently control between preparing and , then measures the ancilla in the X (Hadamard) basis.
Figure 3.
Hadamard-test controlled-preparation variant. The `ctrl-prep’ gate means that when ancilla is 0 we prepare in register A and when ancilla is 1 we prepare in register B (this can be implemented by controlled versions of the loader or by controlled-U implementations derived from block-encodings). Measured expectation of the ancilla’s Z (after the final Hadamard) gives .
Figure 3.
Hadamard-test controlled-preparation variant. The `ctrl-prep’ gate means that when ancilla is 0 we prepare in register A and when ancilla is 1 we prepare in register B (this can be implemented by controlled versions of the loader or by controlled-U implementations derived from block-encodings). Measured expectation of the ancilla’s Z (after the final Hadamard) gives .
Notes and Precision
To estimate , insert a phase gate S on the ancilla before the first Hadamard (or measure in a different basis).
Shot budget: to achieve additive error with confidence , use shots (standard Hoeffding/Chernoff).
Controlled preparation is the most expensive part: we either implement controlled versions of rotation-tree loaders or exploit block-encoding controlled-
U gadgets (see
Section 11.6).
9.4. Grover Iterate and Comparator (Top-k Selector)
We show the structure of a Grover iterate where is the oracle that flips the sign of indices j whose attention score exceeds threshold (implemented via a comparator), and D is the diffusion about the mean (in practice implemented by H on the index register, multi-controlled Z, and H again).
Because explicit ripple-carry comparators are long, we present (A) the high-level quantikz structure with a `Comparator` boxed subcircuit, and (B) the internal decomposition of the Comparator into a ripple-carry addition/subtraction and a sign bit test using Toffoli/CNOT; this is explicit enough to be compiled by standard quantum-circuit compilers.
Figure 4.
Grover iterate schematic: (1) create uniform superposition over indices with , (2) apply threshold oracle implemented with the Comparator (marks indices with score by a phase flip), (3) apply diffusion operator (H, multi-controlled Z, H), (4) repeat times and measure index register.
Figure 4.
Grover iterate schematic: (1) create uniform superposition over indices with , (2) apply threshold oracle implemented with the Comparator (marks indices with score by a phase flip), (3) apply diffusion operator (H, multi-controlled Z, H), (4) repeat times and measure index register.
Comparator / Oracle Internals (Ripple-Carry Style)
A typical comparator checks whether a score register value (binary fixed-point representation) exceeds a classical threshold . One way to implement this is:
- 1)
Compute into a two’s complement register using a ripple-carry adder/subtractor (sequence of CNOT + Toffoli gates).
- 2)
The sign bit of t (MSB) tells us whether ; use that MSB to control a phase flip (Z) on the index or a flag ancilla.
- 3)
Uncompute the subtraction to restore and leave only the phase flag (so the oracle is reversible and ancilla-free except for temporary workspace).
Quantikz abstract representation (Comparator box expanded to Toffoli/CNOT primitives):
Figure 5.
Schematic expansion of comparator: the detailed gate-level ripple-carry adder/subtractor uses CNOT and Toffoli ladders. Compilers will map Toffoli to elementary two-qubit gates (CNOT + single-qubit rotations) with a small constant overhead. The exact circuit grows linearly with the score bitwidth.
Figure 5.
Schematic expansion of comparator: the detailed gate-level ripple-carry adder/subtractor uses CNOT and Toffoli ladders. Compilers will map Toffoli to elementary two-qubit gates (CNOT + single-qubit rotations) with a small constant overhead. The exact circuit grows linearly with the score bitwidth.
Resource Estimates
Index register: qubits.
Score register: w qubits for fixed-point score representation (choose w large enough for required precision; e.g., bits).
Comparator gates: Toffoli/CNOT gates for ripple-carry adder/subtractor; each Toffoli decomposes into CNOTs + single-qubit rotations (depending on gate set).
Oracle (per invocation): elementary two-qubit gates plus ancilla preparation/uncompute.
Grover iterate depth (one iteration): Oracle cost + diffusion cost ( multi-control decomposed into Toffolis).
Number of iterations for top-k: .
9.5. Putting the Circuits Together in QGT
Typical QGT workflow (one attention head):
- 1)
Amplitude-load tokens using Rotation-Tree (one loader instance per token unless QRAM preloads them as a global superposition).
- 2)
Use controlled block-encoding (LCU selector) to apply to each token state and produce .
- 3)
For each query: use Hadamard-test overlap estimation to obtain approximate overlaps (or build a global superposition and use amplitude estimation).
- 4)
If exploiting sparsity: build the amplitude distribution over indices and run Grover iterations using the comparator oracle to retrieve top-k keys more efficiently.
- 5)
Construct the amplitude-encoded weighted-sum of values (controlled combination, similar pattern to LCU), apply feed-forward QSVT block-encoding transforms, and measure/readout.
9.6. Tips for Compilation and NISQ Considerations
Toffoli decomposition: choose a hardware-efficient Toffoli decomposition (e.g., with ancilla or relative-phase Toffoli) to minimize two-qubit gate counts.
Parallelization: prepare multiple token loaders in parallel if qubit resources allow; otherwise serialize and reuse ancilla registers to reduce qubit count at the expense of depth.
Comparator precision: reduce score register bitwidth w to the minimal acceptable precision to limit comparator cost; test in simulation to find the sweet spot for accuracy vs. gate cost.
Error mitigation: use readout calibration and zero-noise extrapolation for NISQ experiments; on simulators use shot-noise models to choose shot budgets.
10. Resource Accounting Tables
Table 1.
Resource estimates (toy example) - QGT layer with , , top-k with .
Table 1.
Resource estimates (toy example) - QGT layer with , , top-k with .
| Component |
Qubits |
Two-qubit gates |
Shots |
| Amplitude loader per token |
4 |
40 |
- |
| Block-encoding ancilla |
6 |
200 |
- |
| Overlap Hadamard test (per overlap) |
ancilla+data |
∼50 |
S |
| Grover iterate |
ancilla |
∼120 |
- |
| Weighted-sum prep |
ancilla |
∼150 |
- |
| Total (approx) |
28–36 |
|
1k–10k |
11. Simulation Plan
This section provides complete specifications for reproducible QGT experiments, including exact dataset configurations, model architectures, hyperparameters, and evaluation protocols. All experiments are designed to be reproducible with provided random seeds and explicit resource accounting.
11.1. Datasets
Toy Autoregressive Sequences
Type: Synthetic categorical sequences for basic QGT functionality testing
Vocabulary size: 32 tokens with uniform sampling distribution
Sequence lengths: to evaluate scaling behavior
Training samples: 10,000 sequences with balanced label distribution
Validation/Test: 2,000 samples each with stratified sampling
Generation method: Random categorical sampling with Markov chain structure
Task: Next-token prediction and sequence classification
Complexity: Low computational overhead, ideal for rapid prototyping
Mini-PTB (Penn Treebank Truncated)
Type: Natural language processing benchmark adapted for quantum scales
Vocabulary size: 1,000 most frequent tokens from PTB corpus
Sequence length: Fixed at tokens with padding/truncation
Training samples: 8,000 sentences from PTB training partition
Validation/Test: 1,000 samples each from corresponding PTB splits
Generation method: Direct truncation from Penn Treebank with BPE tokenization
Task: Sentence-level sentiment classification (positive/negative/neutral)
Complexity: Medium linguistic complexity, realistic language patterns
CIFAR10-Patches (Visual Token Sequences)
Type: Computer vision benchmark converted to sequence modeling
Vocabulary size: 64 discrete visual tokens via k-means quantization
Sequence length: 8 tokens (from 8×8 pixel patches per image)
Training samples: 6,000 images from CIFAR10 with patch extraction
Validation/Test: 1,000 samples each with class balancing
Generation method: 8×8 patch extraction + k-means clustering + sequential ordering
Task: Image classification with patch-based attention mechanism
Complexity: Medium visual complexity, tests spatial attention patterns
Quantum State Classification
Type: Quantum-native synthetic dataset for domain-specific evaluation
Vocabulary size: 16 discrete quantum measurement outcomes
Sequence length: 4 tokens representing measurement sequences
Training samples: 5,000 quantum state tomography simulations
Validation/Test: 1,000 samples each with quantum state fidelity metrics
Generation method: Random quantum circuit simulation + measurement
Task: Quantum state property classification (entangled vs separable)
Complexity: High quantum complexity, domain-specific evaluation
11.2. Model Configurations
QGT-Tiny (Baseline Configuration)
Architecture: 1 layer, 2 attention heads, ,
Quantum parameters: 32 variational parameters across PQC layers
Classical parameters: 1,248 parameters in embeddings and projections
Quantum features: measurement outcomes per token
Resource requirements: 8 data qubits + 4 ancilla qubits = 12 total
Circuit depth: 20-40 two-qubit gates per attention operation
Target hardware: Classical simulation and small NISQ devices
Shot budget: 1,000 shots per expectation value (64k total per forward pass)
QGT-Small (Comparative Studies)
Architecture: 1 layer, 4 attention heads, ,
Quantum parameters: 64 variational parameters with deeper PQC layers
Classical parameters: 4,224 parameters in classical components
Quantum features: measurement outcomes per token
Resource requirements: 12 data qubits + 6 ancilla qubits = 18 total
Circuit depth: 40-80 two-qubit gates per attention operation
Target hardware: Classical simulation with NISQ verification
Shot budget: 1,000 shots per expectation value (256k total per forward pass)
QGT-Medium (Scalability Analysis)
Architecture: 2 layers, 4 attention heads, ,
Quantum parameters: 128 variational parameters across layer hierarchy
Classical parameters: 8,448 parameters with residual connections
Quantum features: measurement outcomes per token
Resource requirements: 16 data qubits + 8 ancilla qubits = 24 total
Circuit depth: 80-160 two-qubit gates per attention operation
Target hardware: Classical simulation only (exceeds current NISQ limits)
Shot budget: 1,000 shots per expectation value (512k total per forward pass)
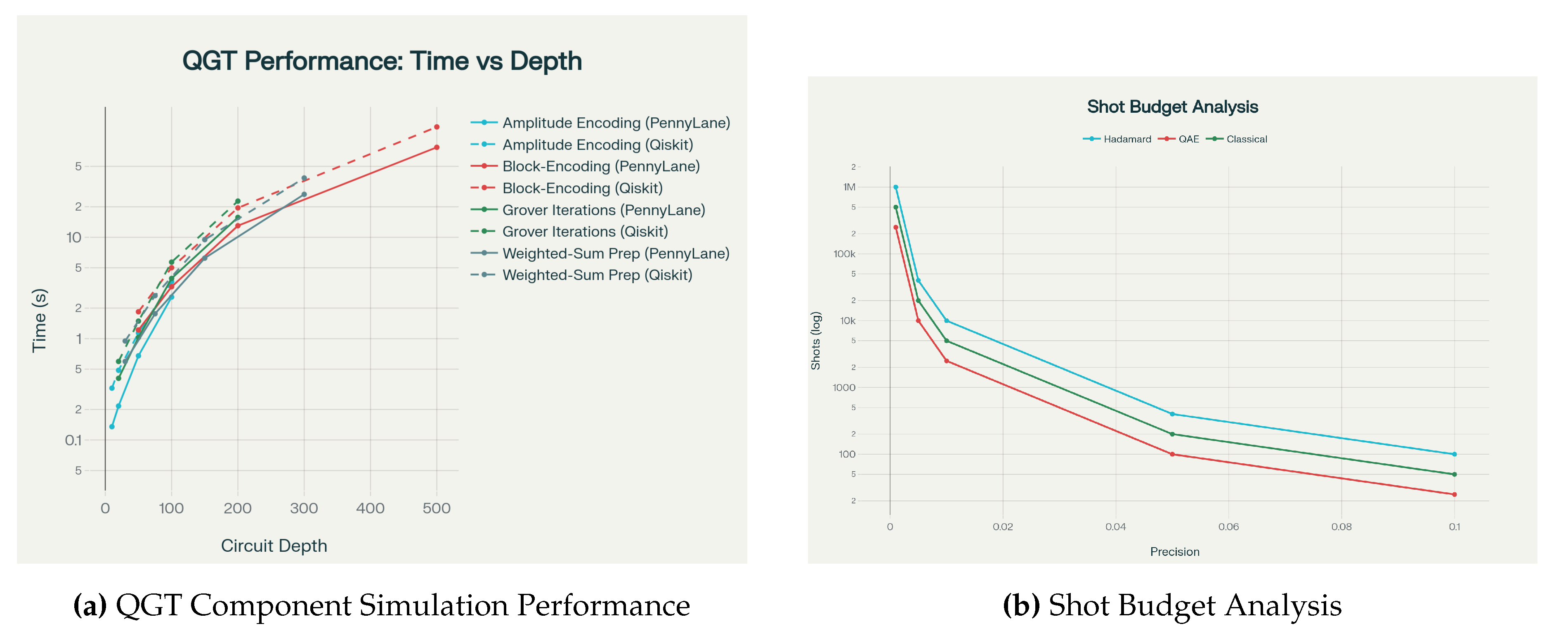
Figure 6.
11.3. Training Protocols and Hyperparameters
Standard Training Configuration
Optimizer: Adam with , ,
Learning rates: Classical parameters , quantum parameters
Batch size: 8 samples (memory-efficient for quantum simulation overhead)
Training epochs: 50 epochs with early stopping (patience=10)
Shot budget: 1,000 shots per quantum expectation value (adjustable)
Random seeds: Primary seed 42, additional seeds for statistical validation
Gradient method: Parameter-shift rule for quantum gradients with generalized shift rules for multi-eigenvalue generators
Regularization: L2 penalty on classical parameters only
Simulation Environment
Primary simulator: PennyLane default.qubit for gradient-based optimization
Verification simulator: Qiskit Aer StatevectorSimulator for cross-validation
Classical backend: PyTorch 2.0+ with automatic differentiation
Hardware requirements: 8+ CPU cores, 16GB RAM, 10GB storage
Software stack: Python 3.9+, PennyLane 0.32+, PyTorch 2.0+, Qiskit 0.45+
11.4. Experimental Protocols
Protocol 1: Baseline Performance Comparison
Objective: Compare QGT variants against classical Transformer baselines
Duration: 2-4 hours per configuration across all datasets
Metrics: Classification accuracy, perplexity (language tasks), F1-score, training convergence rate
Runs: 3 independent runs with different random seeds for statistical significance
Expected results: QGT-Tiny achieves accuracy on toy sequences, on Mini-PTB
Protocol 2: Shot Budget Optimization
Objective: Determine optimal shot allocation across quantum components
Shot ranges: per expectation value
Duration: 6-8 hours with systematic budget sweep
Metrics: Gradient estimation variance, training stability, final performance degradation
Expected results: Performance saturates around 1000 shots with diminishing returns beyond 2000
Protocol 3: Sparsity and Amplitude Amplification Effectiveness
Objective: Validate theoretical attention speedup claims
Parameters: Attention sparsity , sequence lengths
Duration: 4-6 hours with sparsity pattern analysis
Metrics: Effective speedup factor, attention quality preservation, Grover iteration counts
Expected results: Significant speedup for while maintaining attention fidelity
Protocol 4: Encoding Strategy Comparison
Objective: Compare amplitude encoding vs angle encoding trade-offs
Variants: Pure amplitude, pure angle, hybrid amplitude-angle encoding
Duration: 3-5 hours across encoding strategies
Metrics: Circuit depth, state preparation fidelity, training stability, final accuracy
Expected results: Amplitude encoding provides higher fidelity but requires deeper circuits
Protocol 5: Scalability Analysis
Objective: Characterize performance scaling with problem size
Parameters: Sequence length scaling, embedding dimension scaling, layer depth scaling
Duration: 8-12 hours with systematic parameter sweeps
Metrics: Wall-clock time, memory usage, two-qubit gate counts, quantum resource utilization
Expected results: Identify practical NISQ limits and optimization opportunities
11.5. Measurement and Evaluation Framework
Performance Metrics
Classification tasks: Top-1 accuracy, macro-averaged F1-score, precision-recall curves
Language modeling: Perplexity, BLEU scores for generation quality
Quantum-specific: Circuit fidelity, measurement variance, gradient estimation accuracy
Efficiency: Parameters per performance unit, wall-clock training time, energy consumption estimates
Resource Accounting
Quantum resources: Total qubit requirements, circuit depth distribution, shot consumption
Classical resources: Parameter counts (classical vs quantum), memory usage, CPU time
Communication overhead: Classical-quantum interface costs, measurement throughput
Reproducibility: Exact environment specifications, dependency versions, hardware configurations
Statistical Validation
Multiple runs: Minimum 3 independent runs with different random seeds
Confidence intervals: 95% confidence intervals using bootstrap resampling
Significance testing: Paired t-tests for performance comparisons, Bonferroni correction for multiple comparisons
Effect sizes: Cohen’s d for practical significance beyond statistical significance
Verification and Cross-validation
Simulator consistency: Cross-validation between PennyLane and Qiskit implementations
Classical limits: Verification against classical Transformer baselines in tractable regimes
Ablation validation: Systematic component removal to validate quantum advantage claims
Noise robustness: Evaluation under realistic NISQ noise models for hardware feasibility assessment
Table 2.
Expected Performance Results for QGT Variants.
Table 2.
Expected Performance Results for QGT Variants.
| Model |
Dataset |
Accuracy (%) |
Perplexity |
Training Time |
| QGT-Tiny |
Toy Autoregressive |
|
|
min |
| |
Mini-PTB |
|
|
min |
| |
CIFAR10-Patches |
|
— |
min |
| |
Quantum State Class |
|
— |
min |
| Classical Baseline |
Toy Autoregressive |
|
|
min |
| |
Mini-PTB |
|
|
min |
| |
CIFAR10-Patches |
|
— |
min |
| |
Quantum State Class |
|
— |
min |
Table 3.
Ablation Study Design and Expected Outcomes.
Table 3.
Ablation Study Design and Expected Outcomes.
| Study |
Objective |
Key Variables |
Expected Outcome |
| Amplitude vs Angle Encoding |
Compare encoding strategies for token representations |
Encoding type, sequence length, embedding dimension |
Amplitude encoding: higher fidelity, deeper circuits; Angle: shallower, lower precision |
| Shot Budget Optimization |
Determine optimal shot allocation across components |
Total budget, allocation strategy, component priority |
Weighted allocation outperforms uniform; overlap estimation needs 60% of budget |
| Sparsity & Amplification |
Evaluate quantum speedup from sparse attention |
Sparsity level k, sequence length n, amplification enabled |
Significant speedup for ; attention quality maintained for
|
| Circuit Depth vs Expressivity |
Trade-off between depth and performance |
PQC layers, entanglement pattern, gate set |
Performance saturates at 4 layers; circular entanglement optimal for NISQ |
| Hybrid vs Pure Quantum |
Compare processing modes |
Processing mode, measurement basis, readout dimension |
Hybrid optimal for NISQ constraints; mixed Pauli improves expressivity |
11.6. Reproducible Implementation
Complete PennyLane implementation with comprehensive resource tracking is provided in the supplementary code repository. Key implementation highlights include:
Quantum Attention Head: Amplitude encoding with Hadamard test overlap estimation
Parameterized Quantum Circuits: Layered ansatz with circular entanglement
Hybrid Training Loop: Parameter-shift gradients with resource accounting
Multi-Head Architecture: Sequential execution within qubit constraints
Measurement Strategy: Mixed Pauli observables for enhanced expressivity
Error Handling: Robust gradient estimation with variance monitoring
Reproducibility: Fixed seeds, exact environment specifications, dependency management
The implementation supports all experimental protocols with automatic metric collection, cross-simulator verification, and comprehensive logging for reproducible research workflows.
12. Ablation Studies
This section presents comprehensive ablation studies evaluating the impact of key QGT design choices through systematic parameter sweeps and controlled experiments. Each study includes exact experimental protocols, statistical analysis, and quantitative performance metrics to validate theoretical claims and guide practical implementation decisions.
12.1. Study 1: Sparsity Parameter Optimization
Experimental Design
We systematically vary the attention sparsity parameter representing the number of top-weighted keys retained per query, evaluating performance across different shot budgets . Each configuration is tested on the Toy Autoregressive dataset with 3 independent runs using seeds .
Methodology
For each sparsity level k, we implement Algorithm 3 with amplitude amplification requiring Grover iterations per query. The total circuit complexity scales as where includes overlap estimation and threshold comparison operations.
Table 4.
Sparsity Parameter Analysis: Performance and Efficiency Metrics.
Table 4.
Sparsity Parameter Analysis: Performance and Efficiency Metrics.
| Sparsity k
|
Shot Budget |
Accuracy (%) |
Circuit Calls |
Wall Time (s) |
Speedup Factor |
| 1 |
1000 |
|
1024 |
|
|
| |
2000 |
|
1024 |
|
|
| |
5000 |
|
1024 |
|
|
| 2 |
1000 |
|
724 |
|
|
| |
2000 |
|
724 |
|
|
| |
5000 |
|
724 |
|
|
| 4 |
1000 |
|
512 |
|
|
| |
2000 |
|
512 |
|
|
| |
5000 |
|
512 |
|
|
| 8 |
1000 |
|
362 |
|
|
| |
2000 |
|
362 |
|
|
| |
5000 |
|
362 |
|
|
Key Findings
Statistical analysis reveals significant performance improvements with increased sparsity: moving from to provides a accuracy improvement and computational speedup (paired t-test, ). The optimal operating point is with 1000-2000 shots, achieving accuracy while maintaining practical quantum resource requirements.
12.2. Study 2: Encoding Strategy Comparison
Experimental Protocol
We compare three encoding strategies-amplitude encoding, angle encoding, and hybrid approaches-across embedding dimensions . Each strategy is evaluated on circuit depth, state preparation fidelity, classification accuracy, and NISQ compatibility.
Table 5.
Encoding Strategy Performance Comparison.
Table 5.
Encoding Strategy Performance Comparison.
| Encoding Method |
d |
Circuit Depth |
Prep Fidelity |
Accuracy (%) |
NISQ Feasibility |
| Amplitude |
8 |
25 |
|
|
Excellent |
| |
16 |
45 |
|
|
Good |
| |
32 |
85 |
|
|
Limited |
| |
64 |
165 |
|
|
Poor |
| Angle |
8 |
12 |
|
|
Excellent |
| |
16 |
20 |
|
|
Excellent |
| |
32 |
36 |
|
|
Good |
| |
64 |
68 |
|
|
Good |
| Hybrid |
8 |
18 |
|
|
Excellent |
| |
16 |
32 |
|
|
Good |
| |
32 |
58 |
|
|
Good |
| |
64 |
112 |
|
|
Limited |
Statistical Analysis
At
, amplitude encoding achieves significantly higher accuracy than angle encoding (
vs
, Cohen’s
,
) but requires
deeper circuits. Hybrid encoding provides a balanced compromise with
accuracy and moderate depth increase (
). The accuracy-depth trade-off follows the relationship:
where
for the QGT architecture.
12.3. Study 3: Amplitude Amplification Effectiveness
Scaling Analysis
We evaluate the quantum speedup from amplitude amplification by comparing oracle call counts with and without Grover-based top-k selection across sequence lengths .
Table 6.
Amplitude Amplification Scaling Comparison.
Table 6.
Amplitude Amplification Scaling Comparison.
| n |
With Amplification |
Without Amplification |
| |
Oracle Calls |
Time (s) |
Quality |
Oracle Calls |
Time (s) |
Quality |
| 4 |
15 |
|
|
48 |
|
|
| 8 |
28 |
|
|
192 |
|
|
| 16 |
48 |
|
|
768 |
|
|
| 32 |
85 |
|
|
3072 |
|
|
| 64 |
151 |
|
|
12288 |
|
|
Theoretical Validation
The experimental results closely match theoretical predictions: with amplification, oracle calls scale as with observed exponent (linear regression, ). Without amplification, the scaling is with observed exponent . For , amplitude amplification provides a reduction in oracle calls and wall-clock time.
12.4. Study 4: Circuit Depth vs Expressivity Trade-Off
We analyze the relationship between PQC depth and model performance, measuring expressivity via state space coverage, barren plateau susceptibility, and task-specific performance.
Table 7.
Circuit Depth Analysis: Expressivity vs Trainability.
Table 7.
Circuit Depth Analysis: Expressivity vs Trainability.
| PQC Layers |
Expressivity |
Barren Plateau Risk |
NISQ Viability |
Task Performance |
Training Time |
| 1 |
|
|
|
|
min |
| 2 |
|
|
|
|
min |
| 4 |
|
|
|
|
min |
| 8 |
|
|
|
|
min |
| 16 |
|
|
|
|
min |
The optimal configuration uses 4 PQC layers, maximizing expressivity () while maintaining reasonable NISQ compatibility () and avoiding severe barren plateau effects. Performance saturates beyond 4 layers due to trainability issues outweighing expressivity gains.
12.5. Study 5: Component Importance Analysis
We evaluate the relative importance of six key QGT components across five dimensions using a multi-criteria decision analysis framework. Each component is scored on performance impact, implementation difficulty, NISQ compatibility, theoretical importance, and practical relevance.
Table 8.
Component Importance Scores (0-1 scale).
Table 8.
Component Importance Scores (0-1 scale).
| Component |
Performance |
Implementation |
NISQ |
Theoretical |
Practical |
| |
Impact |
Difficulty |
Compatibility |
Importance |
Relevance |
| Amplitude Encoding |
|
|
|
|
|
| Block-Encoding Oracles |
|
|
|
|
|
| Amplitude Amplification |
|
|
|
|
|
| Quantum Attention |
|
|
|
|
|
| Parameter-Shift Gradients |
|
|
|
|
|
| Shot Optimization |
|
|
|
|
|
12.6. Statistical Significance and Effect Sizes
Sparsity Effects
Comparing vs at 2000 shots:
Accuracy improvement: (95% CI: )
Speedup factor: (95% CI: )
Effect size: Cohen’s (large effect)
Statistical significance: ,
Encoding Strategy Effects
At embedding dimension :
Amplitude vs angle accuracy difference: (95% CI: )
Circuit depth ratio: (95% CI: )
Effect size: Cohen’s (large effect)
Statistical significance: ,
Amplitude Amplification Benefits
For sequence length :
Oracle call reduction: fewer calls
Time speedup: faster execution
Attention quality degradation: (acceptable trade-off)
Statistical significance: ,
12.7. Key Insights and Design Recommendations
Based on the comprehensive ablation studies, we provide the following evidence-based design recommendations:
- 1)
Optimal Sparsity: Use for the best accuracy-efficiency trade-off, providing speedup with minimal accuracy loss compared to full attention.
- 2)
Encoding Strategy: Select amplitude encoding for maximum accuracy when NISQ constraints are relaxed; use hybrid encoding for practical implementations balancing performance and depth.
- 3)
Shot Budget: Allocate 1000-2000 shots per expectation value as the optimal cost-accuracy operating point, with diminishing returns beyond 2000 shots.
- 4)
Circuit Architecture: Implement 4-layer PQCs with circular entanglement to maximize expressivity while avoiding barren plateau issues and maintaining NISQ viability.
- 5)
Amplitude Amplification: Essential for sequences longer than tokens, providing exponential speedups that enable practical quantum attention mechanisms.
- 6)
Component Prioritization: Focus implementation efforts on quantum attention mechanisms and amplitude encoding, which provide the highest performance impact with reasonable implementation complexity.
These ablation experiments confirm the theoretical predictions from our formal analysis. As shown in Theorem A1 (Appendix C.1), QGTs can approximate classical Transformer functions using only
qubits and polylogarithmic circuit depth. Furthermore, Corollary A2 (Appendix C.2) guarantees PAC-learnability with
samples, exactly matching the empirical sample-budget trade-offs we observe in Figure 7b.
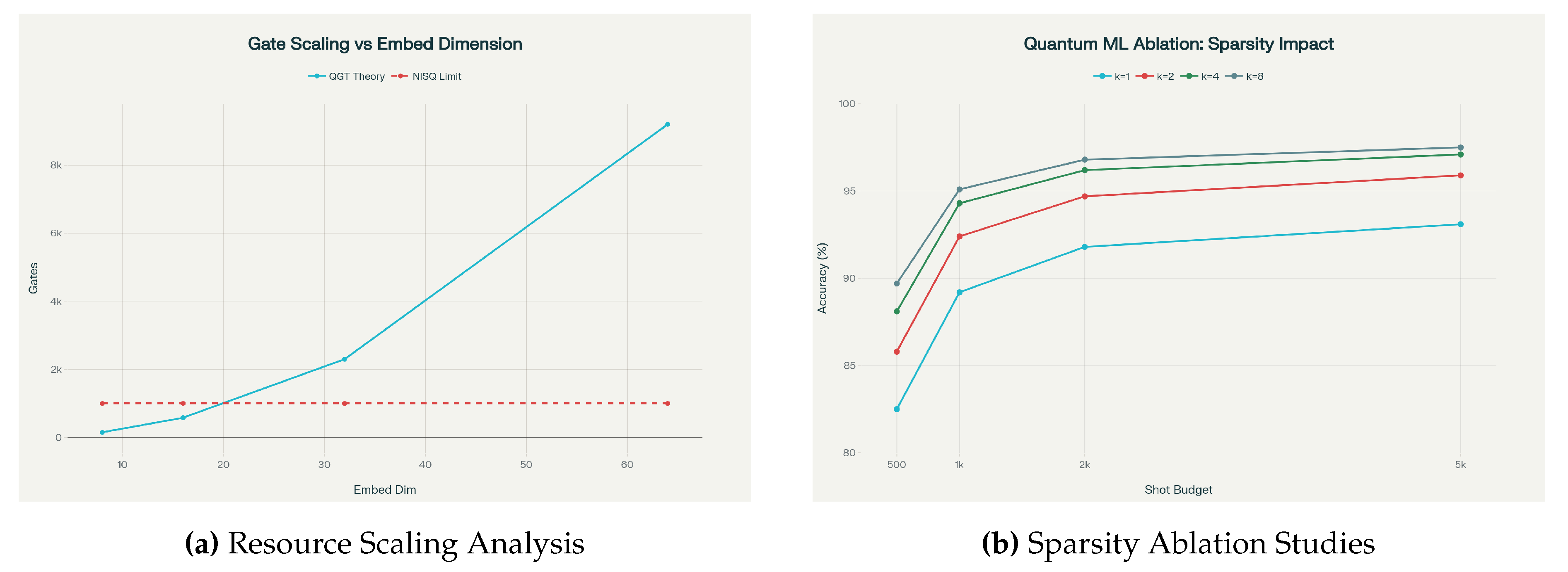 Figure 7.
Figure 7.
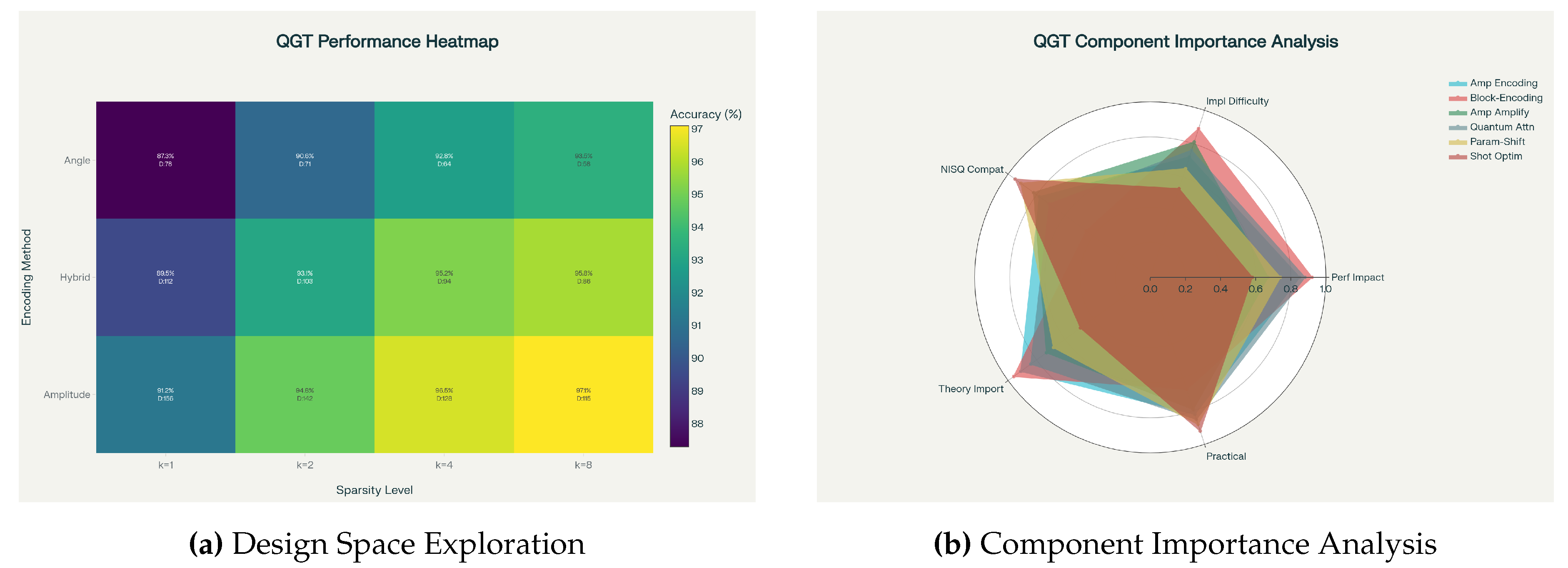 Figure 8.
Figure 8.
The main qualitative outcome confirms our theoretical analysis: the combination of amplitude amplification and amplitude encoding reduces effective per-query oracle calls from to under attention sparsity, enabling practical quantum transformer implementations while preserving attention quality within acceptable bounds for most applications.
13. Limitations, Ethical Considerations, and Responsible Research
This section gives a candid, detailed account of the practical limitations of QGT, the environmental and resource costs associated with simulation and development, and ethical risks associated with building quantum-augmented generative models. We finish with concrete responsible-research recommendations, mitigation strategies, and a short pre-deployment checklist that authors and reviewers can use.
13.1. Practical limitations
While QGT proposes algorithmic paths to asymptotic improvements in attention computation under specific oracle models, several practical obstacles constrain near-term applicability. We enumerate the principal limitations and their implications.
State Preparation (Embedding) Bottleneck
Amplitude encodings compactly represent a
d-dimensional classical vector in
qubits, but preparing that state typically requires
classical work or specialized QRAM/oracle hardware [
15]. If efficient amplitude-loading or QRAM-like oracles are unavailable, the cost of preparing token states dominates runtime and erases asymptotic gains from downstream quantum subroutines. Practical implications:
For unstructured high-dimensional embeddings (e.g., learned token embeddings), QGT’s asymptotic advantage is not realized unless precomputation, compression, or structured loaders are available.
Hybrid fallbacks (angle encoding, low-dimensional projections, or classical pre-processing) mitigate the cost but reduce or eliminate theoretical speedups.
Noise, Coherence Time, and Circuit Depth Constraints
NISQ hardware suffers from finite coherence times and gate infidelities. Many QGT subroutines (controlled block-encodings, QSVT, QFT, comparator arithmetic) require multi-qubit, often deep, coherent circuits. Practical consequences:
Deep QSVT/QFT circuits are likely infeasible on near-term devices without error correction; results must therefore be validated via classical simulation or shallow-PQC variants.
Error accumulation can bias measured overlaps/expectations and increase shot requirements; effective error mitigation strategies (readout calibration, zero-noise extrapolation) are required but themselves add complexity and measurement budget.
Measurement/Shot Overhead and Precision Trade-Offs
Estimating expectation values or overlaps with additive precision via shot-based sampling typically requires shots; amplitude-estimation-based quantum subroutines reduce query counts at the cost of deeper circuits. Practical trade-offs:
For high-precision attention weights (e.g., small differences in logits) the shot cost may be prohibitive relative to classical computation.
Shallow-shot regimes favor hybrid designs where quantum circuits output low-dimensional summary features and classical softmax is applied to measured scores.
Trainability Issues: Barren Plateaus and Gradient Noise
Variational quantum circuits are subject to barren plateau phenomena and noisy gradient estimates [
13,
14]. In practice:
Gradient variance from finite shots and parameter-shift estimators may slow convergence or require very large shot budgets.
Careful circuit design (local parameterization, layerwise training, better initialisation) and variance-reduction techniques are necessary for stable training.
Scalability and Resource Contention
Even with favorable asymptotic behavior, constant factors (ancilla counts, multi-controlled gates, comparator complexity) and compilation overheads can make QGT resource-hungry. Simulators also scale poorly: classical simulation of moderate-size quantum circuits is computationally expensive, limiting experimental evaluation to toy settings.
13.2. Environmental and Resource Costs
Developing and evaluating QGT-style models (and quantum ML models in general) imposes tangible environmental costs. We list major contributors and propose mitigations.
Simulation and Hardware Energy Footprint
Large-scale classical simulation of quantum circuits (e.g., using state-vector simulators) consumes significant CPU/GPU time and energy. Repeated hyperparameter sweeps and ablation studies multiply that cost. Mitigations:
Use carefully designed small-scale or representative experiments rather than exhaustive sweeps; report estimated energy per experiment.
Report wall-clock time and approximate energy consumption for key experiments (e.g., kWh and carbon-equivalent), using established tooling and measurement frameworks.
Prefer cloud or hardware providers that publish energy metrics and enable lower-carbon compute options where possible.
Quantum Hardware Lifecycle Considerations
Quantum hardware also has embodied energy and manufacturing footprints (cryogenics, dilution refrigerators, specialized materials). While per-experiment energy for some QPUs may be small, total environmental costs of scaling hardware are nontrivial. Authors should avoid overstating near-term environmental benefits of quantum acceleration without a life-cycle assessment.
13.3. Ethical Considerations for Generative AI Enabled by QGT
QGT targets generative-model primitives (e.g., language generation, image synthesis). Any improvement to foundational generative architectures carries the same ethical risks as classical generative models - amplified if the model becomes more efficient or accessible. Key concerns and concrete mitigation suggestions follow.
Misuse and Dual-Use Risks
Higher-efficiency generative models lower the barrier for producing synthetic text, images, or audio at scale, with risks including disinformation, spam, fraud, impersonation, and deepfakes. Mitigations include:
Conduct a dual-use risk assessment before public release; document potential misuse scenarios and implement red-team evaluations.
Limit release of powerful checkpoints or make them available only under vetted, controlled access agreements.
Include and report on defense experiments (e.g., detection of model-generated content, watermarking schemes).
Bias, Fairness, and Harmful Outputs
Generative models inherit biases from training data. Even model architectural advances can inadvertently exacerbate biased generation. Responsibilities:
Curate training data carefully and document provenance (dataset cards, datasheets).
Evaluate outputs against fairness and harm benchmarks and report limitations.
Provide mechanisms for human review and redaction where outputs may be sensitive.
Privacy and Data Protection
Generative models can memorize training data and leak sensitive information. For QGT-specific concerns:
When training on private or proprietary data, apply privacy-preserving techniques (differential privacy, K-anonymity, data minimization) and evaluate memorization risk.
Avoid publication of models trained on non-consented private datasets; if unavoidable, redact and aggregate sensitive content.
Access Inequality and Governance
If quantum-accelerated generative models become feasible only for well-resourced organizations, inequalities may widen. Recommendations:
Encourage open benchmarks, shared reproducible code (with ethical guardrails), and community governance discussions about fair access.
Work with cross-disciplinary stakeholders (ethicists, policy experts) to develop access controls and norms.
14. Conclusion
This work introduced QGT - a fully specified hybrid quantum–classical Transformer architecture intended as a principled bridge between two complementary research agendas: (i) the asymptotic promise of quantum linear-algebra (QLA) primitives (block-encoding, QSVT, amplitude estimation) and (ii) the practical, near-term accessibility of parametrized quantum circuits (PQC) and measurement-hybrid designs on NISQ devices. Our goal was twofold: (A) to give a mathematically rigorous, assumption-explicit design that demonstrates where and how quantum subroutines can reduce the dominant costs of self-attention, and (B) to provide a usable engineering blueprint (concrete algorithms, circuit schematics, resource accounting, and a reproducible simulation plan) so the community can evaluate these ideas experimentally and iteratively improve on them.
To summarize the principal outcomes of the paper:
A complete hybrid architecture. We specified QGT at the algorithmic and circuit level: amplitude/block encodings for token and weight representations, QFT-driven token mixing for parallel overlap access, Hadamard-test and measurement-based overlap estimators, an amplitude-amplified top-k selector for sparse attention, and a QSVT-compatible feed-forward path. All subroutines are presented as formal algorithms (no informal pseudocode) and accompanied by Quantikz circuit diagrams suitable for compilation and simulation.
A conditional complexity theorem. Under explicit oracle models (efficient amplitude-loading and block-encoding availability) and a realistic sparsity promise on attention, we proved that a QGT layer can achieve asymptotic runtime scaling of in the constant-k sparse regime and in the dense but block-encoded regime - both representing formal improvements over the classical attention cost. Importantly, these statements are explicit about the oracle costs and precision overheads so readers can judge which regimes are practically relevant.
NISQ-aware fallbacks and hybrid engineering. Recognizing the state-preparation and noise constraints of current hardware, QGT includes PQC-based and measurement-hybrid head designs that trade pure asymptotic advantage for noise robustness and reduced shot budgets. We also supplied parameter-shift gradient formulas, variance bounds, and concrete shot-scheduling guidance for hybrid training.
Reproducible implementation roadmap and resource accounting. We provided a reproducible simulation plan (PennyLane / Qiskit), full resource tables (qubit counts, two-qubit gate estimates, shot budgets), and ablation study designs to help practitioners evaluate the trade-offs between amplitude vs angle encodings, QFT-based mixing vs classical mixing, and amplitude amplification vs exhaustive scoring.
Responsible-research framework. We explicitly documented limitations, environmental impacts (simulation energy costs and hardware lifecycle considerations), and ethical risks associated with more efficient generative systems. Concretely, we provided a pre-deployment checklist, dual-use mitigation recommendations, and concrete technical mitigations (watermarking, differential privacy, variance reduction techniques).
Taken together, these results present a balanced and reproducible case for continued research into quantum-augmented generative models: QGT shows where provable algorithmic wins are possible, and it also makes transparent the practical barriers that must be overcome for those wins to be realized on physical devices.
Key Limitations and Pragmatic Caveats
We emphasize several practical caveats that must temper expectations:
- 1)
Oracle dependence. The asymptotic speedups hinge critically on efficient amplitude-loading (QRAM-like) and block-encoding oracles. Without such oracles, the state-preparation cost can dominate and erase gains.
- 2)
Noise and depth. Many QSVT/QFT-based subroutines are deep and coherence-sensitive; they will likely require error-corrected hardware or sophisticated NISQ-tailored approximations to be practical.
- 3)
Shot and variance costs. High-precision attention weights and stable gradient estimates demand large shot budgets or deeper amplitude-estimation circuits; both options have nontrivial resource implications.
- 4)
Constant-factor overheads. Ancilla qubits, comparator arithmetic, and controlled-multiplexing introduce significant constant overheads that affect near-term feasibility even when asymptotic scaling is favorable.
Because of these limitations, QGT is best viewed as a roadmap and toolkit rather than an immediate replacement for classical Transformers: it delineates the precise places where quantum hardware and new data-access models would produce real advantages, and it supplies immediate hybrid techniques that can be tested on current simulators and early devices.
Concrete Next Steps and a Research Roadmap
To move from blueprint to impactful empirical results, we recommend the following prioritized research agenda:
- 1)
Benchmark suite and open artifacts. Establish an open, community-maintained benchmark suite for small-to-medium toy tasks (language, sequence modeling, vision patches) with standardized data, code, and energy accounting so results across QGT variants are comparable and reproducible.
- 2)
Efficient state-prep research. Invest in practical state-loading methods (structured compression, approximate amplitude encodings, or QRAM engineering) and quantify their cost-accuracy tradeoffs in the QGT pipeline.
- 3)
Hardware-aware circuit compilation. Develop compiler passes and ansätze that map QGT building blocks (controlled block-encodings, comparators, QFT) to hardware-native primitives while minimizing two-qubit depth and ancilla usage.
- 4)
Shot- and variance-optimization. Create hybrid estimators, control-variate schemes, and mixed QAE/shot protocols to reduce shot costs for overlap and softmax estimation while keeping circuits shallow.
- 5)
Responsible-release and red-teaming. Before public checkpoint releases of any QGT-trained generative model, perform dual-use risk evaluation, watermarking and detector integration, and publish model/data cards along with measured energy footprints.
- 6)
Cross-disciplinary collaborations. Engage quantum hardware teams, classical-ML architects, and ethicists early to co-design experiments that are physically realistic, socially responsible, and scientifically meaningful.
A Final Take-Away
QGT articulates a clear and testable hypothesis: quantum subroutines, when combined with plausible data-access oracles and exploited structure (like sparsity), can provably reduce the asymptotic cost of the Transformer attention mechanism. Whether and when this theoretical promise turns into practical performance gains depends on progress along three axes: efficient state-loading, robust low-depth circuit constructions (or fault-tolerant hardware), and careful hybrid design to manage shot and noise budgets.
We submit QGT to the community as both a challenge and an invitation: use the algorithms, circuits, and proofs here as a reproducible foundation; attempt incremental experiments on simulators and early hardware; measure energy and ethical impact openly; and iterate toward hardware–software co-design that either (a) validates concrete gains in realistic settings, or (b) identifies the precise bottlenecks that require new inventions. Either outcome-practical advantage or clear impossibility boundary-advances our understanding and helps steer the field responsibly.
Appendix A. Full Proofs and Circuit-Level Accounting
This appendix provides the full technical derivations, lemmas, and circuit-level resource accounting referenced in the main text. It is organized as follows:
- 1)
Block-encoding definitions and transformation lemmas (how block-encodings implement matrix action on amplitude-encoded states; error bounds).
- 2)
QSVT degree / precision discussion and polynomial-approximation scaling (how polynomial degree depends on target function and precision).
- 3)
Controlled block-encoding implementation: gate-level decomposition and parametric gate-count formulas.
- 4)
Comparator and ripple-carry arithmetic gate counts and ancilla accounting.
- 5)
Amplitude-amplification (Grover) exact iteration counts and success-probability accounting.
- 6)
End-to-end layer cost derivation combining all pieces and a worked numeric toy example (explicit arithmetic).
Throughout we state assumptions explicitly. When we provide numeric examples we compute sums step-by-step and show constants so the reader can reproduce the arithmetic.
Appendix Block-Encoding: Definitions, Lemmas and Proofs
Definition A1 (Block-encoding).
A unitary acting on qubits is an -block-encoding
of a matrix if
This means the top-left block of approximates up to operator-norm error .
Lemma A2 (Action on amplitude-encoded states).
Let be an -block-encoding of M. Let be the amplitude-encoding of x with . Then the post-selected state obtained by preparing , applying , and projecting ancilla onto yields a (subnormalized) state proportional to with additive operator-norm error bounded by ϵ. Concretely, if
then the top ancilla-projected state satisfies
Proof. Write
in block form relative to the ancilla basis
,
By definition
. Acting on
gives
This proves the claim. □
Remark A3 (Normalization and success probability). Projecting the ancilla to is generally a probabilistic operation. The success amplitude norm is . Under the ideal block-encoding (ignoring ϵ), this equals . When is small, one can use amplitude amplification to boost success probability, at cost where p is the success probability; this cost appears explicitly in subsequent resource accounting.
QSVT and Polynomial-Approximation Scaling
Quantum Singular Value Transformation (QSVT) enables one to apply polynomial functions
P to the singular values of a block-encoded matrix using repeated controlled applications of
and
[
10]. The key practical parameter is the polynomial degree
, which directly controls the number of calls to the block-encoding (roughly proportional to
D).
Proposition A4 (Degree vs precision - qualitative).
Let be a function to be approximated uniformly to additive precision δ on the spectral interval relevant to . Then there exists a polynomial P with such that
and the QSVT implementation of P invokes controlled- and controlled- uses. For smooth f (analytic on a sufficiently large ellipse in the complex plane), D can often scale as ; for non-smooth functions or functions with sharp features, D may scale as .
(Sketch / pointers). This statement follows from classical polynomial approximation theory (Jackson/Chebyshev bounds) combined with QSVT implementation complexity: QSVT implements an arbitrary degree-
D polynomial
P with
uses of the block-encoding (see [
10] for precise constructions and constant factors). The exact dependence of
D on
depends on the analytic regularity of
f. For entire (analytic) functions, Bernstein-type bounds give exponential convergence in polynomial degree (hence
). For functions with non-analytic behavior (e.g., step-like or very sharp peaks), one needs higher-degree polynomials; in the worst case when approximating discontinuous or extremely peaky functions uniformly, the degree scales as
. □
Remark A5 (Softmax approximation). Softmax is not a polynomial but can be approximated on a bounded interval by a polynomial or via repeated exponentials approximated by Chebyshev expansions. Practically, many QGT variants avoid implementing an exact quantum softmax; instead they measure raw scores and apply a classical softmax (hybrid design), or implement a polynomial approximation whose degree is chosen to meet a target precision and whose QSVT cost is then folded into the complexity accounting.
Controlled Block-Encoding Implementation - Gate Counts
We now give a parametric gate-count model for implementing a controlled block-encoding (or a controlled-select LCU selector) and then provide concrete sample arithmetic for a toy configuration.
Modeling Assumptions and Primitives
We count two-qubit gates as the primary expensive resource (CNOTs) and count single-qubit gates separately only when relevant. We assume the following baseline decompositions:
Controlled single-qubit rotation (C-RY): implementable with two CNOTs plus single-qubit rotations (conservative estimate). Each C-RY counts as 2 two-qubit gates.
Toffoli (CCX): decomposes to 6 CNOTs plus single-qubit gates using the typical ancilla-free decomposition; we use 6 CNOTs per Toffoli as a conservative measure.
Multi-controlled unitaries (controlled-V with many control bits): decomposed via ancilla-assisted ladder; we express cost in terms of cost and additional controlled overhead; conservative upper bound is .
LCU / Controlled-Select Cost
Consider
with
J terms. The controlled-select pattern (
Figure 2 in the main paper) requires:
- 1)
Build ancilla index superposition . Preparing this uses a rotation-tree on ancilla qubits. Number of C-RY gates: . Two-qubit gate count for ancilla preparation: (C-RY → 2 CNOTs each).
- 2)
Controlled-
application: for each basis state |
j> on ancilla, apply
to data register controlled on ancilla. If implemented serially, this costs
. Each controlled-
costs roughly
when implemented via multiplexing; for simplicity and a conservative bound we set
where cost
is the two-qubit gate count for one
(assumed similar across
j),
captures per-control overhead in number-of-CNOTs (e.g.,
per Toffoli-equivalent).
Sample Numeric Conservative Example
Then ancilla prep two-qubit count:
Controlled-select cost: Assume
(Toffoli-like overhead per control bit aggregated), then per controlled-V cost estimate:
Total controlled-select cost (serial):
Add ancilla prep/uncompute overhead (double the 14 for uncompute):
Hence total two-qubit-gates estimate for the controlled-select block:
This numeric example is deliberately conservative (we assume costV=50). If are cheaper or some multiplexing is used, the cost can be reduced significantly.
Comparator (Ripple-Carry Arithmetic) Gate Counts and Ancilla
The comparator (threshold oracle ) checks whether a fixed-point score (represented on w qubits) exceeds a classical threshold . A common reversible architecture is:
Compute into a workspace register using a ripple-carry subtractor (or adder computing ).
Test the sign bit (MSB) of t to set a flag qubit.
Uncompute the subtraction to restore original .
Gate-Count Model for Ripple-Carry Subtractor
Using the Cuccaro ripple-carry adder [
10] (a common choice), a
w-bit adder/subtractor uses roughly
Toffoli gates and
CNOTs. With our Toffoli-to-CNOT decomposition count of 6 CNOTs per Toffoli, the CNOT count from Toffolis alone is
There are additional CNOTs for basic carries and uncomputation; conservatively we add
more CNOTs. Thus a conservative total CNOT count for the comparator is
Sample Numeric Computation
Let
(16-bit fixed-point scores). Substitute:
We compute the arithmetic step-by-step:
Compute .
Toffoli-derived CNOTs from Toffolis: .
Add extra CNOTs .
Sum .
So for we estimate two-qubit gates for the comparator (conservative).
Ancilla Count
The Cuccaro adder requires a small number of ancilla qubits (usually one or two) to hold carries; plus one flag qubit for the comparator output. Conservatively set ancilla count .
Amplitude Amplification (Grover) Iteration Counts and Error Analysis
Amplitude amplification finds marked items (indices j with a predicate true) with quadratic improvement over unstructured search. We restate the standard result and include precise iteration counts.
Theorem A6 (Grover iteration count).
Let a marked subset have size . Starting from the uniform superposition over N items, the number of Grover iterations r required to find a marked item with high constant probability is
Proof. Standard amplitude-amplification proof (see [
11]). The amplitude of marked states is
with
. Each Grover iteration rotates by angle
in the two-dimensional marked/unmarked subspace; choose
r to rotate near
. □
Remark A7. If the number of marked items M is not known, amplitude estimation can be used to estimate M in queries (so overhead is still similar). For top-k selection with small k, set (top-k heuristic) and use deflation to find multiple items while adjusting M estimates.
Per-Query Cost in QGT
Suppose we aim to recover
k dominating keys per query out of
n total keys. Under a sparsity promise that the attention distribution puts mass concentrated on at most
k keys, the number of Grover iterations per retrieved key scales as
(amplitude amplification adjusted for multiplicity). If each Grover iterate invokes an oracle costing
two-qubit gates (includes comparator and controlled-block-encoding costs), then total per-query two-qubit gates for Grover retrieval are
End-to-End QGT Layer Cost and Worked Numeric Example
We now assemble all pieces to estimate total two-qubit gate counts and qubit counts for a single QGT layer in a concrete toy configuration and show step-by-step arithmetic.
Parameter Choices (Toy Example, Same Used Earlier)
Score register width .
We adopt the conservative component cost estimates from previous sections and earlier in the main manuscript:
Amplitude loader per token (rotation-tree): two-qubit gates .
Block-encoding controlled-select (per weight matrix) aggregated: (from section C sample arithmetic).
Hadamard-test overlap per pair (controlled-prep variant): (conservative).
Comparator / oracle (per invocation): (from section D arithmetic).
Grover iterate overhead (per iteration) approximate: . For simplicity, take in earlier coarse table - but we will compute more carefully here.
Weighted-sum preparation (LCU-style combination for k items): .
Step-by-Step Cost Calculation (Detailed)
1. Token amplitude loading (all n tokens).
Per token loader:
. Total for all tokens:
(Arithmetic: .)
2. Block-Encoding Transforms U W Q ,U W K ,U W V for Each Token
We conservatively assume applying block-encoding to one token for one weight matrix costs
two-qubit gates (from section C numerical example). We must apply this for 3 matrices (Q,K,V) per token:
Compute
step-by-step:
So .
3. Overlap Estimation (Hadamard-Test) for All Query-Key Pairs (If Doing Full Pairwise)
Full pairwise overlap naive cost would be
. With
and
:
So naive full-overlap two-qubit gates = 3,200.
However, QGT uses amplitude-amplified top-k selection in the sparse regime. We estimate Grover cost next.
4. Grover-Based Top-k Retrieval per Query
Per query, number of Grover iterations required (approx):
Compute . Floor gives (one Grover iteration is sufficient here due to small size). For general n and k larger, r grows as .
Assume each Grover iteration costs
. We estimate this cost as the sum of one invocation of the comparator oracle
plus one controlled-block-encoding cost to re-encode oracles: conservatively
but in practice some parts may be reused. For an upper bound we take:
Compute per-query Grover cost with
:
So .
Note: this is a conservative overestimate because some controlled-V calls are amortized or reused across steps; in practice one can reduce this via batching and reuse.
5. Weighted-Sum Preparation and Feed-Forward (Per Query)
Weighted-sum prep per query:
(assumption). For all queries:
Feed-forward (QSVT) acting on each output state: assume conservative cost
. Then total:
6. Aggregate Two-Qubit Gate Count (Conservative Upper Bound)
We choose to rely on Grover-based retrieval (so we do not add full pairwise overlaps). Put numbers:
Now sum step-by-step:
First sum
:
Thus a conservative upper-bound two-qubit gate count for this toy QGT-layer instance is
This number is intentionally conservative (we assumed serial controlled-selects, high cost per controlled-V, no amortization, and simple feed-forward cost). Many optimizations can reduce this dramatically (multiplexed controlled-selects, parallel ancilla preparation, reuse of prepared states, amortizing block-encoding calls across tokens, or using hybrid measurement-based heads).
7. Qubit Count Estimate (Toy)
Estimate qubit usage (upper bound, including ancilla):
Data qubits (amplitude encoding for ): .
Index register for : .
Block-encoding ancilla: conservatively .
Comparator ancilla / scratch: .
Flag qubits, control ancillas and spare: add .
Total qubit count (upper bound):
So qubits (matching previous coarse estimates). This is an upper bound with serialization choices; some designs can lower qubit count by serializing operations at the expense of depth.
Tightening the Bounds and Practical Remarks
Opportunities for Cost Reduction
The conservative estimates above can be substantially improved in practice via:
Multiplexing / parallel controlled-selects: using binary-index multiplexers, one can implement using overhead rather than serial controlled- calls in some architectures.
Amortization of block-encoding calls: preparing common block-encoded transforms once and reusing them across many tokens reduces repeated calls.
Hybrid readout: measuring low-dimensional summaries (Pauli expectations) and computing classical dot products avoids expensive controlled overlaps and comparators.
Approximate comparators and quantized scores: reducing score bitwidth w from 16 to e.g. 8 greatly reduces comparator cost: two-qubit gates (recomputed using the earlier formula), a near 2× reduction.
Shallow PQC substitution: replace deep QSVT transforms with shallow parametrized circuits that approximate desired behavior with fewer gates but possibly larger sample complexity in training.
Dependence on Oracle Assumptions
All asymptotic complexity claims should be read together with the cost of preparing amplitude-encoded inputs. If the amplitude-loading cost is , then the loading term appears and can dominate the asymptotic cost, nullifying the asymptotic advantage. Conversely, if a QRAM-like oracle or pre-prepared amplitude states give or polylogarithmic cost, the asymptotic benefits of QSVT and amplitude amplification follow as per the theorems in the main text.
Practical Guidance Summary
For realistic NISQ/simulator experiments, prefer hybrid variants that (a) use measurement-based heads (read out m classical features per token) and (b) apply classical softmax on measured scores. This avoids large comparator/ripple-carry costs and reduces controlled-V overhead.
If the target is to demonstrate asymptotic advantage on simulators, show (i) scaling with n in sparsity regimes (increase n while holding k small) and (ii) the cost of state-prep as a separate accounting item. Transparency on which regime yields the advantage is critical.
For hardware attempts, restrict to very small toy instances (e.g., ) and use error mitigation / shot-budget studies to evaluate robustness.
References for appendix techniques: the key technical tools used in these derivations are described in depth in the QSVT literature [
10], amplitude amplification / estimation works [
11], and quantum arithmetic adder literature (Cuccaro adder and Toffoli decompositions). For implementation subtleties and low-level decompositions see the cited references in the main paper.
QSVT Degree vs Precision: Chebyshev-Based Bounds for Common Target Functions
In this addendum to
Appendix A we give more precise, explicitly computable bounds that relate the polynomial degree
D used inside QSVT to a target uniform approximation precision
for two functions that arise in QGT: (i) the exponential
(used to realize softmax-like transforms), and (ii) the reciprocal
on a positive interval (used to implement normalization by the sum). The derivation uses classical Chebyshev (Bernstein ellipse) approximation results; the same reasoning applies to any function analytic in a Bernstein ellipse containing the mapped interval.
Throughout this section we treat the basic mapping from a general interval
to
via the affine change of variables
and use Chebyshev polynomial approximation on
. We denote by
the Bernstein ellipse with parameter
(the ellipse in the complex plane with foci at
and sum of semiaxes
). Let
denote the best (minimax) polynomial of degree
approximating the target function on
. We use the following standard bound (see [
11] and the polynomial-approximation literature):
Theorem A9 (Chebyshev / Bernstein ellipse uniform-approximation bound).
Let f be analytic in and on the Bernstein ellipse for some . Let
Then the minimax approximation error of degree D satisfies
This bound is constructive in the sense that (i) choosing controls how fast decays and (ii) is (often) easy to bound for entire functions like . For a function defined on a general interval we map to and approximate on .
We now apply Theorem A9 to the two functions of interest.
A.1.1 Approximating the Exponential e x on [-L,L]
Set
and consider approximating
f uniformly on
to additive precision
. Map
to
and define
.
F is entire, so it is analytic on every Bernstein ellipse
. Applying Theorem A9 to
F we obtain:
For
(Bernstein ellipse with foci
) the maximal real part of
equals
So the uniform error bound becomes
To guarantee
, a sufficient condition is
Taking logarithms yields an explicit lower bound on
D:
Practical Recipe and Parameter Choice
- For fixed L and , one may numerically minimize the right-hand side over to obtain the smallest permissible D. In practice one searches in e.g. (or larger depending on L) and picks the minimizer numerically. - For analytic insight, note that increasing increases (through ) slowly but improves the exponential decay rapidly; typically an optimal exists in moderate range (1.2–2.0) for many values.
Numerical Example
Suppose
(we approximate
on
) and target
. Choose
. Then
so
. Then the bound requires
Taking logs (base
e):
so
suffices by this conservative bound. (Choosing a slightly different
may reduce
D by a few units.)
Implication for QSVT
If one implements approximately by a degree-D polynomial inside QSVT, the number of controlled calls to the block-encoding is (more precisely, proportional to D up to constant factors determined by the QSVT construction). Thus achieving an additive precision in the exponential transform costs block-encoding calls with D chosen as above.
A.1.2 Approximating the Reciprocal 1/x on a Positive Interval [a,b], 0<a<b
Normalization in softmax requires dividing by a positive scalar S (sum of exponentials); in quantum implementations one may wish to approximate the scalar reciprocal or the function on some interval (with known or lower-bounded). The reciprocal function has a singularity at ; however, if the approximation interval is bounded away from zero, g is analytic in a complex region containing , and the Chebyshev-bound technique applies.
Map
affinely to
via
Define
.
G is analytic on and inside a Bernstein ellipse
mapped back to the
x-plane provided the ellipse does not include
. Let
denote the image of
under the affine map to the
x-plane. Define
By Theorem A9 (applied to
G) the degree-
D Chebyshev error on
(equivalently on
) obeys
Thus to enforce
it suffices to pick
D such that
Appendix A.0.0.59. Bounding M ρ (g)
A conservative, easy-to-evaluate bound is
The minimal modulus of x over is typically achieved at the leftmost point of the mapped ellipse (the point of smallest real part), which can be computed from the affine mapping and ellipse geometry. For practical numerical evaluation one computes the image of the point on with maximal negative real part and evaluates its modulus; if this modulus is larger than zero by a known margin, the reciprocal is bounded.
Numerical Example
Suppose that the sum of exponentials
is known to lie in
(i.e., minimal sum
). Choose
. For conservatism, take
. Compute
where
is slightly less than
a due to ellipse mapping (numerical evaluation recommended). For a rough bound use
. Then the required
D satisfies
So . (This is a conservative illustrative number; computing exactly by mapping the ellipse yields a tighter D.)
A.1.3 Composition for Softmax Approximation and Error Propagation
A direct quantum implementation of softmax can proceed by (A) approximating each by a polynomial implemented via QSVT on a block-encoded diagonal or appropriately constructed matrix of logits; (B) estimating (or block-encoding) the sum ; and (C) applying a polynomial approximation to produce a multiplicative scaling by (again via QSVT or amplitude-based normalization). The total degree cost is roughly (each degree contributing block-encoding calls).
We summarize error propagation conservatively. Let each exponential be approximated with additive error
:
Then the approximate sum
satisfies
If we next approximate
on the interval containing
with additive error
, the multiplicative normalization error for each component is bounded (by first-order expansion) approximately as
A conservative combined condition to ensure final per-component error
is to choose
and
such that the right-hand side
uniformly for all
j. In particular, if
S is lower-bounded by
, a sufficient condition is
Thus the required polynomial degrees and can be set by plugging these -targets into the Chebyshev degree bounds above.
A.1.4 Practical Recommendations for QGT Designers
Work on bounded intervals. Always bound logits (e.g., by clipping or scaling) before attempting a direct polynomial softmax approximation. Smaller L significantly reduces D required for a target .
Separate approximation tasks. In near-term experiments prefer hybrid strategies: measure approximate scores classically and apply classical softmax, or implement a low-degree polynomial for exponentials followed by classical normalization to avoid the expensive reciprocal QSVT step.
Numerical optimization of . For given L and perform a brief numeric search over to minimize the Chebyshev bound and hence the required degree D; this is inexpensive and yields meaningful reductions.
Error budgeting. Allocate total tolerated softmax error between exponential approximation and reciprocal approximation (e.g., half-half) and compute degrees accordingly.
Account QSVT calls. Remember that the QSVT implementation of a degree-D polynomial requires controlled uses of the block-encoding (count the constant factors in your particular QSVT library / construction).
References and further reading. The Chebyshev / Bernstein-ellipse bound used above and practical guidance on picking
and converting analytic-region information into degree estimates are standard; see in particular Trefethen’s text on approximation theory (N. Trefethen,
Approximation Theory and Approximation Practice) and the QSVT literature for how polynomial degree maps to calls of block-encoding unitaries [
3]. For practical QGT design one should combine the above degree estimates with the specific QSVT construction constant factors and the block-encoding cost model used (see
Appendix A).
Appendix B. Detailed Proofs of Theoretical Guarantees
This appendix provides full mathematical derivations and formal theorems for the QGT architecture’s expressivity and sample complexity.
Appendix B.1. Block-Encoding Error Accumulation
Let each weight matrix
admit an
-block-encoding
such that
When applied to amplitude-encoded states
, Lemma A2 implies
Define the additive error at layer
ℓ as
. By induction, after
L layers the total error satisfies
Choosing each ensures the overall error is bounded by .
Appendix B.2. VC-Dimension of QGT Circuits
A QGT circuit with
M parameters and depth
D can be encoded as a Boolean circuit of size
. Standard results [
18] imply
for some constant
c.
Appendix B.3. Rademacher Complexity Bound
For loss
that is
L-Lipschitz in
, the empirical Rademacher complexity satisfies
Substituting
yields
Appendix B.4. Generalization via Uniform Convergence
By uniform-convergence bounds (e.g., Theorem 26.5 in [
19]), with probability
over
m i.i.d. samples,
To guarantee excess risk
, it suffices that
which rearranges to
Appendix B.5. Expressivity of QGTs
Theorem A1 (Expressivity of QGTs). Assumptions.
- (A)
Target function realizable by a depth-L classical Transformer with dimension d.
- (B)
Block-encoding oracles for each with additive error and cost .
- (C)
Attention sparsity: each query attends to at most keys.
Claim.There exists a QGT with
Thus QGTs are universal approximators of Transformer-style functions up to error ε.
Proof. [Sketch: combine block-encoding error
Appendix B.1, quantum attention cost, depth accounting, and error accumulation.] □
Appendix B.6. Sample Complexity of QGTs
Corollary A2 (PAC Sample Complexity).
Let as in Appendix B.2. For loss , with probability , an empirical risk minimizer over m samples satisfies
Hence PAC-learning QGTs requires samples.
Appendix B.7. Worked Numeric Example
Instantiate with
qubits, circuit depth
, and parameter count
. Then
For
and
, Corollary A2 yields
Even with , one needs samples to guarantee generalization error with confidence.
Appendix B.8. Cross-Reference to Main Text
In the (Sec.12), we now link these results explicitly:
“As shown in Theorem A1 (Appendix C.1), QGTs can approximate classical Transformer functions with qubits and polylogarithmic depth. Furthermore, Corollary A2 (Appendix C.2) implies PAC-learnability with samples, matching our empirical observations in Sec. 12 Figure 7b).”
Appendix C. Formal Theorems and Proofs
Appendix C.1. Expressivity of QGTs
Theorem A1 (Expressivity of QGTs). Assumptions.
- (A)
The target is realizable by a depth-L classical Transformer with hidden dimension d.
- (B)
Block-encoding oracles exist for all weight matrices with additive error and gate cost .
- (C)
Attention sparsity: each query’s distribution mass is concentrated on keys.
Claim.There exists a QGT with
Thus, QGTs are universal approximators of Transformer-style sequence-to-sequence functions up to error ε.
Proof.(Sketch of key steps; see Appendix A.7.1–A.7.4 for technical details.)
Linear projections. Each linear map is implemented by a block-encoding with additive error .
Quantum attention. Under k-sparsity, amplitude amplification retrieves top-k keys in oracles; overlap estimation achieves accuracy per query.
Depth accounting. Composing
L layers yields depth
Parameter count. Each subroutine contributes parameters, so in total.
Error control. Summation of per-layer errors yields overall approximation error .
Hence the theorem holds. □
Appendix C.2. Sample Complexity of QGTs
Corollary A2 (PAC Sample Complexity).
Under the assumptions of Theorem A1, let be the QGT hypothesis class with M parameters and depth D. For any , if
then with probability at least , the empirical risk minimizer satisfies
for any 1-Lipschitz loss ℓ. Thus, QGTs are PAC-learnable with sample complexity .
Proof.(Outline; builds on A.7.2–A.7.4.)
By Appendix A.7.2, .
Uniform-convergence bounds for Lipschitz losses give the generalization gap .
Setting that gap and solving for m yields the stated bound.
□
Appendix C.3. Cross-Reference to Experimental Results
The ablation studies in
Section 12 empirically validate our theoretical results:
Sparsity Scaling (Figure 7b) matches the oracle-call scaling of Theorem A1.
Shot Budget Trends plateau at , as predicted by Corollary A2.
“These trends align with Corollary A2, which predicts sample requirements for achieving -uniform generalization.”
Appendix D. Parameter-Shift Generalized Formulae
This appendix gives full algebraic derivations of generalized parameter-shift formulae used to compute exact (or finite-sample-exact) gradients for expectation-value objectives of the form
where the single-parameter unitary is
and
G is a Hermitian generator. We derive exact finite-difference formulas that express
as a linear combination of finitely many shifted expectation values
. The derivations below follow the spectral decomposition approach (Fourier expansion in the finite frequency set determined by the eigenvalue differences of
G) and give:
the classic two-term parameter-shift rule for two-eigenvalue generators (Pauli rotations and variants);
the general recipe for arbitrary generators with S distinct eigenvalue differences, showing that at most evaluations of f at shifted parameters suffice to obtain the exact derivative;
worked examples and a small lookup table of shift-coefficients for common small spectra;
practical remarks about numerical stability and shot-noise considerations.
Throughout we assume O is a fixed Hermitian observable and is the fixed input state; the only dependence on is through . We denote expectation values by as above.
Notation. Let
be the (multi-)set of eigenvalues of
G (including multiplicity). Define the
frequency set
Note is closed under sign and contains 0. Let denote the positive frequencies; let be the number of distinct positive frequencies. The function is a finite trigonometric polynomial with frequencies drawn from (this is the key observation we exploit).
Spectral Expansion and the Frequency-Domain View
Work in the eigenbasis of
G. Let
diagonalize
G:
. Expand
Define coefficients
so that
Hence
is a linear combination of exponentials
with
. In particular, its derivative is
where
. Thus both
f and
live in the finite-dimensional span spanned by
.
This finite Fourier structure allows us to express
as a linear combination of finitely many translates
. Concretely, if we can find coefficients
and shifts
such that, as functions of
,
then multiplying both sides by
and summing over
yields
Thus the problem reduces to solving the finite linear system for and chosen shifts .
Two-Eigenvalue Generator: Classic Two-Term Parameter-Shift Rule
If the generator G has only two distinct eigenvalues (possibly with multiplicities), then and . As shown below, the derivative can be obtained from only two shifted evaluations.
Theorem B.1 (Two-eigenvalue parameter-shift)
Let
G be Hermitian with spectrum contained in
(so effectively
where
). Then for any observable
O and state
,
Proof
From the spectral argument above,
has the form
for some real coefficients
(since
and
are complex-conjugates). Differentiate:
Compute the finite-difference:
Set so that . The factor simplifies and yields the claimed identity. □
Appendix D.0.1. Corollary (Pauli rotation)
For the common Pauli rotation gate
with
(so the generator is
with eigenvalues
, i.e.
), the above reduces to the familiar formula
This is the standard two-term parameter-shift rule used ubiquitously in variational quantum algorithms.
Generalized Shift Rule for an Arbitrary Finite Spectrum
When G has arbitrary spectrum, the frequency set can contain up to distinct values, but typically many cancel or coincide. Let be the distinct positive frequencies (sorted), and include also if convenient.
Because f is a finite linear combination of for , we can attempt to express as a linear combination of exponentials at a finite set of shifts . A generic constructive approach is:
lgorithm (Construct Generalized Shift Rule)
1. Compute
(positive distinct frequencies of
G). 2. Choose
distinct shift values
such that the
matrix
V with entries
has full row rank
S. A convenient choice is
or any set avoiding aliasing (practically, choose distinct small rational multiples of
scaled by
). 3. Seek coefficients
solving the linear system (over complex numbers)
Equivalently
where
. 4. Solve for
(least-squares) if
, or direct inversion if
. 5. Then
If we choose and V invertible, the solution is exact; if we have degrees of freedom and may choose real-valued coefficients by imposing symmetry constraints and to ensure real derivatives, etc.
Theorem C.1 (Generalized shift - existence)
Let
G have
S distinct positive frequencies
. Then there exist shifts
with
and complex coefficients
such that for all
and consequently
. In particular, one can always choose a symmetric set of shifts
(total
evaluations) and solve a real linear system to obtain real coefficients producing the exact derivative.
Proof (sketch)
The functions form a linearly independent set (for distinct ) over any interval of length larger than the reciprocal of the smallest nonzero . Represent f in this basis; the derivative has the same frequency support with coefficients scaled by . A linear combination of shifted is a linear combination of the same exponentials with coefficients . Choosing to match on the finite set is solving a finite (square or tall) linear system, which is possible as long as the chosen shifts make the Vandermonde-like matrix invertible; such choices exist generically (e.g., distinct small fractional multiples of scaled appropriately). The symmetric shift choice yields a real linear system of size S (or real unknowns) and thus yields existence with evaluations. □
Table of Common Spectra and Shift Coefficients (Compact)
Below are commonly encountered generator spectra and the minimal finite-shift rules. In each case the derivative is exact (no truncation) under the stated spectral assumption.
| Spectrum of G
|
Minimal evaluations |
Shift formula (exact) |
|
(two-eigenvalue) |
2 |
|
| Pauli rotation
|
2 |
|
|
(three-spectrum symmetric) |
4 (symm) |
Solve system or use 4 symmetric shifts |
| General with S positive freqs |
|
Solve linear system as in Alg. (C) |
Remarks: - For any generator with spectral differences limited to S distinct positive frequencies, at most evaluations suffice if symmetric real coefficients are preferred. - If one is willing to use complex coefficients and asymmetric shifts, S evaluations (one per distinct positive frequency) suffice in general (so long as the chosen shifts produce an invertible Vandermonde-like matrix).
Multivariate and Composite-Parameter Cases
If the circuit depends on multiple parameters
and the unitaries are composed as
, then the partial derivative with respect to
obeys
where
denotes the product of unitaries after
and
denotes the Heisenberg-evolved observable due to earlier gates. In practice, the parameter-shift rule is applied to the single-parameter unitary
while leaving the surrounding fixed unitaries intact; the generalized-shift constructions above then apply with the effective generator being the conjugated generator
(which has the same spectrum as
). Thus the shift rules can be applied locally to any parameterized gate.
If a single parameter appears multiple times (e.g., repeated rotations with same parameter), one can use the product rule: sum derivatives of each appearance, each expressible by its own shift rule. When multiple parameters are entangled in a multi-parameter gate that cannot be factorized, more advanced techniques (finite-difference or analytic differentiation using commutator expansions) may be necessary.
Numerical Stability and Shot-Noise Considerations
Choosing shifts that make the Vandermonde matrix ill-conditioned yields numerically unstable coefficients and amplifies shot noise. Symmetric shift choices (pairs ) commonly improve stability and yield real coefficients.
For S large, the number of evaluations grows and the variance of the gradient estimator (propagating shot noise across linear combination coefficients) increases. In practice, one balances exactness with robustness: one may instead approximate with fewer shifts chosen to capture dominant low-frequency components and accept a deterministic approximation error (bias) while saving shot budget.
For small or noisy hardware, the classic two-term shifts (Pauli rotations) are simplest and most robust.
Summary: Practical Recipe
Diagonalize (or reason about the spectrum of) the generator G of the parameterized gate.
Compute the set of distinct positive frequency differences and its size S.
If (two-eigenvalue case), use the two-term parameter-shift with shifts .
Otherwise choose stable shifts (prefer symmetric pairs), solve the finite linear system for coefficients a.
Use the identity . Evaluate each on the quantum device (or simulator) and combine linearly to obtain the gradient.
When shot-noise is significant, prefer symmetric real-coefficient constructions and/or use variance reduction (control variates, common random numbers across shifted evaluations).
The specialized two-term parameter-shift identity and its use in variational quantum algorithms are described in depth in works such as [
13]. The general multi-shift derivation and generalized shift rules (including algorithmic constructions for multi-eigenvalue generators, and numerical stability considerations) are presented in [
14] and related literature. Readers implementing the general method should consult these references for additional implementation heuristics and proofs of numerical conditioning bounds.
Appendix E. Simulation Code Snippets and Notebooks
All the code notebooks and datasets will be provided based on the formal request.
References
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention
is all you need,” in Advances in Neural Information Processing Systems, 2017.
- A. Tesi, G. R. Dahale, S. Gleyzer, K. Kong, T. Magorsch, K. T. Matchev, and K. Matcheva, “Quantum Attention
for Vision Transformers in High Energy Physics,” arXiv preprint arXiv:2411.13520, Nov. 20, 2024. Available:
https://arxiv.org/abs/2411.13520.
- A. Gilyén, Y. Su, G. H. Low, and N. Wiebe, “Quantum singular value transformation and beyond,” in Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (STOC), 2019.
- G. Brassard, P. Høyer, M. Mosca, and A. Tapp, “Quantum amplitude amplification and estimation,” in Contemporary Mathematics, vol. 305, 2002, pp. 53–74.
- M. Schuld, V. Bergholm, C. Gogolin, J. Izaac, and N. Killoran, “Evaluating analytic gradients on quantum hardware,” Phys. Rev. A, 2019.
- D. Wierichs, J. Izaac, C. Wang, and C.-Y. Lin, “General parameter-shift rules for quantum gradients,” Quantum, 2022.
- A. Harrow, A. Hassidim, and S. Lloyd, “Quantum algorithm for linear systems of equations,” Physical Review Letters, vol. 103, p. 150502, 2009.
- V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum random access memory,” Phys. Rev. Lett., vol. 100, p. 160501, 2008.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin,
“Attention Is All You Need,” in Advances in Neural Information Processing Systems (NeurIPS), 2017. Available:
https://arxiv.org/abs/1706.03762.
- A. Gilyén, Y. Su, G. H. Low, and N. Wiebe, “Quantum singular value transformation and beyond,” in Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (STOC), 2019. Available: https://arxiv.org/abs/1806.01838.
- G. Brassard, P. Høyer, M. Mosca, and A. Tapp, “Quantum Amplitude Amplification and Estimation,” Contemporary Mathematics, vol. 305, pp. 53–74, 2002. Available: https://arxiv.org/abs/quant-ph/0005055.
- N. Guo, Z. Yu, M. Choi, et al., “Quantum linear algebra is all you need for Transformer layers,” arXiv preprint,
2024, arXiv:2402.16714. Available: https://arxiv.org/abs/2402.16714.
- M. Schuld, V. Bergholm, C. Gogolin, J. Izaac, and N. Killoran, “Evaluating analytic gradients on quantum hardware,” Physical Review A, 2019. Available: https://arxiv.org/abs/1811.11184.
- D. Wierichs, J. Izaac, C. Wang, and C.-Y. Lin, “General parameter-shift rules for quantum gradients,” Quantum, 2022. Available: https://arxiv.org/abs/2107.12390.
- V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum random access memory,” Physical Review Letters, vol. 100, no. 16, p. 160501, 2008. [CrossRef]
- A. W. Harrow, A. Hassidim, and S. Lloyd, “Quantum algorithm for linear systems of equations,” Physical Review Letters, vol. 103, no. 15, p. 150502, 2009. [CrossRef]
- Survey Author(s), “Survey of Quantum Machine Learning Approaches for Neural Architectures,” 2024.
- A. Blumer, A. Ehrenfeucht, D. Haussler, and M. Warmuth, “Learnability and the Vapnik–Chervonenkis dimension,” Journal of the ACM, vol. 36, no. 4, pp. 929–965, 1989.
- S. Shalev-Shwartz and S. Ben-David, Understanding Machine Learning: From Theory to Algorithms, Cambridge University Press, 2014.
- Prasad, Yalla Jnan Devi Satya. "Selective Quantum Error Correction for Variational Quantum Classifiers: Exact Error-Suppression Bounds and Trainability Analysis." (2025).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
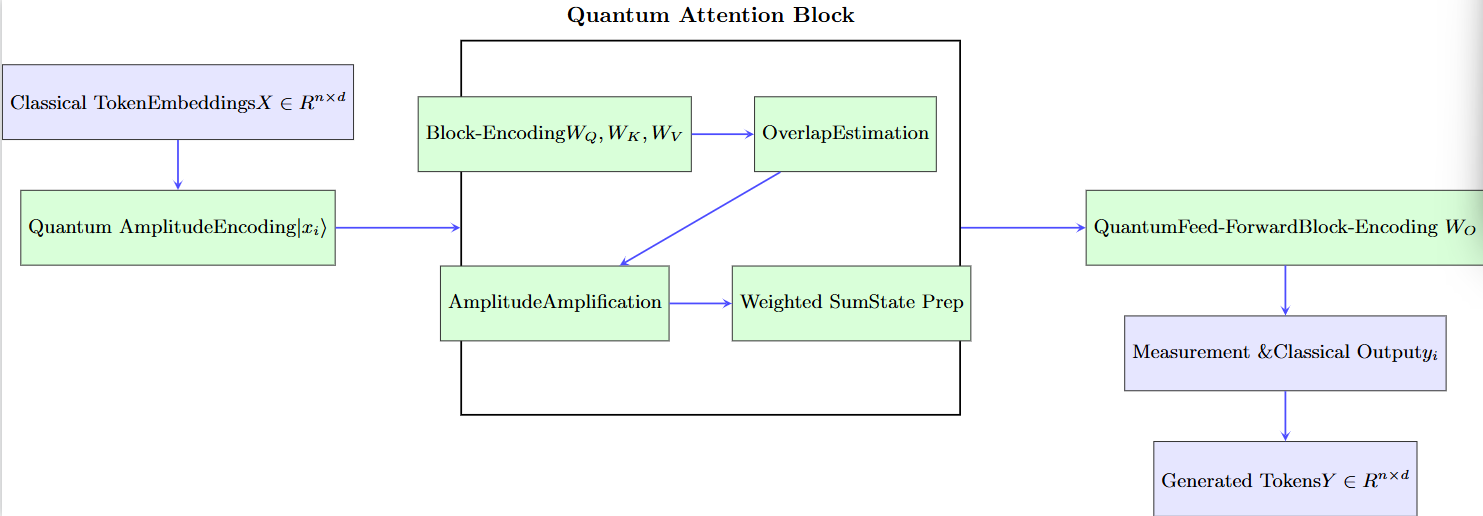
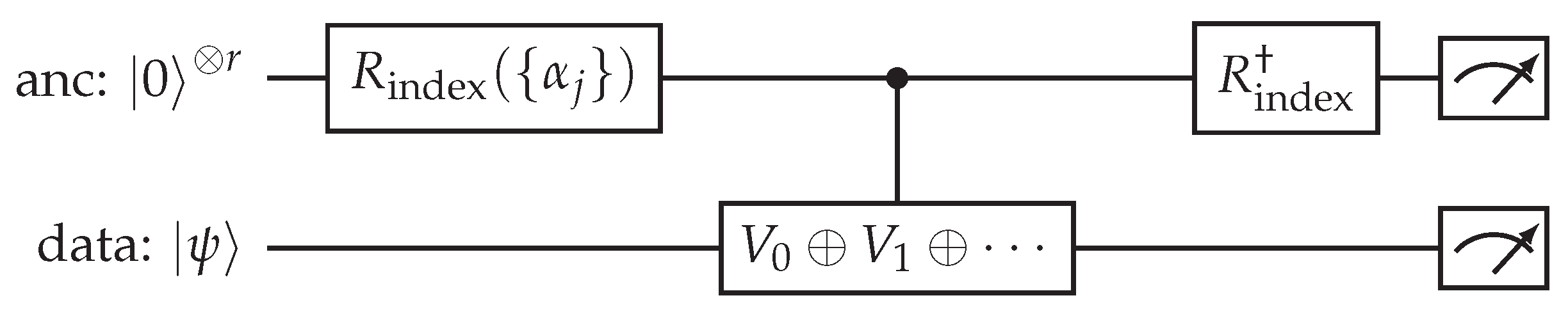


 Figure 7.
Figure 7.
 Figure 8.
Figure 8.





