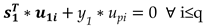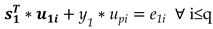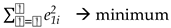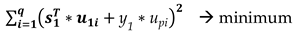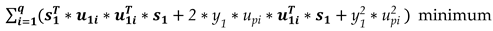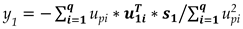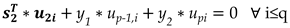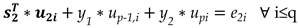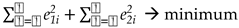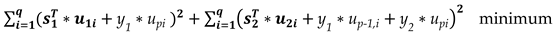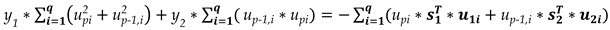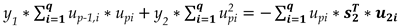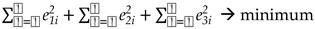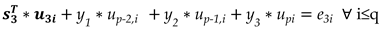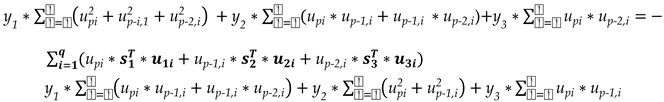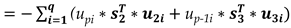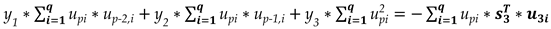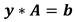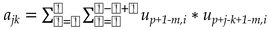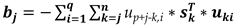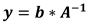A Non-Parametric Algorithm to Estimate Future Samples in Time Series

1. Introduction

Difference equations have been widely used to model time series by means of exponential functions. The parameters of the exponential functions result from an optimization process that minimizes the modelling error. These techniques suffer from numerical problems that affect the accuracy of the computed parameters. The frequencies and the dumping factors of the exponential functions are the roots of polynomials that result from the optimization process. However the numerical computation of roots is rather sensitive leading to compromised accuracy. To overcome this problem, alternative approaches for the computation of the exponential parameters were proposed in literature. Among the most efficient techniques are the well-known ESPRIT and HSVD algorithms that perform well when it comes to spectral estimation but continue having numerical problems to predict future samples [1,2]. In addition round-off errors add-up creating significant deviation from the correct values of the parameters which compromises the prediction based on extrapolation of the exponential functions.

2. Materials and Methods

2.1. The Orthogonal Approach

Let us consider the p_th order Hankel matrix H of a given set x of N samples with N>p and size px(N-p+1). The SVD of H is H=U*S*V where U is a pxp matrix of singular vectors of size p, S is a pxp diagonal matrix of singular values, arranged in ascending order and V is a px(N-p+1) matrix of singular vectors of size (N-p+1) [3]. Assuming that the size of the null space of H is q only p-q singular values in S are non-zero and q of the singular vectors of U namely u₁… u_q span the null space of H. If U_q is a pxq matrix of these vectors then the N-p+1 vectors of H are orthogonal to U_q [4,5,6]. The (N+1)_th unknown sample of the set x, namely x(N+1) along with the p-1 known samples x(N-p+2), x(N-p+3) … x(N) form a new vector of size p, namely x₁ which is part of the augmented Hankel matrix H_a1=[H x₁]. Since all the vectors of H are orthogonal to U_q the same should hold for the vectors of the augmented H_a1, hence x₁ is also orthogonal to U_q. By splitting x₁ into two parts, the known part namely ${\mathit{s}}_1^{\mathit{T}}$=[x(N-p+2) x(N-p+3) … x(N)] and the unknown part y₁=x(N+1) the following equation is obtained.

(1)

Where u_1i consists of the p-1 first components of the i_th singular vector u_i and u_pi is the last component of u_i.

Equation (1) is only theoretically valid. In real life the orthogonality is only approximate and (1) should be reformulated as follows,

(1.1)

where e_1i is the approximation error. Best approximation will be achieved when the accumulated squared error is minimized,

(2)

which leads to the solution of the following minimization problem,

(3)

An equivalent minimization problem results after elaborating the above expression (3),

(4)

By setting to zero the first derivative of (4) with respect to y₁ the following solution is obtained,

(5)

2.2. The Case of Two Unknown Samples

To estimate x(N+1) and x(N+2) simultaneously a similar approach is used. Besides the vector x₁ a second vector x₂ of size p, consisting of p-2 known samples x(N-p+3), x(N-p+4),.. x(N) and two unknown samples, namely x(N+1) and x(N+2) is formed. The augmented Hankel matrix H_a1 becomes H_a2=[H x₁ x₂] and both vectors x₁ and x₂ have to be orthogonal to U_q. Consequently next to equation (1) an additional equation to guarantee the orthogonality of x₂ is needed. Vector x₂ is split into two parts, the known part s₂ and the unknown components y₁ and y₂ with ${\mathit{s}}_2^{\mathit{T}}$=[x(N-p+3) x(N-p+4 … x(N)] and [y₁ y₂]=[x(N+1) x(N+2)]. Due to the orthogonality property the following must hold,

(6)

where u_2i consists of the p-2 first components of the i_th singular vector u_i and u_p-1,i and u_pi are the last two components of u_i.

As it was mentioned before, equation (6) is only theoretically valid. In real life the orthogonality is only approximate and (6) should be reformulated as follows,

(7)

where e_2i is the approximation error. For best estimates of both x(N+1) and x(N+2) the following combined optimization problem must be solved,

(8)

By using (1.1) and (7) the above minimization problem can be expressed as,

(9)

To solve the above the first derivatives of expression (9) with respect to y₁ and y₂ are set to zero. This leads to the following two equations,

(10.1)

(10.2)

The above linear system of equations provides best estimates for y₁ and y₂.

2.3. The General Case of Many Unknown Samples

When three future samples need to be estimated, a third term in the optimization problem (8) is added [7]. By following the same type of notation equation (8) becomes,

(11)

where e_3i is the error due to the third unknown sample x(N+3)=y₃

By following the same notation as in the case of two unknown samples the error e_3i can be expressed as follows,

(12)

where ${\mathit{s}}_3^{\mathit{T}}$=[x(N-p+4) x(N-p+4 … x(N)] , u_3i consists of the p-3 first components of the i_th singular vector u_i and u_p-2,i , u_p-1,i and u_pi are the last three components of u_i.

By setting the first derivatives of expression (11) with respect to y₁, y₂ and y₃ to zero, a linear system of three equations is formed and its solution provides the estimates of the three unknown samples y₁, y₂ and y₃ .

By replacing (1), (7) and (12) into expression (11) and by elaborating on the algebraic manipulations, the following set of equations is obtained,

(13.1)

(13.2)

(13.3)

The above system of equations (13) maybe expressed as,

(14)

where y=[y₁ y₂ y₃], A is a symmetric matrix and b is a vector.

In a more general notation, the elements of the symmetric matrix A for all j ≤ k and k≤n can be expressed as,

(15)

where n stands for the number of samples to be estimated, namely n=3 in this case.

Similarly, the elements of b can be expressed as,

(16)

With A and b known, the estimation of y is straightforward based on equation (14),

(17)

where y is the vector of n unknown future samples of the set x.

3. Results

The proposed algorithm was tested against the well known method ESPRIT that models the signal by means of exponential sinusoids. A large set of signals, four thousands in total, with variable complexity in terms of the rank of their covariance matrix was considered. The comparison was based on the accuracy of predicting future samples as well as on the overall consistency of the two algorithms. The term consistency refers to the homogeneity of the prediction errors. Each signal consists of 2000 to 2500 samples and it was generated from white noise that was filtered using random low pass FIR filters with hundreds of taps. Four sets of future samples were selected for the comparison. The latter is based on the RMSE among the predicted values and the actual values of the signals. The four sets refer to predicting the first, tenth, twentieth and thirtieth future samples using both the proposed and the ESPRIT algorithms and comparing the RMSEs of the two methods. To evaluate the algorithms with respect to their consistency the variance of the errors is used. In order to eliminate variations due to the differences of the signal amplitudes, all errors were normalized with respect to the actual value of the predicted sample.

For the ESPRIT method the prediction for each one of the 4000 signals is based on twenty different models with orders equally spaced between 140 and 900. By averaging these twenty different results the overall prediction is computed.

For the new method the size p of the Hankel matrix H is set to 600. Alternative choices for p were also tested showing no significant change in the results as long as p is not too small compared to the length N of the signals. Regarding the null space not only one single size for each signal is used. Instead, an optimum set of null spaces for each signal is considered and the overall prediction is computed by averaging individual results. There are two constraints while choosing the optimum set of null spaces, a) the sizes of the null spaces of the optimum set are consecutive numbers and b) the variance of the results of the set is minimal. The second constraint is imposed to guarantee maximum consistency of the chosen set.

Table 1 shows the obtained results for the four different setups in predicting future samples. In all cases the new method performs better than ESPRIT in terms of both RMSE and variance.

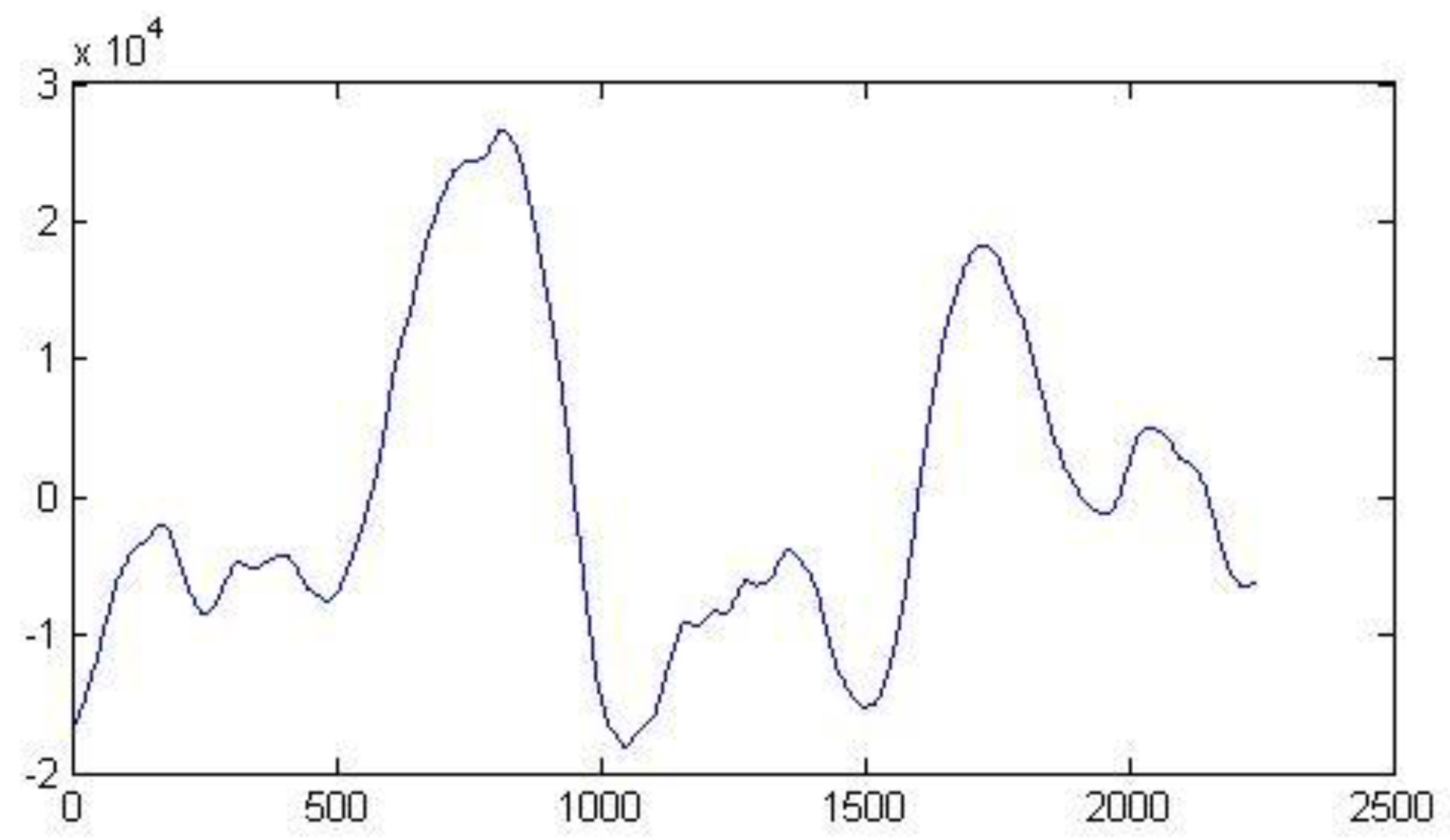
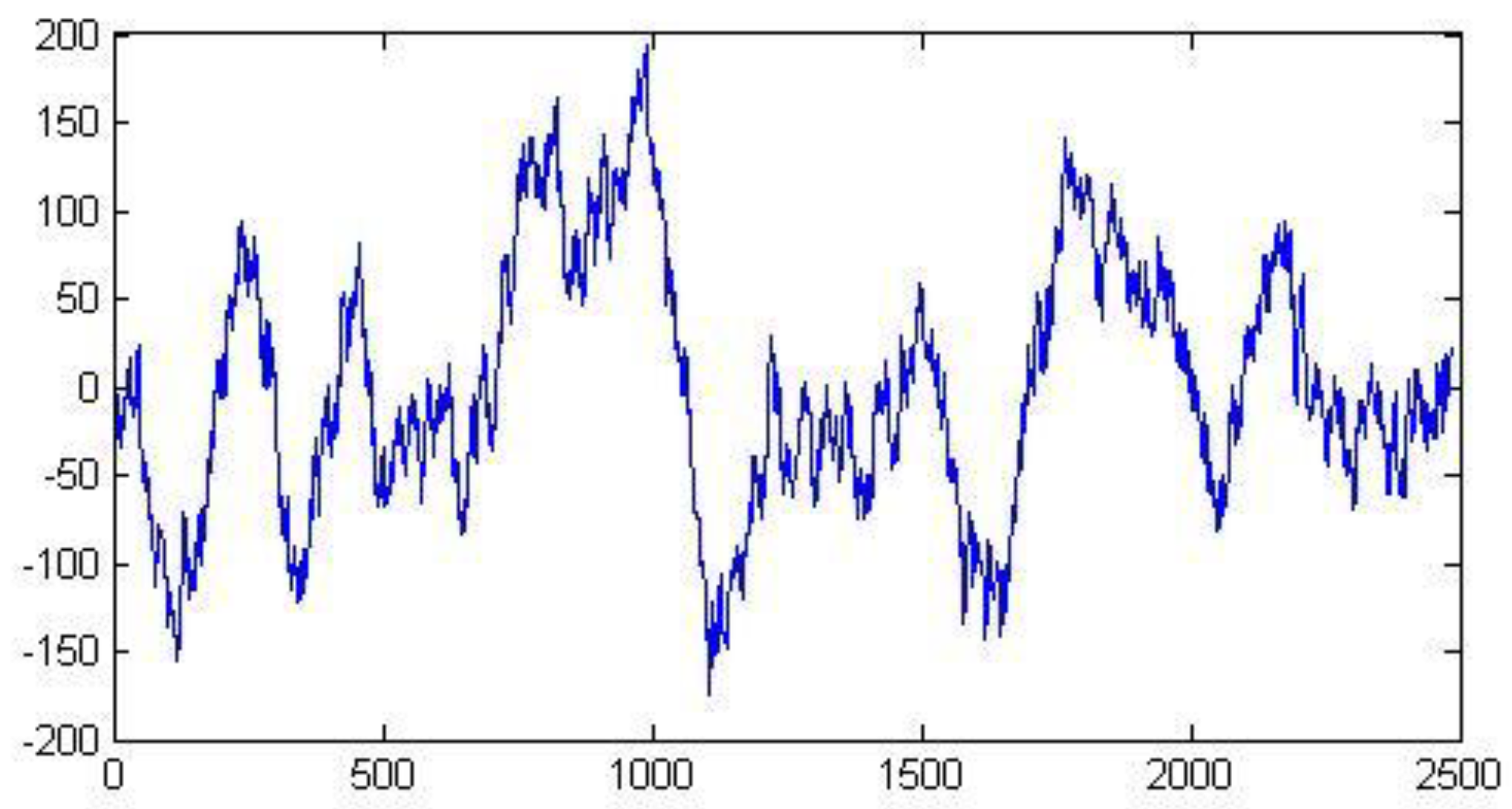
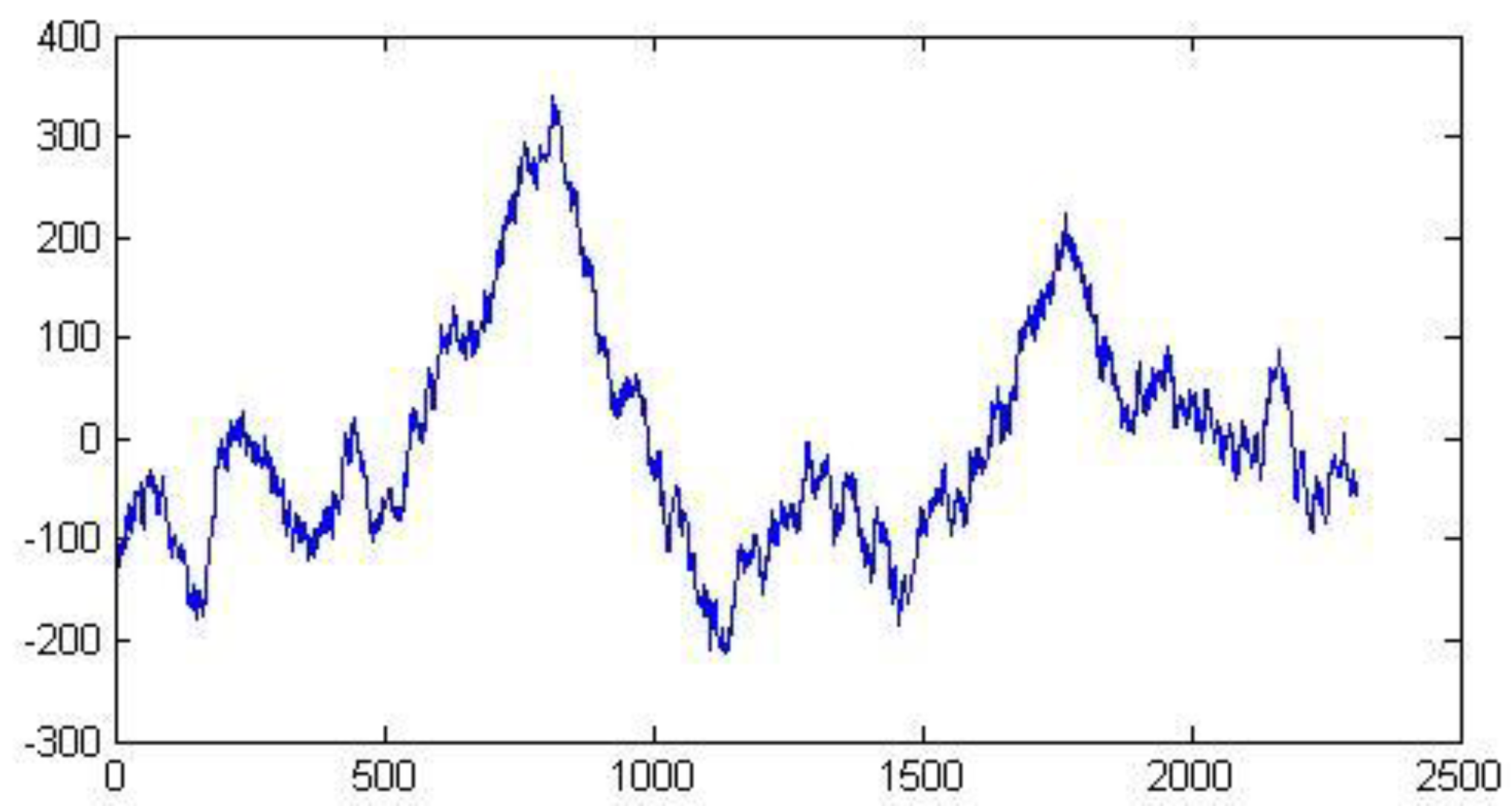
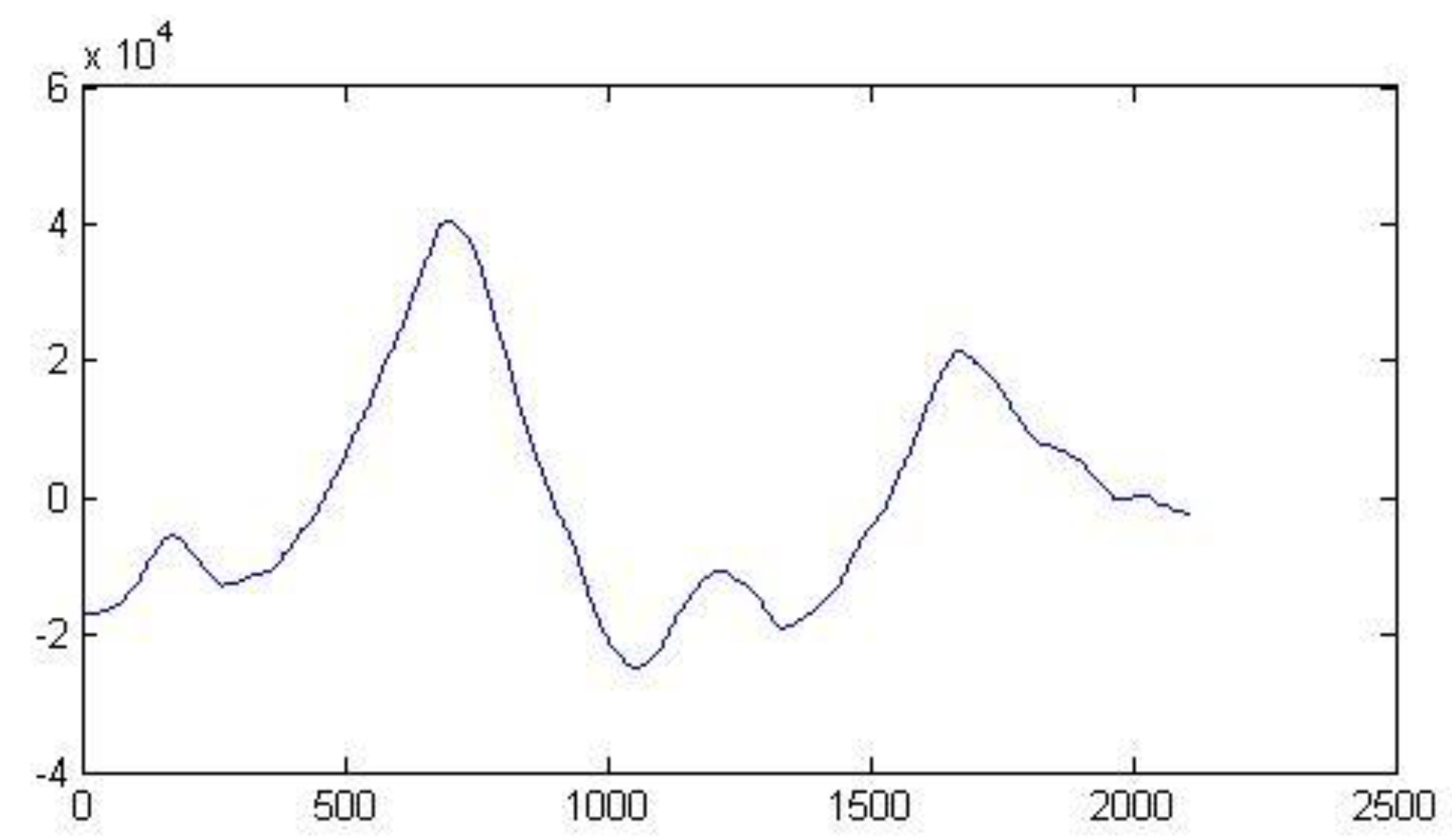
Figure 1, Figure 2, Figure 3 and Figure 4 show the shape of representative signals among the 4000 used. The rank of the covariance matrix of all 4000 signals varies considerably, ranging from low to high rank. This way the results are not biased with respect to the degree of predictability of the signals.

4. Discussion

A new method to predict future samples is presented and it is compared against the ESPRIT method. The new method was proven to be more accurate and more consistent than ESPRIT, based on results from four thousand time series of variable spectral complexity. The new method exploits the properties of the eigenvectors of the Hankel matrix of the time series that are associated with the low eigenvalues. It is fast and stable and can predict any set of future samples. Further research will focus on both the selection of the null space of the time series Hankel matrix and the choice of the matrix size.