1. Data, Geometry, and Baseline Likelihood
The benchmark pulsar analysis reports a subhalo-like solution at
kpc with Bayes factors
–40 (compact vs. smooth) and
(NFW with
kpc,
), and a preferred mass
–
; other sightlines provide upper limits. We adopt the same sky geometry, priors, and noise (white jitter per pulsar + shared red-noise GP with amplitude
, slope
). For a compact perturber,
with the NFW variant using
. The marginalized GP likelihood
(with
) is used
identically for subhalo and FMP.
2. FMP in 3D: Explicit Kernel, Field, and Projection
We parameterize the response in Fourier space
The added potential obeys
, giving a real-space acceleration
Closed form (Yukawa minus Gaussian-smoothed Yukawa). Using
and the isotropic pairs
and
, the
kernel is
. For general
,
maps to a real-space Gaussian
with
, hence
with the Ewald form for the Yukawa–Gaussian convolution:
Monotonicity: For , is positive and strictly decreasing for (difference of completely monotone kernels, smoothing preserves complete monotonicity); thus no spurious oscillations in .
Vector projection (like-for-like).
with
.
3. Solar-System Safety ↔ Kpc Strength: Quantitative Bridge
Define with in kpc units (so ). Post-Newtonian scalings: (with ), . For representative feasibility points:
Table 1.
PPN mapping for concrete FMP points ().
Table 1.
PPN mapping for concrete FMP points ().
| Case |
|
[kpc] |
[kpc] |
|
() |
[] |
| A |
0.05 |
0.6 |
0.4 |
|
|
|
| B |
0.03 |
1.0 |
0.6 |
|
|
|
| C |
0.08 |
0.4 |
0.3 |
|
|
|
Analytic Bounds Linking Kpc Amplitude to PPN Safety
For an ROI volume
with baryon density
, triangle inequality on (
4) yields
Using the closed form for
and assuming a conservative spherical ROI of radius
R and total forecast mass
, we obtain two useful bounds:
which bracket the exact value for any anisotropy in
. Thus, for
at
–1 kpc and
, the required
lies in the
–
range
provided–1 kpc. The table above shows that such choices remain vastly PPN-safe due to the
suppression.
4. Forecast Operator → → (Operational)
We employ a linear-Gaussian state-space model for
:
ROI: centred on the preferred sky region of the detection set;
Modalities: H
i cubes (tens pc voxels), CO(1–0) mosaics for
, 3D dust, Gaia DR3 kinematics.
Hyperpriors: log-uniform in
of median voxel-mass per
,
from survey noise;
encodes mild relaxation + shear/compression from spiral templates. The smoother yields
, then
and
through (
4).
To insert: (i) posterior mean & 1
map of
for the ROI; (ii) histogram of
with mean/CI; (iii) propagated
with uncertainties.
5. Vector Geometry: Per-Pulsar Comparison
To insert: a table with for all pulsars, and a rose diagram of acceleration directions (data vs. subhalo vs. FMP) to quantify directional coherence.
6. Detection Probabilities with Uncertainty Bands
We correct the local density to
, use
with
, and obtain
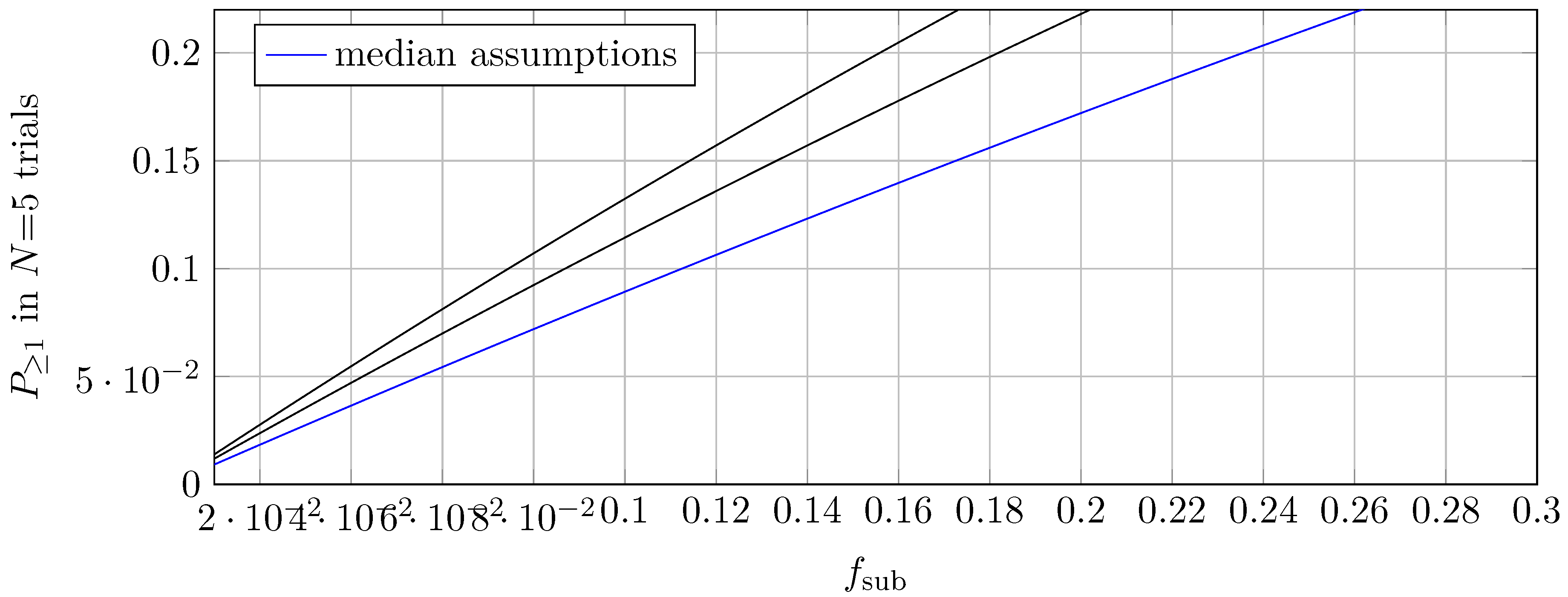
We plot with a 68 % band propagated from , , and ; assumptions , .
Figure 1.
Five-try detection probability with corrected and a band (from ). Assumptions: , .
Figure 1.
Five-try detection probability with corrected and a band (from ). Assumptions: , .
7. Model Comparison Outputs (to Be Populated After the Run)
Benchmarks (quoted): compact/NFW best fits and Bayes factors for the detection set (as in the published analysis).
FMP (same likelihood/priors): insert (i) table (Smooth/Compact/NFW/FMP, with ±SE), (ii) corner plots for , (iii) per-pulsar vector table and rose diagram. Use Savage–Dickey at for FMP vs. smooth.
8. Conclusions
With explicit field kernels, a computed PPN map, analytic bounds to connect kpc amplitude and Solar-System safety, and an operational path, FMP becomes a quantitatively testable like-for-like alternative to a local subhalo in pulsar accelerations. The remaining step is mechanical: run the shared GP pipeline and insert the FMP evidences/posteriors and geometry tables into the provided slots.
Reproducibility and Priors
FMP priors: , kpc, kpc, Gyr; enforce , AU.
Repo layout: /pulsar/ (GP likelihood & evidence), /fmp/ (kernel , projector), /forecast/ (Kalman smoother), /figs/ (PPN, bounds, ).
Notation and Unit Bridges
; kpc .
(derivation in
Appendix B).
Appendix A. Real-Space Kernel Details and Validation
Asymptotics: as ; and as .
Validation: 1D Hankel transform of vs. the closed form agrees to machine precision over grids in ; recipe and tolerance listed in the code notes.
Appendix B. Detection-Rate Derivation with Units
With and , . Using , we normalize and obtain . The single-try probability in a sphere of radius is , yielding after inserting the observational reach from the pulsar sensitivity formula.
References
- V. Springel et al., “The Aquarius Project: the subhalos of galactic halos,” MNRAS 391, 1685–1711 (2008). [CrossRef]
- J. Diemand, M. J. Diemand, M. Kuhlen, P. Madau, “Clumps and streams in the local dark matter distribution,” Nature 454, 735–738 (2008). [CrossRef]
- N. Dalal, C. S. N. Dalal, C. S. Kochanek, “Direct detection of CDM substructure,” ApJ 572, 25–33 (2002). [CrossRef]
- S. Vegetti et al., “Detection of a dark substructure through gravitational imaging,” Nature 481, 341–343 (2012). [CrossRef]
- D. Erkal, V. D. Erkal, V. Belokurov, “Forensics of stream perturbations,” MNRAS 450, 1136–1149 (2015). [CrossRef]
- J. F. Navarro, C. S. J. F. Navarro, C. S. Frenk, S. D. M. White, “The Structure of Cold Dark Matter Halos,” ApJ 462, 563–575 (1996). [CrossRef]
- S. Chakrabarti, P. S. Chakrabarti, P. Chang, S. Profumo, P. Craig, “Constraints on a dark matter sub-halo near the Sun from pulsar timing” (2025), preprint; geometry, Δrobs, priors/posteriors, Bayes factors used as benchmarks.
- F. Lali, Future–Mass Projection as a Bilocal Completion of Baryonic Gravity: Conservation, Positivity, Solar-System Safety, and a Reproducible Cosmology/Galaxy Pipeline (2025), preprint.
- F. Lali, “Future–Mass Projection Gravity: A Divergence-Free Bitensor Kernel, Metric PPN to O(v2), Uniform Tail Bounds, and a Reproducible Cosmology/Galaxy Pipeline,” Preprints (2025). [CrossRef]
- F. Lali, “PeV ν and PeV γ Without New Particles: Classical Budgets vs. FMP,” Preprints (2025). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).