Mathematical Analysis of Entanglement Measures and Maximized Quantum Fisher Information

1. Introduction

Entanglement, a cornerstone of quantum mechanics, is a fundamental resource in quantum computing and quantum information science. For bipartite systems, various measures such as concurrence [1] and negativity [3,5] have been developed to quantify this unique correlation. These measures, by definition, do not increase under Local Operations and Classical Communication (LOCC) [4]. A well-known issue is the state ordering problem [10], where different entanglement measures can assign different ranks to non-maximally entangled states, suggesting that each measure captures a different facet of entanglement [2].

In parallel, Quantum Fisher Information (QFI) [6,7] has emerged as a key metric in quantum metrology [8,9], as it quantifies the ultimate precision with which a parameter can be estimated. A state's QFI, when exceeding a certain threshold, can also serve as a witness for entanglement [9]. However, unlike entanglement measures, QFI is not an entanglement monotone and can be changed via local unitary operations. This necessitates finding the Maximized QFI (MQFI) over all possible local unitary rotations to properly compare a state's metrological potential with its entanglement [11,12,13,14,15,16,17].

In this work, we aim to bridge the gap between these two seemingly different concepts. We perform a large-scale numerical simulation to generate a large number of random two-qubit states and analyze the correlations between their entanglement measures (concurrence and negativity) and their QFI [11]. Our primary goal is to examine how MQFI, a measure of a state's optimal metrological utility, relates to the standard entanglement measures.

2. Methods

Random State Generation: We generated 20,000 random two-qubit density matrices. The states were created by generating random unitary matrices and a set of random positive eigenvalues that sum to one. This method ensures that the generated matrices are valid density operators.

Entanglement Measures:

• Concurrence: For each density matrix ρ, we computed its concurrence C(ρ) using the well-established formula based on the eigenvalues of the spin-flipped state [1]. The concurrence value ranges from 0 for separable states to 1 for maximally entangled states.
• Negativity: We calculated the negativity N(ρ) for each state based on the negative eigenvalues of its partial transpose [3,5]. This value is also bounded between 0 and 1. We also defined a rescaled Negativity, Neg′=2×N(ρ), to better align with the scale of Concurrence for pure states.
• Relative Entropy of Entanglement:

The Relative Entropy of Entanglement (REE) for a given state is defined as the minimum value of the quantum relative entropy,

S(ρ∣∣σ)=Tr(ρ logρ−ρ log σ), where the minimum is taken over the set of all separable states, σ. The formula for this is given as

E(ρ)=minρ∈D S(ρ∣∣σ)=S(ρ∣∣σ). This definition essentially means that REE quantifies entanglement by measuring the distance between a given state and the closest separable state.

Quantum Fisher Information:

• QFI and MQFI: For each state, we calculated the QFI with a fixed generator, specifically the two-qubit Pauli Z-operator, J=σz ⊗σz. We then performed an optimization over local unitary rotations to find the maximum possible QFI for that state, which we refer to as MQFI [11].
• Normalization: All QFI and MQFI values were normalized by dividing by 4, as this allows for a direct comparison with the entanglement measures.

Data Visualization and Analysis: The generated data points were plotted on scatter graphs in Figure 1. Polynomial fits for the upper and lower bounds of the data clouds were calculated to provide a quantitative description of the relationships.

3. Results and Discussions

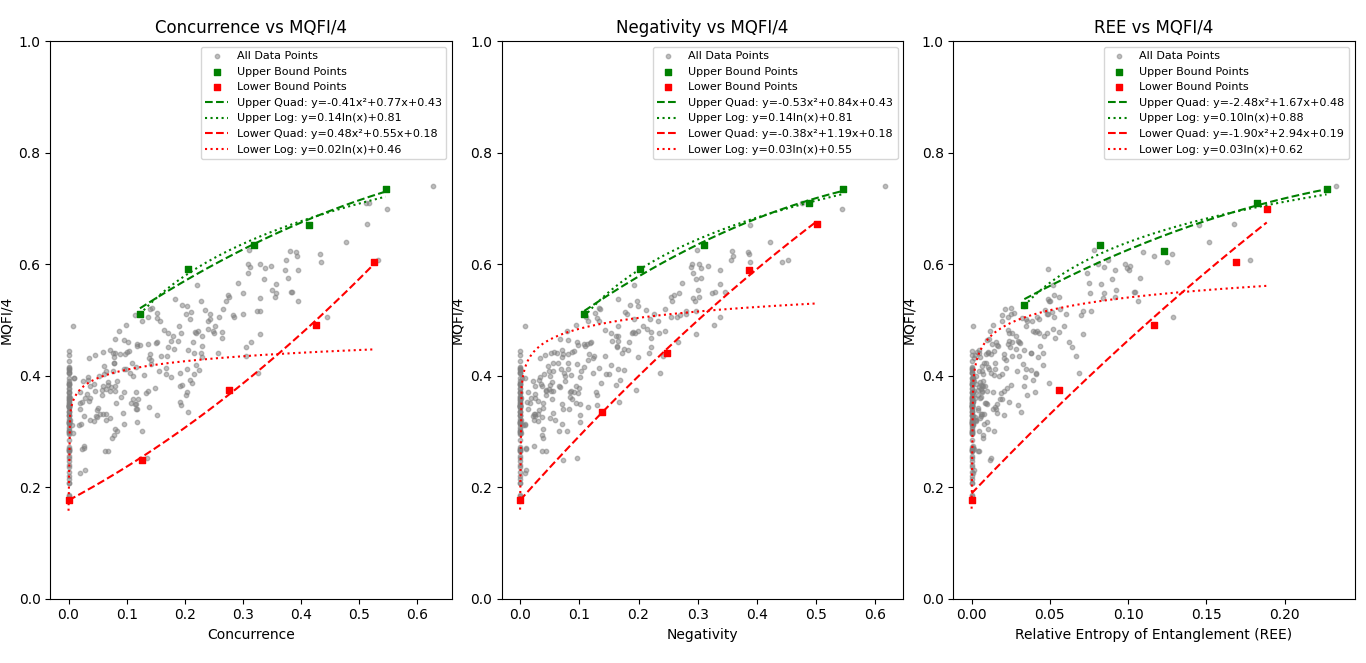
The numerical analysis of entanglement measures and their relationship with Maximized Quantum Fisher Information (MQFI) for general two-qubit systems revealed several key findings, as depicted in Figure 1. This figure presents three distinct subplots, each illustrating the correlation between MQFI/4 and a specific entanglement measure: Concurrence, Negativity, and Relative Entropy of Entanglement (REE). The gray data points represent a large ensemble of randomly generated two-qubit states, exhibiting a clear and predictable envelope that bounds the relationship between entanglement and metrological capacity.

A critical aspect of our analysis involves delineating the upper and lower bounds of MQFI/4 as a function of entanglement. To achieve this, a binning method was employed, grouping data points based on their respective entanglement measure values. For each bin, the maximum and minimum MQFI/4 values were identified, forming the "Upper Bound Points" (green squares) and "Lower Bound Points" (red squares), respectively. These points effectively define the envelope within which all observed MQFI/4 values lie for a given entanglement.

3.1. REE vs. MQFI/4 (Rightmost Subplot):

This subplot investigates the relationship between REE and MQFI/4. The data clearly shows that MQFI/4 generally exceeds REE for low entanglement, with the upper bound approaching the theoretical limit (y=x) for higher entanglement.

The fitted quadratic curves for the bounds are given by:

• Upper Quadratic Fit: y=−2.48x2+1.67x+0.48 (R2=0.98)
• Lower Quadratic Fit: y=−1.90x2+2.94x+0.19 (R2=0.91)

And the logarithmic fits are:

• Upper Logarithmic Fit: y=0.10ln(x)+0.88 (R2=0.97)
• Lower Logarithmic Fit: y=0.03ln(x)+0.62 (R2=0.89)

The positive coefficients for the linear terms in both quadratic and logarithmic fits suggest that MQFI/4 generally increases with REE. The negative quadratic term in the upper fit implies a potential saturation or even a slight decrease in the rate of increase at higher REE values, indicating that beyond a certain point, additional REE provides diminishing returns in enhancing MQFI. The R2 values, particularly for the upper quadratic and logarithmic fits (0.98 and 0.97, respectively), demonstrate an excellent fit to the boundary data. Physically, these bounds represent the maximum and minimum metrological utility for states with a given amount of REE, indicating that while REE quantifies entanglement, its direct relationship with MQFI is more complex than a simple linear scaling.

3.2. Concurrence vs. MQFI/4 (Leftmost Subplot):

This subplot explores the relationship between Concurrence, another widely used entanglement measure, and MQFI/4.

The fitted curves are:

• Upper Quadratic Fit: y=−0.41x2+0.77x+0.43 (R2=0.99)
• Lower Quadratic Fit: y=0.48x2+0.55x+0.18 (R2=0.92)

And the logarithmic fits are:

• Upper Logarithmic Fit: y=0.14ln(x)+0.81 (R2=0.98)
• Lower Logarithmic Fit: y=0.02ln(x)+0.46 (R2=0.89)

Similar to REE, a strong positive correlation is observed, with higher Concurrence generally leading to higher MQFI/4. The quadratic fit for the upper bound (R²=0.99) shows an exceptionally strong fit. The negative coefficient of the x2 term in the upper quadratic fit again suggests a potential saturation effect. The logarithmic fits provide an alternative perspective, showing a less steep increase for the lower bound. This indicates that while entanglement (quantified by Concurrence) is beneficial, its metrological enhancement might follow a different functional form depending on the specific state and the chosen estimation strategy. For non-entangled states (Concurrence=0), MQFI/4 is non-zero (y-intercept of the fits), highlighting that even separable states can possess quantum information useful for metrology.

3.3. Negativity vs. MQFI/4 (Middle Subplot):

The middle subplot illustrates the relationship between Negativity and MQFI/4. Negativity, being an entanglement monotone, also exhibits a clear bounding behavior with MQFI/4.

The fitted curves are:

• Upper Quadratic Fit: y=−0.53x2+0.84x+0.43 (R2=0.98)
• Lower Quadratic Fit: y=0.38x2+1.19x+0.18 (R2=0.92)

And the logarithmic fits are:

• Upper Logarithmic Fit: y=0.14ln(x)+0.81 (R2=0.98)
• Lower Logarithmic Fit: y=0.03ln(x)+0.55 (R2=0.88)

The trends observed for Negativity are highly consistent with those for Concurrence and REE. The quadratic and logarithmic fits for both upper and lower bounds show high R2 values (mostly above 0.90), signifying a robust description of the observed behavior. The similar functional forms and coefficients across different entanglement measures suggest a general underlying relationship between the degree of entanglement and the quantum metrological capabilities of two-qubit systems. The non-zero intercepts for zero Negativity again confirm the metrological utility of separable states.

3.4. Overall Discussion:

The consistent behavior across all three entanglement measures underscores the fundamental connection between entanglement and quantum metrology. The upper bounds, described by the quadratic and logarithmic fits, effectively represent the "optimal" states in terms of metrological performance for a given entanglement. The negative quadratic terms in the upper bound fits for all measures hint at a practical limit to the metrological gain from increasing entanglement, suggesting that beyond a certain point, the sensitivity might not increase as rapidly. Conversely, the lower bounds illustrate the minimum metrological capability, which is still entanglement-dependent.

The fact that MQFI/4 is non-zero even for separable states (where entanglement measures are zero) is physically significant. It indicates that quantum advantage in metrology is not solely predicated on entanglement, though entanglement undeniably enhances it. However, the distinct upward trend of both upper and lower bounds with increasing entanglement measures clearly demonstrates that highly entangled states generally offer superior metrological precision. The differences in the shapes and coefficients of the fit curves across the three entanglement measures suggest subtle distinctions in how each measure correlates with metrological capacity, reflecting their unique mathematical definitions and physical interpretations of entanglement. These findings provide valuable insights for designing and optimizing quantum metrology protocols by leveraging specific entanglement resources.

4. Discussion and Conclusion

Our results confirm the strong relationship between entanglement and metrological utility. Concurrence [1], Negativity [3] and REE when plotted against QFI, show a general trend of increasing QFI with increasing entanglement.

The gray data points (MQFI), which represent the metrological performance after local optimization, form a much tighter and more predictable band [11]. This demonstrates the critical role of local unitary operations in unlocking a state's full metrological potential. By choosing the optimal basis for measurement, a state can achieve its maximum possible QFI.

As expected, all of our data points, representing mixed states, fall below y=x, confirming that mixed states cannot surpass the metrological performance of pure states with the same level of entanglement. The upper bound fit for the MQFI points shows that, at higher entanglement, local optimization can bring the performance of mixed states very close to this theoretical pure-state limit.

Our findings also touch upon the state ordering problem [10,11,12,13,14,15,16,17]. While both Concurrence, Negativity and REE are entanglement monotones, they can rank states differently. Our plots show that the relationship between these measures and MQFI is not a simple one-to-one mapping. This implies that MQFI, while strongly correlated with entanglement, is another distinct measure of a state's quantum properties, related to its metrological capacity.