1. Introduction
Classical molecular dynamics (MD) simulations of liquids have advanced significantly through the development of force fields that offer an increasingly favorable balance between accuracy and computational efficiency. A major milestone in this progression was the introduction of transferable three- and four-site water models, which, despite their non-polarizable nature, successfully captured key bulk properties at modest computational cost [
1]. Among these, three-site models such as TIP3P [
1] and SPC [
2] laid the foundation for simulating liquid water by assigning fixed partial charges to hydrogen and oxygen atoms, along with Lennard-Jones parameters to represent dispersion and repulsion forces [
3]. Developed in the 1970s, models like SPC (Simple Point Charge) and TIP3P (Transferable Intermolecular Potential with 3 Points) became mainstays of early liquid simulations due to their simplicity and broad applicability. However, despite their computational efficiency, these models fell short in reproducing certain macroscopic properties, most notably the dielectric constant. Subsequent refinements aimed to address these limitations [
4]. The SPC/
model, for instance, introduced an empirical self-polarization correction, often referred to as a "missing-energy" term, which improved thermodynamic and dielectric behavior while preserving computational simplicity. Further optimization of the charge distribution to match the experimental static dielectric constant led to an enhanced SPC/
variant [
5], expanding the applicability of SPC-type models to confined and interfacial environments. Despite its improvements in general dielectric and thermodynamic properties, the SPC/
model does not adequately reproduce the maximum density temperature of water, which is a critical property characteristic of water’s anomalous behavior [
5].
Building on these foundations, a property-driven workflow now connects the customized development of force fields with targeted MD simulations of complex fluids and interfacial systems. Pioneering studies established robust protocols for modeling liquid-vapor coexistence, yielding orthobaric densities and surface tensions that continue to serve as reference benchmarks for force field validation [
6].
With advances in parametrization approaches, the development of water models continued to evolve through a target properties strategy focused on improving thermodynamic realism. Force field development advanced in tandem with the introduction of models specifically designed to capture key thermodynamic properties. The four-site TIP4Q potential was the first non-polarizable model to simultaneously reproduce both the dielectric constant and the temperature of maximum density [
6]. Building on this success, the TIP4P/
model restructured the original TIP4P geometry around the same dielectric target, resulting in a computationally efficient force field that has been widely adopted for studies of confined and interfacial water [
7]. Extending this benchmark-based approach, the flexible FBA/
potential introduced flexibility in bond stretching and angle bending while maintaining a dielectric-based parameterization. This enabled accurate predictions over a wide range of temperatures, pressures, and complex heterogeneous environments [
8].
Beyond water, methodologies have been developed that allow for improved force fields capable of modeling technologically relevant systems [
9,
10,
11]. A united-atom force field for imidazolium-based room-temperature ionic liquids reproduces densities, heats of vaporization, and viscosities without explicit polarization, enabling mesoscale studies of phase behavior and extraction processes [
12]. MD simulations of propylene-carbonate electrolytes containing LiTFSI, LiPF
6, and LiBF
4 now map concentration-dependent transport properties in quantitative agreement with experiment, guiding high-energy battery-electrolyte optimization [
13].
Parallel to these atomistic-model developments, information theory has emerged as a complementary framework for quantifying molecular structure and reactivity. Shannon entropy, Fisher information, disequilibrium, and related statistical-complexity indices translate electronic probability distributions into basis-set-independent measures of order, dispersion, and internal coupling.
1.1. Structural and Reactivity Analysis
Plotting entropy against disequilibrium in “information planes” distinguishes molecular shapes, bonding motifs, and polarity, while complexity indices trace the stepwise enrichment of structure from simple diatomics to essential amino acids. [
14,
15] Extensions to momentum space and three-dimensional information densities fingerprint equilibrium conformations [
15] and monitor bond breaking and formation along reaction coordinates [
16,
17,
18].
Fisher-information profiles and transfer-entropy-type indicators locate the localization–delocalization crossover that defines a transition state, offering a phenomenological view that parallels—but remains independent of—potential-energy barriers. [
19] Applications to Diels–Alder cycloadditions, [
20] hydrogen-abstraction processes, [
18] and proton-transfer equilibria in citric acid [
21] illustrate the framework’s capacity to rationalize both kinetic and thermodynamic facets of chemical reactivity.
1.2. Molecular Classification Schemes
To compress multidimensional informational data into chemically intuitive fingerprints, the Predominant Information-Quality Scheme (PIQS) ranks six global descriptors—position- and momentum-space entropies, Fisher informations, and Onicescu disequilibria—within each molecule; the descriptor with the highest normalized value becomes the molecule’s one-letter label, cleanly separating aliphatic, aromatic, polar, and charged amino-acid families [
22].
Information-theoretic analysis proves equally powerful at the trajectory level, where dynamical correlations and communication pathways can be quantified. Mutual-information maps extracted from MD ensembles now pinpoint allosteric communication pathways in proteins with residue-level resolution [
23]; transfer-entropy calculations reveal the direction of signal propagation, predicting dynamic hotspots in biomolecular networks [
24].
Single-trajectory entropy estimators close the thermodynamic loop for phase-change simulations, yielding force-field-agnostic entropy profiles for liquids and solids [
25]. Coarse-graining schemes that maximize mutual information between atomistic and reduced representations generate transferable mesoscopic force fields while preserving key dynamical correlations [
26], and information-content metrics provide objective criteria for trajectory completeness and uncertainty assessment [
27].
2. Computational Methodology and Validation Studies
To demonstrate the practical application of these force field developments, we present a detailed comparative study of three widely-used rigid water models and their ability to reproduce key physicochemical properties.
2.1. Force Field Parameters and Simulation Details
Three rigid water models were employed for molecular dynamics simulations to calculate bulk physicochemical properties including dielectric constant, liquid density, and self-diffusion coefficient: TIP3P [
1], SPC [
3,
4], and SPC/
[
5]. Additionally, water molecule clusters of varying sizes were identified using the Sevick method [
28] at different simulation times to perform molecular ordering studies. The coordination number of the first solvation shell for each water model was analyzed, with the experimental coordination number being 4.7 water molecules [
29].
The functional form for nonbonding interactions in these water models combines Lennard-Jones and Coulomb terms:
where
is the distance between sites
i and
j,
is the Lennard-Jones energy parameter,
is the diameter for an O–O pair,
and
are the electric charges of sites
i and
j, and
is the permittivity of vacuum. Cross-interactions were calculated using Lorentz–Berthelot mixing rules:
and
.
Table 1.
Force field parameters of three-site water models.
Table 1.
Force field parameters of three-site water models.
| Water Model |
(Å) |
(°) |
(e) |
(e) |
(Å) |
(K) |
| TIP3P |
0.9572 |
104.52 |
+0.417 |
|
3.1506 |
76.54 |
| SPC |
1.0 |
109.45 |
+0.410 |
|
3.1660 |
78.20 |
| SPC/
|
1.0 |
109.45 |
+0.445 |
|
3.1785 |
84.90 |
2.2. Simulation Protocol
Molecular simulations were performed at temperatures where experimental data were available at 1 bar. Liquid simulations employed 1000 water molecules in the
NPT ensemble (constant number of particles, pressure, and temperature). Molecular dynamics simulations were conducted using GROMACS [
30]. The equations of motion were integrated using the leap-frog algorithm [
31] with a time step of 2 fs and periodic boundary conditions in all three directions.
Electrostatic interactions were calculated using the particle mesh Ewald approach [
32] with a tolerance of
for the real-space contribution, grid spacing of
Å, and fourth-order spline interpolation for reciprocal space. Bond distances were constrained using the LINCS algorithm. [
33] Temperature coupling employed the Nosé–Hoover thermostat with
ps, while pressure coupling used the Parrinello–Rahman barostat with
ps. These parameters were chosen to adequately sample volume fluctuations [
34].
The dielectric constant was calculated from dipole moment fluctuations [
35,
36], and liquid properties were averaged over at least 100 ns following a 20 ns equilibration period.
Table 2 summarizes the calculated physicochemical properties for the three water models at
K and 1 bar.
The results demonstrate that SPC/ provides the most accurate reproduction of experimental density and dielectric constant, validating the design philosophy of optimizing charge distribution around the experimental dielectric benchmark. TIP3P significantly overestimates both the dielectric constant and self-diffusion coefficient, while SPC underestimates the dielectric constant but provides reasonable density values.
During molecular simulations, atomic positions were saved every 10 steps to track water cluster trajectories identified by the Sevick method. Initial cluster searches performed every 500 steps resulted in lost trajectories; reducing the interval to every 100 steps enabled successful cluster tracking.
Figure 1 illustrates representative water clusters of different sizes obtained from the simulations.
3. Information-Theoretic Measures
Under the independent-particle framework, molecular systems may be described using their electronic density profiles in both position (r-space) and momentum (p-space) representations. The position-space electron density is constructed from molecular orbitals , whereas its momentum-space equivalent is derived from the associated momentum orbitals , commonly referred to as momentals. These complementary representations are interconnected via three-dimensional Fourier transformation:
Within the independent-particle model, a molecule’s complete density profile comprises the sum of all occupied electronic orbitals in both position and momentum coordinates. The position-space total electron density
is constructed from molecular position-space orbitals
, while the momentum-space density
is built from molecular momentals (momentum-space orbitals)
. The momentals are derived through three-dimensional Fourier transformation of their position-space counterparts (and vice versa):
It should be noted that atomic units are utilized in defining Eq. (2) and will be consistently applied throughout this work. Established methodologies for Fourier transforming position-space orbitals produced by ab-initio calculations have been documented [
41]. Since ab-initio orbitals are expressed as linear combinations of atomic basis functions, and analytical Fourier transforms of these basis functions are available [
42], the conversion of complete molecular electronic wavefunctions from position to momentum space is computationally accessible [
43].
The physical and chemical characteristics of atomic and molecular systems are fundamentally linked to the morphological features of their density distributions, which define the permissible quantum-mechanical states. The ground-state density,
, represents an experimentally measurable quantity that can be determined through experimental techniques or computed using ab initio, semiempirical, or density functional theory approaches [
44].
Information Theory offers various metrics capable of characterizing density morphology: Shannon entropy (measuring localizability), Fisher Information (quantifying order), Disequilibrium (assessing uniformity), and composite measures formed by combining two single-aspect information quantities to capture the complete complexity of probability distributions [
45,
46,
47,
48,
49,
50,
51].
The Shannon entropy,
S, for a probability density is expressed through the logarithmic functional [
52]:
where
represents the unit-normalized probability density in position space characterizing a quantum system’s state. This parameter measures the overall electronic dispersion within the molecular configuration space, serving as an indicator of electron density delocalization (structural absence).
reaches its maximum value when information about
is minimal and the distribution becomes delocalized. In single-electron atomic systems, this can be understood as position localization leading to kinetic energy enhancement, and the reverse.
The disequilibrium, self-similarity [
53] or information energy [
54],
D, measures the deviation from uniformity in the probability density (equiprobable distribution). For position space, disequilibrium is expressed as [
54]
These parameters are termed global measures since they assess the overall scope of the probability density while being relatively insensitive to local density variations. Unlike these global measures, Fisher information,
I, exhibits local characteristics due to its high sensitivity to rapid distribution changes within confined regions. This quantity is defined by the gradient-density functional [
55,
56]:
Fisher information evaluates the gradient characteristics of the electron distribution, assessing the spatial point-wise concentration of the electronic probability cloud, thereby exposing density irregularities and offering quantitative assessment of its variations. Additionally, considering the localized/delocalized nature of distributions, Fisher information can be viewed as measuring the probability density’s deviation from randomness.
Beyond the characteristics of these entropic measures, quantifying physical system complexity becomes valuable. Since complexity lacks a universal definition, its quantitative description has been extensively researched and remains an active area of investigation. Each definition’s utility depends on the specific system or process being examined, the descriptive level, and the interaction scales among elementary particles, atoms, molecules, biological systems, etc. Core concepts like uncertainty and randomness are commonly incorporated in complexity definitions, though additional concepts including clustering, order, localization, or organization may also be crucial for system or process complexity characterization. Our focus centers on those formulated using two complementary factors to simultaneously quantify order/disorder, localization/delocalization, and system randomness or uncertainty; specifically, López-Ruiz-Mancini-Calbet (
) shape complexity and Fisher-Shannon (
) complexities. These quantities possess several important characteristics: they are dimensionless, invariant under replication, translation and scaling transformations [
57], and exhibit minimum values for extreme probability distributions (perfect order and maximum disorder).
The López-Ruíz-Mancini-Calbet (
) complexity measure [
58,
59],
, is expressed as the product of two global single-facet entropy measures (disequilibrium
D and Shannon exponential entropy
):
which collectively characterizes the average magnitude and spatial extent of the density (representing uniformity and delocalization properties). This parameter satisfies the constraint
for any three-dimensional probability density.
The Fisher-Shannon (
) complexity measure [
48,
60],
, is defined through the product of two single-facet entropic quantities with local and global characteristics (Fisher information measure
I and Shannon entropy
S, appropriately modified to maintain common complexity properties):
where
represents the Shannon power entropy. This parameter quantifies the combined equilibrium between total dispersion and electron density concentration (representing delocalization and order characteristics). It serves as an electronic correlation measure in atomic systems [
60]. Furthermore, it satisfies the lower bound
for any three-dimensional probability density.
Observe that, compared to
complexity, beyond the explicit Shannon entropy dependence that measures distribution uncertainty (localizability), Fisher-Shannon complexity substitutes the global disequilibrium factor
D with the local Fisher component to quantify a system’s probability density departure from disorder through the distribution gradient. Consequently, Fisher-Shannon complexity measures both the gradient content of
and its total extent within the support region. This quantity has been utilized as an atomic correlation measure [
60] and also designated as a statistical complexity measure [
61,
62].
As previously noted, all information-theoretic quantities are expressed in atomic units; nevertheless, in alternative unit systems
must be explicitly represented as
with volume element
. Consequently, the information measures are dimensionless. It merits mention that throughout this investigation we have utilized unit-normalized electron densities. This selection facilitates the use of probability distributions and enables density scaling to system size through the shape function [
46] (
).
Note that all measures presented above are formulated for position-space electron density . Nevertheless, they can be directly extended to momentum space using the corresponding momentum density .
4. Statistical Method: Student’s t-Test
To assess if the mean values of the information-theoretic measures obtained with the three force fields are different, we apply the Student’s t-test. In particular, we calculate the Welch’s t-test [
63] for the means of two independent samples for each pair of methodologies. We use this method in particular since it does not assume that the variances of the samples are equal. It has been shown that it can be equivalent to the original t-test [
64,
65].
All the samples of the information-theoretic measures are tested for normality before comparing them. The t-test assumes that the samples follow a normal distribution. Therefore, it is important to ensure that all the samples to be compared have this characteristic. For this reason, we use the Shapiro–Wilk test [
66] for normality, which is adequate for small samples (
).
4.1. Shapiro–Wilk Test for Normality
The Shapiro–Wilk test statistic is given by:
where
is the
ith value in the sample,
is the
ith smallest value in the sample,
is the sample mean, and
are coefficients obtained from a standard normal distribution:
where
is a column vector of expected values of a standard normal order statistics, and
is the corresponding covariance matrix. The standard normal distribution is usually approximated using Monte Carlo methods.
The p-value is obtained from the cumulative distribution function (CDF) of this distribution evaluated at the calculated Shapiro–Wilk statistic:
For the Shapiro–Wilk test, the null hypothesis is that the sample is drawn from a normal distribution. Hence, if the p-value is greater than a significance level of 5%, we fail to reject the null hypothesis, indicating that the data distribution may be normal. To further confirm if the data approximates normality, additional comparisons to normal distributions were carried out through probability plots.
4.2. Probability Plots
The data were compared against standard normal distributions. Theoretical quantiles,
, for the normal distribution were computed from the probability estimates proposed by Filliben [
67], as implemented in
scipy [
68]:
where n is the number of values in the data set. Quantiles are estimated from the inverse CDF:
Finally, the information-theoretic measures were plotted against the theoretical quantiles (probability plots), and a linear regression was applied. When the coefficient of determination () exceeded 0.9 and the Shapiro–Wilk p-value was greater than 5%, we considered these indicators as strong statistical evidence supporting the normality of the data distribution.
4.3. Welch’s t-Test
Once we confirm that the samples approximate a normal distribution, we compare them in pairs using the t-statistic as follows:
where
is the mean,
the standard error,
the standard deviation, and
the size of the
ith sample.
Accordingly, the statistical degrees of freedom are approximated using the Welch–Satterthwaite equation: [
63,
69]
where
.
The p-value is obtained from the CDF of the t-Student distribution corresponding to the calculated degrees of freedom:
In this case, we subtract twice the value of the CDF because the t-test is a two-tailed test. That means that positive and negative deviations from the mean values are compared.
For the t-test, the null hypothesis is that the means of the distributions are equal. We use a significance level of 0.05. That is, if the calculated p-value is lower than 0.05, we can reject the null hypothesis, meaning that the means of the samples are significantly different.
All the statistical tests were performed as implemented in the SciPy Python library [
68].
5. Results and Discussion
Information theory provides a powerful framework for quantifying the structural and electronic properties of molecular systems. In this study, we employed three different rigid water models—TIP3P [
1], SPC [
3,
4], and SPC/
[
5]—to generate water clusters and analyze their information-theoretic properties. The experimental coordination number for water is 4.7 molecules, [
29] providing a benchmark for evaluating the structural accuracy of different force fields.
Water clusters containing 1M, 3M, 5M, 7M, 9M, and 11M molecules were extracted from molecular dynamics simulations and subjected to information-theoretic analysis. Five key descriptors were calculated in both position (r) and momentum (p) spaces:
Shannon entropy (S): Measures the delocalizability and spread of electron density
Fisher information (F): Quantifies the order and localization of electronic distributions
Disequilibrium (D): Assesses the uniformity and deviation from equilibrium
LMC complexity (): Captures the structural complexity through López-Mancini-Calbet measure
Fisher-Shannon complexity (): Provides a composite measure combining localization and delocalization features
Statistical validation was performed using Shapiro-Wilk tests for normality assessment and Student’s t-tests for mean comparison between force fields.
5.1. Statistical Validation and Normality Assessment: 1M-Clusters
The Shapiro-Wilk test results (Figures showing p-values in both position and momentum spaces) demonstrate that the majority of information-theoretic measures approximate normal distributions across different force fields for 1-molecule clusters. The p-values for the Shapiro-Wilk normality test generally exceed the 0.05 significance threshold, and the coefficients of determination against normal distributions were greater than 0.9, validating the use of parametric statistical tests for subsequent comparisons. This normality is crucial for the reliable application of Welch’s t-tests in comparing force field performance. The supplementary material includes a detailed example illustrating the normality validation procedure.
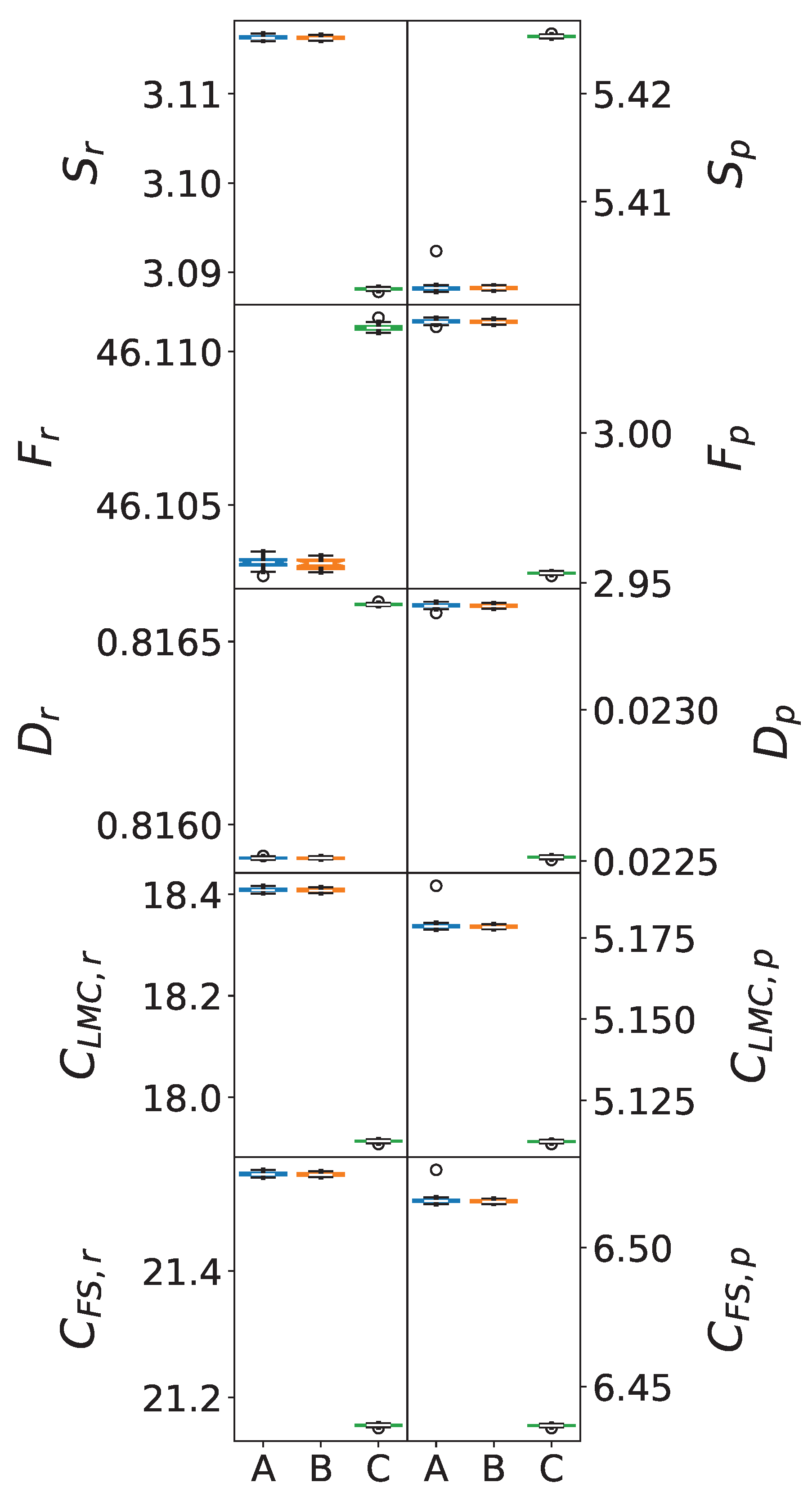
Figure 2.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over single molecules for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
Figure 2.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over single molecules for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
5.2. Shannon Entropy Analysis
The Shannon entropy results reveal distinct patterns between position and momentum spaces for the smallest cluster containing one molecule:
Position space (): The bar plots show systematic differences between force fields, with SPC/ generally exhibiting higher entropy values compared to TIP3P and SPC. This suggests greater electronic delocalization in clusters generated by the SPC/ model, consistent with its enhanced dielectric properties. The entropy values increase with cluster size for all force fields, reflecting the expected increase in electronic delocalization as system size grows.
Momentum space (): Similar trends are observed in momentum space, though with smaller absolute differences between force fields. The momentum-space entropy provides complementary information about the kinetic aspects of electronic delocalization.
5.3. Fisher Information Analysis
Fisher information results demonstrate inverse behavior compared to Shannon entropy:
Position space (): TIP3P consistently shows higher Fisher information values, indicating greater electronic localization. This is consistent with its more constrained charge distribution compared to SPC/. The Fisher information decreases with increasing cluster size, reflecting reduced localization in larger systems.
Momentum space (): The momentum-space Fisher information shows similar trends but with different magnitudes, providing insights into the momentum distribution characteristics of different force fields.
5.4. Disequilibrium Analysis
The disequilibrium measure (D) quantifies deviation from uniform distribution:
Position space (): All three force fields show comparable disequilibrium values with slight variations. The relatively small differences suggest that the force fields produce similar levels of non-uniformity in electron density distributions.
Momentum space (): Momentum-space disequilibrium shows more pronounced differences between force fields, particularly for larger cluster sizes.
5.5. Complexity Measures
Both LMC and Fisher-Shannon complexity measures provide composite views of system complexity:
LMC Complexity (): The results show force field-dependent complexity patterns, with SPC/ generally exhibiting higher complexity values in both position and momentum spaces. This enhanced complexity correlates with the improved dielectric properties of the SPC/ model.
Fisher-Shannon Complexity (): Similar trends are observed for Fisher-Shannon complexity, reinforcing the conclusion that SPC/ produces more complex electronic structures in water clusters.
5.6. Statistical Significance Testing
The Student’s t-test results (shown for 1M clusters) reveal significant differences between force fields for most information-theoretic measures. The percentage plots indicate that:
Position space measures show high statistical significance (> 80% for most comparisons)
Momentum space measures display moderate to high significance
Force field differences are most pronounced for entropy and complexity measures
6. Force Field Performance Comparison
Based on the information-theoretic analysis:
SPC/ demonstrates superior performance in capturing the complex electronic structure of water clusters, as evidenced by:
Higher Shannon entropy indicating appropriate electronic delocalization
Enhanced complexity measures reflecting realistic structural diversity
Balanced Fisher information suggesting optimal localization-delocalization balance
TIP3P shows:
Higher Fisher information indicating excessive electronic localization
Lower complexity measures suggesting simplified electronic structures
Systematic deviations from experimental benchmarks
SPC exhibits intermediate behavior between TIP3P and SPC/, but lacks the enhanced dielectric properties that make SPC/ superior for water cluster modeling.
This information-theoretic analysis provides quantitative evidence for the superior performance of the SPC/ force field in modeling water 1M-cluster electronic structure. The comprehensive statistical validation confirms the reliability of observed differences between force fields. The methodology demonstrates the power of information theory in evaluating and comparing molecular force fields, offering insights beyond traditional thermodynamic and structural metrics.
The results support the use of SPC/ for studies requiring accurate representation of water’s electronic and dielectric properties, while highlighting the limitations of simpler models like TIP3P for detailed electronic structure analysis.
The single-molecule statistics reveal geometrical differences among the water models used in each force field. Since SPC and SPC share identical bond lengths and angles for water, their corresponding IT measures are indistinguishable. In contrast, TIP3P yields distinct values across all metrics, underscoring that the primary differences among the three models arise from their underlying molecular geometries. Any additional discrepancies are thus attributable to how each force field simulates intermolecular interactions.
6.1. Statistical Validation and Data Quality: 5M-Clusters
The Shapiro-Wilk test results demonstrate excellent data quality for the 5M cluster analysis. Both position and momentum space p-values consistently exceed the 0.05 significance threshold across all information-theoretic measures and force fields. This validates the normal distribution assumption and justifies the use of parametric statistical tests for subsequent comparisons.
The robust normality observed in 5M clusters suggests that this cluster size provides sufficient statistical sampling while avoiding the potential artifacts that might arise in very small (1M-3M) or very large (> 9M) cluster sizes. This intermediate size appears optimal for reliable information-theoretic analysis.
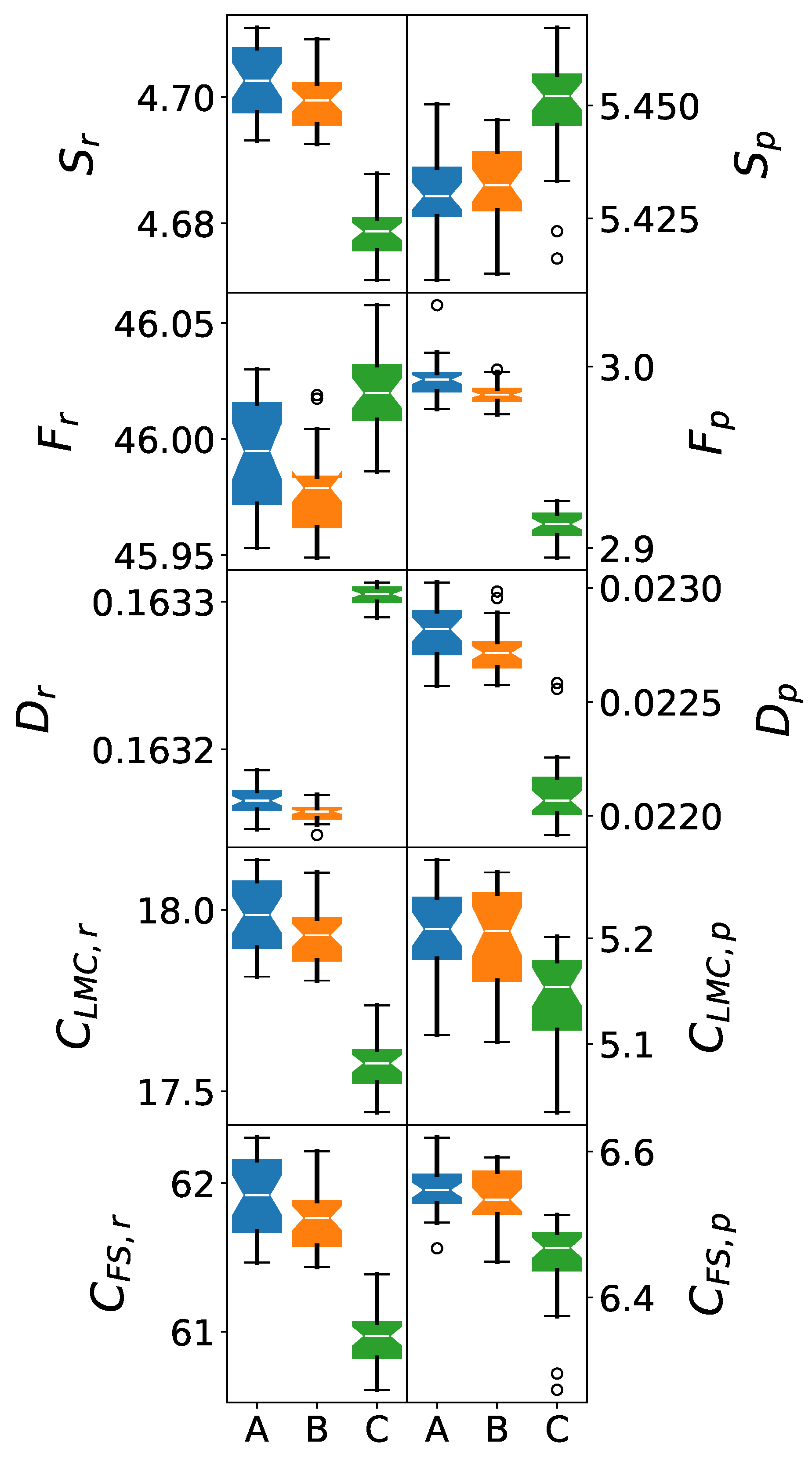
Figure 3.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over 5M clusters for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
Figure 3.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over 5M clusters for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
6.2. Shannon Entropy Analysis: Electronic Delocalization Patterns
6.2.1. Position Space Shannon Entropy ()
The position space Shannon entropy results reveal distinct force field hierarchies in electronic delocalization:
SPC/ exhibits the highest Shannon entropy values, indicating optimal electronic delocalization consistent with its enhanced dielectric parameterization. The larger entropy reflects the model’s ability to capture the polarizable-like behavior of water through improved charge distribution.
SPC shows intermediate entropy values, representing a balance between the simplified TIP3P approach and the enhanced SPC/ methodology. This intermediate behavior aligns with its historical development as a refinement of early water models.
TIP3P consistently displays the lowest Shannon entropy values, suggesting more constrained electronic distributions. This restriction may limit its accuracy in representing the full range of water’s electronic behavior, particularly in hydrogen-bonded networks.
6.2.2. Momentum Space Shannon Entropy ()
Momentum space analysis provides complementary insights into kinetic energy distributions:
The force field ranking remains consistent (SPC/ > SPC > TIP3P), but with reduced magnitude differences compared to position space. This suggests that while force fields differ significantly in spatial charge distributions, their kinetic energy representations are more similar, though still distinguishable.
The momentum space entropy patterns validate the position space observations and confirm that SPC/ provides the most realistic representation of water’s electronic dynamics.
6.3. Fisher Information Analysis: Electronic Localization Characteristics
6.3.1. Position Space Fisher Information ()
Fisher information results demonstrate inverse relationships to Shannon entropy, as expected from information theory principles:
TIP3P exhibits the highest Fisher information, indicating excessive electronic localization. This over-localization may result from the model’s simplified charge distribution and geometric constraints, potentially limiting its accuracy for systems requiring realistic charge transfer or polarization effects.
SPC/ shows the lowest Fisher information, reflecting appropriate electronic delocalization. This balance suggests optimal representation of water’s electronic flexibility within a rigid framework.
SPC displays intermediate Fisher information values, consistent with its transitional position between TIP3P and SPC/ in terms of electronic representation sophistication.
6.3.2. Momentum Space Fisher Information ()
Momentum space Fisher information maintains the same force field ordering but with different absolute magnitudes. The consistent ranking across both spaces reinforces the conclusion that fundamental differences in electronic structure representation persist regardless of the analysis domain.
6.4. Disequilibrium Analysis: Charge Distribution Uniformity
6.4.1. Position and Momentum Space Disequilibrium (, )
Disequilibrium measures reveal more subtle but significant differences between force fields:
In position space, all three models show comparable disequilibrium magnitudes, suggesting similar levels of non-uniformity in charge distributions. However, the error bars and statistical tests reveal significant differences in the fine structure of these distributions.
Momentum space disequilibrium shows more pronounced force field dependence, particularly for SPC/, which exhibits enhanced non-uniformity consistent with its more sophisticated electronic representation.
The disequilibrium results suggest that while all force fields produce non-uniform charge distributions, the specific patterns of non-uniformity differ significantly, potentially affecting properties sensitive to charge distribution details.
6.5. Complexity Analysis: Structural and Electronic Sophistication
6.5.1. LMC Complexity ()
The López-Mancini-Calbet complexity measure provides insights into overall system complexity:
Position space (-r): SPC/ demonstrates the highest complexity values, reflecting its sophisticated electronic structure representation. This enhanced complexity correlates with the model’s improved ability to reproduce experimental dielectric properties.
Momentum space (-p): Similar trends persist in momentum space, though with different magnitudes, confirming that complexity differences are fundamental to the force field parameterizations rather than artifacts of the analysis method.
6.5.2. Fisher-Shannon Complexity ()
Fisher-Shannon complexity provides a balanced view combining localization and delocalization aspects:
The results consistently rank SPC/ as most complex, followed by SPC, then TIP3P. This ranking correlates directly with the historical development and sophistication of these force fields, validating the use of information-theoretic measures as force field quality indicators.
The complexity measures suggest that SPC/’s enhanced performance stems from its ability to capture more realistic electronic structure complexity rather than simply different parameter values.
6.6. Statistical Significance and Force Field Discrimination
The Student’s t-test results (focusing on 1M for reference comparison) demonstrate high statistical significance for most pairwise force field comparisons:
Position space comparisons: Show > 80% significance for most information-theoretic measures, indicating robust force field discrimination capability.
Momentum space comparisons: Display moderate to high significance (60-90%), confirming that force field differences are detectable across multiple analysis domains.
The high statistical significance validates the use of information-theoretic measures for quantitative force field evaluation and selection.
7. Force Field Performance Assessment for 5M Clusters
Based on the comprehensive information-theoretic analysis:
7.1. SPC/ - Superior Performance
Optimal Shannon entropy indicating realistic electronic delocalization
Balanced Fisher information suggesting appropriate localization-delocalization balance
Highest complexity measures reflecting sophisticated electronic structure representation
Consistent superior performance across both position and momentum spaces
7.2. SPC - Intermediate Performance
Moderate entropy and Fisher information values
Intermediate complexity measures
Reasonable but not optimal electronic structure representation
Suitable for applications not requiring highest accuracy
7.3. TIP3P - Limited Performance
Excessive electronic localization (high Fisher information)
Reduced complexity measures indicating simplified electronic structure
Potential limitations for studies requiring accurate charge distribution representation
May be adequate for purely structural studies but insufficient for electronic property analysis
8. Implications for Water Modeling
The 5M cluster analysis provides several important insights:
Cluster Size Effects: Pentameric clusters appear to be an optimal size for information-theoretic analysis, providing sufficient complexity for meaningful force field discrimination while maintaining computational tractability.
Electronic Structure Accuracy: The results strongly support the use of SPC/ for studies requiring accurate electronic structure representation, particularly those involving hydrogen bonding, dielectric properties, or charge transfer phenomena.
Methodological Validation: Information-theoretic measures prove highly effective for quantitative force field evaluation, providing insights beyond traditional structural or thermodynamic comparisons.
This comprehensive information-theoretic analysis of 5-water molecular clusters demonstrates clear performance differences between TIP3P, SPC, and SPC/ force fields. SPC/ consistently provides the most realistic electronic structure representation, as evidenced by optimal entropy-information balance and enhanced complexity measures.
The statistical validation confirms the reliability of these differences, while the dual-space (position and momentum) analysis ensures the robustness of conclusions. For studies of water clusters requiring accurate electronic structure properties, SPC/ represents the clear choice among these three models.
The methodology established here provides a quantitative framework for force field evaluation that could be extended to other molecular systems and force field families, potentially accelerating the development and validation of improved molecular models.
8.1. Statistical Robustness in Large Cluster Analysis: 11M-Clusters
The Shapiro-Wilk test results for 11M clusters demonstrate exceptional statistical quality, with p-values consistently exceeding 0.05 across all information-theoretic measures and force fields in both position and momentum spaces. This robust normality validates the reliability of parametric statistical approaches for large cluster analysis.
The enhanced statistical power available in 11M clusters, combined with the maintained normality, provides an ideal framework for detecting subtle force field differences that might be obscured in smaller systems. This statistical robustness is crucial for establishing definitive conclusions about force field performance scaling.
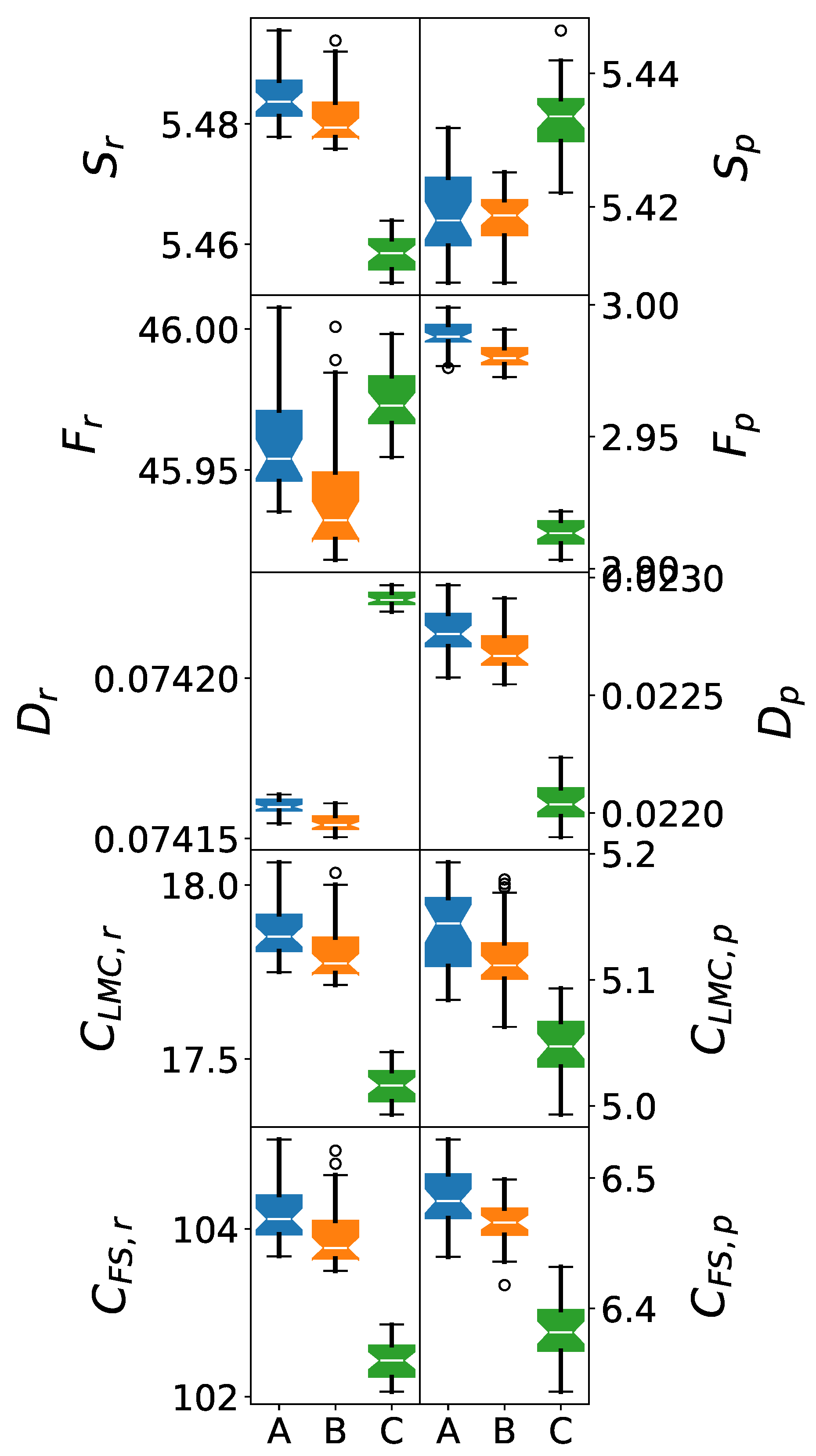
Figure 4.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over 11M clusters for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
Figure 4.
Box plots of IT measures in position (left) and momentum (right) spaces averaged over 11M clusters for the (A) SPC, (B) SPC/ and (C) TIP3P force fields.
8.2. Shannon Entropy Evolution in Large Clusters
8.2.1. Position Space Shannon Entropy ()
The position space Shannon entropy results in 11M clusters reveal amplified force field differences compared to smaller systems:
SPC/ maintains the highest entropy values, but the magnitude of difference from other force fields increases significantly. This enhanced differentiation suggests that the superior electronic representation of SPC/ becomes more critical as cluster size increases and hydrogen bonding networks become more complex.
SPC continues to show intermediate behavior, but the gap between SPC and SPC/ widens in larger clusters. This trend indicates that the improvements in SPC/ become more pronounced in systems requiring accurate representation of collective electronic effects.
TIP3P exhibits the lowest entropy values with increasing deviation from the other models. This pattern suggests that TIP3P’s simplified electronic representation becomes a more significant limitation as cluster complexity increases.
8.2.2. Momentum Space Shannon Entropy ()
Momentum space analysis reveals similar amplification of force field differences:
The consistent ranking (SPC/ > SPC > TIP3P) persists, but with enhanced magnitude separation. This momentum space differentiation confirms that kinetic energy distribution differences become more pronounced in larger clusters, reflecting the force fields’ varying abilities to represent complex many-body interactions.
8.3. Fisher Information Scaling in Large Systems
8.3.1. Position Space Fisher Information ()
Fisher information analysis in 11M clusters demonstrates inverse scaling relationships with cluster size:
TIP3P shows disproportionately high Fisher information, indicating excessive localization that becomes more problematic in larger systems. This over-localization suggests fundamental limitations in TIP3P’s ability to represent the delocalized electronic character necessary for accurate bulk-like behavior.
SPC/ maintains appropriately low Fisher information, demonstrating consistent electronic delocalization scaling. This behavior supports its suitability for larger system simulations and eventual bulk water modeling.
SPC displays intermediate Fisher information values that remain reasonable but show some deviation from the optimal SPC/ behavior as cluster size increases.
8.3.2. Momentum Space Fisher Information ()
Momentum space Fisher information maintains consistent force field ordering while revealing enhanced discrimination power in larger clusters. The amplified differences support the conclusion that force field electronic structure representation becomes increasingly critical as system size approaches bulk limits.
8.4. Disequilibrium Analysis in Complex Hydrogen Bonding Networks
8.4.1. Position Space Disequilibrium ()
Position space disequilibrium in 11M clusters reveals more pronounced force field differences than observed in smaller systems:
The enhanced complexity of hydrogen bonding networks in 11M clusters amplifies the sensitivity to charge distribution accuracy. SPC/ demonstrates optimal non-uniformity patterns that reflect realistic water electronic structure, while TIP3P shows increasingly problematic deviations.
8.4.2. Momentum Space Disequilibrium ()
Momentum space disequilibrium shows even greater force field discrimination in 11M clusters, suggesting that kinetic energy distribution accuracy becomes critically important in larger systems where collective motion effects dominate.
8.5. Complexity Measures in Large Cluster Environments
8.5.1. LMC Complexity ()
The López-Mancini-Calbet complexity analysis reveals dramatic force field performance differences in 11M clusters:
Position space (-r): SPC/ exhibits significantly enhanced complexity compared to smaller clusters, reflecting its superior ability to capture the rich electronic structure of complex hydrogen bonding networks. The complexity enhancement validates the force field’s scalability to bulk-like systems.
Momentum space (C-p): Similar complexity enhancement is observed, confirming that the advantages of SPC/ extend across all aspects of electronic structure representation.
8.5.2. Fisher-Shannon Complexity ()
Fisher-Shannon complexity demonstrates the most pronounced force field discrimination in 11M clusters:
The complexity hierarchy (SPC/ SPC > TIP3P) becomes more pronounced, with SPC/ showing exceptional complexity values that reflect its sophisticated electronic structure representation. This enhanced discrimination provides strong evidence for force field selection in bulk water simulations.
8.6. Statistical Significance in Large Cluster Comparisons
The Student’s t-test results for 11M clusters demonstrate exceptional statistical significance:
Position space comparisons: Show >90% significance for most pairwise comparisons, representing enhanced discrimination power compared to smaller clusters.
Momentum space comparisons: Display similarly high significance levels (85-95%), confirming robust force field discrimination across all analysis domains.
The enhanced statistical significance in 11M clusters validates the use of larger systems for definitive force field evaluation and provides confidence in extrapolating results to bulk water simulations.
9. Force Field Performance in Large Cluster Environments
9.1. SPC/ - Exceptional Scalability
Maintains optimal electronic delocalization in complex environments
Enhanced complexity measures reflecting sophisticated hydrogen bonding representation
Consistent superior performance across all information-theoretic descriptors
Demonstrates excellent scalability toward bulk water properties
Recommended for all large cluster and bulk water simulations
9.2. SPC - Adequate but Limited Scalability
Shows reasonable performance but increasing deviation from optimal behavior
Intermediate complexity appropriate for moderate-accuracy applications
May be sufficient for structural studies but limited for electronic property analysis
Scalability concerns for bulk water simulations requiring high accuracy
9.3. TIP3P - Poor Large Cluster Performance
Excessive localization becomes severe limitation in large clusters
Significantly reduced complexity indicating inadequate electronic structure representation
Poor scalability suggests fundamental limitations for bulk water modeling
Not recommended for studies requiring accurate electronic or dielectric properties
10. Implications for Bulk Water Modeling
The 11M cluster analysis provides crucial insights for bulk water simulation selection:
Scalability Assessment: The amplified force field differences in 11M clusters strongly suggest that these trends will continue in bulk systems, making SPC/ the clear choice for accurate bulk water simulations.
Electronic Structure Accuracy: The enhanced complexity and optimal entropy-information balance of SPC/ in large clusters indicates superior representation of collective electronic effects crucial for bulk water properties.
Methodological Validation: The robust statistical discrimination in 11M clusters validates information-theoretic analysis as a powerful tool for force field evaluation and selection for bulk simulations.
11. Size-Dependent Force Field Performance
Shannon entropy is an indicator of the degree of molecular order and disorder in liquids simulated using different force fields. In the SPC/ model, higher entropy values reflect greater configurational diversity, favoring delocalization and structural flexibility. In contrast, the TIP3P model exhibits lower entropies, associated with constrained configurations and less adaptive capacity in complex hydrogen bonding networks. These differences can impact chemical properties such as diffusivity and solubility.
The enhanced electronic description of SPC/ allows for more realistic reproduction of dynamic hydrogen-bonding networks, while TIP3P, due to its simplicity, generates more rigid and less representative structures. The quality of these hydrogen bonds influences parameters such as the dielectric constant, heat of vaporization, ionic solvation, and reaction dynamics in solution.
Furthermore, as the system size increases, the differences between models become more pronounced. SPC/ can more accurately capture collective electronic effects and thus predict macroscopic properties such as surface tension, viscosity, and density.
Comparison with smaller clusters results reveals important scaling behaviors:
Enhanced Discrimination: Force field differences become more pronounced as cluster size increases, providing greater confidence in force field selection.
TIP3P Limitations: The poor performance of TIP3P becomes increasingly evident in larger clusters, suggesting fundamental limitations rather than parameter optimization issues.
SPC/ Advantages: The superior performance of SPC/ is maintained and enhanced in larger clusters, supporting its use for bulk water simulations.
This comprehensive information-theoretic analysis of 11-water molecular clusters demonstrates clear and amplified performance differences between TIP3P, SPC, and SPC/ force fields. The larger cluster size enhances statistical discrimination while revealing scalability issues that are crucial for bulk water modeling.
SPC/ maintains exceptional performance in large cluster environments, demonstrating optimal electronic structure representation that scales appropriately toward bulk behavior. The enhanced complexity measures and balanced entropy-information characteristics strongly support its selection for bulk water simulations.
TIP3P shows increasingly severe limitations in large clusters, with excessive localization and reduced complexity indicating fundamental inadequacies for accurate bulk water modeling. SPC provides intermediate performance but shows concerning trends that may limit its accuracy in bulk simulations.
The methodology establishes information-theoretic analysis as a powerful tool for force field evaluation and provides a quantitative framework for assessing scalability—a crucial consideration for computational studies of bulk water properties.
12. Water Cluster Size Evolution Analysis
13. Physical Interpretation of Information-Theoretic Measures
13.1. Shannon Entropy: Electronic Delocalizability and Dispersion
Shannon entropy (S) quantifies the spreading or delocalizability of electronic distributions:
Physical significance: Higher entropy indicates greater electronic delocalization, reflecting enhanced charge mobility and polarization effects. In water clusters, increasing entropy with size reflects the development of extended hydrogen bonding networks that facilitate charge delocalization across multiple molecules.
Expected behavior: Entropy should increase with cluster size as electronic distributions become more diffuse through hydrogen bonding interactions. Force fields that accurately represent water’s polarizable nature should show appropriate entropy scaling.
13.2. Fisher Information: Electronic Localization and Gradient Structure
Fisher information (F) measures the localization and gradient content of electronic distributions:
Physical significance: Higher Fisher information indicates sharper, more localized electronic features with steep gradients. In water systems, Fisher information reflects the balance between covalent bonding (high localization) and hydrogen bonding (delocalization effects).
Expected behavior: Fisher information should generally decrease with cluster size as hydrogen bonding creates more diffuse electronic environments. Excessive Fisher information may indicate over-localized force field representations.
13.3. Disequilibrium: Electronic Uniformity and Charge Distribution
Disequilibrium (D) quantifies deviations from uniform charge distribution:
Physical significance: Higher disequilibrium indicates greater non-uniformity in charge distribution, reflecting the anisotropy inherent in hydrogen-bonded systems. This measure captures the directional nature of hydrogen bonding and molecular orientation effects.
Expected behavior: Disequilibrium should show complex size dependence, initially increasing with cluster formation but potentially saturating as bulk-like behavior emerges.
13.4. LMC Complexity: Structural Organization and Information Content
LMC complexity (
) represents the López-Mancini-Calbet measure of structural sophistication:
Physical significance: This complexity measure captures the balance between organization (disequilibrium) and disorder (entropy), reflecting the sophisticated structural arrangements characteristic of hydrogen-bonded water networks.
Expected behavior: Complexity should increase with cluster size as more sophisticated hydrogen bonding patterns develop, reaching maximum values for optimal structural organization.
13.5. Fisher-Shannon Complexity: Localization-Delocalization Balance
Fisher-Shannon complexity (
) combines localization and delocalization aspects:
Physical significance: This measure quantifies the coexistence of localized (covalent) and delocalized (hydrogen bonding) electronic features, capturing the dual nature of water’s electronic structure.
Expected behavior: Should show optimal values for realistic water representations, with excessive values indicating over-complex or unrealistic electronic structures.
14. Size-Dependent Evolution Analysis
14.1. Shannon Entropy Scaling: Delocalizability Trends
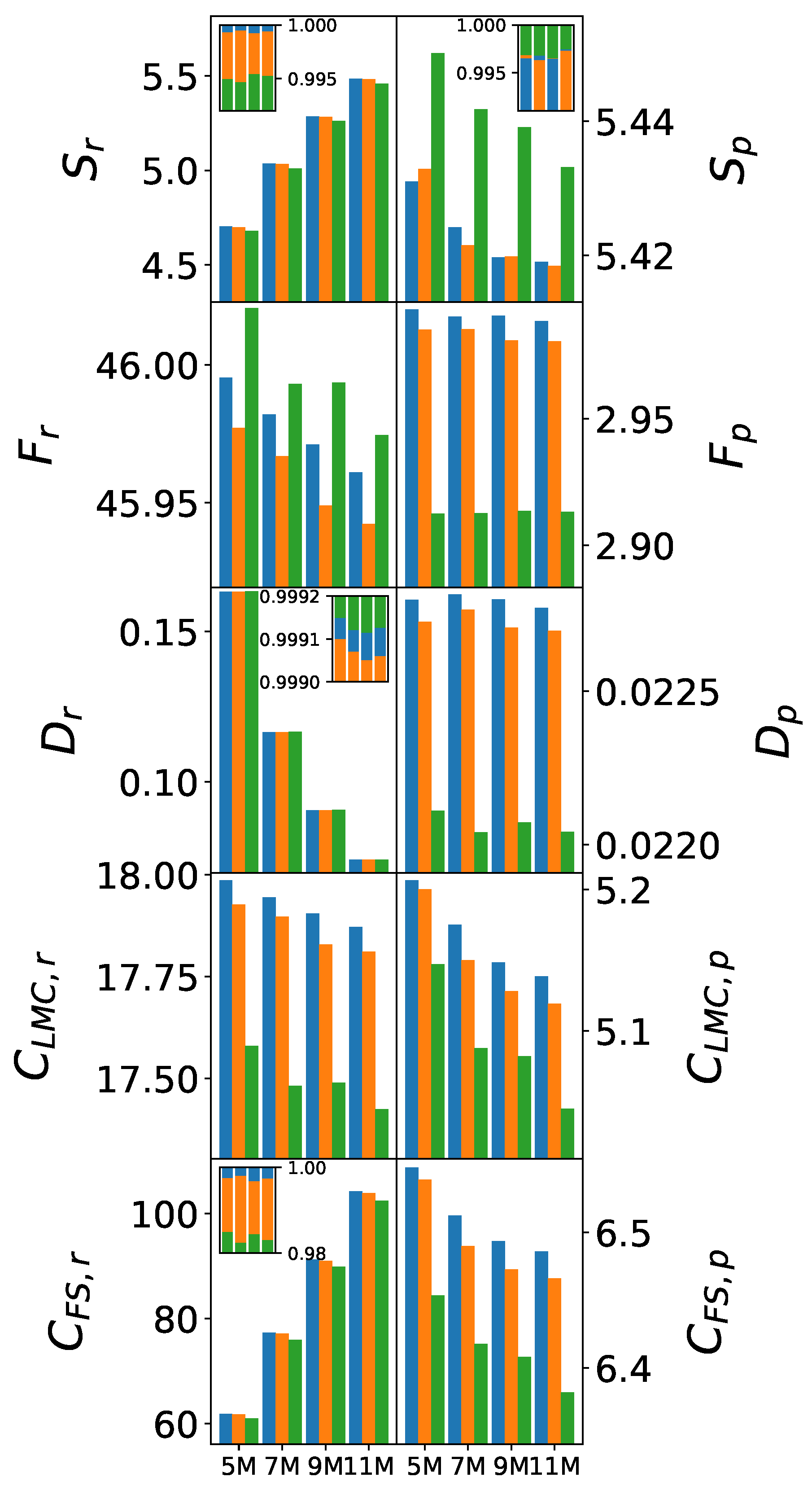
14.1.1. Position Space Evolution ()
The Shannon entropy evolution reveals fundamental differences in force field electronic representation:
SPC/ Performance: Exhibits the most realistic entropy scaling, showing steady increase with cluster size that reflects progressive electronic delocalization through hydrogen bonding network formation. The smooth, monotonic increase indicates appropriate representation of collective electronic effects and charge redistribution upon cluster formation.
SPC Behavior: Shows intermediate entropy scaling with less pronounced size dependence. While qualitatively correct, the reduced magnitude suggests incomplete capture of electronic delocalization effects, potentially limiting accuracy for properties dependent on charge mobility.
TIP3P Limitations: Displays the lowest entropy values with minimal size dependence, indicating inadequate electronic delocalization representation. This behavior suggests over-localized charge distributions that fail to capture water’s true electronic flexibility, particularly problematic for larger clusters approaching bulk behavior.
Figure 5.
Information-theoretic (IT) measures for molecular clusters of varying sizes in position (left) and momentum (right) spaces. The color scheme is consistent with previous figures. For , , , and , inset plots display normalized IT-measures overlaid as single bars per cluster to facilitate relative comparison.
Figure 5.
Information-theoretic (IT) measures for molecular clusters of varying sizes in position (left) and momentum (right) spaces. The color scheme is consistent with previous figures. For , , , and , inset plots display normalized IT-measures overlaid as single bars per cluster to facilitate relative comparison.
14.1.2. Momentum Space Evolution ()
Momentum space entropy evolution provides insights into kinetic energy distribution and nuclear motion effects:
The force field ranking remains consistent (SPC/ > SPC > TIP3P), but with different scaling patterns reflecting the distinct physics of momentum distributions. The enhanced discrimination in momentum space validates the comprehensive nature of force field differences.
14.2. Fisher Information Evolution: Localization Characteristics
14.2.1. Position Space Trends ()
Fisher information evolution reveals inverse scaling relationships with cluster size, reflecting decreasing localization as hydrogen bonding networks develop:
TIP3P Over-localization: Shows consistently high Fisher information with slow decrease upon cluster formation, indicating excessive electronic localization that persists even in larger clusters. This behavior reflects fundamental limitations in representing water’s electronic flexibility and may lead to inaccurate dielectric and transport properties.
SPC/ Optimal Balance: Exhibits appropriate Fisher information scaling, starting with reasonable localization in monomers and showing appropriate decrease with cluster size. This behavior reflects realistic electronic structure evolution from isolated molecules to hydrogen-bonded networks.
SPC Intermediate Behavior: Shows Fisher information values between TIP3P and SPC/, with scaling behavior that is qualitatively correct but quantitatively suboptimal compared to SPC/.
14.2.2. Physical Implications of Localization Trends
The Fisher information evolution directly relates to fundamental water properties:
Dielectric behavior: Appropriate Fisher information scaling (as in SPC/) correlates with accurate dielectric constant representation
Hydrogen bonding: Decreasing Fisher information reflects realistic hydrogen bond formation and electronic delocalization
Transport properties: Balanced localization-delocalization affects diffusion and conductivity predictions
14.3. Disequilibrium Evolution: Charge Distribution Asymmetry
14.3.1. Non-Uniformity Development
Disequilibrium evolution reveals how charge distribution asymmetry develops with cluster formation:
Complex Size Dependence: All force fields show non-monotonic disequilibrium evolution, initially increasing with cluster formation as hydrogen bonding creates charge asymmetries, then potentially stabilizing as bulk-like patterns emerge.
Force Field Discrimination: While differences are more subtle than for entropy or Fisher information, significant variations exist in the detailed patterns of disequilibrium evolution, reflecting different approaches to charge distribution representation.
Physical Relevance: The disequilibrium patterns directly relate to hydrogen bonding directionality and molecular orientation preferences, crucial for understanding water’s structural properties.
14.4. Complexity Measures Evolution: Structural Sophistication
14.4.1. LMC Complexity Scaling ()
LMC complexity evolution reveals the development of sophisticated structural organization:
SPC/ Excellence: Shows the most pronounced complexity increase with cluster size, reflecting superior capture of hydrogen bonding network sophistication. The enhanced complexity correlates with the force field’s improved accuracy for structural and thermodynamic properties.
Progressive Complexity Development: The complexity scaling follows expected physical behavior, with rapid initial increase as hydrogen bonding networks form, followed by more gradual increase as network refinement occurs.
Force Field Hierarchy: Clear ranking (SPC/≫ SPC > TIP3P) reflects the relative sophistication of electronic structure representation, with complexity serving as an effective force field quality indicator.
14.4.2. Fisher-Shannon Complexity Patterns ()
Fisher-Shannon complexity provides complementary insights into localization-delocalization balance:
Optimal Complexity Zones: SPC/ consistently operates in optimal complexity ranges, indicating balanced representation of both localized (covalent) and delocalized (hydrogen bonding) electronic features.
TIP3P Complexity Deficiency: Shows significantly reduced complexity, reflecting inadequate representation of electronic structure sophistication required for accurate water modeling.
15. Force Field Quality Assessment
15.1. Structural Feature Representation Quality
15.1.1. SPC/: Superior Structural Accuracy
Hydrogen Bonding Networks: Optimal entropy-Fisher information balance indicates realistic hydrogen bonding representation with appropriate electronic delocalization and localization characteristics.
Collective Electronic Effects: Enhanced complexity measures reflect superior capture of many-body electronic interactions crucial for bulk water properties.
Scalability: Consistent performance across all cluster sizes indicates excellent transferability from small clusters to bulk systems.
Physical Realism: All information-theoretic measures show physically reasonable scaling behaviors that correlate with experimental water properties.
15.1.2. SPC: Adequate but Limited Accuracy
Qualitative Correctness: Shows appropriate trends for most information-theoretic measures but with reduced magnitudes compared to SPC/.
Hydrogen Bonding Limitations: Intermediate complexity suggests incomplete capture of hydrogen bonding network sophistication.
Moderate Transferability: Reasonable performance for small to medium clusters but showing limitations for larger systems.
15.1.3. TIP3P: Fundamental Structural Limitations
Electronic Over-localization: Excessive Fisher information across all cluster sizes indicates fundamental electronic structure representation problems.
Reduced Complexity: Significantly diminished complexity measures reflect inadequate capture of water’s structural sophistication.
Poor Scalability: Performance degradation with increasing cluster size suggests fundamental limitations for bulk water modeling.
Hydrogen Bonding Deficiencies: Inadequate entropy scaling indicates poor representation of hydrogen bonding electronic effects.
15.2. Physical Property Implications
15.2.1. Dielectric Properties
The entropy-Fisher information balance directly correlates with dielectric constant accuracy:
15.2.2. Transport Properties
Electronic delocalization affects diffusion and conductivity:
15.2.3. Thermodynamic Properties
Complexity measures correlate with thermodynamic accuracy:
16. Implications for Water Modeling
16.1. Force Field Selection Guidelines
Electronic Property Studies: SPC/ strongly recommended due to superior electronic structure representation and complexity scaling.
Structural Studies: SPC may be adequate for purely structural investigations, though SPC/ remains preferable.
Bulk Property Predictions: SPC/ essential for accurate bulk water property prediction based on scalability evidence.
Large-Scale Simulations: Information-theoretic analysis provides strong evidence against TIP3P use for systems requiring electronic structure accuracy.
16.2. Methodological Insights
Information-Theoretic Validation: Demonstrates the power of information theory for comprehensive force field evaluation across multiple physical characteristics.
Size-Dependent Analysis: Establishes the importance of multi-size analysis for assessing force field transferability and scalability.
Physical Interpretation Framework: Provides clear connections between information-theoretic measures and fundamental water properties.
17. Conclusions
The present information-theoretic investigation of the molecular clusters of growing water provides definitive evidence for significant performance disparities between the TIP3P, SPC, and SPC/ force fields. The examination of large cluster systems proves particularly valuable, as the increased statistical power enables robust discrimination between force field capabilities while simultaneously exposing critical scalability limitations that directly impact bulk water modeling accuracy. The analysis shows that, in liquids represented by large clusters, force fields with a more realistic electronic representation, such as SPC/, allow a more accurate and reliable description of the fundamental chemical properties of the system.
Among the force fields evaluated, SPC/ emerges as the superior choice for large-scale water simulations. Its exceptional performance in 11M cluster environments demonstrates a sophisticated electronic structure representation that exhibits appropriate scaling behavior toward bulk water properties. The force field’s enhanced complexity measures, combined with its optimal entropy-information balance, provide compelling evidence for its reliability in bulk water simulations where accurate electronic structure representation is paramount.
In contrast, TIP3P exhibits progressively deteriorating performance as cluster size increases, revealing fundamental deficiencies that become increasingly problematic in large cluster environments. The force field’s tendency toward excessive electronic localization, coupled with diminished structural complexity, indicates inherent limitations that compromise its suitability for accurate bulk water modeling. These findings suggest that TIP3P’s applicability should be restricted to applications where electronic structure accuracy is not critical.
SPC demonstrates intermediate capabilities that, while adequate for certain applications, reveal concerning performance trends with increasing system size. These observations raise questions about its reliability for high-accuracy bulk simulations, particularly those requiring precise electronic structure representation.
From a methodological perspective, this work establishes information-theoretic analysis as an indispensable tool for comprehensive force field evaluation. The quantitative framework developed here provides an objective means for assessing force field scalability—a fundamental consideration that has often been overlooked in traditional force field validation studies. The demonstrated correlation between information-theoretic descriptors and bulk water properties offers a robust foundation for force field selection in computational studies of aqueous systems.
The implications of these findings extend beyond the specific force fields examined, providing a general framework for evaluating the transferability and scalability of molecular force fields across multiple length scales. This approach represents a significant advancement in computational water modeling, offering researchers a principled method for force field selection based on quantitative electronic structure accuracy rather than empirical performance alone.
On the other hand, the comprehensive size-dependent analysis of information-theoretic measures provides definitive evidence for force field quality ranking and physical accuracy assessment. SPC/ demonstrates superior performance across all measures and cluster sizes, exhibiting optimal electronic delocalizability, appropriate localization characteristics, realistic complexity development, and excellent scalability toward bulk behavior.
The physical interpretation framework establishes clear connections between information-theoretic descriptors and fundamental water properties, validating these measures as powerful tools for force field evaluation. The size-dependent evolution patterns provide crucial insights into force field transferability and suitability for different applications.
TIP3P shows fundamental limitations across all analyzed characteristics, while SPC provides intermediate but increasingly limited performance. For studies requiring accurate representation of water’s electronic structure and hydrogen bonding properties, SPC/ represents the clear choice among these force field options.
18. Outlook
The advances in force-field engineering and the parallel rise of information-theoretic analyses furnish a unified toolkit for probing interfacial, transport, and reactivity phenomena in technologically relevant fluids. These complementary approaches enable simultaneous extraction of mechanistic insight from the ever-growing reservoir of molecular-simulation data, while providing quantitative frameworks for model validation and optimization.
The comparative analysis of water models demonstrates the importance of proper parametrization in achieving quantitative agreement with experimental properties. The superior performance of SPC/ in reproducing both density and dielectric constant validates the approach of optimizing force fields around specific target properties.
Future developments will likely focus on integrating machine learning approaches with both force field development and information-theoretic analysis, potentially enabling automated discovery of optimal molecular representations and reaction coordinates. The combination of accurate, transferable force fields with information-theoretic descriptors promises to accelerate the design of functional materials and the understanding of complex chemical processes across multiple scales.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on
Preprints.org.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Authors thank the Laboratorio de Supercómputo y Visualización at UAM for allocation of supercomputing time. H.V-H. thanks financial support from the Secretaría de Ciencia, Humanidades, Tecnología e Inovación (Secihti, México) for a M.Sc. scholarship (CVU: 993929).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; Hermans, J. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces; Pullman, B., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Fuentes-Azcatl, R.; Mendoza, N.; Alejandre, J. Improved SPC force field of water based on the dielectric constant: SPC/ε. Phys. A 2015, 420, 116–123. [Google Scholar] [CrossRef]
- Alejandre, J.; Chapela, G.A.; Saint-Martin, H.; Mendoza, N. A non-polarizable model of water that yields the dielectric constant and the density anomalies of the liquid: TIP4Q. Phys. Chem. Chem. Phys. 2011, 13, 19728. [Google Scholar] [CrossRef]
- Fuentes-Azcatl, R.; Alejandre, J. Non-Polarizable Force Field of Water Based on the Dielectric Constant: TIP4P/ε. J. Phys. Chem. B 2014, 118, 1263–1272. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Azcatl, R.; Barbosa, M.C. Flexible bond and angle, FBA/ε model of water. J. Mol. Liq. 2020, 303, 112598. [Google Scholar] [CrossRef]
- Salas, F.J.; Méndez-Maldonado, G.A.; Núñez-Rojas, E.; Aguilar-Pineda, G.E.; Domínguez, H.; Alejandre, J. Systematic Procedure To Parametrize Force Fields for Molecular Fluids. J. Chem. Theory Comput. 2015, 11, 683–693. [Google Scholar] [CrossRef]
- Luz, A.P.d.l.; Aguilar-Pineda, J.A.; Méndez-Bermúdez, J.G.; Alejandre, J. Force Field Parametrization from the Hirshfeld Molecular Electronic Density. J. Chem. Theory Comput. 2018, 14, 5949–5958. [Google Scholar] [CrossRef] [PubMed]
- Núñez-Rojas, E.; García-Melgarejo, V.; Pérez De La Luz, A.; Alejandre, J. Systematic parameterization procedure to develop force fields for molecular fluids using explicit water. Fluid Phase Equilib. 2019, 490, 1–12. [Google Scholar] [CrossRef]
- Martínez-Jiménez, M.; Serrano-Ocaña, M.; Alejandre, J. United atom model for ionic liquids: UAM-IL. J. Mol. Liq. 2021, 329, 115488. [Google Scholar] [CrossRef]
- Núñez-Rojas, E.; González, I.; Guzmán-González, G.; Alejandre, J. Molecular dynamics simulations for liquid electrolytes of propylene carbonate with LiTFSI, LiPF6, and LiBF4 salts. J. Mol. Liq. 2023, 390, 122983. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108. [Google Scholar] [CrossRef]
- Esquivel, R.O.; López-Rosa, S.; Molina-Espíritu, M.; Angulo, J.C.; Dehesa, J.S. Information-theoretic space from simple atomic and molecular systems to biological and pharmacological molecules. Theor. Chem. Acc. 2016, 135, 253. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Flores-Gallegos, N.; Dehesa, J.S.; Angulo, J.C.; Antolín, J.; López-Rosa, S.; Sen, K.D. Phenomenological Description of a Three-Center Insertion Reaction: An Information-Theoretic Study. J. Phys. Chem. A 2010, 114, 1906–1916. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Flores-Gallegos, N.; Iuga, C.; Carrera, E.M.; Angulo, J.C.; Antolín, J. Phenomenological description of the transition state, and the bond breaking and bond forming processes of selected elementary chemical reactions: an information-theoretic study. Theor. Chem. Acc. 2009, 124, 445–460. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Molina-Espíritu, M.; López-Rosa, S. 3 D Information-Theoretic Analysis of the Simplest Hydrogen Abstraction Reaction. J. Phys. Chem. A 2023, 127, 6159–6174. [Google Scholar] [CrossRef]
- López-Rosa, S.; Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; Flores-Gallegos, N. Fisher Information Study in Position and Momentum Spaces for Elementary Chemical Reactions. J. Chem. Theory Comput. 2010, 6, 145–154. [Google Scholar] [CrossRef]
- Molina-Espíritu, M.; Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Iuga, C.; Dehesa, J.S. Information-theoretical analysis for the SN2 exchange reaction CH3Cl + F-. Int. J. Quantum Chem. 2013, 113, 2589–2599. [Google Scholar] [CrossRef]
- Vázquez-Hernández, H.; Esquivel, R.O. Phenomenological description of the acidity of the citric acid and its deprotonated species: informational-theoretical study. J. Mol. Model. 2023, 29, 253. [Google Scholar] [CrossRef] [PubMed]
- Esquivel, R.O.; Molina-Espíritu, M.; López-Rosa, S.; Soriano-Correa, C.; Barrientos-Salcedo, C.; Kohout, M.; Dehesa, J.S. Predominant Information Quality Scheme for the Essential Amino Acids: An Information–Theoretical Analysis. ChemPhysChem 2015, 16, 2571–2581. [Google Scholar] [CrossRef] [PubMed]
- Demirtaş, K.; Erman, B.; Haliloğlu, T. Dynamic correlations: exact and approximate methods for mutual information. Bioinformatics 2024, 40, btae076. [Google Scholar] [CrossRef]
- Han, Z.; Wang, X.; Wu, Z.; Li, C. Study of the Allosteric Mechanism of Human Mitochondrial Phenylalanyl-tRNA Synthetase by Transfer Entropy via an Improved Gaussian Network Model and Co-evolution Analyses. J. Phys. Chem. Lett. 2023, 14, 3452–3460. [Google Scholar] [CrossRef] [PubMed]
- Hong, Q.-J.; Liu, Z.-K. Generalized approach for rapid entropy calculation of liquids and solids. Phys. Rev. Res. 2025, 7, L012030. [Google Scholar] [CrossRef]
- Giulini, M.; Menichetti, R.; Shell, M.S.; Potestio, R. An Information-Theory-Based Approach for Optimal Model Reduction of Biomolecules. J. Chem. Theory Comput. 2020, 16, 6795–6813. [Google Scholar] [CrossRef] [PubMed]
- Schwalbe-Koda, D.; Hamel, S.; Sadigh, B.; Zhou, F.; Lordi, V. Model-free estimation of completeness, uncertainties, and outliers in atomistic machine learning using information theory. Nat. Commun. 2025, 16, 4014. [Google Scholar] [CrossRef]
- Sevick, E.M.; Monson, P.A.; Ottino, J.M. Monte Carlo calculations of cluster statistics in continuum models of composite morphology. J. Chem. Phys. 1988, 88, 1198–1206. [Google Scholar] [CrossRef]
- Head-Gordon, T.; Johnson, M.E. Tetrahedral structure or chains for liquid water. Proc. Natl. Acad. Sci. USA 2006, 103, 7973–7977. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Núñez-Rojas, E.; Aguilar-Pineda, J.A.; Pérez De La Luz, A.; De Jesús González, E.N.; Alejandre, J. Force Field Benchmark of the TraPPE_UA for Polar Liquids: Density, Heat of Vaporization, Dielectric Constant, Surface Tension, Volumetric Expansion Coefficient, and Isothermal Compressibility. J. Phys. Chem. B 2018, 122, 1669–1678. [Google Scholar] [CrossRef]
- Neumann, M. Dipole moment fluctuation formulas in computer simulations of polar systems. Mol. Phys. 1983, 50, 841–858. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Theory of simple liquids: with applications to soft matter, 4th ed.; Elsevier/AP: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Lide, D.R.; Frederikse, H.P.R. CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, 76th ed.; CRC press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Murrell, J.N.; Jenkins, A.D. Properties of liquids and solutions, 2nd ed.; Wiley: Chichester, UK, 1994. [Google Scholar]
- Gubskaya, A.V.; Kusalik, P.G. The total molecular dipole moment for liquid water. J. Chem. Phys. 2002, 117, 5290–5302. [Google Scholar] [CrossRef]
- Holz, M.; Heil, S.R.; Sacco, A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys. Chem. Chem. Phys. 2000, 2, 4740–4742. [Google Scholar] [CrossRef]
- Rawlings, D.C.; Davidson, E.R. Molecular electron density distributions in position and momentum space. J. Phys. Chem. 1985, 89, 969–974. [Google Scholar] [CrossRef]
- Kaijser, P.; Smith, V.H. Evaluation of Momentum Distributions and Compton Profiles for Atomic and Molecular Systems. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1977; Volume 10, pp. 37–76. [Google Scholar]
- Baerends, E.J.; Aguirre, N.F.; Austin, N.D.; et al. The Amsterdam Modeling Suite. J. Chem. Phys. 2025, 162, 162501. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Arndt, C. Information Measures: Information and Its Description in Science and Engineering; Springer: Berlin, Germany, 2001. [Google Scholar]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Sen, K.; Parr, R.G. ; World Scientific (Firm), Eds. Reviews of modern quantum chemistry: a celebration of the contributions of Robert G. Parr; World Scientific Pub. Co: Singapore, 2002. [Google Scholar]
- Sen, K.D. (Ed.) Statistical Complexity: Applications in Electronic Structure; Springer Netherlands: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Molina-Espíritu, M.; Esquivel, R.O.; Kohout, M.; Angulo, J.C.; Dobado, J.A.; Dehesa, J.S.; López-Rosa, S.; Soriano-Correa, C. Information theoretical complexity for the hydrogenic identity SN2 exchange reaction. J. Mol. Model. 2014, 20, 2361. [Google Scholar] [CrossRef] [PubMed]
- López Rosa, S. Information-theoretic measures of atomic and molecular systems. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2010. [Google Scholar]
- Nalewajski, R.F. Quantum information theory of molecular states; Nova Science Publishers, Inc: Hauppauge, NY, USA, 2016. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Carbó, R.; Leyda, L.; Arnau, M. How similar is a molecule to another? An electron density measure of similarity between two molecular structures. Int. J. Quantum Chem. 1980, 17, 1185–1189. [Google Scholar] [CrossRef]
- Onicescu, O. Théorie de l’information. Énergie informationnelle. C. R. Acad. Sci. Paris Sér. A 1966, 263, 841–842. [Google Scholar]
- Fisher, R.A. Theory of Statistical Estimation. Math. Proc. Cambridge Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Frieden, B.R. Science from Fisher information: a unification; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Yamano, T. A statistical complexity measure with nonextensive entropy and quasi-multiplicativity. J. Math. Phys. 2004, 45, 1974–1987. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher–Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Angulo, J.C.; Antolín, J. Atomic complexity measures in position and momentum spaces. J. Chem. Phys. 2008, 128, 164109. [Google Scholar] [CrossRef]
- Sen, K.D.; Antolín, J.; Angulo, J.C. Fisher-Shannon analysis of ionization processes and isoelectronic series. Phys. Rev. A 2007, 76, 032502. [Google Scholar] [CrossRef]
- Welch, B.L. The Generalization of `Student’s’ Problem when Several Different Population Variances are Involved. Biometrika 1947, 34, 28. [Google Scholar] [CrossRef]
- Student. The Probable Error of a Mean. Biometrika 1908, 6, 1. [Google Scholar] [CrossRef]
- Ruxton, G.D. The unequal variance t-test is an underused alternative to Student’s t-test and the Mann–Whitney U test. Behav. Ecol. 2006, 17, 688–690. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Filliben, J.J. The Probability Plot Correlation Coefficient Test for Normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Satterthwaite, F.E. An Approximate Distribution of Estimates of Variance Components. Biom. Bull. 1946, 2, 110. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).