Submitted:
21 August 2025
Posted:
22 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
2.1. Data Center Layout Issues
2.2. Optimization Models for Siting Problems
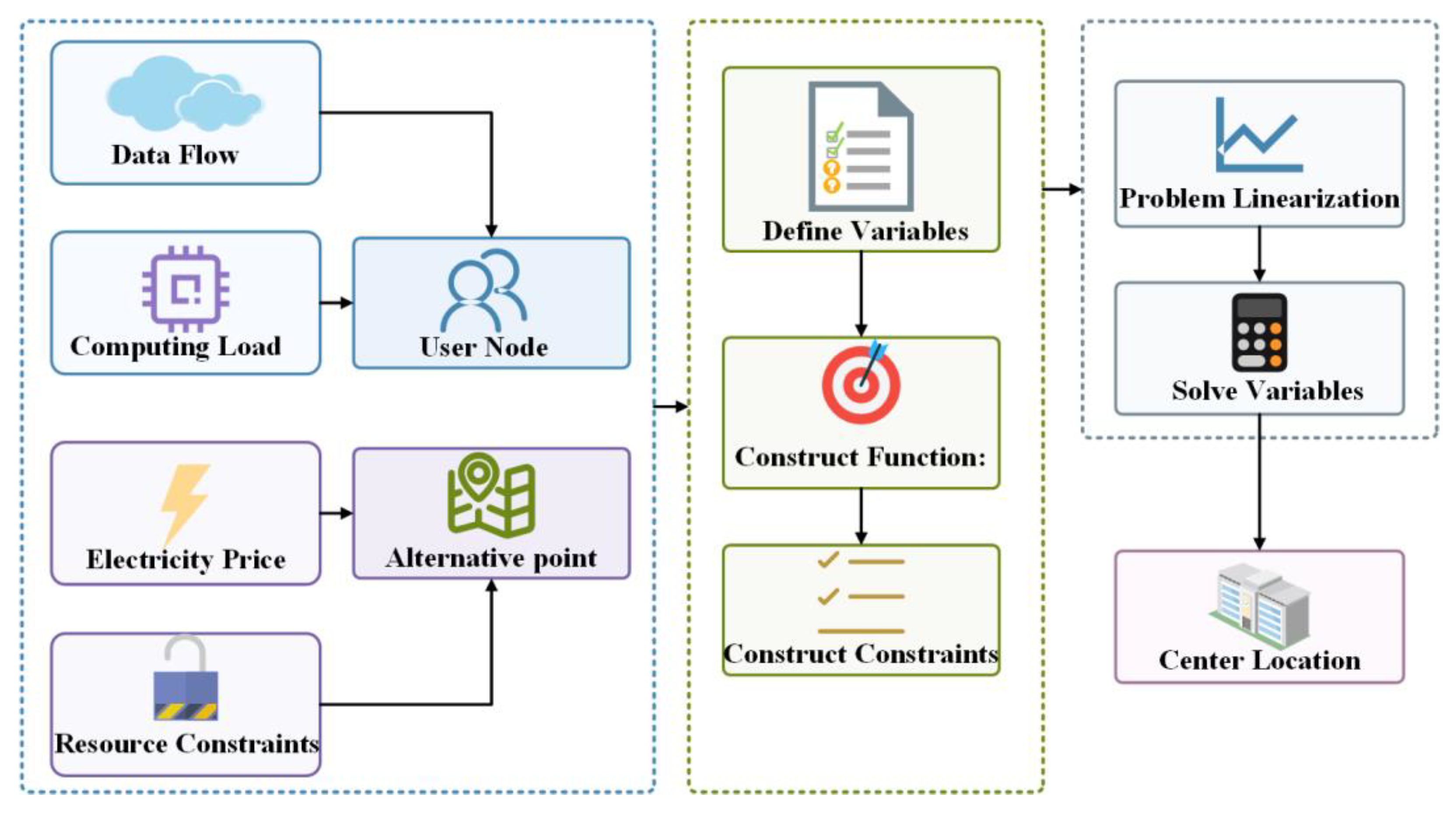
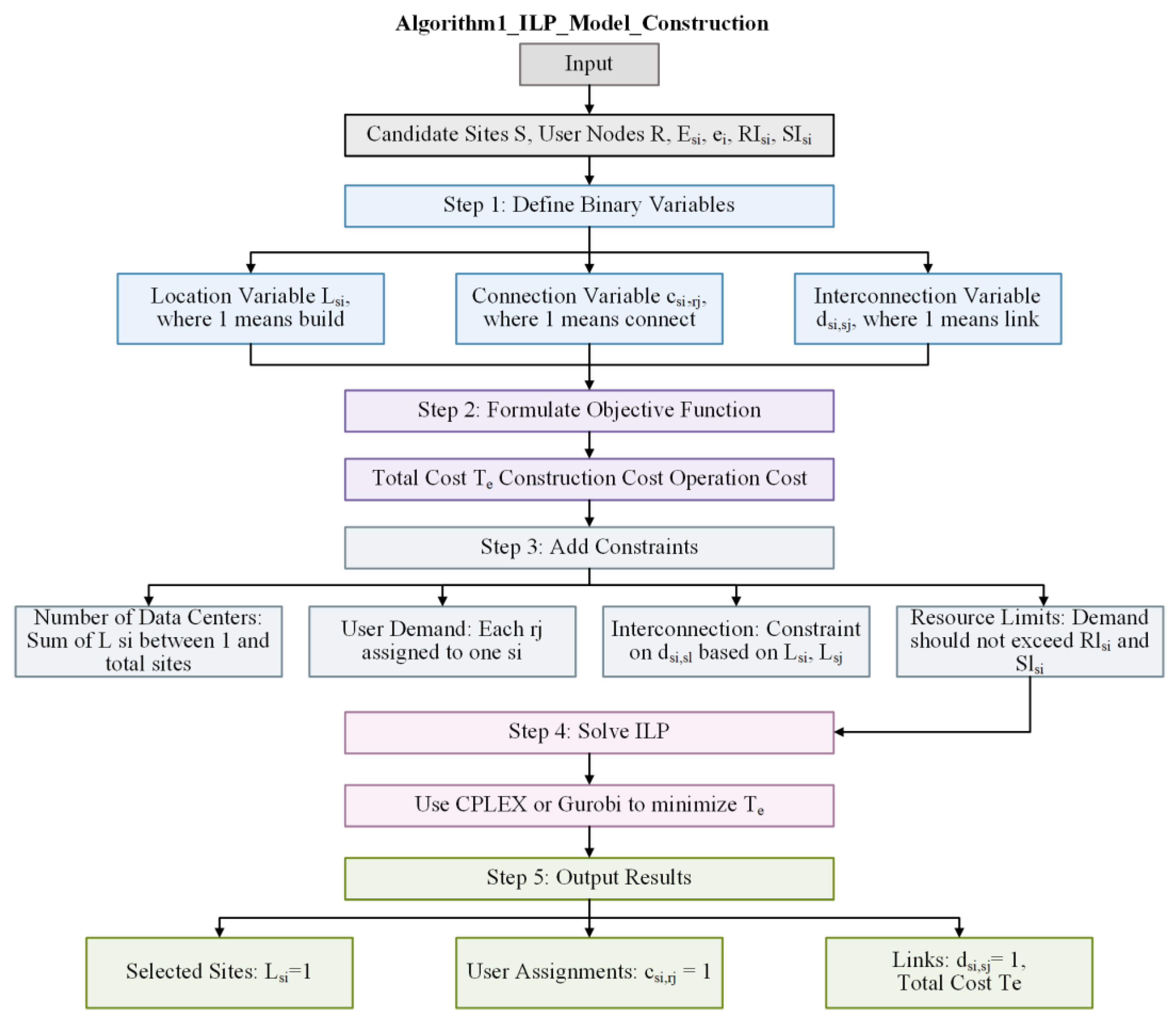
3. Methodology
3.1. Definition and Characteristics of User Demand Nodes and Alternative Points
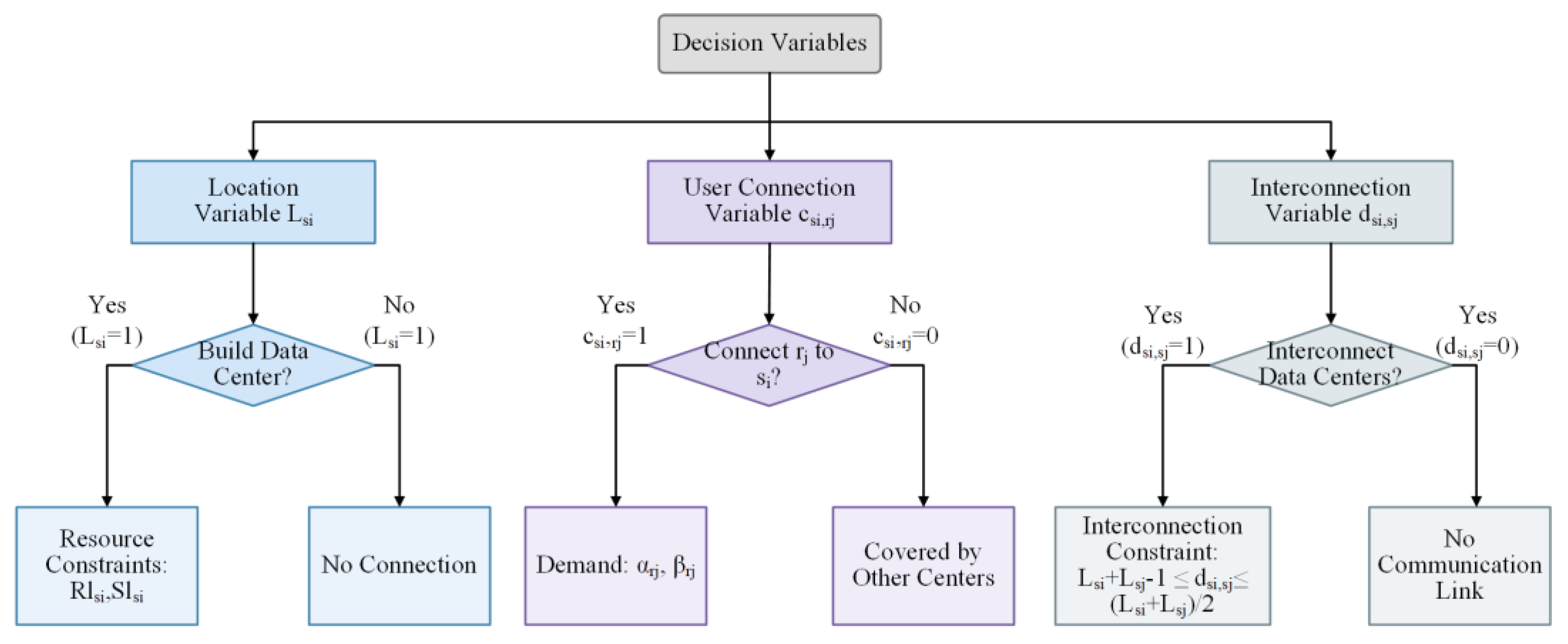
3.2. Identification and Analysis of Decision Variables
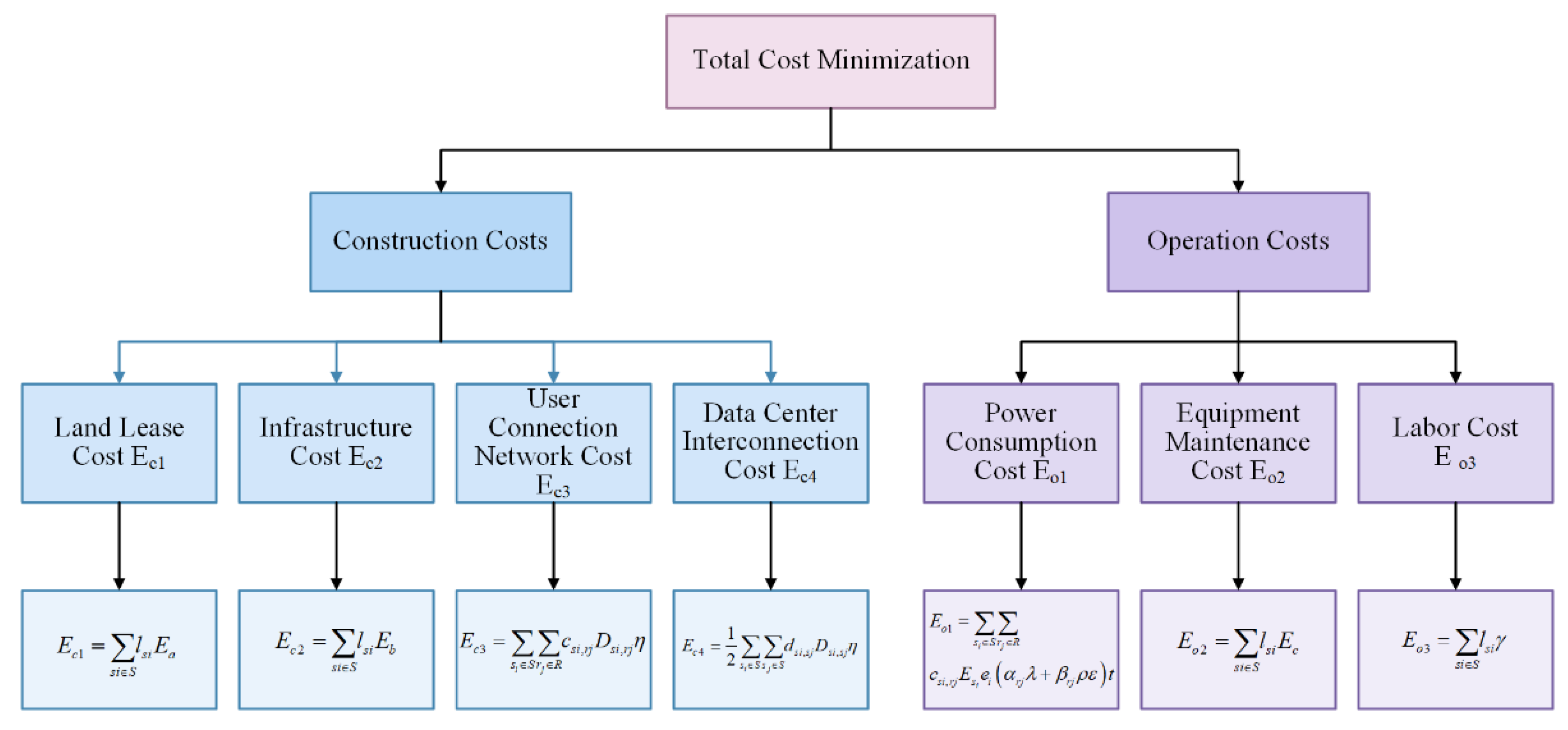
3.2. Design of Objective Function and Constraints
4. Experiment
4.1. Condition Setting
4.2. Experimental Results and Analysis
5. Conclusions
References
- Chen, Zhao, et al. "Scene Chinese Recognition with Local and Global Attention." Pattern Recognition 158.000(2025). [CrossRef]
- Z. Chen, "Arbitrary Shape Text Detection With Discrete Cosine Transform and CLIP for Urban Scene Perception in ITS," in IEEE Transactions on Intelligent Transportation Systems. [CrossRef]
- Wang, Jiao'e, Du Fangye, and Xiao Fan. Spatial evolution of new infrastructure and its determinants: A case study of big data centers. [J] Journal of Geographical Sciences 78.2 (2023): 259-272.
- Li, Yuan, et al. Spatial characteristics and location selection of global data center expansion. [J] Journal of Geographical Sciences 78.8 (2023): 1936-1954.
- Chen, Min, et al. "Internet data centers participating in demand response: A comprehensive review." Renewable and Sustainable Energy Reviews 117 (2020): 109466. [CrossRef]
- Liang, G. U. O., et al. "Research on key technologies of data center parameter automatic optimization based on machine learning." Information and Communications Technology and Policy 46.6 (2020): 21.
- You, Yang, et al. "Imagenet training in minutes." Proceedings of the 47th international conference on parallel processing. 2018.
- Zhang, Qingxia, et al. "A survey on data center cooling systems: Technology, power consumption modeling and control strategy optimization." Journal of Systems Architecture 119 (2021): 102253. [CrossRef]
- Goiri, Ínigo, et al. "Intelligent placement of datacenters for internet services." 2011 31st International Conference on Distributed Computing Systems. IEEE, 2011.
- Hans, Ronny, et al. "Setting Priorities-A Heuristic Approach for Cloud Data Center Selection." CLOSER. 2015.
- Wang, Jiaoe, Du Fangye, and Xiao Fan. "Spatial evolution of new infrastructure and its determinants: A case study of big data centers". Journal of Geographical Sciences, 27.12 (2021): 259 - 272.
- Turek, Dirk, and Peter Radgen. "Optimized data center site selection—Mesoclimatic effects on data center energy consumption and costs." Energy Efficiency 14.3 (2021): 33. [CrossRef]
- Yan, Wenrui, et al. "LT-TCO: A TCO Calculation Model of Data Centers for Long-Term Data Preservation." 2019 IEEE International Conference on Networking, Architecture and Storage (NAS). IEEE, 2019.
- Li, Chenliang, Xiaobing Yu, and Wen-Xuan Zhao. "An integrated approach to site selection for a big data center using PROMETHEE-MCGP methodology." Journal of Intelligent & Fuzzy Systems 41.6 (2021): 6495-6515. [CrossRef]
- Turek, Dirk, and Peter Radgen. "Optimized data center site selection—Mesoclimatic effects on data center energy consumption and costs." Energy Efficiency 14.3 (2021): 33. [CrossRef]
- Wang, Shun, et al. Low carbonlocation-routing problem based on evolutionary hyper-heuristic algorithm of ant colony selection mechanism. [J] Computer Integrated Manufacturing Systems 26.6 (2020): 1702-1716.
- Wang, Yawen. Research on location optimization of power supplies distribution center based on carbon constraints. [J] Shanghai Energy Conservation 12 (2020): 1427-1432.
- Ghaderi, Abdolsalam, and Morteza Momeni. "A multi-period maximal coverage model for locating simultaneous ground and air emergency medical services facilities." Journal of Ambient Intelligence and Humanized Computing 12 (2021): 1577-1600. [CrossRef]
- Colombo, Fabio, Roberto Cordone, and Guglielmo Lulli. "The multimode covering location problem." Computers & operations research 67 (2016): 25-33.
- Drakulić, Darko, Aleksandar Takači, and Miroslav Marić. "New model of maximal covering location problem with fuzzy conditions." Computing and informatics 35.3 (2016): 635-652.
- Sudtachat, Kanchala, Maria E. Mayorga, and Laura A. Mclay. "A nested-compliance table policy for emergency medical service systems under relocation." Omega 58 (2016): 154-168. [CrossRef]
- Stanimirović, Zorica, et al. "A two-phase optimization method for solving the multi-type maximal covering location problem in emergency service networks." Information Technology and Control 46.1 (2017): 100-117. [CrossRef]
- Mišković, Stefan. "A VNS-LP algorithm for the robust dynamic maximal covering location problem." OR Spectrum 39.4 (2017): 1011-1033. [CrossRef]
- Arana-Jiménez, Manuel, Víctor Blanco, and Elena Fernández. "On the fuzzy maximal covering location problem." European Journal of Operational Research 283.2 (2020): 692-705. [CrossRef]
- Wang, Wei, et al. "Emergency facility location problems in logistics: Status and perspectives." Transportation research part E: logistics and transportation review 154 (2021): 102465.
- Toregas, Constantine, et al. "The location of emergency service facilities." Operations research 19.6 (1971): 1363-1373. [CrossRef]
- Perera, Piyaruwan Harindra Kaluthantirige. Recharging infrastructure planning for electric vehicles: a lifecycle thinking approach. Diss. University of British Columbia, 2020.
- Xia, Yangsheng, et al. "Two-layer path planning for multi-area coverage by a cooperative ground vehicle and drone system." Expert Systems with Applications 217 (2023): 119604. [CrossRef]
- Su, Qiang, Qinyi Luo, and Samuel H. Huang. "Cost-effective analyses for emergency medical services deployment: A case study in Shanghai." International Journal of Production Economics 163 (2015): 112-123. [CrossRef]
- Syahputra, Rizki Agam, Prima Denny Sentia, and Riski Arifin. "Determining Optimal New Waste Disposal Facilities Location by Using Set Covering Problem Algorithm." Conference on Broad Exposure to Science and Technology 2021 (BEST 2021). Atlantis Press, 2022.
- Liu, Jingkuang, et al. "Optimization of site selection for emergency medical facilities considering the SEIR model." Computational Intelligence and Neuroscience 2022.1 (2022): 1912272. [CrossRef]
- Çelik, Serdar, and Şeyda Ok. "Electric vehicle charging stations: Model, algorithm, simulation, location, and capacity planning." Heliyon 10.7 (2024).
- Jabbarzadeh, Armin, Behnam Fahimnia, and Stefan Seuring. "Dynamic supply chain network design for the supply of blood in disasters: A robust model with real world application." Transportation research part E: logistics and transportation review 70 (2014): 225-244. [CrossRef]
- Bayram, Vedat, Barbaros Ç. Tansel, and Hande Yaman. "Compromising system and user interests in shelter location and evacuation planning." Transportation research part B: methodological 72 (2015): 146-163. [CrossRef]
- Shahriari, Milad, et al. "Bi-objective approach for placing ground and air ambulance base and helipad locations in order to optimize EMS response." The American journal of emergency medicine 35.12 (2017): 1873-1881. [CrossRef]
- Murad, Abdulkader, et al. "Optimizing health service location in a highly urbanized city: Multi criteria decision making and P-Median problem models for public hospitals in Jeddah City, KSA." Plos one 19.1 (2024): e0294819. [CrossRef]
- Calik, Hatice, Martine Labbé, and Hande Yaman. "p-Center problems." Location science (2015): 79-92.
- Gwalani, Harsha, et al. "A distributed algorithm for solving large-scale p-median problems using expectation maximization." PeerJ Computer Science 10 (2024): e2446. [CrossRef]
- Ren, Zhi-Gang, et al. "New ideas for applying ant colony optimization to the set covering problem." Computers & Industrial Engineering 58.4 (2010): 774-784. [CrossRef]
- Razi, Nasuh, and Mumtaz Karatas. "A multi-objective model for locating search and rescue boats." European Journal of Operational Research 254.1 (2016): 279-293. [CrossRef]
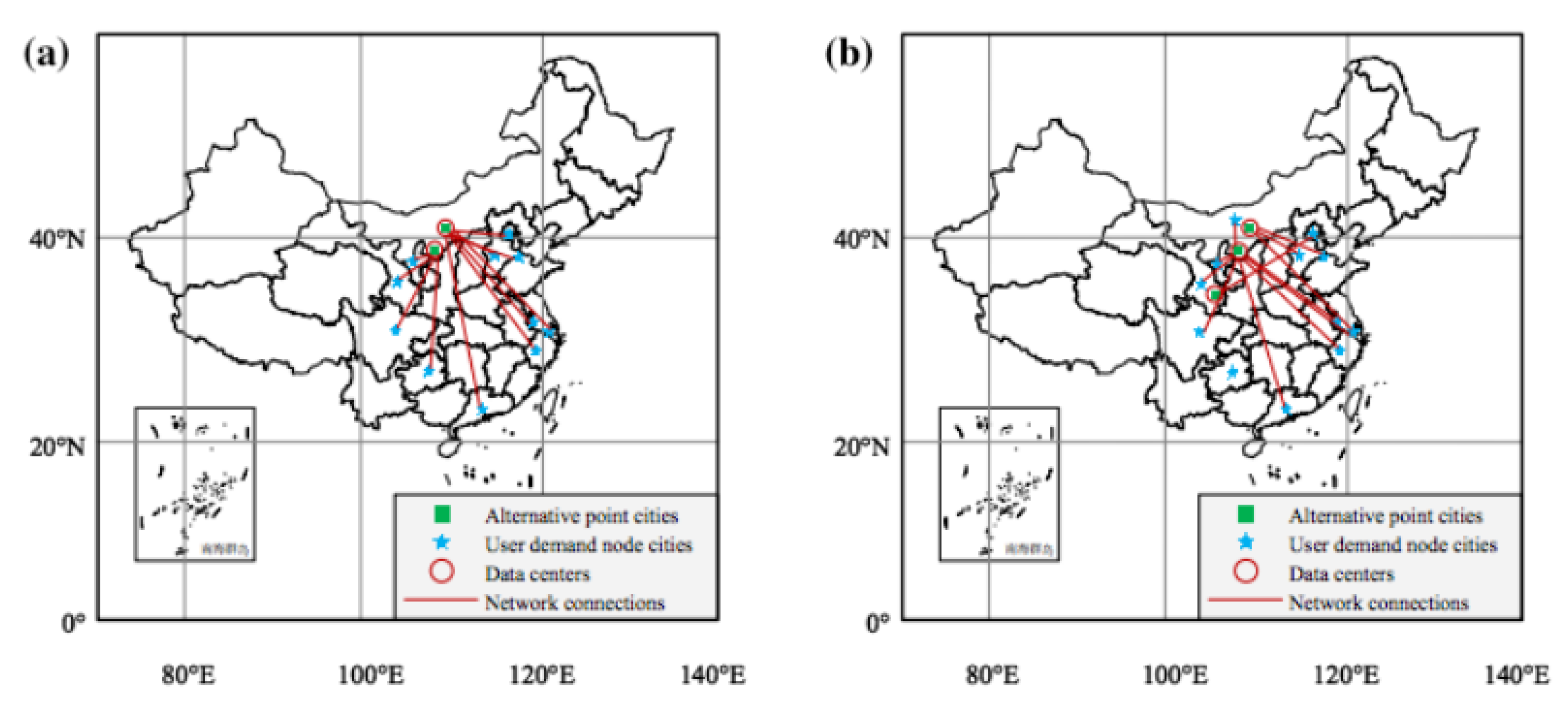
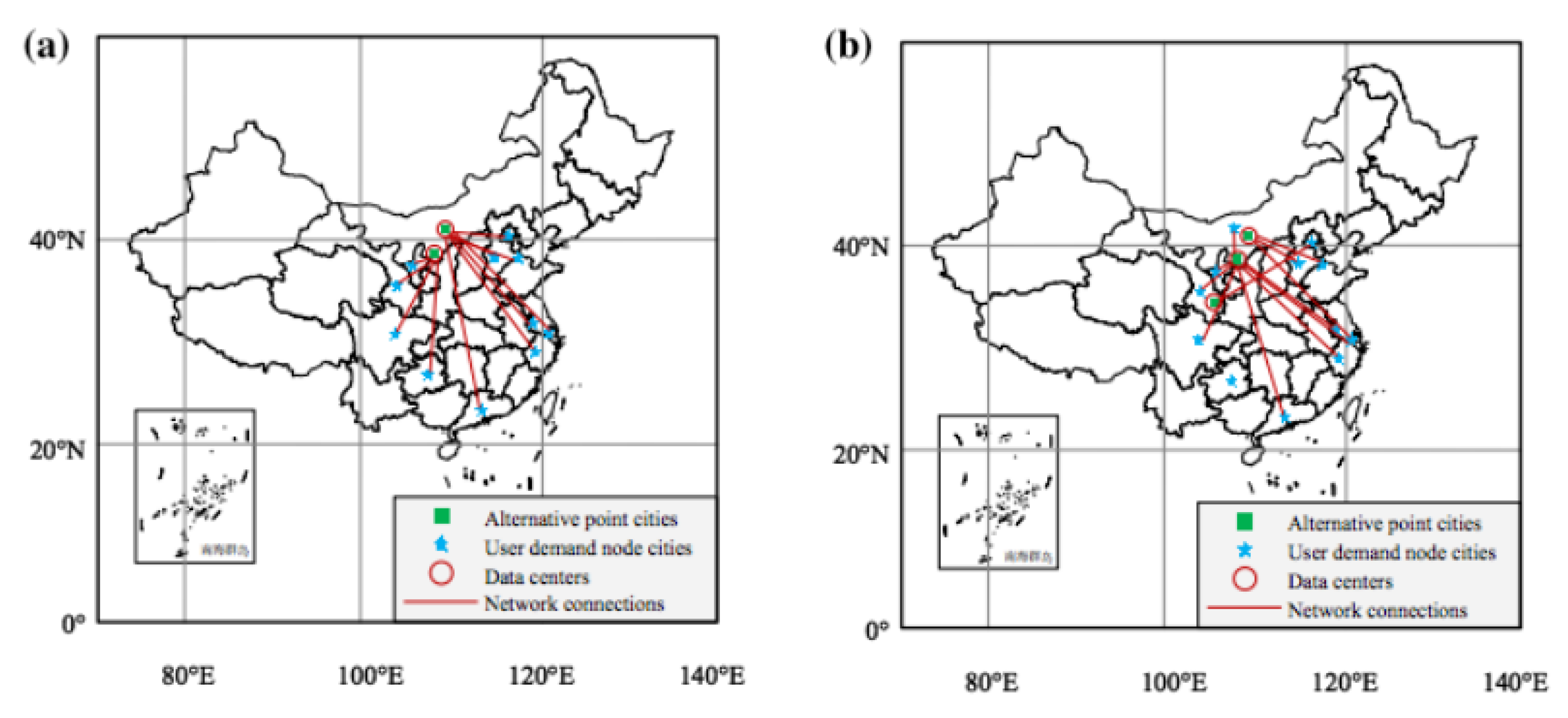
| Alternative point cities | Conventional baseline scenario | Energy efficiency scenario | ||
| Electricity prices | Efficiency | Electricity prices | Efficiency | |
| Langfang | 0.44 | 1.49 | 0.44 | 1.25 |
| Hefei | 0.48 | 1.49 | 0.48 | 1.25 |
| Zhuhai | 0.57 | 1.49 | 0.57 | 1.25 |
| Mianyang | 0.43 | 1.49 | 0.43 | 1.25 |
| Baotou | 0.31 | 1.49 | 0.31 | 1.2 |
| Zunyi | 0.36 | 1.49 | 0.36 | 1.2 |
| Lanzhou | 0.39 | 1.49 | 0.39 | 1.2 |
| Yinchuan | 0.32 | 1.49 | 0.32 | 1.2 |
| Province | User demand node | Longitude/oE | latitude/oE | αri/MIPS | βri/Mbps |
| Inner Mongolia | Hohhot | 111.75 | 40.84 | 1.54×10^11 | 2.64×10^7 |
| Beijing | Beijing | 116.41 | 39.9 | 4.49×10^10 | 7.70×10^7 |
| Tianjin | Tianjin | 117.19 | 39.13 | 3.34×10^10 | 5.91×10^7 |
| Ningxia | Yinchuan | 106.23 | 38.49 | 4.09×10^10 | 7.01×10^7 |
| Hebei | Shijiazhuang | 114.5 | 38.05 | 1.55×10^11 | 2.66×10^7 |
| Gansu | Lanzhou | 103.83 | 36.06 | 5.42×10^10 | 9.30×10^7 |
| Jiangsu | Nanjing | 118.77 | 32.04 | 2.51×10^11 | 4.31×10^7 |
| Shanghai | Shanghai | 121.47 | 31.23 | 6.20×10^10 | 1.06×10^7 |
| Sichuan | Chengdu | 104.07 | 30.57 | 4.53×10^10 | 7.99×10^7 |
| Zhejiang | Hangzhou | 120.15 | 30.29 | 1.90×10^11 | 3.26×10^7 |
| Guizhou | Guiyang | 106.71 | 26.58 | 6.24×10^10 | 1.07×10^7 |
| Guangzhou | Shenzhen | 114.06 | 22.54 | 3.24×10^11 | 5.12×10^7 |
| Province | Alternative point | Longitude/oE | latitude/oE | Rlsi/MIPS | Slsi/Mbps |
| Hebei | Langfang | 116.71 | 39.53 | 1.80×10^12 | 1.01×10^17 |
| Anhui | Hefei | 117.27 | 31.86 | 1.49×10^12 | 7.93×10^16 |
| Guangdong | Zhuhai | 113.56 | 22.27 | 2.95×10^12 | 1.63×10^17 |
| Sichuan | Mianyang | 104.73 | 31.47 | 1.79×10^12 | 1.02×10^17 |
| Inner Mongolia | Baotou | 109.84 | 40.65 | 2.82×10^12 | 1.49×10^17 |
| Guizhou | Zunyi | 106.93 | 27.73 | 1.38×10^12 | 7.13×10^16 |
| Gansu | Tianshui | 105.73 | 34.58 | 1.12×10^12 | 5.71×10^16 |
| Ningxia | Wuzhong | 106.20 | 37.98 | 1.02×10^12 | 5.73×10^16 |
| Parameter | Meaning | Unit | Data |
| ρ | Data Storage Duration | day | 365 |
| λ | Processor Computing Power Consumption | kW/MIPS | 2.8×10^−5 |
| ε | Storage Device Power Consumption | kW/Mbit | 3.7×10^−10 |
| η | Cost per Unit Length of Optical Fiber Network | ¥/km | 7200 |
| t | Design Lifespan of Data Center | year | 12 |
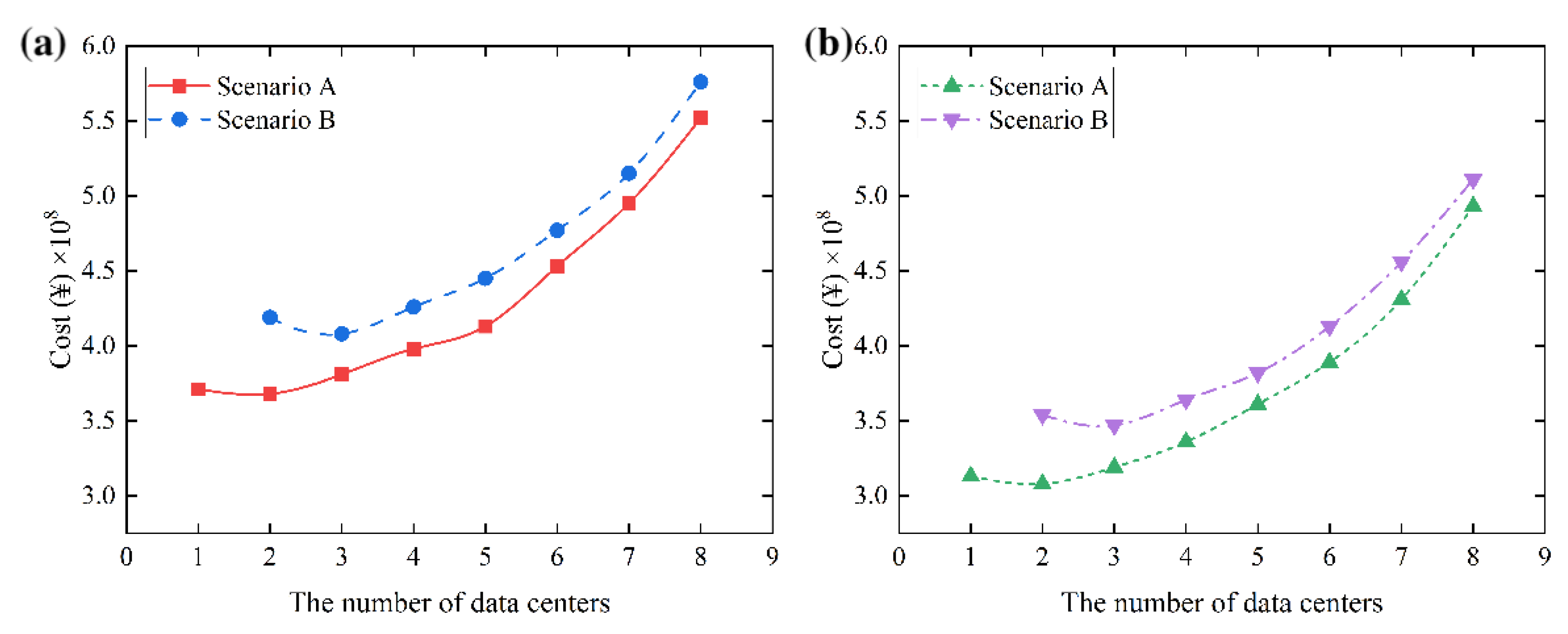
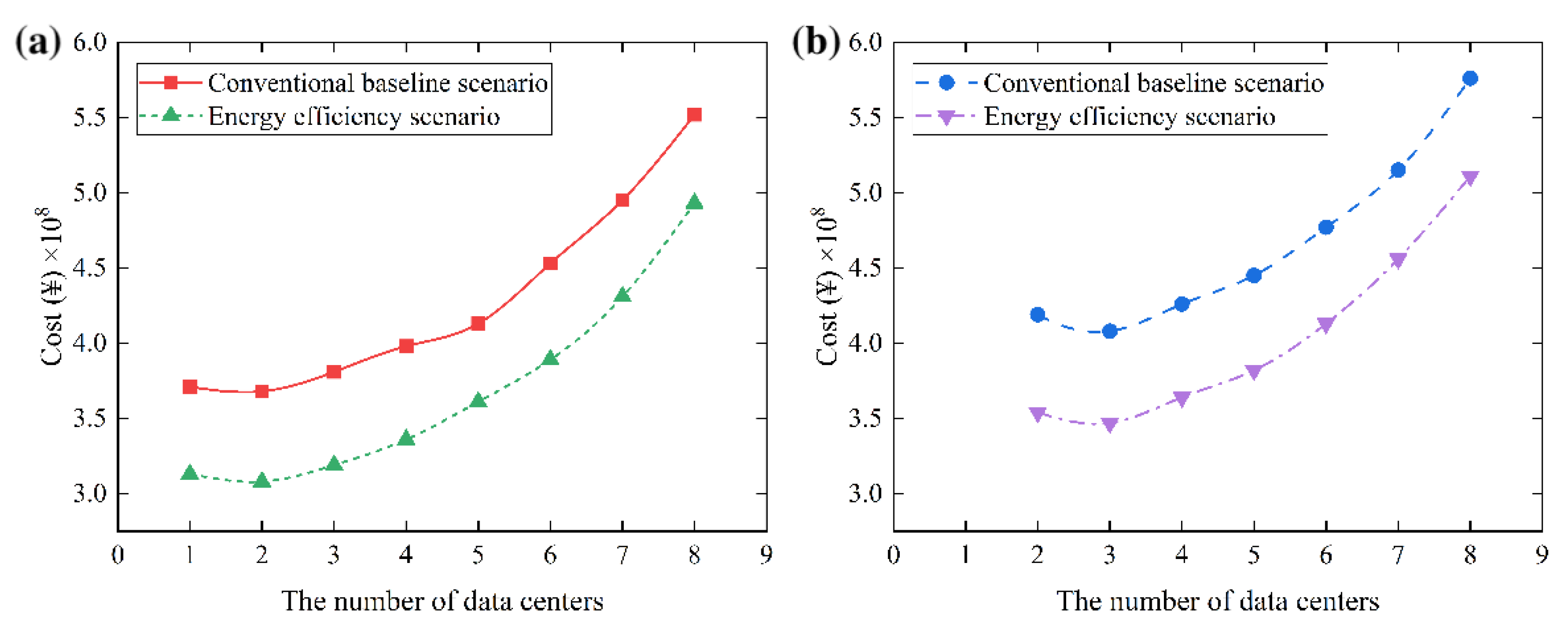
| The number of data center | Total cost (¥) | |
| Scenario A | Scenario B | |
| 1 | 3.71×10^8 | - |
| 2 | 3.68×10^8 | 4.19×10^8 |
| 3 | 3.81×10^8 | 4.08×10^8 |
| 4 | 3.98×10^8 | 4.26×10^8 |
| 5 | 4.13×10^8 | 4.45×10^8 |
| 6 | 4.53×10^8 | 4.77×10^8 |
| 7 | 4.95×10^8 | 5.15×10^8 |
| 8 | 5.52×10^8 | 5.76×10^8 |
| The number of data center | Total cost (¥) | |
| Scenario A | Scenario B | |
| 1 | 3.13×10^8 | - |
| 2 | 3.08×10^8 | 3.54×10^8 |
| 3 | 3.19×10^8 | 3.47×10^8 |
| 4 | 3.36×10^8 | 3.64×10^8 |
| 5 | 3.61×10^8 | 3.82×10^8 |
| 6 | 3.89×10^8 | 4.13×10^8 |
| 7 | 4.31×10^8 | 4.56×10^8 |
| 8 | 4.93×10^8 | 5.11×10^8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





