Submitted:
17 August 2025
Posted:
18 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Complex Metric
2.1. Cosmic Microwave Background
2.2. After the Big Bang
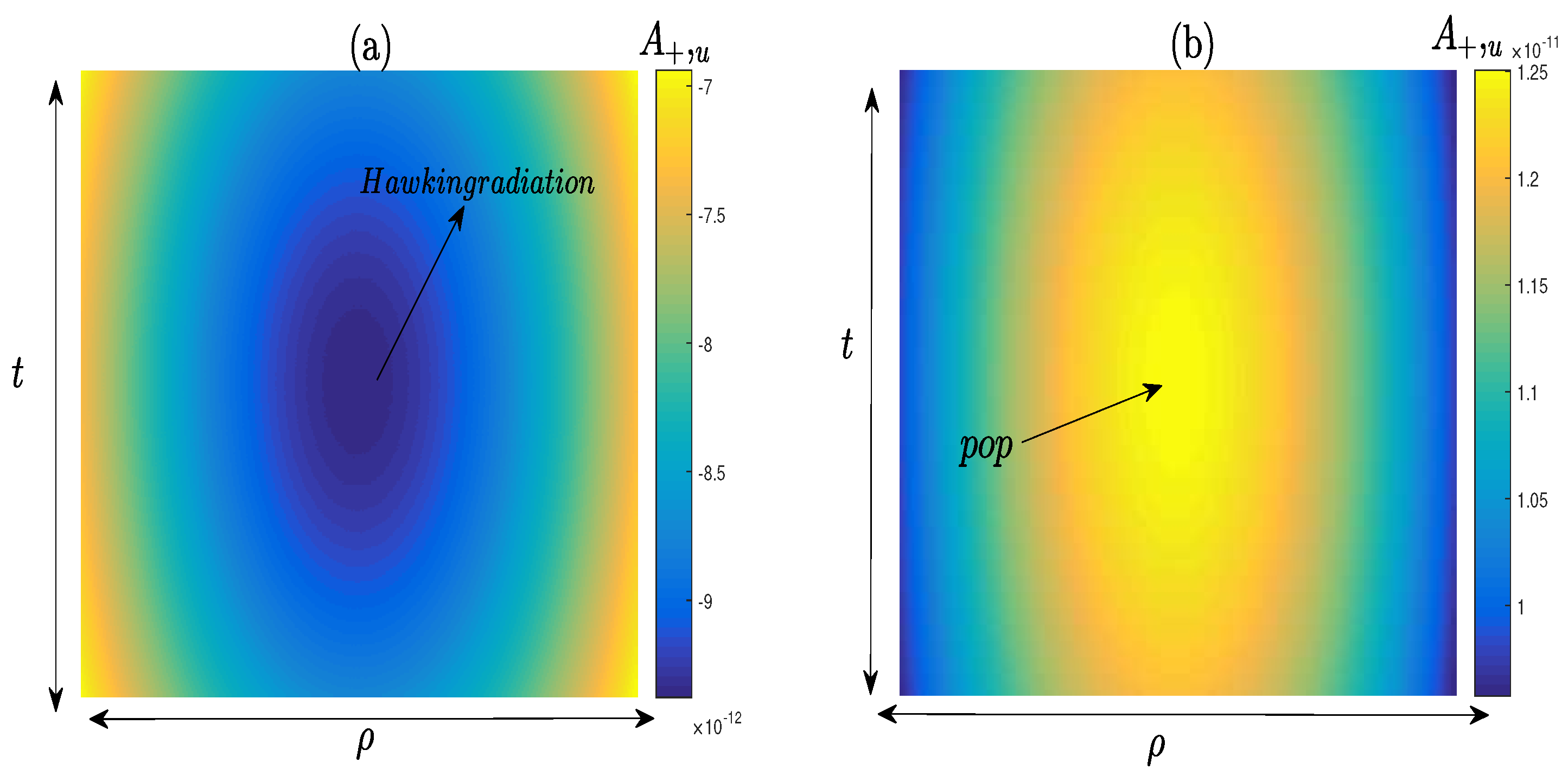
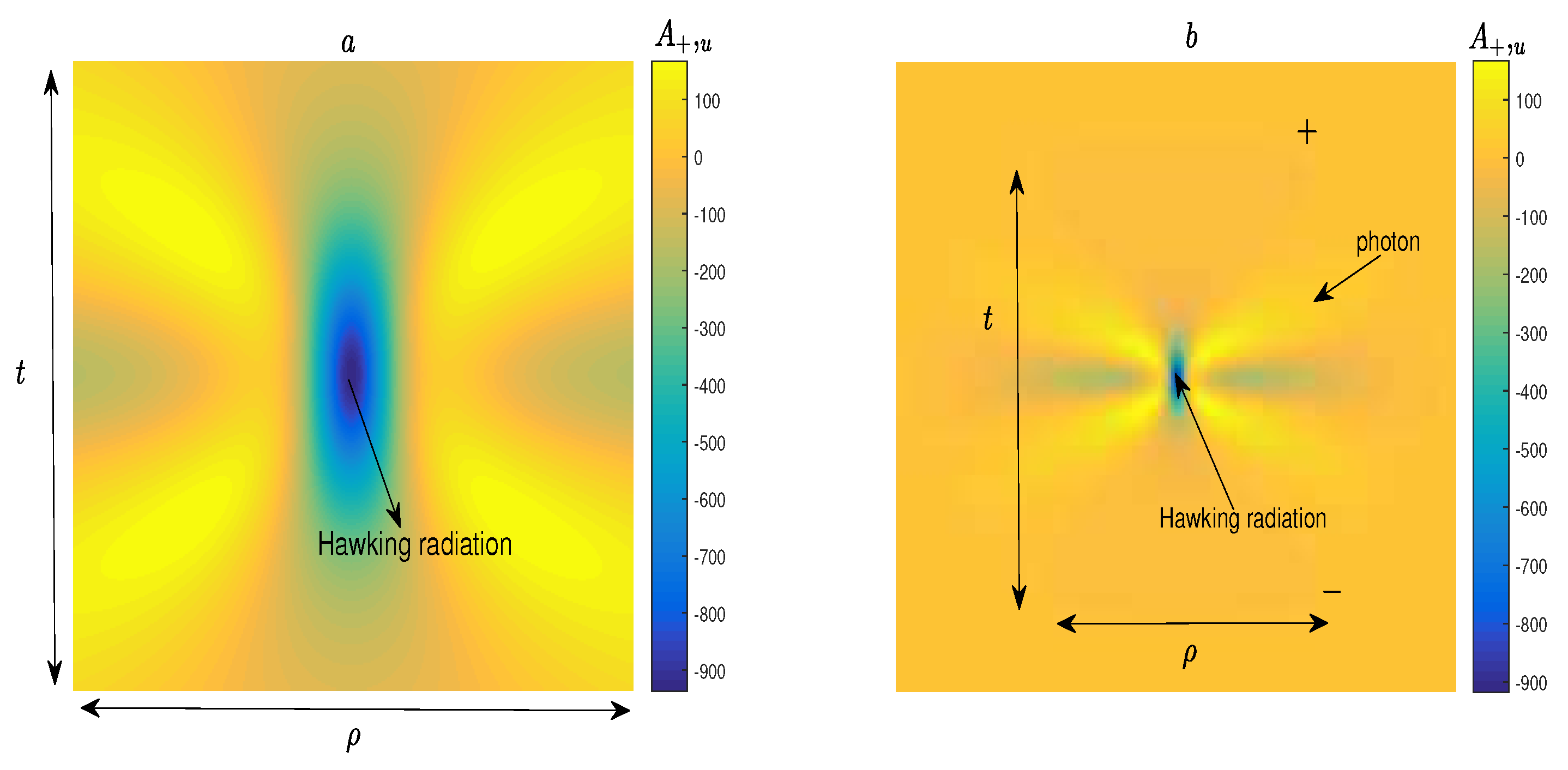
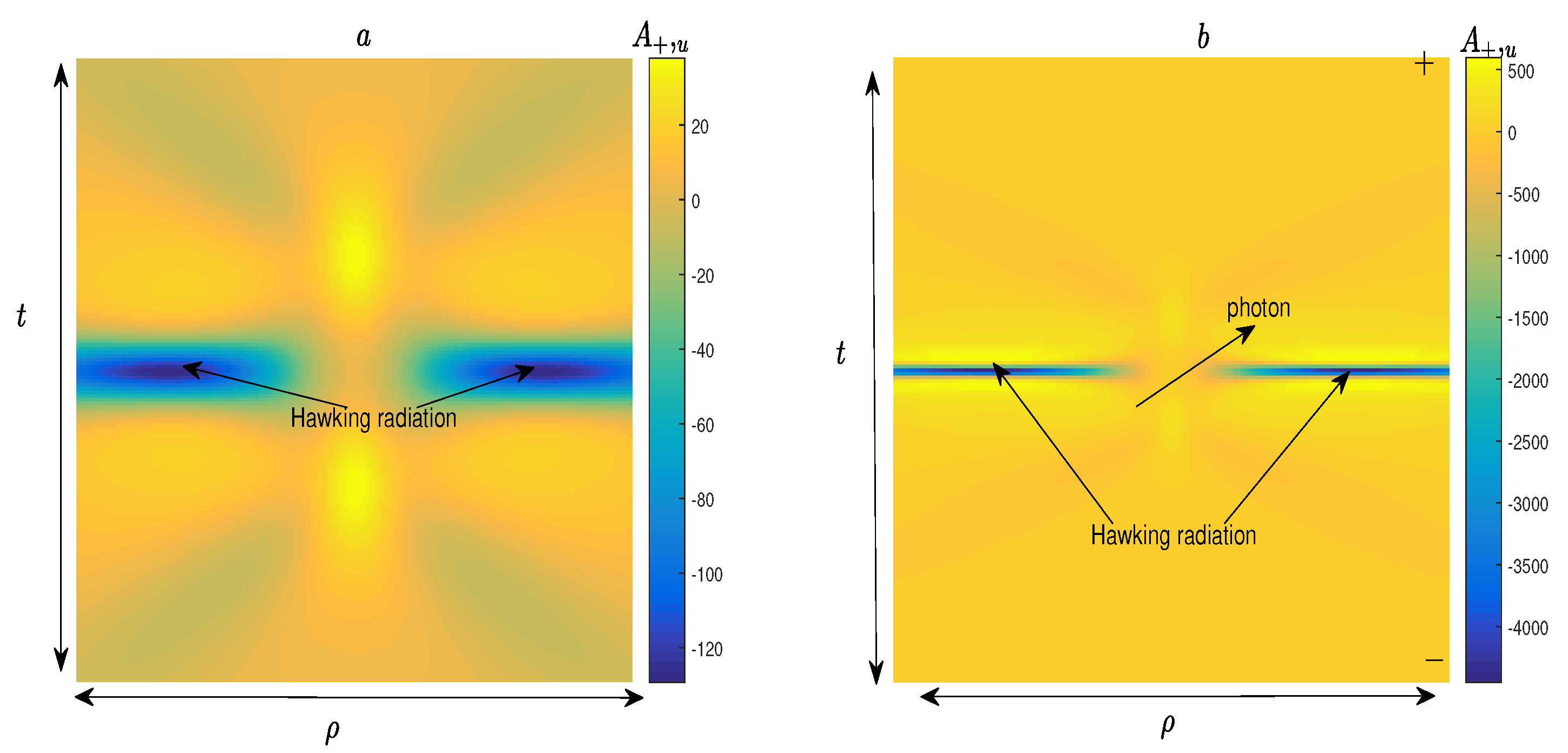
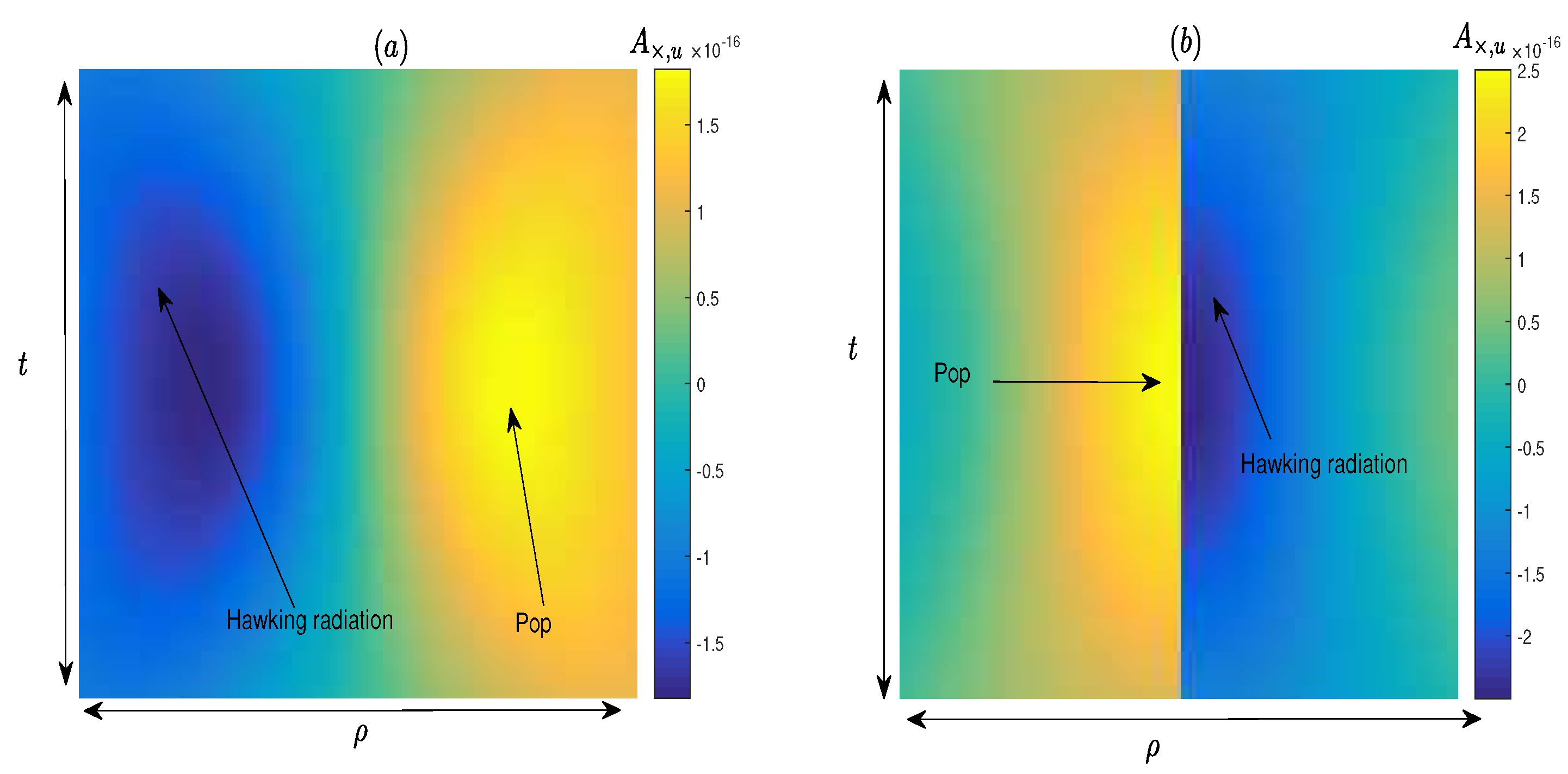
2.3. Phantom Black Hole
3. Conclusion
References
- E. Witten, arXiv:2111.06514.
- J. B. Hartle and S. Hawking, Phys. Rev. D 28 2960 (1983). [CrossRef]
- F. Bricesse, Phys. Rev. D 105 126028 (2022). [CrossRef]
- M. Kontsevich and G. Segal, arXiv:2105.10161.
- R. Penrose, Gen. Relativ. Grav. 7 pp.31-52 (1976).
- R. Penrose, Found. Phys. 44: 557-575 (2014). [CrossRef]
- H. Everett, Rev. Mod. Phys. 29 454 (1957). [CrossRef]
- J. Defo and K. Kuetche, JETP. 135 3 (2022).
- J. Defo and K. Kuetche, arXiv:2506.10053.
- B. P. Abbott and al., LIGO-Virgo scientific collaboration, Phys. Rev. Lett. 116 061102 (2016). [CrossRef]
- M. Parikh, F. Wilczek, and G. Zahariade, arXiv:2005.07211.
- F. Dyson, Int. J. Mod. Phys. A. 28 25 (2013).
- S. Hawking, Phys. Rev. D 13 2 (1976).
- S. Hawking, Nuclear. Physic B239 257-276 (1984).
- M. Carmeli and C. Charach, Found. Phys. 14 , 10, (1984).
- V. Gurzadyan and R. Penrose, arXiv:1011.3706.
- V. Gurzadyan and R. Penrose, arXiv:1302.5162.
- K. Meissner and R. Penrose, arXiv:2503.24263.
- R. Penrose, Found. Phys. 44: 873-890 (2014). [CrossRef]
- G. Gibbons and M. Perry, Phys. Rev. D 22 2 (1980).
- G. Gibbons, Commun. math. Phys. 44 , 245-264 (1975). [CrossRef]
- S. Farnes, arXiv:1712.07962.
- P. Jordan, J. Ehlers, and W. Kundt, Abh. Akad. Wiss. Mainz. Math. Naturwiss; A.S. Kompaneets, Zh. Eksp. Teor. Fiz. 34 953 (1958); Sov. Phys. JETP 7 659 (1958).
- S. Tomizawa and T. Mishima, Phys. Rev. D 91 124058 (2015). [CrossRef]
- A. Tomimatsu, Gen. Relativ. Grav. 21 613 (1989). [CrossRef]
- T. Piran, P. Sarfier and R. Stark, Phys. Rev. D 32 3101 (1985). [CrossRef]
- J. Hartle, S. Hawking and T. Hertog, arXiv:0803.1663.
- A. Pomeransky, Phys. Rev. D 73 044004 (2006). [CrossRef]
- A. Sakharov, Sov. Phys. JETP 52 3 (1980).
- J. Halliwell and S. Hawking, Phys. Rev. D 31 8 (1985). [CrossRef]
- S. Hawking, arXiv:hep-th/0507171.
- R. Penrose, Phys. Rev. Lett. 14 3 (1965). [CrossRef]
- G. Steigman, arXiv:0808.1122.
- A. Dolgov and J. Sil, Phys. Rev. D 47 10 (1993). [CrossRef]
- L. Canetti, M. Drewes and M. Shaposhnikov, arXiv:1204.4186.
- K. Rajeev, Phys. Rev. D 106 023511 (2022). [CrossRef]
- J. Dorronsoro, J. Halliwell, J. Hartle, T. Hertog,and O. Janssen, Phys. Rev. D 96 043505 (2017). [CrossRef]
- T. Shestakova, arXiv:1909.05588.
- J. Lehners, Phys. Rev. D 111 063503 (2025).
- V. Zakharov, ZhETF Pis. Red. 12 9 447-449 (1970).
- C. Rovelli, arXiv:2111.07828.
- W. Bonnor, Gen. Relativ. Grav. 21 11 (1989). [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




