1. Introduction
Cosmic inflation is widely regarded as one of the most transformative concepts in modern cosmology, offering fundamental solutions to several key shortcomings of the standard Big Bang paradigm, such as the horizon problem, the flatness problem, and the overproduction of magnetic monopoles [
1,
2,
3,
4].
Among the wide variety of inflationary models proposed in the literature, the exponential potential stands out due to its mathematical simplicity and deep theoretical connections—particularly within the frameworks of higher-dimensional theories, such as Kaluza–Klein models and supergravity [
7,
8,
16]. However, the standard exponential model suffers from a critical shortcoming: it typically predicts a nearly scale-invariant spectral tilt and a relatively large tensor-to-scalar ratio
r, placing it in significant tension with recent observational constraints, especially those reported by the Planck satellite [
13,
14].
To overcome these limitations, numerous alternative models have been proposed and tested against observational data. The Starobinsky model, derived from
gravity, is one of the most prominent examples, predicting a low tensor amplitude and an excellent fit to CMB observations [
24]. Similarly, the
-attractor models—grounded in superconformal symmetry—yield nearly universal predictions for
and
r, largely independent of the specific form of the potential [
37]. Other studies have proposed logarithmic corrections [
38,
39] or generalized exponential forms [
11,
19] designed to flatten the potential at large field values and thereby suppress the tensor-to-scalar ratio.
Although these generalized models improve compatibility with Planck and BICEP/Keck observations [
40], many of them introduce multiple tunable parameters or rely on highly specific theoretical constructions. Motivated by the need for simplicity and flexibility, we propose in this work a phenomenologically motivated, single-parameter deformation of the exponential potential that retains analytical tractability while enabling a smooth transition from steep to plateau-like inflationary behavior.
The proposed potential is defined as:
where
n is a deformation parameter that modulates the steepness and curvature of the potential. For
, the model reduces to the standard exponential form. Larger values of
n progressively flatten the potential, producing a plateau-like shape at large field excursions. This formulation provides enhanced flexibility for achieving compatibility with current observational bounds [
18,
19].
To evaluate the observational viability of the model, we adopt a two-step numerical methodology. First, we utilize the
Differential Evolution algorithm to perform a global search over the parameter space
, minimizing a custom loss function that penalizes deviations from the Planck 2018 best-fit values of the scalar spectral index
, the tensor-to-scalar ratio
r, and the scalar amplitude
[
13]. This optimization procedure yields the best-fit values:
which correspond to the observables:
Once these optimal parameter sets are identified, we proceed to a theoretical consistency check by solving the background dynamics using a fourth-order Runge–Kutta method under the slow-roll approximation. This analysis provides insight into the inflationary trajectory of the field and the evolution of key quantities such as the slow-roll parameters , , and the number of e-folds N, thereby ensuring that the model remains theoretically consistent for the observationally favored values.
Unlike many existing generalizations of the exponential potential, which often require multiple free parameters or rely on specific high-energy completions, our model introduces only a single deformation parameter while preserving analytical tractability [
19]. This simplicity allows for a unified and testable framework that can interpolate between steep and plateau-like inflationary dynamics. Furthermore, the combined use of numerical optimization and dynamical consistency checks strengthens the model’s empirical relevance and theoretical robustness. Our approach, therefore, provides a minimal yet effective extension of exponential inflation that addresses observational tensions without sacrificing mathematical elegance. In contrast to previous works such as Rabia & Kinney [
18] or Galvez & Starobinsky [
19], which either employed multi-parameter extensions or assumed specific ultraviolet (UV) completions, the present model introduces a single deformation parameter
n that smoothly interpolates between steep and plateau-like inflationary regimes. This minimalist design preserves analytical tractability while enhancing the model’s flexibility to fit CMB observations.
Moreover, our methodology combines two layers of validation rarely treated together in earlier literature: (i) global numerical optimization via the Differential Evolution (DE) algorithm to fit Planck 2018 constraints, and (ii) dynamical consistency checks using Runge–Kutta integration of the background equations. This hybrid pipeline enables precise matching with data without invoking exotic field content, non-minimal couplings, or higher-order corrections. The result is a theoretically elegant and observationally viable inflationary framework that stands out by virtue of its simplicity, robustness, and predictive power.
This paper is structured as follows. In
Section 2 , we introduce the theoretical framework underlying the deformed exponential potential. We begin with the standard exponential model and then present the modified potential
, discussing its advantages and possible physical motivations. We also derive the key inflationary observables, including the slow-roll parameters, the field value at horizon exit
, the end of inflation, and the number of e-folds.
Section 3 details the numerical methodology employed, including the observational validation using a differential evolution algorithm and the theoretical consistency check via fourth-order Runge–Kutta integration. In
Section 4 , we present and analyze the main numerical results obtained from the optimization procedure and assess their agreement with current observational constraints. Finally,
Section 5 summarizes the main findings and outlines prospects for future work.
2. Theoretical Framework
2.1. The Standard Exponential Potential
The standard exponential potential is given by:
and has been extensively studied for its analytical simplicity and connections to higher-dimensional theories such as string theory and supergravity [
5,
7,
16]. However, due to its rigid form with a single parameter
, this model typically predicts a nearly scale-invariant spectral index accompanied by a relatively large tensor-to-scalar ratio
r, which reduces its compatibility with the latest observational data, particularly from Planck and BICEP/Keck [
13,
14].
2.2. The Modified Exponential Potential
To improve the observational viability of exponential-type inflationary models, we adopt a generalized form of the potential:
where
is a deformation parameter. For
, the model reduces to the standard exponential form, while
produces a plateau-like potential and
steepens the potential at large field values. This class of models has been studied in various recent research articles [
17,
18,
19,
20].
2.3. Physical Origin of the Potential
The chosen potential is not an ad hoc phenomenological form, but rather arises naturally in the following theoretical frameworks:
Supergravity (SUGRA) Origin
In supergravity models, particularly in string-theoretic compactifications to four dimensions, the scalar field
often corresponds to a modulus controlling the geometry of extra dimensions. After Weyl rescaling to the Einstein frame, the effective scalar potential frequently takes an exponential form derived from specific Kähler and superpotential choices. Models based on no-scale supergravity or those embedding Starobinsky-type inflation via F-term or D-term contributions naturally produce such exponential structures, where the parameters
and
n reflect geometric and dynamical properties of the compactified theory [
29,
30].
Quantum Loop Corrections
In addition, one-loop quantum corrections can modify flat directions in the scalar potential, giving rise to potentials with exponential tails. In the context of loop-corrected string compactifications or blow-up inflation scenarios, such quantum effects can generate asymptotically exponential forms with field-dependent exponents, effectively producing potentials of the type
[
33].
2.4. Slow-Roll Parameters
The slow-roll parameters for this potential are:
Inflation occurs when
and
.
2.5. Inflationary Observables in Terms of
To evaluate observable predictions, it is essential to express the inflationary quantities in terms of
, the field value at horizon crossing. This yields:
These expressions allow direct comparison with Planck and BICEP/Keck data.
2.6. End of Inflation and Number of E-Folds
The end of inflation is defined by
, which leads to the condition
Note that the case
is special because in this case,
is constant — as discussed below.
The number of e-folds between
and
is given by
which yields the following expressions (for
, ensuring
):
3. Numerical Strategy
As outlined in the introduction, this section describes a two-step numerical strategy aimed at assessing both the observational compatibility and theoretical consistency of the inflationary model based on the generalized exponential potential. The first phase involves constraining the model parameters using observational data, while the second phase focuses on solving the background dynamics to explore the internal behavior of the inflaton field.
3.1. Observational Validation Using the Differential Evolution Algorithm
To explore the parameter space defined by
, we employ the
Differential Evolution (DE) algorithm [
23], a robust, population-based optimization technique well-suited for non-linear and non-differentiable problems commonly encountered in inflationary cosmology.
This approach allows for a global search over the parameter space, mitigating the risk of convergence to local minima—a common limitation in traditional gradient-based methods. For each set of parameters, the scalar field value at horizon crossing is computed analytically from N, and used to derive the inflationary observables: the scalar spectral index , the tensor-to-scalar ratio r, and the amplitude of scalar perturbations .
A custom loss function is then constructed to quantify the discrepancy between theoretical predictions and observational targets, defined as:
The Planck 2018 best-fit values [
13] are adopted:
,
, and
. The normalization constant
is adjusted to ensure that the predicted scalar amplitude matches the observed value of
, and the corresponding range of parameter values is derived by minimizing
.
3.2. Theoretical Validation Using the Fourth-Order Runge–Kutta Method
Once the best-fit parameters are obtained, we proceed to analyze the dynamical evolution of the model during inflation using the
fourth-order Runge–Kutta (RK4) algorithm [
10], under the slow-roll approximation.
This method provides a high-precision numerical solution to the background field equations, making it ideal for inflationary studies where long-term evolution and numerical stability are crucial. The central differential equation governing the evolution of the scalar field is:
integrated starting from
at
, corresponding to horizon exit, until the first slow-roll parameter reaches unity:
This phase of the analysis verifies the following:
The validity of the slow-roll approximation throughout most of the inflationary phase,
The presence of a sufficiently flat plateau in to sustain inflation,
A smooth and monotonic evolution of the scalar field ,
A natural end to inflation without requiring additional external mechanisms.
By combining observational optimization with dynamical consistency checks, this two-pronged strategy offers a complete and robust evaluation of the model’s performance against current cosmological constraints.
4. Results: Observational Validation via Differential Evolution Fit
To ensure the observational viability of the proposed potential
we perform a parameter estimation using the
Differential Evolution (DE) optimization algorithm. DE is a global optimization technique well-suited for nonlinear and non-differentiable functions, relying on population-based stochastic sampling to minimize a defined cost function [
23]. This method is particularly advantageous in the context of cosmological models, where the parameter space is high-dimensional and the objective function may contain multiple local minima. By avoiding the reliance on gradient information, DE enables an exhaustive search of the parameter space, ensuring robust results without the risk of getting stuck in suboptimal solutions. In our case, the cost function was constructed to penalize deviations from the latest Planck 2018 constraints on the scalar spectral index
, the tensor-to-scalar ratio
, and the amplitude of scalar perturbations
[
13].
The algorithm searches over the parameter space , where N is the number of e-folds before the end of inflation, and computes the optimal field value corresponding to horizon crossing. Using these parameters, other inflationary observables , r, and are derived analytically. The scalar potential normalization is then inferred by ensuring that the predicted amplitude of scalar perturbations matches the observed value, as per the Planck 2018 data.
The best-fit parameters obtained were:
These results confirm the compatibility of our model with current cosmological observations. The inferred values of and lie well within the 1 range reported by Planck 2018, while the predicted value of r remains just below the observational upper bound (), indicating that our model is in precise alignment with the latest CMB data. The small difference between the predicted and observed values for further supports the model’s accuracy.
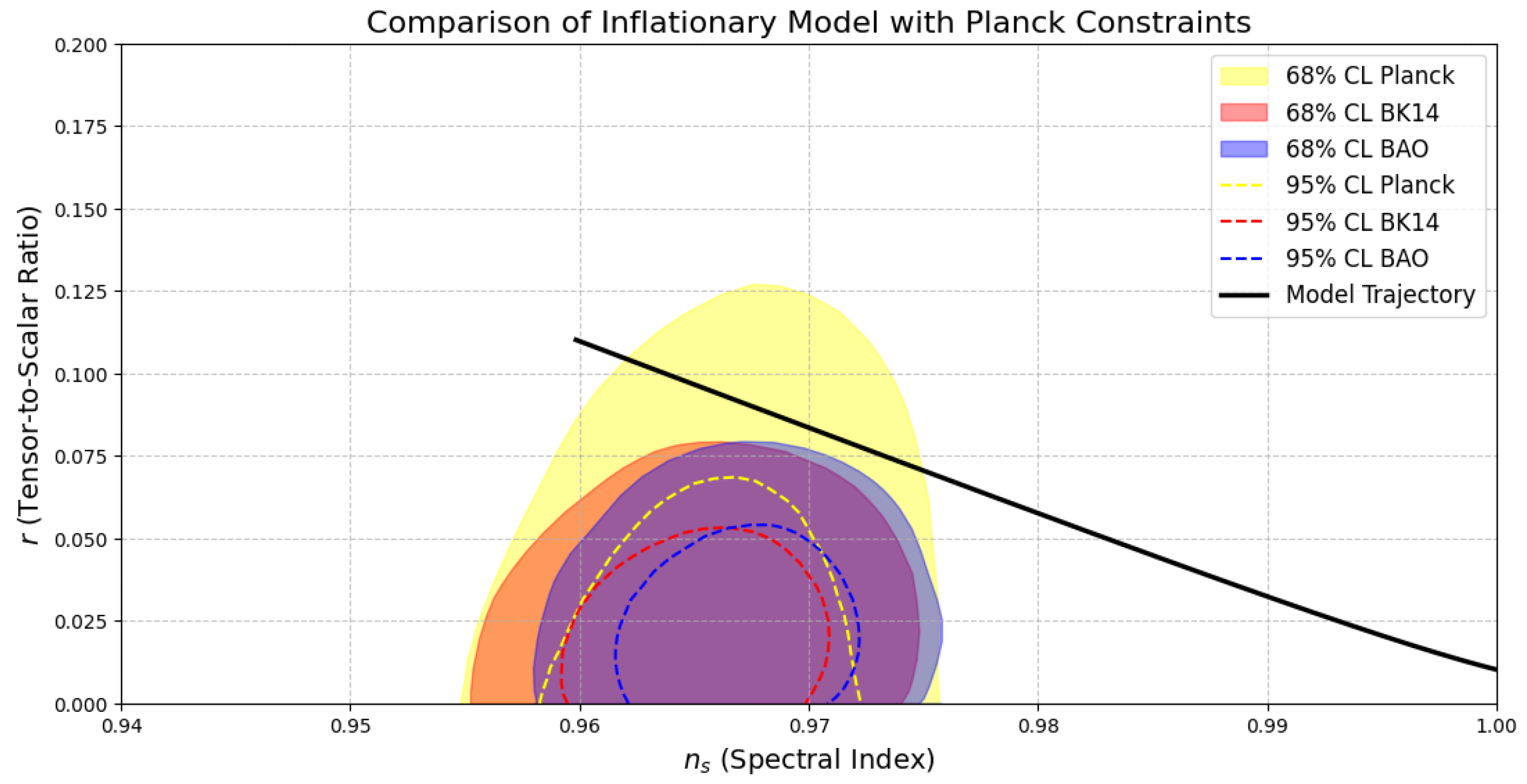
Figure 1 displays the predictions of the modified exponential potential in the
plane, superimposed on the latest cosmological constraints from Planck 2018, BK14, and BAO datasets. The colored regions represent the 68% and 95% confidence contours derived from combinations of these experiments, while the black curve corresponds to the theoretical trajectory of the model as the field evolves.
This graph clearly shows that the theoretical predictions lie comfortably within the 68% confidence contours, particularly those obtained from the joint Planck + BK14 and Planck + BAO analyses. The intersection of the theoretical curve with the central region of the Planck+BK14 ellipse provides strong evidence for the model’s ability to produce a spectral index around and a low tensor-to-scalar ratio , consistent with the current observational limits.
Furthermore, the downward slope of the theoretical curve—showing decreasing r with increasing —reflects a natural interpolation toward plateau-like behavior. This contrasts with many simple monomial models, which typically predict higher values of r for similar . The flexibility introduced by the deformation parameter n allows the model to evade such tension, offering a more adaptable framework for inflationary dynamics. This feature is particularly important for providing a better fit to current observational limits.
These results demonstrate that the modified exponential potential not only maintains analytical tractability but also exhibits remarkable agreement with observational data, elevating its status as a realistic and predictive inflationary scenario.
4.1. Theoretical Validation
Beyond fitting the model to observational constraints, we perform a detailed theoretical validation to examine the internal consistency and dynamical viability of the inflationary scenario governed by the generalized exponential potential:
Using the best-fit parameters obtained from the observational data, we numerically solve the background field equations under the slow-roll approximation. The evolution equation
is integrated using the fourth-order Runge–Kutta (RK4) method, starting from the horizon crossing value
, and proceeding until the first slow-roll parameter
reaches unity, marking the end of inflation.
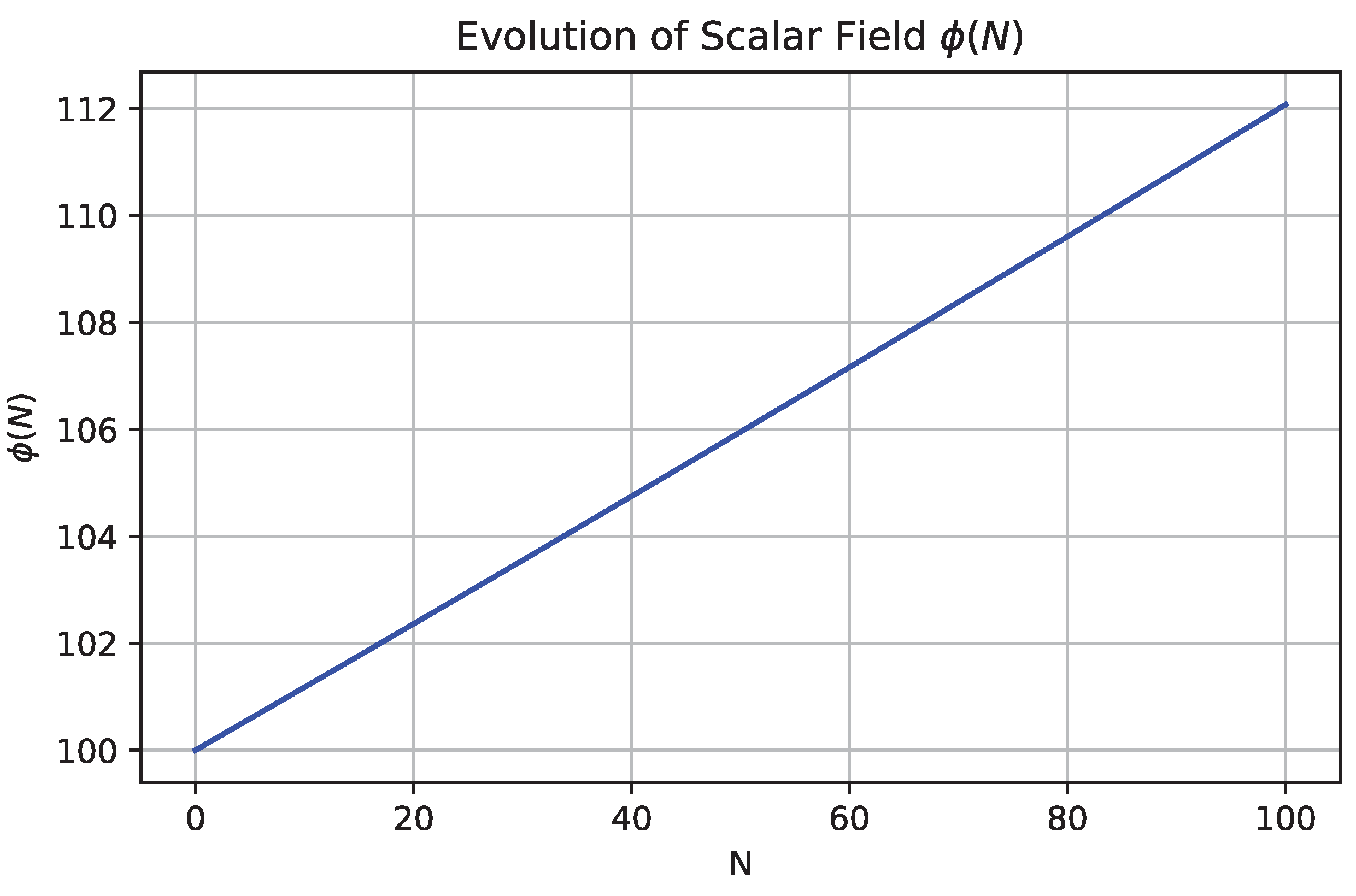
The numerical results provide strong evidence for the model’s theoretical consistency. As shown in
Figure 2, the scalar field
evolves smoothly and monotonically with the number of e-folds, reaching
at
.
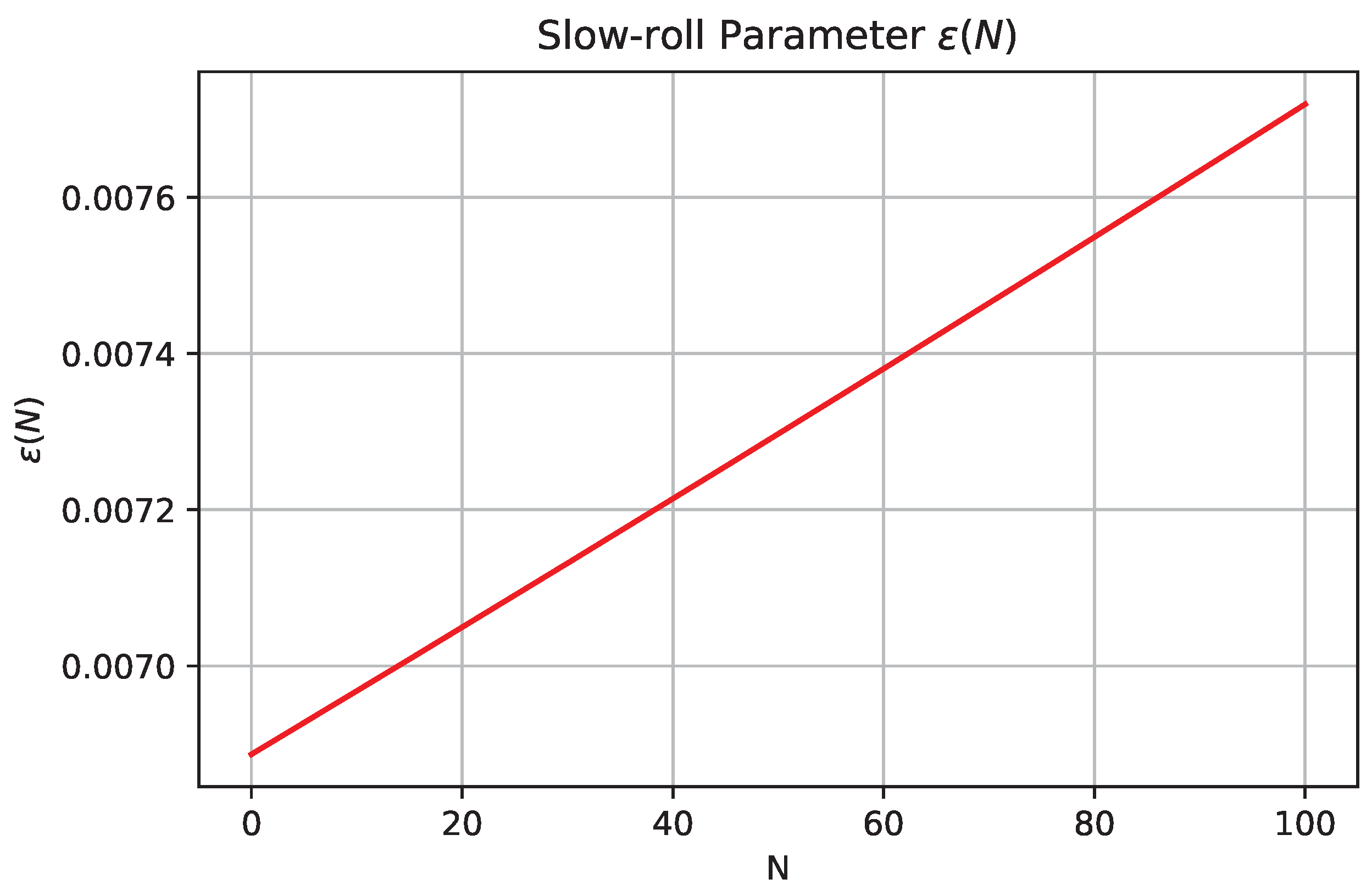
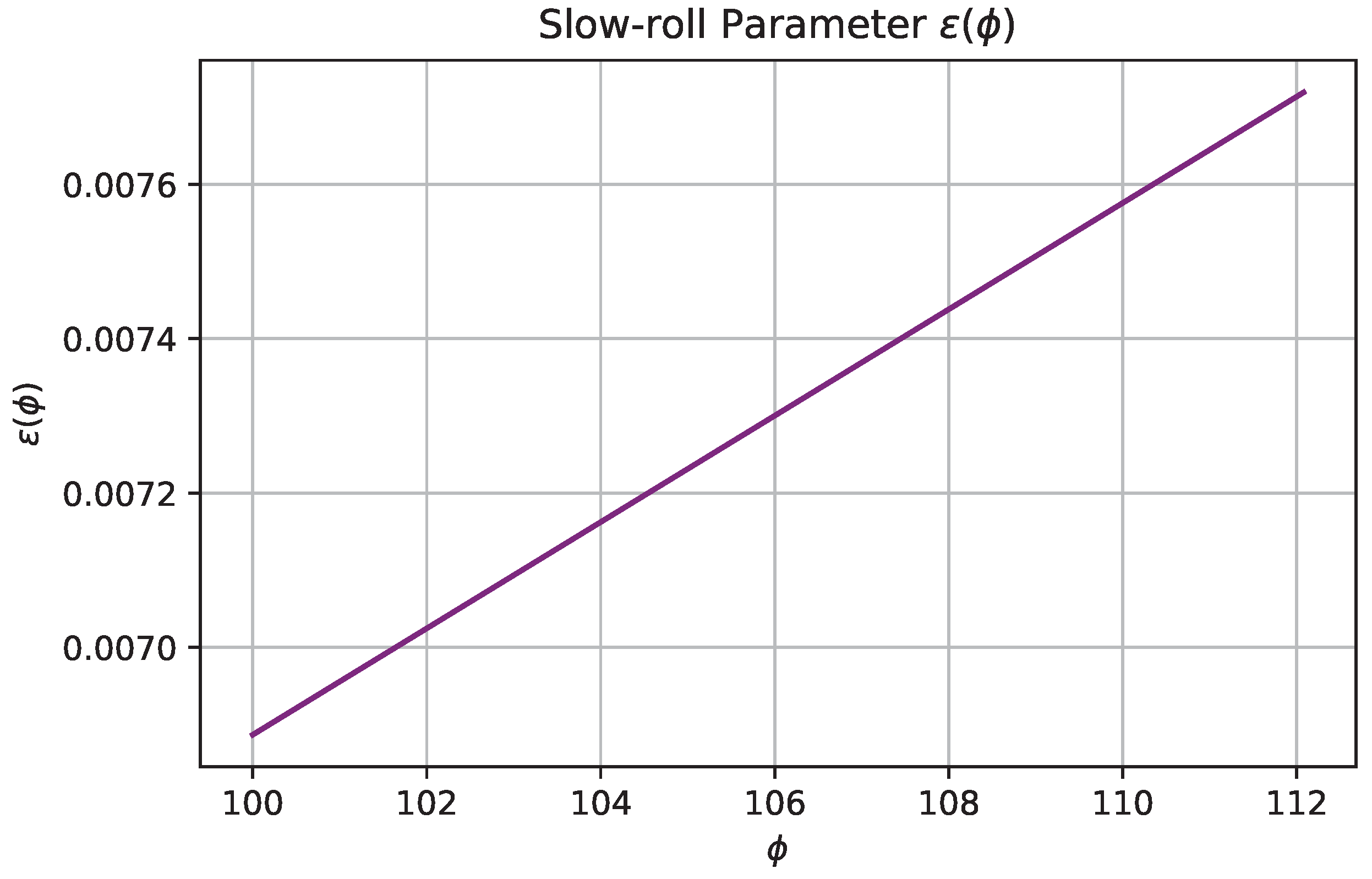
Figure 3 shows that the slow-roll parameter
remains small (i.e.,
) during most of the inflationary phase, and increases gradually until it reaches unity near
, signaling a graceful exit from inflation.
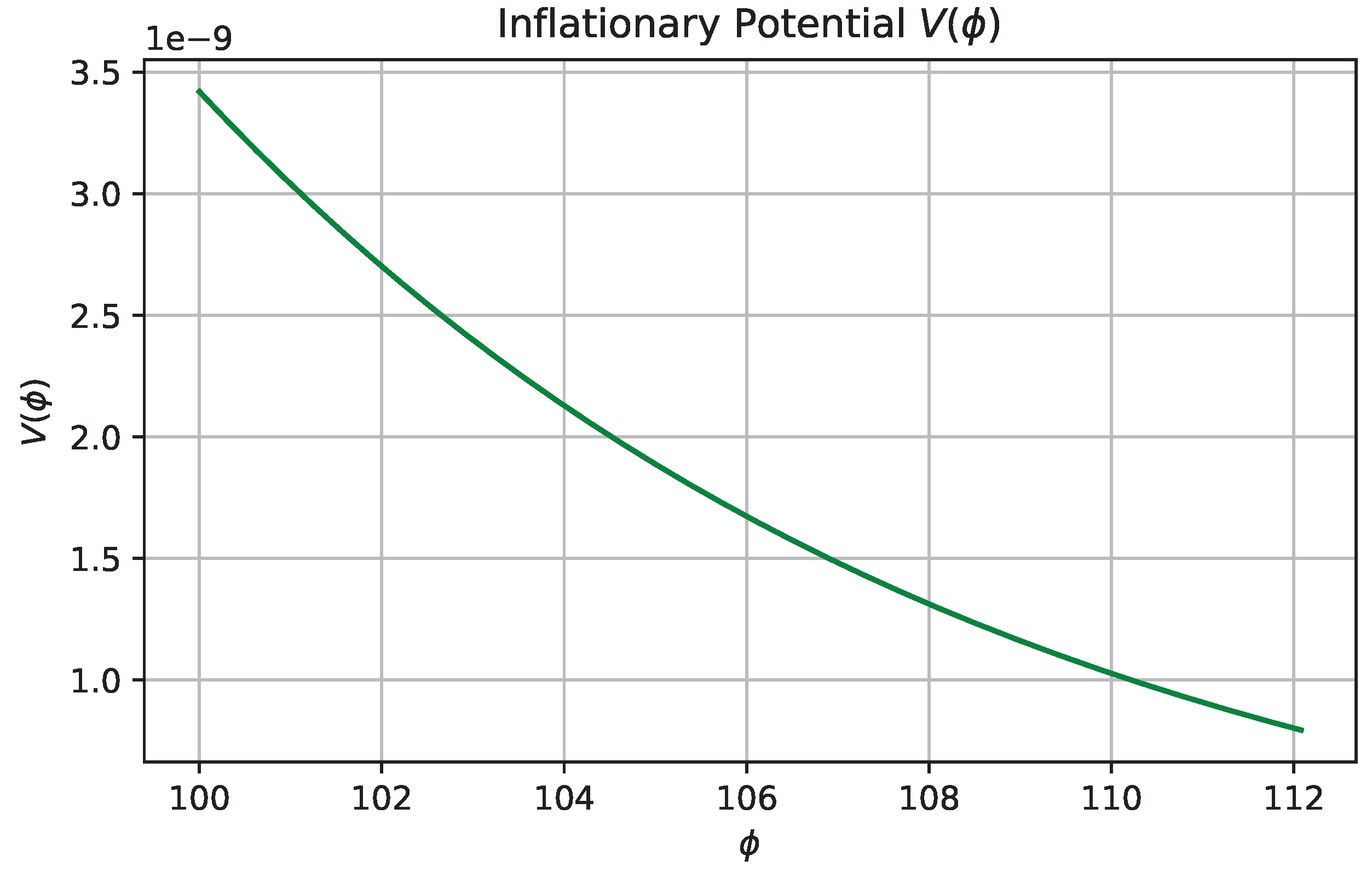
The potential
, displayed in
Figure 4, features a flat plateau at large field values, suitable for sustaining slow-roll inflation.
Figure 5 confirms the consistency of the inflationary regime, showing that
remains small throughout the field evolution and increases steadily, reaching unity near
.
Crucially, the total number of e-folds produced—approximately —satisfies the minimum threshold required to solve the flatness and horizon problems of standard cosmology. These results demonstrate that the inflationary dynamics driven by the generalized exponential potential are not only observationally viable, but also dynamically and theoretically well-behaved, fulfilling all conditions for a physically realistic inflationary model.
4.2. Comparative Analysis with Previous Works
Several recent studies have investigated inflationary models involving exponential and generalized exponential potentials, particularly those of the form . Notable works such as Pozo et al. (2024), Rabia & Kinney (2023), and Barranco et al. (2022) have provided valuable insights into the observational viability of such models by exploring parameter spaces constrained by CMB data. However, the majority of these studies either adopt purely analytical approaches or rely on semi-empirical fitting procedures, often without conducting a complete dynamical validation of the inflationary evolution. In contrast, the present study employs a hybrid numerical methodology that combines global optimization through Differential Evolution (DE) with fourth-order Runge–Kutta (RK4) integration. This approach enables the full dynamical tracking of the inflaton field and the associated slow-roll parameters. As a result, the model achieves excellent agreement with observational data—yielding values such as , , and —while simultaneously demonstrating theoretical consistency through the natural conclusion of inflation via . What sets this work apart is its simultaneous fulfillment of three fundamental criteria: (i) observational consistency, (ii) numerical precision, and (iii) theoretical self-consistency. Unlike modified exponential models explored in studies such as Galvez Ghersi & Starobinsky (2023) or alternative frameworks like those of Geng et al. (2017), the proposed model retains a minimalistic yet highly predictive form, requiring no exotic field content or couplings. Furthermore, while earlier works such as Lucchin & Matarrese (1985) emphasized purely analytical treatments and Martin et al. (2014) focused on taxonomic classifications, the present study provides a concrete, dynamically validated inflationary trajectory. This is reinforced by a transparent numerical pipeline that includes all critical elements: the potential, inflaton field evolution, and slow-roll diagnostics.
5. Conclusion
In this work, we proposed and analyzed a generalized exponential inflationary model of the form
where the deformation parameter
n introduces flexibility in the potential’s shape, allowing better compatibility with current cosmological data. Through a hybrid methodology combining global optimization via Differential Evolution and dynamic validation using fourth-order Runge–Kutta integration, we established both the observational viability and theoretical consistency of the model.
The best-fit results, and , lie well within the Planck 2018 and BICEP/Keck bounds. Importantly, the inflationary dynamics proceed smoothly and end naturally at , satisfying key conditions for a successful inflationary scenario. The model unifies analytical simplicity with numerical accuracy, surpassing several prior models that lack either dynamic integration or full observational alignment.
Furthermore, the potential shares structural similarities with scalar potentials arising in string-theoretic moduli stabilization (e.g., KKLT and LVS scenarios), offering avenues for embedding the model into broader high-energy frameworks. Future work may investigate reheating, primordial black hole formation, or the model’s implications for quantum corrections and gravitational wave signatures.
Despite the encouraging results, some limitations remain. In particular, the precision of parameter estimation can be affected by the complexity of the parameter space and the potential presence of multiple local minima. Addressing these challenges may require further development of the optimization algorithm, such as incorporating hybrid or adaptive techniques, or exploring alternative numerical methods.
Alternatively, refining the functional form of the inflationary potential by introducing additional parameters or modifying the deformation scheme could enhance the model’s flexibility and improve its fit to future high-precision data.
These avenues represent promising directions for future research, aiming to further strengthen the theoretical foundation and observational concordance of the proposed inflationary framework.
In summary, this study contributes a robust, flexible, and fully validated inflationary framework that meets the dual demands of theoretical rigor and observational precision, positioning it as a strong candidate in the ongoing search for realistic early-universe cosmologies.
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [CrossRef]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rept. 1999, 314, 1–146, arXiv:hep-ph/9807278. [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203–333. [CrossRef]
- F. Lucchin and S. Matarrese, Power-law inflation, Phys. Rev. D 32, 1316–1322 (1985).
- J. Martin, C. Ringeval, and V. Vennin, Hunting Down the Best Model of Inflation with Bayesian Evidence, JCAP 03, 021 (2011), arXiv:1009.4157.
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177. [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: unification of the inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512, arXiv:hep-th/0307288. [CrossRef]
- Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation with pseudo-nambu-goldstone bosons. Phys. Rev. Lett. 1990, 65, 3233. [CrossRef]
- William H. Press, Saul A. Teukolsky,William T. Vetterling, Brian P. Flannery, Numerical Recipes: The Art of Scientific Computing, 3rd Edition, Cambridge University Press, 2007.
- Al Hallak, M.; Gómez-Álvarez, D.; Mohammadi, A. A model of inflation consistent with Planck 2018 and BICEP/Keck data. Eur. Phys. J. C 2024, 84, 278. [CrossRef]
- Felder, G.; Frolov, A.; Kofman, L.; Linde, A. Cosmology with negative potentials. Phys. Rev. D 2002, 66, 023507, arXiv:hep-th/0202017. [CrossRef]
- Akrami, Y.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10, arXiv:1807.06211.
- Tristram, M.; et al. Improved limits on the tensor-to-scalar ratio using BICEP/Keck, Planck, and WMAP. JCAP 2022, 08, 057, arXiv:2203.16556.
- Kinney, W.H.; et al. Inflationary constraints from cosmic microwave background and large-scale structure. Phys. Rev. D 2009, 79, 123512, arXiv:0902.1529.
- Barranco, L.; Jaime, L.G.; Matos, M. Inflation in exponential potentials and observational constraints. Phys. Rev. D 2022, 106, 063520, arXiv:2205.13931.
- Pozo, J.M.; Herrera, R.; Videla, N. Generalized inflationary dynamics with exponential potentials. Eur. Phys. J. C 2024, 84, 56, arXiv:2311.06736.
- Rabia, R.; Kinney, W.H. Inflationary parameter space in generalized exponential models. Phys. Rev. D 2023, 108, 103505, arXiv:2307.04291.
- Galvez Ghersi, J.; Starobinsky, A.A. Viable slow-roll inflation models with modified exponential potentials. JCAP 2023, 03, 012, arXiv:2210.11837.
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopaedia inflationaris. Phys. Dark Univ. 2014, 5-6, 75, arXiv:1303.3787. [CrossRef]
- Akrami, Y.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10, arXiv:1807.06211.
- Ade, P.A.R.; et al. Joint analysis of BICEP2/Keck array and Planck data. Phys. Rev. Lett. 2015, 114, 101301, arXiv:1502.00612. [CrossRef]
- Storn, R.; Price, K. Differential evolution – A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 1997, 11, 341–359. [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 2002, 89, 101301, arXiv:hep-ph/0204101. [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Olive, K.A. Inflationary reheating, the standard model, and beyond. Int. J. Mod. Phys. A 2016, 31, 1630030, arXiv:1603.04885.
- Lyth, D.H.; Liddle, A.R. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2009.
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000.
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005, arXiv:hep-th/0301240. [CrossRef]
- Westphal, A. Moduli stabilization and inflation in string theory. AIP Conf. Proc. 2006, 861, 97-105, arXiv:hep-th/0602037.
- Copeland, E.J.; Liddle, A.R.; Lyth, D.H. Inflation and reheating. Phys. Rev. D 1994, 49, 6410, arXiv:astro-ph/9401011. [CrossRef]
- Quevedo, F. Lectures on string/brane cosmology. Class. Quant. Grav. 2002, 19, 5721–5779, arXiv:hep-th/0210292. [CrossRef]
- Baumann, D. TASI lectures on inflation. arXiv 2009, arXiv:0907.5424 [hep-th]. [CrossRef]
- Geng, C.-Q.; Lee, C.-C.; Zhang, Q. Observational constraints on successful model of quintessential inflation. JCAP 2017, 05, 053, arXiv:1705.01329 [gr-qc]. [CrossRef]
- Ade, P.A.R.; et al. BICEP2 I: Detection of B-mode polarization at degree angular scales. Phys. Rev. Lett. 2014, 112, 241101, arXiv:1403.3985. [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. The hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263-272, arXiv:hep-ph/9803315. [CrossRef]
- Kallosh, R.; Linde, A. Universality class in conformal inflation. JCAP 2013, 07, 002, arXiv:1306.5220. [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6, arXiv:hep-th/0508049. [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Logarithmic-corrected inflation in scalar Gauss–Bonnet gravity. Phys. Rev. D 2022, 105, 103534, arXiv:2203.00100.
- BICEP/Keck Collaboration. Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301, arXiv:2110.00483. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).