A Hypothesis for the Down-Type Quark Mass Formula and Its Relation to the 2–3 Rotation of the Cabibbo–Kobayashi–Maskawa Matrix: Half of \( \frac{2}{9} \) and Half of \( \cos{\left(\frac{3}{8}\pi\right)} \)

1. Introduction

1.1. Koide’s Mass Formula

Let the masses of the charged leptons $e^{-}$, ${\mu }^{-}$, and ${\tau }^{-}$ be denoted by $m_{\mathrm{e}}$, $m_{\mu }$, and $m_{\tau }$, respectively.

In 1982, Yoshio Koide proposed a mass formula inspired by the work of Harari, Haut, and Weyers [1], which relates the masses of the three generations of charged leptons [2,3]:

$${\displaystyle \frac{m_e+m_{\mu }+m_{\tau }}{{\left(\sqrt{m_e}+\sqrt{m_{\mu }}+\sqrt{m_{\tau }}\right)}^2}}={\displaystyle \frac{2}{3}}.$$

This empirical formula remarkably reproduces the observed mass hierarchy of the electron, muon, and tauon with surprising precision.

1.2. Extension by Carl A. Brannen

In 2006, Carl A. Brannen proposed an extension of the Koide mass formula in his paper [4].

We now denote the masses of $e^{-}$, ${\mu }^{-}$, and ${\tau }^{-}$ as $m_{e1}$, $m_{e2}$, and $m_{e3}$, respectively.

According to Brannen, the square root of each mass can be parameterized as:

$$\sqrt{m_{en}}=17.716 \left(1+\sqrt{2}\cos \left({\displaystyle \frac{2}{9}}+{\displaystyle \frac{2}{3}}n\mathsf{\pi }\right)\right) \left[\mathrm{Me}{\mathrm{V}}^{{\displaystyle \frac{1}{2}}}\right],\hspace{1em}n=1, 2, 3.$$

Note that the ${\displaystyle \frac{2}{9}}$ inside the cosine is ${\displaystyle \frac{2}{9}}$, not ${\displaystyle \frac{2}{9}}\mathsf{\pi }$.

1.3. Generalization of the Formula

Since

$$\sqrt{m_{e1}}+\sqrt{m_{e2}}+\sqrt{m_{e3}}=53.148 \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right],$$

we use this as a normalization factor.

Following Brannen’s approach, in which the parameters ${\theta }_{\mathrm{\angle }}$ (theta angle) and $\varphi$ are introduced to generalize the mass formula, we adopt the notation ${\theta }_a$in place of ${\theta }_{\mathrm{\angle }}$throughout this work to improve readability.

In this framework, the parameter $T$ is defined as follows:

$$T=\sqrt{{\displaystyle \frac{1+\cos \left({\theta }_a\right)}{2}}}.$$

The two forms are shown below.

(1) Koide form:

$${\displaystyle \frac{m_{e1}+m_{e2}+m_{e3}}{{\left(\sqrt{m_{e1}}+\sqrt{m_{e2}}+\sqrt{m_{e3}}\right)}^2}}={\displaystyle \frac{1+2T^2}{3}}.$$

(2) Brannen form:

$$\sqrt{m_{en}}={\displaystyle \frac{53.148}{3}} \left(1+2T\cos \left({\displaystyle \frac{1}{3}}\varphi +{\displaystyle \frac{2}{3}}n\mathsf{\pi }\right)\right) \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right], \hspace{1em} n=1, 2, 3.$$

Here, for charged leptons, Brannen sets:

$$\cos \left({\theta }_a\right)=0,\hspace{1em}\varphi ={\displaystyle \frac{2}{3}}.$$

1.4. Down-Type Quarks

We obtain the masses of the down-type quarks from the 2024 edition of the Particle Data Group (PDG) [5]. In what follows, all experimental values are taken from that edition. Although the energy scales for $d$, $s$ are given at $2 \left[\mathrm{GeV}\right]$ and for $b$ at $4.2 \left[\mathrm{GeV}\right]$, we use the following representative values.

Let $m_{d1}$, $m_{d2}$, and $m_{d3}$ denote the masses of the $d$, $s$, and $b$ quarks, respectively:

$$\begin{gathered} m_{d1}=4.7\pm 0.07 \left[\mathrm{MeV}\right], \\ {m}_{d2}=93.5\pm 0.8 \left[\mathrm{MeV}\right], \\ {m}_{d3}={4183}_{-30}^{+40} \left[\mathrm{MeV}\right].\hspace{1em} \end{gathered}$$

From these values, we find:

$$\sqrt{m_{d1}}+\sqrt{m_{d2}}+\sqrt{m_{d3}}\approx 76.224-76.880 \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right]\approx 53.148\times 3^{{\displaystyle \frac{1}{3}}} \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right].$$

Based on this observation, we hypothesize that the down-type quark mass formula takes the form:

$$\sqrt{m_{dn}}={\displaystyle \frac{53.148}{3^{\frac{2}{3}}}} \left(1+2T\cos \left({\displaystyle \frac{1}{3}}\varphi +{\displaystyle \frac{2}{3}}n\mathsf{\pi }\right)\right) \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right],\hspace{1em}n=1, 2, 3.$$

First, we set:

$$\varphi ={\displaystyle \frac{1}{3}}.$$

Next, upon substituting $2T=1.543$ into the above hypothetical mass formula, we obtain:

$$\begin{gathered} m_{d1}\approx 4.73 \left[\mathrm{MeV}\right], \hspace{1em} \\ {m}_{d2}\approx 94.98 \left[\mathrm{MeV}\right],\hspace{1em} \\ {m}_{d3}\approx 4190.34 \left[\mathrm{MeV}\right]. \end{gathered}$$

These values are in good agreement with the experimental measurements.

Taking $2T\approx 1.543$ yields $\cos \left({\theta }_a\right)\approx 0.190$.

We thus conjecture:

$$\cos \left({\theta }_a\right)={\displaystyle \frac{1}{2}}\cos \left({\displaystyle \frac{3}{8}}\mathsf{\pi }\right)={\displaystyle \frac{\sqrt{2-\sqrt{2}}}{4}}\approx 0.191342\hspace{1em}\left(\Rightarrow {\theta }_a\approx 1.378267\mathrm{ }\left[\mathrm{rad}\right]\right).$$

1.5. Proposed Mass Formula for Down-Type Quarks

Here we set:

$$\cos \left({\theta }_a\right)={\displaystyle \frac{1}{2}}\cos \left({\displaystyle \frac{3}{8}}\mathsf{\pi }\right),\hspace{1em}\varphi ={\displaystyle \frac{1}{3}}.$$

Thus,

$$T=\sqrt{{\displaystyle \frac{4+\sqrt{2-\sqrt{2}}}{8}}}.$$

We obtain the following two forms.

(1) Koide form:

$${\displaystyle \frac{m_{d1}+m_{d2}+m_{d3}}{{\left(\sqrt{m_{d1}}+\sqrt{m_{d2}}+\sqrt{m_{d3}}\right)}^2}}={\displaystyle \frac{8+\sqrt{2-\sqrt{2}}}{12}}\approx 0.730447.$$

(2) Brannen form:

$$\sqrt{m_{dn}}={\displaystyle \frac{53.148}{3^{\frac{2}{3}}}} \left(1+\sqrt{{\displaystyle \frac{4+\sqrt{2-\sqrt{2}}}{2}}}\cos \left({\displaystyle \frac{1}{9}}+{\displaystyle \frac{2}{3}}n\mathsf{\pi }\right)\right) \left[{\mathrm{MeV}}^{{\displaystyle \frac{1}{2}}}\right],\hspace{1em}n=1, 2, 3.$$

With this formulation, the resulting masses are:

$$\begin{gathered} m_{d1}\approx 4.69 \left[\mathrm{MeV}\right], \hspace{1em} \\ {m}_{d2}\approx 94.86 \left[\mathrm{MeV}\right],\hspace{1em} \\ {m}_{d3}\approx 4192.29 \left[\mathrm{MeV}\right]. \end{gathered}$$

1.6. The Cabibbo–Kobayashi–Maskawa Matrix

We now employ ${\displaystyle \frac{1}{9}}$ and ${\displaystyle \frac{1}{2}}\cos \left({\displaystyle \frac{3}{8}}\mathsf{\pi }\right),$ newly introduced in this work, to explore its potential role in describing the rotational structure of the Cabibbo–Kobayashi–Maskawa (CKM) matrix [6,7].

2. Method

2.1. Construction of the CKM Matrix

First, we denote the mass eigenstates of the down-type quarks by ${\left(d,s,b\right)}^{\mathrm{T}}$ and the flavor eigenstates by ${\left(d^{\prime },s^{\prime },b^{\prime }\right)}^{\mathrm{T}}$.

Similarly, we denote the mass eigenstates of the up-type quarks by ${\left(u,c,t\right)}^{\mathrm{T}}$ and the flavor eigenstates by ${\left(u^{\prime },c^{\prime },t^{\prime }\right)}^{\mathrm{T}}$.

The relationship between flavor and mass eigenstates is given by:

$$\left(\begin{array}{c}{d}^{\prime }\\ s^{\prime }\\ b^{\prime }\end{array}\right)={\mathit{V}}_d\left(\begin{array}{c}d\\ s\\ b\end{array}\right),\hspace{1em}\left(\begin{array}{c}{u}^{\prime }\\ c^{\prime }\\ t^{\prime }\end{array}\right)={\mathit{V}}_u\left(\begin{array}{c}u\\ c\\ t\end{array}\right).$$

These states are connected through the charged-current interaction mediated by the $W$-boson:

$$\left(\begin{array}{c}u\\ c\\ t\end{array}\right)={{\mathit{V}}_u}^{†}\left(\begin{array}{c}{u}^{\prime }\\ c^{\prime }\\ t^{\prime }\end{array}\right)\hspace{1em}\iff \hspace{1em}\left(\begin{array}{c}{d}^{\prime }\\ s^{\prime }\\ b^{\prime }\end{array}\right)={\mathit{V}}_d\left(\begin{array}{c}d\\ s\\ b\end{array}\right).$$

Hence, at first glance, the CKM matrix can be expressed as:

$${\mathit{V}}_{\mathrm{CKM}}={{\mathit{V}}_u}^{†}{\mathit{V}}_d.$$

However, in vacuum, the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix [8] is expected to be expressible as:

$${\mathit{U}}_{\mathrm{PMNS}}={{\mathit{U}}_e}^{†}{\mathit{U}}_{\nu }\left(\begin{array}{ccc}\cos \left({\theta }_{\nu 31}\right)& 0& -e^{i{\delta }_{\nu 31}}\sin \left({\theta }_{\nu 31}\right)\\ 0& 1& 0\\ e^{-i{\delta }_{\nu 31}}\sin \left({\theta }_{\nu 31}\right)& 0& \cos \left({\theta }_{\nu 31}\right)\end{array}\right),$$

where ${{\mathit{U}}_e}^{†}{\mathit{U}}_{\nu }$ is the Tribimaximal mixing matrix [9], ${\theta }_{\nu 31}\approx 0.173478 \left[\mathrm{rad}\right]$, and ${\delta }_{\nu 31}={\displaystyle \frac{1}{2}}\mathsf{\pi } \left[\mathrm{rad}\right]$ [10].

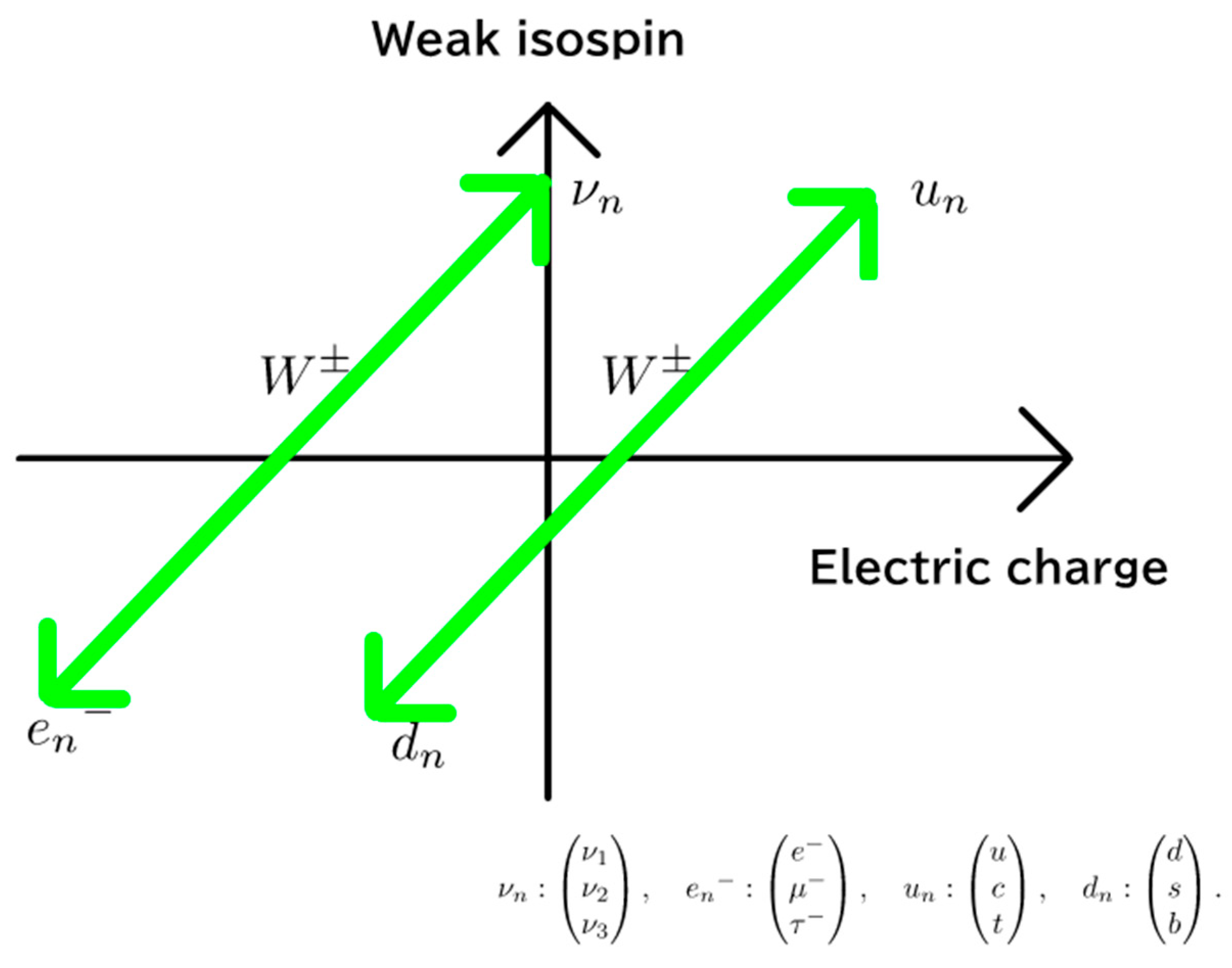
It is therefore predicted that, by the same reasoning and considering the direction of the $W$-boson interaction (see Figure 1), the inverse CKM matrix takes the form:

$${{\mathit{V}}_{\mathrm{CKM}}}^{†}={{\mathit{V}}_d}^{†}{\mathit{V}}_u\left(\begin{array}{ccc}\cos \left({\theta }_{u31}\right)& 0& -e^{i{\delta }_{u31}}\sin \left({\theta }_{u31}\right)\\ 0& 1& 0\\ e^{-i{\delta }_{u31}}\sin \left({\theta }_{u31}\right)& 0& \cos \left({\theta }_{u31}\right)\end{array}\right),$$

where ${\theta }_{u31}$ is the 3–1 angle of the CKM matrix and ${\delta }_{u31}$ is the complex phase in that rotation.

Hence, the CKM matrix can be equivalently expressed as:

$${\mathit{V}}_{\mathrm{CKM}}=\left(\begin{array}{ccc}\cos \left({\theta }_{u31}\right)& 0& e^{i{\delta }_{u31}}\sin \left({\theta }_{u31}\right)\\ 0& 1& 0\\ -e^{-i{\delta }_{u31}}\sin \left({\theta }_{u31}\right)& 0& \cos \left({\theta }_{u31}\right)\end{array}\right) {{\mathit{V}}_u}^{†}{\mathit{V}}_d.$$

2.2. The 1–2 Rotation

We now turn to the 1–2 rotation, commonly referred to as the Cabibbo rotation and parameterized by the Cabibbo angle ${\theta }_{\mathrm{C}}$ [6,11].

The experimentally determined value is given in the PDG:

$$\sin \left({\theta }_{\mathrm{C}}\right)\approx 0.224-0.225\hspace{1em}\left(\Rightarrow {\theta }_{\mathrm{C}}\approx 0.226-0.227 \left[\mathrm{rad}\right]\right).$$

Next, we introduce a "half-Cabibbo" angle ${\theta }_{\mathrm{hC}}$ by defining:

$$\sin \left({\theta }_{\mathrm{hC}}\right)={\displaystyle \frac{1}{2}}\tan \left({\displaystyle \frac{2}{9}}\right)\hspace{1em}\left(\Rightarrow {\theta }_{\mathrm{hC}}\approx 0.113219 \left[\mathrm{rad}\right]\right).$$

We note explicitly that ${\theta }_{\mathrm{hC}}$ need not equal ${\displaystyle \frac{1}{2}}{\theta }_{\mathrm{C}}$.

Denoting the down-type and up-type 1–2 rotation angles by ${\theta }_{d12}$ and ${\theta }_{u12}$, respectively.

Then the individual rotation matrices are:

$$\begin{gathered} {\mathit{V}}_{d12}=\left(\begin{array}{ccc}\cos \left({\theta }_{d12}\right)& \sin \left({\theta }_{d12}\right)& 0\\ -\sin \left({\theta }_{d12}\right)& \cos \left({\theta }_{d12}\right)& 0\\ 0& 0& 1\end{array}\right), \\ {\mathit{V}}_{u12}=\left(\begin{array}{ccc}\cos \left({\theta }_{u12}\right)& \sin \left({\theta }_{u12}\right)& 0\\ -\sin \left({\theta }_{u12}\right)& \cos \left({\theta }_{u12}\right)& 0\\ 0& 0& 1\end{array}\right). \end{gathered}$$

Note that ${\theta }_{d12}$ can in principle be either $\pm {\theta }_{\mathrm{hC}}$.

We now choose:

$${\theta }_{d12}={\theta }_{\mathrm{hC}},\hspace{1em}{\theta }_{u12}=-{\theta }_{d12}=-{\theta }_{\mathrm{hC}}.$$

It follows that the combined rotation takes the form:

$${{\mathit{V}}_{u12}}^{†}{\mathit{V}}_{d12}=\left(\begin{array}{ccc}\cos \left(2{\theta }_{\mathrm{hC}}\right)& \sin \left(2{\theta }_{\mathrm{hC}}\right)& 0\\ -\sin \left(2{\theta }_{\mathrm{hC}}\right)& \cos \left(2{\theta }_{\mathrm{hC}}\right)& 0\\ 0& 0& 1\end{array}\right)\approx \left(\begin{array}{ccc}0.974472& 0.224507& 0\\ -0.224507& 0.974472& 0\\ 0& 0& 1\end{array}\right).$$

The magnitudes of the $\left(\mathrm{1,2}\right)$ and $\left(\mathrm{2,1}\right)$ entries are in good agreement with the experimental values of $\left|V_{us}\right|$ and $\left|V_{cd}\right|$ in the CKM matrix.

2.3. The 2–3 Rotation

In the 2–3 rotation, we denote the down-type quark rotation by ${\theta }_{d23}$ and the up-type quark rotation by ${\theta }_{u23}$.

The individual rotation matrices are:

$$\begin{gathered} {\mathit{V}}_{d23}=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \left({\theta }_{d23}\right)& e^{-i{\delta }_{d23}}\sin \left({\theta }_{d23}\right)\\ 0& -\hspace{0.17em}{e}^{i{\delta }_{d23}}\sin \left({\theta }_{d23}\right)& \cos \left({\theta }_{d23}\right)\end{array}\right), \\ {\mathit{V}}_{u23}=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \left({\theta }_{u23}\right)& e^{-i{\delta }_{u23}}\sin \left({\theta }_{u23}\right)\\ 0& -\hspace{0.17em}{e}^{i{\delta }_{u23}}\sin \left({\theta }_{u23}\right)& \cos \left({\theta }_{u23}\right)\end{array}\right). \end{gathered}$$

We now choose:

$${\theta }_{d23}={\displaystyle \frac{1}{9}},\hspace{1em}{\theta }_{u23}=-{\displaystyle \frac{1}{9}}.$$

For the complex phases, we set:

$${\delta }_{d23}=-{\theta }_a,\hspace{1em}{\delta }_{u23}={\theta }_a.$$

Hence,

$${{\mathit{V}}_{u23}}^{†}{\mathit{V}}_{d23}=\left(\begin{array}{ccc}1& 0& 0\\ 0& {\cos }^2\left({\displaystyle \frac{1}{9}}\right)-e^{2i{\theta }_a}{\sin }^2\left({\displaystyle \frac{1}{9}}\right)& \cos \left({\theta }_a\right)\sin \left({\displaystyle \frac{2}{9}}\right)\\ 0& -\cos \left({\theta }_a\right)\sin \left({\displaystyle \frac{2}{9}}\right)& {\cos }^2\left({\displaystyle \frac{1}{9}}\right)-e^{-2i{\theta }_a}{\sin }^2\left({\displaystyle \frac{1}{9}}\right)\end{array}\right).$$

Numerically, the matrix can be expressed approximately as:

$$\left(\begin{array}{ccc}1& 0& 0\\ 0& 0.999100+0.004618i& 0.042171\\ 0& -0.042171& 0.999100-0.004618i\end{array}\right).$$

The magnitudes of the $\left(\mathrm{2,3}\right)$ and $\left(\mathrm{3,2}\right)$ entries are in good agreement with the experimental values of $\left|V_{cb}\right|$ and $\left|V_{ts}\right|$ in the CKM matrix.

2.4. Combining the Matrices

We define the following matrices:

$$\begin{gathered} {\mathit{V}}_d={\mathit{V}}_{d23}{\mathit{V}}_{d12}, \\ {\mathit{V}}_u={\mathit{V}}_{u23}{\mathit{V}}_{u12}. \end{gathered}$$

It follows that:

$${{\mathit{V}}_u}^{†}{\mathit{V}}_d={{\mathit{V}}_{u12}}^{†}{{\mathit{V}}_{u23}}^{†}{\mathit{V}}_{d23}{\mathit{V}}_{d12}.$$

3. Result

The result is obtained as follows:

$${{\mathit{V}}_u}^{†}{\mathit{V}}_d\approx \left(\begin{array}{ccc}+0.974484-0.000059i& +0.224406+0.000518i& 0.004764+0.000000i\\ -0.224406-0.000518i& +0.973584+0.004559i& 0.041901+0.000000i\\ +0.004764+0.000000i& -0.041901-0.000000i& 0.999100-0.004618i\end{array}\right).$$

The absolute values of each element are:

$$\left(\begin{array}{ccc}0.974484& 0.224407& 0.004764\\ 0.224407& 0.973594& 0.041901\\ 0.004764& 0.041901& 0.999110\end{array}\right).$$

4. Discussion

The absolute values of each element obtained in Section 3, with the exception of the $\left(1,3\right)$ and $\left(3,1\right)$ entries, are close to the experimentally determined values.

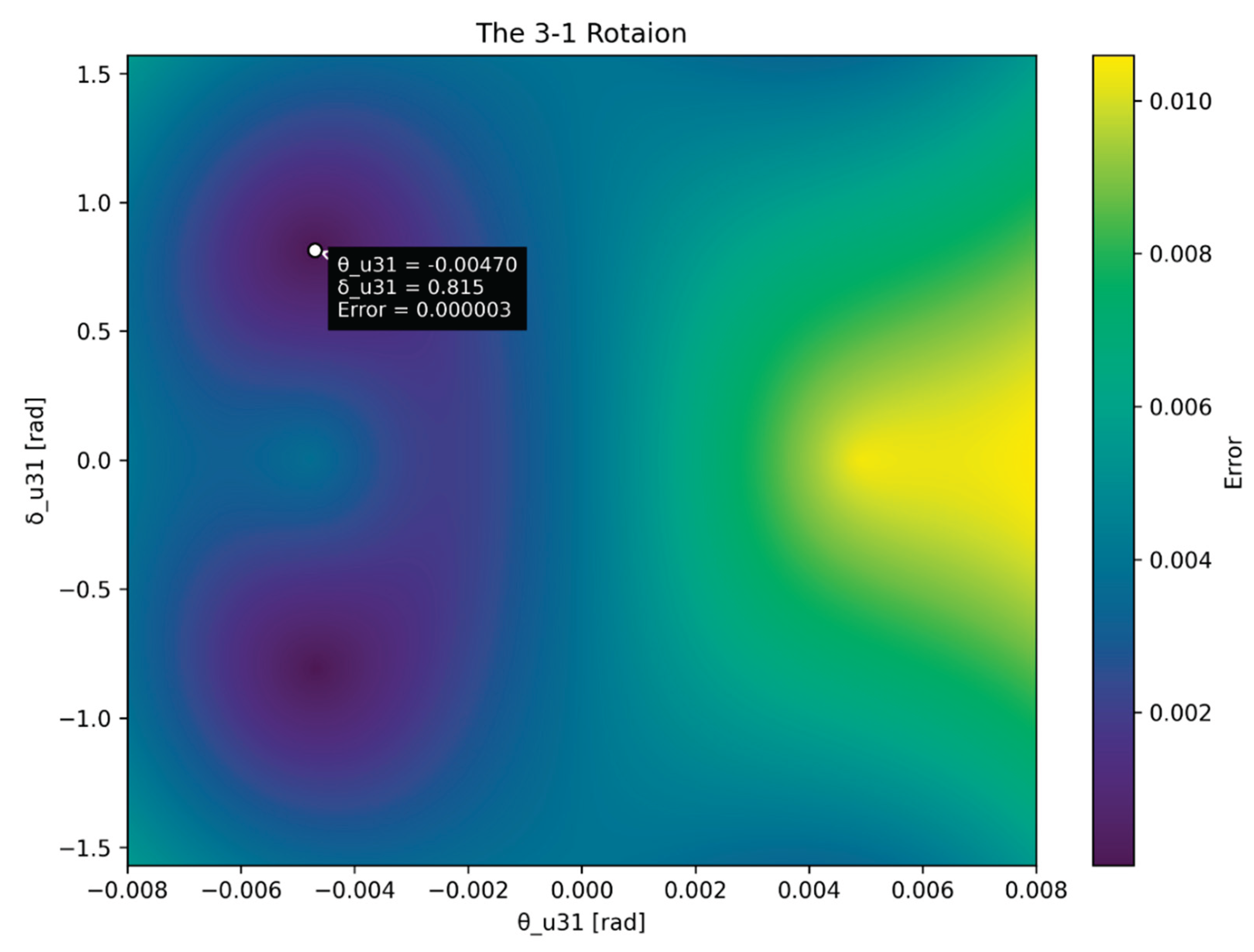
The only remaining free parameters are those of the 3–1 rotation, because the up-type quark mass formula remains unspecified. Hence the parameters ${\theta }_{u31}$ and ${\delta }_{u31}$ cannot be determined in advance. To resolve these, we have performed a two-dimensional grid search over ${\theta }_{u31}$ and ${\delta }_{u31}$, selecting the values that minimize the deviation of $\left|V_{ub}\right|$ and $\left|V_{td}\right|$ from their experimental counterparts. The optimal parameters are found to be:

$${\theta }_{u31}=-0.00470 \left[\mathrm{rad}\right],\hspace{1em}{\delta }_{u31}=0.815 \left[\mathrm{rad}\right]$$

(see Figure 2).

At these values the CKM matrix takes the form:

$${\mathit{V}}_{\mathrm{CKM}}\approx \left(\begin{array}{ccc}0.974458-0.000075i& 0.224539+0.000662i& 0.001528-0.003402i\\ -0.224406-0.000518i& 0.973584+0.004559i& 0.041901+0.000000i\\ 0.007905-0.003333i& -0.041176-0.000766i& 0.999104-0.004634i\end{array}\right).$$

The absolute values of each element are:

$$\left(\begin{array}{ccc}0.974458& 0.224540& 0.003730\\ 0.224407& 0.973594& 0.041901\\ 0.008579& 0.041183& 0.999115\end{array}\right).$$

These values are in excellent agreement with the PDG 2024 global-fit values, with all deviations within 0.7 standard deviations ($0.7\sigma$).

Moreover, the three interior angles of the corresponding unitarity triangle are found to be:

$$\begin{gathered} \alpha =\arg \left(-{\displaystyle \frac{V_{td}{V}_{tb}^{*}}{V_{ud}{V}_{ub}^{*}}}\right)\approx 1.598571\mathrm{ }\left[\mathrm{rad}\right]\approx {91.591}^{\circ }, \\ \beta =\arg \left(-{\displaystyle \frac{V_{cd}{V}_{cb}^{\mathrm{*}}}{V_{td}{V}_{tb}^{\mathrm{*}}}}\right)\approx 0.396689 \left[\mathrm{rad}\right]\approx {22.729}^{\circ }, \\ \gamma =\arg \left(-{\displaystyle \frac{V_{ud}{V}_{ub}^{\mathrm{*}}}{V_{cd}{V}_{cb}^{\mathrm{*}}}}\right)\approx 1.146333 \left[\mathrm{rad}\right]\approx {65.680}^{\circ }. \end{gathered}$$

Hence, we have

$$\sin \left(2\beta \right)\approx 0.713,$$

which is in excellent agreement with the experimental value ${\sin \left(2\beta \right)}_{\exp }=0.709\pm 0.011.$

Finally, we calculate the Jarlskog invariant [12]

$$\left|J\right|=\left|\mathrm{Im}\left(V_{ud}{V}_{cs}{V}_{us}^{*}{V}_{cd}^{*}\right)\right|\approx 3.113\times {10}^{-5},$$

which is in excellent agreement with the experimental value $J_{\exp }=\left({3.12}_{-0.12}^{+0.13}\right)\times {10}^{-5}.$

All parameters are in excellent agreement with the experimental values, but ${\theta }_{u31}\approx -0.00470 \left[\mathrm{rad}\right]$ and ${\delta }_{u31}\approx 0.815 \left[\mathrm{rad}\right]$ cannot be uniquely determined because a corresponding mass formula for up-type quarks remains undetermined. We anticipate that future investigations will shed light on this issue.

5. Conclusion

By postulating a mass formula for down-type quarks—which yields the values:

$${\displaystyle \frac{1}{9}},\hspace{1em}{\displaystyle \frac{1}{2}}\cos \left({\displaystyle \frac{3}{8}}\mathsf{\pi }\right)$$

—and by introducing a "half-Cabibbo" angle:

$${\displaystyle \frac{1}{2}}\tan \left({\displaystyle \frac{2}{9}}\right),$$

we have been able to construct a matrix that closely approximates the CKM matrix except for the 3–1 rotation. However, since no analogous mass formula for up-type quarks has yet been deduced, the 3–1 rotation matrix remains undetermined, and only a rough estimate of its value could be obtained. It is anticipated that, with the successful conjecture of an up-type quark mass formula in future work, a more accurate reconstruction of the CKM matrix will become possible.