Submitted:
07 August 2025
Posted:
08 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Field-Observed RCF
2.1. RCF of Rails
2.1.1. Squats
2.1.2. Head Checks
2.2. RCF of Wheels
2.2.1. Spalling
2.2.2. Shelling
2.2.3. Heavy Shelling
2.2.4. Flat Spalling
3. Field-Observed Wear
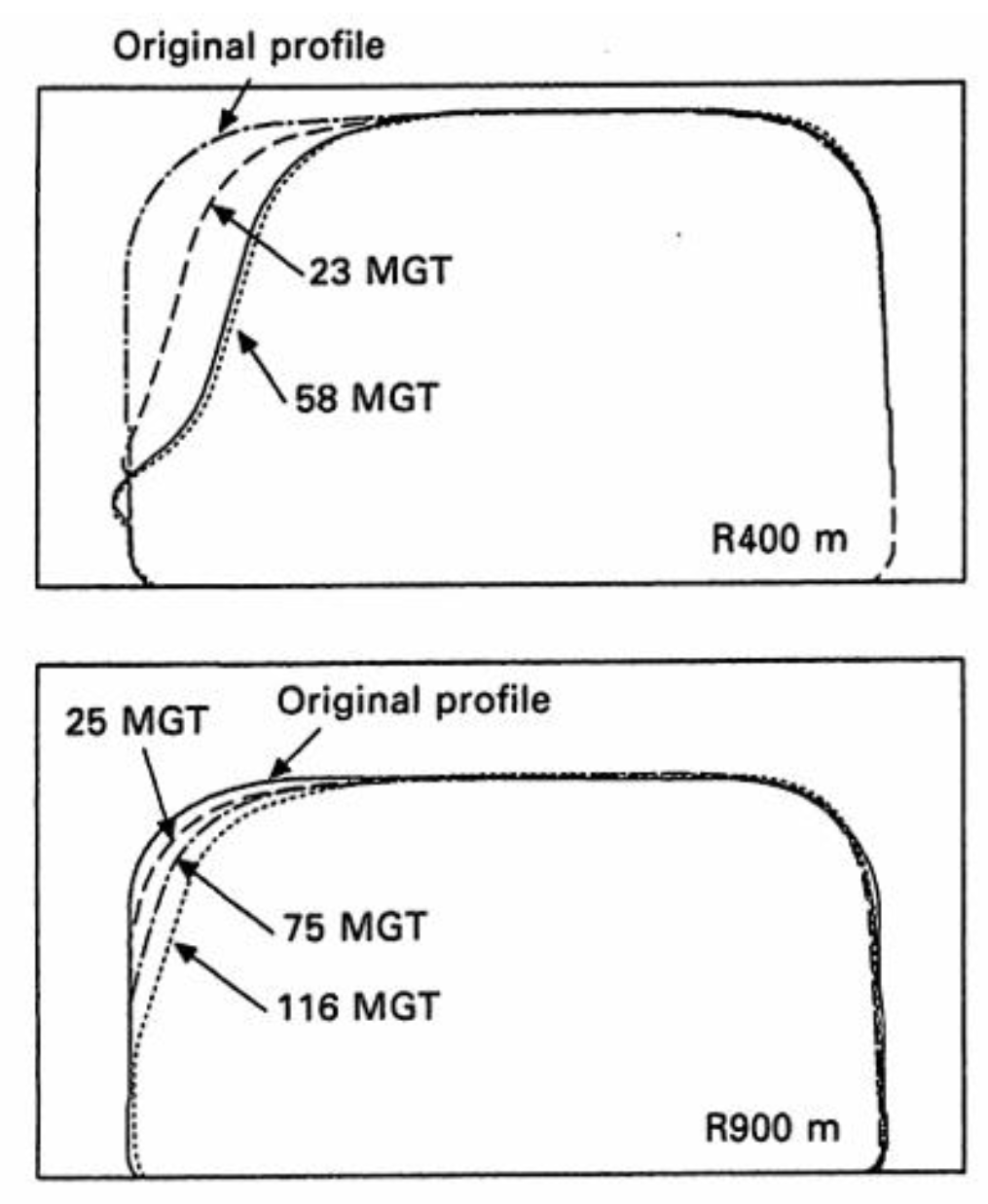
3.1. Wear of Rails
3.1.1. Side Wear
3.1.2. Corrugation
3.2. Wear of Wheels
3.2.1. Hollow Wear and Grooving Wear
3.2.2. Flange Vertical Wear
4. RCF Crack Models
4.1. Crack Initiation
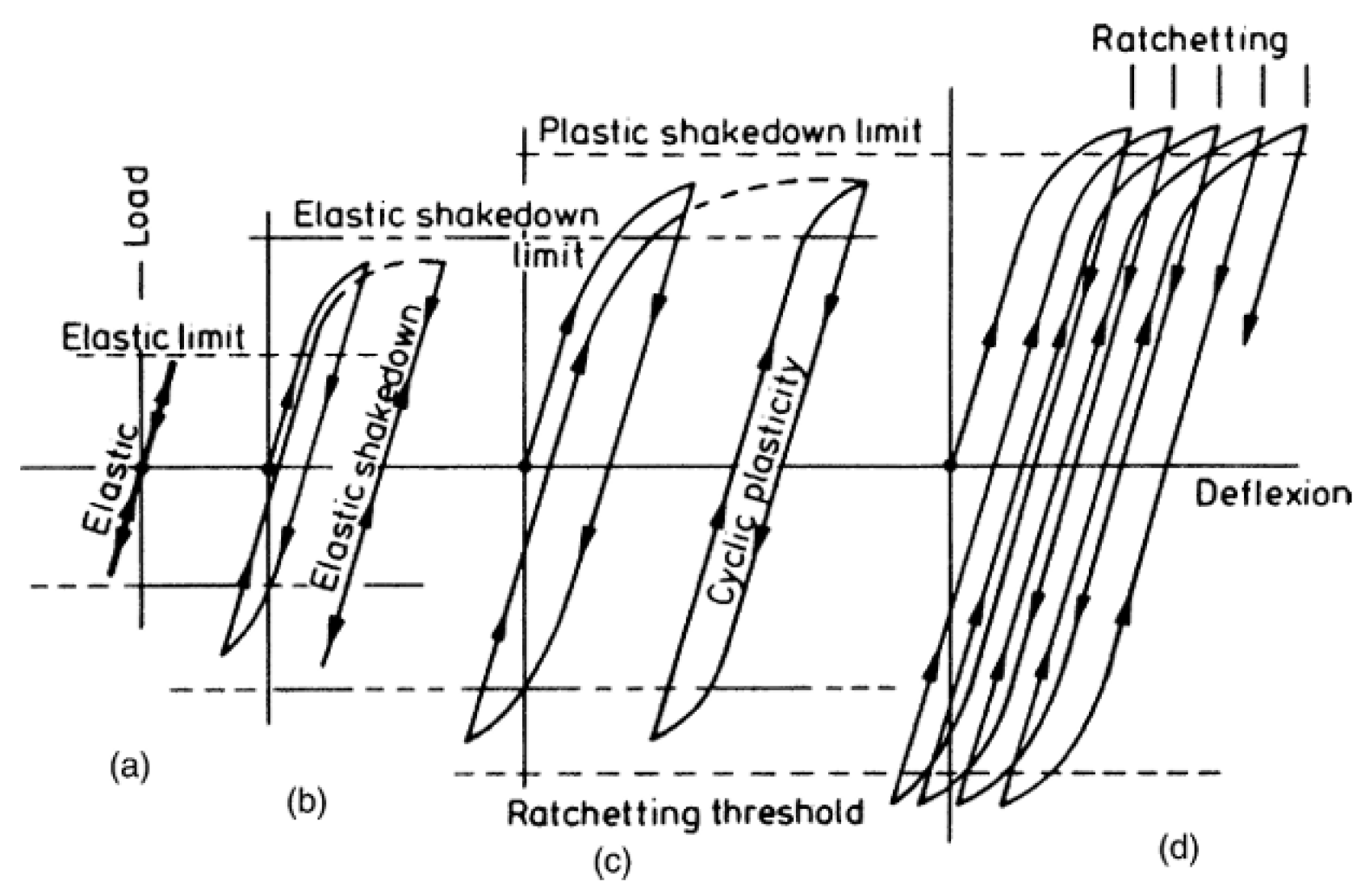
4.1.1. Elastic Shakedown
4.1.2. Plastic Shakedown
4.1.3. Ratcheting
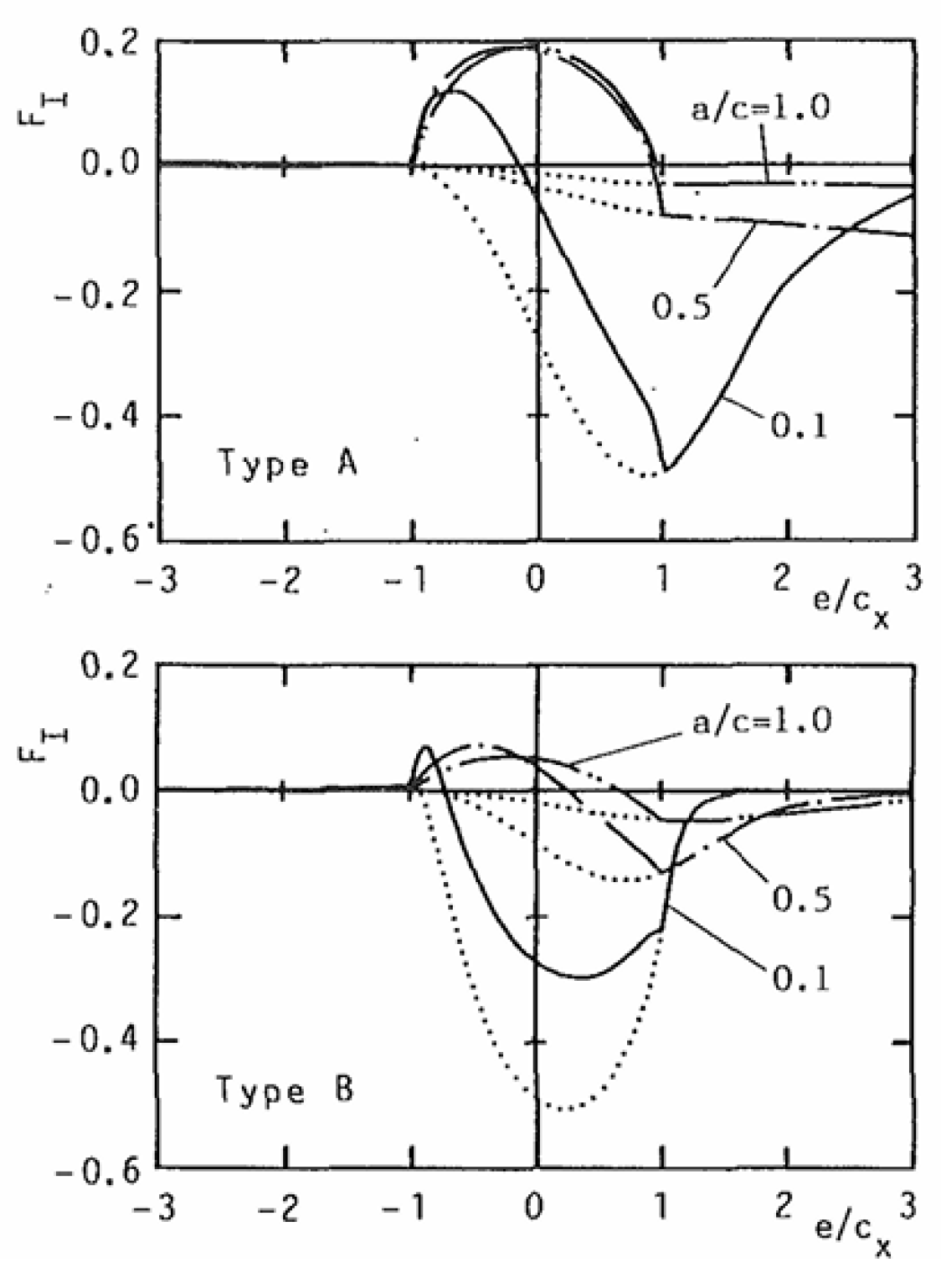
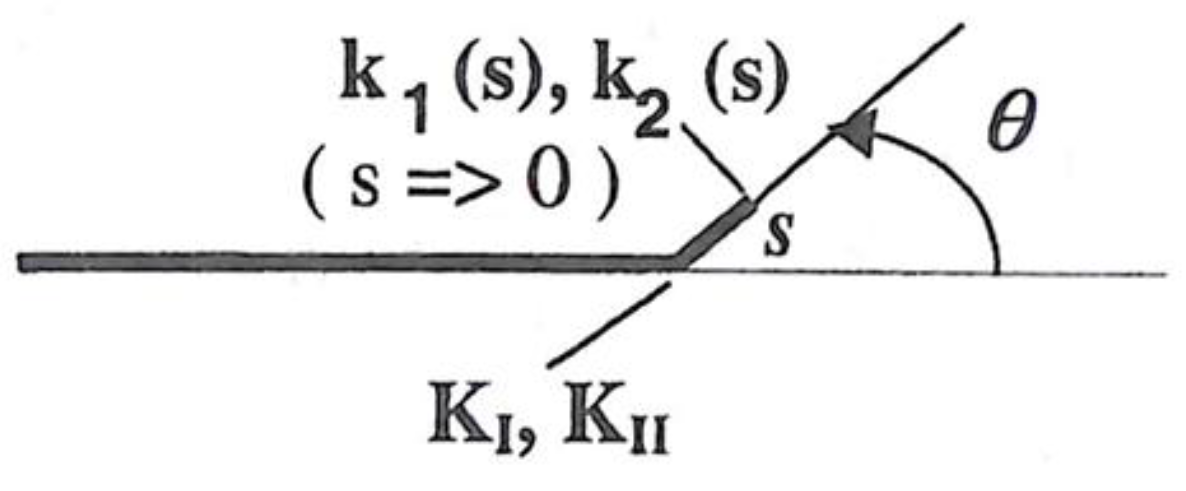
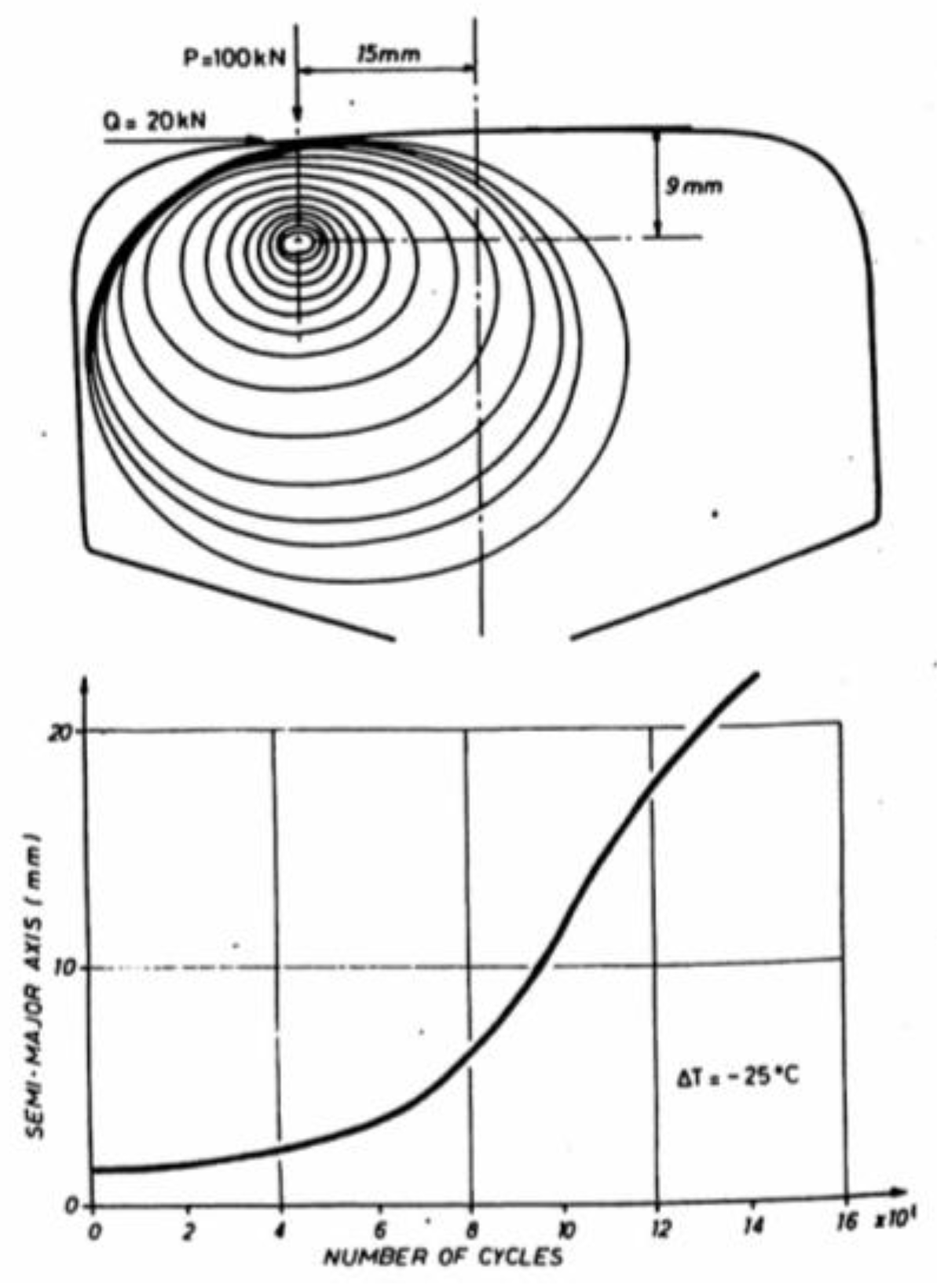
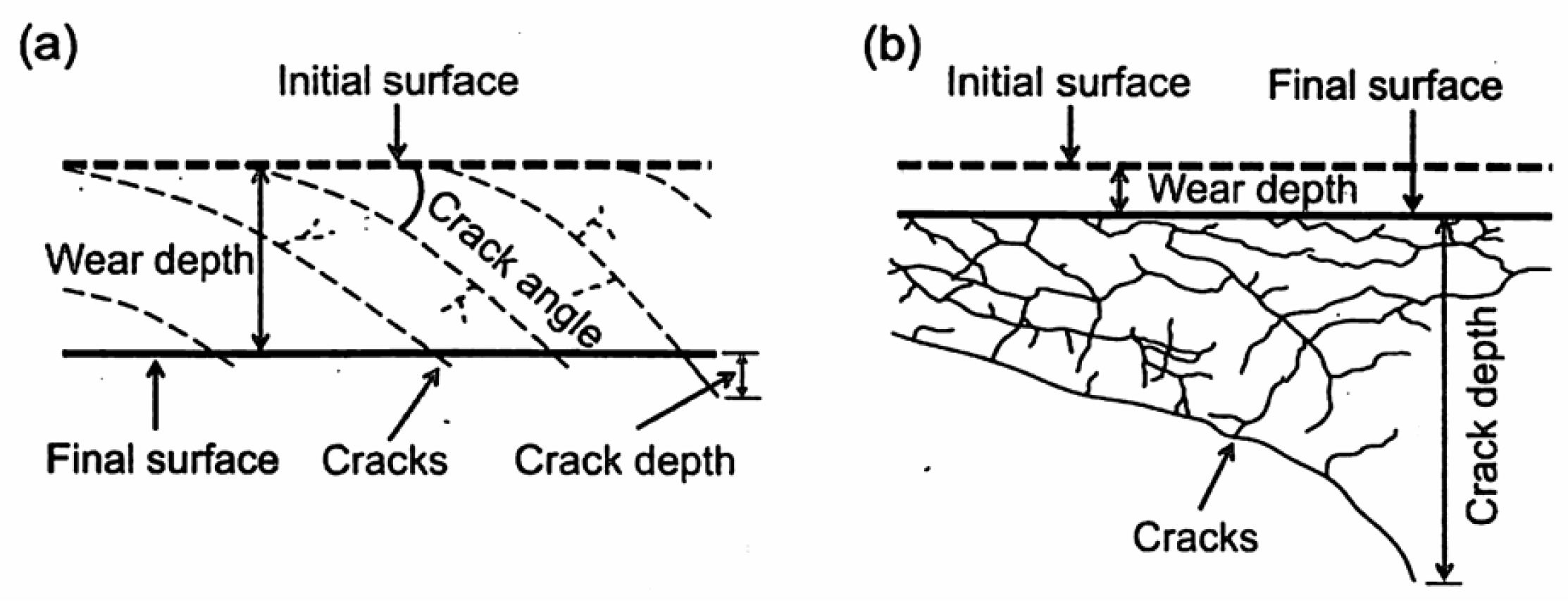
4.2. Crack Growth
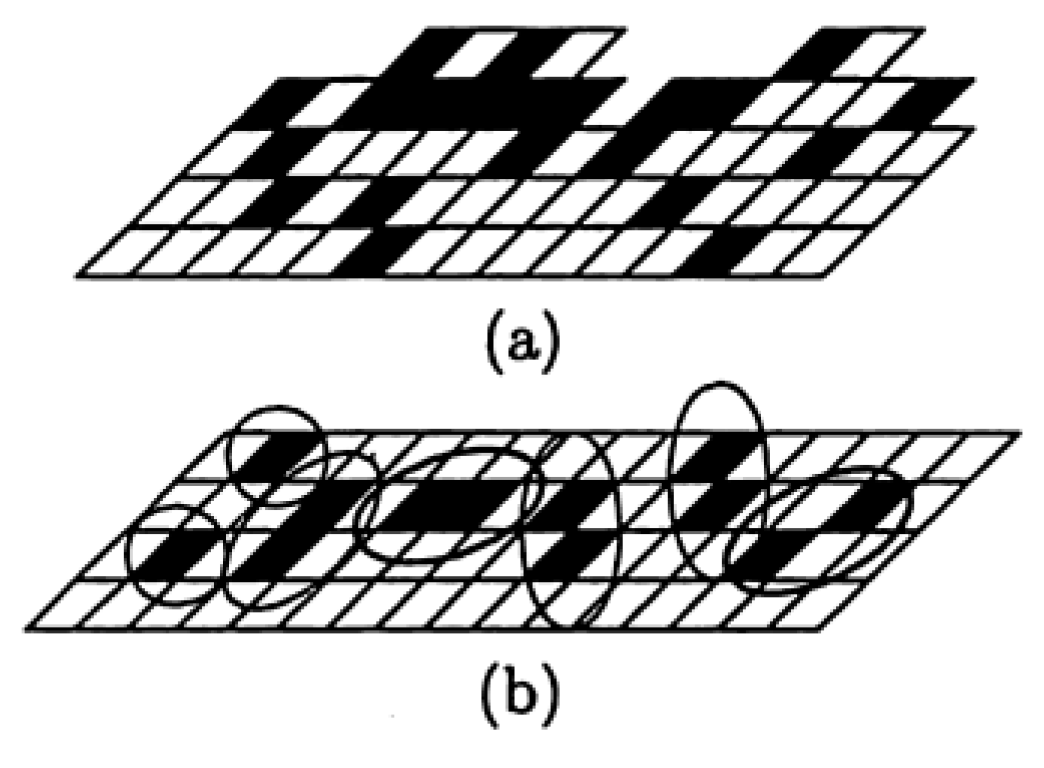
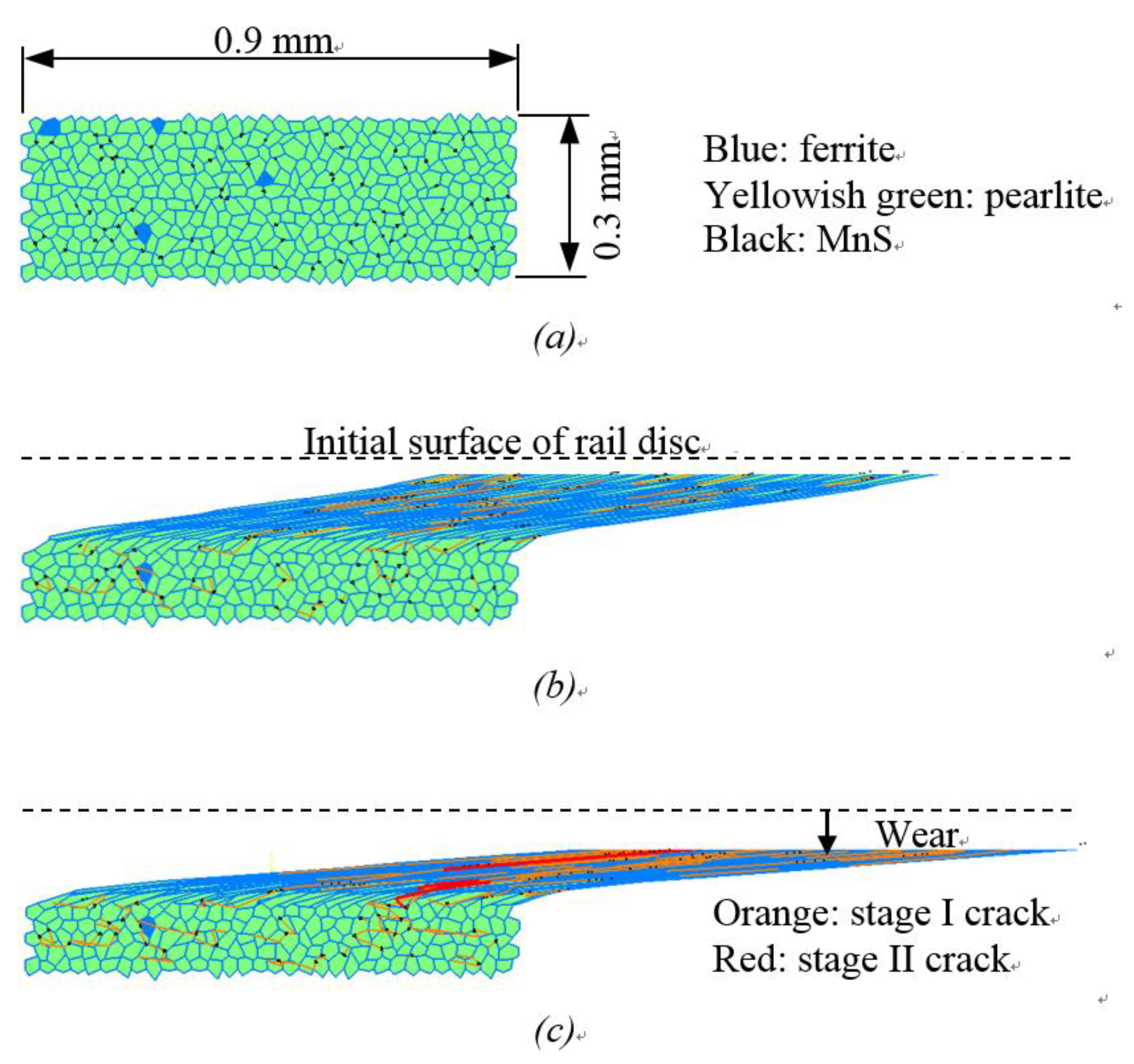
4.2.1. Short Crack
- (a)
- MSC crack growth (Stage I)
- (b)
- PSC crack growth (Stage II)
- (c)
- Coalescence
- (d)
- Surface roughness
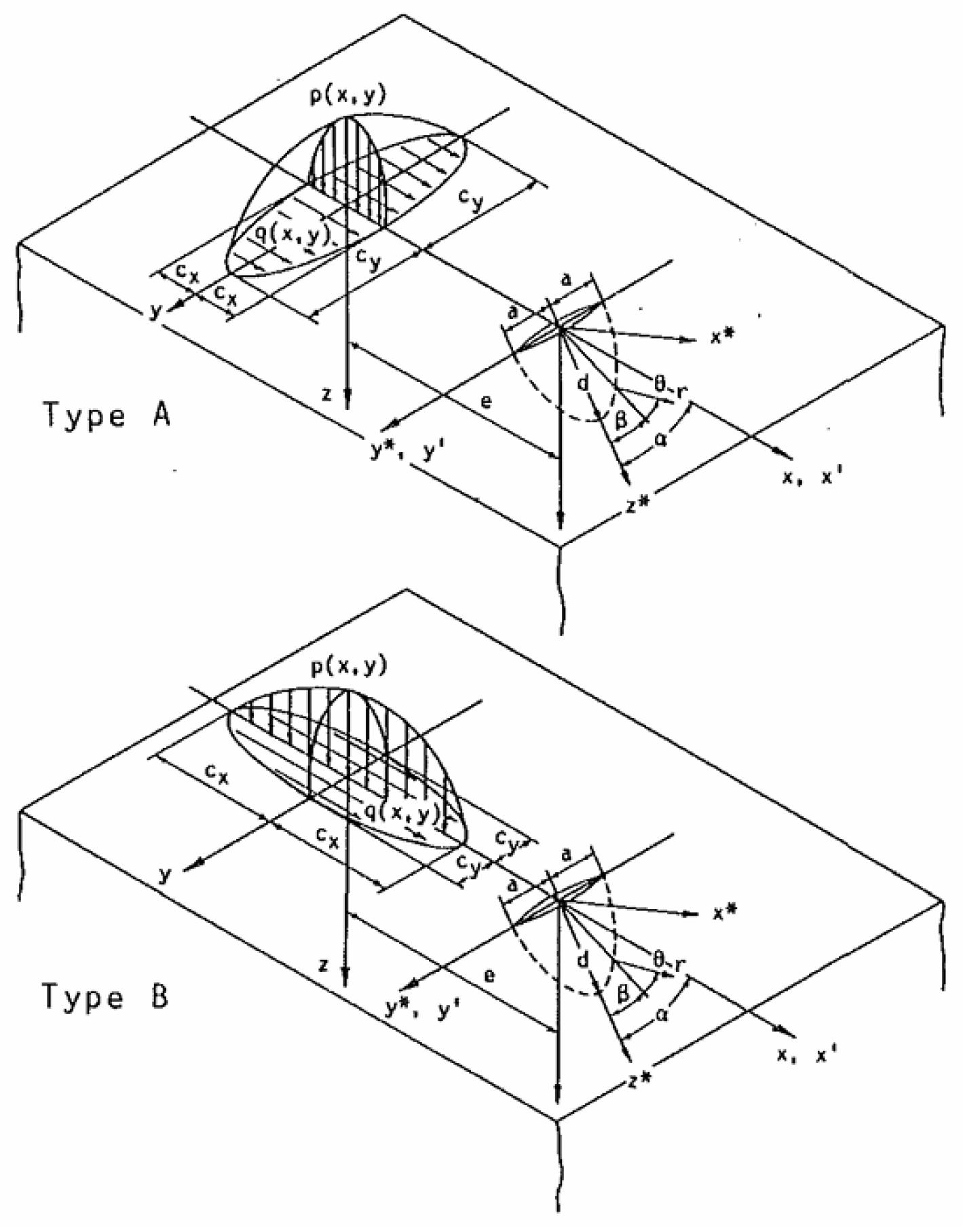
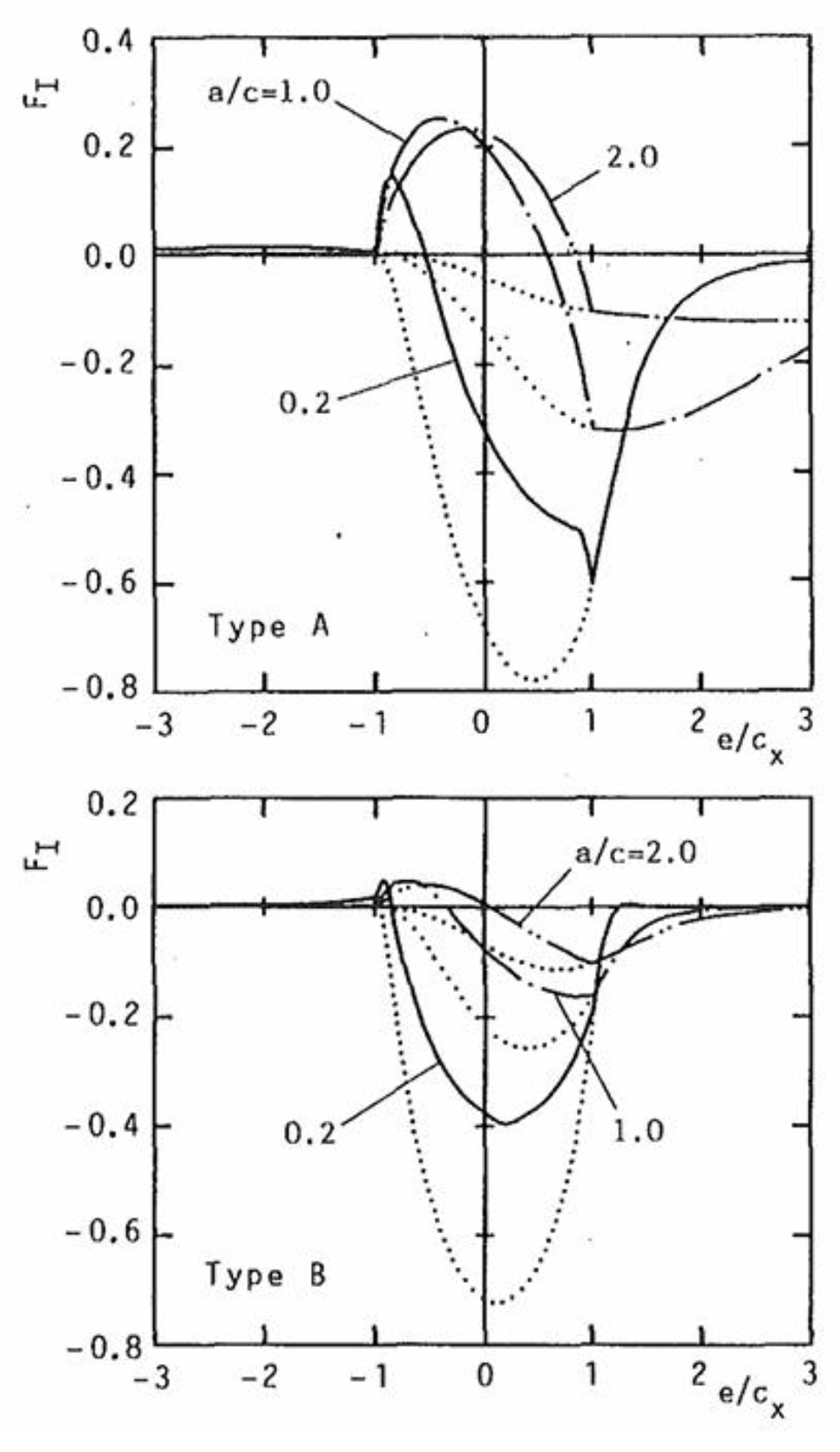
4.2.2. Long Crack
- (a)
- Role of the lubricant
- 1)
- Bending stress
- 2)
- Contact stress
- 3)
- Thermal stress
- 4)
- Residual stress
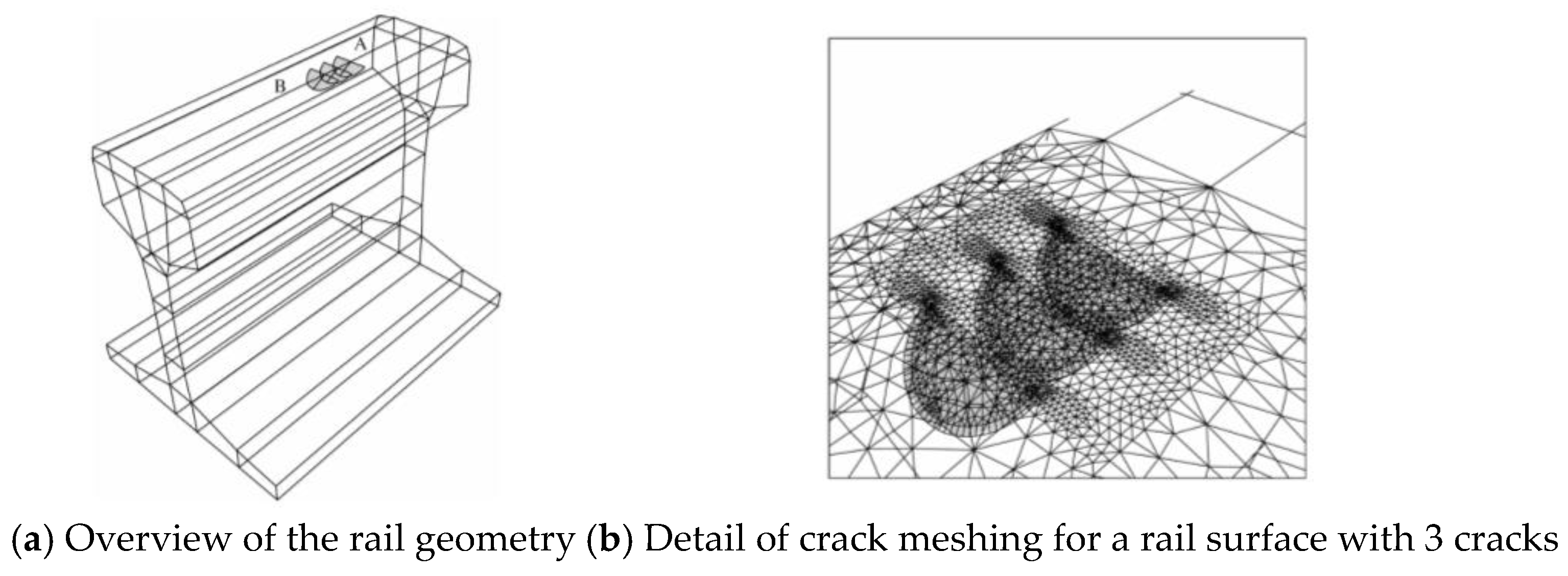
5. Wear Models
5.1. Wear Mechanisms
5.1.1. Adhesive Wear
5.1.2. Abrasive Wear
5.1.3. Fatigue Wear
5.1.4. Corrosive Wear
5.1.5. Delamination Wear
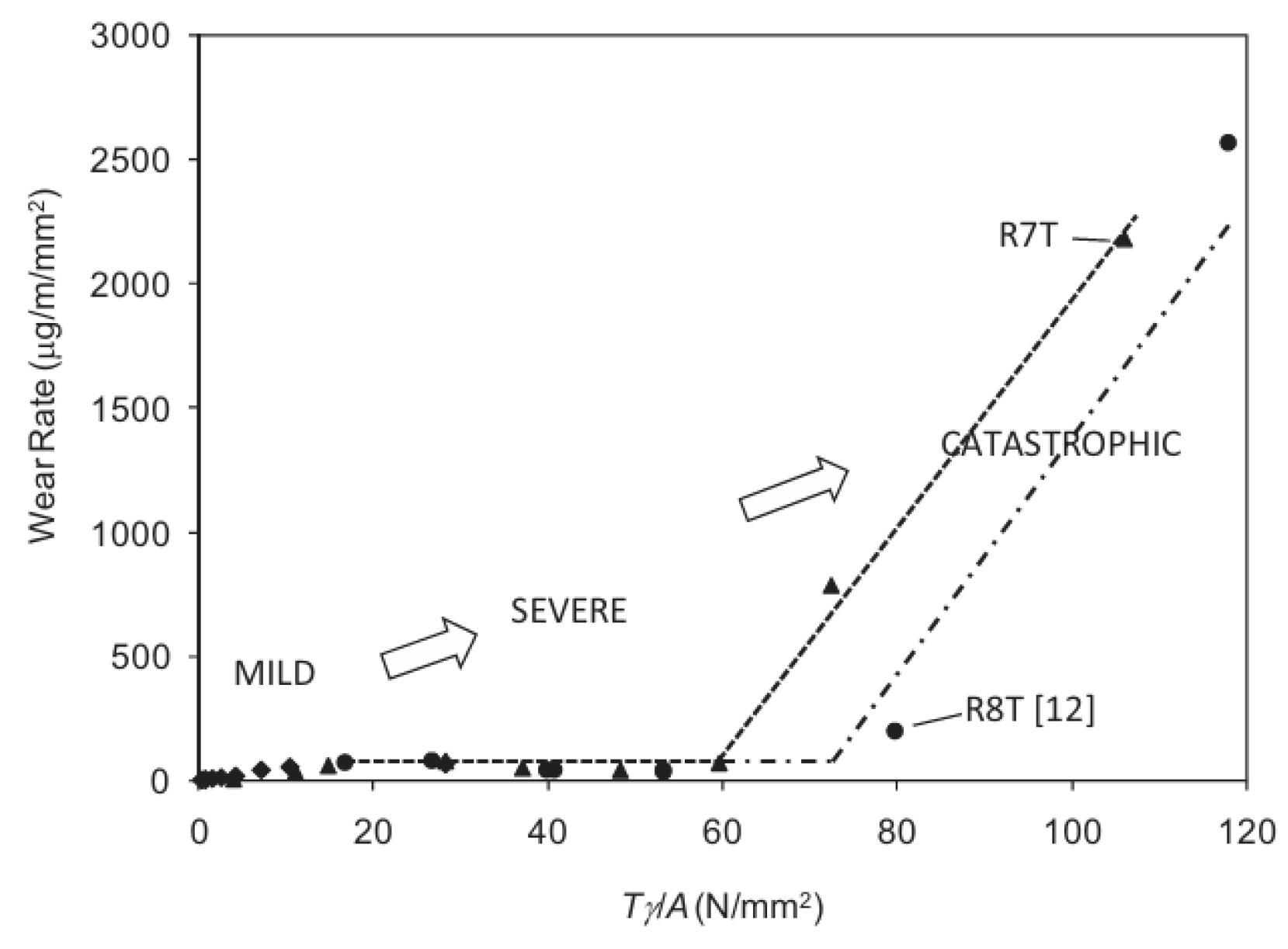
5.2. Wear Regimes
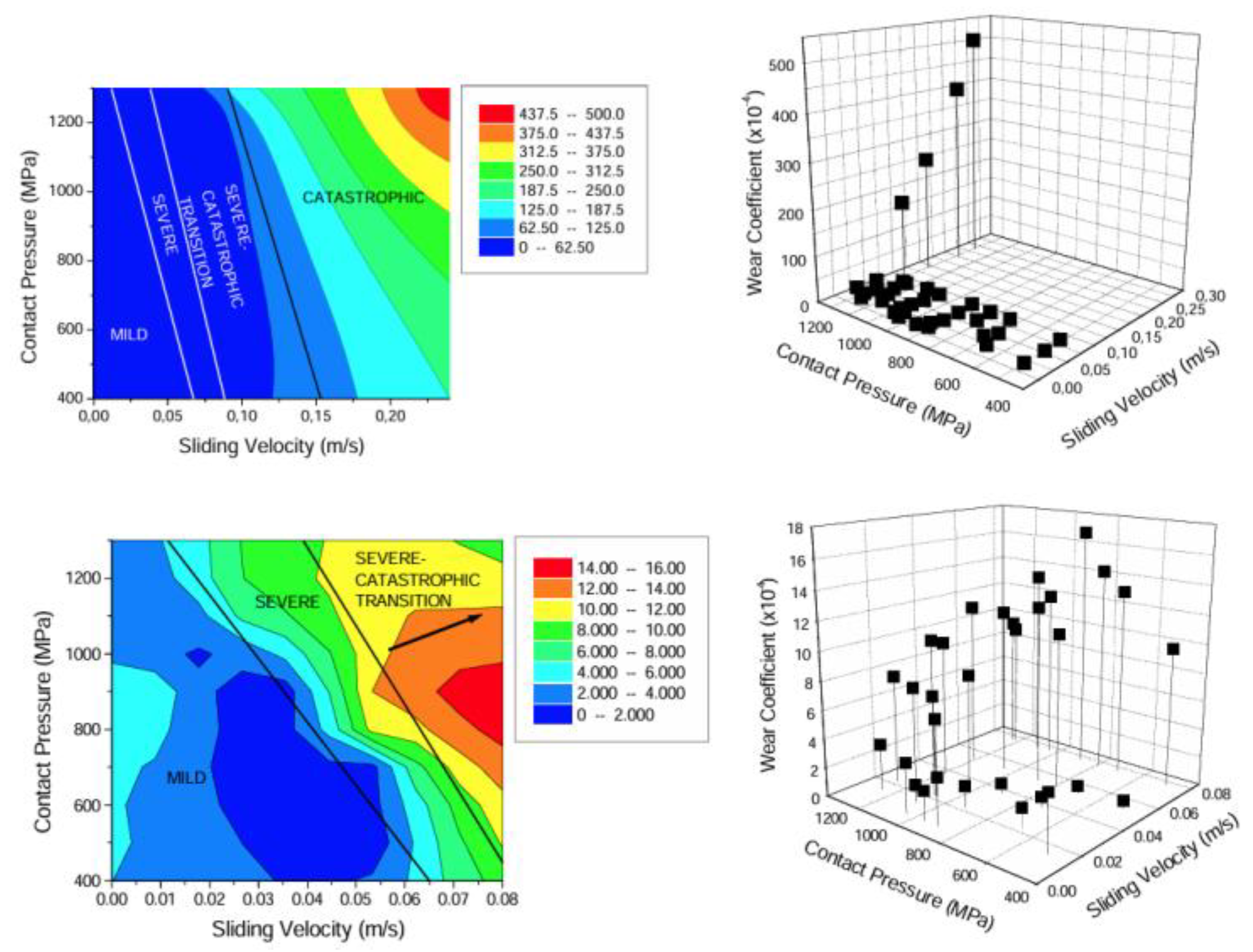
5.3. Wear Coefficient Maps
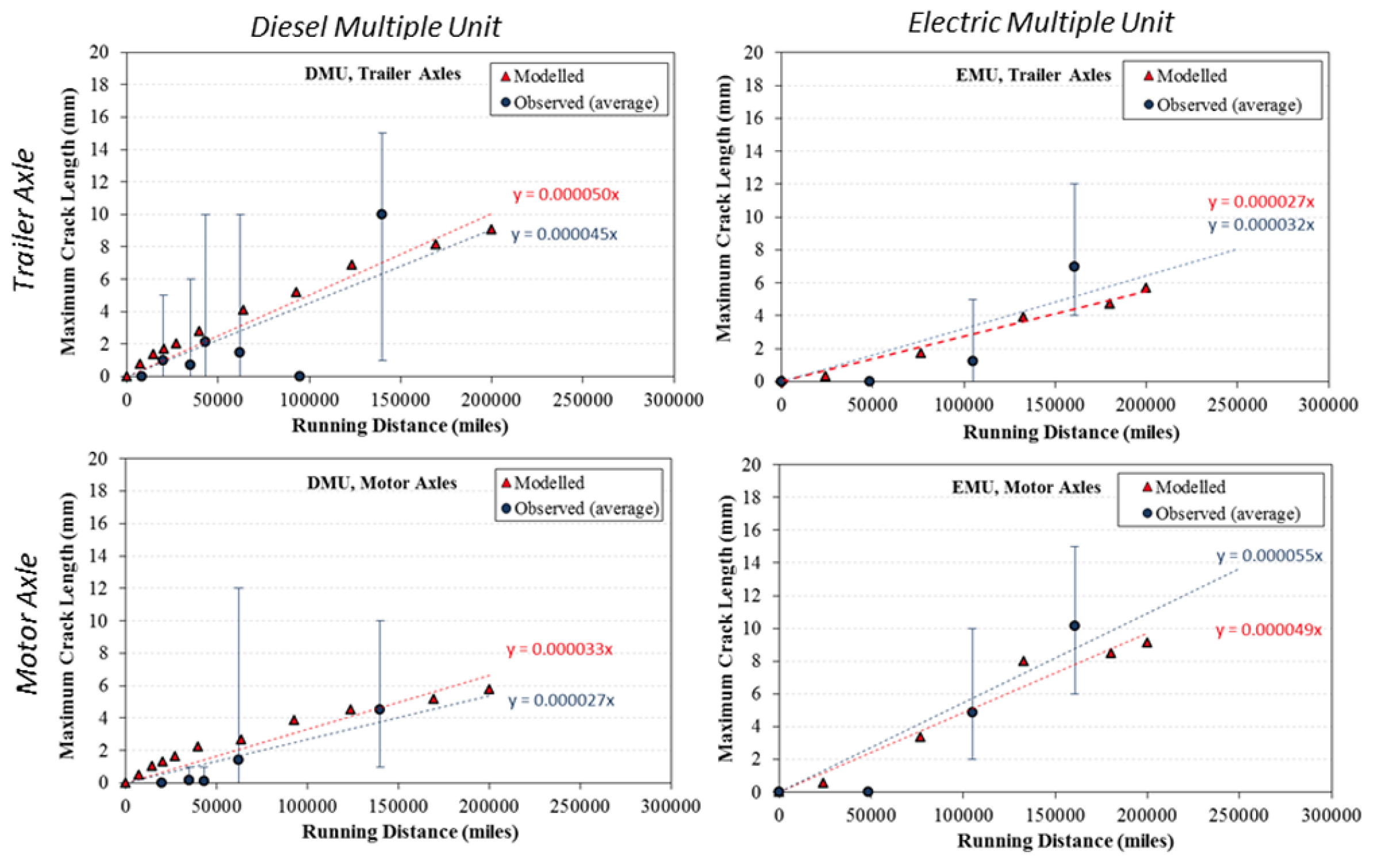
5.4. Wear Prediction
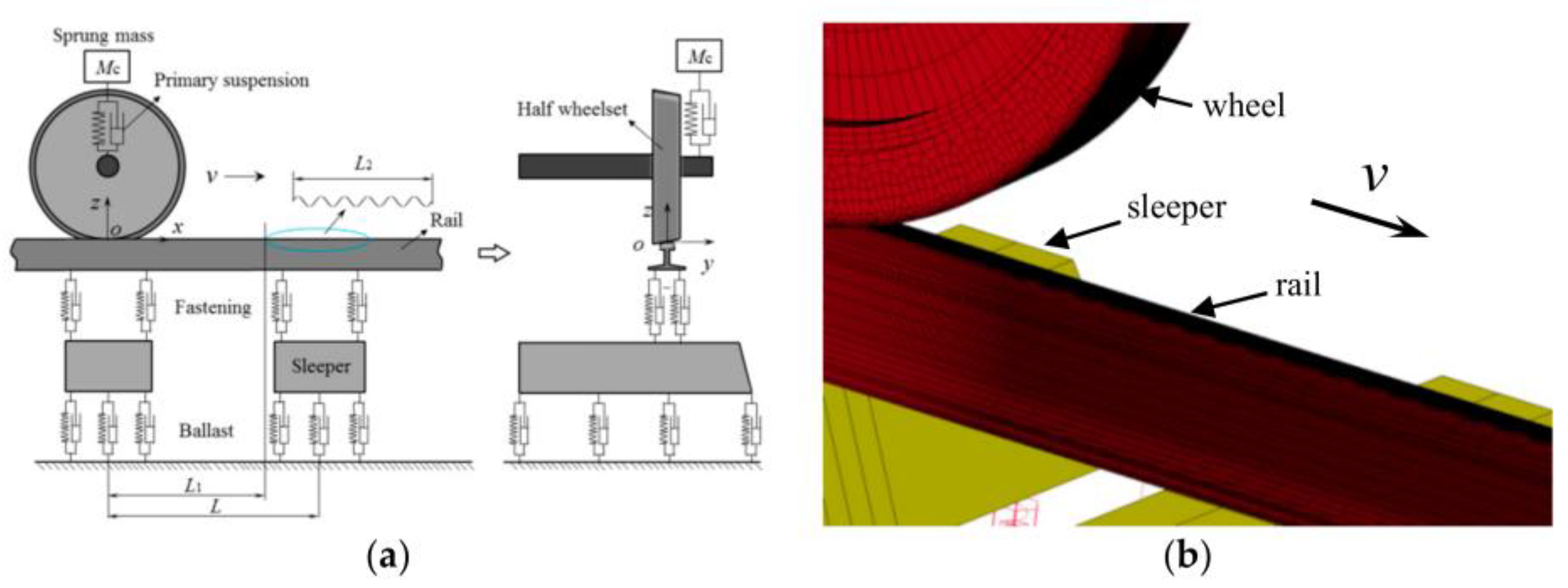
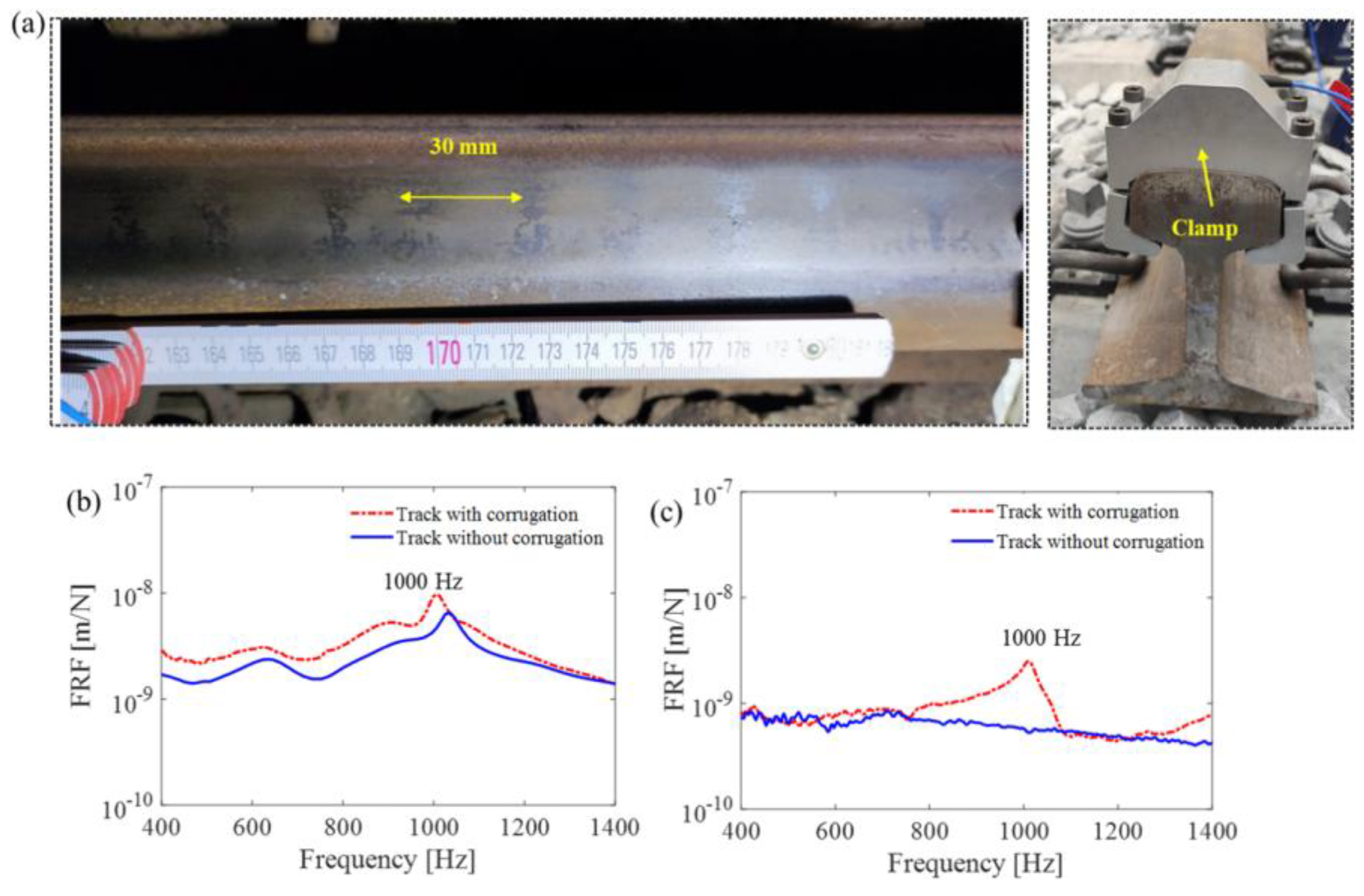
5.5. Corrugation
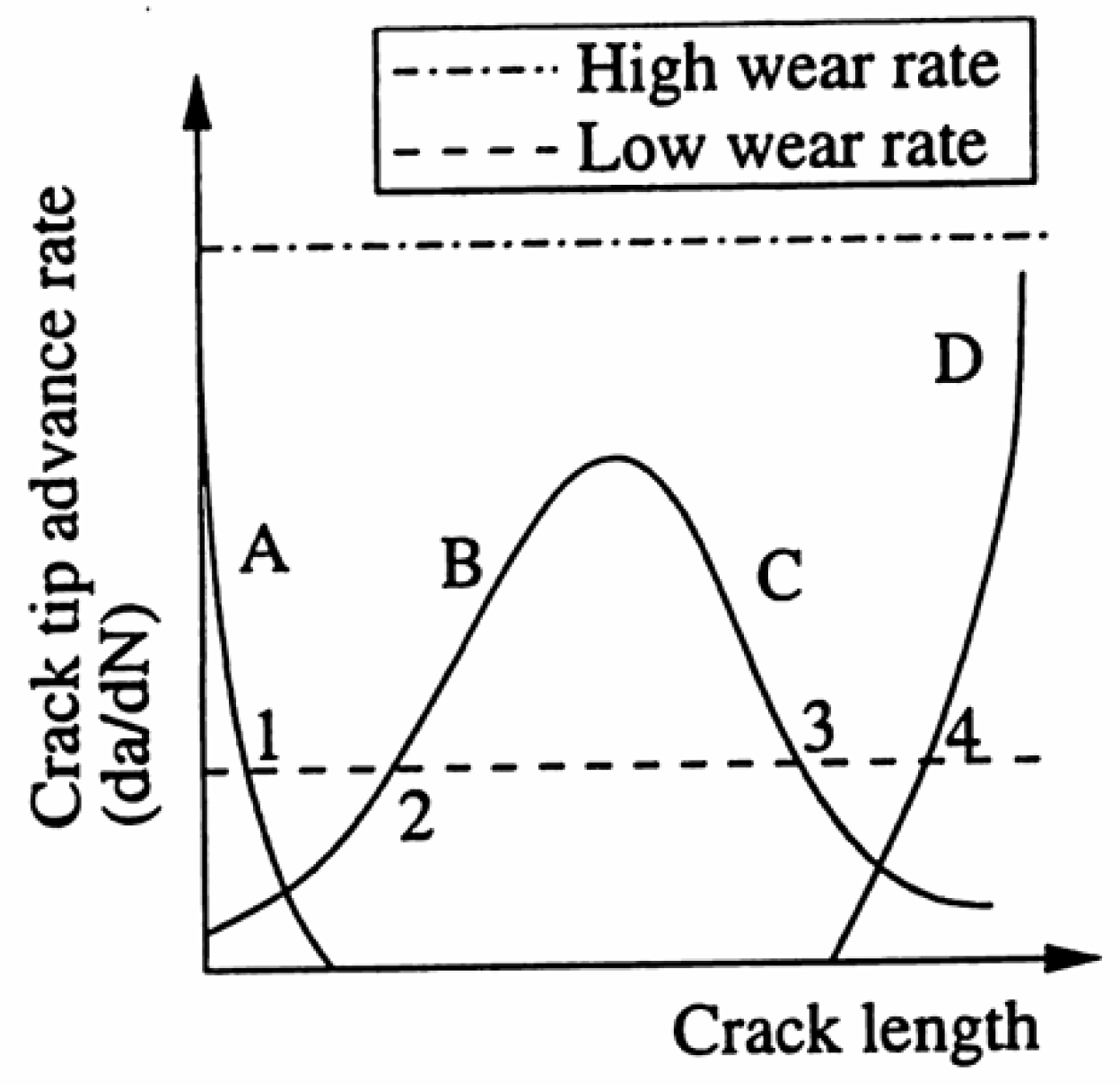
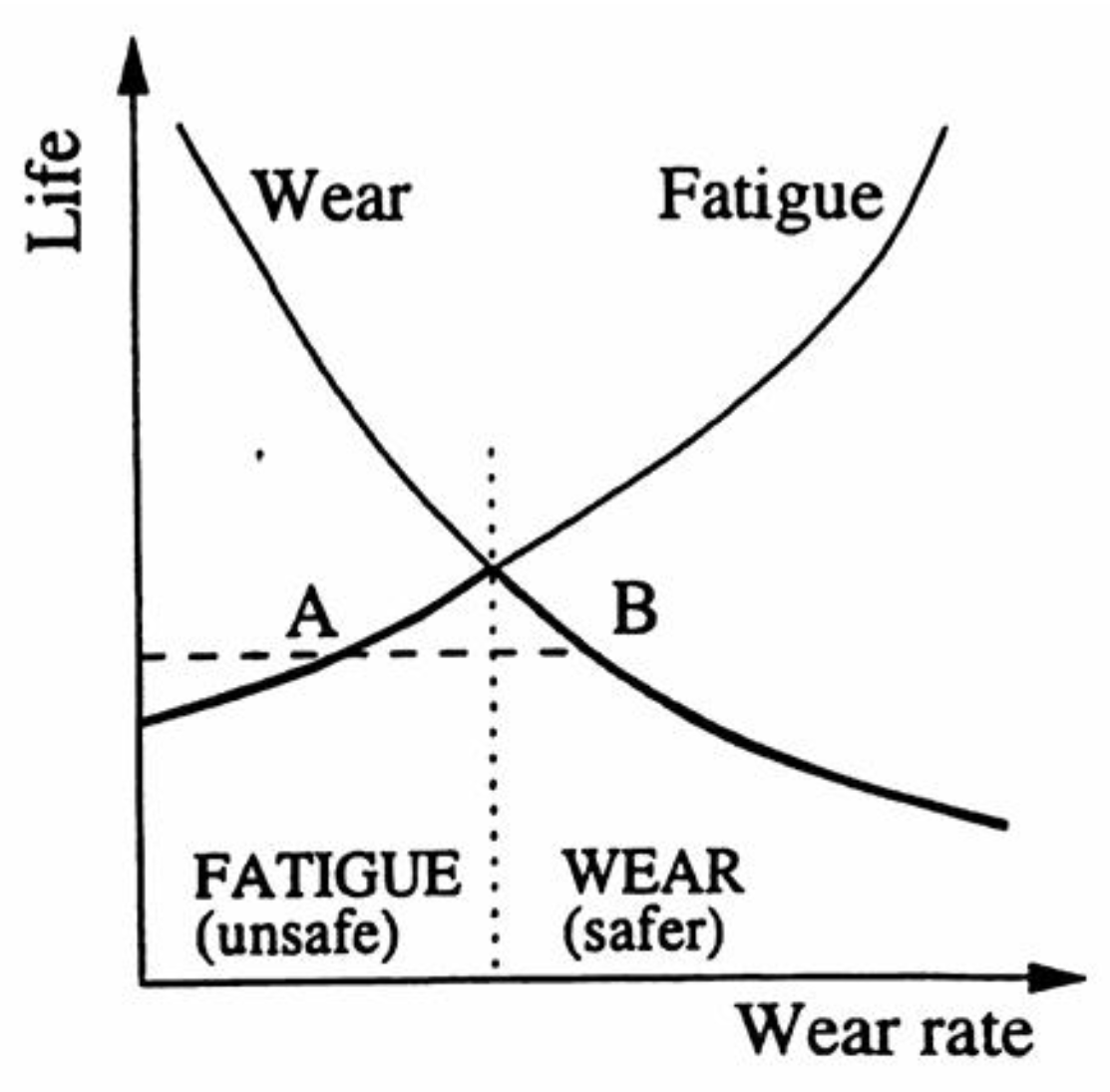
6. Competition Between RCF and Wear
7. Discussion
7.1. Details of Crack Initiation and MSC Growth
7.2. 3D Analysis of Short Cracks
7.3. Modelling for Fatigue Wear
7.4. Complex Shape of Horizontal Crack Growth
7.5. Effects of Rolling Reversal of Wheel
8. Conclusions
References
- Bevan, A.; Iwnicki, S. Review of wheel turning data and identification of other wheel damage modes, T792 project report, RSSB, 2010.
- Kapoor, A.; Fletcher, D.I.; Franklin, F.J. The role of wear in enhancing rail life. Tribol. Series 2003, 41, 331–340. [Google Scholar]
- Magel, E.; Mutton, P.; Ekberg, A.; Kapoor, A. Rolling contact fatigue. wear and broken rail derailments. Wear 2016, 366–367, 249–257. [Google Scholar] [CrossRef]
- Kanematsu, Y. A study on grinding control method considering surface decarburization and rolling contact fatigue of railway rails. PhD thesis, Tokyo University of Science 2023.
- Railway wheelset, Edited by Research Committee for wheelset of high-speed vehicle, Maruzen planet, 2011. (in Japanese).
- Wheel-rail interface handbook, Edited by R. Lewis and U. Olofsson, Woodhead publishing Limited, 2009.
- Matsumoto, A. Prevention of rail corrugation on curve and improvement of bogie curving performance, PhD thesis, The University of Tokyo, 2017.
- Kapoor, A. A re-evaluation of the life to rupture of ductile metals by cyclic plastic strain. Fat. Fract. Eng. Mater. Struct. 1994, 17, 201–219. [Google Scholar] [CrossRef]
- Van, K.D.; Cailletaud, G.; Flavenot, J.F.; Douaron, A.L. Criterion for high cycle fatigue failure under multiaxial loading in biaxial and multiaxial fatigue, 1989, 459–478. Mechanical Engineering Publications, London.
- Ekberg, A.; Bjarnehed, H.; Lundbéan, R. A fatigue life model for general rolling contact with application to wheel/rail damage. Fat. Fract. Engng. Mater. Struct. 1995, 18, 1189–1199. [Google Scholar] [CrossRef]
- Kato, T.; Sugeta, A.; Nakayama, E. Investigation of influence of white layer geometry on spalling property in railway wheel steel. Wear 2011, 18, 400–407. [Google Scholar] [CrossRef]
- Jiang, Y.; Sehitoglu, H. Modeling of cyclic ratchetting plasticity, part I: Development of constitutive relations. Trans. ASME, J. Appi. Mech. 1996, 63, 720–725. [Google Scholar] [CrossRef]
- Ringsberg, J.W. Life prediction of rolling contact fatigue crack initiation. I. J. Fat. 2001, 23, 575–586. [Google Scholar] [CrossRef]
- Akama, M.; Matsuda, H.; Doi, H.; Tsujie, M. Fatigue crack initiation life prediction of rails using theory of critical distance and critical plane approach. J. Comput. Sci. Tech. 2012, 6, 54–69. [Google Scholar] [CrossRef]
- Franklin, F.J.; Widiyarta, I.; Kapoor, A. Computer simulation of wear and rolling contact fatigue. Wear 2001, 251, 949–955. [Google Scholar] [CrossRef]
- Franklin, F.J.; Kapoor, A. Modelling wear and crack initiation in rails. Proc. Instn. Mech. Engrs., Part F, J. Rail Rapid Transit 2007, 221, 23–33. [Google Scholar] [CrossRef]
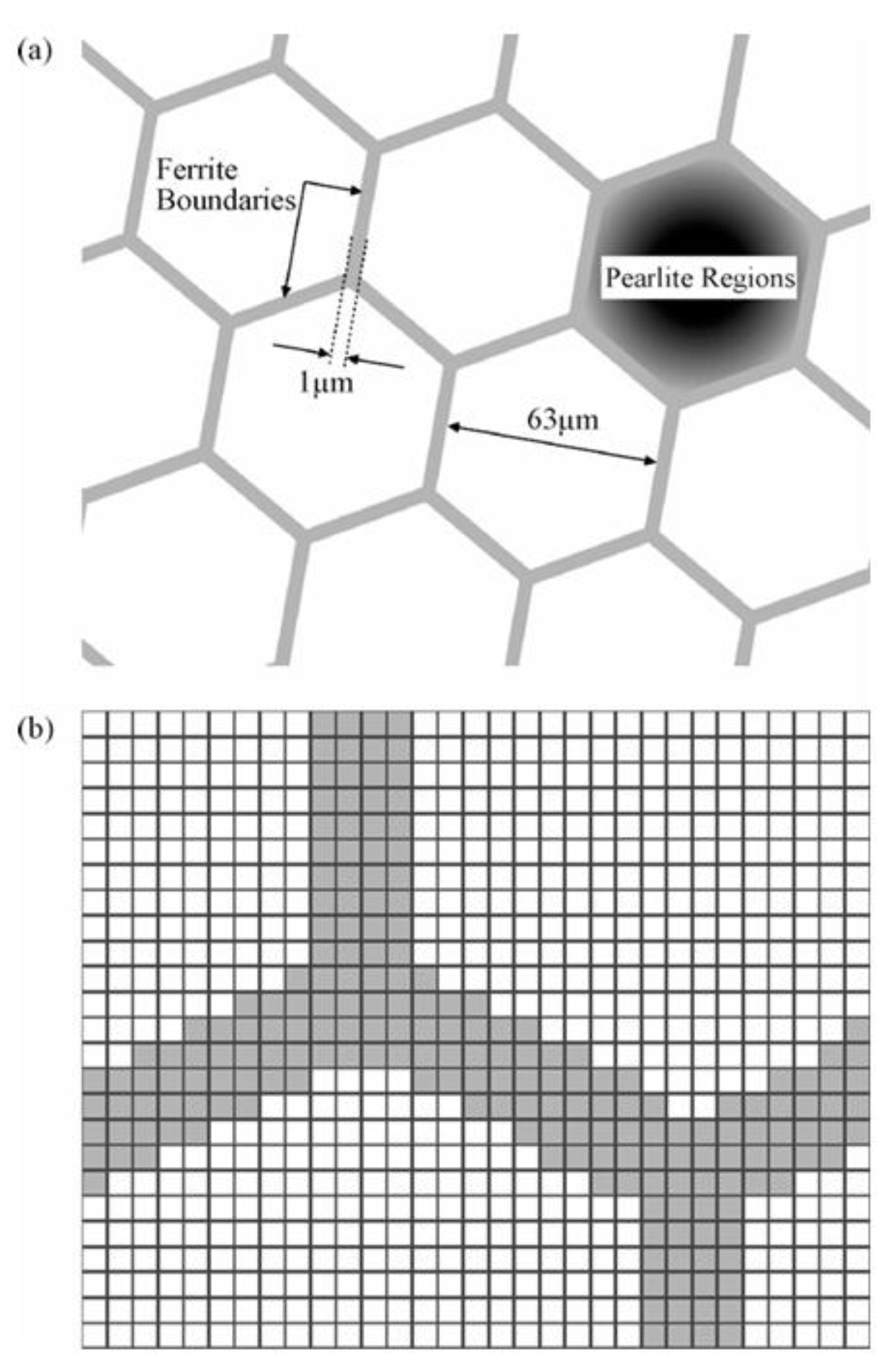
- Franklin, F.J.; Garnham, J.E.; Fletcher, D.I.; Davis, C.L.; Kapoor, A. Modelling rail steel microstructure and its effect on crack initiation. Wear 2008, 265, 1332–1341. [Google Scholar] [CrossRef]
- Garnham, J.E.; Ding, R.-G.; Davis, C.L. Ductile inclusions in rail, subject to compressive rolling-sliding contact. Wear 2010, 269, 733–746. [Google Scholar] [CrossRef]
- Akama, M.; Kimata, T. Numerical simulation model for the competition between short crack propagation and wear in the wheel tread. Wear 2020, 448–449, 203205. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, 1998. [Google Scholar]
- Hoshide, T.; Kusuura, K. Life prediction by simulation of crack growth in notched components with different microstructures and under multiaxial fatigue. Fat. Fract. Engng. Mater. Struct. 1998, 21, 201–213. [Google Scholar] [CrossRef]
- Hobson, P. D. The growth of short fatigue cracks in a medium carbon steel. PhD thesis, University of Sheffield, 1985.
- Socie, D.; Furman, S. Fatigue damage simulation models for multiaxial loading, Fatigue 96, 6th International Fatigue Congress, G. Lutjering and H.Nowack, Eds., Berlin, Germany, 1996, 967–976.
- Kapoor, A.; Franklin, F. J.; Wong, S. K.; Ishida, M. Surface roughness and plastic flow in rail wheel contact. Wear 2002, 253, 257–264. [Google Scholar] [CrossRef]
- Donzella, G.; Faccoli, M.; Ghidini, A.; Mazzu, A.; Roberti, R. The competitive role of wear and RCF in a rail steel. Eng. Fract. Mech. 2005, 72, 287–308. [Google Scholar] [CrossRef]
- Seabra, J.; Berthe, D. Influence of surface waviness and roughness on the normal pressure distribution in the Hertzian contact. Trans. ASME, J. Tribol. 1987, 109, 462–469. [Google Scholar] [CrossRef]
- Ringsberg, J. W.; Bergkvist, A. On propagation of short rolling contact fatigue cracks. Fat. Fract. Engng. Mater. Struct. 2003, 26, 969–983. [Google Scholar] [CrossRef]
- Canadinc, D.; Sehitoglu, H.; Verzal, K. Analysis of surface crack growth under rolling contact fatigue. I. J. Fat. 2008, 30, 1678–1689. [Google Scholar] [CrossRef]
- Chawanat, W.; Akama, M. Crack propagation under rolling contact fatigue near the white etching layer of a railway wheel. Tribol. Online 2024, 19, 277–286. [Google Scholar] [CrossRef]
- Lian, Q.; Deng, G.; Juboori, A.; Li, H.; Liu, Z.; Wang, X.; Zhu, H. Crack propagation behavior in white etching layer on rail steel surface. Eng. Fail. Anal. 2019, 104, 816–829. [Google Scholar] [CrossRef]
- Kráčalík, M.; Daves, W.; Antretter, T. Calculation of crack driving forces of surface cracks subjected to rolling/sliding contact. Eng. Fract. Mech. 2016, 152, 10–25. [Google Scholar] [CrossRef]
- Tillberg, J.; Larsson, F.; Runesson, K. On the role of material dissipation for the crack-driving force. I. J. Plast. 2010, 26, 992–1012. [Google Scholar] [CrossRef]
- Daves, W.; Kráčalík, M.; Scheriau, S. Analysis of crack growth under rolling-sliding contact. I. J. Fat. 2019, 121, 63–72. [Google Scholar] [CrossRef]
- Floros, D.; Ekberg, A.; Larsson, F. Evaluation of mixed-mode crack growth direction criteria under rolling contact conditions. Wear 2020, 448–449, 203184. [Google Scholar] [CrossRef]
- Bold, P. E. Multiaxial fatigue crack growth in rail steel. PhD thesis, University of Sheffield, 1990.
- Way, S. Pitting due to rolling contact. Trans. ASME. J. of Appl. Mech. 1935, 57, A49–A58. [Google Scholar] [CrossRef]
- Keer, L.M.; Bryant., M.D. A Pitting model for rolling contact fatigue. Trans. ASME, J. Tribol. 1983, 105, 198–205. [Google Scholar] [CrossRef]
- Bower, A. F. The influence of crack face friction and trapped fluid on surface initiated rolling contact fatigue cracks. Trans. ASME, J. Tribol. 1988, 110, 704–711. [Google Scholar] [CrossRef]
- Bogdański, S.; Olzak, M.; Stupnicki, J. Numerical stress analysis of rail rolling contact fatigue cracks. Wear 1996, 191, 14–24. [Google Scholar] [CrossRef]
- Murakami, Y.; Kaneta, M.; Yatsuzuka, H. Analysis of surface crack propagation in lubricated rolling contact. ASLE Trans. 1985, 28, 60–68. [Google Scholar] [CrossRef]
- Kaneta, M.; Yatsuzuka, H.; Murakami, Y. Mechanism of crack growth in lubricated rolling/sliding contact. ASLE Trans. 1985, 28, 407–414. [Google Scholar] [CrossRef]
- Kaneta, M.; Murakami, Y. Effects of oil hydraulic pressure on surface crack growth in rolling/sliding contact. Tribol. Int. 1987, 20, 210–217. [Google Scholar] [CrossRef]
- Kaneta, M.; Murakami, Y. Propagation of semi-elliptical surface cracks in lubricated rolling/sliding elliptical contacts. Trans. ASME, J. Tribol. 1991, 113, 270–275. [Google Scholar] [CrossRef]
- Fletcher, D.I.; Beynon, J.H. A simple method of stress intensity factor calculation for inclined surface-breaking cracks with crack face friction under contact loading. Proc. Instn. Mech. Engrs., Part J, J. Engng. Tribol. 1999, 213, 481–486. [Google Scholar] [CrossRef]
- Fletcher, D.I.; Beynon, J.H. A simple method of stress intensity factor calculation for inclined fluid-filled surface-breaking cracks under contact loading. Proc. Instn. Mech. Engrs., Part J, J. Engng. Tribol. 1999, 213, 299–304. [Google Scholar] [CrossRef]
- Kaneta, M.; Matsuda, K.; Murakami, K.; Nishikawa, H. Possible mechanism for rail dark spot defects. Transactions of the ASME: Series F, J. Tribol. 1998, 120, 304–309. [Google Scholar] [CrossRef]
- Akama, M.; Mori, T. Boundary element analysis of surface initiated rolling contact fatigue cracks in wheel/rail contact systems. Wear 2002, 253, 35–41. [Google Scholar] [CrossRef]
- Bogdański, S.; Lewicki, P. 3D model of liquid entrapment mechanism for rolling contact fatigue cracks in rails. Wear 2008, 265, 1356–1362. [Google Scholar] [CrossRef]
- Fletcher, D.I.; Hyde, P.; Kapoor, A. Investigating fluid penetration of rolling contact fatigue cracks in rails using a newly developed full-scale test facility. Proc. IMechE Part F: J. Rail Rapid Transit. 2007, 221, 35–44. [Google Scholar] [CrossRef]
- Bold, P.E.; Brown, M.W.; Allen, R.J. Shear mode crack growth and rolling contact fatigue. Wear 1991, 144, 307–317. [Google Scholar] [CrossRef]
- Akama, M.; Matsubara, K. Simulation for propagation of horizontal fissures in rail squats. Trans. JSCES 2020, 20200017. (in Japanese). [Google Scholar]
- Richard, H.A.; Eberlein, A.; Kullmer, G. Concepts and experimental results for stable and unstable crack growth under 3D-mixed-mode-loadings. Engng. Fract. Mech. 2017, 174, 10–20. [Google Scholar] [CrossRef]
- Akama, M. Fatigue crack growth under non-proportional mixed mode loading in rail and wheel steel part 1: Sequential mode I and mode II loading. Appl. Sci. 2019, 9, 2006. [Google Scholar] [CrossRef]
- Akama, M.; Kiuchi, A. Fatigue crack growth under non-proportional mixed mode loading in rail and wheel steel part 2: Sequential mode I and mode III loading. Appl. Sci. 2019, 9, 2866. [Google Scholar] [CrossRef]
- Otsuka, A.; Mori, K.; Miyata, T. The condition of fatigue crack growth in mixed mode condition. Eng. Fract. Mech. 1975, 7, 429–439. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G. C. On the crack extention in plates under plane loading and transverse shear. ASME J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Dubourg, M.C.; Lamacq, V. A predictive rolling contact fatigue growth model: Onset of branching, direction and growth – role of dry and lubricated conditions on crack patterns. J. Tribol. 2002, 124, 680–688. [Google Scholar] [CrossRef]
- Hourlier, F.; Pineau, A. Propagation of fatigue cracks under polymodal loading. Fat. Fract. Eng. Mater. Struct. 1982, 5, 287–302. [Google Scholar] [CrossRef]
- Amestoy, M.; Leblond, J.B. Crack paths in plane situations—II. Detailed form of the expansion of the stress intensity factors. Int. J. Solids Struc. 1992, 29, 465–501. [Google Scholar]
- Enblom, R.; Berg, M. Impact of non-elliptic contact modelling in wheel wear simulation. Wear 2008, 265, 1532–1541. [Google Scholar] [CrossRef]
- Kashiwaya, K.; Ishida, M. The prediction model of growth rate of rail transverse crack. Proc. Railway Mech. 2003, 7, 79–84. (in Japanese). [Google Scholar]
- Fletcher, D. I.; Hyde, P.; Kapoor, A. Growth of multiple rolling contact fatigue cracks driven by rail bending modelled using a boundary element technique. Proc. IMec, Part F: J. Rail Rapid Transit 2004, 218, 243–253. [Google Scholar] [CrossRef]
- Mair, R.I.; Groenhout, R. The growth of transverse fatigue defects in the head of railway rails. Rail Eng. Int. 1980, 11, 675–686. [Google Scholar]
- Shah, R.C.; Kobayashi, A. Stress intensity factor for an elliptical crack under arbitrary normal loading. Eng. Fract. Mech. 1971, 3, 71–96. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts. Almquist and Wiksells Akademiska Handböcker, Stockholm, 1946.
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Suh, N. P. The delamination theory of wear. Wear 1973, 25, 111–124. [Google Scholar] [CrossRef]
- Kapoor, A.; Franklin, F. J. Tribological layers and the wear of ductile materials. Wear 2000, 245, 204–215. [Google Scholar] [CrossRef]
- Beagley, T. M. Severe wear of rolling/sliding contacts. Wear 1976, 36, 317–335. [Google Scholar] [CrossRef]
- Bolton, P.J.; Clayton, P.; McEwen, I.J. Wear of rail and tyre steels under rolling/sliding conditions. ASLE transactions 1982, 25, 17–24. [Google Scholar] [CrossRef]
- Bolton, P.J.; Clayton, P. Rolling-sliding wear damage in rail and tyre steels. Wear 1984, 93, 145–165. [Google Scholar] [CrossRef]
- Olofsson, U.; Telliskivi, T. Wear, plastic deformation and friction of two rail steels—A full-scale test and a laboratory study. Wear 2003, 254, 80–93. [Google Scholar] [CrossRef]
- Garnham, J.E.; Beynon, J.H. Dry rolling-sliding wear of bainitic and pearlitic steels. Wear 1992, 157, 81–109. [Google Scholar] [CrossRef]
- Lewis, R.; Dwyer-Joyce, R.S. Wear mechanisms and transitions in railway wheel steels. Proc. IMec, Part J: J. Engng. Tribol. 2004, 218, 467–478. [Google Scholar] [CrossRef]
- Lewis, R.; Dwyer-Joyce, R.S.; Olofsson, U.; Pombo, J.; Jambrósio, J.; Pereira, M.; Ariaudo, C.; Kuka, N. Mapping railway wheel material wear mechanisms and transitions. Proc. IMechE Part F: J. Rail Rapid Transit 2010, 224, 125–137. [Google Scholar] [CrossRef]
- Lewis, R.; Olofsson, U. Mapping rail wear regimes and transitions. Wear 2004, 257, 721–729. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J.; Pereira, M.; Lewis, R.; Dwyer-Joyce, R.; Ariaudo, C.; Kuka, N. Development of a wear prediction tool for steel railway wheels using three alternative wear functions. Wear 2011, 271, 238–245. [Google Scholar] [CrossRef]
- Jin, Y.; Ishida, M.; Namura, A. Experimental simulation and prediction of wear of wheel flange and rail gauge corner. Wear 2011, 271, 259–267. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Núñez, A.; Dollevoet, R. New insights into the short pitch corrugation enigma based on 3D-FE coupled dynamic vehicle-track modeling of frictional rolling contact. Appl. Sci. 2017, 7, 807. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Zhang, P.; Núñez, A.; Dollevoet, R. Mechanism of short pitch rail corrugation: Initial excitation and frequency selection for consistent initiation and growth. Int. J. Rail Trans. 2022, 12, 1–36. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Z. The development of short pitch rail corrugation: Extensive field monitoring and validation of numerical predictions. Tribo. Int. 2025, 210, 10821. [Google Scholar] [CrossRef]
- Burstow, M. C. Whole life rail model application and development for RSSB - Development of an RCF damage parameter, Technical Report AEATR-ES-2003-832 Issue 1, Rail Safety & Standards Board (RSSB), 2003.
- Burstow, M. C. Whole life rail model application and development for RSSB - Continued development of an RCF damage parameter, Technical Report AEATR-ES-2004-880 Issue 2, Rail Safety & Standards Board (RSSB), 2004.
- Burstow, M. C.; Watson, A. S.; Beagles, M. Simulation of rail wear and rolling contact fatigue using the Whole Life Rail Model, Proceedings of ‘Railway Engineering 2003’, London 30th April 1st May, 2003.
- Mazzù, A.; Petrogalli, C.; Faccoli, M. An integrated model for competitive damage mechanisms assessment in railway wheel steels. Wear 2015, 322–323, 181–191. [Google Scholar] [CrossRef]
- Mazzù, A.; Donzella, G. A model for predicting plastic strain and surface cracks at steady-state wear and ratcheting regime. Wear 2018, 400–401, 127–136. [Google Scholar] [CrossRef]
- Mazzù, A.; Petrogalli, C.; Lancini, M.; Ghidini, A.; Faccoli, M. Effect of wear on surface crack propagation in rail-wheel wet contact. J. Mater. Eng. Perform 2018, 27, 630–639. [Google Scholar] [CrossRef]
- Karttunen, K.; Kabo, E.; Ekberg, A. Numerical assessment of the influence of worn wheel tread geometry on rail and wheel deterioration. Wear 2014, 317, 77–91. [Google Scholar] [CrossRef]
- Karttunen, K.; Kabo, E.; Ekberg, A. Estimation of gauge corner and flange root degradation from rail. wheel and track geometries. Wear, 2016; 366–367, 294–302. [Google Scholar]
- Ekberg, A.; Kabo, E.; Andersson, H. An engineering model for prediction of rolling contact fatigue of railway wheels. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 899–909. [Google Scholar] [CrossRef]
- Dirks, B.; Enblom, R. Prediction model for wheel profile wear and rolling contact fatigue. Wear 2011, 271, 210–217. [Google Scholar] [CrossRef]
- Bevan, A.; Molyneux-Berry, P.; Eickhoff, B.; Burstow, M. Development and validation of a wheel wear and rolling contact fatigue damage model. Wear 2013, 307, 100–111. [Google Scholar] [CrossRef]
- Brouzoulis, J. Wear impact on rolling contact fatigue crack growth in rails. Wear 2014, 314, 13–19. [Google Scholar] [CrossRef]
- Jun, H.K.; Lee, D.H.; Kim, D.S. Calculation of minimum crack size for growth under rolling contact between wheel and rail. Wear 2015, 344–345, 46–57. [Google Scholar] [CrossRef]
- Fletcher, D.I.; Kapoor, A. Rapid method of stress intensity factor calculation for semi-elliptical surface breaking cracks under three-dimensional contact loading. Proc IMechE, Part F: J. Rail Rapid Transit 2006, 220, 219–234. [Google Scholar] [CrossRef]
- Trummer, G.; Marte, C.; Dietmaier, P.; Sommitsch, C.; Six, K. Modelling surface rolling contact fatigue crack initiation taking severe plastic shear deformation into account. Wear 2016, 352–353, 136–145. [Google Scholar] [CrossRef]
- Hiensch, M.; Steenbergen, M. Rolling contact fatigue on premium rail grades: Damage function development from field data. Wear 2018, 394–395, 187–194. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, L.; Ding, H.H.; Tan, G.X.; Lewis, R.; Liu, Q.Y.; Guo, J.; Wang, W.J. Investigation on wear and rolling contact fatigue of wheel-rail materials under various wheel/rail hardness ratio and creepage conditions. Tribol. Int. 2020, 143, 106091. [Google Scholar] [CrossRef]
- Zhang, R.; Zheng, C.; Chen, C.; Lv, B.; Gao, G.; Yang, Z.; Yang, Y.; Zhang, F. Study on fatigue wear competition mechanism and microstructure evolution on the surface of a bainitic steel rail. Wear 2021, 482–483, 203978. [Google Scholar] [CrossRef]
- Zani, N.; Petrogalli, C. Predictive maps for the rolling contact fatigue and wear interaction in railway wheel steels. Wear 2022, 510–511, 204513. [Google Scholar] [CrossRef]
- Wang, H.H.; Wang, W.J.; Han, Z.Y.; Wang, Y.; Ding, H.H.; Lewis, R.; Lin, Q.; Liu, Q.Y.; Zhou, Z.R. Wear and rolling contact fatigue competition mechanism of different types of rail steels under various slip ratios. Wear 2023, 22, 204721. [Google Scholar] [CrossRef]
- Luo, K.; Liu, X.; Yang, Y.; Cong, T.; Zhang, F.; Wang, W. Modeling the competitive relationship between wear and rolling contact fatigue of railway wheel steel. Wear 2025, 560–561, 205615. [Google Scholar] [CrossRef]
- Tao, G.; Tan, M.; Yuan, X.; Wen, B.; Wen, Z. Influence of wheel wear on the rolling contact fatigue of metro wheels in the central area of the wheel tread. Wear 2025, 571, 205777. [Google Scholar] [CrossRef]
- Urashima, C.; Nishida, S. Fatigue crack initiation and propagation behaviour and fracture surface of eutectoid steels. J. Soc. Mat. Sci., Japan 1994, 43, 515–521. [Google Scholar] [CrossRef]
- Bomidi, J. AR.; Weinzapfel, N.; Sadeghi, F. An improved approach for 3D rolling contact fatigue simulations with microstructure topology. Tribol. Trans. 2013, 56, 385–399. [Google Scholar] [CrossRef]
- Bomidi, J.A.R.; Sadeghi, F. Three-dimensional finite element elastic–plastic model for subsurface initiated spalling in rolling contacts. Trans. ASME, J. Tribol. 2014, 136, 011402. [Google Scholar] [CrossRef]
- Franklin, F.J.; Gahlot, A.; Fletcher, D.I.; Garnham, J.E.; Davis, C. Three-dimensional modelling of rail steel microstructure and crack growth. Wear 2011, 357–363. [Google Scholar] [CrossRef]
- Wang, D.F.; Kato, K. Nano-scale fatigue wear of carbon nitride coatings: Part II—Wear mechanisms. Trans. ASME, J. Tribol. 2003, 125, 437–444. [Google Scholar] [CrossRef]
- Deng, X.; Qian, Z.; Li, Z.; Dollevoet, R. Investigation of the formation of corrugation-induced rail squats based on extensive field monitoring. Int. J. Fat. 2018, 112, 94–105. [Google Scholar] [CrossRef]
- Tyfour, W.R.; Beynon, J.H. The effect of rolling direction reversal on the wear rate and wear mechanism of pearlitic rail steel. Tribol. Int. 1994, 27, 401–412. [Google Scholar] [CrossRef]
- Tyfour, W.R.; Beynon, J.H. The effect of rolling direction reversal on fatigue crack morphology and propagation. Tribol. Int. 1994, 27, 273–282. [Google Scholar] [CrossRef]
- Akama, M.; Takahashi, Y. The influence of rolling direction reversal on wear and RCF cracks on the wheel tread, The 5th International Conference on Railway Technology, 22 – 25 Aug. 2022, Le Corum Congress Center, France.





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




