1. Introduction
Simulation is a valuable tool for evaluating the effective parameters in various processes, especially in water treatment. In fact, it not only enhances understanding of the process but also enables simulation with minimal experimental data.
In recent years, increased computing power and the availability of graphics processors have enabled more complex hydrodynamic models that replicate natural processes using input data. The ability to model processes occurring during electrodialysis opens up opportunities for the practical use of the phenomenon of electroconvection, which is an important step towards a much wider application of electrodialysis on an industrial scale.
Electrodialysis (ED) is an economically and environmentally efficient method for desalination, concentration and separation of natural and industrial solutions. The broader application of this method is hindered by certain limitations encountered in traditional use. These include a low mass transfer rate due to diffusion limitations, membrane surface fouling, and unwanted generation of H⁺ and OH⁻ ions at the membrane/solution interface. Applying high current densities or voltages in ED has been shown to overcome some of these limitations. Based on direct numerical modeling of the Nernst-Planck-Poisson and Navier-Stokes equations, a group of scientists [
1,
2] constructed several 1D-2D-3D mathematical models to describe the transfer of salt ions in a desalination channel under overlimit current conditions. A group of scientists [
3] also created a 2D model describing the combined contribution of spacers, electroconvection, and water dissociation/recombination reactions. It is used to determine the fundamental patterns of interaction between spacer geometry and current density and their influence on the transfer processes and solution flow. The overlimit current mode is economically advantageous for desalination of dilute solutions, since electroconvective vortices developing in this mode allow a significant increase in the rate of useful mass transfer, which saves the area of expensive membranes [
4]. The broader adoption of the overlimit current mode is hindered by limited understanding of the complex physicochemical processes it involves.
The complex relationships between the input and output parameters of the electrodialysis plant setup can be solved by nonlinear methods known as computational intelligence methods [
5]. The most reliable and powerful computational intelligence methods include data-driven systems such as neural networks, genetic algorithms and fuzzy logic models, which have attracted much attention as effective methods for environmental applications. In recent years, water treatment process prediction has been carried out using various models such as artificial neural networks (ANN) [
6,
7], adaptive neuro-fuzzy inference system [
8], least-squares support vector machines [
9], random forest [
10], response surface methodology [
11], genetic algorithm [
12] and fuzzy inference system [
13].
Due to the need to include not only quantitative but also qualitative parameters in the model, fuzzy models have recently become widespread, including the FCM approach described by Kosko [
14]. It has the ability to convey expert experience in the form of indices that can be calculated using uncertain, vague and subjective information. In essence, the fuzzy inference system produces evaluation results in the form of linguistic terms that are understandable to managers, decision makers and non-experts [
15]. There are a small number of published studies that have used the fuzzy logic approach to model the performance of an electrodialysis plant [
16]. Guolin Jing et al. [
17] applied a fuzzy logic model to predict the percentage of NaCl solution separation depending on voltage and flow rate. Hanife Sari et al. [
18] developed an FCC model to simulate a new integrated process (UF-IER-EDBM-FO) consisting of ultrafiltration (UF), ion exchange resins (IER), bipolar membrane electrodialysis (EDBM) and Fenton oxidation units (FO). Kyriakarakos et al. [
19,
20] developed a variable load energy management system (EMS) based on FCM.
These studies confirm the possibility of applying fuzzy logic techniques to water purification problems, in particular, to predict electrodialysis in a membrane system. However, in the known models, the list of parameters used is limited and does not include high-level system parameters such as price or membrane service life, which are included in this work.
2. Materials and Methods
This section describes the general methods used in FCM theory, which are used to construct the model structure and predict the evolution of the system after changing the values of the model components. A brief introduction to FCM theory and the basic equation used for scenario modeling is provided.
FCM is a soft computing method that can be used to describe, analyze, and model complex systems. Originally introduced by Kosko [
14], FCM takes the form of a knowledge graph consisting of nodes representing concepts and links between them. Concepts are nonlinear and represent variables in a causal system, with their states taking values within a specified range
. Links in an FCM model reflect the presence and strength of causal links between concepts. The strength of a link is determined by the weight of an arc of a directed graph and takes a value in the range
if negative causal links are not taken into account in the model, or
if negative causal links are taken into account.
The list of concepts, connections and connection weights are determined based on expert knowledge, research data, statistical properties of the system or historical data about the system. Such a fuzzy model describes the state of the system at a certain point in time in M -dimensional space, where M is the number of concepts in the system.
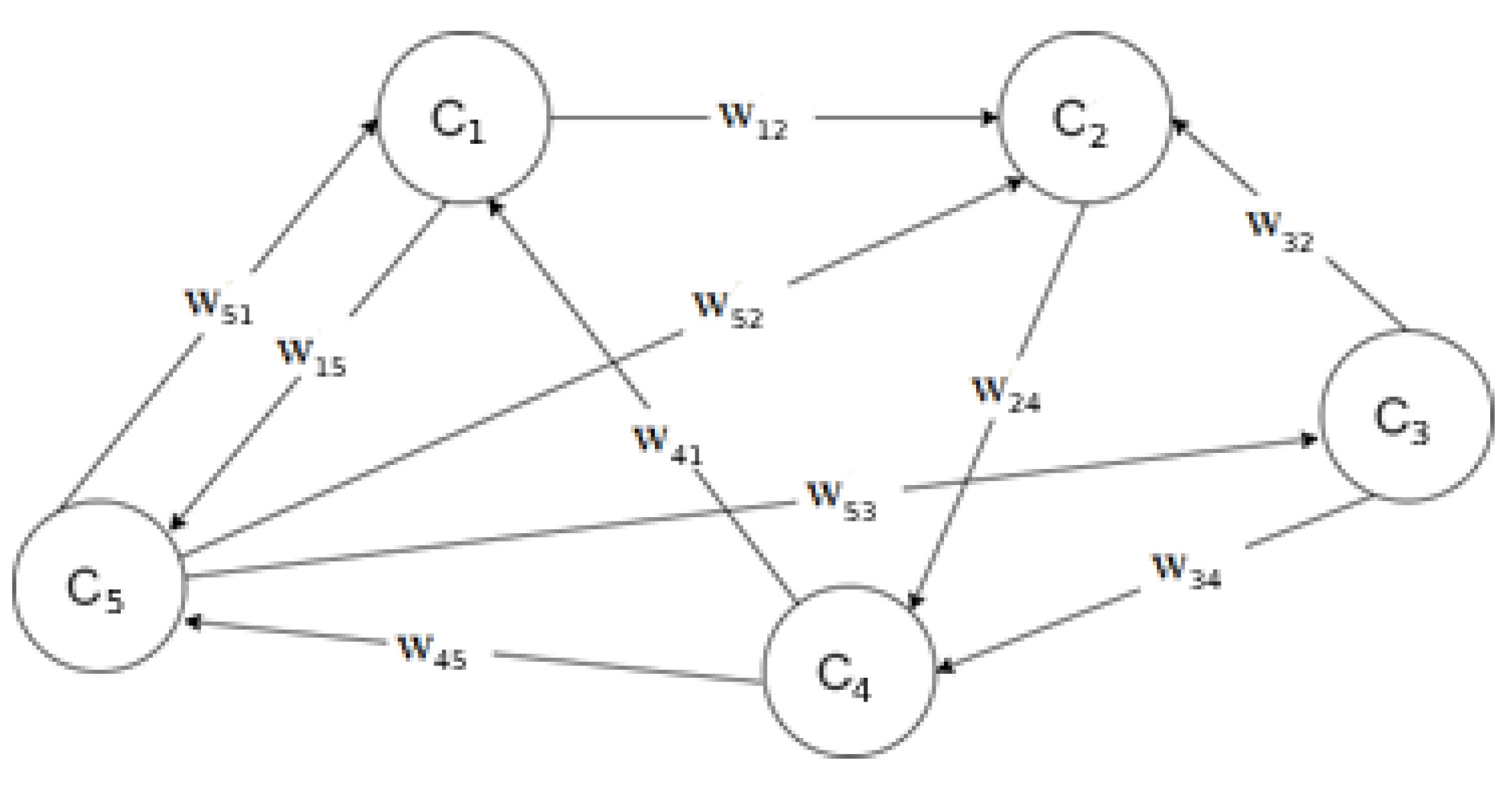
Figure 1 shows a simple FCM with five concepts and ten weighted relationships. FCMs are weighted directed graphs that can model the relationships or causality that exist among the features of a system. The concepts are represented by nodes
,
,
,
and
.
The connection is always directed from the concept of cause to the concept of effect. For example, in
Figure 1, with
, when is said
have an effect on
, that is,
is a causal concept, while
is a concept of effect. If the connection is positive, then the concept
has a positive effect on the concept
, otherwise negative. Each concept is characterized by a number
, which represents its value, and is the result of mapping the real value of the system variable into the interval
.
The model underlying the standard FCM can be characterized by a set of 4 components , where is a set of concepts of dimension , constructed on the basis of fuzzy sets, is a matrix of influence weights , assigned to each pair of concepts dimension . The value determines the sign and weight of the arc connecting the causal concept and the concept of the effect . The function determines the magnitude of the activation of each concept at a discrete moment in time . The activation function aggregates the magnitude of the impact of causal concepts on the target concept and limits the result within the interval . The interpretation of the causal relationship between two concepts, and , is as follows:
if , then strengthening (weakening) of the concept will lead to strengthening (weakening) of the concept with intensity .
if , then strengthening (weakening) of the concept will lead to weakening (strengthening) of the concept with intensity .
if (or is very close to 0), this indicates that there is no causal relationship between and , so there is no corresponding arc in this graph.
The final state of the system at
depends on the initial vector
and the weight matrix
. The activation of the concept
at time
is given in equation (1) and depends on the influences of the other concepts associated with the concept
and the activation value of the concept at time
.
where
is the weight of the connection between concepts
and
,
is the activation of the concept
at time
,
is the fuzzy operator of the triangular norm (T-norm), and
is the fuzzy operator of the triangular conorm (S-norm), which are fuzzy logic operators used to solve problems of accumulation of influence of several control concepts on the target concept and to determine the indirect influence of concepts.
The FCM update rule is applied recursively until a certain termination condition is met. At each discrete time step, the FCM will generate a matrix containing information about the activation degree of all concepts. In the FCM, individual fuzzy influences of control concepts that influence target concepts are combined using S-norms. T-norms and S-norm are operators in fuzzy logic that represent conjunction and disjunction operations on the interval . The most well-known fuzzy logic operators are the T-norm operator minimum , which is used for the intersection operation, and the dual S-norm operator maximum , which represents the sum operation. Using the T-norm operator minimum can be advantageous for those systems in which the information processing method is close to logical, i.e. most of the dependencies between the input and output values of the system are binary in nature.
To add negative cause-and-effect relationships between the concepts of the FCM, the algorithm described by Silov [
18] was used in the work. Its main idea is to create a second matrix describing all negative impacts in the system. To do this, the initial dimensions of the FCM are doubled by separating positive and negative impacts using the rule described by equation (2) to obtain a matrix
containing only positive weights.
Given that the matrix
has the size
, where
is the number of concepts considered in the model, the matrix
will have the size
. Since the weight of the arcs in the FCM usually depends on expert opinion and is not exact, some of the links may be missing and/or their weight may be determined inaccurately. To adjust the weight matrix and identify hidden links between concepts, we used the probabilistic transitive closure (PTC) approach [
19], which consists of calculating a bipolar weighted oriented graph with the same set of concepts as the original FCM, but with links corresponding to the indirect effects in the FCM. The link weight (
,
) in the PTC
matrix is the probability that the FCM has an arc from
in
. The PTC matrix
is obtained from the matrix using Equation (3):
where
is the PTC. After calculating the indirect effects in the FCM using PTC , the matrix
can be reduced to its initial size
by obtaining the matrix
, which is formed using the transformation described in Equation (4):
where
and
represent the positive and negative impact of the concepts, respectively. The matrix
elements are used in scenario modeling and allow for problem-target analysis in complex systems.
The FCM of the electrodialysis plant was constructed using the following steps:
Expert interviews were conducted to identify the concepts of the FCM and the interactions between them. Using the language equivalents of “Very Low”, “Low”, “Average”, “High”, “Very High” and the direction of influence, positive or negative, experts were asked to rate the influence of one concept on another.
Experts' qualitative ratings were converted into a numerical equivalent (0–4) and combined using a weighted mean based on the expert's tenure.
The numerical values were normalized on interval and a matrix of connection strengths was constructed.
The FCM was trained, resulting in a matrix of positive and negative relationships.
The analysis of the constructed FCM was carried out and system indicators were calculated.
After training the FCM and constructing a matrix of positive-negative connections, the resulting system is analyzed. For this purpose, based on the matrix of positive-negative connections , the system indicators of the analyzed weakly structured system are determined.
Weakly structured systems are systems in which qualitative, poorly defined concepts prevail, and the criteria for evaluating the alternatives of the decisions taken are, as a rule, of a subjective nature. The system being evaluated is a representative of this class since it includes qualitative parameters such as the quality of purification and the service life of the membrane. When analyzing system indicators - such as mutual consonance, dissonance, positive and negative influence of concepts on each other and on the system as a whole - determining key factors of the model, and conduct a scenario analysis of the system as described in [
21].
3. Results
As a result of the study, the FCM of the electrodialysis plant at the water treatment facility was constructed, the analysis of positive and negative components of the links and the system analysis of the constructed FCM were carried out. Strategies to increase the efficiency of the water treatment facility were proposed.
In the initial modeling stage, potential system concepts were proposed. Expert interviews were conducted to compile a list of FCM concepts. Obtained list presented in the
Table 1. During second stage of the interviews, experts assessed cause-and-effect relationships using a scale of “Not related”, “Very weakly related”, “Weakly related”, “Related”, “Strongly related”, “Very strongly related”. These assessments were converted to a 0–4 scale and averaged. A matrix representing the mutual influence weights between concepts was then constructed.
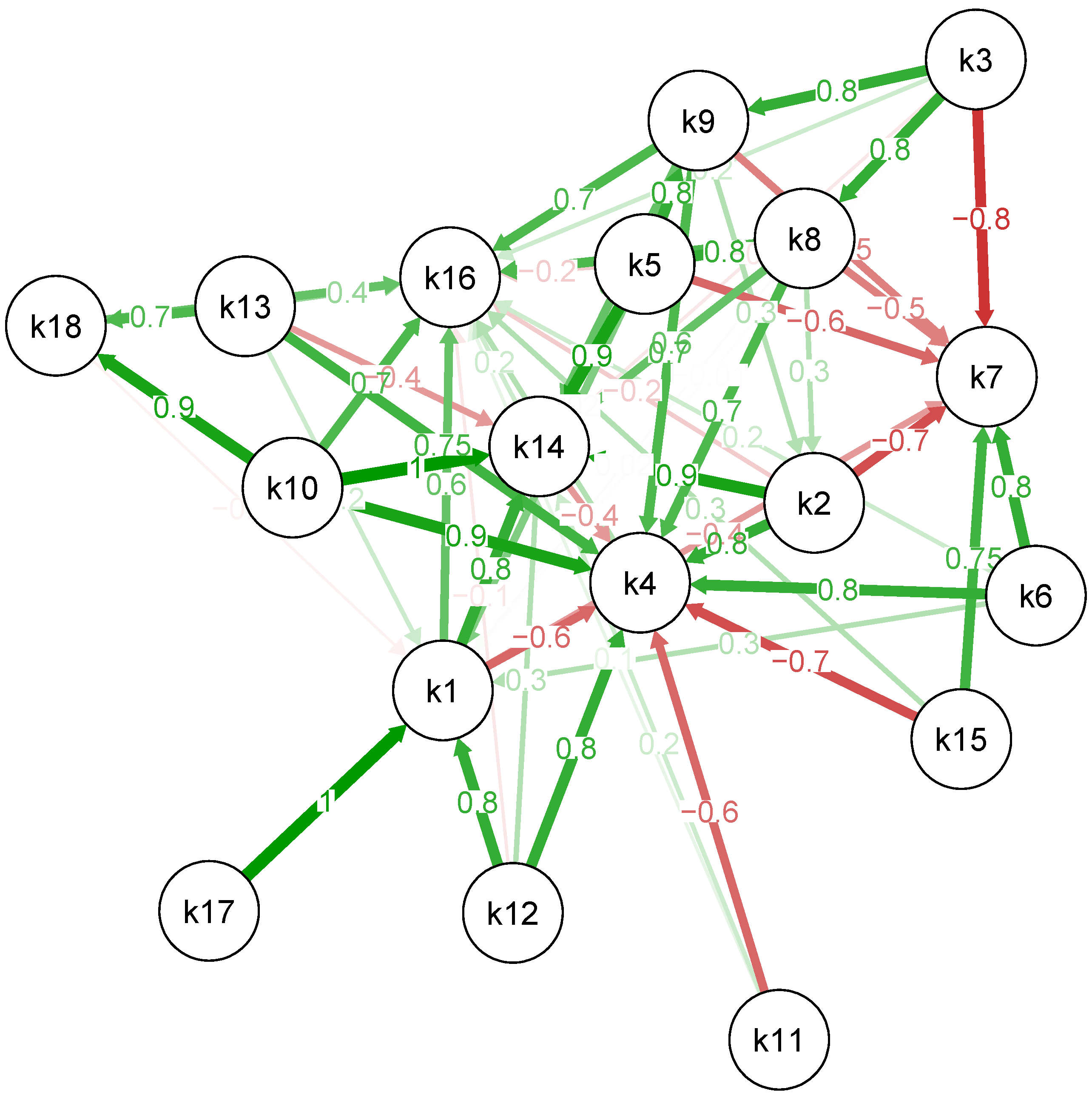
Figure 2 shows the resulting FCM as an oriented weighted graph, and
Table 2a and
Table 2b show the matrix of relationships between the concepts of the resulting system. The third row of the FCM matrix shows that the concept k3 (Concentration of salt ions) is negatively influenced by k1 (Solution flow rate) with a weight of –0.01 and by k7 (Membrane service life) with a weight of –0.8, while it is positively influenced by k8 (Current strength in the system) and k9 (Potential jump in the system), both with a weight of 0.8. For an illustrative example, we selected the target states of the electrodialysis plant at a water treatment facility system as:
Increase in concept k7 (Membrane service life).
Reduction of concept k16 (Power consumption (electrodialysis + pump operation)).
From the original FCM
of dimension
a fuzzy matrix of positive connections was formed
. After that, a transitively closed cognitive matrix of mutual influences was calculated and the system indicators of the FCM were calculated. The system indicators were determined as described in [
21] and presented in
Table 3.
When analyzing the obtained model, we can conclude that the first target concept k7 (membrane service life) is weakened by the system and the dissonance of the weakening effect is below average, therefore the development trend of this concept is negative. The target concept k16 (electricity consumption of electrodialysis and pump operation) is reinforced by the system, with above-average consonance, indicating an optimistic development trend. The concept k5 (membrane conductivity) has the strongest positive influence on the system (impact: 0.219), although the system does not, in turn, reinforce this concept. The consonance of the concept is high, therefore it itself provides strengthening of the system.
The next concept in terms of the degree of positive amplification of the system is the concept k13 (channel length). The concept k19 (installation cost) is provided by the growth under the action of the system, while it has an insignificant effect on the system. The concept k14 (device productivity) is contradictory, the system increases it, and it has a strong negative effect on the system. Since the consonance of the system's influence for k14 is maximum within the framework of the considered model, there is an optimistic development trend. Among all concepts, the system most significantly weakens the target concept k7 (membrane service life).
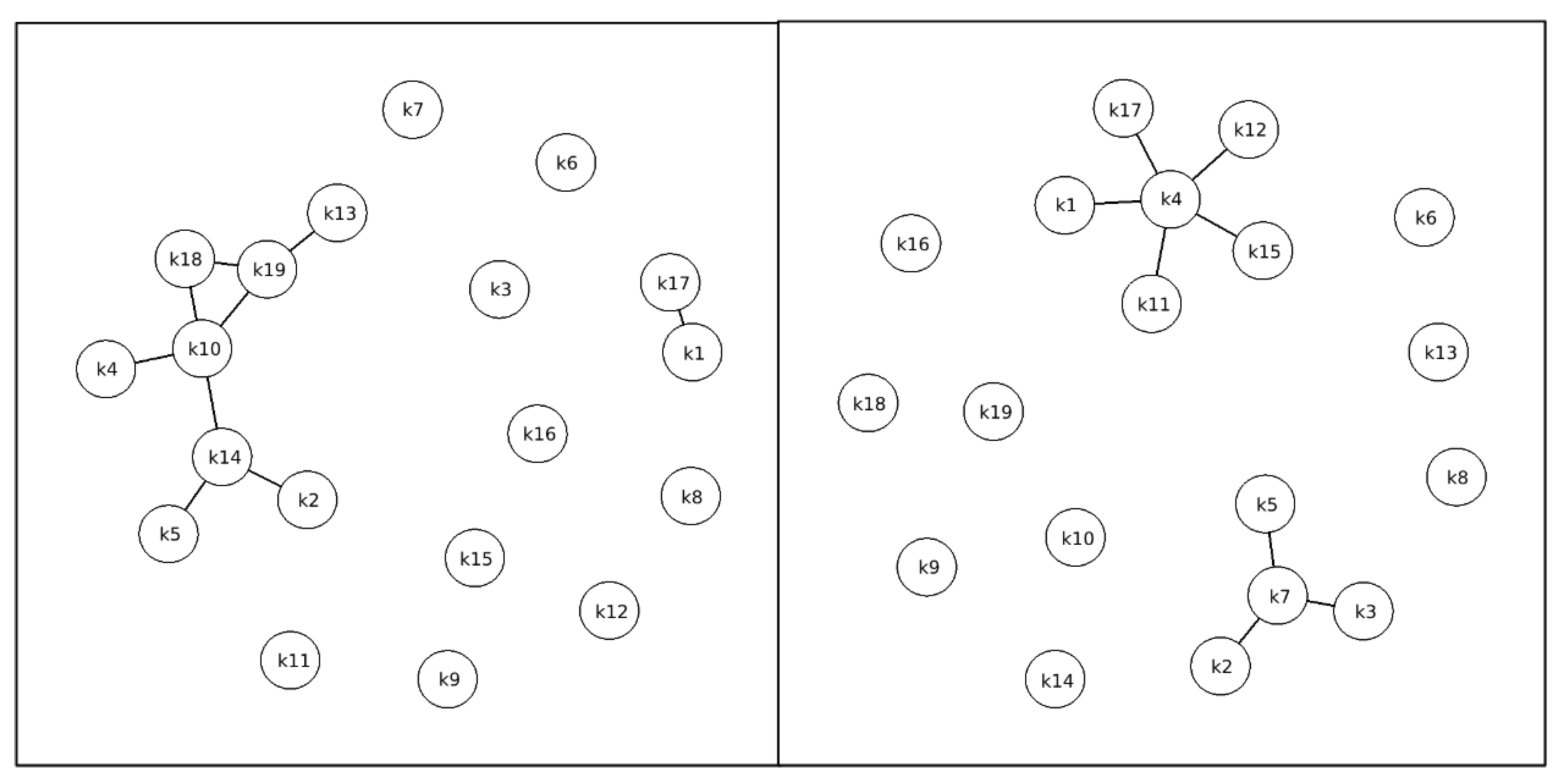
Let us consider the clusters of positive and negative influence available in the system, taking into account the assignment of the corresponding relevance level based on the matrices of positive and negative mutual influence. This allows us to identify groups of similar concepts and analyze the relationships within the clusters of interest. Assigning relevance levels enables graphical evaluation of the clusters and accelerates matrix analysis.
In
Figure 3 (left), the following clusters of mutually reinforcing concepts can be identified: k5 (membrane conductivity), k2 (water temperature at the inlet to the chamber), k14 (device performance) - form the cluster "Purification speed", which is closely related to another cluster - "Installation characteristics", including concepts k4 (purification quality), k13 (channel length), k19 (installation cost), k18 (installation size), k10 (number of paired chambers in the device). A separate cluster includes k16 (electricity consumption), along with k1 (solution flow rate), and k17 (pump efficiency). To examine contradictions within the system,
Figure 3 (right) illustrates groups of opposing concepts. The first cluster is represented by concepts k11 (distance between membranes in the apparatus), k1 (flow rate of the solution), k12 (width of the inlet opening), k15 (amount of salts in the solution), k17 (pump efficiency) with an impact on concept k4 (purification quality). The second cluster, consisting of k2 (water temperature at the inlet to the chamber), k3 (salt ion concentration), k5 (membrane conductivity) has an impact on concept k7 (membrane service life).
To support decision-making, we addressed the inverse problem for FCM model of the electrodialysis plant at a water treatment facility. The methodology used to solve this problem follows the approach detailed by Petukhova et al. [
22], which outlines an optimization algorithm for inverse problem modeling in FCMs. For demonstration purposes,
Table 4 presents the specified increments in the values of selected target concepts used in the illustrative scenario.
Solving the problem yields a vector of control concept increments, presented in
Table 5.
The results presented in
Table 5 can be summarized as follows. The upper-level strategy, corresponding to the Max solution type, is primarily focused on reducing most control concepts, with the exception of k11 (distance between membranes in the device). Notably, increasing this parameter in the direct task by soling Eq. (1), leads to an overall improvement in the target concepts; however, it also causes a significant decrease in the k4 (quality of purification). In contrast, the diverse range of lower-level strategies, represented by the Min solution type, provides flexibility for experts. These strategies enable the selection of optimal control actions tailored to the specific requirements and constraints of the water treatment system.
4. Conclusion
This article presented a detailed analysis of an electrodialysis plant model at a water treatment facility using FCM theory. The model was examined, and an example was provided to demonstrate its application in decision support and the development of system strategies. The analysis revealed that the target concept, ``Membrane service life”, is weakened by the system, reflecting a negative development trend. In contrast, ``Electric power consumption” is positively influenced by the system, suggesting that its value increases in tandem with other system variables. The concept ``Electrical conductivity of membranes” was identified as the most influential factor strengthening the system, a conclusion supported by experimental data.
The study confirms the applicability of the FCM method not only to socio-economic systems but also to physicochemical systems. The developed model demonstrates that FCMs can be effectively used to monitor and control electrodialysis processes in real time by dynamically adjusting system parameters. The implementation of FCM-based decision support tools in operational settings can lead to improved process efficiency, extended membrane lifespan, and significant reductions in energy consumption and maintenance costs.
From a practical standpoint, this approach can support plant operators in identifying system bottlenecks early, optimizing resource use, and making data-driven decisions to ensure stable and cost-effective water treatment operations.
Future research could involve training the proposed model on historical and real-time experimental data using error-dependent learning algorithms. Another promising direction is the incorporation of time delays in concept influence, allowing the model to represent intermediate system states and better capture the dynamic nature of system responses.
Author Contributions
Conceptualization, A.P., A.K.; methodology, A.P.; software, A.P.; validation, A.P., A.K.; formal analysis, A.P.; investigation, A.P.; resources, E.K.; data curation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, E.K.; visualization, A.P.; supervision, E.K.; project administration, A.K. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN |
Artificial neural networks |
| ED |
Electrodialysis |
| EMS |
Energy management system |
| FCM |
Fuzzy Cognitive Map |
References
- Zabolotsky, V.I. , Novak L., Kovalenko A.V., Nikonenko V.V., Urtenov M.Kh., Lebedev K.A., But A.Yu. Electroconvection in systems with heterogeneous ion-exchange membranes. Membrany i membrannye tekhnologii = Membranes and membrane technologies. 2017, 7, 265–276, (In Russ.). [Google Scholar] [CrossRef]
- Pismemsky, A.V. , Urtenov M.K., Nikonenko V.V., Sistat P., Pismeskaya N.D., Kovalenko A.V. Model and experimental studies of gravitational convection in an electromembrane cell. Russian Journal of Electrochemistry. 2012, 48, 756–766. [Google Scholar] [CrossRef]
- Urtenov, M.K. , Kovalenko, A.V., Gudza, V.A., Sukhinov, A.I., Chubyr, N.O. Model and numerical experiment for calculating the theoretical current-voltage characteristic in electro-membrane systems. IOP Conference Series Materials Science and Engineering. 2019, 680, 012030. [Google Scholar] [CrossRef]
- Kovalenko, A.V. , Urtenov, M. K., Yzdenova, A.M., Sukhinov, A.I., Chubyr, N.O. Simulation of galvanic dynamic mode in membrane hydrocleaning systems taking into account space charge. AIP Conference Proceedings 2019, 2188, 050021. [Google Scholar] [CrossRef]
- Badrnezhad, R. , Mirza B. Modeling and optimization of cross-flow ultrafiltration using hybrid neural network-genetic algorithm approach. Journal of Industrial and Engineering Chemistry 2014, 20, 528–543. [Google Scholar] [CrossRef]
- Asl, S.M.H. , Ahmadi M., Ghiasvand M., Tardast A., Katal R. Artificial neural network (ANN) approach for modeling of Cr(VI) adsorption from aqueous solution by zeolite prepared from raw fly ash (ZFA). Journal of Industrial and Engineering Chemistry 2014, 19, 1044–1055. [Google Scholar] [CrossRef]
- Soleimanzade, M.A. , Sadrzadeh M. Deep learning-based energy management of a hybrid photovoltaic-reverse osmosis-pressure retarded osmosis system. Applied Energy 2021, 293, 116959. [Google Scholar] [CrossRef]
- Mandal, S. , Mahapatra S.S., Patel R.K. Neuro fuzzy approach for arsenic(III) and chromium(VI) removal from water. Journal of Water Process Engineering 2015, 5, 58–75. [Google Scholar] [CrossRef]
- Ghaedi, M. , Ghaedi A.M., Hossainpour M., Ansari A., Habibi M.H., Asghari A.R. Least square support vector (LS-SVM) method for modeling of methylene blue dye adsorption using copper oxide loaded on activated carbon: Kinetic and isotherm study. Journal of Industrial and Engineering Chemistry 2014, 20, 1641–1649. [Google Scholar] [CrossRef]
- Dehghanian, N. , Ghaedi M., Ansari A., Ghaedi A., Vafaei A., Asif M., Agarwal S., Tyagi I., Gupta V.K. A random forest approach for predicting the removal of congo red from aqueous solutions by adsorption onto tin sulfide nanoparticles loaded on activated carbon. Desalination and Water Treatment 2016, 57, 9272–9285. [Google Scholar] [CrossRef]
- Hajati, S. , Ghaedi M., Mazaheri H. Removal of methylene blue from aqueous solution by walnut carbon: optimization using response surface methodology. Desalination and Water Treatment 2014, 52, 1–15. [Google Scholar]
- Ghaedi, M. , Zeinali N., Ghaedi A.M., Teimuori M., Tashkhourian J. Artificial neural network genetic algorithm based optimization for the adsorption of methylene blue and brilliant green from aqueous solution by graphite oxide nanoparticle. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2014, 125, 264–277. [Google Scholar] [CrossRef] [PubMed]
- Rahmanian, B. , Pakizeh M., Esfandyari M., Maskooki A. Fuzzy inference system for modeling of zinc removal using micellar-enhanced ultrafiltration. Separation Science and Technology 2011, 46, 1571–1581. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy cognitive maps. International Journal of Man-Machine Studies 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Gharibi, H. , Mahvi A.H., Nabizadeh R., Arabalibeik H., Yunesian M., Sowlat M.H. A novel approach in water quality assessment based on fuzzy logic. Journal of Environmental Management 2012, 112, 87–95. [Google Scholar] [CrossRef]
- Jing, G.L. , Du W.T., Zhou Q., Li S.T. Studying fitting effect by ANFIS in the electrodialysis process. Advanced Materials Research 2011, 268–270, 336–339. [Google Scholar] [CrossRef]
- Jing, G. , Du W. Fuzzy logic-based model for prediction of separation percent of NaCl solution using electrodialysis. Asian Journal of Chemistry 2012, 24, 2216–2220. [Google Scholar]
- Silov, V. Strategic Decision-Making in a Fuzzy Environment. Moscow: INPRO-RES 1995; Vol. 228. (In Russ.).
- Kyriakarakos, G. , Dounis A.I., Arvanitis K.G., Papadakis G. Design of a fuzzy cognitive maps variable-load energy management system for autonomous PV-reverse osmosis desalination systems: A simulation survey. Applied Energy 2017, 187, 575–584. [Google Scholar] [CrossRef]
- Niesink, P. , Poulin K., Šajna M. Computing transitive closure of bipolar weighted digraphs. Discrete Applied Mathematics 2013, 161, 217–243. [Google Scholar] [CrossRef]
- Petukhova, A. , Fachada N. Retail System Scenario Modeling Using Fuzzy Cognitive Maps. Information 2022, 13, 251. [Google Scholar] [CrossRef]
- Petukhova AV, Kovalenko AV, Ovsyannikova AV. Algorithm for Optimization of Inverse Problem Modeling in Fuzzy Cognitive Maps. Mathematics 2022, 10, 3452. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).