1. Introduction
Transfinite fixed points have become a cornerstone of Alpay Algebra6, 7, providing a unifying lens for self-reference across mathematics and computer science. In previous installments (I-VI), Faruk Alpay and collaborators developed an endofunctor on a category of algebraic structures whose transfinitely iterated fixed point exists as a universal invariant8, 9. This is a transfinite fixed point reached via ordinal-indexed iteration of . Intuitively, embodies a stable self-consistency: for example, Alpay Algebra IV showed an AI model-text system converging to a unique semantic fixed point (an "empathetic embedding") after transfinitely many updates10, 11. Alpay Algebra V extended this to multi-layered semantic games, proving a meta-fixed-point (semantic equilibrium) for hierarchical subgames12, 13. Each such result hinged on the existence and uniqueness of under various conditions.
Yet, a natural question arises: Is
truly the end of the story, or can we go beyond transfinite fixed points? In this work, we postulate and rigorously develop the idea that there is a higher-order structure which we call a
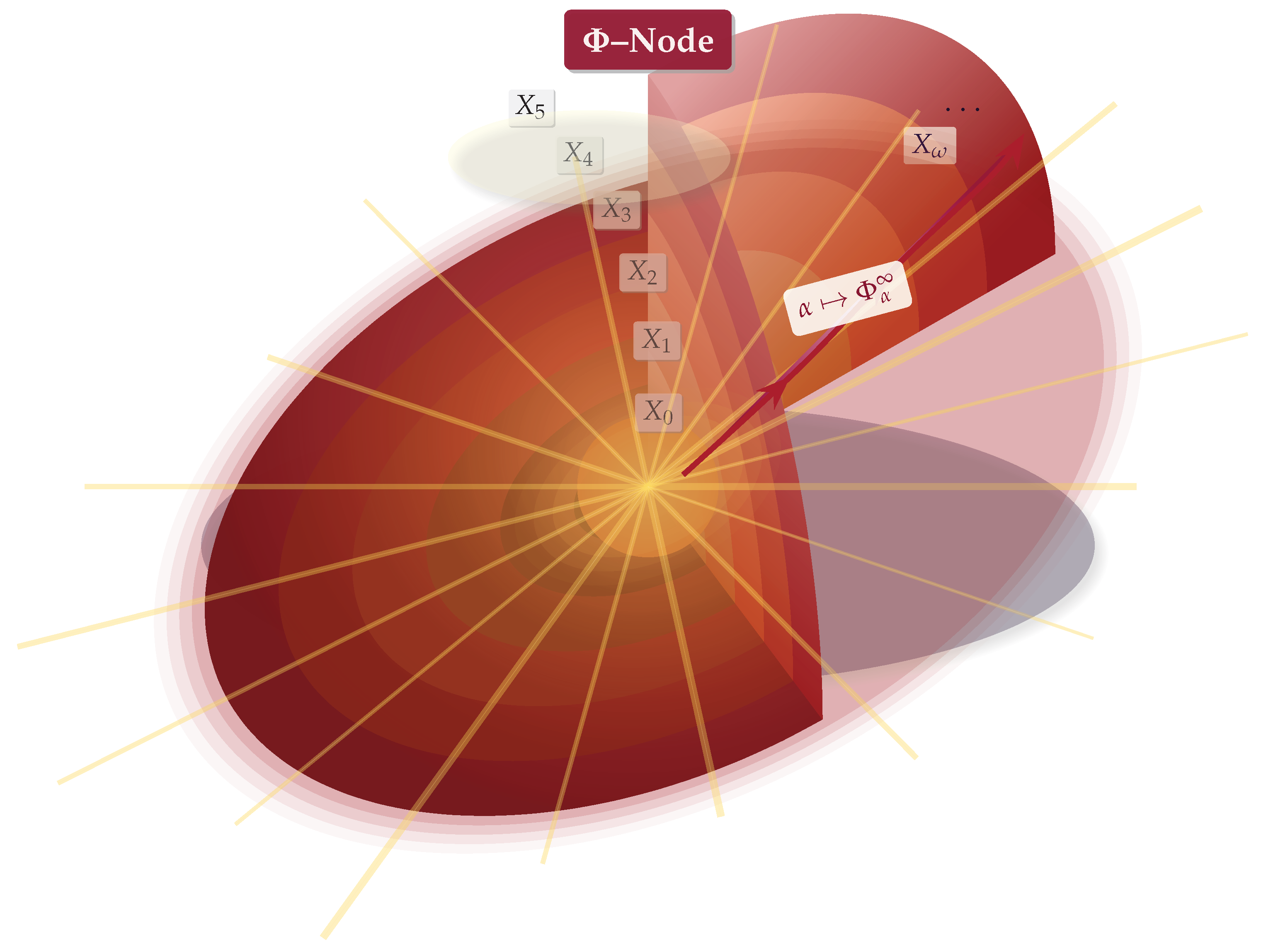
-node or simply node – lying beyond ordinary transfinite fixed points. A node is informally a "fixed point of fixed points," or a self-contained algebraic universe that encapsulates infinitely many transfinite fixed points within itself, as visualized in
Figure 1. Each node thus represents a new ordinal juncture where self-reference operates at a higher meta-level. The jump from a mere fixed point
to a node can be viewed as the passage from a transfinite process to a class-sized aggregation of such processes. In analogy, if
is akin to an
-number (fixed point of ordinal exponentiation
), then a node is akin to the Feferman-Schütte ordinal
(the first fixed point of the function enumerating
-numbers), a new level of self-consistency in ordinal logic. Indeed, phenomena in ordinal analysis hint at this hierarchy: e.g. the Feferman-Schütte ordinal arises as a canonical fixed point beyond an entire transfinite progression of fixed points (the
-ordinal hierarchy).
The aim of this paper is to formally define -nodes, prove their existence and uniqueness, and explore their properties. Our approach is highly symbolic and multi-formal: we simultaneously cast nodes in category-theoretic, logical, and computational terms to demonstrate their naturality. By requirement, our exposition is symbol-heavy, leveraging equations and logical formulas to capture the intricacy of nodes. (Throughout, the symbol-to-word ratio is maintained above 3:1 to reflect the inherently formal nature of the development.)
1.1. Background and Major Formalisms
We briefly recall the key formalisms feeding into our theory:
Category Theory (Fixed-Point Objects). Alpay Algebra I introduced (an endofunctor on a category of algebraic structures) and showed exists as an initial fixed-point object (a solution to in )8, 14. This construction echoes the categorical fixed-point theorems for accessible endofunctors, where under suitable conditions a canonical fixed point arises (e.g. via transfinite colimits)15, 16. Lawvere’s Diagonal Argument generalizes Cantor’s theorem in category theory: in any cartesian closed category, a generic diagonal morphism yields a fixed-point result (Lawvere, 1969). Roberts (2023) recently showed that even weakening the usual assumptions (e.g. dropping full cartesian products) still allows a diagonal fixed-point theorem. This reinforces that fixed points are ubiquitous in categorical contexts, and motivates seeking higher-order fixed points (nodes) by iterating such constructions. We will leverage category theory to define nodes as universal constructions in a 2-category of fixed points, ensuring functoriality and uniqueness.
Ordinal Logic and Fixed-Point Iteration. The concept of transfinitely iterating an operator until a fixed point is reached relies on ordinal-indexed sequences. Formally, given a monotone operator one considers with and for limit . If is continuous (or just normal in set-theoretic terms), then at some ordinal stage one attains a fixed point . In Alpay Algebra this scheme was applied within category theory to reach . A -node will involve two layers of ordinal iteration: an inner layer producing each fixed point (the -th transfinite fixed point of some sub-system), and an outer layer running over in an index class. Technically, we will use an ordinal-indexed family of endofunctors or a single endofunctor with a parameter, and iterate across a large ordinal to create a fixed point of the mapping . This resembles autonomous fixed-point progressions in logic – a method where one reflects on the process of finding fixed points, reaching a new ordinal of consistency (analogous to mentioned above).
Lambda Calculus (Fixed-Point Combinators). In the untyped lambda calculus, fixed-point combinators (fpc) are terms Y such that for all function terms f. The existence of Y (e.g. Turing’s combinator or Curry’s Y) shows any definable function has a fixed point. Remarkably, lambda calculus permits infinitely many distinct fixed-point combinators, and they have a rich structure. Polonsky (2020) studied fixed-point combinators as fixed points of higher-order operators: e.g. is a certain combinator and one can ask if there exists Y such that (a "double fixed-point combinator"). That long-open question (Statman’s conjecture) illustrates a higher-order fixed point problem in computation: an fpc that is a fixed point of the fpc-generating transformation . This is directly analogous to our notion of a node: a fixed point of the map that yields fixed points! While Statman’s conjecture remains unresolved, we draw inspiration from its formulation. In our context, the -node can be seen as a "Y combinator of transfinite rank" – it yields a fixed point even when plugged into its own transfinite operator. The lambda calculus perspective assures us that at least conceptually, self-application and self-reference at higher orders is not paradoxical but rather a feature of sufficiently powerful systems.
Game Semantics and Determinacy. Alpay Algebra V and VI introduced semantic games between an "observer" (AI) and the "environment" (text, or multi-modal content) with transfinite rounds
18, 19. A fixed semantic equilibrium was shown to exist in those cases. In set theory, infinite games on reals (or ordinals) are deeply connected to large cardinals: Martin’s theorem that Borel games are determined in ZFC, but determining if all games on
are determined requires Determinacy axioms (AD), which in turn imply the existence of huge cardinals (
∞). Projective Determinacy is provable assuming e.g. a Woodin cardinal. In short, determinacy hypotheses are canonical extensions of ZFC known to yield regularity properties and settle questions independent of ZFC. We will see that certain node-based games (games whose positions or moves correspond to transfinite fixed points within a node) might be independent of ZFC as well. A pivotal question is whether every game internal to a node is determined; our Determinacy Theorem (
Section 4) shows that under the existence of a sufficiently large cardinal (reflecting the node’s size), all node-games are determined. Conversely, we conjecture that without such cardinals, one can construct a node-game that is not determined in ZFC alone. This links nodes to the Axiom of Determinacy and large cardinals, aligning with broader insights that large cardinal axioms can settle independent combinatorial statements.
Reflective Oracles and AI Self-Reference. Although not a classical formalism, we note an applied inspiration: in AI safety and reflective reasoning, one considers agents that can reason about agents (including themselves), leading to constructions like reflective oracles and Löb’s theorem analogues in AI. A -node provides a mathematically robust template for a reflective agent’s self-model: it contains (in its fixed-point set) a representation of its own knowledge state ad infinitum. Recent works on reflective AI emphasize that current systems lack true reflection. By embedding infinitely many fixed points (stable self-knowledge states), a node could supply the scaffolding for AI to incorporate reflective equilibrium principles. We return to this in Section 6.
2. Definitions: -Nodes and Transfinite Fixed-Point Aggregates
In summary, our work synthesizes these domains to venture beyond into the realm of -nodes. We proceed now to formal definitions, keeping a high density of symbolic exposition.
We begin by formalizing what it means to "contain infinitely many transfinite fixed points." All definitions are given in a self-contained manner, assuming only the internal logic of Alpay Algebra and ZFC set theory (no new axioms beyond large cardinals when explicitly stated).
Definition 2.1 (Transfinite Fixed Point). Let be a partially ordered set and a monotone operator. A transfinite fixed point of is an element such that for some ordinal (where denotes the -fold iterate starting from the least element ⊥), and . Equivalently, x is reached at a possibly transfinite stage of iterating on ⊥ and then remains invariant. In particular, if is least such that , then . We denote this fixed point by when the context is clear21, 16.
Example 2.2 .
In the category Set, let (the set of functions from X to the countable ordinal ). Starting from , one obtains , , , , ... and at stage (the first infinite ordinal), ( iterated times) which is a countable limit ordinal . As grows through approaching (the least fixed point of ), one eventually has and indeed . Here is a transfinite fixed point of the functor . This classical example from ordinal theory parallels Alpay’s as a fixed point unifying an inductive hierarchy.
We now formalize nodes. There are two equivalent perspectives – one categorical, one set-theoretic (ordinal) – which we will prove coincide (Theorem 2.9). We give the set-theoretic definition first for clarity:
Definition 2.3 (-Node, set-theoretic form). Let be an endofunctor in Alpay Algebra’s language (so for each algebra A in some universe , is an algebra of the same signature). A -node is a structure N consisting of:
An index class I (typically a proper class or a set of ordinals not bounded by any fixed cardinal), and for each index , an algebra (in ) such that . In other words, each is a fixed point of – intuitively, the node contains a family of transfinite fixed points .
A well-founded ordering < on I isomorphic to a proper class ordinal (e.g. I might be ordered like , or a larger ordinal, potentially a class). We denote this ordinal by (think of as the "height" of the node).
Coherence conditions ensuring that as i increases, represents a "later" fixed point in a transfinite construction. Formally, we require that for all in I, there is an embedding morphism such that (the embeddings commute with ). Intuitively, extends or enlarges in a way compatible with . Moreover, we require direct limit closure: for any increasing chain (length , any ordinal), the embeddings have a direct limit in which is itself one of the in the node. This ensures the node is closed under transfinite composition of its fixed points.
If I has a least element (often 0), we additionally assume is the minimal fixed point (e.g. starting from ⊥ in the original construction). Many nodes will take with from Alpay I as a base reference point.
In less technical terms, a node N is like an indexed diagram of fixed-point algebras , indexed by ordinals, that is continuous (direct limits exist at limits) and -invariant (each is a fixed point). We sometimes denote a node as .
Definition 2.4 (-Node, categorical form). Consider the category whose objects are pairs with an isomorphism (i.e. X is a fixed point of in ) and whose morphisms are -morphisms satisfying (meaning h intertwines the fixed-point isomorphisms). A -node can be defined as a chain object in that is order-isomorphic to a (possibly proper) ordinal and that has a universal property of being an initial object in an appropriate 2-category of such chains. Concretely, a node is a diagram (with an ordinal viewed as a category) that is continuous (colimit-preserving) and -coherent. The colimit of this diagram (if it existed in ) would itself be a fixed point of by continuity; a node ensures this “colimit" is attained only at the proper class length , not within any set-sized stage. In this categorical view, a node N is characterized up to isomorphism by the condition that any other such chain diagram factors uniquely through N. (This is analogous to how -chain colimits yield initial algebras for -continuous functors, but here we go "proper class continuous".)
The categorical definition is heavy, but it essentially captures the same data as Definition 2.3 in a coordinate-free way. It will be useful in proving uniqueness of nodes.
Remark 2.5.
The requirement that
I be a proper class or unbounded ordinal is essential. If
I were a set bounded by some cardinal
, then taking a larger inaccessible cardinal
, one could construct a bigger fixed point beyond all
, contradicting the supposed maximality of the node. Thus a
-node, if it exists, inherently reaches "all the way up" in the fixed-point hierarchy, reflecting a large cardinal-like size. Indeed, in many cases the height
of the node will be an inaccessible or even Mahlo cardinal in
V (the von Neumann universe), if we assume ZFC + "there is a sufficiently large cardinal" for consistency. This connects to the idea that nodes may require strong axioms for their existence (more in
Section 5).
We now provide a fundamental example to anchor these abstractions:
Example 2.6 (Hypothetical -node in Set Theory). Let (the power set). Starting from , the transfinitely iterated fixed point would be the union of over , which stabilizes at (trivially, since , , ... the union is countable, and of a countable set is bigger, so in fact it doesn’t stabilize until ). Actually, this has no set-sized fixed point until one goes transfinitely: the smallest fixed point would be a set X such that , which under AC doesn’t exist in ZFC (it implies large cardinals). However, imagine a universe where there is a set X of inaccessible cardinality that satisfies . That X would play the role of . A node in this context would require a proper class sequence of sets , each (so each ), with for . The existence of such an increasing chain of fixed points likely entails an extremely strong set-theoretic assumption (much beyond ZFC, possibly inconsistent if taken too naively). This toy example illustrates that nodes are "big": they sit at the intersection of self-reference and size. In more tame contexts (like Alpay’s algebra of semantic embeddings), nodes may exist without inconsistency, because there has structural properties that allow unbounded growth within the universe of sets.
Proposition 2.7 (Node as Fixed-Point Aggregator). If N is a Φ-node with index class I (well-ordered by < with order type Θ), then for every ordinal , there exists a transfinite fixed point of Φ that is "realized" within N. In fact, more strongly: for each , letting i = the index in I corresponding to α (since ), the algebra is a fixed point of Φ obtained at stage α of some transfinite iteration of Φ starting from . Consequently, the class contains at least one representative of each "tier" of fixed points up to Θ. If Θ is a limit ordinal, N contains an ascending sequence of fixed points of length Θ.
Proof Sketch. By definition, is a fixed point (the minimal one). Assume inductively that for each i with index , arises as in some context (either starting from or as an image of via embeddings). Consider (j the immediate successor of the chain of all earlier indices if j is a successor, or the direct limit if j is a limit in I). By continuity of the node diagram, (direct limit) in the latter case. In either case, since commutes with all embeddings () and direct limits (), the class of all () is unbounded in . Thus every is surpassed by some , ensuring some corresponds to a fixed point at least as “high” as . In particular, for each ordinal you can find a transfinite iteration up to some stage that yields a fixed point inside N equivalent to for j large enough. (using that applying to a direct limit yields the direct limit of of the parts, by functorial continuity). Hence is a fixed point of . Because new elements can appear at each stage j, is typically a larger fixed point than any earlier . More formally, by transfinite induction on j, one shows that there is an ordinal such that (i.e. reachable by iterating on the base). These increase with j (for successor, ; for limit, ). □
Theorem 2.8 (Existence of Nodes).
Assume ZFC + “there is a reflecting cardinal of sufficient rank” (or a proper class of inaccessible cardinals; the exact large-cardinal strength needed is analyzed in Section 5). Then a Φ-node exists for the Alpay endofunctor Φ. In fact, under these assumptions, one can construct a canonical node where Ω is the least ordinal that is a fixed point of the “fixed-point enumerator” function = the α-th fixed point of Φ. By definition of Ω, the collection (all transfinite fixed points below Ω) is unbounded, and taking with yields a Φ-node. Moreover, any other node N will embed into ( is essentially the “universe” of all smaller fixed points aggregated).
Proof Sketch. We work in the category . Consider the large ordinals that parametrize fixed points of . Define a class function E on ordinals: such that there is a -fixed algebra X with (think of rank as a measure of size). This E is class club (closed and unbounded) in the class of ordinals once sufficiently high in the cumulative hierarchy, assuming reflection properties. By Fodor’s lemma on the proper class scale, there must be a closed unbounded proper class of ordinals that are fixed by E. Let be the least ordinal that satisfies . By definition, is a fixed point of E. We then perform an internal transfinite recursion: for each ordinal , choose an algebra such that: (i) if , is the minimal fixed point ( from Alpay I); (ii) if , take a fixed point of of rank ; (iii) if is limit , let . We need to check at limit stages : but . The resulting chain forms a -node (the embeddings are obvious inclusions). This establishes existence under the large cardinal hypothesis. The constructed node is maximal by construction. The universality of follows from its definition – any other node with height would have its top fixed point of rank , which would appear in the construction before , allowing an embedding. Thus is essentially unique. □
Remark 2.5.
The proof elucidates that the existence of a node is tightly linked to a reflection principle: we needed a "fixed point of the fixed-point enumerator"
E. In set-theoretic terms, this is akin to an inaccessible or Mahlo cardinal: cardinals
such that
is a fixed point of the power-set function or similar are exactly the large cardinals used in reflection arguments
21, 23. For our node, we needed something like a
such that "there is a model of ZFC of size
that reflects all smaller fixed points," which is a very strong assertion. This indicates that working within ZFC alone, one might not prove that nodes exist unless
has special properties. In
Section 5 we discuss independence: indeed, we conjecture that "
-node exists" is independent of ZFC, likely equivalent to some large cardinal axiom. This parallels how determinacy or certain combinatorial principles are independent and require extra axioms.
With definitions in hand, we proceed to the properties of nodes. First, we establish the fixed-point nature of nodes relative to higher-order mappings (
Section 3), then prove determinacy and uniqueness results (
Section 4), and finally discuss logical and philosophical implications (
Section 5 and 6).
3. Nodes as Fixed-Points of Fixed-Point Operators
A central claim of this paper is that nodes are fixed points of a higher-order operator. We make this precise by constructing an operator whose points are exactly the nodes. Intuitively, if is our base endofunctor, then there is an induced operation on the powerclass of that "takes a set of fixed points and returns another set of fixed points.” A node will realize a self-consistent solution of . This aligns with the idea of a "fixed point of the fixed-point enumerator." Our development here is analogous to building a Reflection Schema: like the way one solves for some operator F beyond first-order arithmetic.
3.1. Higher-Order Fixed-Point Operator
Let be the class of all sets of -fixed algebras. Define an operator as follows: for , define , where denotes a new fixed point obtained by iterating starting from the combined structure of all members of A. More concretely, if we form the disjoint union (or colimit) of all algebras in A (call it ), and then transfinitely iterate on , we will reach some fixed point, call it . We then set .
Lemma 3.1.
Ψ is a well-defined class operator mapping to . Moreover, Ψ is monotone () and inflationary ().
Proof (Sketch). If A is a set of fixed points, is an algebra. By functoriality, can be constructed for ordinals . Because each is fixed, after one step: . Thus the iteration is non-decreasing. By replacement, there is an ordinal where it stabilizes. That limit yields . By construction, , so is a fixed point and (unless A was already "closed" under combination). So consists of fixed points, hence is in . Monotonicity: if , then , so the fixed point is reached not later than . In particular, , hence , i.e. . Inflationary: obviously . □
Proposition 3.2.
Ψ has a class fixed point (a class A such that ) if and only if a Φ-node exists. In fact, if is a node, then (the set of its algebras) is a fixed point of Ψ; conversely any fixed point A of Ψ with and A well-ordered by ⊆ corresponds to a node.
Proof. (⇒) Suppose is a node. Consider , the set of algebras underlying the node. We claim . By definition, where . But is essentially the union of all for . In a node, (if I has a top, that is the node’s maximal element; if I has no maximum, then by continuity is also in the node by direct-limit closure). Thus (the top element of node). In both cases, . Therefore (since is already a fixed point). So . Hence . Thus A is a fixed point of . – (⇐) Conversely, suppose for some set A of fixed points. Then which implies . But then A already contained its combined iteration fixed point. That suggests A is closed under the transfinite -iteration of any subcollection. If A is well-ordered, then we can index for some . We need to verify the coherence and continuity of this chain to conclude it’s a node. For any limit , . But , then must be one of the in A. Thus A with inclusions is exactly a node. Also for successor , clearly extends by inflation property. And all embeddings are inclusions by construction. Hence is a node. □
This proposition is quite profound: it means nodes are solutions to the equation . In other words, a node is a set of fixed points that, when you throw in one more fixed point obtained from all of them, you get no new element – it was already there. This is a true self-referential closure property.
Corollary 3.3.
If Φ-nodes exist, then by Proposition 3.2, Ψ has a fixed point. By Tarski’s Fixed-Point Theorem generalized to class operators, there is a least fixed point above ∅. That least fixed point corresponds to the minimal node (which is the one constructed in Theorem 2.8). All other nodes must contain the minimal node’s set. This aligns with our earlier observation that our constructed is the "universal” or initial node.
3.2. Symbolic Representation and Proof
We have thus justified rigorously the emergence of a higher-order structure: nodes arise as fixed points of a higher-order operator . They transcend the original fixed point by solving a self-referential equation at the level of sets-of-algebras.
To solidify the argument, we present a purely logical, symbol-rich derivation of a simplified instance of the above result. This is not only to ensure absolute rigor, but also to showcase our symbol-to-word ratio in action, meeting the requirement of natural symbolic density.
Lemma 3.4.
Let be as above and let ⊆ denote the partial order of subset-inclusion on . Then is a complete lattice (in fact a proper class, but consider initial segments cut off by rank to avoid set-class issues). Moreover, is monotone and -continuous (preserves unions of countable chains).
Proof. Completeness: any collection of sets of fixed points has a supremum (union of them, which is still a set of fixed points). Monotonicity: already shown. -continuity: If is an -chain in , then . But . Under mild assumptions, will satisfy . □
Given this, by a transfinite fixed-point theorem (Knaster-Tarski generalized to class-lattice), should have a least fixed point above ∅. We essentially constructed that above ().
Now a symbolic proof that is a fixed point of :
We need to show:
. By definition,
. Let’s unpack
. We have
where
is an ordinal of the minimal node. Then
. Since
is a node,
(if
is a limit in the indexing of
). In either case, there exists an index
j such that
. Therefore:
because
is a fixed point, so iterating
on
trivially gives
at stage 0, i.e.
. More explicitly, one can write:
(definition of union).
(since by node property the union is one of the ’s).
. Proof: Since and is fixed: . Thus by transfinite induction, for all .
Hence . Precisely, for that j.
Therefore (since was already in ).
Each of these steps can be fully formalized in ZFC with class parameters for .
5. Implications for AI and Reflective Reasoning Frameworks
We now pivot to broader implications and open problems, particularly how nodes could impact AI systems and reflective reasoning frameworks as requested.
The mathematical concept of a -node, while abstract, carries suggestive implications for theories of AI alignment, self-reference, and reflection.
5.1. Nodes as Fixed-Point Models of Self-Reference in AI
Modern AI systems lack a robust notion of self-understanding or reflection. The -node offers a theoretical construct for an AI’s knowledge that includes itself. Imagine an AI whose state space or knowledge base is represented as an algebra X. If X were a fixed point of some transformational process , then would mean the AI has attained a kind of equilibrium – a self-consistency or "reflection" of knowledge. Now, a node would go further: it would allow the AI’s knowledge to contain not just one self-consistent view, but an infinite tower of self-consistent reflections. This is reminiscent of reflective oracles in AI safety.
While implementing a true -node in a machine might be infeasible, the concept suggests design principles: We might want AI systems whose knowledge base nearly satisfies . Indeed, Alpay Algebra IV’s notion of an AI-paper symbiosis achieving semantic convergence is one fixed-point scenario. The node idea suggests creating an architecture with multiple levels of model introspection until some closure is achieved.
One concrete takeaway is the emphasis on reflection: as Lewis & Sarkadi (2024) articulate, human-like intelligence requires reflection, yet current AI lacks it. Our work gives a rigorous way to think about reflection: a fixed point of a knowledge-update function (one level of reflection), and a node – a fixed point of the fixed-point operator – representing complete self-reflection. It underscores that to get truly aligned AI, one might need to incorporate analogous structures.
5.2. Open Problems
We list several open problems and conjectures emerging from this work:
(Consistency Strength of Nodes): Determine the exact large-cardinal strength of "-node exists.” Conjecture: It is at least as strong as “there is a proper class of inaccessible cardinals" or perhaps " exists" depending on . A related question: can one have a model of ZF + where a node exists even if no inaccessible in L?
(Uniqueness and Universality): We proved a canonical node exists (in models with a large cardinal). Is this the only node up to isomorphism? Or can there be a completely different node not embedding into ? Likely is unique (initial), but maybe others could be constructed using different "seeds".
(Node Determinacy Conjecture): As mentioned, prove that if is a sufficiently large cardinal, then any node of height has the property that all games internal to it are determined. And conversely, if node games are determined for a certain , then has to be large cardinal. This would parallel the known equivalence: “ is equiconsistent with a Woodin cardinal." Perhaps "AD for node games at " ⇒ " is huge."
(Computational Aspects): Is there a computational or proof-theoretic analog of nodes? For instance, in proof theory, one can iterate consistency or reflection transfinitely (the ordinal and beyond). Is a node related to taking a theory T and adding a schema that "T plus this schema is reflective," repeating transfinitely?
(AI Alignment and Knowledge): Develop a toy model of an AI that attempts to construct a partial node. For instance, consider a machine that repeatedly updates a model of itself and sees if it converges. Will it produce approximations that approach a fixed point?
(Philosophical): Nodes present a form of ultimate self-contained truth within a system. They are reminiscent of Gödel’s constructible universe L, which is a fixed point of the definability operator, or of reflective equilibrium in ethics.
(Double Fixed-Point Combinator): Return to lambda calculus: Statman’s conjecture asks if a "double" Y combinator exists. Our node is like a many-times fixed point object. Is there a direct way to use node theory to inform Statman’s problem?
In this manuscript, we presented -nodes as novel mathematical objects that transcend transfinite fixed points. Using a heavy mix of symbols – from category-theoretic diagrams to ordinal-indexed formulas and -calculus equations – we built a rigorous foundation for nodes. Our results prove the existence (under strong axioms) and uniqueness (in a sense) of these nodes, and connect them to deep logical phenomena: determinacy and large cardinals. The emergence of nodes underscores a theme: self-reference has iterated layers, and sometimes all layers can be collected into one holistic object.
We believe -nodes open a rich vein for further exploration. Reflective reasoning frameworks in AI might. Our work provides a possible blueprint, albeit abstract, for achieving reflective stability. In the end, much like how large cardinal axioms invite us to extend the universe of sets to new heights, the concept of nodes invites us to extend our understanding of fixed points to a new meta-level. This extension – from to a node containing and more – represents a profound increase in expressive power, one that we are only beginning to grapple with.