1. Introduction
Polarization-maintaining (PM) fibers play a crucial role in many optical technology fields, such as fiber optic gyroscopes (FOGs) [
1,
2,
3], fiber optic sensors [
4,
5], and fiber lasers [
6,
7,
8]. Researchers have developed various types of solid-core PM fibers (PMFs) [
9]. Currently, solid-core PMFs exhibit the birefringence of higher than 10
-4 and transmission loss of lower than 0.36 dB/km, respectively [
10]. However, the solid-core PMFs have some inherent limitations, such as high material absorption loss, low damage thresholds, and high nonlinearity [
11,
12].
Hollow-core fibers (HCFs) have offered the breakthrough solutions to the technical bottlenecks faced by traditional solid-core fibers. The light-guiding mechanisms of HCFs include the photonic bandgap guidance [
13] and anti-resonant guidance [
14]. Hollow-core photonic bandgap fibers (HC-PBGFs) [
15,
16]can introduce high birefringence by adjusting the quartz walls around the core, leading to anti-cross coupling between the core mode and surface mode. However, for the HC-PBGFs, narrow guidance bandwidth, poor mode purity, and high surface scattering losses limit their application potential [
17,
18,
19]. In contrast, hollow-core anti-resonant fibers (HC-ARFs) have larger design flexibility, wider transmission bandwidth, and lower transmission loss [
20]. Although the HC-ARFs achieve a certain degree of mode overlap between the core and cladding region, the coupling between the fundamental mode and the cladding region is crucial for the fiber performance. However, due to the characteristics of the air core, it does not exhibit the photo elastic effect, which means that we cannot introduce the birefringence within the core structure by using traditional methods [
21]. Therefore, the HC-ARFs face the challenges in achieving high birefringence (>10
-4). Most of works on the HC-ARFs focuses on the birefringence enhancement, which can be achieved by changing the core shape, constructing the wall thickness differences, and modifying the cladding tube materials.
As is known to all, given the established efficacy of elliptical core geometries in inducing high birefringence (Hi-Bi) within conventional solid-core fibers [
22]. Drawing inspiration from this principle, a direct method to introduce an effective refractive index difference in HCFs is to modify the core shape, such as by increasing the ellipticity of the core. This modification leads to differences in the fundamental mode profiles in the x and y directions, thereby achieving high birefringence of HC-ARF [
23]. In 2013, Vincetti et al. conducted the theoretical simulations to investigate the influence of the elliptical aspect ratio of the HC-ARF core on its birefringence characteristics [
24]. The theoretical results revealed that as the elliptical aspect ratio of the core increases, the birefringence also increases. The optimized fiber design achieved a maximum birefringence value of 7×10
-5. However, the elliptical core constructed by the arrangement of cladding glass tubes could not introduce higher birefringence. In 2022, Wei et al. [
25] proposed a quasi-elliptical core HC-ARF. By introducing an asymmetric polarization mode field in the elliptical core, a birefringence of 1.33×10⁻⁴ and a transmission bandwidth of 460 nm were achieved at 1.55 μm. However, this structure supports few-mode transmission, and the proposed fiber structure, which features an elliptical cladding tube, presents significant challenges in fabrication. In 2023, Wang et al. [
26] introduced a crescent-shaped core AR-HCF with excellent birefringence performance, achieving a bandwidth of 300 nm and a loss limit of less than 1 dB/km at a birefringence level of 10⁻⁴. Only the fundamental mode purity is relatively low, Although the performance is superior, the fabrication of the glass cladding wall of this structure cannot be effectively realized through conventional pressure control methods.
Additionally, using tubes of varying thicknesses in orthogonal directions has been proven to be an indirect yet effective method for achieving high birefringence, as demonstrated by numerous studies. In 2016, Mousavi et al. [
27] proposed to achieve high birefringence by constructing resonant and anti-resonant tubes in orthogonal directions. Although this design achieved a high birefringence of 1.5×10⁻⁴ at 1.55 μm, the loss was as high as 43 dB/km, but the higher-order mode suppression ratio (HOMSR) was not discussed. Subsequently, in 2018, Wei et al. [
28] introduced the nested rings into a six-hole anti-resonant structure. Although this design simplified the fiber structure, the loss at 1.55 μm was as high as 20 dB/km, and the birefringence was only at the 10⁻⁵ level. In 2020, Yerolatsitis et al. [
29]achieved a maximum loss of <1000 dB/km at 1.55 μm and a phase birefringence of 2.5×10⁻⁵ by introducing differences in cladding tube thickness in a six-hole HC-ARF. In 2022, Ding et al. designed and fabricated a novel four-hole nested anti-resonant fiber with a semi-circular cladding tube structure [
30]. By constructing a thickness difference in the glass walls in orthogonal directions of the HC-ARF, an asymmetry in mode profiles was introduced, resulting in high birefringence. The fiber achieved a transmission loss of only 4.8 dB/km at 1.52 μm, but the phase birefringence was only 1.8×10⁻⁵, with a bandwidth of 154 nm. But the mode purity value of this fundamental mode is not theoretically specified. In 2024, Wang et al. [
31] proposed a crescent-shaped nested HC-ARF with four-fold rotational symmetry. By designing thickness differences in the walls in orthogonal directions and utilizing the anti-crossing effect between core modes and glass modes, high birefringence was achieved. The fiber achieved a birefringence of 3.62×10⁻⁵ and a loss of 8.5 dB/km at 1.06 μm. Similarly, the high-order mode transmission loss is not mentioned. However, the use of this semi-tube structure imposes extremely stringent requirements on precise pressure control technology, and the fabrication process is highly demanding. Because most of the reported designs have a certain level of complexity or low feasibility in drawing processes, Meanwhile, the current birefringent anti-resonant fiber (ARF) cannot simultaneously achieve a higher higher-order mode suppression ratio and low-loss polarization-dependent transmission, To solve these questions, there is an urgent need to design a kind of polarization-maintaining PM-HC-ARF) which has good optical transmission characteristics while ensuring the practicality and operability of the structure.
In this paper, a PM-HC-ARF with different wall thickness and six-cladding holes is proposed. Unlike the mentioned single-solution designs, This fiber takes into account the combined effects of geometric polarization maintenance and surface mode polarization maintenance by combining the characteristics of an elliptical core and different wall thickness. Theoretical calculations indicate that within the wavelength range of 1420 to 1800 nm, the phase birefringence is greater than 1×10-4, reaching a maximum of 1.45×10-4. In the S+C+L+U communication band (~380 nm), the transmission loss is less than 8.8 dB/km. The higher-order mode suppression ratio is greater than 241 within the considered wavelength band, The purity of the fundamental mode transmission is satisfactory. Moreover, the PM-HC-ARF also exhibits excellent resistance to bending. Even with a bending radius as small as 3 cm, the x-polarized (x-pol) light loss is only 0.0078 dB/m, and the y-polarized (y-pol) light loss is only 0.0052 dB/m.
2. Structure Design and Principle
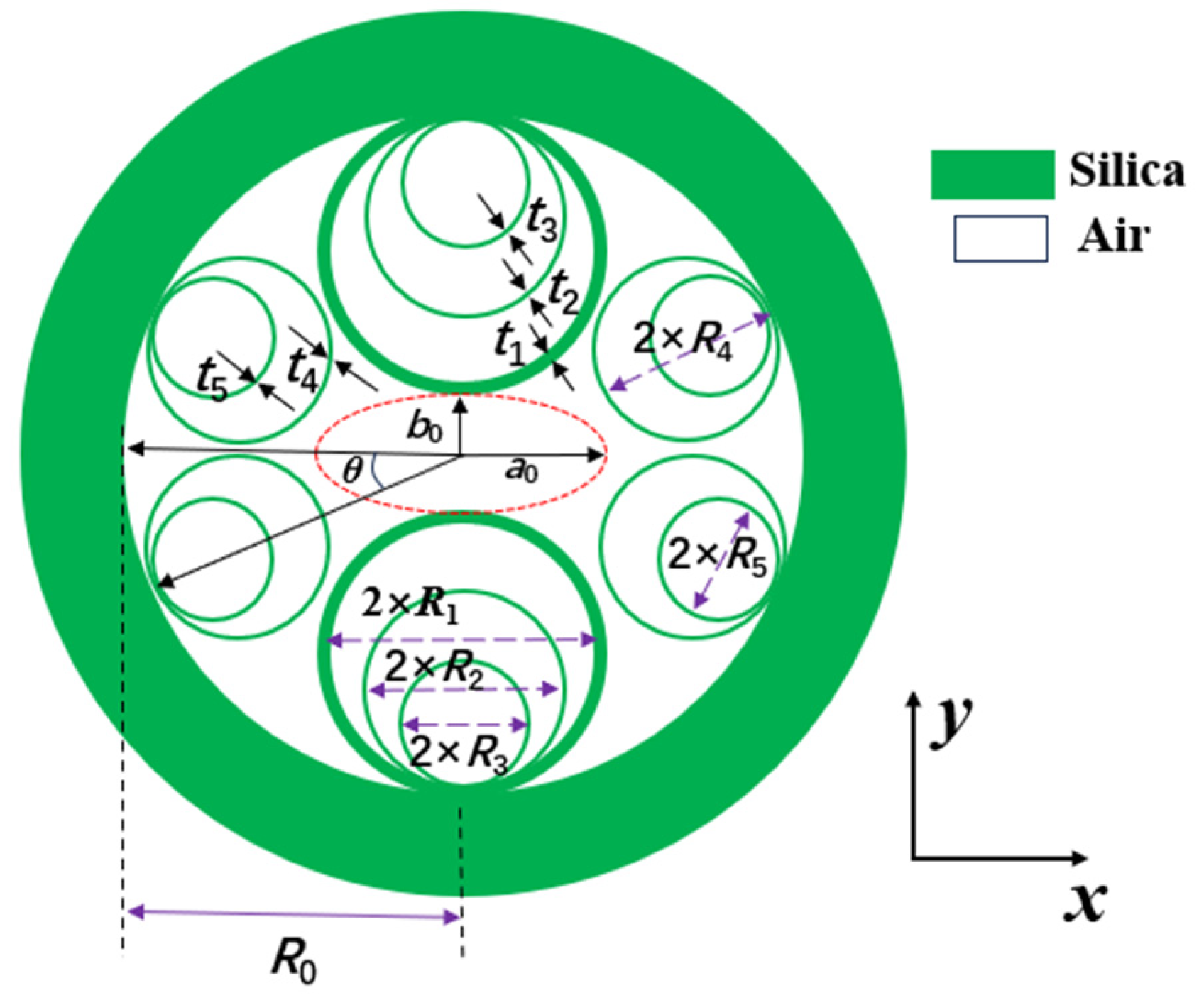
In this work, the cross-section of the proposed PM-HC-ARF that supports two polarization modes of the fundamental mode LP
01 is shown in
Figure 1. From
Figure 1, the cladding structure includes a double-layer nested configuration with six holes, which is used to minimize the confinement loss. In the x-direction and y-direction, two kinds of cladding tubes are utilized. Specifically, in the y-direction, two larger cladding tubes are used to couple one polarization state of the core mode into the cladding mode, thereby enhancing the birefringence through an asymmetric core profile, which facilitates large birefringence while reducing differential loss between the fundamental core modes of the two polarizations. To achieve larger birefringence, it is crucial to ensure that the coupling between the core mode and cladding modes of the two polarization states occurs. Therefore, the wall thicknesses of the cladding tubes are carefully calculated, ensuring that the wall thickness of the four cladding tubes in the x-direction approaches the anti-resonant condition, while the wall thickness of the two cladding tubes in the y-direction approaches the resonant condition. The designed PM-HC-ARF structure exhibits a left-right symmetrical configuration, demonstrating strong feasibility for manufacturing. Additionally, the PM-HC-ARF structure is characterized by the following dimensions: in the y-direction, the radius of the first cladding tube is denoted as
R1, with a wall thickness of
t1; the radius of the first nested cladding tube is
R2, with a wall thickness of
t2; the radius of the second nested cladding tube is
R3, with a wall thickness of
t3. In the x-direction, the radius of the first cladding tube is
R4, with a wall thickness of
t4; the radius of the second nested cladding tube is
R5, with a wall thickness of
t5; the radius of the internal region of the outermost sleeve is
R0. The long and short axes of the elliptical core in the horizontal direction are designated as
a0 and
b0.The angle of deviation
θ=25°.
All simulations were performed using the finite element method. In the simulation, the maximum mesh size in the silica glass region should not exceed λ/5.8, while for air region it should not exceed λ/4. Perfectly Matched Layer (PML) boundaries were applied to the outermost layer of the geometry. The effective refractive index of the silica material was calculated using the following Sellmeier equation [
32].
where λ represents for the wavelength of the incident light. According to the resonance principle of HC-ARF, the light loss in the m-th anti-resonant frequency band is minimized when the resonance equation is satisfied [
33].
where
nsilica is the refractive index of the silica glass,
nair is the refractive index of air, and m is the order of resonance. When the light wavelength meets the specific anti-resonant condition, the light field energy is effectively confined within the core region, significantly reducing the confinement loss. Phase birefringence refers to the effective refractive index difference between the fundamental modes of the x and y-pol lights. This birefringence can be calculated using the following formula.
where the effective refractive indices for the fundamental modes in the x and y directions are represented by
nx and
ny, respectively. The propagation constants for the modes in the two perpendicular directions are denoted as
βx and
βy, respectively. For the HC-ARF, this confinement loss (CL) can be calculated using the following formula [
34].
The higher-order mode extinction ratio (HOMER) plays a critical role in communication transmission. Typically, the single-mode characteristic is determined by the HOMER, which can be expressed as [
35].
where C
LHOM represents the minimum confinement loss of the HOM, and
CL(x, y) −pol denotes the confinement loss of the x-pol and y-pol fundamental modes, respectively. Generally, when the HOMER is greater than 100, good single-mode transmission characteristics can be achieved. The initial structure parameters of the PM-HC-ARF are set as follow,
. According to Eq.(2), the value of
t is chosen to achieve the first anti-resonance band at an incident wavelength of 1550 nm. In the following, we aim to optimize the structure parameters to achieve the good transmission performances at specific wavelengths.
Author Contributions
Conceptualization, H.X. and Z.H.; methodology, H.X. and YY.; software, D.W. and Z.R.; validation, Y.H., Y.Y. and J.L.; formal analysis, H.X. and S.L.; investigation, H.X. and J.Y.; resources, G.Z., C.X. and Z.H.; data curation, H.X. and D.W.; writing—original draft preparation, H.X. ; writing—review and editing, H.X., J.Y. and Z.H.; visualization, C.X. and Y.H. ; supervision, H.X. and J.Y.; project administration, H.X. ; funding acquisition, Z.H. and G.Z. All authors have read and agreed to the published version of the manuscript.
Figure 1.
The cross-section of the proposed PM-HC-ARF.
Figure 1.
The cross-section of the proposed PM-HC-ARF.
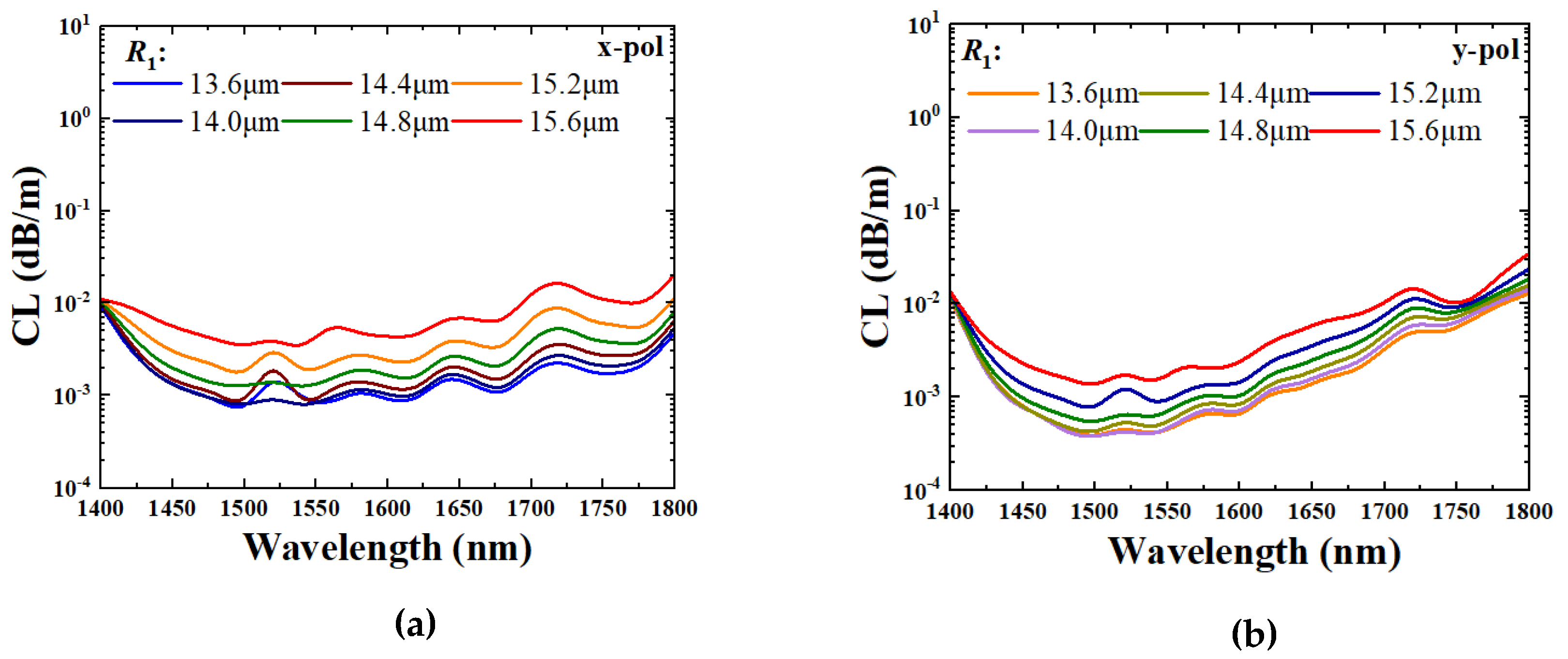
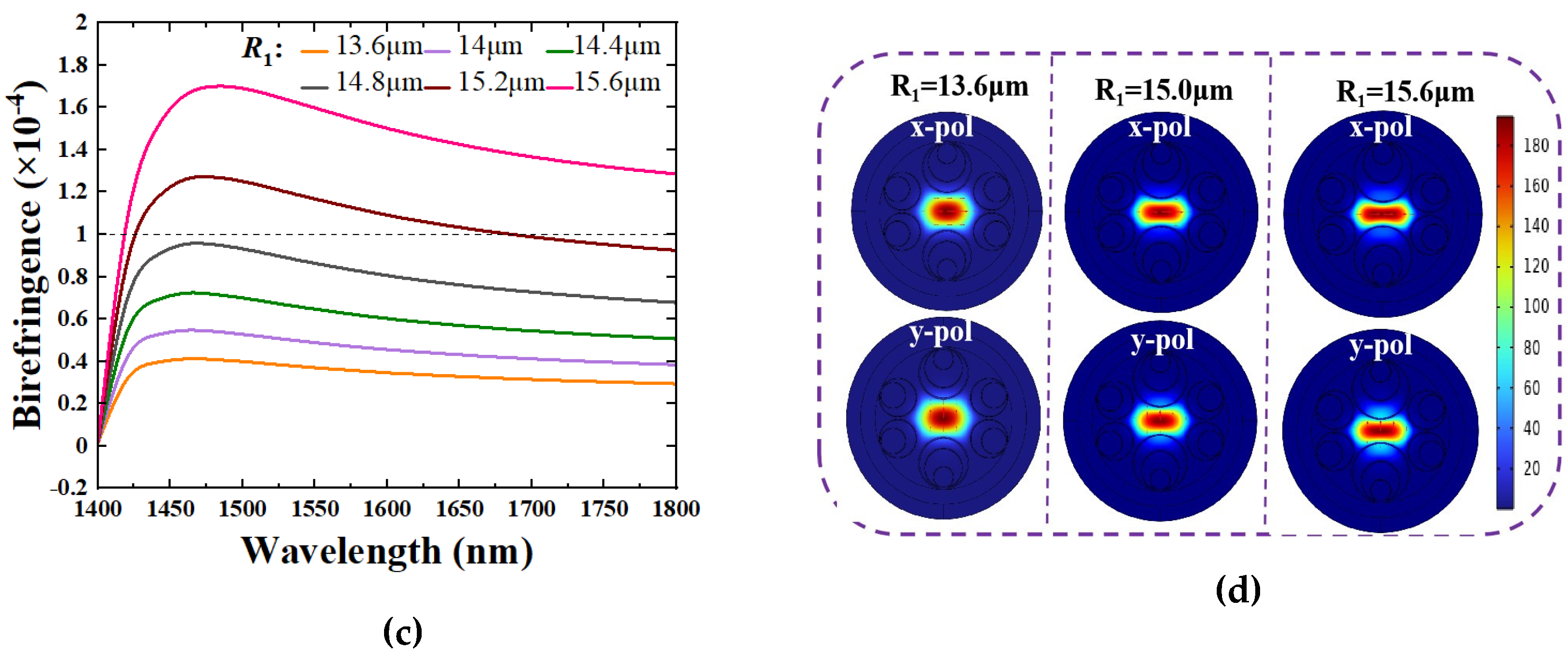
Figure 2.
(a) The effect of changes in R1 on the CL of the x-pol FM, (b) the effect of changes in R1 on the CL of the y-pol FM, (c) the effect of changes in R1 on the birefringence and (d) the FM field patterns calculated at wavelength 1550 nm for R1 values of 13.6 μm, 15 μm, and 15.6 μm, respectively.
Figure 2.
(a) The effect of changes in R1 on the CL of the x-pol FM, (b) the effect of changes in R1 on the CL of the y-pol FM, (c) the effect of changes in R1 on the birefringence and (d) the FM field patterns calculated at wavelength 1550 nm for R1 values of 13.6 μm, 15 μm, and 15.6 μm, respectively.
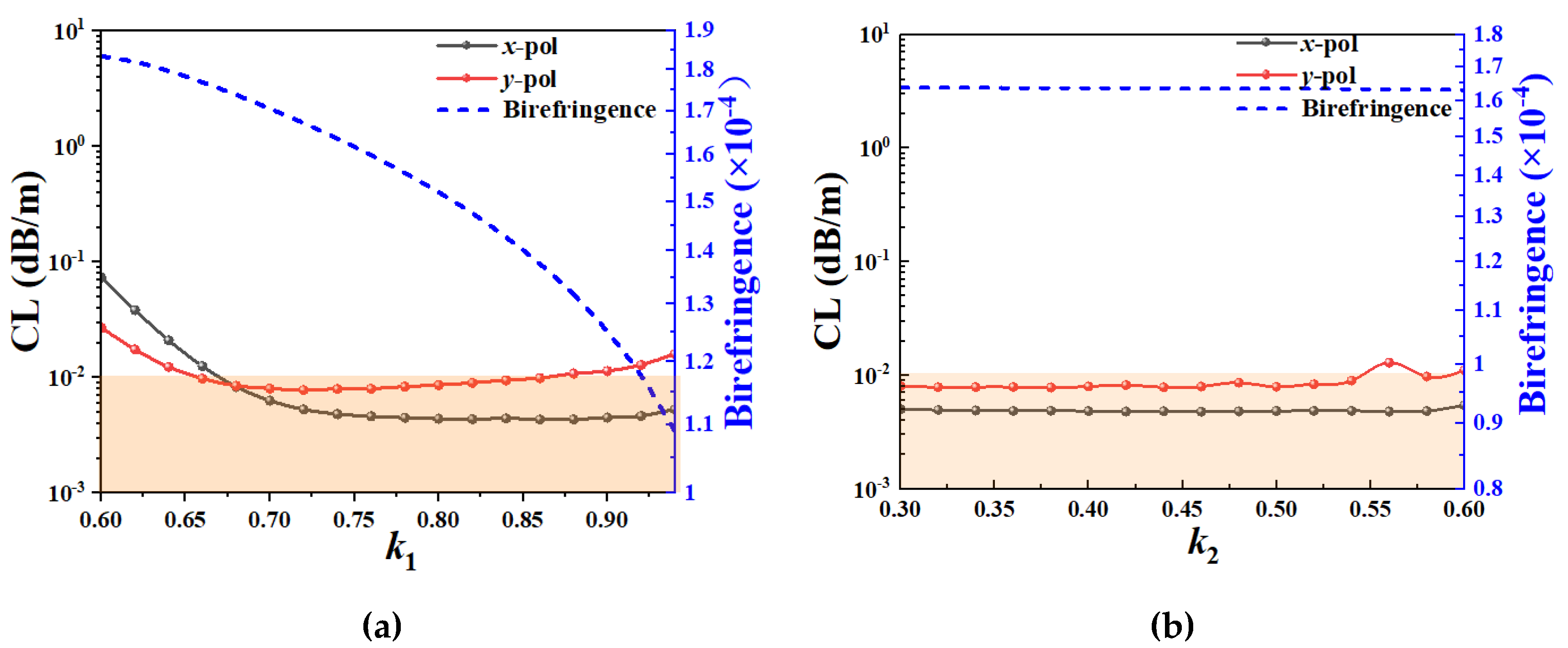
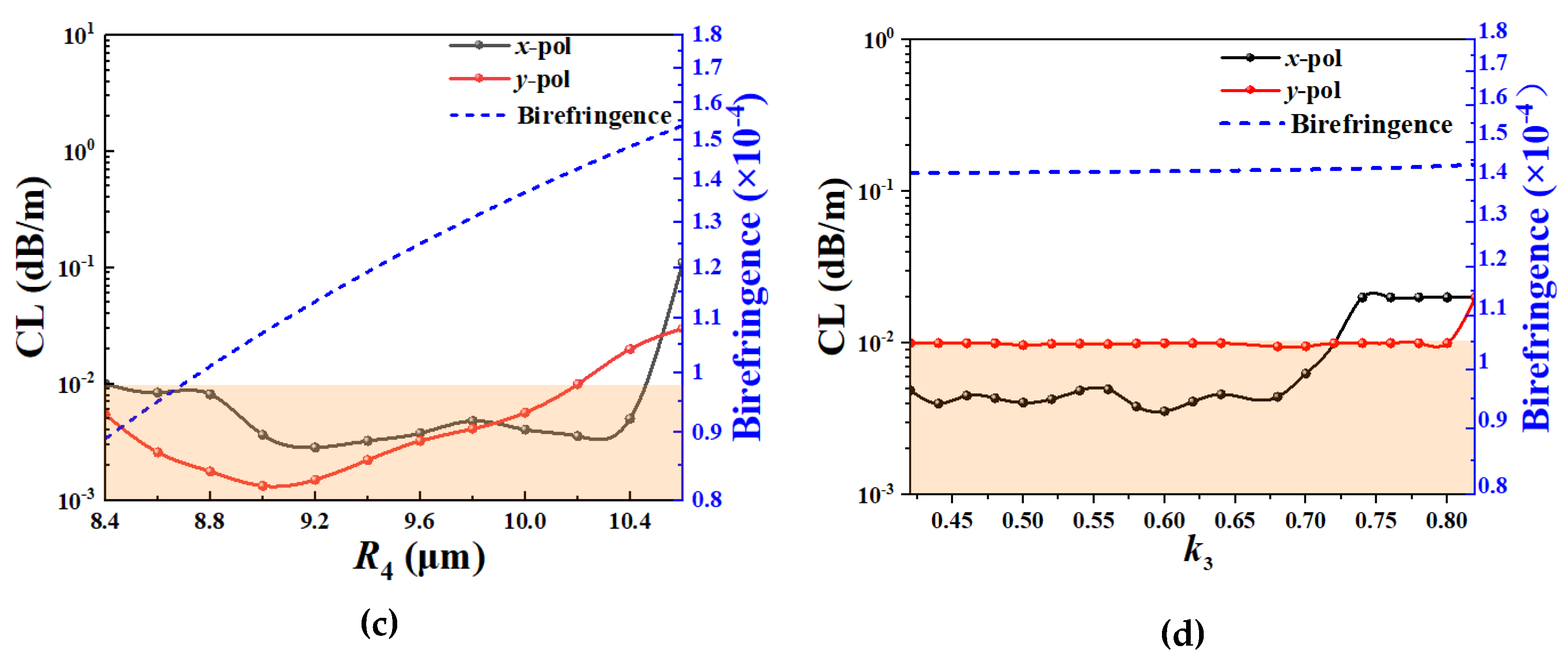
Figure 3.
(a) The effect of k1 on the CL and birefringence, (b) the effect of k2 on the CL and birefringence, (c) the effect of R4 on the CL and birefringence, and (d) the effect of k3 on the CL and birefringence.
Figure 3.
(a) The effect of k1 on the CL and birefringence, (b) the effect of k2 on the CL and birefringence, (c) the effect of R4 on the CL and birefringence, and (d) the effect of k3 on the CL and birefringence.
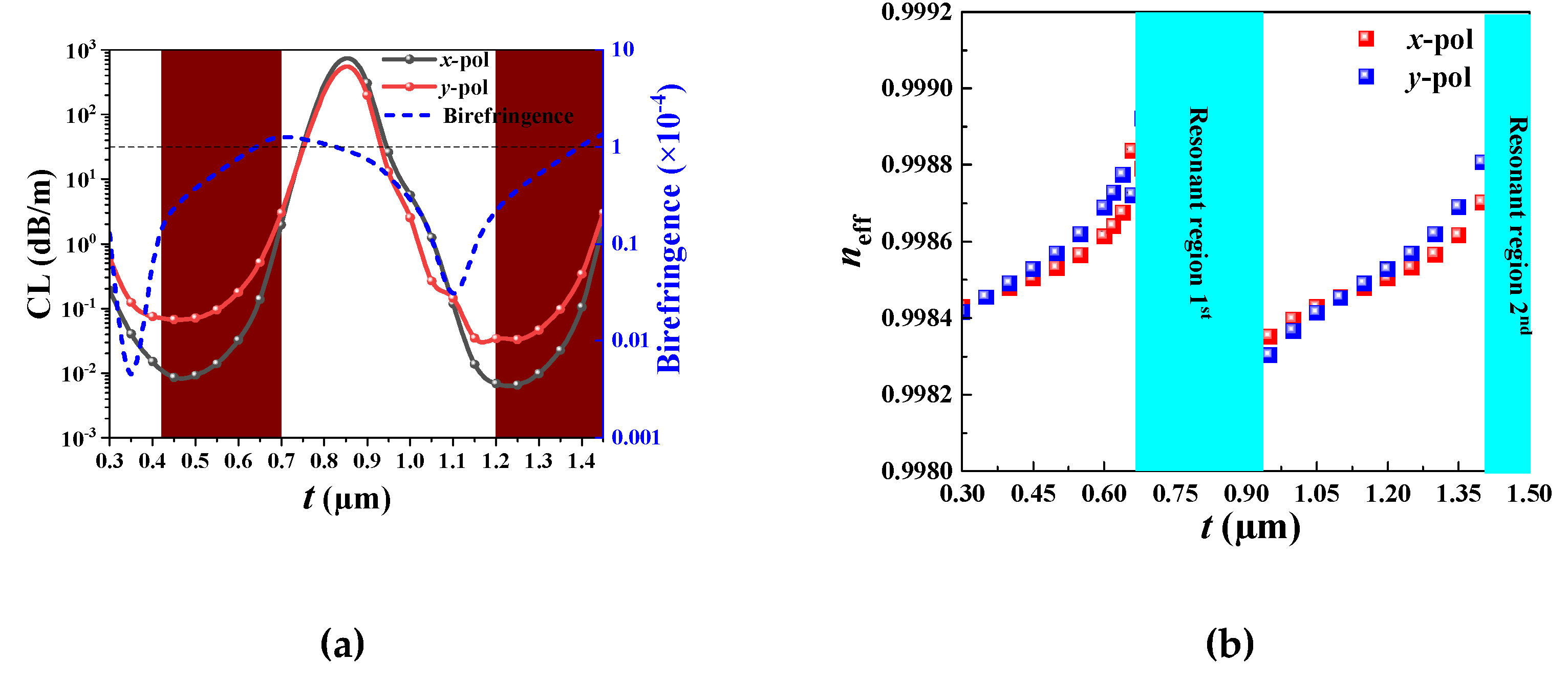
Figure 4.
(a) The effect of t on the CL and birefringence, and (b) the effect of t on the effective refractive index and birefringence.
Figure 4.
(a) The effect of t on the CL and birefringence, and (b) the effect of t on the effective refractive index and birefringence.
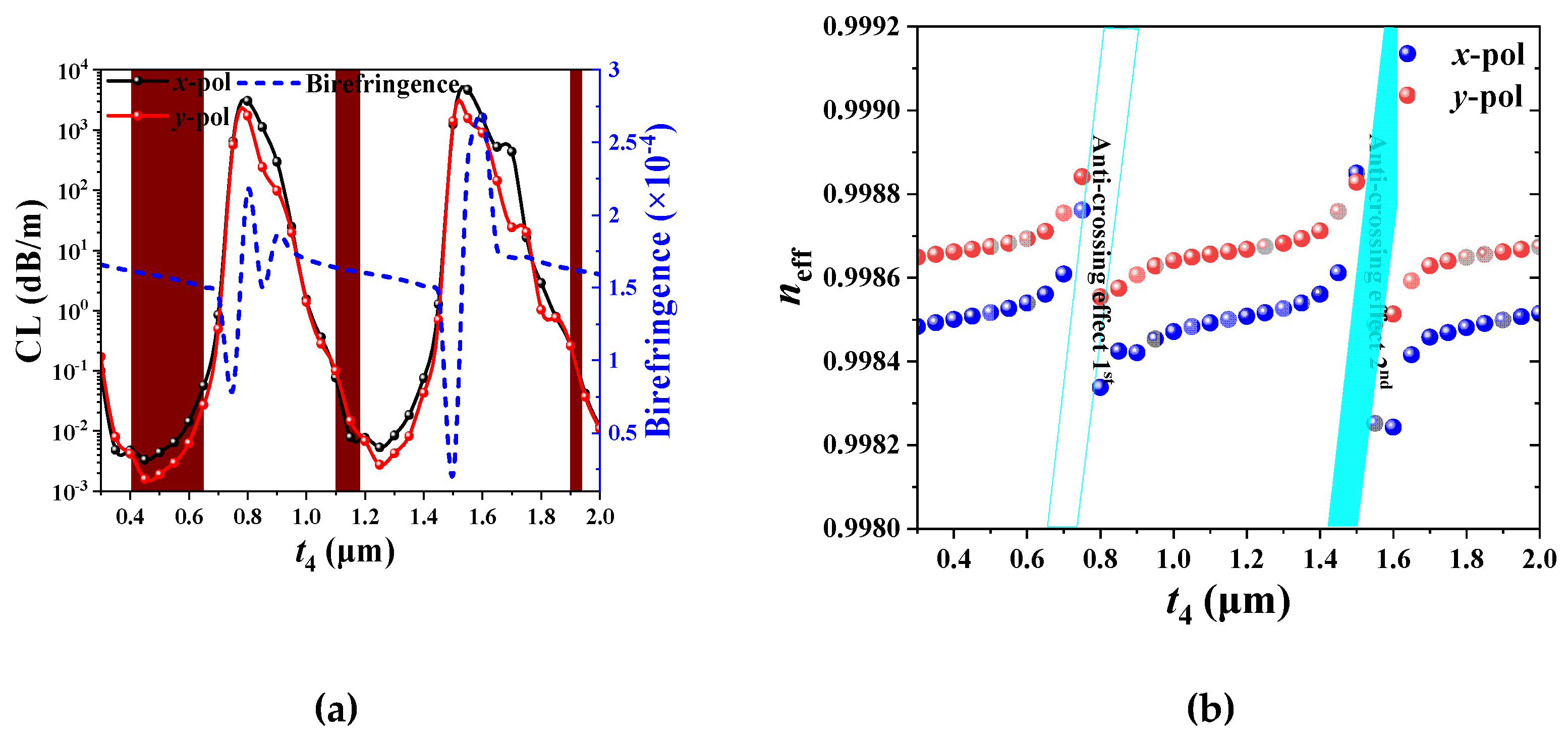
Figure 5.
(a) The effect of t4 on the CL and birefringence, and (b) the effect of t4 on the effective refractive index and birefringence.
Figure 5.
(a) The effect of t4 on the CL and birefringence, and (b) the effect of t4 on the effective refractive index and birefringence.
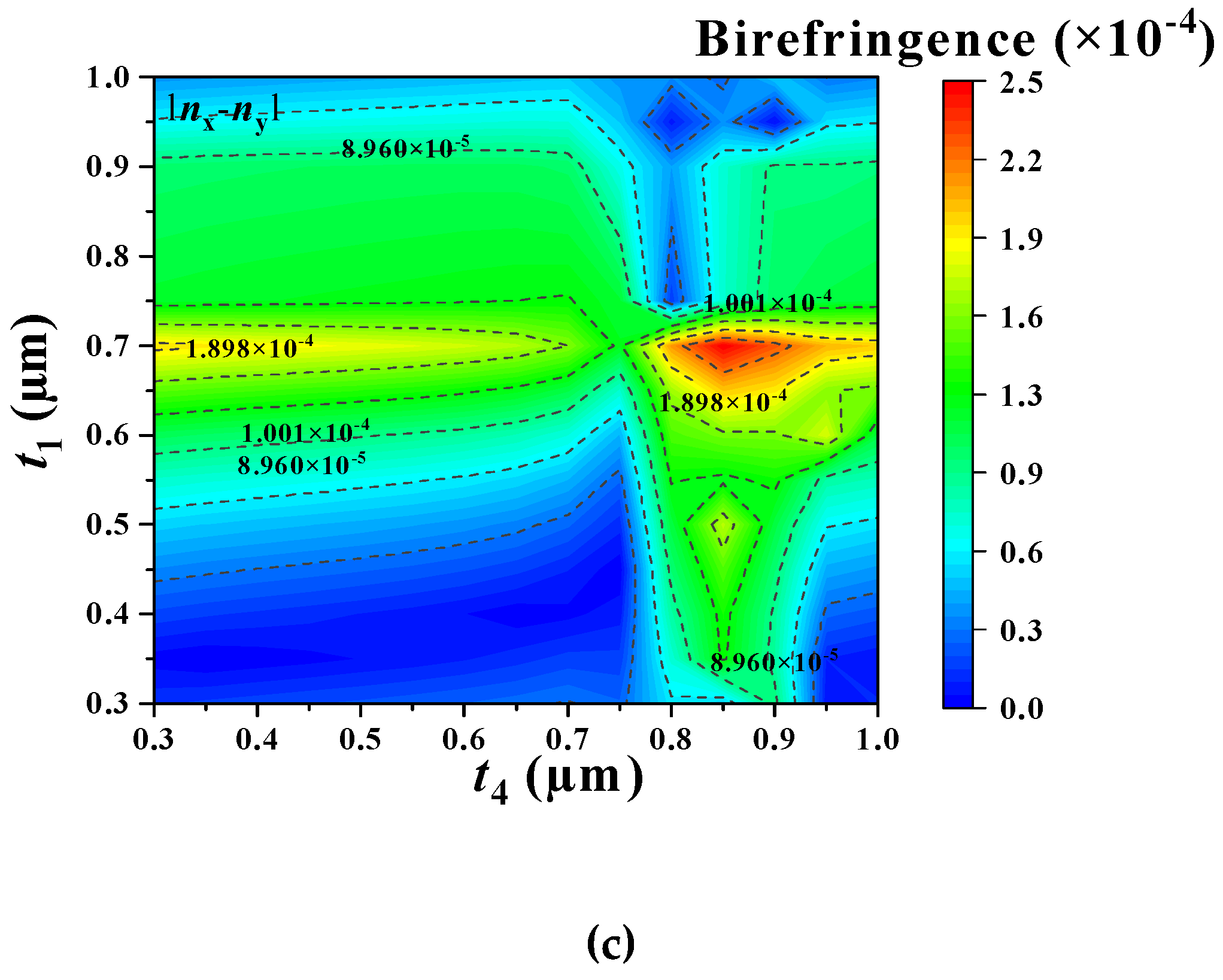
Figure 6.
(a) The x-pol fundamental mode CL and (b) y-pol fundamental mode CL as functions of and , and (c) the birefringence as a function of and at wavelength 1.55 μm.
Figure 6.
(a) The x-pol fundamental mode CL and (b) y-pol fundamental mode CL as functions of and , and (c) the birefringence as a function of and at wavelength 1.55 μm.
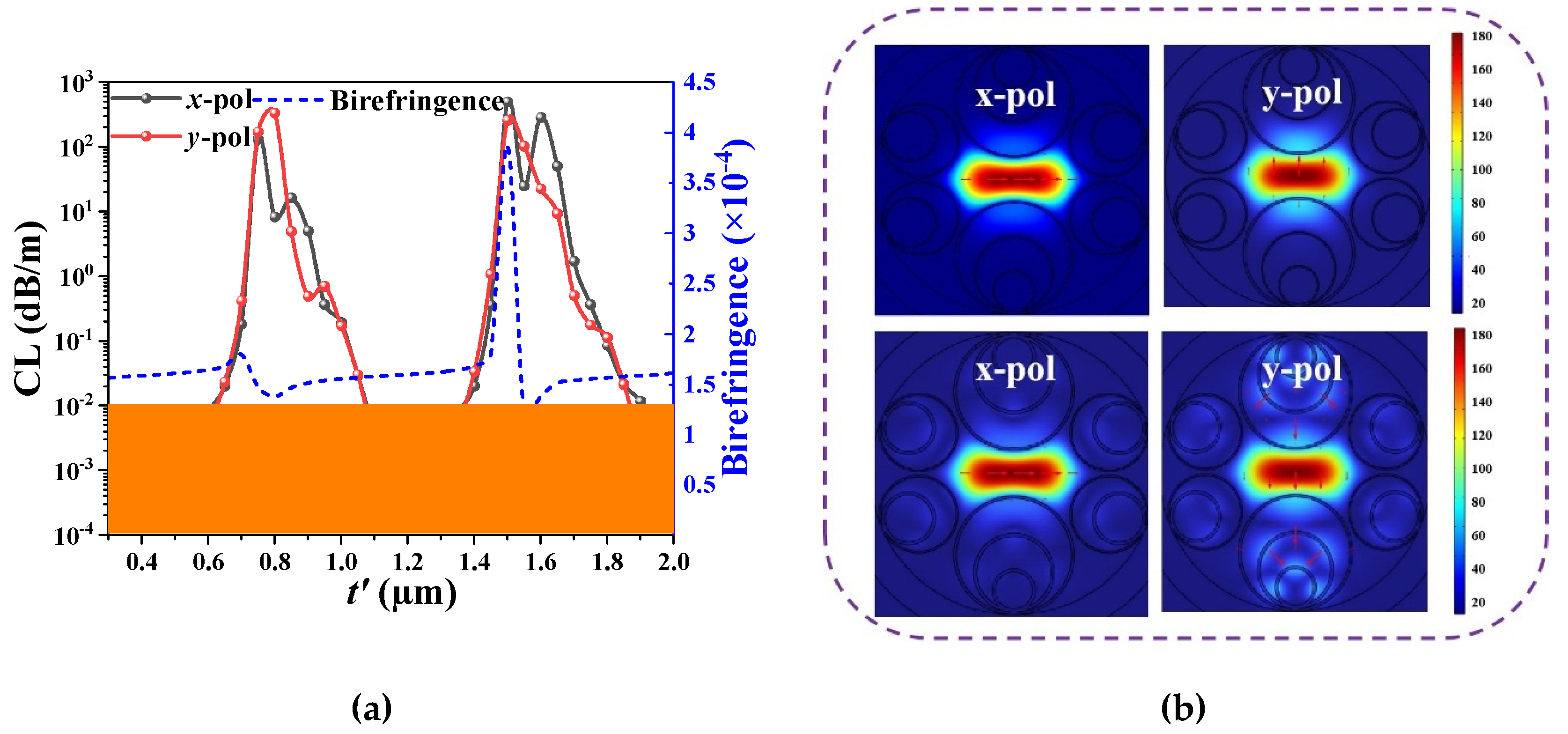
Figure 7.
(a) The effect of t′ on the CL and birefringence, and (b) the electric field distributions of the x-pol and y-pol fundamental modes calculated at wavelength 1.55 μm, along with t′=0.45 μm and t′=0.75 μm.
Figure 7.
(a) The effect of t′ on the CL and birefringence, and (b) the electric field distributions of the x-pol and y-pol fundamental modes calculated at wavelength 1.55 μm, along with t′=0.45 μm and t′=0.75 μm.
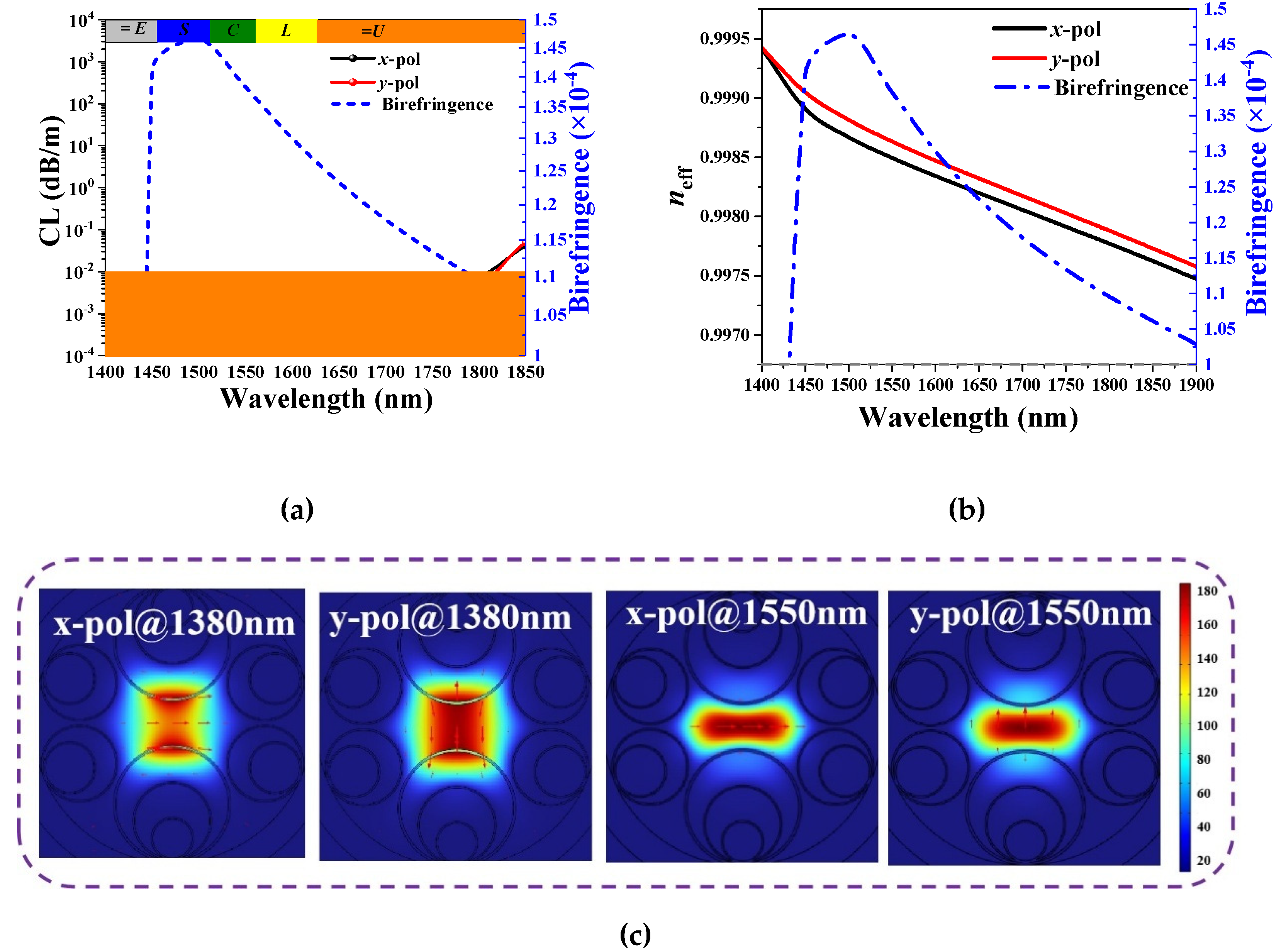
Figure 8.
(a) The x-pol and y-pol fundamental mode CLs as functions of wavelength, (b) the effective refractive indices of the x-pol and y-pol fundamental modes, and birefringence as functions of wavelength, and (c) the electrical field distributions of the x-pol and y-pol fundamental modes calculated at wavelengths 1380 nm and 1550nm.
Figure 8.
(a) The x-pol and y-pol fundamental mode CLs as functions of wavelength, (b) the effective refractive indices of the x-pol and y-pol fundamental modes, and birefringence as functions of wavelength, and (c) the electrical field distributions of the x-pol and y-pol fundamental modes calculated at wavelengths 1380 nm and 1550nm.
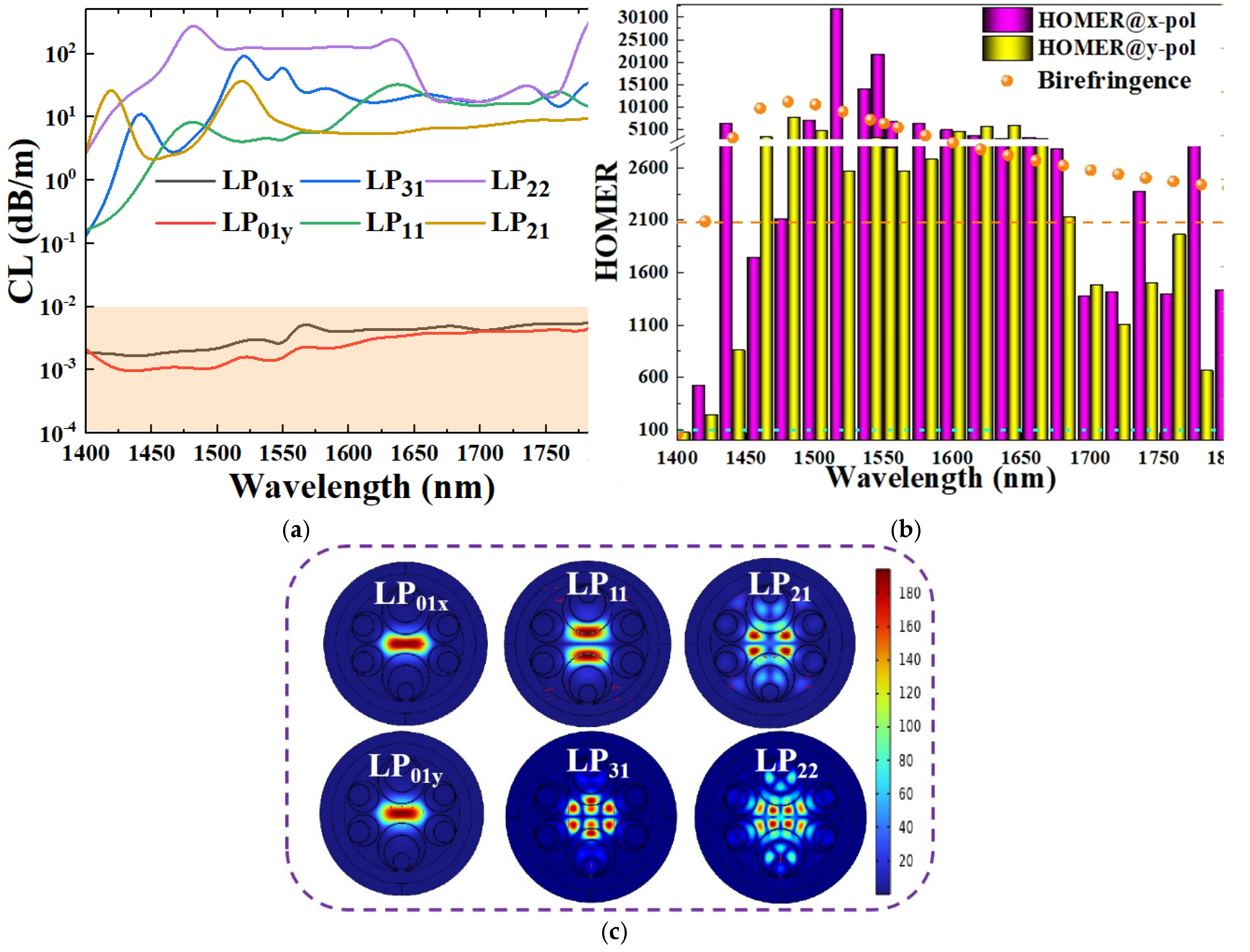
Figure 9.
(a) The CLs of the FM and the HOMs (LP11, LP21, LP31, LP22), (b) the corresponding HOMER and birefringence, and (c) the mode field distributions of the FM and HOMs.
Figure 9.
(a) The CLs of the FM and the HOMs (LP11, LP21, LP31, LP22), (b) the corresponding HOMER and birefringence, and (c) the mode field distributions of the FM and HOMs.
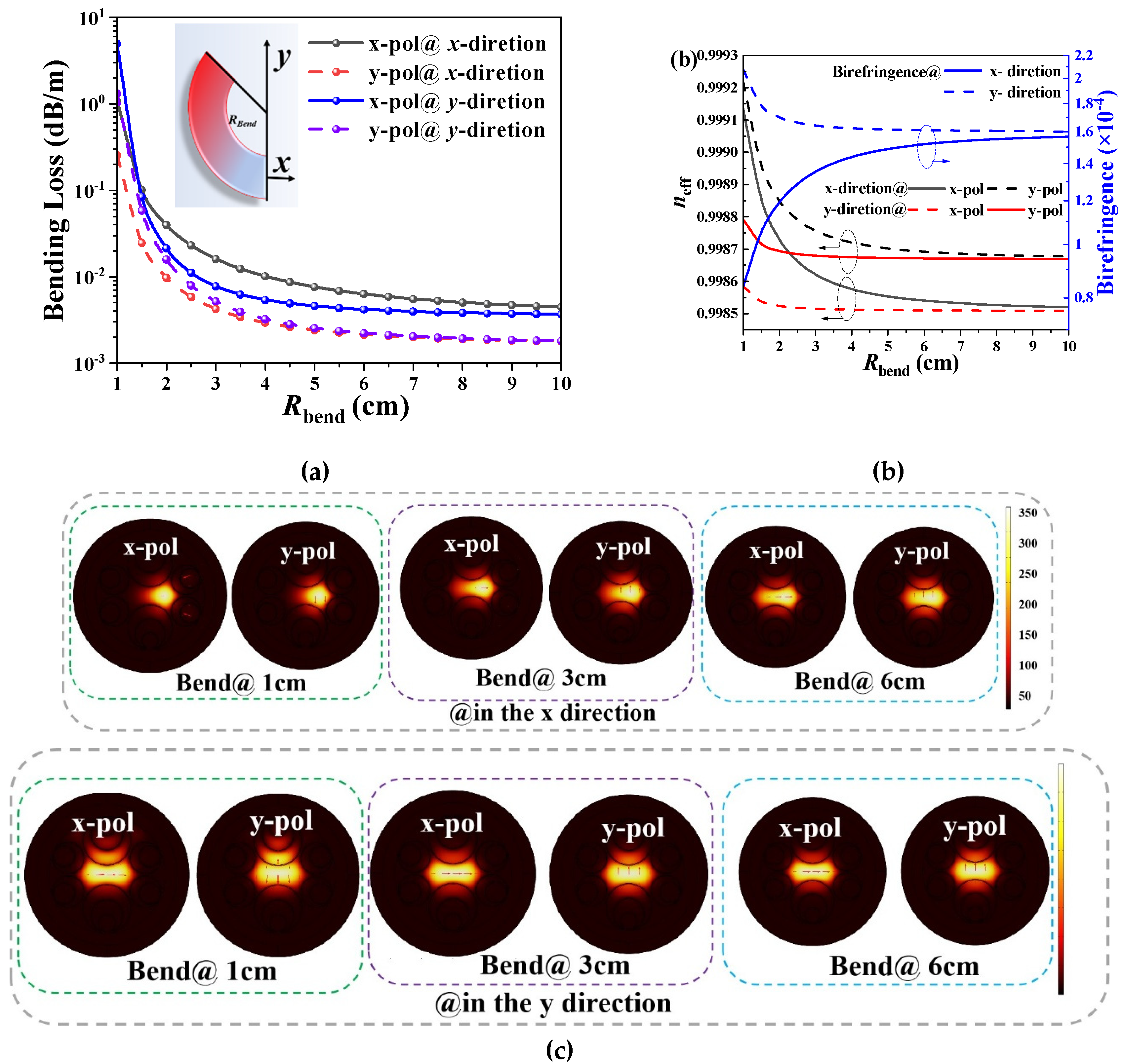
Figure 10.
(a) and (b) The impact of bending radius on various parameters, and (c) mode diagrams with bending of 1 cm and 3 cm, respectively, in the x-direction and 6 cm in the y-direction. ( =74.25μm, =15.6 μm, =10.4 μm, =5.62 μm, =10.2 μm, =6.93 μm, 0.45μm, and =0.67 μm.).
Figure 10.
(a) and (b) The impact of bending radius on various parameters, and (c) mode diagrams with bending of 1 cm and 3 cm, respectively, in the x-direction and 6 cm in the y-direction. ( =74.25μm, =15.6 μm, =10.4 μm, =5.62 μm, =10.2 μm, =6.93 μm, 0.45μm, and =0.67 μm.).
Table 1.
Comparison of the performances of the designed PM-HC-ARF with other reported results.
Table 1.
Comparison of the performances of the designed PM-HC-ARF with other reported results.
| Ref. |
CL |
Birefringence |
Bandwidth |
Bending
resistance |
HOMER |
| [37] |
185.0 dB/km @1.589μm |
9.1 × 10-5
|
133nm |
>10cm |
No report |
| [38] |
30dB/km @1.55μm; |
>1×10-4
|
460nm(<103dB/km) |
>4cm |
No report |
| [39] |
460dB/km @1.55μm |
>2.5×10-5
|
150nm |
------ |
No report |
| [40] |
4.8 dB/km@ 1.522μm |
>1.8×10-5
|
154nm |
>25cm |
No report |
| [41] |
8.5dB/km@1.06μm;
204.1dB/km@1.55μm |
3.62×10-5;
9.83×10-5
|
172nm;
216nm |
>10cm |
No report |
| This work |
1.5dB/km@1.55μm;
0.82dB/km@1.45μm
|
>1.45×10-4 |
>1.05×10-4, ~380nm
|
>3cm
(4.25 dB/km)
|
32,070
(>241)
|