DEMNet: Dual-Encoder-Decoder Multi-Frame Infrared Small Target Detection Network with Motion Encoding

1. Introduction

Infrared thermal imaging systems passively receive infrared radiation from scenes, offering advantages such as good concealment, high angular resolution, and strong anti-interference capabilities. Unlike visible light imaging systems, infrared systems can operate in all weather conditions, making them widely used in fields such as maritime rescue, military reconnaissance, and missile guidance. Among its related technologies, infrared small target detection has attracted widespread attention due to its ability to accurately locate targets of interest within an image. However, infrared targets are typically small in size, lack well-defined texture, possess limited shape and contour information, and are often embedded in low signal-to-noise ratio (SNR) environments. These challenges make it difficult to distinguish such targets from background clutter and noise, significantly complicating the detection task.

1.1. Related Works

1.1.1. Single-Frame Methods

Early methods for infrared small target detection were based on the assumption that the background of the image remained static or exhibited only minor variations, with background pixels showing strong correlation and similarity. Under this assumption, filter-based techniques were widely adopted [1]. However, the presence of prominent edges in the background can disrupt this correlation. To address such issues, some researchers proposed transforming the image from the spatial domain to various transform domains [2], such as the Fourier transform and gradient vector fields.

With the rise of saliency detection techniques in computer vision, infrared small target detection methods inspired by the human visual attention mechanism have also emerged. In 2012, Shao et al. proposed an approach based on the contrast mechanism of the human visual system (HVS), where a Laplacian of Gaussian (LoG) filter was used to suppress noise and enhance target intensity, thereby improving detection performance [3]. Also in 2012, Qi et al. introduced a saliency-based region detection method incorporating attention mechanisms to detect small infrared targets in complex backgrounds [4]. In 2013, Gao et al. developed an adaptive infrared patch-image model constructed from local patches, which was used to segment targets and suppress various types of clutter interference [5].

In addition, in 2013, Chen et al. proposed an algorithm based on the contrast mechanism of the HVS and a derived kernel model, in which local contrast and adaptive thresholding were employed to segment targets [6]. In 2014, Han et al. introduced a thresholding and rapid traversal method based on the attention shift mechanism of the HVS for fast target acquisition [7]. In 2018, Zhang et al. calculated a local intensity and gradient (LIG) map from the original infrared image to enhance targets while suppressing clutter [8]. In the same year, Moradia et al. modeled point targets using multi-scale average absolute gray difference (AAGD) and a Laplacian of point spread function (LoPSF) to reduce false alarm rates [9]. Although these methods significantly improve detection performance, they still struggle to handle complex and dynamically changing background scenarios.

In recent years, deep learning methods have been widely applied to various visual tasks. Dai et al. proposed asymmetric context modulation (ACM), which integrates high-level semantic information and low-level positional details through a comprehensive top-down and bottom-up attention modulation pathway [10]. In their subsequent work, they introduced the attention local contrast network (ALCNet), which refines features based on the idea of local contrast, particularly targeting small targets [11]. Furthermore, the internal attention-aware network (IAANet) first adopts a the region proposal network (RPN) to generate coarse target regions, and then pixel-level self-attention computation is applied to these proposed regions to obtain attention-aware features [12]. Wu et al. designed UIUNet, in which micro-UNet modules are embedded within a UNet architecture to learn multi-level and multi-scale features of infrared images [13]. The dense nested attention network (DNANet) extracts spatial features at multiple scales through a feature pyramid structure and effectively fuses them via densely connected skip pathways, achieving outstanding detection performance [14]. Liu et al. incorporated the Transformer architecture into infrared small target detection, yielding promising results [15]. He et al. employed discrete wavelet transform (DWT) and inverse DWT (IDWT) to extract and fuse frequency-domain and spatial-domain features, enhancing detection accuracy on public datasets [16]. Liu et al. also proposed MSHNet, a network capable of capturing multi-scale spatial location information. Combined with a novel scale and location sensitive loss function, their method achieved superior detection results [17].

To summarize, single-frame detection methods, whether model-driven traditional approaches or data-driven deep learning techniques, often fail to deliver satisfactory results in scenarios involving strong interfering targets or adverse imaging conditions characterized by low signal-to-noise ratios, heavy clutter, and significant noise. In such challenging environments, the detection of infrared small targets typically requires richer feature information for accurate identification. Therefore, multi-frame detection algorithms that are capable of capturing temporal contextual information are better suited for handling the aforementioned complex scenarios

1.1.2. Multi-Frame Methods

In the early stages, traditional multi-frame infrared small target detection algorithms primarily relied on target motion characteristics [18] or differences between adjacent frames to facilitate detection [19]. Subsequently, some methods attempted to extend single-frame detection algorithms into the multi-frame domain, achieving notable improvements. For example, the spatio-temporal local contrast filter (STLCF) [20] and the spatio-temporal local difference measure (STLDM) [21] expanded 2D operators into 3D spatio-temporal operators to compute information across the current and historical frames. These outputs were then fused with temporal saliency features to extract target locations. In 2021, the multi-subspace learning and spatio-temporal patch tensor model (MSLSTIPT) was proposed [22], which similarly extends 2D spatial low-rank decomposition into the 3D spatio-temporal domain for small target detection in multi-frame infrared image sequences. In more recent studies, Wu et al. proposed a 4-D tensor model that processes a sequence of infrared images and utilizes tensor train and its extension, tensor ring, to decompose them into 4-D tensors [23]. Li et al. introduced a twist tensor model based on sparse regularization, which enhances the contrast between targets and background for more effective small target detection [24].However, such approaches often rely heavily on scene-specific prior knowledge and make relatively narrow assumptions about the target types, leading to limited robustness. As a result, detection performance tends to degrade significantly when there are scene changes or variations in target characteristics.

In recent years, with the continuous advancement of deep learning algorithms and the release of infrared sequence image datasets [25,26], deep learning-based multi-frame infrared small target detection methods have gradually become mainstream. The earliest approaches simply extended single-frame detection methods to sequential images by applying single-frame detection to each frame independently [27,28]. Although this strategy enabled processing of consecutive frames, it failed to leverage temporal contextual information and could not fully exploit the advantages of multi-frame analysis. Subsequent research explored the use of motion cues from preceding and succeeding frames to perform super-resolution enhancement on the current frame, thereby improving the detail and visibility of dim infrared targets [29,30]. While this technique can enhance detection performance, it typically results in significant computational overhead due to the resolution upscaling process, which poses challenges for real-time applications. Later, Wang et al. proposed a network incorporating a spatio-temporal multi-scale feature extractor module, which captures multi-scale spatial information across frames in the temporal dimension. This approach significantly improved detection accuracy and fully exploited the advantages of multi-frame detection [31]. As a result, most subsequent studies have adopted similar strategies.

In 2023, Li et al. proposed an effective direction-coded temporal U-shape module in multi-frame detection [26]. In 2024, Chen et al. extended the use of ConvLSTM-based cross-spatiotemporal slice node feature processing to the field of infrared small target detection [32]. Duan et al. introduced frequency information by applying Fourier and inverse Fourier transforms to infrared images, achieving excellent detection performance [33]. Ying et al. enhanced target features by emphasizing specific frequency-domain components and incorporated a feature recurrence framework, yielding promising results on a self-constructed satellite dataset [34]. In 2025, Liu et al. proposed a long-term optical flow-based motion pattern extractor module that improves upon traditional optical flow methods by leveraging motion information for target detection [35]. Peng et al. adapted a dual-branch parallel feature extraction approach from the video domain to infrared small target detection, where one branch extracts global features while the other focuses on key frame features; the fusion of these features achieved competitive performance with low computational cost [36]. Zhu et al. incorporated a Transformer-based attention mechanism to encode and fuse spatiotemporal and channel-wise features for target detection [37]. Zhang et al. utilized the consistent motion direction and strong inter-frame correlation of infrared small targets by designing a spatial saliency feature generation module, which was fused across the temporal dimension for final detection [38]. Similarly, Zhu et al. adopted a parallel dual-branch feature extraction strategy, where spatial features assist in enhancing temporal motion cues, and proposed a complementary symmetric weighting module to fuse spatiotemporal features, resulting in outstanding detection performance [39].

1.2. Motivation

When detecting dim infrared targets in complex environments, the low contrast between the target and the background often renders single-frame infrared small target detection algorithms ineffective, either missing the target or generating a large number of false alarms. In such scenarios, multi-frame infrared small target detection algorithms can leverage temporal contextual information by perceiving differences across consecutive frames, thereby achieving better detection performance. However, despite the improvements over single-frame methods, existing multi-frame detection approaches still suffer from several limitations:

(1) Although these methods adopt various spatiotemporal feature fusion strategies, most rely on implicit extraction via 3D convolutions or attention mechanisms, and they often overlook the motion consistency of the target. Li et al. [26] proposed an explicit encoding method that maps the target’s position within each frame to model its motion features. However, the motion encoding strategy is insufficiently developed and fails to capture the relative positional relationships of the target across frames, leaving substantial room for refinement in motion representation.

(2) Current methods usually integrate spatiotemporal feature extraction into one encode-decode architecture, which may impede the performance for the tight coupling of the spatial and temporal feature extraction process.

(3) The commonly used false alarm rate (Fa) metric presents limitations. Fa is defined as the ratio of non-target pixels incorrectly predicted as targets to the total number of pixels in the image, which fails to intuitively reflect the model’s ability to suppress target level false positive ratio. In practical applications, detection results are typically processed on a per-target basis rather than per-pixel.

This paper proposes a novel Dual-Encoder-decoder Multi-frame infrared small target detection Network with motion encoding, termed DEMNet. The proposed method first employs a Spatial Feature Extractor module, which uses an encoder-decoder structure to extract multi-scale spatial features from input images. Then, a motion information encoder-decoder module is used to map and reconstruct the motion characteristics of the target, thereby capturing rich temporal contextual information. A multi-stage decoder and prediction head are used to generate the target prediction map for the last frame. This process effectively enhances the representation of dim targets embedded in complex backgrounds.

The main contributions of this paper are summarized as follows:

(1) A dual encoder-decoder multi-frame infrared small target detection network, DEMNet, was proposed. The network integrates spatial and temporal contextual features, and employs end-to-end learning to enhance the representation of dim and small targets under complex backgrounds.

(2) Based on the motion consistency of infrared targets, a motion encoding strategy was introduced. It consists of inter-frame motion encoding and intra-frame location encoding to explicitly capture spatiotemporal motion characteristics and improve temporal feature utilization.

(3) A target level false alarm evaluation metric, FaT, was proposed to address the limitations of pixel-level metrics. FaT evaluates false alarms at the object level, providing a more intuitive and accurate assessment of the model's false alarm suppression ability in practical scenarios.

(4) Experimental results on the DAUB [25] and NUDT-MIRST [26] datasets demonstrate that the proposed DEMNet significantly outperforms existing state-of-the-art methods, particularly in detecting dim targets with low signal-to-noise ratios.

2. Methods

In this section, the implementation and application of DEMNet are presented. The main components of the proposed model are introduced in detail, including the design of the spatial feature extractor module and the motion information encoding. Furthermore, the specific implementation of the proposed algorithm on input image sequences is described.

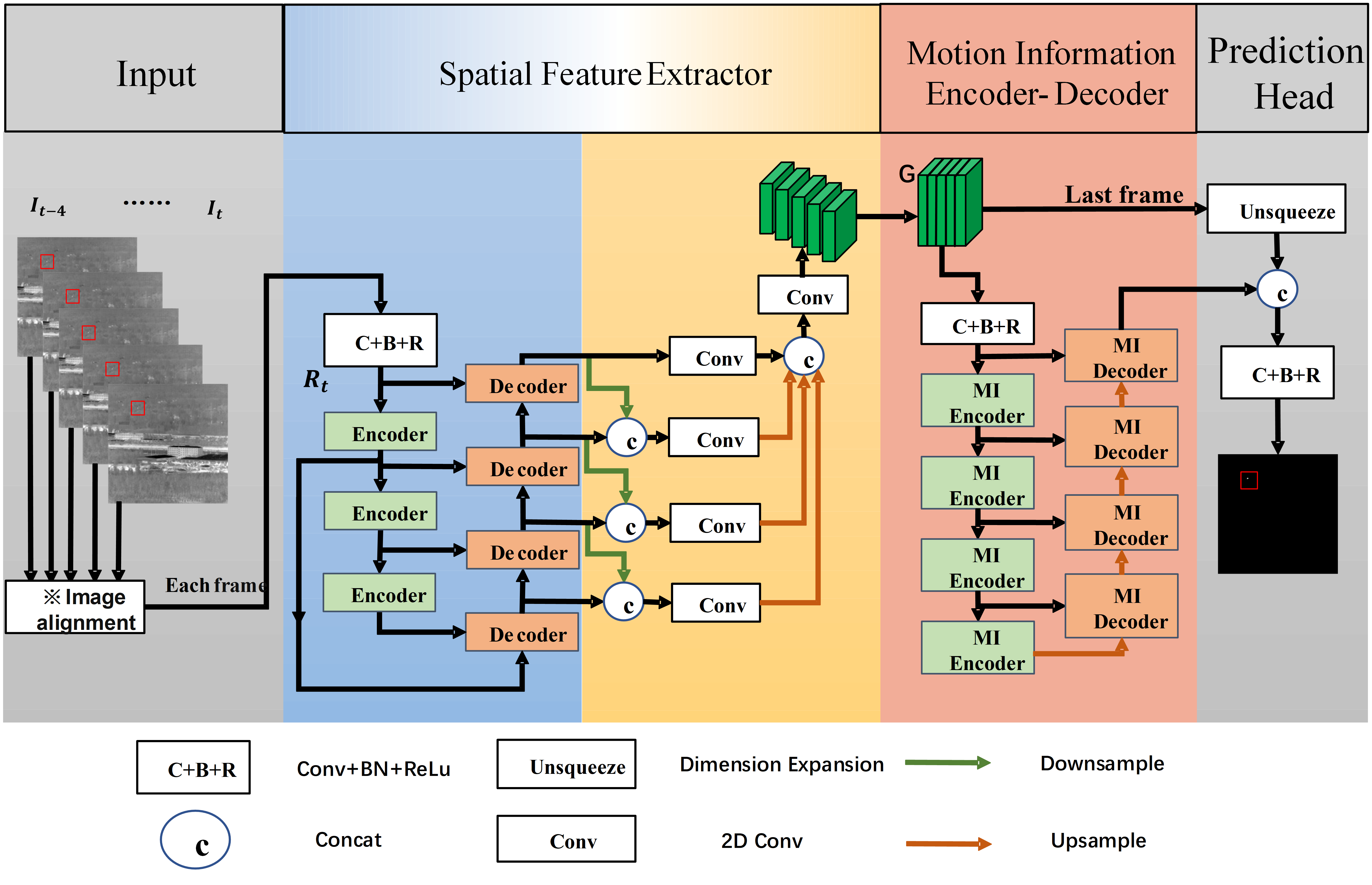
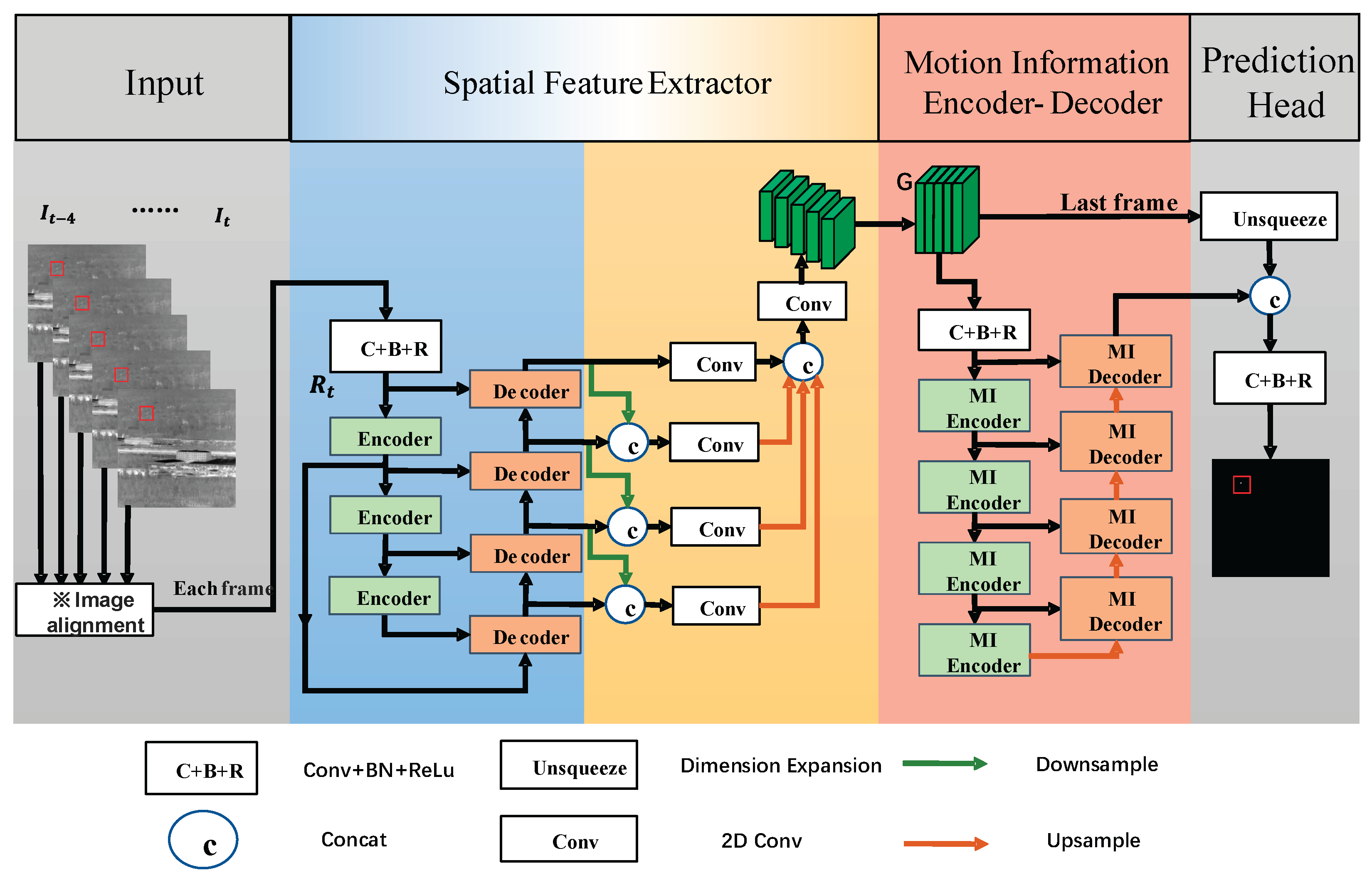
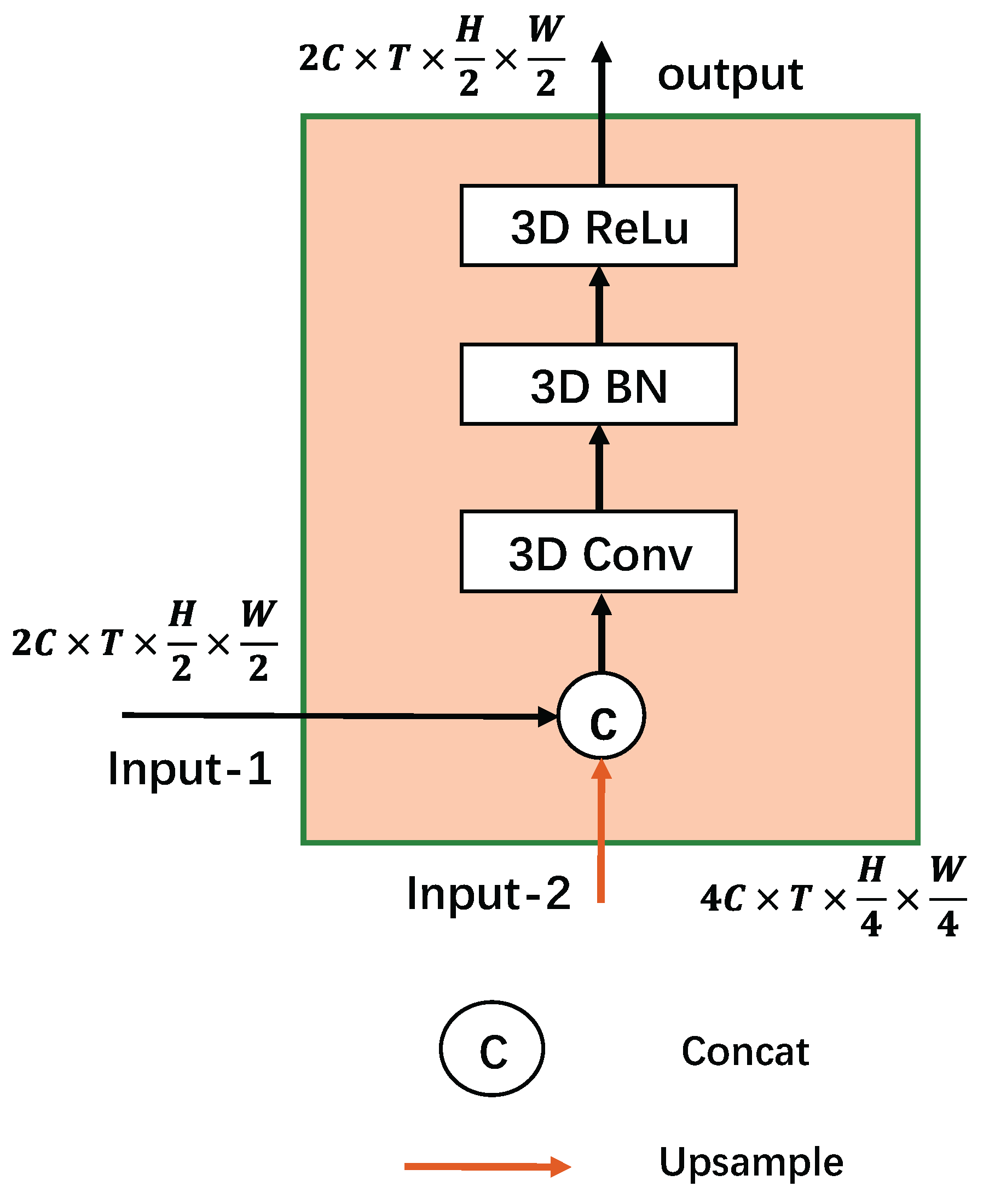
2.1. Overall Architecture

The overall architecture of DEMNet is illustrated in Figure 1. It consists of three major components: Spatial Feature Extractor, the motion information encoder-decoder structure, and a prediction head composed of convolution, normalization, and activation functions.

The input to the network is a sequence of consecutive infrared frames denoted as $I^{1\times T\times H\times W}$, where T denotes the length of the input sequence (5 frames are used in this work). Firstly, all previous frames in the input sequence are aligned with the last frame individually. The image alignment operation consists of four steps: detecting feature points, matching feature points, computing the homography matrix, and performing image transformation. Each aligned frame is sequentially fed into the Spatial Feature Extractor module. The resulting feature maps are then concatenated along the temporal dimension to produce a feature map $G^{C\times T\times H\times W}$.

Subsequently, $G^{C\times T\times H\times W}$ is passed into the multi-stage Motion Information Encoder (MI Encoder) to extract motion features across the multiple frames. These features are then progressively decoded through a multi-stage decoder, where they are fused with shallow features at each stage.

Finally, the output feature map from the highest-level decoder is concatenated with the last frame of $G^{C\times T\times H\times W}$, and this fused representation is passed through the prediction head to generate the final detection map of infrared small targets for the last frame.

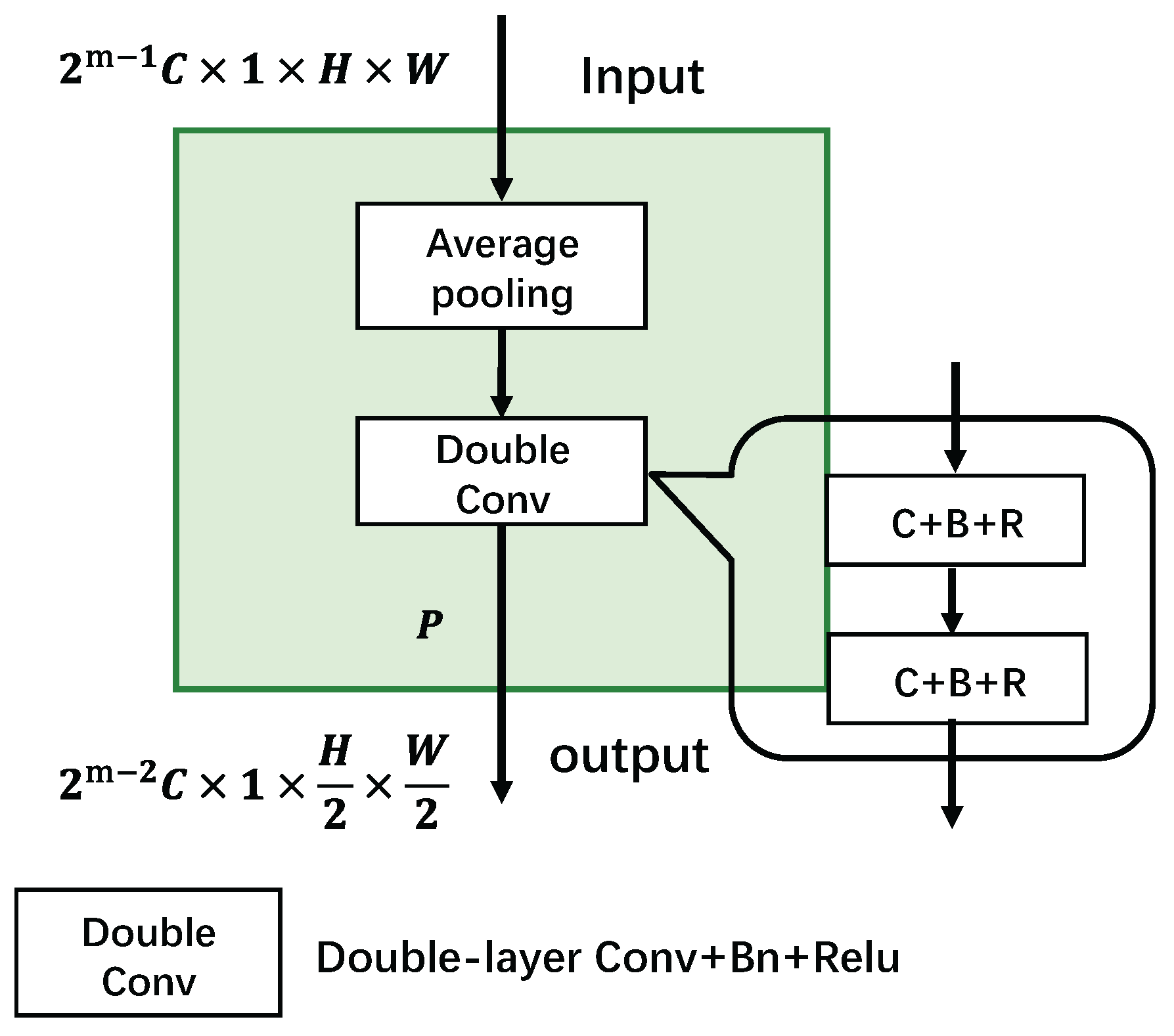
2.2. Spatial Feature Extractor

First, the input image sequence $I^{1\times T\times H\times W}$ is processed frame by frame through channel expansion to obtain T feature maps $R_t^{32\times 1\times H\times W}(t=1,\mathrm{2...}T)$. Each frame is then fed into multi-level encoders to extract feature maps that contain multi-scale spatial information. These features are subsequently passed through a multi-level decoder for feature fusion and decoding. Finally, the decoded features from all T frames are concatenated to form the output feature map $G^{C\times T\times H\times W}$.

2.2.1. Encoder

The encoder uses 2×2 average pooling to obtain the global low-frequency information of the feature map, and its structure is shown in Figure 2.

At the encoder at level m, the output feature map of the average pooling layer has a size of $2^{m-1}C\times 1\times {\displaystyle \frac{\mathrm{H}}{2^m}}\times {\displaystyle \frac{\mathrm{W}}{2^m}}$. It is subsequently processed by two convolutional layers, each convolution is followed with batch normalization and activation, resulting in a refined feature map P whose size is $2^{m-2}C\times 1\times {\displaystyle \frac{\mathrm{H}}{2^m}}\times {\displaystyle \frac{\mathrm{W}}{2^m}}$. This output is forwarded to the encoder at the next level and also to the decoder at level (m+1) for further processing. The final level of the encoder is slightly different, where the feature map P is only transmitted laterally, without being passed down to the next encoder level.

2.2.2. Decoder

The decoder employs channel attention and pixel attention mechanisms to highlight critical features. The output features from different decoding levels are resized and undergo complex top-down and bottom-up information propagation and fusion. Ultimately, a single-frame feature map enriched with multiscale spatial information is obtained, as illustrated in Figure 3.

The pixel attention and channel attention of the received feature maps $P$ and $F$ are calculated and cross multiplied to get the high-level semantic feature map output containing rich context information. The whole process is shown in Equation (1) - (8) as follows:

$$F_{up}=Upsample\left(F\right)$$

(1)

$$F_{mid-1}=AvgPooling\left(Conv\left(F_{up}\right)\right)$$

(2)

$$F_{mid-2}=Relu\left\{Bn\left[Conv\left(F_{mid-1}\right)\right]\right\}$$

(3)

$$F_{CA}=Sigmoid\left\{Bn\left[Conv\left(F_{mid-2}\right)\right]\right\}$$

(4)

$$P_{mid}=Relu\left\{Bn\left[Conv\left(P\right)\right]\right\}$$

(5)

$$P_{PA}=Sigmoid\left\{Bn\left[Conv\left(P_{mid}\right)\right]\right\}$$

(6)

$$G_{mix}=Relu\left\{Bn\left[Conv\left(F_{conv}\ast P_{PA}+P\ast F_{CA}\right)\right]\right\}$$

(7)

$$Output=DoubleConv\left(G_{mix}\right)$$

(8)

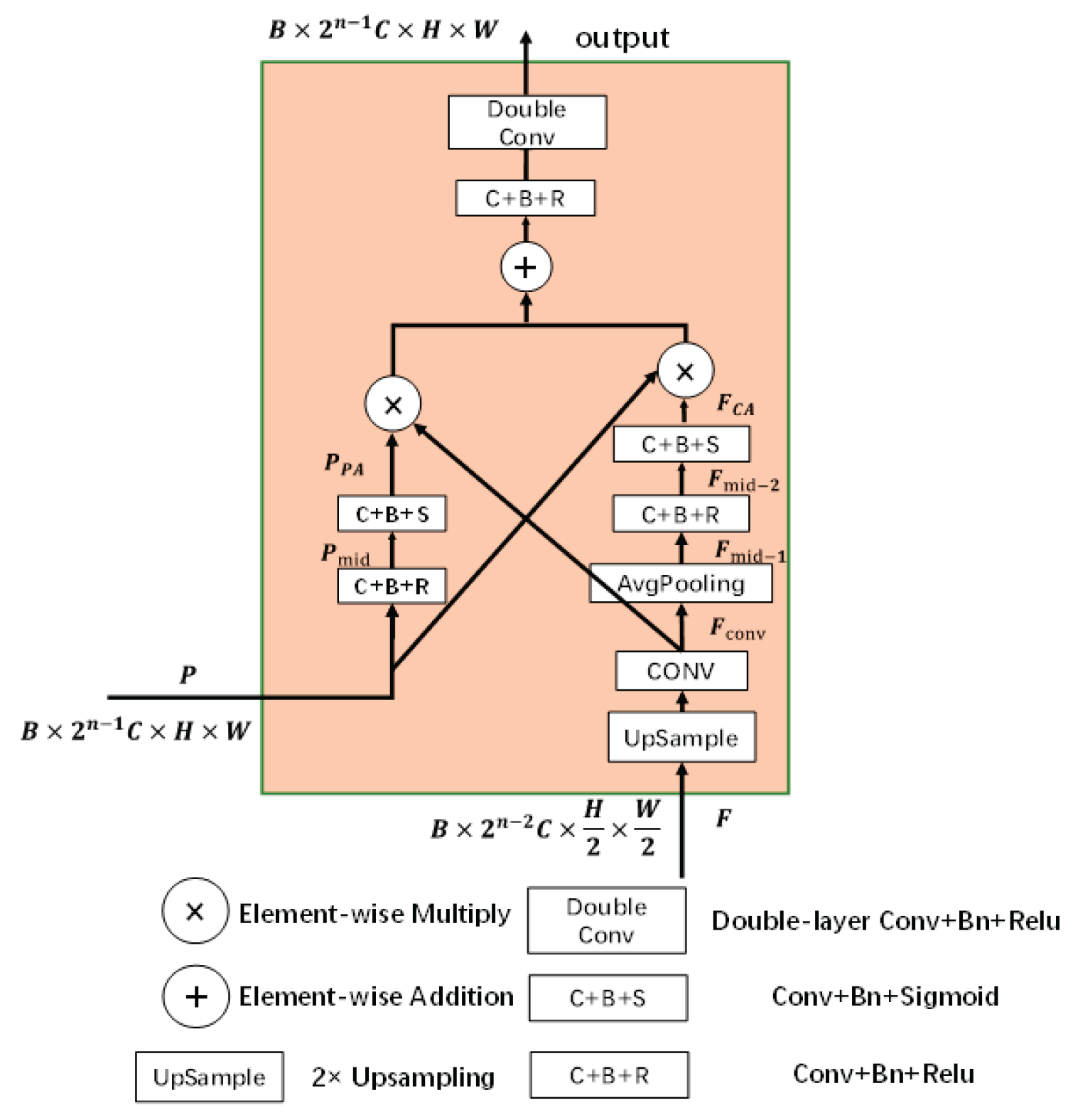
2.3. Motion Information Encoder

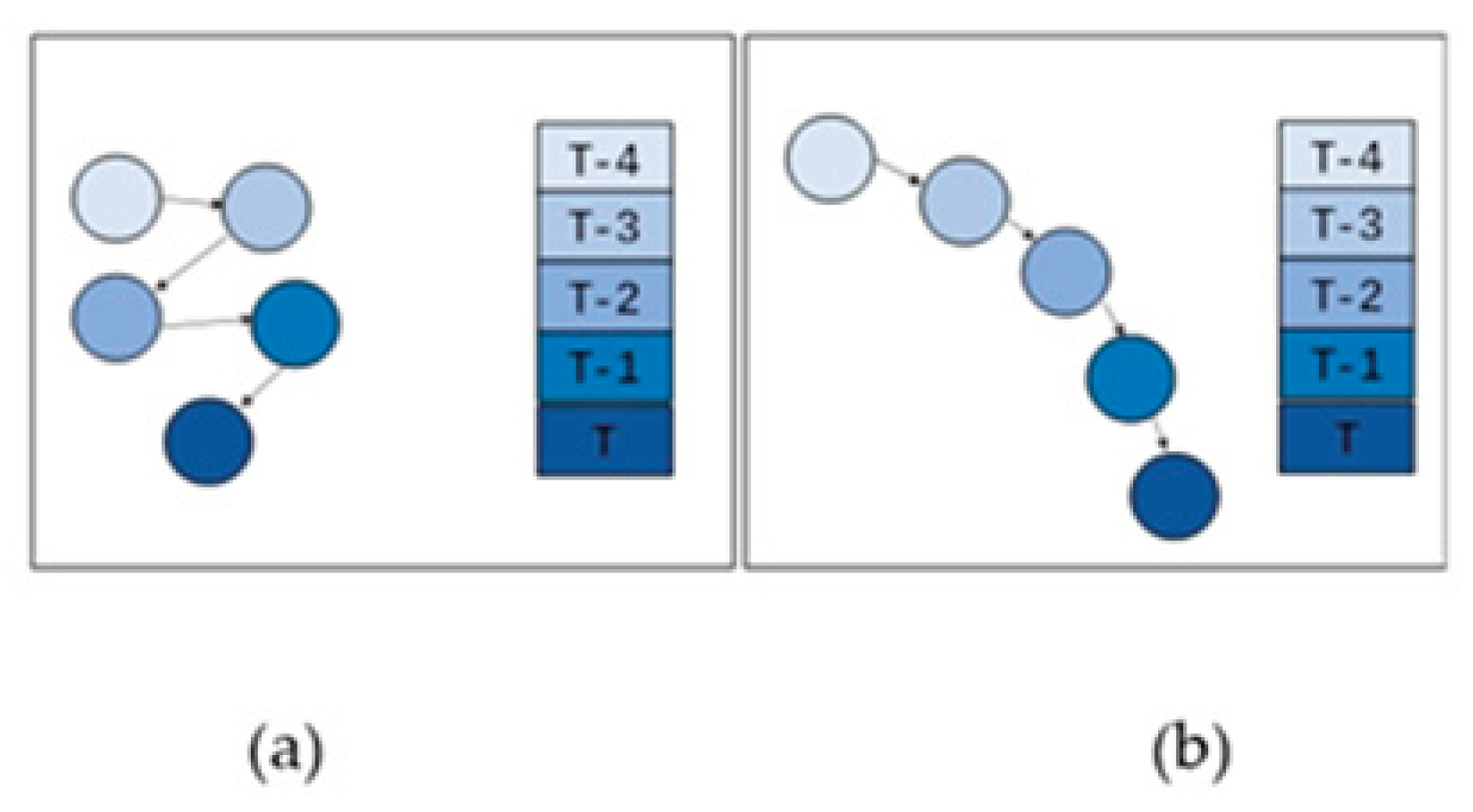
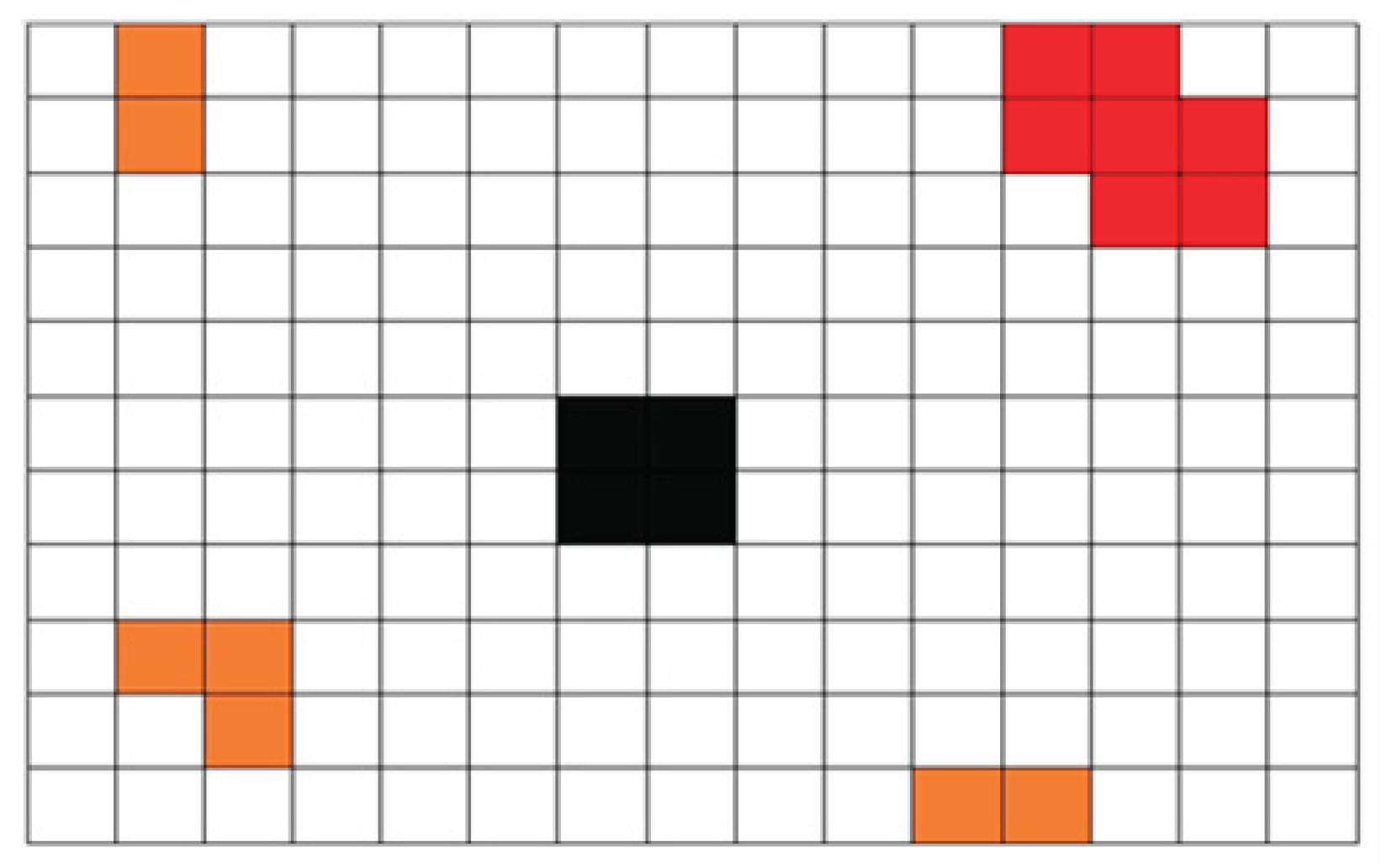
2.3.1. Inter-Frame Motion Encoding Module

Based on the assumption of motion consistency of targets, an inter-frame motion encoding module and an intra-frame position encoding module are proposed. On this basis, a motion information encoder (MI Encoder) is constructed. The feature maps obtained from the spatial feature extractor are concatenated along the temporal dimension and fed into the MI Encoder. This encoder module comprises the inter-frame motion encoding module, intra-frame positional encoding module, as well as 3D maxpooling layer, 3D convolutional layers, batch normalization (BN) layer, and ReLU activation layer. It effectively encodes the motion information of the target and fuses it with multiscale spatial features, yielding feature maps that contain both motion and spatial information of the target, as illustrated in Figure 4.

The inter-frame motion encoding module encodes the directional relationship of the maximum value in each 2×2 pooling region of past frames relative to the current frame, capturing the target’s motion characteristics through variations in directional relationships. As illustrated in Figure 6, in a sequence of consecutive frames, it is assumed that both targets and clutter appear as the brightest regions within their local neighborhoods. However, the motion patterns of targets and clutter differ significantly. Typically, targets move along specific, regular trajectories, while clutter tends to move randomly. Let $V_{p_{i\to t}}$ denotes the directional mapping between the maximum pixel in each pooling region of the past frame $F_{t-i}$ and the corresponding position in the current frame $F_t$. The average of the mapping values across all past frames is defined as P, as expressed in Equation (9):

$$P={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^{t-1}{V}_{p_{i\to t}}}{t}}$$

(9)

where $V_{p_{i\to t}}$ is determined by the horizontal positional mapping $x_{i\to t}$ and the vertical positional mapping $y_{i\to t}$. $x_{i\to t}$ and $y_{i\to t}$ are derived based on the relative directional relationship between the location of the maximum pixel in the pooling region of the past frame and its corresponding position in the current frame. If the maximum pixel in the past frame is located to the left or above its position in the current frame, $x_{i\to t}$ and $y_{i\to t}$ are set to 1, respectively. If the horizontal or vertical position remains unchanged, the values are set to 0. If the direction is to the right or below, $x_{i\to t}$ and $y_{i\to t}$ are set to -1, respectively. The definition of $V_{p_{i\to t}}$ is then given in Equation (10):

$$V_{p_{i\to t}}=\left\{\begin{array}{cc}\sqrt{x_{i\to t}+\alpha \ast y_{i\to t}}& (x_{i\to t}+\alpha \ast y_{i\to t})\ge 0\\ -\sqrt{\left|x_{i\to t}+\alpha \ast y_{i\to t}\right|}& (x_{i\to t}+\alpha \ast y_{i\to t})<0\end{array}\right.$$

(10)

$V_{p_{i\to t}}$ has the following properties:

Figure 5. Motion characteristics of clutter and targets: (a)clutter; (b) target.

Figure 5. Motion characteristics of clutter and targets: (a)clutter; (b) target.

1) When the position of the maximum pixel within the pooling region remains in the same direction across frames, the sign remains unchanged; when the direction changes, the sign is reversed.

2) By setting α=0.8, it ensures that the mapping values are unique under all nine possible directional relationships between the positions of the maximum pixel in the past and current frames.

3) A square root operation is applied to $V_{p_{i\to t}}$ to avoid conflicts where the summation of $V_{p_{i\to t}}$ are the same across different previous frames, but the motion trajectories differ. For example, in one pooling region, the directional encoding for two previous frames may both be 1. In another region, the encodings for the same two frames may be 0 and 2, respectively. So without the square root operation, the summation cannot differ different motion trajectories.

The specific computation process of $V_{p_{i\to t}}$ is shown in the pseudo code of Algorithm 1.

Algorithm 1: Inter-Frame Motion Encoding

Input: Feature map F Output: Mapping value vector V

1.(F_pool,index)=3DMaxpooling(F) 2: index_x(i)=index(i)%W  // index_x $\in$ [0,W) 3. index_y(i)=index(i)//W  // index_y $\in$ [0,H) 4. for i in range(T-1):  if index_x(i)< index_x(t): $x_{i\to t}$ = -1  if index_x(i)= index_x(t): $x_{i\to t}$ = 0  if index_x(i)> index_x(t): $x_{i\to t}$ = 1 // Horizontal direction encoding 5.for i in range(T-1):  if index_y(i)< index_y (t): $y_{i\to t}$ = -1  if index_y (i)= index_y (t): $y_{i\to t}$ = 0  if index_y (i)> index_y (t): $y_{i\to t}$ = 1 // Vertical direction encoding 6. for i in range(T-1):      $\mathrm{v}\left(\mathrm{i}\right)=\left\{\begin{array}{cc}\sqrt{x_{i\to t}+\alpha \ast y_{i\to t}}& (x_{i\to t}+\alpha \ast y_{i\to t})\ge 0\\ -\sqrt{\left|x_{i\to t}+\alpha \ast y_{i\to t}\right|}& (x_{i\to t}+\alpha \ast y_{i\to t})<0\end{array}\right.$ // $\alpha =0.8$    V+= v(i) 7.V=V/(t-1) 8: return V

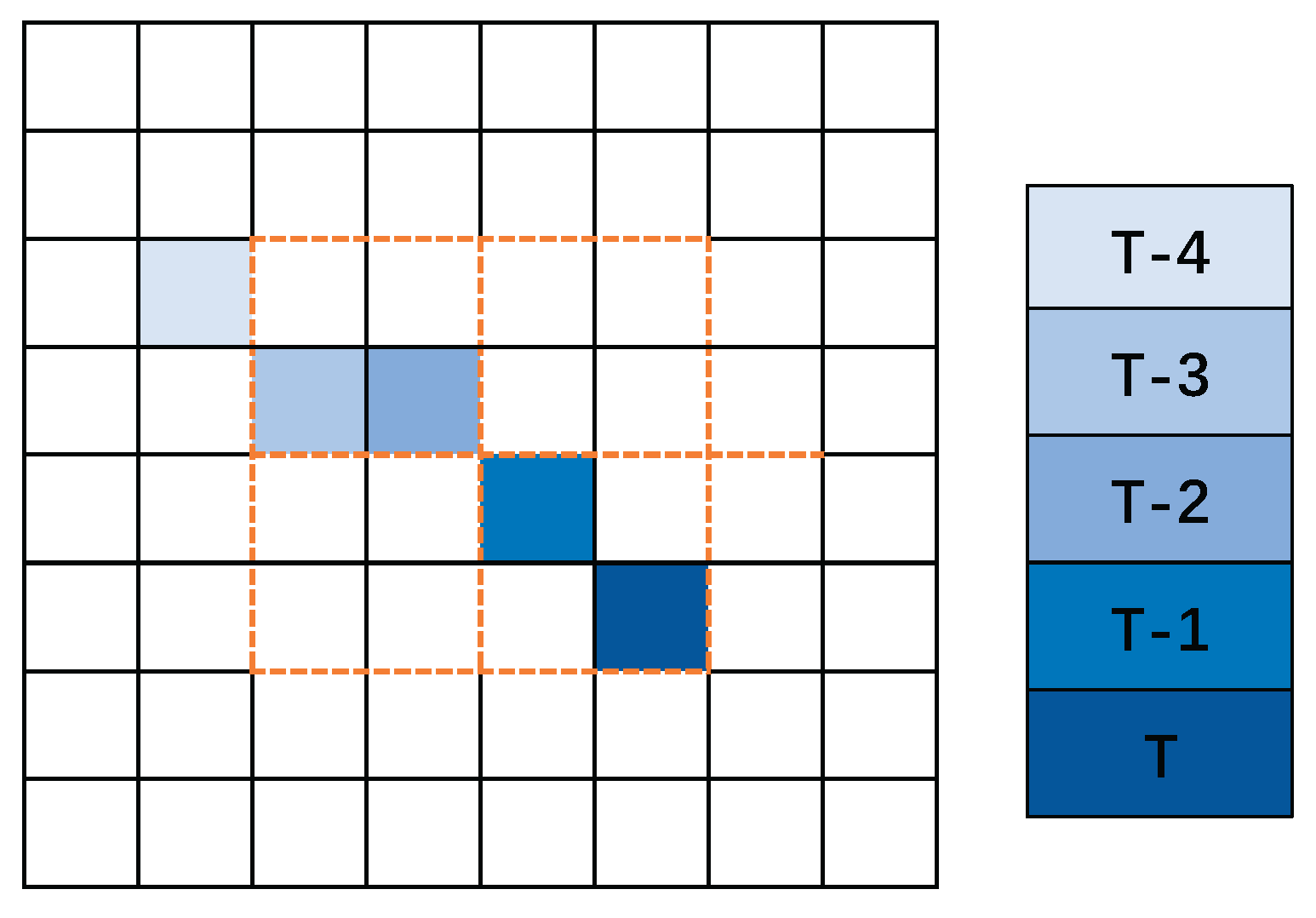
2.3.2. Intra-Frame Position Encoding

The intra-frame position encoding module encodes the position of the maximum value within each pooling regions of a single frame, capturing the motion characteristics of the target based on the positional patterns of maximum values across consecutive frames. As shown in Figure 6, for the four pooling regions within the 4×4 area enclosed by the red dashed box in the feature map, when a target passes through this window over several consecutive frames, both the maximum value and its location within each pooling region change in each frame. The variations in the maximum value and its index position caused by target motion exhibit more regular patterns, whereas those induced by clutter signals or background regions tend to be more random.

Figure 6. The process of the target crossing through four 2×2 pooling windows.

Figure 6. The process of the target crossing through four 2×2 pooling windows.

Therefore, by encoding the index positions of the maximum values during pooling in each frame, the model can perceive the intra-frame variations caused by target motion, distinguish them from the irregular patterns of clutter or background, and thus improve detection performance. Specifically, the encoding process of the intra-frame location information encoding module is presented in Algorithm 2.

Algorithm 2: Intra-Frame Position Encoding Module

Input: Feature map F Output: Mapping value vector D

1: (F_pool,index)=3DMaxpooling(F) 2: index_x(i)=index(i)%2   //The result is 0 or 1, which means on the left or right 3. index_y(i)=(index(i)//W)%2 // The result is 0 or 1, which means in the upper or lower area 4. for i in range(T):  D(i)=1.25+ ${\displaystyle \frac{\mathrm{index}\text{\_}\mathrm{x}\left(\mathrm{i}\right)+2\ast \mathrm{index}\_\mathrm{y}\left(\mathrm{i}\right)}{4}}$ // The codes of the four positions are $\left(\begin{array}{cc}1.25& 1.5\\ 1.75& 2.0\end{array}\right)$ 5: return D

2.4. Motion Information Decoder

The motion information decoder performs simple decoding on the received features, as shown in Figure 7.

In the decoder module, the decoder at level n receives deep features passed upward from the decoder at the lower level (the lowest-level decoder receives features from the corresponding encoder at the same level). After upsampling, these features are concatenated with the shallow features from the encoder at level n–1 along the channel dimension, followed by 3D convolution, BN, and a ReLU activation layer. The output is then passed to the upper-level decoder. The top-level decoder is slightly different in its 3D convolution module, the temporal padding is set to 0, and the output feature map has the shape $B\times C\times 1\times H\times \mathrm{W}$.

3. Experiments and Results

3.1. Dataset

The DAUB dataset [25] was created by B. Hui et al. from the National University of Defense Technology. It consists of 22 video sequences with a total of 16,177 frames, each with a resolution of 256×256 pixels and corresponding annotations. The dataset focuses on detecting fixed-wing UAV targets and includes various backgrounds such as sky and ground across diverse scenes. As a real-world dataset, its annotations include frame index, target index, and the target's center point. Following the work of Yuan et al. [40], binary mask labels were generated from the center point annotations. The training set and test set split follows the protocol provided at https://github.com/UESTC-nnLab/SSTNet.

However, in the test set, sequence 21 contains severe blind pixels, nearly no inter-frame motion of the target, and extremely dim targets, as illustrated in Figure 8, where the red box indicates the target and the blue box marks the blind pixel region. Therefore, this noisy sequence was excluded from evaluation.

The NUDT-MIRST dataset was developed by Li et al. from the National University of Defense Technology [26]. It was generated by embedding targets into real-world captured infrared images, followed by jitter and noise augmentation. The dataset consists of 100 sequences with a total of 10,000 frames, covering diverse scenarios including sky, ocean, and land. Designed to highlight the advantages of multi-frame detection methods under complex backgrounds, the dataset is split based on the signal-to-noise ratio between the target and its surrounding background. The images are categorized into two groups: SNR≤3 and 3<SNR<10. In the training set, the first 10 frames of each sequence are composed of images with SNR≤3, while the remaining 90 frames contain images with 3<SNR<10. The test set includes 8 sequences entirely consisting of images with SNR≤3 and 12 sequences entirely composed of images with 3<SNR<10. The training and testing split follows the protocol available at https://github.com/TinaLRJ/Multi-frame-infrared-small-target-detection-DTUM.

3.2. Performance Evaluation Indices

P_d（Probability of Detection）, used to evaluate the detection performance of the model, is calculated as shown in Equation (11):

$$p_d={\displaystyle \frac{T_{TP}}{T_{All}}}\times 100\%$$

(11)

where T_TP is the number of correctly predicted targets and T_All is the number of all targets in labels. A predicted target is deemed correctly detected if the Euclidean distance between its center and the nearest ground-truth target center is less than or equal to 3 pixels.

F_a (False alarm rate), used to evaluate the model's anti-false-alarm performance, and its calculation method is presented as follows:

$${\mathrm{F}}_{\mathrm{a}}={\displaystyle \frac{P_{FP}}{{\displaystyle \sum _{i=1}^N{H}_i\times W_i}}}$$

(12)

where P_FP represents the number of all pixels falsely predicted as targets, ${\mathrm{H}}_{\mathrm{i}}\times {\mathrm{W}}_{\mathrm{i}}$ is the size of the i-th input image, and N is the number of test images. If the distance between the center of a predicted target and the nearest annotated target center exceeds 3 pixels, or no matching target exists, the pixels contained in the predicted target are considered as false alarms.

In infrared small target detection tasks, the proportion of target pixels in the entire image is extremely small, typically on the order of ${10}^{-7}~{10}^{-5}$. This proportion varies significantly across different datasets and therefore cannot intuitively reflect the performance of the model. Specifically, in some cases, it becomes difficult to distinguish between models based on commonly used metrics. As shown in Figure 9, black pixels represent the ground-truth targets, while red and orange pixels denote false alarms detected by two different models. For this particular image prediction, both models yield the same false alarm F_a score. However, the red model predicts only one false target, whereas the orange model generates three. These two scenarios have distinctly different negative impacts. In general, the model represented by red causes less interference and thus has a relatively smaller impact. Nevertheless, this advantage is not reflected in the F_a metric, highlighting its limitation.

In such scenarios, a new metric, False Alarms of Target (F_aT), is proposed to address this limitation. The definition of F_aT is given as follows:

$$F_{aT}={\displaystyle \frac{T_{FP}}{T_{All}}}\times 100\%$$

(13)

where ${\mathrm{T}}_{\mathrm{FP}}$ represents the number of correctly predicted targets and ${\mathrm{T}}_{\mathrm{All}}$ represents the number of all targets in labels. A prediction target is considered a false alarm if the distance between the center of the predicted target and the nearest annotated target center exceeds 3 pixels, or if no corresponding ground truth target exists. This metric counts the number of false alarm targets, providing a closer alignment with real-world usage scenarios. The numerical value can more intuitively reflect the model's false alarm performance.

Params: Refers to the number of model parameters, which is used to measure the size and complexity of the model. It represents the total sum of all parameters in the model.

FLOPs: Stands for Floating-Point Operations per Second, a metric used to assess the computational complexity of the model. It indicates the number of floating-point operations required for one forward pass through the model. In this study, tests were conducted using images with a resolution of 256×256.

FPS: Represents the model's running speed, defined as the number of frames processed per second.

ROC curve (Receiver Operating Characteristic curve): It is used to evaluate the performance of a model across varying detection thresholds. The P_d and F_a are metrics used to assess model performance at fixed detection thresholds, whereas the ROC curve provides an overview of model performance across a range of sliding thresholds. In the ROC curve, F_a is plotted on the x-axis and P_d on the y-axis. The closer the ROC curve approaches the top-left corner, the better the model's performance.

3.3. Network Training

The model was trained on an Intel(R) Core(TM) i9-10920X @ 3.50GHz CPU and an NVIDIA GeForce RTX 3090 with 24GB of VRAM. The primary software versions used were Python 3.8 and PyTorch 1.8. The optimizer employed was the adam optimizer [41], with an initial learning rate of 0.001. Testing was conducted after 20 epochs of training. The learning strategy adopted was Cosine Annealing LR [42], where the learning rate gradually decreases to its minimum value over the course of 20 epochs. Unless otherwise specified, the loss function used in the following experiments is soft-IoU loss, as shown in Equation (14):

$$Soft-IoULoss=1-{\displaystyle \frac{{\displaystyle \sum _{i,j}{p}_{i,j}}\times t_{i,j}+a}{{\displaystyle \sum _{i,j}{p}_{i,j}}+t_{i,j}-p_{i,j}\times t_{i,j}+a}}$$

(14)

where i and j represent the row and column coordinates of the image, respectively; background pixels are labeled as 0, and target pixels are labeled as 1. t_i,j denotes the ground truth pixel value at the corresponding coordinate, and p_i,j represents the predicted pixel value. a is a small constant added to prevent division by zero.

3.4. Ablation Study

3.4.1. Effectiveness of the MI Encoder

The study constructed four different models to evaluate the effectiveness of the motion information encoding modules:

• Model A: An encoder that uses neither the inter-frame nor intra-frame encoding modules.
• Model B: An encoder that uses only the intra-frame position encoding module.
• Model C: An encoder that uses only the inter-frame motion encoding module.
• Model D: The complete encoder with both inter-frame and intra-frame motion encoding modules.

These models were trained and tested on the DAUB and NUDT-MIRST datasets, and the results are shown in Table 1. The best results are shown in boldface and the second best results are shown in underlined.

On the DAUB dataset, the baseline model A, which uses a conventional encoder without any motion encoding module, achieved a P_d of 94.71%. Using only the intra-frame encoding module (model B) improved Pd by 1.66 percentage points, while using only the inter-frame encoding module (model C) improved Pd by 0.85 percentage points. The complete encoder module (model D) achieved a detection rate of 98.28%, an increase of 3.57 percentage points, outperforming both models B and C.

Regarding false alarm suppression performance, compared to baseline model A, the F_a metric of models B, C, and D improved by 3.14×10⁻⁶, 5.05×10⁻⁶, and 6.25×10⁻⁶, corresponding to improvements of 38.54%, 60.10%, and 76.88%, respectively. In terms of the F_aT metric, compared to model A, the values decreased by 8.987, 13.993, and 14.19 percentage points, respectively.

On the NUDT dataset, model A achieved a Pd of 96.01% as the baseline. Compared to this, models B, C, and D improved Pd by 1.66, 0.85, and 2.2 percentage points, respectively.

In terms of false alarm suppression performance, the F_a metric of models B, C, and D increased by 9.01×10⁻⁶, 16.83×10⁻⁶, and 18.61×10⁻⁶ compared to baseline model A, corresponding to improvements of 33.16%, 61.94%, and 68.49%, respectively. For the F_aT metric, compared to model A, the values decreased by 4.61, 6.27, and 7.43 percentage points, respectively.

Overall, the experimental results demonstrate that the two motion encoding modules indeed enhance the model's target detection capability, resulting in higher detection rates and lower false alarms, thereby improving the overall performance of the model.

3.4.2. Effectiveness of the Spatial Feature Extractor

This section constructs and evaluates three models:

Model A: an encoder module using spatial downsampling and a ResBlock-like [43] residual connection structure for encoding, combined with a decoder module that performs decoding only through concatenation and upsampling.

Model B: an encoder-decoder module without integrating a global attention mechanism during decoding.

Model C: the complete spatial feature extractor module.

These models were trained and tested on the DAUB and NUDT datasets. The results are presented in Table 2.

On the DAUB dataset, Model A achieved a P_d of 94.62% as the baseline. Model B improved P_d by 2.44 percentage points, while Model C, which consists of the complete spatial feature extractor module, improved Pd by 3.66 percentage points. Regarding false alarm performance, the F_a metric for Models B and C increased by 1.08×10⁻⁶ and 7.40×10⁻⁶ compared to baseline Model A, representing improvements of 11.64% and 79.74%, respectively. In terms of F_aT, Models B and C reduced the false alarm rate by 0.41 and 1.47 percentage points compared to Model A.

On the NUDT dataset, Model A had a P_d of 94.39% as baseline. Model B improved P_d by 1.65 percentage points, and Model C improved by 3.82 percentage points. For false alarm performance, the F_a metric of Models B and C decreased by 1.09×10⁻⁶ and 0.72×10⁻⁶ compared to Model A, representing improvements of 11.7% and 7.76%, respectively. In F_aT, Models B and C reduced false alarms by 0.46 and 0.28 percentage points compared to Model A.

Overall, the spatial feature extractor of the encoding-decoding structure can better extract the spatial features of the image, so that the model has a higher detection rate and lower false alarm rate, and the overall performance of the model has been improved.

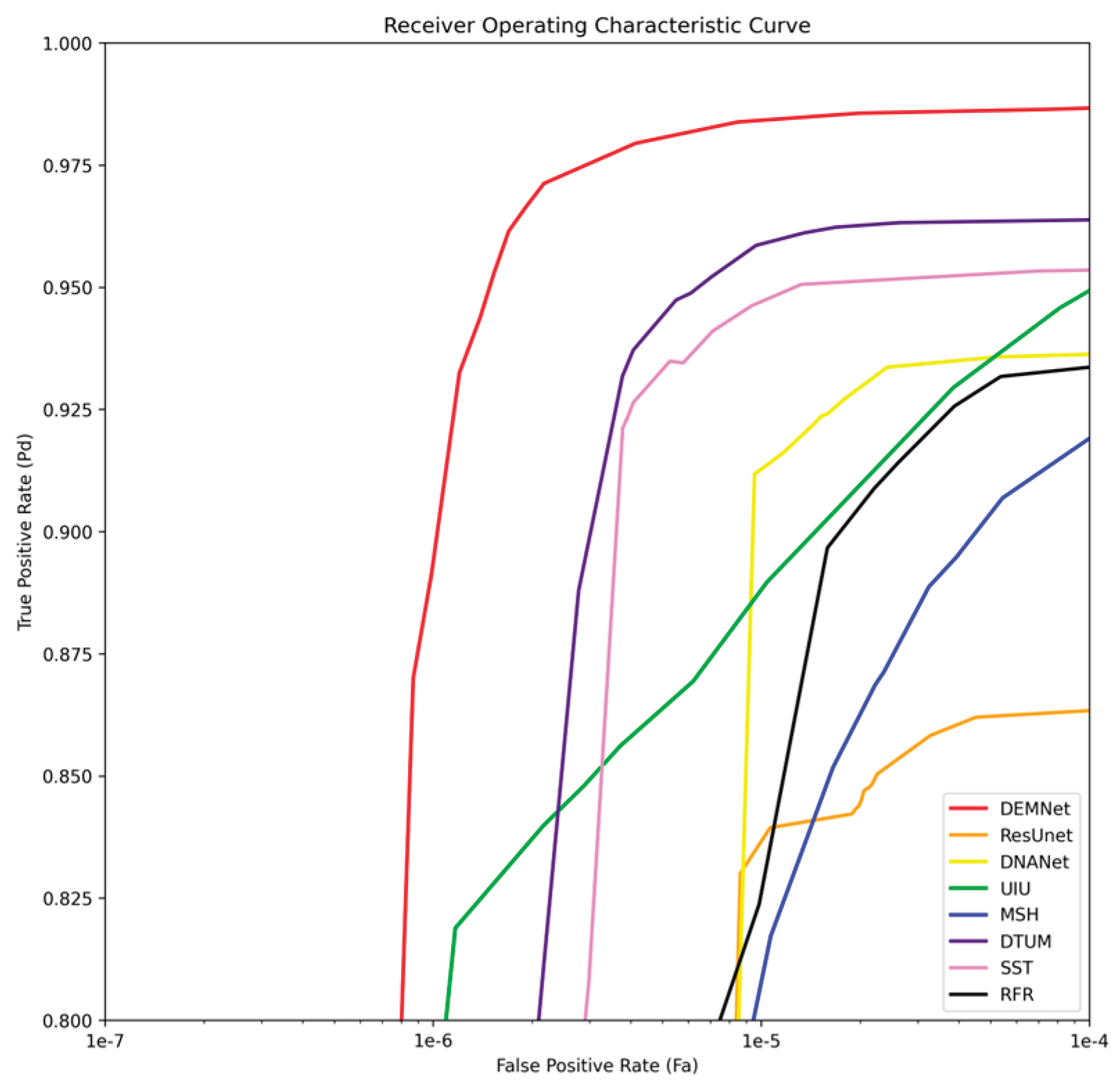
3.5. Comparative Experiments

This paper conducted comparative experiments by evaluating DEMNet against classic single-frame algorithms such as ResUNet [43], DNANet [14], UIUNet [13], MSHNet [17], as well as multi-frame models including RFR [34], DTUM [26], and SST [32] on the DAUB and NUDT datasets. Table 3 and Table 4 present the comparative results on the DAUB and NUDT datasets, respectively.

Note that for the DTUM model trained on the NUDT-MIRST dataset, the hybrid training scheme combining the authors’ proposed HPM loss and soft-IoU loss achieved better performance, and these results are reported here. However, on the DAUB dataset, the hybrid loss scheme underperformed compared to using only soft-IoU loss, so the results shown are based solely on the soft-IoU loss training.

The SST model’s test results were obtained using the original authors’ best model weights and evaluated with the same metrics. However, since SST model’s predictions are bounding boxes, the pixel-level F_a could not be calculated and thus only other metrics besides F_a are presented.

On the DAUB dataset, DEMNet achieved P_d of 98.28%, F_a of 1.88×10⁻⁶, and F_aT of 5.01%, outperforming all other compared models and reaching the best overall performance. Among these, P_d improved by 2.42 percentage points over the second-best model, F_a decreased by 4.13×10⁻⁶ (a reduction of 68.72%), and F_aT improved by 5.3 percentage points compared to the second best.

On the NUDT dataset, DEMNet also demonstrated excellent performance. Across the entire test set, Pd was 98.21%, Fa was 8.56×10⁻⁶, and FaT was 6.19%, all better than the other compared models and achieving the top performance. Compared to the second-best model, Pd increased by 1.68 percentage points, Fa decreased by 0.67×10⁻⁶ (a reduction of 7.26%), and FaT improved by 0.46 percentage points. Notably, on the test sequences with SNR≤ 3, DEMNet’s advantages were even more pronounced, with a Pd of 96.41%, Fa of 6.77×10⁻⁶, and FaT of 11.72%. Here, Pd outperformed the second-best by 5.67 percentage points, Fa decreased by 2.45×10⁻⁶ (a reduction of 26.57%), and FaT led by 2.46 percentage points.

Overall, DEMNet demonstrates excellent performance on both datasets, with a particularly significant advantage in detection rate, while also leading to false alarm suppression.

To more clearly showcase the detection capability of DEMNet and the comparison models for dim and small targets under complex environments, two sets of images were randomly selected from the NUDT test sequences with SNR ≤ 3 and from the DAUB test sequences. The visualized prediction results are shown in Figure 10. Images 1 and 2 are from NUDT, while Images 3 and 4 are from DAUB. Targets are highlighted and zoomed in with red boxes, while false alarm targets are highlighted and zoomed in with green boxes.

For images 1 and 2, the prediction maps from different models show that single-frame methods either fail to detect the target, resulting in blank prediction maps, or detect a large number of false alarm pixels and false targets. Only a few single-frame models manage to detect the target, but their predicted shapes deviate significantly from the real target. In contrast, most multi-frame models can locate the target, although the predicted shapes may vary somewhat, and occasionally some false alarms appear. Among them, DEMNet not only detects the target but also predicts the target’s contour most closely matching the real one.

For image 3, the target is relatively small in the frame, with weak infrared features and interference from other bright spots, making detection challenging. Most single-frame methods fail to identify the true target and instead detect interference targets. While multi-frame methods (except DEMNet) detect the true target, they still produce many false alarms.

For image 4, the target has a good signal-to-noise ratio and high contrast against the background, so all models successfully detect the correct target. However, some models’ prediction results contain false alarms. Among the models without false alarms, DEMNet and DTUM provide the most accurate target contour predictions, demonstrating their performance advantages consistent with the comparative experimental results.

Figure 11 shows the ROC curves of DEMNet and the comparison models on the DAUB dataset. In the figure, the ROC curve of DEMNet envelops those of the other models, meaning that at various F_a levels, DEMNet consistently achieves higher Pd values than the comparison models. This demonstrates that DEMNet’s detection performance under varying threshold settings is also superior to all the other models.

4. Conclusions

For detecting dim and weak targets in complex environments, this paper proposes DEMNet, a multi-frame infrared small target detection algorithm featuring a dual-encoder-decoder architecture with well-designed motion encoding. In the feature extraction phase, the model extracts and fuses features through average pooling and attention mechanism, and obtains multi-scale spatial features. Additionally, based on the motion consistency principle, a frame-to-frame motion information encoding module and an intra-frame position information encoding module are designed. These form the basis of the motion information encoder, which further extracts temporal contextual information of features, especially the inter-frame motion of targets, enabling full utilization of temporal cues. Compared with existing algorithms, DEMNet achieves outstanding detection performance.

Specifically, on the DAUB dataset, compared to the second-best model, DEMNet improves P_d by 2.42 percentage points, reduces F_a by 4.13×10⁻⁶ (reduced by 68.72%), and decreases F_aT by 5.3 percentage points. On the NUDT dataset, it improves P_d by 1.68 percentage points, reduces F_a by 0.67×10⁻⁶ (reduced by 7.26%), and lowers F_aT by 0.46 percentage points compared to the next-best model. Particularly on the low signal-to-noise ratio (SNR≤3) test sequences, DEMNet achieves a P_d of 96.41%, F_a of 6.77×10⁻⁶, and F_aT of 11.72%, outperforming the second-best model by increasing P_d by 5.67 percentage points, reducing F_a by 2.45×10⁻⁶ (26.57% decrease), and lowering F_aT by 2.46 percentage points.