Submitted:
28 June 2025
Posted:
01 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction and Summary
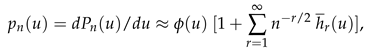
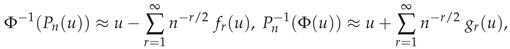
2. Multivariate Edgeworth Expansions
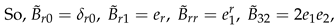
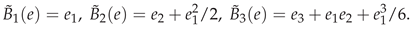
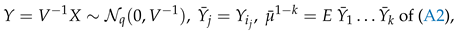
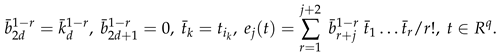
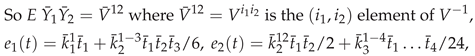
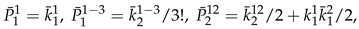
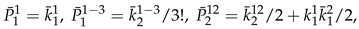
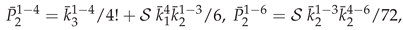
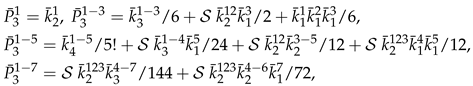
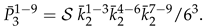
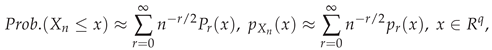
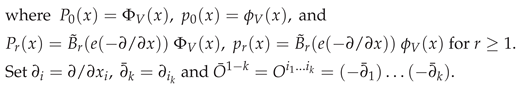
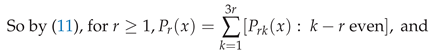
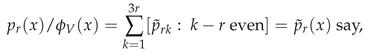
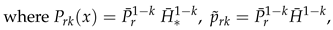
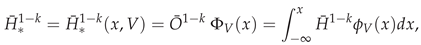
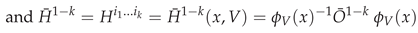
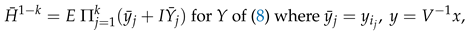
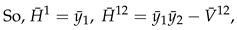
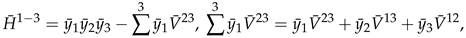
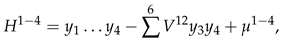
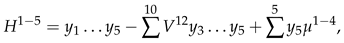
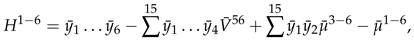
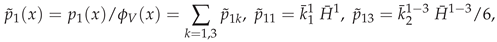
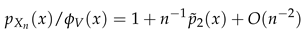
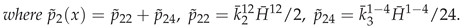
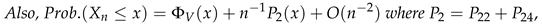
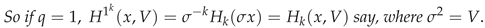
3. Secondary or Derived Expansions
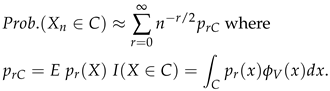
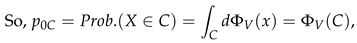
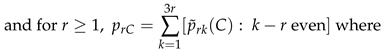

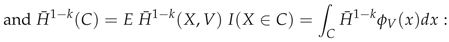
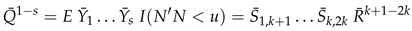
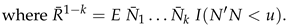
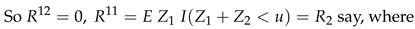
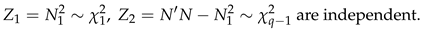
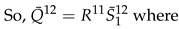
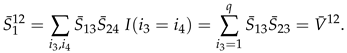
 |
4. The Distribution of for
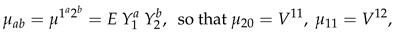
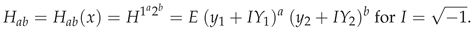
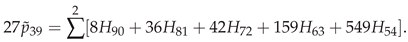
5. Conclusions
6. Discussion
Appendix A: The Edgeworth coefficients needed for (11)
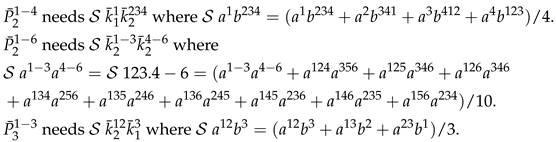
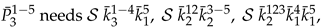
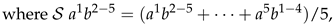
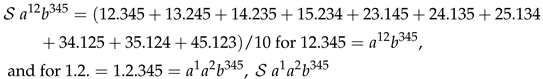
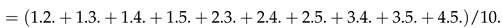
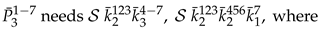
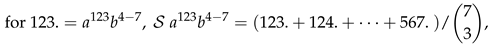
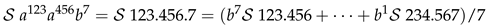

Appendix B: and of (2) for .
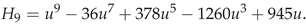
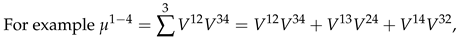
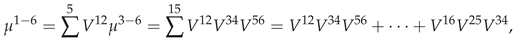
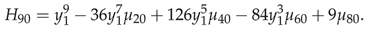
Appendix I Code for Bivariate Normal Moments and Bivariate Hermite Polynomals
References
- Abdel-Wahed, A.R. and Winterbottom, A. (1983) Approximating posterior distributions of system reliability. The Statistician, 32, 224–228. [CrossRef]
- Abramowitz, M. and Stegun, I. A. (1964) Handbook of mathematical functions. U.S. Department of Commerce, National Bureau of Standards, Applied Mathematics Series 55.
- Anderson, T. W. (1958) An introduction to multivariate analysis. John Wiley, New York.
- Comtet, L. Advanced Combinatorics; Reidel: Dordrecht, The Netherlands, 1974.
- Cornish, E.A. and Fisher, R. A. (1937) Moments and cumulants in the specification of distributions. Rev. de l’Inst. Int. de Statist. 5, 307–322. Reproduced in the collected papers of R.A. Fisher, 4. [CrossRef]
- Fisher, R. A. and Cornish, E.A. (1960) The percentile points of distributions having known cumulants. Technometrics, 2, 209–225. [CrossRef]
- Gradshteyn, I.S., and Ryzhik, I.M., (2000) Tables of integrals, series and products. 6th edition. Academic Press, New York. The generalized hypergeometric function is defined in §9.14.
- Gradshteyn, I.S., and Ryzhik, I.M., (2000) Tables of integrals, series and products. 6th edition. Academic Press, New York. The generalized hypergeometric function is defined in §9.14.
- Hill, G.W. and Davis, A.W. (1968) Generalised asymptotic expansions of Cornish-Fisher type. Ann. Math. Statist., 39, 1264–1273. [CrossRef]
- On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables. Biometrika, 12, 134–139. JSTOR 2331932.
- Jensen, J.L. (1988) Uniform saddlepoint approximations, Adv. Appl. Prob. 20, 622-634.
- Simonato, J.G. (2011) The performance of Johnson distributions for computing value at risk and expected shortfall. Journal of Derivatives (19) 7–24. [CrossRef]
- Skovgaard, I.M. (1981a) Edgeworth expansions of the distributions of maximum likelihood estimators in the general (non i.i.d.) case. Scand. J. Statist., 8, 227-236.
- Skovgaard, I. M. (1981b) Transformation of an Edgeworth expansion by a sequence of smooth functions. Scand. J. Statist., 8, 207-217.
- Skovgaard, I. M. (1986) On multivariate Edgeworth expansions. Int. Statist. Rev., 54, 169–186. [CrossRef]
- Stuart, A. and Ord, K. (1991). Kendall’s advanced theory of statistics, 2. 5th edition. Griffin , London.
- Takemura, A. and Takeuchi, K. (1988) Some results on univariate and multivariate Cornish-Fisher expansions: algebraic properties and validity. Sankhya, Series A50, 111–136.
- Takeuchi, K. (1978) A multivariate generalization of Cornish-Fisher expansion and its applications. (In Japanese.) Keizaigaku Ronshu, 44, (2), 1–12.
- Teal, P. (2024) A code to calculate bivariate Hermite polynomials.https://github.com/paultnz/bihermite/blob/main/bihermite.py Its input is V11,V12,V22 and y1,y2, not V11,V12,V22 and x1,x2.
- TianLi, S., ShuNing, W. and WeiLian, A. (2009) GPS positioning accuracy estimation using Cornish-Fisher expansions. International Conference on comms. and mobile computing, IEEE Computer Soc., 152–155.
- Winterbottom, A. (1980) Asymptotic expansions to improve large sample confidence intervals for system reliability. Biometrika, 67, 351–357. [CrossRef]
- Winterbottom, A. (1984) The interval estimation of system reliability component test data. Operations Research, 32, 628–640. [CrossRef]
- Withers, C.S. (1984) Asymptotic expansions for distributions and quantiles with power series cumulants. Journal Royal Statist. Soc. B, 46, 389–396. Corrigendum (1986) 48, 256. For typos, see p23–24 of Withers (2024). [CrossRef]
- Withers, C.S. (1989) Accurate confidence intervals when nuisance parameters are present. Comm. Statist. - Theory and Methods, 18, 4229–4259. [CrossRef]
- Withers, C.S. (2000) A simple expression for the multivariate Hermite polynomials. Statistics and Prob. Letters, 47, 165–169. [CrossRef]
- Withers, C.S. (2024) 5th-Order multivariate Edgeworth expansions for parametric estimates. Mathematics, 12,905, Advances in Applied Prob. and Statist. Inference. https://www.mdpi.com/2227-7390/12/6/905/pdf. [CrossRef]
- Withers, C.S. (2025) New methods for multivariate normal moments. Stats. 8(2), 46. [CrossRef]
- Withers, C.S. and Nadarajah, S.N. (2009) Charlier and Edgeworth expansions via Bell polynomials. Probability and Mathematical Statistics, 29, 271–280. For typos, see p24–25 of Withers (2024).
- Withers, C.S. and Nadarajah, S. (2010) Tilted Edgeworth expansions for asymptotically normal vectors. Annals of the Institute of Statistical Mathematics, 62 (6), 1113–1142. [CrossRef]
- Withers, C.S. and Nadarajah, S. (2011) Generalized Cornish-Fisher expansions. Bull. Brazilian Math. Soc., New Series, 42 (2), 213–242. [CrossRef]
- Withers, C.S. and Nadarajah, S.N. (2012a) Improved confidence regions based on Edgeworth expansions. Computational Statistics and Data Analysis, 56 (12), 4366–4380. [CrossRef]
- Withers, C.S. and Nadarajah, S.N. (2012b) Cornish-Fisher expansions about the F-distribution. Applied Mathematics and Computation, 218 (15), 7947–7957. [CrossRef]
- Withers, C.S. and Nadarajah, S. (2014) Expansions about the gamma for the distribution and quantiles of a standard estimate. Methodology and Computing in Applied Prob., 16 (3), 693-713. [CrossRef]
- Withers, C.S. and Nadarajah, S. (2015) Edgeworth-Cornish-Fisher-Hill-Davis expansions for normal and non-normal limits via Bell polynomials. Stochastics An International Journal of Probability and Stochastic Processes, 87 (5), 794–805. [CrossRef]
- Withers, C.S. and Nadarajah, S. (2020) The distribution and percentiles of channel capacity for multiple arrays. Sadhana, SADH, Indian Academy of Sciences, 45 (1), 1–25. [CrossRef]
- Xu, J. and Gupta, A.K. (2006) Improved confidence regions for a mean vector under general conditions. Computational Stat. and Data Analysis, 51 1051-1062. [CrossRef]
- Zhang, L., Mykland, P.A. and Ait-Sahalia, Y. (2011) Edgeworth expansions for realised volatility and related estimators. Journal of Econometrics (160) 190–203. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




