Submitted:
17 June 2025
Posted:
18 June 2025
You are already at the latest version
Abstract
Keywords:
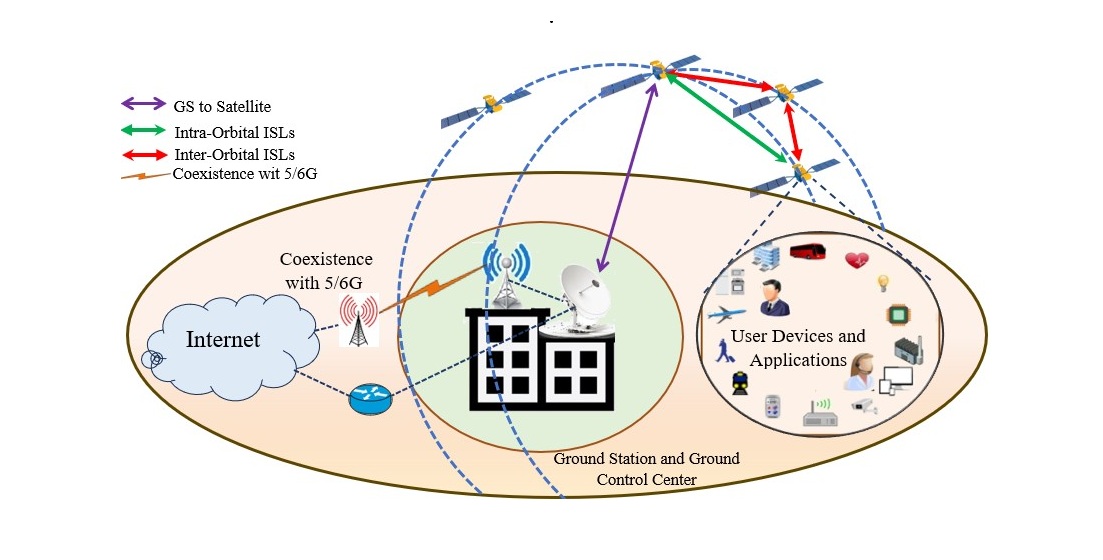
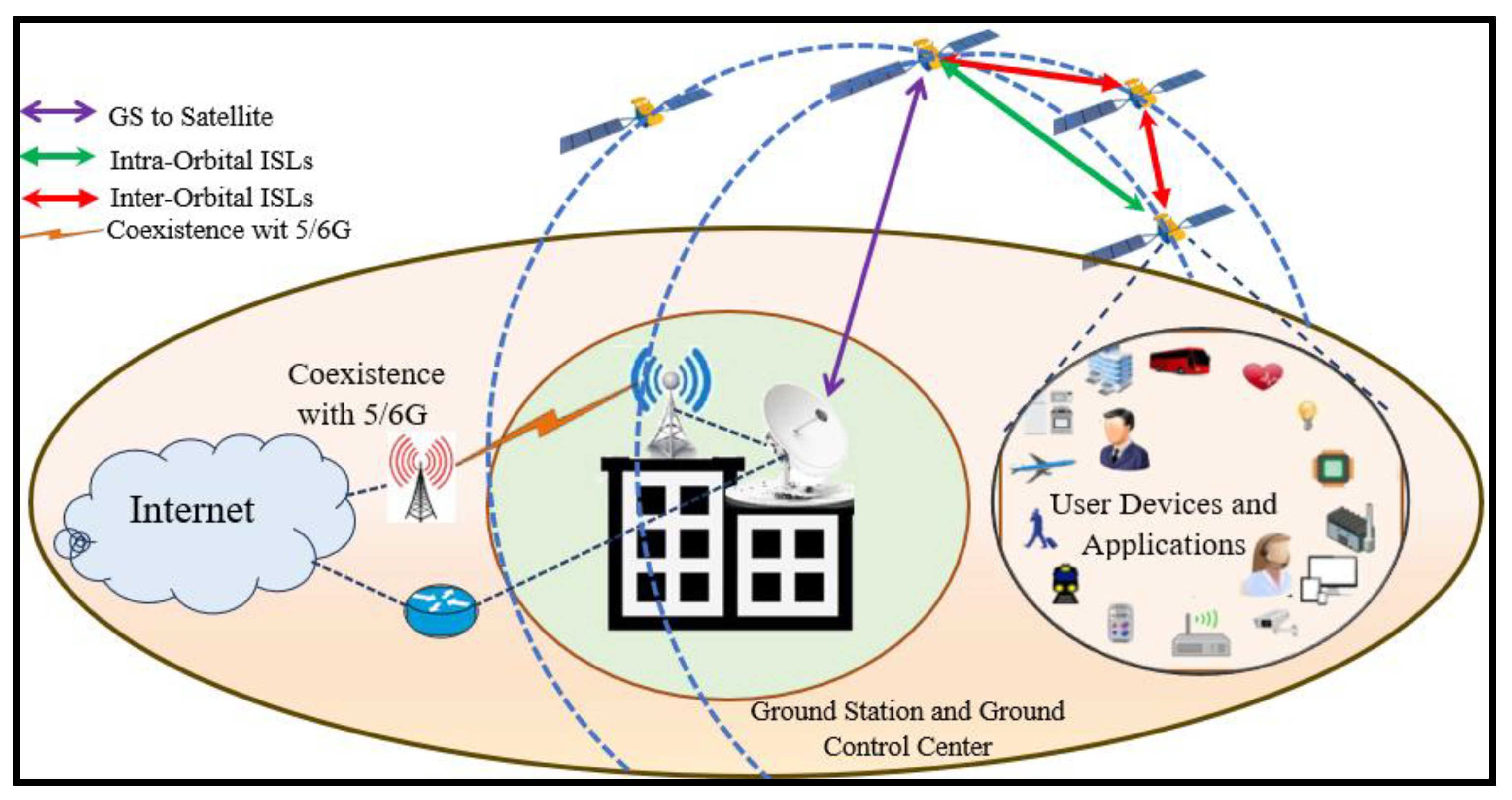
1. Introduction
1.1. Satellite Constellation Architecure
1.2. Operation of LEO Satellite Networks
- Direct Connection: The user device connects directly to the satellites that cover the user device area.
- Satellite Relay: the satellites are equipped with an onboard LTE/5/6G modem (eNodeB) which acts like a cell tower in space that can receive from and transmit to user devices.
- Inter-Satellite Links (ISLs): the satellite uses laser ISLs to transmit the signal across the satellite network toward the satellite that is positioned over a GS.
- Ground Station Link: the signal is then downlinked to a GS connected to terrestrial networks that can provide internet backbone.
1.3. Problem Statement and Research Motivation
1.4. Research Contribution
- It reviews the optimizing methods of satellite orbital placement and coverage for LEO networks. It highlights the main parameters that have been considered in increasing Internet connectivity, coverage area and reliability.
- It analyses the LEO orbital parameters that can mitigate the signal impairments and space debris, and it enhances the swath width for LEO satellite network.
- It suggests two solutions for satellite orbital placement and coverage optimization for LEO networks based on effective machine learning algorithms.
2. Related Works
2.1. Related Work on Satellite Orbital Placement
2.2. Related Work on Optimization of LEO Coverage Area
2.3. Related Work on LEO Orbital Signal Impairments
3.0. Analysis of Satellite Orbital Placement and Coverage Optimization for LEO
3.1. Orbital Parameters and Their Impact
3.1.1. Satellite Coverage Area
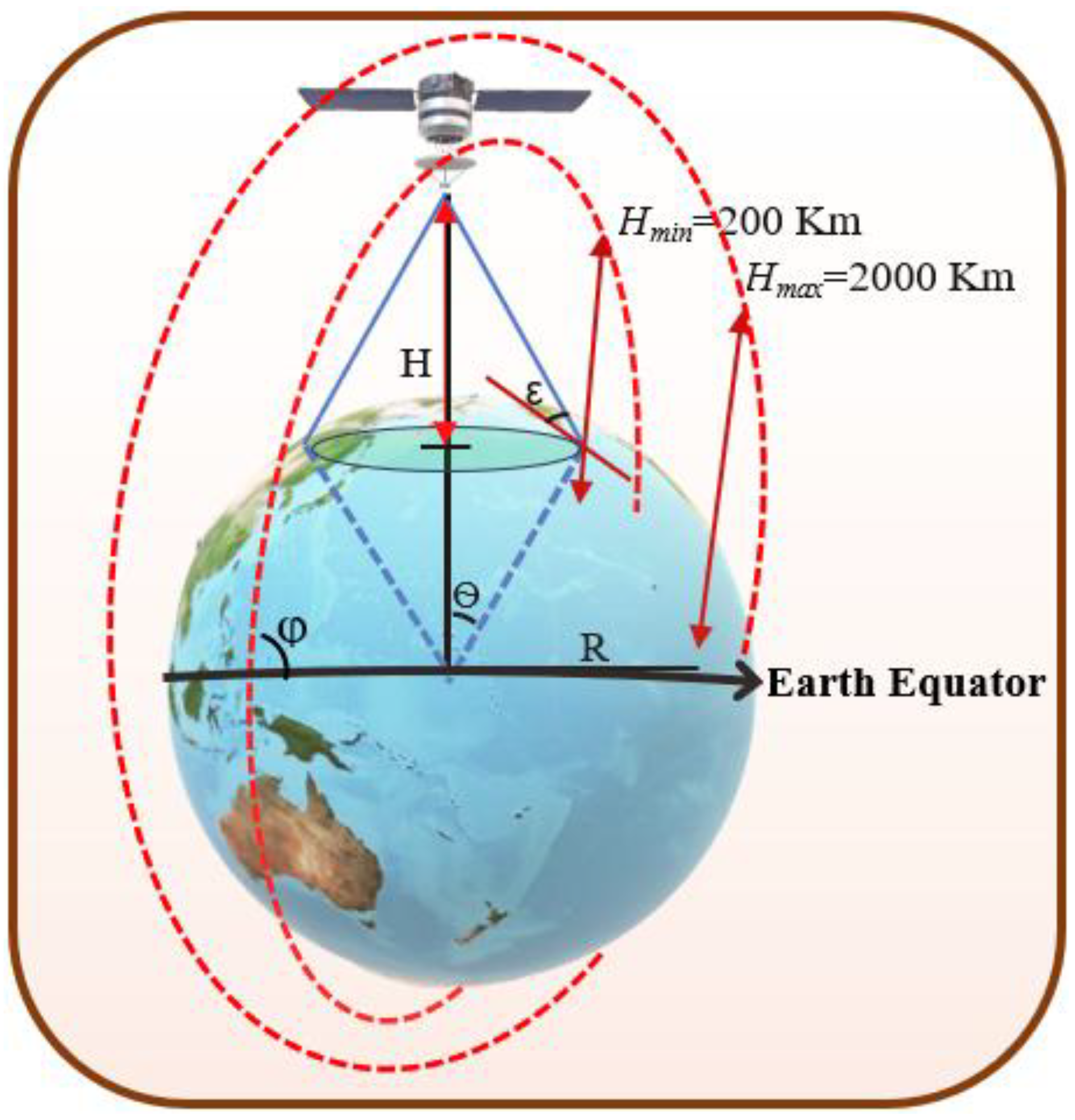
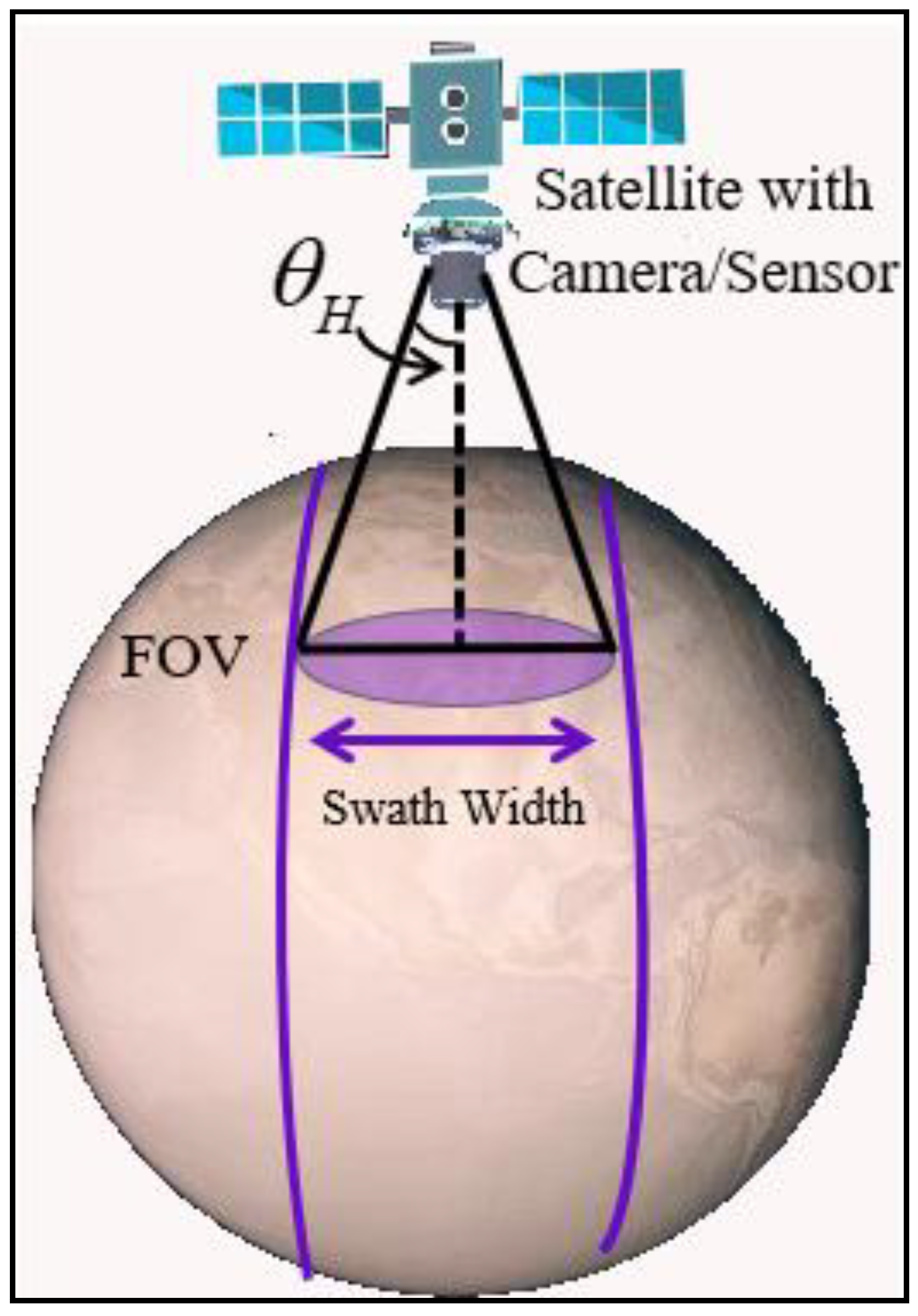
3.1.2. Satellite Swath Width
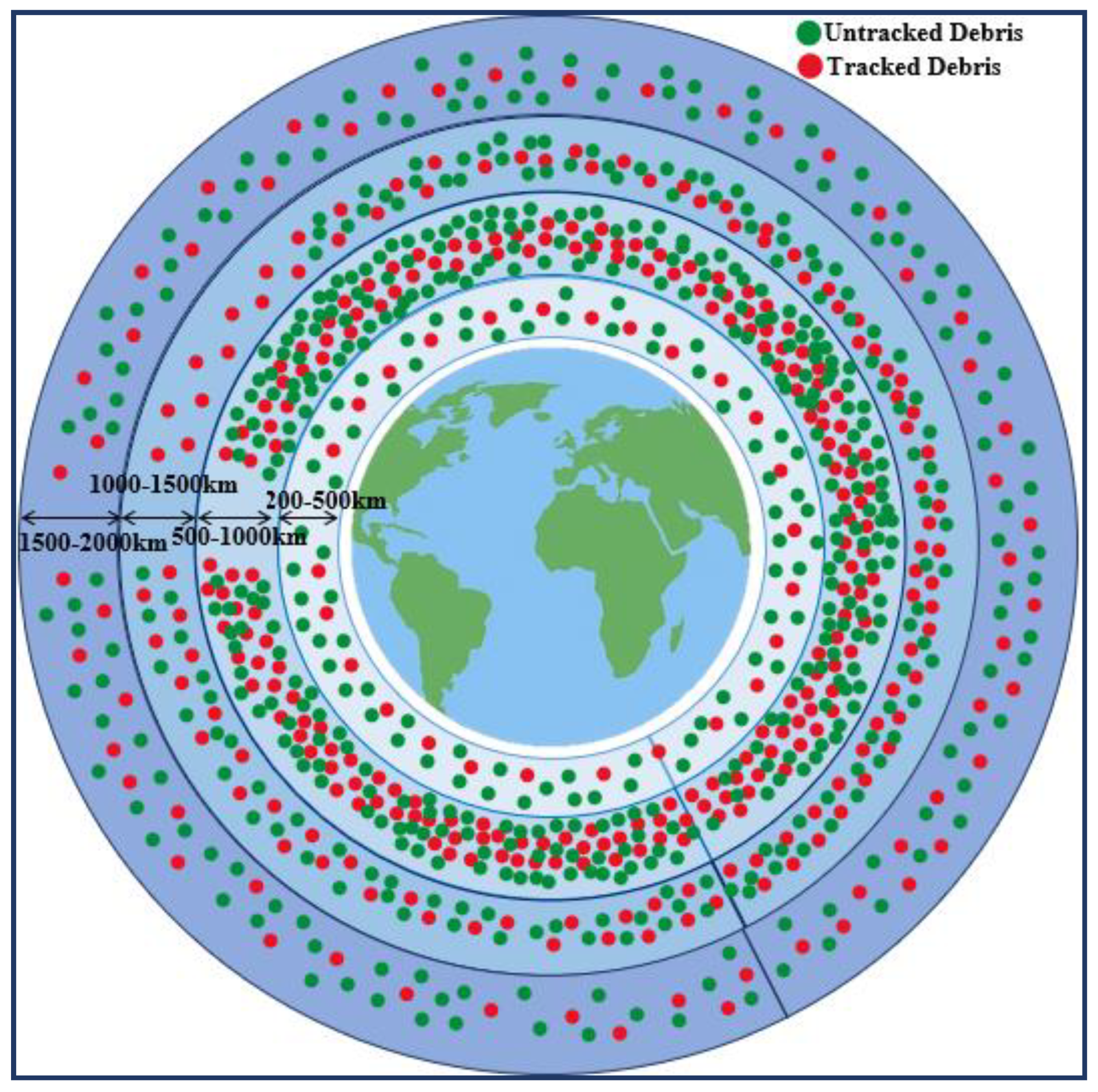
3.1.3. LEO Space Debris
| Altitude Range (km) | Tracked Debris (>10 cm) | Estimated Untracked Debris (1 mm–10 cm) | Description |
| 200–500 | ~1,200 | ~60,000 | Lower density; frequent orbital decay due to atmospheric drag. Debris typically re-enters within years. |
| 500–800 | ~4,500 | ~150,000 | Moderate density; long-lived orbits. Popular for remote sensing missions. |
| 800–1,000 | ~6,800 | ~200,000 | Densest zone, called “congested LEO belt.” Site of several breakup events (e.g., Iridium-Cosmos collision). |
| 1,000–1,500 | ~3,000 | ~80,000 | Includes old satellites and upper stages. Low drag means debris remains for centuries. |
| 1,500–2,000 | ~1,000 | ~30,000 | Sparse compared to lower LEO, but debris is persistent due to low atmospheric influence. |
3.1.4. LEO Signal Impairments
- Intra-System Interference: Beams from adjacent satellites can overlap which causes interference for users on the ground.
- Inter-System Interference: Interference from satellites in different LEO constellations or from satellites in higher orbits (MEO/GEO) that use adjacent frequency bands.
- Terrestrial Interference: Signals from ground-based systems such as 5G towers, Wi-Fi networks, and microwave signals are a major source of interference.
- Space Weather: Solar flares and geomagnetic storms cause signal attenuation or noise.
- Intentional Interference (Jamming): Malicious attempts to transmit powerful signals at a satellite to disrupt its communication link.
- Multipath and Doppler Effects: Due to fast satellite movement and terrain-based signal reflection.
3.1.5. LEO Signal Impairments
- Intra-System Interference: Beams from adjacent satellites can overlap which causes interference for users on the ground.
- Inter-System Interference: Interference from satellites in different LEO constellations or from satellites in higher orbits (MEO/GEO) that use adjacent frequency bands.
- Terrestrial Interference: Signals from ground-based systems such as 5G towers, Wi-Fi networks, and microwave signals are a major source of interference.
- Space Weather: Solar flares and geomagnetic storms cause signal attenuation or noise.
- Intentional Interference (Jamming): Malicious attempts to transmit powerful signals at a satellite to disrupt its communication link.
- Multipath and Doppler Effects: Due to fast satellite movement and terrain-based signal reflection.
4.0. Discussion of Satellite Orbital Placement Proposed Solutions
4.1. Satellite Orbital Placement Proposed Solution
-
Step 1: Select affective placement parameters.
- The most affective parameters in satellite placement are SINR, end-to-end delay, optimal altitude, number of tracked and untracked debris, etc.
-
Step 2: Initialize the matrix Q of DRL.
- The Q-matrix must be constructed and initialized to 0. The columns represent all possible actions while the rows represent the states for each action.
-
Step 3: Choose and perform action.
- For each episode, a random initial state and possible action are selected by the agent to go to the next state. After that, the maximum Q value for the next state is estimated as:where α represents the learning rate, γ is the discount factor, is the new value of Q, is the current Q value, and is the maximum predicted rewards by given new states and possible actions.
-
Step 4: Reward estimation.
- The reward function is calculated based on R (State, Action(selected parameters)).
-
Step 5: Q-Learning evaluation.
- The function Q(State, Action) should be maximized, and the Q-Table should be updated until the learning is stopped.
-
Step 6: Debris Avoidance.
- The suggested proposed algorithm should utilize a collision avoidance system that autonomously detects potential collisions with other satellites or debris. Consequently, AI system with advance detection systems should be applied for each satellite to perform real-time orbital adjustments.
4.2. Coverage Optimization Proposed Solution
-
Step 1: Obtain value of Satellite Orbital Placement.
- The latitude (H) should be estimated from previous algorithm of orbital placement because it is an important parameter in coverage area equation.
-
Step 2: Determine the weightage for each involved parameter.
- The satellite should autonomously adjust values of inclination angle, elevation angle, and swath width. The number of satellites in each orbit is determined to reliably cover the whole ground. Based on the effectiveness of each parameter, the weightage of each one of them is estimated.
-
Step 3: Use optimization function.
- One of the real-time optimization algorithms such heuristic, and metaheuristics should be used to obtain the optimal value of satellite coverage area. The metaheuristics algorithms perform better optimization, including genetic algorithms, particle swarm optimization, and simulated annealing, ant colony optimization.
-
Step 4: Communication evaluation.
- The link quality and reliable internet connectivity should be evaluated for each coverage optimization selection.
-
Step 5: Select optimal coverage area parameters.
- After evaluation of each selection, the most optimal value of inclination angle, elevation angle, and swath width are determined based on the latitude value that is estimated in Equations (3) and (5).
5.0. Limitations and Future Works
6.0. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- K. Çelikbilek, E. S. K. Çelikbilek, E. S. Lohan, and J. Praks (2024), Optimization of a LEO-PNT Constellation: Design Considerations and Open Challenges, Int J Satell Commun Network. 2024;01-16. [CrossRef]
- Prol FS, Bhuiyan MZH, Kaasalainen S, et al. Simulations of Dedicated LEO-PNT Systems for Precise Point Positioning: Methodology, Parameter Analysis, and Accuracy Evaluation. to appear in IEEETransactions on AerospaceandElectronic Systems 2024: 8. [CrossRef]
- Liu, J. , et al.: Design optimisation of low earth orbit constellation based on BeiDou Satellite Navigation System precise point positioning. IET Radar Sonar Navig. 16(8), 1241–1252 (2022). [CrossRef]
- Nardin A, Dovis F, Fraire JA. Empowering the Tracking Performance of LEO-Based Positioning by Means of Meta Signals. IEEE Journal of Radio Frequency Identification 2021; 5(3): 244–253. [CrossRef]
- M. Frąckiewicz, Sky-Fi Revolution: How Starlink Is Reshaping Global Internet Access, access on May 2025.
- Wu, Z.; Ni, S.; Xiao, W.; Li, Z.; Liu, H. Study on the Feasibility and Performance Evaluation of High-Orbit Spacecraft Orbit Determination Based on GNSS/SLR/VLBI. Remote Sens. 2024, 16, 4214. [Google Scholar] [CrossRef]
- Page, Pranav S., Kaustubh S. Bhargao, Hrishikesh V. Baviskar, and Gaurav S. Kasbekar. "Distributed probabilistic congestion control in LEO satellite networks." In 2023 15th International Conference on COMmunication Systems & NETworkS (COMSNETS), pp. 335-339. IEEE, 2023. [CrossRef]
- Ekici, Eylem, Ian F. Akyildiz, and Michael D. Bender. "Datagram routing algorithm for LEO satellite networks." In Proceedings IEEE INFOCOM 2000. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No. 00CH37064), vol. 2, pp. 500-508. IEEE, 2000. [CrossRef]
- The many locations for space science missions, Satellite Orbits, https://www.teledyne, access on April 2025.
- Wang, Ruibo, Mustafa A. Kishk, and Mohamed-Slim Alouini. "Stochastic geometry-based low latency routing in massive LEO satellite networks." IEEE Transactions on Aerospace and Electronic Systems 58, no. 5 (2022): 3881-3894. [CrossRef]
- Guo, Jianming, David Rincon, Sebastia Sallent, Lei Yang, Xiaoqian Chen, and Xianqi Chen. "Gateway placement optimization in LEO satellite networks based on traffic estimation." IEEE Transactions on Vehicular Technology 70, no. 4 (2021): 3860-3876. [CrossRef]
- G. Fontanesi, F. G. Fontanesi, F. Ortíz, E. Lagunas, V. Monzón Baeza, M. Vázquez, J.A. Vásquez-Peralvo, M. Minardi, H.-N. Vu, P. Jubba Honnaiah, C. Lacoste, Y. Drif, T.S. Abdu, G. Eappen, J. Rehman, L.M. García-Socorrás, W.A. Martins, P. Henarejos, H. Al-Hraishawi, J.C. Merlano Duncan, T.X. Vu, and S. Chatzinotas, "Artificial Intelligence for Satellite Communication and Non-Terrestrial Networks: A Survey," 2023. [CrossRef]
- Shang, Zixia. "Towards Future Communication: AI-Based Satellite Constellation Orbit Optimization and Design for Underserved Areas." Authorea Preprints (2025).
- Prol, Fabricio S., R. Morales Ferre, Zainab Saleem, Petri Välisuo, Christina Pinell, Elena Simona Lohan, Mahmoud Elsanhoury et al. "Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities." IEEE access 10 (2022): 83971-84002. [CrossRef]
- Ge, Haibo, Bofeng Li, Liangwei Nie, Maorong Ge, and Harald Schuh. "LEO constellation optimization for LEO enhanced global navigation satellite system (LeGNSS)." Advances in Space Research 66, no. 3 (2020): 520-532. [CrossRef]
- Çelikbilek, Kaan, Zainab Saleem, Ruben Morales Ferre, Jaan Praks, and Elena Simona Lohan. "Survey on optimization methods for LEO-satellite-based networks with applications in future autonomous transportation." Sensors 22, no. 4 (2022): 1421. [CrossRef]
- Liu, Jing, Jinming Hao, Yan Yang, Zheyu Xu, Weiping Liu, and Renzhe Wu. "Design optimisation of low earth orbit constellation based on BeiDou Satellite Navigation System precise point positioning." IET radar, sonar & navigation 16, no. 8 (2022): 1241-1252. [CrossRef]
- Guo, Junqi, Yang Wang, Xingxiang Xie, and Chenyang Sun. "A fast satellite selection algorithm for positioning in LEO constellation." Advances in Space Research 73, no. 1 (2024): 271-285. [CrossRef]
- Çelikbilek, Kaan, Elena Simona Lohan, and Jaan Praks. "Optimization of a LEO-PNT Constellation: Design Considerations and Open Challenges." International Journal of Satellite Communications and Networking (2025). [CrossRef]
- Ghoniem, Ibrahim Fouad, Ashraf El-Kutb Mousa, and Gamal El-Fiky. "GNSS-RO LEO satellite orbit optimization for Egypt and the Middle East region." Alexandria Engineering Journal 59, no. 1 (2020): 389-397. [CrossRef]
- Imoto, Yuta, Satoshi Satoh, Toshihiro Obata, and Katsuhiko Yamada. "Optimal constellation design based on satellite ground tracks for Earth observation missions." Acta Astronautica 207 (2023): 1-9.
- Xue, W.; Hu, M.; Ruan, Y.; Wang, X.; Yu, M. Research on Design and Staged Deployment of LEO Navigation Constellation for MEO Navigation Satellite Failure. Remote Sens. 2024, 16, 3667. [Google Scholar] [CrossRef]
- Cakaj, Shkelzen. "The coverage belt for low earth orbiting satellites." Proc. 39th Int. Convent. Info. Commun. Technol., Electron. Microelectron.(ICICTEM), Opatija, Croatia: 554-557, 2016.
- Cakaj, Shkelzen, Bexhet Kamo, Algenti Lala, and Alban Rakipi. "The coverage analysis for low earth orbiting satellites at low elevation. International Journal of Advanced Computer Science and Applications 5, no. 6.:6-10, 2014. [CrossRef]
- Zhu, Titus Gramacy, Shi-soon Solosa, and Periera Maniani. "Modeling and optimization of multi-altitude leo satellite networks using cox point processes: Towards efficient coverage and performance analysis." International Journal of Enterprise Modelling 17, no. 1 (2023): 35-44.
- Silvirianti, X. , and Georges Kaddoum. "Quantum Adaptive Learning for Coverage Optimization in LEO Satellite Network.", TechRxiv., Authorea Preprints. , 2025. 19 March. [CrossRef]
- Shin, Jinyoung, Sang-Young Park, Jihae Son, and Sung-Chan Song. "Design of regional coverage low earth orbit (LEO) constellation with optimal inclination." Journal of Astronomy and Space Sciences 38, no. 4 (2021): 217-227. [CrossRef]
- Lluch, Ignasi, and Alessandro Golkar. "Satellite-to-satellite coverage optimization approach for opportunistic inter-satellite links." In 2014 IEEE Aerospace Conference, pp. 1-13. IEEE, 2014.
- Lee, Miyeon, Sucheol Kim, Minje Kim, Dong-Hyun Jung, and Junil Choi. "Analyzing downlink coverage in clustered low Earth orbit satellite constellations: A stochastic geometry approach." IEEE Transactions on Communications (2025). [CrossRef]
- Zong, Peng, and Saeid Kohani. "Optimal satellite LEO constellation design based on global coverage in one revisit time." International Journal of Aerospace Engineering 2019, no. 1 (2019): 4373749. [CrossRef]
- Hassan, Sheikh Salman, Yu Min Park, Yan Kyaw Tun, Walid Saad, Zhu Han, and Choong Seon Hong. "SpaceRIS: LEO satellite coverage maximization in 6G sub-THz networks by MAPPO DRL and whale optimization." IEEE Journal on Selected Areas in Communications (2024). [CrossRef]
- Zhao, Yuhan, and Quanyan Zhu. "Autonomous and resilient control for optimal leo satellite constellation coverage against space threats. arXiv:2203.02050 (2022).
- Pinell, Christina, Fabricio S. Prol, M. Zahidul H. Bhuiyan, and Jaan Praks. "Receiver architectures for positioning with low earth orbit satellite signals: a survey." EURASIP Journal on Advances in Signal Processing 2023, no. 1 (2023): 60. [CrossRef]
- Ning, Qian, Xinjing Yang, Bingcai Chen, and Xinzhi Zhou. "The performance analysis of NOMA in LEO satellite rain attenuation and fading hybrid channel." International Journal of Satellite Communications and Networking 40, no. 4 (2022): 256-267. [CrossRef]
- JIA Min,MENG Shiyao,GUO Qing,GU Xuemai. "Analysis of inter-system interference of large-scale LEO satellite constellation." Journal of Terahertz Science and Electronic Information Technology 20, no. JIA Min,MENG Shiyao,GUO Qing,GU Xuemai. "Analysis of inter-system interference of large-scale LEO satellite constellation." Journal of Terahertz Science and Electronic Information Technology 20, no. 1 (2022): 34-39.
- Liu, Jiawei, Kan Wang, Ahmed El-Mowafy, and Xuhai Yang. "PCO and hardware delay calibration for LEO satellite antenna downlinking navigation signals." Measurement Science and Technology 35, no. 8 (2024): 086314. [CrossRef]
- Dwivedi, Ayush Kumar, Sachin Chaudhari, Neeraj Varshney, and Pramod K. Varshney. "Performance analysis of LEO satellite-based IoT networks in the presence of interference." IEEE Internet of Things Journal 11, no. 5 (2023): 8783-8799. [CrossRef]
- Miteva, R.; Samwel, S.W.; Tkatchova, S. Space Weather Effects on Satellites. Astronomy 2023, 2, 165–179. [Google Scholar] [CrossRef]
- Radojkovic, I.; Anastasov, J.; Milic, D.N.; Ivaniš, P.; Djordjevic, G.T. Secrecy Analysis of LEO Satellite-to-Ground Station Communication System Influenced by Gamma-Shadowed Ricean Fading. Electronics 2025, 14, 293. [Google Scholar] [CrossRef]
- Beidas, Bassel F. "Low cost per bit for LEO satellite systems: radio-frequency impairments compensation.", Non-Geostationary Satellite Communications Systems, Chapter 5, pp.: 89-111, 2022.
- Ma, J.; Kang, R.; Li, R.; Zhang, Q.; Liu, L.; Wang, X. Uncertainty Theory-Based Resilience Analysis for LEO Satellite Communication Systems. Symmetry 2022, 14, 1568. [Google Scholar] [CrossRef]
- Zhang, Zhenghao. "ChirpPair: packet acquisition in uncoordinated access channels of Low Earth Orbit (LEO) satellite networks." EURASIP Journal on Wireless Communications and Networking 2024, no. 1 (2024): 47. [CrossRef]
- Sun, Y.; Rao, P.; Hu, T. Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera. Sensors 2021, 21, 4106. [Google Scholar] [CrossRef] [PubMed]
- "3 DEBRIS POPULATION DISTRIBUTION." National Research Council. 1995. Orbital Debris: A Technical Assessment. Washington, DC: The National Academies Press. [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. 1995. Orbital Debris: A Technical Assessment. Washington, DC: The National Academies Press. [CrossRef]
- ESA’S ANNUAL SPACE ENVIRONMENT REPORT, https://sdup.esoc.esa.int/discosweb/statistics/, https://www.sdo.esoc.esa.int/environment_report/Space_Environment_Report_latest.pdf, accessed on May 2025.
- Astromaterials Research & Exploration Science, NASA ORBITAL DEBRIS PROGRAM OFFICE, https://orbitaldebris.jsc.nasa.gov/faq/, accessed on May 2025.
- SPACE SAFETY, About space debris, https://www.esa.int/Space_Safety/Space_Debris/About_space_debris, accessed on May 2025.
- Ahmed, A.A.; Malebary, S.J.; Ali, W.; Barukab, O.M. Smart Traffic Shaping Based on Distributed Reinforcement Learning for Multimedia Streaming over 5G-VANET Communication Technology. Mathematics 2023, 11, 700. [Google Scholar] [CrossRef]
- Ahmed, Adel A. "An effective handover management based on SINR and software-defined network over urban vehicular ad hoc networks." Transactions on Emerging Telecommunications Technologies 30, no. 12 (2019): e3787. [CrossRef]
- Ahamed, A. A real-time routing protocol with adaptive traffic shaping for multimedia streaming over next-generation of Wireless Multimedia Sensor Networks. Pervasive Mob Comput. 2017; 40: 495-511.
| Research Work | Publish Year | Short Description | Limitation |
|---|---|---|---|
| Z. Shang [13] | 2024 | Utilized deep reinforcement learning for optimizing satellite constellations, enhancing communication speed and coverage in challenging regions. | Focused on specific regions; generalizability to other areas not addressed. |
| F.S. Prol et al. [14] | 2023 | Reviewed requirements for building LEO-PNT systems, including signal design and system segments. | Lacked clear recommendations due to limited simulations in existing literature. |
| G. Haibo et al. [15] | 2020 | Analyzed orbital parameters to optimize LEO constellations for GNSS, promoting uniform satellite distribution. | Did not consider dynamic environmental factors affecting satellite visibility. |
| Kaan et al. [16] | 2022 | Presented an overview of LEO optimization methods across various applications and system segments. | Comparative analysis may not cover all emerging optimization techniques. |
| L. Jing et al. [17] | 2021 | Applied NSGA-III algorithm to design hybrid LEO constellations, reducing satellite count for BeiDou enhancement. | Potential trade-offs in coverage and redundancy are not fully explored. |
| G. Junqi et al. [18] | 2023 | Proposed a fast satellite selection algorithm using geometric methods for optimal positioning. | Performance under real-world signal conditions not extensively validated. |
| Kaan et al. [19] | 2023 | It studied LEO-PNT constellation design, evaluating optimization approaches and performance metrics. | May require further empirical validation for specific application scenarios. |
| I.F. Ghoniem et al. [20] | 2020 | Proposed GNSS-LEO orbit optimization for Egypt and the Middle East, analyzing over 100 orbit cases. | Focused on a specific geographic region; applicability to other regions uncertain. |
| Yuta et al. [21] | 2010 | Suggested a metaheuristic optimization method for constellation design in interferometric applications. | Limited by the computational complexity of metaheuristic approaches. |
| W. Xue et al. [22] | 2024 | It studied LEO navigation constellation design considering deployment stages and task requirements. | Solutions for performance degradation issues need further testing. |
| Research Work | Publish Year | Short Description | Limitation |
|---|---|---|---|
| S. Cakaj [23,24] | 2016, 2014 | Developed a mathematical model for LEO coverage belt, identifying optimal orbital altitudes (5633–8177 km) and elevation angles (2°–10°) for maximum coverage area. | Models may not account for dynamic environmental factors or real-time operational constraints. |
| Z. Titus et al. [25] | 2023 | Proposed a mathematical model using Cox point processes to optimize multi-altitude LEO satellite networks, assessing performance via coverage probability, signal strength, interference levels, capacity, and quality of service. | The model's complexity may pose challenges for real-time implementation and scalability. |
| Silvirianti et al. [26] | 2025 | Suggested a Quantum Adaptive Learning (QAL) approach leveraging quantum computing and adaptive learning for coverage optimization in stochastic geometry-based LEO satellite networks. | Quantum computing applications are still emerging; practical implementation may be limited by current technological capabilities. |
| J. Shin et al. [27] | 2021 | Proposed an analytical constellation design for discontinuous regional coverage, introducing an optimal inclination search algorithm to maximize coverage for specific ground regions. | Focused on regional coverage may not address global coverage requirements or dynamic reconfiguration needs. |
| I. Lluch et al. [28] | 2014 | Introduced an optimization approach for satellite-to-satellite coverage, demonstrating that increasing inter-satellite link range beyond 6,000 km yields diminishing returns at LEO altitudes. | The study may not consider advancements in inter-satellite communication technologies or varying orbital dynamics. |
| Miyeon et al. [29] | 2025 | Conducted mathematical analysis on cluster area, Line-of-Sight (LOS) intensity, and Signal-to-Interference Ratio (SIR) thresholds to enhance coverage probability in satellite cluster networks. | The model may require extensive data for accurate predictions and might not adapt well to rapidly changing network conditions. |
| Peng Zong et al. [30] | 2019 | Utilized a genetic algorithm to optimize constellation satellite coverage in one revisit, focusing on regional coverage at defined latitudes and demonstrating that inclinations above 90° can cover Earth's poles. | The approach may not fully address the trade-offs between coverage frequency and resource constraints. |
| Hassan et al. [31] | 2024 | Proposed the integration of Reconfigurable Intelligent Surfaces (RISs) within 6G sub-THz networks to maximize LEO satellite coverage and optimize network performance parameters. | Implementation depends on the maturity of RIS technology and its integration with existing satellite infrastructure. |
| Zhao et al. [32] | 2022 | Developed an autonomous self-healing framework aiming to maximize coverage performance, minimize control efforts for satellite constellation adaptation, and enhance resilience against various threats. | The framework's effectiveness in diverse operational scenarios and its scalability require further validation. |
| Research Work | Year | Short Description | Limitation |
|---|---|---|---|
| Christina et al. [33] | 2023 | Surveyed receiver designs for LEO satellite signals, discussing challenges like Doppler shifts and signal attenuation, and exploring augmentation methods such as Satellite Timing and Location (STL) services. | STL services provide lower accuracy compared to GNSS; augmentation methods may not be globally available. |
| Qian Ning et al. [34] | 2022 | Proposed a system model of shadow fading and rain attenuation in the satellite downlink channel for LEO. Analyzed the application of Non-Orthogonal Multiple Access (NOMA) in LEO satellite communications under rain attenuation and fading, demonstrating improved ergodic capacity. | Performance gains depend on accurate channel state information; practical implementation complexity may be high. |
| JIA Min et al. [35] | 2022 | Investigated inter-satellite link interference in large-scale LEO constellations, analyzing attenuation characteristics and time-frequency distributions. Used simulations to demonstrate noticeable interference in higher frequency links among large-scale LEO satellite constellation systems. | Simulation-based study; real-world validation needed for diverse operational scenarios. |
| Jiawei Liu et al. [36] | 2024 | Proposed an approach for in-orbit calibration of the phase center offsets (PCOs) and code hardware delays of the LEO downlink navigation signal, enhancing signal accuracy. Found that increasing the number of tracking stations and processing periods can improve the formal precision of PCOs and hardware delay. | Requires extensive ground station networks; calibration precision depends on observational data quality. |
| A.K. Dwivedi et al. [37] | 2023 | Studied successive interference cancellation (SIC) and captured model (CM)-based decoding schemes at the ground station to mitigate interference. Derived average outage probability for the CM-based and SIC schemes analytically under high signal-to-noise ratio (SNR), utilized to optimize system parameters for achieving a target outage probability. | Assumes ideal synchronization; real-world asynchronous transmissions may pose challenges. |
| R. Miteva et al. [38] | 2023 | Introduced an overview of how space weather phenomena, such as geomagnetic storms and solar flares, impact satellite operations. Discussed how sequences of geomagnetic disturbances, even if individually weak, can cumulatively lead to significant atmospheric drag, potentially resulting in satellite service disruptions or losses. | Focuses on cumulative effects and may not address immediate mitigation strategies. |
| Radojkovic et al. [39] | 2025 | Presented the impact of gamma-shadowed Ricean fading on the secrecy capacity of LEO satellite-to-ground communications. Analyzed the secrecy performance of a LEO satellite and ground user downlink in the presence of an eavesdropper over gamma-shadowed Ricean fading channels. | Assumes specific fading models; applicability to varying environmental conditions may be limited. |
| Bassel F. Beidas [40] | 2022 | Presented a digital compensation algorithm with immunity to frequency offset, minimizing I/Q imbalance introduced by analog frequency-conversion circuits in LEO satellite systems. | Implementation may require complex calibration; effectiveness under varying hardware conditions needs assessment. |
| Ji Ma et al. [41] | 2022 | Proposed a resilience measure for LEO satellite networks utilizing uncertainty theory to define belief instantaneous availability. Developed an uncertain satellite network evolution model considering various impairments to describe the operating pattern of dynamic LEO and estimate resilience. | Relies on uncertainty theory; may require extensive data for accurate modeling. |
| Zhenghao Zhang [42] | 2024 | Proposed a packet acquisition method using chirp signals to improve detection in weak signal environments and reduce peak-to-average power ratio. | Effectiveness may vary with signal conditions; integration into existing systems requires evaluation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





