Impact of Sharp Soil Interfaces on Solute Transport: Insights from Reactive Tracer Test in a 2D Intermediate-Scale Experiment

1. Introduction

Groundwater remediation has become a critical global concern due to the persistent challenge of aquifer pollution and the growing demand for clean water resources [1,2]. Understanding how contaminants are transported, mixed, and react is essential for the successful remediation of polluted aquifers [3,4]. Among various remediation methods, in situ treatment technologies have attracted significant attention in recent years [5,6] because they offer cost-effective and minimally invasive solutions [7]. In this context, the effective mixing of two solutes is crucial to enhancing the performance of in situ treatments [8,9]. Since mixing governs the interaction between the injected remediation fluids and the contaminated groundwater, improved mixing facilitates mass transfer, accelerates chemical reactions, and ultimately leads to a more efficient remediation process [10,11,12]. However, mixing is frequently hindered in porous media by the inherent structural complexities of natural geological formations, which can result in unexpected behavior [13,14,15]. Sharp soil interfaces constitute an important building block of a wide variety of heterogeneous geological systems, representing abrupt transitions between materials with differing permeability and grain size.[16,17,18]. These interfaces, commonly found at sedimentary layer boundaries, fractured rock formations, and engineered remediation barriers [19,20,21], play a pivotal role in controlling transport and mixing. Advancing a quantitative and comprehensive understanding of plume-interface mixing processes is crucial for optimizing remediation strategies, ensuring that injected agents can effectively interact with contaminants [22,23,24], and for refining predictive models of contaminant transport in subsurface systems [12,25,26].

Research over the past decades has demonstrated that sharp interfaces significantly alter solute transport dynamics [17,27,28]. One of the first experimental works on this topic, conducted by Sternberg [27], revealed that sharp interfaces produce transport behaviors that classical advection-dispersion models cannot accurately represent [29,30,31]. These models assume that dispersion across an interface is a simple weighted average of the properties of both media [32]. However, experimental results show that dispersion adjusts to expected values much faster than predicted, suggesting the presence of an additional mechanism at the interface that accelerates this process [28]. Building upon this, Marseguerra and Zoia [28] investigated solute transport across sharp interfaces between coarse and fine media using the random walk method for particle transport simulations. They observed a discontinuity in concentration profiles when solutes crossed the interface [32,33,34], attributing it to solute accumulation on the coarse side before gradually dispersing into the finer medium. This behavior was further suggested by Berkowitz et al. [17], who, through laboratory column experiments on solute migration in composite porous media, indicated that a conservative tracer moving through a coarse-grained segment encounters resistance when entering a finer medium [35,36]. This results in a "slow release" effect, causing a delayed breakthrough curve and increased dispersion. Similarly, Cortis and Zoia [37] showed that particles crossing an interface between materials with different dispersion properties experience asymmetric random forces. These forces disrupt the symmetry assumed in classical transport models, leading to a delayed and spatially uneven arrival of the solute, which further complicates predictions of solute migration [38].

According to mixing processes, although several studies have focused on understanding the effect of heterogeneity on mixing [39,40,41], few works have specifically addressed the impact of sharp interfaces on the mixing [42]. It is well understood that sharp soil interfaces generate steep transverse concentration gradients [17], which can have significant chemical and biological implications. In such contexts, mixing is most pronounced at the contact zones between regions of differing permeability, where reactions are especially intense along these interfaces [43]. In line with this, Perujo et al. [44] demonstrated that coarse-to-fine transitions facilitate the accumulation and transformation of organic matter at the interface. This transition zone thus becomes a region of enhanced microbial activity, promoting increased biomass growth and organic matter degradation. However, the finer sediments limit biofilm development, which ultimately impacts the efficiency of the overall reaction [45]. Despite these insights, there is still much to understand regarding solute transport behavior and the mixing plume dynamics due to sharp soil interfaces [17,42,46]. Specifically, further investigation is needed to visualize the role of sharp soil interfaces on solute transport, the mixing plume evolution, the impact of interfaces on concentration gradients, as well as their role on mixing efficiency in two and three dimensions. Understanding the role of sharp soil interfaces on solute transport and where mixing is most promoted within each medium will provide valuable information for optimizing remediation strategies and improving our overall understanding of subsurface processes [22,23,24].

As a contribution, this article builds upon the results of a novel laboratory-scale experiment, discussing the impact of sharp soil interfaces in both non-reactive transport and mixing processes. Conservative and reactive transport experiments were conducted in a 2D intermediate-scale horizontal tank composed of a bilayer porous medium with a sharp soil interface. To achieve this, a set of four experiments were conducted, considering four different porous medium configurations (porous media packing)—fine (F), coarse (C), fine-to-coarse (FC), and coarse-to-fine (CF). Conservative tracer tests were conducted to visualize solute pulse evolution and obtain concentration breakthrough curves (BTCs), which characterize non-reactive solute transport behavior. In the reactive experiments, colored products were generated and quantified using pixel-by-pixel calibration, converting light intensities into concentration values. The experimental setup allows to monitor and visualize in real-time the spatiotemporal evolution of the tracer and the mixing plume. In this sense, this work aims to demonstrate that: (i) Transport behavior and mixing processes strongly depend on the flow direction. (ii) The sharp soil interface plays distinct roles in solute transport. (iii) The sharp soil interface influences both solute reactivity and mixing efficiency.

The structure of this article is as follows. The Materials and Methods section describes the experimental setup, the porous medium configurations used, the procedure for the reactive transport experiments and tracer tests, the chemical solutions employed, the image acquisition and processing techniques used to capture the evolution of non-reactive and reactive transport, and the explanation of key variables and metrics used for analysis. The Results and Discussion section presents the main findings, including the analysis and discussion of non-reactive solute transport, the spatiotemporal evolution of the reaction product, longitudinal profiles of the reaction product, and mixing metrics and their corresponding profiles. Finally, the Conclusions section provides a summary of the key insights from the study, emphasizing the impact of sharp soil interfaces in mixing processes and transport behavior.

2. Materials and Method

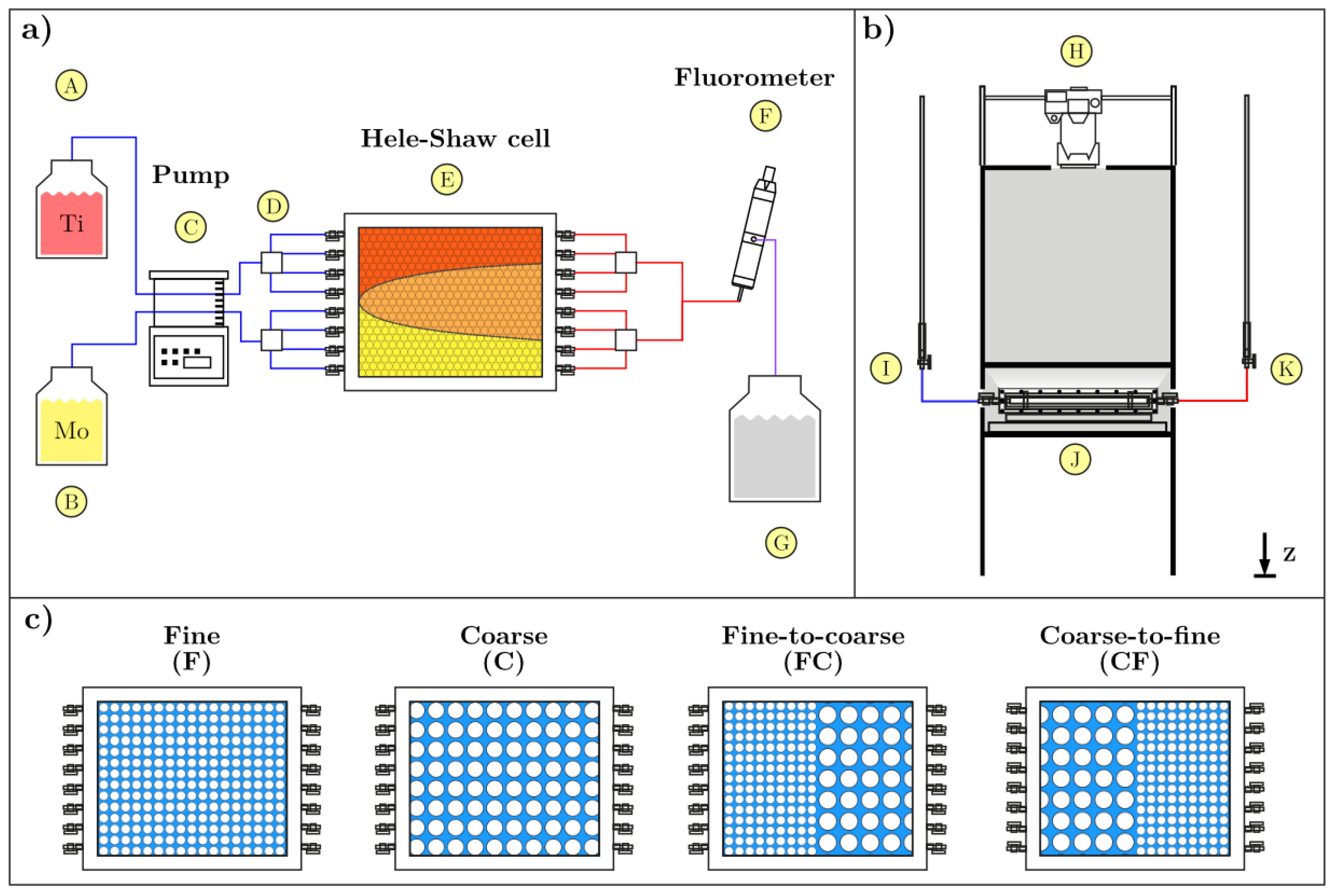
2.1. Experimental Setup

Experiments were conducted in a transparent intermediate-scale horizontal tank made of plexiglass with dimensions of 26 cm in length (L), 20 cm in width (W), and 2 cm in height (H) (refer to Figure 1a). To provide uniform flow conditions, the tank has eight inlet and outlet ports evenly spaced 2 cm apart. All inlet ports are connected to a high-precision multichannel pump (Ismatec IP-N Digital Peristaltic Pump, 24 channels, Pressure Lever Cartridge; 230 VAC). Inlet ports are divided into two groups by means of two 4-channel flow cells to allow the injection of two different fluids, in parallel, through the inlet face of the tank. Outlet ports are ultimately connected to a single tube that freely discharges into a waste container at atmospheric pressure. The height of this tube provides a fixed constant head boundary condition during the experiments. When required for the conservative tracer test, the outlet tube is connected to an Albillia FL24 fluorimeter (see Figure 1a). A pair of piezometers are installed, one at the inlet and the other at the outlet of the tank to measure the effective hydraulic conductivity of the porous medium. The experiments were carried out in a dark room to prevent interference from external light (Figure 1b). Images were captured during both reactive and conservative tracer tests using a Nikon D7100 camera equipped with a Tamron SP AF 17-50mm F/2.8 XR Di II LD Aspherical (IF) Model A16 lens. Transmitted light was used for both experiments, with an LED light placed underneath the tank. Continuous monitoring was performed throughout the experiment, with a fluorometer recording data every second (BTC) and photographs taken every 30 seconds.

2.2. Porous Media Configurations

The horizontal tank was packed in four different porous medium configurations (refer to Figure 1c): a) fine (F), using 1 mm glass beads; b) coarse (C), using 2 mm glass beads; c) fine-to-coarse (FC), with a vertical sharp interface transitioning from 1 mm to 2 mm glass beads; and d) coarse-to-fine (CF), with a vertical sharp interface transitioning from 2 mm to 1 mm glass beads. In the configurations with the sharp soil interface, the interface was positioned at the midpoint of the tank at $x\approx 13$ cm. This vertical interface was created using a 0.1 mm thick methacrylate bar. During packing, the bar was inserted in the middle of the tank to separately distribute the fine and coarse grains, and was carefully removed before sealing the tank. In each porous medium configuration, the tank was wet packed with deionized water (Milli-Q), ensuring that the tank was always filled with water before adding the glass beads. This step was crucial to maintain saturated conditions and prevent the incorporation of air bubbles into the system.

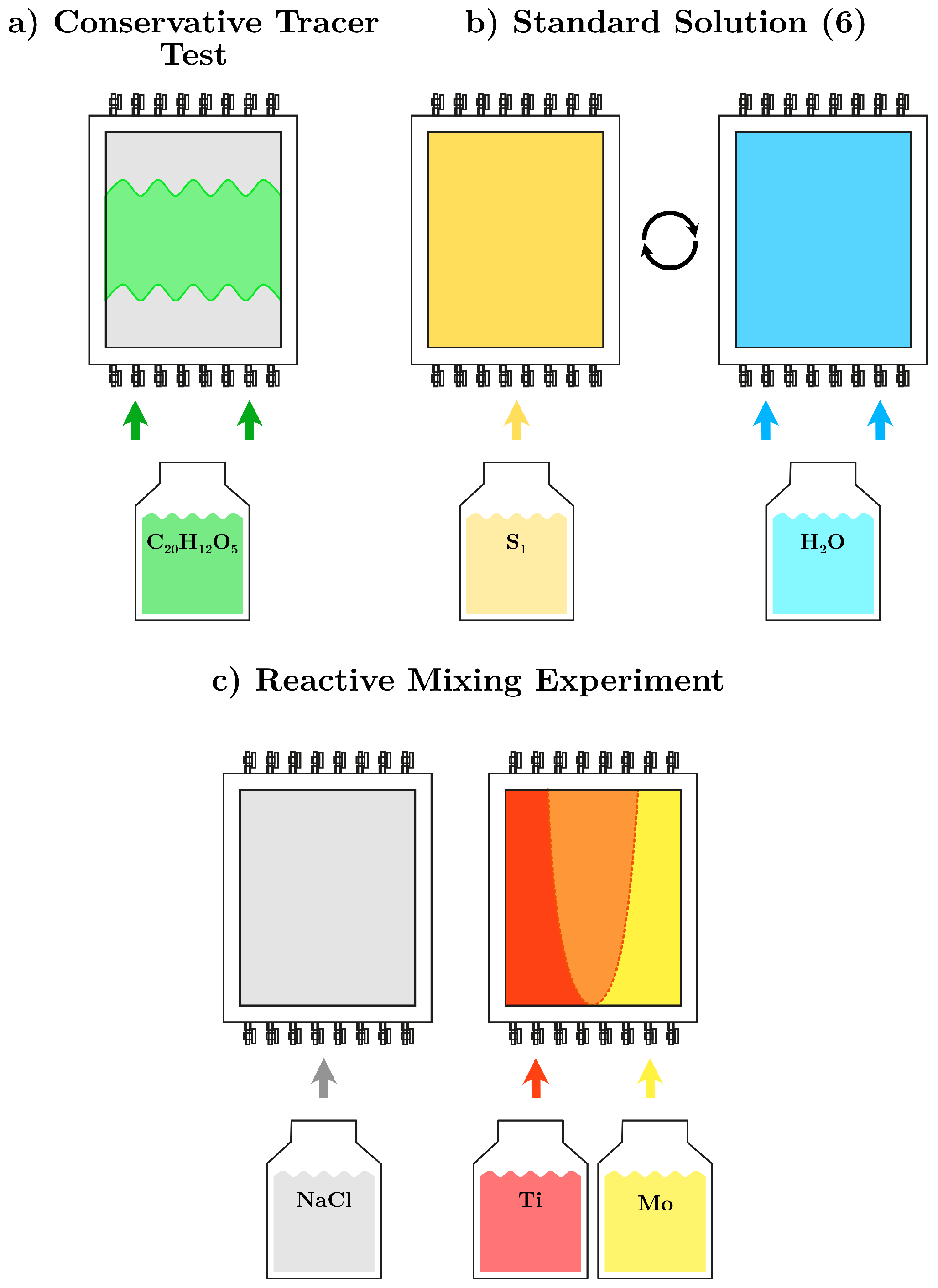
2.3. Reactive Transport Experiments and Tracer Tests

For each porous medium configuration, the experiment was divided into three stages (Figure 2): a) The injection of a conservative tracer test pulse (Figure 2a). This stage was conducted with the purpose of characterizing non-reactive solute transport. This consisted of measuring concentration breakthrough curves (BTCs) at the tank outlet and recording images that show the spatio-temporal evolution of the pulse. This test involved injecting a fluorescein pulse (0.05 mg/L) at a constant flow rate (Q=7.96 ml/min) for 10 minutes. Following the injection, deionized water was injected for 120 minutes to flush the tracer; b) The injection of six standard solutions with known concentrations of Tiron Molybdate (${\mathrm{MoTi}}_2^{-4}$) (Figure 2b). In this stage, six light intensity images of Tiron Molybdate at a constant steady-state concentration were recorded with the purpose of establishing a clear relationship between concentration and color intensity pixel-wise. Each standard solution was sequentially injected into the tank, starting from the lowest concentration (C₁) to the highest (C₆). Each was injected for 1 hour and 30 minutes before imaging. The tank was flushed with distilled water for another hour and a half between injections; c) The simultaneous injection of Molybdate solution ($W_1$) and Tiron solution ($W_2$) through the two separate groups of inlet ports. This setup allows the chemical solutions to uniformly enter into the porous medium through half of the tank’s inlet area, promoting interaction and mixing in the midsection of the tank (Figure 2c). This stage defines the reactive transport experiment, aimed at investigating the role of the sharp interface on solute transport. The total injected flow rate (Q) was 7.96 ml/min. This total flow was equally distributed between the two 4-channel flow cells (Q/2), with each receiving a flow rate of 3.98 ml/min. At the tank outlet, the constant head imposed was 90 cm above tank elevation. The reactive transport experiment lasted 3 hours to ensure that concentrations reach the steady state solution. To prevent density issues, since both $W_1$ and $W_2$ had higher densities than distilled water, the tank was pre-saturated with a 0.4363 M NaCl solution before conducting the reactive transport experiment.

Transport experiments were conducted under advection dominated flow conditions (the properties of each porous medium configuration are presented in Table 1). The grain Péclet number for each porous medium configuration was calculated using $\mathrm{Pe}=vd/D$, where, v represents the fluid velocity (calculated from the total inflow rate Q, the cross-sectional area A and the porosity $\varphi$ through $v=Q/A\varphi$), d represents the diameter of the glass beads, and D represents the molecular diffusion coefficient of water. The Reynolds number was calculated using $\mathrm{Re}=vd/\nu$, where $\nu$ is the kinematic viscosity of the fluid. The kinematic viscosity is calculated as $\nu =\mu /\rho$, where $\mu$ is the dynamic viscosity and $\rho$ is the fluid density. In our experiment, the dynamic viscosity of water was $\mu =1.003\times {10}^{-3}\mathrm{kg}/(\mathrm{m}·\mathrm{s})$ (estimated for a temperature of 20 °C), and the density of water $\rho =1.0136{\mathrm{kg}/\mathrm{m}}^3$ (measured for water with NaCl), resulting in a kinematic viscosity of $\nu =9.91\times {10}^{-7}{\mathrm{m}}^2/\mathrm{s}$. The hydraulic conductivity (K) for each porous medium configuration was obtained through Darcy’s law from the piezometric head difference of the tank ($\Delta h$). The porosity ($\varphi$) for each porous medium configuration was determined by converting the weight of the glass beads used to fill the tank into volume.

2.4. Chemical Solutions

The reactive transport experiment was conducted using a colorimetric reaction involving two solutions: $W_1$, containing 0.01 M (mol/L) of sodium molybdate dihydrate (MoNa₂O₄$·2$H₂O), and $W_2$, containing 0.02 M of Tiron (1,2-dihydroxybenzene-3,5-disulfonic acid, Ti-2) (refer to Table 2). This reaction resulted in the formation of Tiron Molybdate (${\mathrm{MoTi}}_2^{-3}$ and ${\mathrm{MoTi}}_2^{-4}$) through the following reaction scheme:

$$M{o}^{-1}+T{i}^{-2}\rightleftharpoons MoT{i}^{-3}+2H_{2}O,$$

(1)

$$MoT{i}^{-3}+T{i}^{-2}\rightleftharpoons MoT{i}_2^{-4}+O{H}^{-}+H_{2}O.$$

(2)

During this process, the colorimetric reaction occurs almost instantaneously, with ${\mathrm{MoTi}}_2^{-4}$ being the colorimetric species [48] and thereby the only component quantified in the image analysis. The color of ${\mathrm{MoTi}}_2^{-4}$ varies from yellow to dark red. The preparation of the solutions used in the mixing experiment followed the chemical protocol described by Oates and Harvey [49] and Bertran Oller [42], with slight modifications in this study. To prepare the molybdate solution $W_1$ and the Tiron solution $W_2$, a buffered solution of succinic acid and NaOH was first prepared to maintain the appropriate pH range for the colorimetric reaction. Since ${\mathrm{MoTi}}_2^{-4}$ remains stable within a pH range of approximately 6.6–7.5, it was essential to ensure that the pH remained within this range during preparation. Finally, Ti and Mo (${\mathrm{MoNa}}_2$O₄) were added to their respective buffer solutions to obtain $W_2$ and $W_1$. To further balance the solutions, NaCl was added to the molybdate solution $W_1$ to compensate for the slightly higher density of the Tiron solution $W_2$. For the quantification of ${\mathrm{MoTi}}_2^{-4}$, a visual calibration was created based on the relationship between the image color intensity and the concentration of the generated product. To achieve this, several standard solutions were prepared by combining different volumes of a 0.05 M Ti stock solution and a 0.025 M molybdate stock solution, both buffered to pH 6.6 with 0.13 M succinate and 0.26 M NaOH (refer to Table 2). In addition to a blank, six standard solutions were prepared with concentrations of 0.0002 M, 0.0011 M, 0.0029 M, 0.0042 M, 0.0059 M, and 0.0090 M (refer to Table 3). These solutions were then used to create a calibration curve, which allowed the interpolation of product values based on the observed color. To perform the conservative tracer test and capture the breakthrough curves for each configuration, a 0.05 mg/L fluorescein solution was used, prepared with distilled water.

2.5. Image Acquisition and Processing

During experiments, the camera continuously captured 24-bit RGB color images to record the spatio-temporal evolution of the solute plume in each porous medium configuration (${\mathrm{MoTi}}_2^{-4}$ or fluorescein). The camera settings were manually adjusted and kept constant throughout the experiment, with a relative aperture of f/2.8, a shutter speed of 1/30 seconds, and an ISO setting of 200. The ${\mathrm{MoTi}}_2^{-4}$ images were processed using the OpenCV library in Python [50,51], following the methodology proposed by Bertran Oller [42]. The concentration of ${\mathrm{MoTi}}_2^{-4}$ was determined pixel-by-pixel following the method outlined by Castro-Alcalá et al. [43], where the light intensity of each pixel was correlated with those of the standard solutions. This was done using piecewise linear interpolation, with the known concentrations derived from standard solution images obtained prior to the reactive transport experiment. The processing workflow consisted of the following steps: a) Converting both the experimental images and the standard images obtained from each experiment from the raw format (NEF) to 16-bit TIFF images; b) Cropping the images to focus on the region of interest (ROI) with a resolution of 3975 x 3000 pixels, each measuring 0.0066 mm²; c) Centering all images from the reactive transport experiment and the standard solutions to the same (x, y) coordinates to ensure proper interpolation; d) Subtracting the background $I_{\mathrm{bg}}$ (chosen for each porous medium configuration) from all standard and experimental images:

$${\overline{I}}_{\exp }(x,y,t)=I_{\exp }(x,y,t)-I_{\mathrm{bg}}(x,y),$$

(3)

$${\overline{I}}_i(x,y,t)=I_i(x,y,t)-I_{\mathrm{bg}}(x,y),$$

(4)

where $I_i(x,y,t)$ is the light intensity image of the ith standard solution, and $I_{\mathrm{bg}}(x,y)$ is the light intensity of a blank image obtained under steady-state flow conditions prior to each experiment; e) Channel selection, considering only the green band $I_i^{\ast }(x,y,t)$ and $I_{\exp }^{\ast }(x,y,t)$ for the ith standard and experimental images, respectively. The green channel was chosen because it provided an accurate differentiation of the intensities for each standard solution recorded. e) Calculating the concentrations $C(x,y,t)$ using a piecewise linear interpolation model that relates the green band intensities from the experiment $I_{\exp }^{\ast }(x,y,t)$ with those of the standard solutions $I_{\mathrm{std}}^{\ast }(x,y)$ and their corresponding concentrations $C_i$. The concentration is calculated as follows:

$$C(x,y,t)=C_i+{\displaystyle \frac{C_{i+1}-C_i}{I_{i+1}^{\ast }(x,y)-I_i^{\ast }(x,y)}}\left(I_{\exp }^{\ast }(x,y,t)-I_i^{\ast }(x,y)\right),$$

(5)

where $I_{\exp }^{\ast }(x,y,t)$ lies in the range $[I_i^{\ast }(x,y),I_{i+1}^{\ast }(x,y)]$, and the $I_i^{\ast }(x,y)$ values for each calibration point represent the green band intensity for each pixel in the ith standard image. The concentration $C_i$ is the known concentration associated with the ith standard solution.

2.6. Key Variables and Metrics for Analysis

To evaluate the results, we will use key variables and metrics that characterize transport behavior and mixing processes within the system. The transverse extent of the product plume ($ϵ$) defines the influence of mixing along the transverse direction to mean flow. For each porous medium configuration, the transverse extent $ϵ$ was determined by binarizing the steady-state plume image using a concentration threshold of $C(x,y,t)={10}^{-5}\mathrm{M}$, which was established through visual calibration to accurately define the plume edges. After binarization, the plume extent was quantified by measuring the maximum transverse distance (in the y-direction) for each position along the x-axis. In the binary images, black pixels represented the plume region (above threshold), while white pixels indicated the absence of the solute product. From this, an apparent transverse dispersivity (${\alpha }_T$) was calculated using the relationship between the transverse extent of the plume and transverse dispersion reported by De Simoni et al. [52] in homogeneous porous media for the same problem. This can be written as

$${\alpha }_T={\displaystyle \frac{{ϵ}^2}{24x}}.$$

(6)

Two other mixing metrics will be also used to analyze the results. On the one hand, the total mass produced by the reaction, i.e., the total mass of ${\mathrm{MoTi}}_2^{-4}$ (g), was calculated for each configuration by integrating the concentration $C(x,y,t)$ (mol/L) of ${\mathrm{MoTi}}_2^{-4}$ throughout the volume of the domain (V) (see Table 1):

$$M\left(t\right)=\varphi {\int }_{V}C(x,y,t)dV.$$

(7)

This formulation assumes a uniform porosity $\varphi$ across the entire domain. However, in the C–F and F–C configurations, the porous medium is composed of two distinct materials with different porosities. In such cases, using a single porosity value leads to an inaccurate estimation of the total reacted mass. To account for the spatial variation in porosity, the calculation must be adjusted by including the porosity inside the integral. Specifically, the domain is divided into two subdomains: $V_1$ and $V_2$, corresponding to the coarse and fine materials with porosities ${\varphi }_1$ and ${\varphi }_2$, respectively (see Table 1). The corrected expression for the total mass becomes:

$$M\left(t\right)={\int }_{V_1}{\varphi }_1·C(x,y,t)dV+{\int }_{V_2}{\varphi }_2·C(x,y,t)dV.$$

(8)

Concentrations in mol/L were converted to g/L using the molecular mass of ${\mathrm{MoTi}}_2^{-4}$, 841.37 g/mol, based on $M_{\mathrm{Mo}}=175.95$ g/mol and $M_{\mathrm{Ti}}=332.21$ g/mol. On the other, mixing will also be characterized through the scalar dissipation rate, defined by Le Borgne et al. [40] as

$$\chi \left(t\right)={\int }_V{C}^2(x,y,t)dV.$$

(9)

In both cases, the unit volume was defined as the product of the pixel area in the $x,y$-plane and the tank height W as $V_{\mathrm{pixel}}=W\Delta x\Delta y$. In addition, results will analyze the longitudinal distribution of the reaction product, which provides insight about the temporal evolution of the longitudinal front of the product plume. To do this, we will use the vertical average of concentrations along the tank width, defined as

$$\overline{C}(x,t)={\displaystyle \frac{1}{W}}{\int }_0^{W}C(x,y,t)dy.$$

(10)

Results will be presented using a dimensionless time expressed as pore volume with respect to half of the volume of the tank ($V/2$). Let us denote as $V_A$ the volume of the first half of the tank and $V_B=V-V_A$ the remaining volume. In our experiment, A can be one material type and B a different one. The water residence time in $V_A$ and $V_B$ can be estimated as $t_A^{\ast }=V_A{\varphi }_A/Q$ and $t_B^{\ast }=V_B{\varphi }_B/Q$, respectively. From this, the pore volume is defined as

$$P_V\left(t\right)=\left\{\begin{array}{cc}t/t_A^{\ast },\hfill & \mathrm{if}t<t_A^{\ast },\hfill \\ 1+(t-t_A^{\ast })/t_B^{\ast },\hfill & \mathrm{if}t\ge t_A^{\ast },\hfill \end{array}\right.$$

(11)

This way, when $P_V=1$ the injected water has occupied the first half of the porous medium, and when $P_V=2$ the injected water has occupied the entire porous medium.

3. Results and Discussion

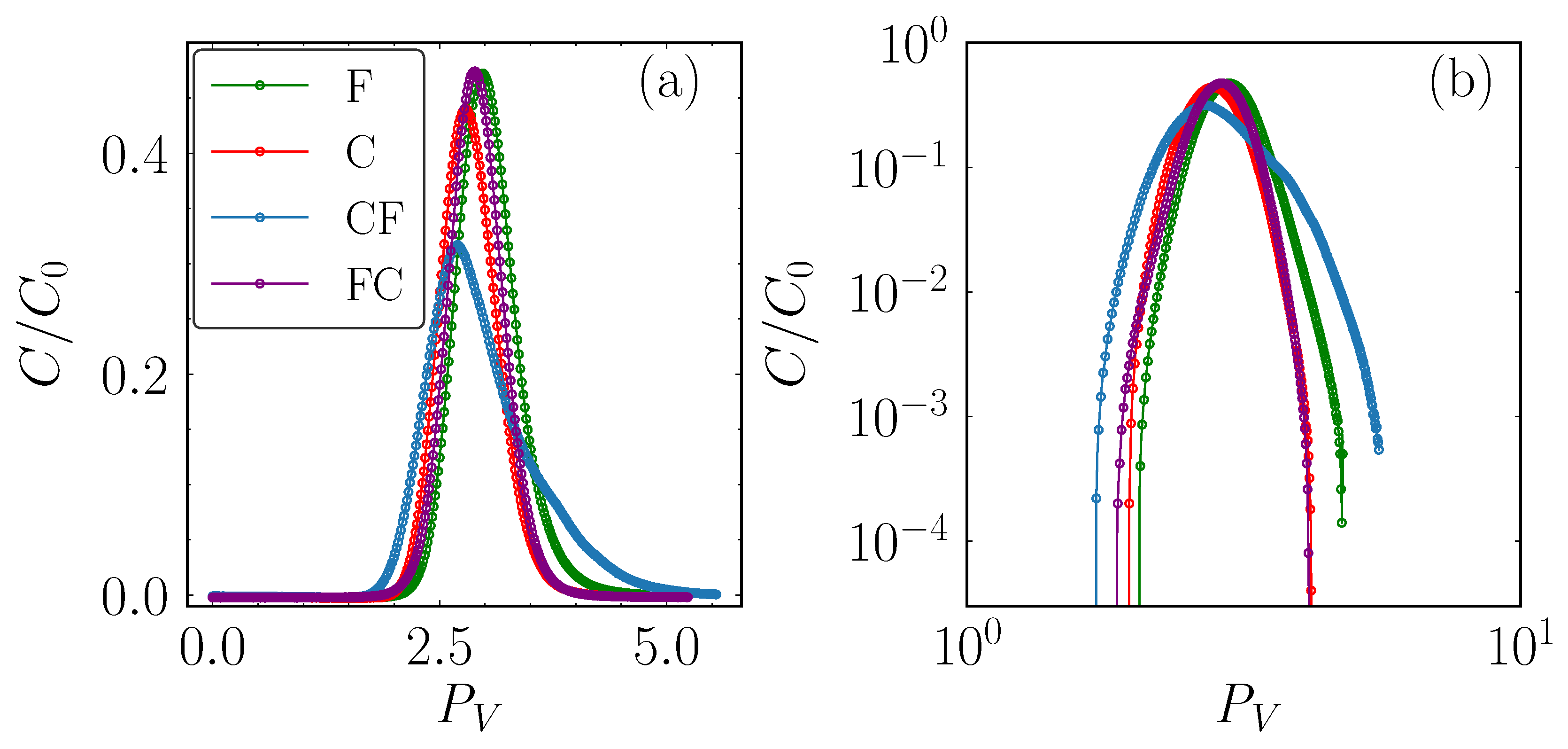
3.1. Non-reactive Solute Transport

The impact of the sharp soil interface was first evaluated by analyzing the behavior of the breakthrough curves (BTCs) of the conservative solute pulse obtained for each porous medium configuration and its spatiotemporal evolution through a series of images, as shown in Figure 3 and Figure 4. Figure 3(a) presents the BTCs in terms of normalized concentration (${\mathrm{C}/\mathrm{C}}_0$) and pore volumes $P_V$. For a closer look at the arrival and tailing, they are also shown on a logarithmic scale in Figure 3(b). The results obtained from the non-reactive transport experiments demonstrate a clear direction-dependent transport behavior, which aligns with previous experimental observations [17,46,53]. The BTCs for the coarse (C) and fine (F) porous media exhibit Fickian-Gaussian behavior, a typical characteristic of homogeneous porous systems. When comparing the BTCs, the coarse medium (C) shows an earlier arrival, a lower peak, and a faster tail exit compared to the fine one (F), in line with theoretical expectations [54]. The BTC of the fine-to-coarse (FC) medium also exhibits Gaussian behavior. In Figure 3(a), it can be observed that both the arrival time and the tailing behavior are similar to those of the coarse medium (C), while the peak value is similar to that of the fine medium (F). This suggests that the fine-to-coarse (FC) porous medium behaves as if it were a single homogeneous porous medium, incorporating characteristics of both media; however, previous experiments have indicated that this behavior may depend on the flow rate [55]. In contrast, the BTC obtained for the coarse-to-fine (CF) medium exhibits an asymmetric, non-Fickian behavior, consistent with the experimental results reported by Berkowitz et al. [17]. It presents an early arrival, a low peak value and a long tail typical of BTCs obtained from porous media with mass transfer processes [56,57].

The impact of the sharp interface on solute transport is clearly observed through the spatiotemporal evolution of the solute pulse. Previous solute transport experiments only captured breakthrough curves (BTC), limiting the ability to fully visualize transport processes at the interface [17,53]. In the present study, three key moments are identified for both the fine-to-coarse (FC) and coarse-to-fine (CF) porous medium configurations: just before the plume front reaches the interface ($P_V=1$), when the plume front is at the interface ($P_V=1.4$), and just after the plume tail exits the interface ($P_V=1.8$). In the fine-to-coarse (FC) porous medium configuration, before crossing the interface (Figure 4a), the pulse presents a relatively regular front, with a slight tendency to develop more rapidly on the upper side of the tank. As it passes through the interface (Figure 4b), this tendency becomes more pronounced. When the pulse passes almost through the interface, it begins to resemble its previous shape. After completely crossing the interface (Figure 4c), the pulse does not show significant variation, maintaining a shape similar to what it appeared before crossing the interface. On the other hand, in the coarse-to-fine (CF) porous medium configuration, a slight tendency for the pulse to move faster along the bottom side of the tank is observed before reaching the interface (Figure 4d). Upon reaching the interface (Figure 4e), this tendency becomes more pronounced as the pulse shows a strong inclination to develop along the bottom side of the tank, forming small-scale preferential flow channels, a phenomenon reported in Fine-scale heterogeneity of alluvial aquifers [58,59]. The upper side of the pulse experiences a significant delay, resulting in a pulse that no longer resembles its previous shape after passing through the interface (Figure 4f). The pulse becomes distorted, adopting an asymmetrical sigmoidal form.

The results obtained from the non-reactive transport experiments demonstrate that the sharp interface play a different role in transport behavior. In the fine-to-coarse (FC) porous medium configuration, the breakthrough curve (BTC) display a Gaussian distribution, suggesting that the entire medium behaves as a single, homogeneous porous system. The BTC combines features of both porous materials: the arrival time is similar to that observed in the coarse medium BTC, while the peak concentration closely aligns with the BTC from the fine configuration. Regarding the role of the sharp interface, a smooth transition in transport properties is observed, suggesting that the interface apparently acts as a continuous boundary, allowing solute transport to occur as if through a homogeneous medium. In contrast, in the coarse-to-fine (CF) configuration, the resulting breakthrough curves (BTCs) exhibit strong non-Fickian features which align with previous experimental results obtained by Berkowitz et al. [17], including an apparent double peak and an extended tail, which suggests that the coarse-to-fine (CF) porous medium behaves like a dual-permeability system with the interface limiting the mass transfer [6,38]. Visual analysis of the tracer shows that the sharp interface acts as a hydraulic barrier. When the solute pulse reaches the transition, it appears to collide with a wall, which distorts the flow field as it crosses into the fine porous material. This distortion forces the solute pulse to redistribute through localized preferential flow paths.

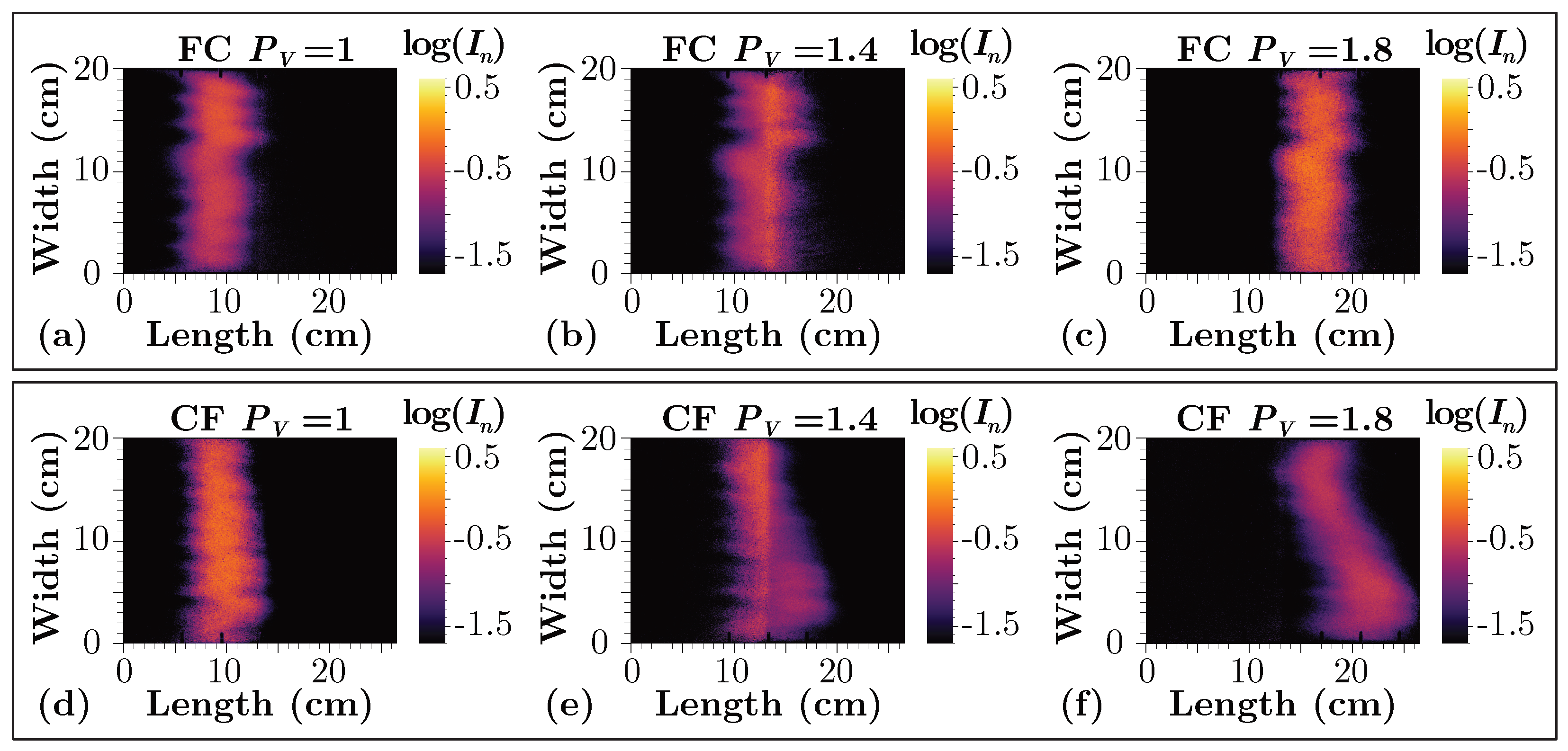
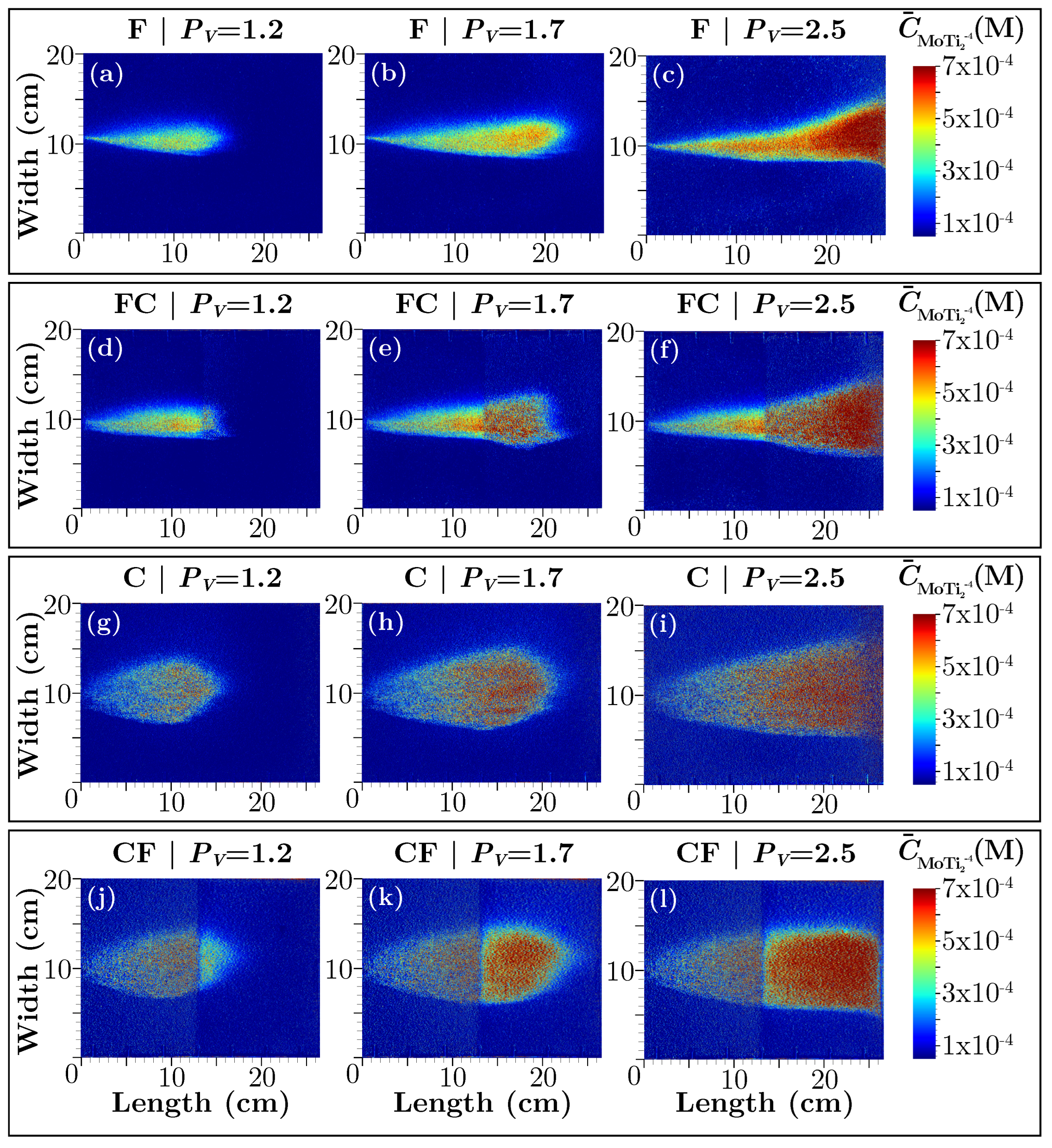
3.2. Spatiotemporal Evolution of the Reaction Product

We now examine the spatiotemporal evolution of the reaction product plume through a selected series of three images for each porous medium configuration, capturing different stages: at the interface ($P_V=1.2$), after passing through it ($P_V=1.7$), and upon reaching a steady state ($P_V=2.5$), as shown in Figure 5. Upon comparing all cases, we immediately observe that the morphology of the reaction product plume varies depending on the direction, acquiring different transverse extents based on the grain size, which aligns with previous experimental results [60,61]. In the fine (F) medium, in Figure 5(a) the plume initially exhibits an elliptical shape $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 4\times {10}^{-4})$, elongating and widening at the front as it progresses (Figure 5b). By the third stage (Figure 5c), it adopts a final horn-like form, characterized by concave edges, a narrow initial section, and a wider final shape $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 7\times {10}^{-4})$. In the fine-to-coarse (FC) medium, in Figure 5(d) the plume also begins with an elliptical shape $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 4\times {10}^{-4})$. As it advances into the coarse medium (Figure 5e), it expands transversely, adopting a significantly greater transverse extent than it had in the fine medium. In the final stage (Figure 5f), the plume exhibits a narrow shape in the fine medium, transitioning into a much wider form, ultimately resembling a funnel-like shape $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 7\times {10}^{-4})$. In the coarse (C) medium, the plume initially reaches a much greater width than in the fine medium $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 5\times {10}^{-4})$, associated with increased transverse dispersion (Figure 5g). As it advances, it maintains convex edges and an overall oval shape. In the final stage (Figure 5i), the plume develops a bell-like form, adopting a significantly greater thickness than in the fine-grained medium $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 7\times {10}^{-4})$. In the coarse-to-fine (CF) medium, the plume initially presents a thickness similar to that in the coarse medium $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 5\times {10}^{-4})$ but ceases to spread laterally upon entering the fine medium, maintaining a constant thickness. After crossing the interface, it adopts a rectangular form with straight edges $({\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)\sim 7\times {10}^{-4})$, eventually transitioning into a bullet-like shape in the final stage (Figure 5l).

The results indicate that the shape of the reaction product plume is direction-dependent and. Grain size governs dispersion [60,61], which in turn determines the transverse extent of the mixing plume [62,63,64,65]. This implies that in coarse media, the transverse extent is greater than in fine media, as previously reported by Sternberg [27]. Consequently, the sharp interface plays a different role in shaping the morphology of the plume depending on the direction: in the fine-to-coarse (FC) configuration, the interface enhances lateral spreading due to increased dispersion in the coarse region, while in the coarse-to-fine (CF) configuration, it restricts lateral spreading, resulting in a constant uniform plume width.

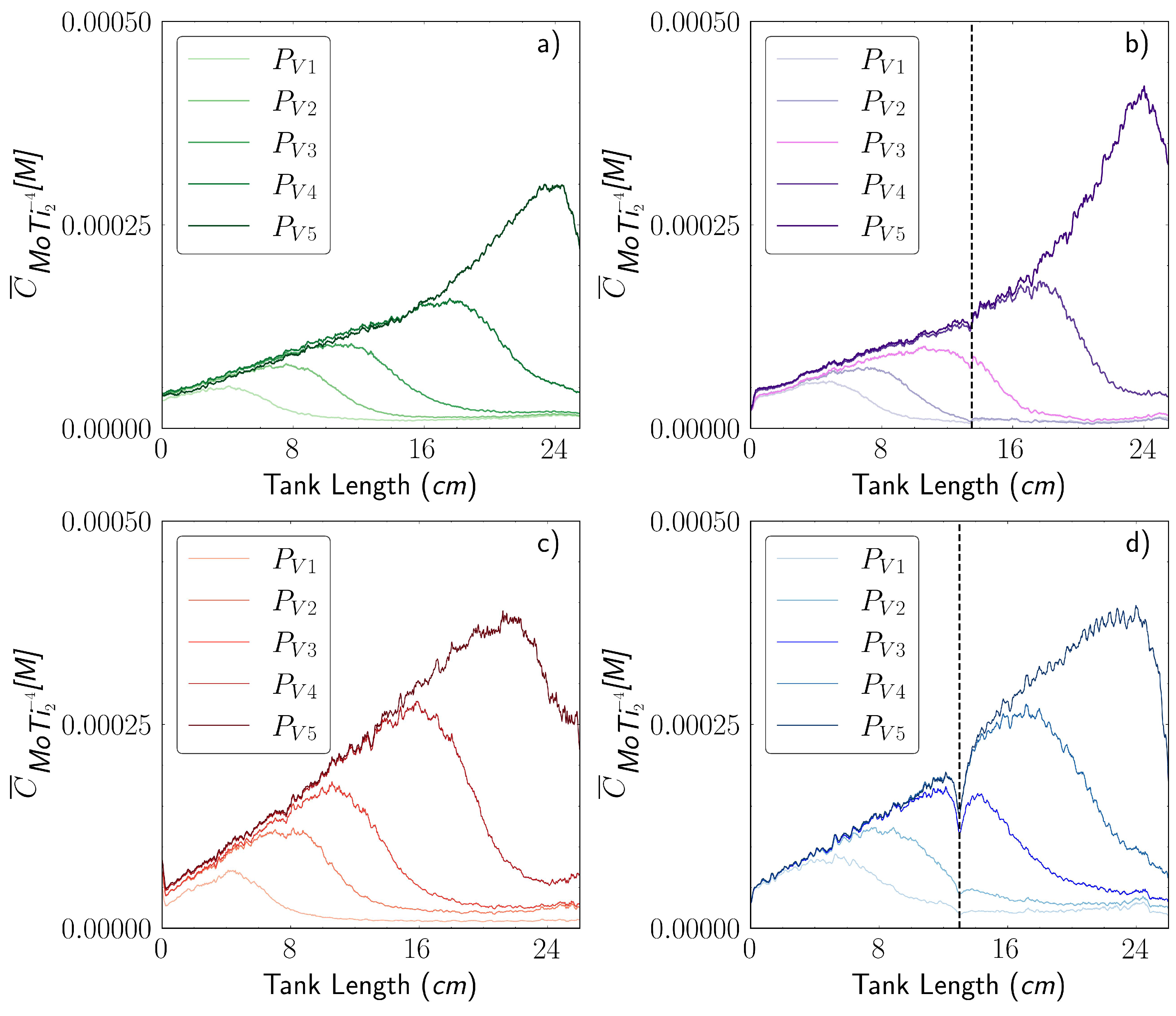
3.3. Longitudinal Profiles of the Reaction Product

The effect that sharp soil interfaces have on reactive transport and mixing processes can be analyzed in greater detail by examining the temporal evolution of the longitudinal distribution of the reaction product. Figure 6 shows the longitudinal profiles of ${\overline{\mathit{C}}}_{{\mathrm{MoTi}}_2^{-4}}\left(M\right)$ concentrations for each porous medium configuration at five different times $P_{V_1}$= 0.7, $P_{V_2}$= 1, $P_{V_3}$= 1.5, $P_{V_4}$= 2, y $P_{V_5}$= 2.8, illustrating the temporal evolution of the reaction product front along the tank length. The most notable result is that the reaction product encounters anomalous resistance when crossing the interface between coarse and fine material. This effect is much less pronounced in the fine-to-coarse (FC) configuration when the direction of flow is reversed. To analyze this behavior, we begin with the fine-to-coarse (FC) configuration, as shown in Figure 6(b). Initially, the concentration profiles follow a trend similar to that of the fine medium ($P_{V_1}=0.7$, $P_{V_2}=1$). However, at $P_{V_3}=1.5$, a marked discontinuity appears in the concentration profile. Before reaching the interface, the concentration gradually decreases, but upon arrival at the transition zone, it suddenly drops, followed immediately by a significant jump in concentrations. One possible explanation for this behavior comes from the numerical simulations of Leij et al. [33], who demonstrated that concentration discontinuities can result from the way boundary conditions are defined in systems with differing porous media. In their model, a constant solute concentration is maintained in the fine porous layer—representing a so-called first-type boundary condition, commonly used in solute injection experiments. At the interface between the two media, however, they apply a third-type boundary condition, in which the solute flux is governed by both the flow velocity and the transport properties of the medium. The inconsistency between these boundary conditions at different locations in the system leads to a nonuniform redistribution of the solute near the interface, which may account for the concentration jumps observed in our experimental data. At later times, specifically $P_{V_4}=2$ and $P_{V_5}=2.8$, the concentration profiles reach significantly higher values (${\overline{\mathit{C}}}_{{\mathrm{MoTi}}_2^{-4}}\sim 4\times {10}^{-4}\mathrm{M}$) than those observed in the fine medium at equivalent times, suggesting enhanced mixing upon entering the coarse medium.

In the coarse-to-fine (CF) configuration (Figure 6d), the profiles of the reactive product at times $P_{V_1}=0.7$ and $P_{V_2}=1$ exhibit behavior similar to that of the coarse medium (C). However, at $P_{V_3}=1.5$, a discontinuity in concentration is also observed. Initially, the profile follows a trend consistent with that of the coarse medium, but as it approaches the interface, the concentration drops sharply to very low values—lower than those observed in the fine-to-coarse (FC) configuration. However, contrary to previously reported one-dimensional results [17,28,37], this asymmetric anomalous resistance to crossing the interface does not produce solute accumulation behind the interface in the coarse to fine (CF) configuration. After the initial drop, the concentrations begin to increase again, but in a gradual manner, rather than the abrupt jump observed in the FC case. For times $P_{V_4}=2$ and $P_{V_5}=2.8$, the sharp drop in concentration remains evident and can also be observed in the longitudinal profiles. Following this, the concentrations gradually recover and eventually reach similar trend to those observed in the coarse medium.

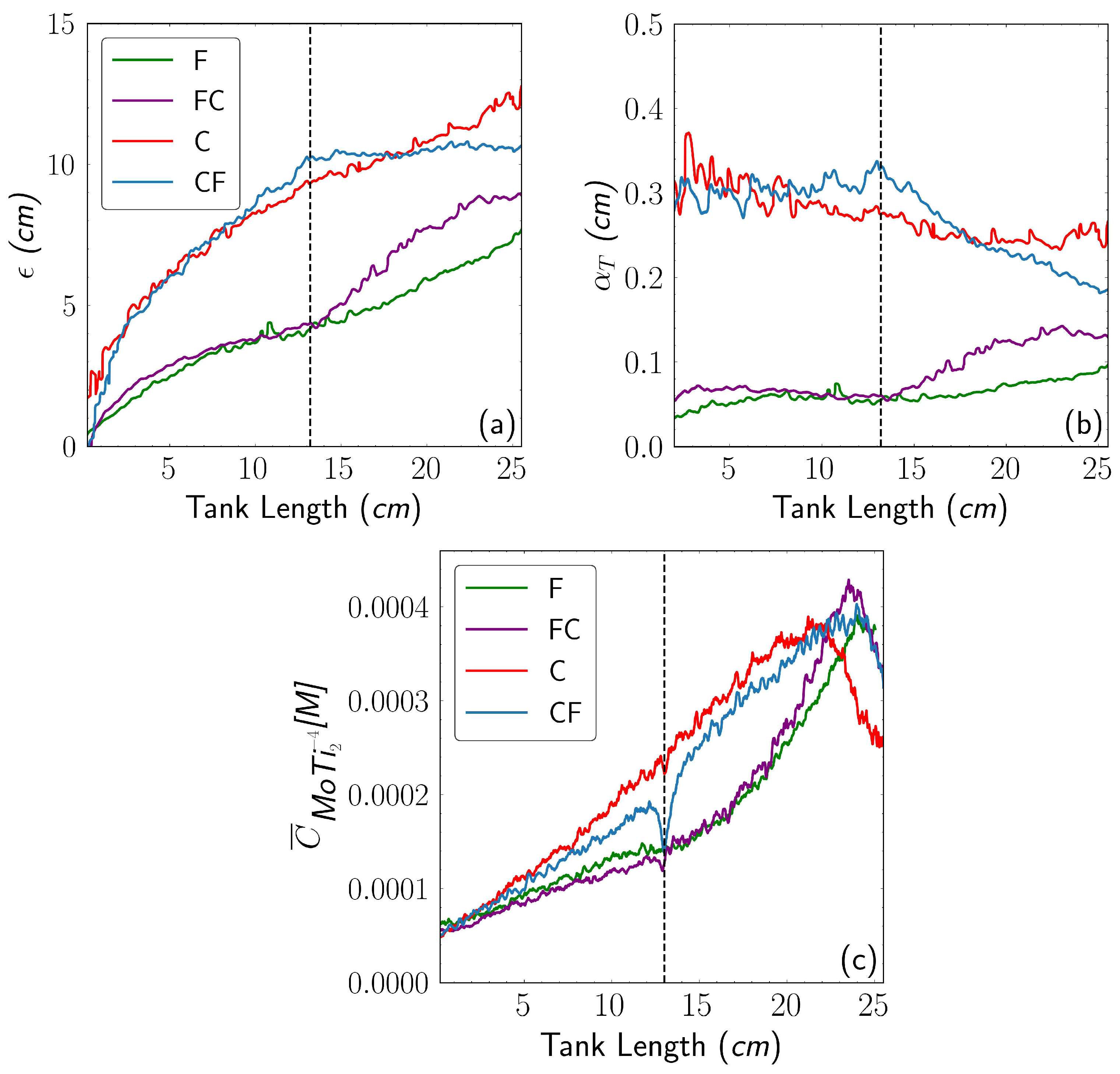
3.4. Mixing Metrics and Profiles of the Reaction Product

To further investigate the impact of the sharp soil interface on the reactive product concentration, we jointly analyze the transverse extent of mixing ($ϵ$), the apparent transverse dispersivity (${\alpha }_T$), and the longitudinal concentration profile ($\overline{C}$). These metrics allow us to characterize the behavior of the solute plume as it crosses the interface under each porous medium configuration. Our results shows an unexpected significant enhancement of the transverse spread of the reaction product in the coarse-to-fine (CF) configuration with a slow release in the fine material —an effect that is not observed in the fine-to-coarse (FC) configuration and cannot be explained by standard modeling approaches based on Fickian flux continuity and the advection-dispersion equation. We summarize the evidence supporting this behavior below.

• In the coarse-to-fine (CF) porous medium configuration, the transverse extent ($ϵ$) initially follows a similar trend to that of the coarse medium ($ϵ>2\mathrm{cm}$) (Figure 7a); however, it surprisingly increases just before reaching the interface ($ϵ>10\mathrm{cm}$), indicating an unexpected greater transverse dispersion of the plume. After crossing the interface, the transverse extent ($ϵ$) stabilizes ($ϵ\sim 10.5\mathrm{cm}$) and remains constant until the end of the tank. Similarly, the apparent transverse dispersivity (${\alpha }_T$) starts with values similar to those obtained in the coarse (C) porous medium (${\alpha }_T\sim 0.3\mathrm{cm}$) (Figure 7b), but as the interface is approaching, the value significantly increases to about ${\alpha }_T\sim 0.32\mathrm{cm}$. Beyond this point, the apparent transverse dispersivity (${\alpha }_T$) decreases linearly, finishing at roughly $0.2\mathrm{cm}$. Regarding the longitudinal concentration profile ($\overline{C}$), a clear discontinuity is observed, reaching its minimum value at the sharp interface (${\overline{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(\mathrm{M}\right)\sim 1.5\times {10}^{-4}$); see Figure 7(c). Afterward, the concentration begins to rapidly rise again, although the values remain significantly lower than those observed in the coarse medium.
• In the fine-to-coarse (FC) configuration, the transverse extent of the reaction product plume ($ϵ$) exhibits a dual behavior (Figure 7a), with an inflection point at the interface ($\mathrm{length}=13\mathrm{cm}$) where the curve abruptly dips before rising in a sigmoidal manner. From the interface to the end of the tank, the transverse extent ($ϵ$) remains significantly larger than in the fine medium, ultimately reaching a final value that exceeds it ($ϵ>8\mathrm{cm}$). Regarding the transverse dispersivity (${\alpha }_T$), in the first half of the tank, a constant value of ${\alpha }_T\sim 0.05\mathrm{cm}$ is obtained (Figure 7b), which then increases significantly after crossing the interface, reaching final values of ${\alpha }_T\sim 0.14\mathrm{cm}$. Regarding the longitudinal concentration profile ($\overline{C}$) (Figure 7c) in the fine-to-coarse (FC) media, the curve initially exhibit similar slope that the fine (F) medium. However, upon reaching the interface, the FC curve experiences a slight decline before steepening significantly, leading to notably higher concentration values (${\overline{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(\mathrm{M}\right)>3.5\times {10}^{-4}$)

Although the importance of heterogeneity in controlling solute mixing and reactivity has been widely recognized in previous studies [17,39,40,41,66], no direct studies have specifically analyzed the role of mixing affected by soil interfaces. In this section, we assess the mixing metrics for each scenario by analyzing the mixing efficiency through two key variables: the total reaction product mass of ${\mathrm{MoTi}}_2^{-4}$, denoted as ${\mathit{M}}_{{\mathrm{MoTi}}_2^{-4}}$ (g), and its corresponding scalar dissipation rate $\chi$, as shown in Figure 8. This analysis is crucial for understanding where mixing is most promoted within a discontinuous heterogeneous porous medium. Upon comparing all cases, we observe different behaviors in the scalar dissipation rate and total mass production near the interface, indicating an asymmetric flow-direction dependence on mixing efficiency and reactivity. To reflect this behavior more clearly, we present below a summary of the evidences.

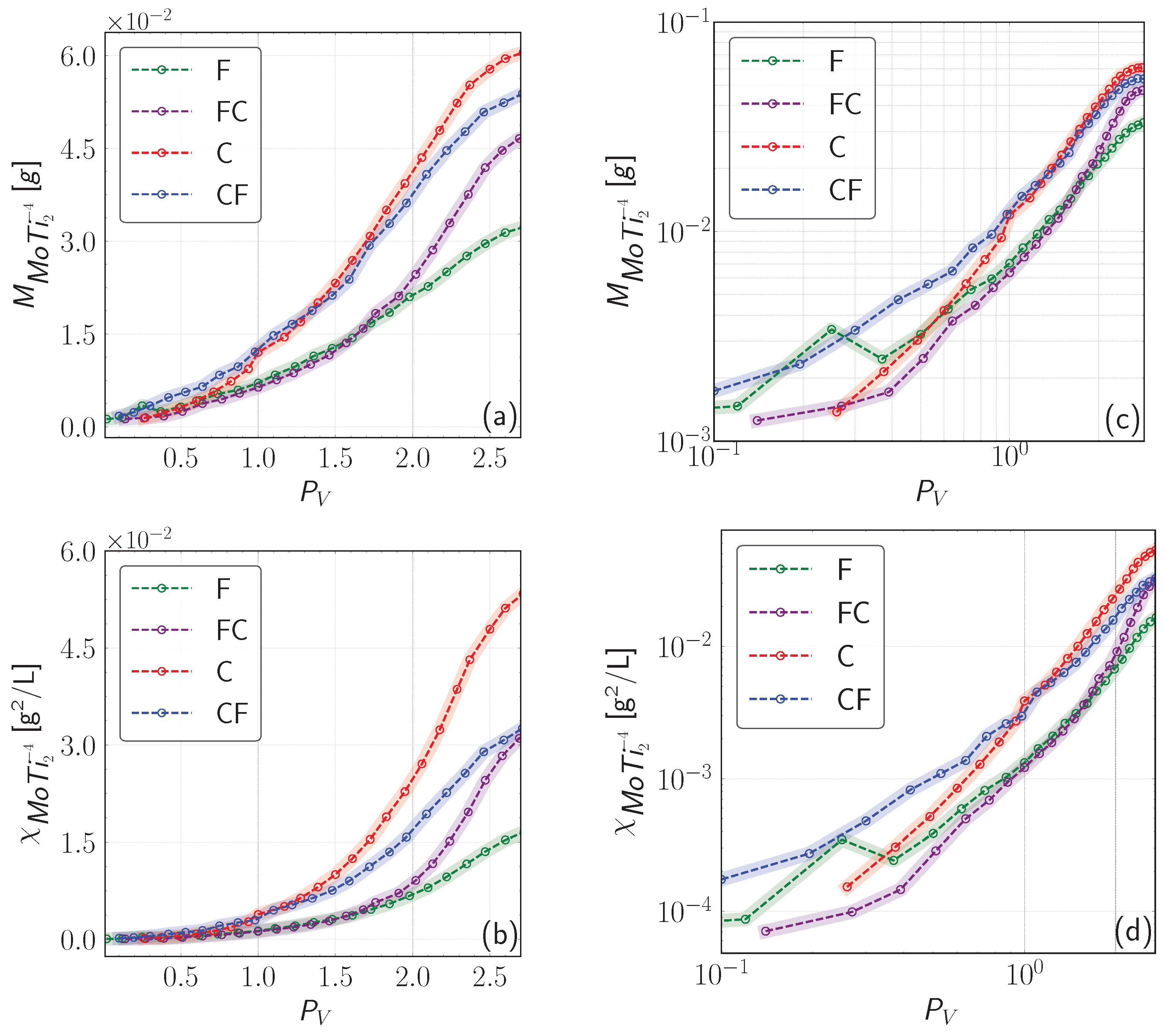
• In the coarse-to-fine (CF) configuration, the total reaction product mass follows the same trend of the coarse medium up to around $P_V$ = 1.6 (Figure 8a). From this point onward, the total reaction product begins to decline, resulting in lower final values compared to the coarse medium (${\mathit{M}}_{{\mathrm{MoTi}}_2^{-4}}\left(\mathrm{g}\right)\sim 5.5\times {10}^{-2}$). Nevertheless, the CF configuration consistently produces a higher total product mass than the FC transition along the entire length of the tank, indicating that even after the decline, mixing and reactivity remain more efficient than in the reverse flow configuration. Regarding the scalar dissipation in the (Figure 8b), the coarse-to-fine (CF) curve reaches a similar final scalar dissipation value as the fine-to-coarse (FC) curve (${\chi }_{{\mathrm{MoTi}}_2^{-4}}$ (${\mathrm{g}}^2/\mathrm{L}$) $\sim 3\times {10}^{-2}$). However, their temporal evolution is notably different. In particular, the CF configuration consistently exhibits higher values throughout the tank length.
• In the fine-to-coarse (FC) configuration, the total reaction product mass initially follows a pattern similar to that of the fine medium up to approximately $P_V=1.8$ (Figure 8a). Beyond this point, the total reaction product mass increases exponentially, eventually surpassing the values observed in the fine medium (${\mathit{C}}_{{\mathrm{MoTi}}_2^{-4}}\left(\mathrm{g}\right)>4.5\times {10}^{-2}$). Regarding the scalar dissipation (Figure 8b), the curve exhibits a sigmoidal behavior, similar to the coarse medium. However, after passing through the interface, the slope decreases significantly, eventually reaching much lower values.

Corresponding mixing metrics show that as the apparent transverse dispersivity increases when approaching the interface in the CF transition, the scalar dissipation rate and the total mass reacted also increases, indicating that the CF configuration tends to promote greater solute reactivity near the interface than the FC configuration.

3.5. Conclusions

Sharp soil interfaces formed in porous media between materials with differing grain sizes introduced unexpected effects on solute transport, challenging conventional assumptions about solute transport and reactivity. Understanding their impact on mixing processes and transport behavior is crucial for improving groundwater remediation strategies and predictive models of contaminant migration in subsurface systems. While the impact of sharp soil interfaces had been extensively explored through numerical solute transport models, Darcy-scale experiments designed to visually assess the mechanisms governing their impact on transport behavior and mixing remained largely unknown. To address this gap, we presented well-controlled laboratory experiments conducted in an intermediate-scale horizontal tank simulating sharp transitions between fine and coarse porous materials. The experimental setup allowed for the real-time monitoring and visualization of the spatiotemporal evolution of solute plumes. Finally, we conclude that:

• The sharp soil interface play a different role in transport behavior. In the coarse-to-fine (CF) porous medium, the sharp interface acts as a hydraulic barrier, distorting the flow as it crosses into the fine material, forcing solute redistribution through small-scale preferential flow paths. This leads to an apparently dual-permeability system, with a breakthrough curve (BTC) displaying non-Fickian features, including early arrival, a low peak value, and a long tail. In contrast, the fine-to-coarse (FC) configuration shows a smooth transition of transport properties, behaving apparently as a single homogeneous medium, with a BTC that follows a Gaussian distribution and integrates characteristics of both porous materials.
• Reaction product encounters anomalous resistance when crossing the interface between coarse and fine material. This effect is much less pronounced in the fine-to-coarse (FC) transition when the direction of flow is reversed. However, contrary to the reported one-dimensional results (column experiments), this asymmetric anomalous resistance to cross the interface does not produce solute accumulation behind the interface. Instead, results show an unexpected significant enhancement of the transverse spread of the reaction product in the coarse-to-fine transition (CF) with a slow release in the fine material. As a result, a sudden decrease in the longitudinal resident concentration profile across the heterogeneity interface is observed. Corresponding mixing metrics show that as the apparent transverse dispersivity increases when approaching the interface in the CF transition, the scalar dissipation rate and the total mass reacted also increases, indicating that the CF configuration tends to promote greater solute reactivity near the interface than the FC configuration.