Submitted:
14 June 2025
Posted:
16 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
Bilinski & Emanuel, 2020; Bustos Sierra et al., 2020; Félix-Cardoso et al., 2020; Fouillet et al., 2020; Kontis et al., 2020; Mannucci et al., 2020; Mills et al., 2020; Olson et al., 2020; Piccininni et al., 2020; Sinnathamby et al., 2020; Tadbiri et al., 2020; Vestergaard et al., 2020; Villani et al., 2020; Achilleos et al., 2021; Al Wahaibi et al., 2021; Anand et al., 2021; Böttcher et al., 2021; Chan et al., 2021; Dahal et al., 2021; Das-Munshi et al., 2021; Deshmukh et al., 2021; Faust et al., 2021; Gallo et al., 2021; Islam, et al., 2021a, 2021b; Jacobson & Jokela, 2021; Jdanov et al., 2021; Joffe, 2021; Karlinsky & Kobak, 2021; Kobak, 2021; Kontopantelis et al., 2021a, 2021b; Kung et al., 2021a, 2021b; Liu et al., 2021; Locatelli & Rousson, 2021; Miller et al., 2021; Nørgaard et al., 2021; Panagiotou et al., 2021; Pilkington et al., 2021; Polyakova et al., 2021; 2021b; Rossen et al., 2021; Sanmarchi et al., 2021; Sempé et al., 2021; Soneji et al. 2021; Stein et al., 2021; Stokes et al., 2021; Vila-Corcoles et al., 2021; Wilcox et al., 2021; Woolf et al., 2021a, 2021b; Yorifuji et al., 2021; Ackley et al., 2022; Acosta et al., 2022; Engler, 2022; Faust et al., 2022; Ghaznavi et al., 2022; Gobiņa et al., 2022; He et al., 2022; Henry et al., 2022; Jha et al., 2022; Juul et al., 2022; Kontis et al., 2022; Kontopantelis et al., 2022; Lee et al., 2022; Leffler et al., 2022; Lewnard et al., 2022; McGrail, 2022; Neil et al., 2022; Neil & Fenton, 2022; Pálinkás & Sándor, 2022; Ramírez-Soto & Ortega-Cáceres, 2022; Razak et al., 2022; Redert, 2022a, 2022b; Rossen et al., 2022; Safavi-Naini et al., 2022; Schöley et al., 2022; Thoma & Declercq, 2022; Wang et al., 2022; Aarstad & Kvitastein, 2023; Bilinski et al., 2023; de Boer et al., 2023; de Gier et al., 2023; Demetriou et al., 2023; Alessandria et al., 2025; Haugen, 2023; Jones & Ponomarenko, 2023; Kuhbandner & Reitzner, 2023; Masselot et al., 2023; Matveeva & Shabalina, 2023; Neil & Fenton, 2023; Paglino et al., 2023; Redert, 2023; Schellekens, 2023; Scherb & Hayashi, 2023; Šorli et al., 2023; Woolf et al., 2023; Rancourt et al., 2024; Rancourt & Hickey, 2023; Rancourt et al., 2023a; Rancourt et al., 2023b; Rancourt et al., 2022a; Rancourt, 2022; Rancourt et al., 2022b; Rancourt et al., 2022c; Rancourt, 2021; Rancourt et al., 2021a; Rancourt et al., 2021b; Rancourt et al., 2020; Rancourt, 2020; Johnson & Rancourt, 2022; Aune et al., 2023; Bonnet et al., 2024; Faisant et al., 2024; Foster et al., 2024; Korsgaard, 2024; Léger & Rizzi, 2024; Matthes et al., 2024; Mostert et al., 2024; Nørgaard et al., 2024; Paganuzzi et al., 2024; Paglino et al., 2024; Pallari et al., 2024; Pulido et al., 2024; Zawisza et al., 2024; Zou et al., 2024.
- the sharpness of the peaks, with full-width at half-maxima of approximately 4 weeks
- the timing of the peaks, being late in the winter season, surging after week 11 of 2020, which is unprecedented for any large sharp-peak feature in all-cause mortality data
- the synchronicity of the onset of the surge in all-cause mortality, across continents and immediately following the WHO’s pandemic declaration
- the state-to-state (USA) absence or presence of the mortality peaks, being correlated with nursing home events and government public health measures.
1.1. Data Sources
1.1. Technical Points About Mortality Data
2. Results
2.1. Excess Mortality at the Continental Scale in the USA and Europe in 2020
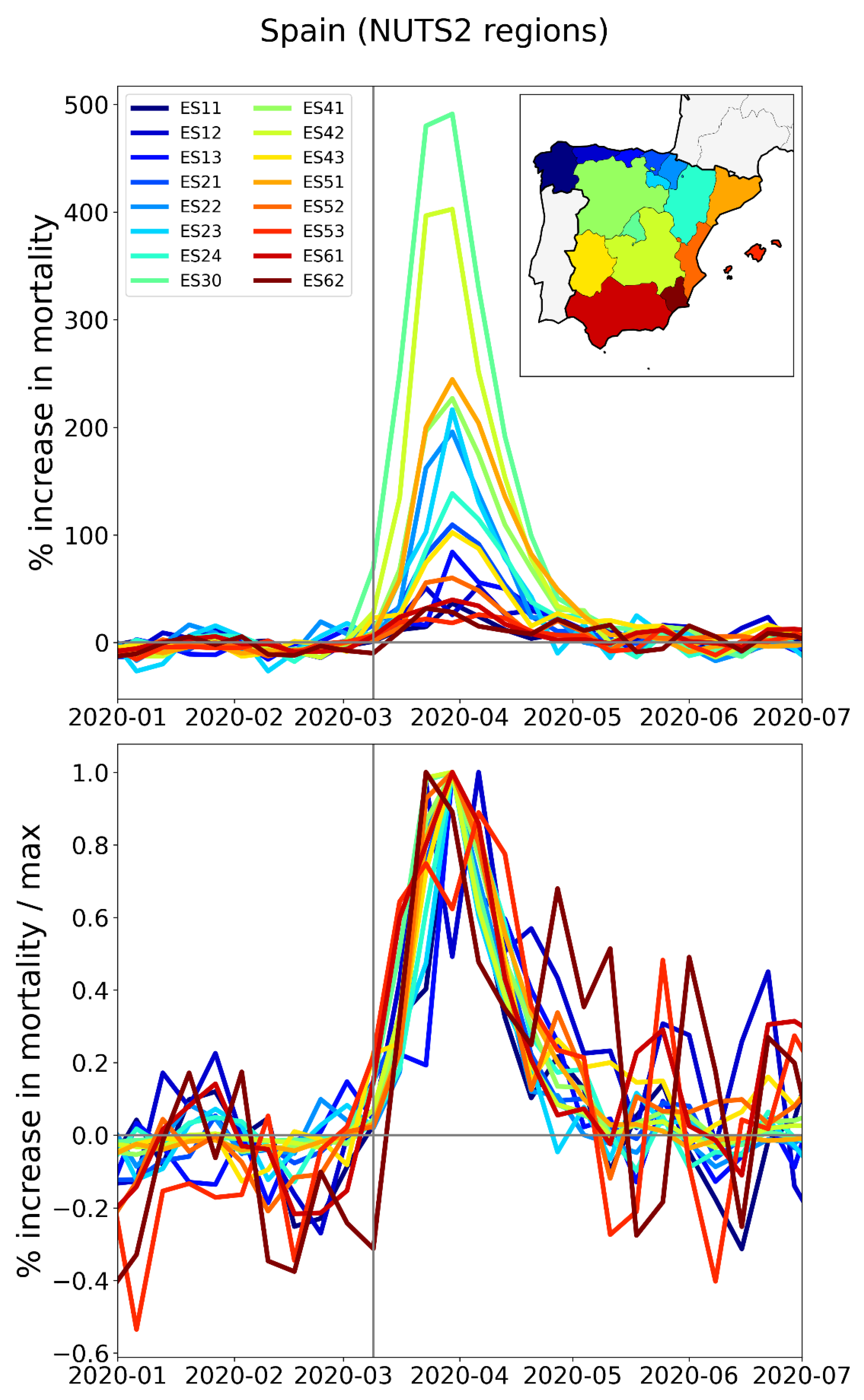
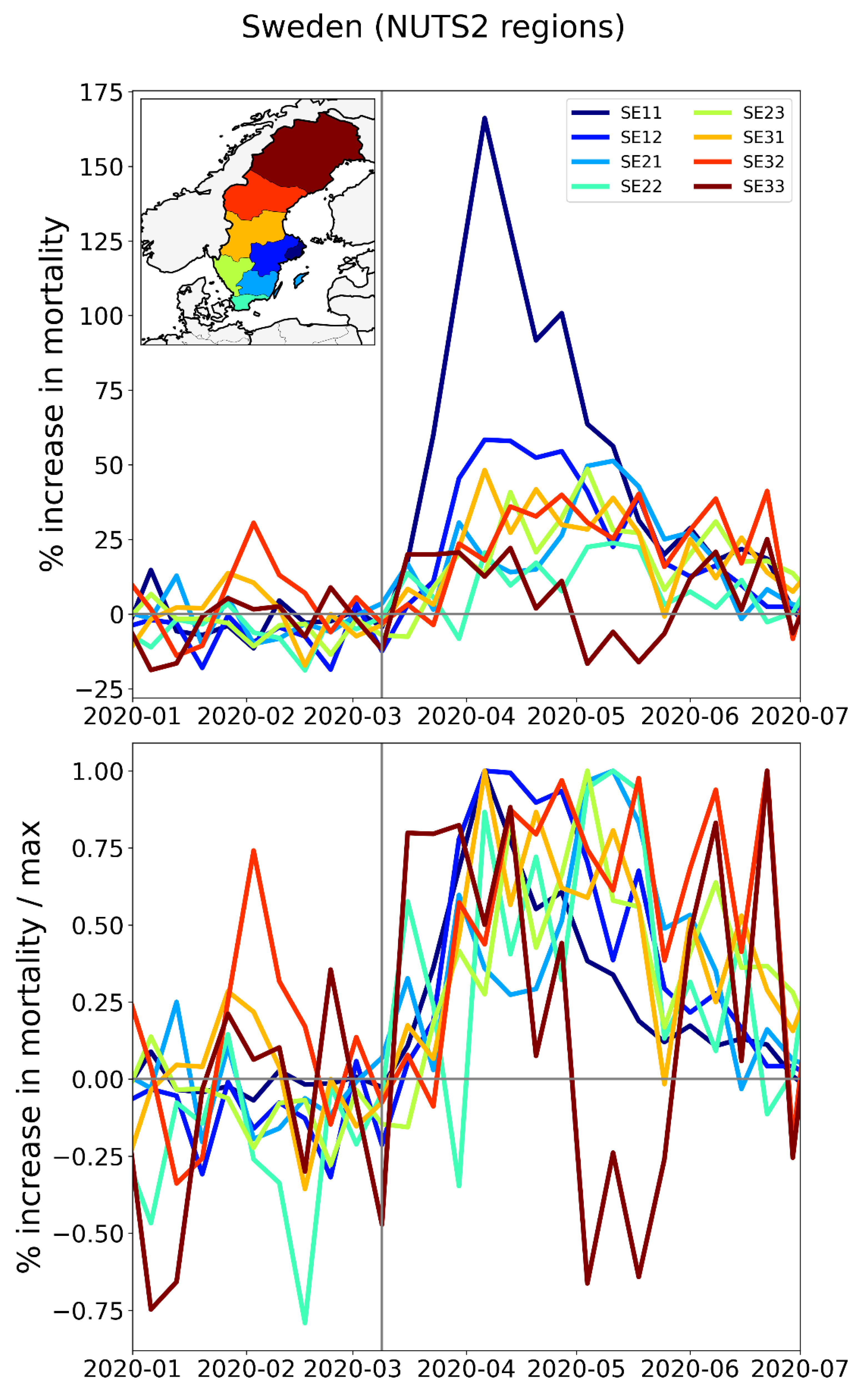
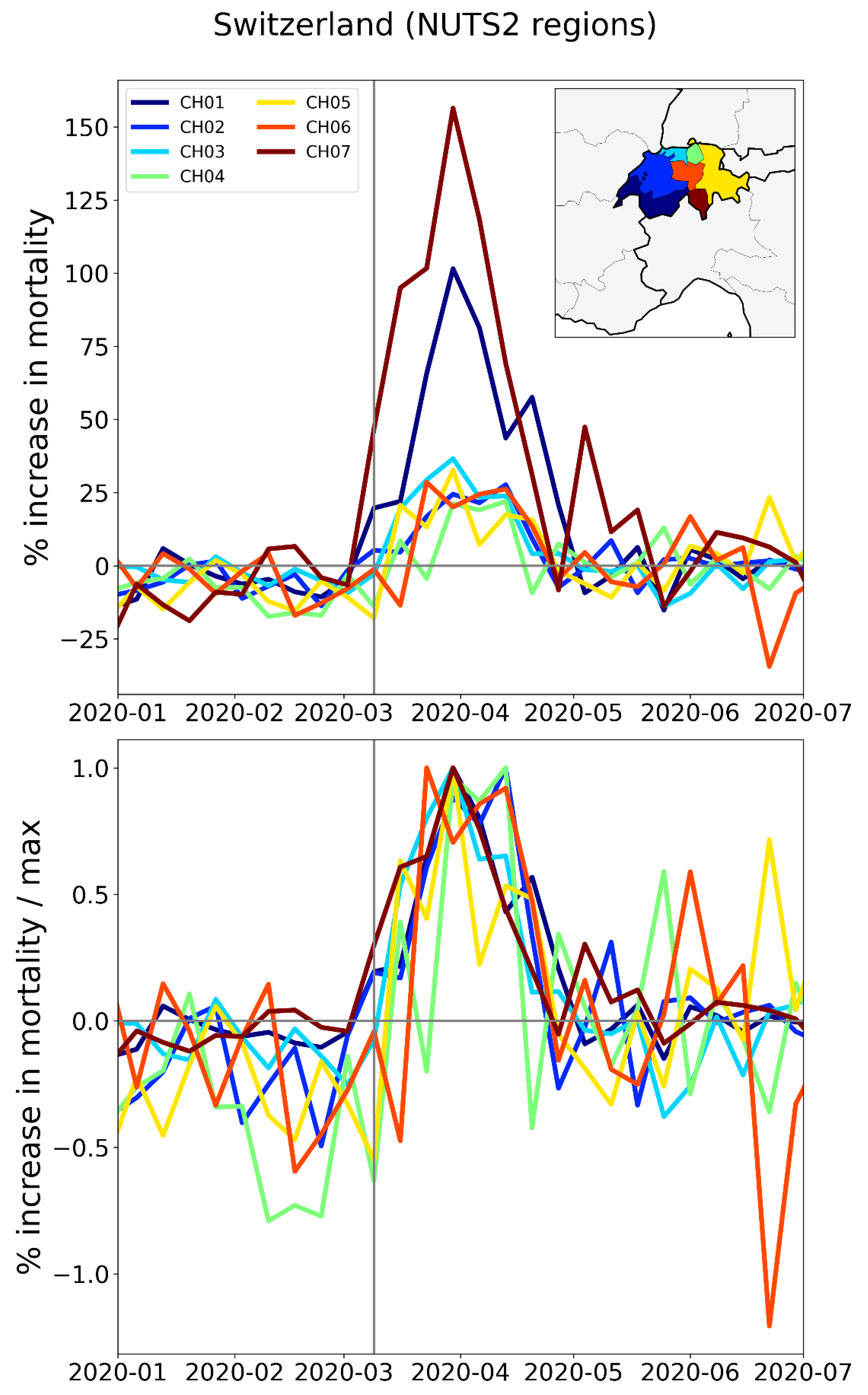
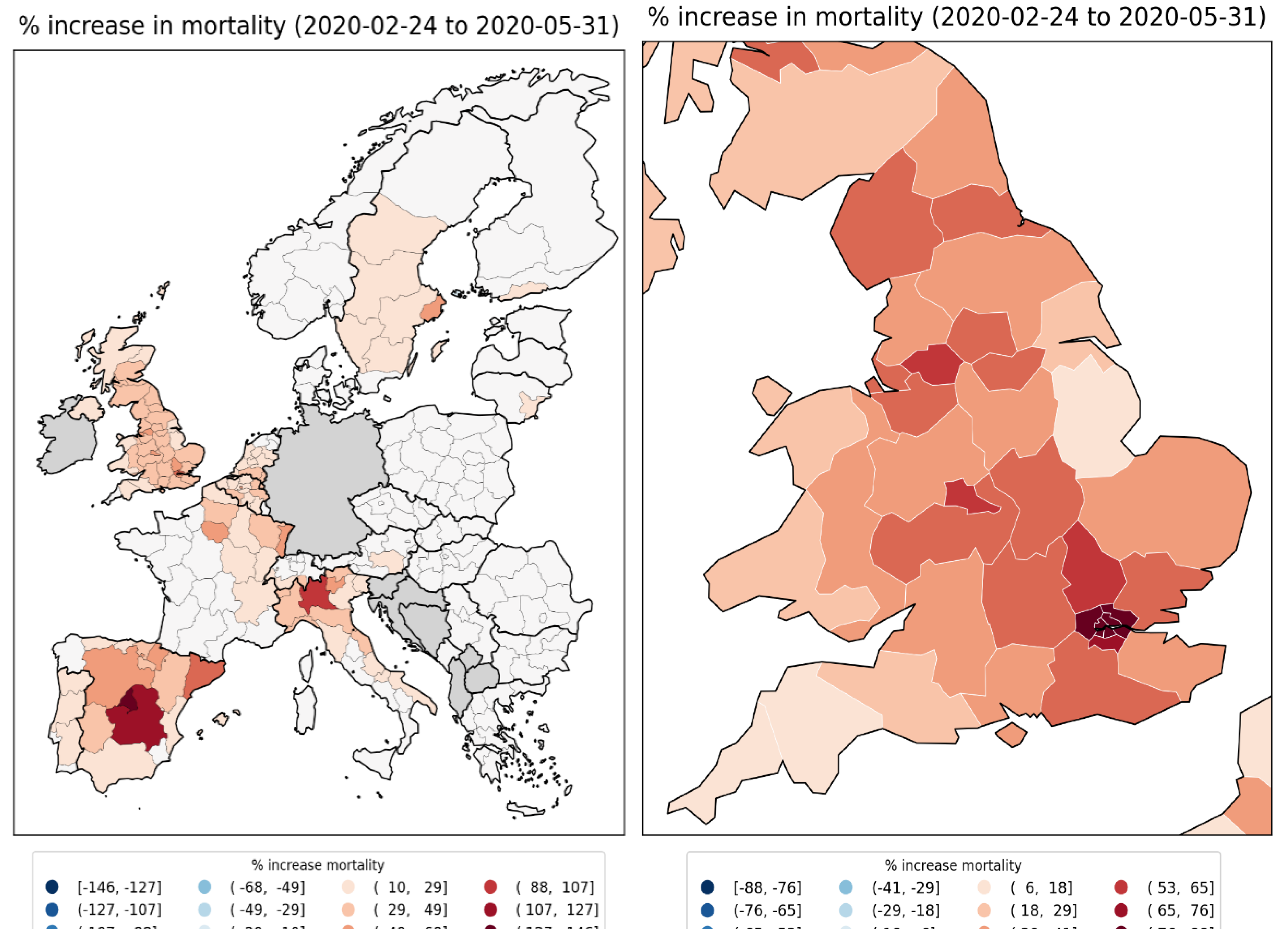
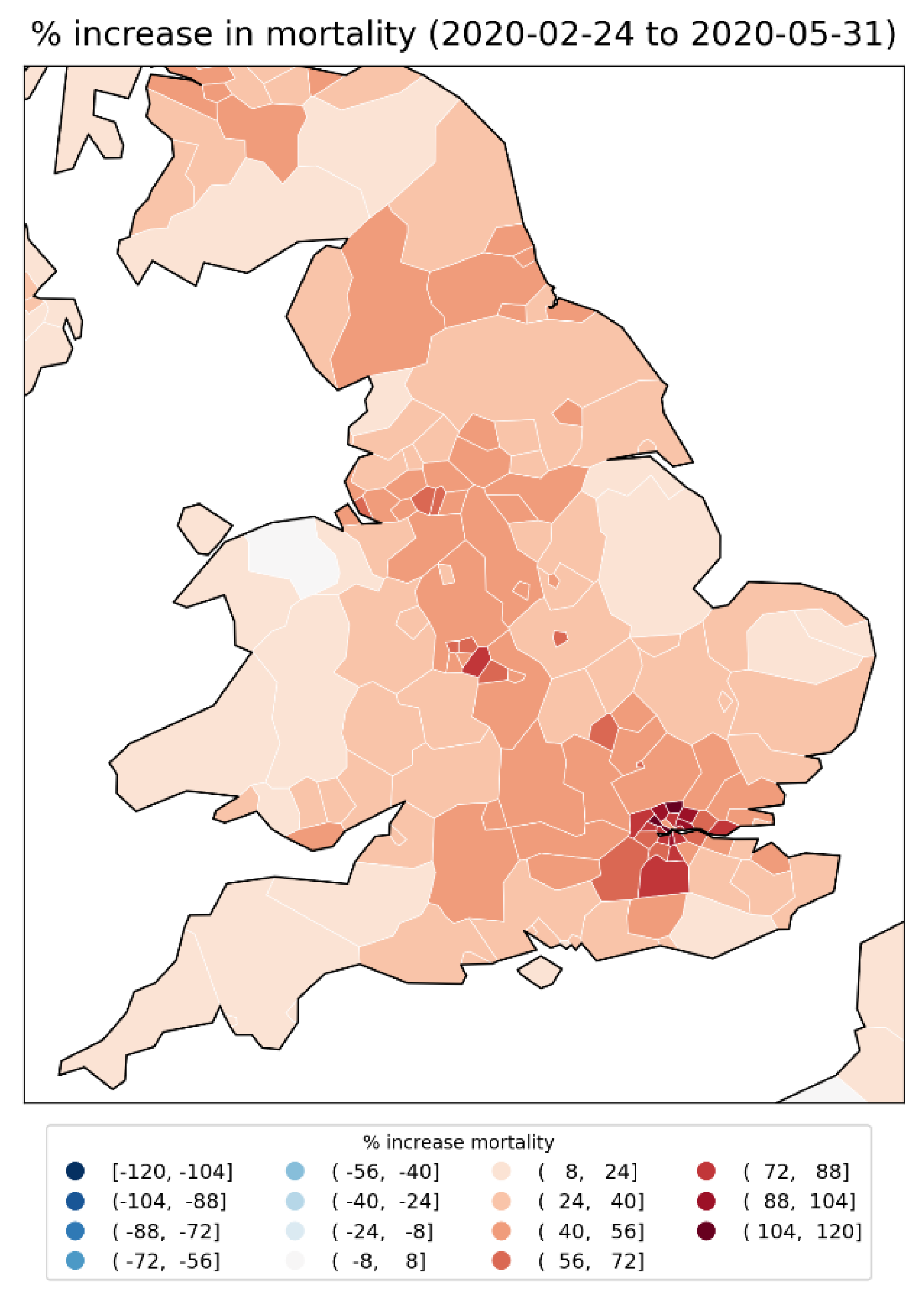
2.1.1. Europe Excess Mortality by NUTS2 Region
2.1.2. Europe Excess Mortality by NUTS3 Region
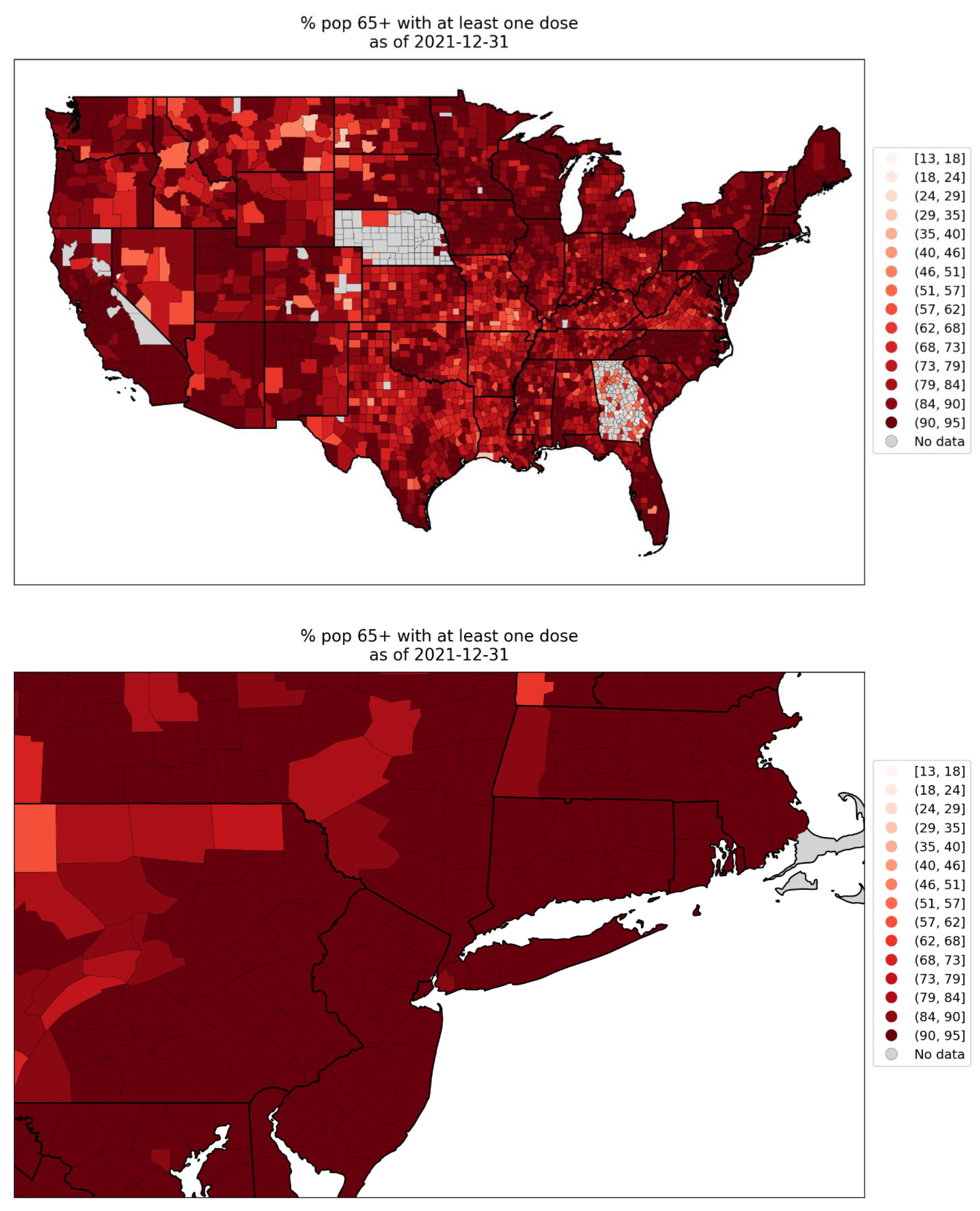
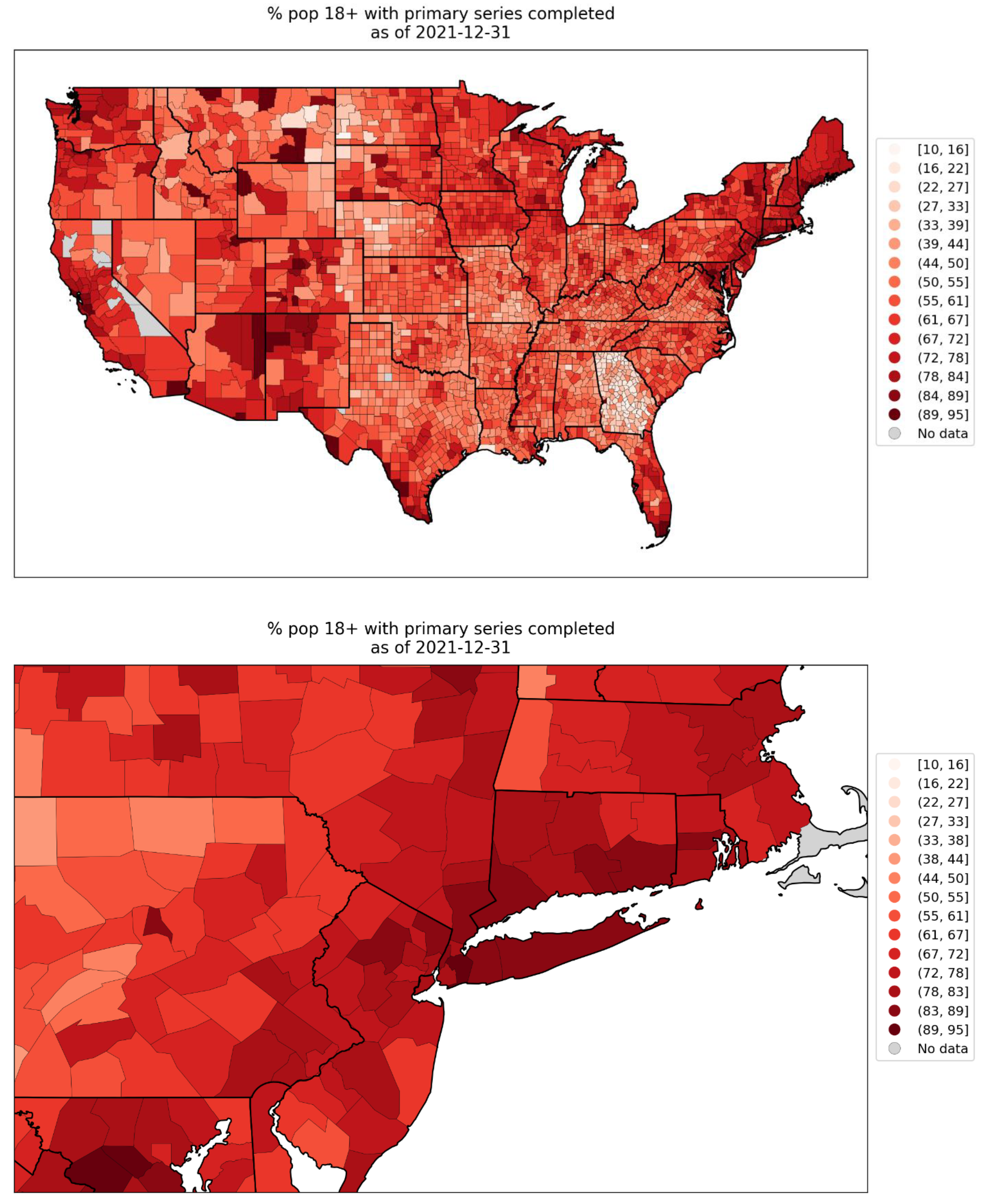
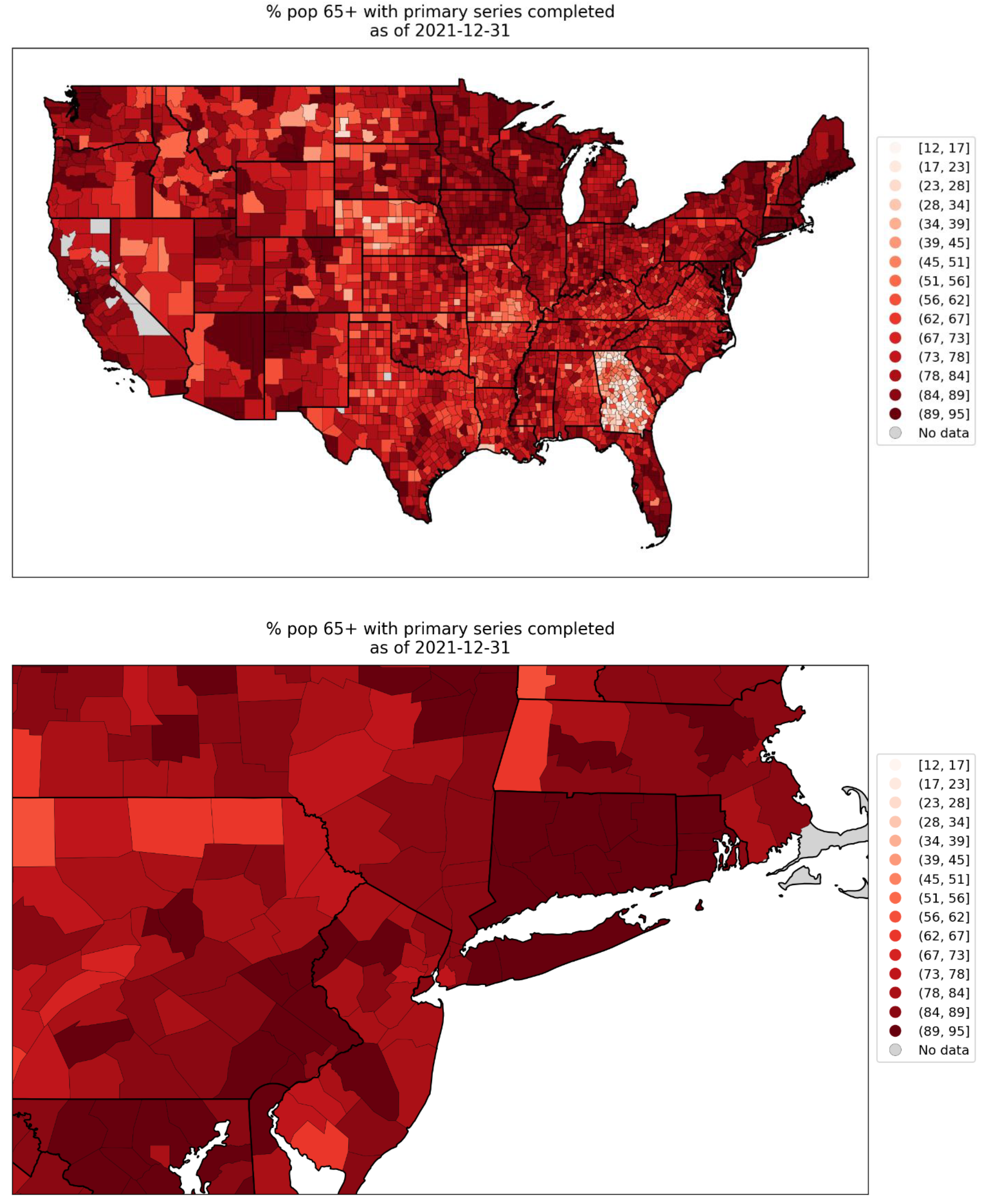
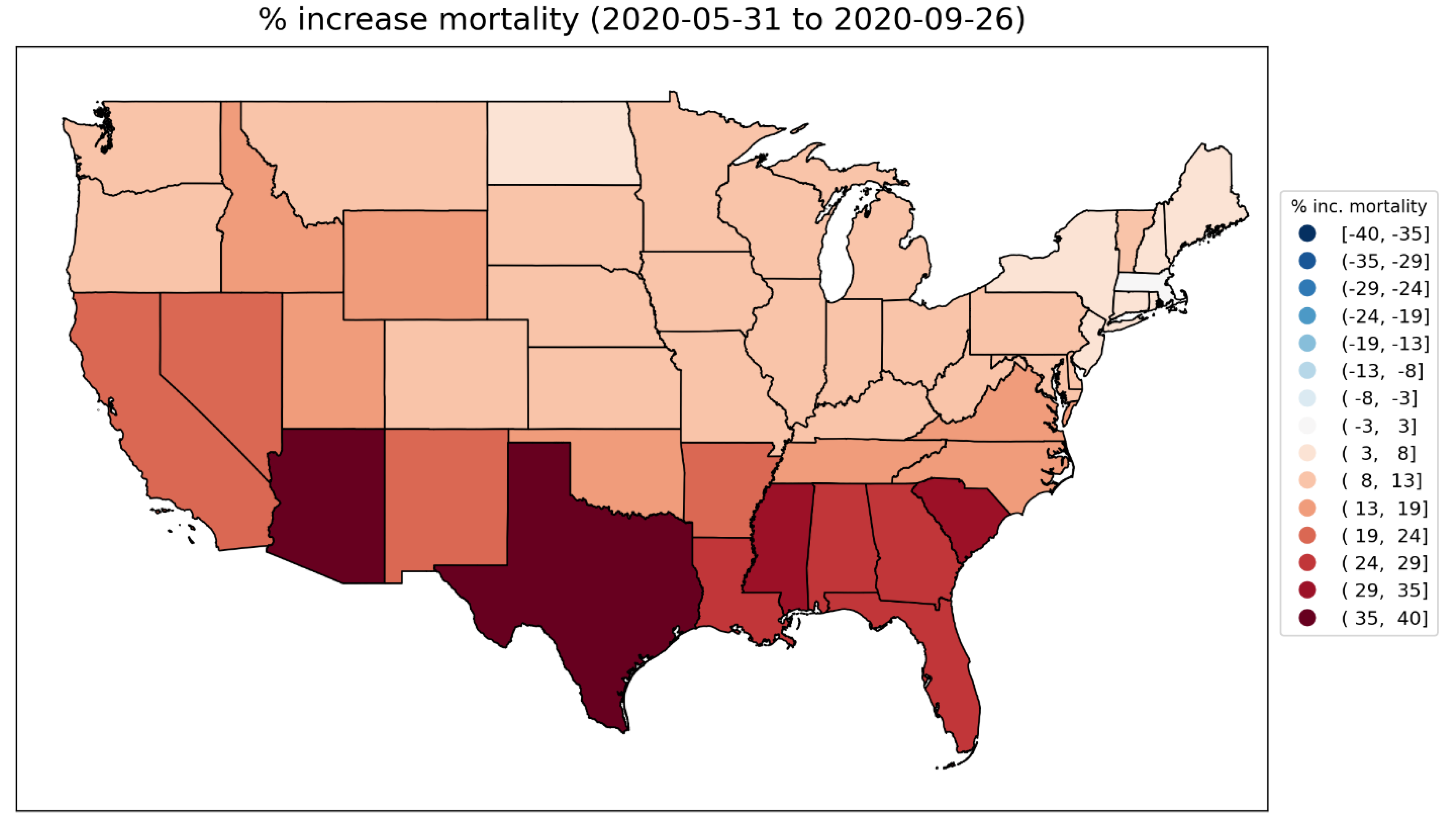
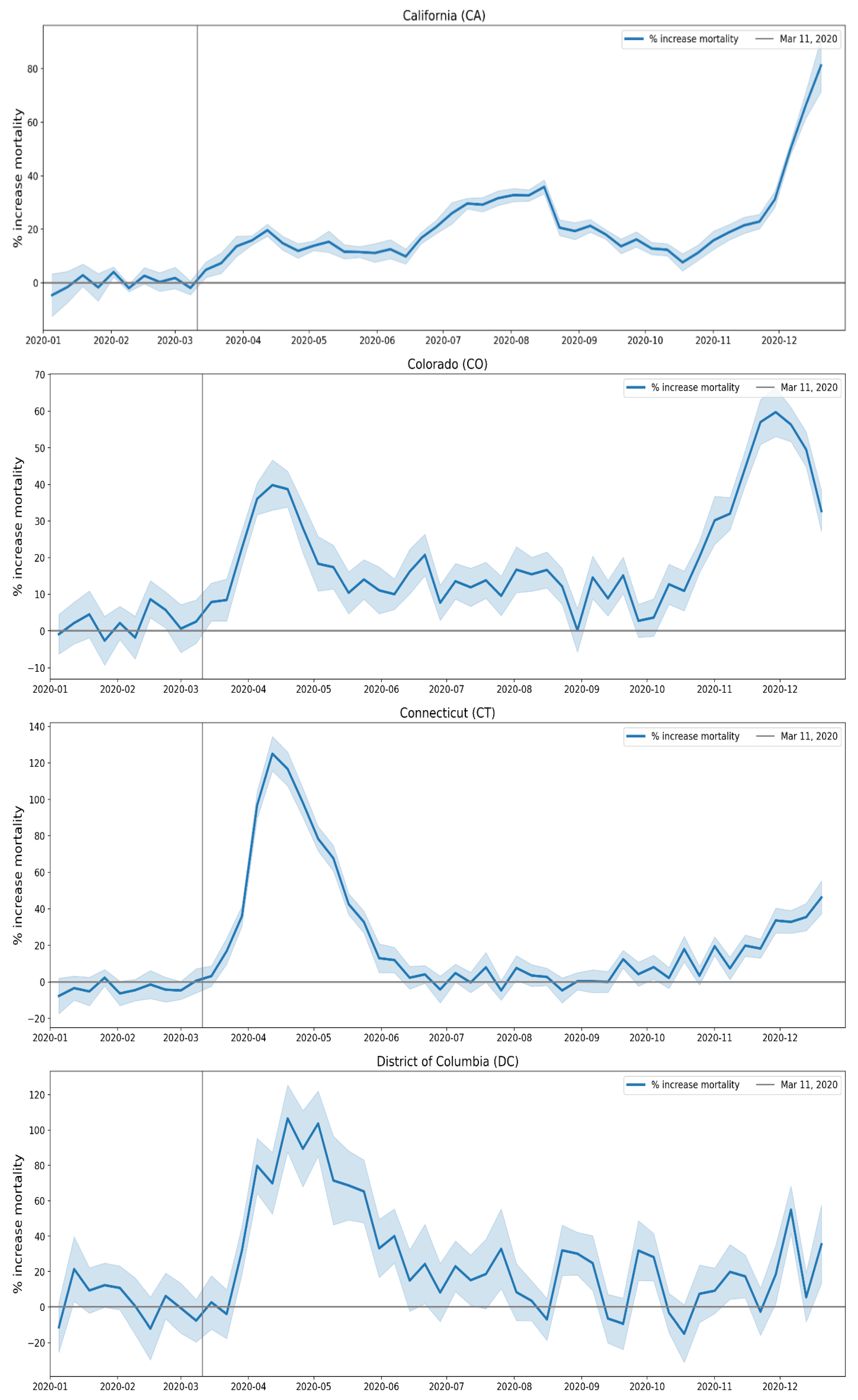
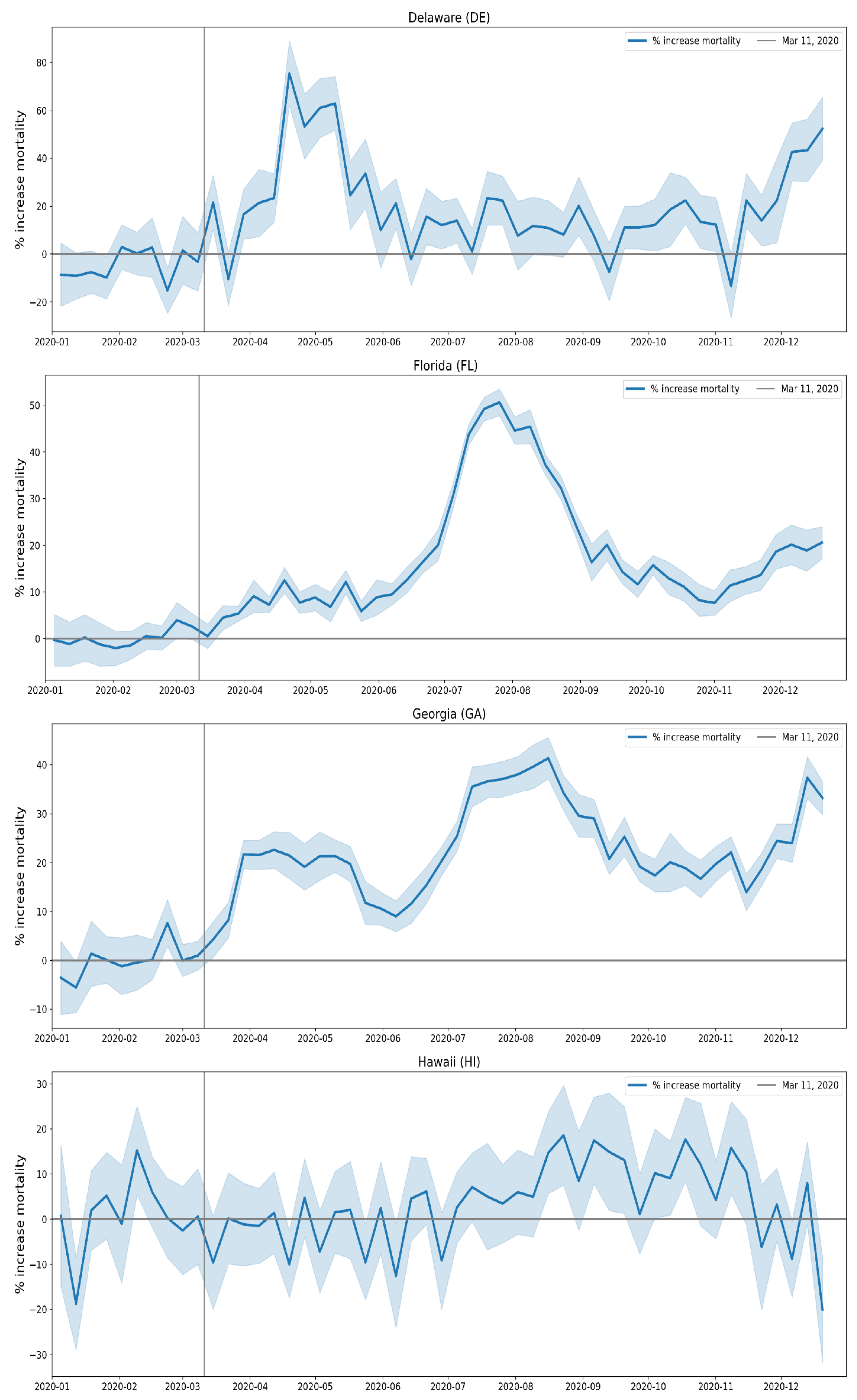
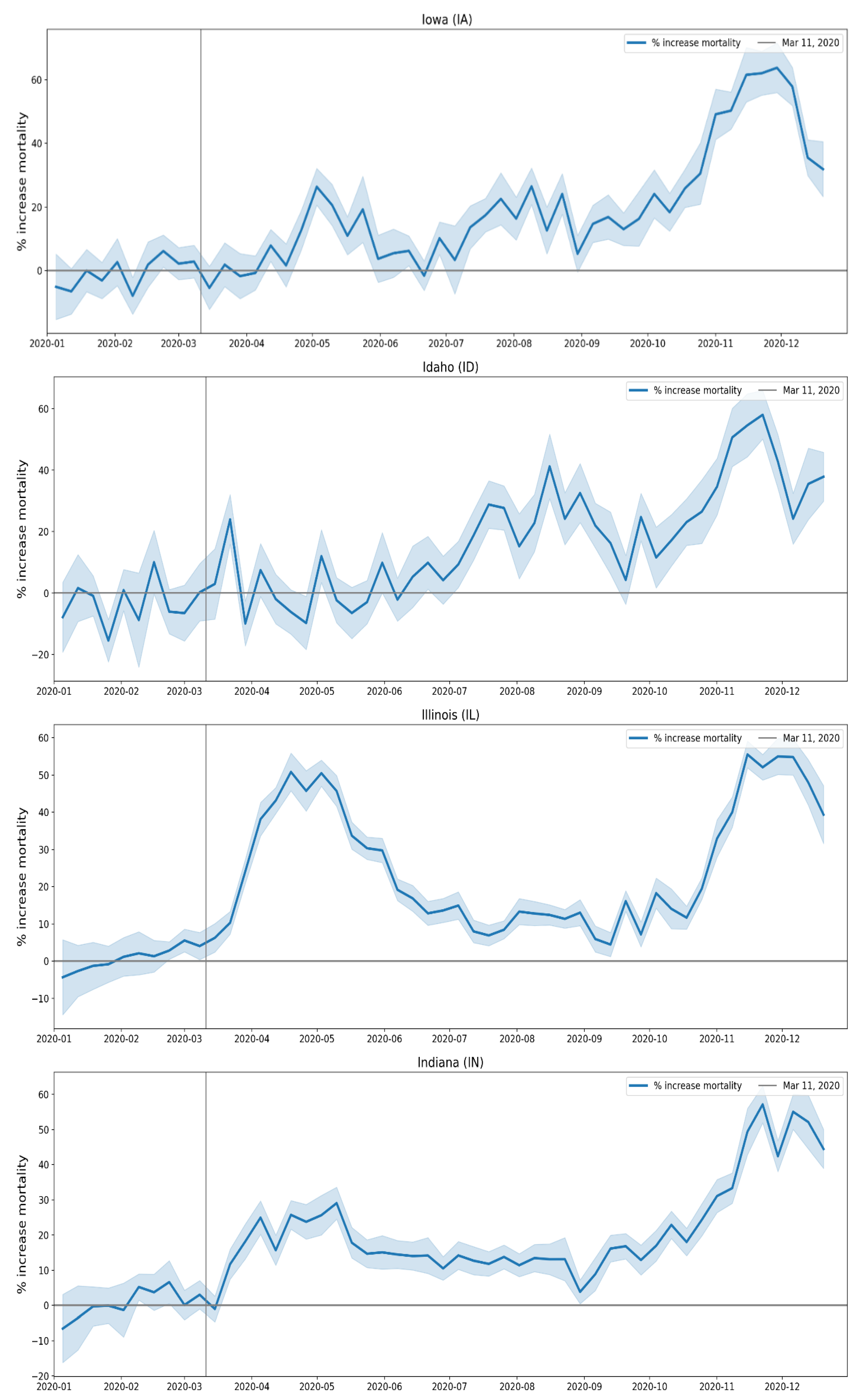
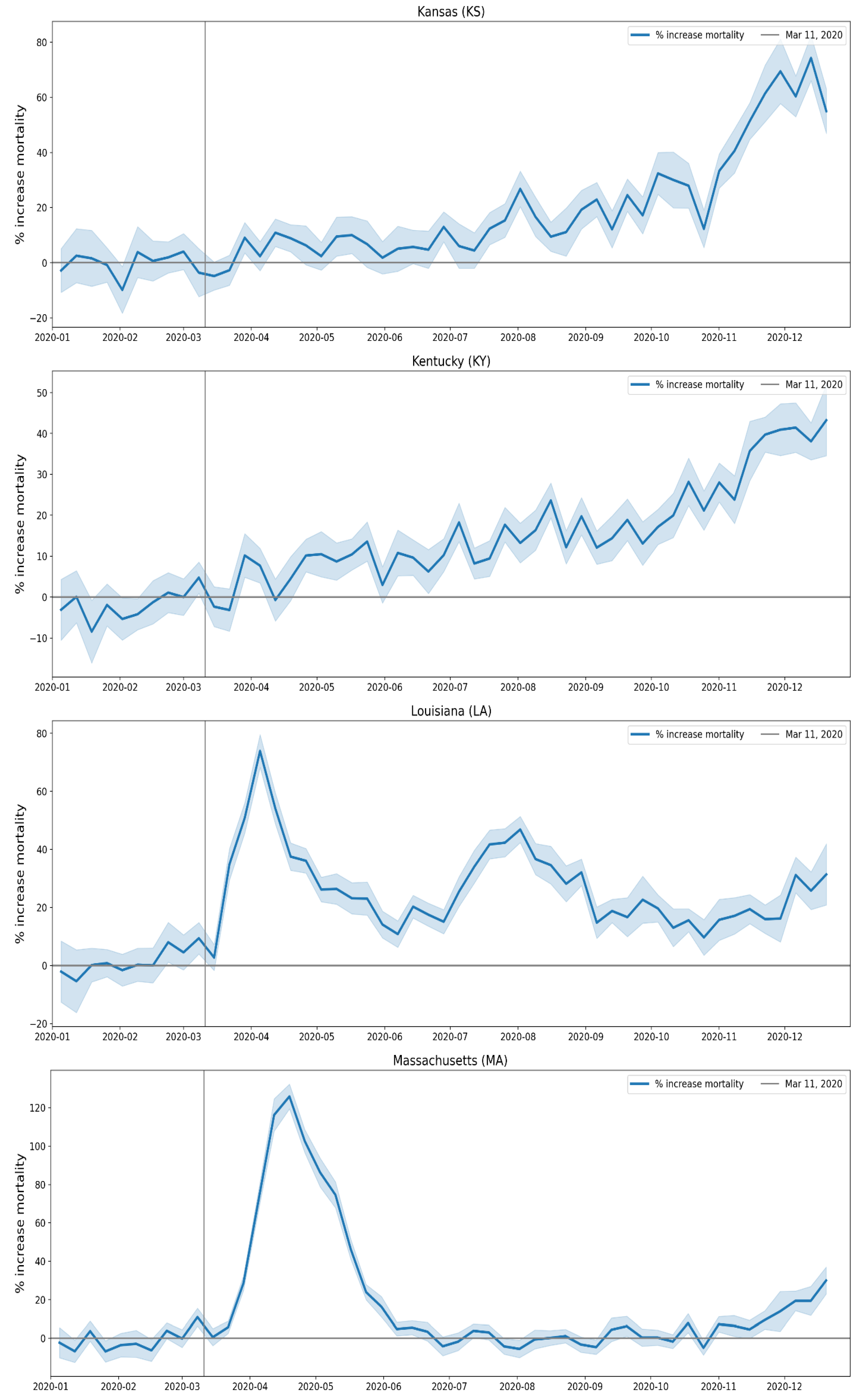
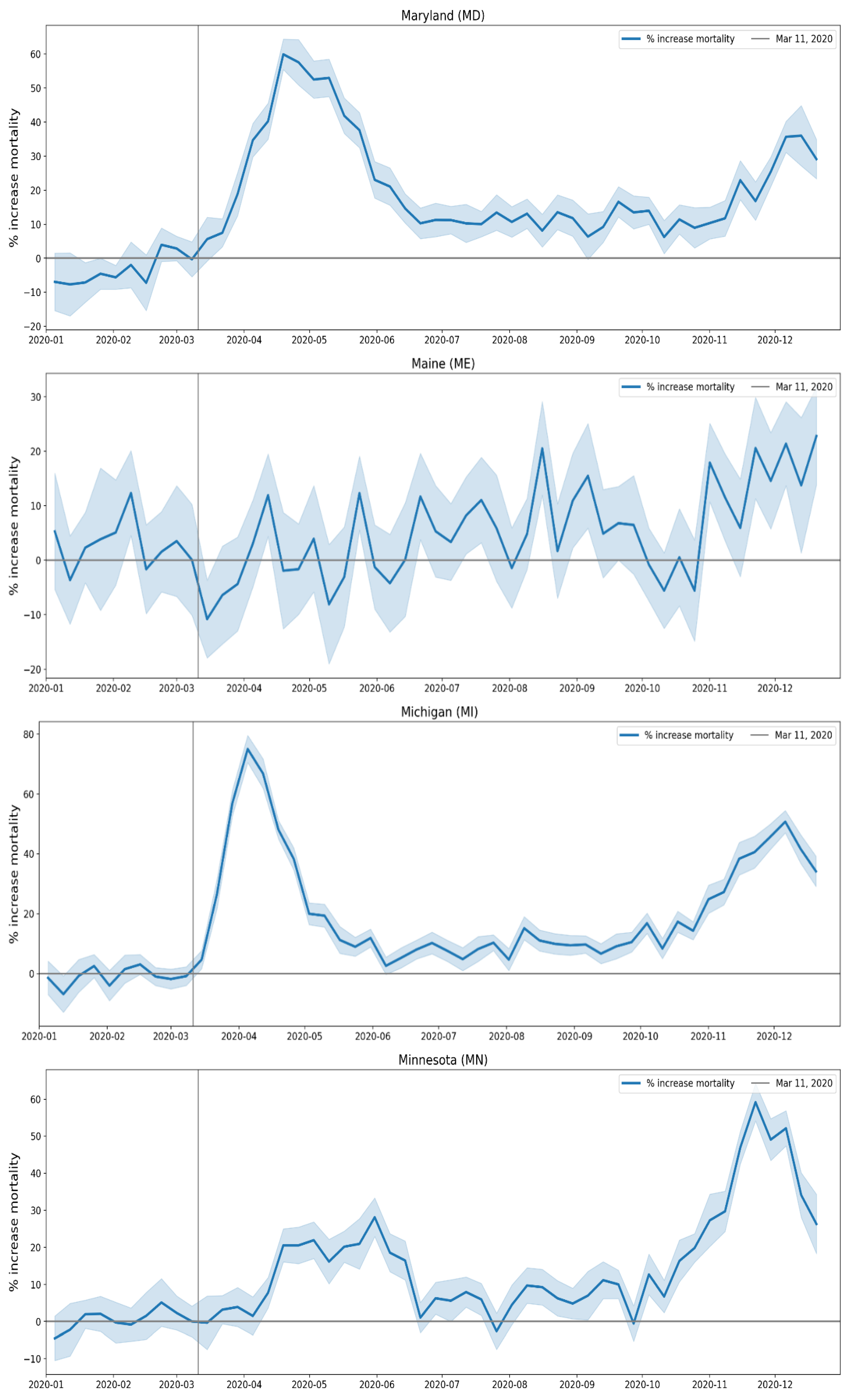
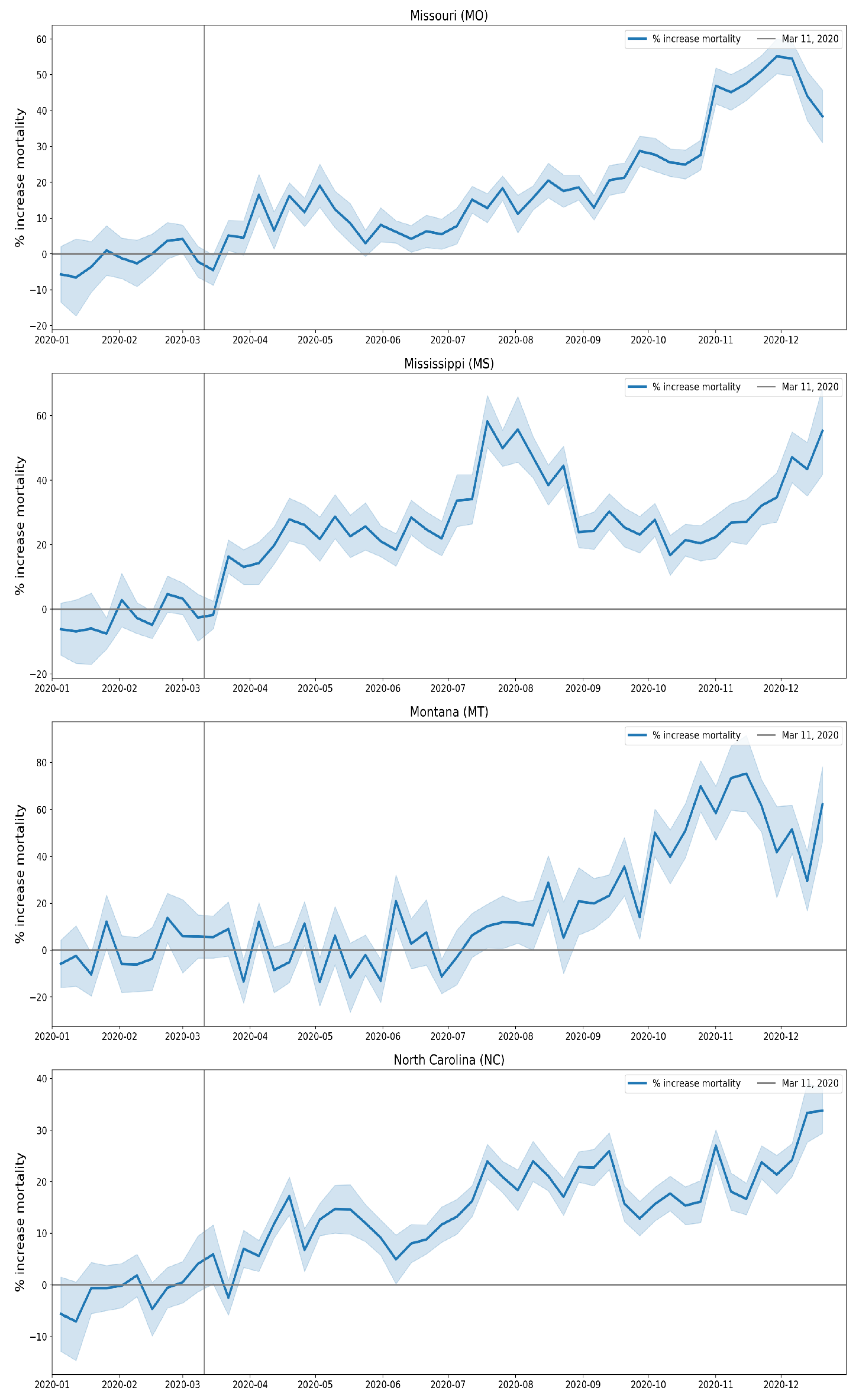
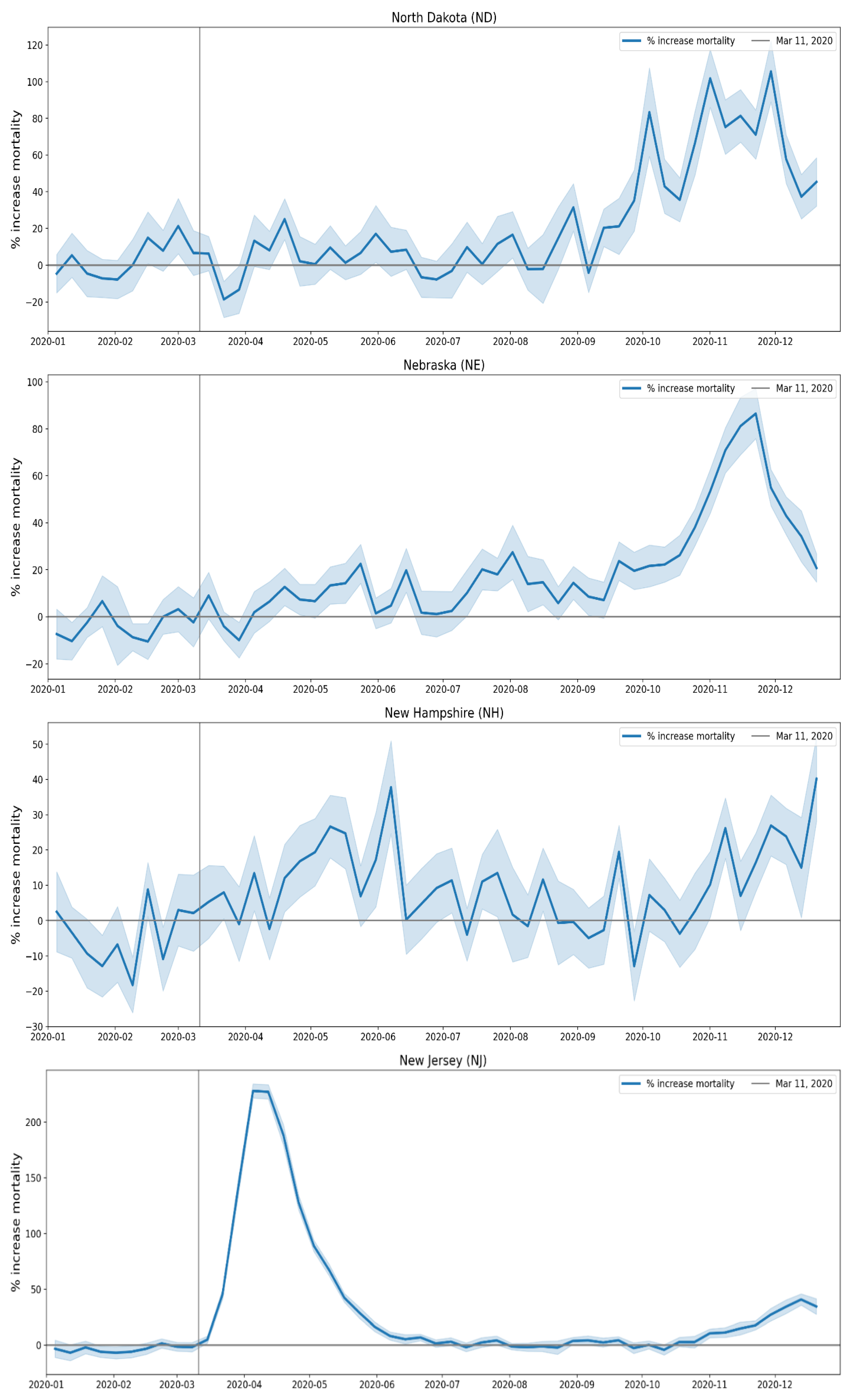
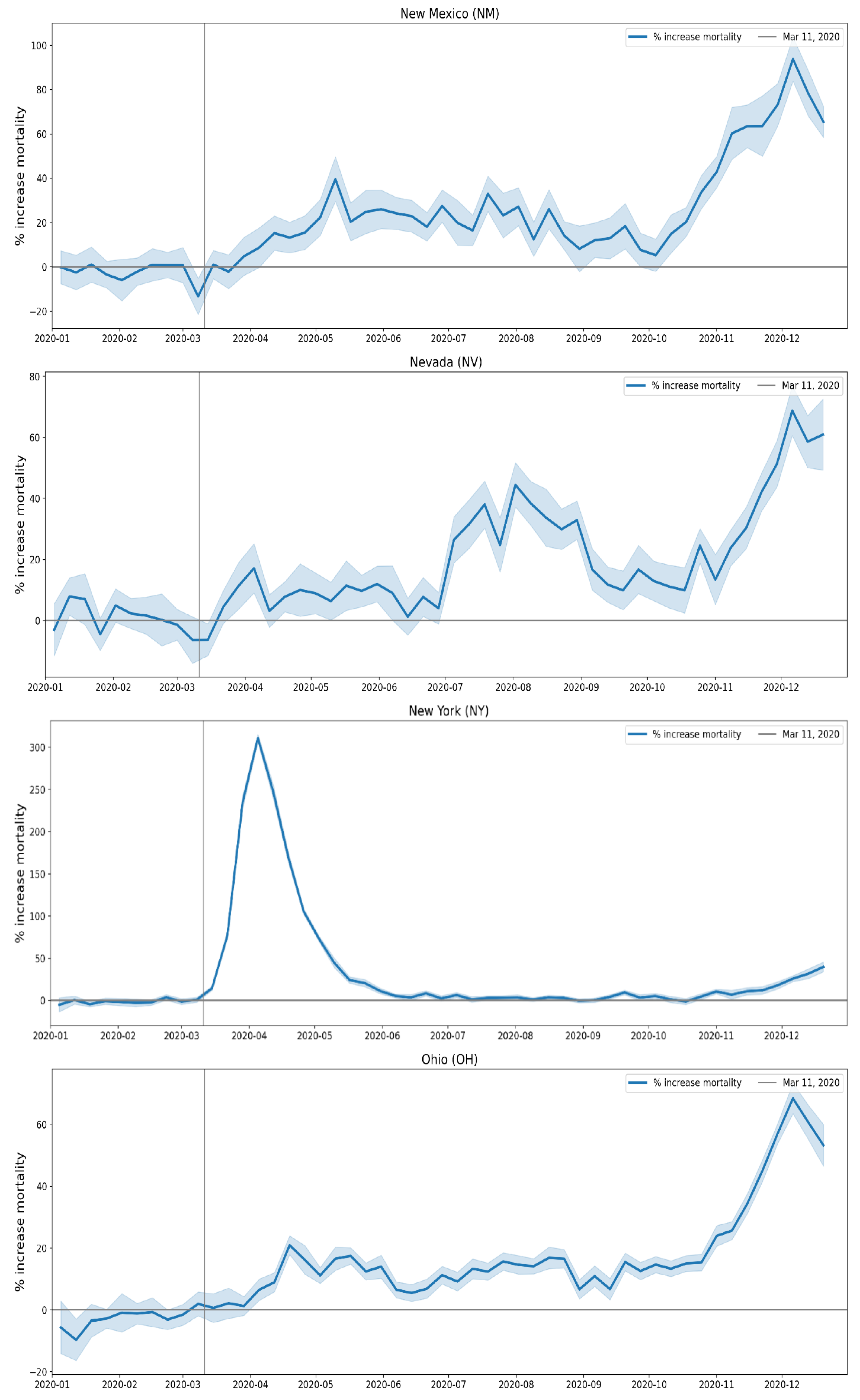
2.1.3. USA Excess Mortality by State
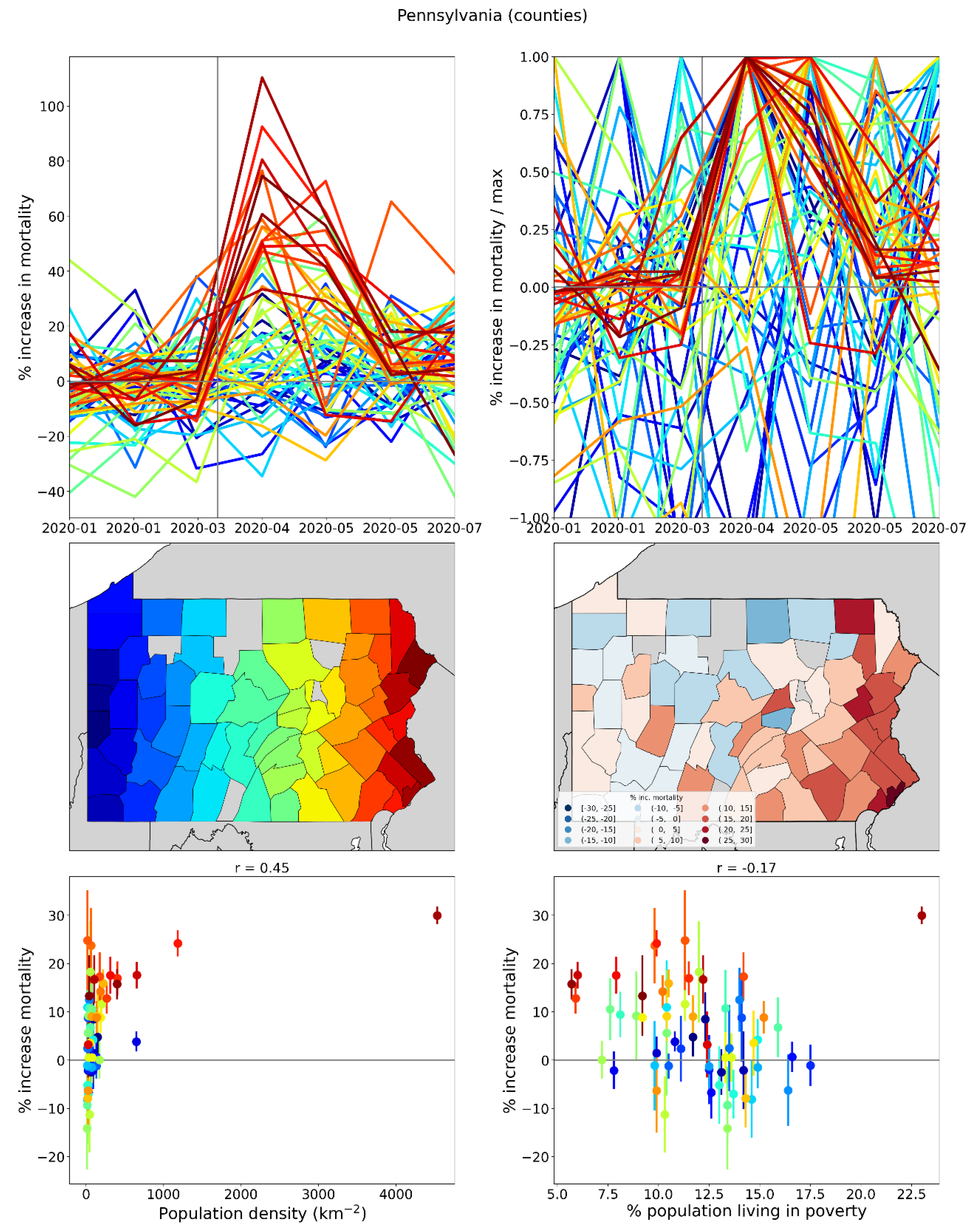
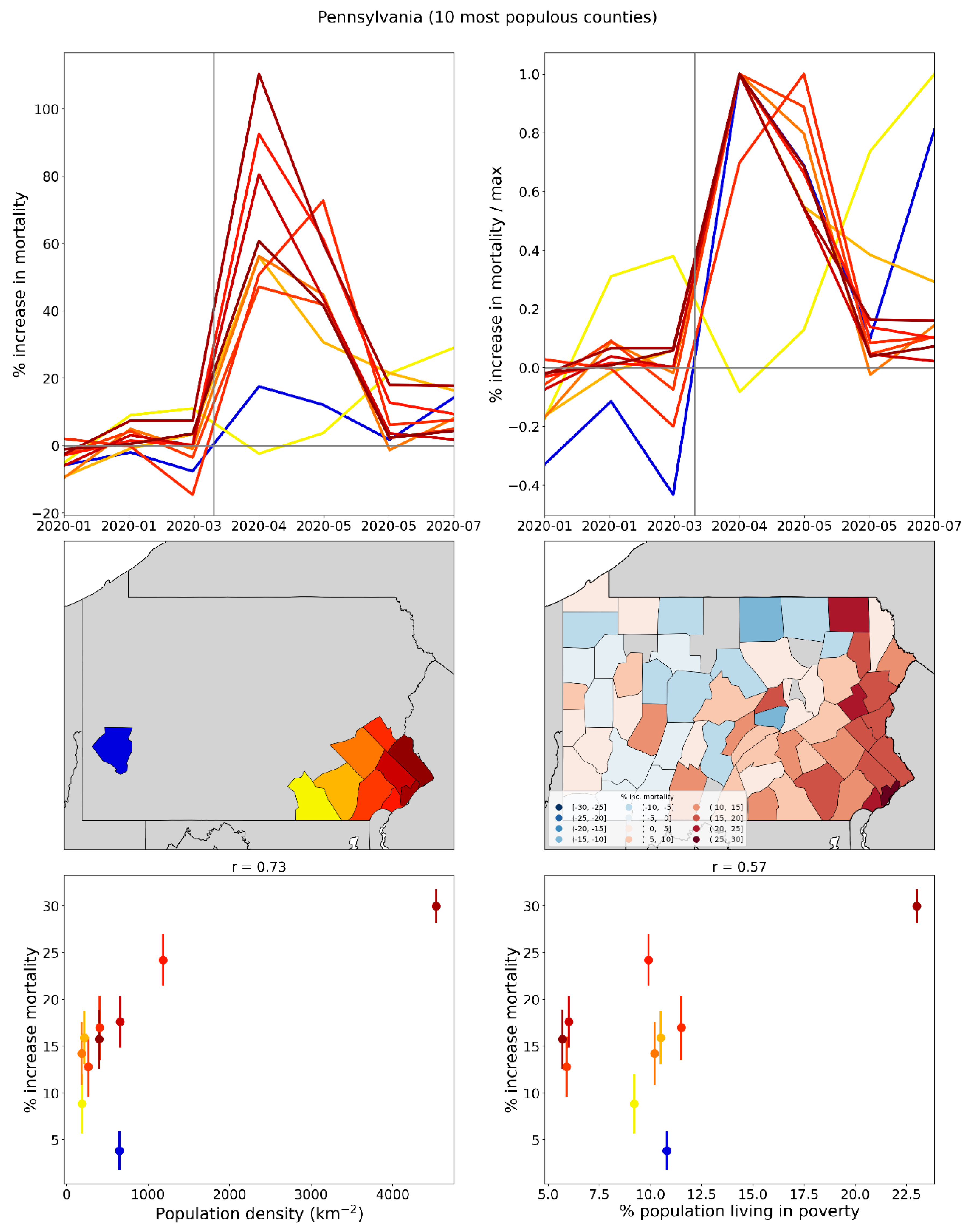
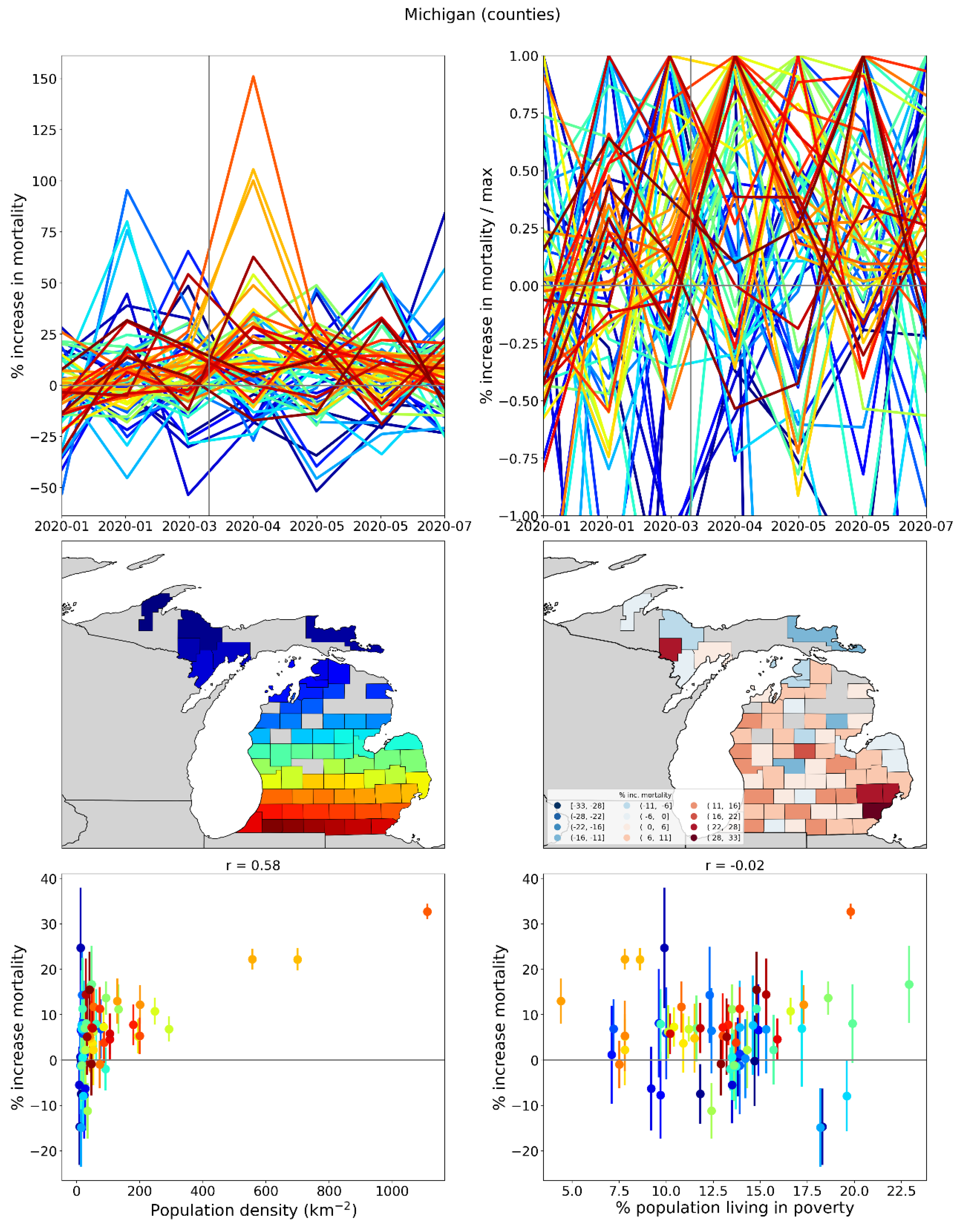
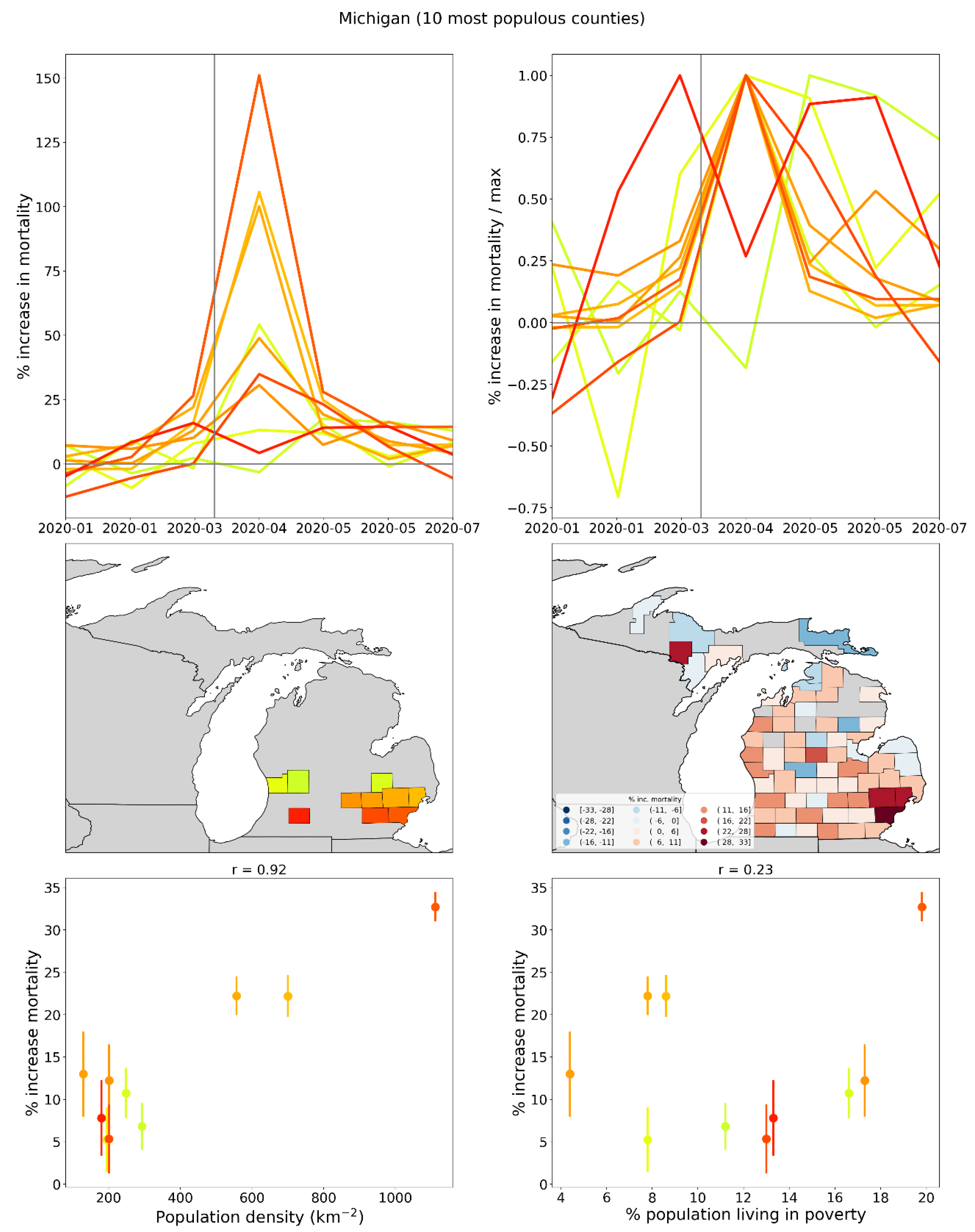
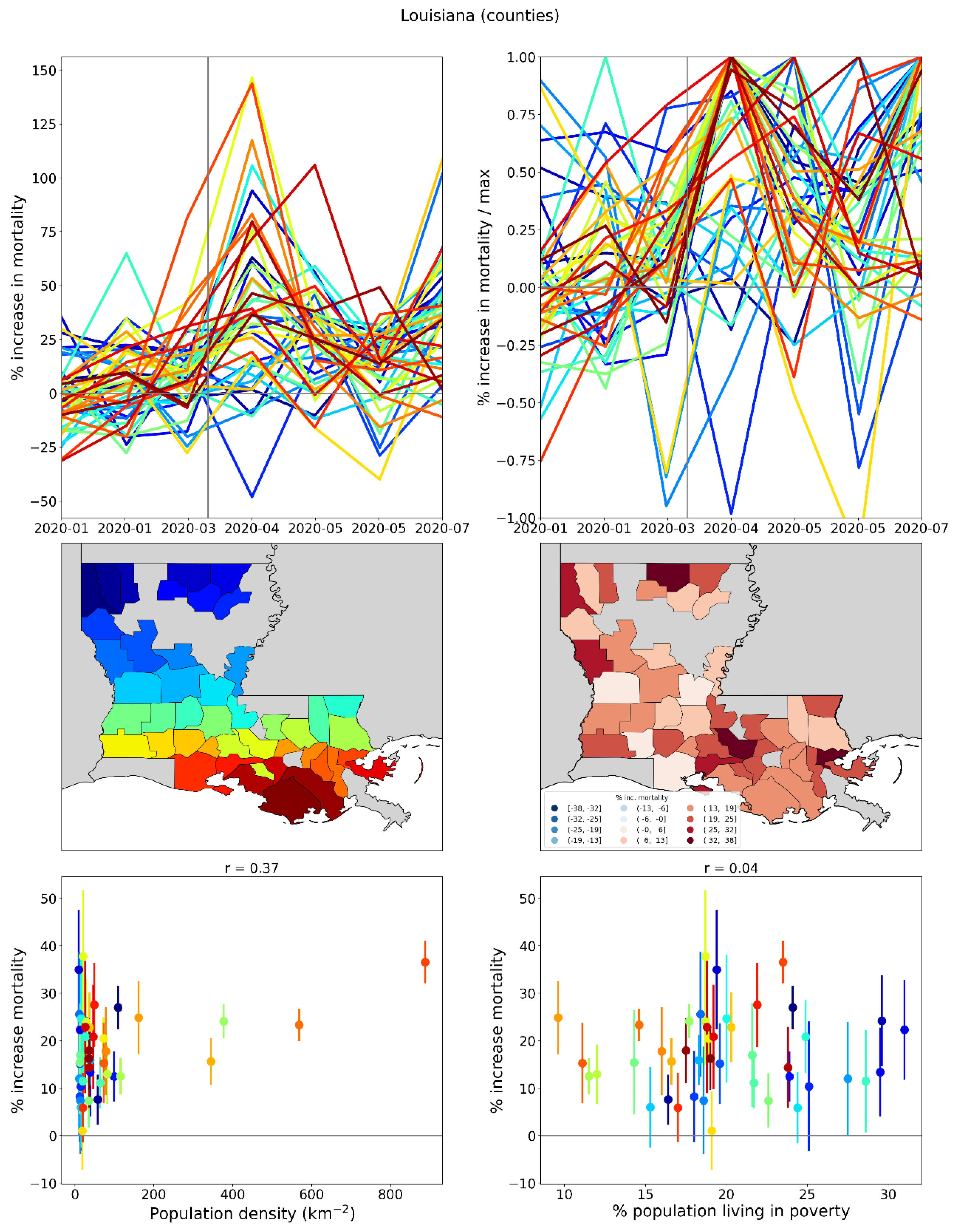
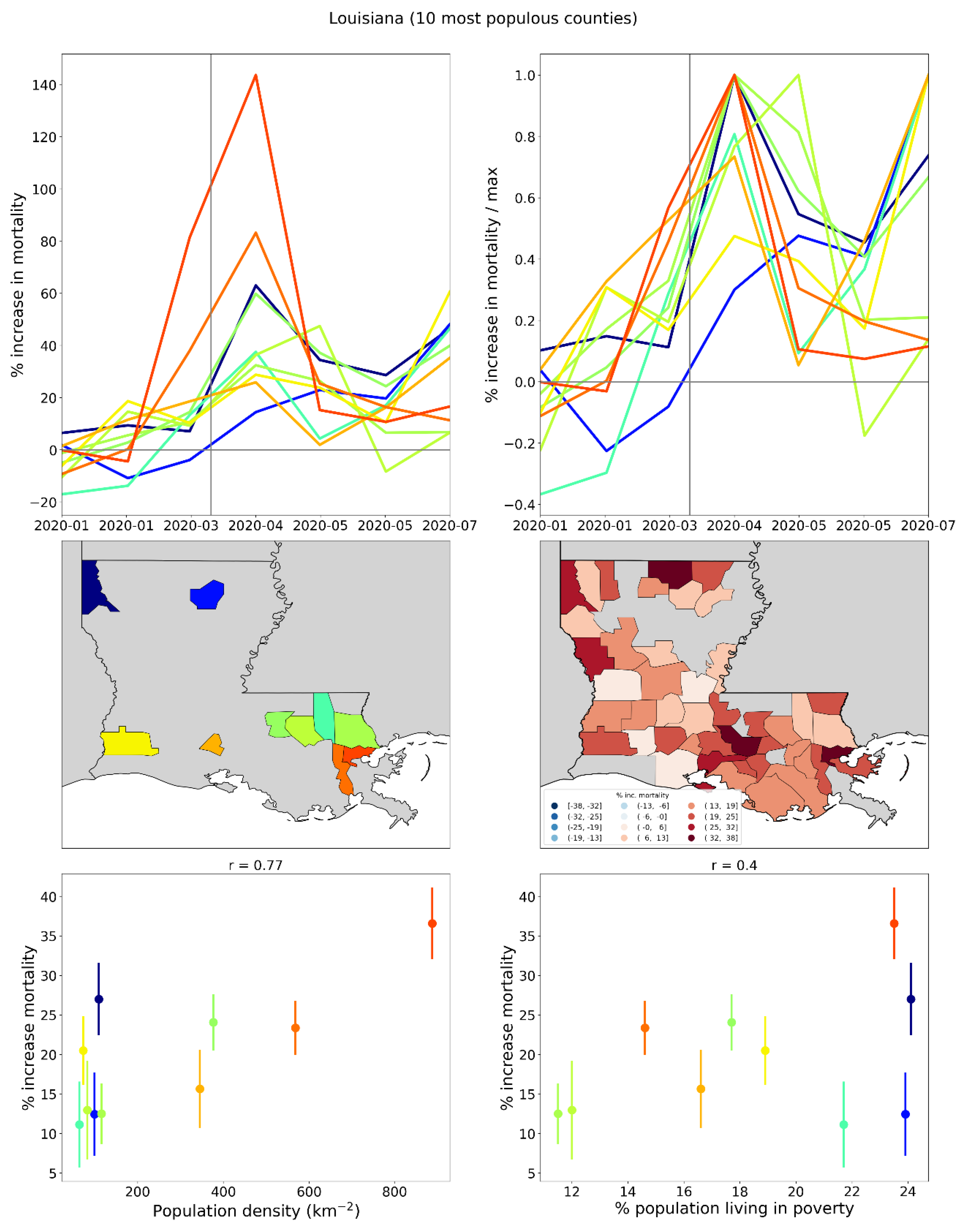
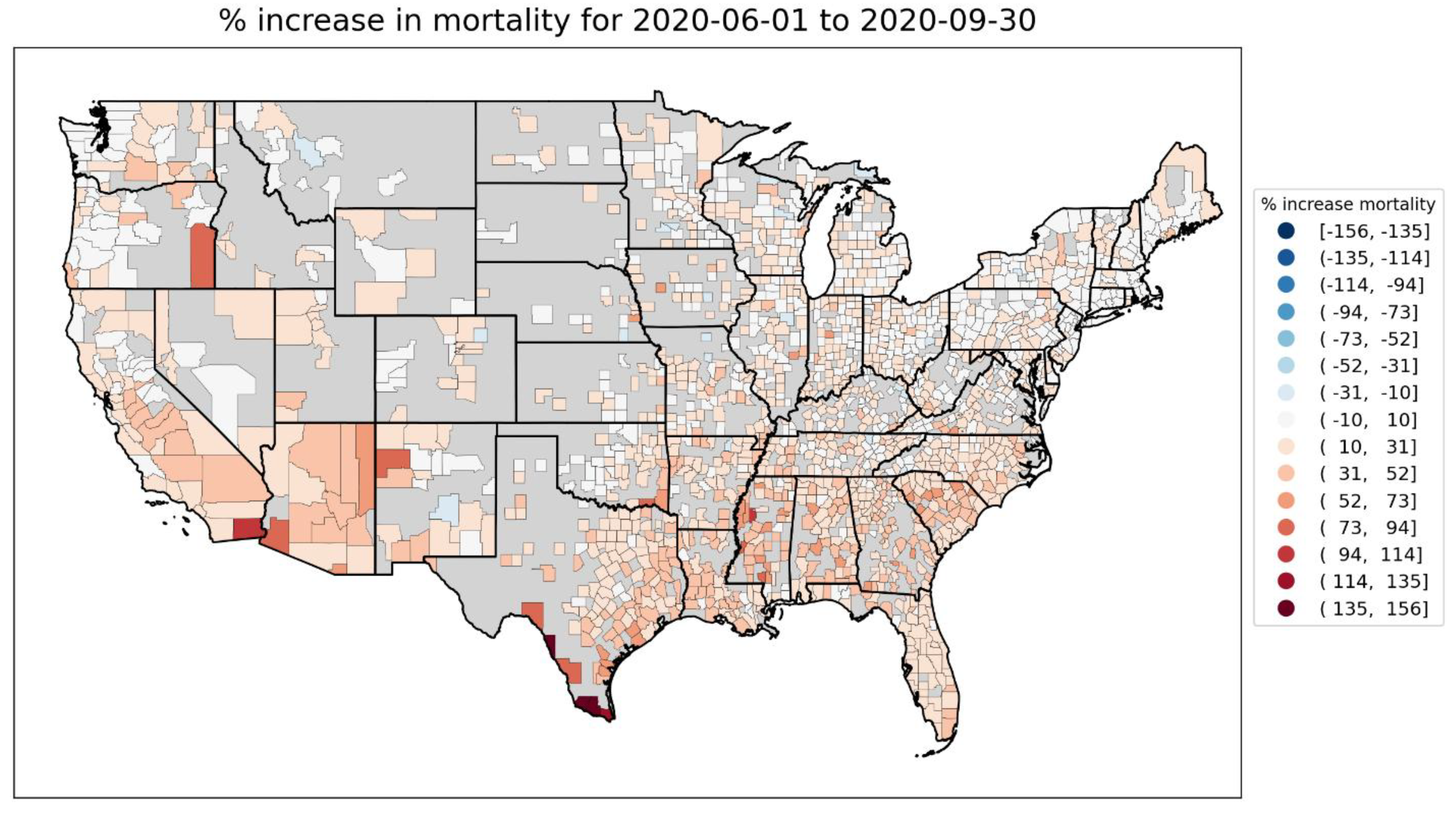
2.1.4. USA Excess Mortality by County
2.2. Timing of F-Peaks at Different Geographic Scales
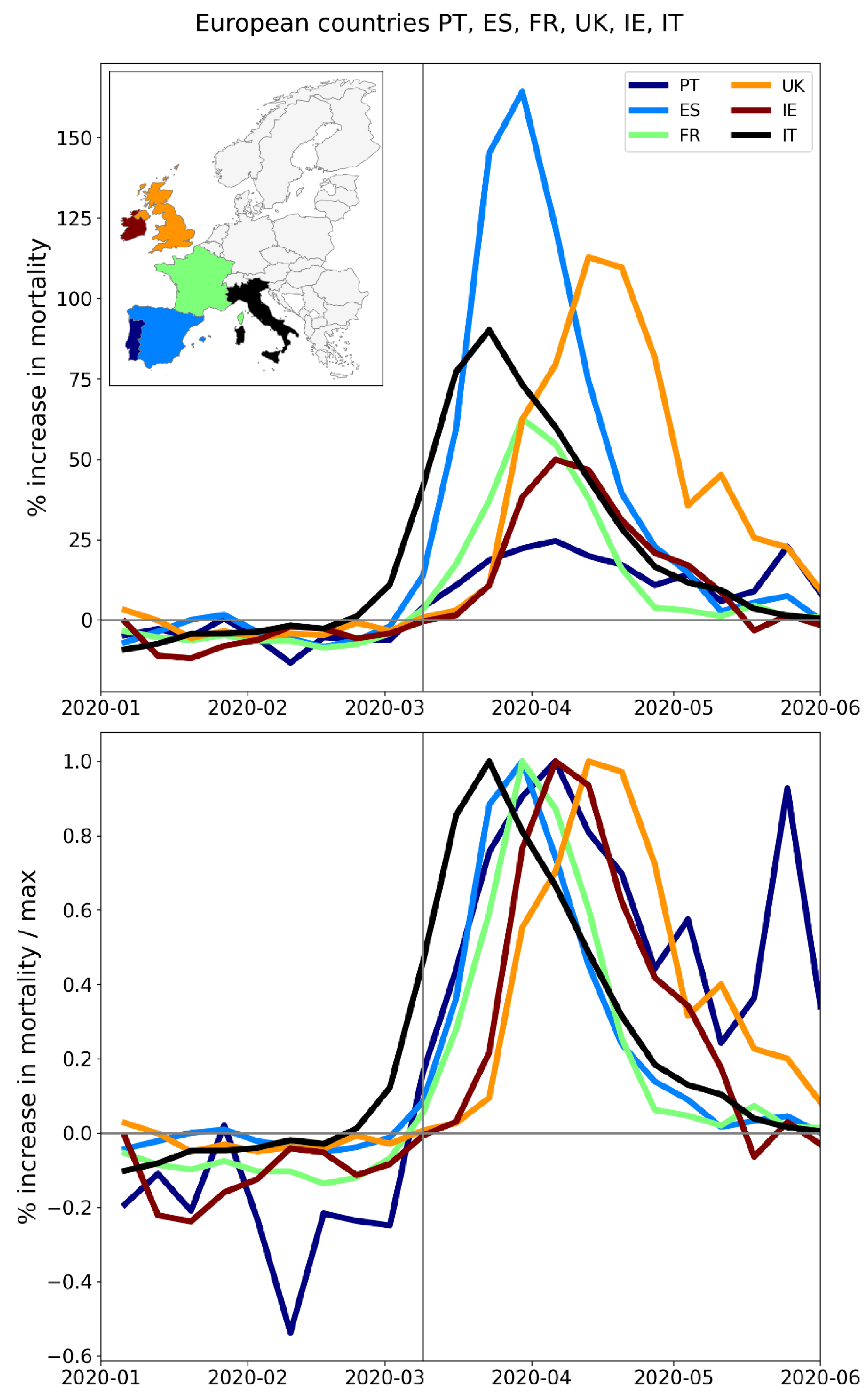
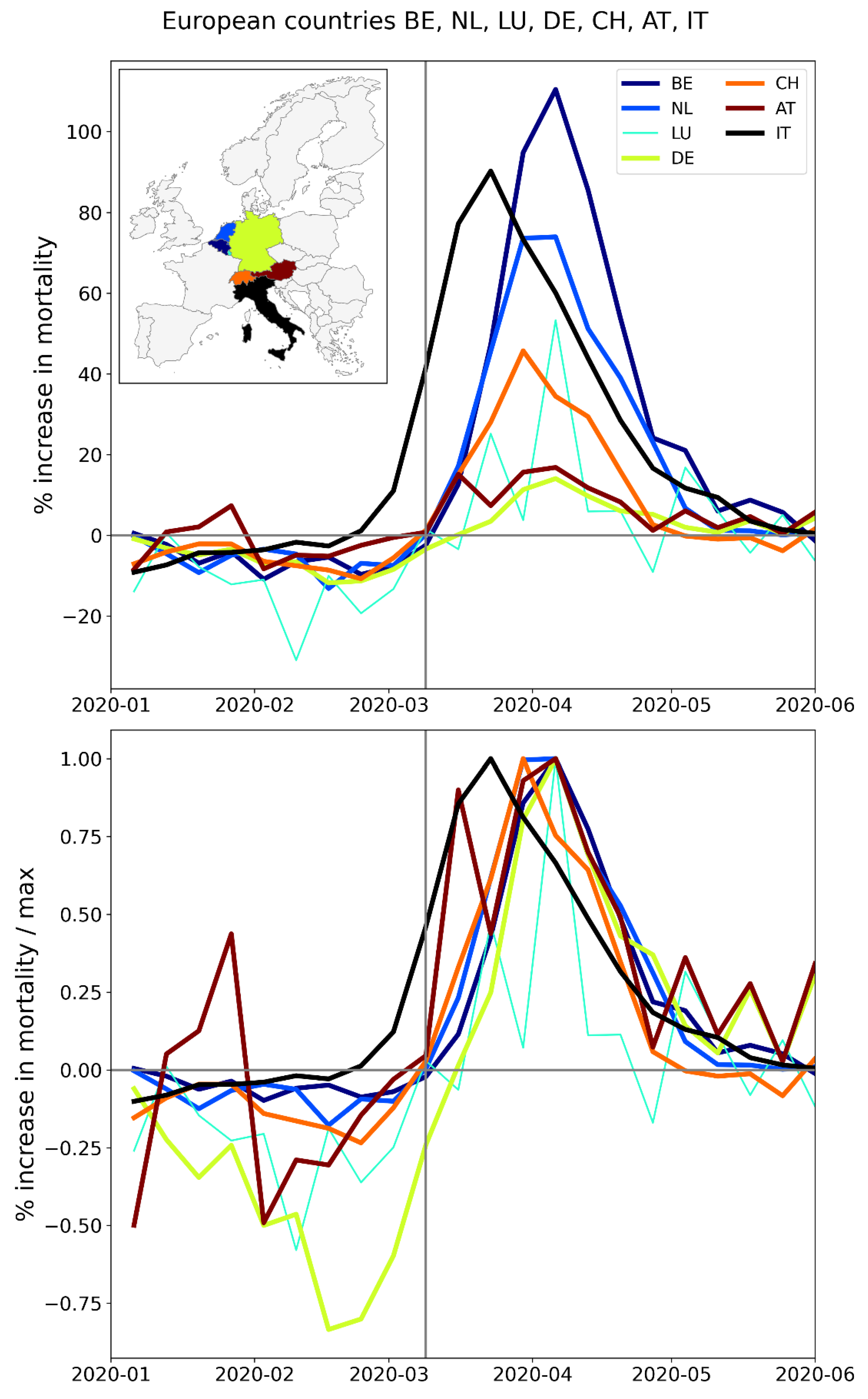
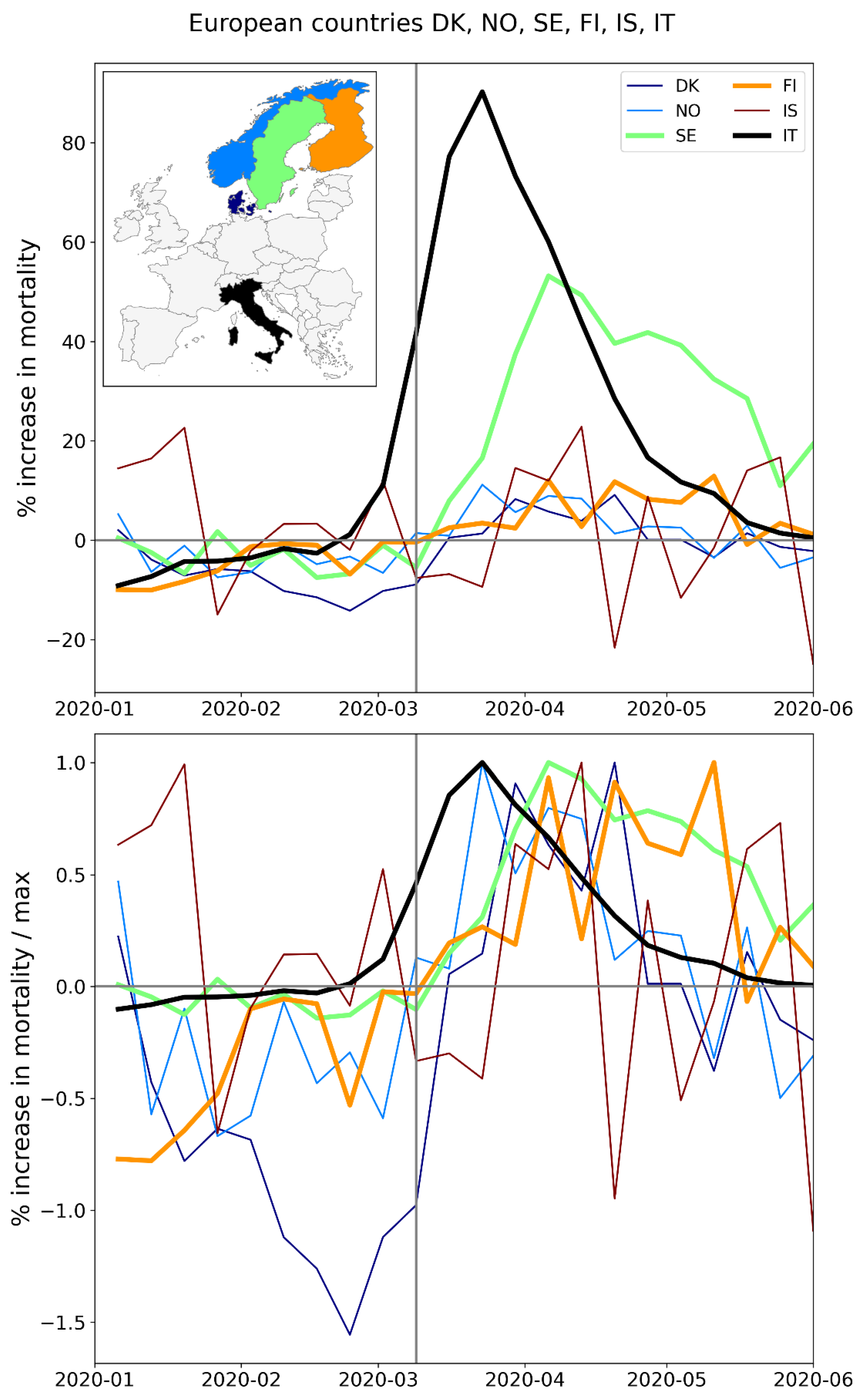
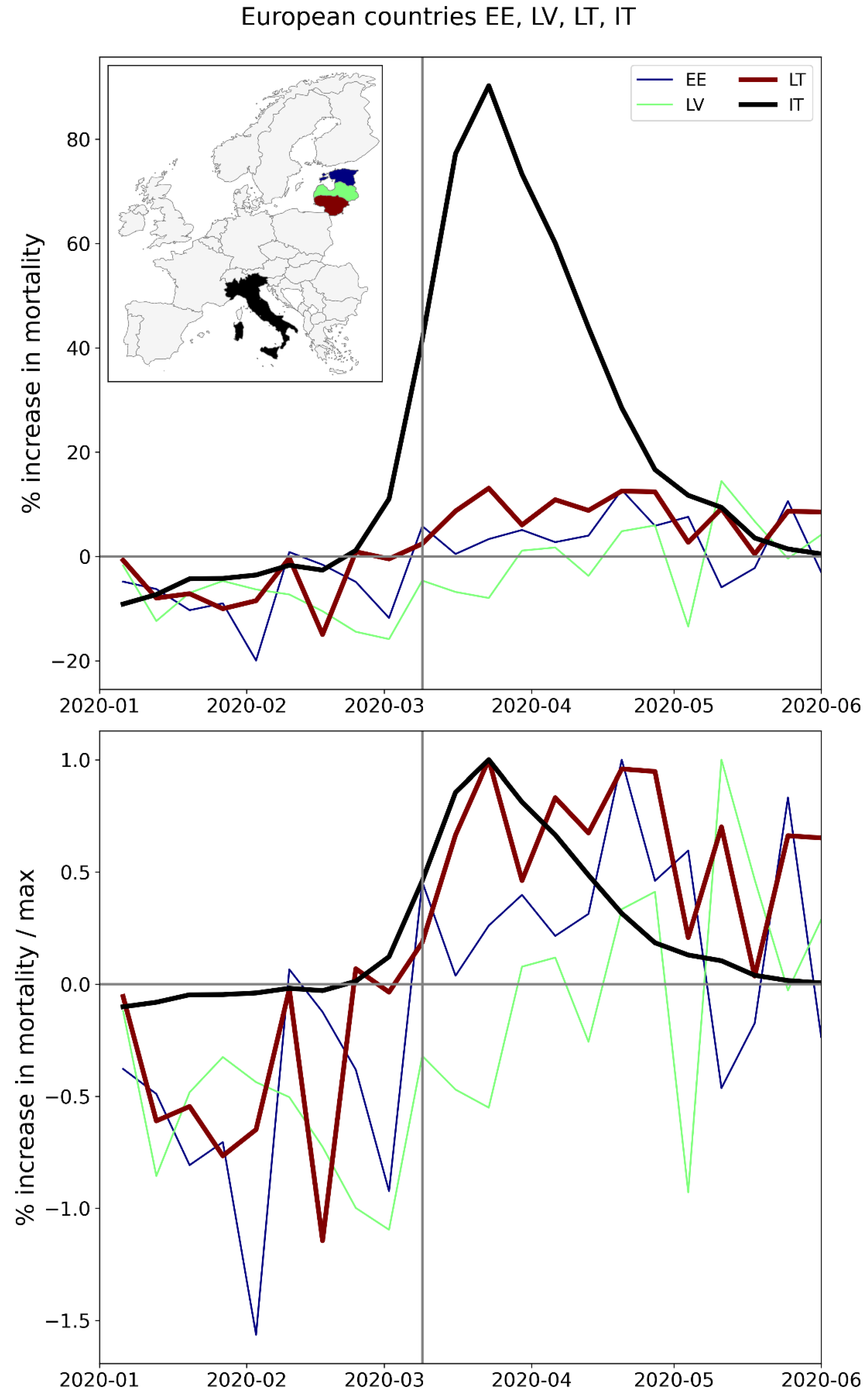
2.2.1. Europe – National Level (NUTS0)
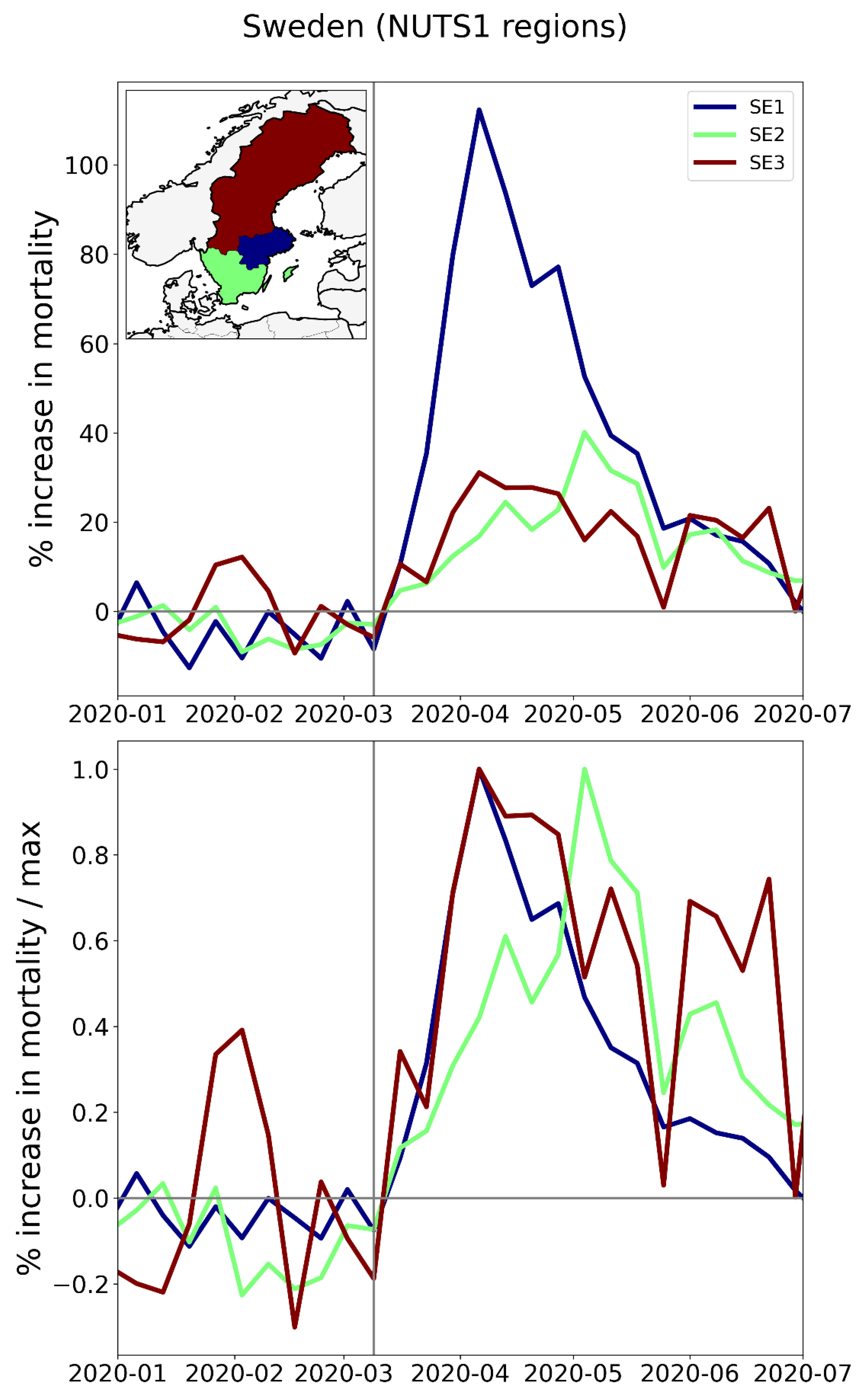
2.2.2. Europe – NUTS1 Level Subnational Regions
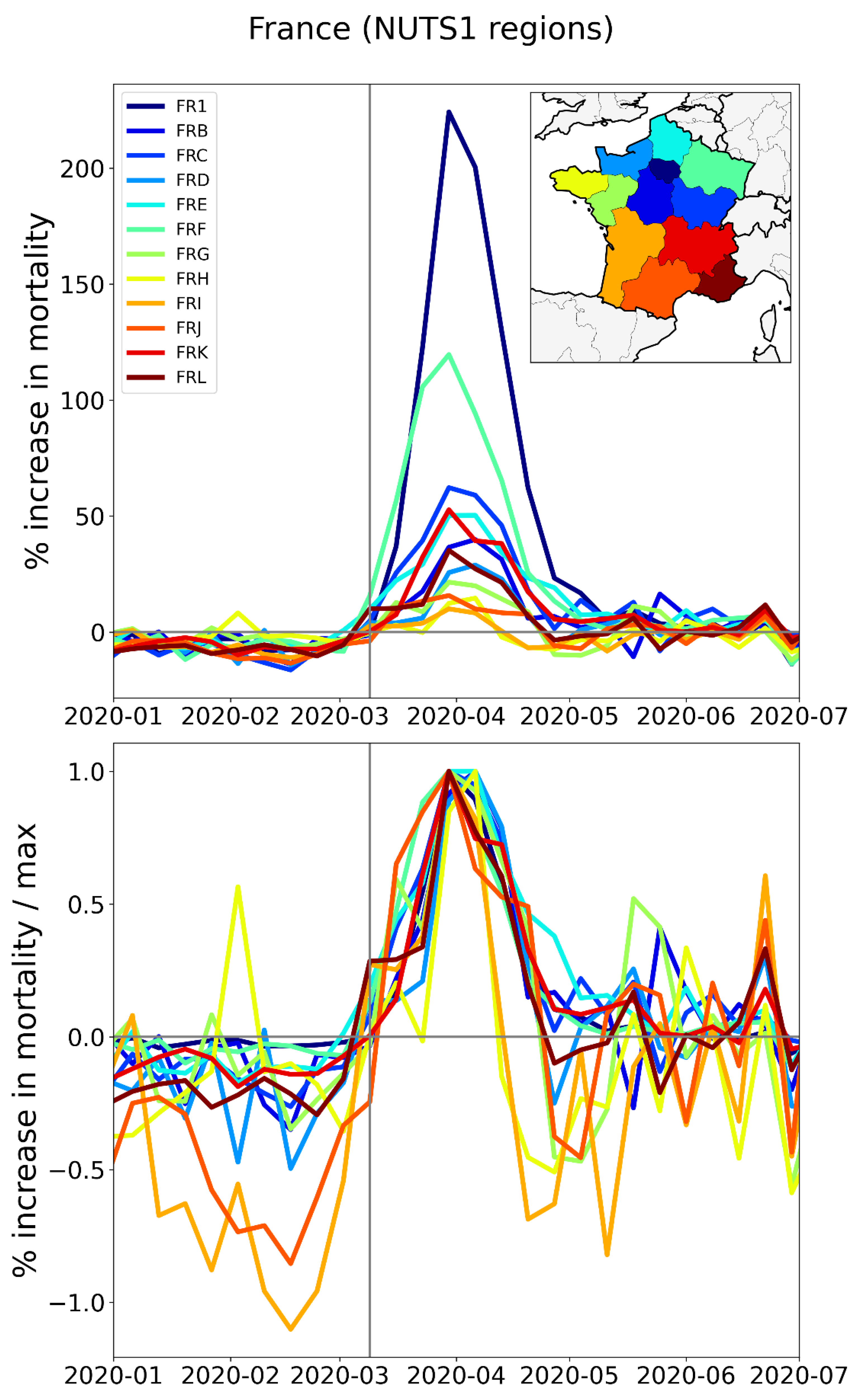
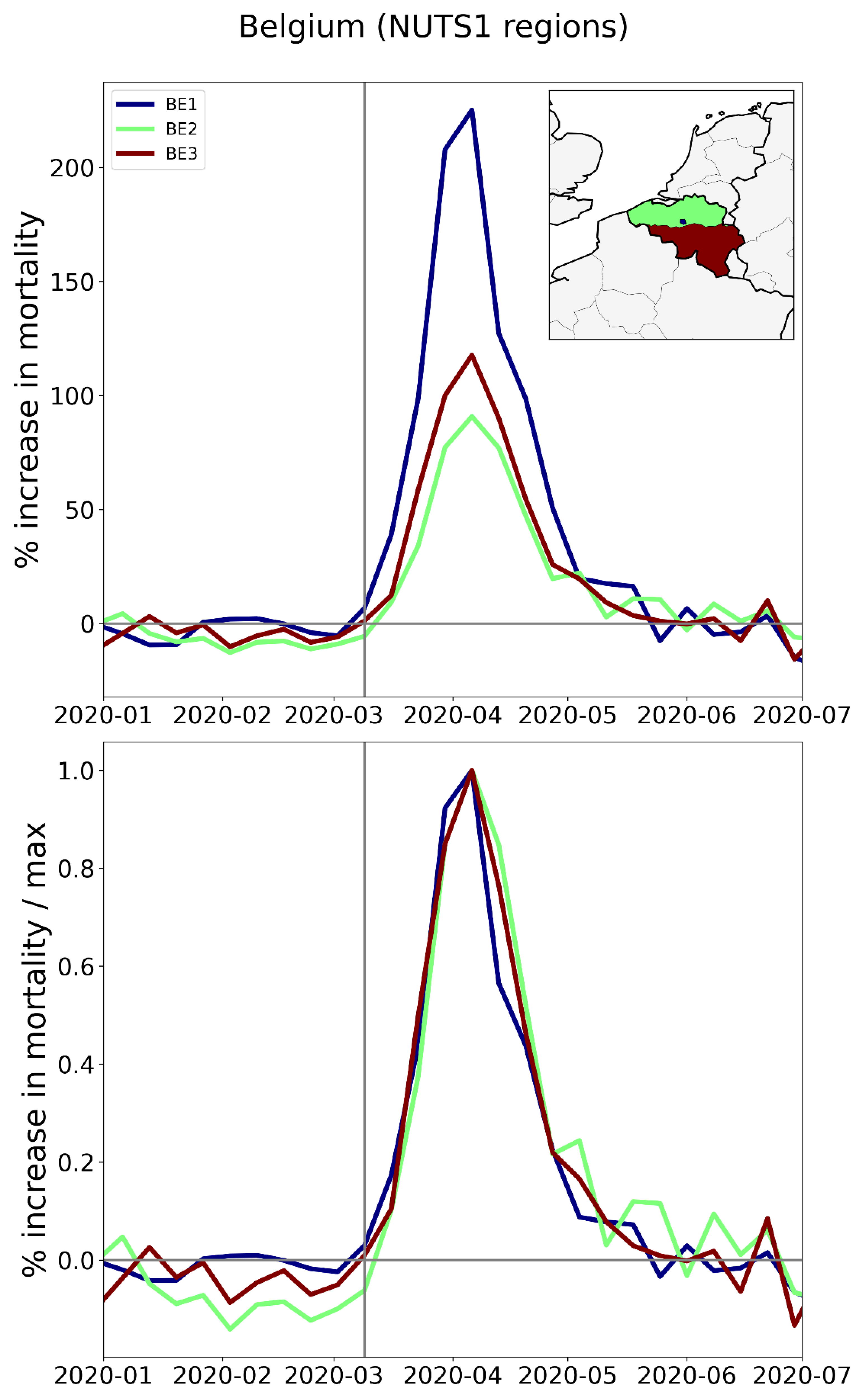
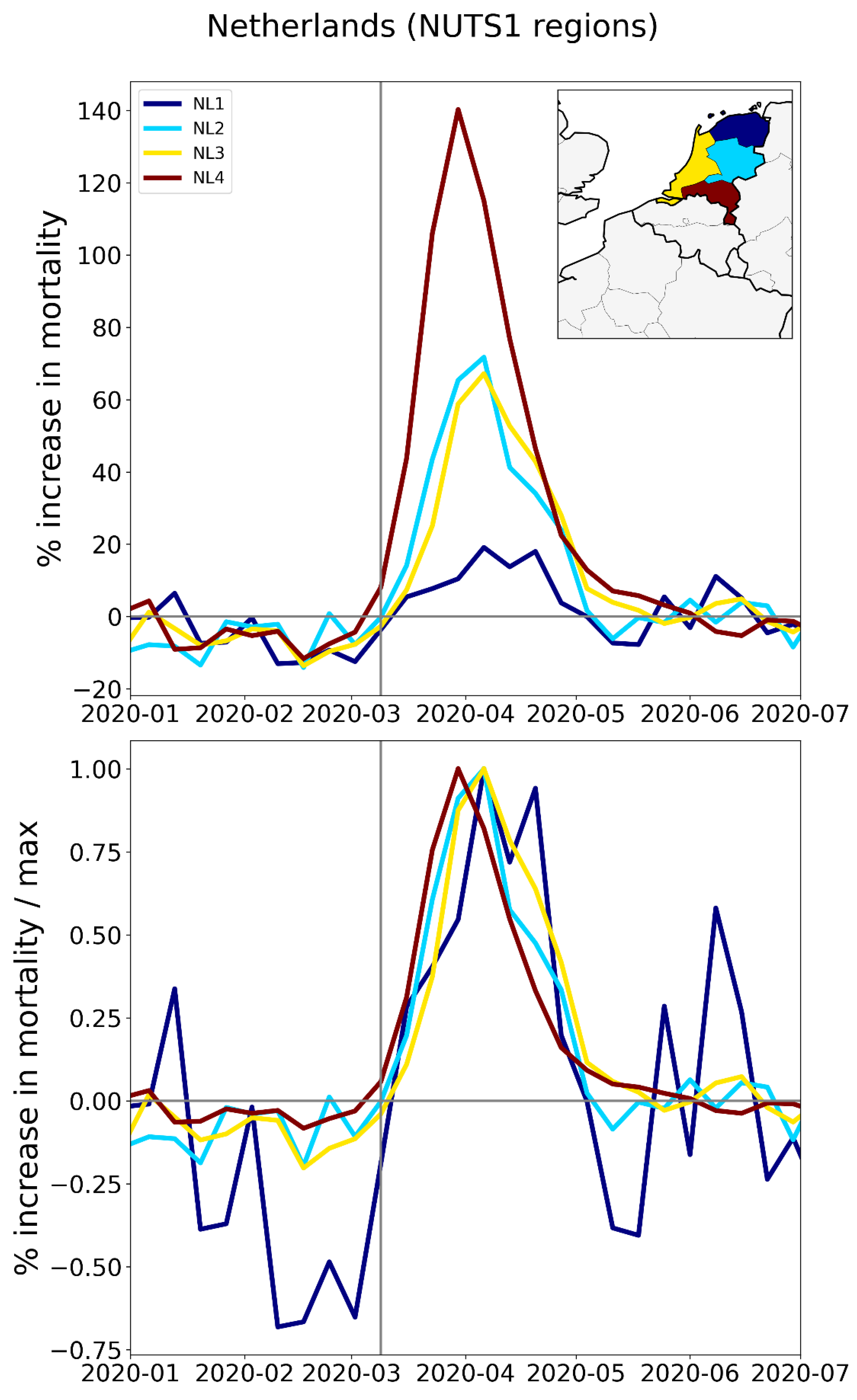
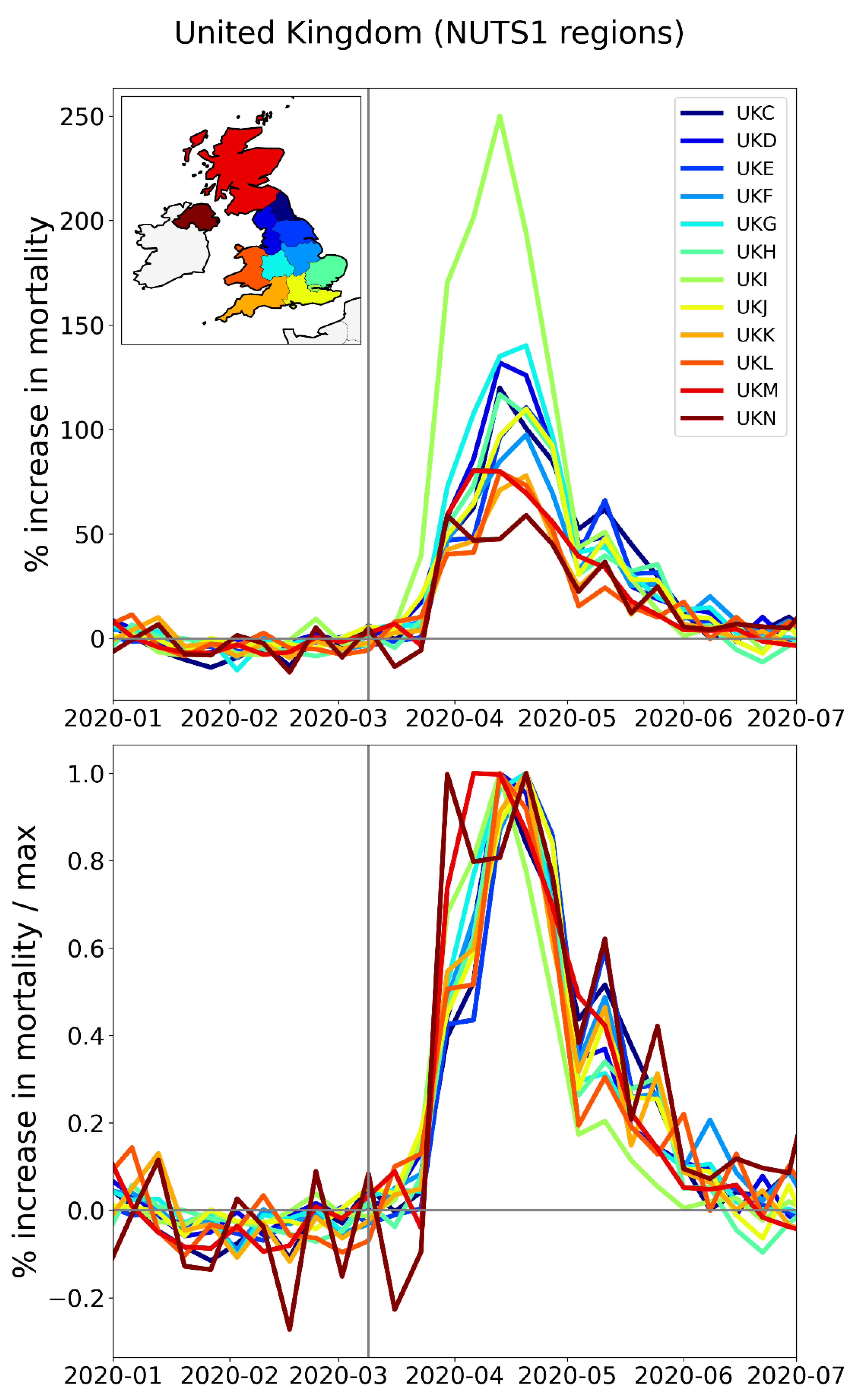
2.2.3. Europe – NUTS2 Level Subnational Regions
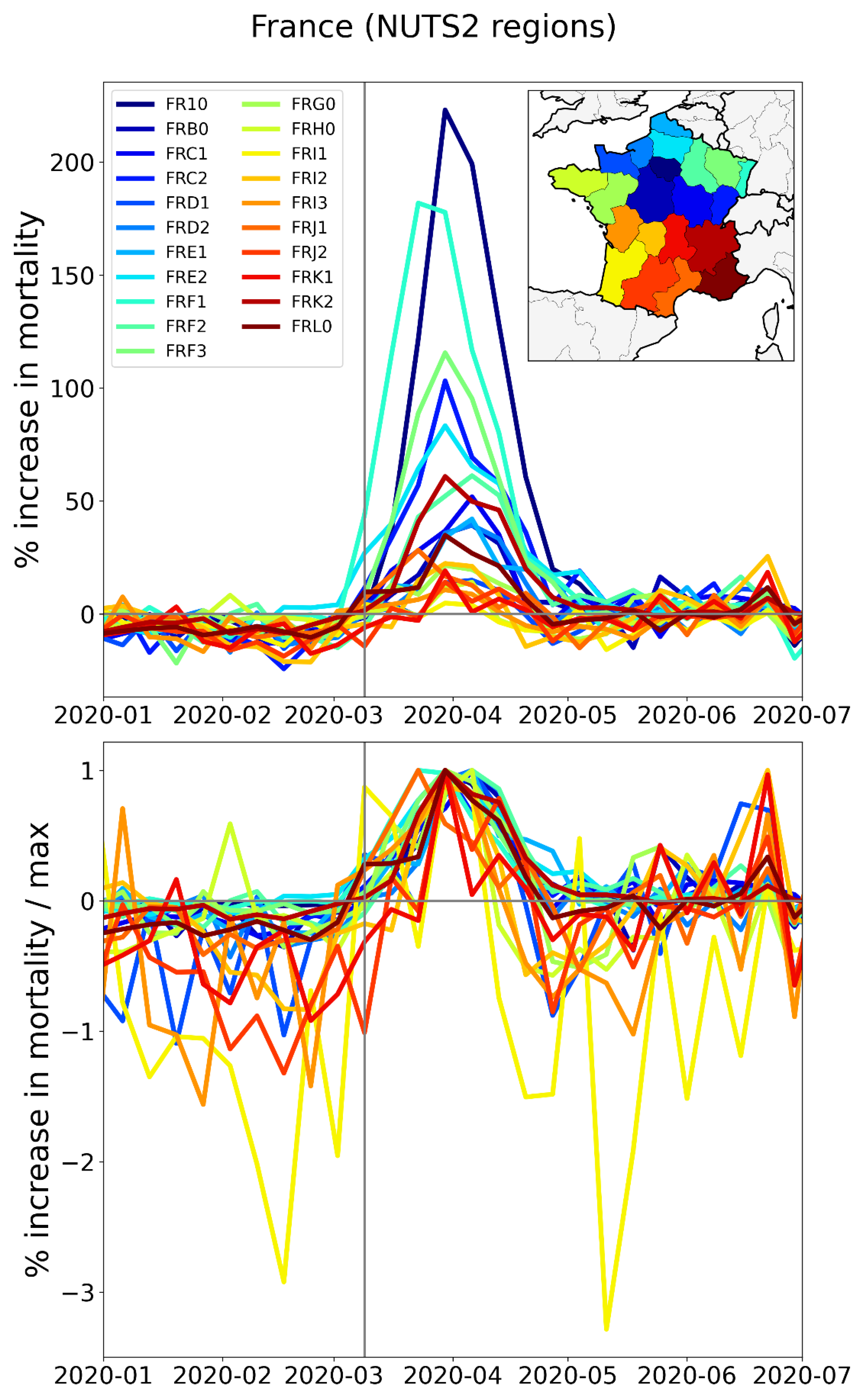
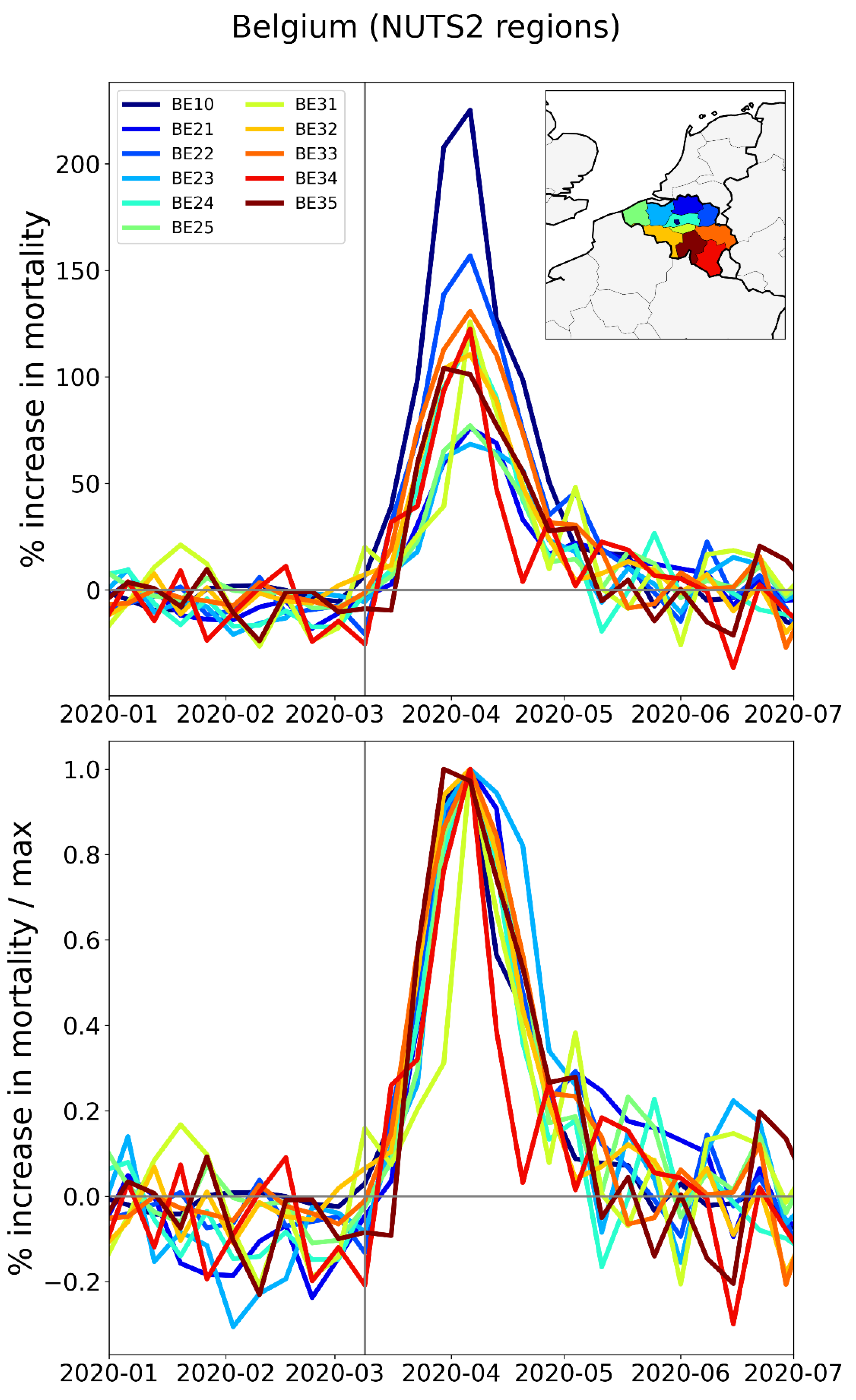
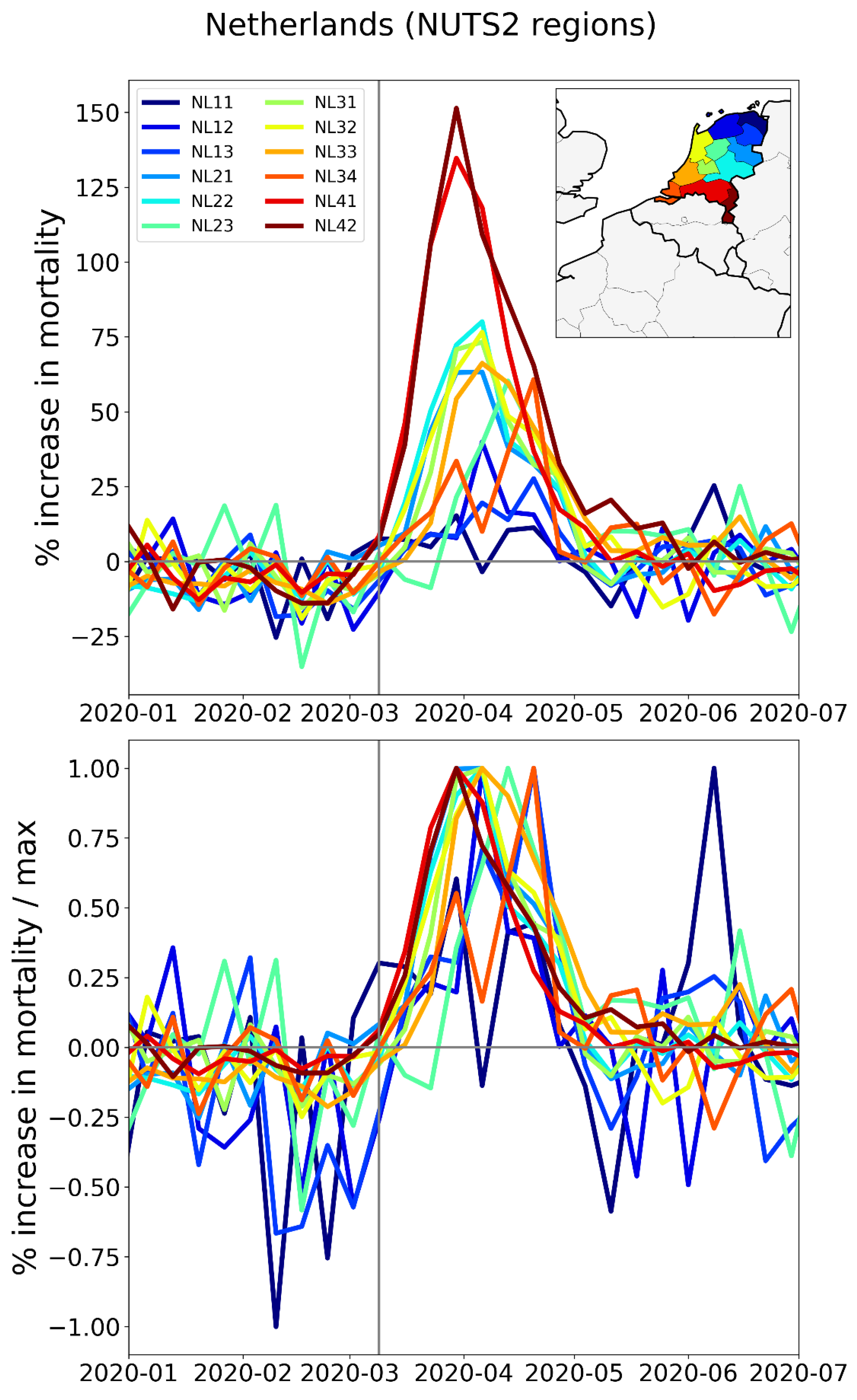
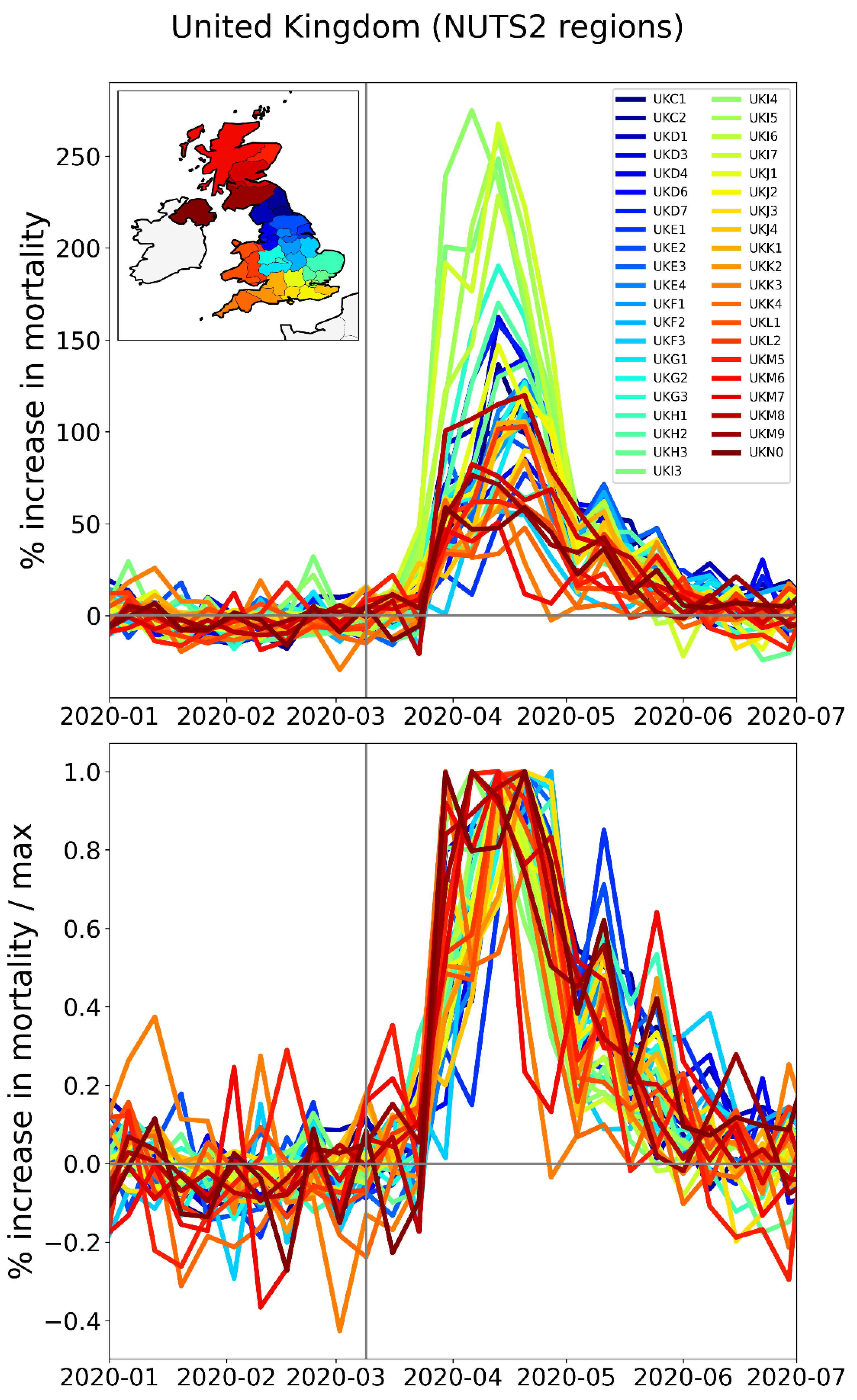
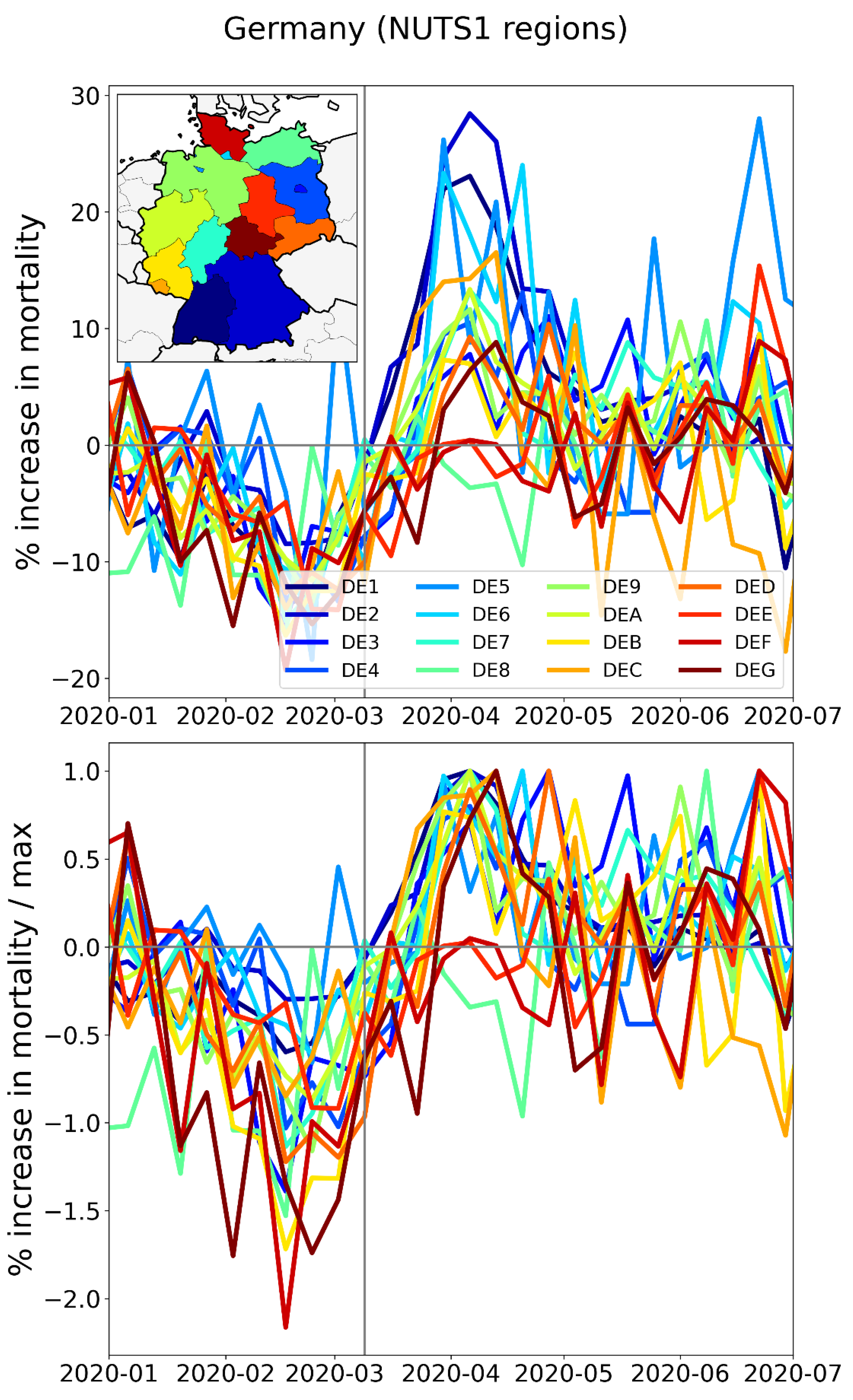
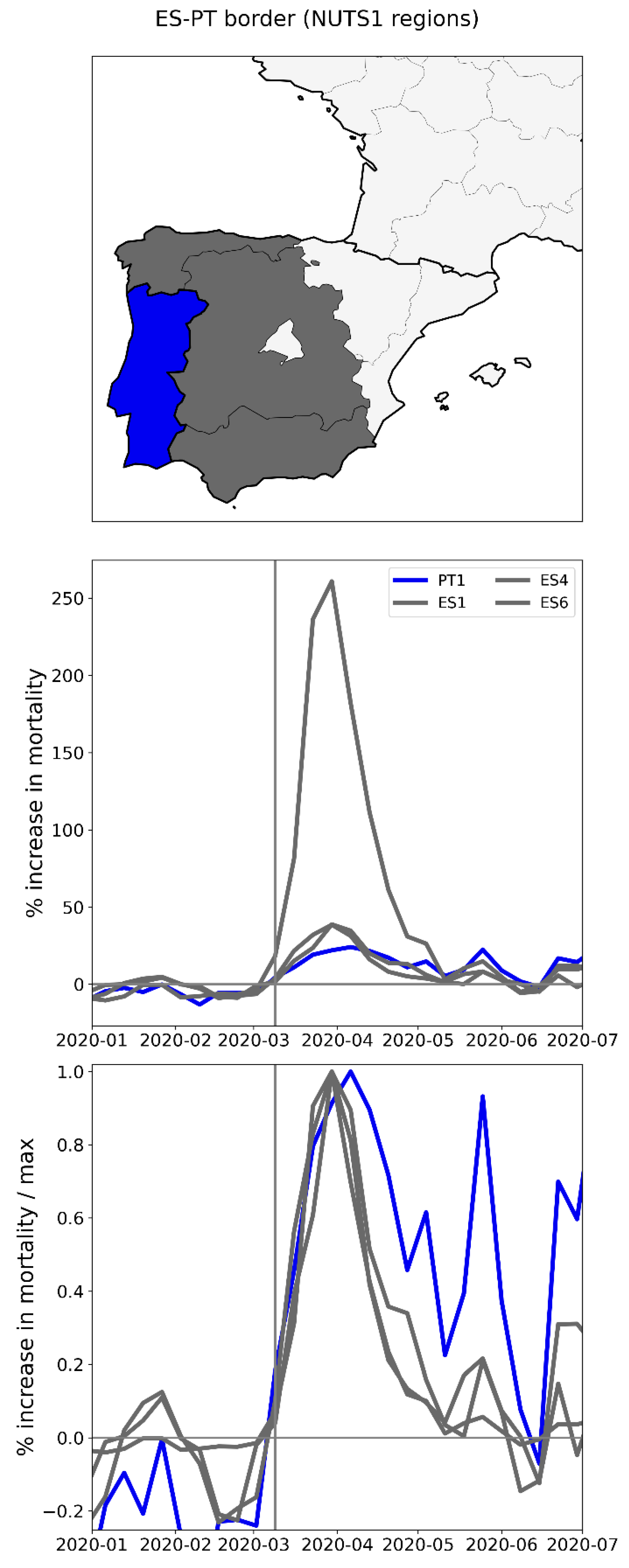
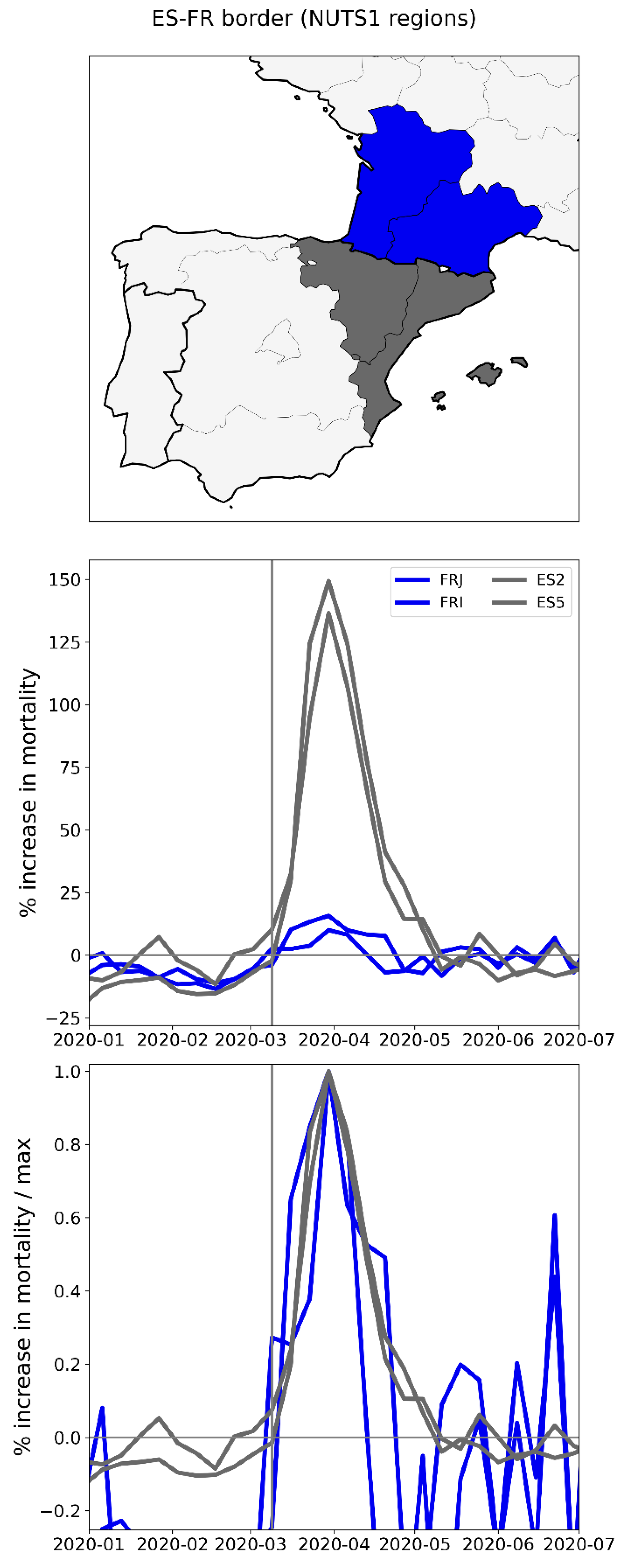
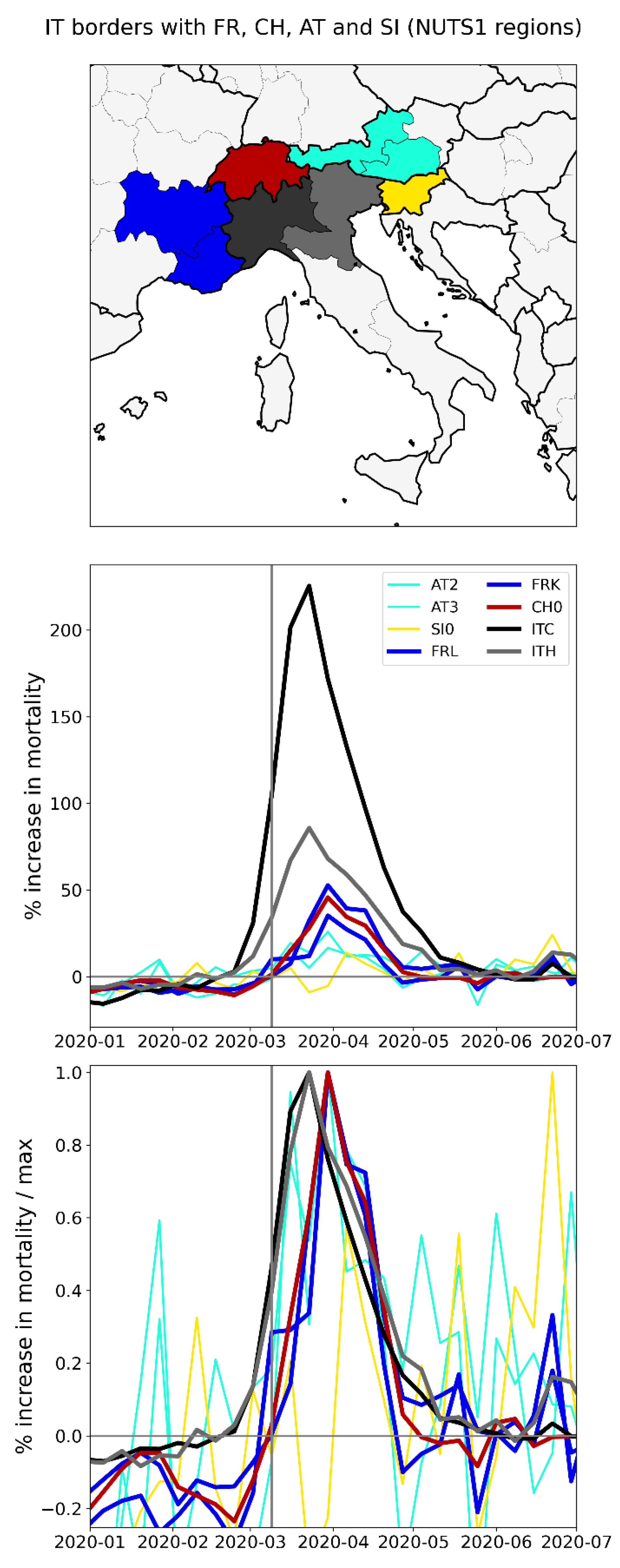
2.2.4. Europe – International Border Regions (NUTS1 Level)
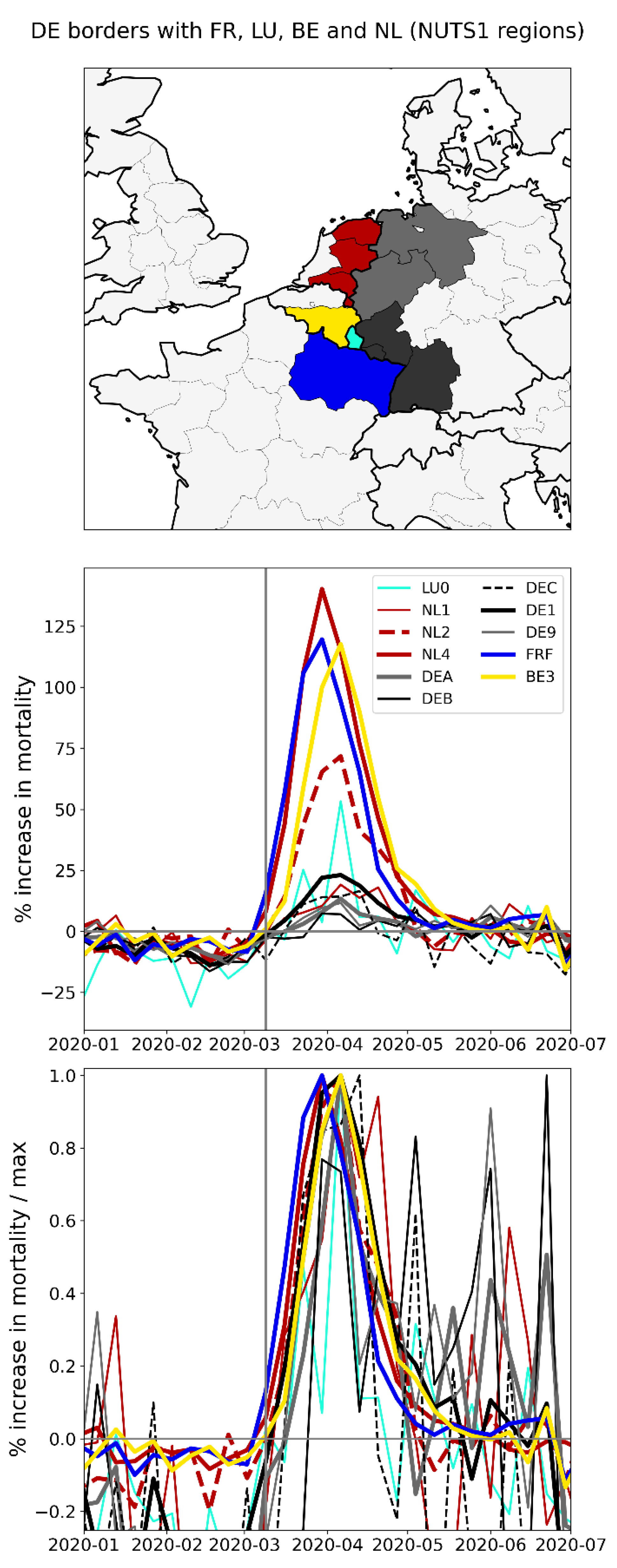
- All the western border regions of Germany had small first-peak period excess mortality. No border regions of Germany had large excess mortality peaks during the first-peak period.
- The German NUTS1 region DEB (Rhineland-Palatinate: thin solid black lines in middle and bottom panels, northern black-shaded region in top panel) essentially did not have an F-peak, whereas bordering NUTS1 regions in France (FRF) and Belgium (BE3) had large F-peaks and large integrated first-peak period P-scores (see Figure 3)
- The other four German NUTS1 regions had F-peaks with the same or nearly the same widths as, but with significantly smaller (up to more than five times smaller) peak heights than, the regions that share borders with them in France, Belgium, and the Netherlands. The Dutch NUTS1 region NL1 (North Netherlands: thin red lines, northernmost red-shaded region) is similar to the German regions in that it had a small F-peak height, whereas the other two Dutch NUTS1 border regions NL2 (East Netherlands: dashed red lines, middle red-shaded region) — which shares an internal border with NL1 — and NL4 (South Netherlands: thick solid red lines, southernmost red-shaded region) had large peak heights.
- The F-peaks in the bordering regions of the four countries France, Belgium, the Netherlands, and Germany all had essentially the same width (FWHM) while having significantly different peak heights.
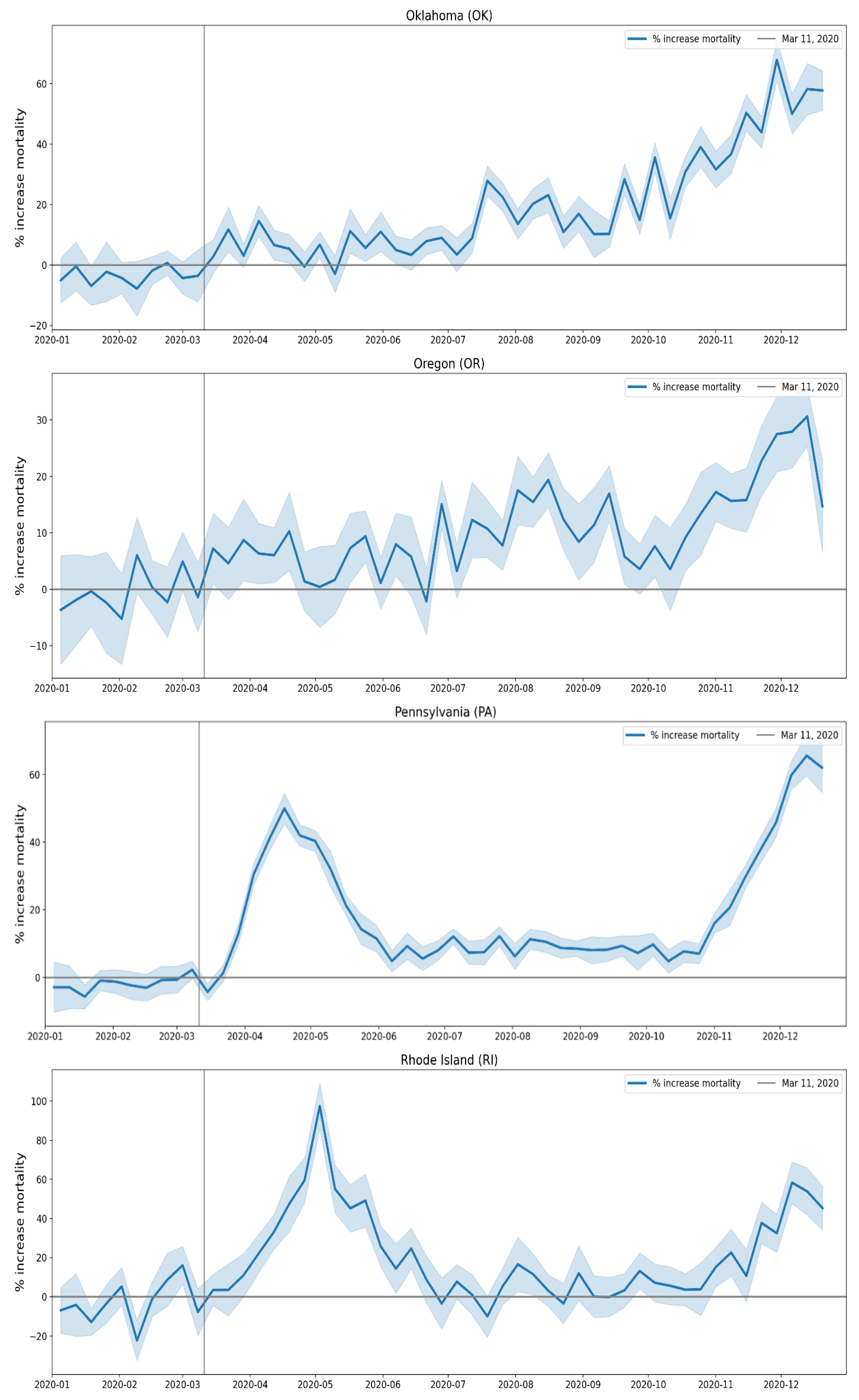
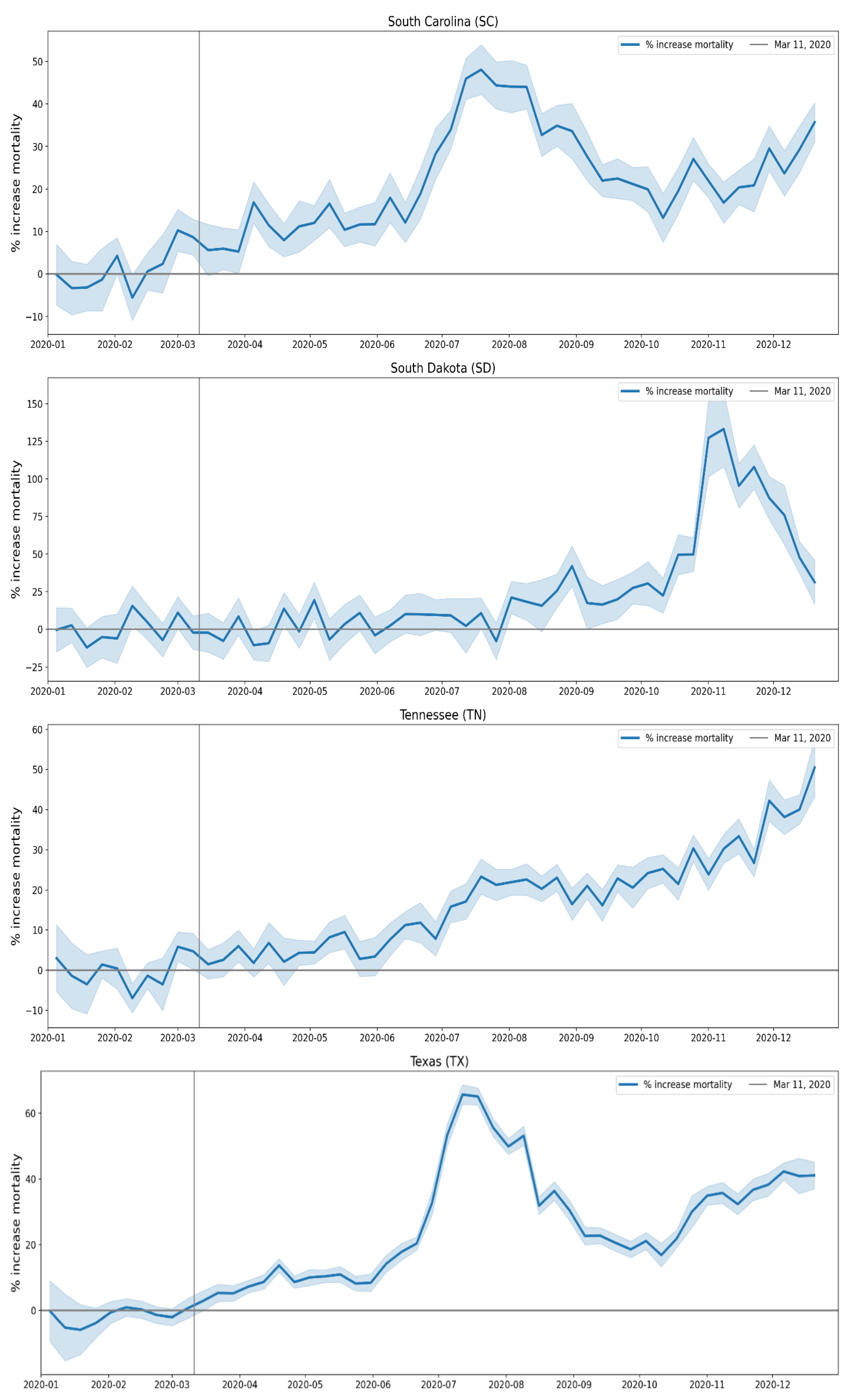
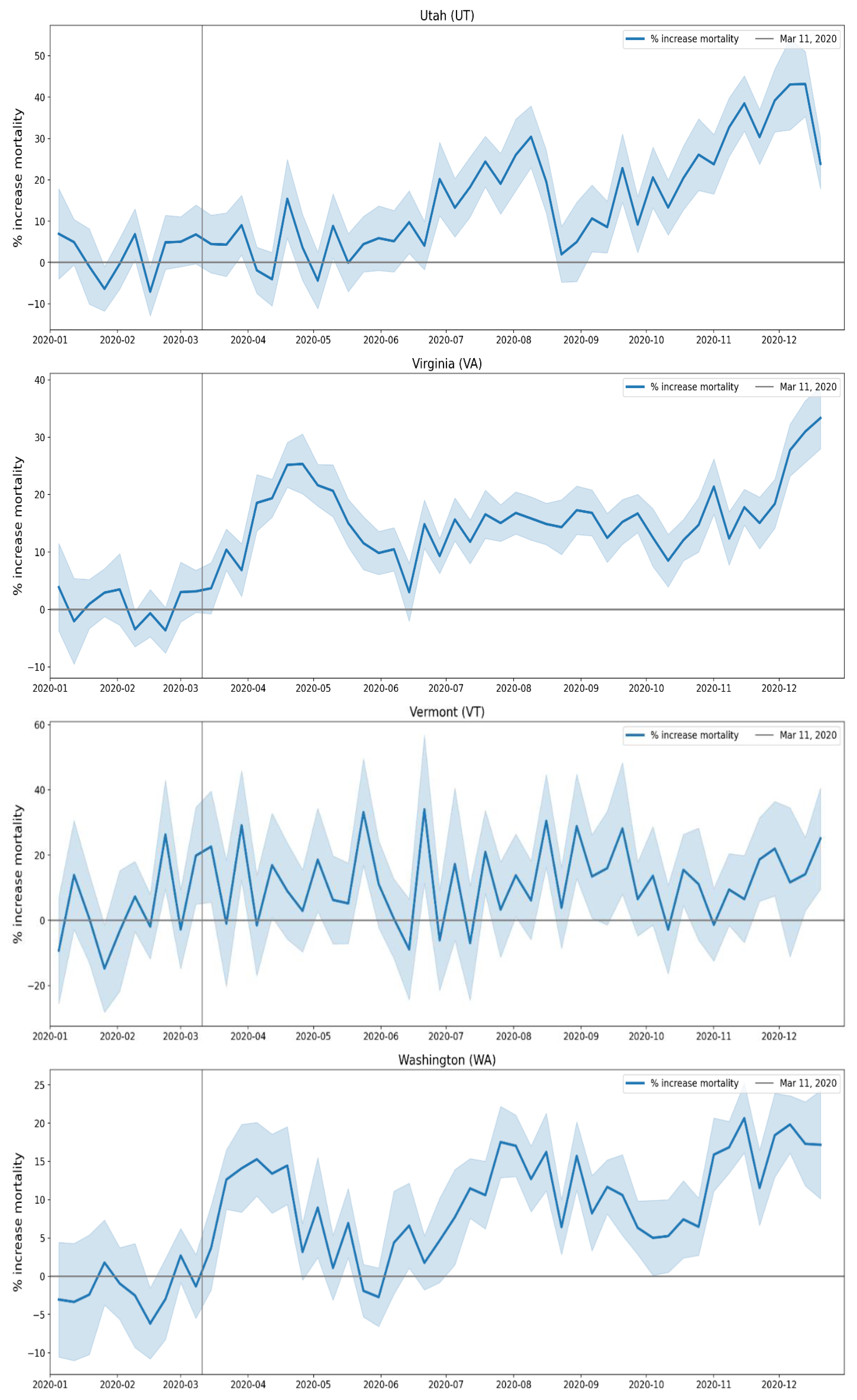
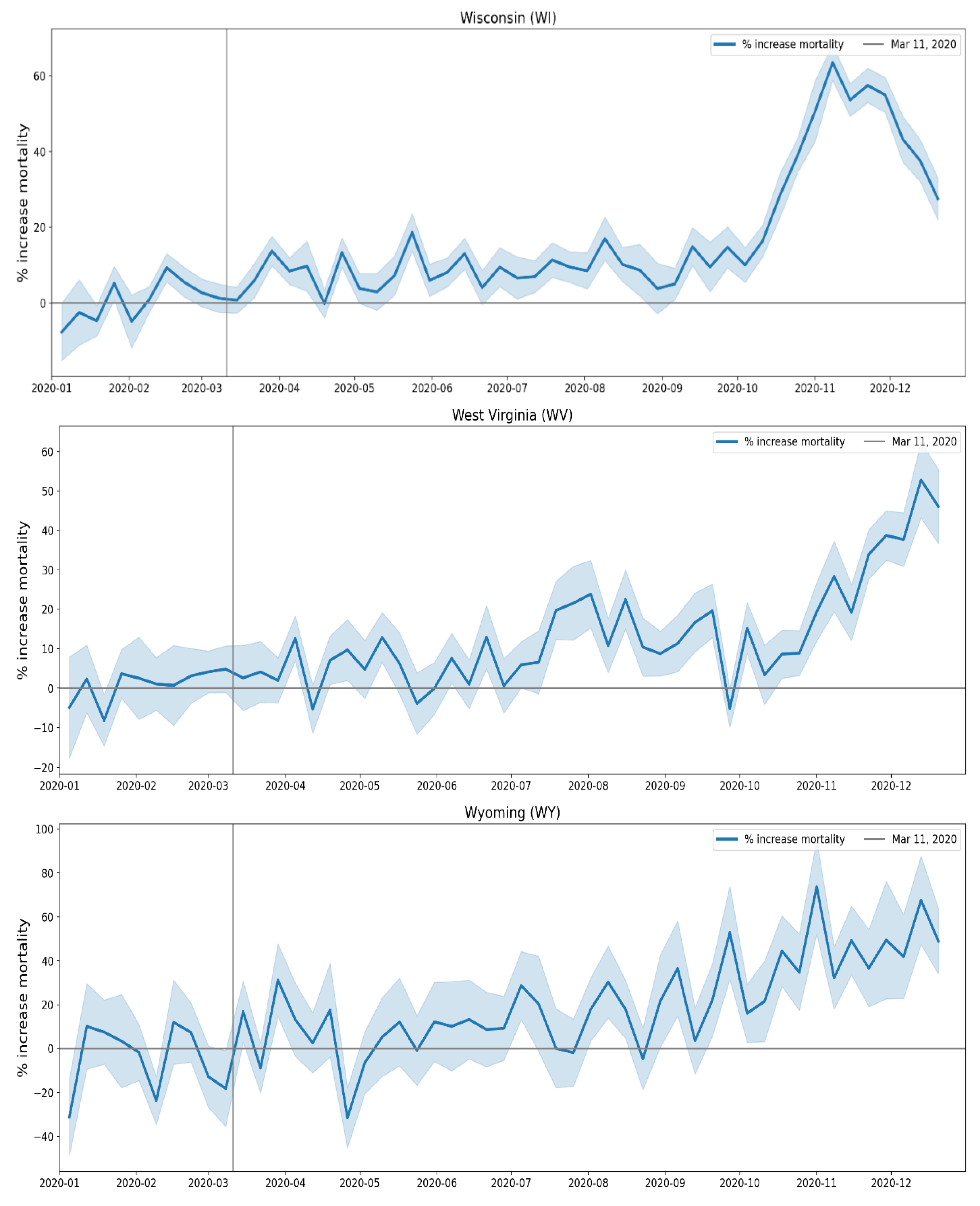
2.2.5. USA States
2.2.6. USA Counties
2.3. Differing Excess Mortalities Between Regions with Large International Airports
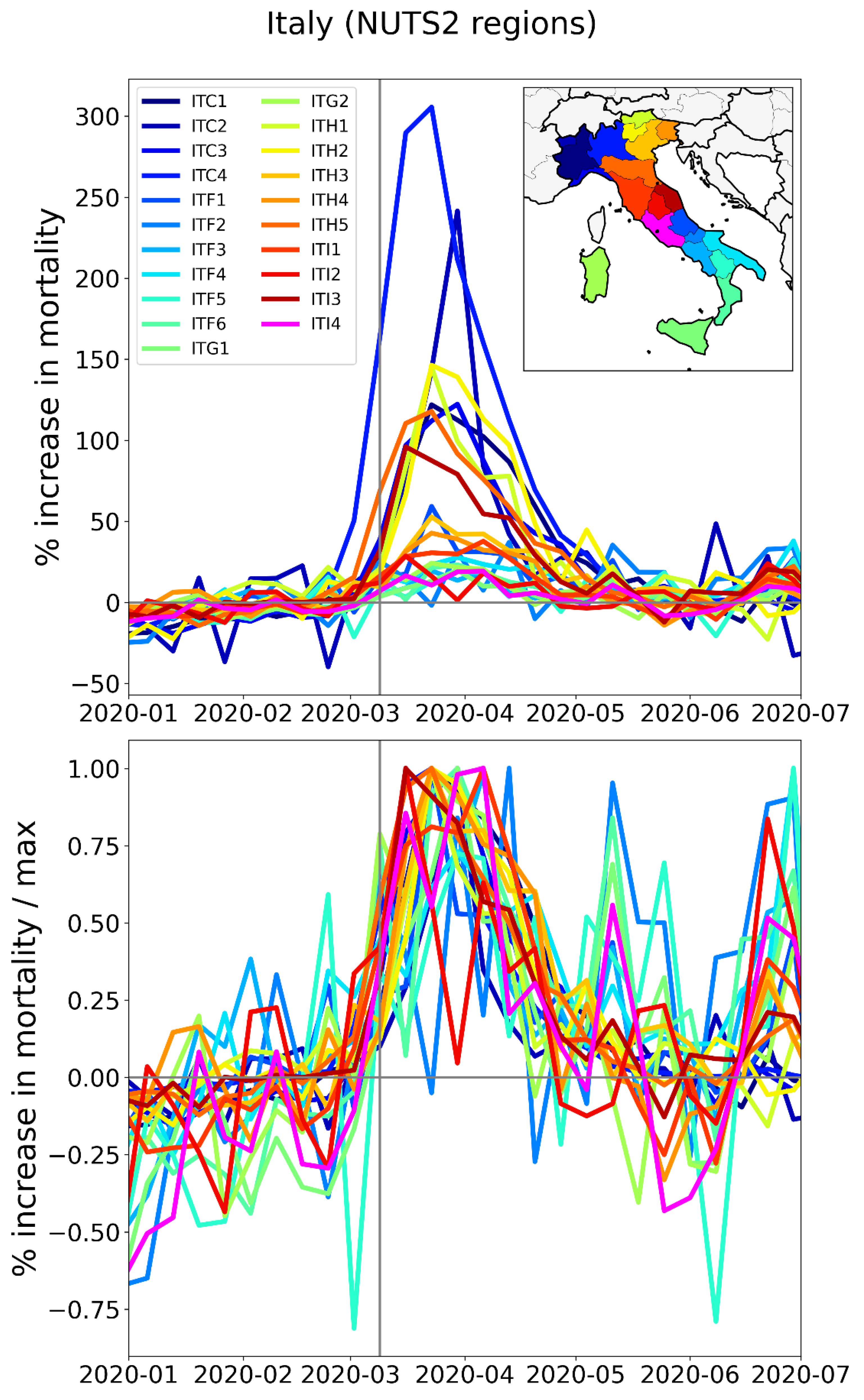
2.3.1. The Case of Rome vs Milan in Italy
- Rome Fiumicino (FCO), in the Lazio NUTS2 region
- Milan Malpensa (MXP) in the Lombardy NUTS2 region, which also serves the Piedmont NUTS2 region
- Milan Bergamo (BGY) in the Lombardy NUTS2 region
- Venice Marco Polo (VCE) in the Veneto NUTS2 region
- Naples International Airport (NAP) in the Campania NUTS2 region
2.3.2. The Case of New York City vs Los Angeles and San Francisco in the USA
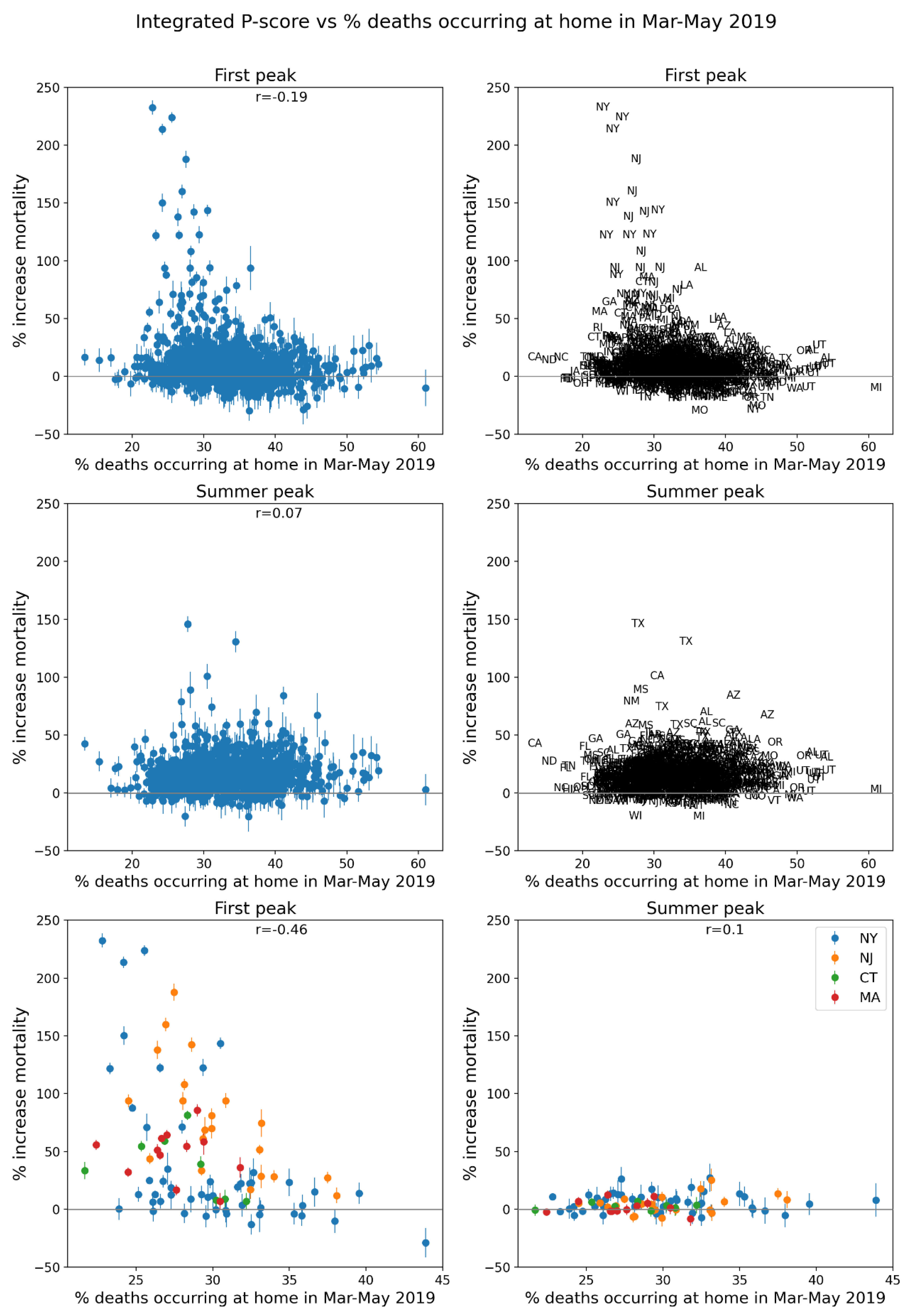
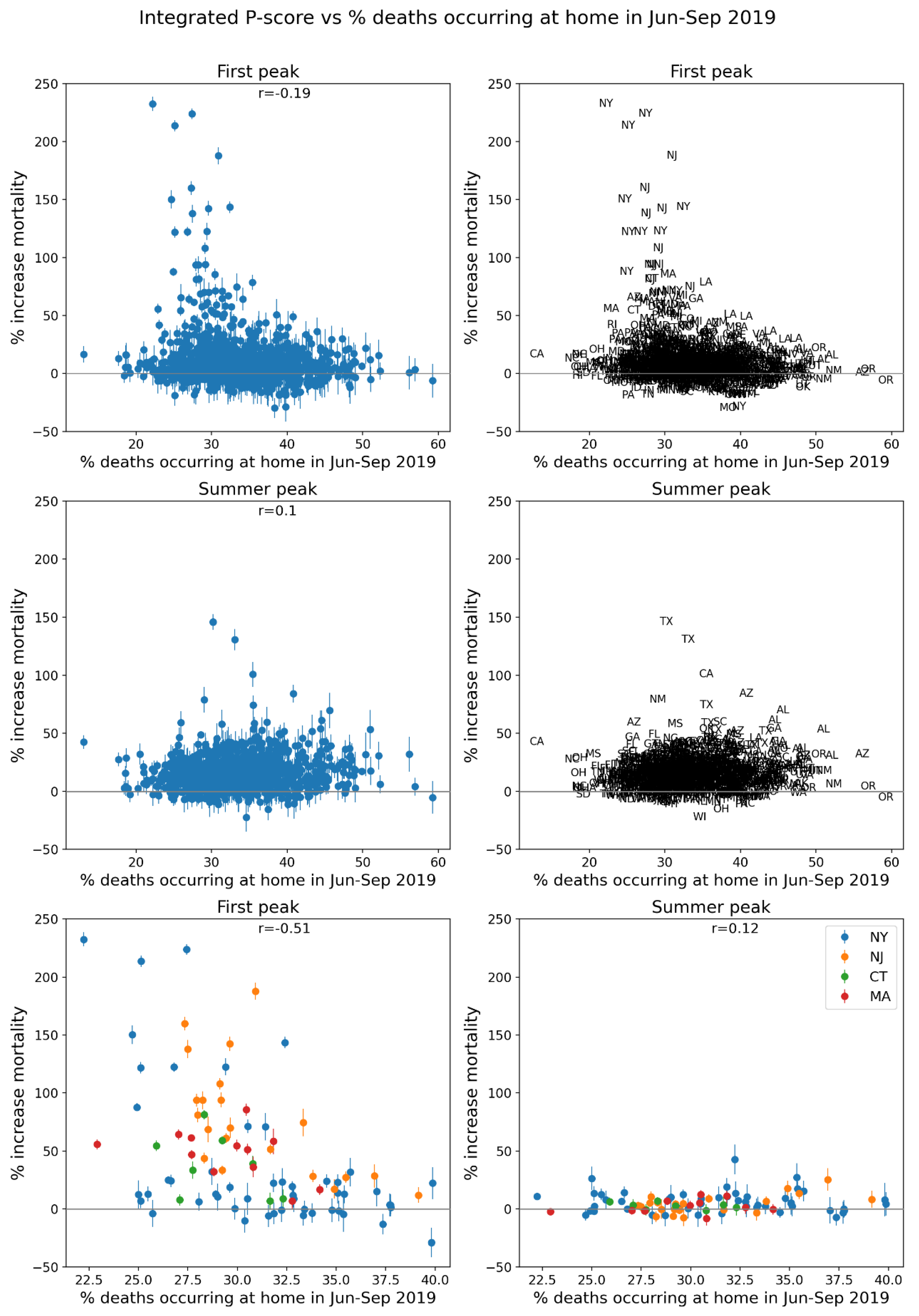
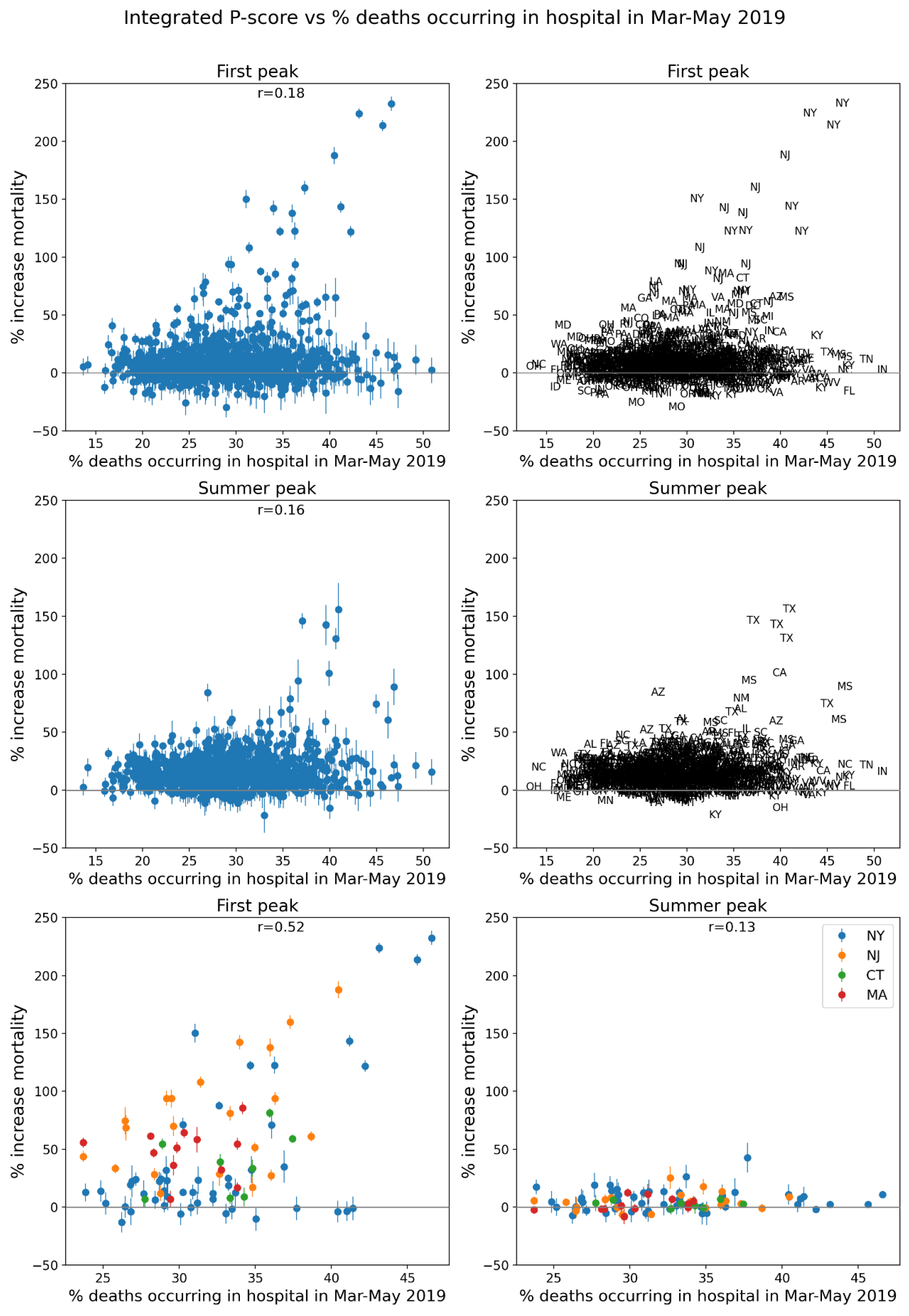
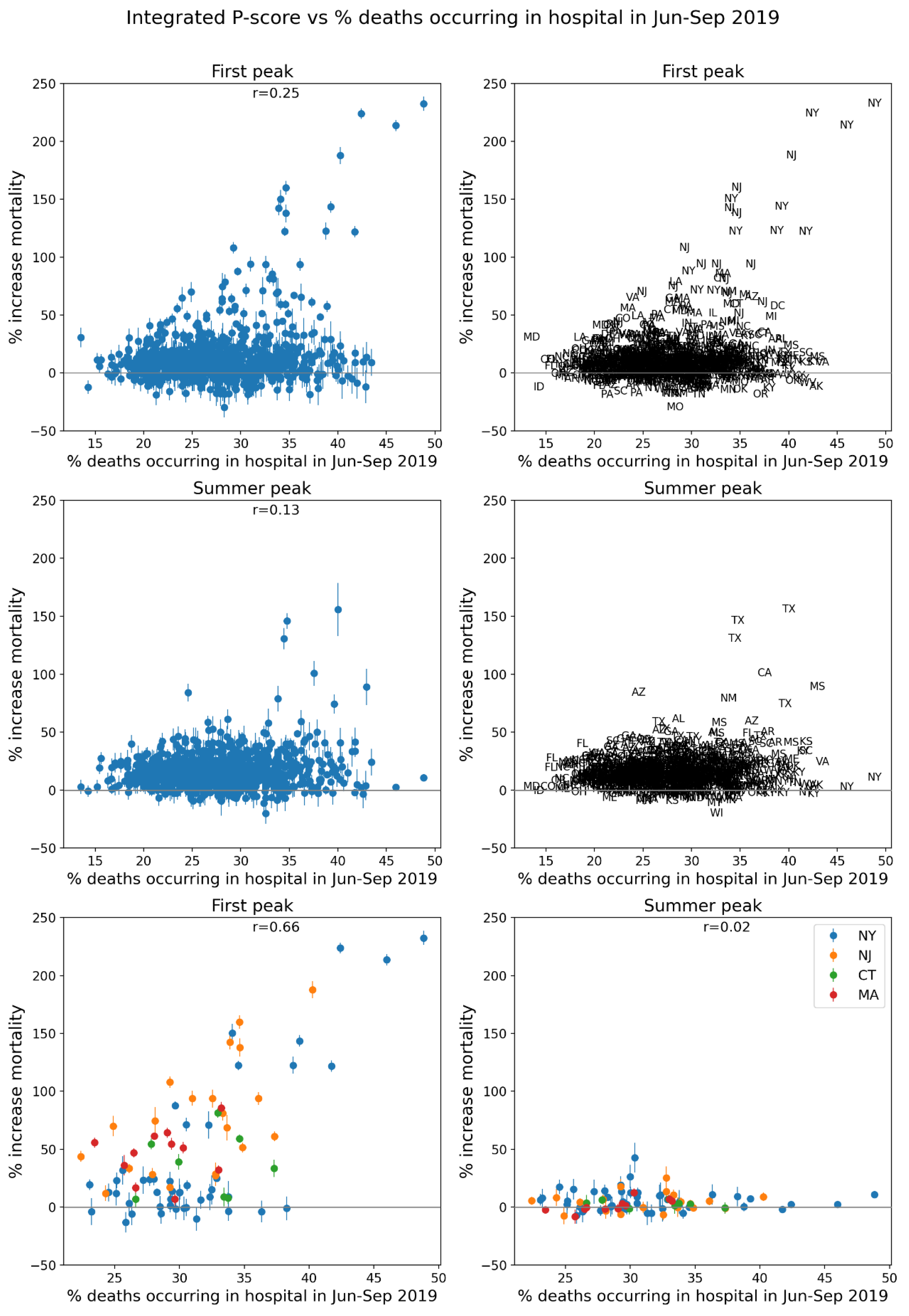
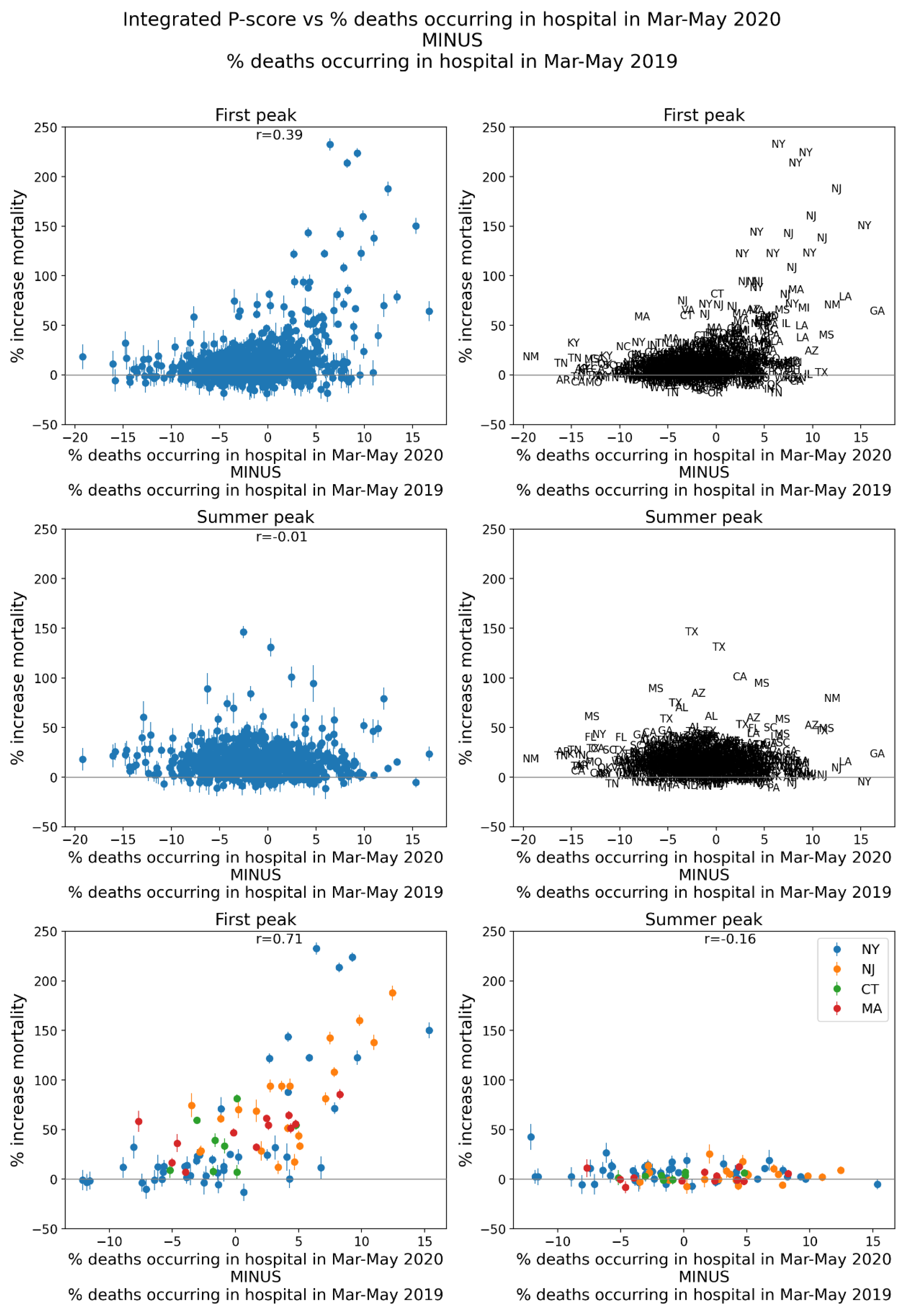
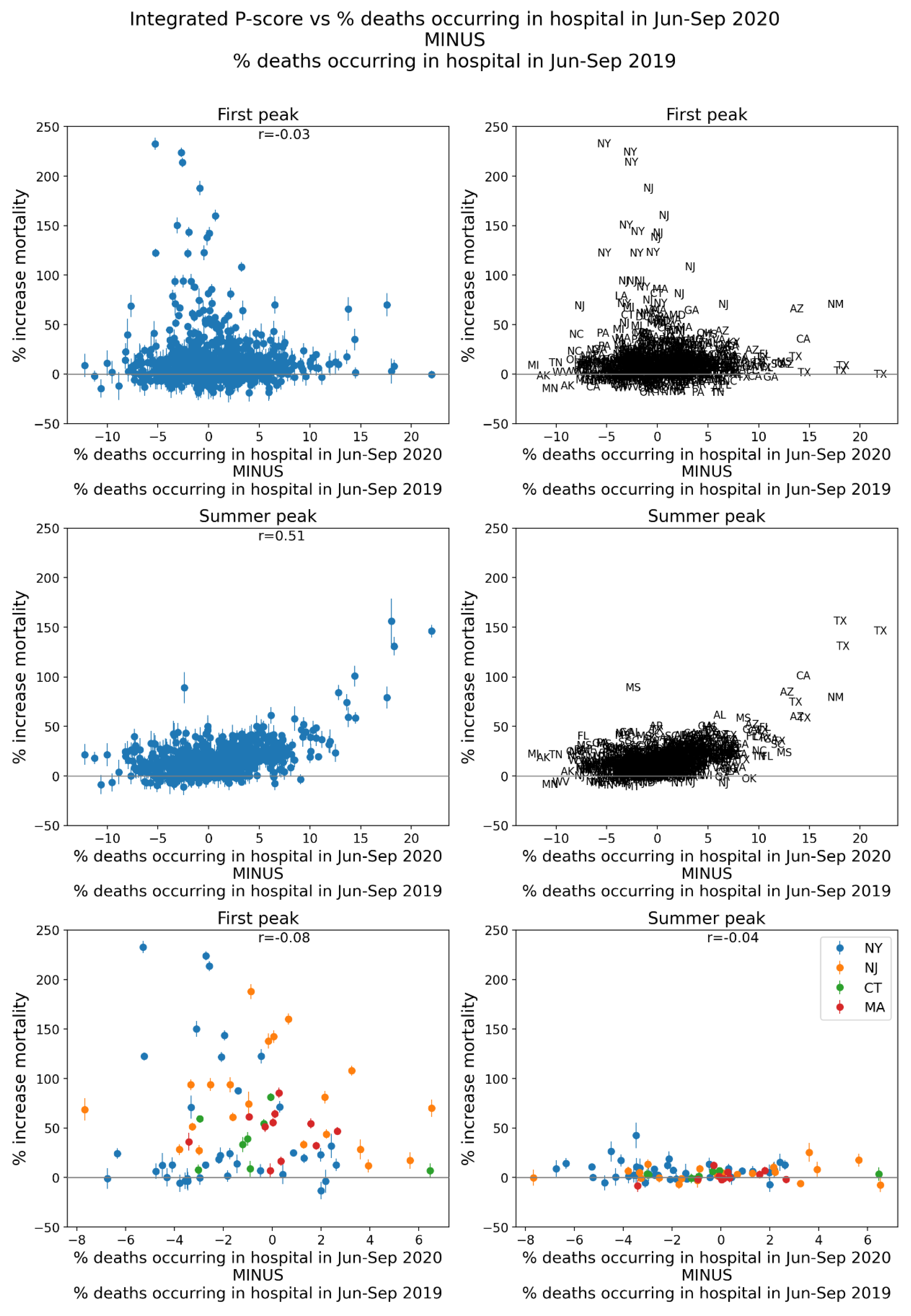
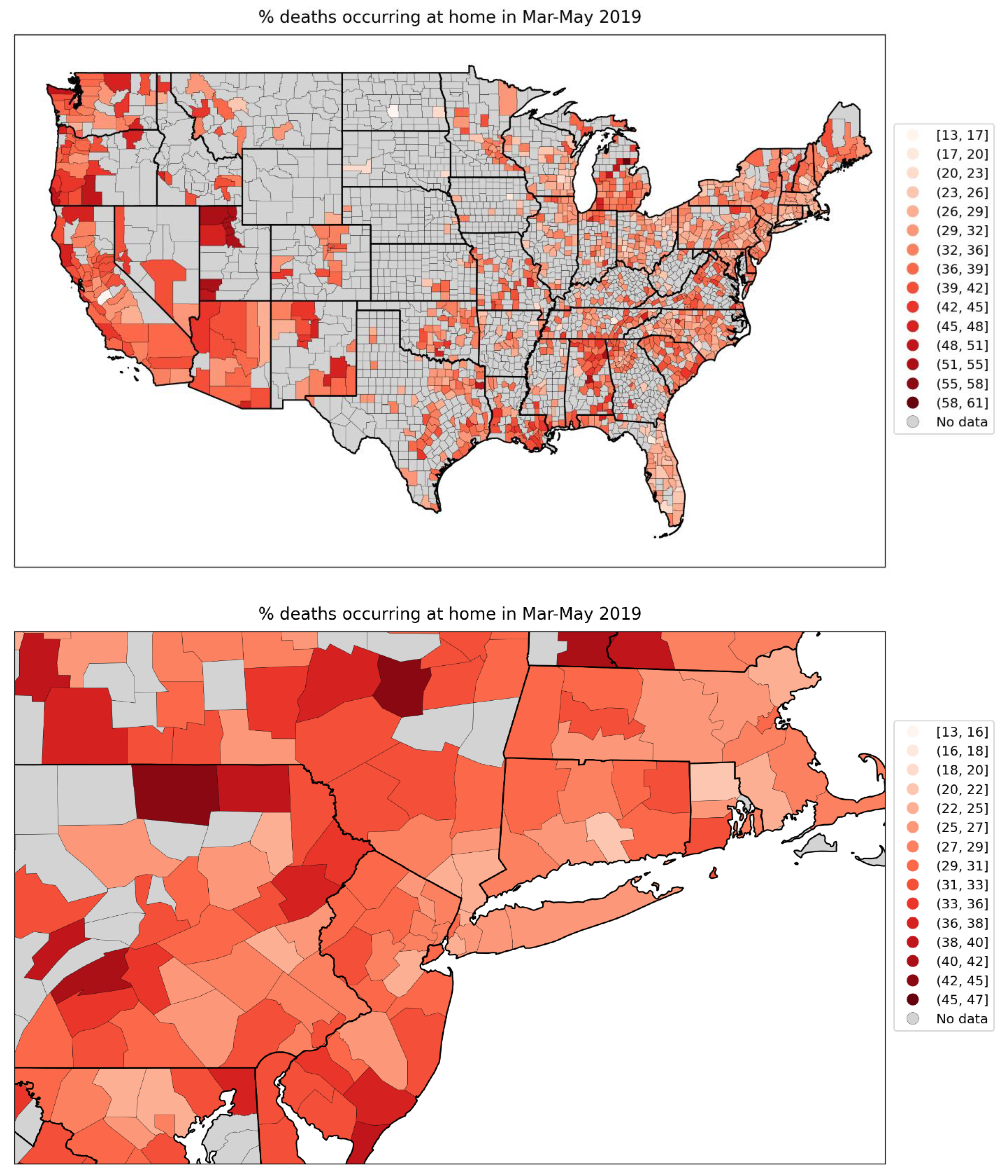
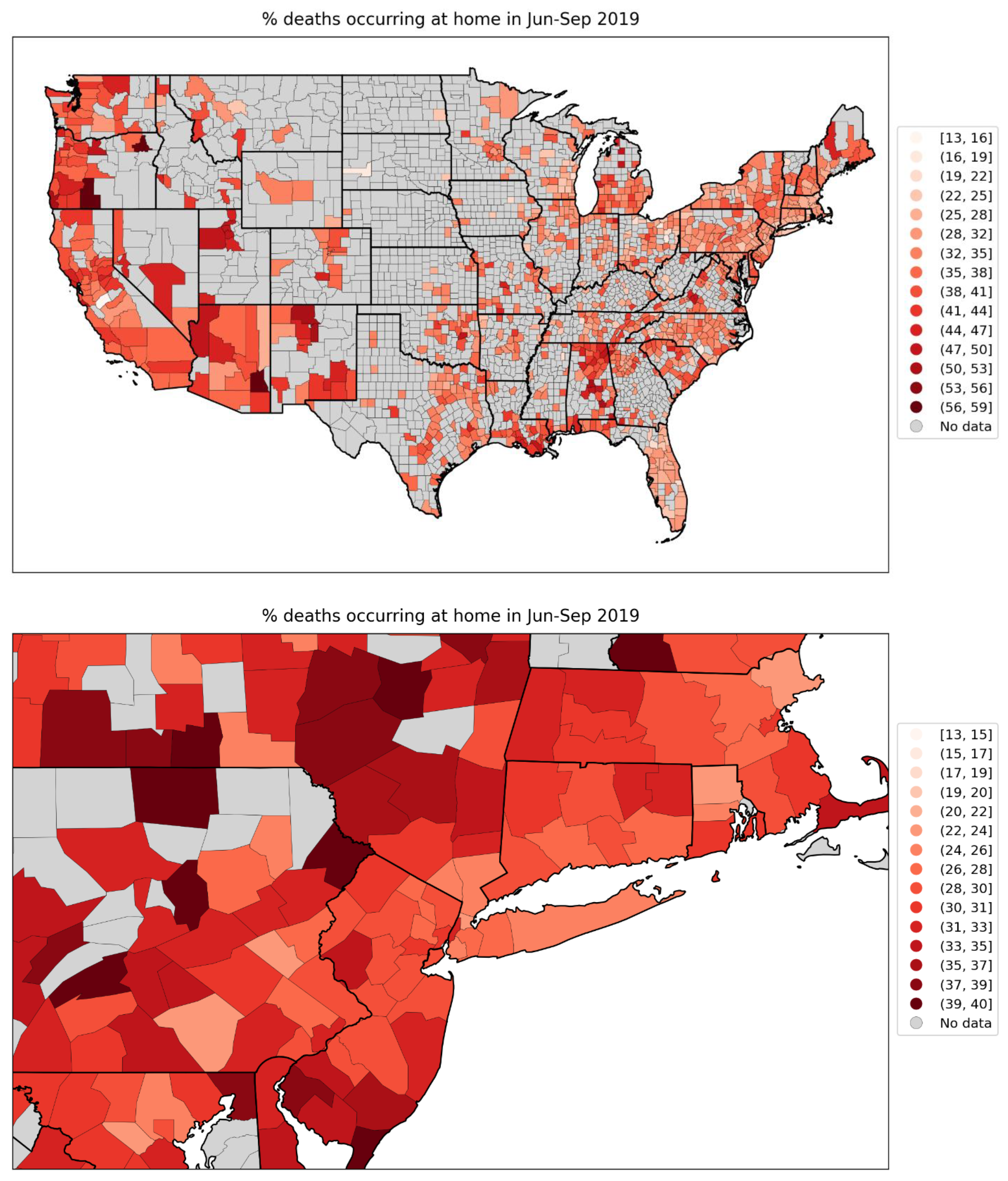
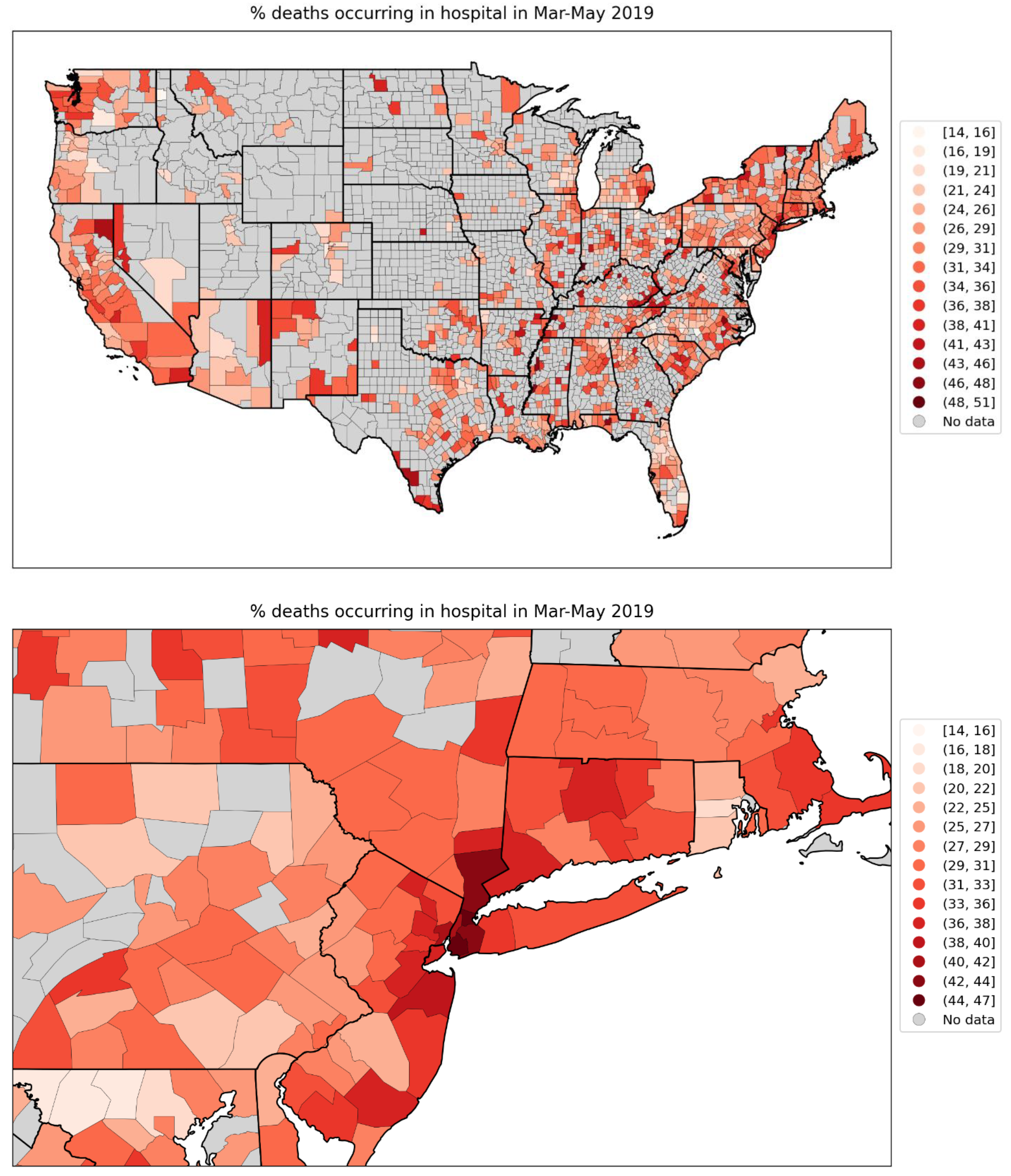
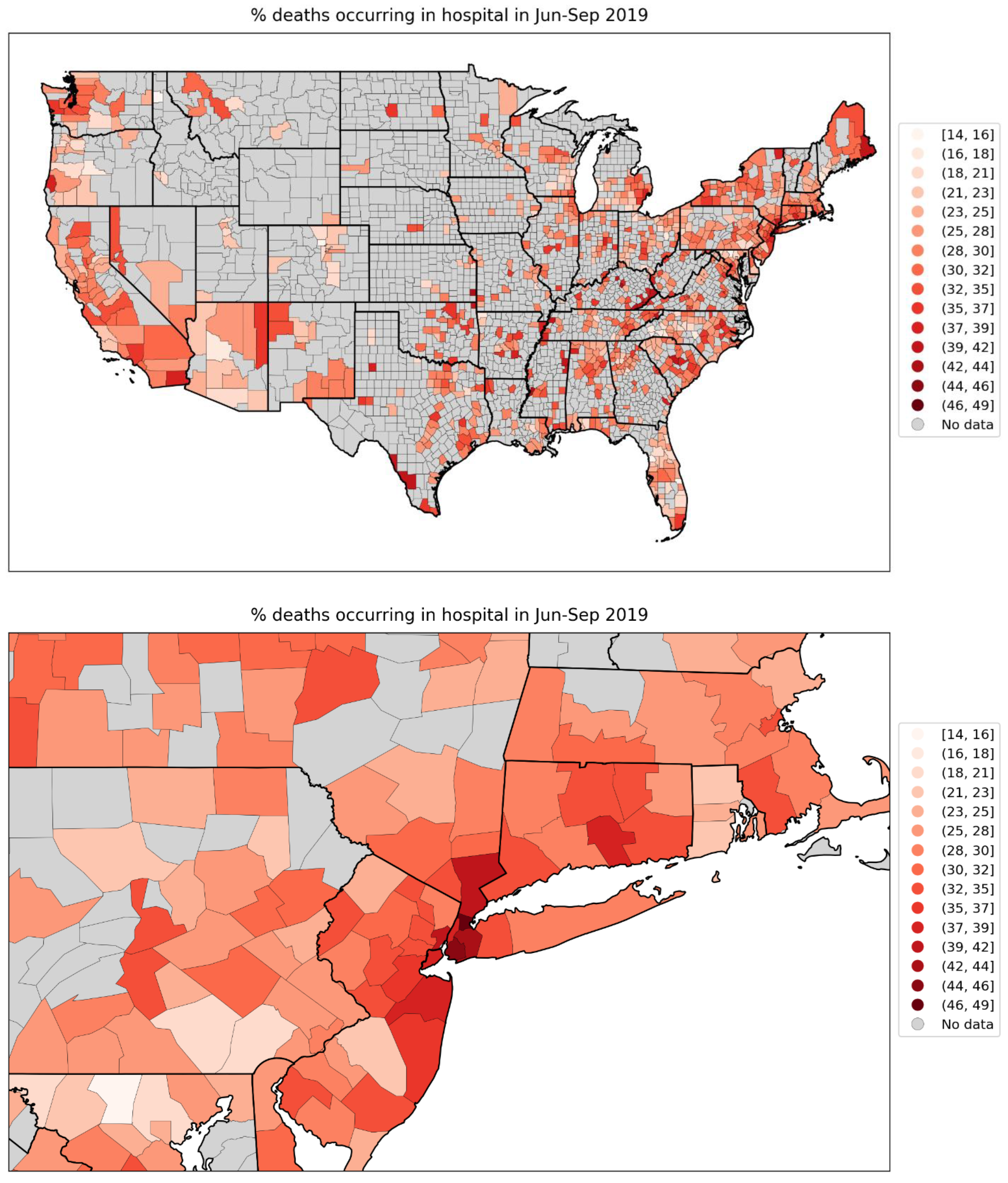
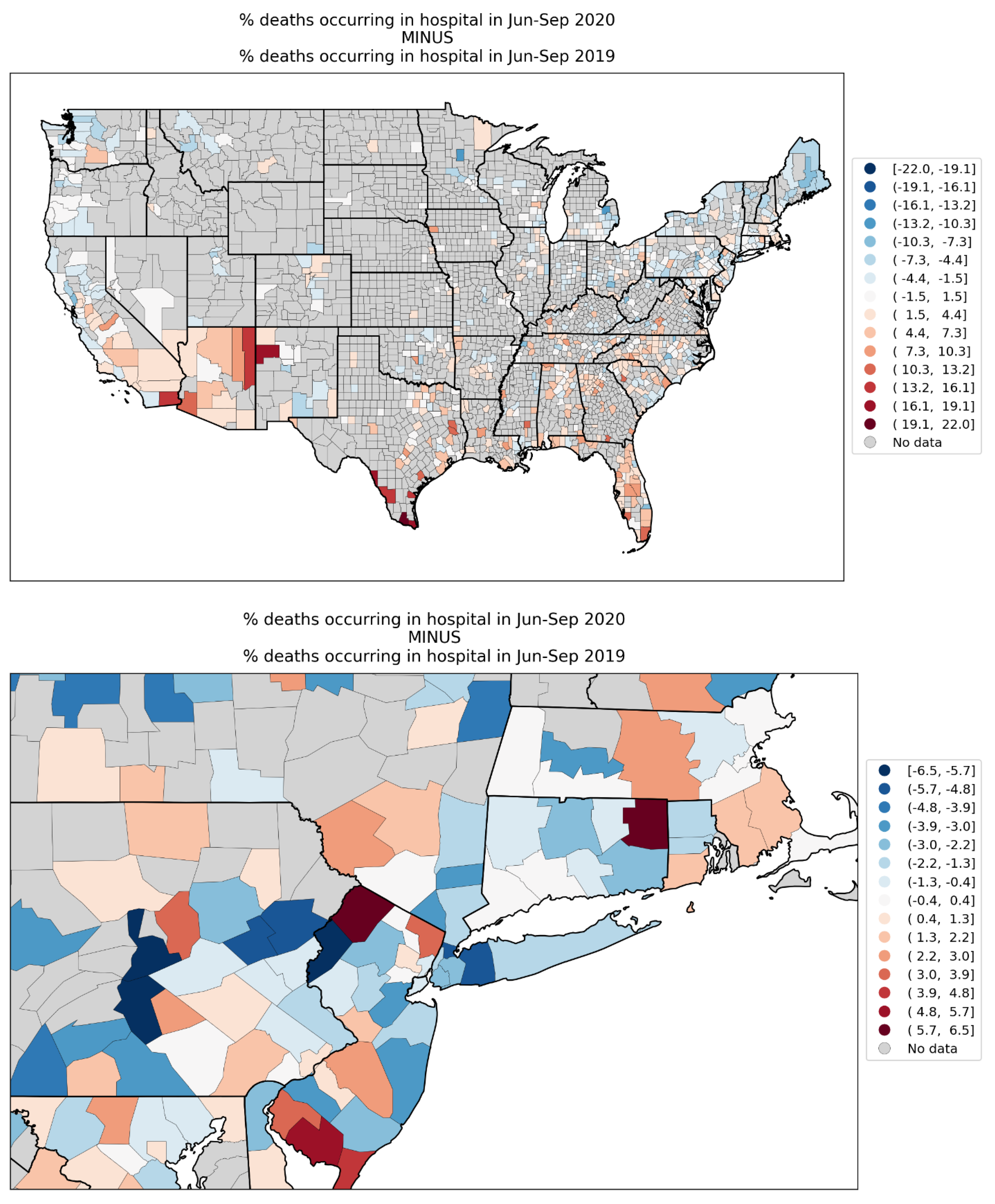
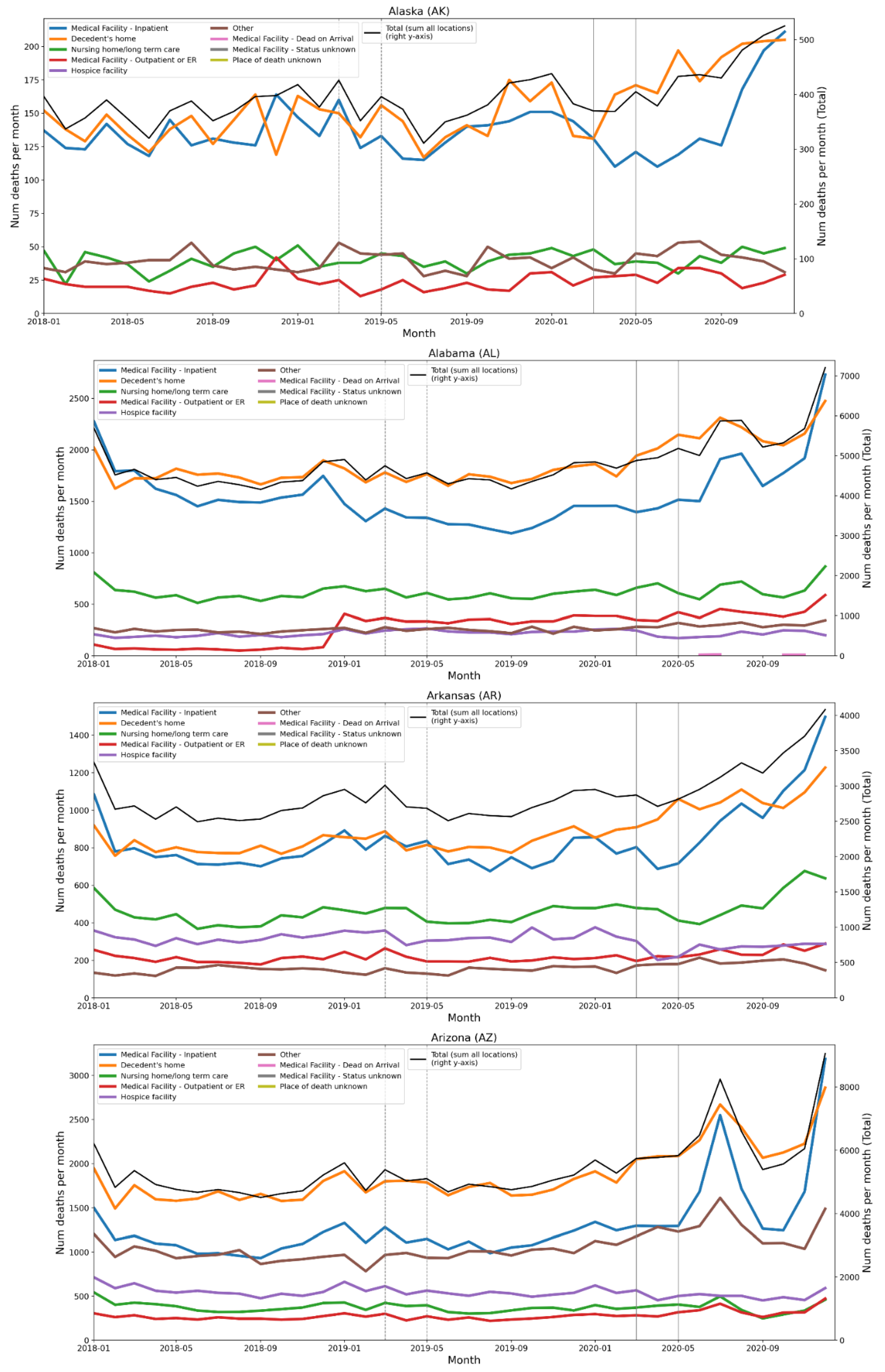
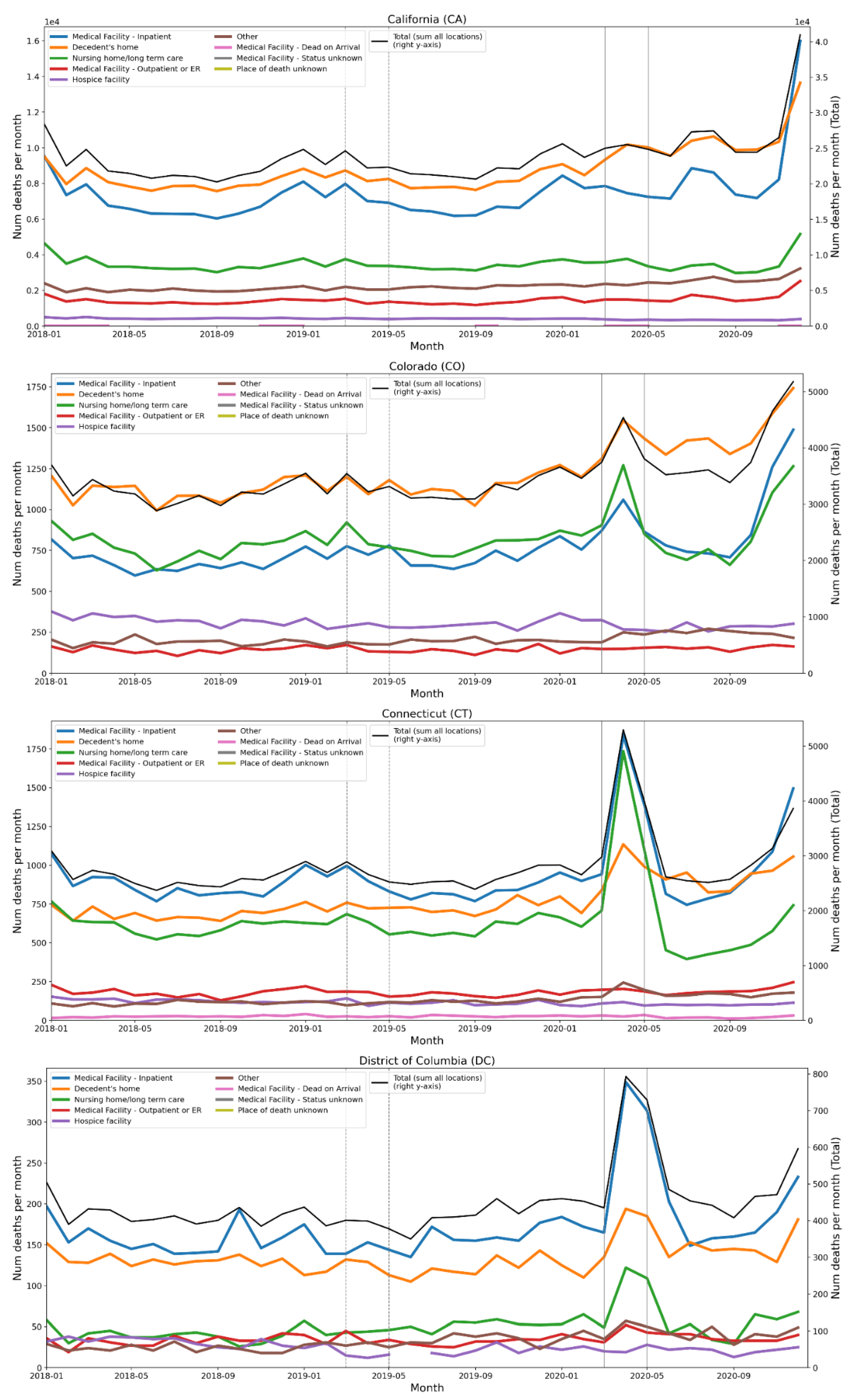
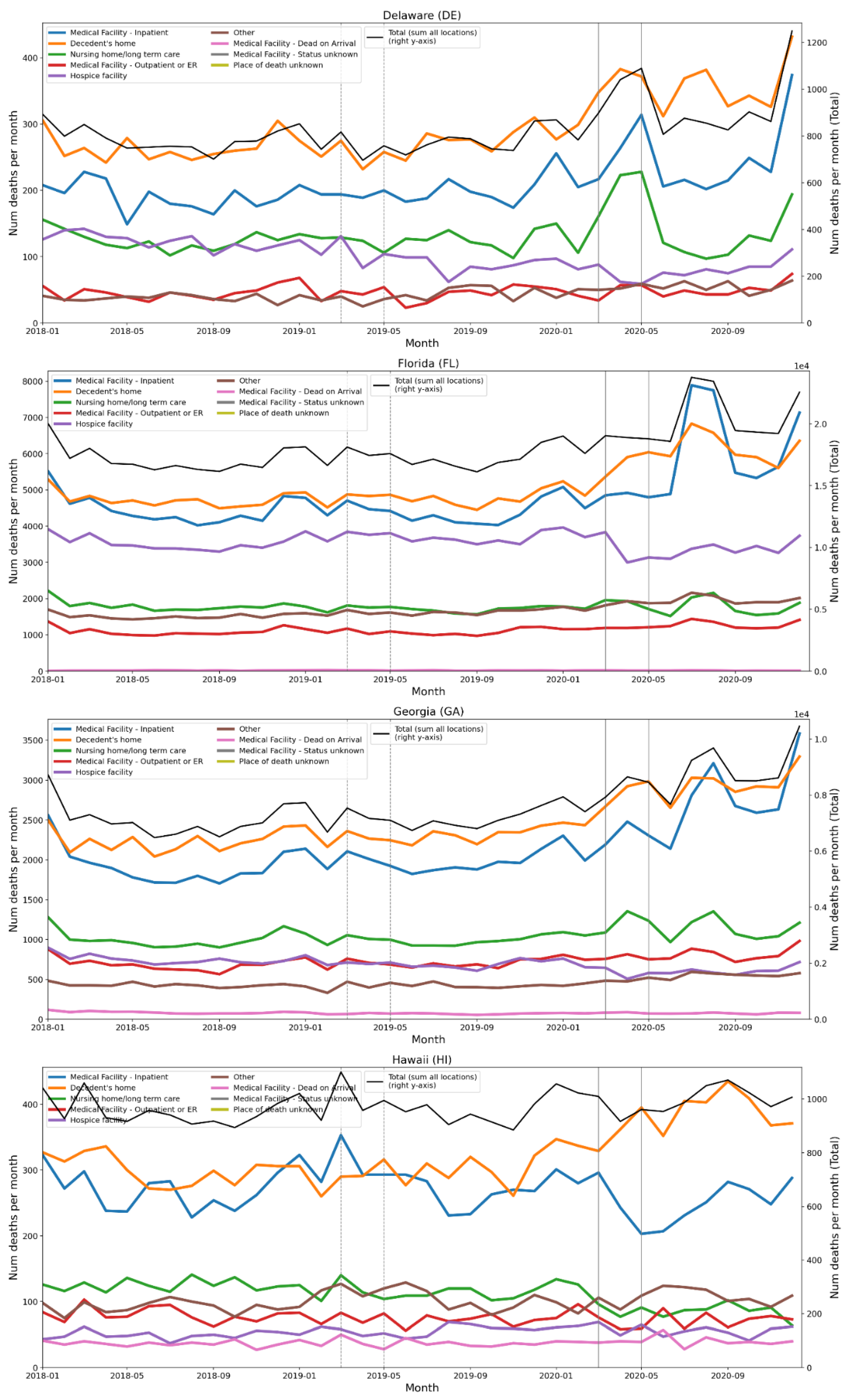
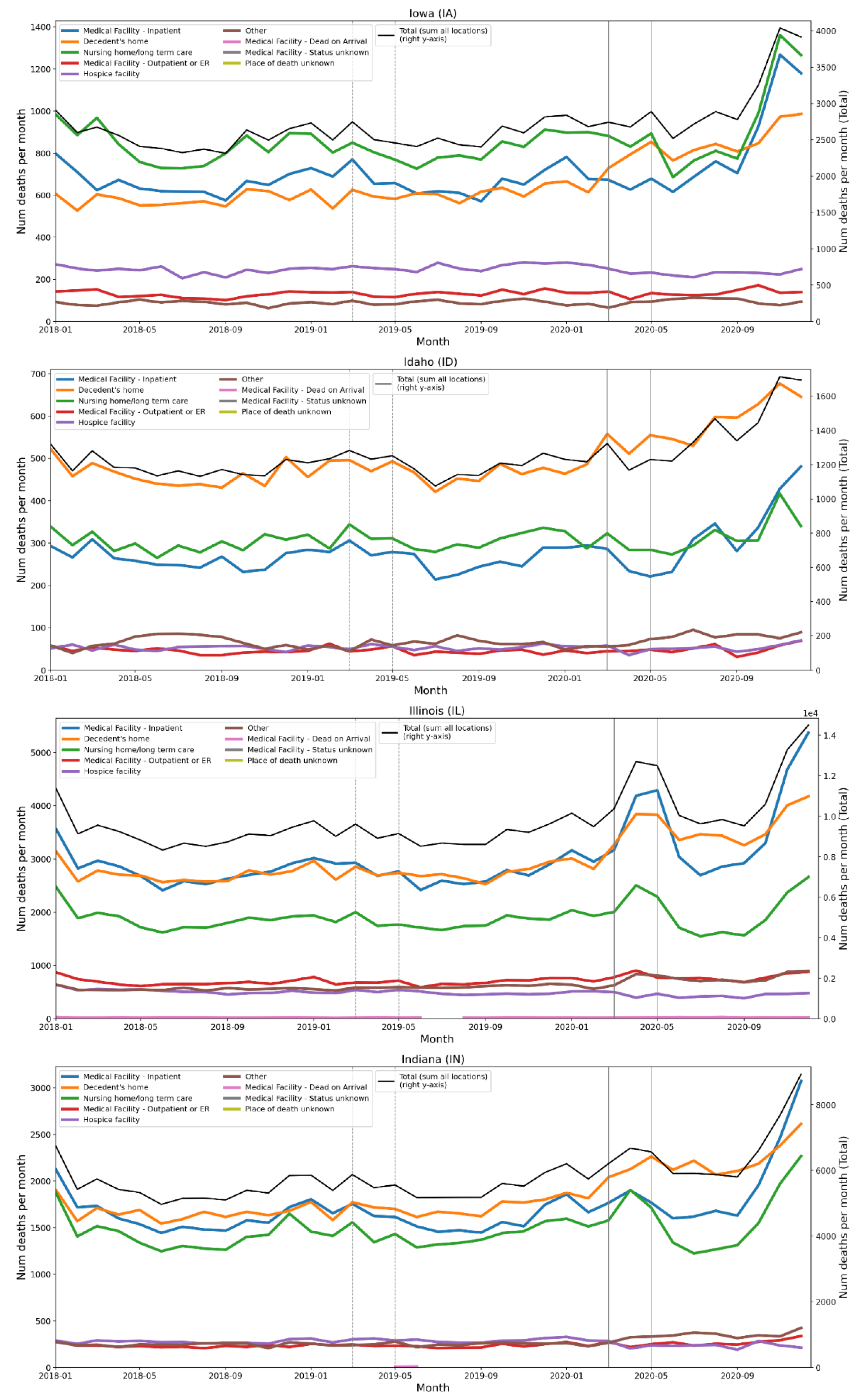
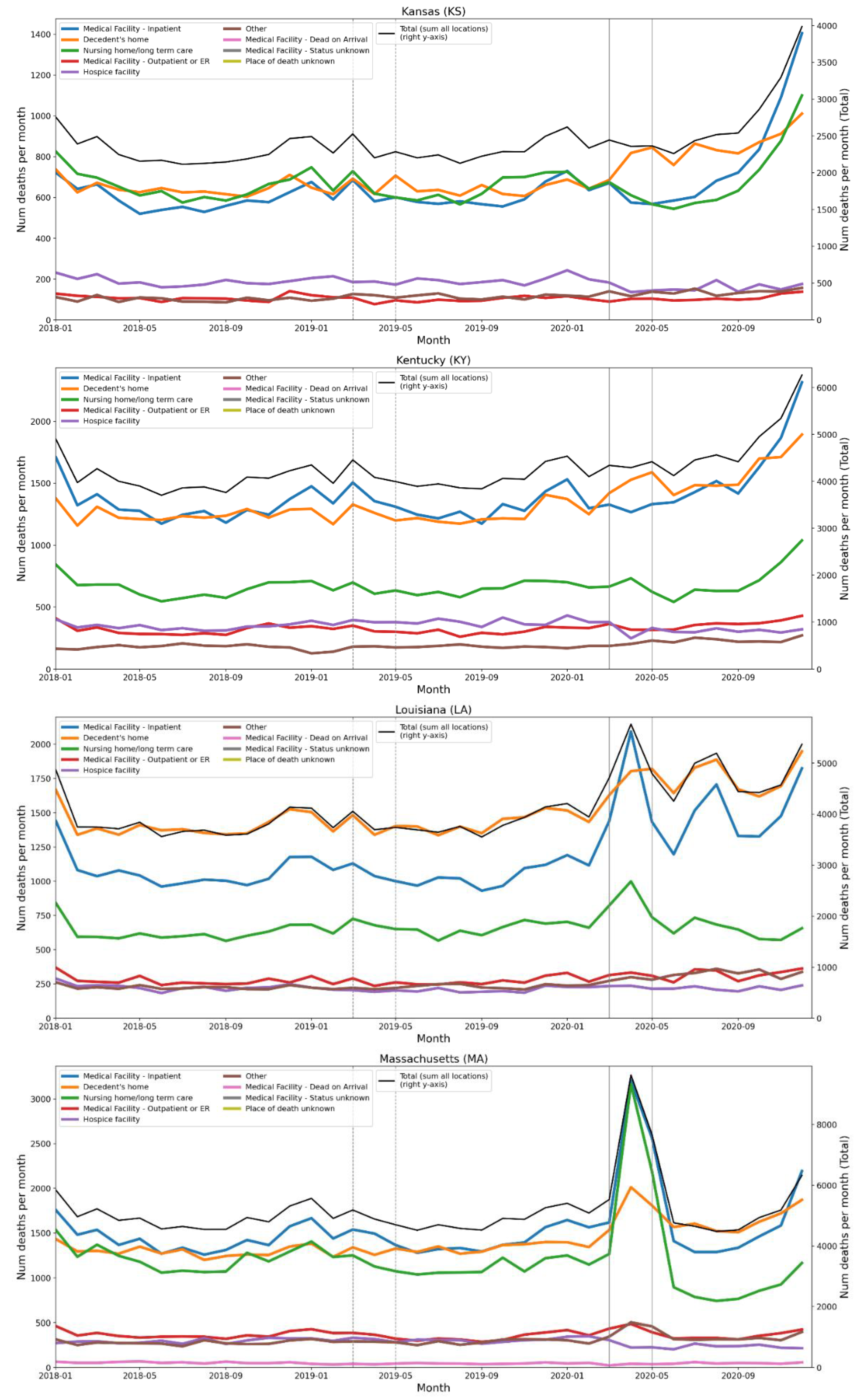
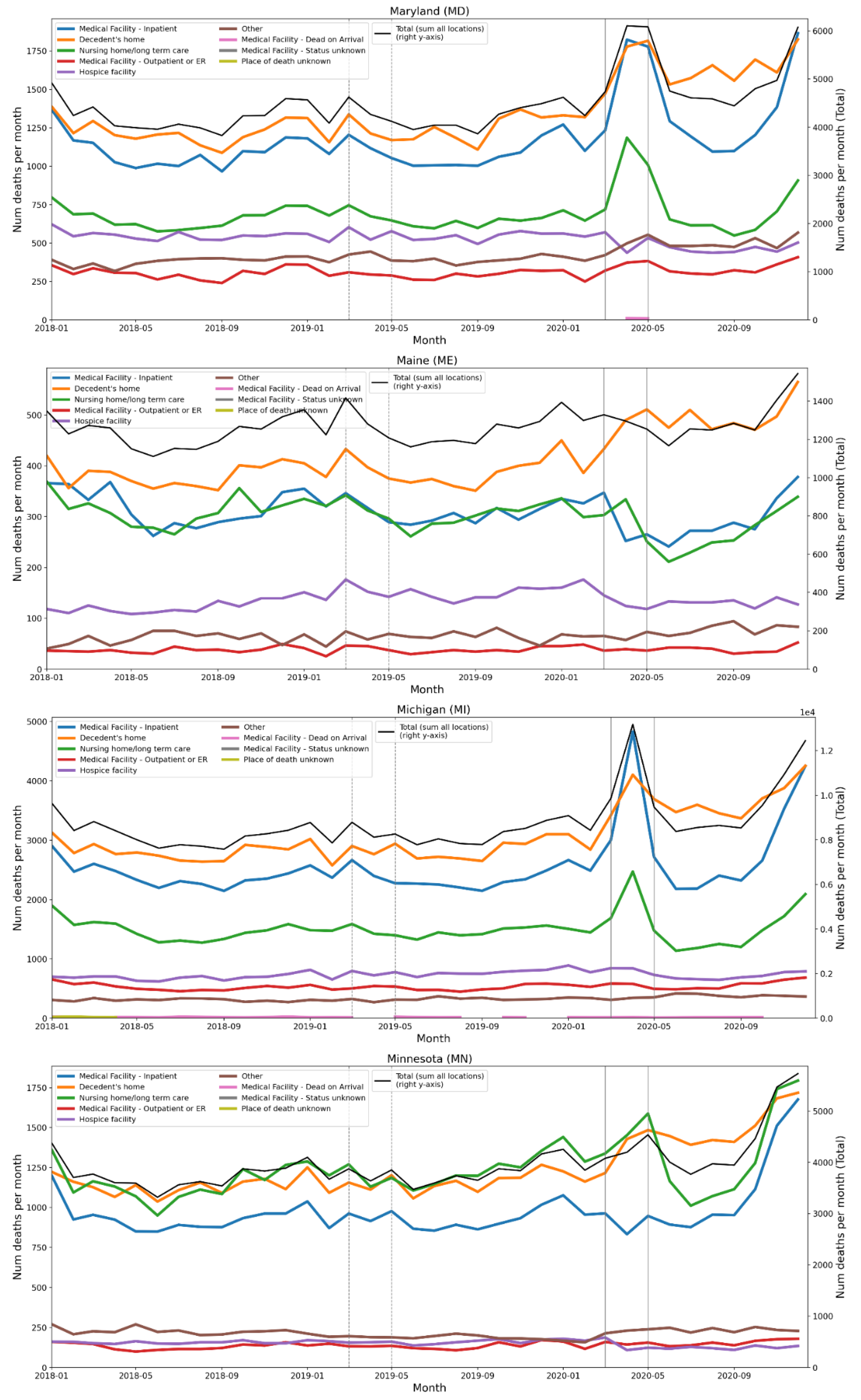
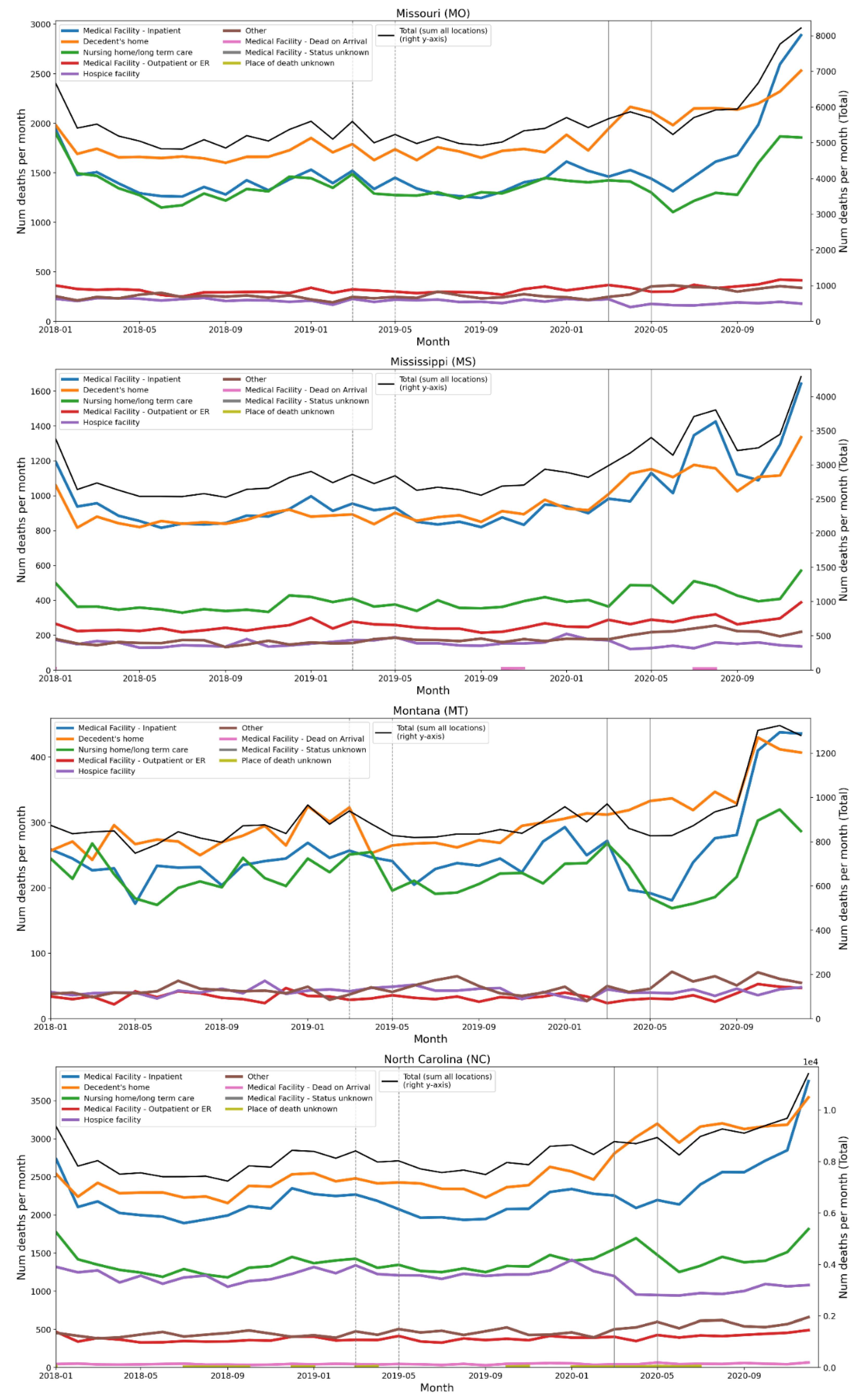
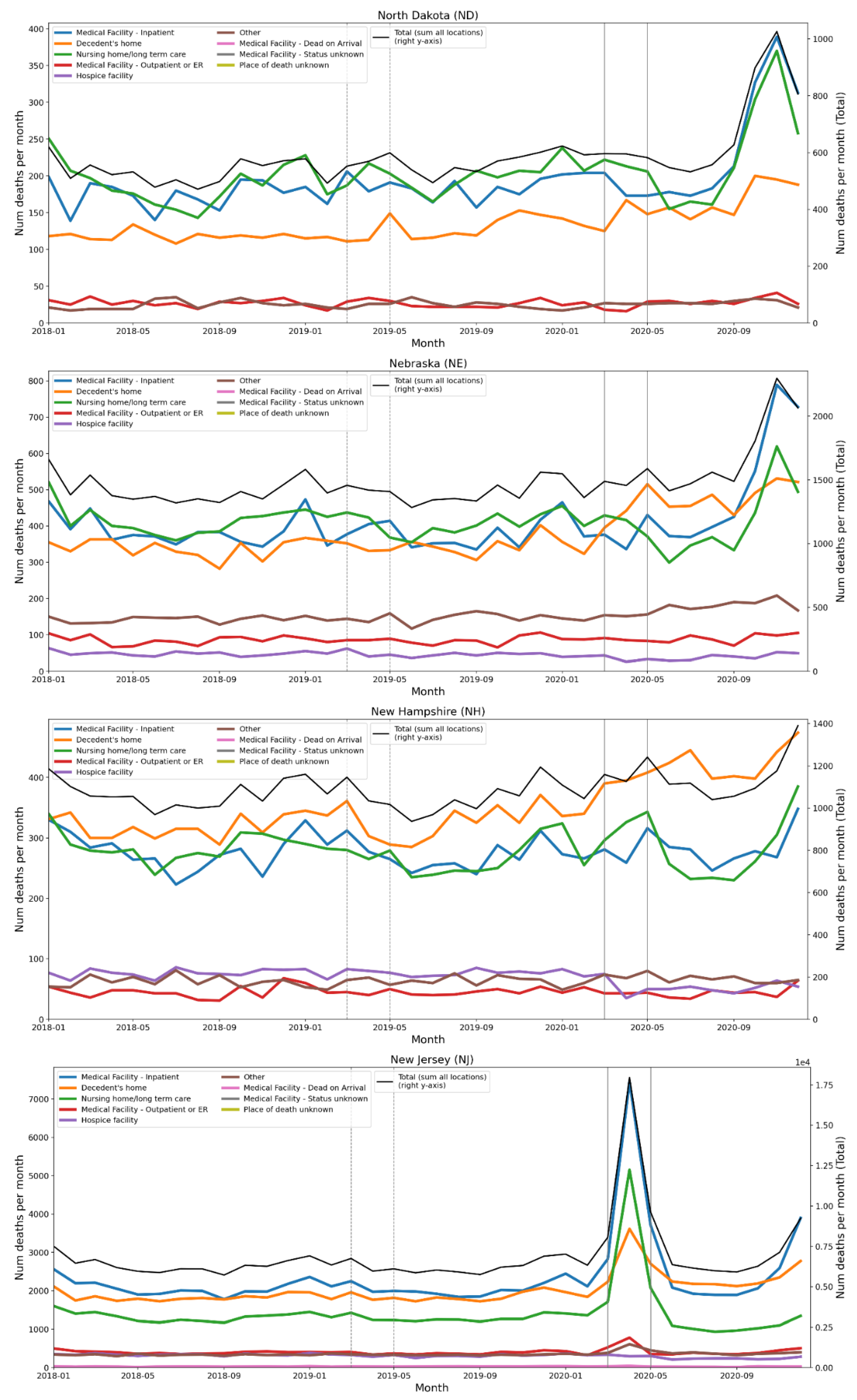
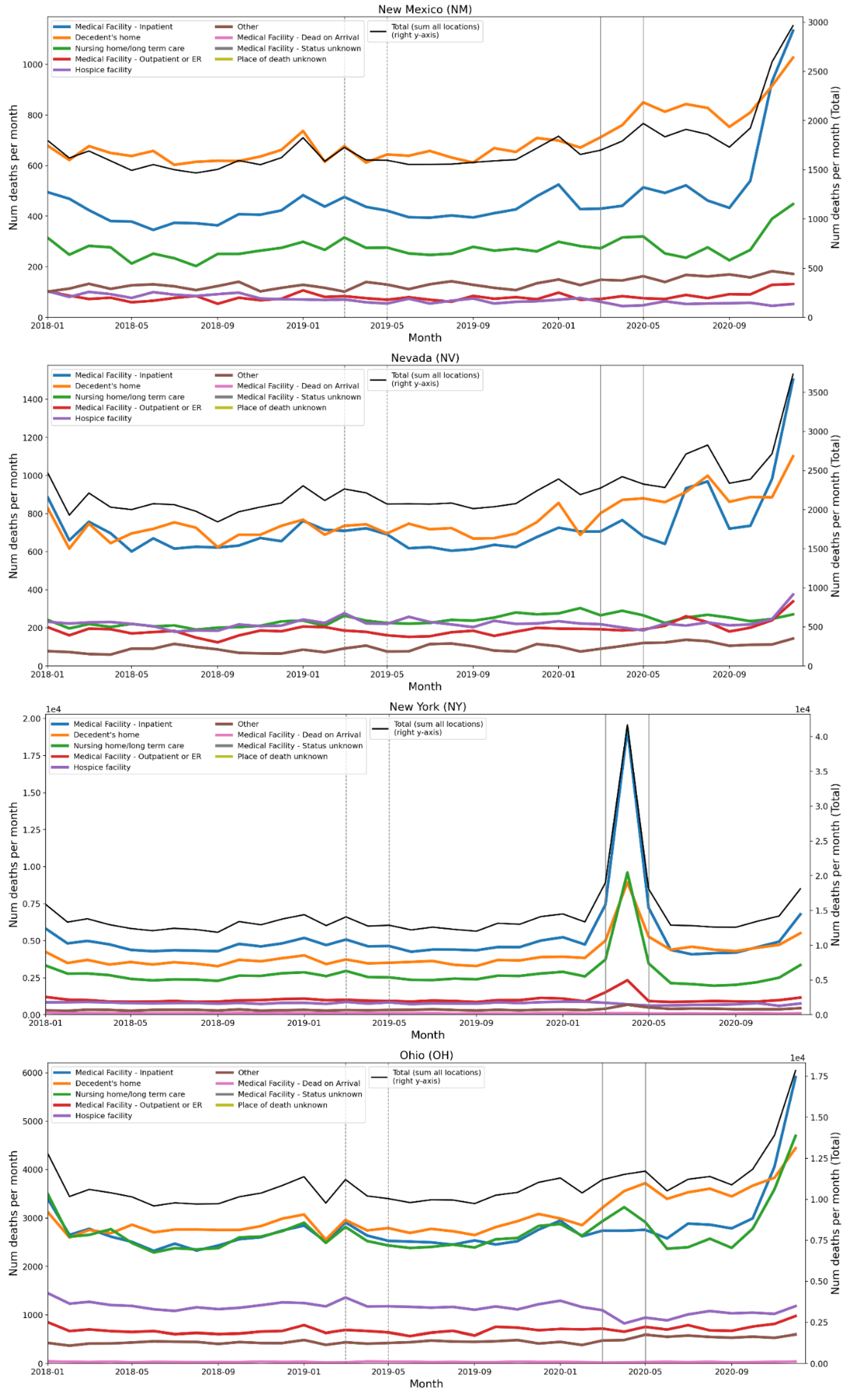
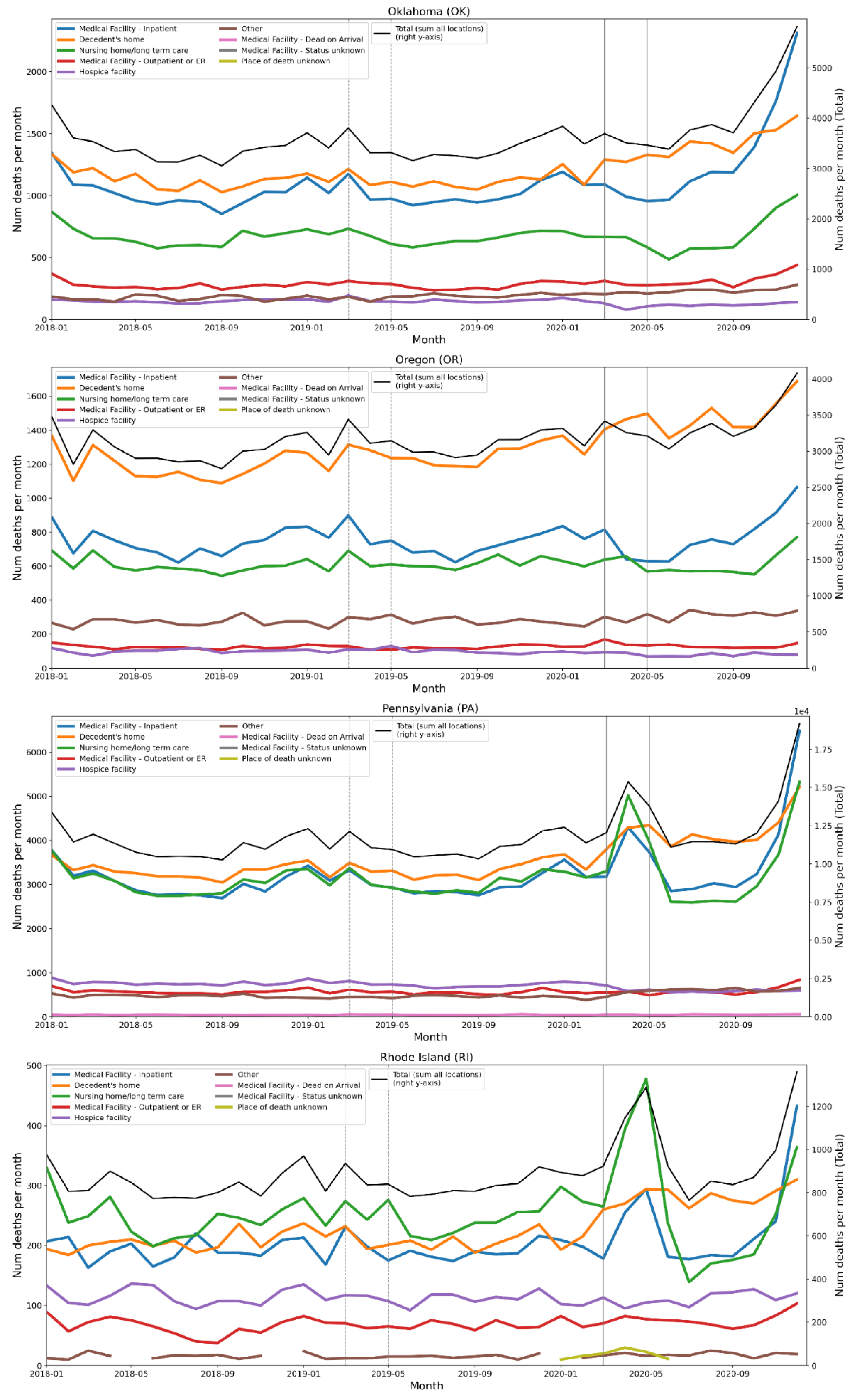
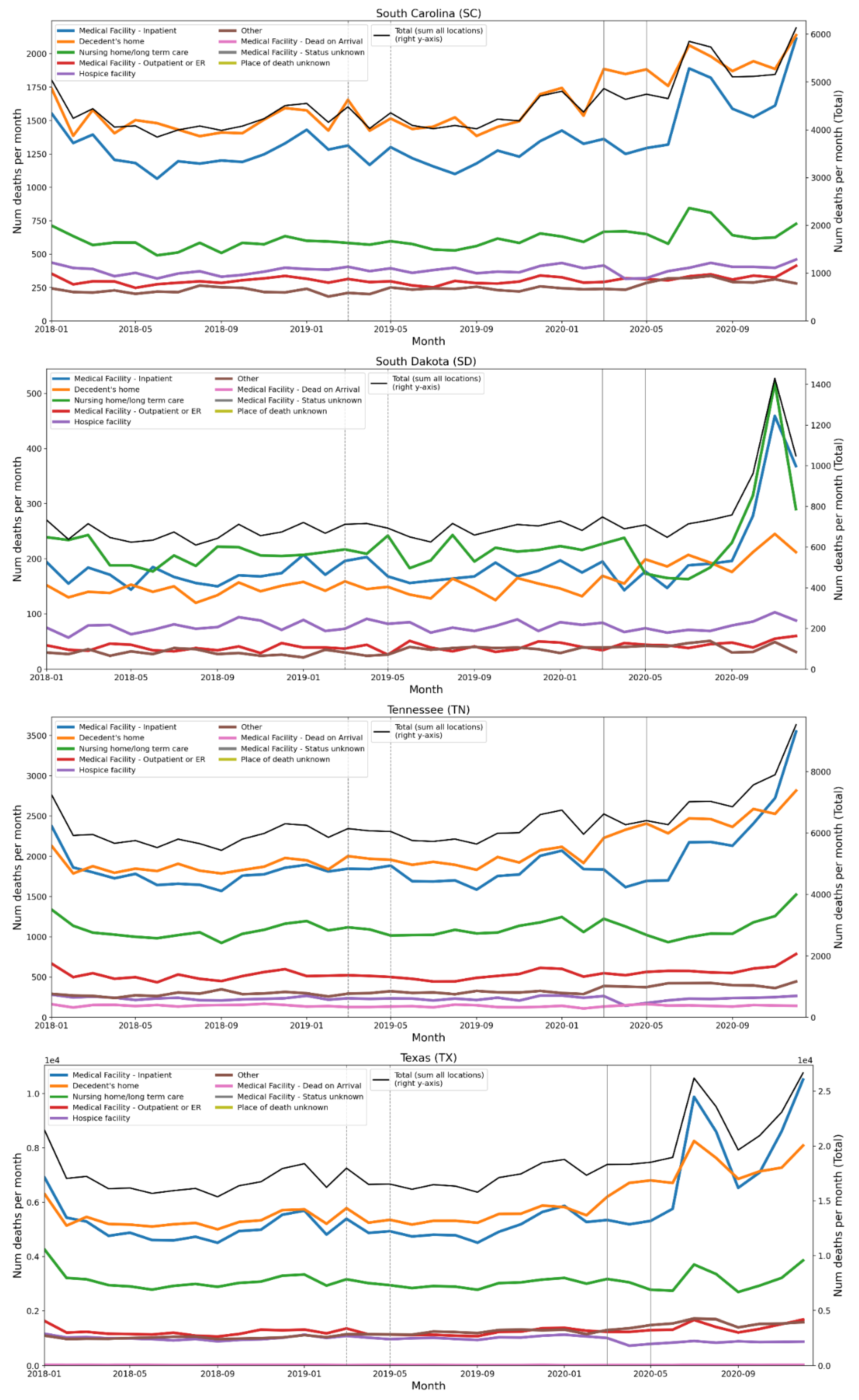
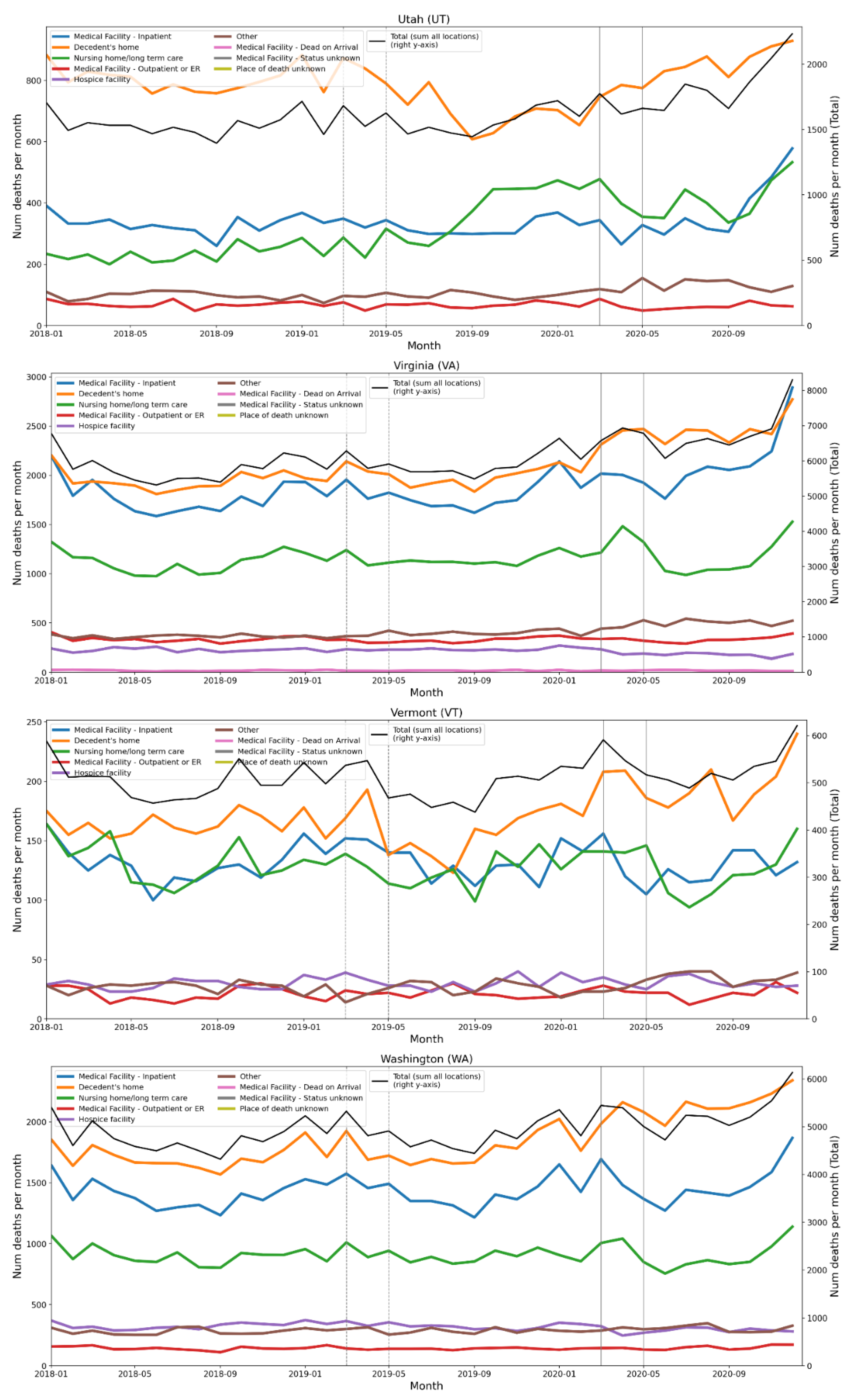
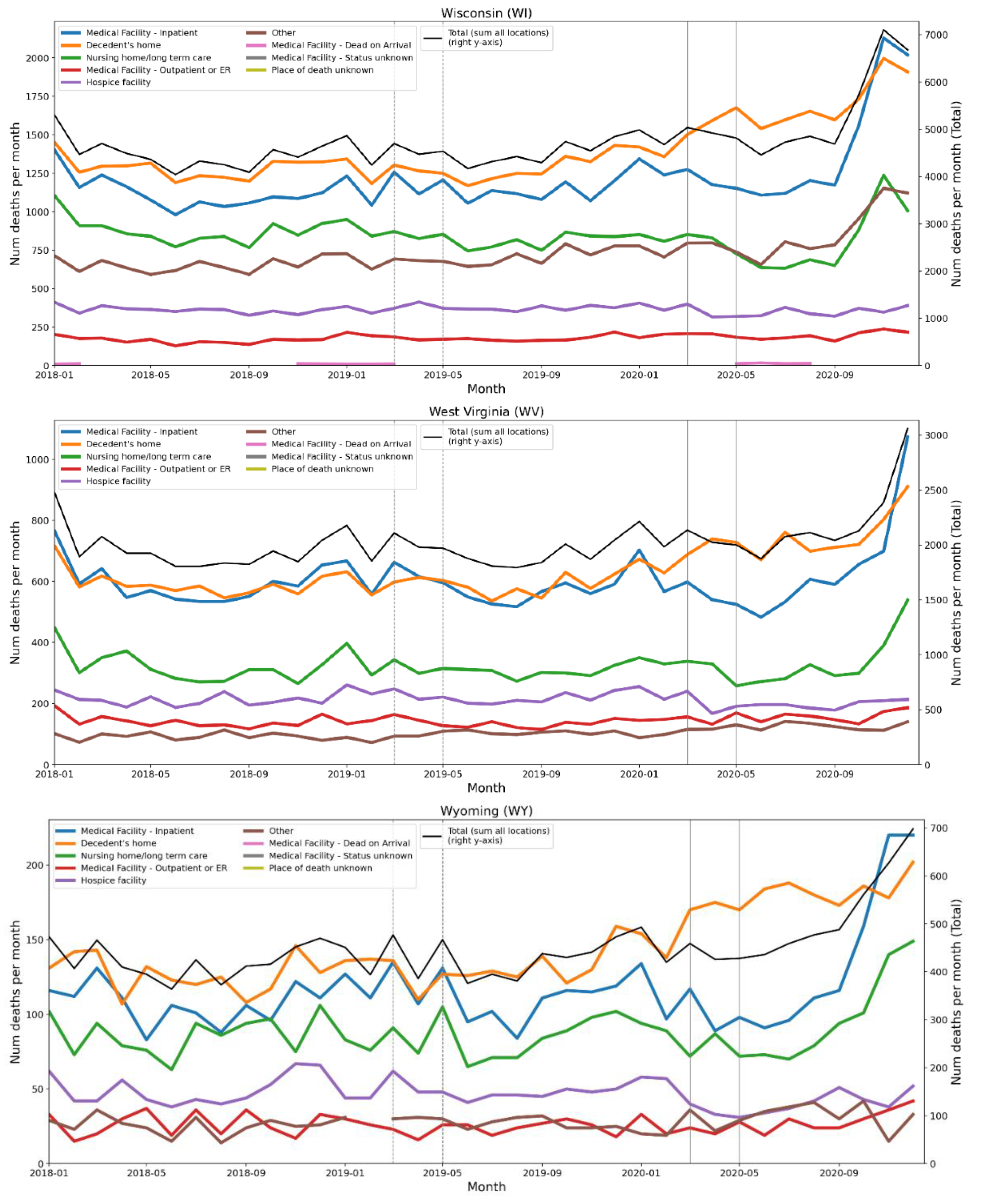
2.4. Deaths by Institutional Location for USA States and Counties
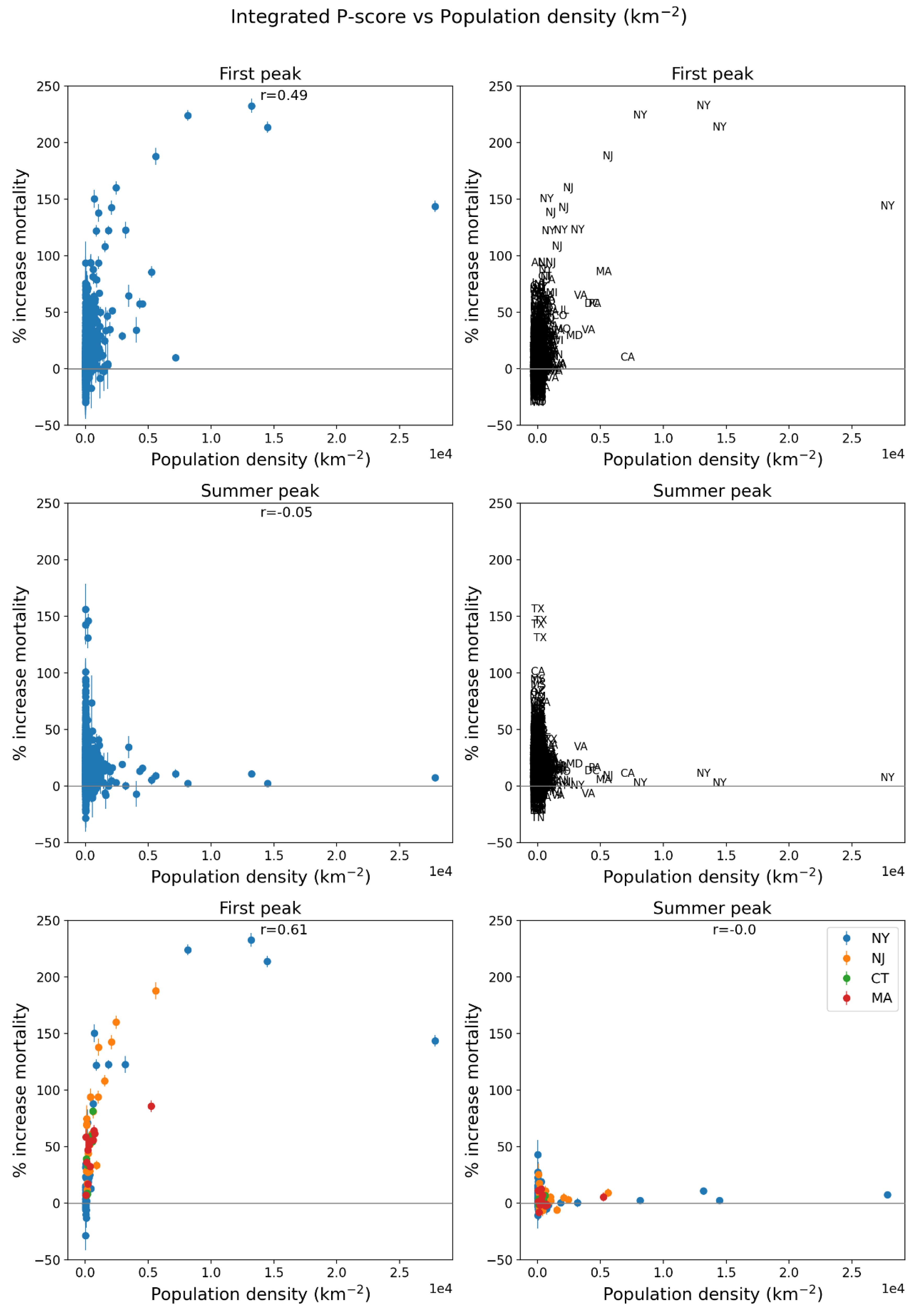
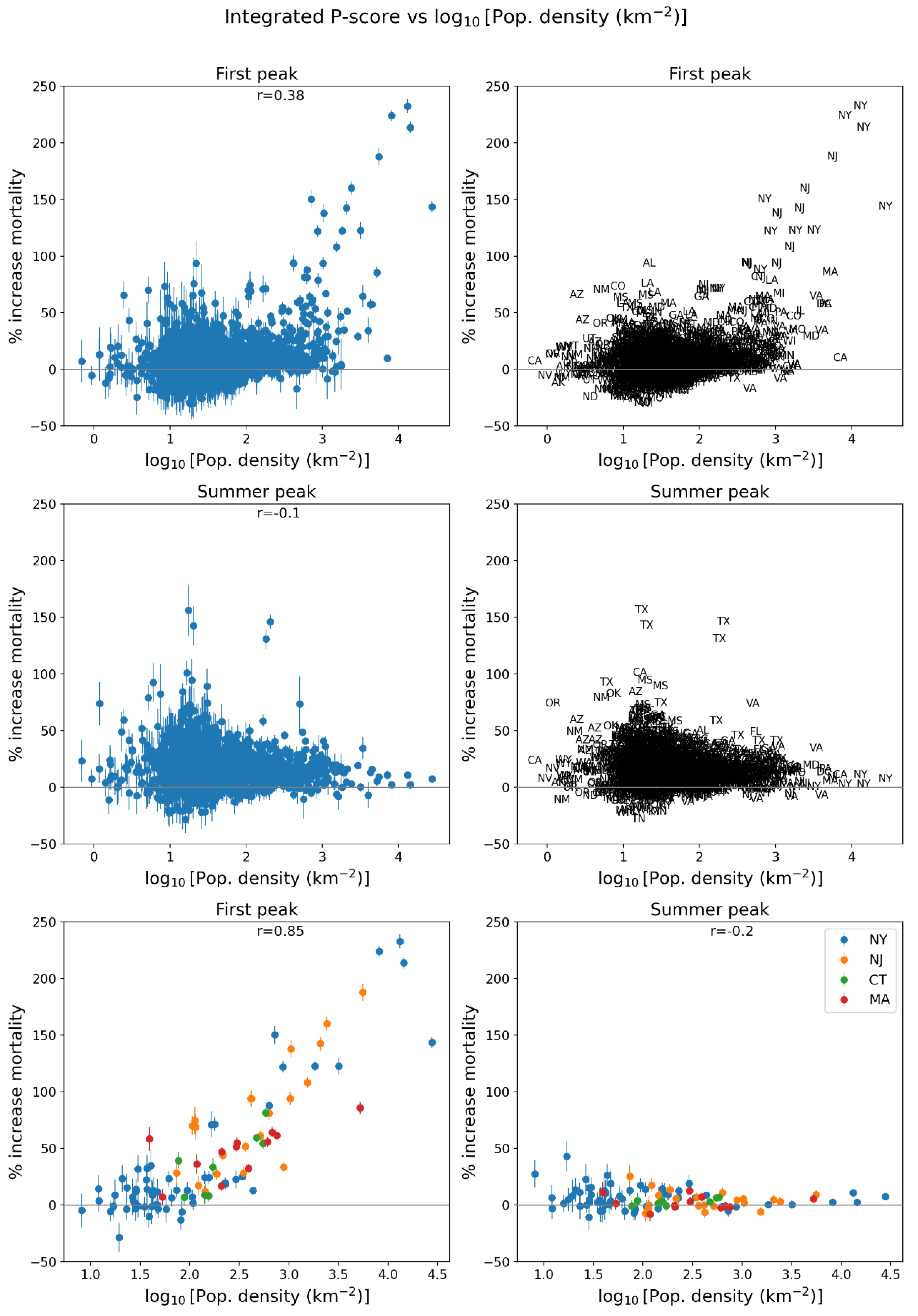
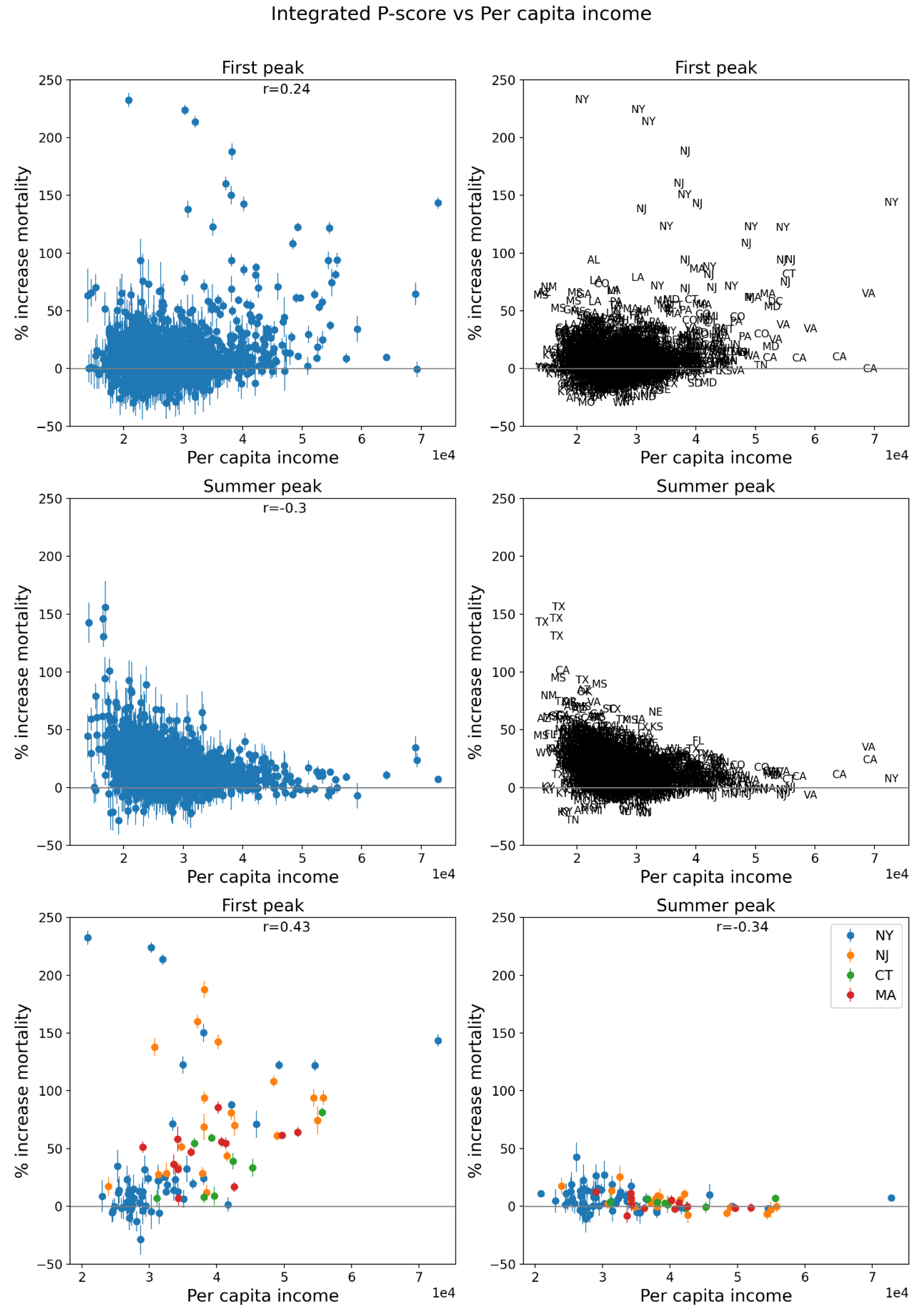
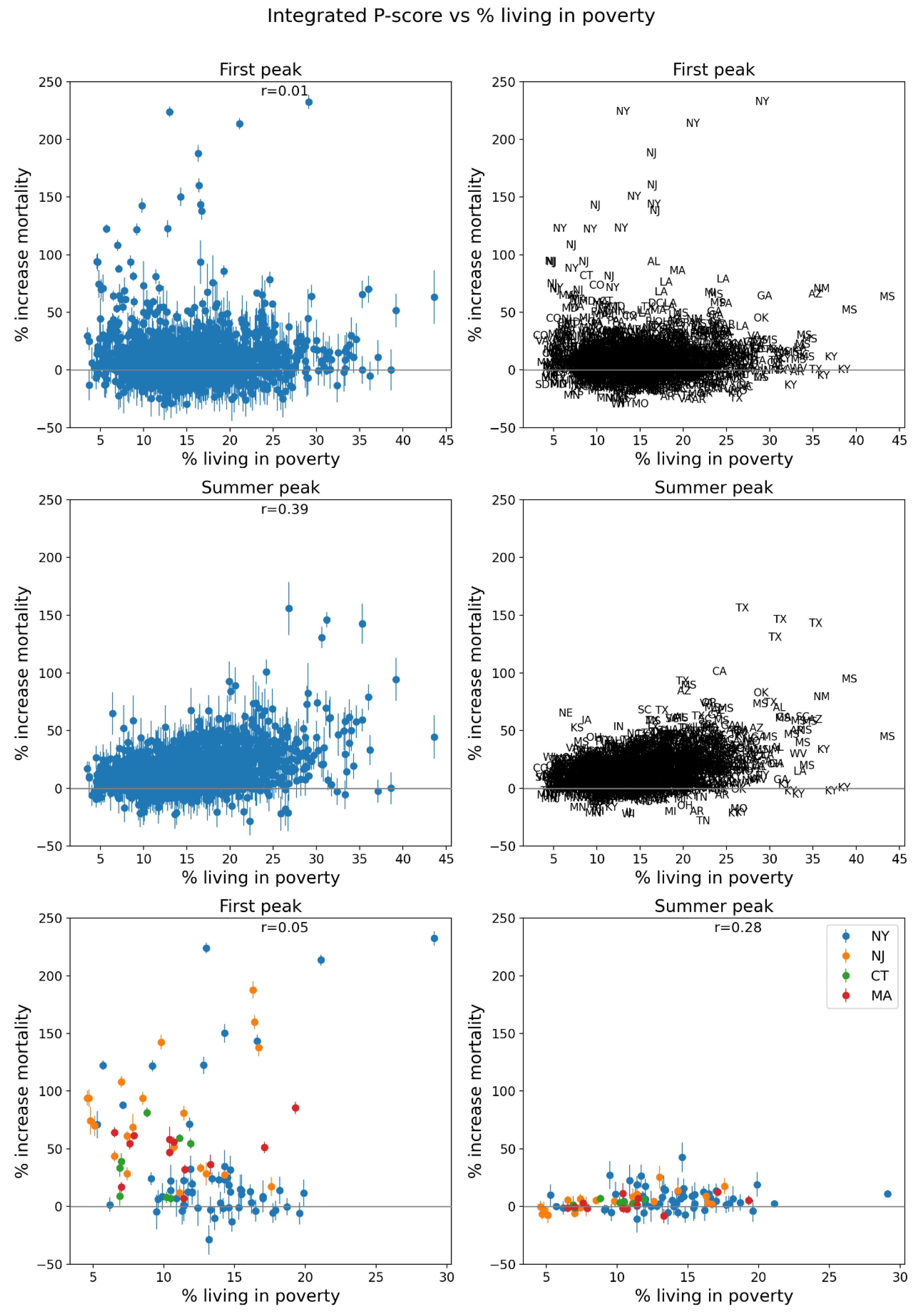
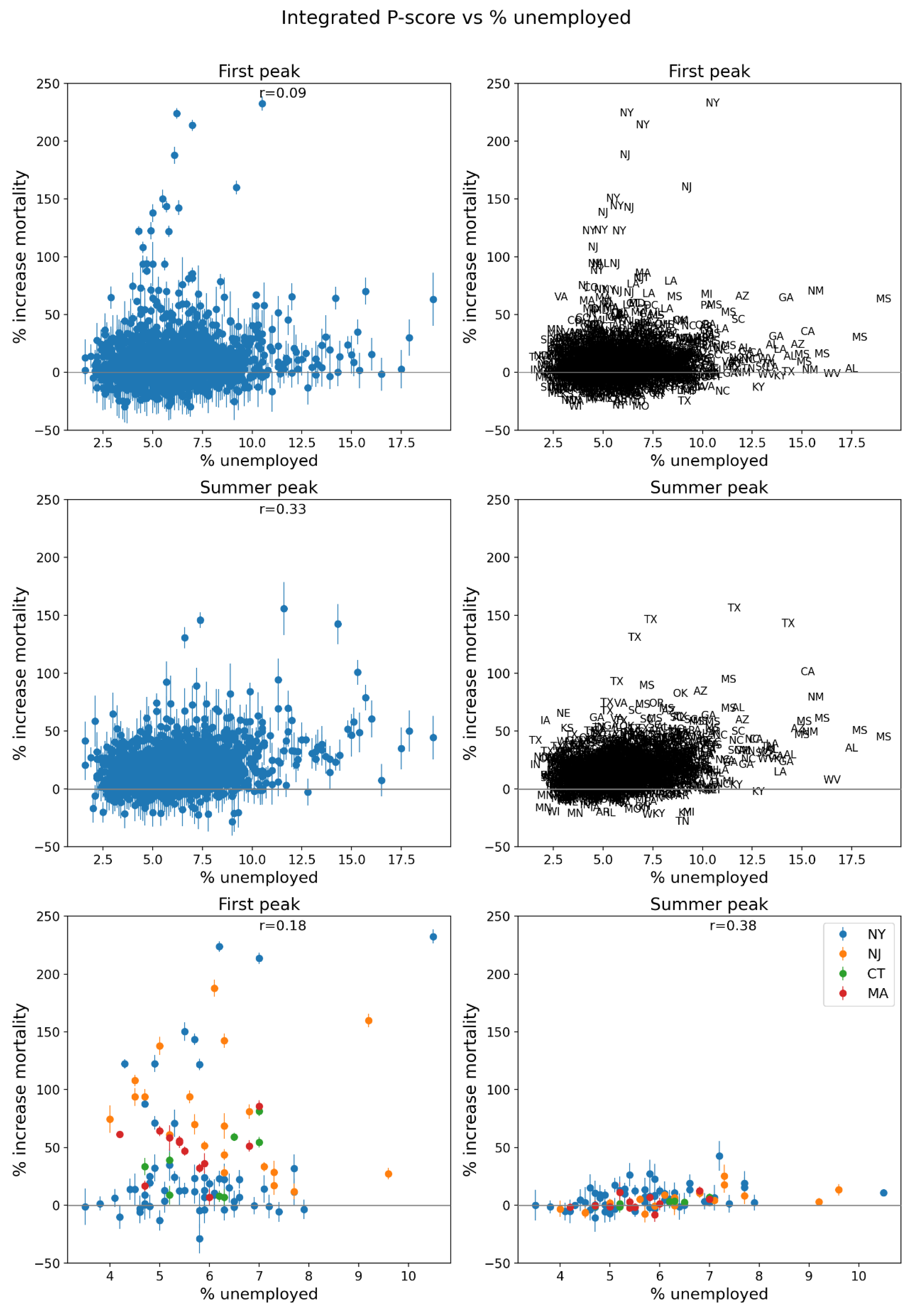
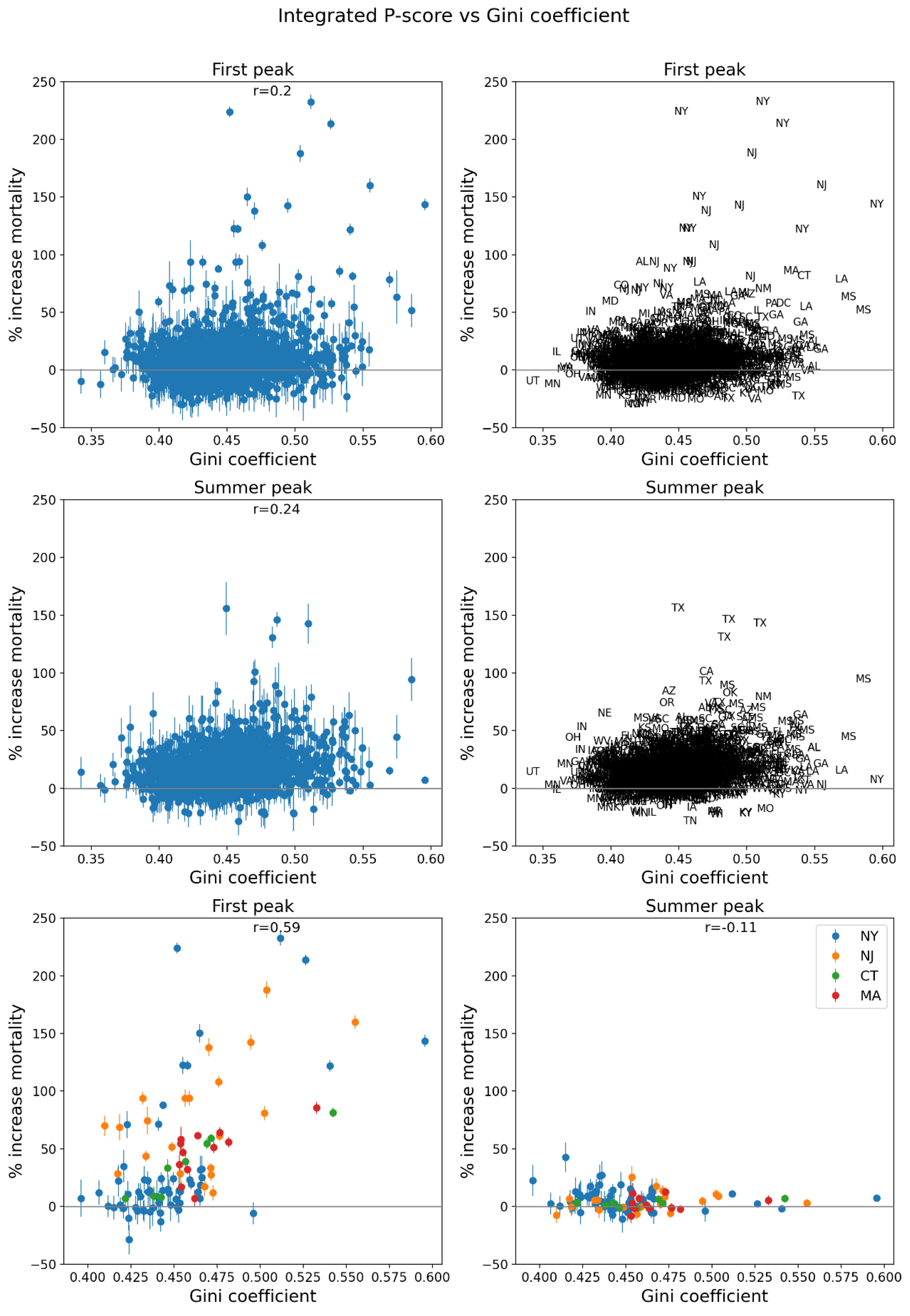
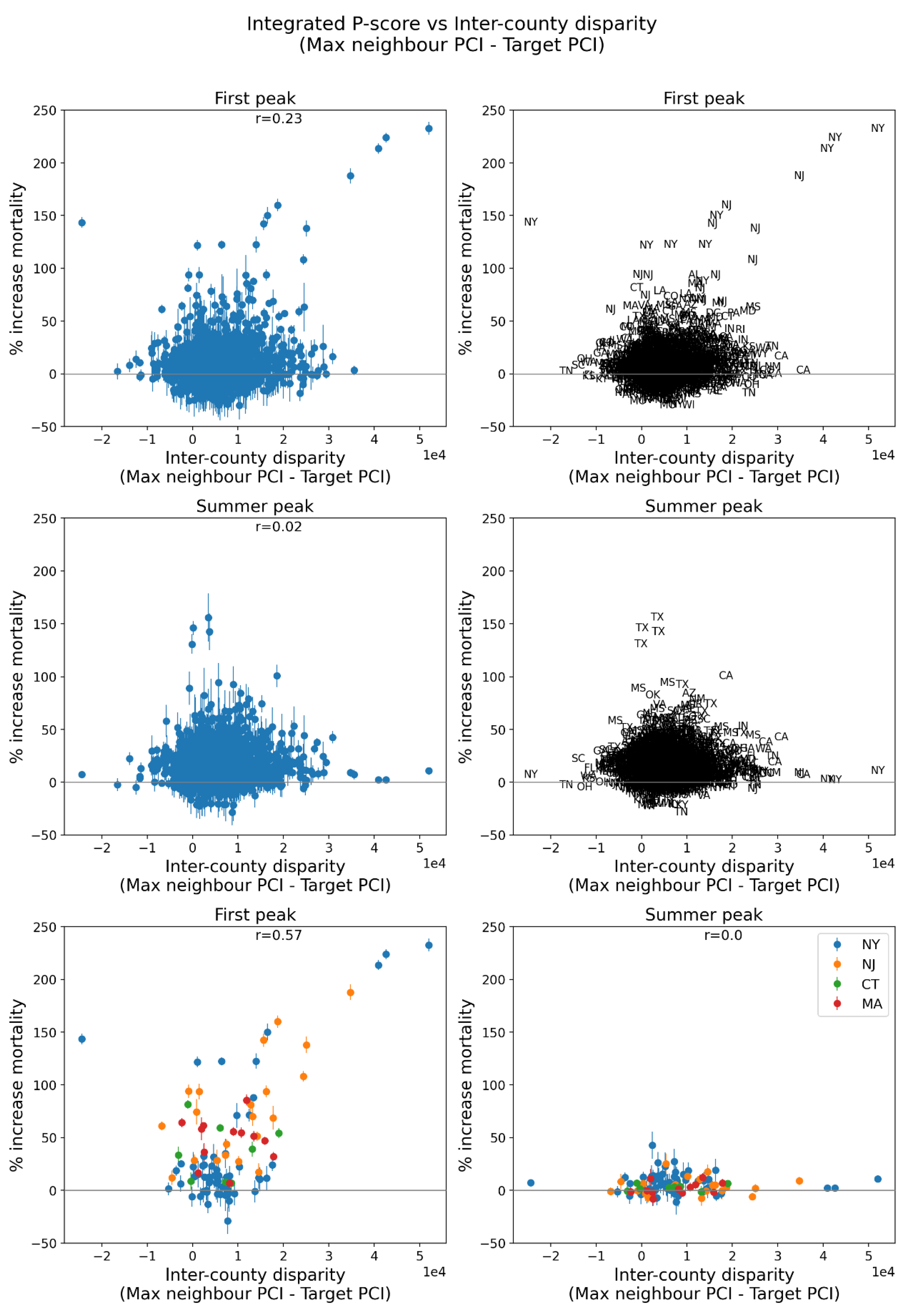
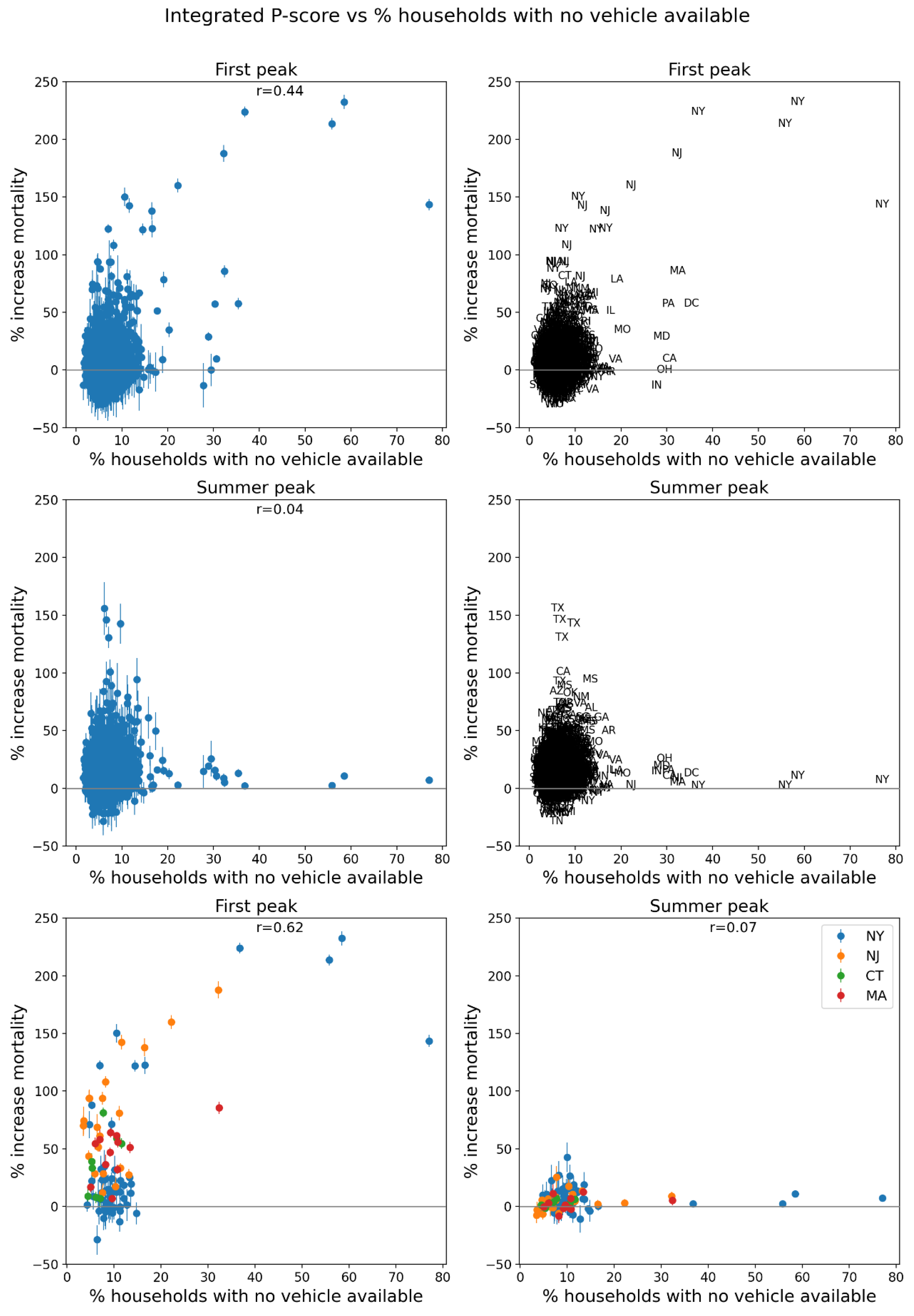
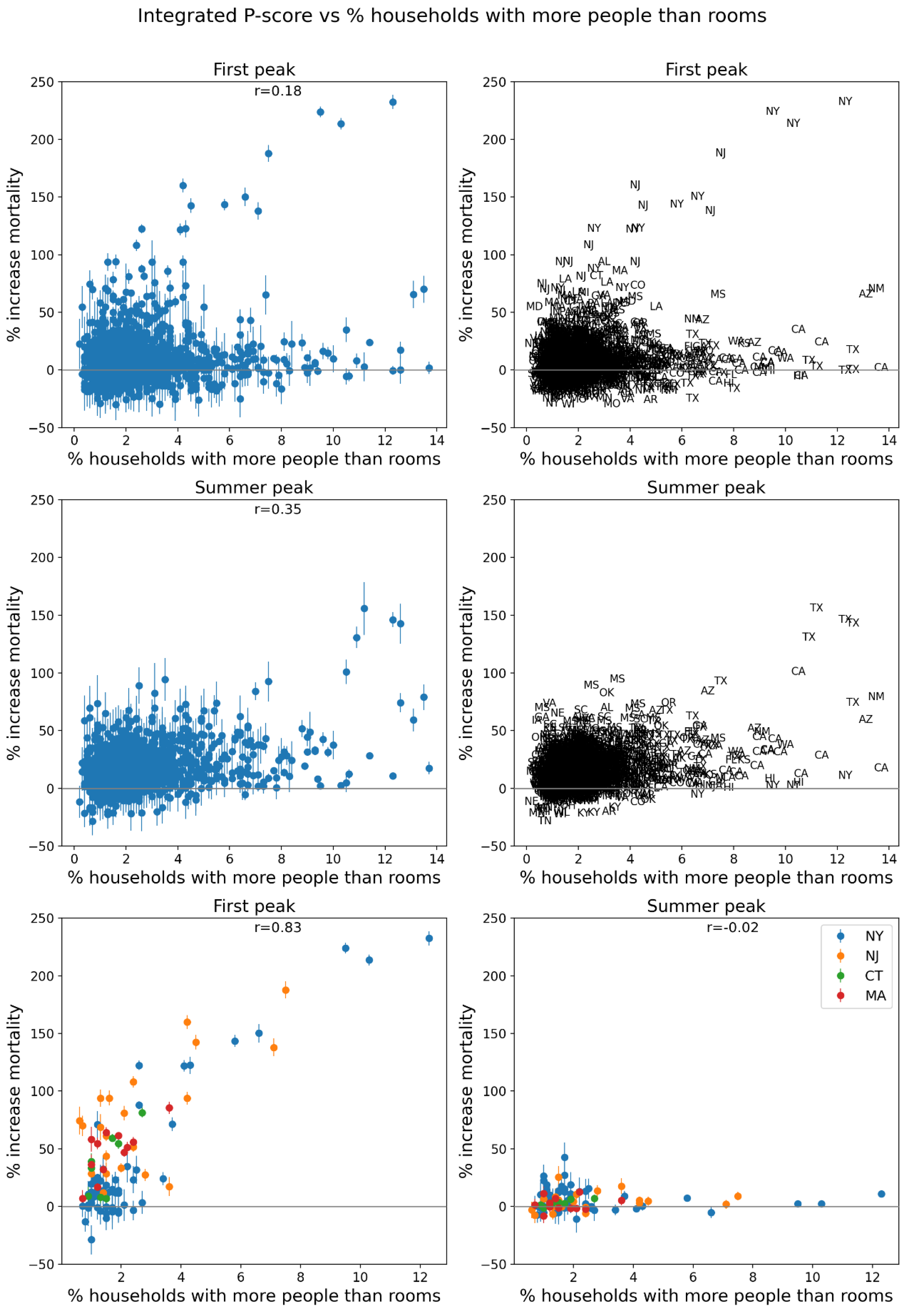
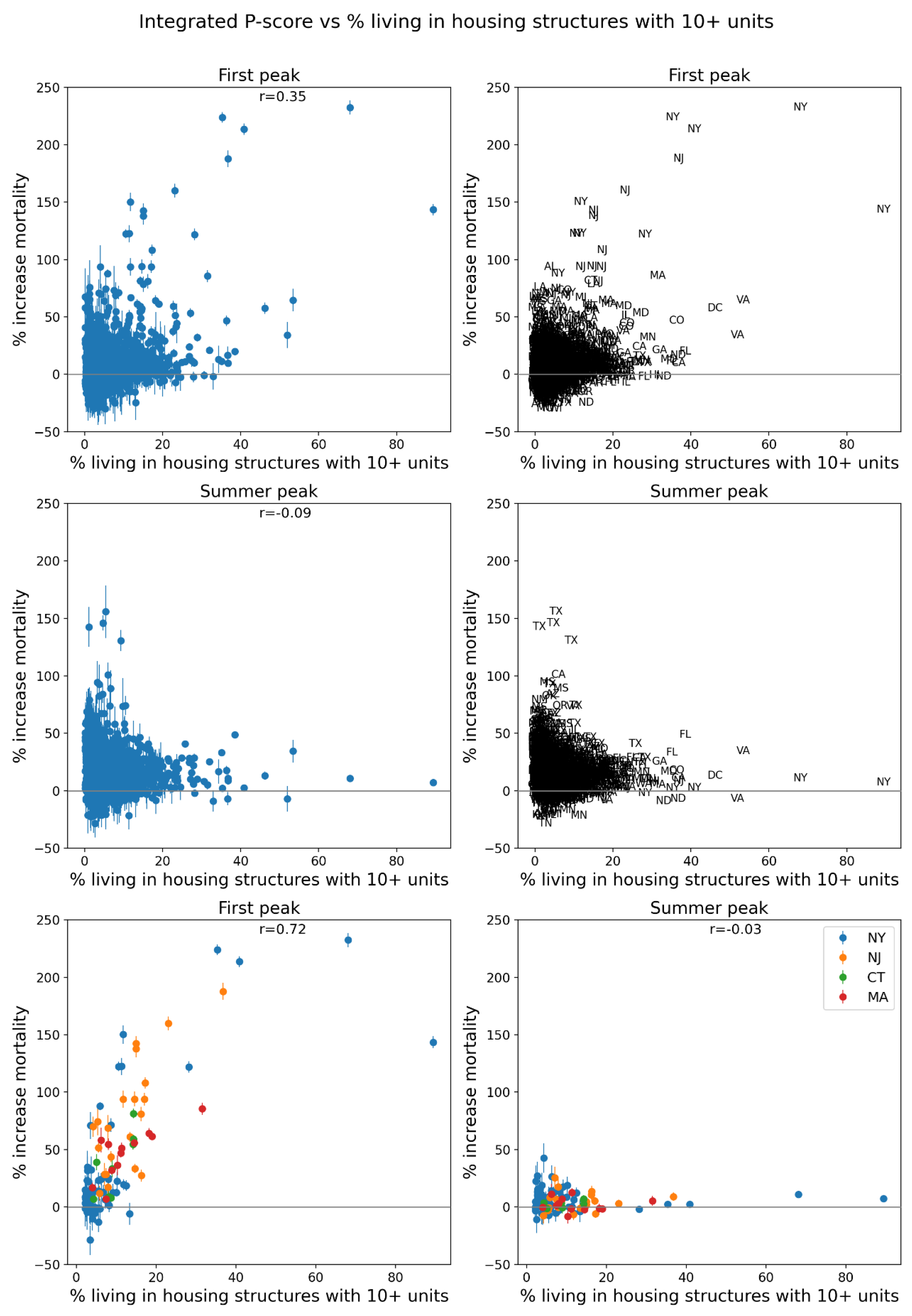
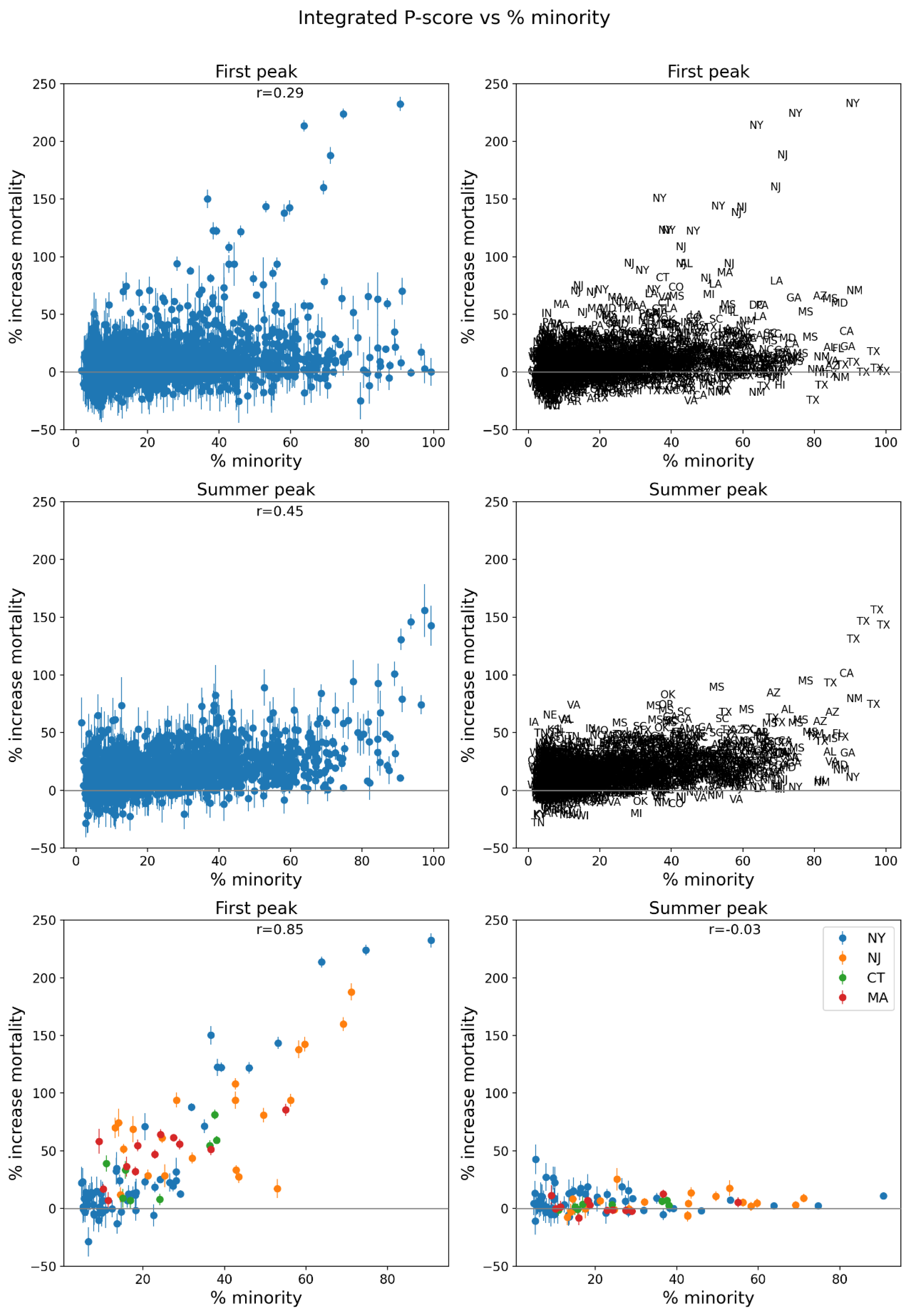
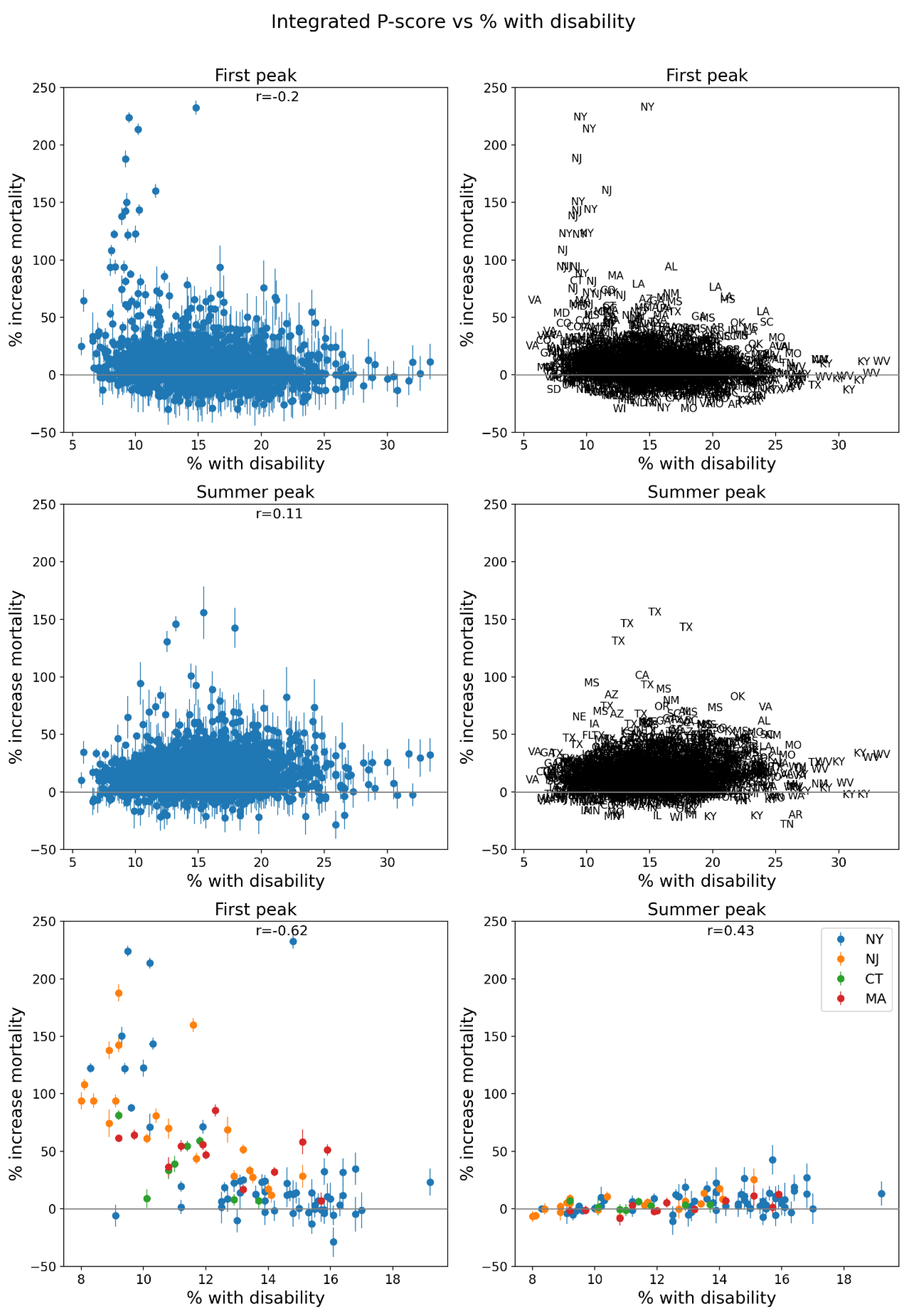
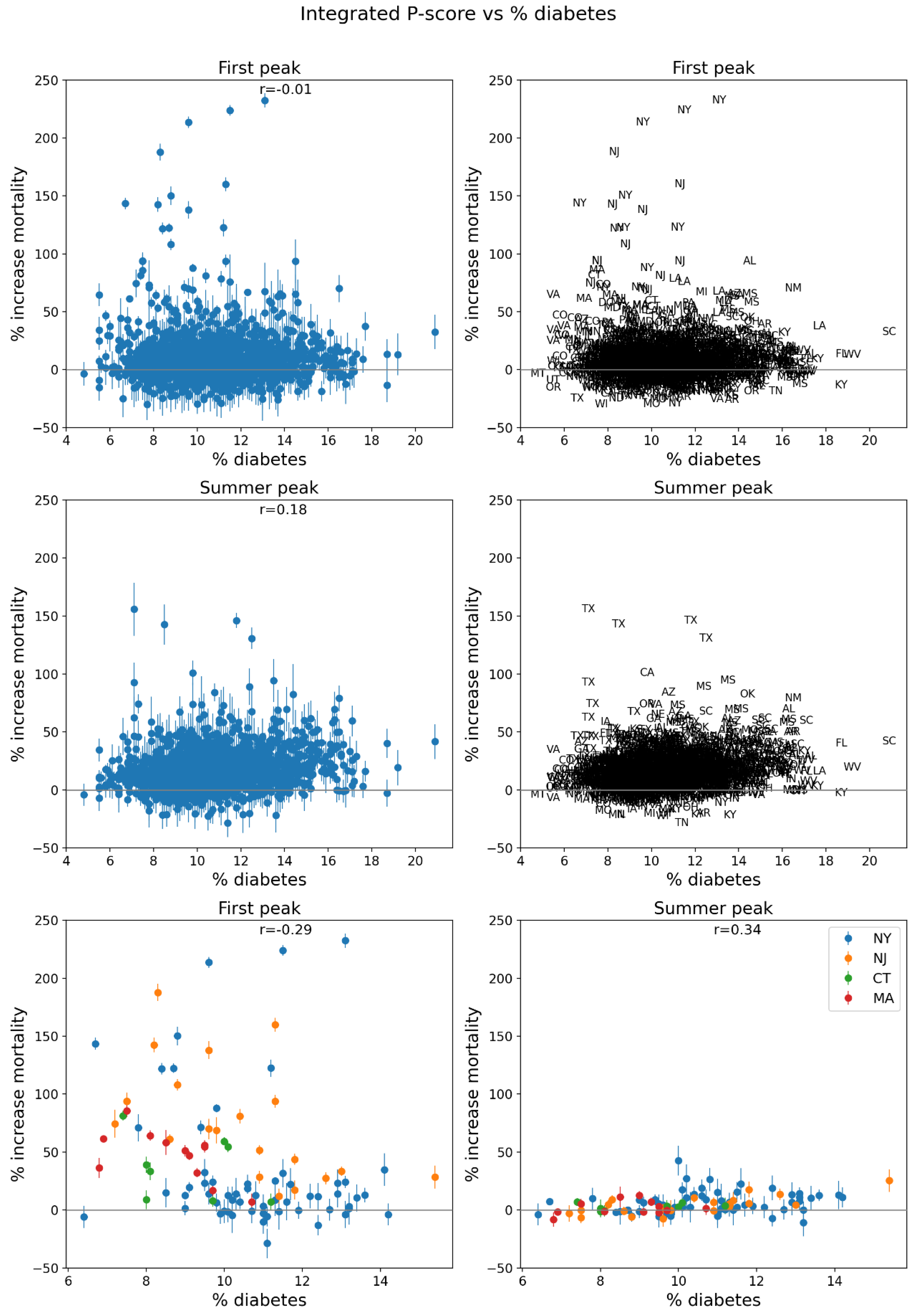
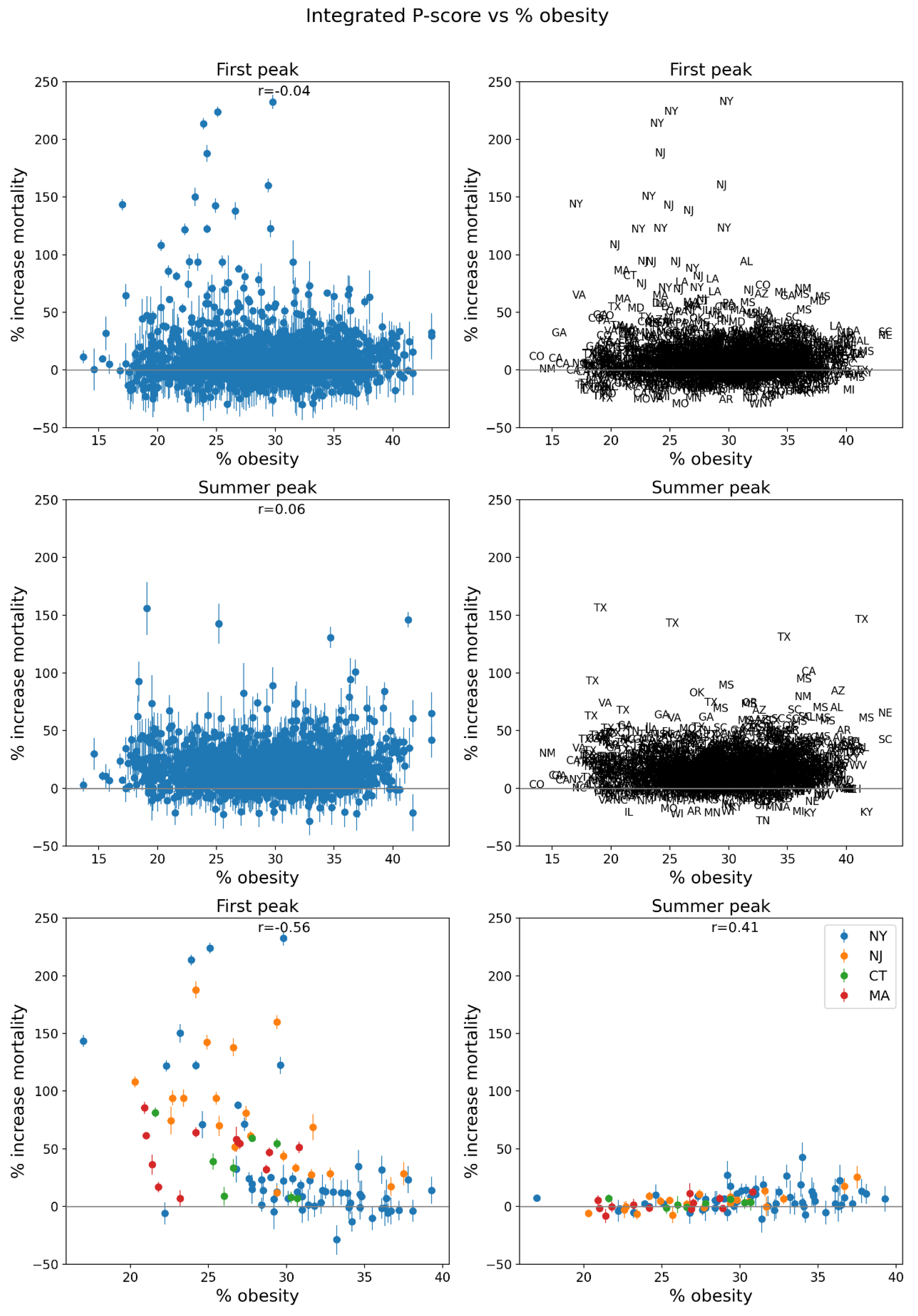
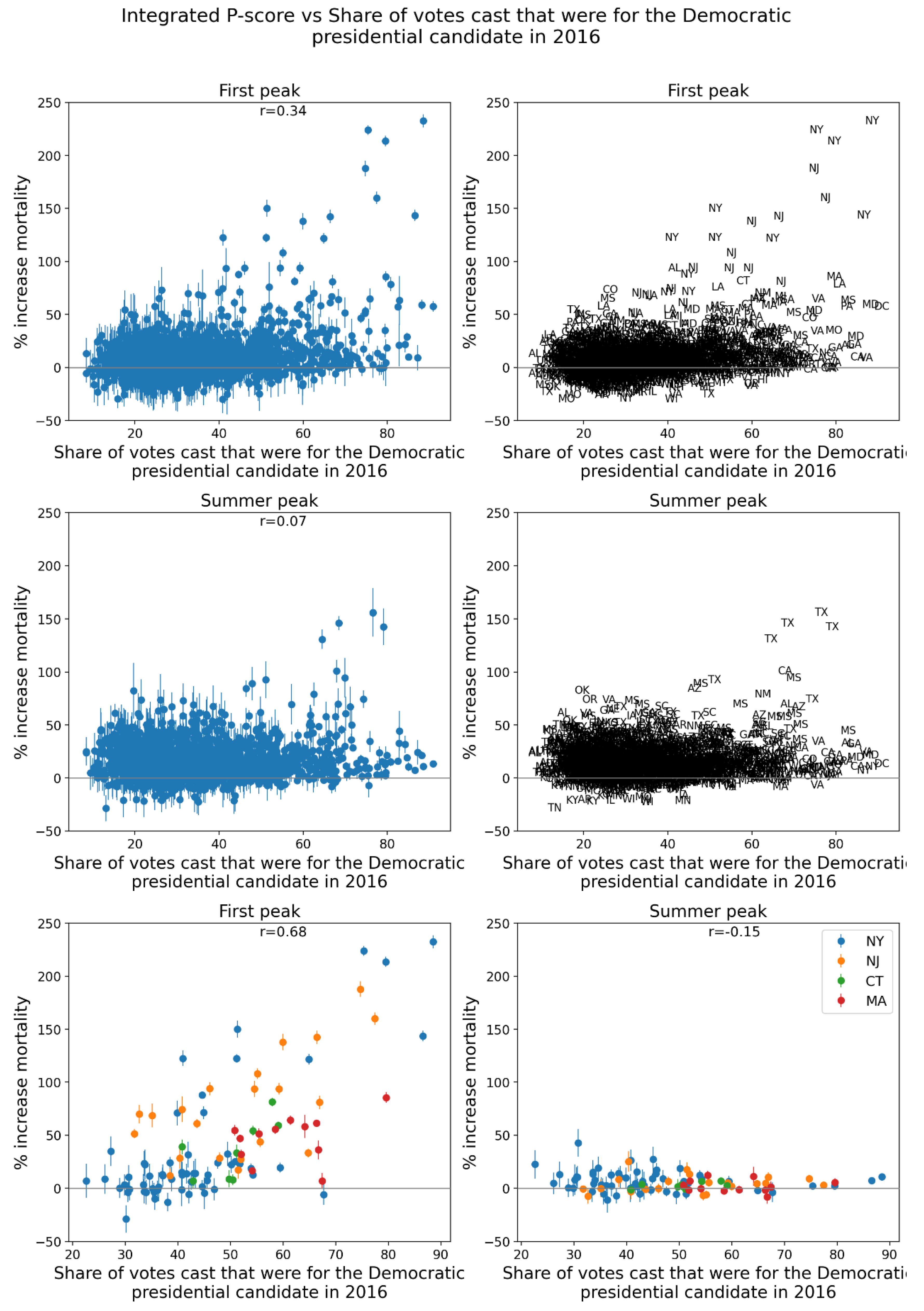
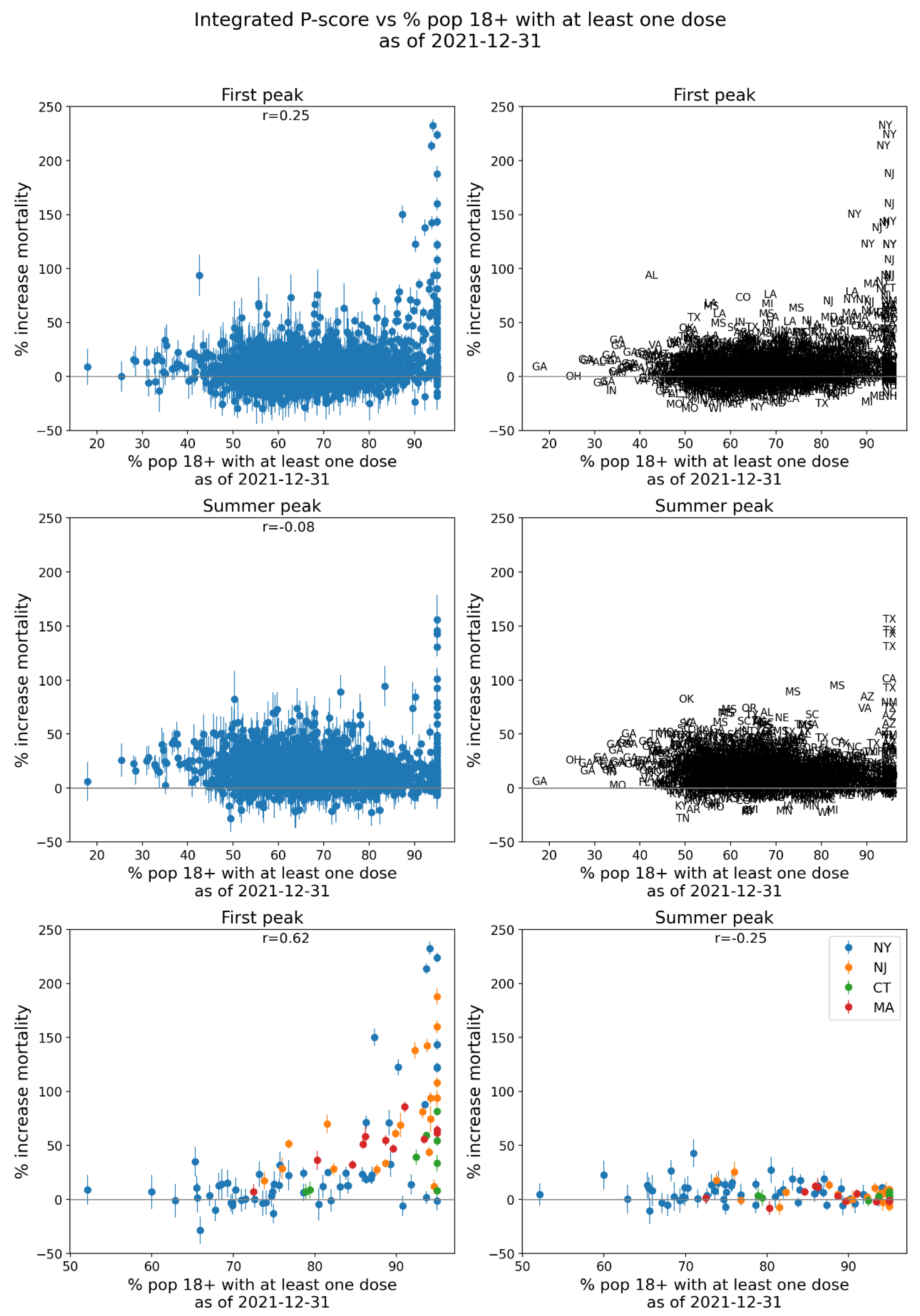
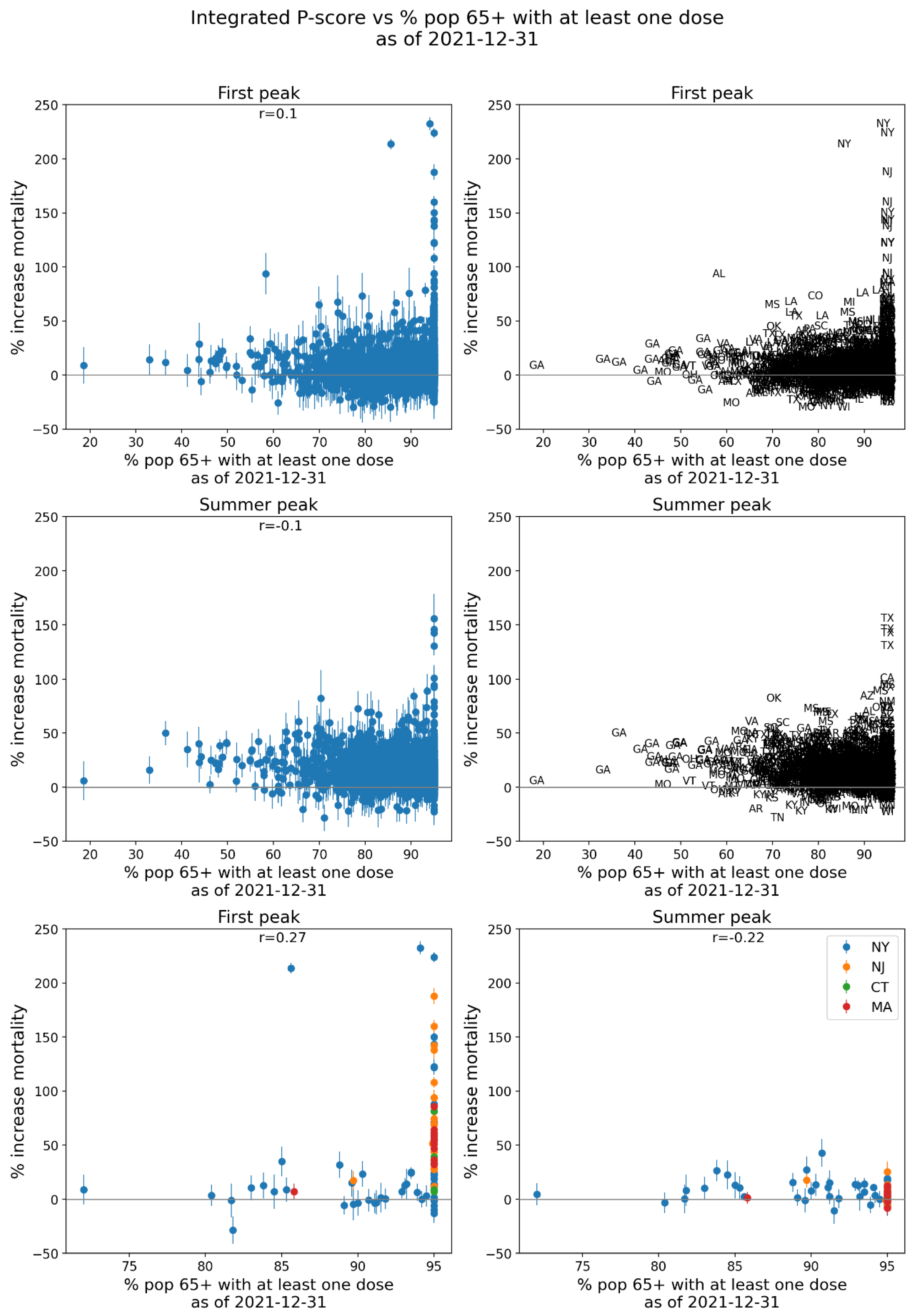
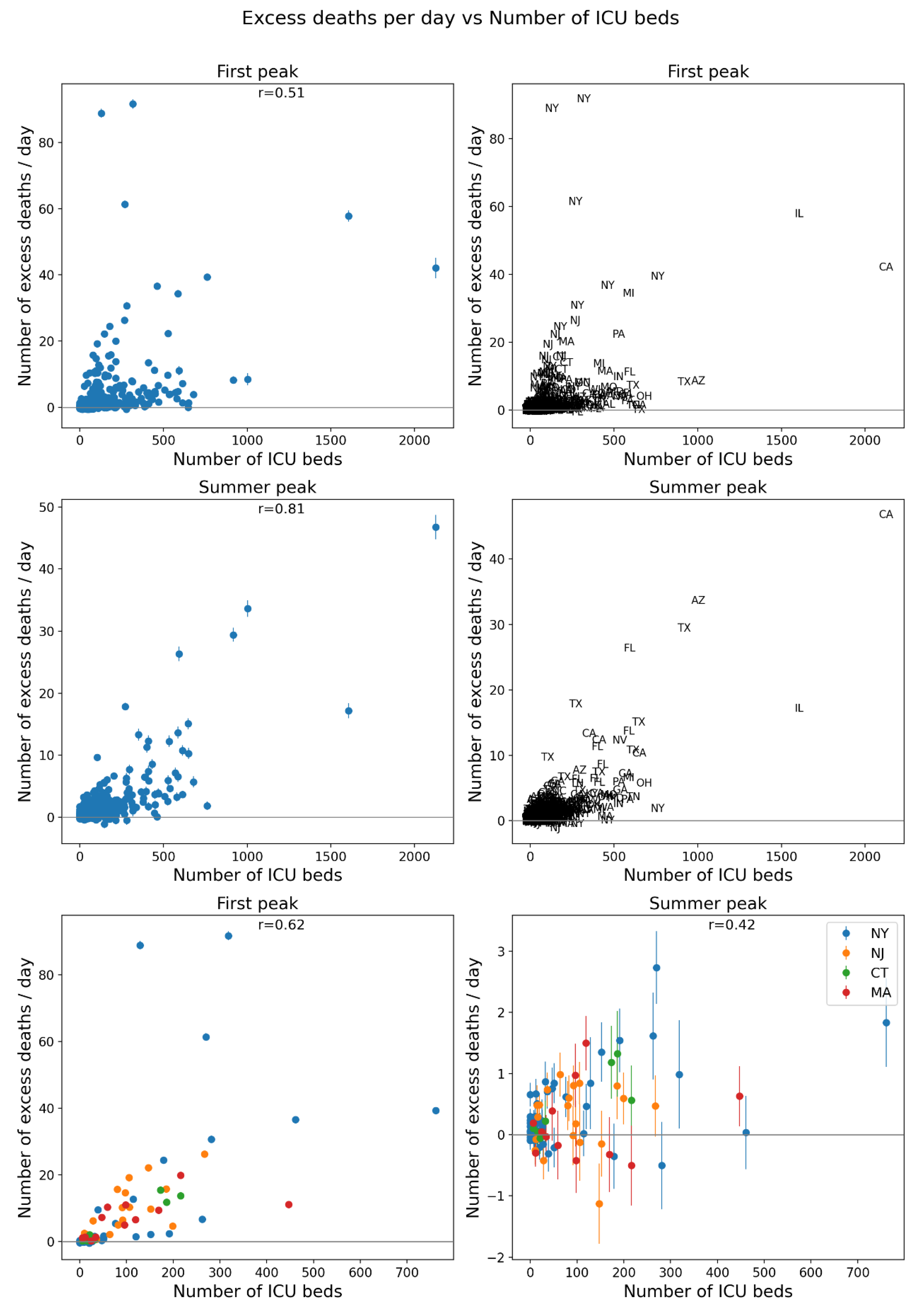
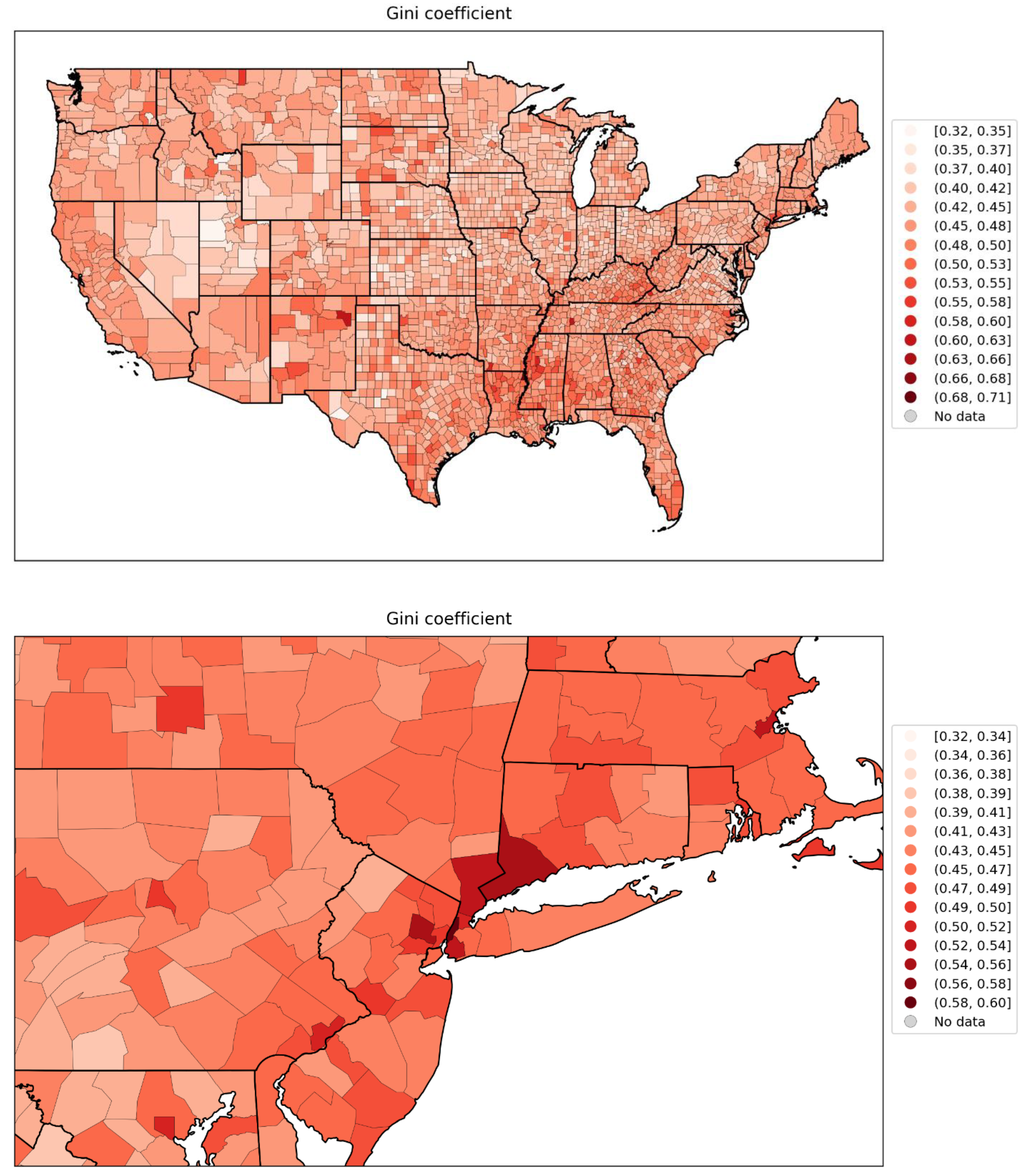
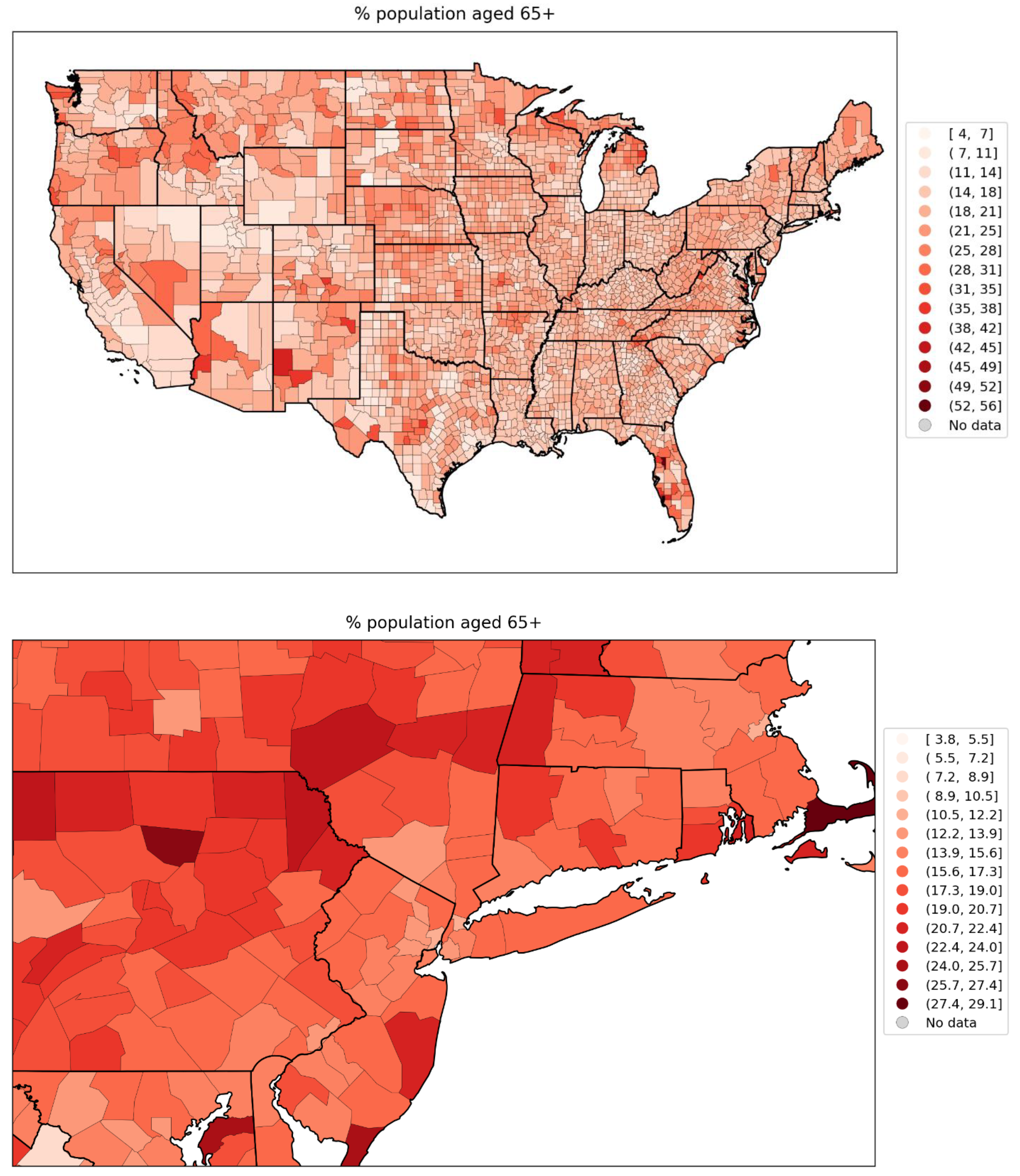
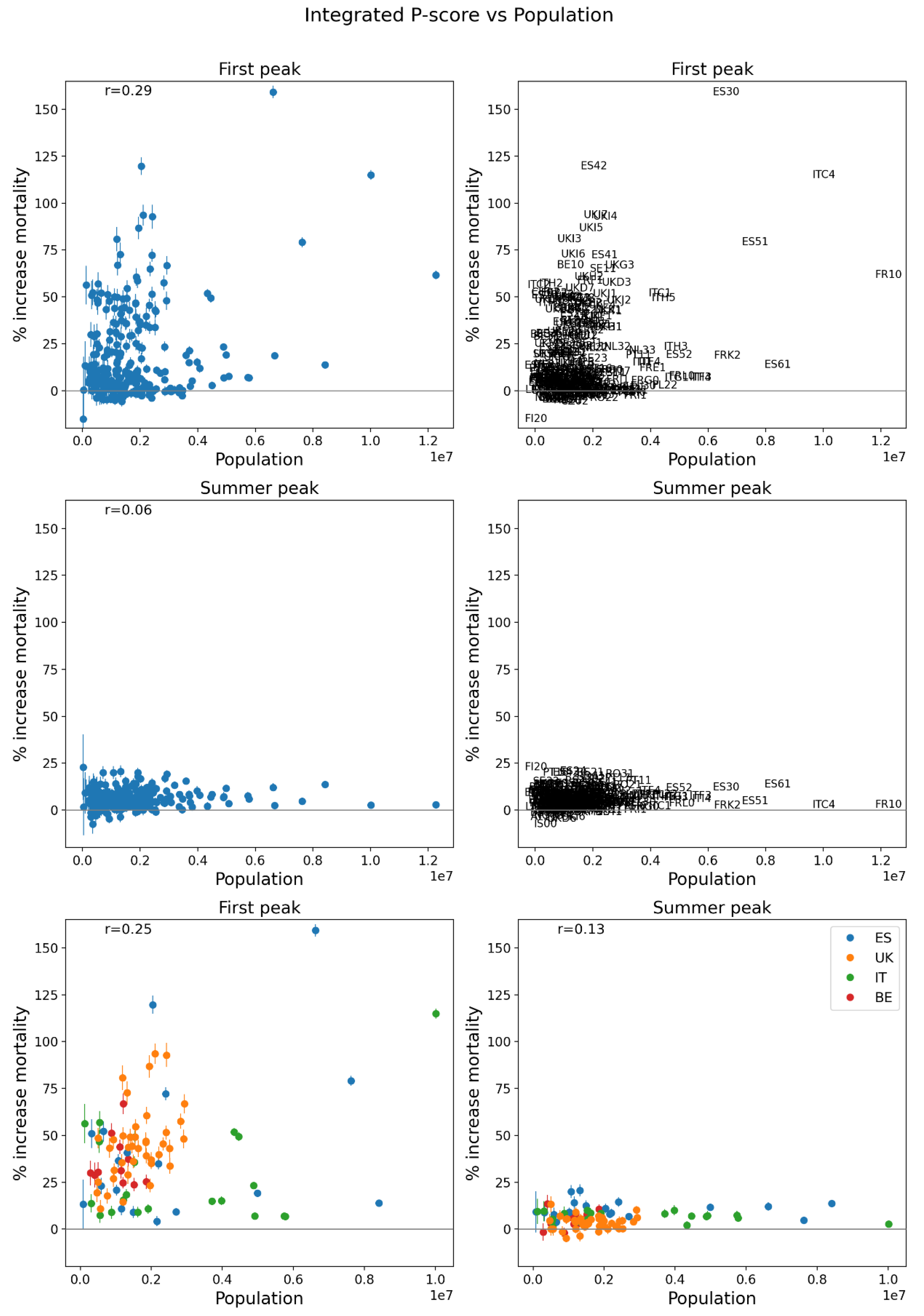
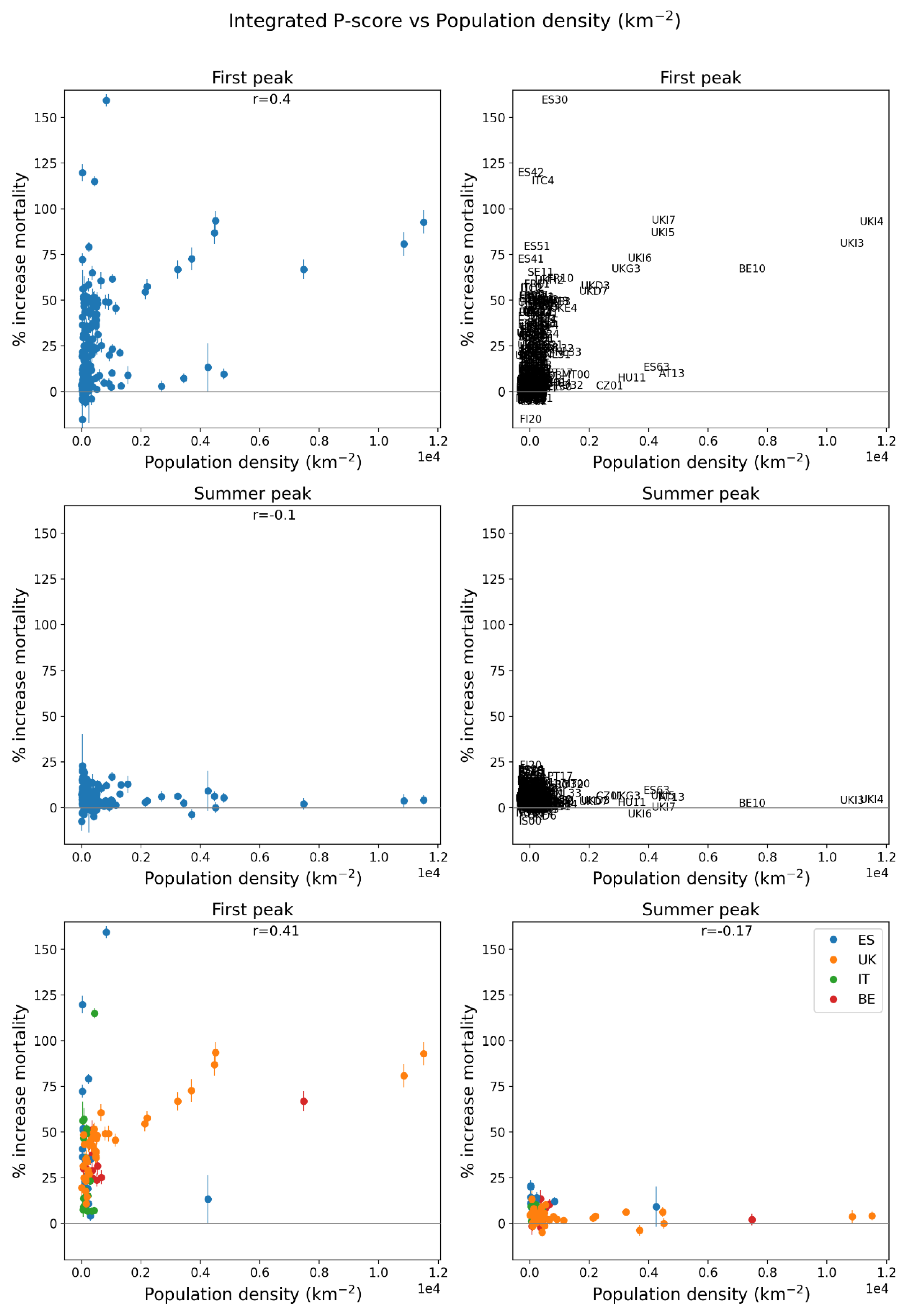
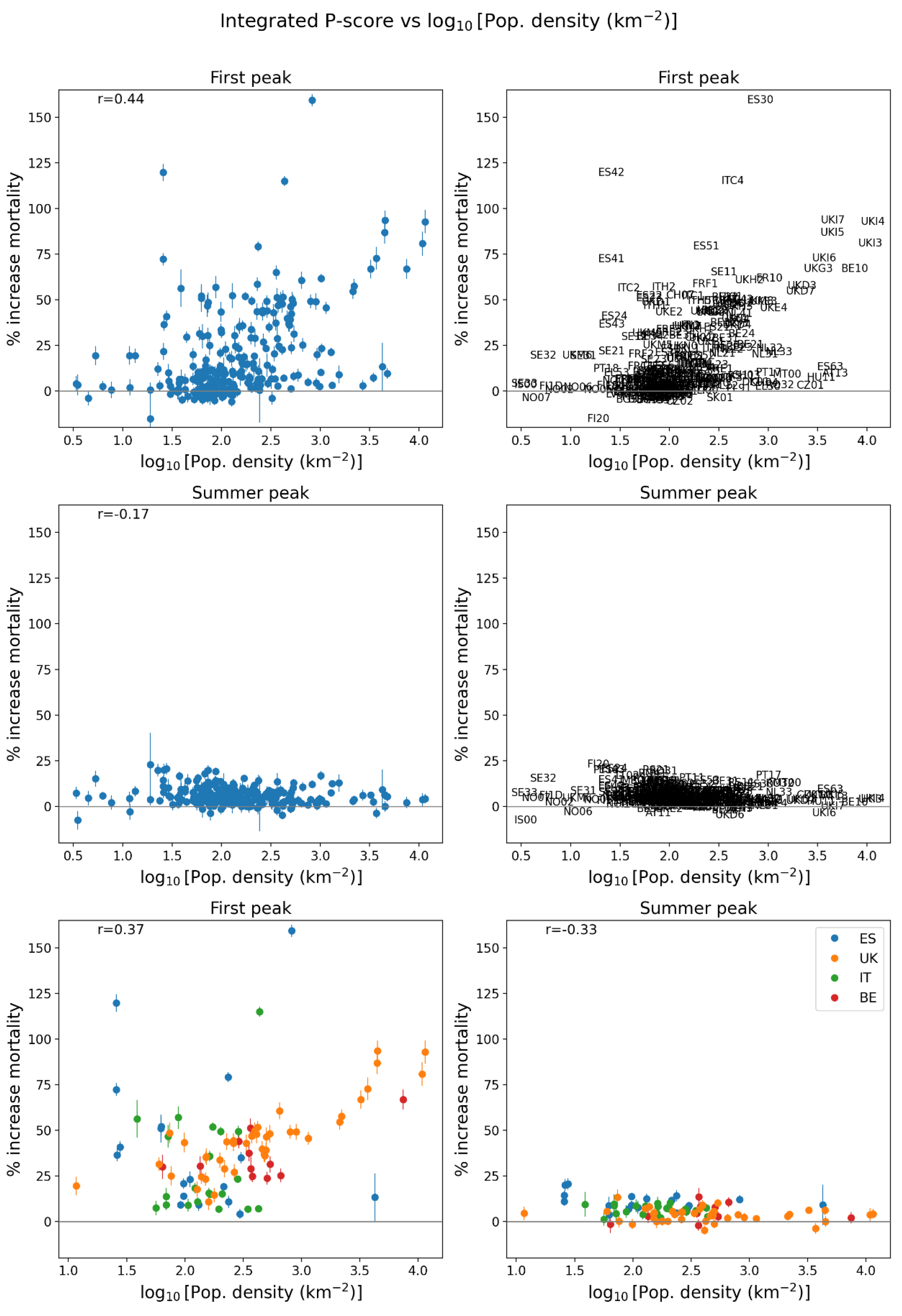
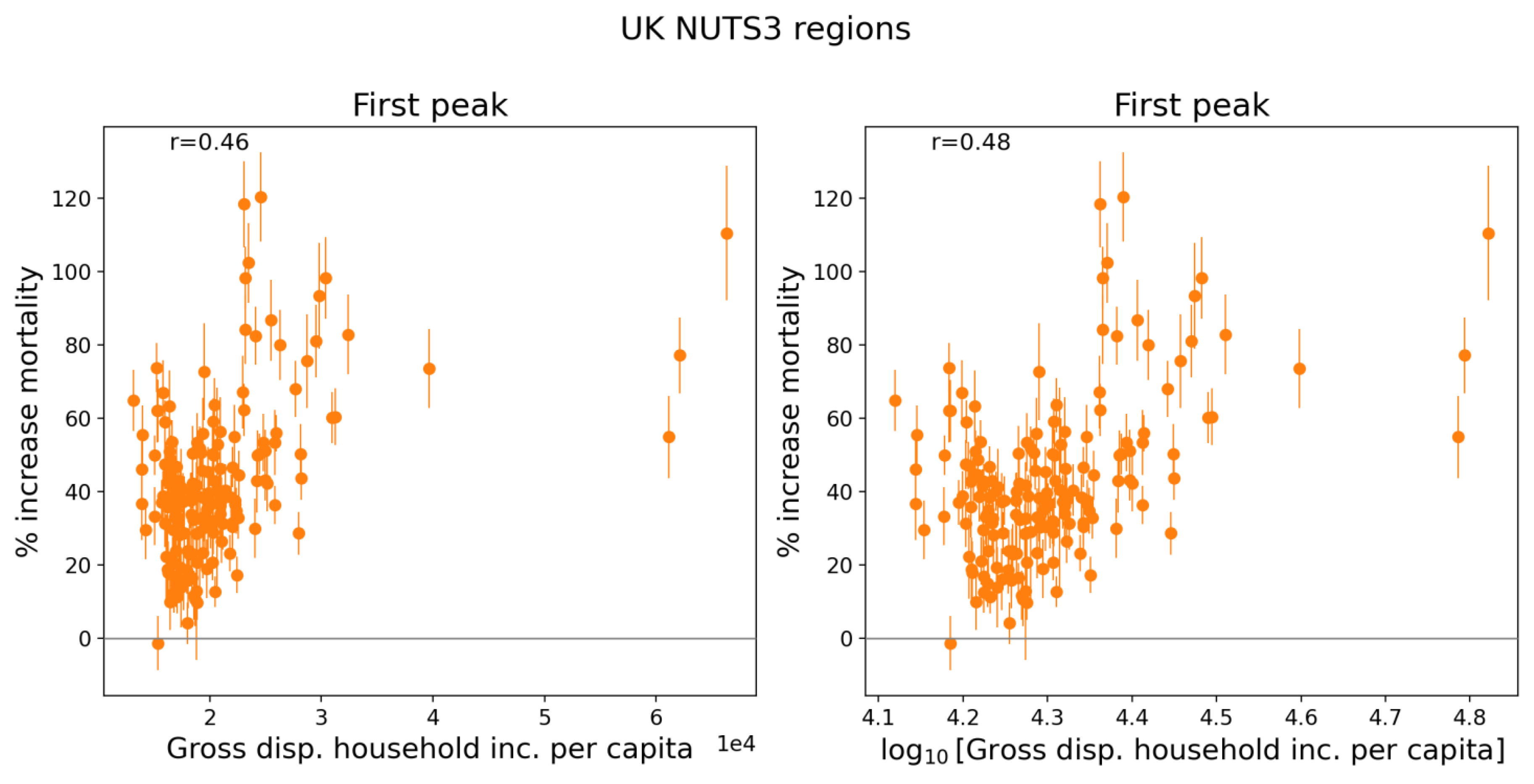
2.5. Excess Mortality P-Scores vs Socioeconomic Variables
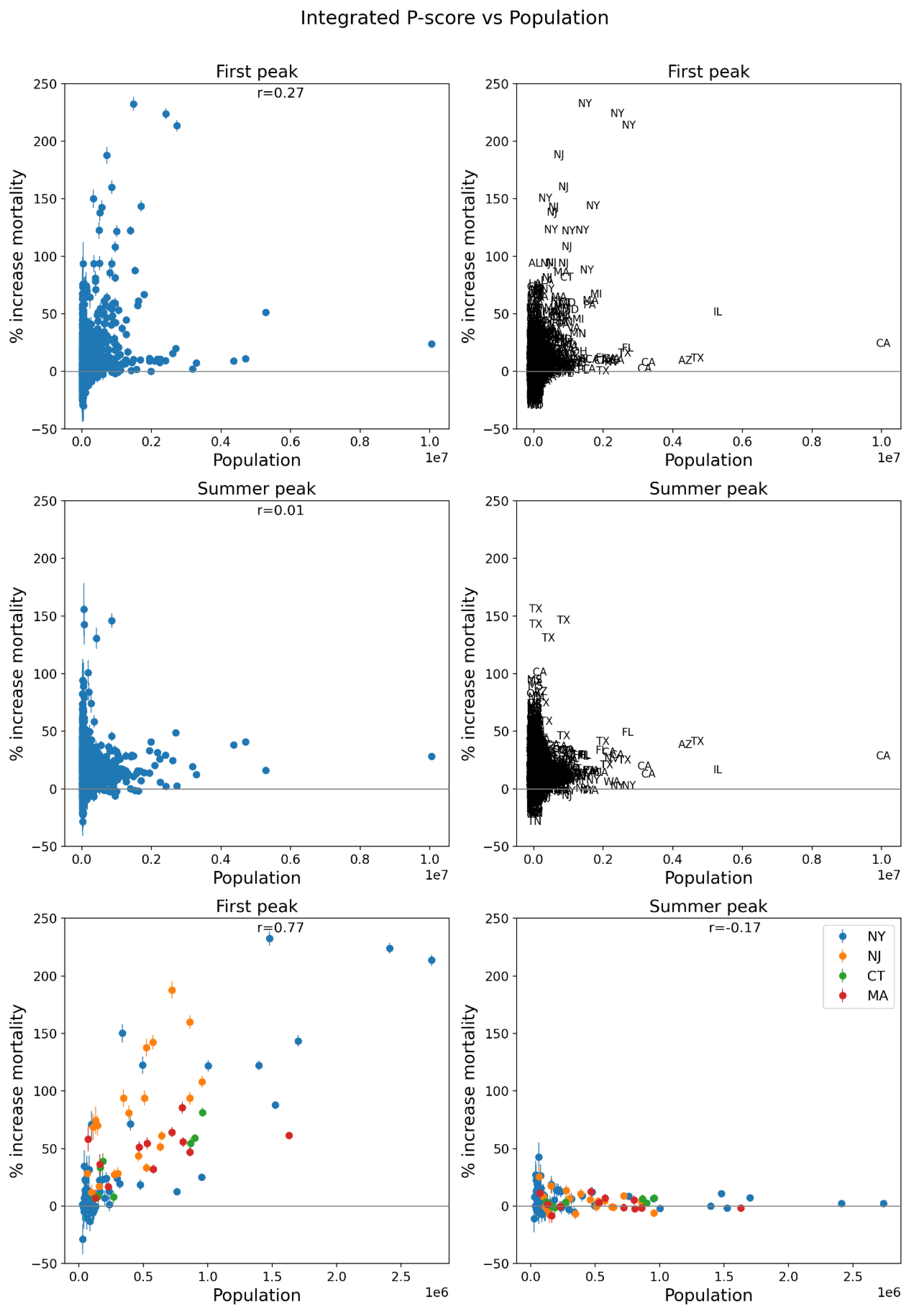
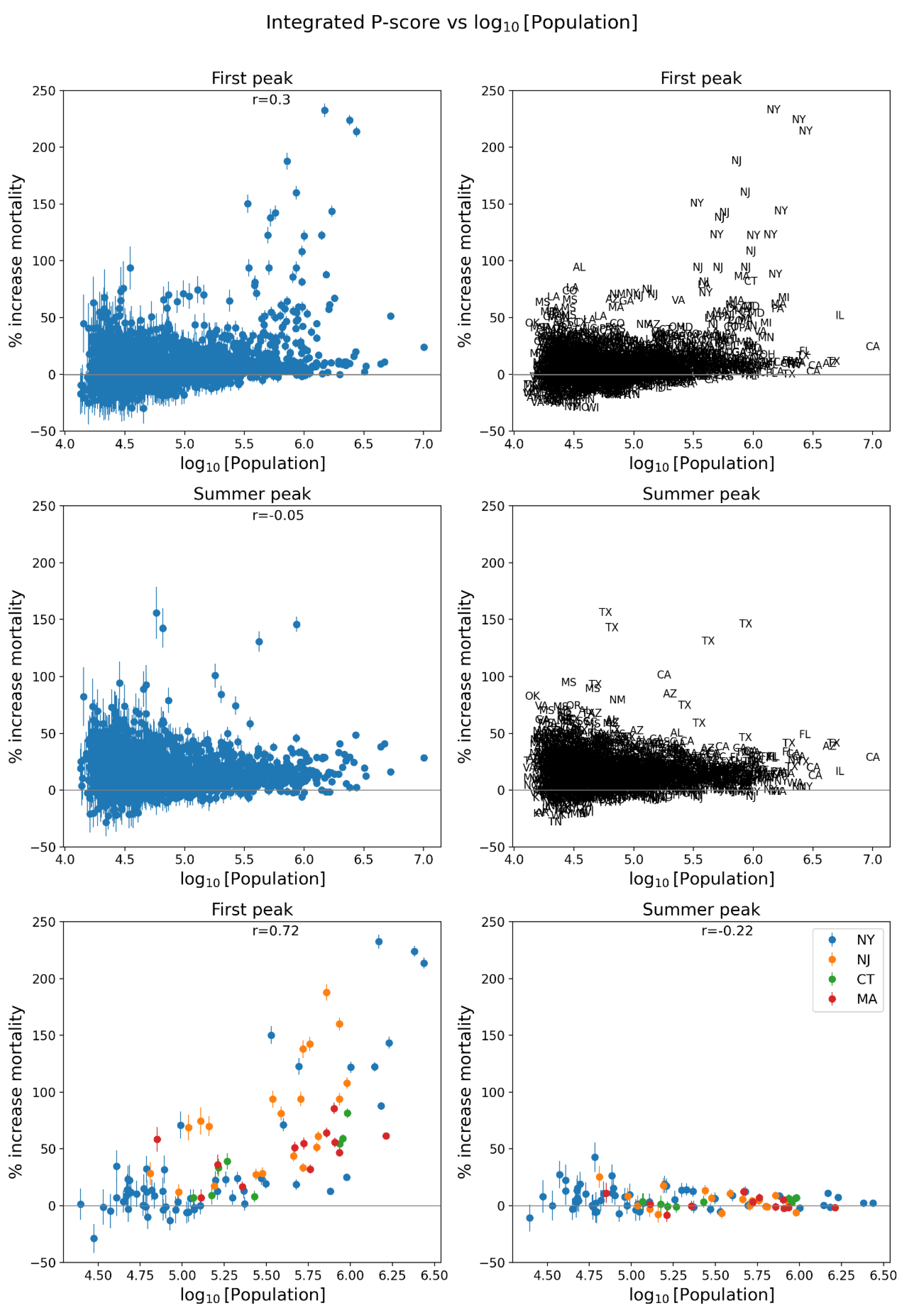
2.5.1. USA Counties
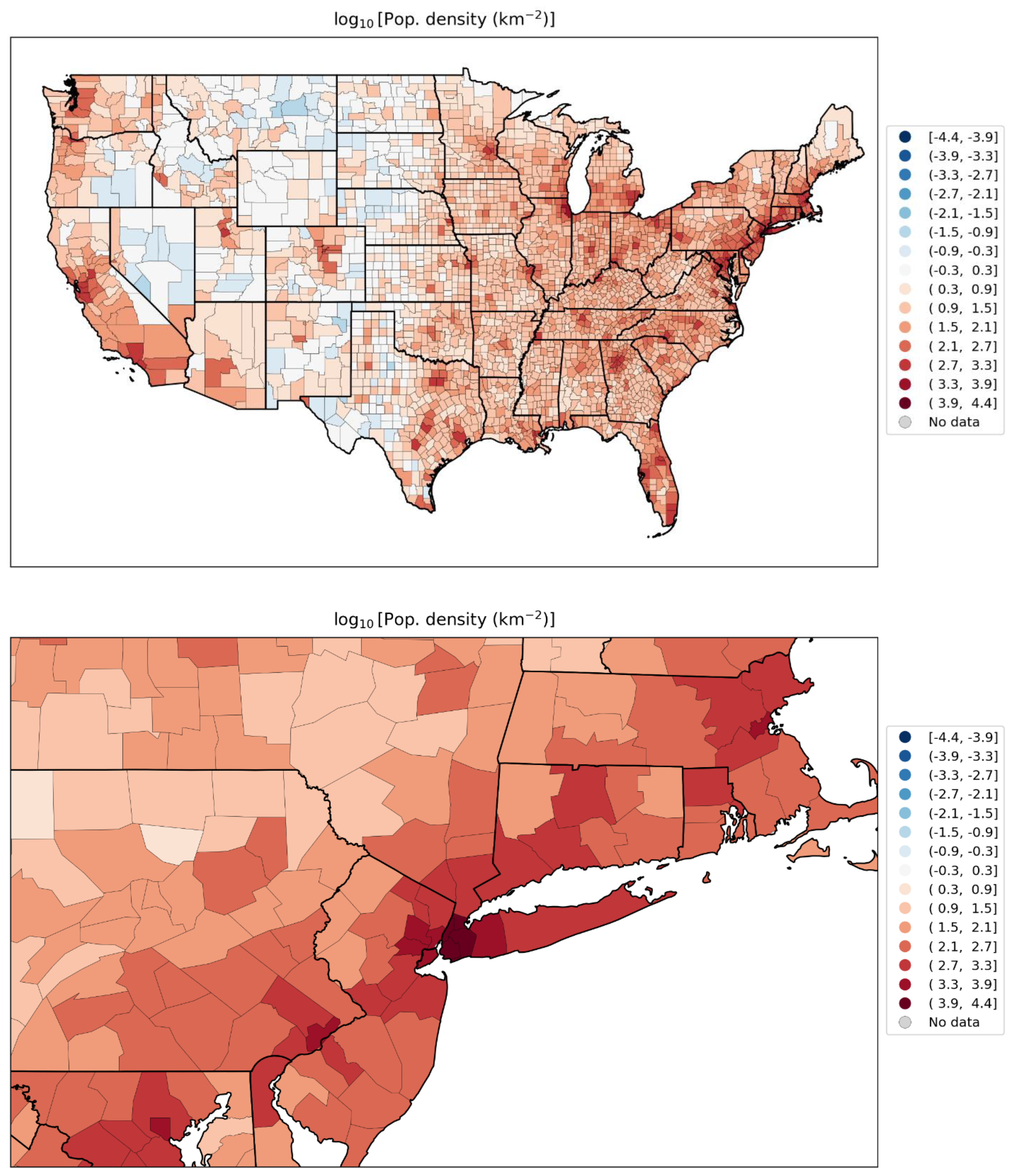
- log[population density] (Figure 67, r = 0.85);
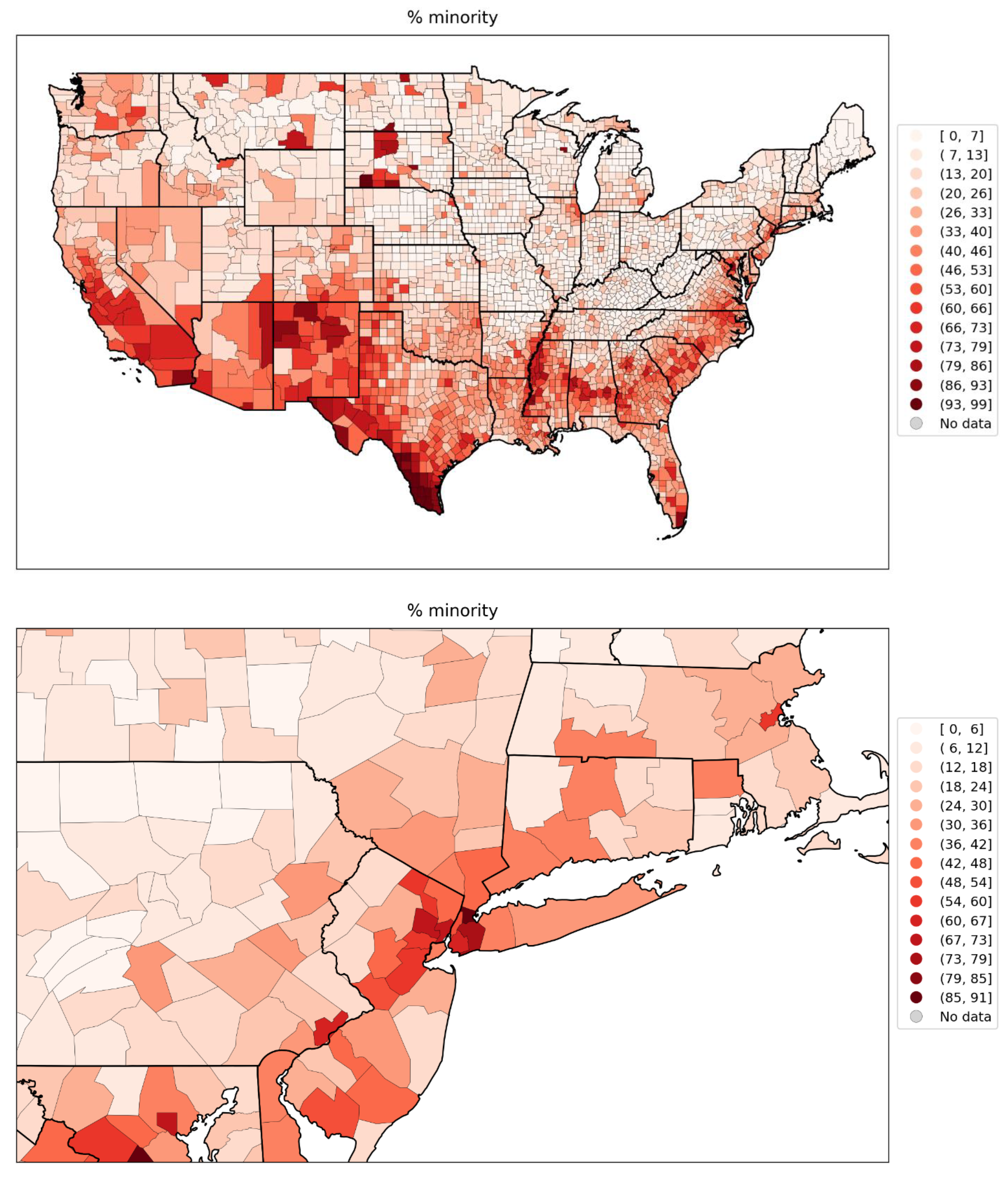
- % minority (Figure 77, r = 0.85);
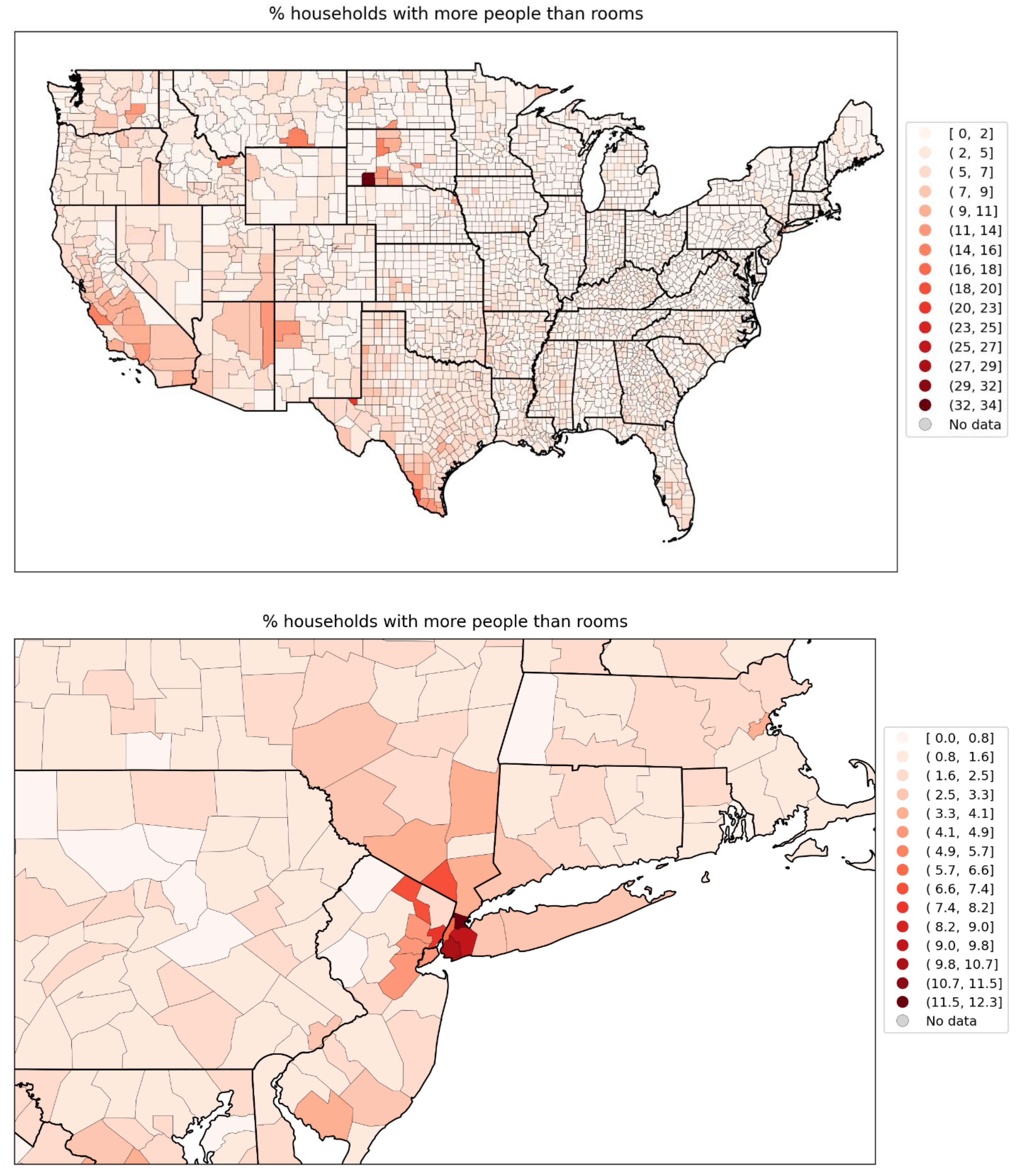
- % households with more people than rooms (Figure 74, r = 0.83);
- population (Figure 64, r = 0.77);
- log[population] (Figure 65, r = 0.72);
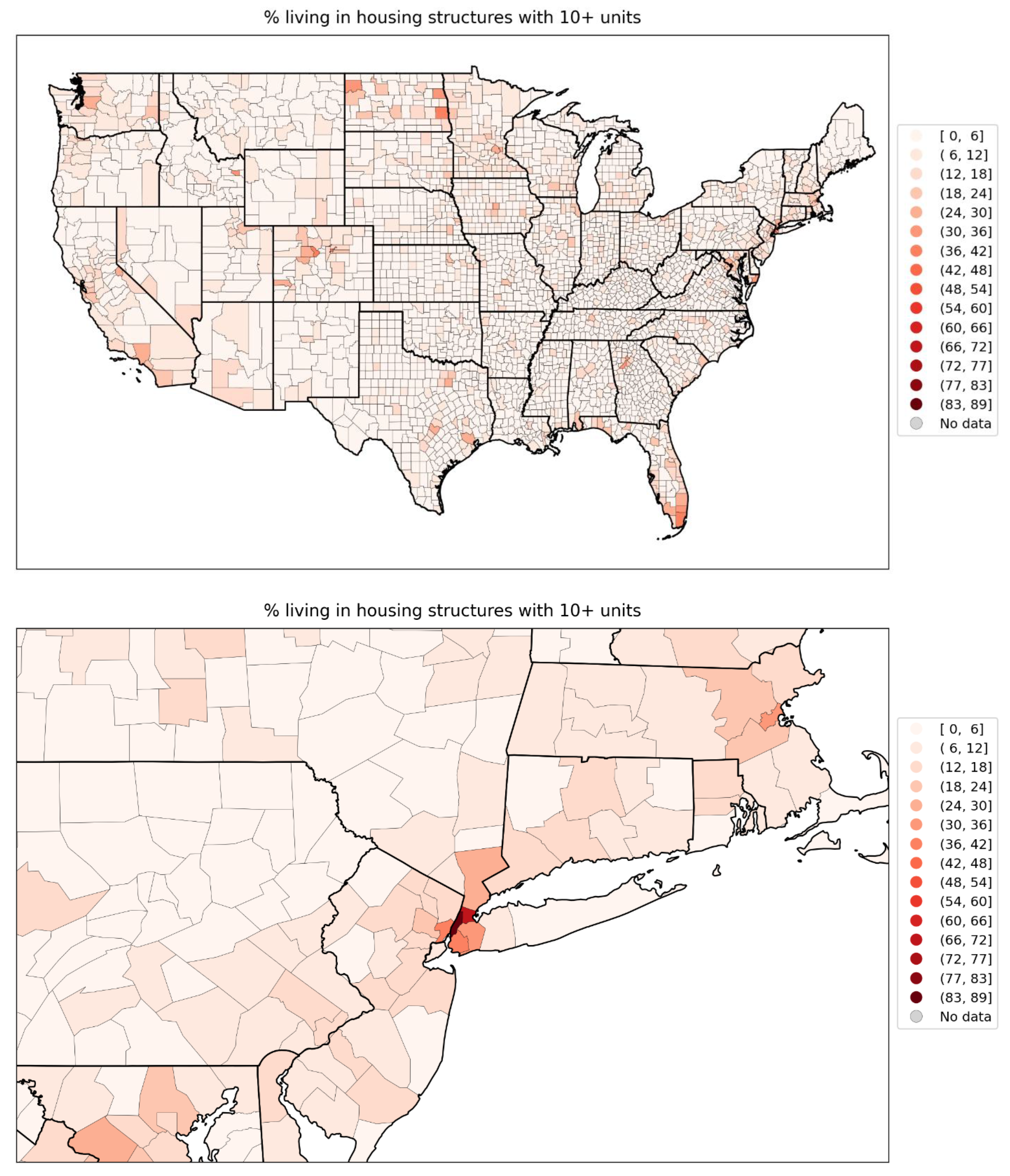
- % living in housing structures with more than 10 units (Figure 75, r = 0.72); and
- share of votes cast in the 2016 election that were for the Democratic presidential candidate (Figure 85, r = 0.68).
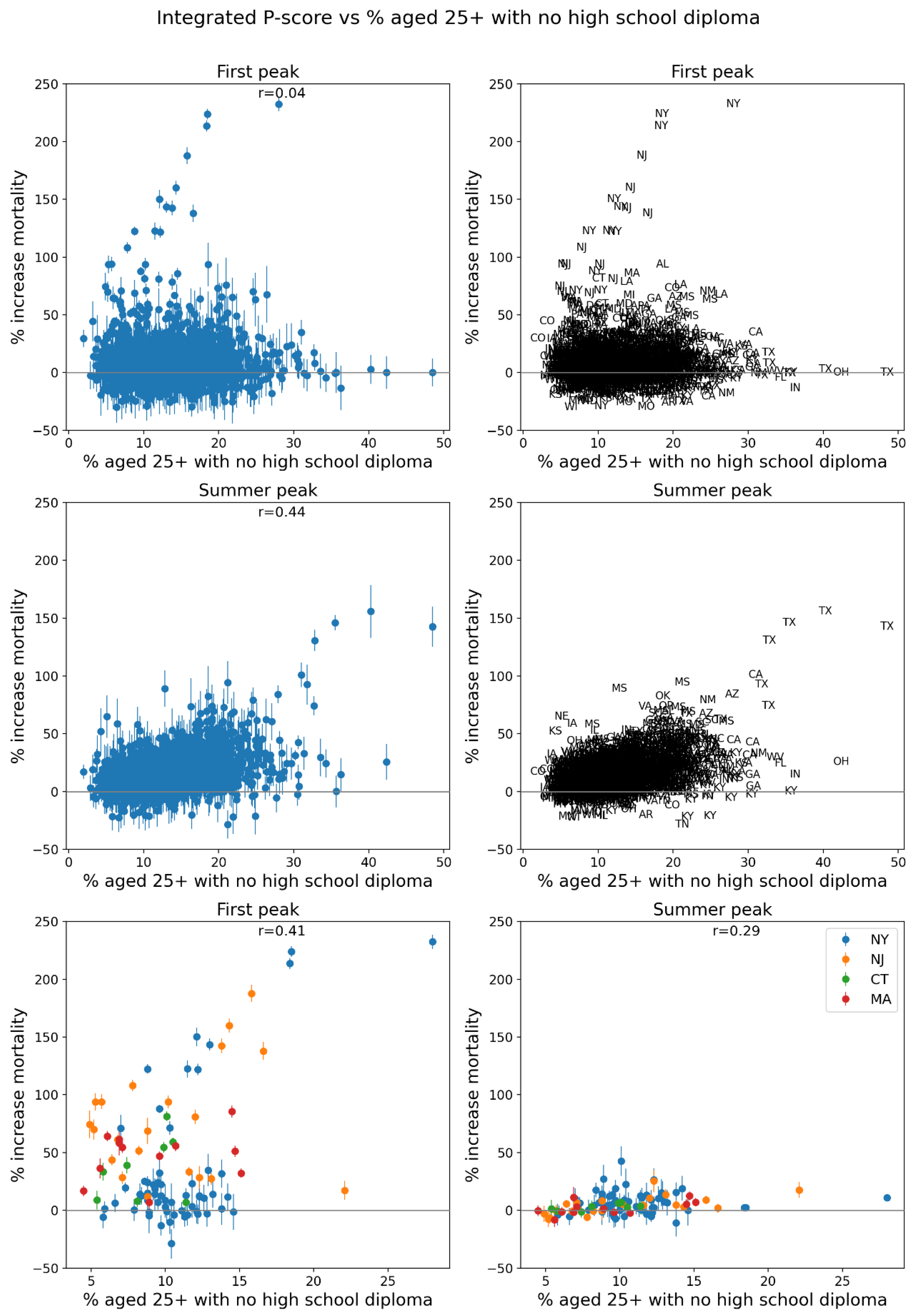
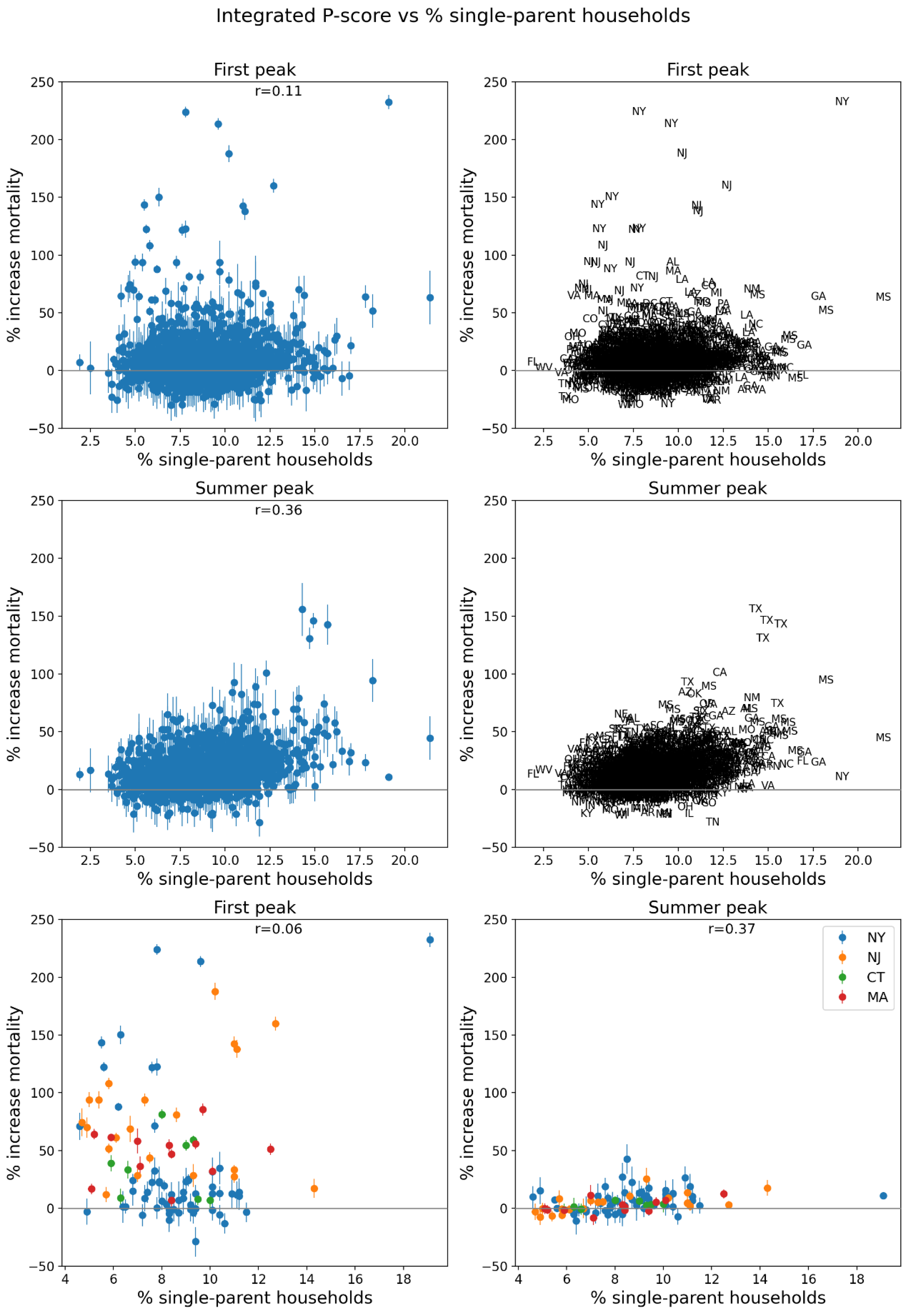
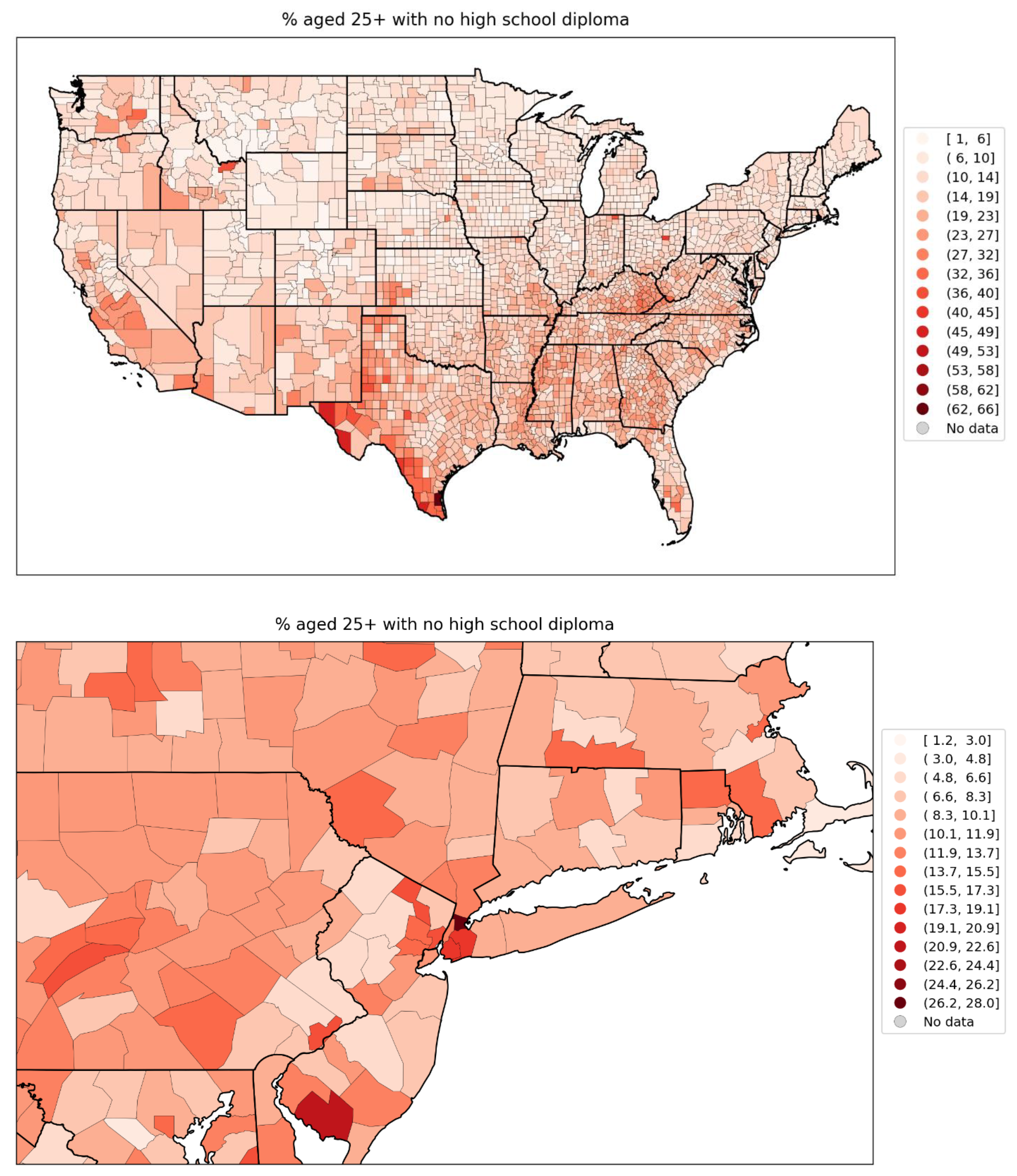
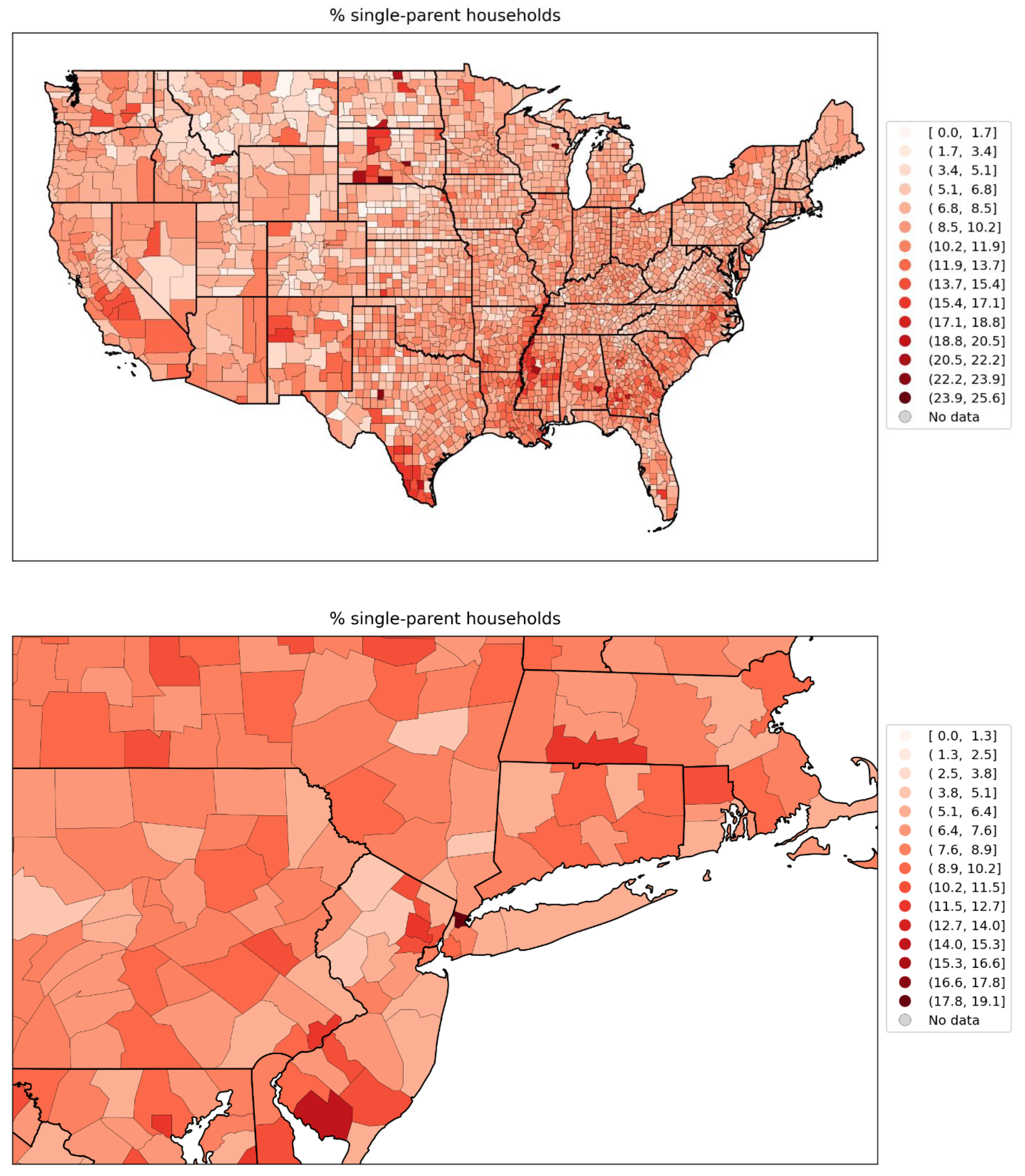
- the percentage of the county’s population aged 25+ with no high school diploma (Figure 78, lower-left panel, and see the map for this variable in Figure 113, bottom panel); and
- the percentage of single-parent households (Figure 81, lower-left panel and map in Figure 116, bottom panel).
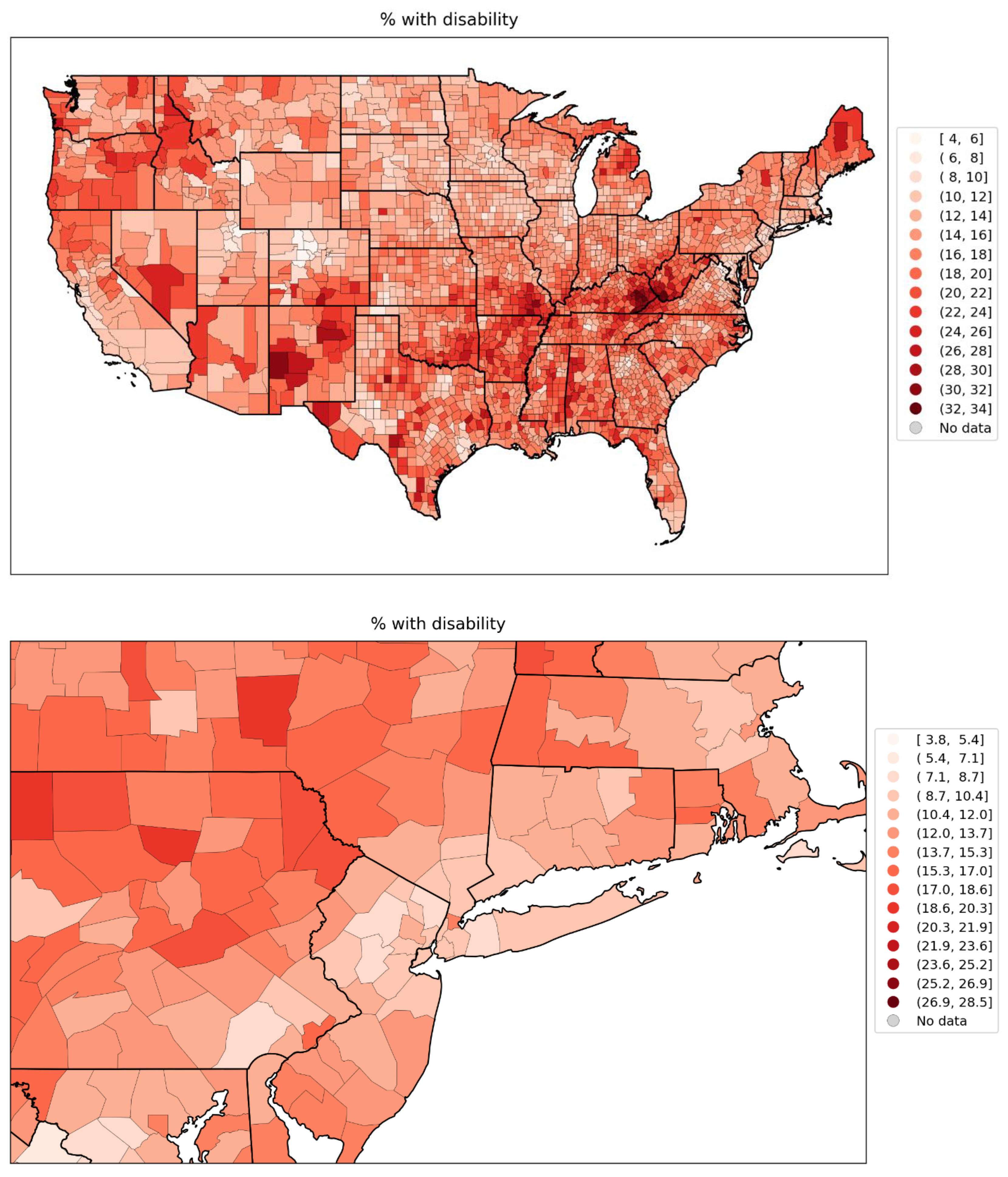
- the percentage of the population with a disability (Figure 82, lower-left panel, and map in Figure 117, bottom panel);
- the percentage of the population with diabetes (Figure 83, lower-left panel, and map in Figure 118, bottom panel); and
- the percentage of the population with obesity (Figure 84, lower-left panel, and map in Figure 119, bottom panel).
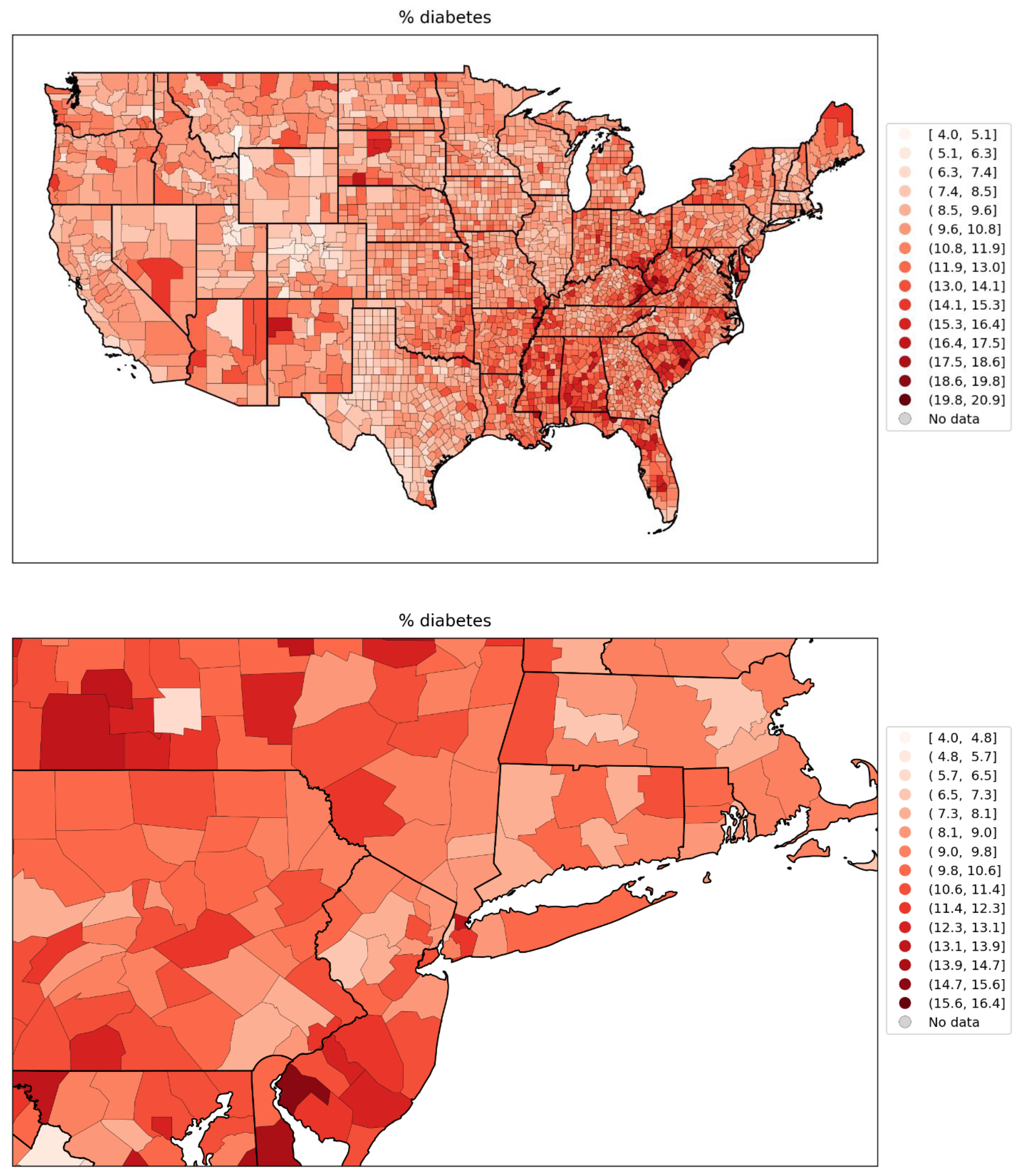
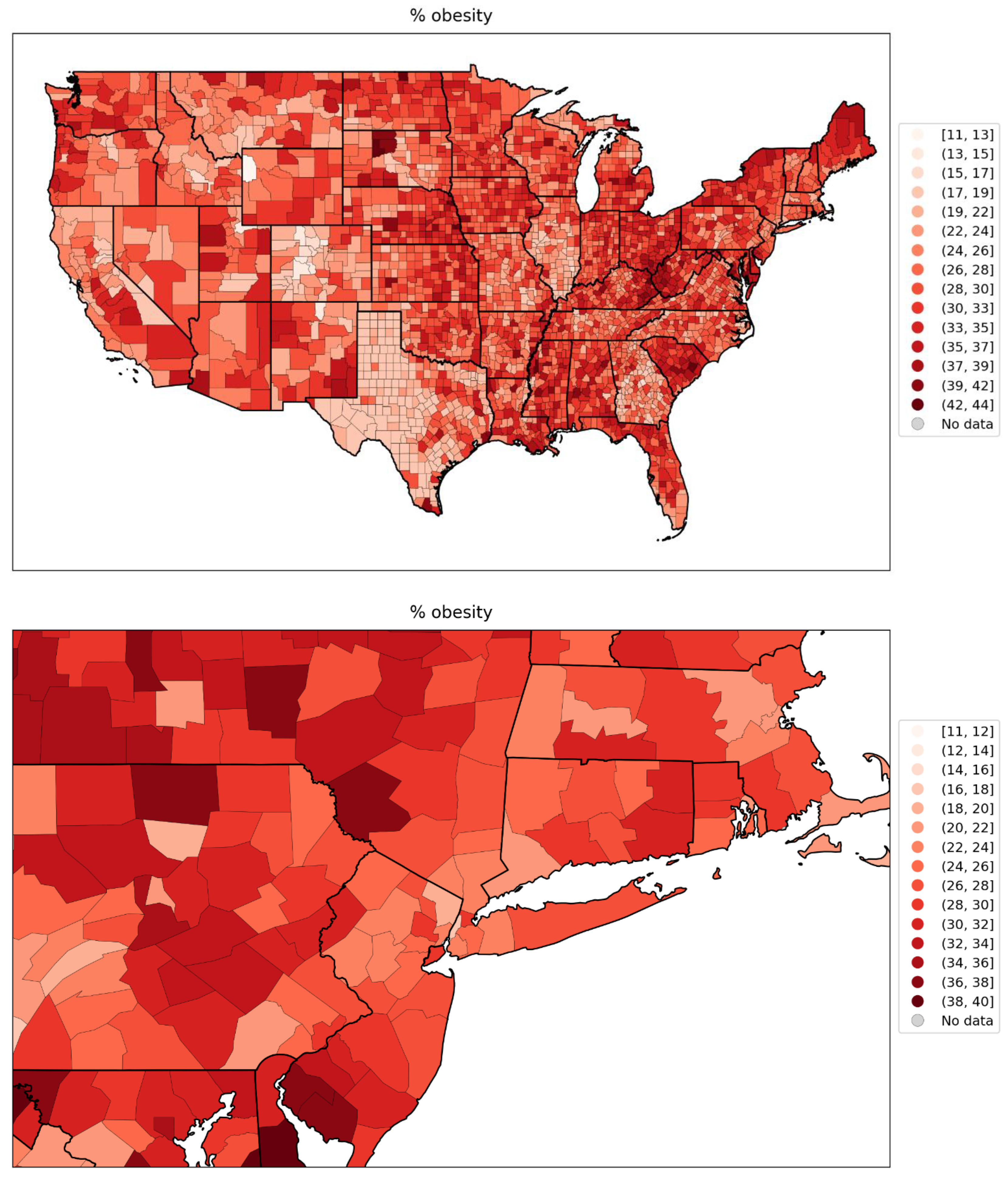
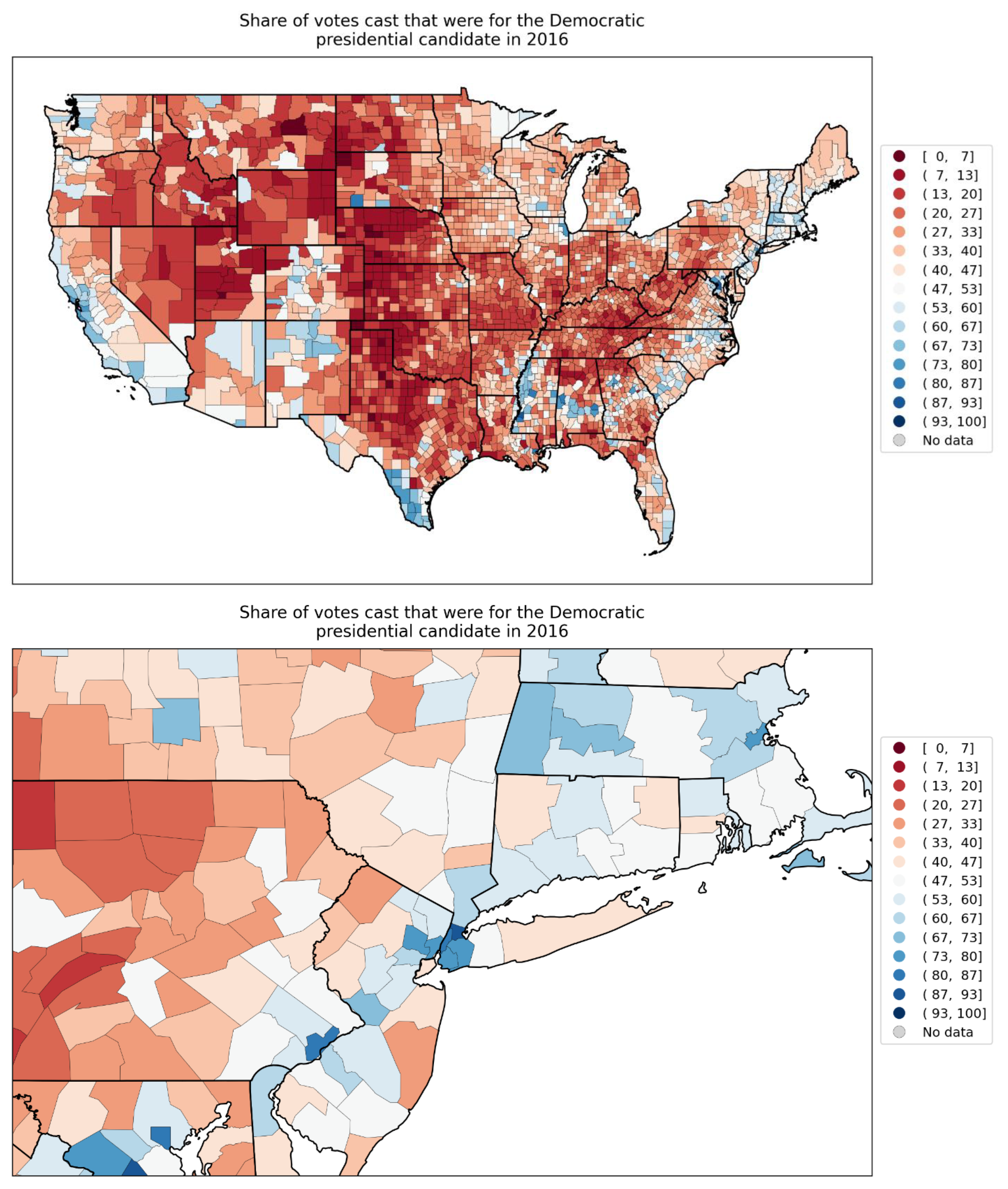
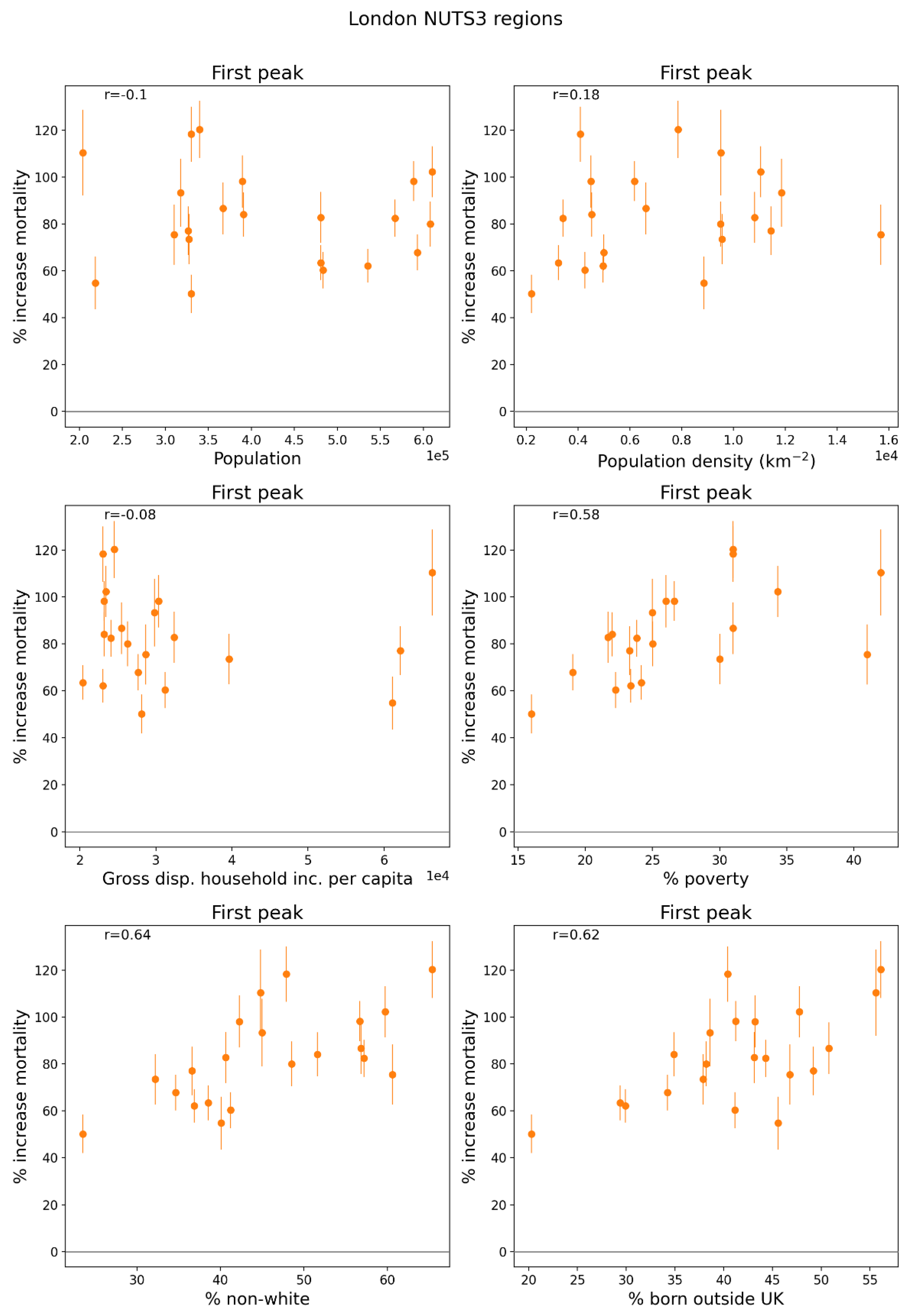
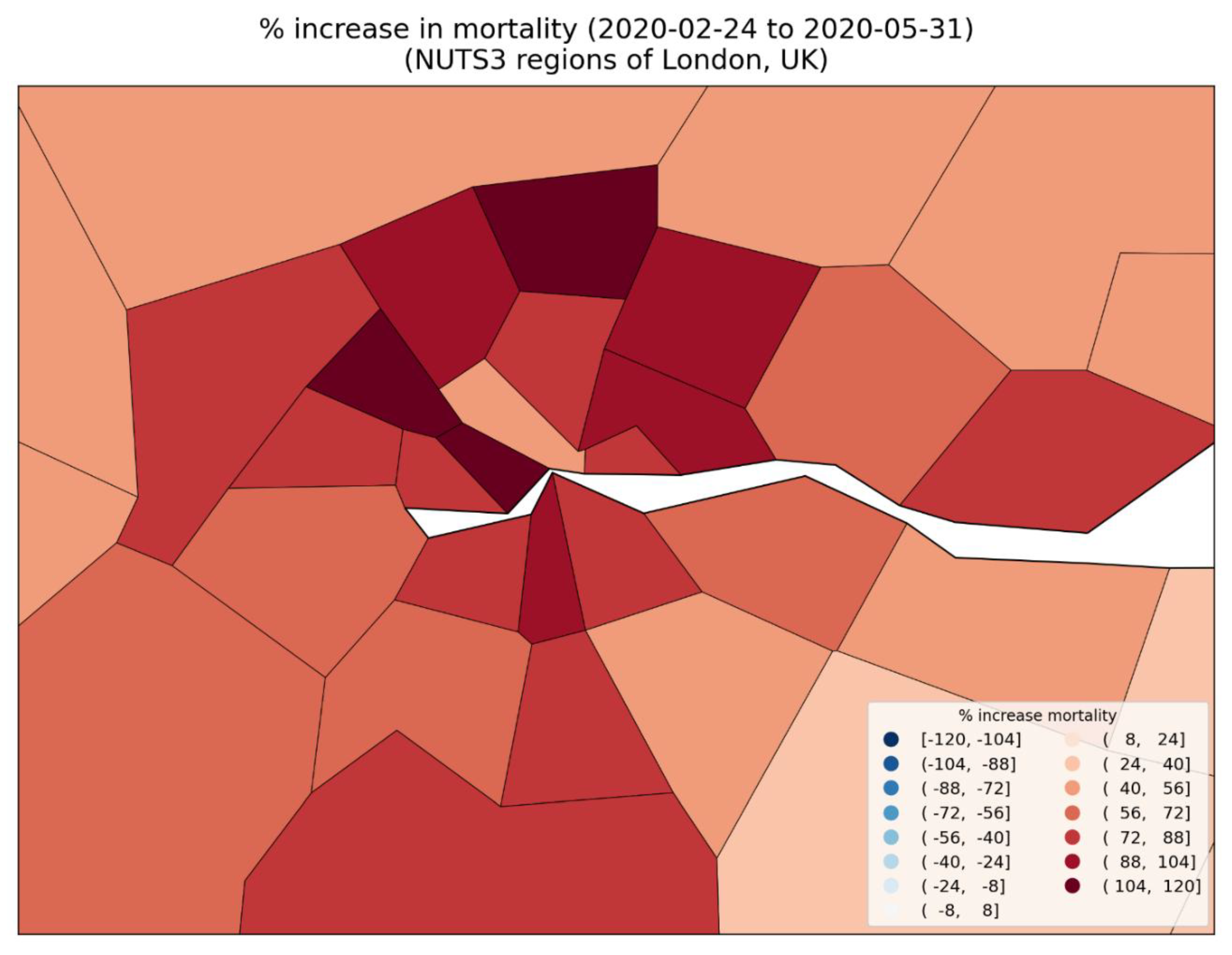
2.5.2. European Subnational Regions
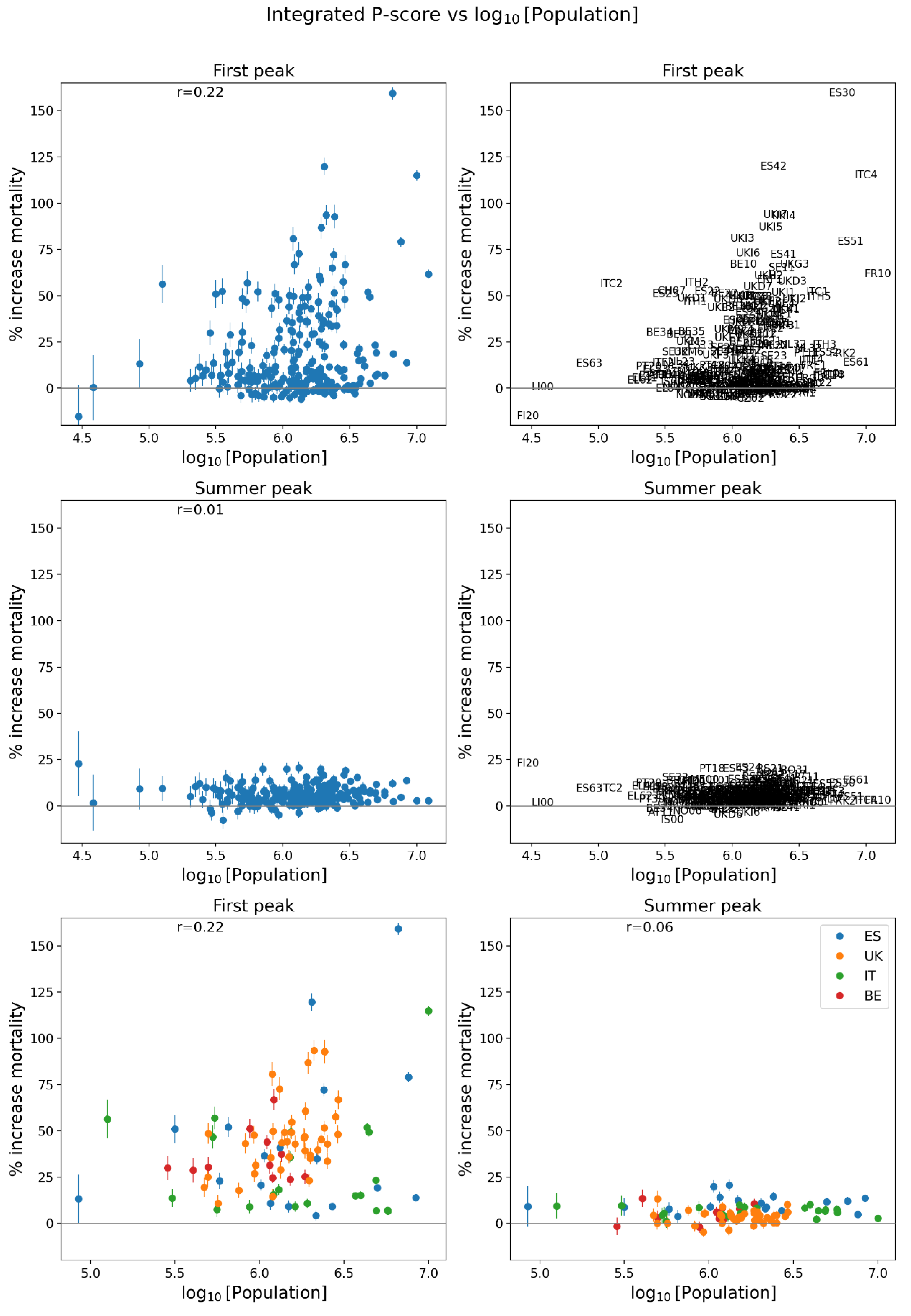
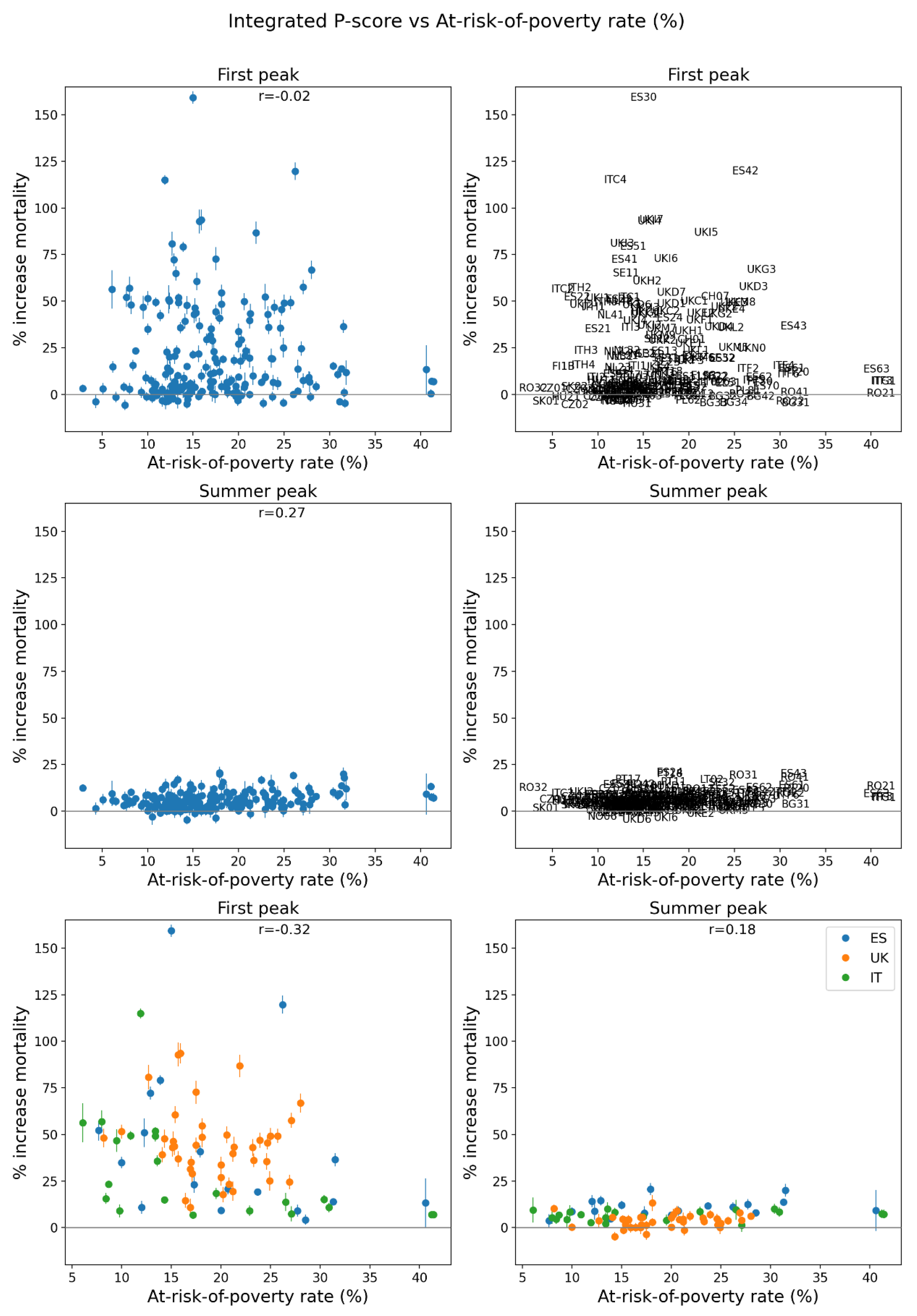


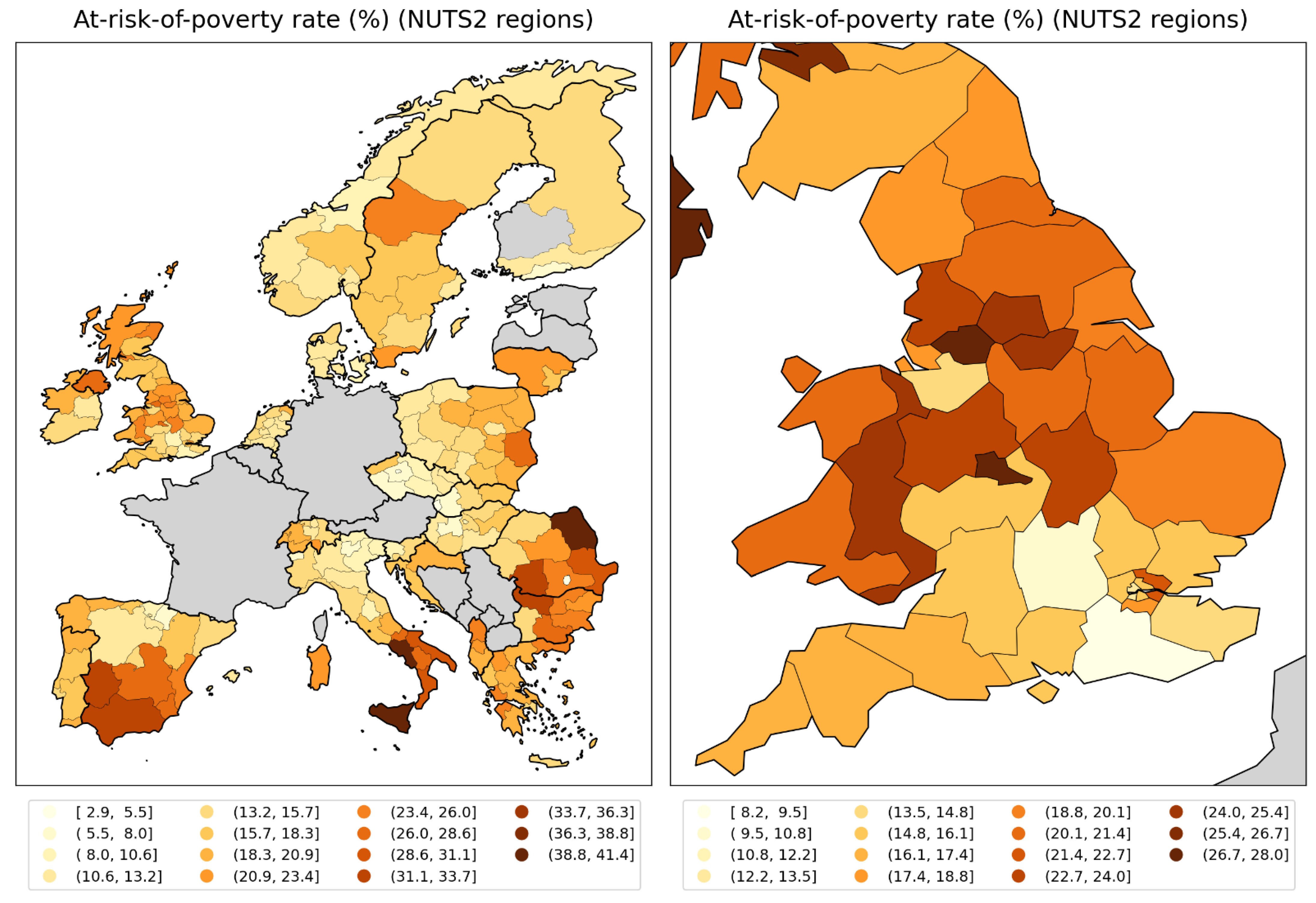

- the rate of poverty (Figure 150, middle row, right panel) with r = 0.58;
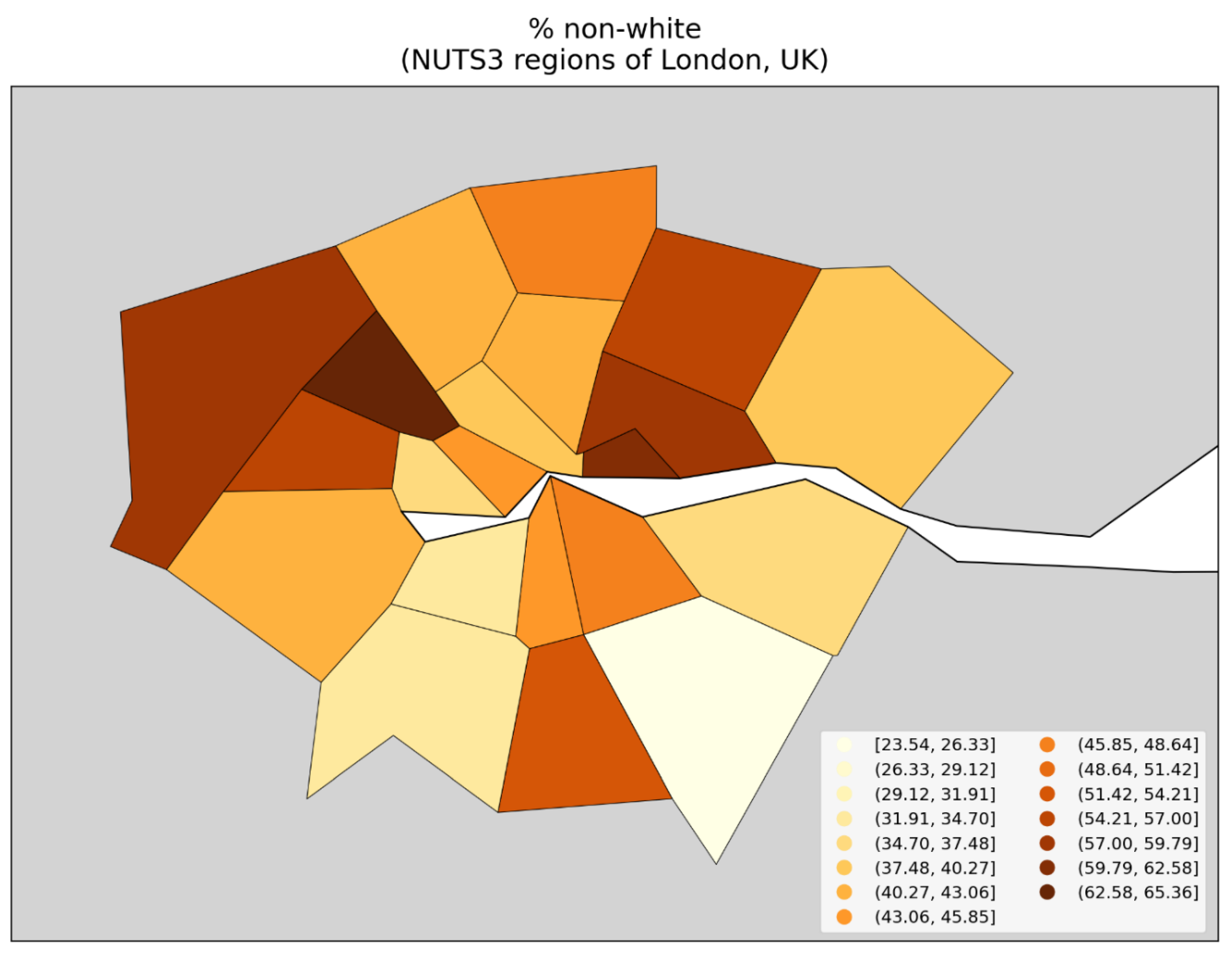
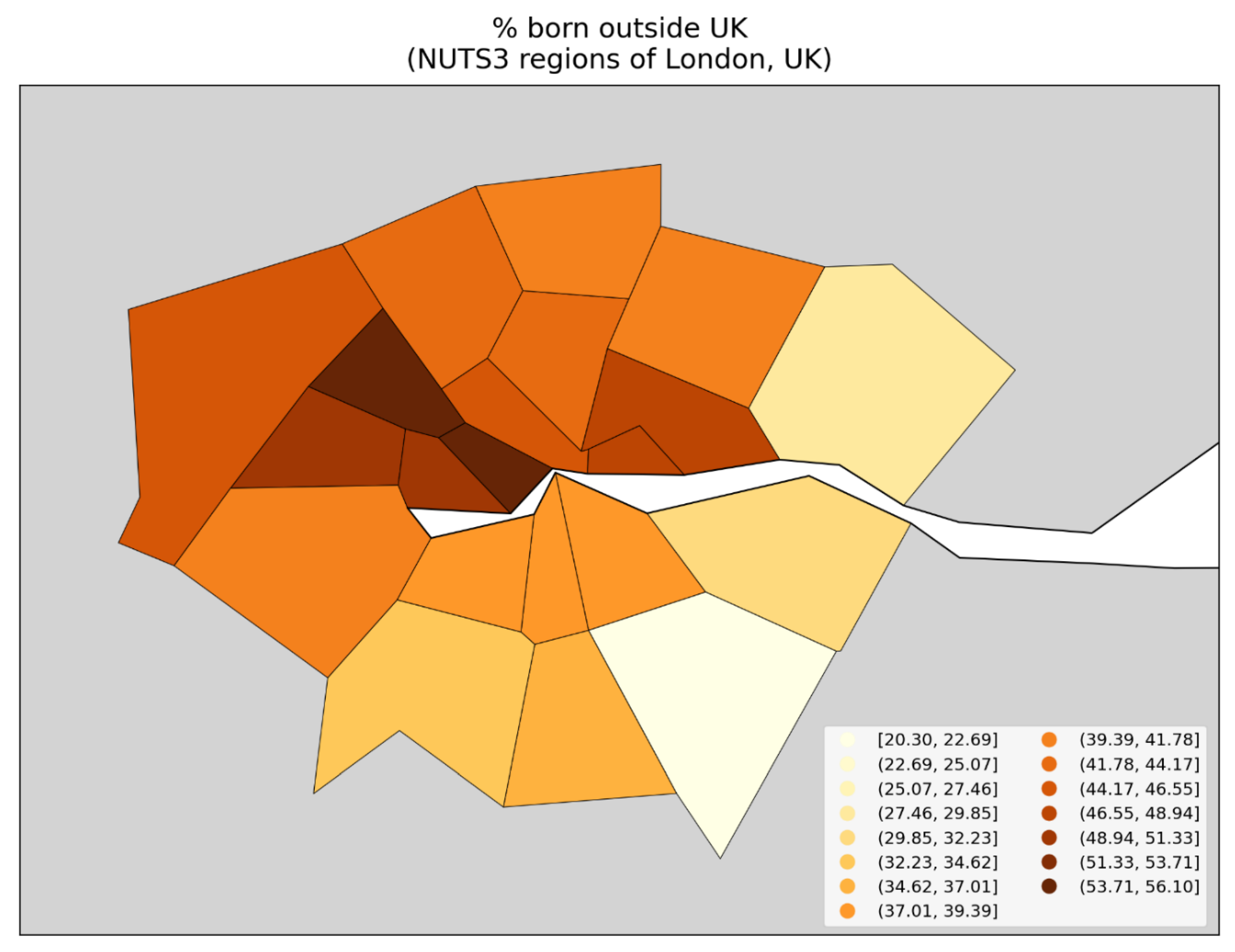
- the percent of the population that is non-white (Figure 150, bottom row, left panel) with r = 0.64; and
- the percent of the population born outside of the UK (Figure 150, bottom row, right panel) with r = 0.62.
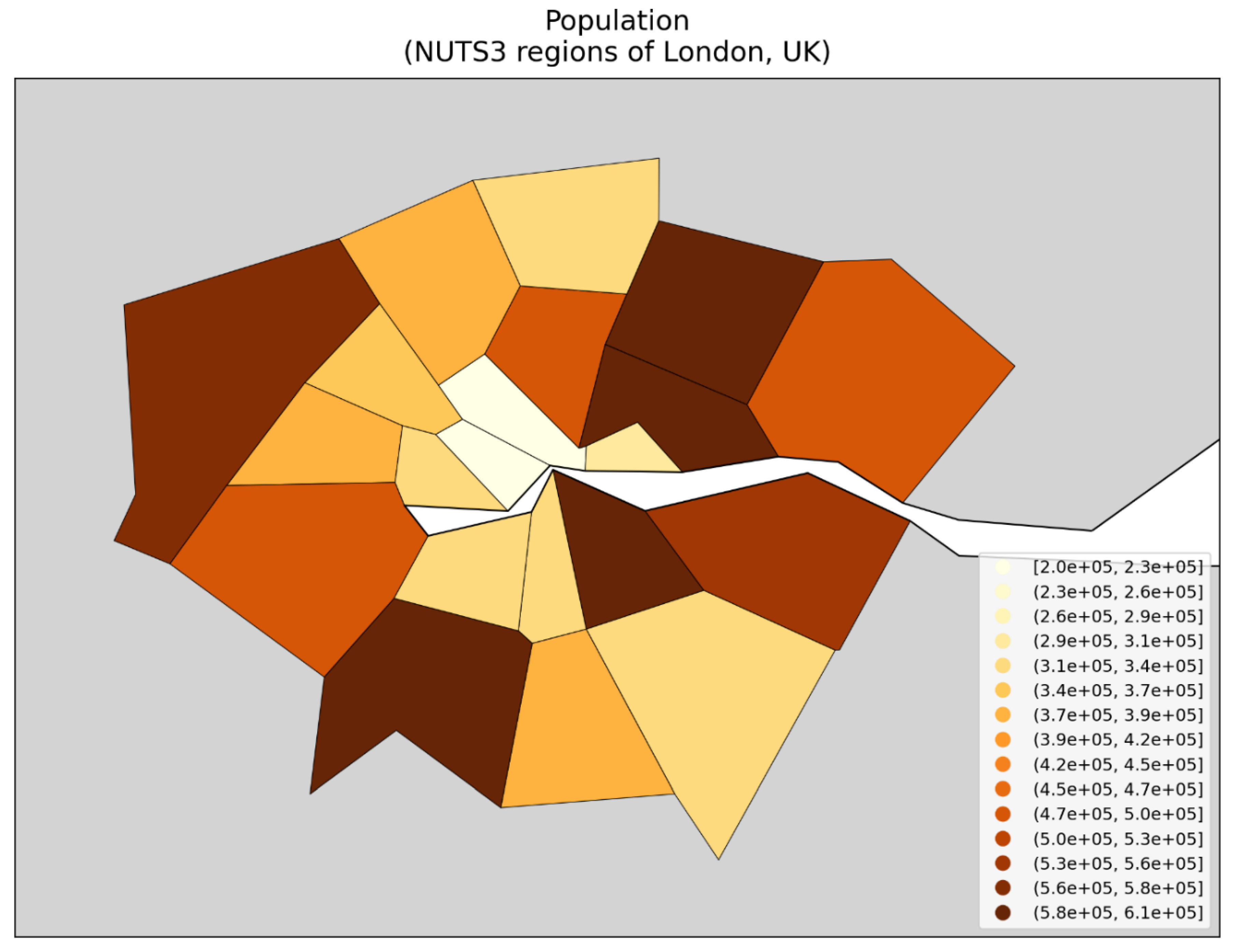
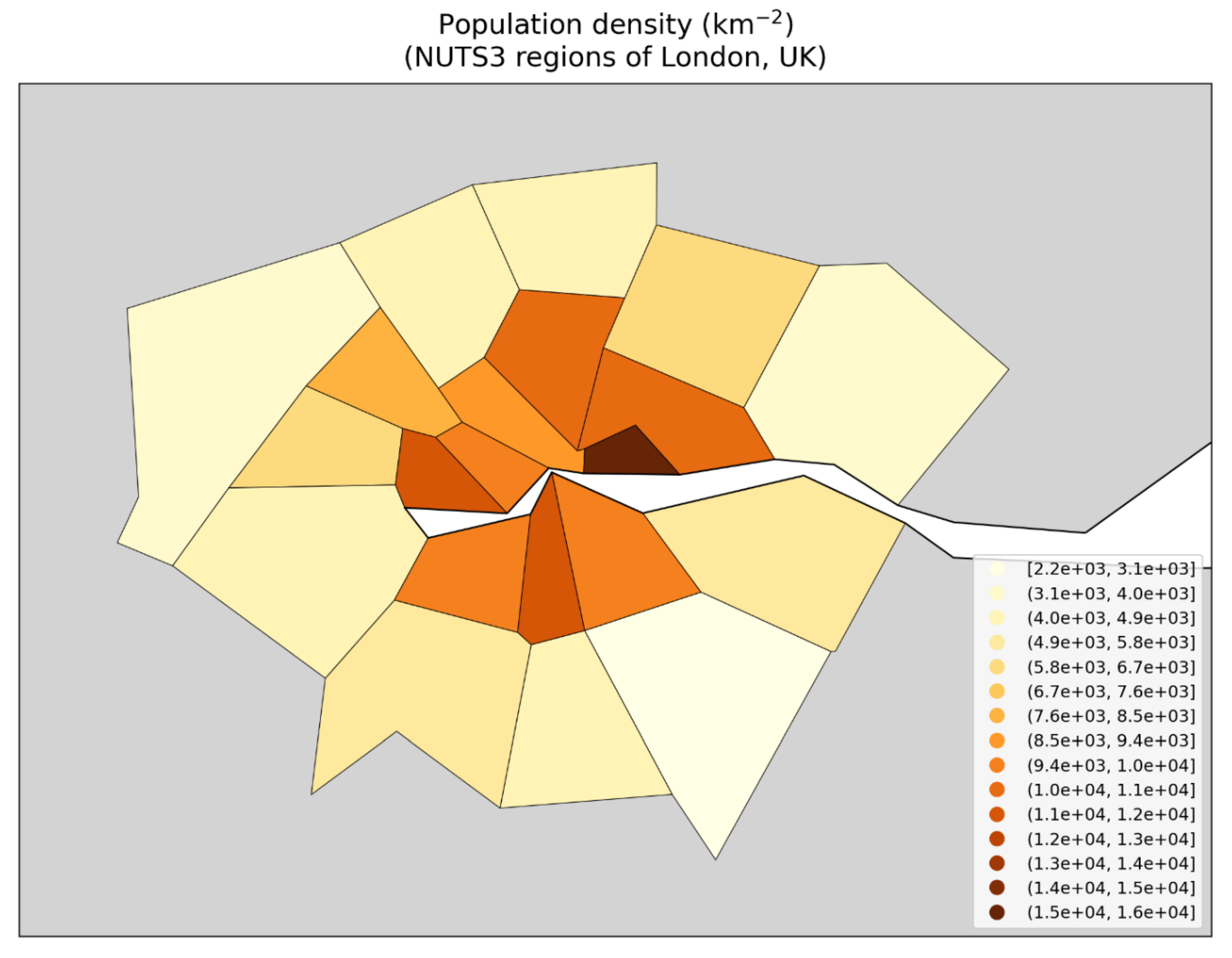
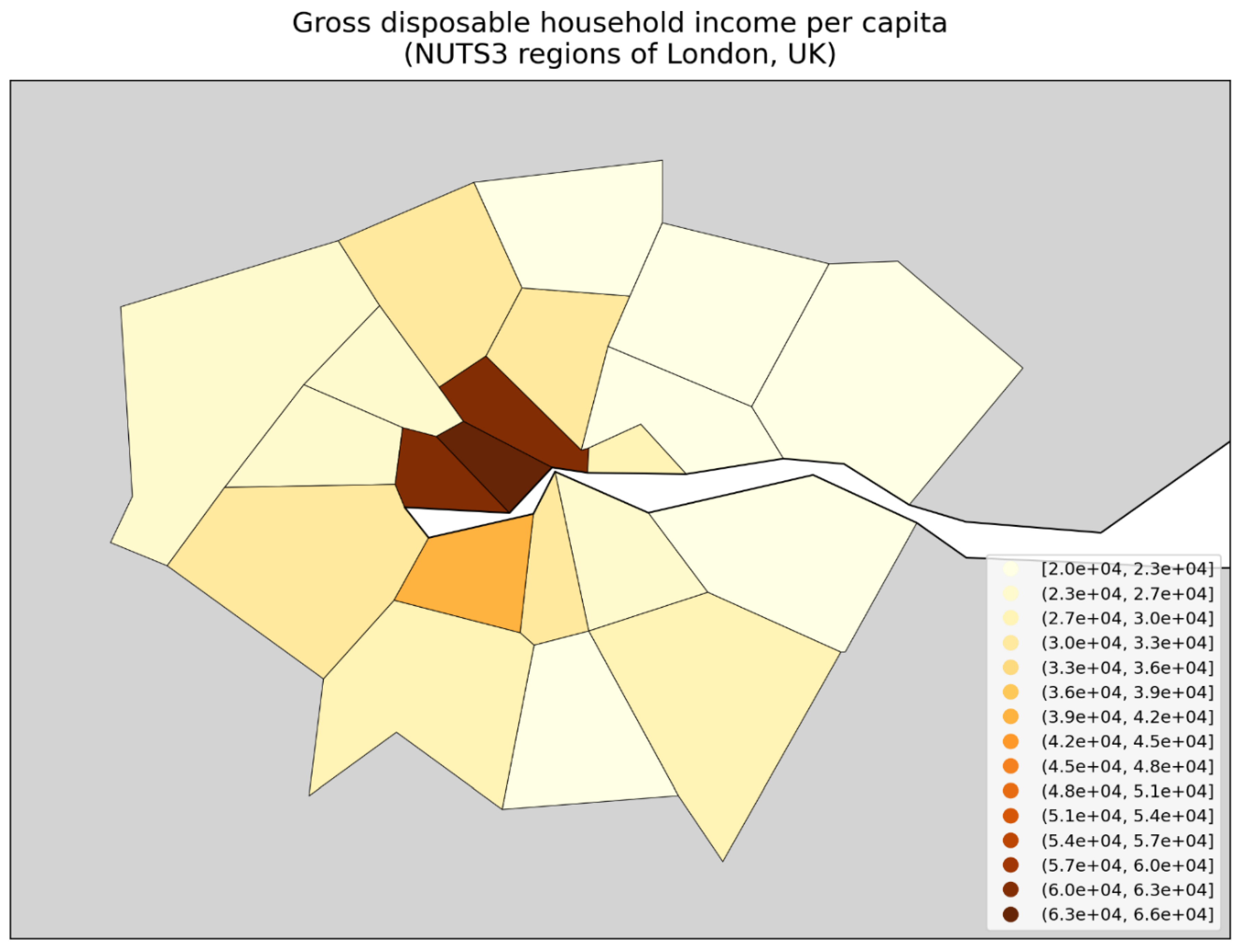
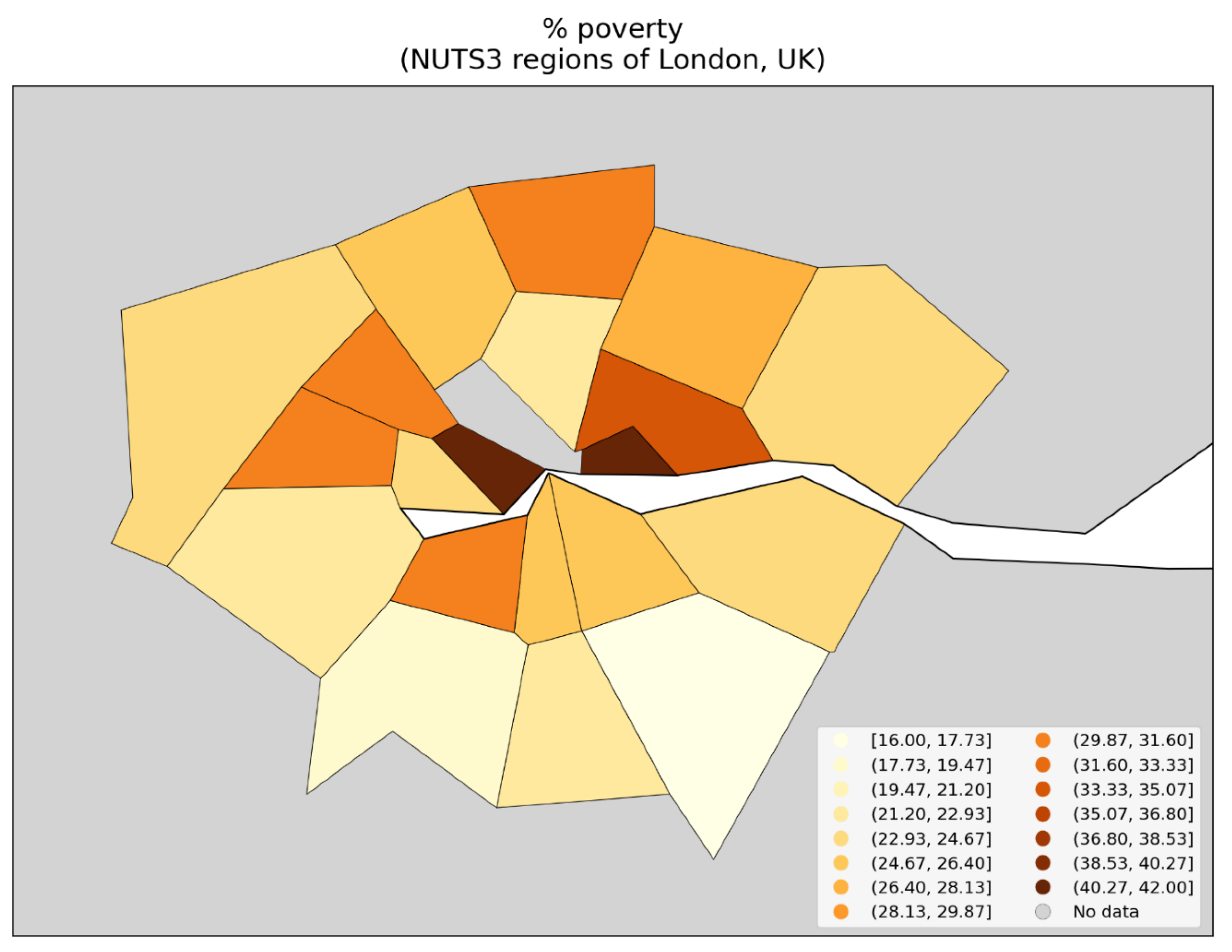
3. Discussion
3.1. Overview of the Discussion
3.1.1. Summary of Main Features of the Results
- Geographic heterogeneity of first-peak period excess mortality: Section 3.1 and Section 3.2 demonstrate that there was a high degree of geographic heterogeneity in excess mortality in the USA and Europe, with a handful of geographic regions having essentially synchronous (within weeks of each other) large peaks of first-peak period excess mortality (“F-peaks”) and all other regions having low or negligible excess mortality in the said first-peak period.
- Temporal synchrony of first-peak period excess mortality: Section 3.3 shows that F-peaks for USA states and European countries were almost all positioned within three or four weeks of one another and no earlier than the week of the WHO’s pandemic declaration. For a given large-F-peak European country, the F-peaks for all subnational regions rose and fell in lockstep synchrony but showed large variation in peak height and total integrated excess mortality. A similar result was seen for the counties of large-F-peak USA states.
- Dramatic differences in first-peak period excess mortality for comparable cities with large airports in the same countries: Section 3.4 compares cities with large airports in the same country (Rome vs Milan in Italy, and Los Angeles and San Francisco vs New York City in the USA) and shows that there was a dramatic difference in first-peak period excess mortality between the compared cities, despite their having similar demographics, health care systems, and international air travel traffic, including from China and East Asia.
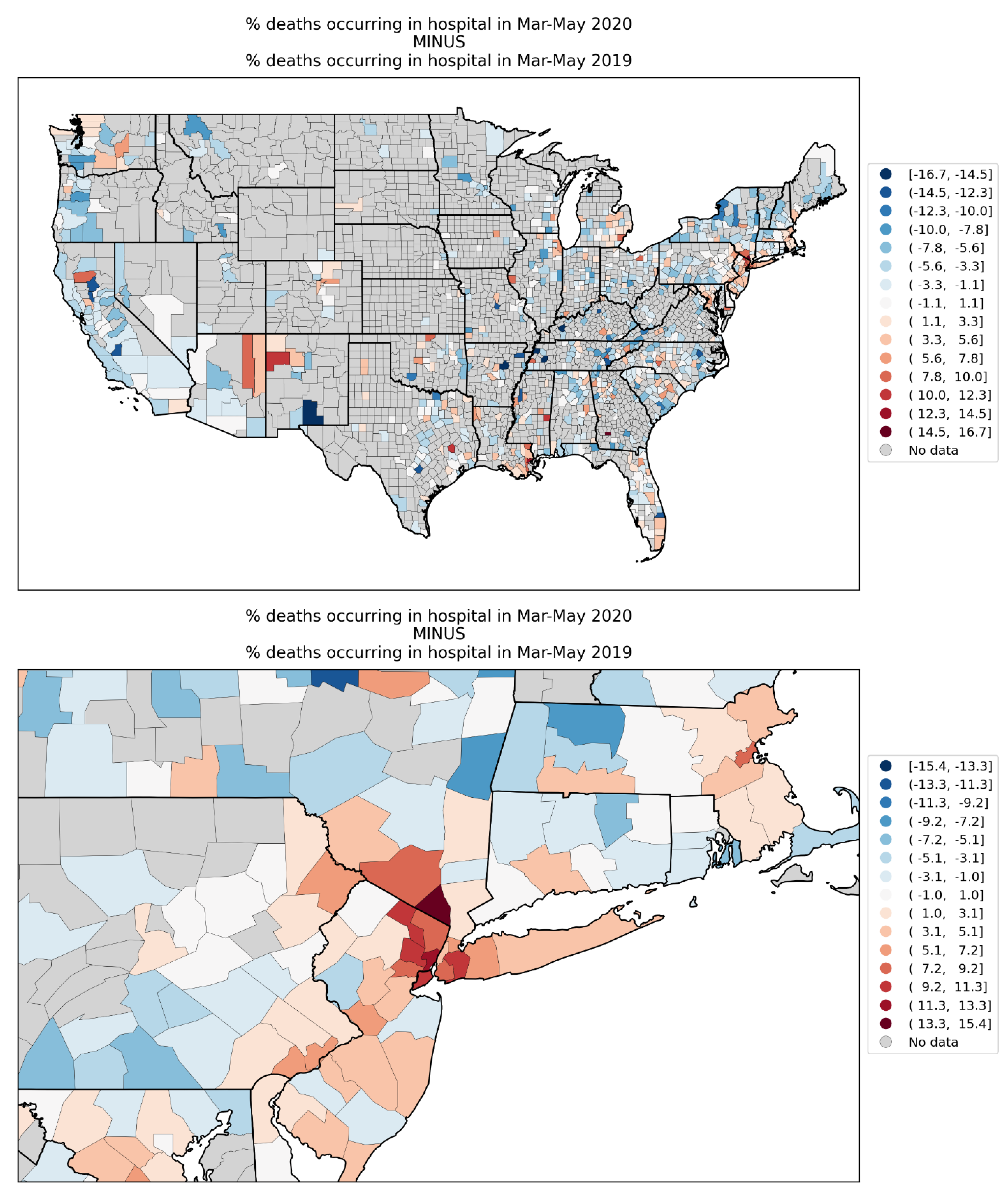
- Increased share of deaths occurring in hospitals for jurisdictions with large F-peaks: Section 3.5 shows that the share of deaths occurring in hospitals and in nursing homes increased during the first-peak period (March-May 2020) compared to March-May 2019, for the USA states or counties with the largest F-peaks, and the share of home deaths increased compared to 2019 in the large majority of studied USA states or counties having small, negligible or undetected F-peaks.
- Correlations with socioeconomic vulnerability in regions with large F-peaks: Section 3.6 shows that integrated first-peak period P-scores were correlated with increasing socioeconomic vulnerability for the counties of the USA states with the largest F-peaks, and for the boroughs of London, UK, while much structure and complexity in the all-jurisdiction scatter plots occurs due to geo-socioeconomic gradients and heterogeneity. Furthermore, there are large qualitative differences between first-peak and summer-peak period scatter plots.
3.1.2. Large-Scale Spatial Epidemic Models and Their Caveats
3.1.3. Incompatibility of First-Peak Period Excess Mortality Outcomes with the Paradigm of Infectious Disease Spread, and Alternative Hypothesis of Iatrogenic Cause of Excess Mortality
3.2. Geographic Heterogeneity of First-Peak Period Excess Mortality is Incompatible with the Paradigm of Infectious Respiratory Disease Spread
3.2.1. National-Level (Europe) and State-Level (USA) Heterogeneity of Excess Mortality
3.2.2. Subnational (Europe) and County-Level (USA) Excess Mortality
3.2.3. Near Synchronous Timing of F-peaks across Europe and the USA
- -
- one week (Washington State and Oregon)
- -
- two weeks (14 states, including New York State and New Jersey, which had the largest first-peak period integrated P-scores among USA states)
- -
- three weeks (12 states, including Connecticut, Massachusetts, and District of Columbia, which had the third, fourth, and fifth highest integrated first-peak period P-scores among USA states, respectively)
- -
- four weeks (North Carolina)
- -
- five weeks (Rhode Island, Delaware, Minnesota, Ohio, and New Hampshire)
- -
- six weeks (Iowa)
- -
- seven weeks (New Mexico)
3.2.4 Simultaneous Rise and Fall of F-Peaks for Subnational Regions Within a Given European Country and for Counties of a Given USA State
3.2.5. Staggering in Time of F-Peaks of Different Countries in Europe Linked to Date of First National Lockdown
3.3. Deadly Medical Treatments Were Prevalent in First-Peak Period Mortality Hotspots
3.3.1. Italy
-
that the onset of outbreaks in Northern Italy occurred before national containment measures were implemented, whereas the onset of outbreaks in other regions of Italy occurred after measures were implemented (La Maestra et al., 2020)
- →
- →
- this would also be contradicted by the dominant view that the SARS-CoV-2 pathogen was circulating in Italy weeks before the first reported case of locally acquired infection dated February 20, 2020 (La Maestra et al., 2020; Zehender et al, 2020; Cereda et al., 2021; Apolone et al., 2021; Alteri et al., 2021; Davis et al., 2021).
-
that poor air quality in Northern Italy, including Lombardy, could have increased infectiousness and severity of infection with COVID-19, causing higher mortality in the northern regions (Coker et al., 2020; Ottaiano et al., 2021)
- →
- this is contradicted by a recent systematic review and meta-analysis of the relationship between particulate matter air pollution and COVID-19 infection severity and mortality, which found no reliable evidence of an increase in mortality risk due to air pollution (Sheppard et al., 2023)
- →
- regardless, the magnitude of the effect would be much smaller than necessary to account for the observed large difference in first-peak period excess mortality between Lombardy and Lazio, Campania and other Italian regions
- →
- also, there are a number of areas in Eastern Europe with comparable annual mean air pollution levels to Northern Italy, including in Central and Southern Poland, Central Serbia, and the area around the Bulgarian capital (see the map in Figure 166, reproduced from European Environment Agency (2018)), but these areas had essentially zero excess mortality during the first-peak period, as shown in the maps in Section 3.2.
- that, within Italy’s decentralized health system, different regions adopted different strategies in response to the perceived threat of COVID-19 (Capano & Lippi, 2021; Bosa et al., 2021), which is addressed as follows.
3.3.2. USA
3.3.3. Other European Countries
3.4. Socioeconomic Characteristics of First-Peak Period Mortality Hotspots
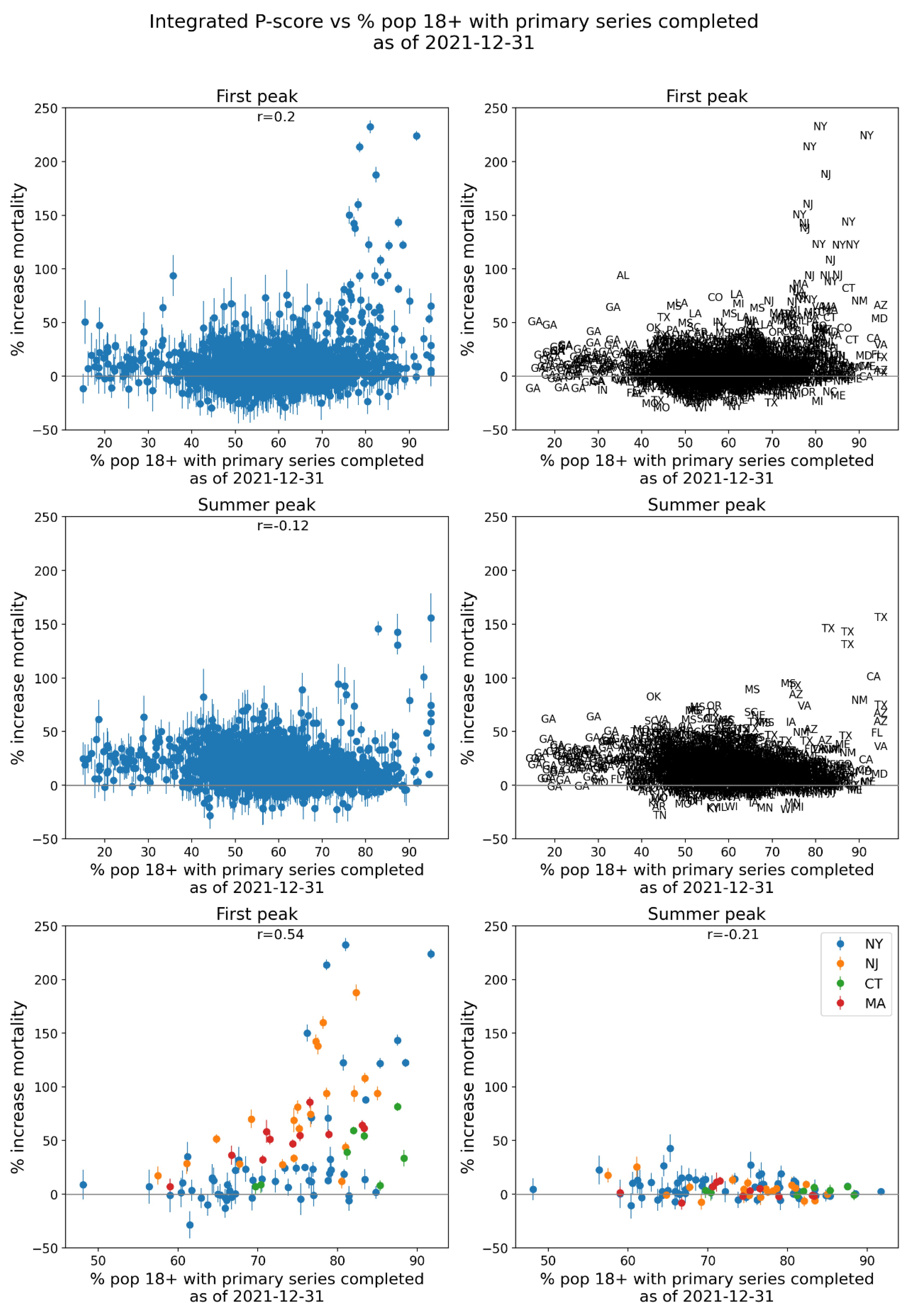
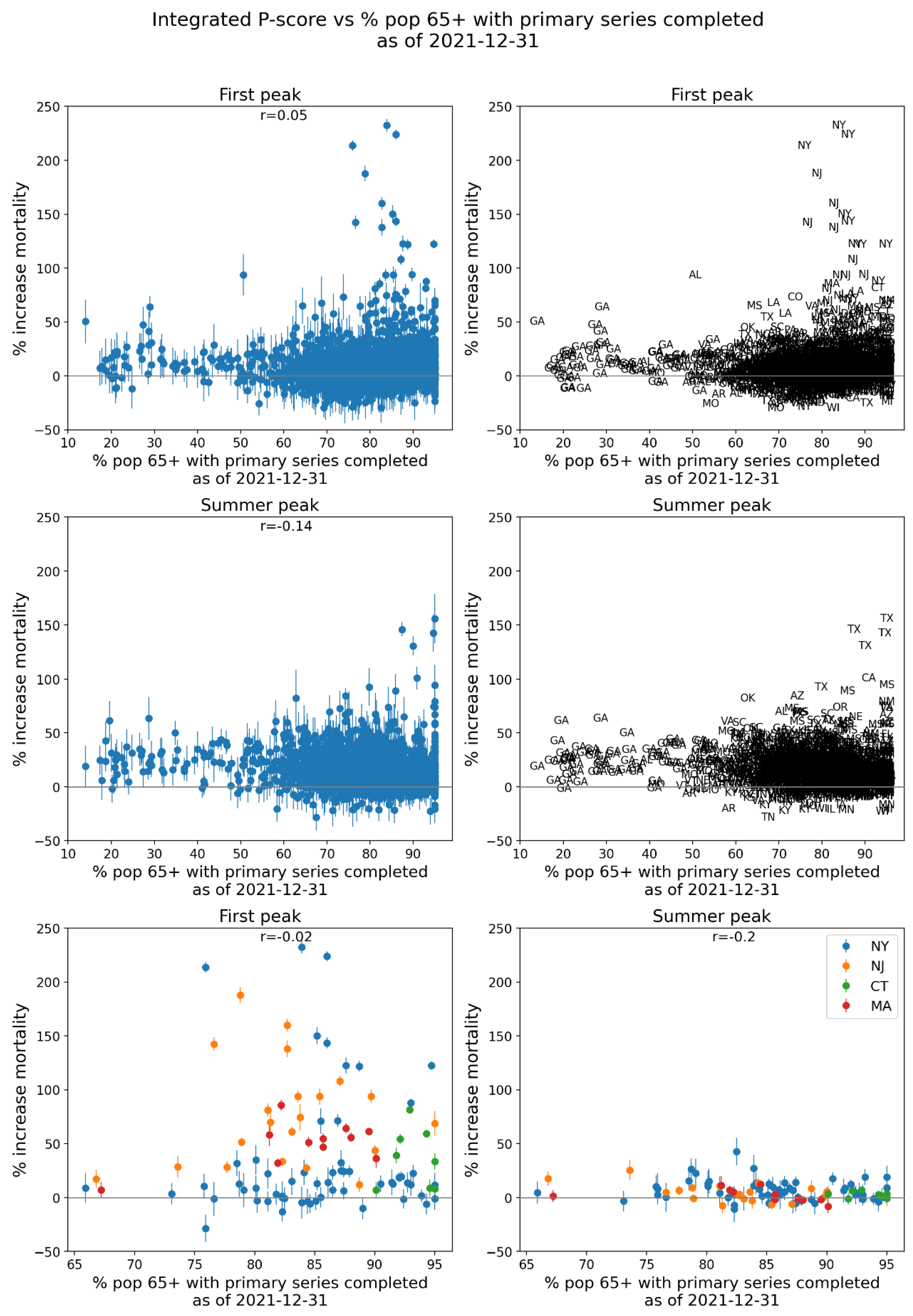
3.4.1. Integrated First-Peak Period P-Scores vs Socioeconomic Variables for USA Counties
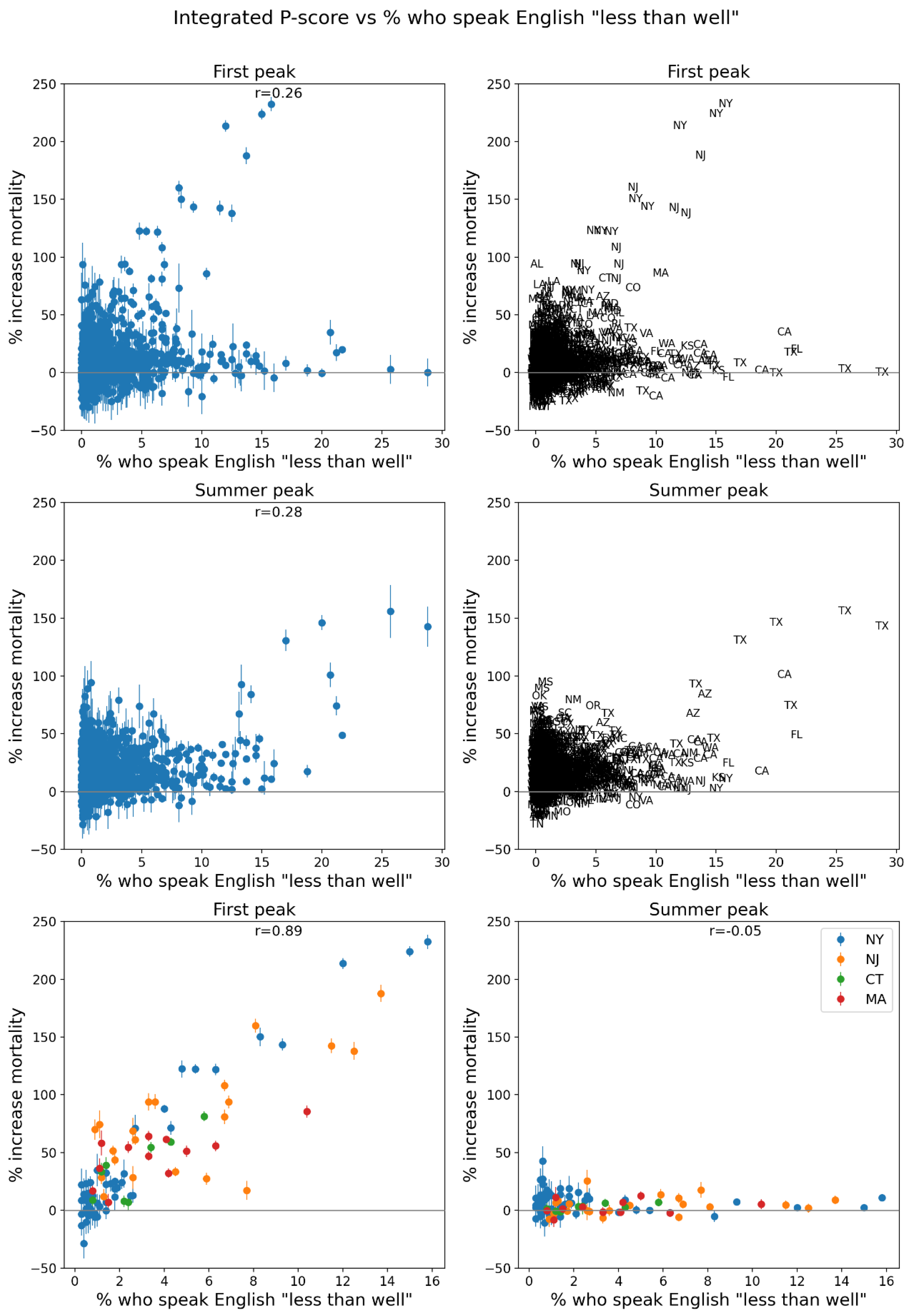
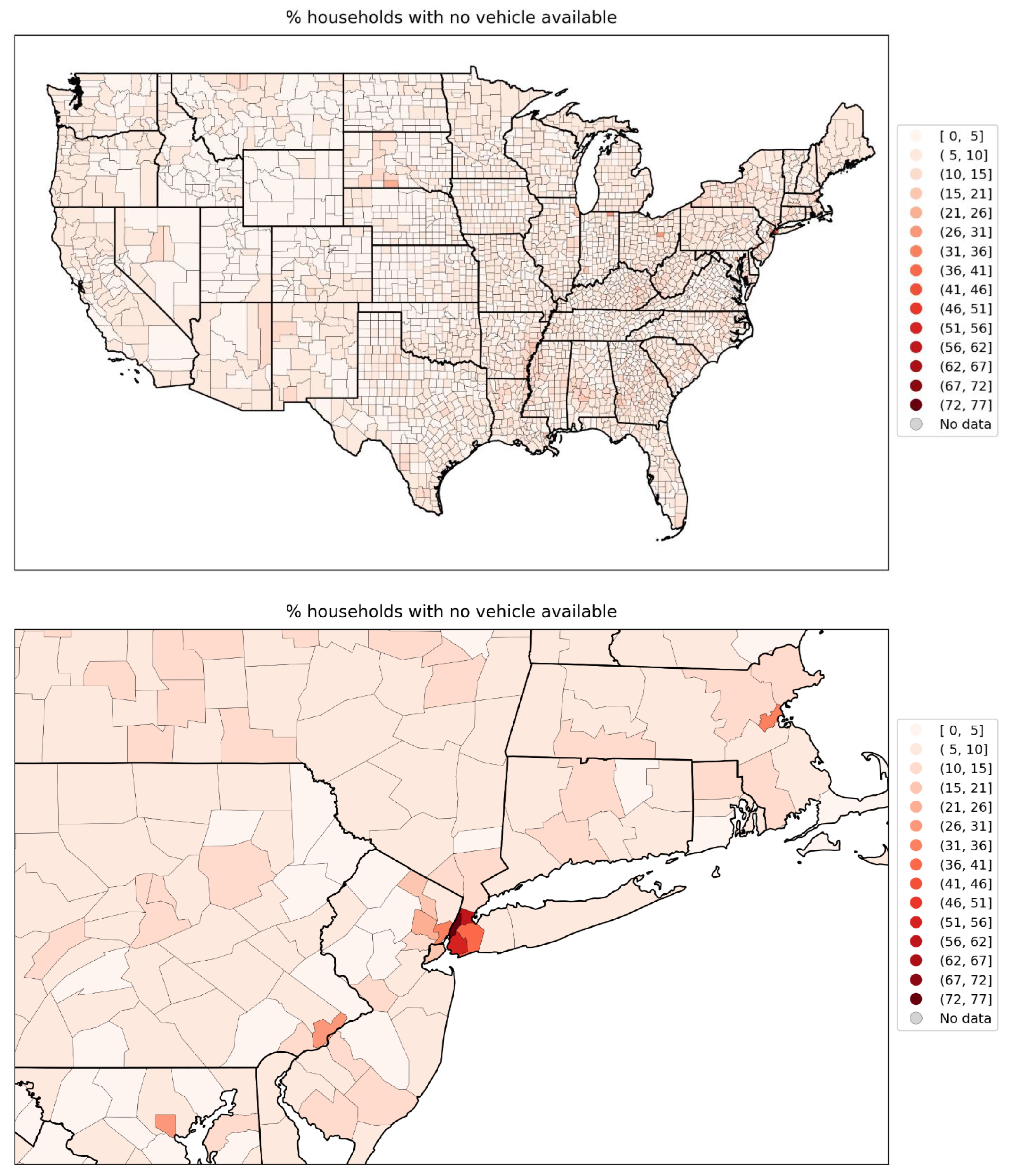
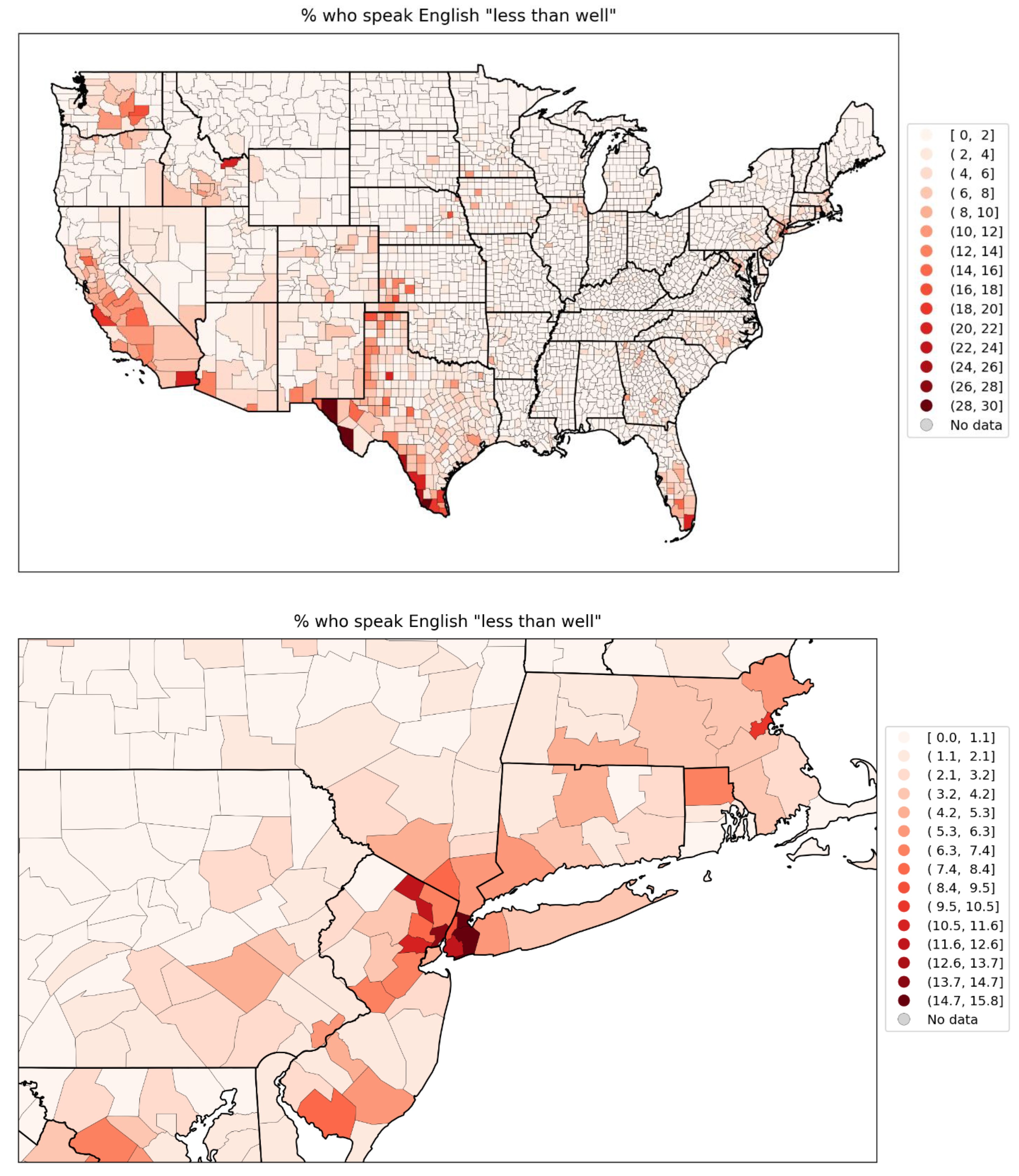
- % who speak English “less than well” (Figure 76, r = 0.89),
- log[population density] (Figure 67, r = 0.85),
- % minority (Figure 77, r = 0.85),
- % households with more people than rooms (Figure 74, r = 0.83),
- population (Figure 64, r = 0.77),
- log[population] (Figure 65, r = 0.72), and
- % living in housing structures with more than 10 units (Figure 75, r = 0.72).
3.4.2. Integrated Summer-Peak Period P-Score vs Socioeconomic Variables for USA Counties
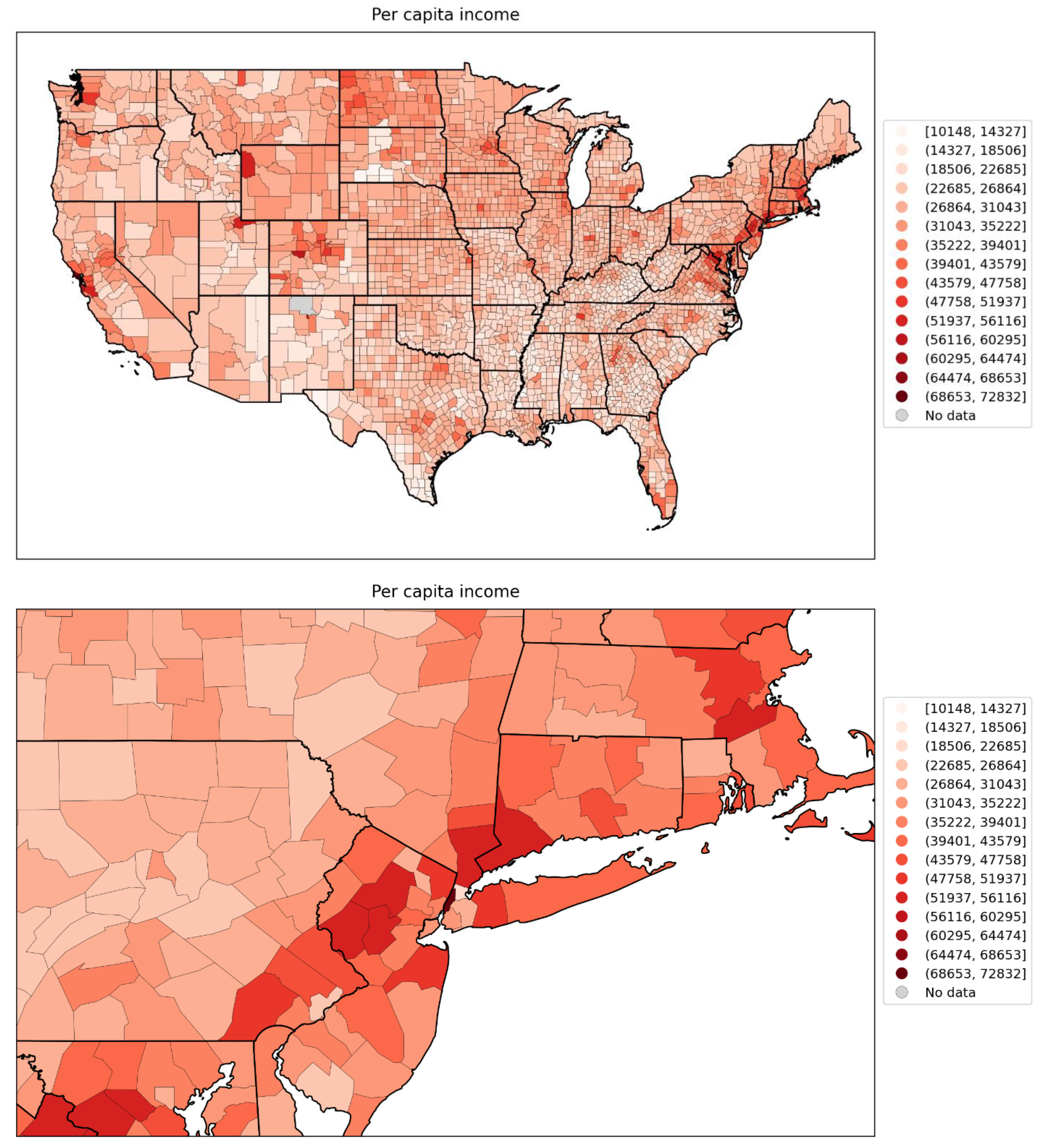
- low per capita income (Figure 68),
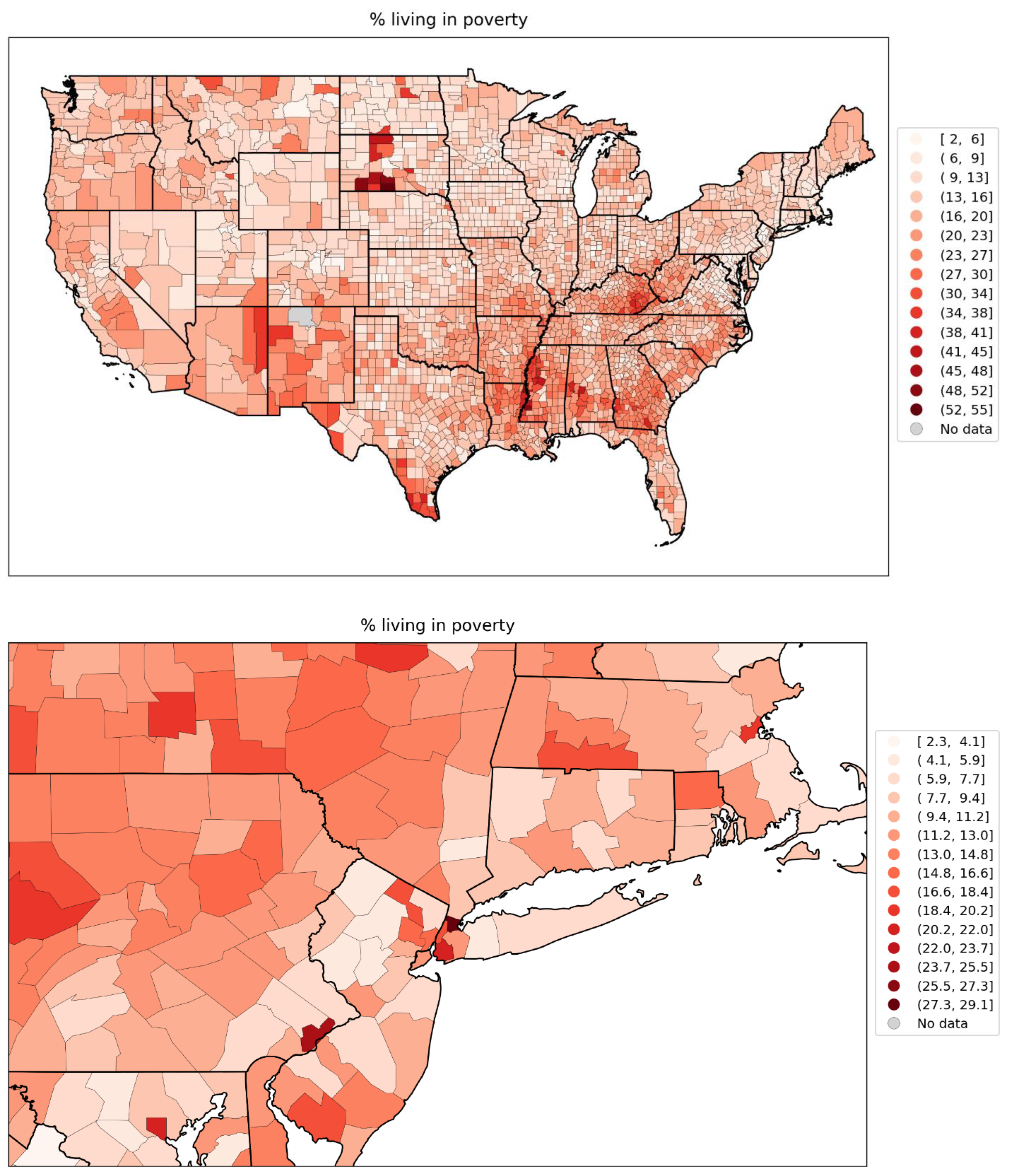
- high poverty (Figure 69),
- high prevalence of crowded living conditions (Figure 74),
- low rates of speaking English, especially for the counties near the Mexican border (Figure 76, map in Figure 111),
- high percentage minority (Figure 77),
-
high percentage of the population aged 25+ with no high school diploma (Figure 78), andhigh rate of single-parent households (Figure 81).
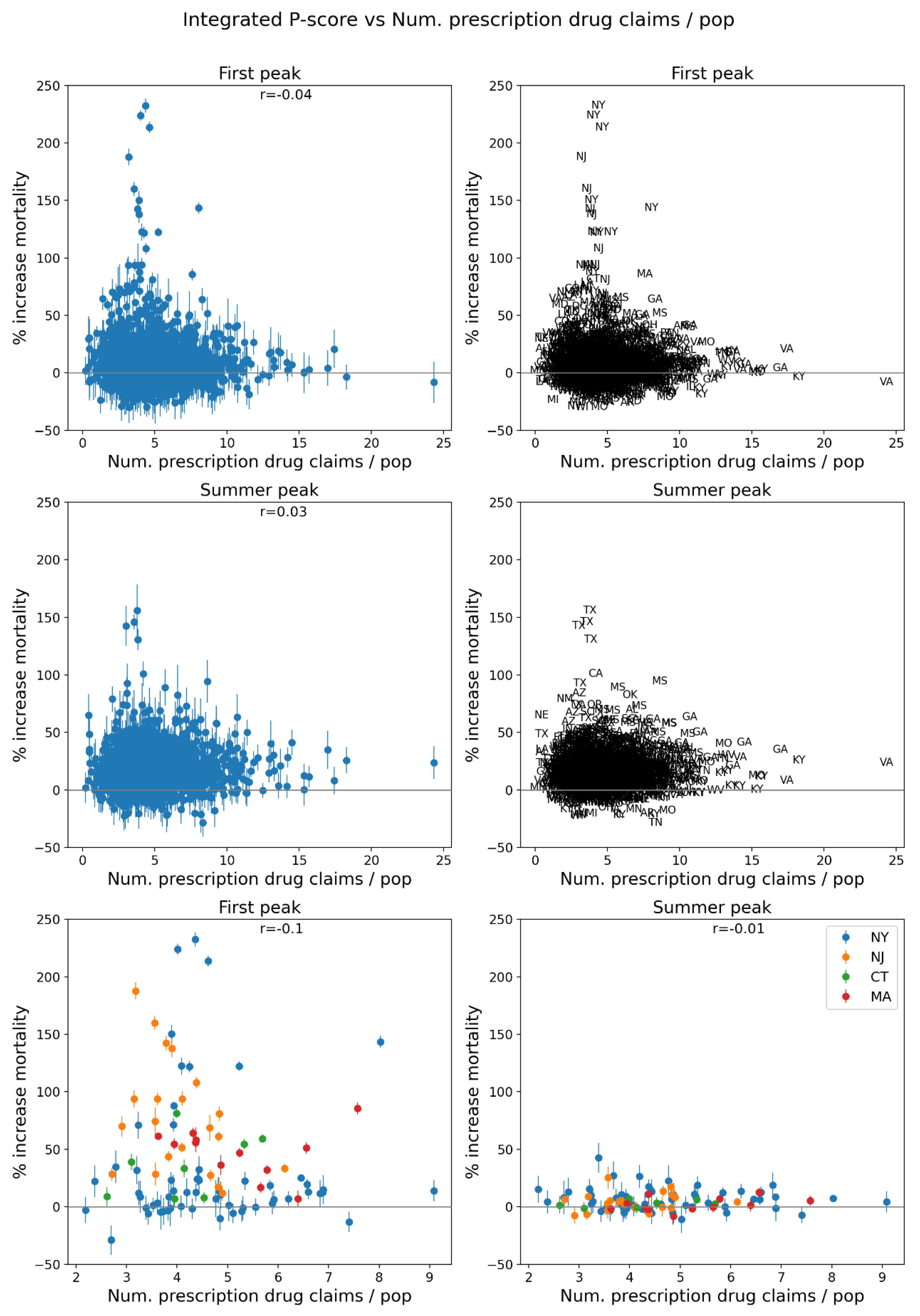
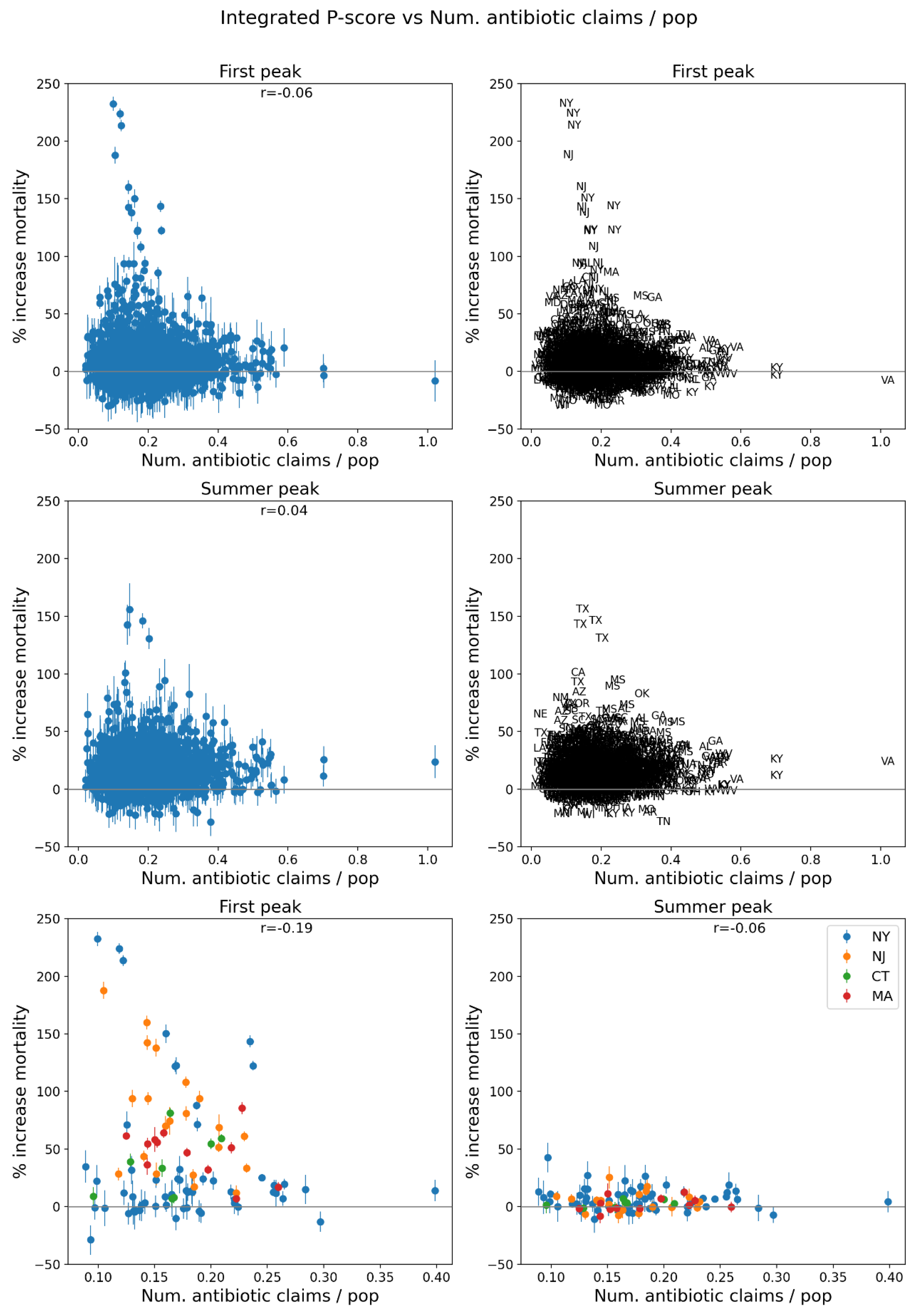
3.4.3. Correlation Between P-Scores and Degree of Interaction with the Medical System
3.4.5. The Bronx
3.4.6. The Role of Large “Safety Net” Hospital Complexes in Regions with High Inequality
3.5. Pneumonia Induced by Biological Stress of Lockdown Measures
- Many studies find that the excess all-ages all-cause mortality in the first-peak period is closely equal to assigned COVID-19 deaths in this period (e.g., Rancourt et al., 2021a, for the USA). That is, that the first-peak period excess deaths are associated with respiratory conditions.
- The geotemporal evolution of the F-peak excess mortality is inconsistent with the paradigm of a spreading viral respiratory disease, as discussed above in sections 4.2 and 4.3.
- A significant portion of first-peak period excess mortality may have been caused by the application of dangerous medical treatments in excess mortality hotspots such as New York City, Lombardy, Madrid, and London, as discussed above in sections 4.4 and 4.5.
4. Conclusion
- the essential synchrony (within weeks) in mortality hotspots (large “first peaks” or “F-peaks”) immediately following the WHO’s March 11, 2020 announcement of a pandemic, across countries and states on two continents in the Northern Hemisphere,
- the absence of a single F-peak-like excess mortality event (i.e., rise—peak—fall or rise—plateau) prior to the WHO’s March 11, 2020 declaration of a pandemic,
- the extreme geographical heterogeneity of the magnitude of any excess all-cause mortality as P-score in the time period (“first-peak period”) of the said hotspots,
- the striking differences in the occurrences of hotspots (presence or absence) in entirely comparable large cities in the same countries (Milan vs Rome in Italy; New York City vs Los Angeles and California in the USA),
- the systematic increases in shares of institutional (versus home) deaths in mortality hotspot jurisdictions, and
- the strong correlations to socioeconomic vulnerability of hotspot intensity in high-geographical-resolution sectors within hotspot urban regions,
A. Additional Graphs Pertaining to Section 3.3
A.1 Europe, Weekly P-Scores for National-Level (NUTS0) Jurisdictions, All Countries, Geographic Subsets
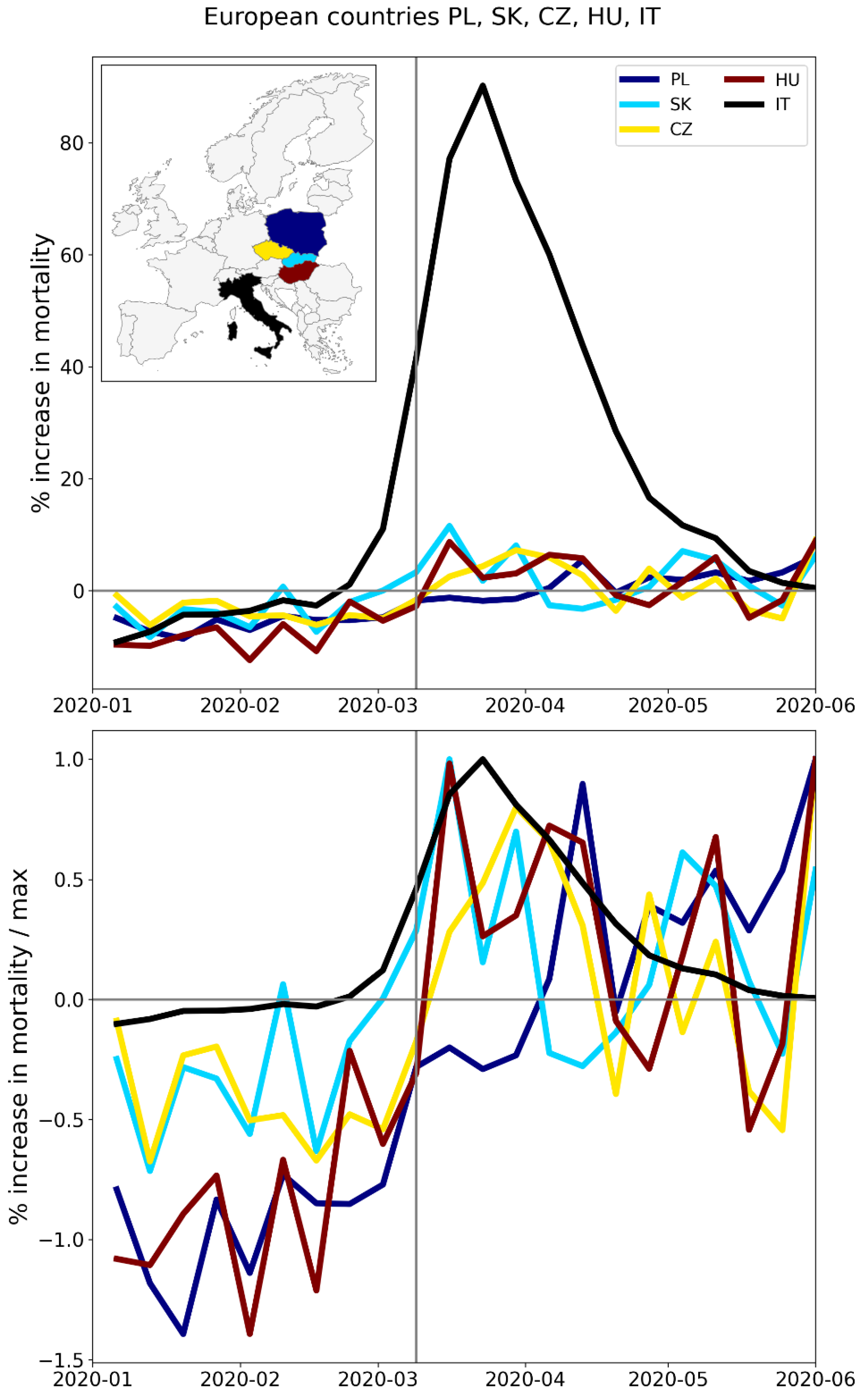
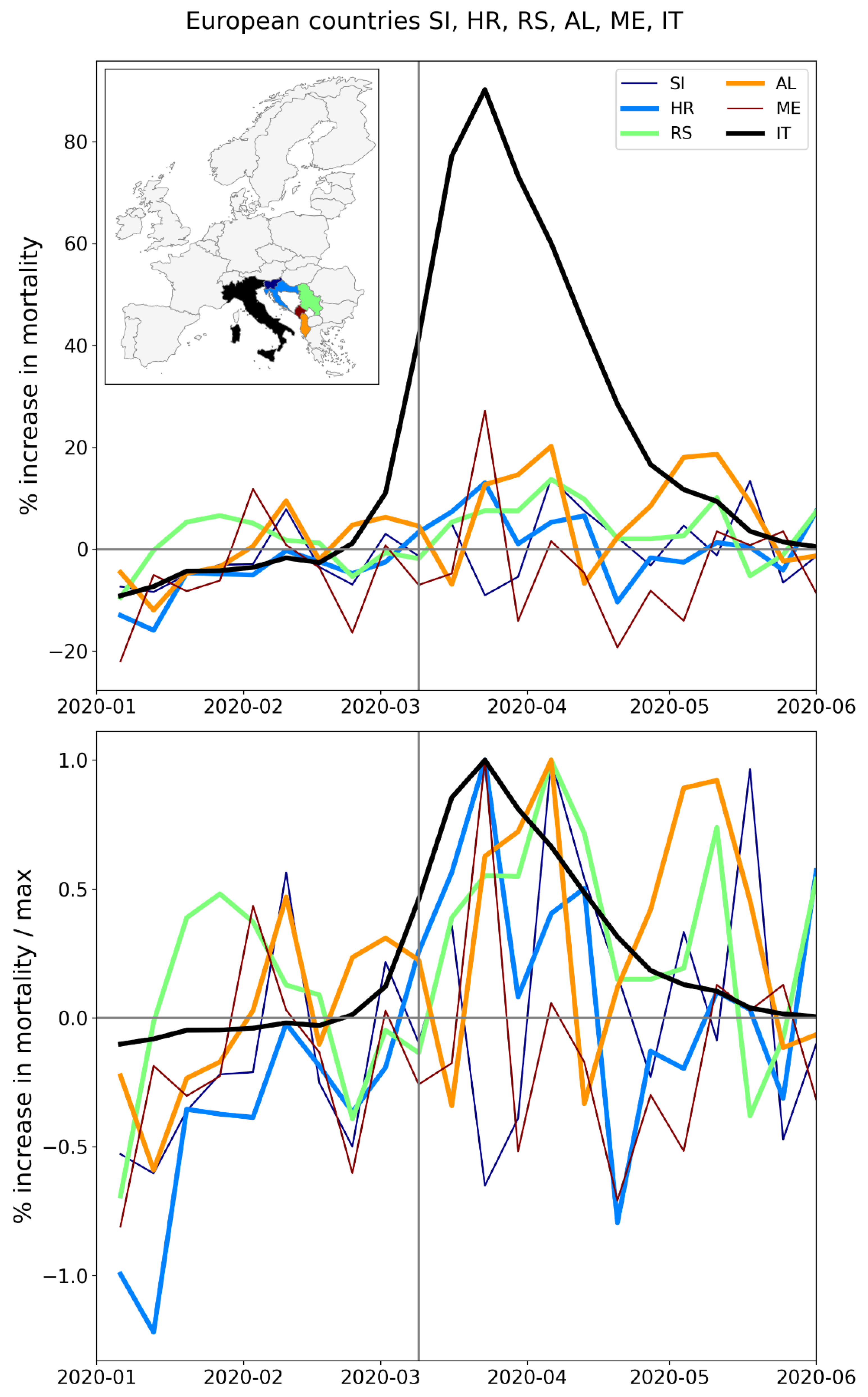
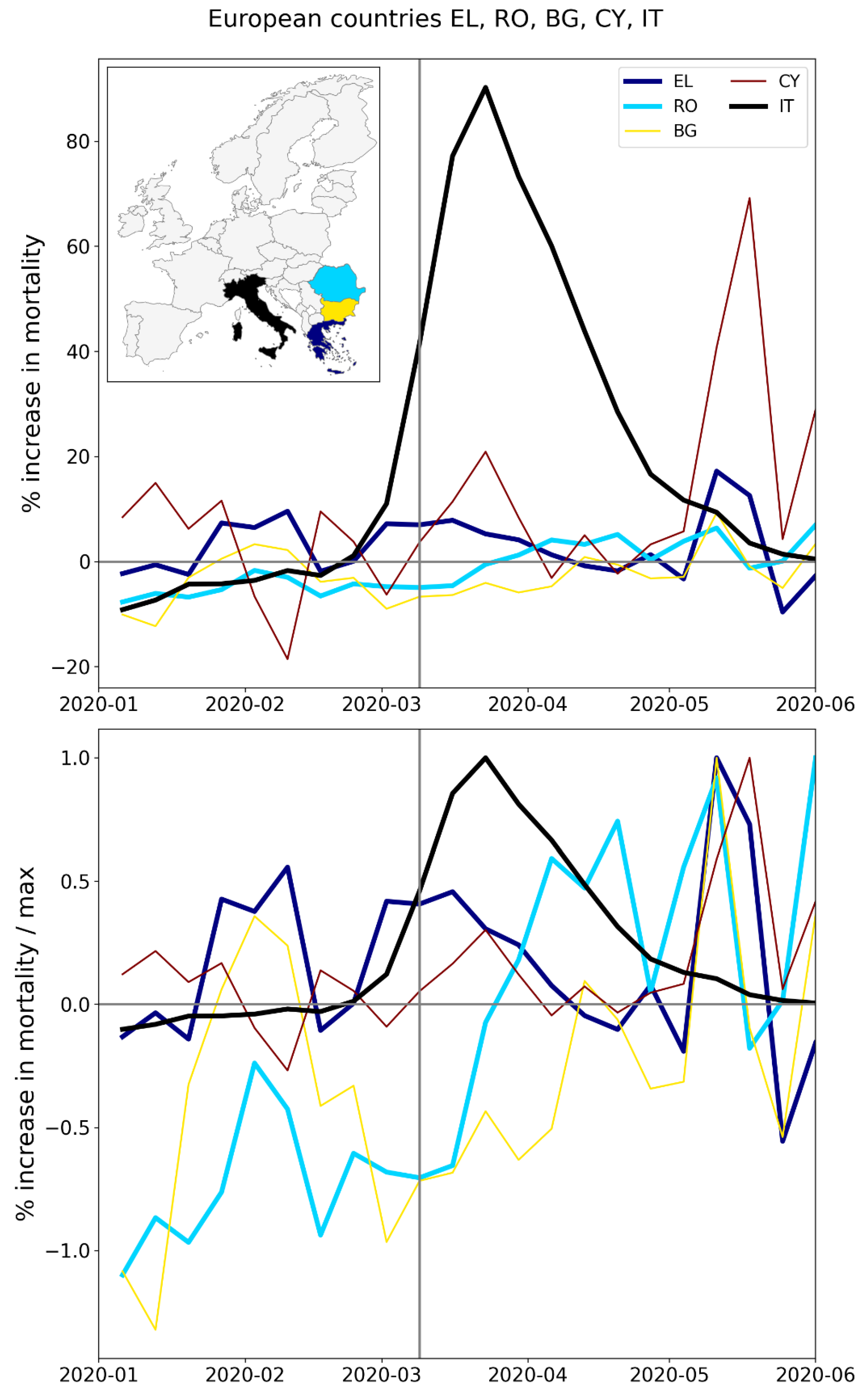
A.2. USA, Weekly P-Scores for All States, Organized Geographically by Census Division
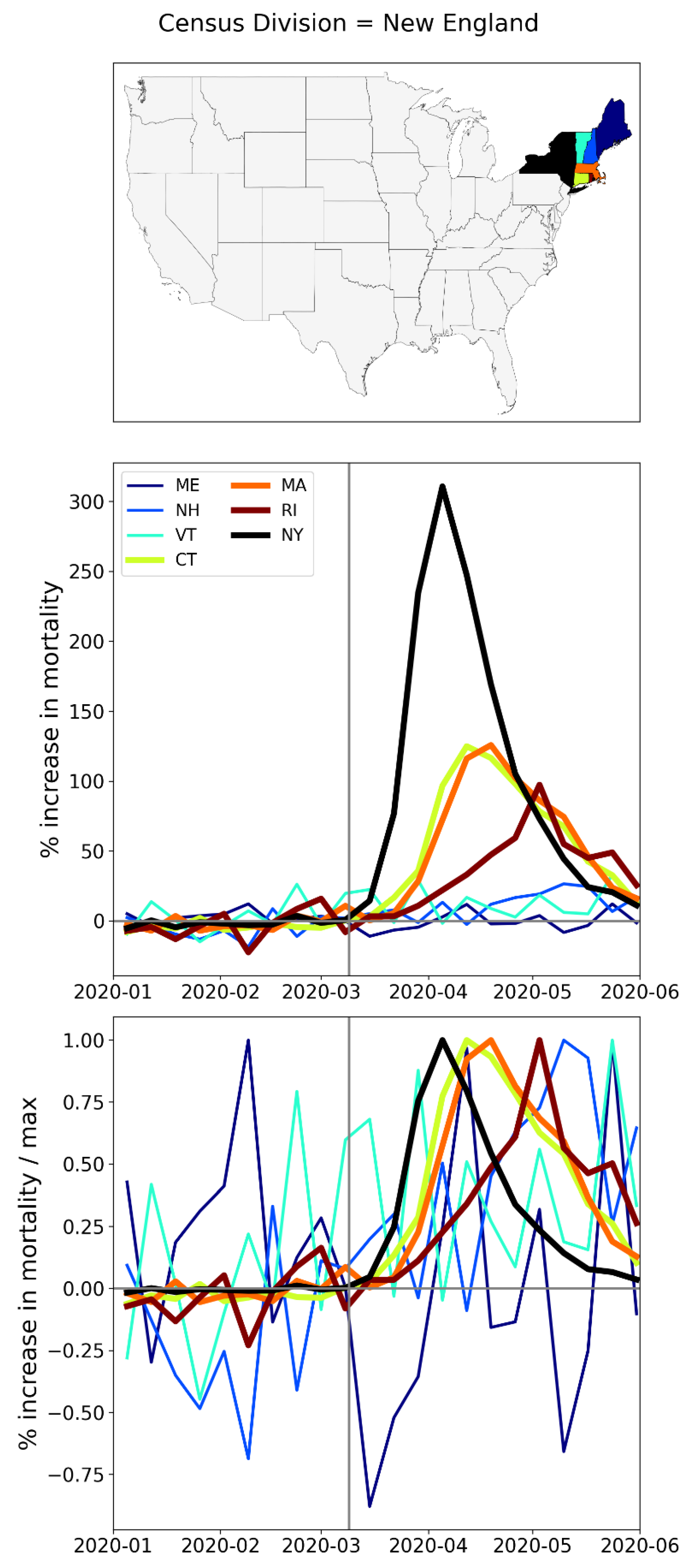
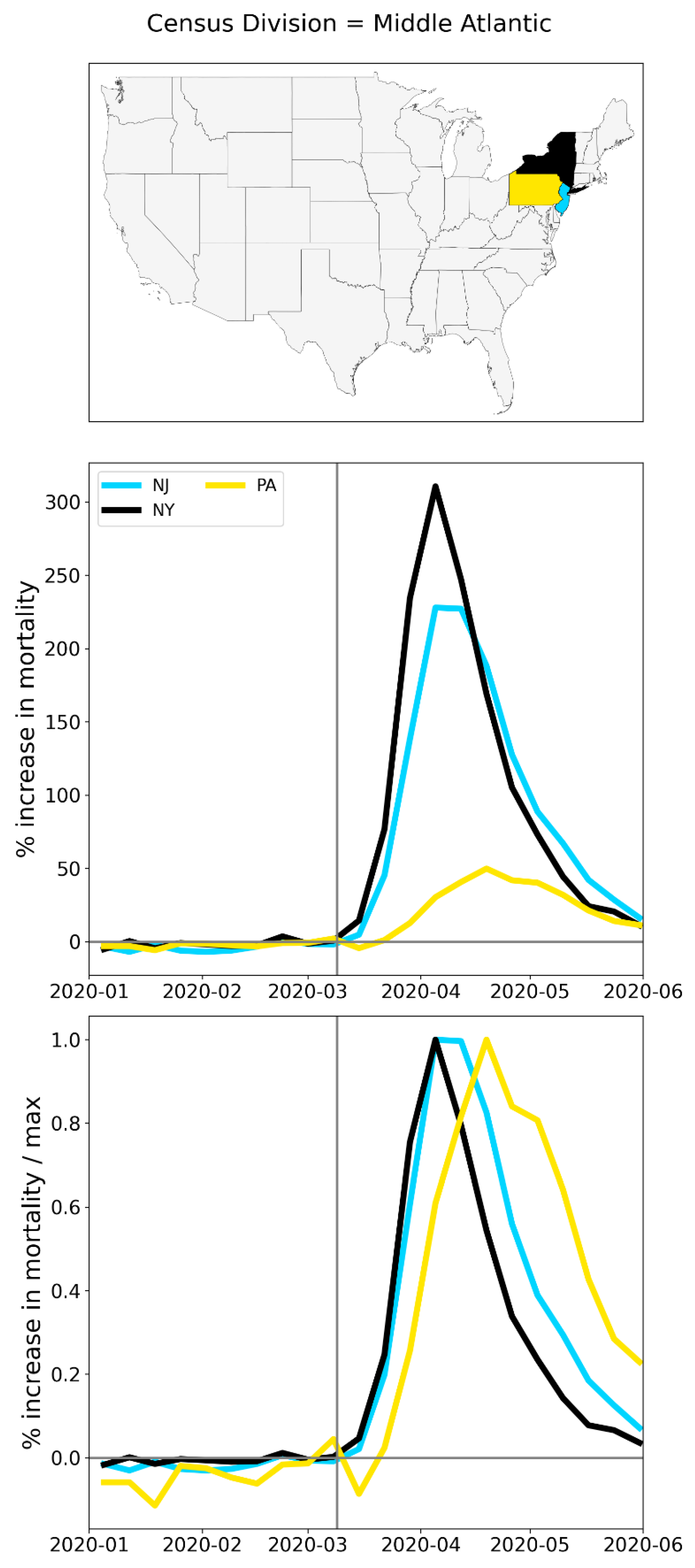
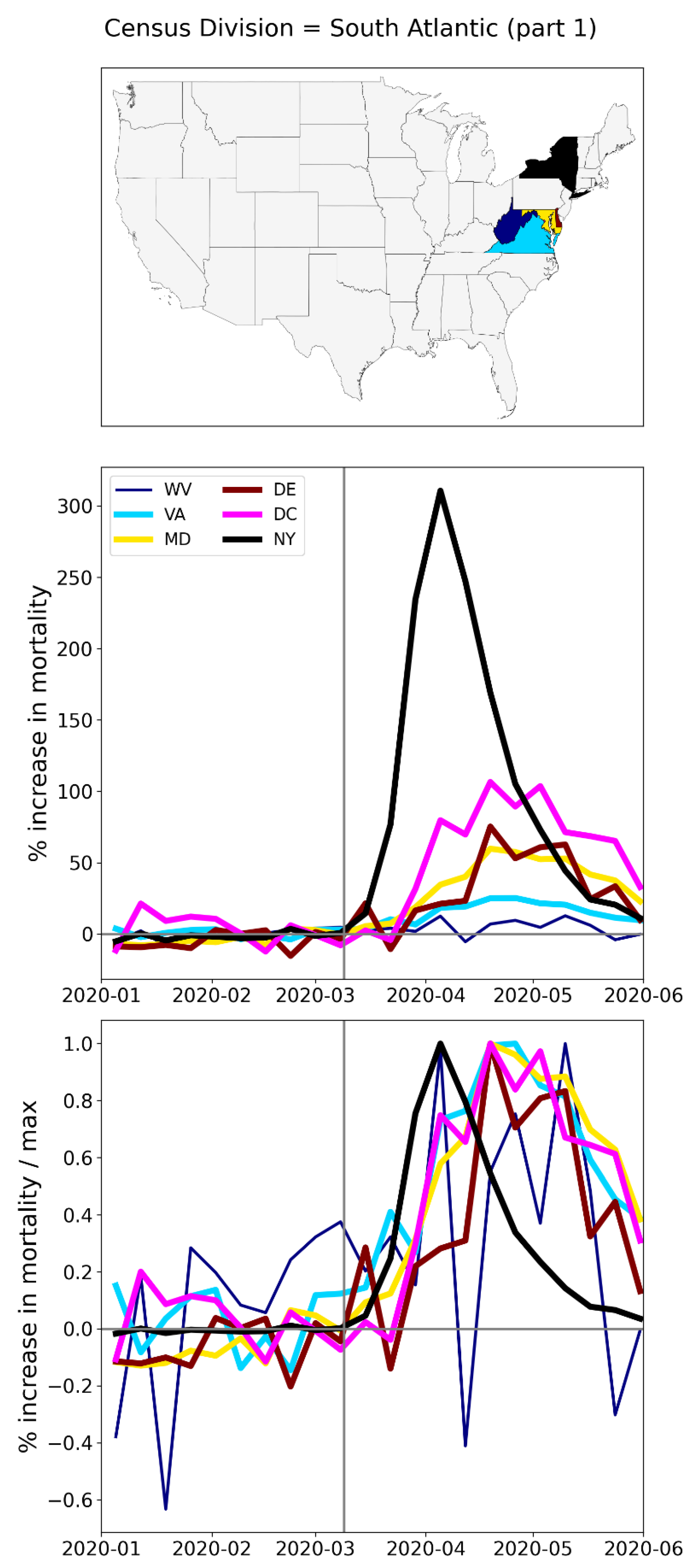
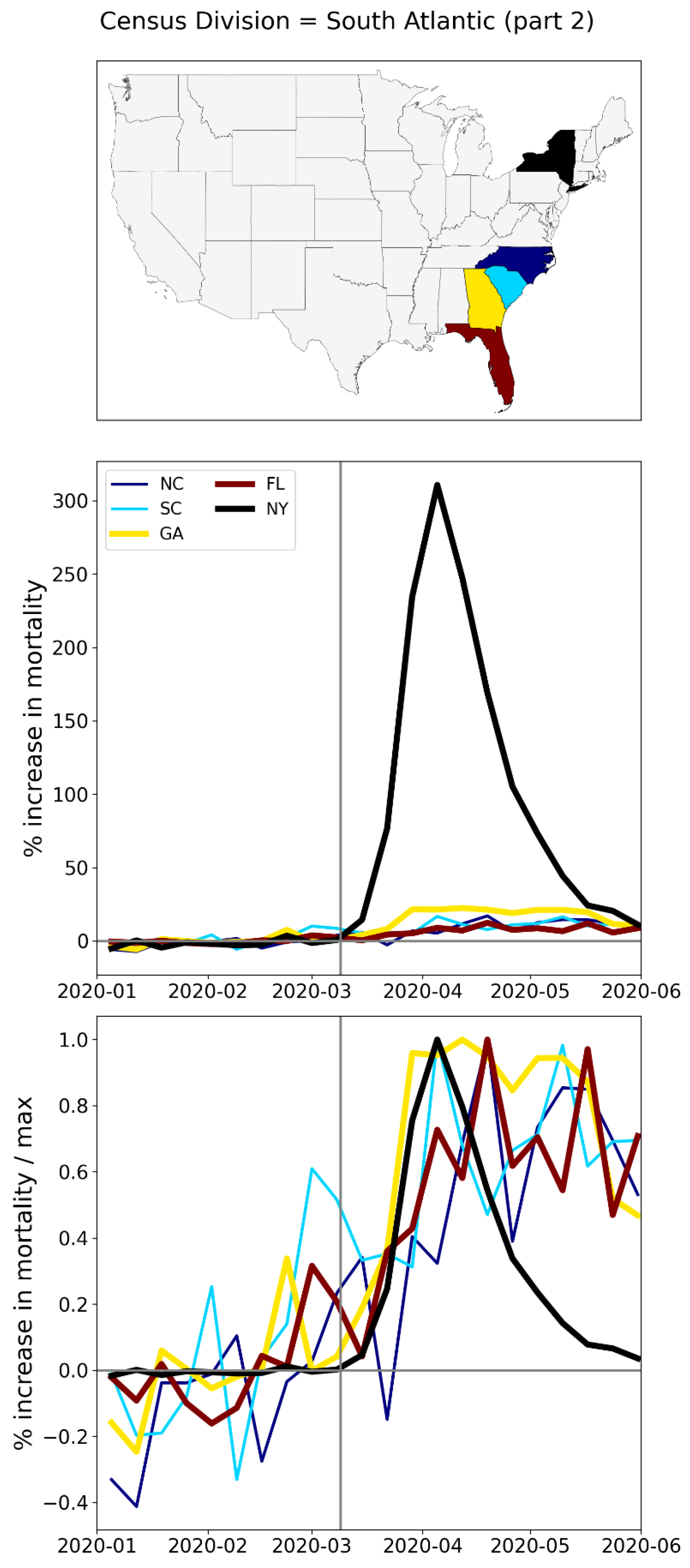
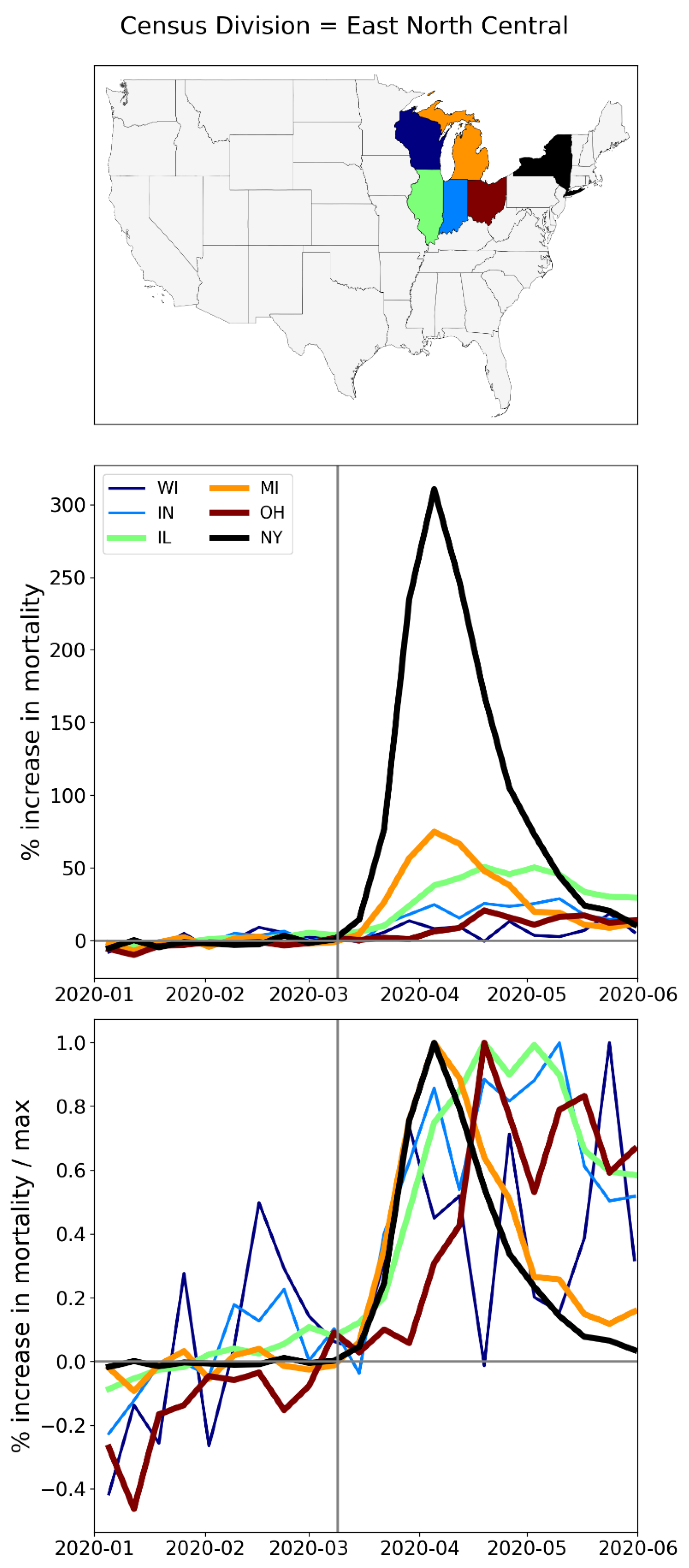
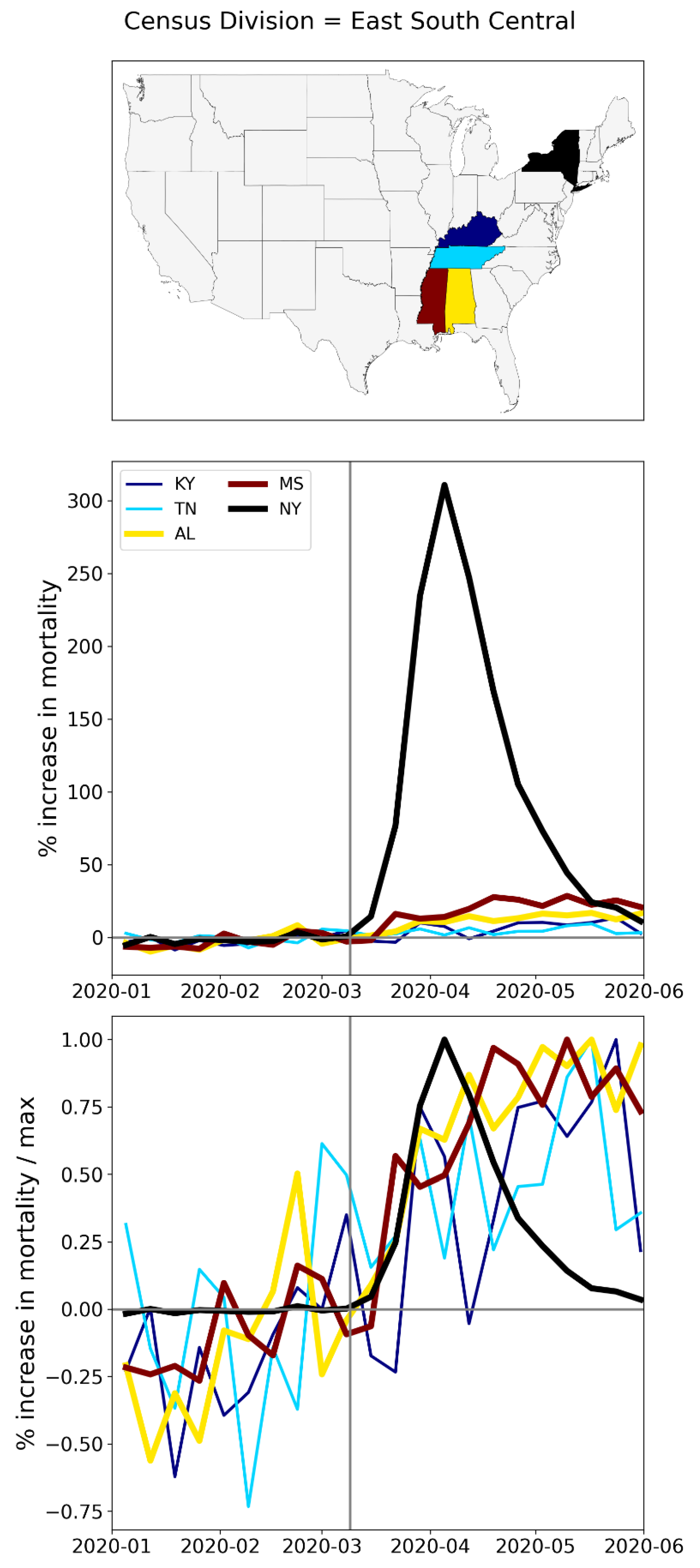
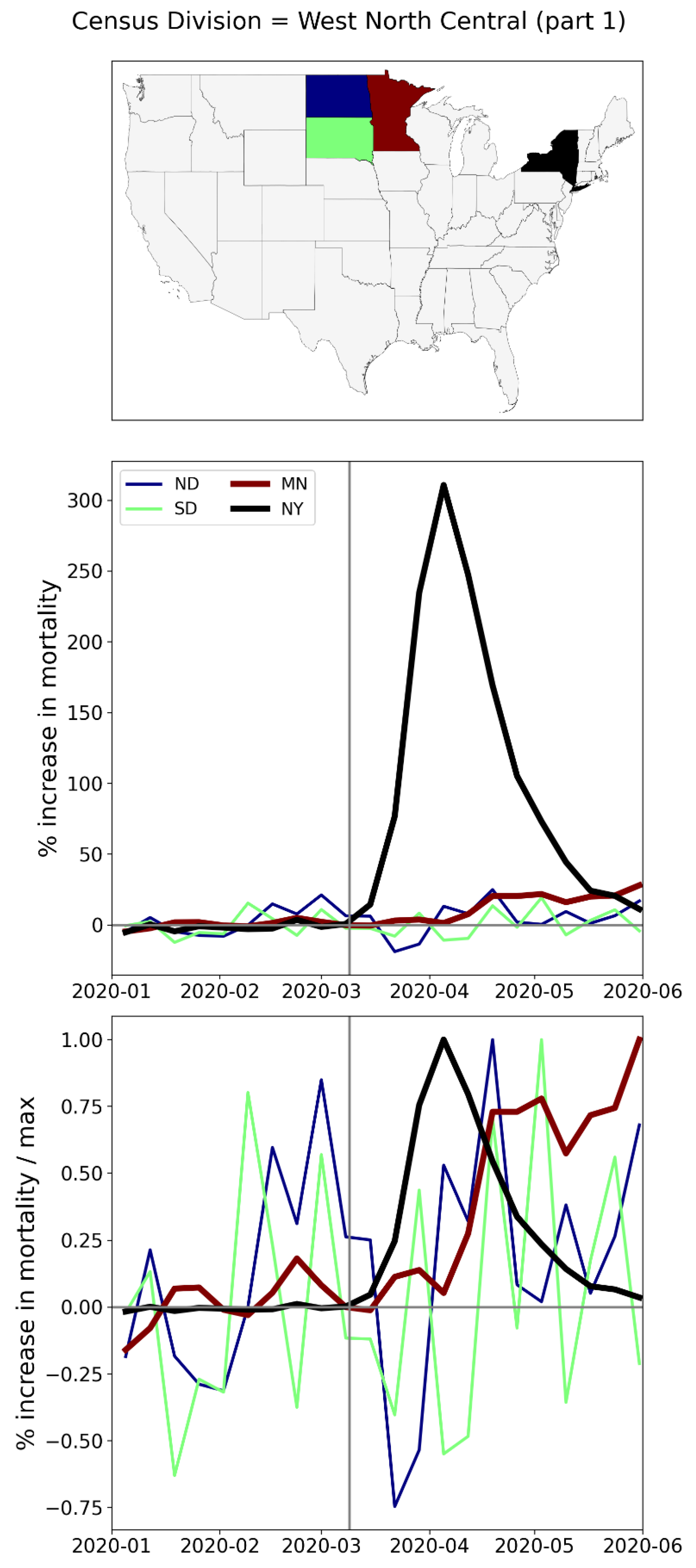
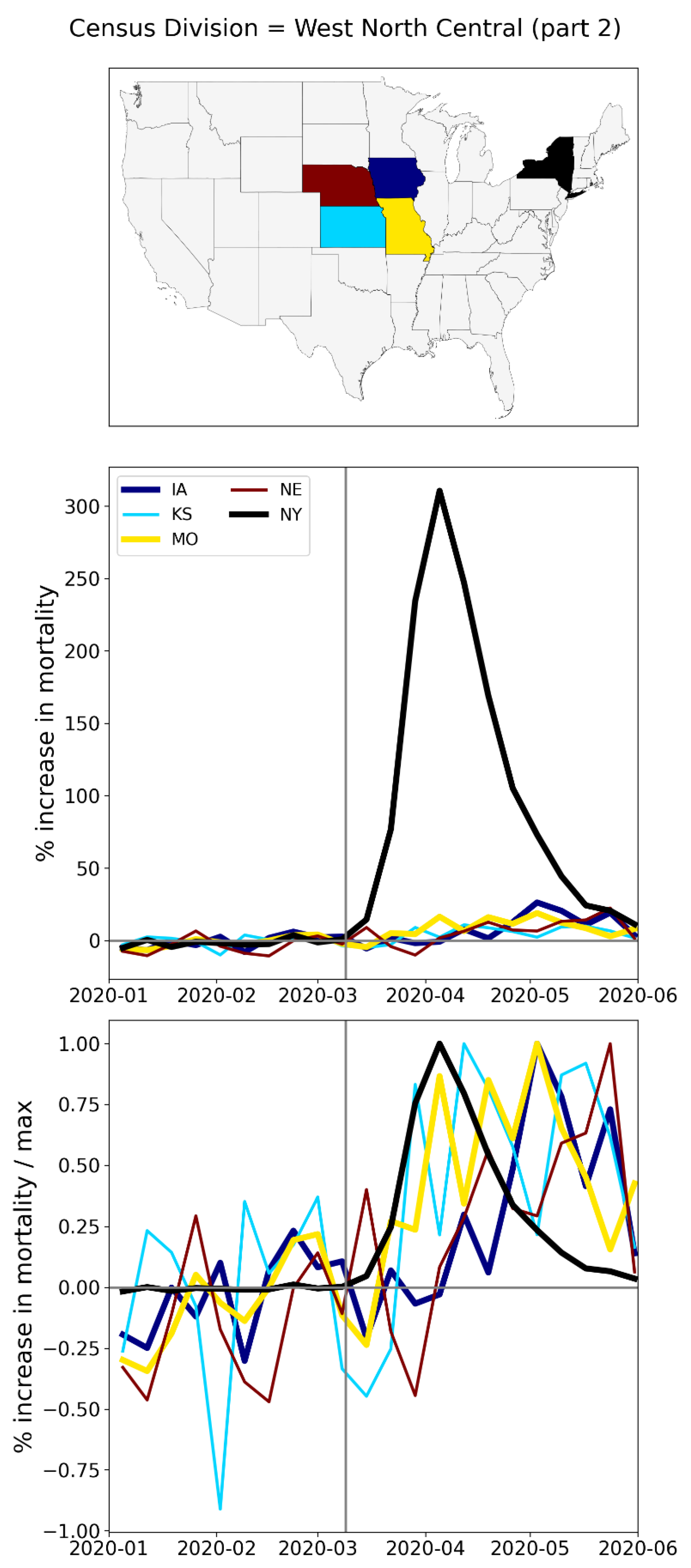
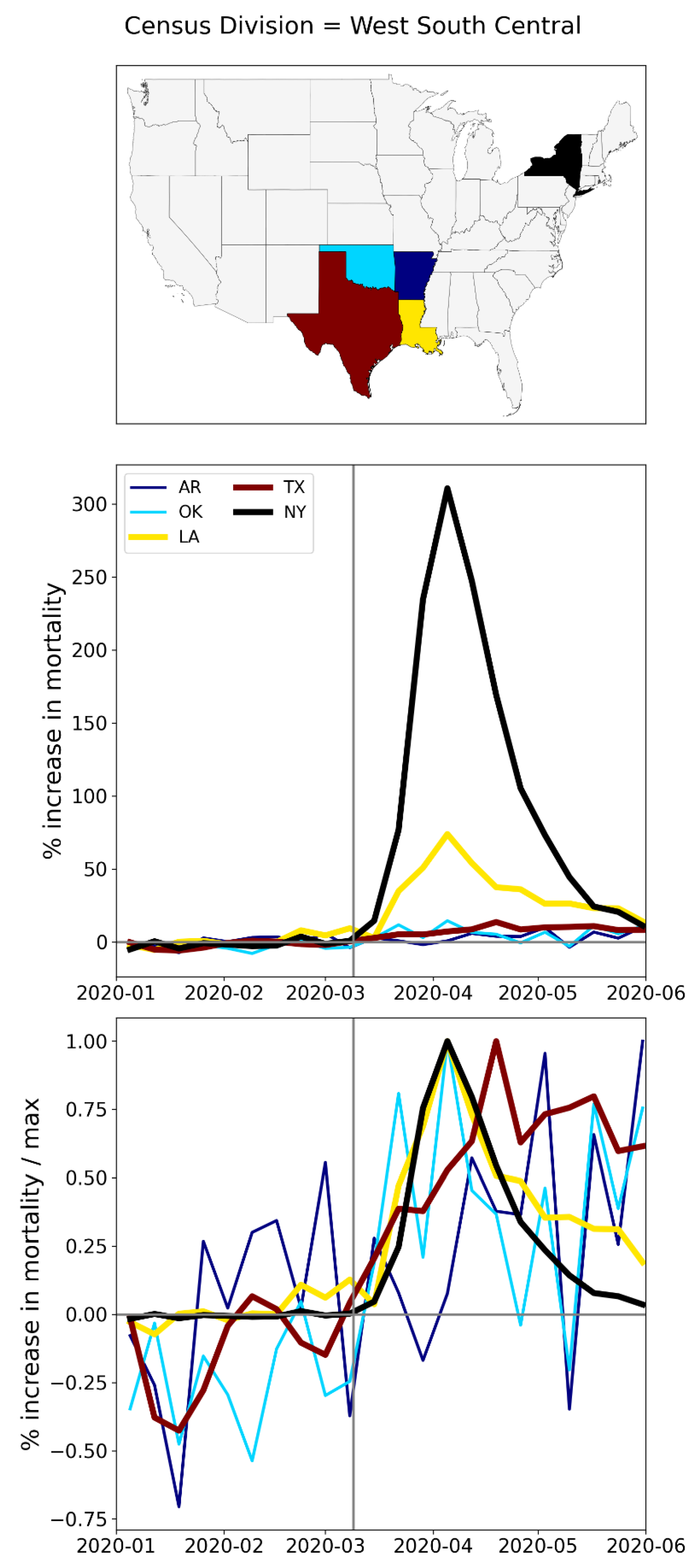
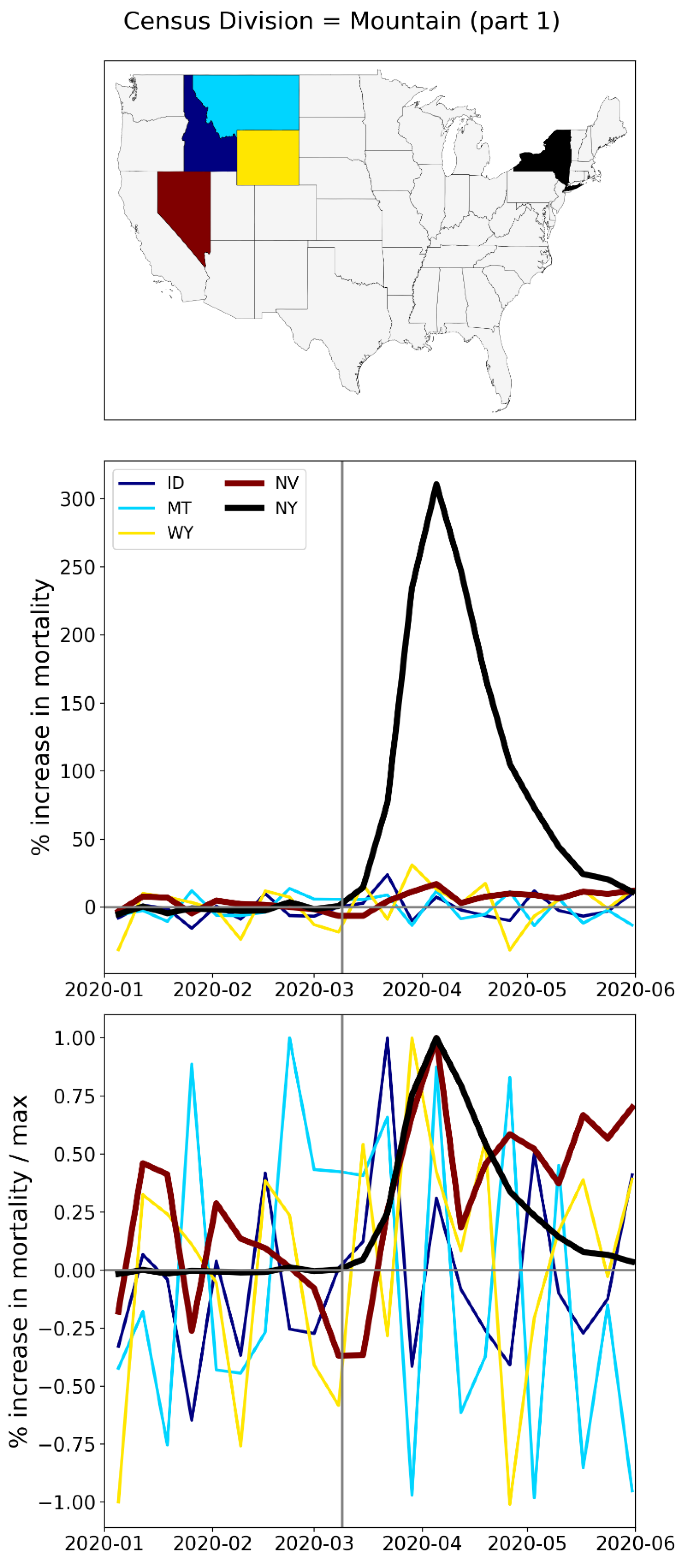
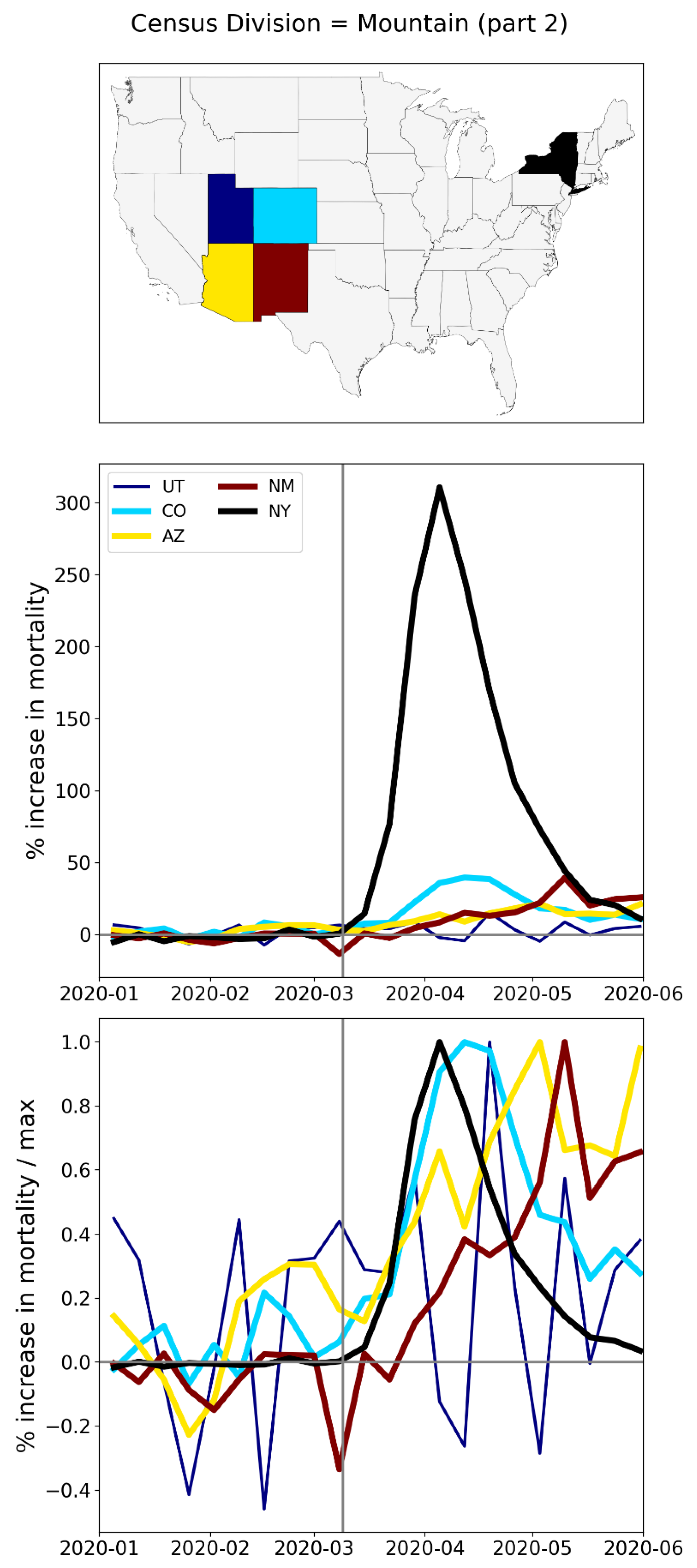
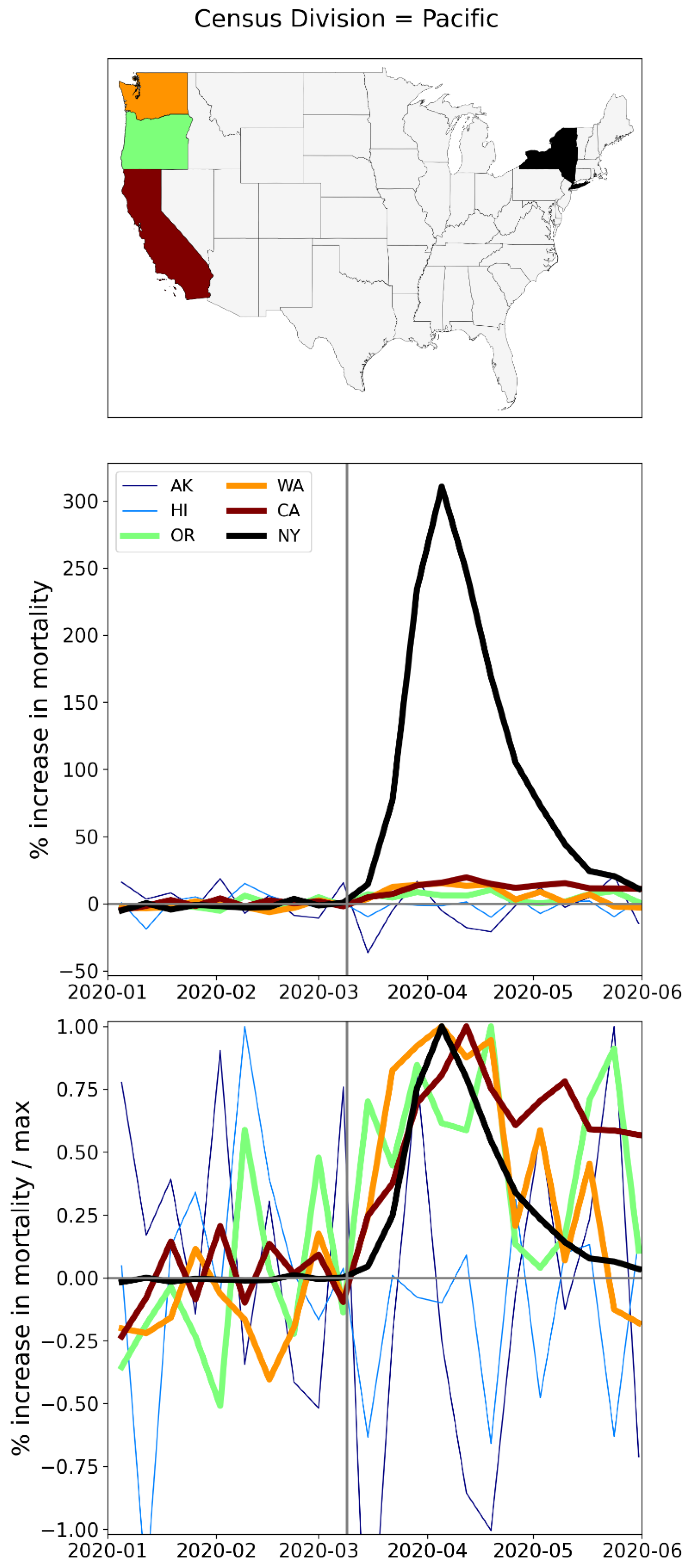
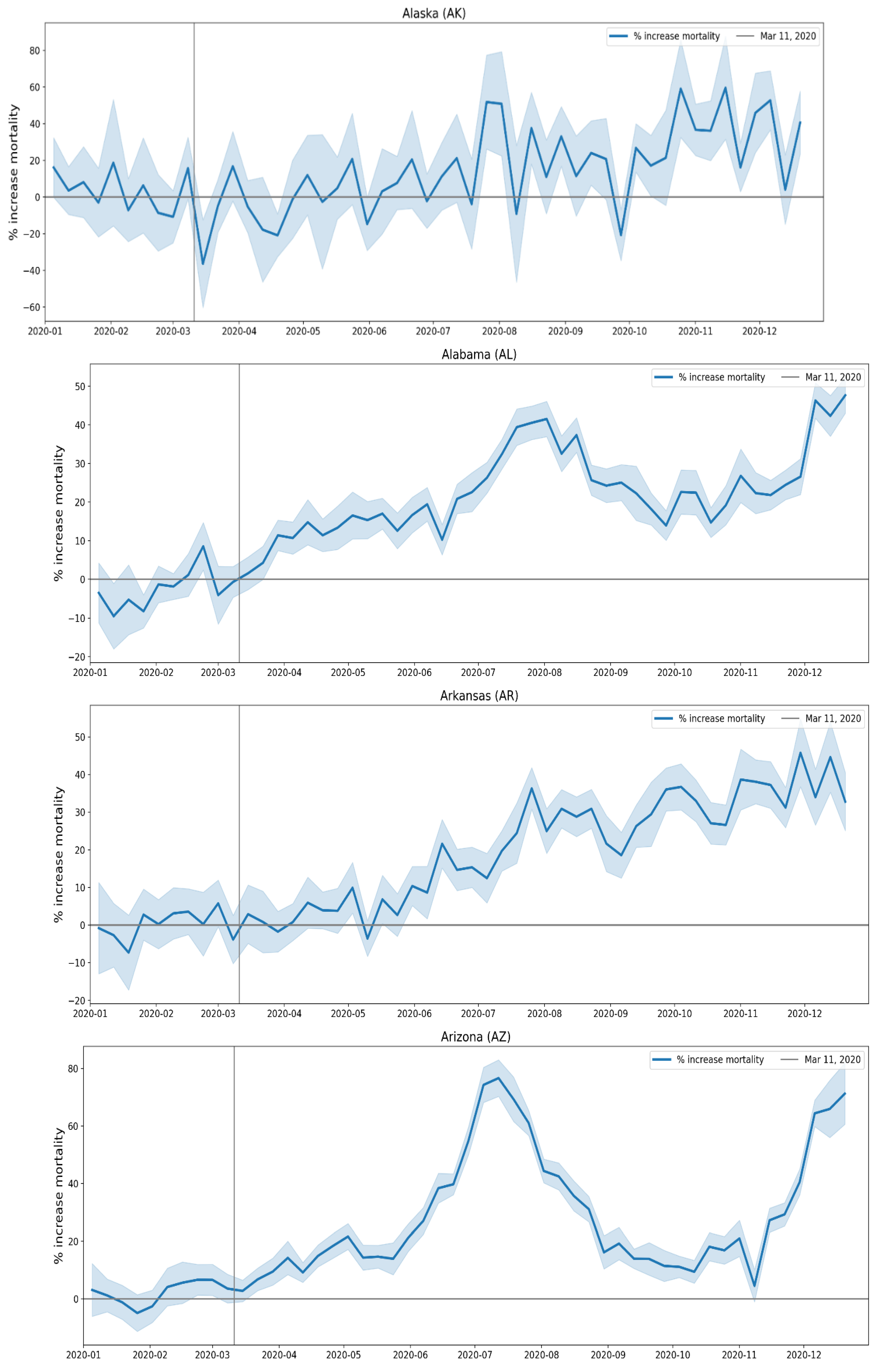
A.3. USA, Weekly P-Scores for Each State, for the Year 2020
B. Additional Graphs Pertaining to Section 3.5
C. Tables of European Regions by NUTS Level, Ordered by Integrated First-Peak Period P-Score
C.1 NUTS0 Level (Countries)
| Rank | NUTS Code | NUTS Level | Country | P-score (%) | (1σ) Err (%) | P-score / Err | Rise-side half-maximum (weeks after Mar 9-15, 2020)* |
| 1 | ES | 0 | Spain | 47.6 | 1.7 | 28 | 1 |
| 2 | UK | 0 | United Kingdom | 41.3 | 2.7 | 15 | 3 |
| 3 | IT | 0 | Italy | 34 | 1.5 | 23 | 0 |
| 4 | BE | 0 | Belgium | 31 | 2.6 | 12 | 2 |
| 5 | SE | 0 | Sweden | 23.7 | 2.1 | 11 | 3 |
| 6 | NL | 0 | Netherlands | 22.2 | 2 | 11 | 2 |
| 7 | FR | 0 | France | 16.4 | 1.5 | 11 | 2 |
| 8 | IE | 0 | Ireland | 14.9 | 2.1 | 7.1 | 3 |
| 9 | PT | 0 | Portugal | 11.6 | 1.7 | 6.8 | 1 |
| 10 | CY | 0 | Cyprus | 11 | 4.2 | 2.6 | - |
| 11 | CH | 0 | Switzerland | 10.5 | 2 | 5.3 | 2 |
| 12 | AL | 0 | Albania | 7.1 | 2.6 | 2.7 | - |
| 13 | MT | 0 | Malta | 6.8 | 5.1 | 1.3 | - |
| 14 | LT | 0 | Lithuania | 6.7 | 1.9 | 3.5 | 1 |
| 15 | AT | 0 | Austria | 6.1 | 1.9 | 3.2 | 1 |
| 16 | LU | 0 | Luxembourg | 4.5 | 4.6 | 0.98 | - |
| 17 | FI | 0 | Finland | 4.1 | 1.8 | 2.3 | - |
| 18 | EL | 0 | Greece | 3.4 | 1.5 | 2.3 | - |
| 19 | RS | 0 | Serbia | 3.3 | 1.8 | 1.8 | - |
| 20 | IS | 0 | Iceland | 3 | 5.4 | 0.56 | - |
| 21 | EE | 0 | Estonia | 2.1 | 2.6 | 0.81 | - |
| 22 | DE | 0 | Germany | 2 | 2 | 1.0 | - |
| 24 | NO | 0 | Norway | 1.9 | 1.7 | 1.0 | - |
| 23 | SK | 0 | Slovakia | 1.9 | 1.9 | 1.0 | - |
| 25 | HU | 0 | Hungary | 1 | 1.8 | 0.56 | - |
| 27 | HR | 0 | Croatia | 0.9 | 2 | 0.45 | - |
| 26 | SI | 0 | Slovenia | 0.9 | 2.2 | 0.41 | - |
| 28 | CZ | 0 | Czechia | 0.3 | 1.8 | 0.17 | - |
| 29 | RO | 0 | Romania | 0.1 | 1.6 | 0.06 | - |
| 30 | PL | 0 | Poland | 0 | 1.7 | 0 | - |
| 31 | LI | 0 | Liechtenstein | 0 | 17 | 0 | - |
| 32 | DK | 0 | Denmark | -0.8 | 1.6 | -0.50 | - |
| 33 | LV | 0 | Latvia | -2.7 | 2.1 | -1.3 | - |
| 34 | BG | 0 | Bulgaria | -3.1 | 1.5 | -2.1 | - |
| 35 | ME | 0 | Montenegro | -4 | 3.4 | -1.2 | - |
C.2. NUTS1 Level
| Rank | NUTS Code | NUTS Level | Region Name | Country | P-score (%) | (1σ) Err (%) |
| 1 | ES3 | 1 | COMUNIDAD DE MADRID | Spain | 145.6 | 3.2 |
| 2 | ITC | 1 | NORD-OVEST | Italy | 80.6 | 2 |
| 3 | UKI | 1 | LONDON | United Kingdom | 80.5 | 4 |
| 4 | ES4 | 1 | CENTRO (ES) | Spain | 73.8 | 2.7 |
| 5 | BE1 | 1 | RÉGION DE BRUXELLES-CAPITALE/BRUSSELS HOOFDSTEDELIJK GEWEST | Belgium | 60.9 | 5.2 |
| 6 | FR1 | 1 | ILE-DE-FRANCE | France | 58 | 2.4 |
| 7 | UKG | 1 | WEST MIDLANDS (ENGLAND) | United Kingdom | 49.5 | 3.7 |
| 8 | UKD | 1 | NORTH WEST (ENGLAND) | United Kingdom | 46.4 | 2.8 |
| 9 | UKC | 1 | NORTH EAST (ENGLAND) | United Kingdom | 43.2 | 3.1 |
| 10 | SE1 | 1 | ÖSTRA SVERIGE | Sweden | 42.5 | 2.8 |
| 11 | UKJ | 1 | SOUTH EAST (ENGLAND) | United Kingdom | 40.6 | 3.3 |
| 12 | NL4 | 1 | ZUID-NEDERLAND | Netherlands | 40.6 | 2.9 |
| 13 | UKH | 1 | EAST OF ENGLAND | United Kingdom | 40.3 | 3.5 |
| 14 | ES5 | 1 | ESTE | Spain | 39.4 | 2.1 |
| 15 | UKE | 1 | YORKSHIRE AND THE HUMBER | United Kingdom | 39 | 2.9 |
| 16 | ES2 | 1 | NORESTE | Spain | 37 | 2.5 |
| 17 | FRF | 1 | ALSACE-CHAMPAGNE-ARDENNE-LORRAINE | France | 35.4 | 2.8 |
| 18 | UKF | 1 | EAST MIDLANDS (ENGLAND) | United Kingdom | 35 | 3.2 |
| 19 | BE3 | 1 | RÉGION WALLONNE | Belgium | 33.2 | 3.1 |
| 20 | ITH | 1 | NORD-EST | Italy | 32.6 | 1.5 |
| 21 | UKM | 1 | SCOTLAND | United Kingdom | 31.7 | 2.4 |
| 22 | UKK | 1 | SOUTH WEST (ENGLAND) | United Kingdom | 26.6 | 3.6 |
| 23 | BE2 | 1 | VLAAMS GEWEST | Belgium | 25.6 | 2.7 |
| 24 | UKL | 1 | WALES | United Kingdom | 24.8 | 3.2 |
| 25 | UKN | 1 | NORTHERN IRELAND | United Kingdom | 23 | 3.8 |
| 26 | NL2 | 1 | OOST-NEDERLAND | Netherlands | 19.7 | 2.8 |
| 27 | FRC | 1 | BOURGOGNE-FRANCHE-COMTÉ | France | 18.8 | 2.4 |
| 28 | NL3 | 1 | WEST-NEDERLAND | Netherlands | 18.8 | 2 |
| 29 | FRE | 1 | NORD-PAS DE CALAIS-PICARDIE | France | 17.9 | 2.3 |
| 30 | IE0 | 1 | IRELAND | Ireland | 14.9 | 2.1 |
| 31 | FRK | 1 | AUVERGNE-RHÔNE-ALPES | France | 14 | 1.8 |
| 32 | SE3 | 1 | NORRA SVERIGE | Sweden | 13.7 | 2.7 |
| 33 | SE2 | 1 | SÖDRA SVERIGE | Sweden | 13.7 | 2.3 |
| 34 | ITI | 1 | CENTRO (IT) | Italy | 12.1 | 1.6 |
| 35 | ES1 | 1 | NOROESTE | Spain | 11.9 | 1.7 |
| 36 | PT1 | 1 | CONTINENTE | Portugal | 11.8 | 1.8 |
| 37 | ES6 | 1 | SUR | Spain | 11.5 | 1.6 |
| 38 | CY0 | 1 | Kypros | Cyprus | 11 | 4.2 |
| 39 | ITF | 1 | SUD | Italy | 10.9 | 1.5 |
| 40 | FRB | 1 | CENTRE - VAL DE LOIRE | France | 10.6 | 2.1 |
| 41 | CH0 | 1 | SCHWEIZ/SUISSE/SVIZZERA | Switzerland | 10.5 | 2 |
| 42 | PT2 | 1 | REGIÃO AUTÓNOMA DOS AÇORES | Portugal | 9.9 | 6.4 |
| 43 | AT2 | 1 | SÜDÖSTERREICH | Austria | 8.6 | 2.7 |
| 44 | DE2 | 1 | BAYERN | Germany | 8 | 2.1 |
| 45 | FRM | 1 | CORSE | France | 7.2 | 5.4 |
| 46 | FRL | 1 | PROVENCE-ALPES-CÔTE D’AZUR | France | 6.9 | 1.5 |
| 47 | MT0 | 1 | MALTA | Malta | 6.8 | 5.1 |
| 48 | LT0 | 1 | LIETUVA | Lithuania | 6.7 | 1.9 |
| 49 | AT1 | 1 | OSTÖSTERREICH | Austria | 6.5 | 2.1 |
| 50 | ITG | 1 | ISOLE | Italy | 6.4 | 1.7 |
| 51 | FRD | 1 | NORMANDIE | France | 6.3 | 2.1 |
| 52 | DE1 | 1 | BADEN-WÜRTTEMBERG | Germany | 5.6 | 2.2 |
| 53 | FRG | 1 | PAYS DE LA LOIRE | France | 5 | 1.9 |
| 54 | HU1 | 1 | KÖZÉP-MAGYARORSZÁG | Hungary | 4.9 | 2.1 |
| 55 | EL6 | 1 | KENTRIKI ELLADA | Greece | 4.6 | 2.2 |
| 56 | PT3 | 1 | REGIÃO AUTÓNOMA DA MADEIRA | Portugal | 4.6 | 5.4 |
| 57 | LU0 | 1 | LUXEMBOURG | Luxembourg | 4.5 | 4.6 |
| 58 | EL4 | 1 | NISIA AIGAIOU, KRITI | Greece | 4.2 | 2.7 |
| 59 | FI1 | 1 | MANNER-SUOMI | Finland | 4.1 | 1.8 |
| 60 | RS2 | 1 | Srbija - jug | Serbia | 4.1 | 2 |
| 61 | AT3 | 1 | WESTÖSTERREICH | Austria | 3.9 | 2.4 |
| 62 | DE6 | 1 | HAMBURG | Germany | 3.6 | 2.6 |
| 63 | EL5 | 1 | VOREIA ELLADA | Greece | 3.6 | 2 |
| 64 | DE5 | 1 | BREMEN | Germany | 3.4 | 4.4 |
| 65 | RO4 | 1 | MACROREGIUNEA PATRU | Romania | 3.1 | 2.1 |
| 66 | ES7 | 1 | CANARIAS | Spain | 3.1 | 2.6 |
| 67 | IS0 | 1 | ÍSLAND | Iceland | 3 | 5.4 |
| 68 | NL1 | 1 | NOORD-NEDERLAND | Netherlands | 2.9 | 2.7 |
| 69 | FRJ | 1 | LANGUEDOC-ROUSSILLON-MIDI-PYRÉNÉES | France | 2.7 | 1.5 |
| 70 | RS1 | 1 | Srbija - sever | Serbia | 2.3 | 2 |
| 71 | EL3 | 1 | ATTIKI | Greece | 2.2 | 1.9 |
| 72 | PL2 | 1 | MAKROREGION POŁUDNIOWY | Poland | 2.1 | 1.8 |
| 73 | EE0 | 1 | EESTI | Estonia | 2 | 2.6 |
| 74 | SK0 | 1 | SLOVENSKO | Slovakia | 1.9 | 1.9 |
| 75 | NO0 | 1 | NORGE | Norway | 1.9 | 1.7 |
| 76 | DE7 | 1 | HESSEN | Germany | 1.8 | 2.1 |
| 77 | DE3 | 1 | BERLIN | Germany | 1.6 | 2.2 |
| 78 | DE9 | 1 | NIEDERSACHSEN | Germany | 1.3 | 2.1 |
| 79 | DEA | 1 | NORDRHEIN-WESTFALEN | Germany | 1.2 | 2.2 |
| 80 | HU2 | 1 | DUNÁNTÚL | Hungary | 1.1 | 2.1 |
| 81 | DEC | 1 | SAARLAND | Germany | 1.1 | 3.5 |
| 82 | PL9 | 1 | MAKROREGION WOJEWÓDZTWO MAZOWIECKIE | Poland | 1 | 1.7 |
| 83 | SI0 | 1 | SLOVENIJA | Slovenia | 0.9 | 2.2 |
| 84 | PL8 | 1 | MAKROREGION WSCHODNI | Poland | 0.9 | 1.8 |
| 85 | HR0 | 1 | HRVATSKA | Croatia | 0.9 | 2 |
| 86 | RO3 | 1 | MACROREGIUNEA TREI | Romania | 0.6 | 1.7 |
| 87 | PL7 | 1 | MAKROREGION CENTRALNY | Poland | 0.5 | 2.3 |
| 88 | FRY | 1 | RUP FR - RÉGIONS ULTRAPÉRIPHÉRIQUES FRANÇAISES | France | 0.4 | 2.4 |
| 89 | CZ0 | 1 | ČESKÁ REPUBLIKA | Czechia | 0.3 | 1.8 |
| 90 | RO1 | 1 | MACROREGIUNEA UNU | Romania | 0.3 | 1.8 |
| 91 | DEB | 1 | RHEINLAND-PFALZ | Germany | -0.2 | 2.4 |
| 92 | LI0 | 1 | LIECHTENSTEIN | Liechtenstein | 0 | 17 |
| 93 | FRH | 1 | BRETAGNE | France | -0.3 | 1.9 |
| 94 | PL5 | 1 | MAKROREGION POŁUDNIOWO-ZACHODNI | Poland | -0.8 | 2.5 |
| 95 | FRI | 1 | AQUITAINE-LIMOUSIN-POITOU-CHARENTES | France | -0.8 | 1.7 |
| 96 | DK0 | 1 | DANMARK | Denmark | -0.8 | 1.6 |
| 97 | DED | 1 | SACHSEN | Germany | -0.8 | 2.7 |
| 98 | DE4 | 1 | BRANDENBURG | Germany | -1.1 | 2.5 |
| 99 | HU3 | 1 | ALFÖLD ÉS ÉSZAK | Hungary | -1.6 | 2.1 |
| 100 | DE8 | 1 | MECKLENBURG-VORPOMMERN | Germany | -2.1 | 2.5 |
| 101 | PL6 | 1 | MAKROREGION PÓŁNOCNY | Poland | -2.2 | 1.7 |
| 102 | RO2 | 1 | MACROREGIUNEA DOI | Romania | -2.2 | 1.8 |
| 103 | PL4 | 1 | MAKROREGION PÓŁNOCNO-ZACHODNI | Poland | -2.3 | 2 |
| 104 | BG4 | 1 | YUGOZAPADNA I YUZHNA TSENTRALNA BULGARIA | Bulgaria | -2.4 | 1.9 |
| 105 | DEG | 1 | THÜRINGEN | Germany | -2.7 | 3 |
| 106 | LV0 | 1 | LATVIJA | Latvia | -2.7 | 2.1 |
| 107 | DEF | 1 | SCHLESWIG-HOLSTEIN | Germany | -3 | 2.4 |
| 108 | BG3 | 1 | SEVERNA I YUGOIZTOCHNA BULGARIA | Bulgaria | -3.7 | 1.7 |
| 109 | ME0 | 1 | CRNA GORA | Montenegro | -4 | 3.4 |
| 110 | DEE | 1 | SACHSEN-ANHALT | Germany | -4.1 | 2.6 |
| 111 | FI2 | 1 | ÅLAND | Finland | -15 | 16 |
C.3. NUTS2 Level
| Rank | NUTS Code | NUTS Level | Region Name | Country | P-score (%) | (1σ) Err (%) |
| 1 | ES30 | 2 | Comunidad de Madrid | Spain | 145.6 | 3.2 |
| 2 | ES42 | 2 | Castilla-La Mancha | Spain | 108.7 | 4.4 |
| 3 | ITC4 | 2 | Lombardia | Italy | 106.2 | 2.5 |
| 4 | UKI4 | 2 | Inner London - East | United Kingdom | 87.3 | 6 |
| 5 | UKI7 | 2 | Outer London - West and North West | United Kingdom | 86.4 | 5 |
| 6 | UKI5 | 2 | Outer London - East and North East | United Kingdom | 80.2 | 5.5 |
| 7 | UKI3 | 2 | Inner London - West | United Kingdom | 77.2 | 6.2 |
| 8 | ES51 | 2 | Cataluña | Spain | 72.4 | 2.8 |
| 9 | UKI6 | 2 | Outer London - South | United Kingdom | 67.2 | 5.8 |
| 10 | ES41 | 2 | Castilla y León | Spain | 66.3 | 3.3 |
| 11 | UKG3 | 2 | West Midlands | United Kingdom | 61.3 | 4.6 |
| 12 | BE10 | 2 | Région de Bruxelles-Capitale/ Brussels Hoofdstedelijk Gewest | Belgium | 60.9 | 5.2 |
| 13 | SE11 | 2 | Stockholm | Sweden | 59.4 | 3.6 |
| 14 | FR10 | 2 | Ile-de-France | France | 56.2 | 2.4 |
| 15 | UKH2 | 2 | Bedfordshire and Hertfordshire | United Kingdom | 55.5 | 4.3 |
| 16 | FRF1 | 2 | Alsace | France | 53.7 | 3.6 |
| 17 | ITH2 | 2 | Provincia Autonoma di Trento | Italy | 53.5 | 5.6 |
| 18 | UKD3 | 2 | Greater Manchester | United Kingdom | 53.1 | 3.5 |
| 19 | UKD7 | 2 | Merseyside | United Kingdom | 51.2 | 4 |
| 20 | ES22 | 2 | Comunidad Foral de Navarra | Spain | 49.5 | 5 |
| 21 | ITC2 | 2 | Valle d'Aosta/Vallée d'Aoste | Italy | 48.1 | 9.4 |
| 22 | ITC1 | 2 | Piemonte | Italy | 47.9 | 2.1 |
| 23 | ES23 | 2 | La Rioja | Spain | 47.8 | 7.2 |
| 24 | CH07 | 2 | Ticino | Switzerland | 47.8 | 6.7 |
| 25 | UKJ1 | 2 | Berkshire, Buckinghamshire and Oxfordshire | United Kingdom | 47.3 | 3.4 |
| 26 | BE22 | 2 | Prov. Limburg (BE) | Belgium | 46.2 | 5.2 |
| 27 | UKC1 | 2 | Tees Valley and Durham | United Kingdom | 46.2 | 4.2 |
| 28 | ITH5 | 2 | Emilia-Romagna | Italy | 45.9 | 2.3 |
| 29 | UKD1 | 2 | Cumbria | United Kingdom | 45.4 | 5.2 |
| 30 | UKM8 | 2 | West Central Scotland | United Kingdom | 45.4 | 3.7 |
| 31 | ITH1 | 2 | Provincia Autonoma di Bolzano/Bozen | Italy | 44.7 | 6.2 |
| 32 | ITC3 | 2 | Liguria | Italy | 44.6 | 3.2 |
| 33 | NL42 | 2 | Limburg (NL) | Netherlands | 44.6 | 4.2 |
| 34 | UKE3 | 2 | South Yorkshire | United Kingdom | 44.2 | 4 |
| 35 | UKJ2 | 2 | Surrey, East and West Sussex | United Kingdom | 44 | 4.5 |
| 36 | UKD6 | 2 | Cheshire | United Kingdom | 43.9 | 4.5 |
| 37 | UKF2 | 2 | Leicestershire, Rutland and Northamptonshire | United Kingdom | 43 | 3.8 |
| 38 | UKH3 | 2 | Essex | United Kingdom | 41.9 | 4.8 |
| 39 | UKE4 | 2 | West Yorkshire | United Kingdom | 41.8 | 3.2 |
| 40 | UKG1 | 2 | Herefordshire, Worcestershire and Warwickshire | United Kingdom | 41.3 | 4.2 |
| 41 | UKC2 | 2 | Northumberland and Tyne and Wear | United Kingdom | 40.6 | 3.7 |
| 42 | BE33 | 2 | Prov. Liège | Belgium | 39.8 | 3.6 |
| 43 | UKK1 | 2 | Gloucestershire, Wiltshire and Bristol/Bath area | United Kingdom | 39.6 | 4.4 |
| 44 | UKE2 | 2 | North Yorkshire | United Kingdom | 39.4 | 4.9 |
| 45 | UKG2 | 2 | Shropshire and Staffordshire | United Kingdom | 38.8 | 4.2 |
| 46 | NL41 | 2 | Noord-Brabant | Netherlands | 38.5 | 3 |
| 47 | ES24 | 2 | Aragón | Spain | 37.4 | 3.1 |
| 48 | UKF1 | 2 | Derbyshire and Nottinghamshire | United Kingdom | 36.7 | 4.1 |
| 49 | UKJ4 | 2 | Kent | United Kingdom | 35.7 | 3.8 |
| 50 | UKJ3 | 2 | Hampshire and Isle of Wight | United Kingdom | 33.6 | 3.8 |
| 51 | BE32 | 2 | Prov. Hainaut | Belgium | 33.6 | 4.3 |
| 52 | ES43 | 2 | Extremadura | Spain | 33.4 | 3.3 |
| 53 | UKD4 | 2 | Lancashire | United Kingdom | 33.4 | 3.4 |
| 54 | ITI3 | 2 | Marche | Italy | 33.1 | 2.8 |
| 55 | UKM7 | 2 | Eastern Scotland | United Kingdom | 32.9 | 3.1 |
| 56 | UKL2 | 2 | East Wales | United Kingdom | 32.4 | 4.2 |
| 57 | ES21 | 2 | País Vasco | Spain | 31.8 | 3 |
| 58 | UKH1 | 2 | East Anglia | United Kingdom | 30.3 | 3.9 |
| 59 | FRF3 | 2 | Lorraine | France | 30 | 3.3 |
| 60 | FRE2 | 2 | Picardie | France | 29.9 | 3 |
| 61 | UKM9 | 2 | Southern Scotland | United Kingdom | 29.3 | 3.6 |
| 62 | BE35 | 2 | Prov. Namur | Belgium | 27.8 | 5.1 |
| 63 | FRC2 | 2 | Franche-Comté | France | 27 | 3.9 |
| 64 | BE24 | 2 | Prov. Vlaams-Brabant | Belgium | 27 | 4.1 |
| 65 | UKK2 | 2 | Dorset and Somerset | United Kingdom | 26.5 | 4.4 |
| 66 | UKE1 | 2 | East Yorkshire and Northern Lincolnshire | United Kingdom | 25.8 | 4.2 |
| 67 | CH01 | 2 | Région lémanique | Switzerland | 25.8 | 3.7 |
| 68 | SE12 | 2 | Östra Mellansverige | Sweden | 25.5 | 3.2 |
| 69 | BE34 | 2 | Prov. Luxembourg (BE) | Belgium | 24.9 | 6.3 |
| 70 | BE31 | 2 | Prov. Brabant Wallon | Belgium | 24 | 6.1 |
| 71 | UKM5 | 2 | North Eastern Scotland | United Kingdom | 23.1 | 5 |
| 72 | UKN0 | 2 | Northern Ireland | United Kingdom | 23 | 3.8 |
| 73 | BE25 | 2 | Prov. West-Vlaanderen | Belgium | 21.9 | 3 |
| 74 | BE23 | 2 | Prov. Oost-Vlaanderen | Belgium | 21.7 | 3.4 |
| 75 | BE21 | 2 | Prov. Antwerpen | Belgium | 21.5 | 3.5 |
| 76 | ES13 | 2 | Cantabria | Spain | 21.2 | 4.1 |
| 77 | UKL1 | 2 | West Wales and The Valleys | United Kingdom | 21.1 | 3.4 |
| 78 | NL32 | 2 | Noord-Holland | Netherlands | 21 | 2.6 |
| 79 | ITH3 | 2 | Veneto | Italy | 21 | 1.7 |
| 80 | NL22 | 2 | Gelderland | Netherlands | 20.9 | 3.1 |
| 81 | SE21 | 2 | Småland med öarna | Sweden | 19.5 | 4.3 |
| 82 | NL21 | 2 | Overijssel | Netherlands | 19.1 | 4 |
| 83 | NL33 | 2 | Zuid-Holland | Netherlands | 18.4 | 2.4 |
| 84 | ITF1 | 2 | Abruzzo | Italy | 18.2 | 3 |
| 85 | UKM6 | 2 | Highlands and Islands | United Kingdom | 18.2 | 4.8 |
| 86 | ES12 | 2 | Principado de Asturias | Spain | 18 | 2.8 |
| 87 | NL31 | 2 | Utrecht | Netherlands | 17.9 | 3.4 |
| 88 | SE31 | 2 | Norra Mellansverige | Sweden | 17.8 | 3.8 |
| 89 | FRF2 | 2 | Champagne-Ardenne | France | 17.5 | 3.3 |
| 90 | SE32 | 2 | Mellersta Norrland | Sweden | 17.2 | 5 |
| 91 | ES52 | 2 | Comunidad Valenciana | Spain | 17 | 2.1 |
| 92 | FRK2 | 2 | Rhône-Alpes | France | 16.7 | 1.8 |
| 93 | PT11 | 2 | Norte | Portugal | 16.5 | 2.2 |
| 94 | UKF3 | 2 | Lincolnshire | United Kingdom | 16.5 | 4 |
| 95 | ES63 | 2 | Ciudad Autónoma de Ceuta | Spain | 16 | 13 |
| 96 | ITF4 | 2 | Puglia | Italy | 15.1 | 2.2 |
| 97 | ITH4 | 2 | Friuli-Venezia Giulia | Italy | 14.8 | 3 |
| 98 | SE23 | 2 | Västsverige | Sweden | 14.6 | 2.7 |
| 99 | UKK4 | 2 | Devon | United Kingdom | 13.4 | 3.8 |
| 100 | ITI1 | 2 | Toscana | Italy | 13.4 | 2 |
| 101 | FI1B | 2 | Helsinki-Uusimaa | Finland | 13.2 | 3 |
| 102 | NL23 | 2 | Flevoland | Netherlands | 12.5 | 6.4 |
| 103 | ES61 | 2 | Andalucía | Spain | 12 | 1.7 |
| 104 | FRC1 | 2 | Bourgogne | France | 11.9 | 2.5 |
| 105 | NL34 | 2 | Zeeland | Netherlands | 11.7 | 5 |
| 106 | ITF2 | 2 | Molise | Italy | 11.4 | 4.6 |
| 107 | CY00 | 2 | Kypros | Cyprus | 11 | 4.2 |
| 108 | PT18 | 2 | Alentejo | Portugal | 10.9 | 3.7 |
| 109 | PT16 | 2 | Centro (PT) | Portugal | 10.3 | 2.5 |
| 110 | AT22 | 2 | Steiermark | Austria | 10.2 | 3.2 |
| 111 | FRE1 | 2 | Nord-Pas de Calais | France | 10.2 | 2.4 |
| 112 | LT01 | 2 | Sostinės regionas | Lithuania | 10.1 | 3.4 |
| 113 | PT20 | 2 | Região Autónoma dos Açores | Portugal | 9.9 | 6.4 |
| 114 | ES53 | 2 | Illes Balears | Spain | 9.8 | 3.5 |
| 115 | FRB0 | 2 | Centre - Val de Loire | France | 9.7 | 2.1 |
| 116 | ITF6 | 2 | Calabria | Italy | 9.7 | 2.5 |
| 117 | UKK3 | 2 | Cornwall and Isles of Scilly | United Kingdom | 9.7 | 4.6 |
| 118 | EL53 | 2 | Dytiki Makedonia | Greece | 9.3 | 4.9 |
| 119 | PT17 | 2 | Área Metropolitana de Lisboa | Portugal | 9.2 | 2.2 |
| 120 | ITG2 | 2 | Sardegna | Italy | 8.8 | 3 |
| 121 | RS22 | 2 | Region Južne i Istočne Srbije | Serbia | 8.7 | 2.7 |
| 122 | SE22 | 2 | Sydsverige | Sweden | 8.7 | 3.3 |
| 123 | AT13 | 2 | Wien | Austria | 8.5 | 2.9 |
| 124 | ITF5 | 2 | Basilicata | Italy | 8.1 | 4 |
| 125 | ES62 | 2 | Región de Murcia | Spain | 8 | 3.1 |
| 126 | FRD2 | 2 | Haute-Normandie | France | 7.8 | 2.5 |
| 127 | ES11 | 2 | Galicia | Spain | 7.8 | 1.9 |
| 128 | ITI2 | 2 | Umbria | Italy | 7.6 | 3.5 |
| 129 | CH03 | 2 | Nordwestschweiz | Switzerland | 7.5 | 3.3 |
| 130 | EL61 | 2 | Thessalia | Greece | 7.4 | 3.4 |
| 131 | AT33 | 2 | Tirol | Austria | 7.2 | 4 |
| 132 | RS11 | 2 | Beogradski region | Serbia | 7.1 | 2.4 |
| 133 | EL63 | 2 | Dytiki Ellada | Greece | 7 | 3.9 |
| 134 | HU11 | 2 | Budapest | Hungary | 7 | 2.6 |
| 135 | MT00 | 2 | Malta | Malta | 6.8 | 5.1 |
| 136 | ITF3 | 2 | Campania | Italy | 6.6 | 1.8 |
| 137 | FRL0 | 2 | Provence-Alpes-Côte d’Azur | France | 6.2 | 1.5 |
| 138 | EL42 | 2 | Notio Aigaio | Greece | 6.1 | 5.4 |
| 139 | AT34 | 2 | Vorarlberg | Austria | 6.1 | 6 |
| 140 | CH02 | 2 | Espace Mittelland | Switzerland | 5.9 | 2.7 |
| 141 | RO42 | 2 | Vest | Romania | 5.8 | 2.3 |
| 142 | AT11 | 2 | Burgenland | Austria | 5.8 | 5 |
| 143 | ITI4 | 2 | Lazio | Italy | 5.8 | 1.7 |
| 144 | LT02 | 2 | Vidurio ir vakarų Lietuvos regionas | Lithuania | 5.7 | 2 |
| 145 | ITG1 | 2 | Sicilia | Italy | 5.7 | 1.7 |
| 146 | SK04 | 2 | Východné Slovensko | Slovakia | 5.7 | 3.1 |
| 147 | FRM0 | 2 | Corse | France | 5.5 | 5.3 |
| 148 | EL51 | 2 | Anatoliki Makedonia, Thraki | Greece | 5.4 | 3.4 |
| 149 | NO01 | 2 | Oslo og Akershus | Norway | 5.3 | 3.3 |
| 150 | AT21 | 2 | Kärnten | Austria | 5 | 4 |
| 151 | AT12 | 2 | Niederösterreich | Austria | 5 | 2.5 |
| 152 | NO03 | 2 | Sør-Østlandet | Norway | 4.9 | 3.1 |
| 153 | FRJ1 | 2 | Languedoc-Roussillon | France | 4.6 | 2 |
| 154 | EL41 | 2 | Voreio Aigaio | Greece | 4.6 | 6.2 |
| 155 | PT30 | 2 | Região Autónoma da Madeira | Portugal | 4.6 | 5.4 |
| 156 | LU00 | 2 | Luxembourg | Luxembourg | 4.5 | 4.6 |
| 157 | SE33 | 2 | Övre Norrland | Sweden | 4.4 | 3.9 |
| 158 | CH06 | 2 | Zentralschweiz | Switzerland | 4.4 | 4 |
| 159 | PT15 | 2 | Algarve | Portugal | 4.4 | 4.2 |
| 160 | FRG0 | 2 | Pays de la Loire | France | 4.3 | 1.9 |
| 161 | EL62 | 2 | Ionia Nisia | Greece | 4.3 | 5.8 |
| 162 | AT32 | 2 | Salzburg | Austria | 4 | 4 |
| 163 | PL72 | 2 | Świętokrzyskie | Poland | 3.7 | 3.1 |
| 164 | NL12 | 2 | Friesland (NL) | Netherlands | 3.7 | 3.8 |
| 165 | DK01 | 2 | Hovedstaden | Denmark | 3.6 | 2.4 |
| 166 | NL13 | 2 | Drenthe | Netherlands | 3.4 | 4.1 |
| 167 | EL65 | 2 | Peloponnisos | Greece | 3.4 | 3.5 |
| 168 | CZ01 | 2 | Praha | Czechia | 3.3 | 3 |
| 169 | CZ08 | 2 | Moravskoslezsko | Czechia | 3.2 | 2.9 |
| 170 | SK02 | 2 | Západné Slovensko | Slovakia | 3.2 | 2.7 |
| 171 | EL43 | 2 | Kriti | Greece | 3.2 | 3.6 |
| 172 | ES70 | 2 | Canarias | Spain | 3.1 | 2.6 |
| 173 | CH05 | 2 | Ostschweiz | Switzerland | 3 | 3.1 |
| 174 | IS00 | 2 | Ísland | Iceland | 3 | 5.4 |
| 175 | EL52 | 2 | Kentriki Makedonia | Greece | 2.9 | 2.2 |
| 176 | CZ04 | 2 | Severozápad | Czechia | 2.8 | 2.8 |
| 177 | PL22 | 2 | Śląskie | Poland | 2.8 | 2 |
| 178 | HU22 | 2 | Nyugat-Dunántúl | Hungary | 2.7 | 3.1 |
| 179 | CH04 | 2 | Zürich | Switzerland | 2.6 | 3 |
| 180 | RO32 | 2 | Bucureşti - Ilfov | Romania | 2.5 | 1.9 |
| 181 | CZ03 | 2 | Jihozápad | Czechia | 2.5 | 3.3 |
| 182 | CZ07 | 2 | Střední Morava | Czechia | 2.3 | 2.9 |
| 183 | FI19 | 2 | Länsi-Suomi | Finland | 2.2 | 2.7 |
| 184 | EL30 | 2 | Attiki | Greece | 2.2 | 1.9 |
| 185 | FI1D | 2 | Pohjois- ja Itä-Suomi | Finland | 2.2 | 2.7 |
| 186 | HU12 | 2 | Pest | Hungary | 2 | 2.5 |
| 187 | EE00 | 2 | Eesti | Estonia | 2 | 2.6 |
| 188 | AT31 | 2 | Oberösterreich | Austria | 2 | 3.1 |
| 189 | PL81 | 2 | Lubelskie | Poland | 1.7 | 2.2 |
| 190 | HU23 | 2 | Dél-Dunántúl | Hungary | 1.7 | 2.8 |
| 191 | FRD1 | 2 | Basse-Normandie | France | 1.5 | 2.6 |
| 192 | NL11 | 2 | Groningen | Netherlands | 1.4 | 4.2 |
| 193 | PL21 | 2 | Małopolskie | Poland | 1.1 | 1.9 |
| 194 | PL92 | 2 | Mazowiecki regionalny | Poland | 1 | 2.1 |
| 195 | PL91 | 2 | Warszawski stołeczny | Poland | 1 | 1.9 |
| 196 | RO11 | 2 | Nord-Vest | Romania | 0.9 | 2.2 |
| 197 | NO06 | 2 | Trøndelag | Norway | 0.8 | 4.3 |
| 198 | RO41 | 2 | Sud-Vest Oltenia | Romania | 0.8 | 2.6 |
| 199 | NO02 | 2 | Hedmark og Oppland | Norway | 0.6 | 4.5 |
| 200 | NO05 | 2 | Vestlandet | Norway | 0.6 | 3.6 |
| 201 | HU33 | 2 | Dél-Alföld | Hungary | 0.5 | 2.3 |
| 202 | PL84 | 2 | Podlaskie | Poland | 0.5 | 2.9 |
| 203 | PL82 | 2 | Podkarpackie | Poland | 0.3 | 2.6 |
| 204 | RS21 | 2 | Region Šumadije i Zapadne Srbije | Serbia | 0.2 | 2.2 |
| 205 | EL64 | 2 | Sterea Ellada | Greece | 0 | 3.8 |
| 206 | HU32 | 2 | Észak-Alföld | Hungary | 0 | 2.9 |
| 207 | NO04 | 2 | Agder og Rogaland | Norway | 0 | 3.7 |
| 208 | FI1C | 2 | Etelä-Suomi | Finland | -0.1 | 2.8 |
| 209 | PL52 | 2 | Opolskie | Poland | -0.1 | 3.1 |
| 210 | LI00 | 2 | Liechtenstein | Liechtenstein | 0 | 17 |
| 211 | RO12 | 2 | Centru | Romania | -0.4 | 2.1 |
| 212 | DK02 | 2 | Sjælland | Denmark | -0.4 | 2.9 |
| 213 | RO21 | 2 | Nord-Est | Romania | -0.4 | 2.2 |
| 214 | RO31 | 2 | Sud - Muntenia | Romania | -0.5 | 2 |
| 215 | HU21 | 2 | Közép-Dunántúl | Hungary | -0.9 | 2.8 |
| 216 | PL51 | 2 | Dolnośląskie | Poland | -1 | 2.6 |
| 217 | FRI2 | 2 | Limousin | France | -1 | 3.1 |
| 218 | PL71 | 2 | Łódzkie | Poland | -1 | 2.5 |
| 219 | SK03 | 2 | Stredné Slovensko | Slovakia | -1.2 | 2.2 |
| 220 | EL54 | 2 | Ipeiros | Greece | -1.2 | 4.8 |
| 221 | FRH0 | 2 | Bretagne | France | -1.2 | 1.9 |
| 222 | FRI3 | 2 | Poitou-Charentes | France | -1.3 | 2.4 |
| 223 | PL63 | 2 | Pomorskie | Poland | -1.4 | 2.2 |
| 224 | BG42 | 2 | Yuzhen tsentralen | Bulgaria | -1.4 | 2.5 |
| 225 | BG32 | 2 | Severen tsentralen | Bulgaria | -1.4 | 2.7 |
| 226 | PL61 | 2 | Kujawsko-pomorskie | Poland | -1.4 | 2.2 |
| 227 | FRJ2 | 2 | Midi-Pyrénées | France | -1.4 | 1.7 |
| 228 | DK04 | 2 | Midtjylland | Denmark | -1.5 | 2.8 |
| 229 | RS12 | 2 | Region Vojvodine | Serbia | -1.5 | 2.3 |
| 230 | PL41 | 2 | Wielkopolskie | Poland | -1.5 | 2.3 |
| 231 | CZ06 | 2 | Jihovýchod | Czechia | -2 | 2.5 |
| 232 | FRK1 | 2 | Auvergne | France | -2 | 2.6 |
| 233 | PL42 | 2 | Zachodniopomorskie | Poland | -2.3 | 2.4 |
| 234 | LV00 | 2 | Latvija | Latvia | -2.7 | 2.1 |
| 235 | FRI1 | 2 | Aquitaine | France | -2.8 | 1.9 |
| 236 | CZ05 | 2 | Severovýchod | Czechia | -3 | 2.8 |
| 237 | BG41 | 2 | Yugozapaden | Bulgaria | -3.1 | 2 |
| 238 | NO07 | 2 | Nord-Norge | Norway | -3.1 | 4 |
| 239 | BG34 | 2 | Yugoiztochen | Bulgaria | -3.8 | 2.3 |
| 240 | SK01 | 2 | Bratislavský kraj | Slovakia | -3.9 | 3.4 |
| 241 | ME00 | 2 | Crna Gora | Montenegro | -4 | 3.4 |
| 242 | DK03 | 2 | Syddanmark | Denmark | -4.1 | 2.5 |
| 243 | PL62 | 2 | Warmińsko-mazurskie | Poland | -4.5 | 2.8 |
| 244 | BG31 | 2 | Severozapaden | Bulgaria | -4.5 | 2.4 |
| 245 | RO22 | 2 | Sud-Est | Romania | -4.5 | 1.9 |
| 246 | DK05 | 2 | Nordjylland | Denmark | -4.7 | 4 |
| 247 | PL43 | 2 | Lubuskie | Poland | -4.7 | 3.3 |
| 248 | CZ02 | 2 | Střední Čechy | Czechia | -4.8 | 2.8 |
| 249 | BG33 | 2 | Severoiztochen | Bulgaria | -5.2 | 2.8 |
| 250 | HU31 | 2 | Észak-Magyarország | Hungary | -5.5 | 2.6 |
| 251 | FI20 | 2 | Åland | Finland | -15 | 16 |
C.4. NUTS3 Level
| Rank | NUTS Code | NUTS Level | Region Name | Country | P-score (%) | (1σ) Err (%) |
| 1 | ITC46 | 3 | Bergamo | Italy | 241 | 8.6 |
| 2 | ITC4A | 3 | Cremona | Italy | 210 | 11 |
| 3 | ITC49 | 3 | Lodi | Italy | 170 | 14 |
| 4 | ES416 | 3 | Segovia | Spain | 167 | 15 |
| 5 | ITH51 | 3 | Piacenza | Italy | 146.9 | 9.9 |
| 6 | ES300 | 3 | Madrid | Spain | 145.6 | 3.2 |
| 7 | ITC47 | 3 | Brescia | Italy | 145.5 | 6 |
| 8 | ES424 | 3 | Guadalajara | Spain | 136 | 12 |
| 9 | ES422 | 3 | Ciudad Real | Spain | 135.1 | 8.3 |
| 10 | UKI72 | 3 | Brent | United Kingdom | 120 | 12 |
| 11 | ES417 | 3 | Soria | Spain | 119 | 17 |
| 12 | UKI54 | 3 | Enfield | United Kingdom | 118 | 12 |
| 13 | ITH52 | 3 | Parma | Italy | 113.3 | 7.2 |
| 14 | ITC43 | 3 | Lecco | Italy | 111.6 | 8.8 |
| 15 | UKI32 | 3 | Westminster | United Kingdom | 110 | 18 |
| 16 | ES423 | 3 | Cuenca | Spain | 109.3 | 9.9 |
| 17 | ES421 | 3 | Albacete | Spain | 105.9 | 8.6 |
| 18 | ITC48 | 3 | Pavia | Italy | 104.3 | 6.4 |
| 19 | UKI41 | 3 | Hackney and Newham | United Kingdom | 102 | 11 |
| 20 | UKI53 | 3 | Redbridge and Waltham Forest | United Kingdom | 98.3 | 8.5 |
| 21 | UKI71 | 3 | Barnet | United Kingdom | 98 | 11 |
| 22 | UKI45 | 3 | Lambeth | United Kingdom | 93 | 14 |
| 23 | ES415 | 3 | Salamanca | Spain | 89.5 | 7 |
| 24 | ES511 | 3 | Barcelona | Spain | 87.9 | 2.9 |
| 25 | UKI73 | 3 | Ealing | United Kingdom | 87 | 11 |
| 26 | UKI62 | 3 | Croydon | United Kingdom | 84 | 9.4 |
| 27 | UKI43 | 3 | Haringey and Islington | United Kingdom | 83 | 11 |
| 28 | UKI74 | 3 | Harrow and Hillingdon | United Kingdom | 82.4 | 7.9 |
| 29 | UKJ26 | 3 | East Surrey | United Kingdom | 81 | 9.9 |
| 30 | ES425 | 3 | Toledo | Spain | 80.4 | 6.5 |
| 31 | UKI44 | 3 | Lewisham and Southwark | United Kingdom | 80 | 9.6 |
| 32 | ES411 | 3 | Ávila | Spain | 78.8 | 9.6 |
| 33 | ITC4C | 3 | Milano | Italy | 78.6 | 3.4 |
| 34 | FR106 | 3 | Seine-Saint-Denis | France | 77.7 | 5.1 |
| 35 | UKI33 | 3 | Kensington & Chelsea and Hammersmith & Fulham | United Kingdom | 77 | 10 |
| 36 | UKI42 | 3 | Tower Hamlets | United Kingdom | 76 | 13 |
| 37 | FRF12 | 3 | Haut-Rhin | France | 75.1 | 5.3 |
| 38 | ITC4B | 3 | Mantova | Italy | 75.1 | 6.8 |
| 39 | UKG31 | 3 | Birmingham | United Kingdom | 73.7 | 6.7 |
| 40 | UKI34 | 3 | Wandsworth | United Kingdom | 73 | 11 |
| 41 | ITI31 | 3 | Pesaro e Urbino | Italy | 73.3 | 6.2 |
| 42 | UKH32 | 3 | Thurrock | United Kingdom | 73 | 13 |
| 43 | FR105 | 3 | Hauts-de-Seine | France | 72.4 | 5.1 |
| 44 | ITC13 | 3 | Biella | Italy | 71.6 | 8.7 |
| 45 | UKI63 | 3 | Merton, Kingston upon Thames and Sutton | United Kingdom | 67.9 | 7.7 |
| 46 | UKG32 | 3 | Solihull | United Kingdom | 67.1 | 9.9 |
| 47 | UKD33 | 3 | Manchester | United Kingdom | 66.9 | 8.9 |
| 48 | ITC18 | 3 | Alessandria | Italy | 66.4 | 5.5 |
| 49 | BE323 | 3 | Arr. Mons | Belgium | 66 | 7.9 |
| 50 | ITC4D | 3 | Monza e della Brianza | Italy | 65.8 | 4.5 |
| 51 | FR108 | 3 | Val-d'Oise | France | 65.6 | 4.6 |
| 52 | UKF21 | 3 | Leicester | United Kingdom | 64.8 | 8.4 |
| 53 | UKI52 | 3 | Barking & Dagenham and Havering | United Kingdom | 63.5 | 7.4 |
| 54 | UKH21 | 3 | Luton | United Kingdom | 63.2 | 9.8 |
| 55 | ES432 | 3 | Cáceres | Spain | 63 | 6.2 |
| 56 | FR107 | 3 | Val-de-Marne | France | 62.2 | 4.3 |
| 57 | UKI51 | 3 | Bexley and Greenwich | United Kingdom | 62.1 | 7.1 |
| 58 | UKG38 | 3 | Walsall | United Kingdom | 62 | 8.4 |
| 59 | UKG39 | 3 | Wolverhampton | United Kingdom | 62 | 8.7 |
| 60 | NL413 | 3 | Noordoost-Noord-Brabant | Netherlands | 61.9 | 6 |
| 61 | ES418 | 3 | Valladolid | Spain | 61.9 | 5.9 |
| 62 | BE100 | 3 | Arr. de Bruxelles-Capitale/Arr. van Brussel-Hoofdstad | Belgium | 60.9 | 5.2 |
| 63 | UKI75 | 3 | Hounslow and Richmond upon Thames | United Kingdom | 60.3 | 7.7 |
| 64 | UKJ25 | 3 | West Surrey | United Kingdom | 60.1 | 6.9 |
| 65 | ES211 | 3 | Araba/Álava | Spain | 59.6 | 7.2 |
| 66 | SE110 | 3 | Stockholms län | Sweden | 59.4 | 3.6 |
| 67 | UKD34 | 3 | Greater Manchester South West | United Kingdom | 59.1 | 6.2 |
| 68 | UKD72 | 3 | Liverpool | United Kingdom | 58.9 | 5.9 |
| 69 | ITC12 | 3 | Vercelli | Italy | 57.7 | 8.6 |
| 70 | ITC15 | 3 | Novara | Italy | 57.3 | 5.9 |
| 71 | FR104 | 3 | Essonne | France | 56.3 | 5 |
| 72 | UKJ12 | 3 | Milton Keynes | United Kingdom | 56.2 | 9.5 |
| 73 | UKH23 | 3 | Hertfordshire | United Kingdom | 55.9 | 4.9 |
| 74 | UKK14 | 3 | Swindon | United Kingdom | 55.7 | 9.8 |
| 75 | UKG37 | 3 | Sandwell | United Kingdom | 55.4 | 7.9 |
| 76 | UKH25 | 3 | Central Bedfordshire | United Kingdom | 54.9 | 8.6 |
| 77 | UKI31 | 3 | Camden and City of London | United Kingdom | 55 | 11 |
| 78 | ITC44 | 3 | Sondrio | Italy | 54.2 | 8.6 |
| 79 | UKC14 | 3 | Durham CC | United Kingdom | 53.5 | 6 |
| 80 | ITH20 | 3 | Trento | Italy | 53.5 | 5.6 |
| 81 | UKD74 | 3 | Wirral | United Kingdom | 53.4 | 7.9 |
| 82 | UKJ28 | 3 | West Sussex (North East) | United Kingdom | 53.3 | 7.8 |
| 83 | UKH35 | 3 | West Essex | United Kingdom | 53.2 | 8.9 |
| 84 | ES413 | 3 | León | Spain | 53.2 | 5.1 |
| 85 | UKD12 | 3 | East Cumbria | United Kingdom | 52.7 | 7.2 |
| 86 | ITC42 | 3 | Como | Italy | 52.2 | 5.5 |
| 87 | UKD35 | 3 | Greater Manchester South East | United Kingdom | 51.7 | 6 |
| 88 | UKJ11 | 3 | Berkshire | United Kingdom | 51.1 | 5.6 |
| 89 | ITC33 | 3 | Genova | Italy | 51 | 4 |
| 90 | UKD37 | 3 | Greater Manchester North East | United Kingdom | 50.9 | 5.6 |
| 91 | UKM83 | 3 | Inverclyde, East Renfrewshire and Renfrewshire | United Kingdom | 50.5 | 6.5 |
| 92 | UKD73 | 3 | Sefton | United Kingdom | 50.3 | 7.6 |
| 93 | UKM75 | 3 | Edinburgh, City of | United Kingdom | 50.2 | 5.6 |
| 94 | UKE21 | 3 | York | United Kingdom | 50.2 | 9.7 |
| 95 | UKI61 | 3 | Bromley | United Kingdom | 50.2 | 8.2 |
| 96 | ITH53 | 3 | Reggio nell'Emilia | Italy | 50.1 | 4.9 |
| 97 | BE221 | 3 | Arr. Hasselt | Belgium | 50.1 | 6.6 |
| 98 | FR102 | 3 | Seine-et-Marne | France | 50 | 4.6 |
| 99 | UKJ43 | 3 | Kent Thames Gateway | United Kingdom | 49.9 | 6.9 |
| 100 | UKE41 | 3 | Bradford | United Kingdom | 49.9 | 5.4 |
| 101 | UKD62 | 3 | Cheshire East | United Kingdom | 49.9 | 6.8 |
| 102 | ES220 | 3 | Navarra | Spain | 49.5 | 5 |
| 103 | UKM81 | 3 | East Dunbartonshire, West Dunbartonshire and Helensburgh & Lomond | United Kingdom | 49 | 7.7 |
| 104 | UKE32 | 3 | Sheffield | United Kingdom | 48.7 | 6.5 |
| 105 | ITC20 | 3 | Valle d'Aosta/Vallée d'Aoste | Italy | 48.1 | 9.4 |
| 106 | NL421 | 3 | Noord-Limburg | Netherlands | 48 | 7.1 |
| 107 | ES230 | 3 | La Rioja | Spain | 47.8 | 7.2 |
| 108 | CH070 | 3 | Ticino | Switzerland | 47.8 | 6.7 |
| 109 | UKC23 | 3 | Sunderland | United Kingdom | 47.3 | 6.7 |
| 110 | UKC12 | 3 | South Teesside | United Kingdom | 47.1 | 6.4 |
| 111 | UKM82 | 3 | Glasgow City | United Kingdom | 46.7 | 5.6 |
| 112 | FR103 | 3 | Yvelines | France | 46.7 | 3.9 |
| 113 | UKG13 | 3 | Warwickshire | United Kingdom | 46.6 | 5.5 |
| 114 | UKH24 | 3 | Bedford | United Kingdom | 46 | 10 |
| 115 | UKF14 | 3 | Nottingham | United Kingdom | 45.9 | 9 |
| 116 | FR101 | 3 | Paris | France | 45.6 | 3.1 |
| 117 | UKG24 | 3 | Staffordshire CC | United Kingdom | 45.6 | 5.1 |
| 118 | UKF13 | 3 | South and West Derbyshire | United Kingdom | 45.4 | 6.7 |
| 119 | ITC11 | 3 | Torino | Italy | 45.1 | 2.5 |
| 120 | ITC17 | 3 | Asti | Italy | 45.1 | 6.6 |
| 121 | NL422 | 3 | Midden-Limburg | Netherlands | 45 | 7.4 |
| 122 | BE335 | 3 | Arr. Verviers - communes francophones | Belgium | 44.8 | 8.1 |
| 123 | UKG36 | 3 | Dudley | United Kingdom | 44.8 | 6.4 |
| 124 | ITH10 | 3 | Bolzano-Bozen | Italy | 44.7 | 6.2 |
| 125 | UKD36 | 3 | Greater Manchester North West | United Kingdom | 44.5 | 4.7 |
| 126 | UKK15 | 3 | Wiltshire CC | United Kingdom | 44.4 | 6.6 |
| 127 | ES412 | 3 | Burgos | Spain | 44.3 | 5.6 |
| 128 | UKG33 | 3 | Coventry | United Kingdom | 44.3 | 8 |
| 129 | FRE22 | 3 | Oise | France | 43.9 | 4.8 |
| 130 | UKJ13 | 3 | Buckinghamshire CC | United Kingdom | 43.6 | 6 |
| 131 | BE332 | 3 | Arr. Liège | Belgium | 43.5 | 4.8 |
| 132 | ITC14 | 3 | Verbano-Cusio-Ossola | Italy | 43.3 | 9 |
| 133 | NL423 | 3 | Zuid-Limburg | Netherlands | 43.2 | 4.9 |
| 134 | UKJ14 | 3 | Oxfordshire | United Kingdom | 43 | 5.6 |
| 135 | BE222 | 3 | Arr. Maaseik | Belgium | 42.9 | 9.2 |
| 136 | UKD61 | 3 | Warrington | United Kingdom | 42.9 | 7.5 |
| 137 | UKJ37 | 3 | North Hampshire | United Kingdom | 42.9 | 8.7 |
| 138 | UKD71 | 3 | East Merseyside | United Kingdom | 42.8 | 5.3 |
| 139 | UKC22 | 3 | Tyneside | United Kingdom | 42.7 | 4.7 |
| 140 | UKF11 | 3 | Derby | United Kingdom | 42.7 | 7.9 |
| 141 | ITC31 | 3 | Imperia | Italy | 42.5 | 6.8 |
| 142 | FRF34 | 3 | Vosges | France | 42.3 | 7.5 |
| 143 | UKL22 | 3 | Cardiff and Vale of Glamorgan | United Kingdom | 42.2 | 6.8 |
| 144 | UKH36 | 3 | Heart of Essex | United Kingdom | 42.2 | 7.6 |
| 145 | UKM95 | 3 | South Lanarkshire | United Kingdom | 41.6 | 6.3 |
| 146 | UKE31 | 3 | Barnsley, Doncaster and Rotherham | United Kingdom | 41.5 | 4.5 |
| 147 | UKC13 | 3 | Darlington | United Kingdom | 41 | 10 |
| 148 | BE223 | 3 | Arr. Tongeren | Belgium | 40.7 | 8.8 |
| 149 | ITH59 | 3 | Rimini | Italy | 40.4 | 5.4 |
| 150 | UKM66 | 3 | Shetland Islands | United Kingdom | 40 | 28 |
| 151 | UKH37 | 3 | Essex Thames Gateway | United Kingdom | 40.3 | 7 |
| 152 | ES243 | 3 | Zaragoza | Spain | 40.2 | 3.9 |
| 153 | FRF11 | 3 | Bas-Rhin | France | 40 | 4 |
| 154 | UKE44 | 3 | Calderdale and Kirklees | United Kingdom | 40 | 5.3 |
| 155 | UKE42 | 3 | Leeds | United Kingdom | 40 | 5.2 |
| 156 | ITC41 | 3 | Varese | Italy | 40 | 3.6 |
| 157 | UKF22 | 3 | Leicestershire CC and Rutland | United Kingdom | 39.6 | 5 |
| 158 | UKG12 | 3 | Worcestershire | United Kingdom | 38.9 | 5.3 |
| 159 | NL212 | 3 | Zuidwest-Overijssel | Netherlands | 38.9 | 9.9 |
| 160 | UKF25 | 3 | North Northamptonshire | United Kingdom | 38.7 | 5.6 |
| 161 | NL412 | 3 | Midden-Noord-Brabant | Netherlands | 38.7 | 5.5 |
| 162 | UKL15 | 3 | Central Valleys | United Kingdom | 38.6 | 6.8 |
| 163 | UKN06 | 3 | Belfast | United Kingdom | 38.5 | 6.7 |
| 164 | UKF24 | 3 | West Northamptonshire | United Kingdom | 38.4 | 6.5 |
| 165 | UKJ35 | 3 | South Hampshire | United Kingdom | 38.4 | 5.9 |
| 166 | UKE45 | 3 | Wakefield | United Kingdom | 38.4 | 5.4 |
| 167 | FRC21 | 3 | Doubs | France | 38.4 | 6.3 |
| 168 | UKK13 | 3 | Gloucestershire | United Kingdom | 38.3 | 6.3 |
| 169 | UKD47 | 3 | Chorley and West Lancashire | United Kingdom | 38.2 | 7.3 |
| 170 | BE342 | 3 | Arr. Bastogne | Belgium | 38 | 15 |
| 171 | BE336 | 3 | Bezirk Verviers - Deutschsprachige Gemeinschaft | Belgium | 38 | 13 |
| 172 | UKD63 | 3 | Cheshire West and Chester | United Kingdom | 37.7 | 6 |
| 173 | UKM71 | 3 | Angus and Dundee City | United Kingdom | 37.5 | 6.6 |
| 174 | UKK12 | 3 | Bath and North East Somerset, North Somerset and South Gloucestershire | United Kingdom | 37.5 | 5.5 |
| 175 | UKD11 | 3 | West Cumbria | United Kingdom | 37.5 | 7.5 |
| 176 | UKH14 | 3 | Suffolk | United Kingdom | 37.4 | 4.7 |
| 177 | UKM73 | 3 | East Lothian and Midlothian | United Kingdom | 37.2 | 7.3 |
| 178 | UKJ32 | 3 | Southampton | United Kingdom | 37.1 | 7.8 |
| 179 | UKD46 | 3 | East Lancashire | United Kingdom | 37 | 6.1 |
| 180 | NL414 | 3 | Zuidoost-Noord-Brabant | Netherlands | 36.9 | 5 |
| 181 | UKD41 | 3 | Blackburn with Darwen | United Kingdom | 36.6 | 9.8 |
| 182 | ES242 | 3 | Teruel | Spain | 36.6 | 8.9 |
| 183 | UKE22 | 3 | North Yorkshire CC | United Kingdom | 36.5 | 5.3 |
| 184 | BE334 | 3 | Arr. Waremme | Belgium | 36 | 13 |
| 185 | UKJ36 | 3 | Central Hampshire | United Kingdom | 36.3 | 5.3 |
| 186 | UKH31 | 3 | Southend-on-Sea | United Kingdom | 36.2 | 9.1 |
| 187 | UKE12 | 3 | East Riding of Yorkshire | United Kingdom | 36.1 | 6 |
| 188 | BE343 | 3 | Arr. Marche-en-Famenne | Belgium | 36 | 14 |
| 189 | UKD42 | 3 | Blackpool | United Kingdom | 35.8 | 8.4 |
| 190 | EL532 | 3 | Kastoria | Greece | 36 | 14 |
| 191 | ES414 | 3 | Palencia | Spain | 35.6 | 7.9 |
| 192 | ITC32 | 3 | Savona | Italy | 35.4 | 5.8 |
| 193 | UKJ44 | 3 | East Kent | United Kingdom | 35.1 | 5.5 |
| 194 | BE352 | 3 | Arr. Namur | Belgium | 35 | 6.2 |
| 195 | UKM84 | 3 | North Lanarkshire | United Kingdom | 34.9 | 5.7 |
| 196 | NL224 | 3 | Zuidwest-Gelderland | Netherlands | 34.8 | 8.5 |
| 197 | UKJ27 | 3 | West Sussex (South West) | United Kingdom | 34.7 | 6.2 |
| 198 | FRE21 | 3 | Aisne | France | 34.6 | 5.5 |
| 199 | ITI11 | 3 | Massa-Carrara | Italy | 34.6 | 6.7 |
| 200 | BE321 | 3 | Arr. Ath | Belgium | 35 | 11 |
| 201 | ES512 | 3 | Girona | Spain | 34.1 | 4.9 |
| 202 | FRF33 | 3 | Moselle | France | 34 | 3.6 |
| 203 | CH013 | 3 | Genève | Switzerland | 34 | 5.6 |
| 204 | ITC34 | 3 | La Spezia | Italy | 33.9 | 6.5 |
| 205 | UKG11 | 3 | Herefordshire, County of | United Kingdom | 33.8 | 7.9 |
| 206 | UKM76 | 3 | Falkirk | United Kingdom | 33.7 | 8.9 |
| 207 | UKG21 | 3 | Telford and Wrekin | United Kingdom | 33.4 | 9.2 |
| 208 | UKG23 | 3 | Stoke-on-Trent | United Kingdom | 33.2 | 7.9 |
| 209 | ES419 | 3 | Zamora | Spain | 32.9 | 6.6 |
| 210 | UKJ41 | 3 | Medway | United Kingdom | 32.9 | 8 |
| 211 | UKC11 | 3 | Hartlepool and Stockton-on-Tees | United Kingdom | 32.9 | 7.4 |
| 212 | BE242 | 3 | Arr. Leuven | Belgium | 32.8 | 6.1 |
| 213 | UKH12 | 3 | Cambridgeshire CC | United Kingdom | 32.8 | 5.8 |
| 214 | UKN13 | 3 | Antrim and Newtownabbey | United Kingdom | 32.7 | 9.3 |
| 215 | UKL21 | 3 | Monmouthshire and Newport | United Kingdom | 32.6 | 8.1 |
| 216 | SE214 | 3 | Gotlands län | Sweden | 33 | 15 |
| 217 | ITH31 | 3 | Verona | Italy | 32.5 | 3.8 |
| 218 | UKD45 | 3 | Mid Lancashire | United Kingdom | 32.4 | 6 |
| 219 | UKM78 | 3 | West Lothian | United Kingdom | 32.3 | 9 |
| 220 | SE122 | 3 | Södermanlands län | Sweden | 31.9 | 6.1 |
| 221 | UKH34 | 3 | Essex Haven Gateway | United Kingdom | 31.8 | 6.1 |
| 222 | BE353 | 3 | Arr. Philippeville | Belgium | 32 | 13 |
| 223 | UKK11 | 3 | Bristol, City of | United Kingdom | 31.6 | 6.7 |
| 224 | SE312 | 3 | Dalarnas län | Sweden | 31.5 | 6.7 |
| 225 | UKJ45 | 3 | Mid Kent | United Kingdom | 31.5 | 6.4 |
| 226 | ES213 | 3 | Bizkaia | Spain | 31.5 | 3.5 |
| 227 | UKF12 | 3 | East Derbyshire | United Kingdom | 31.5 | 6.5 |
| 228 | BE324 | 3 | Arr. Mouscron | Belgium | 31 | 12 |
| 229 | UKM93 | 3 | East Ayrshire and North Ayrshire mainland | United Kingdom | 31.4 | 6.1 |
| 230 | NL211 | 3 | Noord-Overijssel | Netherlands | 31.3 | 6.5 |
| 231 | UKK21 | 3 | Bournemouth and Poole | United Kingdom | 31.3 | 7.1 |
| 232 | ITH55 | 3 | Bologna | Italy | 31.3 | 3.3 |
| 233 | ITF13 | 3 | Pescara | Italy | 31.2 | 6.3 |
| 234 | UKL16 | 3 | Gwent Valleys | United Kingdom | 31.2 | 6.3 |
| 235 | BE322 | 3 | Arr. Charleroi | Belgium | 30.9 | 6.4 |
| 236 | BE231 | 3 | Arr. Aalst | Belgium | 30.8 | 6.8 |
| 237 | UKF16 | 3 | South Nottinghamshire | United Kingdom | 30.8 | 6.3 |
| 238 | BE254 | 3 | Arr. Kortrijk | Belgium | 30.7 | 6 |
| 239 | ITH54 | 3 | Modena | Italy | 30.6 | 4.1 |
| 240 | UKC21 | 3 | Northumberland | United Kingdom | 30.3 | 6.6 |
| 241 | UKK22 | 3 | Dorset CC | United Kingdom | 30.3 | 6.2 |
| 242 | RS225 | 3 | Nišavska oblast | Serbia | 30.3 | 5.5 |
| 243 | UKH16 | 3 | North and West Norfolk | United Kingdom | 30.2 | 6.8 |
| 244 | UKJ21 | 3 | Brighton and Hove | United Kingdom | 29.9 | 8.1 |
| 245 | PT16D | 3 | Região de Aveiro | Portugal | 29.8 | 5.6 |
| 246 | SE125 | 3 | Västmanlands län | Sweden | 29.6 | 6.2 |
| 247 | UKL18 | 3 | Swansea | United Kingdom | 29.5 | 7.4 |
| 248 | ES514 | 3 | Tarragona | Spain | 29.5 | 4.3 |
| 249 | UKE11 | 3 | Kingston upon Hull, City of | United Kingdom | 29.5 | 8 |
| 250 | BE344 | 3 | Arr. Neufchâteau | Belgium | 29 | 13 |
| 251 | BE257 | 3 | Arr. Tielt | Belgium | 29 | 11 |
| 252 | UKM65 | 3 | Orkney Islands | United Kingdom | 29 | 19 |
| 253 | NL221 | 3 | Veluwe | Netherlands | 28.9 | 4.8 |
| 254 | UKG22 | 3 | Shropshire CC | United Kingdom | 28.8 | 5.9 |
| 255 | UKF15 | 3 | North Nottinghamshire | United Kingdom | 28.7 | 5.8 |
| 256 | ES513 | 3 | Lleida | Spain | 28.6 | 5.5 |
| 257 | UKJ46 | 3 | West Kent | United Kingdom | 28.6 | 5.9 |
| 258 | BE232 | 3 | Arr. Dendermonde | Belgium | 28.5 | 7.9 |
| 259 | ITI33 | 3 | Macerata | Italy | 28.5 | 5.7 |
| 260 | UKM94 | 3 | South Ayrshire | United Kingdom | 28.4 | 8 |
| 261 | FRF32 | 3 | Meuse | France | 28.4 | 8 |
| 262 | UKM61 | 3 | Caithness & Sutherland and Ross & Cromarty | United Kingdom | 28 | 11 |
| 263 | UKH11 | 3 | Peterborough | United Kingdom | 28.1 | 8.6 |
| 264 | ITC16 | 3 | Cuneo | Italy | 27.6 | 4.7 |
| 265 | ITH44 | 3 | Trieste | Italy | 27.6 | 5.6 |
| 266 | BE325 | 3 | Arr. Soignies | Belgium | 27.4 | 8.6 |
| 267 | FRK26 | 3 | Rhône | France | 27.4 | 3.2 |
| 268 | FRC23 | 3 | Haute-Saône | France | 27.1 | 7.1 |
| 269 | NL329 | 3 | Groot-Amsterdam | Netherlands | 27 | 3.7 |
| 270 | ES241 | 3 | Huesca | Spain | 26.5 | 6.6 |
| 271 | UKM77 | 3 | Perth & Kinross and Stirling | United Kingdom | 26.3 | 5.9 |
| 272 | BE258 | 3 | Arr. Veurne | Belgium | 26 | 11 |
| 273 | NL328 | 3 | Alkmaar en omgeving | Netherlands | 26 | 6.9 |
| 274 | FRB03 | 3 | Indre | France | 25.5 | 5.4 |
| 275 | AT334 | 3 | Tiroler Oberland | Austria | 25 | 12 |
| 276 | BE213 | 3 | Arr. Turnhout | Belgium | 25.1 | 5.3 |
| 277 | FRF24 | 3 | Haute-Marne | France | 25.1 | 8.1 |
| 278 | CH011 | 3 | Vaud | Switzerland | 25 | 4.8 |
| 279 | SE123 | 3 | Östergötlands län | Sweden | 24.7 | 5.1 |
| 280 | PT112 | 3 | Cávado | Portugal | 24.7 | 5.9 |
| 281 | ITH58 | 3 | Forlì-Cesena | Italy | 24.7 | 5.1 |
| 282 | PT11D | 3 | Douro | Portugal | 24.7 | 7.5 |
| 283 | NL323 | 3 | IJmond | Netherlands | 24.4 | 7.5 |
| 284 | SE121 | 3 | Uppsala län | Sweden | 24 | 6.7 |
| 285 | FRK28 | 3 | Haute-Savoie | France | 24 | 4.4 |
| 286 | BE310 | 3 | Arr. Nivelles | Belgium | 24 | 6.1 |
| 287 | ITG16 | 3 | Enna | Italy | 23.9 | 7.5 |
| 288 | BE253 | 3 | Arr. Ieper | Belgium | 23.8 | 9.6 |
| 289 | SE211 | 3 | Jönköpings län | Sweden | 23.8 | 6.4 |
| 290 | UKL23 | 3 | Flintshire and Wrexham | United Kingdom | 23.8 | 5.7 |
| 291 | UKD44 | 3 | Lancaster and Wyre | United Kingdom | 23.7 | 6.1 |
| 292 | BE251 | 3 | Arr. Brugge | Belgium | 23.7 | 6.2 |
| 293 | UKN12 | 3 | Causeway Coast and Glens | United Kingdom | 23.7 | 8.8 |
| 294 | FRB02 | 3 | Eure-et-Loir | France | 23.7 | 4.9 |
| 295 | FRF23 | 3 | Marne | France | 23.5 | 4.9 |
| 296 | ES614 | 3 | Granada | Spain | 23.4 | 4.3 |
| 297 | UKH17 | 3 | Breckland and South Norfolk | United Kingdom | 23.1 | 7 |
| 298 | ES522 | 3 | Castellón / Castelló | Spain | 23.1 | 4.9 |
| 299 | UKM50 | 3 | Aberdeen City and Aberdeenshire | United Kingdom | 23.1 | 5 |
| 300 | UKN09 | 3 | Ards and North Down | United Kingdom | 23 | 7.6 |
| 301 | UKL24 | 3 | Powys | United Kingdom | 22.9 | 8.2 |
| 302 | ITI32 | 3 | Ancona | Italy | 22.6 | 4.1 |
| 303 | NL324 | 3 | Agglomeratie Haarlem | Netherlands | 22.5 | 6.4 |
| 304 | FRC22 | 3 | Jura | France | 22.4 | 7.1 |
| 305 | UKN16 | 3 | Fermanagh and Omagh | United Kingdom | 22 | 11 |
| 306 | NL325 | 3 | Zaanstreek | Netherlands | 22.1 | 8.3 |
| 307 | BE241 | 3 | Arr. Halle-Vilvoorde | Belgium | 22.1 | 4.7 |
| 308 | BE256 | 3 | Arr. Roeselare | Belgium | 21.9 | 8 |
| 309 | ITF46 | 3 | Foggia | Italy | 21.7 | 3.9 |
| 310 | CH063 | 3 | Schwyz | Switzerland | 22 | 10 |
| 311 | CH064 | 3 | Obwalden | Switzerland | 22 | 19 |
| 312 | UKM63 | 3 | Lochaber, Skye & Lochalsh, Arran & Cumbrae and Argyll & Bute | United Kingdom | 21.5 | 9.7 |
| 313 | ITH34 | 3 | Treviso | Italy | 21.5 | 3.8 |
| 314 | ES212 | 3 | Gipuzkoa | Spain | 21.5 | 4 |
| 315 | AL014 | 3 | Lezhë | Albania | 21.5 | 9.5 |
| 316 | ES130 | 3 | Cantabria | Spain | 21.2 | 4.1 |
| 317 | ITH32 | 3 | Vicenza | Italy | 21.2 | 3.5 |
| 318 | BE211 | 3 | Arr. Antwerpen | Belgium | 21.1 | 4.1 |
| 319 | FRF31 | 3 | Meurthe-et-Moselle | France | 21 | 4.2 |
| 320 | ITF12 | 3 | Teramo | Italy | 21 | 5.9 |
| 321 | UKL17 | 3 | Bridgend and Neath Port Talbot | United Kingdom | 21 | 6.6 |
| 322 | UKK23 | 3 | Somerset | United Kingdom | 20.7 | 4.9 |
| 323 | UKN14 | 3 | Lisburn and Castlereagh | United Kingdom | 20.7 | 9.6 |
| 324 | BE236 | 3 | Arr. Sint-Niklaas | Belgium | 20.6 | 6.6 |
| 325 | NL33C | 3 | Groot-Rijnmond | Netherlands | 20.3 | 3.2 |
| 326 | BE233 | 3 | Arr. Eeklo | Belgium | 20 | 11 |
| 327 | NL332 | 3 | Agglomeratie's-Gravenhage | Netherlands | 20.2 | 3.8 |
| 328 | RS229 | 3 | Toplička oblast | Serbia | 20.1 | 8.3 |
| 329 | UKJ31 | 3 | Portsmouth | United Kingdom | 19.2 | 8.6 |
| 330 | ITH35 | 3 | Venezia | Italy | 19.2 | 3.3 |
| 331 | ITI14 | 3 | Firenze | Italy | 19.1 | 3.4 |
| 332 | UKM91 | 3 | Scottish Borders | United Kingdom | 18.9 | 8.1 |
| 333 | UKN07 | 3 | Armagh City, Banbridge and Craigavon | United Kingdom | 18.8 | 8.6 |
| 334 | PT11A | 3 | Área Metropolitana do Porto | Portugal | 18.7 | 2.9 |
| 335 | ITH41 | 3 | Pordenone | Italy | 18.5 | 6.4 |
| 336 | ITF44 | 3 | Brindisi | Italy | 18.5 | 5.6 |
| 337 | UKH15 | 3 | Norwich and East Norfolk | United Kingdom | 18.4 | 6.3 |
| 338 | ITF62 | 3 | Crotone | Italy | 18.4 | 9.4 |
| 339 | BE212 | 3 | Arr. Mechelen | Belgium | 18.3 | 5.5 |
| 340 | ITF34 | 3 | Avellino | Italy | 18.2 | 5.1 |
| 341 | FRC24 | 3 | Territoire de Belfort | France | 18.1 | 6.2 |
| 342 | FRE23 | 3 | Somme | France | 18 | 4.1 |
| 343 | FI1D5 | 3 | Keski-Pohjanmaa | Finland | 18 | 12 |
| 344 | ES120 | 3 | Asturias | Spain | 18 | 2.8 |
| 345 | CH012 | 3 | Valais | Switzerland | 17.9 | 7.2 |
| 346 | NL310 | 3 | Utrecht | Netherlands | 17.9 | 3.4 |
| 347 | UKN08 | 3 | Newry, Mourne and Down | United Kingdom | 17.8 | 8.5 |
| 348 | SE124 | 3 | Örebro län | Sweden | 17.8 | 6 |
| 349 | ITG25 | 3 | Sassari | Italy | 17.7 | 5.4 |
| 350 | PT11E | 3 | Terras de Trás-os-Montes | Portugal | 17.7 | 7.8 |
| 351 | ITI35 | 3 | Fermo | Italy | 17.7 | 6.6 |
| 352 | NL33B | 3 | Oost-Zuid-Holland | Netherlands | 17.5 | 6.2 |
| 353 | SE321 | 3 | Västernorrlands län | Sweden | 17.3 | 6.2 |
| 354 | FRK25 | 3 | Loire | France | 17.3 | 3.6 |
| 355 | FRC11 | 3 | Côte-d’Or | France | 17.3 | 4 |
| 356 | UKJ22 | 3 | East Sussex CC | United Kingdom | 17.2 | 5 |
| 357 | NL411 | 3 | West-Noord-Brabant | Netherlands | 17.2 | 4.2 |
| 358 | SE322 | 3 | Jämtlands län | Sweden | 17 | 8.3 |
| 359 | BE326 | 3 | Arr. Thuin | Belgium | 16.8 | 7.9 |
| 360 | NL226 | 3 | Arnhem/Nijmegen | Netherlands | 16.8 | 4.2 |
| 361 | UKN11 | 3 | Mid Ulster | United Kingdom | 16.8 | 9.9 |
| 362 | CH054 | 3 | Appenzell Innerrhoden | Switzerland | 17 | 25 |
| 363 | ITH33 | 3 | Belluno | Italy | 16.6 | 6.5 |
| 364 | BE235 | 3 | Arr. Oudenaarde | Belgium | 16.5 | 9.5 |
| 365 | UKF30 | 3 | Lincolnshire | United Kingdom | 16.5 | 4 |
| 366 | ITF14 | 3 | Chieti | Italy | 16.5 | 4.7 |
| 367 | SE232 | 3 | Västra Götalands län | Sweden | 16.4 | 3 |
| 368 | RO215 | 3 | Suceava | Romania | 16.4 | 3.8 |
| 369 | ES521 | 3 | Alicante / Alacant | Spain | 16.3 | 2.9 |
| 370 | CH025 | 3 | Jura | Switzerland | 16 | 12 |
| 371 | FRK22 | 3 | Ardèche | France | 16.2 | 5 |
| 372 | ES617 | 3 | Málaga | Spain | 16.2 | 2.8 |
| 373 | ES523 | 3 | Valencia / València | Spain | 16.1 | 2.3 |
| 374 | NL33A | 3 | Zuidoost-Zuid-Holland | Netherlands | 16.1 | 5.4 |
| 375 | UKM72 | 3 | Clackmannanshire and Fife | United Kingdom | 16 | 4.8 |
| 376 | FRD21 | 3 | Eure | France | 16 | 4.4 |
| 377 | UKN15 | 3 | Mid and East Antrim | United Kingdom | 16 | 8.5 |
| 378 | PT16E | 3 | Região de Coimbra | Portugal | 16 | 4.5 |
| 379 | ITI42 | 3 | Rieti | Italy | 15.9 | 7.5 |
| 380 | AT221 | 3 | Graz | Austria | 15.9 | 4.9 |
| 381 | BE234 | 3 | Arr. Gent | Belgium | 15.7 | 4.4 |
| 382 | UKK42 | 3 | Torbay | United Kingdom | 15.7 | 7.6 |
| 383 | ITH37 | 3 | Rovigo | Italy | 15.7 | 5.2 |
| 384 | ES630 | 3 | Ceuta | Spain | 16 | 13 |
| 385 | BE345 | 3 | Arr. Virton | Belgium | 16 | 14 |
| 386 | SE213 | 3 | Kalmar län | Sweden | 15.6 | 6.9 |
| 387 | FRF22 | 3 | Aube | France | 15.4 | 5.9 |
| 388 | ITF45 | 3 | Lecce | Italy | 15.1 | 3.5 |
| 389 | EL624 | 3 | Lefkada | Greece | 15 | 17 |
| 390 | FRC13 | 3 | Saône-et-Loire | France | 14.9 | 3.9 |
| 391 | UKK41 | 3 | Plymouth | United Kingdom | 14.9 | 6.4 |
| 392 | ITI16 | 3 | Livorno | Italy | 14.7 | 5.2 |
| 393 | NL333 | 3 | Delft en Westland | Netherlands | 14.7 | 7.6 |
| 394 | ITF47 | 3 | Bari | Italy | 14.6 | 3.2 |
| 395 | EL621 | 3 | Zakynthos | Greece | 15 | 15 |
| 396 | NL341 | 3 | Zeeuwsch-Vlaanderen | Netherlands | 14.6 | 8.6 |
| 397 | AT113 | 3 | Südburgenland | Austria | 14.6 | 8.6 |
| 398 | CH022 | 3 | Freiburg | Switzerland | 14.5 | 7.2 |
| 399 | PT185 | 3 | Lezíria do Tejo | Portugal | 14.5 | 5.6 |
| 400 | ITH56 | 3 | Ferrara | Italy | 14.4 | 4.6 |
| 401 | PT184 | 3 | Baixo Alentejo | Portugal | 14.2 | 7.4 |
| 402 | FRM01 | 3 | Corse-du-Sud | France | 14 | 8.6 |
| 403 | ES431 | 3 | Badajoz | Spain | 13.9 | 3.6 |
| 404 | AL032 | 3 | Fier | Albania | 13.9 | 6.6 |
| 405 | ITH36 | 3 | Padova | Italy | 13.9 | 3.2 |
| 406 | UKL11 | 3 | Isle of Anglesey | United Kingdom | 14 | 11 |
| 407 | ITG2B | 3 | Medio Campidano | Italy | 13.8 | 9.3 |
| 408 | FI1D8 | 3 | Kainuu | Finland | 13.7 | 9.5 |
| 409 | FRB05 | 3 | Loir-et-Cher | France | 13.7 | 5 |
| 410 | ES616 | 3 | Jaén | Spain | 13.7 | 3.9 |
| 411 | BE331 | 3 | Arr. Huy | Belgium | 13.7 | 8.8 |
| 412 | AT224 | 3 | Oststeiermark | Austria | 13.6 | 6.5 |
| 413 | SE313 | 3 | Gävleborgs län | Sweden | 13.4 | 5.8 |
| 414 | SE212 | 3 | Kronobergs län | Sweden | 13.3 | 7.5 |
| 415 | EL512 | 3 | Xanthi | Greece | 13.3 | 8.5 |
| 416 | ITI13 | 3 | Pistoia | Italy | 13.3 | 4.9 |
| 417 | FRL04 | 3 | Bouches-du-Rhône | France | 13.3 | 2.4 |
| 418 | FI1B1 | 3 | Helsinki-Uusimaa | Finland | 13.2 | 3 |
| 419 | FRE11 | 3 | Nord | France | 13.2 | 2.8 |
| 420 | CH024 | 3 | Neuchâtel | Switzerland | 13.1 | 7.6 |
| 421 | FRK23 | 3 | Drôme | France | 13.1 | 4.1 |
| 422 | CH023 | 3 | Solothurn | Switzerland | 13 | 6.4 |
| 423 | NL337 | 3 | Agglomeratie Leiden en Bollenstreek | Netherlands | 13 | 4.8 |
| 424 | ITF22 | 3 | Campobasso | Italy | 12.9 | 6.2 |
| 425 | AL015 | 3 | Shkodër | Albania | 12.8 | 7.3 |
| 426 | UKM64 | 3 | Na h-Eileanan Siar (Western Isles) | United Kingdom | 13 | 19 |
| 427 | ITI17 | 3 | Pisa | Italy | 12.7 | 4.4 |
| 428 | CH032 | 3 | Basel-Landschaft | Switzerland | 12.6 | 6.4 |
| 429 | UKK43 | 3 | Devon CC | United Kingdom | 12.6 | 4.2 |
| 430 | SE332 | 3 | Norrbottens län | Sweden | 12.6 | 5.6 |
| 431 | NL230 | 3 | Flevoland | Netherlands | 12.5 | 6.4 |
| 432 | ES113 | 3 | Ourense | Spain | 12.5 | 4.5 |
| 433 | EL526 | 3 | Serres | Greece | 12.4 | 6.4 |
| 434 | FRK27 | 3 | Savoie | France | 12.4 | 5 |
| 435 | UKE13 | 3 | North and North East Lincolnshire | United Kingdom | 12.4 | 5.3 |
| 436 | ITF65 | 3 | Reggio di Calabria | Italy | 12.3 | 4.5 |
| 437 | PT181 | 3 | Alentejo Litoral | Portugal | 12.2 | 8.8 |
| 438 | ITF48 | 3 | Barletta-Andria-Trani | Italy | 12.2 | 5.3 |
| 439 | PT11C | 3 | Tâmega e Sousa | Portugal | 12 | 5.5 |
| 440 | EE004 | 3 | Lääne-Eesti | Estonia | 11.9 | 7.4 |
| 441 | ES532 | 3 | Mallorca | Spain | 11.8 | 3.7 |
| 442 | UKM92 | 3 | Dumfries & Galloway | United Kingdom | 11.6 | 6.7 |
| 443 | EL434 | 3 | Chania | Greece | 11.5 | 7.4 |
| 444 | NO032 | 3 | Buskerud | Norway | 11.4 | 6.4 |
| 445 | EL633 | 3 | Ileia | Greece | 11.2 | 7.2 |
| 446 | UKL14 | 3 | South West Wales | United Kingdom | 11.2 | 4.5 |
| 447 | ITI12 | 3 | Lucca | Italy | 11.2 | 4.2 |
| 448 | RO421 | 3 | Arad | Romania | 11.1 | 3.9 |
| 449 | AT126 | 3 | Wiener Umland/Nordteil | Austria | 11 | 5.3 |
| 450 | CY000 | 3 | Kypros | Cyprus | 11 | 4.2 |
| 451 | NO011 | 3 | Oslo | Norway | 11 | 4.6 |
| 452 | ITG2C | 3 | Carbonia-Iglesias | Italy | 10.8 | 7.9 |
| 453 | FRK24 | 3 | Isère | France | 10.7 | 2.9 |
| 454 | UKJ34 | 3 | Isle of Wight | United Kingdom | 10.5 | 7.3 |
| 455 | NL342 | 3 | Overig Zeeland | Netherlands | 10.5 | 5.9 |
| 456 | ITG19 | 3 | Siracusa | Italy | 10.5 | 4.5 |
| 457 | PT16H | 3 | Beira Baixa | Portugal | 10.4 | 8.1 |
| 458 | BE327 | 3 | Arr. Tournai | Belgium | 10.3 | 7 |
| 459 | FRK21 | 3 | Ain | France | 10.2 | 4.4 |
| 460 | AT213 | 3 | Unterkärnten | Austria | 10.2 | 6.6 |
| 461 | LT011 | 3 | Vilniaus apskritis | Lithuania | 10.1 | 3.4 |
| 462 | LT022 | 3 | Kauno apskritis | Lithuania | 10 | 3.7 |
| 463 | RS215 | 3 | Pomoravska oblast | Serbia | 9.9 | 5.5 |
| 464 | AT335 | 3 | Tiroler Unterland | Austria | 9.9 | 6.6 |
| 465 | PT200 | 3 | Região Autónoma dos Açores | Portugal | 9.9 | 6.4 |
| 466 | PT187 | 3 | Alentejo Central | Portugal | 9.9 | 6.5 |
| 467 | UKL12 | 3 | Gwynedd | United Kingdom | 9.9 | 7.6 |
| 468 | EL632 | 3 | Achaia | Greece | 9.8 | 5.8 |
| 469 | CH031 | 3 | Basel-Stadt | Switzerland | 9.7 | 6.2 |
| 470 | EL613 | 3 | Magnisia, Sporades | Greece | 9.7 | 6.1 |
| 471 | UKK30 | 3 | Cornwall and Isles of Scilly | United Kingdom | 9.7 | 4.6 |
| 472 | PT16G | 3 | Viseu Dão Lafões | Portugal | 9.7 | 5.8 |
| 473 | NL225 | 3 | Achterhoek | Netherlands | 9.6 | 4.7 |
| 474 | FRJ12 | 3 | Gard | France | 9.6 | 3.9 |
| 475 | FRC14 | 3 | Yonne | France | 9.5 | 4.6 |
| 476 | BG311 | 3 | Vidin | Bulgaria | 9.5 | 7.3 |
| 477 | PT16I | 3 | Médio Tejo | Portugal | 9.5 | 5.6 |
| 478 | EL305 | 3 | Anatoliki Attiki | Greece | 9.5 | 4.5 |
| 479 | PT119 | 3 | Ave | Portugal | 9.4 | 5 |
| 480 | ITG28 | 3 | Oristano | Italy | 9.3 | 5.8 |
| 481 | FRF21 | 3 | Ardennes | France | 9.3 | 6 |
| 482 | AL022 | 3 | Tiranë | Albania | 9.3 | 4.6 |
| 483 | PT170 | 3 | Área Metropolitana de Lisboa | Portugal | 9.2 | 2.2 |
| 484 | SE224 | 3 | Skåne län | Sweden | 9.1 | 3.4 |
| 485 | ES111 | 3 | A Coruña | Spain | 9 | 2.8 |
| 486 | ITI1A | 3 | Grosseto | Italy | 9 | 5.8 |
| 487 | ITH57 | 3 | Ravenna | Italy | 9 | 4.6 |
| 488 | FRD12 | 3 | Manche | France | 9 | 4 |
| 489 | ITG13 | 3 | Messina | Italy | 9 | 4.1 |
| 490 | ITF52 | 3 | Matera | Italy | 8.9 | 6.8 |
| 491 | NL321 | 3 | Kop van Noord-Holland | Netherlands | 8.9 | 5.3 |
| 492 | ITF61 | 3 | Cosenza | Italy | 8.9 | 3.7 |
| 493 | HU233 | 3 | Tolna | Hungary | 8.8 | 5.2 |
| 494 | ES618 | 3 | Sevilla | Spain | 8.8 | 2.6 |
| 495 | EL515 | 3 | Thasos, Kavala | Greece | 8.8 | 6.8 |
| 496 | ES612 | 3 | Cádiz | Spain | 8.8 | 3.4 |
| 497 | ITI22 | 3 | Terni | Italy | 8.7 | 5.4 |
| 498 | RO423 | 3 | Hunedoara | Romania | 8.7 | 3.8 |
| 499 | FI1C5 | 3 | Etelä-Karjala | Finland | 8.7 | 6.9 |
| 500 | ITI34 | 3 | Ascoli Piceno | Italy | 8.7 | 6.4 |
| 501 | FRG04 | 3 | Sarthe | France | 8.7 | 4.1 |
| 502 | UKM62 | 3 | Inverness & Nairn and Moray, Badenoch & Strathspey | United Kingdom | 8.7 | 6.5 |
| 503 | EL514 | 3 | Drama | Greece | 8.6 | 8 |
| 504 | ITH42 | 3 | Udine | Italy | 8.6 | 3.8 |
| 505 | AT130 | 3 | Wien | Austria | 8.5 | 2.9 |
| 506 | RO415 | 3 | Vâlcea | Romania | 8.4 | 6 |
| 507 | SE311 | 3 | Värmlands län | Sweden | 8.4 | 5.7 |
| 508 | EL612 | 3 | Larisa | Greece | 8.4 | 5.8 |
| 509 | NL213 | 3 | Twente | Netherlands | 8.3 | 4.3 |
| 510 | ES613 | 3 | Córdoba | Spain | 8.3 | 3.7 |
| 511 | RS224 | 3 | Jablanička oblast | Serbia | 8.2 | 5.6 |
| 512 | EL411 | 3 | Lesvos, Limnos | Greece | 8.2 | 8.5 |
| 513 | AL021 | 3 | Elbasan | Albania | 8.1 | 6.3 |
| 514 | AT222 | 3 | Liezen | Austria | 8.1 | 9.1 |
| 515 | LT023 | 3 | Klaipėdos apskritis | Lithuania | 8.1 | 4.4 |
| 516 | AT124 | 3 | Waldviertel | Austria | 8.1 | 5.8 |
| 517 | ES620 | 3 | Murcia | Spain | 8 | 3.1 |
| 518 | FRE12 | 3 | Pas-de-Calais | France | 8 | 3 |
| 519 | ITF43 | 3 | Taranto | Italy | 8 | 4 |
| 520 | NL327 | 3 | Het Gooi en Vechtstreek | Netherlands | 8 | 5.5 |
| 521 | ITF21 | 3 | Isernia | Italy | 7.9 | 8.4 |
| 522 | DK012 | 3 | Københavns omegn | Denmark | 7.9 | 4.1 |
| 523 | ES615 | 3 | Huelva | Spain | 7.8 | 4.8 |
| 524 | BE255 | 3 | Arr. Oostende | Belgium | 7.8 | 6 |
| 525 | EL521 | 3 | Imathia | Greece | 7.8 | 7.1 |
| 526 | BG343 | 3 | Yambol | Bulgaria | 7.8 | 6.1 |
| 527 | AT121 | 3 | Mostviertel-Eisenwurzen | Austria | 7.7 | 5.4 |
| 528 | ITF51 | 3 | Potenza | Italy | 7.7 | 4.9 |
| 529 | FRB01 | 3 | Cher | France | 7.7 | 4.7 |
| 530 | PT111 | 3 | Alto Minho | Portugal | 7.7 | 5.6 |
| 531 | NL126 | 3 | Zuidoost-Friesland | Netherlands | 7.7 | 7.2 |
| 532 | ITF33 | 3 | Napoli | Italy | 7.6 | 2.3 |
| 533 | AT122 | 3 | Niederösterreich-Süd | Austria | 7.6 | 5.6 |
| 534 | EL531 | 3 | Grevena, Kozani | Greece | 7.5 | 5.9 |
| 535 | SK021 | 3 | Trnavský kraj | Slovakia | 7.5 | 4.3 |
| 536 | ITI44 | 3 | Latina | Italy | 7.4 | 4.1 |
| 537 | CH055 | 3 | St. Gallen | Switzerland | 7.4 | 4.7 |
| 538 | ITH43 | 3 | Gorizia | Italy | 7.3 | 7.3 |
| 539 | FRL03 | 3 | Alpes-Maritimes | France | 7.3 | 2.6 |
| 540 | FRG02 | 3 | Maine-et-Loire | France | 7.3 | 3.5 |
| 541 | ITI45 | 3 | Frosinone | Italy | 7.2 | 3.8 |
| 542 | SK042 | 3 | Košický kraj | Slovakia | 7.2 | 3.8 |
| 543 | FRD22 | 3 | Seine-Maritime | France | 7.2 | 2.8 |
| 544 | ITI21 | 3 | Perugia | Italy | 7.1 | 4 |
| 545 | RS110 | 3 | Beogradska oblast | Serbia | 7.1 | 2.4 |
| 546 | HU110 | 3 | Budapest | Hungary | 7 | 2.6 |
| 547 | EL421 | 3 | Kalymnos, Karpathos, Kos, Rodos | Greece | 7 | 7.1 |
| 548 | EL527 | 3 | Chalkidiki | Greece | 6.9 | 8.4 |
| 549 | AT342 | 3 | Rheintal-Bodenseegebiet | Austria | 6.9 | 6.4 |
| 550 | RS216 | 3 | Rasinska oblast | Serbia | 6.8 | 4.8 |
| 551 | FRJ25 | 3 | Lot | France | 6.8 | 6 |
| 552 | BE341 | 3 | Arr. Arlon | Belgium | 7 | 11 |
| 553 | FRI22 | 3 | Creuse | France | 6.7 | 7.6 |
| 554 | ES611 | 3 | Almería | Spain | 6.7 | 4 |
| 555 | LT025 | 3 | Panevėžio apskritis | Lithuania | 6.6 | 5.1 |
| 556 | BE351 | 3 | Arr. Dinant | Belgium | 6.5 | 8.2 |
| 557 | FRC12 | 3 | Nièvre | France | 6.5 | 5.2 |
| 558 | ITG27 | 3 | Cagliari | Italy | 6.5 | 4.4 |
| 559 | PT11B | 3 | Alto Tâmega | Portugal | 6.4 | 8.1 |
| 560 | RS228 | 3 | Pčinjska oblast | Serbia | 6.4 | 6 |
| 561 | SE221 | 3 | Blekinge län | Sweden | 6.4 | 6.8 |
| 562 | FRJ24 | 3 | Gers | France | 6.4 | 6.2 |
| 563 | RO412 | 3 | Gorj | Romania | 6.3 | 4.7 |
| 564 | AT314 | 3 | Steyr-Kirchdorf | Austria | 6.2 | 7.5 |
| 565 | RO125 | 3 | Mureş | Romania | 6.2 | 3.8 |
| 566 | FRI14 | 3 | Lot-et-Garonne | France | 6.2 | 4.6 |
| 567 | AT225 | 3 | West- und Südsteiermark | Austria | 6.2 | 6.5 |
| 568 | PL815 | 3 | Puławski | Poland | 6.1 | 4 |
| 569 | EL644 | 3 | Fthiotida | Greece | 6.1 | 7.2 |
| 570 | PL22A | 3 | Katowicki | Poland | 6.1 | 3.4 |
| 571 | AT322 | 3 | Pinzgau-Pongau | Austria | 6.1 | 7.3 |
| 572 | FRG03 | 3 | Mayenne | France | 6.1 | 5.3 |
| 573 | FRJ26 | 3 | Hautes-Pyrénées | France | 6 | 5.7 |
| 574 | RS122 | 3 | Južnobanatska oblast | Serbia | 6 | 4.6 |
| 575 | FI1D2 | 3 | Pohjois-Savo | Finland | 5.9 | 5.5 |
| 576 | AT111 | 3 | Mittelburgenland | Austria | 6 | 13 |
| 577 | PL721 | 3 | Kielecki | Poland | 5.8 | 3.8 |
| 578 | SE231 | 3 | Hallands län | Sweden | 5.7 | 5.4 |
| 579 | ITF63 | 3 | Catanzaro | Italy | 5.7 | 4.3 |
| 580 | ITI43 | 3 | Roma | Italy | 5.6 | 1.9 |
| 581 | ITG15 | 3 | Caltanissetta | Italy | 5.6 | 4.6 |
| 582 | FRJ11 | 3 | Aude | France | 5.5 | 4.6 |
| 583 | PL415 | 3 | Miasto Poznań | Poland | 5.4 | 3.9 |
| 584 | RO322 | 3 | Ilfov | Romania | 5.4 | 4.5 |
| 585 | PL228 | 3 | Bytomski | Poland | 5.4 | 4.2 |
| 586 | ES114 | 3 | Pontevedra | Spain | 5.4 | 3.1 |
| 587 | ITF11 | 3 | L'Aquila | Italy | 5.4 | 4.7 |
| 588 | BG324 | 3 | Razgrad | Bulgaria | 5.4 | 6.6 |
| 589 | ITI18 | 3 | Arezzo | Italy | 5.3 | 4.5 |
| 590 | PL22B | 3 | Sosnowiecki | Poland | 5.3 | 3.3 |
| 591 | ITI15 | 3 | Prato | Italy | 5.2 | 5.6 |
| 592 | FRJ13 | 3 | Hérault | France | 5.2 | 2.7 |
| 593 | DK041 | 3 | Vestjylland | Denmark | 5.2 | 4.5 |
| 594 | EL301 | 3 | Voreios Tomeas Athinon | Greece | 5.1 | 3.8 |
| 595 | FI197 | 3 | Pirkanmaa | Finland | 5.1 | 4.8 |
| 596 | NO051 | 3 | Hordaland | Norway | 5.1 | 4.9 |
| 597 | LT026 | 3 | Šiaulių apskritis | Lithuania | 5 | 4.6 |
| 598 | ES705 | 3 | Gran Canaria | Spain | 5 | 3.5 |
| 599 | EL611 | 3 | Karditsa, Trikala | Greece | 5 | 5 |
| 600 | NL113 | 3 | Overig Groningen | Netherlands | 4.9 | 5.1 |
| 601 | LT027 | 3 | Tauragės apskritis | Lithuania | 4.9 | 7 |
| 602 | FRI33 | 3 | Deux-Sèvres | France | 4.9 | 5.2 |
| 603 | EL422 | 3 | Andros, Thira, Kea, Milos, Mykonos, Naxos, Paros, Syros, Tinos | Greece | 4.9 | 8 |
| 604 | PL224 | 3 | Częstochowski | Poland | 4.9 | 3.7 |
| 605 | EL651 | 3 | Argolida, Arkadia | Greece | 4.8 | 5.6 |
| 606 | FRG01 | 3 | Loire-Atlantique | France | 4.8 | 2.8 |
| 607 | PL926 | 3 | Żyrardowski | Poland | 4.7 | 4.9 |
| 608 | ITF64 | 3 | Vibo Valentia | Italy | 4.7 | 6.7 |
| 609 | AT211 | 3 | Klagenfurt-Villach | Austria | 4.7 | 5.6 |
| 610 | ES112 | 3 | Lugo | Spain | 4.7 | 4.1 |
| 611 | PL911 | 3 | Miasto Warszawa | Poland | 4.6 | 2.3 |
| 612 | AT332 | 3 | Innsbruck | Austria | 4.6 | 6.1 |
| 613 | AT313 | 3 | Mühlviertel | Austria | 4.6 | 6.9 |
| 614 | PT300 | 3 | Região Autónoma da Madeira | Portugal | 4.6 | 5.4 |
| 615 | DK011 | 3 | Byen København | Denmark | 4.6 | 3.8 |
| 616 | FRB06 | 3 | Loiret | France | 4.6 | 3.9 |
| 617 | NL132 | 3 | Zuidoost-Drenthe | Netherlands | 4.5 | 6.4 |
| 618 | LU000 | 3 | Luxembourg | Luxembourg | 4.5 | 4.6 |
| 619 | ES709 | 3 | Tenerife | Spain | 4.5 | 3.7 |
| 620 | EL413 | 3 | Chios | Greece | 4 | 12 |
| 621 | AL034 | 3 | Korcë | Albania | 4.5 | 6.4 |
| 622 | AT223 | 3 | Östliche Obersteiermark | Austria | 4.5 | 6.8 |
| 623 | ES533 | 3 | Menorca | Spain | 4 | 12 |
| 624 | NL131 | 3 | Noord-Drenthe | Netherlands | 4.4 | 6.6 |
| 625 | PT150 | 3 | Algarve | Portugal | 4.4 | 4.2 |
| 626 | ITG26 | 3 | Nuoro | Italy | 4.3 | 6.3 |
| 627 | FRD13 | 3 | Orne | France | 4.3 | 5.7 |
| 628 | RO113 | 3 | Cluj | Romania | 4.2 | 3.5 |
| 629 | LT024 | 3 | Marijampolės apskritis | Lithuania | 4.1 | 5.8 |
| 630 | RO126 | 3 | Sibiu | Romania | 4.1 | 4.1 |
| 631 | ITG18 | 3 | Ragusa | Italy | 4.1 | 5.2 |
| 632 | UKL13 | 3 | Conwy and Denbighshire | United Kingdom | 4.1 | 5.6 |
| 633 | SK041 | 3 | Prešovský kraj | Slovakia | 4 | 3.7 |
| 634 | HU222 | 3 | Vas | Hungary | 4 | 5.1 |
| 635 | RS212 | 3 | Kolubarska oblast | Serbia | 4 | 5.4 |
| 636 | ITF31 | 3 | Caserta | Italy | 4 | 3.6 |
| 637 | EL653 | 3 | Lakonia, Messinia | Greece | 4 | 5.4 |
| 638 | PL921 | 3 | Radomski | Poland | 4 | 3.8 |
| 639 | FI193 | 3 | Keski-Suomi | Finland | 4 | 5.2 |
| 640 | RO112 | 3 | Bistriţa-Năsăud | Romania | 4 | 4.6 |
| 641 | NL125 | 3 | Zuidwest-Friesland | Netherlands | 3.9 | 7.8 |
| 642 | HU331 | 3 | Bács-Kiskun | Hungary | 3.9 | 3.6 |
| 643 | CZ031 | 3 | Jihočeský kraj | Czechia | 3.9 | 3.8 |
| 644 | CH033 | 3 | Aargau | Switzerland | 3.9 | 4.2 |
| 645 | FI1C2 | 3 | Kanta-Häme | Finland | 3.9 | 6.8 |
| 646 | BG325 | 3 | Silistra | Bulgaria | 3.8 | 6.5 |
| 647 | FI1C3 | 3 | Päijät-Häme | Finland | 3.8 | 6.1 |
| 648 | AT226 | 3 | Westliche Obersteiermark | Austria | 3.8 | 8.2 |
| 649 | ITG12 | 3 | Palermo | Italy | 3.8 | 2.7 |
| 650 | PL924 | 3 | Ostrołęcki | Poland | 3.8 | 4.8 |
| 651 | ITF32 | 3 | Benevento | Italy | 3.7 | 5.1 |
| 652 | ITG17 | 3 | Catania | Italy | 3.6 | 2.8 |
| 653 | ITG11 | 3 | Trapani | Italy | 3.6 | 4.1 |
| 654 | BG415 | 3 | Kyustendil | Bulgaria | 3.6 | 5.4 |
| 655 | AT341 | 3 | Bludenz-Bregenzer Wald | Austria | 3 | 11 |
| 656 | IS002 | 3 | Landsbyggð | Iceland | 3.4 | 9 |
| 657 | PT16J | 3 | Beiras e Serra da Estrela | Portugal | 3.4 | 5.1 |
| 658 | CZ041 | 3 | Karlovarský kraj | Czechia | 3.4 | 5.4 |
| 659 | HU221 | 3 | Győr-Moson-Sopron | Hungary | 3.4 | 4.5 |
| 660 | NO031 | 3 | Østfold | Norway | 3.3 | 5.5 |
| 661 | CZ010 | 3 | Hlavní město Praha | Czechia | 3.3 | 3 |
| 662 | CZ080 | 3 | Moravskoslezský kraj | Czechia | 3.2 | 2.9 |
| 663 | RO424 | 3 | Timiş | Romania | 3.2 | 3.7 |
| 664 | FRJ15 | 3 | Pyrénées-Orientales | France | 3.2 | 3.9 |
| 665 | PL214 | 3 | Krakowski | Poland | 3.2 | 3.7 |
| 666 | RO212 | 3 | Botoşani | Romania | 3.2 | 4 |
| 667 | CZ072 | 3 | Zlínský kraj | Czechia | 3.2 | 3.8 |
| 668 | AT323 | 3 | Salzburg und Umgebung | Austria | 3.1 | 5 |
| 669 | DK021 | 3 | Østsjælland | Denmark | 3.1 | 6 |
| 670 | EE001 | 3 | Põhja-Eesti | Estonia | 3 | 3.9 |
| 671 | FRH04 | 3 | Morbihan | France | 2.9 | 3.1 |
| 672 | BG422 | 3 | Haskovo | Bulgaria | 2.9 | 5 |
| 673 | EL302 | 3 | Dytikos Tomeas Athinon | Greece | 2.9 | 4.4 |
| 674 | FRJ14 | 3 | Lozère | France | 2.7 | 9.4 |
| 675 | NO033 | 3 | Vestfold | Norway | 2.7 | 6.1 |
| 676 | EL306 | 3 | Dytiki Attiki | Greece | 2.7 | 7.6 |
| 677 | IS001 | 3 | Höfuðborgarsvæði | Iceland | 2.7 | 6.9 |
| 678 | PL517 | 3 | Wałbrzyski | Poland | 2.6 | 3.9 |
| 679 | AT125 | 3 | Weinviertel | Austria | 2.6 | 6.6 |
| 680 | CZ042 | 3 | Ústecký kraj | Czechia | 2.6 | 3 |
| 681 | AT312 | 3 | Linz-Wels | Austria | 2.6 | 4.4 |
| 682 | CH040 | 3 | Zürich | Switzerland | 2.6 | 3 |
| 683 | PL518 | 3 | Wrocławski | Poland | 2.6 | 3.7 |
| 684 | EL431 | 3 | Irakleio | Greece | 2.5 | 4.9 |
| 685 | AL011 | 3 | Dibër | Albania | 2.5 | 9.5 |
| 686 | SK022 | 3 | Trenčiansky kraj | Slovakia | 2.5 | 4.2 |
| 687 | HU231 | 3 | Baranya | Hungary | 2.5 | 4.6 |
| 688 | FRK13 | 3 | Haute-Loire | France | 2.5 | 5.8 |
| 689 | BG424 | 3 | Smolyan | Bulgaria | 2.5 | 6.4 |
| 690 | AT321 | 3 | Lungau | Austria | 2 | 20 |
| 691 | FRL05 | 3 | Var | France | 2.4 | 3 |
| 692 | HU323 | 3 | Szabolcs-Szatmár-Bereg | Hungary | 2.4 | 4.2 |
| 693 | ITG14 | 3 | Agrigento | Italy | 2.4 | 3.7 |
| 694 | EL522 | 3 | Thessaloniki | Greece | 2.3 | 2.8 |
| 695 | PL225 | 3 | Bielski | Poland | 2.3 | 3.2 |
| 696 | PT186 | 3 | Alto Alentejo | Portugal | 2.3 | 6.7 |
| 697 | AL031 | 3 | Berat | Albania | 2.3 | 8 |
| 698 | PL841 | 3 | Białostocki | Poland | 2.2 | 4.1 |
| 699 | CH061 | 3 | Luzern | Switzerland | 2.2 | 5.5 |
| 700 | HU213 | 3 | Veszprém | Hungary | 2.1 | 4.3 |
| 701 | EL524 | 3 | Pella | Greece | 2.1 | 6.7 |
| 702 | PL814 | 3 | Lubelski | Poland | 2.1 | 3.4 |
| 703 | HU120 | 3 | Pest | Hungary | 2 | 2.5 |
| 704 | PL218 | 3 | Nowosądecki | Poland | 2 | 4 |
| 705 | RS227 | 3 | Podunavska oblast | Serbia | 2 | 5.7 |
| 706 | ITF35 | 3 | Salerno | Italy | 2 | 2.9 |
| 707 | RO321 | 3 | Bucureşti | Romania | 2 | 2.1 |
| 708 | EL541 | 3 | Arta, Preveza | Greece | 2 | 7 |
| 709 | RS123 | 3 | Južnobačka oblast | Serbia | 1.9 | 3.9 |
| 710 | LT021 | 3 | Alytaus apskritis | Lithuania | 1.8 | 6.1 |
| 711 | EL622 | 3 | Kerkyra | Greece | 1.7 | 7.5 |
| 712 | PL638 | 3 | Starogardzki | Poland | 1.7 | 4.6 |
| 713 | RO311 | 3 | Argeş | Romania | 1.7 | 3.3 |
| 714 | HU212 | 3 | Komárom-Esztergom | Hungary | 1.6 | 4.8 |
| 715 | CZ071 | 3 | Olomoucký kraj | Czechia | 1.5 | 3.9 |
| 716 | NO021 | 3 | Hedmark | Norway | 1.5 | 6.1 |
| 717 | PL416 | 3 | Kaliski | Poland | 1.4 | 4 |
| 718 | RS125 | 3 | Severnobačka oblast | Serbia | 1.4 | 5.6 |
| 719 | PL524 | 3 | Opolski | Poland | 1.3 | 3.7 |
| 720 | PL217 | 3 | Tarnowski | Poland | 1.3 | 4.5 |
| 721 | FRI32 | 3 | Charente-Maritime | France | 1.3 | 3.1 |
| 722 | AL012 | 3 | Durrës | Albania | 1.3 | 6.1 |
| 723 | AL033 | 3 | Gjirokastër | Albania | 1.3 | 9.9 |
| 724 | EL307 | 3 | Peiraias, Nisoi | Greece | 1.3 | 4 |
| 725 | FRB04 | 3 | Indre-et-Loire | France | 1.3 | 3.5 |
| 726 | NL124 | 3 | Noord-Friesland | Netherlands | 1.2 | 5 |
| 727 | PL823 | 3 | Rzeszowski | Poland | 1.1 | 4 |
| 728 | PL812 | 3 | Chełmsko-zamojski | Poland | 1.1 | 3.3 |
| 729 | FRM02 | 3 | Haute-Corse | France | 1.1 | 6.2 |
| 730 | FRH02 | 3 | Finistère | France | 1.1 | 3 |
| 731 | NO042 | 3 | Vest-Agder | Norway | 1.1 | 7.2 |
| 732 | PL824 | 3 | Tarnobrzeski | Poland | 1.1 | 4.1 |
| 733 | FRK11 | 3 | Allier | France | 1 | 4.6 |
| 734 | FI1D9 | 3 | Pohjois-Pohjanmaa | Finland | 1 | 4.4 |
| 735 | CZ032 | 3 | Plzeňský kraj | Czechia | 1 | 4.3 |
| 736 | CH056 | 3 | Graubünden | Switzerland | 1 | 6.5 |
| 737 | NO034 | 3 | Telemark | Norway | 0.9 | 7 |
| 738 | RO114 | 3 | Maramureş | Romania | 0.9 | 3.5 |
| 739 | PT16B | 3 | Oeste | Portugal | 0.9 | 4.2 |
| 740 | LV006 | 3 | Rīga | Latvia | 0.9 | 3.4 |
| 741 | ITI19 | 3 | Siena | Italy | 0.9 | 4.9 |
| 742 | FRJ22 | 3 | Aveyron | France | 0.9 | 4.6 |
| 743 | RS213 | 3 | Mačvanska oblast | Serbia | 0.8 | 4.8 |
| 744 | NO043 | 3 | Rogaland | Norway | 0.8 | 5 |
| 745 | NO060 | 3 | Trøndelag | Norway | 0.8 | 4.3 |
| 746 | RO314 | 3 | Giurgiu | Romania | 0.8 | 4.2 |
| 747 | PL617 | 3 | Inowrocławski | Poland | 0.8 | 4.5 |
| 748 | SK023 | 3 | Nitriansky kraj | Slovakia | 0.7 | 3.6 |
| 749 | PL715 | 3 | Skierniewicki | Poland | 0.7 | 4.4 |
| 750 | NO022 | 3 | Oppland | Norway | 0.7 | 7 |
| 751 | HU223 | 3 | Zala | Hungary | 0.6 | 4.8 |
| 752 | BG322 | 3 | Gabrovo | Bulgaria | 0.6 | 6.4 |
| 753 | PT16F | 3 | Região de Leiria | Portugal | 0.6 | 5.3 |
| 754 | NL133 | 3 | Zuidwest-Drenthe | Netherlands | 0.5 | 7.7 |
| 755 | PL722 | 3 | Sandomiersko-jędrzejowski | Poland | 0.5 | 4.1 |
| 756 | EL652 | 3 | Korinthia | Greece | 0.5 | 6.6 |
| 757 | PL713 | 3 | Piotrkowski | Poland | 0.4 | 3.9 |
| 758 | FI194 | 3 | Etelä-Pohjanmaa | Finland | 0.4 | 6.1 |
| 759 | CH052 | 3 | Schaffhausen | Switzerland | 0.4 | 8.8 |
| 760 | PL21A | 3 | Oświęcimski | Poland | 0.4 | 3.7 |
| 761 | PL843 | 3 | Suwalski | Poland | 0.4 | 5.3 |
| 762 | EL631 | 3 | Aitoloakarnania | Greece | 0.4 | 5.5 |
| 763 | LT028 | 3 | Telšių apskritis | Lithuania | 0.4 | 6.8 |
| 764 | FRK14 | 3 | Puy-de-Dôme | France | 0.4 | 3.5 |
| 765 | CH053 | 3 | Appenzell Ausserrhoden | Switzerland | 0 | 12 |
| 766 | RO315 | 3 | Ialomiţa | Romania | 0.4 | 4.7 |
| 767 | PL619 | 3 | Włocławski | Poland | 0.4 | 4.2 |
| 768 | CH021 | 3 | Bern | Switzerland | 0.3 | 3.2 |
| 769 | PL925 | 3 | Siedlecki | Poland | 0.3 | 4.1 |
| 770 | EL304 | 3 | Notios Tomeas Athinon | Greece | 0.3 | 3.8 |
| 771 | RO121 | 3 | Alba | Romania | 0.3 | 4.2 |
| 772 | RS126 | 3 | Srednjobanatska oblast | Serbia | 0.2 | 5.5 |
| 773 | EL513 | 3 | Rodopi | Greece | 0.1 | 6.9 |
| 774 | NO012 | 3 | Akershus | Norway | 0 | 4.2 |
| 775 | FI195 | 3 | Pohjanmaa | Finland | 0 | 5.9 |
| 776 | RO317 | 3 | Teleorman | Romania | 0 | 3.7 |
| 777 | RO312 | 3 | Călăraşi | Romania | -0.1 | 4.6 |
| 778 | PL213 | 3 | Miasto Kraków | Poland | -0.1 | 3.6 |
| 779 | SK031 | 3 | Žilinský kraj | Slovakia | -0.1 | 3.5 |
| 780 | FI1D1 | 3 | Etelä-Savo | Finland | -0.1 | 6.2 |
| 781 | RO413 | 3 | Mehedinţi | Romania | -0.2 | 5 |
| 782 | RS222 | 3 | Braničevska oblast | Serbia | -0.2 | 5.3 |
| 783 | BG313 | 3 | Vratsa | Bulgaria | -0.2 | 5 |
| 784 | RO111 | 3 | Bihor | Romania | -0.2 | 3.5 |
| 785 | HU321 | 3 | Hajdú-Bihar | Hungary | -0.3 | 4.2 |
| 786 | NL112 | 3 | Delfzijl en omgeving | Netherlands | 0 | 11 |
| 787 | LI000 | 3 | Liechtenstein | Liechtenstein | 0 | 17 |
| 788 | PL822 | 3 | Przemyski | Poland | -0.3 | 4.8 |
| 789 | FRG05 | 3 | Vendée | France | -0.3 | 3.3 |
| 790 | AT112 | 3 | Nordburgenland | Austria | -0.4 | 6.6 |
| 791 | HU332 | 3 | Békés | Hungary | -0.4 | 3.9 |
| 792 | PL227 | 3 | Rybnicki | Poland | -0.4 | 4 |
| 793 | NO071 | 3 | Nordland | Norway | -0.4 | 6.1 |
| 794 | FRL06 | 3 | Vaucluse | France | -0.5 | 3.8 |
| 795 | PL229 | 3 | Gliwicki | Poland | -0.5 | 4.3 |
| 796 | EL511 | 3 | Evros | Greece | -0.5 | 6.1 |
| 797 | PL427 | 3 | Szczecinecko-pyrzycki | Poland | -0.5 | 3.9 |
| 798 | CZ053 | 3 | Pardubický kraj | Czechia | -0.6 | 3.9 |
| 799 | AT212 | 3 | Oberkärnten | Austria | -0.7 | 7.2 |
| 800 | FRI31 | 3 | Charente | France | -0.7 | 4.7 |
| 801 | EL303 | 3 | Kentrikos Tomeas Athinon | Greece | -0.7 | 2.8 |
| 802 | RO316 | 3 | Prahova | Romania | -0.8 | 2.9 |
| 803 | EL645 | 3 | Fokida | Greece | -1 | 12 |
| 804 | CZ063 | 3 | Kraj Vysočina | Czechia | -0.8 | 4 |
| 805 | DK013 | 3 | Nordsjælland | Denmark | -0.9 | 4.1 |
| 806 | PL219 | 3 | Nowotarski | Poland | -0.9 | 5.2 |
| 807 | PL613 | 3 | Bydgosko-toruński | Poland | -0.9 | 3.1 |
| 808 | AT315 | 3 | Traunviertel | Austria | -0.9 | 5.9 |
| 809 | AT127 | 3 | Wiener Umland/Südteil | Austria | -1 | 5.1 |
| 810 | AT311 | 3 | Innviertel | Austria | -1 | 5.2 |
| 811 | RO422 | 3 | Caraş-Severin | Romania | -1 | 4.5 |
| 812 | BE252 | 3 | Arr. Diksmuide | Belgium | -1 | 11 |
| 813 | PL821 | 3 | Krośnieński | Poland | -1.2 | 4.3 |
| 814 | PL711 | 3 | Miasto Łódź | Poland | -1.2 | 3.2 |
| 815 | FRI21 | 3 | Corrèze | France | -1.3 | 4.9 |
| 816 | EE008 | 3 | Lõuna-Eesti | Estonia | -1.3 | 4.6 |
| 817 | FRJ23 | 3 | Haute-Garonne | France | -1.3 | 2.5 |
| 818 | PL842 | 3 | Łomżyński | Poland | -1.3 | 4.1 |
| 819 | UKN10 | 3 | Derry City and Strabane | United Kingdom | -1.4 | 7.4 |
| 820 | FI1C4 | 3 | Kymenlaakso | Finland | -1.4 | 5.8 |
| 821 | DK022 | 3 | Vest- og Sydsjælland | Denmark | -1.5 | 3.3 |
| 822 | FI1D3 | 3 | Pohjois-Karjala | Finland | -1.5 | 6 |
| 823 | AL013 | 3 | Kukës | Albania | -2 | 12 |
| 824 | FRI13 | 3 | Landes | France | -1.6 | 4.6 |
| 825 | FI196 | 3 | Satakunta | Finland | -1.6 | 5.2 |
| 826 | PL424 | 3 | Miasto Szczecin | Poland | -1.6 | 4.2 |
| 827 | PL634 | 3 | Gdański | Poland | -1.6 | 3.8 |
| 828 | RO414 | 3 | Olt | Romania | -1.7 | 3.5 |
| 829 | CH057 | 3 | Thurgau | Switzerland | -1.7 | 6.3 |
| 830 | PL633 | 3 | Trójmiejski | Poland | -1.7 | 3.3 |
| 831 | AL035 | 3 | Vlorë | Albania | -1.8 | 7 |
| 832 | CH051 | 3 | Glarus | Switzerland | -2 | 13 |
| 833 | PL637 | 3 | Chojnicki | Poland | -1.9 | 5.9 |
| 834 | FRD11 | 3 | Calvados | France | -1.9 | 3.1 |
| 835 | RO214 | 3 | Neamţ | Romania | -1.9 | 3.8 |
| 836 | FRL02 | 3 | Hautes-Alpes | France | -1.9 | 6.9 |
| 837 | ES531 | 3 | Eivissa y Formentera | Spain | -2 | 9.9 |
| 838 | RS214 | 3 | Moravička oblast | Serbia | -2 | 5.3 |
| 839 | RO115 | 3 | Satu Mare | Romania | -2 | 4.7 |
| 840 | ITI41 | 3 | Viterbo | Italy | -2 | 4.7 |
| 841 | FRI34 | 3 | Vienne | France | -2.1 | 3.9 |
| 842 | EL543 | 3 | Ioannina | Greece | -2.1 | 6.6 |
| 843 | EL642 | 3 | Evvoia | Greece | -2.2 | 5.2 |
| 844 | PL618 | 3 | Świecki | Poland | -2.2 | 6.8 |
| 845 | SK032 | 3 | Banskobystrický kraj | Slovakia | -2.2 | 3 |
| 846 | RO411 | 3 | Dolj | Romania | -2.2 | 3.8 |
| 847 | RS217 | 3 | Raška oblast | Serbia | -2.2 | 4.5 |
| 848 | PL523 | 3 | Nyski | Poland | -2.3 | 4.7 |
| 849 | BG423 | 3 | Pazardzhik | Bulgaria | -2.3 | 4.6 |
| 850 | RO223 | 3 | Constanţa | Romania | -2.4 | 2.9 |
| 851 | BG342 | 3 | Sliven | Bulgaria | -2.4 | 5.3 |
| 852 | FRI12 | 3 | Gironde | France | -2.4 | 2.4 |
| 853 | FRI23 | 3 | Haute-Vienne | France | -2.4 | 4.3 |
| 854 | PL712 | 3 | Łódzki | Poland | -2.4 | 4.7 |
| 855 | FRH03 | 3 | Ille-et-Vilaine | France | -2.4 | 3.2 |
| 856 | LT029 | 3 | Utenos apskritis | Lithuania | -2.5 | 5.5 |
| 857 | PL418 | 3 | Poznański | Poland | -2.5 | 4 |
| 858 | CZ064 | 3 | Jihomoravský kraj | Czechia | -2.6 | 2.8 |
| 859 | ES708 | 3 | Lanzarote | Spain | -2.6 | 9 |
| 860 | HU322 | 3 | Jász-Nagykun-Szolnok | Hungary | -2.6 | 3.8 |
| 861 | EL641 | 3 | Voiotia | Greece | -2.6 | 6.7 |
| 862 | FRI15 | 3 | Pyrénées-Atlantiques | France | -2.6 | 3.4 |
| 863 | BG331 | 3 | Varna | Bulgaria | -2.7 | 4 |
| 864 | ES707 | 3 | La Palma | Spain | -2.8 | 8.7 |
| 865 | BG421 | 3 | Plovdiv | Bulgaria | -2.8 | 3.1 |
| 866 | DK032 | 3 | Sydjylland | Denmark | -2.9 | 3.1 |
| 867 | HU333 | 3 | Csongrád | Hungary | -2.9 | 3.6 |
| 868 | BG413 | 3 | Blagoevgrad | Bulgaria | -2.9 | 4.3 |
| 869 | BG323 | 3 | Ruse | Bulgaria | -2.9 | 4.6 |
| 870 | PL714 | 3 | Sieradzki | Poland | -2.9 | 4 |
| 871 | BG333 | 3 | Shumen | Bulgaria | -2.9 | 5 |
| 872 | LV003 | 3 | Kurzeme | Latvia | -2.9 | 4.7 |
| 873 | NO073 | 3 | Finnmark | Norway | -3 | 9.4 |
| 874 | EL433 | 3 | Rethymni | Greece | -3 | 8.7 |
| 875 | PL514 | 3 | Miasto Wrocław | Poland | -3 | 4 |
| 876 | RO226 | 3 | Vrancea | Romania | -3 | 3.9 |
| 877 | BG414 | 3 | Pernik | Bulgaria | -3.1 | 5.7 |
| 878 | FRL01 | 3 | Alpes-de-Haute-Provence | France | -3 | 13 |
| 879 | FRH01 | 3 | Côtes-d’Armor | France | -3.2 | 3.3 |
| 880 | EL412 | 3 | Ikaria, Samos | Greece | -3 | 13 |
| 881 | PL922 | 3 | Ciechanowski | Poland | -3.3 | 4.2 |
| 882 | RS124 | 3 | Severnobanatska oblast | Serbia | -3.3 | 6.2 |
| 883 | LV005 | 3 | Latgale | Latvia | -3.3 | 4 |
| 884 | HU311 | 3 | Borsod-Abaúj-Zemplén | Hungary | -3.3 | 3.3 |
| 885 | PL623 | 3 | Ełcki | Poland | -3.4 | 5.4 |
| 886 | BG411 | 3 | Sofia (stolitsa) | Bulgaria | -3.4 | 2.6 |
| 887 | PL426 | 3 | Koszaliński | Poland | -3.4 | 4.5 |
| 888 | RO122 | 3 | Braşov | Romania | -3.4 | 3.4 |
| 889 | RO124 | 3 | Harghita | Romania | -3.4 | 4.8 |
| 890 | LV009 | 3 | Zemgale | Latvia | -3.4 | 4.7 |
| 891 | PL636 | 3 | Słupski | Poland | -3.5 | 4.1 |
| 892 | EL432 | 3 | Lasithi | Greece | -3.5 | 9 |
| 893 | PL411 | 3 | Pilski | Poland | -3.5 | 4.2 |
| 894 | PL912 | 3 | Warszawski wschodni | Poland | -3.5 | 3.4 |
| 895 | RO224 | 3 | Galaţi | Romania | -3.5 | 3.3 |
| 896 | FRJ27 | 3 | Tarn | France | -3.5 | 4 |
| 897 | NO053 | 3 | Møre og Romsdal | Norway | -3.5 | 5.8 |
| 898 | PL621 | 3 | Elbląski | Poland | -3.7 | 4.2 |
| 899 | PL432 | 3 | Zielonogórski | Poland | -3.7 | 3.9 |
| 900 | PL428 | 3 | Szczeciński | Poland | -3.8 | 3.7 |
| 901 | SK010 | 3 | Bratislavský kraj | Slovakia | -3.9 | 3.4 |
| 902 | PL515 | 3 | Jeleniogórski | Poland | -4 | 3.8 |
| 903 | ME000 | 3 | Crna Gora | Montenegro | -4 | 3.4 |
| 904 | BG425 | 3 | Kardzhali | Bulgaria | -4 | 5.9 |
| 905 | CZ052 | 3 | Královéhradecký kraj | Czechia | -4.1 | 3.7 |
| 906 | RS211 | 3 | Zlatiborska oblast | Serbia | -4.1 | 4.2 |
| 907 | NO041 | 3 | Aust-Agder | Norway | -4.2 | 8.7 |
| 908 | CH062 | 3 | Uri | Switzerland | -4 | 15 |
| 909 | HU232 | 3 | Somogy | Hungary | -4.2 | 4.4 |
| 910 | PL414 | 3 | Koniński | Poland | -4.4 | 3.7 |
| 911 | PL516 | 3 | Legnicko-głogowski | Poland | -4.4 | 4.5 |
| 912 | SE331 | 3 | Västerbottens län | Sweden | -4.4 | 5 |
| 913 | PL811 | 3 | Bialski | Poland | -4.4 | 4.7 |
| 914 | CZ051 | 3 | Liberecký kraj | Czechia | -4.4 | 4.4 |
| 915 | FI1D7 | 3 | Lappi | Finland | -4.6 | 5.6 |
| 916 | RO116 | 3 | Sălaj | Romania | -4.6 | 4.8 |
| 917 | FRJ21 | 3 | Ariège | France | -4.6 | 5.7 |
| 918 | RO313 | 3 | Dâmboviţa | Romania | -4.6 | 3.5 |
| 919 | DK050 | 3 | Nordjylland | Denmark | -4.7 | 4 |
| 920 | RS226 | 3 | Pirotska oblast | Serbia | -4.8 | 8 |
| 921 | FRI11 | 3 | Dordogne | France | -4.8 | 3.8 |
| 922 | CZ020 | 3 | Středočeský kraj | Czechia | -4.8 | 2.8 |
| 923 | RO221 | 3 | Brăila | Romania | -4.9 | 4.1 |
| 924 | PL923 | 3 | Płocki | Poland | -4.9 | 4.2 |
| 925 | HU211 | 3 | Fejér | Hungary | -5 | 3.7 |
| 926 | DK042 | 3 | Østjylland | Denmark | -5.1 | 3.2 |
| 927 | ITG2A | 3 | Ogliastra | Italy | -5 | 10 |
| 928 | NL111 | 3 | Oost-Groningen | Netherlands | -5.3 | 6.4 |
| 929 | AT333 | 3 | Osttirol | Austria | -5 | 13 |
| 930 | PL913 | 3 | Warszawski zachodni | Poland | -5.5 | 3.1 |
| 931 | RO211 | 3 | Bacău | Romania | -5.5 | 3.1 |
| 932 | FI1C1 | 3 | Varsinais-Suomi | Finland | -5.7 | 4.3 |
| 933 | PL622 | 3 | Olsztyński | Poland | -5.7 | 3.6 |
| 934 | LV007 | 3 | Pierīga | Latvia | -5.8 | 4 |
| 935 | PL22C | 3 | Tyski | Poland | -5.9 | 3.9 |
| 936 | DK031 | 3 | Fyn | Denmark | -5.9 | 3.4 |
| 937 | RO213 | 3 | Iaşi | Romania | -5.9 | 3.1 |
| 938 | BG341 | 3 | Burgas | Bulgaria | -6 | 3.3 |
| 939 | PL616 | 3 | Grudziądzki | Poland | -6 | 4 |
| 940 | PL431 | 3 | Gorzowski | Poland | -6.2 | 4.2 |
| 941 | DK014 | 3 | Bornholm | Denmark | -6.3 | 9.9 |
| 942 | BG412 | 3 | Sofia | Bulgaria | -6.3 | 3.8 |
| 943 | PL417 | 3 | Leszczyński | Poland | -6.3 | 3.7 |
| 944 | LV008 | 3 | Vidzeme | Latvia | -6.5 | 4.8 |
| 945 | AT123 | 3 | Sankt Pölten | Austria | -6.5 | 6.6 |
| 946 | FRJ28 | 3 | Tarn-et-Garonne | France | -6.6 | 4.6 |
| 947 | BG321 | 3 | Veliko Tarnovo | Bulgaria | -6.6 | 4.2 |
| 948 | CH066 | 3 | Zug | Switzerland | -6.7 | 8.1 |
| 949 | NO052 | 3 | Sogn og Fjordane | Norway | -6.7 | 8.9 |
| 950 | EL623 | 3 | Ithaki, Kefallinia | Greece | -7 | 13 |
| 951 | BG344 | 3 | Stara Zagora | Bulgaria | -6.9 | 4 |
| 952 | RS127 | 3 | Sremska oblast | Serbia | -7.1 | 3.9 |
| 953 | EL525 | 3 | Pieria | Greece | -7.2 | 6 |
| 954 | RO222 | 3 | Buzău | Romania | -7.3 | 3 |
| 955 | NO072 | 3 | Troms | Norway | -7.5 | 7 |
| 956 | EL533 | 3 | Florina | Greece | -8 | 10 |
| 957 | EL523 | 3 | Kilkis | Greece | -7.6 | 8 |
| 958 | BG314 | 3 | Pleven | Bulgaria | -7.8 | 3.8 |
| 959 | BG315 | 3 | Lovech | Bulgaria | -7.9 | 4.9 |
| 960 | HU312 | 3 | Heves | Hungary | -8 | 4 |
| 961 | BG332 | 3 | Dobrich | Bulgaria | -8.2 | 5 |
| 962 | EL542 | 3 | Thesprotia | Greece | -8 | 11 |
| 963 | RO216 | 3 | Vaslui | Romania | -8.5 | 4 |
| 964 | HU313 | 3 | Nógrád | Hungary | -8.5 | 4.5 |
| 965 | FRK12 | 3 | Cantal | France | -8.6 | 5.9 |
| 966 | RS218 | 3 | Šumadijska oblast | Serbia | -8.6 | 4.7 |
| 967 | RO225 | 3 | Tulcea | Romania | -8.6 | 5.1 |
| 968 | ITG29 | 3 | Olbia-Tempio | Italy | -8.8 | 6.7 |
| 969 | EL643 | 3 | Evrytania | Greece | -9 | 16 |
| 970 | CH065 | 3 | Nidwalden | Switzerland | -9 | 14 |
| 971 | BG312 | 3 | Montana | Bulgaria | -10.6 | 4.8 |
| 972 | BG334 | 3 | Targovishte | Bulgaria | -11.9 | 5.5 |
| 973 | ES704 | 3 | Fuerteventura | Spain | -12 | 11 |
| 974 | RS121 | 3 | Zapadnobačka oblast | Serbia | -14.2 | 4.8 |
| 975 | RO123 | 3 | Covasna | Romania | -14.8 | 4.7 |
| 976 | FI200 | 3 | Åland | Finland | -15 | 16 |
| 977 | AT331 | 3 | Außerfern | Austria | -17 | 13 |
D. Tables of USA Regions (States and Counties), Ordered by Integrated First-Peak Period P-Score
D.1 USA States
| Rank (by P-score) | State Name | State Abbrev. | P-score (%) | (1σ) Err (%) | P-score / Err | Rise-side half-maximum (weeks after March 8-14, 2020)* |
| 1 | New York | NY | 101.9 | 1.6 | 63.7 | 2 |
| 2 | New Jersey | NJ | 90.3 | 1.8 | 50.2 | 2 |
| 3 | Connecticut | CT | 54 | 2.2 | 24.6 | 3 |
| 4 | Massachusetts | MA | 52.5 | 1.7 | 30.9 | 3 |
| 5 | District of Columbia | DC | 51.1 | 5.5 | 9.3 | 3 |
| 6 | Rhode Island | RI | 32.9 | 3.5 | 9.4 | 5 |
| 7 | Maryland | MD | 31.1 | 1.7 | 18.3 | 3 |
| 8 | Louisiana | LA | 30.9 | 1.6 | 19.3 | 2 |
| 9 | Illinois | IL | 29.4 | 1.2 | 24.5 | 3 |
| 10 | Michigan | MI | 28.7 | 1.2 | 23.9 | 2 |
| 11 | Delaware | DE | 27.9 | 3.9 | 7.2 | 5 |
| 12 | Pennsylvania | PA | 21.2 | 1.1 | 19.3 | 3 |
| 13 | Colorado | CO | 18.8 | 1.8 | 10.4 | 2 |
| 14 | Mississippi | MS | 16.2 | 1.8 | 9.0 | 2 |
| 15 | Indiana | IN | 15.8 | 1.3 | 12.2 | 2 |
| 16 | Georgia | GA | 14.7 | 1.1 | 13.4 | 2 |
| 17 | Virginia | VA | 14 | 1.3 | 10.8 | 3 |
| 18 | Vermont | VT | 11.9 | 4.5 | 2.6 | - |
| 19 | Arizona | AZ | 11.4 | 1.3 | 8.8 | 3 |
| 20 | New Mexico | NM | 11.1 | 2.4 | 4.6 | 7 |
| 21 | California | CA | 10.63 | 0.88 | 12.1 | 2 |
| 22 | Minnesota | MN | 10.4 | 1.5 | 6.9 | 5 |
| 23 | South Carolina | SC | 10.2 | 1.4 | 7.3 | 3 |
| 24 | New Hampshire | NH | 10.1 | 2.8 | 3.6 | 5 |
| 25 | Alabama | AL | 9.3 | 1.5 | 6.2 | 2 |
| 26 | Ohio | OH | 8.5 | 1.1 | 7.7 | 5 |
| 27 | North Carolina | NC | 8.3 | 1.2 | 6.9 | 4 |
| 28 | Missouri | MO | 7.6 | 1.4 | 5.4 | 3 |
| 29 | Iowa | IA | 7.2 | 1.9 | 3.8 | 6 |
| 30 | Washington | WA | 7.1 | 1.4 | 5.1 | 1 |
| 31 | Texas | TX | 6.77 | 0.69 | 9.8 | 3 |
| 32 | Wisconsin | WI | 6.7 | 1.2 | 5.6 | 2 |
| 33 | Florida | FL | 6.61 | 0.78 | 8.5 | 3 |
| 34 | Nebraska | NE | 5.9 | 2.4 | 2.5 | - |
| 35 | Nevada | NV | 5.7 | 1.9 | 3.0 | 2 |
| 36 | Kentucky | KY | 5.5 | 1.3 | 4.2 | 2 |
| 37 | Oregon | OR | 5.1 | 1.7 | 3.0 | 1 |
| 38 | North Dakota | ND | 5 | 3.4 | 1.5 | - |
| 39 | West Virginia | WV | 4.8 | 1.9 | 2.5 | - |
| 40 | Tennessee | TN | 4.6 | 1.2 | 3.8 | 2 |
| 41 | Kansas | KS | 4.3 | 1.8 | 2.4 | - |
| 42 | Oklahoma | OK | 4.2 | 1.6 | 2.6 | - |
| 43 | Utah | UT | 3.9 | 2 | 2.0 | - |
| 44 | Arkansas | AR | 2.6 | 1.8 | 1.4 | - |
| 45 | South Dakota | SD | 1.8 | 3.3 | 0.6 | - |
| 46 | Wyoming | WY | 1.4 | 4.4 | 0.3 | - |
| 47 | Montana | MT | 0.1 | 3 | 0.03 | - |
| 48 | Idaho | ID | -0.1 | 2.4 | -0.04 | - |
| 49 | Maine | ME | -0.2 | 2.5 | -0.08 | - |
| 50 | Alaska | AK | -2.1 | 5.9 | -0.4 | - |
| 51 | Hawaii | HI | -2.4 | 2.6 | -0.9 | - |
D.2 USA Counties
| Rank | County Name | State Abbrev. | P-score (%) | (1σ) Err (%) |
| 1 | Bronx County | NY | 232.5 | 7.4 |
| 2 | Queens County | NY | 223.9 | 5.6 |
| 3 | Kings County | NY | 213.6 | 6 |
| 4 | Hudson County | NJ | 187.8 | 8.6 |
| 5 | Essex County | NJ | 160 | 7.1 |
| 6 | Rockland County | NY | 150.2 | 9.1 |
| 7 | New York County | NY | 143.5 | 6.4 |
| 8 | Union County | NJ | 142.4 | 7.4 |
| 9 | Passaic County | NJ | 137.9 | 9.7 |
| 10 | Richmond County | NY | 122.6 | 9.3 |
| 11 | Nassau County | NY | 122.4 | 5 |
| 12 | Westchester County | NY | 121.8 | 6.2 |
| 13 | Bergen County | NJ | 108.1 | 6.2 |
| 14 | Morris County | NJ | 93.9 | 7.9 |
| 15 | Middlesex County | NJ | 93.7 | 7 |
| 16 | Somerset County | NJ | 93.7 | 9.2 |
| 17 | Chambers County | AL | 94 | 23 |
| 18 | Suffolk County | NY | 87.8 | 4.4 |
| 19 | Suffolk County | MA | 85.6 | 6.2 |
| 20 | Fairfield County | CT | 81.4 | 4.8 |
| 21 | Mercer County | NJ | 81 | 7.2 |
| 22 | Orleans Parish | LA | 78.6 | 8.1 |
| 23 | Iberville Parish | LA | 76 | 30 |
| 24 | Hunterdon County | NJ | 74 | 14 |
| 25 | Morgan County | CO | 73 | 25 |
| 26 | Orange County | NY | 71.3 | 6.7 |
| 27 | Putnam County | NY | 71 | 13 |
| 28 | McKinley County | NM | 70 | 13 |
| 29 | Sussex County | NJ | 70 | 10 |
| 30 | Warren County | NJ | 69 | 13 |
| 31 | Assumption Parish | LA | 68 | 30 |
| 32 | Wayne County | MI | 67 | 2.8 |
| 33 | Apache County | AZ | 66 | 14 |
| 34 | Neshoba County | MS | 65 | 20 |
| 35 | Arlington County | VA | 65 | 11 |
| 36 | Norfolk County | MA | 64.3 | 5.3 |
| 37 | Dougherty County | GA | 64 | 11 |
| 38 | Holmes County | MS | 63 | 28 |
| 39 | Middlesex County | MA | 61.4 | 3.5 |
| 40 | Monmouth County | NJ | 61.1 | 5.1 |
| 41 | Hartford County | CT | 59.3 | 4.1 |
| 42 | Prince George's County | MD | 59.2 | 6.1 |
| 43 | Franklin County | MA | 58 | 12 |
| 44 | Copiah County | MS | 58 | 23 |
| 45 | Union Parish | LA | 58 | 22 |
| 46 | District of Columbia | DC | 57.6 | 6 |
| 47 | Philadelphia County | PA | 57.4 | 2.8 |
| 48 | Essex County | MA | 55.7 | 5.3 |
| 49 | Pointe Coupee Parish | LA | 55 | 22 |
| 50 | Plymouth County | MA | 54.6 | 6.2 |
| 51 | Kent County | MD | 55 | 21 |
| 52 | New Haven County | CT | 54.4 | 5.8 |
| 53 | Panola County | TX | 54 | 21 |
| 54 | Montgomery County | MD | 53.4 | 4.9 |
| 55 | Leflore County | MS | 52 | 16 |
| 56 | Ocean County | NJ | 51.5 | 5.1 |
| 57 | Cook County | IL | 51.3 | 1.9 |
| 58 | Hampden County | MA | 51.3 | 6 |
| 59 | St. Charles Parish | LA | 51 | 15 |
| 60 | Dodge County | GA | 50 | 23 |
| 61 | Decatur County | IN | 50 | 22 |
| 62 | Delaware County | PA | 50.1 | 5.4 |
| 63 | Tippah County | MS | 49 | 22 |
| 64 | Jefferson Parish | LA | 49 | 6 |
| 65 | Macomb County | MI | 48.3 | 3.7 |
| 66 | St. John the Baptist Parish | LA | 48 | 14 |
| 67 | Butts County | GA | 47 | 18 |
| 68 | Worcester County | MA | 46.9 | 4.6 |
| 69 | Denver County | CO | 46.6 | 5.3 |
| 70 | Washington County | TX | 45 | 16 |
| 71 | Clarendon County | SC | 45 | 14 |
| 72 | Choctaw County | OK | 45 | 30 |
| 73 | Oakland County | MI | 44.7 | 2.8 |
| 74 | Broomfield County | CO | 44 | 20 |
| 75 | Burlington County | NJ | 43.8 | 5.4 |
| 76 | San Juan County | NM | 44 | 10 |
| 77 | Coconino County | AZ | 43 | 12 |
| 78 | Juniata County | PA | 42 | 25 |
| 79 | Marion County | IN | 42.3 | 3.4 |
| 80 | Providence County | RI | 41.9 | 5.2 |
| 81 | Arapahoe County | CO | 41.3 | 5.5 |
| 82 | Mahoning County | OH | 41.3 | 6 |
| 83 | Toombs County | GA | 41 | 21 |
| 84 | Carbon County | PA | 41 | 14 |
| 85 | Frederick County | MD | 41 | 7.1 |
| 86 | Poweshiek County | IA | 41 | 26 |
| 87 | Clarke County | MS | 41 | 25 |
| 88 | Drew County | AR | 41 | 28 |
| 89 | Jefferson County | OR | 40 | 21 |
| 90 | Montgomery County | PA | 40.3 | 4 |
| 91 | Vance County | NC | 40 | 19 |
| 92 | Lauderdale County | MS | 40 | 13 |
| 93 | Pike County | PA | 40 | 16 |
| 94 | Litchfield County | CT | 39.1 | 7.9 |
| 95 | Columbia County | AR | 39 | 19 |
| 96 | Columbus County | NC | 38 | 15 |
| 97 | Howard County | TX | 38 | 20 |
| 98 | Orange County | IN | 38 | 18 |
| 99 | Fairfax County | VA | 37.4 | 4.6 |
| 100 | Washington Parish | LA | 37 | 14 |
| 101 | East Baton Rouge Parish | LA | 37.1 | 5.1 |
| 102 | Palo Pinto County | TX | 37 | 21 |
| 103 | McLeod County | MN | 37 | 15 |
| 104 | Iberia Parish | LA | 36 | 14 |
| 105 | Hampshire County | MA | 36 | 10 |
| 106 | Pasquotank County | NC | 36 | 13 |
| 107 | Fayette County | IN | 36 | 19 |
| 108 | Imperial County | CA | 35 | 13 |
| 109 | St. Louis city | MO | 34.9 | 7.3 |
| 110 | Orleans County | NY | 35 | 15 |
| 111 | Lackawanna County | PA | 34.6 | 7.9 |
| 112 | Prince William County | VA | 34.5 | 6.8 |
| 113 | Bucks County | PA | 34.5 | 4.7 |
| 114 | Lyon County | KS | 34 | 21 |
| 115 | Carroll County | TN | 34 | 18 |
| 116 | Alexandria city | VA | 34 | 13 |
| 117 | Union County | SC | 34 | 16 |
| 118 | Lehigh County | PA | 34.1 | 5.2 |
| 119 | Lincoln County | MS | 34 | 20 |
| 120 | Rockingham County | VA | 34 | 13 |
| 121 | Manassas city | VA | 34 | 24 |
| 122 | Jackson County | GA | 34 | 13 |
| 123 | Caddo Parish | LA | 33.6 | 8.8 |
| 124 | Middlesex County | CT | 33.5 | 8.6 |
| 125 | Attala County | MS | 33 | 23 |
| 126 | Camden County | NJ | 33.4 | 4.6 |
| 127 | Morgan County | MO | 33 | 23 |
| 128 | Lee County | SC | 33 | 19 |
| 129 | Sussex County | DE | 33 | 5.9 |
| 130 | Northampton County | PA | 33 | 5.5 |
| 131 | Northampton County | NC | 33 | 32 |
| 132 | Berks County | PA | 32.7 | 5.7 |
| 133 | Page County | VA | 33 | 20 |
| 134 | Williamsburg County | SC | 33 | 17 |
| 135 | Clay County | MN | 33 | 15 |
| 136 | Benton County | WA | 32.5 | 8.6 |
| 137 | De Soto Parish | LA | 32 | 18 |
| 138 | Columbia County | NY | 32 | 13 |
| 139 | Bristol County | MA | 32.2 | 4.5 |
| 140 | Hennepin County | MN | 32.1 | 3.9 |
| 141 | Hopkins County | KY | 32 | 13 |
| 142 | Clinton County | IN | 32 | 15 |
| 143 | Upson County | GA | 32 | 16 |
| 144 | Benton County | MO | 32 | 19 |
| 145 | Sullivan County | NY | 32 | 14 |
| 146 | Charles County | MD | 31.7 | 7.5 |
| 147 | Putnam County | TN | 31 | 12 |
| 148 | Hillsdale County | MI | 31 | 13 |
| 149 | Lake County | IL | 31.3 | 5.3 |
| 150 | Montgomery County | AL | 31.1 | 7.6 |
| 151 | Wapello County | IA | 31 | 13 |
| 152 | Mitchell County | GA | 31 | 21 |
| 153 | Pontotoc County | MS | 31 | 18 |
| 154 | Carroll County | MD | 30.7 | 10 |
| 155 | Burke County | GA | 31 | 25 |
| 156 | Waller County | TX | 31 | 18 |
| 157 | Livingston Parish | LA | 30.4 | 8.3 |
| 158 | Allen Parish | LA | 30 | 17 |
| 159 | Lafourche Parish | LA | 30 | 10 |
| 160 | Coahoma County | MS | 30 | 17 |
| 161 | Sabine Parish | LA | 30 | 19 |
| 162 | Henry County | IN | 30 | 17 |
| 163 | Douglas County | CO | 29.6 | 8.3 |
| 164 | Duplin County | NC | 29 | 13 |
| 165 | Cass County | NE | 29 | 22 |
| 166 | Lucas County | OH | 29.3 | 5.6 |
| 167 | St. Mary Parish | LA | 29 | 13 |
| 168 | Covington County | MS | 29 | 20 |
| 169 | Henderson County | TN | 29 | 18 |
| 170 | Harrisonburg city | VA | 29 | 14 |
| 171 | Lancaster County | PA | 29.1 | 4.5 |
| 172 | Bremer County | IA | 29 | 23 |
| 173 | Carroll County | VA | 29 | 14 |
| 174 | Franklin County | AL | 29 | 17 |
| 175 | Jefferson County | AR | 29 | 11 |
| 176 | Baltimore city | MD | 29 | 4.4 |
| 177 | Geauga County | OH | 29 | 12 |
| 178 | Fairfield County | SC | 29 | 21 |
| 179 | Portsmouth city | VA | 29 | 11 |
| 180 | Bartow County | GA | 28.7 | 9.9 |
| 181 | DuPage County | IL | 28.7 | 4.7 |
| 182 | Washington County | IA | 29 | 19 |
| 183 | Rabun County | GA | 28 | 22 |
| 184 | Salem County | NJ | 28 | 11 |
| 185 | Gloucester County | NJ | 28.3 | 6 |
| 186 | Lincoln County | NC | 28 | 10 |
| 187 | Johnson County | MO | 28 | 15 |
| 188 | Monroe County | PA | 28.1 | 7.5 |
| 189 | Brown County | SD | 28 | 16 |
| 190 | St. Clair County | IL | 27.5 | 7.8 |
| 191 | Spalding County | GA | 27 | 13 |
| 192 | Baltimore County | MD | 27.4 | 4.3 |
| 193 | Atlantic County | NJ | 27.4 | 5.5 |
| 194 | Chester County | PA | 27.3 | 5.1 |
| 195 | Fluvanna County | VA | 27 | 21 |
| 196 | Box Elder County | UT | 27 | 16 |
| 197 | Union County | GA | 27 | 15 |
| 198 | Bolivar County | MS | 27 | 15 |
| 199 | Lamar County | MS | 27 | 16 |
| 200 | Cape Girardeau County | MO | 27 | 12 |
| 201 | Caroline County | MD | 27 | 17 |
| 202 | Susquehanna County | PA | 27 | 19 |
| 203 | Lincoln County | KY | 26 | 24 |
| 204 | Colonial Heights city | VA | 26 | 20 |
| 205 | Fauquier County | VA | 26 | 12 |
| 206 | Ascension Parish | LA | 26 | 11 |
| 207 | Kane County | IL | 26.3 | 7.1 |
| 208 | Delaware County | OK | 26 | 16 |
| 209 | Hickman County | TN | 26 | 23 |
| 210 | Henrico County | VA | 25.9 | 6.6 |
| 211 | Livingston County | MI | 25.8 | 7.2 |
| 212 | Wyandotte County | KS | 25.6 | 7.6 |
| 213 | Monroe County | FL | 26 | 13 |
| 214 | Fillmore County | MN | 26 | 19 |
| 215 | McHenry County | IL | 25.5 | 7.4 |
| 216 | Oktibbeha County | MS | 26 | 20 |
| 217 | Marion County | MS | 26 | 23 |
| 218 | Russell County | AL | 25 | 15 |
| 219 | Berkeley County | WV | 25 | 11 |
| 220 | Staunton city | VA | 25 | 15 |
| 221 | Grant County | KY | 25 | 20 |
| 222 | Miami County | IN | 25 | 18 |
| 223 | Erie County | NY | 25.1 | 3.5 |
| 224 | Will County | IL | 24.9 | 4.7 |
| 225 | Warren County | MO | 25 | 21 |
| 226 | Loudoun County | VA | 24.8 | 8.5 |
| 227 | Milwaukee County | WI | 24.7 | 4.6 |
| 228 | Habersham County | GA | 25 | 16 |
| 229 | Yakima County | WA | 24.6 | 9.1 |
| 230 | Marengo County | AL | 25 | 19 |
| 231 | Dallas County | IA | 24 | 14 |
| 232 | New Castle County | DE | 24.3 | 4.8 |
| 233 | Marion County | AL | 24 | 14 |
| 234 | Robertson County | TN | 24 | 11 |
| 235 | Niagara County | NY | 24.2 | 5.8 |
| 236 | Dutchess County | NY | 24.1 | 6.3 |
| 237 | Sumter County | GA | 24 | 15 |
| 238 | Shenandoah County | VA | 24 | 14 |
| 239 | Suffolk city | VA | 24 | 11 |
| 240 | Los Angeles County | CA | 23.9 | 2.1 |
| 241 | Bryan County | GA | 24 | 17 |
| 242 | Buchanan County | VA | 24 | 21 |
| 243 | Navajo County | AZ | 23.7 | 8 |
| 244 | Van Wert County | OH | 24 | 21 |
| 245 | Macon County | NC | 24 | 15 |
| 246 | Escambia County | AL | 24 | 16 |
| 247 | Dearborn County | IN | 23 | 16 |
| 248 | Johnson County | IN | 23.4 | 8.3 |
| 249 | Monroe County | MS | 23 | 13 |
| 250 | Custer County | OK | 23 | 20 |
| 251 | Chenango County | NY | 23 | 13 |
| 252 | Ulster County | NY | 23.2 | 7.5 |
| 253 | St. Tammany Parish | LA | 23.1 | 5.8 |
| 254 | Haralson County | GA | 23 | 18 |
| 255 | St. Bernard Parish | LA | 23 | 16 |
| 256 | Henry County | AL | 23 | 21 |
| 257 | Clay County | MS | 23 | 23 |
| 258 | Franklin County | GA | 23 | 16 |
| 259 | Gage County | NE | 23 | 24 |
| 260 | Harnett County | NC | 22.7 | 9.2 |
| 261 | Adams County | PA | 23 | 11 |
| 262 | Genesee County | MI | 22.7 | 4 |
| 263 | Clark County | IN | 22.7 | 9.7 |
| 264 | Caldwell County | TX | 23 | 16 |
| 265 | Finney County | KS | 23 | 22 |
| 266 | Allegany County | MD | 22.5 | 8.6 |
| 267 | Rowan County | KY | 23 | 20 |
| 268 | St. Louis County | MO | 22.5 | 4.1 |
| 269 | LaPorte County | IN | 22.5 | 8 |
| 270 | Schenectady County | NY | 22.4 | 8.8 |
| 271 | Jackson County | NC | 22 | 15 |
| 272 | Scott County | MN | 22 | 13 |
| 273 | Douglas County | GA | 22.4 | 9.5 |
| 274 | Fayette County | TN | 22 | 15 |
| 275 | Cherokee County | AL | 22 | 14 |
| 276 | Walker County | GA | 22 | 13 |
| 277 | Tioga County | NY | 22 | 15 |
| 278 | Davie County | NC | 22 | 17 |
| 279 | Sequoyah County | OK | 22 | 13 |
| 280 | Stark County | ND | 22 | 21 |
| 281 | Pike County | MS | 22 | 12 |
| 282 | Lincoln County | WI | 22 | 16 |
| 283 | Clay County | IN | 22 | 17 |
| 284 | Baldwin County | GA | 22 | 12 |
| 285 | Martin County | NC | 22 | 15 |
| 286 | Clayton County | GA | 21.8 | 8.2 |
| 287 | Dinwiddie County | VA | 22 | 17 |
| 288 | St. Martin Parish | LA | 22 | 14 |
| 289 | Saginaw County | MI | 21.7 | 5.7 |
| 290 | Kent County | DE | 21.7 | 6.9 |
| 291 | Curry County | OR | 22 | 14 |
| 292 | Branch County | MI | 22 | 16 |
| 293 | Elmore County | AL | 22 | 11 |
| 294 | Monroe County | IN | 21 | 12 |
| 295 | Williamson County | IL | 21 | 10 |
| 296 | DeKalb County | IL | 21 | 11 |
| 297 | Fulton County | GA | 20.9 | 3.4 |
| 298 | Macon County | AL | 21 | 22 |
| 299 | Jennings County | IN | 21 | 17 |
| 300 | Somerset County | MD | 21 | 18 |
| 301 | Salem city | VA | 21 | 18 |
| 302 | Hancock County | IN | 21 | 16 |
| 303 | Calcasieu Parish | LA | 20.6 | 6.6 |
| 304 | Union County | AR | 21 | 13 |
| 305 | St. Landry Parish | LA | 20.6 | 8.4 |
| 306 | Lavaca County | TX | 21 | 20 |
| 307 | Taylor County | KY | 20 | 17 |
| 308 | Wood County | OH | 20.5 | 7.8 |
| 309 | Lincoln County | NE | 20 | 18 |
| 310 | Lincoln County | MT | 20 | 21 |
| 311 | Marshall County | IA | 20 | 15 |
| 312 | Delaware County | IN | 20.4 | 8.9 |
| 313 | Fayette County | GA | 20 | 13 |
| 314 | Hamilton County | IN | 20.1 | 6.7 |
| 315 | Weld County | CO | 20.1 | 7.6 |
| 316 | Bristol County | RI | 20 | 15 |
| 317 | Houston County | AL | 20 | 8.2 |
| 318 | Decatur County | GA | 20 | 15 |
| 319 | Miami-Dade County | FL | 19.8 | 2.8 |
| 320 | Hart County | GA | 20 | 20 |
| 321 | Pinal County | AZ | 19.8 | 5 |
| 322 | Pearl River County | MS | 20 | 10 |
| 323 | Mercer County | OH | 20 | 16 |
| 324 | Muscatine County | IA | 20 | 13 |
| 325 | Carroll County | GA | 19.5 | 8.8 |
| 326 | Sweetwater County | WY | 20 | 19 |
| 327 | Monroe County | GA | 19 | 23 |
| 328 | Albany County | NY | 19.5 | 4.8 |
| 329 | Coffee County | TN | 19 | 12 |
| 330 | Natchitoches Parish | LA | 19 | 14 |
| 331 | Perry County | OH | 19 | 16 |
| 332 | Indiana County | PA | 19 | 12 |
| 333 | Cobb County | GA | 19.3 | 4 |
| 334 | Jefferson County | CO | 19.3 | 4.3 |
| 335 | Madison County | IN | 19.3 | 7.8 |
| 336 | Gratiot County | MI | 19 | 16 |
| 337 | Fayette County | IA | 19 | 19 |
| 338 | Tillamook County | OR | 19 | 17 |
| 339 | Morehouse Parish | LA | 19 | 15 |
| 340 | Marion County | IL | 19 | 13 |
| 341 | Dauphin County | PA | 19.2 | 5.3 |
| 342 | Kershaw County | SC | 19 | 12 |
| 343 | Webster County | IA | 19 | 13 |
| 344 | Woodbury County | IA | 19 | 12 |
| 345 | Whitley County | KY | 19 | 18 |
| 346 | Owen County | IN | 19 | 22 |
| 347 | Hertford County | NC | 19 | 15 |
| 348 | Montgomery County | NC | 19 | 14 |
| 349 | Fremont County | WY | 19 | 14 |
| 350 | Gwinnett County | GA | 18.7 | 4 |
| 351 | Grundy County | IL | 19 | 15 |
| 352 | Washtenaw County | MI | 18.6 | 6.3 |
| 353 | Lake County | IN | 18.6 | 4.6 |
| 354 | Onondaga County | NY | 18.6 | 5.1 |
| 355 | Tate County | MS | 19 | 15 |
| 356 | Howard County | MD | 18.6 | 10 |
| 357 | Clinton County | IL | 19 | 20 |
| 358 | Olmsted County | MN | 19 | 11 |
| 359 | Washington County | RI | 18.4 | 9 |
| 360 | DeKalb County | GA | 18.4 | 3.5 |
| 361 | Lincoln Parish | LA | 18 | 16 |
| 362 | Hall County | GA | 18.3 | 7.2 |
| 363 | Wayne County | NC | 18.3 | 7.6 |
| 364 | Levy County | FL | 18 | 12 |
| 365 | Otero County | NM | 18 | 14 |
| 366 | Accomack County | VA | 18 | 13 |
| 367 | Jo Daviess County | IL | 18 | 21 |
| 368 | Madison County | OH | 18 | 15 |
| 369 | Pemiscot County | MO | 18 | 24 |
| 370 | Linn County | IA | 17.9 | 7.2 |
| 371 | Auglaize County | OH | 18 | 14 |
| 372 | Dixie County | FL | 18 | 22 |
| 373 | DeSoto County | FL | 18 | 17 |
| 374 | Tangipahoa Parish | LA | 17.9 | 8.8 |
| 375 | Albemarle County | VA | 18 | 11 |
| 376 | Henry County | IL | 18 | 13 |
| 377 | Jackson County | AL | 18 | 10 |
| 378 | Vernon County | MO | 18 | 19 |
| 379 | Dickinson County | MI | 18 | 17 |
| 380 | Summit County | OH | 17.7 | 4.5 |
| 381 | Centre County | PA | 17.7 | 9.6 |
| 382 | Terrebonne Parish | LA | 18 | 10 |
| 383 | Crisp County | GA | 18 | 16 |
| 384 | Wyandot County | OH | 18 | 19 |
| 385 | Muskegon County | MI | 17.6 | 8.2 |
| 386 | Hillsborough County | NH | 17.5 | 4.8 |
| 387 | Lawrence County | SD | 17 | 21 |
| 388 | Fentress County | TN | 17 | 18 |
| 389 | Rockingham County | NH | 17.4 | 5.3 |
| 390 | Webb County | TX | 17.4 | 7.7 |
| 391 | Isabella County | MI | 17 | 14 |
| 392 | Jackson County | WV | 17 | 18 |
| 393 | Bullitt County | KY | 17 | 12 |
| 394 | Richland County | SC | 17.3 | 6.1 |
| 395 | Hendricks County | IN | 17.3 | 7.6 |
| 396 | Wayne County | KY | 17 | 22 |
| 397 | Ogle County | IL | 17 | 12 |
| 398 | Cumberland County | NJ | 17.2 | 9.1 |
| 399 | Pitt County | NC | 17.2 | 6.9 |
| 400 | Hall County | NE | 17 | 15 |
| 401 | Stoddard County | MO | 17 | 16 |
| 402 | Bedford County | VA | 17 | 10 |
| 403 | Linn County | OR | 17 | 6.9 |
| 404 | Porter County | IN | 17 | 7.9 |
| 405 | Peach County | GA | 17 | 19 |
| 406 | Coryell County | TX | 17 | 14 |
| 407 | Franklin County | OH | 16.9 | 3.6 |
| 408 | Victoria County | TX | 17 | 12 |
| 409 | Highland County | OH | 17 | 17 |
| 410 | Brown County | TX | 17 | 15 |
| 411 | Barnstable County | MA | 16.7 | 4.8 |
| 412 | Madison County | TN | 17 | 13 |
| 413 | Wayne County | WV | 17 | 17 |
| 414 | Cass County | ND | 16.5 | 8.2 |
| 415 | Knox County | KY | 16 | 15 |
| 416 | Merced County | CA | 16.5 | 7.8 |
| 417 | Henry County | GA | 16.5 | 7.7 |
| 418 | Henderson County | NC | 16.4 | 8.6 |
| 419 | Manistee County | MI | 16 | 15 |
| 420 | McDonald County | MO | 16 | 18 |
| 421 | Adams County | CO | 16.3 | 5.4 |
| 422 | Wilson County | NC | 16.3 | 9.6 |
| 423 | Greene County | IN | 16 | 16 |
| 424 | Beaver County | PA | 16.3 | 6.7 |
| 425 | Colleton County | SC | 16 | 13 |
| 426 | Charlotte County | FL | 16.1 | 4.8 |
| 427 | Mobile County | AL | 16.1 | 5 |
| 428 | Lyon County | NV | 16 | 10 |
| 429 | Montrose County | CO | 16 | 16 |
| 430 | Union County | PA | 16 | 14 |
| 431 | Okmulgee County | OK | 16 | 17 |
| 432 | Mendocino County | CA | 16 | 11 |
| 433 | Sutter County | CA | 15.9 | 9.9 |
| 434 | Allen County | KY | 16 | 19 |
| 435 | Columbiana County | OH | 15.9 | 8.1 |
| 436 | Dallas County | TX | 15.8 | 2 |
| 437 | Troup County | GA | 16 | 13 |
| 438 | Newberry County | SC | 16 | 15 |
| 439 | Erie County | OH | 16 | 11 |
| 440 | Georgetown County | SC | 15.7 | 9.6 |
| 441 | Ingham County | MI | 15.7 | 6.4 |
| 442 | Whitman County | WA | 16 | 20 |
| 443 | Colquitt County | GA | 16 | 16 |
| 444 | Paulding County | GA | 15.7 | 8.1 |
| 445 | Elbert County | GA | 16 | 20 |
| 446 | Vernon County | WI | 16 | 19 |
| 447 | Sunflower County | MS | 16 | 15 |
| 448 | Dorchester County | MD | 16 | 15 |
| 449 | Beauregard Parish | LA | 15 | 16 |
| 450 | Luzerne County | PA | 15.5 | 5.6 |
| 451 | Goodhue County | MN | 15 | 14 |
| 452 | Chilton County | AL | 15 | 15 |
| 453 | Cleburne County | AR | 15 | 14 |
| 454 | Webster Parish | LA | 15 | 13 |
| 455 | Kendall County | IL | 15 | 11 |
| 456 | Lafayette Parish | LA | 15.3 | 7.2 |
| 457 | Ray County | MO | 15 | 22 |
| 458 | Harrison County | TX | 15 | 13 |
| 459 | Coles County | IL | 15 | 13 |
| 460 | Shiawassee County | MI | 15 | 12 |
| 461 | Steuben County | IN | 15 | 17 |
| 462 | Alamance County | NC | 15.2 | 7 |
| 463 | Jasper County | IA | 15 | 22 |
| 464 | Yazoo County | MS | 15 | 17 |
| 465 | Ellis County | TX | 15.2 | 9.3 |
| 466 | Franklin County | VA | 15 | 13 |
| 467 | Simpson County | MS | 15 | 17 |
| 468 | Tuolumne County | CA | 15 | 12 |
| 469 | Sumter County | SC | 15 | 9.4 |
| 470 | Otsego County | NY | 15 | 14 |
| 471 | Weakley County | TN | 15 | 16 |
| 472 | Douglas County | OR | 14.9 | 7.3 |
| 473 | Kankakee County | IL | 14.9 | 8.3 |
| 474 | Campbell County | VA | 15 | 12 |
| 475 | Wagoner County | OK | 15 | 12 |
| 476 | Craven County | NC | 14.7 | 8.7 |
| 477 | Putnam County | GA | 15 | 21 |
| 478 | Fayette County | KY | 14.7 | 5.7 |
| 479 | Newport News city | VA | 14.7 | 8.1 |
| 480 | Tulare County | CA | 14.6 | 5.5 |
| 481 | Winnebago County | IL | 14.6 | 4.9 |
| 482 | Sarpy County | NE | 14.6 | 8.3 |
| 483 | Mecklenburg County | NC | 14.6 | 4.2 |
| 484 | Lebanon County | PA | 14.6 | 8.3 |
| 485 | Dakota County | MN | 14.6 | 5.6 |
| 486 | Clarke County | GA | 15 | 10 |
| 487 | Rockingham County | NC | 14.5 | 8.1 |
| 488 | Rankin County | MS | 14.5 | 7.5 |
| 489 | Graves County | KY | 15 | 12 |
| 490 | Meriwether County | GA | 15 | 17 |
| 491 | Washington County | ME | 14 | 16 |
| 492 | Brown County | OH | 14 | 14 |
| 493 | Walton County | GA | 14 | 13 |
| 494 | Lafayette County | MS | 14 | 15 |
| 495 | Fannin County | GA | 14 | 15 |
| 496 | Morton County | ND | 14 | 15 |
| 497 | Carson City | NV | 14 | 11 |
| 498 | Giles County | TN | 14 | 18 |
| 499 | Ross County | OH | 14.2 | 9.3 |
| 500 | Washington County | VT | 14 | 13 |
| 501 | Rogers County | OK | 14.2 | 8.4 |
| 502 | Iredell County | NC | 14.1 | 7.5 |
| 503 | Colorado County | TX | 14 | 17 |
| 504 | Anne Arundel County | MD | 14 | 4.7 |
| 505 | Franklin County | NY | 14 | 12 |
| 506 | Calvert County | MD | 14 | 12 |
| 507 | Warren County | NC | 14 | 17 |
| 508 | Delaware County | OH | 14 | 8.8 |
| 509 | Cortland County | NY | 14 | 15 |
| 510 | Macoupin County | IL | 14 | 12 |
| 511 | Burleigh County | ND | 14 | 11 |
| 512 | Talbot County | MD | 14 | 17 |
| 513 | Warren County | NY | 13.8 | 9.7 |
| 514 | Grant County | IN | 14 | 11 |
| 515 | Davidson County | NC | 13.8 | 9.2 |
| 516 | Buncombe County | NC | 13.8 | 6.6 |
| 517 | Clarke County | AL | 14 | 14 |
| 518 | Carlton County | MN | 14 | 18 |
| 519 | Wicomico County | MD | 13.7 | 8.2 |
| 520 | Jackson County | MO | 13.7 | 3.8 |
| 521 | Roanoke city | VA | 13.7 | 7.9 |
| 522 | Green County | WI | 14 | 16 |
| 523 | Allegan County | MI | 13.6 | 8.6 |
| 524 | Monroe County | IL | 14 | 16 |
| 525 | Laurel County | KY | 13.6 | 9.1 |
| 526 | Hardin County | TN | 14 | 15 |
| 527 | Warren County | MS | 14 | 14 |
| 528 | Shawano County | WI | 14 | 13 |
| 529 | Nez Perce County | ID | 14 | 15 |
| 530 | McDowell County | NC | 14 | 11 |
| 531 | Lawrence County | TN | 14 | 13 |
| 532 | Durham County | NC | 13.5 | 7.1 |
| 533 | Mason County | MI | 13 | 16 |
| 534 | Douglas County | WA | 13 | 22 |
| 535 | Hockley County | TX | 13 | 19 |
| 536 | Shelby County | IN | 13 | 12 |
| 537 | Portage County | OH | 13.4 | 8.3 |
| 538 | Jefferson County | TX | 13.4 | 5.9 |
| 539 | DeKalb County | TN | 13 | 18 |
| 540 | Windham County | VT | 13 | 13 |
| 541 | Gadsden County | FL | 13 | 14 |
| 542 | Berrien County | MI | 13.3 | 7.5 |
| 543 | Texas County | MO | 13 | 16 |
| 544 | Ozaukee County | WI | 13 | 11 |
| 545 | Hood County | TX | 13 | 13 |
| 546 | James City County | VA | 13.3 | 9.7 |
| 547 | Pickaway County | OH | 13 | 12 |
| 548 | Pine County | MN | 13 | 17 |
| 549 | Rutherford County | TN | 13.2 | 7.2 |
| 550 | Morgan County | IN | 13 | 12 |
| 551 | Rapides Parish | LA | 13.2 | 6.8 |
| 552 | Cumberland County | NC | 13.2 | 4.8 |
| 553 | Yolo County | CA | 13.2 | 9.4 |
| 554 | Malheur County | OR | 13 | 26 |
| 555 | Winston County | AL | 13 | 15 |
| 556 | White County | IN | 13 | 17 |
| 557 | Pima County | AZ | 13.1 | 4.1 |
| 558 | Boone County | WV | 13 | 19 |
| 559 | Van Buren County | MI | 13 | 13 |
| 560 | Worcester County | MD | 13 | 13 |
| 561 | Franklin County | PA | 13 | 7.2 |
| 562 | Greenville County | SC | 13 | 4.5 |
| 563 | Elko County | NV | 13 | 15 |
| 564 | Oneida County | NY | 12.9 | 6.9 |
| 565 | Montgomery County | KS | 13 | 18 |
| 566 | Lee County | AL | 12.9 | 9.1 |
| 567 | Dillon County | SC | 13 | 13 |
| 568 | Robeson County | NC | 12.9 | 6.8 |
| 569 | Cecil County | MD | 12.8 | 8.1 |
| 570 | Acadia Parish | LA | 12.8 | 9.3 |
| 571 | Marshall County | AL | 12.8 | 8.4 |
| 572 | Ionia County | MI | 13 | 11 |
| 573 | Monroe County | NY | 12.7 | 3.4 |
| 574 | Hunt County | TX | 12.7 | 9.8 |
| 575 | Caroline County | VA | 13 | 16 |
| 576 | Rensselaer County | NY | 12.7 | 8 |
| 577 | Anoka County | MN | 12.7 | 6.3 |
| 578 | Anderson County | SC | 12.7 | 6.4 |
| 579 | Potter County | TX | 12.6 | 8.8 |
| 580 | San Miguel County | NM | 13 | 19 |
| 581 | Guernsey County | OH | 13 | 15 |
| 582 | Kent County | RI | 12.6 | 8.4 |
| 583 | Fayette County | TX | 13 | 17 |
| 584 | Bartholomew County | IN | 13 | 12 |
| 585 | Cayuga County | NY | 13 | 13 |
| 586 | Tipton County | TN | 13 | 13 |
| 587 | Tishomingo County | MS | 12 | 19 |
| 588 | Jefferson County | KY | 12.3 | 3.6 |
| 589 | Thomas County | GA | 12 | 13 |
| 590 | Spotsylvania County | VA | 12.3 | 8.7 |
| 591 | Bertie County | NC | 12 | 16 |
| 592 | Adams County | NE | 12 | 15 |
| 593 | Polk County | TX | 12 | 13 |
| 594 | Cass County | MI | 12 | 12 |
| 595 | Jones County | MS | 12 | 13 |
| 596 | Meigs County | OH | 12 | 16 |
| 597 | Iroquois County | IL | 12 | 15 |
| 598 | Freeborn County | MN | 12 | 14 |
| 599 | Pike County | AL | 12 | 14 |
| 600 | Valencia County | NM | 12 | 11 |
| 601 | Washington County | NY | 12 | 11 |
| 602 | Ramsey County | MN | 11.9 | 5.8 |
| 603 | Pettis County | MO | 12 | 15 |
| 604 | Muscogee County | GA | 11.9 | 8.7 |
| 605 | Cape May County | NJ | 11.9 | 6.9 |
| 606 | Cabarrus County | NC | 11.8 | 7.8 |
| 607 | Lapeer County | MI | 11.8 | 8.5 |
| 608 | Forrest County | MS | 11.8 | 9.3 |
| 609 | Hinds County | MS | 11.8 | 6.4 |
| 610 | Blue Earth County | MN | 12 | 12 |
| 611 | Monroe County | MI | 11.7 | 6.6 |
| 612 | Putnam County | IN | 12 | 14 |
| 613 | Nicollet County | MN | 12 | 17 |
| 614 | Laurens County | GA | 12 | 12 |
| 615 | Cass County | TX | 12 | 15 |
| 616 | Snohomish County | WA | 11.6 | 4.2 |
| 617 | Rock County | WI | 11.6 | 6.4 |
| 618 | Grand Traverse County | MI | 12 | 12 |
| 619 | Montgomery County | NY | 12 | 12 |
| 620 | Montgomery County | VA | 12 | 12 |
| 621 | Pulaski County | AR | 11.5 | 4.5 |
| 622 | Bedford County | PA | 11 | 15 |
| 623 | Wyoming County | WV | 11 | 16 |
| 624 | Fayette County | OH | 11 | 19 |
| 625 | Grant County | WA | 11 | 11 |
| 626 | Jackson County | IL | 11 | 12 |
| 627 | Boone County | KY | 11 | 10 |
| 628 | Pickens County | GA | 11 | 14 |
| 629 | Scotland County | NC | 11 | 15 |
| 630 | Broward County | FL | 11.4 | 2.4 |
| 631 | Warrick County | IN | 11 | 11 |
| 632 | Boulder County | CO | 11.4 | 5.9 |
| 633 | Kalamazoo County | MI | 11.3 | 6.6 |
| 634 | Howard County | IN | 11.3 | 7.6 |
| 635 | Jasper County | IN | 11 | 15 |
| 636 | Citrus County | FL | 11.3 | 5.3 |
| 637 | Bastrop County | TX | 11 | 11 |
| 638 | Lawrence County | PA | 11.2 | 8.1 |
| 639 | Clarion County | PA | 11 | 15 |
| 640 | Dyer County | TN | 11 | 13 |
| 641 | Calhoun County | MI | 11.2 | 7.8 |
| 642 | Antrim County | MI | 11 | 20 |
| 643 | Adams County | MS | 11 | 14 |
| 644 | Wilson County | TN | 11.1 | 9.2 |
| 645 | Sedgwick County | KS | 11.1 | 4.1 |
| 646 | Sawyer County | WI | 11 | 18 |
| 647 | Ohio County | WV | 11 | 12 |
| 648 | Ouachita Parish | LA | 11 | 8.1 |
| 649 | Sanilac County | MI | 11 | 12 |
| 650 | Ottawa County | MI | 11 | 5.3 |
| 651 | Harris County | TX | 11 | 1.5 |
| 652 | Bell County | KY | 11 | 16 |
| 653 | Belmont County | OH | 11 | 10 |
| 654 | Columbia County | GA | 10.8 | 7.9 |
| 655 | Marion County | SC | 11 | 12 |
| 656 | Mecklenburg County | VA | 11 | 12 |
| 657 | Stark County | OH | 10.8 | 3.9 |
| 658 | Covington County | AL | 11 | 12 |
| 659 | Polk County | IA | 10.8 | 4.9 |
| 660 | King County | WA | 10.7 | 2.6 |
| 661 | San Bernardino County | CA | 10.7 | 2.4 |
| 662 | Champaign County | OH | 11 | 15 |
| 663 | St. Lucie County | FL | 10.7 | 4.4 |
| 664 | Sumner County | TN | 10.7 | 6 |
| 665 | Cleveland County | OK | 10.7 | 6.2 |
| 666 | Scott County | IA | 10.7 | 7.7 |
| 667 | Phelps County | MO | 11 | 15 |
| 668 | Racine County | WI | 10.7 | 7.2 |
| 669 | Brazos County | TX | 10.6 | 9 |
| 670 | St. Clair County | MI | 10.6 | 6.3 |
| 671 | Spartanburg County | SC | 10.6 | 4.5 |
| 672 | Davis County | UT | 10.6 | 5.8 |
| 673 | Washington County | OK | 11 | 10 |
| 674 | Comanche County | OK | 11 | 10 |
| 675 | Shelby County | TX | 11 | 17 |
| 676 | Carter County | TN | 10.6 | 9.1 |
| 677 | Peoria County | IL | 10.6 | 6.1 |
| 678 | Lancaster County | SC | 10.5 | 8.8 |
| 679 | Churchill County | NV | 10 | 17 |
| 680 | Shelby County | TN | 10.5 | 3.9 |
| 681 | Lenoir County | NC | 10 | 11 |
| 682 | Fulton County | NY | 10 | 12 |
| 683 | Washington County | OR | 10.5 | 4.9 |
| 684 | Somerset County | ME | 10 | 11 |
| 685 | Montgomery County | KY | 10 | 17 |
| 686 | Seminole County | OK | 10 | 14 |
| 687 | Palm Beach County | FL | 10.3 | 2.8 |
| 688 | Bell County | TX | 10.3 | 7.7 |
| 689 | St. Louis County | MN | 10.3 | 7 |
| 690 | Newton County | GA | 10.2 | 8.8 |
| 691 | Barnwell County | SC | 10 | 18 |
| 692 | Coffee County | GA | 10 | 13 |
| 693 | St. Francis County | AR | 10 | 21 |
| 694 | Catoosa County | GA | 10 | 11 |
| 695 | Dallas County | AL | 10 | 15 |
| 696 | Franklin County | TN | 10 | 11 |
| 697 | Nacogdoches County | TX | 10 | 12 |
| 698 | Alameda County | CA | 10.1 | 2.9 |
| 699 | Cuyahoga County | OH | 10.1 | 2.6 |
| 700 | Howell County | MO | 10 | 13 |
| 701 | Overton County | TN | 10 | 14 |
| 702 | Windsor County | VT | 10 | 15 |
| 703 | Smith County | TX | 10 | 6.6 |
| 704 | Manatee County | FL | 10 | 4.3 |
| 705 | New Madrid County | MO | 10 | 17 |
| 706 | Pontotoc County | OK | 10 | 14 |
| 707 | Knox County | OH | 10 | 14 |
| 708 | Chatham County | NC | 10 | 11 |
| 709 | Ripley County | IN | 10 | 18 |
| 710 | Aransas County | TX | 10 | 24 |
| 711 | Travis County | TX | 9.9 | 3.1 |
| 712 | Cheatham County | TN | 10 | 21 |
| 713 | Worth County | GA | 10 | 17 |
| 714 | Jefferson County | MO | 9.9 | 5.6 |
| 715 | San Francisco County | CA | 9.8 | 3.3 |
| 716 | Marion County | OR | 9.8 | 5.3 |
| 717 | York County | SC | 9.8 | 6.2 |
| 718 | Jefferson County | WV | 10 | 11 |
| 719 | Greenwood County | SC | 9.8 | 8.4 |
| 720 | Franklin County | WA | 10 | 12 |
| 721 | Scott County | TN | 10 | 17 |
| 722 | Madison County | MS | 9.7 | 9.1 |
| 723 | Yuma County | AZ | 9.7 | 6.2 |
| 724 | DeSoto County | MS | 9.6 | 8 |
| 725 | Chittenden County | VT | 9.6 | 7.9 |
| 726 | Belknap County | NH | 10 | 10 |
| 727 | Walworth County | WI | 10 | 11 |
| 728 | Grays Harbor County | WA | 9.5 | 9.6 |
| 729 | Jessamine County | KY | 10 | 13 |
| 730 | Sarasota County | FL | 9.5 | 4.1 |
| 731 | Riverside County | CA | 9.5 | 2.5 |
| 732 | Otsego County | MI | 9 | 16 |
| 733 | Chesterfield County | VA | 9.5 | 5.7 |
| 734 | Waynesboro city | VA | 9 | 18 |
| 735 | Umatilla County | OR | 9.5 | 9.4 |
| 736 | Clackamas County | OR | 9.5 | 5.5 |
| 737 | Gregg County | TX | 9.4 | 7.1 |
| 738 | Lexington County | SC | 9.4 | 5.1 |
| 739 | Independence County | AR | 9 | 14 |
| 740 | Ward County | ND | 9 | 11 |
| 741 | Rowan County | NC | 9.3 | 6.3 |
| 742 | Wayne County | IN | 9.3 | 9.2 |
| 743 | Houston County | TX | 9 | 15 |
| 744 | Jackson County | MI | 9.3 | 8.2 |
| 745 | Brown County | WI | 9.3 | 6.2 |
| 746 | Boone County | IL | 9 | 17 |
| 747 | Floyd County | IN | 9 | 11 |
| 748 | Calloway County | KY | 9 | 13 |
| 749 | Dorchester County | SC | 9.3 | 8.8 |
| 750 | Tazewell County | IL | 9.3 | 9.9 |
| 751 | Sauk County | WI | 9 | 13 |
| 752 | Florence County | SC | 9.2 | 6.5 |
| 753 | Hamilton County | OH | 9.2 | 4.4 |
| 754 | Hamblen County | TN | 9 | 11 |
| 755 | Santa Clara County | CA | 9.2 | 2.7 |
| 756 | Montgomery County | TX | 9.2 | 5.1 |
| 757 | Orange County | TX | 9 | 10 |
| 758 | Petersburg city | VA | 9 | 12 |
| 759 | Lubbock County | TX | 9.2 | 5.9 |
| 760 | Lee County | MS | 9.1 | 9.4 |
| 761 | Chaves County | NM | 9 | 11 |
| 762 | Putnam County | FL | 9.1 | 8.3 |
| 763 | Butler County | KS | 9.1 | 9.7 |
| 764 | Fulton County | OH | 9 | 16 |
| 765 | Maricopa County | AZ | 9.1 | 2.1 |
| 766 | Jefferson County | IL | 9 | 13 |
| 767 | Macon County | TN | 9 | 17 |
| 768 | Crawford County | KS | 9 | 16 |
| 769 | Kanawha County | WV | 9 | 6.8 |
| 770 | Harris County | GA | 9 | 18 |
| 771 | Garrett County | MD | 9 | 15 |
| 772 | Tarrant County | TX | 9 | 2.4 |
| 773 | Bibb County | GA | 9 | 7.9 |
| 774 | Amador County | CA | 9 | 12 |
| 775 | Iron County | UT | 9 | 15 |
| 776 | Coffee County | AL | 9 | 12 |
| 777 | Floyd County | KY | 9 | 12 |
| 778 | Armstrong County | PA | 9 | 10 |
| 779 | Merrimack County | NH | 8.9 | 6.7 |
| 780 | Johnston County | NC | 8.9 | 6.9 |
| 781 | Dawson County | GA | 9 | 17 |
| 782 | Oconee County | GA | 9 | 14 |
| 783 | Starke County | IN | 9 | 18 |
| 784 | Catawba County | NC | 8.9 | 7.3 |
| 785 | Stokes County | NC | 9 | 10 |
| 786 | Cumberland County | ME | 8.9 | 6.4 |
| 787 | Bradley County | TN | 8.8 | 8.2 |
| 788 | Tolland County | CT | 8.8 | 8.3 |
| 789 | Burke County | NC | 8.8 | 8.4 |
| 790 | Chatham County | GA | 8.8 | 7.6 |
| 791 | Minnehaha County | SD | 8.8 | 7.1 |
| 792 | Shelby County | KY | 9 | 14 |
| 793 | Madison County | NY | 9 | 12 |
| 794 | Allegany County | NY | 9 | 15 |
| 795 | Leavenworth County | KS | 9 | 14 |
| 796 | Martin County | FL | 8.7 | 6.3 |
| 797 | Washington County | MS | 9 | 13 |
| 798 | San Joaquin County | CA | 8.7 | 4.7 |
| 799 | Greenup County | KY | 9 | 12 |
| 800 | San Mateo County | CA | 8.7 | 4.9 |
| 801 | Buffalo County | NE | 9 | 14 |
| 802 | Stanly County | NC | 9 | 11 |
| 803 | Tuscola County | MI | 9 | 12 |
| 804 | Butler County | OH | 8.6 | 4.6 |
| 805 | Orange County | NC | 8.6 | 9.4 |
| 806 | Rutland County | VT | 8.6 | 9.4 |
| 807 | Randolph County | NC | 8.6 | 6.4 |
| 808 | LaSalle County | IL | 8.6 | 8.9 |
| 809 | Cheboygan County | MI | 9 | 14 |
| 810 | Grant County | WI | 9 | 13 |
| 811 | Kendall County | TX | 8 | 16 |
| 812 | Itasca County | MN | 8 | 14 |
| 813 | Brooke County | WV | 8 | 15 |
| 814 | Davidson County | TN | 8.4 | 3.9 |
| 815 | Christian County | IL | 8 | 13 |
| 816 | Pope County | AR | 8 | 13 |
| 817 | Jackson County | MS | 8.4 | 6.6 |
| 818 | Aiken County | SC | 8.4 | 5.8 |
| 819 | Lake County | MT | 8 | 17 |
| 820 | Berkeley County | SC | 8.4 | 7.6 |
| 821 | Hanover County | VA | 8.3 | 9.2 |
| 822 | Warren County | KY | 8.2 | 8.8 |
| 823 | Harford County | MD | 8.2 | 6 |
| 824 | Lowndes County | MS | 8 | 12 |
| 825 | Franklin County | VT | 8 | 13 |
| 826 | Prentiss County | MS | 8 | 14 |
| 827 | Beaufort County | SC | 8.2 | 6.8 |
| 828 | Cass County | IN | 8 | 13 |
| 829 | Perry County | PA | 8 | 12 |
| 830 | Doña Ana County | NM | 8.1 | 7.1 |
| 831 | Caledonia County | VT | 8 | 18 |
| 832 | Cameron County | TX | 8.1 | 6.6 |
| 833 | Logan County | KY | 8 | 14 |
| 834 | Granville County | NC | 8 | 12 |
| 835 | Grimes County | TX | 8 | 14 |
| 836 | Greene County | OH | 7.9 | 7.6 |
| 837 | Weber County | UT | 7.9 | 7.9 |
| 838 | Gilmer County | GA | 8 | 14 |
| 839 | Schuylkill County | PA | 7.9 | 5.9 |
| 840 | New London County | CT | 7.9 | 5.2 |
| 841 | Otter Tail County | MN | 8 | 11 |
| 842 | Sullivan County | TN | 7.9 | 6.2 |
| 843 | Bulloch County | GA | 8 | 11 |
| 844 | Jefferson County | AL | 7.8 | 3.3 |
| 845 | Spokane County | WA | 7.8 | 4.7 |
| 846 | Clark County | WA | 7.8 | 4.6 |
| 847 | Rusk County | TX | 8 | 16 |
| 848 | Tulsa County | OK | 7.7 | 3.5 |
| 849 | Barry County | MI | 8 | 13 |
| 850 | Clark County | NV | 7.7 | 2.5 |
| 851 | Hillsborough County | FL | 7.7 | 3.1 |
| 852 | Meade County | KY | 8 | 19 |
| 853 | Washington County | VA | 7.7 | 9.7 |
| 854 | Oneida County | WI | 8 | 14 |
| 855 | Richmond County | NC | 8 | 11 |
| 856 | Coweta County | GA | 7.6 | 9.8 |
| 857 | Columbia County | PA | 7.6 | 9.7 |
| 858 | Gloucester County | VA | 8 | 12 |
| 859 | Leelanau County | MI | 8 | 17 |
| 860 | Franklin County | AR | 8 | 19 |
| 861 | Mille Lacs County | MN | 8 | 16 |
| 862 | Marshall County | MS | 8 | 15 |
| 863 | Ottawa County | OH | 8 | 10 |
| 864 | Casey County | KY | 8 | 19 |
| 865 | Murray County | GA | 8 | 13 |
| 866 | St. Clair County | AL | 7.5 | 8.9 |
| 867 | Austin County | TX | 8 | 16 |
| 868 | Bristol city | VA | 8 | 22 |
| 869 | Darlington County | SC | 7.5 | 8.5 |
| 870 | Knox County | TN | 7.4 | 4.1 |
| 871 | Cleveland County | NC | 7.4 | 7.6 |
| 872 | Fort Bend County | TX | 7.4 | 5.5 |
| 873 | Tuscaloosa County | AL | 7.4 | 8.7 |
| 874 | McLean County | IL | 7 | 11 |
| 875 | Madison County | IL | 7.3 | 4.9 |
| 876 | San Diego County | CA | 7.3 | 1.9 |
| 877 | Edgefield County | SC | 7 | 17 |
| 878 | Dane County | WI | 7.3 | 5 |
| 879 | Contra Costa County | CA | 7.2 | 3.6 |
| 880 | Northumberland County | PA | 7.2 | 8.8 |
| 881 | Hardeman County | TN | 7 | 17 |
| 882 | Sumter County | FL | 7.2 | 7.1 |
| 883 | Oceana County | MI | 7 | 16 |
| 884 | Lycoming County | PA | 7.2 | 7.4 |
| 885 | Bradford County | FL | 7 | 14 |
| 886 | Inyo County | CA | 7 | 19 |
| 887 | Glynn County | GA | 7.1 | 9 |
| 888 | Mifflin County | PA | 7 | 13 |
| 889 | Broome County | NY | 7.1 | 6.8 |
| 890 | Montgomery County | IL | 7 | 18 |
| 891 | Whatcom County | WA | 7.1 | 6.7 |
| 892 | Moore County | NC | 7 | 7.8 |
| 893 | Van Zandt County | TX | 7 | 11 |
| 894 | Wyoming County | NY | 7 | 17 |
| 895 | Limestone County | AL | 7 | 11 |
| 896 | Ware County | GA | 7 | 11 |
| 897 | White County | GA | 7 | 17 |
| 898 | Horry County | SC | 7 | 4.9 |
| 899 | Mohave County | AZ | 6.9 | 4.8 |
| 900 | Berkshire County | MA | 6.9 | 7.6 |
| 901 | Brazoria County | TX | 6.9 | 6 |
| 902 | Sioux County | IA | 7 | 18 |
| 903 | Allegheny County | PA | 6.9 | 2.8 |
| 904 | Mercer County | WV | 6.9 | 9.4 |
| 905 | Windham County | CT | 6.9 | 7.5 |
| 906 | Wilkes County | NC | 7 | 11 |
| 907 | Beaufort County | NC | 7 | 11 |
| 908 | Walla Walla County | WA | 7 | 14 |
| 909 | El Paso County | CO | 6.7 | 3.9 |
| 910 | Sandoval County | NM | 6.7 | 7.8 |
| 911 | Kalkaska County | MI | 7 | 18 |
| 912 | Stevens County | WA | 7 | 13 |
| 913 | Jackson County | OR | 6.7 | 5.4 |
| 914 | Bladen County | NC | 7 | 14 |
| 915 | Scott County | MO | 7 | 13 |
| 916 | Fresno County | CA | 6.6 | 3.3 |
| 917 | Boone County | IA | 7 | 16 |
| 918 | Chesapeake city | VA | 6.5 | 6.4 |
| 919 | Spencer County | IN | 7 | 22 |
| 920 | Upshur County | TX | 7 | 14 |
| 921 | Beltrami County | MN | 7 | 15 |
| 922 | Barrow County | GA | 7 | 11 |
| 923 | Washburn County | WI | 7 | 20 |
| 924 | Vilas County | WI | 7 | 14 |
| 925 | Washington County | MD | 6.5 | 6.7 |
| 926 | Callaway County | MO | 6 | 18 |
| 927 | Hill County | TX | 6 | 14 |
| 928 | Calumet County | WI | 6 | 18 |
| 929 | Henderson County | KY | 6 | 13 |
| 930 | Wayne County | OH | 6.4 | 7.2 |
| 931 | Ontario County | NY | 6.4 | 8.1 |
| 932 | Taney County | MO | 6 | 12 |
| 933 | Angelina County | TX | 6.3 | 8.2 |
| 934 | Johnson County | IA | 6 | 11 |
| 935 | Trumbull County | OH | 6.3 | 5.9 |
| 936 | Yankton County | SD | 6 | 19 |
| 937 | Talladega County | AL | 6.3 | 8.2 |
| 938 | Wayne County | PA | 6 | 11 |
| 939 | Sanpete County | UT | 6 | 19 |
| 940 | Salt Lake County | UT | 6.2 | 3.5 |
| 941 | St. Francois County | MO | 6.2 | 8.8 |
| 942 | Ector County | TX | 6.2 | 7.7 |
| 943 | Franklin County | KY | 6 | 12 |
| 944 | Walker County | AL | 6.2 | 10 |
| 945 | Athens County | OH | 6 | 12 |
| 946 | Lee County | FL | 6.2 | 4.8 |
| 947 | Jefferson County | WA | 6 | 15 |
| 948 | Carroll County | AR | 6 | 18 |
| 949 | Forsyth County | GA | 6.2 | 8.3 |
| 950 | Yamhill County | OR | 6.1 | 8.8 |
| 951 | Stephenson County | IL | 6 | 10 |
| 952 | Suwannee County | FL | 6 | 12 |
| 953 | El Dorado County | CA | 6 | 7.1 |
| 954 | Chesterfield County | SC | 6 | 11 |
| 955 | Carver County | MN | 6 | 14 |
| 956 | Cherokee County | OK | 6 | 11 |
| 957 | Rock Island County | IL | 6 | 6.7 |
| 958 | Forsyth County | NC | 5.9 | 5.1 |
| 959 | El Paso County | TX | 5.9 | 3.9 |
| 960 | Washington County | TN | 5.9 | 6.4 |
| 961 | Allen County | IN | 5.9 | 4.4 |
| 962 | Grenada County | MS | 6 | 16 |
| 963 | Hardin County | KY | 5.9 | 9 |
| 964 | Clinton County | MI | 6 | 14 |
| 965 | Madison County | KY | 5.7 | 9.8 |
| 966 | St. Charles County | MO | 5.7 | 5.4 |
| 967 | Gem County | ID | 6 | 21 |
| 968 | Grainger County | TN | 6 | 16 |
| 969 | Waukesha County | WI | 5.7 | 4.4 |
| 970 | Houston County | GA | 5.7 | 8.3 |
| 971 | Indian River County | FL | 5.6 | 6.3 |
| 972 | Craighead County | AR | 5.6 | 9.1 |
| 973 | Newport County | RI | 6 | 11 |
| 974 | Randolph County | AL | 6 | 17 |
| 975 | Caddo County | OK | 6 | 15 |
| 976 | Sangamon County | IL | 5.6 | 6 |
| 977 | Kern County | CA | 5.6 | 3.6 |
| 978 | Berrien County | GA | 6 | 17 |
| 979 | Scioto County | OH | 5.5 | 8.1 |
| 980 | Bernalillo County | NM | 5.5 | 3.9 |
| 981 | Lee County | NC | 5 | 11 |
| 982 | Baker County | OR | 5 | 19 |
| 983 | Caswell County | NC | 5 | 18 |
| 984 | Scott County | IN | 5 | 16 |
| 985 | Kings County | CA | 5.4 | 9.4 |
| 986 | Halifax County | NC | 5 | 10 |
| 987 | Kent County | MI | 5.4 | 3.9 |
| 988 | Tuscarawas County | OH | 5.3 | 7.5 |
| 989 | Roane County | TN | 5.3 | 9.8 |
| 990 | Orangeburg County | SC | 5.3 | 8 |
| 991 | Twin Falls County | ID | 5 | 11 |
| 992 | Ouachita County | AR | 5 | 17 |
| 993 | Autauga County | AL | 5 | 12 |
| 994 | Bosque County | TX | 5 | 17 |
| 995 | Medina County | OH | 5.2 | 8.1 |
| 996 | Alexander County | NC | 5 | 14 |
| 997 | Santa Cruz County | AZ | 5 | 15 |
| 998 | Cerro Gordo County | IA | 5 | 13 |
| 999 | Frederick County | VA | 5.1 | 9.9 |
| 1000 | McCracken County | KY | 5.1 | 9.8 |
| 1001 | Lancaster County | NE | 5.1 | 5.4 |
| 1002 | Sheboygan County | WI | 5.1 | 7.5 |
| 1003 | Lee County | IA | 5 | 14 |
| 1004 | Gaston County | NC | 5.1 | 5.9 |
| 1005 | Hardin County | OH | 5 | 19 |
| 1006 | Collin County | TX | 5.1 | 3.7 |
| 1007 | Washoe County | NV | 5.1 | 6 |
| 1008 | Nevada County | CA | 5.1 | 8.7 |
| 1009 | Williamson County | TX | 5 | 4.8 |
| 1010 | Ashe County | NC | 5 | 12 |
| 1011 | Washington County | UT | 5 | 6.1 |
| 1012 | McMinn County | TN | 5 | 11 |
| 1013 | Winona County | MN | 5 | 18 |
| 1014 | Blair County | PA | 4.9 | 6.3 |
| 1015 | Hopkins County | TX | 5 | 13 |
| 1016 | Galveston County | TX | 4.9 | 5.7 |
| 1017 | Polk County | GA | 5 | 13 |
| 1018 | Lyon County | MN | 5 | 23 |
| 1019 | Jackson County | OK | 5 | 19 |
| 1020 | Guilford County | NC | 4.7 | 4.6 |
| 1021 | Midland County | MI | 5 | 11 |
| 1022 | Roscommon County | MI | 5 | 14 |
| 1023 | Henderson County | TX | 4.6 | 7.2 |
| 1024 | Virginia Beach city | VA | 4.6 | 4.7 |
| 1025 | Douglas County | NE | 4.6 | 3.7 |
| 1026 | Huntington County | IN | 5 | 16 |
| 1027 | Charlottesville city | VA | 5 | 23 |
| 1028 | St. Joseph County | IN | 4.5 | 5.2 |
| 1029 | Randolph County | IL | 5 | 16 |
| 1030 | Duval County | FL | 4.5 | 3.1 |
| 1031 | Taylor County | FL | 4 | 22 |
| 1032 | Hancock County | MS | 4 | 15 |
| 1033 | Flathead County | MT | 4.4 | 8 |
| 1034 | McCurtain County | OK | 4 | 16 |
| 1035 | Whitfield County | GA | 4 | 10 |
| 1036 | Marlboro County | SC | 4 | 17 |
| 1037 | St. Mary's County | MD | 4.4 | 8.9 |
| 1038 | Volusia County | FL | 4.4 | 3.6 |
| 1039 | Panola County | MS | 4 | 15 |
| 1040 | Lynchburg city | VA | 4 | 11 |
| 1041 | Clark County | OH | 4.3 | 7.3 |
| 1042 | Baxter County | AR | 4.3 | 9.6 |
| 1043 | Vernon Parish | LA | 4 | 13 |
| 1044 | Gillespie County | TX | 4 | 14 |
| 1045 | Etowah County | AL | 4.3 | 7.1 |
| 1046 | York County | PA | 4.2 | 5.1 |
| 1047 | Ventura County | CA | 4.2 | 4.2 |
| 1048 | Jones County | GA | 4 | 16 |
| 1049 | Campbell County | KY | 4.1 | 9.7 |
| 1050 | Cumberland County | PA | 4.1 | 5.3 |
| 1051 | Evangeline Parish | LA | 4 | 17 |
| 1052 | Black Hawk County | IA | 4.1 | 7.9 |
| 1053 | Sebastian County | AR | 4 | 6.5 |
| 1054 | Erath County | TX | 4 | 18 |
| 1055 | Chester County | SC | 4 | 12 |
| 1056 | Fond du Lac County | WI | 3.9 | 8.2 |
| 1057 | Kerr County | TX | 4 | 11 |
| 1058 | Plymouth County | IA | 4 | 17 |
| 1059 | Jasper County | TX | 4 | 14 |
| 1060 | Somerset County | PA | 3.8 | 7.8 |
| 1061 | Pottawattamie County | IA | 3.8 | 9.8 |
| 1062 | Lewis and Clark County | MT | 4 | 12 |
| 1063 | DeKalb County | IN | 4 | 12 |
| 1064 | Island County | WA | 3.8 | 9.8 |
| 1065 | Washington County | OH | 3.8 | 9.6 |
| 1066 | Gila County | AZ | 3.7 | 9.9 |
| 1067 | Raleigh County | WV | 3.7 | 8.2 |
| 1068 | Humphreys County | TN | 4 | 17 |
| 1069 | Lenawee County | MI | 3.7 | 7 |
| 1070 | Hopewell city | VA | 4 | 16 |
| 1071 | Oconto County | WI | 4 | 13 |
| 1072 | Jackson County | FL | 4 | 12 |
| 1073 | Elkhart County | IN | 3.6 | 6.9 |
| 1074 | Vanderburgh County | IN | 3.6 | 6 |
| 1075 | Wayne County | GA | 4 | 14 |
| 1076 | Ada County | ID | 3.5 | 4.8 |
| 1077 | Westmoreland County | VA | 3 | 15 |
| 1078 | Delaware County | NY | 3 | 10 |
| 1079 | Montgomery County | IN | 3 | 16 |
| 1080 | Franklin County | IL | 3 | 14 |
| 1081 | New Hanover County | NC | 3.4 | 7.6 |
| 1082 | Charleston County | SC | 3.4 | 4.9 |
| 1083 | Logan County | OH | 3 | 11 |
| 1084 | Pueblo County | CO | 3.4 | 5.8 |
| 1085 | Huron County | OH | 3 | 10 |
| 1086 | Washington County | MN | 3.4 | 6.1 |
| 1087 | Lincoln County | OK | 3 | 14 |
| 1088 | Kaufman County | TX | 3.3 | 9.3 |
| 1089 | Augusta County | VA | 3.3 | 8.6 |
| 1090 | Montgomery County | TN | 3.3 | 5.7 |
| 1091 | DeKalb County | AL | 3.3 | 9.2 |
| 1092 | Pulaski County | KY | 3.3 | 8.7 |
| 1093 | Gladwin County | MI | 3 | 14 |
| 1094 | Solano County | CA | 3.3 | 4.6 |
| 1095 | Klamath County | OR | 3 | 10 |
| 1096 | Mesa County | CO | 3.3 | 6.4 |
| 1097 | Camden County | MO | 3 | 13 |
| 1098 | Wood County | TX | 3.2 | 9.5 |
| 1099 | Steuben County | NY | 3 | 10 |
| 1100 | Arkansas County | AR | 3 | 19 |
| 1101 | Richmond County | GA | 3.2 | 6.6 |
| 1102 | Columbia County | WI | 3 | 12 |
| 1103 | Miller County | MO | 3 | 18 |
| 1104 | Norfolk city | VA | 3.1 | 5.6 |
| 1105 | Kennebec County | ME | 3 | 6.9 |
| 1106 | Skagit County | WA | 3 | 7.5 |
| 1107 | Vermilion Parish | LA | 3 | 12 |
| 1108 | Noble County | IN | 3 | 12 |
| 1109 | Del Norte County | CA | 3 | 16 |
| 1110 | Johnson County | TX | 3 | 6.6 |
| 1111 | Marathon County | WI | 3 | 9.3 |
| 1112 | Hot Spring County | AR | 3 | 13 |
| 1113 | Multnomah County | OR | 2.9 | 3.9 |
| 1114 | Osceola County | MI | 3 | 16 |
| 1115 | Avoyelles Parish | LA | 3 | 11 |
| 1116 | Maverick County | TX | 3 | 13 |
| 1117 | Douglas County | WI | 3 | 12 |
| 1118 | Utah County | UT | 2.9 | 5.5 |
| 1119 | Bennington County | VT | 3 | 11 |
| 1120 | Shelby County | AL | 2.9 | 8 |
| 1121 | McNairy County | TN | 3 | 13 |
| 1122 | Whiteside County | IL | 3 | 11 |
| 1123 | Crook County | OR | 3 | 16 |
| 1124 | Anderson County | TX | 3 | 12 |
| 1125 | Audrain County | MO | 3 | 18 |
| 1126 | Monroe County | AL | 3 | 17 |
| 1127 | Grayson County | KY | 3 | 15 |
| 1128 | Pasco County | FL | 2.8 | 3.3 |
| 1129 | Boyd County | KY | 3 | 12 |
| 1130 | Stearns County | MN | 2.7 | 7.6 |
| 1131 | Harrison County | MS | 2.7 | 5.2 |
| 1132 | Larimer County | CO | 2.7 | 5.4 |
| 1133 | Polk County | FL | 2.7 | 2.6 |
| 1134 | Marion County | FL | 2.6 | 5.2 |
| 1135 | Escambia County | FL | 2.6 | 4.7 |
| 1136 | Boone County | IN | 3 | 11 |
| 1137 | Bingham County | ID | 3 | 11 |
| 1138 | Cooke County | TX | 3 | 13 |
| 1139 | Calhoun County | AL | 2.6 | 7.9 |
| 1140 | Oklahoma County | OK | 2.6 | 3 |
| 1141 | Matanuska-Susitna Borough | AK | 3 | 10 |
| 1142 | Platte County | MO | 3 | 11 |
| 1143 | Crawford County | MO | 3 | 16 |
| 1144 | Monongalia County | WV | 3 | 10 |
| 1145 | Iosco County | MI | 2 | 15 |
| 1146 | Atascosa County | TX | 2 | 12 |
| 1147 | Danville city | VA | 2 | 10 |
| 1148 | Mason County | WA | 2 | 10 |
| 1149 | Newton County | MO | 2 | 10 |
| 1150 | Jefferson County | WI | 2.4 | 9.8 |
| 1151 | Claiborne County | TN | 2 | 14 |
| 1152 | Burnet County | TX | 2 | 11 |
| 1153 | Pittsburg County | OK | 2 | 10 |
| 1154 | Knox County | IN | 2 | 11 |
| 1155 | York County | VA | 2 | 13 |
| 1156 | McLennan County | TX | 2.3 | 5.2 |
| 1157 | Clinton County | PA | 2 | 14 |
| 1158 | Fairbanks North Star Borough | AK | 2 | 13 |
| 1159 | Orange County | CA | 2.3 | 1.9 |
| 1160 | Clay County | FL | 2.3 | 5.7 |
| 1161 | Tippecanoe County | IN | 2.3 | 7.4 |
| 1162 | Stafford County | VA | 2.3 | 8.9 |
| 1163 | Williamson County | TN | 2.2 | 8 |
| 1164 | Portage County | WI | 2 | 12 |
| 1165 | Napa County | CA | 2.2 | 7.8 |
| 1166 | Morgan County | WV | 2 | 23 |
| 1167 | Matagorda County | TX | 2 | 14 |
| 1168 | Morgan County | IL | 2 | 13 |
| 1169 | Fairfield County | OH | 2.2 | 6 |
| 1170 | Bowie County | TX | 2.1 | 8.4 |
| 1171 | Pottawatomie County | OK | 2.1 | 9.5 |
| 1172 | Baker County | FL | 2 | 17 |
| 1173 | Trempealeau County | WI | 2 | 17 |
| 1174 | Edgecombe County | NC | 2.1 | 9.2 |
| 1175 | Aroostook County | ME | 2.1 | 9.6 |
| 1176 | Walker County | TX | 2 | 13 |
| 1177 | Santa Fe County | NM | 2.1 | 7.7 |
| 1178 | Lawrence County | AL | 2 | 14 |
| 1179 | Carroll County | OH | 2 | 15 |
| 1180 | Flagler County | FL | 2 | 6.2 |
| 1181 | Concordia Parish | LA | 2 | 19 |
| 1182 | Warren County | PA | 2 | 13 |
| 1183 | Union County | OH | 2 | 12 |
| 1184 | La Plata County | CO | 2 | 14 |
| 1185 | Rockdale County | GA | 1.9 | 9.9 |
| 1186 | Outagamie County | WI | 1.9 | 6.9 |
| 1187 | Door County | WI | 2 | 15 |
| 1188 | Roanoke County | VA | 1.8 | 8.7 |
| 1189 | Putnam County | WV | 2 | 12 |
| 1190 | Dubois County | IN | 2 | 12 |
| 1191 | Monterey County | CA | 1.8 | 5.3 |
| 1192 | Highlands County | FL | 1.8 | 6.8 |
| 1193 | Logan County | AR | 2 | 15 |
| 1194 | Siskiyou County | CA | 2 | 11 |
| 1195 | Pierce County | WA | 1.7 | 3.1 |
| 1196 | Sheridan County | WY | 2 | 14 |
| 1197 | Cibola County | NM | 2 | 15 |
| 1198 | Osceola County | FL | 1.7 | 5 |
| 1199 | Sacramento County | CA | 1.7 | 2.7 |
| 1200 | Codington County | SD | 2 | 17 |
| 1201 | Vigo County | IN | 1.7 | 8.1 |
| 1202 | Rice County | MN | 2 | 13 |
| 1203 | Benton County | MN | 2 | 13 |
| 1204 | Macon County | IL | 1.6 | 6.9 |
| 1205 | Henry County | TN | 2 | 12 |
| 1206 | Huntingdon County | PA | 2 | 13 |
| 1207 | Franklin County | MO | 1.6 | 9 |
| 1208 | Daviess County | IN | 2 | 14 |
| 1209 | Jasper County | SC | 2 | 15 |
| 1210 | Baldwin County | AL | 1.6 | 5.1 |
| 1211 | Ford County | KS | 2 | 17 |
| 1212 | Yavapai County | AZ | 1.5 | 5.4 |
| 1213 | Clay County | MO | 1.5 | 7.1 |
| 1214 | Saratoga County | NY | 1.5 | 6 |
| 1215 | Riley County | KS | 1 | 15 |
| 1216 | Hawkins County | TN | 1.5 | 9.6 |
| 1217 | Caldwell County | NC | 1.4 | 8.3 |
| 1218 | Dickson County | TN | 1 | 12 |
| 1219 | Lincoln County | TN | 1 | 15 |
| 1220 | Nueces County | TX | 1.3 | 5.6 |
| 1221 | McDowell County | WV | 1 | 15 |
| 1222 | Yates County | NY | 1 | 14 |
| 1223 | Barbour County | AL | 1 | 14 |
| 1224 | Gallia County | OH | 1 | 12 |
| 1225 | Alpena County | MI | 1 | 14 |
| 1226 | Midland County | TX | 1.2 | 7.7 |
| 1227 | Wakulla County | FL | 1 | 14 |
| 1228 | Parker County | TX | 1.1 | 7.6 |
| 1229 | Pickens County | SC | 1.1 | 7 |
| 1230 | Pike County | OH | 1 | 12 |
| 1231 | Walton County | FL | 1 | 8.5 |
| 1232 | Yellowstone County | MT | 1 | 6.5 |
| 1233 | Wake County | NC | 1 | 4.5 |
| 1234 | Pulaski County | MO | 1 | 14 |
| 1235 | Dunklin County | MO | 1 | 15 |
| 1236 | Langlade County | WI | 1 | 17 |
| 1237 | Waupaca County | WI | 1 | 12 |
| 1238 | Carroll County | IA | 1 | 17 |
| 1239 | Washington County | IN | 1 | 19 |
| 1240 | Geneva County | AL | 1 | 14 |
| 1241 | Patrick County | VA | 1 | 17 |
| 1242 | Montgomery County | OH | 0.8 | 4.4 |
| 1243 | Graham County | AZ | 1 | 14 |
| 1244 | Lorain County | OH | 0.8 | 4.5 |
| 1245 | Morgan County | AL | 0.8 | 7.6 |
| 1246 | Butler County | MO | 1 | 13 |
| 1247 | Marshall County | IN | 1 | 13 |
| 1248 | Jefferson County | TN | 0.7 | 9.6 |
| 1249 | Pittsylvania County | VA | 0.7 | 10 |
| 1250 | Lawrence County | IN | 1 | 11 |
| 1251 | Orange County | FL | 0.7 | 3.2 |
| 1252 | Campbell County | TN | 1 | 12 |
| 1253 | Clearfield County | PA | 0.6 | 7.9 |
| 1254 | Tazewell County | VA | 0.6 | 9.4 |
| 1255 | Lake County | FL | 0.6 | 3.4 |
| 1256 | Woodford County | IL | 1 | 14 |
| 1257 | Pennington County | SD | 0.6 | 7.9 |
| 1258 | Boone County | AR | 1 | 11 |
| 1259 | Grayson County | TX | 0.6 | 7.4 |
| 1260 | Ben Hill County | GA | 1 | 17 |
| 1261 | Clermont County | OH | 0.5 | 7.3 |
| 1262 | Kenosha County | WI | 0.4 | 6.9 |
| 1263 | Shelby County | OH | 0 | 15 |
| 1264 | Carroll County | NH | 0.4 | 9.5 |
| 1265 | Sherburne County | MN | 0 | 11 |
| 1266 | Hampton city | VA | 0.4 | 7.8 |
| 1267 | Taos County | NM | 0 | 18 |
| 1268 | Randolph County | AR | 0 | 14 |
| 1269 | Vermilion County | IL | 0.4 | 7.9 |
| 1270 | Hancock County | ME | 0 | 12 |
| 1271 | Denton County | TX | 0.3 | 4 |
| 1272 | Genesee County | NY | 0.3 | 9.4 |
| 1273 | Marinette County | WI | 0 | 10 |
| 1274 | Muskogee County | OK | 0 | 11 |
| 1275 | Strafford County | NH | 0.2 | 9.9 |
| 1276 | Putnam County | OH | 0 | 13 |
| 1277 | Reno County | KS | 0.1 | 9.7 |
| 1278 | Adams County | IL | 0 | 10 |
| 1279 | Washington County | MO | 0 | 15 |
| 1280 | Clay County | KY | 0 | 18 |
| 1281 | Holmes County | OH | 0 | 14 |
| 1282 | Crawford County | AR | 0 | 12 |
| 1283 | Starr County | TX | 0 | 12 |
| 1284 | Bexar County | TX | 0 | 2 |
| 1285 | Mecosta County | MI | 0 | 11 |
| 1286 | Sonoma County | CA | -0.1 | 4.3 |
| 1287 | Brunswick County | NC | -0.1 | 6.2 |
| 1288 | Coshocton County | OH | 0 | 14 |
| 1289 | Union County | TN | 0 | 15 |
| 1290 | Missoula County | MT | 0 | 10 |
| 1291 | Snyder County | PA | 0 | 12 |
| 1292 | Lauderdale County | AL | -0.2 | 7.3 |
| 1293 | Randolph County | IN | 0 | 14 |
| 1294 | Chautauqua County | NY | -0.2 | 7.5 |
| 1295 | Chelan County | WA | 0 | 11 |
| 1296 | Laurens County | SC | 0 | 11 |
| 1297 | Orleans County | VT | 0 | 16 |
| 1298 | Kenton County | KY | -0.2 | 6.9 |
| 1299 | Becker County | MN | 0 | 14 |
| 1300 | Rutherford County | NC | 0 | 11 |
| 1301 | Wythe County | VA | 0 | 15 |
| 1302 | Adams County | IN | 0 | 15 |
| 1303 | Greene County | MO | -0.3 | 5.4 |
| 1304 | Wise County | VA | 0 | 12 |
| 1305 | Harvey County | KS | 0 | 12 |
| 1306 | Cass County | MN | 0 | 16 |
| 1307 | Buchanan County | MO | -0.4 | 8.7 |
| 1308 | Floyd County | GA | -0.4 | 7.8 |
| 1309 | Hidalgo County | TX | -0.5 | 3.8 |
| 1310 | Marshall County | TN | -1 | 14 |
| 1311 | Gibson County | TN | -0.5 | 9.5 |
| 1312 | Luna County | NM | -1 | 13 |
| 1313 | Randall County | TX | -0.6 | 8.3 |
| 1314 | Erie County | PA | -0.6 | 4.7 |
| 1315 | Marin County | CA | -0.6 | 6.8 |
| 1316 | Okeechobee County | FL | -1 | 12 |
| 1317 | San Benito County | CA | -1 | 13 |
| 1318 | Hamilton County | TN | -0.6 | 4.9 |
| 1319 | Dodge County | WI | -0.7 | 7.9 |
| 1320 | Honolulu County | HI | -0.8 | 3.6 |
| 1321 | Rhea County | TN | -1 | 16 |
| 1322 | Union County | FL | -1 | 17 |
| 1323 | Crittenden County | AR | -0.8 | 9.5 |
| 1324 | Emmet County | MI | -1 | 17 |
| 1325 | Rockbridge County | VA | -1 | 16 |
| 1326 | Jasper County | MO | -0.8 | 6.9 |
| 1327 | Osage County | OK | -1 | 11 |
| 1328 | Deschutes County | OR | -0.9 | 6 |
| 1329 | Lamar County | TX | -0.9 | 9.7 |
| 1330 | Fayette County | WV | -1 | 13 |
| 1331 | Clinton County | IA | -1 | 13 |
| 1332 | Lonoke County | AR | -1 | 11 |
| 1333 | Herkimer County | NY | -1 | 10 |
| 1334 | Hernando County | FL | -1 | 5.2 |
| 1335 | Brevard County | FL | -1 | 2.9 |
| 1336 | Jackson County | AR | -1 | 18 |
| 1337 | Richmond city | VA | -1 | 6 |
| 1338 | Bonneville County | ID | -1 | 7.5 |
| 1339 | Carter County | OK | -1 | 9.5 |
| 1340 | Clinton County | NY | -1 | 10 |
| 1341 | Seminole County | FL | -1 | 5 |
| 1342 | Guadalupe County | TX | -1 | 7.5 |
| 1343 | Harrison County | IN | -1 | 14 |
| 1344 | Le Flore County | OK | -1 | 10 |
| 1345 | St. Johns County | FL | -1.2 | 5.3 |
| 1346 | Halifax County | VA | -1 | 14 |
| 1347 | Liberty County | GA | -1 | 12 |
| 1348 | Gray County | TX | -1 | 18 |
| 1349 | Polk County | NC | -1 | 15 |
| 1350 | Bay County | MI | -1.3 | 7.1 |
| 1351 | Warren County | IA | -1 | 13 |
| 1352 | Seneca County | NY | -1 | 15 |
| 1353 | Marion County | AR | -1 | 17 |
| 1354 | Humboldt County | CA | -1.3 | 7 |
| 1355 | Leon County | FL | -1.3 | 5.5 |
| 1356 | Calaveras County | CA | -1 | 10 |
| 1357 | Dubuque County | IA | -1.3 | 9 |
| 1358 | Mayes County | OK | -1 | 12 |
| 1359 | Upshur County | WV | -1 | 18 |
| 1360 | Stanislaus County | CA | -1.5 | 4.4 |
| 1361 | Mercer County | PA | -1.5 | 6.6 |
| 1362 | Mineral County | WV | -1 | 15 |
| 1363 | Lincoln County | ME | -1 | 14 |
| 1364 | Lee County | IL | -1 | 13 |
| 1365 | Morgan County | TN | -1 | 14 |
| 1366 | Miami County | OH | -1.5 | 7.5 |
| 1367 | Winnebago County | WI | -1.6 | 7.6 |
| 1368 | Transylvania County | NC | -2 | 12 |
| 1369 | Cherokee County | GA | -1.6 | 7.1 |
| 1370 | Union County | NC | -1.6 | 5.7 |
| 1371 | Cabell County | WV | -1.6 | 7.1 |
| 1372 | Jefferson County | NY | -1.6 | 8.8 |
| 1373 | Mingo County | WV | -2 | 14 |
| 1374 | Santa Cruz County | CA | -1.7 | 6.4 |
| 1375 | Phillips County | AR | -2 | 17 |
| 1376 | Tioga County | PA | -2 | 13 |
| 1377 | Nicholas County | WV | -2 | 13 |
| 1378 | Dodge County | NE | -2 | 12 |
| 1379 | Shasta County | CA | -1.8 | 5.9 |
| 1380 | Bedford County | TN | -2 | 14 |
| 1381 | Person County | NC | -2 | 11 |
| 1382 | Garland County | AR | -1.8 | 6.7 |
| 1383 | Clark County | WI | -2 | 12 |
| 1384 | Clare County | MI | -2 | 12 |
| 1385 | Pinellas County | FL | -1.8 | 2.5 |
| 1386 | Chattooga County | GA | -2 | 13 |
| 1387 | Huron County | MI | -2 | 13 |
| 1388 | Shawnee County | KS | -1.9 | 7.1 |
| 1389 | Grand Forks County | ND | -2 | 11 |
| 1390 | Jay County | IN | -2 | 16 |
| 1391 | Fayette County | PA | -1.9 | 6.2 |
| 1392 | Labette County | KS | -2 | 17 |
| 1393 | Ashtabula County | OH | -1.9 | 7.5 |
| 1394 | Tom Green County | TX | -1.9 | 9.6 |
| 1395 | Cumberland County | TN | -2 | 7.9 |
| 1396 | Hawaii County | HI | -2 | 6.1 |
| 1397 | Lawrence County | AR | -2 | 15 |
| 1398 | Holmes County | FL | -2 | 15 |
| 1399 | Lane County | OR | -2 | 3.9 |
| 1400 | McPherson County | KS | -2 | 14 |
| 1401 | McDonough County | IL | -2 | 13 |
| 1402 | Anchorage Muny | AK | -2.1 | 5.6 |
| 1403 | Cowlitz County | WA | -2.1 | 7.3 |
| 1404 | Wood County | WV | -2.1 | 8.5 |
| 1405 | Madison County | AL | -2.1 | 4.6 |
| 1406 | Placer County | CA | -2.1 | 4.3 |
| 1407 | Smyth County | VA | -2 | 11 |
| 1408 | Eau Claire County | WI | -2 | 10 |
| 1409 | Cherokee County | SC | -2.2 | 9.8 |
| 1410 | Monroe County | TN | -2 | 10 |
| 1411 | Lincoln County | OR | -2 | 12 |
| 1412 | Preston County | WV | -2 | 13 |
| 1413 | Lake County | OH | -2.2 | 4.5 |
| 1414 | Haywood County | NC | -2 | 11 |
| 1415 | Fairfax city | VA | -2 | 17 |
| 1416 | Collier County | FL | -2.3 | 4.7 |
| 1417 | Logan County | WV | -2 | 10 |
| 1418 | Greenbrier County | WV | -2 | 12 |
| 1419 | Botetourt County | VA | -2 | 16 |
| 1420 | Grady County | OK | -2 | 11 |
| 1421 | Westmoreland County | PA | -2.4 | 3.7 |
| 1422 | Newaygo County | MI | -2 | 11 |
| 1423 | Madera County | CA | -2.4 | 8.9 |
| 1424 | Cowley County | KS | -2 | 13 |
| 1425 | Houghton County | MI | -2 | 14 |
| 1426 | Val Verde County | TX | -2 | 14 |
| 1427 | Story County | IA | -2 | 12 |
| 1428 | Blount County | TN | -2.4 | 6.1 |
| 1429 | Alachua County | FL | -2.4 | 5.4 |
| 1430 | Randolph County | MO | -2 | 15 |
| 1431 | Johnson County | KS | -2.5 | 4.9 |
| 1432 | Stephens County | GA | -2 | 14 |
| 1433 | Randolph County | WV | -3 | 12 |
| 1434 | Pike County | KY | -2.5 | 8.7 |
| 1435 | Hart County | KY | -3 | 21 |
| 1436 | Alleghany County | VA | -3 | 18 |
| 1437 | Wells County | IN | -3 | 14 |
| 1438 | Butler County | PA | -2.6 | 6.2 |
| 1439 | Young County | TX | -3 | 17 |
| 1440 | Seneca County | OH | -3 | 13 |
| 1441 | Fremont County | CO | -2.7 | 9.4 |
| 1442 | Douglas County | KS | -3 | 11 |
| 1443 | Lawrence County | KY | -3 | 19 |
| 1444 | Allen County | OH | -2.7 | 8.5 |
| 1445 | Hoke County | NC | -3 | 14 |
| 1446 | Sandusky County | OH | -2.9 | 9.1 |
| 1447 | Benton County | TN | -3 | 15 |
| 1448 | Licking County | OH | -2.9 | 6.7 |
| 1449 | Green Lake County | WI | -3 | 14 |
| 1450 | Knox County | ME | -3 | 9.6 |
| 1451 | Greene County | NY | -3 | 11 |
| 1452 | Clatsop County | OR | -3 | 13 |
| 1453 | Monroe County | WI | -3 | 11 |
| 1454 | Tallapoosa County | AL | -3 | 10 |
| 1455 | Hays County | TX | -3.1 | 8.6 |
| 1456 | Lowndes County | GA | -3.1 | 7.6 |
| 1457 | Kitsap County | WA | -3.2 | 5 |
| 1458 | Garfield County | CO | -3 | 13 |
| 1459 | Fannin County | TX | -3 | 14 |
| 1460 | Anderson County | TN | -3.2 | 7.9 |
| 1461 | Washington County | WI | -3.3 | 7.5 |
| 1462 | Grant County | NM | -3 | 12 |
| 1463 | Manitowoc County | WI | -3 | 10 |
| 1464 | Miller County | AR | -3 | 12 |
| 1465 | York County | ME | -3.4 | 6.1 |
| 1466 | Camden County | GA | -3 | 11 |
| 1467 | Steele County | MN | -3 | 16 |
| 1468 | Oswego County | NY | -3.4 | 8.2 |
| 1469 | Christian County | KY | -3 | 11 |
| 1470 | Lewis County | WA | -3.4 | 9 |
| 1471 | Loudon County | TN | -3.4 | 9.5 |
| 1472 | Perry County | KY | -3 | 11 |
| 1473 | Gibson County | IN | -4 | 16 |
| 1474 | Polk County | MN | -4 | 13 |
| 1475 | Hampton County | SC | -4 | 15 |
| 1476 | Wichita County | TX | -3.5 | 7.4 |
| 1477 | Gallatin County | MT | -4 | 10 |
| 1478 | Faulkner County | AR | -3.6 | 8.7 |
| 1479 | Wasco County | OR | -4 | 15 |
| 1480 | Adams County | OH | -4 | 13 |
| 1481 | Waldo County | ME | -4 | 11 |
| 1482 | Darke County | OH | -3.6 | 9.7 |
| 1483 | Daviess County | KY | -3.7 | 6.9 |
| 1484 | Cocke County | TN | -4 | 11 |
| 1485 | Bossier Parish | LA | -3.7 | 7.3 |
| 1486 | Henry County | OH | -4 | 15 |
| 1487 | Cattaraugus County | NY | -3.8 | 9.1 |
| 1488 | Wayne County | NY | -4 | 11 |
| 1489 | Navarro County | TX | -4 | 14 |
| 1490 | Wise County | TX | -4 | 11 |
| 1491 | Boone County | MO | -3.8 | 7.8 |
| 1492 | Garfield County | OK | -3.9 | 9.5 |
| 1493 | Warren County | OH | -3.9 | 6 |
| 1494 | San Patricio County | TX | -3.9 | 9.8 |
| 1495 | Sharp County | AR | -4 | 15 |
| 1496 | Obion County | TN | -4 | 12 |
| 1497 | Park County | WY | -4 | 13 |
| 1498 | Shelby County | IL | -4 | 19 |
| 1499 | Christian County | MO | -4 | 12 |
| 1500 | Posey County | IN | -4 | 17 |
| 1501 | Columbia County | OR | -4 | 11 |
| 1502 | Leon County | TX | -4 | 17 |
| 1503 | Jackson County | OH | -4 | 14 |
| 1504 | Prince Edward County | VA | -4 | 16 |
| 1505 | Cherokee County | TX | -4.2 | 9.8 |
| 1506 | Eaton County | MI | -4.3 | 7.9 |
| 1507 | Kay County | OK | -4.3 | 8.7 |
| 1508 | Kandiyohi County | MN | -4 | 15 |
| 1509 | Ravalli County | MT | -4 | 12 |
| 1510 | Hendry County | FL | -4 | 12 |
| 1511 | Lewis County | WV | -5 | 19 |
| 1512 | Isle of Wight County | VA | -5 | 13 |
| 1513 | Brown County | MN | -5 | 13 |
| 1514 | La Crosse County | WI | -4.7 | 7.1 |
| 1515 | Des Moines County | IA | -5 | 13 |
| 1516 | Essex County | NY | -5 | 14 |
| 1517 | Russell County | VA | -5 | 16 |
| 1518 | Oldham County | KY | -5 | 12 |
| 1519 | Effingham County | GA | -5 | 12 |
| 1520 | Lassen County | CA | -5 | 18 |
| 1521 | Anson County | NC | -5 | 19 |
| 1522 | Juneau County | WI | -5 | 14 |
| 1523 | Rio Arriba County | NM | -5 | 11 |
| 1524 | Santa Barbara County | CA | -5 | 4.6 |
| 1525 | Wood County | WI | -5 | 8 |
| 1526 | Sampson County | NC | -5 | 8.9 |
| 1527 | Delta County | CO | -5 | 11 |
| 1528 | Harlan County | KY | -5 | 12 |
| 1529 | Benton County | AR | -5.2 | 5.8 |
| 1530 | Comal County | TX | -5.2 | 7.1 |
| 1531 | Madison County | NE | -5 | 11 |
| 1532 | Douglas County | MN | -5 | 12 |
| 1533 | Scott County | VA | -5 | 14 |
| 1534 | Lauderdale County | TN | -5 | 15 |
| 1535 | Columbia County | FL | -5.3 | 8.2 |
| 1536 | Madison County | GA | -5 | 18 |
| 1537 | Marion County | MO | -5 | 14 |
| 1538 | Nassau County | FL | -5.4 | 7.9 |
| 1539 | Carteret County | NC | -5.4 | 8 |
| 1540 | Henry County | VA | -5.5 | 9.1 |
| 1541 | Knox County | IL | -5 | 12 |
| 1542 | Bannock County | ID | -5.5 | 9.8 |
| 1543 | Franklin County | KS | -5 | 14 |
| 1544 | Logan County | IL | -6 | 14 |
| 1545 | Blount County | AL | -5.5 | 8.5 |
| 1546 | Nye County | NV | -5.5 | 8.4 |
| 1547 | Canyon County | ID | -5.6 | 5.3 |
| 1548 | Saline County | MO | -6 | 17 |
| 1549 | Bee County | TX | -6 | 15 |
| 1550 | Maui County | HI | -5.6 | 7 |
| 1551 | Medina County | TX | -6 | 13 |
| 1552 | Jackson County | IN | -6 | 12 |
| 1553 | White County | AR | -6 | 11 |
| 1554 | St. Lawrence County | NY | -5.7 | 8.3 |
| 1555 | Nash County | NC | -5.7 | 7.2 |
| 1556 | Preble County | OH | -6 | 13 |
| 1557 | Polk County | OR | -5.8 | 9.4 |
| 1558 | Taylor County | TX | -5.8 | 6.5 |
| 1559 | Nelson County | KY | -6 | 11 |
| 1560 | Tift County | GA | -6 | 12 |
| 1561 | Penobscot County | ME | -6 | 6.2 |
| 1562 | Tompkins County | NY | -6 | 9.3 |
| 1563 | Alcorn County | MS | -6 | 13 |
| 1564 | Barry County | MO | -6 | 13 |
| 1565 | San Jacinto County | TX | -6 | 14 |
| 1566 | Pacific County | WA | -6 | 15 |
| 1567 | Cascade County | MT | -6.1 | 7.8 |
| 1568 | Livingston County | IL | -6 | 14 |
| 1569 | Union County | OR | -6 | 14 |
| 1570 | Polk County | AR | -6 | 16 |
| 1571 | White County | TN | -6 | 13 |
| 1572 | Jefferson County | OH | -6 | 10 |
| 1573 | Culpeper County | VA | -6 | 12 |
| 1574 | Richland Parish | LA | -6 | 16 |
| 1575 | Okaloosa County | FL | -6.5 | 5.4 |
| 1576 | Okanogan County | WA | -6 | 13 |
| 1577 | Lawrence County | OH | -6 | 11 |
| 1578 | St. Croix County | WI | -6.5 | 9.8 |
| 1579 | Grafton County | NH | -6.5 | 7.5 |
| 1580 | Mason County | WV | -7 | 13 |
| 1581 | Mississippi County | AR | -6.5 | 9.5 |
| 1582 | Dale County | AL | -7 | 11 |
| 1583 | Hardin County | TX | -7 | 10 |
| 1584 | Jersey County | IL | -7 | 17 |
| 1585 | Josephine County | OR | -6.7 | 6.6 |
| 1586 | Scott County | MS | -7 | 14 |
| 1587 | Saline County | KS | -6.7 | 9.7 |
| 1588 | Wexford County | MI | -7 | 13 |
| 1589 | Orange County | VA | -7 | 12 |
| 1590 | Ottawa County | OK | -7 | 15 |
| 1591 | Wright County | MN | -6.9 | 8.3 |
| 1592 | Androscoggin County | ME | -6.9 | 6.5 |
| 1593 | Tehama County | CA | -7 | 11 |
| 1594 | Itawamba County | MS | -7 | 16 |
| 1595 | Marshall County | KY | -7 | 14 |
| 1596 | Laramie County | WY | -7 | 8.2 |
| 1597 | Marshall County | WV | -7 | 12 |
| 1598 | Bay County | FL | -7.1 | 6.1 |
| 1599 | Oxford County | ME | -7.2 | 9.8 |
| 1600 | Thurston County | WA | -7.2 | 4.9 |
| 1601 | Unicoi County | TN | -7 | 15 |
| 1602 | Ashley County | AR | -7 | 17 |
| 1603 | Champaign County | IL | -7.3 | 7.1 |
| 1604 | Cass County | MO | -7.3 | 7.5 |
| 1605 | Ohio County | KY | -7 | 13 |
| 1606 | Woodford County | KY | -7 | 15 |
| 1607 | Webster County | MO | -7 | 14 |
| 1608 | Muskingum County | OH | -7.4 | 9.2 |
| 1609 | Venango County | PA | -7 | 11 |
| 1610 | Limestone County | TX | -7 | 14 |
| 1611 | Logan County | OK | -7 | 12 |
| 1612 | Butte County | CA | -7.4 | 6.1 |
| 1613 | Surry County | NC | -7.4 | 8.1 |
| 1614 | Sevier County | TN | -7.5 | 8.1 |
| 1615 | Effingham County | IL | -8 | 16 |
| 1616 | Greene County | AR | -8 | 10 |
| 1617 | Grant Parish | LA | -8 | 16 |
| 1618 | Lincoln County | NM | -8 | 16 |
| 1619 | Elk County | PA | -8 | 14 |
| 1620 | Union County | MS | -8 | 15 |
| 1621 | Cambria County | PA | -7.8 | 7.2 |
| 1622 | Asotin County | WA | -8 | 15 |
| 1623 | Washington County | AR | -7.9 | 6.8 |
| 1624 | Garvin County | OK | -8 | 12 |
| 1625 | Jefferson County | IN | -8 | 13 |
| 1626 | Prince George County | VA | -8 | 15 |
| 1627 | Cole County | MO | -8 | 9.7 |
| 1628 | McKean County | PA | -8 | 11 |
| 1629 | Rockwall County | TX | -8 | 12 |
| 1630 | Payne County | OK | -8.1 | 9.2 |
| 1631 | Onslow County | NC | -8.2 | 7.3 |
| 1632 | Cheshire County | NH | -8 | 10 |
| 1633 | Sullivan County | NH | -8 | 10 |
| 1634 | Winchester city | VA | -8 | 17 |
| 1635 | Cullman County | AL | -8.3 | 7.5 |
| 1636 | Yadkin County | NC | -8 | 13 |
| 1637 | St. Joseph County | MI | -8.5 | 9.8 |
| 1638 | Washington County | PA | -8.5 | 4.7 |
| 1639 | Pender County | NC | -8 | 10 |
| 1640 | Waushara County | WI | -9 | 14 |
| 1641 | McClain County | OK | -9 | 15 |
| 1642 | Curry County | NM | -9 | 12 |
| 1643 | San Luis Obispo County | CA | -8.7 | 5.1 |
| 1644 | Amherst County | VA | -9 | 12 |
| 1645 | Meeker County | MN | -9 | 13 |
| 1646 | Morrow County | OH | -9 | 14 |
| 1647 | Hancock County | WV | -9 | 13 |
| 1648 | Lafayette County | MO | -9 | 11 |
| 1649 | Johnson County | KY | -9 | 13 |
| 1650 | Orange County | VT | -9 | 13 |
| 1651 | Kittitas County | WA | -9 | 16 |
| 1652 | Ashland County | OH | -9 | 11 |
| 1653 | Addison County | VT | -9 | 15 |
| 1654 | Cache County | UT | -9.2 | 9.9 |
| 1655 | Charlevoix County | MI | -9 | 13 |
| 1656 | Fulton County | IL | -9 | 11 |
| 1657 | Polk County | MO | -9 | 12 |
| 1658 | Trinity County | TX | -10 | 14 |
| 1659 | Polk County | WI | -10 | 12 |
| 1660 | Tooele County | UT | -10 | 11 |
| 1661 | Clinton County | OH | -10 | 11 |
| 1662 | Fayette County | IL | -10 | 18 |
| 1663 | Abbeville County | SC | -10 | 14 |
| 1664 | Jefferson Davis Parish | LA | -10 | 10 |
| 1665 | Louisa County | VA | -10 | 13 |
| 1666 | Wadena County | MN | -10 | 17 |
| 1667 | Natrona County | WY | -10 | 10 |
| 1668 | Ogemaw County | MI | -10 | 15 |
| 1669 | Canadian County | OK | -10 | 7.4 |
| 1670 | Warren County | VA | -10 | 12 |
| 1671 | Cherokee County | NC | -10 | 13 |
| 1672 | Livingston County | NY | -10.1 | 9.8 |
| 1673 | Yuba County | CA | -10.1 | 9.9 |
| 1674 | Mower County | MN | -10 | 12 |
| 1675 | Marion County | OH | -10.2 | 7.8 |
| 1676 | Adams County | WI | -10 | 13 |
| 1677 | Jefferson County | PA | -10 | 11 |
| 1678 | Cochise County | AZ | -10.4 | 6.5 |
| 1679 | Lincoln County | WV | -10 | 14 |
| 1680 | Hancock County | OH | -10.5 | 8.5 |
| 1681 | Marion County | TN | -11 | 12 |
| 1682 | Lincoln County | MO | -11 | 12 |
| 1683 | Marion County | WV | -10.6 | 9.2 |
| 1684 | Wyoming County | PA | -11 | 13 |
| 1685 | Clallam County | WA | -10.7 | 7.4 |
| 1686 | Edgar County | IL | -11 | 17 |
| 1687 | Saline County | AR | -11 | 7.4 |
| 1688 | Gordon County | GA | -11 | 9.2 |
| 1689 | Scotts Bluff County | NE | -11 | 12 |
| 1690 | Santa Rosa County | FL | -11.3 | 6.1 |
| 1691 | Greene County | PA | -11 | 11 |
| 1692 | Martin County | MN | -11 | 17 |
| 1693 | Pulaski County | VA | -11.5 | 9.9 |
| 1694 | Harrison County | KY | -11 | 18 |
| 1695 | Muhlenberg County | KY | -12 | 14 |
| 1696 | Richland County | OH | -11.6 | 7.1 |
| 1697 | Lumpkin County | GA | -12 | 13 |
| 1698 | Jim Wells County | TX | -12 | 15 |
| 1699 | Kauai County | HI | -12 | 11 |
| 1700 | Johnson County | TN | -12 | 13 |
| 1701 | Grady County | GA | -12 | 17 |
| 1702 | McIntosh County | OK | -12 | 13 |
| 1703 | Wharton County | TX | -12 | 12 |
| 1704 | Kenai Peninsula Borough | AK | -12 | 13 |
| 1705 | Stephens County | OK | -12 | 11 |
| 1706 | Winston County | MS | -12 | 16 |
| 1707 | Kootenai County | ID | -12.4 | 5.7 |
| 1708 | Saline County | IL | -12 | 13 |
| 1709 | Lee County | VA | -12 | 16 |
| 1710 | Chisago County | MN | -13 | 11 |
| 1711 | Liberty County | TX | -12.6 | 8.5 |
| 1712 | Franklin County | NC | -13 | 12 |
| 1713 | Hale County | TX | -13 | 13 |
| 1714 | Queen Anne's County | MD | -13 | 10 |
| 1715 | Defiance County | OH | -13 | 13 |
| 1716 | Bonner County | ID | -13 | 11 |
| 1717 | Platte County | NE | -13 | 15 |
| 1718 | Crawford County | OH | -13.1 | 9.7 |
| 1719 | Chemung County | NY | -13.1 | 8.1 |
| 1720 | Lincoln County | SD | -13 | 12 |
| 1721 | Scott County | KY | -13 | 11 |
| 1722 | Harrison County | WV | -13.2 | 7.3 |
| 1723 | Lake County | CA | -13.2 | 8.2 |
| 1724 | Arenac County | MI | -13 | 15 |
| 1725 | LaGrange County | IN | -13 | 17 |
| 1726 | Llano County | TX | -13 | 12 |
| 1727 | Barron County | WI | -13.5 | 9.2 |
| 1728 | Letcher County | KY | -13 | 13 |
| 1729 | Rockcastle County | KY | -14 | 16 |
| 1730 | Creek County | OK | -13.7 | 9.1 |
| 1731 | Whitley County | IN | -14 | 16 |
| 1732 | Lawrence County | MO | -14 | 12 |
| 1733 | Emanuel County | GA | -14 | 11 |
| 1734 | Warren County | TN | -14 | 12 |
| 1735 | Clark County | KY | -14 | 12 |
| 1736 | Franklin County | ME | -14 | 13 |
| 1737 | Chippewa County | WI | -14.1 | 9.2 |
| 1738 | Bryan County | OK | -14.2 | 9.5 |
| 1739 | Marquette County | MI | -14 | 10 |
| 1740 | Colbert County | AL | -14.3 | 9.9 |
| 1741 | Dare County | NC | -15 | 12 |
| 1742 | Kosciusko County | IN | -14.8 | 8.7 |
| 1743 | Crow Wing County | MN | -14.8 | 8.5 |
| 1744 | Silver Bow County | MT | -15 | 12 |
| 1745 | Yell County | AR | -15 | 15 |
| 1746 | Mercer County | KY | -15 | 13 |
| 1747 | Marion County | IA | -15 | 11 |
| 1748 | Wabash County | IN | -15 | 11 |
| 1749 | Wilson County | TX | -15 | 11 |
| 1750 | Watauga County | NC | -15 | 12 |
| 1751 | DeWitt County | TX | -15 | 16 |
| 1752 | Benton County | OR | -15 | 10 |
| 1753 | Sumner County | KS | -15 | 14 |
| 1754 | Washington County | FL | -16 | 13 |
| 1755 | Pierce County | WI | -16 | 15 |
| 1756 | Delta County | MI | -16 | 12 |
| 1757 | Oconee County | SC | -15.9 | 7.4 |
| 1758 | Morrison County | MN | -16 | 14 |
| 1759 | Barren County | KY | -16.3 | 9.5 |
| 1760 | George County | MS | -16 | 15 |
| 1761 | Bibb County | AL | -16 | 13 |
| 1762 | Chowan County | NC | -16 | 16 |
| 1763 | Titus County | TX | -16 | 12 |
| 1764 | Chippewa County | MI | -17 | 12 |
| 1765 | Milam County | TX | -17 | 15 |
| 1766 | Burleson County | TX | -17 | 14 |
| 1767 | Hempstead County | AR | -17 | 13 |
| 1768 | Martinsville city | VA | -17 | 16 |
| 1769 | Williams County | OH | -17 | 12 |
| 1770 | Bradford County | PA | -17.5 | 7.7 |
| 1771 | Montcalm County | MI | -17.6 | 9.5 |
| 1772 | Eddy County | NM | -17.8 | 8.8 |
| 1773 | Perry County | IL | -18 | 15 |
| 1774 | Lea County | NM | -18 | 9.6 |
| 1775 | Maury County | TN | -18.3 | 6.9 |
| 1776 | Coos County | NH | -18 | 11 |
| 1777 | Adair County | MO | -18 | 14 |
| 1778 | Sagadahoc County | ME | -19 | 12 |
| 1779 | Greene County | TN | -18.6 | 7.7 |
| 1780 | Coos County | OR | -18.7 | 7.2 |
| 1781 | Beckham County | OK | -19 | 15 |
| 1782 | Crawford County | PA | -18.7 | 7.9 |
| 1783 | Boyle County | KY | -19 | 12 |
| 1784 | Johnson County | AR | -19 | 12 |
| 1785 | Hocking County | OH | -19 | 12 |
| 1786 | Miami County | KS | -19 | 16 |
| 1787 | Cross County | AR | -19 | 13 |
| 1788 | Carter County | KY | -20 | 12 |
| 1789 | Glenn County | CA | -21 | 14 |
| 1790 | Clay County | AR | -21 | 13 |
| 1791 | Henry County | MO | -21 | 14 |
| 1792 | Cherokee County | KS | -22 | 13 |
| 1793 | Isanti County | MN | -22 | 11 |
| 1794 | Bureau County | IL | -23 | 11 |
| 1795 | Eastland County | TX | -23 | 12 |
| 1796 | Conway County | AR | -23 | 12 |
| 1797 | Menominee County | MI | -24 | 11 |
| 1798 | Stutsman County | ND | -25 | 13 |
| 1799 | Hubbard County | MN | -25 | 14 |
| 1800 | Kleberg County | TX | -25 | 14 |
| 1801 | Nottoway County | VA | -25 | 16 |
| 1802 | Stone County | MO | -25.7 | 9.5 |
| 1803 | Poinsett County | AR | -26 | 12 |
| 1804 | Schoharie County | NY | -29 | 11 |
| 1805 | Laclede County | MO | -29.7 | 8.1 |
| 1806 | Dunn County | WI | -30 | 11 |
References
- Aarstad & Kvitastein, 2023: Aarstad J, Kvitastein OA. Is there a Link between the 2021 COVID-19 Vaccination Uptake in Europe and 2022 Excess All-Cause Mortality? Asian Pacific Journal of Health Science. 2023;10:25-31. [CrossRef]
- Accinelli et al., 2021: Accinelli RA, Ynga-Meléndez GJ, León-Abarca JA, López LM, Madrid-Cisneros JC, Mendoza-Saldaña JD. Travel Med Inf Dis. 2021;44:102163. [CrossRef]
- Achilleos, S. et al., 2021: Achilleos S, Quattrocchi A, Gabel J, Heraclides A, Kolokotroni O, Constantinou C, et al. Excess all-cause mortality and COVID-19-related mortality: a temporal analysis in 22 countries, from January until August 2020. Int J Epidemiol. 2022;51:35-53. [CrossRef]
- Ackley et al., 2021: Ackley CA, Lundberg DJ, Ma L, Ela IT, Preston SH, Stokes AC.County-level estimates of excess mortality associated with COVID-19 in the United States. SSM - Population Health. 2022;17:101021. [CrossRef]
- Acosta et al., 2022: Acosta RJ, Patnaik B, Buckee C, Kiang MV, Irizarry RA, Balsari S, et al. All-cause excess mortality across 90 municipalities in Gujarat, India, during the COVID-19 pandemic (March 2020-April 2021). PLOS Glob Public Health. 2022;2:e0000824. [CrossRef]
- Al Wahaibi et al., 2021: Al Wahaibi A, Al-Maani A, Alyaquobi F, Al Harthy K, Al-Jardani A, Al Rawahi B, et al. Effects of COVID-19 on mortality: A 5-year population-based study in Oman. Int J Infect Dis. 2021;104:102-107. [CrossRef]
- Alessandria et al., 2025: Alessandria M, Malatesta G, Di Palmo G, Cosentino M, Donzelli A. All-cause mortality according to COVID-19 vaccination status: An analysis of the UK office for National statistics public data [version 2; peer review: 2 approved]. F1000Research. 2025;13:886. [CrossRef]
- Alteri et al., 2021: Alteri C, Cento V, Piralla A, Costabile V, Tallarita M, Colagrossi L, et al. Genomic epidemiology of SARS-CoV-2 reveals multiple lineages and early spread of SARS-CoV-2 infections in Lombardy, Italy. Nat Commun. 2021;12:434. [CrossRef]
- Amaro, 2020: Amaro S. Germany seals off borders as European countries report record jump in coronavirus deaths. CNBC. 16 March 2020. Accessed on 2024-10-01 from: https://www.cnbc.com/2020/03/16/coronavirus-update-germany-seven-other-eu-countries-close-borders.html [Archived at: https://archive.is/j9RX7].
- American Thoracic Society, 2005: American Thoracic Society. Guidelines for the Management of Adults with Hospital-acquired, Ventilator-associated, and Healthcare-associated Pneumonia. Am J Respir Crit Care Med. 2005;171:388–416. [CrossRef]
- Anand et al., 2021: Anan A, Sandefur J, Subramanian A. Three New Estimates of India’s All-Cause Excess Mortality during the COVID-19 Pandemic. CGD Working Paper 589. Washington, DC: Center for Global Development. Accessed on 2025-03-12 from: https://cgdev.org/publication/three-new-estimates-indias-all-cause-excess-mortality-during-covid-19-pandemic.
- Apolone et al., 2021: Apolone G, Montomoli E, Manenti A, Boeri M, Sabia F, Hyseni I, et al. Unexpected detection of SARS-CoV-2 antibodies in the prepandemic period in Italy. Tumori J. 2021;107:446-451. [CrossRef]
- ASA et al., 2020: Joint Statement on Multiple Patients Per Ventilator. American Society of Anesthesiologists. 25 March 2020. Accessed 2025-05-08 from: https://www.asahq.org/about-asa/newsroom/news-releases/2020/03/joint-statement-on-multiple-patients-per-ventilator.
- ATSDR, 2024: Agency for Toxic Substances and Disease Registry. SVI Data & Documentation Download. Accessed on 2024-10-31 from: https://www.atsdr.cdc.gov/placeandhealth/svi/data_documentation_download.html.
- Aune et al., 2023: Aune KT, Grantz KH, Menezes NP, Robsky KO, Gurley ES, Marx MA, et al. Demographic and Geographic Characterization of Excess Mortality During the COVID-19 Pandemic in Baltimore City, Maryland, March 2020 to March 2021. American Journal of Epidemiology. 2024 Feb 1;193(2):267–76.
- Babaev et al., 2022: Babaev A, Martin-Johnson T, Klion M. Respiratory therapy and proning. In: Shabsigh R, editor. Health crisis management in acute care hospitals: Lessons learned from COVID-19 and beyond. Cham: Springer; 2022. pp. 165-182. [CrossRef]
- Bailey & Köhnlein, 2020: Bailey S, Köhnlein C. PCR Pandemic: Interview with Virus Mania's Dr Claus Köhnlein. 26 October 2020. Accessed 2025-05-07 from: https://odysee.com/@drsambailey:c/pcr-pandemic-interview-with-virus-mania:9.
- Bajardi et al., 2011: Bajardi P, Poletto C, Ramasco JJ, Tizzoni M, Colizza V, Vespignani A. Human Mobility Networks, Travel Restrictions, and the Global Spread of 2009 H1N1 Pandemic. PLOS One. 2011;6:e16591. [CrossRef]
- Balcan et al., 2010: Balcan D, Gonçalves B, Hu H, Ramasco JJ, Colizza V, Vespignani A. Modeling the spatial spread of infectious diseases: The GLobal Epidemic and Mobility computational model. J Comput Sci. 2010;1:132-145. [CrossRef]
- Basellini & Camarda, 2022: Basellini U, Camarda CG. Explaining regional differences in mortality during the first wave of Covid-19 in Italy. Population Studies. 2022;76:99-118. [CrossRef]
- Beitler et al., 2020: Beitler JR, Mittel AM, Kallet R, Kacmarek R, Hess D, Branson R, et al. Ventilator Sharing during an Acute Shortage Caused by the COVID-19 Pandemic. Am J Resp Crit Care Med. 2020;202:600-604. [CrossRef]
- Bilinski & Emanuel, 2020: Bilinski A, Emanuel EJ. COVID-19 and Excess All-Cause Mortality in the US and 18 Comparison Countries. JAMA. 2020;324(20):2100–2102. https://jamanetwork.com/journals/jama/fullarticle/2771841. [CrossRef]
- Bilinski et al., 2023: Bilinski A, Thompson K, Emanuel E. COVID-19 and Excess All-Cause Mortality in the US and 20 Comparison Countries, June 2021-March 2022. JAMA. 2023;329:92–94. [CrossRef]
- Boccia et al., 2020: Boccia S, Ricciardi W, Ioannidis JPA. What Other Countries Can Learn From Italy During the COVID-19 Pandemic. JAMA Intern Med. 2020;180(7):927-928. [CrossRef]
- Bonnet et al., 2024: Bonnet F, Grigoriev P, Sauerberg M, Alliger I, Mühlichen M, Camarda CG. Spatial Variation in Excess Mortality Across Europe: A Cross-Sectional Study of 561 Regions in 21 Countries. Journal of Epidemiology and Global Health. 2024 Jun 1;14(2):470–9.
- Borba et al., 2020: Borba M, Val F, Sampaio V, Alexandre M, Melo G, Brito M, et al. Effect of High vs Low Doses of Chloroquine Diphosphate as Adjunctive Therapy for Patients Hospitalized With Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) Infection: A Randomized Clinical Trial. JAMA Network Open. 2020;3:e208857. [CrossRef]
- Bosa et al., 2021: Bosa I, Castelli A, Castelli M, Ciani O, Compagni A, Galizzi MM, et al. Corona-regionalism? Differences in regional responses to COVID-19 in Italy. Health Policy. 2021;125:1179-1187. [CrossRef]
- Böttcher et al., 2021: Böttcher L, D’Orsogna MR, Chou T. Using excess deaths and testing statistics to determine COVID-19 mortalities. Eur J Epidemiol. 2021;36:545–558. [CrossRef]
- Bottiroli et al., 2021: Bottiroli M, Calini A, Pinciroli R, Mueller A, Siragusa A, Anelli C, et al. The repurposed use of anesthesia machines to ventilate critically ill patients with coronavirus disease 2019 (COVID-19). BMC Anesthesiology. 2021;21:155. [CrossRef]
- Bouadma et al., 2015: Bouadma L, Sonneville R, Garrouste-Orgeas M, Darmon M, Souweine B, Voiriot G, et al. Ventilator-Associated Events: Prevalence, Outcome, and Relationship With Ventilator-Associated Pneumonia. Critical Care Medicine. 2015;43:1798-1806. [CrossRef]
- Brockmann & Helbing, 2013: Brockmann D, Helbing D. The Hidden Geometry of Complex, Network-Driven Contagion Phenomena. Science. 2013;342:1337. [CrossRef]
- Burton et al., 2010: Burton DC, Flannery B, Bennett NM, Farley MM, Gershman K, Harrison LH, et al. Socioeconomic and Racial/Ethnic Disparities in the Incidence of Bacteremic Pneumonia Among US Adults. American Journal of Public Health. 2010;100:1904-1911. [CrossRef]
- Bustos Sierra et al., 2020: Bustos Sierra N, Bossuyt N, Braeye T, Leroy M, Moyersoen I, Peeters I, et al. All-cause mortality supports the COVID-19 mortality in Belgium and comparison with major fatal events of the last century. Arch Public Health. 2020;78:117. [CrossRef]
- Caballero et al., 2024: Caballero J, García-Sánchez M, Vich JG-E. Current role of midazolam in the sedation of the ventilated critically ill patient: against. Medicina Intensiva. 2024;48:177-179. [CrossRef]
- Campitelli et al., 2021: Campitelli MA, Bronskill SE, Maclagan LC. Comparison of Medication Prescribing Before and After the COVID-19 Pandemic Among Nursing Home Residents in Ontario, Canada. JAMA Network Open. 2021;4:e2118441. [CrossRef]
- Capano & Lippi, 2021: Capano G, Lippi A. Decentralization, policy capacities, and varieties of first health response to the COVID-19 outbreak: evidence from three regions in Italy. Journal of European Public Policy. 2021;28:1197-1218. [CrossRef]
- Casas-Rojo et al., 2020: Casas-Rojo JM, Antón-Santos JM, Millán-Núñez-Cortés J, Lumbreras-Bermejo C, Ramos-Rincón JM, Roy-Vallejo E, et al. Clinical characteristics of patients hospitalized with COVID-19 in Spain: results from the SEMI-COVID-19 Registry. Rev Clin Esp. 2020;220:480-494. [CrossRef]
- Cassidy, 2022: Cassidy RE. Pharmacy. In: Shabsigh R, editor. Health crisis management in acute care hospitals: Lessons learned from COVID-19 and beyond. Cham: Springer; 2022. pp. 183-200. [CrossRef]
- CDC, 2024a: Centers for Disease Control and Prevention. Weekly Counts of Deaths by Jurisdiction and Age. Accessed on 2024-02-13 from: https://data.cdc.gov/NCHS/Weekly-Counts-of-Deaths-by-Jurisdiction-and-Age/y5bj-9g5w/about_data.
- CDC, 2024b: Centers for Disease Control and Prevention. National Center for Health Statistics Mortality Data on CDC WONDER. Accessed on 2024-02-15 from: https://wonder.cdc.gov/mcd.html.
- CDC, 2024c: Centers for Disease Control and Prevention. US Diabetes Surveillance System Application. Accessed on 2024-10-29 from: https://gis.cdc.gov/grasp/diabetes/diabetesatlas-surveillance.html.
- CDC, 2025. Centers for Disease Control and Prevention. COVID-19 Vaccinations in the United States,County. Acccessed on 2025-01-05 from: https://data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh/about_data.
- Cereda et al., 2021: Cereda D, Manica M, Tirani M, Rovida F, Demicheli V, Ajelli M, et al. The early phase of the COVID-19 epidemic in Lombardy, Italy. Epidemics. 2021;37:100528. [CrossRef]
- Chaillot, 2024: Chaillot P. Covid 19: Decoding Official Data: Mortality, tests, vaccines, hospitals. The truth emerges. Paris: L'Artilleur; 2024. ISBN-10: 2810012393, ISBN-13: 978-2810012398.
- Chan et al., 2021: Chan EYS, Cheng D, Martin J. Impact of COVID-19 on excess mortality, life expectancy, and years of life lost in the United States. PLOS ONE. 2021;16(9:e0256835. [CrossRef]
- Chastre & Fagon, 2002: Chastre J, Fagon J-Y. Ventilator-associated Pneumonia. Am J Respir Crit Care Med. 2002;165:867-903. [CrossRef]
- Chinazzi et al., 2020: Chinazzi M, Davis JT, Ajelli M, Gioannini C, Litvinova M, Merler S, et al. The effect of travel restrictions on the spread of the2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368:395-400. [CrossRef]
- Clark & Shabsigh, 2022: Clark S, Shabsigh R. Background, the hospital system, the patient community, and the Bronx. In: Shabsigh R, editor. Health crisis management in acute care hospitals: Lessons learned from COVID-19 and beyond. Cham: Springer; 2022. pp. 1-7. [CrossRef]
- Coker et al., 2020: Coker ES, Cavalli L, Fabrizi E, Guastella G, Lippo E, Parisi ML, et al. The Effects of Air Pollution on COVID-19 Related Mortality in Northern Italy. Environmental and Resource Economics. 2020;76:611–634. [CrossRef]
- Colizza et al., 2007: Colizza V, Barrat A, Barthelemy M, Valleron A-J, Vespignani A. Modeling the Worldwide Spread of Pandemic Influenza: Baseline Case and Containment Interventions. PLOS Med. 2007;4:e13. [CrossRef]
- Cook, 2020: Cook DC. Implementing shared ventilation must be scientific and ethical, or it risks harm. British Journal of Anesthesiology. 2020;125:E181-E183. [CrossRef]
- Cooper et al., 2006: Cooper BS, Pitman RJ, Edmunds WJ, Gay NJ. Delaying the International Spread of Pandemic Influenza. PLOS Med. 2006;3:e212. [CrossRef]
- Dahal et al., 2021: Dahal S, Banda JM, Bento AI, Mizumoto K, Chowell G. Characterizing all-cause excess mortality patterns during COVID-19 pandemic in Mexico. BMC Infect Dis. 2021;21:432. [CrossRef]
- Das-Munshi et al., 2021: Das-Munshi J, Kuo Chang C, Bakolis I, Broadbent M, Dregan A, Hotopf M, et al. All-cause and cause-specific mortality in people with mental disorders and intellectual disabilities, before and during the COVID-19 pandemic: cohort study. Lancet Reg Health Eur. 2021;11:100228. [CrossRef]
- Davis, 2006: Davis KA. Ventilator-Associated Pneumonia: A Review. J Intensive Care Med. 2006;21:211-226. [CrossRef]
- Davis et al., 2021: Davis JT, Chinazzi M, Perra N, Mu K, Pastore y Piontti A, Ajelli M, et al. Cryptic transmission of SARS-CoV-2 and the first COVID-19 wave. Nature. 2021;600:127-132. [CrossRef]
- de Boer et al., 2023: de Boer PT, van de Kassteele J, Vos ERA, van Asten L, Dongelmans DA, van Gageldonk-Lafeber AB, et al. Age-specific severity of SARS-CoV-2 in February 2020 – June 2021 in the Netherlands. medRxiv. 2023.02.09.23285703. [CrossRef]
- de Freytas-Tamura et al., 2020: de Freytas-Tamura K, Hu W, Cook LR. “It’s the death towers”: How the Bronx became New York’s virus hot spot. New York Times. 26 May 2020. Accessed on 2025-02-04 from: https://www.nytimes.com/2020/05/26/nyregion/bronx-coronavirus-outbreak.html.
- de Gier et al., 2023: de Gier B, van Asten L, Boere TM, van Roon A, van Roekl C, Pijpers J, et al. Effect of COVID-19 vaccination on mortality by COVID-19 and on mortality by other causes, the Netherlands, January 2021–January 2022. Vaccine. 2023;41:4488-4496. [CrossRef]
- de Terwangne et al., 2021: de Terwangne C, Sorgente A, Tortora R, Cheung D, Duprez F, Place S, et al. Mortality Rate and Predictors among Patients with COVID-19 Related Acute Respiratory Failure Requiring Mechanical Ventilation: A Retrospective Single Centre Study. The Journal of Critical Care Medicine. 2021;7:21-27. [CrossRef]
- Demetriou et al., 2023: Demetriou CA, Achilleos S, Qattrocchi A, Gabel J, Critselis E, Constantinou C, et al. Impact of the COVID-19 pandemic on total, sex- and age-specific all-cause mortality in 20 countries worldwide during 2020: results from the C-MOR project. Int J Epidemiol. 2023;52:664–676. [CrossRef]
- Department of Transportation, 2024: Department of Transportation. U.S. International Air Passenger and Freight Statistics. December 2020. Accessed on 2024-11-25 from: https://www.transportation.gov/sites/dot.gov/files/2020-12/US%20International%20Air%20Passenger%20and%20Freight%20Statistics%20for%20December%202019.pdf.
- Deshmukh et al., 2021: Deshmukh Y, Suraweera W, Tumbe C, et al. Excess mortality in India from July 2020 to July 2021 during the COVID pandemic: death registration, health facility deaths, and survey data. medRxiv 2021.07.20.21260872. [CrossRef]
- Docquier et al., 2022: Docquier F, Golenvaux N, Nijssen S, Schaus P, Stips F. Cross-border mobility responses to COVID-19 in Europe: new evidence from facebook data. Globalization and Health. 2022;18:41. [CrossRef]
- Doyno et al., 2020: Doyno C, Sobieraj DM, Baker WL. Toxicity of chloroquine and hydroxychloroquine following therapeutic use or overdose. Clinical Toxicology. 2021;59:12-23. [CrossRef]
- Eder et al., 2020: Eder S, Fountain H, Keller MH, Xiao M, Stevenson A. 430,000 people have traveled from China to U.S. since coronavirus surfaced. New York Times. 4 April 2020. Accessed on 2024-11-25 from: https://www.nytimes.com/2020/04/04/us/coronavirus-china-travel-restrictions.html [Archived at: https://archive.is/8pjIn].
- ENAC, 2017: Ente Nazionale per l’Avazione Civile. Traffic Data 2017. Sapia P, Di Agostino M, editors. Accessed on 2024-10-11 from: https://www.enac.gov.it/app/uploads/2024/04/ENAC_Traffic_data_2017_en.pdf.
- ENAC, 2018: Ente Nazionale per l’Avazione Civile. Traffic Data 2018. Sapia P, Di Agostino M, editors. Accessed on 2024-10-11 from: https://www.enac.gov.it/app/uploads/2019/06/ENAC_Traffic-data_2018.pdf.
- ENAC, 2019: Ente Nazionale per l’Avazione Civile. Dati di Traffico 2019. Dolci S, Sgrelli E, Petrini R, editors. Accessed on 2024-10-11 from: http://web.unibas.it/donatociampa/wp-content/uploads/2020/09/ENAC-Dati-di-traffico-2019.pdf.
- Engler, 2022: Engler J. Were the unprecedented excess deaths curves in Northern Italy in spring 2020 caused by the spread of a novel deadly virus? A reassessment of the available evidence suggests another factor was involved. BizNews. 14 September 2022. Accessed on 2025-03-14 from: https://www.biznews.com/health/2022/09/14/excess-deaths-healthcare-panic. [See also: The Lombardy Analysis: Lombardy deaths in March 2020 reveal a pattern which seems difficult to explain by viral spread. PANDA Uncut, 22 August 2022. Accessed on 2025-03-12 from: https://pandauncut.substack.com/p/the-lombardy-analysis].
- Epstein et al., 2007: Epstein JM, Goedecke DM, Yu F, Morris RJ, Wagener DK, Bobashev GV. Controlling Pandemic Flu: The Value of International Air Travel Restrictions. PLOS One. 2007;2:e401. [CrossRef]
- European Environment Agency, 2018: European Environment Agency. PM2.5 annual mean in 2018. Published 2020-09-09, Modified 2024-09-20. Accessed on 2024-10-11 from: https://www.eea.europa.eu/en/analysis/maps-and-charts/pm2-5-annual-mean-in-2 [Archived at: https://archive.is/O0ucK].
- Eurostat, 2021: Eurostat. Commuting between regions. 10 June 2021. Accessed on 2024-10-01 from: https://ec.europa.eu/eurostat/web/products-eurostat-news/-/ddn-20210610-1.
- Eurostat, 2024a: Eurostat. Deaths by week, sex and NUTS 3 region. Accessed on 2024-02-10 from: https://ec.europa.eu/eurostat/databrowser/view/DEMO_R_MWK3_TS/default/table?lang=en&category=demo.demomwk.
- Eurostat, 2024b: Eurostat. Population on 1 January by NUTS 2 region. Accessed on 2024-10-07 from: https://ec.europa.eu/eurostat/databrowser/view/tgs00096/default/table?lang=en.
- Eurostat, 2024c: Eurostat. Population density by NUTS 2 region. Accessed on 2024-02-26 from: https://ec.europa.eu/eurostat/databrowser/view/tgs00024/default/table?lang=en.
- Eurostat, 2024d: Eurostat. At-risk-of-poverty rate by NUTS 2 region. Accessed on 2024-03-22 from: https://ec.europa.eu/eurostat/databrowser/view/tgs00103/default/table?lang=en.
- Eurostat, 2024e: Eurostat. International road freight transport - loaded goods in reporting country by country of unloading and type of transport (t, tkm) - quarterly data. Accessed on 2024-10-02 from: https://ec.europa.eu/eurostat/databrowser/view/road_go_iq_ltt__custom_13116607/default/table?lang=en.
- Eurostat, 2024f: Eurostat. International road freight transport - unloaded goods in reporting country by country of loading and type of transport (t, tkm) - quarterly data. Accessed on 2024-10-02 from: https://ec.europa.eu/eurostat/databrowser/view/road_go_iq_utt/default/table?lang=en&category=road.road_go.road_go_int.
- Eurostat, 2024g: Eurostat. Available beds in hospitals by NUTS 2 region. Accessed on 2024-10-11 from: https://ec.europa.eu/eurostat/databrowser/view/hlth_rs_bdsrg2/default/table?lang=en&category=hlth.hlth_care.hlth_res.hlth_facil.
- Eurostat, 2025: Eurostat. NUTS – NOMENCLATURE OF TERRITORIAL UNITS FOR STATISTICS. Accessed on 2025-01-17 from: https://ec.europa.eu/eurostat/web/nuts.
- Fagiuoli et al., 2020: Fagiuoli S, Lorini FL, Remuzzi G. Adaptations and Lessons in the Province of Bergamo. New England Journal of Medicine. 2020;382:e71. [CrossRef]
- Faisant et al., 2024: Faisant M, Vincent N, Hubert B, le Tertre A. Regional excess mortality in France during COVID-19 pandemic: the first three epidemic periods (March 2020–June 2021). European Journal of Public Health. 2024 Jun 1;34(3):606–12.
- Faust et al., 2021. Faust JS, Krumholz HM, Du C. All-Cause Excess Mortality and COVID-19–Related Mortality Among US Adults Aged 25-44 Years, March-July 2020. JAMA. 2020;325:785–787. [CrossRef]
- Faust et al., 2022: Faust JS, Renton B, Chen AJ, Du C, Liang C, Li S-X, et al. Uncoupling of all-cause excess mortality from COVID-19 cases in a highly vaccinated state. The Lancet. 2022;22:1419-1420. [CrossRef]
- Félix-Cardoso et al., 2020: Félix-Cardoso F, Vasconcelos H, Pereira Rodrigues P, Cruz-Correia R. Excess mortality during COVID-19 in five European countries and a critique of mortality data analysis. medRxiv 2020.04.28.20083147. [CrossRef]
- Ferguson et al., 2006: Ferguson NM, Cummings DAT, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448-452. [CrossRef]
- Ferguson et al., 2020: Ferguson NM, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M, et al. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. MRC Centre for Global Infectious Disease Analysis, Imperial College London. 16 March 2020. Accessed 2025-04-30 from: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/disease-areas/covid-19/report-9-impact-of-npis-on-covid-19/.
- Fiolet et al., 2021: Fiolet T, Guihur A, Rebeaud ME, Mulot M, Peiffer-Smadja N, Mahamat-Saleh Y. Effect of hydroxychloroquine with or without azithromycin on the mortality of coronavirus disease 2019 (COVID-19) patients: a systematic review and meta-analysis. Clin Microbiol Inf. 2021;27:19-27. [CrossRef]
- Financial Mirror, 2020: Financial Mirror. Cyprus melted under hottest May on record. Financial Mirror. 4 June 2020. Accessed 2025-04-17 from: https://www.financialmirror.com/2020/06/04/cyprus-melted-under-hottest-may-on-record/.
- Flory et al., 2009: Flory JH, Joffe M, Fishman NO, Edelstein PH, Metlay JP. Socioeconomic risk factors for bacteraemic pneumococcal pneumonia in adults. Epidemiol Infect. 2009;137:717-726. [CrossRef]
- Foster et al., 2024: Foster TB, Fernandez L, Porter SR, Pharris-Ciurej N. Racial and Ethnic Disparities in Excess All-Cause Mortality in the First Year of the COVID-19 Pandemic. Demography. 2024 Feb 1;61(1):59–85.
- Fouillet et al., 2020: Fouillet A, Pontais I, Caserio-Schönemann C. Excess all-cause mortality during the first wave of the COVID-19 epidemic in France, March to May 2020. Euro Surveill. 2020;25:2001485. [CrossRef]
- Gallo et al., 2021: Gallo E, Prosepe I, Lorenzoni G, Akar AS, Lanera C, Berchialla P, et al. Excess of all-cause mortality is only partially explained by COVID-19 in Veneto (Italy) during spring outbreak. BMC Public Health. 2021;21:797. [CrossRef]
- Gattinoni et al., 2017: Gattinoni L, Marini JJ, Collino F, Maiolo G, Rapetti F, Tonetti T, et al. The future of mechanical ventilation: lessons from the present and the past. Critical Care. 2017;21:183. [CrossRef]
- Gautret et al., 2020: Gautret P, Lagier J-C, Parola P, Hoang VT, Meddeb L, Mailhe M, et al. Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial. Int J Antimicrob Agents. 2020;56:105949. [CrossRef]
- Gautret et al., 2025: Gautret P, Lagier J-C, Parola P, Hoang VT, Meddeb L, Mailhe M, et al. Retraction notice to “Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial”[International Journal of Antimicrobial Agents 56 (2020), 105949]. Int J Antimicrob Agents. 2025;65:107416. [CrossRef]
- Ghaznavi et al., 2022: Ghaznavi C, Eguchi A, Tanoue Y, Yoneoka D, Kawashima T, Suzuki M, et al. Pre- and post-COVID-19 all-cause mortality of Japanese citizens versus foreign residents living in Japan, 2015–2021. SSM - Population Health. 2022;18:101114. [CrossRef]
- Gil-Rodrigo et al., 2020: Gil-Rodrigo A, Miró Ò, Piñera P, Burillo-Putze G, Jiménez S, Martín A, et al. Analysis of clinical characteristics and outcomes in patients with COVID-19 based on a series of 1000 patients treated in Spanish emergency departments. Emergencias. 2020;32:233-241.
- Gilbertoni et al., 2021: Gilbertoni D, Adja KYC, Golinelli D, Reno C, Regazzi L, Lenzi J, et al. Patterns of COVID-19 related excess mortality in the municipalities of Northern Italy during the first wave of the pandemic. Health and Place. 2021;67:102508. [CrossRef]
- Gobiņa et al., 2022: Gobiņa I, Avotiņš A, Kojalo U, Strēle I, Pildava S, Villeruša A, et al. Excess mortality associated with the COVID-19 pandemic in Latvia: a population-level analysis of all-cause and noncommunicable disease deaths in 2020. BMC Public Health. 2022;22:1109. [CrossRef]
- Gonzalez-Zorn, 2021: Gonzalez-Zorn B. Antibiotic use in the COVID-19 crisis in Spain. Clin Microbiol Inf. 2021;27:646-647. [CrossRef]
- Goodall et al., 2020: Goodall JW, Reed TAN, Ardissino M, Bassett P, Whittington AM, Cohen DL, et al. Risk factors for severe disease in patients admitted with COVID-19 to a hospital in London, England: a retrospective cohort study. Epidemiol Infect. 2020;148:e251. [CrossRef]
- Grasselli et al., 2020a: Grasselli G, Pesenti A, Cecconi M. Critical Care Utilization for the COVID-19 Outbreak in Lombardy, Italy: Early Experience and Forecast During an Emergency Response. JAMA. 2020;323(16):1545–1546. [CrossRef]
- Grasselli et al., 2020b: Grasselli G, Zangrillo A, Zanella A, Antonelli M, Cabrini L, Castelli A. Baseline Characteristics and Outcomes of 1591 Patients Infected With SARS-CoV-2 Admitted to ICUs of the Lombardy Region, Italy. JAMA. 2020;323(16):1574–1581. [CrossRef]
- Grasselli et al., 2020c: Grasselli G, Greco M, Zanella A, Albano G, Antonelli M, Bellani G, et al. Risk Factors Associated With Mortality Among Patients With COVID-19 in Intensive Care Units in Lombardy, Italy. JAMA Internal Medicine. 2020;180(10):1345–1355. [CrossRef]
- Greater London Authority, 2023: Greater London Authority. Land Area and Population Density, Ward and Borough. 17 August 2023. Accessed on 2024-12-05 from: https://www.data.gov.uk/dataset/a76f46f9-c10b-4fe7-82f6-aa928471fcd1/land-area-and-population-density-ward-and-borough.
- Grenfell et al. 2001: Grenfell BT, Bjørnstad, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716-723. [CrossRef]
- Gutíerrez-Abejón et al., 2020: Gutíerrez-Abejón E, Tamayo E, Martín-García D, Álvarez FJ, Herrera-Gómez F. Clinical Profile, Treatment and Predictors during the First COVID-19Wave: A Population-Based Registry Analysis from Castile and Leon Hospitals. Int J Environ Res Public Health. 2020;17:9360. [CrossRef]
- Haugen, 2023: Haugen M. Excess mortality compared to vaccination in the covid era. Substack. 20 January 2023. Accessed on 2025-03-12 from: https://electricgerms.substack.com/p/excess-mortality-compared-to-vaccination.
- He et al., 2022: He G, Xiao J, Lin Z, Ma W. Excess mortality, rather than case fatality rate, is a superior indicator to assess the impact of COVID-19 pandemic. The Innovation. 2022;3:100298. [CrossRef]
- Henry et al., 2022: Henry NJ, Elagali A, Nguyen M, Chipeta MG, Moore CE. Variation in excess all-cause mortality by age, sex, and province during the first wave of the COVID-19 pandemic in Italy. Sci Rep. 2022;12:1077. [CrossRef]
- Hentschke-Lopes et al., 2022: Hentschke-Lopes M, Botton MR, Borges P, Freitas M, Mancuso ACB, Matte U. Cad Saúde Pública. 2022;38:e00001022. [CrossRef]
- Hess et al., 2020: Hess DR, Kallet RH, Beitler JR. Ventilator Sharing: The Good, the Bad, and the Ugly. Resp Care. 2020;65:1059-1062. [CrossRef]
- HHS, 2024: US Department of Health and Human Services. Part D Prescriber Data CY 2017. Accessed on 2024-11-13 from: https://www.hhs.gov/guidance/document/part-d-prescriber-data-cy-2017-0. [Alternative link: https://www.hhs.gov/guidance/document/part-d-prescriber-data-cy-2017].
- Hickey & Rancourt, 2023a: Hickey J, Rancourt DG. Predictions from standard epidemiological models of consequences of segregating and isolating vulnerable people into care facilities. PLOS ONE. 2023;18:e0293556. [CrossRef]
- Hickey & Rancourt, 2023b: Hickey J, Rancourt DG. Viral Respiratory Epidemic Modeling of Societal Segregation Based on Vaccination Status. Cureus. 2023;15:e50520. [CrossRef]
- Institute for Government Analysis, 2022: Institute for Government Analysis. Timeline of UK government coronavirus lockdowns and measures, March 2020 to December 2021. 9 December 2022. Accessed on 2025-01-27 from: https://www.instituteforgovernment.org.uk/sites/default/files/2022-12/timeline-coronavirus-lockdown-december-2021.pdf.
- Ioannidis et al., 2023: Ioannidis JPA, Zonta F, Levitt M. Variability in excess deaths across countries with different vulnerability during 2020–2023. PNAS. 2023;120:e2309557120. [CrossRef]
- Islam, et al., 2021a: Islam N, Jdanov DA, Shkolnikov VM, Khunti K, Kawachi I, White M, et al. Effects of covid-19 pandemic on life expectancy and premature mortality in 2020: time series analysis in 37 countries. BMJ. 2021;375:e066768. [CrossRef]
- Islam, et al., 2021b: Islam N, Shkolnikov VM, Acosta RJ, Klimkin I, Kawachi I, Irizarry RA, et al. Excess deaths associated with covid-19 pandemic in 2020: age and sex disaggregated time series analysis in 29 high income countries. BMJ. 2021;373:n1137. [CrossRef]
- Jacobson & Jokela, 2021: Jacobson SH, Jokela JA. Beyond COVID-19 deaths during the COVID-19 pandemic in the United States. Health Care Management Science. 2021;24:661–665. [CrossRef]
- Jdanov et al., 2021: Jdanov DA, Galarza AA, Shkolnikov VM, Jasilionis D, Németh L, Leon DA, et al. The short-term mortality fluctuation data series, monitoring mortality shocks across time and space. Scientific Data. 2021;8:235. [CrossRef]
- Jha et al., 2022: Jha P, Deshmukh Y, Tumbe C, Suraweera W, Bhowmick A, Sharma S, et al. COVID mortality in India: National survey data and health facility deaths. Science. 2022;375:667–671. [CrossRef]
- Joffe, 2021: Joffe AR. COVID-19: Rethinking the Lockdown Groupthink. Front Public Health. 2021;9: 625778. [CrossRef]
- Johnson & Rancourt, 2022: Johnson JA, Rancourt DG. Evaluating the Effect of Lockdowns On All-Cause Mortality During the COVID Era: Lockdowns Did Not Save Lives. ResearchGate. 9 July 2022. Accessed on 2025-03-12 from. Also available at: https://correlation-canada.org/effect-of-lockdowns-in-usa/. [CrossRef]
- Jones & Ponomarenko, 2023: Jones RP, Ponomarenko A. Effect of Age, Sex, and COVID-19 Vaccination History on All-Cause Mortality: Unexpected Outcomes in a Complex Biological and Social System. Preprints. 2023; 2023040248. https://www.preprints.org/manuscript/202304.0248/v1.
- Joseph et al., 2010: Joseph NM, Sistla S, Dutta TK, Badhar AS, Parija SC. Ventilator-associated pneumonia: A review. European Journal of Internal Medicine. 2010;21:360-388. [CrossRef]
- Juul et al., 2022: Juul FE, Jodal HC, Barua I, Refsum E, Olsvik Ø, Helsingen LM, et al. Mortality in Norway and Sweden during the COVID-19 pandemic. Scandinavian Journal of Public Health. 2022;50:38-45. [CrossRef]
- Juurlink, 2020: Juurlink DN. Safety considerations with chloroquine, hydroxychloroquine and azithromycin in the management of SARS-CoV-2 infection. CMAJ. 2020;192:E450. [CrossRef]
- Karlinsky & Kobak, 2021: Karlinsky A, Kobak D. Tracking excess mortality across countries during the COVID-19 pandemic with the World Mortality Dataset. eLife. 2021;10:e69336. [CrossRef]
- Keane, 2023: Keane D. One of London’s busiest A&Es needs urgent funding for more beds. The Standard. 20 February 2023. Accessed on 2025-02-04 from: https://www.standard.co.uk/news/health/northwick-park-hospital-funding-accident-and-emergency-beds-b1061659.html.
- Kobak, 2021: Kobak D. Excess mortality reveals Covid’s true toll in Russia. Significance. 2021;18:16-19. [CrossRef]
- Kontis et al., 2020: Kontis V, Bennett JE, Rashid T, Parks RM, Pearson-Stuttard J, Guillot M, et al. Magnitude, demographics and dynamics of the effect of the first wave of the COVID-19 pandemic on all-cause mortality in 21 industrialized countries. Nature Med. 2020;26:1919–1928. [CrossRef]
- Kontis et al., 2022: Kontis V, Bennett JE, Parks RM, Rashid T, Pearson-Stuttard J, Asaria P, et al. Lessons learned and lessons missed: impact of the coronavirus disease 2019 (COVID-19) pandemic on all-cause mortality in 40 industrialised countries and US states prior to mass vaccination. [version 2; peer review: 2 approved]. Wellcome Open Res. 2022;6:279. [CrossRef]
- Kontopantelis et al., 2021a. Kontopantelis E, Mamas MA, Webb RI, Castro A, Rutter MK, Gale CP, et al. Excess deaths from COVID-19 and other causes by region, neighbourhood deprivation level and place of death during the first 30 weeks of the pandemic in England and Wales: A retrospective registry study. Lancet Reg Health Eur. 2021;7:100144. [CrossRef]
- Kontopantelis et al., 2021b. Kontopantelis E, Mamas MA, Deanfield J, Asaria M, Doran T. Excess mortality in England and Wales during the first wave of the COVID-19 pandemic. J Epidemiol Community Health. 2021;75:213–223. https://jech.bmj.com/content/75/3/213.
- Kontopantelis et al., 2022. Kontopantelis E, Mamas MA, Webb RT, Castro A, Rutter MK, Gale CP, et al. Excess years of life lost to COVID-19 and other causes of death by sex, neighbourhood deprivation, and region in England and Wales during 2020: A registry-based study. PLOS Medicine. 2022;19:e1003904. [CrossRef]
- Korosec, 2020: Korosec M. Extreme Heatwave with up to +43C in Turkey, 41.5C in Cyprus, +40C in Greece, and South Italy today, May 16th. 16 May 2020. Accessed 2025-04-17 from: https://www.severe-weather.eu/mcd/heatwave-above-40-degrees-turkey-mk/.
- Korsgaard, 2024: Korsgaard SR. All-cause mortality and Japan’s early countermeasures. Health Science Reports. 2024;7:e1905. [CrossRef]
- Kotfis et al., 2020: Kotfis K, Williams Roberson S, Wilson JE, Dabrowski W, Pun BT, Ely EW. COVID-19: ICU delirium management during SARS-CoV-2 pandemic. Critical Care. 2020;24:176. [CrossRef]
- Kuhbandner & Reitzner, 2023: Kuhbandner C, Reitzner M. Excess mortality in Germany 2020-2022. Cureus. 2023;15:e39371. [CrossRef]
- Kung et al., 2021a: Kung S, Doppen M, Black M, Brathwaite I, Kearns C, Weatherall M, et al. Underestimation of COVID-19 mortality during the pandemic. ERJ Open Res. 2021;7:00766-2020. [CrossRef]
- Kung et al., 2021b: Kung S, Doppen M, Black M, Hills T, Kearns N. Reduced mortality in New Zealand during the COVID-19 pandemic. The Lancet. 2020;397:25. [CrossRef]
- Lacout et al., 2021: Lacout A, Perronne C, Lounnas V. Hydroxychloroquine in Hospitalized Patients with Covid-19. New England Journal of Medicine. 2021;389:881-882. [CrossRef]
- LaHue et al., 2020: LaHue SC, James TC, Newman JC, Esmaili AM, Ormseth CH, Ely EW. Collaborative Delirium Prevention in the Age of COVID-19. Journal of the American Geriatrics Society. 2020;68:947-949. [CrossRef]
- La Maestra et al., 2020: La Maestra S, Abbondandolo A, De Flora S. Epidemiological trends of COVID-19 epidemic in Italy over March 2020: From 1000 to 100 000 cases. Journal of Medical Virology. 2020;92:1956-1961. [CrossRef]
- Lane et al., 2020: Lane JCE, Weaver J, Kostka K, Duarte-Salles T, Abrahao MTF, Alghoul H, et al. Risk of hydroxychloroquine alone and in combination with azithromycin in the treatment of rheumatoid arthritis: a multinational, retrospective study. Lancet Rheumatol. 2020;2:e698-711. [CrossRef]
- Lee et al., 2022: Lee W-E, Park SW, Weinberger DM, Olson D, Simonsen L, Grenfell BT, et al. Direct and indirect mortality impacts of the COVID-19 pandemic in the US, March 2020-April 2021. medRxiv. 2022.02.10.22270721. [CrossRef]
- Leffler et al., 2022: Leffler CT, Lykins V JD, Das S, Yang E, Konda S. Preliminary Analysis of Excess Mortality in India During the COVID-19 Pandemic. Am J Trop Med Hyg. 2022;106:1507-1510. [CrossRef]
- Léger & Rizzi, 2024: Léger AE, Rizzi S. Month-to-month all-cause mortality forecasting: a method allowing for changes in seasonal patterns. American Journal of Epidemiology. 2024;193:898–907. [CrossRef]
- Lewnard et al., 2022: Lewnard JA, Mahmud A, Narayan T, Wahl B, Selvavinayagam TS, Mohan C, et al. All-cause mortality during the COVID-19 pandemic in Chennai, India: an observational study. Lancet Infect Dis. 2022;22:463-472. [CrossRef]
- Liu et al., 2021: Liu J, Zhang L, Yan Y, Zhou Y, Yin P, Qi J et al. Excess mortality in Wuhan city and other parts of China during the three months of the covid-19 outbreak: findings from nationwide mortality registries. BMJ. 2021;372:n415. [CrossRef]
- Locatelli & Rousson, 2021: Locatelli I, Rousson V. A first analysis of excess mortality in Switzerland in 2020. PLOS ONE. 2021;16:e0253505. [CrossRef]
- Maantay, 2007: Maantay J. Asthma and air pollution in the Bronx: Methodological and data considerations in using GIS for environmental justice and health research. Health & Place. 2007;13:32-56. [CrossRef]
- Machado-Duque et al., 2022: Machado-Duque ME, Gaviria-Mendoza A, Valladales-Restrepo LF, Albanés-Beltrán JP, Machado-Alba JE. Trends in the Use of Sedative-Hypnotics, Opioids, and Neuromuscular Blockers in Hospitalized Patients During the COVID-19 Pandemic: Observational Retrospective Study. Drugs – Real World Outcomes. 2022;9:629-638. [CrossRef]
- Mackenzie, 1983: Mackenzie AH. Dose Refinements in Long-Term Therapy of Rheumatoid Arthritis with Antimalarials. Am J Med. 1983;75:40-45. [CrossRef]
- Mahase, 2020: Mahase E. Covid-19: most patients require mechanical ventilation in first 24 hours of critical care. BMJ. 2020;368:m1201 . [CrossRef]
- Mannucci et al., 2020: Mannucci E, Besmir N, Monami M. Factors associated with increased all-cause mortality during the COVID-19 pandemic in Italy. Int J Infect Dis. 2020;98:121–124. [CrossRef]
- Marinella, 1997: Marinella MA. Propofol for sedation in the intensive care unit: essentials for the clinician. Respir med. 1997;91:505-510. [CrossRef]
- Marliot et al., 2020: Marliot G, Penel N, Gamblin V. Switch in use of midazolam for cancer patients during the COVID-19 pandemic. J Oncol Pharm Pract. 2020;26:1817-1818. [CrossRef]
- Marquardt & Albertson, 2001: Marquardt K, Albertson TE. Treatment of Hydroxychloroquine Overdose. Therapeutics. 2001;19:420-424. [CrossRef]
- Martínez-Sanz et al., 2021. Martínez-Sanz J, Muriel A, Ron R, Herrera S, Pérez-Molina JA, Moreno S, et al. Clin Microbiol Inf. 2021;27:238-243. [CrossRef]
- Masselot et al., 2023: Masselot P, Mistry M, Vanoli J, Schneider R, Iungman T, Garcia-Leon D, et al. Excess mortality attributed to heat and cold: a health impact assessment study in 854 cities in Europe. Lancet Planet Health. 2023;7:e271-e281. [CrossRef]
- Mathews et al., 2021: Mathews KS, Seitz KP, Vranas KC, Druggal A, Valley TS, Zhao B, et al. Variation in Initial U.S. Hospital Responses to the Coronavirus Disease 2019 Pandemic. Critical Care Medicine. 2021;49:1038-1048. [CrossRef]
- Matthes et al., 2024: Matthes KL, Floris J, Merzouki A, Junker C, Weitkunat R, Rühli F, et al. Spatial pattern of all cause excess mortality in Swiss districts during the pandemic years 1890, 1918 and 2020. Spatial and Spatio-temporal Epidemiology [Internet]. 2024 Nov;51:100697. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1877584524000649.
- Matveeva & Shabalina, 2023: Matveeva O, Shabalina SA. Comparison of vaccination and booster rates and their impact on excess mortality during the COVID-19 pandemic in European countries. Front Immunol. 2023;14:1151311. [CrossRef]
- Maxwell et al., 2024: Maxwell CJ, Dampf H, Alkabbani W, Cotton CA, Gamble J-M, Hogan DB, et al. Psychotropic, Anticonvulsant, and Opioid Use in Assisted Living Residents Before and During the COVID-19 Pandemic. Journal of the American Medical Directors Association. 2024;25:121-129. [CrossRef]
- McCrae & Watson, 2023: McCrae N, Watson R. The mad rush for ventilators in the Covid killing fields, Part 1. The Conservative Woman. 17 April 2023. Accessed on 2024-10-16 from: https://www.conservativewoman.co.uk/the-mad-rush-for-ventilators-in-the-covid-killing-fields-part-1/ [Archived at: https://archive.is/YIIGy].
- McDermid et al., 2023: McDermid J, Ballard C, Khan Z, Aarsland D, Fox C, Fossey J, et al. Impact of the Covid-19 pandemic on neuropsychiatric symptoms and antipsychotic prescribing for people with dementia in nursing home settings. Int J Geriatr Psychiatry. 2023;38:e5878. [CrossRef]
- McGrail, 2022: McGrail K. Excess mortality, COVID-19 and health care systems in Canada. CMAJ. 2022;194:E741-E745. [CrossRef]
- Melsen et al., 2011: Melsen WG, Rovers MM, Koeman M, Bonten MJM. Estimating the attributable mortality of ventilator-associated pneumonia from randomized prevention studies. Crit Care Med. 2011; 39:2736-2742. [CrossRef]
- Merler & Ajelli, 2010: Merler S, Ajelli M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proc R Soc B. 2010;277:557-565. [CrossRef]
- Melsen et al., 2013: Melsen WG, Rovers MM, Groenwald RHH, Bergmans DCJJ, Camus C, Bauer TT et al. Attributable mortality of ventilator-associated pneumonia: a meta-analysis of individual patient data from randomised prevention studies. Lancet Infect Dis. 2013;13:665-671. [CrossRef]
- Miller et al., 2021: Miller S, Wherry LR, Mazumder B. Estimated Mortality Increases During The COVID-19 Pandemic By Socioeconomic Status, Race, And Ethnicity. Health Affairs. 2021;40:1252-1260. [CrossRef]
- Mills et al., 2020: Mills EHA., Møller AL, Gnesin F, Zylyftari N, Broccia M, Schou M, et al. National all-cause mortality during the COVID-19 pandemic: a Danish registry-based study. Eur J Epidemiol. 2020;35:1007–1019. [CrossRef]
- MIT Election Data Science Lab, 2018: MIT Election Data and Science Lab. County Presidential Election Returns 2000-2020. Accessed on 2024-11-19 from: . [CrossRef]
- Mitropoulos et al., 2023: Mitropoulos D, Pytharoulis I, Zanis P, Anagnostopoulou C. Subseasonal-to-Seasonal Predictability Assessment of an Early HeatWave in the Eastern Mediterranean in May 2020. Environ Sci Proc. 2023;26:42. [CrossRef]
- Mostert et al., 2024: Mostert S, Hoogland M, Huibers M, Kaspers G. Excess mortality across countries in the Western World since the COVID-19 pandemic: ‘Our World in Data’ estimates of January 2020 to December 2022. BMJ Public Health. 2024 May;2(1):e000282.
- Neil et al., 2022: Neil M, Fenton N, Smalley J, Craig CEH, Guetzkow J, McLachlan S, et al. Official mortality data for England suggest systematic miscategorisation of vaccine status and uncertain effectiveness of Covid-19 vaccination. ResearchGate. 12 January 2022. [CrossRef]
- Neil & Fenton, 2022: Neil M, Fenton N. The Devil's Advocate: An Exploratory Analysis of 2022 Excess Mortality - What is causing excess deaths: Covid, long-covid, lockdowns, healthcare or the vaccines? Where are the numbers? Substack. 14 December 2022. Accessed on 2025-03-12 from: https://wherearethenumbers.substack.com/p/the-devils-advocate-an-exploratory.
- Neil & Fenton, 2023: Neil M, Fenton N. The Very Best of Cheap Trick..... How widespread is the (mal)practice of miscategorising vaccination status? Where are the numbers? Substack. 29 July 2023. Accessed on 2025-03-12 from: https://wherearethenumbers.substack.com/p/the-very-best-of-cheap-trick.
- Nikishimi et al., 2022 : Nikishimi M, Jafari D, Singh N, Shinozaki K, Sison CP, Shoaib M, et al. Mortality of Mechanically Ventilated COVID-19 Patients in Traditional versus Expanded Intensive Care Units in New York. Ann Am Thorac Soc. 2022;19:1346-1354. [CrossRef]
- Nørgaard et al., 2021: Nørgaard SK, Vestergaard LS, Nielsen J, Richter L, Schmid D, Bustos N, et al. Real-time monitoring shows substantial excess all-cause mortality during second wave of COVID-19 in Europe, October to December 2020. Euro Surveill. 2021;26:2002023. [CrossRef]
- Nørgaard et al., 2024: Nørgaard SK, Nielsen J, Nordholm AC, Richter L, Chalupka A, Sierra NB, et al. Excess mortality in Europe coincides with peaks of COVID-19, influenza and respiratory syncytial virus (RSV), November 2023 to February 2024. Eurosurveillance. 2024 Apr 11;29(15).
- Núñez-Gil et al., 2020: Núñez-Gil IJ, Estrada V, Fernández-Pérez C, Fernández-Rozas I, Martín-Sánchez FJ, Macaya C. Curva pandémica COVID-19, sobrecarga sanitaria y mortalidad. Emergencias. 2020;32:290-299.
- Olson et al., 2020: Olson DR, Huynh M, Fine A, Baumgartner J, Castro A, Tai Chan H, et al. Preliminary Estimate of Excess Mortality During the COVID-19 Outbreak — New York City, March 11–May 2, 2020. MMWR Morb Mortal Wkly Rep. 2020;69:603–605. [CrossRef]
- ONS, 2021: Office for National Statistics. Poverty rate by NUTS 2 region, UK, financial year ending 2018 to financial year ending 2020. Accessed on 2024-12-03 from: https://www.ons.gov.uk/peoplepopulationandcommunity/personalandhouseholdfinances/incomeandwealth/adhocs/13572povertyratebynuts2regionukfinancialyearending2018tofinancialyearending2020.
- ONS, 2022a: Office for National Statistics. Regional ethnic diversity. 22 December 2022. Accessed on 2024-12-05 from: https://www.ethnicity-facts-figures.service.gov.uk/uk-population-by-ethnicity/national-and-regional-populations/regional-ethnic-diversity/latest/.
- ONS, 2022b: Office for National Statistics. International migration, England and Wales: Census 2021. 2 November 2022. Accessed on 2024-12-05 from: https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/internationalmigration/bulletins/internationalmigrationenglandandwales/census2021.
- ONS, 2024: Office for National Statistics. Regional gross disposable household income: all International Territorial Level (ITL) regions. Accessed on 2024-12-04 from: https://www.ons.gov.uk/economy/regionalaccounts/grossdisposablehouseholdincome/datasets/regionalgrossdisposablehouseholdincomegdhi.
- Ottaiano et al., 2021: Ottaiano A, Santorsola M, Tamburini M, Corrado F, Scrima M, Bocchetti M, et al. Journal of Epidemiology and Global Health. 2021;11:253-256. [CrossRef]
- Paganuzzi et al., 2024: Paganuzzi M, Nattino G, Ghilardi GI, Costantino G, Rossi C, Cortellaro F, et al. Assessing the heterogeneity of the impact of COVID-19 incidence on all-cause excess mortality among healthcare districts in Lombardy, Italy, to evaluate the local response to the pandemic: an ecological study. BMJ Open. 2024;14:e077476. [CrossRef]
- Paglino et al., 2023: Paglino E, Lundberg DJ, Zhou Z, Wasserman JA, Raquib R, Luck AN, et al. Monthly excess mortality across counties in the United States during the COVID-19 pandemic, March 2020 to February 2022. Sci Adv. 2023;9:eadf9742. [CrossRef]
- Paglino et al., 2024: Paglino E, Lundberg DJ, Wrigley-Field E, Zhou Z, Wasserman JA, Raquib R, et al. Excess natural-cause mortality in US counties and its association with reported COVID-19 deaths. Proceedings of the National Academy of Sciences of the United States of America. 2024;121(6).
- Pálinkás & Sándor, 2022: Pálinkás A; Sándor J. Effectiveness of COVID-19 Vaccination in Preventing All-Cause Mortality among Adults during the Third Wave of the Epidemic in Hungary: Nationwide Retrospective Cohort Study. Vaccines. 2022;10:1009. [CrossRef]
- Pallari et al., 2024: Pallari CT, Achilleos S, Quattrocchi A, Gabel J, Critselis E, Athanasiadou M, et al. Magnitude and determinants of excess total, age-specific and sex-specific all-cause mortality in 24 countries worldwide during 2020 and 2021: results on the impact of the COVID-19 pandemic from the CMOR project. BMJ Global Health. 2024 Apr 18;9(4).
- Panagiotou et al., 2021: Panagiotou OA, Kosar CM, White EM, Bantis LE, Yang X, Santostefano CM, et al. Risk Factors Associated With All-Cause 30-Day Mortality in Nursing Home Residents With COVID-19. JAMA Intern Med. 2021;181(4):439–448. [CrossRef]
- Pastor-Satorras et al., 2015: Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys. 2015;87:925-979. [CrossRef]
- Pecoraro et al., 2020: Pecoraro F, Clemente F, Luzi D. The efficiency in the ordinary hospital bed management in Italy: An in-depth analysis of intensive care unit in the areas affected by COVID-19 before the outbreak. PLOS One. 2020;15:e0239249. [CrossRef]
- Pérez-Belmonte et al., 2020. Pérez-Belmonte LM, Torres-Peña JD, López-Carmona MD, Ayala-Gutiérrez MM, Fuentes-Jiménez F, et al. Mortality and other adverse outcomes inpatients with type 2 diabetes mellitus admitted for COVID-19 in association with glucose-lowering drugs: a nationwide cohort study. BMC Medicine. 2020;18:359. [CrossRef]
- Piccininni et al., 2020: Piccininni M, Rohmann J L, Foresti L, Lurani C, Kurth T. Use of all cause mortality to quantify the consequences of covid-19 in Nembro, Lombardy: descriptive study. BMJ. 2020; 369:m1835. [CrossRef]
- Pilkington et al., 2021: Pilkington H, Feuillet T, Rican S, Goupil de Bouillé J, Bouchaud O, Caihol J, et al. Spatial determinants of excess all-cause mortality during the first wave of the COVID-19 epidemic in France. BMC Public Health. 2021;21:2157. [CrossRef]
- Polyakova et al., 2021: Polyakova M, Udalova V, Kocks G, Genadek K, Finlay K, Finkelstein AN. Racial Disparities In Excess All-Cause Mortality During The Early COVID-19 Pandemic Varied Substantially Across States. Health Affairs. 2021;40:307-316. [CrossRef]
- Pradelle et al., 2024a: Pradelle A, Mainbourg S, Provencher S, Massy E, Grenet G, Lega J-C. Deaths induced by compassionate use of hydroxychloroquine during the first COVID-19 wave: an estimate. Biomed Pharmacother. 2024;171:116055. [CrossRef]
- Pradelle et al., 2024b. Pradelle A, Mainbourg S, Provencher S, Massy E, Grenet G, Lega J-C. Retraction notice to 'Deaths induced by compassionate use of hydroxychloroquine during the first COVID-19 wave: an estimate' [Biomedicine & Pharmacotherapy, Volume 171 (2024) 116055]. Biomed Pharmacother. 2024;179:117353. [CrossRef]
- Prats-Uribe et al., 2021: Prats-Uribe A, Sena AG, Hui Lai LY, Ahmed W-U-R, Alghoul H, Alser O, et al. Use of repurposed and adjuvant drugs in hospital patients with covid-19: multinational network cohort study. BMJ. 2021;373:n1038. [CrossRef]
- Pulido et al., 2024: Pulido J, Barrio G, Donat M, Politi J, Moreno A, Cea-Soriano L, et al. Excess Mortality During 2020 in Spain: The Most Affected Population, Age, and Educational Group by the COVID-19 Pandemic. Disaster Medicine and Public Health Preparedness. 2024 Feb 19;18.
- Puliyel, 2020: Puliyel J. Rapid Response: Dose Related Toxicity of Hydroxychloroquine. BMJ. 12 July 2020. Accessed 2025-05-07 from: https://www.bmj.com/content/370/bmj.m2670/rr-1.
- Rancourt, 2020: Rancourt DG. All-cause mortality during COVID-19 — No plague and a likely signature of mass homicide by government response. ResearchGate, 2 June 2020. Accessed on 2025-03-12 from: https://correlation-canada.org/no-plague-mass-homicide-2020/. [CrossRef]
- Rancourt, 2021: Rancourt DG. Do Face Masks Reduce COVID-19 Spread in Bangladesh? Are the Abaluck et al. Results Reliable? denisrancourt.ca. 20 September 2021. Accessed on 2025-03-12 from: https://denisrancourt.ca/entries.php?id=106. Also available at: https://correlation-canada.org/do-face-masks-work-in-bangladesh/.
- Rancourt, 2022: Rancourt DG. Probable causal association between India’s extraordinary April-July 2021 excess-mortality event and the vaccine rollout. Correlation Research in the Public Interest. 5 December 2022. Accessed on 2025-03-12 from: https://correlation-canada.org/report-probable-causal-association-between-indias-extraordinary-april-july-2021-excess-mortality-event-and-the-vaccine-rollout/.
- Rancourt, 2024: Rancourt DG. Medical Hypothesis: Respiratory epidemics and pandemics without viral transmission. Correlation Research in the Public Interest. 2 December 2024. Accessed on 2025-03-12 from: https://correlation-canada.org/respiratory-epidemics-without-viral-transmission/. [Also available at: . [CrossRef]
- Rancourt et al., 2020: Rancourt DG, Baudin M, Mercier J. Evaluation of the virulence of SARS-CoV-2 in France, from all-cause mortality 1946-2020. ResearchGate. 20 August 2020. Accessed on 2025-03-12 from. [CrossRef]
- Rancourt et al., 2021a: Rancourt DG, Baudin M, Mercier J. Nature of the COVID-era public health disaster in the USA, from all-cause mortality and socio-geo-economic and climatic data. ResearchGate. 25 Ocbtober 2021. Accessed on 2025-03-12 from. Also available at: https://correlation-canada.org/Mortality-public-health-disaster-USA/. [CrossRef]
- Rancourt et al., 2021b: Rancourt DG, Baudin M, Mercier J. Analysis of all-cause mortality by week in Canada 2010-2021, by province, age and sex: There was no COVID-19 pandemic, and there is strong evidence of response-caused deaths in the most elderly and in young males. ResearchGate. 6 August 2021. Accessed on 2025-03-12 from. Also available at: https://correlation-canada.org/all-cause-mortality-in-canada-2021/. [CrossRef]
- Rancourt et al., 2022a: Rancourt DG, Baudin M, Mercier J. Probable causal association between Australia’s new regime of high all-cause mortality and its COVID-19 vaccine rollout. Correlation Research in the Public Interest. 20 December 2022. Accessed on 2025-03-12 from: https://correlation-canada.org/report-probable-causal-association-between-australias-new-regime-of-high-all-cause-mortality-and-its-covid-19-vaccine-rollout/.
- Rancourt et al., 2022b: Rancourt DG, Baudin M, Mercier J. COVID-Period Mass Vaccination Campaign and Public Health Disaster in the USA: From age/state-resolved all-cause mortality by time, age-resolved vaccine delivery by time, and socio-geo-economic data. ResearchGate. 2 August 2022. Accessed on 2025-03-12 from. Also available at: https://vixra.org/abs/2208.0023 and archived at: https://archive.ph/lFNwK. [CrossRef]
- Rancourt et al., 2022c: Rancourt DG, Baudin M, Mercier J. Proof that Canada’s COVID-19 mortality statistics are incorrect. Correlation Research in the Public Interest. 5 October 2022. Accessed on 2025-03-12 from: https://correlation-canada.org/report-proof-that-canadas-covid-19-mortality-statistics-are-incorrect/.
- Rancourt et al., 2023a: Rancourt DG, Baudin M, Hickey J, Mercier J. COVID-19 vaccine-associated mortality in the Southern Hemisphere. Correlation Research in the Public Interest. 17 September 2023. Accessed on 2025-03-12 from: https://correlation-canada.org/covid-19-vaccine-associated-mortality-in-the-Southern-Hemisphere/.
- Rancourt et al., 2023b: Rancourt DG, Baudin M, Hickey J, Mercier J. Age-stratified COVID-19 vaccine-dose fatality rate for Israel and Australia. Correlation Research in the Public Interest. 9 February 2023. Accessed on 2025-03-12 from: https://correlation-canada.org/report-age-stratified-covid-19-vaccine-dose-fatality-rate-for-israel-and-australia/.
- Rancourt & Hickey, 2023: Rancourt DG, Hickey J. Quantitative evaluation of whether the Nobel-Prize-winning COVID-19 vaccine actually saved millions of lives. Correlation Research in the Public Interest. 08 October 2023. Accessed on 2025-03-12 from: https://correlation-canada.org/nobel-vaccine-and-all-cause-mortality/. Also available at. [CrossRef]
- Rancourt et al., 2024: Rancourt DG, Hickey J, Linard C. Spatiotemporal variation of excess all-cause mortality in the world (125 countries) during the Covid period 2020-2023 regarding socio economic factors and public-health and medical interventions. Correlation Research in the Public Interest. 19 July 2024. Accessed on 2025-03-12 from: https://correlation-canada.org/covid-excess-mortality-125-countries/. Also available at. [CrossRef]
- Rafferty et al., 2018: Rafferty S, Smallman-Raynor MR, Cliff AD. J Hist Geog. 2018;59:2-14. [CrossRef]
- Ramírez-Soto & Ortega-Cáceres, 2022: Ramírez-Soto MC, Ortega-Cáceres G. Analysis of Excess All-Cause Mortality and COVID-19 Mortality in Peru: Observational Study. Trop Med Infect Dis. 2022;7:44. [CrossRef]
- Razak et al., 2022: Razak F, Shin S, Naylor CD, Slutsky AS. Canada’s response to the initial 2 years of the COVID-19 pandemic: a comparison with peer countries. CMAJ. 2022;194:E870-7. [CrossRef]
- RECOVERY Collaborative Group, 2020: The RECOVERY Collaborative Group. Effect of Hydroxychloroquine in Hospitalized Patients with Covid-19. New England Journal of Medicine. 2020;383:2030-2040. [CrossRef]
- Redert, 2022a: Redert A. Short-term Vaccine Fatality Ratio of booster and 4th dose in The Netherlands. ResearchGate. October 2022. Accessed on 2025-03-12 from: . [CrossRef]
- Redert, 2022b. Redert A. Covid-19 vaccinations and all-cause mortality -a long-term differential analysis among municipalities. ResearchGate. July 2022. Accessed on 2025-03-12 from: . [CrossRef]
- Redet, 2023: Redert A. Causal effect of covid vaccination on mortality in Europe. ResearchGate. 24 February 2023. Accessed on 2025-03-12 from: https://www.researchgate.net/publication/368777703_Causal_effect_of_covid_vaccination_on_mortality_in_Europe.
- Redondo-Bravo et al., 2020: Redondo-Bravo L, Sierra Moros MJ, Martínez Sánchez EV, Lorusso N, Carmona Ubago A, Gallardo García V, Sánchez Villanueva P, et al. The first wave of the COVID-19 pandemic in Spain: characterisation of cases and risk factors for severe outcomes, as at 27 April 2020. Euro Surveill. 2020:25;2004131. [CrossRef]
- Rezoagli et al., 2021: Rezoagli E, Magliocca A, Bellani G, Pesenti A, Grasselli G. Development of a Critical Care Response – Experiences from Italy During the Coronavirus Disease 2019 Pandemic. Anesthesiology Clin. 2021;39:265-284. [CrossRef]
- RHIhub, 2024: Rural Health Information Hub. Rural Data Explorer. Accessed on 2024-11-12 from: https://www.ruralhealthinfo.org/data-explorer.
- Riccardo et al., 2020: Riccardo F, Ajelli M, Andrianou XD, Bella A, Del Manso M, Fabiana M, et al. Epidemiological characteristics of COVID-19 cases and estimates of the reproductive numbers 1 month into the epidemic, Italy, 28 January to 31 March 2020. Euro Surveill. 2020;25:2000790. [CrossRef]
- Rich, 2020: Rich D. Covid-19: In Cameroon, chloroquine therapy hailed by French expert becomes state protocol. France 24. 3 May 2020. Accessed on 2025-01-31 from: https://www.france24.com/en/20200503-covid-19-in-cameroon-a-chloroquine-therapy-hailed-by-french-expert-becomes-state-protocol.
- Richardson et al., 2020: Richardson S, Hirsch JS, Narasimhan M, Crawford JM, McGinn T, Davidson KW, et al. Presenting Characteristics, Comorbidities, and Outcomes Among 5700 Patients Hospitalized With COVID-19 in the New York City Area. JAMA. 2020;323(20):2052–2059. [CrossRef]
- Rossen et al., 2021: Rossen LM, Ahmad FB, Anderson RN, Branum AM, Du C, Krumholz HM, et al. Disparities in Excess Mortality Associated with COVID-19 — United States, 2020. MMWR Morb Mortal Wkly Rep. 2021;70:1114–1119. [CrossRef]
- Rossen et al., 2022: Rossen LM, Nørgaard SK, Sutton PD, Krause TG, Ahmad FB, Vestergaard LS, et al. Excess all-cause mortality in the USA and Europe during the COVID-19 pandemic, 2020 and 2021. Sci Rep. 2022;12:18559. [CrossRef]
- Safavi-Naini et al., 2022: Safavi-Naini SAA, Farsi Y, Alali WQ, Sohlpour A, Pourhoseingholi MA. Excess all-cause mortality and COVID-19 reported fatality in Iran (April 2013–September 2021): age and sex disaggregated time series analysis. BMC Res Notes. 2022;15:130. [CrossRef]
- Sanmarchi et al., 2021: Sanmarchi F, Golinelli D, Lenzi J, Capodici A, Reno C, Gibertoni D. Exploring the Gap Between Excess Mortality and COVID-19 Deaths in 67 Countries. JAMA Network Open. 2021;4:e2117359. [CrossRef]
- Sattenspiel & Dietz, 1995: Sattenspiel L, Dietz K. A Structured Epidemic Model Incorporating Geographic Mobility Among Regions. Math Biosci. 1995;128:71-91. [CrossRef]
- Schellekens, 2023: Schellekens P. Excess mortality and vaccination: How front-runners in the vaccination space compare across countries on excess mortality. pandem-ic. Updated 6 April 2024. Accessed on 2025-03-12 from: https://pandem-ic.com/excess-mortality-and-vaccination/.
- Scherb & Hayashi, 2023: Scherb H, Hayashi K. Annual All-Cause Mortality Rate in Germany and Japan (2005 to 2022) With Focus on The Covid-19 Pandemic: Hypotheses And Trend Analyses. Med Clin Sci. 2023;5:1-7. Accessed on 2025-03-12 from: https://www.sciencexcel.com/articles/RZ2ZUhxdYkEj0DhgjZAtR9kZitZyJDfKaVQhO3JP.pdf.
- Schöley et al., 2022: Schöley J, Aburto JM, Kashnitsky I, Kniffka MS, Zhang L, Jaadia H, et al. Life expectancy changes since COVID-19. Nat Hum Behav. 2022;6:1649–1659. [CrossRef]
- Schulte et al., 2020: Schulte F, Lucas E, Rau J, Szabo L, Hancock J. Millions Of Older Americans Live In Counties With No ICU Beds As Pandemic Intensifies. 20 March 2020. Accessed on 2024-10-25 from: https://kffhealthnews.org/news/as-coronavirus-spreads-widely-millions-of-older-americans-live-in-counties-with-no-icu-beds/. [Archived at: https://archive.is/OrUTD].
- Sempé et al., 2021: Sempé L, Lloyd-Sherlock P, Martínez R, Ebrahim S, McKee M, Acosta E. Estimation of all-cause excess mortality by age-specific mortality patterns for countries with incomplete vital statistics: a population-based study of the case of Peru during the first wave of the COVID-19 pandemic. Lancet Reg Health Am. 2021;2:100039. [CrossRef]
- Shabsigh, 2022: Shabsigh R. Prologue. In: Shabsigh R, editor. Health crisis management in acute care hospitals: Lessons learned from COVID-19 and beyond. Cham: Springer; 2022. pp. ix-x. [CrossRef]
- Sheppard et al., 2023. Sheppard N, Carroll M, Gao C, Lane T. Particulate matter air pollution and COVID-19 infection, severity, and mortality: A systematic review and meta-analysis. Science of the Total Environment. 2023;880:163272. [CrossRef]
- Silverio et al., 2020. Silverio A, Di Maio M, Ciccarelli M, Carrizzo A, Vecchione C, Galasso G. Timing of national lockdown and mortality in COVID-19: The Italian experience. Int J Infect Dis. 2020;100:193-195. [CrossRef]
- Simon & Ebbs, 2020: Simon E, Ebbs S. Poverty, pollution and neglect: How the Bronx became a coronavirus “formula for disaster”. ABC News. 11 April 2020. Accessed on 2025-02-04 from: https://abcnews.go.com/Health/poverty-pollution-neglect-bronx-coronavirus-formula-disaster/.
- Sinnathamby et al., 2020: Sinnathamby MA, Whitaker H, Coughlan L, Lopez Bernal J, Ramsay M, Andrews N. All-cause excess mortality observed by age group and regions in the first wave of the COVID-19 pandemic in England. Euro Surveill. 2020;25:2001239. [CrossRef]
- Slutsky & Ranieri, 2013: Slutsky AS, Ranieri VM. Ventilator-Induced Lung Injury. New England Journal of Medicine. 2013;369:2126-2136. [CrossRef]
- Soneji et al., 2021: Soneji S, Beltrán-Sánchez H, Yang JW, Mann C. Population-level mortality burden from novel coronavirus (COVID-19) in Europe and North America. Genus. 2021;77:7. [CrossRef]
- Šorli et al., 2023: Šorli AS, Makovec T, Krevel Z, Gorjup R. Forgotten “Primum Non Nocere” and Increased Mortality after COVID-19 Vaccination. Qual Prim Care. 2023;31:006. Accessed on 2025-03-12 from: https://www.primescholars.com/articles/forgotten-primum-non-nocere-and-increased-mortality-after--covid19-vaccination.pdf.
- Spiteri et al., 2020: Spiteri G, Fielding J, Diercke M, Campese C, Enouf V, Gaymard A, et al. First cases of coronavirus disease 2019 (COVID-19) in the WHO European Region, 24 January to 21 February 2020. Euro Surveill. 2020;25(9):pii=2000178. [CrossRef]
- Stein et al., 2021: Stein RE, Corcoran KE, Colyer CJ, Mackay AM, Guthrie SK. Closed but Not Protected: Excess Deaths Among the Amish and Mennonites During the COVID-19 Pandemic. J Relig Health. 2021;60:3230–3244. [CrossRef]
- Stokes et al., 2021: Stokes AC, Lundberg DJ, Elo IT, Hempstead K, Bor J, Preston SH. COVID-19 and excess mortality in the United States: A county-level analysis. PLoS Med. 2021;18:e1003571. [CrossRef]
- Sy, 2024: Sy W. Excess Deaths in the United Kingdom: Midazolam and Euthanasia in the COVID-19 Pandemic. Med Clin Res. 2024;9:1-21. https://www.medclinrese.org/open-access/excess-deaths-in-the-united-kingdom-midazolam-and-euthanasia-in-the-covid19-pandemic.pdf.
- Tadbiri et al., 2020: Tadbiri H, Moradi-Lakeh M, Naghavi M. All-cause excess mortality and COVID-19-related deaths in Iran. Med J Islam Repub Iran. 2020;34:8. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7711045/.
- Tarazi et al., 2022: Tarazi W, Welch P, Nguyen N, Bosworth A, Sheingold S, De Lew N, et al. Medicare Beneficiary Enrollment Trends and Demographic Characteristics. Assistant Secretary for Planning and Evaluation, Office of Health Policy. 2 March 2022. Accessed on 2024-12-07 from: https://aspe.hhs.gov/sites/default/files/documents/b9ac26a13b4fdf30c16c24e79df0c99c/medicare-beneficiary-enrollment-ib.pdf.
- Taccone et al., 2021: Taccone FS, Van Goethem N, De Pauw R, Wittebole X, Blot K, Van Oyen H, et al. The role of organizational characteristics on the outcome of COVID-19 patients admitted to the ICU in Belgium. The Lancet Regional Health – Europe. 2021;2:100019. [CrossRef]
- Thoma & Declercq, 2022: Thoma ME, Declercq ER. All-Cause Maternal Mortality in the US Before vs During the COVID-19 Pandemic. JAMA Netw Open. 2022;5:e2219133. [CrossRef]
- Thomas et al., 2020: Thomas LJ, Huang P, Yin F, Lui XI, Almquist ZW, Hipp JR, et al. Spatial heterogeneity can lead to substantial local variations in COVID-19 timing and severity. PNAS. 2020;117:24180-24187. [CrossRef]
- Torjesen, 2021: Torjesen I. Covid-19: When to start invasive ventilation is “the million dollar question”. BMJ. 2021;372:n121. [CrossRef]
- Trust for London, 2024: Trust for London. Poverty rates by London borough. Last updated September 2024. Accessed on 2024-12-04 from: https://trustforlondon.org.uk/data/poverty-borough/.
- US Census Bureau, 2023: United States Census Bureau. American Community Survey 1-year estimates. Accessed on 2025-04-17 from: http://censusreporter.org/profiles/31000US35620-new-york-newark-jersey-city-ny-nj-metro-area/.
- US Census Bureau, 2024a: United States Census Bureau. County Intercensal Population Totals: 2010-2020. Accessed on 2024-11-14 from: https://www.census.gov/data/tables/time-series/demo/popest/intercensal-2010-2020-counties.html.
- US Census Bureau, 2024b: United States Census Bureau. COVID-19 Demographic and Economic Resources (V3). Accessed on 2024-03-13 from: https://covid19.census.gov/datasets/21843f238cbb46b08615fc53e19e0daf/explore?location=3.618777%2C0.315550%2C0.51. Alternative link: https://covid19.census.gov/.
- US Census Bureau, 2024c: United States Census Bureau. 2020 Census Urban Areas Facts. Accessed on 2024-11-25 from: https://www.census.gov/programs-surveys/geography/guidance/geo-areas/urban-rural/2020-ua-facts.html.
- van der Velde et al., 2021: van der Velde M, Sijtsma D, Goossens M, Maartense B. The Dutch–German Border: Open in Times of Coronavirus Lockdowns. Borders in Globalization Review. 2021;2:149-155. [CrossRef]
- Vestergaard et al., 2020: Vestergaard LS, Nielsen J, Richter L, Schmid D, Bustos N, Braeye T, et al. Excess all-cause mortality during the COVID-19 pandemic in Europe – preliminary pooled estimates from the EuroMOMO network, March to April 2020. Euro Surveill. 2020;25:2001214. [CrossRef]
- Vila-Corcoles et al., 2021: Vila-Corcoles A, Satue-Gracia E, Vila-Rovira A, de Diego-Cabanes, C, Forcadell-Peris MJ, Hospital-Guardiola I, et al. COVID19-related and all-cause mortality risk among middle-aged and older adults across the first epidemic wave of SARS-COV-2 infection: a population-based cohort study in Southern Catalonia, Spain, March–June 2020. BMC Public Health. 2021;21:1795. [CrossRef]
- Villani, L. et al., 2020: Villani L, McKee M, Cascini F, Ricciardi W, Boccia S. Comparison of Deaths Rates for COVID-19 across Europe During the First Wave of the COVID-19 Pandemic. Front Public Health. 2020;8:620416. [CrossRef]
- Wang et al., 2022: Wang H, Paulson KR, Pease SA, Watson S, Comfort H, Zheng P, et al. Estimating excess mortality due to the COVID-19 pandemic: a systematic analysis of COVID-19-related mortality, 2020–21. The Lancet. 2022;399:1513–1536. [CrossRef]
- Watson et al., 2020: Watson JA, Tarning J, Hoglund RM, Baud FJ, Megarbane B, Clemessy J-L, et al. Concentration-dependent mortality of chloroquine in overdose. eLife. 2020;9:e58631. [CrossRef]
- WHO, 2020: World Health Organization. WHO Director-General's opening remarks at the media briefing on COVID-19 - 11 March 2020. 11 March 2020. Accessed on 2025-05-13 from: https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020.
- WHO, 2023: World Health Organization. WHO chief declares end to COVID-19 as a global health emergency. 5 May 2023. Accessed on 2025-05-13 from: https://news.un.org/en/story/2023/05/1136367.
- Wilcox et al., 2021: Wilcox CR, Islam N, Dambha-Miller H. Association between influenza vaccination and hospitalisation or all-cause mortality in people with COVID-19: a retrospective cohort study. BMJ Open Resp Res. 2021;8:e000857. [CrossRef]
- Williams, 2024: Williams G. New acute unit to cut A&E waits at Northwick Park Hospital. Brent & Kilburn Times. 2 August 2024. Accessed on 2025-02-04 from: https://www.kilburntimes.co.uk/news/24494062.new-acute-unit-cut-e-waits-northwick-park-hospital/.
- Wise & Coombes, 2020: Wise J, Coombes R. Covid-19: The inside story of the RECOVERY trial. BMJ. 2020;370:m2670. [CrossRef]
- Woolf et al., 2021a. Woolf SH, Chapman DA, Sabo RT, Zimmerman EB. Excess Deaths From COVID-19 and Other Causes in the US, March 1, 2020, to January 2, 2021. JAMA. 2021;325:1786–1789. 1.
- Woolf et al., 2021b: Woolf SH, Masters RK, Aron LY. Effect of the covid-19 pandemic in 2020 on life expectancy across populations in the USA and other high income countries: simulations of provisional mortality data. BMJ. 2021;373n1343. [CrossRef]
- Woolf et al., 2023: Woolf SH, Wolf ER, Rivara FP. The New Crisis of Increasing All-Cause Mortality in US Children and Adolescents. JAMA. 2023;329:975–976. [CrossRef]
- Wunsch, 2020. Wunsch H. Mechanical Ventilation in COVID-19: Interpreting the Current Epidemiology. American Journal of Respiratory and Critical Care Medicine. 2020;202:1-21. [CrossRef]
- Yorifuji et al., 2021: Yorifuji T, Matsumoto N, Takao S. Excess All-Cause Mortality During the COVID-19 Outbreak in Japan. Journal of Epidemiology. 2021;31:90-92. [CrossRef]
- Zawisza et al., 2024: Zawisza K, Sekuła P, Gajdzica M, Tobiasz-Adamczyk B. Social capital and all-cause mortality before and during the COVID-19 pandemic among middle-aged and older people: Prospective cohort study in Poland. Social Science and Medicine. 2024;343:116573. [CrossRef]
- Zehender et al., 2020: Zehender G, Lai A, Bergna A, Meroni L, Riva A, Balotta C, et al. Genomic characterization and phylogenetic analysis of SARS-COV-2 in Italy. Journal of Medical Virology. 2020;92:1637-1640. [CrossRef]
- Zou et al., 2024: Zou F, Xiao J, Jin Y, Jian R, Hu Y, Liang X, et al. Multilayer factors associated with excess all-cause mortality during the omicron and non-omicron waves of the COVID-19 pandemic: time series analysis in 29 countries. BMC Public Health. 2024;24:350. [CrossRef]
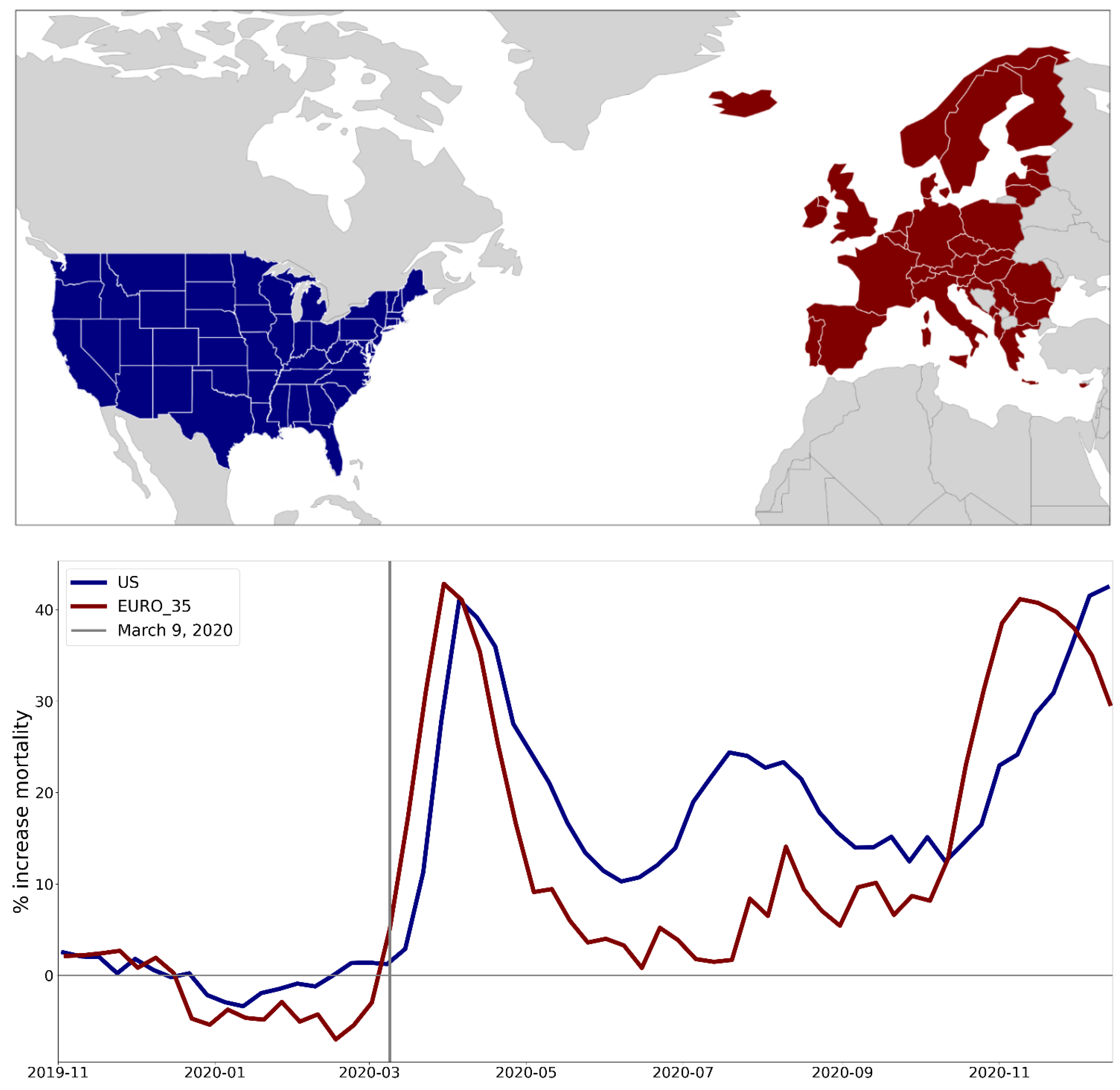
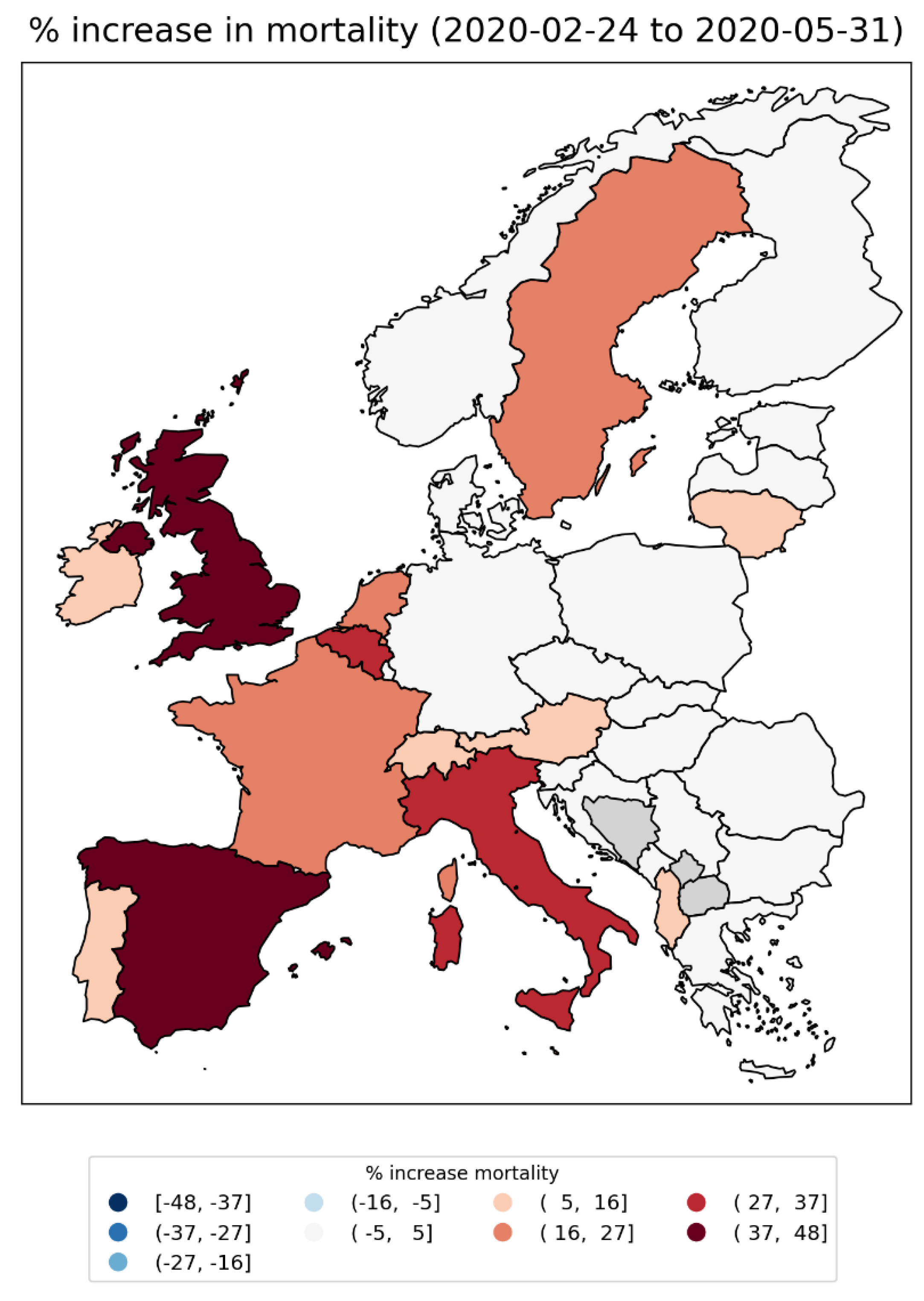
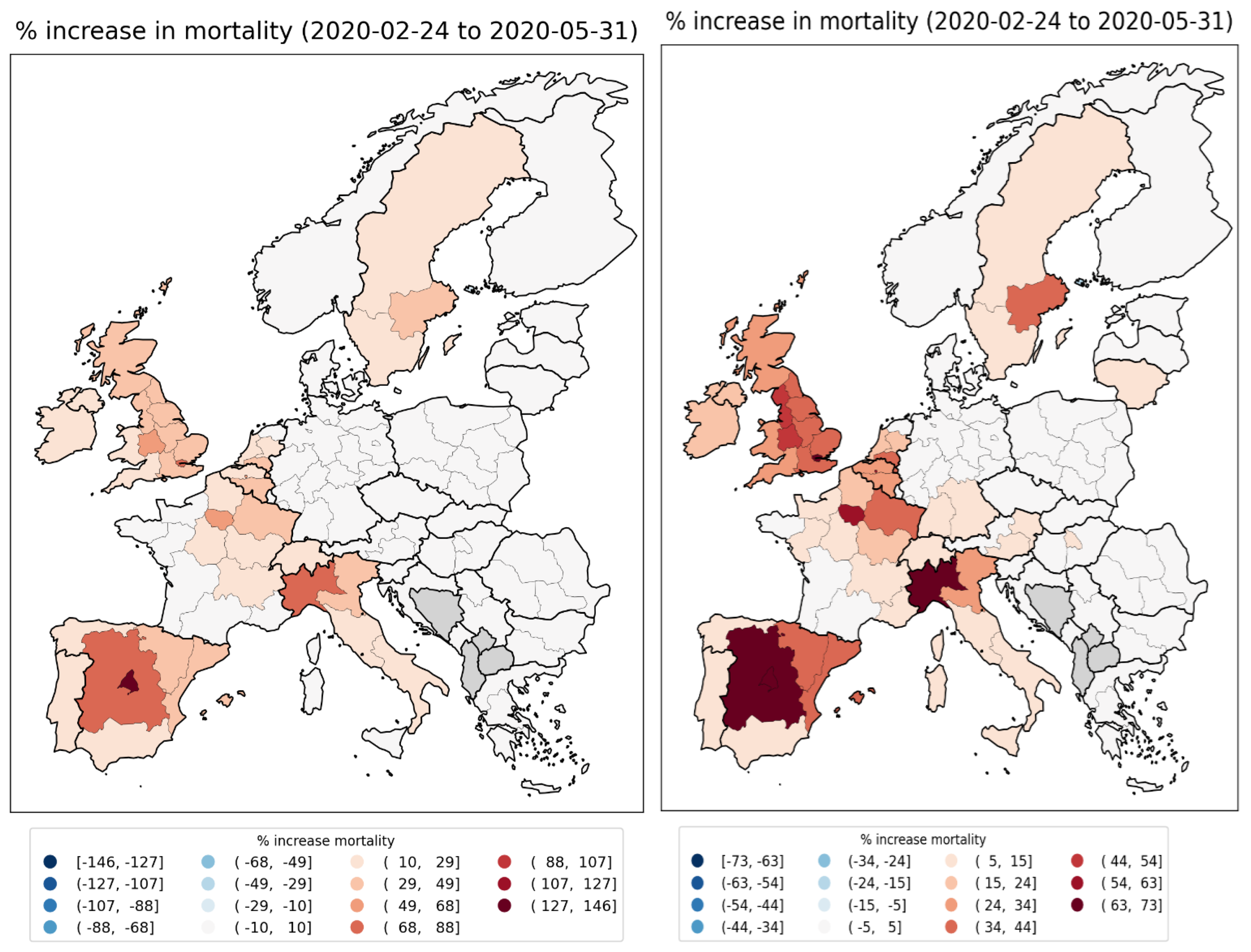
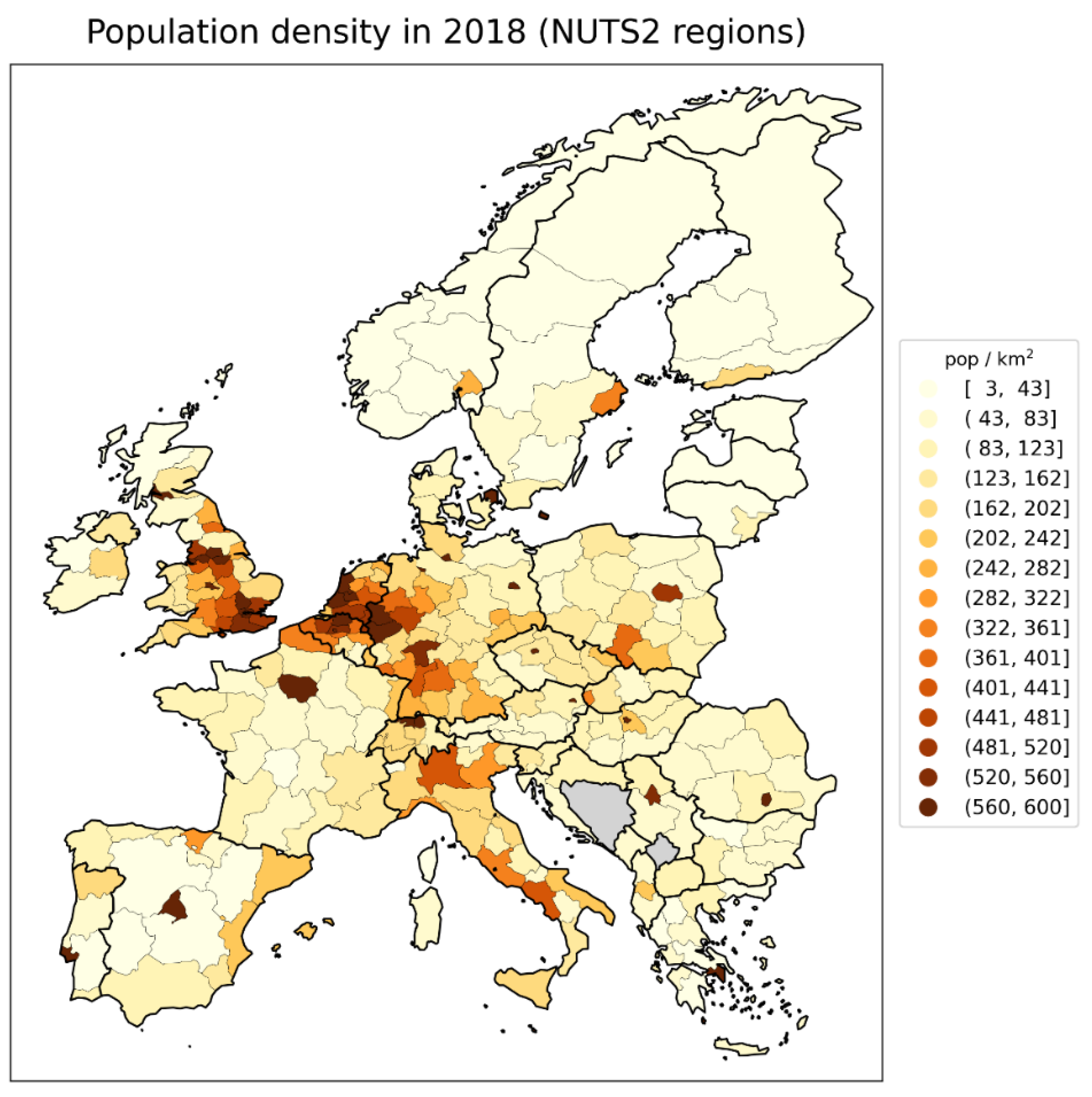
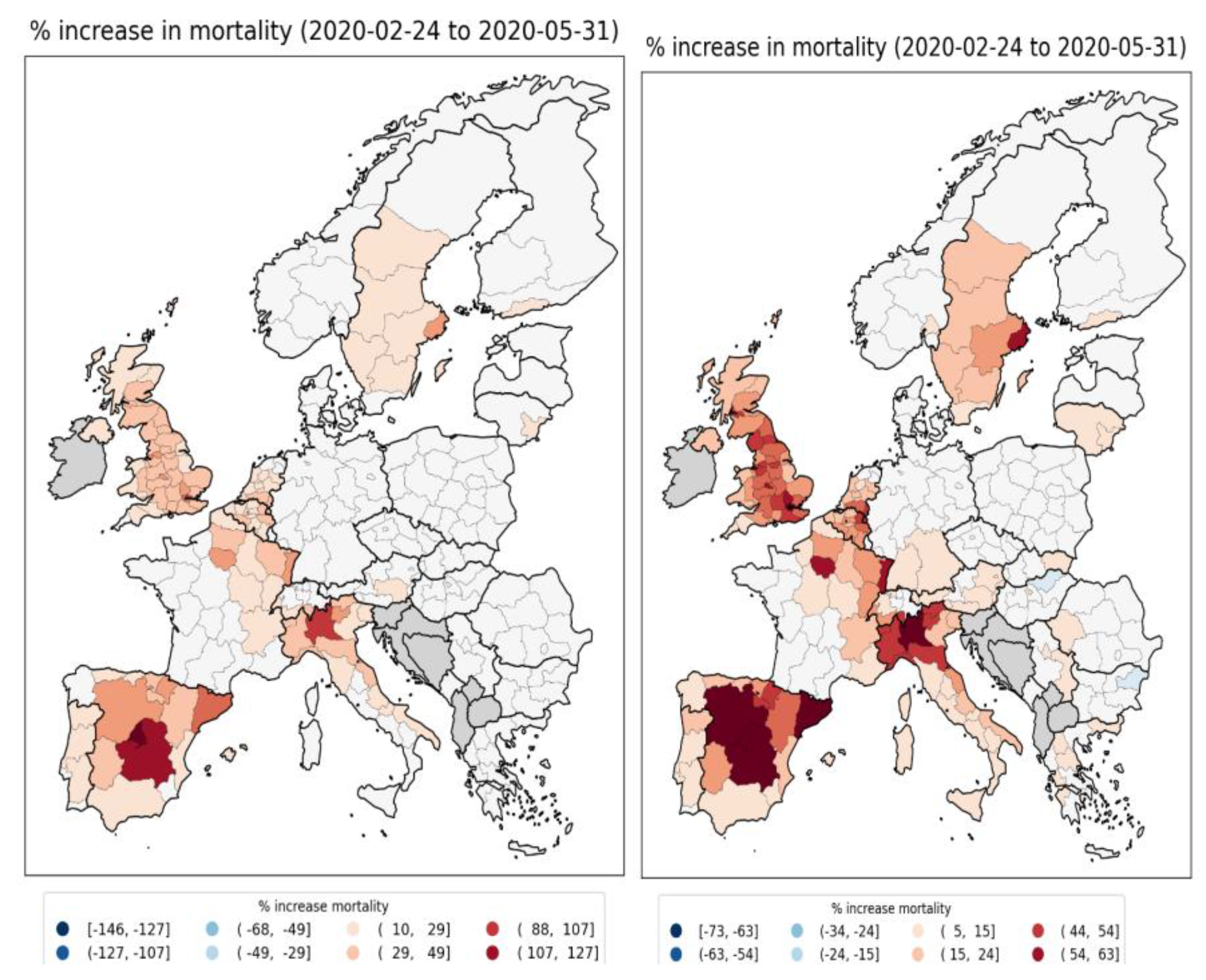
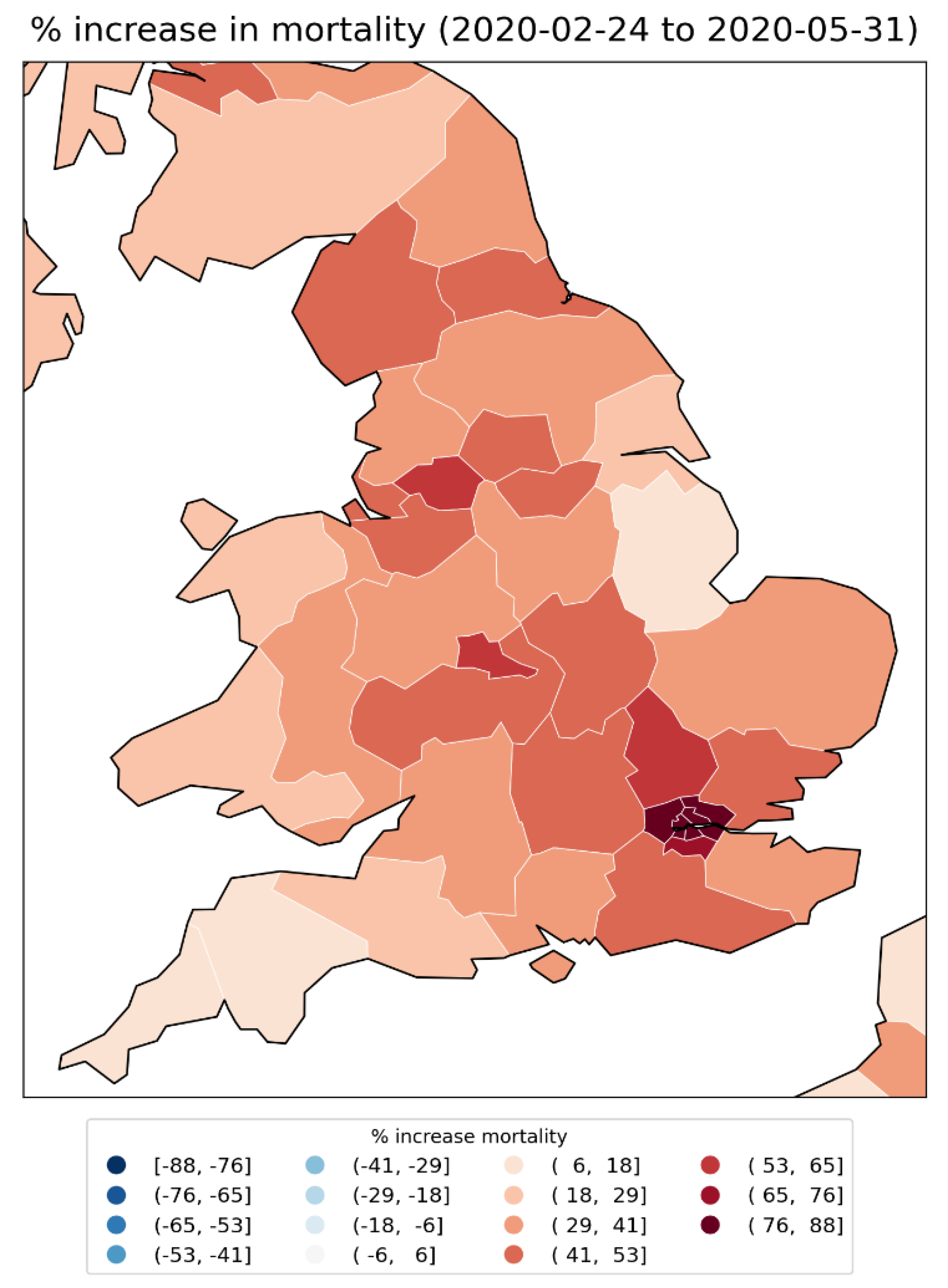
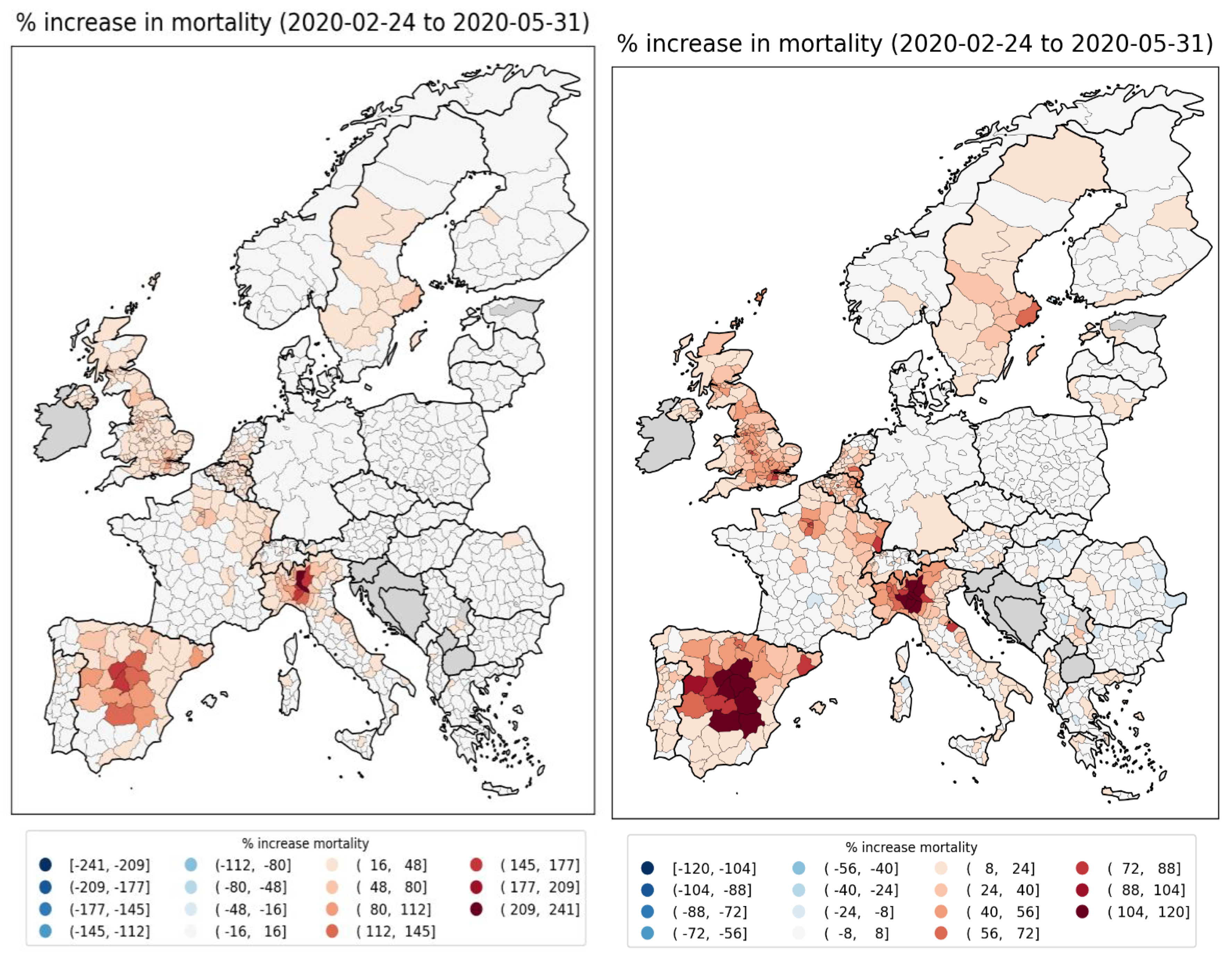
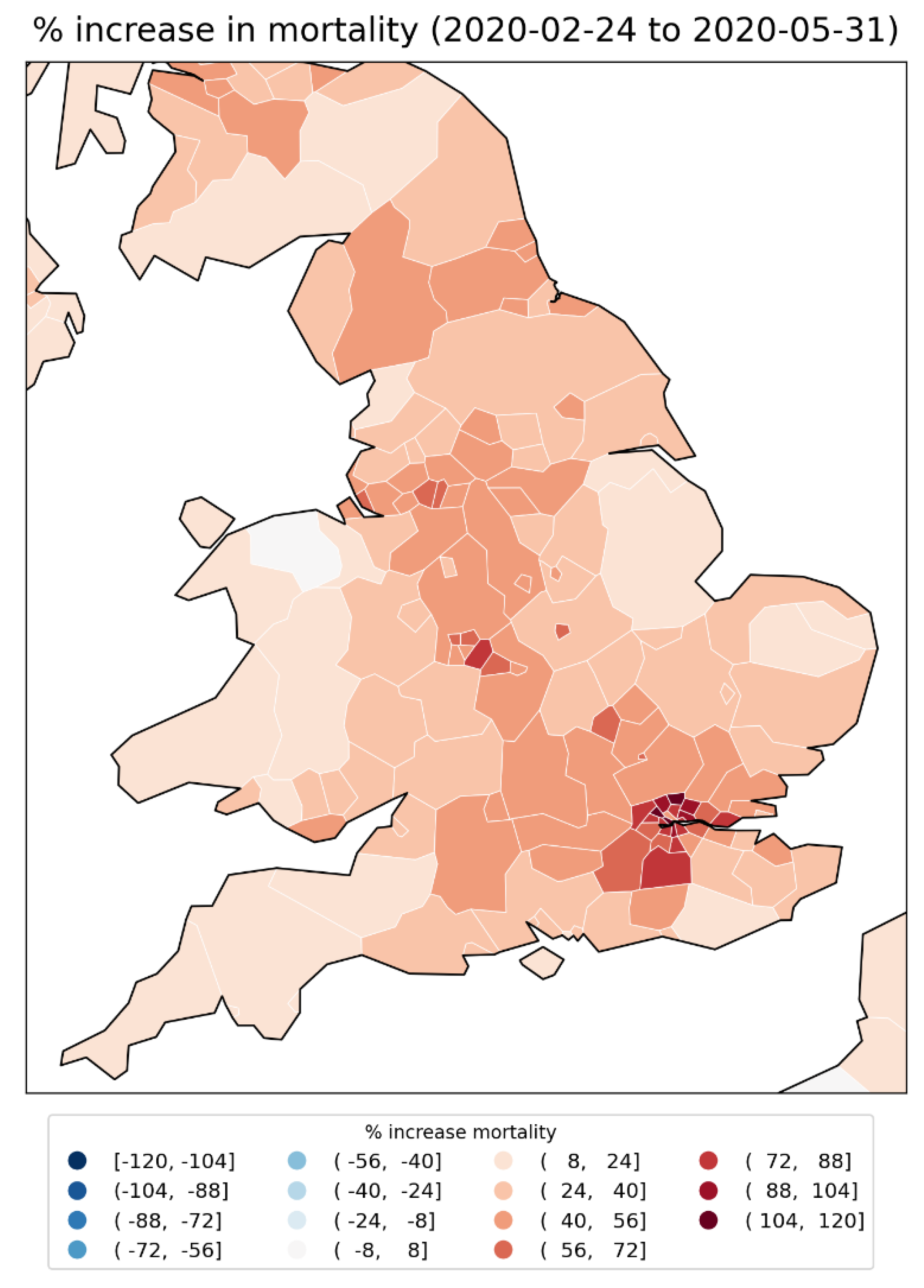
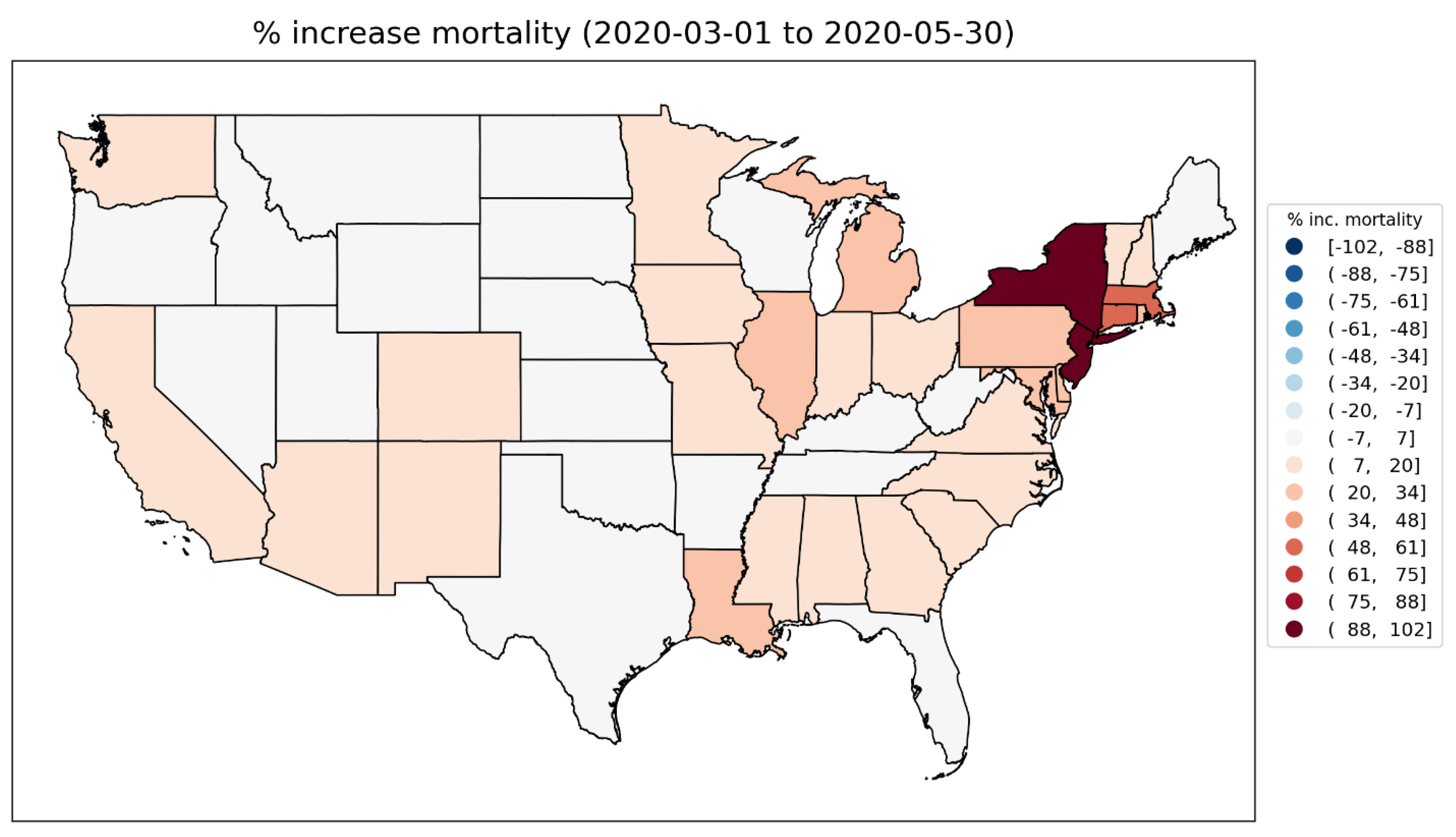
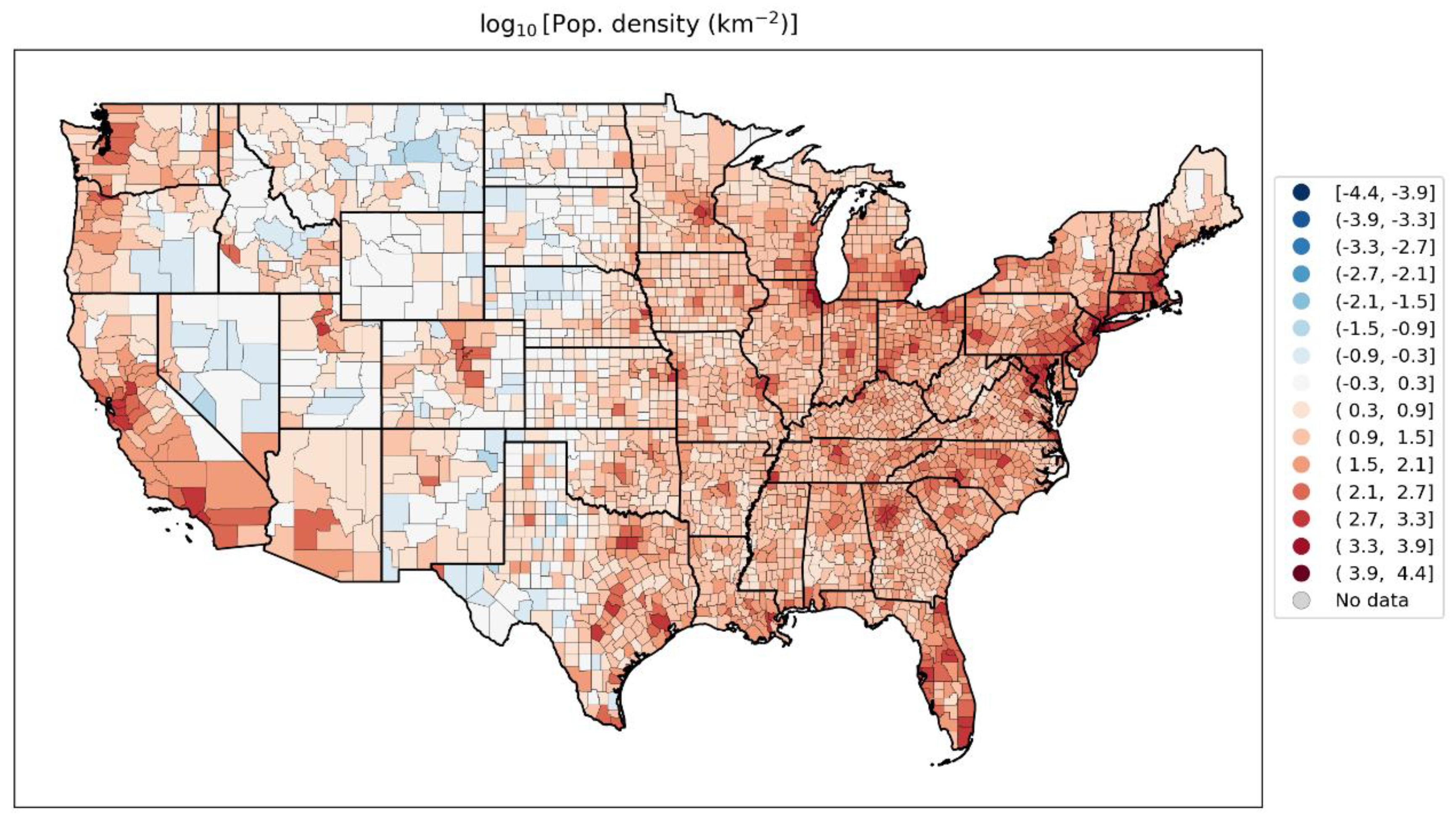
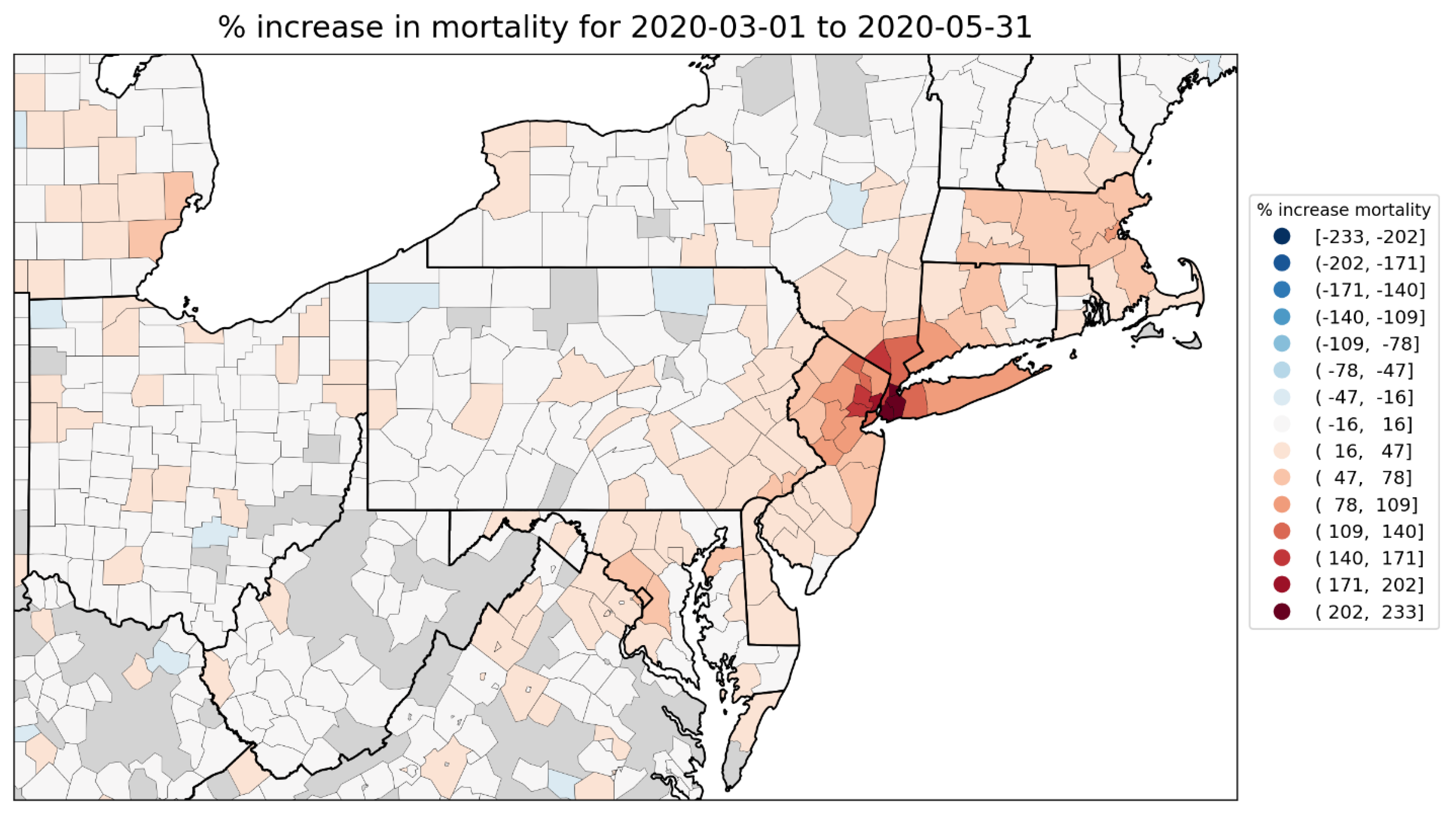
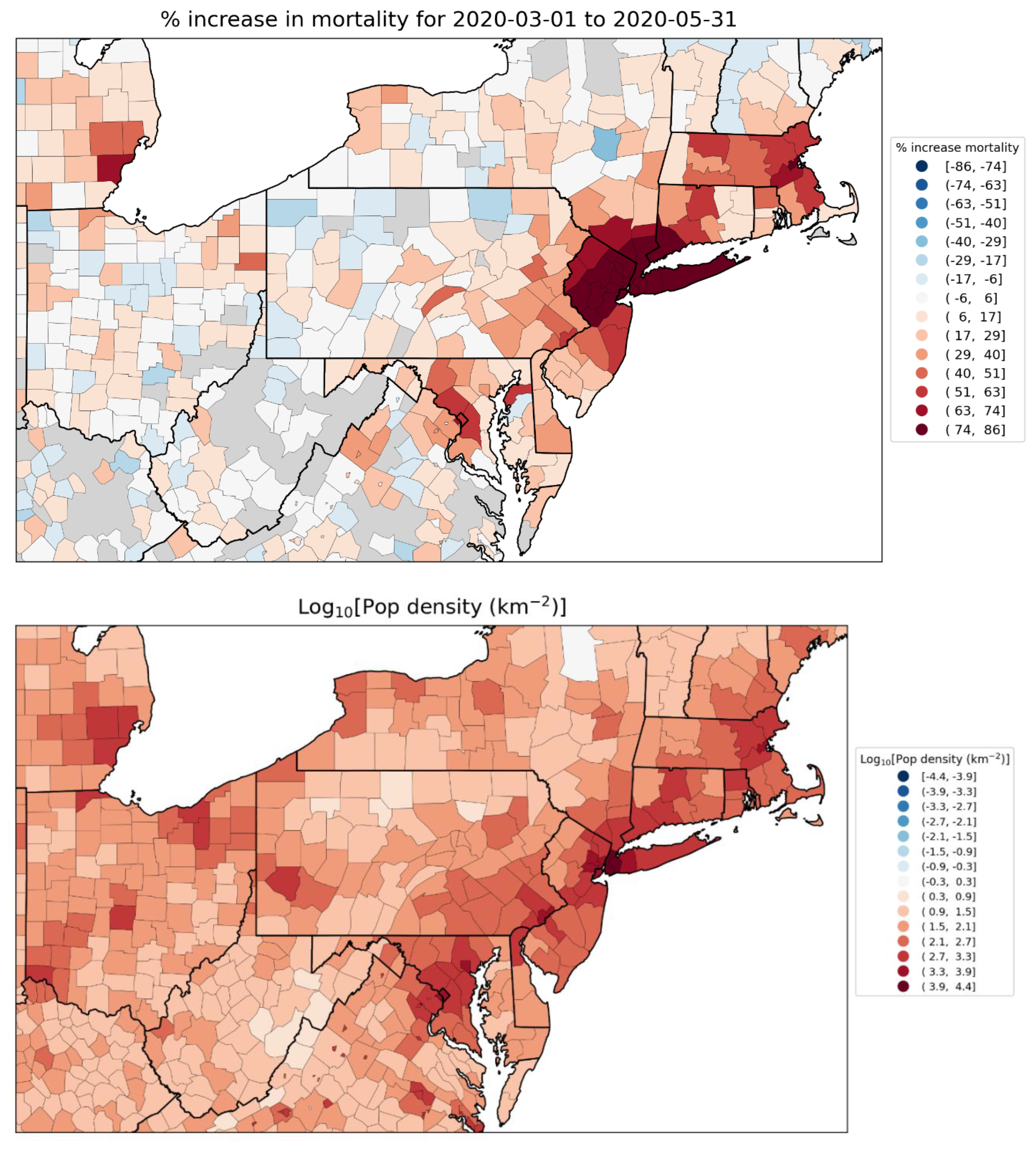
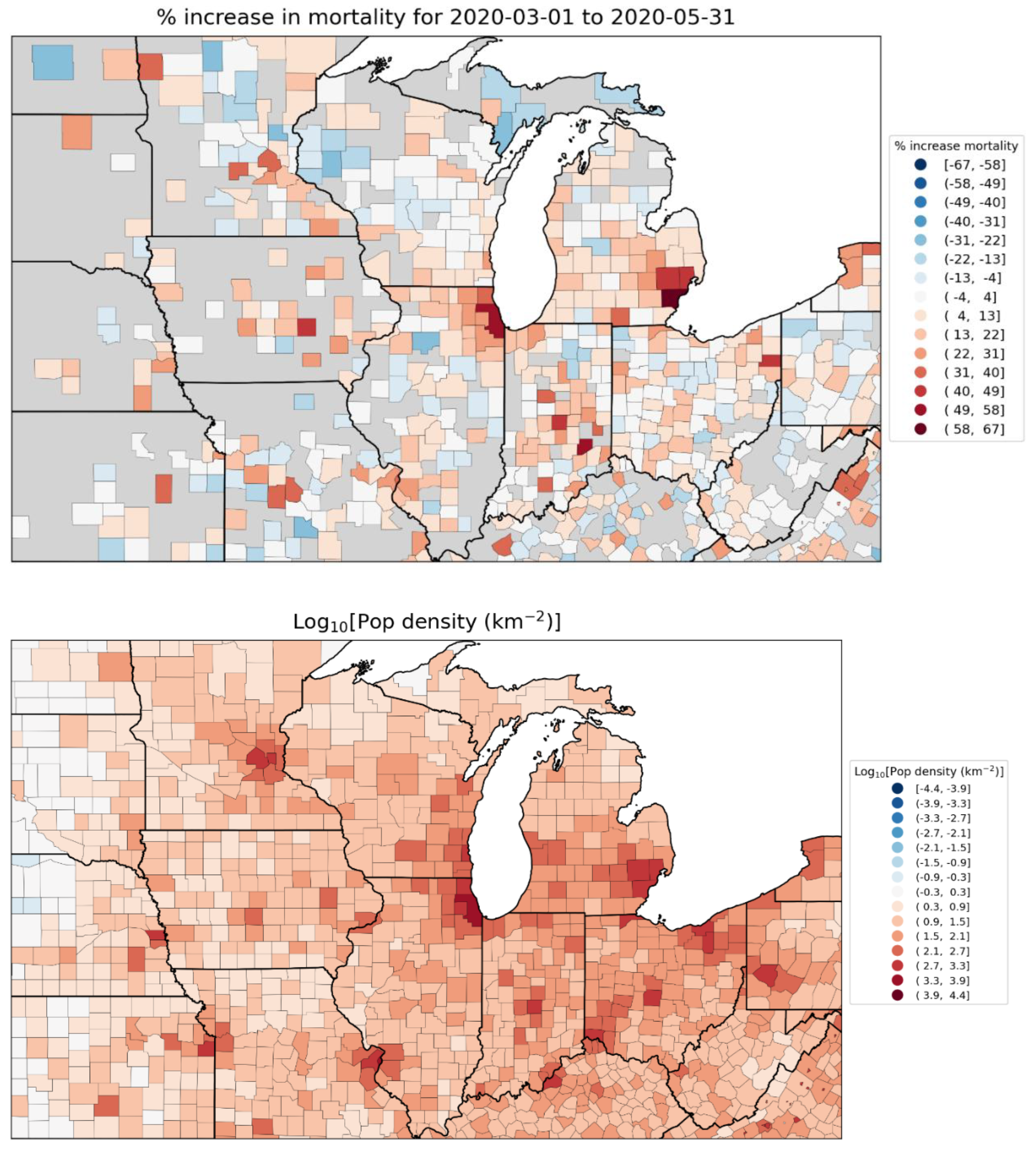
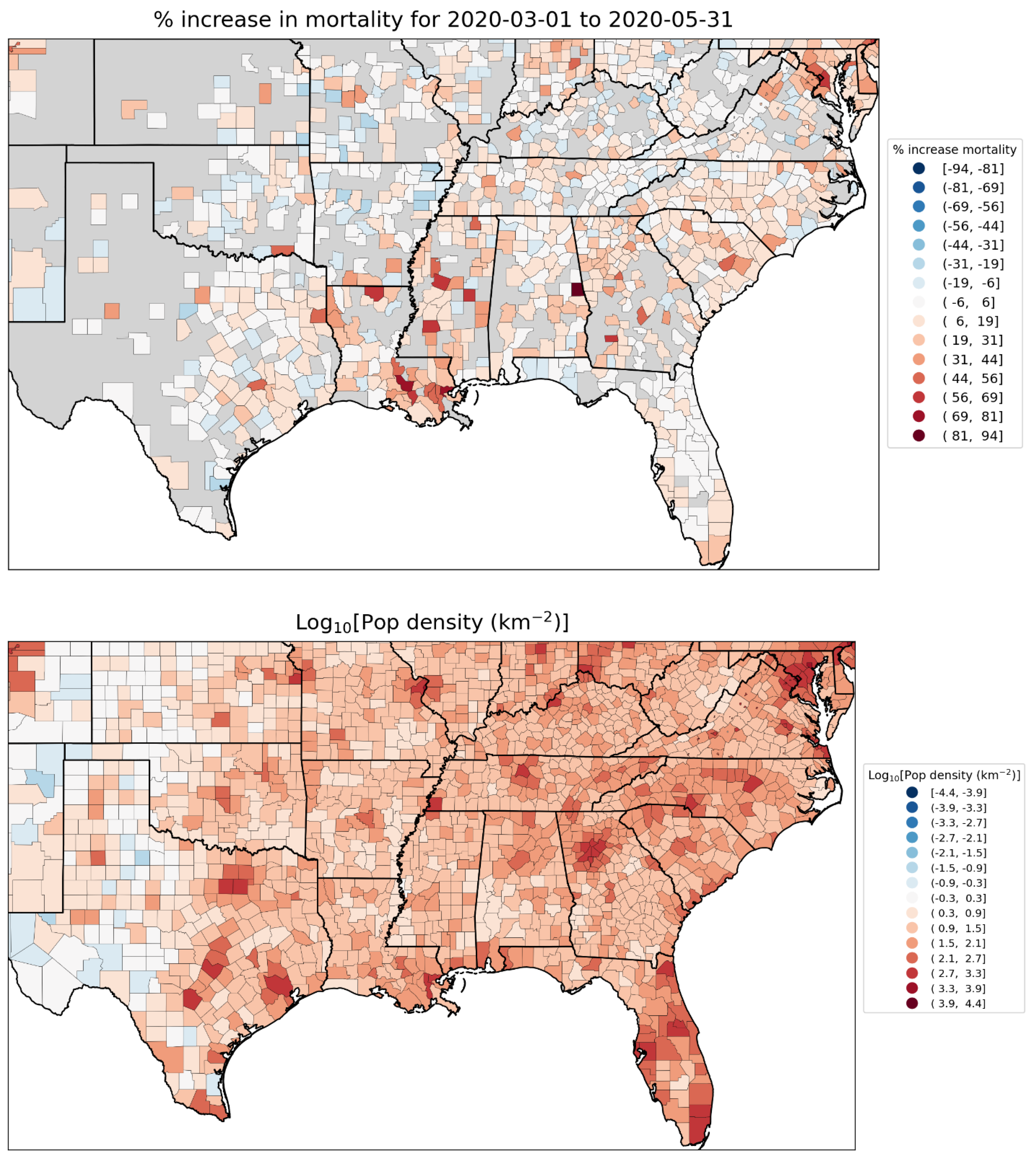
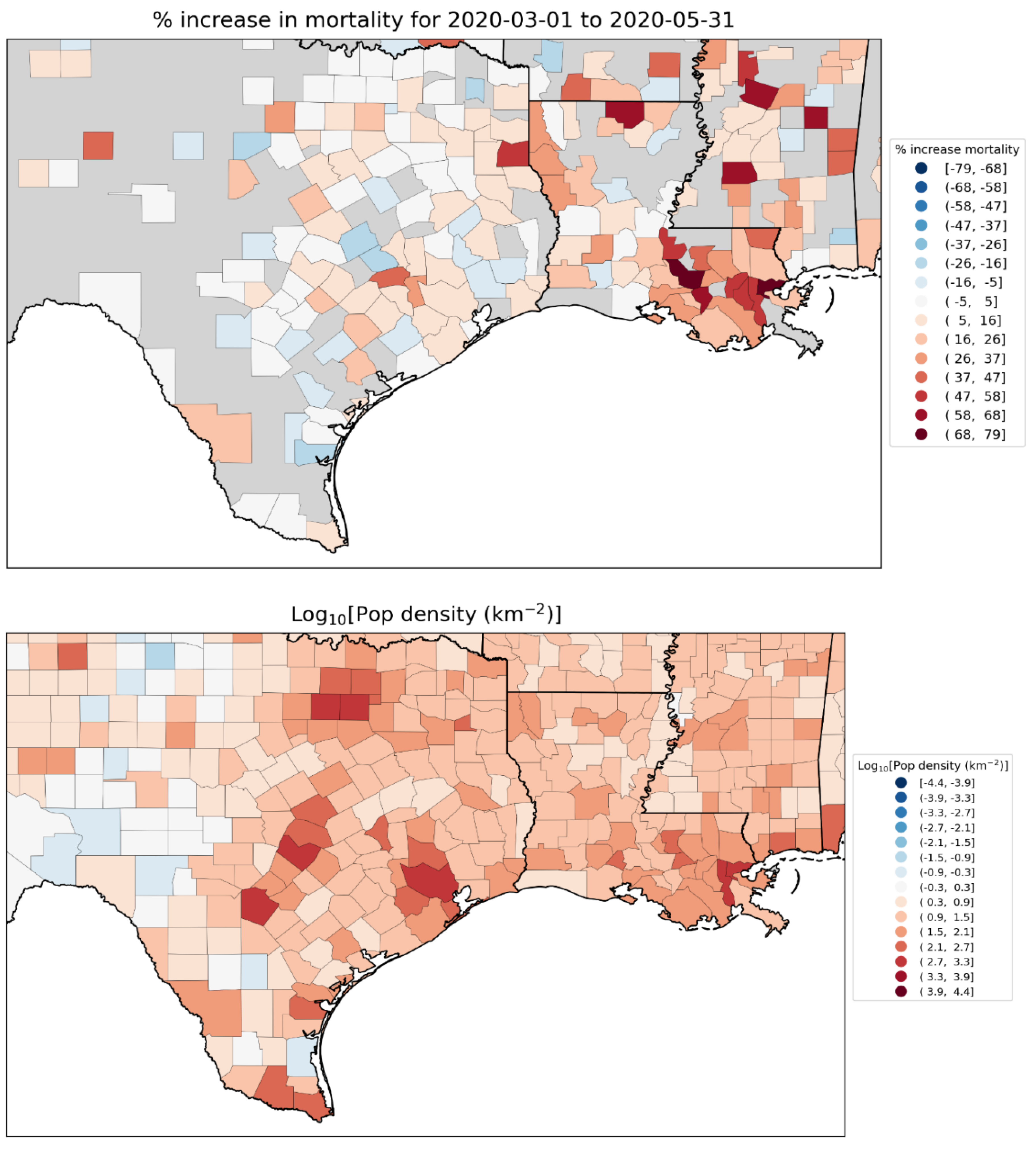
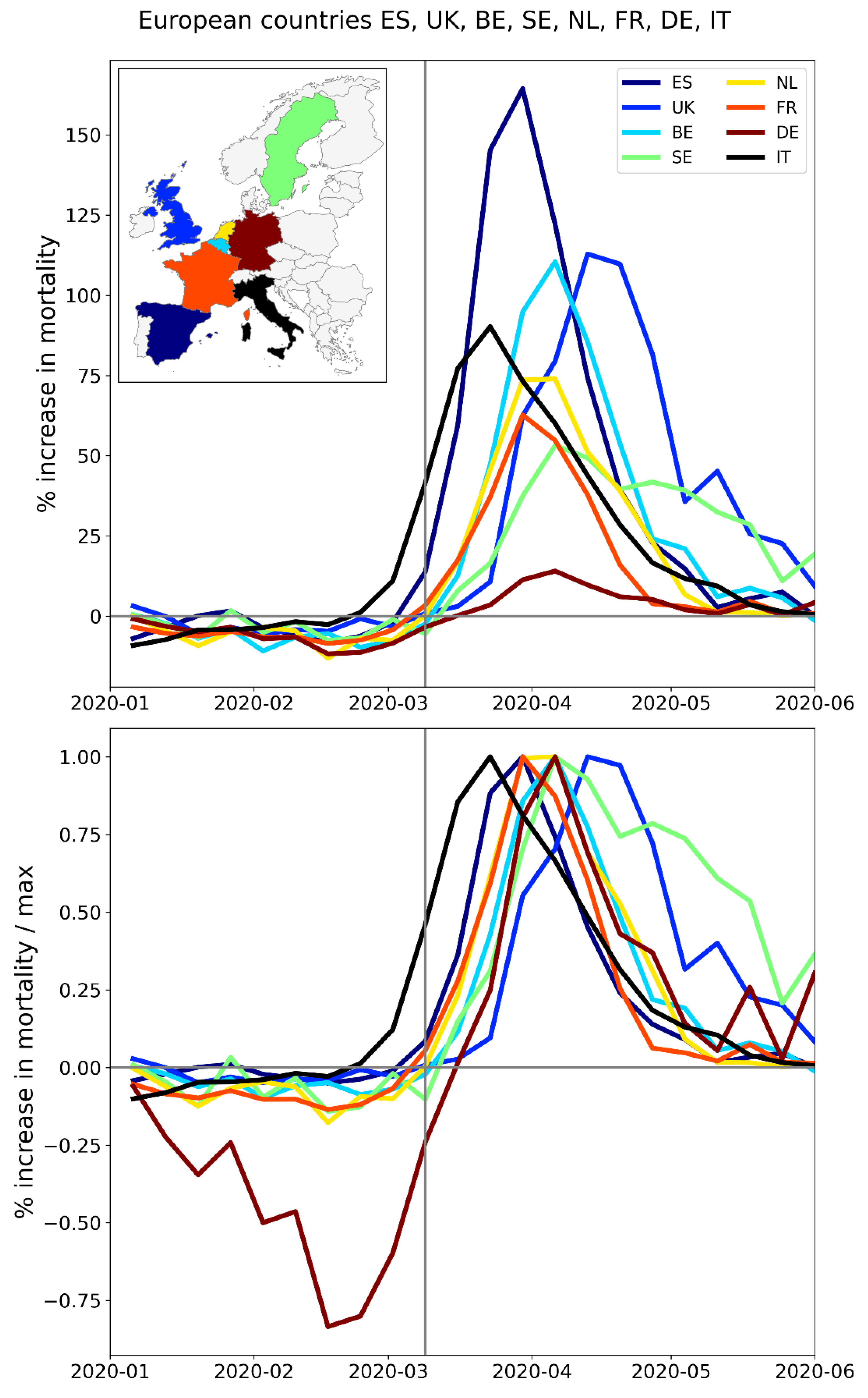
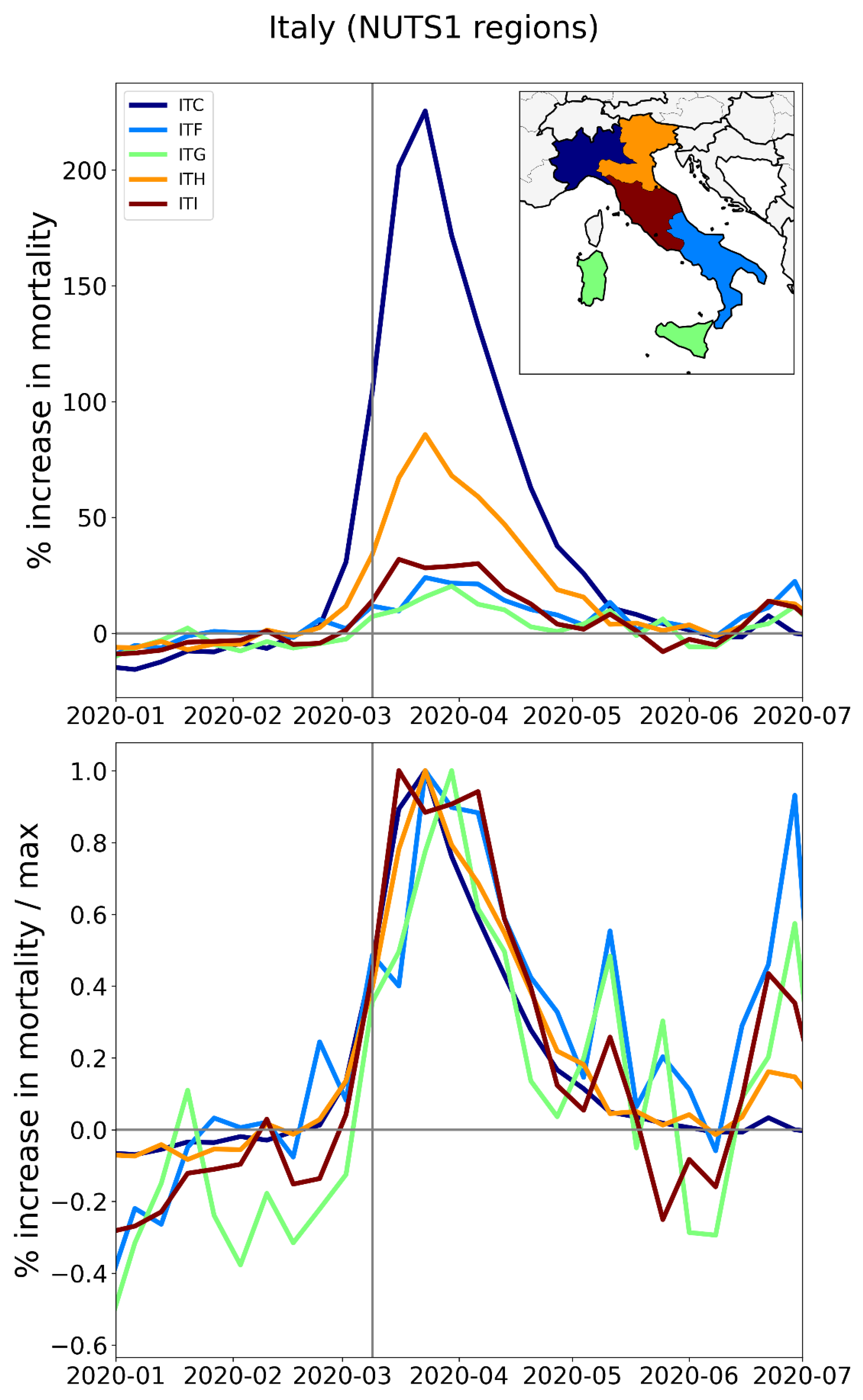
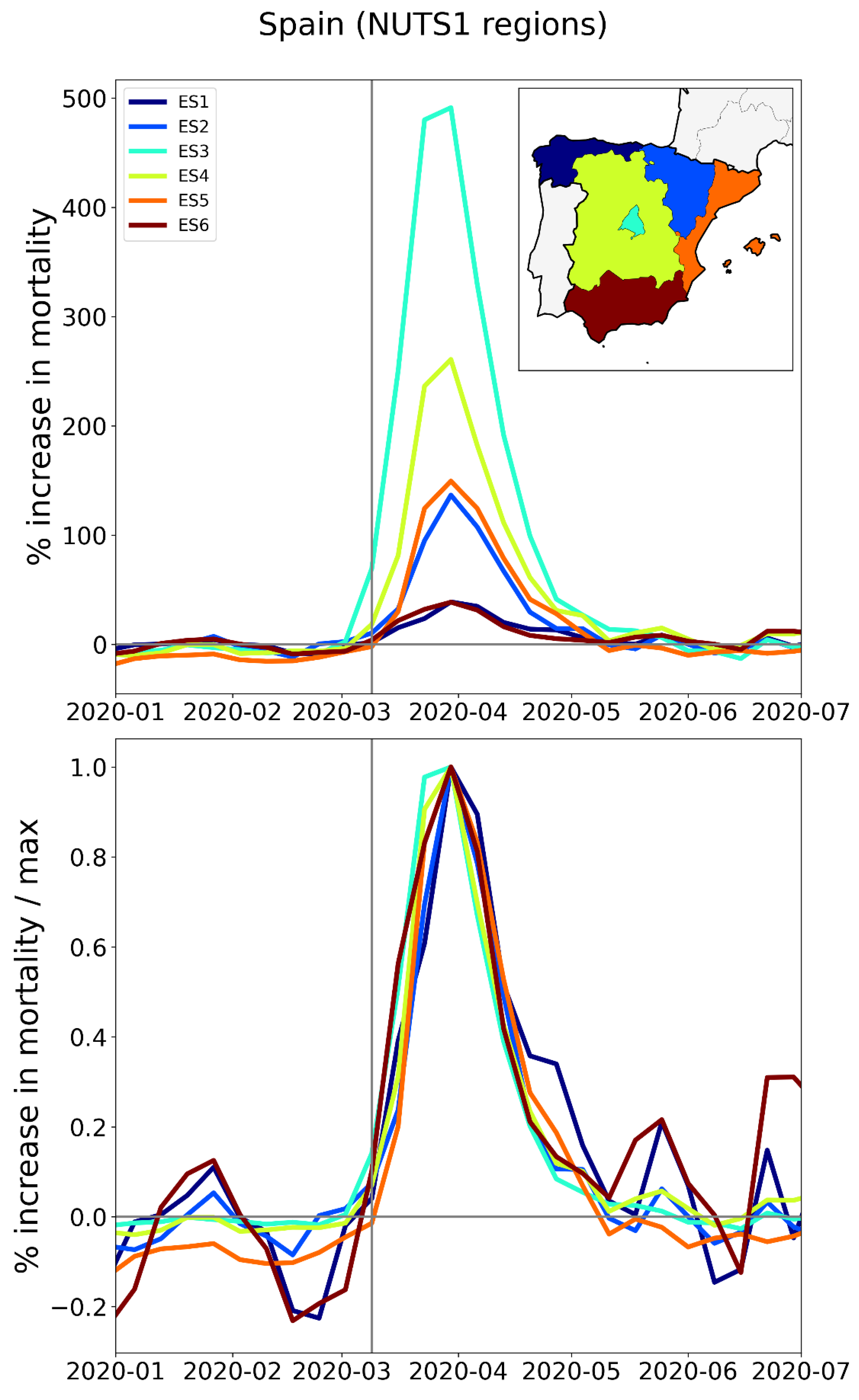
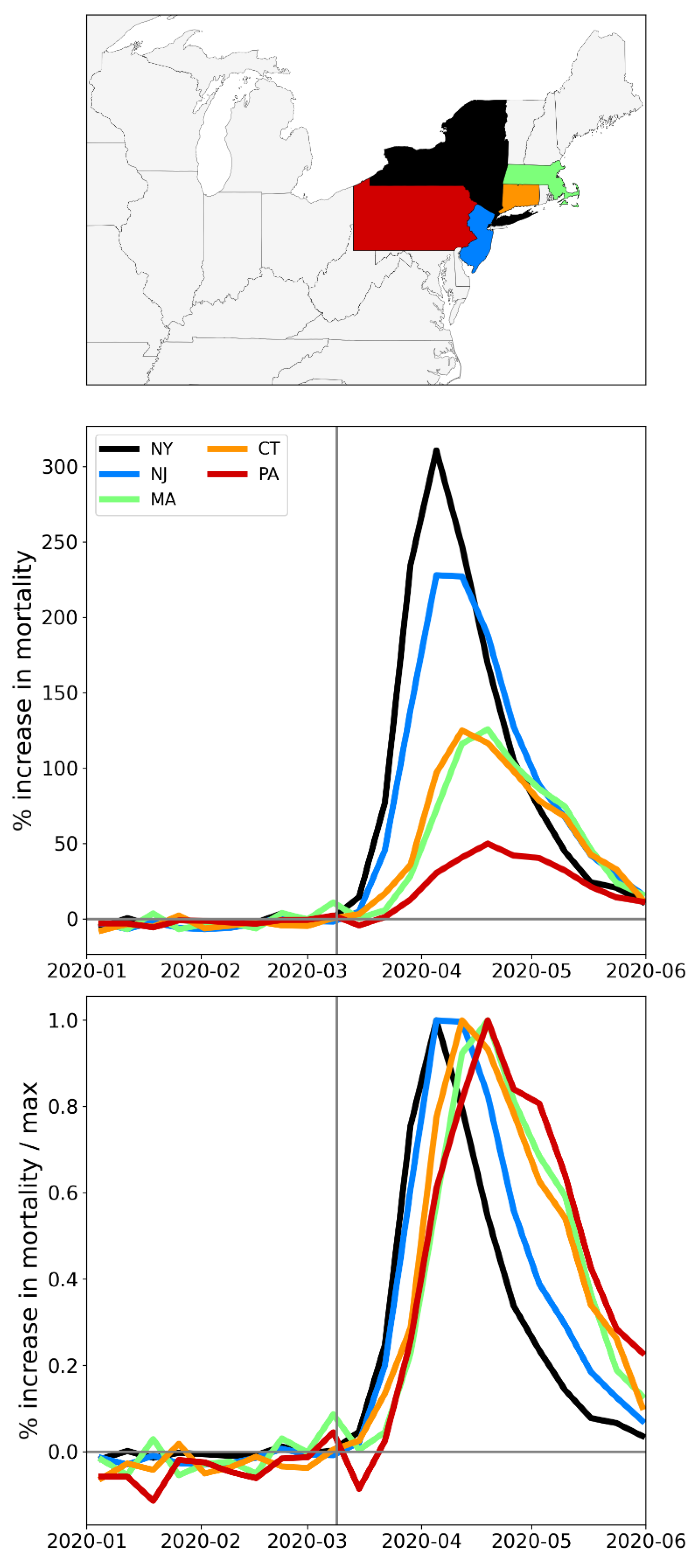
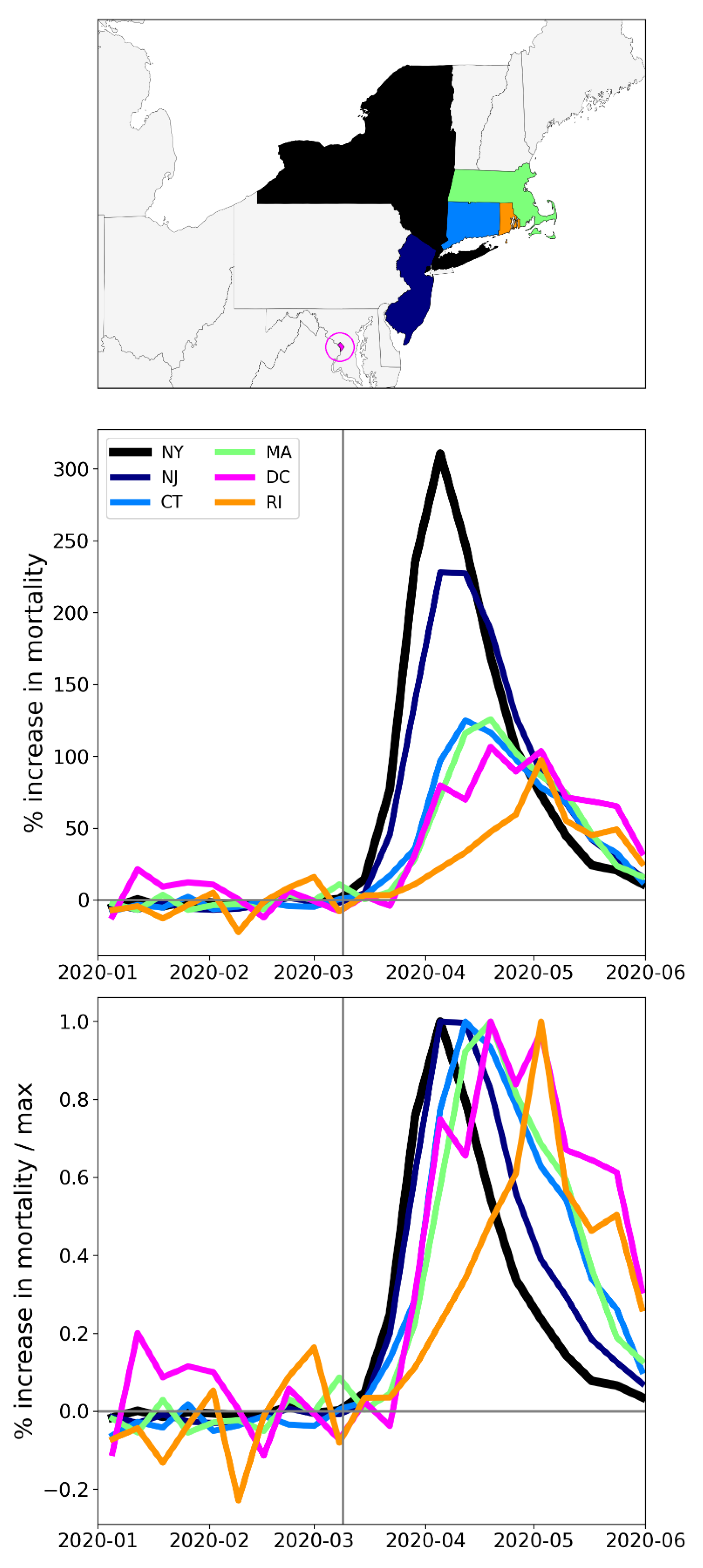
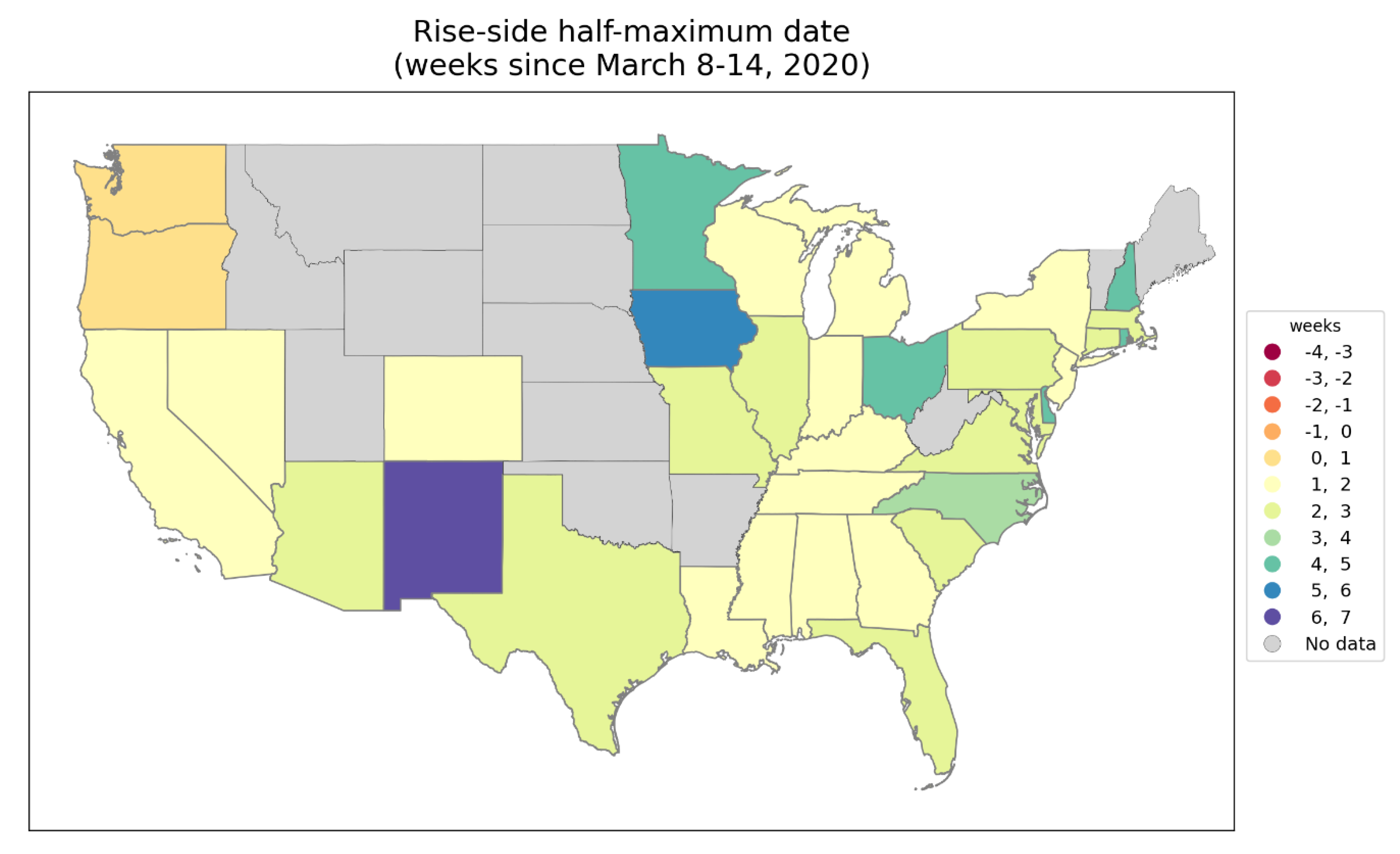
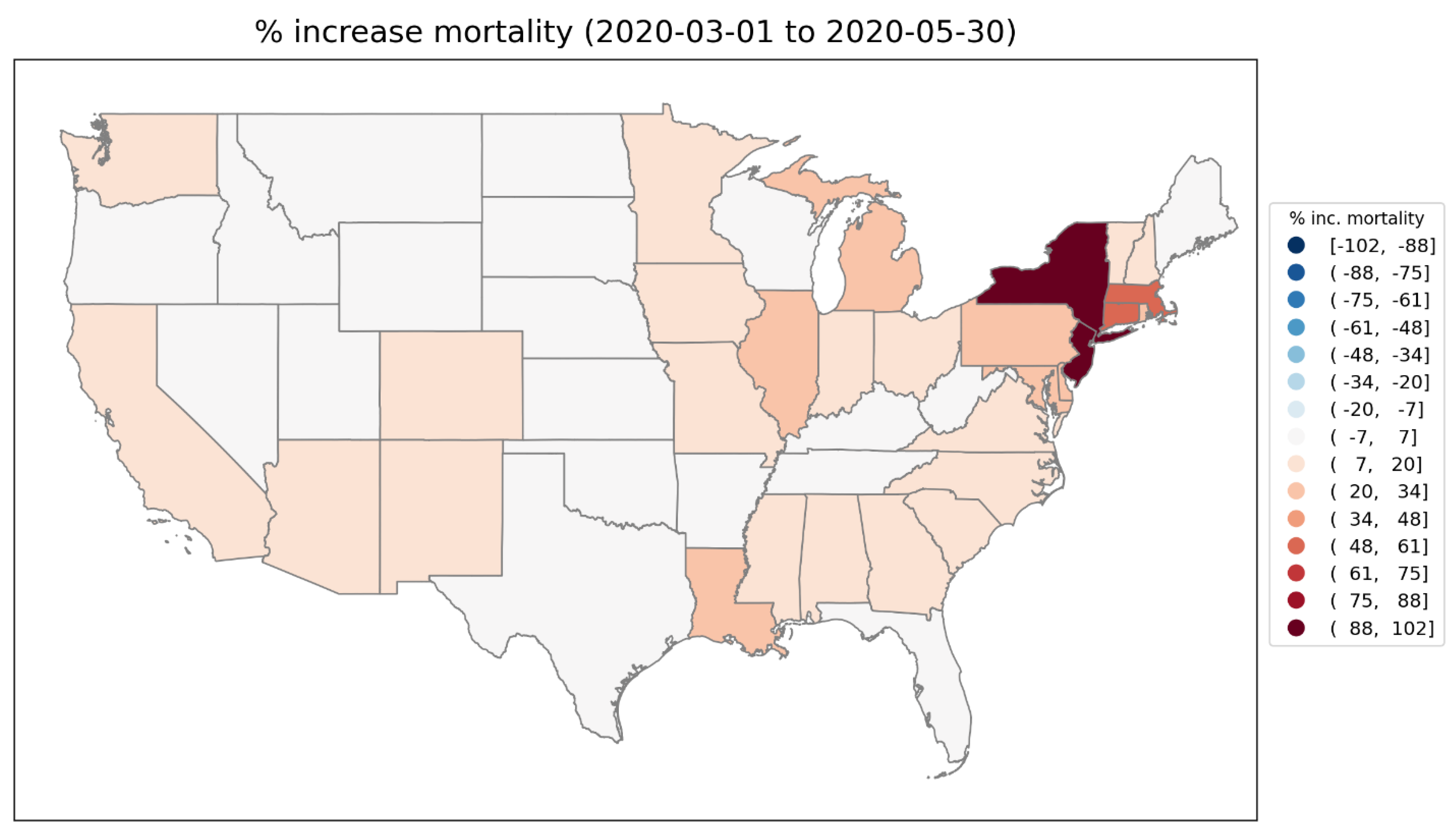
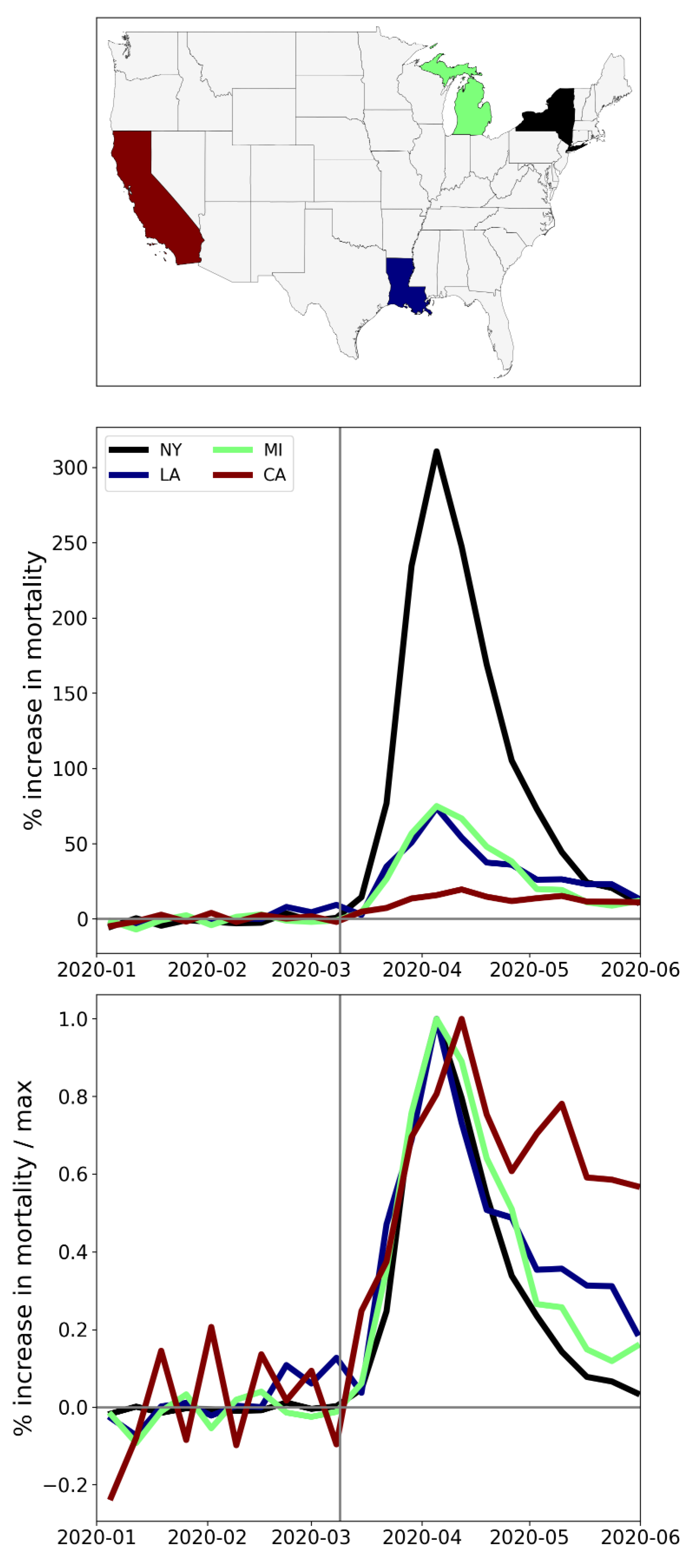
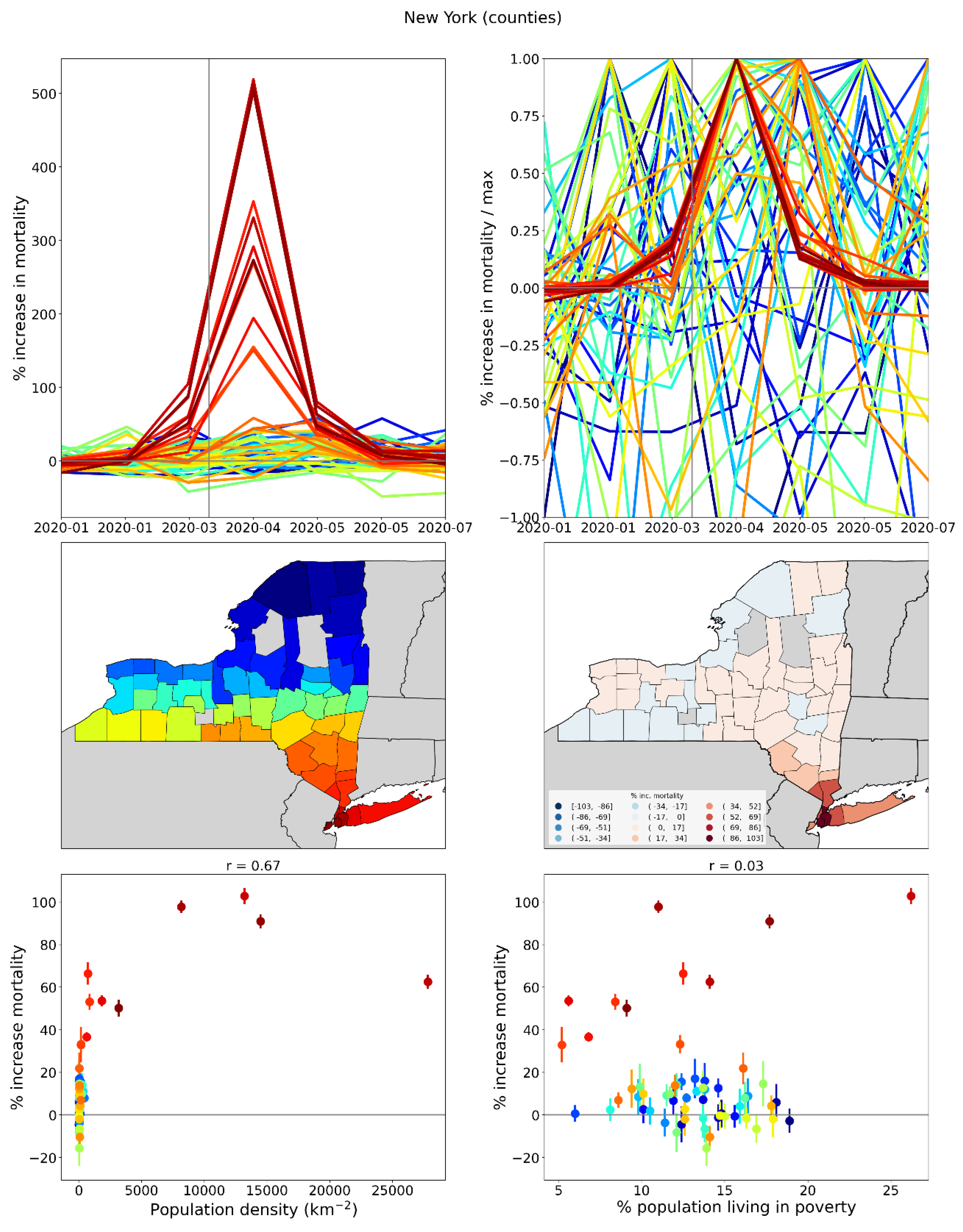
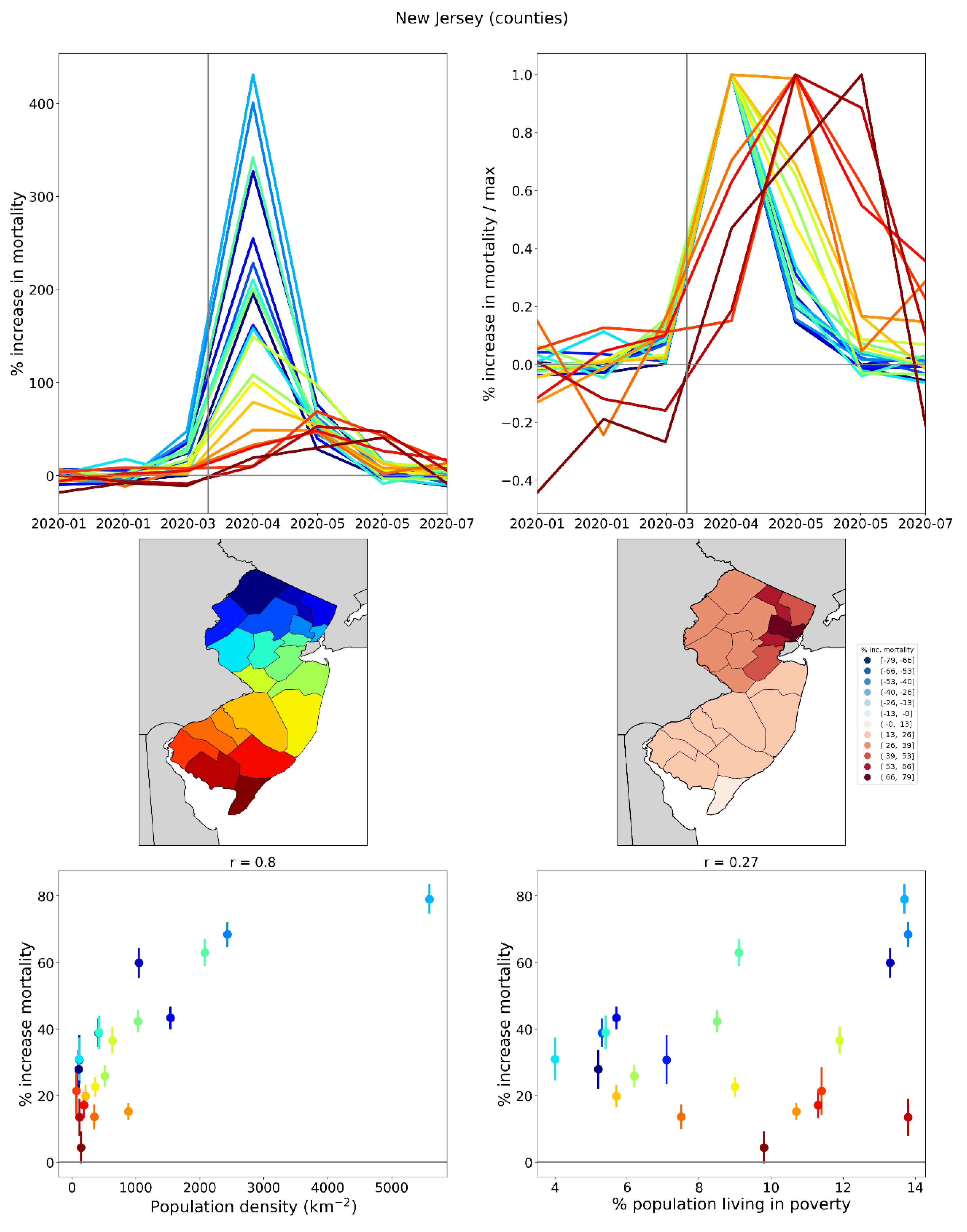
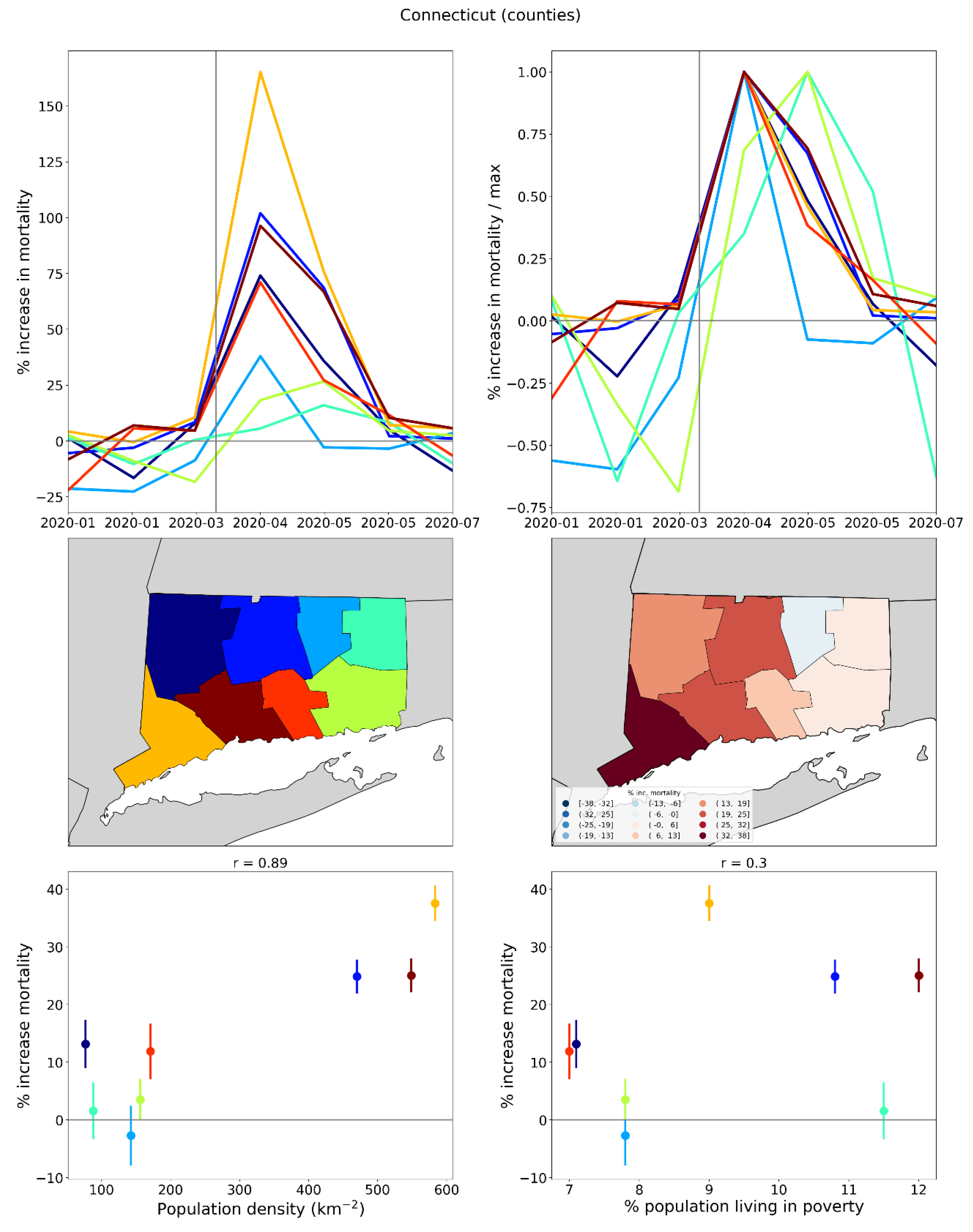
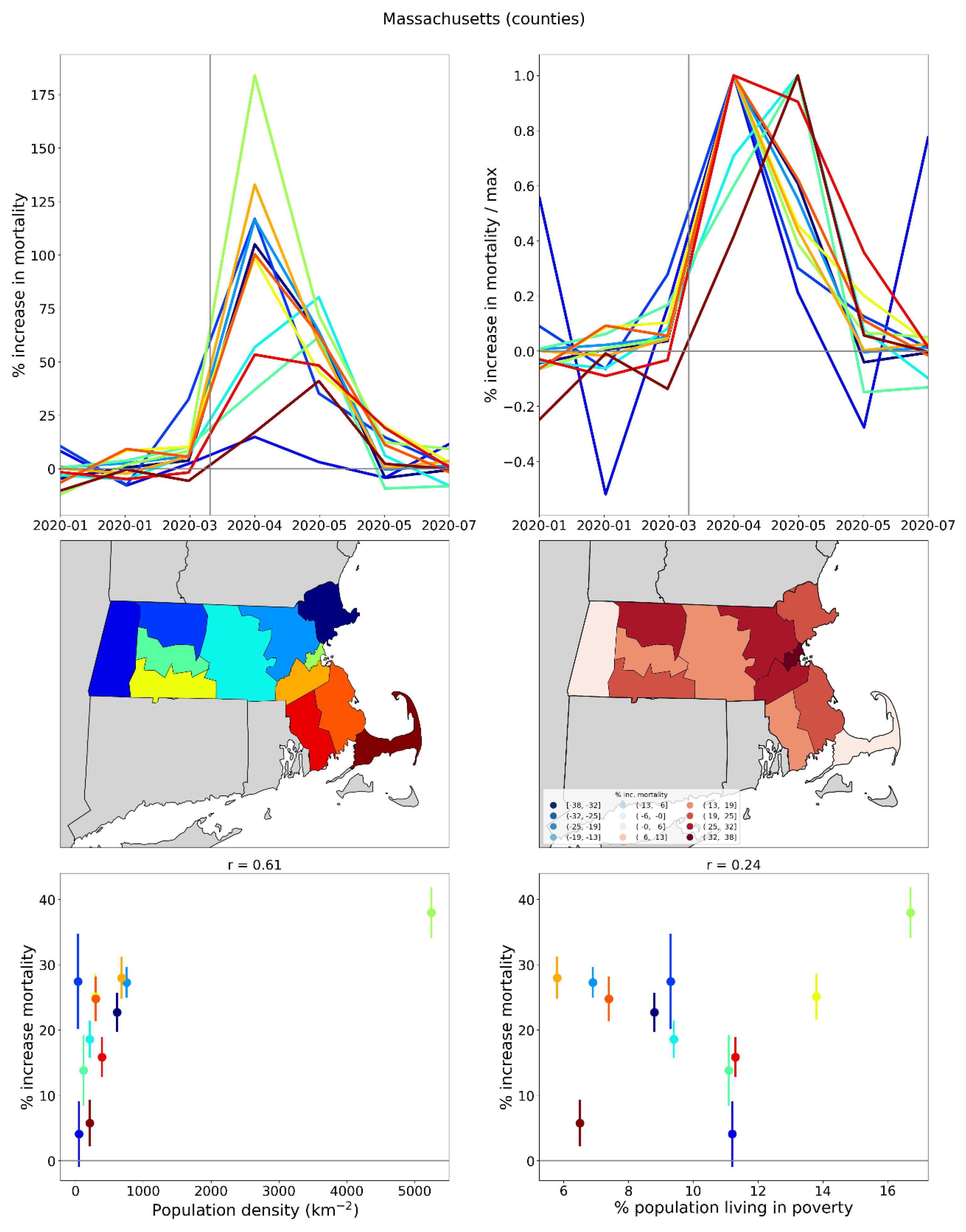
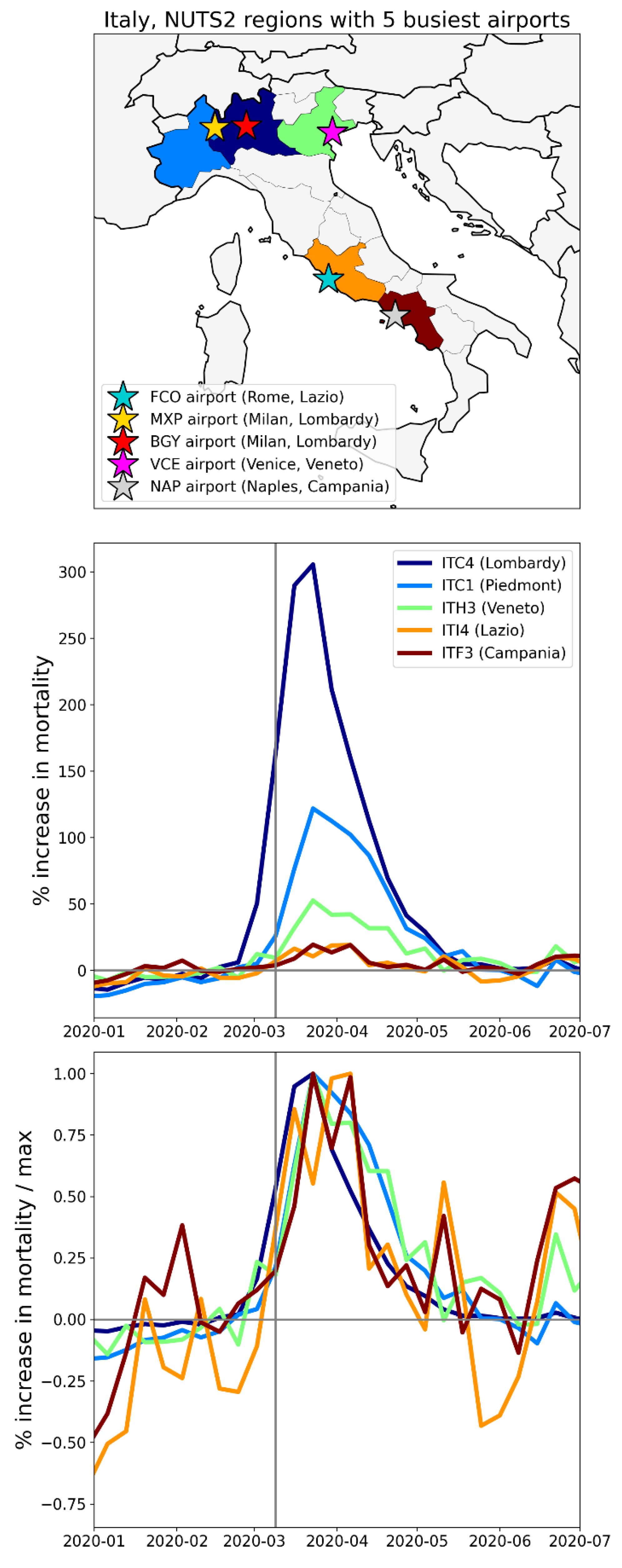
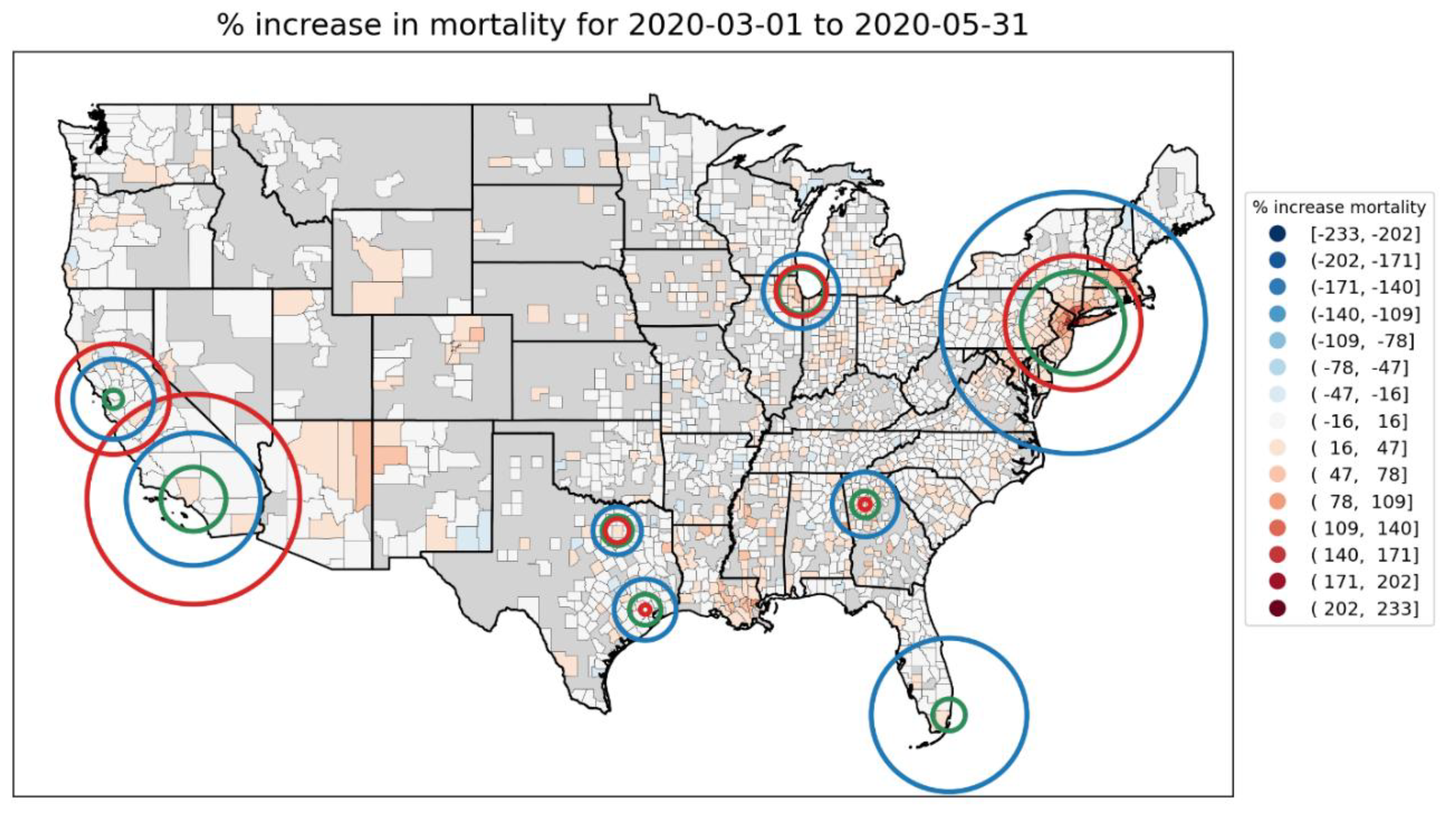
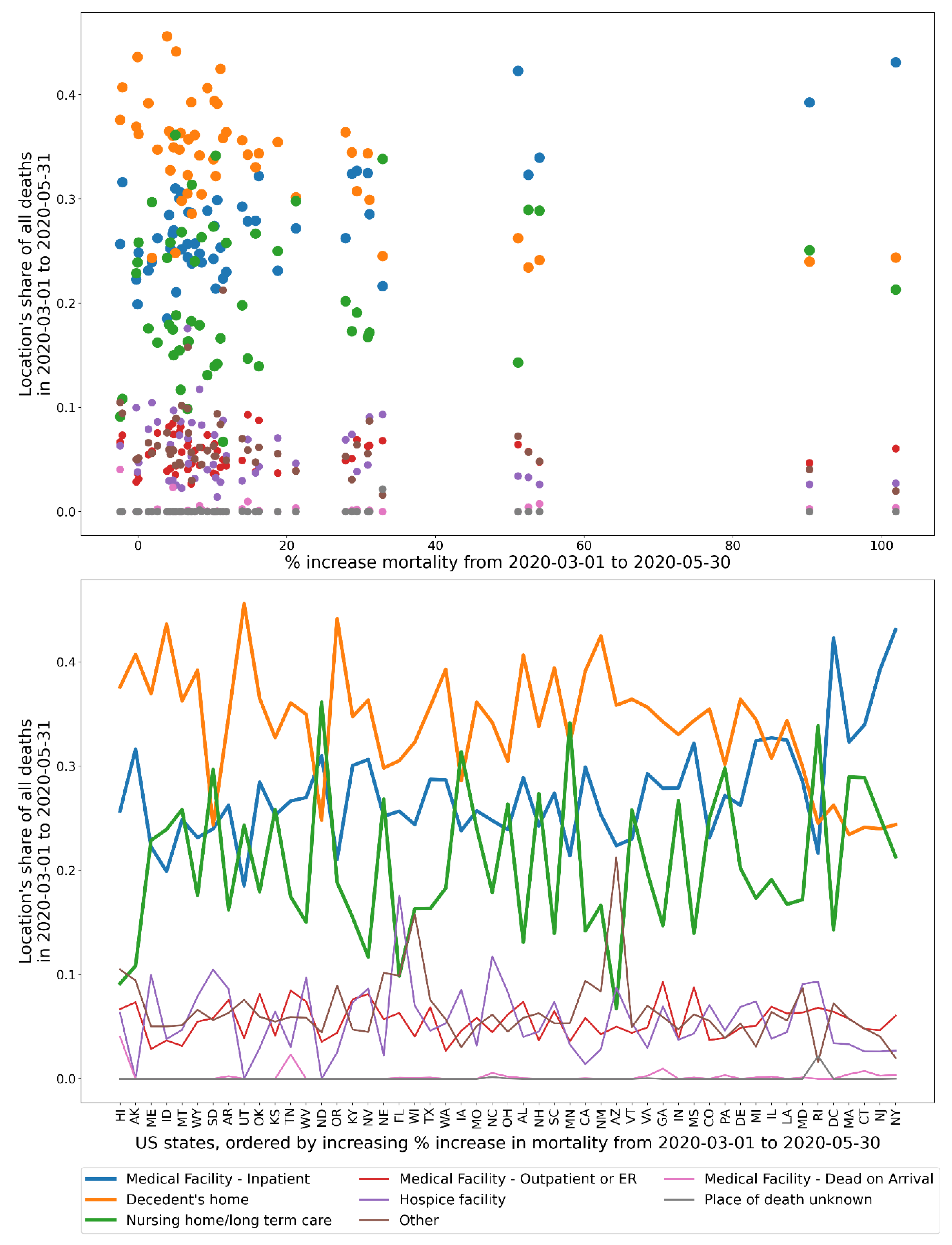
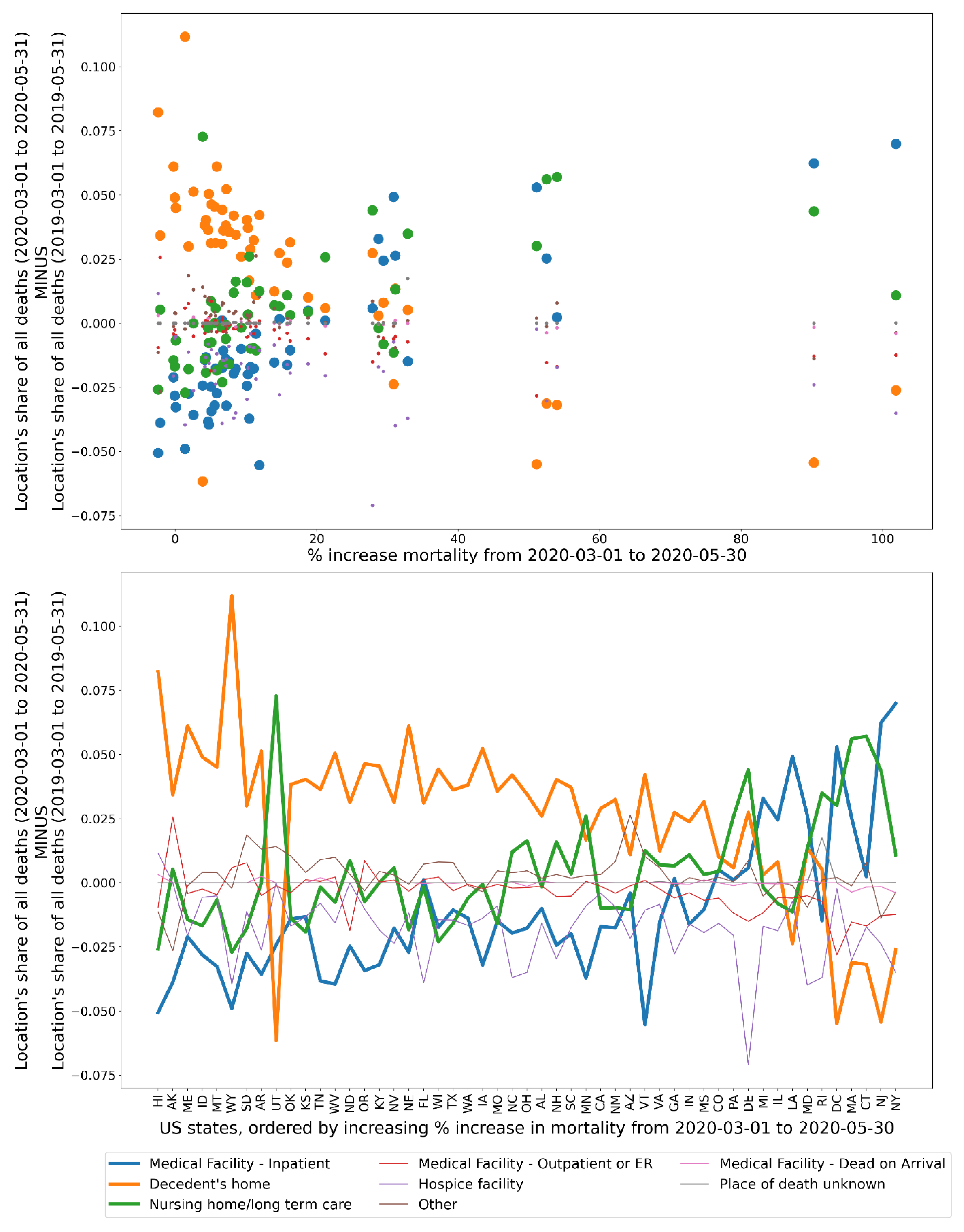
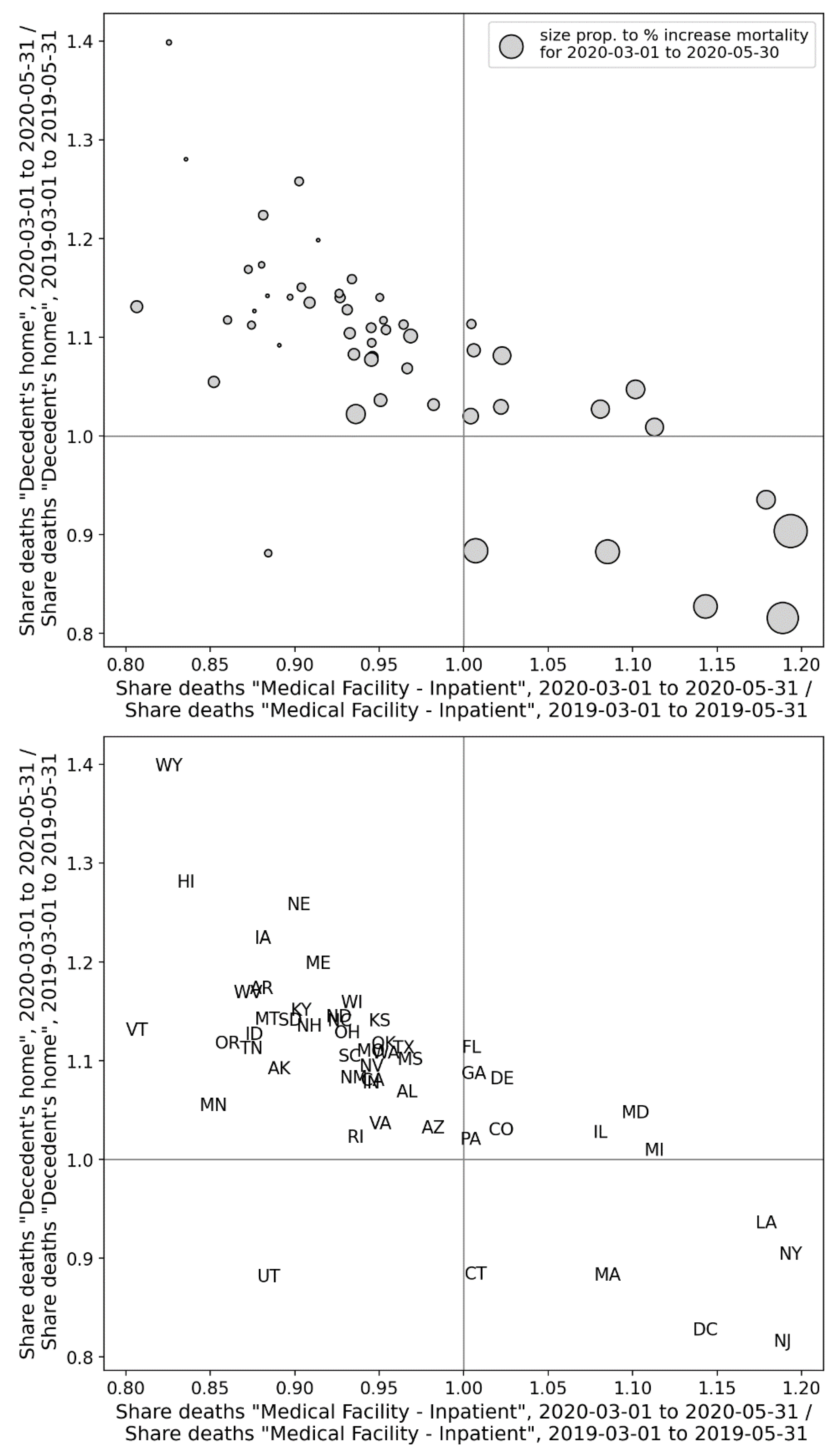
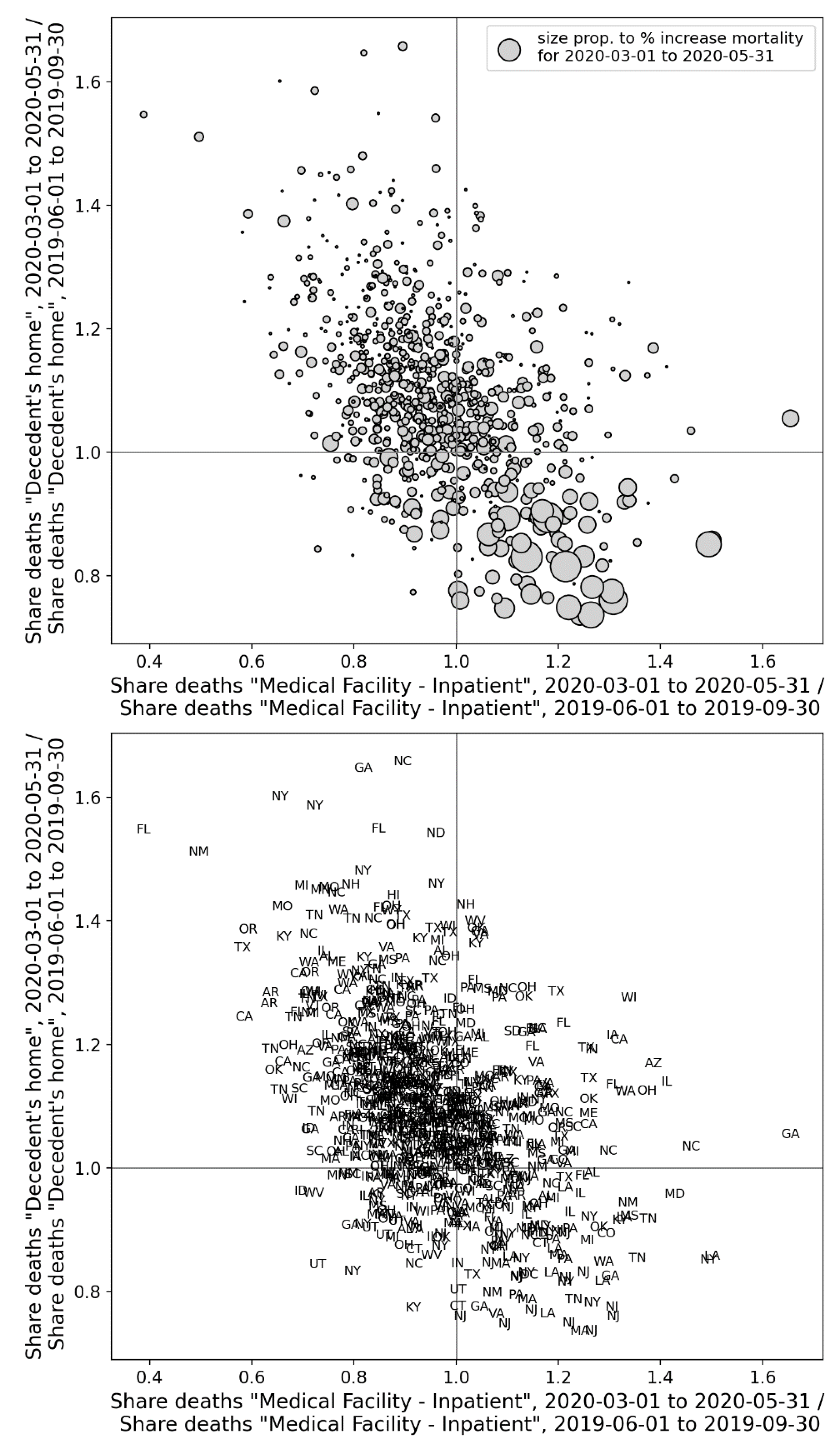
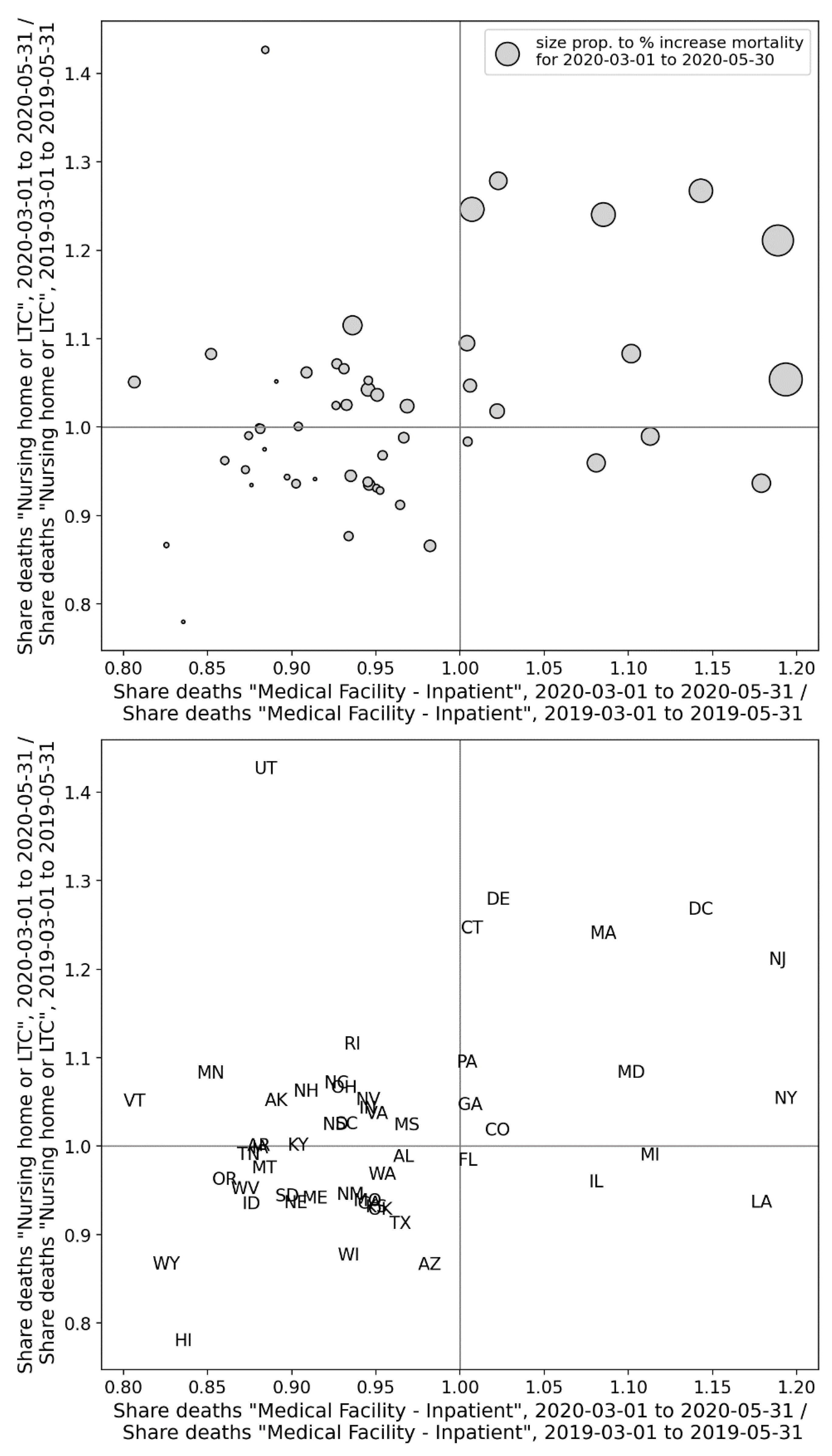
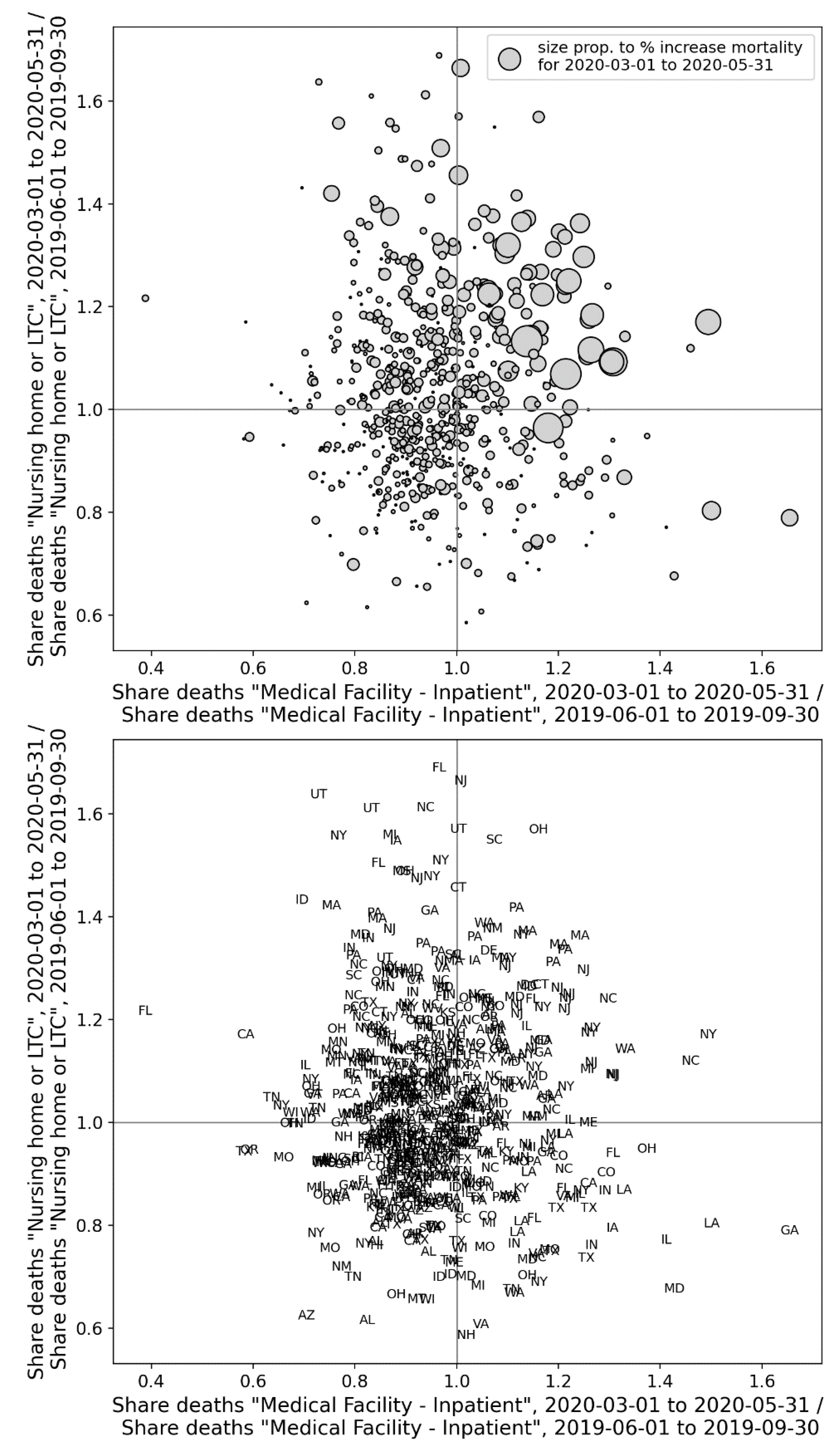
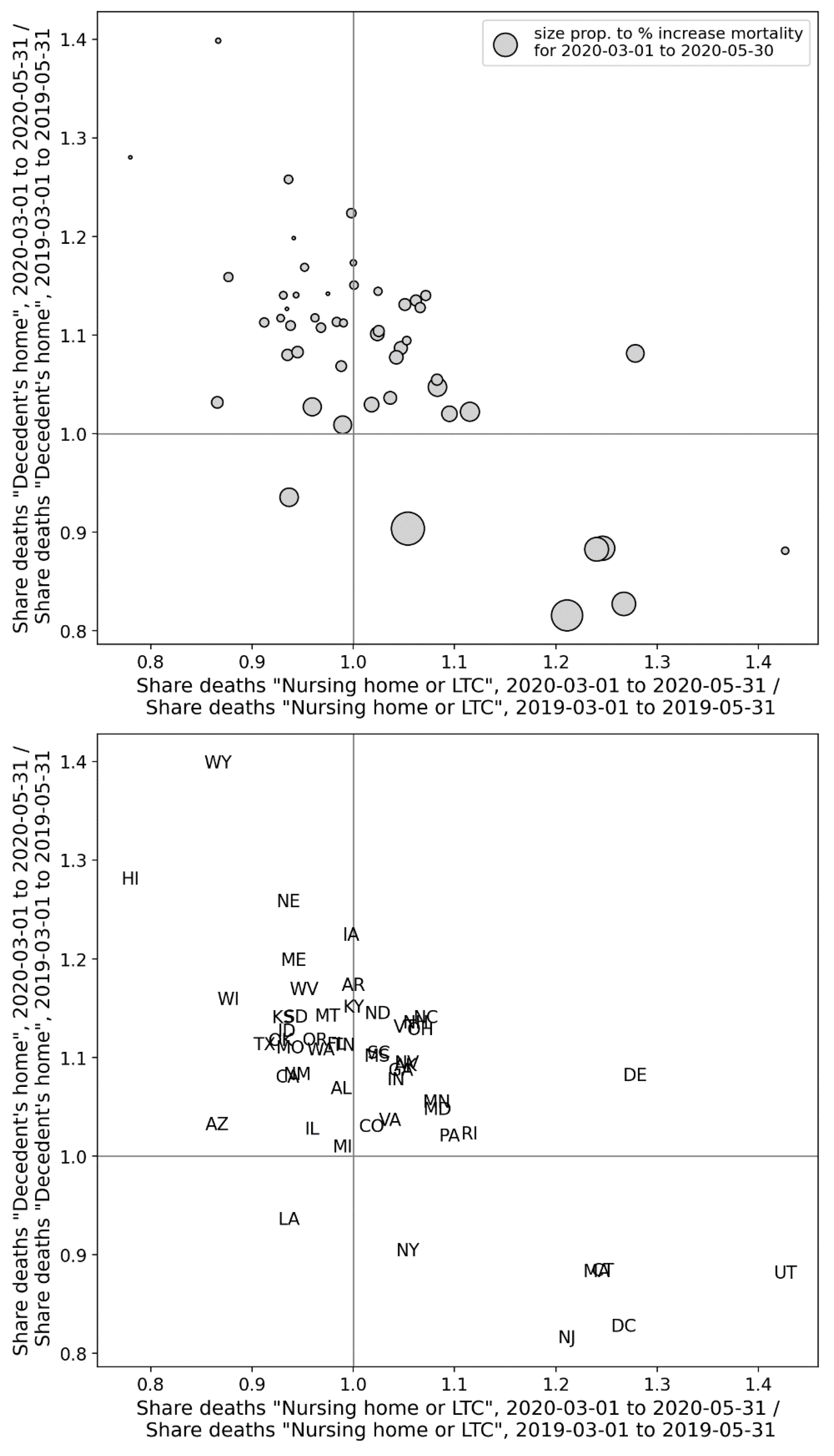
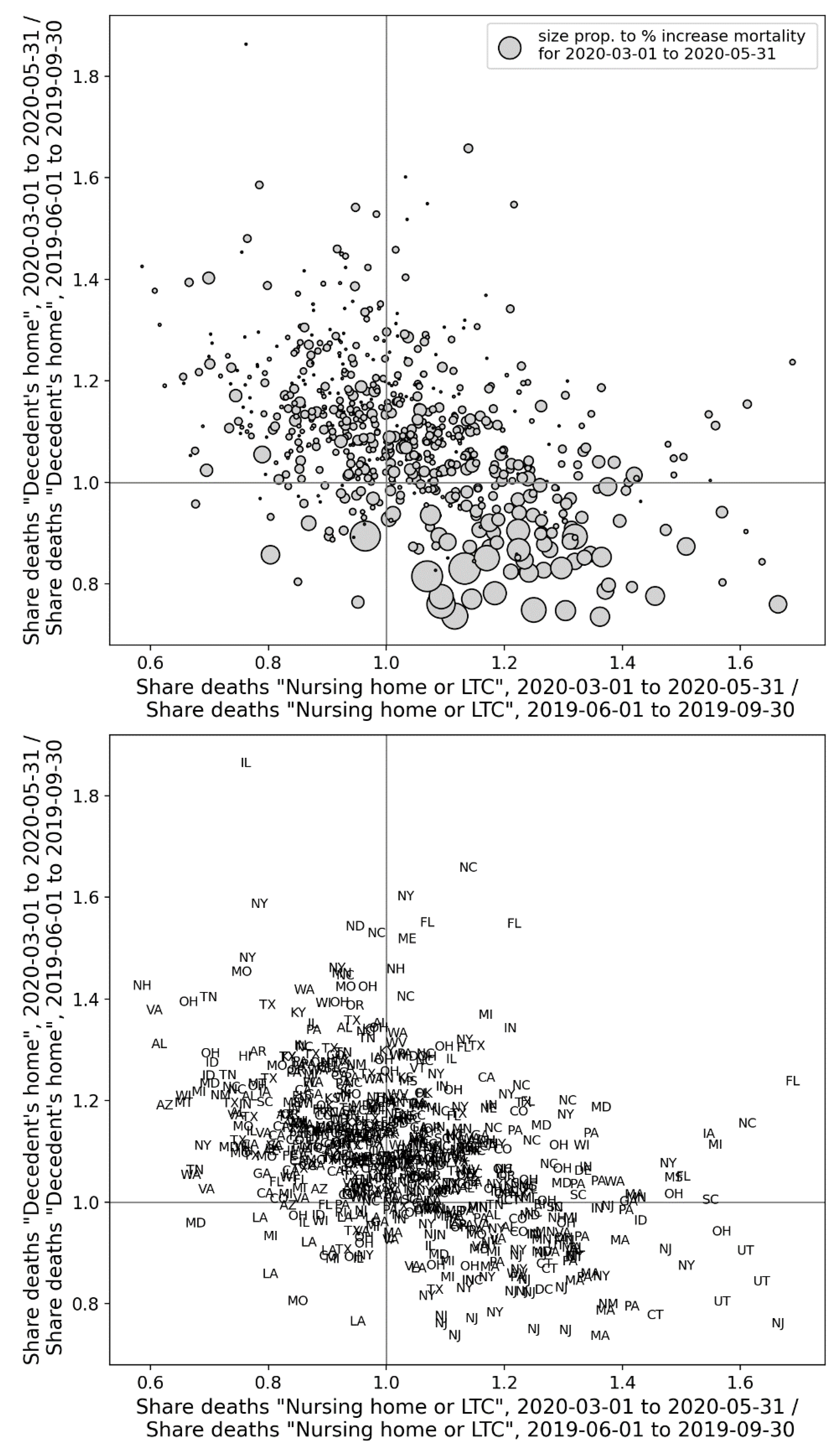
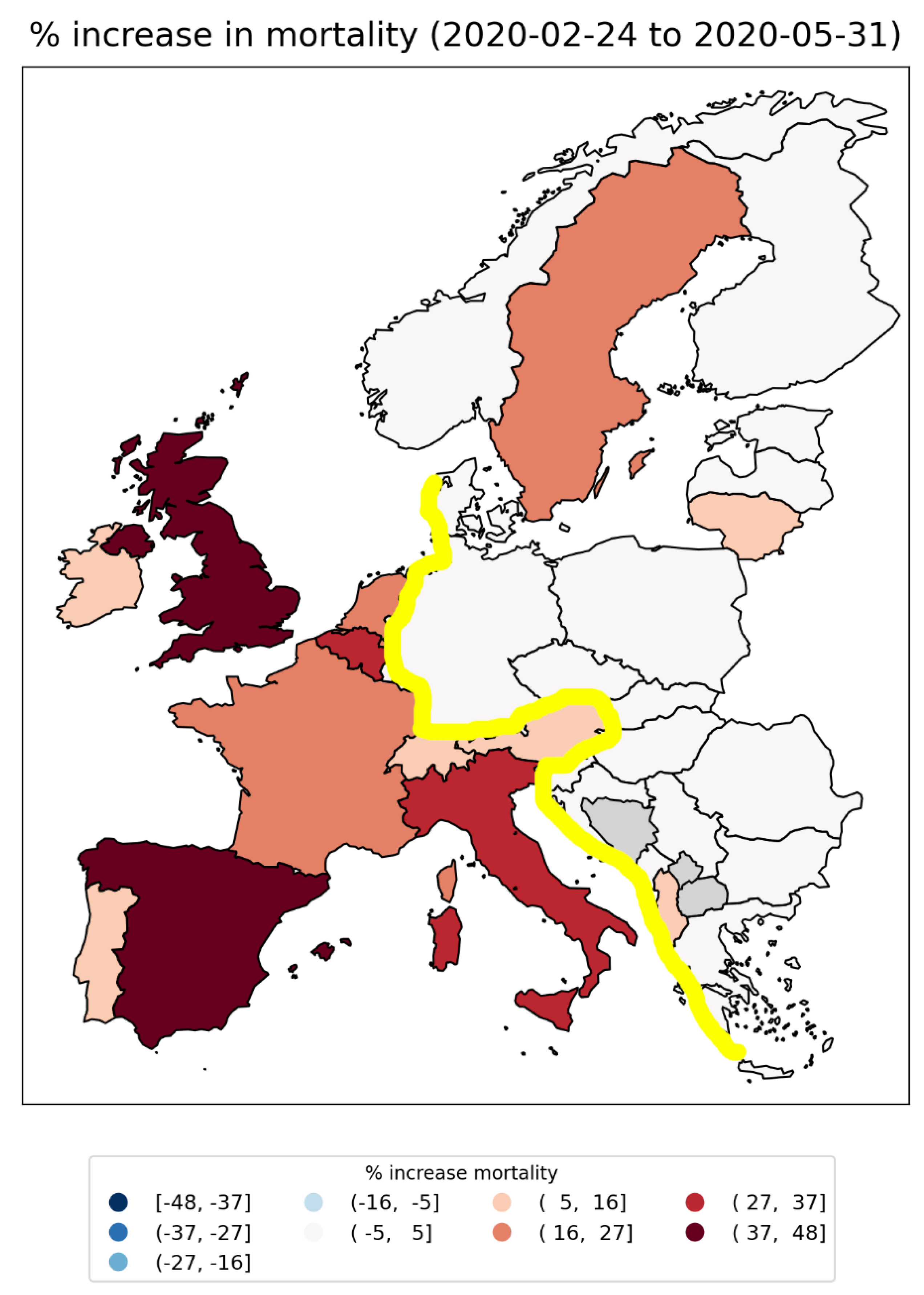
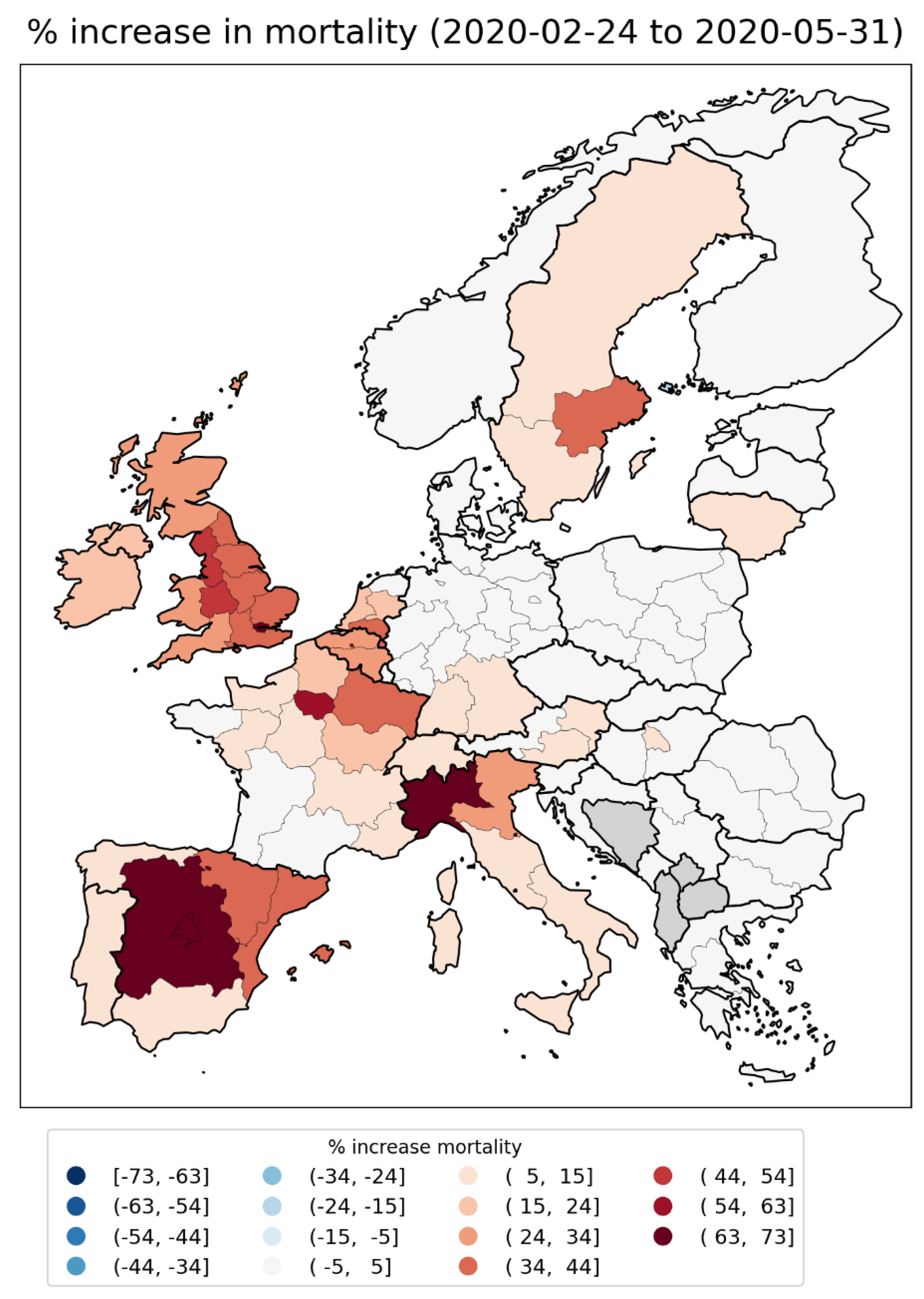
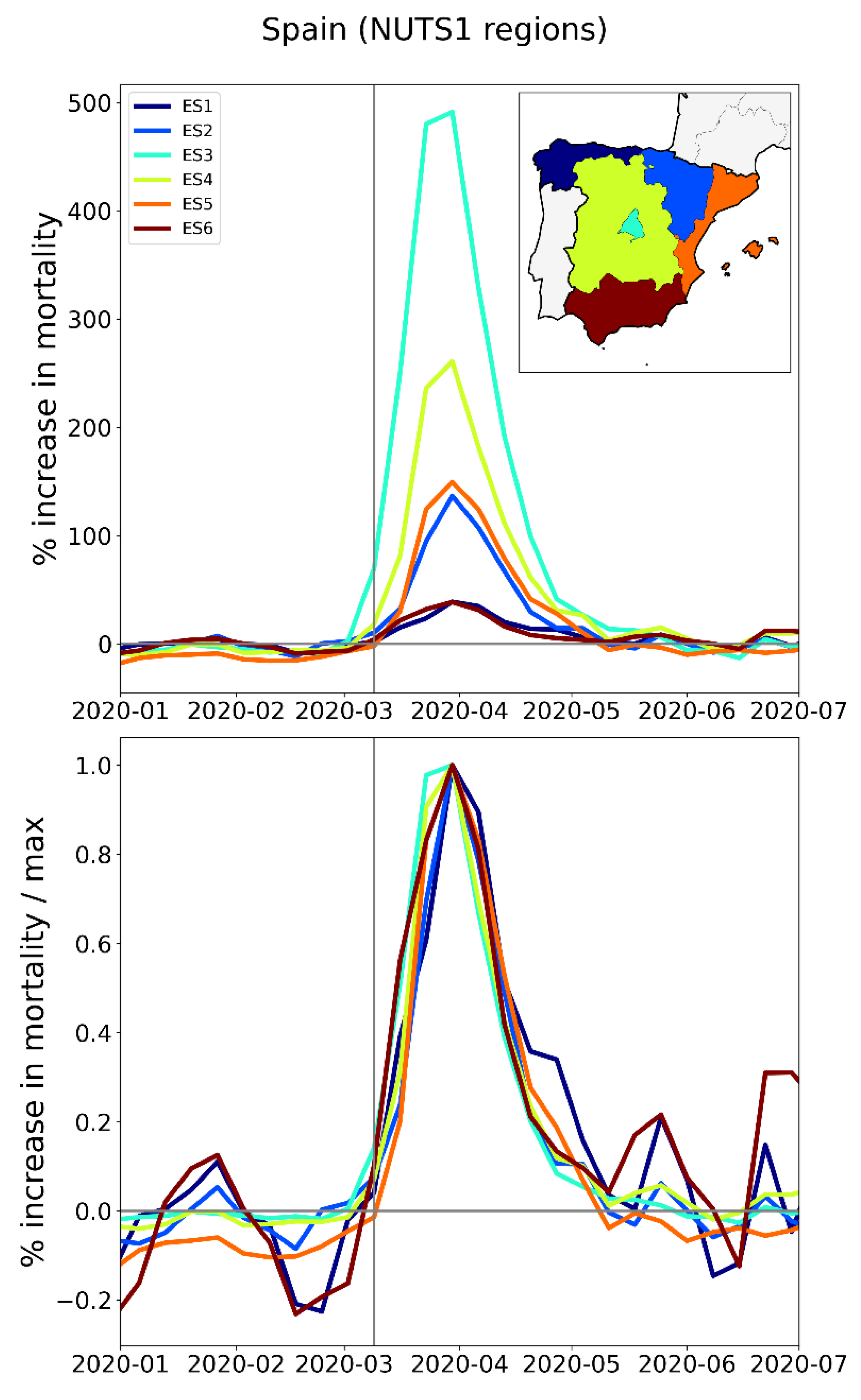
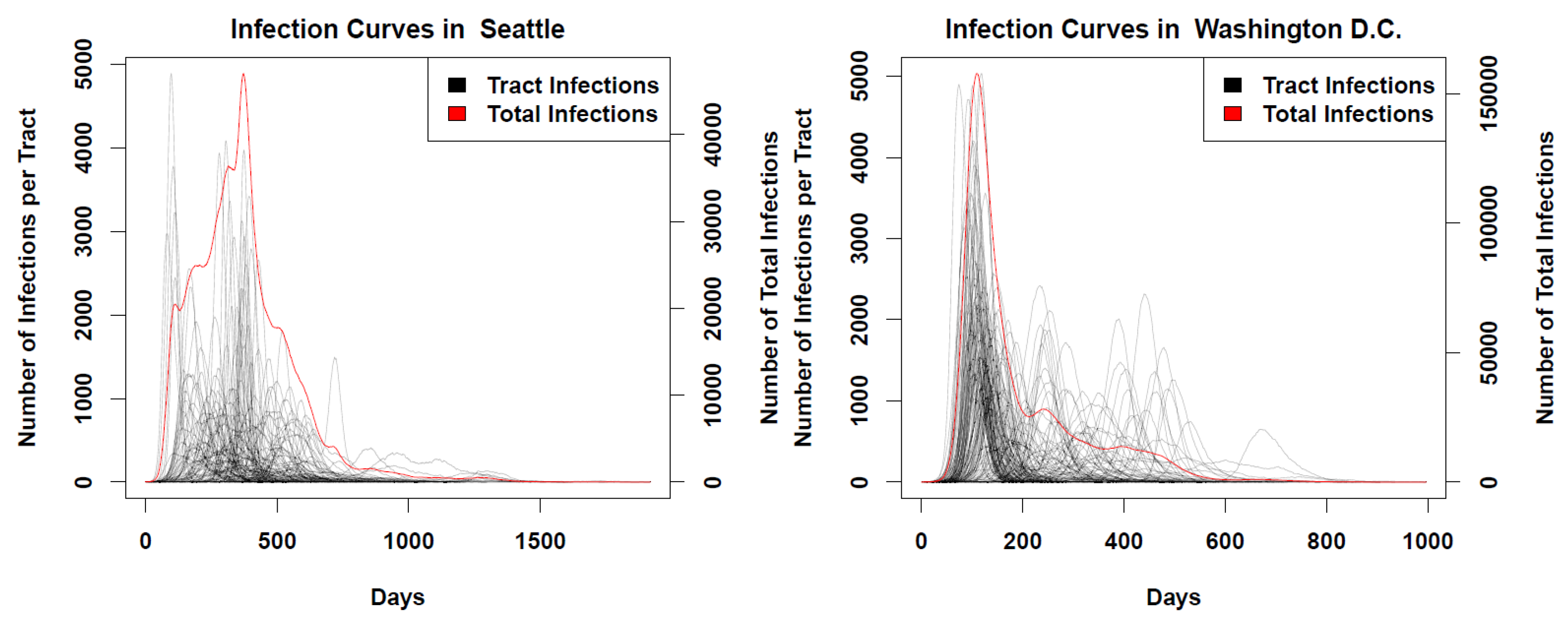
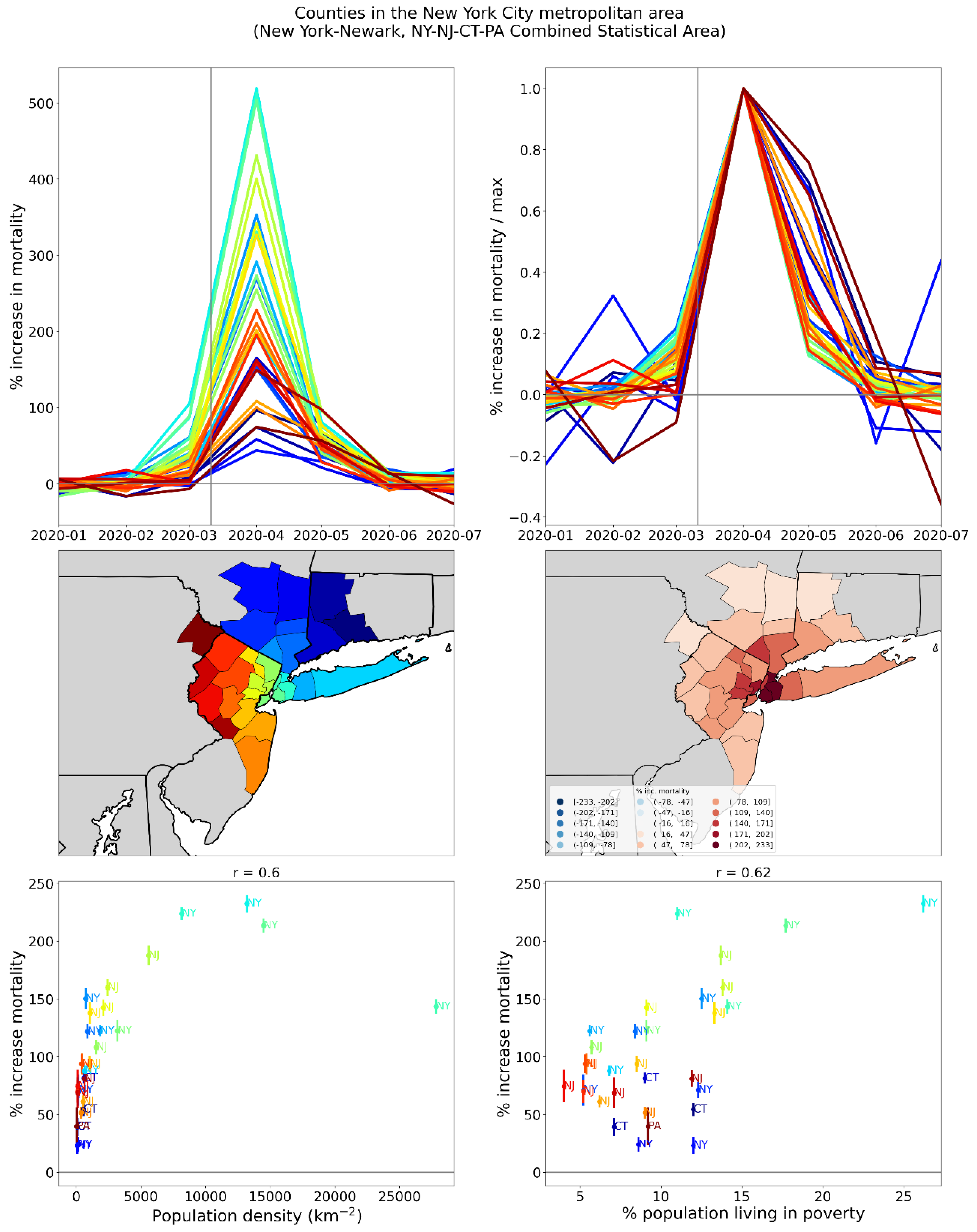
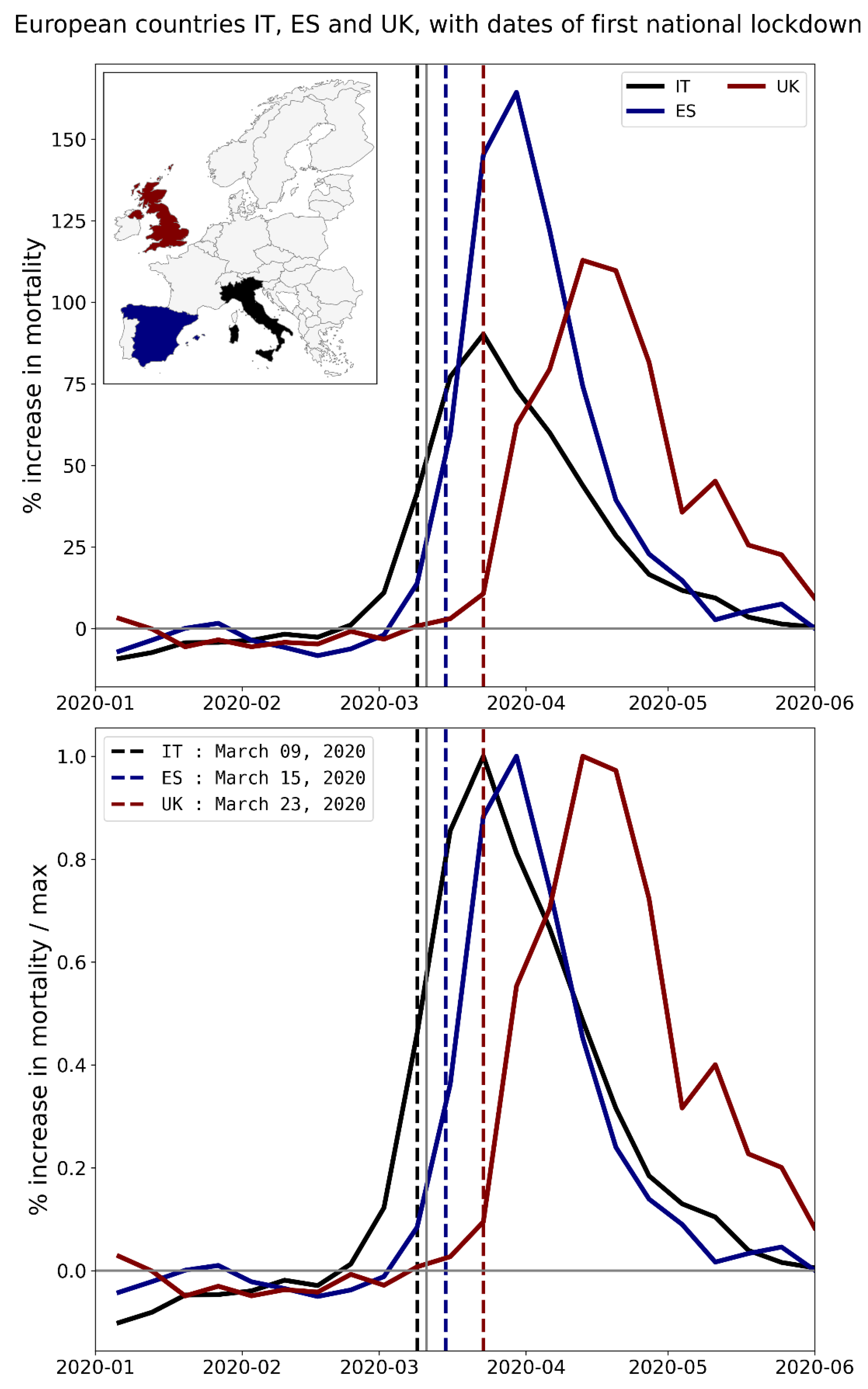
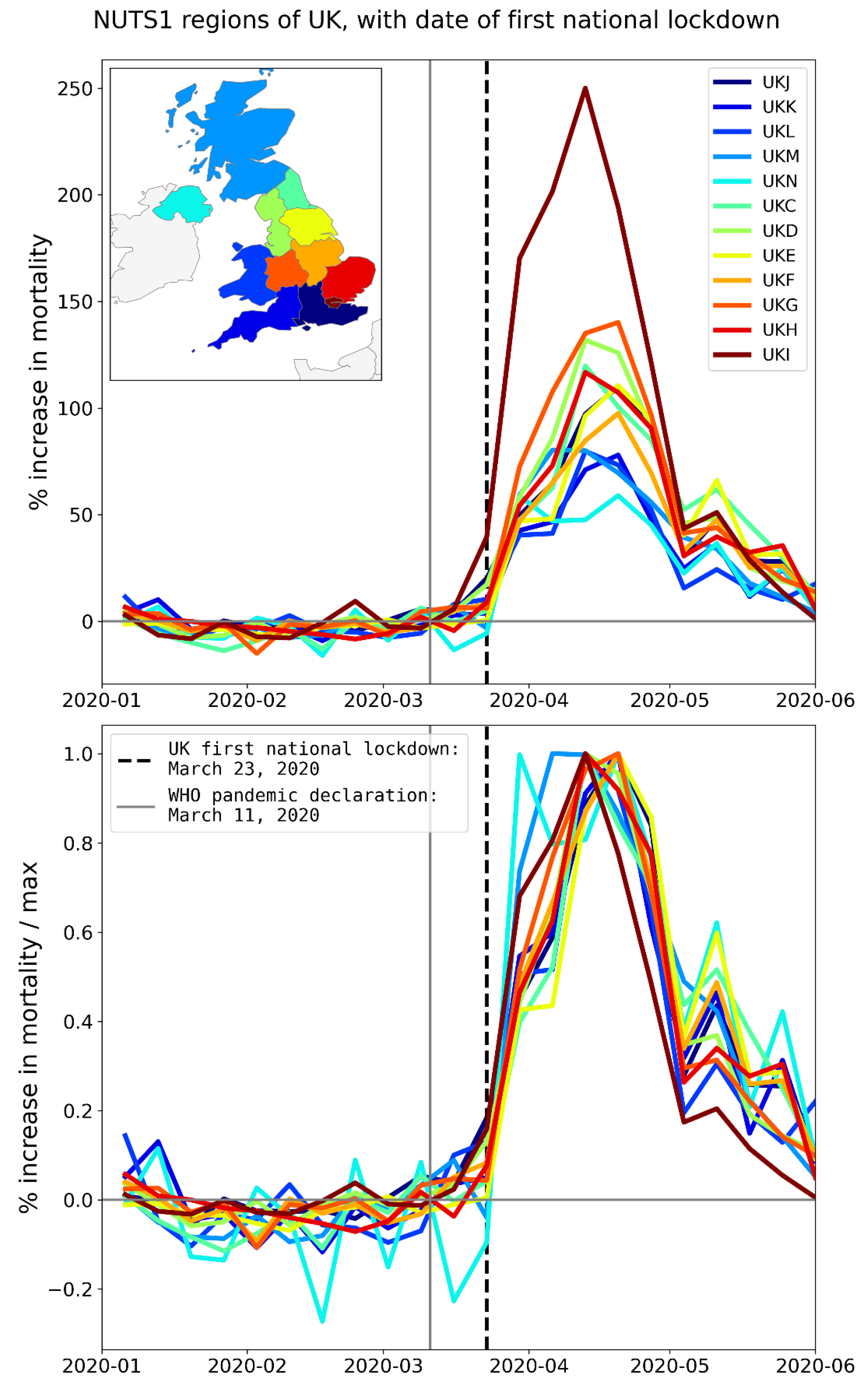
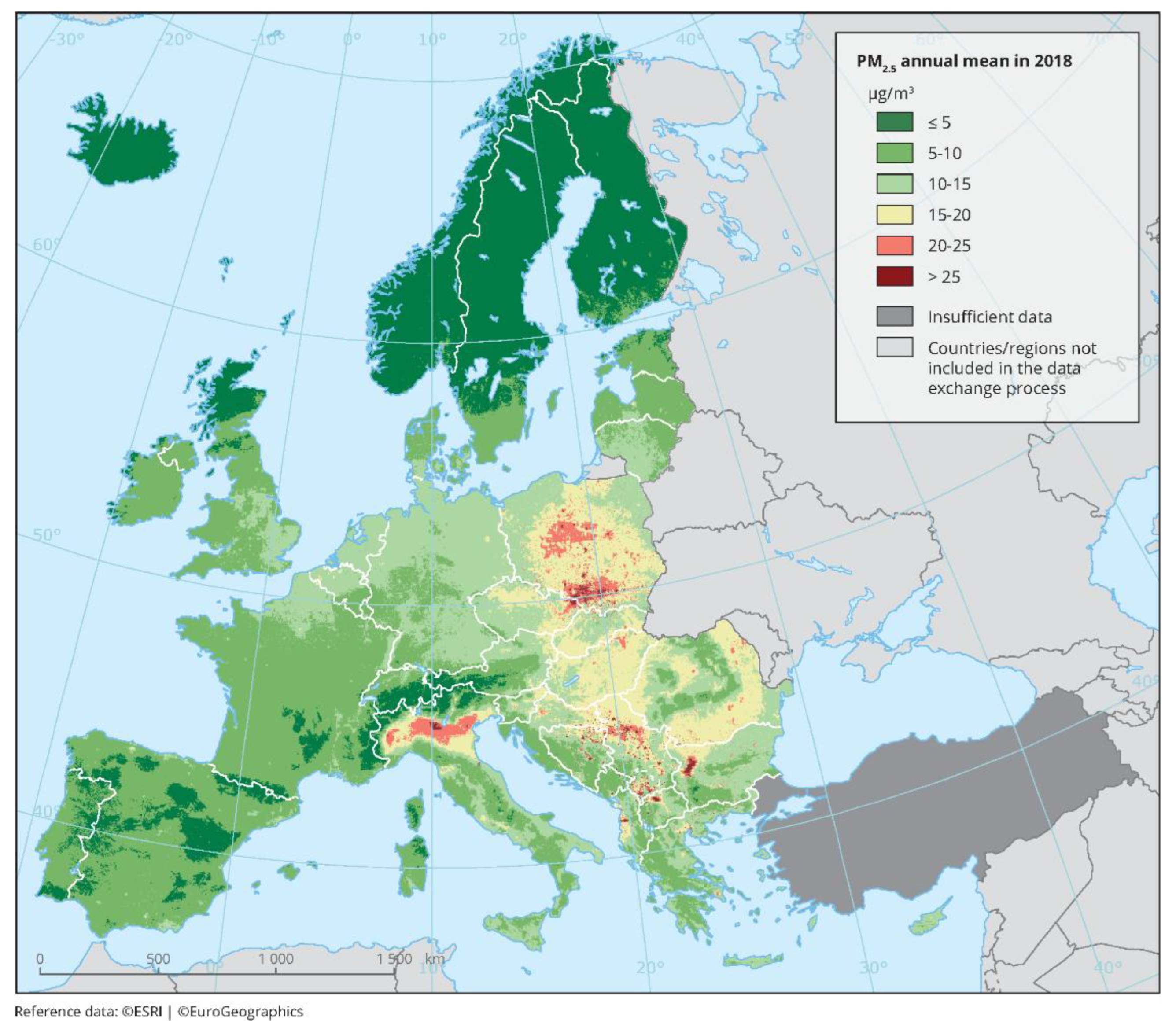
| Airport Name | Code | NUTS2 region | Total Passengers (2019)* | Num. passengers arriving directly from or traveling directly to a Chinese airport‡ | Num. passengers directly to or from an Asia Pacific airport*** (2019) |
||
|---|---|---|---|---|---|---|---|
| 2017* | 2018** | 2019*** | |||||
| Rome Leonardo da Vinci-Fiumicino | FCO | ITI4 (Lazio) |
43,354,887 | 443,762 | 413,882 | 506,898 | 2,019,300 |
| Milan Malpensa | MXP | ITC4 (Lombardy) ITC1 (Piedmont) |
28,705,638 | 246,437 | 272,783 | 346,887 | 1,269,474 |
| Milan Bergamo | BGY | ITC4 (Lombardy) |
13,792,266 | none reported | none reported | none reported | 0 |
| Venice Marco Polo | VCE | ITH3 (Veneto) | 11,507,301 | none reported | none reported | none reported | 73,247 |
| Naples International Airport | NAP | ITF3 (Campania) | 10,796,590 | none reported | none reported | none reported | 208 |
| NUTS2 region | ITI4 (Lazio) | ITC4 (Lombardy) | ITC1 (Piedmont) | ITH3 (Veneto) | ITF3 (Campania) |
|---|---|---|---|---|---|
| Population in 2020 (millions) * | 5.76 | 10.03 | 4.31 | 4.88 | 5.71 |
| All-ages mortality rate in 2019 (per 1000 persons) * | 10.1 | 10.1 | 12.4 | 10.1 | 9.5 |
| Share pop. aged 65+ in 2020 (%) * | 22.2 | 22.9 | 25.9 | 23.3 | 19.3 |
| Share pop. aged 80+ in 2020 (%) * | 7 | 7.4 | 8.6 | 7.3 | 5.3 |
| Num. beds in hospitals in region in 2020 ** | 20,268 | 36,383 | 15,332 | 15,799 | 14,582 |
| Num. beds in hospitals in region in 2020 / Population of region in 2020 | 1.59 | 1.58 | 1.34 | 1.35 | 1.33 |
| Num. ICU beds in region in 2017 ‡ | 486 | 738 | 299 | 468 | 427 |
| Num. ICU beds in region in 2017 / Num. people in region aged 65+ in 2020 (%) | 0.038 | 0.032 | 0.027 | 0.041 | 0.039 |
| Integrated first-peak period P-score and 1σ error (%) | 5.8 ± 1.7 | 106.2 ± 2.5 | 47.9 ± 2.1 | 21.0 ± 1.7 | 6.6 ± 1.8 |
| New York City | Los Angeles | San Francisco | |
|---|---|---|---|
| Total population (millions) | 8.44 | 10.1 | 7.68 |
| Total area (km2) | 778 | 10500 | 17900 |
| Population density (km-2) | 10800 | 962 | 429 |
| % population aged 65+ | 14.1 | 12.9 | 14.6 |
| % living in poverty | 18.6 | 15.7 | 9.1 |
| % minority | 67.9 | 73.7 | 60.3 |
| % pop. that speaks English "less than well" | 11.7 | 12.8 | 7.6 |
| % pop. aged 25+ with no high school diploma | 12.9 | 14.5 | 8.1 |
| % households with more people than rooms | 9.0 | 11.4 | 6.7 |
| % single-parent households | 9.6 | 9.4 | 6.6 |
| Num. ICU beds per total pop. (%) | 0.019 | 0.021 | 0.020 |
| Num. ICU beds per pop. aged 65+ (%) | 0.13 | 0.16 | 0.13 |
| Integrated first-peak period P-score and 1σ error (%) | 200.2 ± 2.5 | 23.9 ± 1.8 | 7.3 ± 1.3 |
| Figure (scatter) | Figure (heatmap) | USA county-level socioeconomic variable | Year(s) |
|---|---|---|---|
| Figure 64 | Figure 99 | Population | 2019 |
| Figure 65 | Figure 100 | Log(Population) | 2019 |
| Figure 66 | Figure 101 | Population density | 2017-2021 ACS * |
| Figure 67 | Figure 102 | Log(Population density) | 2017-2021 ACS |
| Figure 68 | Figure 103 | Per capita income | 2014-2018 ACS ** |
| Figure 69 | Figure 104 | % living in poverty | 2014-2018 ACS |
| Figure 70 | Figure 105 | % unemployed | 2014-2018 ACS |
| Figure 71 | Figure 106 | Gini coefficient | 2014-2018 ACS |
| Figure 72 | Figure 107 | Inter-county disparity | 2014-2018 ACS |
| Figure 73 | Figure 108 | % households with no vehicle available | 2014-2018 ACS |
| Figure 74 | Figure 109 | % households with more people than rooms | 2014-2018 ACS |
| Figure 75 | Figure 110 | % living in housing structures with 10+ units | 2014-2018 ACS |
| Figure 76 | Figure 111 | % of population that speaks English “less than well” | 2014-2018 ACS |
| Figure 77 | Figure 112 | % minority | 2014-2018 ACS |
| Figure 78 | Figure 113 | % aged 25+ with no high school diploma | 2014-2018 ACS |
| Figure 79 | Figure 114 | % aged 65+ | 2014-2018 ACS |
| Figure 80 | Figure 115 | % aged 17 and under | 2014-2018 ACS |
| Figure 81 | Figure 116 | % households that are single-parent households | 2014-2018 ACS |
| Figure 82 | Figure 117 | % with a disability | 2014-2018 ACS |
| Figure 83 | Figure 118 | % with diabetes | 2018 |
| Figure 84 | Figure 119 | % with obesity | 2018 |
| Figure 85 | Figure 120 | % of votes cast in the 2016 election that were for the Democratic presidential candidate | 2016 |
| Figure 86 | Figure 121 | % deaths occurring at home in March-May 2019 | 2019 |
| Figure 87 | Figure 122 | % deaths occurring at home in June-September 2019 | 2019 |
| Figure 88 | Figure 123 | % deaths occurring in hospital in March-May 2019 | 2019 |
| Figure 89 | Figure 124 | % deaths occurring in hospital in June-September 2019 | 2019 |
| Figure 90 | Figure 125 | % deaths in hospital in March-May 2020 minus % deaths occurring in hospital in March-May 2019 | 2019, 2020 |
| Figure 91 | Figure 126 | % deaths in hospital in June-September 2020 minus % deaths occurring in hospital in June-September 2019 | 2019, 2020 |
| Figure 92 | Figure 127 | Number of prescription drug claims per person | 2017 |
| Figure 93 | Figure 128 | Number of antibiotic prescription drug claims per person | 2017 |
| Figure 94 | Figure 129 | % aged 18+ with at least one dose of a COVID vaccine by 2021-12-31 | 2020, 2021 |
| Figure 95 | Figure 130 | % aged 65+ with at least one dose of a COVID vaccine by 2021-12-31 | 2020, 2021 |
| Figure 96 | Figure 131 | % aged 18+ with completed primary series of a COVID vaccine by 2021-12-31 | 2020, 2021 |
| Figure 97 | Figure 132 | % aged 65+ with completed primary series of a COVID vaccine by 2021-12-31 | 2020, 2021 |
| Figure 98 | Figure 133 | Number of ICU beds per county | 2018, 2019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





