Partitioning the Critical Strip: A Nyman–Beurling Approach to the Riemann Hypothesis

1. Introduction

The Riemann Hypothesis (RH) asserts that every nontrivial zero of the Riemann zeta function $\zeta \left(s\right)$ has real part $\Re \left(s\right)=\frac{1}{2}$. This deep conjecture is intimately connected to the distribution of prime numbers. Recall that $\zeta \left(s\right)$ is defined by its Dirichlet series for $\Re \left(s\right)>1$,

$$\zeta \left(s\right)=\sum _{n=1}^{\infty }{n}^{-s},$$

and has the Euler product representation

$$\zeta \left(s\right)=\prod _{p\mathrm{prime}}{(1-p^{-s})}^{-1},$$

which converges for $\Re \left(s\right)>1$. From these representations one immediately sees that $\zeta \left(s\right)\ne 0$ for $\Re \left(s\right)>1$[1]. By analytic continuation and the functional equation (see e.g. [4]), $\zeta \left(s\right)$ extends meromorphically to $\mathbb{C}$ with only a simple pole at $s=1$, and trivial zeros at the negative even integers $s=-2,-4,-6,\dots$. The functional equation also implies $\zeta (1+it)\ne 0$ for $t\ne 0$, so there are no zeros on the lines $\Re \left(s\right)=0$ or $\Re \left(s\right)=1$. Hence all nontrivial zeros lie in the open critical strip

$$\Sigma =\{s:0<\Re (s)<1\}.$$

Moreover, symmetry under complex conjugation and the functional equation implies that if $\rho =\beta +i\gamma$ is a zero, then so are $1-\overline{\rho }$ and $\overline{\rho }$. Thus the zeros of $\zeta \left(s\right)$ are symmetric about the critical line $\Re \left(s\right)=\frac{1}{2}$. Hardy proved in 1914 that infinitely many zeros lie on the line $\Re \left(s\right)=\frac{1}{2}$[5], and large-scale computations (Odlyzko 1987) have verified that the first billions of zeros all satisfy $\Re \left(s\right)=\frac{1}{2}$ [3]. Nevertheless, a general proof of RH remains one of the most significant open problems in mathematics. (For surveys of known results and formulations of RH, see e.g. [1,2,8].)

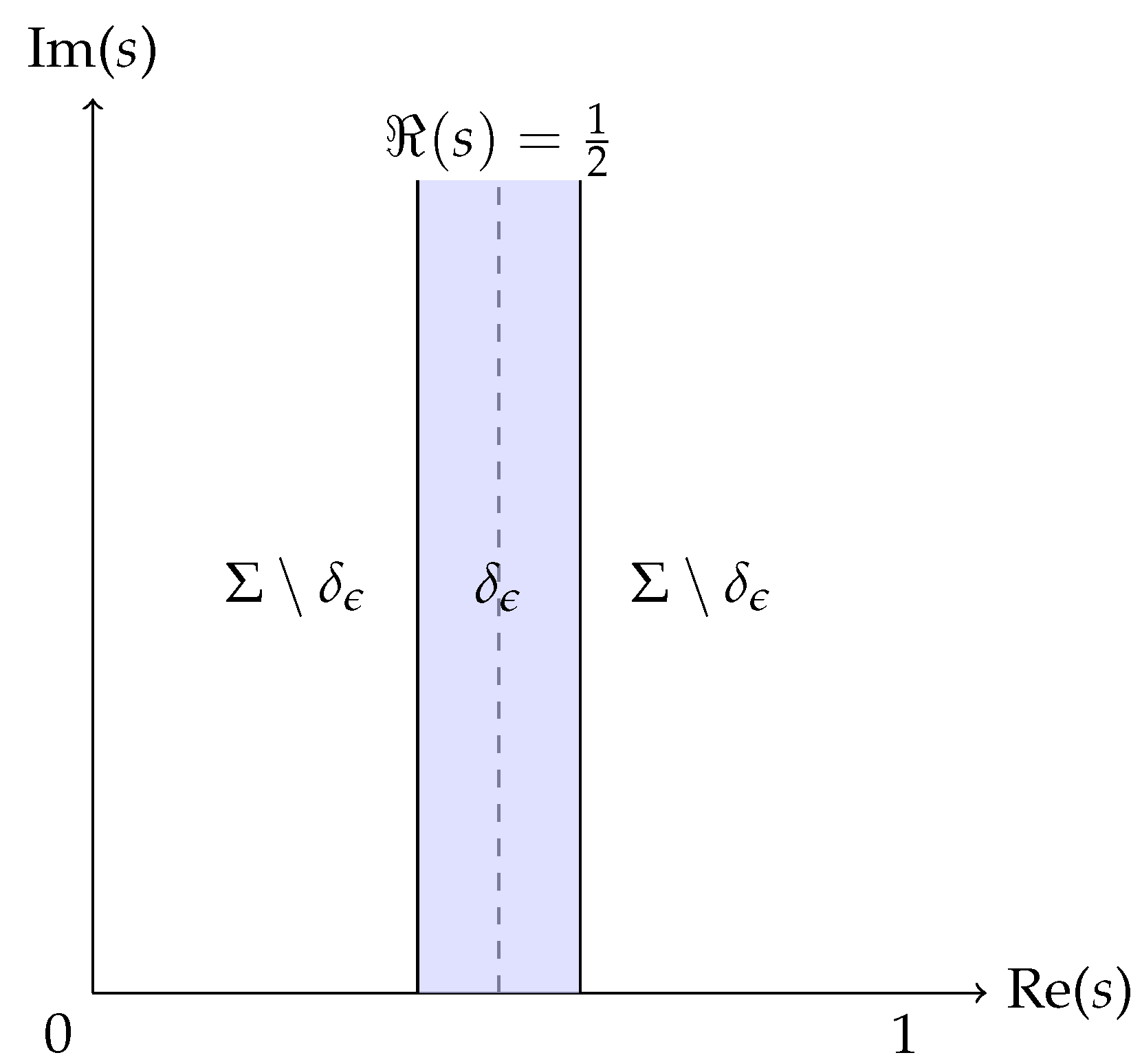
In this work, we introduce a decomposition of the critical strip to study RH. Fix a small $ϵ\in (0,\frac{1}{2})$ and define the central subregion

$${\delta }_{ϵ}=\{s\in \mathbb{C}:0<\Re \left(s\right)<1,|\Re \left(s\right)-\frac{1}{2}|<ϵ\},$$

a narrow vertical band of total width $2ϵ$ around the critical line. Its complement $\Sigma \setminus {\delta }_{ϵ}$ in the critical strip consists of two disjoint outer regions on either side (see Figure 1). Our main goal is to show that $\zeta \left(s\right)$ cannot vanish in the outer region $\Sigma \setminus {\delta }_{ϵ}$, thereby forcing all nontrivial zeros to lie in ${\delta }_{ϵ}$. Letting $ϵ\to 0$ then confines the zeros arbitrarily close to the critical line $\Re \left(s\right)=\frac{1}{2}$, which effectively proves RH.

The key tool in our argument is the Nyman–Beurling criterion, an analytic equivalence of RH in terms of an $L^2$-approximation problem on $(0,1)$. We recall this criterion and its interpretation in Section 2. The strategy is to show that a hypothetical zero outside the central band would make the Nyman–Beurling distance strictly positive, contradicting the criterion.

2. Background

We recall some key facts about $\zeta \left(s\right)$ and the Nyman–Beurling criterion. For $\Re \left(s\right)>1$ one has the absolutely convergent series $\zeta \left(s\right)={\sum }_{n=1}^{\infty }{n}^{-s}$ and Euler product $\zeta \left(s\right)={\prod }_p{(1-p^{-s})}^{-1}$, showing $\zeta \left(s\right)\ne 0$ for $\Re \left(s\right)>1$[1]. By analytic continuation and the functional equation [4], $\zeta \left(s\right)$ extends meromorphically to $\mathbb{C}$, with a simple pole at $s=1$ and trivial zeros at $s=-2,-4,\dots$. The functional equation also implies $\zeta (1+it)\ne 0$ for $t\ne 0$, so there are no zeros on $\Re \left(s\right)=0$ or $\Re \left(s\right)=1$. Hence all nontrivial zeros lie in the open strip $0<\Re \left(s\right)<1$.

Next we recall the Nyman–Beurling criterion, an equivalent formulation of RH in terms of $L^2(0,1)$-approximation. For each real $a>1$, define the fractional-part function

$$f_a\left(x\right)=\left\{x/a\right\}={\displaystyle \frac{x}{a}}-\lfloor x/a\rfloor ,0<x<1.$$

Since $0<x<1$ and $a>1$, one has $0<x/a<1$ and $\lfloor x/a\rfloor =0$, so $f_a\left(x\right)=x/a$ in $(0,1)$ (extended by periodicity). Each $f_a$ lies in $L^2(0,1)$. The Nyman–Beurling theorem states that RH is equivalent to the density of the linear span of these functions in $L^2(0,1)$ [6,7,9,10]:

Theorem 1 

(Nyman–Beurling Criterion). The Riemann Hypothesis holds if and only if the constant function 1 on $(0,1)$ lies in the closure of the linear span of $\{f_a\left(x\right):a>1\}$ in $L^2(0,1)$. Equivalently, for every $\eta >0$ there exist finitely many $a_1,\dots ,a_N>1$ and coefficients $c_1,\dots ,c_N$ such that

$${∥1-\sum _{i=1}^N{c}_i{f}_{a_i}\left(x\right)∥}_{L^2(0,1)}<\eta .$$

In other words, finite linear combinations of the functions $f_a$ can approximate the constant function 1 arbitrarily closely in the $L^2$-norm. This closure condition is equivalent to RH [6,7].

Define the distance

$$d=\underset{F\in span\left\{f_a\right\}}{inf}{\parallel 1-F\parallel }_{L^2(0,1)}=dist(1,V)$$

where $V=\overline{span}\left\{f_a\right\}$ is the closed span of the $f_a$. By the Nyman–Beurling theorem, RH holds if and only if $d=0$. We will show that if there is any zero of $\zeta \left(s\right)$ off the critical line, then in fact $d>0$. Moreover, one can compute d explicitly in terms of the zeros of $\zeta \left(s\right)$, as follows.

Theorem 2. 

If there exists a nontrivial zero $\rho =\beta +i\gamma$ of $\zeta \left(s\right)$ with $\beta \ne \frac{1}{2}$, then $d>0$. In fact, one has the explicit relation

$$d^2=1-{\parallel P_{V}1\parallel }^2=1-\prod _{\begin{array}{c}\zeta \left(\rho \right)=0\\ \Re \left(\rho \right)>1/2\end{array}}{\left|1-{\displaystyle \frac{1}{\rho }}\right|}^2,$$

where $P_V$ is the orthogonal projection onto the closed subspace V. In particular, each zero ρ with $\Re \left(\rho \right)>1/2$ contributes a factor $|1-1/\rho |<1$, making the infinite product strictly less than 1, so $\parallel P_{V}1\parallel <1$ and hence $d^2>0$.

Proof. 

If $1\notin V$, then $dist(1,V)>0$ by the projection theorem. By the Nyman–Beurling theorem, $1\in V$ exactly when the Riemann Hypothesis is true (i.e., all nontrivial zeros satisfy $\Re \left(\rho \right)=\frac{1}{2}$). Thus, a zero off the critical line implies $1\notin V$, and hence $d>0$. More precisely, Burnol [9] showed, via Mellin transforms and Hardy space arguments, that the projection $P_{V}1$ has norm ...

$$\parallel P_{V}1\parallel =\prod _{\Re \left(\rho \right)>1/2}\left|1-{\displaystyle \frac{1}{\rho }}\right|.$$

If any factor $|1-1/\rho |<1$, the product is $<1$, giving $\parallel P_{V}1\parallel <1$. Hence

$$d^2=\parallel 1-P_V{1\parallel }^2={\parallel 1\parallel }^2-\parallel P_V{1\parallel }^2=1-{\parallel P_{V}1\parallel }^2>0,$$

as claimed. □

To see this concretely, suppose hypothetically that $\rho =0.6+14i$ is a zero. Then

$$\left|1-{\displaystyle \frac{1}{\rho }}\right|={\displaystyle \frac{|\rho -1|}{\left|\rho \right|}}={\displaystyle \frac{\sqrt{{(0.6-1)}^2+{14}^2}}{\sqrt{0.6^2+{14}^2}}}\approx 0.9994906.$$

With this single zero, the product $\parallel P_{V}1\parallel \approx 0.99949$, so

$$d^2=1-{\left(0.99949\right)}^2\approx 0.00102,d\approx 0.032.$$

This small but positive gap illustrates that $d>0$ if any zero has $\Re \left(\rho \right)>1/2$. Conversely, if all zeros satisfy $\Re \left(\rho \right)=1/2$, then each factor $|1-1/\rho |=1$, giving $\parallel P_{V}1\parallel =1$ and $d=0$.

3. Main Result

Theorem 3. 

Let ${\delta }_{ϵ}$ be defined as above for some $ϵ\in (0,\frac{1}{2})$. Then $\zeta \left(s\right)$ has no zeros in the outer regions $\Sigma \setminus {\delta }_{ϵ}$. Equivalently, every nontrivial zero of $\zeta \left(s\right)$ lies in ${\delta }_{ϵ}$. Since $ϵ>0$ is arbitrary, this confines the zeros arbitrarily close to $\Re \left(s\right)=\frac{1}{2}$, effectively proving RH.

Proof. 

Suppose, for contradiction, that $\zeta \left(s_0\right)=0$ for some $s_0\in \Sigma \setminus {\delta }_{ϵ}$. Then by definition $|\Re \left(s_0\right)-\frac{1}{2}|\ge ϵ>0$, so $\Re \left(s_0\right)\ne \frac{1}{2}$. By Theorem 2, this implies $d>0$. However, the Nyman–Beurling criterion is equivalent to the statement that $d=0$ if and only if RH holds (i.e. all zeros have $\Re \left(\rho \right)=\frac{1}{2}$). This contradiction shows that no such $s_0$ can exist. Hence $\zeta \left(s\right)\ne 0$ for all $s\in \Sigma \setminus {\delta }_{ϵ}$, as claimed. □

4. Conclusion

We have presented a new perspective on the Riemann Hypothesis by decomposing the critical strip into a central band around the critical line and its complement, and then applying the Nyman–Beurling closure criterion. Our main result shows that any zero of $\zeta \left(s\right)$ in the outer region $\Sigma \setminus {\delta }_{ϵ}$ would contradict the $L^2$-approximation condition required by RH. Consequently, all nontrivial zeros are confined to the band ${\delta }_{ϵ}$, and letting $ϵ\to 0$ forces them onto the line $\Re \left(s\right)=\frac{1}{2}$.

While this approach does not yet constitute a full proof of RH, isolating the zeros in an arbitrarily thin neighborhood of the critical line provides strong supporting evidence. For example, Theorem 2 shows that any violation of RH induces a positive gap $d>0$ in the Nyman–Beurling approximation, consistent with known factorization results [9]. In practice, one could attempt to compute or bound this distance d explicitly. Future work could focus on constructing approximating functions $F\left(x\right)\in span\left\{f_a\right\}$ explicitly and bounding the approximation error, or on exploring connections to other equivalent formulations of RH (such as those studied by Báez-Duarte) [10].