1. Introduction
Plastics are used in the manufacture of various products such as clothing, tires, cosmetics, paints, bags, rope, and netting. Plastics, made from a specific type of polymer, are lightweight, flexible, corrosion resistant, dielectric, thermal insulators, insoluble in water, most are not biodegradable, have the potential to absorb, release and transport chemicals, and gradually decompose by erosion or fragmentation through biological, chemical, and physical processes until they become solid microplastic (MP) particles with a size of 1 μm to 5 mm [
1], or nanoplastics with a size of 1 nm to 1 μ [
2].
In the analysis of plastic particles, it is desirable to know the shape, size, concentration, refractive index (RI), and effective refractive index of the sample (colloid or suspension). Tuoriniemi J. et al. [
3] determined the mean diameters (
: 100, 300, and 460 nm) and number concentrations (
) of polystyrene (PS) particles by fitting coherent scattering theory (CST) to the effective refractive index (
) measured by SPR for a series of dilutions. R. Márquez-Islas et al. [
4] obtained the refractive index, size (radii of ~25 nm), and concentration of non-absorbing spherical nanoparticles in a colloid, using a mathematical method and measurements with the Abbe refractometer and with dynamic light scattering (DLS).
R.C. Thompson et al.[
5] collected and quantified microplastic debris on beaches, estuarine and subtidal sediments, where nine polymers were identified : acrylic, alkyd, poly (ethylene: propylene), polyamide (nylon), polyester, polyethylene, polymethacrylate, polypropylene, and polyvinyl alcohol ; and demonstrated in small aquariums, that species would ingest microplastics within a few days. Microplastic debris is found throughout the natural environment, as it is transported through air and water, and has been detected in food, beverages, terrestrial animals, birds, and fish, with emerging evidence of negative effects [
6]. A study of water distribution networks across Britain, from the treatment plant to the customer's tap, detected mainly polyamide (PA), polyethylene terephthalate (PET), polypropylene (PP), and polystyrene (PS), among 19 types of polymer particles, for sizes greater than 25 µm diameter [
7].
Other research provides the presence, distribution, and potential ecological risks of MPs in terrestrial ecosystems [
8], in water and aquatic systems [
9], and ecotoxicological effects on aquatic organisms [
10]. But MPs have not only been found in the environment; they have also been found in the human body, including blood. MPs are absorbed by the human body and transported through the bloodstream. In a study of 20 healthy volunteers, blood concentrations ranged from 1.84−4.65 μg/mL, with an average length of 7−3000 μm and an average width of 5−800 μm, and with 24 polymer types, with an abundance of polyethylene (32%), ethylene propylene diene (14%), and ethylene-vinyl-acetate/alcohol (12%), whose presence poses the risk of potential detrimental effects, such as vascular inflammation, accumulation in major organs, and alterations in immune response, hemostasis, and thrombosis [
11]. The MPs have been found in food products like table salt, shellfish, fish, processed foods like honey, milk, sugar, sardines, sprats, dried fish, and tea bags[
12]. Different studies have been carried out to assess the effects of the ingestion of MPs: Sapkale et al evaluated the oxidative damage caused by microplastics with size from in 8–100 µm in the ram's horn snail
Indoplanorbis exustus, and found that the lethal concentration 50 (LC
50) was calculated to be 872 mg L-
1 (or 0.087% w/v) after 96 h of exposure [
13]. In another study, Berber evaluated the genotoxicity of polystyrene microplastic in the aquatic species
Daphnia magna, calculating an LC
50 of 808.97 μg mL
-1 (or 0.08 % w/v) [
14]. The common techniques used to determine one or more characteristics for nanoparticle detection are electron microscopy (EM) [
3], spectroscopy, dynamic light scattering (DLS)[
3,
4] , and to detect microparticles, there are microspectroscopy, Fourier Transform Infrared (FTIR) [
5,
7,
15], and Raman[
16]. Therefore, it is important to establish regulations for industries that produce plastic, implement corrective measures for pollution, investigate the effects on living beings, and develop methods to detect and analyze nanoplastics and microplastic particles.
In this investigation, it is important to estimate the thickness of the thin gold film adhered to the prism surface by means of the theoretical experimental adjustment of the SPR curves[
17]. The surface plasmon resonance technique[
18,
19,
20,
21] is employed to obtain the reflectance and resonance angle when the suspensions are placed in a cell prism. To determine the effective refractive index and the percentage of the fill fraction f (hereafter concentration) that corresponds to each reflectance, the scattering theory [
22]and the Mie scattering theory[
23] are applied. To simulate reflectance and calculate the effective refractive index of colloids (nanoparticles in distilled water) and suspensions (microparticles in distilled water), the formulas of coherent scattering theory [
24,
25] and the van der Hulst model [
26] are used, respectively. In the experiments, we used a portable optomechatronic system and applications developed in LabVIEW and MATLAB [
27], where the optical sensor (semicircular prism, thin gold film, and cell for samples) was placed in a Kretschmann-Raether configuration. Suspensions of 5 µm diameter SPSP in distilled water are prepared with different concentrations (0.00, 0.02, 0.05, 0.50, and 1.00 %). Each suspension is then scanned by the system to obtain its reflectance, which is normalized and adjusted to the reference point of the distilled water sample. Finally, its effective refractive index and corresponding concentration are determined using reflectance (resonance angle, depth) and the van de Hulst formula (real part and imaginary part of effective refractive index).
2. Theory
In physics, chemistry, and biology, surface plasmon resonance (SPR), and coherent scattering theory (CST) have gained significant importance in the research of diverse topics, including the study of colloids and suspensions (fluids containing nanoparticles and microparticles, respectively), as they allow us to understand the iterations of light with samples [
3,
4,
17,
22,
23].
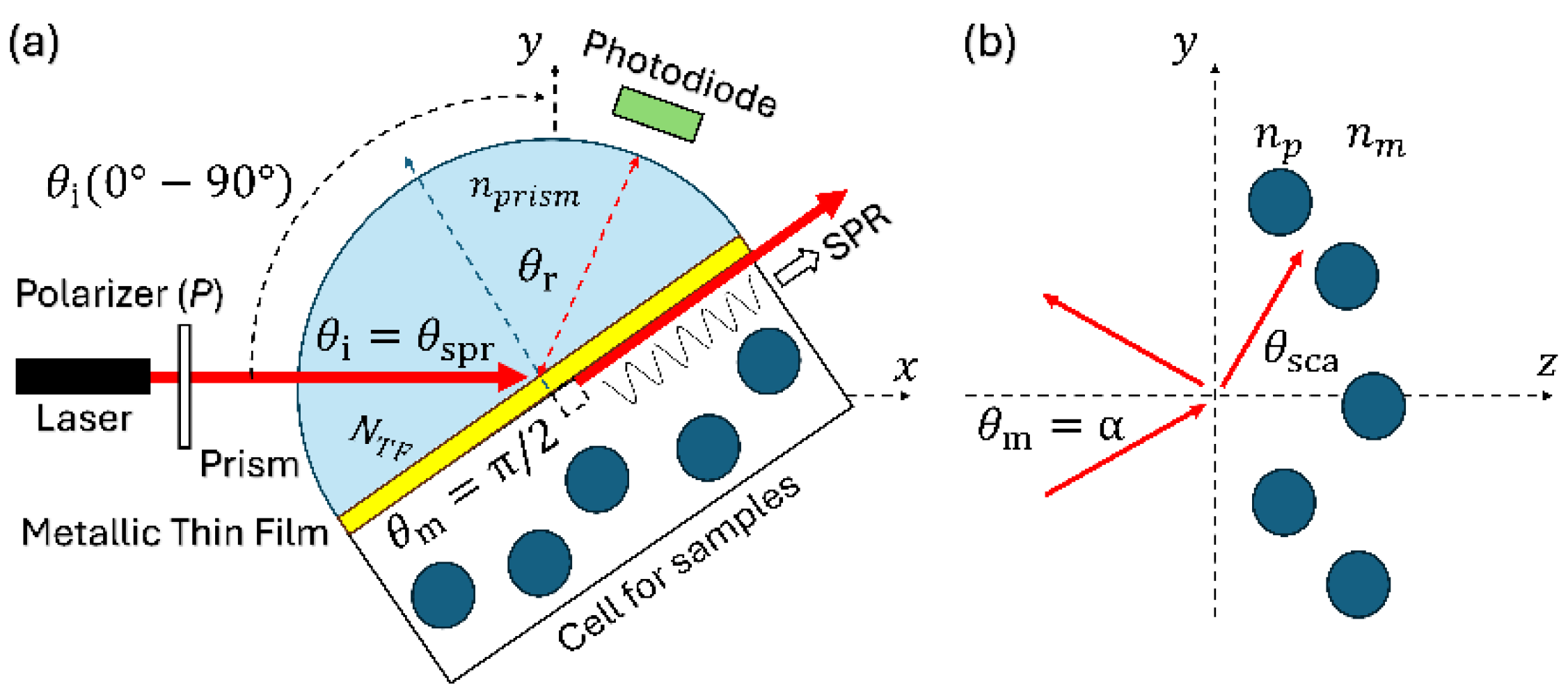
Figure 1 shows a sensor with a coherent light source, a polarizer (
), a photodiode, a semicircular prism, a metallic thin film (TF), and particles in a dielectric medium to illustrate the phenomena of SPR and coherent scattering.
A film is considered thin when all interference effects in reflected or transmitted coherent light can be detected. Interference effects depend on the illumination source and the thickness and refractive index (RI) of each layer, where each layer is represented by a 2x2 matrix. In normal coatings, the films (metals and dielectrics) will be thin, while the substrates will be thick. The reflectance, admittance, and the characteristic matrix, of an assembly of thin films for oblique incidence in absorbing media, are expressed respectively as [
28]:
where
is the reflection coefficient,
is the tilted admittance on the incident medium,
is the tilted admittance of the substrate or emergent medium,
is the optical admittance of the multilayer system,
and
represent the amplitude of the magnetic and electric fields, respectively.
is the phase thickness,
is the wavelength,
is the physical thickness,
is the complex refractive index,
is the angle of incidence,
is the layer number from 1 to
,
, for
- polarization
, for
- polarization
, and
the optical admittance in free space equal to
.
SPR was developed over time by several researchers[
18,
19,
20,
21] . In SPR, surface plasmon excitation occurs at the interface of a metallic thin film and a dielectric medium, when a coherent light source undergoes total internal reflection. The coherent light beam then excites the surface electrons of the metallic film, causing them to interact with the dielectric medium containing the sample (biomolecules, analytes, or particles). The SPR technique allows the detection of very small changes in the refractive index of a metallic surface (which has surface plasmons, or collective electron oscillations) when the molecules or particles in the sample bind to the metal surface while scattering (plasmonic scattering) detects the light scattered by these molecules/particles at the surface.
From CST researchers, two formulas are presented here to calculate the effective refractive index. Equation (4) for a dilute monodisperse system of randomly located spherical particles, developed by García-Valenzuela et. al [
24,
25], and equation (5) for a monodisperse system (isotropic and independent of polarization) of spherical particles, developed by H.C. van de Hulst [
26]:
where
is the refractive index of the medium surrounding the particles,
is the imaginary unit (
),
is the number concentration of the particles,
is the wavenumber of the incident wave in the medium, and the functions
that can be
,
or
) is the forward-scattering amplitude,
for s-polarization (TE: Transverse Electric) and
for p-polarization (TM: Transverse Magnetic) are the components of the amplitude scattering matrix, calculated by Mie scattering theory [
23].
, which has the form
[
3], is the angle of incidence in the dielectric medium for the evanescent field, and
[
24,
25] is the scattering angle.
can be calculated from the resonance angle
by sequentially applying Snell's law at the interfaces (Prism – Thin film of gold – Matrix material, dielectric medium, colloid, or suspension) [
3,
24,
25]. Also
is the relative refractive index,
is the size parameter,
is the wavelength in vacuum,
is the wavelength of the incident light in the surrounding medium,
is the refractive index of a spherical particle,
is the radius of the spherical particle,
is the particle fill fraction, and
is the volume of a spherical particle.
In CST [
22], the study of incident coherent light and coherent light scattered in a certain direction, passing through spherical particles of any size and material immersed in a surrounding medium (transparent, homogeneous, and isotropic), is described with formulas that are exact solutions to Maxwell's equations, which were developed by Gustav Mie [
23]. Light scattering is the phenomenon where light is redirected by an object. The scattered wave is composed of several partial waves, whose amplitudes depend on
(mth electric partial wave),
(mth magnetic partial wave),
and
:
where
and
are the amplitude functions,
and
are the angular functions,
is the number of terms in the summation,
is the maximum number rounded to the nearest integer,
and
are the partial derivatives of
and
respectively, the argument
takes on the values
or
,
and
are the Bessel functions of positive and negative half-order, respectively. The angular functions
and
containing the scattering angle
,
is the Legendre polynomial of degree
, and
.
In this work, with an optomechatronic system and applications that we have developed, the processing of the signals for SPR and CTS is carried out in real-time and post-processing for the analysis of the signals, from the measurement of the thin film deposited on the prism to the detection of spherical polystyrene particles in a solution and the calculation of effective refractive index.
3. System and Methodology
The Optomechatronic System [
27] is formed of a laser diode with a wavelength of
(Mod. LPM690-30C, Newport Corporation, Irvine, California, USA), a linear polarizer
(Mod. 5511 General Purpose Sheet Polarizer, 450-750 nm, Newport Corporation, Irvine, California, USA), a semicircular prism (FK5, n=1.4585 [
29]) with gold metallic thin film (Purity of 99.99%, Kurt J. Lesker Co., Clairton, PA, USA) and glass cell to colloids or suspension samples (5 μm diameter SPSP, Number 02705-AB, SPI Supplies, West Chester, Pennsylvania, USA), a silicon photodiode (Mod. S1226-8BK, Hamamatsu Photonics K.K., Hamamatsu City, Japan), two motorized rotation stages (Mod. 8MR180-2, Standa LTD, Lithuania), a cabinet with power and control electronics, control program (LabVIEW, Version 2020, National Instruments, Ciudad Juárez, México), simulation and post-processing program (MATLAB, Version 2024, MathWorks, Inc., Massachusetts, USA), ana personal computer (Windows 10, Intel Core i7, 2.6 GHz, 12 GB RAM, 1 TB SSD).
According to the concentration and volume formula for dilutions (), for an initial concentration of 1% of SPSP in distilled water and a final volume of 3000 μL, by adding an initial volume of 0, 60, 150, 1500, and 3000 μL, a final concentration percentage of 0.00, 0.20, 0.05, 0.50 and 1.00 % of PS in distilled water can be obtained.
Once the samples are obtained, the system is adjusted with the laser and prism at 0 and 90 degrees. Each homogenized sample of the PS solution is placed in the prism cell, and an angular scan of 30 to 80 degrees is performed to obtain the reflectance signal with SPR-Scattering.
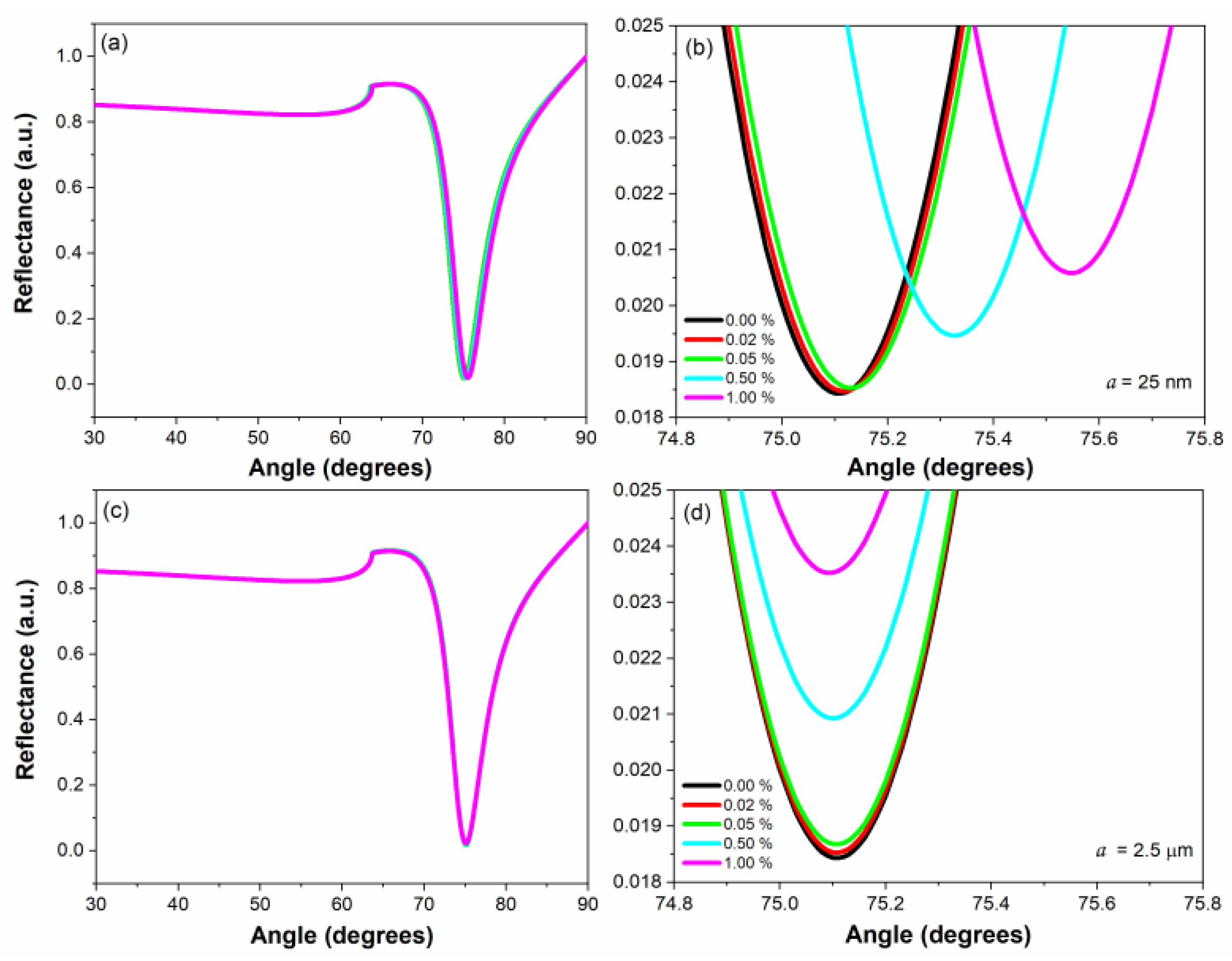
The reflectance (Eq. 1-3) of the sensor (
Figure 1) with SPR-Scattering can be simulated (
Figure 2a-b, signal in black) when the coherent light (
is p-polarized, the gold thin film (
[
30], the thickness of 51 nm) in the prism (
) adjoins a dielectric medium (for example, distilled water with
, and there is a total internal reflection (
). From the reflectance, the resonance angle
is obtained, which is used to obtain the angle of incidence in the medium
i using Snell's law, and the scattering angle
.
Then, to calculate the effective refractive index (Eq. 4, 6-14) for spherical (radius
) polystyrene (
) particles in distilled water with a concentration of
, it is necessary to calculate
(1.2125
4.36
),
(1.2126
4.3934
) and
(1.6082
) for the corresponding relative refractive index
, the wavenumber of the incident wave in the medium
, the size parameter
3273,
number of terms in the summation
,
+
, and
, where
-
;
, and
for
,
8.0816
2.8428
and
1.2067
3.4738
. The result of the calculation is
=
, which is simulated as a medium in reflectance (Eq. 1), is graphed in
Figure 2a-b (red signal). The same procedure is performed for concentrations of 0.05, 0.50, and 1.00 % (
Figure 2a-b, signals in green, cyan, and magenta, respectively).
For particles with radii greater than 850 nm, Eq. (4) takes values greater than
and then values that grow exponentially, so Eq. (5) or Eq. (15) can be used to calculate the
of 5 µm diameter or 2.5 µm radius SPSP in distilled water with different concentrations.
Table 1 shows the effective refractive indices calculated for SPSP of 25 nm and 2.5 µm radius, using Eq. (4) and Eq. (5) or (15), respectively.
As can be seen in
Figure 2a-b and
Table 1, for nanoparticles, the resonance angle shifts to the right as particle concentration increases, and their refractive index can be differentiated from the fifth digit. Whereas in
Figure 2c-d and
Table 1, for microparticles, the reflectance has almost the same resonance angle and the depth tends to be smaller as particle concentration increases, and the refractive index can be differentiated from the sixth digit.
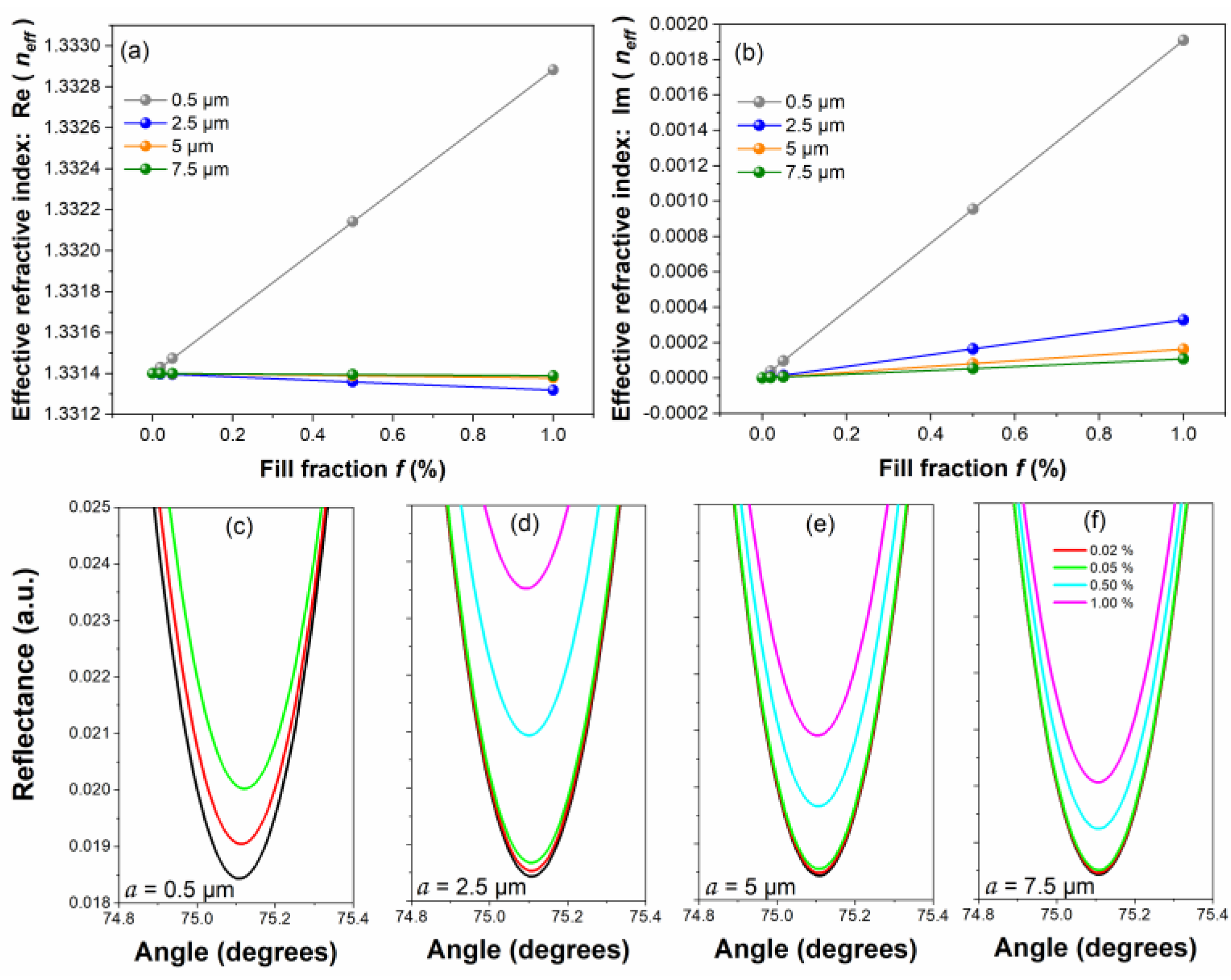
Figure 3 a-b shows the real and imaginary parts of the effective refractive index for different solutions with spherical particles of 0.5 µm, 2.5 µm, 5 µm, and 7.5 µm radius in distilled water, with concentrations of 0-1%. Figures 3 c-f show the respective reflectances, where the reflectance depth values for spherical particles with a radius of 7.5 µm (
Figure 3f) are within the reflectance of the 5 µm ones (
Figure 3e), the 5 µm reflectance depth values are within the reflectance of the 2.5 µm ones (
Figure 3d), and the 2.5 µm values are within the reflectance of 0.5 µm (
Figure 3c). Therefore, with the angular scanning technique in SPR, the size of the particles can only be differentiated from 1% of the filling fraction, if the diameter or radius of the particle is not known as a priori.
From Eq. (15), the real and imaginary parts of the effective refractive index will be given by:
where
is equal to
if
and
.
Knowing the refractive index of the prism (
), the metallic film (
) and its thickness (51 nm), and the water (
) as the base sample, we have an initial reference point (
) for
:
and
. Thus, the real part will be affected by changes in the resonance angle and the imaginary part by the depth of the reflectance. As mentioned above, different mathematical methods have already been demonstrated to know the three main parameters (
), so in this situation we are only going to measure the concentration knowing a priori the refractive index (
) and the radius (
) of the spherical particle. For the deeper points of the signals (
Figure 2d and 3d), the effective refractive index (sample in the dielectric medium) can be calculated by giving values to
in equations 15 b-c until they coincide with the minimum value of its reflectance.
In this way, the methodology consists of obtaining the theoretical value of the effective refractive index () for each concentration of the colloid or solution sample, substitute it in the reflectance formula as the dielectric medium, and graph the expected theoretical SPR-Scattering signal. The experimental air reflectance is then fitted to the theoretical signal (simulated) to determine the thickness of the gold film deposited on the flat face of the semicircular prism. Finally, the experimental reflectance of the distilled water is adjusted to the simulated one, to know the displacements (degrees), amplitudes (reflectance), and losses or gains, which must be applied to all the experimental signals to find their respective effective refractive index and concentration using Eq. 15 b-c.
4. Results and Discussion
Suspensions must be homogenized before use, they must not be frozen or shaken vigorously, at least ten particles must be measured in image visualization, store at room temperature with the bottle tightly covered, and in case of spillage, be sure to rinse with plenty of water and dispose of it as normal laboratory waste. To ensure a homogeneous suspension of samples with 5 µm diameter or 2.5 radius SPSP (manufactured by SPI Supplies), the bottle was gently inverted several times until no sediment or clumps were observed. It was then immersed in an ultrasonic water bath (C008 40 KHz, AcmeSonic Ltd., Shenzhen, China) for one minute at low power. The desired sample was immediately withdrawn from the bottle using a pipette (Ecopipette 20-200 & 100-1000 µL, CAPP AHN Biotechnologie GmbH, Nordhausen, Germany). The concentration of SPSP was 0.00, 0.02, 0.05, 0.50, and 1.00 % in distilled water.
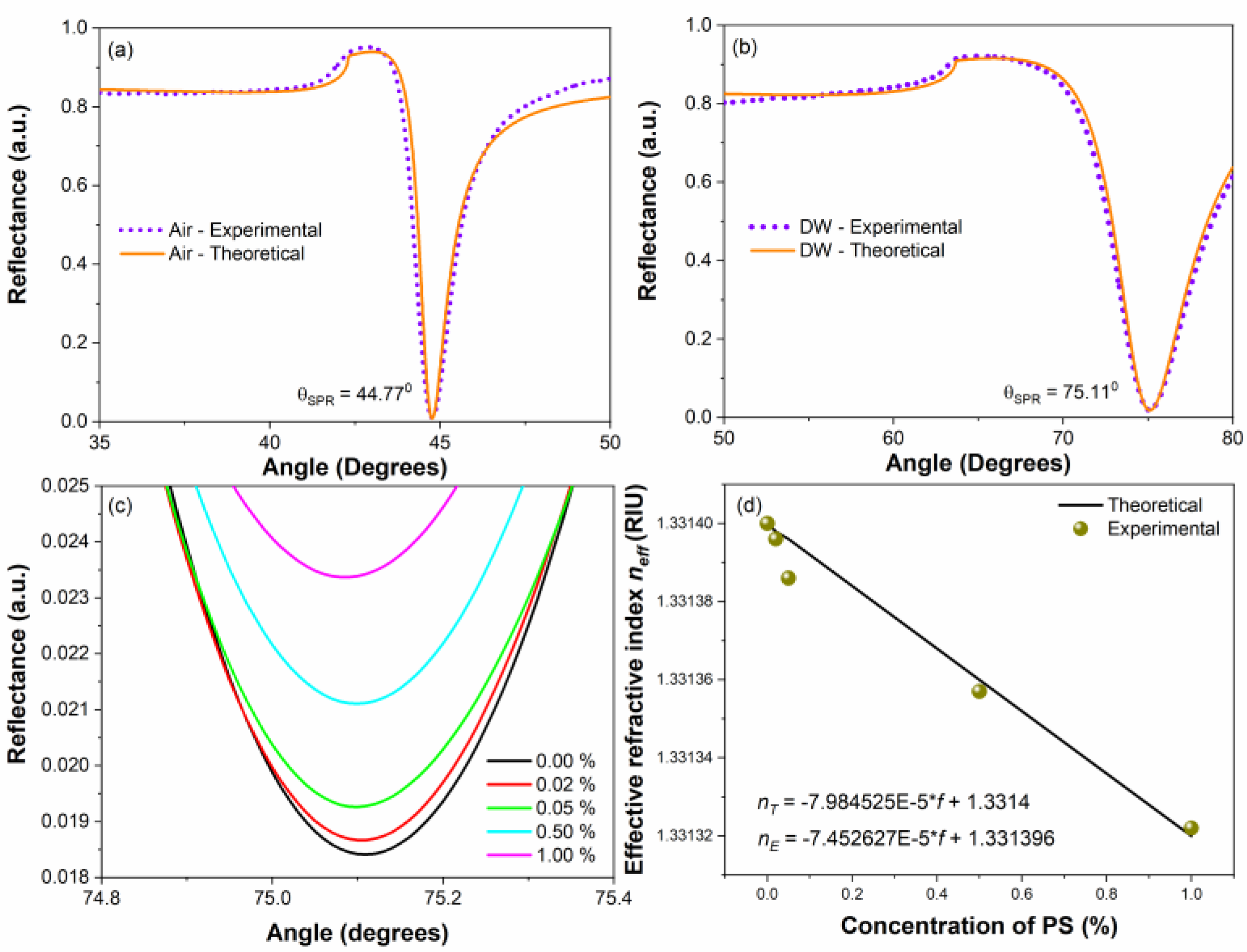
Figure 4 (a) shows the adjustment of the experimental air sample with the theoretical signal to determine the thickness of the thin gold film deposited on the flat face of the prism, resulting in a 51 nm thin gold film.
Figure 4 (b) shows the adjustment of the reflectance of the distilled water sample to the theoretical signal with a reference point at 75.11°, 0.0184 depth. The displacement, amplitude, and gain/loss parameters used in the adjustment are subsequently applied to all samples, resulting in
Figure 4 (c).
To calculate
and
from the magenta signal shown in
Figure 4c with its resonance angle and depth of
and
, respectively, with relative refractive index (
=1.1920), particle size (
=32.7286), and forward scattering
, the value of
is introduced in equations (15b) and (15c), from 0.00 with increments of 0.01, until the value of
+
introduced in the external medium of thin films gives us the value of the angle of resonance and the depth of the reflectance. So, in this case (magenta signal of
Figure 4c), the effective refractive index is
for a concentration of 0.97 %. The effective refractive indices and their concentrations obtained for the reflectances in
Figure 4c are shown in
Table 2, where the smallest error was 0.03 % (
and
).
The optoelectronic system has a resolution of 0.01 degrees and a precision of 0.0071 RIU (Refractive Index Unit). For very small concentrations (0.00, 0.02, 0.05, 0.50, and 1.00 %) of 2.5 μm radii SPSP in distilled water, the experiment provides a good linear fitting of
=0.986, a sensitivity of -7.4526
RIU/% (
Figure 4d), LOD=0.001% and LOQ=0.0035%. It is very important to correctly determine the thickness of the thin gold film (51 nm), since it determines the measurement range in the reflectance amplitude, equal to 0.0051 nm, where the concentrations and the extinction coefficient are mainly measured since
is approximately equal to 1.3314 for all solutions. To avoid potential errors when the laser power varies, a beam splitter and a photodiode were added to the portable optoelectronic system to provide reference power.
After each test, it is recommended to recover the sample by subtracting the solution with the corresponding or labeled syringe for each sample, then clean the cell with methanol by introducing it into its corresponding syringe and leaving it for 1 minute, finally rinsing about 5 times with distilled water.
A sample of 5 µm diameter or 2.5 radius SPSP suspension was taken from the manufacturer's bottle and allowed to dry on a slide for microscopic observation (
Figure 5). The diameter measurements (4.6; 4.2; 3.8; 4.6; 4.7; 5.1; 4.9; 5.5; 5.3; and 5.2) yielded an average of 4.76 μm and a standard deviation of 0.45 μm.
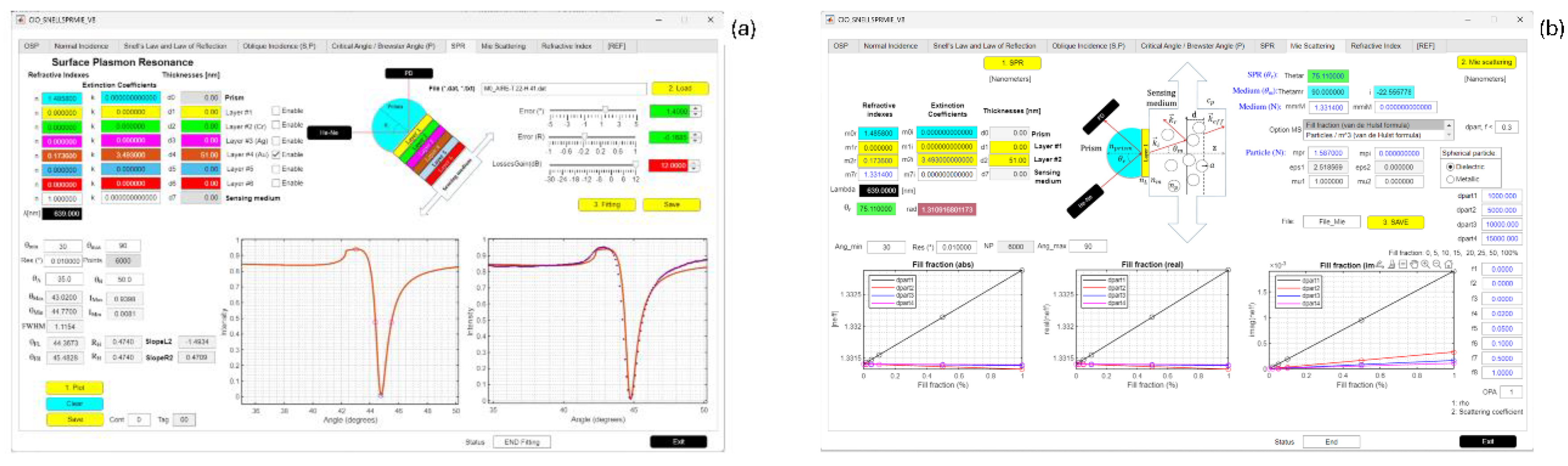
Figure 6 shows two main functions of the application developed in MATLAB for our portable optomechatronic system. The reflectance function with SPR (
Figure 6a) is used to simulate a semicircular prism with 1-6 thin films and a dielectric medium at a given wavelength and to fit an experimental signal to a simulated theoretical signal. The reflectance function with Mie Scattering (
Figure 6b) is used to simulate a semicircular prism with 1-2 thin films and a dielectric medium at a given wavelength and to calculate the effective refractive index (Eq. 4 or 5) using Mie scattering theory.
For the simulation of SPR curves based on the Fresnel formalism, there is the free software WinSpall 3.01 [
31]. There are also tables [
32,
33,
34], MATLAB functions [
35], calculator [
36], and software [
37] that can help us verify, obtain, or display, the Mie theory's scattering functions for spherical particles.
Figure 1.
(a) Sensor, with Kretschmann-Raether configuration, for the detection of particles in a colloid or suspension, and (b) reflection and transmission of coherent light in a dielectric medium with particles. .
Figure 1.
(a) Sensor, with Kretschmann-Raether configuration, for the detection of particles in a colloid or suspension, and (b) reflection and transmission of coherent light in a dielectric medium with particles. .
Figure 2.
Simulation of reflectance for a solution containing SPSP of 25 nm (a-b) and 2.5 µm (c-d) of radius, with concentrations of 0.00, 0.02, 0.05, 0.50, and 1.00 % in distilled water. The prism is an FK5, which has a thin film of gold (51 nm of thickness) and a cell for the sample of colloid or solution.
Figure 2.
Simulation of reflectance for a solution containing SPSP of 25 nm (a-b) and 2.5 µm (c-d) of radius, with concentrations of 0.00, 0.02, 0.05, 0.50, and 1.00 % in distilled water. The prism is an FK5, which has a thin film of gold (51 nm of thickness) and a cell for the sample of colloid or solution.
Figure 3.
Simulation of scattering and SPR. (a) refractive index, (b) extinction coefficient, and (c-f) respective reflectances, for solutions with spherical particles of 0.5 µm, 2.5 µm, 5 µm, and 7.5 µm radius in distilled water.
Figure 3.
Simulation of scattering and SPR. (a) refractive index, (b) extinction coefficient, and (c-f) respective reflectances, for solutions with spherical particles of 0.5 µm, 2.5 µm, 5 µm, and 7.5 µm radius in distilled water.
Figure 4.
(a) Fitting of the experimental reflectance of air to the theoretical signal, (b) fitting of the experimental reflectance of distilled water to the theoretical signal, (c) SPR-Scattering reflectance signals for different percentages of PS in distilled water, and (d) theoretical calculation and experimental measurement for different concentrations.
Figure 4.
(a) Fitting of the experimental reflectance of air to the theoretical signal, (b) fitting of the experimental reflectance of distilled water to the theoretical signal, (c) SPR-Scattering reflectance signals for different percentages of PS in distilled water, and (d) theoretical calculation and experimental measurement for different concentrations.
Figure 5.
Polystyrene microspheres of 5 μm µm diameter or 2.5 radius SPSP viewed with a digital microscope (VHX-5000, Keyence Corporation, Osaka, Japan).
Figure 5.
Polystyrene microspheres of 5 μm µm diameter or 2.5 radius SPSP viewed with a digital microscope (VHX-5000, Keyence Corporation, Osaka, Japan).
Figure 6.
Application developed in MATLAB to process the theoretical and experimental signals of (a) SPR and (b) Scattering.
Figure 6.
Application developed in MATLAB to process the theoretical and experimental signals of (a) SPR and (b) Scattering.
Table 1.
Theoretical effective refractive indices for spherical polystyrene particles with a radius of 25 nm and 2.5 µm with concentrations of 0.00, 0.02, 0.05, 0.50, and 1.00% immersed in distilled water.
Table 1.
Theoretical effective refractive indices for spherical polystyrene particles with a radius of 25 nm and 2.5 µm with concentrations of 0.00, 0.02, 0.05, 0.50, and 1.00% immersed in distilled water.
| |
(Eq. 4)
|
(Eq. 5 or Eq. 15)
|
| % PS |
|
|
|
|
| 0.00 |
1.331400 |
0 |
1.331400 |
0 |
| 0.02 |
1.331450 |
1.3816E-7 |
1.331398 |
6.5749E-6 |
| 0.05 |
1.331524 |
3.4548E-7 |
1.331396 |
1.6437E-5 |
| 0.50 |
1.332644 |
3.4656E-6 |
1.331360 |
1.6437E-4 |
| 1.00 |
1.333893 |
6.9550E-6 |
1.331320 |
3.2874E-4 |
Table 2.
Experimental effective refractive indices for SPSP in distilled water. The spherical PS particles have a 5 μm diameter or 2.5 radius, a refractive index of , and different concentrations (%).
Table 2.
Experimental effective refractive indices for SPSP in distilled water. The spherical PS particles have a 5 μm diameter or 2.5 radius, a refractive index of , and different concentrations (%).
|
(Eq. 15b and Eq. 15c)
|
|
|
|
| 0.00 |
1.331400 |
0 |
| 0.05 |
1.331396 |
1.6437E-5 |
| 0.17 |
1.331386 |
5.5856E-5 |
| 0.53 |
1.331357 |
1.7423E-4 |
| 0.97 |
1.331322 |
3.1888E-4 |