Elastic Curves and Euler-Bernoulli Constrained Beams from the Perspective of Geometric Algebra

1. Geometric Algebra

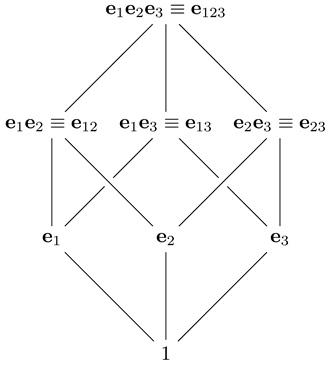
In the following section we use the convention of denoting the scalars with Greek letters, the vectors with lowercase Latin letters, and multi-vectors and blades with capital Latin letters. The planar Euclidean geometric algebra ${\mathbb{G}}^3\equiv C{\ell }_{3,0}\left(\mathbb{R}\right)$ is generated by the set of orthonormal basis vectors $E=\{e_1,e_2,e_3\}$ for which the so-called geometric product is defined with properties

$$\begin{array}{}\mathrm{(1)}& \hfill e_i{e}_i& =1\hfill \mathrm{(2)}& \hfill e_i{e}_j& =-e_j{e}_i,i\ne j\hfill \end{array}$$

The pseudoscalar is denoted by $I_3$. The structure of the algebra can be illustrated in the diagram below

Blades are also denoted by index concatenation as above. An overview of the topic, including its applications to physics, can be found in the books of MacDonald [6] and Hestenes [7], Doran and Lasenby [8].

1.1. Products in GA

The geometric product of two vectors can be decomposed into a symmetrical scalar product and an antisymmetrical wedge product:

$$ab=a\ast b+a\wedge b,a\ast b=b\ast a,a\wedge b=-b\wedge a$$

The wedge product is called also exterior by some authors. For higher-dimensional objects, the scalar product is defined simply as the scalar part of the geometric product between multivectors:

$$A\ast B:={〈AB〉}_0$$

(3)

where the notation 〈〉_k denotes the part of the multivector of grade k.

Furthermore, the wedge product is extended for blades (products of basis vectors) as

$$a\wedge A_k:={\displaystyle \frac{1}{2}}\left(a{A}_k+{(-1)}^k{A}_{k}a\right)$$

(4)

The interior product, called sometimes also Hestenes contraction (see the discussion in [12]), is a symmetrical operation defined for multi-vectors of grades r and l, respectively, as

$$A_r·B_l:=\sum _{|r-s|>0}{〈AB〉}_{|r-s|}$$

while for scalars $\alpha ·A=0$. Therefore, for vectors $a·b=a\ast b$ as expected from the vector calculus.

It is noteworthy also that for a vector and a blade [9] [Ch. 1, p.3]

$$a·A_k={\displaystyle \frac{1}{2}}\left(a{A}_k-{(-1)}^k{A}_{k}a\right)$$

which extends the geometric product decomposition also to the products of vectors and blades:

$$aA=a·A+a\wedge A$$

(5)

It should be noted that unlike the scalar product the contraction is not associative in the general case.

The cross product for the 3 dimensional space can be expressed as

$$a\times b=-I_3(a\wedge b)$$

1.2. Principal Automorphisms

Three principle automorphisms can be identified in Geometric Algebra:

• vector reflection: $v\mapsto -v$
• geometric product reversion: ${\left(ab\right)}^{\sim }:=ba$
• inverse blade, or Hermite, automorphism (IBA): $A^{\#}:=A^{-1}$, for the respective blade

While the first two automorphisms are broadly recognized, the third one is appreciated less. The IBA is obviously defined only for non-nilpotent blades. Technically speaking, the reversion and IBA are anti-automorphisms [10].

1.3. Norm

For Clifford algebras with unspecified signatures the norm of a multivector can be defined as

$$\left|\right|A\left|\right|:=\sqrt{A\ast A^{\#}}$$

(6)

For vectors we have the special case $\left|\right|v\left|\right|=\sqrt{v·v}=\sqrt{v^2}$, which reminds of the formula for the absolute value of a scalar. For positive signatures, i.e. for ${\mathbb{G}}^3$, we have the equivalent formula

$$\left|\right|A\left|\right|=\sqrt{A\ast A^{\sim }}$$

1.4. Elements of Geometric Calculus

The geometric derivative subsumes divergence, curl and gradient operations of the vector calculus. Introduction on the topic can be found in [11]. It is defined in the simplest way as

$$\nabla f:=e^j{\partial }_{j}f,{\partial }_j\equiv {\displaystyle \frac{\partial }{\partial x_j}}$$

where $e^j$ are the components of the dual or reciprocal basis, such that

$$x=x_i{e}^j=x^i{e}_i$$

for an arbitrary vector x. For the dual basis $e^i\ast x=x_i$ since $e^i{e}_j=e^i\ast e_j={\delta }_{ij}$, where the $\delta$ denotes the Kronecker’s symbol.

The geometric derivative is co-ordinate independent. Moreover, it splits into a grade-lowering and grade-increasing parts

$$\nabla f=\nabla ·f+\nabla \wedge f$$

Therefore, in many cases ∇ can be treated as a vector.

2. Frenet, Gradient and Inertial Frames in 3D

In the present section, the approach outlined above will be applied to the 3D Euclidean space. Differential geometry can be readily analyzed with the tools provided by geometric algebra. The approach pioneered by Hestenes, Sobczyk, Doran, and Lasenby is to use the shape operator as the main tool for the differential geometry described by the tools of the geometric algebra [7,8] [Ch. 6], [13]. It uses the tangent vectors on the surface to build the pseudoscalar $I\left(x\right)$ at every point from the tangent vectors of the parameter curves on the surface. Although general in nature this approach can be simplified for curves and given explicit form for engineering and physical applications.

In the subsequent discussion we work in ${\mathbb{G}}^3$. The pesudoscalar is denoted by $I_3$ and it commutes with all elements of the algebra. Consider the scalar equation $F(x,y,z)=0$, which defines a surface in 3D. We can use it to specify also a vector field defining curve embedded in that surface in the following way.

Definition 1.

Define the curve specified by $F(x,y,z)=0$ by the vector field $\gamma \left(s\right)$, for which

$$F(x,y,z)=0\mapsto \gamma \left(s\right):=r{|}_{x=f\left(s\right),y=g\left(s\right),z=h\left(s\right)}=f\left(s\right)e_1+g\left(s\right)e_2+h\left(s\right)e_3$$

for suitable functions $f,g,h$, such that

$$F\left(f\right(s),g(s),h(s\left)\right)=0$$

holds identically.

Considering a curve in the 3D space, there is a parametrization by the length s, such that

$$\left|\right|{\gamma }^{\prime }\left(s\right)\left|\right|=1\Rightarrow s={\int }_0^s\left|\right|{\gamma }^{\prime }\left(t\right)\left|\right|dt={\int }_0^{s}dt$$

The assumption here is that $\gamma \left(s\right)$ is non-singular except at $s=0$. Then define the tangent vector as

$$t:={\gamma }^{\prime }⟹\gamma \left(s\right)=\gamma \left(0\right)+{\int }_0^{s}t\left(u\right)du$$

Then

$$0=F^{\prime }=r^{\prime }\left(s\right)·\nabla F⟹t·{\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}=t·n=0$$

(7)

Therefore, the gradient $\nabla F$ is orthogonal to t. Furthermore,

$$t·\nabla F=(t·\nabla )F⟹(t·\nabla )F=0$$

We also obtain the equivalence

$${\displaystyle \frac{d}{ds}}=t·\nabla$$

Furthermore, identically

$$\nabla \wedge \gamma =\nabla \wedge r=0$$

2.1. Frenet Frames

Consider the normalization constraint $t·t=1$. Differentiate the equation to obtain

$$t·t^{\prime }=0$$

Therefore, $t^{\prime }$ is orthogonal to t. Define the curve normal as

$$n:=t^{\prime }/\left|\right|t^{\prime }\left|\right|=t^{\prime }/\left|\kappa \right|$$

(8)

where the unsigned curvature is defined as the norm of the acceleration

$$\left|\kappa \right|:=\left|\right|t^{\prime }\left|\right|$$

(9)

Therefore, we can compute the signed curvature as $\kappa =t^{\prime }·n$ and use this expression throughout. The bi-normal vector b is orthogonal to the osculating plane $t\wedge n$:

$$b:=-I_{3}tn=-I_3·(t\wedge n)$$

(10)

It also holds that

$$n^{\prime }·n=b^{\prime }·b=0$$

Define the torsion as

$$\tau :=b·n^{\prime }$$

(11)

The torsion measures the amount of rotation of the Frenet frame around the tangent t as the arc length increases (see Figure 1). Differentiating orthogonality relations

$$t·b=n·b=t·n=0$$

yields the anti-symmetric frame coefficient matrix

$$\Omega =\left(\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right)$$

(12)

The frame derivative can be computed concisely from the matrix equation

$${\mathbf{E}}^{\prime }=\Omega \mathbf{E},\mathbf{E}=\left(\begin{array}{c}t\\ n\\ b\end{array}\right)$$

On the other hand, the following identity holds

$$(t^{\prime }\wedge t)·t=t^{\prime }(t·t)=t^{\prime }$$

Therefore, we can identify a frame bi-vector $\Omega$ up to an orthogonal bi-vector B,

$$\Omega :=t^{\prime }\wedge t+B$$

such that $B·t=0$ and $t^{\prime }=\Omega ·t$. The bi-vector B can be completely specified as follows.

Proposition 1.

For the case of Frenet frame the Darboux or angular velocity bi-vector is

$$\Omega =t^{\prime }\wedge t+b^{\prime }\wedge b$$

(13)

and its dual Darboux vector is

$$\omega =\tau t+\kappa b$$

(14)

Proof. 

To demonstrate the statement we compute first the inner product

$$(b^{\prime }\wedge b)·t=(b·t)b^{\prime }-(b^{\prime }·t)b=\tau (n·t)b=0$$

Therefore,

$$\begin{array}{cc}\hfill \Omega ·b& =(t^{\prime }\wedge t)·b+(b^{\prime }\wedge b)·b=b^{\prime }=-\tau n\hfill \\ \hfill \Omega ·n& =\left(t^{\prime }\wedge t\right)·n+\left(b^{\prime }\wedge b\right)·n=-(t^{\prime }·n)t-(b^{\prime }·n)b=-\kappa t+\tau b\hfill \end{array}$$

Compute

$$\omega =\Omega I_3=(\kappa nt-\tau nb)tnb=\kappa b-\tau nbtnb=\kappa b-\tau t{\left(nb\right)}^2=\kappa b+\tau t$$

□

Therefore, the trajectory can be recovered by quadrature starting from the integral

$$t\left(s\right)=t\left(0\right)+{\int }_0^s\Omega ·tds=t\left(0\right)+{\int }_0^s\kappa (n\wedge t)·tds=t\left(0\right)+{\int }_0^s\kappa nds=t\left(0\right)+{\int }_0^s{t}^{\prime }ds$$

so that

$$t\left(s\right)=t\left(0\right)+{\int }_0^s\kappa nds$$

(15)

Remark 1.

The analogy between the frame matrix and frame bi-vector is not complete. The frame matrix Ω is singular since $\det (\Omega )=0$. This is not the case for the frame bi-vector Ω since the product ${\Omega }^{\sim }\Omega ={\kappa }^2+{\tau }^2$ results in a scalar, which is also the determinant of the bi-vector, so that its inverse is

$${\Omega }^{-1}={\Omega }^{\sim }/\left({\Omega }^{\sim }\Omega \right)$$

2.2. Gradient (Darboux) Frame

Define the surface normal vector as

$$n:={\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}$$

(16)

Remark 2.

The above relationship defines the Gauss map $G:\mathbb{R}\mapsto {〈{\mathbb{G}}^3〉}_1$ of the surface $F(x,y,z)$:

$$G:F\mapsto {\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}$$

Define the osculating plane by the bi-vector $O:=t\wedge n$ and the tangent plane by $T_2:=I_3·n$. Define the bi-normal vector b to be orthogonal to the osculating plane O:

$$b:=-I_{3}tn=-I_3(t\wedge n)$$

(17)

Then $T_2=-t\wedge b$. It also holds that

$$t·t^{\prime }=n^{\prime }·n=b^{\prime }·b=0$$

as before. Differentiating the orthogonality relations

$$t·b=n·b=t·n=0$$

yields anti-symmetric coefficient frame matrix as before.

We will look for a Darboux bi-vector as before starting from the identity

$$(n^{\prime }\wedge n)·n=n^{\prime }$$

Then

$$\Omega =(n^{\prime }\wedge n)+B$$

such that $n·B=0$ so that

$$\Omega ·n=n^{\prime }$$

Consider the constraint equation

$$\Omega ·t=(n^{\prime }\wedge n)·t+B·t=-(n^{\prime }·t)n+B·t=t^{\prime }$$

Therefore

$$n^{\prime }·t=n·t^{\prime }=0$$

(18)

Consider the bi-vector

$$\Omega =t^{\prime }\wedge t+n^{\prime }\wedge n$$

(19)

On the other hand,

$$\begin{array}{c}{b}^{\prime }=-I_3(t^{\prime }n+t{n}^{\prime })=-I_3(t^{\prime }\wedge n+t\wedge n^{\prime })=n·\left(I_3{t}^{\prime }\right)-t·\left(I_3{n}^{\prime }\right)\hfill \\ \hfill =n·(I_3\Omega ·t)-t·(I_3\Omega ·n)=n·(\omega \wedge t)-t·(\omega \wedge n),\omega :=\Omega I_3\end{array}$$

in terms of the dual vector. Therefore,

$$b^{\prime }=(n·\omega )t-(t·\omega )n$$

(20)

Furthermore,

$$\begin{array}{}\mathrm{(21)}& \hfill (n^{\prime }\wedge n)I_3& =n^{\prime }·(n·(t\wedge n\wedge b)=-n^{\prime }·(t\wedge b)=(n^{\prime }·b)t-(n^{\prime }·t)b=(n^{\prime }·b)t\hfill \mathrm{(22)}& \hfill (t^{\prime }\wedge t)I_3& =t^{\prime }·(t·(t\wedge n\wedge b)=t^{\prime }·(n\wedge b)=(t^{\prime }·n)b-(t^{\prime }·b)n=-(t^{\prime }·b)n\hfill \end{array}$$

Therefore, the Darboux vector is

$$\omega =(n^{\prime }·b)t-(t^{\prime }·b)n$$

(23)

Therefore,

$$n·\omega =-(t^{\prime }·b),t·\omega =(n^{\prime }·b)$$

However,

$$\Omega ·b=-(n^{\prime }·b)n-(t^{\prime }·b)t$$

Therefore,

$$b^{\prime }=-(t^{\prime }·b)t-(n^{\prime }·b)n=\Omega ·b$$

Therefore, $\Omega$ is the Darboux bi-vector of the gradient frame.

Proposition 2.

For the case of Gradient frame the Darboux or angular velocity bi-vector is

$$\Omega =t^{\prime }\wedge t+n^{\prime }\wedge n$$

(24)

Define the coefficients

$$k_1:=t^{\prime }·b,k_2:=n^{\prime }·b$$

To determine explicitly $k_1$ and $k_2$ we use the following approach. Define the unit vector (i.e. the Frenet normal)

$$\eta :=t^{\prime }/\kappa$$

Then also $n·\eta =(n·t^{\prime })/\kappa =0$. On the other hand,

$$\eta \wedge b=-\eta \wedge \left(I_3(t\wedge n)\right)=-I_3(\eta ·(t\wedge n))=-I_3(n(\eta ·t)-t(\eta ·n))=I_{3}t(\eta ·n)=0$$

Therefore, $\eta$ and b are co-linear. Moreover, since both are unit vectors it follows that $\eta =\pm b$. Therefore, $k_1=t^{\prime }·(\pm \eta )=\pm \kappa$. Therefore, there are 2 possible combinations $(k_1=\kappa ,\eta =b)$ and $(k_1=-\kappa ,\eta =-b)$. Considering the planar case we observe that the second option realizes. Therefore, $k_1=-\kappa$.

Define the dual vector

$$\beta :=-I_3(t\wedge \eta )$$

Then

$$n\wedge \beta =-n\wedge \left(I_3(t\wedge \eta )\right)=-I_3(n·(t\wedge \eta ))=I_{3}t(n·\eta )=0$$

Therefore, n and $\beta$ are co-linear. Furthermore,

$$n·\beta =-n·\left(I_3(t\wedge \eta )\right)=-I_3(n\wedge t\wedge (-b))=I_3(n\wedge t\wedge b)=-I_3{I}_3=1$$

Therefore, $n=\beta$ and $k_2=-n^{\prime }·\eta =-{\beta }^{\prime }·\eta$. Therefore,

$$\tau =\beta ·{\eta }^{\prime }=-{\beta }^{\prime }·\eta =k_2$$

To summarize, the Frenet and Gradient frames are related by the transformation

$$\left(\begin{array}{c}t\\ -b\\ n\end{array}\right)={\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right)}^T\left(\begin{array}{c}t\\ n\\ b\end{array}\right),\mathbf{U}:=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right)$$

or in shortened matrix notation

$${\mathbf{E}}_g={\mathbf{U}}^T\mathbf{E}$$

(25)

From the above equation it is apparent that U is an orthogonal matrix – $\mathbf{U}{\mathbf{U}}^T=\mathbf{I}$. The frame matrix is

$${\Omega }_g=\left(\begin{array}{ccc}0& 0& -\kappa \\ 0& 0& \tau \\ \kappa & -\tau & 0\end{array}\right)$$

The two frame matrices are related by:

$${\Omega }_g=\mathbf{U}\Omega {\mathbf{U}}^T$$

(26)

Remark 3.

The name Darboux frame is justified since we can identify the plane as the surface "arena" where the equations evolve. Since the Darboux frame is represented by the matrix

$${\Omega }_d=\left(\begin{array}{ccc}0& {\kappa }_g& {\kappa }_n\\ -{\kappa }_g& 0& \tau \\ -{\kappa }_n& -\tau & 0\end{array}\right)$$

Then for the plane ${\kappa }_g=0$; so up to the orientation of the normal vector one can identify ${\Omega }_g$ with ${\Omega }_d$.

The tangent field can be recovered by quadrature as

$$t\left(s\right)-t\left(0\right)={\int }_0^s\Omega ·tds=-{\int }_0^s\kappa bds$$

(27)

The gradient frame can be recognized as the Darboux frame for the plane, where the geodesic curvature ${\kappa }_g=0$.

Remark 4.

The gradient frame can be suitable for immersed elastic curves and also in the case where one wishes to characterize the interaction of the elastica with the medium. There, one could specify a normal forcing field as a constraint of the equations. Therefore, by duality, in a deformed body (under a strain field) the strength of interaction can be given by the value of ${\kappa }_g$.

2.3. Bishop (Inertial) Frames

The Bishop or parallel transport frame [14] is an alternative description that is well-defined even when the curve has vanishing acceleration. The Bishop frame $(t,\eta ,\beta )$ is such that

$$t^{\prime }:=k_1\eta +k_2\beta$$

(28)

and furthermore the frame matrix is computed as

$${\Omega }_b=\left(\begin{array}{ccc}0& k_1& k_2\\ -k_1& 0& 0\\ -k_2& 0& 0\end{array}\right)$$

To connect with the approach discussed so far we observe that

$$\left|\right|t^{\prime }{\left|\right|}^2=k_1^2+k_2^2={\kappa }^2$$

Therefore, one can posit the rotation relationship

$$k_1=\kappa cos\varphi \left(s\right),k_2=\kappa sin\varphi \left(s\right),tan\varphi ={\displaystyle \frac{k_2}{k_1}}$$

for some phase function $\varphi \left(s\right)$ of the arc-length to be determined further. We look for a Darboux bi-vector of the form

$$\Omega :=t^{\prime }\wedge t+B$$

Then

$$t^{\prime }=\Omega ·t=t^{\prime }+B·t⟶B·t=0$$

Furthermore

$${\eta }^{\prime }=\Omega ·\eta =-(t^{\prime }·\eta )t+B·\eta =-k_{1}t+B·\eta ⟶B·\eta =0$$

and finally

$${\beta }^{\prime }=\Omega ·\beta =-(t^{\prime }·\beta )t+B·\beta =-k_{2}t+B·\beta ⟶B·\beta =0$$

Therefore, we can conclude that $B=0$ and the Darboux bi-vector has the especially simple form [7, Ch. 6, p. 238]

$${\Omega }_b=t^{\prime }\wedge t$$

(29)

To determine the function $\varphi$ we proceed as follows. Using the Frenet frame we form the invariant volume:

$$\omega :=t\wedge t^{\prime }\wedge t^{″}=\kappa t\wedge n\wedge ({\kappa }^{\prime }n+\kappa n^{\prime })=\kappa t\wedge n\wedge \underset{t^{″}}{\underbrace{({\kappa }^{\prime }n+\kappa (-\kappa t+\tau b))}}={\kappa }^2\tau I_3$$

(30)

Observe that

$$t^{″}\wedge t=(k_1^{\prime }\eta +k_1{\eta }^{\prime }+k_2^{\prime }\beta +k_2{\beta }^{\prime })\wedge t=k_1^{\prime }\eta \wedge t+k_2^{\prime }\beta \wedge t$$

Then

$$\begin{array}{c}t\wedge t^{\prime }\wedge t^{\prime \prime }=-(k_1{k}_2^{\prime }-k_2{k}_1^{\prime })\eta \wedge \beta \wedge t=\hfill \\ (k_1{k}_2^{\prime }-k_2{k}_1^{\prime })I_3=((\kappa cos\varphi ){(\kappa sin\varphi )}^{\prime }-(\kappa sin\varphi ){(\kappa cos\varphi )}^{\prime })I_3=\\ (\kappa cos\varphi ({\kappa }^{\prime }sin\varphi +\kappa cos\varphi {\varphi }^{\prime })-\kappa sin\varphi ({\kappa }^{\prime }cos\varphi -\kappa sin\varphi {\varphi }^{\prime }))I_3=\\ \hfill \left({\kappa }^2{cos}^2\varphi {\varphi }^{\prime }+{\kappa }^2{sin}^2\varphi {\varphi }^{\prime }\right)I_3={\kappa }^2{\varphi }^{\prime }{I}_3\end{array}$$

Therefore, from eq. 30 it follows that

$${\varphi }^{\prime }=\tau$$

(31)

as also determined in [15]. In other words, $\varphi$ is the integral or cumulative torsion. It is a $2\pi$ multiple of the twisting number. Therefore, the frame matrix becomes

$${\Omega }_b=\kappa \left(\begin{array}{ccc}0& cos\varphi \left(s\right)& sin\varphi \left(s\right)\\ -cos\varphi \left(s\right)& 0& 0\\ -sin\varphi \left(s\right)& 0& 0\end{array}\right)$$

(32)

From this presentation it is apparent that geometric calculus streamlines calculations.

3. Euler-Lagrange Formulation of the Elastica Problem

A beam is defined to be a three-dimensional deformable body whose length is much larger than its other two dimensions. Such a body can be described by a curve threading its center line in $R^3$ and a cross section at every point of the curve whose intersection is precisely the barycenter of the section. A comprehensive variational analysis has been presented in [16].

3.1. Free Elastica Equations

The elastica theory is the oldest variational model of elastic rods. The core of the presented approach is coordinate free. The constrained Lagrangian energy density functional is identified as

$$\mathcal{L}(t,t^{\prime }):={\displaystyle \frac{1}{2}}{t}^{\prime 2}+{\displaystyle \frac{\lambda }{2}}\left(t^2-1\right)$$

(33)

where its independent variables are vectors and the multiplier is scalar while t is not assumed a priori to be the tangent field. This Lagrangian is manifestly translationally invariant. The above Lagrangian corresponds to the traditional definition given in [15,17] since

$$\mathcal{L}(t,t^{\prime })={\displaystyle \frac{1}{2}}{\kappa }^2+{\displaystyle \frac{\lambda }{2}}\left(t^2-1\right)={\displaystyle \frac{1}{2}}{\kappa }^2$$

under nomralization. Furthermore assume that $t\in {\mathbb{G}}^n$, $n\ge 3$. The tangent field and its derivative are varied independently. To enact the variations we use the generalized partial gradient operator:

$${\nabla }_y:=\sum _{i=1}^n{e}^i{\partial }_{y_i}$$

(34)

The free elastica equation can be derived as follows. Observe the relations

$${\nabla }_{\gamma }\mathcal{L}=0,{\pi }_1:={\nabla }_t\mathcal{L}=\lambda t,{\pi }_2:={\nabla }_{t^{\prime }}\mathcal{L}=t^{\prime },{\partial }_{\lambda }\mathcal{L}=t^2-1$$

Therefore, the Euler-Lagrange equations are

$${\displaystyle \frac{d}{ds}}{\nabla }_t\mathcal{L}-{\displaystyle \frac{d^2}{d{s}^2}}{\nabla }_{t^{\prime }}\mathcal{L}={\nabla }_{\gamma }\mathcal{L},{\partial }_{\lambda }\mathcal{L}=0$$

That is, up to sign it holds that

$${\displaystyle \frac{d}{ds}}\lambda t-{\displaystyle \frac{d^2}{d{s}^2}}{t}^{\prime }\equiv {\left(\lambda t\right)}^{\prime }-t^{‴}=0,t^2-1=0$$

(35)

3.2. Symmetries of the Lagrangian

The first equation integrates to the constant vector field J, which is also the Noether current, such that

$$J=\lambda t-t^{″},J^{\prime }=0$$

(36)

Furthermore, define the pseudoscalar

$$w:=t\wedge t^{\prime }\wedge J=-t\wedge t^{\prime }\wedge t^{″}$$

and differentiate it to obtain

$$w^{\prime }={(t\wedge t^{\prime }\wedge J)}^{\prime }={(t\wedge t^{\prime })}^{\prime }\wedge J=t\wedge t^{″}\wedge J=t\wedge (\lambda t-J)\wedge J=0$$

using the equation of motion. Therefore, w is also constant. Denote its magnitude by $c=\left|\right|w\left|\right|$. Observe that it is an invariant which does not depend on the used basis.

Furthermore, we establish the stronger result that

$$w\wedge t^{‴}=-t\wedge t^{\prime }\wedge t^{″}\wedge t^{‴}=-t\wedge t^{\prime }\wedge t^{″}\wedge ({\lambda }^{\prime }t+\lambda t^{\prime })=0$$

without explicitly using the dimensionality of Euclidean space. Therefore, we claim:

Proposition 3.

An elastica is confined to a 3 dimensional subspace of ${\mathbb{G}}^n$.

Therefore, without loss of generality we assume further that $n=3$.

Furthermore, by the Ostrogradski principle for higher-order Lagrangians [18], the equation for the Hamiltonian is given by

$$\mathcal{H}=\left({\pi }_1-{\displaystyle \frac{d}{dt}}{\pi }_2\right)·t+{\pi }_2·t^{\prime }-\mathcal{L}=J·t+t^{\prime 2}-\mathcal{L}$$

(37)

Differentiate the Hamiltonian and use the equations of motion to obtain

$${\mathcal{H}}^{\prime }=J·t^{\prime }+2t^{″}·t^{\prime }-{\mathcal{L}}^{\prime }=(\lambda t-t^{\prime \prime })·t^{\prime }+t^{″}·t^{\prime }=-t^{″}·t^{\prime }+t^{″}·t^{\prime }=0$$

by the orthogonality of t and $t^{\prime }$. Therefore, it was just established that the Hamiltonian is a first integral of the system – i.e. a constant.

Furthermore, the conservation of the Hamiltonian can be interpreted as the energy conservation law for the elastic energy density:

$$\mathcal{H}=J·t+{\displaystyle \frac{1}{2}}{t}^{\prime 2}-{\displaystyle \frac{1}{2}}\lambda (t^2-1)=J·t+{\displaystyle \frac{1}{2}}{\kappa }^2=H$$

(38)

applying the normalization of t and the definition of $\kappa$.

The torque can be identified with the bi-vector

$$\mathcal{M}=\gamma \wedge J+t\wedge t^{\prime }=\gamma \wedge J-{\Omega }_b$$

(39)

relating to the Bishop frame bi-vector. Therefore,

$${\mathcal{M}}^{\prime }=t\wedge J+t\wedge t^{″}=-t\wedge t^{″}+t\wedge t^{″}=0$$

is the expression of the conservation law of angular momentum. Therefore, $\mathcal{M}$ can be identified with some constant M – i.e. $\mathcal{M}=M$.

Remark 5.

We can define the generalized, multi-vector Hamiltonian, which combines both conservation laws, as an even element of the algebra as

$$\mathcal{F}:=\mathcal{H}+\mathcal{M}=J·t+{\displaystyle \frac{1}{2}}{t}^{\prime 2}+\gamma \wedge J+t\wedge t^{\prime }$$

(40)

In this formulation, $\mathcal{F}$ corresponds to a constant quaternion. Therefore, we have just established that an elastica can be suitably parametrizied, and therefore classified, by a quaternion up to a rigid motion.

Observe that

$$\mathcal{M}\wedge J=-t\wedge t^{\prime }\wedge t^{″}=-w=c{I}_3$$

up to sign. Therefore, we can attribute the volumetric invariant to the torque.

Note that up to the last equation the approach is completely frame-independent! Thus, the choice of a specific frame and coordinates is a matter of utility guided by the need to simplify computations.

3.3. Derivation of the Curvature Equation

Observe that

$$J·t=\lambda -t^{″}·t=H-{\displaystyle \frac{1}{2}}{\kappa }^2$$

(41)

Having derived the relevant symmetries of the system at this point we specialize the discussion and employ the Frenet frames to express J.

$$t^{″}={\kappa }^{\prime }n+\kappa n^{\prime }={\kappa }^{\prime }n+\kappa (-\kappa t+\tau b)={\kappa }^{\prime }n-{\kappa }^{2}t+\kappa \tau b$$

(42)

Therefore,

$$J=({\kappa }^2+\lambda )t-{\kappa }^{\prime }n-\kappa \tau b$$

(43)

in the Frenet frame. The magnitude of the momentum vector can be calculated from the scalar product:

$$J·J:=j^2={({\kappa }^2+\lambda )}^2+{\kappa }^{\prime 2}+{\left(\kappa \tau \right)}^2$$

(44)

for some constant j giving the norm of J. Observe that the above equation is also frame-independent.

Furthermore, compute the pseudoscalar $w=t\wedge t^{\prime }\wedge J=-{\kappa }^2\tau I_3$ and identify the constraint

$${\kappa }^2\tau =c$$

(45)

coupling curvature and torsion.

Lastly, the Lagrange multiplier’s functional form is determined in the following way. Project J onto the tangent vector to obtain:

$$J·t=\lambda -t^{″}·t=\lambda +{\kappa }^2\Rightarrow t^{″}·t=-{\kappa }^2$$

Substitute in eq. 41 to obtain the Lagrange multiplier

$$\lambda =H-{\displaystyle \frac{3}{2}}{\kappa }^2$$

(46)

Project J onto the normal vector to obtain:

$$J·n=-t^{″}·n=-{\kappa }^{\prime }$$

Differentiate to obtain

$$J·n^{\prime }=J·(-\kappa t+\tau b)=-\kappa ({\kappa }^2+\lambda )-\kappa {\tau }^2=-{\kappa }^{″}$$

Substitute $\lambda$ from eq. 46 to obtain

$${\kappa }^{″}-{\kappa }^3-\left(H-{\displaystyle \frac{3}{2}}{\kappa }^2\right)\kappa ={\kappa }^{″}+{\displaystyle \frac{1}{2}}{\kappa }^3-H\kappa =\kappa {\tau }^2$$

(47)

agreeing with the result in [19].

Remark 6.

The traditional derivation of the elastic equation proceeds as follows [20]. Differentiate J and use the Frenet frame equations

$$(3\kappa {\kappa }^{\prime }+{\lambda }^{\prime })t-({\kappa }^{″}-{\kappa }^3-\lambda \kappa -\kappa {\tau }^2)n-(\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau )b=0$$

to obtain a system of 3 constraints:

$$3\kappa {\kappa }^{\prime }+{\lambda }^{\prime }=0,{\kappa }^{″}-{\kappa }^3-\lambda \kappa -\kappa {\tau }^2=0,\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau =0$$

Solve the constraint for the torsion

$$\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau =0⟹{\tau }^{\prime }/\tau +2{\kappa }^{\prime }/\kappa =0⟹log\tau {\kappa }^2=logc⟹\tau ={\displaystyle \frac{c}{{\kappa }^2}}$$

and the Lagrange multiplier

$$3\kappa {\kappa }^{\prime }+{\lambda }^{\prime }=0⟹\lambda =H-{\displaystyle \frac{3}{2}}{\kappa }^2$$

Substitute the solutions in the remaining constraint. Observe that using the traditional approach the role of the constant H is not apparent.

The advantage of the geometric-algebraic approach is that one does not need to solve a differential equation for the torsion. Instead, the role of the invariant pseudoscalar is put to the front. From the present discussion it transpires that choice of frame is a matter of convenience for the problem at hand.

The preceding discussion can be formulated concisely as the following theorem:

Theorem 1.

The elastica system is equivalent to the first order ODE

$${\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2+{\kappa }^{\prime 2}-j^2=-c\tau =-{\displaystyle \frac{c^2}{{\kappa }^2}}$$

(48)

which can be differentiated into the second order differential equation

$${\kappa }^{″}+{\displaystyle \frac{1}{2}}{\kappa }^3-H\kappa =\kappa {\tau }^2={\displaystyle \frac{c^2}{{\kappa }^3}}$$

(49)

where H is the Hamiltonian energy density of the system, c is the torsion coupling and j is the magnitude of the generalized momentum J. The vector field J can be expressed in the Frenet frame as

$$J=\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)t-{\kappa }^{\prime }n-\kappa \tau b,J^{\prime }=0$$

(50)

3.4. Classification of Elastic Curves

The torsion coupling condition $\tau {\kappa }^2=c$ requires some attention. On the first place,

$$t^{″}={\kappa }^{\prime }n+\kappa n^{\prime }⟹t^{″}·b=\kappa \tau$$

Also $\kappa b=-\kappa I_3(t\wedge n)=-I_3(t\wedge t^{\prime })$. Therefore,

$${\kappa }^2\tau =\kappa t^{″}·b=-t^{″}·\left(I_3(t\wedge t^{\prime })\right)=-I_3(t\wedge t^{\prime }\wedge t^{″})$$

or equivalently,

$${\kappa }^2\tau I_3=c{I}_3=t\wedge t^{\prime }\wedge t^{″}=\omega$$

(51)

in terms of the volume invariant. Therefore, in the non-trivial case, linear dependence between the 3 vectors ($t\wedge t^{\prime }\wedge t^{″}=0$) implies that the curve is planar (i.e. $\tau =0$). Let $\sigma :=t\wedge t^{\prime }$. Obviously, whenever t and $t^{\prime }$ are linearly dependent then $\sigma =0$. On the other hand, suppose that only ${\sigma }^{\prime }=0$. Then

$$t\wedge t^{″}=0⟹t^{″}·b=0⟹\tau =0$$

While

$${\sigma }^2=(t\wedge t^{\prime })·(t\wedge t^{\prime })=t·(t^{\prime }·(t\wedge t^{\prime }))=-t·\left(t{t}^{\prime 2}\right)=-{\kappa }^2$$

(52)

Furthermore, $t^{‴}$ is in the span of ($t,t^{\prime },t^{″}$) since $t\wedge t^{\prime }\wedge t^{″}\wedge t^{‴}={\kappa }^2\tau I_3\wedge t^{‴}=0$. The above results can be neatly summarized in the following diagram:

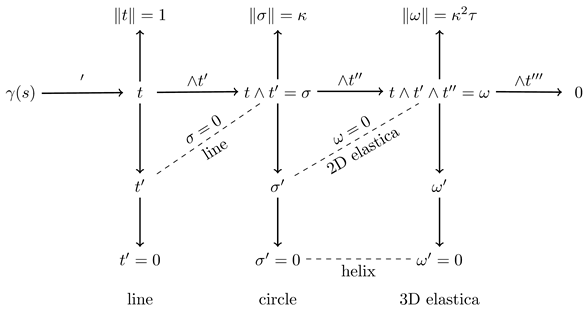The above diagram is generated by the consecutive action of two operators – the covariant arc length differentiation and exterior multiplication.

4. Applications

4.1. Planar Elastica

Then $\tau =c=0$. The curvature differential equation becomes

$${\kappa }^{\prime }=\pm \sqrt{j^2-{\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2}$$

(53)

The equation is resolved by variation of parameters using the generic ansatz

$$\kappa =A\mathrm{dn}\left(qs\right|m)$$

This leads to the algebraic system for the parameters A, q and m:

$$\begin{array}{}\mathrm{(54)}& \hfill A^2{m}^2(4q^2-A^2)=0\mathrm{(55)}& \hfill A^{2}m(2m{q}^2+2H-A^2)=0\mathrm{(56)}& \hfill (2j-2H+A^2)(2j+2H-A^2)=0\end{array}$$

This leads to a general solution of the form

$$\kappa =2q\mathrm{dn}\left(qs\right|m),q>0$$

(57)

The non trivial solutions are given by the set

$$\begin{array}{c}\left\{q=\pm \sqrt{{\displaystyle \frac{j+H}{2}}},m={\displaystyle \frac{2j}{j+H}},A=\mp \sqrt{2j+2H}\right\}\cup \\ \left\{q=\pm \sqrt{{\displaystyle \frac{j+H}{2}}},m={\displaystyle \frac{2j}{j+H}},A=\pm \sqrt{2j+2H}\right\}\cup \\ \left\{q=\pm \sqrt{{\displaystyle \frac{H-j}{2}}},m={\displaystyle \frac{2j}{j-H}},A=\mp \sqrt{2H-2j}\right\}\cup \\ \left\{q=\pm \sqrt{{\displaystyle \frac{H-j}{2}}},m={\displaystyle \frac{2j}{j-H}},A=\pm \sqrt{2H-2j}\right\}\end{array}$$

Geometrically admissible are only the solutions where A is positive. This corresponds to the results given in [21] after a suitable reparametrization.

4.2. Generic 3D Elastica

We follow the method described in [20] where the equation is proven.

Proposition 4.

The substitution $u={\kappa }^2$ results in an autonomous ODE for u:

$${\left({\displaystyle \frac{u^{\prime }}{2}}\right)}^2=u{j}^2-c^2-u{\left(H-{\displaystyle \frac{u}{2}}\right)}^2$$

(58)

Proof. 

Suppose that $u={\kappa }^2\ne 0$. Observe that wherever $\kappa \ne 0$

$${\kappa }^{\prime }={\displaystyle \frac{u^{\prime }}{2\kappa }}={\displaystyle \frac{u^{\prime }}{2\sqrt{u}}}$$

Therefore,

$${\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2+{\kappa }^{\prime 2}-j^2={\left(H-{\displaystyle \frac{u}{2}}\right)}^2+{\left({\displaystyle \frac{u^{\prime }}{2\sqrt{u}}}\right)}^2-j^{2}c\tau =-{\displaystyle \frac{c^2}{{\kappa }^2}}=-{\displaystyle \frac{c^2}{u}}$$

and multiply by u. □

This equation can be integrated in elliptic functions as follows [15,19,22,23]. We make the ansatz

$${\kappa }^2=u=p-Am{\mathrm{sn}}^2\left(\sqrt{q}s\right|m)=p-A+A{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

Observe that the 2D case corresponds to $A=p$.

Using some identities for the elliptic functions, one arrives at the following system of polynomial equations for the parameters

$$\begin{array}{}\mathrm{(59)}& \hfill A^2{m}^3\left(4q-A\right)=0\mathrm{(60)}& \hfill A^2{m}^2\left(4mq+4q-3p+4H\right)=0\mathrm{(61)}& \hfill Am\left(4Amq-3p^2+8Hp+4j^2-4H^2\right)=0\mathrm{(62)}& \hfill p^3-4H{p}^2+4(H^2-j^2)p+4c^2=0\end{array}$$

Therefore, $A=4q$.

The last equation contains only the integration constants H, c and j besides the unknown parameter p. Therefore, the solutions can be parameterized by the roots of the equation for p. Then

$$\begin{array}{cc}\hfill m_1& ={\displaystyle \frac{(3p-4H)\sqrt{-3p^2+8Hp+16j^2}+3p^2-8Hp+8j^2+8H^2}{2\left(3p^2-8Hp-4j^2+4H^2\right)}},\hfill \\ \hfill q_1& =-{\displaystyle \frac{\sqrt{-3p^2+8Hp+16j^2}-3p+4H}{8}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill m_2& =-{\displaystyle \frac{(3p-4H)\sqrt{-3p^2+8Hp+16j^2}-3p^2+8Hp-8j^2-8H^2}{2\left(3p^2-8Hp-4j^2+4H^2\right)}},\hfill \\ \hfill q_2& ={\displaystyle \frac{\sqrt{-3p^2+8Hp+16j^2}+3p-4H}{8}}\hfill \end{array}$$

This leads to a parametric solution of the form

$${\kappa }^2=p-4q+4q{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

(63)

In another parametrization we have the system of equations

$$\begin{array}{}\mathrm{(64)}& \hfill p={\displaystyle \frac{4}{3}}(H+q(m+1))\mathrm{(65)}& \hfill mq(H^2+3j^2-4(1-m+m^2)q^2)=0\mathrm{(66)}& \hfill 4H^3+27c^2-36H{j}^2+12(H^2+3j^2)(1+m)q+16{\left(1+m\right)}^3{q}^3=0\end{array}$$

which couples the p an q parameters algebraically. The advantage here is the linear relationship between p and H. The positive solution is

$$q={\displaystyle \frac{\sqrt{H^2+3j^2}}{2\sqrt{1-m+m^2}}}$$

The denominator is always positive. Then the solutions are parametrized by the value of m. In the 2D case, as observed

$$4q={\displaystyle \frac{4}{3}}(H+q(m+1))⟹H=q(2-m)\ge 0⟹m\le 2$$

Otherwise,

$${\kappa }^2={\displaystyle \frac{4}{3}}(H+q(m-2))+4q{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

(67)

Remark 7.

The torsion is

$$\tau ={\displaystyle \frac{c}{p-4qm{\mathrm{sn}}^2\left(\sqrt{q}s\right|m)}}$$

which determines the Frenet frame. This can be integrated into an incomplete elliptical integral of the third kind.

$$\varphi \left(s\right)={\displaystyle \frac{c}{p\sqrt{q}}}\Pi \left({\displaystyle \frac{4qm}{p}},\mathrm{am}\left(\sqrt{q}s\right|m)|m\right)={\displaystyle \frac{c}{p\sqrt{q}}}\mathcal{P}\left({\displaystyle \frac{4qm}{p}},\sqrt{q}s|m\right)$$

allowing for calculation of the Bishop frame.

4.3. Integration of the Elastica in Terms of the Bishop Frame

Observe that equation 38 can be integrated as

$$J·\gamma +{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds=Hs$$

(68)

Adding both conservation laws allows one to solve for the $\gamma$ field using the invertivbility of the geometric product:

$$\gamma \left(s\right)=\left(Hs+M-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds-\sigma \right)J^{-1},\sigma =t\wedge t^{\prime }=\kappa t\wedge n=-{\Omega }_b$$

(69)

Observe, that the above formulation is coordinate-free demonstrating the advantage of Geometric Algebra approach. Therefore, we establish that the elastica is a completely integrable system in terms of the Bishop frame.

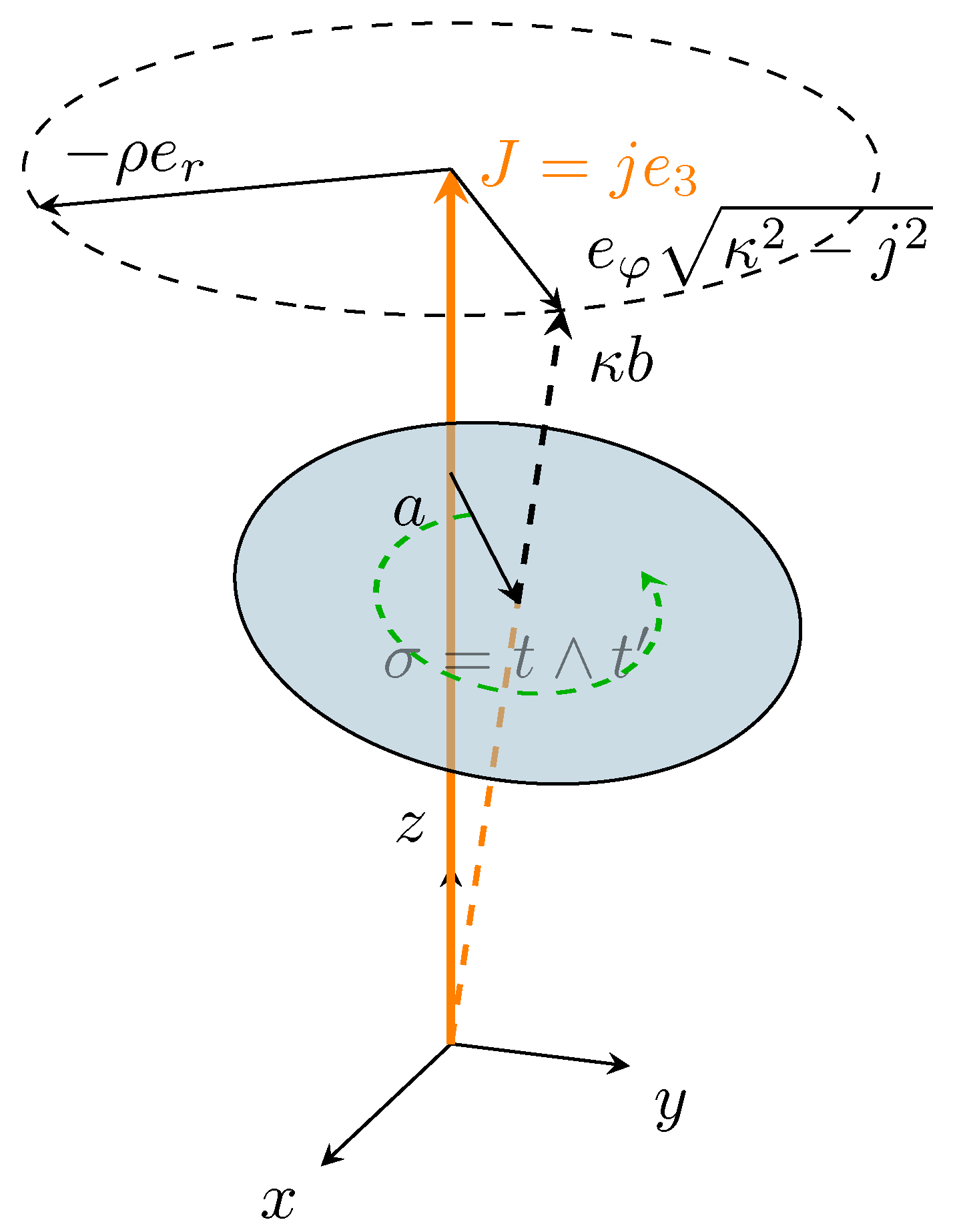
The conserved momentum allows for aligning the solution to a global basis and identifying a corresponding coordinate system. Such a convenient coordinate system is the cylindrical [19,22] one aligned with the momentum J (see Figure 2). We define the constant altitude unit vector along the direction of J as

$$e_3:=J/j$$

(70)

In summary, we can formulate following result:

Theorem 2.

Suppose that the Bishop frame ${\Omega }_b$, j, H, M and $e_3$ are specified. Then the elastica curve can be reconstructed by quadrature as:

$$j\gamma \left(s\right)=\left(Hs-{\displaystyle \frac{1}{2}}{\int }_0^s{\kappa }^{2}ds\right)e_3+\left(M+{\Omega }_b\right)·e_3$$

(71)

under the compatibility condition

$${\Omega }_b^{\prime }=jt\wedge e_3=t\wedge J$$

Proof. 

Consider the identity $e_3\wedge (M-\sigma )=e_3\wedge \gamma \wedge J={〈\gamma 〉}_3=0$ (eq. 39). Therefore, we are led to a new equation in terms of the preferred direction, which splits into translational and rotational components as follows:

$$j\gamma \left(s\right)=\left(Hs-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds\right)e_3+\left(M+{\Omega }_b\right)·e_3$$

Furthermore, the first term can be interpreted as a sum of translations, while the second term – as a sum of rotations.

Eq. 69 implies the compatibility condition

$$jt{e}_3=H-{\displaystyle \frac{1}{2}}{\kappa }^2-{\sigma }^{\prime }\Rightarrow jt\wedge e_3=-{\sigma }^{\prime }={\Omega }_b^{\prime }$$

Therefore, formally the Bishop frame can be determined by quadrature as

$$\sigma =j\int e_3\wedge tds$$

from the tangent field, so the total angular momentum can be identified with the integration constant of the Bishop frame. □

Geometrically eq. 71 amounts to establishing a preferred orientation of the system (i.e. a global cylindrical symmetry). Using these coordinates, the solutions can be represented conveniently in a cylindrical coordinate system [22]. Then for the altitude we have

$$j{e}_3·\gamma =jz=Hs-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds$$

So we can identify the altitude (i.e. the z-axis) with the direction of translation. Using eq. 63 one obtains directly

$$jz\left(s\right)=Hs-{\displaystyle \frac{1}{2}}(p-4q)s-2\sqrt{q}\mathcal{E}\left(\sqrt{q}s\right|m)={\displaystyle \frac{H}{3}}s-{\displaystyle \frac{2m}{3}}(q-2)s-2\sqrt{q}\mathcal{E}\left(\sqrt{q}s\right|m)$$

(72)

in terms of the Jacobi epsilon function.

Consider the identity

$$m_3\equiv M·e_3=-\underset{jz{e}_3}{\underbrace{j(\gamma ·e_3)e_3}}+\gamma j+\sigma ·e_3=j\rho e_r+\sigma ·e_3,m_3=M·J/j$$

We can solve for the radial component as

$$j\rho e_r=m_3-\sigma ·e_3$$

(73)

To obtain the angular coordinate proceed as follows and furthermore,

$$j^2{\rho }^2=m_3^2+{(\sigma ·e_3)}^2-2m_3·\sigma ·e_3$$

Differentiate eq. 73 as

$$j\rho {\phi }^{\prime }{e}_{\phi }+j{\rho }^{\prime }{e}_r=e_3·{\sigma }^{\prime }$$

Take the inner products

$$j\rho {\phi }^{\prime }=e_3·{\sigma }^{\prime }·e_{\phi },j{\rho }^{\prime }=e_3·{\sigma }^{\prime }·e_r$$

Integrate to obtain the polar coordinates

$$\begin{array}{}\mathrm{(74)}& \hfill j\rho \left(s\right)& =e_3·\int {\sigma }^{\prime }·e_{r}ds\hfill \mathrm{(75)}& \hfill j\phi \left(s\right)& =e_3·\int {\displaystyle \frac{{\sigma }^{\prime }·e_{\phi }}{\rho }}ds\hfill \end{array}$$

The procedure can be explicated in the next section.

4.4. Construction of the Preferred Coordinate System

The exposition follows the approach of [22] taking into account the differences in the employed formalism.

Observe that $\kappa I_{3}b=\kappa tn=t\wedge t^{\prime }=\sigma =-{\Omega }_b$ so that $\kappa b=I_3\sigma$ (see Figure 2). The solid angle between the planes $\sigma$ and $R=I_{3}J=j{e}_r\wedge e_{\phi }$ is given by

$$cos\theta ={\displaystyle \frac{\sigma ·R}{\left|\right|R\left|\right|\left|\right|\sigma \left|\right|}}=I_3{\displaystyle \frac{\sigma \wedge J}{j\left|\kappa \right|}}={\displaystyle \frac{I_{3}w}{j\left|\kappa \right|}}={\displaystyle \frac{c}{j\kappa }}$$

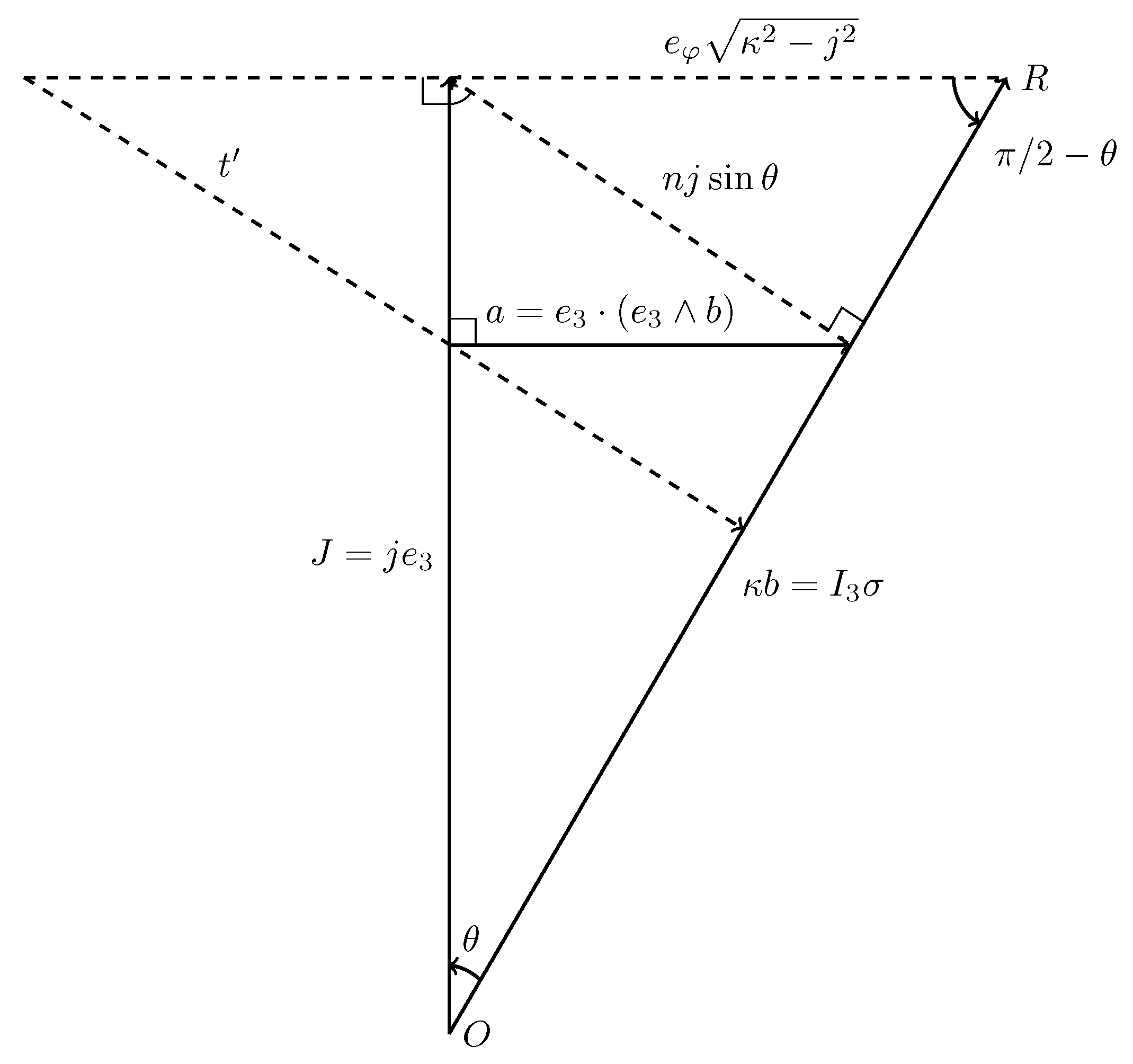
To construct $e_{\phi }$ compute the rejection vector to b in the plane $e_3\wedge b$ (see Figure 3)

$$a:=e_3·(e_3\wedge b)=b-(e_3·b)e_3=b-(J·b)J/j^2=\left|\right|a\left|\right|e_{\phi }$$

Furthermore, we have the identity

$$a^2={(e_3·(e_3\wedge b))}^2=1-{(e_3·b)}^2={sin}^2\theta$$

Therefore, the norm of the vector a can be computed as

$$\left|\right|a\left|\right|=|sin\theta |={\displaystyle \frac{\sqrt{j^2-{\kappa }^2{\tau }^2}}{j}}={\displaystyle \frac{\sqrt{j^2{\kappa }^2-c^2}}{j\kappa }}=\sqrt{1-{\left({\displaystyle \frac{c}{j\kappa }}\right)}^2}$$

(76)

after substitution in eq. 43 since $J·b=-\kappa \tau$.

Observe that in cylindrical coordinates $(\rho ,\phi ,z)$

$$r=\rho e_r+e_{3}z⟶t={\rho }^{\prime }{e}_r+\rho {\phi }^{\prime }{e}_{\phi }+z^{\prime }{e}_3$$

(77)

The two remaining coordinate equations can be obtained as the scalar products

$$t·e_r={\rho }^{\prime },t·e_{\phi }=\rho {\phi }^{\prime }$$

Direct representation of a in terms of the Frenet frame using eq. 50 results in

$$\begin{array}{c}a{j}^2=b{j}^2-(J·b)J=t\left({\kappa }^2+\lambda \right)\kappa \tau -n\kappa \tau {\kappa }^{\prime }+b\left(j^2-{\kappa }^2{\tau }^2\right)=\hfill \\ \hfill t\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)\kappa \tau -n\kappa \tau {\kappa }^{\prime }+b\left(j^2-{\kappa }^2{\tau }^2\right)\end{array}$$

(78)

Furthermore, the third basis vector can be computed as $e_r=R{e}_{\phi }=-I_3{e}_{\phi }{e}_3$.

$${\rho }^{\prime }=t·e_r=-t·\left(I_3{e}_{\phi }{e}_3\right)=-I_3(t\wedge e_{\phi }\wedge e_3)=-{\displaystyle \frac{I_3}{\left|\right|a\left|\right|j}}(t\wedge a\wedge J)$$

(79)

Then

$$a\wedge J=\left(b-{\displaystyle \frac{J·b}{j^2}}J\right)\wedge J=b\wedge J$$

so that

$$t\wedge a\wedge J=t\wedge b\wedge (\lambda t-t^{″})=t\wedge b\wedge t^{″}=t\wedge b\wedge ({\kappa }^{\prime }n-k{n}^{\prime })={\kappa }^{\prime }t\wedge b\wedge n={\kappa }^{\prime }{I}_3$$

Therefore,

$$-{\displaystyle \frac{I_3}{\left|\right|a\left|\right|j}}t\wedge a\wedge J={\displaystyle \frac{{\kappa }^{\prime }}{\left|\right|a\left|\right|j}}={\displaystyle \frac{j\kappa {\kappa }^{\prime }}{j\sqrt{j^2{\kappa }^2-c^2}}}={\rho }^{\prime }$$

from eqs. 76 and 79, which directly integrates to

$$j^2\rho =\sqrt{j^2{\kappa }^2-c^2}=j\kappa \left|\right|a\left|\right|$$

(80)

Furthermore,

$$\rho {\phi }^{\prime }=t·e_{\phi }=t·{\displaystyle \frac{a}{\left|\right|a\left|\right|}}={\displaystyle \frac{\kappa \tau ({\kappa }^2+\lambda )}{j\sqrt{j^2-{\kappa }^2{\tau }^2}}}={\displaystyle \frac{c(2H-{\kappa }^2)}{2j\sqrt{j^2{\kappa }^2-c^2}}}$$

so that

$${\phi }^{\prime }={\displaystyle \frac{jc(H-{\kappa }^2)}{2(j^2{\kappa }^2-c^2)}}=-{\displaystyle \frac{c}{2j}}+{\displaystyle \frac{c}{2j}}{\displaystyle \frac{(2H{j}^2-c^2)}{(j^2{\kappa }^2-c^2)}}$$

This can be integrated into

$$\phi \left(s\right)=-{\displaystyle \frac{cs}{2j}}+{\displaystyle \frac{c}{2j}}{\displaystyle \frac{(2H{j}^2-c^2)}{\sqrt{q}(j^{2}p-c^2)}}\Pi \left({\displaystyle \frac{4mq{j}^2}{j^{2}p-c^2}},\mathrm{am}\left(\sqrt{q}s|m\right)|m\right)$$

(81)

in terms of the incomplete elliptic integral of the 3^rd kind, corresponding to the result in [24]. This is, however, not the most convenient representation as noted in [23]. It is produced here only to demonstrate the correspondence of the approach.

4.5. Specialization to 2D

To connect with the 2D application we use the frames {$e_1,e_3$} with pseudoscalar $I_2=e_1\wedge e_3$. Observe that the Bishop frame is simply $\sigma =\kappa I_2=2q\mathrm{dn}\left(sq\right|m)I_2$ and the torque bi-vector is $M=m_3{I}_2$.

Then one immediately obtains the solution

$$j\gamma =\left(Hs-2q\mathcal{E}\left(qs\right|m)\right)e_3+\left(m_3-2q\mathrm{dn}\left(qs\right|m)\right)e_1$$

(82)

Furthermore, the linear momentum becomes

$$J=\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)t-{\kappa }^{\prime }n=(H-2q^2{\mathrm{dn}}^2\left(qs\right|m))t+2m{q}^2\mathrm{cn}\left(qs\right|m)\mathrm{sn}\left(qs\right|m)n$$

(83)

Example 1.

One of the solutions are the set of equations

$$\begin{array}{}\mathrm{(84)}& \hfill \kappa \left(s\right)& =\sqrt{2}\sqrt{j+H}\mathrm{dn}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)\hfill \mathrm{(85)}& \hfill x\left(s\right)& ={\displaystyle \frac{\sqrt{2}\sqrt{j+H}}{j}}\mathrm{dn}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)={\displaystyle \frac{\kappa \left(s\right)}{j}}\hfill \mathrm{(86)}& \hfill z\left(s\right)& ={\displaystyle \frac{Hs}{j}}-{\displaystyle \frac{\sqrt{2}\sqrt{j+H}}{j}}\mathcal{E}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)\hfill \end{array}$$

5. Discussion

The present contribution considers the problem of 2D and 3D non-extendable elastic beams and rods from the perspective of Geometric algebra. This allows for a great simplification of the problem due to the considerable expression power of the Geometric algebra approach. Notably, the approach obviates the use of a non-Euclidean configuration space [5]. Instead, all calculations are performed in the physical Euclidean space.

The paper demonstrates the forms of Frenet, Darboux, and Bishop frames in ${\mathbb{G}}^3$. It furthermore offers a new Lagrangian formulation of the elastica theory. This allows for construction of the fundamental Notherian conserved quantities. The Geometric algebra approach also enables an intuitive classification of the elastica system using its geometric invariants.

Concise expressions of the elastica equations are found using the Bishop frame. The Geometric algebra approach demonstrates natural correspondence of the free elastic problem with the Kirchhoff beam theory. Finally, we have determined a coordinate-free formulation of the solution.

Possible applications of the approach are inverse problems, image analysis and Finite Element Modeling, FEM.

Appendix A.1. Elliptic Integrals of the First Kind

Incomplete elliptic integral of the 1^st kind:

$$\mathcal{F}\left(\varphi |m\right):={\int }_0^{\varphi }{\displaystyle \frac{du}{\sqrt{1-m{sin}^{2}u}}}$$

(A1)

The Jacobi amplitude function is the inverse of the $\mathcal{F}$ integral:

$$u=\mathcal{F}\left(\varphi |m\right)⟹\mathrm{am}\left(u\right|m):=\varphi$$

(A2)

Its derivative is denoted by $\mathrm{dn}$:

$$\mathrm{dn}\left(x\right|m)={\displaystyle \frac{d}{dx}}\mathrm{am}\left(x\right|m)=\sqrt{1-m{\mathrm{sn}}^2\left(x\right|m)}$$

Therefore, we have the identity

$$\mathrm{dn}{\left(x\right|m)}^2+m{\mathrm{sn}}^2\left(x\right|m)=1$$

The complete elliptic integral is defined as

$$\mathcal{F}\left({\displaystyle \frac{\pi }{2}}|m\right)=:\mathcal{K}\left(m\right)$$

(A3)

The elliptic sine and cosine are defined by

$$\mathrm{sn}\left(x\right|m):=sin\mathrm{am}(x\left|m\right),\mathrm{cn}\left(x\right|m):=cos\mathrm{am}(x\left|m\right)$$

(A4)

Therefore, we have the identity

$$\mathrm{sn}{\left(x\right|m)}^2+{\mathrm{cn}}^2\left(x\right|m)=1$$

Appendix A.2. Elliptic Integrals of the Second Kind

Incomplete elliptic integral of the 2^nd kind:

$$E\left(\varphi |m\right):={\int }_0^{\varphi }\sqrt{1-m{sin}^{2}u}du$$

(A5)

The complete elliptic integral is defined as $E\left({\displaystyle \frac{\pi }{2}}|m\right)=:E\left(m\right)$.

The Jacobi epsilon function $\mathcal{E}\left(x\right|m)$ is defined as

$$\mathcal{E}\left(x\right|m):={\int }_0^x{\mathrm{dn}}^2\left(t\right|m)dt$$

(A6)

The epsilon function is related to the incomplete elliptic integral of the 2^nd kind as

$$E\left(\mathrm{am}\right(x\left|m\right)\left|m\right)=\mathcal{E}\left(x\right|m)$$

(A7)

Appendix A.3. Elliptic Integrals of the Third Kind

The incomplete elliptic integral of the third kind is given by

$$\Pi \left(n,\varphi |m\right)={\int }_0^{\varphi }{\displaystyle \frac{1}{1-n{sin}^2\theta }}{\displaystyle \frac{d\theta }{\sqrt{1-m{sin}^2\theta }}}$$

(A8)

Furthermore, the integral can be analytically continued to a quasi-periodic function as

$$\Pi \left(n,\varphi |m\right)=\Pi \left(n,\left\{\varphi \right\}|m\right)+2⌊{\displaystyle \frac{\mathrm{Re}\left(\varphi \right)}{\pi }}⌋\Pi (n\mid m)$$

where $\left\{\varphi \right\}:=\varphi mod\pi$ denotes the fractional part of $\varphi$ modulo $\pi$. The integral is related to the elliptic functions by the integral equation

$$\Pi \left(n,\varphi |m\right)={\int }_0^z{\displaystyle \frac{du}{1-n{\mathrm{sn}}^2\left(u\right|m)}},z=\mathcal{F}\left(\varphi |m\right)$$

(A9)

This formula follows from the substitution $\theta =\mathrm{am}\left(u\right|m)$ so that $z=\mathcal{F}\left(\varphi |m\right)$ in the original argument. Therefore, we have also the formula

$$\Pi \left(n,\mathrm{am}\left(\varphi \right|m\left)\right|m\right)={\int }_0^{\varphi }{\displaystyle \frac{du}{1-n{\mathrm{sn}}^2\left(u\right|m)}}=:\mathcal{P}(n,\varphi |m)$$

The complete elliptic integral of the third kind is given by

$$\Pi \left(n|m\right)=\Pi \left(n,{\displaystyle \frac{\pi }{2}}|m\right)={\int }_0^{{\displaystyle \frac{\pi }{2}}}{\displaystyle \frac{1}{1-n{sin}^2\theta }}{\displaystyle \frac{d\theta }{\sqrt{1-m{sin}^2\theta }}}$$

(A10)

Appendix A.4. Integral Identities

$$\begin{array}{cc}\hfill {\int }_0^s\mathrm{sn}\left(u\right|m)\mathrm{cn}\left(u\right|m)du& =-{\displaystyle \frac{1}{m}}(\mathrm{dn}\left(s\right|m)-1)\hfill \end{array}$$

(A11)

$$\begin{array}{cc}\hfill {\int }_0^s{\mathrm{cn}}^2\left(u\right|m)du& ={\displaystyle \frac{\mathcal{E}\left(s\right|m)-(1-m)s}{m}},\hfill \end{array}$$

(A12)

$$\begin{array}{cc}\hfill {\int }_0^s{\mathrm{sn}}^2\left(u\right|m)du& =-{\displaystyle \frac{\mathcal{E}\left(s\right|m)-s}{m}},\hfill \end{array}$$

(A13)