A Mathematical Approach to Context-Free Languages

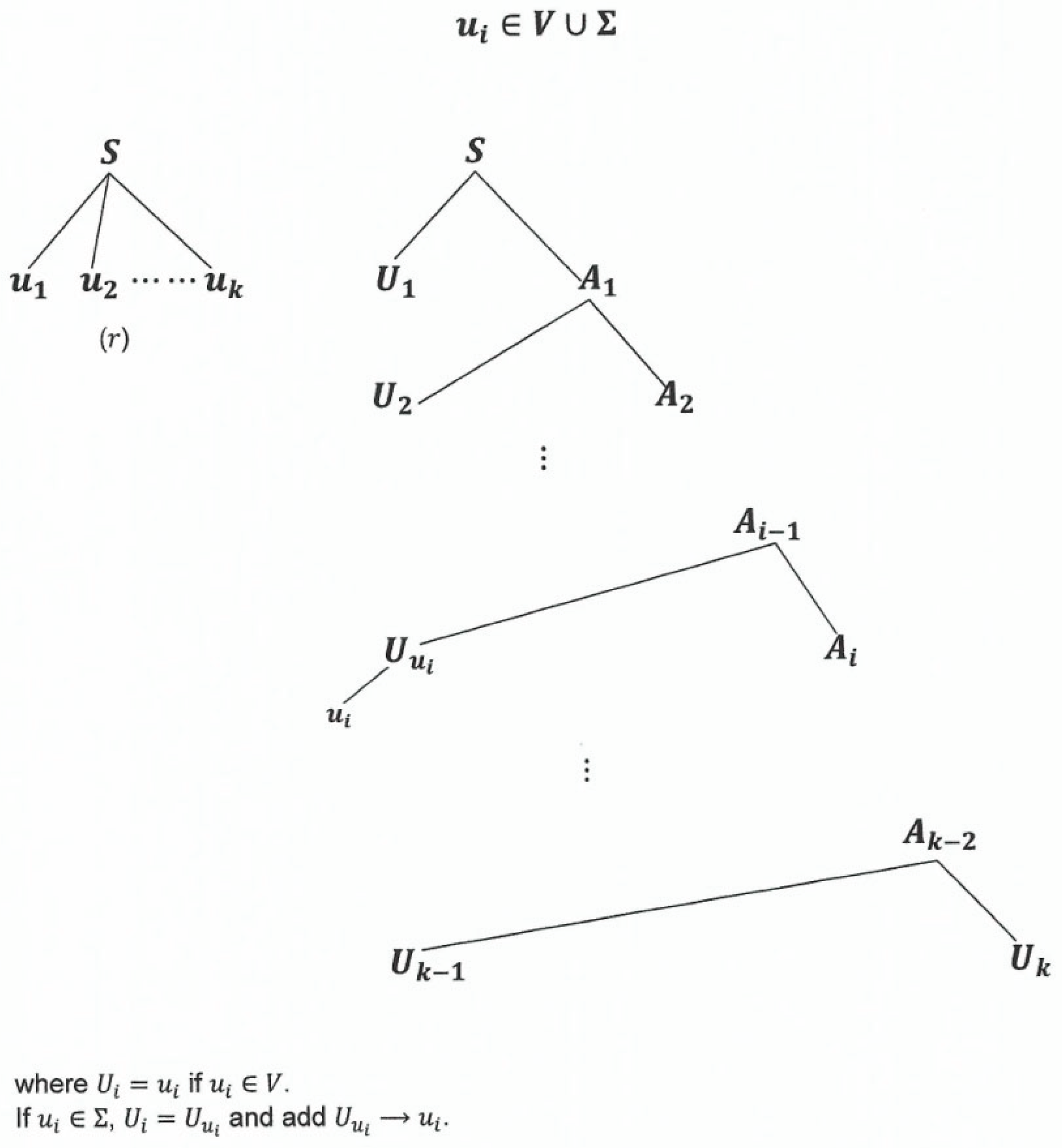
2.1. Context-Free Grammars (CFG)

In Chapter 1, we use finite automata and regular expressions to describe regular languages. In this chapter, we introduce the concept of Context-Free Grammar which is a more powerful tool for describing languages.

A Context-Free Grammar is formally defined as follows.

Definition 2.1. 

A Context-Free Grammar denoted by $CFG$ is a 4-tuple $G=(V, \mathsf{\Sigma }, R, S)$, where

(i)

$V$ is a finite set of variables;

(ii)

$\mathsf{\Sigma }$ is a finite set of terminals such that $V\cap \mathsf{\Sigma }=\mathrm{\varnothing }$;

(iii)

$S\in V$ is the start variable; and

(iv)

$R\subset V\times {(V\cup \mathsf{\Sigma })}^{*}$ is a finite relation

For any $(A,u)\in R$, we usually write $A\to u$ and call it a rule.

Accordingly, the relation $R$ is also called the set of rules for the $CFG$.

$A$ is sometimes called the head of the rule whereas $u$ is called the body of the rule.

Example 2.2. 

Let $V=\{<SENTENSE>,<NOUN PHRASE>,<VERB PHRASE>,<PREP PHRASE>,$

$<CMPLX NOUN>,<CMPLX VERB>,<PREP>,<ARTICLE>,<NOUN>,<VERB>\}$

$\mathsf{\Sigma }=\{\mathrm{a},\mathrm{t}\mathrm{h}\mathrm{e},\mathrm{b}\mathrm{o}\mathrm{y},\mathrm{g}\mathrm{i}\mathrm{r}\mathrm{l},\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r},\mathrm{t}\mathrm{o}\mathrm{u}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s},\mathrm{l}\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{s},\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{s},\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\}$

$S=<SENTENSE>$

Let $R$ consist of the following rules:

$<SENTENSE>⟶<NOUN PHRASE><VERB PHRASE>$

$<NOUN PHRASE>⟶<CMPLX NOUN>|<CMPLX NOUN><PREP PHRASE>$

$<VERB PHRASE>⟶<CMPLX VERB>|<CMPLX VERB><PREP PHRASE>$

$<PREP PHRASE>⟶<PREP><CMPLX NOUN>$

$<CMPLX NOUN>⟶<ARTICLE><NOUN>$

$<CMPLX VERB>⟶<VERB>|<VERB><NOUN PHRASE>$

$<ARTICLE>⟶a | the$

$<NOUN>⟶boy \left| girl \right| flower$

$<VERB>⟶touches \left| likes \right| sees$

$<PREP>⟶with$

$G=(V, \mathsf{\Sigma }, R, S)$ is a $CFG$.

The following are examples of strings in ${\mathsf{\Sigma }}^{*}$ that can be derived by $G$.

$(i) <SENTENSE>$

$⟶<NOUN PHRASE><VERB PHRASE>$

$⟶<CMPLX NOUN><VERB PHRASE>$

$⟶<ARTICLE><NOUN><VERB PHRASE>$

$⟶ a<NOUN><VERB PHRASE>$

$⟶ a boy<VERB PHRASE>$

$⟶ a boy<CMPLX VERB>$

$⟶ a boy<VERB>$

$⟶ a boy sees$

$(ii) <SENTENSE>$

$⟶<NOUN PHRASE><VERB PHRASE>$

$⟶<CMPLX NOUN><VERB PHRASE>$

$⟶<ARTICLE><NOUN><VERB PHRASE>$

$⟶ the boy<VERB PHRASE>$

$⟶ the boy<CMPLX VERB>$

$⟶ the boy<VERB><NOUN PHRASE>$

$⟶ the boy sees<CMPLX NOUN>$

$⟶ the boy sees<ARTICLE><NOUN>$

$⟶ the boy sees a flower$

$(iii)<SENTENSE>$

$⟶<NOUN PHRASE><VERB PHRASE>$

$⟶<CMPLX NOUN><PREP PHRASE><VERB PHRASE>$

$⟶<ARTICLE><NOUN><PREP><CMPLX NOUN><VERB PHRASE>$

$⟶ a girl with<ARTICLE><NOUN><VERB PHRASE>$

$⟶ a girl with a flower<CMPLX VERB>$

$⟶ a girl with a flower<VERB><NOUN PHRASE>$

$⟶ a girl with a flower likes<CMPLX NOUN>$

$⟶ a girl with a flower likes<ARTICLE><NOUN>$

$⟶ a girl with a flower likes the boy$

Definition 2.3. 

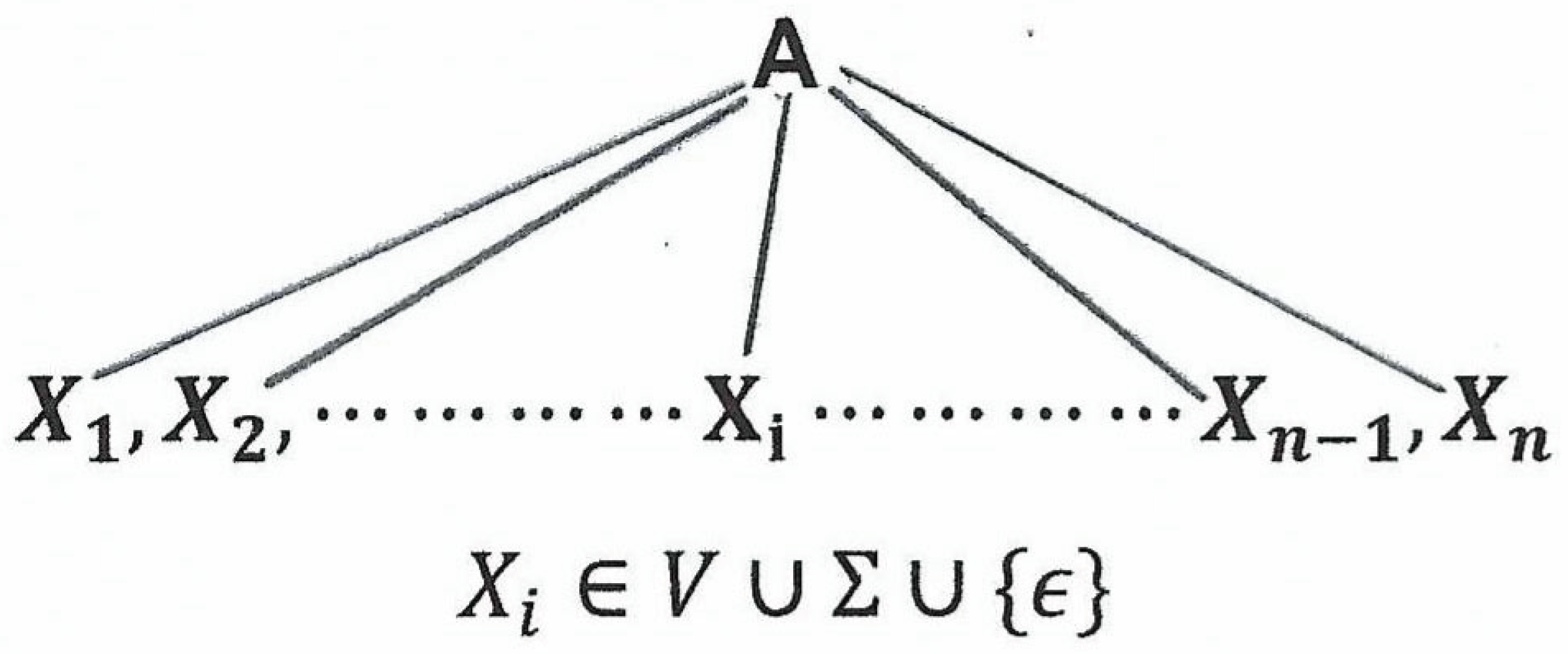
Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

For any $u,v\in {(V\cup \mathsf{\Sigma })}^{*}$, we say $u$ yields $v$ (or $v$ is derivable from $u$) in one step (written as $u\stackrel{1}{\Rightarrow }v$or simply $u⟹v$) if and only if

$\exists A\in V, \gamma ,\alpha ,\beta \in {(V\cup \mathsf{\Sigma })}^{*}$ and a rule $A⟶\gamma$ such that $u=\alpha A\beta$ and $v=\alpha \gamma \beta$.

Note that the process of deriving $v$ from $u$ is basically a replacement of a variable in $u$ by the body of the variable’s rule to obtain $v$.

In addition, we define $u\stackrel{0}{\Rightarrow }v$ iff $u=v$.

For any integer $n\ge 0$, we say $u$ yields $v$ (or $v$ is derivable from $u$) in $n+1$ steps (written as $u\stackrel{n+1}{\Rightarrow }v$) iff $\exists w\in {(V\cup \mathsf{\Sigma })}^{*}$ such that $u\stackrel{n}{\Rightarrow }w$and $w\stackrel{1}{\Rightarrow }v$.

If there are more than one $CFG$ to be considered, (e.g. $G$ and $G^{\text{'}}$) and if we need to distinguish between derivations in $G$ from derivations in $G^{\text{'}}$, we can write

$u\stackrel{n,G}{\Rightarrow }v$to mean $v$ is derivable from $u$ in $n$ steps by use of rules in $G$; and

$u\stackrel{n,G^{\text{'}}}{\Rightarrow }v$ to mean $v$ is derivable from $u$ in $n$ steps by use of rules in $G^{\text{'}}$.

Furthermore, if we need to specify the rule to be applied in each step, we can use

$u\stackrel{n,G,(R_1,R_2,\dots R_n)}{\Rightarrow }v$to mean $v$ is derivable from $u$ in $n$ steps by use of rules in $G$ with rule $R_i$ to be applied in the $i^{th}$ step; and

$u\stackrel{n,G^{\text{'}},(R_1^{\text{'}},R_2^{\text{'}},\dots R_n^{\text{'}})}{\Rightarrow }v$to mean $v$ is derivable from $u$ in $n$ steps by use of rules in $G^{\text{'}}$ with rule $R_i^{\text{'}}$ to be applied in the $i^{th}$ step.

Since there can be more than one way of deriving a string, it is sometimes useful to require the derivation to be leftmost. A leftmost derivation is a derivation in which the leftmost variable at every step is replaced by the body of its rule.

Formally, we define leftmost derivation as follows.

For any $u,v\in {(V\cup \mathsf{\Sigma })}^{*}$, $v$ is a leftmost derivation of $u$ in one step (written as$u\stackrel{1,lm}{\Rightarrow }v$or simply $u\stackrel{lm}{\Rightarrow }v$) iff $\exists w\in {\mathsf{\Sigma }}^{*}$, $w^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$, $A\in V, \alpha \in {(V\cup \mathsf{\Sigma })}^{*}$ and a rule $A⟶\alpha$ such that $u=wA{w}^{\text{'}}$ and $v=w\alpha w^{\text{'}}$.

For any integer $n\ge 0, u\stackrel{n,lm}{\Rightarrow }v$is defined similarly as $u\stackrel{n}{\Rightarrow }v$.

Definition 2.4 

. Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$; $\stackrel{*}{\Rightarrow }$ be a subset of ${(V\cup \mathsf{\Sigma })}^{*}\times {(V\cup \mathsf{\Sigma })}^{*}$ .

We define the relation $\stackrel{*}{\Rightarrow }$ as follows:

$\forall u,v\in {(V\cup \mathsf{\Sigma })}^{*},u\stackrel{*}{\Rightarrow }v$ if and only if $u\stackrel{n}{\Rightarrow }v$ for some integer $n\ge 0$.

$n$ is called the length of the derivation of $v$ from $u$.

Note that whenever there is an $n$ such that $u\stackrel{n}{\Rightarrow }v$, there is a minimum $n^{\text{'}}$ such that $u\stackrel{n^{\text{'}}}{\Rightarrow }v$.

If there are more than one $CFG$ to be considered,

$u\stackrel{*,G}{\Rightarrow }v$ if and only if $u\stackrel{n,G}{\Rightarrow }v$ for some integer $n\ge 0$.

$\stackrel{*,lm}{\Rightarrow }$is defined similarly as $\stackrel{*}{\Rightarrow }$.

Proposition 2.5. 

$\stackrel{*}{\Rightarrow }$ (respectively $\stackrel{*,lm}{\Rightarrow }$) is reflexive and transitive.

Proof. 

Since $u\stackrel{0}{\Rightarrow }u$ for all $u\in {(V\cup \mathsf{\Sigma })}^{*}$, $u\stackrel{*}{\Rightarrow }u$ for all $u\in {(V\cup \mathsf{\Sigma })}^{*}$.

Therefore, $\stackrel{*}{\Rightarrow }$ is reflexive.

For transitivity, assume $u\stackrel{*}{\Rightarrow }v$and $v\stackrel{*}{\Rightarrow }w$.

There exist integers $m\ge 0$ and $n\ge 0$ such that

$u\stackrel{m}{\Rightarrow }v$and $v\stackrel{n}{\Rightarrow }w$.

There are two cases to examine, $n=0$ or $n\ne 0$

$(i) n=0$

$$v\stackrel{0}{\Rightarrow }w$$

By definition, $v=w$.

Since $u\stackrel{m}{\Rightarrow }v$, $u\stackrel{m}{\Rightarrow }w$.

Therefore, $u\stackrel{*}{\Rightarrow }w .$

$(ii) n\ne 0$

$v\stackrel{n}{\Rightarrow }w$

$v\stackrel{n-1}{\Rightarrow }{\alpha }_{n-1}\stackrel{1}{\Rightarrow }w$ for some ${\alpha }_{n-1}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

With a backward induction argument, we have

$v⟹{\alpha }_1⟹{\alpha }_2\dots \dots \dots ⟹{\alpha }_{n-1}⟹w$ for some ${{\alpha }_{1,}{\alpha }_{2,}\dots \alpha }_{n-1}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

We now have

$u\stackrel{m}{\Rightarrow }v⟹{\alpha }_1⟹{\alpha }_2\dots \dots \dots ⟹{\alpha }_{n-1}⟹w$.

Since $\left(u\stackrel{m}{\Rightarrow }v⟹{\alpha }_1\right)⟹\left(u\stackrel{m+1}{\Rightarrow }{\alpha }_1\right)$,

$(u\stackrel{m+1}{\Rightarrow }{\alpha }_1⟹{\alpha }_2)⟹\left(u\stackrel{m+2}{\Rightarrow }{\alpha }_2\right)$,

$⋮$

With a forward induction argument, we have

$u\stackrel{m+n-1}{\Rightarrow }{\alpha }_{n-1}$.

Finally, $(u\stackrel{m+n-1}{\Rightarrow }{\alpha }_{n-1}⟹w)⟹\left(u\stackrel{m+n}{\Rightarrow }w\right)$.

Therefore, $u\stackrel{*}{\Rightarrow }w$.

Combining (i) and (ii), $\stackrel{*}{\Rightarrow }$ is transitive.

With a similar argument, we can establish $\stackrel{*,lm}{\Rightarrow }$ is also reflexive and transitive.

Definition 2.6. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

The language of $G$ is defined as

$L\left(G\right)=\left\{w{\in \mathsf{\Sigma }}^{\mathrm{*}}\right|S\stackrel{\mathrm{*}}{\Rightarrow }w\}$.

Note that if $S\stackrel{n}{\Rightarrow }w$, $n\ge 1$ because $S\stackrel{0}{\Rightarrow }w$ implies $S=w$ which is a contradiction.

Definition 2.7. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $Q$ represent the rule $A\to \alpha$ in $R$.

$\forall u,v\in {(V\cup \mathsf{\Sigma })}^{*},$ we say $u$ yields $v$ (or $v$ is derivable from $u$) using the rule $Q$ (written as

$u\stackrel{Q}{\Rightarrow }v$) if and only if there exist $w_1,w_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $u=w_{1}A{w}_2$ and $v=w_1\alpha w_2$.

Proposition 2.8. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

For any $A\in V,$ $\alpha \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ and $x,y,z\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$,

(i)

$\left(A⟶\alpha \right)⟺(A⟹\alpha )$

(ii)

If there is no $\alpha$ in ${(V\cup \mathsf{\Sigma })}^{*}$ such that $S⟶\alpha$ is a rule, $L\left(G\right)=\varnothing$.

(iii)

If $\left\{\alpha \in {\left(V\cup \mathsf{\Sigma }\right)}^{*}|A⟶\alpha \right\}=\varnothing$ and $x⟹y$, then $A$ appears in $x⟹A$ appears in $y$.

(iv)

Let $S⟹u_1⟹u_2\dots \dots \dots ⟹u_n⟹w$, where $u_i\in {(V\cup \mathsf{\Sigma })}^{*}$ for all $i\in \{\mathrm{1,2},3,\dots n\}$, $w\in {\mathsf{\Sigma }}^{*}$ and $n\ge 1$.

If $A\in V$ and $A$ appears in $u_i$ for some $i\in \{\mathrm{1,2},3,\dots n\},$then $\exists \alpha \in {(V\cup \mathsf{\Sigma })}^{*}$ such that $A⟶\alpha$ is a rule.

Proof. 

(i)

If $A⟶\alpha$ is a rule, since $ϵ$ is in ${(V\cup \mathsf{\Sigma })}^{*}$, $ϵAϵ⟹ϵ\alpha ϵ$.

Therefore, $A⟹\alpha$.

Conversely if $A⟹\alpha$, $\exists Q\in V,\beta ,w_1,w_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $A=w_{1}Q{w}_2$ and

$\alpha =w_1\beta w_2$ and $Q⟶\beta$ is a rule.

Since $A=w_{1}Q{w}_2$, $w_1,w_2$ must be $ϵ$ and $A=Q$.

Therefore, $\alpha =\beta$ and $Q⟶\beta$ becomes $A⟶\alpha$.

(ii)

Assume for contradiction that $L\left(G\right)\ne \varnothing$.

$\exists w\in L\left(G\right).$

$\exists k\in \mathbb{N}\cup \left\{0\right\},w_1,w_2,\dots \dots \dots w_k\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $S⟹w_1⟹w_2\dots \dots \dots ⟹w_k⟹w$ or $S⟹w$. (Note that $k=0⟹S=w_k$.)

By (i), $S⟶w_1$ or $S⟶w$.

This contradicts the assumption that there is no $\alpha$ in ${(V\cup \mathsf{\Sigma })}^{*}$ such that $S⟶\alpha$ is a rule.

(iii)

Since $x⟹y$, $\exists B\in V,w_1,w_2,\beta \in {(V\cup \mathsf{\Sigma })}^{*}$ such that $x=w_{1}B{w}_2$, $y=w_1\beta w_2$ and $B⟶\beta$ is a rule.

Since $A⟶\alpha$ is not a rule $\forall \alpha \in {\left(V\cup \mathsf{\Sigma }\right)}^{*},A\ne B$.

Since $A$ appears in $x$, $A$ appears either in $w_1 or w_2$.

In either case, $A$ appears in $y$.

(iv)

Assume for contradiction $\exists A$ which appears in $u_i$ for some $i\in \{\mathrm{1,2},3\dots n\}$ such that $A⟶\alpha$ is not a rule for all $\alpha \in {\left(V\cup \mathsf{\Sigma }\right)}^{*}$.

By (iii), $A$ appears in $u_{i+1}$.

By repeated application of (iii), we can conclude that $A$ appears in $u_{i+2}, u_{i+3},\dots u_n$and $w$, which is a contradiction because $w$ contains no variables.

Example 2.9. 

Let $G=\left(\right\{S\}, \{\mathrm{0,1}\}, R, S)$ be a $CFG$.

Create the rules in $R$ so that $L\left(G\right)=\left\{0^n{1}^{2n+1}\right|n\in \mathbb{N}\}$.

The rule is $S⟶0S11 | 1$ as can be seen from the following applications of the rule.

$S⟶0S11$ (1^st application of $S⟶0S11$)

$⟶00S1111$ (2^nd application of $S⟶0S11$)

$⟶000S111111$ (3^rd application of $S⟶0S11$)

$⋮$

$⋮$

$⟶0^{n}S{1}^{2n}$ ($n^{th}$ application of $S⟶0S11$)

$⟶0^n{1}^{2n+1}$ (Application of $S⟶1$)

Example 2.10. 

Let $G=\left(\right\{S\}, \{\mathrm{0,1}\}, R, S)$ be a $CFG$.

Create the rules in $R$ so that $L\left(G\right)=\left\{0^{2n}{1}^{3n}\right|n\in \mathbb{N}\}$.

The rule is $S⟶00S111 | ϵ$ as can be seen from the following applications of the rule.

$S⟶00S111$ (1^st application of $S⟶00S111$)

$⟶0000S111111$ (2^nd application of $S⟶00S111$)

$⟶000000S111111111$ (3^rd application of $S⟶00S111$)

$⋮$

$⋮$

$⟶0^{2n}S{1}^{3n}$ ($n^{th}$ application of $S⟶00S111$)

$⟶0^{2n}{ϵ1}^{3n}$ (Application of $S⟶ϵ$)

$⟶0^{2n}{1}^{3n}$

Example 2.11. 

Let $G=\left(\right\{S\}, \{\mathrm{0,1}\}, R, S)$ be a $CFG$.

Create the rules in $R$ so that $L\left(G\right)=\left\{0^{2n+7}{1}^{3n+9}\right|n\in \mathbb{N}\}$.

The rule is $S⟶00S111 | 0^7{1}^9$ as can be seen from the following applications of the rule.

$S⟶00S111$ (1^st application of $S⟶00S111$)

$⟶0000S111111$ (2^nd application of $S⟶00S111$)

$⟶000000S111111111$ (3^rd application of $S⟶00S111$)

$⋮$

$⋮$

$⟶0^{2n}S{1}^{3n}$ ($n^{th}$ application of $S⟶00S111$)

$⟶0^{2n}{0}^7{1}^9{1}^{3n}$ (Application of $S⟶0^7{1}^9$)

$⟶0^{2n+7}{1}^{3n+9}$

Definition 2.12. Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $R_1,R_2,R_3,\dots \dots R_n and Q$ be rules in $R$ where $n\ge 1$.

$\left(R_1,R_2,R_3,\dots \dots R_n\right)$ and $Q$ are equivalent if $\forall u\in {\left(V\cup \mathsf{\Sigma }\right)}^{\mathrm{*}},$there exists $v\in {\left(V\cup \mathsf{\Sigma }\right)}^{\mathrm{*}}$ such that $u\stackrel{n,(R_1,R_2,\dots R_n)}{\Rightarrow }v$if and only if $u\stackrel{Q}{\Rightarrow }v$

Proposition 2.13. 

(i)

$A\stackrel{A\to \alpha }{\Rightarrow }\alpha$ if and only if $A\to \alpha$ is a rule.

(ii)

If $A$ does not appear in $\alpha$ and $A$ does not appear in $\beta$ and $A\to \alpha$ is a rule, then

$\alpha A\beta \stackrel{A\to \gamma }{\Rightarrow }x iff x=\alpha \gamma \beta$.

Proof. 

(i)

If $A\to \alpha$ is a rule, $ϵAϵ\stackrel{A\to \alpha }{\Rightarrow }ϵ\alpha ϵ$ and therefore, $A\stackrel{A\to \alpha }{\Rightarrow }\alpha$.

(ii)

If $x=\alpha \gamma \beta$, since $A\to \gamma$, by definition $\alpha A\beta \stackrel{A\to \gamma }{\Rightarrow }\alpha \gamma \beta$. Therefore, $\alpha A\beta \stackrel{A\to \gamma }{\Rightarrow }x$.

Conversely, if $A\stackrel{A\to \alpha }{\Rightarrow }\alpha$, by definition $A\to \alpha$ is a rule.

Conversely, if $\alpha A\beta \stackrel{A\to \gamma }{\Rightarrow }x$, $\exists u_1,u_2\in {\left(V\cup \mathsf{\Sigma }\right)}^{*}$ such that $\alpha A\beta =u_{1}A{u}_2$ and $x=u_1\gamma u_2$.

Since $A$ does not appear in $\alpha$ and $A$ does not appear in $\beta$, there is only one appearance of $A$ in $\alpha A\beta$.

Therefore, there is only one appearance of $A$ in $u_{1}A{u}_2$.

Therefore, $\left(\alpha A\beta =u_{1}A{u}_2\right)⟹\left(\alpha =u_1 \& \beta =u_2\right)$.

Therefore, $x=\alpha \gamma \beta$.

Proposition 2.14. 

$(A⟶\alpha )$ & $(B⟶\beta )$ are equivalent if and only if $(A=B)$ & $(\alpha =\beta )$.

Proof. 

If $(A⟶\alpha )$ & $(B⟶\beta )$ are equivalent,

$\left(A⟶\alpha \right)⟹\left(A\stackrel{A\to \alpha }{\Rightarrow }\alpha \right)$ (Proposition 2.13)

Since $(A⟶\alpha )$ & $(B⟶\beta )$ are equivalent, $A\stackrel{B\to \beta }{\Rightarrow }\alpha$.

There exist $w_1,w_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $A=w_{1}B{w}_2$ and $\alpha =w_1\beta w_2$.

$A=w_{1}B{w}_2⟹A=B$ since $A$ and $B$ are both variables.

$A=w_{1}A{w}_2⟹w_1=w_2=ϵ$.

Therefore, $\alpha =\beta$.

Conversely, if $(A=B)$ & $\left(\alpha =\beta \right)$, $(A⟶\alpha )$ & $(B⟶\beta )$ are the same rule and hence they are equivalent.

Proposition 2.15. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

$\forall A,B\in V$ and $x,y,z\in {(V\cup \mathsf{\Sigma })}^{*}$, $\left(A⟶xBz\right) \& (B⟶y)$ are equivalent to $A⟶xyz$.

Proof.$\forall u\in {(V\cup \mathsf{\Sigma })}^{*}$, let

$R_1$ be $A⟶xBz$

$R_2$ be $B⟶y$

$R_3$ be $A⟶xyz$If $u\stackrel{2,(R_1,R_2)}{\Rightarrow }v$, $\exists w_1\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $u\stackrel{R_1}{\Rightarrow }{w}_1\stackrel{R_2}{\Rightarrow }v$Since $u\stackrel{R_1}{\Rightarrow }{w}_1$, $u={\alpha }_{1}A{\alpha }_2$ and $w_1={\alpha }_{1}xBz{\alpha }_2$ for some ${\alpha }_1,{\alpha }_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

Since $R_2=(B⟶y)$, ${\alpha }_{1}xBz{\alpha }_2\stackrel{R_2}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

That is, $w_1\stackrel{R_2}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

Therefore, $\exists v={\alpha }_{1}xyz{\alpha }_2$ such that $u\stackrel{2,(R_1,R_2)}{\Rightarrow }v$.

Since $R_3=(A⟶xyz)$, ${\alpha }_{1}A{\alpha }_2\stackrel{R_3}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

That is, $u\stackrel{R_3}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

Therefore, $u\stackrel{R_3}{\Rightarrow }v$.

Conversely, if $u\stackrel{R_3}{\Rightarrow }v$, $u={\alpha }_{1}A{\alpha }_2$ and $v={\alpha }_{1}xyz{\alpha }_2$ for some ${\alpha }_1,{\alpha }_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

Let $w_1={\alpha }_{1}xBz{\alpha }_2$.

Since $R_1=(A⟶xBz)$, ${\alpha }_{1}A{\alpha }_2\stackrel{R_1}{\Rightarrow }{\alpha }_{1}xBz{\alpha }_2$.

Since $R_2=(B⟶y)$, ${\alpha }_{1}xBz{\alpha }_2\stackrel{R_2}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

Therefore, ${\alpha }_{1}A{\alpha }_2\stackrel{R_1}{\Rightarrow }{\alpha }_{1}xBz{\alpha }_2\stackrel{R_2}{\Rightarrow }{\alpha }_{1}xyz{\alpha }_2$.

That is, $u\stackrel{R_1}{\Rightarrow }{w}_1\stackrel{R_2}{\Rightarrow }v$.

That is, $u\stackrel{2,(R_1,R_2)}{\Rightarrow }v$Combining both directions, $(R_1,R_2)$ and $R_3$ are equivalent.

Proposition 2.16. Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

(a)

$\forall A,B\in V$, $x,y,z\in {(V\cup \mathsf{\Sigma })}^{*}$, if $A⟹xBz \& B⟹y$ then $A\stackrel{*}{\Rightarrow }xyz$.

(b)

$\forall \alpha ,\beta ,\gamma ,{\beta }^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$, if $\beta ⟹{\beta }^{\text{'}}$ then $\alpha \beta \gamma ⟹\alpha {\beta }^{\text{'}}\gamma$.

(c)

$\forall \alpha ,\beta ,\gamma ,{\beta }^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$, if $\beta \stackrel{*}{\Rightarrow }{\beta }^{\text{'}}$ then $\alpha \beta \gamma \stackrel{*}{\Rightarrow }\alpha {\beta }^{\text{'}}\gamma$.

(d)

Let ${\alpha }_1,{\alpha }_2,\dots {\alpha }_n,{\beta }_1,{\beta }_2,\dots {\beta }_n,{\gamma }_1,{\gamma }_2,\dots {\gamma }_n\in {(V\cup \mathsf{\Sigma })}^{*}$.

If ${\beta }_i\stackrel{*}{\Rightarrow }{\gamma }_i$ for $i\in \{\mathrm{1,2},3,\dots n\}$, then ${\alpha }_1{\beta }_1{\alpha }_2{\beta }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n\stackrel{*}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\gamma }_3\dots {\alpha }_n{\gamma }_n$.

In the special case of ${\alpha }_1={\alpha }_2,\dots ={\alpha }_n=ϵ$, ${\beta }_1{\beta }_2{\beta }_3\dots {\beta }_n\stackrel{*}{\Rightarrow }{\gamma }_1{\gamma }_2{\gamma }_3\dots {\gamma }_n$.

Proof. 

(a)

By Proposition 2.8 (i), $(B⟹y)⟺\left(B⟶y\right)$.

By definition of derivation, $xBz⟹xyz$.

Therefore, $A⟹xBz⟹xyz$.

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }xyz$.

(b)

Since $\beta ⟹{\beta }^{\mathrm{\text{'}}}$, $\exists {\beta }_1,{\beta }_2\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$, $A\in V$, $\eta \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ and a rule $A⟶\eta$ such that

$\beta ={\beta }_{1}A{\beta }_2$, ${\beta }^{\mathrm{\text{'}}}={\beta }_1\eta {\beta }_2$.

Therefore, $\alpha \beta \gamma =\alpha {\beta }_{1}A{\beta }_2\gamma$ and $\alpha {\beta }^{\mathrm{\text{'}}}\gamma =\alpha {\beta }_1\eta {\beta }_2\gamma$.

Therefore, $\alpha \beta \gamma ⟹\alpha {\beta }^{\mathrm{\text{'}}}\gamma$.

(c)

Since $\beta \stackrel{\mathrm{*}}{\Rightarrow }{\beta }^{\mathrm{\text{'}}}$, $\exists u_1,u_2\dots u_n\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ where $n\ge 0$ such that

$\beta ⟹u_1⟹u_2⟹u_3\dots u_{n-1}⟹u_n⟹{\beta }^{\mathrm{\text{'}}}$.

$\alpha \beta \gamma ⟹\alpha u_1\gamma$ ($\beta ⟹u_1$ & (b))

$⟹\alpha u_2\gamma$ ($u_1⟹u_2$ & (b))

$⋮$

$⟹\alpha u_n\gamma$ ($u_{n-1}⟹u_n$ & (b))

$⟹\alpha {\beta }^{\mathrm{\text{'}}}\gamma$ ($u_n⟹{\beta }^{\mathrm{\text{'}}}$. & (b))

Therefore, $\alpha \beta \gamma \stackrel{\mathrm{*}}{\Rightarrow }\alpha {\beta }^{\mathrm{\text{'}}}\gamma$.

(d)

${\alpha }_1{\beta }_1{\alpha }_2{\beta }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\beta }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n$ (${\beta }_1\stackrel{\mathrm{*}}{\Rightarrow }{\gamma }_1$ & (c))

$\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n$ (${\beta }_2\stackrel{\mathrm{*}}{\Rightarrow }{\gamma }_2$ & (c))

$\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\gamma }_3\dots {\alpha }_n{\beta }_n$ (${\beta }_3\stackrel{\mathrm{*}}{\Rightarrow }{\gamma }_3$ & (c))

$⋮$

$\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\gamma }_3\dots {\alpha }_n{\gamma }_n$ (${\beta }_n\stackrel{\mathrm{*}}{\Rightarrow }{\gamma }_n$ & (c))

Therefore, ${\alpha }_1{\beta }_1{\alpha }_2{\beta }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\gamma }_3\dots {\alpha }_n{\gamma }_n$.

This completes the proof of Proposition 2.16.

By replacing $⟹$ with $\stackrel{lm}{\Rightarrow }$ and $\stackrel{*}{\Rightarrow }$ with $\stackrel{*,lm}{\Rightarrow }$, we have the following proposition.

Proposition 2.17. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

(a)

$\forall A,B\in V$, $x,y,z\in {(V\cup \mathsf{\Sigma })}^{*}$, if $A\stackrel{lm}{\Rightarrow }xBz \& B\stackrel{lm}{\Rightarrow }y$ then $A\stackrel{*,lm}{\Rightarrow }xyz$.

(b)

$\forall \alpha ,\beta ,\gamma ,{\beta }^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$, if $\beta \stackrel{lm}{\Rightarrow }{\beta }^{\text{'}}$ then $\alpha \beta \gamma \stackrel{lm}{\Rightarrow }\alpha {\beta }^{\text{'}}\gamma$.

(c)

$\forall \alpha ,\beta ,\gamma ,{\beta }^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$, if $\beta \stackrel{*,lm}{\Rightarrow }{\beta }^{\text{'}}$ then $\alpha \beta \gamma \stackrel{*,lm}{\Rightarrow }\alpha {\beta }^{\text{'}}\gamma$.

(d)

Let ${\alpha }_1,{\alpha }_2,\dots {\alpha }_n,{\beta }_1,{\beta }_2,\dots {\beta }_n,{\gamma }_1,{\gamma }_2,\dots {\gamma }_n\in {(V\cup \mathsf{\Sigma })}^{*}$.

If ${\beta }_i\stackrel{\mathrm{*},lm}{\Rightarrow }{\gamma }_i$ for $i\in \{\mathrm{1,2},3,\dots n\}$, then ${\alpha }_1{\beta }_1{\alpha }_2{\beta }_2{\alpha }_3{\beta }_3\dots {\alpha }_n{\beta }_n\stackrel{\mathrm{*},lm}{\Rightarrow }{\alpha }_1{\gamma }_1{\alpha }_2{\gamma }_2{\alpha }_3{\gamma }_3\dots {\alpha }_n{\gamma }_n$.

In the special case of ${\alpha }_1={\alpha }_2,\dots ={\alpha }_n=ϵ$, ${\beta }_1{\beta }_2{\beta }_3\dots {\beta }_n\stackrel{\mathrm{*},lm}{\Rightarrow }{\gamma }_1{\gamma }_2{\gamma }_3\dots {\gamma }_n$.

Proposition 2.18. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

$A,A_1,A_2,\dots \dots A_n\in V$, ${\alpha }_1,{\alpha }_2,\dots {\alpha }_n,{\beta }_1,{\beta }_2,\dots {\beta }_n\in {(V\cup \mathsf{\Sigma })}^{*}$.

If $A⟶{\alpha }_1{A}_1{\beta }_1$, $A_1⟶{\alpha }_2{A}_2{\beta }_2$, $\dots A_{n-1}⟶{\alpha }_n{A}_n{\beta }_n$, then $A\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1\dots {\alpha }_{n-1}{\alpha }_n{A_n\beta }_n{\beta }_{n-1}\dots {\beta }_1$.

Proof. 

The proof is by induction on $n$.

($n=1$)

If $A⟶{\alpha }_1{A}_1{\beta }_1$, by Proposition 2.8 (i), $A{⟹\alpha }_1{A}_1{\beta }_1$.

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1{A}_1{\beta }_1$.

($n=k+1,k\ge 1$)

Assume $A⟶{\alpha }_1{A}_1{\beta }_1$, $A_1⟶{\alpha }_2{A}_2{\beta }_2$, $\dots A_{k-1}⟶{\alpha }_k{A}_k{\beta }_k$, $A_k⟶{\alpha }_{k+1}{A}_{k+1}{\beta }_{k+1}$.

By induction hypothesis, $A\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{A_k\beta }_k{\beta }_{k-1}\dots {\beta }_1$.

Since $A_k⟶{\alpha }_{k+1}{A}_{k+1}{\beta }_{k+1}$, by definition of derivation,

${\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{A_k\beta }_k{\beta }_{k-1}\dots {\beta }_1⟹{\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{{\alpha }_{k+1}{A}_{k+1}{\beta }_{k+1}\beta }_k{\beta }_{k-1}\dots {\beta }_1$.

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{A_k\beta }_k{\beta }_{k-1}\dots {\beta }_1⟹{\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{{\alpha }_{k+1}{A}_{k+1}{\beta }_{k+1}\beta }_k{\beta }_{k-1}\dots {\beta }_1$.

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }{\alpha }_1\dots {\alpha }_{k-1}{\alpha }_k{{\alpha }_{k+1}{A}_{k+1}{\beta }_{k+1}\beta }_k{\beta }_{k-1}\dots {\beta }_1$.

This completes the proof of Proposition 2.18.

Proposition 2.19. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$, $B\in V,R_1, R_2, R_3, \dots \dots R_n$be rules in $R$ where $n\ge 0$.

Let ${\alpha }_1,{\alpha }_2,{\alpha }_1^{\mathrm{\text{'}}},{\alpha }_2^{\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

If ${\alpha }_{1}B{\alpha }_2\stackrel{n,(R_1,R_2,\dots R_n)}{\Rightarrow }{\alpha }_1^{\mathrm{\text{'}}}B{\alpha }_2^{\mathrm{\text{'}}}$ then ${\alpha }_{1}x{\alpha }_2\stackrel{n,(R_1,R_2,\dots R_n)}{\Rightarrow }{\alpha }_1^{\mathrm{\text{'}}}x{\alpha }_2^{\mathrm{\text{'}}}\forall x\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ where the two $B\mathrm{’}s$ in the two strings are the same $B$ (Note that there can be more than one $B$ in the string ${\alpha }_{1}B{\alpha }_2$) and $B$ is not the head of any rule $R_i(i=\mathrm{1,2},\dots \dots n)$.

(Note that when $n=0$, the statement becomes

${(\alpha }_{1}B{\alpha }_2={\alpha }_1^{\mathrm{\text{'}}}B{\alpha }_2^{\mathrm{\text{'}}})⟹{(\alpha }_{1}x{\alpha }_2={\alpha }_1^{\mathrm{\text{'}}}x{\alpha }_2^{\mathrm{\text{'}}}\forall x\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$)

Proof. 

For $n=0$, ${\alpha }_{1}B{\alpha }_2={\alpha }_1^{\mathrm{\text{'}}}B{\alpha }_2^{\mathrm{\text{'}}}$

Since the two $B’s$ in the two strings are the same $B$, replacing them with $x$ must yield two equal strings.

Therefore, ${\alpha }_{1}x{\alpha }_2={\alpha }_1^{\mathrm{\text{'}}}x{\alpha }_2^{\mathrm{\text{'}}}$.

Therefore, the statement is true for $n=0$.

For $n=1$, if ${\alpha }_{1}B{\alpha }_2\stackrel{R_1}{\Rightarrow }{\alpha }_1^{\mathrm{\text{'}}}B{\alpha }_2^{\mathrm{\text{'}}}$,

Let $A⟶\alpha$ be the rule represented by $R_1$.

By definition of yielding, $\exists u_1,u_2\in {(V\cup \mathsf{\Sigma })}^{*}$ such that

${\alpha }_{1}B{\alpha }_2=u_{1}A{u}_2$ and ${\alpha }_1^{\mathrm{\text{'}}}B{\alpha }_2^{\mathrm{\text{'}}}=u_1\alpha u_2$.

The $B$ that appears in ${\alpha }_{1}B{\alpha }_2$ must also appear in $u_{1}A{u}_2$.

Since $R_1$does not originate from this particular $B$, $A$ and $B$ cannot be the same object in the string ${\alpha }_{1}B{\alpha }_2$or $u_{1}A{u}_2$ and hence there are only two cases to examine: $B$ appears in $u_1$ or $B$ appears in $u_2$.

(i)

If $B$ appears in $u_1$

Let $u_1^{\text{'}}$ be the string obtained by replacing $B$ in $u_1$ with $x$.

Since ${\alpha }_{1}B{\alpha }_2=u_{1}A{u}_2$, replacing $B$ with $x$ on both sides would yield two equal strings.

That is, ${\alpha }_{1}x{\alpha }_2=u_1^{\mathrm{\text{'}}}A{u}_2$.

Since ${\alpha }_1^{\text{'}}B{\alpha }_2^{\text{'}}=u_1\alpha u_2$, replacing $B$ with $x$ on both sides would yield two equal strings.

That is, ${\alpha }_1^{\mathrm{\text{'}}}x{\alpha }_2^{\mathrm{\text{'}}}=u_1^{\mathrm{\text{'}}}\alpha u_2$.

However, $u_1^{\mathrm{\text{'}}}A{u}_2\stackrel{R_1}{\Rightarrow }{u}_1^{\mathrm{\text{'}}}\alpha u_2$ since $A⟶\alpha$ is a rule.

Therefore, ${\alpha }_{1}x{\alpha }_2\stackrel{R_1}{\Rightarrow }{\alpha }_1^{\mathrm{\text{'}}}x{\alpha }_2^{\mathrm{\text{'}}}$.

Therefore, the statement is true for $n=1$.

(ii)

If $B$ appears in $u_2$, with a similar argument, we can show that the statement is also true for $n=1$.

With the results established on $n=0$ and $n=1$ and an induction argument, we can conclude that for $n\ge 0$,

$\left({\alpha }_{1}B{\alpha }_2\stackrel{n,\left(R_1,R_2,\dots R_n\right)}{\Rightarrow }{\alpha }_1^{\text{'}}B{\alpha }_2^{\text{'}}\right){⟹(\alpha }_{1}x{\alpha }_2\stackrel{n,(R_1,R_2,\dots R_n)}{\Rightarrow }{\alpha }_1^{\text{'}}x{\alpha }_2^{\text{'}} \forall x\in {(V\cup \mathsf{\Sigma })}^{*}$)

Proposition 2.20. 

If $G=(V, \mathsf{\Sigma }, R, S)$ is a $CFG$ and there exist $u_1,u_2,\dots u_k\in {(V\cup \mathsf{\Sigma })}^{*}$, $w\in {\mathsf{\Sigma }}^{*}$ such that

$S⟹u_1⟹u_2⟹u_3\dots ⟹u_r⟹\dots ⟹u_k⟹w$, then

The # of variables in $u_r\le$ the # of steps remaining from $u_r$ to $w$.

Proof. Let $n$ be the number of steps remaining from $u_r$ to $w$.

$n=k+1-r$

We’ll prove this proposition by induction on $n$.

(For $n=1$)

$r=k$

Therefore, $u_r=u_k⟹w$.

Since $u_k⟹w$, $\exists \alpha ,\beta ,\gamma \in {(V\cup \mathsf{\Sigma })}^{*}$ and a rule $A⟶\gamma$ such that

$u_k=\alpha A\beta$ and $w=\alpha \gamma \beta$.

Since $w\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $\alpha ,\beta \in {\mathsf{\Sigma }}^{\mathrm{*}}$.

Therefore, $u_k$ has only one variable.

Therefore, $u_r$ has only one variable.

Therefore, # of variables in $u_r\le$ the # of steps remaining from $u_r$ to $w$.

(For induction)

The # of steps remaining from $u_{r-1}$ to $w$ is $n+1=k+2-r$.

Since $u_{r-1}⟹u_r$, $\exists \alpha ,\beta ,\gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ and a rule $A⟶\gamma$ such that

$u_{r-1}=\alpha A\beta$ and $u_r=\alpha \gamma \beta$.

Let $m$ be the number of variables in $u_{r-1}$.

# of variables in $u_r=m-1+$ (# of variables in $\gamma$) $\ge m-1$.

By induction hypothesis, # of variables in $u_r\le n=k+1-r$.

Therefore, $m-1\le$ # of variables in $u_r\le n=k+1-r$.

Therefore, $m-1\le k+1-r$.

Therefore, $m\le k+2-r$.

Therefore, number of variables in $u_{r-1}\le$ # of steps remaining from $u_{r-1}$ to $w$.

This completes the proof of Proposition 2.20.

Example 2.21. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$ and there exist $u_1,u_2,\dots u_k\in {(V\cup \mathsf{\Sigma })}^{*}$, $w\in {\mathsf{\Sigma }}^{*}$ such that

$S⟹u_1⟹u_2⟹u_3\dots ⟹u_r⟹\dots ⟹u_k⟹w$. Show that the statement

(# of variables in $u_r=$ the # of steps remaining from $u_r$ to $w$) is not always true.

(Hint: Consider $V=\left\{S,A,B,C\right\},\mathsf{\Sigma }=\left\{a,b,c\right\},R=\{S⟶AB,A⟶C,C⟶c,B⟶b\}$ and

$S\stackrel{S⟶AB}{\Rightarrow }AB\stackrel{A⟶C}{\Rightarrow }CB\stackrel{C⟶c}{\Rightarrow }cB\stackrel{B⟶b}{\Rightarrow }cb$.)

Definition 2.22. 

$\forall \alpha ,\beta \in {(V\cup \mathsf{\Sigma })}^{*}, \alpha$ is a substring of $\beta$ (written as $\alpha ⊏\beta$) if $\exists {\alpha }^{\text{'}},{\alpha }^{\text{'}\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$ such that

$\beta ={\alpha }^{\text{'}}\alpha {\alpha }^{\text{'}\text{'}}$. ${\alpha }^{\text{'}}$ is called the left complement of $\alpha$ in $\beta$, written as $LC\left(\alpha \right)$. ${\alpha }^{\text{'}\text{'}}$ is called the right complement of $\alpha$ in $\beta$, written as $RC\left(\alpha \right)$.

Proposition 2.23. 

For any strings ${\alpha }_1,{\alpha }_2,u$ such that ${\alpha }_1,{\alpha }_2⊏u$, if ${\alpha }_1⊏{\alpha }_2$, then

(i)

$LC\left({\alpha }_2\right)⊏LC\left({\alpha }_1\right)$ & $LC\left({\alpha }_2\right)\bullet r=LC\left({\alpha }_1\right)$ for some string $r$

(ii)

$RC\left({\alpha }_2\right)⊏RC\left({\alpha }_1\right)$ & $l\bullet RC\left({\alpha }_2\right)=RC\left({\alpha }_1\right)$ for some string $l$.

Proof. 

${\alpha }_1⊏u⟹u=x_1{\alpha }_1{y}_1$ for some strings $x_1,y_1$.

${\alpha }_2⊏u⟹u=x_2{\alpha }_2{y}_2$ for some strings $x_2,y_2$.

$x_1=LC\left({\alpha }_1\right)$ ; $y_1=RC\left({\alpha }_1\right)$.

$x_2=LC\left({\alpha }_2\right)$ ; $y_2=RC\left({\alpha }_2\right)$.

${\alpha }_1⊏{\alpha }_2⟹{\alpha }_2=r{\alpha }_{1}l$ for some strings $r$ & $l$.

Therefore, $u=x_2{\alpha }_2{y}_2=x_{2}r{\alpha }_{1}l{y}_2$.

Since $u=x_1{\alpha }_1{y}_1$, $x_1{\alpha }_1{y}_1=x_{2}r{\alpha }_{1}l{y}_2$.

Therefore, $x_1=x_{2}r$ and $y_1=l{y}_2$.

Therefore, $LC\left({\alpha }_1\right)=LC\left({\alpha }_2\right)\bullet r$ and $RC\left({\alpha }_1\right)=l\bullet RC\left({\alpha }_2\right)$.

Therefore, $LC\left({\alpha }_2\right)⊏LC\left({\alpha }_1\right)$ and $RC\left({\alpha }_2\right)⊏RC\left({\alpha }_1\right)$.

This completes the proof of Proposition 2.23.

Definition 2.24. 

For any strings ${\alpha }_1,{\alpha }_2,u$ such that ${\alpha }_1,{\alpha }_2⊏u$, ${\alpha }_1$ is said to be on the left of ${\alpha }_2$ if there exist strings $x, y, z$ such that $u=x{\alpha }_{1}y{\alpha }_{2}z$.

Proposition 2.25. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $u_0⟹u_1⟹u_2⟹u_3\dots \dots ⟹u_n$, where $u_0,u_1,u_2,u_3\dots u_n\in {(V\cup \mathsf{\Sigma })}^{*}$.

Let $0\le i<j\le n$.

If ${\alpha }_i⊏u_i$, then $\exists {\alpha }_{i+1},{\alpha }_{i+2},\dots {\alpha }_j$ where ${\alpha }_{i+1}⊏u_{i+1},{\alpha }_{i+2}⊏u_{i+2},\dots {\alpha }_j⊏u_j$ such that

${\alpha }_i\stackrel{{\lambda }_1}{\Rightarrow }{\alpha }_{i+1}\stackrel{{\lambda }_2}{\Rightarrow }{\alpha }_{i+2}\stackrel{{\lambda }_3}{\Rightarrow }{\alpha }_{i+3}\dots \dots \stackrel{{\lambda }_{j-i}}{\Rightarrow }{\alpha }_j$ where ${\lambda }_1,{\lambda }_2,\dots \dots {\lambda }_{j-i}\in \left\{\mathrm{0,1}\right\}$.

Hence, ${\alpha }_i\stackrel{*}{\Rightarrow }{\alpha }_j$ in no more than $j-i$ steps.

${\alpha }_j$ is called the $(j-i)$-step expansion of ${\alpha }_i$ within the derivation of $u_0\stackrel{*}{\Rightarrow }{u}_n$ and it is written as ${\alpha }_j=Expan({\alpha }_i,j-i)$.

Proof. Let $k=j-i$.

$1\le k\le n$This proposition can be proved by induction on $k$.

($k=1$):

$j=i+1$

Since $u_i⟹u_{i+1}$, $\exists \alpha ,\beta ,\gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ and a rule $A⟶\gamma$ such that

$u_i=\alpha A\beta$ and $u_{i+1}=\alpha \gamma \beta$.

Since ${\alpha }_i⊏u_i$, $\exists {\alpha }^{\mathrm{\text{'}}},{\beta }^{\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $u_i={\alpha }^{\mathrm{\text{'}}}{\alpha }_i{\beta }^{\mathrm{\text{'}}}$.

(i)

If $A⊏{\alpha }_i$

$\exists {\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}},{\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that ${\alpha }_i={\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}$.

$u_i={\alpha }^{\mathrm{\text{'}}}{\alpha }_i{\beta }^{\mathrm{\text{'}}}={\alpha }^{\mathrm{\text{'}}}{\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}$.

Also, $u_i=\alpha A\beta$.

Therefore, $\alpha A\beta ={\alpha }^{\mathrm{\text{'}}}{\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}$.

Therefore, $\alpha ={\alpha }^{\mathrm{\text{'}}}{\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}$ and $\beta ={\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}$.

Since $u_{i+1}=\alpha \gamma \beta$, $u_{i+1}={\alpha }^{\mathrm{\text{'}}}{\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}\gamma {\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}$.

Take ${\alpha }_{i+1}={\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}\gamma {\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}$.

Since ${\alpha }_i={\alpha }^{\mathrm{\text{'}}\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}\mathrm{\text{'}}}$ and $A⟶\gamma$ is a rule, ${\alpha }_i⟹{\alpha }_{i+1}$.

(ii)

If $A$ is not a substring of ${\alpha }_i$Since $u_i=\alpha A\beta$ and ${\alpha }_i⊏u_i$, either ${\alpha }_i⊏\alpha$ or ${\alpha }_i⊏\beta$.

Since $u_{i+1}=\alpha \gamma \beta$, $\alpha ⊏u_{i+1}$ and $\beta ⊏u_{i+1}$.

Therefore (${\alpha }_i⊏\alpha$ or ${\alpha }_i⊏\beta$)$⟹{\alpha }_i⊏u_{i+1}$.

Take ${\alpha }_{i+1}={\alpha }_i$.

Therefore, ${\alpha }_i\stackrel{0}{\Rightarrow }{\alpha }_{i+1}$.

Combining (i) and (ii), ${\alpha }_i\stackrel{{\lambda }_1}{\Rightarrow }{\alpha }_{i+1}$ where ${\lambda }_1\in \left\{\mathrm{0,1}\right\}$.

(Induction):

By induction assumption,

${\alpha }_i\stackrel{{\lambda }_1}{\Rightarrow }{\alpha }_{i+1}\stackrel{{\lambda }_2}{\Rightarrow }{\alpha }_{i+2}\stackrel{{\lambda }_3}{\Rightarrow }{\alpha }_{i+3}\dots \dots \stackrel{{\lambda }_{j-i}}{\Rightarrow }{\alpha }_j$ where ${\lambda }_1,{\lambda }_2,\dots \dots {\lambda }_{j-i}\in \left\{\mathrm{0,1}\right\}$ and

${\alpha }_{i+1}⊏u_{i+1},{\alpha }_{i+2}⊏u_{i+2},\dots {\alpha }_j⊏u_j$.

Since ${\alpha }_j⊏u_j$ and $u_j⟹u_{j+1}$, by applying the same argument as in the case of ($k=1$), we can find ${\alpha }_{j+1}⊏u_{j+1}$ such that ${\alpha }_j\stackrel{{\lambda }_{j-i+1}}{\Rightarrow }{\alpha }_{j+1}$ where ${\lambda }_{j-i+1}\in \left\{\mathrm{0,1}\right\}$.

We now have ${\alpha }_i\stackrel{{\lambda }_1}{\Rightarrow }{\alpha }_{i+1}\stackrel{{\lambda }_2}{\Rightarrow }{\alpha }_{i+2}\stackrel{{\lambda }_3}{\Rightarrow }{\alpha }_{i+3}\dots \dots \stackrel{{\lambda }_{j-i}}{\Rightarrow }{\alpha }_j\stackrel{{\lambda }_{j-i+1}}{\Rightarrow }{\alpha }_{j+1}$ where

${\lambda }_1,{\lambda }_2,\dots \dots {\lambda }_{j-i},{\lambda }_{j-i+1}\in \left\{\mathrm{0,1}\right\}$ and ${\alpha }_{i+1}⊏u_{i+1},{\alpha }_{i+2}⊏u_{i+2},\dots {\alpha }_j⊏u_j,{\alpha }_{j+1}⊏u_{j+1}$.

This completes the proof of Proposition 2.25.

Proposition 2.26. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $u_0⟹u_1⟹u_2⟹u_3\dots \dots ⟹u_n$, where $u_0,u_1,u_2,u_3\dots u_n\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

Let $0\le i<j\le n$, ${\alpha }_i⊏u_i$, ${\alpha }_i^{\mathrm{\text{'}}}⊏u_i$, ${\alpha }_j=Expan({\alpha }_i,j-i)$ & ${\alpha }_j^{\mathrm{\text{'}}}=Expan({\alpha }_i^{\mathrm{\text{'}}},j-i)$.

If ${\alpha }_i$ is to the left of ${\alpha }_i^{\text{'}}$ within $u_i$, then ${\alpha }_j$ is to the left of ${\alpha }_j^{\text{'}}$ within $u_j$.

Proof. 

Let $k=j-1$.

$0\le k\le n$.

We can prove this proposition by induction on $k$.

($k=0$)

$j=i⟹{\alpha }_i={\alpha }_j$ & ${\alpha }_i^{\mathrm{\text{'}}}={\alpha }_j^{\mathrm{\text{'}}}$.

Therefore, ${\alpha }_i\stackrel{0}{\Rightarrow }{\alpha }_j$ & ${\alpha }_i^{\mathrm{\text{'}}}\stackrel{0}{\Rightarrow }{\alpha }_j^{\mathrm{\text{'}}}$.

${\alpha }_j=Expan({\alpha }_i,0)$ and ${\alpha }_j^{\mathrm{\text{'}}}=Expan({\alpha }_i^{\mathrm{\text{'}}},0)$.

${\alpha }_i$ is to the left of ${\alpha }_i^{\text{'}}⟹{\alpha }_j$ is to the left of ${\alpha }_j^{\text{'}}$.

The statement is true for $k=0$.

(Induction)

Induction Hypothesis:

$({\alpha }_i$ is to the left of ${\alpha }_i^{\mathrm{\text{'}}})⟹({\alpha }_{i+k}$ is to the left of ${\alpha }_{i+k}^{\mathrm{\text{'}}})$.

Since ${\alpha }_{i+k}$ is to the left of ${\alpha }_{i+k}^{\text{'}}$, there exist $x, y, z$ $\in {(V\cup \mathsf{\Sigma })}^{*}$ such that

$u_{i+k}=x{\alpha }_{i+k}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$.

Since $u_{i+k}⟹u_{i+k+1}$, there exists a rule $A⟶\gamma$ such that

$u_{i+k}=\alpha A\beta$ & $u_{i+k+1}=\alpha \gamma \beta$.

We now have five situations to examine: $A⊏x,A⊏{\alpha }_{i+k},A⊏y,A⊏{\alpha }_{i+k}^{\mathrm{\text{'}}},A⊏z$.

(i)

$A⊏x$

$RC\left(A\right)=l\bullet RC\left(x\right)$ (Proposition 2.23)

$\beta =l\bullet {\alpha }_{i+k}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$ ($RC\left(A\right)=\beta$, $RC\left(x\right)={\alpha }_{i+k}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$)

$u_{i+k+1}=\alpha \gamma \beta =\alpha \gamma l{\alpha }_{i+k}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$.

Take ${\alpha }_{i+k+1}={\alpha }_{i+k}$ and ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}={\alpha }_{i+k}^{\mathrm{\text{'}}}$.

Therefore, ${\alpha }_{i+k}\stackrel{0}{\Rightarrow }{\alpha }_{i+k+1}$ & ${\alpha }_{i+k}^{\mathrm{\text{'}}}\stackrel{0}{\Rightarrow }{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$.

In addition, $u_{i+k+1}=\alpha \gamma l{\alpha }_{i+k+1}y{\alpha }_{i+k+1}^{\mathrm{\text{'}}}z$.

Therefore, ${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\text{'}}$.

(ii)

$A⊏{\alpha }_{i+k}$

$\exists {\alpha }^{\mathrm{\text{'}}},{\beta }^{\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that

${\alpha }_{i+k}={\alpha }^{\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}}$

$u_{i+k}=x{\alpha }_{i+k}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z=x{\alpha }^{\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$Since $u_{i+k}=\alpha A\beta$, $\alpha =x{\alpha }^{\mathrm{\text{'}}}$ & $\beta ={\beta }^{\mathrm{\text{'}}}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$.

Therefore, $u_{i+k+1}=\alpha \gamma \beta =x{\alpha }^{\mathrm{\text{'}}}\gamma {\beta }^{\mathrm{\text{'}}}y{\alpha }_{i+k}^{\mathrm{\text{'}}}z$.

Take ${\alpha }_{i+k+1}={\alpha }^{\mathrm{\text{'}}}\gamma {\beta }^{\mathrm{\text{'}}}$ & ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}={\alpha }_{i+k}^{\mathrm{\text{'}}}$.

Now, $u_{i+k+1}=x{\alpha }_{i+k+1}y{\alpha }_{i+k+1}^{\mathrm{\text{'}}}z$.

So, ${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}$.

In addition, ${\alpha }_{i+k}⟹{\alpha }_{i+k+1}$ because ${\alpha }_{i+k}={\alpha }^{\mathrm{\text{'}}}A{\beta }^{\mathrm{\text{'}}}$ & ${\alpha }_{i+k+1}={\alpha }^{\mathrm{\text{'}}}\gamma {\beta }^{\mathrm{\text{'}}}$.

Also, ${\alpha }_{i+k}^{\mathrm{\text{'}}}\stackrel{0}{\Rightarrow }{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ because ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}={\alpha }_{i+k}^{\mathrm{\text{'}}}$.

(iii)

$A⊏y$

With a similar argument as in (i), we can show that $\exists {\alpha }_{i+k+1},{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ in $u_{i+k+1}$ such that ${\alpha }_{i+k}\stackrel{\lambda }{\Rightarrow }{\alpha }_{i+k+1}$ & ${\alpha }_{i+k}^{\mathrm{\text{'}}}\stackrel{{\lambda }^{\mathrm{\text{'}}}}{\Rightarrow }{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ where $\lambda ,{\lambda }^{\mathrm{\text{'}}}\in \left\{\mathrm{0,1}\right\}$ and

${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}$.

(iv)

$A⊏{\alpha }_{i+k}^{\text{'}}$

With a similar argument as in (ii), we can show that $\exists {\alpha }_{i+k+1},{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ in $u_{i+k+1}$ such that ${\alpha }_{i+k}\stackrel{\lambda }{\Rightarrow }{\alpha }_{i+k+1}$ & ${\alpha }_{i+k}^{\mathrm{\text{'}}}\stackrel{{\lambda }^{\mathrm{\text{'}}}}{\Rightarrow }{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ where $\lambda ,{\lambda }^{\mathrm{\text{'}}}\in \left\{\mathrm{0,1}\right\}$ and

${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}$.

(v)

$A⊏z$

With a similar argument as in (i), we can show that $\exists {\alpha }_{i+k+1},{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ in $u_{i+k+1}$ such that ${\alpha }_{i+k}\stackrel{\lambda }{\Rightarrow }{\alpha }_{i+k+1}$ & ${\alpha }_{i+k}^{\mathrm{\text{'}}}\stackrel{{\lambda }^{\mathrm{\text{'}}}}{\Rightarrow }{\alpha }_{i+k+1}^{\mathrm{\text{'}}}$ where $\lambda ,{\lambda }^{\mathrm{\text{'}}}\in \left\{\mathrm{0,1}\right\}$ and

${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\mathrm{\text{'}}}$.

Combining all (i) to (v) and the induction hypothesis, we now have:

If ${\alpha }_i$ is to the left of ${\alpha }_i^{\text{'}}$ within $u_i$, then ${\alpha }_{i+k+1}$ is to the left of ${\alpha }_{i+k+1}^{\text{'}}$ within $u_{i+k+1}$.

This completes the proof of Proposition 2.26.

Proposition 2.27. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $u_0⟹u_1⟹\dots ⟹u_i⟹u_{i+1}\dots ⟹u_n$, where $u_0,u_1,\dots u_i,u_{i+1}\dots u_n\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ & $0\le i<n$.

Let ${\alpha }_i,{\beta }_i\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

If ${\alpha }_i{\beta }_i⊏u_i$, then $Expan\left({\alpha }_i{\beta }_i,1\right)=Expan\left({\alpha }_i,1\right)Expan\left({\beta }_i,1\right)$.

Proof. 

Since ${\alpha }_i{\beta }_i⊏u_i,$

$u_i=x{\alpha }_i{\beta }_{i}y$ for some $x,y\in {(V\cup \mathsf{\Sigma })}^{*}$.

Since $u_i⟹u_{i+1}$, $\exists \alpha ,\beta ,\gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ and a rule $A⟶\gamma$ such that

$u_i=\alpha A\beta$ & $u_{i+1}=\alpha \gamma \beta$.

Since $A⊏u_i$ & $u_i=x{\alpha }_i{\beta }_{i}y$, we have four cases to examine:

$A⊏x$, $A⊏{\alpha }_i$, $A⊏{\beta }_i$, $A⊏y$.

(i)

$A⊏x$

$x=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}$ for some $x^{\mathrm{\text{'}}},y^{\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

$u_i=x{\alpha }_i{\beta }_{i}y=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\alpha }_i{\beta }_{i}y$.

Since $u_i$ is also equal to $\alpha A\beta$, $\alpha A\beta =x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\alpha }_i{\beta }_{i}y$.

Therefore, $\alpha =x^{\mathrm{\text{'}}}$ and $\beta =y^{\mathrm{\text{'}}}{\alpha }_i{\beta }_{i}y$.

Since $u_{i+1}=\alpha \gamma \beta$, $u_{i+1}=x^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}{\alpha }_i{\beta }_{i}y$.

Now we have ${\alpha }_i,{\beta }_i,{\alpha }_i{\beta }_i⊏u_i$ & ${\alpha }_i,{\beta }_i,{\alpha }_i{\beta }_i⊏u_{i+1}$.

In addition, ${\alpha }_i\stackrel{0}{\Rightarrow }{\alpha }_i$, ${\beta }_i\stackrel{0}{\Rightarrow }{\beta }_i$, ${\alpha }_i{\beta }_i\stackrel{0}{\Rightarrow }{\alpha }_i{\beta }_i$.

Therefore, $Expan\left({\alpha }_i{\beta }_i,1\right)={\alpha }_i{\beta }_i$, $Expan\left({\alpha }_i,1\right)={\alpha }_i$ and $Expan\left({\beta }_i,1\right)={\beta }_i$.

Therefore, $Expan\left({\alpha }_i{\beta }_i,1\right)=Expan\left({\alpha }_i,1\right)Expan\left({\beta }_i,1\right)$.

(ii)

$A⊏{\alpha }_i$

${\alpha }_i=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}$ for some $x^{\mathrm{\text{'}}},y^{\mathrm{\text{'}}}\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

Since $u_i=x{\alpha }_i{\beta }_{i}y$, $u_i=x{x}^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\beta }_{i}y$.

Since $u_i=\alpha A\beta$, $\alpha A\beta =x{x}^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\beta }_{i}y$.

Therefore, $\alpha =x{x}^{\mathrm{\text{'}}}$ and $\beta =y^{\mathrm{\text{'}}}{\beta }_{i}y$.

Since $u_{i+1}=\alpha \gamma \beta$, $u_{i+1}=x{x}^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}{\beta }_{i}y$.

Let ${\alpha }_{i+1}=x^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}$. Then $u_{i+1}=x{\alpha }_{i+1}{\beta }_{i}y$.

Since ${\alpha }_i=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}$ and $A⟶\gamma$ is a rule, ${\alpha }_i⟹{\alpha }_{i+1}$.

Since ${\alpha }_i⊏u_i$ and ${\alpha }_{i+1}⊏u_{i+1}$, $Expan\left({\alpha }_i,1\right)={\alpha }_{i+1}$.

Since ${\beta }_i⊏u_i$ and ${\beta }_i⊏u_{i+1}$ and ${\beta }_i\stackrel{0}{\Rightarrow }{\beta }_i$, $Expan\left({\beta }_i,1\right)={\beta }_i$.

Since ${\alpha }_i=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}$, ${\alpha }_i{\beta }_i=x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\beta }_i$.

$x^{\mathrm{\text{'}}}A{y}^{\mathrm{\text{'}}}{\beta }_i⟹x^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}{\beta }_i$ because $A⟶\gamma$ is a rule.

Therefore, ${\alpha }_i{\beta }_i⟹x^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}{\beta }_i$.

Therefore, ${\alpha }_i{\beta }_i⟹{\alpha }_{i+1}{\beta }_i$ (${\alpha }_{i+1}=x^{\mathrm{\text{'}}}\gamma y^{\mathrm{\text{'}}}$)

Since ${\alpha }_i{\beta }_i⊏u_i$ and ${\alpha }_{i+1}{\beta }_i⊏u_{i+1}$, $Expan\left({\alpha }_i{\beta }_i,1\right)={\alpha }_{i+1}{\beta }_i$.

Therefore, $Expan\left({\alpha }_i{\beta }_i,1\right)=Expan\left({\alpha }_i,1\right)Expan\left({\beta }_i,1\right)$.

(iii)

$A⊏{\beta }_i$

With a similar argument as in (ii), we can show that $Expan\left({\alpha }_i{\beta }_i,1\right)=Expan\left({\alpha }_i,1\right)Expan\left({\beta }_i,1\right)$.

(iv)

$A⊏y$

With a similar argument as in (i), we can show that

$Expan\left({\alpha }_i{\beta }_i,1\right)=Expan\left({\alpha }_i,1\right)Expan\left({\beta }_i,1\right)$.

This completes the proof of Proposition 2.27.

Proposition 2.28. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

Let $u_0⟹u_1⟹\dots ⟹u_i\dots ⟹u_n$, where $u_0,u_1,\dots u_i,\dots u_n\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ & $0\le i\le n$.

(i)

For $0\le k\le n-i$, $Expan\left({\alpha }_{i_1}{\alpha }_{i_2}\dots {\alpha }_{i_m},k\right)=Expan\left({\alpha }_{i_1},k\right)Expan\left({\alpha }_{i_2},k\right)\dots Expan\left({\alpha }_{i_m},k\right)$ where

${\alpha }_{i_1}{\alpha }_{i_2}\dots {\alpha }_{i_m}⊏u_i$.

(ii)

If $u_0=X_1{X}_2\dots X_m$ where $X_1{,X}_2,\dots X_m\in V\cup \mathsf{\Sigma }$ & $u_n=w\in {\mathsf{\Sigma }}^{*}$, then $\exists w_1,w_2\dots w_m\in {\mathsf{\Sigma }}^{*}$ such that $X_i\stackrel{*}{\Rightarrow }{w}_i$ in no more than $n$ steps &

$w=w_1{w}_2\dots w_m$.

Proof. 

Claim.

$\forall {\alpha }_i,{\beta }_i\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that ${\alpha }_i{\beta }_i⊏u_i$ and $0\le k\le n-i$,

$Expan\left({\alpha }_i{\beta }_i,k\right)=Expan\left({\alpha }_i,k\right)Expan\left({\beta }_i,k\right)$

This Claim can be proved by induction on $k$.

($k=0$)

$Expan\left({\alpha }_i{\beta }_i,0\right)={\alpha }_i{\beta }_i$.

$Expan\left({\alpha }_i,0\right)={\alpha }_i$ and $Expan\left({\beta }_i,0\right)={\beta }_i$.

Therefore, $Expan\left({\alpha }_i{\beta }_i,0\right)=Expan\left({\alpha }_i,0\right)Expan\left({\beta }_i,0\right)$.

The statement is true for $k=0$.

(Induction)

Induction Hypothesis:

$Expan\left({\alpha }_i{\beta }_i,k\right)=Expan\left({\alpha }_i,k\right)Expan\left({\beta }_i,k\right)$ where

$Expan\left({\alpha }_i{\beta }_i,k\right),Expan\left({\alpha }_i,k\right),Expan\left({\beta }_i,k\right)⊏u_{i+k}$.

$Expan\left({\alpha }_i{\beta }_i,k+1\right)=Expan(Expan\left({\alpha }_i{\beta }_i,k\right),1)$

$=Expan(Expan\left({\alpha }_i,k\right)Expan\left({\beta }_i,k\right),1)$ (Induction Hypothesis)

$=Expan(Expan\left({\alpha }_i,k\right),1)Expan(Expan\left({\beta }_i,k\right),1)$ (Proposition 2.27)

$=Expan\left({\alpha }_i,k+1\right)Expan\left({\beta }_i,k+1\right)$This completes the proof of Claim.

The proof of (i) is by induction on $m$.

($m=1$)

$LHS=Expan\left({\alpha }_{i1},k\right)$.

$RHS=Expan\left({\alpha }_{i1},k\right)$.

Therefore, the statement is true for $m=1$.

(Induction)

Induction Hypothesis: $Expan\left({\alpha }_{i_1}{\alpha }_{i_2}\dots {\alpha }_{i_m},k\right)=Expan\left({\alpha }_{i_1},k\right)Expan\left({\alpha }_{i_2},k\right)\dots Expan\left({\alpha }_{i_m},k\right)$.

$Expan\left({\alpha }_{i_1}{\alpha }_{i_2}\dots {\alpha }_{i_m}{\alpha }_{i_{m+1}},k\right)=Expan\left({\alpha }_{i_1}{\alpha }_{i_2}\dots {\alpha }_{i_m},k\right)Expan\left({\alpha }_{i_{m+1}},k\right)$ (Claim)

$=Expan\left({\alpha }_{i_1},k\right)Expan\left({\alpha }_{i_2},k\right)\dots Expan\left({\alpha }_{i_m},k\right)Expan\left({\alpha }_{i_{m+1}},k\right)$ (Induction Hypothesis)

This completes the proof of (i).

(i)

Set $i=0$ & $k=n$ for the result in (i).

${\alpha }_{0_1}=X_1$,${\alpha }_{0_2}=X_2$,$\dots {\alpha }_{0_m}=X_m$.

$u_0=X_1{X}_2\dots X_m={\alpha }_{0_1}{\alpha }_{0_2}\dots {\alpha }_{0_m}$Therefore, ${\alpha }_{0_1}{\alpha }_{0_2}\dots {\alpha }_{0_m}⊏u_0$.

By (i), $Expan\left({\alpha }_{0_1}{\alpha }_{0_2}\dots {\alpha }_{0_m},n\right)=Expan\left({\alpha }_{0_1},n\right)Expan\left({\alpha }_{0_2},n\right)\dots Expan\left({\alpha }_{0_m},n\right)$Therefore, $Expan\left(X_1{X}_2\dots X_m,n\right)=Expan\left(X_1,n\right)Expan\left(X_2,n\right)\dots Expan\left(X_m,n\right)$.

$Expan\left(X_1{X}_2\dots X_m,n\right)=Expan\left(u_0,n\right)=u_n=w$.

Therefore, $Expan\left(X_1,n\right)Expan\left(X_2,n\right)\dots Expan\left(X_m,n\right)=w$.

Therefore, $Expan\left(X_i,n\right)=w_i$ for some $w_i\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $i\in \{\mathrm{1,2},\dots n\}$.

Therefore, $w=w_1{w}_2\dots w_m$ &

$X_i\stackrel{*}{\Rightarrow }{w}_i$ in no more than $n$ steps.

Proposition 2.29. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$, $\alpha ,\beta \in {(V\cup \mathsf{\Sigma })}^{*}$, $X\in V$ and $w\in {\mathsf{\Sigma }}^{*}$.

If $\alpha X\beta \stackrel{\mathrm{*}}{\Rightarrow }w$, then $X\stackrel{\mathrm{*}}{\Rightarrow }{w}^{\mathrm{\text{'}}}$ for some $w^{\mathrm{\text{'}}}\in {\mathsf{\Sigma }}^{\mathrm{*}}$.

Proof. 

$\exists n\ge 1$ such that $\alpha X\beta \stackrel{n}{\Rightarrow }w$.

$Expan\left(\alpha X\beta ,n\right)=w$.

$Expan\left(\alpha ,n\right)Expan\left(X,n\right)Expan\left(\beta ,n\right)=w$ (Proposition 2.28)

$Expan\left(X,n\right)=w^{\mathrm{\text{'}}}$ for some $w^{\mathrm{\text{'}}}\in {\mathsf{\Sigma }}^{\mathrm{*}}$

$X\stackrel{*}{\Rightarrow }{w}^{\text{'}}$ for some $w^{\text{'}}\in {\mathsf{\Sigma }}^{*}$ (Proposition 2.25)

This completes the proof of Proposition 2.29.

Example 2.30. Prove that the non-regular set $A=\left\{a^n{b}^n\right| n\ge 0\}$ is a $CFL$.

Proof. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$ such that

$V=\left\{S\right\}$, $\mathsf{\Sigma }=\{\mathrm{a},\mathrm{b}\}$, $R=\{S⟶aSb,S⟶ϵ\}$.

In short form, $S⟶aSb|ϵ$.

Claim 1. 

If $S\stackrel{n+1}{\Rightarrow }\alpha \forall n\ge 0$ where $\alpha \in {(V\cup \mathsf{\Sigma })}^{*}$, then

$\exists \gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $S\stackrel{n}{\Rightarrow }\gamma$ and $\gamma \stackrel{1}{\Rightarrow }\alpha$ and $\gamma =a^{n}S{b}^n$.

Claim 1 can be proved by induction on $n$.

For $n=0$, if $S\stackrel{1}{\Rightarrow }\alpha$, by definition, $\exists \gamma \in {(V\cup \mathsf{\Sigma })}^{*}$ such that $S\stackrel{0}{\Rightarrow }\gamma$ and $\gamma \stackrel{1}{\Rightarrow }\alpha$.

Therefore, $S=\gamma$.

Therefore, $\gamma =a^{0}S{b}^0$.

Therefore, the statement is true for $n=0$.

Assume the statement is true for $n=k$ for $k\ge 0$.

That is, $\left(S\stackrel{k+1}{\Rightarrow }\alpha \right)⟹\left(\exists \gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}suchthatS\stackrel{k}{\Rightarrow }\gamma \&\gamma \stackrel{1}{\Rightarrow }\alpha \&\gamma =a^{k}S{b}^k\right)$ for $k\ge 0$ and $\alpha \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

For $n=k+1$, assume $S\stackrel{k+2}{\Rightarrow }\alpha$.

By definition, $\exists {\gamma }^{\text{'}}\in {(V\cup \mathsf{\Sigma })}^{*}$ such that

$S\stackrel{k+1}{\Rightarrow }{\gamma }^{\mathrm{\text{'}}}$ and ${\gamma }^{\mathrm{\text{'}}}\stackrel{1}{\Rightarrow }\alpha$.

By induction assumption, $\exists \gamma \in {(V\cup \mathsf{\Sigma })}^{*}$ such that $S\stackrel{k}{\Rightarrow }\gamma$ and $\gamma \stackrel{1}{\Rightarrow }{\gamma }^{\text{'}}$ and $\gamma =a^{k}S{b}^k$.

Since there are only two rules in $R$, namely $S⟶aSb or S⟶ϵ$.

If we use $S⟶ϵ$ on $\gamma \stackrel{1}{\Rightarrow }{\gamma }^{\mathrm{\text{'}}}$, then $a^{k}S{b}^k\stackrel{S⟶ϵ}{\Rightarrow }{\gamma }^{\mathrm{\text{'}}}$.

By Proposition 2.13 (ii), ${\gamma }^{\mathrm{\text{'}}}=a^kϵb^k=a^k{b}^k$.

This contradicts the conclusion ${\gamma }^{\text{'}}\stackrel{1}{\Rightarrow }\alpha$ we derive above because $a^k{b}^k$ does not contain a variable.

Therefore, we must use rule $S⟶aSb$.

Therefore, $\gamma \stackrel{S⟶aSb}{\Rightarrow }{\gamma }^{\mathrm{\text{'}}}$.

Therefore, $a^{k}S{b}^k\stackrel{S⟶aSb}{\Rightarrow }{\gamma }^{\mathrm{\text{'}}}$.

Again by Proposition 2.13 (ii), ${\gamma }^{\mathrm{\text{'}}}=a^{k}aSb{b}^k=a^{k+1}S{b}^{k+1}$.

This completes the proof of Claim 1.

Claim 2. 

$S\stackrel{n+1}{\Rightarrow }{a}^n{b}^n \forall n\ge 0$.

For $n=0$, $S\stackrel{S⟶ϵ}{\Rightarrow }ϵ$ by Proposition 2.13 (i).

Therefore, $S\stackrel{1}{\Rightarrow }{a}^0{b}^0$ and hence the statement is true for $n=0$.

For $n\ge 1$, by Proposition 2.13 (i) & (ii),

$S\stackrel{S⟶aSb}{\Rightarrow }aSb\stackrel{S⟶aSb}{\Rightarrow }{a}^{2}S{b}^2\stackrel{S⟶aSb}{\Rightarrow }{a}^{3}S{b}^3\dots \dots \stackrel{S⟶aSb}{\Rightarrow }{a}^{n}S{b}^n$.

Therefore, $S\stackrel{n}{\Rightarrow }{a}^{n}S{b}^n$.

In addition, $a^{n}S{b}^n\stackrel{S⟶ϵ}{\Rightarrow }{a}^n{b}^n$ by Proposition 2.13 (ii).

Therefore, $S\stackrel{n+1}{\Rightarrow }{a}^n{b}^n$.

This completes the proof of Claim 2.

It remains to show that $L\left(G\right)=A$.

$u\in A⟹u=a^n{b}^n$

$⟹S\stackrel{n+1}{\Rightarrow }u$ (by Claim 2)

$⟹u\in L\left(G\right)$Conversely, if $u\in L\left(G\right)$, $u\in {\mathsf{\Sigma }}^{*}$ and

$S\stackrel{n+1}{\Rightarrow }u$ for some $n\ge 0$.

$\exists \gamma \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that $S\stackrel{n}{\Rightarrow }\gamma$ and $\gamma \stackrel{1}{\Rightarrow }u$ and $\gamma =a^{n}S{b}^n$ by Claim 1.

Since there are only two rules in $R$, either $\gamma \stackrel{S⟶aSb}{\Rightarrow }u$ or $\gamma \stackrel{S⟶ϵ}{\Rightarrow }u$.

$\left(\gamma \stackrel{S⟶aSb}{\Rightarrow }u\right)$

$⟹\left(a^{n}S{b}^n\stackrel{S⟶aSb}{\Rightarrow }u\right)$

$⟹a^{n+1}S{b}^{n+1}=u$ (Proposition 2.13 (ii))

$⟹$ a contradiction to $u\in {\mathsf{\Sigma }}^{*}$.

Therefore, we must use $\gamma \stackrel{S⟶ϵ}{\Rightarrow }u$.

Therefore, $a^{n}S{b}^n\stackrel{S⟶ϵ}{\Rightarrow }u$.

$a^nϵb^n=u$ by Proposition 2.13 (ii).

Therefore, $u=a^n{b}^n$ and hence $u\in A$.

Combining both directions, $L\left(G\right)=A$.

Before proceeding to the proof of some important theorems in $CFG$, we need to review some Tree terminology and Graph Theory. The readers are assumed to have some background in the subject matter and the following are stated without proof.

T1. A tree is a directed acyclic graph (DAG).

T2. Trees are collections of nodes and edges.

T3. If $(A, B)$ is the directed edge from node $A$ to node $B$, $A$ is called the parent and $B$ is called the child.

T4. A node has at most one parent, drawn above the node and zero or more children, drawn below.

T5. There is one node that has no parent. This node is called the root and appears at the top of the tree. Nodes that have no children are called leaves. Nodes that are not leaves are called interior nodes.

T6. A simple directed path from $v_0$ to $v_n$ is represented by $(v_0, v_1, v_2,\dots v_n)$ where $(v_i,v_{i+1})$ with $i\in \{\mathrm{0,1},2,\dots n-1\}$ are directed edges joining the nodes, $v_0, v_1, v_2,\dots v_n$ of the tree and $v_i\ne v_j$ for $i\ne j$. The length of the simple directed path is equal to the number of directed edges connecting the nodes $v_0, v_1, v_2,\dots v_n$ and is equal to $n$ in this case.

T7. For any two nodes $A$ and $B$, if there is a simple directed path from $A$ to $B$, $B$ is a descendant of $A$ and $A$ is the ancestor of $B$. Since every simple directed path from $A$ to $B$ must pass through a child of $A$, there is simple directed path from one of $A’s$ children to $B$.

T8. There is a unique simple directed path from the root to any other node.

T9. Let $d\left(r,l\right)=$ the length of the path from the root $r$ to a leaf$l$. The height of the tree is defined as $h=Max\left\{d\right(r,l\left)\right|r=root;l=a leaf\}$. Therefore, the height of a tree is the longest path from the root to a leaf.

T10. The length of the path from the root to a node $v$ is called the level of $v$.

T11. The simple directed path from an interior node to a leaf is called a branch. The combination of all branches is the largest subtree with the interior node as the root. The length of any branch is no longer than the height of the subtree which in turn is no longer than the height of the parent tree.

T12. The children of a node are ordered from left to right. If node $A$ is to the left of node $B$, then all the descendants of $A$ are to be to the left of all the descendants of $B$ at the same level.

T13. A subtree is a tree of which the vertices and edges are also the vertices and edges of the parent tree. If a subtree has a leaf, the leaf is also a leaf of the parent tree.

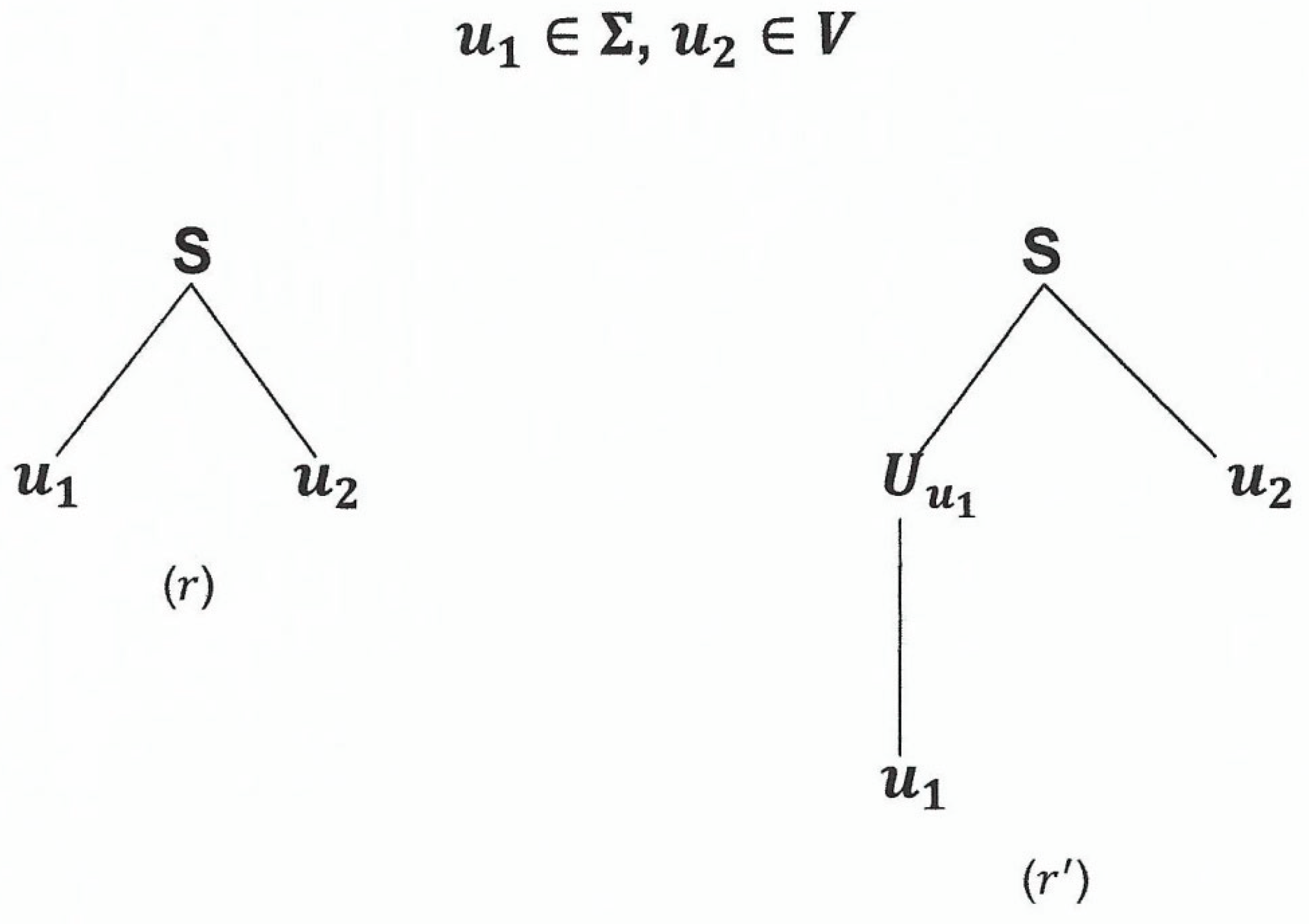
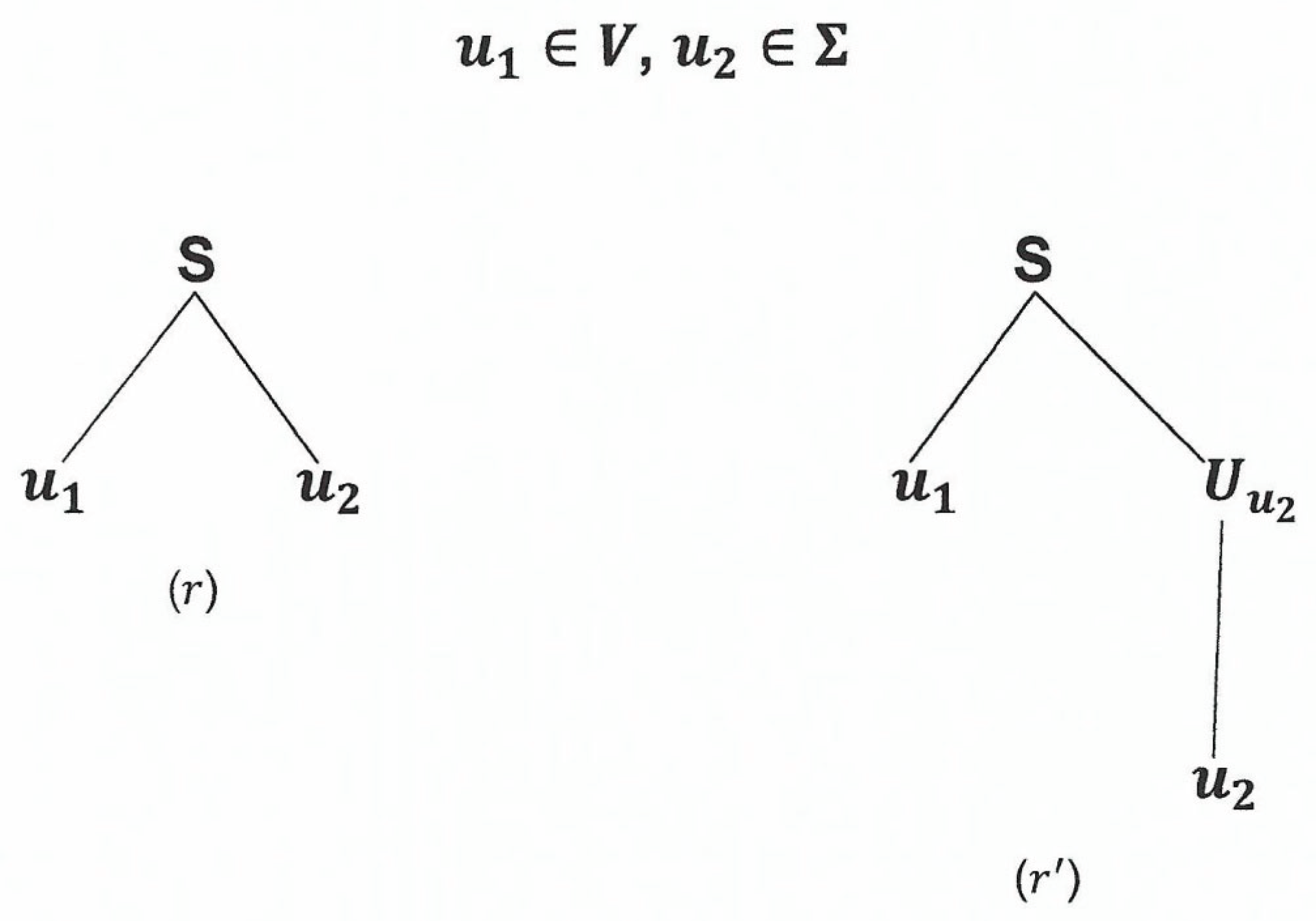
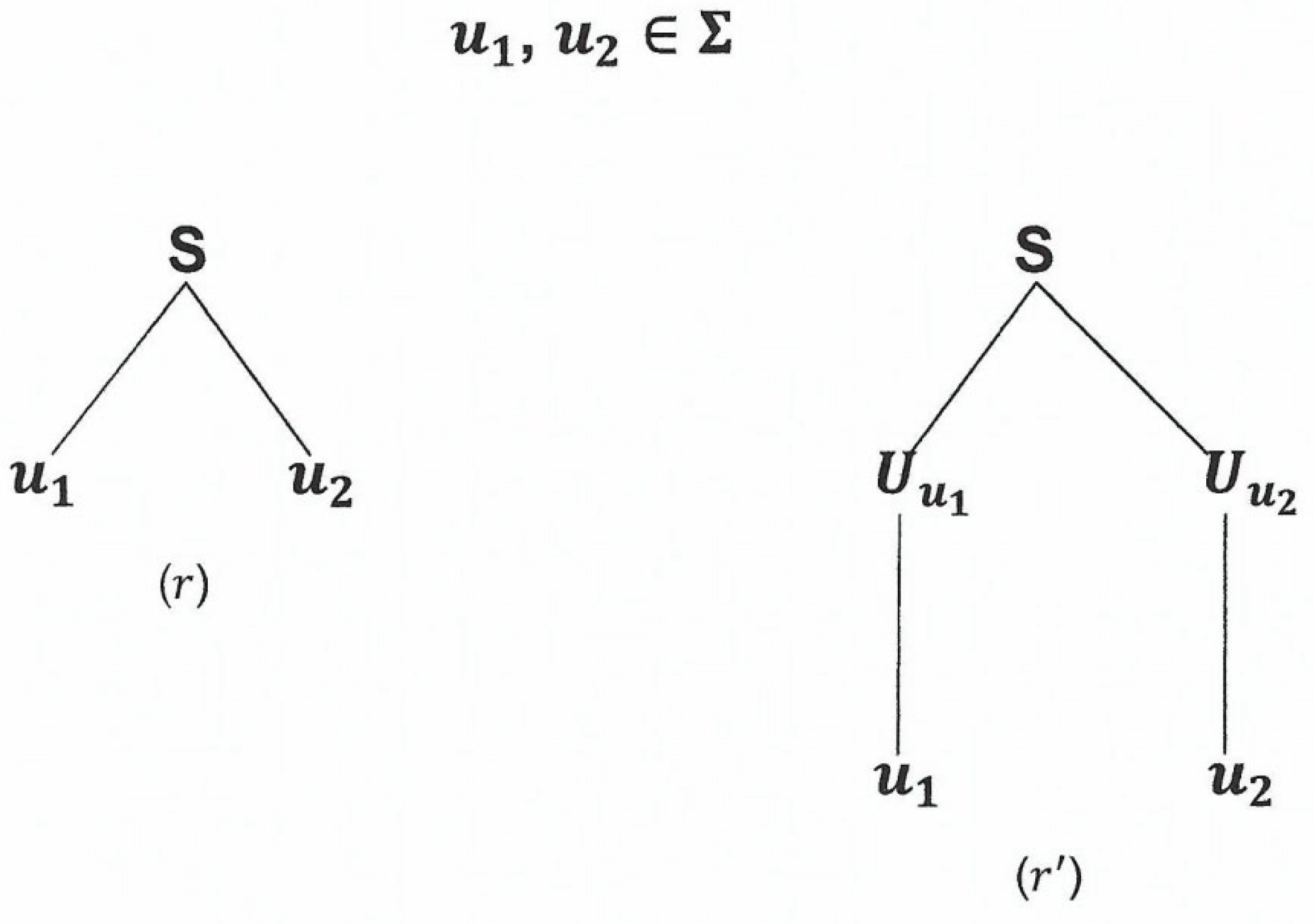
Definition 2.31. 

For any context-free grammar, $G=(V, \mathsf{\Sigma }, R, S)$, a parse tree for $G$ is a tree that satisfies the following conditions:

(i)

Each interior node is labeled as a variable in $V$.

(ii)

Each leaf is labeled either as a variable in $V$, a terminal in $\mathsf{\Sigma }$ or $ϵ$.

(iii)

If an interior node labeled $A$ (a variable) has children $X_1,X_2,X_3,\dots X_n$ where $X_i\in V\cup \mathsf{\Sigma }$ for $i\in \{\mathrm{1,2},\dots n\}$, then

$A⟶X_1{X}_2{X}_3\dots X_n$ is a rule in $R$.

(iv)

If an interior node labeled $A$ (a variable) has $ϵ$ as a child, then $ϵ$ is the only child of $A$ and $A⟶ϵ$ is a rule in $R$.

Note that any subtree of a parse tree is also a parse tree.

Definition 2.32. The yield of a parse tree is the concatenation of all the leaves of the tree from left to right.

Theorem 2.33. Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$. The following statements are equivalent.

(i)

$\exists$ a parse tree with root $A\in V$ and a yield $w\in {\mathsf{\Sigma }}^{*}$.

(ii)

$A\stackrel{*,lm}{\Rightarrow }w,w\in {\mathsf{\Sigma }}^{*}$.

(iii)

$A\stackrel{*}{\Rightarrow }w$, $w\in {\mathsf{\Sigma }}^{*}$.

Proof. “(i)$⟹$(ii)”

This can be proved by an induction on the height of the tree in statement (i).

Let $h (\ge 1)$ be the height of the parse tree in statement (i).

“$h=1$”

The parse tree looks like the following figure.

Figure 2.1. Caption.

Figure 2.1. Caption.

By definition of parse tree, $A⟶X_1{X}_2{X}_3\dots X_n$ is a rule in $R$.

By Proposition 2.8(i), $A⟹X_1{X}_2{X}_3\dots X_n$.

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }{X}_1{X}_2{X}_3\dots X_n$.

The yield of this tree is $X_1{X}_2{X}_3\dots X_n$ which is equal to $w$ by statement (i).

Therefore, $A\stackrel{*}{\Rightarrow }w$.

Since $A$ is the only variable in the string $A$, it is therefore also the leftmost variable in the string $A$.

Therefore, $A\stackrel{*,lm}{\Rightarrow }w$.

Hence, the statement “(i)$⟹$(ii)” is true for $h=1$.

“Induction”

Let $k$ be an integer such that $k\ge 1$.

Induction Hypothesis:

The statement “(i)$⟹$(ii)” is true for any parse tree with height $h$ if $h\le k$.

Consider now a parse tree $Pt(A,w,k+1)$ that has root $A$, yield $w$ and a height of $k+1$.

This parse tree looks like the following figure.

Figure 2.2. Caption.

Figure 2.2. Caption.

$\forall i\in \{\mathrm{1,2},\dots n\}$, $X_i\in V\cup \mathsf{\Sigma }$.

There are 2 cases to examine.

(a)

$X_i\in \mathsf{\Sigma }$

$X_i=w_i$ for some $w_i\in \mathsf{\Sigma }$.

$X_i\stackrel{0}{\Rightarrow }{w}_i$.

$X_i\stackrel{\mathrm{*}}{\Rightarrow }{w}_i$.

$X_i\stackrel{*,lm}{\Rightarrow }{w}_i$ ($X_i$ is the only variable in the head)

Furthermore, since $X_i\in \mathsf{\Sigma }$, $X_i=w_i$ is a leaf.

Therefore, $w_i⊏w$.

(b)

$X_i\in V$

By T11 and T13, the combination of all branches of $X_i$ forms a subtree of $Pt(A,w,k+1)$ and every leaf of the subtree is also a leaf of the parent tree.

Let $w_i$ be the yield of $X_i$.

By definition of yield, every symbol in $w_i$ is a leaf and therefore a symbol in $w$.

Therefore, $w_i⊏w$.

Since $w\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $w_i\in {\mathsf{\Sigma }}^{\mathrm{*}}$.

Claim: $w=w_1{w}_2\dots w_n$.

By T12, $w_i$ is to the left of $w_j$ for $i<j$ since $X_i$ is to the left of $X_j$.

Therefore, $w=x_0{w}_1{x}_1{w}_2\dots w_n{x}_n$ where $x_0,x_1,\dots x_n\in {\mathsf{\Sigma }}^{\mathrm{*}}$.

Let $l$ be a symbol in $w$.

$l$ is a leaf in $Pt(A,w,k+1)$ because $w$ is the yield.

By T8, there is a simple directed path from $A$ to $l$.

By T7, there is a simple directed path from $X_i$ to $l$ for some $i\in \{\mathrm{1,2},\dots n\}$.

Since $l$ has no children, $l$ must be a leaf descendant of $X_i$.

Therefore, $l$ is a symbol in $w_i$ because $w_i$ is the yield of the subtree with root $X_i$.

Therefore, $l$ is a symbol in $w⟹l$ is a symbol in $w_i$ for some $i\in \{\mathrm{1,2},\dots n\}$.

Therefore, $\left|w\right|\le \left|w_1{w}_2\dots w_n\right|$.

Therefore, $\left|x_0{w}_1{x}_1{w}_2\dots w_n{x}_n\right|\le \left|w_1{w}_2\dots w_n\right|$.

This means that $x_0=x_1=\dots =x_n=ϵ$.

Therefore, $w=w_1{w}_2\dots w_n$.

Now, back to the subtree with root $X_i$ and yield $w_i$.

The height of this subtree = the length of the longest branch in the subtree

= the length of a simple directed path in the parent tree

from $X_i$ to a leaf $l$= the length of a simple directed path in the parent tree

from $A$ to a leaf $l$ minus $1$ (By T7 & $X_i$ is a child of $A$)

$\le$ the height of the parent tree minus $1$= $k+1-1$= $k$By induction hypothesis, $X_i\stackrel{*,lm}{\Rightarrow }{w}_i$.

Combining (a) & (b), we now have $X_i\stackrel{\mathrm{*},lm}{\Rightarrow }{w}_i$ for all $i\in \{\mathrm{1,2},\dots n\}$ and $w=w_1{w}_2\dots w_n$.

For the parent tree $Pt(A,w,k+1)$,

$A⟹X_1{X}_2{X}_3\dots X_n$ (Proposition 2.8(i))

$A\stackrel{lm}{\Rightarrow }{X}_1{X}_2{X}_3\dots X_n$ ($A$ is the only variable in the head)

Since $X_i\stackrel{*,lm}{\Rightarrow }{w}_i$ and by Proposition 2.17,

$X_1{X}_2{X}_3\dots X_n\stackrel{\mathrm{*},lm}{\Rightarrow }{w}_1{w}_2\dots w_n$.

Therefore, $A\stackrel{lm}{\Rightarrow }{X}_1{X}_2{X}_3\dots X_n\stackrel{\mathrm{*},lm}{\Rightarrow }{w}_1{w}_2\dots w_n$.

$A\stackrel{\mathrm{*},lm}{\Rightarrow }{w}_1{w}_2\dots w_n$.

Since $w=w_1{w}_2\dots w_n$, $A\stackrel{\mathrm{*},lm}{\Rightarrow }w$.

The statement “(i)$⟹$(ii)” is true for $h=k+1$.

This completes the proof of “(i)$⟹$(ii)”.

“(ii)$⟹$(iii)”

The proof of this statement is trivial because every leftmost derivation is a derivation.

“(iii)$⟹$(i)”

Since $A\stackrel{*}{\Rightarrow }w$, $\exists n\ge 1$ such that $A\stackrel{n}{\Rightarrow }w$. (Note that $n\ne 0$ because $A\in V$ and $w\in {\mathsf{\Sigma }}^{*}$.)

The proof of this statement, “(iii)$⟹$(i)”, is by induction on $n$.

($n=1)$

$\exists w_1,w_2\dots w_m\in \mathsf{\Sigma }$ such that $w=w_1{w}_2\dots w_m$ & $A⟹w_1{w}_2\dots w_m$.

By Proposition 2.8(i), $A⟶w_1{w}_2\dots w_m$.

The following is a parse tree with root $A$ and yield $w$.

Figure 2.3. Caption.

Figure 2.3. Caption.

Therefore, the statement is true for $n=1$.

(Induction)

Induction Hypothesis:

Let $k$ be an integer such that $k\ge 1$.

For any $n\le k$, if $A\stackrel{n}{\Rightarrow }w$, then $\exists$ a parse tree with root $A$ and yield $w$.

Now, consider $n=k+1$.

If $A\stackrel{k+1}{\Rightarrow }w$,

$\exists u_1,u_2,\dots u_k\in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$ such that

$A⟹u_1⟹u_2\dots \dots ⟹u_k⟹w$.

$\exists X_1,X_2,\dots X_m\in V\cup \mathsf{\Sigma }$ such that $u_1=X_1{X}_2\dots X_m$.

Therefore, $X_1{X}_2\dots X_m⟹u_2\dots \dots ⟹u_k⟹w$.

By Proposition 2.28(ii),

$X_i\stackrel{n_i}{\Rightarrow }{w}_i$ with $n_i\le k$ and $w_1{w}_2\dots w_m=w$.

By induction hypothesis, $\exists$ a parse tree with root $X_i$ and yield $w_i$ which looks like the following figure.

Figure 2.4. Caption.

Figure 2.4. Caption.

We now can construct a parse tree, $Pt(A,w,k+1)$ as follows.

(1)

Start with a one level parse tree that has root $A$ and yield $X_1{X}_2\dots X_m$ that looks like the following figure.

Figure 2.5. Caption.

Figure 2.5. Caption.

(2)

For each $i\in \{\mathrm{1,2},\dots m\}$, if $X_i\in \mathsf{\Sigma }$, set $X_i=w_i$ for some $w_i\in \mathsf{\Sigma }$.

If $X_i\in V$, add the parse tree as shown in Figure 2.4 to the parse tree as shown in Figure 2.5. The resulting tree would look like the following figure.

$$Pt(A,w,k+1)$$

Figure 2.6. Caption.

Figure 2.6. Caption.

Clearly, this tree ($Pt(A,w,k+1)$) with root $A$ is a parse tree since the one level tree and all the subtrees with root $X_i$ and yield $w_i$ are parse trees.

In addition, since $w_1{w}_2\dots w_m=w$, the yield of this parse tree is $w$.

Therefore, the statement “(iii)$⟹$(i)” is true for $n=k+1$.

This completes the proof of “(iii)$⟹$(i)” and also the proof of Theorem 2.33.

2.2. Chomsky Normal Form (CNF)

Definition 2.34. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$.

$G$ is in Chomsky normal form if very rule of $G$ is of the following form:

$A⟶BC$ where $AϵV$ and $B,CϵV\backslash \left\{S\right\}$

$A⟶a$ where $aϵ\mathsf{\Sigma }$

$S⟶ϵ$ where $S=$ Start Variable

Lemma 2.35. 

For every $CFG G=(V,\mathsf{\Sigma },R,S)$, there is a $CFG G^{\text{'}}$ with no $ϵ$-rule ($A⟶ϵ$ where $A\ne S$) or unit rule ($A⟶B$ where $A,B\in V$) such that $L\left(G\right)=L\left(G^{\text{'}}\right)$.

Proof. 

We can inductively construct a new set of rules, $R^{\text{'}}$ using the following procedure:

(i)

Copy all the rules in $R$ to $R^{\text{'}}$.

(ii)

If $B\ne S,A⟶\alpha B\beta$ and $B⟶ϵ$ are in $R^{\text{'}}$, create $A⟶\alpha \beta$ in $R^{\text{'}}$.

(iii)

If $A⟶B$ and $B⟶\gamma$ are in $R^{\text{'}}$, create $A⟶\gamma$ in $R^{\text{'}}$.

We can further assume that $R^{\text{'}}$ is the smallest one of all the sets that can be thus created because we can always rename the smallest one to $R^{\text{'}}$ knowing that the minimum exists.

Let $G^{\mathrm{\text{'}}}=(V,\mathsf{\Sigma },R^{\mathrm{\text{'}}},S)$.

It’s clear from construction that $R\subset R^{\text{'}}$.

Therefore, every derivation in $G$ is a derivation in $G^{\text{'}}$ and hence $L\left(G\right)\subset L\left(G^{\text{'}}\right)$.

On the other hand, every new rule that is created in $G^{\text{'}}$ is equivalent to the two rules that it is created from by Proposition 2.15 and therefore, every derivation in $G^{\text{'}}$ can be simulated by either the same rules or equivalent rules in $G$.

Hence, $L\left(G^{\mathrm{\text{'}}}\right)\subset L\left(G\right)$.

It remains to show that all the $ϵ$ and unit rules in $G^{\text{'}}$ are redundant for the production of any $x\in L\left(G^{\text{'}}\right)$.

Since $L\left(G^{\text{'}}\right)=\left\{x{\in \mathsf{\Sigma }}^{*} \right| S\stackrel{*,G^{\text{'}}}{\Rightarrow }x\}$, knowing that minimum derivations exist, we can assume every derivation of $x\in L\left(G^{\text{'}}\right)$ is the one of minimum length.

Claim 1. 

Any derivation $S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$ does not use an $ϵ$-rule.

Proof of Claim 1. 

Assume for contradiction that $B⟶ϵ$ where $B\ne S$ is used at some point of the derivation.

$S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$ can be rewritten as

$S\stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma B\delta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma \delta \stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }x$ where $\gamma ,\delta \in {\left(V\cup \mathsf{\Sigma }\right)}^{\mathrm{*}}$.

This $B$ must have been generated at an earlier point of the derivation in the form of

$\eta A\theta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \alpha B\beta \theta$ where $\eta ,\alpha ,\beta ,\theta \in {\left(V\cup \mathsf{\Sigma }\right)}^{\mathrm{*}}$.

Therefore, $S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$ can be further rewritten as

$S\stackrel{m,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta A\theta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \alpha B\beta \theta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma B\delta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma \delta \stackrel{k,G^{\mathrm{\text{'}}}}{\Rightarrow }x$ where $k,m,n\ge 0$.

(Note that $\eta \alpha B\beta \theta \stackrel{n,G^{\text{'}}}{\Rightarrow }\gamma B\delta$ is a derivation in which the rule in each step does not originate from this particular $B$.)

Since $A⟶\alpha B\beta$ and $B⟶ϵ$ are in $R^{\text{'}}$, by construction (ii), $A⟶\alpha \beta$ is in $R^{\text{'}}$.

Therefore, $\eta A\theta \stackrel{1,G^{\text{'}}}{\Rightarrow }\eta \alpha \beta \theta$ is a valid production in $G^{\text{'}}$.

Furthermore, since $\eta \alpha B\beta \theta \stackrel{n,G^{\text{'}}}{\Rightarrow }\gamma B\delta$, by Proposition 2.19, we can substitute $ϵ$ for $B$ to obtain the following valid production in $G^{\text{'}}$:

$\eta \alpha \beta \theta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma \delta$.

If we apply these two new productions at the corresponding points of the original derivation of $x$, we have the following valid derivation:

$S\stackrel{m,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta A\theta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \alpha \beta \theta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\gamma \delta \stackrel{k,G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

We note that this new derivation of $x$ has a length of $k+m+n+1$ which is shorter than the original one of $k+m+n+2$.

This contradicts the assumption that the original derivation is of minimum length.

Claim 2. Any derivation $S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$ does not use a unit rule.

Proof of Claim 2. Assume for contradiction that a unit rule $A⟶B$ is used at some point of the derivation $S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$.

We can rewrite this derivation as

$S\stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha A\beta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha B\beta \stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

This $B$ must be eventually gotten rid of before reaching the final product of $x{\in \mathsf{\Sigma }}^{*}$ and the production that we need for getting rid of $B$ is:

$\eta B\theta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \gamma \theta$ where $B⟶\gamma$ is a rule in $G^{\mathrm{\text{'}}}$.

We can now rewrite $S\stackrel{*,G^{\text{'}}}{\Rightarrow }x$ as

$S\stackrel{m,G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha A\beta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha B\beta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta B\theta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \gamma \theta \stackrel{k,G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

Since $A⟶B$ and $B⟶\gamma$ are rules in $R^{\text{'}}$, $A⟶\gamma$ is a rule in $R^{\text{'}}$ by construction (iii).

$\alpha A\beta \stackrel{1,G^{\text{'}}}{\Rightarrow }\alpha \gamma \beta$ is a valid production in $G^{\text{'}}$.

Furthermore, since $\alpha B\beta \stackrel{n,G^{\text{'}}}{\Rightarrow }\eta B\theta$, by Proposition 2.19, we can substitute $\gamma$ for $B$ to obtain the following valid production:

$\alpha \gamma \beta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \gamma \theta$.

By applying these two new productions at the corresponding points of the derivation of $x$, we have the following derivation:

$S\stackrel{m,G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha A\beta \stackrel{1,G^{\mathrm{\text{'}}}}{\Rightarrow }\alpha \gamma \beta \stackrel{n,G^{\mathrm{\text{'}}}}{\Rightarrow }\eta \gamma \theta \stackrel{k,G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

This new derivation has a length of $k+m+n+1$ which is shorter than the original one of $k+m+n+2$.

This contradicts the assumption that the original given derivation of $x$ is of minimum length.

Combining Claim 1 and Claim 2, we can conclude Lemma 2.35.

We now examine a method for converting a $CFG$ into one in Chomsky Normal form.

Definition 2.36 (The Method$\left(\mathit{M}\right)$).

From every $CFG$, $G=(V, \mathsf{\Sigma }, R, S)$, that doesn’t have $ϵ$-rules or unit rules, we can construct a $CFG$, $G^{\text{'}}=(V^{\text{'}}, \mathsf{\Sigma }, R^{\text{'}}, S)$ using a method called Method $\left(M\right)$ as described in the following steps:

Step 1

For every $a\in \mathsf{\Sigma }$, create a variable $A_a$ and a rule $A_a⟶a$. Note that $A_a$ is a newly and uniquely created variable such that $A_a\notin V$ and $A_a\ne A_b$ for any $a,b\in \mathsf{\Sigma }$ such that $a\ne b$.

Step 2

$\forall r\in R$, $r$ can be expressed as $A⟶u_1{u}_2\dots u_k$ where $A\in V$, $u_1,u_2,\dots u_k\in V\cup \mathsf{\Sigma }$ & $k\ge 0$. Create a set of rules (called $P\left(r\right)$) and a set of nodes (called $V\left(r\right)$) according to the following steps:

(i)

For $k=0$

$r$ becomes $A⟶ϵ$.

Since $R$ doesn’t have any $ϵ$-rule, except $S⟶ϵ$, $A$ must be equal to $S$ and $r$ becomes $S⟶ϵ$.

Copy $S⟶ϵ$ into $P\left(r\right)$.

In this case, $P\left(r\right)=\left\{S⟶ϵ\right\}=\left\{r\right\}$ and $V\left(r\right)=\varnothing$.

(ii)

For $k=1$

$r$ becomes $A⟶u_1$.

Since $R$ doesn’t have any unit rule, $u_1\in \mathsf{\Sigma }$.

Copy $r$ into $P\left(r\right)$.

In this case, $P\left(r\right)=\left\{A⟶u_1\right\}=\left\{r\right\}$ and $V\left(r\right)=\varnothing$.

(iii)

For $k=2$

$r$ becomes $A⟶u_1{u}_2$.

If $u_1,u_2\in V$, copy $r$ into $P\left(r\right)$. In this case, $P\left(r\right)=\left\{ A⟶u_1{u}_2\right\}=\left\{r\right\}$ and $V\left(r\right)=\varnothing$.

If $u_1\in \mathsf{\Sigma }$ & $u_2\in V$, create $A⟶U_{u_1}{u}_2$ and add this rule and $U_{u_1}⟶u_1$ to $P\left(r\right)$. Add $U_{u_1}$ to $V\left(r\right)$.

(Note that $U_{u_1}⟶u_1$ was created in Step 1 above).

In this case, $P\left(r\right)=\{A⟶U_{u_1}{u}_2,U_{u_1}⟶u_1\}$ and $V\left(r\right)=\left\{U_{u_1}\right\}$.

If $u_1\in V$ & $u_2\in \mathsf{\Sigma }$, create $A⟶u_1{U}_{u_2}$ and add this rule and $U_{u_2}⟶u_2$ to $P\left(r\right)$. Add $U_{u_2}$ to $V\left(r\right)$.

(Note that $U_{u_2}⟶u_2$ was created in Step 1 above).

In this case, $P\left(r\right)=\{A⟶u_1{U}_{u_2},U_{u_2}⟶u_2\}$ and $V\left(r\right)=\left\{U_{u_2}\right\}$.

If both $u_1,u_2\in \mathsf{\Sigma }$, create $A⟶U_{u_1}{U}_{u_2}$ and add it along with $U_{u_1}⟶u_1$, $U_{u_2}⟶u_2$ to $P\left(r\right)$. Add $U_{u_1}$, $U_{u_2}$ to $V\left(r\right)$.

(Note that $U_{u_1}⟶u_1$ and $U_{u_2}⟶u_2$ were created in Step 1 above).

In this case, $P\left(r\right)=\{A⟶U_{u_1}{U}_{u_2},U_{u_1}⟶u_1,U_{u_2}⟶u_2\}$ and $V\left(r\right)=\{U_{u_1},U_{u_2}\}$.

(iv)

For $k\ge 3$

Figure 2.7. Caption.

Figure 2.7. Caption.

As depicted by the above figure, create the following rules and add them to $P\left(r\right)$.

$A⟶U_1{A}_1$

$A_1⟶U_2{A}_2$

$A_2⟶U_3{A}_3$

$⋮$

$A_i⟶U_{i+1}{A}_{i+1}$

$⋮$

$A_{k-2}⟶U_{k-1}{U}_k$ where $A_1,A_2,\dots A_{k-2}$ are variables newly and uniquely created for each $r$ and therefore, they are not in $V$.

For any $i\in \{\mathrm{1,2},3,\dots k\}$, if $u_i\in V$, $U_i=u_i$ and if $u_i\in \mathsf{\Sigma }$, set $U_i=U_{u_i}$ and add $U_{u_i}⟶u_i$ to $P\left(r\right)$. Add $U_{u_i}$ to $V\left(r\right)$.

(Note that $U_{u_i}⟶u_i$ for each $u_i\in \mathsf{\Sigma }$ were created in Step 1 above).

In this case, $P\left(r\right)$ includes all the rules:

$A⟶U_1{A}_1$

$A_1⟶U_2{A}_2$

$A_2⟶U_3{A}_3$

$⋮$

$A_i⟶U_{i+1}{A}_{i+1}$

$⋮$

$A_{k-2}⟶U_{k-1}{U}_k$and the rules $U_{u_i}⟶u_i$ for any $u_i\in \mathsf{\Sigma }$ whereas

$V\left(r\right)=\left\{U_{u_i}|u_i\in \mathsf{\Sigma }\right\}\cup \left\{A_i\right|i=\mathrm{1,2},\dots k-2\}$Step 3

Set

$$V^{\mathrm{\text{'}}}=V\cup {\displaystyle \bigcup _{r\in R}}V\left(r\right)$$

And

$R^{\mathrm{\text{'}}}={\displaystyle \bigcup _{r\in R}}P\left(r\right)$

We note the following properties of the rules created by Method $\left(M\right)$:

N1. All the rules in $R^{\text{'}}$ are in Chomsky Normal Form.

N2. For any $r^{\mathbf{\text{'}}}\in R^{\mathrm{\text{'}}}$, there exists $r\in R$ such that $r^{\mathbf{\text{'}}}\in P\left(r\right)$. Furthermore, $P\left(r_1\right)\ne P\left(r_2\right)$ for any $r_1,r_2\in R$ such that $r_1\ne r_2$.

N3. For any $r\in R$, $r$ is equivalent to the rules in $P\left(r\right)$ by Proposition 2.15.

N4. $V$ and ${\displaystyle \bigcup _{r\in R}}V\left(r\right)$ are disjoint. That is $V\cap {\displaystyle \bigcup _{r\in R}}V\left(r\right)=\mathrm{\varnothing }$.

N5. For any $r^{\mathbf{\text{'}}}\in P\left(r\right)$, either $Head\left(r^{\mathbf{\text{'}}}\right)=Head\left(r\right)$ or $Head\left(r^{\mathbf{\text{'}}}\right)\notin V$. Or equivalently, $Head\left(r^{\mathbf{\text{'}}}\right)\in V⟹Head\left(r^{\mathbf{\text{'}}}\right)=Head\left(r\right)$.

N6. $\forall r^{\mathbf{\text{'}}}\in P\left(r\right)$, if $\left|Body\left(r^{\mathbf{\text{'}}}\right)\right|=2$, then $r^{\mathbf{\text{'}}}$ is unique for $P\left(r\right)$. That is,

$r^{\mathbf{\text{'}}}\notin P\left(r_1\right)$ for any $r_1\in R$ such that $r\ne r_1$.

N7. If $k=0$ or $\left|Body\left(r\right)\right|=0$, $P\left(r\right)=\left\{S⟶ϵ\right\}=\left\{r\right\}$ and $V\left(r\right)=\mathrm{\varnothing }$.

N8. If $k=1$ or $\left|Body\left(r\right)\right|=1$, $P\left(r\right)=\left\{A⟶u_1\right\}=\left\{r\right\}$ and $V\left(r\right)=\mathrm{\varnothing }$ where $u_1\in \mathsf{\Sigma }$.

We now have the following theorem.

Theorem 2.37. Every context-free language is generated by a $CFG$ in Chomsky normal form ($CNF$).

Proof. Since every context-free language is generated by a $CFG$, we need to show that every $CFG$ can be converted to an equivalent $CFG$ in Chomsky normal form.

Also, because of Lemma 2.35, we can start with a $CFG$ that has no $ϵ$-rule ($A⟶ϵ$ where $A\ne S$) or unit rule ($A⟶B$ where $A,B\in V$).

Let $G=(V,\mathsf{\Sigma },R,S)$ be the $CFG$ that has no $ϵ$-rule or unit rule except $S⟶ϵ$.

Let $G^{\text{'}}=(V^{\text{'}}, \mathsf{\Sigma }, R^{\text{'}}, S)$ be a $CFG$ constructed from $G$ by use of Method $\left(M\right)$.

In the following, we shall show $L\left(G\right)=L\left(G^{\mathrm{\text{'}}}\right)$ by showing $x\in L\left(G\right)⟺x\in L\left(G^{\mathrm{\text{'}}}\right)$ $\forall x\in {\mathsf{\Sigma }}^{\mathrm{*}}$.

$"⟹"$ (If $x\in L\left(G\right)$)

$S\stackrel{\mathrm{*},G}{\Rightarrow }x$.

$\exists r_1,r_2,\dots r_i,\dots r_n,r_{n+1}\in R$ and $u_1,u_2,\dots u_i,\dots u_n\in {(V\cup \Sigma )}^{\mathrm{*}}$ such that

$S\stackrel{r_1,G}{\Rightarrow }{u}_1\stackrel{r_2,G}{\Rightarrow }{u}_2\dots \dots u_{i-1}\stackrel{r_i,G}{\Rightarrow }{u}_i\dots \dots \stackrel{r_n,G}{\Rightarrow }{u}_n\stackrel{r_{n+1},G}{\Rightarrow }x$.

By N3, for any $i\in \{\mathrm{1,2},\dots ,n+1\}$, $r_i$ is equivalent to a sequence of rules from $P\left(r_i\right)$ which is a subset of $R^{\text{'}}$.

Therefore, $S\stackrel{P\left(r_1\right),G^{\mathrm{\text{'}}}}{\Rightarrow }{u}_1\stackrel{{P(r}_2),G^{\mathrm{\text{'}}}}{\Rightarrow }{u}_2\dots \dots u_{i-1}\stackrel{P\left(r_i\right),G^{\mathrm{\text{'}}}}{\Rightarrow }{u}_i\dots \dots \stackrel{P\left(r_n\right),G^{\mathrm{\text{'}}}}{\Rightarrow }{u}_n\stackrel{{P(r}_{n+1}),G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

Note that $u_1,u_2,\dots u_i,\dots u_n\in {(V^{\mathrm{\text{'}}}\cup \Sigma )}^{\mathrm{*}}$ because $V\subset V^{\mathrm{\text{'}}}$.

Therefore, $S\stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

Therefore, $x\in L\left(G^{\mathrm{\text{'}}}\right)$.

“$⟸$” (If $x\in L\left(G^{\mathrm{\text{'}}}\right)$)

$S\stackrel{\mathrm{*},G^{\mathrm{\text{'}}}}{\Rightarrow }x$.

By Theorem 2.33, $\exists$ a parse tree (in $G^{\text{'}}$) with root $S\in V^{\text{'}}$ and a yield $x\in {\mathsf{\Sigma }}^{*}$.

Let’s call this parse tree $\left(T^{\text{'}}\right)$.

By definition of parse tree, $S$ and its children must be the head and body of a rule in $R^{\text{'}}$.

Let’s call this rule $r^{\text{'}}$ and hence $Head\left(r^{\text{'}}\right)=S$.

By N1, $r^{\text{'}}$ must be in one of the following forms:

• $S⟶ϵ$
• $A⟶a$ where $a\in \mathsf{\Sigma }$, $A\in V^{\text{'}}$
• $A⟶U_1{U}_2$ where $A\in V^{\text{'}}$, $U_1,U_2\in V^{\text{'}}\backslash \left\{S\right\}$

If $r^{\text{'}}$ is $S⟶ϵ$, $ϵ$ is the only child of $S$.

Since $ϵ$ has no children and $x$ is a descendant of $S$, this is possible only if $ϵ=x$.

Furthermore, by construction of $\left(M\right)$, $S⟶ϵ$ in $R^{\text{'}}$ is created from $S⟶ϵ$ in $R$.

Therefore, $S⟶ϵ$ is also a rule in $R$.

Therefore, $S\stackrel{1,G}{\Rightarrow }ϵ$. (Proposition 2.8(i))

Therefore, $S\stackrel{1,G}{\Rightarrow }x$.

Therefore, $S\stackrel{*,G}{\Rightarrow }x$.

Therefore, $x\in L\left(G\right)$If $r^{\mathrm{\text{'}}}$ is $A⟶a$, since $S=Head\left(r^{\mathrm{\text{'}}}\right)$, $S=A$.

Therefore, $r^{\text{'}}$ is $S⟶a$ and $S$ has only one child which is $a$.

Since $x$ is a descendant of $S$ and $a$ has no children, $a=x$.

By construction of $\left(M\right)$, $A⟶a$ in $R^{\text{'}}$ is created from $A⟶a$ in $R$.

Therefore, $A⟶a$ is also a rule in $R$.

Therefore, $S⟶x$ is a rule in $R$.

Therefore, $S\stackrel{1,G}{\Rightarrow }x$. (Proposition 2.8(i))

Therefore, $S\stackrel{*,G}{\Rightarrow }x$.

Therefore, $x\in L\left(G\right)$.

If $r^{\mathrm{\text{'}}}$ is $A⟶U_1{U}_2$ where $A\in V^{\mathrm{\text{'}}}$, $U_1,U_2\in V^{\mathrm{\text{'}}}\backslash \left\{S\right\}$Since $Head\left(r^{\mathrm{\text{'}}}\right)=S$ and $S\in V$, $Head\left(r^{\mathrm{\text{'}}}\right)\in V$.

Since $Head\left(r^{\mathrm{\text{'}}}\right)=A$, $A=S$.

Therefore, $r^{\mathrm{\text{'}}}$ becomes $S⟶U_1{U}_2$ where $U_1,U_2\in V^{\mathrm{\text{'}}}\backslash \left\{S\right\}$.

By N2, $\exists r\in R$ such that $r^{\text{'}}\in P\left(r\right)$.

Let $r$ be $A^{\mathrm{\text{'}}}⟶u_1{u}_2\dots u_k$ where $A\mathrm{\text{'}}\in V$, $u_1,u_2,\dots u_k\in V\cup \mathsf{\Sigma }$.

By N5, $Head\left(r^{\mathrm{\text{'}}}\right)\in V⟹Head\left(r^{\mathrm{\text{'}}}\right)=Head\left(r\right)$.

Therefore, $S=A^{\text{'}}$.

Therefore, $r$ becomes $S⟶u_1{u}_2\dots u_k$.

We now analyze the different situations for different values of $k$.

If $k=0$, $r$ becomes $S⟶ϵ$.

By construction of $\left(M\right)$, $P\left(r\right)=\{S⟶ϵ\}$.

Since $r^{\mathrm{\text{'}}}\in P\left(r\right)$, $r^{\mathrm{\text{'}}}$ is $S⟶ϵ$.

This contradicts the underlying assumption that $r^{\text{'}}$ is $A⟶U_1{U}_2$ where $A\in V^{\text{'}}$, $U_1,U_2\in V^{\text{'}}\backslash \left\{S\right\}$.

Therefore, $k$ cannot be $0$.

If $k=1$, $r$ becomes $S⟶u_1$.

Since $R$ doesn’t have any unit rule, $u_1\in \mathsf{\Sigma }$.

By construction of $\left(M\right)$, $P\left(r\right)=\{S⟶u_1\}$.

Therefore, $r^{\text{'}}$ is $S⟶u_1$ where $u_1\in \mathsf{\Sigma }$.

This contradicts the underlying assumption that $r^{\text{'}}$ is $A⟶U_1{U}_2$ where $A\in V^{\text{'}}$, $U_1,U_2\in V^{\text{'}}\backslash \left\{S\right\}$.

Therefore, $k$ cannot be $1$.

Therefore, we can exclude the cases of $k\in \left\{\mathrm{0,1}\right\}$ under the assumption that $r^{\text{'}}$ is $A⟶U_1{U}_2$ where $A\in V^{\text{'}}$, $U_1,U_2\in V^{\text{'}}\backslash \left\{S\right\}$.

If $k=2$, $r$ becomes $S⟶u_1{u}_2$.

By construction of $\left(M\right)$, $P\left(r\right)$ is one of the following:

(i)

$P\left(r\right)=\{S⟶u_1{u}_2\}$ if $u_1,u_2\in V$

(ii)

$P\left(r\right)=\{S⟶U_{u_1}{u}_2,U_{u_1}⟶u_1\}$ if $u_1\in \mathsf{\Sigma }\& u_2\in V$

(iii)

$P\left(r\right)=\{S⟶u_1{U}_{u_2},U_{u_2}⟶u_2\}$ if $u_1\in V\& u_2\in \mathsf{\Sigma }$

(iv)

$P\left(r\right)=\{S⟶U_{u_1}{U}_{u_2},U_{u_1}⟶u_1,U_{u_2}⟶u_2\}$ if $u_1,u_2\in \mathsf{\Sigma }$

For (i), $r^{\mathrm{\text{'}}}$ is $S⟶u_1{u}_2$.

In this case, $r$ and $r^{\text{'}}$ are the same and the sub parse tree in $\left(T^{\text{'}}\right)$ with root $S$ and children $u_1,u_2$ as shown on the right of the following figure can be replaced by a parse tree in $G$ with the same root and children as shown on the left.

Figure 2.8. Caption.

Figure 2.8. Caption.

For (ii), $r^{\mathrm{\text{'}}}$ is either $S⟶U_{u_1}{u}_2$ or $U_{u_1}⟶u_1$.

However, since $Head\left(r^{\mathrm{\text{'}}}\right)=S$ which is in $V$ and $U_{u_1}\notin V$, $r^{\mathrm{\text{'}}}$ cannot be $U_{u_1}⟶u_1$.

$r^{\mathrm{\text{'}}}$ must be $S⟶U_{u_1}{u}_2$.

By N3, $S⟶u_1{u}_2$ is equivalent to $S⟶U_{u_1}{u}_2$ and $U_{u_1}⟶u_1$.

We have the following equivalent parse trees with the same root and yield.

Figure 2.9. Caption.

Figure 2.9. Caption.

The one on the left is a parse tree in $G$ whose root and its children are the head and body of a rule in $R$ whereas the one on the right is a sub parse tree of $\left(T^{\text{'}}\right)$.

Therefore we can replace a sub parse tree of $\left(T^{\text{'}}\right)$ with an equivalent parse tree in $G$ whose root and yield are the head and body of a rule in $R$.

For (iii), by a similar argument, we have the following equivalent parse trees with the same root and yield.

Figure 2.10. Caption.

Figure 2.10. Caption.

The one on the left is a parse tree in $G$ whose root and its children are the head and body of a rule in $R$ whereas the one on the right is a sub parse tree of $\left(T^{\text{'}}\right)$.

Therefore we can replace a sub parse tree of $\left(T^{\text{'}}\right)$ with an equivalent parse tree in $G$ whose root and yield are the head and body of a rule in $R$.

For (iv), by a similar argument, we have the following equivalent parse trees with the same root and yield.

Figure 2.11. Caption.

Figure 2.11. Caption.

The one on the left is a parse tree in $G$ whose root and its children are the head and body of a rule in $R$ whereas the one on the right is a sub parse tree of $\left(T^{\text{'}}\right)$.

Therefore we can replace a sub parse tree of $\left(T^{\text{'}}\right)$ with an equivalent parse tree in $G$ whose root and yield are the head and body of a rule in $R$.

If $k\ge 3$, $r$ is $S⟶u_1{u}_2\dots u_k$.

$P\left(r\right)$ consists of the following rules:

$S⟶U_1{A}_1$

$A_1⟶U_2{A}_2$

$A_2⟶U_3{A}_3$

$⋮$

$A_i⟶U_{i+1}{A}_{i+1}$

$⋮$

$A_{k-2}⟶U_{k-1}{U}_k$

$U_{u_i}⟶u_i$ if $u_i\in \mathsf{\Sigma }$ $\forall i\in \{\mathrm{1,2},3,\dots k\}$where $U_i=u_i$ if $u_i\in V$ and $U_i=U_{u_i}$ if $u_i\in \mathsf{\Sigma }$.

Since $Head\left(r^{\mathrm{\text{'}}}\right)=S$, $r^{\mathrm{\text{'}}}$ is $S⟶U_1{A}_1$.

Since $\left(T^{\text{'}}\right)$ is a parse tree of $G^{\text{'}}$, by definition of parse tree,

$U_1{A}_1$ are children of $S$.

$U_2{A}_2$ are children of $A_1$.

$U_3{A}_3$ are children of $A_2$.

$⋮$

$U_{k-1}{U}_k$ are children of $A_{k-2}$.

By N3, $r$ is equivalent to the sequence of rules contained in $P\left(r\right)$.

Therefore, we have the following equivalent parse trees with the same root and yield.

Figure 2.12. Caption.

Figure 2.12. Caption.

The one on the left is a parse tree in $G$ whose root and its children are the head and body of a rule in $R$ whereas the one on the right is a sub parse tree of $\left(T^{\text{'}}\right)$.

Therefore we can replace a sub parse tree of $\left(T^{\text{'}}\right)$ with an equivalent parse tree in $G$ whose root and yield are the head and body of a rule in $R$.

Combining all cases, we conclude that there is a sub parse tree in $\left(T^{\text{'}}\right)$ with root $S$ that can be replaced by an equivalent parse tree in $G$ whose root and yield are the head and body of a rule in $R$.

We can write this rule in$R$ as $S⟶u_1{u}_2\dots u_k$ where $k\ge 0$ and $u_i\in V\cup \mathsf{\Sigma }$ for $i\in \{\mathrm{1,2},\dots k\}$

(a) If all $u_i$’s are terminals

In this case, $u_1{u}_2\dots u_k=x$, the yield of the parent tree $\left(T^{\text{'}}\right)$.

The reason is that a leaf of a subtree is also a leaf of the parent tree.

Therefore, $u_i⊏x\forall i\in \{\mathrm{1,2},\dots k\}$.

On the other hand, if $l$ is a leaf in $x$, there is a simple directed path from $S$ to $l$. This simple directed path must pass through one of the nodes $u_1,u_2\dots u_k$ because $u_1{u}_2\dots u_k$ is the yield of a sub parse tree in $\left(T^{\text{'}}\right)$ which is obtained by branching out from $S$ in all possible directions.

Therefore, $l$must be one of the nodes $u_1,u_2\dots u_k$.

After replacement, we now have a new tree which is a parse tree in $G$, and furthermore, the root and yield of this tree are respectively $S$ and $x$.

By Theorem 2.33, $S\stackrel{*,G}{\Rightarrow }x$.

Therefore, $x\in L\left(G\right)$.

(b) If some $u_i$’s are variables

For each $u_i$ that is a variable, we can repeat the above replacement process to replace the sub parse tree (with root $u_i$) in $\left(T^{\text{'}}\right)$ with a parse tree in $G$ whose root ($u_i$) and the root’s children are the head and body of a rule in $R$.

Since every time we do a replacement, we get down to a lower level of $\left(T^{\text{'}}\right)$ and since the height of $\left(T^{\text{'}}\right)$ and the number of subtrees of $\left(T^{\text{'}}\right)$ are both finite, this process of replacement must come to a stop after a finite number of operations. When this happens, we have a new tree in which every interior node and its children are the head and body of a rule in $R$. This means that the new tree thus created is a parse tree in $G$.

Furthermore, this replacement process only affects the nodes which are variables. Therefore, the yield of $\left(T^{\text{'}}\right)$, namely $x$, is untouched and remains at the bottom after the replacement is complete.

This means that $x$ is also the yield of the newly created tree.

We now have a new tree with root $S$ and yield $x$ and the tree is also a parse tree in $G$.

By Theorem 2.33, $S\stackrel{*,G}{\Rightarrow }x$.

Therefore, $x\in L\left(G\right)$.

Combining (a) and (b), we complete the proof of Theorem 2.37.

On the basis of Theorem 2.37 and the results proved in Lemma 2.35, we can now develop a set of operational rules for the conversion of a $CFG$ to one in $CNF$.

Let $G=(V,\mathsf{\Sigma },R,S)$ be the $CFG$ to be converted.

Let $G^{\mathrm{\text{'}}}=(V^{\mathrm{\text{'}}},\mathsf{\Sigma },R^{\mathrm{\text{'}}},S_0)$ be the $CFG$ to be created in $CNF$.

$\mathit{C}\mathit{R}-1.$

Create $S_0⟶S$ and add it to $R^{\text{'}}$.

(Note that this creation will ensure that the start variable will not occur on the right hand side of a rule.)

$\mathit{C}\mathit{R}-2.$

(Elimination of $ϵ$-rules)

If $\exists$ a rule $B⟶ϵ$ in $R$, do the following:

(i)

For every rule in $R$ in the form $A⟶u_{1}B{u}_{2}B{u}_{3}B{u}_4\dots \dots u_{n-1}B{u}_{n}B{u}_{n+1}$

(1)

For each single occurrence of $B$, on the $RHS$, create a rule with that occurrence deleted and add it to $R^{\text{'}}$.

For example, $A⟶u_1{u}_{2}B{u}_{3}B{u}_4\dots \dots u_{n-1}B{u}_{n}B{u}_{n+1}$

$A⟶u_{1}B{u}_2{u}_{3}B{u}_4\dots \dots u_{n-1}B{u}_{n}B{u}_{n+1}$

$⋮$

$A⟶u_{1}B{u}_{2}B{u}_{3}B{u}_4\dots \dots u_{n-1}B{u}_n{u}_{n+1}$

(2)

For each group occurrence of $2 B’s$ on the $RHS$, create a rule with that group occurrence deleted and add it to $R^{\text{'}}$.

For example, $A⟶u_1{u}_2{u}_{3}B{u}_4\dots \dots u_{n-1}B{u}_{n}B{u}_{n+1}$

$A⟶u_1{u}_{2}B{u}_3{u}_4\dots \dots u_{n-1}B{u}_{n}B{u}_{n+1}$

$⋮$

$A⟶u_{1}B{u}_{2}B{u}_{3}B{u}_4\dots \dots u_{n-1}{u}_n{u}_{n+1}$.

$⋮$

$⋮$

(n) For each group occurrence of $n B’s$ on the $RHS$, create a rule with that group occurrence deleted and add it to $R^{\text{'}}$.

For example, $A⟶u_1{u}_2{u}_3{u}_4\dots \dots u_{n-1}{u}_n{u}_{n+1}$.

(ii)

Repeat (i) until all rules of the form of $B⟶ϵ$ are eliminated.

$\mathit{C}\mathit{R}-3.$ (Elimination of unit rules)

If $\exists$ rules $A⟶B$ and $B⟶u$ in $R$, do the following:

(i)

Create $A⟶u$ and add it to $R^{\text{'}}$.

(ii)

Copy $B⟶u$ to $R^{\text{'}}$ .

(iii)

Do not copy $A⟶B$ to $R^{\text{'}}$.

(iv)

Repeat (i) and (ii) until all unit rules of the form $A⟶B$ are eliminated.

$\mathit{C}\mathit{R}-4.$ (Conversion of remaining rules)

For every remaining rule $A$ in $R$, $A⟶u_1{u}_2\dots \dots u_k$ where each $u_i\in V\cup \mathsf{\Sigma }$ for $i\in \{\mathrm{1,2},\dots \dots k\}$.

Create in $R^{\text{'}}$ the following sequence of rules and add the corresponding created variables to $V^{\text{'}}$:

$A⟶U_1{A}_1$

$A_1⟶U_2{A}_2$

$A_2⟶U_3{A}_3$

$⋮$

$A_{k-2}⟶U_{k-1}{A}_{k-1}$

$A_{k-1}⟶U_k$

where $U_i=u_i$ if $u_i\in V$ and if $u_i\in \mathsf{\Sigma }$, add $U_i⟶u_i$.

Example 2.38. Let $G=(V,\mathsf{\Sigma },R,S)$ be the $CFG$ consisting of the following rules:

$S⟶ASA|aB$

$A⟶B|S$

   $B⟶b|ϵ$

   Convert $G$ to $G^{\mathrm{\text{'}}}=(V^{\mathrm{\text{'}}},\mathsf{\Sigma },R^{\mathrm{\text{'}}},S_0)$ in $CNF$.

   Step 1. (Applying $\mathit{C}\mathit{R}-1$.)

   $S_0⟶S$

$S⟶ASA|aB$

$A⟶B|S$

   $B⟶b|ϵ$

   Step 2. (Removing $B⟶ϵ$ using $\mathit{C}\mathit{R}-2$)

   $S_0⟶S$

$S⟶ASA\left|aB\right|a$

   $A⟶B\left|S\right|ϵ$

   $B⟶b$

   Step 3 (Removing $A⟶ϵ$ using $\mathit{C}\mathit{R}-2$)

   $S_0⟶S$

   $S⟶ASA\left|aB\right|a\left|SA\right|AS|S$

   $A⟶B|S$

   $B⟶b$

   Step 4 (Removing $S⟶S$ because of redundancy)

$S_0⟶S$

   $S⟶ASA\left|aB\right|a\left|SA\right|AS$

   $A⟶B|S$

   $B⟶b$

   Step 5 (Removing $S_0⟶S$ using $\mathit{C}\mathit{R}-3$)

   $S_0⟶ASA\left|aB\right|a\left|SA\right|AS$

   $S⟶ASA\left|aB\right|a\left|SA\right|AS$

   $A⟶B|S$

   $B⟶b$

   Step 6 (Removing $A⟶B$ using $\mathit{C}\mathit{R}-3$)

   $S_0⟶ASA\left|aB\right|a\left|SA\right|AS$

   $S⟶ASA\left|aB\right|a\left|SA\right|AS$

   $A⟶b|S$ $B⟶b$Step 7 (Removing $A⟶S$ using $\mathit{C}\mathit{R}-3$)

   $S_0⟶ASA\left|aB\right|a\left|SA\right|AS$

   $S⟶ASA\left|aB\right|a\left|SA\right|AS$

   $A⟶b\left|ASA\right|aB\left|a\right|SA|AS$

   $B⟶b$

   Step 8 (Conversion of remaining rules into $CNF$)

   Since $S_0⟶ASA⟺\left\{\begin{array}{c}{S}_0⟶A{A}_1\\ A_1⟶SA\end{array}\right.$ and $S_0⟶aB⟺\left\{\begin{array}{c}{S}_0⟶UB\\ U⟶a\end{array}\right.$,

   $S⟶ASA⟺\left\{\begin{array}{c}S⟶A{A}_1\\ A_1⟶SA\end{array}\right.$ and $S⟶aB⟺\left\{\begin{array}{c}S⟶UB\\ U⟶a\end{array}\right.$, and

   $A⟶ASA⟺\left\{\begin{array}{c}A⟶A{A}_1\\ A_1⟶SA\end{array}\right.$ and $A⟶aB⟺\left\{\begin{array}{c}A⟶UB\\ U⟶a\end{array}\right.$,

   the rules in $R^{\text{'}}$ now become

   $S_0⟶A{A}_1\left|UB\right|a\left|SA\right|AS$

   $S⟶A{A}_1\left|UB\right|a\left|SA\right|AS$

   $A⟶b\left|A{A}_1\right|UB\left|a\right|SA|AS$

   $B⟶b$

$A_1⟶SA$

$U⟶a$

Example 2.39. 

Convert $S⟶aSb|ϵ$ to $CNF$ where $S\in V$ and $a,b\in \mathsf{\Sigma }$ and show that there is more than one way of deriving the string $a^2{b}^2$ using rules in $CNF$.

Conversion of rules.

$S⟶aSb|ϵ$

$⟺S⟶aSb|ab$

$⟺\left\{\begin{array}{c}S⟶ASB|AB\\ A⟶a \\ B⟶b \end{array}\right.$

$⟺\left\{\begin{array}{c}S⟶AC|AB;C⟶SB\\ A⟶a;B⟶b \end{array}\right.$

Derivation of a²b²

There is more than one way of deriving the string $a^2{b}^2$. Below are a few examples.

(i)

$S\stackrel{S⟶AC}{\Rightarrow }AC\stackrel{C⟶SB}{\Rightarrow }ASB\stackrel{A⟶a}{\Rightarrow }aSB\stackrel{B⟶b}{\Rightarrow }aSb\stackrel{S⟶AB}{\Rightarrow }aABb\stackrel{A⟶a}{\Rightarrow }aaBb\stackrel{B⟶b}{\Rightarrow }aabb$.

(ii)

$S\stackrel{S⟶AC}{\Rightarrow }AC\stackrel{C⟶SB}{\Rightarrow }ASB\stackrel{S⟶AB}{\Rightarrow }AABB\stackrel{A⟶a}{\Rightarrow }aABB\stackrel{A⟶a}{\Rightarrow }aaBB\stackrel{B⟶b}{\Rightarrow }aabB\stackrel{B⟶b}{\Rightarrow }aabb$.

(iii)

$S\stackrel{S⟶AC}{\Rightarrow }AC\stackrel{C⟶SB}{\Rightarrow }ASB\stackrel{S⟶AB}{\Rightarrow }AABB\stackrel{B⟶b}{\Rightarrow }AABb\stackrel{B⟶b}{\Rightarrow }AAbb\stackrel{A⟶a}{\Rightarrow }Aabb\stackrel{A⟶a}{\Rightarrow }aabb$.

2.3. Pushdown Automata ($\mathit{P}\mathit{D}\mathit{A}$)

Pushdown automata is another kind of nondeterministic computation model similar to nondeterministic finite automata except that they have an extra component called stack. The purpose of the stack is to provide additional memory beyond what is available in finite automata.

Pushdown automata are equivalent in power to context-free grammars which will be proved later. In addition to reading symbols from the input alphabet $\mathsf{\Sigma }$, a $PDA$ also reads and writes symbols on the stack. Writing and reading on the stack must be done at the top. Either symbol from input or stack can be $ϵ$ thereby allowing the machine to move without actually reading or writing. Upon reading a symbol from the input alphabet, the $PDA$ decides to make one of the following moves on the stack before entering the next state:

(i) Replace

Replace the symbol at the top of the stack with another symbol. This move is referred to as the “Replace” move.

(ii) Push

Add a symbol to the top of the stack. This move is referred to as the “Push” move.

(iii) Pop

Erase or remove a symbol from the top of the stack. This move is referred to as the “Pop” move.

(iv) Untouched

Do nothing to change the stack. This move is referred to as “Untouched” move.

A $PDA$ is formally defined as follows.

Definition 2.40. 

A $PDA$ is a 7-tuple, $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ where $Q,\mathsf{\Sigma },\mathsf{\Gamma }\& F$ are finite sets such that

(a) $Q$ is the set of states

(b) $\mathsf{\Sigma }$ is the input alphabet

(c) $\mathsf{\Gamma }$ is the stack alphabet

(d) $\delta :Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}⟶\wp (Q\times {\mathsf{\Gamma }}_{ϵ})$ is the transition function

(e) $q_0\in Q$ is the start state

(f) $⟂\in \mathsf{\Gamma }$ is the initial stack symbol signaling an empty stack

(g) $F\subset Q$ is the set of accept states.

$M$ computes as follows.

Let $w=w_1{w}_2\dots w_m$ where $w_i\in {\mathsf{\Sigma }}_{ϵ}$ for $1\le i\le m$.

$M$ accepts $w$ iff $\exists r_0, r_1\dots r_m\in Q$ and $s_0, s_1\dots s_m\in {\mathsf{\Gamma }}^{*}$ such that the following conditions are satisfied:

(i) $r_0=q_0$ and $s_0=⟂$

(ii) $\left(r_{i+1},b_i\right)\in \delta \left(r_i,w_{i+1},a_i\right)$) for $0\le i\le m-1$ where $a_i,b_i\in {\mathsf{\Gamma }}_{ϵ}$ and $s_i=a_i{t}_i$, $s_{i+1}=b_i{t}_i$ where $t_i\in {\mathsf{\Gamma }}^{*}$

(iii) $r_m\in F$

When $m=0, w=ϵ$ and only conditions (i) and (iii) are valid which then becomes $r_0=q_0$ and $s_0=⟂$ and $r_0\in F$.

Therefore, we define a $PDA$ to accept $ϵ$ whenever the start state is also an accept state and the stack is signaled to be empty.

If we write $r_i\stackrel{w_{i+1},a_i⟶b_i,\delta }{\to }{r}_{i+1}$ for $\left(r_{i+1},b_i\right)\in \delta \left(r_i,w_{i+1},a_i\right)$, conditions (i), (ii) and (iii) can be written as follows:

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\delta }{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\delta }{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}\dots r_{m-1}\stackrel{w_m,a_{m-1}⟶b_{m-1,}\delta }{\to }{r}_m,r_m\in F$.

When there is only one transition function under consideration, the showing of $\delta$ in the computation is usually omitted and the following shorthand is used instead:

$q_0=r_0\stackrel{w_1,a_0⟶b_0}{\to }{r}_1\stackrel{w_2,a_1⟶b_1}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_i}{\to }{r}_{i+1}\dots r_{m-1}\stackrel{w_m,a_{m-1}⟶b_{m-1}}{\to }{r}_m,r_m\in F$.

For simplicity, we sometimes can use the notation $q_0\stackrel{w,*,\delta }{\to }{r}_m$ to represent a computation of $w$ from $q_0$ to $r_m$ without showing the intermediate states.

We now can use the transition function to describe the four basic moves of the $PDA$ as mentioned above:

(i) Replace

$r\stackrel{a,b⟶c}{\to }{r}^{\text{'}}$ signifies a replacement of $b$ by $c$ at the top of the stack upon reading symbol $a$ from input.

(ii) Push

$r\stackrel{a,ϵ⟶c}{\to }{r}^{\text{'}}$ signifies adding the symbol $c$ to the top of the stack upon reading symbol $a$ from input.

(iii) Pop

$r\stackrel{a,b⟶ϵ}{\to }{r}^{\text{'}}$ signifies removing the symbol $b$ from the top of the stack upon reading symbol $a$ from input.

(iv) Untouched

$r\stackrel{a,ϵ⟶ϵ}{\to }{r}^{\text{'}}$ signifies nothing is done to change the stack upon reading symbol $a$ from input.

We further note that when $a=ϵ$, $r\stackrel{ϵ,ϵ⟶ϵ}{\to }{r}^{\text{'}}$ signifies a change of state from $r$ to $r^{\text{'}}$ with no input read and no change made to the stack.

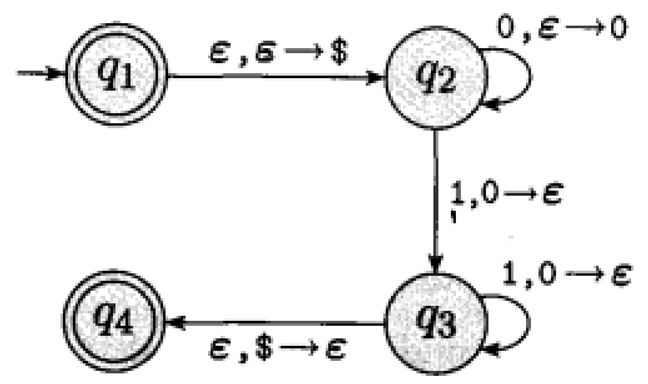
Example 2.41. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_1,⟂,F)$ be a $PDA$ where

$Q=\{q_1,q_2,q_3,q_4\}$, $\mathsf{\Sigma }=\left\{\mathrm{0,1}\right\}$, $\mathsf{\Gamma }=\{0,\mathrm{⟂},\mathrm{\$}\}$, $F=\{q_1,q_4\}$ with the following state diagram:

$M$ recognizes the language $\left\{0^n{1}^n\right| n\ge 0\}$.

If the stack is signaled to be empty at the beginning, $M$ accepts the empty string ($ϵ=0^0{1}^0$), because $q_1$ is both a start and accept state. Furthermore, if the input string is not empty at the start state, the $PDA$ would not read anything from the string except to push $\$$ onto the stack.

$M$ accepts the string $0^3{1}^3$ with the following computation:

$q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2\stackrel{0,ϵ⟶0}{\to }{q}_2\stackrel{0,ϵ⟶0}{\to }{q}_2\stackrel{0,ϵ⟶0}{\to }{q}_2\stackrel{\mathrm{1,0}⟶ϵ}{\to }{q}_3\stackrel{\mathrm{1,0}⟶ϵ}{\to }{q}_3\stackrel{\mathrm{1,0}⟶ϵ}{\to }{q}_3\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_4$, $q_4\in F$.

Note that the above illustration is not a proof that $M$ recognizes the language

$\left\{0^n{1}^n\right| n\ge 0\}$. To make such a proof, one must argue that every string of the form $0^n{1}^n$ is accepted by $M$ and every string accepted by $M$ is of the form $0^n{1}^n$.

Note also that the steps $q_1\stackrel{ϵ,ϵ⟶\$}{\to }{q}_2$ and $q_3\stackrel{ϵ,\$⟶ϵ}{\to }{q}_4$ can be replaced by $q_1\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_2$ and $q_3\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_4$ to transition to another state without making a change to the stack.

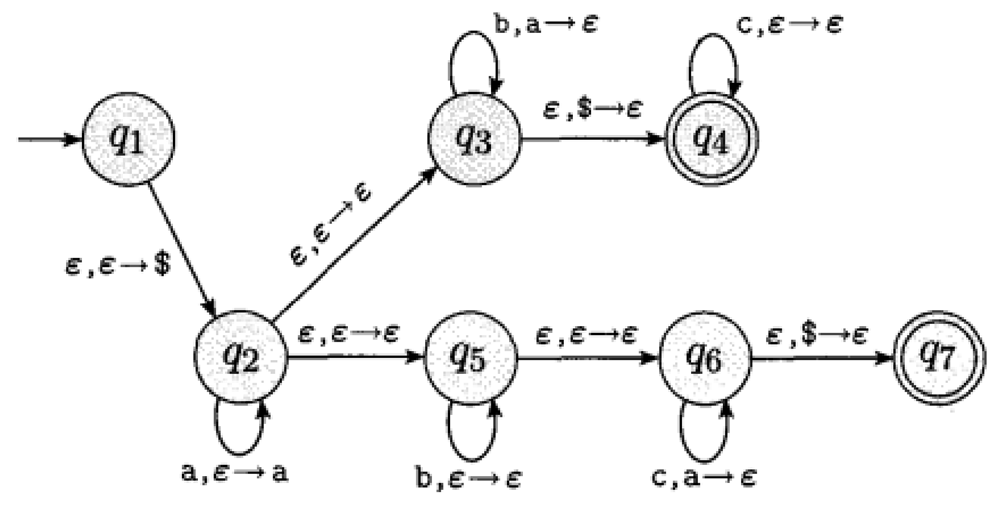
Example 2.42. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_1,⟂,F)$ be a $PDA$ where

$Q=\{q_1,q_2,q_3,q_4,q_5,q_6,q_7\}$, $\mathsf{\Sigma }=\{a,b,c\}$, $\mathsf{\Gamma }=\{\mathrm{a},\mathrm{⟂},\mathrm{\$}\}$, $F=\{q_4,q_7\}$ with the following state diagram:

$M$ recognizes the language $\left\{a^i{b}^j{c}^k\right|i,j,k\ge 0andi=jori=k\}$.

$M$ accepts the empty string ($ϵ=a^0{b}^0{c}^0$) with the following computation:

$q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_3\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_4$, $q_4\in F$.

$M$ accepts the string $a^2{b}^2{c}^3$ with the following computation:

$q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2\stackrel{a,ϵ⟶a}{\to }{q}_2\stackrel{a,ϵ⟶a}{\to }{q}_2\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_3\stackrel{b,a⟶ϵ}{\to }{q}_3\stackrel{b,a⟶ϵ}{\to }{q}_3\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_4\stackrel{c,ϵ⟶ϵ}{\to }{q}_4\stackrel{c,ϵ⟶ϵ}{\to }{q}_4\stackrel{c,ϵ⟶ϵ}{\to }{q}_4$, $q_4\in F$.

$M$ accepts the string $a^2{b}^3{c}^2$ with the following computation:

$q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2\stackrel{a,ϵ⟶a}{\to }{q}_2\stackrel{a,ϵ⟶a}{\to }{q}_2\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_5\stackrel{b,ϵ⟶ϵ}{\to }{q}_5\stackrel{b,ϵ⟶ϵ}{\to }{q}_5\stackrel{b,ϵ⟶ϵ}{\to }{q}_5\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_6\stackrel{c,a⟶ϵ}{\to }{q}_6\stackrel{c,a⟶ϵ}{\to }{q}_6\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_7$, $q_7\in F$.

Note also that the computations $q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2$, $q_3\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_4$, and $q_6\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_7$ can be replaced by $q_1\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_2$ and $q_3\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_4$ and $q_6\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_7$ to transition to another state without making a change to the stack.

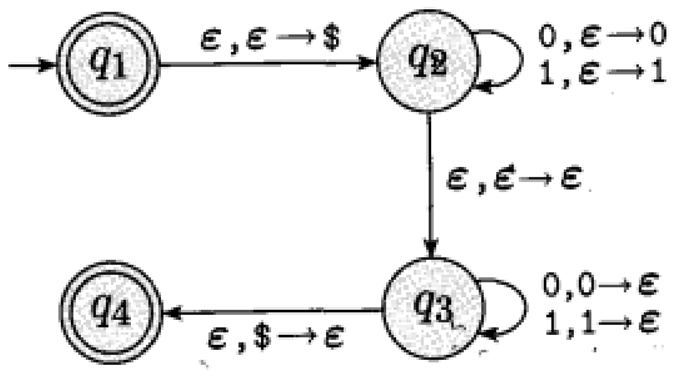
Example 2.43. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_1,\mathrm{⟂},F)$ be a $PDA$ where

$Q=\{q_1,q_2,q_3,q_4\}$, $\mathsf{\Sigma }=\left\{\mathrm{0,1}\right\}$, $\mathsf{\Gamma }=\{\mathrm{0,1},\mathrm{⟂},\mathrm{\$}\}$, $F=\{q_1,q_4\}$ with the following state diagram:

$M$ recognizes the language $\left\{w{w}^R\right|w\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{*}}\}$.

If the stack is signaled to be empty at the beginning, $M$ accepts the empty string

($ϵ=ϵ{ϵ}^R$), because $q_1$ is both a start and accept state.

$M$ accepts the string $001100$ with the following computation:

$q_1\stackrel{ϵ,ϵ⟶\mathrm{\$}}{\to }{q}_2\stackrel{0,ϵ⟶0}{\to }{q}_2\stackrel{0,ϵ⟶0}{\to }{q}_2\stackrel{1,ϵ⟶1}{\to }{q}_2\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_3\stackrel{\mathrm{1,1}⟶ϵ}{\to }{q}_3\stackrel{\mathrm{0,0}⟶ϵ}{\to }{q}_3\stackrel{\mathrm{0,0}⟶ϵ}{\to }{q}_3\stackrel{ϵ,\mathrm{\$}⟶ϵ}{\to }{q}_4$, $q_4\in F$.

Note also that the steps $q_1\stackrel{ϵ,ϵ⟶\$}{\to }{q}_2$ and $q_3\stackrel{ϵ,\$⟶ϵ}{\to }{q}_4$ can be replaced by $q_1\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_2$ and $q_3\stackrel{ϵ,ϵ⟶ϵ}{\to }{q}_4$ to transition to another state without making a change to the stack.

Instead of writing symbols one at a time to the stack, we can actually design $PDA$s which can write a string of symbols to the stack in one step. These $PDA$s are called extended $PDA$s. It turns out that the two kinds of $PDA$s are equivalent in power in that given one, we can construct the other such that the two recognize the same language. The equivalence of these two kinds of $PDA$s will be proved later.

Definition 2.44. 

An extended $PDA$ is a 7-tuple, $M_E=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\widehat{\delta },q_0,⟂,F)$ where $Q,\mathsf{\Sigma },\mathsf{\Gamma }\& F$ are finite sets such that

(a) $Q$ is the set of states

(b) $\mathsf{\Sigma }$ is the input alphabet

(c) $\mathsf{\Gamma }$ is the stack alphabet

(d) $\widehat{\delta }:Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}⟶\wp (Q\times {\mathsf{\Gamma }}^{*})$ is the transition function

(e) $q_0\in Q$ is the start state

(f) $⟂\in \mathsf{\Gamma }$ is the initial stack symbol signaling an empty stack

(g) $F\subset Q$ is the set of accept states.

$M$ computes as follows.

Let $w=w_1{w}_2\dots w_m$ where $w_i\in {\mathsf{\Sigma }}_{ϵ}$ for $1\le i\le m$.

$M$ accepts $w$ iff $\exists r_0, r_1\dots r_m\in Q$ and $s_0, s_1\dots s_m\in {\mathsf{\Gamma }}^{*}$ such that the following conditions are satisfied:

(1) $r_0=q_0$ and $s_0=⟂$

(2) $\left(r_{i+1},b_i\right)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$) for $0\le i\le m-1$ where $a_i\in {\mathsf{\Gamma }}_{ϵ}$, $b_i\in {\mathsf{\Gamma }}^{*}$ and $s_i=a_i{t}_i$, $s_{i+1}=b_i{t}_i$ where $t_i\in {\mathsf{\Gamma }}^{*}$

(3) $r_m\in F$

When $m=0, w=ϵ$ and only conditions (i) and (iii) are valid which then becomes $r_0=q_0$ and $s_0=⟂$ and $r_0\in F$.

Therefore, we define the extended $PDA$ to accept $ϵ$ whenever the start state is also an accept state and the stack is signaled to be empty.

If we write $r_i\stackrel{w_{i+1},a_i⟶b_i,\widehat{\delta }}{\to }{r}_{i+1}$ for $\left(r_{i+1},b_i\right)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$, conditions (i), (ii) and (iii) can be written as follows:

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\widehat{\delta }}{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\widehat{\delta }}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}\dots r_{m-1}\stackrel{w_m,a_{m-1}⟶b_{m-1,}\widehat{\delta }}{\to }{r}_m,r_m\in F$.

When there is only one transition function under consideration, the showing of $\widehat{\delta }$ in the computation is usually omitted and the following shorthand is used instead:

$q_0=r_0\stackrel{w_1,a_0⟶b_0}{\to }{r}_1\stackrel{w_2,a_1⟶b_1}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_i}{\to }{r}_{i+1}\dots r_{m-1}\stackrel{w_m,a_{m-1}⟶b_{m-1}}{\to }{r}_m,r_m\in F$.

For simplicity, we sometimes can use the notation $q_0\stackrel{w,*,\widehat{\delta }}{\to }{r}_m$ to represent a computation of $w$ from $q_0$ to $r_m$ without showing the intermediate states.

Theorem 2.45. 

For any extended $PDA$, ($M_E$), there is a $PDA (M$), such that $L\left(M_E\right)=L\left(M\right)$ and vice versa.

Proof. 

Construction of $M$ from $M_E$.

Let $M_E=(Q_E,\mathsf{\Sigma },\mathsf{\Gamma },\widehat{\delta },q_0,\mathrm{⟂},F)$ be an extended $PDA$.

Construct $PDA$, $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ where $Q$ and $\delta$ are to be defined as follows.

For every $(q,a,s)\in Q_E\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$, we define $\delta (q,a,s)$ as follows.

If $\widehat{\delta }\left(q,a,s\right)=\varnothing$, $\delta \left(q,a,s\right)=\varnothing$.

If $\widehat{\delta }\left(q,a,s\right)\ne \varnothing$, $\exists$ at least one $(r,u)\in \widehat{\delta }\left(q,a,s\right)$.

Let ${\delta }_1\left(q,a,s\right)=\left\{\right(r,ϵ\left)\right|(r,ϵ)\in \widehat{\delta }\left(q,a,s\right)\}$.

$\forall (r,u)\in \widehat{\delta }\left(q,a,s\right)$ where $(r,u)\in Q_E\times {\mathsf{\Gamma }}^{\mathrm{*}}$ and $u\ne ϵ$, $\exists u_1,u_2\dots u_l\in \mathsf{\Gamma }$, $l\ge 1$ such that $u=u_1{u}_2\dots u_l$.

(Note that none of $u_1,u_2\dots u_l$ is $ϵ$.)

Create new states $q_1,q_2,\dots q_{l-1}$ that satisfy the following conditions:

$q\stackrel{a,s⟶u_l,\delta }{\to }{q}_1$ (by making ${(q}_1,u_l)\in \delta \left(q,a,s\right)$)

$q_1\stackrel{ϵ,ϵ⟶u_{l-1},\delta }{\to }{q}_2$ (by making $\delta \left(q_1,ϵ,ϵ\right)=\{q_2,u_{l-1}\}$)

$q_2\stackrel{ϵ,ϵ⟶u_{l-2},\delta }{\to }{q}_3$ (by making $\delta \left(q_2,ϵ,ϵ\right)=\{q_3,u_{l-2}\}$)

$⋮$

$q_{l-1}\stackrel{ϵ,ϵ⟶u_1,\delta }{\to }r$ (by making $\delta \left(q_{l-1},ϵ,ϵ\right)=\{r,u_1\}$)

Note that the states $q_1,q_2,\dots q_{l-1}$ thus created are not in $Q_E$ and that

$\delta \left(q_i,a,s\right)=\mathrm{\varnothing }$ for any other combinations of $\left(a,s\right)\ne \left(ϵ,ϵ\right)$ and $i\in \{\mathrm{1,2},\dots l-1\}$.

Note also that there can be more than one set of states $q_1,q_2,\dots q_{l-1}$ and stack symbols $u_1,u_2\dots u_l$ to be created from each combination of $\left(q,a,s\right)$ because there can be more than one $(r,u)\in \widehat{\delta }\left(q,a,s\right)$ based on which the states and the stack symbols are created.

Let ${\delta }_2\left(q,a,s\right)=\bigcup _{(r,u)\in \widehat{\delta }\left(q,a,s\right)}\left\{\left(q_1,u_l\right)\right\}$ where $u=u_1{u}_2\dots u_l$, $l\ge 1$, $u_i\in \mathsf{\Gamma }$ and

$q_1$ is created from (ii) above.

Let $\delta \left(q,a,s\right)={\delta }_1\left(q,a,s\right)\cup {\delta }_2\left(q,a,s\right)$.

For each $\left(q,a,s,r,u\right)\in Q_E\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}\times Q_E\times {\mathsf{\Gamma }}^{\mathrm{*}}$, where $(r,u)\in \widehat{\delta }\left(q,a,s\right)$ and $u\ne ϵ$, define

$Q\left(q,a,s,r,u\right)=\left\{q_i\right|1\le i\le l-1;l \& q_i are created from \left(ii\right);(r,u)\in \widehat{\delta }\left(q,a,s\right);u\ne ϵ\}$(Note that $q_i\in Q\left(q,a,s,r,u\right)⟹q_i\notin Q_E$.)

Let $P\left(q,a,s\right)=\bigcup _{\left(r,u\right)\in \widehat{\delta }\left(q,a,s\right);u\ne ϵ}Q\left(q,a,s,r,u\right)$Set $Q=Q_E\cup \left({\bigcup }_{(q,a,s)\in Q_E\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}}P\left(q,a,s\right)\right)$.

So, $M=\left(Q_E\cup \left({\bigcup }_{(q,a,s)\in Q_E\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}}P\left(q,a,s\right)\right),\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,\mathrm{⟂},F\right)$.

The construction is now complete and it remains to show that $L\left(M_E\right)=L\left(M\right)$.

Suppose $w\in L\left(M\right)$.

$\exists w_1,w_2\dots w_n\in {\mathsf{\Sigma }}_{ϵ}$ such that $w=w_1,w_2\dots w_n$ where $n\ge 1$.

$\exists r_0,r_1\dots r_n\in Q$, $a_i,b_i\in {\mathsf{\Gamma }}_{ϵ}$ such that

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\delta }{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\delta }{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\delta }{\to }{r}_n,r_n\in F$.

Claim: 

$\forall 0\le i\le n-1,$

if $r_i\in Q_E$, then

$\exists j$ and $u\in {\mathsf{\Gamma }}^{\mathrm{*}}$ such that $i<j\le n$, $r_i\stackrel{w_{i+1},a_i⟶u,\widehat{\delta }}{\to }{r}_j$ and $w_k=ϵ$ for $i+2\le k\le j$.

Proof of Claim. 

From $r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}$ in the given computation, it follows that $(r_{i+1},b_{i,})\in \delta \left(r_i,w_{i+1},a_i\right)$.

By assumption, $r_i\in Q_E$.

By construction (ii), $\delta \left(r_i,w_{i+1},a_i\right)={\delta }_1\left(r_i,w_{i+1},a_i\right)\cup {\delta }_2\left(r_i,w_{i+1},a_i\right)$.

Either $(r_{i+1},b_{i,})\in {\delta }_1\left(r_i,w_{i+1},a_i\right)$ or $(r_{i+1},b_{i,})\in {\delta }_2\left(r_i,w_{i+1},a_i\right)$.

If $(r_{i+1},b_{i,})\in {\delta }_1\left(r_i,w_{i+1},a_i\right)$Since ${\delta }_1\left(r_i,w_{i+1},a_i\right)=\left\{\right(r,ϵ\left)\right|(r,ϵ)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)\}$, $b_{i,}=ϵ$ and

$(r_{i+1},ϵ)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$.

Therefore, $r_i\stackrel{w_{i+1},a_i⟶ϵ,\widehat{\delta }}{\to }{r}_{i+1}$.

Since $i<i+1\le n$ and $ϵ\in {\mathsf{\Gamma }}^{*}$, Claim is proved by taking $j=i+1$ and $u=ϵ$.

If $(r_{i+1},b_{i,})\in {\delta }_2\left(r_i,w_{i+1},a_i\right)$Since ${\delta }_2\left(r_i,w_{i+1},a_i\right)=\bigcup _{(r,u)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)}\left\{\left(q_1,u_l\right)\right\}$, $\left(r_{i+1},b_{i,}\right)=(q_1,u_l)$ for some $(r,u)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$ where $u=u_1{u}_2\dots u_l$, $l\ge 1$, $u_i\in \mathsf{\Gamma }$ and $q_1$ is created from construction (ii) above.

Therefore $r_{i+1}=q_1$ and $b_{i,}=u_l$.

$r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}$ now becomes $r_i\stackrel{w_{i+1},a_i⟶u_l,\delta }{\to }{r}_{i+1}$.

Furthermore, from $r_{i+1}\stackrel{w_{i+2},a_{i+1}⟶b_{i+1,}\delta }{\to }{r}_{i+2}$ in the given computation, we have

$\left(r_{i+2},b_{i+1}\right)\in \delta \left(r_{i+1},w_{i+2},a_{i+1}\right)=\delta \left(q_1,w_{i+2},a_{i+1}\right)$.

Since $\delta \left(q_1,a,s\right)=\mathrm{\varnothing }$ for all ($a,s$) $\ne$ ($ϵ,ϵ$), we must have $w_{i+2}=a_{i+1}=ϵ$.

Therefore, $\left(r_{i+2},b_{i+1}\right)\in \delta \left(q_1,ϵ,ϵ\right)=\left\{\left(q_2,u_{l-1}\right)\right\}$.

Therefore, $r_{i+2}=q_2$ and $b_{i+1}=u_{l-1}$.

$r_{i+1}\stackrel{w_{i+2},a_{i+1}⟶b_{i+1,}\delta }{\to }{r}_{i+2}$ becomes $r_{i+1}\stackrel{ϵ,ϵ⟶u_{l-1},\delta }{\to }{r}_{i+2}$.

By repeating the above argument, we can obtain the following computation:

$r_i\stackrel{w_{i+1},a_i⟶u_l,\delta }{\to }{r}_{i+1}\stackrel{ϵ,ϵ⟶u_{l-1},\delta }{\to }{r}_{i+2}\stackrel{ϵ,ϵ⟶u_{l-2},\delta }{\to }{r}_{i+3}\dots r_{i+l-1}\stackrel{ϵ,ϵ⟶u_1,\delta }{\to }{r}_{i+l}$.

where $r_{i+1}=q_1$, $r_{i+2}=q_2$, $\dots$ $r_{i+l-1}=q_{l-1}$, $r_{i+l}=r$ and $w_{i+2}=w_{i+3}\dots =w_{i+l}=ϵ$.

Let $j=i+l$.

$r_j=r_{i+1}=r$ and $r\in Q_E⟹r_j\in Q_E$.

Also, $w_{i+2}=w_{i+3}\dots =w_j=ϵ$.

$\left(r,u\right)=(r_j,u)$.

Since $(r,u)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$, $(r_j,u)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$.

Therefore, $r_i\stackrel{w_{i+1},a_i⟶u,\widehat{\delta }}{\to }{r}_j$.

$l\ge 1⟹i+l>i⟹j>i$.

Assume for contradiction that $j>n$.

$i<n\le j-1$.

$i<n\le i+l-1$.

Therefore $r_n\in \left\{r_{i+1},r_{i+2},r_{i+3}\dots r_{i+l-1}\right\}=\{q_1,q_2,q_3,\dots q_{l-1}\}$.

This implies $r_n\notin Q_E$, which is a contradiction because $r_n\in F$ and $F\subset Q_E$.

Therefore, $i<j\le n$.

Claim is also true under condition (b).

Combining (a) and (b), we conclude the proof of Claim.

Since $r_0=q_0\in Q_E$, we can apply Claim on $r_0$ to obtain $j_0$ such that

$0<j_0\le n$; $w_2=w_3=\dots =w_{j_0}=ϵ$; $r_0\stackrel{w_1,a_0⟶u_0,\widehat{\delta }}{\to }{r}_{j_0}$ with $r_{j_0}$ also in $Q_E$ and $u_0\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Since $r_{j_0}\in Q_E$, we can again apply Claim on $r_{j_0}$ to get $r_{j_1}$ such that

$0<j_0<j_1\le n$; $w_{j_0+2}=w_{j_0+3}\dots =w_{j_1}=ϵ$; $r_{j_0}\stackrel{w_{j_0+1},a_{j_0}⟶u_{j_0},\widehat{\delta }}{\to }{r}_{j_1}$ with $r_{j_1}$ also in $Q_E$ & $u_{j_0}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

By repeating this process a number of times, we will obtain $0<j_0<j_1<\dots <j_{m-1}<j_m\le n$ such that

$r_0\stackrel{w_1,a_0⟶u_0,\widehat{\delta }}{\to }{r}_{j_0}\stackrel{w_{j_0+1},a_{j_0}⟶u_{j_0},\widehat{\delta }}{\to }{r}_{j_1}\dots \dots r_{j_{m-1}}\stackrel{w_{j_{m-1}+1},a_{j_{m-1}}⟶u_{j_{m-1}},\widehat{\delta }}{\to }{r}_{j_m}$, where $u_0,u_{j_0}\dots u_{j_{m-1}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Since $n$ is finite, this process of creation must stop at some point and at this point, $j_m=n$.

Therefore, $M_E$ accepts $w_1{w}_{j_0+1}{w}_{j_1+1}\dots w_{j_{m-1}+1}$.

By Claim, we have

$w_2=w_3=\dots =w_{j_0}=ϵ$

$w_{j_0+2}=w_{j_0+3}\dots =w_{j_1}=ϵ$

$⋮$

$w_{j_{m-1}+2}=w_{j_{m-1}+3}\dots =w_{j_m}=ϵ$ where $j_m=n$.

Therefore, $w_1{w}_{j_0+1}{w}_{j_1+1}\dots w_{j_{m-1}+1}=w_1{w}_2\dots w_n=w$.

Therefore, $M_E$ accepts $w_1,w_2\dots w_n=w$.

Therefore, $w\in L\left(M_E\right)$ and hence $L\left(M\right)\subset L\left(M_E\right)$.

Conversely, assume $w\in L\left(M_E\right)$.

$\exists r_0,r_1\dots r_n\in Q_E;$ $a_i\in {\mathsf{\Gamma }}_{ϵ}$, $b_i\in {\mathsf{\Gamma }}^{\mathrm{*}}$ for $0\le i\le n-1$; $w_1,w_2\dots w_n\in {\mathsf{\Sigma }}_{ϵ}$ such that

${w=w}_1{w}_2\dots w_n$ and

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\widehat{\delta }}{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\widehat{\delta }}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\widehat{\delta }}{\to }{r}_n,r_n\in F$.

Since $Q_E\subset Q$, $r_0,r_1\dots r_n\in Q$.

For all $0\le i\le n-1$, $(r_{i+1},b_i)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)⟹\widehat{\delta }\left(r_i,w_{i+1},a_i\right)\ne \mathrm{\varnothing }$.

[If $b_i=ϵ$]

$(r_{i+1},ϵ)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$By construction (ii), ${\delta }_1\left(r_i,w_{i+1},a_i\right)=\left\{\right(r,ϵ\left)\right|(r,ϵ)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)\}$.

Therefore, $(r_{i+1},ϵ)\in {\delta }_1\left(r_i,w_{i+1},a_i\right)$.

Also by construction (ii), $\delta \left(r_i,w_{i+1},a_i\right)={\delta }_1\left(r_i,w_{i+1},a_i\right)\cup {\delta }_2\left(r_i,w_{i+1},a_i\right)$.

Therefore, $(r_{i+1},ϵ)\in \delta \left(r_i,w_{i+1},a_i\right)$.

Therefore, $r_i\stackrel{w_{i+1},a_i⟶ϵ,\delta }{\to }{r}_{i+1}$.

Therefore, $r_i\stackrel{w_{i+1},\mathrm{*},\delta }{\to }{r}_{i+1}$.

[If $b_i\ne ϵ$]

$\exists b_i\left(1\right),b_i\left(2\right)\dots b_i\left(l\right)\in \mathsf{\Gamma }$, $l\ge 1$ such that $b_i=b_i\left(1\right)b_i\left(2\right)\dots b_i\left(l\right)$.

By construction (ii), $\exists q_1,q_2,\dots q_{l-1}\in Q$ such that

$r_i\stackrel{w_{i+1},a_i⟶b_i\left(l\right),\delta }{\to }{q}_1$

$q_1\stackrel{ϵ,ϵ⟶b_i(l-1),\delta }{\to }{q}_2$

$q_2\stackrel{ϵ,ϵ⟶b_i(l-2),\delta }{\to }{q}_3$

$⋮$

$q_{l-1}\stackrel{ϵ,ϵ⟶b_i\left(1\right),\delta }{\to }{r}_{i+1}$.

Therefore, $r_i\stackrel{w_{i+1},\mathrm{*},\delta }{\to }{r}_{i+1}$.

Combining both cases of [$b_i=ϵ$] and [$b_i\ne ϵ$], we have

$r_i\stackrel{w_{i+1},\mathrm{*},\delta }{\to }{r}_{i+1}$ for all $0\le i\le n-1$.

Therefore,

$q_0=r_0\stackrel{w_1,\mathrm{*},\delta }{\to }{r}_1\stackrel{w_2,\mathrm{*},\delta }{\to }{r}_2\dots r_i\stackrel{w_{i+1},\mathrm{*}\delta }{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,\mathrm{*}\delta }{\to }{r}_n,r_n\in F$.

Therefore, $M$ accepts $w_1{w}_2\dots w_n=w$.

$w\in L\left(M\right)$.

$L\left(M_E\right)\subset L\left(M\right)$.

This completes the proof of $L\left(M_E\right)=L\left(M\right)$ for the construction of $M$ from $M_E$.

Construction of $M_E$ from $M$.

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,\mathrm{⟂},F)$ be a $PDA$.

Construct $M_E=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\widehat{\delta },q_0,\mathrm{⟂},F)$ where

$\widehat{\delta }:Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}⟶\mathrm{\wp }(Q\times {\mathsf{\Gamma }}^{\mathrm{*}})$ such that

$\forall \left(q,a,s\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ},\widehat{\delta }\left(q,a,s\right)=\delta (q,a,s)$.

(Note that this is possible because ${\mathsf{\Gamma }}_{ϵ}\subset {\mathsf{\Gamma }}^{*}$.)

It remains to show that $L\left(M_E\right)=L\left(M\right)$.

Let $w=w_1{w}_2\dots w_n$ where $w_i\in {\mathsf{\Sigma }}_{ϵ}$ for $1\le i\le n$ & $n\ge 1$.

Suppose $w\in L\left(M\right)$.

$\exists r_0,r_1\dots r_n\in Q$, $a_i\in {\mathsf{\Gamma }}_{ϵ}$, $b_i\in {\mathsf{\Gamma }}_{ϵ}$ for $0\le i\le n-1$ such that

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\delta }{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\delta }{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\delta }{\to }{r}_n,r_n\in F$.

For $0\le i\le n-1$,

since $r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}$, $(r_{i+1},b_i)\in \delta \left(r_i,w_{i+1},a_i\right)$.

since $\widehat{\delta }\left(r_i,w_{i+1},a_i\right)=\delta (r_i,w_{i+1},a_i)$, $(r_{i+1},b_i)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$.

Therefore, $r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}$ for $0\le i\le n-1$.

Therefore,

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\widehat{\delta }}{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\widehat{\delta }}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\widehat{\delta }}{\to }{r}_n,r_n\in F$.

$M_E$ accepts $w$.

$w\in L\left(M_E\right)$.

$L\left(M\right)\subset L\left(M_E\right)$.

Conversely, suppose $w\in L\left(M_E\right)$.

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\widehat{\delta }}{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\widehat{\delta }}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\widehat{\delta }}{\to }{r}_n,r_n\in F$,

where $a_i\in {\mathsf{\Gamma }}_{ϵ}$, $b_i\in {\mathsf{\Gamma }}^{\mathrm{*}}$ for $0\le i\le n-1$.

For $0\le i\le n-1$, $r_i\stackrel{w_{i+1},a_i⟶b_{i,}\widehat{\delta }}{\to }{r}_{i+1}⟹(r_{i+1},b_i)\in \widehat{\delta }\left(r_i,w_{i+1},a_i\right)$.

Since $\widehat{\delta }\left(r_i,w_{i+1},a_i\right)=\delta (r_i,w_{i+1},a_i)$, $(r_{i+1},b_i)\in \delta \left(r_i,w_{i+1},a_i\right)$.

Therefore, $r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}$ for $0\le i\le n-1$.

Therefore,

$q_0=r_0\stackrel{w_1,a_0⟶b_0,\delta }{\to }{r}_1\stackrel{w_2,a_1⟶b_1,\delta }{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_{i,}\delta }{\to }{r}_{i+1}\dots r_{n-1}\stackrel{w_n,a_{n-1}⟶b_{n-1,}\delta }{\to }{r}_n,r_n\in F$.

Therefore $M$ accepts $w$ and hence $w\in L\left(M\right)$.

Therefore, $L\left(M_E\right)\subset L\left(M\right)$.

This completes the proof of $L\left(M_E\right)=L\left(M\right)$ for the construction of $M_E$ from $M$.

Combining (A) and (B), we conclude the proof of Theorem 2.45.

Now that we have proved the equivalence of $PDA$ and extended $PDA$, we shall no longer distinguish between $M$ and $M_E$ or between $\delta$ and $\widehat{\delta }$. From here on, we shall be using extended $PDA$ exclusively because it is a much more convenient tool for solving problems. We shall be using $M$ and $\delta$ for all $PDA$s with the understanding that the $PDA$s that we are dealing with can write a string to the stack in one single step.

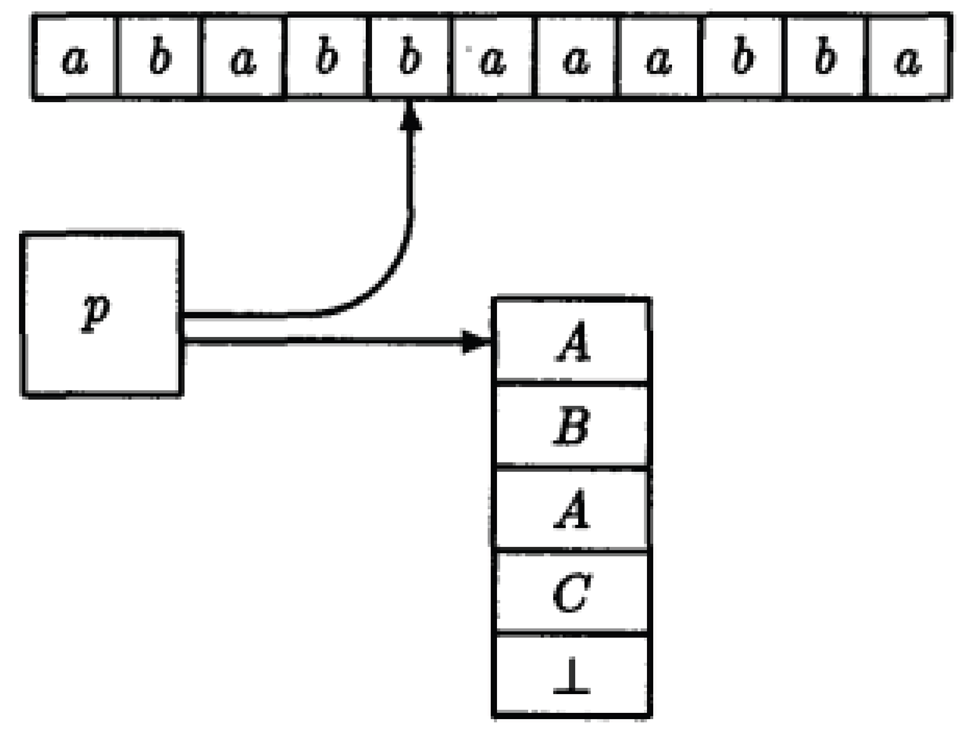
Definition 2.46 (Configurations of a$\mathit{P}\mathit{D}\mathit{A}$). A configuration of a $PDA, M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ is an element of $Q\times {\mathsf{\Sigma }}^{*}\times {\mathsf{\Gamma }}^{*}$ describing the current state, the portion of the input still unread and the current stack contents at some point of a computation. For example, the configuration

$(p,baaabba,ABAC⟂)$ describes the situation as shown in the following diagram.

Note that the portion of the input to the left of the input head, namely $abab$, has been read and cannot affect the computation hereon.

The start configuration on input $w$ is defined as $(q_0,w,⟂)$. That is, the $PDA$ always starts in its start state $q_0$, with the input head pointing to the leftmost input symbol and the stack containing only the start stack symbol $⟂$.

The next-configuration relation (denoted by $\stackrel{1,M}{\to }$ or simply $\stackrel{M}{\to }$ ) describes how the $PDA$ moves from one configuration to another in one step. It is formally defined as follows.

Definition 2.47. Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ be a $PDA$.

$\forall p,q\in Q,a\in {\mathsf{\Sigma }}_{ϵ},A\in {\mathsf{\Gamma }}_{ϵ},y\in {\mathsf{\Sigma }}^{\mathrm{*}},\beta \in {\mathsf{\Gamma }}^{\mathrm{*}},\gamma \in {\mathsf{\Gamma }}^{\mathrm{*}}$,

$\left(p\stackrel{a,A⟶\gamma ,\delta }{\to }q\right)\stackrel{def}{\iff }\left(\left(p,ay,A\beta \right)\stackrel{1,M}{\to }(q,y,\gamma \beta )\right)$.

For any configurations $C$, $D$ of $M$,

$\left(C\stackrel{0,M}{\to }D\right)\stackrel{def}{\iff }\left(C=D\right)$.

$\left(C\stackrel{n+1,M}{\to }D\right)\stackrel{def}{\iff }\left(\exists EC\stackrel{n,M}{\to }E\&E\stackrel{1,M}{\to }D\right)$.

$\left(C\stackrel{\mathrm{*},M}{\to }D\right)\stackrel{def}{\iff }\left(\exists n\ge 0C\stackrel{n,M}{\to }D\right)$.

Proposition 2.48. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ be a $PDA$.

For any $w=w_1{w}_2\dots w_m$ where $w_1,w_2\dots w_m\in {\mathsf{\Sigma }}_{ϵ}$, $M$ accepts $w$ iff $\left(q_0,w,\mathrm{⟂}\right)\stackrel{\mathrm{*},M}{\to }(q,ϵ,\gamma )$ for some $q\in F$ and $\gamma \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Proof. 

By Definition 2.44, $M$ accepts $w=w_1{w}_2\dots w_m$ iff $\exists r_0, r_1\dots r_m\in Q$, $a_i\in {\mathsf{\Gamma }}_{ϵ}$, $b_i\in {\mathsf{\Gamma }}^{*}$ for $0\le i\le m-1$ such that

$q_0=r_0\stackrel{w_1,a_0⟶b_0}{\to }{r}_1\stackrel{w_2,a_1⟶b_1}{\to }{r}_2\dots r_i\stackrel{w_{i+1},a_i⟶b_i}{\to }{r}_{i+1}\dots r_{m-1}\stackrel{w_m,a_{m-1}⟶b_{m-1}}{\to }{r}_m,r_m\in F$.

By Definition 2.47, each one-step transitional movement is equivalent to one step of configuration movement.

For all $0\le i\le m-1$, $\exists$ configurations $C_i$ and $C_{i+1}$ such that

$\left(r_i\stackrel{w_{i+1},a_i⟶b_i}{\to }{r}_{i+1}\right)⟺\left(C_i\stackrel{1,M}{\to }{C}_{i+1}\right)$The above transitional computation is equivalent to

$C_0\stackrel{1,M}{\to }{C}_1\stackrel{1,M}{\to }{C}_2\dots C_i\stackrel{1,M}{\to }{C}_{i+1}\dots C_{m-1}\stackrel{1,M}{\to }{C}_m$, $r_m\in F$.

That is, $C_0\stackrel{n,M}{\to }{C}_m$, $r_m\in F$.

That is, $C_0\stackrel{\mathrm{*},M}{\to }{C}_m$, $r_m\in F$.

Since $C_0=(q_0,w,⟂)$ and $C_m=(r_m,ϵ,\gamma )$ where $\gamma \in {\mathsf{\Gamma }}^{*}$ is the final stack content, we have

$(q_0,w,\mathrm{⟂})\stackrel{\mathrm{*},M}{\to }(r_m,ϵ,\gamma )$, $r_m\in F$.

Therefore, $\left(q_0,w,\mathrm{⟂}\right)\stackrel{\mathrm{*},M}{\to }(q,ϵ,\gamma )$ for some $q\in F$ and $\gamma \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

This completes the proof of Proposition 2.48.

Proposition 2.49. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ and $M^{\text{'}}=(Q^{\text{'}},\mathsf{\Sigma },{\mathsf{\Gamma }}^{\mathrm{\text{'}}},{\delta }^{\text{'}},q_0^{\text{'}},{⟂}^{\text{'}},F^{\text{'}})$ be two $PDA$s such that

$Q\subset Q^{\text{'}}$, $\mathsf{\Gamma }\subset {\mathsf{\Gamma }}^{\mathrm{\text{'}}}$ and

${\delta }^{\mathrm{\text{'}}}\left(q,a,A\right)=\delta \left(q,a,A\right)\forall \left(q,a,A\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$.

$\forall p,q\in Q$, $u,v\in {\mathsf{\Sigma }}^{*}$ and $\alpha ,\beta \in {\mathsf{\Gamma }}^{*}$, the following statements hold:

(a) $\left[\left(p,u,\alpha \right)\stackrel{1,M}{\to }\left(q,v,\beta \right)\right]⟺\left[\left(p,u,\alpha \right)\stackrel{1,M^{\text{'}}}{\to }\left(q,v,\beta \right)\right]$

(b) $\left[\left(p,u,\alpha \right)\stackrel{n,M}{\to }\left(q,v,\beta \right)\right]⟺\left[\left(p,u,\alpha \right)\stackrel{n,M^{\text{'}}}{\to }\left(q,v,\beta \right)\right]$ for any $n\ge 0$

Proof.

(a)

$\left(p,u,\alpha \right)\stackrel{1,M}{\to }\left(q,v,\beta \right)⟺p\stackrel{a,A⟶\gamma ,\delta }{\to }q$ where $u=av$, $a\in {\mathsf{\Sigma }}_{ϵ}$, $\alpha =A\eta$, $\beta =\gamma \eta$, $A\in {\mathsf{\Gamma }}_{ϵ}$, $\gamma ,\eta \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Since $Q\subset Q^{\mathrm{\text{'}}}$, $p,q\in Q⟹p,q\in Q^{\mathrm{\text{'}}}$.

Since $\mathsf{\Gamma }\subset {\mathsf{\Gamma }}^{\mathrm{\text{'}}}$, $A\in {\mathsf{\Gamma }}_{ϵ}⟹A\in {\mathsf{\Gamma }}_{ϵ}^{\mathrm{\text{'}}}$.

Since $\mathsf{\Gamma }\subset {\mathsf{\Gamma }}^{\mathrm{\text{'}}}$, ${\mathsf{\Gamma }}^{*}\subset {\left({\mathsf{\Gamma }}^{\mathrm{\text{'}}}\right)}^{*}$ and hence $\gamma \in {\mathsf{\Gamma }}^{*}⟹\gamma \in {\left({\mathsf{\Gamma }}^{\mathrm{\text{'}}}\right)}^{*}$.

Since ${\delta }^{\mathrm{\text{'}}}\left(p,a,A\right)=\delta \left(p,a,A\right)$ for all $\left(p,a,A\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$, we have

$p\stackrel{a,A⟶\gamma ,\delta }{\to }q⟹p\stackrel{a,A⟶\gamma ,{\delta }^{\mathrm{\text{'}}}}{\to }q$

$⟹\left(p,av,A\eta ,\right)\stackrel{1,M^{\mathrm{\text{'}}}}{\to }\left(q,v,\gamma \eta \right)$

$⟹\left(p,u,\alpha \right)\stackrel{1,M^{\mathrm{\text{'}}}}{\to }\left(q,v,\beta \right)$Conversely,

$\left(p,u,\alpha \right)\stackrel{1,M^{\mathrm{\text{'}}}}{\to }\left(q,v,\beta \right)$ where $p,q\in Q$, $u,v\in {\mathsf{\Sigma }}^{\mathrm{*}}$ and $\alpha ,\beta \in {\mathsf{\Gamma }}^{\mathrm{*}}$

$⟺p\stackrel{a,A⟶\gamma ,{\delta }^{\mathrm{\text{'}}}}{\to }q$ where $p,q\in Q$, $u,v\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $\alpha ,\beta \in {\mathsf{\Gamma }}^{\mathrm{*}}$, $a\in {\mathsf{\Sigma }}_{ϵ}$, $A\in {\mathsf{\Gamma }}_{ϵ}^{\mathrm{\text{'}}}$, $\gamma \in {\left({\mathsf{\Gamma }}^{\mathrm{\text{'}}}\right)}^{\mathrm{*}}$, $\alpha =A\eta$, $\beta =\gamma \eta$.

Since $\alpha \in {\mathsf{\Gamma }}^{\mathrm{*}}$ & $\alpha =A\eta$, $A\in {\mathsf{\Gamma }}_{ϵ}$ and $\eta \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Since $\beta \in {\mathsf{\Gamma }}^{\mathrm{*}}$ & $\beta =\gamma \eta$, $\gamma \in {\mathsf{\Gamma }}^{\mathrm{*}}$ and $\eta \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Therefore $\left(p,a,A\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$ and hence ${\delta }^{\mathrm{\text{'}}}\left(p,a,A\right)=\delta \left(p,a,A\right)$.

Therefore,

$p\stackrel{a,A⟶\gamma ,{\delta }^{\mathrm{\text{'}}}}{\to }q⟹p\stackrel{a,A⟶\gamma ,\delta }{\to }q⟹\left(p,u,\alpha \right)\stackrel{1,M}{\to }\left(q,v,\beta \right)$.

(b)

This part can be proved by using the result of (a) along with an induction argument on the number of steps.

This completes the proof of Proposition 2.49.

Proposition 2.50. 

Let $M=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,⟂,F)$ be a $PDA$. It is true that $\forall p,q\in Q,x,y,w\in {\mathsf{\Sigma }}^{*},\alpha ,\beta ,\gamma \in {\mathsf{\Gamma }}^{*},$integer $n\ge 1$,

$\left(\left(p,x,\alpha \right)\stackrel{n,M}{\to }(q,y,\beta )\right)⟹\left(\left(p,xw,\alpha \gamma \right)\stackrel{n,M}{\to }(q,yw,\beta \gamma )\right)$

Proof. 

The proof is by induction on $n$.

For $n=1$, assume $\left(p,x,\alpha \right)\stackrel{1,M}{\to }(q,y,\beta )$.

$\exists a\in {\mathsf{\Sigma }}_{ϵ}$, $A\in {\mathsf{\Gamma }}_{ϵ}$ and $\eta ,\theta \in {\mathsf{\Gamma }}^{\mathrm{*}}$ such that

$x=ay$, $\alpha =A\eta$, $\beta =\theta \eta$ and $p\stackrel{a,A⟶\theta ,\delta }{\to }q$.

Since $p\stackrel{a,A⟶\theta ,\delta }{\to }q$, and $xw=ayw$, $\alpha \gamma =A\eta \gamma$, and $\beta \gamma =\theta \eta \gamma$,

$\left(p,xw,\alpha \gamma \right)\stackrel{1,M}{\to }(q,yw,\beta \gamma )$.

Therefore, the statement is true for $n=1$.

For induction hypothesis,

$\left(\left(p,x,\alpha \right)\stackrel{k,M}{\to }(q,y,\beta )\right)⟹\left(\left(p,xw,\alpha \gamma \right)\stackrel{k,M}{\to }(q,yw,\beta \gamma )\right)$ for any integer $k\ge 1$.

For $n=k+1$, assume $\left(p,x,\alpha \right)\stackrel{k+1,M}{\to }(q,y,\beta )$.

$\exists p^{\mathrm{\text{'}}}\in Q,$ $x^{\mathrm{\text{'}}}\in {\mathsf{\Sigma }}^{\mathrm{*}}$, ${\alpha }^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$ such that

$\left(p,x,\alpha \right)\stackrel{k,M}{\to }(p^{\mathrm{\text{'}}},x^{\mathrm{\text{'}}},{\alpha }^{\mathrm{\text{'}}})$ and $(p^{\mathrm{\text{'}}},x^{\mathrm{\text{'}}},{\alpha }^{\mathrm{\text{'}}})\stackrel{1,M}{\to }(q,y,\beta )$.

By induction hypothesis, we have

$\left(p,xw,\alpha \gamma \right)\stackrel{k,M}{\to }(p^{\mathrm{\text{'}}},x^{\mathrm{\text{'}}}w,{\alpha }^{\mathrm{\text{'}}}\gamma )$.

Since the statement is true for $n=1$, we also have

$(p^{\mathrm{\text{'}}},x^{\mathrm{\text{'}}}w,{\alpha }^{\mathrm{\text{'}}}\gamma )\stackrel{1,M}{\to }(q,yw,\beta \gamma )$.

Combining the two computations, we have

$\left(p,xw,\alpha \gamma \right)\stackrel{k+1,M}{\to }(q,yw,\beta \gamma )$.

This completes the proof of Proposition 2.50.

The $PDA$s that we have dealt with thus far accept an input by entering an accept state upon reading the entire input. We call this kind of $PDA$ a $PDA$ that accepts by final state. There is another kind of $PDA$ that accepts an input by popping the last symbol off the stack (without pushing any other symbol back on) upon reading the entire input. We call this kind of $PDA$ a $PDA$ that accepts by empty stack. It turns out that the two kinds of $PDA$s are equivalent in that given one, we can construct the other such that the two recognize the same language. Before we prove the equivalence of these two kinds of $PDA$s, we need a formal definition for $PDA$s that accept by empty stack.

Definition 2.51. 

A $PDA$ that accepts by empty stack is a 6-tuple, $M_e=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,{⟂}_e)$ where $Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,{⟂}_e$ are defined similarly as in a $PDA$ that accepts by final state.

$M_e$ computes as follows:

Let $w=w_1{w}_2\dots w_m$ where $w_i\in {\mathsf{\Sigma }}_{ϵ}$ for $1\le i\le m$ & $m\ge 1$.

$M_e$ accepts $w$ iff $\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{\mathrm{*},M_e}{\to }(q,ϵ,ϵ)$ for any $q\in Q$.

(Note that the set of accept states, namely $F$, is not needed in the definition of acceptance by empty state.)

Lemma 2.52. For any $PDA$, $M_e$, that accepts by empty stack, there is a $PDA$, $M_f$, that accepts by final state such that $L\left(M_e\right)=L\left(M_f\right)$.

Proof. 

Let $M_e=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,{⟂}_e)$ where ${⟂}_e\in \mathsf{\Gamma }$ is the initial stack symbol of $M_e$.

Construct $M_f=\left(Q_f,\mathsf{\Sigma },{\mathsf{\Gamma }}_f,{\delta }_f,q_{start},{\mathrm{⟂}}_f,\left\{q_{accept}\right\}\right)$ where $q_{start}$ and $q_{accept}$ are newly created states (not in $Q$) with $q_{start}$ serving as the start state of $M_f$ and $\left\{q_{accept}\right\}$ serving as the set of accept states of $M_f$.

${⟂}_f$ is a newly created stack symbol (not in $\mathsf{\Gamma }$) serving as the initial stack symbol of $M_f$.

$Q_f=Q\cup \{q_{start},q_{accept}\}$

${\mathsf{\Gamma }}_f=\mathsf{\Gamma }\cup \left\{{\mathrm{⟂}}_f\right\}$The transition function ${\delta }_f$ of $M_f$ is defined as follows.

T1: ${\delta }_f\left(q_{start},ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_0,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\right\}$ $\left(⟺q_{start}\stackrel{ϵ,{\mathrm{⟂}}_f⟶{\mathrm{⟂}}_e{\mathrm{⟂}}_f,{\delta }_f}{\to }{q}_0\right)$T2: ${\delta }_f\left(q,ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_{accept},ϵ\right)\right\}\forall q\in Q$ $\left(⟺q\stackrel{ϵ,{\mathrm{⟂}}_f⟶ϵ,{\delta }_f}{\to }{q}_{accept}\right)$T3: ${\delta }_f\left(q,a,A\right)=\delta (q,a,A)$ for any $\left(q,a,A\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$ where

$\delta :Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}⟶\mathrm{\wp }(Q\times {\mathsf{\Gamma }}^{\mathrm{*}})$.

T4: ${\delta }_f\left(q,a,A\right)=\mathrm{\varnothing }$ for any other $\left(q,a,A\right)\in Q_f\times {\mathsf{\Sigma }}_{ϵ}\times {\left({\mathsf{\Gamma }}_f\right)}_{ϵ}$.

The construction is now complete. It remains to show $L\left(M_e\right)=L\left(M_f\right)$.

Suppose $w\in L\left(M_e\right)$.

$\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{n,M_e}{\to }(q,ϵ,ϵ)$ for some $n\ge 0$ & $q\in Q$.

By T1, ${\delta }_f\left(q_{start},ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_0,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\right\}$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$.

By Proposition 2.49, we have

$\left\{\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{n,M_e}{\to }\left(q,ϵ,ϵ\right)\right\}⟺\left\{\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{n,M_f}{\to }\left(q,ϵ,ϵ\right)\right\}$.

By Proposition 2.50, we have

$\left\{\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{n,M_f}{\to }\left(q,ϵ,ϵ\right)\right\}⟹\left\{\left(q_0,wϵ,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\stackrel{n,M_f}{\to }\left(q,ϵϵ,ϵ{\mathrm{⟂}}_f\right)\right\}$.

That is, $\left\{\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{n,M_f}{\to }\left(q,ϵ,ϵ\right)\right\}⟹\left\{\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\stackrel{n,M_f}{\to }\left(q,ϵ,{\mathrm{⟂}}_f\right)\right\}$.

Also by T2, ${\delta }_f\left(q,ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_{accept},ϵ\right)\right\}$.

Therefore, $\left(q,ϵ,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_{accept},ϵ,ϵ\right)$.

Combining, we have

$\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\stackrel{n,M_f}{\to }\left(q,ϵ,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_{accept},ϵ,ϵ\right)$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{\mathrm{*},M_f}{\to }\left(q_{accept},ϵ,ϵ\right)$.

Therefore, $M_f$ accepts $w$.

$w\in L\left(M_f\right)$Therefore, $L\left(M_e\right)\subset L\left(M_f\right)$.

Conversely, assume $w\in L\left(M_f\right)$.

$\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{\mathrm{*},M_f}{\to }\left(q_{accept},ϵ,\gamma \right)$ for some $\gamma \in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Since there exists no transition in one step to go from $q_{start}$ to $q_{accept}$, there must exist configurations $(q_1,u_1,{\gamma }_1)$, $(q_2,u_2,{\gamma }_2)$, $\dots (q_i,u_i,{\gamma }_i)$, $\dots \left(q_n,u_n,{\gamma }_n\right)$ where $n\ge 1$, $u_i\in {\mathsf{\Sigma }}^{\mathrm{*}}$, ${\gamma }_i$ $\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$ for $1\le i\le n$, such that

$\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }(q_1,u_1,{\gamma }_1)\stackrel{1,M_f}{\to }\dots \stackrel{1,M_f}{\to }(q_i,u_i,{\gamma }_i)\stackrel{1,M_f}{\to }\dots \stackrel{1,M_f}{\to }\left(q_n,u_n,{\gamma }_n\right)\stackrel{1,M_f}{\to }$ $\left(q_{accept},ϵ,\gamma \right)$.

Note that $q_i\ne q_{start}$ because each $q_i$ has both incoming and outgoing arrows whereas $q_{start}$ has only outgoing arrows and $q_i\ne q_{accept}$ because $q_{accept}$ has only incoming arrows.

Therefore, for $1\le i\le n$, $q_i\in Q$.

Claim 1. $\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$.

${\delta }_f\left(q_{start},ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_0,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)\right\}$ by T1.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$.

Since $\left(q_{start},w,{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }(q_1,u_1,{\gamma }_1)$, and by T4, ${\delta }_f\left(q_{start},a,A\right)=\mathrm{\varnothing }$ for any other combination of $\left(a,A\right)\ne (ϵ,{\mathrm{⟂}}_f)$, we must have

$\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$.

Claim 2. For $1\le i\le n$, $\exists {\gamma }_i^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$ such that ${\gamma }_i={\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Claim 2 can be proved by induction on $i$.

For $i=1$,

$\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$ (By Claim 1)

Therefore, ${\gamma }_1={\mathrm{⟂}}_e{\mathrm{⟂}}_f$.

Take ${\gamma }_1^{\mathrm{\text{'}}}={\mathrm{⟂}}_e$.

${\gamma }_1={\gamma }_1^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

${\mathrm{⟂}}_e\in \mathsf{\Gamma }⟹{\mathrm{⟂}}_e\in {\mathsf{\Gamma }}^{\mathrm{*}}⟹{\gamma }_1^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

The statement is true for $i=1$.

For induction hypothesis ($i=k)$, assume ${\gamma }_k={\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$ for $1\le k\le n-1$, ${\gamma }_k^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Consider configuration move of

$\left(q_k,u_k,{\gamma }_k\right)\stackrel{1,M_f}{\to }\left(q_{k+1},u_{k+1},{\gamma }_{k+1}\right)$ which is equivalent to $q_k\stackrel{a,b⟶c,{\delta }_f}{\to }{q}_{k+1}$ where

$a\in {\mathsf{\Sigma }}_{ϵ}$, $b\in {\left({\mathsf{\Gamma }}_f\right)}_{ϵ}$, $c\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$, $u_k=a{u}_{k+1}$, ${\gamma }_k=b{\gamma }_k^{"}$, ${\gamma }_{k+1}=c{\gamma }_k^{"}$, ${\gamma }_k^{"}\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Since $1\le k<k+1\le n$, $q_k,q_{k+1}\in Q$.

This configuration move could not have come from T1 because $q_k\ne q_{start}$.

By induction hypothesis, ${\gamma }_k={\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$ & ${\gamma }_k^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

We examine two situations: (i) ${\gamma }_k^{\text{'}}=ϵ$ and (ii) ${\gamma }_k^{\text{'}}\ne ϵ$.

(i) If ${\gamma }_k^{\mathrm{\text{'}}}=ϵ$

${\gamma }_k={⟂}_f$

$b=ϵ$ or $b={\mathrm{⟂}}_f$.

If $b={\mathrm{⟂}}_f$, $q_k\stackrel{a,{\mathrm{⟂}}_f⟶c,{\delta }_f}{\to }{q}_{k+1}$.

This transition must have come from T2 where

${\delta }_f\left(q_k,ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_{accept},ϵ\right)\right\}$, $a=ϵ$, $c=ϵ$.

Therefore, $q_{k+1}=q_{accept}$, which contradicts $q_{k+1}\in Q$.

Therefore, $b=ϵ$.

Therefore, $\left(q_k,a,b\right)=\left(q_k,a,ϵ\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$.

By T3, ${\delta }_f\left(q_k,a,b\right)=\delta \left(q_k,a,b\right)$.

Therefore, $q_k\stackrel{a,ϵ⟶c,\delta }{\to }{q}_{k+1}$.

Therefore, $c\in {\mathsf{\Gamma }}^{*}$.

${\gamma }_k={\mathrm{⟂}}_f=b{\gamma }_k^{"}$.

Since $b=ϵ$, ${\gamma }_k^{"}={\mathrm{⟂}}_f$.

Therefore, ${\gamma }_{k+1}=c{\gamma }_k^{"}=c{\mathrm{⟂}}_f$.

The statement is true for $i=k+1$.

(ii) If ${\gamma }_k^{\mathrm{\text{'}}}\ne ϵ$Since ${\gamma }_k^{\text{'}}\in {\mathsf{\Gamma }}^{*}$, ${⟂}_f$ is not a symbol in ${\gamma }_k^{\text{'}}$.

Since ${\gamma }_k={\gamma }_k^{\text{'}}{⟂}_f$, the leftmost symbol of ${\gamma }_k$ cannot be ${⟂}_f$.

Therefore, the configuration move of $\left(q_k,u_k,{\gamma }_k\right)\stackrel{1,M_f}{\to }\left(q_{k+1},u_{k+1},{\gamma }_{k+1}\right)$ could not have come from T2.

Therefore, it must have come from T3 where $\delta ={\delta }_f$.

Therefore, $\left(q_k,u_k,{\gamma }_k\right)\stackrel{1,M_e}{\to }\left(q_{k+1},u_{k+1},{\gamma }_{k+1}\right)$ by Proposition 2.49.

Therefore, $q_k\stackrel{a,b⟶c,\delta }{\to }{q}_{k+1}$ where

$a\in {\mathsf{\Sigma }}_{ϵ}$, $b\in {\mathsf{\Gamma }}_{ϵ}$, $c\in {\mathsf{\Gamma }}^{\mathrm{*}}$, $u_k=a{u}_{k+1}$, ${\gamma }_k=b{\gamma }_k^{"}$, ${\gamma }_{k+1}=c{\gamma }_k^{"}$, ${\gamma }_k^{"}\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Note that $b\ne {⟂}_f$ because ${⟂}_f\notin {\mathsf{\Gamma }}_{ϵ}$.

By induction hypothesis, ${\gamma }_k={\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$ & ${\gamma }_k^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Therefore, ${{\gamma }_k=\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=b{\gamma }_k^{"}$.

${\gamma }_k^{"}=ϵ⟹{\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=b⟹{\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f\in {\mathsf{\Gamma }}_{ϵ}$, which is a contradiction because ${\mathrm{⟂}}_f\notin {\mathsf{\Gamma }}_{ϵ}$.

Therefore, ${\gamma }_k^{"}\ne ϵ$.

The rightmost symbol of ${\gamma }_k^{"}$ must be ${⟂}_f$.

$\exists {\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$ such that ${\gamma }_k^{"}={\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=b{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_k^{\mathrm{\text{'}}}=b{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}$.

Since ${\gamma }_k^{\text{'}}\in {\mathsf{\Gamma }}^{*}$ by induction hypothesis, ${\gamma }_k^{\text{'}\text{'}\text{'}}{\in \mathsf{\Gamma }}^{*}$.

${\gamma }_{k+1}=c{\gamma }_k^{"}=c{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_f={\gamma }_{k+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$ where ${\gamma }_{k+1}^{\mathrm{\text{'}}}=c{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}$.

Since $c\in {\mathsf{\Gamma }}^{\mathrm{*}}$ & ${\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$, ${\gamma }_{k+1}^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

The statement is also true for $i=k+1$.

Therefore, the statement is true for $i=k+1$ whether or not ${\gamma }_k^{\text{'}}=ϵ$.

This completes the proof of Claim 2.

Claim 3. 

$\left(q_n,u_n,{\gamma }_n\right)=\left(q_n,ϵ,{\mathrm{⟂}}_f\right)$.

We know from above that $\left(q_n,u_n,{\gamma }_n\right)\stackrel{1,M_f}{\to }$ $\left(q_{accept},ϵ,\gamma \right)$.

The only way to transition from a state in $Q$ to $q_{accept}$ is via T2 where

${\delta }_f\left(q_n,ϵ,{\mathrm{⟂}}_f\right)=\left\{\left(q_{accept},ϵ\right)\right\}$.

Equivalently, $q_n\stackrel{ϵ,{\mathrm{⟂}}_f⟶ϵ,{\delta }_f}{\to }{q}_{accept}$.

Therefore, $\left(q_n,u_n,{\gamma }_n\right)\stackrel{1,M_f}{\to }$ $\left(q_{accept},u_n,{\gamma }_n^{"}\right)$ where ${\gamma }_n={\mathrm{⟂}}_f{\gamma }_n^{"}$ & ${\gamma }_n^{"}\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Therefore, $\left(q_{accept},u_n,{\gamma }_n^{"}\right)=\left(q_{accept},ϵ,\gamma \right)$.

Therefore, $u_n=ϵ$ & $\gamma ={\gamma }_n^{"}$.

By Claim 2, ${\gamma }_n={\gamma }_n^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$ where ${\gamma }_n^{\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$.

Therefore, ${\gamma }_n={\gamma }_n^{\mathrm{\text{'}}}{\mathrm{⟂}}_f={\mathrm{⟂}}_f{\gamma }_n^{"}$.

If ${\gamma }_n^{"}\ne ϵ$, its rightmost symbol must be ${⟂}_f$.

Let ${\gamma }_n^{"}={\gamma }_n^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_f$ for some ${\gamma }_n^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Therefore, ${\gamma }_n^{\mathrm{\text{'}}}{\mathrm{⟂}}_f={\mathrm{⟂}}_f{\gamma }_n^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_n^{\text{'}}={⟂}_f{\gamma }_n^{\text{'}\text{'}\text{'}}$, which is a contradiction because by Claim 2, ${\gamma }_n^{\text{'}}{\in \mathsf{\Gamma }}^{*}$ but ${⟂}_f$ is not in ${\mathsf{\Gamma }}^{*}$.

Therefore, ${\gamma }_n^{"}=ϵ$.

$\gamma ={\gamma }_n^{"}=ϵ$.

${\gamma }_n={\mathrm{⟂}}_f{\gamma }_n^{"}={\mathrm{⟂}}_f$.

$\left(q_n,u_n,{\gamma }_n\right)=\left(q_n,ϵ,{\mathrm{⟂}}_f\right)$ and Claim 3 is proved.

Claim 4. 

$(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}})\stackrel{1,M_e}{\to }(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}})$ for $1\le i\le n-1$.

From above, we have $\left(q_i,u_i,{\gamma }_i\right)\stackrel{1,M_f}{\to }\left(q_{i+1},u_{i+1},{\gamma }_{i+1}\right)$.

By Claim 2, $\left(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_f\right)\stackrel{1,M_f}{\to }\left(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_f\right)$ where

${\gamma }_i^{\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$, ${\gamma }_{i+1}^{\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$, $a{\in \mathsf{\Sigma }}_{ϵ}$, $u_i=a{u}_{i+1}$, $u_i$, $u_{i+1}\in {\mathsf{\Sigma }}^{\mathrm{*}}$.

Equivalently, $q_i\stackrel{a,b⟶c,{\delta }_f}{\to }{q}_{i+1}$ where ${\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=b\eta$ & ${\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=c\eta$, $b\in {\left({\mathsf{\Gamma }}_f\right)}_{ϵ}$, $c\in {\mathsf{\Gamma }}_f^{\mathrm{*}}$, $\eta \in {\mathsf{\Gamma }}_f^{\mathrm{*}}$.

Since $q_i\ne q_{start}$, the above computation could not have come from T1.

Since $q_{i+1}\ne q_{accept}$, the above computation could not have come from T2.

Therefore, it must have come from T3 where ${\delta }_f\left(q_i,a,b\right)=\delta (q_i,a,b)$.

Therefore, $b\in {\mathsf{\Gamma }}_{ϵ}$ & $c{\in \mathsf{\Gamma }}^{\mathrm{*}}$ and $q_i\stackrel{a,b⟶c,\delta }{\to }{q}_{i+1}$.

Since ${\gamma }_i^{\text{'}}{⟂}_f=b\eta$, the rightmost symbol of $\eta$ must be ${⟂}_f$.

Therefore, $\eta =\theta {⟂}_f$ for some $\theta \in {\mathsf{\Gamma }}_f^{*}$.

Therefore, ${\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=b\theta {\mathrm{⟂}}_f$ and ${\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_f=c\theta {\mathrm{⟂}}_f$.

Therefore, ${\gamma }_i^{\mathrm{\text{'}}}=b\theta$ and ${\gamma }_{i+1}^{\mathrm{\text{'}}}=c\theta$.

Since ${\gamma }_i^{\text{'}}{\in \mathsf{\Gamma }}^{*}$ by Claim 2, $\theta {\in \mathsf{\Gamma }}^{*}$.

Therefore, $(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}})\stackrel{1,M_e}{\to }(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}})$.

This completes the proof of Claim 4.

By Claim 4, we now have

$(q_1,u_1,{\gamma }_1^{\mathrm{\text{'}}})\stackrel{1,M_e}{\to }(q_2,u_2,{\gamma }_2^{\mathrm{\text{'}}})\stackrel{1,M_e}{\to }\dots \stackrel{1,M_e}{\to }(q_{n-1},u_{n-1},{\gamma }_{n-1}^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }\left(q_n,u_n,{\gamma }_n^{\mathrm{\text{'}}}\right)$.

By Claim 1, $\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_e{\mathrm{⟂}}_f\right)$.

Therefore, $q_1=q_0$, $u_1=w$, ${\gamma }_1={\mathrm{⟂}}_e{\mathrm{⟂}}_f$.

By Claim 2, ${\gamma }_1={\gamma }_1^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_1^{\mathrm{\text{'}}}{\mathrm{⟂}}_f={\mathrm{⟂}}_e{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_1^{\mathrm{\text{'}}}={\mathrm{⟂}}_e$.

Therefore, $\left(q_1,u_1,{\gamma }_1^{\mathrm{\text{'}}}\right)=\left(q_0,w,{\mathrm{⟂}}_e\right)$.

By Claim 3, $\left(q_n,u_n,{\gamma }_n\right)=\left(q_n,ϵ,{\mathrm{⟂}}_f\right)$.

$u_n=ϵ$ & ${\gamma }_n={\mathrm{⟂}}_f$.

By Claim 2, ${\gamma }_n={\gamma }_n^{\mathrm{\text{'}}}{\mathrm{⟂}}_f$.

Therefore, ${\gamma }_n^{\mathrm{\text{'}}}{\mathrm{⟂}}_f={\mathrm{⟂}}_f$.

Therefore, ${\gamma }_n^{\text{'}}=ϵ$.

$\left(q_n,u_n,{\gamma }_n^{\mathrm{\text{'}}}\right)=\left(q_n,ϵ,ϵ\right)$.

Therefore,

$\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }(q_2,u_2,{\gamma }_2^{\mathrm{\text{'}}})\stackrel{1,M_e}{\to }\dots \stackrel{1,M_e}{\to }(q_{n-1},u_{n-1},{\gamma }_{n-1}^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }\left(q_n,ϵ,ϵ\right)$.

$\left(q_0,w,{\mathrm{⟂}}_e\right)\stackrel{\mathrm{*},M_e}{\to }\left(q_n,ϵ,ϵ\right)$.

$M_e$ accepts $w$.

$w\in L\left(M_e\right)$.

$w\in L\left(M_e\right)\iff w\in L\left(M_f\right)$.

This completes the proof of Lemma 2.52.

Lemma 2.53. For any $PDA$, $M_f$, that accepts by final state, there is a $PDA$, $M_e$, that accepts by empty stack such that $L\left(M_e\right)=L\left(M_f\right)$.

Proof. Let $M_f=(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,{⟂}_f,F)$ where ${⟂}_f\in \mathsf{\Gamma }$ is the initial stack symbol of $M_f$.

Construct $M_e=\left(Q_e,\mathsf{\Sigma },{\mathsf{\Gamma }}_e,{\delta }_e,q_{start},{\mathrm{⟂}}_e\right)$ where

$Q_e=Q\cup \{q_{start},q_{empty}\}$; ${\mathsf{\Gamma }}_e=\mathsf{\Gamma }\cup {\mathrm{⟂}}_e$;

$q_{start}$ and $q_{empty}$ are newly created states (not in $Q$) with $q_{start}$ serving as the start state of $M_e$ and $q_{empty}$ serving as the state in which $M_e$ begins the process of emptying the stack (without further consuming input);

${⟂}_e$ is a newly created stack symbol (not in $\mathsf{\Gamma }$) serving as the initial stack symbol of $M_e$.

The transition function ${\delta }_e$ of $M_e$ is defined as follows.

T1: ${\delta }_e\left(q_{start},ϵ,{\mathrm{⟂}}_e\right)=\left\{\left(q_0,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\right\}$ $\left(⟺q_{start}\stackrel{ϵ,{\mathrm{⟂}}_e⟶{\mathrm{⟂}}_f{\mathrm{⟂}}_e,{\delta }_e}{\to }{q}_0\right)$T2: $\forall$ $\left(q,a,A\right)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}$ where $\delta :Q\times {\mathsf{\Sigma }}_{ϵ}\times {\mathsf{\Gamma }}_{ϵ}⟶\mathrm{\wp }(Q\times {\mathsf{\Gamma }}^{\mathrm{*}})$, ${\delta }_e\left(q,a,A\right)=\delta (q,a,A)$.

T3: $\forall$ $q\in F$, ${\delta }_e\left(q,ϵ,ϵ\right)=\left\{\left(q_{empty},ϵ\right)\right\}$ $\left(⟺q\stackrel{ϵ,ϵ⟶ϵ,{\delta }_e}{\to }{q}_{empty}\right)$.

T4: $\forall A\in {\left({\mathsf{\Gamma }}_e\right)}_{ϵ}$, ${\delta }_e\left(q_{empty},ϵ,A\right)=\left\{\left(q_{empty},ϵ\right)\right\}$ $\left(⟺q_{empty}\stackrel{ϵ,A⟶ϵ,{\delta }_e}{\to }{q}_{empty}\right)$.

T5: For any other $\left(q,a,A\right)\in Q_e\times {\mathsf{\Sigma }}_{ϵ}\times {\left({\mathsf{\Gamma }}_e\right)}_{ϵ}$, ${\delta }_e\left(q,a,A\right)=\mathrm{\varnothing }$.

The construction is now complete. It remains to show $L\left(M_e\right)=L\left(M_f\right)$.

Suppose $w\in L\left(M_f\right)$.

$\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{n,M_f}{\to }(q,ϵ,\gamma )$ for some $n\ge 0$ & $q\in F$, $\gamma \in {\mathsf{\Gamma }}^{\mathrm{*}}$.

By T1, ${\delta }_e\left(q_{start},ϵ,{\mathrm{⟂}}_e\right)=\left\{\left(q_0,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\right\}$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$.

By Proposition 2.49, we have

$\left\{\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{n,M_f}{\to }\left(q,ϵ,\gamma \right)\right\}⟺\left\{\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{n,M_e}{\to }\left(q,ϵ,\gamma \right)\right\}$. ($Q\subset Q_e\&{\delta }_e\left(q,a,A\right)=\delta (q,a,A)$)

By Proposition 2.50, we have

$\left\{\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{n,M_e}{\to }\left(q,ϵ,\gamma \right)\right\}⟹\left\{\left(q_0,wϵ,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\stackrel{n,M_e}{\to }\left(q,ϵϵ,{\gamma \mathrm{⟂}}_e\right)\right\}$.

That is, $\left\{\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{n,M_e}{\to }\left(q,ϵ,\gamma \right)\right\}⟹\left\{\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\stackrel{n,M_e}{\to }\left(q,ϵ,{\gamma \mathrm{⟂}}_e\right)\right\}$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\stackrel{n,M_e}{\to }\left(q,ϵ,{\gamma \mathrm{⟂}}_e\right)$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,{\gamma \mathrm{⟂}}_e\right)$.

By T3, $\left(q,ϵ,{\gamma \mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }(q_{empty},ϵ,\gamma {\mathrm{⟂}}_e)$.

By repeated application of T4, $(q_{empty},ϵ,\gamma {\mathrm{⟂}}_e)\stackrel{\mathrm{*},M_e}{\to }(q_{empty},ϵ,ϵ)$.

Combined, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,{\gamma \mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }(q_{empty},ϵ,\gamma {\mathrm{⟂}}_e)\stackrel{\mathrm{*},M_e}{\to }(q_{empty},ϵ,ϵ)$.

Therefore, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{\mathrm{*},M_e}{\to }(q_{empty},ϵ,ϵ)$.

Therefore, $M_e$ accepts $w$.

$w\in L\left(M_e\right)$Therefore, $L\left(M_f\right)\subset L\left(M_e\right)$.

Conversely, assume $w\in L\left(M_e\right)$.

There exist configurations $(q_1,u_1,{\gamma }_1)$, $(q_2,u_2,{\gamma }_2)$, $\dots (q_i,u_i,{\gamma }_i)$, $\dots \left(q_n,u_n,{\gamma }_n\right)$ where

$n\ge 0$, $u_i\in {\mathsf{\Sigma }}^{\mathrm{*}}$, ${\gamma }_i$ $\in {\mathsf{\Gamma }}_e^{\mathrm{*}}$ for $1\le i\le n$, $q_1,q_1\dots q_n\in Q_e$ such that

$\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }(q_1,u_1,{\gamma }_1)\stackrel{1,M_e}{\to }\dots \stackrel{1,M_e}{\to }(q_i,u_i,{\gamma }_i)\stackrel{1,M_e}{\to }\dots \stackrel{1,M_e}{\to }\left(q_n,u_n,{\gamma }_n\right)\stackrel{1,M_e}{\to }$ $\left(q,ϵ,ϵ\right)$.

Note that $q_{start}\notin \{q_1,q_1\dots q_n\}$ because $q_{start}$ doesn’t have incoming arrows.

If $n=0$, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }\left(q,ϵ,ϵ\right)$.

By T1, $\left(q_{start},w,{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$ and this is the only configuration move out of $\left(q_{start},w,{\mathrm{⟂}}_e\right)$ because ${\delta }_e\left(q_{start},ϵ,{\mathrm{⟂}}_e\right)=\left\{\left(q_0,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)\right\}$.

Therefore, $\left(q,ϵ,ϵ\right)=\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$, which is a contradiction because ${\mathrm{⟂}}_f{\mathrm{⟂}}_e\ne ϵ$.

Therefore, $n\ge 1$.

In addition, we have $\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$.

To move from $\left(q_0,w,{⟂}_f{⟂}_e\right)$ to the final configuration $\left(q,ϵ,ϵ\right)$, $M_e$ must pop ${⟂}_e$ at some point which can only be done by T4 because T1 does not pop ${⟂}_e$ and T2 and T3 cannot move on ${⟂}_e$.

Therefore, we must have a $q_{empty}$ somewhere between $\left(q_0,w,{⟂}_f{⟂}_e\right)$ and $\left(q,ϵ,ϵ\right)$.

However, we can only transition into $q_{empty}$ via a state $p\in F$ (T3).

Therefore, there must be a $p\in F$ somewhere between $\left(q_0,w,{⟂}_f{⟂}_e\right)$ and $\left(q,ϵ,ϵ\right)$.

$\exists m=$ Max$\left\{i\right|1\le i\le n;q_i\in F\}$.

Claim 1. For $1\le i\le m$, $q_i\ne q_{empty}$ and hence ${\gamma }_i$ has ${⟂}_e$ as its rightmost symbol.

To prove Claim 1, we assume for contradiction $\exists k$ such that $1\le k\le m$ & $q_k=q_{empty}$.

By T4, $q_{k+1}=q_{k+2}=\dots =q_m=q_{empty}$.

This contradicts $q_m\in F$.

Therefore, $q_i\ne q_{empty}$ for $1\le i\le m$.

As mentioned above, $\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$.

Therefore, ${\gamma }_1={\mathrm{⟂}}_f{\mathrm{⟂}}_e$.

Since the only way to pop ${⟂}_e$ is by using T4 that requires the existence of $q_{empty}$ and we cannot have any $q_{empty}$ between $q_1$ and $q_m$, we must conclude that ${⟂}_e$ remains sitting at the bottom of the stack as the machine moves from $q_1$ to $q_m.$Therefore, ${\gamma }_i$ has ${⟂}_e$ as its rightmost symbol for $1\le i\le m$.

Claim 2. For configuration $\left(q_m,u_m,{\gamma }_m\right)$, $u_m=ϵ$.

To prove Claim 2, we assume for contradiction $u_m\ne ϵ$.

At this configuration, there are two possible ways for the machine to move: (i) is to continue to simulate $M_f$ using T2 and (ii) is to enter $q_{empty}$ using T3.

For (i), the machine will continue to read the input but will never enter an accept state again because it has passed $q_m$ which is the highest accept state in this computation. By the time the machine completes reading the entire input it will come to a stop and has never had a chance to enter the state $q_{empty}$. Thus, ${⟂}_e$ remains sitting in the stack when everything comes to stop. This is contradictory to the assumption that the computation ends at $\left(q,ϵ,ϵ\right)$.

For (ii), the machine enters $q_{empty}$ using T3 transition:

$q_m\stackrel{ϵ,ϵ⟶ϵ,{\delta }_e}{\to }{q}_{empty}$.

$q_{m+1}=q_{empty}$, $u_{m+1}=u_m$, ${\gamma }_{m+1}={\gamma }_m$.

$\left(q_m,u_m,{\gamma }_m\right)\stackrel{1,M_e}{\to }\left(q_{empty},u_m,{\gamma }_m\right)$Once the machine has entered $q_{empty}$, it will follow T4, which is $q_{empty}\stackrel{ϵ,A⟶ϵ,{\delta }_e}{\to }{q}_{empty}$, to continue to pop symbols from the stack while remaining in $q_{empty}$ and not reading any input.

Therefore, $q_{m+1}=q_{m+2}=\dots =q_n=q=q_{empty}$ &

$u_m=u_{m+1}=u_{m+2}=\dots =u_n=ϵ$ (Last configuration is $\left(q,ϵ,ϵ\right)$).

Therefore, both (i) and (ii) contradict the original assumption that $u_m\ne ϵ$.

Therefore, $u_m=ϵ$.

Claim 3. 

For $1\le i\le m$, $\exists {\gamma }_i^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$ such that ${\gamma }_i={\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e$.

The proof of Claim 3 is by induction on $i$.

We show at the beginning that $\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$Therefore, ${\gamma }_1={\mathrm{⟂}}_f{\mathrm{⟂}}_e$.

Since ${\mathrm{⟂}}_f\in \mathsf{\Gamma }\subset {\mathsf{\Gamma }}^{\mathrm{*}}$, ${\mathrm{⟂}}_f\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

If we take ${\gamma }_1^{\mathrm{\text{'}}}={\mathrm{⟂}}_f$, ${\gamma }_1={{\gamma }_1^{\mathrm{\text{'}}}\mathrm{⟂}}_e$.

The statement is true for $i=1$.

For induction hypothesis, ${\gamma }_k={\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_e$ for $1\le k\le m-1$, ${\gamma }_k^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

We show at the beginning that $q_{start}\notin \{q_1,q_2\dots q_n\}$ & $q_{empty}\notin \{q_1,q_2\dots q_m\}$ by Claim 1.

Therefore, $q_1,q_1\dots q_m\in Q$.

Consider configuration move of

$\left(q_k,u_k,{\gamma }_k\right)\stackrel{1,M_e}{\to }\left(q_{k+1},u_{k+1},{\gamma }_{k+1}\right)$.

This move could not have come from T3 or T4 because $q_k\ne q_{empty}$ & $q_{k+1}\ne q_{empty}$.

The move must have come from T2 where ${\delta }_e=\delta$.

By Proposition 2.49, we have

$\left(q_k,u_k,{\gamma }_k\right)\stackrel{1,M_f}{\to }\left(q_{k+1},u_{k+1},{\gamma }_{k+1}\right)$.

Therefore, $q_k\stackrel{a,b⟶c,\delta }{\to }{q}_{k+1}$ where

$a\in {\mathsf{\Sigma }}_{ϵ}$, $b\in {\mathsf{\Gamma }}_{ϵ}$, $c\in {\mathsf{\Gamma }}^{\mathrm{*}}$, $u_k=a{u}_{k+1}$, ${\gamma }_k=b{\gamma }_k^{"}$, ${\gamma }_{k+1}=c{\gamma }_k^{"}$, ${\gamma }_k^{"}\in {\mathsf{\Gamma }}_e^{\mathrm{*}}$.

Note that $b\in {\mathsf{\Gamma }}_{ϵ}⟹b\ne {\mathrm{⟂}}_e$.

By induction hypothesis, ${\gamma }_k={\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_e$ & ${\gamma }_k^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

Therefore, ${\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b{\gamma }_k^{"}$.

${\gamma }_k^{"}=ϵ⟹{\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b⟹\left({\gamma }_k^{\mathrm{\text{'}}}=ϵ\right)\&(b={\mathrm{⟂}}_e)⟹$ Contradiction.

Therefore, ${\gamma }_k^{"}\ne ϵ$.

The rightmost symbol of ${\gamma }_k^{"}$ must be ${⟂}_e$ (because ${\gamma }_k^{\text{'}}{⟂}_e=b{\gamma }_k^{"}$)

$\exists {\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}\in {\mathsf{\Gamma }}_e^{\mathrm{*}}$ such that ${\gamma }_k^{"}={\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_e$.

Therefore, ${\gamma }_k^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_e$.

Therefore, ${\gamma }_k^{\mathrm{\text{'}}}=b{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}$.

Since ${\gamma }_k^{\text{'}}\in {\mathsf{\Gamma }}^{*}$ by induction hypothesis, ${\gamma }_k^{\text{'}\text{'}\text{'}}{\in \mathsf{\Gamma }}^{*}$.

${\gamma }_{k+1}=c{\gamma }_k^{"}=c{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\mathrm{⟂}}_e={\gamma }_{k+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_e$ where ${\gamma }_{k+1}^{\mathrm{\text{'}}}=c{\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}$.

Since $c\in {\mathsf{\Gamma }}^{\mathrm{*}}$ & ${\gamma }_k^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$, ${\gamma }_{k+1}^{\mathrm{\text{'}}}\in {\mathsf{\Gamma }}^{\mathrm{*}}$.

The statement is also true for $i=k+1$.

This completes the proof of Claim 3.

Claim 4. 

$(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}})$ for $1\le i\le m-1$.

By assumption, $\left(q_i,u_i,{\gamma }_i\right)\stackrel{1,M_e}{\to }\left(q_{i+1},u_{i+1},{\gamma }_{i+1}\right)$.

By Claim 3, $\left(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e\right)\stackrel{1,M_e}{\to }\left(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_e\right)$By Claim 1, $q_i\ne q_{empty}$ & $q_{i+1}\ne q_{empty}$ for $1\le i\le m-1$.

Also, we point out at the beginning that $q_i\ne q_{start}$ for $1\le i\le n$.

Therefore, this computation must have come from T2 where ${\delta }_e=\delta$.

By Proposition 2.49, $\left(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e\right)\stackrel{1,M_f}{\to }\left(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_e\right)$.

Equivalently, $q_i\stackrel{a,b⟶c,\delta }{\to }{q}_{i+1}$ where

$a{\in \mathsf{\Sigma }}_{ϵ}$, $b\in {\mathsf{\Gamma }}_{ϵ}{,c{\in \mathsf{\Gamma }}^{\mathrm{*}},\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b\eta$ & ${\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=c\eta$, $\eta \in {\mathsf{\Gamma }}_e^{\mathrm{*}}$, $u_i=a{u}_{i+1}$.

Note that $b\in {\mathsf{\Gamma }}_{ϵ}⟹b\ne {\mathrm{⟂}}_e$.

$\eta =ϵ⟹{\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b⟹\left({\gamma }_i^{\mathrm{\text{'}}}=ϵ\right)\&(b={\mathrm{⟂}}_e)⟹$ Contradiction.

Therefore, $\eta \ne ϵ$.

The rightmost symbol of $\eta$ must be ${⟂}_e$ (because ${\gamma }_i^{\text{'}}{⟂}_e=b\eta$).

Let $\eta =\theta {\mathrm{⟂}}_e$ where $\theta \in {\mathsf{\Gamma }}_e^{\mathrm{*}}$.

Therefore, ${\gamma }_i^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=b\theta {\mathrm{⟂}}_e$ & ${\gamma }_{i+1}^{\mathrm{\text{'}}}{\mathrm{⟂}}_e=c\theta {\mathrm{⟂}}_e$.

Therefore, ${\gamma }_i^{\mathrm{\text{'}}}=b\theta$ & ${\gamma }_{i+1}^{\mathrm{\text{'}}}=c\theta$.

Since ${\gamma }_i^{\text{'}}{\in \mathsf{\Gamma }}^{*}$ by Claim 3, $\theta {\in \mathsf{\Gamma }}^{*}$.

$c{\in \mathsf{\Gamma }}^{\mathrm{*}}$ & $\theta {\in \mathsf{\Gamma }}^{\mathrm{*}}⟹{\gamma }_{i+1}^{\mathrm{\text{'}}}{\in \mathsf{\Gamma }}^{\mathrm{*}}$.

Therefore, $(q_i,u_i,{\gamma }_i^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }(q_{i+1},u_{i+1},{\gamma }_{i+1}^{\mathrm{\text{'}}})$.

This completes the proof of Claim 4.

By Claim 4, we now have,

$(q_1,u_1,{\gamma }_1^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }(q_2,u_2,{\gamma }_2^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }\dots \stackrel{1,M_f}{\to }(q_{m-1},u_{m-1},{\gamma }_{m-1}^{\mathrm{\text{'}}})\stackrel{1,M_f}{\to }(q_m,u_m,{\gamma }_m^{\mathrm{\text{'}}})$.

$\left(q_1,u_1,{\gamma }_1\right)=\left(q_0,w,{\mathrm{⟂}}_f{\mathrm{⟂}}_e\right)$ as shown at the beginning.

Therefore, ${\gamma }_1={\mathrm{⟂}}_f{\mathrm{⟂}}_e$.

By Claim 3, ${\gamma }_1={\gamma }_1^{\mathrm{\text{'}}}{\mathrm{⟂}}_e$.

Therefore, ${\gamma }_1^{\mathrm{\text{'}}}={\mathrm{⟂}}_f$.

Therefore, $\left(q_1,u_1,{\gamma }_1^{\mathrm{\text{'}}}\right)=\left(q_0,w,{\mathrm{⟂}}_f\right)$.

By definition, $q_m\in F$.

By Claim 2, $u_m=ϵ$.

Therefore, $\left(q_m,u_m,{\gamma }_m^{\mathrm{\text{'}}}\right)=(q_m,ϵ,{\gamma }_m^{\mathrm{\text{'}}})$.

Therefore, $\left(q_0,w,{\mathrm{⟂}}_f\right)\stackrel{\mathrm{*},M_f}{\to }(q_m,ϵ,{\gamma }_m^{\mathrm{\text{'}}})$ where $q_m\in F$.

Therefore, $M_f$ accepts $w$.

$w\in L\left(M_f\right)$.

$L\left(M_e\right)\subset L\left(M_f\right)$.

This completes the proof of Lemma 2.53.

Combining Lemma 2.52 and Lemma 2.53, we have the following theorem.

Theorem 2.54. 

For any $PDA$, $M_e$, that accepts by empty stack, there is a $PDA$, $M_f$, that accepts by final state such that $L\left(M_e\right)=L\left(M_f\right)$.

Conversely, For any $PDA$, $M_f$, that accepts by final state, there is a $PDA$, $M_e$, that accepts by empty stack such that $L\left(M_e\right)=L\left(M_f\right)$.

2.4. Equivalence of $\mathbf{C}\mathbf{F}\mathbf{G}$

and$\mathbf{P}\mathbf{D}\mathbf{A}$In this section, we shall prove that context-free grammars and pushdown automata are equivalent in power in that any language that is context-free is recognized by a pushdown automata and vice versa.

Definition 2.54. 

Let $G=(V,\mathsf{\Sigma },R,S)$ be a $CFG$.

Let $A\in V$, $y\in {(V\cup \Sigma )}^{\mathrm{*}}$.

$A$ is called the leftmost variable in $y$ iff $\exists x\in {\mathsf{\Sigma }}^{*}$ and $\alpha \in {(V\cup \Sigma )}^{*}$ such that $y=xA\alpha$.

$x$ is called the head of $y$ (written as $x=Head\left(y\right)$), $A\alpha$ is called the body of $y$ (written as $A\alpha =Body\left(y\right)$) and $\alpha$ is called the tail of $y$ (written as $\alpha =Tail\left(y\right)$).

It is clear from this definition that $y=Head\left(y\right)ATail\left(y\right)=Head\left(y\right)Body\left(y\right)$ and if $y\in {\mathsf{\Sigma }}^{\mathrm{*}}$, then $Head\left(y\right)=y$ and $Body\left(y\right)=Tail\left(y\right)=ϵ$.

Definition 2.55. Let $G=(V,\mathsf{\Sigma },R,S)$ be a $CFG$.

$\forall x,y\in {(V\cup \Sigma )}^{*}$, $x$ is a prefix of $y$ (written as $x{\le }_{PRE}y$) iff $\exists z\in {(V\cup \Sigma )}^{*}$ such that $xz=y$.

Proposition 2.56.${\le }_{PRE}$ is a reflexive and transitive relation from ${(V\cup \Sigma )}^{*}$ to ${(V\cup \Sigma )}^{*}$.

Proof. 

$\forall x\in {(V\cup \Sigma )}^{*}$, $\exists ϵ\in {(V\cup \Sigma )}^{*}$ and $xϵ=x$.

Therefore, $x{\le }_{PRE}x$ and ${\le }_{PRE}$ is a reflexive.

$\forall x,y,z\in {(V\cup \Sigma )}^{\mathrm{*}}$, if $x{\le }_{PRE}y$ and $y{\le }_{PRE}z$,

$\exists x^{\mathrm{\text{'}}},y^{\mathrm{\text{'}}}\in {(V\cup \Sigma )}^{\mathrm{*}}$ such that $x{x}^{\mathrm{\text{'}}}=y$ and $y{y}^{\mathrm{\text{'}}}=z$.

Therefore, $x{x}^{\mathrm{\text{'}}}{y}^{\mathrm{\text{'}}}=z$.

Since $x^{\mathrm{\text{'}}}{y}^{\mathrm{\text{'}}}\in {(V\cup \Sigma )}^{\mathrm{*}}$, $x{\le }_{PRE}z$.

Therefore, ${\le }_{PRE}$ is transitive.

This completes the proof of Proposition 2.56.

Proposition 2.57. 

Let $G=(V,\mathsf{\Sigma },R,S)$ be a $CFG$.

Let $w\in {\mathsf{\Sigma }}^{\mathrm{*}}$, ${\gamma }_i\in {(V\cup \Sigma )}^{\mathrm{*}}$ for all $i\in \{\mathrm{1,2},3,\dots n\}$.

Let $A_i$ be the leftmost variable in ${\gamma }_i$ and $A_i⟶{\beta }_i$ be the rule such that ${\gamma }_i\stackrel{A_i⟶{\beta }_i,lm}{\to }{\gamma }_{i+1}$ for all $i\in \{\mathrm{1,2},3,\dots n\}$.

Let $S={\gamma }_1\stackrel{lm}{\Rightarrow }{\gamma }_2\stackrel{lm}{\Rightarrow }{\gamma }_3\dots \stackrel{lm}{\Rightarrow }{\gamma }_n=w$.

The following statements are true:

(a) $Head\left({\gamma }_i\right){\le }_{PRE}Head\left({\gamma }_{i+1}\right)$

(b) $\forall 1\le i<j\le n$, $Head\left({\gamma }_i\right){\le }_{PRE}Head\left({\gamma }_j\right)$ & hence

$Head\left({\gamma }_1\right){\le }_{PRE}Head\left({\gamma }_2\right){\le }_{PRE}\dots {\le }_{PRE}Head\left({\gamma }_n\right)=w$

(c) $Head\left({\gamma }_{i+1}\right)=Head\left({\gamma }_i\right)Head\left({\beta }_i\right)$ & $Body\left({\gamma }_{i+1}\right)=Body\left({\beta }_i\right)Tail\left({\gamma }_i\right)$

(d) If $y_i\in {(V\cup \Sigma )}^{*}$ such that $Head\left({\gamma }_i\right)y_i=w$, then $Head\left({\beta }_i\right)$ ${\le }_{PRE}{y}_i$.

Proof. 

Since ${\gamma }_i\stackrel{A_i⟶{\beta }_i,lm}{\to }{\gamma }_{i+1}$, & ${\gamma }_i=Head\left({\gamma }_i\right)A_{i}Tail\left({\gamma }_i\right)$, we have ${\gamma }_{i+1}=Head\left({\gamma }_i\right){\beta }_{i}Tail\left({\gamma }_i\right)$.

Therefore, ${\gamma }_{i+1}=Head\left({\gamma }_i\right)Head\left({\beta }_i\right)B_{i}Tail\left({\beta }_i\right)Tail\left({\gamma }_i\right)$ where $B_i$ is the leftmost variable in ${\beta }_i$.

Since $Head\left({\gamma }_i\right)\in {\mathsf{\Sigma }}^{\mathrm{*}}$ & $Head\left({\beta }_i\right)\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $B_i$ is also the leftmost variable in ${\gamma }_{i+1}$.

Therefore, $Head\left({\gamma }_{i+1}\right)=Head\left({\gamma }_i\right)Head\left({\beta }_i\right)$.

Therefore, $Head\left({\gamma }_i\right){\le }_{PRE}Head\left({\gamma }_{i+1}\right)$.

This follows (a) to be true because ${\le }_{PRE}$ is transitive.

$Head\left({\gamma }_{i+1}\right)=Head\left({\gamma }_i\right)Head\left({\beta }_i\right)$ is established in the proof of (a).

It is also established in the proof of (a) that ${\gamma }_{i+1}=Head\left({\gamma }_i\right)Head\left({\beta }_i\right)B_{i}Tail\left({\beta }_i\right)Tail\left({\gamma }_i\right)$.

$Body\left({\gamma }_{i+1}\right)=B_{i}Tail\left({\beta }_i\right)Tail\left({\gamma }_i\right)$.

$=Body\left({\beta }_i\right)Tail\left({\gamma }_i\right)$ ($B_i$ is the leftmost variable in ${\beta }_i$)

From (b), $Head\left({\gamma }_{i+1}\right){\le }_{PRE}Head\left({\gamma }_n\right)=w$.

Therefore, $\exists y_{i+1}\in {\mathsf{\Sigma }}^{\mathrm{*}}$ such that $Head\left({\gamma }_{i+1}\right)y_{i+1}=w$.

Therefore, $Head\left({\gamma }_{i+1}\right)y_{i+1}=Head\left({\gamma }_i\right)y_i$.

By (c), $Head\left({\gamma }_i\right)Head\left({\beta }_i\right)y_{i+1}=Head\left({\gamma }_i\right)y_i$.

Therefore, $Head\left({\beta }_i\right)y_{i+1}=y_i$.

Therefore, $Head\left({\beta }_i\right){\le }_{PRE}{y}_i$.

Lemma 2.58. For any $CFG G$, $\exists$ a $PDA$ $M_e$ such that $L\left(G\right)=L\left(M_e\right)$.

Proof. 

Let $G=(V,\mathsf{\Sigma },R,S)$ be a $CFG$.

Construct $M_e=(\left\{q\right\},\mathsf{\Sigma },\mathrm{V}\cup \mathsf{\Sigma },\delta ,q,S)$ where $\delta$ is the transition function defined as follows.

T1: $\delta \left(q,ϵ,A\right)=\left\{\right(q,\beta \left)\right|A⟶\beta$ is a rule in $R\}$.

T2: $\delta \left(q,a,a\right)=\left\{\left(q,ϵ\right)\right\}$ $\forall a\in {\mathsf{\Sigma }}_{ϵ}$.

T3: For all other $\left(q,a,A\right)\in \left\{q\right\}\times {\mathsf{\Sigma }}_{ϵ}\times {\left(\mathrm{V}\cup \mathsf{\Sigma }\right)}_{ϵ}$, $\delta \left(q,a,A\right)=\mathrm{\varnothing }$.

Note that the start variable of $G$ is the start stack symbol of $M_e$.

It remains to show $L\left(G\right)=L\left(M_e\right)$.

To prove $L\left(G\right)\subset L\left(M_e\right)$, suppose $w\in L\left(G\right)$.

$\exists {\gamma }_1,{\gamma }_2,\dots {\gamma }_n\in {\left(\mathrm{V}\cup \mathsf{\Sigma }\right)}^{\mathrm{*}}$ such that

$S={\gamma }_1\stackrel{lm}{\Rightarrow }{\gamma }_2\stackrel{lm}{\Rightarrow }{\gamma }_3\dots {\gamma }_i\stackrel{lm}{\Rightarrow }{\gamma }_{i+1}\dots \stackrel{lm}{\Rightarrow }{\gamma }_n=w$.

$\forall i\in \{\mathrm{1,2},3,\dots n\}$, $Head\left({\gamma }_i\right){\le }_{PRE}w$ by Proposition 2.57(b).

Therefore, $\exists y_i$ such that $Head\left({\gamma }_i\right)y_i=w$.

Claim. 

$\forall i\in \{\mathrm{1,2},3,\dots n\}$, $\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,y_i,Body\left({\gamma }_i\right)\right)$ where $Head\left({\gamma }_i\right)y_i=w$.

This Claim can be proved by induction $i$.

For $i=1$, $S={\gamma }_1$ because $S={\gamma }_1\stackrel{lm}{\Rightarrow }{\gamma }_2\stackrel{lm}{\Rightarrow }{\gamma }_3\dots {\gamma }_i\stackrel{lm}{\Rightarrow }{\gamma }_{i+1}\dots \stackrel{lm}{\Rightarrow }{\gamma }_n=w$.

$Head\left({\gamma }_1\right)=Head\left(S\right)=ϵ$. $Body\left({\gamma }_1\right)=Body\left(S\right)=S$.

$\left(q,w,S\right)\stackrel{0,M_e}{\to }\left(q,w,S\right)=(q_1,y_1,{\alpha }_1)$.

Therefore, $q=q_1$, $y_1=w$ & ${\alpha }_1=S$.

Therefore, $q=q_1$, $Head\left({\gamma }_1\right)y_1=ϵw=w$ & ${\alpha }_1=Body\left({\gamma }_1\right)$.

$\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }(q,y_1,Body\left({\gamma }_1\right)$.

The statement is true for $i=1$.

For induction hypothesis, we have

$\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,y_k,Body\left({\gamma }_k\right)\right)$ where $Head\left({\gamma }_k\right)y_k=w$ for $1\le k<n-1$.

Let $A_k$ be the leftmost variable in ${\gamma }_k$.

Since ${\gamma }_k\stackrel{lm}{\Rightarrow }{\gamma }_{k+1}$, $\exists A_k⟶{\beta }_k$ where ${\beta }_k\in {\left(\mathrm{V}\cup \mathsf{\Sigma }\right)}^{\mathrm{*}}$.

$\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,y_k,Body\left({\gamma }_k\right)\right)$= $\left(q,y_k,A_{k}Tail\left({\gamma }_k\right)\right)$

$\stackrel{1,M_e}{\to }$ $\left(q,y_k,{\beta }_{k}Tail\left({\gamma }_k\right)\right)$ (by T1)

= $\left(q,y_k,{Head(\beta }_k\left)Body\right({\beta }_k)Tail\left({\gamma }_k\right)\right)$By Proposition 2.57, $Head\left({\beta }_k\right){\le }_{PRE}{y}_k$.

$\exists y_{k+1}\in {(V\cup \Sigma )}^{\mathrm{*}}$ such that $Head\left({\beta }_k\right)y_{k+1}=y_k$.

Therefore, $\left(q,y_k,{Head(\beta }_k\left)Body\right({\beta }_k)Tail\left({\gamma }_k\right)\right)=\left(q,Head\left({\beta }_k\right)y_{k+1},{Head(\beta }_k\left)Body\right({\beta }_k)Tail\left({\gamma }_k\right)\right)$

$\stackrel{\left|{Head(\beta }_k)\right|,M_e}{\to }\left(q,y_{k+1},Body\left({\beta }_k\right)Tail\left({\gamma }_k\right)\right)$ (by repeated applications of T2 $\left|{Head(\beta }_k)\right|$ times)

= $\left(q,y_{k+1},Body\left({\gamma }_{k+1}\right)\right)$ (by Proposition 2.57(c))

Therefore, $\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,y_{k+1},Body\left({\gamma }_{k+1}\right)\right)$.

Since $Head\left({\beta }_k\right)y_{k+1}=y_k$,

$Head\left({\gamma }_k\right)Head\left({\beta }_k\right)y_{k+1}=Head\left({\gamma }_k\right)y_k$.

By Proposition 2.57(c), $Head\left({\gamma }_{k+1}\right)=Head\left({\gamma }_k\right)Head\left({\beta }_k\right)$.

By induction hypothesis, $Head\left({\gamma }_k\right)y_k=w$.

Therefore, $Head\left({\gamma }_{k+1}\right)y_{k+1}=w$.

Therefore, the statement is true for$i=k+1$.

To complete the proof of $L\left(G\right)\subset L\left(M_e\right)$, set $i=n$ in Claim.

$\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,y_n,Body\left({\gamma }_n\right)\right)$ where $Head\left({\gamma }_n\right)y_n=w$.

Since ${\gamma }_n=w$, $Head\left({\gamma }_n\right)=Head\left(w\right)=w$ & $Body\left({\gamma }_n\right)=Body\left(w\right)=ϵ$.

($Head\left({\gamma }_n\right)=w$) & ($Head\left({\gamma }_n\right)y_n=w$)$⟹w{y}_n=w⟹y_n=ϵ$.

Therefore, $\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)$.

$w\in L\left(M_e\right)$.

Therefore, $L\left(G\right)\subset L\left(M_e\right)$.

(Note that at this final configuration of $\left(q, ϵ,ϵ\right)$, we could have used the transition, $\delta \left(q,ϵ,ϵ\right)=\left\{\left(q,ϵ\right)\right\}$ or $q\stackrel{ϵ,ϵ⟶ϵ,\delta }{\to }q$, to loop on without stopping. However, this machine is nondeterministic, which means that we don’t have to take an option which is a bad one. On the other hand, if bad choices are made, we can loop ourselves to infinity.)

To prove $L\left(M_e\right)\subset L\left(G\right)$, let $w\in L\left(M_e\right)$.

$\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)$.

Claim. 

$\forall x\in {\mathsf{\Sigma }}^{\mathrm{*}}$, if $(q,x,A)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)$, then $A\stackrel{\mathrm{*}}{\Rightarrow }x$.

Proof of this Claim is by induction on the number of steps.

$\exists n\ge 1$, such that $(q,x,A)\stackrel{n,M_e}{\to }\left(q,ϵ,ϵ\right)$.

For $n=1$, $(q,x,A)\stackrel{1,M_e}{\to }\left(q,ϵ,ϵ\right)$.

Since $A\in V$, we must use T1 and that is, $\delta \left(q,ϵ,A\right)=\left\{\right(q,\beta \left)\right|A⟶\beta$ is a rule in $R\}$.

Therefore, $\left(q,x,A\right)\stackrel{1,M_e}{\to }\left(q,x,\beta \right)=\left(q,ϵ,ϵ\right)$.

Therefore, $x=\beta =ϵ$.

Therefore, $A⟶ϵ$ is a rule.

$A⟹ϵ$ by Proposition 2.8(i).

Therefore, $A\stackrel{*}{\Rightarrow }ϵ$.

The statement is true for $n=1$.

For induction hypothesis, assume the statement is true for all $n\le k$ with $k\ge 1$.

That is, if $(q,x,A)\stackrel{n,M_e}{\to }\left(q,ϵ,ϵ\right)$, then $A\stackrel{\mathrm{*}}{\Rightarrow }x$ for all $n\le k$.

For $n=k+1$, assume $(q,x,A)\stackrel{k+1,M_e}{\to }\left(q,ϵ,ϵ\right)$.

Since $A\in V$, the first move must be based on T1.

Therefore, $\left(q,x,A\right)\stackrel{1,M_e}{\to }(q,x,Y_1{Y}_2\dots Y_m)\stackrel{k,M_e}{\to }\left(q,ϵ,ϵ\right)$ where

$A⟶Y_1{Y}_2\dots Y_m$ & $Y_i\in \mathrm{V}\cup \mathsf{\Sigma }$ for $i\in \{\mathrm{1,2},\dots m\}$.

Since $(q,x,Y_1{Y}_2\dots Y_m)\stackrel{k,M_e}{\to }\left(q, ϵ,ϵ\right)$, the machine must pop all the $Y_{i}s$ off the stack by the time it finishes reading input $x$ and empties the stack.

Let $x_i$ be the portion of $x$ that the machine consumes while popping $Y_i$ off the stack and returning its stack head to the position right before popping $Y_{i+1}$ off for $i=\mathrm{1,2},3,\dots m-1$.

Let also $x_m$ be the last portion of $x$ that the machine consumes while popping $Y_m$ off the stack and emptying the stack eventually.

Note that if $Y_i$ is a terminal, $x_i=Y_i$. The $PDA$ will pop $Y_i$ using T2 and then scan the same symbol $x_i$ from the input. The stack head will then point at $Y_{i+1}$.

By these assumptions, we have $x=x_1{x}_2\dots x_m$.

In addition, we have the following sequence of computations:$(q,x_1{x}_2\dots x_m,Y_1{Y}_2\dots Y_m)\stackrel{\mathrm{*},M_e}{\to }(q,x_2{x}_3\dots x_m,Y_2{Y}_3\dots Y_m)\stackrel{\mathrm{*},M_e}{\to }(q,x_3{x}_4\dots x_m,Y_3{Y}_4\dots Y_m)$ $\stackrel{\mathrm{*},M_e}{\to }\dots \stackrel{\mathrm{*},M_e}{\to }\left(q,x_i{x}_{i+1}\dots x_m,Y_i{Y}_{i+1}\dots Y_m\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,x_{i+1}\dots x_m,Y_{i+1}\dots Y_m\right)$

$\stackrel{\mathrm{*},M_e}{\to }\dots \stackrel{\mathrm{*},M_e}{\to }(q,x_m,Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)$.

Since the stack head does not go below $Y_{i+1}$ while the $PDA$ consumes $x_i$, we have the following equivalent computations:

$(q,x_1,Y_1)\stackrel{\mathrm{*},M_e}{\to }(q,ϵ,ϵ)$

$(q,x_2,Y_2)\stackrel{\mathrm{*},M_e}{\to }(q,ϵ,ϵ)$

$⋮$

$(q,x_i,Y_i)\stackrel{\mathrm{*},M_e}{\to }(q,ϵ,ϵ)$

$⋮$

$(q,x_m,Y_m)\stackrel{\mathrm{*},M_e}{\to }(q,ϵ,ϵ)$

Since the sum of all the numbers of steps in all these computations is equal to $k$, the number of steps in each of these computations is less than or equal to $k$.

Therefore, we can use the induction hypothesis to derive the following:

$Y_1\stackrel{\mathrm{*}}{\Rightarrow }{x}_1$

$Y_2\stackrel{\mathrm{*}}{\Rightarrow }{x}_2$

$⋮$

$Y_i\stackrel{\mathrm{*}}{\Rightarrow }{x}_i$

$⋮$

$Y_m\stackrel{\mathrm{*}}{\Rightarrow }{x}_m$Since $A⟶Y_1{Y}_2\dots Y_m$, $A⟹Y_1{Y}_2\dots Y_m$ by Proposition 2.8(i).

Since $Y_i\stackrel{\mathrm{*}}{\Rightarrow }{x}_i$ $\forall i\in \{\mathrm{1,2},\dots m\}$, $Y_1{Y}_2\dots Y_m\stackrel{\mathrm{*}}{\Rightarrow }{x}_1{x}_2\dots x_m$ by Proposition 2.16(d).

Therefore, $A\stackrel{\mathrm{*}}{\Rightarrow }{x}_1{x}_2\dots x_m$.

Therefore, $A\stackrel{*}{\Rightarrow }x$.

The statement is true for $n=k+1$.

To complete the proof of $L\left(M_e\right)\subset L\left(G\right)$, put $A=S$ & $x=w$ in Claim.

$\left[\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)\right]⟹\left[S\stackrel{\mathrm{*}}{\Rightarrow }w\right]$.

$w\in L\left(M_e\right)⟹\left[\left(q,w,S\right)\stackrel{\mathrm{*},M_e}{\to }\left(q,ϵ,ϵ\right)\right]⟹\left[S\stackrel{\mathrm{*}}{\Rightarrow }w\right]⟹w\in L\left(G\right)$.

This completes the proof of $L\left(M_e\right)\subset L\left(G\right)$ and hence the proof of Lemma 2.58.

Lemma 2.59. 

For any$PDA$ $M_e$, $\exists$ a $CFGG$ such that $L\left(G\right)=L\left(M_e\right)$.

Proof.

Let $M_e=\left(Q,\mathsf{\Sigma },\mathsf{\Gamma },\delta ,q_0,{⟂}_e\right)$ be a $PDA$ that accepts by empty stack.

Construct $CFG$ $G=(V,\mathsf{\Sigma },R,S)$ where $V$ & $R$ are defined as follows.

$V=\left\{S\right\}\cup \left\{\right[pXq\left]\right|p,q\in Q,X\in \mathsf{\Gamma }\}$Note that $V$ is finite because $Q$ & $\mathsf{\Gamma }$ are finite.

Let $\left(P\right)$ be the procedure for creating rules in $R$ defined as follows.

$\forall (q,a,X)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times \mathsf{\Gamma }$, if $\delta (q,a,X)\ne \mathrm{\varnothing }$, $\exists (r_0,Y_1{Y}_2\dots Y_m)\in \delta (q,a,X)$.

That is, $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$.

For every $r_1,r_2,\dots r_m\in Q$, $a\in {\mathsf{\Sigma }}_{ϵ}$, let

$\left[qX{r}_m\right]⟶a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_m{r}_m\right]$ be a rule in $R$.

Note that the total number of rules thus created based on each

$(r_0,Y_1{Y}_2\dots Y_m))\in \delta (q,a,X)$ is finite because $Q$, $m$, & ${\mathsf{\Sigma }}_{ϵ}$ are finite.

Furthermore, the set $\delta (q,a,X)$ is finite & the total number of such sets, $\delta (q,a,X)$ is finite because the total number of $(q,a,X)\in Q\times {\mathsf{\Sigma }}_{ϵ}\times \mathsf{\Gamma }$ is finite.

Therefore, the total number of rules thus created for any given $PDA$, $M_e$ is finite.

Let $R_1=$ the set of rules created by $\left(P\right)$.

$R_2=\{S⟶[q_0{\mathrm{⟂}}_{e}p\left]\right|p\in Q\}$.

$R=R_1\cup R_2$.

The construction of $G$ is complete and we now proceed to prove $L\left(G\right)=L\left(M_e\right)$.

Claim 1. $S\stackrel{\mathrm{*}}{\Rightarrow }w$ iff $\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{\mathrm{*}}{\Rightarrow }w$ for some $p\in Q$.

<Proof of Claim 1>

$"$If $S\stackrel{\mathrm{*}}{\Rightarrow }w"$

$\exists n\ge 1$ such that $S\stackrel{n}{\Rightarrow }w$.

$S\stackrel{1}{\Rightarrow }\beta \stackrel{n-1}{\Rightarrow }w$ where $\beta \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

By Proposition 2.8(i), $S⟶\beta$ is a rule.

This rule must be from $R_2$.

Therefore, $S⟶\left[q_0{\mathrm{⟂}}_{e}p\right]$ for some $p\in Q$.

Therefore, $S\stackrel{1}{\Rightarrow }\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{n-1}{\Rightarrow }w$.

Therefore, $\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{n-1}{\Rightarrow }w$.

Therefore, $\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{\mathrm{*}}{\Rightarrow }w$ for some $p\in Q$.

$"$If $\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{\mathrm{*}}{\Rightarrow }wforsomep\in Q"$By construction, $S⟶\left[q_0{⟂}_{e}p\right]$ is a rule in $R_2$.

By Proposition 2.8(i), $S\stackrel{1}{\Rightarrow }\left[q_0{⟂}_{e}p\right]$.

Therefore, $S\stackrel{1}{\Rightarrow }\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{\mathrm{*}}{\Rightarrow }w$.

Therefore, $S\stackrel{*}{\Rightarrow }w$.

This completes the proof of Claim 1.

Claim 2. $\forall p,q\in Q$, $X\in \mathsf{\Gamma }$, $w\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w$ iff $(q,w,X)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$.

<Proof of Claim 2>

“If”

Assume $(q,w,X)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$.

$\exists n\ge 1$ such that $(q,w,X)\stackrel{n,M_e}{\to }\left(p,ϵ,ϵ\right)$.

The proof of $\left[qXp\right]\stackrel{*}{\Rightarrow }w$ is by induction on $n$.

For $n=1$, $(q,w,X)\stackrel{1,M_e}{\to }\left(p,ϵ,ϵ\right)$Therefore, $q\stackrel{a,X⟶ϵ}{\to }p$ where $a\in {\mathsf{\Sigma }}_{ϵ}$ & $w=aϵ=a$.

By $\left(P\right)$, if $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$, then $\exists$ a rule $\left[qX{r}_m\right]⟶a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_m{r}_m\right]$ for some $r_1,r_2,\dots r_m\in Q$.

In this case, $Y_1{Y}_2\dots Y_m=ϵ$ which means $m=0$ and hence $r_m=r_0$.

Therefore, $\exists$ a rule $\left[qX{r}_0\right]⟶a$.

Since $p=r_0$ & $w=a$, the rule becomes $\left[qXp\right]⟶w$.

By Proposition 2.8(i), $\left[qXp\right]⟹w$.

Therefore, $\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w$.

The statement is true for $n=1$.

Assume the statement is true for all $n\le k$ where $k\ge 1$.

That is, $\left\{\left(q,w,X\right)\stackrel{n,M_e}{\to }\left(p,ϵ,ϵ\right)\right\}⟹\left\{\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w\right\}$ for all $n\le k$.

For $n=k+1$, assume $\left(q,w,X\right)\stackrel{k+1,M_e}{\to }\left(p,ϵ,ϵ\right)$.

$\exists Y_1,Y_2,\dots Y_m\in \mathsf{\Gamma }$, $a\in {\mathsf{\Sigma }}_{ϵ}$, $x\in {\mathsf{\Sigma }}^{\mathrm{*}}$, $w=ax$, $r_0\in Q$ such that $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$.

Therefore, $\left(q,w,X\right)\stackrel{1,M_e}{\to }(r_0,x,Y_1{Y}_2\dots Y_m)\stackrel{k,M_e}{\to }\left(p,ϵ,ϵ\right)$.

Since $(r_0,x,Y_1{Y}_2\dots Y_m)\stackrel{k,M_e}{\to }\left(p, ϵ,ϵ\right)$, using the same argument as used in the proof of Lemma 2.58, we can deduce the following computations:

$(r_0,x_1,Y_1)\stackrel{\mathrm{*},M_e}{\to }\left(r_1,ϵ,ϵ\right)$

$(r_1,x_2,Y_2)\stackrel{\mathrm{*},M_e}{\to }\left(r_2,ϵ,ϵ\right)$

$⋮$

$(r_{i-1},x_i,Y_i)\stackrel{\mathrm{*},M_e}{\to }\left(r_i,ϵ,ϵ\right)$

$⋮$

$(r_{m-1},x_m,Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(r_m,ϵ,ϵ\right)$ where

$r_1,$ $r_2\dots r_{m-1}\in Q$, $r_m=p$,

$x_i$ is the portion of $x$ that the machine consumes while popping $Y_i$ off the stack and returning its stack head to the position right before popping $Y_{i+1}$ off for $i=\mathrm{1,2},3,\dots m-1$ and $x_m$ is the last portion of $x$ that the machine consumes while popping $Y_m$ off the stack and emptying the stack eventually.

Note that the machine goes from state $r_{i-1}$ to state $r_i$ after completing the above actions & $x=x_1{x}_2\dots x_m$.

Since each computation $(r_{i-1},x_i,Y_i)\stackrel{\mathrm{*},M_e}{\to }\left(r_i,ϵ,ϵ\right)$ is part of the computation $(r_0,x,Y_1{Y}_2\dots Y_m)\stackrel{k,M_e}{\to }\left(p,ϵ,ϵ\right)$, each one makes no more than $k$ moves.

By induction hypothesis, $\left[r_{i-1}{Y}_i{r}_i\right]\stackrel{\mathrm{*}}{\Rightarrow }{x}_i$ for $i=\mathrm{1,2},\dots m$.

As shown above, $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$ & since $r_1,$ $r_2\dots r_{m-1},p\in Q$, by $\left(P\right)$,

$\exists$ a rule $\left[qXp\right]⟶a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]$.

By Proposition 2.8(i), $\left[qXp\right]⟹a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]$.

Since $a\stackrel{0}{\Rightarrow }a$ & $\left[r_{i-1}{Y}_i{r}_i\right]\stackrel{\mathrm{*}}{\Rightarrow }{x}_i$ for $i=\mathrm{1,2},\dots m$.

$a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]\stackrel{\mathrm{*}}{\Rightarrow }a{x}_1{x}_2\dots x_m$ by Proposition 2.16(d).

Therefore, $\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }a{x}_1{x}_2\dots x_m$.

Since $w=ax=a{x}_1{x}_2\dots x_m$, $\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w$.

Therefore, $\left\{\left(q,w,X\right)\stackrel{k+1,M_e}{\to }\left(p,ϵ,ϵ\right)\right\}⟹\left\{\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w\right\}$Therefore, the statement is true for $n=k+1$.

This completes the proof of the “If” part of Claim 2.

“Only if”

Assume $\left[qXp\right]\stackrel{\mathrm{*}}{\Rightarrow }w$.

$\exists n\ge 1$ such that $\left[qXp\right]\stackrel{n}{\Rightarrow }w$.

The proof of $\left(q,w,X\right)\stackrel{*,M_e}{\to }\left(p, ϵ,ϵ\right)$ is by induction on $n$.

For $n=1$, $\left[qXp\right]\stackrel{1}{\Rightarrow }w$.

By Proposition 2.8(i), $\left[qXp\right]⟶w$ is a rule in $R_1$ (It’s not in $R_2$ because $\left[qXp\right]\ne S$).

Since every rule in $R_1$ is of the form $\left[qX{r}_m\right]⟶a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_m{r}_m\right]$ where

$q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$ & $r_1,$ $r_2\dots r_{m-1},r_m\in Q$.

In this particular case, $w$ is not a variable.

Therefore, $\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_m{r}_m\right]=ϵ$ or $m=0$.

Therefore, $a=w$ & $r_m=r_0$.

Since $\left[qXp\right]=\left[qX{r}_m\right]$, $p=r_m=r_0$.

We must have $q\stackrel{a,X⟶ϵ}{\to }p$.

Therefore, $\left(q,w,X\right)\stackrel{1,M_e}{\to }\left(p,x,ϵ\right)$ where $w=ax$.

As shown above, $a=w$.

Therefore, $x=ϵ$.

Therefore, $\left(q,w,X\right)\stackrel{1,M_e}{\to }\left(p,ϵ,ϵ\right)$.

Therefore, $\left(q,w,X\right)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$.

The statement is true for $n=1$.

For induction hypothesis, assume it is true that

$\left\{\left[qXp\right]\stackrel{n}{\Rightarrow }w\right\}⟹\left\{\left(q,w,X\right)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)\right\}$ for all $n\le k$ where $k\ge 1$.

For $n=k+1$, assume $\left[qXp\right]\stackrel{k+1}{\Rightarrow }w$.

Therefore, $\left[qXp\right]\stackrel{1}{\Rightarrow }\beta \stackrel{k}{\Rightarrow }w$ where $\beta \in {(V\cup \mathsf{\Sigma })}^{\mathrm{*}}$.

By Proposition 2.8(i), $\left[qXp\right]⟶\beta$ is a rule in $R_1$.

This rule must be of the form $\left[qXp\right]⟶a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]$ where

${r_0,r}_1,$ $r_2\dots r_{m-1}\in Q$, $a\in {\mathsf{\Sigma }}_{ϵ}$, $Y_1,Y_2,\dots Y_m\in \mathsf{\Gamma }$, $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$.

$\left[qXp\right]\stackrel{1}{\Rightarrow }a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]$ by Proposition 2.8(i).

Therefore, $\left[qXp\right]\stackrel{1}{\Rightarrow }a\left[r_0{Y}_1{r}_1\right]\left[r_1{Y}_2{r}_2\right]\dots \left[r_{m-1}{Y}_{m}p\right]\stackrel{k}{\Rightarrow }w$.

By Proposition 2.28(ii), $\exists w_1,w_2\dots w_m\in {\mathsf{\Sigma }}^{\mathrm{*}}$ such that $\left[r_{i-1}{Y}_i{r}_i\right]\stackrel{\mathrm{*}}{\Rightarrow }{w}_i$ in no more than $k$ steps for $i=\mathrm{1,2},\dots m$ and $w=a{w}_1{w}_2\dots w_m$.

By induction hypothesis, $(r_{i-1},w_i,Y_i)\stackrel{\mathrm{*},M_e}{\to }\left(r_i,ϵ,ϵ\right)$ for $i=\mathrm{1,2},\dots m$.

By Proposition 2.50,

$(r_{i-1},w_i{w}_{i+1}\dots w_m,Y_i{Y}_{i+1}\dots Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(r_i,w_{i+1}\dots w_m,Y_{i+1}\dots Y_m\right)$ for $i=\mathrm{1,2},\dots m$.

$(r_0,w_1{w}_2\dots w_m,Y_1{Y}_2\dots Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(r_1,w_2\dots w_m,Y_2\dots Y_m\right)$ for $i=1$.

$(r_1,w_2\dots w_m,Y_2\dots Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(r_2,w_3\dots w_m,Y_3\dots Y_m\right)$ for $i=2$.

$⋮$

$(r_{m-1},w_m,Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(r_m,ϵ,ϵ\right)$ for $i=m-1$ where $r_m=p$.

Furthermore, as shown above, $q\stackrel{a,X⟶Y_1{Y}_2\dots Y_m}{\to }{r}_0$.

Therefore, $(q,a{w}_1{w}_2\dots w_m,X)\stackrel{1,M_e}{\to }(r_0,w_1{w}_2\dots w_m,Y_1{Y}_2\dots Y_m)$.

Since $w=a{w}_1{w}_2\dots w_m$, $(q,w,X)\stackrel{1,M_e}{\to }(r_0,w_1{w}_2\dots w_m,Y_1{Y}_2\dots Y_m)$.

Connecting all the computations, we have

$\left(q,w,X\right)\stackrel{1,M_e}{\to }\left(r_0,w_1{w}_2\dots w_m,Y_1{Y}_2\dots Y_m\right)\stackrel{\mathrm{*},M_e}{\to }\left(r_1,w_2\dots w_m,Y_2\dots Y_m\right)$

$\stackrel{\mathrm{*},M_e}{\to }\left(r_2,w_3\dots w_m,Y_3\dots Y_m\right)\stackrel{\mathrm{*},M_e}{\to }\dots \stackrel{\mathrm{*},M_e}{\to }(r_{m-1},w_m,Y_m)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$.

Therefore, $\left(q,w,X\right)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$.

Therefore, $\left\{\left[qXp\right]\stackrel{k+1}{\Rightarrow }w\right\}⟹\left\{\left(q,w,X\right)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)\right\}$.

This completes the proof of Claim 2.

We now get back to the proof of $L\left(G\right)=L\left(M_e\right)$.

$w\in L\left(G\right)⟺S\stackrel{\mathrm{*}}{\Rightarrow }W$

$⟺\left[q_0{\mathrm{⟂}}_{e}p\right]\stackrel{\mathrm{*}}{\Rightarrow }w$ for some $p\in Q$ (Claim 1)

$⟺(q_0,w,{\mathrm{⟂}}_e)\stackrel{\mathrm{*},M_e}{\to }\left(p,ϵ,ϵ\right)$ (Claim 2)

$⟺M_e$ accepts $w$

$⟺w\in L\left(M_e\right)$Therefore, $L\left(G\right)=L\left(M_e\right)$.

This completes the proof of Lemma 2.59.

Combining Lemma 2.58 and Lemma 2.59, we have the following theorem.

Theorem 2.60. For any $CFGG$, $\exists$ a $PDA$ $M_e$ such that $L\left(G\right)=L\left(M_e\right)$.

Conversely, for any$PDA$ $M_e$, $\exists$ a $CFG G$ such that $L\left(G\right)=L\left(M_e\right)$.

2.5. The Pumping Lemma for Context Free Languages

In this section, we shall develop a tool for showing that a language is not context free. This tool is called “The Pumping Lemma for context free languages.” This Pumping Lemma is analogous to the pumping lemma we study in Chapter 1 for regular languages. The difference this time is we are pumping two strings rather than one and the string that we are dealing with is broken down into five substrings in contrast to three substrings in the case of regular languages.

Theorem 2.61. 

Let $G=(V, \mathsf{\Sigma }, R, S)$ be a $CFG$ in Chomsky Normal Form.

Let $Pt(A,w,h)$ be the parse tree corresponding to this grammar in accordance with the meaning of Theorem 2.33 where $A(\in V)$ is the root, $w(\in {\mathsf{\Sigma }}^{*})$ is the yield and $h$ is the height of the parse tree. Then it is true that $\left|w\right|\le 2^{h-1}$.

Proof. 

The proof of this theorem is by induction on $h$.

For $h=1$, $Pt(A,w,h)$ is a 1-level tree with $A$ at the zero level and $w$ at the first level.

The only forms of rules in Chomsky Normal Form are:

$A⟶BC$ where $AϵV$ and $B,CϵV\backslash \left\{S\right\}$

$A⟶a$ where $aϵ\mathsf{\Sigma }\subset {\mathsf{\Sigma }}^{\mathrm{*}}$

$S⟶ϵ$ where $S=$ Start Variable.

Since $w\in {\mathsf{\Sigma }}^{*}$, we have either $A⟶a$ or $S⟶ϵ$.

Therefore, $w=a$ or $w=ϵ$.

$w=a\Rightarrow \left|w\right|=1\Rightarrow \left|w\right|=2^0\le 2^{h-1}$.

$w=ϵ\Rightarrow \left|w\right|=0\Rightarrow \left|w\right|\le 2^0\le 2^{h-1}$.

Either case, we have statement being true for $h=1$.

For induction hypothesis, assume the statement is true for all $h\le k$ where $k\ge 1$.

Consider a parse tree, $Pt(A,w,k+1)$, that correspond to $G$ according to the meaning of Theorem 2.33.

Since $k\ge 1$, the height of $Pt(A,w,k+1)$ is greater than or equal to $2$. Hence the children of A which appear in the first level cannot be $a$ or $ϵ$.

They must be $B$ and $C$ with $B,CϵV\backslash \left\{S\right\}$.

Using similar argument as we use in proving Theorem 2.33, we can show the following:

(i) The combination of all branches of $B$ (respectively $C$) form a subtree $Pt(B,w_1,h_1)$ (respectively$Pt(C,w_2,h_2)$)

(ii) $h_1\le k$ & $h_2\le k$

(iii) $w=w_1{w}_2$.

By (ii) and induction hypothesis, $\left|w_1\right|\le 2^{h_1-1}$ & $\left|w_2\right|\le 2^{h_2-1}$.

$\left|w\right|=\left|w_1\right|+\left|w_2\right|$

$\le 2^{h_1-1}+2^{h_2-1}$

$\le 2^{k-1}+2^{k-1}$

$=2\bullet 2^{k-1}$

$=2^k$

$=2^{\left(k+1\right)-1}$This completes the induction proof of Theorem 2.61.

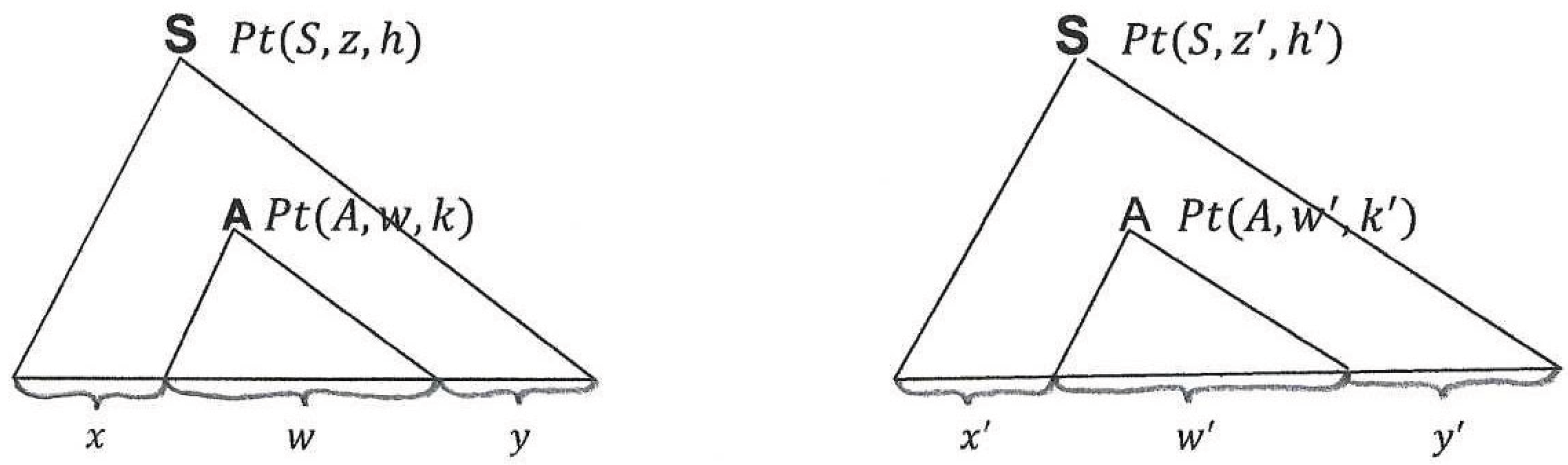
Proposition 2.62. 

Let $Pt(A,z,h)$ be a parse tree for $CFG,G=(V, \mathsf{\Sigma }, R, S)$ and $Pt(B,w,k)$ be the largest subtree of $Pt(A,z,h)$ where $w$, $z\in {\mathsf{\Sigma }}^{*}$. Then $\exists x,y\in {\mathsf{\Sigma }}^{*}$ such that $z=xwy$. Furthermore, the nodes on any path from $A$ to $x$ (respectively $y$) cannot be a node in $Pt(B,w,k)$.

Proof. By T13, every leaf of a subtree is also a leaf of the parent tree.

Therefore, $w⊏z$.

Therefore, $z=xwy$ for some $x,y\in {\mathsf{\Sigma }}^{*}$.

Let $(A,v_1,v_2,\dots v_n,l)$ be a path from $A$ to$l$ where $l$ is a symbol in $x$.

There exists a $v_i(i=\mathrm{1,2},\dots n)$ on this path such that $v_i$ and $B$ are at the same level.

If $v_i$ and $B$ are the same node, $(v_i,\dots v_n,l)$ is a branch rooted at $B$ and by T11, it is a path inside $Pt(B,w,k)$.

This means that $l$ is a symbol in $w$ and this contradicts the assumption that $l$ is a symbol in $x$.

Therefore, $v_i$ cannot be the same node as $B$.

Since $l$ is to the left of every symbol in $w$ and $v_i$ is an ancestor of $l$, by T12, $v_i$ is to the left of $B$.

Let $v_j$ be a node on the path $(A,v_1,v_2,\dots v_i\dots v_n,l)$.

If $j<i$, $v_j$ is above the level of $B$ and hence $v_j$ is not a node in $Pt(B,w,k)$.

If $j>i$, $v_j$ is a descendant of $v_i$ and hence by T12, $v_j$ is to the left of all descendants of B at the same level.

Therefore, $v_j$ cannot be a node in $Pt(B,w,k)$.

With similar argument, we can also prove that if $v_j$ is a node on a path from $A$ to any $l^{\text{'}}$ in $y$, $v_j$ cannot be a node in $Pt(B,w,k)$.

This completes the proof of Proposition 2.62.

Theorem 2.63. Let $Pt(S,z,h)$ be a parse tree for $CFG,G=(V, \mathsf{\Sigma }, R, S)$ and $Pt(A,w,k)$ be the largest subtree of $Pt(S,z,h)$ rooted at $A$ such that $z=xwy$ where $x,y,w,z\in {\mathsf{\Sigma }}^{*}$.

If $Pt(A,w,k)$ is replaced by another parse tree $Pt(A,w^{\text{'}},k^{\text{'}})$, to form a new tree $Pt(S,z^{\text{'}},h^{\text{'}})$, then $z^{\text{'}}=x{w}^{\text{'}}y$.

Proof. 

By Proposition 2.62, we can write $z^{\text{'}}=x^{\text{'}}{w}^{\text{'}}{y}^{\text{'}}$ for some $x^{\text{'}}$, $y^{\text{'}}\in {\mathsf{\Sigma }}^{*}$ because $Pt(A,w^{\text{'}},k^{\text{'}})$ is a subtree of $Pt(S,z^{\text{'}},h^{\text{'}})$.

See Figure 2.13 below.

Figure 2.13. Caption.

Figure 2.13. Caption.

Let $l$ be a leaf in $x$.

By T8, there is a unique path from $S$ to $l$ in $Pt(S,z,h)$.

Let’s call this path $(S,v_1,v_2,\dots v_i\dots v_n,l)$ where $v_i$ is at the same level of $A$.

By Proposition 2.62, $(S,v_1,v_2,\dots v_i\dots v_n,l)$ is not affected by the removal of $Pt(A,w,k)$ and in addition, $v_i$ is to the left of $A$.

Therefore, $(S,v_1,v_2,\dots v_i\dots v_n,l)$ remains a path in the new $Pt(S,z^{\mathrm{\text{'}}},h^{\mathrm{\text{'}}})$.

Therefore, $l$ is a leaf in $z^{\text{'}}$.

$l$ is not in $w^{\text{'}}$ because $w^{\text{'}}$ consists of all the leaves created from the addition of $Pt(A,w^{\text{'}},k^{\text{'}})$.

If $l$ is in $y^{\text{'}}$, the ancestor of $l$ at the level of $A$, namely $v_i$, must be to the right of $A$ which contradicts what we have shown above and that is $v_i$ is to the left of $A$.

Therefore, $l$ cannot be in $y^{\text{'}}$.

Therefore, $l$ is in $x^{\text{'}}$.

Therefore, $x⊏x^{\text{'}}$.

Conversely, if $l^{\text{'}}$ is a leaf in $x^{\text{'}}$,

by T8, there is a unique path from $S$ to $l^{\text{'}}$ in $Pt(S,z^{\text{'}},h^{\text{'}})$.

Let’s call this path $(S,v_1^{\mathrm{\text{'}}},v_2^{\mathrm{\text{'}}},\dots v_i^{\mathrm{\text{'}}}\dots v_n^{\mathrm{\text{'}}},l^{\mathrm{\text{'}}})$ where $v_i^{\mathrm{\text{'}}}$ and $A$ are at the same level.

By Proposition 2.62, $v_1^{\mathrm{\text{'}}},v_2^{\mathrm{\text{'}}},\dots v_i^{\mathrm{\text{'}}}\dots v_n^{\mathrm{\text{'}}},l^{\mathrm{\text{'}}}$ are not in $Pt(A,w^{\mathrm{\text{'}}},k^{\mathrm{\text{'}}})$ and $v_i^{\mathrm{\text{'}}}$ is to the left of $A$.

These nodes must have come from $Pt(S,z,h)$.

In addition, they are not in $Pt(A,w,k)$ either because if they were, they would have been eliminated by the replacement of $Pt(A,w,k)$.

Therefore, $l^{\text{'}}$ is not in $w$.

If $l^{\text{'}}$ is in $y$, $v_i^{\text{'}}$ would be to the right of $A$, which contradicts what we have shown above and that is $v_i^{\text{'}}$ is to the left of $A$.

Therefore, $l^{\text{'}}$ cannot be in $y$.

Therefore, $l^{\text{'}}$ is in $x$.

Therefore, $x^{\text{'}}⊏x$.

Therefore, $x=x^{\text{'}}$.

With similar argument, we can also prove that $y=y^{\text{'}}$.

This completes the proof of Theorem 2.63.

Theorem 2.64A (The Pumping Lemma for 

$\mathit{C}\mathit{F}\mathit{L}$s). Let $L$ be a $CFL$.

$\exists p>0$ such that if $z\in L$ and $\left|z\right|\ge p$, then

$z=uvwxy$ for some $u,v,w,x,y\in {\mathsf{\Sigma }}^{*}$ with the following conditions satisfied:

(i) $\forall i\ge 0$, $u{v}^{i}w{x}^{i}y\in L$

(ii) $vx\ne ϵ$

(iii) $\left|vwx\right|\le p$

Proof. 

By Theorem 2.37, there exists a $CFG$, $G=(V, \mathsf{\Sigma }, R, S)$ in Chomsky Normal Form such that $L=L\left(G\right)$. Let $p=2^m$ where $m=\left|V\right|=$ the number of variables in $V$.

If $z\in L$, $z\in L\left(G\right)$.

$S\stackrel{\mathrm{*}}{\Rightarrow }z$By Theorem 2.33, there is a parse tree for $G$ with root $S$ and yield $z$.

Let this parse tree be represented by $Pt(S,z,h)$ where $h$ is the height of the tree.

By Theorem 2.61, $\left|z\right|\le 2^{h-1}$.

If $\left|z\right|\ge p=2^m$, $2^m\le 2^{h-1}$.

$m\le h-1$.

$h\ge m+1$.

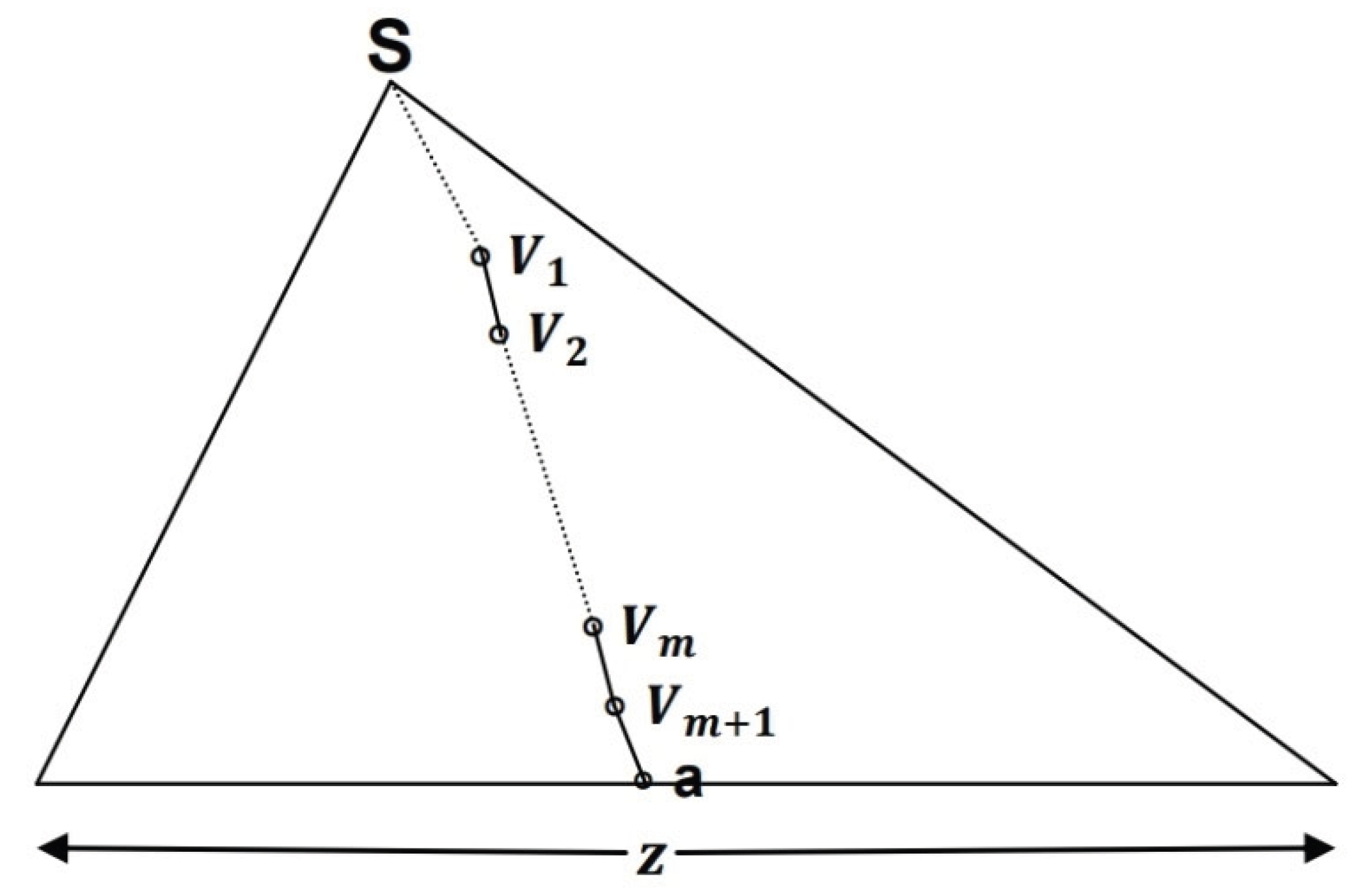
By T9, $\exists$ a path from $S$ to $a$ where $a$ is a leaf in $z$ such that the length of this path is equal to $h$.

(Note that this is the longest path in the tree.)

Since $h\ge m+1$, there are at least $m+2$ nodes on this path.

Let $(V_1,V_2,\dots \dots V_m,V_{m+1},a)$ be the lowest portion of this path where

$V_1,V_2,\dots \dots V_m,V_{m+1}\in V$.

See Figure 2.14 below.

Figure 2.13. Caption.

Figure 2.13. Caption.

Note that this is the longest path from $V_1$ to a leaf.

Since $m=\left|V\right|$, by the pigeonhole principle, $\exists 1\le i<j\le m+1$ such that $V_i=V_j$.

Let $Pt(V_j,w,h_j)$ be the largest subtree rooted at $V_j$ and $Pt(V_i,w^{\text{'}},h_i)$ be the largest subtree rooted at $V_i$.

See Figure 2.15 below.

Figure 2.13. Caption.

Figure 2.13. Caption.

As can be seen in Figure 2.15, $Pt(V_j,w,h_j)$ is a subtree of $Pt(V_i,w^{\text{'}},h_i)$ which in turn is a subtree of the parent tree $Pt(S,z,h)$.

By Proposition 2.62, we can write the yield of $Pt(V_i,w^{\text{'}},h_i)$ as $vwx$ where $v,x\in {\mathsf{\Sigma }}^{*}$ and the yield of $Pt(S,z,h)$ as $uvwxy$ where $u,y\in {\mathsf{\Sigma }}^{*}$.

That is, $z=uvwxy$ and $w^{\mathrm{\text{'}}}=vwx$.

Since $V_i=V_j$, we can replace $Pt(V_j,w,h_j)$ by $Pt(V_i,vwx,h_i)$ to form a new parse tree.

By Theorem 2.63, the yield of this new parse tree is $uvvwxxy=u{v}^{2}w{x}^{2}y$.

By repeated application of this replacement procedure, we can create new parse trees $Pt(S,u{v}^{i}w{x}^{i}y,k_i)$ for $i\ge 2$.

By Theorem 2.33, $S\stackrel{\mathrm{*}}{\Rightarrow }u{v}^{i}w{x}^{i}y$ for $i\ge 2$.

If we replace $Pt(V_i,vwx,h_i)$ by $Pt(V_j,w,h_j)$, we obtain a new parse tree $Pt(S,uwy,k_0)$.

Again by Theorem 2.33, $S\stackrel{*}{\Rightarrow }uwy$.

Or $S\stackrel{\mathrm{*}}{\Rightarrow }u{v}^{0}w{x}^{0}y$.

When $i=1$, $z=uvwxy$ and we know $S\stackrel{\mathrm{*}}{\Rightarrow }z$.

Therefore, $S\stackrel{\mathrm{*}}{\Rightarrow }u{v}^{i}w{x}^{i}y$ for $i\ge 0$.

Therefore, $u{v}^{i}w{x}^{i}y\in L$ for $i\ge 0$.

This proves Condition (i) is satisfied.

The only three forms of rules in a $CFG$ in $CNF$ are:

$A⟶BC$ where $AϵV$ and $B,CϵV\backslash \left\{S\right\}$

$A⟶a$ where $aϵ\mathsf{\Sigma }$

$S⟶ϵ$ where $S=$ Start Variable

$a$ and $ϵ$ cannot be the children of $V_i$ because $a$ and $ϵ$ cannot have descendant $V_j$.

Let $B, C\in V$ be the two children of $V_i$.

Let $Pt(B,b,h_b)$ & $Pt(C,c,h_c)$ be the largest sub parse tree with yields $b,c\in {\mathsf{\Sigma }}^{*}$ and roots $B, C\in V$.

Using similar argument as used in the proof Theorem 2.33, we can show that $bc=vwx$.

By T7, $V_j$ is either a descendant of $B$ or $C$.

If $V_j$ is a descendant of $B$, $Pt(V_j,w,h_j)$ is a subtree of $Pt(B,b,h_b)$.

By Proposition 2.62, $w⊏b$ and $b=w_{1}w{w}_2$ for some $w_1$, $w_2\in {\mathsf{\Sigma }}^{*}$.

Therefore, $vwx=bc=w_{1}w{w}_{2}c$.

$v=w_1$ & $x=w_{2}c$.

Since $C$ and all its descendants are not $S$, $c$ cannot be $ϵ$.

$x\ne ϵ$.

Therefore, $vx\ne ϵ$.

If $V_j$ is a descendant of $C$, with similar argument, we can show that $v\ne ϵ$ and hence $vx\ne ϵ$.

In all cases, Condition (ii) is satisfied.

Since $V_i$ is a descendant of $V_1$, $Pt(V_i,vwx,h_i)$ is a subtree of $Pt(V_1,z_1,h_1)$.

By Proposition 2.62, $vwx⊏z_1$.

$\left|vwx\right|\le \left|z_1\right|$.

By Theorem 2.61, $\left|z_1\right|\le 2^{h_1-1}$.

Therefore, $\left|vwx\right|\le 2^{h_1-1}$.

Since $(V_1,V_2,\dots \dots V_m,V_{m+1},a)$ is the longest path from $V_1$ to a leaf,

$h_1=$ the length of $\left(V_1,V_2,\dots \dots V_m,V_{m+1},a\right)=m+1$.

Therefore, $\left|vwx\right|\le 2^{m+1-1}=2^m=p$.

Therefore, Condition (iii) is satisfied.

This completes the proof of Theorem 2.64A.

Theorem 2.64B Pumping Lemma (contra positive form). 

$~\left(S\right)⟹L$ is not context free where

$~\left(S\right)$ is equivalent to:

$\forall p\ge 1, \exists s\in L$ with $\left|s\right|\ge p$ such that whenever $s=uvwxy$, at least one of the conditions (i), (ii), or (iii) cannot be satisfied.

The contra positive form of the Pumping Lemma is used to prove a language is not context free. The general strategy is to find an $s\in L$ with $\left|s\right|\ge p$ for any given $p\ge 1$ so that whenever $s$ is broken into $s=uvwxy$, at least one of the conditions of (i), (ii), or (iii) must be false. This can be usually accomplished by showing one of the following:

(1) Condition (i) alone is false.

(2) Condition (iii) $⟹~$ Condition (i)

(3) (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

Example 2.65. 

Show that $L=\left\{a^n{b}^n{c}^n|n\ge 0\right\}$ is not $CFL$.

$\forall p\ge 1$, construct $s=a^p{b}^p{c}^p$.

See figure below.

$\mathit{S}=\underset{\mathit{p}}{\underbrace{\mathit{a}\dots \dots \dots \mathit{a}}}\underset{\mathit{p}}{\underbrace{\mathit{b}\dots \dots \dots \mathit{b}}}\underset{\mathit{p}}{\underbrace{\mathit{c}\dots \dots \dots \mathit{c}}}$

$s\in L$ and $\left|s\right|\ge p$.

Assume $s=uvwxy$.

If Condition (iii) is true, $\left|vwx\right|\le p$.

There are 5 cases for consideration.

(1) $vwx=a^n$ where $n\le p$(2) $vwx=a^n{b}^m$ where $n\le p\&m\le p$(3) $vwx=b^n$ where $n\le p$(4) $vwx=b^n{c}^m$ where $n\le p\&m\le p$(5) $vwx=c^n$ where $n\le p$For case (1), $vwx=a^n⟹v^{2}w{x}^2=a^{n^{\mathrm{\text{'}}}}$.

If Condition (ii) is true, $vx\ne ϵ$.

Either $v\ne ϵ$ or $x\ne ϵ$.

This means $n^{\text{'}}>n$.

$s=uvwxy=u{a}^{n}y$ contains the same number of $a\mathrm{’}s$, $b\mathrm{’}s$ and $c\mathrm{’}s$.

$u{v}^{2}w{x}^{2}y=u{a}^{n^{\text{'}}}y$ contains more $a’s$ than $s$ and therefore has more $a’s$ than $b’s$ and $c’s$ in itself.

Therefore, $u{v}^{2}w{x}^{2}y$ is not in $L$.

Therefore, (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

Similar arguments can be made in cases (3) and (5) to arrive at the same conclusion as in case (1).

For case (2), $s=uvwxy=u{a}^n{b}^{m}y$ contains the same number of $a’s$, $b’s$and $c’s$.

If Condition (ii) is true, $vx\ne ϵ$.

Either $v\ne ϵ$ or $x\ne ϵ$.

$vwx=a^n{b}^m⟹v^{2}w{x}^2$ will increase the number of $a’s$ or the number of $b’s$ or both.

$u{v}^{2}w{x}^{2}y$ will have more $a\mathrm{’}s$ than $c\mathrm{’}s$ or more $b\mathrm{’}s$ than $c\mathrm{’}s$.

Either way, $u{v}^{2}w{x}^{2}y$ is not in $L$.

Therefore, (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

Similar arguments can be made in cases (4) to arrive at the same conclusion as in case (2).

Combining all 5 cases, we conclude (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

By Theorem 2.64B, $L$ is not context free.

Example 2.66. 

Show that $L=\left\{w\#w|w\in {\left\{\mathrm{0,1}\right\}}^{*}\right\}$ is not $CFL$.

$\forall p\ge 1$, construct $s=0^p{1}^p\#0^p{1}^p$.

$s\in L$ and $\left|s\right|=4p+1>p$.

Assume $s=uvwxy$.

If both Conditions (ii) & (iii) are true, we have the following cases to consider.

(1) $vwx$is to the left of #

See figure below.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$#$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$Condition (3) $⟹\left|vwx\right|\le p$ which makes it possible for $vwx$ to be contained in $0^p{1}^p$.

Since Condition (ii) is true, $vx\ne ϵ$.

Pumping up to $u{v}^{2}w{x}^{2}y$ will increase the number of symbols on the left of the # sign while not changing the symbols on the right.

This makes it impossible for $u{v}^{2}w{x}^{2}y$ to remain in $L$.

Therefore, (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

(2) $vwx$is to the right of #

Similar argument can be made to lead to same conclusion as in (1).

(3) $vwx$ contains the # sign

(i) $w$ contains # (See figure below.)

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$#$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}⇥⇤\mathit{w}⇥⇤\mathit{x}⇥$Condition (iii) $⟹\left|vwx\right|\le p⟹\left(\begin{array}{c}v contains only 1^{\mathrm{\text{'}}}s if v\ne ϵ and \\ x contains only 0^{\mathrm{\text{'}}}s if x\ne ϵ\end{array}\right)$.

Condition (ii) $⟹vx\ne ϵ⟹$ one of $v$ or $x$ is not $ϵ$.

Pumping down $⟹uwy=0^p{1}^i\#0^j{1}^p$.

$v\ne ϵ⟹i<p⟹0^p{1}^i\#0^j{1}^p\notin L⟹uwy\notin L$.

$x\ne ϵ⟹j<p⟹0^p{1}^i\#0^j{1}^p\notin L⟹uwy\notin L$.

Therefore, (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

(ii) $w$ is to the left of # (See figure below.)

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$#$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}⇥⇤\mathit{x}⇥$Since $vwx$ contains the # sign, $x\ne ϵ$.

Therefore, $x$ contains #. (See figure above.)

Pumping down will eliminate the # sign making it impossible for $uwy$ to remain in $L$.

Therefore, $uwy$ is not in $L$ and Condition (i) cannot be satisfied.

(iii) $w$ is to the right of #

Similar argument will lead to the same conclusion as in case 3(ii) above.

Combining all possible cases, (Condition (ii) and Condition (iii))$⟹~$ Condition (i).

By Theorem 2.64B, $L$ is not context free.

Example 2.67. 

Show that the intersection of two $CFL$s may not be a $CFL$.

Let $L_1=\left\{a^n{b}^n{c}^m|n,m\in \mathbb{N}\right\}$

$L_2=\left\{a^n{b}^m{c}^m|n,m\in \mathbb{N}\right\}$

$L_1\cap L_2=\left\{a^n{b}^n{c}^n|n\in \mathbb{N}\right\}$, which is not context free as shown in Example 2.65.

$L_1$ can be generated by the following $CFG$ rules:

$S⟶TD$

$T⟶aTb|ϵ$

$D⟶Dc|ϵ$

$L_2$ can be generated by the following $CFG$ rules:

$S⟶AB$

$A⟶Aa|ϵ$

$B⟶bBc|ϵ$Therefore, $L_1$ and $L_2$ are $CFL$s.

Example 2.68. 

Show that Show that $L=\left\{ww|w\in {\left\{\mathrm{0,1}\right\}}^{*}\right\}$ is not $CFL$.

$\forall p\ge 1$, construct $s=0^p{1}^p{0}^p{1}^p$.

$s\in L$ and $\left|s\right|=4p>p$.

Assume $s=uvwxy$ for some $u,v,w,x,y\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{*}}$.

Claim 1. If $i<p$, the strings $0^i{1}^p{0}^p{1}^p,0^p{1}^i{0}^p{1}^p,0^p{1}^p{0}^i{1}^p,0^p{1}^p{0}^p{1}^i$ are not in $L$.

Assume for contradiction that $0^i{1}^p{0}^p{1}^p\in L$.

$\exists r\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{*}}$ such that $0^i{1}^p{0}^p{1}^p=rr$.

Therefore, $\left|rr\right|=\left(i+p\right)+(p+p)$

$\left|r\right|={\displaystyle \frac{\left(i+p\right)+(p+p)}{2}}$Since $\left|r\right|$ is the arithmetic mean of $\left(i+p\right)$ and $(p+p)$ and $\left(i+p\right)<(p+p)$,

$\left|r\right|>i+p$ and $\left|r\right|<p+p$.

Therefore, $\left|r\right|\ge i+p+1$.

The leftmost $i+p+1$ symbols of $0^i{1}^p{0}^p{1}^p$ form the substring $0^i{1}^{p}0$.

The leftmost $\left|r\right|$ symbols of $0^i{1}^p{0}^p{1}^p$ form the substring $r$.

Since $\left|r\right|\ge i+p+1$, $0^i{1}^{p}0⊏r$.

Therefore, $10⊏0^i{1}^{p}0⊏r$.

Similarly, the rightmost 2$p$ symbols of $0^i{1}^p{0}^p{1}^p$ form the substring $0^p{1}^p$ and the rightmost $\left|r\right|$ symbols of $0^i{1}^p{0}^p{1}^p$ form the substring $r$.

Since $\left|r\right|<p+p$, $r⊏0^p{1}^p$.

Therefore, $10⊏r⊏0^p{1}^p$.

This is a contradiction because $10$ cannot be a substring of $0^p{1}^p$.

Therefore, $0^i{1}^p{0}^p{1}^p\notin L$.

Similar arguments can be made to show $0^p{1}^i{0}^p{1}^p,0^p{1}^p{0}^i{1}^p,0^p{1}^p{0}^p{1}^i$ are not in $L$.

Claim 2.

If at least one of $i,j$ is less than $p$, the strings $0^i{1}^j{0}^p{1}^p,0^p{1}^i{0}^j{1}^p,0^p{1}^p{0}^i{1}^j$ are not in $L$.

Assume for contradiction $0^i{1}^j{0}^p{1}^p$ is in $L$.

$0^i{1}^j{0}^p{1}^p=rr$ for some $r\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{*}}$.

Therefore, $\left|rr\right|=\left(i+j\right)+(p+p)$

$\left|r\right|={\displaystyle \frac{\left(i+j\right)+(p+p)}{2}}$Since $\left|r\right|$ is the arithmetic mean of $\left(i+j\right)$ and $(p+p)$ and $\left(i+j\right)<(p+p)$,

$\left|r\right|>i+j$ and $\left|r\right|<p+p$.

Therefore, $\left|r\right|\ge i+j+1$.

The leftmost $i+j+1$ symbols of $0^i{1}^j{0}^p{1}^p$ form the substring $0^i{1}^{j}0$.

The leftmost $\left|r\right|$ symbols of $0^i{1}^j{0}^p{1}^p$ form the substring $r$.

Since $\left|r\right|\ge i+j+1$, $0^i{1}^{j}0⊏r$.

Therefore, $10⊏0^i{1}^{j}0⊏r$.

Similarly, the rightmost 2$p$ symbols of $0^i{1}^j{0}^p{1}^p$ form the substring $0^p{1}^p$ and the rightmost $\left|r\right|$ symbols of $0^i{1}^j{0}^p{1}^p$ form the substring $r$.

Since $\left|r\right|<p+p$, $r⊏0^p{1}^p$.

Since $10⊏r$ & $r⊏0^p{1}^p$, $10⊏0^p{1}^p$.

This is a contradiction because $10$ cannot be a substring of $0^p{1}^p$.

Therefore, $0^i{1}^j{0}^p{1}^p\notin L$.

Similar arguments can be made to show that $0^p{1}^i{0}^j{1}^p,0^p{1}^p{0}^i{1}^j$ are not in $L$.

Returning to the proof that $L$ is not $CFL$, we assume both Condition (ii) and Condition (iii) are true.

Since $\left|vwx\right|\le p$, we have 7 cases to consider.

(1) $vwx$ is a substring of the first block of $0^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(2) $vwx$ is a substring of the first block of $1^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(3) $vwx$ is a substring of the second block of $0^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(4) $vwx$ is a substring of the second block of $1^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(5) $vwx$ straddles the first block of $0^p$ and the first block of $1^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(6) $vwx$ straddles the first block of $1^p$ and the second block of $0^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$(7) $vwx$ straddles the second block of $0^p$ and the second block of $1^p$.

$\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}\stackrel{\mathit{p}}{\overbrace{00\dots \dots \dots \dots 00}}\stackrel{\mathit{p}}{\overbrace{11\dots \dots \dots \dots 11}}$

$⇤\mathit{v}\mathit{w}\mathit{x}⇥$

In case (1), $v$ consists of all $0$’s if $v\ne ϵ$ and $x$ consists of all $0$’s if $x\ne ϵ$.

Pumping down would only affect the first block of $0^p$ and not the other 3 blocks.

Therefore, $uwy=0^i{1}^p{0}^p{1}^p$.

Since $vx\ne ϵ$ by Condition (ii), one of $v$ and $x$ is not $ϵ$.

Pumping down would reduce the number of $0$’s in the first block of $0^p$.

Therefore, $i<p$.

By Claim 1, $u{v}^{0}w{x}^{0}y=uwy=0^i{1}^p{0}^p{1}^p\notin L$.

Therefore, Condition (i) is not satisfied.

For cases (2), (3) and (4), similar arguments can be made to lead to the same conclusion as in (1).

For case (5), $\left|vwx\right|\le p$ $⟹$ pumping down can only affect the first and second blocks of symbols.

We can write $uwy=0^i{1}^j{0}^p{1}^p$.

Furthermore, the first symbol of $vwx$ is $0$ and the last symbol of $vwx$ is $1$.

If $v\ne ϵ$, the first symbol of $v$ is $0$.

If $x\ne ϵ$, the last symbol of $x$ is $1$.

Since Condition (ii) is true, $vx\ne ϵ$.

One of $v$ and $x$ is not $ϵ$.

Pumping down will either reduce the number of $0$’s in $0^p$ or the number of $1$’s in $1^p$.

Therefore, either $i<p$ or $j<p$.

By Claim 2, $uwy=0^i{1}^j{0}^p{1}^p$ is not in $L$.

Therefore, Condition (i) is not satisfied.

For cases (6) and (7), similar arguments can be made to lead to the same conclusion as in (5).

Combining all 7 cases, we conclude that

(Condition (ii) and Condition (iii))$⟹~$ Condition (i).

Hence, by Theorem 2.64B, $L$ is not context free.