Bifurcation and Optimal Control Analysis of an HIV/AIDS Model with Saturated Incidence Rate

1. Introduction

The Human Immunodeficiency Virus (HIV) is a virus that attacks the body’s immune system by targeting white blood cells, increasing susceptibility to infections such as tuberculosis and certain cancers, and continues to pose a serious global public health challenge, particularly when transmitted through unprotected sexual intercourse. Acquired Immunodeficiency Syndrome (AIDS) represents the most advanced stage of HIV infection, typically developing after years without treatment [1]. Prevention strategies are essential and include consistent and correct condom use, comprehensive sexual health education, and public education campaigns. Early diagnosis and the timely initiation of antiretroviral therapy (treatment) are crucial to controlling the infection and preventing progression to severe immunodeficiency, opportunistic infections, increased mortality, and reduced quality of life. Globally, an estimated 39.9 million people were living with HIV in 2023, with 1.3 million new cases. Sub-Saharan Africa remains the most affected region, accounting for over two-thirds of the global HIV burden. The global prevalence among adults aged 15-49 is about 0.6%, with women and girls representing 53% of all HIV cases [2]. Despite significant progress in expanding access to antiretroviral therapy (ART), which now reaches 30.7 million people, the HIV epidemic continues to be a major public health issue. Timely screening and widespread ART availability are crucial to reducing transmission and improving health outcomes. The global spread of the HIV/AIDS epidemic has established it as a significant worldwide issue and an increasingly urgent public health challenge. The study of HIV/AIDS transmission dynamics has great attention from both mathematicians and biologists due to the multidimensional crisis, particularly in the health sector. To effectively accelerate HIV/AIDS prevention efforts, it is essential to integrate both behavioral and biomedical control strategies [3].

Due to its ability to provide both short-term and long-term forecasts of HIV and AIDS prevalence, the mathematical modelling approach has become an essential tool in analyzing the transmission and control of HIV/AIDS. There are many models in the literature that describe the dynamics of HIV/AIDS spread using a system of nonlinear differential equations. The model in [4,5,6,7], for example, incorporates behavior control through public education campaigns. These studies concluded that such campaigns, based on the ABC (Abstinence, Be faithful, use Condoms) strategy, can effectively reduce HIV/AIDS transmission. Antiretroviral treatment plays a crucial role in mitigating the spread of diseases such as HIV/AIDS. The model in [7] integrates behavioral intervention through education campaigns with biomedical treatment during the pre-AIDS stage. It introduces compartments for individuals practicing abstinence or faithfulness, condom users, and those under treatment. Thus, a compartmental HIV/AIDS model with seven population groups was developed to assess the impact of education campaigns and pre-AIDS treatment. The study used nonlinear differential equations to analyze stability and derive the effective reproduction number. The study concludes that treatment is the most effective among the three strategies. Furthermore, studies [8,9,10] indicate that well-designed public health education campaigns significantly influence HIV/AIDS transmission dynamics by highlighting their essential role in prevention efforts.

In mathematical epidemiology, disease incidence plays an important role in the study of epidemiological mathematical models. The incidence rate of disease is the rate at which new cases of infection appear in the population due to significant contact between susceptible individuals and infected individuals. Several types of incidence rates have been introduced in classical epidemiological modeling. The incidence rate of the form $\beta SI$ is called the bilinear incidence rate. In contrast, the incidence of the form ${\displaystyle \frac{\beta SI}{N}}$, where$\beta$is the contact rate between susceptible and infected individuals, $S$ is the number of susceptible individuals, $I$ is the number of infectious individuals, and $N$ is the total population, is known as the standard incidence rate [11]. Both types have been widely used in literature [7,8,9,10]. However, there are various reasons to modify these traditional incidence formulations. For instance, if the assumption of homogeneous mixing within the population does not hold, a nonlinear transmission function may be introduced to better reflect heterogeneous mixing and realistic population structures. A more accurate alternative is the saturated incidence rate, expressed as ${\displaystyle \frac{\beta SI}{1+cI }}$, which incorporates the inhibitory effect (c) associated with high levels of infective individuals. To capture the inhibitory effects arising from behavioral changes or the density of infected individuals, neither the mass action incidence nor the standard incidence function is sufficient. The saturated incidence form lies between the bilinear and standard incidence rates in terms of behavioral realism. Several mathematical models have been formulated using saturated functions to represent disease incidence or control measures such as treatment [12,13,14,15,16] and references therein.

Optimal control theory is a powerful tool for designing intervention strategies to minimize infection rates while considering implementation costs in epidemiological models [17,18]. This approach has been widely applied to HIV/AIDS dynamics. For example, Yusuf and Benyah [19] incorporated behavior change and antiretroviral therapy (ART), showing that early ART combined with behavioral interventions reduces HIV incidence and prevalence. Joshi et al. [4] emphasized the impact of information campaigns and awareness-based stratification in reducing HIV transmission. According to Safiel et al. [8], screening individuals unaware of their HIV status and treating identified cases are both effective in reducing the transmission of HIV/AIDS within a population. Building upon this framework, Okosun et al. [9] extended this by including condom use, screening, and treatment in a time-dependent control model. Through the application of optimal control theory and cost-effectiveness analysis, the research highlighted the significant impact of awareness among infectives on disease transmission and associated costs. The findings concluded that the most cost-effective intervention involves the combined implementation of all control strategies. A related study [7] also examined the impact of information campaigns and treatment using optimal control and numerical simulations, confirming treatment as the most cost-effective strategy among those evaluated. The authors suggested incorporating the progression rate from asymptomatic infection to pre-AIDS as a control variable, given its high sensitivity index. Extending this to a co-infection setting, a model in [20,21] incorporated a protected class for HIV/AIDS and pneumonia, and a model in [22] incorporated a protected class and three time-dependent control measures for HIV and Hepatitis B Virus (HBV). The results show that integrating protective classes improves intervention outcomes and resource allocation. Collectively, these studies highlight the value of optimal control and cost-effectiveness analysis in guiding public health strategies to manage the transmission of diseases other than HIV/AIDS [23,24,25,26,27,28,29].

Motivated by the above studies, this study refers to the HIV/AIDS model presented in [7] by adding a screening intervention for the unaware infected individuals and assuming a saturation incidence rate. A deterministic compartmental model is proposed to capture the dynamics of HIV/AIDS transmission, followed by a comprehensive qualitative and quantitative analysis. Specifically, the study establishes the existence and stability of the disease-free and endemic equilibria and investigates the occurrence of bifurcations and their epidemiological implications. The model is further formulated as an optimal control problem by introducing time-dependent control variables representing educational campaigns, screening of unaware infectives, and treatment of aware infectives. The pairwise effectiveness of these controls is analyzed, and the most cost-effective strategy is identified using the Incremental Cost-Effectiveness Ratio (ICER) metrics. The novelty of this study lies in the comprehensive integration of three interventions (educational campaigns, screening, and treatment) into a unified modelling framework with saturated incidence. Additionally, the study evaluates the role of preventive interventions, including antiretroviral therapy, public health campaigns, and condom use, with particular emphasis on education for susceptible individuals, screening for the unaware infected, and treatment for the aware infected. By combining rigorous mathematical analysis with optimal control and cost-effectiveness evaluation, the study provides valuable insights for designing efficient and sustainable interventions for HIV/AIDS control.

This paper is organized as follows: Section 2 describes the formulation of a deterministic model for HIV/AIDS with a saturated incidence rate. In Section 3, we conduct a detailed analysis of the model, including its basic properties, the characterization of equilibrium points, and the derivation of the effective reproduction number. The section further investigates the local and global equilibria, bifurcation phenomena, and sensitivity analysis. In Section 4, the model is extended to an optimal control framework, and Pontryagin’s Maximum Principle is employed to characterize the optimal control strategies. Section 5 presents numerical simulations based on selected parameter values to illustrate the analytical results of the model and includes a cost-effectiveness analysis of the proposed control strategies. Finally, Section 6 concludes the study with a summary of the key findings and potential directions for future research.

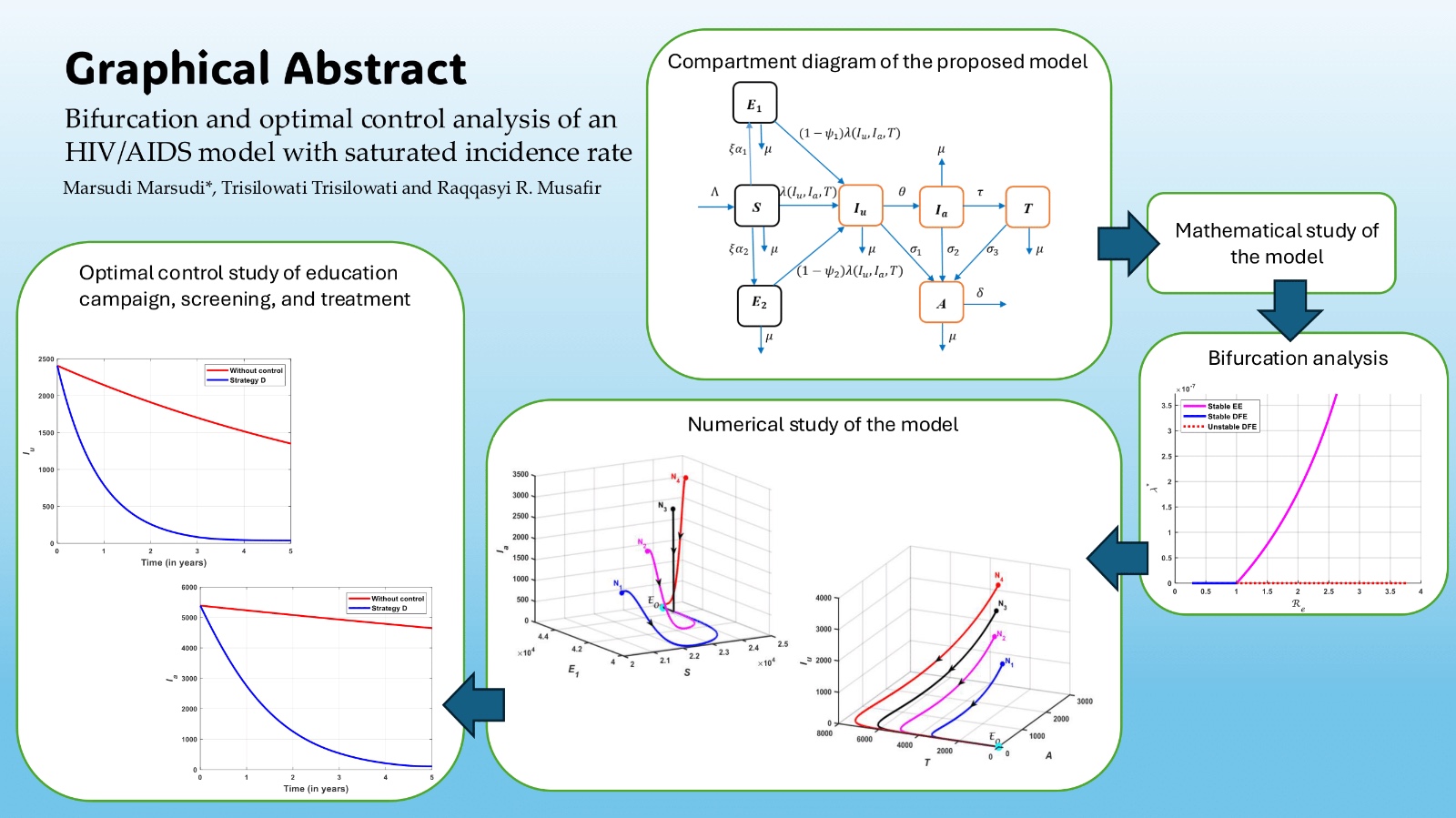
2. Formulation of the Model

In this section, we formulate a mathematical model for the transmission dynamics of HIV/AIDS in a population under the influence of three control strategies with a saturated incidence rate. The total human population$,$ $N$ is divided into seven compartments based on the epidemiological status of individuals, namely: $S$ is the number of susceptible individuals, $E_1$ is the number of educated susceptible individuals who practice abstinence or be faithful (AB behavior), $E_2$ is the number of educated susceptible individuals who use condoms (C behavior), $I_u$is the number of unaware infective individuals, $I_a$is the number of aware (screened) infective individuals, $T$is the number of individuals receiving antiretroviral (ARV) treatment, and $A$is the number of individuals at the critical stage of infection caused by HIV (full-blown AIDS). We consider a sexually active population, and the total population at time $t$is given by

$$N(t)=S(t)+E_1(t)+E_2(t)+I_u(t)+I_a(t)+T(t)+A(t).$$

Educational campaigns result in the division of the susceptible individuals $S$into three subclasses, with a proportion transitioning to $E_1$and $E_2$at the rate ${\alpha }_1$and ${\alpha }_2$ is ${\xi \alpha }_1$and ${\xi \alpha }_2,$ where $\xi$ is rate of educational campaigns. Susceptible individuals are uninfected but at risk of acquiring HIV through contact with three actively infectious classes, $I_u, I_a,$and $T.$ The treated class consists of individuals receiving antiretroviral treatment for the screened infective class. The model assumes that the transmission follows a saturated incidence rate. The number of susceptible individuals $S$ is assumed to increase at a new individuals enter the sexually active population at a constant recruitment rate $\mathsf{\Lambda }.$ Susceptible individuals are reduced by the force of infection

$$\lambda (I_u,I_a,T)={\displaystyle \frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)}{1+\omega (I_u+I_a+T)}},$$

where $\beta$ is the effective contact rate, and ${\eta }_1, {\eta }_1\in (0, 1)$ is the modification parameter relative infectivity of individuals in $I_u$ and $I_a$, respectively. The parameter that represents the psychological or inhibitory effect is denoted by $\omega$. Moreover, susceptible individuals can become educated through education campaigns and move to the compartments$E_1$and$E_2$at a constant rate ${\alpha }_1$and ${\alpha }_2,$respectively. It is further reduced by a natural death at a rate $\mu .$ Therefore, the rate of change of the susceptible individuals with time is given by

$${\displaystyle \frac{dS}{dt}}=\Lambda -\lambda (I_u,I_a,T)S-(\xi {\alpha }_1+\xi {\alpha }_2+\mu )S.$$

(1)

The population of educated susceptible individuals who practice AB behavior increases as susceptible receive educational campaigns at a rate ${\alpha }_1,$and decrease due to the force of infection at the rate $\left(1-{\psi }_1\right)\lambda \left(I_u, I_a, T\right),$ where ${\psi }_1$ represents the effectiveness of these campaigns in promoting AB behavior. Additionally, the population is further reduced by natural death at a rate $\mu .$ Therefore, the rate of change of susceptible individuals practicing AB behavior due to educational campaigns is given by

$${\displaystyle \frac{d{E}_1}{dt}}=\xi {\alpha }_{1}S-(1-{\psi }_1)\lambda (I_u,I_a,T)E_1-\mu E_1.$$

(2)

The population of educated susceptible individuals who practice C behavior increases as susceptible receive educational campaigns at a rate ${\alpha }_2.$ It decreases due to the force of infection at the rate $\left(1-{\psi }_2\right)\lambda \left(I_u, I_a, T\right),$ where ${\psi }_2$ denotes the effectiveness of the campaigns in promoting C behavior. This population also declines due to natural death at a rate $\mu .$ Therefore, the rate of change of susceptible individuals practicing C behavior because of educational campaigns is given by

$${\displaystyle \frac{d{E}_2}{dt}}=\xi {\alpha }_{2}S-(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-\mu E_2.$$

(3)

The population of unaware infected individuals is generated by the force of infections $\lambda \left(I_u, I_a, T\right),\left(1-{\psi }_1\right)\lambda \left(I_u, I_a, T\right),$ and $\left(1-{\psi }_2\right)\lambda \left(I_u, I_a, T\right)$. It decreases due to screening interventions among unaware infected individuals at a rate $\theta ,$ and is further reduced by progression to full-blown AIDS at a rate ${\sigma }_1,$as well as by natural death at a rate $\mu .$ Thus, the rate of change of the unaware infected individuals is given by

$${\displaystyle \frac{d{I}_u}{dt}}=\lambda (I_u,I_a,T)S+(1-{\psi }_1)\lambda (I_u,I_a,T)E_1+(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-(\theta +{\sigma }_1+\mu )I_u.$$

(4)

The population of aware infected individuals increases through screening of unaware infectives at a rate $\theta .$ This population decreases due to the intervention of antiretroviral treatment at a rate $\tau$, and is further reduced by progression to full-blown AIDS at a rate ${\sigma }_2,$ and natural death at a rate $\mu .$ Therefore, the rate of change of the aware individuals over time is given by

$${\displaystyle \frac{d{I}_a}{dt}}=\theta I_u-(\tau +{\sigma }_2+\mu )I_a$$

(5)

The population of treated infective individuals increases due to the intervention of antiretroviral treatment to aware infectives at a rate $\tau .$ This population decreases due to progression to full-blown AIDS at a rate ${\sigma }_3$and natural death at a rate $\mu$ $.$Therefore, the rate of change of the treated infective individuals over time is given by

$${\displaystyle \frac{dT}{dt}}=\tau I_a-({\sigma }_3+\mu )T.$$

(6)

The population of AIDS individuals increases due to the progression of unaware infectives, aware infectives, and treated individuals to the AIDS class, at rates ${\sigma }_1, {\sigma }_2,$and ${\sigma }_3$respectively. This population decreases due to natural death at a rate $\mu$ and further decreased by AIDS-induced death at a rate $\delta .$ Therefore, the rate of change of the full-blown AIDS individuals over time is given by

$${\displaystyle \frac{dA}{dt}}={\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-(\delta +\mu )A.$$

(7)

A Compartment diagram of the HIV/AIDS model incorporating education campaigns, screening, and antiretroviral treatment interventions with saturated incidence rate is presented in Figure 1. Table 1 provides detailed descriptions of each model parameter.

Based on the compartmental diagram, the model describing the dynamics of HIV/AIDS transmission with a saturated incidence rate is represented by a seven-dimensional nonlinear system of ordinary differential equations, as shown in Equation (8).

$$\begin{array}{c}{\displaystyle \frac{dS}{dt}}=\Lambda -\lambda (I_u,I_a,T)S-(\xi {\alpha }_1+\xi {\alpha }_2+\mu )S,\hfill \\ {\displaystyle \frac{d{E}_1}{dt}}=\xi {\alpha }_{1}S-(1-{\psi }_1)\lambda (I_u,I_a,T)E_1-\mu E_1,\hfill \\ {\displaystyle \frac{d{E}_2}{dt}}=\xi {\alpha }_{2}S-(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-\mu E_2,\hfill \\ {\displaystyle \frac{d{I}_u}{dt}}=\lambda (I_u,I_a,T)S+(1-{\psi }_1)\lambda (I_u,I_a,T)E_1+(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-(\theta +{\sigma }_1+\mu )I_u,\hfill \\ {\displaystyle \frac{d{I}_a}{dt}}=\theta I_u-(\tau +{\sigma }_2+\mu )I_a,\hfill \\ {\displaystyle \frac{dT}{dt}}=\tau I_a-({\sigma }_3+\mu )T,\hfill \\ {\displaystyle \frac{dA}{dt}}={\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-(\delta +\mu )A.\hfill \end{array}$$

(8)

with nonnegative initial conditions,

$$\begin{array}{l}S(0)=S^0,\hspace{0.33em}{E}_1(0)=E_1^0,\hspace{0.33em}{E}_2(0)=E_2^0,\hspace{0.33em}{I}_u(0)=I_u^0,\\ I_a(0)=I_a^0,\hspace{0.33em}T(0)=T^0,\hspace{0.33em}A(0)=A^0.\hspace{0.33em}\end{array}$$

(9)

3. Analysis of the Model

3.1. Positivity and Boundedness of Solutions

Lemma 1.

If $S(0),\hspace{0.33em}{E}_1(0),\hspace{0.33em}{E}_2(0),I_u(0),\hspace{0.33em}{I}_a(0),\hspace{0.33em}T(0),\hspace{0.33em}A(0)$ are nonnegative, then the solutions of the model (8) are nonnegative for all $t\ge 0$.

Proof. 

To prove this, we employ a proof by contradiction to demonstrate that each state variable remains non-negative for all $\mathrm{t}\ge 0$. Let us denote

$$m(t)=\min \left\{S(t),\hspace{0.33em}{E}_1(t),\hspace{0.33em}{E}_2(t),I_u(t),\hspace{0.33em}{I}_a(t),\hspace{0.33em}T(t),\hspace{0.33em}A(t)\right\}.$$

Given that all initial conditions are nonnegative, it follows that $m(0)\ge 0$. Without loss of generality, assume$m(t)=S(t)$. We will use proof by contradiction to show that $S(t)\ge 0$ for all $\mathrm{t}\ge 0$. Suppose on the contrary, that this is not the case. Then, there exists a first time $t_1$ such that hold

$$S(t_1-\epsilon )\ge 0,\hspace{0.33em}\hspace{0.33em}S(t_1)=0,\hspace{0.33em}\mathrm{and} S(t_1+\epsilon )<0,$$

(10)

for some positive constant $\epsilon$. From the first equation of model (8) and evaluating at $t_1$, we have

$${\displaystyle \frac{dS(t_1)}{dt}}=\Lambda -\lambda (I_u(t_1),I_a(t_1),T(t_1))S(t_1)-(\xi {\alpha }_1+\xi {\alpha }_2+\mu )S(t_1).$$

Since $\Lambda >0$ and$S(t_1)=0$, this simplifies to

$${\displaystyle \frac{dS(t_1)}{dt}}=\Lambda >0$$

By the Monotonicity Theorem, it follows that $S(t_1+\epsilon )\ge 0$ for all$\epsilon >0$, which contradicts the assumption in Equation (10) that$S(t_1+\epsilon )<0$. Therefore, the contradiction implies that $S(t)\ge 0$ for all $\mathrm{t}\ge 0$Using a similar argument, it can be shown that$E_1(t)\ge 0,\hspace{0.33em}{E}_2(t)\ge 0,$$I_u(t)\ge 0,\hspace{0.33em}{I}_a(t)\ge 0,\hspace{0.33em}T(t)\ge 0,$ and$A(t)\ge 0$ for all $\mathrm{t}\ge 0$. This completes the proof. □

Lemma 2.

Solution of the model (8) with nonnegative initial values are bounded.

Proof. 

Let $(S,E_1,E_2,\hspace{0.17em}{I}_u,\hspace{0.17em}{I}_a,\hspace{0.17em}T,A)\in R_{+}^7$ is an arbitrary non-negative solution of the model (8) with initial conditions given in Equation (9). The total population $N(t)=S(t)+E_1(t)+E_2(t)+I_u(t)+I_a(t)+T(t)+I(t)$. Now adding all the differential equations given in Equation (1) we have got the derivative of the total population$N(t)$to time $t$, we have

$${\displaystyle \frac{dN(t)}{dt}}=\Lambda -\mu N(t)-\delta A(t).$$

Next, disregarding the infections $A(t)$, we have determined that

$${\displaystyle \frac{dN(t)}{dt}}\le \Lambda -\mu N(t).$$

(11)

Thus, for the initial condition $0\le N\le \frac{\Lambda }{\mu }$ , and by applying the Standard Comparison Theorem [30], we get

$$0\le N(t)\le {\displaystyle \frac{\Lambda }{\mu }}.$$

(12)

Therefore, the solutions$S(t),\hspace{0.33em}{E}_1(t),\hspace{0.33em}{E}_2(t),I_u(t),\hspace{0.33em}{I}_a(t),\hspace{0.33em}T(t),\hspace{0.33em}$and$A(t)$ of the model (8) are bounded above by $\Lambda /\mu$. This completes the proof. □

Hence, the biologically feasible region of the HIV/AIDS model (8) is given the following positively invariant region:

$$\Omega =\left\{(S,E_1,E_2,\hspace{0.17em}{I}_u,\hspace{0.17em}{I}_a,\hspace{0.17em}T,A)\in {ℝ}_{+}^7|\hspace{0.33em}0\le S+E_1+E_2+\hspace{0.17em}{I}_u+\hspace{0.17em}{I}_a+\hspace{0.17em}T+A\le {\displaystyle \frac{\Lambda }{\mu }}\right\}.$$

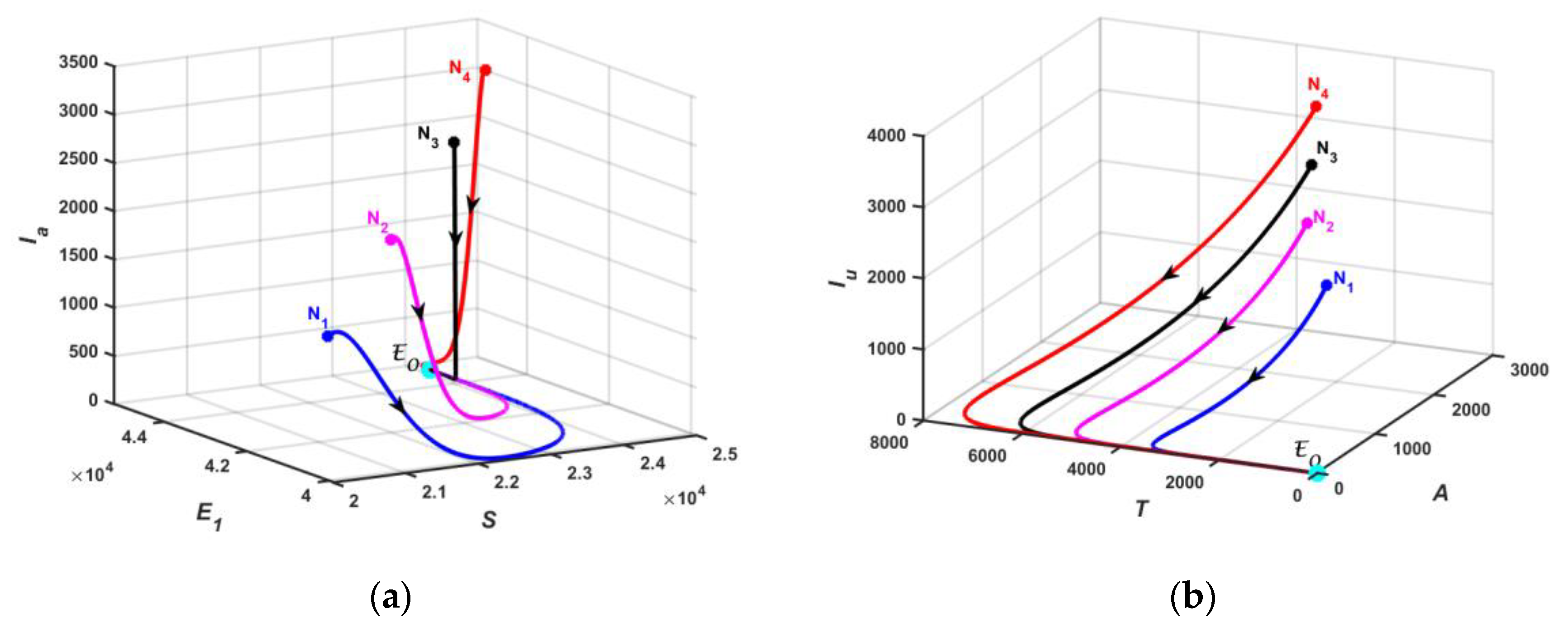
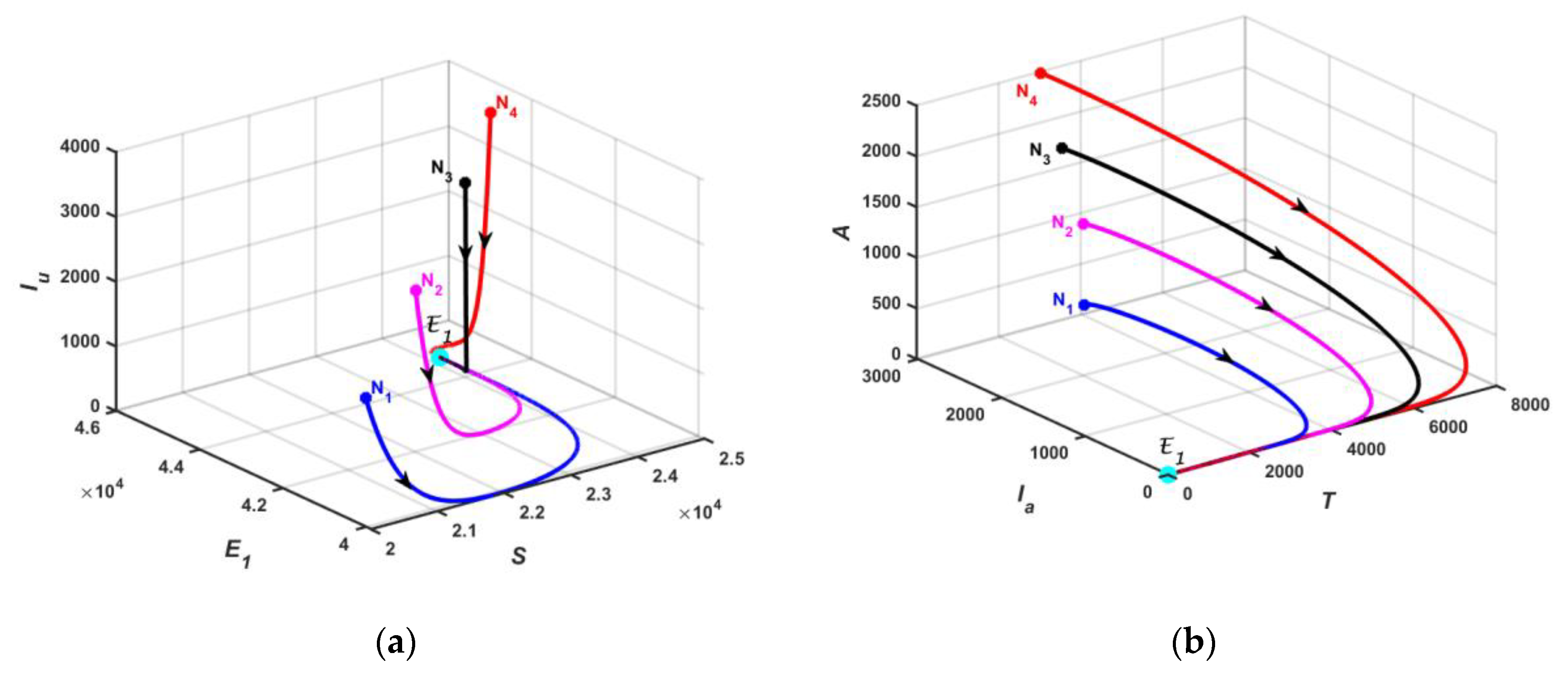
3.2. Existence of Equilibrium Points

To compute the equilibrium solutions of the model (8), we set the right-hand sides of the equations for model (8) to zero.

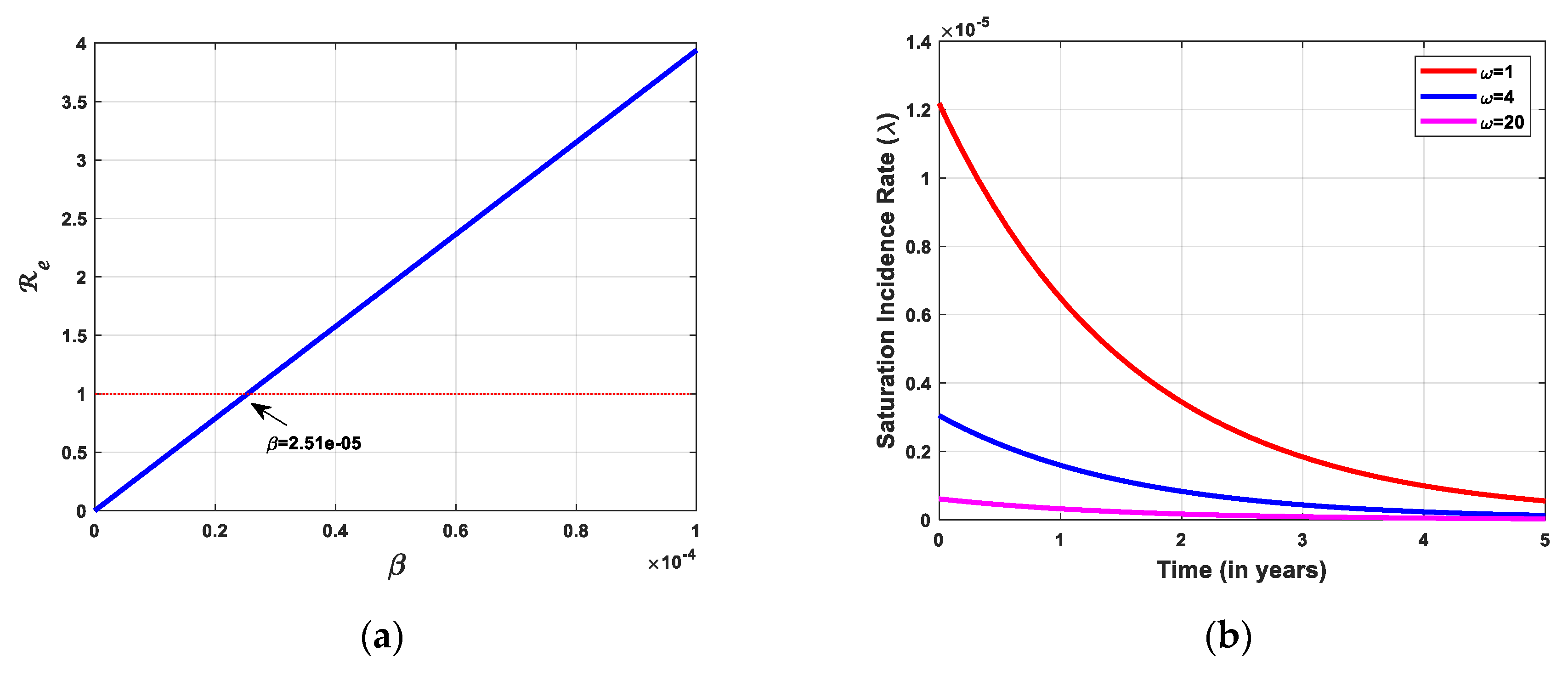
3.2.1. Disease-Free Equilibrium (DFE) and Effective Reproduction Number

The disease-free equilibrium (DFE) of the HIV/AIDS model (8) is given by

$$\begin{array}{l}{\mathcal{E}}_0=\left(S^0,\hspace{0.33em}{E}_1^0,\hspace{0.17em}{E}_2^0,\hspace{0.33em}{I}_u^0,\hspace{0.33em}{I}_a^0,\hspace{0.33em}{T}^0,\hspace{0.33em}{A}^0\right)\\ =\left({\displaystyle \frac{\Lambda }{\xi {\alpha }_1+\xi {\alpha }_2+\mu }},\hspace{0.33em}{\displaystyle \frac{\xi {\alpha }_1\Lambda }{\mu (\xi {\alpha }_1+\xi {\alpha }_2+\mu (\xi {\alpha }_1+\xi {\alpha }_2+\mu )}},\hspace{0.17em}{\displaystyle \frac{\xi {\alpha }_2\Lambda }{\mu (\xi {\alpha }_1+\xi {\alpha }_2+\mu )}},\hspace{0.33em}0,\hspace{0.33em}0,\hspace{0.33em}0,\hspace{0.33em}0\right)\end{array}$$

(13)

To determine the effective reproduction number for model (8), we employ the next-generation matrix method as presented in [31]. Following the approach described in [31,32], we construct the matrix $\mathcal{F}$ and $\mathcal{V}$, which represent the matrix of new infections and transition matrix between the compartments of the system, respectively. Considering the infected compartments $x={\left(I_u,\hspace{0.33em}{I}_a,\hspace{0.33em}T,\hspace{0.33em}A\right)}^T,$ the right-hand side of model (8) can be rewritten by

$${\displaystyle \frac{dx}{dt}}=\mathcal{F}(x)-\mathcal{V}(x)$$

(14)

where

$$\mathcal{F}=\left[\begin{array}{c}\lambda (I_u,I_a,T)S+c_1\lambda (I_u,I_a,T)E_1+c_2(I_u,I_a,T)\lambda E_2\\ 0\\ 0\\ 0\end{array}\right]\hspace{0.33em},\hspace{0.33em}\mathcal{V}=\left[\begin{array}{c}L{I}_u\\ -\theta I_u+M{I}_a\\ -\tau I_a+WT\\ -{\sigma }_1{I}_u-{\sigma }_2{I}_a-{\sigma }_{3}T+PA\end{array}\right].$$

The matrix $F$is the Jacobian matrix of $\mathcal{F}$ evaluated at the disease-free equilibrium ${\mathcal{E}}_0$, and the matrix $V$ is the Jacobian matrix of $\mathcal{V}$ evaluated at the disease-free equilibrium ${\mathcal{E}}_0$, we have

$$F\hspace{0.33em}\hspace{0.17em}=\left[\begin{array}{cccc}\frac{\beta Q\Lambda }{\mu K}& \frac{\beta {\eta }_{1}Q\Lambda }{\mu K}& \frac{\beta {\eta }_{2}Q\Lambda }{\mu K}& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hspace{0.17em}\mathrm{and} V\hspace{0.33em}\hspace{0.17em}=\left[\begin{array}{cccc}L& 0& 0& 0\\ -\theta & M& 0& 0\\ 0& -\tau & W& 0\\ -{\sigma }_1& -{\sigma }_2& -{\sigma }_3& P\end{array}\right].$$

(15)

The next-generation matrix $(F{V}^{-1})$ is

$$F{V}^{-1}\hspace{0.33em}\hspace{0.17em}=\left[\begin{array}{cccc}\frac{\beta \Lambda Q}{\mu KL}+\frac{\beta \Lambda {\eta }_1\theta Q}{\mu KLM}+\frac{\beta \Lambda {\eta }_2\theta \tau Q}{\mu KLMW}& \frac{\beta \Lambda {\eta }_{1}Q}{\mu KM}+\frac{\beta \Lambda {\eta }_2\tau Q}{\mu KMW}& \frac{\beta \Lambda {\eta }_{1}Q}{\mu KW}& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hspace{0.17em}$$

where

$$\begin{gathered} K=\xi {\alpha }_1+\xi {\alpha }_2+\mu ,\hspace{0.33em}L=\theta +{\sigma }_1+\mu ,\hspace{0.33em}M=\tau +{\sigma }_2+\mu ,\hspace{0.33em}W={\sigma }_3+\hspace{0.33em}\mu ,\hspace{0.33em}P=\delta +\mu ,\hspace{0.33em}{c}_1=1-{\psi }_1,\hspace{0.33em}{c}_2=1-{\psi }_2, \\ Q=c_1\xi {\alpha }_1+c_2\xi {\alpha }_2+\mu . \end{gathered}$$

Hence, the effective reproduction number of model (8) is defined as the maximum of the absolute values of the eigenvalues of the next-generation matrix, $F{V}^{-1}$ given by

$${\mathcal{R}}_e={\displaystyle \frac{\beta \Lambda Q}{\mu KL}}+{\displaystyle \frac{\beta \Lambda {\eta }_1\theta Q}{\mu KLM}}+{\displaystyle \frac{\beta \Lambda {\eta }_2\theta \tau Q}{\mu KLMW}}={\mathcal{R}}_{I_u}+{\mathcal{R}}_{I_a}+{\mathcal{R}}_T,$$

(16)

where ${\mathcal{R}}_{I_u}=\frac{\beta \Lambda Q}{\mu KL},\hspace{0.33em}{\mathcal{R}}_{I_a}=\frac{\beta \Lambda Q{\eta }_1\theta }{\mu KLM},\hspace{0.33em}$ and ${\mathcal{R}}_T=\frac{\beta \Lambda Q{\eta }_2\theta \tau }{\mu KLMW}$. Here, ${\mathcal{R}}_{I_u}$ is the contribution to the reproduction number with intervention by unaware infective individuals $I_u$, ${\mathcal{R}}_{I_a}$ is the contribution to the reproduction number with intervention by aware (screened) infective individuals $I_a$, and ${\mathcal{R}}_T$ is the contribution to the reproduction number with treated individuals T.

When education campaigns, screening, and treatment are implemented to control and eradicate the disease, the effective reproduction number represents the average number of new infections generated by a single HIV-infected individual in a susceptible population, under the influence of these control strategies.

3.2.2. Existence of Endemic Equilibrium

In this subsection, we will find conditions for the existence of an endemic equilibrium (EE) for the model (8). Let's determine the effective reproduction number. The equilibrium of model (8) and its stability denote an arbitrary endemic equilibrium of model (8). Solving the equilibrium conditions of the model (8) at a steady state gives

$$\begin{array}{l}{S}^{*}={\displaystyle \frac{\Lambda }{{\lambda }^{*}+K}},\hspace{0.33em}{E}_1^{*}={\displaystyle \frac{\xi {\alpha }_1\Lambda }{(c_1{\lambda }^{*}+\mu )({\lambda }^{*}+K)}},\hspace{0.33em}{E}_2^{*}={\displaystyle \frac{\xi {\alpha }_2\Lambda }{(c_2{\lambda }^{*}+\mu )({\lambda }^{*}+K)}},\\ I_u^{*}={\displaystyle \frac{{\lambda }^{*}\Lambda }{L({\lambda }^{*}+K)}}+{\displaystyle \frac{c_1{\lambda }^{*}\xi {\alpha }_1\Lambda }{L(c_1{\lambda }^{*}+\mu )({\lambda }^{*}+K)}}+{\displaystyle \frac{c_2{\lambda }^{*}\xi {\alpha }_2\Lambda }{L(c_2{\lambda }^{*}+\mu )({\lambda }^{*}+K)}},\\ I_a^{*}=y_1{I}_u^{*},\hspace{0.33em}{T}^{*}=y_2{I}_u^{*},\hspace{0.33em}{A}^{*}=y_3{I}_u^{*},\hspace{0.33em}\end{array}$$

(17)

where $y_1=\frac{\theta }{M},\hspace{0.33em}{y}_2=\frac{\theta \tau }{MW},\hspace{0.33em}{y}_3=\frac{{\sigma }_1+{\sigma }_2{y}_1+{\sigma }_3{y}_2}{P},$and

$${\lambda }^{*}={\displaystyle \frac{\beta (I_u^{*}+{\eta }_2{I}_a^{*}+{\eta }_3{T}^{*})}{1+\omega (I_u^{*}+I_a^{*}+T^{*})}}$$

(18)

Substituting the value of $I_u^{*},\hspace{0.33em}{I}_a^{*},\hspace{0.33em}{T}^{*}$ in (17) into (18), we obtain

$${\lambda }^{*}(a_3{\lambda }^{*3}+a_2{\lambda }^{*2}+a_1{\lambda }^{*}+a_0)=0,$$

(19)

where

$$\begin{array}{l}{a}_3=c_1{c}_2[\Lambda \omega (1+y_1+y_2)+L],\\ a_2=[\Lambda \omega (c_1{c}_2\xi ({\alpha }_1+{\alpha }_2)+ (c_1+c_2)\mu )]\hspace{0.33em}(1+y_1+y_2)-\Lambda c_1{c}_2\beta (1+{\eta }_1{y}_1+{\eta }_2{y}_2)\\ +L[\mu (c_1+c_2)+Q{c}_1{c}_2],\end{array}$$

$$\begin{array}{l}{a}_1=\Lambda \omega \mu Q(1+y_1+y_2)+L\mu [K(c_1+c_2)+\mu ]-\Lambda \beta [c_1{c}_2\xi ({\alpha }_1+{\alpha }_2)+(c_1+c_2)\mu ](1+{\eta }_1{y}_1+{\eta }_2{y}_2),\\ a_0=LK{\mu }^2(1-{\mathcal{R}}_e).\end{array}$$

From Equation (19), one solution is ${\lambda }^{*}=0$ corresponds to the disease-free equilibrium. Another solution is given by the roots of a cubic polynomial (20),

$$a_3{\lambda }^{*3}+a_2{\lambda }^{*2}+a_1{\lambda }^{*}+a_0=0,$$

(20)

which is related to situations where the HIV disease persists. For the endemic equilibrium to exist, ${\lambda }^{*}$ is a positive real root of the cubic polynomial (20). It is clear that $a_3>0$ (since all model parameters are nonnegative) and $a_0<0$ when ${\mathcal{R}}_e>1$. Thus, the number of possible positive real roots of the cubic polynomial (20) depends on the signs of $a_1$ and${ a}_2$. By applying Descarte’s Rule of Signs to the cubic polynomial in Equation (20), the number of positive real roots can be determined. In addition, according to [7], using Cardan’s formula, the polynomial (13) has one positive real root and a pair of complex conjugate roots if the discriminant$\Delta =r^2+q^3>0$, given by

$${\lambda }_1^{*}=u+v-{\displaystyle \frac{a_2}{3a_3}},\hspace{0.33em}{\lambda }_2^{*}=-{\displaystyle \frac{u+v}{2}}-{\displaystyle \frac{a_2}{3a_3}}+{\displaystyle \frac{i\sqrt{3}(u-v)}{2}},\hspace{0.33em}\hspace{0.17em}{\lambda }_3^{*}=-{\displaystyle \frac{u+v}{2}}-{\displaystyle \frac{a_2}{3a_3}}-{\displaystyle \frac{i\sqrt{3}(u-v)}{2}},$$

(21)

where $u=\sqrt[3]{r+\sqrt{r^2+q^3}},\hspace{0.33em}v=\sqrt[3]{r-\sqrt{r^2+q^3}},\hspace{0.33em}$and $q=\frac{3a_3{a}_1-a_2^2}{9a_3^2},\hspace{0.33em}r=\frac{9a_3{a}_2{a}_1-27a_3^2{a}_0-2a_2^2}{54a_3^2}.$

Furthermore, if Equation (20) has a single positive real root, then the components of the endemic equilibrium ${\mathcal{E}}_1=(S^{*},\hspace{0.17em}{E}_1^{*},\hspace{0.17em}{E}_2^{*},I_u^{*},\hspace{0.17em}{I}_a^{*},\hspace{0.17em}{T}^{*},\hspace{0.17em}{A}^{*})$ can be obtained by substituting the value of $\lambda ={\lambda }_1^{*}$ into the expression for each state in Equation (20). This result is summarized in the following lemma.

Lemma 3.

The model (8) has a unique endemic equilibrium ${\mathcal{E}}_1$ whenever ${\mathcal{R}}_e>1$ with $\lambda ={\lambda }_1^{*}$ are the positive real roots of Equation (20).

3.3. Stability Analysis

3.3.1. Local Stability of Disease-Free Equilibrium

Theorem 1.

The disease-free equilibrium of the model (8), ${\mathcal{E}}_0$, is locally asymptotically stable if ${\mathcal{R}}_e<1,$ and unstable if ${\mathcal{R}}_e>1$.

Proof. 

The Jacobian matrix of the model (8) at the disease-free equilibrium ${\mathcal{E}}_0$, denoted by $J({\mathcal{E}}_0)$ is given as

$$J({\mathcal{E}}_0)=\left(\begin{array}{ccccccc}-K& 0& 0& -\frac{\beta \Lambda }{K}& -\frac{\beta \Lambda {\eta }_1}{K}& -\frac{\beta \Lambda {\eta }_2}{K}& 0\\ \xi {\alpha }_1& -\mu & 0& -\frac{\beta \Lambda c_1\xi {\alpha }_1}{\mu K}& -\frac{\beta \Lambda {\eta }_1{c}_1\xi {\alpha }_1}{\mu K}& -\frac{\beta \Lambda {\eta }_2{c}_1\xi {\alpha }_1}{\mu K}& 0\\ \xi {\alpha }_2& 0& -\mu & -\frac{\beta \Lambda c_2\xi {\alpha }_2}{\mu K}& -\frac{\beta \Lambda {\eta }_1{c}_2\xi {\alpha }_2}{\mu K}& -\frac{\beta \Lambda {\eta }_2{c}_2\xi {\alpha }_2}{\mu K}& 0\\ 0& 0& 0& \frac{\beta \Lambda Q}{\mu K}-L& \frac{\beta \Lambda {\eta }_{1}Q}{\mu K}& \frac{\beta \Lambda {\eta }_{2}Q}{\mu K}& 0\\ 0& 0& 0& \theta & -M& 0& 0\\ 0& 0& 0& 0& \tau & -W& 0\\ 0& 0& 0& {\sigma }_1& {\sigma }_2& {\sigma }_3& -P\end{array}\right).$$

(22)

There are seven eigenvalues of the matrix $J({\mathcal{E}}_0)$; four of the eigenvalues are ${\lambda }_1={\lambda }_2=-\mu ,\hspace{0.33em}{\lambda }_3=-K,\hspace{0.33em}{\lambda }_4=-P$, and the remaining eigenvalues are the solutions of the following into the $3\times 3$matrix as shown below,

$$J_1=\left(\begin{array}{ccc}\frac{\beta \Lambda Q}{\mu K}-L& \frac{\beta \Lambda {\eta }_{1}Q}{\mu K}& \frac{\beta \Lambda {\eta }_{2}Q}{\mu K}\\ \theta & -M& 0\\ 0& \tau & -W\end{array}\right).$$

(23)

The characteristic equational corresponding to $J_1$ is

$${\lambda }^{*3}+h_1{\lambda }^{*2}+h_2{\lambda }^{*}+h_3=0\hspace{0.17em},$$

(24)

where

$$\begin{array}{l}{h}_1=L\hspace{0.33em}(1-{\mathcal{R}}_{I_u})+M+W,\\ h_2=LM\hspace{0.33em}(1-{\mathcal{R}}_{I_a})+W(L+M)-{\mathcal{R}}_{I_u}(M+W),\\ h_3=LMW(1-{\mathcal{R}}_e).\end{array}$$

As $-\mu ,\hspace{0.33em}-K,\hspace{0.33em}-P$ are negative, the Routh-Hurwitz Criteria depicted that, Equation (24) has three negative roots if $h_1>0,\hspace{0.33em}{h}_2>0,\hspace{0.33em}{h}_3>0,$ and $h_1{h}_2>h_3.$ Thus, this is possible only ${\mathcal{R}}_e<1$. As a result, the disease-free equilibrium of the model (8), ${\mathcal{E}}_0$, is locally asymptotically stable in Ω if ${\mathcal{R}}_e<1$. If ${\mathcal{R}}_e>1$, the Jacobian matrix $J({\mathcal{E}}_0)$ has at least one eigenvalue with a positive real part. Thus, the disease-free equilibrium ${\mathcal{E}}_0$is locally asymptotically unstable. This completes the proof. □

3.3.2. Global Stability of Disease-Free Equilibrium

To establish the global stability of the disease-free equilibrium ${\mathcal{E}}_0$, we apply the method used in [33]. To do this, let the model (8) be rewritten in the form

$$\begin{array}{l}{\displaystyle \frac{dX}{dt}}=F(X,Y)\hspace{0.17em},\\ {\displaystyle \frac{dZ}{dt}}=G(X,Z),\hspace{0.33em}G(X,0)=0\hspace{0.17em},\end{array}$$

(25)

where $X=(S,\hspace{0.33em}{E}_1,\hspace{0.33em}{E}_2)\in {ℝ}^3$ is the uninfected compartments, $Z=(I_u,\hspace{0.33em}{I}_a,\hspace{0.33em}T,\hspace{0.33em}A)\in {ℝ}^4$ is the infected compartments. Let ${\mathcal{E}}_0=(X^0,\hspace{0.17em}0,\hspace{0.17em}0,\hspace{0.17em}0,\hspace{0.17em}0)$, where $X^0=\left(S^0,\hspace{0.17em}{E}_1^0,\hspace{0.17em}{E}_2^0\right)$ denotes the disease-free equilibrium of model (8). To establish the global asymptotic stability of the disease-free equilibrium of model (8), the following conditions must be satisfied:

• (${\mathrm{H}}_1$) For ${\displaystyle \frac{dX}{dt}}=F(X,0),\hspace{0.33em}{X}^0$ is globally asymptotically stable.
• (${\mathrm{H}}_2$) $G(X,Z)=BZ-\widehat{G}(X,Z),\hspace{0.33em}\widehat{G}(X,Z)\ge 0$ for $(X,\hspace{0.33em}Z)\in \Omega$ and $B=D_{Z}G(X^0,\hspace{0.33em}0)$ is a Metzler-matrix (the off-diagonal elements of$B$are nonnegative).

Theorem 2.

The disease-free equilibrium points of the model ${\mathcal{E}}_0$ is globally asymptotically stable for ${\mathcal{R}}_e<1$.

Proof. 

System (8) can be written as the system (25) form, and we get $X=(S,\hspace{0.33em}{E}_1,\hspace{0.33em}{E}_2)\in {ℝ}^3$, $Z=(I_u,\hspace{0.33em}{I}_a,\hspace{0.33em}T,\hspace{0.33em}A)\in {ℝ}^4$. Next, we have identified the following matrices:

$$F(X,Z)=\left(\begin{array}{c}\Lambda -\frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)}{1+\omega (I_u+I_a+T)}S-KS\\ \xi {\alpha }_{1}S-\frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)}{1+\omega (I_u+I_a+T)}{c}_1{E}_1-\mu E_1\\ \xi {\alpha }_{2}S-\frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)}{1+\omega (I_u+I_a+T)}{c}_2{E}_2-\mu E_2\end{array}\right),\hspace{0.33em}G(X,Z)=\left(\begin{array}{c}\frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)}{1+\omega (I_u+I_a+T)}(S+c_1{E}_1+c_2{E}_2)-L{I}_u\\ \theta I_u-M{I}_a\\ \tau I_a-WT\\ {\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-PA\end{array}\right)\hspace{0.17em}.$$

From the first equation of system (25),

$${\displaystyle \frac{dX}{dt}}=F(X,0)=\left(\begin{array}{c}\Lambda -KS\\ \xi {\alpha }_{1}S-\mu E_1\\ \xi {\alpha }_{2}S-\mu E_2\end{array}\right)\hspace{0.17em}.$$

(26)

The Jacobian matrix of $F(X,0)$ is given by

$$J(F(X,0))=\left(\begin{array}{ccc}-K& 0& 0\\ \xi {\alpha }_1& -\mu & 0\\ \xi {\alpha }_2& 0& -\mu \end{array}\right).$$

(27)

The eigen values of the matrix $J(F(X,0))$ in system (27) are $-K,\hspace{0.33em}-\mu ,$ and $-\mu$. Since the eigenvalues of the given matrix (27) are clearly negative, then the system (26) is globally asymptotically stable. At $F(X,\hspace{0.33em}0)=0,$ $X^0=\left(S^0,\hspace{0.33em}{E}_1^0,\hspace{0.33em}{E}_2^0\right)=\left(\frac{\Lambda }{K},\hspace{0.33em}\frac{\xi {\alpha }_1\Lambda }{\mu K},\hspace{0.33em}\frac{\xi {\alpha }_2\Lambda }{\mu K}\right).$ As $t\to \infty ,$ $S\to S^0,\hspace{0.17em}{E}_1\to E_1^0,\hspace{0.33em}{E}_2\to E_2^0$. Thus, condition (${\mathrm{H}}_1$) is satisfied and $X^0$ is globally asymptotically stable. Additionally, we demonstrate that $G(X,\hspace{0.33em}Z)$ satisfies the second requirements stated in (${\mathrm{H}}_2$). It is clear that $G(X,\hspace{0.33em}0)=0$. We derive from the second equation in Equation (25),

$$\begin{array}{l}B=D_{X}G(X^0,0)\\ =\left(\begin{array}{cccc}\beta (S^0+c_1{E}_1^0+c_2{E}_2^0)-L& \beta {\eta }_1(S^0+c_1{E}_1^0+c_2{E}_2^0)& \beta {\eta }_2(S^0+c_1{E}_1^0+c_2{E}_2^0)& 0\\ \theta & -M& 0& 0\\ 0& \tau & -W& 0\\ {\sigma }_1& {\sigma }_2& {\sigma }_3& -P\end{array}\right)\hspace{0.17em}\end{array}.$$

(28)

B is a Metzler-matrix because all off-diagonal entries of the matrix B are not negative and

$$\begin{array}{l}\widehat{G}(X,\hspace{0.33em}Z)=BZ-G(X,\hspace{0.33em}Z)\\ =\left(\begin{array}{c}\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)[\frac{(S^0-S)+\omega (I_u+I_a+T)S^0}{1+\omega (I_u+I_a+T)}+c_1(\frac{(E_1^0-E_1)+\omega (I_u+I_a+T)E_1^0}{1+\omega (I_u+I_a+T)}+c_2(\frac{(E_2^0-E_2)+\omega (I_u+I_a+T)E_2^0}{1+\omega (I_u+I_a+T)})]\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right)\end{array}$$

Clearly, $\stackrel{⌢}{G}(X,\hspace{0.33em}Z)\ge 0$ is true, since $0\le S\le S^0,\hspace{0.33em}0\le E_1\le E_1^0,\hspace{0.33em}0\le E_2\le E_2^0$. As a result, condition (${\mathrm{H}}_2$) is satisfied. Therefore, both conditions are satisfied, and the proof of Theorem 2 is completed. □

3.3.3. Global Stability of Endemic Equilibrium

To analyze the global dynamics of model (8) around the unique endemic equilibrium point ${\mathcal{E}}_1$, we present the following result.

Theorem 3.

If ${\mathcal{R}}_e>1$, then the endemic equilibrium ${\mathcal{E}}_1$ of the model (8) is globally asymptotically stable in $\Omega$.

Proof of Theorem 3.

Let ${\mathcal{R}}_e>1$ such that the endemic equilibrium ${\mathcal{E}}_1$exist. Furthermore, considering the following function ${\mathcal{L}}_2$, inspired by Muthu and Kumar [34] as follows:

$$\begin{array}{l}{\mathcal{L}}_2=(S+E_1+E_2+I_u+I_a+T+A)-(S^{*}+E_1^{*}+E_2^{*}+I_u^{*}+I_a^{*}+T^{*}+A^{*})\\ -(S^{*}+E_1^{*}+E_2^{*}+I_u^{*}+I_a^{*}+T^{*}+A^{*})\ln \left({\displaystyle \frac{S+E_1+E_2+I_u+I_a+T+A}{S^{*}+E_1^{*}+E_2^{*}+I_u^{*}+I_a^{*}+T^{*}+A^{*}}}\right)\\ =N-N^{*}-N^{*}\ln \left({\displaystyle \frac{N}{N^{*}}}\right).\end{array}$$

(29)

By direct calculating the derivative of ${\mathcal{L}}_2$ with respect to t along the solutions of the model (8), we have

$${\displaystyle \frac{d{\mathcal{L}}_2}{dt}}=\left(1-{\displaystyle \frac{N^{*}}{N}}\right){\displaystyle \frac{dN}{dt}}=\left(1-{\displaystyle \frac{N^{*}}{N}}\right)\left(\Lambda -\delta A-\mu N\right).$$

From the right-hand sides of (5) at steady state, we have $\Lambda =\delta A^{*}+\mu N^{*}$. Thus,

$$\begin{array}{l}{\displaystyle \frac{d{\mathcal{L}}_2}{dt}}=\left(1-{\displaystyle \frac{N^{*}}{N}}\right)\left(\delta A^{*}+\mu N^{*}-\delta A-\mu N\right)={\displaystyle \frac{N-N^{*}}{N}}\left(-\mu (N-N^{*})-\delta (A-A^{*})\right)\\ =-{\displaystyle \frac{\mu {(N^{*}-N)}^2}{N}}-{\displaystyle \frac{\delta (N^{*}-N)(A^{*}-A)}{N}}.\end{array}.$$

(30)

Clearly, $d{\mathcal{L}}_2/dt<0$ because $S\le S^{*},\hspace{0.33em}{E}_1\le E_1^{*},\hspace{0.33em}{E}_2\le E_2^{*},\hspace{0.33em}{I}_u\le I_u^{*},\hspace{0.17em}{I}_a\le I_a^{*},\hspace{0.33em}T\le T^{*},\hspace{0.33em}A\le A^{*},$which implies $0\le N\le N^{*}$. Additionally, $d{\mathcal{L}}_2/dt=0$if and only if $S=S^{*},\hspace{0.33em}{E}_1=E_1^{*},\hspace{0.33em}{E}_2=E_2^{*},$ $I_u=I_u^{*},\hspace{0.33em}{I}_a=I_a^{*},\hspace{0.33em}T=T^{*},\hspace{0.33em}A=A^{*}$. Hence, ${\mathcal{L}}_2$is a Lyapunov function on Thus, $S_1\to S^{*},\hspace{0.17em}$ $E_1\to E_1^{*}, E_2\to E_2^{*}, I_1\to I_1^{*}, I_2\to I_2^{*}, T\to T^{*} ,A\to A^{*}$ as $t\to \infty$. Therefore, the largest compact invariant set in $\{(S,\hspace{0.17em}{E}_1,\hspace{0.17em}{E}_2,\hspace{0.17em}{I}_u,\hspace{0.17em}{I}_a,\hspace{0.17em}T,\hspace{0.17em}A)\in \Omega |\hspace{0.33em}\frac{d{L}_2}{dt}=0\}$is the singleton set $\left\{{\mathcal{E}}_1\right\}$. By LaSalle’s Invariance Principle [35], the unique endemic equilibrium of the model (8) is globally asymptotically stable in $\Omega$. The proof of Theorem 3 is completed. □

The epidemiological implication of the above result is that the HIV/AIDS epidemic will persist in the community despite education campaigns, screening, and antiretroviral treatment programs if the threshold quantity (${\mathcal{R}}_e$) exceeds unity.

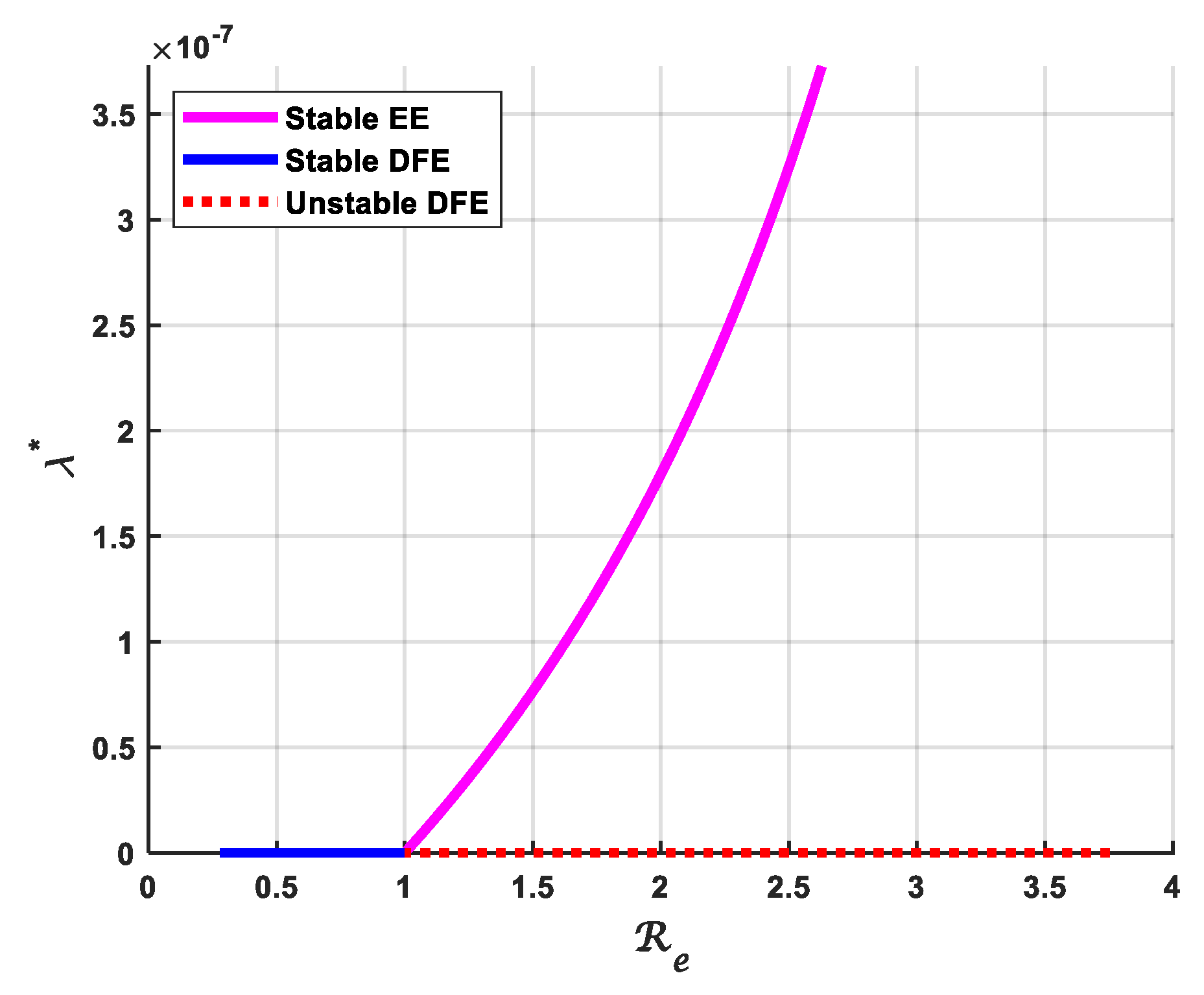
3.4. Bifurcation Analysis

An important phenomenon in compartmental epidemiological modelling, particularly in HIV/AIDS transmission, is the occurrence of a bifurcation at the critical point where ${\mathcal{R}}_e=1$. To investigate the existence of a bifurcation for the model (8), we employ the center manifold theory as described by Castillo-Chavez and song in [33].

Theorem 4.

The HIV/AIDS model (8) exhibits a forward bifurcation at ${\mathcal{R}}_e=1$ whenever $B_0<0$ holds, with

$$\begin{array}{l}{B}_0=\left(K{\beta }^{*}\xi \left({\alpha }_1{c}_1{\psi }_1+{\alpha }_2{c}_2{\psi }_2\right)+{\beta }^{*}\mu \xi \left({\alpha }_1+{\alpha }_2\right)\right)\left(W{\eta }_1\theta +{\eta }_2\tau \theta +MW\right)\\ +K\mu \omega \left(W\theta \xi +MW+\tau \theta \right)\left({\alpha }_1{\psi }_1+{\alpha }_2{\psi }_2\right)\\ -\left(K{\beta }^{*}\xi \left({\alpha }_1{c}_1+{\alpha }_2{c}_2\right)+{\beta }^{*}\mu \xi \left({\alpha }_1{\psi }_1+{\alpha }_2{\psi }_2\right)+{\beta }^{*}{\mu }^2\right)\left(W{\eta }_1\theta +MW+{\eta }_2\tau \theta \right)\\ -K{\mu }^2\omega \left(MW+W\theta +\tau \theta \right)-K\theta \xi \mu \omega \left(MW+\tau +W\right)\left({\alpha }_1+{\alpha }_2\right).\end{array}$$

Proof of Theorem 4.

We simplify model (8) by choosing, $S=x_1,\hspace{0.33em}{E}_1=x_2,E_2=x_3,\hspace{0.33em}{I}_u=x_4,$$I_a=x_5,\hspace{0.33em}T=x_6,A=x_7.$ If we set, $X={\left(x_1,\hspace{0.33em}{x}_2,\hspace{0.33em}{x}_3,x_4,x_5,x_6,x_7\right)}^T,$ then our model (8) can be written in the form $\frac{dX}{dt}=f(X)$ with $f={(f_1,f_2,f_3,f_4,f_5,f_6,f_7)}^T$. Thus, we have

$$\begin{array}{l}\begin{array}{l}{f}_1=\Lambda -\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_1-K{x}_1,\\ f_2=\xi {\alpha }_1{x}_1-c_1\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_2-\mu x_2,\end{array}\\ \begin{array}{l}{f}_3=\xi {\alpha }_2{x}_1-c_2\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_3-\mu x_3,\\ f_4=\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_1+c_1\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_2+c_2\left(\frac{\beta (x_4+{\eta }_1{x}_5+{\eta }_2{x}_6}{1+\omega (x_4+x_5+x_6)}\right)x_3,\\ f_5=\theta x_4-M{x}_5,\\ f_6=\tau x_5-W{x}_6,\\ f_7={\sigma }_1{x}_4+{\sigma }_2{x}_5+{\sigma }_3{x}_6-P{x}_7.\end{array}\end{array}$$

The characteristic equation in Equation (20) produces an eigenvalue of zero if $h_3=LMW(1-{\mathcal{R}}_e).$ We simplify this equation and considering ${\mathcal{R}}_e$ stated in Equation (16), we get ${\mathcal{R}}_e=1$. By selecting $\beta$ as the bifurcation parameter at the point where ${\mathcal{R}}_e=1,$ we obtain the critical value of $\beta$ as follows:

$$\beta ={\beta }^{*}={\displaystyle \frac{\mu KLMW}{\Lambda Q(MW+{\eta }_1\theta W+{\eta }_2\theta \tau )}},$$

(31)

The Jacobian matrix of the model (8), evaluated at the disease-free equilibrium ${\mathcal{E}}_0$ and $\beta ={\beta }^{*},$ is given by

$$J({\mathcal{E}}_0,{\beta }^{*})=\left(\begin{array}{ccccccc}-K& 0& 0& -\frac{{\beta }^{*}\Lambda }{K}& -\frac{{\beta }^{*}\Lambda {\eta }_1}{K}& -\frac{{\beta }^{*}\Lambda {\eta }_2}{K}& 0\\ \xi {\alpha }_1& -\mu & 0& -\frac{{\beta }^{*}\Lambda \xi c_1{\alpha }_1}{\mu K}& -\frac{{\beta }^{*}\Lambda {\eta }_1\xi c_1{\alpha }_1}{\mu K}& -\frac{{\beta }^{*}\Lambda {\eta }_2\xi c_1{\alpha }_1}{\mu K}& 0\\ \xi {\alpha }_2& 0& -\mu & -\frac{{\beta }^{*}\Lambda \xi c_2{\alpha }_2}{\mu K}& -\frac{{\beta }^{*}\Lambda {\eta }_1\xi c_2{\alpha }_2}{\mu K}& -\frac{{\beta }^{*}\Lambda {\eta }_2\xi c_2{\alpha }_2}{\mu K}& 0\\ 0& 0& 0& \frac{{\beta }^{*}\Lambda Q}{\mu K}-L& \frac{{\beta }^{*}\Lambda {\eta }_{1}Q}{\mu K}& \frac{{\beta }^{*}\Lambda {\eta }_{2}Q}{\mu K}& 0\\ 0& 0& 0& \theta & -M& 0& 0\\ 0& 0& 0& 0& \tau & -W& 0\\ 0& 0& 0& {\sigma }_1& {\sigma }_2& {\sigma }_3& -P\end{array}\right).$$

(32)

The characteristic equation in (32), given by $|J({\mathcal{E}}_0,{\beta }^{*})-\lambda I|=0$, gives a simple zero eigenvalues with other six eigenvalues having negative real part. The eigenvalues of the characteristic equation are ${\lambda }_1={\lambda }_2=-\mu ,\hspace{0.33em}{\lambda }_3=-K,\hspace{0.33em}{\lambda }_4=-P,\hspace{0.33em}{\lambda }_5=0\hspace{0.33em}$and the remaining eigenvalues are the solutions of the following characteristic equation

$${\lambda }^2+h_1\lambda +h_2=0,$$

(33)

with $h_1,\hspace{0.33em}{h}_2$ as in Equation (24). The Equation (33) has negative roots (${\lambda }_6<0,\hspace{0.33em}{\lambda }_7<0$) when satisfies the discriminant $D=h_1^2-4h_2$ is positive, ${\lambda }_6.{\lambda }_7=h_2>0$ and ${\lambda }_6+{\lambda }_7=h_1<0$.

Further, the right eigenvector associated with the zero eigenvalues is denoted by $w={(w_1,w_2,\hspace{0.17em}\dots ,\hspace{0.17em}{w}_7)}^T$can be obtained from $J({\mathcal{E}}_0,{\beta }^{*})w=0$,

$$\begin{array}{l}{w}_1=-{\displaystyle \frac{\Lambda {\beta }^{*}{w}_4(MW+W{\eta }_1\theta +{\eta }_2\tau \theta )}{K^{2}MW}},\hspace{0.33em}{w}_2=-{\displaystyle \frac{\Lambda {\beta }^{*}\xi {\alpha }_1{w}_4(MW+W{\eta }_1\theta +{\eta }_2\tau \theta )(K{c}_1+\mu )}{u^2{K}^{2}MW}}\\ w_3=-{\displaystyle \frac{\Lambda {\beta }^{*}\xi {\alpha }_2{w}_4(MW+W{\eta }_1\theta +{\eta }_2\tau \theta )(K{c}_2+\mu )}{{\mu }^2{K}^{2}MW}},\hspace{0.33em}{w}_4=w_4,w_5={\displaystyle \frac{\theta w_4}{M}},\hspace{0.33em}{w}_6={\displaystyle \frac{\tau \theta w_4}{MW}},\hspace{0.33em}\\ w_7={\displaystyle \frac{w_4(MW{\sigma }_1+W{\sigma }_2\theta +{\sigma }_3\tau \theta )}{MWP}}.\end{array}$$

Thus, it was chosen$w_4>0$results in $w_2,\hspace{0.33em}{w}_3,\hspace{0.33em}{w}_5,\hspace{0.33em}{w}_6,\hspace{0.33em}{w}_7$ being positive. Moreover, the left eigenvector $v=(v_1,v_2,\hspace{0.17em}{v}_3,\hspace{0.33em}{v}_4,\hspace{0.33em}{v}_5,v_6,\hspace{0.17em}{v}_7)$ satisfying $v\cdot w=1$ is given by

$$\begin{gathered} v_1=0,\hspace{0.33em}{v}_2=0,\hspace{0.33em}{v}_3=0,\hspace{0.33em}{v}_4={\displaystyle \frac{1}{w_4}}\left({\displaystyle \frac{\mu K{M}^2{W}^2}{\mu K{M}^2{W}^2+{\beta }^{*}\theta \Lambda Q(W^2{\eta }_1+{\eta }_2\tau W+{\eta }_2\tau M)}}\right), \\ {v}_5={\displaystyle \frac{v_4{\beta }^{*}\Lambda Q(W{\eta }_1+{\eta }_2\tau )}{\mu KMW}},v_6={\displaystyle \frac{v_4{\beta }^{*}\Lambda {\eta }_{2}Q}{KW}},\hspace{0.33em}{v}_7=0. \end{gathered}$$

According to Theorem 4.1 in [33], we calculate the bifurcation coefficient $\tilde{a}$ and $\tilde{b}$ , we have

$$\begin{array}{l}\tilde{a}={\displaystyle \sum _{k,i,j=1}^7{v}_k{w}_i}{w}_j{\displaystyle \frac{{\partial }^2{f}_k({\mathcal{E}}_0,{\beta }^{*})}{\partial x_i\partial x_j}}\\ ={\displaystyle \frac{1}{K^3{M}^4{W}^4{\mu }^3}}\left\{2{\beta }^{*}\Lambda w_4\left({\beta }^{*}\Lambda {\eta }_2\tau \theta (M+W)+{\beta }^{*}\Lambda W^2{\eta }_1\theta )Q+K{M}^2{W}^2\mu \right)\right\}\\ \times \left(W{\eta }_1\theta +{\eta }_2\tau \theta +MW\right)B_0\end{array}$$

and

$$\begin{array}{l}\tilde{b}={\displaystyle \sum _{k,i=1}^7{v}_k{w}_i}{\displaystyle \frac{{\partial }^2{f}_k({\mathcal{E}}_0,{\beta }^{*})}{\partial x_i\partial \beta }}=v_4{w}_4{\displaystyle \frac{{\partial }^2{f}_4({\mathcal{E}}_0,{\beta }^{*})}{\partial x_4\partial \beta }}+v_4{w}_5{\displaystyle \frac{{\partial }^2{f}_4({\mathcal{E}}_0,{\beta }^{*})}{\partial x_5\partial \beta }}+v_{4}w6{\displaystyle \frac{{\partial }^2{f}_4({\mathcal{E}}_0,{\beta }^{*})}{\partial x_6\partial \beta }}\\ ={\displaystyle \frac{\Lambda MQW\left(W{\eta }_1\theta +{\eta }_2\tau \theta +MW\right)}{{\beta }^{*}\Lambda Q\theta \left(M{\eta }_2\tau +W^2{\eta }_1+W{\eta }_2\theta \right)+\mu K{M}^2{W}^2}},\end{array}$$

where

$$\begin{array}{l}{B}_0=\left(K{\beta }^{*}\xi \left({\alpha }_1{c}_1{\psi }_1+{\alpha }_2{c}_2{\psi }_2\right)+{\beta }^{*}\mu \xi \left({\alpha }_1+{\alpha }_2\right)\right)\left(W{\eta }_1\theta +{\eta }_2\tau \theta +MW\right)\\ +K\mu \omega \left(W\theta \xi +MW+\tau \theta \right)\left({\alpha }_1{\psi }_1+{\alpha }_2{\psi }_2\right)\\ -\left(K{\beta }^{*}\xi \left({\alpha }_1{c}_1+{\alpha }_2{c}_2\right)+{\beta }^{*}\mu \xi \left({\alpha }_1{\psi }_1+{\alpha }_2{\psi }_2\right)+{\beta }^{*}{\mu }^2\right)\left(W{\eta }_1\theta +MW+{\eta }_2\tau \theta \right)\\ -K{\mu }^2\omega \left(MW+W\theta +\tau \theta \right)-K\theta \xi \mu \omega \left(MW+\tau +W\right)\left({\alpha }_1+{\alpha }_2\right).\end{array}$$

It is important to highlight that the coefficient $\tilde{b}$ is always positive. Consequently, the local dynamics around the disease-free equilibrium point are determined by the sign of the coefficient$\tilde{a}$. A backward bifurcation of system (8) occurs if $\tilde{a}$ is positive, whereas a forward bifurcation occurs if $\tilde{a}$ is negative. Alternatively, model (8) exhibits a forward bifurcation if $B_0<0$. Thus, the proof of Theorem 4 is completed. □

To demonstrate this phenomenon in relation to the above Theorem 4, the same parameter values used in Table 1 are used and forward bifurcation diagrams are depicted in Figure 2. For this set of parameter values, the associated forward bifurcation coefficient are $\tilde{a}=-513.753554$ with $B_0=-1.517129\times {10}^{-5}$ and $\tilde{b}=13,433.84676$. The bifurcation parameter at the point where ${\mathcal{R}}_e=1$ is${\beta }^{*}=1.389119\times {10}^{-5}$.

Figure 2 illustrates the system’s behaviour as the effective reproduction number ${\mathcal{R}}_e$varies. When ${\mathcal{R}}_e<1$ , the disease-free equilibrium (DFE) ${\mathcal{E}}_0$ is locally asymptotically stable, as shown by the solid blue line. However, when ${\mathcal{R}}_e>1$, the DFE ${\mathcal{E}}_0$ becomes unstable, indicated by the dashed blue line. The ascending magenta line in Figure 2 represents a stable endemic equilibrium (EE) ${\mathcal{E}}_1,$ indicating a transition from the DFE to the EE, which suggests the sustained presence of the virus in the population.

For${\mathcal{R}}_e>1$, the applying Descartes’ Rule of Signs, along with the conditions $a_3>0$ and$a_1<0,$ the cubic polynomial in Equation (24), the number of positive real roots can be determined, as summarized in Table 2. In contrast, when ${\mathcal{R}}_e<1$, no endemic equilibrium exists. Figure 2 depicts these equilibria, highlighting a forward bifurcation occurring at ${\mathcal{R}}_e=1$. In the figure, the solid blue line represents the stable disease-free equilibrium ${\mathcal{E}}_0$ for${\mathcal{R}}_e<1$, while the dashed blue line shows the unstable DFE for ${\mathcal{R}}_e>1$. The ascending magenta curve represents the stable branch of the endemic equilibrium ${\mathcal{E}}_1$. Consequently, ${\mathcal{E}}_1$is stable when ${\mathcal{R}}_e>1$ and unstable when ${\mathcal{R}}_e<1$. Similarly, ${\mathcal{E}}_0$is stable for ${\mathcal{R}}_e<1$ and becomes unstable for ${\mathcal{R}}_e>1$.

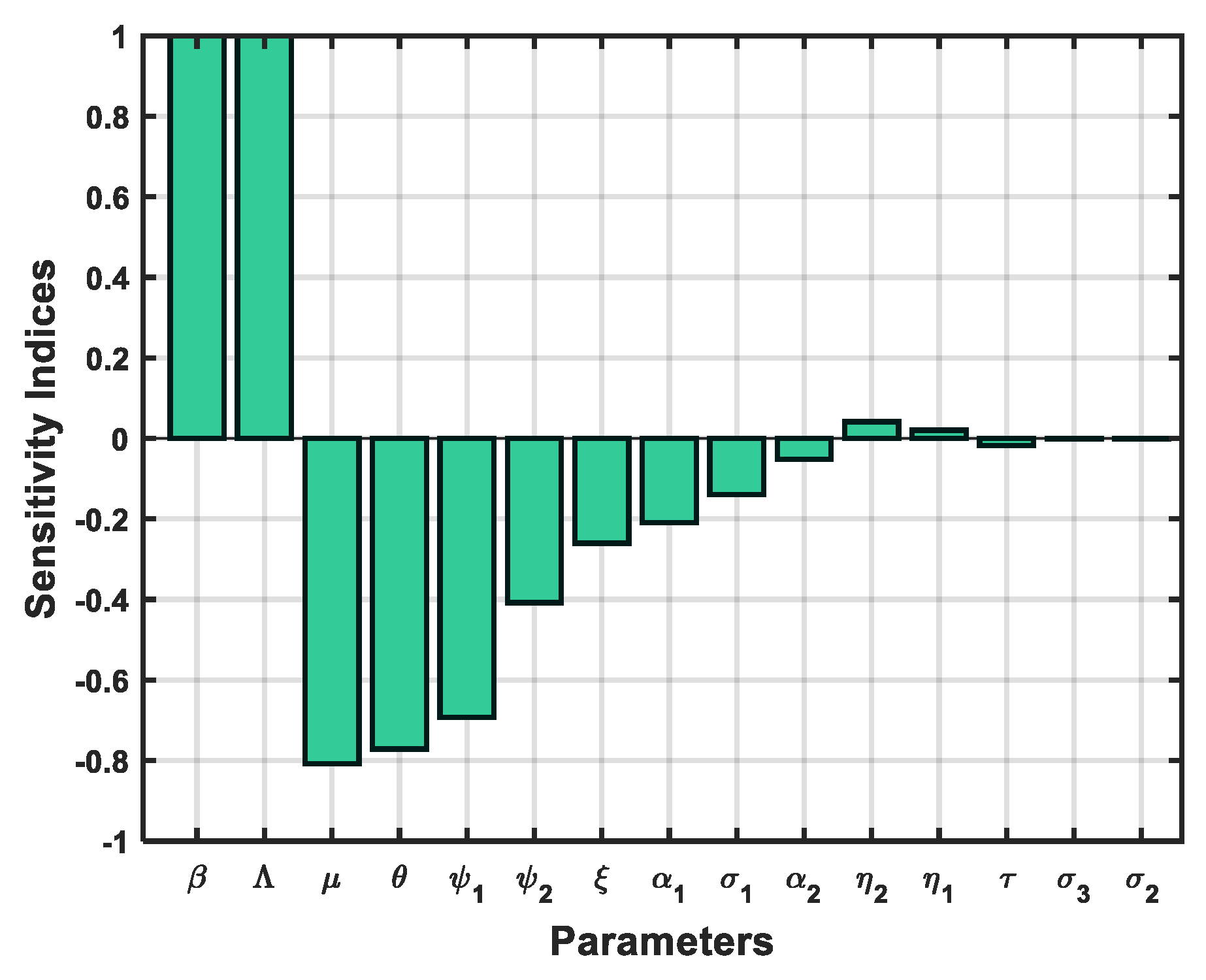
3.5. Sensitivity Analysis

The sensitivity analysis of model parameters is an important aspect of the present study. This analysis identifies the relevant sensitivity indices for each parameter, highlighting its role in the disease dynamics. In this section, we present a sensitivity analysis of various model parameters concerning the threshold quantity ${\mathcal{R}}_e$. Furthermore, this analysis helps to identify the parameters that have a significant influence on ${\mathcal{R}}_e$, making them potential targets for intervention. A parameter that has a significant impact on ${\mathcal{R}}_e$ indicates its dominant role in determining the endemicity of HIV/AIDS.

Following the methods described in [36], we perform the analysis by calculating the sensitivity indices of the model parameters. To conduct the sensitivity analysis, the normalized forward sensitivity index of a variable concerning a given parameter is determined. The sensitivity index of ${\mathcal{R}}_e$ concerning the parameter $\phi$ is defined by the following formula:

$${{\rm Y}}_{\phi }^{{\mathcal{R}}_e}={\displaystyle \frac{\partial {\mathcal{R}}_e}{\partial \phi }}{\displaystyle \frac{\phi }{{\mathcal{R}}_e}}.$$

(34)

A parameter with a larger sensitivity index value has greater influence than a parameter with a smaller sensitivity index value. The sign of the sensitivity indices ${\mathcal{R}}_e$ concerning a parameter indicates whether the parameter has a positive or negative effect on ${\mathcal{R}}_e$. Specifically, if the sign of the sensitivity indices is positive, then the value of${\mathcal{R}}_e$ increases as the parameter increases; conversely, if the sign of the sensitivity indices is negative, then the value of ${\mathcal{R}}_e$ decreases as the parameter increases. The sensitivity indices of various model parameters, calculated using the expression given in (34), are presented in Table 2. The effective reproduction number of the model (8) depends on fifteen parameters, namely, $\Lambda ,\hspace{0.17em}\beta ,\hspace{0.17em}\mu ,\hspace{0.17em}\theta ,\hspace{0.17em}{\psi }_1,\hspace{0.17em}{\psi }_2,\hspace{0.17em}\xi ,\hspace{0.33em}{\sigma }_1,\hspace{0.33em}{\sigma }_2,\hspace{0.33em}{\sigma }_3,\hspace{0.17em}{\alpha }_1,\hspace{0.17em}{\alpha }_2,{\eta }_1,\hspace{0.17em}{\eta }_2,$ and $\tau$. Table 2 presents the sensitivity index values and ranks the parameters from most to least sensitive. Parameters $\beta ,\hspace{0.33em}\Lambda ,\hspace{0.33em}{\eta }_1,$ and ${\eta }_2$ with positive sensitivity indices indicate that the remaining parameters have negative sensitivity indices.

Figure 3 presents the sensitivity index values of various model parameters, calculated using expression (34), and arranged in descending order from the most sensitive to the least sensitive (left to right). An absolute value of the sensitive index greater than 0.5 is considered to have a significant effect on ${\mathcal{R}}_e$. The most sensitive parameter is the effect-contact rate ($\beta$) and with a sensitivity index value given by 1. This means that if the value of $\beta$ is increased (decreased) by 10% while other parameter values are constant, the value of ${\mathcal{R}}_e$ increased (decreased) by 10%. Conversely, the sensitive index value of $\theta$ is -0.7716, indicating that increasing (decreasing) the value of $\theta$ while other parameter values are constant, will be followed by a decrease (increase) in the value of ${\mathcal{R}}_e$ by 7.716 %. The same interpretation applies to the other parameters.

We have illustrated the impact of several key parameters graphically in Figure 4. Figure 4(a) shows the effect of parameter $\beta$ on the transmission dynamics of HIV. According to the graph, HIV infection is eradicated when the effective contact rate is reduced to 0.0000251. This demonstrates that HIV transmission can be stopped by reducing the rate of contact between susceptible and infective individuals below this threshold.

The effects of increasing the saturation rate are evaluated through numerical simulations presented in Figure 4(b). The psychological or inhibitory effect (denoted by $\omega$) is used to assess the influence of saturation, even though it does not directly affect the effective reproduction number. The numerical results indicate that the saturation rate decreases as the inhibitory effects increase.

4. Optimal Control Model

In this section, the deterministic model (8) is developed into a control problem by considering the parameters $\xi ,\hspace{0.33em}\theta ,$ and $\tau$as continuous variables that depend on time. The optimal control parameters and conditions are considered as follows:

• The parameter $u_1 (0\le u_1\le 1)$ represents the proportion of the susceptible subpopulation that receives the educational campaign and adopts AB (Abstinence, Be faithful) and C (use Condoms) behaviours.
• The parameter $u_2 (0\le u_2\le 1)$ represents the proportion of the unaware infective subpopulation that receives screening per unit of time.
• The parameter $u_3 \left(0\le u_3\le 1\right)$ represents the proportion of the aware infective subpopulation that receives antiretroviral treatment per unit time.

The control variables $u_1,\hspace{0.33em}{u}_2,$ and $u_3$ are defined on the closed interval $[0, T_f]$, where $T_f$ denotes the final time of the control implementations. By integrating the three previously described control strategies into the dynamic system (1), the corresponding system of differential equations is reformulated as follows:

$$\begin{array}{l}{\displaystyle \frac{dS}{dt}} =\hspace{0.17em}\Lambda -\lambda (I_u,I_a,T)S-(u_1{\alpha }_1+u_1{\alpha }_2+\mu )S,\\ {\displaystyle \frac{d{E}_1}{dt}}=\hspace{0.33em}{u}_1{\alpha }_{1}S-(1-{\psi }_1)\lambda (I_u,I_a,T)E_1-\mu E_1,\\ {\displaystyle \frac{d{E}_2}{dt}}=u_1{\alpha }_{2}S-(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-\mu E_2,\\ {\displaystyle \frac{d{I}_u}{dt}}=\lambda (I_u,I_a,T)S+(1-{\psi }_1)\lambda (I_u,I_a,T)E_1+(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-(u_2+{\sigma }_1+\mu )I_u,\\ {\displaystyle \frac{d{I}_a}{dt}}=u_2{I}_u-(u_3+{\sigma }_2+\mu )I_a,\\ {\displaystyle \frac{dT}{dt}}=u_3{I}_a-({\sigma }_3+\mu )T,\\ {\displaystyle \frac{dA}{dt}}={\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-(\gamma +\mu )A,\end{array}$$

(35)

with the corresponding initial conditions are given in Equation (9).

4.1. Optimal Control Problem

In this section, we analyze the behaviour of the given model by using optimal control theory. The main objective is to minimizes the number of infected individuals ($I_u$ and $I_a$) and the control costs associated with the educational campaigns ($u_1$), screening of the unaware infective subpopulation ($u_2$), and antiretroviral therapy for the aware infective subpopulation ($u_3$). The objective functional for a fixed time $T_f$, given by

$$J(u_1,u_2,\hspace{0.17em}{u}_3)={\displaystyle \underset{0}{\overset{T_f}{\int }}\left[B_1{I}_u+B_2{I}_a+\frac{1}{2}(C_1{u}_1^2+C_2{u}_2^2+C_3{u}_3^2)\right]}\hspace{0.33em}dt,$$

(36)

where $B_1\ge 0,\hspace{0.33em}{B}_2\ge 0$ are nonnegative weight constant on the unaware and aware infected individuals, whereas $C_i\hspace{0.33em}(i=1,\hspace{0.33em}2,\hspace{0.33em}3)$ are the relative costs of the controls associated control $u_i\hspace{0.33em}(i=1,\hspace{0.33em}2,\hspace{0.33em}3)$.

The main goal of this part is to find the optimal control strategies $u^{*}=(u_1^{*},u_2^{*},u_3^{*})$, subject to (35) and minimizing the objective functional Eq (36) such that

$$J(u_1^{*},u_2^{*},u_3^{*})=\min \left\{J(u_1,u_2,u_3):\hspace{0.33em}{u}_1,u_2,u_3\in U\right\}$$

(37)

where $U=\left\{(u_1,u_2,u_3)\in {ℝ}^3: 0\le u_i\le 1,\hspace{0.33em}i=1,\hspace{0.17em}2,3\hspace{0.17em},\hspace{0.33em}\hspace{0.33em}t\in [0,\hspace{0.33em}{T}_f]\right\}$ is the control set.

4.2. Existence of an Optimal Controls

This section investigates the existence of an optimal control triple that minimize the objective functional J defined in Equation (36). To establish this, we employ the existence theorem by Fleming and Rishel [37].

Theorem 5.

Given the objective functional J defined on the control set U, there exists an optimal control triple $u^{*}=(u_1^{*},u_2^{*},u_3^{*})$ such that Equation (37) is satisfied, provided the five following conditions hold [37]:

(i) 

The optimal control set, and state variables set are nonempty.

(ii) 

The control set U is closed and convex.

(iii) 

The right-hand side of the state system (35) is continuous and bounded by a linear function in both the state and control variables.

(iv) 

The integrand of the objective functional J in Equation (36) is convex concerning the control set U.

(v) 

There exist constants  $d_1>0,\hspace{0.33em}{d}_2>0,$  and  $d_3>1$  such that the integrand of the objective functional J in (36) is bound below by

$$d_1{\left({\displaystyle \sum _{i=1}^3|u_i}{|}^2\right)}^{d_3/2}-d_2.$$

Proof. 

We must confirm the validity of the fife conditions specified in Theorem 5.

(i) Clearly, U is a nonempty set of measurable functions in$ℝ$, and the corresponding solutions exist and remain bounded.

(ii) Given the control set $U=\left\{u=(u_1, u_2, u_{3)}ϵ{\mathbb{R}}^3 :0\le u_i\le 1, i=\mathrm{1,2},3\right\}$. This set can be expressed as $U=U_1\times U_2\times U_3$, where each $U_i\subseteq [0,\hspace{0.33em}1]$, indicating U is bounded for all $t\in \left[0, T_f\right]$. Consequently, U is closed. Now, let $a=(a_1,\hspace{0.33em}{a}_2,\hspace{0.33em}{a}_3)$ and $b=(b_1,\hspace{0.33em}{b}_2,\hspace{0.33em}{b}_3)$ any two arbitrary elements in U. By the definition of a convex set [38], it follows that $\phi a_j+(1-\phi )b_j\in [0,\hspace{0.33em}1]$ for all $j=1,\hspace{0.33em}2,\hspace{0.33em}3.$ Hence, $\phi a+(1-\phi )b\in U,$ which implies that U is a convex set.

(iii) Let $x=(S,\hspace{0.33em}{E}_1,\hspace{0.33em}{E}_2,\hspace{0.33em}{I}_u,\hspace{0.33em}{I}_a,\hspace{0.33em}T,\hspace{0.33em}A)$ be the state variables of the model (8) and $(u_1,u_2,\hspace{0.17em}{u}_3)\in U.$Then the right-hand side of the system (35) can be written as $g(t,\hspace{0.33em}x,\hspace{0.33em}u)=g_1(t,\hspace{0.33em}x)+g_2(t,\hspace{0.33em}x)u,$where

$$g(t,\hspace{0.33em}x,\hspace{0.33em}u)=\left(\begin{array}{c}\Lambda -\lambda (I_u,I_a,T)S-(u_1{\alpha }_1+u_2{\alpha }_2+\mu )S\\ u_1{\alpha }_{1}S-\lambda (I_u,I_a,T)c_1{E}_1-\mu E_1\\ u_1{\alpha }_{2}S-\lambda (I_u,I_a,T)c_2{E}_2-\mu E_2\\ \lambda (I_u,I_a,T)(S+c_1{E}_1+c_2{E}_2)-(u_2+{\sigma }_1+\mu )I_u\\ u_2{I}_u-(u_3+{\sigma }_2+\mu )I_a\\ u_3{I}_a-WT\\ {\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-PA\end{array}\right),$$

$$g_1(t,\hspace{0.33em}x)=\left(\begin{array}{c}\Lambda -\lambda (I_u,I_a,T)S-\mu S\\ -\lambda (I_u,I_a,T)c_1{E}_1-\mu E_1\\ -\lambda (I_u,I_a,T)c_2{E}_2-\mu E_2\\ \lambda (I_u,I_a,T)(S+c_1{E}_1+c_2{E}_2)-({\sigma }_1+\mu )I_u\\ -({\sigma }_2+\mu )I_a\\ -WT\\ {\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-PA\end{array}\right),\hspace{0.33em} g_2(t,\hspace{0.33em}x)=\left(\begin{array}{ccc}-{\alpha }_{1}S& -{\alpha }_{2}S& 0\\ {\alpha }_{1}S& 0& 0\\ {\alpha }_{2}S& 0& 0\\ 0& -I_u& 0\\ 0& I_u& -I_a\\ 0& 0& I_a\\ 0& 0& 0\end{array}\right).$$

Derived from the Euclidean norm of a matrix as indicated in [26,28], we obtain $‖g(t,\hspace{0.33em}x,\hspace{0.33em}u)‖=‖g_1(t,\hspace{0.33em}x)‖+‖g_2(t,\hspace{0.33em}x)‖‖u‖$. This means that the right-hand side of the model (8) can be expressed as a linear function of the controls $u_1,\hspace{0.33em}{u}_2,$and $u_3$ with coefficients depending on state variables.

(iv) The integrand of the objective functional (36) can be expressed in the form of a Lagrangian as $L=B_1{I}_u+B_2{I}_a+\frac{1}{2}(C_1{u}_1^2+C_2{u}_2^2+C_3{u}_3^2)=h_1(t,x)+h_2(t,u)$. To establish convexity, it is sufficient to show that the term $h_2\left(t, u\right)={\displaystyle \frac{1}{2}} \sum _{i=1}^3{C_{i}u}_i^2$ is convex on the control set U. Notice that $h_2\left(t, u\right)$ is formed as a finite linear sum of the functions $q_i={\displaystyle \frac{1}{2}} u_i^2$. Therefore, it is easier to show that the function $q:U\to \mathbb{R}$ given by $q={\displaystyle \frac{1}{2}} u^2$ is convex. Let $y, z\in U$ and $\varphi \in \left[0. 1\right]$. Then,

$$\begin{array}{ll}q\left(\varphi y+(1-\varphi )z\right)-\left(\varphi q(y)+(1-\varphi )q(z)\right)& =\frac{1}{2}{\left(\varphi y+(1-\varphi )z\right)}^2-\frac{1}{2}\left(\varphi y^2+(1-\varphi )z^2\right)\\ & =\frac{1}{2}\left({\varphi }^2-\varphi \right){\left(y-z\right)}^2\le 0, \sin \mathrm{ce} \varphi \in [0,\hspace{0.33em}1].\end{array}$$

Hence, $q\left(\varphi y+(1-\varphi )z\right)\le \left(\varphi q\left(y\right)+\left(1-\varphi \right)q\left(z\right)\right).$ Thus, the condition satisfies the definition of a convex function as stated in [45]. As a result, the function$h_2(t,\hspace{0.33em}u)$is convex function on U.

(v) By applying the Lagrangian equation $\mathcal{L}$, we demonstrate the final condition as follows:

$$\begin{array}{l}\mathcal{L}=B_1{I}_u+B_2{I}_a+\frac{1}{2}\left(C_1{u}_1^2+C_2{u}_2^2+C_3{u}_3^2\right)\ge \frac{1}{2}\hspace{0.33em}\left(C_1{u}_1^2+C_2{u}_2^2+C_3{u}_3^2\right)\\ \ge \min \left\{\frac{1}{2}{C}_1,\hspace{0.33em}\frac{1}{2}{C}_2,\frac{1}{2}{C}_3\right\}{\left({\displaystyle \sum _{i=1}^3{u}_i^2}\right)}^{\frac{2}{2}}-C_2\ge d_1\hspace{0.17em}{\left({\displaystyle \sum _{i=1}^3{\left|u_i\right|}^2}\right)}^{\frac{d_3}{2}}-d_2,\end{array}$$

where $d_1=\min \left\{\frac{1}{2}{C}_1,\hspace{0.33em}\frac{1}{2}{C}_2,\frac{1}{2}{C}_3\right\},\hspace{0.33em}{d}_3=2,$ and $d_2=C_2>0$.

The proof of Theorem 5 is completed. □

4.3. Characterization of the Optimal Control

We characterize the optimal control triple $u^{*}=\left(u_1^{*},u_2^{*}, u_3^{*}\right)$ of the system and the corresponding states $x^{*}=(S^{*},\hspace{0.17em}{E}_1^{*},\hspace{0.17em}{E}_2^{*},I_u^{*},\hspace{0.17em}{I}_a^{*},\hspace{0.17em}{T}^{*},\hspace{0.17em}{A}^{*})$ with its control function $u_1,\hspace{0.33em}{u}_2,$and $u_3$, with the objective functional Equation (36). Using Pontryagin’s Maximal Principle [8,9], we obtain the necessary conditions for the optimal controls. Pontryagin’s Maximal Principle convert Equation (35) and Equation (37) into a problem of minimizing pointwise a Hamiltonian, $\mathcal{H}$ concerning $u_1,\hspace{0.33em}{u}_2,$ and $u_3$. The Hamiltonian $\mathcal{H}$ is defined as follows:

$$\begin{array}{l}\mathcal{H}=B_1{I}_u+B_2{I}_a+\frac{1}{2}(C_1{u}_1^2+C_2{u}_2^2+C_3{u}_3^2)+{\lambda }_1\left(\Lambda -\lambda (I_u,I_a,T)S-u_1({\alpha }_1+{\alpha }_2)S-\mu S\right)\\ +{\lambda }_2\left(u_1{\alpha }_{1}S-(1-{\psi }_1)\lambda (I_u,I_a,T)E_1-\mu E_1\right)+{\lambda }_3\left(u_1{\alpha }_{2}S-(1-{\psi }_2)\lambda (I_u,I_a,T)E_2-\mu E_2\right) \\ +{\lambda }_4\left(\lambda (I_u,I_a,T)S+1-{\psi }_1)\lambda (I_u,I_a,T)E_1\right.+\hspace{0.33em}\left.1-{\psi }_2)\lambda (I_u,I_a,T)E_2-\left(u_2+{\sigma }_1+\mu \right)I_u\right)\\ +{\lambda }_5\left(u_2\hspace{0.17em}{I}_u-(u_3+{\sigma }_2+\mu )I_a\right)+{\lambda }_6\left(u_3\hspace{0.17em}{I}_a-({\sigma }_3+\mu )\right)+{\lambda }_7\left({\sigma }_1{I}_u+{\sigma }_2{I}_a+{\sigma }_{3}T-(\gamma +\mu )A\right).\end{array}$$

(38)

where ${\lambda }_1,\hspace{0.33em}{\lambda }_2,\hspace{0.33em}{\lambda }_3,\hspace{0.33em}{\lambda }_4,\hspace{0.33em}{\lambda }_5,\hspace{0.33em}{\lambda }_6,$and ${\lambda }_7$are the adjoint variables.

The following result gives the necessary conditions for the optimal control.

Theorem 6.

Given an optimal controls $\left(u_1^{*},u_2^{*}, u_3^{*}\right)$ that minimizes the objective functional J over the control set U subject to system (1), then there exist the adjoint variables ${\lambda }_1,\hspace{0.33em}{\lambda }_2,\hspace{0.33em}{\lambda }_3,\hspace{0.33em}{\lambda }_4,\hspace{0.33em}{\lambda }_5,\hspace{0.33em}{\lambda }_6,$ and ${\lambda }_7$ satisfying the following equations:

$$\begin{array}{l}{\displaystyle \frac{d{\lambda }_1}{dt}}=({\lambda }_1-{\lambda }_4){\displaystyle \frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S}{1+\omega (I_u+I_2+T)}}+({\lambda }_1-{\lambda }_2)u_1{\alpha }_1+({\lambda }_1-{\lambda }_3)u_1{\alpha }_2+{\lambda }_1\mu ,\\ {\displaystyle \frac{d{\lambda }_2}{dt}}=({\lambda }_2-{\lambda }_4){\displaystyle \frac{c_1\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S}{1+\omega (I_u+I_2+T)}}+{\lambda }_2\mu ,\\ {\displaystyle \frac{d{\lambda }_3}{dt}}=({\lambda }_3-{\lambda }_4){\displaystyle \frac{c_2\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S}{1+\omega (I_u+I_2+T)}}+{\lambda }_3\mu ,\\ {\displaystyle \frac{d{\lambda }_4}{dt}}=-B_1+({\lambda }_1-{\lambda }_4)\left({\displaystyle \frac{\beta S}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_2-{\lambda }_4)\left({\displaystyle \frac{c_1\beta E_1}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_1\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_1\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)\\ +({\lambda }_3-{\lambda }_4)\left({\displaystyle \frac{c_2\beta E_2}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_2\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_2\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_4-{\lambda }_7){\sigma }_1+({\lambda }_4-{\lambda }_5)u_2+{\lambda }_4\mu ,\end{array}$$

$$\begin{array}{l}{\displaystyle \frac{d{\lambda }_5}{dt}}=-B_2+({\lambda }_1-{\lambda }_4)\left({\displaystyle \frac{\beta {\eta }_{1}S}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_2-{\lambda }_4)\left({\displaystyle \frac{c_1\beta {\eta }_1{E}_1}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_1\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_1\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)\\ +({\lambda }_3-{\lambda }_4)\left({\displaystyle \frac{c_2\beta {\eta }_1{E}_2}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_2\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_2\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_5-{\lambda }_6)u_3+({\lambda }_5-{\lambda }_7){\sigma }_2+{\lambda }_5\mu ,\\ {\displaystyle \frac{d{\lambda }_6}{dt}}=({\lambda }_1-{\lambda }_4)\left({\displaystyle \frac{\beta {\eta }_{2}S}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)S\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_2-{\lambda }_4)\left({\displaystyle \frac{c_1\beta {\eta }_2{E}_1}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_1\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_1\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)\\ +({\lambda }_3-{\lambda }_4)\left({\displaystyle \frac{c_2\beta {\eta }_2{E}_2}{1+\omega (I_u+I_2+T)}}-{\displaystyle \frac{c_2\beta (I_u+{\eta }_1{I}_a+{\eta }_{2}T)E_2\omega }{{(1+\omega (I_u+I_2+T))}^2}}\right)+({\lambda }_6-{\lambda }_7){\sigma }_3+{\lambda }_6\mu ,\\ {\displaystyle \frac{d{\lambda }_7}{dt}}=({\lambda }_7-{\lambda }_6)\delta +(\gamma +\mu ){\lambda }_7.\end{array}$$

(39)

with transversality conditions,

$${\lambda }_j(T_f)=0,\hspace{0.33em}j=1,\hspace{0.33em}2,\hspace{0.33em}3,\hspace{0.33em}4,\hspace{0.33em}5,\hspace{0.33em}6,\hspace{0.33em}7.$$

Furthermore, the optimal, denoted as  $u^{*}=\left(u_1^{*},u_2^{*}, u_3^{*}\right)$ is expressed as follows:

$$\begin{array}{l}{u}_1^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\displaystyle \frac{\left(({\lambda }_1-{\lambda }_2){\alpha }_1+({\lambda }_1-{\lambda }_3){\alpha }_2\right)S^{*}}{C_1}}\right)\hspace{0.33em},\hspace{0.33em}1\right\},\hspace{1em}\\ u_2^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\displaystyle \frac{({\lambda }_4-{\lambda }_5)\hspace{0.17em}{I}_u^{*}}{C_2}}\right),\hspace{0.33em}1\right\},\\ u_3^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\displaystyle \frac{({\lambda }_5-{\lambda }_6)\hspace{0.17em}{I}_a^{*}}{C_3}}\right),\hspace{0.33em}1\right\}.\end{array}$$

(40)

Proof. 

We apply Pontryagin’s Maximum Principle to derive the adjoint variables, the transversality conditions, and the optimal control triplet. The system of adjoint equations (39) is obtained by taking the partial derivatives of the Hamiltonian in Equation (38) with respect to the corresponding state variables, $S,\hspace{0.33em}{E}_1,\hspace{0.33em}{E}_2,\hspace{0.33em}{I}_u,\hspace{0.33em}{I}_a,\hspace{0.33em}T,\hspace{0.33em}A,$ as follows:

$$\begin{array}{l}{\displaystyle \frac{\partial {\lambda }_1}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial S}}\hspace{0.33em}, \hspace{0.33em}{\lambda }_1(T_f)=0;{\displaystyle \frac{\partial {\lambda }_2}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial E_1}},\hspace{0.33em} \hspace{0.33em}{\lambda }_2(T_f)=0;{\displaystyle \frac{\partial {\lambda }_3}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial E_2}},\hspace{0.33em} \hspace{0.33em}{\lambda }_3(T_f)=0; \\ {\displaystyle \frac{\partial {\lambda }_4}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial I_u}}, {\lambda }_4(T_f)=0;\hspace{0.33em}{\displaystyle \frac{\partial {\lambda }_5}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial I_a}}\hspace{0.33em}, \hspace{0.33em}{\lambda }_5(T_f)=0;{\displaystyle \frac{\partial {\lambda }_6}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial T}}, \hspace{0.33em} {\lambda }_6(T_f)=0;\\ {\displaystyle \frac{\partial {\lambda }_7}{\partial t}}=-{\displaystyle \frac{\partial \mathcal{H}}{\partial A}},\hspace{0.33em} {\lambda }_7(T_f)=0.\end{array}$$

Finally, the optimal controls can be characterized from$\mathcal{H}$in Equation (38) by applying the optimality conditions for each control measure $u_i,$ where $0\le u_i\le 1$, for $i=1,\hspace{0.33em}2,\hspace{0.33em}3.$ Thus,

$${\displaystyle \frac{\partial \mathcal{H}}{\partial u_1}}=0,\hspace{0.33em}\hspace{0.33em}{\displaystyle \frac{\partial \mathcal{H}}{\partial u_1}}=0,\hspace{0.33em}\hspace{0.33em}{\displaystyle \frac{\partial \mathcal{H}}{\partial u_1}}=0.$$

(41)

By solving Equation (41) with the optimal controls $u_1^{*},u_2^{*},$ and $u_3^{*}$, we derive the following characterization:

$${\tilde{u}}_1={\displaystyle \frac{\left(({\lambda }_1-{\lambda }_2){\alpha }_1+({\lambda }_1-{\lambda }_3){\alpha }_2\right)S^{*}}{C_1}},\hspace{0.33em}\hspace{0.33em}{\tilde{u}}_2={\displaystyle \frac{({\lambda }_4-{\lambda }_5)I_u^{*}}{C_2}},\hspace{0.33em}\hspace{0.33em}{\tilde{u}}_3={\displaystyle \frac{({\lambda }_5-{\lambda }_6)I_a^{*}}{C_3}}.$$

(42)

Since all three control measures are bounded between 0 and 1, we have

$$u_i^{*}=\left\{\begin{array}{ccc}0& \mathrm{if}& {\tilde{u}}_i^{*}\le 0,\\ {\tilde{u}}_i^{*}& \mathrm{if}& 0<{\tilde{u}}_i^{*}<1,\\ 1& i\mathrm{f}& {\tilde{u}}_i^{*}\ge 1.\end{array}\right.$$

where

$${\tilde{u}}_1={\displaystyle \frac{\left(({\lambda }_1-{\lambda }_2){\alpha }_1+({\lambda }_1-{\lambda }_3){\alpha }_2\right)S^{*}}{C_1}},\hspace{0.33em}\hspace{0.33em}{\tilde{u}}_2={\displaystyle \frac{({\lambda }_4-{\lambda }_5)I_u^{*}}{C_2}},\hspace{0.33em}\hspace{0.33em}{\tilde{u}}_3={\displaystyle \frac{({\lambda }_5-{\lambda }_6)I_a^{*}}{C_3}}.$$

Hence, for these controls $u_1^{*},\hspace{0.33em}{u}_2^{*},\hspace{0.33em}$and $u_3^{*}$ given in the Equation (40) are characterized by

$$u_1^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\tilde{u}}_1\right)\hspace{0.33em},\hspace{0.33em}1\right\},\hspace{0.33em}{u}_2^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\tilde{u}}_2\right),\hspace{0.33em}1\right\},\hspace{0.33em}{u}_3^{*}=\min \left\{\max \hspace{0.17em}\left(0,\hspace{0.17em}{\tilde{u}}_3\right),\hspace{0.33em}1\right\}.$$

The proof of Theorem 6 is complete. □

5. Numerical Simulations and Cost-Effectiveness Analysis

5.1. Numerical Simulation of Model

In this section, we present several numerical simulations of the model (8) to illustrate the dynamics of HIV transmission, using the parameter values estimated and shown in Table 2. These results aim to explore the dynamic effects of education, screening, and therapy interventions on HIV incidence. To perform the simulations, both models are solved numerically using the fourth-order Runge-Kutta method and implemented in MATLAB. We set the initial population as follows:

$$\left(S(0),\hspace{0.33em}{E}_1(0),\hspace{0.33em}{E}_2(0),I_u(0),\hspace{0.33em}{I}_a(0),\hspace{0.33em}T(0),\hspace{0.33em}A(0)\right)=\left(2904903,\hspace{0.17em}5000,\hspace{0.17em}2500,\hspace{0.17em}2408,\hspace{0.17em}5390,\hspace{0.17em}519,\hspace{0.33em}1024\right).$$

(43)

First, we set parameter value $\beta =0.00001$ and the other parameters as given in Table 1. We obtain ${\mathcal{R}}_e=0.719881<1$. Theorem 1 is numerically illustrated in Figure 5, demonstrating the global stability of the DFE $E_0=(24154.59,\hspace{0.17em}67287.79,\hspace{0.17em}49541.66,\hspace{0.33em}0,\hspace{0.17em}0,\hspace{0.17em}0,\hspace{0.17em}0)$ within its region of attraction in both the$S-E_1-I_a$ and$A-T-I_u$ spaces. Figure 5(a) shows that all solution trajectories starting within the area of attraction converge to the point $\left(S^0, E_1^0, I_a^0\right)=\left(24154.59, 67287.79, 0\right)$. Similarly, Figure 5(b) indicates that all trajectories originating within the region of attraction tend toward the point $\left(A^0, T, I_u^0\right)=\left(0, 0, 0\right).$Three different initial values are used in constructing the stability diagram of ${\mathcal{E}}_0$ in three different state spaces, as follows: ${\mathrm{N}}_1$(20000, 40000, 30000, 2000, 1500, 1000, 1000), ${\mathrm{N}}_2$(22000, 42000, 32000, 2500, 2000, 2000, 1000), ${\mathrm{N}}_3$(24000, 44000, 34000, 3000, 2500, 2500, 2000), and ${\mathrm{N}}_4$(25000, 45000, 35000, 3500, 3000, 3000, 2500). This approach can also be extended to demonstrate the global asymptotic stability of the disease-free equilibrium ${\mathcal{E}}_0$ in other subspaces of the model.

Second, we set parameter value $\beta =0.00004$ while the remaining parameters are taken from Table 1. This results in the effective reproduction number of ${\mathcal{R}}_e=2.879523>1.$ Theorem 2 is numerically illustrated in Figure 6, demonstrating the global stability of the endemic equilibrium ${\mathcal{E}}_1=\left(24151.41,\hspace{0.17em}\hspace{0.17em}44846.37,\hspace{0.33em}33015.99,\hspace{0.33em}0.68,\hspace{0.33em}0.64,\right.\hspace{0.33em}10.31,\hspace{0.33em}0.24)$ within its region of attraction in both the $S-E_1-I_a$ and $T-I_a-A$ spaces. In Figure 6(a), all solution trajectories that begin within the region of attraction ${\mathrm{N}}_1, {\mathrm{N}}_2, {\mathrm{N}}_3,$and${\mathrm{N}}_4$converge to the point$\left(S^0, E_1^0, I_a^0\right)=\left(\mathrm{24151.41,44846.37}, 0\right)$. Figure 6(b) indicates that all trajectories that begin within the region of attraction tend toward the point $\left( T, I_a^0, A^0\right)=\left(10.31, 0.64, 0.24\right).$ This methodology can further be applied to verify the global asymptotic stability of the endemic equilibrium ${\mathcal{E}}_1$in other subspaces of the model.

5.2. Optimal Control Simulation

We compute the numerical solution to the optimal control problem by solving the optimality system, which consists of the state and adjoint equations, using the forward-backward sweep method. This involves numerical integration using the fourth-order Runge-Kutta method implemented in MATLAB. Initially, the state system (35) is solved forward in time, with initial values determined by the transversality condition. Subsequently, the adjoint system (39) is solved backwards in time, utilizing the current iteration of state variables. The control variables are updated through a convex combination of their previous values and the new estimate derived from Equation (40). This iterative process is repeated until convergence of the state equations is achieved [18].

For numerical simulation purposes, the weight factors $B_1=1$ and $B_2=1$ are utilized, alongside cost coefficients $C_1=20, C_2=55,$and $C_3=75$. Simulations were conducted over a period of 5 years. These cost values are determined based on the efforts to implement the strategies under consideration. The parameter values presented in Table 1 and $\beta =0.00004$ are employed in the simulations for cases where ${\mathcal{R}}_e=2.879523>1$. To assess the impact of various optimal control strategies on the spread of HIV infection within the community, we will examine and compare the numerical results of interventions that implement multiple strategies. Strategies involving a single intervention are excluded, as they do not ensure the complete eradication of the disease from the community. This study considers the following four combined intervention strategies:

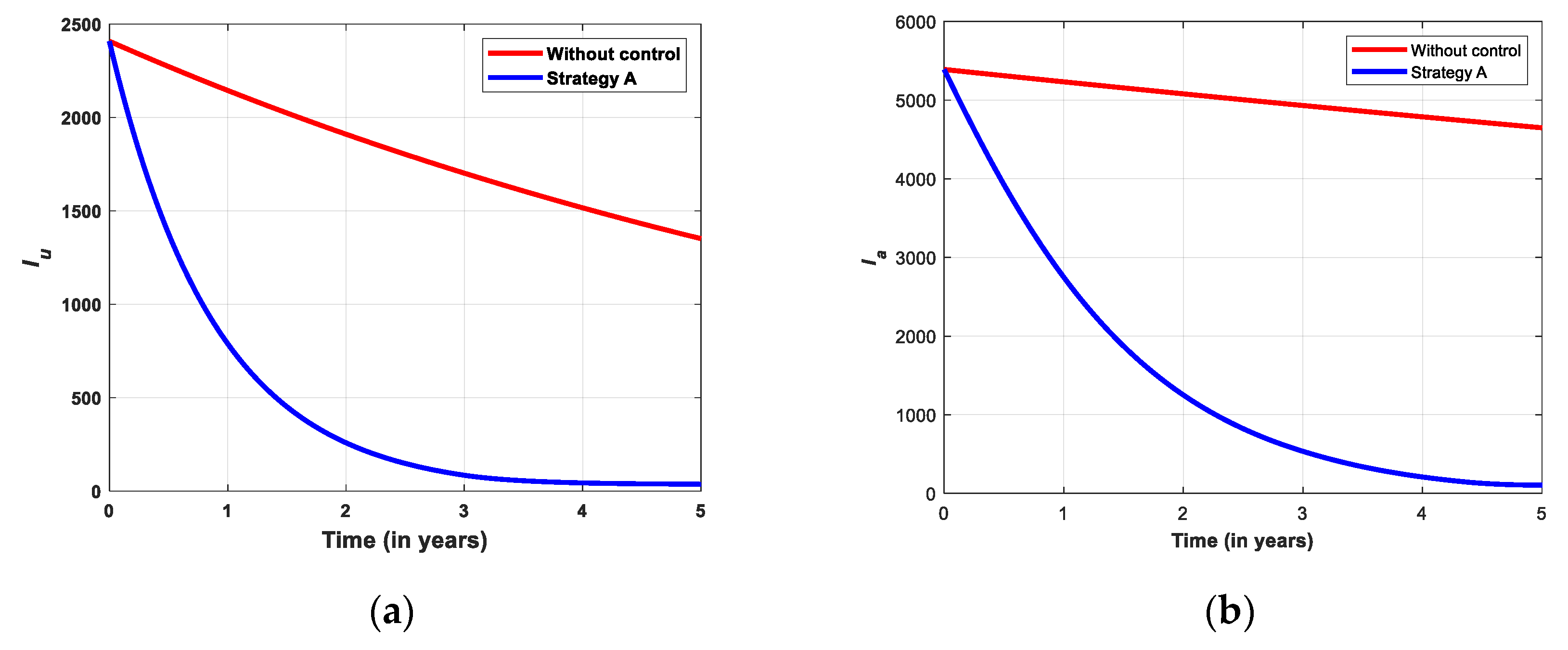
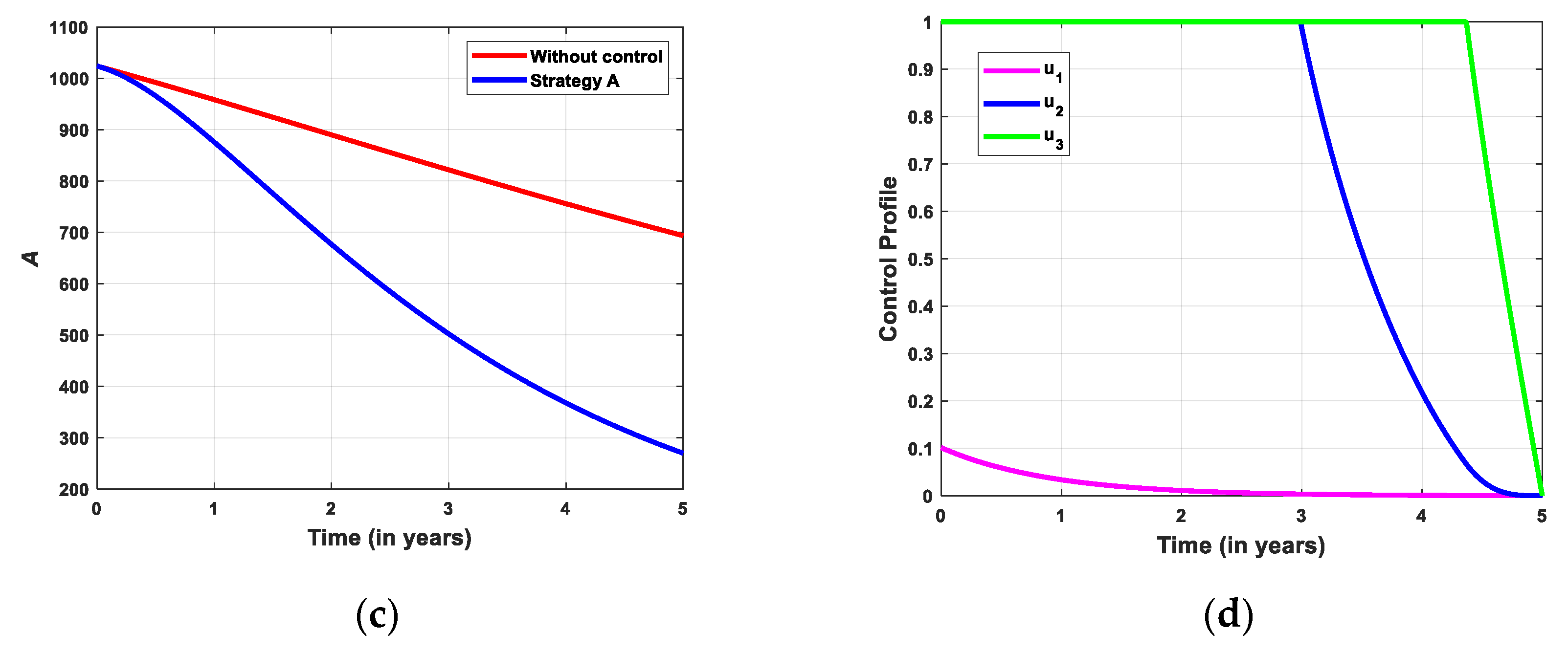
• Strategy A: Educational campaign combined with screening ${(u}_1\ne 0, u_2\ne 0, u_3\ne 0).$
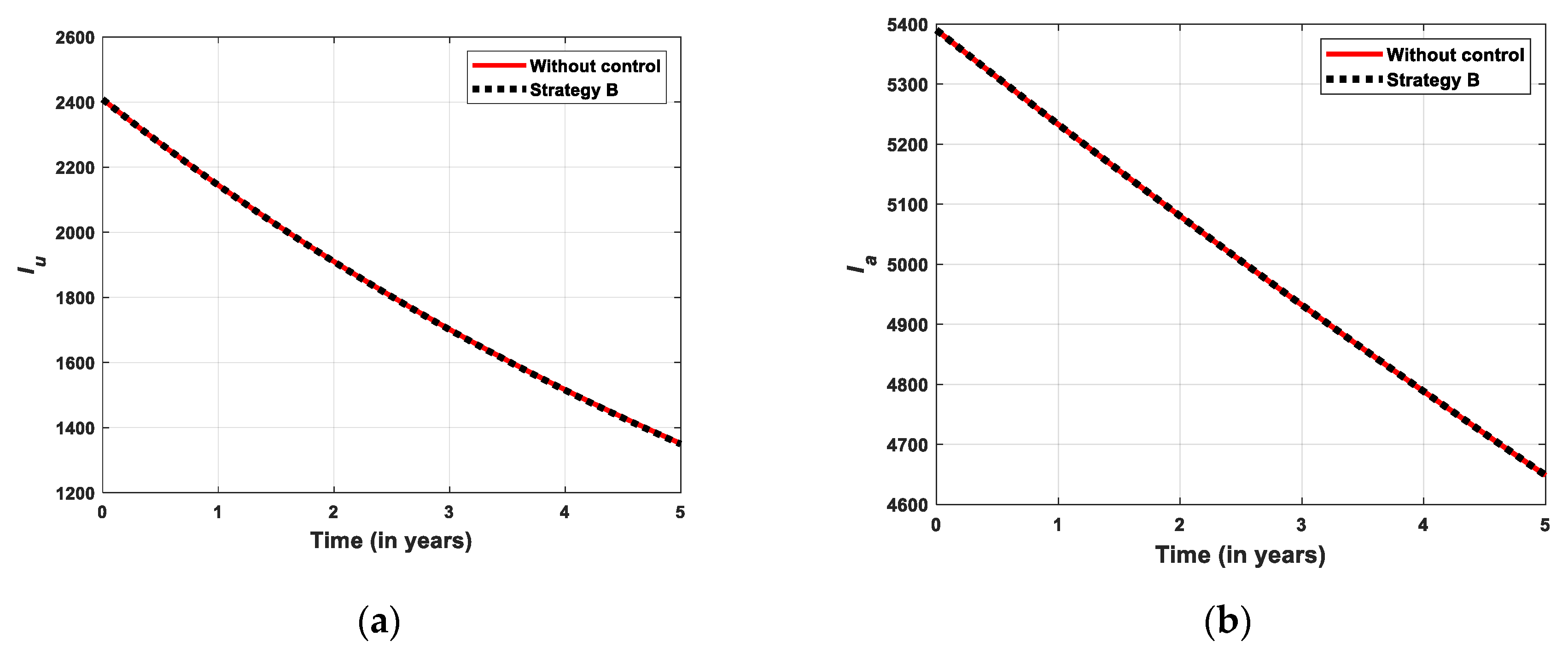
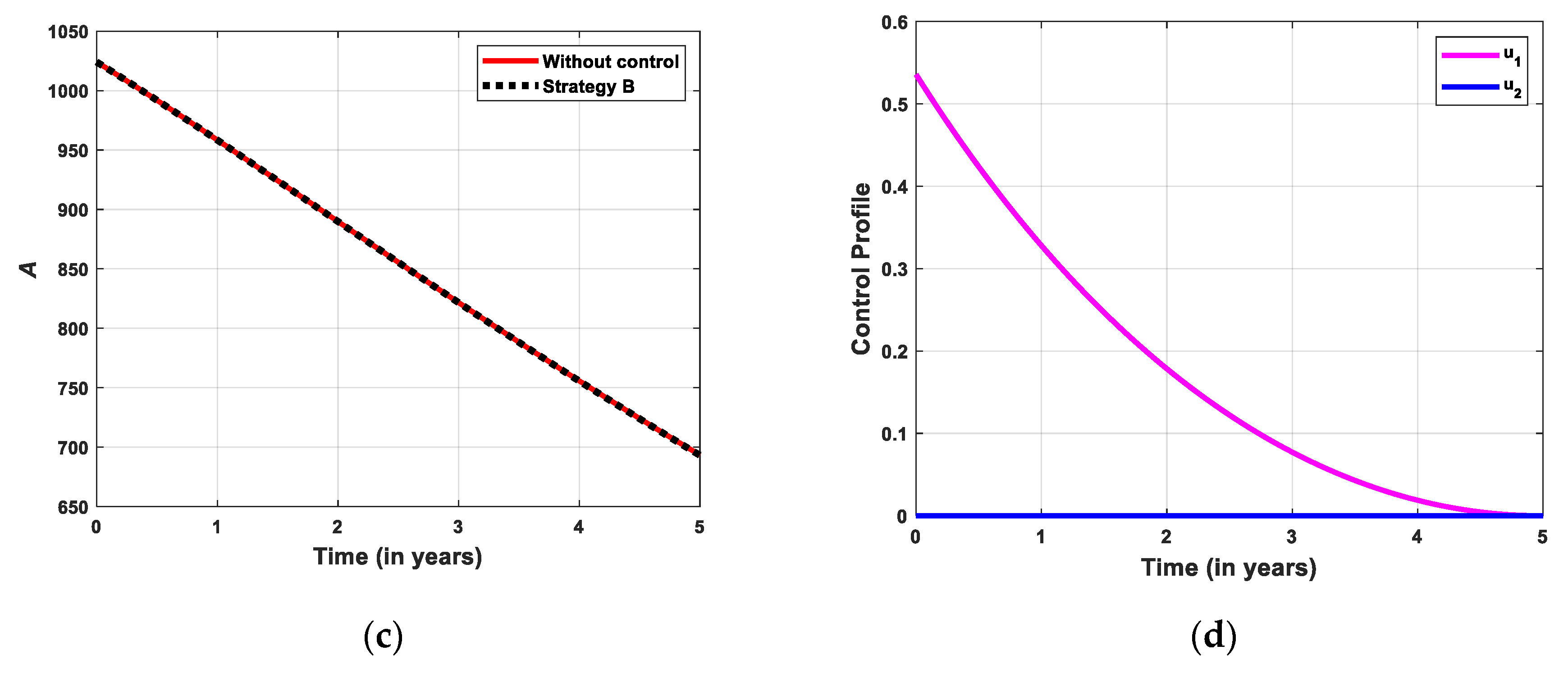
• Strategy B: Educational campaign combined with treatment ${(u}_1\ne 0, u_2\ne 0, u_3=0).$
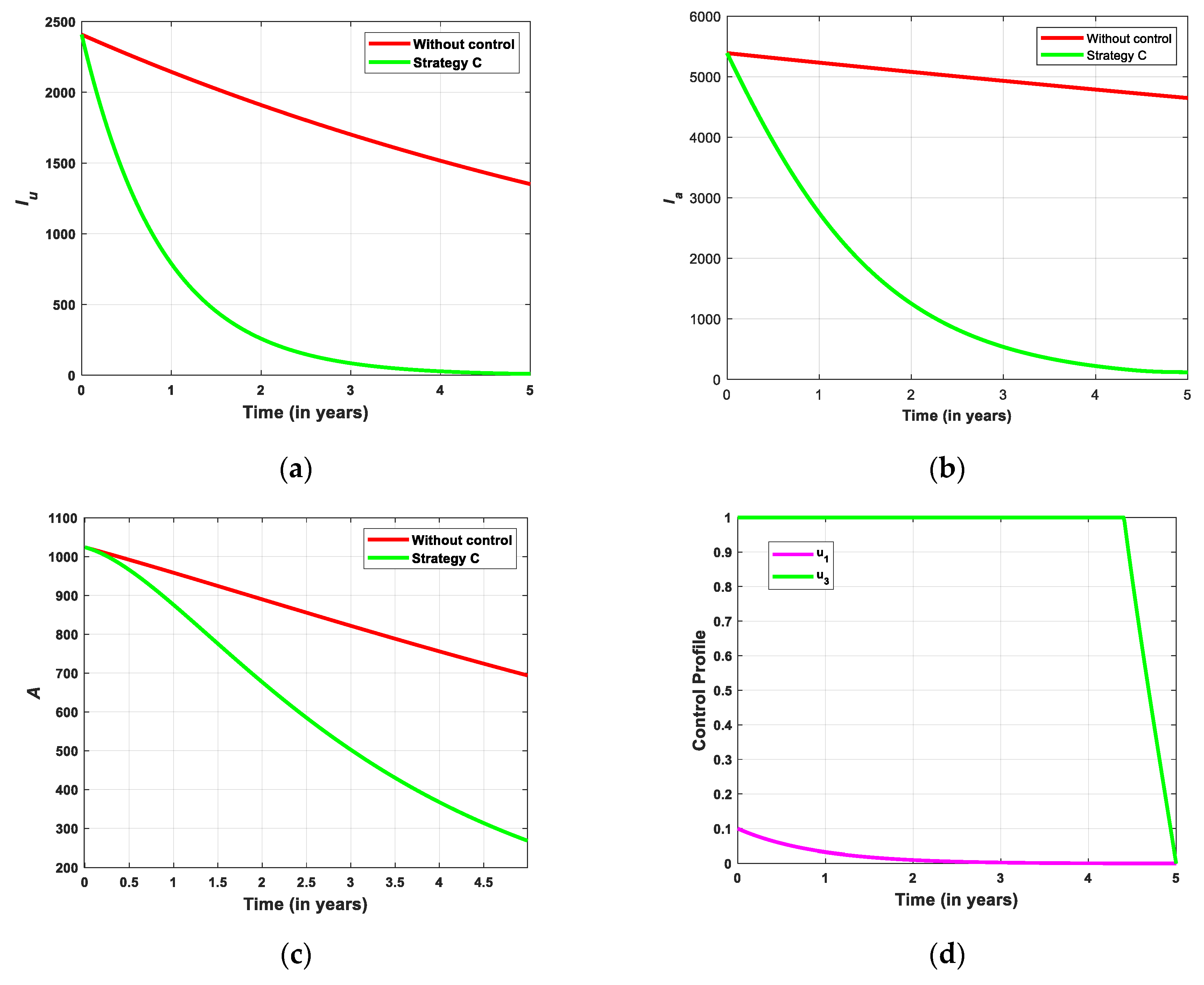
• Strategy C: Screening combined with treatment $(u_1\ne 0, u_2=0, u_3\ne 0).$
• Strategy D: Implementation of all control ${(u}_1=0, u_2\ne 0, u_3\ne 0).$

5.2.1. Simulation for Strategi A ${(\mathrm{u}}_1\ne 0,{\mathrm{u}}_2\ne 0,{\mathrm{u}}_3\ne 0).$

By implementing the triple control strategies simultaneously, we observed that Strategy A, which involves the simultaneous implementation of educational campaign control ($u_1$), screening control ($u_2$), and antiretroviral treatment control ($u_3$), significantly reduces the number of infected individuals (Figure 7). Specifically, at the final time ($T_f=5 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}$), the total number of unaware infectives under control is 36.7, compared to 1351.2 without control (Figure 7(a)). Similarly, the total number of aware infectives at time $T_f$ is reduced to 105.36 with control, whereas it reaches 4648.5 in the absence control, which is significantly different (Figure 7(b)). Additionally, the total number of individuals with AIDS at time $T_f$ is reduced to 269.8 with control, whereas it reaches 693.5 in the absence of control. These results demonstrate that the optimal control strategy is highly effective for both groups of HIV-infected individuals and AIDS cases. Furthermore, Figure 7(d) illustrates the control profiles for Strategy A over time. To minimize the number of HIV infections and associated costs, the control $u_1$is maintained at its upper limit for approximately 2.98 years before gradually decreasing to zero at the end of the control period. Similarly, the controls $u_2$and $u_3$are kept at their upper limit for 2.98 years and 4.35 years, respectively, before dropping to their lower bounds at the end of the control period.

5.2.2. Simulation for Strategi B

This strategy implements both intervention measures $u_1$(educational campaign control) and $u_2$ (screening controls). It is observed from Figure 8(a) to 8(c) that due to this control strategy, the number of unaware infectives, aware infectives, and AIDS individuals decreased only slightly during the control period. This result shows that the Strategy B has no significant effect on the subpopulation of the unaware infected individuals, aware infected individuals, and AIDS individuals. The control profile for the educational campaigns control $u_1$ at the beginning of the control period is at 0.53, then gradually decreases to zero at the end of the control period, while the control profile for screening control $u_2$ is maintained at its lower bound for the whole period (Figure 8(d)) .

5.2.3. Simulation for Strategi C

The simultaneous implementation of double control strategies demonstrates that Strategy C (i.e., applying educational campaign control and antiretroviral treatment) significantly reduces the number of infected individuals (Figure 9). Specifically, at the final time, the total number of unaware infectives under control is 9.7, compared to 1351.2 without control (Figure 9(a)). Similarly, the total number of aware infectives at time 5 years is reduced to 118.2 with control, whereas it reaches 4648.5 in the absence control, which is significantly different (Figure 9(b)). Additionally, at the final time, applying Strategy C leads to a significant decrease in the number of AIDS individuals (267.6) compared to the uncontrolled case (Figure 9(c)). Furthermore, Figure 9(d) illustrates the control profiles for Strategy C over time. The control profiles for the educational campaigns control $u_1$at the beginning of the control period; it is at 0.09 then gradually decreases to zero at the end of the control period. The control profiles for the antiretroviral treatment control $u_3$ should be maintained at it upper bound for the first 4.4 years. After which both controls gradually decrease to it lower bound at the end of the period (Figure 9(d)). The optimal control profiles for $u_1$ and $u_3$ in Strategy C are identical to those in Strategy A.

5.2.3. Simulation for Strategi C

The simultaneous implementation of double control strategies demonstrates that Strategy C (i.e., applying educational campaign control and antiretroviral treatment) significantly reduces the number of infected individuals (Figure 8). Specifically, at the final time, the total number of unaware infectives under control is 9.7, compared to 1351.2 without control (Figure 8(a)). Similarly, the total number of aware infectives at time 5 years is reduced to 118.2 with control, whereas it reaches 4648.5 in the absence control which is significantly different (Figure 9(b). Additionally, at the final time, applying Strategy C leads to a significant in the number of AIDS individuals (267.6) compared to the uncontrolled case (Figure 9(c)). The control profiles for the educational campaigns control $u_1$at the beginning of the control period it is at 0.09 then gradually decreases to zero at the end of the control period. The control profiles for the antiretroviral treatment control $u_3$ should be maintained at its upper bound for the first 4.4 years. After which both controls gradually decrease to its lower bound at the end of the period (Figure 9(d)). The optimal control profiles for $u_1$ and $u_3$ in Strategy C are identical to those in Strategy A.

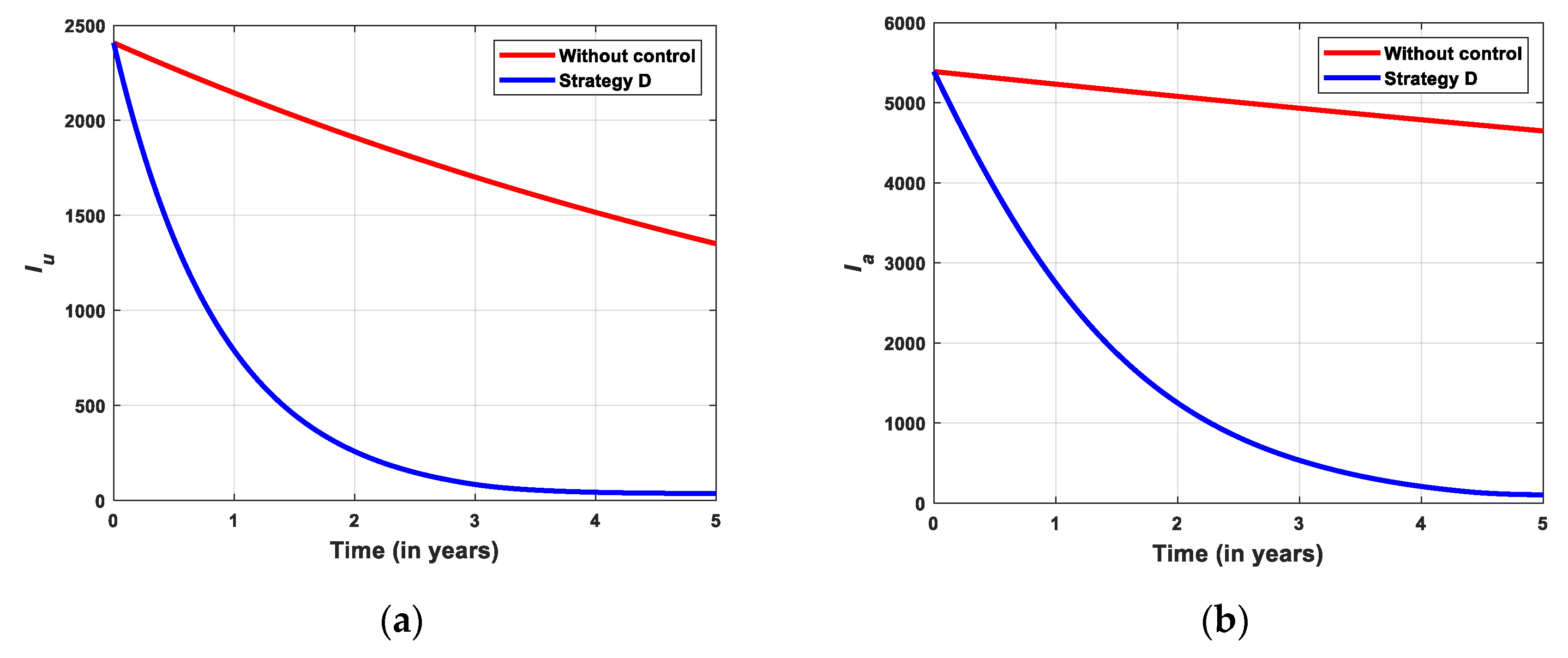
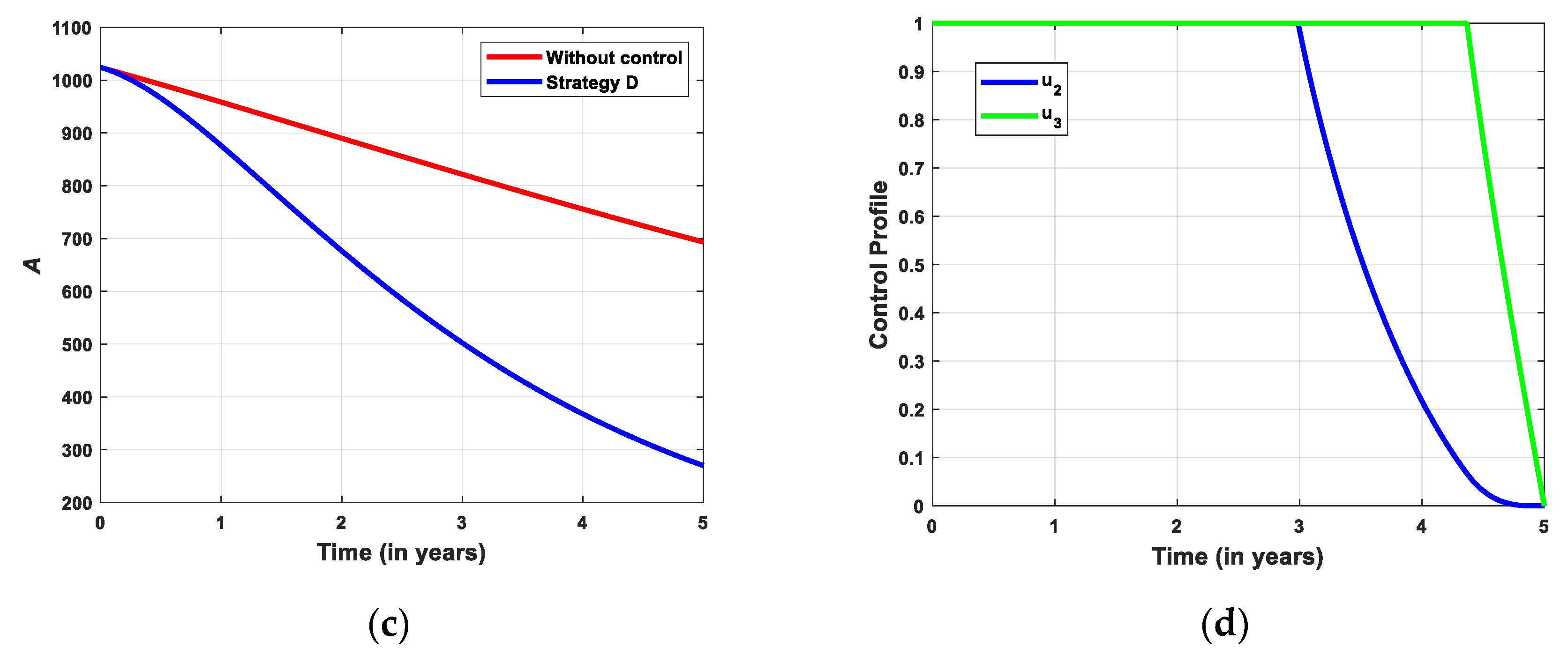
5.2.4. Simulation for Strategi D

This strategy implements both intervention measures $u_2$(screening control) and $u_3$ (antiretroviral treatment). Specifically, at the final time (5 years), the total number of unaware infectives under control is 36.7, compared to 1351.2 without control (Figure 10(a)). Similarly, the total number of aware infectives at time $T_f$ is reduced to 105.3 with control, whereas it reaches 4648.5 in the absence control, which is significantly different (Figure 10(b)). Additionally, at the final time, applying Strategy A leads to a significant decrease in the number of AIDS individuals (269.8) compared to the uncontrolled case (Figure 10(c)). The control profiles for the screening control $u_2$ should be maintained at it upper bound for the first 2.98 years, while the control profile for the antiretroviral treatment control ($u_3$) should be maintained at it upper bound for the first 4.36 years. After which both controls gradually decrease to it lower bound at the end of the period. The optimal control profiles for $u_2$ and $u_3$ in Strategy D are identical to those in Strategy A.

5.3. Cost-Effectiveness Analysis

To determine which control strategy is most effective, this subsection evaluates the economic implications of educational campaign strategies for susceptible individuals, screening for unaware infectives, and antiretroviral therapy for aware infectives in the dynamics of HIV/AIDS, using cost-effectiveness analysis (CEA). CEA helps identify and propose the most efficient or cost-effective strategy for implementation under limited sources. In this study, the evaluation will be conducted using the incremental cost-effectiveness ratio (ICER), which compares the difference in costs and health outcomes between two competing intervention strategies. Each intervention is compared to the next less effective alternative in terms of the number of infections averted [9]. When comparing two competing intervention strategies, p and q, The ICER is defined as follows [21,25].

$$\mathrm{ICER}={\displaystyle \frac{\mathrm{Change} \mathrm{in} \mathrm{total} \mathrm{costs} \mathrm{associated} \mathrm{with} \mathrm{strategies} p \mathrm{and} q }{\mathrm{Change} \mathrm{in} \mathrm{control} \mathrm{benefits} \mathrm{obtained} \mathrm{by} \mathrm{implementing} \mathrm{the} \mathrm{strategies} p \mathrm{and} q}}.$$

(44)

The total averted infections, used in the cost-effectiveness analysis table, is determined by the difference between the total number of infected individuals without any control and the total number with the implementation of a control strategy. The total cost associated with a control strategy is directly proportional to the number of controls applied. In this study, the ICER values were computed using formula (31). Specifically, the total cost (TC) and total averted infections (TA) for each strategy $i$were calculated using the following formulas:

$$TC(i)={\displaystyle {\int }_{i=1}^{T_f}\left[w_3{(u_1^{*}(t))}^2+w_4{(u_2^{*}(t))}^2+w_5{(u_3^{*}(t))}^2\right]}\hspace{0.33em}dt,$$

(45)

$$TA(i)={\displaystyle {\int }_{i=1}^{T_f}\left[(I_u(t)-I_u^{*}(t))+(I_a(t)-I_a^{*}(t))+(A(t)-A^{*}(t))\right]}\hspace{0.33em}dt.$$

(46)

Table 3 presents the control strategies ranked in ascending order of total averted infections. Here, the ICER is calculated for Strategies B and D to enable a comparative evaluation of their relative effectiveness, defined as:

$$\begin{array}{l}\mathrm{CER}(B)={\displaystyle \frac{TC(B)}{TA(B)}}={\displaystyle \frac{4.0169}{4.7007}}=\mathrm{0.8545.}\\ \mathrm{ICER}(D)={\displaystyle \frac{TC(D)-TC(B)}{TA(D)-TA(B)}}={\displaystyle \frac{526.3404-4.0169}{25999.8318-4.7007}}=\mathrm{0.0201.}\\ \mathrm{ICER}(A)={\displaystyle \frac{TC(A)-TC(D)}{TA(A)-TA(D)}}={\displaystyle \frac{526.4049-526.3404}{25999.9067-25999.8318}}=0,8612\\ \mathrm{ICER}(C)={\displaystyle \frac{TC(C)-TC(A)}{TA(C)-TA(A)}}={\displaystyle \frac{344.4764-526.4049}{26013.4355-25999.9067}}=-\mathrm{13.4475.}\end{array}$$

Table 3 presents a summary of the ICER calculations of Strategies B, D, A, and C. From the table, the comparison between Strategy B and Strategy D shows that the ICER of Strategy B is higher than that of Strategy D, indicating that Strategy B is both more costly and less effective. Consequently, Strategy B should be excluded from the set of alternative control intervention strategies competing for the same limited resources. Furthermore, the ICER for Strategies D and A are recalculated using the same procedure, as presented in the fourth column of Table 4.

From Table 4, the comparison between Strategy D and Strategy A shows that the ICER of Strategy A is higher than that of Strategy D, which indicates that Strategy A is both more costly and less effective. Consequently, Strategy A should be excluded from the set of alternative control intervention strategies competing for the same limited resources. Furthermore, the ICER for Strategies D and C are recalculated, with the results presented in the fourth column of Table 5.

The comparison of ICER values for intervention Strategies D and C, as shown in Table 5, indicates that the ICER for Strategy D is higher than that of Strategy C. Consequently, Strategy D is excluded from the set of remaining alternative strategies to prevent the inefficient allocation of limited resources. We observed that Strategy C, which involves the simultaneous implementation of educational campaigns and antiretroviral treatment measures (i.e., $u_1\ne 0, u_3\ne 0$ and $u_2=0$), is identified as the most cost-effective among the four proposed control strategies aimed at reducing and controlling the spread of HIV/AIDS in the community considered in this study.