Time as the Experience of Information: An Epistemic Reformulation of Temporal Dynamics

1. Introduction

The nature of time continues to provoke foundational inquiry across physics, philosophy, and information theory. In Newtonian mechanics, time is treated as a universal, absolute parameter. In contrast, relativity entwines time with space, rendering it local and observer-dependent. Meanwhile, quantum gravity suggests time may not exist as a fundamental entity at all, as exemplified by the Wheeler–DeWitt equation, which omits time entirely [9,11]. These conceptual tensions motivate a reassessment: what, fundamentally, is time?

In parallel, the emergence of information-centric worldviews has reshaped multiple disciplines. Information theory [1], epistemic logic [2], and digital metaphysics [14] emphasize knowledge, distinctions, and observer-system interactions. However, these perspectives have largely sidestepped the temporal question: how does time emerge from or relate to information?

This paper proposes a reformulation: time is the experience of information. Specifically, we define epistemic time as a function of the rate of change of accessible information about a system, relative to an embedded observer. Rather than treating time as external to a system, we embed it within the observer’s epistemic interaction with that system. This view diverges sharply from block universe models or thermodynamic asymmetries alone, instead rooting temporal experience in informational flux.

To formalize this idea, we construct a metric space, an epistemic manifold, in which time increments are defined as the differential accumulation of distinguishable information. We derive this structure from first principles, linking it to curvature, geodesics, and the observer’s resolution limit. This allows us to reinterpret classic paradoxes, such as why photons, despite mediating causality, do not experience time, as boundary conditions of zero informational change.

We situate our work within ongoing debates on the origin and direction of time, including relational theories [12], informational physics [7], and multiverse formulations [13]. While prior models invoke entropy or event correlation, our contribution centers on the observer’s epistemic state, offering a complementary and unifying framework.

This reconceptualization not only advances foundational theory but also holds practical value for fields where time is indexed to belief change, such as imprecise probability theory, agentic AI, and decision intelligence. Our formalism enables temporally grounded reasoning that adapts to the structure and content of information, rather than an externally imposed clock.

Because we make mention of it in this paper, GaiaGraph is an agentic AI-powered knowledge graph architecture designed to encode, infer, and act upon epistemic structures such as uncertainty, ambiguity, and temporal change. It models information flow across semantically rich, dynamically updating subgraphs where reasoning and decision-making occur through possibilistic inference rather than deterministic computation.

In line with Entropy’s mission, we present a rigorous and generalizable framework for temporal dynamics based on uncertainty, distinguishability, and observer knowledge. Our central thesis is that epistemic time is a measurable, modelable, and potentially observable phenomenon that bridges physics and cognition. This paper develops that thesis in full and outlines key implications for future research.

2. A Definition of Time as Informational Experience

2.1. Postulate from First Principles

Let a system $\mathcal{S}$ be any physically bounded, internally coherent entity capable of distinguishing among informational states. We define an epistemic state of $\mathcal{S}$ as a configuration in which the system possesses a definite pattern of internal distinctions that are meaningful relative to its structural or functional encoding.

Let $\mathcal{I}\left(t\right)$ be a scalar function representing the cumulative epistemically accessible information within $\mathcal{S}$ at coordinate time t. This includes:

• Sensory data or internal observations,
• Computed or inferred quantities from prior states,
• Any distinguishable symbolic, analog, or dynamical representation that contributes to the system’s internal configuration.

We postulate:

Epistemic Time Postulate: A system experiences time if and only if it undergoes a change in epistemically accessible information. That is, time is the rate at which a system internally distinguishes its own evolution.

This postulate reinterprets time not as an external parameter but as a consequence of state distinction, grounded in information-theoretic change.

2.2. Formal Derivation

Let $t\in \mathbb{R}$ denote coordinate or parametric time, and let $\mathcal{I}\left(t\right)$ be a non-decreasing function measuring the accumulation of distinct informational events by the system. Define the rate of informational change as:

$$\dot{\mathcal{I}}\left(t\right):={\displaystyle \frac{d\mathcal{I}\left(t\right)}{dt}}.$$

(1)

We define epistemic time $\mathcal{T}$ as an internal clock governed by the flux of informational change:

$${\displaystyle \frac{d\mathcal{T}}{dt}}=f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right),$$

(2)

where $f:{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ is a continuous, monotonic function satisfying:

• $f\left(0\right)=0$: No informational change implies no experienced time.
• $f^{\prime }\left(x\right)>0$ for $x>0$: Faster informational change implies faster epistemic time accrual.
• Optional smoothness: $f\in C^1$ or higher if differentiability is required for dynamical systems modeling.

In the simplest case, let $f\left(x\right)=x$. Then:

$$d\mathcal{T}=d\mathcal{I}.$$

(3)

This means that one unit of epistemic time corresponds exactly to one unit of distinguishable informational transition.

2.3. Interpretation as a Path Integral

If $\mathcal{I}\left(t\right)$ is integrable over an interval $[t_0,t_1]$, then the total epistemic time experienced by the system is:

$$\mathcal{T}\left(t_1\right)-\mathcal{T}\left(t_0\right)={\int }_{t_0}^{t_1}f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right)dt.$$

(4)

This integral defines epistemic time as the accumulation of informational flux. For discrete systems (e.g., symbol-processing agents), this can be approximated as:

$${\mathcal{T}}_n=\sum _{k=1}^{n}f\left(\Delta {\mathcal{I}}_k\right),$$

(5)

where $\Delta {\mathcal{I}}_k$ is the amount of distinct information registered during the k-th timestep.

2.4. Implications

• If $\dot{\mathcal{I}}\left(t\right)=0$ on some interval, then ${\displaystyle \frac{d\mathcal{T}}{dt}}=0$: the system does not experience time during that interval.
• If the system enters a state of informational stasis (e.g., cryopreservation, complete sensory deprivation), its internal clock halts.
• Subsystems ${\mathcal{S}}_i\subset \mathcal{S}$ may each possess distinct ${\mathcal{I}}_i\left(t\right)$, resulting in localized epistemic times ${\mathcal{T}}_i\left(t\right)$. This explains heterochronicity, why different components age at different rates.
• Systems in identical physical conditions (same coordinate time t) may experience different epistemic times $\mathcal{T}$ due to different internal information flux.
• Epistemic time is non-uniform, non-linear, and intrinsic, emerging from within the system, not imposed from without.

2.5. Contrast with Parametric Time

Traditional parametric time t is symmetric, uniform, and global. In contrast, epistemic time $\mathcal{T}$ is:

• Local to each system or subsystem.
• Asymmetric and path-dependent.
• A function of internal change, not external duration.
• Emergent from distinguishable state transitions.

This reframing allows us to decouple time from geometry or thermodynamics and instead anchor it in information, providing a common framework for interpreting relativistic clocks, biological aging, and conscious experience.

3. Integration with Relativity

We distinguish two fundamental temporal measures: proper time, denoted $\tau$, and epistemic time, denoted $\mathcal{T}$. Proper time $\tau$ is the relativistically invariant interval experienced by a system along its worldline, as determined by spacetime geometry. Epistemic time $\mathcal{T}$, by contrast, quantifies the cumulative experience of internal informational change—the accrual of epistemically distinguishable states.

While $\tau$ is governed by the spacetime metric, $\mathcal{T}$ is governed by an information-theoretic metric internal to the system. They coincide only when the system’s informational capacity is unconstrained and fully synchronized with geometric flow. In general, the relation is:

$${\displaystyle \frac{d\mathcal{T}}{d\tau }}=\Phi \left(x^{\mu }\right),$$

(6)

where $\Phi \left(x^{\mu }\right)$ is a spacetime-dependent function encoding the system’s epistemic bandwidth—its capacity to register and integrate distinctions. In vacuum and inertial conditions, $\Phi \approx 1$, so that epistemic time tracks proper time. Under strong curvature, decoherence, or energy constraints, $\Phi \ll 1$, suppressing the flow of epistemic time relative to geometric proper time.

Einstein’s theory of relativity revolutionized the conception of time by abandoning the Newtonian view of a global, absolute clock. In special relativity, time is relative to an observer’s velocity; in general relativity, it is also shaped by spacetime curvature induced by mass-energy. These formulations are geometric and covariant, describing how time flows differently along different worldlines.

In this section, we reinterpret relativistic time not merely as geometric deformation but as modulation in a system’s ability to distinguish internal informational change. Specifically, we propose that relativistic effects alter the system’s epistemic bandwidth, its capacity to experience time, by scaling the rate at which it processes distinguishable events.

3.1. Proper Time as Informational Accrual

In general relativity, the infinitesimal proper time $d\tau$ along a worldline parameterized by a four-velocity $u^{\mu }=d{x}^{\mu }/d\lambda$ is given by the spacetime line element:

$$d{\tau }^2=-g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }.$$

(7)

Proper time is maximal for geodesics, paths that minimize the action functional:

$$S=\int \sqrt{-g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }}.$$

(8)

This is interpreted physically as the passage of time for an inertial observer. From an epistemic perspective, we reinterpret this geodesic as the trajectory that minimizes internal disturbance to a system’s informational configuration.

Let $\mathcal{I}\left(\tau \right)$ denote the cumulative epistemically accessible information within a system $\mathcal{S}$ evolving along a timelike worldline. Then epistemic time $\mathcal{T}$ accrues as a function of the rate of internal informational change relative to proper time:

$${\displaystyle \frac{d\mathcal{T}}{d\tau }}=f\left({\displaystyle \frac{d\mathcal{I}}{d\tau }}\right),$$

(9)

where f is a monotonic function with $f\left(0\right)=0$. When the system registers no distinguishable events, $d\mathcal{T}=0$ even if $d\tau >0$. Hence, epistemic time halts despite the continuous flow of proper time.

3.2. Gravitational Time Dilation as Informational Suppression

In Schwarzschild spacetime, the metric outside a non-rotating, spherically symmetric mass M is:

$$d{s}^2=-\left(1-{\displaystyle \frac{2GM}{r{c}^2}}\right)c^{2}d{t}^2+{\left(1-{\displaystyle \frac{2GM}{r{c}^2}}\right)}^{-1}d{r}^2+r^{2}d{\Omega }^2.$$

(10)

For a stationary observer at radius r, proper time relates to coordinate time via:

$$d\tau =\sqrt{1-{\displaystyle \frac{2GM}{r{c}^2}}}dt.$$

(11)

This time dilation implies that internal processes, clocks, metabolism, neural firing, slow relative to an observer at infinity. From our informational perspective, this corresponds to a reduction in $d\mathcal{I}/dt$, caused by curvature-induced constraints on energy throughput or signal propagation.

Hence, gravitational curvature suppresses a system’s ability to distinguish and integrate change:

$${\displaystyle \frac{d\mathcal{I}}{dt}}\propto \sqrt{1-{\displaystyle \frac{2GM}{r{c}^2}}}.$$

(12)

$$\begin{array}{|c|}\hline {\displaystyle \frac{d\mathcal{T}}{dt}}=f\left({\displaystyle \frac{d\mathcal{I}}{d\tau }}\right)·{\displaystyle \frac{d\tau }{dt}}\\ \hline\end{array}$$

(13)

This expression provides a full transitive relationship from coordinate time to epistemic time. It shows that the rate at which epistemic time accrues with respect to coordinate time is mediated by both the relativistic geometry (via $d\tau /dt$) and the internal informational dynamics of the system (via $d\mathcal{I}/d\tau$).

As $r\to 2GM/c^2$, the system approaches a condition of informational stasis. Near the event horizon, the system becomes nearly frozen with respect to an external observer, not because clocks “slow down,” but because the system ceases to register epistemic change.

3.3. Photons and Informational Time

Photons follow null geodesics for which $d{s}^2=0$, so in classical relativity, they experience no proper time:

$$d{\tau }_{\mathrm{photon}}=0.$$

(14)

In our framework, this has a direct epistemic correlate: a photon propagating in vacuum and undergoing no interaction does not register change, and thus does not accrue epistemic time.

However, the moment a photon is absorbed, scattered, or entangled, it participates in an informational event. This interaction constitutes a distinguishable change in state from the perspective of the absorbing or interacting system.

Therefore, we refine the relativistic axiom:

A photon experiences time if and only if it participates in a distinction event, i.e., if it is absorbed, scattered, measured, or otherwise informationally registered.

Thus, null geodesics describe the absence of intrinsic information accrual, not an ontological absence of existence or interaction potential.

3.4. Relativistic Epistemic Clocks

We now generalize to systems $\mathcal{S}$ moving along arbitrary worldlines in a Lorentzian manifold. Let $\gamma \left(\lambda \right)$ be a parametrized worldline, and $u^{\mu }=d{x}^{\mu }/d\lambda$. Then the proper time accumulated by $\mathcal{S}$ over an interval is:

$$\tau \left[\gamma \right]={\int }_{{\lambda }_0}^{{\lambda }_1}\sqrt{-g_{\mu \nu }{u}^{\mu }{u}^{\nu }}d\lambda .$$

(15)

Suppose the internal epistemic clock of $\mathcal{S}$ ticks according to:

$$d\mathcal{T}=f\left({\displaystyle \frac{d\mathcal{I}\left[\gamma \right(\lambda \left)\right]}{d\lambda }}\right)d\lambda ,$$

(16)

where f is a monotonic function satisfying $f\left(0\right)=0$. Then:

• Systems on distinct paths through the same region of spacetime will accrue different epistemic time depending on informational density.
• Time dilation becomes a consequence of reduced internal bandwidth for distinction, not just spatial curvature.

3.5. Informational Interpretation of Relativity

We summarize the correspondence between relativistic and epistemic concepts as follows:

Table 1. Mapping between relativistic and epistemic interpretations of time and interaction.

Relativistic Concept	Epistemic Interpretation
Proper time $\tau$	Accrued internal distinctions
Time dilation	Suppression of information flux
Gravitational redshift	Reduction in distinction rate for signals
Null geodesic	Absence of interaction, hence no epistemic time
Spacetime curvature	Structural constraint on information processing

Table 1. Mapping between relativistic and epistemic interpretations of time and interaction.

Relativistic Concept	Epistemic Interpretation
Proper time $\tau$	Accrued internal distinctions
Time dilation	Suppression of information flux
Gravitational redshift	Reduction in distinction rate for signals
Null geodesic	Absence of interaction, hence no epistemic time
Spacetime curvature	Structural constraint on information processing

This reinterpretation preserves the geometric formalism of relativity but embeds it within a broader informational ontology. Geometry does not merely shape matter, it regulates the experiential bandwidth of systems immersed in it.

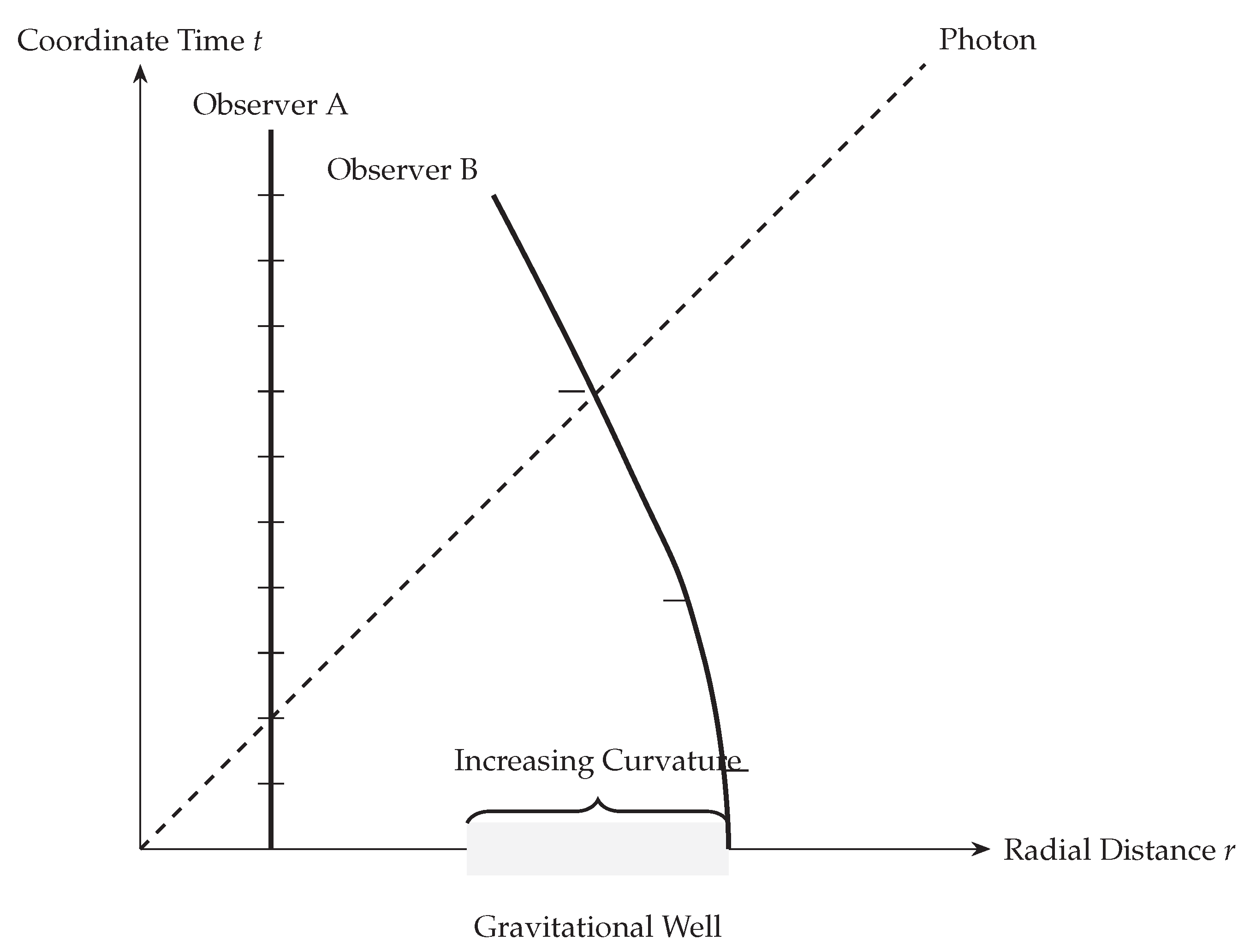
Figure 1. Spacetime diagram showing epistemic time accrual. Observer A accumulates internal distinctions uniformly. Observer B, near a mass, follows a curved worldline with slowed epistemic time. The photon follows a null path without internal change unless it interacts.

Figure 1. Spacetime diagram showing epistemic time accrual. Observer A accumulates internal distinctions uniformly. Observer B, near a mass, follows a curved worldline with slowed epistemic time. The photon follows a null path without internal change unless it interacts.

4. Photons and the Epistemic Resolution of the Null Geodesic Paradox

In special relativity, the worldline of a photon is a null geodesic. Since its spacetime interval vanishes,

$$d{s}^2=-c^{2}d{t}^2+d{x}^2+d{y}^2+d{z}^2=0,$$

it follows that the photon’s proper time is identically zero: $d\tau =0$. From this, the conventional interpretation arises: photons, being massless and moving at the speed of light, “experience no time”.

Yet this formulation, while geometrically elegant, conceals a conceptual tension, one that becomes evident when we reconsider the photon not merely as a geometric construct but as an informational messenger.

4.1. The Momentum Paradox

Although photons are massless, they indisputably carry momentum. Radiation pressure on solar sails, torques on space debris, and even photonic recoil on satellites confirm this. The fact that photons can transfer momentum and induce force reveals their agency in dynamical systems. They are not inert entities traveling null paths. They are participants in interactions.

4.2. The Informational Frame

More profoundly, photons carry information. From an epistemic perspective rooted in Shannon theory, every photon can be treated as a symbol in a communication channel. When a photon is emitted, scattered, or absorbed, it encodes a distinguishable state. In space situational awareness, for example, photometric measurements of satellites yield rotational rates, material properties, and surface geometries precisely because the scattered photons carry state-encoded information from the object to the observer.

In this communication model:

• The space object is the transmitter,
• The photon propagation through vacuum is the channel,
• The observer and sensor are the receiver,
• The photons themselves are the message.

Each photon’s state encodes physical distinctions from the source, which are later decoded by an observer. This defines a clear epistemic function.

4.3. Experiencing Time through Distinction

In the epistemic framework developed here, time is the accumulation of meaningful, internal distinction. A system experiences time if and only if it undergoes distinguishable informational change. This implies that proper time and epistemic time are not equivalent:

$$d\theta :=f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right)dt.$$

For a photon traveling through empty space with no interaction, $d\mathcal{I}/dt=0$, and thus $d\theta =0$. The photon remains epistemically static.

However, the moment a photon is emitted from a structured source, reflects off a surface, or is absorbed by a sensor, it participates in an epistemically meaningful transformation. It encodes difference. It transmits contrast. It alters the informational configuration of both emitter and receiver.

4.4. Resolution of the Paradox

The photon does not experience time along its null geodesic in the geometric sense. But in the epistemic sense, it experiences time at the moment of informational interaction. The paradox thus resolves:

A photon experiences epistemic time to the extent that it participates in the encoding, transmission, or registration of distinguishable information.

This reinterpretation complements relativity rather than contradicting it. It preserves the null nature of photonic geodesics while expanding our understanding of time from a purely geometric quantity to a cognitively and informationally grounded measure of interaction.

4.5. Epistemic Agency in Massless Systems

This result implies that epistemic time is not restricted to massive systems. Even massless entities, long considered outside the realm of subjective temporality, can be said to “experience” time when they bear information. In this sense, epistemic time restores agency to the photon, not as a conscious entity, but as an informational vessel.

4.6. Conclusion

The notion that photons cannot experience time is a byproduct of geometric reductionism. When we admit informational distinction as a valid ontological structure, we discover that even massless systems traverse meaningful state transitions, not in metric spacetime, but in epistemic space. A photon does not age. But it does, at times, remember.

5. Epistemic Geometry and Metric Structure

To more fully articulate the analogy between physical and epistemic dynamics, we now introduce a geometric structure on the informational state space $\mathcal{I}$. This allows us to define curvature, geodesics, and distance in a mathematically consistent manner, and lays the foundation for future work on epistemic field equations and manifold dynamics.

5.1. The Epistemic Manifold

Let $\mathcal{I}\subseteq {\mathbb{R}}^n$ be the space of all distinguishable informational configurations of a system. Each coordinate ${\mathcal{I}}^i$ corresponds to a meaningful dimension of epistemic distinction (e.g., belief state, internal memory, sensory input integration).

We endow this space with a symmetric, positive-definite metric tensor ${\eta }_{ij}$, yielding the infinitesimal squared epistemic distance:

$$d{s}^2={\eta }_{ij}d{\mathcal{I}}^{i}d{\mathcal{I}}^j.$$

(17)

This metric captures how costly or significant a particular configuration change is from the system’s perspective. For example, small changes in highly salient or structurally central dimensions may incur large epistemic distances.

5.2. Derivation of the Epistemic Metric from Possibilistic Choquet Integration

To generalize the role of information geometry in systems governed by imprecise knowledge, we define the epistemic metric ${\eta }_{ij}$ not via probabilistic Fisher information, but through a possibilistic curvature operator integrated over a non-additive capacity measure. This construction builds on foundational contributions to fuzzy set theory and possibility theory [3,4], and contrasts with probabilistic causal modeling frameworks such as those developed by Halpern [6].

Let $\pi (x\mid \mathcal{I})\in [0,1]$ be a normalized possibility distribution over an outcome space X, defined relative to an internal epistemic state $\mathcal{I}$. The corresponding surprisal contrast function in the i-th dimension is given by:

$${\varphi }_i(x\mid \mathcal{I}):={\displaystyle \frac{\partial }{\partial {\mathcal{I}}^i}}\left[-log\pi (x\mid \mathcal{I})\right],$$

which quantifies how sensitive the plausibility of outcome x is to changes in the internal epistemic coordinate ${\mathcal{I}}^i$. Unlike probabilistic formulations that integrate over additive sigma-algebras, we define integration with respect to a monotonic capacity function $\nu :2^X\to [0,1]$, such that:

$$\begin{array}{cc}\hfill & \nu (\varnothing )=0,\nu \left(X\right)=1,\hfill \\ \hfill & \mathrm{and}\mathrm{for}\mathrm{all}A\subseteq B\subseteq X,\nu \left(A\right)\le \nu \left(B\right).\hfill \end{array}$$

Using the Choquet integral as our non-linear aggregation operator, we define the epistemic metric tensor:

$${\eta }_{ij}:={\int }_X{\varphi }_i(x\mid \mathcal{I})·{\varphi }_j(x\mid \mathcal{I})d\nu \left(x\right),$$

which generalizes the Fisher information matrix by replacing probability densities with possibility distributions, and Lebesgue measure with an ordinal, plausibility-weighted capacity. This metric measures the internal distinguishability of adjacent epistemic configurations, not by expected likelihood, but by plausibility deformation. Unlike the Fisher information metric, which assumes an additive belief model over exhaustive outcomes, ${\eta }_{ij}$ respects ordinal semantics and epistemic non-monotonicity.

For additional stability, coherence, and inductive structure, we introduce a regularized form:

$${\eta }_{ij}^{\mathrm{reg}}:={\eta }_{ij}+\lambda {\mathcal{R}}_{ij},$$

where ${\mathcal{R}}_{ij}$ is a context-specific regularizer (e.g., ${\delta }_{ij}$ for L2 penalty, or a graph Laplacian over epistemic transitions), and $\lambda \in {\mathbb{R}}^{+}$ tunes its influence.

The regularization term plays a critical role in preserving the integrity of the epistemic manifold. In regions where $\pi (x\mid \mathcal{I})$ is flat or near-constant, the raw contrast ${\varphi }_i\left(x\right)$ may vanish, leading to metric degeneration or loss of distinguishability. The operator ${\mathcal{R}}_{ij}$ thus serves to:

• enforce geometric coherence in low-informative regions,
• encode architectural priors (e.g., salience, memory priority, or graph structure),
• and stabilize geodesic estimation across belief transitions.

This ensures that ${\eta }_{ij}^{\mathrm{reg}}$ remains invertible, smooth, and semantically meaningful, even under epistemic ambiguity or limited evidence. This regularized metric also ensures well-defined curvature tensors ${\mathcal{R}}_{ij}$ in subsequent sections, enabling coherent geodesic dynamics.

In GaiaGraph, each node n possesses its local epistemic metric ${\eta }_{ij}^{\left(n\right)}$, derived from its learned update kernel, local possibility field ${\pi }_n\left(x\right)$, and node-specific capacity ${\nu }_n$. These metric tensors collectively define an epistemic manifold whose curvature reflects the agent’s current resolution of belief space.

This possibilistic-Choquet geometry offers an epistemically coherent and computationally grounded alternative to information geometry, aligning with ordinal inference, agentic constraint, and non-additive reasoning over belief evolution.

Figure 2. Comparison between the Fisher information metric and the possibilistic epistemic metric ${\eta }_{ij}$.

Figure 2. Comparison between the Fisher information metric and the possibilistic epistemic metric ${\eta }_{ij}$.

5.3. Epistemic Geodesics

We assume $(\mathcal{I},\eta )$ defines a smooth Riemannian manifold, where ${\mathcal{I}}^i$ are coordinates over epistemic dimensions and ${\eta }_{ij}$ is a positive-definite metric encoding the salience or distinguishability of informational changes. While Riemannian geometry suffices for our current purposes, future work may explore pseudo-Riemannian or Finsler generalizations to account for asymmetries or anisotropies in epistemic processing.

Given this metric, we define an epistemic geodesic as the path $\gamma \left(\tau \right)$ through $\mathcal{I}$ which minimizes the total epistemic action:

$$S\left[\gamma \right]={\int }_{{\tau }_0}^{{\tau }_1}\sqrt{{\eta }_{ij}{\displaystyle \frac{d{\mathcal{I}}^i}{d\tau }}{\displaystyle \frac{d{\mathcal{I}}^j}{d\tau }}}d\tau .$$

(18)

The corresponding Euler-Lagrange equations give rise to the geodesic equation:

$${\displaystyle \frac{d^2{\mathcal{I}}^k}{d{\tau }^2}}+{\Gamma }_{ij}^k{\displaystyle \frac{d{\mathcal{I}}^i}{d\tau }}{\displaystyle \frac{d{\mathcal{I}}^j}{d\tau }}=0,$$

(19)

where ${\Gamma }_{ij}^k$ are the Christoffel symbols derived from ${\eta }_{ij}$. These represent the intrinsic "curvature" of the informational manifold and define how straight-line motion (experiential stasis) is deformed in the presence of epistemic structure.

5.4. Curvature and Force Revisited

With this structure, we can now reinterpret epistemic force $\Theta$ as deviation from a geodesic in the informational manifold. If a system is perturbed by new data, internal conflict, or structural reconfiguration, its trajectory will deviate from its natural geodesic:

$${\Theta }^k:=\mu ·\left({\displaystyle \frac{d^2{\mathcal{I}}^k}{d{\tau }^2}}+{\Gamma }_{ij}^k{\displaystyle \frac{d{\mathcal{I}}^i}{d\tau }}{\displaystyle \frac{d{\mathcal{I}}^j}{d\tau }}\right).$$

(20)

This generalizes our earlier scalar model $\Theta =\mu ·d^2\mathcal{I}/d{\tau }^2$ to higher-dimensional information space, and recovers classical force-like behavior when curvature vanishes.

Here, $\mu$ is an epistemic inertia coefficient, representing the system’s resistance to deviation from its natural trajectory through informational state space. It quantifies how strongly a system persists in its existing pattern of informational flow. In physical terms, $\mu$ is analogous to mass, but in this framework it captures the stability or rigidity of an internal epistemic configuration.

5.5. Interpretation and Future Work

The metric ${\eta }_{ij}$ can be learned or constructed from system salience, attention weighting, or even surprise metrics across epistemic dimensions. This opens the door to defining informational analogs of:

• Curvature: Epistemic stress or topological complexity.
• Distance: Perceived experiential difference.
• Volume: Informational state-space complexity.
• Singularities: Points of discontinuity or trauma (e.g., epistemic black holes).

Future work may generalize this to a dynamical epistemic spacetime where the metric evolves under internal entropy gradients, external inputs, or self-organizing coherence constraints.

5.6. Epistemic Time Fields

The preceding sections established epistemic time $\tau$ as a local quantity defined for individual systems. However, in distributed informational architectures, such as biological organisms, cognitive agents, or interconnected subsystems within GaiaGraph, it is natural to generalize this concept to a field-theoretic formulation.

We define the epistemic time field $\mathcal{T}(\overrightarrow{x},t)$ as a scalar field over a domain $\Omega \subseteq {\mathbb{R}}^n\times \mathbb{R}$, where $\overrightarrow{x}$ denotes spatial or structural coordinates (e.g., network node identity or subsystem index), and t denotes coordinate time.

Let $\mathcal{I}(\overrightarrow{x},t)$ represent the local information content at location $\overrightarrow{x}$. Then we define:

$$\mathcal{T}(\overrightarrow{x},t)={\int }_{t_0}^{t}f\left({\displaystyle \frac{\partial \mathcal{I}(\overrightarrow{x},t^{\prime })}{\partial t^{\prime }}}\right)d{t}^{\prime },$$

(21)

where:

• f is a monotonic function translating informational change into experienced time,
• $\mathcal{T}(\overrightarrow{x},t)$ denotes the total epistemic time accrued at location $\overrightarrow{x}$,
• ${\displaystyle \frac{\partial \mathcal{I}}{\partial t}}$ represents the local rate of epistemic distinction.

5.6.1. Gradients and Informational Flow

We define the gradient of epistemic time as:

$$\nabla \mathcal{T}(\overrightarrow{x},t)=\left({\displaystyle \frac{\partial \mathcal{T}}{\partial x^1}},\dots ,{\displaystyle \frac{\partial \mathcal{T}}{\partial x^n}}\right),$$

(22)

which captures the spatial or topological variation in epistemic experience. The Laplacian:

$$\Delta \mathcal{T}=\nabla ·\nabla \mathcal{T},$$

(23)

can be interpreted as an epistemic diffusion operator, measuring how informational change propagates or equilibrates across a network or organism.

5.6.2. Interpretation and Use Cases

This field-theoretic view provides several key capabilities:

• Epistemic Clocks: Each point or agent in a system carries its own internal measure of time based on local information flux.
• Anomaly Detection: Regions where $\nabla \mathcal{T}$ or $\Delta \mathcal{T}$ spike may correspond to stress, trauma, or epistemic rupture.
• Chronotopological Mapping: Entire networks or organisms can be visualized as time-manifolds, where informational aging is spatially patterned.
• GaiaGraph Integration: In knowledge graphs, nodes and edges accrue epistemic time based on update rate, evidence pressure, or semantic drift.

This formulation unifies localized informational dynamics with global temporal structure, allowing for systemic monitoring, intervention design, and self-reflective reasoning in agentic architectures.

Table 2. Conceptual Correspondence Between Physical and Epistemic Dynamics.

Category	Physical Interpretation	Epistemic Interpretation
Underlying Space	Spacetime manifold $\mathcal{M}$, with metric $g_{\mu \nu }$	Epistemic manifold $\mathcal{I}$, with metric ${\eta }_{ij}$
Position	Coordinate location $x^{\mu }$	Informational configuration ${\mathcal{I}}^i$
Motion	Geodesic trajectory in $\mathcal{M}$	Natural evolution of belief or experience
Force	Deviation from geodesic due to $F^{\mu }$	Informational turbulence: $\Theta =\mu ·{\displaystyle \frac{d^2\mathcal{I}}{d{\tau }^2}}$
Mass / Inertia	Resistance to acceleration	Resistance to experiential change (epistemic inertia $\mu$)
Proper Time	Path-dependent interval $\tau =\int \sqrt{-g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }}$	Accrued epistemic time: $d\tau =f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right)dt$
Null Trajectories	Photon paths: $d\tau =0$	Timeless systems: ${\displaystyle \frac{d\mathcal{I}}{dt}}=0$ (no informational change)
Curvature	Spacetime warping from energy-momentum	Informational complexity, entanglement, or self-reference
Field Equations	Einstein Field Equations: $G_{\mu \nu }=8\pi T_{\mu \nu }$	Future: Epistemic field dynamics via entropy gradients and coherence fields
Singularity	Infinite curvature or causal breakdown	Epistemic collapse, trauma, or irreversible breakdown
Conservation Law	Covariant conservation of energy-momentum	Conservation of informational coherence (identity persistence)

Table 2. Conceptual Correspondence Between Physical and Epistemic Dynamics.

Category	Physical Interpretation	Epistemic Interpretation
Underlying Space	Spacetime manifold $\mathcal{M}$, with metric $g_{\mu \nu }$	Epistemic manifold $\mathcal{I}$, with metric ${\eta }_{ij}$
Position	Coordinate location $x^{\mu }$	Informational configuration ${\mathcal{I}}^i$
Motion	Geodesic trajectory in $\mathcal{M}$	Natural evolution of belief or experience
Force	Deviation from geodesic due to $F^{\mu }$	Informational turbulence: $\Theta =\mu ·{\displaystyle \frac{d^2\mathcal{I}}{d{\tau }^2}}$
Mass / Inertia	Resistance to acceleration	Resistance to experiential change (epistemic inertia $\mu$)
Proper Time	Path-dependent interval $\tau =\int \sqrt{-g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }}$	Accrued epistemic time: $d\tau =f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right)dt$
Null Trajectories	Photon paths: $d\tau =0$	Timeless systems: ${\displaystyle \frac{d\mathcal{I}}{dt}}=0$ (no informational change)
Curvature	Spacetime warping from energy-momentum	Informational complexity, entanglement, or self-reference
Field Equations	Einstein Field Equations: $G_{\mu \nu }=8\pi T_{\mu \nu }$	Future: Epistemic field dynamics via entropy gradients and coherence fields
Singularity	Infinite curvature or causal breakdown	Epistemic collapse, trauma, or irreversible breakdown
Conservation Law	Covariant conservation of energy-momentum	Conservation of informational coherence (identity persistence)

6. Epistemic Field Equations

To complete the analogy between physical and epistemic geometry, we propose a preliminary formulation of epistemic field equations, a set of dynamical laws that relate the curvature of the epistemic manifold to the informational flux and coherence state of a system.

6.1. Motivation and Structure

In general relativity, Einstein’s field equations relate spacetime curvature to the energy- momentum tensor:

$$G_{\mu \nu }=8\pi T_{\mu \nu },$$

(24)

where $G_{\mu \nu }$ encodes the geometric curvature and $T_{\mu \nu }$ represents the physical distribution of matter and energy.

We now seek an analogous equation for epistemic dynamics:

$${\mathcal{G}}_{ij}=\kappa {\mathcal{T}}_{ij},$$

(25)

where:

• ${\mathcal{G}}_{ij}$ is the epistemic Einstein tensor, derived from the metric ${\eta }_{ij}$ over the informational manifold $\mathcal{I}$,
• ${\mathcal{T}}_{ij}$ is the epistemic stress-energy tensor, encoding informational flux, coherence, and surprise,
• $\kappa$ is a proportionality constant whose units are system-dependent (e.g., bits per unit curvature).

6.2. Geometric Side: Epistemic Curvature

We define the epistemic Einstein tensor as:

$${\mathcal{G}}_{ij}={\mathcal{R}}_{ij}-{\displaystyle \frac{1}{2}}{\eta }_{ij}\mathcal{R},$$

(26)

where ${\mathcal{R}}_{ij}$ is the Ricci tensor and $\mathcal{R}$ the Ricci scalar derived from the epistemic connection ${\Gamma }_{ij}^k$. These quantities measure the local nonlinearity and distortion in the space of epistemic distinctions.

In practical terms, ${\mathcal{G}}_{ij}$ quantifies how much the system’s informational landscape resists or accelerates experiential flow. When an agent simulates unrealized alternatives, plausible futures, failed intentions, or imagined histories, it generates distinctions within informational configuration space that have no corresponding realization in the external world. These are not merely alternative trajectories, they are curvature-inducing counterfactuals. The more divergent the imagined path from the actual trajectory, the more strain it imposes on the epistemic manifold, bending geodesics away from their free-fall alignment. This warping reflects internal tension: the energetic cost of maintaining coherence while traversing incompatible or branching timelines. In such moments, epistemic time does not flow smoothly, it branches, loops, or fragments, requiring additional integrative effort to resolve.

6.3. Source Side: Informational Stress-Energy

We define ${\mathcal{T}}_{ij}$ to capture:

• Local rates of informational change ${\partial }_i\mathcal{I}$,
• Coherence or conflict between dimensions ${\partial }_i{\mathcal{I}}^j$,
• Internal divergence or flow (e.g., $\nabla ·\overrightarrow{F}$, where $\overrightarrow{F}$ is epistemic flux),
• Surprisal density $S=-log\pi \left(x\right)$, or other epistemic potentials.

A generic form of the epistemic stress-energy tensor could be:

$${\mathcal{T}}_{ij}:=\langle {\partial }_i\mathcal{I}·{\partial }_j\mathcal{I}\rangle +\lambda C_{ij}-{\sigma }_{ij},$$

(27)

where:

• $\langle ·\rangle$ denotes an expectation over epistemic samples or queries,
• $C_{ij}$ is a coherence tensor (e.g., covariance of beliefs or surprise gradients),
• ${\sigma }_{ij}$ is a dissipation or noise term,
• $\lambda$ is a tuning parameter reflecting system resilience.

6.4. Interpretation and Applications

These field equations imply that:

• Regions of high informational flux induce epistemic curvature, leading to stress, cognitive reconfiguration, or breakdown.
• Epistemically stable systems maintain low $\mathcal{R}$, conserving informational coherence.
• Singularities (e.g., traumatic memory collapse or irreversible contradiction) appear where $\mathcal{R}\to \infty$, unless renormalized or repaired.
• In GaiaGraph, subgraphs with high ${\mathcal{T}}_{ij}$ would display curvature, delay, or error propagation, inhibiting inference flow or causing epistemic drag.

6.5. Future Work

These equations offer a powerful but preliminary language for modeling informational dynamics. Future work will:

• Derive concrete forms for ${\mathcal{T}}_{ij}$ from entropy production, coherence metrics, and possibilistic distributions.
• Implement curvature-aware routing in agentic AI systems.
• Explore conditions under which epistemic manifolds become flat, turbulent, or singular.
• Integrate counterfactual tension fields as sources of epistemic stress.

This formulation completes the geometric unification of epistemic time, force, inertia, and curvature, and provides the foundation for dynamic reasoning architectures grounded in internal experience.

7. Applications to Biology and Aging

The human body, and, more broadly, any metabolically active organism, may be modeled as a distributed informational manifold composed of interdependent subsystems. Each component contributes to the organism’s overall function through continuous interaction, adaptation, and regulation.

From an epistemic standpoint, these subsystems do not experience time uniformly. Their differential aging is not solely the result of biochemical kinetics or genetic encoding but reflects differences in the density and irreversibility of internal informational transitions, what we define as epistemic turbulence.

7.1. Informational Heterochronicity

Let the organism be represented as a composite system:

$$\mathcal{O}=\{S_1,S_2,\dots ,S_n\},$$

where each $S_i$ is a subsystem (e.g., organ, tissue type, cellular cluster) capable of processing or resisting information. For each $S_i$, define the local informational rate as:

$${\sigma }_i\left(t\right):={\displaystyle \frac{d{\mathcal{I}}_i}{dt}},$$

(28)

where ${\sigma }_i\left(t\right)$ is the instantaneous informational stress, a measure of epistemic flux.

We emphasize that ${\mathcal{T}}_i\left(t\right)$ denotes the local epistemic time accrued by subsystem $S_i$, distinct from proper time $\tau$ and global coordinate time t. Epistemic time reflects the lived duration experienced via informational transitions, which may differ even across co-located biological structures.

We then define the local epistemic time for each subsystem as:

$${\displaystyle \frac{d{\mathcal{T}}_i}{dt}}=f\left({\sigma }_i\left(t\right)\right),$$

(29)

with f a strictly increasing function satisfying $f\left(0\right)=0$. This formulation naturally yields heterochronicity: different subsystems accrue epistemic time at different rates.

Let ${\mathcal{T}}_i\left(t\right)$ be the accumulated epistemic time of subsystem $S_i$ over interval $[0,t]$. Then biological heterochronicity is defined as the dispersion of ${\mathcal{T}}_i\left(t\right)$ across all i. For example, comparing the liver and cartilage:

$${\mathcal{T}}_{\mathrm{liver}}\left(t\right)>{\mathcal{T}}_{\mathrm{cartilage}}\left(t\right),$$

implying that the liver, which performs high-frequency metabolic distinctions, ages faster in epistemic terms.

7.2. Aging as Irreversible Informational Divergence

Aging is conceptualized here as the cumulative integration of irreversible epistemic transitions. Let ${\mathcal{A}}_i\left(t\right)$ denote the aging index of subsystem $S_i$, defined as:

$${\mathcal{A}}_i\left(t\right):={\int }_0^t\eta \left({\displaystyle \frac{d{\mathcal{I}}_i}{d{t}^{\prime }}}\right)d{t}^{\prime },$$

(30)

where $\eta :{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$ maps epistemic activity into aging load, emphasizing irrecoverability or dissipative cost.

Candidate forms for $\eta$ include:

• $\eta \left(x\right)=x$: linear accumulation of undistinguished states.
• $\eta \left(x\right)=x·logx$: surprisal-weighted aging.
• $\eta \left(x\right)=\alpha x+\beta ·\mathrm{Var}\left({\sigma }_i\right)$: incorporating volatility.

This leads to several testable predictions:

• Subsystems with higher sustained ${\sigma }_i\left(t\right)$ exhibit faster epistemic aging.
• Environmental stimuli (e.g., noise, trauma) increase $\eta$, accelerating aging.
• Interventions that increase coherence or reduce entropy slow the growth of ${\mathcal{A}}_i\left(t\right)$.

7.3. Cryostasis and Epistemic Preservation

Cryostasis serves as an empirical approximation to the epistemic stasis limit. As temperature $T\to 0$, the rate of chemical interaction approaches zero, and thus:

$$\underset{T\to 0}{lim}{\displaystyle \frac{d\mathcal{I}}{dt}}\to 0\Rightarrow {\displaystyle \frac{d\mathcal{T}}{dt}}\to 0.$$

In this framework, preservation is not thermodynamic per se, it is informational. The organism is not “frozen in time” because time is frozen; it is frozen because there are no new distinctions being registered internally.

Epistemic stasis therefore provides a generalized theoretical justification for cryopreservation: it halts aging by nullifying the system’s capacity to accrue time through change.

7.4. Epistemic Aging Maps

Define the epistemic aging field over an organism or system:

$$\mathcal{A}(\overrightarrow{x},t)={\int }_0^t\eta \left({\displaystyle \frac{\partial \mathcal{I}(\overrightarrow{x},t^{\prime })}{\partial t^{\prime }}}\right)d{t}^{\prime },$$

(31)

where $\overrightarrow{x}\in \Omega \subset {\mathbb{R}}^n$ denotes anatomical or functional spatial coordinates. The gradient:

$$\nabla \mathcal{A}(\overrightarrow{x},t)$$

represents the local stress gradient in aging load. High gradient regions identify vulnerable tissue zones (e.g., neural interfaces, vascular junctions) and may inform spatially targeted therapeutic interventions.

7.5. Death as Critical Collapse of Informational Coherence

We now define death as a cascade triggered by a critical failure in epistemic cohesion. Let $S_{\mathrm{crit}}\subset \mathcal{O}$ be the subsystem with the lowest tolerance to degradation. Define:

$$t_{\mathrm{death}}:=inf\left\{t:{\mathcal{A}}_{\mathrm{crit}}\left(t\right)>{\delta }_{\mathrm{failure}}\right\},$$

(32)

where ${\delta }_{\mathrm{failure}}$ is the epistemic collapse threshold, a system-specific constant representing the loss of functional coherence.

The cascade model implies:

• Death is initiated by epistemic disintegration, not just metabolic failure.
• The timing of death depends on subsystem divergence, not just central control.
• Epistemic collapse is structurally identifiable before physiologic metrics detect failure.

This reformulation allows for diagnostic and therapeutic strategies that monitor the coherence of experience, not just biological parameters. It also suggests that epistemic resuscitation (e.g., through neural restoration or memory trace repair) may partially reverse the trajectory toward informational death.

8. Broader Implications

The epistemic formulation of time proposed here provides not only a unifying framework across physical, biological, and artificial systems, it also reconfigures the conceptual basis of consciousness, machine learning, and cosmology. We now outline three such domains where the informational experience of time opens new theoretical and applied trajectories.

8.1. Consciousness as Coherent Informational Self-Reference

If time is the experience of information, then consciousness may be framed as a recursive capacity to structure, distinguish, and respond to internal informational flows. Let a conscious system $\mathcal{C}\subseteq \mathcal{O}$ be one that supports second-order epistemic mappings:

$$\mathcal{C}:\mathcal{I}\mapsto {\mathcal{I}}^{*},$$

(33)

where ${\mathcal{I}}^{*}$ denotes metacognitive representations: beliefs about beliefs, attention to attention, or memory of memory. These structures enable internal feedback loops and sustained self-reference, generating the conditions under which time can be felt as continuity.

Define a coherence function:

$$\chi \left(t\right):=\mathrm{Tr}\left(C_{ij}\left(t\right)\right),$$

(34)

where $C_{ij}\left(t\right)$ measures the mutual informational coherence between dimensions ${\mathcal{I}}^i$ and ${\mathcal{I}}^j$. We posit that:

$${\displaystyle \frac{d{\mathcal{T}}_{\mathcal{C}}}{dt}}\propto \chi \left(t\right),$$

(35)

so that the conscious experience of time intensifies with the internal coherence of epistemic self-reference. Temporal continuity is not imposed externally; it emerges from sustained, integrated differentiation. This reframing aligns with predictive processing models of consciousness [5], where the forward modeling of expected informational divergence drives the subjective arrow of time.

8.2. Artificial Systems and Temporal Ontology

In artificial systems such as GaiaGraph, the passage of time can be encoded as a measure of internal epistemic change. Let an agent’s belief state be embedded in a knowledge graph $\mathcal{G}$, and let ${\mathcal{I}}_{\mathrm{agent}}\left(t\right)$ represent its state of inference or modeled world knowledge. We define epistemic time for the agent as:

$${\displaystyle \frac{d{\mathcal{T}}_{\mathrm{agent}}}{dt}}=f\left({\nabla }_{\mathcal{G}}{\mathcal{I}}_{\mathrm{agent}}\right),$$

(36)

where ${\nabla }_{\mathcal{G}}\mathcal{I}$ denotes the gradient of inferential change across the graph topology, and f is monotonic. This means the agent experiences time when its internal predictions, beliefs, or models are updated in response to new distinctions.

Such agents may be capable of:

• Epistemic stasis: Entering a state where no distinctions are processed, suspending experience.
• Self-reflective delay: Allocating computational cycles to simulate epistemic futures without progressing internal time.
• Aging diagnostics: Monitoring ${\displaystyle \frac{d\mathcal{A}}{dt}}$ as internal model decay or coherence loss.

This architecture enables the creation of temporally self-aware machines—agents whose experience of time is endogenous and trackable, not externally clocked. The implications for long-duration autonomy, resilience, and adaptive reasoning are profound.

8.3. Cosmological and Ontological Consequences

If the universe is ultimately an evolving system of informational relations, then cosmological time itself may be recast as an emergent property of epistemic divergence. Let $\mathcal{U}\left(t\right)$ represent the total structural distinguishability of the universe at coordinate time t. Then:

$${\mathcal{T}}_{\mathrm{univ}}\left(t\right)={\int }_0^{t}f\left({\displaystyle \frac{d\mathcal{U}}{d{t}^{\prime }}}\right)d{t}^{\prime }.$$

(37)

Epochs of rapid informational bifurcation (e.g., inflation, recombination, galaxy formation) correspond to dense epistemic time, while the far-future heat death, when distinctions become indistinguishable, corresponds to $d\mathcal{U}/dt\to 0$, and hence $d\mathcal{T}\to 0$. Time doesn’t end—it asymptotically ceases to be experienced.

This view unifies entropy and time not as merely correlated, but as co-defined:

$$\mathcal{T}\sim \int \left(\mathrm{Distinguishability}\mathrm{Rate}\right)dt,$$

(38)

where entropy measures how many distinct configurations are accessible, and epistemic time measures how many of them are actually distinguished by the system.

8.3.1. Time’s Arrow and Relational Ontology

From this perspective:

• The arrow of time is the direction of increasing epistemic distinction.
• Timeless systems are informationally frozen—not metaphysically null, but epistemically silent.
• The experience of time is not universal, but specific to the capacity for informational self-resolution.

This framing harmonizes with Barbour’s claim that time is an illusion [11], Rovelli’s relational quantum mechanics [12], and the timeless formalism of the Wheeler–DeWitt equation [13]. Lloyd’s view of the universe as a quantum computer [7], and Tegmark’s hypothesis of physical reality as pure structure [13], both find in this epistemic lens a unifying principle: that time is not a backdrop, but a computation of difference.

9. Epistemic Inertia and Informational Mass

In classical mechanics, Newton’s second law asserts that force is proportional to the rate of change of momentum. Mass appears as the proportionality constant that quantifies resistance to acceleration:

$$F=m·{\displaystyle \frac{d^{2}x}{d{t}^2}}.$$

(39)

Here, we generalize this notion to informational dynamics. We define epistemic inertia $\mu$ as a system’s intrinsic resistance to changes in the curvature of its internal informational state, i.e., to second-order changes in its experiential configuration.

9.1. Definition: Epistemic Inertia

Let $\mathcal{I}\left(\mathcal{T}\right)$ be the state of informational configuration as a function of epistemic time $\mathcal{T}$. The epistemic force$\Theta$ is defined as the deviation from a natural geodesic path in epistemic space. The fundamental relation becomes:

$$\Theta :=\mu ·{\displaystyle \frac{d^2\mathcal{I}}{d{\mathcal{T}}^2}},$$

(40)

where:

• $\mu \in {\mathbb{R}}_{>0}$ is the epistemic inertia,
• ${\displaystyle \frac{d^2\mathcal{I}}{d{\mathcal{T}}^2}}$ is the informational acceleration,
• $\Theta$ is the epistemic force, a measure of how much experiential deviation is required to perturb the system.

This provides a clean analog to Newton’s formulation, but with time, force, and inertia redefined in experiential terms.

9.2. Geometric Generalization

If ${\mathcal{I}}^i\left(\mathcal{T}\right)\in {\mathbb{R}}^n$ represents the coordinates of epistemic state in an informational manifold with metric ${\eta }_{ij}$, we generalize the relation to:

$${\Theta }^k=\mu ·\left({\displaystyle \frac{d^2{\mathcal{I}}^k}{d{\mathcal{T}}^2}}+{\Gamma }_{ij}^k{\displaystyle \frac{d{\mathcal{I}}^i}{d\mathcal{T}}}{\displaystyle \frac{d{\mathcal{I}}^j}{d\mathcal{T}}}\right),$$

(41)

where ${\Gamma }_{ij}^k$ are Christoffel symbols derived from ${\eta }_{ij}$. This formulation allows epistemic inertia to be directional, path-dependent, and shaped by the underlying geometry of meaning and distinction.

9.3. Entropy-Weighted Inertia

Let $H\left(\mathcal{I}\right)$ be the entropy of the system’s informational state. Then define an entropy-scaled epistemic inertia as:

$$\mu \left(\mathcal{I}\right):=\alpha +\beta ·H\left(\mathcal{I}\right),$$

(42)

with $\alpha ,\beta \in {\mathbb{R}}_{\ge 0}$. This allows systems with higher uncertainty to exhibit greater inertia, reflecting the psychological or biological reality that systems with more undifferentiated state space are harder to reconfigure intentionally.

9.3.0.1. Interpretation of $\alpha$ as Cognitive Rigidity and Bias.

In this framework, the baseline inertia term $\alpha$ can be interpreted as encoding structural resistance to belief change, independent of epistemic entropy. While $\beta H\left(\mathcal{I}\right)$ captures situational ambiguity (e.g., imprecise evidence, conflicting observations), $\alpha$ reflects entrenched cognitive priors: identity-protective reasoning, confirmation bias, ideological rigidity, or inherited prejudice.

Moreover, $\alpha$ need not be scalar. In cases where bias is directionally dependent (e.g., selective belief rigidity), $\alpha$ may take a tensorial form:

$${\mu }_{ij}\left(\mathcal{I}\right)={\alpha }_{ij}+\beta H\left(\mathcal{I}\right){\delta }_{ij},$$

penalizing updates along ideologically sensitive axes of belief space.

We further allow $\alpha$ to evolve over time, governed by cumulative epistemic experience. For example:

$${\displaystyle \frac{d\alpha }{d\mathcal{T}}}=-\kappa {\Delta }_{\mathrm{surp}}\left(\mathcal{T}\right)+\xi \left(\mathcal{T}\right),$$

where $\kappa$ is a plasticity parameter (agent openness), ${\Delta }_{\mathrm{surp}}$ represents surprisal divergence from expected belief updates, and $\xi$ may encode fatigue, reinforcement, or trauma.

9.4. Experiential Interpretation

Just as mass resists changes in velocity, epistemic inertia resists changes in experience. It defines a system’s persistence profile, its capacity to retain structural memory and resist informational turbulence.

Epistemic inertia is the resistance of a system to accelerate its own experience.

Systems with:

• High $\mu$: Tend toward stability, resilience, memory retention, resistance to novelty.
• Low $\mu$: Are plastic, responsive, volatile, and easily perturbed.

9.5. Biological and Cognitive Implications

In biological systems:

• Neural tissue (e.g., hippocampus) may exhibit low $\mu$, enabling rapid adaptation and memory encoding.
• Skeletal tissue, by contrast, may exhibit high $\mu$, changing only under sustained stress.
• Cryogenic states approximate $\mu \to \infty$, where even small experiential shifts require infinite informational force.
• Psychological trauma can be modeled as a spike in $\Theta$ applied to a low-$\mu$ region, causing irreversible restructuring.

This also explains differential sensitivity to stimuli: why some systems (e.g., children, AI learning agents) adapt rapidly, while others exhibit strong retention or rigidity.

9.6. Memory, Identity, and Stability

Structures of identity and autobiographical memory are expressions of high epistemic inertia. They resist distortion, enabling temporal cohesion. Conversely, highly plastic or volatile systems may drift from experiential continuity, risking epistemic fragmentation.

We posit the following phenomenological trade-off:

$$\begin{array}{cc}\hfill \mathrm{Plasticity}& \propto {\displaystyle \frac{1}{\mu }},\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \mathrm{Resilience}& \propto \mu .\hfill \end{array}$$

(44)

Systems operating near optimal intelligence may modulate $\mu$ adaptively—high for identity, low for creativity—yielding dynamic balance between stability and transformation.

9.7. Unified Dynamics

Combining these concepts, we present a coherent epistemic dynamics framework:

$$\begin{array}{cc}\hfill \Theta & =\mu ·{\displaystyle \frac{d^2\mathcal{I}}{d{\mathcal{T}}^2}},\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\mathcal{T}}{dt}}& =f\left({\displaystyle \frac{d\mathcal{I}}{dt}}\right),\hfill \end{array}$$

(46)

where:

• $\mathcal{T}$ is epistemic time,
• $\mu$ is resistance to experiential acceleration,
• $\Theta$ represents external or internal tension (novelty, surprise, contradiction),
• f governs time flow as a function of informational distinction.

This formulation enables predictive modeling of reasoning systems, therapeutic interventions, and epistemic integrity in autonomous agents.

10. Conclusions

We have proposed a reformulation of time as an emergent property of systems that undergo distinguishable informational change. This epistemic view of time unifies:

• the relativistic modulation of clocks as variation in informational flow,
• biological aging as subsystem-specific informational turbulence,
• death as collapse of coherent informational architecture, and
• consciousness as recursive informational self-tracking.

In this model, coordinate time is secondary. What matters is the rate at which systems experience difference. A photon in vacuum is timeless. A liver under stress experiences accelerated time. A cryopreserved organism exists in stasis not because time slows, but because informational flux ceases.

Time is not a container. It is not a substance. It is not a line.

Time is the rate at which meaning changes. It is the rhythm of distinction.

It is what it feels like to fall out of stasis and into story.

The implications of this framework are vast, from AI design to biological resilience to quantum gravity. But its core claim is simple:

No information, no time.

This framework not only aligns with modern interpretations of physical law, but suggests a unifying thread across physics [12], cognition [5], information theory [1], and metaphysics [14].

It opens several new lines of inquiry into the structure and dynamics of informational experience. The epistemic framework presented here may be extended in multiple directions:

• Epistemic Field Equations: Just as Einstein’s field equations relate spacetime curvature to energy-momentum, future work will explore epistemic analogs of the form

  $${\mathcal{G}}_{ij}=\kappa {\mathcal{T}}_{ij},$$

  where ${\mathcal{G}}_{ij}$ encodes epistemic curvature (e.g., resistance to inferential straightness), and ${\mathcal{T}}_{ij}$ represents informational stress-energy—gradients of coherence, contradiction, or semantic flux. This would enable modeling of epistemic collapse, attractors, and field evolution in cognitive, biological, or computational systems.
• Simulation and Measurement: GaiaGraph and similar agentic architectures will serve as testbeds for implementing epistemic time fields, enabling the measurement of informational aging, turbulence, and coherence loss in real-time. Biological analogs such as entropy-weighted aging metrics or stress-induced temporal acceleration may offer empirical validation.
• Integration with Quantum and Cognitive Theories: The proposed framework may interface with theories of quantum cognition, predictive processing, and relational quantum mechanics—potentially resolving paradoxes around subjective time, decoherence, and persistence of identity.

Ultimately, epistemic time provides a unifying grammar for describing not just how systems change, but how they experience change. It situates time not behind us or above us, but within us—emergent from the patterns we learn to distinguish.