1. Introduction
Large language models (LLMs), such as GPT, Gemini, and Llama, have shown a strong ability in natural language understanding and generation. The strong capabilities of LLMs made them a key component for many solutions regarding natural language processing tasks, especially for generic question answering, where LLMs are capable to generate convincing answers [
1]. However, the hallucination problem of those models limits their usage in real scenarios [
2]. In the case of domain-specific question answering, the hallucination can be seen as factual wrong, outdated, or irrelevant responses by the LLMs [
3]. To decrease the effect of hallucination and help the LLMs to generate more accurate answers, Retrieval Augmented Generation (RAG) was proposed [
4]. The RAG method helps the underlying LLM by embedding a set of relevant textual documents with the given question, and the task of the LLM becomes extracting the answer from this set of documents.
The simplicity of applying the RAG method makes it very common in multiple fields such as Finance [
5], Medicine [
6], Religion [
7], to name a few. However, the RAG method struggle to solve the hallucination in multi-hop (complex) questions that require the underlying LLM to reason over multiple documents. The semantic similarity-based document retrieval in RAG fails at retrieving the necessary documents to answer multi-hop questions. The recent LLMs, such as Gemini 2.0, provided a longer context window to enable sharing more knowledge with the LLMs; however, the LLMs have shown that they do not leverage all the knowledge shared with them, as they are focusing only on part of the shared knowledge [
8]. This problem is known in the literature as the lost-in-the-middle problem.
Another attempt to alleviate the limitations of the RAG method is the GraphRAG method [
9]. The first appearance of the GraphRAG was in a blog by Microsoft Research [
10]. The authors in the Microsoft blog suggested converting the knowledge from the unstructured textual format into a knowledge graph (KG), where knowledge can be well structured, as a solution to the limitation of RAG in multi-hop questions. Previously, we proposed SubGraph Retrieval Augmented Generation (SG-RAG) as a GraphRAG method for multi-hop knowledge graph question answering [
11]. SG-RAG depends on Cypher queries to retrieve the necessary subgraphs from the KG to answer the given questions. Since LLMs expect textual data, SG-RAG transforms the retrieved subgraphs into a textual representation in triplet format. We showed that SG-RAG outperforms RAG for 1-hop, 2-hop, and 3-hop questions using Llama-3 8B Instruct and GPT-4 Tubro as underlying LLMs. Although SG-RAG has shown a high performance, the textual transformation step in SG-RAG does not impose an order on the triplets shared with the underlying LLM, leaving us unaware of how the ordering might affect the performance of SG-RAG. We have also observed that the shared triplets contain many redundant triplets, which makes the context shared with the LLM longer. Lastly, our previous experiments were bound by Llama-3 8B Instruct as the only open-source LLM we experimented with and by RAG as a baseline.
In order to fill the gap in our previous work and further enhance our method, we propose an extension to the methodology of SG-RAG that is based on injecting an additional step after the textual transformation called Merging and Ordering Triplets (MOT). The goal of MOT is to merge highly overlapped subgraphs, which leads to removing the redundant triplets, and then defining an ordering among them. We have also extended our experiments to cover more open-source LLMs with different sizes and more advanced baselines. The chosen LLMs are Llama-3.1 8B Instruct, Llama-3.2 3B Instruct, Qwen-2.5 7B Instruct, and Qwen-2.5 3B Instruct. Our results show that SG-RAG MOT outperforms Chain-of-Thought and Graph Chain-of-Thought, which is a state-of-the-art GraphRAG method. The ablation study on the effect of ordering triplets indicates that defining an order using graph traversal algorithms, such as Breadth First Search (BFS) and Depth First Search (DFS), helps the underlying LLM in reasoning on the given triplets and decreases the effect of the lost-in-the-middle problem.
The rest of this article is structured as follows.
Section 2 presents the background information and related works.
Section 3 provides the definition of the preliminary concepts and the definition of the problem we are targeting. We present our previous work in
Section 4 with explaining the methodology of SG-RAG and the main findings, and highlighting the potential improvements. We describe the Merging and Ordering Triplets (MOT) step as an extension to the SG-RAG method in
Section 5.
Section 6 and
Section 7 provide the setup of the experiments and the results with the ablation studies and the case studies.
Section 8 concludes the article with a summary of the work and highlights the future work.
2. Background and Related Work
Large Language Models have shown significantly high performance in many tasks regarding Natural Language Understanding and Generation [
1,
12]. However, for domain-specific question answering task, LLMs are suffering from providing factually wrong, out-of-context, outdated, or irrelevant responses. This problem is known in the literature as hallucination [
2]. Because of the large scale of those models, task or domain-specific fine-tuning becomes challenging. One of the most promising and commonly used solutions is Retrieval Augmented Generation (RAG) [
4,
13]. The RAG method is based on injecting a set of domain knowledge with the user input and sending them together to the LLM. The selection process of the set of knowledge shared by the LLM is based on measuring the semantic similarity between the user input and the entire set of domain knowledge. The top-k most similar piece of knowledge is sent to the LLM. Although the RAG method has shown an improvement on simple questions, it is still struggling with complex questions where reasoning is required [
10].
In parallel to the domain-specific question answering, the high performance of LLMs attracts researchers to investigate the potential of LLMs with graph-related tasks [
14], such as classifying graph nodes [
15]. The potential of using graphs and LLMs leads to the idea of using knowledge graphs and LLMs. Edge et al. [
16] works on answering the domain-specific questions that are on a global level, which require an understanding and awareness of the domain. To achieve their goal, they used LLMs to transform the unstructured domain knowledge into a knowledge graph, and then they divided the knowledge graph into small subgraphs (communities) where each subgraph holds summarized information about the subgraph. After that, the concept of GraphRAG has been raised and intensively studied as an improvement of the traditional RAG method [
9], where the domain knowledge in GraphRAG is represented as a knowledge graph. Graph Cain-of-Thought (Graph-CoT) proposed by Jin et al. [
17] is an example of the GraphRAG method. Graph-CoT tackles the questions that require reasoning by giving the LLM the ability to interact directly with the knowledge graph through a set of predefined functions. For any input question, it starts from the node that is semantically similar to the input question and then traverses the knowledge graph, collecting the required information to answer the question. Another GraphRAG method is Think-on-Graph(ToG), proposed by Sun et al. [
18]. ToG is based on iteratively applying beam search on the given knowledge for building multiple reasoning paths starting with the nodes containing the entities that appear in the given question. The task of the LLM in ToG is scoring the candidate paths, determining whether the reasoning paths contain enough knowledge to answer the question, and lastly generating the response based on the retrieved paths. The last example of the GraphRAG method is the SubGraph Retrieval Augmented Generation (SG-RAG) that we proposed earlier [
11]. We discuss SG-RAG in detail later in
Section 4.
3. Preliminaries and Problem Definition
In this section, we define preliminary concepts that we used in the problem definition and the rest of this paper.
Definition 1.
Graph: Graph is a data structure that consists of a set of nodes denoted by V and a set of edges denoted by E. For each edge , there exist two nodes, , such that e connects and . With respect to E, a graph can be categorized as directed or undirected. The difference between them is that for each edge in the directed graph, there exist two nodes, , where e connects from to . In the context of the directed graph, we call the as source and destination, respectively.
Definition 2.
Subgraph: Let and be two graphs. We call a subgraph of G if and only if and .
Definition 3. Multigraph: A graph is called a multigraph if loops and multiple edges connecting the same two vertices are permitted [19]. Similar to graph, a multigraph can be either directed or undirected.
Definition 4.
Knowledge Graph: Knowledge Graph, denoted by , refers to the knowledge stored in a multigraph . Each vertex represent an entity, while each edge determines the relationship between the two entities in . The nodes and edges are labeled to specify the type of information they carry.
The nodes and edges in
may include a set of attributes to embed additional information in a structured format.
can be hosted in a graph database such as Neo4j
1, where graph-specific query language can be used to search and retrieve subgraphs. An example of a graph-specific query language is Cypher query language developed by Neo4j [
20].
Definition 5.
-hop Question in context: Let q be a question expressed in Natural Language where the answer to q consists of multiple entities in the . We call q an n-hop question if answering q requires one or more subgraphs, where each subgraph has n edges. The number of necessary subgraphs is equal to the number of entities in the expected answer to q.
The question "The films staged by Sharon Tate have been released during which years" is an example of a 2-hop question. To find the correct answer to the question, which is "1967, 1968", you need two subgraphs. Each of these subgraphs has 2 edges, "STARRED_ACTORS" and "RELEASE_YEAR".
Problem Definition: Let D be a domain where its knowledge is represented by a knowledge graph . The task of domain-specific Multi-hop Knowledge Graph Question Answering (KGQA) can be defined as generating answers to the n-hop questions about D. The generation of the answer is based on the retrieved knowledge from the .
4. SubGraph Retrieval Augmented Generation
Subgraph Retrieval Augmented Generation (
SG-RAG) is a zero-shot GraphRAG method we proposed in [
11] for domain-specific Multi-hop KGQA. In this section, we first provide an overview of the
SG-RAG method. Then, we highlight the experimental setup and the main findings in our previous work [
11]. Lastly, we discuss the potential improvements that we cover in our extension.
4.1. Overview of the SG-RAG
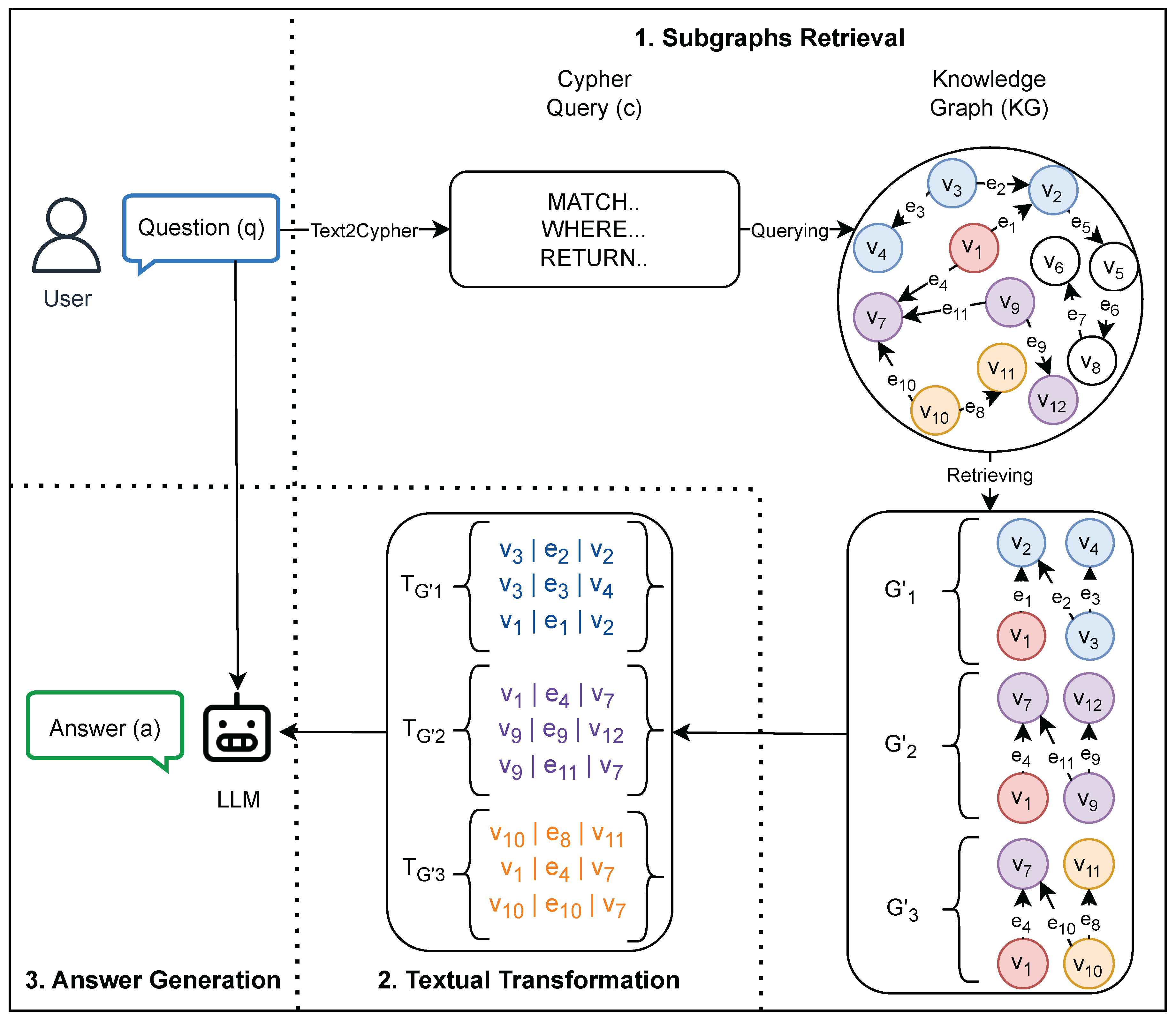
As
Figure 1 shows, the
SG-RAG method comprises three main steps: 1. Subgraphs Retrieval, 2. Textual Transformation, and 3. Answer generation. For a user question
q, the
SG-RAG method starts with the Subgraphs Retrieval step for retrieving the necessary subgraphs to answer
q. The retrieval process is based on mapping
q into a Cypher query
(Text2Cypher mapping):
such that querying the
using
retrieves the set of matched and filtered subgraphs
S containing the necessary information to answer
q:
where,
. We applied Text2Cypher mapping using a template-based approach where the templates are manually generated. Examples of the templates are provided in
Figure A1.
After retrieving the set of subgraphs
S, the second step of transforming the retrieved subgraphs into a textual representation starts. For each retrieved subgraph
, the transformation is based on converting each directed edge
with its corresponding source and destination nodes
into a triplet, denoted by
t, in the form of "subject | relation | object". In the triplet format, the "subject" and "object" refer to
and
respectively, while "relation" refers to the label of
e. During the textual transformation, the triplets that belong to the same subgraph are grouped, such that
Since
is a set, there is no pre-defined order among the triplets
.
Lastly, the answer
A to the question
q is generated using the underlying LLM as
where
I refers to the instructions explaining the task and the inputs to the LLM. The prompt templates represented by
I is shown in
Figure A2.
4.2. Experimental Setup and Main Results
In our previous work [
11], we experimented with the MetaQA benchmark dataset proposed by Zhang et al. [
21], which is a benchmark for Multi-hop KGQA. It contains a
about the Movies domain and a set of question-answer pairs grouped into 1-hop, 2-hop, and 3-hop. The ground truth answers are lists of entities.
As baseline methods to compare SG-RAG with, we considered the following methods:
The performance of the
SG-RAG and the baseline methods are measured using the answer-matching rate metric, which is inspired by the notion of entity-matching rate metric proposed by Wen et al. [
22] for measuring the performance of dialogue systems. The answer-matching rate, denoted by AMR, is based on measuring the intersection between the ground truth answer
and the generated answer
A, normalized by the number of entities in
Initially, we compared the performance of
SG-RAG with the
Direct and
RAG methods, where
RAG used Wikipedia documents regarding the entities in the MetaQA dataset as external knowledge. This experiment was conducted on a test sample of 15K question-answer pairs divided equally among 1-hop, 2-hop, and 3-hop questions. The underlying LLM is the Llama-3 8B Instruct version [
23]. From the results shown in
Table 1, we can observe that the performance of the
Direct method is poor compared to other methods. This shows that depending only on the internal knowledge of Llama-3 8B is not enough for the domain-specific task. On the other hand, the traditional
RAG method provides a significant
2 increase in the performance in 1-hop and 2-hop questions (
and
increase in 1-hop and 2-hop respectively using Top-10) compared to the
Direct method; however, the performance increase for 3-hop questions is very low (maximum increase is
using Top-1) that may due to the limitation of the semantic-based retrieval to find the necessary documents to answer multi-hop questions. This limitation of traditional
RAG is addressed in
SG-RAG, which is seen in the significant increase in the performance for 1-hop, 2-hop, and 3-hop questions.
One of the possible reasons behind the lower performance of the traditional
RAG method compared to
SG-RAG on 1-hop questions can be that Wikipedia documents may not contain all the information required to answer the question. To address this issue further, we generated textual documents based on the MetaQA-KG using the Gemini model
3. To generate the documents, we first extract the entity names from the questions. Then, for each entity, we extracted the node
representing the targeted entity and the 1-hop neighborhood around it. Lastly, we converted the extracted subgraph into a set of triplets and sent it to the Gemini model to generate a paragraph regarding the given triplets. During this experiment, we used Gemini 1.5 Flash version. This experiment was conducted on a test sample of 1547 1-hop questions, 1589 2-hop questions, and 1513 3-hop questions. From the results in
Table 2, we can see that applying
RAG on generated documents based on the
(
RAG-Gen) increases the performance in 1-hop questions compared to
RAG-Wiki. Moreover, we can still notice that the performance of
SG-RAG is higher than the
RAG-Gen performance, even for 1-hop questions. The reason behind the high performance of
SG-RAG is that the knowledge sent to the LLM is in the triplet format, which helps the LLM in extracting the information and applying reasoning on it.
Lastly, to analyze the effect of the underlying LLM, we re-applied
SG-RAG and
RAG-Gen on the GPT-4 Turbo [
24] using the same sample we used earlier. We can notice from the results in
Table 3 that
SG-RAG still outperformed the traditional
RAG method for 1-hop, 2-hop, and 3-hop questions. We can also see a general increase in the performance of all the methods compared to the results on Llama-3 8B instruct. This increase is because of the high capability of the GPT-4 model compared to Llama-3 8B.
4.3. Potential Improvements
LLMs generally struggle to pay enough attention to the knowledge that appears in the middle of the context and focus only on the knowledge at the beginning and end of the context. This problem in LLMs is known as lost-in-the-middle [
8]. For multi-hop QA, the lost-in-the-middle problem increases when the necessary parts of information are far away from each other [
25]. A possible solution to this problem is to apply an ordering on the knowledge in the context [
26,
27]. In our previous work, we did not propose any ordering mechanism among the subgraph’s triplets
; however, specifying an order among the triplets can decrease the effect of the lost-in-the-middle problem by supporting the LLM in reasoning on
T and generating a more accurate answer to
q.
Moreover, the textual transformation step in SG-RAG converts the set of retrieved subgraphs to the set so that each subgraph is represented by the set of triplets . In the triplets representation, the subgraphs in T can overlap. This means that the set of subgraphs’ triplets T that is shared with the LLM to generate an answer to q can contain repetitive triplets. These redundant triplets unnecessarily increase the size of the context shared with the LLM. During our experiments, we noticed that on average, of the retrieved triplets in a 2-hop question are redundant. This percentage is increased to around in the case of the 3-hop question.
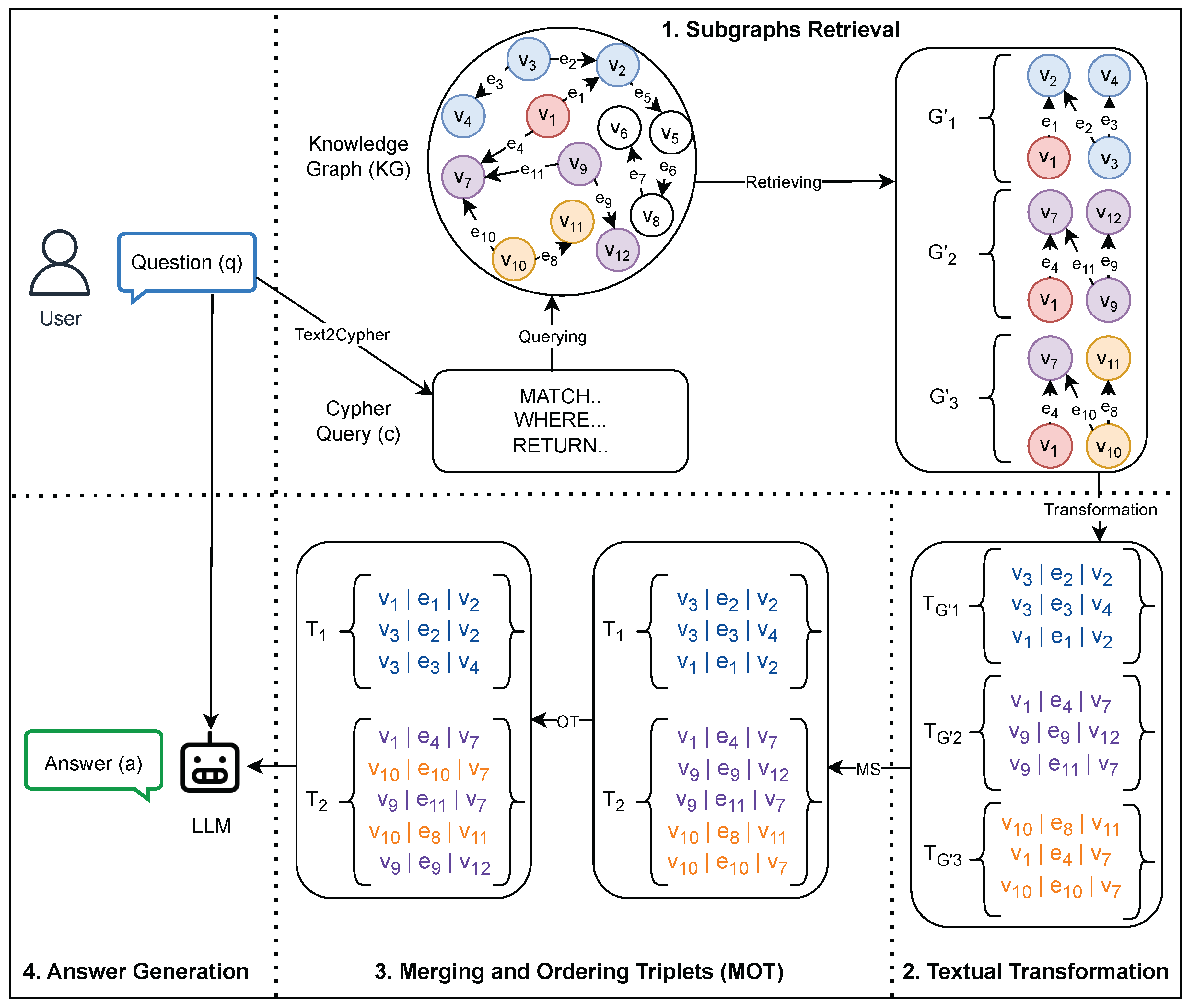
5. Merging and Ordering Triplets
To address the potential improvements discussed in
Section 4.3, we introduce an additional step to the
SG-RAG method after the textual transformation step, as demonstrated in
Figure 2. The new step is called Merging and Ordering Triplets (
MOT) that works to reduce the redundant triplets in
T by merging the subgraphs that have a high overlap with each other. After that, the MOT step sets an order among the triplets in each subgraph’s triplets
using a graph traversal algorithm. In the following sub-sections, we explain in detail the process of the Merging Subgraphs (MS) and the Ordering Triplets (OT).
5.1. Merging Subgraphs (MS)
The redundant triplets in T are due to the overlap among the subgraphs’ triplet set . Let such that there exists a triplet t where and . Removing t from one of them makes the information in the cropped subgraph incomplete. For that reason, MOT reduces the redundancy by applying agglomerative (bottom-up) hierarchical merging on T as demonstrated in Algorithm 1. Initially, the hierarchical merging algorithm starts with the set of subgraphs’ triplets T, which is created by the textual transformation step of SG-RAG. In each iteration, it merges the two sets of triplets such that the overlap between and is the maximum and above the threshold . The merging forms a new set of triplets . Both and are removed from T and replaced with . The MS algorithm stops when the overlap between each two sets is below .
To measure the overlap between two sets of triplets, we use the Jaccard similarity:
The result of the MS is:
where
is a set of triplets.
The result of the MS depends on the threshold
, which is a hyperparameter. The threshold
can take a value between 0 and 1, where 0 leads to merge all
into a single subgraph, while 1 prevents any merging process. This hyperparameter controls the trade-off between decreasing the size of the context shared with the LLM by removing redundant triplets and the performance of the LLM. We discuss the effect of this hyperparameter later in
Section 7.2.
|
Algorithm 1: Merging Subgraphs |
 |
5.2. Ordering Triplets (OT)
After completing Merging Subgraphs (MS), the Ordering Triplets (OT) works to order the triplets in each set of triplets
independently. Our ordering mechanism uses the Breadth First Search (BFS) as a triplet traversal algorithm. As shown in Algorithm 2, the OT requires as inputs the set of triplets
, and the node
where
represents the entity appearing in the question
q. OT defines a queue, called
in Algorithm 2, to hold the nodes that have been reached but not explored yet. The
contains the node
initially. Besides the
queue, OT also defined an empty list, called
in Algorithm 2, to carry the traversed triplets. On each iteration, OT gets the first node
from the
queue, then it retrieves the set of triplets
as:
After that, for each triplet
,
t is appended to the
list if
, and the algorithm adds the node
, defined as
where
, to the end of the queue
.
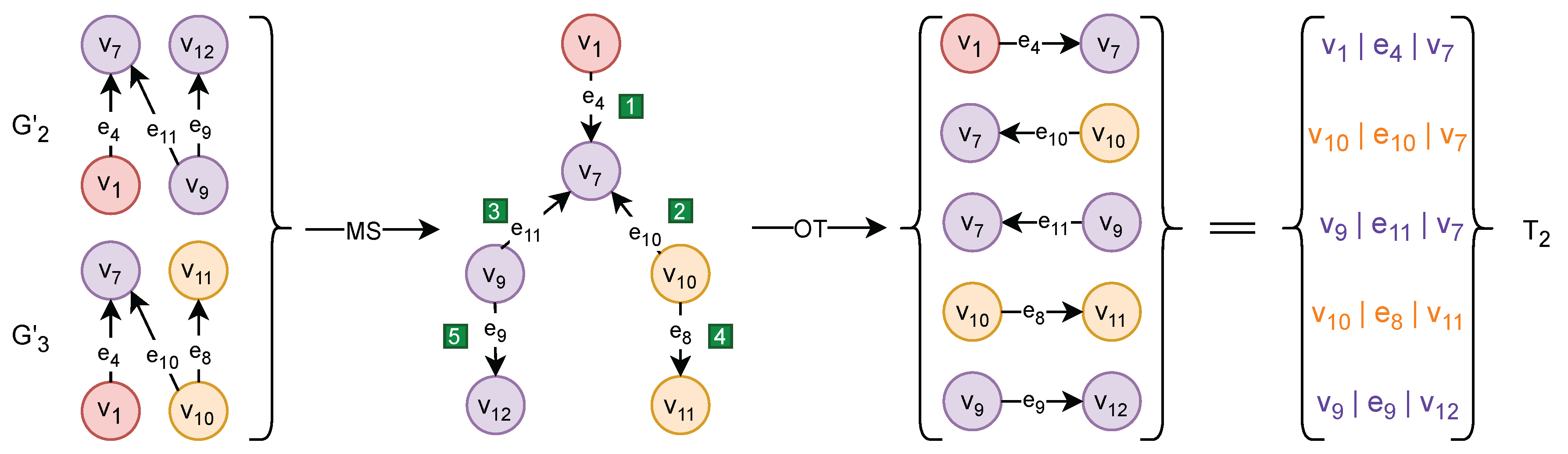
Figure 3 provides a zoomed-in visualization of the
MOT on the subgraphs
and
from
Figure 2. We can see that
and
merged into a larger subgraph where the redundant triplet "
|
|
" is removed. After that, BFS traversed the merged subgraph. The numbers in the green squares are the traversing order of the triplets.
|
Algorithm 2: BFS Ordering Triplets |
 |
6. Experimental Settings
In this section, we provide the settings of our experiments. First, we list the baseline methods we considered. Then, we specify our test set and the evaluation metric we used. Lastly, we discuss the implementation setup of the experiments.
6.1. Baselines
In our results, we compared the performance of the SG-RAG MOT on the following state-of-the-art methods:
Direct: Similar to the
Direct baseline used by Saleh et al. [
11]. The prompt used with this method in shown in
Figure A3.
Chain-of-Thought (
CoT) [
28]: In the
CoT method, the LLM answers the question
q in a step-by-step approach based on its internal knowledge until it reaches the final answer to
q. To give the LLM this ability, we applied the few-shot setup by providing 7 examples as context in the prompt. The prompt template for CoT is in
Figure A4.
Triplet-based RAG: This method integrates the top-
k related knowledge, which is retrieved from the
in triplet format, with the LLM prompt to generate the answer to
q. The retrieval process is based on the semantic similarity between the
q and the triplets in the
. In our experiments, we applied this method three times with
k being 5, 10, and 20. the prompt used with this method is same as
SG-RAG which is shown in
Figure A2.
Graph Chain-of-Thought (
Graph-CoT) [
17]: We applied the
Graph-CoT in the few-shot setup using the implementation of Jin et al. [
17] published on GitHub
4.
We discarded the Think-on-Graph (
ToG) [
18] method from our baselines. During our initial experiment, we applied
ToG using the implementation of Sun et al. [
18] published on GitHub
5; however, we noticed incompatibility between
ToG and the MetaQA benchmark we used for testing, which led to a low performance on
ToG.
6.2. Dataset and Evaluation Metric
Following our previous work [
11], we applied our experiments to the MetaQA benchmark dataset proposed by Zhang et al. [
21]. All the experiments were conducted on a sample of 3942 question-answer pairs, around
of the test set in the MetaQA, divided equally among the number of hops. We hosted MetaQA
in the Neo4j Graph Database. To evaluate the performance of the
SG-RAG MOT and the baseline methods, we continued using Answer-Matching Rate(AMR) metric.
6.3. Experimental Setup
We tested our method and the baseline on multiple open-source LLMs with different sizes. From the Llama family, we chose Llama-3.1 8B Instruct and Llama 3.2 3B Instruct. From the Qwen family, we chose Qwen-2.5 7B Instruct and Qwen-2.5 3B Instruct [
29].
The MOT step requires specifying the entity name that appears in the question. To do that, we use a general open-source NER model from Hugging Face
6 that is built based on the Roberta Large model. Since the
Graph-CoT and the
Triplet-based RAG methods need to apply a semantic-based retrieval as part of their methods, we used "all-mpnet-base-v2"
7 as an embedding model. This model is the default embedding model used by the
Graph-CoT [
17].
Lastly, we ran the methods 3 times for each question, except for the Graph-CoT, to decrease the effect of the randomization that can come from the underlying LLMs. For the Graph-CoT, we executed it only once per question due to the high cost in terms of time and resources, as it requires multiple calls to the LLM.
7. Results and Discussion
In this section, we first highlight the overall performance of our method and the baselines. Then, we discuss the ablation studies for further analysis. Lastly, we provide case studies as empirical examples of our method and the baseline, and show some of the failure cases of SG-RAG MOT.
7.1. Overall Performance
The main results are shown in
Table 4. From the results, we can observe that: 1) The performance of
SG-RAG MOT achieved a higher performance than other baselines, especially for 2-hop and 3-hop questions. 2) When we look at the performance of
Triplet-based RAG for 2-hop and 3-hop questions, we can observe that its performance is the lowest. Based on our experiments, we notice that the triplets retrieved by the semantic similarity are factually irrelevant to the 2-hop and 3-hop questions, which misleads the underlying LLMs to generate factually wrong answers. 3) For the
CoT, we notice that it did not provide a performance boost to the Direct method for 2-hop and 3-hop questions. We noticed that answering the multi-hop question step-by-step requires stronger knowledge in the targeted domain. 4) The performance of
Graph-CoT is highly sensitive to the underlying LLM, where its performance changes significantly from one LLM to another. For example, the performance difference between Qwen-2.5 7B Instruct and Llama-3.1 8B Instruct is
,
, and
in 1-hop, 2-hop, and 3-hop, respectively. Based on our experiments, we noticed that the iterative approach that the
Graph-CoT used to traverse the
to reach the answer requires a high capability from the underlying LLM, where any small hallucination in one iteration leads the LLM to hallucinate in all upcoming iterations.
7.2. Ablation Study
How do different open-source LLMs with different sizes perform in SG-RAG MOT? In the main results, we showed the performance of
SG-RAG MOT using Llama-3.1 8B Instruct. In this experiment, we want to explore its performance using different open-source LLMs that have different sizes. The results of
SG-RAG MOT with different underlying LLMs are shown in
Table 5. From the results, we can see that the performance of
SG-RAG MOT changes with the different underlying LLMs. However, we can observe that the performance is not related to the size of the model, as we can see that the best performance is achieved with Qwen-2.5 7B Instruct, which is higher than Llama-3.1 8B Instruct by
,
, and
for 1-hop, 2-hop and 3-hop respectively. Moreover, the performance of Llama-3.1 8B and Llama-3.2 3B are similar to each other for 2-hop and 3-hop questions. Our results indicate that the LLM with a higher ability to reason and extract answers from the given subgraphs triplets can achieve a higher performance in
SG-RAG MOT.
What is the effect of the Breadth First Search (BFS) traversal algorithm on the performance of SG-RAG MOT? To answer this question, we re-applied
SG-RAG MOT with the merging threshold
set as 0 and using different ordering strategies. We applied this experiment with
to have only one big subgraph where the effect of the ordering can reach the maximum. The ordering strategies we tested are: 1) Breadth First Search (BFS) traversal algorithm, which we used as the main ordering strategy, 2) the reverse of BFS, which reverses upside down the order defined by BFS, 3) Depth First Search (DFS) traversal algorithm, 4) the reverse of DFS, and 5) Random ordering following the standard SG-RAG [
11]. The results of
SG-RAG MOT with the selected ordering strategies are shown in
Table 6. From the results, we can find that the performance of the Random ordering is always lower than the performance of BFS and DFS. Moreover, we can also see that DFS and BFS achieved comparable results without any significant difference in performance. This result indicates that defining an order among the triplets in the subgraph helps the LLMs to reason over the given subgraph and extract the right answer, which leads to a decrease in the hallucination problem. When we look at the performance of the reverse BFS, we can see that it is lower than the performance of BFS and closer to the performance of the Random ordering. We can observe the same for the performance of reverse DFS. The advantage of BFS and DFS over their reverse versions is that the first (top) triplets in the BFS and DFS ordering contain the entity appearing in the question
q, and the following triplets are connected to the previous one, which helps the LLMs to concentrate on all given triplets until the last triplet.
What is the importance of the Merging Threshold on the performance of SG-RAG MOT? To answer this question, we tested the
SG-RAG MOT with different values of merging threshold
. The selected values are from 0 to
and 1. We did not test the values between
to
because there is no merging happening among the subgraphs for those values, which makes them exactly similar when
in our test set. When
is set to 0, all subgraphs are merged to create one subgraph, which means that all redundant triplets are removed. As the value of
increases, we have more subgraphs and more redundant triplets, until
reaches 1. When
is 1, the subgraphs are kept as they are without merging and without removing redundant triplets.
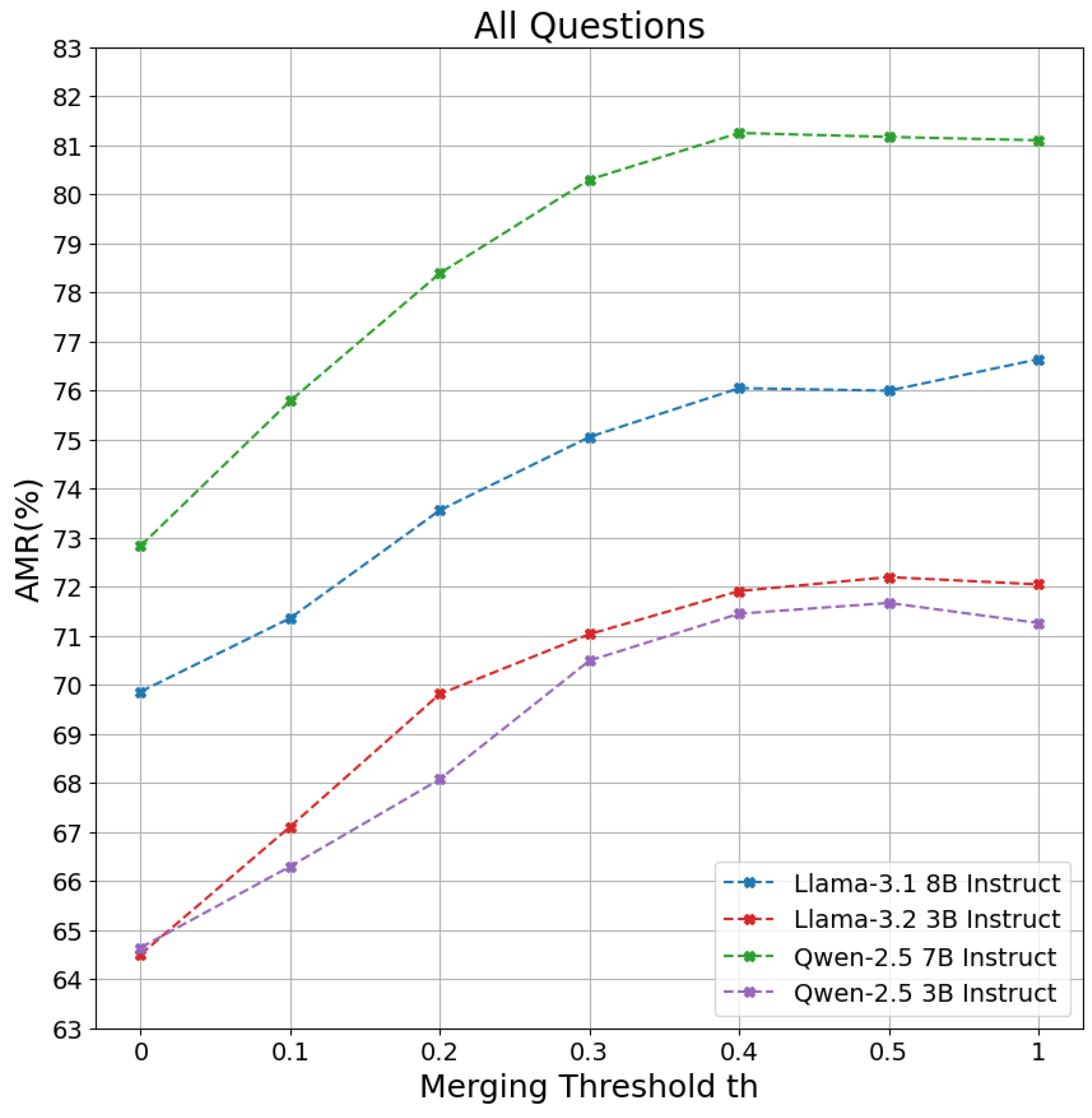
Figure 4 shows the performance of
SG-RAG MOT with the different values of
in all the questions in our test set. We can observe from the results that the performance increases as the value of
increases until a specific value, which is
in our case. After that value, the performance does not change significantly. This observation highlights the importance of the merging threshold
in controlling the trade-off between the performance of
SG-RAG MOT and the redundancy in the triplets. Decreasing the value of
to be close to 0 leads to a decrease in the duplicated triplets, which makes the context shared with the underlying LLM shorter and helps the LLM to infer faster; however, this comes with a sacrifice in the performance of the method, in our case there is a performance decrease of
on average compared to the peak of the performance. We can see a deeper look in
Figure 5, which shows the performance of the
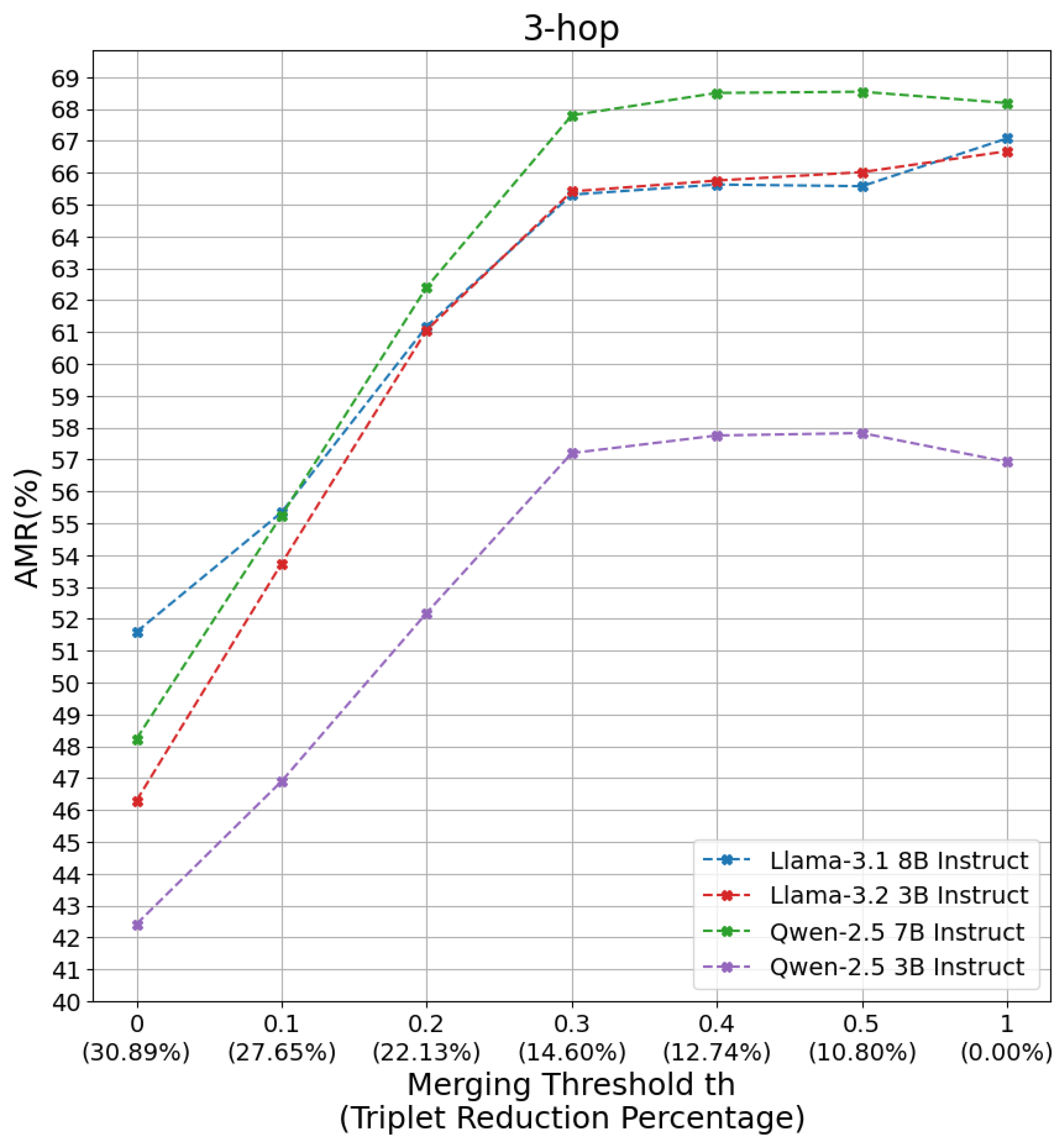
SG-RAG MOT on the 3-hop questions only. The percentage enclosed by parentheses on the x-axis shows the percentage of reduction in the number of triplets. We can see that when
is
, we decrease the number of triplets by
and obtain high performance on different underlying LLMs.
7.3. Case Studies
We conduct case studies for two main reasons. 1) Provide an empirical example of the responses generated with
SG-RAG MOT and the other baseline. 2) Highlight the weakness of
SG-RAG MOT. In
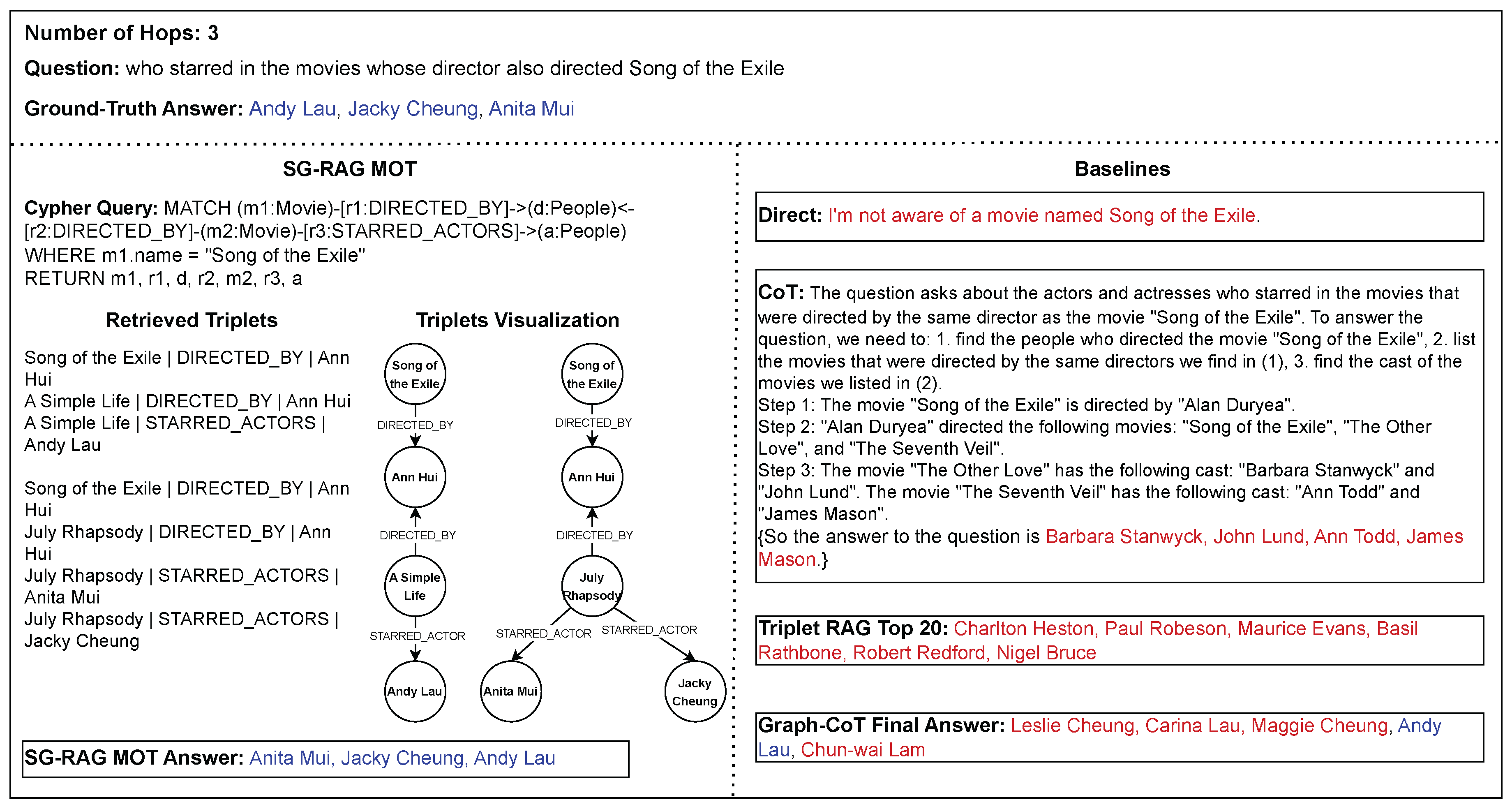
Figure 6, we can see an example of a 3-hop question from MetaQA. The question given in this example is a 3-hop because it requires identifying the director of the "Song of the Exile" movie, then finding the movies that were directed by the director of "Song of the Exile", and lastly finding the names of the actors and actresses who appeared in these movies. From the
SG-RAG MOT, we can see that the Cypher query searches for the required knowledge in the KG and retrieves it as triplets, which leads the LLM to generate the correct and precise answer. For
Graph-CoT, one of the names in the final answer is correct, while the rest are wrong. This may be due to the underlying LLM controlling the traversal process of the knowledge graph, where a small hallucination of the underlying LLM can wrongly turn the direction of the traversal. In the case of the
CoT and
Triplet-based RAG methods, they both failed to generate correct answers.
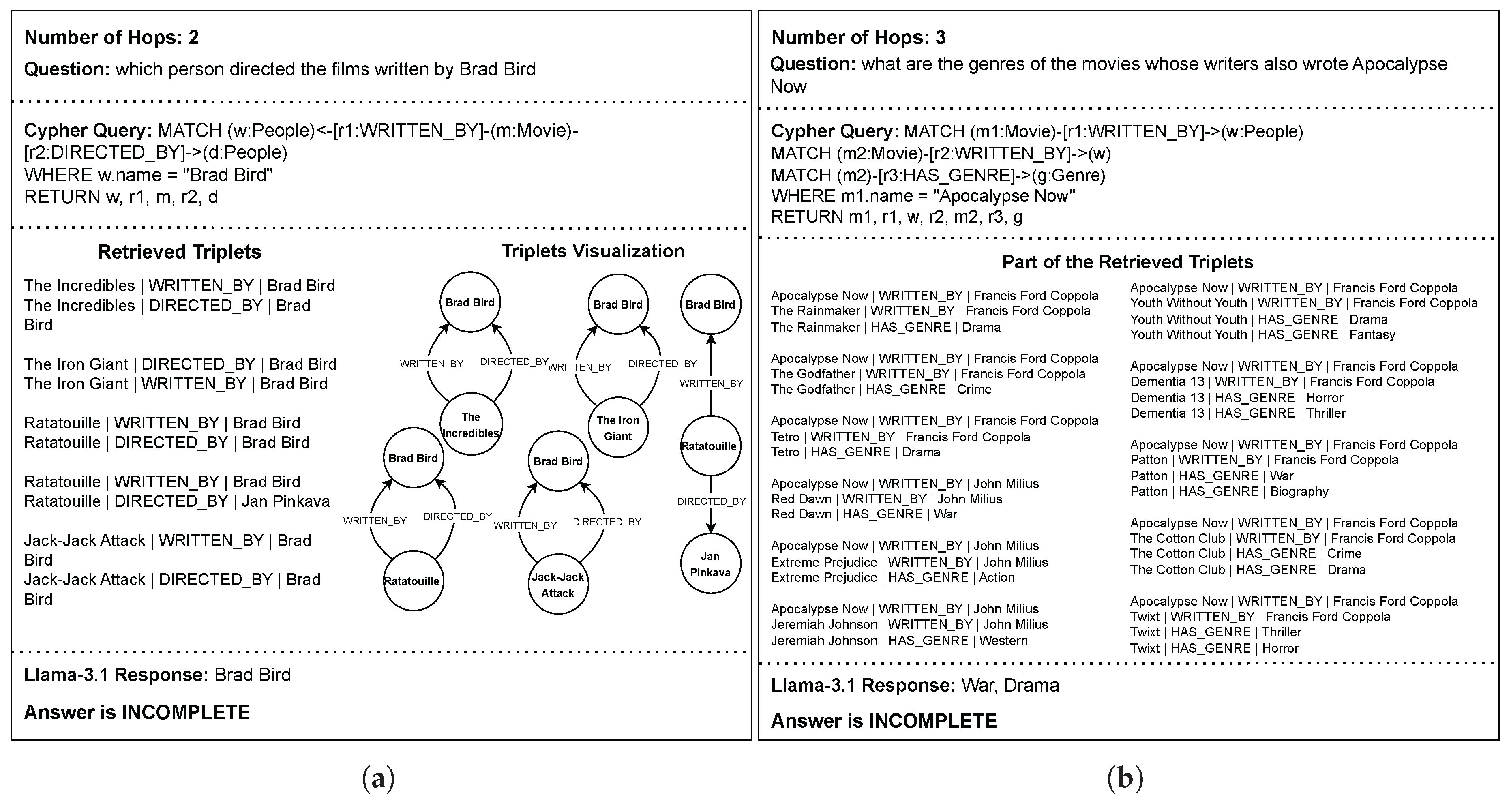
In
Figure 7, we can see two examples where
SG-RAG MOT failed to generate complete answers. Each of these examples represents a limitation in our method. The left example in the figure is a 2-hop question where the "Brad Bird" entity is repeated 9 times in the retrieved triplets. This high repetition of an entity confuses the underlying LLM and misleads it to think it is the right answer. Such a kind of entity (node) level repetition is not addressed by the
MOT step since our method catches the redundancy on the triplet level. Another weakness of
SG-RAG MOT can be seen in the right example in
Figure 7, where the number of retrieved triplets is high. The total number of retrieved triplets is 76, but we cropped them in the figure because of space limitations. Although the triplets provided the necessary knowledge to answer the question fully and precisely, the long context prevents the LLM from leveraging the entire provided knowledge.
8. Conclusions and Future Work
In our previous work, we proposed SubGraph Retrieval Augmented Generation (
SG-RAG) as a GraphRAG method for multi-hop knowledge graph question answering [
11]. We also showed that the performance of
SG-RAG outperforms the traditional
RAG method using Llama-3 8B Instruct and the GPT-4 Turbo. In this work, we aim to further enhance the performance of
SG-RAG by introducing a new step called Merging and Ordering Triplets (
MOT). The
MOT step seeks to decrease the redundancy in the retrieved subgraph triplets by applying hierarchical merging, where highly overlapped subgraphs are merged. It also defines an order among the triplets using the Breadth First Search traversal algorithm. We conducted our experiments on 4 different open-source LLMs. The
SG-RAG MOT performed better than Chaint of Thought (
CoT),
Triplet-based RAG, and Graph Chain-of-Thoughts (
Graph-CoT) on the chosen LLMs. During our ablation studies, we tested different ordering strategies. Our results indicate that using a graph traversal algorithm, such as Breadth First Search and Depth First Search, helps the LLM in reasoning on the given triplets and decreases the effect of the lost-in-the-middle problem.
Although SG-RAG MOT achieved good performance on the MetaQA benchmark, there is still room for improvement. Besides the weakness of SG-RAG MOT we described in our case studies, the template-based Text2Cypher mapping is one of the main limitations in our method. Working on a domain-agnostic Text2Cypher mapping is a promising direction that can help facilitate applying our method to real scenarios.
Author Contributions
Conceptualization, Ahmmad O. M. Saleh, Gokhan Tur and Yucel Saygin; Formal analysis, Ahmmad O. M. Saleh, Gokhan Tur and Yucel Saygin; Investigation, Ahmmad O. M. Saleh; Methodology, Ahmmad O. M. Saleh; Software, Ahmmad O. M. Saleh; Supervision, Gokhan Tur and Yucel Saygin; Validation, Ahmmad O. M. Saleh, Gokhan Tur and Yucel Saygin; Visualization, Ahmmad O. M. Saleh; Writing – original draft, Ahmmad O. M. Saleh; Writing – review and editing, Yucel Saygin. All authors will be updated at each stage of manuscript processing, including submission, revision, and revision reminder, via emails from our system or the assigned Assistant Editor.
Funding
This research was partially funded by the Scientific and Technological Research Council of Turkey (TUBITAK)’s Industrial PhD program under project number 118C056.
Data Availability Statement
Data sharing is not applicable
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this article:
| LLM |
Large Language Model |
| KG |
Knowledge Graph |
| RAG |
Retrieval Augmented Generation |
| SG-RAG |
SubGraph Retrieval Augmented Generation |
| MOT |
Merging and Ordering Triplets |
| MS |
Merging Subgraph |
| OT |
Ordering Triplets |
| BFS |
Breadth First Search |
| DFS |
Depth First Search |
| CoT |
Chain-of-Though |
| ToG |
Think-on-Graph |
Appendix A. Cypher Query Templates
Figure A1.
Example of Our Cypher Query Templates for MetaQA KG.
Figure A1.
Example of Our Cypher Query Templates for MetaQA KG.
Appendix B. Prompt Templates
Figure A2.
The Prompt Template used with SG-RAG, SG-RAG MOT, and Triplet-based RAG.
Figure A2.
The Prompt Template used with SG-RAG, SG-RAG MOT, and Triplet-based RAG.
Figure A3.
The Prompt Template used with the Direct Method.
Figure A3.
The Prompt Template used with the Direct Method.
Figure A4.
The Prompt Template used with the Chain-of-Thought (CoT) Method.
Figure A4.
The Prompt Template used with the Chain-of-Thought (CoT) Method.
References
- Touvron, H.; Martin, L.; Stone, K.; Albert, P.; Almahairi, A.; Babaei, Y.; Bashlykov, N.; Batra, S.; Bhargava, P.; Bhosale, S.; et al. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288 2023. [CrossRef]
- Tonmoy, S.; Zaman, S.; Jain, V.; Rani, A.; Rawte, V.; Chadha, A.; Das, A. A comprehensive survey of hallucination mitigation techniques in large language models. arXiv preprint arXiv:2401.01313 2024. [CrossRef]
- Li, J.; Chen, J.; Ren, R.; Cheng, X.; Zhao, W.X.; Nie, J.Y.; Wen, J.R. The dawn after the dark: An empirical study on factuality hallucination in large language models. arXiv preprint arXiv:2401.03205 2024. [CrossRef]
- Lewis, P.; Perez, E.; Piktus, A.; Petroni, F.; Karpukhin, V.; Goyal, N.; Küttler, H.; Lewis, M.; Yih, W.t.; Rocktäschel, T.; et al. Retrieval-augmented generation for knowledge-intensive nlp tasks. Advances in Neural Information Processing Systems 2020, 33, 9459–9474.
- Setty, S.; Jijo, K.; Chung, E.; Vidra, N. Improving Retrieval for RAG based Question Answering Models on Financial Documents. arXiv preprint arXiv:2404.07221 2024. [CrossRef]
- Zakka, C.; Shad, R.; Chaurasia, A.; Dalal, A.R.; Kim, J.L.; Moor, M.; Fong, R.; Phillips, C.; Alexander, K.; Ashley, E.; et al. Almanac—retrieval-augmented language models for clinical medicine. NEJM AI 2024, 1, AIoa2300068. [CrossRef]
- Alan, A.Y.; Karaarslan, E.; Aydin, O. A RAG-based Question Answering System Proposal for Understanding Islam: MufassirQAS LLM. arXiv preprint arXiv:2401.15378 2024. [CrossRef]
- Liu, N.F.; Lin, K.; Hewitt, J.; Paranjape, A.; Bevilacqua, M.; Petroni, F.; Liang, P. Lost in the middle: How language models use long contexts. arXiv preprint arXiv:2307.03172 2023. [CrossRef]
- Zhang, Q.; Chen, S.; Bei, Y.; Yuan, Z.; Zhou, H.; Hong, Z.; Dong, J.; Chen, H.; Chang, Y.; Huang, X. A Survey of Graph Retrieval-Augmented Generation for Customized Large Language Models. arXiv preprint arXiv:2501.13958 2025. [CrossRef]
- Larson, J.; Truitt, S. GraphRAG: Unlocking LLM discovery on narrative private data, 2024. Accessed 25/06/2024.
- Saleh, A.O.; Tür, G.; Saygin, Y. SG-RAG: Multi-Hop Question Answering With Large Language Models Through Knowledge Graphs. In Proceedings of the Proceedings of the 7th International Conference on Natural Language and Speech Processing (ICNLSP 2024), 2024, pp. 439–448.
- Reid, M.; Savinov, N.; Teplyashin, D.; Lepikhin, D.; Lillicrap, T.; Alayrac, J.b.; Soricut, R.; Lazaridou, A.; Firat, O.; Schrittwieser, J.; et al. Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context. arXiv preprint arXiv:2403.05530 2024. [CrossRef]
- Gao, Y.; Xiong, Y.; Gao, X.; Jia, K.; Pan, J.; Bi, Y.; Dai, Y.; Sun, J.; Wang, H. Retrieval-augmented generation for large language models: A survey. arXiv preprint arXiv:2312.10997 2023. [CrossRef]
- Jin, B.; Liu, G.; Han, C.; Jiang, M.; Ji, H.; Han, J. Large language models on graphs: A comprehensive survey. arXiv preprint arXiv:2312.02783 2023. [CrossRef]
- Chen, Z.; Mao, H.; Li, H.; Jin, W.; Wen, H.; Wei, X.; Wang, S.; Yin, D.; Fan, W.; Liu, H.; et al. Exploring the potential of large language models (llms) in learning on graphs. ACM SIGKDD Explorations Newsletter 2024, 25, 42–61. [CrossRef]
- Edge, D.; Trinh, H.; Cheng, N.; Bradley, J.; Chao, A.; Mody, A.; Truitt, S.; Larson, J. From local to global: A graph rag approach to query-focused summarization. arXiv preprint arXiv:2404.16130 2024. [CrossRef]
- Jin, B.; Xie, C.; Zhang, J.; Roy, K.K.; Zhang, Y.; Li, Z.; Li, R.; Tang, X.; Wang, S.; Meng, Y.; et al. Graph chain-of-thought: Augmenting large language models by reasoning on graphs. arXiv preprint arXiv:2404.07103 2024. [CrossRef]
- Sun, J.; Xu, C.; Tang, L.; Wang, S.; Lin, C.; Gong, Y.; Ni, L.M.; Shum, H.Y.; Guo, J. Think-on-graph: Deep and responsible reasoning of large language model on knowledge graph. arXiv preprint arXiv:2307.07697 2023. [CrossRef]
- Shafie, T. A multigraph approach to social network analysis 2015. [CrossRef]
- Francis, N.; Green, A.; Guagliardo, P.; Libkin, L.; Lindaaker, T.; Marsault, V.; Plantikow, S.; Rydberg, M.; Selmer, P.; Taylor, A. Cypher: An evolving query language for property graphs. In Proceedings of the Proceedings of the 2018 international conference on management of data, 2018, pp. 1433–1445. [CrossRef]
- Zhang, Y.; Dai, H.; Kozareva, Z.; Smola, A.J.; Song, L. Variational Reasoning for Question Answering with Knowledge Graph. In Proceedings of the AAAI, 2018. [CrossRef]
- Wen, T.H.; Vandyke, D.; Mrkšić, N.; Gašić, M.; Rojas-Barahona, L.M.; Su, P.H.; Ultes, S.; Young, S. A Network-based End-to-End Trainable Task-oriented Dialogue System. In Proceedings of the Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 1, Long Papers; Lapata, M.; Blunsom, P.; Koller, A., Eds., Valencia, Spain, 2017; pp. 438–449. [CrossRef]
- AI@Meta. Llama 3 Model Card 2024.
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman, F.L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Anadkat, S.; et al. Gpt-4 technical report. arXiv preprint arXiv:2303.08774 2023. [CrossRef]
- Baker, G.A.; Raut, A.; Shaier, S.; Hunter, L.E.; von der Wense, K. Lost in the Middle, and In-Between: Enhancing Language Models’ Ability to Reason Over Long Contexts in Multi-Hop QA. arXiv preprint arXiv:2412.10079 2024. [CrossRef]
- Peysakhovich, A.; Lerer, A. Attention sorting combats recency bias in long context language models. arXiv preprint arXiv:2310.01427 2023. [CrossRef]
- Tang, R.; Zhang, X.; Ma, X.; Lin, J.; Ture, F. Found in the middle: Permutation self-consistency improves listwise ranking in large language models. arXiv preprint arXiv:2310.07712 2023. [CrossRef]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Xia, F.; Chi, E.; Le, Q.V.; Zhou, D.; et al. Chain-of-thought prompting elicits reasoning in large language models. Advances in neural information processing systems 2022, 35, 24824–24837.
- Team, Q. Qwen2.5: A Party of Foundation Models, 2024.
| 1 |
|
| 2 |
The p-value calculated by one-tailed paired t-test
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
Figure 1.
An Overview of SG-RAG.
Figure 1.
An Overview of SG-RAG.
Figure 2.
An Overview of SG-RAG with Merging and Ordering Triplets Extension.
Figure 2.
An Overview of SG-RAG with Merging and Ordering Triplets Extension.
Figure 3.
Zoomed-in Visualization of the
MOT on the subgraphs
and
from
Figure 2.
Figure 3.
Zoomed-in Visualization of the
MOT on the subgraphs
and
from
Figure 2.
Figure 4.
The Performance of SG-RAG MOT with Different Merging Threshold Values Over All Questions.
Figure 4.
The Performance of SG-RAG MOT with Different Merging Threshold Values Over All Questions.
Figure 5.
The Performance of SG-RAG MOT with Different Merging Threshold Values Over 3-hop Questions.
Figure 5.
The Performance of SG-RAG MOT with Different Merging Threshold Values Over 3-hop Questions.
Figure 6.
Example of the Responses generated with SG-RAG MOT and the other baseline on a 3-hop Question.
Figure 6.
Example of the Responses generated with SG-RAG MOT and the other baseline on a 3-hop Question.
Figure 7.
Failure Cases of SG-RAG MOT: (a) Failed Because of High Repetition of "Brad Bird" Entity in the Retrieved Triplets. (b) Failed Because of High Number of Retrieved Triplets.
Figure 7.
Failure Cases of SG-RAG MOT: (a) Failed Because of High Repetition of "Brad Bird" Entity in the Retrieved Triplets. (b) Failed Because of High Number of Retrieved Triplets.
Table 1.
Comparison between the performance of Direct, RAG on Wikipedia documents (RAG-Wiki), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on Llama-3.1 8B Instruct.
Table 1.
Comparison between the performance of Direct, RAG on Wikipedia documents (RAG-Wiki), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on Llama-3.1 8B Instruct.
| Method |
1-hop |
2-hop |
3-hop |
| Direct |
0.24 |
0.13 |
0.17 |
| RAG-Wiki Top-1 |
0.33 |
0.19 |
0.21 |
| RAG-Wiki Top-2 |
0.36 |
0.20 |
0.20 |
| RAG-Wiki Top-3 |
0.38 |
0.22 |
0.20 |
| RAG-Wiki Top-5 |
0.40 |
0.23 |
0.18 |
| RAG-Wiki Top-10 |
0.42 |
0.27 |
0.19 |
| SG-RAG |
0.90 |
0.73 |
0.58 |
Table 2.
Comparison between the performance of RAG on Wikipedia documents (RAG-Wiki), RAG on Gemini generated documents (RAG-Gen), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on Llama-3.1 8B Instruct.
Table 2.
Comparison between the performance of RAG on Wikipedia documents (RAG-Wiki), RAG on Gemini generated documents (RAG-Gen), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on Llama-3.1 8B Instruct.
| Method |
1-hop |
2-hop |
3-hop |
| RAG-Wiki Top-1 |
0.33 |
0.19 |
0.21 |
| RAG-Wiki Top-2 |
0.35 |
0.20 |
0.20 |
| RAG-Wiki Top-3 |
0.36 |
0.22 |
0.20 |
| RAG-Gen Top-1 |
0.64 |
0.15 |
0.17 |
| RAG-Gen Top-2 |
0.66 |
0.12 |
0.13 |
| RAG-Gen Top-3 |
0.66 |
0.12 |
0.16 |
| SG-RAG |
0.91 |
0.72 |
0.60 |
Table 3.
Comparison between the performance of RAG on Gemini generated documents (RAG-Gen), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on GPT-4 Turbo.
Table 3.
Comparison between the performance of RAG on Gemini generated documents (RAG-Gen), and SG-RAG. We show the performance based on Answer-Matching Rate(AMR). We conducted this experiment on GPT-4 Turbo.
| Method |
1-hop |
2-hop |
3-hop |
| RAG-Gen Top-1 |
0.765 |
0.286 |
0.204 |
| RAG-Gen Top-2 |
0.776 |
0.181 |
0.177 |
| RAG-Gen Top-3 |
0.784 |
0.179 |
0.180 |
| SG-RAG |
0.941 |
0.815 |
0.520 |
Table 4.
Comparison between the performance of Direct, CoT, Triplet-based RAG, Graph-CoT, and SG-RAG MOT. We show the performance based on Answer-Matching Rate(AMR) as a percentage. For SG-RAG MOT we set the merging threshold as and used Llama-3.1 8B Instruct as the underlying LLM.
Table 4.
Comparison between the performance of Direct, CoT, Triplet-based RAG, Graph-CoT, and SG-RAG MOT. We show the performance based on Answer-Matching Rate(AMR) as a percentage. For SG-RAG MOT we set the merging threshold as and used Llama-3.1 8B Instruct as the underlying LLM.
| Method |
LLM |
1-hop |
2-hop |
3-hop |
| Direct |
Llama-3.1 8B Instruct |
36.43 |
22.77 |
18.01 |
| Llama-3.2 3B Instruct |
21.30 |
12.13 |
8.72 |
| Qwen-2.5 7B Instruct |
16.46 |
18.61 |
15.14 |
| Qwen-2.5 3B Instruct |
11.85 |
12.96 |
8.05 |
| CoT |
Llama-3.1 8B Instruct |
39.27 |
21.81 |
14.25 |
| Llama-3.2 3B Instruct |
23.01 |
13.95 |
13.38 |
| Qwen-2.5 7B Instruct |
18.45 |
18.99 |
15.62 |
| Qwen-2.5 3B Instruct |
13.08 |
14.36 |
8.79 |
| Triplet RAG Top 5 |
Llama-3.1 8B Instruct |
54.94 |
4.58 |
9.85 |
| Llama-3.2 3B Instruct |
52.24 |
5.27 |
12.83 |
| Qwen-2.5 7B Instruct |
56.73 |
5.91 |
11.68 |
| Qwen-2.5 3B Instruct |
53.60 |
3.71 |
12.13 |
| Triplet RAG Top 10 |
Llama-3.1 8B Instruct |
60.28 |
6.06 |
12.66 |
| Llama-3.2 3B Instruct |
58.25 |
6.42 |
15.23 |
| Qwen-2.5 7B Instruct |
61.82 |
6.53 |
13.20 |
| Qwen-2.5 3B Instruct |
57.31 |
4.27 |
13.87 |
| Triplet RAG Top 20 |
Llama-3.1 8B Instruct |
63.87 |
7.18 |
14.63 |
| Llama-3.2 3B Instruct |
61.46 |
7.12 |
16.79 |
| Qwen-2.5 7B Instruct |
64.68 |
6.75 |
14.14 |
| Qwen-2.5 3B Instruct |
58.55 |
5.58 |
14.62 |
| Graph-CoT |
Llama-3.1 8B Instruct |
47.98 |
15.38 |
4.33 |
| Llama-3.2 3B Instruct |
25.11 |
9.92 |
6.41 |
| Qwen-2.5 7B Instruct |
81.40 |
57.42 |
25.35 |
| Qwen-2.5 3B Instruct |
51.83 |
13.65 |
6.48 |
| SG-RAG MOT |
85.26 |
77.27 |
65.63 |
Table 5.
Comparison between the performance of different open-source LLMs in SG-RAG MOT. We show the performance based on Answer-Matching Rate(AMR) as a percentage. We set the merging threshold as .
Table 5.
Comparison between the performance of different open-source LLMs in SG-RAG MOT. We show the performance based on Answer-Matching Rate(AMR) as a percentage. We set the merging threshold as .
| LLM |
1-hop |
2-hop |
3-hop |
| Llama-3.1 8B Instruct |
85.26 |
77.27 |
65.63 |
| Llama-3.2 3B Instruct |
72.62 |
77.43 |
65.75 |
| Qwen-2.5 7B Instruct |
88.80 |
86.52 |
68.50 |
| Qwen-2.5 3B Instruct |
81.40 |
75.25 |
57.75 |
Table 6.
Comparison among different ordering strategies on SG-RAG MOT with merging threshold .
Table 6.
Comparison among different ordering strategies on SG-RAG MOT with merging threshold .
| LLM |
Ordering Strategy |
2-hop |
3-hop |
| Llama-3.1 8B Instruct |
Random |
67.69 |
45.81 |
| DFS |
73.24 |
50.98 |
| Reverse DFS |
68.82 |
46.68 |
| BFS |
72.64 |
51.59 |
| Reverse BFS |
69.39 |
50.37 |
| Llama-3.2 3B Instruct |
Random |
69.75 |
42.93 |
| DFS |
73.98 |
46.52 |
| Reverse DFS |
69.44 |
43.60 |
| BFS |
74.78 |
46.29 |
| Reverse BFS |
69.65 |
43.34 |
| Qwen-2.5 7B Instruct |
Random |
77.07 |
43.81 |
| DFS |
82.58 |
50.45 |
| Reverse DFS |
80.98 |
45.98 |
| BFS |
81.88 |
48.23 |
| Reverse BFS |
79.76 |
49.36 |
| Qwen-2.5 3B Instruct |
Random |
65.12 |
36.98 |
| DFS |
69.47 |
41.25 |
| Reverse DFS |
67.77 |
38.42 |
| BFS |
70.49 |
42.42 |
| Reverse BFS |
67.28 |
38.26 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).