Submitted:
20 May 2025
Posted:
22 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
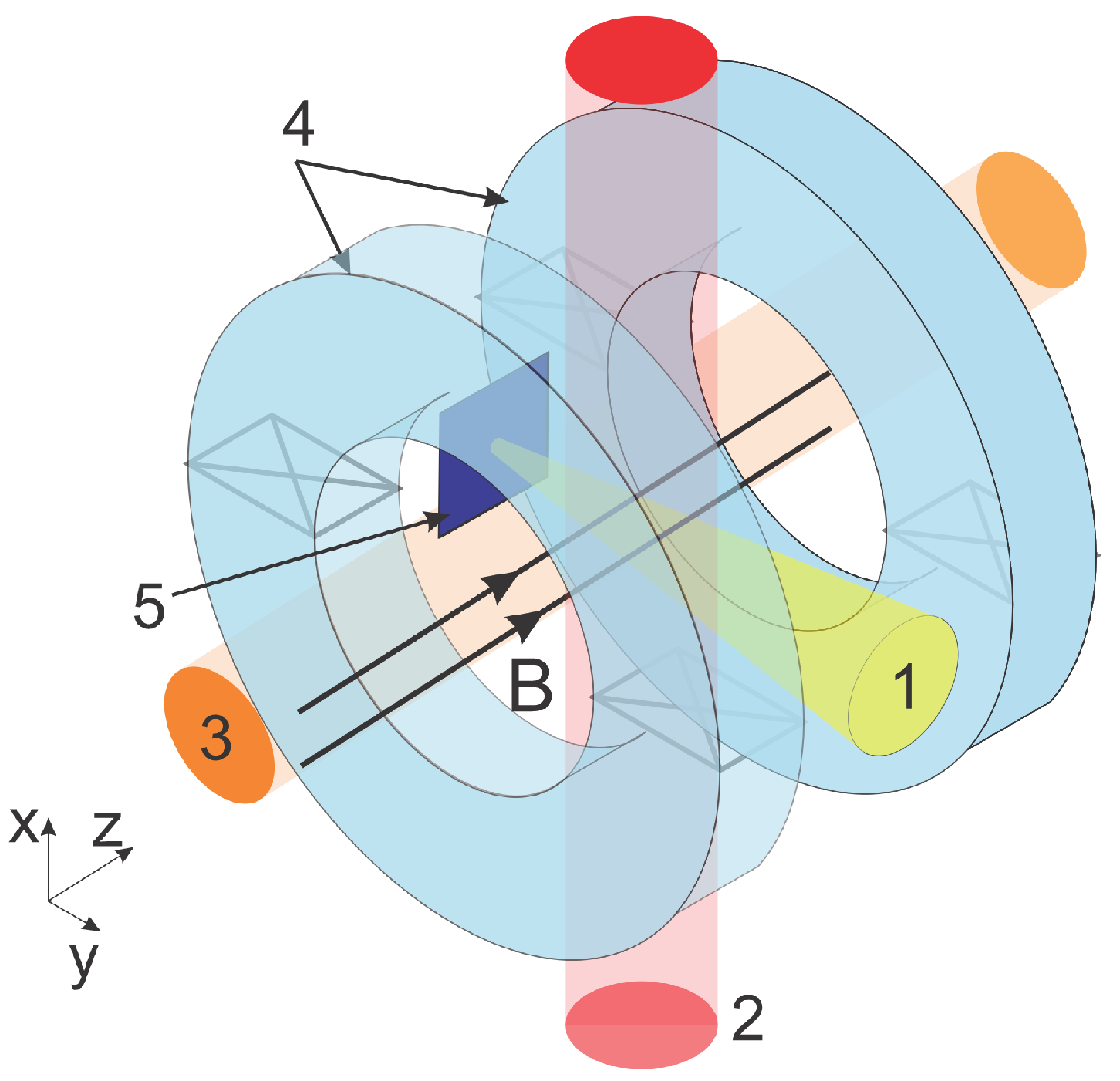
2. Methods
3. Results
3.1. Expansion of Femtosecond and Nanosecond Flows into Vacuum
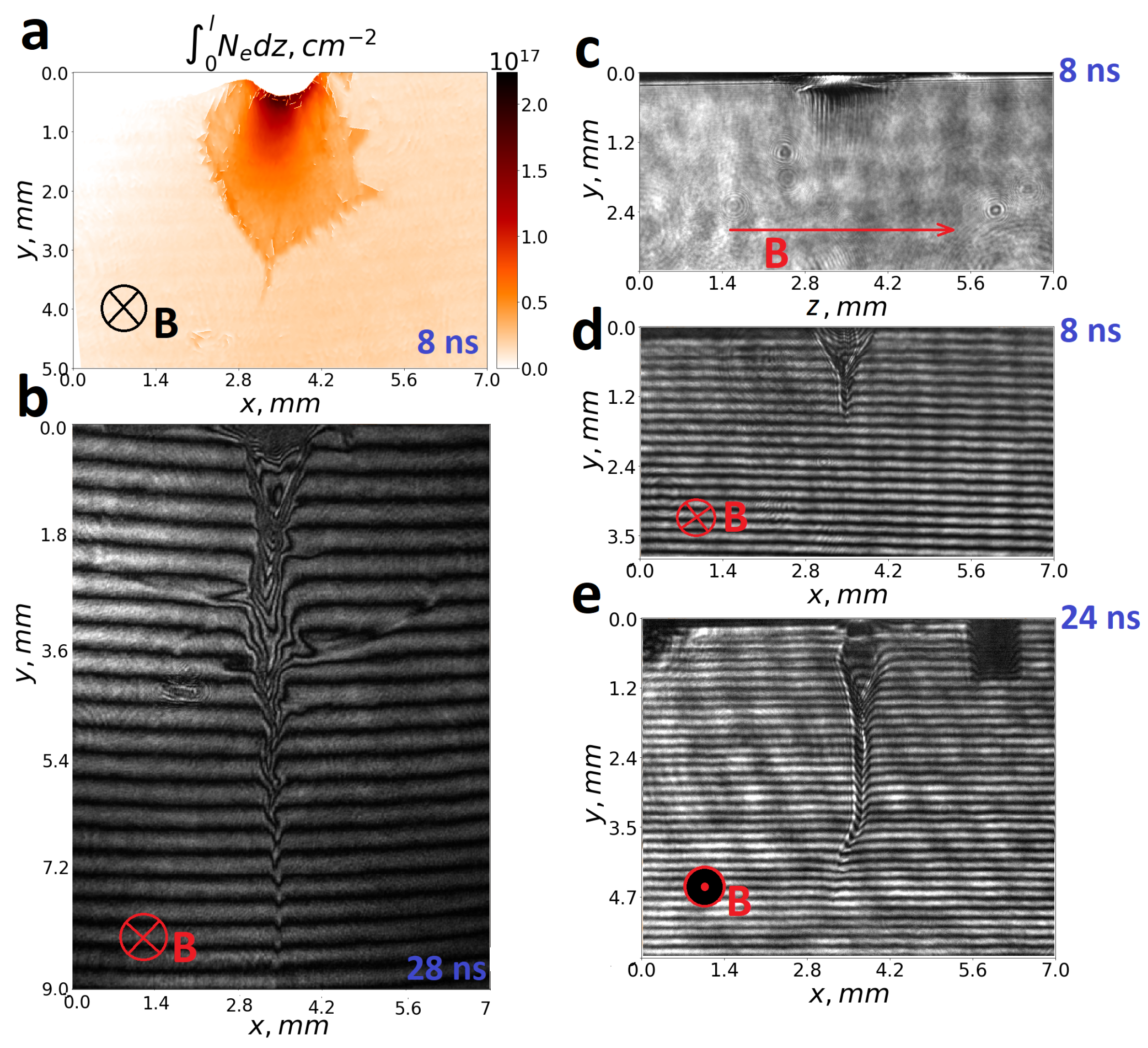
3.2. Features of the Expansion of <<Femtosecond>> and <<Nanosecond>> Plasma Flows into an External Transverse Magnetic Field of 14 T
3.3. Interaction of Elongated Laser Plasma Slab with Transverse Magnetic Field
| Fs flow | Ns flow | Astro | |
|---|---|---|---|
| Material | H | ||
| Z | |||
| A | |||
| B | |||
| L | |||
| [eV] | |||
| [eV] | |||
| V | |||
| 43 | 81 | ||
| 15 | |||
| (directed) | |||
| (directed) | |||
| c/ | |||
| 14 | 370 | ||
| Re | 320 | 670 | |
| Eu | 3 | ||
| 1 | |||
| HN |
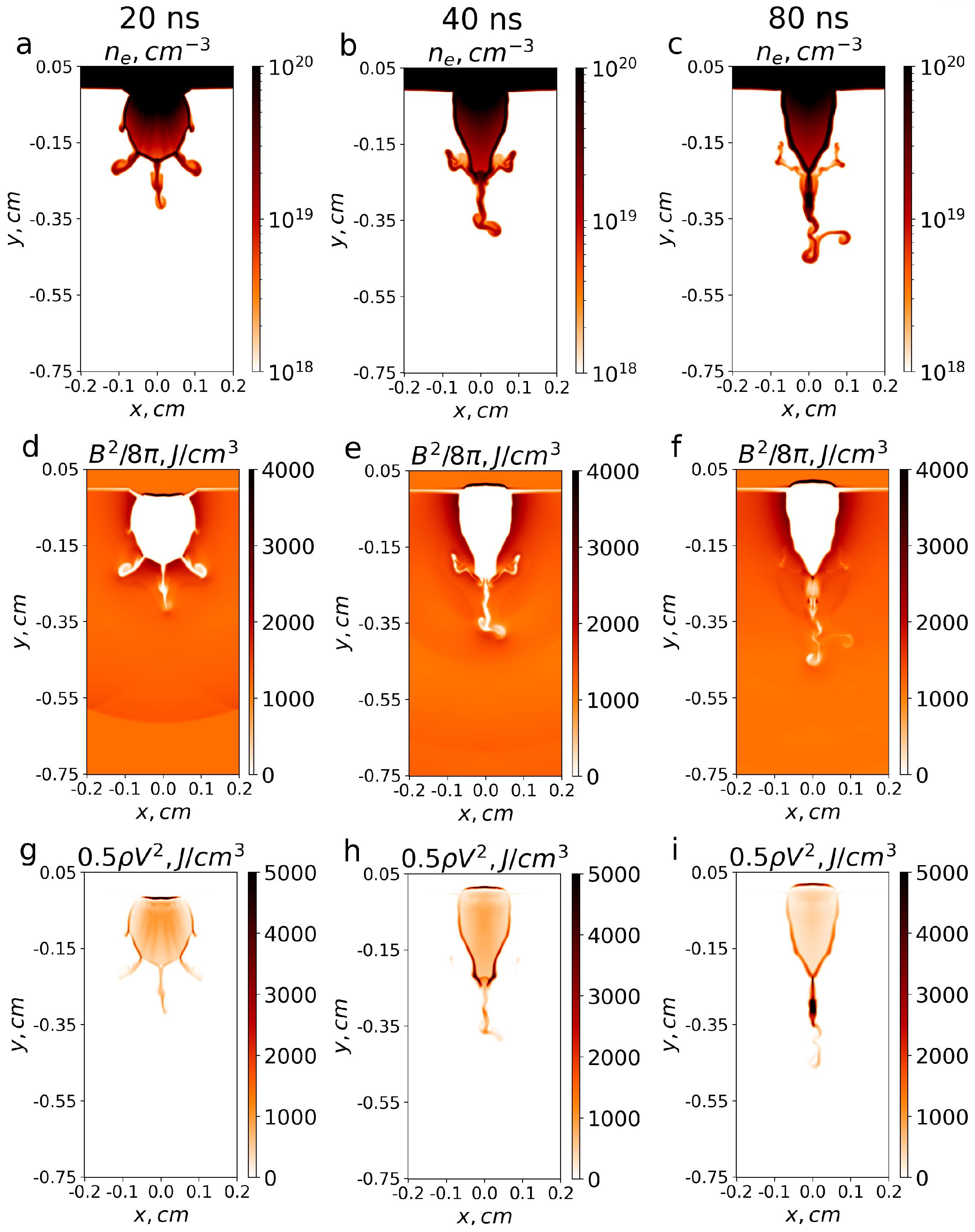
4. Simulation
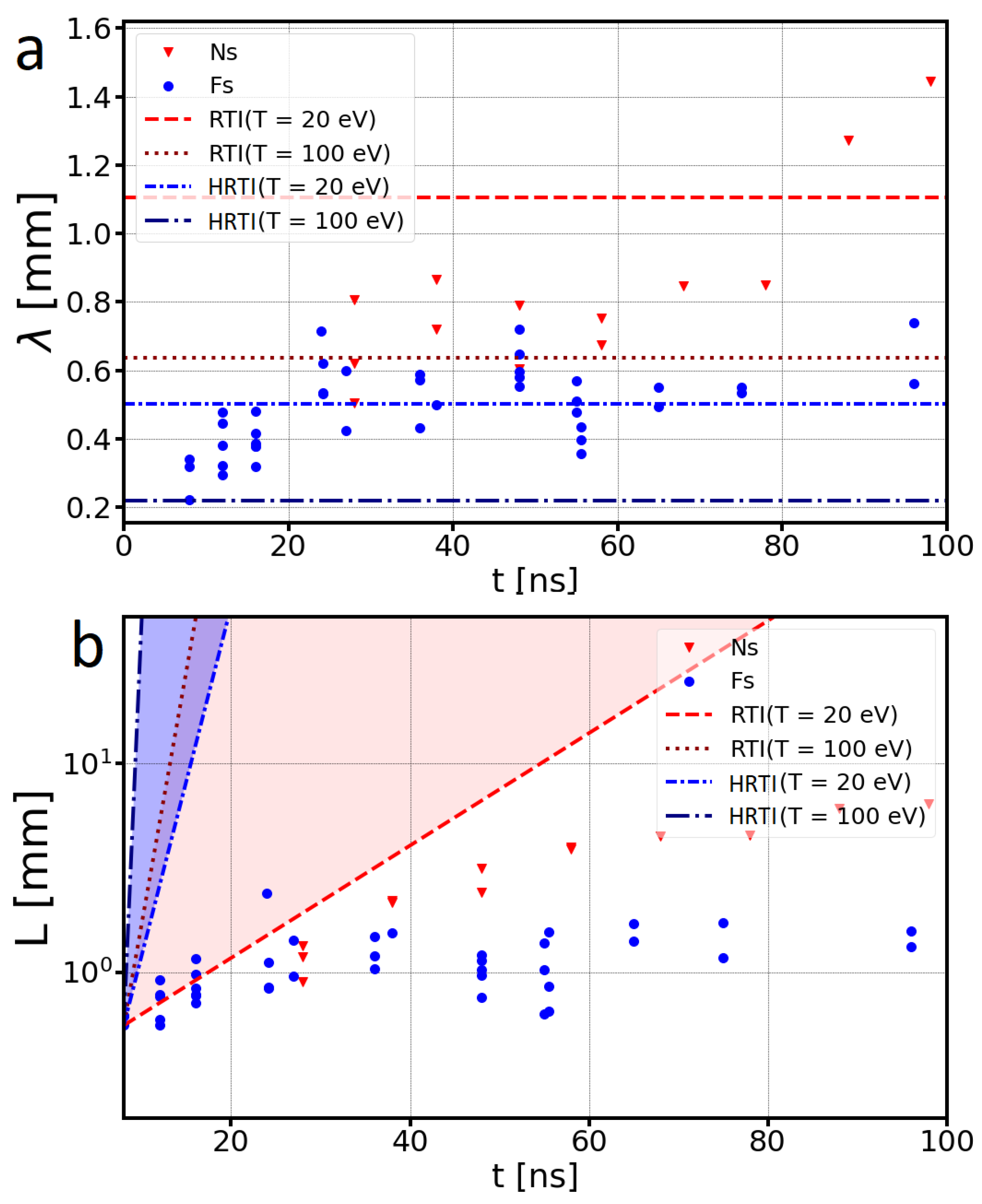
5. Discussion
5.1. Astrophysical Implication
6. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basov, N.; Krokhin, O. Conditions for heating up of a plasma by the radiation from an optical generator. Sov. Phys. JETP 1964, 19, 123–126. [Google Scholar]
- Chang, P.; Fiksel, G.; Hohenberger, M.; Knauer, J.; Betti, R.; Marshall, F.; Meyerhofer, D.; Séguin, F.; Petrasso, R. Fusion yield enhancement in magnetized laser-driven implosions. Physical review letters 2011, 107, 035006. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Optics communications 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Zakharov, Y.; Antonov, V.; Boyarintsev, E.; Melekhov, A.; Posukh, V.; Shaikhislamov, I.; Pickalov, V. Role of the Hall flute instability in the interaction of laser and space plasmas with a magnetic field. Plasma Physics Reports 2006, 32, 183–204. [Google Scholar] [CrossRef]
- Ripin, B.; McLean, E.; Manka, C.; Pawley, C.; Stamper, J.; Peyser, T.; Mostovych, A.; Grun, J.; Hassam, A.; Huba, J. Large-Larmor-radius interchange instability. Physical review letters 1987, 59, 2299. [Google Scholar] [CrossRef]
- Khiar, B.; Revet, G.; Ciardi, A.; Burdonov, K.; Filippov, E.; Béard, J.; Cerchez, M.; Chen, S.; Gangolf, T.; Makarov, S.; et al. Laser-produced magnetic-Rayleigh-Taylor unstable plasma slabs in a 20 T magnetic field. Physical Review Letters 2019, 123, 205001. [Google Scholar] [CrossRef]
- Hassam, A.; Huba, J. Structuring of the AMPTE magnetotail barium releases. Geophysical research letters 1987, 14, 60–63. [Google Scholar] [CrossRef]
- Fujioka, S.; Zhang, Z.; Ishihara, K.; Shigemori, K.; Hironaka, Y.; Johzaki, T.; Sunahara, A.; Yamamoto, N.; Nakashima, H.; Watanabe, T.; et al. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser. Scientific reports 2013, 3, 1170. [Google Scholar] [CrossRef]
- Froula, D.; Ross, J.; Pollock, B.; Davis, P.; James, A.; Divol, L.; Edwards, M.; Offenberger, A.; Price, D.; Town, R.; et al. Quenching of the Nonlocal Electron Heat Transport by Large External Magnetic Fields<? format?> in a Laser-Produced Plasma Measured with Imaging Thomson Scattering. Physical review letters 2007, 98, 135001. [Google Scholar]
- Zemskov, R.; Burdonov, K.; Soloviev, A.; Sladkov, A.; Korzhimanov, A.; Fuchs, J.; Bisikalo, D.; Zhilkin, A.; Barkov, M.; Ciardi, A.; et al. Laboratory modeling of YSO jets collimation by a large-scale divergent interstellar magnetic field. Astronomy & Astrophysics 2024, 681, A37. [Google Scholar]
- Burdonov, K.; Yao, W.; Sladkov, A.; Bonito, R.; Chen, S.; Ciardi, A.; Korzhimanov, A.; Soloviev, A.; Starodubtsev, M.; Zemskov, R.; et al. Laboratory modelling of equatorial ‘tongue’accretion channels in young stellar objects caused by the Rayleigh-Taylor instability. Astronomy & Astrophysics 2022, 657, A112. [Google Scholar]
- Fazzini, A.; Yao, W.; Burdonov, K.; Beard, J.; Chen, S.; Ciardi, A.; d’Humieres, E.; Diab, R.; Filippov, E.; Kisyov, S.; et al. Particle energization in colliding subcritical collisionless shocks investigated in the laboratory. Astronomy & Astrophysics 2022, 665, A87. [Google Scholar]
- Burdonov, K. .; Revet, G..; Bonito, R..; Argiroffi, C..; Béard, J..; Bolanõs, S..; Cerchez, M..; Chen, S. N..; Ciardi, A..; Espinosa, G..; et al. Laboratory evidence for an asymmetric accretion structure upon slanted matter impact in young stars. Astronomy & Astrophysics 2020, 642, A38. [Google Scholar] [CrossRef]
- Burdonov, K.; Bonito, R.; Giannini, T.; Aidakina, N.; Argiroffi, C.; Béard, J.; Chen, S.; Ciardi, A.; Ginzburg, V.; Gubskiy, K.; et al. Inferring possible magnetic field strength of accreting inflows in EXor-type objects from scaled laboratory experiments. Astronomy & Astrophysics 2021, 648, A81. [Google Scholar]
- Albertazzi, B.; Ciardi, A.; Nakatsutsumi, M.; Vinci, T.; Beard, J.; Bonito, R.; Billette, J.; Borghesi, M.; Burkley, Z.; Chen, S.N.; et al. Laboratory formation of a scaled protostellar jet by coaligned poloidal magnetic field. Science 2014, 346, 325–328, [https://science.sciencemag.org/content/346/6207/325.full.pdf]. [Google Scholar] [CrossRef]
- Yao, W.; Fazzini, A.; Chen, S.; Burdonov, K.; Antici, P.; Beard, J.; Bolanos, S.; Ciardi, A.; Diab, R.; Filippov, E.; et al. Laboratory evidence for proton energization by collisionless shock surfing. Nature Physics 2021, 17, 1177–1182. [Google Scholar] [CrossRef]
- Ryutov, D.; Drake, R.P.; Kane, J.; Liang, E.; Remington, B.A.; Wood-Vasey, W.M. Similarity Criteria for the Laboratory Simulation of Supernova Hydrodynamics. The Astrophysical Journal 1999, 518, 821–832. [Google Scholar] [CrossRef]
- Ryutov, D.D.; Drake, R.P.; Remington, B.A. Criteria for Scaled Laboratory Simulations of Astrophysical MHD Phenomena. The Astrophysical Journal Supplement Series 2000, 127, 465–468. [Google Scholar] [CrossRef]
- Ryutov, D.D. Scaling laws for dynamical plasma phenomena. Physics of Plasmas 2018, 25, 100501. [Google Scholar] [CrossRef]
- Roth, M.; Cowan, T.; Key, M.; Hatchett, S.; Brown, C.; Fountain, W.; Johnson, J.; Pennington, D.; Snavely, R.; Wilks, S.; et al. Fast ignition by intense laser-accelerated proton beams. Physical review letters 2001, 86, 436. [Google Scholar] [CrossRef]
- Tabak, M.; Clark, D.; Hatchett, S.; Key, M.; Lasinski, B.; Snavely, R.; Wilks, S.; Town, R.; Stephens, R.; Campbell, E.; et al. Review of progress in fast ignition. Physics of Plasmas 2005, 12. [Google Scholar] [CrossRef]
- Albert, F.; Thomas, A.G. Applications of laser wakefield accelerator-based light sources. Plasma Physics and Controlled Fusion 2016, 58, 103001. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Burdonov, K.F.; Ginzburg, V.N.; Glyavin, M.Y.; Zemskov, R.S.; Kotov, A.V.; Kochetkov, A.A.; Kuzmin, A.A.; Murzanev, A.A.; Mukhin, I.B.; et al. Research in plasma physics and particle acceleration using the PEARL petawatt laser. Uspekhi Fizicheskikh Nauk 2024, 194, 313–335. [Google Scholar] [CrossRef]
- Perevalov, S.E.; Kotov, A.V.; Zemskov, R.S.; Burdonov, K.F.; Ginzburg, V.N.; Kuzmin, A.A.; Stukachev, S.E.; Yakovlev, I.V.; Shaykin, A.; Lopatin, A.Y.; et al. Acceleration of Electrons upon Interaction of Laser Pulses with Solid Targets in the Laser Peeler Regime. Bulletin of the Lebedev Physics Institute 2024, 51, S305–S315. [Google Scholar] [CrossRef]
- Perevalov, S.; Burdonov, K.; Kotov, A.; Romanovskiy, D.; Soloviev, A.; Starodubtsev, M.; Golovanov, A.; Ginzburg, V.; Kochetkov, A.; Korobeinikova, A.; et al. Experimental study of strongly mismatched regime of laser-driven wakefield acceleration. Plasma Physics and Controlled Fusion 2020, 62, 094004. [Google Scholar] [CrossRef]
- Schoenlein, R.; Elsaesser, T.; Holldack, K.; Huang, Z.; Kapteyn, H.; Murnane, M.; Woerner, M. Recent advances in ultrafast X-ray sources. Philosophical Transactions of the Royal Society A 2019, 377, 20180384. [Google Scholar] [CrossRef]
- Liao, G.Q.; Li, Y.T. Review of intense terahertz radiation from relativistic laser-produced plasmas. IEEE Transactions on Plasma Science 2019, 47, 3002–3008. [Google Scholar] [CrossRef]
- Zemskov, R.; Perevalov, S.; Kotov, A.; Bodrov, S.; Stepanov, A.; Solov’ev, A.; Bakunov, M.; Luchinin, A.; Ginzburg, V.; Kuz’min, A.; et al. Experimental Study of Terahertz Radiation Generation in the Interaction of Ultrashort Laser Pulse with Gas Targets. Radiophysics and Quantum Electronics 2023, 65, 877–887. [Google Scholar] [CrossRef]
- Chen, H.; Fiuza, F. Perspectives on relativistic electron–positron pair plasma experiments of astrophysical relevance using high-power lasers. Physics of Plasmas 2023, 30. [Google Scholar] [CrossRef]
- Gurevich, E.; Hergenröder, R. Femtosecond laser-induced breakdown spectroscopy: physics, applications, and perspectives. Applied spectroscopy 2007, 61, 233A–242A. [Google Scholar] [CrossRef]
- Singh, J.P.; Thakur, S.N. Laser-induced breakdown spectroscopy; Elsevier, 2020. [Google Scholar]
- Harilal, S.S.; Freeman, J.R.; Diwakar, P.K.; Hassanein, A. Femtosecond laser ablation: Fundamentals and applications. In Laser-Induced Breakdown Spectroscopy: Theory and Applications; Springer, 2014; pp. 143–166. [Google Scholar]
- Amoruso, S.; Bruzzese, R.; Spinelli, N.; Velotta, R. Characterization of laser-ablation plasmas. Journal of Physics B: Atomic, Molecular and Optical Physics 1999, 32, R131. [Google Scholar] [CrossRef]
- Antici, P.; Gremillet, L.; Grismayer, T.; Mora, P.; Audebert, P.; Borghesi, M.; Cecchetti, C.; Mančic, A.; Fuchs, J. Modeling target bulk heating resulting from ultra-intense short pulse laser irradiation of solid density targets. Physics of Plasmas 2013, 20. [Google Scholar] [CrossRef]
- Dubois, J.L.; Lubrano-Lavaderci, F.; Raffestin, D.; Ribolzi, J.; Gazave, J.; Fontaine, A.C.L.; d’Humières, E.; Hulin, S.; Nicolaï, P.; Poyé, A.; et al. Target charging in short-pulse-laser–plasma experiments. Physical Review E 2014, 89, 013102. [Google Scholar] [CrossRef]
- Soloviev, A.; Burdonov, K.; Chen, S.; Eremeev, A.; Korzhimanov, A.; Pokrovskiy, G.; Pikuz, T.; Revet, G.; Sladkov, A.; Ginzburg, V.; et al. Experimental evidence for short-pulse laser heating of solid-density target to high bulk temperatures. Scientific Reports 2017, 7, 12144. [Google Scholar] [CrossRef] [PubMed]
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Reports on progress in physics 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
- Sarri, G.; Macchi, A.; Cecchetti, C.; Kar, S.; Liseykina, T.; Yang, X.; Dieckmann, M.E.; Fuchs, J.; Galimberti, M.; Gizzi, L.; et al. Dynamics of Self-Generated, Large Amplitude Magnetic Fields Following<? format?> High-Intensity Laser Matter Interaction. Physical review letters 2012, 109, 205002. [Google Scholar]
- Albertazzi, B.; Chen, S.; Antici, P.; Böker, J.; Borghesi, M.; Breil, J.; Dervieux, V.; Feugeas, J.; Lancia, L.; Nakatsutsumi, M.; et al. Dynamics and structure of self-generated magnetics fields on solids following high contrast, high intensity laser irradiation. Physics of Plasmas 2015, 22. [Google Scholar] [CrossRef]
- Shaikh, M.; Lad, A.D.; Jana, K.; Sarkar, D.; Dey, I.; Kumar, G.R. Megagauss magnetic fields in ultra-intense laser generated dense plasmas. Plasma Physics and Controlled Fusion 2016, 59, 014007. [Google Scholar] [CrossRef]
- Borghesi, M.; Mackinnon, A.; Gaillard, R.; Willi, O.; Pukhov, A.; Meyer-ter Vehn, J. Large quasistatic magnetic fields generated by a relativistically intense laser pulse propagating in a preionized plasma. Physical review letters 1998, 80, 5137. [Google Scholar] [CrossRef]
- Gopal, A.; Tatarakis, M.; Beg, F.; Clark, E.; Dangor, A.; Evans, R.; Norreys, P.; Wei, M.; Zepf, M.; Krushelnick, K. Temporally and spatially resolved measurements of multi-megagauss magnetic fields in high intensity laser-produced plasmas. Physics of Plasmas 2008, 15. [Google Scholar] [CrossRef]
- Weibel, E.S. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Physical Review Letters 1959, 2, 83. [Google Scholar] [CrossRef]
- Ruyer, C.; Bolaños, S.; Albertazzi, B.; Chen, S.; Antici, P.; Böker, J.; Dervieux, V.; Lancia, L.; Nakatsutsumi, M.; Romagnani, L.; et al. Growth of concomitant laser-driven collisionless and resistive electron filamentation instabilities over large spatiotemporal scales. Nature Physics 2020, 16, 983–988. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Makur, K.; Ramakrishna, B. Observation of resistive Weibel instability in intense laser plasma. Laser and Particle Beams 2020, 38, 152–158. [Google Scholar] [CrossRef]
- Quinn, K.; Romagnani, L.; Ramakrishna, B.; Sarri, G.; Dieckmann, M.E.; Wilson, P.; Fuchs, J.; Lancia, L.; Pipahl, A.; Toncian, T.; et al. Weibel-induced filamentation during an ultrafast laser-driven plasma expansion. Physical review letters 2012, 108, 135001. [Google Scholar] [CrossRef]
- Biermann, L. Über den Ursprung der Magnetfelder auf Sternen und im interstellaren Raum (miteinem Anhang von A. Schlüter). Zeitschrift Naturforschung Teil A 1950, 5, 65. [Google Scholar]
- Ciardi, A.; Vinci, T.; Fuchs, J.; Albertazzi, B.; Riconda, C.; Pépin, H.; Portugall, O. Astrophysics of Magnetically Collimated Jets Generated from Laser-Produced Plasmas. Physical review letters 2013, 110, 025002. [Google Scholar] [CrossRef]
- Ciardi, A.; Lebedev, S.; Frank, A.; Blackman, E.; Chittenden, J.; Jennings, C.; Ampleford, D.; Bland, S.; Bott, S.; Rapley, J.; et al. The evolution of magnetic tower jets in the laboratory. Physics of Plasmas 2007, 14, 056501. [Google Scholar] [CrossRef]
- Ryu, D.; Schleicher, D.R.; Treumann, R.A.; Tsagas, C.G.; Widrow, L.M. Magnetic fields in the large-scale structure of the universe. Space Science Reviews 2012, 166, 1–35. [Google Scholar] [CrossRef]
- Ryutov, D.; Kugland, N.; Park, H.; Plechaty, C.; Remington, B.; Ross, J. Basic scalings for collisionless-shock experiments in a plasma without pre-imposed magnetic field. Plasma Physics and Controlled Fusion 2012, 54, 105021. [Google Scholar] [CrossRef]
- Lozhkarev, V.; Freidman, G.; Ginzburg, V.; Katin, E.; Khazanov, E.; Kirsanov, A.; Luchinin, G.; Mal’Shakov, A.; Martyanov, M.; Palashov, O.; et al. Compact 0.56 petawatt laser system based on optical parametric chirped pulse amplification in KD* P crystals. Laser Physics Letters 2007, 4, 421. [Google Scholar] [CrossRef]
- Ginzburg, V.; Yakovlev, I.; Kochetkov, A.; Kuzmin, A.; Mironov, S.; Shaikin, I.; Shaykin, A.; Khazanov, E. 11 fs, 1.5 PW laser with nonlinear pulse compression. Optics express 2021, 29, 28297–28306. [Google Scholar] [CrossRef]
- Soloviev, A.; Kotov, A.; Martyanov, M.; Perevalov, S.; Zemskov, R.; Starodubtsev, M.; Alexandrov, A.; Galaktionov, I.; Samarkin, V.; Kudryashov, A.; et al. Improving focusability of post-compressed PW laser pulses using a deformable mirror. Optics Express 2022, 30, 40584–40591. [Google Scholar] [CrossRef] [PubMed]
- Soloviev, A.; Burdonov, K.; Kotov, A.; Perevalov, S.; Zemskov, R.; Ginzburg, V.; Kochetkov, A.; Kuzmin, A.; Shaikin, A.; Shaikin, I.; et al. Experimental study of the interaction of a laser plasma flow with a transverse magnetic field. Radiophysics and Quantum Electronics 2021, 63, 876–886. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Barkov, M.V.; Khangulyan, D. Scenarios for Ultrafast Gamma-Ray Variability in AGN. apj 2017, 841, 61, [arXiv:astro-ph.HE/1704.08148]. [Google Scholar] [CrossRef]
- Luchinin, A.; Malyshev, V.; Kopelovich, E.; Burdonov, K.; Gushchin, M.; Morozkin, M.; Proyavin, M.; Rozental, R.; Soloviev, A.; Starodubtsev, M.; et al. Pulsed magnetic field generation system for laser-plasma research. Review of Scientific Instruments 2021, 92. [Google Scholar] [CrossRef] [PubMed]
- Faenov, A.Y.; Colgan, J.; Hansen, S.; Zhidkov, A.; Pikuz, T.; Nishiuchi, M.; Pikuz, S.; Skobelev, I.Y.; Abdallah, J.; Sakaki, H.; et al. Nonlinear increase of X-ray intensities from thin foils irradiated with a 200 TW femtosecond laser. Scientific reports 2015, 5, 13436. [Google Scholar] [CrossRef]
- Faenov, A.Y. X-ray spectroscopic methods for measuring the parameters of high-temperature dense plasma. Measurement techniques 1997, 40, 94–100. [Google Scholar] [CrossRef]
- Hipp, M.; Woisetschlager, J.; Reiterer, P.; Neger, T. Digital evaluation of interferograms. Measurement 2004, 36, 53–66. [Google Scholar] [CrossRef]
- Basov, N.; Zakharenkov, Y.A.; Rupasov, A.; Sklizkov, G.; Shikanov, A. Diagnostics of Dense Plasma. Nauka, Moscow 1989, 11, 9. [Google Scholar]
- Tatarakis, M.; Gopal, A.; Watts, I.; Beg, F.; Dangor, A.; Krushelnick, K.; Wagner, U.; Norreys, P.; Clark, E.; Zepf, M.; et al. Measurements of ultrastrong magnetic fields during relativistic laser–plasma interactions. Physics of Plasmas 2002, 9, 2244–2250. [Google Scholar] [CrossRef]
- Tatarakis, M.; Watts, I.; Beg, F.; Clark, E.; Dangor, A.; Gopal, A.; Haines, M.; Norreys, P.; Wagner, U.; Wei, M.S.; et al. Measuring huge magnetic fields. Nature 2002, 415, 280–280. [Google Scholar] [CrossRef] [PubMed]
- Zemskov, R.; Burdonov, K.; Kuzmin, A.; et al. Laboratory study of Rayleigh-Taylor instability in laser plasma interacting with an external magnetic field of 14 T. Radiophysics and Quantum Electronics 2024, 57. [Google Scholar]
- Korobkov, S.; Nikolenko, A.; Gushchin, M.; Strikovsky, A.; Zudin, I.Y.; Aidakina, N.; Shaikhislamov, I.; Rumenskikh, M.; Zemskov, R.; Starodubtsev, M. Features of Dynamics and Instability of Plasma Jets Expanding into an External Magnetic Field in Laboratory Experiments with Compact Coaxial Plasma Generators on a Large-Scale “Krot” Stand. Astronomy Reports 2023, 67, 93–103. [Google Scholar] [CrossRef]
- Winske, D.; Huba, J.D.; Niemann, C.; Le, A. Recalling and updating research on diamagnetic cavities: Experiments, theory, simulations. Frontiers in Astronomy and Space Sciences 2019, 5, 51. [Google Scholar] [CrossRef]
- Tang, H.b.; Hu, G.y.; Liang, Y.h.; Wang, Y.l.; Tao, T.; Hu, P.; Yuan, P.; Zhu, P.; Zuo, Y.; Zhao, B.; et al. Observation of large Larmor radius instability in laser plasma expanding into a 10 T external magnetic field. Physics of Plasmas 2020, 27. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dynamics 1969, 4, 101–104. [Google Scholar] [CrossRef]
- Richardson, A.S. 2019 NRL plasma formulary; Naval Research Laboratory: Washington, DC, 2019. [Google Scholar]
- Fryxell, B.; Olson, K.; Ricker, P.; Timmes, F.X.; Zingale, M.; Lamb, D.; MacNeice, P.; Rosner, R.; Truran, J.; Tufo, H. FLASH: An Adaptive Mesh Hydrodynamics Code for ModelingAstrophysical Thermonuclear Flashes. The Astrophysical Journal Supplement Series 2000, 131, 273. [Google Scholar] [CrossRef]
- Wollaeger, R.T.; Van Rossum, D.R. Radiation transport for explosive outflows: opacity regrouping. The Astrophysical Journal Supplement Series 2014, 214, 28. [Google Scholar] [CrossRef]
- Chatzopoulos, E.; Weide, K. Gray radiation hydrodynamics with the FLASH code for astrophysical applications. The Astrophysical Journal 2019, 876, 148. [Google Scholar] [CrossRef]
- Braginskii, S. Transport processes in a plasma. Reviews of plasma physics 1965, 1, 205. [Google Scholar]
- Huba, J.; Gladd, N.; Papadopoulos, K. The lower-hybrid-drift instability as a source of anomalous resistivity for magnetic field line reconnection. Geophysical Research Letters 1977, 4, 125–128. [Google Scholar] [CrossRef]
- Okada, S.; Sato, K.; Sekiguchi, T. Possibility of lower-hybrid-drift instability in laser produced plasma in a uniform magnetic field. Journal of the Physical Society of Japan 1979, 46, 355–356. [Google Scholar] [CrossRef]
- Peyser, T.; Manka, C.; Ripin, B.; Ganguli, G. Electron–ion hybrid instability in laser-produced plasma expansions across magnetic fields. Physics of Fluids B: Plasma Physics 1992, 4, 2448–2458. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and hydromagnetic stability; Courier Corporation, 2013. [Google Scholar]
- Sharp, D.H. Overview of Rayleigh-taylor instability. Technical report, Los Alamos National Laboratory (LANL), Los Alamos, NM (United States), 1983.
- Winske, D. Short-wavelength modes on expanding plasma clouds. Journal of Geophysical Research: Space Physics 1988, 93, 2539–2552. [Google Scholar] [CrossRef]
- Zakharov, Y.P. Collisionless laboratory astrophysics with lasers. IEEE transactions on plasma science 2003, 31, 1243–1251. [Google Scholar] [CrossRef]
- Huba, J.; Lyon, J.; Hassam, A. Theory and simulation of the Rayleigh-Taylor instability in the limit of large Larmor radius. Physical review letters 1987, 59, 2971. [Google Scholar] [CrossRef]
- Huba, J.; Hassam, A.; Satyanarayana, P. Nonlocal theory of the Rayleigh–Taylor instability in the limit of unmagnetized ions. Physics of Fluids B: Plasma Physics 1989, 1, 931–941. [Google Scholar] [CrossRef]
- Hassam, A.; Huba, J. Nonlinear evolution of the unmagnetized ion Rayleigh–Taylor instability. Physics of Fluids B: Plasma Physics 1990, 2, 2001–2006. [Google Scholar] [CrossRef]
- Huba, J. Hall magnetohydrodynamics in space and laboratory plasmas. Physics of Plasmas 1995, 2, 2504–2513. [Google Scholar] [CrossRef]
- Bernhardt, P.; Roussel-Dupre, R.; Pongratz, M.; Haerendel, G.; Valenzuela, A.; Gurnett, D.; Anderson, R. Observations and theory of the AMPTE magnetotail barium releases. Journal of Geophysical Research: Space Physics 1987, 92, 5777–5794. [Google Scholar] [CrossRef]
- Huba, J.; Hassam, A.; Winske, D. Stability of sub-Alfvénic plasma expansions. Physics of Fluids B: Plasma Physics 1990, 2, 1676–1697. [Google Scholar] [CrossRef]
- Zhu, P.; Sovinec, C.; Hegna, C. The formation of blobs from a pure interchange process. Physics of Plasmas 2015, 22. [Google Scholar] [CrossRef]
- Faenov, A.Y.; Pikuz, S.; Erko, A.; Bryunetkin, B.; Dyakin, V.; Ivanenkov, G.; Mingaleev, A.; Pikuz, T.; Romanova, V.; Shelkovenko, T. High-performance x-ray spectroscopic devices for plasma microsources investigations. Physica Scripta 1994, 50, 333. [Google Scholar] [CrossRef]
- Filippov, E.D.; Makarov, S.S.; Burdonov, K.F.; Yao, W.; Revet, G.; Béard, J.; Bolaños, S.; Chen, S.N.; Guediche, A.; Hare, J.; et al. Enhanced X-ray emission arising from laser-plasma confinement by a strong transverse magnetic field. Scientific Reports 2021, 11, 8180. [Google Scholar] [CrossRef]
- Hassam, A.; Huba, J. Magnetohydrodynamic equations for systems with large Larmor radius. The Physics of fluids 1988, 31, 318–325. [Google Scholar] [CrossRef]
- Ryutov, D.; Kugland, N.; Levy, M.; Plechaty, C.; Ross, J.; Park, H. Magnetic field advection in two interpenetrating plasma streams. Physics of Plasmas 2013, 20. [Google Scholar] [CrossRef]
- Gordeev, A.V.; Kingsep, A.S.; Rudakov, L.I. Electron magnetohydrodynamics. Physics Reports 1994, 243, 215–315. [Google Scholar] [CrossRef]
- Gushchin, M.E.; Korobkov, S.V.; Terekhin, V.A.; Strikovskiy, A.; Gundorin, V.I.; Zudin, I.Y.; Aidakina, N.A.; Nikolenko, A. Laboratory simulation of the dynamics of a dense plasma cloud expanding in a magnetized background plasma on a Krot large-scale device. JETP Letters 2018, 108, 391–395. [Google Scholar] [CrossRef]
- Nikolenko, A.; Gushchin, M.; Korobkov, S.; Zudin, I.Y.; Aidakina, N.; Strikovskiy, A.; Loskutov, K. Dynamics of a Plasma Cloud Generated by a Compact Coaxial Gun upon Expansion into Vacuum and Large-Volume Background Plasma in an External Magnetic Field. Plasma Physics Reports 2023, 49, 1284–1299. [Google Scholar] [CrossRef]
- Collette, A.; Gekelman, W. Structure of an exploding laser-produced plasma. Physical review letters 2010, 105, 195003. [Google Scholar] [CrossRef]
- Collette, A.; Gekelman, W. Structure of an exploding laser-produced plasma. Physics of Plasmas 2011, 18. [Google Scholar] [CrossRef]
- Chibranov, A.; Shaikhislamov, I.; Berezutskiy, A.; Posukh, V.; Trushin, P.; Zakharov, Y.P.; Miroshnichenko, I.; Rumenskikh, M.; Terekhin, V. Hall Effects and Diamagnetic Cavity Collapse during a Laser Plasma Cloud Expansion into a Vacuum Magnetic Field. Astronomy Reports 2024, 68, 418–428. [Google Scholar] [CrossRef]
- Winske, D. Regimes of the magnetized Rayleigh–Taylor instability. Physics of Plasmas 1996, 3, 3966–3974. [Google Scholar] [CrossRef]
- Huba, J.; Winske, D. Rayleigh–Taylor instability: Comparison of hybrid and nonideal magnetohydrodynamic simulations. Physics of Plasmas 1998, 5, 2305–2316. [Google Scholar] [CrossRef]
- Umeda, T.; Wada, Y. Non-MHD effects in the nonlinear development of the MHD-scale Rayleigh-Taylor instability. Physics of Plasmas 2017, 24. [Google Scholar] [CrossRef]
- Aliu, E.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Bouvier, A.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; Byrum, K.; et al. VERITAS Observations of Day-scale Flaring of M 87 in 2010 April. apj 2012, 746, 141, [arXiv:astro-ph.CO/1112.4518]. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berenji, B.; et al. Fermi Gamma-ray Space Telescope Observations of the Gamma-ray Outburst from 3C454.3 in November 2010. apjl 2011, 733, L26, [arXiv:astro-ph.HE/1102.0277]. [Google Scholar] [CrossRef]
- Barkov, M.V.; Aharonian, F.A.; Bosch-Ramon, V. Gamma-ray Flares from Red Giant/Jet Interactions in Active Galactic Nuclei. apj 2010, 724, 1517–1523, [arXiv:astro-ph.HE/1005.5252]. [Google Scholar] [CrossRef]
- Barkov, M.V.; Aharonian, F.A.; Bogovalov, S.V.; Kelner, S.R.; Khangulyan, D. Rapid TeV Variability in Blazars as a Result of Jet-Star Interaction. apj 2012, 749, 119, [arXiv:astro-ph.HE/1012.1787]. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Perucho, M.; Barkov, M.V. Clouds and red giants interacting with the base of AGN jets. aap 2012, 539, A69, [arXiv:astro-ph.HE/1201.5279]. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





