Derivatives, Integrals and Polynomials Arising from the Inhomogeneous Airy's Equation

1. Introduction

Airy’s differential equation and its associated Airy’s functions date back to the nineteenth century, [1]. They are as relevant today as they were then due to their many applications in mathematical physics, optics, electromagnetism and fluid dynamic modeling, among other fields of endeavour (cf. [2,3,4] and the references therein). A large number of differential equations in quantum theory can be reduced to Airy’s equation by an appropriate change of variables, thus adding to the importance and relevance of studies of Airy’s functions and other related special functions, [3,4].

Although Airy’s equation has been largely studied in its homogeneous form, it is considered in this work in the following inhomogeneous form, suggested by Miller and Mursi [5], wherein $f\left(x\right)$ is a continuous function of the non-negative, real variable $x$, and prime notation denotes ordinary differentiation with respect to the independent variable:

$$y^{\prime \prime }-xy=f\left(x\right).$$

(1)

When $f\left(x\right)\equiv 0$, general solution to Equation (1) can be expressed in the form:

$$y=a_1{A}_i\left(x\right)+b_1{B}_i\left(x\right),$$

(2)

where $a_1 \mathrm{a}\mathrm{n}\mathrm{d} b_1$ are arbitrary constants, and $A_i\left(x\right)$ and $B_i\left(x\right)$ are Airy’s functions of the first- and second-kind, respectively, [2].

When $f\left(x\right)=\mp 1/\pi$ , Scorer [6] obtained the following general solutions using variation of parameters. For $f\left(x\right)=-1/\pi$, general solution to Equation (1) is given by:

$$y=a_2{A}_i\left(x\right)+b_2{B}_i\left(x\right)+G_i\left(x\right),$$

(3)

and when $f\left(x\right)=1/\pi$, general solution is given by:

$$y=a_3{A}_i\left(x\right)+b_3{B}_i\left(x\right)+H_i\left(x\right),$$

(4)

where $a_2, { b_2, a}_3\mathrm{a}\mathrm{n}\mathrm{d} b_3$are arbitrary constants.

The functions $G_i\left(x\right)$ and $H_i\left(x\right)$ are known as the Scorer functions, [2,4], or the inhomogeneous Airy’s functions, and arise in Raman scattering in chemical physics and in some engineering applications, [7,8]. The Scorer functions are related to Airy’s functions by:

$$G_i\left(x\right)+H_i\left(x\right)=B_i\left(x\right),$$

(5)

$$G_i\left(x\right)=A_i\left(x\right){\int }_0^x{B}_i\left(t\right)dt+B_i\left(x\right){\int }_x^{\infty }{A}_i\left(t\right)dt,$$

(6)

$$H_i\left(x\right)=B_i\left(x\right){\int }_{-\infty }^x{A}_i\left(t\right)dt-A_i\left(x\right){\int }_{-\infty }^x{B}_i\left(t\right)dt.$$

(7)

When $f\left(x\right)=\kappa$, where $\kappa$ is any constant, general solution to Equation (1) has been obtained in the following form, [9,10]:

$$y=a_4{A}_i\left(x\right)+b_4{B}_i\left(x\right)-{\kappa \pi N}_i\left(x\right),$$

(8)

where $a_4$ and $b_4$ are arbitrary constants, and $N_i\left(x\right)$ is defined by:

$$N_i\left(x\right)=A_i\left(x\right){\int }_0^x{B}_i\left(t\right)dt-B_i\left(x\right){\int }_0^x{A}_i\left(t\right)dt.$$

(9)

The function $N_i\left(x\right)$ was introduced by Nield and Kuznetsov [10] in their analysis of flow in the transition layer where the governing Brinkman’s equation was reduced to the inhomogeneous Airy’s equation by a special choice of the permeability function. The function $N_i\left(x\right)$ is referred to as the standard Nield-Kuznetsov function of the first-kind, and its main properties were studied by Hamdan and Kamel [9], including the following relationships between $G_i\left(x\right), H_i\left(x\right)$ and $N_i\left(x\right)$:

$$G_i\left(x\right)=N_i\left(x\right)+{\displaystyle \frac{1}{3}}{B}_i\left(x\right),$$

(10)

$$H_i\left(x\right)={\displaystyle \frac{2}{3}}{B}_i\left(x\right)-N_i\left(x\right).$$

(11)

Using (10) and (11) in (3) and (4), respectively, it is easily seen that solutions (3) and (8) are equivalent when $a_4=a_2 \mathrm{a}\mathrm{n}\mathrm{d} b_4=b_2+1/3$ , while solutions (4) and (8) are equivalent when $a_4=a_3; b_4=b_3+2/3.$

In an attempt to offer modelling flexibility in the study of flow through the transition layer, Abu Zaytoon and Hamdan [11] introduced a permeability model that reduced Brinkman’s equation to the following generalized inhomogeneous Airy’s equation of integer index $n$:

$$y_n^{\prime \prime }-x^n{y}_n=f\left(x\right).$$

(12)

The homogeneous part of (12), that is when $f\left(x\right)\equiv 0$, was studied by Swanson and Headley [12] who expressed its general solution as:

$$y_n=a_n{A}_n\left(x\right)+b_n{B}_n\left(x\right),$$

(13)

wherein $a_n$ and $b_n$ are arbitrary constants, and the functions $A_n\left(x\right)$ and $B_n\left(x\right)$ are the generalized Airy’s functions of the first- and second-kind, respectively, defined as:

$$A_n\left(x\right)={\displaystyle \frac{2p}{\pi }}sin\left(p\pi \right)(x{)}^{{\displaystyle \frac{1}{2}}}{K}_p\left(\zeta \right),$$

(14)

$$B_n\left(x\right)=(px{)}^{{\displaystyle \frac{1}{2}}}\left(I_{-p}\left(\zeta \right)+I_p\left(\zeta \right)\right),$$

(15)

where $p={\displaystyle \frac{1}{n+2}}$, $\zeta =2p{\left(x\right)}^{{\displaystyle \frac{1}{2p}}}$, and $\Gamma (.)$ is the gamma function. The Wronskian of $A_n\left(x\right)$ and $B_n\left(x\right)$ is given by:

$$W\left(A_n\left(x\right),B_n\left(x\right)\right)={\displaystyle \frac{2}{\pi }}{p}^{{\displaystyle \frac{1}{2}}}\sin \left(p\pi \right),$$

(16)

and the terms $I_p \mathrm{a}\mathrm{n}\mathrm{d} K_p$ are the modified Bessel functions defined by the following formulas in which $j=\sqrt{-1}$ :

$$I_p\left(\zeta \right)={\left(j\right)}^{-p}{K}_p\left(j\zeta \right)=\sum _{m=1}^{\infty }{\displaystyle \frac{1}{m!\Gamma \left(m+p+1\right)}}({\displaystyle \frac{\zeta }{2}}{)}^{2m+p},$$

(17)

$$K_p\left(\zeta \right)={\displaystyle \frac{\pi }{2}}{\displaystyle \frac{\left(I_{-p}\left(\zeta \right)-I_p\left(\zeta \right)\right)}{\sin \left(p\pi \right)}}.$$

(18)

It should be noted that when the index $n=1$ in Equations (12)–(15), Airy’s equation and its solutions are recovered, although subscript $“i”$ is used instead of 1 for consistency with notation in the literature.

When $f\left(x\right)=\kappa$, Abu Zaytoon and Hamdan [11] obtained and expressed the general solution to the inhomogeneous generalized Airy’s Equation (12) as:

$$y_n=a_n{A}_n\left(x\right)+b_n{B}_n\left(x\right)-{\displaystyle \frac{\kappa \pi }{2\sqrt{p}\sin \left(p\pi \right)}}{N}_n\left(x\right),$$

(19)

where the function $N_n\left(x\right)$ is the generalized Nield-Kuznetsov function of the first-kind, defined as:

$$N_n\left(x\right)=A_n\left(x\right){\int }_0^x{B}_n\left(t\right)dt-B_n\left(x\right){\int }_0^x{A}_n\left(t\right)dt.$$

(20)

Related to the Nield-Kuznetsov functions, $N_i\left(x\right) \mathrm{a}\mathrm{n}\mathrm{d} N_n\left(x\right)$, that arise and play a significant role in the solution to the inhomogeneous Airy’s equations, is the parametric Nield-Kuznetsov function of the first-kind, $N_w\left(a,x\right)$, with parameter a, which arises in the particular solution of the inhomogeneous Weber’s equation of the form:

$$y^{\prime \prime }+\left({\displaystyle \frac{x^2}{4}}-a\right)y=\kappa .$$

(21)

General solution to (21) is expressed as:

$$y_w=a_{1}W\left(a,x\right)+b_{1}W\left(a,-x\right)-\kappa N_w\left(a,x\right),$$

(22)

where $N_w\left(a,x\right)$ is defined by:

$$N_w\left(a,x\right)=W\left(a,x\right){\int }_0^{x}W\left(a,-t\right)dt-W\left(a,-x\right){\int }_0^{x}W\left(a,t\right)dt.$$

(23)

The functions $N_i\left(x\right), N_n\left(x\right) \mathrm{a}\mathrm{n}\mathrm{d} N_w\left(a,x\right)$ are known as the Nield-Kuznetsov functions of the first kind. Their analysis and applications have been extensivley discussed and documented, [9,10,13], and include solution methodologies and methods of computations of the inhomogeneous Airy’s and Weber’s equations with initial and boundary conditions.

Recent work in this field includes the elegant work of Dunster, (cf. [14] and the references therein), on the Nield-Kuznetsov functions and the use of Laplace transform and uniform asymptotic expansions. Dunster [14] introduced the concept of a compelemtary function to the parametric Nield-Kuznetsov function and studied its convergence and its favourable properties, and discussed its role in the solution of (21).

Analysis of Airy’s polynomials that arise in higher derivatives of Airy’s functions has been carried out in the elaborate work of Abramochkin and Razueva, [15]. The same Airy’s polynomials, together with other polynomials, arise in the higher derivatives of $N_i\left(x\right)$ and are important from both a theoretical and a practical point of view, as discussed by Hamdan et.al. [16].

Recent developments in the field include analysis of generalized forms of Airy’s equations due to either their associated applications or due to the arise of many interesting associated special functions. These include the work of Askari and Ansari (cf. [17] and the references therein) on higher-order differential equations and the Mainardi function, and the work of Cinque and Orsingher (cf. [18] and the references therein) on higher-order, Airy-type equations.

The recent work reported in [11,14,15,17,18], and the references therein, clearly represents an advancement of the state of knowledge in this field of Airy’s and generalized Airy’s equations, their solutions and applications. It motivate the current work in which we derive further properties and representations of these functions, and relate them to other special functions. In particular, specific objectives of the current work are as follows:

• Fill-in some knowledge gaps that exit in the available literature. To this end, the Scorer solutions to Equation (1), as given by Equations (3) and (4), are used to obtain solutions to Equation (1) when $f\left(x\right)=\kappa \ne \mp 1/k$.
• Introduce complementary functions, albeit divergent, to $N_i\left(x\right)$ and $N_n\left(x\right)$ that might be of importance in asymptotic analysis.
• Provide representations of all special functions arising in this work in terms of modified Bessel functions.
• Advance the state of knowledge by introducing a generalized Scorer function, $G_n\left(x\right)$.
• Discuss higher derivatives of all generalized functions arising in this work and obtain their associated polynomials.
• Introduce a computational procedure for the newly introduced generalized Scorer function and applying it to computing and graphing the generalized Scorer function over a subinterval of the X-axis.
• Provide a solution to an initial value problem involving the generalized Scorer function.

In order to accomplish the above objectives, this work is organized as follows. In Section 2, solutions to Equation (1) when $f\left(x\right)=\kappa \ne \mp 1/\pi$ are expressed in terms of the Scorer functions $G_i\left(x\right)$ and $H_i\left(x\right)$. The function $N_i\left(x\right)$ is expressed in terms of the primitives of the Scorer functions, and its complement is derived. The Nield-Kuznetsov and Scorer functions are then expressed in terms of the modified Bessel functions.

In Section 3, the generalized Scorer function, $G_n\left(x\right)$, is derived and expressed it in terms of generalized Airy’s functions and the generalized Nield-Kuznetsov function $N_n\left(x\right)$. General solution to Equation (12) when $f\left(x\right)=\kappa$ is then derived and discussed. All generalized functions are expressed in terms of the modified Bessel functions, and a computational procedure for $G_n\left(x\right)$and$N_n\left(x\right)$ is derived and applied to graphing $G_n\left(x\right)$ for different values of $n$. Solution to an initial value problem involving $G_n\left(x\right)$ is obtained.

In Section 4, higher derivatives of all generalized functions appearing in this work are discussed, and generalizations of these derivatives are derived and expressed in terms of generalized Airy’s and other polynomials. Degrees of the resulting polynomials are and expressed in terms of the orders of the derivatives. Dependence of the polynomials on index $n$, of the generalized Airy’s equation, is discussed.

A conclusion to the current work is provided to summarize the key findings, and to define a direction for future work.

2. Further Representations of Airy’s Related Special Functions

2.1. Solutions to Equation (1) when $f\left(x\right)=\kappa \ne \mp 1/\pi$

Solutions to Equation (1) when $f\left(x\right)=\kappa \ne \mp 1/\pi$ are not readily available in terms of the Scorer functions. However, with the help of the Nield-Kuznetsov $N_i\left(x\right)$ function and its connections to the Scorer functions the following proposition provides the form of solutions.

Proposition 1.

General solutions to the inhomogeneous Airy’s Equation (1) with  $f\left(x\right)=\kappa$  are given by:

$$y=a_1{A}_i\left(x\right)+{[b}_1+{\displaystyle \frac{\kappa \pi }{3}}]B_i\left(x\right)-\kappa \pi G_i\left(x\right),$$

(24)

$$y=a_1{A}_i\left(x\right)+\left[b_1-{\displaystyle \frac{2}{3}}{\kappa \pi ]B}_i\left(x\right)+\kappa \pi H_i\left(x\right)\right].$$

(25)

Proof. 

Substituting $N_i\left(x\right)=G_i\left(x\right)-{\displaystyle \frac{1}{3}}{B}_i\left(x\right)$ from (10) in (8), and $N_i\left(x\right)={\displaystyle \frac{2}{3}}{B}_i\left(x\right)-H_i\left(x\right)$ from (11) in (8), yields (24) and (25), respectively. □

2.2. Relationship of $N_i\left(x\right)$ to the Primatives of the Scorer Functions

In what follows, the relationships between $Ni\left(x\right)$ and the Wronskians that involve Airy’s and Scorer’s functions are established. The following Wronskians have been reported in [4]:

$$W_1=W\left(A_i\left(x\right),G_i\left(x\right)\right)=A_i\left(x\right){G^{\prime }}_i\left(x\right)-G_i\left(x\right){A^{\prime }}_i\left(x\right),$$

(26)

$$W_2=W\left(A_i\left(x\right),H_i\left(x\right)\right)=A_i\left(x\right){H^{\prime }}_i\left(x\right)-H_i\left(x\right){A^{\prime }}_i\left(x\right),$$

(27)

$$W_3=W\left(B_i\left(x\right),G_i\left(x\right)\right)=B_i\left(x\right){G^{\prime }}_i\left(x\right)-G_i\left(x\right){B^{\prime }}_i\left(x\right),$$

(28)

$$W_4=W\left(B_i\left(x\right),H_i\left(x\right)\right)=B\left(x\right){H^{\prime }}_i\left(x\right)-H_i\left(x\right){B^{\prime }}_i\left(x\right).$$

(29)

The right-hand-sides of (26)-(29) have also been expressed in terms of ${\int }_0^x{A}_i\left(t\right)dt$ and ${\int }_0^x{B}_i\left(t\right)dt$, [4], as:

$${\int }_0^x{A}_i\left(t\right)dt={\displaystyle \frac{1}{3}}+\pi \left\{{G_i\left(x\right){A^{\prime }}_i\left(x\right)-A}_i\left(x\right){G^{\prime }}_i\left(x\right)\right\}={\displaystyle \frac{1}{3}}-\pi W_1,$$

(30)

$${\int }_0^x{A}_i\left(t\right)dt=-{\displaystyle \frac{2}{3}}-\pi \left\{{H_i\left(x\right){A^{\prime }}_i\left(x\right)-A}_i\left(x\right){H^{\prime }}_i\left(x\right)\right\}=-{\displaystyle \frac{2}{3}}+\pi W_2,$$

(31)

$${\int }_0^x{B}_i\left(t\right)dt=\pi \left\{{G_i\left(x\right){B^{\prime }}_i\left(x\right)-B}_i\left(x\right){G^{\prime }}_i\left(x\right)\right\}=-\pi W_3,$$

(32)

$${\int }_0^x{B}_i\left(t\right)dt=-\pi \left\{{H_i\left(x\right){B^{\prime }}_i\left(x\right)-B}_i\left(x\right){H^{\prime }}_i\left(x\right)\right\}=\pi W_4.$$

(33)

Using (30)-(33) in (9) renders the following expressions for $Ni\left(x\right)$:

$$N_i\left(x\right)=\pi \left\{W_1{B}_i\left(x\right)-W_3{A}_i\left(x\right)\right\}-{\displaystyle \frac{1}{3}}{B}_i\left(x\right),$$

(34)

$$N_i\left(x\right)=\pi \left\{W_4{A}_i\left(x\right)-W_2{B}_i\left(x\right)\right\}+{\displaystyle \frac{2}{3}}{B}_i\left(x\right).$$

(35)

2.3. Bessel Function Representation of Airy’s, Scorer’s and the Nield-Kuznetsov Functions

Airy’s functions, their derivatives and integrals take the following forms in terms of the modified Bessel functions, [2,4], obtained from (14) and (15) with $n=1$, $p={\displaystyle \frac{1}{n+2}}={\displaystyle \frac{1}{3}}$, and $\zeta =2p{\left(x\right)}^{{\displaystyle \frac{1}{2p}}}={\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}:$

$$A_i\left(x\right)={\displaystyle \frac{\sqrt{x}}{3}}\left[I_{-{\displaystyle \frac{1}{3}}}\left(\zeta \right)-I_{{\displaystyle \frac{1}{3}}}\left(\zeta \right)\right],$$

(36)

$$B_i\left(x\right)=\sqrt{{\displaystyle \frac{x}{3}}} \left[I_{{\displaystyle \frac{1}{3}}}\left(\zeta \right)+I_{-{\displaystyle \frac{1}{3}}}\left(\zeta \right)\right],$$

(37)

$${A\prime }_i\left(x\right)=-{\displaystyle \frac{x}{3}}\left[I_{-{\displaystyle \frac{2}{3}}}\left(\zeta \right)-I_{{\displaystyle \frac{2}{3}}}\left(\zeta \right)\right],$$

(38)

$${B\prime }_i\left(x\right)={\displaystyle \frac{x}{\sqrt{3}}} \left[I_{-{\displaystyle \frac{2}{3}}}\left(\zeta \right)+I_{{\displaystyle \frac{2}{3}}}\left(\zeta \right)\right],$$

(39)

$${\int }_0^x{A}_i\left(t\right)dt={\displaystyle \frac{1}{3}}{\int }_0^x\sqrt{t}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)-I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)\right]dt,$$

(40)

$${\int }_0^x{B}_i\left(t\right)dt={\displaystyle \frac{1}{\sqrt{3}}}{\int }_0^x\sqrt{t}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)+I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)\right]dt,$$

(41)

where the function $I_{\mp 1/3}$ is obtained from (17) and (18) as:

$$I_{\mp 1/3}\left(\zeta \right)=\sum _{m=1}^{\infty }{\displaystyle \frac{1}{m!\Gamma \left(m\mp \frac{1}{3}+1\right)}}({\displaystyle \frac{\zeta }{2}}{)}^{2m\mp {\displaystyle \frac{1}{3}}}.$$

(42)

Using (36), (37), (40) and (41) in (9)-(11), the functions $N_i\left(x\right)$, $G_i\left(x\right)$ and $H_i\left(x\right)$ can be written in the following forms:

$$N_i\left(x\right)={\displaystyle \frac{2\sqrt{x}}{3\sqrt{3}}}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right){\int }_0^x \sqrt{t}{I}_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)dt-I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right){\int }_0^x \sqrt{t}{I}_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)dt\right]$$

(43)

$$G_i\left(x\right)={\displaystyle \frac{\sqrt{x}}{3\sqrt{3}}}\left[\begin{array}{c}\left(I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)-I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)\right){\int }_0^x \sqrt{t}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)+I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{{\displaystyle \frac{3}{2}}}\right)\right]dt+\\ \left(I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)+I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)\right)\left(1-{\int }_0^x \sqrt{t}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)-I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)\right]dt\right)\end{array}\right]$$

(44)

$$\begin{gathered} H_i\left(x\right)={\displaystyle \frac{2\sqrt{x}}{3\sqrt{3}}}\left[I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)+I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right)\right] \\ -{\displaystyle \frac{2\sqrt{x}}{3\sqrt{3}}}\left[I_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right){\int }_0^x \sqrt{t}{I}_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)dt-I_{{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{x}^{{\displaystyle \frac{3}{2}}}\right){\int }_0^x \sqrt{t}{I}_{-{\displaystyle \frac{1}{3}}}\left({\displaystyle \frac{2}{3}}{t}^{3/2}\right)dt\right] \end{gathered}$$

(45)

2.4. Complementary Function of $N_i\left(x\right)$

Aspnes [19,20] introduced a function $A_{i1}\left(x\right)$ that can be thought of as the complement of ${\int }_0^x{A}_i\left(x\right)dx$, and is defined by:

$$A_{i1}\left(x\right)={\int }_x^{\infty }{A}_i\left(x\right)=\pi \left\{A_i\left(x\right){G^{\prime }}_i\left(x\right)-{A^{\prime }}_i\left(x\right)G_i\left(x\right)\right\}.$$

(46)

Dunster [14] introduced the concept of a complementary function to $N_w\left(a,x\right)$ by extending its definition to $[x,+\infty )$, and discussed its convergence and favourable properties. This complement is defined by:

$${\tilde{N}}_w\left(a,x\right)=W\left(a,x\right){\int }_x^{\infty }W\left(a,-t\right)dt-W\left(a,-x\right){\int }_x^{\infty }W\left(a,t\right)dt.$$

(47)

Now, defining $N_w^{\mathrm{*}}(a,x)={N_w\left(a,x\right)+\tilde{N}}_w\left(a,x\right)$, equations (23) and (47) give

$$N_w^{*}\left(a,x\right)=W\left(a,x\right){\int }_0^{\infty }W\left(a,-t\right)dt-W\left(a,-x\right){\int }_0^{\infty }W\left(a,t\right)dt.$$

(48)

Following the definition introduced by Dunster, [14], the complement of $N_i\left(x\right)$ is defined as:

$${\tilde{N}}_i\left(x\right)=A_i\left(x\right){\int }_x^{\infty }{B}_i\left(t\right)dt-B_i\left(x\right){\int }_x^{\infty }{A}_i\left(t\right)dt.$$

(49)

From (30) the integral ${\int }_x^{\infty }{A}_i\left(t\right)dt$ is expressed as:

$${\int }_x^{\infty }{A}_i\left(t\right)dt=\pi W_1,$$

(50)

and using (50) in (49) yields:

$${\tilde{N}}_i\left(x\right)=A_i\left(x\right){\int }_x^{\infty }{B}_i\left(t\right)dt-{\pi W_{1}B}_i\left(x\right).$$

(51)

Defining $N_i^{*}\left(x\right)=N_i\left(x\right)+{\tilde{N}}_i\left(x\right)$, the following expression is obtained:

$${N_i^{*}\left(x\right)=A}_i\left(x\right){\int }_0^{\infty }{B}_i\left(t\right)dt-B_i\left(x\right){\int }_0^{\infty }{A}_i\left(t\right)dt.$$

(52)

Equation (52) can be written, with the help of the value ${\int }_0^{\infty }{A}_i\left(t\right)dt={\displaystyle \frac{1}{3}}$ as:

$$N_i^{*}\left(x\right)=A_i\left(x\right){\int }_0^{\infty }{B}_i\left(t\right)dt-{{\displaystyle \frac{1}{3}}B}_i\left(x\right).$$

(53)

Both functions ${\tilde{N}}_i\left(x\right)$ and $N_i^{*}\left(x\right)$, defined by Equations (51) and (53), respectively, involve a divergent integral, namely ${\int }_0^{\infty }{B}_i\left(t\right)dt$. However, they might be of value in future study of asymptotic behaviour and could serve as comparison functions of other improper integrals or infinite series.

3. Generalized Airy’s Inhomogeneous Equation

3.1. Generalized Airy’s and Nield-Kuznetsov Functions

Consider the generalized, inhomogeneous Airy’s Equation (12) in which $n>-2$ is an integer and $f\left(x\right)$ is a smooth function of its real, non-negative variable $x$. Solution to the homogeneous part of this equation is given by (13), with the generalized Airy’s functions given by (14) and (15). The following derivatives of the functions $A_n\left(x\right)$ and $B_n\left(x\right)$ are obtained from Equations (14) and (15), respectively:

$${A\prime }_n\left(x\right)=p {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{1-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)-I_{p-1}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right],$$

(54)

$${B\prime }_n\left(x\right)=p^{1/2} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{p-1}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)+I_{1-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right].$$

(55)

Integrals of the generalized Airy’s functions, obtained from (14) and (15), can be written as:

$${\int }_0^x{A}_n\left(t\right)dt=p{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}[I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)-I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)]dt,$$

(56)

$${\int }_0^x{B}_n\left(t\right)dt=\sqrt{p}{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt.$$

(57)

Upon using (14), (15), (20) and (54)-(57), the following expressions for $N_n\left(x\right)$ and ${N^{\prime }}_n\left(x\right)$ are obtained:

$$N_n\left(x\right)=p\sqrt{p}\left(I_{-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)-I_p\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right){\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt-p(x{)}^{{\displaystyle \frac{1}{2}}}\left(I_{-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)+I_p\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right){\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt,$$

(58)

$$\begin{gathered} N_n^{\prime }\left(x\right)=-p^{3/2} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{1-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)-I_{p-1}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt \\ {p}^{3/2} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{p-1}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{1-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)-I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt. \end{gathered}$$

(59)

Complementary function to the generalized Nield-Kuznetsov function of the first-kind is defined by:

$${\tilde{N}}_n\left(x\right)=A_n\left(x\right){\int }_x^{\infty }{B}_n\left(t\right)dt-B_n\left(x\right){\int }_x^{\infty }{A}_n\left(t\right)dt,$$

(60)

and the sum of $N_n\left(x\right)$ and its complement is the function $N_n^{*}\left(x\right)$, defined by:

$${N_n^{*}\left(x\right)=N}_n\left(x\right)+{\tilde{N}}_n\left(x\right)=A_n\left(x\right){\int }_0^{\infty }{B}_n\left(t\right)dt-B_n\left(x\right){\int }_0^{\infty }{A}_n\left(t\right)dt.$$

(61)

Again, both ${\tilde{N}}_n\left(x\right)$ and $N_n^{*}\left(x\right)$ involve the divergent integral ${\int }_0^{\infty }{B}_n\left(t\right)dt$, hence both are divergent.

3.2. Generalized Scorer Function

For the special cases of $f\left(x\right)=\kappa =\mp 1/\pi$, general solutions to the inhomogeneous Airy’s equation (1) are expressed in terms of Airy’s and Scorer’s functions given by (6) and (7). When $f\left(x\right)=\kappa =-1/\pi$, the function $G_i\left(x\right)$ satisfies equation (1) and when $f\left(x\right)=\kappa =1/\pi$, then both ${-G}_i\left(x\right)$ and $H_i\left(x\right)$ satisfy Airy’s inhomogeneous equation (1). In what follows, a generalized Scorer function $G_n\left(x\right)$, valid for $x\ge 0$, is introduced to satisfy the generalized Airy’s Equation (12) for any $f\left(x\right)=\kappa$, including $\kappa =\mp 1/\pi .$Define the generalized Scorer function $G_n\left(x\right)$ in terms of the generalized Airy’s functions as:

$$G_n\left(x\right)=A_n\left(x\right){\int }_0^x{B}_n\left(t\right)dt+B_n\left(x\right){\int }_x^{\infty }{A}_n\left(t\right)dt,$$

(62)

in such a way that when $n=1$, equation (6) is recovered. An expression for $G_n\left(x\right)$ is provided by the following proposition.

Proposition 2.

The generalized Scorer function  $G_n\left(x\right)$  is expressed in terms of  $N_n\left(x\right)$  and  $B_n\left(x\right)$  as:

$$G_n\left(x\right)=N_n\left(x\right)+{\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}{B}_n\left(x\right).$$

(63)

Proof. 

Equation (62) can be written as:

$$G_n\left(x\right)=A_n\left(x\right){\int }_0^x{B}_n\left(t\right)dt+B_n\left(x\right)\left[{\int }_0^{\infty }{A}_n\left(t\right)dt-{\int }_0^x{A}_n\left(t\right)dt\right].$$

(64)

Using (20), Equation (64) takes the form:

$$G_n\left(x\right)=N_n\left(x\right)+B_n\left(x\right){\int }_0^{\infty }{A}_n\left(t\right)dt.$$

(65)

The integral ${\int }_0^{\infty }{A}_n\left(t\right)dt$ can be evaluated by applying formula 10.43.19 from DLMF( NIST), [21]. Using (14), ${\int }_0^{\infty }{A}_n\left(t\right)dt$ takes the form:

$${\int }_0^{\infty }{A}_n\left(x\right)dx={\displaystyle \frac{2p}{\pi }}sin\left(p\pi \right){\int }_0^{\infty }\left(x{)}^{{\displaystyle \frac{1}{2}}}{K}_p\right(2p{\left(x\right)}^{{\displaystyle \frac{1}{2p}}})dx.$$

(66)

Using the substitution $x={\left({\displaystyle \frac{u}{2p}}\right)}^{2p}$, integral (66) takes the form:

$${\int }_0^{\infty }{A}_n\left(x\right)dx={\displaystyle \frac{1}{\pi }}sin\left(p\pi \right)\cdot (2p{)}^{2-3p}{\int }_0^{\mathrm{\infty }} u^{3p-1}{K}_p\left(u\right)du.$$

(67)

Applying the following integral identity for the modified Bessel function of the second kind, valid for $\left|Re\left(\nu \right)\right|<Re\left(\mu \right)$, namely:

$${\int }_0^{\mathrm{\infty }} t^{\mu -1}{K}_{\nu }\left(t\right)\mathrm{d}t=2^{\mu -2}\mathsf{\Gamma }\left({\displaystyle \frac{1}{2}}\mu -{\displaystyle \frac{1}{2}}\nu \right)\mathsf{\Gamma }\left({\displaystyle \frac{1}{2}}\mu +{\displaystyle \frac{1}{2}}\nu \right),$$

(68)

with $\nu =p \mathrm{a}\mathrm{n}\mathrm{d} \mu =3p,$ integral (67) takes the form:

$${\int }_0^{\infty }{A}_n\left(t\right)dt={\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}.$$

(69)

Equation (69) reduces to the known value ${\int }_0^{\infty }{A}_i\left(t\right)dt={\displaystyle \frac{1}{3}}$ when $n=1$ and $p={\displaystyle \frac{1}{n+2}}={\displaystyle \frac{1}{3}}.$

Upon using (69) in (65), the expression for $G_n\left(x\right)$ in (63) is obtained. □

With $G_n\left(x\right)$ given by (63), general solution to Equation (12) can be obtained according to the following proposition.

Proposition 3.

General solution to the inhomogeneous generalized Airy’s Equation (12) when  $f\left(x\right)=\kappa$  is given by:

$$y_n=a_n{A}_n\left(x\right)+c_n{B}_n\left(x\right)-{{\displaystyle \frac{\kappa \pi }{2\sqrt{p}\sin \left(p\pi \right)}}G}_n\left(x\right).$$

(70)

Proof. 

Equation (63) provides the following expression for $N_n\left(x\right)$:

$${N_n\left(x\right)=G}_n\left(x\right)-{\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}{B}_n\left(x\right).$$

(71)

Using (70) in (19) yields:

$$y_n=a_n{A}_n\left(x\right)+\left[b_n+\kappa {\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2p^{\left(3p-3/2\right)}}}\right]{ B}_n\left(x\right)-{{\displaystyle \frac{\kappa \pi }{2\sqrt{p}\sin \left(p\pi \right)}}G}_n\left(x\right).$$

(72)

Letting $c_n=b_n+\kappa {\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2p^{\left(3p-3/2\right)}}}$ in (72), result (70) follows. □

It is worth noting that when $f\left(x\right)=\kappa =1/\pi$, the general solution (72) becomes:

$$y_n=a_n{A}_n\left(x\right)+\left[b_n+{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2\pi p^{\left(3p-3/2\right)}}}\right]{ B}_n\left(x\right)-{{\displaystyle \frac{1}{2\sqrt{p}\sin \left(p\pi \right)}}G}_n\left(x\right),$$

(73)

and when $f\left(x\right)=\kappa =-1/\pi$, the general solution (72) takes the form:

$$y_n=a_n{A}_n\left(x\right)+\left[b_n-{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2\pi p^{\left(3p-3/2\right)}}}\right]{ B}_n\left(x\right)+{{\displaystyle \frac{1}{2\sqrt{p}\sin \left(p\pi \right)}}G}_n\left(x\right).$$

(74)

3.3. Bessel Function Representation of the Generalized Scorer Function

The generalized Scorer function, $G_n\left(x\right)$ and its first derivative take the following forms, respectively, in terms of Bessel’s modified functions, obtained by substituting (15) and (59) in (63), then differentiating:

$$\begin{gathered} G_n\left(x\right)=-\left(px{)}^{{\displaystyle \frac{1}{2}}}\right(I_{-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right) \\ +p\sqrt{p}\left(I_{-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)-I_p\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right){\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt \\ +I_p\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right))\sqrt{p}{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt \\ +{\displaystyle \frac{\sin \mathrm{p}\mathsf{\pi }}{\mathsf{\pi }}}.{\displaystyle \frac{\mathsf{\Gamma }\left(\mathrm{p}\right).\mathsf{\Gamma }\left(2\mathrm{p}\right)}{{\mathrm{p}}^{\left(3\mathrm{p}-2\right)}}}(px{)}^{{\displaystyle \frac{1}{2}}}\left[I_{-p}\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)+I_p\left(2p{x}^{{\displaystyle \frac{1}{2p}}}\right)\right], \end{gathered}$$

(75)

$$\begin{gathered} G_n^{\prime }\left(x\right)=p^{{\displaystyle \frac{3}{2}}} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left\{\left[I_{p-1}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{1-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)-I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt\right\} \\ -p^{{\displaystyle \frac{3}{2}}} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{1-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)-I_{p-1}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]{\int }_0^x{t}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left[I_p\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]dt \\ +{\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}\left\{p^{1/2} {\left(x\right)}^{{\displaystyle \frac{n+1}{2}}}\left[I_{p-1}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)+I_{1-p}\left(2p{t}^{{\displaystyle \frac{1}{2p}}}\right)\right]\right\}. \end{gathered}$$

(76)

3.4. Values at $x=0$ of the Generalized Scorer Function and Its Derivative

The value $G_n\left(0\right)$ is obtained from (63) as:

$$G_n\left(0\right)={\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{\mathsf{\Gamma }(1-p)}}.p^{({\displaystyle \frac{5}{2}}-4p)},$$

(77)

where $B_n\left(0\right)={\displaystyle \frac{{\left(p\right)}^{1/2-p}}{\mathsf{\Gamma }(1-p)}}$ and $N_n\left(0\right)=0$ have been used. With the knowledge that for a non-integer p, $\mathsf{\Gamma }(1-p)\mathsf{\Gamma }\left(p\right)={\displaystyle \frac{\pi }{\mathrm{s}\mathrm{i}\mathrm{n}p\pi }}$, Equation (77) can be written as:

$$G_n\left(0\right)={\left({\displaystyle \frac{\mathsf{\Gamma }\left(p\right)\sin p\pi }{\pi }}\right)}^2.\mathsf{\Gamma }\left(2p\right).p^{({\displaystyle \frac{5}{2}}-4p)}.$$

(78)

First derivative of $G_n\left(x\right)$ is given by:

$$G_n^{\prime }\left(x\right)=N_n^{\prime }\left(x\right)+{\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}{B}_n^{\prime }\left(x\right),$$

(79)

with value at zero given by:

$$G_n^{\prime }\left(0\right)=-{\displaystyle \frac{\sin p\pi }{\pi }}.\mathsf{\Gamma }\left(2p\right).p^{\left({\displaystyle \frac{3}{2}}-2p\right)},$$

(80)

wherein the values ${B^{\mathrm{\text{'}}}}_n\left(0\right)=-{\displaystyle \frac{{\left(p\right)}^{p-\frac{1}{2}}}{\mathsf{\Gamma }\left(p\right)}}$ and ${N^{\mathrm{\text{'}}}}_n\left(0\right)=0$ have been used.

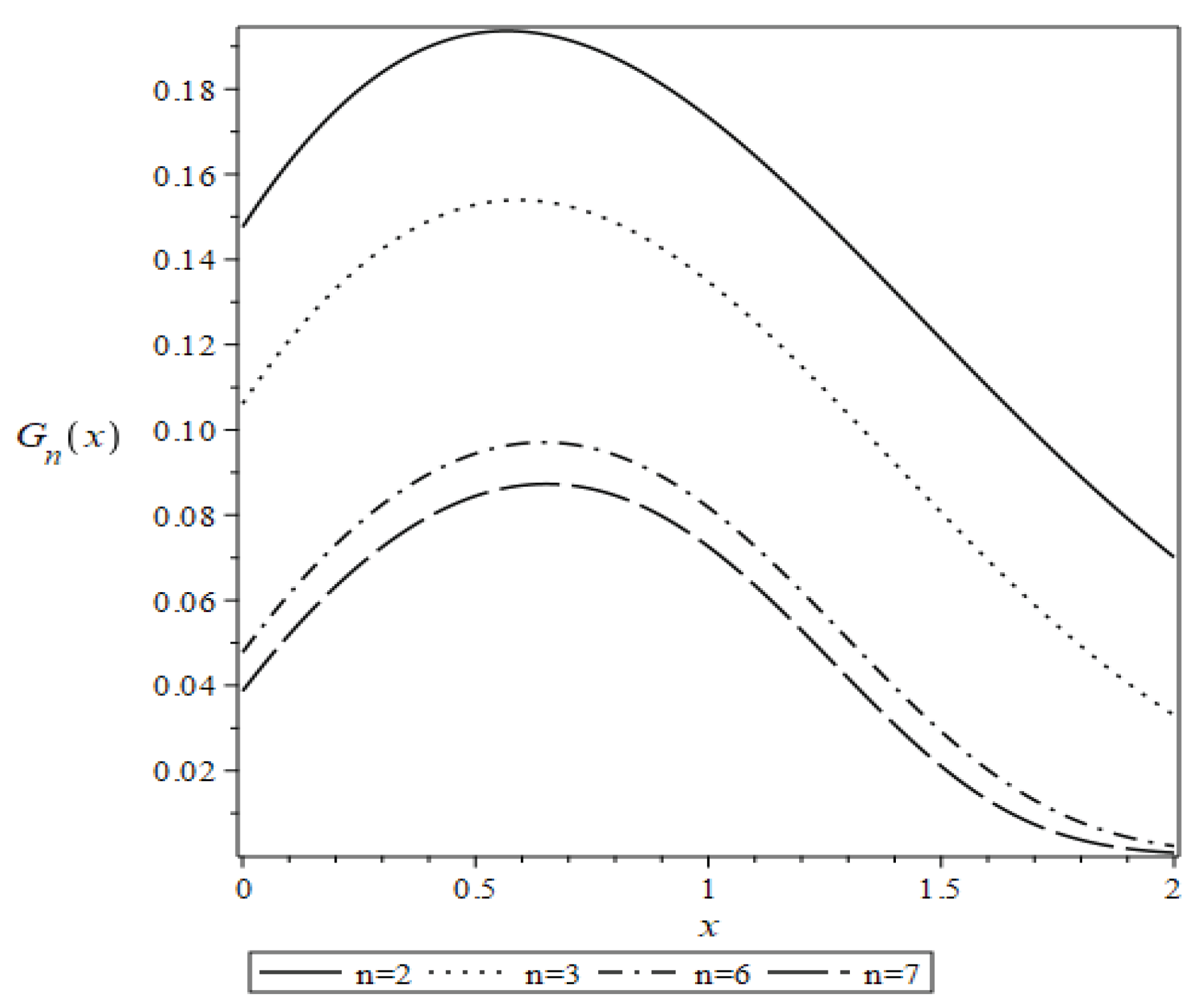
3.5. Computational Algorithm of the Generalized Functions

Following Swanson and Headley, [12], the generalized Airy’s functions are evaluated using the following relationships:

$${\rho }_n={\displaystyle \frac{({p)}^{1-p}}{\mathsf{\Gamma }(1-p)}} \mathrm{and} {\phi }_n={\displaystyle \frac{{\left(p\right)}^p}{\mathsf{\Gamma }\left(p\right)}},$$

(81)

$$g_{n1}\left(x\right)=1+\sum _{k=1}^{\infty }{p}^{2k}\prod _{j=1}^k{\displaystyle \frac{x^{\left(n+2\right)k}}{j\left(j-p\right)}},$$

(82)

$$g_{n2}\left(x\right)=x\left[1+\sum _{k=1}^{\infty }{p}^{2k}\prod _{j=1}^k{\displaystyle \frac{x^{\left(n+2\right)k}}{j\left(j+p\right)}}\right],$$

(83)

$$A_n\left(x\right)={\rho }_n{g}_{n1}\left(x\right)-{\phi }_n{g}_{n2}\left(x\right),$$

(84)

$$B_n\left(x\right)={{\displaystyle \frac{1}{\sqrt{p}}}[\rho }_n{g}_{n1}\left(x\right)+{\phi }_n{g}_{n2}\left(x\right)].$$

(85)

Based on the above, the generalized Nield-Kuznetsov function of the first-kind and the generalized Scorer function can be evaluated using the following expressions, obtained using (81)-(85) in (20) and (63), respectively:

$$N_n\left(x\right)={\displaystyle \frac{2}{\sqrt{p}}}{\rho }_n{\phi }_n\left\{g_{n1}\left(x\right){\int }_0^x{g}_{n2}\left(t\right)dt-g_{n2}\left(y\right){\int }_0^x{g}_{n1}\left(t\right)dt\right\}$$

(86)

$$G_n\left(x\right)={\omega }_n{[\rho }_n{g}_{n1}\left(x\right)+{\phi }_n{g}_{n2}\left(x\right)]+N_n\left(x\right),$$

(87)

where

$${\omega }_n={\displaystyle \frac{\sin p\pi }{\pi }}.{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{p^{\left(3p-2\right)}}}.$$

(88)

For the sake of illustrating the above computational procedure, the generalized Scorer function $G_n\left(x\right)$ is computed for the index values $n=2, 3, 6 \mathrm{a}\mathrm{n}\mathrm{d} 7$, over the interval $0\le x\le 2$, and plotted in Figure 1, which shows the possibility of turning points at values $x>2.$ However, verification of turning points requires more extensive calculations using the above procedure. It should be noted that all computations were carried out using Maple.

3.6. Initial Value Problem Involving the Generalized Scorer Function

Consider the problem of solving Equation (12) with $f\left(x\right)=-1/\pi$ subject to the conditions: $y_n\left(0\right)=\alpha$ and $y_n^{\prime }\left(0\right)=\beta$, where $\alpha$ and $\beta$ are real numbers. From general solution (74) and the given initial conditions, the following system of two equations in the two arbitrary constants $a_n$ and $b_n$ is obtained:

$$a_n{A}_n\left(0\right)+{ B}_n\left(0\right)b_n=\alpha -{{\displaystyle \frac{1}{2\sqrt{p}\sin \left(p\pi \right)}}G}_n\left(0\right)+\left[{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2\pi p^{\left(3p-\frac{3}{2}\right)}}}\right]{ B}_n\left(0\right),$$

(89)

$$a_n{A\prime }_n\left(0\right)+b_n{ B\prime }_n\left(0\right)=\beta -{\displaystyle \frac{1}{2\sqrt{p}\sin \left(p\pi \right)}}{G}_n^{\prime }\left(0\right)+\left[{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)}{2\pi p^{\left(3p-\frac{3}{2}\right)}}}\right]{ B^{\prime }}_n\left(0\right).$$

(90)

Solution of the above system of equations is given by:

$$a_n={\displaystyle \frac{\pi \left[\alpha { B^{\prime }}_n\left(0\right)-\beta { B}_n\left(0\right)\right]}{2\sqrt{p}\sin \left(p\pi \right)}}+{\displaystyle \frac{\pi \left[G_n^{\prime }\left(0\right){ B}_n\left(0\right)-G_n\left(0\right){ B^{\prime }}_n\left(0\right)\right]}{4p(\sin \left(p\pi \right){)}^2}},$$

(91)

$$\begin{gathered} b_n={\displaystyle \frac{\pi \left[\beta A_n\left(0\right)-\alpha A_n^{\prime }\left(0\right)\right]}{2\sqrt{p}\sin \left(p\pi \right)}}+{\displaystyle \frac{\pi \left[{G_n\left(0\right)A_n^{\prime }\left(0\right)-G}_n^{\prime }\left(0\right)A_n\left(0\right)\right]}{4p(\sin \left(p\pi \right){)}^2 }} \\ +{\displaystyle \frac{\mathsf{\Gamma }\left(p\right).\mathsf{\Gamma }\left(2p\right)\left[{A_n\left(0\right)B_n^{\prime }\left(0\right)-B}_n\left(0\right)A_n^{\prime }\right(0\left)\right]}{4\sin \left(p\pi \right)p^{\left(3p-1\right)}}}. \end{gathered}$$

(92)

Determination of values of $a_n$ and $b_n$ requires a knowledge of the values at zero of $A_n\left(0\right)$, $A_n^{\prime }\left(0\right)$, $B_n\left(0\right)$ and $B_n^{\prime }\left(0\right)$, which are given by:

$$A_n\left(0\right)={\displaystyle \frac{{\left(p\right)}^{1-p}}{\mathsf{\Gamma }(1-p)}}\mathrm{and} {A^{\prime }}_n\left(0\right)=-{\displaystyle \frac{{\left(p\right)}^p}{\mathsf{\Gamma }\left(p\right)}},$$

(93)

$$B_n\left(0\right)={\displaystyle \frac{{\left(p\right)}^{1/2-p}}{\mathsf{\Gamma }(1-p)}}\mathrm{and} {B^{\prime }}_n\left(0\right)=-{\displaystyle \frac{{\left(p\right)}^{p-\frac{1}{2}}}{\mathsf{\Gamma }\left(p\right)}},$$

(94)

$$N_n\left(0\right)={N^{\prime }}_n\left(0\right)=0,$$

(95)

and $G_n\left(0\right)$ and $G_n^{\prime }\left(0\right)$, which are given by (78) and (80), respectively. For the sake of illustration, computations have been carried using the values of $\alpha =1, \beta =2$. Once $a_n$ and $b_n$ are calculated, solution $y_n\left(x\right)$, as given by (74), is computed using the computational procedure of Section 3.5, above.

Solutions to the given initial value problem are shown in Figure 2, below, for $n=2 \mathrm{a}\mathrm{n}\mathrm{d} 3.$

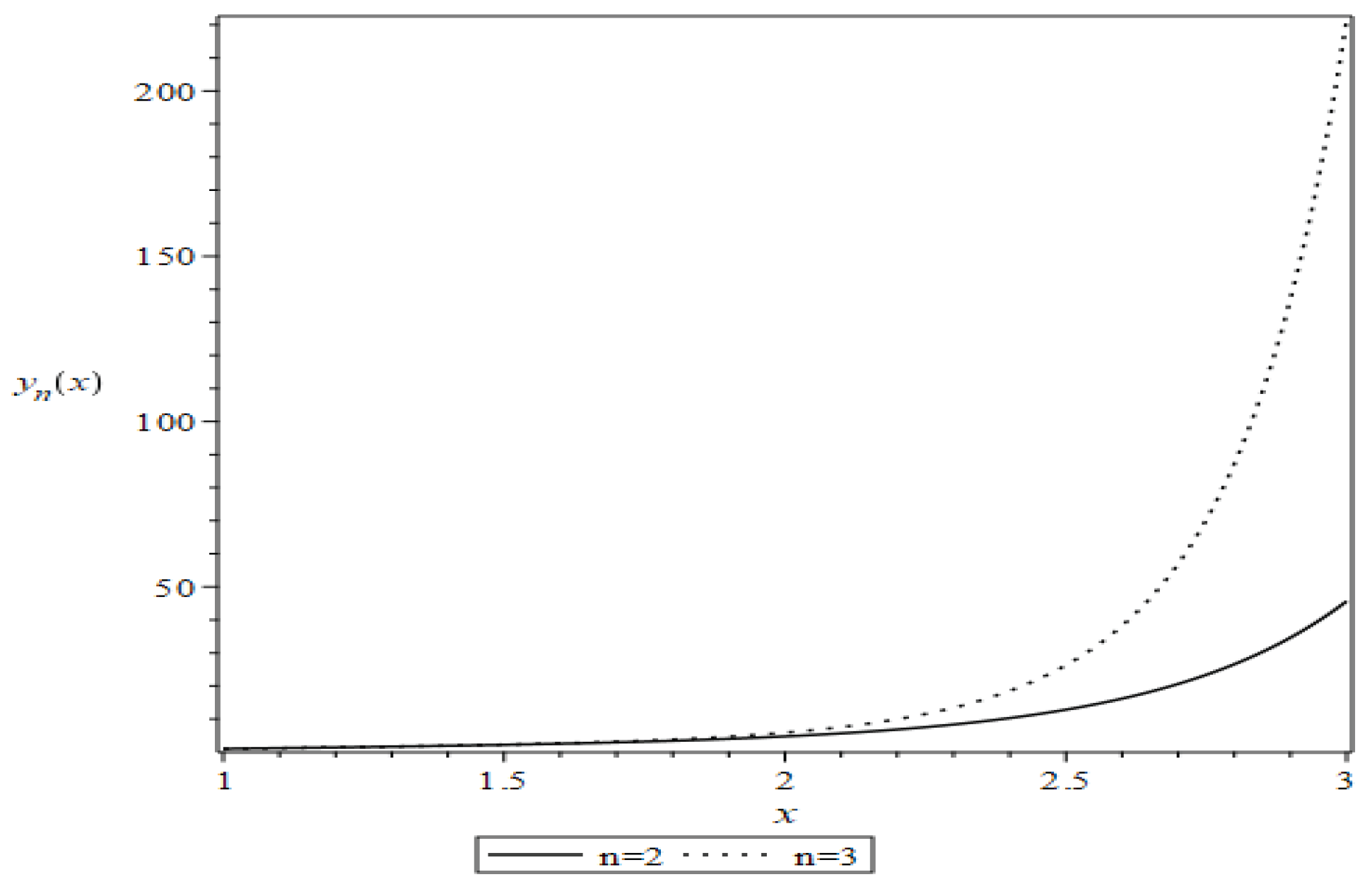
4. Higher Derivatives of ${\mathit{N}}_{\mathit{i}}\left(\mathit{x}\right),{\mathit{A}}_{\mathit{n}}\left(\mathit{x}\right),{\mathbf{B}}_{\mathbf{n}}\left(\mathbf{x}\right)\mathbf{a}\mathbf{n}\mathbf{d}{\mathbf{N}}_{\mathbf{n}}\left(\mathbf{x}\right)$

In a previous article, Hamdan et.al. [16] discussed higher derivatives of the Nield-Kuznetsov function $N_i\left(x\right)$ and the polynomials arising from its derivatives. In what follows, expressions for higher derivatives of the generalized functions $A_n\left(x\right), B_n\left(x\right)$, $N_n\left(x\right)$, and $G_n\left(x\right)$ are obtained.

4.1. Higher Derivatives of $A_n\left(x\right)and{B}_n\left(x\right)$

Consider the homogeneous generalized Airy’s equation, written in the form

$$y_n^{\prime \prime }=x^n{y}_n.$$

(96)

The following few higher derivatives are obtained by repeated differentiation of (96):

$$y_n^{\prime \prime \prime }=x^n{y}_n^{\prime }+n{x}^{n-1}{y}_n,$$

(97)

$$y_n^{iv}=2n{x}^{n-1}{y}_n^{\prime }+{[x}^{2n}+n\left(n-1\right)x^{n-2}]y_n,$$

(98)

$$y_n^v={[x}^{2n}+3n\left(n-1\right)x^{n-2}]y_n^{\prime }+{[4nx}^{2n-1}+n\left(n-1\right)(n-2\left)x^{n-3}\right]y_n,$$

(99)

$$\begin{gathered} y_n^{vi}={[6nx}^{2n-1}+4n\left(n-1\right)(n-2)x^{n-3}]y_n^{\prime } \\ +{{[x}^{3n}+n(11n-7)x}^{2n-2}+n\left(n-1\right)(n-2)(n-3)x^{n-4}]y_n, \end{gathered}$$

(100)

$$\begin{gathered} y_n^{vii}={[x^{3n}+n(23n-13)x}^{2n-2}+5n\left(n-1\right)(n-2)(n-3)x^{n-4}]y_n^{\prime } \\ +{{[9nx}^{3n-1}+2n\left(n-1\right)(13n-11)x}^{2n-3}+n\left(n-1\right)(n-2)(n-3)(n-4)x^{n-5}]y_n, \end{gathered}$$

(101)

Each of the above derivatives of $y_n$ is expressed in terms of $y_n$ and $y_n^{\prime }$, whose coefficients are polynomials. The generalized Airy’s functions, $A_n\left(x\right)$ and $B_n\left(x\right)$ satisfy Equation (96) and the derivatives above. The kth derivatives of $A_n\left(x\right)$ and $B_n\left(x\right)$ can thus be expressed in the following forms:

$$A_n^{\left(k\right)}\left(x\right)=P_k\left(x\right){A^{\prime }}_n\left(x\right)+Q_k\left(x\right)A_n\left(x\right),$$

(102)

$$B_n^{\left(k\right)}\left(x\right)=P_k\left(x\right){B^{\prime }}_n\left(x\right)+Q_k\left(x\right)B_n\left(x\right),$$

(103)

where $P_k\left(x\right)$ is the polynomial coefficient of $A_n^{\prime }\left(x\right)$ and of $B_n^{\prime }\left(x\right)$, and $Q_k\left(x\right)$ is the polynomial coefficient of $A_n\left(x\right)$ and of $B_n\left(x\right)$ in the kth derivative of $A_n\left(x\right)$ and $B_n\left(x\right)$. A few of these polynomials are shown in the Table 1, below.

4.2. Higher Derivatives of $N_n\left(x\right)$

The inhomogeneous generalized Airy’s Equation (1), with $f\left(x\right)=\kappa$, can be written as:

$$y_n^{\prime \prime }=x^n{y}_n+\kappa ,$$

(104)

and the function $N_n\left(x\right)$ satisfies the particular solution to the inhomogeneous generalized Airy’s Equation (104). We thus have:

$$N_n^{\prime \prime }\left(x\right)=x^n{N}_n\left(x\right)-W(A_n\left(x\right),B_n\left(x\right)).$$

(105)

The following few higher derivatives are obtained by repeated differentiation of (105):

$$N_n^{\prime \prime \prime }\left(x\right)=x^n{N}_n^{\prime }\left(x\right)+n{x}^{n-1}{N}_n\left(x\right),$$

(106)

$$N_n^{iv}\left(x\right)=2n{x}^{n-1}{N}_n^{\prime }\left(x\right)+\left[x^{2n}+n\left(n-1\right)x^{n-2}\right]N_n\left(x\right)-x^{n}W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(107)

$$N_n^v\left(x\right)=[x^{2n}+3n\left(n-1\right)x^{n-2}]N_n^{\prime }\left(x\right)+\left[{4nx}^{2n-1}+n\left(n-1\right)(n-2)x^{n-3}\right]N_n\left(x\right)-{3nx}^{n-1}W(A_n\left(x\right),B_n\left(x\right)),$$

(108)

$$\begin{gathered} N_n^{vi}\left(x\right)=\left[{6nx}^{2n-1}+4n\left(n-1\right)\left(n-2\right)x^{n-3}\right]N_n^{\prime }\left(x\right)+ \\ [{x^{3n}+n\left(11n-7\right)x}^{2n-2}+n\left(n-1\right)\left(n-2\right)(n-3\left)x^{n-4}\right]N_n\left(x\right)-{[x^{2n}+6n(n-1)x}^{n-2}\left]W\right(A_n\left(x\right),B_n\left(x\right)), \end{gathered}$$

(109)

$$\begin{gathered} N_n^{vii}\left(x\right)=\left[x^{3n}+{n(23n-13)x}^{2n-2}+5n\left(n-1\right)\left(n-2\right)\left(n-3\right)x^{n-4}\right]N_n^{\prime }\left(x\right)+\left[{9nx}^{3n-1}+2n\left(n-1\right)\left(13n-11\right)x^{2n-3}+n\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)x^{n-5}\right]N_n\left(x\right) \\ -{[8n{x}^{2n-1}+10n(n-1\left)\right(n-2)x}^{n-3}\left]W\right(A_n\left(x\right),B_n\left(x\right)). \end{gathered}$$

(110)

Each of the above derivatives of $N_n\left(x\right)$ is expressed in terms of $N_n\left(x\right)$ and $N_n^{\prime }\left(x\right)$. The kth derivatives of $N_n\left(x\right)$ is thus expressed in the following form:

$$N_n^{\prime \prime }\left(x\right)=x^n{N}_n\left(x\right)-W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(111)

where $P_k\left(x\right)$, $Q_k\left(x\right)$ and $R_k\left(x\right)$ are the polynomial coefficients of $N_n^{\prime }\left(x\right)$, $N_n\left(x\right)$ and the Wronskian $W(A_n\left(x\right),B_n\left(x\right))$, respectively, in the kth derivative of $N_n\left(x\right)$. A few of these polynomials are shown in the Table 1, below.

4.3. Higher Derivatives of $G_n\left(x\right)$

The generalized Scorer function $G_n\left(x\right)$ is defined by Equation (67), which can be written in the form:

$$G_n\left(x\right)=N_n\left(x\right)+{\omega }_n{B}_n\left(x\right),$$

(112)

where ${\omega }_n$ is defined by Equation (88). The following few higher derivatives of $G_n\left(x\right)$ are obtained by repeated differentiation of (112):

$${G_n^{\prime \prime }\left(x\right)=x}^n{G}_n\left(x\right)-W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(113)

$$G_n^{\prime \prime \prime }\left(x\right)=x^n{G}_n^{\prime }\left(x\right)+n{x}^{n-1}{G}_n\left(x\right),$$

(114)

$$G_n^{iv}\left(x\right)=2n{x}^{n-1}{G}_n^{\prime }\left(x\right)+\left[x^{2n}+n\left(n-1\right)x^{n-2}\right]G_n\left(x\right)-x^{n}W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(115)

$$G_n^v\left(x\right)=\left[x^{2n}+3n\left(n-1\right)x^{n-2}\right]G_n^{\prime }\left(x\right)+\left[{4nx}^{2n-1}+n\left(n-1\right)\left(n-2\right)x^{n-3}\right]G_n\left(x\right)-{3nx}^{n-1}W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(116)

$$\begin{gathered} G_n^{vi}\left(x\right)=\left[{6nx}^{2n-1}+4n\left(n-1\right)\left(n-2\right)x^{n-3}\right]G_n^{\prime }\left(x\right) \\ \left[{x^{3n}+n\left(11n-7\right)x}^{2n-2}+n\left(n-1\right)\left(n-2\right)\left(n-3\right)x^{n-4}\right]G_n\left(x\right) \\ -{[x^{2n}+6n(n-1)x}^{n-2}\left]W\right(A_n\left(x\right),B_n\left(x\right)), \end{gathered}$$

(117)

$$\begin{gathered} G_n^{vii}\left(x\right)=\left[x^{3n}+{n\left(23n-13\right)x}^{2n-2}+5n\left(n-1\right)\left(n-2\right)\left(n-3\right)x^{n-4}\right]G_n^{\prime }\left(x\right)+\left[{9nx}^{3n-1}+2n\left(n-1\right)\left(13n-11\right)x^{2n-3}+n\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)x^{n-5}\right]G_n\left(x\right) \\ -{[8n{x}^{2n-1}+10n(n-1\left)\right(n-2)x}^{n-3}\left]W\right(A_n\left(x\right),B_n\left(x\right)). \end{gathered}$$

(118)

Each of the above derivatives of $G_n\left(x\right)$ is expressed in terms of $G_n\left(x\right)$ and $G_n^{\prime }\left(x\right)$. The kth derivatives of $G_n\left(x\right)$ is thus expressed in the following form:

$$G_n^{\left(k\right)}\left(x\right)=P_k\left(x\right)G_n^{\prime }\left(x\right)+Q_k\left(x\right)G_n\left(x\right)-R_k\left(x\right)W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(119)

where $P_k\left(x\right)$, $Q_k\left(x\right)$ and $R_k\left(x\right)$ are the polynomial coefficients of $G_n^{\prime }\left(x\right)$, $G_n\left(x\right)$ and $W(A_n\left(x\right),B_n\left(x\right))$, respectively, in the kth derivative of $G_n\left(x\right)$. A few of these polynomials are shown in Table 1, below.

4.4. The Polynomial Coefficients and Iterative Definition of the Higher Derivatives

Polynomial coefficients $P_k\left(x\right)$, $Q_k\left(x\right)$ and $R_k\left(x\right)$ obtained in the above higher derivatives are presented in Table 1. Degrees of the polynomials $P_k\left(x\right)$, $Q_k\left(x\right)$ and $R_k\left(x\right)$ are shown in Table 2 and are expressed in terms of the order of the derivative, k, and the index, n, of the generalized Airy’s equation. These polynomials are needed to define higher derivatives iteratively, as discussed in what follows.

The k+1st derivatives of the generalized functions $A_n\left(x\right)$, $B_n\left(x\right)$, $N_n\left(x\right)$ and $G_n\left(x\right)$ take the following forms:

$$A_n^{\left(k+1\right)}\left(x\right)=P_{k+1}\left(x\right){A^{\prime }}_n\left(x\right)+Q_{k+1}\left(x\right)A_n\left(x\right),$$

(120)

$$B_n^{\left(k+1\right)}\left(x\right)=P_{k+1}\left(x\right){B^{\prime }}_n\left(x\right)+Q_{k+1}\left(x\right)B_n\left(x\right),$$

(121)

$$N_n^{\left(k+1\right)}\left(x\right)=P_{k+1}\left(x\right){N^{\prime }}_n\left(x\right)+{Q_{k+1}\left(x\right)N}_n\left(x\right)-R_{k+1}\left(x\right)W\left(A_n\left(x\right),B_n\left(x\right)\right),$$

(122)

$$G_n^{\left(k+1\right)}\left(x\right)=P_{k+1}\left(x\right){G^{\prime }}_n\left(x\right)+{Q_{k+1}\left(x\right)G}_n\left(x\right)-R_{k+1}\left(x\right)W\left(A_n\left(x\right),B_n\left(x\right)\right).$$

(123)

The polynomial coefficients $P_{k+1}\left(x\right)$, $Q_{k+1}\left(x\right)$ and $R_{k+1}\left(x\right)$, in the k+1st derivative are obtained from $P_k\left(x\right)$, $Q_k\left(x\right)$ and $R_k\left(x\right)$, in the kth derivative using the following relationships:

$$P_{k+1}\left(x\right)=P_k^{\prime }\left(x\right)+Q_k\left(x\right),$$

(124)

$${{Q_{k+1}\left(x\right)=Q_k^{\prime }\left(x\right)+x}^{n}P}_k\left(x\right),$$

(125)

$$R_{k+1}\left(x\right)=R_k^{\prime }\left(x\right)+P_k\left(x\right),$$

(126)

Equations (120)-(123) can thus be written in the following final forms that include the value of the Wronskian, $W\left(A_n\left(x\right),B_n\left(x\right)\right)$, as given by Equation (16):

$$A_n^{\left(k+1\right)}\left(x\right)=\left\{P_k^{\prime }\right(x)+Q_k(x\left)\right\}{A^{\prime }}_n\left(x\right)+{{\left\{Q_k^{\prime }\right(x)+x}^{n}P}_k\left(x\right)\}{A}_n\left(x\right),$$

(127)

$$B_n^{\left(k+1\right)}\left(x\right)=\left\{P_k^{\prime }\right(x)+Q_k(x\left)\right\}{B^{\prime }}_n\left(x\right)+{{\left\{Q_k^{\prime }\right(x)+x}^{n}P}_k\left(x\right)\}{B}_n\left(x\right),$$

(128)

$$\begin{gathered} N_n^{\left(k+1\right)}\left(x\right)=\left\{P_k^{\prime }\left(x\right)+Q_k\left(x\right)\right\}{N^{\prime }}_n\left(x\right)+{{\left\{Q_k^{\prime }\right(x)+x}^{n}P}_k\left(x\right)\}{N}_n\left(x\right) \\ -{\displaystyle \frac{2}{\pi }}{p}^{{\displaystyle \frac{1}{2}}}\sin \left(p\pi \right)\left\{R_k^{\prime }\left(x\right)+P_k\left(x\right)\right\}, \end{gathered}$$

(129)

$$\begin{gathered} G_n^{\left(k+1\right)}\left(x\right)=\left\{P_k^{\prime }\left(x\right)+Q_k\left(x\right)\right\}{G^{\prime }}_n\left(x\right)+{{\left\{Q_k^{\prime }\right(x)+x}^{n}P}_k\left(x\right)\}{G}_n\left(x\right) \\ -{\displaystyle \frac{2}{\pi }}{p}^{{\displaystyle \frac{1}{2}}}\sin \left(p\pi \right)\left\{R_k^{\prime }\left(x\right)+P_k\left(x\right)\right\}. \end{gathered}$$

(130)

It is worth noting that the k+1st derivatives of the generalized Scorer function can be obtained in terms of the k+1st derivatives of $N_n\left(x\right)$ and $B_n\left(x\right)$ by differentiating (112) as follows:

$$G_n^{\left(k+1\right)}\left(x\right)=N_n^{\left(k+1\right)}\left(x\right)+{\omega }_n{B}_n^{\left(k+1\right)}\left(x\right).$$

(131)

Using (121) and (122) in (131) yields:

$$G_n^{\left(k+1\right)}\left(x\right)=P_{k+1}\left(x\right)\left[{N^{\prime }}_n\left(x\right)+{\omega }_n{B^{\prime }}_n\left(x\right)\right]+{Q_{k+1}\left(x\right)[N}_n\left(x\right)+{\omega }_n{B}_n\left(x\right)]-R_{k+1}\left(x\right)W(A_n\left(x\right),B_n\left(x\right)\left)\right],$$

(132)

and using (124)-(126) in (132) gives:

$$G_n^{\left(k+1\right)}\left(x\right)=\left\{P_k^{\prime }\left(x\right)+Q_k\left(x\right)\right\}\left[{N^{\prime }}_n\left(x\right)+{\omega }_n{B^{\prime }}_n\left(x\right)\right]+{\left\{{{Q_k^{\prime }\left(x\right)+x}^{n}P}_k\left(x\right)\right\}[N}_n\left(x\right)+{\omega }_n{B}_n\left(x\right)]-{\displaystyle \frac{2}{\pi }}{p}^{{\displaystyle \frac{1}{2}}}\sin \left(p\pi \right)\left\{R_k^{\prime }\left(x\right)+P_k\left(x\right)\right\}.$$

(133)

4.5. Dependence of the Coefficient Polynomials on Index n

For a given value of index n, if a term in a polynomial involves x to a negative power, that term is dropped out. For the sake of illustration consider Table 1 when $n=3$. The polynomials take the forms shown in Table 3, below.