1. Introduction
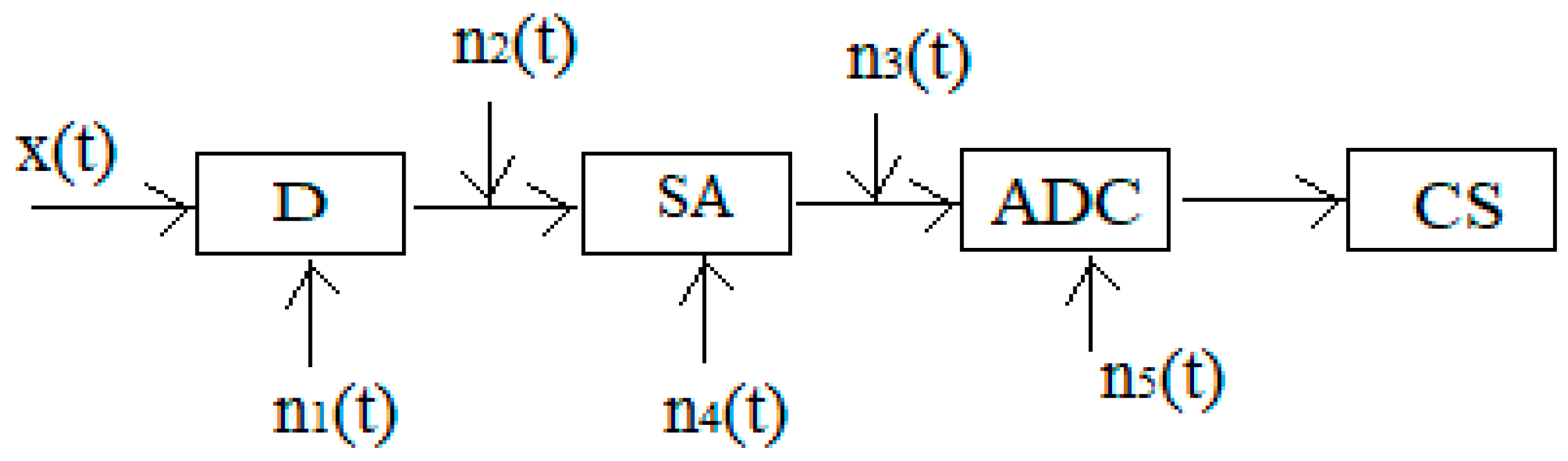
The task of detecting signals in radio engineering systems is, as a rule, to measure the informative parameters of the signal and resolve the signal against the background of noise. In this case, the structure of the input information can be represented by
Figure 1, where the following designations are adopted:
– signal sensor,
– input signal amplifier,
– analog-to-digital converter,
– computing system,
- input signal,
- external noise distorting the signal,
– additional noise introduced by the equipment during the conversion.
External noise , which distorts the input signal, can be eliminated based on statistical differences between the noise and a mixture of the input signal and noise .
Currently, quite a lot of work is devoted to the issues of signal detection against the background of noise. For example, an adaptive signal detection and carrier frequency offset (CFO) estimation method based on a virtual array is proposed in this [
1]. This is a data-aided method that utilizes a training sequence composed of three segments of sub-training sequences with different symbols. This method first uses spatial spectrum estimation to obtain the coarse frequency estimations of interference signals and CFO from virtual array signals constructed from the first two sub-training sequences. Then, beamforming is conducted accordingly on the virtual array signals constructed from the third sub-training sequence to suppress the in-band interferences and protrude the expected signal. Finally, improved performance of signal detection and CFO estimation is obtained with the beamformed signals. In [
2], to solve the problem of reducing the noise level of radio signals, a radio communication signal denoising method based on the relativistic average generative adversarial networks (RaGAN) is proposed. This method combines the bidirectional long short-term memory (Bi-LSTM) model, which is good at processing time-series data with RaGAN, and uses the weighted loss function to construct a noise reduction model suitable for radio communication signals, which realizes the end-to-end denoising of radio signals. There are papers dealing with noise abatement in a narrow subject area. Thus, the work [
3] is devoted to the study of interference detection in the wireless communication system of railway transport. In this paper, the fourth-order cyclic cumulant (FOCC) of signals with different modulation modes is analyzed for the narrow-band wireless communications system of rail transit. Based on the analysis results, an adjacent-frequency interference detection algorithm is proposed according to the FOCC of the received signal within the predetermined cyclic frequency range. To detect interference with the same carrier frequency, a same frequency interference detection algorithm using the relationship between the FOCC and the received power is proposed. For example, work [
4] considers the detection of underwater acoustic signals against the background of non-stationary sea noise. This article discusses a new effective approach to the problem of signal detection against background noise based on a nonlinear residual functional called the neuron-like criterion function (NCF). A detailed comparison of the NCF-based technique and the conventional correlation criterion function (CCF)-based matched-signal detection is performed. approach to the problem of detecting a signal against a background of noise. It is also possible to pay attention to the work [
5], which considers an adaptive feedback-controlled signal detection scheme for diffusion-based molecular communication systems. This paper proposes a simple and practical method that enables receiver nanomachines to automatically estimate signal detection times according to the measured molecular concentrations and weighted feedback errors.
In contrast to the listed works, this article is devoted to nonparametric methods of signal detection, the use of which is advisable when the statistical parameters of noise are a priori unknown [
6,
7,
8].
Nonparametric signal detection methods in radio communication systems were first used to minimize the likelihood of accepting a false hypothesis about the presence of a signal in the receiving path. In this regard, in the literature, nonparametric methods are understood to be methods of minimizing the level of false alarms in the absence of a priori information about the statistical characteristics of noise.
The insensitivity (invariance) of nonparametric procedures to the statistical properties of noise is achieved by converting the observed sample data to quantities whose statistical properties are known in advance and do not depend on the probabilistic characteristics of the observed data. For example, in radio reception technology, to combat the level instability of noise [
9,
10,
11], the conversion of the input signal into the so-called sign function is widely used. The essence of the sign function is to convert the signal samples observed at the input of the radio receiver into a sequence of zeros and ones, depending on the sign of the conversion, the appearance of which is equally likely if only the distribution of the input samples is symmetrical with respect to the restriction level.
The procedure for ranking input samples has the broadest invariant properties, which converts them into a sequence of integers - ranks depending on the relative position of this sample in the ranked series of the entire observed population. Ranks have many properties useful for practice, and the theory of rank procedures is most deeply developed compared to nonparametric methods of other classes and is best prepared for practical implementation.
There are a number of fundamental monographs and reference books in the field of rank signal processing [
12], the bibliography of journal articles [
13] has hundreds of titles. The methods of rank detection of signals are divided into pre-detector and post-detector [
14]. Post-detector detectors are much simpler in terms of technical implementation. However, the disadvantage of the post-detector ranking method is the small volume of ranked samples, which reduces the noise immunity of detection compared to optimal methods. Therefore, consideration of the issues of noise immunity of post-vector rank information processing is an urgent task.
2. Method
The detection task allows us to interpret the data at the input of the detection system as a random array of sample data with certain statistical properties. The randomness of the array is due to the very physical nature of the observed quantities (electromagnetic field strength, sound pressure, light flux), the effects of extraneous random noise, as well as measurement errors or transformations of physical quantities, noise from receiving and amplifying devices, etc. Based on a priori information about the properties of the array of sample values of in situations of absence and presence of a signal, the null and alternative statistical hypotheses are formulated, respectively, i.e. some assumptions about the form of probability distributions of .
Depending on the degree of concretization of these assumptions and the accepted quality criterion, statistics
, i.e. some functionality from the input data, and a threshold constant
(threshold) are selected [
15]. The decision is made by comparing the value of
obtained for this particular implementation of the array
with the threshold of
. If
≥
, then a decision is made in favor of an alternative hypothesis, about the presence of a signal, in the opposite case, in favor of the null hypothesis, i.e. about the absence of a signal. Thus, the detection system must contain a
statistics calculator and a threshold device.
The result of the detection system can generally be interpreted as an estimate of
of some formal parameter
, equal to 0 in the absence of a signal, and equal to 1 in its presence [
16]. Due to the presence of random noise measured value of
does not always coincide with the true value of
, but only with some probability, which, when
=1 and
=1 is called the probability of correct detection
, and when
=1 and
= 0, the probability of false alarm
. The parameters
and
fully characterize the performance of the detection system, which is the higher the smaller
and more
. They usually strive to organize the decision–making procedure in such a way that the value of
does not exceed the pre-agreed standard level
, and the value of
is possibly the maximum (the so-called Neumann-Pearson criterion [
17]). The values of
and
depend on the type of statistics
. The possibility of optimal choice of
is determined by the completeness and reliability of a priori information about the properties of the distributions of the array of sample values of
. Depending on the level of detail of this information, various statistical processing methods are used – optimal, adaptive, and nonparametric.
Nonparametric methods [
18,
19] are used when the functional type of the input data distribution is unknown, and only the most general differences between the situations of presence and absence of a signal are specified.
Almost all nonparametric detection systems contain devices as a component element that perform some invariant transformation
of an array of sample values
. The result of the transformation is a new array
, the distribution of the elements of which, in the absence of a signal (
= 0), is exactly known. The
transformation makes it possible to reduce the problem of detecting a signal against the background of noise with an unknown distribution to the problem of testing a simple hypothesis regarding the distribution of the
array. Accordingly, the synthesis of nonparametric detection systems is performed in two steps: on the first, the type of invariant transformation
is chosen, on the second, the method of processing the transformed data. The simplest and well-known example of such a transformation is the sign statistics [
20]
If the symmetry hypothesis is correct, then it is not difficult to verify that the appearance of ones and zeros at the output of the limiter (1) is equally likely, i.e.
Therefore, transformation (1) translates an array with an arbitrary distribution symmetric relative to the zero level into a new array with a uniform distribution regardless of the specific type of the initial distribution. If the symmetry of the distribution is violated when a signal appears, then the detection problem can be formulated as a test of a null hypothesis (2) against an alternative hypothesis.
The optimal solution to this problem is the sign criterion [
21,
22,
23], which prescribes the summation of the signs of the sample elements.
and comparing the accumulated value with the threshold. Statistics (3) represents the number of successes in a series of n independent experiments, i.e. it obeys a binomial distribution, and in the absence of a signal, the probability of success is 1/2, and in the presence of a signal, it is more than 1/2. Thus, statistic (3) satisfies the two above requirements: at
, its distribution is precisely known and unchanged, whatever the initial symmetric distribution
, and at
, the distribution of statistic (3) is sensitive to the presence of a signal.
If the initial sample
is ordered by magnitude, then a so-called variation series is formed, in which
is the smallest element of the sample;
is the second largest element;
is the
-
th largest element;
is the maximum element, while
The random variable
is called the
-
th ordinal statistic and its invariant property is that as the sample size increases, the value
converges in probability to the quantile of the level
regardless of the type of distribution of the initial sample [
24,
25].
The rank of the
-th element
, an array of sample values
, is the ordinal number
of this element in the variation series, i.e.
Formally, the rank calculation procedure can be represented as
The set of ranks {
of all the elements of the sample
forms a certain permutation of integers from 1 to
. According to the hypothesis of randomness, all such permutations are equally probable. Therefore, regardless of the specific distribution law of the initial sample
, the joint distribution of ranks {
is uniform:
According to the classical theory of signal detection [
26], the array of sample values
must be supplemented with an array
. In the theory of radiolocation, sample values of
are usually referred to as a signal sample containing information about the signal. The
sample is called a reference or noise sample and coincides in its properties with the
sample in the absence of a signal.
In this regard, the first stage of synthesis of rank detectors is reduced to the organization of arrays
and
. Usually, the elements of sample arrays are voltage samples at the output of signal sensors, followed by sampling with a certain interval
. The set of discrete samples formed in this way forms the set
, which is the initial one for the formation of all sample arrays. From the set
, it is necessary to select a signal sample
, which is formed for each resolution cell according to the informative parameters of the signal. In accordance with the principles of radiolocation, a resolution cell is an area in the signal parameter space, the center of which corresponds to the settings of a given detection channel, and the dimensions along the coordinate axes correspond to the dimensions of the uncertainty zones according to the corresponding parameters [
27]. Array
, like array
, is formed from elements of the set
, however, unlike
, array
can include elements related to different resolution cells.
Then, instead of expression (6), we obtain the following definition of ranks
Obviously, with such a rank determination, any change in the distribution of sample compared to sample leads to a deviation in the distribution of ranks from a uniform one.
The structure of post-detector rank processing can be conventionally represented in the form of the following blocks (
Figure 2):
- is a preprocessing unit,
- is a sampling unit,
- is a ranking unit,
- is a ranking statistics calculation unit,
- is a threshold device;
- is a random array of sample data,
- is an array of ranks obtained after random ordering an array of sample data,
- is some rank statistics.
The S (sampling unit) provides the preparation of the initial data for rank processing: signal samples and reference samples , related to the checked resolution cell based on the informative parameters of the received signal. The source material for the formation of samples and is the sequence of samples at the output of the signal preprocessing unit . The sample includes samples with numbers , where is a set containing elements and corresponding to the numbers of the signal samples of the resolution cell. The sample includes samples with numbers , where is a set containing m elements and corresponding to the numbers of the reference samples of the resolution cell and the signal sample.
The type of a particular ranking algorithm depends on the relationship between the sets and or the equivalent relationship between the sets and . Therefore, in post-detector rank detectors , since ranking without reference samples is unacceptable.
The choice of the composition of the reference sample is determined by a priori information about the properties of noise. We will not describe the principles of selecting reference samples here, as they are described in detail in textbooks on radiolocation. Note that for any methods of forming a reference sample, the condition of statistical uniformity of its elements must be fulfilled [
28,
29]. Due to the limited quasi-uniformity intervals of noise, the volumes of reference samples are usually small and lie within
[E], which causes difficulties in setting low false alarm levels
. These difficulties are caused by the discrete nature of the ranks, which, in turn, leads to the discreteness of rank statistics. Therefore, the threshold level with which the rank statistics are compared to make a decision about the presence of a signal cannot take arbitrary values, but is limited from above by the maximum value of the rank statistics. The maximum threshold value corresponds to the minimum achievable non-zero false alarm level
. You can write it down
Therefore, the lower the required false alarm level, the higher the values of and .
3. Theories
The problem of signal detection can be formulated as a test of two hypotheses: a null hypothesis that the distribution of ranks is uniform, and an alternative hypothesis about a violation of the uniformity of the distribution of ranks when a signal appears. With this formulation of the problem, further processing can be performed based on the well-known Neumann-Pearson criterion. Processing according to this criterion is reduced to calculating the likelihood ratio of the ranks to test the hypothesis
against the alternative hypothesis
:
where
) is the probability distribution of the ranks.
Rank independence allows us to write the following expression
Since any monotone likelihood ratio function has optimal properties, then prolog expression (11), we obtain
where
Optimal signal detection can also be performed based on other quality criteria. The choice of criterion depends on the possibility of performing specific calculations and the ease of use of optimal detection results. In contrast to the classical Neumann-Pearson criterion, which consists in maximizing the probability of correct detection of
at a fixed false alarm level
, we can use the criterion for minimizing the RMS error of measuring the situation parameter, which we will call the
– criterion.:
where
is the symbol of mathematical expectation.
The function can be calculated in advance and stored in a long-term storage device (ROM). Then the optimal rank processing is reduced to extracting the value from the ROM at address and accumulating these values for all .
First of all, it is necessary to specify the class of processing algorithms within which we will search for the optimal one. For the reasons mentioned above, algorithms similar in structure to algorithm (12), but not tied to a specific ranking method, are a suitable class [
30]. The type of nonlinear transformation
in these algorithms is found using the
– criterion. To do this, we represent the function
by an l -
th degree polynomial in R:
where
is a one–dimensional moment of the ranks of the
- th order.
Then the problem is reduced to optimizing the coefficient matrix
by minimizing the functional
which is obtained from expression (14) after substituting statistics (12) with the function
of the form (15) instead of
. Varying this functional by
and assuming the events
and
to be equally probable, we obtain a system of linear algebraic equations with respect to the coefficients
:
or after statistical averaging, we get
where
(
is the two–dimensional moment of the ranks.
In the solution of the given system, we do not need to provide an a priori unknown signal-to-noise ratio. It is difficult to get pregnant, it is a preposition, it is a sign of the weak. This is how it is allowed to apply and to use the criterion of Neumann-Pearson. In this case, the system (14) has the form:
If the signal sample is statistically homogeneous, then the moments of the ranks do not depend on the reference number. Then the coefficients
are independent of
and the system of equations (25) is significantly simplified:
Thus, rank processing according to the - criterion consists in calculating the moments of ranks from the first to the - th order, calculating the coefficients of the systems of equations (16) or (17) and solving these equations relative to . Based on the values of . found, the function table (15) is calculated, which is then used in rank processing.
4. Simulation Studies
The use of rank processing algorithms often encounters difficulties due to either purely technical reasons (the inability to perform calculations, the cumbersomeness of the results obtained), or reasons of a fundamental nature, for example, the dependence of the structure of optimal processing algorithms on an a priori unknown signal-to-noise ratio. Any attempts to overcome these difficulties are associated with the need to move away from strict optimality and, consequently, with some loss of detection efficiency.
An exhaustive characteristic of the detector's effectiveness is the relationship linking the probability of correct detection , the false alarm level , and the signal-to-noise ratio . However, it is usually not possible to obtain accurate mathematical expressions for the probabilities and α of rank detectors due to the non-linearity of the ranking procedure and subsequent rank processing. Therefore, approximate methods for determining and are used: Gaussian approximation and statistical modeling.
The first method is based on the central limit theorem, according to which, for large sample sizes, the distribution of many rank statistics
can be approximated by a normal law. In this case, the relationship between the probabilities of correct detection and false alarm is described by a simple relation
where
and
are the mathematical expectation and variance of the rank statistics
in the situation
;
is the Laplace integral, the function
is the inverse function of
.
However, not all rank statistics (for example, optimal rank statistics or a rank code detector) are asymptotically normal. In addition, the sample sizes used in ranked detection systems are usually small. Therefore, the Gaussian approximation of their distributions turns out to be too rough. It should also be noted that calculating even the first two moments of rank statistics is in many cases a difficult and not always solvable task. Therefore, additional simplifying assumptions are often resorted to, in particular, the signal is considered weak [
31,
32].
The statistical modeling method is free from these disadvantages [
33]. However, it is very time-consuming when estimating low false alarm levels. Therefore, we can propose an algorithm for calculating the probabilities
and
, which ensures high computational accuracy with sample sizes typical of rank detectors. The algorithm is based on the well-known formulas for
and
:
where the summation is carried out for all rank implementations for which the value of the studied statistic
exceeds the threshold level
, i.e. for the critical region of the studied rank decision rule.
It follows from formulas (19) and (20) that calculations can be organized as an enumeration of all possible values of ranks . At each point in the space of rank values, the value of the rank statistic should be calculated and compared with the threshold. If Если , then it is necessary to calculate the probability of the occurrence of this realization in situations and and include it in the sums (19) and (20). Otherwise, you should move on to the next point, and so on. The total number of iterations is , which can be very large for real values of and .
The number of iterations can be reduced if the statistics
and the distribution of ranks
are invariant to permutations of arguments. Then it is enough to limit ourselves to bypassing the range of rank values in which
The reduction of the values being viewed is easy to account for if the probabilities
are multiplied by the number of equivalent points in the entire space of rank values equal to
As a result, instead of viewing
points, it is enough to limit ourselves to traversing
(m+n)/n points. The traversal order is also important, which is advisable to start from the point
and then move in such an order that the rank codes
decrease. For example, with
n = 2 and
= 3, the traversal order will be as follows: {33, 32, 31, 30, 22, 21, 20, 11, 10, 00}. This traversal procedure allows for the minimum number of steps to select all points related to the critical area of the studied decisive rule and stop the traversal long before the final point
. The practice of calculations shows [
34,
35] that for the vast majority of rank statistics, the enumeration of possible rank implementations can be stopped if, at the next exit to the main diagonal, where
, the statistic value is below the threshold. In this case, all further points in the above order of traversal either do not fall into the critical region, or their contribution is very insignificant. As a result, the number of iterated rank implementations is reduced by several orders of magnitude, which reduces computational costs.
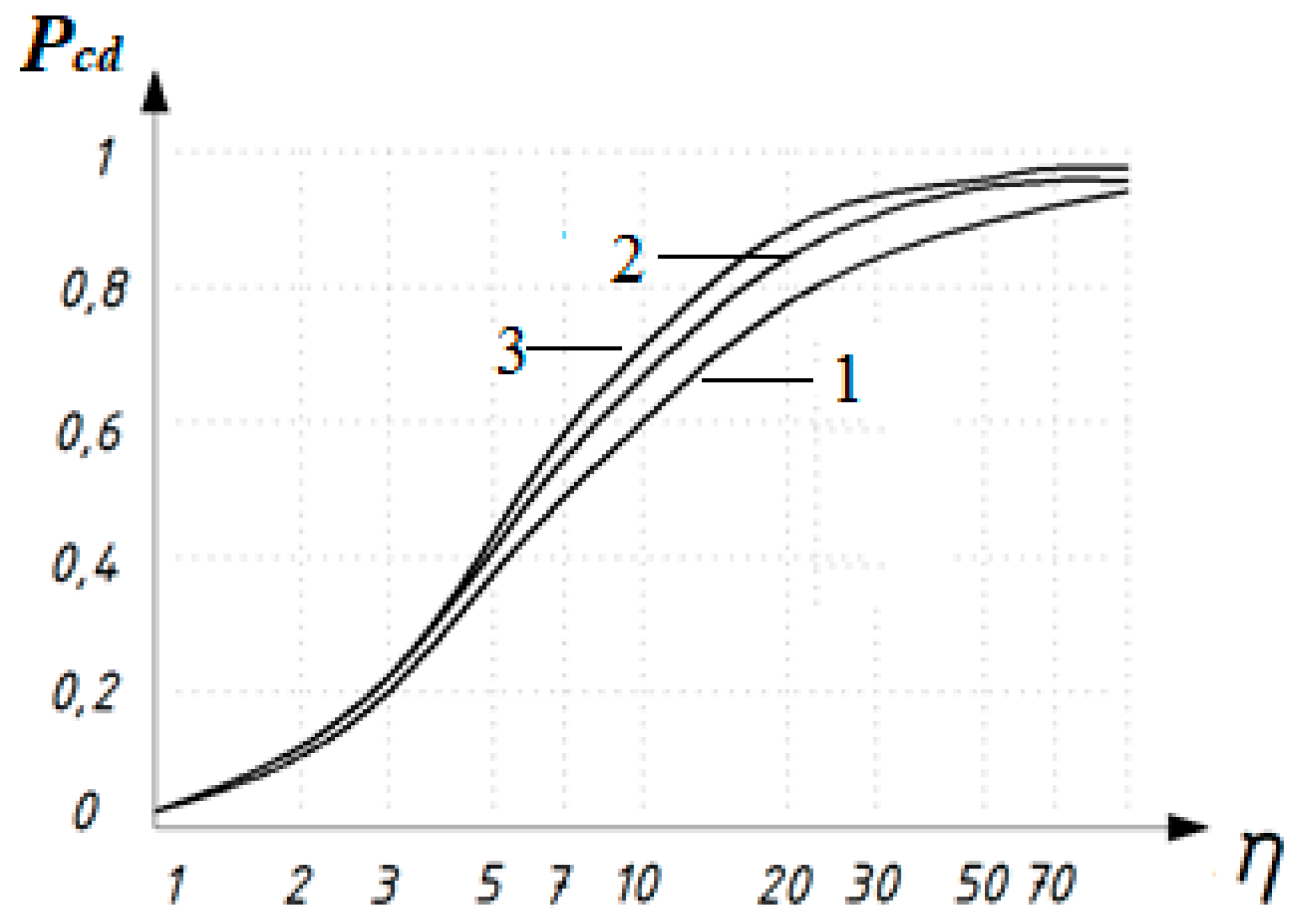
Let's analyze the effectiveness of the – detection criterion.
The dependence of the probability of correct detection on the signal-to-noise ratio for various degrees of the polynomial
for the Rayleigh distribution is shown in
Figure 3: 1 -
, 2 -
;
.
The dependence of the probability of correct detection on the signal-to-noise ratio for the various degrees of the polynomial
for the Gaussian distribution are shown in
Figure 4: 1 -
, 2 -
;
.
To evaluate the effectiveness of the
–detection criterion, we will use such an important characteristic of signal detection as the threshold signal–to-noise ratio - the minimum ratio at which the signal is still detected with a given probability
against the background of noise causing a "false alarm". Let us introduce the concept of losses in the threshold signal-to-noise ratio [
36] in comparison with optimal detection
where
is the threshold signal-to-noise ratio, providing a given probability of detecting
at some fixed probability of false alarm
, for optimal detection;
is the threshold signal-to-noise ratio, providing a given probability of detecting
at some fixed probability of false alarm
, for detection by the
– criterion.
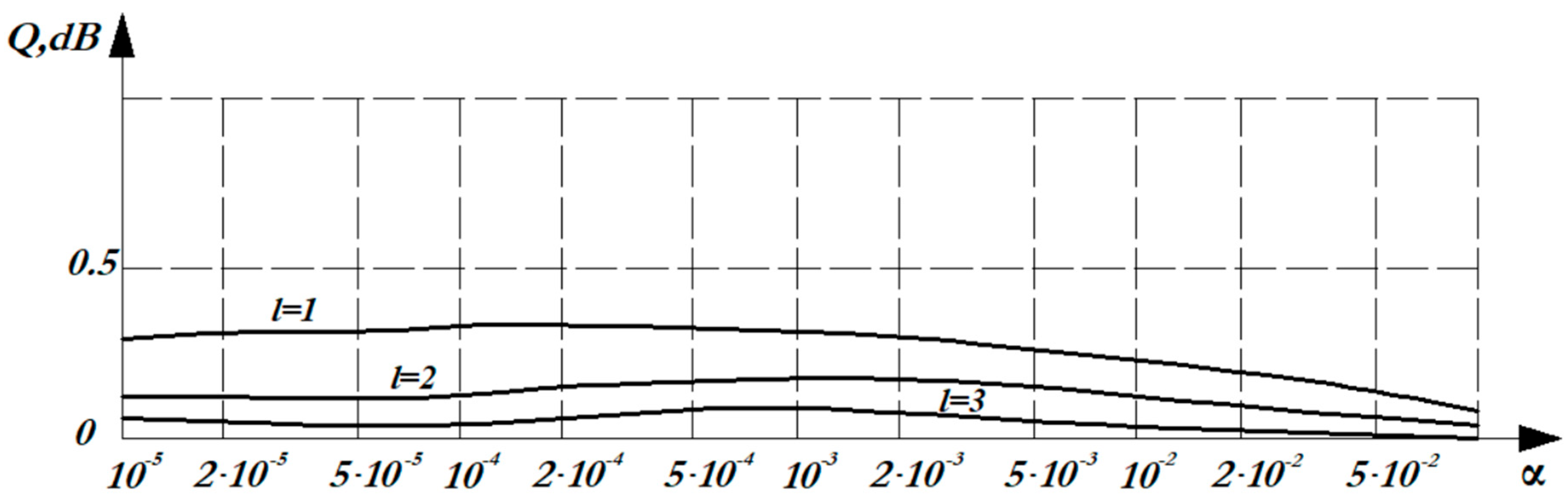
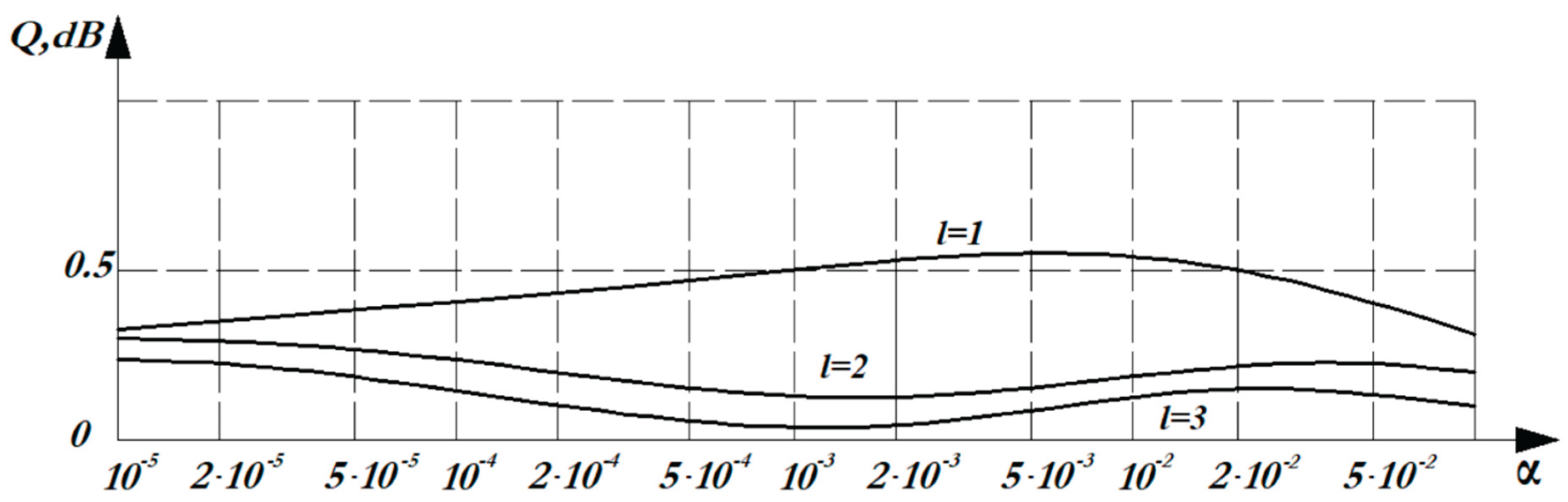
Figure 5 shows the dependence of losses in the signal–to-noise threshold ratio on the probability of a false alarm of the
- detection criterion compared with the optimal detection for the Gaussian distribution. Threshold losses are calculated for various degrees of the polynomial
and for
.
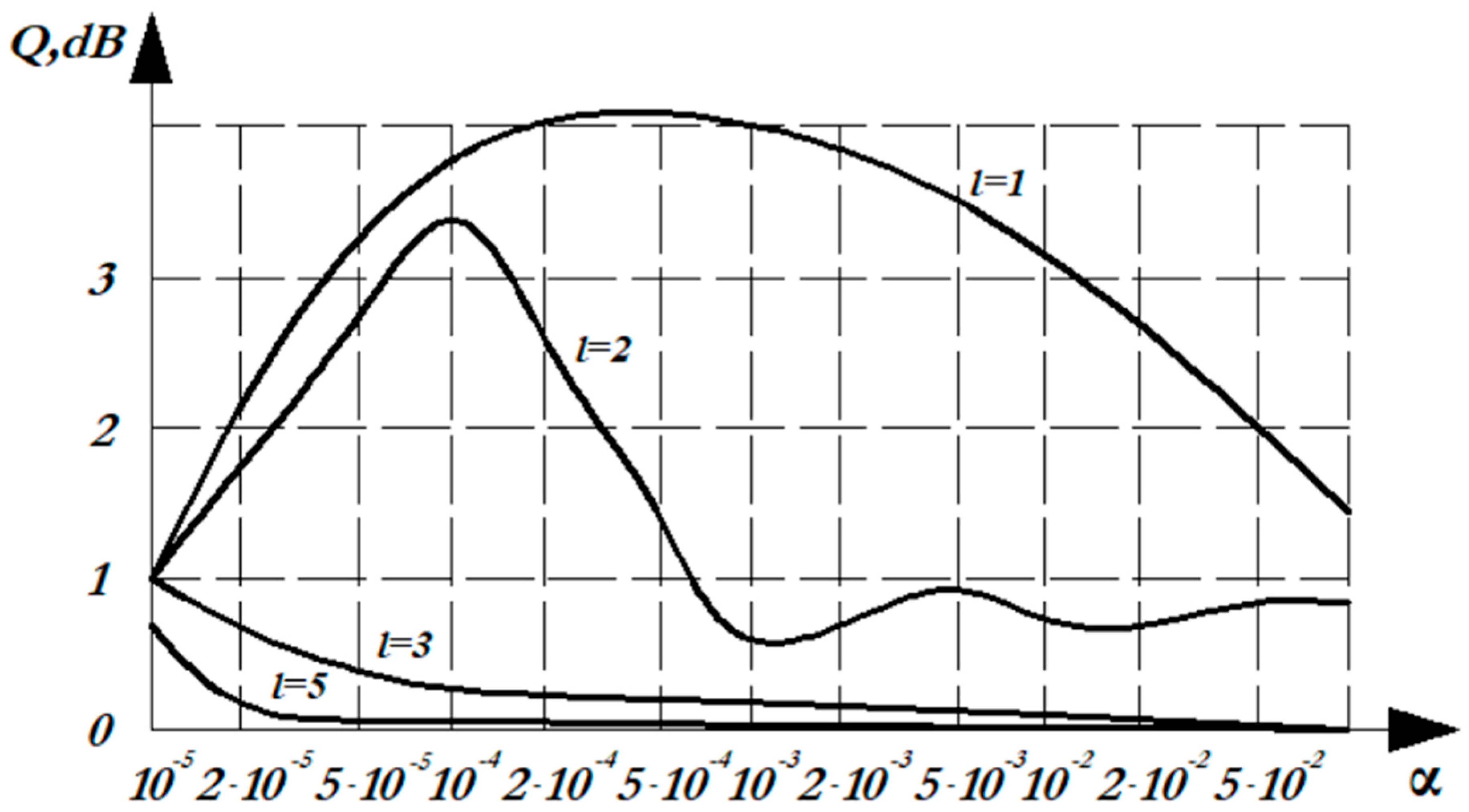
Figure 6 and
Figure 7 show a similar relationship for the Rayleigh distribution and the Rayleigh-Rice distribution.